Алгоритм и его свойства. Примеры алгоритмов
Цель занятия: познакомить учащихся с понятием алгоритма, исполнителями алгоритмов, примерами алгоритмов в жизни, алгоритмическим способом решения задач, закрепить полученные знания с помощью электронного теста, развивать навыки самоконтроля.
Ход урока
- Организационный момент.
- Подготовка к изучению нового материала. (ознакомление с планом и целью занятия) .
- Изучение нового материала. (просмотр электронного урока с использованием мультимедиа проектора) . Слайды + текст лекции.
- По ходу урока учащиеся конспектируют определения и отвечают на вопросы.
- Закрепление темы занятия (работа уч-ся на компьютере) . Электронный тест с последующей самопроверкой. Решение алгоритмических задач.
- Подведение итогов.
 Выставление оценок с учетом
процентного выполнения теста.
Выставление оценок с учетом
процентного выполнения теста. - Задание на дом. (выучить определения, привести примеры алгоритмов из жизненной практики.)
Изучение нового материала.
Один из важнейших этапов решения задач на ЭВМ – составление алгоритма. О том, что такое алгоритмы, какими общими свойствами они обладают и как исполняются, мы и поговорим на этом уроке.
В 1983 году отмечалось 1200-летие со дня рождения одного из величайших ученых Средней Азии и средневекового Востока Мухамада ибн Мусы аль-Хорезми. Он написал ряд трактатов по арифметике и алгебре, в том числе книгу «Арифметика индусскими цифрами» – о счете с помощью десяти цифр и правилах арифметических действий с числами.
Имя ученого аль-Хорезми превратилось в понятие
algorithmi, первоначально обозначавшее десятичную
систему исчисления и правила арифметических
действий в этой системе. Отсюда и возник
современный научный термин «алгоритм».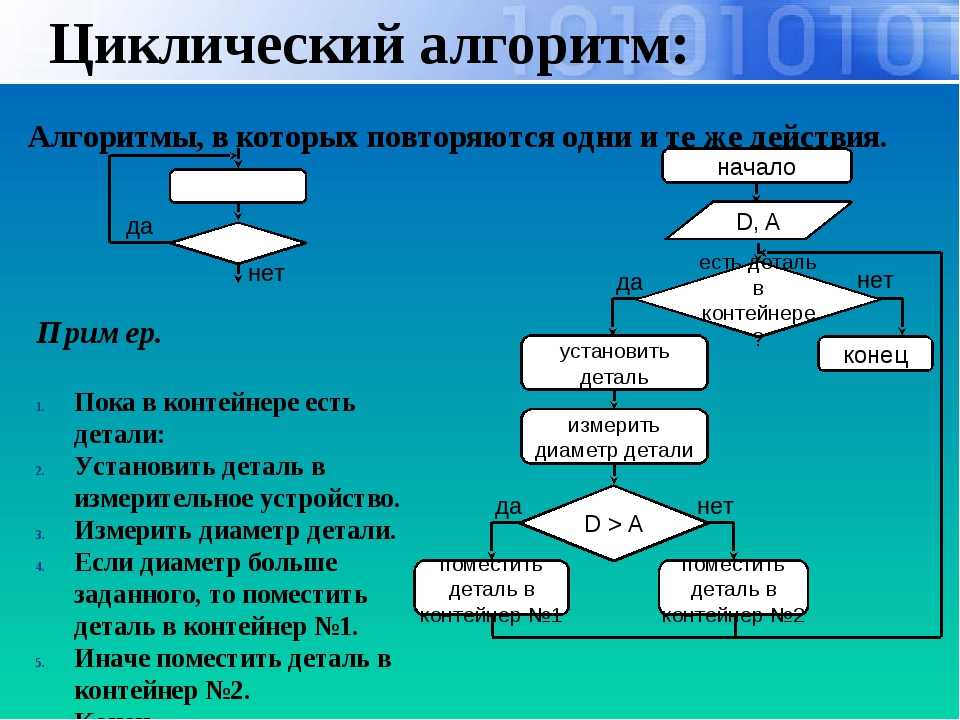
Каждый из нас ежедневно использует различные алгоритмы: инструкции, правила, рецепты и т.п. Обычно мы это делаем не задумываясь. Например, открывая дверь ключом, никто не размышляет над тем, в какой последовательности выполнять действия. Однако чтобы научить кого-нибудь открывать дверь, придется четко указать и сами действия, и порядок их выполнения. То же потребуется и при указании маршрута поездки.
Сравним эти алгоритмы. На первый взгляд, между ними нет ничего общего. Одно дело – открывать дверь, другое – ехать в гости. Но если приглядеться внимательно, можно заметить существенное сходство между ними. Прежде всего, это строгий порядок выполнения действий.
Демонстрация слайда 1. /Приложение/
Мы можем теперь сказать, что алгоритм – это
организованная последовательность действий.
Данную формулировку, конечно, нельзя считать
определением алгоритма. Например, мы не
объяснили, что означают слова
«организованная» и «действия».
На слайде еще одно задание. Выполните его, используя для записи ответа любой текстовый редактор или бумагу и карандаш.
Демонстрация слайда 2. /Приложение/
Сравните свой ответ с правильным.
Правильный алгоритм:
- Налить в чайник воду.
- Зажечь спичку.
- Открыть кран газовой горелки.
- Поднести спичку к горелке.
- Поставить чайник на плиту.
- Ждать, пока вода закипит.
- Выключить газ.
Демонстрация слайда 3. /Приложение/
Рассмотренные нами алгоритмы составлены для
исполнения человеком. Но человек далеко не
единственный возможный исполнитель алгоритмов.
Все живые существа и даже отдельные клетки
исполняют различные алгоритмы. Способны на это и
созданные человеком устройства –
роботы-манипуляторы и станки с программным
управлением. Но прежде чем составлять алгоритм
решения задачи, нужно узнать, какие действия
предполагаемый исполнитель способен выполнить.
Но человек далеко не
единственный возможный исполнитель алгоритмов.
Все живые существа и даже отдельные клетки
исполняют различные алгоритмы. Способны на это и
созданные человеком устройства –
роботы-манипуляторы и станки с программным
управлением. Но прежде чем составлять алгоритм
решения задачи, нужно узнать, какие действия
предполагаемый исполнитель способен выполнить.
Поясним сказанное на примере. Допустим, нужно решить квадратное уравнение.
Десятикласснику требуется минимум инструкций, потому что он уже знает способ решения.
Восьмикласснику понадобятся намного более сложные инструкции, потому что он этого еще не проходил.
Теперь мы можем уточнить понятие алгоритма: это организованная последовательность действий, допустимых для некоторого исполнителя.
Рассмотрим информационный процесс
редактирования текста. При работе с текстом
возможны различные операции: удаление,
копирование, перемещение или замена его
фрагментов.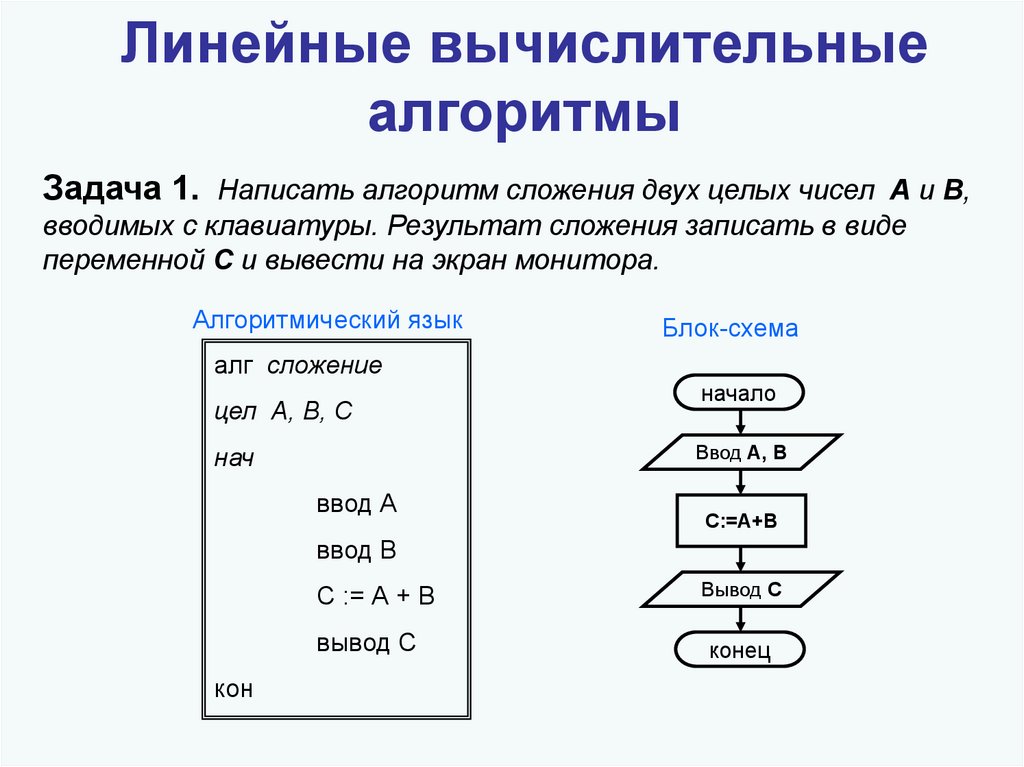 Что необходимо для того, чтобы
преобразовать текст?
Что необходимо для того, чтобы
преобразовать текст?
- Первое. Требуется исполнитель.
- Второе. Процесс должен быть разбит на этапы, понятные исполнителю.
- Третье. Должно быть определено начальное состояние текста и его требуемое конечное состояние.
Теория алгоритмов имеет большое практическое значение. Алгоритмический тип деятельности важен не только как одна из эффективных форм труда человека. Через алгоритмизацию, через расчленение сложных действий на всё более простые, на действия, выполнение которых доступно машинам, пролегает путь к автоматизации различных процессов.
Далее под алгоритмом будет пониматься конечная
последовательность указаний, адресованных
исполнителю, четко и однозначно задающая процесс
решения задач какого-либо типа во всех деталях и
позволяющая получить за конечное число шагов
результат, однозначно определяемый исходными
данными.
Такое свойство алгоритма, как однозначность результата при заданных исходных данных, называется определенностью (детерминированностью) .
Заметим, что большинство алгоритмов могут выполняться при достаточно разнообразных наборах исходных данных, то есть использоваться для решения не какой-либо одной задачи, а целого класса подобных задач. Это свойство алгоритма называется массовостью.
С алгоритмами человек встречается на каждом шагу.
Пример 1. Дан угол. Необходимо провести биссектрису. (Есть способ, как, пользуясь линейкой и циркулем, можно решить эту задачу.)
Пример 2. Даны два целых числа. Необходимо найти их разность. (Имеется правило, в котором ясно изложен весь порядок действий с цифрами данных чисел.)
В приведенных примерах речь идет о том, как
сложную работу представить в виде
последовательности простых действий. Вычитание
многоразрядных чисел сводится к действиям с
цифрами. При делении угла пополам выполняются
несложные построения линейкой и циркулем.
Вычитание
многоразрядных чисел сводится к действиям с
цифрами. При делении угла пополам выполняются
несложные построения линейкой и циркулем.
Однако высказанные соображения следует дополнить. Ведь правила вычитания формулируются для любых многоразрядных чисел, а не для каких-то конкретных двух. Инструкция проведения биссектрисы тоже такова, что, пользуясь ею, можно разделить пополам любой угол. То есть каждому алгоритму присуща массовость – пригодность для решения не какой-либо одной, а целого класса задач.
Далее под алгоритмом будет пониматься конечная последовательность указаний, адресованных исполнителю, четко и однозначно задающая процесс решения задач какого-либо типа во всех деталях и позволяющая получить за конечное число шагов результат, однозначно определяемый исходными данными.
Такое свойство алгоритма, как однозначность
результата при заданных исходных данных,
называется определенностью
(детерминированностью) . На этом занятии мы
познакомились с такими важнейшими понятиями, как
алгоритм, исполнитель, система команд
исполнителя, узнали основные свойства
алгоритма.
На этом занятии мы
познакомились с такими важнейшими понятиями, как
алгоритм, исполнитель, система команд
исполнителя, узнали основные свойства
алгоритма.
Закрепление темы:
Алгоритмические задачи
№1. Старик должен переправить на лодке через реку волка, козу и капусту. Лодка может выдержать только старика и одного “пассажира”. В каком порядке старик перевезет пассажиров? Не забудь, что волк может съесть козу, а коза – капусту. Найди 2 варианта решения.
Алгоритм решения задачи:
| 1 вариант | 2 вариант |
| 1) __________________________ | 1) _________________________ |
| 2) _________________________ | 2) _________________________ |
| 3) __________________________ | 3) _________________________ |
и т. д.
д.
№2 Два мальчика и двое взрослых должны переправиться на другую сторону реки на плоту, который выдерживает либо двух мальчиков, либо одного мальчика и одного взрослого. Как осуществить переправу? Найди несколько способов решения этой задачи.
Алгоритм решения задачи:
| 1 способ | 2 способ | 3 способ | |
| 1 шаг | |||
| 2 шаг | |||
| 3 шаг | |||
| 4 шаг | |||
| 5 шаг |
Обозначения: 1м- один мальчик, 2м – два мальчика,
1в – один взрослый.
1. Практикум по решению задач
Злоумышленник поменял местами действия в алгоритме вычисления среднего арифметического из квадратного корня трёх чисел:
Присвоить а значение (а2+в2+с2) /3.
Вести а,в,с
Сообщить “Среднее арифметическое квадратов равно”
Сообщить а.
Восстановите правильный порядок действий.
2. Исправьте следующий алгоритм решения уравнения (х-2) (х+2) =0:
Присвоить х значение +-2.
Сообщить “Корни уравнения равны”.
Сообщить первое значение х.
Сообщить второе значение х.
3. Автомобиль проехал три участка пути разной длины с разными скоростями. Составьте алгоритм нахождения средней скорости автомобиля.
4. Проснувшись утром, школьник почувствовал недомогание. Находившийся рядом злоумышленник тут же составил для него следующий алгоритм:
Измерить температуру.
Если температура выше 370, то:
Вызвать врача.
Пойти в школу.
Несмотря на недомогание, школьник исправил этот алгоритм, добавив всего две строки. Какие строки добавил школьник?
5. Запишите в виде алгоритмов правила определения знака:
А) произведения двух действительных чисел;
Б) суммы двух действительных чисел.
6. В записи алгоритма вычисления значения выражения (х2— 5х+5) / (х6— 4х2+3)
Злоумышленник одно действие поставил не на свое место. Вот как стал выглядеть алгоритм:
- ввести х
- если х6— 4х2 + 3=0, то:
- сообщить “При таком х значение выражения не определено”.
- иначе:
- присвоить у значение (х2— 5х +5) /(х6- 4х2+3) .
- конец ветвления.
- сообщить у.
Верните действие на свое место.
Электронный тест
1. Которые из документов являются алгоритмами?
Которые из документов являются алгоритмами?
а) Правило правописания приставок, оканчивающихся на з,с(да)
б) Программа телепередач
в) Кулинарный рецепт приготовления блюда
г) Инструкция по сборке проданного в разобранном виде шкафа
2. В каких случаях правильно заканчивается предложение: Алгоритм – это
а) конечная последовательность действий, приводящая к искомому результату при любых допустимых исходных данных
б) указание на выполнение действий
в) конечный набор понятных некоторому исполнителю команд, выполнение которых приводит к однозначному решению поставленной задачи
г) программа в машинных кодах
3. Расчлененность алгоритма на отдельные элементарные действия – это
а) Дискретность
б) Определенность
в) Массовость
г) Детерминированность
4. Которые из документов являются алгоритмами?
А) Каталог книг в библиотеке
Б) Порядок набора международного телефонного номера
В) Рецепт приготовления клея
Г) Настенный календарь на текущий год
Подведение итогов. Выставление оценок с учетом
процентного выполнения теста.
Выставление оценок с учетом
процентного выполнения теста.
Задание на дом. (выучить определения, привести примеры алгоритмов из жизненной практики.)
Виды алгоритмов в информатике: примеры
При изучении информатики немало внимания уделяется изучению алгоритмов и их видам. Не зная основных сведений о них, нельзя написать программу или проанализировать ее работу. Изучение алгоритмов начинается еще в школьном курсе информатики. Сегодня мы рассмотрим понятие алгоритма, свойства алгоритма, виды.
Понятие
Алгоритм – это определенная последовательность действий, которая приводит к достижению того или иного результата. Составляя алгоритм, детально прописывают каждое действие исполнителя, которое в дальнейшем приведет его к решению поставленной задачи.
Довольно часто алгоритмы используют в математике для решения тех или иных задач. Так, многим известен алгоритм решения квадратных уравнений с поиском дискриминанта.
Свойства
Прежде чем рассматривать виды алгоритмов в информатике, необходимо выяснить их основные свойства.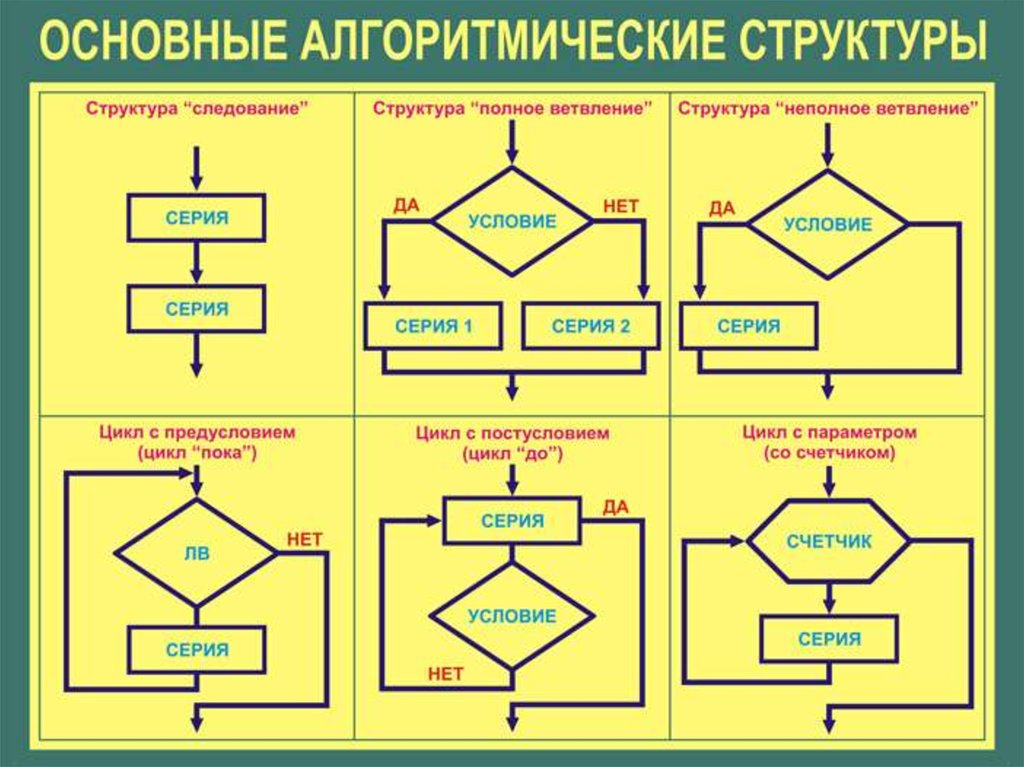
Среди основных свойств алгоритмов необходимо выделить следующие:
- Детерминированность, то есть определенность. Заключается в том, что любой алгоритм предполагает получение определенного результата при заданных исходных.
- Результативность. Означает, что при наличии ряда исходных данных после выполнения ряда шагов будет достигнут определенный, ожидаемый результат.
- Массовость. Написанный единожды алгоритм может использоваться для решения всех задач заданного типа.
- Дискретность. Она подразумевает, что любой алгоритм можно разбить на несколько этапов, каждый из которых имеет свое назначение.
Способы записи
Вне зависимости от того, какие виды алгоритмов в информатике вы рассматриваете, существует несколько способов их записи.
- Словесный.
- Формульно-словесный.
- Графический.
- Язык алгоритма.
Наиболее часто изображают алгоритм в виде блок-схемы, используя специальные обозначения, зафиксированные ГОСТами.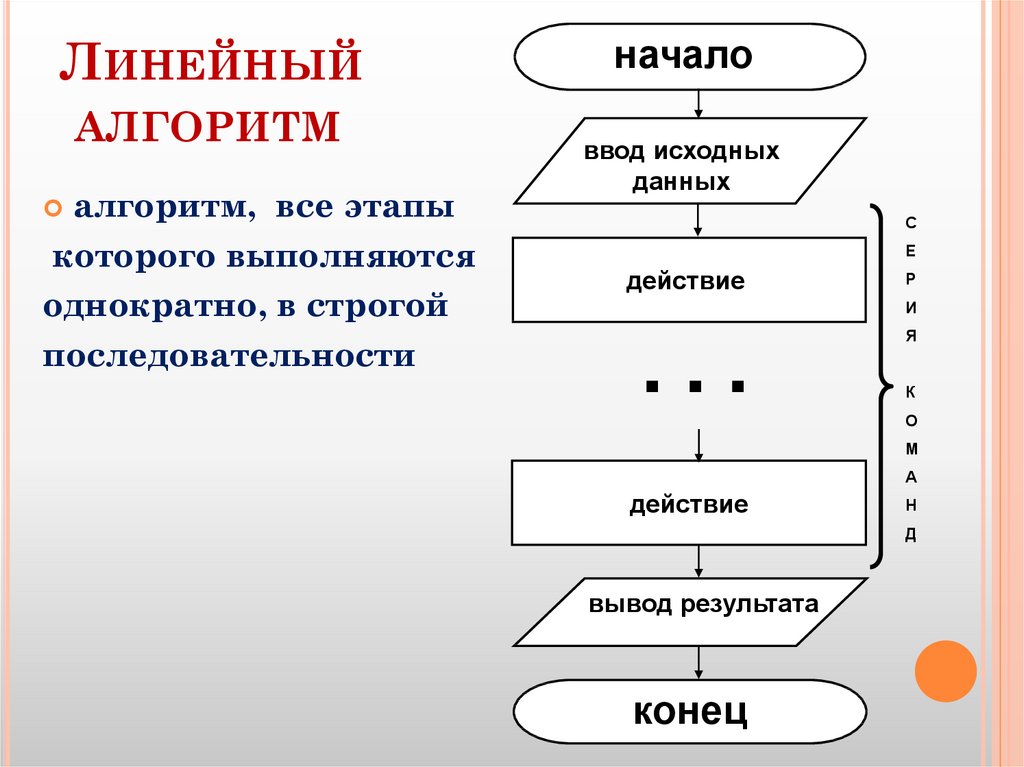
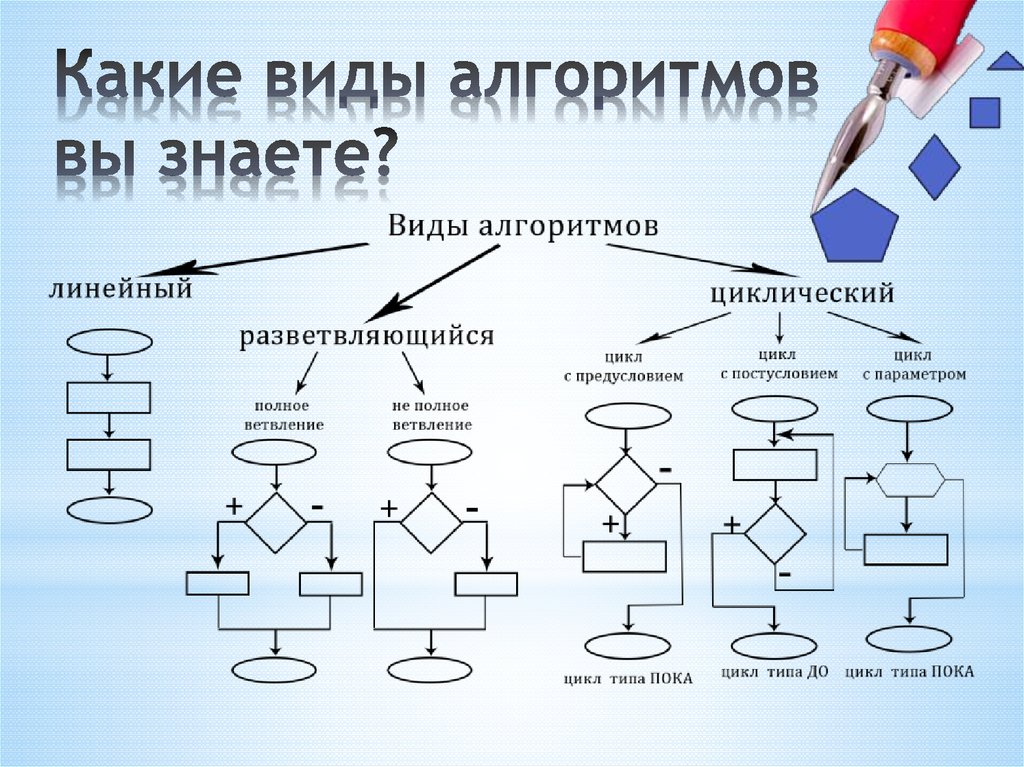
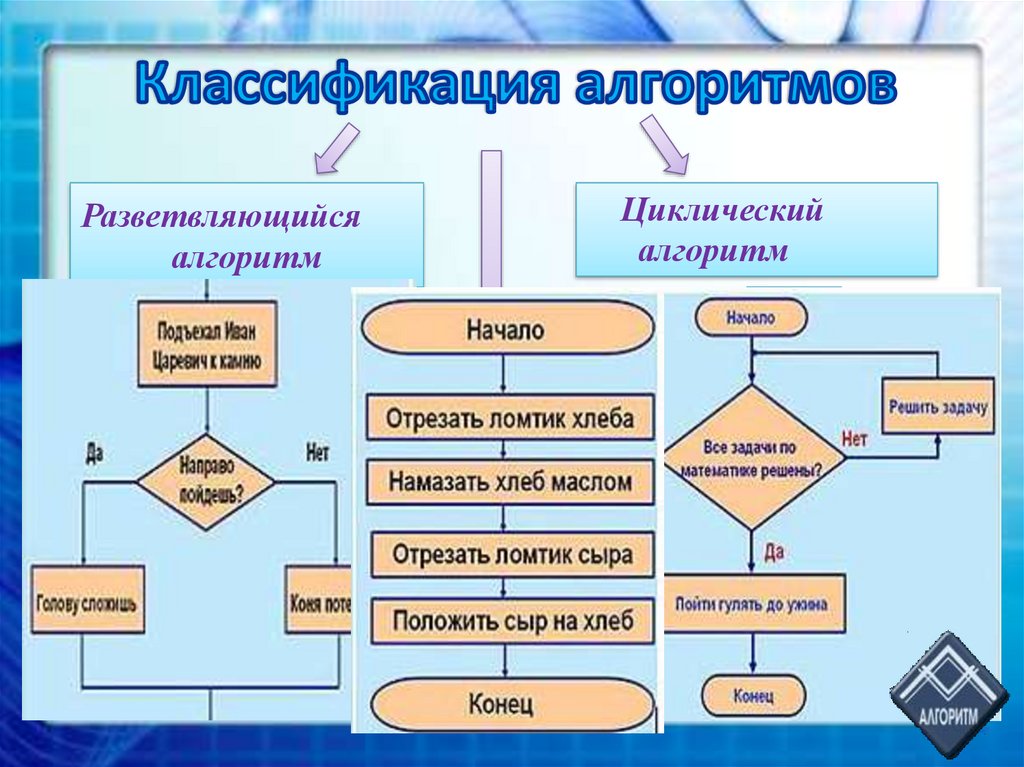
Основные виды
Выделяют три основных схемы:
- Линейный алгоритм.
- Ветвящийся алгоритм, или разветвленный.
- Циклический.
Далее мы рассмотрим виды алгоритмов в информатике, примеры, которые помогут более детально понять, как они работают.
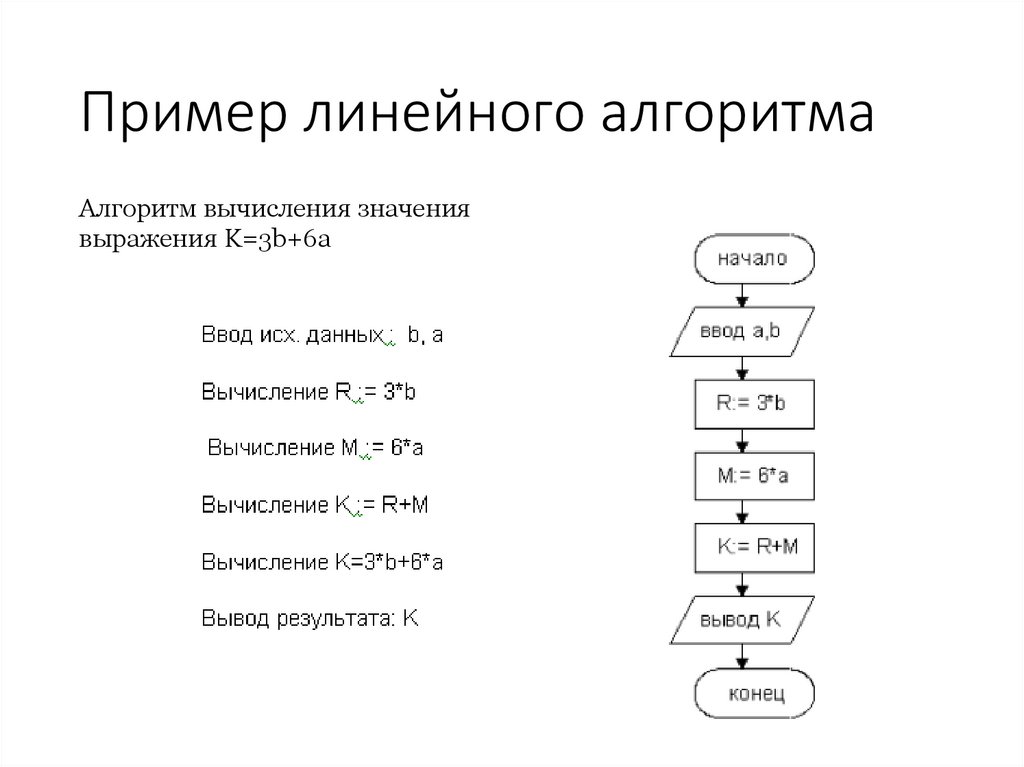
Линейный
Наиболее простым в информатике считается линейный алгоритм. Он предполагает последовательность выполнения действий. Приведем наиболее простой пример алгоритма такого вида. Назовем его «Сбор в школу».
1. Встаем, когда звенит будильник.
2. Умываемся.
3. Чистим зубы.
4. Делаем зарядку.
5. Одеваемся.
6. Кушаем.
7. Обуваемся и идем в школу.
8. Конец алгоритма.
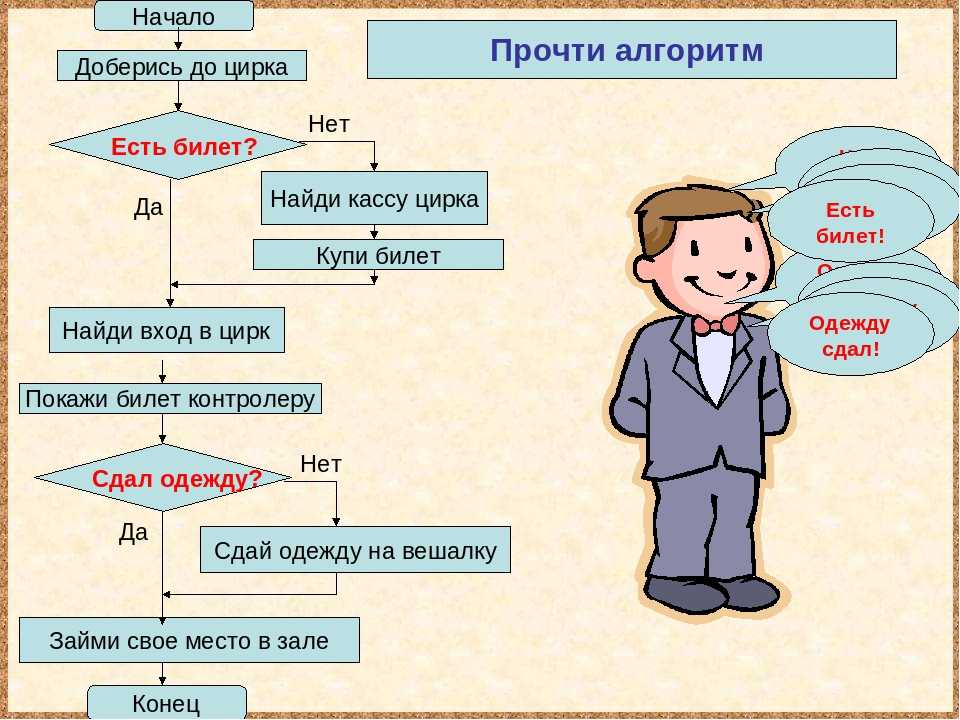
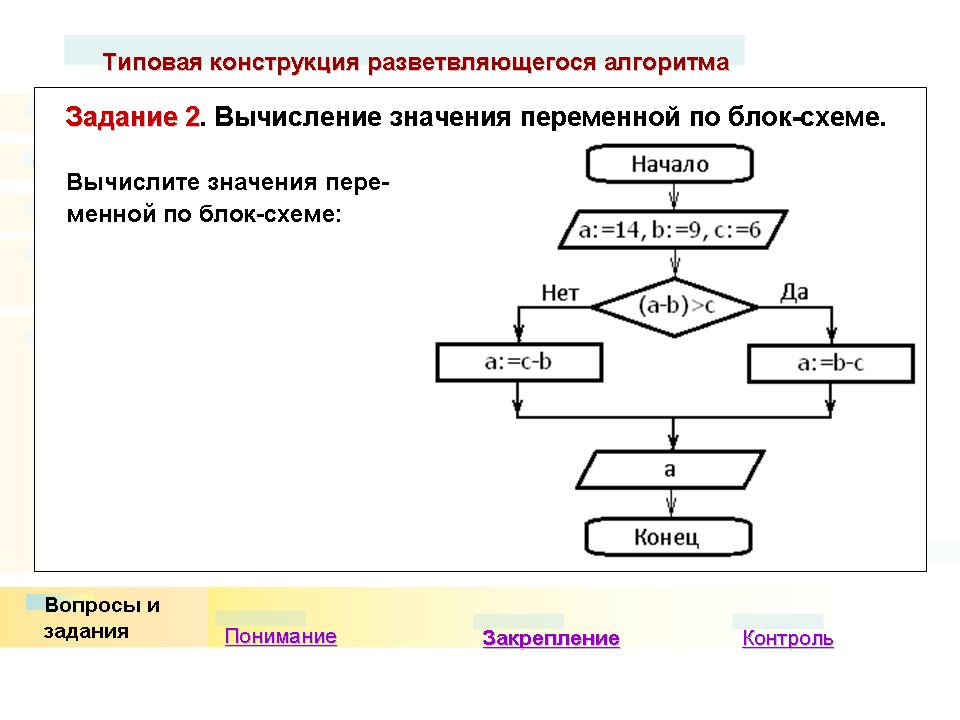
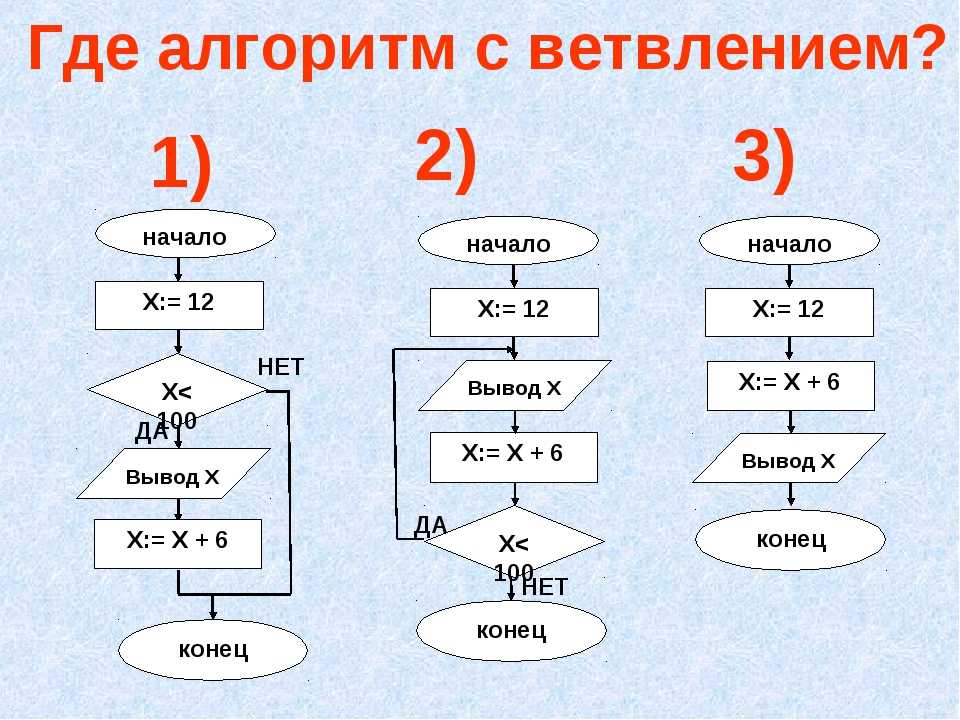
Разветвляющийся алгоритм
Рассматривая виды алгоритмов в информатике, нельзя не вспомнить о разветвляющейся структуре. Данный вид предполагает наличие условия, при котором в случае его выполнения действия выполняются в одном порядке, а в случае невыполнения – в другом.
Например, возьмем следующую ситуацию – переход дороги пешеходом.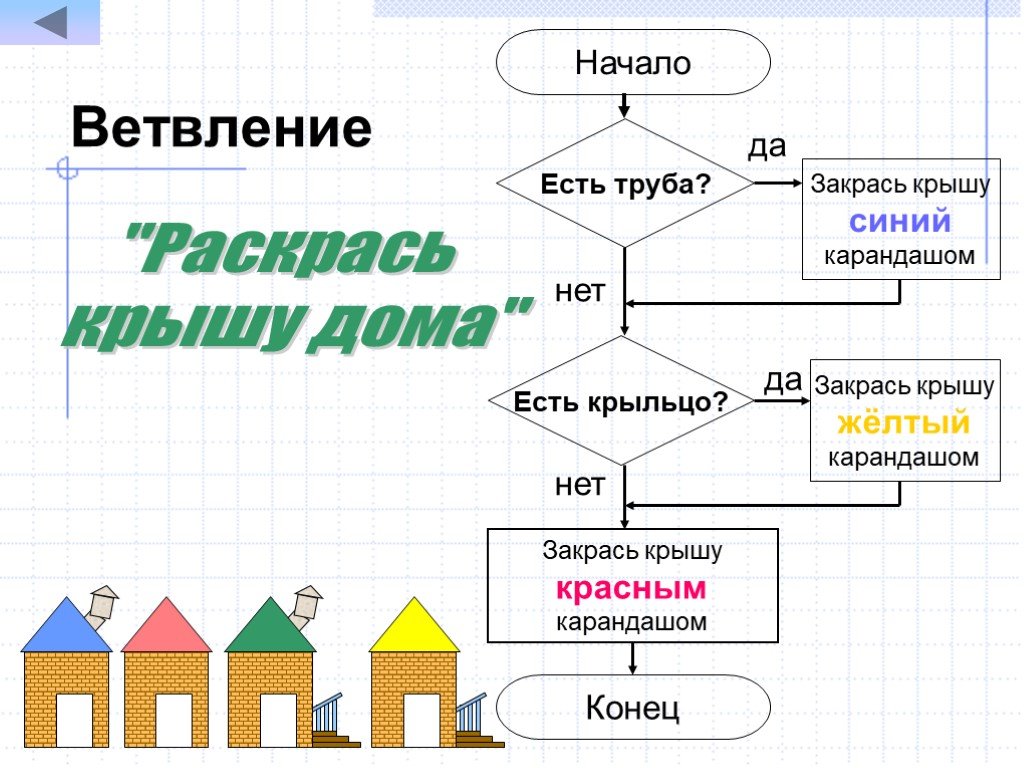
1. Подходим к светофору.
2. Смотрим на сигнал светофора.
3. Он должен быть зеленым (это условие).
4. Если условие выполняется, мы переходим дорогу.
4.1 Если нет – ждем, пока загорится зеленый.
4.2 Переходим дорогу.
5. Конец алгоритма.
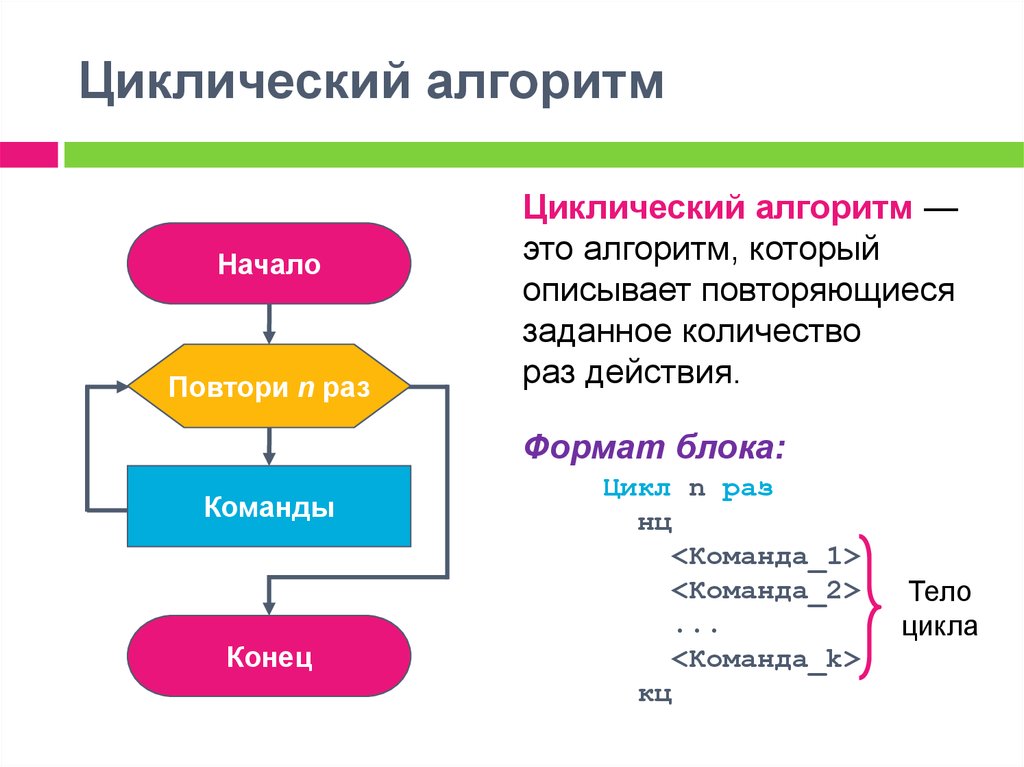
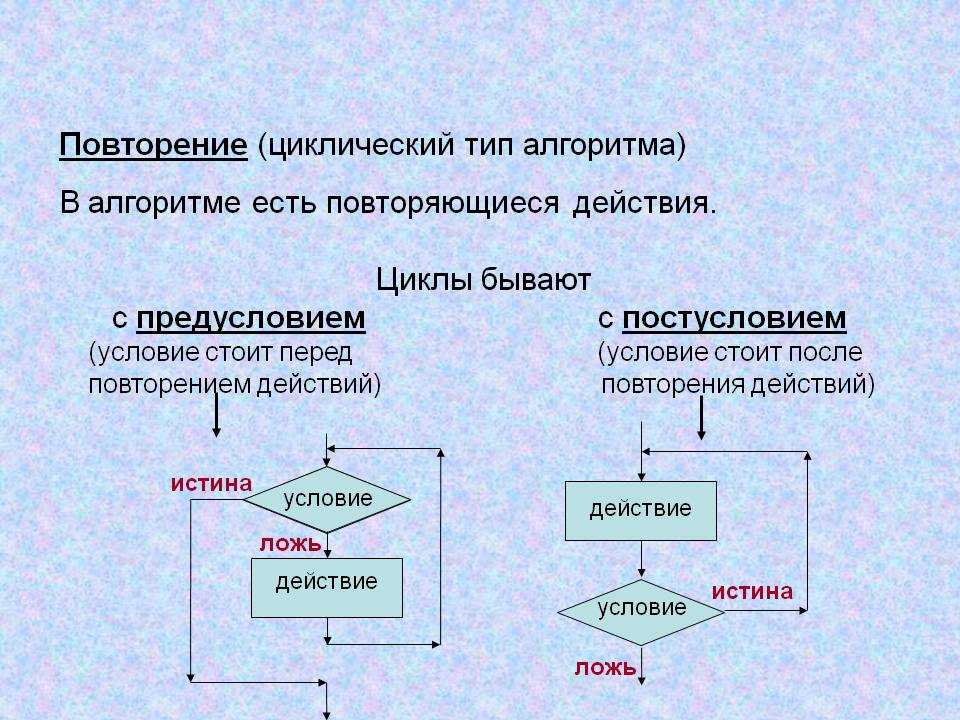
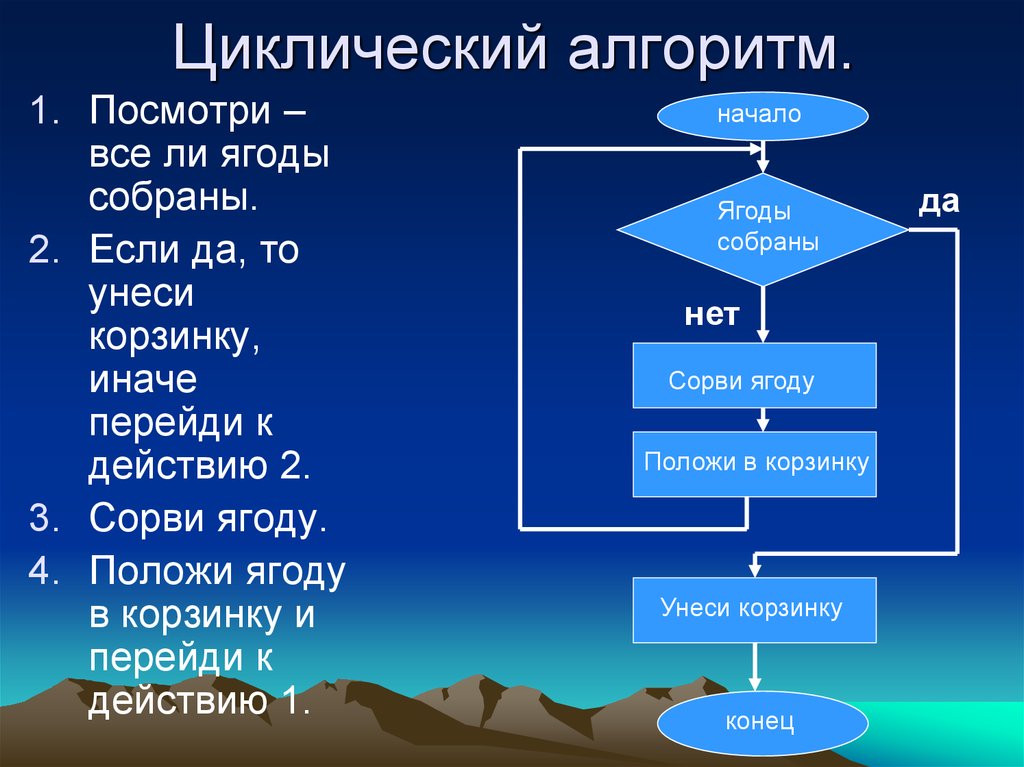
Циклический алгоритм
Изучая виды алгоритмов в информатике, детально следует остановиться на циклическом алгоритме. Данный алгоритм предполагает участок вычислений или действий, который выполняется до выполнения определенного условия.
Возьмем простой пример. Если ряд чисел от 1 до 100. Нам необходимо найти все простые числа, то есть те, которые делятся на единицу и себя. Назовем алгоритм «Простые числа».
1. Берем число 1.
2. Проверяем, меньше ли оно 100.
3. Если да, проверяем простое ли это число.
4. Если условие выполняется, записываем его.
5. Берем число 2.
6. Проверяем, меньше ли оно 100.
7. Проверяем, простое ли оно.
…. Берем число 8.
Проверяем, меньше ли оно 100.
Проверяем, простое ли число.
Нет, пропускаем его.
Берем число 9.
Таким образом перебираем все числа, до 100.
Как видите, шаги 1 – 4 будут повторяться некоторое число раз.
Среди циклических выделяют алгоритмы с предусловием, когда условие проверяется в начале цикла, или с постусловием, когда проверка идет в конце цикла.
Другие варианты
Алгоритм может быть и смешанным. Так, он может быть циклическим и разветвленным одновременно. При этом используются разные условия на разных отрезках алгоритма. Такие сложные структуры приеняются при написании сложных программ и игр.
Обозначения в блок-схеме
Мы с вами рассмотрели, какие виды алгоритмов есть в информатике. Но мы не рассказали о том, какие обозначения используются при их графической записи.
- Начало и конец алгоритма записываются в овальной рамке.
- Каждая команда фиксируется в прямоугольнике.
- Условие прописывается в ромбе.
- Все части алгоритма соединяются при помощи стрелок.

Выводы
Мы с вами рассмотрели тему «Алгоритмы, виды, свойства». Информатика уделяет немало времени изучению алгоритмов. Их используют при написании различных программ как для решения математических задач, так и для создания игр и различного рода приложений.
3 основных примера алгоритмов, которые вы должны знать
Некоторые алгоритмы встречаются снова и снова. В этом руководстве мы рассмотрим три наиболее распространенных: поиск, сортировка и добавление/удаление из связанного списка. Идеи, окружающие эти примеры алгоритмов, проникают во многие другие алгоритмы. Понимание этих трех примеров поможет нам создать прочную основу, чтобы мы могли уверенно решать будущие проблемы с алгоритмами!
Примеры алгоритмов, № 1: Двоичный поискДвоичный поиск — это важный алгоритм поиска, который принимает отсортированный массив и возвращает индекс искомого значения. Мы делаем это со следующими шагами:
- Найдите середину отсортированного массива.

- Сравните среднюю точку с интересующим значением.
- Если средняя точка больше значения, выполнить двоичный поиск в правой половине массива.
- Если средняя точка меньше значения, выполнить бинарный поиск в левой половине массива.
- Повторяйте эти шаги до тех пор, пока значение средней точки не сравняется с интересующим значением или мы не узнаем, что значение отсутствует в массиве.
Из приведенных выше шагов ясно, что наше решение может быть рекурсивным. Мы будем передавать меньший массив в наш метод на каждой итерации, пока наш массив не будет содержать только интересующее нас значение. Сложные части правильно индексируют наш массив и отслеживают смещение нашего индекса на каждой итерации, чтобы мы могли вернуть индекс нашего значения из исходного массива. См. ниже нашу версию алгоритма бинарного поиска.
по определению двоичный_поиск (обр, значение, смещение = 0) середина = (длина обр.) / 2 if value < arr[mid] binary_search(arr[0...mid], value, offset) elsif value > arr[mid] двоичный_поиск (обр [(середина + 1)..-1], значение, смещение + середина + 1) еще смещение возврата + середина конец конец
Двоичный поиск имеет временную сложность O(logn) . Мы знаем это, потому что если мы удвоим размер нашего входного массива, нам понадобится только еще одна итерация нашего алгоритма, чтобы получить окончательный ответ. Вот почему бинарный поиск является таким важным алгоритмом в информатике.
Сортировка слиянием использует аналогичную методологию «разделяй и властвуй» для эффективной сортировки массивов. См. следующие шаги для реализации сортировки слиянием.
- Возврат, если массив состоит только из одного элемента, поскольку он уже отсортирован.
- Разделить массив на две половины до тех пор, пока его больше нельзя будет разделить.
- Объединяйте меньшие массивы в отсортированном порядке, пока не получите исходный отсортированный массив.

Для реализации сортировки слиянием мы определим два метода. Один позаботится о разделении массива, а другой позаботится о слиянии двух несортированных массивов обратно в один отсортированный массив. Мы рекурсивно вызываем метод разделения ( merge_sort ) до тех пор, пока наш массив не будет состоять только из одного элемента. Затем мы объединяем их вместе и, наконец, возвращаем наш отсортированный массив. См. ниже:
def merge_sort (массив) вернуть массив, если array.length == 1 mid_point = массив.длина/2 слева = массив [0... середина_точки] справа = массив [mid_point..-1] слияние (сортировка слиянием (слева), сортировка слиянием (справа)) конец
слияние по определению (слева, справа)
объединенный_арр = []
пока не осталось.пусто? && право.пусто?
если левая.длина == 0
merged_arr << правый.shift
Эльсиф право.длина == 0
merged_arr << влево.shift
elsif слева[0] <= справа[0]
merged_arr << влево. shift
elsif справа[0] <= слева[0]
merged_arr << правый.shift
конец
конец
слитный_arr
конец
shift
elsif справа[0] <= слева[0]
merged_arr << правый.shift
конец
конец
слитный_arr
конец
Сортировка слиянием имеет временную сложность O(nlogn) , что является наилучшей возможной временной сложностью для алгоритма сортировки. Разделяя и властвуя, мы значительно повышаем эффективность сортировки, которая и без того требует значительных вычислительных ресурсов.
Связанный список — это фундаментальная структура данных информатики, которая наиболее полезна благодаря постоянному времени вставки и удаления. Используя узлы и указатели, мы можем выполнять некоторые процессы намного эффективнее, чем если бы мы использовали массив. См. схему ниже:
Связный список состоит из узлов, каждый из которых имеет часть данных и указатель на следующий узел. Мы представляем это в Ruby, создавая структуру Node с двумя аргументами: :data и :next_node . Теперь нам просто нужно определить два метода,
Теперь нам просто нужно определить два метода, insert_node и delete_node , которые принимают узел head и местоположение места вставки/удаления. Метод insert_node имеет дополнительный аргумент, узел , который является структурой узла, которую мы хотим вставить. Затем мы зацикливаемся, пока не найдем место, в которое мы хотели бы вставить или удалить. Когда мы доберемся до нужного места и переставим указатели, чтобы отразить нашу вставку/удаление.
Узел = Struct.new(:data, :next_node)
def insert_node (головка, узел, местоположение)
текущий_узел = голова
текущее_местоположение = 0
до текущего_местоположения == местоположение
предыдущий_узел = текущий_узел
текущий_узел = текущий_узел.следующий_узел
текущее_местоположение += 1
конец
если предыдущий_узел
предыдущий_узел.следующий_узел = узел
узел.следующий_узел = текущий_узел
еще
узел.следующий_узел = текущий_узел
конец
голова
конец
def delete_node (голова, местоположение)
текущий_узел = голова
текущее_местоположение = 0
до текущего_местоположения == местоположение
предыдущий_узел = текущий_узел
текущий_узел = текущий_узел. следующий_узел
текущее_местоположение += 1
конец
если предыдущий_узел
предыдущий_узел.следующий_узел = текущий_узел.следующий_узел
еще
голова = текущий_узел.следующий_узел
конец
голова
конец
следующий_узел
текущее_местоположение += 1
конец
если предыдущий_узел
предыдущий_узел.следующий_узел = текущий_узел.следующий_узел
еще
голова = текущий_узел.следующий_узел
конец
голова
конец
С помощью связанного списка мы можем удалять элементы из середины коллекции без необходимости перемещаться по остальной структуре данных в памяти, как если бы мы использовали массив. Выбирая лучшую структуру данных для наших нужд, мы можем достичь оптимальной эффективности!
Что дальше?Эти три примера алгоритмов — лишь поверхностная часть фундаментальных алгоритмов, которые мы должны знать, чтобы создавать эффективные программы и успешно проходить технические собеседования. Вот еще несколько алгоритмов, которые мы можем изучить самостоятельно, чтобы углубить наши знания.
- Быстрая сортировка
- Обход двоичного дерева поиска
- Минимальное остовное дерево
- Хипсорт
- Перевернуть строку на месте
Это трудные для понимания концепции, поэтому нам просто нужно продолжать практиковаться и понимать больше примеров алгоритмов!
Другие руководства, которые могут быть вам интересны:
- Введение в жадные алгоритмы
- Два алгоритма решения шифра Виженера в Ruby
- Внедрение двухэтапной аутентификации Google в ваше приложение
- 6 лучших практик Ruby, которые должны знать новички
Биография автора
Ханна Сквайер — разработчик программного обеспечения-самоучка, имеющая опыт работы в области ГИС и гражданского строительства.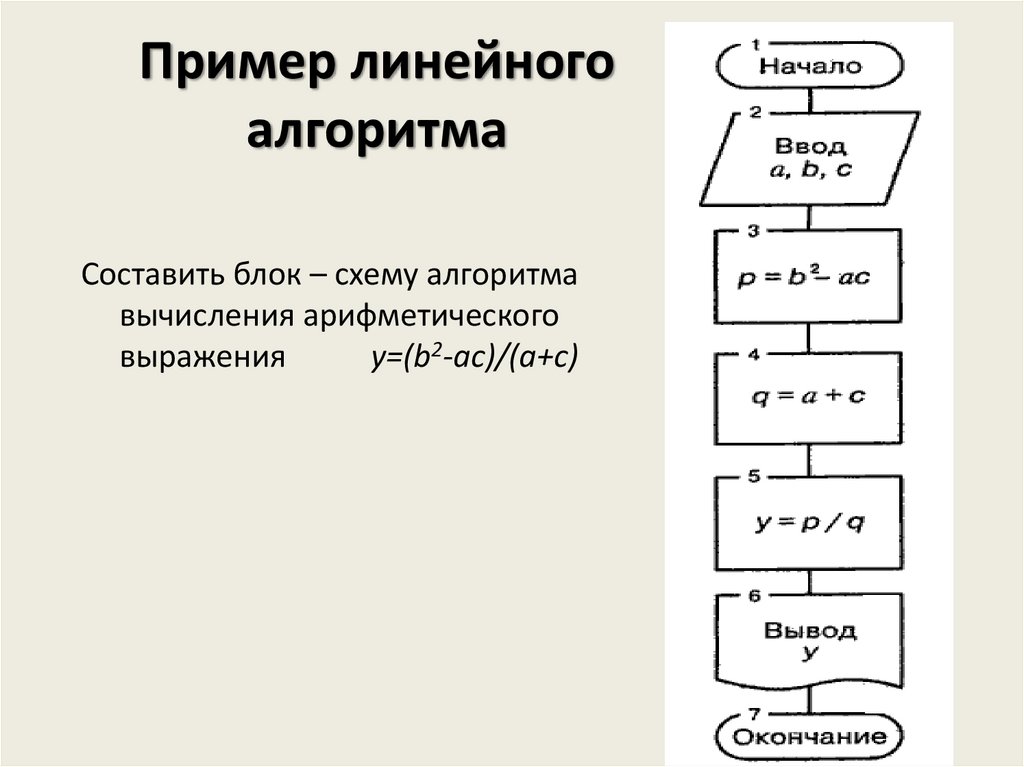 Будучи выпускником Калифорнийского университета в Беркли и одним из первых сотрудников стартапа, она справилась со многими сложными задачами благодаря своим техническим ноу-хау и настойчивости. Готовясь к своему следующему приключению, чтобы стать инженером-программистом на полную ставку, она пишет учебные пособия для сообщества разработчиков. В свободное от программирования время Ханна играет во фрисби и думает о том, как сделать города лучше для жизни. Пишите по адресу [email protected].
Будучи выпускником Калифорнийского университета в Беркли и одним из первых сотрудников стартапа, она справилась со многими сложными задачами благодаря своим техническим ноу-хау и настойчивости. Готовясь к своему следующему приключению, чтобы стать инженером-программистом на полную ставку, она пишет учебные пособия для сообщества разработчиков. В свободное от программирования время Ханна играет во фрисби и думает о том, как сделать города лучше для жизни. Пишите по адресу [email protected].
Что такое алгоритм? Определение, типы, сложность, примеры
Алгоритм — это четко определенный последовательный вычислительный метод, который принимает значение или набор значений в качестве входных данных и производит выходные данные, необходимые для решения проблемы.
Или мы можем сказать, что алгоритм считается точным тогда и только тогда, когда он останавливается с правильным выводом для каждого входного экземпляра.
НЕОБХОДИМОСТЬ АЛГОРИТМОВ:
Алгоритмы используются для систематического и эффективного решения проблем или автоматизации задач.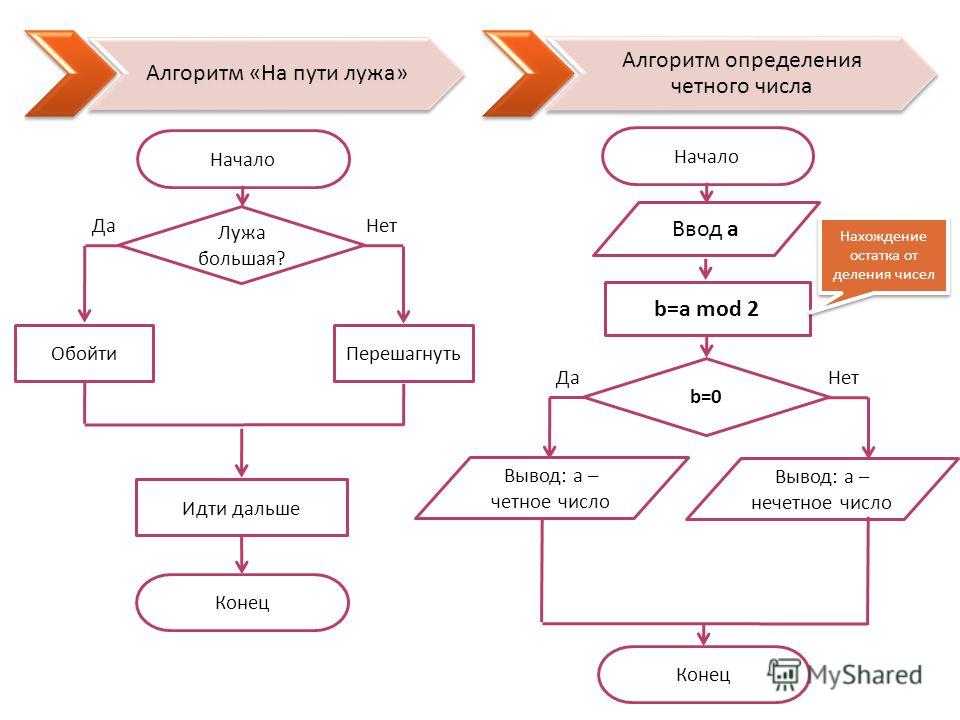 Они представляют собой набор инструкций или правил, которые направляют компьютер или программное обеспечение при выполнении конкретной задачи или решении проблемы.
Они представляют собой набор инструкций или правил, которые направляют компьютер или программное обеспечение при выполнении конкретной задачи или решении проблемы.
Мы используем алгоритмы по нескольким причинам:
- Эффективность: Алгоритмы могут выполнять задачи быстро и точно, что делает их важным инструментом для задач, требующих большого количества вычислений или обработки данных.
- Непротиворечивость: Алгоритмы воспроизводимы и дают согласованные результаты при каждом выполнении. Это важно при работе с большими объемами данных или сложными процессами.
- Масштабируемость: Алгоритмы можно масштабировать для обработки больших наборов данных или сложных задач, что делает их полезными для приложений, требующих обработки больших объемов данных.
- Автоматизация: Алгоритмы могут автоматизировать повторяющиеся задачи, снижая потребность в человеческом вмешательстве и освобождая время для других задач.

- Стандартизация: Алгоритмы могут быть стандартизированы и распространены между различными группами или организациями, что упрощает совместную работу и обмен знаниями.
В целом, алгоритмы являются важным инструментом для решения проблем в различных областях, включая информатику, инженерию, анализ данных, финансы и многие другие.
Пример:Рассмотрим ящик, в котором никто не может видеть, что происходит внутри, мы называем его черным ящиком.
Мы вводим данные в коробку, и она дает нам нужный результат, но процедура, которую нам может понадобиться знать для преобразования ввода в желаемый вывод, является АЛГОРИТМОМ.
Алгоритм не зависит от используемого языка. Он сообщает программисту логику, используемую для решения проблемы. Таким образом, это логическая пошаговая процедура, которая действует как план для программистов.
Примеры из жизни, определяющие использование алгоритмов:- Рассмотрим часы.
 Мы знаем, что часы тикают, но как производитель устанавливает эти гайки и болты так, чтобы они продолжали двигаться каждые 60 секунд, минутная стрелка должна двигаться, а часовая стрелка должна двигаться каждые 60 минут? Поэтому, чтобы решить эту проблему, за ней должен стоять алгоритм.
Мы знаем, что часы тикают, но как производитель устанавливает эти гайки и болты так, чтобы они продолжали двигаться каждые 60 секунд, минутная стрелка должна двигаться, а часовая стрелка должна двигаться каждые 60 минут? Поэтому, чтобы решить эту проблему, за ней должен стоять алгоритм. - Видели, как кто-то готовил для вас вашу любимую еду? Нужен ли рецепт для этого? Да, это необходимо, так как рецепт представляет собой последовательную процедуру, которая превращает сырую картошку в холодную картошку. Вот что такое алгоритм: следование процедуре для получения желаемого результата. Нужно ли соблюдать последовательность? Да, последовательность — это самое важное, что нужно соблюдать, чтобы получить то, что мы хотим.
- Алгоритмы сортировки: Пузырьковая сортировка, сортировка вставками и многое другое. Эти алгоритмы используются для сортировки данных в определенном формате.
- Алгоритмы поиска: Линейный поиск, двоичный поиск и т.
 д. Эти алгоритмы используются для поиска значения или записи, которые требуются пользователю.
д. Эти алгоритмы используются для поиска значения или записи, которые требуются пользователю. - Алгоритмы графов : Он используется для поиска решений таких задач, как поиск кратчайшего пути между городами, и реальных задач, таких как задачи коммивояжера.
Пузырьковая сортировка: Простой алгоритм сортировки, который многократно проходит по списку, сравнивает соседние элементы и меняет их местами, если они расположены в неправильном порядке.
Сортировка вставками: Простой алгоритм сортировки, который создает окончательный отсортированный массив по одному элементу за раз, сравнивая каждый новый элемент с уже отсортированными элементами и вставляя его в правильную позицию.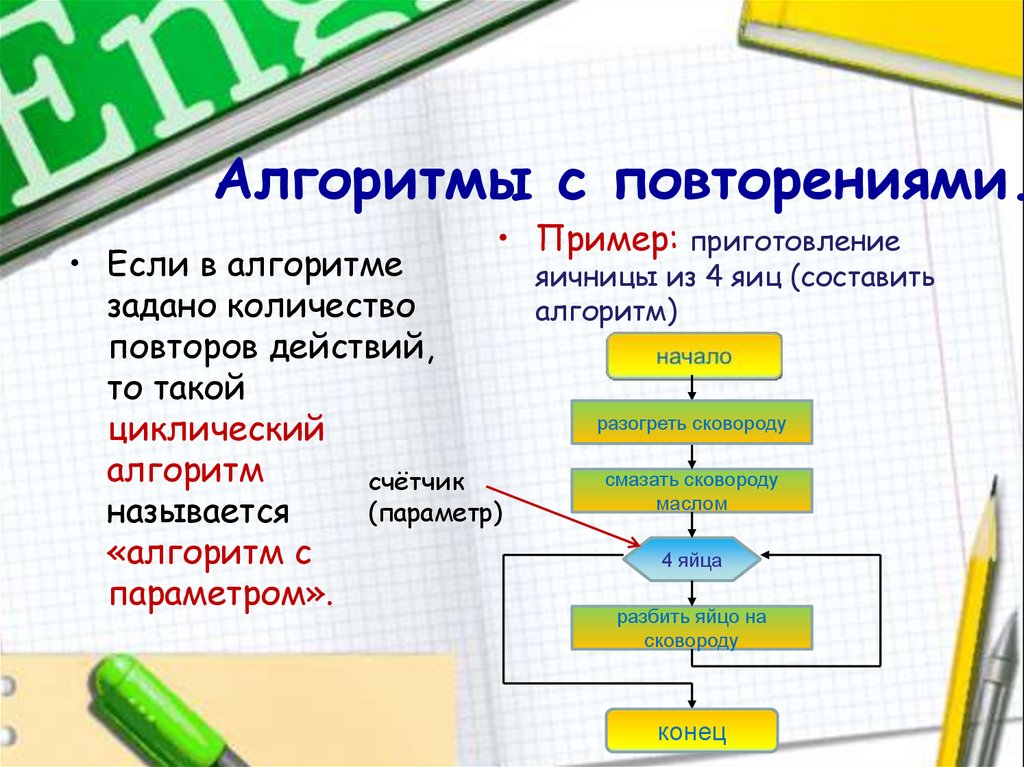
Сортировка выбором: Простой алгоритм сортировки, который многократно выбирает минимальный элемент из несортированной части массива и перемещает его в конец отсортированной части.
Сортировка слиянием: Алгоритм сортировки по принципу «разделяй и властвуй», который работает, разделяя несортированный список на n подсписков, сортируя каждый подсписок, а затем снова объединяя их в один отсортированный список.
Быстрая сортировка: Алгоритм сортировки по принципу «разделяй и властвуй», который работает путем выбора «осевого» элемента из массива и разделения других элементов на два подмассива в зависимости от того, меньше они или больше, чем опорный . Затем подмассивы сортируются рекурсивно.
Каждый из этих алгоритмов имеет разную временную и пространственную сложность, что делает некоторые из них более подходящими для определенных случаев использования, чем другие.
Алгоритмы поиска — это алгоритмы поиска определенного элемента или значения в структуре данных (например, в массиве или связанном списке).
 Некоторые из наиболее часто используемых алгоритмов поиска включают:
Некоторые из наиболее часто используемых алгоритмов поиска включают:Линейный поиск: Простой алгоритм поиска, который перебирает каждый элемент списка, пока не найдет совпадение.
Бинарный поиск: Алгоритм поиска, который работает путем многократного деления отсортированного списка пополам, пока не будет найден нужный элемент или не будет определено, что элемент отсутствует.
Поиск с переходом: Алгоритм поиска, который работает путем перехода вперед на фиксированные шаги в списке, пока не будет найден подходящий кандидат, а затем выполняет линейный поиск в окружающих элементах.
Поиск с интерполяцией : Алгоритм поиска, использующий информацию о диапазоне значений в списке для оценки положения нужного элемента и последующей проверки его наличия.
Поиск в хэш-таблице: Алгоритм поиска, использующий хеш-функцию для сопоставления элементов с индексами в массиве, а затем выполняющий поиск в массиве с постоянным временем для поиска нужного элемента.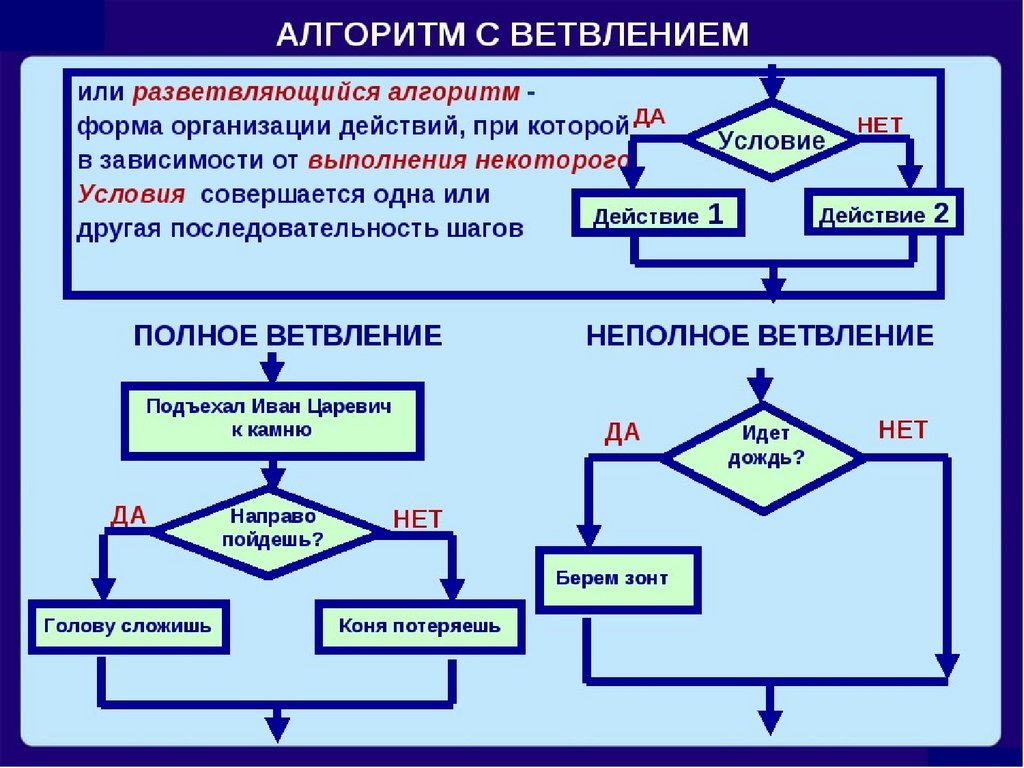
Каждый из этих алгоритмов имеет разную временную и пространственную сложность, что делает некоторые из них более подходящими для определенных случаев использования, чем другие. Выбор используемого алгоритма зависит от конкретных требований задачи, таких как размер структуры данных, распределение значений и желаемая временная сложность.
Алгоритмы графов — это набор алгоритмов, используемых для обработки, анализа и понимания структур данных графов. Графики — это математические структуры, используемые для моделирования отношений между объектами, где объекты представлены в виде вершин (или узлов), а отношения между ними представлены в виде ребер. Алгоритмы графов используются в различных приложениях, таких как сетевой анализ, анализ социальных сетей, рекомендательные системы и во многих других областях, где важно понимание взаимосвязей между объектами. Некоторые из распространенных графовых алгоритмов включают:
Алгоритмы поиска кратчайшего пути (например, Dijkstra's, Bellman-Ford, A*)
Алгоритмы минимального связующего дерева (например, Kruskal, Prim)
Алгоритмы максимального потока (например, Ford Network-Fulkerson, Edmonds-Karp)
9 Алгоритмы потока
(например, двудольное сопоставление)Алгоритмы подключения (например, поиск в глубину, поиск в ширину) Зачем мы используем алгоритмы?
Рассмотрим двух детей, Амана и Рохана, собирающих кубик Рубика.
Аман знает, как решить ее за определенное количество шагов. С другой стороны, Рохан знает, что он это сделает, но не знает о процедуре. Аман собирает куб за 2 минуты, тогда как Рохан все еще застрял, и к концу дня ему каким-то образом удалось его решить (возможно, он сжульничал, поскольку процедура необходима).
Таким образом, время, необходимое для решения с помощью процедуры/алгоритма, намного эффективнее, чем без какой-либо процедуры. Следовательно, необходимость в алгоритме является обязательной.
С точки зрения разработки решения ИТ-проблемы, компьютеры быстры, но не бесконечно быстры. Память может быть недорогой, но не бесплатно. Таким образом, время вычислений является ограниченным ресурсом, как и пространство в памяти. Поэтому мы должны использовать эти ресурсы с умом, и алгоритмы, эффективные с точки зрения времени и пространства, помогут вам в этом.
Создание алгоритма:
Поскольку алгоритм не зависит от языка, мы записываем шаги, чтобы продемонстрировать логику решения, которое будет использоваться для решения проблемы.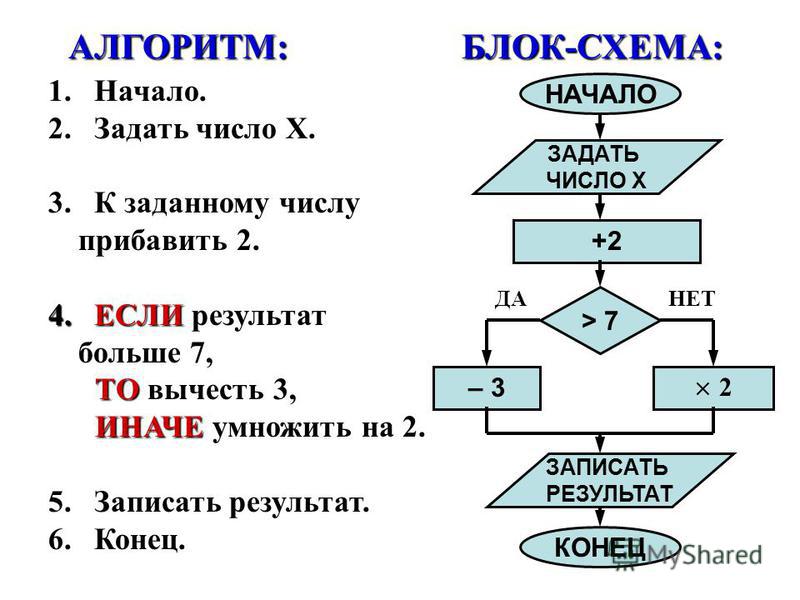 Но прежде чем писать алгоритм, учтите следующие моменты:
Но прежде чем писать алгоритм, учтите следующие моменты:
- Алгоритм должен быть четким и однозначным.
- В алгоритме должно быть 0 или более четко определенных входных данных.
- Алгоритм должен производить один или несколько четко определенных выходных данных, которые эквивалентны желаемому выходному сигналу. После определенного количества шагов алгоритмы должны остановиться.
- Алгоритмы должны останавливаться или заканчиваться после конечного числа шагов.
- Алгоритм должен содержать пошаговые инструкции, не зависящие от какого-либо компьютерного кода.
Пример: Алгоритм умножения 2 чисел и вывода результата:
Шаг 1: Запуск
Шаг 2: Получите знания о вводе. Здесь нам нужны 3 переменные; a и b будут пользовательским вводом, а c будет содержать результат.
Шаг 3: Объявите переменные a, b, c.
Шаг 4: Получить ввод для переменных a и b от пользователя.
Шаг 5: Знайте проблему и найдите решение, используя операторы, структуры данных и логикуНам нужно перемножить переменные a и b, поэтому мы используем оператор * и присваиваем результат c.
То есть c <- a * bШаг 6: Проверьте, как выводить вывод. Здесь нам нужно напечатать вывод. Итак, напишите print c
Шаг 7: Конец
Пример 1: Напишите алгоритм для нахождения максимума всех элементов, присутствующих в массиве.
Следуйте приведенному ниже алгоритму:
Шаг 1: Запустите программу
Шаг 2: Объявите переменную max со значением первого элемента массива.
Шаг 3: Сравните max с другими элементами, используя цикл.
Шаг 4: Если max < значения элемента массива, измените max на новый max.
Шаг 5: Если элементов не осталось, верните или выведите max, в противном случае перейдите к шагу 3.
Шаг 6: Конец решения
Пример 2: Напишите алгоритм для нахождения среднего значения для 3 субъектов.
Следуйте приведенному ниже алгоритму:
Шаг 1: Запустите программу
Шаг 2: Объявите и прочитайте 3 Тема, скажем, S1, S2, S3
Шаг 3: Подсчитайте сумму все 3 значения субъекта и сохранить результат в переменной Sum (Сумма = S1+S2+S3)
Шаг 4: Разделите сумму на 3 и присвойте ее средней переменной. (Среднее = Сумма/3)
Шаг 5: Выведите значение Среднее из 3 субъектов
Шаг 6: Конец решения
Знать об алгоритме Сложность относится к алгоритмам:
9 90 количество ресурсов (таких как время или память), необходимых для решения проблемы или выполнения задачи. Наиболее распространенной мерой сложности является временная сложность, которая относится к количеству времени, которое требуется алгоритму для получения результата в зависимости от размера входных данных. Сложность памяти относится к объему памяти, используемому алгоритмом. Разработчики алгоритмов стремятся разрабатывать алгоритмы с минимально возможной сложностью времени и памяти, поскольку это делает их более эффективными и масштабируемыми.
Сложность памяти относится к объему памяти, используемому алгоритмом. Разработчики алгоритмов стремятся разрабатывать алгоритмы с минимально возможной сложностью времени и памяти, поскольку это делает их более эффективными и масштабируемыми.
Алгоритм анализируется с использованием временной и пространственной сложности. Написание эффективного алгоритма помогает потреблять минимальное количество времени на обработку логики. Для алгоритма A он оценивается на основе двух параметров для входных данных размера n:
- Время Сложность: Время, затраченное алгоритмом на решение задачи. Измеряется путем подсчета итераций циклов, количества сравнений и т. д.
- Пространство Сложность: Пространство, занимаемое алгоритмом для решения задачи. Он включает пространство, используемое необходимыми входными переменными, и любое дополнительное пространство (исключая пространство, занимаемое входными данными), используемое алгоритмом.
Например, если мы используем хеш-таблицу (разновидность структуры данных), нам нужен массив для хранения значений, поэтому
- это занятое дополнительное пространство, поэтому оно будет учитываться при расчете сложности алгоритма. Это дополнительное пространство известно как вспомогательное пространство.
случаев сложности:
В алгоритмах обычно изучаются два случая сложности:
работы (например, занимает наименьшее количество времени, использует наименьшее количество памяти и т. д.).
2. Сложность в наихудшем случае: Наихудшим сценарием для алгоритма является сценарий, в котором алгоритм выполняет максимальный объем работы (например, занимает наибольшее количество времени, использует наибольшее количество памяти и т. д.) .
При анализе сложности алгоритма часто более информативно изучать сценарий наихудшего случая, так как это дает гарантированную верхнюю границу производительности алгоритма.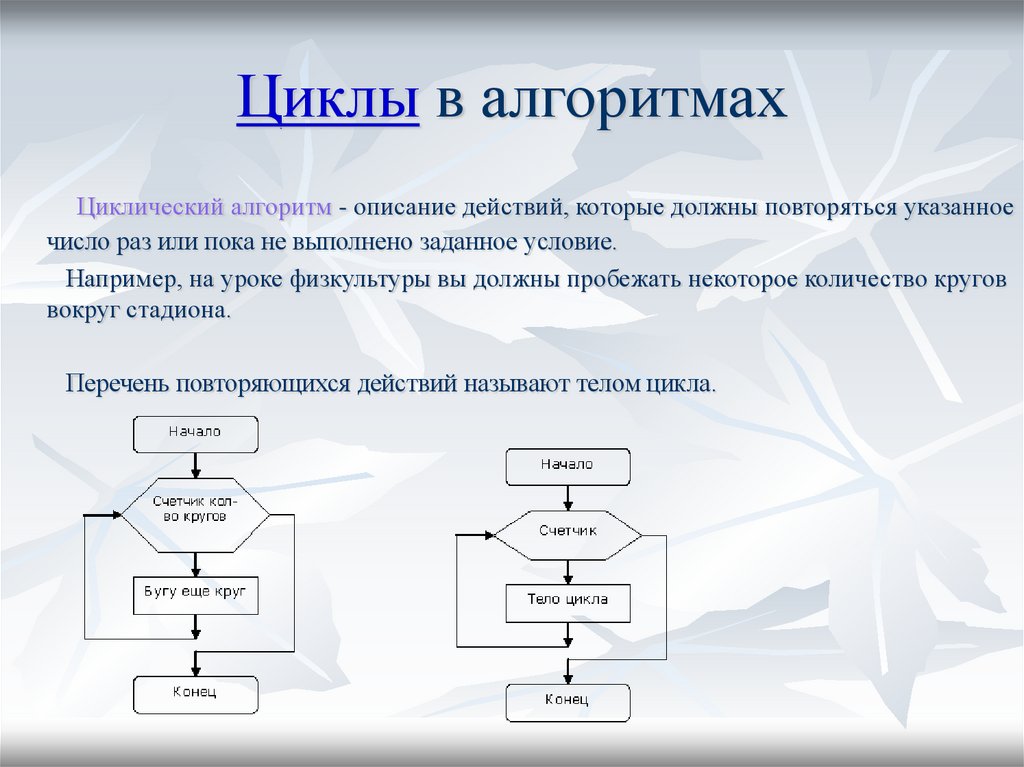


 Выставление оценок с учетом
процентного выполнения теста.
Выставление оценок с учетом
процентного выполнения теста.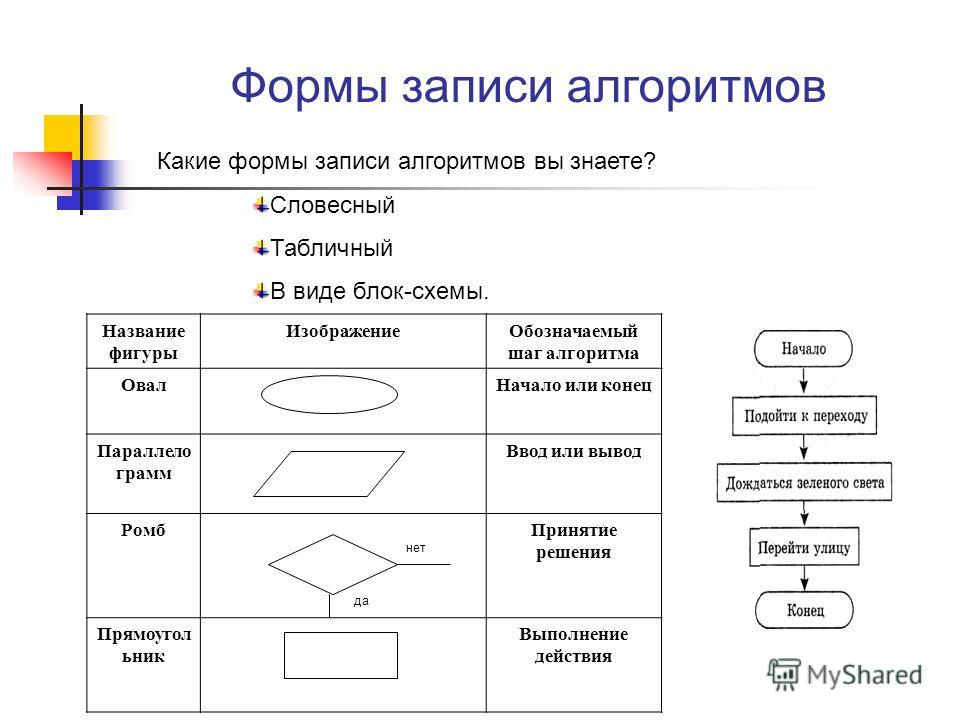
 ..mid], value, offset) elsif value > arr[mid]
двоичный_поиск (обр [(середина + 1)..-1], значение, смещение + середина + 1)
еще
смещение возврата + середина
конец
конец
..mid], value, offset) elsif value > arr[mid]
двоичный_поиск (обр [(середина + 1)..-1], значение, смещение + середина + 1)
еще
смещение возврата + середина
конец
конец
 shift
elsif справа[0] <= слева[0]
merged_arr << правый.shift
конец
конец
слитный_arr
конец
shift
elsif справа[0] <= слева[0]
merged_arr << правый.shift
конец
конец
слитный_arr
конец
 следующий_узел
текущее_местоположение += 1
конец
если предыдущий_узел
предыдущий_узел.следующий_узел = текущий_узел.следующий_узел
еще
голова = текущий_узел.следующий_узел
конец
голова
конец
следующий_узел
текущее_местоположение += 1
конец
если предыдущий_узел
предыдущий_узел.следующий_узел = текущий_узел.следующий_узел
еще
голова = текущий_узел.следующий_узел
конец
голова
конец
 Мы знаем, что часы тикают, но как производитель устанавливает эти гайки и болты так, чтобы они продолжали двигаться каждые 60 секунд, минутная стрелка должна двигаться, а часовая стрелка должна двигаться каждые 60 минут? Поэтому, чтобы решить эту проблему, за ней должен стоять алгоритм.
Мы знаем, что часы тикают, но как производитель устанавливает эти гайки и болты так, чтобы они продолжали двигаться каждые 60 секунд, минутная стрелка должна двигаться, а часовая стрелка должна двигаться каждые 60 минут? Поэтому, чтобы решить эту проблему, за ней должен стоять алгоритм. д. Эти алгоритмы используются для поиска значения или записи, которые требуются пользователю.
д. Эти алгоритмы используются для поиска значения или записи, которые требуются пользователю.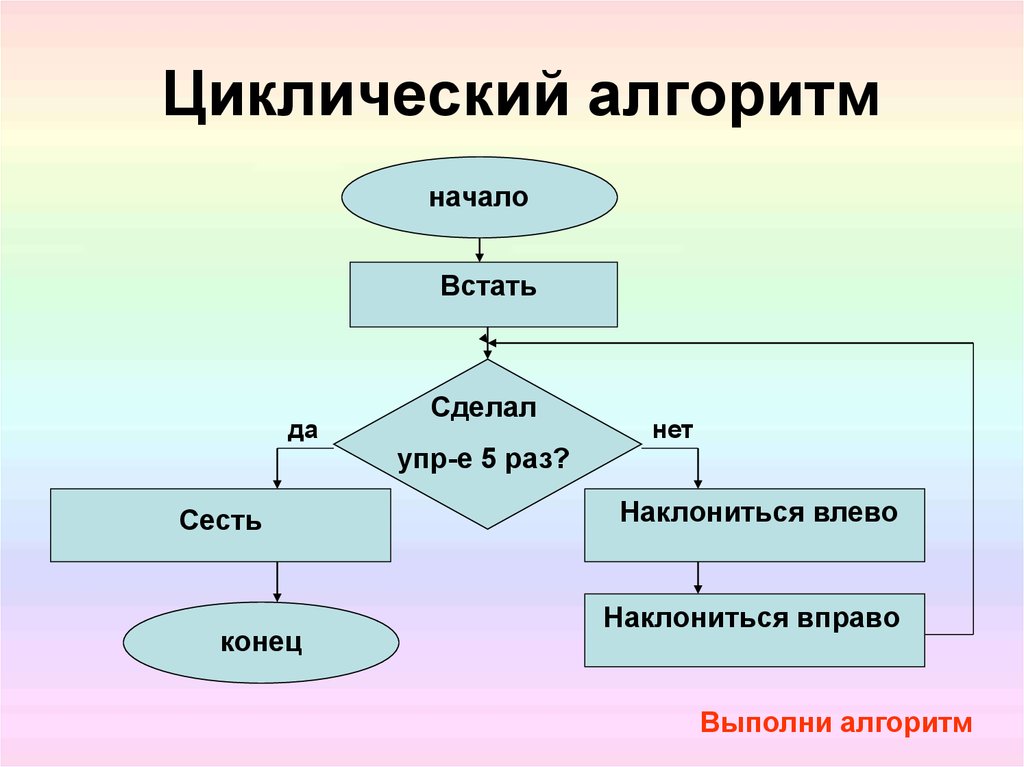 Аман знает, как решить ее за определенное количество шагов. С другой стороны, Рохан знает, что он это сделает, но не знает о процедуре. Аман собирает куб за 2 минуты, тогда как Рохан все еще застрял, и к концу дня ему каким-то образом удалось его решить (возможно, он сжульничал, поскольку процедура необходима).
Аман знает, как решить ее за определенное количество шагов. С другой стороны, Рохан знает, что он это сделает, но не знает о процедуре. Аман собирает куб за 2 минуты, тогда как Рохан все еще застрял, и к концу дня ему каким-то образом удалось его решить (возможно, он сжульничал, поскольку процедура необходима).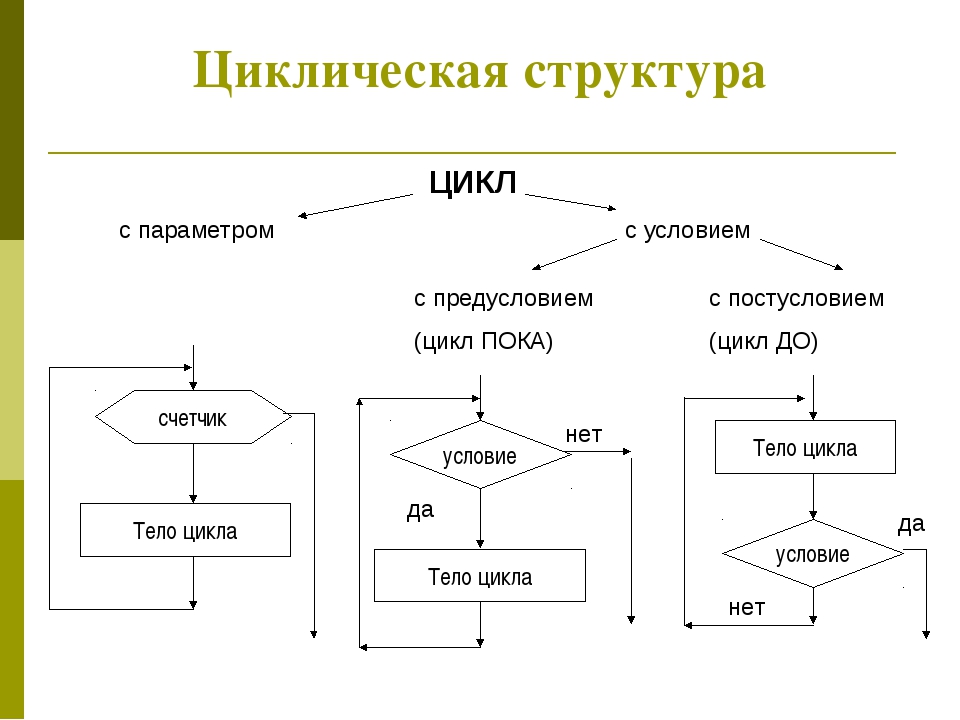
 Например, если мы используем хеш-таблицу (разновидность структуры данных), нам нужен массив для хранения значений, поэтому
Например, если мы используем хеш-таблицу (разновидность структуры данных), нам нужен массив для хранения значений, поэтому