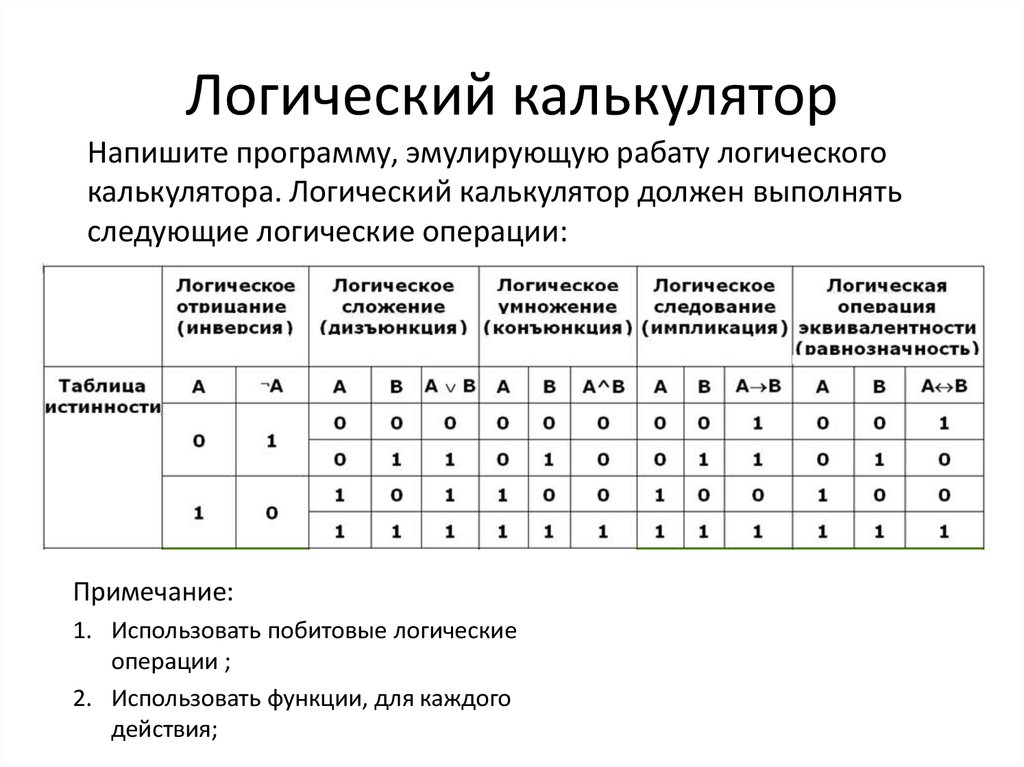
Информатика алгебра логики калькулятор: Калькулятор логических выражений — RC74 — интернет-магазин радиоуправляемых моделей

Содержание

Калькулятор логических выражений

Программа предназначена для получения таблиц истинности логических функций с числом переменных от одной до пяти. Логической (булевой) функцией n переменных y = f(x₁, x₂, …, x_n) называется такая функция, у которой все переменные и сама функция могут принимать только два значения: 0 и 1.

A B C D

0 1

· + ¬

⊕ ⇒ ⇔

↓ |

( )

Решить!

Другой тип калькулятора для таблицы истинности

Шпаргалка по работе с калькулятором.

Переменные, которые могут принимать только два значения 0 и 1 называются логическими переменными (или просто переменными). Заметим, что логическая переменная х может подразумевать под числом 0 некоторое высказывание, которое ложно, и под числом 1 высказывание, которое истинно.

Из определения логической функции следует, что функция n переменных – это отображение Bⁿ в B, которое можно задать непосредственно таблицей, называемой таблицей истинности данной функции.

Основные функции логики – это функции двух переменных z = f(x,y).

Число этих функций равно 2⁴ = 16. Перенумеруем и расположим их в естественном порядке.

Рассмотрим более подробно эти функции. Две из них f₀ = 0 и f₁₅ = 1 являются константами. Функции f₃, f₅, f₁₀ и f₁₂ являются по существу функциями одной переменной.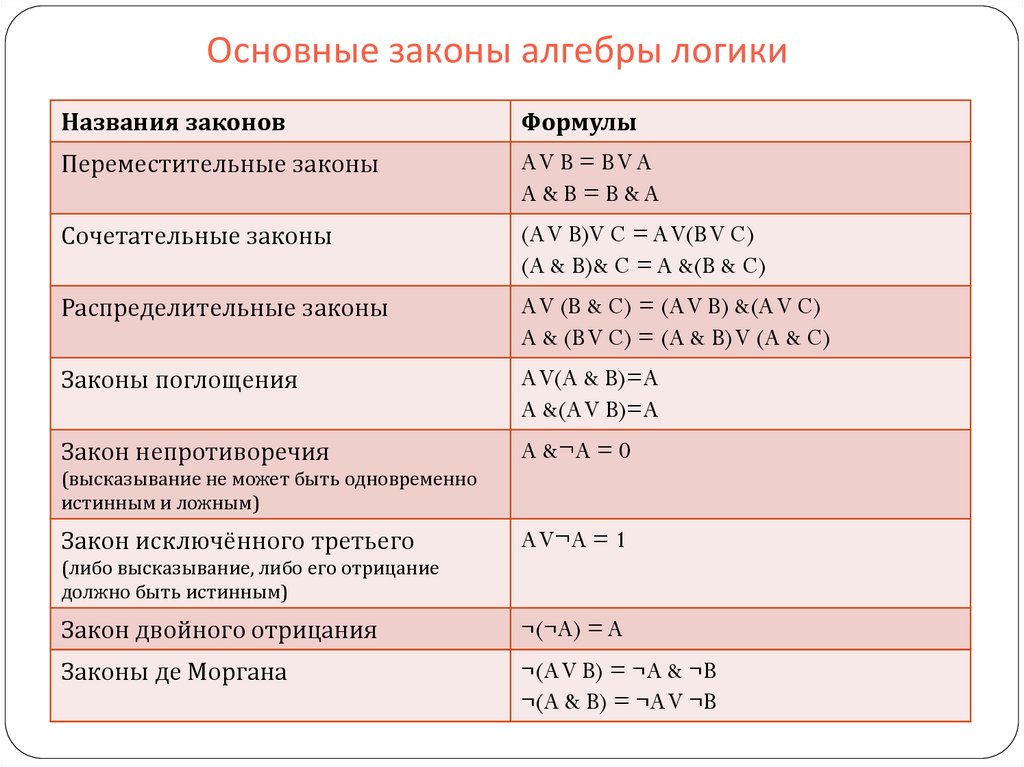

Наиболее важные функции двух переменных имеют специальные названия и обозначения.

1) f₁ – конъюнкция (функция И)
Заметим, что конъюнкция – это фактически обычное умножение (нулей и единиц). Эту функцию обозначают x&y;

2) f₇ – дизъюнкция (функция или). Обозначается V.

3) f₁₃ – импликация (следование). Обозначается ->
Это очень важная функция, особенно в логике. Ее можно рассматривать следующим образом: если х = 0 (т. е. х “ложно”), то из этого факта можно вывести и “ложь”, и “истину” (и это будет правильно), если у = 1 (т. е. у “истинно”), то истина выводится и из “лжи” и из “истины”, и это тоже правильно. Только вывод “из истины ложь” является неверным. Заметим, что любая теорема всегда фактически содержит эту логическую функцию;

4) f₆ – сложение по модулю 2. Обозначается знаком “+” или знаком “+” в кружке.

5) f₉ – эквивалентность или подобие. Эта f₉ = 1 тогда и только тогда, когда х = у. Обозначается х ~ у.

6) f₁₄ – штрих Шеффера. Иногда эту функцию называют “не и” (так как она равна отрицанию конъюнкции). Обозначается x|y.

7) f₈ – стрелка Пирса (иногда эту функцию называют штрих Лукасевича).

Три оставшиеся функции, (f₂ , f₄ и f₁₁) особого обозначения не имеют.

Заметим, что часто в логике рассматриваются функции от функций, т.е. суперпозиции перечисленных выше функций. При этом последовательность действий указывается (как обычно) скобками.

Также можно скачать программу “Логический калькулятор” для Windows.

На данный момент логический калькулятор умеет выполнять следующее:

Ввод и проверка переменных на корректность. Под корректностью подразумевается правильное написание букв и операций над ними
Вывод таблицы истинности для выражения
СКНФ и СДНФ

Калькулятор логических выражений онлайн

Можно также попробовать работу калькулятора логики онлайн (это другая версия, а не та, которую можно скачать выше по ссылке). c*d/+

Польская инверсная запись

Диаграммы Эйлера-Венна

Диаграмма Эйлера-Венна — наглядное средство для работы со множествами. На этих диаграммах изображаются все возможные варианты пересечения множеств. Данная программа относится к таким разделам как

Информатика, Дискретная математика.

ABC

Диаграммы Эйлера-Венна

Редактор схемы логических элементов

Возможности калькулятора позволяют создавать любые сложные схемы логических элементов с последующей минимизацией булевой функции. Имеется поддержка редактирования карты Карно. Данная программа относится к таким разделам как Информатика, Дискретная математика.

Редактор схем

Таблица истинности

(a→c)→b→a
По заданной булевой функции формируется таблица истинности, по которой находятся СКНФ, СДНФ и полином Жегалкина.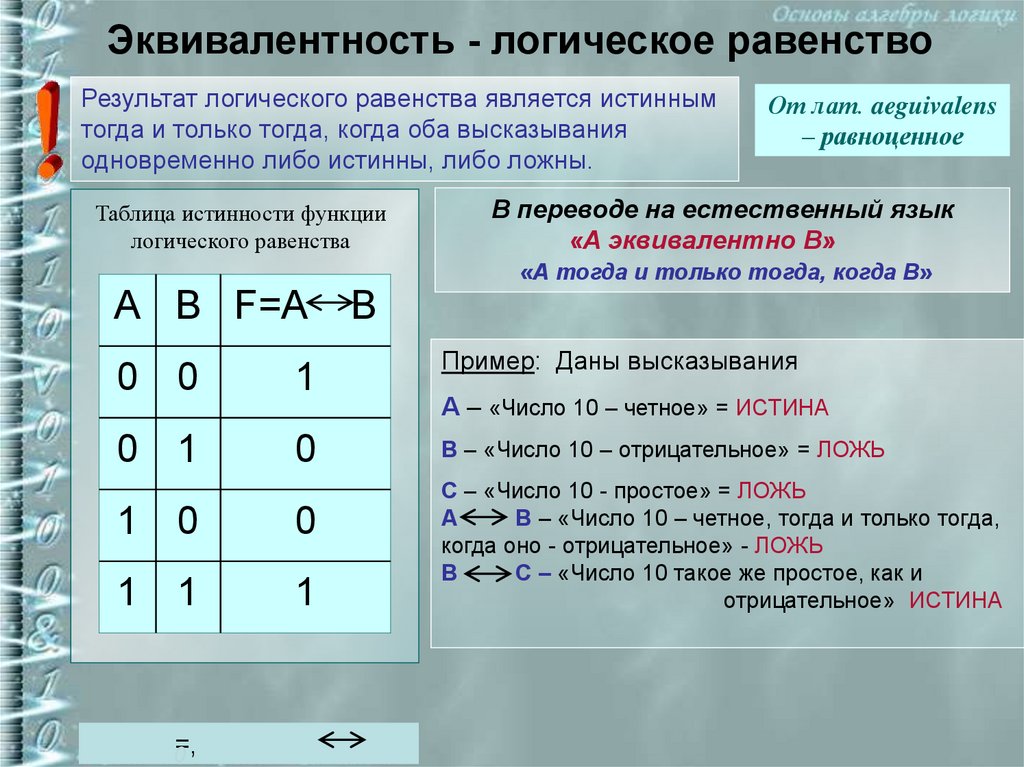

Данная программа относится к таким разделам как Информатика, Дискретная математика.
Этот же калькулятор можно использовать для упрощения логического выражения (через равносильные преобразования).

Таблица истинности

Карты Карно

С помощью этого калькулятора производится минимизация булевой функции методом Карно-Вейча. Данная программа относится к таким разделам как Информатика, Дискретная математика.

x2x3x100000000

Карты Карно

Полином Жегалкина

Многочлен Жегалкина можно получить различными способами. В следующих программах рассмотренны построения многочлена Жегалкина с помощью треугольника Паскаля и согласно методу неопределенных коэффициентов.

Ввод данных можно осуществить в виде вектора значений логической функции, либо через формулу.

Генерация перестановок

Выводит все возможные сочетания из N чисел: N!

Варианты	Вид №1	Вид №2
123	A1A2A3	A₁A₂A₃
132	A1A3A2	A₁A₃A₂
213	A2A1A3	A₂A₁A₃
231	A2A3A1	A₂A₃A₁
312	A3A1A2	A₃A₁A₂
321	A3A2A1	A₃A₂A₁

Генерация перестановок

Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).

Калькулятор булевой алгебры — онлайн-упрощение булевых логических выражений

Поиск инструмента

Найдите инструмент в dCode по ключевым словам:

Просмотрите полный список инструментов dCode

Калькулятор логических выражений

Инструмент/калькулятор для упрощения или минимизации логических выражений (булева алгебра), содержащих логические выражения с И, ИЛИ, НЕ, XOR.

Результаты

Калькулятор логических выражений — dCode

Метки: Символьные вычисления, Электроника

dCode и многое другое

dCode бесплатен, а его инструменты являются ценным подспорьем в играх, математике, геокэшинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !

Упрощение логических выражений

Калькулятор логических выражений/упрощение/минификатор
Формат результата
Любой формат
Дизъюнктивная нормальная форма DNF (сумма произведений/SOP/Minterms)
Конъюнктивная нормальная форма CNF (произведение сумм/POS/Maxterms)
Только вентили НЕ-И (НЕ-И ⊼)
Только вентили ИЛИ-НЕ (НЕ-ИЛИ ⊽)

Нотация

Алгебраические (*, +, !)
Логические (∧, ∨, ¬)
Программирование (& ||, ~)
Буквенное (И, ИЛИ, НЕ)

См. также: Таблица истинности — Решатель уравнений — Двоичный код

Ответы на вопросы (FAQ)

Что такое логическое выражение? (Определение)

A Логическое выражение (или Логическое выражение) — это математическое выражение, использующее Булева алгебра , которая использует логические значения (0 или 1, истина или ложь) в качестве переменных и имеет логические значения в качестве результата/упрощения. Выражение может содержать такие операторы, как конъюнкция (И), дизъюнкция (ИЛИ) и отрицание (НЕ).

Как упростить/минимизировать логическое выражение?

Для упрощения булевых уравнений можно использовать различные методы: помимо классического развития через ассоциативность, коммутативность, дистрибутивность и т. д., таблицы истинности или диаграммы Венна обеспечивают хороший обзор выражений.

Пример: Исходное выражение (LaTeX) $$ \overline{a \land b \land (c \lor \bar{d})} \lor \bar{b} $$

dCode допускает несколько синтаксисов:

Алгебраическая запись

Пример: !(ab(c+!d))+!b с неявным умножением ab = a AND b и ! (восклицательный знак) для строки : логический НЕ .

Логические/компьютерные обозначения

Пример: !(a&&b&&(c||!d))||!b с двойным символом и (амперсанд) для И и двойным символом | (прямая, вертикальная черта) для логического ИЛИ .

Буквенное обозначение

Пример: НЕ (a И b И (c ИЛИ НЕ d)) ИЛИ НЕ b

Для одного и того же выражения может быть несколько минимальных представлений, dCode предоставляет решение и выводит алгебраическое обозначение.

Некоторые обозначения неоднозначны, избегайте функционального обозначения ‘XOR(a,b)’ для записи a XOR b , также избегайте суффикса штрих/апостроф перед `a’ и предпочтите !a .

Что такое методы упрощения булевой алгебры?

Булева алгебра обладает многими свойствами (булевыми законами):

1 — Элемент тождества: $0$ нейтрален для логического ИЛИ, тогда как $1$ нейтрален для логического И

$$a + 0 = a \\a . 1 = a $$

2 — Поглощение: $1$ поглощает для логического ИЛИ, а $0$ поглощает для логического И

$$ a + 1 = 1 \\ a.0 = 0 $$

3 — Идемпотентность: многократное применение одной и той же операции не меняет значение

$$ a + a = a + a + \cdots + а = а \ а . а = а . а . \cdots . a = a $$

4 — Инволюция или двойное дополнение: противоположность противоположности $ a $ est $ a $

$$ a = \overline{\overline{a}} = !(!a) $$

5 — Дополнительность по противоречию: $ a $ AND $ \text{not}(a) $ невозможно, поэтому ложно и равно $ 0 $

$$ а . \overline{a} = 0 $$

6 — Дополнительность по исключенному третьему: $ a $ OR $ \text{not}(a) $ всегда истинно, поэтому $ 1 $

$$ a + \overline{ a} = 1 $$

7 — Закон ассоциативности: скобки между одинаковыми операторами бесполезны

$$ a.(b.c) = (a.b).c = a.b.c \\ a+(b+c) = (a+b) +c = a+b+c $$

8 — Закон коммуникативности: порядок не имеет значения

$$ a.b = b. a \\ a+b = b+a $$

9 — Закон распределения: И распределено над ИЛИ, но также ИЛИ распределяется по И

$$ a.(b+c) = a.b + a.c \\ a+(b.c) = (a+b).(a+c) $$

10 — Законы Де Моргана (подробнее см. ниже)

$$ \overline{a+b} = \overline{a}.\overline{b} \\ \overline{a.b} = \overline{a}+\overline{b} $$

11 — Другие упрощения комбинации указанных выше

$$ a.(a+b) = a \\ a+(a.b) = a \\ (a.b) + (a.!b) = a \\ (a+b).(a+ !b) = a \\ a + (!a.b) = a + b \\ a.(!a + b) = a.b \\ a.b + \overline{a}.c = a.b + \overline{a}.c + b.c $$

Как показать/продемонстрировать, что 2 логических выражения равны?

Метод 1: упростите их , пока не получите то же самое написание в булевой алгебре .

Метод 2: путем вычисления их таблицы истинности , которая должна быть идентичной.

Что такое закон де Моргана?

Законы де Моргана часто используются для перезаписи логических выражений.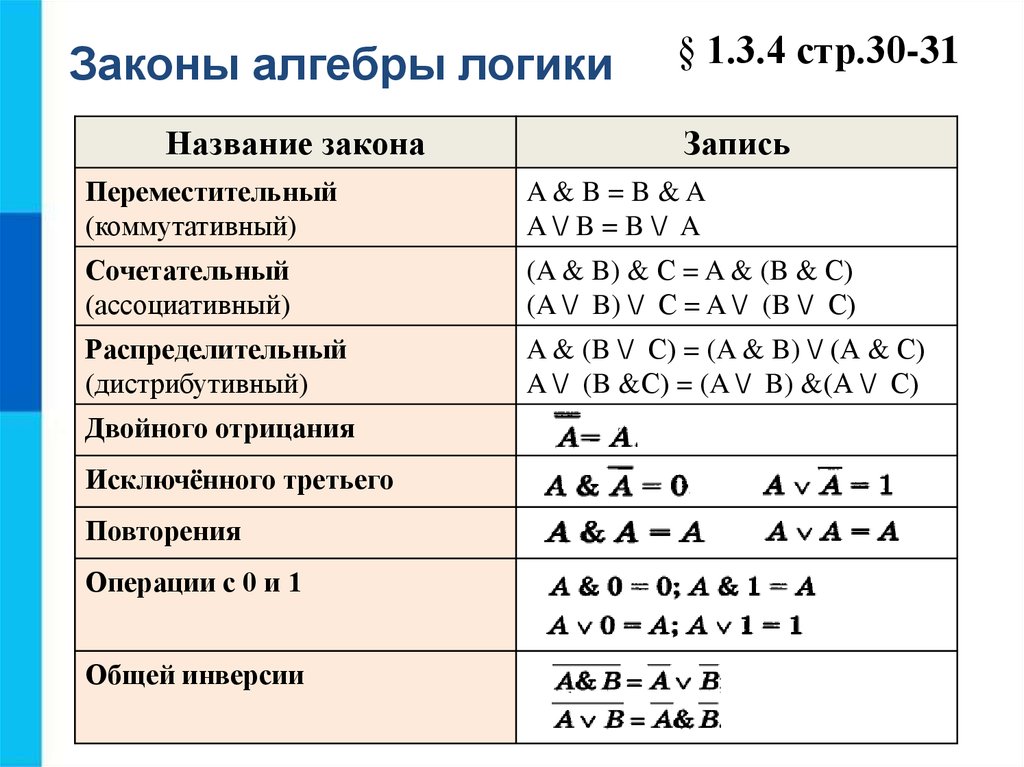 Обычно они формулируются так: не (а и б) = (не а) или (не б) и не (а или б) = (не а) и (не б) . Вот эквивалентные логические записи:

$$ \overline{(a \land b)} \leftrightarrow (\overline{a}) \lor (\overline{b}) \iff \overline{AB} = \overline{a} + \overline{b } $$

$$ \overline{(a \lor b)} \leftrightarrow (\overline{a}) \land (\overline{b}) \iff \overline{a+b} = \overline{a} . \overline{b} $$

Что такое дизъюнктивная или конъюнктивная нормальная форма?

В логике можно использовать разные форматы для обеспечения лучшей читабельности или удобства использования.

Нормальная дизъюнктивная форма (DNF) использует сумму произведений (SOP):

Пример: (a&&c)||b

Нормальная конъюнктивная форма (CNF) или клаузальная форма использует произведение сумм (POS):

Пример: (a+b).(b). +c)

Как показать пошаговые расчеты?

Шаги расчета, какими их может себе представить человек, для решателя не существуют. Выполняемые операции являются бинарными побитовыми и не соответствуют выполняемым при разрешении с помощью карандаша и бумаги.

Исходный код

dCode сохраняет право собственности на исходный код «Калькулятора логических выражений». За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Калькулятор логических выражений», апплета или фрагмента (преобразователь, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или «Булевых выражений». Функции калькулятора (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д.) и загрузка всех данных, script или доступ к API для «Калькулятора логических выражений» не являются общедоступными, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android!

Напоминание: dCode можно использовать бесплатно.

Cite dCode

Копирование и вставка страницы «Калькулятор логических выражений» или любых его результатов разрешено, если вы цитируете dCode!
Экспорт результатов в виде файла .csv или .txt можно выполнить бесплатно, щелкнув значок export . 10, https://www.dcode.fr/boolean-expressions-calculator

Сводка

Упрощение логических выражений
Что такое логическое выражение? (Определение)
Как упростить/минимизировать логическое выражение?
Что такое методы упрощения булевой алгебры?
Как показать/продемонстрировать, что 2 логических выражения равны?
Что такое закон де Моргана?

Что такое дизъюнктивная или конъюнктивная нормальная форма?
Как показать пошаговые расчеты?

Похожие страницы

Truth Table
Equation Solver
Boolean Dual
Boolean Minterms and Maxterms
Binary Code
Math Expression Simplifier
Remove Parentheses
DCODE’S TOOLS LIST

Support

Paypal
Patreon
Подробнее

Форум/Справка

Ключевые слова

bool,boole,boolean,выражение,алгебра,логика,логический,упрощение,упрощение,и,или,не,xor,амперсанд,труба,восклицательный знак,морган

Ссылки

▲

Калькулятор булевой алгебры — онлайн-упрощение логических выражений

Поиск инструмента

Найдите инструмент в dCode по ключевым словам:

Просмотрите полный список инструментов dCode

Калькулятор логических выражений

Результаты

Калькулятор логических выражений — dCode

Теги: Символьные вычисления, Электроника

dCode и многое другое

Программа dCode бесплатна, а ее инструменты оказывают ценную помощь в играх, математике, геокэшинге, головоломках и задачах, которые нужно решать каждый день!

Предложение? обратная связь? Жук ? идея ? Запись в dCode !