Цепь переменного тока с индуктивностью
В статье «ЭДС самоиндукции и индуктивность цепи» говорится, что при включении и при всяком изменении тока в электрической цепи вследствие пересечения проводника своим же собственным магнитным полем в нем возникает индуктированная электродвижущая сила (ЭДС). Эту ЭДС мы назвали ЭДС самоиндукции. ЭДС самоиндукции имеет реактивный характер. Так, например, при увеличении тока в цепи ЭДС самоиндукции будет направлена против ЭДС источника напряжения, и поэтому ток в электрической цепи не может установиться сразу. И, наоборот, при уменьшении тока в цепи индуктируется ЭДС самоиндукции такого направления, что, мешая току исчезать, она поддерживает этот убывающий ток.
Рисунок 1. Цепь переменного тока, содержащая индуктивность
Как нам уже известно, ЭДС самоиндукции зависит от скорости изменения тока в цепи и от индуктивности этой цепи (числа витков, наличия стальных сердечников).
В цепи переменного тока ЭДС самоиндукции возникает непрерывно, так как ток в цепи непрерывно изменяется.
На рисунке 1 представлена схема цепи переменного тока, содержащей катушку с индуктивностью L без стального сердечника. Для простоты будем считать сначала, что активное сопротивление катушки очень мало и им можно пренебречь.
Рассмотрим внимательнее изменение переменного тока за время одного периода. На рисунке 2 показана кривая изменения переменного тока. Первая половина периода разбита на мелкие одинаковые части.
Рисунок 2. Определение скорости изменения переменного тока
За промежуток времени 0 – 1 величина тока изменилась от нуля до 1 – 1’. Прирост величины тока за это время равен а.
За время, обозначенное отрезком 1 – 2, мгновенная величина выросла до 2 – 2’, причем прирост величины тока равен б.
В течение времени, обозначенного отрезком 2 – 3, ток увеличивается до 3 – 3’, прирост тока показывает отрезок в и так далее.
Так, с течением времени переменный ток возрастет до максимума (при 90°). Но, как видно из чертежа, прирост тока делается все меньше и меньше, пока, наконец, при максимальном значении тока этот прирост не станет равным нулю.
При дальнейшем изменении тока от максимума до нуля убыль величины тока становится все больше и больше, пока, наконец, около нулевого значения ток, изменяясь с наибольшей скоростью, не исчезнет, но тут же появляется вновь, протекая в обратном направлении.
Рассматривая изменение тока в течение периода, мы видим, что с наибольшей скоростью изменяется ток около своих нулевых значений. Около максимальных значений скорость изменения тока падает, а при максимальном значении тока прирост его равен нулю. Таким образом, переменный ток меняется не только по величине и направлению, но также и по скорости своего изменения. Переменный ток, проходя по виткам катушки, создает переменное магнитное поле. Магнитные линии этого поля, пересекая витки своей же катушки, индуктируют в них ЭДС самоиндукции.
На рисунке 3 кривая i показывает изменение переменного тока в катушке. Как было уже указано, величина ЭДС самоиндукции зависит от скорости изменения тока и от индуктивности катушки. Но так как индуктивность катушки в нашем случае остается без изменения, ЭДС самоиндукции будет зависеть только от скорости изменения тока. Выше было показано, что наибольшая скорость изменения тока имеет место около нулевых значений тока. Следовательно, наибольшее изменение ЭДС самоиндукции имеет те же моменты.
Рисунок 3. ЭДС самоиндукции в катушке, включенной в цепь переменного тока
В момент а ток резко и быстро увеличивается от нуля, а поэтому, как следует из вышеприведенной формулы, ЭДС самоиндукции (кривая eL) имеет отрицательное максимальное значение. Так как ток увеличивается, то ЭДС самоиндукции по правилу Ленца должна препятствовать изменению (здесь увеличению) тока. Поэтому ЭДС самоиндукции при возрастании тока будет иметь направление, обратное току (положение б), что следует также из указанной формулы.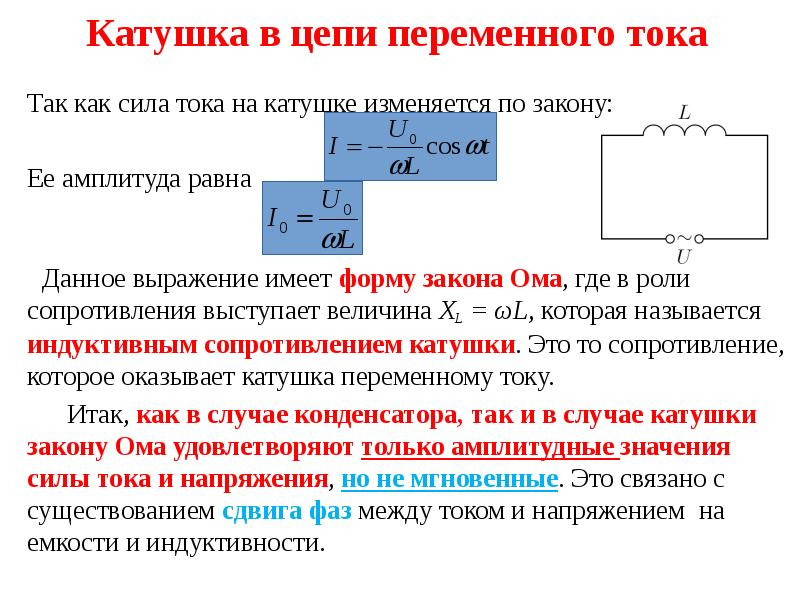
Скорость изменения тока по мере приближения его к максимуму уменьшается. Поэтому ЭДС самоиндукции также уменьшается, пока, наконец, при максимуме тока, когда изменения его будут равны нулю, она не станет равной нулю (положение в).
Переменный ток, достигнув максимума, начинает убывать. По правилу Ленца ЭДС самоиндукции будет мешать току убывать и, направленная уже в сторону протекания тока, будет его поддерживать (положение г).
При дальнейшем изменении переменный ток быстро убывает до нуля. Резкое уменьшение тока в катушке повлечет за собой также быстрое уменьшение магнитного поля и в результате пересечения магнитными линиями витков катушки в них будет индуктироваться наибольшая ЭДС самоиндукции (положение д).
Рисунок 4. Ток в катушке опережает ЭДС самоиндукции по фазе на 90°
Во вторую половину периода изменения тока картина повторяется и снова при возрастании тока ЭДС самоиндукции будет мешать ему, имея направление, обратное току (положение е).
При убывании тока ЭДС самоиндукции, имея направление в сторону тока, будет поддерживать его, не давая ему исчезнуть сразу (положение з).
На рисунке видно, что ЭДС самоиндукции отстает по фазе от тока на 90° или на ¼ периода. Так как магнитный поток совпадает по фазе с током, то можно сказать, что ЭДС, наводимая магнитным потоком, отстает от него по фазе на 90° или на ¼ периода.
Нам уже известно, что две синусоиды, сдвинутые одна относительно другой на 90°, можно изобразить векторами, расположенными под углом 90° (рисунок 4).
Так как ЭДС самоиндукции в цепях переменного тока непрерывно противодействует изменениям тока, то, чтобы дать возможность току протекать по виткам катушки, напряжение сети должно уравновешивать ЭДС самоиндукции. Иными словами, напряжение сети в каждый момент времени должно быть равно и противоположно ЭДС самоиндукции.
Рисунок 5. Приложенное к катушке напряжение сети опережает ток на 90° и противоположно ЭДС самоиндукции
Вектор напряжения сети, равный и противоположный ЭДС самоиндукции eL, мы обозначим через U (рисунок 5).
Только при условии, что к зажимам катушки будет приложено напряжение сети, равное и противоположное ЭДС самоиндукции, и, стало быть, это напряжение сети U уравновесит ЭДС самоиндукции eL, по катушке сможет проходить переменный ток I.
Но в этом случае напряжение сети U будет опережать по фазе ток I на 90°.
Таким образом, в цепях переменного тока ЭДС самоиндукции, возникая непрерывно, вызывает сдвиг фаз между током и напряжением. Возвращаясь к рисунку 3, мы видим, что ток i по катушке будет проходить и тогда, когда напряжение сети (кривая uL) равно нулю (положение в), и даже тогда, когда напряжение сети направлено в сторону, обратную току (положение г и з).
Итак отметим, что в цепи переменного тока, когда ЭДС самоиндукции отсутствует, напряжение сети и ток совпадают по фазе. Индуктивная же нагрузка в цепях переменного тока (обмотки электродвигателей и генераторов, обмотки трансформаторов, индуктивные катушки) всегда вызывает сдвиг фаз между током и напряжением.
Можно показать, что скорость изменения тока пропорциональна угловой частоте ω. Следовательно, действующее значение ЭДС самоиндукции eL может быть найдено по формуле:
eL = ω × L × I = 2 × π × f × L × I .
Как было отмечено выше, напряжение, приложенное к зажимам цепи, содержащей индуктивность, в каждый момент времени должно быть по величине равно ЭДС самоиндукции:
uL = eL.
Поэтому
uL = 2 × π × f × L × I .
Обозначая 2 × π × f × L = xL , получим
uL = xL × I .
Формула закона Ома для цепи переменного тока, содержащего индуктивность, будет такова:
Величина xL называется индуктивным сопротивлением цепи, или реактивным сопротивлением индуктивности, и измеряется в омах.
Таким образом, реактивное индуктивное сопротивление представляет собой своеобразное препятствие, которое оказывает цепь изменениям тока в ней. Оно равно произведению индуктивности на угловую частоту. Формула индуктивного сопротивления имеет вид:
xL = ω × L .
Индуктивное сопротивление проводника зависит от частоты переменного тока и индуктивности проводника. Поэтому индуктивное сопротивление катушки, включаемой в цепь токов различной частоты, будет различным. Например, если имеется катушка индуктивностью 0,05 Гн, то путем расчета индуктивного сопротивления выяснится, что в цепи частотой 50 Гц ее индуктивное сопротивление будет:
xL1 = 2 × π × f1 × L = 2 × 3,14 × 50 × 0,05 = 15,7 Ом ,
а в цепи тока частотой 400 Гц
xL2 = 2 × π × f2 × L = 2 × 3,14 × 400 × 0,05 = 125,6 Ом .
youtube.com/embed/52N9s6gsuD0?wmode=transparent» allowfullscreen=»»> Та часть напряжения сети, которая идет на преодоление (уравновешивание) ЭДС самоиндукции, называется индуктивным падением напряжения или реактивной слагающей напряжения.
uL = xL × I .
Рассмотрим теперь, какая мощность потребляется от источника переменного напряжения, если к его зажимам подключена индуктивность.
Рисунок 6. Кривые мгновенных значений напряжения, тока и мощности для цепи, содержащей индуктивность
На рисунке 6 даны кривые мгновенных значений напряжения, тока и мощности для этого случая. Мгновенное значение мощности равно произведению мгновенных значений напряжения и тока:
p = u × i .
Из чертежа видно, что если u и i имеют одинаковые знаки, то кривая p положительная и располагается выше оси ωt.
Если же u и i имеют разные знаки, то кривая p отрицательна и располагается ниже оси ωt.
В первую четверть периода ток, а в месте с ним и магнитный поток катушки увеличиваются. Катушка забирает из сети мощность. Площадь, заключенная между кривой p и осью ωt, есть работа (энергия) электрического тока. За первую четверть периода энергия, забираемая из сети, идет на создание магнитного поля вокруг витков катушки (мощность положительная). Количество энергии, запасаемое в магнитном поле за время роста тока, можно определить по формуле:
За вторую четверть периода ток убывает. ЭДС самоиндукции, которая в первую четверть периода стремилась помешать возрастанию тока, теперь, когда ток начинает уменьшаться, будет мешать ему уменьшаться. Сама катушка становится как бы генератором электрической энергии. Она возвращает в сеть энергию, запасенную в ее магнитном поле. Мощность отрицательна, и на рисунке 6 кривая p располагается ниже оси ωt.
За вторую половину периода явление повторяется. Таким образом, между источником переменного напряжения и катушкой, содержащей индуктивность, происходит обмен мощностью. В течение первой и третьей четвертей периода мощность поглощается катушкой, в течение второй и четвертой мощность возвращается источнику.
В этом случае, в среднем, расхода мощности не будет, несмотря на то, что на зажимах цепи есть напряжение U и в цепи протекает ток I.
Тот же результат мы получим, если вычислим среднюю или активную мощность по формуле, приведенной выше:
P = U × I × cos φ .
В нашем случае между напряжением и током существует сдвиг фаз, равный 90°, и cos φ = 90° = 0.
Поэтому активная мощность также равна нулю, то есть расхода мощности нет.
Источник: Кузнецов М. И., «Основы электротехники» — 9-е издание, исправленное — Москва: Высшая школа, 1964 — 560 с.
Катушка индуктивности в цепи переменного тока
Если катушка индуктивности включена в цепь переменного тока, то в такой цепи, фаза тока всегда отстает от фазы напряжения.
Разберем причины этого отставания на простейшем примере, когда в цепи имеется только индуктивное сопротивление, а омического сопротивления нет вовсе, или вернее омическим сопротивлением провода катушки самоиндукции можно пренебречь, так как оно мало.
Для удобства рассмотрения явлений будем считать, что мы присоединяем катушку индуктивности к источнику переменного тока в тот момент, когда напряжение U на его зажимах имеет максимальное амплитудное значение (рис. 1а.). Этот момент будем считать началом периода.
Рисунок 1. Самоиндукция-инерция. а) соотношения фаз тока, напряжения и ЭДС самоиндукции при включение катушки индуктивности в цепь переменного тока; б) соотношение фаз скорости движения, внешней силы и силы инерции
В момент включения катушки в ней немедленно возникнет электрический ток. Но ток не может сразу достичь своего амплитудного значения потому, что при его возникновении вокруг катушки начнет появляться магнитное поле, которое будет наводить в катушке ЭДС самоиндукции, направленную против внешнего напряжения, т.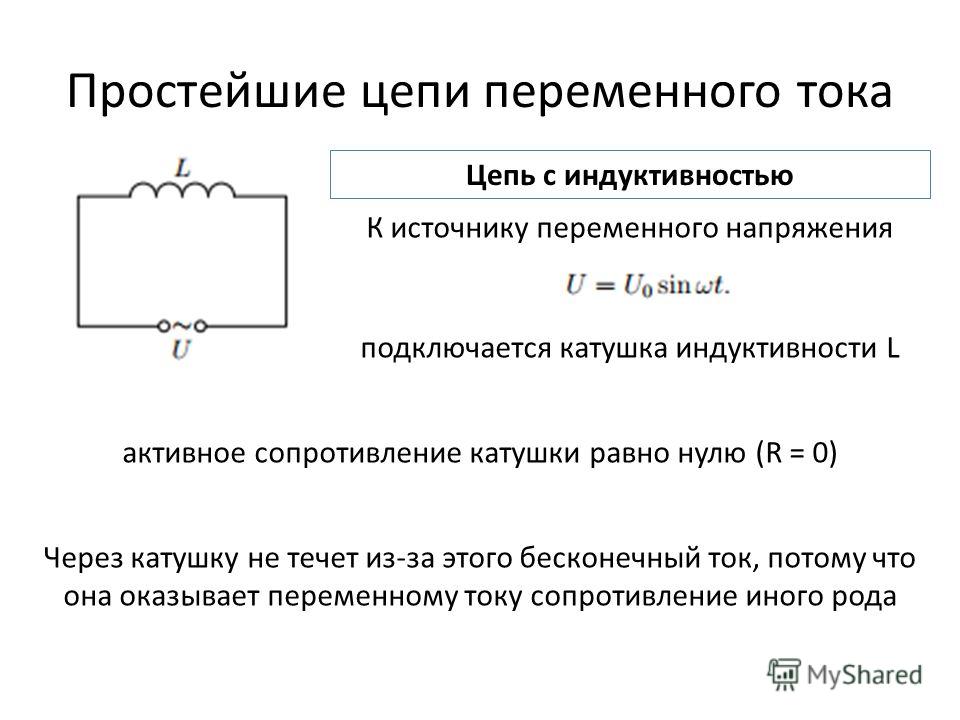
е. напряжения источника переменного тока. Электродвижущая сила самоиндукции будет препятствовать быстрому нарастанию силы тока в катушке. Поэтому нарастание тока будет длиться целую четверть периода.
По мере приближения к концу первой четверти периода скорость нарастания тока в катушке постепенно уменьшается.
Но вместе с тем ослабевает и ЭДС самоиндукции, так как величина ее зависит от скорости изменения силы тока.
Итак, в конце первой четверти периода внешнее напряжение, приложенное к катушке, будет равно нулю, ЭДС самоиндукции также будет, равна нулю, а ток в катушке и магнитный поток вокруг нее будут иметь максимальные амплитудные значения. В магнитном поле катушки будет запасено некоторое количество энергии, полученной от источника тока.
С началом второй четверти периода внешнее напряжение, переменив свое направление, будет возрастать, вследствие чего ток в катушке, текущий все еще в прежнем направлении, начнет уменьшаться. Но теперь в катушке снова возникнет ЭДС самоиндукции, обусловленная уменьшением магнитного потока, которая будет поддерживать ток в прежнем направлении.
В течение всей второй четверти периода внешнее напряже¬ние будет увеличиваться, а сила тока — уменьшаться. Ско¬рость уменьшения силы тока, оставаясь небольшой в начале второй четверти, станет постепенно нарастать и в конце этой четверти достигнет наибольшей величины.
Итак, к концу второй четверти периода внешнее напряжение приближается к амплитудному значению, а сила тока и магнитный ноток приближаются к нулю, убывая все с большей скоростью, вследствие чего ЭДС самоиндукции достигает своего амплитудного значения. Направление ЭДС самоиндукции, как всегда, остается противоположным направлению внешнего напряжения. Энергия, запасенная в магнитном поле за первую четверть периода, теперь возвращается обратно в цепь.
В течение второй половины (третья и четвертая четверти) периода все явления будут происходить в том же порядке, с той лишь разницей, что направления тока, внешнего напряжения и ЭДС самоиндукции изменяются на противоположные (рис. 1а.).
Таким образом, фаза тока все время отстает от фазы напряжения, причем нетрудно заметить, что сдвиг фаз тока и напряжения равен 90°.
Представим себе, что мы толкаем вдоль по рельсам груженую вагонетку. В первый момент, когда вагонетка только начинает трогаться с места, мы прилагаем к ней максимум усилий, которые по мере увеличения скорости вагонетки будем постепенно уменьшать. При этом мы почувствуем, что вагонетка, обладая инерцией, как бы сопротивляется нашим усилиям. Это противодействие (реакция) вагонетки будет особенно сильным вначале, по мере же ослабления наших усилий будет ослабевать и противодействие вагонетки, она постепенно будет переставать «упрямиться» и покорно покатится по рельсам.
Затем мы вовсе перестанем толкать вагонетку и даже, наоборот, начнем понемногу тянуть ее в обратном направлении. При этом мы почувствуем, что вагонетка снова сопротивляется нашим усилиям. Если мы будем все сильнее и сильнее тянуть вагонетку назад, то и ее противодействие будет соответственно все более и более возрастать. Наконец, нам удастся остановить вагонетку и даже изменить направление ее движения.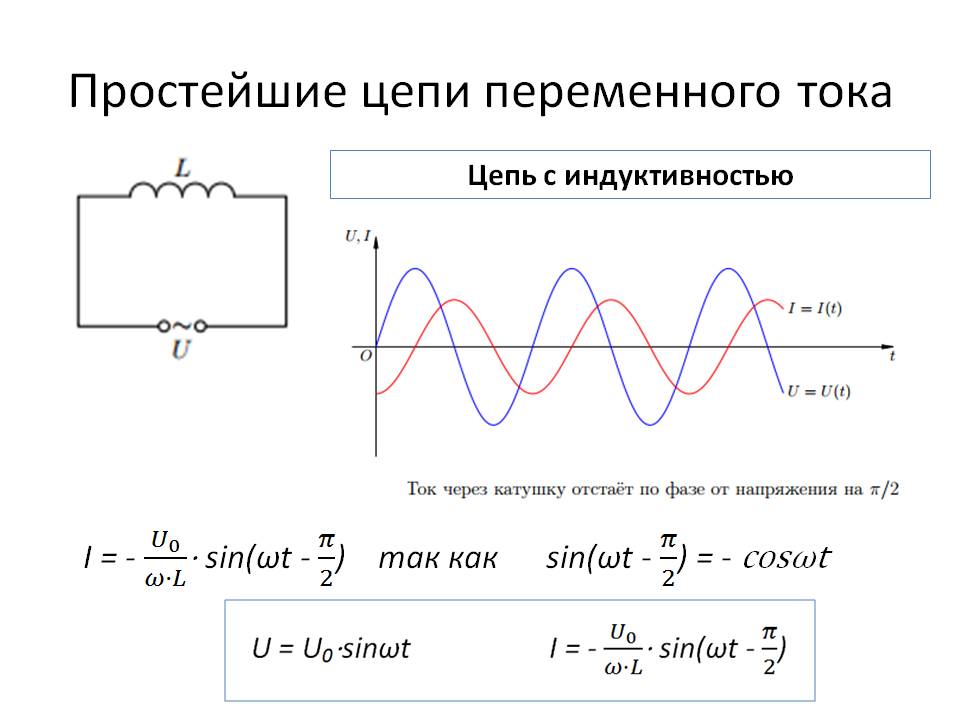
Когда вагонетка покатится обратно, мы будем постепенно ослаблять наши усилия, т. е. будем тянуть ее все слабее и слабее, однако, несмотря на это, скорость вагонетки будет все-таки увеличиваться (при слабом трении в подшипниках).
Когда вагонетка пройдет половину пути в обратном направлении, мы совсем перестанем тянуть ее и снова переменим направление наших усилий, т. е. начнем ее снова задерживать, постепенно увеличивая силу торможения до тех пор, пока вагонетка не остановится, заняв первоначальное (исходное) положение. После этого мы можем продолжать все наши действия сначала.
В этом примере наши усилия, прилагаемые к вагонетке, соответствуют внешней ЭДС, противодействие вагонетки, обусловленное ее инерцией, — ЭДС самоиндукции, а скорость вагонетки — электрическому току. Если изобразить графически изменение наших усилий, а также изменение противодействия вагонетки и ее скорости с течением времени, то мы получим графики (рис.
1б), в точности соответствующие графикам рис.1а.
Из этого примера становится более понятной сущность реактивного (безваттного) сопротивления. В самом деле, в течение первой четверти периода мы толкали вагонетку, а она противодействовала нашим усилиям; в течение второй четверти периода она катилась сама, а мы «упирались»; в течение третьей четверти периода мы опять тянули ее, а вагонетка снова оказывала противодействие нашим усилиям и, наконец, в течение четвертой четверти периода она снова катилась сама, а мы ее тормозили.
Короче говоря, в течение первой и третьей четверти периода мы работали «на вагонетку», а в течение второй и четвертой четвертей она работала «на нас», возвращая обратно полученную то нас энергию. В результате наша работа оказалась «безваттной».
Таким образом катушка индуктивности в цепи переменного тока может работать как безваттный резистор.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Дроссель в цепи переменного тока — Дроссель отставания переменного тока
- Задачи проектирования
Войти
Добро пожаловать! Войдите в свою учетную запись
ваше имя пользователя
ваш пароль
Забыли пароль?
Создать учетную запись
Политика конфиденциальности
Регистрация
Добро пожаловать!Зарегистрируйте аккаунт
ваш адрес электронной почты
ваше имя пользователя
Пароль будет отправлен вам по электронной почте.
Политика конфиденциальности
Восстановление пароля
Восстановить пароль
ваш адрес электронной почты
Поиск
Изменено:
Изделия категории
Катушка индуктивности (иногда называемая соленоидом) состоит из электрического проводника, намотанного на петли, которые обычно представляют собой множество катушек и часто несколько слоев. В случае цепи постоянного тока ток I, протекающий через катушку, создает индукционное магнитное поле B, напряженность которого ɸ внутри нее пропорциональна току: ɸ=LI. Этот коэффициент пропорциональности L можно описать как коэффициент индукции или индуктивность катушки (мера индуктивности называется генр). Оно прямо связано с коэффициентом витка, а также размером поперечного сечения катушки и обратно пропорционально длине катушки. Многократное увеличение величины индуктивности конкретной катушки может быть достигнуто за счет использования ферромагнитного сердечника (например, железа).
Явление самоиндукции объясняется формулой:
Или в дифференциальной форме:
При работе в цепях переменного тока емкость и индуктивность действуют по-разному по отношению к сопротивлению. В случае сопротивления, согласно закону Ома:
, протекающее через резистор R, прямо пропорционально напряжению на его концах:
, а коэффициентом пропорциональности является сопротивление:
U = IR
Уравнение справедливо для обоих мгновенные напряжения и токи:
, а также амплитуды:
или действующие значения.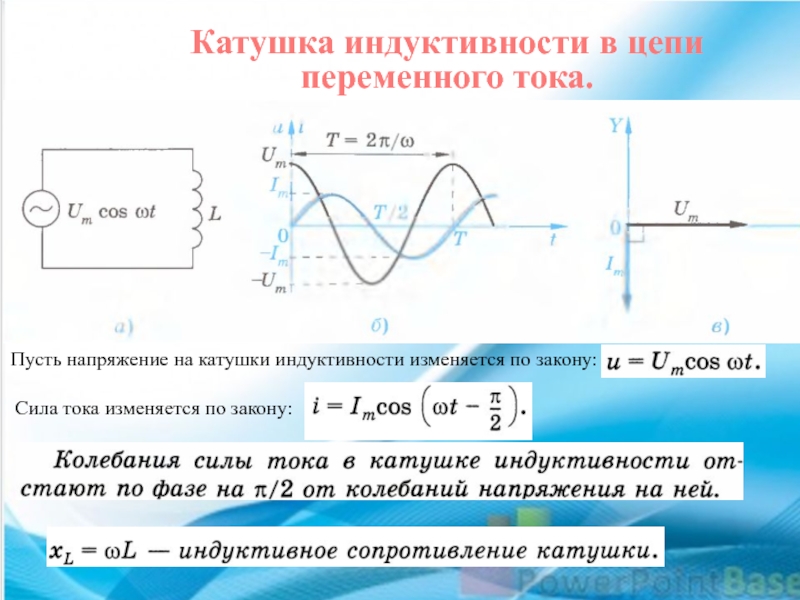
В случае емкости и индуктивности ток, протекающий через них, также зависит от напряжения, однако оба они вызывают фазовый сдвиг φ между током и напряжением. Ток, протекающий через конденсатор, опережает напряжение на конденсаторе на π/2. Для индуктивности ток задерживается по отношению к напряжению на π/2.
Величина, характеризующая соотношение между током и напряжением в цепях переменного тока
цепей называется наклоном, который может быть выражен формулой:
, где X обозначает реактивное сопротивление. Это число представляет собой сопротивление, проявляемое емкостными и индуктивными компонентами и индуктивными элементами при переменном токе определенной частоты ω.
Чтобы в цепи протекал ток, внешнее напряжение uL должно быть уравновешено напряжением электродвижущей силы. Это означает, что напряжение uL должно все время быть одинаковым и противоположным SEM eL. Эта сила достигает своего наибольшего значения, когда скорость изменения тока самая высокая.
Это происходит, когда текущий сигнал меняет направление (пересекает ось времени, проходя через нулевое значение). В результате напряжение uL на катушке индуктивности в цепи переменного тока сдвинуто по фазе относительно электродвижущей силы eL на угол π [рад] = 180, обгоняя ток (i), протекающий в цепи, на угол π/ 2 [рад] = 90.
Угол π/2 — это угол фазового сдвига напряжения uL на катушке индуктивности по отношению к току i. Напряжение uL на выводах катушки можно выразить уравнением:
Мощность может учитывать как отрицательные, так и положительные значения и колеблется во времени в два раза быстрее, чем напряжение и ток. Это означает, что идеальный индуктор вытягивает электричество из источника в течение определенного периода времени, а затем возвращает эту энергию источнику в другом временном интервале. При увеличении промежутка времени, в течение которого мгновенная величина электрического тока увеличивается, он используется для генерации магнитных полей (прибор накапливает энергию).
Единицей измерения индуктивной реактивной мощности является вар [вар].
Ссылки:
http://www.zspgrot.edu.pl/www_mechatronika/files/technik.mechatronik_311-50-_o1.04_u.pdf
http://fizyka.ur.krakow.pl/cwicz36.pdf
Михал
Инженер электроники и телекоммуникаций с дипломом магистра электроэнергетики. Светодизайнер опытный инженер. В настоящее время работает в сфере IT.
Английский
Индуктивность в цепях переменного тока
ЗАДАЧИ:
• обсудить свойства индуктивности в цепи переменного тока.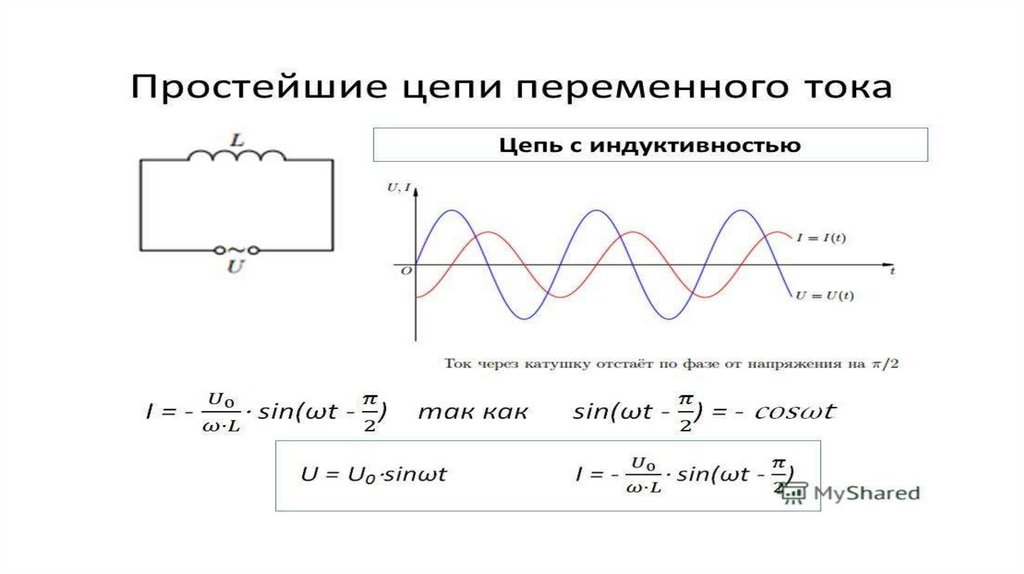
• обсудить индуктивное сопротивление.
• вычислить значения индуктивного сопротивления и индуктивности.
• обсудить взаимосвязь напряжения и тока в чисто индуктивной схема.
• уметь вычислять значения для катушек индуктивности, соединенных последовательно или параллельно.
• обсудить реактивную мощность (вар).
• определить добротность катушки.
ИНДУКТИВНОСТЬ В ЦЕПЯХ ПЕРЕМЕННОГО ТОКА УСЛОВИЯ
- ток отстает от напряжения — соотношение тока и напряжения в чисто индуктивная цепь
- импеданс (Z) — общее ограничение тока в цепи переменного тока
- индуцированное напряжение — напряжение, подводимое к проводнику путем разрезания линии магнитного потока
- индуктивность (L) — свойство электрической цепи, при котором напряжение производится путем разрезания линий магнитного потока
- индуктивное сопротивление (XL) — токоограничивающий эффект чистого индуктор
- качество (Q) — отношение индуктивного реактивного сопротивления к сопротивлению
- реактивное сопротивление — свойство цепи, ограничивающее ток с помощью кроме сопротивления
- реактивная мощность (ВАр) — Вольт Ампер Реактивная; часто называют безваттная мощность
———————————
В этом разделе обсуждается влияние индуктивности на цепи переменного тока.
ИНДУКТИВНОСТЬ
Индуктивность (L) является одним из основных типов нагрузок переменного тока. схемы. Некоторая индуктивность присутствует во всех сетях переменного тока. цепи из-за постоянно меняющегося магнитного поля (РИС. 1). Величина индуктивности одного проводника чрезвычайно мала, и в большинстве случаев это не учитывается при расчетах схемы.
Обычно считается, что цепи содержат индуктивность, если любой тип нагрузки, содержащей катушку. Для цепей, содержащих катушку, индуктивность учитывается при расчетах схемы. Нагрузки, такие как двигатели, трансформаторы, осветительный балласт и дроссели содержат катушки с проволокой.
РИС. 1 Постоянно меняющееся магнитное поле индуцирует напряжение в
любой проводник.
РИС.
2 Когда ток течет по катушке, создается магнитное поле
вокруг катушки.
РИС. 3 По мере уменьшения тока магнитное поле разрушается.
В разделе 10 обсуждалось, что всякий раз, когда ток течет через катушки с проволокой, вокруг проволоки создается магнитное поле (рис. 2). Если величина тока уменьшится, магнитное поле разрушится (РИС. 3). Напомним из раздела 10 несколько фактов, касающихся индуктивности:
1. Когда магнитные линии потока пересекают катушку, индуцируется напряжение в катушке.
2. Наведенное напряжение всегда противоположно по полярности приложенному напряжению. Это часто называют противо-ЭДС (CEMF).
3. Величина индуцированного напряжения пропорциональна скорости изменения тока.
4. Катушка индуктивности препятствует изменению тока.
Катушки индуктивности на фиг. 2 и 3 подключены к переменному
Напряжение. Поэтому магнитное поле постоянно увеличивается, уменьшается,
и меняет полярность.
Поскольку магнитное поле постоянно меняет величину
и направлении, в катушке постоянно индуцируется напряжение. Этот
Индуцированное напряжение не совпадает по фазе с приложенным напряжением на 180° и всегда
против приложенного напряжения (фиг. 4). Поскольку наведенное напряжение
всегда противоположно приложенному напряжению, приложенное напряжение должно
преодолеть наведенное напряжение до того, как ток сможет протекать по цепи.
Например, предположим, что катушка индуктивности подключена к линии переменного тока 120 В. Теперь предположим
что индуктор имеет индуцированное напряжение 116 В. Так как равная величина
приложенного напряжения должны использоваться для преодоления наведенного напряжения, там
будет всего 4 В, чтобы протолкнуть ток через сопротивление провода катушки
(120 — 116 = 4).
РИС. 4 Приложенное напряжение и наведенное напряжение не совпадают по фазе на 180°.
друг с другом.
РИС.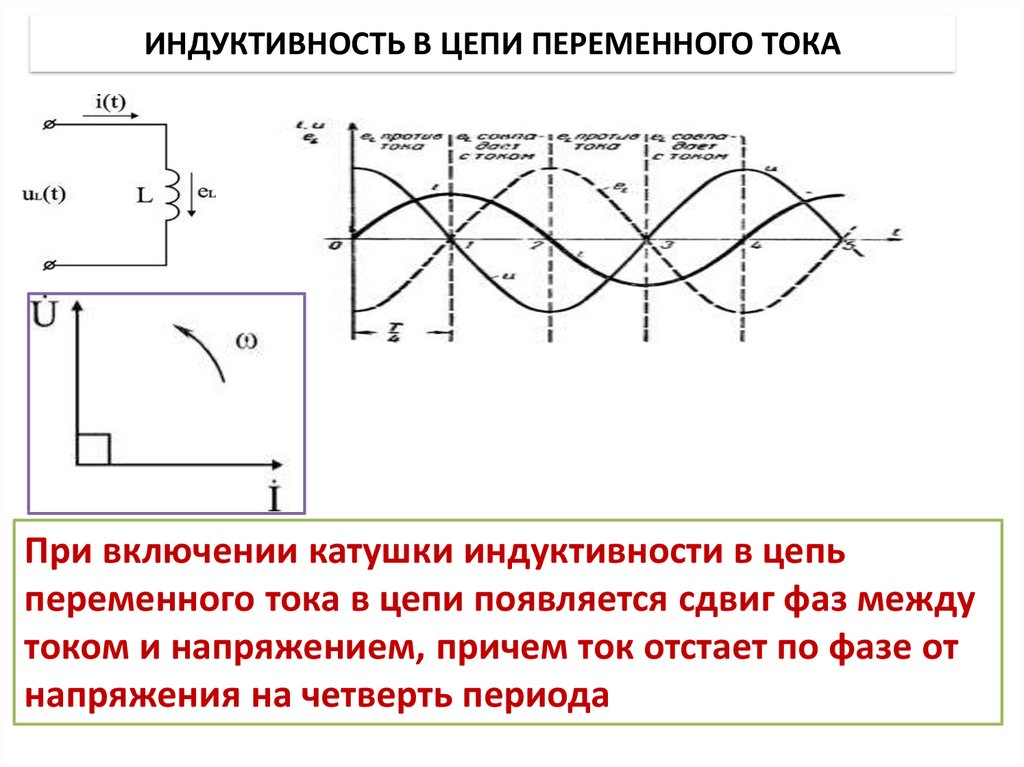
5 Измерение сопротивления катушки.
РИС. 6 Измерение тока цепи амперметром.
ВЫЧИСЛЕНИЕ ИНДУЦИРОВАННОГО НАПРЯЖЕНИЯ
Величину индуцированного напряжения в катушке индуктивности можно вычислить, если сопротивление провода в катушке и величина тока в цепи известны. Для Например, предположим, что омметр используется для измерения фактического количества сопротивление в катушке, а катушка содержит 6 Ом сопротивления провода (РИС. 5).
Теперь предположим, что катушка подключена к цепи переменного тока 120 В и амперметру. измеряет ток 0,8 А (РИС. 6). Теперь можно использовать закон Ома. определить величину напряжения, необходимого для пропускания тока 0,8 А через 6 Ом сопротивления.
Е = I х R
Е = 0,8 х 6
Е = 4,8 В
Поскольку для проталкивания тока через сопротивление провода требуется всего 4,8 В.
катушки индуктивности, оставшаяся часть 120 В используется для преодоления сопротивления катушки.
индуктивное напряжение 1192] = 119:9В). Обратитесь к векторам
в разделе 13.
ИНДУКТИВНАЯ РЕАКТИВНОСТЬ
Обратите внимание, что индуцированное напряжение способно ограничить протекание тока через цепь аналогично сопротивлению. Это индуцированное напряжение равно не сопротивление, но может ограничивать протекание тока так же, как сопротивление делает. Это токоограничивающее свойство катушки индуктивности называется реактивным сопротивлением. и обозначается буквой X. Это реактивное сопротивление обусловлено индуктивностью, поэтому это называется индуктивным сопротивлением и обозначается буквой XL, произносится как «X». sub L.» Индуктивное сопротивление измеряется в омах так же, как сопротивление и может быть вычислено, когда значения индуктивности и частоты известен. Для определения индуктивного сопротивления можно использовать следующую формулу.
XL = 2πFL
где:
XL = индуктивное сопротивление
2 = константа
пи или π = 3,1416
Ф = частота в герцах (Гц)
L = индуктивность в генри (Гн)
Индуктивное сопротивление представляет собой наведенное напряжение и, следовательно, пропорционально к трем факторам, определяющим наведенное напряжение:
1.
Количество витков провода
2. Напряженность магнитного поля
3. Скорость режущего действия (относительное движение между индуктором и магнитные линии потока)
РИС. 7 Катушки с более близкими витками производят большую индуктивность, чем
катушки с витками далеко друг от друга.
Количество витков провода и напряженность магнитного поля определяются физической конструкцией индуктора. Такие факторы, как размер используемого провода, количество витков, насколько близко витки расположены друг к другу, и тип материала сердечника определяют величину индуктивности (в генри, H) катушки (фиг. 7). Скорость резания пропорциональна к частоте (Гц). Увеличение частоты вызовет магнитное линии потока, чтобы сократить проводники с большей скоростью, и, таким образом, будет производить более высокое индуктивное напряжение или более высокое индуктивное сопротивление.
РИС. 9 Схематические обозначения катушек индуктивности.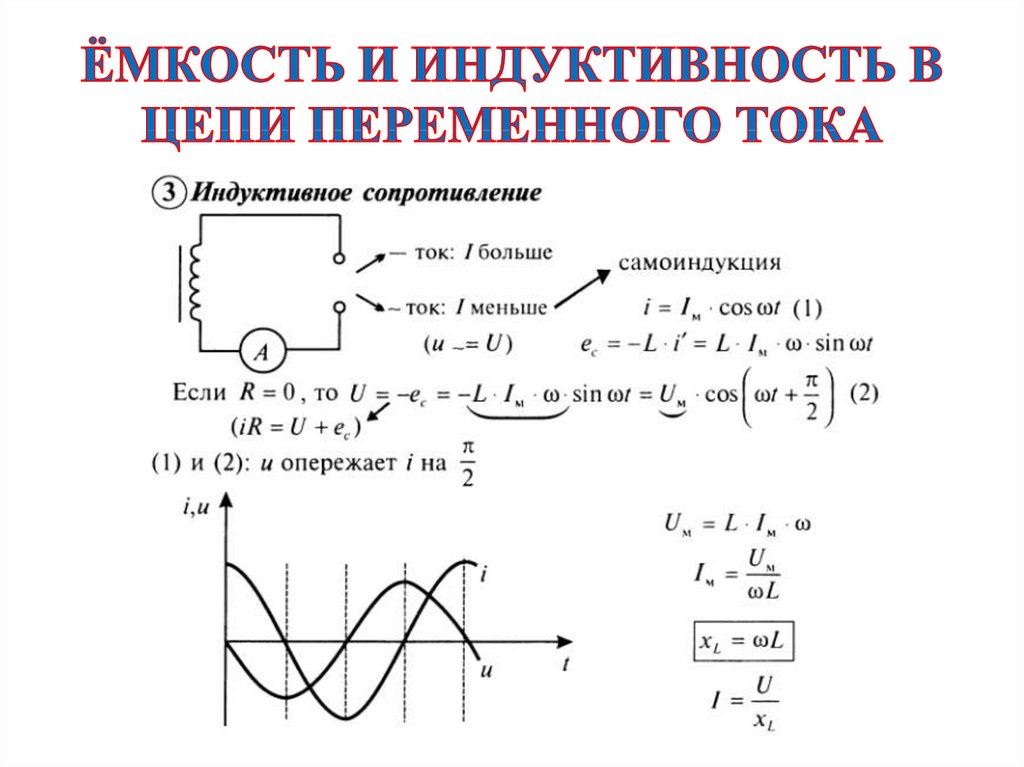
СХЕМАТИЧЕСКИЕ СИМВОЛЫ
Схематическое обозначение, используемое для обозначения индуктора, изображает катушку провода. Несколько символов для катушек индуктивности показаны на фиг. 9. Показанные символы с двумя параллельными линиями представляют индукторы с железным сердечником, а символы без параллельных линий представляют катушки индуктивности с воздушным сердечником.
ИНДУКТОРЫ, СОЕДИНЕННЫЕ ПОСЛЕДОВАТЕЛЬНО
При последовательном соединении катушек индуктивности (РИС. 10) общая индуктивность цепи (LT) равна сумме индуктивностей всех катушек индуктивности.
ЛТ = Л1 + Л2 + Л3
Суммарное индуктивное сопротивление (XLT) катушек индуктивности, соединенных последовательно, равно сумма индуктивных сопротивлений всех катушек индуктивности.
XLT = XL1 + XL2 + XL3
ИНДУКТОРЫ, СОЕДИНЕННЫЕ ПАРАЛЛЕЛЬНО
При параллельном соединении катушек индуктивности (РИС.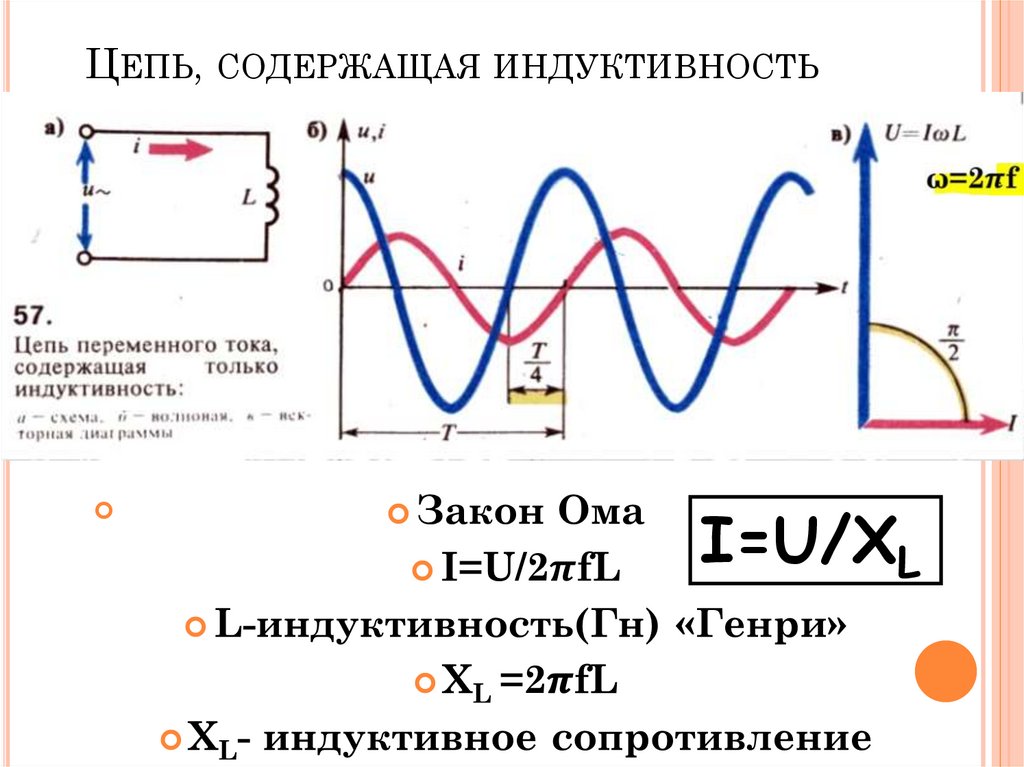
11) общая индуктивность
можно найти аналогично нахождению полного сопротивления параллельного
схема. Обратная величина полной индуктивности равна сумме
обратные величины всех катушек индуктивности.
РИС. 10 индукторов, соединенных последовательно.
РИС. 11 индукторов, соединенных параллельно.
Формулу произведения на сумму можно также использовать для определения общей индуктивности. параллельных индукторов.
LT = L1 x L2/L1 + L2
Если значения всех катушек индуктивности одинаковы, общая индуктивность может найти путем деления индуктивности одного индуктора на общее число индукторов.
LT = L/N
Аналогичные формулы можно использовать для определения полного индуктивного сопротивления катушки индуктивности соединены параллельно.
1/XLT = 1/XL1 + 1/XL2 + 1/XL3
ВЗАИМООТНОШЕНИЯ НАПРЯЖЕНИЯ И ТОКА В ИНДУКТИВНОЙ ЦЕПИ
РИС.
12 Наведенное напряжение пропорционально скорости изменения
текущий.
РИС. 13 Напряжение не индуцируется, когда ток не изменяется.
РИС. 14 Ток отстает от приложенного напряжения на 90°.
В разделе 11 обсуждалось, что при протекании тока через чистый
в резистивной цепи ток и напряжение совпадают по фазе.
В чисто индуктивной цепи ток отстает от напряжения на 90°. Сначала
это может показаться невыполнимым условием до тех пор, пока отношения применяемых
учитывается напряжение и наведенное напряжение. Как действующий и прикладной
напряжение может стать на 90° несовпадающим по фазе относительно друг друга, что лучше всего объяснить
путем сравнения соотношения тока и наведенного напряжения (фиг. 12). Напомним, что индуцированное напряжение пропорционально скорости
изменение тока (скорость режущего действия). В начале
осциллограммы, ток отображается с максимальным значением в отрицательном направлении.
В это время ток не меняется, поэтому индуцированное напряжение равно нулю.
По мере того, как ток начинает уменьшаться в значении, магнитное поле, создаваемое
потоком тока уменьшается или разрушается и начинает индуцировать напряжение
в катушку, когда она прорезает проводники (РИС. 13).
Наибольшая скорость изменения тока возникает, когда ток проходит от отрицательное, через ноль, и начинает возрастать в положительном направлении (РИС. 13). Поскольку ток изменяется с наибольшей скоростью, индуцированное напряжение максимальное.
Когда ток приближается к своему пиковому значению в положительном направлении, скорость изменения уменьшается, вызывая уменьшение наведенного напряжения. Индуцированный напряжение снова будет равно нулю, когда ток достигнет своего пикового значения и магнитное поле перестает расширяться.
Видно, что ток, протекающий через дроссель, опережает
индуцированное напряжение на 90°.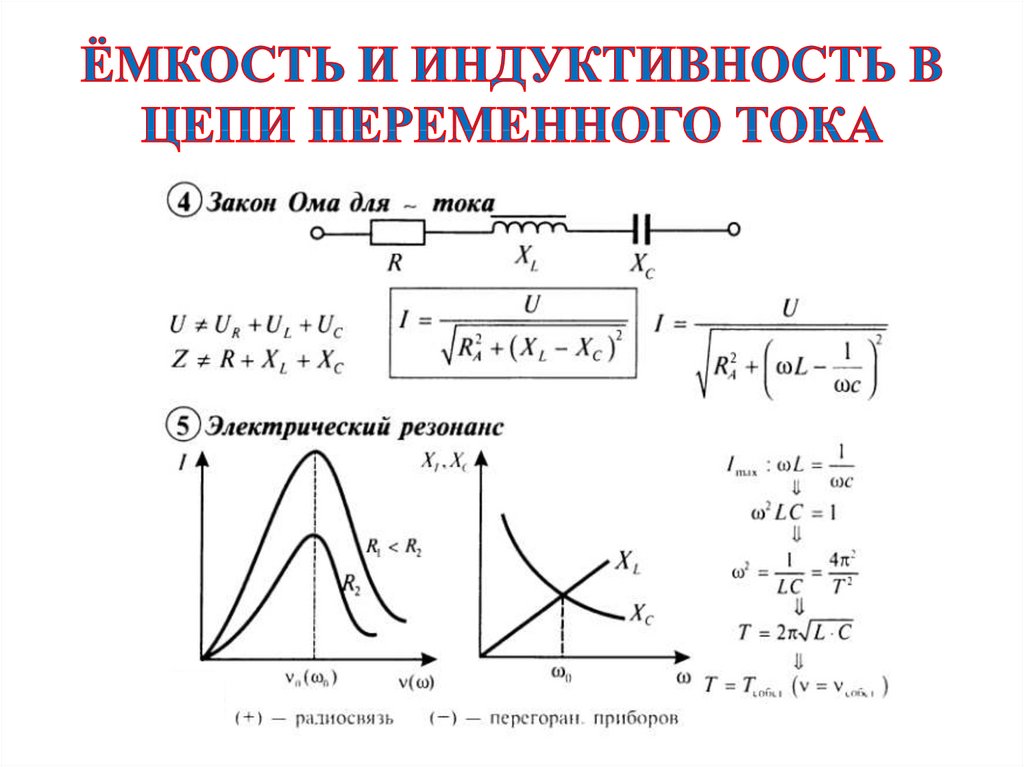
Поскольку наведенное напряжение не совпадает по фазе с приложенным напряжением на 180°, ток будет отставать от приложенного напряжения на 90° (РИС. 14).
ПИТАНИЕ В ИНДУКТИВНОЙ ЦЕПИ
В чисто резистивной цепи реальная мощность, или ватты, равна произведение напряжения и силы тока.
Однако в чисто индуктивной цепи не производится никакой реальной мощности или ватт.
Напомним, что напряжение и ток должны быть либо положительными, либо отрицательными.
прежде чем можно будет произвести истинную силу. Так как напряжение и ток равны 90°
в противофазе друг с другом в чисто индуктивной цепи ток и
напряжение будет разной полярности 50% времени и в то же время
полярность 50% времени. За период времени, в течение которого текущая и
напряжения имеют одинаковую полярность, питание подается на цепь в
форма создания магнитного поля. Когда ток и напряжение равны
с противоположной полярностью энергия возвращается в цепь как магнитное поле.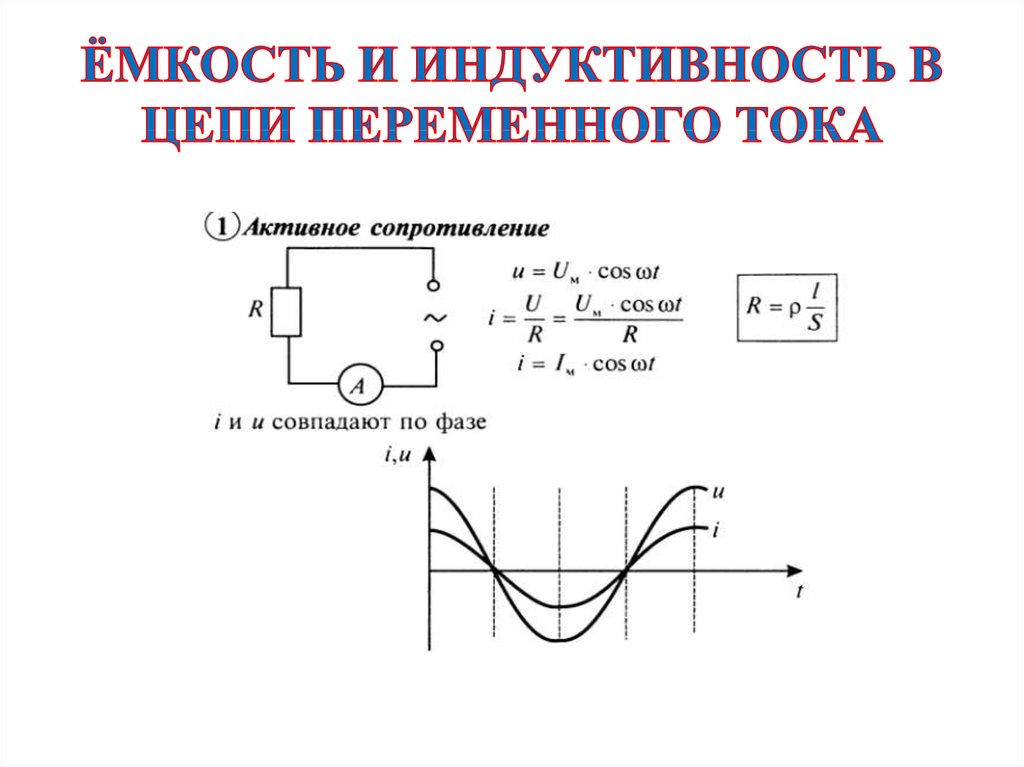
поле схлопывается и индуцирует напряжение обратно в цепь. 92 R-потери, потери на вихревые токи и гистерезис
потери.
РИС. 15 Соотношение напряжения и тока в разных частях цикла.
Форма волны тока и напряжения на РИС. 15 были разделены на четыре секции:
A, B, C и D. В течение первого периода времени, обозначенного A, текущий
отрицательное, а напряжение положительное. В этот период энергия
отдается цепи, когда магнитное поле разрушается. В течение
второй период времени, раздел B, как напряжение, так и ток положительны.
Энергия используется для создания магнитного поля. В третий период времени,
C, ток положительный, а напряжение отрицательное. Сила снова
возвращается в цепь, когда поле разрушается. Во время четвертого
период времени D, как напряжение, так и ток отрицательны. Сила снова
используется для создания магнитного поля. Если количество энергии, используемой для
магнитное поле вычитается из возвращаемой мощности,
результат будет нулевой.
РЕАКТИВНАЯ МОЩНОСТЬ
Хотя, по сути, настоящая сила не используется, за исключением ранее упомянутых потерь, электрическое измерение, называемое реактивной мощностью, используется для измерения реактивная мощность в чисто индуктивной цепи. ВАР — это аббревиатура. для вольт-ампер-реактивных. VAR можно вычислять как ватты, за исключением того, что индуктивная значения сопротивления заменяются на значения сопротивления в формулах.
ВАР равно количеству тока, протекающего через индуктивную цепь. раз больше напряжения, приложенного к индуктивной части цепи. Несколько формулы для вычисления VAR 92 Д x XL
где
EL = напряжение, подаваемое на катушку индуктивности
IL = текущий расход через индуктор
XL = индуктивное сопротивление
Q ИНДУКТОРА
РИС. 16 Катушки индуктивности содержат внутреннее сопротивление.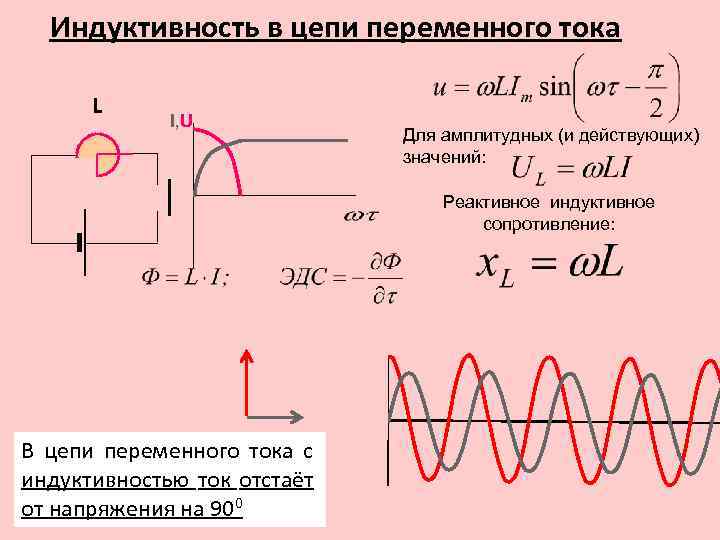
РИС. 17 Q индуктора представляет собой отношение индуктивного реактивного сопротивления как
по сравнению с сопротивлением. Буква Q означает качество.
До сих пор в этом разделе обычно предполагалось, что катушка индуктивности не имеет сопротивления, и что индуктивное сопротивление является единственным токоограничивающим фактор. На самом деле это не так. Поскольку катушки индуктивности на самом деле являются катушками провода, все они имеют некоторое внутреннее сопротивление. Индукторы на самом деле выглядит как катушка, соединенная последовательно с некоторым сопротивлением (РИС. 16). Величина сопротивления по сравнению с индуктивным реактивным сопротивлением определяет добротность катушки. Буква Q означает качество.
Катушки индуктивности с более высоким отношением индуктивного реактивного сопротивления к сопротивлению
считаются индукторами более высокого качества. Индуктор, построенный
с большим проводом будет иметь низкое сопротивление провода и, следовательно, более высокое
Q (фиг.
17). Катушки индуктивности, состоящие из множества витков тонкой проволоки, имеют
гораздо более высокое сопротивление и, следовательно, более низкая добротность.
Чтобы определить добротность катушки индуктивности, разделите индуктивное сопротивление на сопротивление.
Q = XL/R
РИС. 18 Импеданс катушки представляет собой комбинацию сопротивления провода и индуктивности.
реактивное сопротивление.
Хотя катушки индуктивности имеют некоторое сопротивление, катушки индуктивности с
Q 10 или выше обычно считаются чистыми катушками индуктивности. Один раз
отношение индуктивного сопротивления становится в 10 раз больше сопротивления,
величина сопротивления считается незначительной. Например, предположим
катушка индуктивности имеет индуктивное сопротивление 100 Ом и сопротивление провода
10 Ом. Индуктивная реактивная составляющая в цепи равна 90° вне
фазы с резистивной составляющей. Это отношение порождает право
треугольник (РИС.
18). Суммарный токоограничивающий эффект катушки индуктивности
представляет собой комбинацию индуктивного реактивного сопротивления и сопротивления. Это общее
токоограничивающий эффект называется импедансом и обозначается буквой
Z. Полное сопротивление цепи представлено гипотенузой
прямоугольный треугольник, образованный индуктивным сопротивлением и сопротивлением. К
вычислить значение импеданса катушки, индуктивное реактивное сопротивление и
необходимо добавить сопротивление. Поскольку эти два компонента образуют ноги
прямоугольный треугольник и импеданс образует гипотенузу, сложение векторов
должны быть трудоустроены.
Обратите внимание, что значение полного импеданса катушки индуктивности составляет всего 0,5 O больше, чем значение индуктивного сопротивления.
ОБЗОР
• Наведенное напряжение пропорционально скорости изменения тока.
• Наведенное напряжение всегда противоположно по полярности приложенному напряжению.
• Индуктивное сопротивление – это встречное напряжение, которое ограничивает протекание тока, как и сопротивление.
• Индуктивное сопротивление измеряется в омах.
• Индуктивное сопротивление пропорционально индуктивности катушки и частота линии.
• Индуктивное сопротивление обозначается XL.
• Индуктивность измеряется в генри (Гн) и обозначается буквой л.
• Когда катушки индуктивности соединены последовательно, общая индуктивность равна сумме всех индукторов.
• Когда катушки индуктивности соединены параллельно, величина, обратная общей индуктивность равна сумме обратных величин всех катушек индуктивности.
• Ток отстает от приложенного напряжения на 90° в чисто индуктивной цепи.
• Все катушки индуктивности имеют определенное сопротивление.
• Q катушки индуктивности представляет собой отношение индуктивного реактивного сопротивления к
сопротивление.
• Катушки индуктивности с добротностью 10 обычно считаются «чистыми» катушками индуктивности.
• Чисто индуктивные цепи не содержат фактической мощности или ватт.
• Реактивная мощность измеряется в ВАр.
• ВАр – это сокращение от вольт-ампер-реактивный.
ВИКТОРИНА
1. На сколько градусов ток и напряжение не совпадают по фазе с каждым другое в чисто резистивной цепи?
2. На сколько градусов ток и напряжение не совпадают по фазе с каждым другое в чисто индуктивной цепи?
3. Чему пропорционально индуктивное сопротивление?
4. Четыре катушки индуктивности, каждая с индуктивностью 0,6 Гн, соединены в ряд. Чему равна полная индуктивность цепи?
5. Три индуктора соединены параллельно. Катушка индуктивности 1 имеет индуктивность 0,06 Н; индуктор 2 имеет индуктивность 0,05 Гн; а индуктор 3 имеет индуктивность 0,1Гн. Какова общая индуктивность этой цепи?
6.
Если бы три катушки индуктивности в вопросе 5 были соединены последовательно, что
будет индуктивное сопротивление цепи? Предположим, что катушки индуктивности
подключен к сети 60 Гц.
7. Катушка индуктивности подключена к линии 240 В, 1000 Гц. Ток цепи составляет 0,6 А. Какова индуктивность катушки индуктивности?
8. Катушка индуктивности 3,6 Гн подключена к сети 480 В, 60 Гц. линия. Какой ток будет течь в этой цепи?
9. Если рассматриваемая частота 8 уменьшится до 50 Гц, какой ток будет течь в цепи?
10. Катушка индуктивности имеет индуктивное сопротивление 250 Ом при подключении к линия 60 Гц. Чему будет равно индуктивное сопротивление, если катушку индуктивности подключить к линии 400 Гц?
РЕАЛЬНЫЕ ПРИМЕНЕНИЯ
1. Вы работаете электриком, устанавливающим люминесцентные лампы. Ты
обратите внимание, что огни были сделаны в Европе и что балласты оценены
для работы в системе 50 Гц.
Будут ли эти балласты повреждены более чем
ток, если они подключены к 60 Гц? Если есть проблема с этими
фары, что может быть наиболее вероятной причиной неисправности?
2. Вам нужно заказать индуктор на замену того, который
стать дефективным. Информация на шильдике закрашена
и не может быть прочитан. Машина, содержащая индуктор, работает на
480 В при частоте 60 Гц. Другая машина имеет идентичный индуктор
в нем, но и его табличка была закрашена. Накладной амперметр
показывает ток 18 А, а вольтметр показывает падение напряжения
324 В через индуктор в машине, которая все еще работает. После
отключив питание и заблокировав панель, вы отсоединяете дроссель
в действующей машине и измерьте сопротивление провода 1,2 Ом с
омметр. Использование идентичного индуктора в рабочей машине в качестве
например, какое значение индуктивности вы должны заказать, и что будет
минимальная номинальная реактивная мощность катушки индуктивности? Если вас беспокоит сумма
сопротивления провода в индукторе при заказе? Поясните свой ответ.
