Самоиндукция. Индуктивность

 «Науку часто смешивают с знанием.

Это глубокое недоразумение.

Наука есть не только знание, но и сознание,

т.е. умение пользоваться знанием»

В.О. Ключевский

Явление электромагнитной индукции состоит в том, что в замкнутом контуре при изменении магнитного потока в нем возникает электрический ток, который называют индукционным.

Закон электромагнитной индукции гласит: среднее значение ЭДС индукции в проводящем контуре пропорционально скорости изменения магнитного потока через поверхность, ограниченную контуром.

Знак «минус», в математической записи закона, учитывает правило Ленца, согласно которому электромагнитная индукция создает в контуре индукционный ток такого направления, что созданное им магнитное поле препятствует изменению магнитного потока, вызывающего этот ток.

Электромагнитная индукция проявляется во всех случаях изменения магнитного потока через поверхность, ограниченную контуром.

Современник Фарадея американский физик Джозеф Генри независимо от своего английского коллеги открыл некоторые из электромагнитных эффектов. В 1829 году Генри обнаружил, что ЭДС индукции возникает в неподвижном контуре и в отсутствии изменения внешнего магнитного поля. Оказалось, что изменяющийся электрический ток, проходящий в контуре, создает изменяющийся магнитный поток. Это явление было названо явлением самоиндукции.

Примечательно то, что и Генри и Фарадей работали над одной и той же проблемой. И пришли к одним и тем же выводам, касающихся как явления электромагнитной индукции, так и явления самоиндукции. При этом, Генри сделал свои открытия на несколько лет раньше, чем Майкл Фарадей. Но Генри был безответственно нетороплив при опубликовании результатов экспериментов, и Фарадей первым сообщил о своем успехе. Наконец, приоритет открытия электромагнитной индукции был отдан Фарадею, а Генри — открытие явления самоиндукции, которое он описал в той же самой статье, что и явление индукции,— в 1832 г.

Самоиндукция является важным частным случаем явления электромагнитной индукции

. Если электрический ток в замкнутом проводящем контуре по каким-либо причинам изменяется, то изменяется и магнитное поле этого тока (т.е. индукция магнитного поля пропорциональна силе тока в контуре). Но при изменении индукции магнитного поля, создаваемого током, проходящим в контуре, изменяется и магнитный поток (т.е. магнитный поток будет пропорционален индукции магнитного поля). Следовательно, магнитный поток через поверхность, ограниченную контуром, пропорционален силе тока в контуре.

Коэффициент пропорциональности между магнитным потоком и силой тока Томсон (в последствии лорд Кельвин) в 1853 году предложил назвать «

коэффициентом самоиндукции».

Коэффициент самоиндукции, который часто называют просто индуктивностью контура, обозначают L.

Индуктивность в СИ измеряют в Гн (генри).

[L] = [Гн]

Эта единица определяется на основании формулы

Индуктивность контура равна 1 Гн, если при силе постоянного тока в контуре 1 А магнитный поток через поверхность, ограниченную этим контуром, равен 1 Вб.

Индуктивность зависит от размеров и формы контура, а также от магнитных свойств среды, в которой этот контур находится

.

Например, если взять однослойный соленоид, то его индуктивность будет определяться по формуле

где  — это число витков, приходящихся на единицу длины соленоида,

S — площадь поверхности, ограниченной витком,

l — длина соленоида,

m — магнитная проницаемость среды.

Из формулы для магнитного потока следует, что изменить его можно изменяя силу тока в контуре, или его индуктивность, или и то и другое одновременно.

Согласно закону электромагнитной индукции изменяющийся магнитный поток создает в контуре ЭДС.

Возникновение ЭДС индукции в контуре, которое вызвано изменением магнитного поля тока, проходящего в этом же контуре, называют явлением самоиндукции, а появляющуюся ЭДС — электродвижущей силой самоиндукции или ЭДС самоиндукции.

Обозначается ЭДС самоиндукции греческой буквой x_Si. Измеряется ЭДС самоиндукции в В (вольт).

[x_Si] = [В]

По закону электромагнитной индукции среднее значение ЭДС самоиндукции, возникающей в контуре прямо пропорциональна индуктивности контура и скорости изменения силы тока в контуре (при учете, что индуктивность контура остается постоянной).

Из этой формулы следует, что индуктивность — это физическая величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.

Используя это выражение, можно дать второе определение единицы индуктивности: элемент электрической цепи обладает индуктивностью в 1 Гн, если при равномерном изменении силы тока в цепи на 1 А за 1 с в нем возникает ЭДС самоиндукции 1 В.

Поскольку контур замкнут, ЭДС самоиндукции создает в нем ток самоиндукции, силу которого определяют по закону Ома

где R — сопротивление контура.

Знак минус в формуле для ЭДС самоиндукции учитывает правило Ленца, согласно которому ток самоиндукции всегда направлен так, что он противодействует изменению тока, создаваемого источником. Если основной ток возрастает, то ток самоиндукции направлен против тока источника, если уменьшается, то направление тока источника и тока самоиндукции совпадают.

Как же пронаблюдать явление самоиндукции?

Для этого соберем электрическую цепь, состоящую из катушки с большой индуктивностью, резистора с электрическим сопротивлением, равным сопротивлению обмотки катушки, двух одинаковых лампочек, ключа и источника постоянного тока.

При замыкании цепи лампочка 2 начинает светиться практически сразу, а лампочка 1 с заметным опозданием. Происходит это из-за того, что при возрастании силы тока I₁, созданного источником, на участке, образованном катушкой и лампочкой 1, ЭДС самоиндукции в катушке имеет такую полярность, что создаваемый ею ток самоиндукции направлен навстречу тока источника. В результате  рост силы тока на этом участке цепи замедляется, и сила тока не сразу достигает своего максимального значения.

Явление самоиндукции можно также пронаблюдать и при размыкании цепи. Для этого соберем цепь, состоящую из катушки с большим количеством витков, намотанных на железном сердечнике, к зажимам которой параллельно подключена лампочка с большим электрическим сопротивлением по сравнению с сопротивлением обмотки катушки. В качестве источника тока возьмем источник с небольшим ЭДС.

При размыкании ключа сохраняется замкнутой часть цепи, состоящая из уже последовательно соединенных катушки и лампочки. Пока ключ замкнут, лампочка будет тускло светиться, так как отношение сил токов, проходящих через лампочку и катушку, обратно отношению их сопротивлений.

Однако при размыкании ключа можно увидеть, что лампочка ярко вспыхивает.

Почему это происходит?

Все дело в том, что при размыкании цепи сила тока в катушке убывает, что приводит к возникновению ЭДС самоиндукции. Возникающий в цепи ток самоиндукции, согласно правилу Ленца, совпадает по направлению с током катушки, не позволяя ему резко уменьшать силу тока. Это и обеспечивает вспышку лампочки.

Заметим, что явление самоиндукции имеет место в любых случаях изменения силы тока в цепи, содержащей индуктивность, или изменения самой индуктивности.

Вообще, явление самоиндукции подобно явлению инерции в механике.

Известно, что автомобиль не может мгновенно приобрести определенное значение скорости, как не может и мгновенно остановиться, как бы  велика не была тормозящая сила.

Точно так же, за счет самоиндукции при замыкании цепи, сила тока не сразу достигает своего максимального значения, а нарастает постепенно. При выключении источника, ток сразу не прекращается — самоиндукция будет поддерживать его некоторое время, даже не смотря на большое сопротивление цепи.

Упражнения.

Задача: За промежуток времени 9,5 мс сила тока в катушке индуктивности равномерно возросла от 1,6 А до 2,4 А. При этом в катушке возникла ЭДС самоиндукции –14 В. Определите собственный магнитный поток в конце процесса нарастания тока.

Основные выводы:

– Явление возникновения ЭДС индукции в электрической цепи в результате изменения силы тока в этой же цепи, называют явлением самоиндукции.

– ЭДС самоиндукции равна произведению индуктивности контура и скорости изменения силы тока в нем.

– Индуктивность — это физическая величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.

– Единицей измерения индуктивности в СИ является Гн (генри).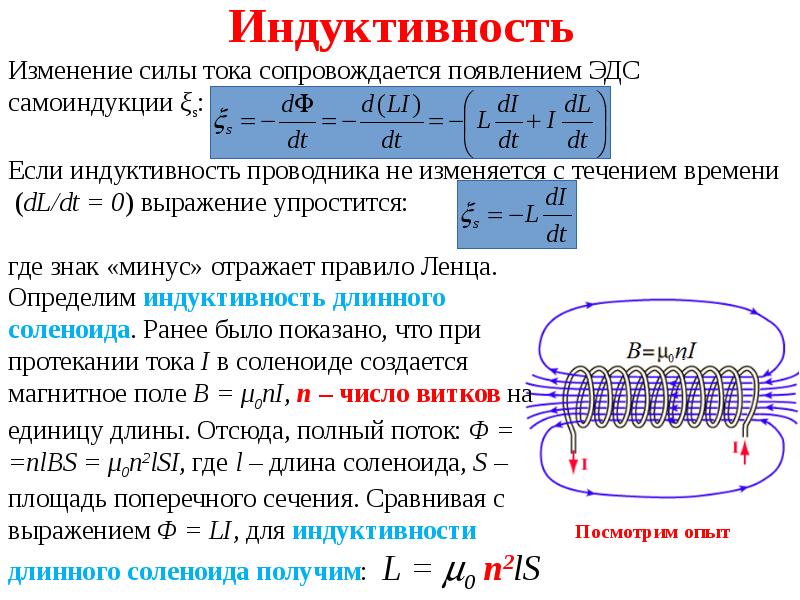

– Индуктивность контура равна 1 Гн, если при силе тока в контуре 1 А магнитный поток через поверхность, ограниченную этим контуром, равен 1 Вб.

Элеком37, Индуктивность. Самоиндукция. Энергия магнитного поля. Правило Ленца.

Индуктивность. Самоиндукция. Энергия магнитного поля. Правило Ленца.

---

Индуктивность. Самоиндукция. Энергия магнитного поля.

Самоиндукция является важным частным случаем электромагнитной индукции, когда изменяющийся магнитный поток, вызывающий ЭДС индукции, создается током в самом контуре. Если ток в рассматриваемом контуре по каким-то причинам изменяется, то изменяется и магнитное поле этого тока, а, следовательно, и собственный магнитный поток, пронизывающий контур. В контуре возникает ЭДС самоиндукции, которая согласно правилу Ленца препятствует изменению тока в контуре. Собственный магнитный поток Φ, пронизывающий контур или катушку с током, пропорционален силе тока I:

Коэффициент пропорциональности L в этой формуле называется коэффициентом самоиндукции или индуктивностью катушки. Единица индуктивности в СИ называется Генри (Гн).

Запомните: индуктивность контура не зависит ни от магнитного потока, ни от силы тока в нем, а определяется только формой и размерами контура, а также свойствами окружающей среды. Поэтому при изменении силы тока в контуре индуктивность остается неизменной. Индуктивность катушки можно рассчитать по формуле:

где: n — концентрация витков на единицу длины катушки:

ЭДС самоиндукции, возникающая в катушке с постоянным значением индуктивности, согласно формуле Фарадея равна:

Итак ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в ней.

Магнитное поле обладает энергией. Подобно тому, как в заряженном конденсаторе имеется запас электрической энергии, в катушке, по виткам которой протекает ток, имеется запас магнитной энергии. Энергия Wм магнитного поля катушки с индуктивностью L, создаваемого током I, может быть рассчитана по одной из формул (они следуют друг из друга с учётом формулы Φ = LI):

Соотнеся формулу для энергии магнитного поля катушки с её геометрическими размерами можно получить формулу для объемной плотности энергии магнитного поля (или энергии единицы объёма):

Правило Ленца.

Инерция – явление, происходящее и в механике (при разгоне автомобиля мы отклоняемся назад, противодействуя увеличению скорости, а при торможении отклоняемся вперёд, противодействуя уменьшению скорости), и в молекулярной физике (при нагревании жидкости увеличивается скорость испарения, самые быстрые молекулы покидают жидкость, уменьшая скорость нагревания) и так далее. В электромагнетизме инерция проявляется в противодействии изменению магнитного потока, пронизывающего контур. Если магнитный поток нарастает, то возникающий в контуре индукционный ток направлен так, чтобы препятствовать нарастанию магнитного потока, а если магнитный поток убывает, то возникающий в контуре индукционный ток направлен так, чтобы препятствовать убыванию магнитного потока.

Правило Ленца для определения направления индукционного тока: возникающий в контуре индукционный ток имеет такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, которое вызывало этот ток.

---

---

Другие стаьи по теме «Электричество»

1.     Электрический ток в газах и в вакууме.

2.     Электрический ток. Сила тока. Сопротивление.

3.     Закон Ома. Последовательное и параллельное соединение проводников.

4.     ЭДС. Закон Ома для полной цепи.

5.     Работа и мощность тока. Закон Джоуля-Ленца.

6.     Электролиз.

7.     Электрический заряд и его свойства.

8.     Закон Кулона.

9.     Электрическое поле и его напряженность.

10.   Принцип суперпозиции. Потенциальная энергия взаимодействия зарядов.

11.   Потенциал. Разность потенциалов. Напряжение.

12.   Электрическая емкость. Плоский конденсатор. Соединения конденсаторов.

13.   Проводящая сфера. Свойства проводника в электрическом поле.

14.   Сила Ампера. Сила Лоренца.

15.   Теория о магнитном поле.

16.   Магнитный поток. Электромагнитная индукция. Движение проводника в магнитном поле.

17.   Индуктивность. Самоиндукция. Энергия магнитного поля. Правило Ленца.

18.   Гармонические колебания.

19.   Математический маятник. Пружинный маятник. Механические волны.

20.   Электрический контур.

21.   Переменный ток. Трансформатор.

Собственная индуктивность

Собственная индуктивность
Далее: Энергия, хранящаяся в Вверх: Индуктивность Предыдущий: Взаимная индуктивность Нам не обязательно нужны две цепи, чтобы иметь индуктивные эффекты. Учитывать единая проводящая цепь, по которой течет ток течет. Этот ток создает магнитное поле, которое возникает магнитный поток, связывающий схема. Мы ожидаем, что поток будет прямо пропорционален к току , учитывая линейный характер законов магнитостатики, и определение магнитного потока. Таким образом, мы можем написать

(241)

где константа пропорциональности называется собственной индуктивностью схема. Как и взаимная индуктивность, собственная индуктивность цепи измеряется в генри и представляет собой чисто геометрическая величина, зависящая только от форма цепи и количество витков в цепи.

Если ток, протекающий по цепи, изменяется на сумма за временной интервал, то магнитный поток, связывающий цепь, изменяется на величину в том же интервале времени. В соответствии с Закон Фарадея, ЭДС

(242)

генерируется вокруг цепи. С , эту ЭДС также можно записать

(243)

Таким образом, ЭДС, создаваемая вокруг цепи за счет собственного тока, непосредственно пропорциональна скорости изменения тока. закон Ленца и здравый смысл требует, что если ток увеличивается, то ЭДС должна всегда действовать, чтобы уменьшить ток, и наоборот . Это легко оценить, так как если ЭДС действовала на увеличение ток, когда ток увеличивался, то мы явно получили бы нефизический положительный отзыв эффект, при котором ток продолжал увеличиваться без ограничений. Отсюда следует, из уравнение (243), что собственная индуктивность цепи обязательно равна положительному числу . Этот это не относится к взаимным индуктивностям, которые могут быть как положительными, так и отрицательными.

Рассмотрим соленоид длиной и поперечным сечением область . Предположим, что соленоид имеет витки. При протекании тока в соленоиде возникает однородное осевое поле величиной

(244)

генерируется в сердечнике соленоида. Напряженность поля вне ядра является незначительный. Магнитный поток, связывающий один виток соленоида, равен . Таким образом, магнитный поток, связывающий все витки соленоид

(245)

Согласно уравнению (241) собственная индуктивность соленоида определяется выражением , что сводится к

(246)

Заметьте, положительный. Кроме того, является геометрической величиной, зависящей только от размеров соленоида и количества витков в соленоиде.

Инженеры нравится сводить все части электрических устройств, какими бы сложными они ни были, к эквивалентная схема , состоящая из сети всего четыре разных типа компонента. Эти четыре основных компонента ЭДС , резисторы , конденсаторы , и катушки индуктивности . Катушка индуктивности представляет собой просто чистую собственную индуктивность и обычно представлял собой маленький соленоид на принципиальных схемах. На практике катушки индуктивности обычно состоят из коротких соленоидов с воздушным сердечником, намотанных из эмалированной медной проволоки.

---

Далее: Энергия, хранящаяся в Вверх: Индуктивность Предыдущий: Взаимная индуктивность

Ричард Фицпатрик 2007-07-14

Заметки о различиях между собственной индуктивностью и взаимной индуктивностью

Сэр Генри Джозеф дал нам первое представление о собственной индуктивности и взаимной индуктивности в 1831 году. Индуктивность является одним из наиболее уважаемых понятий в изучении физики. Единицей СИ для собственной и взаимной индуктивности является генри (Гн). Один генри определяется как взаимная индуктивность катушки для производства эквивалента одного вольта, когда скорость изменения тока составляет один ампер в секунду. Основные различия между собственной индуктивностью и взаимной индуктивностью заключаются в факторах, влияющих на индуктивность, некоторые из которых обсуждаются далее.

Введение в самоиндукцию

Известно, что:

• Катушка, по которой течет ток, создает магнитное поле (ЭДС) наводится за счет электромагнитной индукции

Таким образом, при изменении тока, протекающего через катушку или цепь, в ней создается ЭДС самоиндукции. Согласно закону известного физика Ленца, ЭДС самоиндукции пытается противостоять своей причине создания.

Это явление создания ЭДС самоиндукции, которая позже препятствует любому изменению в катушке или электрическом состоянии цепи, известно как самоиндукция.

Введение во взаимную индуктивность

Взаимная индуктивность, фундаментальное свойство в изучении физики, говорит о двух катушках, расположенных рядом друг с другом.

Предположим, две катушки названы A и B. Рассмотрим сценарий, когда ток пропускают через катушку A. В катушке, расположенной рядом с A, т. е. катушке B, индуцируется ЭДС. 

• Катушка А, в которой создается ток, называется первичной катушкой
• Катушка В, в которой индуцируется ЭДС, называется вторичной катушкой
• Изменение тока, создаваемого в первичной катушке, вызывает ЭДС индуцироваться во вторичной обмотке по принципу электромагнитной индукции
• По этой причине это явление известно как взаимная индуктивность

Коэффициенты собственной и взаимной индуктивности

1. Собственная индуктивность

Магнитный поток (ɸ), связанный с катушкой, прямо пропорционален току (I), протекающему через нее в любой конкретный момент.

ɸ∝ I

Чтобы удалить знак пропорциональности, мы можем написать уравнение как:

ɸ = L I

Где L — постоянная, также известная как коэффициент собственной индуктивности.

Таким образом, коэффициент собственной индуктивности любой катушки или цепи может быть определен как магнитный поток, связанный с ней из-за протекающего через нее тока в один ампер.

• Единица СИ L определяется как Вольт/(Ампер/сек) = сек – вольт/ампер = Ом-сек

2. Взаимная индуктивность вторичная катушка будет индуцировать ЭДС.

Таким образом, магнитный поток (ɸ2) зависит от изменения тока в первичной обмотке. Он прямо пропорционален току (I1).

ɸ2 ∝ I1 

Символ пропорциональности «∝» заменяется константой, обозначаемой «M». Это взаимная индуктивность двух катушек, А и В.

ɸ2 = M I1 

Отсюда коэффициент взаимной индуктивности для данной пары катушек определяется следующим образом:

• Магнитный поток (ɸ), связанный с одной из катушек за счет тока в один ампер в другой катушка равна одному веберу

или

• Величина ЭДС, индуцированной в одной из катушек из-за изменения тока со скоростью один ампер в секунду в другой катушке, равна одному вольту

Факторы, влияющие на себя и Взаимная индуктивность

Ниже приведены факторы, влияющие на константу собственной индуктивности ‘L’:

• Геометрия катушек: Спиральное расположение с большей вероятностью улавливает большее количество силовых линий магнитного поля, чем прямолинейное расположение проводов
• Природа среды между двумя катушками: Если в качестве сердечника катушки используется изолированный ферромагнитный материал, это, вероятно, приведет к тому, что больше силовых линий магнитного поля свяжутся, а это, в свою очередь, повысит значение коэффициент собственной индуктивности
• Длина катушек: Магнитный поток (ɸ), индуцированный в более длинной катушке, всегда меньше, чем поток, индуцированный в более короткой катушке

Ниже приведены факторы, влияющие на постоянную взаимной индуктивности «M»:

Количество витков в катушках A и B: Чем больше количество витков, тем выше взаимная индуктивность между двумя катушками

Размер и форма обеих катушек: Взаимная индуктивность будет различной для катушек различных форм и размеров

Расстояние между двумя катушками: Взаимная индуктивность будет меньше, если расстояние между двумя катушками больше; если расстояние между двумя катушками меньше, взаимная индуктивность будет больше

Магнитное поле первичной катушки может встречаться с магнитным полем вторичной катушки, когда расстояние меньше, вызывая большую ЭДС, индуцируемую во вторичной катушке.