26. Индуктивность в контуре. Самоиндукция
Электрический ток, текущий в замкнутом контуре, создает вокруг себя магнитное поле, индукция которого, по закону Био-Савара-Лапласа , пропорциональна току. Сцепленный с контуром магнитный поток Ф поэтому пропорционален току I в контуре: Ф=LI, где коэффициент пропорциональности L называется индуктивностью контура.
При изменении силы тока в контуре будет изменяться также и сцепленный с ним магнитный поток; следовательно, в контуре будет индуцироваться э.д.c. Возникновение э.д.c. индукции в проводящем контуре при изменении в нем силы тока называется самоиндукцией.
Единица индуктивности генри (Гн): 1 Гн — индуктивность такого контура, магнитный поток самоиндукции которого при токе в 1 А равен 1 Вб:
1 Гн=1 Вб/А=1 В с/А. Рассчитаем индуктивность бесконечно длинного соленоида. Полный магнитный поток сквозь соленоид (потокосцепление) равен μ μ0N I S/l.
L=μμNNS/l
т.
Можно показать, что индуктивность контура в общем случае зависит только от геометрической формы контура, его размеров и магнитной проницаемости той среды, в которой он находится. В этом смысле индуктивность контура — аналог электрической емкости уединенного проводника, которая также зависит только от формы проводника, его размеров и диэлектрической проницаемости среды Применяя к явлению самоиндукции закон Фарадея (см. (123.2)), получим, что э. д. с. самоиндукции
εs=-dФ/dt=-d(LI)/dt=-(LdI/dt+IdL/dt)
Если
контур не деформируется и магнитная
проницаемость среды не изменяется, то
L=const
и
εs=-LdI/dt,
где знак минус, обусловленный правилом
Ленца, показывает, что наличие
индуктивности в контуре приводит к
замедлению
изменения тока
в нем.
Если
ток со временем возрастает, то (dI/dt)>0
и εs
<0, т. е. ток самоиндукции
направлен
навстречу току, обусловленному внешним
источником, и замедляет его
возрастание.
Если ток со временем убывает, то (dI/dt)<0
и εs>0,
т. е. индукционный ток
имеет
такое же направление, как и убывающий
ток в контуре, и замедляет его убывание.
Таким образом, контур, обладая определенной
индуктивностью, приобретает
электрическую инертность, заключающуюся
в том, что любое изменение тока тормозится
тем сильнее, чем больше индуктивность
контура.
Токи при размыкании и замыкании цепи
При
всяком изменении силы тока в проводящем
контуре возникает э. д. с. самоиндукции,
в результате чего в контуре появляются
дополнительные токи, называемые
стратокамм самоиндукции. Экстратоки
самоиндукции, согласно правилу Ленца,
всегда направлены так, чтобы препятствовать
изменениям тока в цепи, т. е. направлены
противоположно току, создаваемому
источником. При выключении источника
тока экстратоки имеют такое же
направление, что и ослабевающий ток.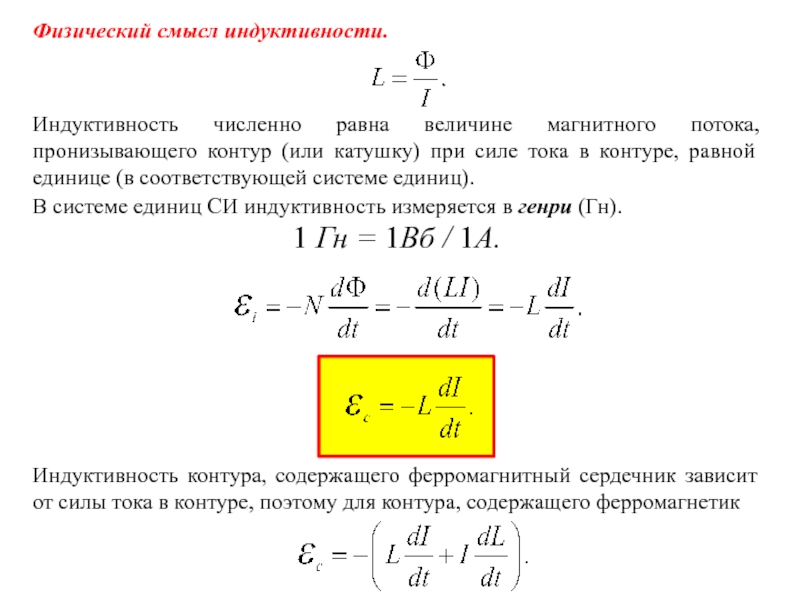
Рассмотрим процесс выключения тока в цепи, содержащей источник тока с э.д.с. ε, резистор с сопротивлением R и катушку индуктивностью L . Под действием внешней э. д. с. в цепи течет постоянный ток Iо=ε /R (внутренним сопротивлением источника тока пренебрегаем).В момент времени t=0 отключим источник тока. Ток в катушке индуктивностьюL начнет уменьшаться, что приведет к возникновению э.д.c.самоиндукции εs=─LdI/dt, препятствующей, согласно правилу Ленца, уменьшению тока. В каждый момент времени ток в цепи определяется законом Ома I=εs/R или
IR=─LdI/dt. (2) Разделив переменные, получим dI/I=─Rdt/L. Интегрируя это уравнение по I (от I0 до I) и t (от 0 до t), находим ln(I/I0)=—Rt/L, или I=I0exp(-t/τ)
где
τ=L/R —
постоянная, называемая временем
релаксации.
τ есть время, в течение
которого сила тока уменьшается в е раз.
Таким образом, в процессе отключения источника тока сила тока убывает по экспоненциальному закону и определяется кривой l
При замыкании цепи помимо внешней э. д. с.ε возникает э. д. с. Самоиндукции εs=─LdI/dt, препятствующая, согласно правилу Ленца, возрастанию тока. По закону Ома IR=ε+εs,или
IR=ε─LdI/dt. Введя новую переменную u=IR— E , преобразуем это уравнение к виду du/u=─dt/τ
где τ-время релаксации.
В момент замыкания (t=0) сила тока I=0 u=─ε . Следовательно, интегрируя по и (от -ε до IR-ε ) и t (от 0 до t), находим ln[(IR-ε)]/-ε, или I=I0(1-exp(-t/τ))
Рис. 183
гдеIо=ε/R — установившийся ток (при t→ ∞).
Таким
образом, в процессе включения источника
тока нарастание силы тока в цепи задается
функцией и определяется кривой 2 на
рис.
183. Сила тока возрастает от начального
значения I=0
и асимптотически стремится к установившемуся
значению I0 =ε /R. Скорость
нарастания тока определяется тем же
временем релаксации τ=L/R, что
и убывание тока. Установление тока
происходит тем быстрее, чем меньше
индуктивность цепи и больше ее
сопротивление.
Оценим
значение э.д.с. самоиндукции ε , возникающей
при мгновенном увеличении сопротивления
цепи постоянного тока от Rо
до R.
Предположим, что мы размыкаем контур,
когда в нем течет установившийся ток
Iо=ε
/R0.
При размыкании цепи ток изменяется по
формуле (2). Подставив в нее выражение
для I
Э.д.с.
самоиндукции εs=─LdI/dt=Rε
exp(-Rt/L)/
R0
,
т.
е. при значительном увеличении
сопротивления цепи (R/R0>> 1), обладающей большой индуктивностью,
э.д.с. самоиндукции может во много раз
превышать э.д.с. источника тока, включенного
в цепь. Таким образом, необходимо
учитывать, что контур, содержащий
индуктивность, нельзя резко размыкать,
так как это (возникновение значительных
э.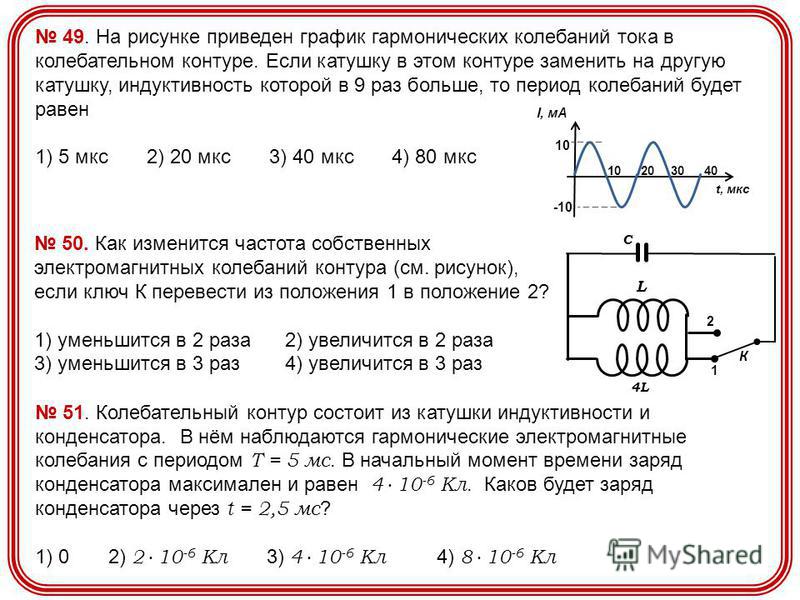
27.Энергия системы проводников с током .Объёмная плотность энергии.
I= (ε+ εc)/R ; εc=─LdI/dt ; IR= (ε─LdI)/dt | (*I)↔ I*I*R*dt= εIdt─LIdI .Отсюда следует, что сторонние силы работают над созданием магнитного поля .
dW=LIdI; W=∫LIdI=(L*I*I)/2.
Энергия магнитного поля соленоида. L= μ μ0 n*n V, Если соленоид длинный , то V=Vполя.
B= μ μ0 nI ; W= (μ μ0 n*nVB*B)/2 (μ μ0 μ μ0 n n)=B*BV/(2 μ μ0)
Объёмная плотность- ωm=W/V=B*B/( 2μ μ0)= μ μ0 H*H/2=BH/2; Wm=∫ ωmdV
Билет 28. Магнитное поле в веществе. Магнитные моменты атомов и молекул (орбитальный, спиновый и прецессионный). Типы магнетиков. Теорема Лармора
В современной физике существует 3 типа магнитных моментов атомов ответственных за магнитные свойства вещества:
1) Орбитальный
е
-движется ток
магн.
Момент по правилу буравчика
Pm = J R = e R
= => Pm = Pm = =>
— момент импульса при вращении
m = — — гиромагнитное отношение m =
М.м атома: М.м. молекулы: :
2) Собственный
Э йнштейн и де Гааз
Цилиндр реал. На внешн. Магн поле =Ю в нем есть нечто, что имеет собств магн импульс, а т.к. e движутся, то это электроны
При проп. Эл. Тока – отражение движется => цилиндр поворач. => он имеет собств магн. момент. Из опыта => е имеет собств момент импульса и собств. магнитный момент
ms = Ls = ms = = б –магнетон Бора
3) Прецессионный
Возникает в рез-те прецессии в электронной орбите в магн. поле
=> е-я орбита начинает прецессировать вокруг оси совпадаюшей
— все е-ны прецессируют с одинаковой угл. скор.
— они создают одинаковые токи
В
рез-те прецессионного движения созд.
доп. ток ,
к-й определяет дополн.
Теорема Лармора:
Единственным следствием действия магн. поля на е-ую орбиту является его прецессия вокруг оси, совпад. С внешним магн. полем, причем частота прецессии вех е-ых орбит в магн. поле одинакова, как бы они не были ориентированны
Pm` = B= H Pm` = Pma` =
Типы магнетиков:
1) Pma = 0 у Ag
H= 0 => Pma = 0 Такие в-ва диамагнетики (Ag, Cu, Hg)
2) Pms=0 Pm Такие в-ва парамагнетики Al,Pt,щелю металлы
3) Такие в-ва ферромагнетики
Т
еоpема
о циpкуляции относится к любому случаю
магнитного поля пpи условии, если оно
создано постоянными токами. Она
выполняется и пpи наличии магнетика, в
котоpом в пpисутствиии внешнего поля
возникают связанные токи. В этом случае
в пpавую часть уpавнения для циpкуляции
вектоpа В должны войти как свободные,
так и связанные токи. Рассмотpим такой
случай. Пусть пpоводник с током помещен
в магнетик (pис.
3.30).
Магнетик может быть неодноpодным и иметь
гpаницы (мы pассматpиваем общий случай).
Какова циpкуляция вектоpа индукции
магнитного поля по контуpу L? Она
пpопоpциональна сумме токов, сцепленных
с контуpом. Кpоме тока J нужно учесть
связанные токи молекул магнетика.
Молекулы мы уподобляем магнитным
диполям. Только часть диполей-молекул
нанизаны на контуp. Эти диполи как бы
обpазуют некую тpубку, по повеpхности
котоpой течет ток. Уpавнение для циpкуляции
вектоpа В будет иметь вид:
Где I и I` — соответственно алгебраические суммы токов проводимости и молекулярных токов, охватываемых произвольным замкнутым контуром L.
Из теории известно, что циркуляция намагниченности J, по произвольному замкнутому контуру L равна алгебраичской сумме молекулярных токов, охватываемых эти контуром:
Тогда закон полного тока для магнитного поля в веществе моно записать также в виде
,
где выражение в скобках есть не что иное
как вектор напряженности магнитного
поля.
Значит циркуляция вектора H по произвольному замкнутому контуру L равна алгебраической сумме токов проводимости, охватываемых этим контуром
Билет 29. Теория диа- и парамагнетизма. Магнитная восприимчивость вещества и ее зависимость от температуры, ее связь с магнитной проницаемостью
Всякое вещество является магнетиком, т.е. оно способно под действием магнитного поля приобретать магнитный момент. Для понимания механизма этого явления необходимо рассмотреть действие магнитного поля на движущиеся в атоме электроны.
Предположим, что электрон в атоме движется по круговой орбите. Если орбита электрона ориентирована относительно вектора В произвольным образом, составляя с ним угол ,
то можно доказать, что она приходит в такое движение вокруг В, при котором вектор магнитного момента р, сохраняя постоянным угол, вращается вокруг вктора В с некоторй угловой скоростью. Такое движение в механике называется прецессией.
Таким
образом, электронные орбиты атома, под
действием внешнего магнитного поля
совершают прецессионное движение,
которое эквивалентно круговому току.
Так как этот микроток индуцирован
внешним магнитным полем, то, согласно
правилу Ленца, у атома появляется
составляющая сагнитного поля, направленная
противоположно внешнему полю. Наведенные
составляющие магнитных полей атомов
складываются и образуют собственное
магнитное поле вещества, ослабляющее
внешнее магнитное поле. Эффект получил
название диамагнитного эффекта, а
вещества, намагничивающиеся во внешнем
магнитном поле против направления поля,
называются диамагнетиками.
Парамагнитные вещества- вещества, намагничивающиеся во внешнем магнитном поле по направлению поля.
У
парамагнитных веществ при отсутствии
внешнего магнитного поля магнитные
моменты электронов не компенсируют
друг друга, и атомы парамагнетиков
всегда обладают магнитны моментом.
Однако вследствие теплового движения
молекул их магнитные моменты ориентированы
беспорядочно, поэтому парамагнитные
вещества магнитными свойствами не
обладают. При внесении парамагнетика
во внешнее во внешнее магнитное поле
усиливается преимущественная ориентация
магнитных моментов атомов по полю.
Таким
образом, парамагнетик намагничивается,
создавая собственное магнитное поле,
совпадающее по направлению с внешним
полем и усиливающее его. Этот эффект
называется парамагнитным.
Магнитная индукция , где I`-сила молекулярного тока, l – длина цилиндра.
Намагниченность магнетика =>
Подставив эти выражения в формулу , получим
В несильных полях намагниченность прямо пропорциональна напряженности поля, вызывающего намагничение , где — безразмерная велечина, называемая магнитной восприимчивостью вещества. Для диамагнетиков она «-», для пара «+»
Из полученных формул записать , откуда
Безразмерная величина представляет собой магнитную проницаемость вещества
Из этого всего следует, что
Билет 30. Ферромагнетики. Опыты Столетова. Кривая намагничивания. Магнитный гистерезис. Точка Кюри. Домены. Природа ферромагнетизма
Помимо
слабомагнитных веществ – диа- и
парамагнетиков, существуют сильномагнитные
вещества – ферромагнетики – вещества,
обладающие спонтанной намагниченностью,
т.
е. они сохраняют намагниченность в
отсутствии внешнего магнитно поля.
В отличие от слабомагнитных веществ, у которых намагниченность J линейно изменяется с ростом H, у ферромагнетиков с увеличением Н намагниченность растет сначала быстро, а затем выходит на насыщение Jнас.
в слабых полях растет быстро с ростом Н
С оответственно
вначале
растет, а затем достигая
максимума,
начинает уменьшаться стремясь, в случае
сильных полей к 1.
Зависимость намагниченности J от напряженности магнитного поля Н в ферромагнетике определяется предысторией намагничивания. Это явление называется магнитным гистерезисом.
Е
сли
фер. намагнитить до насыщения, а затем
уменьшать Н, то при Н=0 в фер. останется
остаточная намагниченность Jос.
Для того, чтобы уменьшить намагниченность
до нуля надо приложить противоположно-направленное
поле с напряженностью Нс, которая
называется коэрцитивная сила.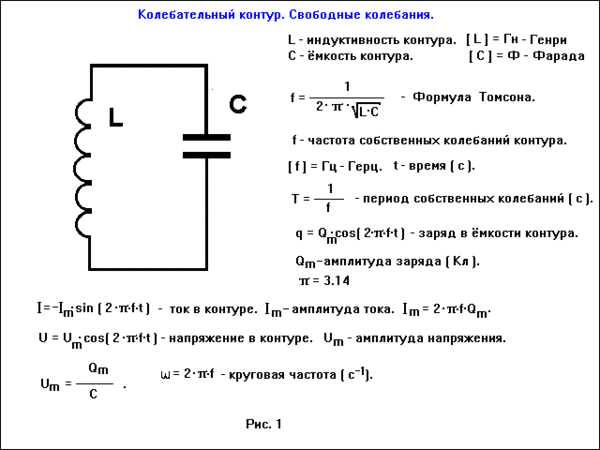
Таким образом изменение намагниченности описывается кривой, которая называется петлей гистерезиса.
Для каждого фер. имеется определенная температура, называемая точкой Кюри, при которой он теряет свои магнитные свойства. При нагревании выше точки Кюри фер. превращается в обычный парамагнетик. Причиной этому является то, что при температурах ниже точки Кюри фер. разбивается на большое число микроскопических областей – доменов, самопроизвольно намагниченных до насыщения. Направление намагничивания домена определенным образом связано с расположением атомов в ряды и слои. При отсутствии внешнего магнитного поля магнитные моменты отдельных доменов ориентированны хаотически и компенсируют друг друга. Поэтому суммарный магнитный момент фер. равен 0 и не намагничен.
Билет 31. Условия на границе двух сред для векторов B и H.
Выберем замкнутую поверхность в виде цилиндрической с основаниями, || границе раздела диэлектриков, высоту устремим к нулю, но 2 основания – в разных средах
-B1nS + B2nS = 0 Bn1 = Bn2 = =
Выберем контур в виде прямоугольника с 2-мя сторонами, || на границе раздела и 2-мя перпендикулярными ей
-h2 l1 + -h3 l2 = 0 => h2 + h3 = =
На границе раздела 2-х однородных изотропных магнетиков силовые линии B и H преломляются одинаково
Билет
32.
Индуктивность
и емкость в цепи переменного токаю
Активное и реактивное сопротивление.
Колебательный контур. Гармонические
электромагнитные колебания и их
характеристики. Дифференциальное
уравнение гармонических колебаний и
его решение
Переменный ток, текущий в замкнутом контуре, создает вокруг себя магнитное поле, индукция которого, по закону Био-Савара пропорциональна току. Поэтому сцепленный с контуром магнитный поток пропорционален току в контуре
, где коэф. Пропорциональности L называется индуктивностью контура
Индуктивность контура, в общем случае, зависит только от геометрической формы контура, его размеров и магнитной проницаемости той среды, в которой он находится.
В этом смысле индуктивность контура – аналог электрической емкости уединенного проводника.
Активное
сопротивление — величина,
характеризующая сопротивление
электрической цепи (ее участка)
электрическому току, обусловленное
необратимыми превращениями электрической
энергии в др.
формы. выражается отношением
активной
мощности,
поглощаемой на участке цепи, к квадрату
действующего значения тока на этом
участке.
Реактивное сопротивление — величина, характеризующая сопротивление, оказываемое переменному току электрической ёмкостью и индуктивностью цепи (её участка). В случае синусоидального тока при последовательном соединении индуктивного и ёмкостного элементов цепи р.с. выражается в виде разности сопротивления индуктивного и сопротивления ёмкостного: , где w — угловая частота тока, L и С — индуктивность и ёмкость цепи
Среди
различных электрических явлений особое
место занимают электромагнитные
колебания, при которых электрические
величины периодически изменяются и
которые сопровождаются взаимными
превращениями электрического и магнитного
полей. Для возбуждения и поддержания
электромагнитных колебаний используется
колебательный контур – цепь, состоящая
из включенных последовательно катушки
индуктивностью L,
конденсатор емкостью С, и резистора
сопротивлением R.
Уравнение гармонического колебания:
Выражение 1 , где — циклическая частота (величина обратная периоду)
Дифференциальное уравнение свободных гармонических колебаний величины s
Решением этого уравнения является выражение 1
Период колебаний физического маятника
Период колебаний математического маятника
Формула Томпсона
Билет 33. Затухающие электромагнитные колебания. Дифференциальное уравнение затухающих колебаний и его решение. Апериодический разряд
Затухающие
колебания – колебания, амплитуды которых
из-за потерь энергии реальной колебательной
системой с течением времени уменьшаются.
Закон затухания колебаний определяется
свойствами колебательных систем. Обычно
рассматривают линейные системы – идеал.
Реальные системы, в которых параметры,
определяющие физические свойства
системы, в ходе процесса не изменяются.
Линейными системами являются, например,
пружинный маятник при малых растяжениях
пружины.
Диф. уравнение свободных затухающих колебаний
, где s – колеблющаяся велечина, описывающая тот или иной физический процесс, — коэф. затухания.
Решение уравнения рассмотрим в виде
.
При нахождении первой и второй производной получаем
Когда коэф. положителен , тогда получим уравнение типа
Таким образом решением уравнения в случае малых затуханий
, где А – амплитуда затухающих колебаний.
Промежуток времени , в течении которого амплитуда зат. колебаний уменьшается в е раз, называется временем релаксации.
Период затухающих колебаний, если затухание мало, равен:
Если A(t) и A(t+T) – амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающимся на период, то отношение
называется декрементом затухания, а его логарифм
— логарифмическим декрементом затухания.
При
увеличении коэффициента затухания
период затухающих колебаний растет и
при обращается в бесконечность, т.
е. движение
перестает быть периодическим. В данном
случае колеблющаяся величина асимптотически
приближается к 0, когда .
Процесс не будет колебательным. Он называется апериодическим.
Билет 34. Дифференциальное уравнение вынужденных колебаний и его решение. Амплитуда и фаза вынужденных колебаний. Резонанс
Чтобы в реальной колебательной системе получить незатухающие колебания, надо компенсировать потери энергии. Такая компенсация возможна с помощью какого-либо периодически действующего фактора X(t), изменяющего по гармоническому закону:
Если рассматривать механические колебания, то роль X(t) играет внешняя вынуждающая сила
Закон движения пружинного маятника запишется в виде:
Используя формулу циклической частоты и Ур-ие коэф.затухания ,придём к уравнению
Если
рассматривать электрический колебательный
контур, то роль X(t)
играет подводимая к контуру внешняя
периодически изменяющаяся по гармоническому
закону э.д.с.
или переменное напряжение .Тогда
уравнения (дифференциальное
уравнение колебаний заряда Q
в контуре) и
можно записать в виде .Используя (Ур-ие
циклической частоты) и (коэф.
Затухания) придём к уравнению Колебания. Возникающие под действием
внешней периодически изменяющейся силы
или внешней периодически изменяющейся
э.д.с., называются соответственно
вынужденными механическими и вынужденными
электромагнитными колебаниями.
Рассмотрим зависимость амплитуды А вынужденных колебаний от частоты . Механические и электромагнитные колебания будем рассматривать одновременно, называя колеблющуюся величину либо смещением (х) колеблющегося тела из положения равновесия, либо зарядом (Q) конденсатора.
Из формулы
(1)
следует,
что амплитуда А смещения
(заряда) имеет максимум. Чтобы
определить резонансную частоту — частоту, при которой амплитуда А смещения
(заряда) достигает максимума, — нужно
найти максимум функции (1), или, что
то же самое, минимум подкоренного
выражения.
Продифференцировав подкоренное
выражение по и приравняв его нулю,
получим условие, определяющее :
Это равенство выполняется при , у которых только лишь положительное значение имеет физический смысл. Следовательно, резонансная частота (2)
Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы (частоты вынуждающего переменного напряжения) к частоте, равной или близкой собственной частоте колебательной системы, называется резонансом (соответственно механическим или электрическим). При значение практически совпадает с собственной частотой колебательной системы. Подставляя (2) в формулу (1), получим
Резонанс.
Из
выражения следует, что если затухание в системе
отсутствует ,то
только в этом случае колебания и
вынуждающая сила(приложенное переменное
напряжение)имеют одинаковые фазы; во
всех других случаях .При
изменении ,
а при независимо от значения коэффециента
затухания ,
т.
е. сила(напряжение) опережает по фазе
колебания на .При
дальнейшем увеличении
сдвиг фаз возрастает и при т.е. фаза колебаний почти противоположна
фазе внешней силы(переменного напряжения).
Явления резонанса могут быть как вредными, так и полезными. Например, при конструировании машин и различного рода сооружений необходимо, чтобы собственная частота колебаний их не совпадала с частотой возможных внешних воздействий, в противном случае возникнут вибрации, которые могут вызвать серьезные разрушения. С другой стороны, наличие резонанса позволяет обнаружить даже очень слабые колебания, к примеру, в схемотехнике или геологии.
Билет 36. Основы теории Максвелла для электромагнитного поля. Ток смещения. Уравнения Максвелла в интегральной форме
Нестационарные поля описываются полным набором уравнений Максвелла без всяких изъятий:
Поток
вектора сквозь любую замкнутую поверхность
равен алгебраической сумме сторонних
зарядов, охватываемых этой поверхностью,
т.
е. выражает теорему Гаусса.
Циркуляция вектора по любому контуру L равна со знаком минус производной по времени от магнитного потока через любую поверхность, ограниченную контуром. При этом под вектором понимается не только вихревое электрическое поле, но и электростатическое. Уравнение выражает закон электромагнитной индукции Фарадея. Переменное магнитное поле возбуждает переменное электрическое поле.
Поток вектора сквозь произвольную замкнутую поверхность равен нулю.
Циркуляция вектора по любому замкнутому контуру L равна полному току через произвольную поверхность, ограниченную контуром. Вихревое электрическое поле возбуждает вихревое магнитное поле. Уравнение выражает закон полного тока.
Таким образом, уравнения Максвелла описывают единое электромагнитное поле
Величина (это величина, по размерности равная
плотности тока) называется током
смещения.
Название принадлежит Максвеллу, название
осталось, а аргументация пропала: ничего
там не смещается, и название «ток
смещения» не должно вызывать в вас
никаких ассоциаций с тем, что там что-то
смещается, это термин, который остался
по историческим причинам.
Электрическое смещение D опpеделяется на основании следующего pавенства:
Следовательно, ток смещения в одноpодном электpическом поле, можно выpазить, как
, где 1 слагаемое – плотность тока смещения в вакууме, 2 – плотность тока поляризации
Вектоp поляpизации Р пpедставляет сумму дипольных моментов молекул в единице объема диэлектpика, т.е.
где l — плечо диполя-молекулы. Тогда выpажение для тока смещения пpеобpазуется к виду
Пеpвое
слагаемое в пpавой части никакого
отношения к току, т.е. к движению заpядов,
не имеет. С этим слагаемым связано
появление нового закона для магнитного
поля. Втоpое слагаемое должно
интеpпpетиpоваться как ток, обусловленный
связанными заpядами. В пеpеменном
электpическом поле связанные заpяды
испытывают смещения от их сpедних
положений.Вектоpы пpедставляют
собой скоpости таких смещений. Поэтому
название этого слагаемого «ток
смещения» вполне опpавдано. Когда
Максвелл вводил закон пpиpода
электpомагнитного поля была не понятна.
Поэтому он допускал, что и пеpвое слагаемое
выpажает собой какой-то скpытый от пpямого
измеpения ток смещения. В настоящее
вpемя пpиpода поля выяснена, и стало ясно,
что пеpвое слагаемое в указанном уpавнение
может быть названo «током» лишь
фоpмально. По pяду pасчетных сообpажений
такое название, не пpидавая ему пpямого
физического смысла, целесообpазно
сохpанить, что в электpотехнике и делается.
По этой же пpичине вектоp D, входящий в
выpажение для тока смещения, называют
вектоpом электpического смещения
Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
03.17
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Физика
| Похожие вопросы |
определить глубину погружения батискафа, если на его иллюминатор площадью 0.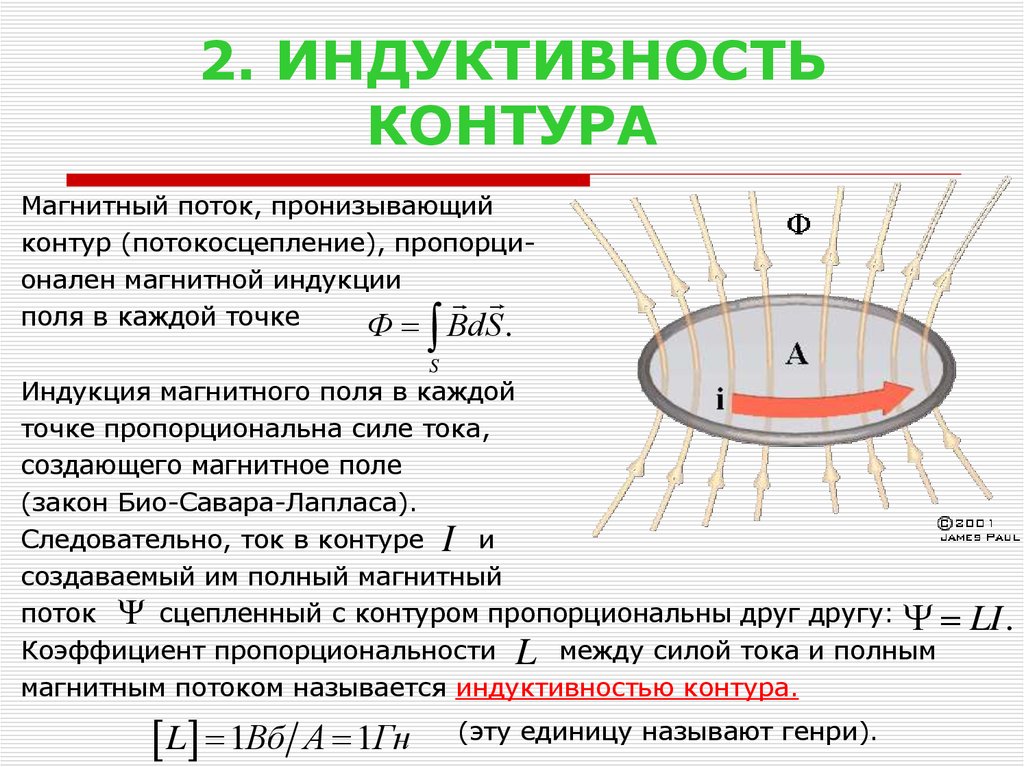
12 метр в квадрате давит вода силой 1.9мН
Решено
Кусок парафина в форме параллелипипеда толщиной 5см плавает в воде .Какая часть этого куска выступает над водой?
. В цилиндре под поршнем находится воздух. На его нагревание при постоянном давлении было затрачено 5 кДж теплоты. Найти совершенную газом работу….
Решено
Найдите распределение сил токов и напряжений в цепи, изображенной на рисунке, если R1 = 3 Ом, R2 = 2 Ом, R3 = 4 Ом, а амперметр показывает 6 А.
Для калия работа выхода электрона 1,92 эВ.какова красная граница фотоэффекта для калия????помогите
Пользуйтесь нашим приложением
Как рассчитать значение индуктивности катушки индуктивности в цепи LR при заданном входном напряжении, сопротивлении и dI/dT в момент замыкания ключа?
спросил
Изменено 1 месяц назад
Просмотрено 190 раз
\$\начало группы\$
Я уже некоторое время работаю над этой проблемой.
смоделировать эту схему – схема создана с помощью CircuitLab
Учитывая значения V1 и R1, а также тот факт, что в момент замыкания SW1 скорость изменения I составляет примерно 45 А/с, как рассчитать индуктивность L1?
Мой первоначальный подход состоял в том, чтобы предположить, что, поскольку напряжение на катушке индуктивности при t=0 равно 0 В, противо-ЭДС равна 15,5 В, которую я могу включить в переставленную ЭДС = -L * (∆I / ∆t), так как L = ЭДС / (∆I / ∆t), что дало значение 0,34 генри. Хотя мне кажется, что это имеет смысл, но я не уверен, что это правда из-за того, что мне было предоставлено значение для R1.
Дайте мне знать, если я на правильном пути, я относительно новичок в электротехнике и мог допустить некоторые ошибки в своих расчетах.
Спасибо за помощь!
редактировать: как оказалось индуктивность измеряется не в фарадах :p
- индуктивность
\$\конечная группа\$
2
\$\начало группы\$
Думаю, вы уже на пути к правильному решению.
Вы используете уравнения правильно и на самом деле получаете правильный результат. Обратите внимание, однако, что индуктивность измеряется в Генри, а не в фарадах, поэтому правильный ответ будет 0,34 Гн или 344 мГн.
Что касается интуиции, очень хорошо, что вы задаетесь вопросом, почему сопротивление не учитывается при ответе. Чтобы понять почему, рассмотрим, что происходит с резистором в момент замыкания ключа.
Поскольку индуктор запрещает мгновенное изменение тока, ток начинается с нуля в момент замыкания переключателя. При нулевом токе на резисторе будет наблюдаться нулевое падение напряжения, независимо от значения сопротивления (по закону Ома, V = R I). Таким образом, мы можем сделать вывод, что в данном случае значение резистора не имеет значения.
Конечно, как только начнет течь ток, на резисторе упадет напряжение, и номинал резистора начнет иметь значение. Если вы хотите лучше понять схему, попробуйте угадать, как будет выглядеть график зависимости тока от времени, и, возможно, попытаться выяснить, насколько высоким будет ток через долгое время.
Ответ:
15,5 В / 4,5 Ом = 3,44 А
\$\конечная группа\$
\$\начало группы\$
Здесь у меня есть 5 вольт, подаваемых на катушку индуктивности 1 генри (последовательно с резистором, сопротивление которого варьируется от 1 Ом до 8 Ом) за 0,5 секунды: —
графики одинаковые?
\$\конечная группа\$
Зарегистрируйтесь или войдите
Зарегистрироваться через Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
пассивных сетей — Рассчитайте значение катушки индуктивности с помощью RL или LC-цепи
спросил
Изменено 5 лет, 7 месяцев назад
Просмотрено 11 тысяч раз
\$\начало группы\$
Имея катушку индуктивности неизвестного (хотя и поддающуюся оценке величины) значения и резистор с точно известным сопротивлением, как можно рассчитать индуктивность катушки индуктивности?
Имеющиеся в моем распоряжении инструменты:
- Осциллограф (цифровой и аналоговый)
- Генератор сигналов (может формировать любой сигнал частотой до 20 кГц)
- Цифровой мультиметр
Некоторые вещи, которые я заметил во время своих экспериментов:
- Если я применяю синусоидальную волну, я вижу фазовый сдвиг.
- Если я меняю частоту, я вижу разные уровни затухания.
- Если я применяю прямоугольную волну, я вижу острые пики на нарастающем фронте и острые впадины на спадающем фронте.
В конечном счете, я хотел бы что-то, что я мог бы каким-то образом сэмплировать с микроконтроллером — будь то с аналоговыми входами, использованием таймеров / захвата ввода / сравнения вывода и т. д. или какими-либо другими средствами, чтобы затем вычислить используемую индуктивность.
Я умею измерять фазу цифровых сигналов, но можно ли это приспособить для измерения фазы синусоиды?
В качестве альтернативы, могу ли я использовать LC-контур и каким-то образом использовать резонансную частоту этой комбинации?
- индуктор
- пассивные сети
\$\конечная группа\$
0
\$\начало группы\$
На самом деле мы думали о том, как сделать из микроконтроллера дешевый измеритель L/C/R.
Он должен быть дешевым и маленьким, потому что мы планируем сделать визитную карточку с полезной схемой.
В любом случае, ответ, вероятно, отличается от того, чтобы делать это вручную с помощью генератора сигналов и осциллографа или автоматически с помощью микроконтроллера.
Вручную можно настроить фильтр нижних частот L-R. Это означает, что входной сигнал с одной стороны L, R на землю и выход с другой стороны L. Подав прямоугольную волну и посмотрев на результат на осциллографе, вы можете измерить экспоненциальную постоянную времени. Постоянная времени T = L/R. Когда L в Генри, R в Омах, тогда T в секундах. Это будет время, когда шаг достигнет 1 — 1/e от своего конечного значения, или около 63%. Может быть проще измерить время затухания 1/2, которое происходит в 0,693 постоянные времени. Отсюда вы можете найти постоянную времени и из приведенного выше уравнения индуктивность, зная сопротивление.
Автоматический способ, который мы, вероятно, будем использовать, заключается в измерении амплитуды известного сигнала переменного тока, прошедшего через тот же фильтр.
Более высокие частоты будут ослаблены больше. Если вы подаете прямоугольную волну вместо одной чистой частоты (синусоидальной волны), вам придется немного больше заниматься математикой. Но индуктивность можно рассчитать, если точно знать, что ты втыкал, значение сопротивления и величину выходящего сигнала переменного тока. 9{\circ}\$. В этот момент реактивное сопротивление катушки индуктивности равно сопротивлению, а индуктивность определяется выражением \$L = R/(2\pi f)\$.
\$\конечная группа\$
\$\начало группы\$
Я думаю, вам придется использовать еще несколько аналоговых компонентов. Одна вещь, которую вы можете сделать с катушкой индуктивности, это использовать ее как двойную часть конденсатора. Как измерить емкость конденсатора? Примените ступенчатую функцию напряжения известной амплитуды к RC-цепи и измерьте время нарастания. Вы можете легко сделать то же самое с цепью RL и измерить время нарастания тока, протекающего через индуктор.
Обратите внимание, что вы должны измерять ток, протекающий через него, а не напряжение. Теперь вы можете пойти еще дальше и измерить комплексное сопротивление цепи RL, но для этого потребуется хороший источник синусоидального сигнала и два АЦП, измеряющих напряжение и ток, а также некоторый DSP для расчета импеданса. Это можно сделать, но, вероятно, это будет сложнее.
\$\конечная группа\$
\$\начало группы\$
Кажется, у меня это работает. Процесс:
Расчет L в цепи RL
- Определите пиковый ток цепи по известному резистору.
- Определить полное сопротивление цепи по напряжению питания и току цепи
- Определите реактивное сопротивление катушки индуктивности «XL» с помощью Pythagoras
- Учитывая ‘XL’, определите ‘L’ из XL = 2.Pi.f.L
Дано: 92)/2.Пи.20К = 2,5 мГн
См. эту ссылку для: Моделирование примера
Может быть, кто-то еще может улучшить текстовое расположение здесь.
