Тепловую индуктивность создали при комнатной температуре

Японские физики обнаружили тепловую индуктивность в проводящей пластине, прикладывая к ее концам переменное напряжение и изучая тепловые потоки, вызванные эффектом Пельтье. Индуктивность выражалась в отставании фазы тепловых волн от фазы напряжения, из-за чего в образце появлялся инвертированный градиент температуры. Исследование опубликовано в Communications Physics.

Если какое-то одно физическое явление похоже на другое, то, скорее всего, оно будет описываться сильно схожей математикой. Можно найти множество примеров этого, но, пожалуй, самым понятным из них оказались законы, описывающие электрический ток и течение воды в трубах. В этом случае можно получить понятную аналогию, если сопоставить электрическое напряжение с давлением, а электрический ток — с потоком воды.

Оказывается, похожим образом можно поступить, если рассматривать процессы теплопереноса. Физикам удалось создать множество тепловых аналогов для простейших элементов электрических цепей, таких как диоды, транзисторы, логические вентили и так далее. До недавнего времени единственным не воспроизведенным тепловым элементом оставалась тепловая индуктивность. Это связано с тем, что колебательное поведение с изменением направления теплового потока от холодного к горячему обычно считается нарушением второго закона термодинамики. Предыдущие попытки создания термоиндуктивного элемента опирались либо на громоздкие неизолированные системы, либо на гелиевые температуры.

Кэндзиро Окава (Kenjiro Okawa) с коллегами из Национального института передовой промышленной науки и технологий (AIST) смогли создать тепловую индуктивность при комнатной температуре на основе эффекта Пельтье, прикладывая переменное напряжение к разным концам проводящей пластины. Меняя частоту напряжения, они нашли режим задержки тепловой фазы, что выражается в отрицательном градиенте температуры в середине образца.

Эффект Пельтье заключается в нагреве или охлаждении в точке контакта двух разнородных проводящих материалов. Локальное увеличение или уменьшение температуры создает ее градиент в окрестности контакта, указывающий направление теплового тока. Тепло не распространяется мгновенно: для оценки скорости процессов теплопроводности используется тепловая постоянная времени, которая помогает понять, насколько быстро в образце выровняется градиент температуры.

При этом ток не обязательно должен быть постоянным. Если период колебания напряжения, приложенного с разных концов образца, много больше тепловой постоянной времени, температурный профиль будет успевать перестраиваться в линейный закон от координаты (в случае справедливости одномерного приближения), а тепловой поток будет повсеместно однородным. Для противоположного случая, когда частота колебаний очень большая, температурное распределение станет постоянным, а поток нулевым за исключением краевых точек. Но когда тепловая постоянная времени оказывается сопоставимой с периодом колебаний напряжения, тепловой профиль представляет собой волнообразную зависимость с двумя точками экстремума. Тепловой поток между этими двумя точками становится отрицательным по отношению к разности температур на концах образца. Из-за возникающей задержки тепловой фазы по отношению к фазе тока этот обратный тепловой поток можно интерпретировать как термоиндуктивность, вызванную эффектом Пельтье.

Физики построили математическую модель этого эффекта для нескольких темроэлектрических материалов: меди и теллуридов висмута и сурьмы. В последнем случае оказалось, что отрицательный локальный температурный градиент может достигать 20 процентов от разности на концах образца. Однако из-за того, что амплитуда колебаний температуры составляет при этом всего 25 милликельвин, эффект невозможно обнаружить прямыми калориметрическими измерениями.

Вместо этого авторы предложили проводить измерения электрического импеданса в области образца, в которой модель предсказывает обратный градиент. Согласно расчетам, пассивная проводимость в ней должна быть несколько ниже, чем в среднем по образцу, а реактивная часть сопротивления может стать положительной. Физики убедились в этом экспериментально, получив хорошее согласие с теорией.

Ученые отмечают, что обнаруженный ими эффект существует при комнатной температуре и легко может быть настроен изменением частоты напряжения. Если удастся сформировать таким образом тепловой аналог самоиндукции, это откроет дорогу к созданию тепловых колебательных контуров.

В последнее время появляется все больше материалов, демонстрирующих необычную теплопроводность. Мы уже рассказывали про концепцию ткани с асимметричной терморегуляцией, а также про достижение рекордного коэффициента тепловой анизотропии в слоистых структурах.

Марат Хамадеев

Нашли опечатку? Выделите фрагмент и нажмите Ctrl+Enter.

Физика, 9 кл. (Буховерцев Б.Б.)

Физика, 9 кл. (Буховерцев Б.Б.)

Буховцев Б.Б., Климонтович Ю.Л., Мякишев Г.Я. Физика. 9 класс. Учебник. — 6-е изд. — М.: Просвещение, 1982. — 272 с. В учебнике на современном уровне изложены фундаментальные вопросы школьной программы, представлены основные технические применения законов физики, рассмотрены методы решения задач. Книга адресована учащимся средних школ, слушателям и преподавателям подготовительных отделений вузов, а также читателям, занимающимся самообразованием и готовящимся к поступлению в вуз. Оглавление ТЕПЛОВЫЕ ЯВЛЕНИЯ. МОЛЕКУЛЯРНАЯ ФИЗИКА Глава I. ОСНОВЫ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ 1. ОСНОВНЫЕ ПОЛОЖЕНИЯ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ. РАЗМЕРЫ МОЛЕКУЛ 2. МАССА МОЛЕКУЛ. ПОСТОЯННАЯ АВОГАДРО 3. БРОУНОВСКОЕ ДВИЖЕНИЕ. 4. СИЛЫ ВЗАИМОДЕЙСТВИЯ МОЛЕКУЛ 5. СТРОЕНИЕ ГАЗООБРАЗНЫХ, ЖИДКИХ И ТВЕРДЫХ ТЕЛ 6. ИДЕАЛЬНЫЙ ГАЗ В МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ 7. ОСНОВНОЕ УРАВНЕНИЕ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ I Глава II. ТЕМПЕРАТУРА. ЭНЕРГИЯ ТЕПЛОВОГО ДВИЖЕНИЯ МОЛЕКУЛ 8. ТЕПЛОВОЕ РАВНОВЕСИЕ. ТЕМПЕРАТУРА 9. ИЗМЕРЕНИЕ ТЕМПЕРАТУРЫ 10. АБСОЛЮТНАЯ ТЕМПЕРАТУРА. ТЕМПЕРАТУРА — МЕРА СРЕДНЕЙ КИНЕТИЧЕСКОЙ ЭНЕРГИИ МОЛЕКУЛ 11. ИЗМЕРЕНИЕ СКОРОСТЕЙ МОЛЕКУЛ ГАЗА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ II Глава III. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА. ГАЗОВЫЕ ЗАКОНЫ 12. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА 13. ПРИМЕНЕНИЕ УРАВНЕНИЯ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА К РАЗЛИЧНЫМ ПРОЦЕССАМ 14. ПРИМЕНЕНИЕ ГАЗОВ В ТЕХНИКЕ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ III Глава IV. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ 16. РАБОТА В ТЕРМОДИНАМИКЕ 17. КОЛИЧЕСТВО ТЕПЛОТЫ 18. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ 19. ПРИМЕНЕНИЕ ПЕРВОГО ЗАКОНА ТЕРМОДИНАМИКИ К РАЗЛИЧНЫМ ПРОЦЕССАМ 20. НЕОБРАТИМОСТЬ ПРОЦЕССОВ В ПРИРОДЕ 21. ПРИНЦИПЫ ДЕЙСТВИЯ ТЕПЛОВЫХ ДВИГАТЕЛЕЙ 22. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ (КПД) ТЕПЛОВОГО ДВИГАТЕЛЯ. ТЕПЛОВЫЕ ДВИГАТЕЛИ И ОХРАНА ПРИРОДЫ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ IV Глава V. ВЗАИМНЫЕ ПРЕВРАЩЕНИЯ ЖИДКОСТЕЙ И ГАЗОВ 23. НАСЫЩЕННЫЙ ПАР 24. ЗАВИСИМОСТЬ ДАВЛЕНИЯ НАСЫЩЕННОГО ПАРА ОТ ТЕМПЕРАТУРЫ. КИПЕНИЕ. КРИТИЧЕСКАЯ ТЕМПЕРАТУРА 25. ВЛАЖНОСТЬ ВОЗДУХА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ V Глава VI. ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ ЖИДКОСТЕЙ 27. СИЛА ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ 28. КАПИЛЛЯРНЫЕ ЯВЛЕНИЯ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ VI Глава VII. ТВЕРДЫЕ ТЕЛА 29. КРИСТАЛЛИЧЕСКИЕ ТЕЛА 30. АМОРФНЫЕ ТЕЛА 31. ДЕФОРМАЦИЯ. ВИДЫ ДЕФОРМАЦИИ ТВЕРДЫХ ТЕЛ 32. МЕХАНИЧЕСКИЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ. ДИАГРАММА РАСТЯЖЕНИЯ 33. ПЛАСТИЧНОСТЬ И ХРУПКОСТЬ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ VII ОСНОВЫ ЭЛЕКТРОДИНАМИКИ 34. ЧТО ТАКОЕ ЭЛЕКТРОДИНАМИКА? Глава VIII. ЭЛЕКТРОСТАТИКА 35. ЭЛЕКТРИЧЕСКИЙ ЗАРЯД И ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ 36. ЗАРЯЖЕННЫЕ ТЕЛА. ЭЛЕКТРИЗАЦИЯ ТЕЛ 37. ЗАКОН СОХРАНЕНИЯ ЭЛЕКТРИЧЕСКОГО ЗАРЯДА 38. ОСНОВНОЙ ЗАКОН ЭЛЕКТРОСТАТИКИ — ЗАКОН КУЛОНА 39. ЕДИНИЦА ЭЛЕКТРИЧЕСКОГО ЗАРЯДА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ 40. БЛИЗКОДЕЙСТВИЕ И ДЕЙСТВИЕ НА РАССТОЯНИИ 41. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ 42. НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ. ПРИНЦИП СУПЕРПОЗИЦИИ ПОЛЕЙ 43. СИЛОВЫЕ ЛИНИИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ 44. ПРОВОДНИКИ В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ 45. НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ РАВНОМЕРНО ЗАРЯЖЕННОГО ПРОВОДЯЩЕГО ШАРА И БЕСКОНЕЧНОЙ ПЛОСКОСТИ 46. ДИЭЛЕКТРИКИ В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ. ДВА ВИДА ДИЭЛЕКТРИКОВ 47. ПОЛЯРИЗАЦИЯ ДИЭЛЕКТРИКОВ. ДИЭЛЕКТРИЧЕСКАЯ ПРОНИЦАЕМОСТЬ 48. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ЗАРЯЖЕННОГО ТЕЛА В ОДНОРОДНОМ ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ 49. ПОТЕНЦИАЛ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ И РАЗНОСТЬ ПОТЕНЦИАЛОВ 50. ПОТЕНЦИАЛ ЭЛЕКТРИЧЕСКОГО ПОЛЯ ТОЧЕЧНОГО ЗАРЯДА 51. СВЯЗЬ МЕЖДУ НАПРЯЖЕННОСТЬЮ ЭЛЕКТРИЧЕСКОГО ПОЛЯ И РАЗНОСТЬЮ ПОТЕНЦИАЛОВ. ЭКВИПОТЕНЦИАЛЬНЫЕ ПОВЕРХНОСТИ 52. ИЗМЕРЕНИЕ РАЗНОСТИ ПОТЕНЦИАЛОВ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ 53. ЭЛЕКТРОЕМКОСТЬ. ЕДИНИЦЫ ЭЛЕКТРОЕМКОСТИ 54. КОНДЕНСАТОРЫ. ЭЛЕКТРОЕМКОСТЬ ПЛОСКОГО КОНДЕНСАТОРА 55. ЭНЕРГИЯ ЗАРЯЖЕННОГО КОНДЕНСАТОРА. ПРИМЕНЕНИЯ КОНДЕНСАТОРОВ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ X Глава IX. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК 56. ЭЛЕКТРИЧЕСКИЙ ТОК. СИЛА ТОКА 57. УСЛОВИЯ, НЕОБХОДИМЫЕ ДЛЯ СУЩЕСТВОВАНИЯ ЭЛЕКТРИЧЕСКОГО ТОКА 58. ЗАКОН ОМА ДЛЯ УЧАСТКА ЦЕПИ. СОПРОТИВЛЕНИЕ 59. ЗАВИСИМОСТЬ СОПРОТИВЛЕНИЯ ПРОВОДНИКА ОТ ТЕМПЕРАТУРЫ 60. СВЕРХПРОВОДИМОСТЬ 61. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ. ПОСЛЕДОВАТЕЛЬНОЕ И ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЯ ПРОВОДНИКОВ 62. ИЗМЕРЕНИЕ СИЛЫ ТОКА И НАПРЯЖЕНИЯ 63. РАБОТА И МОЩНОСТЬ ПОСТОЯННОГО ТОКА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ 64. ЭЛЕКТРОДВИЖУЩАЯ СИЛА 65. ЗАКОН ОМА ДЛЯ ЗАМКНУТОЙ ЦЕПИ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ IX Глава X. ЭЛЕКТРИЧЕСКИЙ ТОК В РАЗЛИЧНЫХ СРЕДАХ 66. ЭЛЕКТРИЧЕСКАЯ ПРОВОДИМОСТЬ РАЗЛИЧНЫХ ВЕЩЕСТВ 67. ЭЛЕКТРОННАЯ ПРОВОДИМОСТЬ МЕТАЛЛОВ 68. ЭЛЕКТРИЧЕСКИЙ ТОК В ЖИДКОСТЯХ 69. ЗАКОН ЭЛЕКТРОЛИЗА 70. ЭЛЕКТРИЧЕСКИЙ ТОК В ГАЗАХ 71. НЕСАМОСТОЯТЕЛЬНЫЙ И САМОСТОЯТЕЛЬНЫЙ РАЗРЯДЫ 72. РАЗЛИЧНЫЕ ТИПЫ САМОСТОЯТЕЛЬНОГО РАЗРЯДА И ИХ ТЕХНИЧЕСКИЕ ПРИМЕНЕНИЯ 73. ПЛАЗМА 74. ЭЛЕКТРИЧЕСКИЙ ТОК В ВАКУУМЕ 75. ДВУХЭЛЕКТРОДНАЯ ЭЛЕКТРОННАЯ ЛАМПА-ДИОД 76. ЭЛЕКТРОННЫЕ ПУЧКИ. ЭЛЕКТРОННОЛУЧЕВАЯ ТРУБКА 77. ЭЛЕКТРИЧЕСКИЙ ТОК В ПОЛУПРОВОДНИКАХ 78. ЭЛЕКТРИЧЕСКАЯ ПРОВОДИМОСТЬ ПОЛУПРОВОДНИКОВ ПРИ НАЛИЧИИ ПРИМЕСЕЙ 79. ЭЛЕКТРИЧЕСКИЙ ТОК ЧЕРЕЗ КОНТАКТ ПОЛУПРОВОДНИКОВ p- И n- ТИПОВ 80. ПОЛУПРОВОДНИКОВЫЙ ДИОД 81. ТРАНЗИСТОР 82. ТЕРМИСТОРЫ И ФОТОРЕЗИСТОРЫ ПРИМЕР РЕШЕНИЯ ЗАДАЧИ КРАТКИЕ ИТОГИ ГЛАВЫ X Глава XI. МАГНИТНОЕ ПОЛЕ 83. ВЗАИМОДЕЙСТВИЕ ТОКОВ. МАГНИТНОЕ ПОЛЕ 84. ВЕКТОР МАГНИТНОЙ ИНДУКЦИИ 85. ЛИНИИ МАГНИТНОЙ ИНДУКЦИИ 86. ЭЛЕКТРОИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ 87. МОДУЛЬ ВЕКТОРА МАГНИТНОЙ ИНДУКЦИИ. МАГНИТНЫЙ ПОТОК 88. ЗАКОН АМПЕРА 89. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ДВИЖУЩИЙСЯ ЗАРЯД. СИЛА ЛОРЕНЦА 90. МАГНИТНЫЕ СВОЙСТВА ВЕЩЕСТВА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ XI Глава XII. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ 91. ОТКРЫТИЕ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ 92. НАПРАВЛЕНИЕ ИНДУКЦИОННОГО ТОКА. ПРАВИЛО ЛЕНЦА 93. ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ 94. ВИХРЕВОЕ ЭЛЕКТРИЧЕСКОЕ ПОЛЕ 95. ЭДС ИНДУКЦИИ В ДВИЖУЩИХСЯ ПРОВОДНИКАХ 96. САМОИНДУКЦИЯ. ИНДУКТИВНОСТЬ 97. ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ ТОКА 98. ОСНОВНЫЕ ЗАКОНЫ ЭЛЕКТРОДИНАМИКИ И ИХ ТЕХНИЧЕСКОЕ ПРИМЕНЕНИЕ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ XII ЗАКЛЮЧЕНИЕ ЛАБОРАТОРНЫЕ РАБОТЫ ОТВЕТЫ К УПРАЖНЕНИЯМ

23.12: Индуктивность — Физика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

2715

• OpenStax
• OpenStax

Цели обучения

К концу этого раздела вы сможете:

• Рассчитать индуктивность катушки индуктивности.
• Рассчитайте энергию, запасенную в катушке индуктивности.
• Рассчитайте ЭДС, создаваемую катушкой индуктивности.

Катушки индуктивности

Индукция — это процесс, при котором ЭДС индуцируется за счет изменения магнитного потока. До сих пор обсуждалось множество примеров, некоторые из которых более эффективны, чем другие. Трансформаторы, например, спроектированы таким образом, чтобы быть особенно эффективными при наведении желаемого напряжения и тока с очень небольшой потерей энергии в другие формы. Существует ли полезная физическая величина, связанная с тем, насколько «эффективно» данное устройство? Ответ положительный, и эта физическая величина называется индуктивностью.

Взаимная индуктивность — это действие закона индукции Фарадея для одного устройства на другое, например, когда первичная катушка передает энергию вторичной обмотке в трансформаторе. См. рисунок, где простые катушки наводят друг в друге ЭДС.

Рисунок \(\PageIndex{1}\): Эти катушки могут индуцировать ЭДС друг в друге, как неэффективный трансформатор. Их взаимная индуктивность М указывает на эффективность связи между ними. Здесь видно, что изменение тока в катушке 1 индуцирует ЭДС в катушке 2. (Обратите внимание, что «\(E_2\) индуцируется» представляет ЭДС индукции в катушке 2.)

Во многих случаях, когда геометрия устройств фиксирована, поток изменяется за счет изменения тока. Поэтому мы сосредоточимся на скорости изменения тока \(\Delta I/\delta t\) как причине индукции. Изменение тока \(I_1\) в одном устройстве, катушка 1 на рисунке, индуцирует \(I_2\) в другом. Мы выражаем это в виде уравнения как

\[ЭДС_2 = — M\dfrac{\Delta I_1}{\Delta t},\], где \(M\) определяется как взаимная индуктивность между двумя устройствами. Знак минус является выражением закона Ленца. Чем больше взаимная индуктивность \(M\), тем эффективнее связь. Например, катушки на рисунке имеют небольшой \(M\) по сравнению с катушками трансформатора в [ссылка]. Единицами для \(M\) являются (V\cdot s)/A = \Omega \cdot s\), который называется генри (H) в честь Джозефа Генри. То есть \(1 \, H = 1 \, \Omega \cdot s\).

Природа здесь симметрична. Если мы изменим ток \(I_2\) в катушке 2, мы индуцируем \(ЭДС_1\) в катушке 1, которая определяется как

\[ЭДС_1 = -M \dfrac{\Delta I_2}{\Delta t} ,\] где \(М\) то же, что и для обратного процесса. Трансформаторы работают в обратном направлении с той же эффективностью или взаимной индуктивностью \(M\).

Большая взаимная индуктивность \(M\) может быть или не быть желательной. Мы хотим, чтобы трансформатор имел большую взаимную индуктивность. Но такой прибор, как электрическая сушилка для белья, может индуцировать на своем корпусе опасную ЭДС, если взаимная индуктивность между его катушками и корпусом велика. Один из способов уменьшить взаимную индуктивность \(M\) состоит в том, чтобы встречно обмотать катушки, чтобы нейтрализовать создаваемое магнитное поле. (См. рис.)

Рисунок \(\PageIndex{2}\): Нагревательные спирали электрической сушилки для белья могут быть намотаны в противоположных направлениях, так что их магнитные поля компенсируют друг друга, что значительно снижает взаимную индуктивность с корпусом сушилки.

Самоиндукция, действие закона Фарадея об индукции устройства на себя, также существует. Когда, например, ток через катушку увеличивается, магнитное поле и поток также увеличиваются, индуцируя противо-ЭДС, как того требует закон Ленца. И наоборот, если ток уменьшается, индуцируется ЭДС, препятствующая уменьшению. Большинство устройств имеют фиксированную геометрию, поэтому изменение потока полностью связано с изменением тока \(\Delta I\) через устройство. ЭДС индукции связана с физической геометрией устройства и скоростью изменения тока. Это дается

\[ЭДС = -L \dfrac{\Delta I}{\Delta t},\] где \(L\) — собственная индуктивность устройства. Устройство, обладающее значительной собственной индуктивностью, называется катушкой индуктивности и обозначается символом на рисунке.

Рисунок \(\PageIndex{3}\):

Знак минус является выражением закона Ленца, указывающим, что ЭДС противодействует изменению тока. Единицами самоиндукции являются генри (Гн), как и для взаимной индуктивности. Чем больше собственная индуктивность \(L\) устройства, тем больше его сопротивление любому изменению тока через него. Например, большая катушка с большим количеством витков и железным сердечником имеет большое \(L\) и не позволит току быстро меняться. Чтобы избежать этого эффекта, необходимо добиться малого \(L\), например, за счет встречной обмотки катушек, как показано на рисунке.

Катушка индуктивности 1 Гн представляет собой большую катушку индуктивности. Чтобы проиллюстрировать это, рассмотрим устройство с \(L = 1,0 \, H\), через которое протекает ток 10 А. Что произойдет, если мы попытаемся отключить ток быстро, возможно, всего за 1,0 мс? ЭДС, заданная выражением \(ЭДС = -L(\Delta I/\Delta t)\), будет препятствовать изменению. Таким образом, ЭДС будет индуцироваться по формуле \). Положительный знак означает, что это большое напряжение направлено в том же направлении, что и ток, противодействуя его уменьшению. Такие большие ЭДС могут вызывать искрение, повреждая коммутационное оборудование, поэтому может потребоваться более медленное изменение тока.

Для такого большого наведенного напряжения есть применение. Вспышки камеры используют батарею, две катушки индуктивности, которые функционируют как трансформатор, и систему переключения или осциллятор для создания больших напряжений. (Помните, что нам нужно изменяющееся магнитное поле, вызванное изменяющимся током, чтобы индуцировать напряжение в другой катушке.) Система генератора будет делать это много раз, когда напряжение батареи увеличится до более чем одной тысячи вольт. (Вы можете услышать пронзительный вой трансформатора во время зарядки конденсатора.) Конденсатор сохраняет высокое напряжение для последующего использования при питании вспышки. (См. рис.)

Рисунок \(\PageIndex{4}\): Благодаря быстрому переключению катушки индуктивности батареи на 1,5 В можно использовать для наведения ЭДС в несколько тысяч вольт. Это напряжение можно использовать для хранения заряда в конденсаторе для последующего использования, например, во вспышке фотоаппарата.

Можно рассчитать \(L\) для индуктора, зная его геометрию (размер и форму) и зная создаваемое им магнитное поле. В большинстве случаев это сложно из-за сложности создаваемого поля. Итак, в этом тексте индуктивность \(L\) обычно является заданной величиной. Единственным исключением является соленоид, потому что он имеет очень однородное поле внутри, почти нулевое поле снаружи и простую форму. Поучительно вывести уравнение для его индуктивности. Начнем с того, что заметим, что ЭДС индукции определяется законом индукции Фарадея как \(ЭДС = -N(\Delta \Phi /\Delta t)\) и, по определению самоиндукции, как \(ЭДС = — L(\Дельта I/\Дельта t)\). Приравнивая эти выходы

\[ЭДС = -N\dfrac{\Delta \Phi}{\Delta t} = -L \dfrac{\Delta I}{\Delta t}.\]

Решение для \(L\) дает \ [L = N\dfrac{\Delta \Phi}{\Delta I}.\]

Это уравнение для собственной индуктивности \(L\) устройства всегда справедливо. Это означает, что собственная индуктивность \(L\) зависит от того, насколько эффективно ток создает поток; чем эффективнее, тем больше \(\Delta \phi /\Delta I\).

Воспользуемся последним уравнением, чтобы найти выражение для индуктивности соленоида. Поскольку площадь \(A\) соленоида фиксирована, изменение потока равно \(\Delta \Phi = \Delta (BA) = A\Delta B\). Чтобы найти \(\Delta B\), заметим, что магнитное поле соленоида определяется выражением \(B = \mu_0 n I = \mu_0 \frac{\Delta I}{l}\). (Здесь \(n = N/l\), где \(N\) — число витков и длина соленоида.) Изменяется только ток, так что \(\Delta \Phi = A \delta B= \ mu_0 NA \frac{\Delta I}{l}\). Подстановка \(\Delta\Phi\) в \(L = N \frac{\Delta \Phi}{\Delta I}\) дает 92 A}{l} (соленоид).\]

Это собственная индуктивность соленоида с площадью поперечного сечения \(A\) и длиной \(l\). Обратите внимание, что индуктивность зависит только от физических характеристик соленоида, соответствующих его определению.

Пример \(\PageIndex{1}\): расчет собственной индуктивности соленоида среднего размера

Рассчитайте собственную индуктивность соленоида длиной 10,0 см и диаметром 4,00 см с 200 витками.

Стратегия

Это прямое применение \(L = \frac{\mu_0 N^2 A}{l}\), поскольку все величины в уравнении, кроме \(L\), известны. 92)}{0,100 \, м}\]

\[= 0,632 \, мГн.\]

Обсуждение

Этот соленоид средних размеров. Его индуктивность около миллигенри также считается умеренной.

Одно из распространенных применений индуктивности используется в светофорах, которые могут определять, когда транспортные средства ожидают на перекрестке. Электрическая цепь с индуктором размещена на дороге под местом остановки ожидающего автомобиля. Кузов автомобиля увеличивает индуктивность, и схема меняется, посылая сигнал светофору изменить цвет. Точно так же металлоискатели, используемые для обеспечения безопасности в аэропортах, используют ту же технику. Катушка или индуктор в корпусе металлоискателя действует как передатчик и приемник. Импульсный сигнал в катушке передатчика индуцирует сигнал в приемнике. На самоиндукцию цепи влияет любой металлический предмет на пути. Такие детекторы могут быть настроены на чувствительность, а также могут указывать примерное местонахождение обнаруженного на человеке металла. (Но они не смогут обнаружить пластиковую взрывчатку, подобную той, что была найдена на «подрывнике в нижнем белье».) См. рисунок.

Рисунок \(\PageIndex{5}\): Знакомые ворота безопасности в аэропорту могут не только обнаруживать металлы, но и указывать их приблизительную высоту над полом. (кредит: Alexbuirds, Wikimedia Commons)

Энергия, запасенная в катушке индуктивности

Из закона Ленца мы знаем, что индуктивность сопротивляется изменениям тока. Есть альтернативный взгляд на эту оппозицию, основанный на энергии. Энергия хранится в магнитном поле. Требуется время, чтобы накопить энергию, и также нужно время, чтобы истощить энергию; следовательно, существует оппозиция быстрым изменениям. В индукторе магнитное поле прямо пропорционально току и индуктивности устройства. Можно показать, что энергия 92 = 0,284 \, Дж.\]

Обсуждение

Этого количества энергии, безусловно, достаточно, чтобы вызвать искру, если ток внезапно отключится. Он не может быть построен мгновенно, если только потребляемая мощность не бесконечна.

Резюме

• Индуктивность — это свойство устройства, которое показывает, насколько эффективно оно индуцирует ЭДС в другом устройстве.
• Взаимная индуктивность — это действие двух устройств, индуцирующих ЭДС друг в друге.
• Изменение тока \(\Delta I_1/\Delta t\) в одном индуцирует \(ЭДС_2\) во втором: \[ЭДС_2 = — M\dfrac{\Delta I_1}{\Delta t},\] где \(M\) определяется как взаимная индуктивность между двумя устройствами, а знак минус соответствует закону Ленца.
• Симметрично изменение тока \(\Delta I_2/\Delta t\) через второе устройство индуцирует \(ЭДС_2\) в первом: \[ЭДС_1 = -M\dfrac{\Delta I_2}{\Delta t },\] где \(M\) — та же взаимная индуктивность, что и в обратном процессе.
• Текущие изменения в устройстве индуцируют ЭДС в самом устройстве.
• Самоиндукция — это эффект устройства, индуцирующего ЭДС само по себе.
• Устройство называется катушкой индуктивности, а ЭДС, индуцируемая в нем изменением тока через него, равна \[ЭДС = -L\dfrac{\Delta I}{\Delta t},\], где \(L\) собственная индуктивность катушки индуктивности, а \(\Delta I/\Delta t\) — скорость изменения тока через нее. Знак минус указывает на то, что ЭДС противодействует изменению тока, как того требует закон Ленца. 92.\]

Глоссарий

индуктивность

свойство устройства, описывающее, насколько эффективно оно создает ЭДС в другом устройстве

взаимная индуктивность

насколько эффективно пара устройств индуцирует ЭДС друг в друге

Генри

единица индуктивности; \(1 \, H = 1 \Омега \cdot s\)

самоиндукция 92\)

Авторы

Пол Питер Урон (почетный профессор Калифорнийского государственного университета, Сакраменто) и Роджер Хинрихс (Государственный университет Нью-Йорка, Колледж в Освего) с соавторами: Ким Диркс (Оклендский университет) и Манджула Шарма (Сиднейский университет) ). Эта работа находится под лицензией OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4. 0).

---

Эта страница под названием 23.12: Inductance распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   ОпенСтакс

   Лицензия

   СС BY

   Версия лицензии

   4,0

   Программа OER или Publisher

   ОпенСтакс

   Показать оглавление

   нет

2. Теги

   1. энергия, запасенная в катушке индуктивности
   2. Генри
   3. индуктивность
   4. индуктор
   5. взаимная индуктивность
   6. самоиндукция
   7. источник@https://openstax. org/details/books/college-physics

23.9 Индуктивность – Колледж физики

Резюме

• Расчет индуктивности катушки индуктивности.
• Рассчитайте энергию, запасенную в катушке индуктивности.
• Рассчитайте ЭДС, создаваемую катушкой индуктивности.

Индукция – это процесс, при котором ЭДС индуцируется изменением магнитного потока. До сих пор обсуждалось множество примеров, некоторые из которых более эффективны, чем другие. Трансформаторы, например, спроектированы таким образом, чтобы быть особенно эффективными при наведении желаемого напряжения и тока с очень небольшой потерей энергии в другие формы. Существует ли полезная физическая величина, связанная с тем, насколько «эффективно» данное устройство? Ответ положительный, и эта физическая величина называется 9.0090 индуктивность .

Взаимная индуктивность — это действие закона индукции Фарадея для одного устройства на другое, например, первичная катушка при передаче энергии вторичной обмотке в трансформаторе. См. рис. 1, где простые катушки наводят друг в друге ЭДС.

Рис. 1. Эти катушки могут индуцировать ЭДС друг в друге, как неэффективный трансформатор. Их взаимная индуктивность М указывает на эффективность связи между ними. Здесь видно, что изменение тока в катушке 1 индуцирует ЭДС в катушке 2. (Обратите внимание, что « E ₂ индуцируемая» представляет ЭДС индукции в катушке 2.)

Во многих случаях, когда геометрия устройств фиксирована, поток изменяется при изменении тока. Поэтому мы сосредоточимся на скорости изменения тока, [латекс]\жирныйсимвол{\Delta I / \Delta t}[/латекс], как на причине индукции. Изменение тока [latex]\boldsymbol{I_1}[/latex] в одном устройстве, катушка 1 на рисунке, индуцирует [latex]\boldsymbol{\textbf{emf}_2}[/latex] в другом. Выразим это в виде уравнения как

[латекс]\boldsymbol{\textbf{emf}_2 = -M}[/латекс] [латекс]\boldsymbol{\frac{\Delta I_1}{\Delta t}}[/латекс],

, где [латекс]\boldsymbol{M}[/латекс] определяется как взаимная индуктивность между двумя устройствами. Знак минус является выражением закона Ленца. Чем больше взаимная индуктивность [латекс]\boldsymbol{M}[/латекс], тем эффективнее связь. Например, катушки на рисунке 1 имеют маленький [латекс]\жирныйсимвол{M}[/латекс] по сравнению с катушками трансформатора в главе 23.7. Рисунок 3. Единицы для [латекс]\жирныйсимвол{М}[/латекс] равны [ латекс]\boldsymbol{(\textbf{V} \cdot \;\textbf{s})/ \textbf{A} = \Omega \cdot \;\textbf{s}}[/latex], который называется Генри (H), в честь Джозефа Генри. То есть [латекс]\boldsymbol{1 \;\textbf{H} = 1 \Omega \cdot \;\textbf{s}}[/latex].

Природа здесь симметрична. Если мы изменим ток [latex]\boldsymbol{I_2}[/latex] в катушке 2, мы индуцируем [latex]\boldsymbol{\textbf{emf}_1}[/latex] в катушке 1, который определяется как

[латекс]\boldsymbol{\textbf{emf}_1 = -M}[/латекс] [латекс]\boldsymbol{\frac{\Delta I_2}{\Delta t}}[/латекс],

, где [latex]\boldsymbol{M}[/latex] — то же, что и для обратного процесса. Трансформаторы работают в обратном направлении с той же эффективностью или взаимной индуктивностью [латекс]\boldsymbol{M}[/латекс] .

Большая взаимная индуктивность [латекс]\boldsymbol{M}[/латекс] может быть как желательной, так и нежелательной. Мы хотим, чтобы трансформатор имел большую взаимную индуктивность. Но такой прибор, как электрическая сушилка для белья, может индуцировать на своем корпусе опасную ЭДС, если взаимная индуктивность между его катушками и корпусом велика. Один из способов уменьшить взаимную индуктивность [латекс]\boldsymbol{M}[/латекс] – это встречная обмотка катушек, чтобы нейтрализовать создаваемое магнитное поле. (См. рис. 2.)

Рисунок 2. Нагревательные катушки электрической сушилки для белья могут быть встречно намотаны, так что их магнитные поля компенсируют друг друга, что значительно снижает взаимную индуктивность с корпусом сушилки.

Самоиндукция , действие закона Фарадея об индукции устройства на себя, также существует. Когда, например, ток через катушку увеличивается, магнитное поле и поток также увеличиваются, индуцируя противо-ЭДС, как того требует закон Ленца. И наоборот, если ток уменьшается, индуцируется ЭДС, препятствующая уменьшению. Большинство устройств имеют фиксированную геометрию, поэтому изменение потока полностью связано с изменением тока [латекс]\boldsymbol{\Delta I}[/латекс] через устройство. ЭДС индукции связана с физической геометрией устройства и скоростью изменения тока. Это дается

[латекс]\boldsymbol{\textbf{emf}= -L}[/латекс] [латекс]\boldsymbol{\frac{\Delta I}{\Delta t}}[/латекс],

, где [latex]\boldsymbol{L}[/latex] – собственная индуктивность устройства. Устройство, обладающее значительной собственной индуктивностью, называется катушкой индуктивности и обозначено символом на рисунке 3.

Рис. 3.

Знак минус является выражением закона Ленца, указывающим, что ЭДС противодействует изменению тока. Единицами самоиндукции являются генри (Гн), как и для взаимной индуктивности. Чем больше собственная индуктивность [латекс]\boldsymbol{L}[/латекс] устройства, тем больше его сопротивление любому изменению тока через него. Например, большая катушка с большим количеством витков и железным сердечником имеет большой [латекс]\жирныйсимвол{L}[/латекс] и не позволит току быстро измениться. Чтобы избежать этого эффекта, необходимо добиться небольшого [латекса]\жирного символа{L}[/латекса], например, путем встречной намотки катушек, как показано на рис. 2.9.0032

Катушка индуктивности 1 Гн представляет собой большую катушку индуктивности. Чтобы проиллюстрировать это, рассмотрим устройство с [латекс]\boldsymbol{L = 1,0 \;\textbf{H}}[/латекс], через которое протекает ток 10 А. Что произойдет, если мы попытаемся отключить ток быстро, возможно, всего за 1,0 мс? ЭДС, заданная формулой [латекс]\жирныйсимвол{\текстбф{ЭДС} = -L(\Delta I/\Delta t)}[/латекс], будет препятствовать изменению. Таким образом, ЭДС будет индуцироваться следующим образом: A})/(1,0 \;\textbf{ms})]=10 000 \;\textbf{V}}[/latex]. Положительный знак означает, что это большое напряжение направлено в том же направлении, что и ток, противодействуя его уменьшению.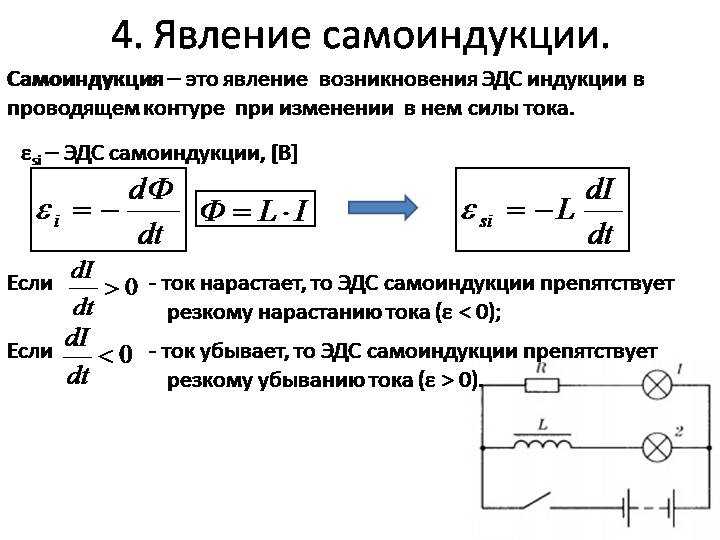 Такие большие ЭДС могут вызывать искрение, повреждая коммутационное оборудование, поэтому может потребоваться более медленное изменение тока.

Для такого большого наведенного напряжения есть применение. Вспышки камеры используют батарею, две катушки индуктивности, которые функционируют как трансформатор, и систему переключения или осциллятор для создания больших напряжений. (Помните, что нам нужно изменяющееся магнитное поле, вызванное изменяющимся током, чтобы индуцировать напряжение в другой катушке.) Система генератора будет делать это много раз, когда напряжение батареи увеличится до более чем одной тысячи вольт. (Вы можете услышать пронзительный вой трансформатора во время зарядки конденсатора.) Конденсатор сохраняет высокое напряжение для последующего использования при питании вспышки. (См. рис. 4.)

Рис. 4. Благодаря быстрому переключению катушки индуктивности батареи напряжением 1,5 В можно использовать для наведения ЭДС в несколько тысяч вольт. Это напряжение можно использовать для хранения заряда в конденсаторе для последующего использования, например, во вспышке фотоаппарата.

Можно рассчитать [латекс]\boldsymbol{L}[/латекс] для индуктора, зная его геометрию (размер и форму) и зная создаваемое им магнитное поле. В большинстве случаев это сложно из-за сложности создаваемого поля. Итак, в этом тексте индуктивность [латекс]\жирный символ{L}[/латекс] обычно является заданной величиной. Единственным исключением является соленоид, потому что он имеет очень однородное поле внутри, почти нулевое поле снаружи и простую форму. Поучительно вывести уравнение для его индуктивности. Начнем с того, что заметим, что ЭДС индукции задается законом индукции Фарадея как собственной индуктивности, как [латекс]\boldsymbol{\textbf{ЭДС}=-L(\Delta I/ \Delta t)}[/latex]. Приравнивая эти выходы

[латекс]\boldsymbol{\textbf{emf} = -N}[/латекс] [латекс]\boldsymbol{\frac{\Delta \phi}{\Delta t}}[/латекс] [латекс]\boldsymbol{ = -L}[/latex] [латекс]\boldsymbol{\frac{\Delta I}{\Delta t}}[/latex].

Решение для [латекс]\boldsymbol{L}[/латекс] дает

[латекс]\boldsymbol{L = N}[/латекс] [латекс]\boldsymbol{\frac{\Delta \phi}{\Delta I}}[/latex].

Это уравнение для собственной индуктивности [латекс]\boldsymbol{L}[/латекс] устройства всегда справедливо. Это означает, что самоиндукция [латекс]\boldsymbol{L}[/латекс] зависит от того, насколько эффективен ток в создании потока; чем эффективнее, тем больше [латекс]\boldsymbol{\Delta \phi \Delta I}[/latex].

Воспользуемся этим последним уравнением, чтобы найти выражение для индуктивности соленоида. Поскольку площадь [латекс]\жирныйсимвол{А}[/латекс] соленоида фиксирована, изменение потока составляет [латекс]\жирныйсимвол{\Дельта \фи = \Дельта (ВА) = А \Дельта В}[/ латекс]. Чтобы найти [латекс]\boldsymbol{\Delta B}[/латекс], заметим, что магнитное поле соленоида определяется выражением [латекс]\жирный символ{В = \mu _0 nI = \mu 0 \frac{NI} {\ell}}[/латекс]. (Здесь [латекс]\boldsymbol{n = N/ \ell}[/latex], где [латекс]\boldsymbol{N}[/латекс] — количество витков, а [латекс]\boldsymbol{\ell}[/ латекс] — длина соленоида. ) Изменяется только ток, так что [латекс]\жирныйсимвол{\Delta \phi = A \Delta B = \mu_0 NA \frac{\Delta I}{\ell}}[/latex] . Замена [латекс]\boldsymbol{\Delta \phi}[/latex] на [латекс]\boldsymbol{L = N \frac{\Delta \phi}{\Delta I}}[/latex] дает 92A}{\ell}}[/latex][latex]\boldsymbol{(\textbf{соленоид})}.[/latex]

Это собственная индуктивность соленоида с площадью поперечного сечения [латекс]\boldsymbol{A}[/латекс] и длиной [латекс]\boldsymbol{\ell}[/латекс]. Обратите внимание, что индуктивность зависит только от физических характеристик соленоида, соответствующих его определению.

Пример 1. Расчет собственной индуктивности соленоида среднего размера

Рассчитайте собственную индуктивность соленоида длиной 10,0 см и диаметром 4,00 см с 200 витками. 92) {0,100 \;\textbf{м}} \\[1em] & \boldsymbol{0,632 \;\textbf{мГн}} \end{массив}[/latex].

Обсуждение

Этот соленоид средних размеров. Его индуктивность около миллигенри также считается умеренной.

Одно из распространенных приложений индуктивности используется в светофорах, которые могут определять, когда транспортные средства ожидают на перекрестке. Электрическая цепь с индуктором размещена на дороге под местом остановки ожидающего автомобиля. Кузов автомобиля увеличивает индуктивность, и схема меняется, посылая сигнал светофору изменить цвет. Точно так же металлоискатели, используемые для обеспечения безопасности в аэропортах, используют ту же технику. Катушка или индуктор в корпусе металлоискателя действует как передатчик и приемник. Импульсный сигнал в катушке передатчика индуцирует сигнал в приемнике. На самоиндукцию цепи влияет любой металлический предмет на пути. Такие детекторы могут быть настроены на чувствительность, а также могут указывать примерное местонахождение обнаруженного на человеке металла. (Но они не смогут обнаружить пластиковую взрывчатку, подобную той, что была обнаружена на «подрывнике в нижнем белье».) См. рис. 5.

Рисунок 5 Знакомые ворота безопасности в аэропорту могут не только обнаруживать металлы, но и указывать их приблизительную высоту над полом.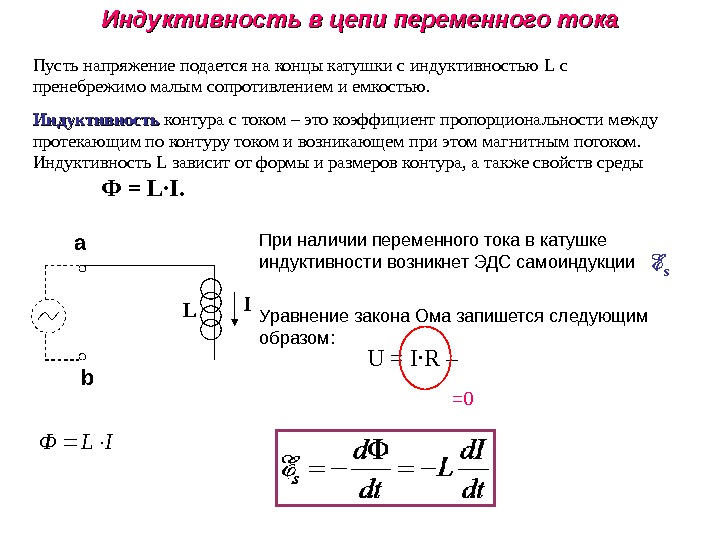 (кредит: Alexbuirds, Wikimedia Commons)

Из закона Ленца мы знаем, что индуктивности противодействуют изменениям тока. Есть альтернативный взгляд на эту оппозицию, основанный на энергии. Энергия хранится в магнитном поле. Требуется время, чтобы накопить энергию, и также нужно время, чтобы истощить энергию; следовательно, существует оппозиция быстрым изменениям. В индукторе магнитное поле прямо пропорционально току и индуктивности устройства. Можно показать, что 92 = 0,284 \;\textbf{J}}. \end{array}[/latex]

Обсуждение

Этого количества энергии определенно достаточно, чтобы вызвать искру, если ток внезапно отключится. Он не может быть построен мгновенно, если только потребляемая мощность не бесконечна.

• Индуктивность — это свойство устройства, которое показывает, насколько эффективно оно индуцирует ЭДС в другом устройстве.
• Взаимная индуктивность — это действие двух устройств, индуцирующих ЭДС друг в друге.
• Изменение тока [латекс]\boldsymbol{\Delta I_1 / \Delta t}[/латекс] в одном индуцирует ЭДС [латекс]\boldsymbol{\textbf{ЭДС}_2}[/латекс] во втором:

  [латекс]\boldsymbol{\textbf{emf}_2 = — M}[/latex][латекс]\boldsymbol{\frac{\Delta I_1}{\Delta t}}[/latex],

  , где [латекс]\жирныйсимвол{М}[/латекс] определяется как взаимная индуктивность между двумя устройствами, а знак минус соответствует закону Ленца.

• Симметрично, изменение тока [латекс]\boldsymbol{\Delta I_2/ \Delta t}[/латекс] через второе устройство индуцирует ЭДС [латекс]\boldsymbol{\textbf{ЭДС}_1}[/латекс] в первый:

  [латекс]\boldsymbol{\textbf{emf}_1 = — M}[/latex][латекс]\boldsymbol{\frac{\Delta I_2}{\Delta t}}[/latex] ,

  , где [латекс]\boldsymbol{M}[/латекс] — та же взаимная индуктивность, что и в обратном процессе.

• Текущие изменения в устройстве индуцируют ЭДС в самом устройстве.
• Самоиндукция — это эффект устройства, индуцирующего ЭДС само по себе.
• Прибор называется индуктором, а ЭДС, индуцируемая в нем изменением тока через него, равна

  [латекс]\boldsymbol{ЭДС = -L}[/латекс][латекс]\boldsymbol{\frac{\Delta I}{\Delta t}}[/latex],

  , где [latex]\boldsymbol{L}[/latex] — собственная индуктивность катушки индуктивности, а [latex]\boldsymbol{\Delta I / \Delta t}[/latex] — скорость изменения тока через это. Знак минус указывает на то, что ЭДС противодействует изменению тока, как того требует закон Ленца.

• Единицей собственной и взаимной индуктивности является генри (H), где [latex]\boldsymbol{1 \;\textbf{H} = 1 \Omega \cdot \;\textbf{s}}[/latex].
• Собственная индуктивность [латекс]\boldsymbol{L}[/латекс] катушки индуктивности пропорциональна тому, насколько поток изменяется с током. Для [латексного]\boldsymbol{N}[/латексного]-виткового индуктора

  [латекс]\boldsymbol{L = N}[/латекс][латекс]\boldsymbol{\frac{\Delta \phi}{\Delta T}}[/latex]

• Самоиндукция соленоида 92}[/латекс].

Задачи и упражнения

1: Две катушки расположены близко друг к другу в физической лаборатории, чтобы продемонстрировать закон индукции Фарадея. Ток 5,00 А в одном отключается за 1,00 мс, индуцируя ЭДС 9,00 В в другом. Чему равна их взаимная индуктивность?

2: Если две катушки, расположенные рядом, имеют взаимную индуктивность 5,00 мГн, какое напряжение индуцируется в одной, когда ток 2,00 А в другой отключается через 30,0 мс?

3: Ток 4,00 А через дроссель 7,50 мГн отключается за 8,33 мс. Какая ЭДС индуцирует противодействие этому?

4: Устройство включено, и через него через 0,100 мс проходит ток 3,00 А. Чему равна собственная индуктивность прибора, если ей противодействует ЭДС наведенного напряжения 150 В?

5: Начиная с [латекс]\boldsymbol{\textbf{эдс}_2 = -M \frac{\Delta I_1}{\Delta t}}[/latex], покажите, что единицами измерения индуктивности являются [латекс ]\boldsymbol{(\textbf{V} \cdot \;\textbf{s})/ \textbf{A} = \Omega \cdot \;\textbf{s}}[/latex].

6: Фотовспышки заряжают конденсатор до высокого напряжения, быстро включая и выключая ток через катушку индуктивности. За какое время необходимо включить или выключить ток 0,100 А через катушку индуктивности 2,00 мГн, чтобы индуцировать ЭДС 500 В?

7: Большой исследовательский соленоид имеет собственную индуктивность 25,0 Гн. а) Какая ЭДС наведения препятствует его отключению, если ток 100 А через него отключается за 80,0 мс? б) Сколько энергии запасается в катушке индуктивности при полном токе? в) С какой скоростью в ваттах должна рассеиваться энергия, чтобы ток выключился за 80,0 мс? (d) Принимая во внимание ответ на последнюю часть, удивительно ли, что так быстро закрыть его сложно?

8: (a) Рассчитайте самоиндукцию соленоида длиной 50 см и диаметром 10 см, имеющего 1000 витков. б) Сколько энергии запасается в этом индукторе при протекании через него тока силой 20,0 А? в) Как быстро его можно выключить, если ЭДС индукции не может превышать 3,00 В?

9: Прецизионный лабораторный резистор изготовлен из витка проволоки диаметром 1,50 см и длиной 4,00 см и имеет 500 витков. а) Чему равна его собственная индуктивность? б) Какая средняя ЭДС индуцируется, если ток 12,0 А через него включается за 5,00 мс (одна четвертая периода для переменного тока частотой 50 Гц)? в) Какова его индуктивность, если его укоротить наполовину и намотать встречно (два слоя по 250 витков в противоположных направлениях)?

10: Нагревательные спирали в фене имеют диаметр 0,800 см, общую длину 1,00 м и 400 витков. а) Какова их полная собственная индуктивность, если предположить, что они действуют как одиночный соленоид? б) Сколько энергии запасается в них при токе 6,00 А? (c) Какая средняя ЭДС препятствует их отключению, если это делается за 5,00 мс (одна четвертая часть цикла для переменного тока с частотой 50 Гц)?

11: Когда ток 20,0 А через индуктор отключается за 1,50 мс, индуцируется ЭДС 800 В, противодействующая изменению.