Определение параметров 3Х фазного трансформатора. Сопротивление обмоток и намагничивающей сети. Угол магнитных потерь

Группа 364 ЭАПУ

Электрические машины. Задание № 1. Вариант № 15.

Определить параметры 3^Х фазного трансформатора.

1. Сопротивление обмоток r₁ х₁ r₂ х₂.

2. Сопротивление намагничивающей ветви Z_m r_m x_m.

3. Угол магнитных потерь.

4. Коэффициент трансформации.

5. Построить векторную характеристику трансформатора U₂ = f(b), b – коэффициент нагрузки трансформатора (коэффициент мощности cosj  = 0,75)

6. Построить зависимость коэффициента полезного действия от нагрузки.

7. Построить векторную диаграмму тр-ра при b = 0,8, коэффициенте мощности cosj  = 0,75.

8. Составить Т- образную схему замещения тр-ра.

Данные для расчета.

Группа соединений                                        

Y/Y_H – 12

Номинальная мощность                               S_H = 40 кВА    

Номинальное напряжение                           U_1H = 6000 В U_2H = 230 В

Напряжение К.З.                                            U_K = 4,5 %

Мощность К.З.                                                Р_K = 880 Вт

Мощность Х.Х.                                               Р_О = 180 Вт

Ток Х.Х.                                                           I_O = 3,0 %

Расчет трансформатора.

1. Схема соединения рисунок 1.

 Определим фазное напряжение первичной обмотки при соединении Y.

2. Из уравнения полной мощности определим  номинальный ток. При соединении обмоток трансформатора Y, I_1Ф = I_1Л.

    I_1Ф = 3,8 А

1. Определим коэффициент трансформации:

  k = 26

2. Используя опыт короткого замыкания,  определим сопротивление обмоток r₁ х₁r₂ х₂.

Условие кз: z_{m >> zk сопротивлением zm пренебрегаем. Сопротивление нагрузки zH = 0.}

  U_1K = 155.9 B

Полное сопротивление цепи:

  z_K = 41 Ом

Активное сопротивление цепи:

  r_K = 20.3 Ом

Реактивное сопротивление цепи:

  x_K = 35.6 Ом

По схеме замещения:

  где k – коэффициент трансформации

  r₂ = 0.015 Ом   r₁ = 10.

15 Ом

 x₂ = 0.026 Ом   x₁ = 17.8 О

3. Используя опыт холостого хода, определим  сопротивление намагничивающей ветви z_mr_mx_m.

Условие хх: z_{m >> zk сопротивлением z К пренебрегаем. Сопротивление нагрузки zH = ¥ (нагрузка отсутствует).}

  m = 3 (трехфазный трансформатор)

Активное сопротивление:

r_m = 4.6 кОм

Полное сопротивление:

   z_m = 30.4 кОм

Реактивное сопротивление:

  x_m = 30.05 кОм

4. Т-образная схема замещения трансформатора.

5. Угол магнитных потерь g:

     g =8,6°  j₀ = 81,4°

6. КПД трансформатора.

å Р –– сумма потерь   å Р = Р_Э + P_С

Р_Э –– потери в обмотках, Р_С » Р₀ –– потери в стали = мощности хх.

    h = 0,97 = 97 %

Диаграмма зависимости КПД от нагрузки:

7. Построим векторную характеристику трансформатора

U₂ = f(b), b – коэффициент нагрузки трансформатора (коэффициент мощности cosj  = 0,75)

Рассчитаем изменение напряжения в процентах:

 

U_KA – активная составляющая

   U_{KA= 2,2 %}

U_Ks  –– реактивная составляющая:

     U_Ks  = 3,9 %

 

8. Построим векторную диаграмму тр-ра при b = 0,8, коэффициенте мощности cosj  = 0,75.

1). Зададим произвольно направление вектора I₂’ и — I₂’

2). Отложим вектор U₂’ на угол от I₂’ cosj  = 0,75 (задан)

3). Строим вектор ЭДС  Е

2 = — Е₁ на угол b = 0,8 от U₂’ и вектор Ф⁰ 90° от Е. I₁’r₁

Длины векторов в комплексном виде, вычислять длины только тех которые не получены путем построения. Направление вектора   I₂’ задается произвольно.

ОПЫТНОЕ ОПРЕДЕЛЕНИЕ ПЕРВИЧНЫХ И ВТОРИЧНЫХ ИНДУКТИВНОСТЕЙ РАССЕЯНИЯ СИЛОВОГО ТРАНСФОРМАТОРА С УЧЕТОМ НЕОДНОЗНАЧНОСТИ ЭТИХ ИНДУКТИВНОСТЕЙ

1

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Билоус О.А. 1

---

1 ФГБОУ ВПО «Пермский национальный исследовательский политехнический университет»

На основании теоретически доказанной неоднозначности влияния вторичной и первичной индуктивностей рассеяния питающего трансформатора тиристорного преобразователя на процесс коммутации токов в фазах вторичных обмоток предложен экспериментальный метод определения величины первичного и вторичного индуктивного сопротивлений рассеяния питающего трансформатора. Для выполнения опыта используется экспериментальный тиристорный электропривод постоянного тока.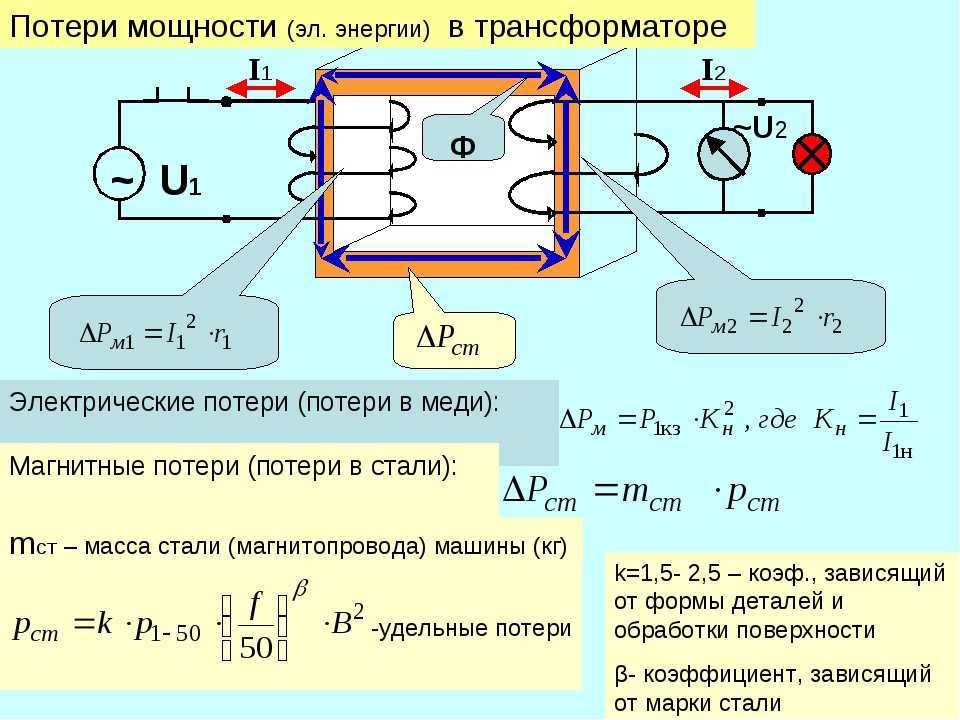 В качестве нагрузки тиристорного преобразователя используется электродвигатель постоянного тока. В результате двух этапов опыта определяются величины действующего значения линейного напряжения, тока нагрузки, углов управления и коммутации, а также мгновенные значения выпрямленного напряжения в зоне коммутации. Это позволяет вычислить совместное индуктивное сопротивление рассеяния трансформатора и сети, индуктивное сопротивление короткого замыкания трансформатора и сети, а затем величины первичного и вторичного индуктивного сопротивлений рассеяния питающего трансформатора. От этих значений зависит степень воздействия на питающую сеть тиристорного электропривода и выбор правильного соотношения мощностей электропривода и сети.

электропривод

тиристорный преобразователь

коммутация токов

первичная и вторичная индуктивности рассеяния

1. Билоус О.А., Иванов А. П. Индуктивное сопротивление сети переменного тока // Информационные управляющие системы: сб. научн. тр. – Пермь, 2004. – С. 36–42.

2. Билоус О.А., Сагизов Э.Б. Математическое моделирование влияния работы непосредственного преобразователя частоты на сеть электроснабжения // Вестник Пермского национального исследовательского политехнического университета. Электротехника, информационные технологии, системы управления. – 2013. – № 8. – С. 106–113.

3. Иванов А.П., Билоус О.А. Анализ процессов коммутации в тиристорных преобразователях с учетом неоднозначности первичных и вторичных индуктивностей рассеяния питающих трансформаторов // Информационные управляющие системы: сб. научн. тр. – Пермь, 2002. – С. 11–21.

4. Кузнецов М.И., Ромодин А.В., Костыгов А.М. Экспериментальное исследование управления потоком реактивной мощности в системе с трехобмоточным трансформатором // Электротехника. – 2011. – № 11. – С. 46–50.

5. Ромодин А.В., Кузнецов М.И. Экспериментальное исследование управления потоком реактивной мощности в системе с двумя источниками питания // Электротехника.

 – 2010. – № 6. – С. 44–49.

Работающий тиристорный электропривод оказывает на питающую сеть неблагоприятное воздействие. Одним из видов такого воздействия являются высокочастотные искажения напряжения питания. В синусоидальном напряжении сети появляются так называемые коммутационные провалы, оказывающие на другие потребители электрической энергии вредное влияние. Основным фактором, определяющим глубину этих провалов, является величина индуктивности сети, которая, в свою очередь, зависит от соотношения первичных и вторичных индуктивностей рассеяния питающего трансформатора [2, 3]. Соотношение первичных и вторичных индуктивностей рассеяния питающих трансформаторов также важно знать при расчетах электропривода переменного тока. Проблему можно решить, используя теорию неоднозначности составляющих индуктивностей рассеяния трансформаторов.

Экспериментальное определение характеристик коммутации вентилей

При исследовании можно пренебречь активными сопротивлениями обмоток трансформаторов и падением напряжения в вентилях при протекании по ним рабочего тока. Для выполнения опыта используется экспериментальный тиристорный электропривод постоянного тока (рис. 1), питаемый от трансформатора, в котором определяется соотношение первичных и вторичных индуктивностей рассеяния. В качестве нагрузки тиристорного преобразователя используется электродвигатель постоянного тока (ДПТ). Его мощность может быть в несколько раз меньше мощности электропривода, который будет установлен в действительности для реализации нужной технологии. Должна быть предусмотрена возможность плавно регулировать вращающий момент ДПТ. Для этого вал двигателя механически соединяется с валом генератора (ГПТ), тормозной момент которого плавно регулируется.

 

Рис. 1. Трехфазная электрическая схема ТП для снятия характеристик коммутации вентилей

Первый этап эксперимента – определение совместного индуктивного сопротивления рассеяния трансформатора и сети (χγ), влияющего на процесс коммутации фазных токов.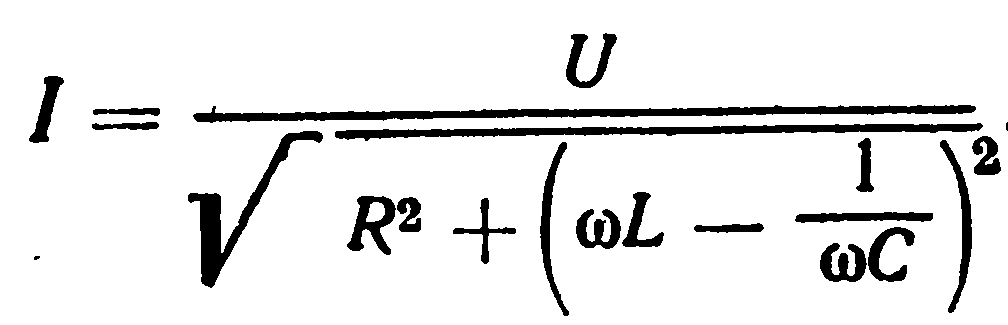 Производится разгон электропривода до максимально возможной скорости. При этом угол управления ТП должен быть близок к нулевому значению (α ≈ 0). Затем осуществляется увеличение момента сопротивления на валу двигателя путем воздействия на тормозной момент генератора. Ток нагрузки устанавливается приблизительно на уровне Id ном двигателя. Снимаются замеры: действующее значение линейного напряжения питания тиристорного преобразователя U2, тока нагрузки двигателя Id, и по осциллографу, включенному на напряжение нагрузки, измеряются величины угла управления α и угла коммутации γ. По этим данным, используя формулу

,

определяется индуктивное сопротивление коммутирующего контура χγ.

Если α = 0, величина χγ определяется по более простой формуле:

Индуктивное сопротивление χγ определяет процесс коммутации токов с учетом неоднозначности составляющих суммарного индуктивного сопротивления χ2 и χ1Σ. Для определения индуктивного сопротивления короткого замыкания трансформатора и сети нужно знать величину отношения:

Здесь χ2 – индуктивное сопротивление рассеяния вторичных обмоток трансформатора;  – коэффициент трансформации питающего трансформатора; χ1Σ – суммарное индуктивное сопротивление первичных обмоток трансформатора с индуктивным сопротивлением сети

χ1Σ = χ1ТР + χc.

Для вычисления Nkγ производится второй этап эксперимента. Воздействуя на СИФУ ТП, угол управления α устанавливается равным . При этом Ud = 0 и Id = 0. Эксперимент проводится при неподвижном заторможенном якоре электродвигателя. Затем, постепенно уменьшая угол α, увеличивают ток якоря до значения, при котором он становится непрерывным, а на экране осциллографа, включенного на напряжение нагрузки, отчетливо просматривается коммутация токов в виде кратковременного импульса. В трехфазной мостовой схеме мгновенные значения выпрямленного напряжения ub в зоне коммутации не равны полусумме ЭДС коммутируемых фаз [1]. Напряжение ub смещается в отрицательную или в положительную сторону от среднего значения. Эти смещения чередуются в четных и нечетных импульсах пульсаций напряжения. В рассматриваемой схеме на каждом такте переключений в коммутации участвуют две фазы. Одна из них коммутирует с отставанием от предыдущей коммутации этой фазы на угол Ψ1 = 60°, другая – на угол Ψ2 = 120°.

На рис. 2 приведена диаграмма напряжения на нагрузке, имеющая место в этой схеме при переключениях фаз (α ≈ 90°). Участвующие в коммутациях фазы обозначены a, b, c. Дальше от нулевой линии коммутирует фаза с отставанием на данном такте от предыдущей коммутации этой фазы на угол Ψ1 = 60°, ближе к нулевой линии – фаза с отставанием Ψ2 = 120°. Величина индуктивности коммутирующего контура в соответствии с [1] определяется выражением:

.

Рис. 2. Диаграмма напряжения на нагрузке в трехфазном мостовом ТП при α ≈ 90°

Из этого выражения видно, что Lγ зависит от значения угла Ψ. В процессе одной коммутации Lγ не остается постоянной величиной и, следовательно, в соответствии с [1] меняется темп изменения токов и . Строго говоря, в коммутации участвуют две фазы одновременно, но на первом этапе влияние фазы, имеющей сдвиг Ψ2 = 120°, незначительно по сравнению с быстродействующей фазой. Здесь ub максимально отстоит от нулевой линии. На втором этапе влияние этой фазы уже завершается и процесс коммутации определяется «медленнодействующей» фазой. Величина ub становится ближе к нулевому значению.

По диаграмме напряжения на нагрузке определяется значение ub. Для этого используются бóльшие отклонения от среднего значения напряжения, имеющие место при Ψ1 = 60°. Для удобства измерения мгновенного напряжения на экране осциллографа, изменив развертку изображения во времени, совмещают четные и нечетные импульсы пульсаций [1] (рис. 3).

Рис. 3. Диаграмма напряжения при совмещении четных и нечетных импульсов пульсаций

Измерив величину 2ub, определяется в вольтах значение ub. По значениям u2 и ub определяется Nkγ. В работе [1] получены уравнения, в которых содержится параметр Nkγ. Для его определения решается одно из этих уравнений относительно Nkγ. Получаем:

(*)

При и формула (*) упрощается:

Для трехфазной мостовой схемы тиристорного преобразователя , , и выражения становятся еще проще:

Вторичное индуктивное сопротивление питающего трансформатора определяется по формуле:

Следующий этап – теоретическое исследование изолированной системы электропривода. Исходя из каталожных данных питающего трансформатора, определяется индуктивное сопротивление короткого замыкания трансформатора χkТР. Затем определяется индуктивное сопротивление коммутирующего контура для трансформатора, питающегося от сети бесконечно большой мощности:

Здесь величина NγТР определена из формулы:

Откуда:

Заключение

Таким образом, определены значения первичного и вторичного индуктивных сопротивлений рассеяния питающего трансформатора, от которых зависит выбор правильного соотношения мощностей электропривода.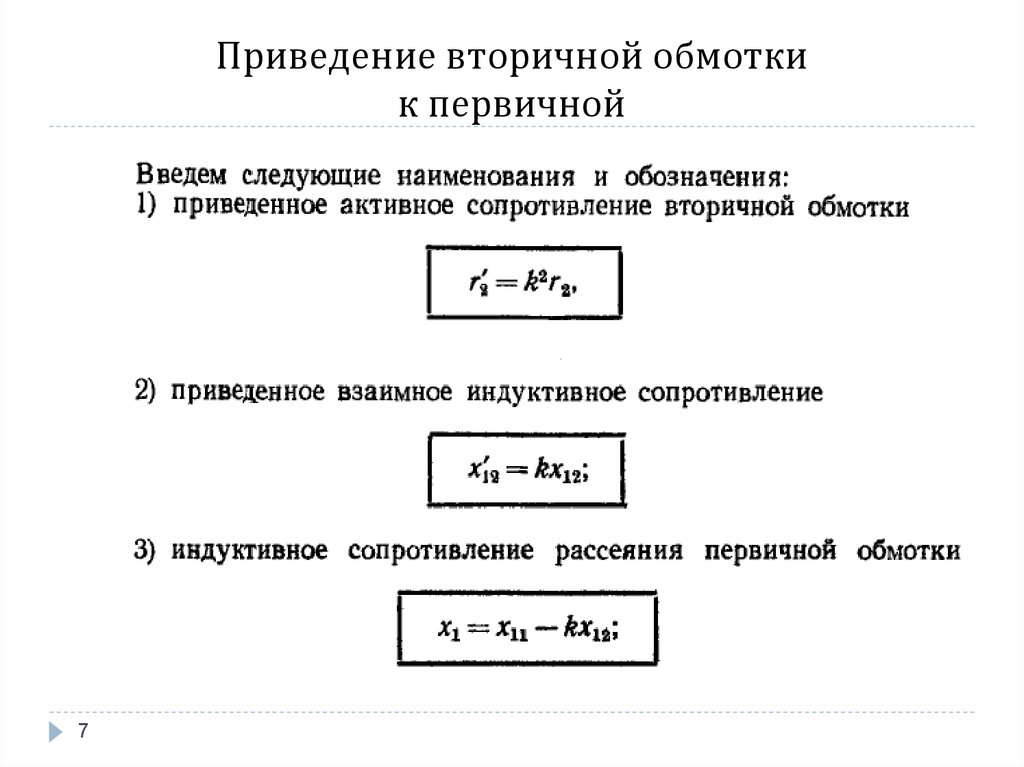

Рецензенты:

Казанцев В.П., д.т.н., доцент, профессор кафедры микропроцессорных средств автоматизации, ФГБОУ ВПО «Пермский национальный исследовательский политехнический университет», г. Пермь;

Бочкарев С.В., д.т.н., доцент, профессор кафедры микропроцессорных средств автоматизации, ФГБОУ ВПО «Пермский национальный исследовательский политехнический университет», г. Пермь.

Работа поступила в редакцию 18.04.2014.

---

Библиографическая ссылка

Билоус О.А. ОПЫТНОЕ ОПРЕДЕЛЕНИЕ ПЕРВИЧНЫХ И ВТОРИЧНЫХ ИНДУКТИВНОСТЕЙ РАССЕЯНИЯ СИЛОВОГО ТРАНСФОРМАТОРА С УЧЕТОМ НЕОДНОЗНАЧНОСТИ ЭТИХ ИНДУКТИВНОСТЕЙ // Фундаментальные исследования. – 2014. – № 6-4. – С. 694-697;
URL: https://fundamental-research.ru/ru/article/view?id=34222 (дата обращения: 01.02.2023).

---

Конструкция трансформатора и катушки индуктивности — Switchcraft

Трансформаторы и катушки индуктивности являются важными компонентами силовых электронных преобразователей. Они используются для хранения энергии, фильтрации и преобразования напряжений и токов.

Целью этой статьи является рассмотрение основных аспектов проектирования, которые необходимо учитывать. Однако невозможно охватить все практические аспекты, поэтому эту статью следует рассматривать только как введение в тему.

Трансформаторы состоят из двух или более обмоток, магнитно связанных друг с другом. Чтобы улучшить эту связь, обмотки обычно размещают на сердечнике из материала с низким магнитным сопротивлением. т.е. материал с низким магнитным сопротивлением.

 

Коэффициент трансформации

Большинству инженеров-электриков хорошо известно, что коэффициент трансформации напряжения (и тока) равен коэффициенту трансформации. Это можно понять, осознав, что все витки обмоток вокруг железного сердечника подвергаются воздействию одного и того же магнитного потока.

Напряжение, индуцируемое в катушке, определяется законом индукции Фарадея как: {уравнение}

Следовательно, можно сделать вывод, что, пока каждая катушка подвергается одинаковому изменению магнитного потока, общее индуцированное напряжение определяется по формуле:

\begin{equation}
V = — N \cdot \frac{\mathrm{ d}\Phi}{\mathrm{d}t}
\end{equation}

Где \(N\) — количество витков в катушке. Когда на обмотку подается внешнее напряжение, это напряжение будет делиться поровну между витками катушки. Точно так же на каждый виток второй обмотки вокруг того же магнитного сердечника будет воздействовать заданное количество вольт на виток обмотки.

Однако проблема и важный параметр при проектировании трансформатора заключается в том, сколько витков нужно использовать для каждого вольта.

Когда вторичная обмотка трансформатора нагружена, повышенный ток вызывает падение напряжения на сопротивлении обмотки. Это приводит к тому, что плотность потока в сердечнике немного снижается, поскольку доступно меньшее напряжение намагничивания. Однако в идеале плотность потока в сердечнике должна оставаться постоянной независимо от нагрузки.

Преобразование импеданса

Иногда полезно рассматривать трансформатор как устройство преобразования импеданса.

Если коэффициент трансформации трансформатора определяется как:

\[ n = \frac{N_2}{N_1} \]

Вторичное напряжение и ток, выраженные в первичном, тогда определяются как:

\[ V_2 = V_1 \cdot n \]

\[ I_2 = \frac{I_1}{n} \]

Коэффициент преобразования импеданса может быть получен следующим образом:

\[ Z_2 = \frac{V_2}{ I_2} = \frac{V_1 \cdot n}{\frac{I_1}{n}} = n^2 \cdot \frac{V_1}{I_1} = n^2 \cdot Z_1 \]

Следовательно, коэффициент преобразования импеданса равен квадрату коэффициента трансформации.

Transformer specifications

Which parameters are important depend on the application, but include:

• Primary voltage and current
• Secondary voltage and current
• Power rating
• Primary inductance
• Leakage inductance

For power transformers the испытания на холостом ходу и короткое замыкание обычно используются для получения электрических параметров трансформатора.

Эквивалентная схема

Эквивалентная схема полезна при анализе характеристик трансформатора. Точную модель получить сложно, но этой упрощенной модели достаточно для большинства трансформаторов. Заметным исключением, однако, являются трансформаторы высокого напряжения, используемые в энергосистеме, но это выходит за рамки данной статьи.

\(R_1\) и \(X_1\) представляют сопротивление и реактивность первичной обмотки, а \(R_2\) и \(X_2\) представляют собой вторичную обмотку.

\(X_m\) и \(R_m\) представляют реактивное сопротивление намагничивания и потери в сердечнике соответственно.

В действительности реактивные сопротивления являются частотно-зависимыми величинами, описываемыми соответствующими индуктивностями. Кроме того, индуктивность намагничивания подвержена нелинейности из-за нелинейных характеристик намагничивания сердечника трансформатора.

Конденсатор \(C_p\) представляет емкость между витками первичной обмотки, как и \(C_s\) вторичной обмотки. \(C_{ps}\) представляет собой емкостную связь между первичной и вторичной обмотками. Емкостью часто пренебрегают, особенно в силовых трансформаторах.

Точно такая же схема может использоваться (и часто используется) для анализа трехфазных трансформаторов. Единственное отличие состоит в том, что необходимо учитывать соотношение между фазовыми и линейными величинами.

Испытание без нагрузки

Испытание без нагрузки выполняется путем приложения номинального напряжения (при номинальной частоте) к первичной обмотке, когда вторичная цепь разомкнута. Напряжение и ток (и их смещение) измеряются.

Мощность, потребляемая без нагрузки, называется потерями холостого хода и состоит в основном из потерь на гистерезис и вихревых токов.

\begin{equation}
P_0 = P_E + P_H
\end{equation}

Вычисляется с учетом только активной части тока, т.е.:

\begin{equation}
P_0 = V_N \cdot I_0 \cdot \cos(\phi_0)
\end{equation}

Где \(\cos(\phi_0)\) — коэффициент мощности смещения.

Эквивалентное полное сопротивление без нагрузки определяется как:

\begin{equation}
Z_m = R_m + jX_m
\end{equation}

сопротивление нагрузки} и \ref{eq:no-load-impedance} соответственно. 92}{P_0}
\label{eq:сопротивление без нагрузки}
\end{equation}

\begin{equation}
Z_m = \frac{V_N}{I_0}
\label{eq:no-load -impedance}
\end{equation}

Испытание можно легко провести и на вторичной стороне трансформатора, с той лишь разницей, что вычисленные импедансы будут относиться к этой стороне.

Путем измерения вторичного напряжения во время испытания без нагрузки также можно определить коэффициент трансформации.

Испытание на короткое замыкание

Испытание на короткое замыкание выполняется путем короткого замыкания вторичной обмотки и подачи синусоидального напряжения, необходимого для получения номинального тока в первичной обмотке. Как и при испытании без нагрузки, измеряются ток, напряжение и коэффициент мощности смещения.

\begin{equation}
P_{sc} = V_{sc} \cdot I_{N} \cdot \cos(\phi_{sc})
\label{eq:sc-power}
\end{equation}

Эквивалентное сопротивление, относящееся к стороне высокого напряжения, определяется по формуле:

\begin{equation} 92}{P_{sc}}
\label{eq:sc-resistance}
\end{equation}

Эквивалентный импеданс равен:

\begin{equation}
Z_{e} = \frac{ V_{sc}}{I_{N}}
\label{eq:sc-impedance}
\end{equation}

Определить постоянную вольт/виток

Если вы собираетесь воспроизвести уже существующий трансформатор, этот тест может быть полезным.

Добавьте небольшую обмотку на сердечник поверх существующих обмоток. Количество витков не имеет решающего значения, если вы за ними следите. Подайте номинальное напряжение на первичную (или вторичную) обмотку и измерьте напряжение, индуцируемое в тестовой обмотке. Разделите это напряжение на количество витков в тестовой обмотке, чтобы получить константу вольт/виток.

Зная номинальные напряжения трансформатора, можно рассчитать количество витков в каждой обмотке.

\begin{equation}
N = \frac{V_N}{K_{emf}}
\end{equation}

Определить частотную характеристику

Нижний предел частоты трансформатора определяется первичной индуктивностью. По мере уменьшения частоты уменьшается и реактивное сопротивление, и, таким образом, трансформатор нагружает цепь возбуждения. Верхняя частотная характеристика определяется индуктивностью рассеяния. Эта индуктивность включена последовательно с трансформатором, и по мере увеличения частоты она будет действовать как более высокий импеданс.

Частотная характеристика обычно не важна для силовых трансформаторов, работающих на частоте сети. Однако это очень важно для трансформаторов, предназначенных для передачи сигналов в диапазоне частот.

Этот тест лучше всего выполнять с помощью сетевого анализатора и получения диаграммы Боде. Однако, если у вас нет доступа к такому оборудованию, можно также использовать генератор сигналов и вольтметр/осциллограф.

Приложите синусоидальное напряжение с постоянной амплитудой и переменной частотой к первичной обмотке и измерьте амплитуду вторичной обмотки. Затухание в дБ определяется как:

\begin{equation}
дБ = 20\cdot \log(\frac{V_{out}}{V_{in}})
\end{equation}

Напр. когда первичное напряжение равно \(1\;В\), соотношение между затуханием \(-3дБ\) и вторичным напряжением: (\frac{0.707}{1})
\end{equation*}

Однако для аудиоприложений вам, вероятно, следует использовать \(-1dB\) в качестве критерия проектирования.

Есть несколько (относительно) дешевых анализаторов цепей для низкочастотного тестирования. Я не буду рекомендовать какую-либо конкретную модель или производителя, но если вам нравятся (аудио)трансформаторы, возможно, стоит изучить их подробнее.

Трансформаторы импеданса

Трансформаторы иногда указываются как имеющие определенный коэффициент трансформации импеданса. Типичным примером является коэффициент трансформации \(600:600 \Omega\), часто встречающийся в аудиотрансформаторах. Новичков это может немного сбить с толку, поскольку идеальному трансформатору не свойственен собственный импеданс. Коэффициент преобразования напряжения и тока в этом примере равен \(1:1\). Трансформатор \(600:1200 \Омега\) будет иметь коэффициент трансформации \(1:2\).

Частотная характеристика аудиопреобразователя обычно определяется как предел \(-3дБ\), относящийся к \(1000\;Гц\). т.е. частоты, на которых уровень напряжения упал до \(70,7\%\) от уровня напряжения при \(1000\;Гц\).

Причина указания импеданса заключается в том, что трансформатор рассчитан на адекватную частотную характеристику при нагрузке \(600\; \Омега\). Индуктивное сопротивление обмотки должно быть выше (или равно) \(600\; \Омега\) на самой низкой интересующей частоте. Таким образом, требуемая индуктивность обмотки определяется как:

\begin{equation}
L = \frac{Z}{2 \pi f}
\end{equation}

Для звукового преобразователя, используемого в качестве примера, с более низким пределом частоты (-3 дБ) \( 50 Гц\), требуемая индуктивность будет иметь вид:

\begin{equation*}
L = \frac{600}{2 \pi 50} = 1,9H
\end{equation*}

Иногда -1 дБ используется ответ. Это дает нам следующую индуктивность:

\begin{equation*}
L = \frac{600}{\pi 50} = 3,8H
\end{equation*}

Далее, если указана номинальная мощность трансформатора, номинальное напряжение определяется номинальной нагрузкой как:

\begin{equation}
В = \sqrt{P \cdot Z}
\end{equation}

Опять же, для нашего примера (который имеет рейтинг \(0,25 \; W\)), это будет оцениваться как:

\begin{equation*}
V = \sqrt{0,25 \cdot 600} = 12,3 \;V
\end{equation*}

Конструкция трансформатора

В этой вводной части рассматриваются только однофазные трансформаторы. Однако основные принципы одинаковы для многофазных конструкций.

Первым шагом в процедуре проектирования трансформатора является определение и сборка исходных данных для проектирования. Обычно они включают:

• Номинальное первичное напряжение и ток
• Рабочая частота
• Коэффициент трансформации, т.е. коэффициент трансформации
• Температурные ограничения, т.е. максимальная температура тела и окружающей среды

Магнитная конструкция

Один из наиболее важных параметров ограничения на вольт на виток для применения линейной частоты, это максимальная плотность потока в сердечнике трансформатора. Типичные значения от \(1\) до \(1,7\) Тесла.

По мере увеличения рабочей частоты (выше нескольких сотен герц) ограничивающим фактором будут потери в сердечнике. Изменение магнитного потока является основной причиной потерь в сердечнике, поэтому магнитный поток должен быть ограничен в соответствии со спецификацией производителя для данного сердечника и частоты. Типичные значения находятся в диапазоне \(0,2 — 0,05T\), но вам действительно нужно проверить таблицу данных.

Магнитный поток, измеренный в Вебере, в проволочной петле определяется по формуле:

\begin{equation}
\Phi = B \cdot A = V \cdot t
\end{equation}

Где \(\Phi\) — магнитный поток, \(B\) — плотность магнитного потока, а \(A\) площадь, окруженная катушкой. \(V\) — напряжение, подаваемое на контур, а \(t\) — продолжительность (время).

При добавлении дополнительных витков к катушке приложенное напряжение можно разделить поровну между витками, следовательно:

\begin{equation}
\Phi = \frac{V \cdot t}{N}
\end{equation }

Где \(N\) — количество витков. Другой способ взглянуть на это состоит в том, что увеличение числа витков увеличивает индуктивность, следовательно, ток уменьшается (а поток зависит от тока).

\begin{equation}
\Phi = L \cdot I
\label{eq:inductor-flux}
\end{equation}

Напряжение, индуцированное в катушке провода, определяется дифференциальным уравнением:

\begin{equation}
V = -L \cdot \frac{\mathrm{d}i}{\mathrm{d}t}
\label{eq:inductor-voltage}
\end{equation}

Отсюда индуктивность катушки определяется по формуле:

\begin{equation}
L = \frac{V \cdot t}{I}
\label{eq:inductance-definition}
\end{equation}

Где \(I\) — сила тока в проводе. Уравнение \eqref{eq:inductance-definition} может быть получено как из уравнения \eqref{eq:inductor-flux}, так и из \eqref{eq:inductor-voltage}. Сделайте ваш выбор.

Индуктивность рассеяния

Индуктивность рассеяния вызвана частями магнитного потока, которые не связывают первичную и вторичную обмотки.

В большинстве трансформаторов индуктивность рассеяния должна быть сведена к минимуму. Неблагоприятная индуктивность рассеяния может вызывать перенапряжения в импульсном преобразователе мощности, что создает дополнительные требования к демпферным цепям.

Заметным исключением из этого правила являются трансформаторы для микроволновых печей, в которые добавлены магнитные шунты для увеличения индуктивности рассеяния. Причина этих шунтов в том, что трансформатор предназначен для управления емкостной нагрузкой. Вторичная обмотка трансформатора микроволновой печи обычно подключается к удвоителю напряжения, и емкостное сопротивление этого удвоителя должно идеально соответствовать индуктивному сопротивлению трансформатора.

Точный расчет индуктивности рассеяния затруднителен, но доступны приблизительные аналитические формулы для различных конфигураций сердечников и обмоток. Для сердечника прямоугольной формы (E) и без чередования обмоток индуктивность рассеяния может быть аппроксимирована выражением: 92 h_w} \left( \frac{b_{Cu}}{3} + b_i \right)
\end{equation}

Где \(p\) — количество сопряженных секций, \(b_{Cu}\ ) — ширина меди в окне обмоток, а \(b_{i}\) — толщина изоляции между обмотками. , на частоте 50Гц.

Обычно у нас есть заданное энергопотребление, накладывающее ограничения на выбор железного ядра, но предположим для этого примера, что у нас уже есть ядро. Хотя это предположение может показаться странным, любители нередко используют (или, по крайней мере, пытаются использовать) ядро, которое оказалось у них в мусорном ящике. 92\) и максимальной плотности потока \(1,3 Тл\).

 

Затем максимальный поток в сердечнике рассчитывается как: сердечник может быть намагничен в обоих направлениях, т. е. \(0,00352 Вб\).

Количество витков, необходимое для получения этого потока, определяется как:

\begin{equation*}
N = \frac{V \cdot t}{\Phi}
\end{equation*}

9{\pi} \]

\( \cos(0) = 1 \) и \( \cos(\pi) = -1 \), следовательно:

\[ V_{avg} = \frac{2 V_p }{\pi} \]

В нашем примере среднее напряжение вычисляется как:

\[ V_{avg} = \frac{2 \cdot 230 \cdot \sqrt{2}}{\pi} = 207 V \]

Необходимое количество витков вычисляется как:

\[ N = \frac{207 \cdot 0,01}{0,00352} = 588\]

Следовательно, выраженное в среднеквадратичных значениях, мы имеем 0,39 вольта на виток или 2,56 витка на вольт. Затем для вторичной обмотки необходимое количество витков просто рассчитывается путем умножения 2,56 на желаемое напряжение.

Напр. если требуемое вторичное напряжение равно \(18\;В\) (что может подойти для линейного регулируемого источника питания 12 В), необходимое количество витков будет:

\begin{equation*}
2,56 \cdot 18 = 46
\end{equation*}

Допустимая мощность

Вычислить мощность не так просто, как вычислить требуемое количество витков. Однако для небольших трансформаторов обычно безопасно делать некоторые предположения, основанные на опыте. Одно из этих предположений состоит в том, что эффективность 92}{R} = \frac{230 \cdot 0,05}{8,59} = 15,4 Вт \]

Тогда номинальная входная мощность трансформатора рассчитывается как:

\[ P = \frac{15,4}{0,1} = 154 Вт \]

Примечание о постоянном токе

Постоянный ток в трансформаторе обычно не очень хорош. Он будет , а не , вносить вклад в мощность, отдаваемую трансформатором, но он будет вносить вклад в магнитный поток в сердечнике. Это означает, что ядро ​​будет ближе к насыщению. Если трансформатор спроектирован таким образом, чтобы быть на грани насыщения без постоянного тока, он будет насыщаться.

Если вы предполагаете, что в трансформаторе будет постоянный ток, вы должны применить те же конструктивные ограничения, что и при проектировании катушки индуктивности, предназначенной для постоянного тока. Обычно это означает добавление воздушного зазора к сердечнику, чтобы уменьшить эффективную проницаемость.

Индуктивность – параметр любой электрической сети, характеризующий ее способность сопротивляться изменению тока.

\begin{equation}
\text{ЭДС} = -L\frac{\mathrm{d}i}{\mathrm{d}t} \Rightarrow L =  — \text{ЭДС} \frac{\mathrm{ д} т} {\ mathrm {д} я} 92
\end{equation}

Где \(I\) — ток намагничивания. т.е. при расчете запаса энергии в трансформаторе он будет меньше полного тока.

Коэффициент добротности

Коэффициент добротности катушки индуктивности описывает устройство по отношению к идеальному компоненту. Это имеет особое значение в радиочастотных приложениях.

Добротность индуктора определяется по формуле:

\begin{equation}
Q_L = \frac{X_L}{R_L} = \frac{2\pi f L}{R_L}
\end{equation} 92\) площадь поперечного сечения. Лучший способ увеличить мощность — уменьшить индуктивность и, следовательно, увеличить ток в сердечнике. Помните, что мощность зависит от тока в квадрате.

Вводя воздушный зазор в магнитопровод, эффективная магнитная проницаемость уменьшится, и, следовательно, уменьшится значение \(A_L\).

Энергия, запасенная в сердечнике, может извлекаться второй обмоткой на том же сердечнике, как и в топологии обратного хода. В качестве альтернативы его можно использовать, подключив катушку индуктивности к другой цепи после ее зарядки, как в топологиях buck/boost.

Тороидальные сердечники

Тороидальные сердечники можно разделить на две основные категории в зависимости от материала, из которого они изготовлены. Сердечники из феррита и железного порошка.

Феррит обладает самой высокой проницаемостью, но не подходит для высоких частот. Кроме того, как мы видели, высокая проницаемость не всегда является преимуществом.

Полезный веб-сайт со спецификациями для различных тороидальных сердечников находится по адресу: http://toroids.info/

Как упоминалось ранее, плотность потока должна быть ограничена, чтобы избежать насыщения сердечника. Для ферритовых тороидальных сердечников это накладывает ограничение:

\begin{equation}
\frac{V}{2 f N A} \le 0,3
\end{equation}

Где \(N\) — число витков обмотки, а \(A\) — площадь поперечного сечения сердечника.

Катушки индуктивности и индуктивное сопротивление | Электромагнитная индукция и цепи переменного тока

Сделать 5 мин. прочитать

Многие цепи также содержат конденсаторы и катушки индуктивности, помимо резисторов и источника переменного напряжения. Мы видели, как конденсаторы и катушки индуктивности реагируют на постоянное напряжение при его включении и выключении. Теперь мы рассмотрим, как катушки индуктивности и конденсаторы реагируют на синусоидальное переменное напряжение.

Предположим, что катушка индуктивности подключена непосредственно к источнику переменного напряжения, как показано на этом рисунке. Разумно предположить пренебрежимо малое сопротивление, так как на практике мы можем сделать сопротивление катушки индуктивности настолько малым, что оно окажет незначительное влияние на цепь. Также показан график зависимости напряжения и тока от времени.

(a) Источник переменного напряжения, включенный последовательно с катушкой индуктивности, имеющей незначительное сопротивление. (б) График тока и напряжения на катушке индуктивности в зависимости от времени.

График на этом рисунке (b) начинается с максимального напряжения. Обратите внимание, что ток начинается с нуля и достигает своего пика 90 483 после 90 484 управляющего им напряжения, как это было в случае, когда в предыдущем разделе было включено постоянное напряжение. Когда напряжение в точке а становится отрицательным, ток начинает уменьшаться; он становится равным нулю в точке b, где напряжение является самым отрицательным. Затем ток становится отрицательным, снова следуя за напряжением. Напряжение становится положительным в точке с и начинает делать ток менее отрицательным. В точке d ток проходит через нуль как раз в тот момент, когда напряжение достигает своего положительного пика, чтобы начать новый цикл. Это поведение резюмируется следующим образом:

Напряжение переменного тока в катушке индуктивности

Когда к катушке индуктивности приложено синусоидальное напряжение, оно опережает ток на одну четвертую периода или на \(\text{90º}\) фазовый угол.

Ток отстает от напряжения, так как катушки индуктивности препятствуют изменению тока. Изменение тока индуцирует противо-ЭДС \(V=-L(\Delta I/\Delta t)\). Это считается эффективным сопротивлением катушки индуктивности переменному току. Действующее значение тока \(I\) через катушку индуктивности \(L\) определяется версией закона Ома:

\(I=\cfrac{V}{{X}_{L}}\text{,}\)

где \(V\) — среднеквадратичное напряжение на катушке индуктивности и \({X}_{ L}\) определяется как

\({X}_{L}=2\pi \text{fL}\text{,}\)

с \(f\) частотой источника переменного напряжения в герцах (анализ схемы с использованием правила цикла Кирхгофа и исчисления фактически дает это выражение). \({X}_{L}\) называется индуктивным сопротивлением , потому что индуктор реагирует на сопротивление току. \({X}_{L}\) имеет единицы измерения в омах (\(1 H=1 \Omega \cdot \text{s}\), так что частота, умноженная на индуктивность, имеет единицы измерения \((\text{циклы/ s})(\Omega \cdot \text{s})=\Omega \)), в соответствии с его ролью эффективного сопротивления.