Переменный электрический ток

1 Прямоугольная рамка площади S=100 см2 вращается в горизонтальном однородном магнитном поле с частотой n= 50 об/с (рис. 145). Магнитная индукция поля В = 0,2 Тл. Найти закон изменения магнитного потока через рамку в зависимости от времени t, если в начальный момент времени плоскость рамки: а) расположена горизонтально; б) составляет с горизонтальной плоскостью угол φ = 30°.

Решение:

где Фо=2 мВб. Отсчет начальной фазы j производится от горизонтальной плоскости в сторону вращения рамки.

2 В условиях задачи 1 найти амплитуду э.д.с, индуцируемой в рамке. Как изменится амплитуда э. д. с, если частоту вращения рамки увеличить в три раза?

Решение:

Рамка, занимавшая в начальный момент времени горизонтальное положение, вращаясь с угловой скоростью ω=2πn, в момент времени t будет составлять с горизонтальной плоскостью угол ωt=2πnt (рис. 379). В течение последующего очень малого промежутка времени Δt она повернется еще на малый угол ωΔt. Пусть сторона рамки, параллельная оси 00, равна а и сторона рамки, перпендикулярная к оси, равна b. За время Δt проводник рамки cd переместится в положение c’d’ и «заметет» при этом площадь

где S=ab — площадь рамки. Магнитный поток через площадь, «заметаемую» проводником cd,

где α — угол между нормалью N к плоскости cc’d’d и направлением магнитной индукции В.
Если промежуток времени Δt очень мал, то угол α практически равен углу ωt, так как направление нормали n мало отличается от направления стороны рамки kd, а вектор В по условию направлен горизонтально. Таким образом,

Следовательно, в момент времени t в проводнике cd индуцируется э.д.с.

Вектор В параллелен плоскостям, в которых при вращении рамки движутся проводники kd и lс. Поэтому через «заметаемые» этими проводниками площади магнитный поток равен нулю и э.д.с. не возникает. В проводнике ad, как легко видеть, индуцируется э.д.с. ε₂. равная по модулю ε₁; но направленная так, что при обходе по контуру рамки эти э. д.с. складываются. В результате суммарная э.д.с, индуцируемая в рамке,

Наибольшее значение э.д.с. принимает в те моменты времени, когда cosωt максимален, т. е. равен единице. Поэтому амплитуда э.д.с.

При увеличении частоты вращения рамки в три раза амплитуда э.д.с. также увеличится в три раза, т.е.

3 Найти максимальный магнитный поток через прямоугольную рамку, вращающуюся в однородном магнитном поле с частотой n=10 об/с, если амплитуда индуцируемой в рамке э. д. с. ε₀ = 3 В (рис. 145).

Решение:

4 Найти частоту вращения прямоугольной рамки в однородном магнитном поле с индукцией B= 0,5 Тл, если амплитуда индуцируемой в рамке э. д. с. ε₀ = 10 В (рис. 145). Площадь рамки S=200 см2, число витков рамки w = 20.

Решение:

5 Напряжение на концах участка цепи, по которому течет переменный ток, изменяется с течением времени по закону

, где φ=π/6— начальная фаза напряжения. В момент времени t=T/12 мгновенное значение напряжения V=10В. Найти амплитуду напряжения Vo, круговую частоту ω и частоту f тока, если период колебаний T=0,01 с. Представить графически зависимость напряжения от времени t.

Решение:

Круговая частота тока

частота тока f=1/T=100 Гц. В момент времени t=T/12 мгновенное значение напряжения

отсюда

График зависимости напряжения от времени представлен на рис. 380.

6 Найти индуктивность катушки, если амплитуда напряжения на ее концах Vo = 160B, амплитуда тока в ней Iо = 10А и частота тока f=50 Гц.

Решение:
Индуктивное сопротивление катушки

где ω=2πf — круговая частота тока. Амплитуда тока

отсюда

7 Индуктивное сопротивление катушки XL = 500 Ом, эффективное напряжение сети, в которую включена катушка, Vэ = 100 В, частота тока f=1 кГц. Найти амплитуду тока в цепи и индуктивность катушки.

Решение:

8 Найти сдвиг фаз φ между напряжением

и током для цепи, состоящеи из последовательно включенных резистора с сопротивлением R = 1 кОм, катушки с индуктивностью L = 0,5 Гн и конденсаторах емкостью С= 1 мкФ.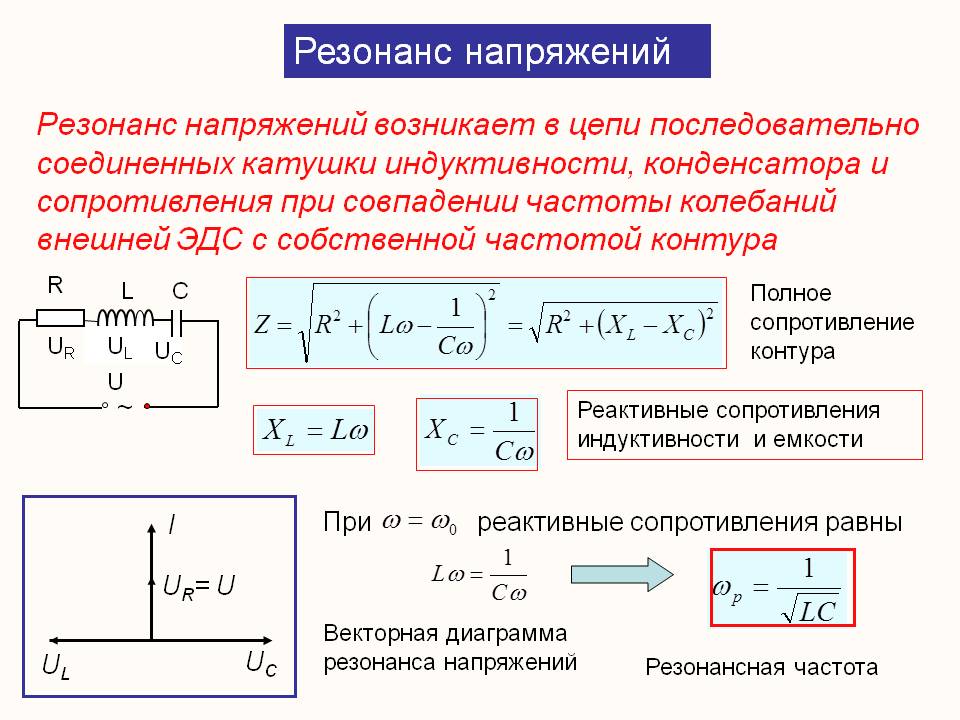 Найти мощность, выделяемую в цепи, если амплитуда напряжения Vo = 100 В, а частота тока f=50 Гц.

Решение:
Полное сопротивление

Мощность

9 В цепь последовательно включены резистор с сопротивлением R = 1 кОм, катушка с индуктивностью L = 0,5 Гн и конденсатор с емкостью С= 1 мкФ. Найти индуктивное сопротивление XL, емкостное сопротивление Хc и полное сопротивление Z цепи при частотах тока f1 = 50Гц и f2 = 10кГц.

Решение:
Индуктивное сопротивление

емкостное сопротивление

и полное сопротивление

где ω=2πf — круговая частота тока. При


при

10 К зажимам генератора присоединен конденсатор с емкостью С=0,1 мкФ. Найти амплитуду напряжения на зажимах, если амплитуда тока Io = 2,2 А, а период тока T = 0,2 мс.

Решение:

11 В сеть переменного тока с эффективным напряжением Vэ=127 В последовательно включены резистор с сопротивлением R=100 Ом и конденсатор с емкостью С = 40 мкФ.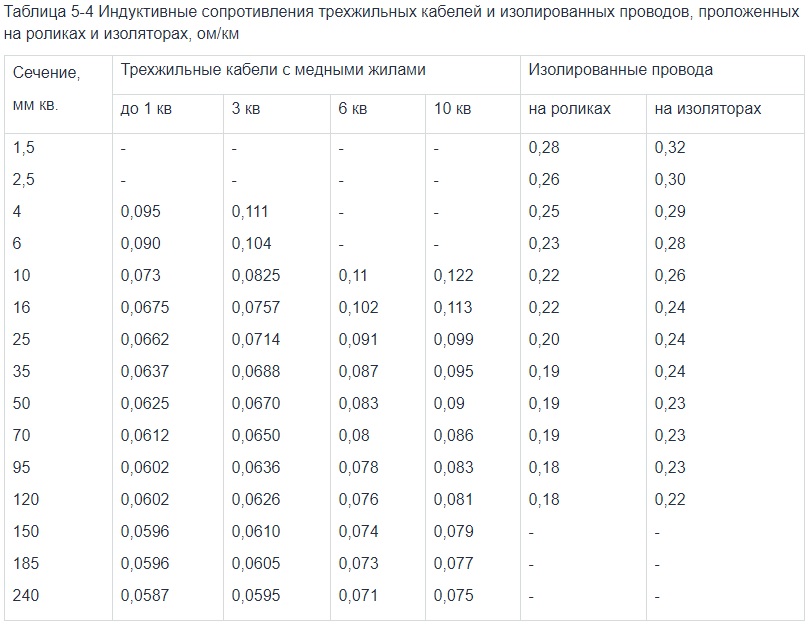 Найти амплитуду тока в цепи.

Решение:

12 В сеть переменного тока с эффективным напряжением Vэ=120 В последовательно включены проводник с сопротивлением R=15 Ом и катушка с индуктивностью L=50 мГн. Найти частоту тока f, если амплитуда тока в цепи Io = 7 А.

Решение:

13 Найти полное сопротивление цепи, состоящей из последовательно включенных конденсатора с емкостью С=0,1 мкФ и катушки с индуктивностью L= 0,5 Гн, при частоте тока f=1 кГц. При какой частоте fo полное сопротивление цепи равно нулю?

Решение:
Полное сопротивление цепи

Из условия, что при частоте f0 полное сопротивление цепи равно нулю, имеем

отсюда

14 В колебательный контур (рис. 146) включен источник переменного тока с э. д. с.

, где амплитуда э. д. с. ε₀ = 2 В. При резонансе амплитуда напряжения на отдельных элементах контура, например на конденсаторе, значительно увеличивается. Найти резонансную амплитуду напряжения на конденсаторе, если известно, что она во столько раз больше амплитуды э.д.с, во сколько раз индуктивное сопротивление XL (или емкостное сопротивление Хс) при резонансе больше сопротивления R. Резонансная частота контура fо = 0,1 МГц, индуктивность катушки L= 1мГн, сопротивление контура R=3 Ом.

Решение:

15 Соленоид с железным сердечником (дроссель), имеющий индуктивность L = 2 Гн и сопротивление обмотки R = 10 Ом, включен сначала в сеть постоянного тока с напряжением V=20 В, а затем в сеть переменного тока с эффективным напряжением Vэ=20 В и частотой тока f=0,4 кГц. Найти ток, текущий через соленоид, в первом случае и амплитуду тока во втором случае.

Решение:
В цепи постоянного тока I=V/R=2 А. Индуктивное сопротивление соленоида

Амплитуда напряжения Так как то амплитуда переменного тока

16 Найти коэффициент мощности cosj электрической цепи, если генератор отдает в цепь мощность N=8 кВт, амплитуда тока в цепи Io=100 А и амплитуда напряжения на зажимах генератора Vo = 200 В.

Решение:
Мощность

отсюда

17 От генератора переменного тока питается электропечь с сопротивлением R = 22 Ом. Найти количество теплоты Q, выделяемое печью за время τ = 1 ч, если амплитуда тока Io=10 А.

Решение:
Эффективный ток

Количество теплоты, выделяемое печью,

18 Кипятильник работает от сети переменного тока с эффективным напряжением Vэ=100В. При температуре tо = 20° С сопротивление фехралевой спирали R = 25 Ом. Какая масса кипящей воды превращается кипятильником в пар за время τ = 1 мин? Удельная теплота парообразования воды r = 2,3 МДж/кг. Температурный коэффициент сопротивления фехраля

.

Решение:

где t=100° С-температура кипения воды.

19 Неоновая лампа включена в сеть переменного тока с эффективным напряжением Vэ=71 В и периодом T= (1/50) с. Найти промежуток времени Δt, в течение которого длится вспышка лампы, и частоту вспышек лампы n.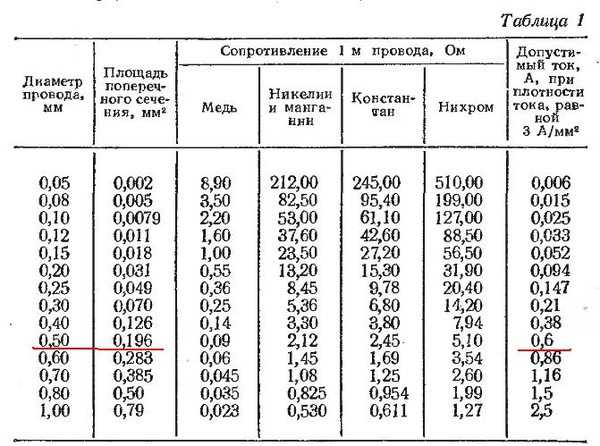 Напряжение зажигания лампы Vэ=86,7 В считать равным напряжению гашения Vг.

Решение:

В сети с эффективным напряжением Vэ амплитуда напряжения

Принимая начальную фазу напряжения равной нулю, запишем закон изменения напряжения с течением времени:

Зажигания (гашения) лампы происходят в моменты времени когда мгновенное напряжение в сети равно напряжению зажигания (рис. 381):

Наименьшее положительное значение, которое может иметь величина

стоящая под знаком синуса, составляет 60° = π/З. В общем случае

где т=0,1, 2, … Следовательно,

Знак плюс здесь соответствует моментам зажигания лампы (напряжение в эти моменты возрастает по модулю), а знак минус-моментам гашения лампы (напряжение убывает по модулю). В частности, первая вспышка . происходит при tо=T/6 и первое гашение — при

Таким образом, длительность вспышки

Вспышки и гашения, происходят в течение каждой половины периода; следовательно, частота вспышек n= 2/T=100.

20 Найти частоту вспышек неоновой лампы, включенной в сеть переменного тока по схеме, изображенной на рис. 147. Э.д.с. батареи элементов ε = 60 В, эффективное напряжение, снимаемое с автотрансформатора, Vэ= 28,3 В, напряжение зажигания лампы Vз = 86,7 В. Частота переменного тока f=200 Гц.

Решение:
Амплитуда переменного напряжения на выходе автотрансформатора

Это напряжение с течением времени изменяется по закону

Напряжение между электродами лампы

(график зависимости этого напряжения от времени приведен на рис. 382).
При

напряжение V2 принимает наибольшее значение

При

напряжение V2 принимает наименьшее значение

Таким образом, напряжение на электродах лампы становится больше напряжения зажигания лишь один раз в течение периода, поэтому частота вспышек неоновой лампы равна частоте тока f=200 Гц.

21 Ток в первичной обмотке трансформатора I1=0,5 А, напряжение на ее концах V1 = 220 В.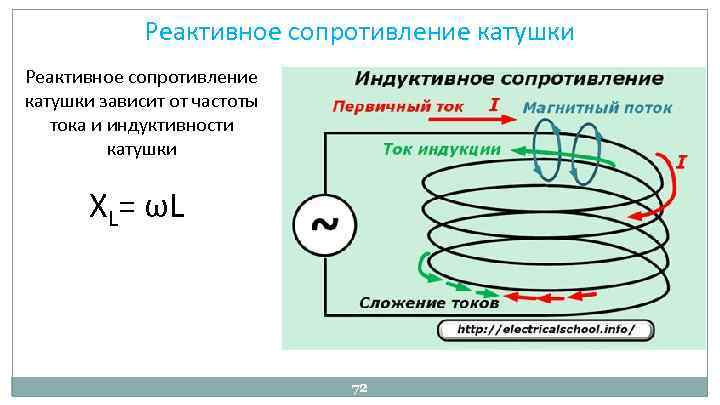 Ток во вторичной обмотке трансформатора I2 = 11 А, напряжение на ее концах V2 = 9,5 В. Найти к.п.д. трансформатора.

Решение:
Мощность, подводимая к первичной обмотке (затраченная мощность), N1=I1V1. Мощность, отдаваемая вторичной обмоткой нагрузке (полезная мощность), N2=I2V2. К. п. д. трансформатора

22 Первичная обмотка понижающего трансформатора с коэффициентом трансформации k=8 включена в сеть переменного тока с напряжением V1=220 В. Сопротивление вторичной обмотки r=2 Ом, ток в ней I=3 А. Найти напряжение V2 на зажимах вторичной обмотки.

Решение:
Индуцируемая во вторичной обмотке э.д.с .

Напряжение на ее зажимах

23 Первичная обмотка трансформатора для питания накала радиоприемника имеет w1= 12000 витков и включена в сеть переменного тока с напряжением V1= 120 В. Какое число витков w2 должна иметь вторичная обмотка, если ее сопротивление r=0,5 Ом? Напряжение накала радиоприемника V2 = 3,5 В при токе I=1А.

Решение:
Индуцируемая во вторичной обмотке э.д.с. должна быть равна напряжению накала V2 и падению напряжения на сопротивлении обмотки Ir. Поэтому отношение чисел витков в обмотках

отсюда

24 Первичная обмотка понижающего трансформатора включена в сеть переменного тока с напряжением V1=220 В. Напряжение на зажимах вторичной обмотки V2 = 20 В, ее сопротивление r=1 Ом, ток в ней I=2 А. Найти коэффициент трансформации k и к.п.д. η трансформатора.

Решение:
Индуцируемая во вторичной обмотке э.д.с.

Коэффициент трансформации трансформатора

Ток в первичной обмотке находим из условия

К.п.д. трансформатора (отношение мощности на зажимах вторичной обмотки к мощности, потребляемой первичной обмоткой)

25 Первичная обмотка понижающего трансформатора с коэффициентом трансформации k=10 включена в сеть переменного тока с напряжением V1=120 В. Сопротивление вторичной обмотки r=1,2 Ом, ток в ней I=5 А. Найти сопротивление R нагрузки трансформатора и напряжение V2 на зажимах вторичной обмотки.

Решение:

26 Найти амплитуду и фазу напряжения в сети, питаемой двумя последовательно включенными генераторами переменного тока, напряжения на зажимах которых

. Амплитуды напряжения генераторов V10 = 60 В и V20=100 В; частота тока f=50 Гц; начальная фаза напряжения второго генератора φ₀ = 30°.

Решение:
Амплитуда напряжения

Сопротивление, индуктивность и емкость в цепи переменного тока

Похожие презентации:

Электрические цепи переменного тока

Сопротивления в цепи переменного тока

Сопротивление в цепи переменного тока. (11 класс)

Электрические цепи переменного тока. Тема 2-5

Переменный ток

Электрические колебания. Переменный ток

Практическое занятие 8. Постоянный ток и его законы. Переменный ток. Импеданс цепи переменного тока. Импульсные токи

Электрические цепи постоянного тока • Электрические цепи синусоидального тока • Трёхфазные цепи

Электрические однофазные цепи синусоидального тока

Электрические цепи синусоидального тока. Лекция 2

Получение переменной ЭДС.
Сопротивление, индуктивность и
емкость в цепи переменного тока.
Закон Ома для цепей переменного
тока. Резонанс в последовательной
и параллельной цепи. Проблема
передачи электроэнергии на

расстояние, трансформатор
20.1. Получение переменной ЭДС.
20.2. Сопротивление, индуктивность и
емкость в цепи переменного тока. Закон Ома
для цепей переменного тока.
20.3. Резонанс в последовательной и
параллельной цепи.
20.4. Проблема передачи электроэнергии на
расстояние, трансформатор.
20.1. Получение переменной ЭДС
Рассмотрим контур АВСД, вращающийся с частотой , в постоянном
магнитном поле, причем АВ(СД) всегда перпендикулярна направлению
поля.
Рис.20.1.
При этом на электроны в контуре действует сила Лоренца,
направление которой указано на рисунке 20.2.
Рис. 20.2.
:
Под действием этой силы электроны в контуре
приходят в движение, т. е. возникает

электрический ток
от
от
ВкА
ДкС
T
и спустя t =
2
от С к Д
от А к В
Через половину периода направление тока в рамке изменяется на
противоположное. Угол поворота рамки определится как:
= t.
По закону Фарадея, ЭДС в контуре определяется соотношением:
инд
di
d
L
,
dt
dt
где =BScos – магнитный поток, пронизывающий рамку.
Получим:
d
d
( BS cos ) ( BS cos t ) BS sin t
dt
dt
m sin t , где m BS .
Вывод: ЭДС индукции в
рамке изменяется по
гармоническому закону.
Рис.20.3.
К оглавлению
20.2. Сопротивление, индуктивность и емкость
цепи
переменного тока. Закон Ома для цепей переменного тока
1.
2.
3.
4.
5.
6.
7.
8.
.
Опыт 20.1. Сдвиги фаз в цепи с емкостью и индуктивностью
Оборудование:
Осциллограф электронный.
Коммутатор к осциллографу.
Батарея конденсаторов на 60 мкФ.
Катушка дроссельная с сердечником.
Реостат на 500 Ом.
Лампа на 127 В, 60 Вт на подставке с
зажимами.
Проводники соединительные.
Ящик – подставка.
Рис.20.4.
Ход работы:
1.Собрать схему рис. 20.4.
2.Катушка
индуктивности,
установленная
на
стенде,
имеет
значительное активное сопротивление, которое следует учитывать в
дальнейших измерениях.
3.Конденсатор, установленный на стенде, не является идеальным, т.е.
в процессе работы он дает утечки тока через изоляцию
4.Для наблюдения явления резонанса можно следить за изменением в
зависимости от частоты5. Включите генератор и дайте ему прогреться
несколько минут.
6.Особо следует определить точное значение резонансной частоты.
Для этого надо, медленно вращая ручку регулировки частоты в
диапазоне и внимательно наблюдая за показаниями амперметра,
«поймать» частоту, при которой сила тока в цепи принимает
максимальное значение. Значение резонансной частоты заносится в
отчет.
7. Находясь на резонансной частоте, измерьте падение напряжения на
конденсаторе
8.С помощью осциллографа определить сдвиги фаз.
Вывод: между током и напряжением существует фазовый сдвиг
Активное сопротивление в цепи переменного тока
Схема:
Для данной цепи: U=U0sin t.
По закону Ома
Рис. 20.5.
U U0
i
sin t I 0 sin t ,
r
r
где
U0
I0
r
амплитудное значение тока.
Вывод: ток и напряжение совпадают по фазе.
График:
Векторная диаграмма:
Рис. 20.6.
Рис. 20.7.
В цепи происходит необратимый процесс преобразования энергии
электрического тока в тепловую энергию (нагрев).
Индуктивность в цепи переменного тока
Индуктивным элементом называется элемент, преобразующий
энергию электрического тока в энергию магнитного поля, окружающего
проводник.
В отличие от предыдущего случая, этот процесс является
обратимым, т. е. энергия источника переходит в энергию магнитного
поля, затем энергия магнитного поля возвращается в цепь в виде
энергии электрического тока. Индуктивный элемент называют
реактивным, т. к. он характеризует реакцию электрической цепи на
протекание в ней электрического тока.
Схема:
Запишем второй закон Кирхгофа для этой цепи. ЭДС

самоиндукции будет полностью компенсировать
падение напряжения на концах катушки:
Рис. 20.8.
di
U L C 0 U L C L .
dt
Имеем:
i=I0sin t U=LI0 cos t=U0cos t,
где U0=LI0 – амплитуда напряжения.
Запишем U0 в виде:
U0=RI0=XLI0,
где XL= L – индуктивное сопротивление катушки.
Таким образом запишем закон Ома:
U0
I0
.
L
График: представим U в виде: UL=U0sin( t+ /2), тогда:
Векторная диаграмма:
Рис. 20.9.
Рис. 20.10.
Вывод: напряжение опережает ток на 90 .
Емкость в цепи переменного тока.
Емкостью называется элемент, который преобразует энергию
источника электрического тока в энергию электрического поля
конденсатора.
По определению
Схема:
t
q
C
,
UC
dq
i
q idt
dt
0
t
1
1
U C q idt , т. к. i I 0 cos t , то
C
C0
t
Рис. 20.11.
I0
1
U C I 0 cos tdt
sin t U 0 sin t ,
C0
C
I0
U0
амплитудное значение напряжения.
C
1
Далее: U
I 0 X C I 0 , где XC – емкостное реактивное
0
C
сопротивление конденсатора.
где
Таким образом запишем закон Ома:
I0
U0
1
C
.
График:
Векторная диаграмма:
Рис. 20.12.
Рис. 20.13.
Вывод: в цепи с емкостной нагрузкой напряжение отстает от
тока на 90 .
Последовательное соединение активного сопротивления,
индуктивности и емкости в цепи переменного тока
Схема:
Запишем второй закон Кирхгофа для
этой цепи. Результирующее напряжение
равно:
ток.
Рис. 20.14.
U=Ur+UL+UC.
Ток i=ir=iL=iC. Опорный вектор –
Из векторной диаграммы
следует:
U2=U2r+(UL+UC)2 или
(IR)2=(Ir)2+I2(XL-XC)2
R2=r2+(XL-XC)=Z, тогда
Рис. 20.15
I0
U0
r 2 ( X L X C )2
закон Ома для цепи переменного тока,
содержащей
активное
сопротивление,
индуктивность и емкость.
К оглавлению

English     Русский Правила

Лекция 25

Лекция 25 Резюме

• Закон Фарадея
• Генераторы
• Закон Ленца
• Наведенные электрические поля

POP5 23. OQ.15
Как направлен ток в резисторе в момент времени сразу после переключения? закрывается?

А. ушел
Б. справа
C. ток равен нулю
Ответ

Точка4 23.30
Каков магнитный поток через каждый виток катушки из 500 витков, когда ЭДС 24 мВ индуцируется ток 4,0 А, который изменяется со скоростью 10 А/с?

А. 96,0 нТл·м ²
Б. 19.2 мк Т·м ²
C. 500 мкм Т·м ²
D. 47,5 мТл·м ²
Ответ

ТП5 23.37а
Батарея 12,0 В включена в последовательную цепь, содержащую резистор 10,0 Ом. и индуктор 2,00 Гн. Через какой промежуток времени ток достигнет 50,0% своего конечного значение после замыкания переключателя?
А. 3,47 мкс с
Б. 288 мк с
С. 9,85 мс
Д. 0,139 с
Ответ

ПСЭ6 32.20
На рисунке ε = 12,0 В постоянная времени 500 мк с и I _макс = 200 мА.

Что такое л ?
А. 500 мкм Н
Б. 2,75 мГн
С. 30,0 мГн
Д. 1.20 Н

Ответ

ТП5 23.48
Сколько энергии запасается в сверхпроводящем соленоиде диаметром 6,20 см и длиной 26,0 см, когда он создает магнитное поле 4,50 Тл?
А. 8.06 МДж
Б. 522 кДж
С. 6,32 кДж
D. 1.77 J
Ответ

Рыцарь2 ул 34,6
Потенциал в точке (а) выше, чем потенциал в (б). Какое из следующих утверждений о токе катушки индуктивности I может быть верным?
A. I от (а) до (б) и устойчивый.
B. I от (а) до (б) и по возрастанию.

C. I от (а) до (б) и уменьшается.
D. I от (b) до (a) и устойчивый.
E. I — от (б) до (а) и по возрастанию.
F. I — от (б) до (а) по убыванию.
Ответ

Walker5e EYU 23,8
Рассмотрим схему, показанную ниже. Ток, подаваемый аккумуляторной батареей сразу после замыкания ключа, равен _____ току, который она выдает через долгое время после замыкания ключа.
А. больше
Б. менее
C. равно
Ответ

 
Яркий
Аккумулятор выдает ток против часовой стрелки I ₁ дюймов первичной обмотке, поэтому ее магнитное поле B ₁ направлено вправо и увеличивается сразу после замыкания переключателя. Вторичная катушка будет противодействовать изменению с левым полем B ₂ , который возникает от индуцированного тока по часовой стрелке I ₂ который идет справа в резисторе.

 

Б. 19,2 мк Т·м ²

 

Д. 0,139 с

 

C. 30,0 мГн

 

С. 6,32 кДж

 

B. I от (а) до (б) и по возрастанию.
В этом случае ЭДС индукции пытается бороться с током вправо (от a к b), потому что ток увеличивается. Обратная ЭДС всегда противодействует изменению магнитного потока через индуктор, что означает, что она всегда противодействует изменение тока через индуктор. Когда ток увеличивается вправо, индуктор представляет собой временный источник ЭДС, пытающийся подтолкнуть ток влево.
F. I — от (б) до (а) по убыванию.
В этом случае ЭДС индукции пытается поддерживать ток влево (от b к a), потому что ток уменьшается. Обратная ЭДС всегда противодействует изменению магнитного потока через индуктор, что означает, что она всегда противодействует изменение тока через индуктор. Когда ток уменьшается по мере того, как он течет влево, индуктор представляет собой временный источник ЭДС, пытающийся подтолкнуть ток влево.

 

Б. меньше чем
Первоначально через катушку индуктивности не протекает ток из-за противо-ЭДС. Следовательно, катушка индуктивности действует как разомкнутая цепь, и ток, подаваемый батареей, равен I ₀  = ℰ/ R (весь ток протекает через левосторонний резистор). По прошествии длительного времени ток перестает меняться, а противо-ЭДС в катушке индуктивности равна нулю. Затем катушка индуктивности действует как провод, ток равномерно распределяется между двумя резисторами, эквивалентное сопротивление цепи составляет 9 Ом.0087 R /2, а ток от батареи равен I _∞  = 2ℰ/ R .

Ответ

23.9 Индуктивность – Колледж физики, главы 1-17

23 Электромагнитная индукция, цепи переменного тока и электрические технологии

Индуктивность

• Расчет индуктивности катушки индуктивности.
• Рассчитайте энергию, запасенную в катушке индуктивности.
• Рассчитайте ЭДС, создаваемую катушкой индуктивности.

Индукция – это процесс, при котором ЭДС индуцируется изменением магнитного потока. До сих пор обсуждалось множество примеров, некоторые из которых более эффективны, чем другие. Трансформаторы, например, спроектированы таким образом, чтобы быть особенно эффективными при наведении желаемого напряжения и тока с очень небольшой потерей энергии в другие формы. Существует ли полезная физическая величина, связанная с тем, насколько «эффективно» данное устройство? Ответ положительный, и эта физическая величина называется индуктивностью.

Взаимная индуктивность — это действие закона индукции Фарадея для одного устройства на другое, например, первичная катушка при передаче энергии вторичной обмотке в трансформаторе. См. [ссылка], где простые катушки наводят друг в друге ЭДС.

Эти катушки могут индуцировать ЭДС друг в друге, как неэффективный трансформатор. Их взаимная индуктивность М указывает на эффективность связи между ними. Здесь видно, что изменение тока в катушке 1 индуцирует ЭДС в катушке 2. (Обратите внимание, что «E2E2 размер 12{E rSub { размер 8{2} } } {}
индуцируется» представляет ЭДС индукции в катушке 2.)

Во многих случаях, когда геометрия устройств фиксирована, поток изменяется при изменении тока. Поэтому мы сосредоточимся на скорости изменения тока, ΔI/ΔtΔI/Δt size 12{ΔI} {}, как на причине индукции. Изменение тока I1I1 размера 12{I rSub { размера 8{1} } } {} в одном устройстве, катушка 1 на рисунке, индуцирует ЭДС2ЭДС2 размера 12{«ЭДС» rSub {размер 8{2} } } { } в другом. Мы выражаем это в форме уравнения как

ЭДС2=-MΔI1Δt, ЭДС2=-MΔI1Δt, размер 12{«ЭДС» rSub {размер 8{2} } = – M {{ΔI rSub {размер 8{1} } } свыше {Δt} } } {}

, где размер MM 12{M} {} определяется как взаимная индуктивность между двумя устройствами. Знак минус является выражением закона Ленца. Чем больше взаимная индуктивность ММ размером 12{M}{}, тем эффективнее связь. Например, катушки в [ссылка] имеют малый размер ММ 12{М} {} по сравнению с катушками трансформатора в [ссылка]. Единицы для MM размера 12{M} {} составляют (В⋅с)/A=Ω⋅с(В⋅с)/A=Ω⋅с размер 12{ ( V cdot s ) “/A”= %OMEGA cdot s } {}, который назван Генри (H), в честь Джозефа Генри. То есть 1 H=1Ω⋅s1 H=1Ω⋅s size 12{1`H=1` %OMEGA cdot s} {}.

Природа здесь симметрична. Если мы изменим текущий размер I2I2 12{I rSub { размер 8{2} } } {} в катушке 2, мы индуцируем ЭДС1emf1 размера 12{«ЭДС» rSub { размер 8{1} } } {} в катушке 1, который дается

ЭДС1=-MΔI2Δt, ЭДС1=-MΔI2Δt, размер 12{«ЭДС» rSub { размер 8{1} } = – M { {ΔI rSub { размер 8{2} } } свыше {Δt} } } {}

, где размер ММ 12{M} {} такой же, как и для обратного процесса. Трансформаторы работают в обратном направлении с той же эффективностью, или ММ взаимной индуктивности типоразмера 12{М} {} .

Большая взаимная индуктивность MM размера 12{M} {} может быть или не быть желательной. Мы хотим, чтобы трансформатор имел большую взаимную индуктивность. Но такой прибор, как электрическая сушилка для белья, может индуцировать на своем корпусе опасную ЭДС, если взаимная индуктивность между его катушками и корпусом велика. Один из способов уменьшить взаимную индуктивность MM размера 12 {M} {} — это встречная обмотка катушек, чтобы нейтрализовать создаваемое магнитное поле. (См. [ссылка].)

Нагревательные катушки электрической сушилки для белья могут быть встречно намотаны, так что их магнитные поля компенсируют друг друга, что значительно снижает взаимную индуктивность с корпусом сушилки.

Самоиндукция, действие закона Фарадея об индукции устройства на себя, также существует. Когда, например, ток через катушку увеличивается, магнитное поле и поток также увеличиваются, индуцируя противо-ЭДС, как того требует закон Ленца. И наоборот, если ток уменьшается, индуцируется ЭДС, препятствующая уменьшению. Большинство устройств имеют фиксированную геометрию, поэтому изменение потока полностью обусловлено изменением тока ΔIΔI размером 12{ΔI} {} через устройство. ЭДС индукции связана с физической геометрией устройства и скоростью изменения тока. Это дается

ЭДС=-L∆I∆t, ЭДС=-L∆I∆t, размер 12{«ЭДС»= – L { {∆I} над {∆t} } } {}

, где размер LL 12{L} {} — собственная индуктивность устройства. Устройство, обладающее значительной собственной индуктивностью, называется катушкой индуктивности и обозначается символом в [ссылка]. Знак минус является выражением закона Ленца, указывающим, что ЭДС противодействует изменению тока. Единицами самоиндукции являются генри (Гн), как и для взаимной индуктивности. Чем больше величина собственной индуктивности LL 12{L}{} устройства, тем больше его сопротивление любому изменению тока через него. Например, большая катушка с большим количеством витков и железным сердечником имеет большой размер LL 12{L}{} и не позволит току быстро меняться. Чтобы избежать этого эффекта, необходимо добиться небольшого размера LL 12{L} {}, например, путем встречной обмотки катушек, как в [ссылка].

Катушка индуктивности 1 Гн представляет собой большую катушку индуктивности. Чтобы проиллюстрировать это, рассмотрим устройство с L=1,0 HL=1,0 H размером 12{L=1 «.» 0`H} {}, через который протекает ток 10 А. Что произойдет, если мы попытаемся отключить ток быстро, возможно, всего за 1,0 мс? ЭДС, определяемая как ЭДС=-L(ΔI/Δt)ЭДС=-L(ΔI/Δt) размер 12{«ЭДС»= – L (ΔI/Δt)} {}, будет противодействовать изменению. Таким образом, будет индуцироваться ЭДС, равная ЭДС=-L(ΔI/Δt)=(1,0 Гн)[(10 А)/(1,0 мс)]=10000 ВЭДС=-L(ΔI/Δt)=(1,0 Гн) [(10 А)/(1,0 мс)] = 10 000 В. Положительный знак означает, что это большое напряжение имеет то же направление, что и ток, и препятствует его уменьшению. Такие большие ЭДС могут вызывать искрение, повреждая коммутационное оборудование, поэтому может потребоваться более медленное изменение тока.

Для такого большого наведенного напряжения есть применение. Вспышки камеры используют батарею, две катушки индуктивности, которые функционируют как трансформатор, и систему переключения или осциллятор для создания больших напряжений. (Помните, что нам нужно изменяющееся магнитное поле, вызванное изменяющимся током, чтобы индуцировать напряжение в другой катушке.) Система генератора будет делать это много раз, когда напряжение батареи увеличится до более чем одной тысячи вольт. (Вы можете услышать пронзительный вой трансформатора во время зарядки конденсатора.) Конденсатор сохраняет высокое напряжение для последующего использования при питании вспышки. (См. [ссылка].)

Благодаря быстрому переключению катушки индуктивности батареи напряжением 1,5 В можно использовать для наведения ЭДС в несколько тысяч вольт. Это напряжение можно использовать для хранения заряда в конденсаторе для последующего использования, например, во вспышке фотоаппарата.

Можно рассчитать размер LL 12{L} {} для индуктора, учитывая его геометрию (размер и форму) и зная создаваемое им магнитное поле. В большинстве случаев это сложно из-за сложности создаваемого поля. Так что в этом тексте индуктивность LL размером 12{L}{} обычно является заданной величиной. Единственным исключением является соленоид, потому что он имеет очень однородное поле внутри, почти нулевое поле снаружи и простую форму. Поучительно вывести уравнение для его индуктивности. Начнем с того, что заметим, что ЭДС индукции определяется законом индукции Фарадея как ЭДС=-N(ΔΦ/Δt)ЭДС=-N(ΔΦ/Δt) размер 12{«ЭДС»= – N ( ΔΦ/Δt ) } {} и, по определению собственной индуктивности, как ЭДС= −L(ΔI/Δt)ЭДС=−L(ΔI/Δt) размер 12{«ЭДС»= – L ( ΔI/Δt ) } {}. Приравнивание этих выходов

ЭДС=-NΔΦΔt=-LΔIΔt.ЭДС=-NΔΦΔt=-LΔIΔt. размер 12{«ЭДС»= – N {{ΔΦ} над {Δt} } = – L {{ΔI} над {Δt} } } {}

Решение для размера LL 12{L} {} дает

L=NΔΦΔI.L=NΔΦΔI. размер 12{L=N { {ΔΦ} свыше {ΔI} } } {}

Это уравнение для собственной индуктивности LL размера 12{L} {} устройства всегда справедливо. Это означает, что величина собственной индуктивности LL 12{L} {} зависит от того, насколько эффективно ток создает поток; тем эффективнее, чем больше ΔΦΔΦ размер 12{ΔΦ} {}/ ΔIΔI размер 12{ΔI} {}.

Воспользуемся этим последним уравнением, чтобы найти выражение для индуктивности соленоида. Поскольку площадь соленоида AA фиксирована, изменение потока равно

.

ΔΦ=Δ(BA)=AΔBΔΦ=Δ(BA)=AΔB.

Чтобы найти
ΔBΔB, заметим, что магнитное поле соленоида задается как B=μ0nI=μ0NIℓB=μ0nI=μ0NIℓ размер 12{B=μ rSub { размер 8{0} } ital «nI»=μ rSub { размер 8{0} } { {итал. «NI»} более {ℓ} } } {}. (Здесь n=N/ℓn=N/ℓ размер 12{n=N/ℓ} {}, где
NN — количество витков, а
ℓℓ — длина соленоида.) Изменяется только ток, так что ΔΦ=AΔB =μ0NAΔIℓΔΦ=AΔB=μ0NAΔIℓ размер 12{ΔΦ=AΔB=μ rSub { размер 8{0} } итал. «NA» {{ΔI} более {ℓ} } } {}. Замена
ΔΦΔΦ в L=NΔΦΔIL=NΔΦΔI размер 12{L=N { {ΔΦ} над {ΔI} } } {} дает

L=NΔΦΔI=Nμ0NAΔIℓΔI.L=NΔΦΔI=Nμ0NAΔIℓΔI. размер 12 {L = N { {ΔΦ} над {ΔI} } = N { {μ rSub { размер 8 {0} } ital «NA» { {ΔI} над {ℓ} } } над {ΔI} } } {}

Это упрощается до

L=μ0N2Aℓ(соленоид).L=μ0N2Aℓ(соленоид). размер 12 {L = { {μ rSub { размер 8 {0} } N rSup { размер 8 {2} } A} более {ℓ} } } {}

Это собственная индуктивность соленоида с площадью поперечного сечения AA и длиной
ℓℓ. Обратите внимание, что индуктивность зависит только от физических характеристик соленоида, соответствующих его определению.

Расчет собственной индуктивности соленоида среднего размера

Рассчитайте собственную индуктивность соленоида длиной 10,0 см и диаметром 4,00 см с 200 витками.

Стратегия

Это прямое применение L=μ0N2AℓL=μ0N2Aℓ размер 12{L= { {μ rSub { размер 8{0} } N rSup { размер 8{2} } A} более {ℓ} } } {}, поскольку все величины в уравнении, кроме LL size 12{L} {}, известны.

Решение

Используйте следующее выражение для самоиндукции соленоида:

L=μ0N2Aℓ.L=μ0N2Aℓ. размер 12{L= { {µ rSub { размер 8{0} } N rSup { размер 8{2} } A} более {ℓ} } } {}

Площадь поперечного сечения в этом примере равна A=πr2= (3,14…)(0,0200 м)2=1,26×10−3м2A=πr2=(3,14…)(0,0200 м)2=1,26×10−3м2 размер 12{A=πr rSup { размер 8{2} } = ( 3 «.» «14» «.» «.» «.» ) ( 0 «.» «0200»`м ) rSup { размер 8{2} } =1 «.» «26» умножить на «10» rSup {размер 8{ – 3} } `m rSup {размер 8{2} } } {}, NN равно 200, а длина ℓℓ равна 0,100 м. Мы знаем, что проницаемость свободного пространства равна µ0=4π×10−7T⋅м/Aµ0=4π×10−7T⋅м/A. Подставляя их в выражение для
LL дает

L=(4π×10−7 T⋅м/A)(200)2(1,26×10−3 м2)0,100 м=0,632 мH.L=(4π×10−7 T⋅m/A )(200)2(1,26×10-3 м2)0,100 м=0,632 мГн.

Обсуждение

Этот соленоид средних размеров. Его индуктивность около миллигенри также считается умеренной.

Одно из распространенных применений индуктивности используется в светофорах, которые могут определять, когда транспортные средства ожидают на перекрестке. Электрическая цепь с индуктором размещена на дороге под местом остановки ожидающего автомобиля. Кузов автомобиля увеличивает индуктивность, и схема меняется, посылая сигнал светофору изменить цвет. Точно так же металлоискатели, используемые для обеспечения безопасности в аэропортах, используют ту же технику. Катушка или индуктор в корпусе металлоискателя действует как передатчик и приемник. Импульсный сигнал в катушке передатчика индуцирует сигнал в приемнике. На самоиндукцию цепи влияет любой металлический предмет на пути. Такие детекторы могут быть настроены на чувствительность, а также могут указывать примерное местонахождение обнаруженного на человеке металла. (Но они не смогут обнаружить пластиковую взрывчатку, подобную той, что была найдена на «подрывнике в нижнем белье».) См. [ссылка].

Знакомые ворота безопасности в аэропорту могут не только обнаруживать металлы, но и указывать их приблизительную высоту над полом. (кредит: Alexbuirds, Wikimedia Commons)

Из закона Ленца мы знаем, что индуктивности противодействуют изменениям тока. Есть альтернативный взгляд на эту оппозицию, основанный на энергии. Энергия хранится в магнитном поле. Требуется время, чтобы накопить энергию, и также нужно время, чтобы истощить энергию; следовательно, существует оппозиция быстрым изменениям. В индукторе магнитное поле прямо пропорционально току и индуктивности устройства. Можно показать, что энергия, запасенная в катушке индуктивности EindEind size 12{E rSub { size 8{“ind”} } } {} определяется как

Eind=12LI2. Eind=12LI2. size 12{E rSub { size 8{«ind»} } = {{1} over {2} } ital «LI» rSup { size 8{2} } } {}

Это выражение похоже на выражение для энергии, запасенной в конденсаторе.

Расчет энергии, запасенной в поле соленоида

Сколько энергии сохраняется в катушке индуктивности 0,632 мГн из предыдущего примера, когда через нее протекает ток 30,0 А?

Стратегия

Энергия определяется уравнением 8{2} } } {}, и известны все величины, кроме EindEind size 12{E rSub { size 8{«ind»} } } {}.

Решение

Подставив значение размера LL 12{L} {} из предыдущего примера и заданный ток в Eind=12LI2Eind=12LI2 size 12{E rSub { size 8{«ind»} } = { {1} свыше {2} } итал. «LI» rSup {размер 8{2} } } {} дает

Eind=12LI2=0,5(0,632×10−3 H)(30,0 A)2=0,284 J.Eind= 12LI2=0,5(0,632×10−3 Гн)(30,0 А)2=0,284 Дж.

Обсуждение

Этого количества энергии, безусловно, достаточно, чтобы вызвать искру при внезапном отключении тока. Он не может быть построен мгновенно, если только потребляемая мощность не бесконечна.

• Индуктивность — это свойство устройства, которое показывает, насколько эффективно оно индуцирует ЭДС в другом устройстве.
• Взаимная индуктивность — это действие двух устройств, индуцирующих ЭДС друг в друге.
• Изменение тока ΔI1/ΔtΔI1/Δt размер 12{ΔI rSub { размер 8{1} } /Δt} {} в одном индуцирует ЭДС emf2emf2 размер 12{«ЭДС» rSub { размер 8{2} } } {} В секунду:

  ЭДС2=-MΔI1Δt, ЭДС2=-MΔI1Δt, размер 12{«ЭДС» rSub {размер 8{2} } = – M {{ΔI rSub {размер 8{1} } } свыше {Δt} } } {}

  , где
  MM определяется как взаимная индуктивность между двумя устройствами, а знак минус соответствует закону Ленца.

• Симметрично, изменение тока ΔI2/ΔtΔI2/Δt размер 12{ΔI rSub { размер 8{2} } /Δt} {} через второе устройство индуцирует ЭДС emf1emf1 размер 12{«ЭДС» rSub { размер 8{1} } } {} во-первых:

  ЭДС1=-MΔI2Δt, ЭДС1=-MΔI2Δt, размер 12{«ЭДС» rSub { размер 8{1} } = – M { {ΔI rSub { размер 8{2} } } свыше {Δt} } } {}

  , где
  ММ — та же взаимная индуктивность, что и в обратном процессе.

• Текущие изменения в устройстве индуцируют ЭДС в самом устройстве.
• Самоиндукция — это эффект устройства, индуцирующего ЭДС само по себе.
• Прибор называется индуктором, а ЭДС индуцируемая в нем изменением тока через него равна {Δt} } } {}где ЛЛ размер 12{L} {} — собственная индуктивность дросселя, а ΔI/ΔtΔI/Δt размер 12{ΔI/Δt} {} — скорость изменения тока через него. Знак минус указывает на то, что ЭДС противодействует изменению тока, как того требует закон Ленца.
• Единицей собственной и взаимной индуктивности является генри (Гн), где 1 H=1 Ω⋅s1 H=1 Ω⋅s размер 12{1`H=1` %OMEGA cdot s} {}.
• Размер собственной индуктивности LL 12{L} {} катушки индуктивности пропорционален тому, насколько поток изменяется с током. Для 12 {N} {}-виткового индуктора размера NN

  L=NΔΦΔI.L=NΔΦΔI. размер 12{L=N { {ΔΦ} свыше {ΔI} } } {}

• Самоиндукция соленоида

  L = μ0N2Aℓ (соленоид), L = μ0N2Aℓ (соленоид), размер 12 {L = { {μ rSub { размер 8 {0} } N rSup { размер 8 {2} } A} свыше {ℓ} } } {}

  , где размер NN 12{N} {} — число витков в соленоиде, размер AA 12{A} {} – площадь поперечного сечения, ℓℓ размера 12{ℓ} {} – длина, а µ0=4π ×10−7T⋅м/Aµ0=4π×10−7T⋅м/A размер 12{μ rSub { размер 8{0} } =4π умножить на «10» rSup { размер 8{“-7”} } `T cdot «m/A»} {} — проницаемость свободного пространства.

• Энергия, запасенная в катушке индуктивности EindEind size 12{E rSub { size 8{«ind»} } } {} is

  Eind=12LI2.Eind=12LI2. size 12{E rSub { size 8{«ind»} } = {{1} over {2} } ital «LI» rSup { size 8{2} } } {}

Как бы вы поместили две одинаковые плоские катушки в контакт, чтобы они имели наибольшую взаимную индуктивность? В мере?

Как бы вы сформировали провод заданной длины, чтобы придать ему наибольшую самоиндукцию? В мере?

Проверить, как было сделано без доказательства в [ссылка], что единицы T⋅m2/A=Ω⋅s=HT⋅m2/A=Ω⋅s=H size 12{T cdot m rSup { size 8{2} } /A= %OMEGA cdot s=H} {}.

Две катушки расположены близко друг к другу в физической лаборатории, чтобы продемонстрировать закон индукции Фарадея. Ток 5,00 А в одном отключается за 1,00 мс, вызывая 9ЭДС 0,00 В в другом. Чему равна их взаимная индуктивность?

1,80 мГн

Если две катушки, расположенные рядом друг с другом, имеют взаимную индуктивность 5,00 мГн, какое напряжение индуцируется в одной, когда ток 2,00 А в другой отключается через 30,0 мс?

Ток 4,00 А через катушку индуктивности 7,50 мГн отключается за 8,33 мс. Какая ЭДС индуцирует противодействие этому?

3,60 В

Устройство включено, и через него через 0,100 мс проходит ток 3,00 А. Чему равна собственная индуктивность прибора, если ей противодействует ЭДС наведенного напряжения 150 В?

Начиная с emf2=-MΔI1Δtemf2=-MΔI1Δt размер 12{«ЭДС» rSub { размер 8{2} } = – M { {ΔI rSub { размер 8{1} } } свыше {Δt} } } {}, покажите, что единицы индуктивности: (В⋅с)/A=Ω⋅с(В⋅с)/A=Ω⋅с size 12{ ( V cdot s ) “/A”= %OMEGA cdot s} {}.

Фотовспышки заряжают конденсатор до высокого напряжения, быстро включая и выключая ток через катушку индуктивности. За какое время необходимо включить или выключить ток 0,100 А через катушку индуктивности 2,00 мГн, чтобы индуцировать ЭДС 500 В?

Большой исследовательский соленоид имеет собственную индуктивность 25,0 Гн. а) Какая ЭДС наведения препятствует его отключению, если ток 100 А через него отключается за 80,0 мс? б) Сколько энергии запасается в катушке индуктивности при полном токе? в) С какой скоростью в ваттах должна рассеиваться энергия, чтобы ток выключился за 80,0 мс? (d) Принимая во внимание ответ на последнюю часть, удивительно ли, что так быстро закрыть его сложно?

(а) 31,3 кВ

(б) 125 кДж

(в) 1,56 МВт

(г) Нет, не удивительно, так как эта мощность очень велика.

(a) Рассчитайте собственную индуктивность соленоида длиной 50,0 см и диаметром 10,0 см, имеющего 1000 витков. б) Сколько энергии запасается в этом индукторе при протекании через него тока силой 20,0 А? в) Как быстро его можно выключить, если ЭДС индукции не может превышать 3,00 В?

Прецизионный лабораторный резистор изготовлен из витка проволоки диаметром 1,50 см и длиной 4,00 см и имеет 500 витков. а) Чему равна его собственная индуктивность? б) Какая средняя ЭДС индуцируется, если ток 12,0 А через него включается за 5,00 мс (одна четвертая периода для переменного тока частотой 50 Гц)? в) Какова его индуктивность, если его укоротить наполовину и намотать встречно (два слоя по 250 витков в противоположных направлениях)?

(а) 1,39 мГн

(б) 3,33 В

(в) Ноль

Нагревательные спирали в фене имеют диаметр 0,800 см, общую длину 1,00 м и 400 витков. а) Какова их полная собственная индуктивность, если предположить, что они действуют как одиночный соленоид? б) Сколько энергии запасается в них при токе 6,00 А? (c) Какая средняя ЭДС препятствует их отключению, если это делается за 5,00 мс (одна четвертая часть цикла для переменного тока с частотой 50 Гц)?

Когда ток 20,0 А через индуктор отключается за 1,50 мс, индуцируется ЭДС 800 В, противодействующая изменению.