Ёмкостное сопротивление. Индуктивное сопротивление
Физика – какая ёмкость слова,
Физика для нас не просто звук,
Физика – опора и основа,
Всех без исключения наук!
Задача 1. В цепи переменного тока с частотой 50 Гц при напряжении 220 В возникает сила тока 4 А. Известно, что в эту цепь включена катушка с ничтожно малым активным сопротивлением. Какова индуктивность катушки?
|
ДАНО:
|
РЕШЕНИЕ Индуктивное сопротивление определяется по формуле
Циклическую частоту можно рассчитать по выражению
Запишем закон Ома для участка цепи
Приравняем две последних формулы для расчёта индуктивного сопротивления и выразим индуктивность катушки
|
|
|
Ответ: 175 мГн.
Задача 2. . При увеличении частоты от 50 Гц до 60 Гц, ёмкостное сопротивление конденсатора с постоянной ёмкостью уменьшилось на 10 Ом. Найдите электроёмкость конденсатора.
|
ДАНО:
|
РЕШЕНИЕ Ёмкостное сопротивление определяется по формуле
Циклическую частоту можно определить по выражению
Тогда ёмкостное сопротивление
Применим данную формулу для двух значений частоты
Изменение ёмкостного сопротивления конденсатора определяется по формуле
Тогда электроёмкость конденсатора
|
|
|
Ответ: 53 мкФ.
Задача 3. Известно, что через катушку, включенную в цепь переменного тока с частотой 200 Гц, проходит ток не более 3 А. Найдите напряжение на катушке, в момент времени
|
ДАНО:

|
СИ
|
РЕШЕНИЕ Из закона Ома для участка цепи следует
Индуктивное сопротивление определяется по формуле
Амплитудное напряжение рассчитывается по выражению
Запишем уравнение гармонических колебаний напряжения
Циклическая частота равна
Тогда уравнение гармонических колебаний напряжения будет иметь вид
Тогда в момент времени t
|
|
|
Ответ: 18,3 В.
Задача 4. Докажите, что если частота переменного тока равна собственной частоте, то по катушке индуктивности и конденсатору будет протекать одинаковый ток, а также на катушке и на конденсаторе будет одинаковое напряжение.
|
ДАНО:
|
РЕШЕНИЕ Собственная циклическая частота в колебательном контуре равна
По определению, собственная частота – это частота свободных колебаний (то есть, колебаний при отсутствии активного сопротивления)
Таким образом, имеется два случая: либо катушка и конденсатор подключены параллельно, либо они подключены последовательно. Активное сопротивление отсутствует. Рассмотрим параллельное соединение
Из закона Ома для участка цепи
Индуктивное сопротивление определяется по формуле
Ёмкостное сопротивление определяется по формуле
С учётом двух последних формул и равенства напряжений получаем
Теперь рассмотрим последовательное соединение
При последовательном соединении
Из закона Ома для участка цепи
Индуктивное сопротивление определяется по формуле
Ёмкостное сопротивление определяется по формуле
С учётом двух последних формул и равенства силы тока получаем
|
|
Доказать |
Ответ: доказано.
С АКТИВНЫМ, ИНДУКТИВНЫМ И ЕМКОСТНЫМ
СОПРОТИВЛЕНИЯМИ
При расчетах цепей переменного тока, так же как и цепей постоянного тока, используют законы Ома и Кирхгофа. Отличие в применении этих законов заключается в том, что в цепях переменного тока необходимо учитывать углы сдвига фаз между токами и напряжениями.
Цепь переменного тока, в которую включены последовательно активное сопротивление R, индуктивность L, обладающая индуктивным сопротивлением , и емкость С, имеющая емкостное сопротивление, 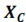 изображена на рис. .8, а.
изображена на рис. .8, а.
Под действием переменного напряжения и в этой цепи протекает переменный ток iСогласно закону Ома определим падения напряжения на каждом элементе цепи:
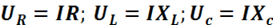
Эти падения напряжения имеют соответствующие углы сдвига фаз по отношению к общему току цепи I.
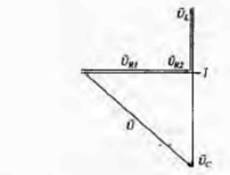
Построим векторную диаграмму тока и напряжений для рассматриваемой цепи (рис. .8,б). Так как сопротивления соединены последовательно, то в них протекает одинаковый ток. Отложим по горизонтали в выбранном масштабе вектор тока I. В цепи с активным сопротивлением ток и напряжение совпадают по фазе, поэтому вектор напряжения откладываем по вектору токаI . Напряжение на индуктивности опережает ток на угол 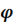 = 90°. Поэтому вектор
= 90°. Поэтому вектор 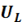 откладываем вверх под углом 90° к вектору тока I . В цепи семкостьюи наоборот, напряжение отстает от тока на угол
откладываем вверх под углом 90° к вектору тока I . В цепи семкостьюи наоборот, напряжение отстает от тока на угол 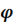 = 90°, поэтому вектор откладываем на диаграмме вниз под углом 90° к вектору тока I.
= 90°, поэтому вектор откладываем на диаграмме вниз под углом 90° к вектору тока I.
Рис. .8. Цепь переменного тока с последовательно включенными сопротивлением ,индуктивностью и емкостью:
а — электрическая схема; б — векторная диаграмма; в — треугольник сопротивлений
Для определения общего напряжения, приложенного к зажимам
цепи, сложим векторы 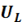 и.
и. 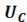 Для этого вычтем из большего вектора
Для этого вычтем из большего вектора 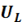 и
и
вектор и получим вектор ( ,) выражающий векторную сумму этих двух напряжений. Теперь сложим векторы ( ) .
Суммой этих векторов будет диагональ параллелограмма — вектор Uявляющийся общим напряжением на зажимах цепи:
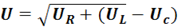 2или 2
2или 2
Полное сопротивление цепи переменного тока, содержащей активное, индуктивное и емкостное сопротивления,
2
Полная проводимость цепи:
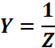
Угол сдвига фаз между током и напряжением цепи определяется тригонометрическими функциями:
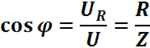
Если >, 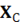 то вектор напряжения U опережает вектор тока I, а если <
то вектор напряжения U опережает вектор тока I, а если < 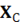 то Uотстает от тока I.Треугольник сопротивлений изображен на рис..8, в
то Uотстает от тока I.Треугольник сопротивлений изображен на рис..8, в
Пример .4. В электрическую цепь, приведенную на рисунке, с напряжением U = 220 В последовательно включены: резистор с активным сопротивлением , = 5 Ом, индуктивная катушка Lс активным сопротивлением
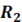 = 3 Ом и индуктивным сопротивлением = 4 Ом, конденсатор С с емкостным сопротивлением
= 3 Ом и индуктивным сопротивлением = 4 Ом, конденсатор С с емкостным сопротивлением 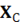 = 10 Ом. Определить ток в цепи и напряжение на отдельных элементах цепи. Нарисовать векторную диаграмму.
= 10 Ом. Определить ток в цепи и напряжение на отдельных элементах цепи. Нарисовать векторную диаграмму.
Решение
Определяем общее сопротивление
2 = =10Ом
Ток в цепи
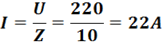
Напряжение на отдельных элементах цепи:
В
В
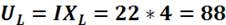 В
В
В
Векторная диаграмма приведена на рисунке ниже.
Рассмотрим электрическую цепь, состоящую из двух приемников, подключенных параллельно к зажимам источника синусоидального напряжения u= 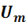 sin
sin 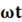
(рис. .9,а). В первом приемнике включены последовательно элементы и L, во втором соответственно 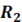 и С. Оба приемника находятся под действием одного общего напряженияu. Запишем выражения для мгновенных значений токов для первой и второй ветви:
и С. Оба приемника находятся под действием одного общего напряженияu. Запишем выражения для мгновенных значений токов для первой и второй ветви:
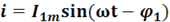
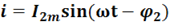
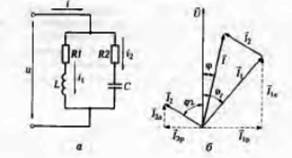
Рис. 9. Цепь переменного тока с параллельно соединенными элементам
а — электрическая схема: б — векторная диаграмма
Так как в первую ветвь включена индуктивная катушка, а во вторую— конденсатор, то электрические цепи соответственно носят индуктивны й и емкостной характер.
Действующее значение тока I и косинус угла 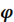 определяем из следующих выражений:
определяем из следующих выражений:

Значение тока I в неразветвленной части цепи определяют как геометрическую сумму токов в ветвях, т.е.I = + 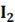
Векторная диаграмма приведена на рис. 9, б. Токи, протекающие через ветви, состоят из активной 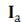 и реактивной
и реактивной 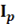 составляющих и соответственно имеют индуктивный и емкостной характер.
составляющих и соответственно имеют индуктивный и емкостной характер.
Ветвь с активной составляющей характеризуется активной проводимостью
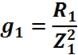
Ветвь с реактивной составляющей характеризуется реактивной проводимостью . Для первой ветви реактивная проводимость
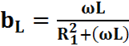 2
2
Реактивная проводимость не является величиной, обратной реактивному сопротивлению, так как при ее определении учитывается и активное сопротивлении ветви. Полная проводимость ветви
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какие законы используют при расчете цепей переменного тока?
2.В чем состоит принципиальное отличие расчета цепей переменного
тока от расчета цепей постоянного тока?
РЕЗОНАНС НАПРЯЖЕНИЙ
В цепи переменного тока с активным, индуктивным и емкостным сопротивлениями, соединенными последовательно (рис. 10, а), может возникнуть резонанс напряжений
Резонанс напряжений наступает в том случае, если индуктивное сопротивление и емкостное сопротивление  равны между собой, т.е.
равны между собой, т.е.
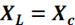
Так как эти сопротивления зависят от частоты, резонанс наступает при определенной резонансной частоте :
При заданной частоте резонанс напряжений может быть достигнут изменением L и С.
Рис. 10. Цепь переменного тока при резонансе напряжения:
а — электрическая схема; б — векторная диаграмма
Когда цепь не настроена в резонанс, ее полное сопротивление
2
При резонансе напряжений в рассматриваемой цепи, когда = 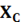 ее полное сопротивление
ее полное сопротивление
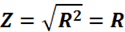
Запомните
1. Полное сопротивление цепи при резонансе напряжений равно активному сопротивлениюR.
2. Угол сдвига фаз 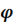 между током и напряжением при резонансе равен нулю. Это значит, что ток и напряжение совпадают по фазе (как в цепи сактивным сопротивлением)
между током и напряжением при резонансе равен нулю. Это значит, что ток и напряжение совпадают по фазе (как в цепи сактивным сопротивлением)
Уменьшение полного сопротивления цепи приводит к тому, что сила тока в ней возрастает. Напряжение генератора переменного тока, включенного в цепь, расходуется на активном сопротивлении:
Напряжение на индуктивности и емкости определяется согласно закону Ома. В связи стем что в последовательно соединенных сопротивлениях протекает одинаковый ток и при резонансе индуктивное сопротивление 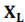 =
= 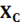 напряжения на индуктивности и емкости тоже равны:
напряжения на индуктивности и емкости тоже равны:
Векторная диаграмма для рассматриваемой цепи при резонансе напряжения приведена на рис 10, б. На векторной диаграмме видно, что напряжения на индуктивности и емкости равны, сдвинуты по фазе друг относительно друга на 180° и взаимно компенсируются.
Если одновременно увеличить оба реактивных сопротивления и  , не нарушая при этом условия резонанса =,
, не нарушая при этом условия резонанса =,  то соответственно возрастут оба частичных напряжения
то соответственно возрастут оба частичных напряжения 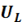 и,
и, 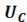 а сила тока в цепи при этом не изменится. Таким образом, можно получить и во много раз большие, чем напряжение U на зажимах цепи, поэтому резонанс напряжений — опасное явление для энергетических установок.
а сила тока в цепи при этом не изменится. Таким образом, можно получить и во много раз большие, чем напряжение U на зажимах цепи, поэтому резонанс напряжений — опасное явление для энергетических установок.
В электроустановках большой мощности резонанс напряжений, который может наступить внезапно, например при изменении емкостного сопротивления, может привести к опасным перенапряжениям и рассматривается как аварийный. В технике связи и автоматике явление резонанса напряжений широко используют для настройки приемных и передающих устройств на определенную частоту
Пример.5. В цепь переменного тока включены последовательно активное сопротивление R = 3 Ом, индуктивность L= 0,005 Гн и емкость С = 63,5 мкф. Генератор, включенный в цепь, вырабатывает переменное напряжение U = 2,5 В с резонансной частотой = 285 Гц. Определить индуктивное и емкостное сопротивления, полное сопротивление цепи, токпротекающий в цепи, напряжения на емкости и индуктивности.
Решение
Индуктивное сопротивление
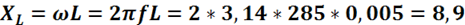 Ом
Ом
Емкостное сопротивление
Индуктивное сопротивление равно емкостному, следовательно, в цепи наступает резонанс напряжения.
Полное сопротивление цепи при резонансе напряжения
2 = 2 = 3Ом
Сила тока в цепи
Напряжение на индуктивности
Напряжение на емкости
Как видно из представленного примера, в режиме резонанса напряжения на индуктивности и емкости равны и превышают напряжение генератора.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что называется резонансом напряжений?
2. Чему равно полное сопротивление цепи при резонансе напряжений?
3. Чему равен угол сдвига фаз 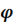 между током и напряжением при резонансе напряжений?
между током и напряжением при резонансе напряжений?
4. Какую опасность представляет резонанс напряжений в технике?
РЕЗОНАНС ТОКОВ
В цепи переменного тока, в которой индуктивность L, емкость Си сопротивлениеR соединены параллельно (рис. .11, а), может возникнуть резонанс токов при условии равенства реактивных сопротивлений:
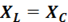
Ток при резонансе достигает минимального значения I = U/R, a cos 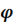 = 1, т. е. достигает своего максимального значения.
= 1, т. е. достигает своего максимального значения.
Значение резонансной частоты определяется формулой
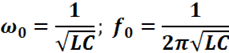
Из формулы следует, что, изменяя величину емкости или индуктивности контура, можно изменять (регулировать) частоту свободных колебаний, т. е. настраивать контур на определенную частоту.
Векторная диаграмма изображена на рис..11, б в режиме резонанса токов.
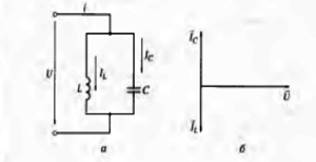
Рис .11. Цепь переменного тока при резонансе тока:
а-электрическая схема; б — векторная диаграмма
Свободные электрические колебания, возникающие в колебательном контуре, всегда затухающие. Затухание колебаний в контуре объясняется тем, что при прохождении электрического то в контуре энергия тратится на нагревание провода, из которого изготовлены индуктивная катушка и соединительные провода.
Потеря энергии в контуре вызывает постепенное уменьшение амплитуды свободных колебаний и их полное прекращение. Скорость затухания колебаний в контуре связана с потерей энергии в нем и зависит от сопротивления контура.
Запомните
■ Токи в ветвях, содержащих L и С, при резонансе тока могут быть
больше общего тока цепи.
■ Индуктивный и емкостной токи противоположны по фазе, равны по значению и по отношению к источнику энергии взаимно
компенсируются, т. е. идет обмен энергией между индуктивной
катушкой и конденсатором.
■ Реактивная мощность цепи при резонансе токов равна нулю, поскольку равны и противоположно направлены токи . Иными словами, реактивная мощность, потребляемая в индуктивной катушке, равна реактивной мощности, генерируемой в конденсаторе.
В результате резонанса токов общий ток в цепи может быть относительно мал, а в ветвях индуктивности и емкости, где происходят электрические колебания, переменный ток значительно больше общего.
Пример 6. Разветвленная цепь, приведенная на рисунке слева, имеет
следующие параметры: = 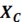 = 10 Ом, R = 40 Ом, U= 120 В. Определить токи в ветвях и общий ток цепи. Построить векторную диаграмму.
= 10 Ом, R = 40 Ом, U= 120 В. Определить токи в ветвях и общий ток цепи. Построить векторную диаграмму.
Решение
Определим токи в ветвях:
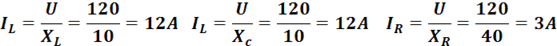
Рассчитаем общий ток цепи

Векторная диаграмма изображена на рисунке справа. Общий ток цепи при резонансе токов в четыре раза меньше тока в ветвях, содержащих реактивные элементы.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. При каких условиях возникает резонанс токов?
2. От чего зависит скорость затухания колебаний в контуре?
3. Чему равна реактивная мощность цепи при резонансе токов?
Элементы сопротивления, индуктивности и ёмкости
⇐ ПредыдущаяСтр 2 из 5Следующая ⇒
Электри́ческое сопротивле́ние — физическая величина, характеризующая свойства проводника препятствовать прохождению электрического тока и равная отношению напряжения на концах проводника к силе тока, протекающего по нему. Сопротивление для цепей переменного тока и для переменных электромагнитных полей описывается понятиями импеданса и волнового сопротивления. Сопротивлением (резистором) также называют радиодеталь, предназначенную для введения в электрические цепи активного сопротивления.
Сопротивление (часто обозначается буквой R или r) считается, в определённых пределах, постоянной величиной для данного проводника; её можно рассчитать как
Где
R — сопротивление;
U — разность электрических потенциалов на концах проводника;
I — сила тока, протекающего между концами проводника под действием разности потенциалов
Реактивное сопротивление — электрическое сопротивление, обусловленное передачей энергии переменным током электрическому или магнитному полю (и обратно).
Реактивное сопротивление определяет мнимую часть импеданса:
, где 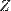 — импеданс, — величина активного сопротивления, — величина реактивного сопротивления, — мнимая единица.
— импеданс, — величина активного сопротивления, — величина реактивного сопротивления, — мнимая единица.
В зависимости от знака величины 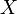 какого-либо элемента электрической цепи говорят о трёх случаях:
какого-либо элемента электрической цепи говорят о трёх случаях:
 — элемент проявляет свойства индуктивности.
— элемент проявляет свойства индуктивности.- — элемент имеет чисто активное сопротивление.
 — элемент проявляет ёмкостные свойства.
— элемент проявляет ёмкостные свойства.
Величина реактивного сопротивления может быть выражена через величины индуктивного и ёмкостного сопротивлений: 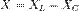
Индуктивное сопротивление ( 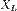 ) обусловлено возникновением ЭДС самоиндукции в элементе электрической цепи. Изменение тока и, как следствие, изменение его магнитного поля вызывает препятствующее изменению этого тока ЭДС самоиндукции. Величина индуктивного сопротивления зависит от индуктивности
) обусловлено возникновением ЭДС самоиндукции в элементе электрической цепи. Изменение тока и, как следствие, изменение его магнитного поля вызывает препятствующее изменению этого тока ЭДС самоиндукции. Величина индуктивного сопротивления зависит от индуктивности 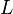 элемента и частоты
элемента и частоты 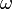 протекающего тока:
протекающего тока:
Ёмкостное сопротивление ( ). Величина ёмкостного сопротивления зависит от ёмкости элемента и также частоты протекающего тока :
Здесь 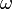 — циклическая частота, равная .
— циклическая частота, равная .
Прямая и обратная зависимость этих сопротивлений от частоты тока приводит к тому, что с увеличением частоты всё большую роль начинает играть индуктивное сопротивление и всё меньшую ёмкостное.
Электрическая ёмкость — характеристика проводника, мера его способности накапливать электрический заряд. В теории электрических цепей ёмкостью называют взаимную ёмкость между двумя проводниками; параметр ёмкостного элемента электрической схемы, представленного в виде двухполюсника. Такая ёмкость определяется как отношение величины электрического заряда к разности потенциалов между этими проводниками.
В системе СИ ёмкость измеряется в фарадах. В системе СГС в сантиметрах.
Для одиночного проводника ёмкость равна отношению заряда проводника к его потенциалу в предположении, что все другие проводники бесконечно удалены и что потенциал бесконечно удалённой точки принят равным нулю. В математической форме данное определение имеет вид
где Q — заряд, U — потенциал проводника.
Ёмкость определяется геометрическими размерами и формой проводника и электрическими свойствами окружающей среды (её диэлектрической проницаемостью) и не зависит от материала проводника. К примеру, ёмкость проводящего шара радиуса R равна (в системе СИ):C = 4πε0εR.
Понятие ёмкости также относится к системе проводников, в частности, к системе двух проводников, разделённых диэлектриком — конденсатору. В этом случае взаимная ёмкость этих проводников (обкладок конденсатора) будет равна отношению заряда, накопленного конденсатором, к разности потенциалов между обкладками.
где S — площадь одной обкладки (подразумевается, что они равны), d — расстояние между обкладками, ε — относительная диэлектрическая проницаемость среды между обкладками, ε0 = 8.854×10−12 Ф/м — электрическая постоянная
Индуктивность (или коэффициент самоиндукции) — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность, краем которой является этот контур.
В формуле
— магнитный поток, I — ток в контуре, L — индуктивность.
Иногда говорят об индуктивности прямого бесконечного провода (при этом подразумевается магнитный поток, создаваемый им через полуплоскость, им ограниченную).
Через индуктивность выражается ЭДС самоиндукции в контуре, возникающая при изменении в нём тока:
.
Из этой формулы следует, что индуктивность численно равна ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.
При заданной силе тока индуктивность определяет энергию магнитного поля тока:
.
Практически участки цепи со значительной индуктивностью выполняют в виде катушек индуктивности.
Рекомендуемые страницы:
Активное сопротивление, индуктивность, емкость в цепях синусоидального тока
Цепь с резистором (рис. 22).
Пусть приложенное напряжение изменяется по закону: . Определить закон изменения тока через резистор.
По закону Ома для участка цепи, содержащего резистор,
, следовательно, ток и напряжение на резисторе совпадают по фазе.
закон Ома для действующих значений напряжения и тока на резисторе.
Перейдем к комплексным выражениям тока и напряжения:
Закон Ома в комплексной форме для цепи с активным сопротивлением:
В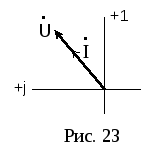 екторная
диаграмма для участка цепи синусоидального
тока, содержащего активное сопротивление,
показана на рис.23.
екторная
диаграмма для участка цепи синусоидального
тока, содержащего активное сопротивление,
показана на рис.23.
Цепь с индуктивностью (рис. 24).
Пусть приложенное
напряжение изменяется по закону: 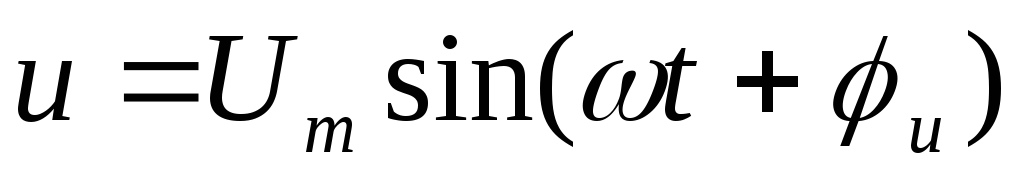 .
Определить закон изменения тока через
индуктивность
.
Определить закон изменения тока через
индуктивность .
.
По закону электромагнитной индукции:

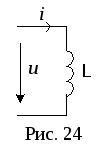
А=0 (постоянная интегрирования), т.к. ток должен быть синусоидальным и не должен иметь постоянную составляющую.

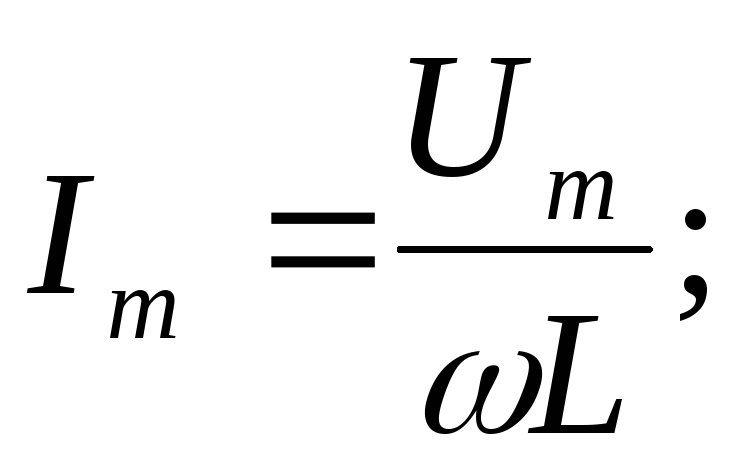 — индуктивное
сопротивление.
— индуктивное
сопротивление.
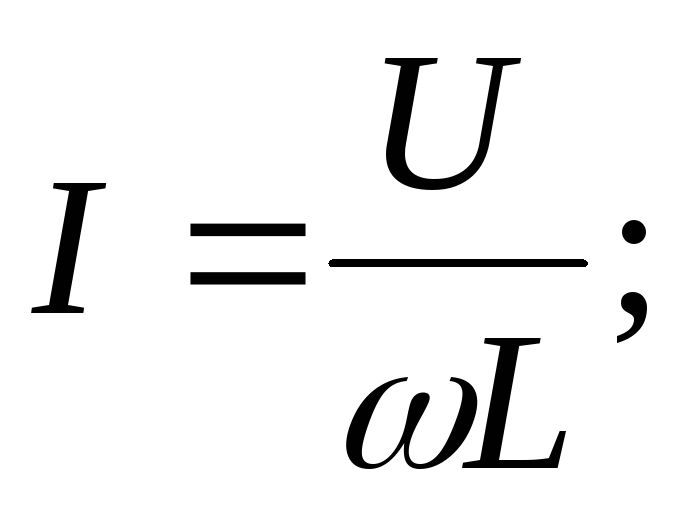
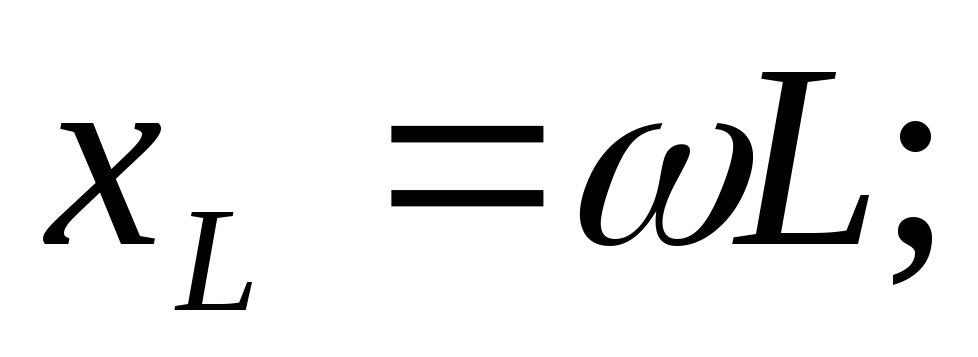
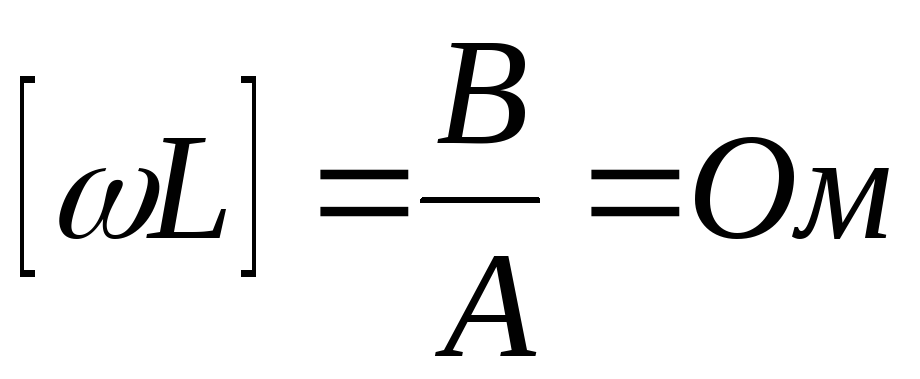
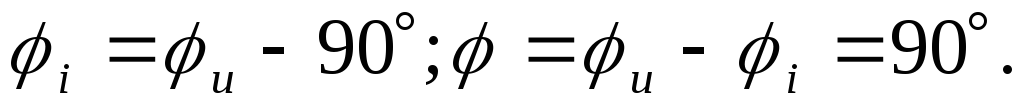
Ток на участке
цепи синусоидального тока, содержащем
индуктивность, отстает от напряжения
на угол 
Перейдем к комплексам тока и напряжения.
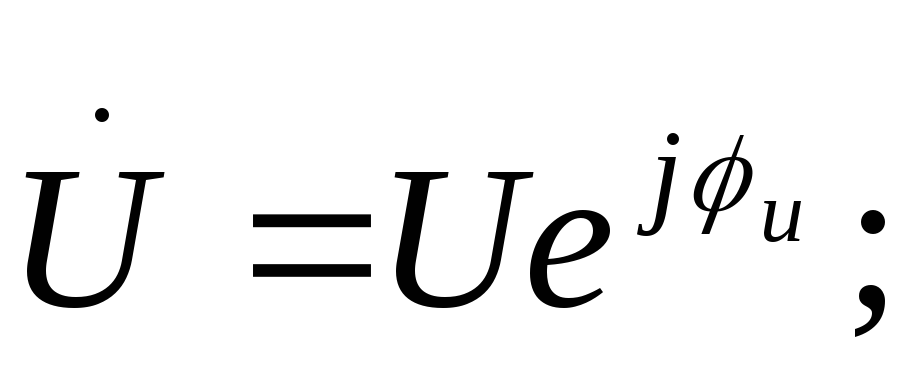
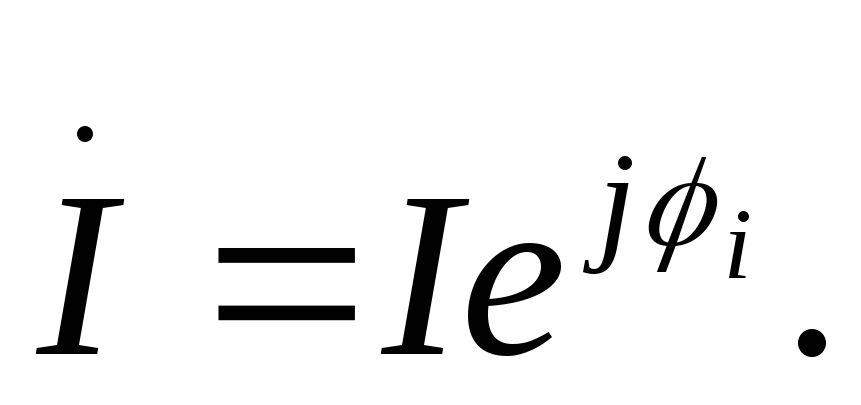
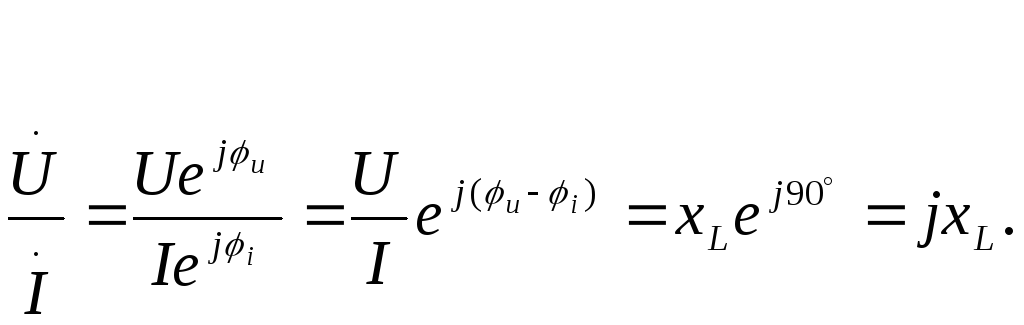
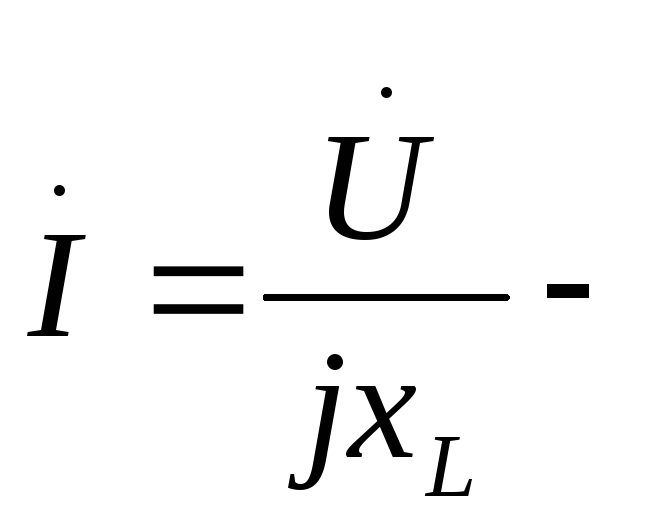 закон Ома для
участка цепи, содержащего индуктивность,
в комплексной форме;
закон Ома для
участка цепи, содержащего индуктивность,
в комплексной форме;
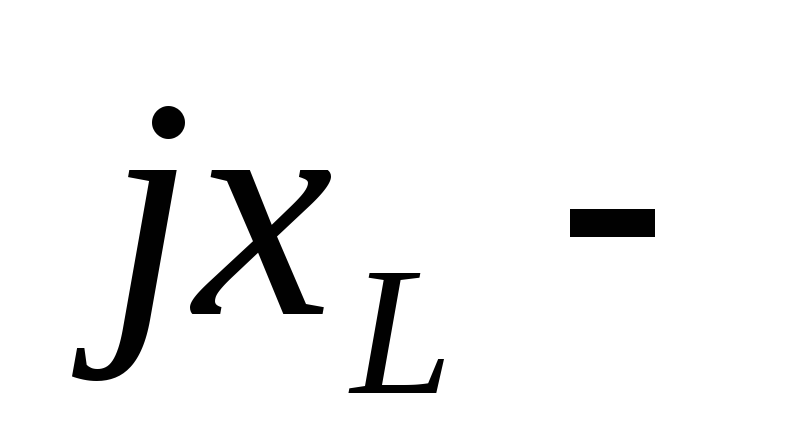 индуктивное
сопротивление в комплексной форме.
индуктивное
сопротивление в комплексной форме.
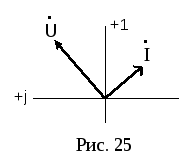
Векторная диаграмма для участка цепи, содержащего индуктивность, показана на рис. 25.
Цепь с емкостью (рис. 26).
Пусть приложенное
напряжение изменяется по закону: 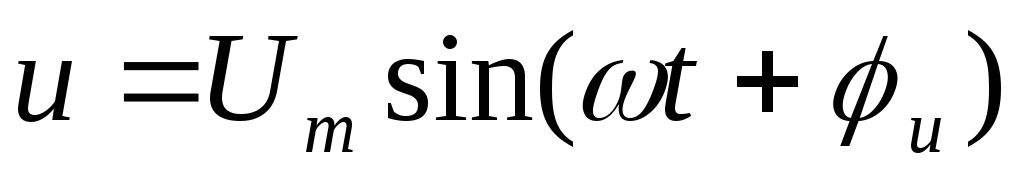 .
Определить закон изменения тока через
емкость
.
Определить закон изменения тока через
емкость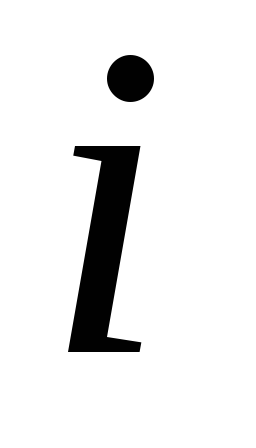 .
.
Т.к. электрический ток, протекающий через конденсатор, есть скорость изменения заряда на его обкладках, то
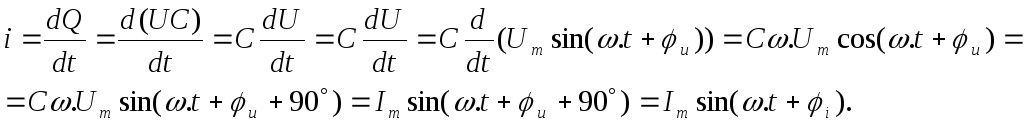
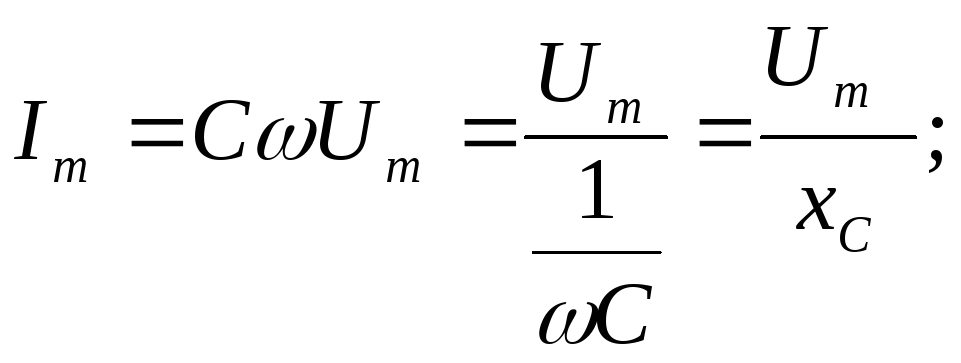
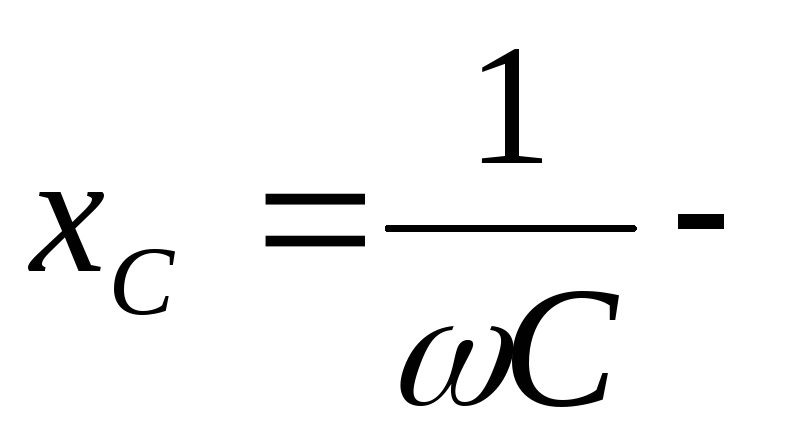 емкостное
сопротивление;
емкостное
сопротивление;
 закон Ома для
действующих значений тока и напряжения
на участке цепи, содержащем емкость.
закон Ома для
действующих значений тока и напряжения
на участке цепи, содержащем емкость.
Ток на емкости
опережает напряжение на угол 
Перейдем к комплексам напряжений и токов:
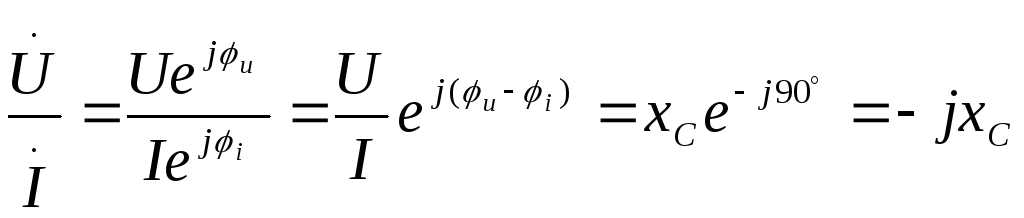
 — закон Ома в
комплексной форме;
— закон Ома в
комплексной форме;
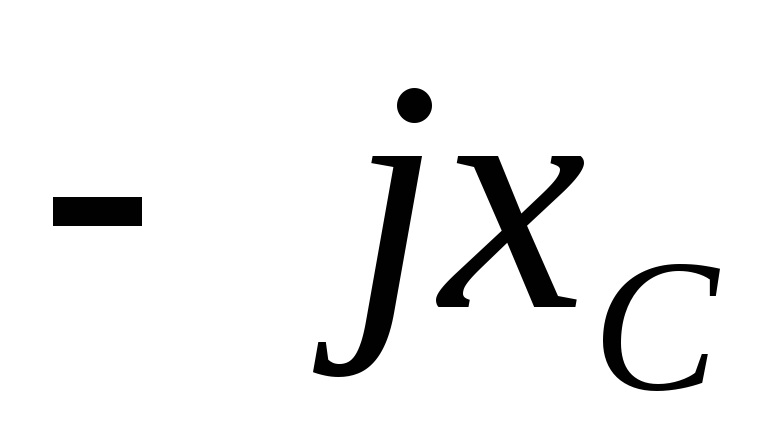 — емкостное
сопротивление в комплексной форме.
— емкостное
сопротивление в комплексной форме.
Векторная диаграмма для участка цепи, содержащего емкость, приведена на рис. 27.
Последовательное включение активного, индуктивного и емкостного сопротивлений в цепи синусоидального тока. Резонанс напряжений
Пусть приложенное
напряжение изменяется по закону: 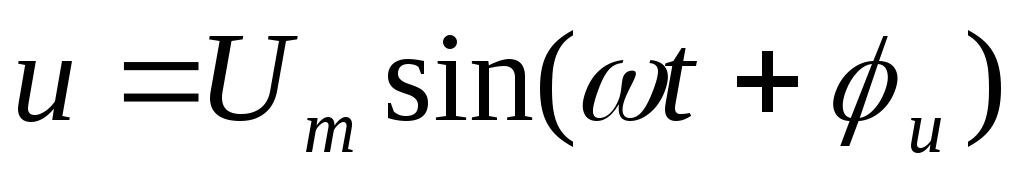 .
Участок цепи содержит последовательно
включенные резистор сопротивлениемR,
индуктивность L,
емкость С (рис. 28). Определить закон изменения тока
на этом участке цепи.
.
Участок цепи содержит последовательно
включенные резистор сопротивлениемR,
индуктивность L,
емкость С (рис. 28). Определить закон изменения тока
на этом участке цепи.
По второму закону
Кирхгофа: 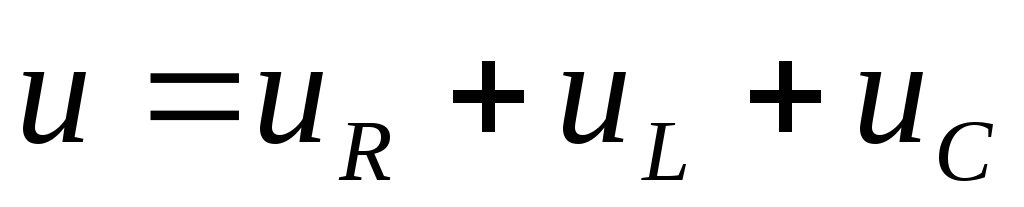 ,
или в комплексной форме:
,
или в комплексной форме: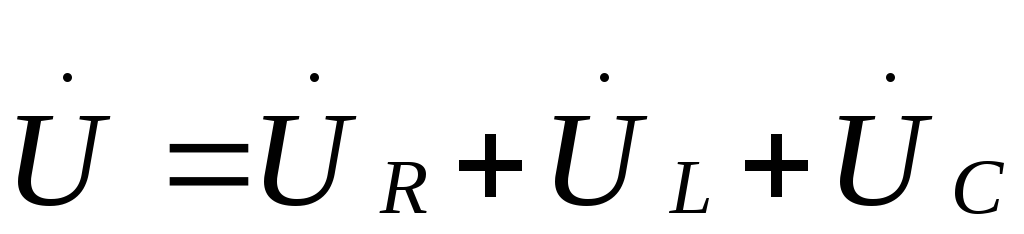 .
Подставим в эту формулу выражения для
падений напряжения на различных
элементах:
.
Подставим в эту формулу выражения для
падений напряжения на различных
элементах:
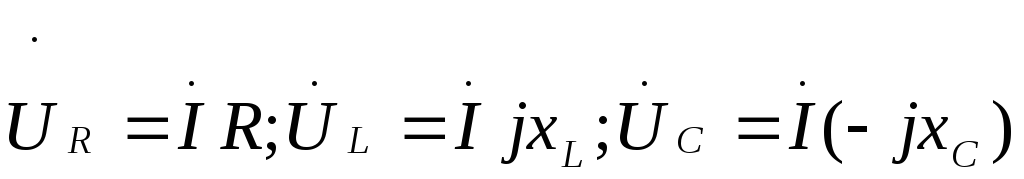 .
.
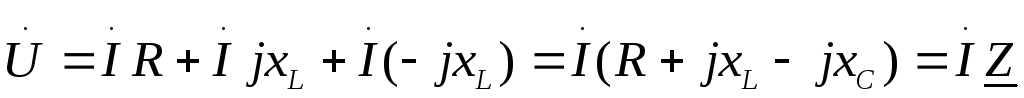 .
.
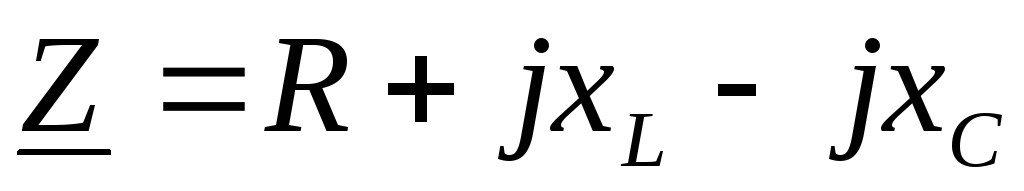
 — комплексное
сопротивление цепи.
— комплексное
сопротивление цепи.
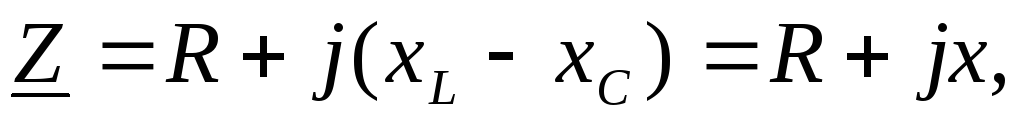 где
где 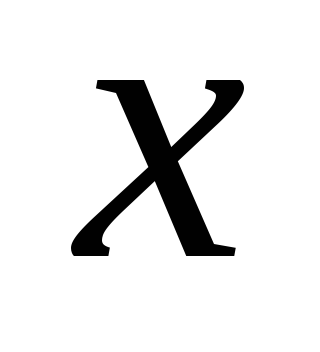 —
реактивное сопротивление.
—
реактивное сопротивление.
Представим комплексное сопротивление в показательной форме:
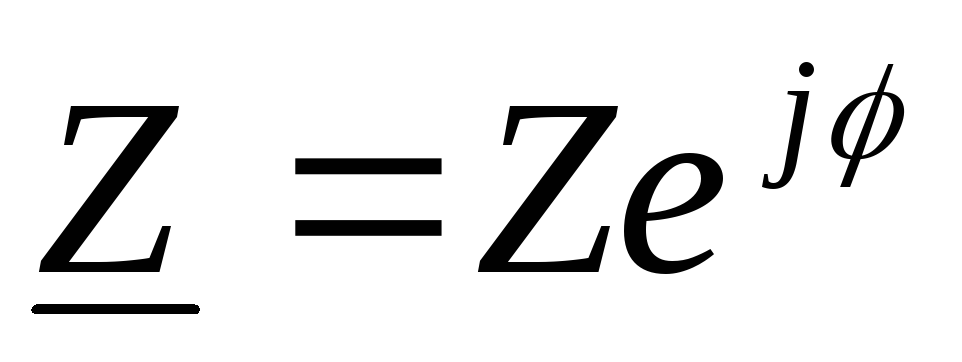 ,
, 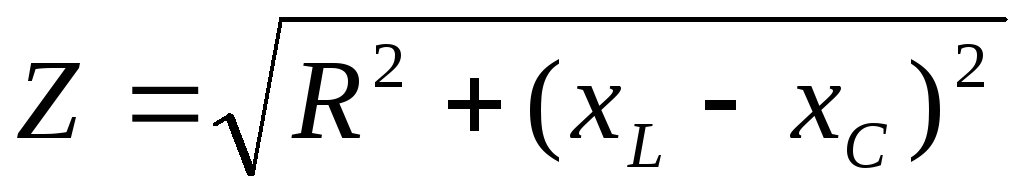 ;
;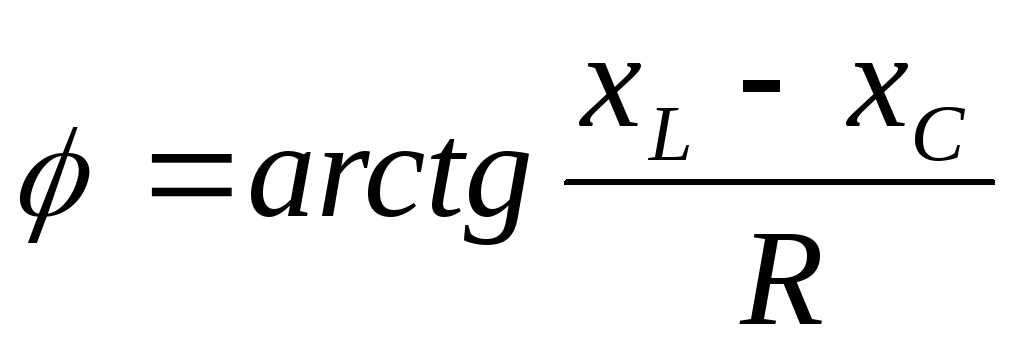 ,
,
где 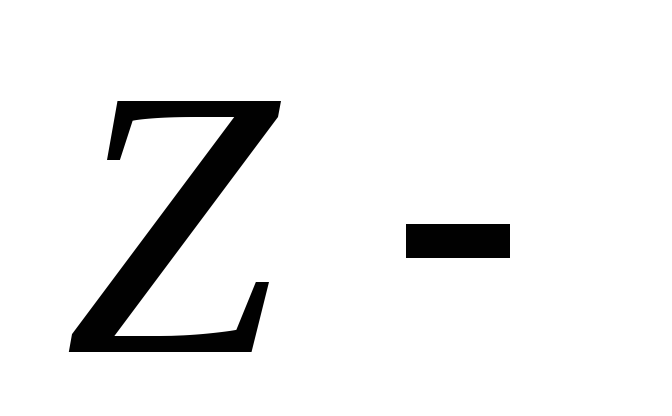 модуль
комплексного сопротивления; полное
сопротивление цепи.
модуль
комплексного сопротивления; полное
сопротивление цепи.
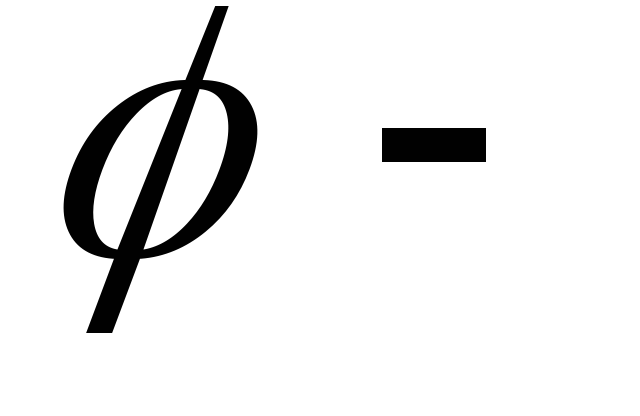 аргумент
(фаза) сопротивления.
аргумент
(фаза) сопротивления.
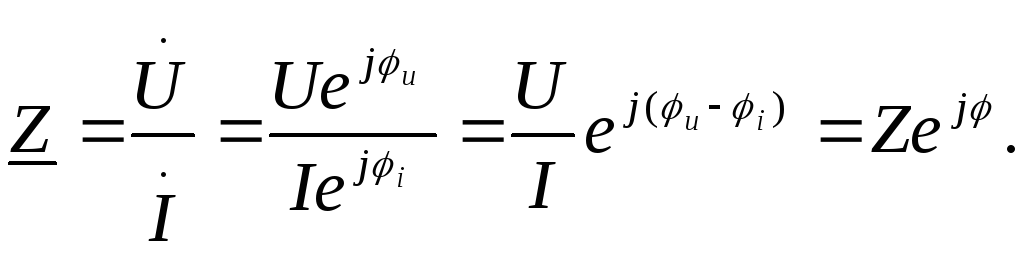
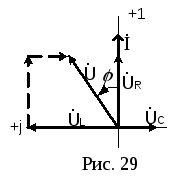
Векторная диаграмма приведена на рис. 29.
Выводы:
В цепи с последовательным соединением R, L, C справедлив закон Ома:
 .
.Угол сдвига фаз между напряжением и током равен аргументу комплексного сопротивления. Знак угла сдвига определяется знаком реактивного сопротивления.
а)  — участок имеет активно-индуктивный
характер, ток отстает от напряжения на
угол, меньше 90
(см. рис. 29).
— участок имеет активно-индуктивный
характер, ток отстает от напряжения на
угол, меньше 90
(см. рис. 29).
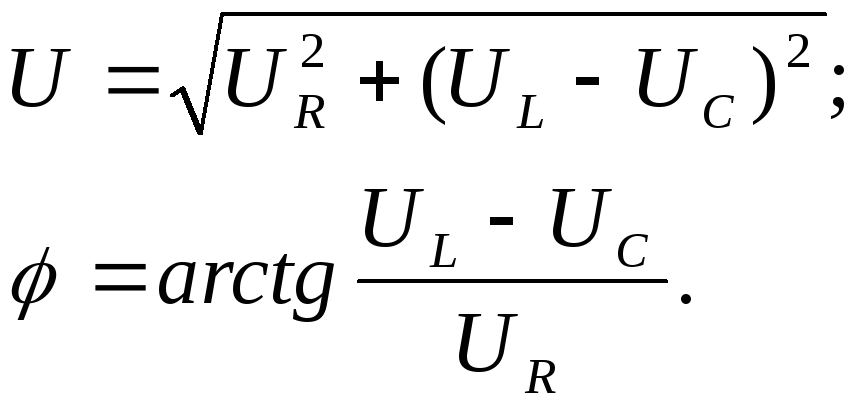
б) 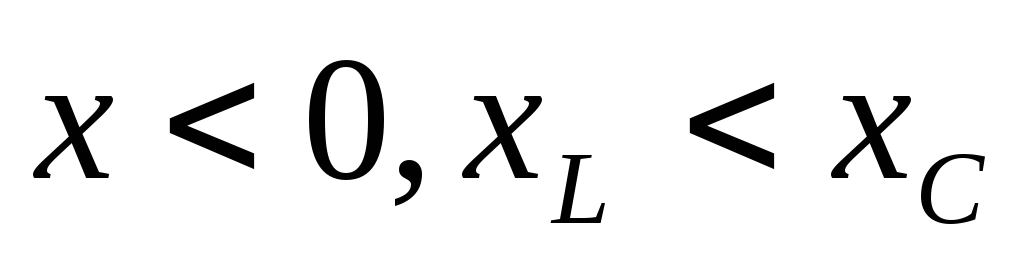 — участок имеет активно-емкостный
характер, ток опережает напряжение на
угол, меньше 90
(рис. 30).
— участок имеет активно-емкостный
характер, ток опережает напряжение на
угол, меньше 90
(рис. 30).
в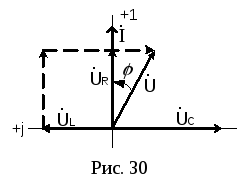 )
)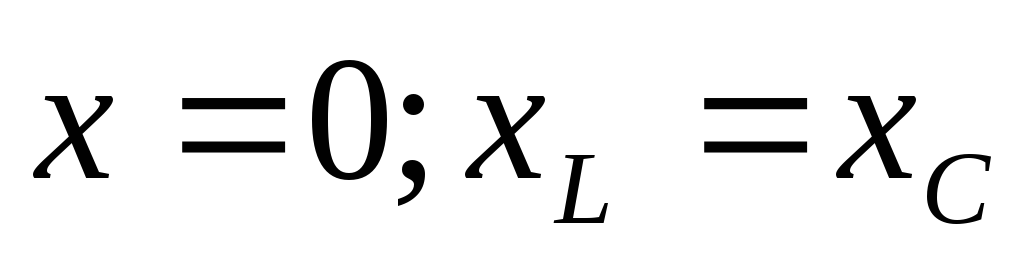 — участок имеет активный характер, ток
и напряжение совпадают по фазе (рис.
31). В цепи наблюдается резонанс напряжений.
— участок имеет активный характер, ток
и напряжение совпадают по фазе (рис.
31). В цепи наблюдается резонанс напряжений.
Р езонансом
в электрических цепях называется режим
участка цепи, содержащий индуктивный
и емкостный элементы, при котором угол
сдвига фаз между напряжением и током
равен 0.
езонансом
в электрических цепях называется режим
участка цепи, содержащий индуктивный
и емкостный элементы, при котором угол
сдвига фаз между напряжением и током
равен 0.
резонанс напряжений – при последовательном соединении элементов;
резонанс токов – при параллельном соединении элементов.
При последовательном соединении элементов (см. рис. 31) во время резонанса напряжений
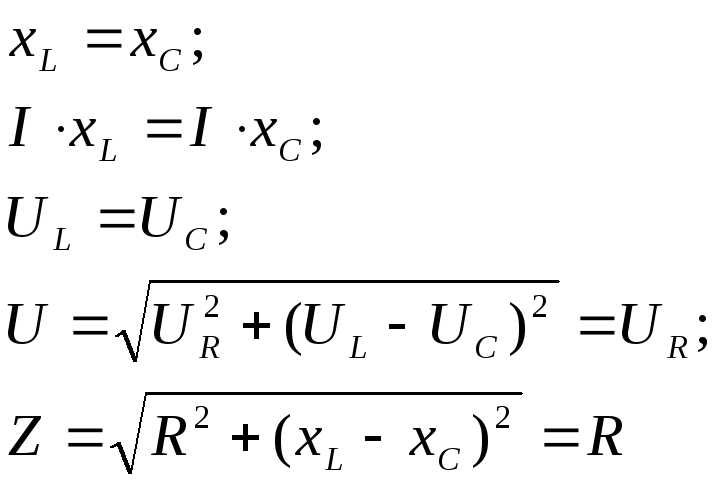
Таким образом, при резонансе напряжений полное сопротивление цепи минимально в сравнении с нерезонансными режимами, следовательно, ток максимален (по закону Ома), возможен перегрев элементов. В то же время напряжение на реактивных элементах может в несколько раз превышать напряжение питания, если реактивные сопротивления больше активного.
Явление резонанса напряжения используется в радиотехнике, но, в то же время, опасно, т.к. возможен пробой изоляции проводов.
По условию резонанса
напряжений 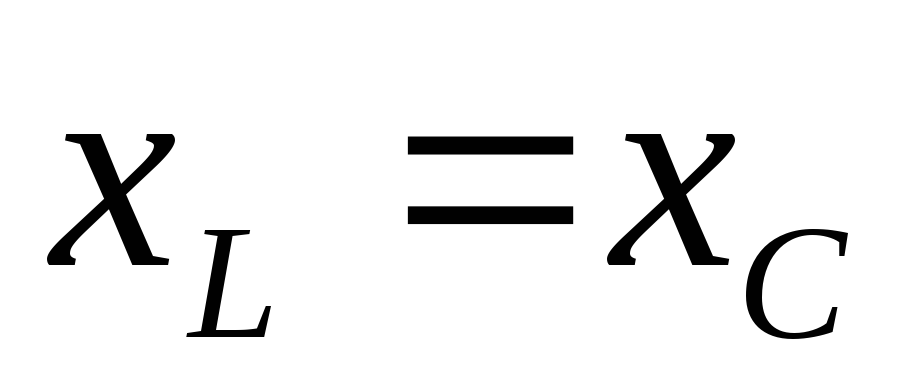 .
Тогда
.
Тогда 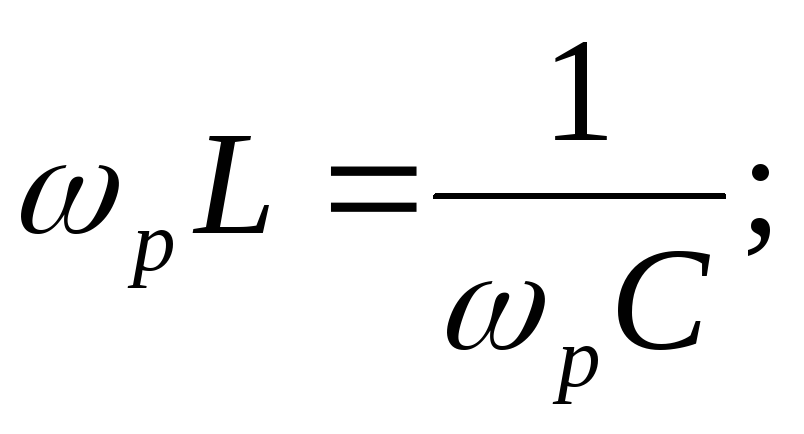
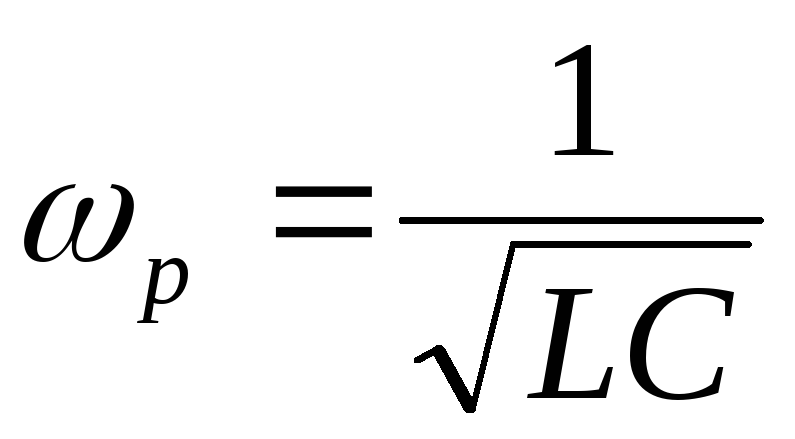 ,
где
,
где 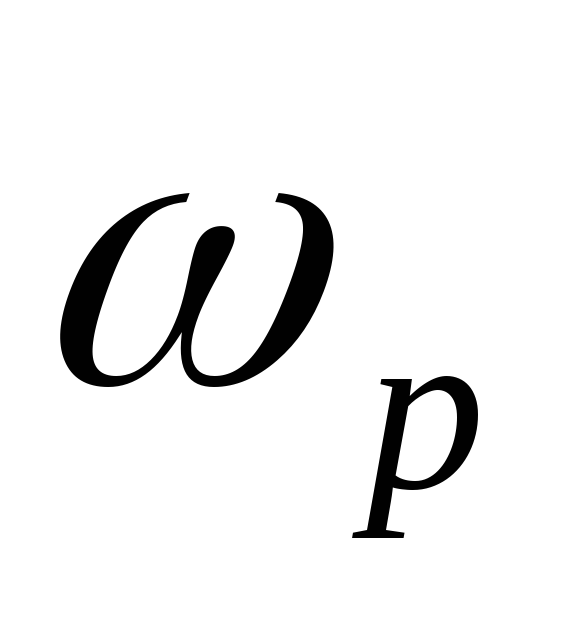 —
частота питающей сети, при которой в
цепи может наступить резонанс.
—
частота питающей сети, при которой в
цепи может наступить резонанс.
Получение резонанса напряжений возможно изменением индуктивности, емкости и частоты.

























































 — элемент проявляет свойства индуктивности.
— элемент проявляет свойства индуктивности.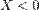 — элемент проявляет ёмкостные свойства.
— элемент проявляет ёмкостные свойства.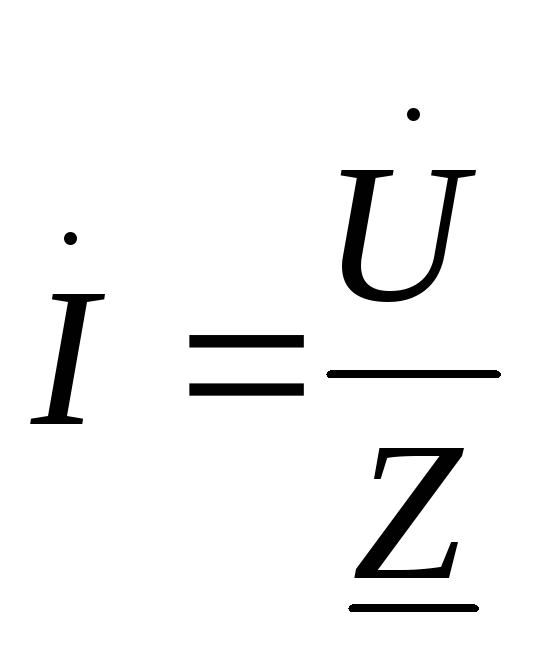 .
.