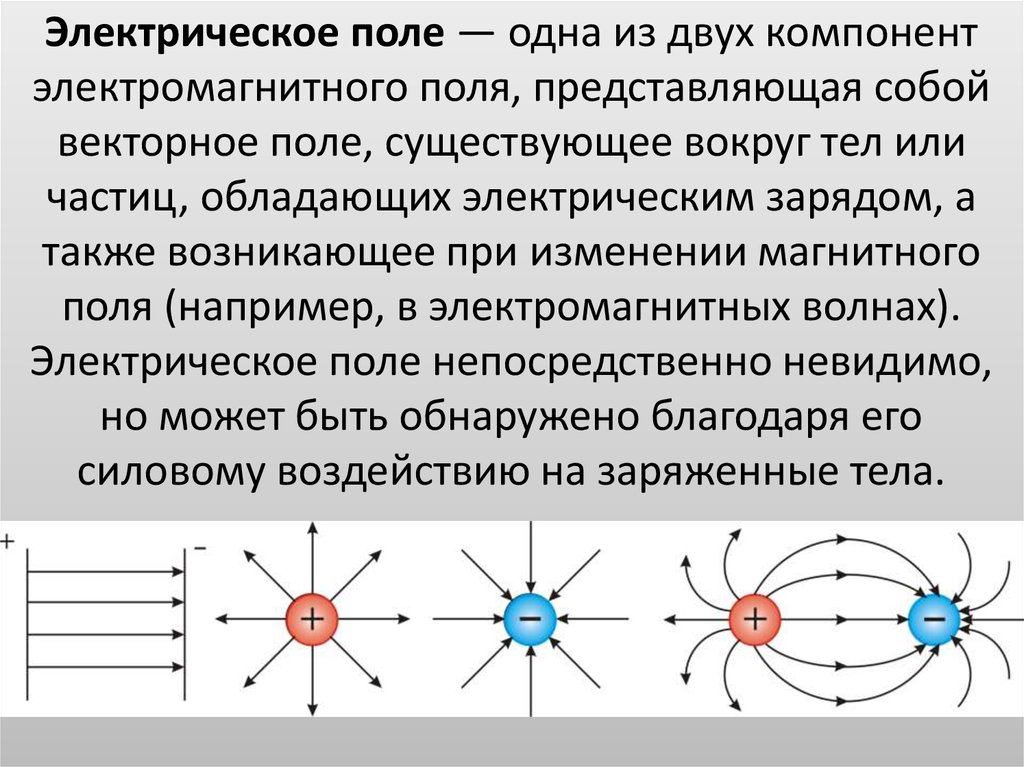
Вихревое электрическое поле

Причина возникновения электрического тока в неподвижном проводнике — электрическое поле. Всякое изменение магнитного поля порождает индукционное электрическое поле независимо от наличия или отсутствия замкнутого контура, при этом если проводник разомкнут, то на его концах возникает разность потенциалов; если проводник замкнут, то в нем наблюдается индукционный ток.

Индукционное электрическое поле является вихревым. Направление силовых линий вихревого эл. поля совпадает с направлением индукционного тока Индукционное электрическое поле имеет совершенно другие свойства в отличии от электростатического поля.

электростатическое поле	индукционное электрическое поле ( вихревое электр. поле )
1. создается неподвижными электр. зарядами	1. вызывается изменениями магнитного поля
2. силовые линии поля разомкнуты — -потенциальное поле	2. силовые линии замкнуты — — вихревое поле
3. источниками поля являются электр. заряды	3. источники поля указать нельзя
4. работа сил поля по перемещению пробного заряда по замкнутому пути = 0.	4. работа сил поля по перемещению пробного заряда по замкнутому пути = ЭДС индукции

Вихревые токи

Индукционные токи в массивных проводниках называют токами Фуко. Токи Фуко могут достигать очень больших значений, т. к. сопротивление массивных проводников мало.Поэтому сердечники трансформаторов делают из изолированных пластин. В ферритах -магнитных изоляторах вихревые токи практически не возникают.

Использование вихревых токов: нагрев и плавка металлов в вакууме; демпферы в электроизмерительных приборах.

Вредное действие вихревых токов: потери энергии в сердечниках трансформаторов и генераторов из-за выделения большого количества тепла.

Эдс индукции в движущихся проводниках

Прямолинейный проводник АВ движется в магнитном поле с индукцией В по проводящим шинам, которые замкнуты на гальванометр.

На электрические заряды, перемещающиеся вместе с проводником в магнитном поле, действует сила Лоренца: Fл = /q/vB sin a Её направление можно определить по правилу левой руки. Под действием Fл внутри проводника происходит распределение положительных и отрицательных зарядов вдоль всей длины проводника l.

Сила Лоренца является в данном случае сторонней силой, и в проводнике возникает ЭДС индукции, а на концах проводника АВ возникает разность потенциалов.

Причина возникновения ЭДС индукции в движущемся проводнике объясняется действием силы Лоренца на свободные заряды.

Готовимся к проверочной работе!

1. При каком направлении движения контура в магнитном поле в контуре будет возникать индукционный ток?

2. Укажите направление индукционного тока в контуре при введении его в однородное магнитное поле.

3. Как изменится магнитный поток в рамке, если рамку повернуть на 90 градусов из положения 1 в положение 2 ?

4. Будет ли возникать индукционный ток в проводниках, если они движутся так, как показано на рисунке?

5. Определить направление индукционного тока в проводнике АБ, движущемся в однородном магнитном поле.

6. Указать правильное направление индукционного тока в контурах.

материалы к зачету физика_11-4

11 класс

Материалы к зачету по теме «Электромагнитная индукция»

1. Явление электромагнитной индукции, открытое Майклом Фарадеем, состоит в возникновении ЭДС индукции в замкнутом контуре при изменении магнитного потока через площадь, ограниченную этим контуром. Согласно закону электромагнитной индукции ЭДС индукции в замкнутом контуре равна скорости изменения магнитного потока, взятой со знаком «минус»:

.

Здесь — поток магнитной индукции через площадь контура S, В

n — проекция вектора магнитной индукции на нормаль к контуру.
Знак «минус» объясняется правилом Ленца, определяющим направление индукционного тока: индукционный ток в замкнутом контуре имеет такое направление, что созданный им магнитный поток через площадь, ограниченную контуром, стремится компенсировать то изменение магнитного потока, которое порождает данный ток.

2. В неподвижном проводнике сторонней силой, создающей ЭДС индукции, является вихревое (индукционное) электрическое поле, порождаемое переменным магнитным полем. В движущемся проводнике источником ЭДС индукции является магнитная сила Лоренца, действующая на движущиеся вместе с проводником заряженные частицы.

3. При движении проводника длиной со скоростью в однородном магнитном поле с индукций В возникает ЭДС индукции

,

где α — угол между векторами скорости и магнитной индукции .

4. Важный частный случай электромагнитной индукции — самоиндукция. При самоиндукции изменяющееся магнитное поле индуцирует ЭДС в том проводнике, по которому течет ток, создающий это поле.

ЭДС самоиндукции прямо пропорциональна скорости изменения силы тока в проводнике:

.

Коэффициент пропорциональности L называют индуктивностью. Индуктивность зависит от размеров и формы проводника, а также от свойств среды, в которой находится проводник. Измеряют ее в генри:

.

5. Энергия магнитного поля тока

равна той работе, которую должен совершить источник, чтобы создать данный ток.

6. Магнитное поле без электрического поля, так же как электрическое поле без магнитного, могут существовать только в определенной системе отсчета. Они являются проявлением единого целого — электромагнитного поля, особой формой существования материи.

Фундаментальное свойство электромагнитного поля: изменяясь во времени, магнитное поле порождает переменное электрическое поле и наоборот.

В разделе справочные материалы можно найти полезную информацию

---

вернуться на страницу «Физика»

вверх

23.4: Наведенное электрическое поле и вихревые токи

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

19544

• Howard Martin пересмотрено Аланом Нг
• University of Wisconsin-Madison

До сих пор мы описывали электромагнитную индукцию в терминах напряжения, индуцируемого изменяющимся магнитным полем.

B \vec E \cdot d\vec l\end{aligned}\] В случае индуцированного напряжения на контуре точки \(A\) и \(B\) совпадают. Таким образом, интеграл находится по замкнутому пути: \[\begin{aligned} \Delta V = \oint \vec E\cdot d\vec l\end{aligned}\] Мы можем включить это в закон Фарадея, используя электрическое поле вместо разности потенциалов:

\[\begin{выровнено} \Delta V=-\frac{d\Phi_{B}}{dt} \end{выровнено}\]

\[\поэтому\oint\vec E\cdot d\vec l=-\frac{d\Phi_{B}}{dt}\]

, где последняя строка представляет собой более общую форму закона Фарадея. Обратите внимание, что в случае электростатики, где электрическое поле создается распределением зарядов, интеграл \(\oint \vec E\cdot d\vec l\) должен быть равен нулю, поскольку электрическая сила консервативна; работа, совершаемая электрическим полем над зарядом \(q\) на замкнутом пути, которая представляет собой просто заряд \(q\), умноженный на этот интеграл, должна быть равна нулю. Сила электрического поля, индуцируемая изменяющимся во времени магнитным полем, не является консервативной!

Закон Фарадея, выраженный с помощью электрического поля, является гораздо более общим и подразумевает, что изменяющееся во времени магнитное поле будет индуцировать электрическое поле. Это верно, независимо от того, существует ли физический провод для передачи индуцированного тока.

Пример \(\PageIndex{1}\)

Круглая область пространства с радиусом \(R\) содержит однородное магнитное поле, величина которого уменьшается со временем: \[\begin{aligned} \ vec B(t) = B_0(1-at)\hat z\end{aligned}\], где \(a\) и \(B_0\) — положительные константы. Определить электрическое поле на расстоянии \(r\) от центра области, внутри и вне области с магнитным полем.

Решение :

На рисунке \(\PageIndex{2}\) показана круговая область магнитного поля, а также круговая траектория радиуса \(r\), которая определяет область, для которой мы вычисляем поток магнитного поля.

Рисунок \(\PageIndex{2}\): Линии индуцированного электрического поля образуют замкнутые круги при изменении магнитного поля.

Сначала рассмотрим индуцированное электрическое поле в области с магнитным полем, где \(r 2\\ 2E &= B_0ar\ \ \поэтому E&=\frac{B_0a}{2}r\quad\text{(внутри области магнитного поля)}\end{aligned}\] и мы видим, что внутри области с магнитным полем напряженность индуцированного электрического поля пропорциональна расстоянию от центра области (т. е. линейно возрастает с \(r\)). 92}{2r}\quad\text{(вне области магнитного поля)}\end{aligned}\] Вне области с магнитным полем величина электрического поля уменьшается по мере удаления от центра области .

Обсуждение:

В этом примере мы определили электрическое поле, которое индуцируется переменным магнитным полем. В этом случае силовые линии электрического поля образуют замкнутые круги и приводят к неконсервативной силе. Когда электрическое поле формируется распределением электрических зарядов, силовые линии начинаются и заканчиваются на зарядах, чего не происходит в случае индуцированного электрического поля.

Когда проводящий материал перемещается в область магнитного поля, в материале индуцируется электрическое поле, образующее замкнутые петли, в результате чего возникают небольшие токовые петли, называемые «вихревыми токами». Затем магнитное поле может воздействовать на эти токи, что фактически приводит к силе воздействия на материал. Это принцип магнитного торможения, который используется в некоторых поездах и в других приложениях.

На рисунке \(\PageIndex{3}\) показано, как можно использовать магнитный тормоз для замедления вращения колеса, сделанного из проводящего материала (материал должен проводить ток, иначе индуцированное электрическое поле не будет производить ток). Магнитное поле создается (например, фиксированным постоянным магнитом) в направлении, перпендикулярном колесу, на небольшой площади (показано внизу колеса на рисунке \(\PageIndex{3}\)).

Рисунок \(\PageIndex{3}\): Вращающееся колесо из проводящего материала имеет небольшую область с магнитным полем. Вихревые токи в области изменяющегося потока приводят к чистому нисходящему току в центре области. Магнитная сила, действующая на этот ток, замедляет колесо.

Для материала, расположенного внизу слева от колеса, магнитный поток увеличивается, так как материал перемещается из области без магнитного поля в область с магнитным полем. В этой части области будут образовываться вихревые токи, направленные по часовой стрелке, которые приводят к возникновению магнитного поля на странице, чтобы противодействовать возрастающему магнитному потоку (закон Ленца). Нижняя правая сторона колеса покидает магнитное поле и, таким образом, будет иметь вихревые токи в противоположном направлении. Токи с обеих сторон складываются в центре, что приводит к чистому нисходящему току. Магнитная сила этого нисходящего тока направлена ​​влево, что приводит к крутящему моменту, замедляющему колесо. Это магнитное торможение.

Опять же, это не более чем сохранение энергии в игре. Поскольку мы индуцируем токи, заставляя колесо двигаться в область магнитного поля или из нее, электрическая энергия в этих токах должна откуда-то поступать (либо мы делаем работу, чтобы колесо вращалось, либо колесо теряет кинетическую энергию). Всякий раз, когда мы пытаемся провести проводник через магнитное поле так, чтобы индуцировался ток, нам придется приложить силу и совершить работу. В случае магнитного торможения колесо будет преобразовывать свою кинетическую энергию вращения в тепло (вихревые токи будут нагревать колесо). Основная проблема с магнитным торможением заключается в том, что нужно рассеивать тепло. Основным преимуществом является отсутствие изнашиваемых деталей, в отличие от торможения с трением. Кроме того, магнитное торможение очень плавное и действует только при наличии движения. Как только колесо перестает вращаться, магнитный поток везде постоянен и вихревые токи исчезают.

Упражнение \(\PageIndex{1}\)

Предположим, что магнитное поле на рисунке \(\PageIndex{3}\) указывает на страницу. Будет ли работать магнитный тормоз?

1. Да.
2. №

Ответить

---

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Райан Мартин и др.

   Лицензия

   CC BY-SA

   Показать оглавление

   нет

2. Теги

   На этой странице нет тегов.

Физика для науки и техники II

9.2 Наведенные электрические поля из Office of Academic Technologies на Vimeo.

9.2 Наведенные электрические поля

Ранее мы видели, что если магнитный поток, проходящий через область, окруженную проводящей петлей, изменяется, то мы получаем индуцируемую электродвижущую силу, усиленную индуцированным током вдоль этой петли непосредственно из закона Фарадея.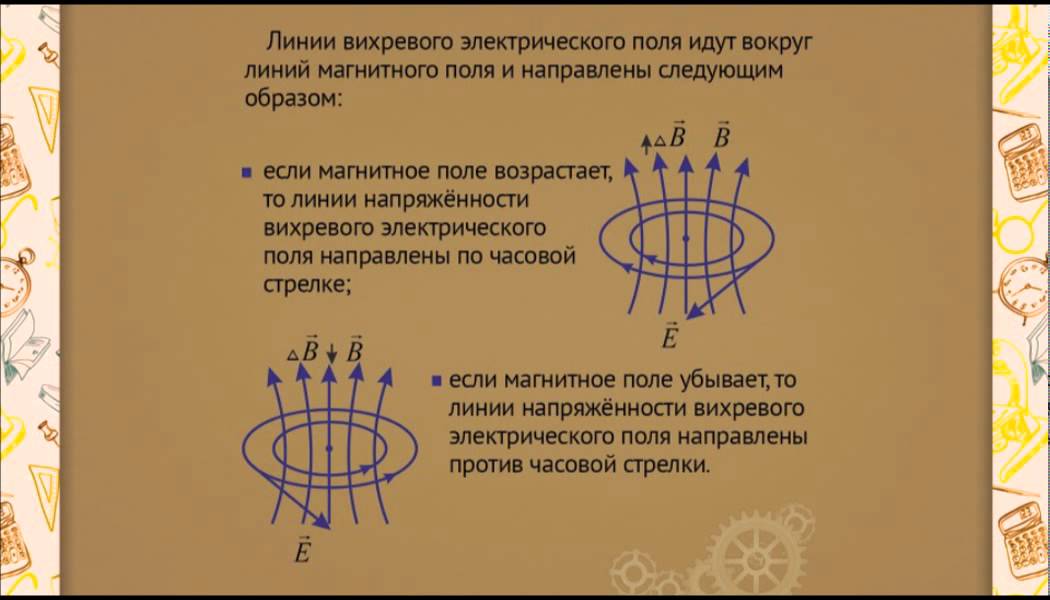 Если мы рассмотрим магнитное поле, скажем, направленное в плоскость, как-то так, то допустим, что оно нарастает в плоскость. И если мы поместим внутри этой области замкнутую проводящую петлю, скажем, круглую петлю, то поток через область, окруженную этой петлей, будет меняться. В результате мы получим индуцированную электродвижущую силу по закону Фарадея, которая, в свою очередь, вызовет индуцированный ток, протекающий через эту петлю.

И из закона Ленца, как только мы определяем направление тока, который говорит, что он должен течь в таком направлении, что он будет противодействовать его курсу, и его курс представляет собой возрастающее магнитное поле в плоскости, поэтому единственное способ, которым он может противодействовать этому, генерируя ток, магнитное поле которого будет направлено в противоположную сторону этому внешнему магнитному полю, и для того, чтобы ток протекал в этом направлении по этой петле, используя правило правой руки, мы хотим, чтобы магнитное поле выходит из плоскости через область, окруженную этой петлей, поэтому ток должен течь в направлении против часовой стрелки через эту петлю.

Что ж, когда мы смотрим на этот процесс, это в каком-то смысле эквивалентно тому, чтобы сказать, что то же самое магнитное поле, которое у нас есть здесь, направлено в плоскость, и если мы просто рассмотрим один из зарядов, движущихся по этому пути, , чтобы заряд, чтобы точечный заряд двигался в этом направлении, по этой круговой траектории, мы должны иметь электрическое поле в среде, в круговой форме, вот так. Другими словами, это электрическое поле будет воздействовать на этот заряд кулоновской силой, так что заряд будет двигаться в направлении этой силы. Чтобы двигаться по такой круговой орбите, эта сила должна быть всегда касательной к окружности, что-то вроде этого. Для этого соответствующая линия электрического поля должна иметь круглую форму.

Другими словами, это будет эквивалентно случаю, когда у нас будет индуцированная линия электрического поля, которая будет иметь форму круга. Что-то вроде этого. А если мы поместим заряд, то для простоты рассмотрим здесь положительный заряд, и этот заряд будет находиться под действием кулоновской силы, которая будет касаться всегда этой силовой линии, а эта силовая линия есть электрическое поле, и при каждом точки вдоль этой траектории под действием этой кулоновской силы, заряд будет двигаться вдоль этой круговой линии электрического поля.

Таким образом, мы можем связать этот случай со следующим, сказав, что, хотя мы начинаем с изменения магнитного поля, которое увеличивается в плоскости, мы заканчиваем с электрическим полем в форме концентрических линий электрического поля. Другими словами, изменение магнитного поля порождает электрическое поле, силовые линии которого имеют форму концентрических окружностей в этой среде. Конечно, если B не изменяется, если оно постоянно, то магнитный поток через этот круговой провод или через область, окруженную круговым проводом, будет равен константе, а так как он не меняется, то по закону Фарадея , производная от константы даст нам 0, мы не получим никакой индуцированной электродвижущей силы и, следовательно, тока. Но если оно меняется, то это изменение будет результатом индукции электрического поля в среде, вот так.

Таким образом, если мы подведем итоги до этого момента, мы можем сказать, что в этом случае i индуцированные будут отображаться в направлении против часовой стрелки. Это из закона Ленца и закона Фарадея. И i индуцируется, конечно, непосредственно связано с индуцируемым электрическим полем, и мы можем видеть, связывая этот первый случай с этим случаем, что это в некотором смысле эквивалентно этому случаю, потому что если мы просто рассмотрим движение одного заряда и его будет выглядеть так. И в этом случае изменяющееся магнитное поле порождало электрическое поле.

Если мы посмотрим на эту часть, скажем, наша проволока имеет радиус r , поэтому мы смотрим на линию поля, индуцированную линию поля, с таким же радиусом r здесь. Согласно закону Фарадея, индуцированная ЭДС представляет собой изменение потока во времени, и если мы посмотрим на этот процесс здесь, то, конечно, кулоновская сила будет совершать работу по перемещению заряда по этому наклону. Работа, выполненная в этом процессе, если обозначить ее через W , будет равна силе, усеянной смещением, интегрированным по всему пути, назовем ее F точка d l , встроенный общий путь.

Здесь d l вектор приращения смещения в направлении, или вдоль направления траектории, и куда мы пойдем, мы увидим, что угол между F и d l идет быть равным 0, поэтому проделанная работа будет равна, следовательно, интегралу от величины F умножить на dl умножить на косинус угла между ними, который равен 0 градусов. Косинус 0 равен 1, а величина F здесь постоянно, и это кулоновская сила, равная q , умноженная на индуцированное электрическое поле E .

Таким образом, проделанная работа будет равна qE умножить на dl , и эти величины постоянны, мы можем взять их за пределы интеграла. Следовательно, проделанная работа на этом пути становится интегралом qE , умноженным на dl . Конечно путь закрытый путь, и по мере того, как мы идем по этому пути и добавляем все эти dl друг к другу по этому пути, мы получим длину этого пути, и это будет длина окружности, которая равна 2 πr . Таким образом, проделанная работа будет равна qE умножить на 2 πr .

С другой стороны, как вы помните из определения потенциала, в котором мы определяли потенциал как работу, совершаемую на единицу заряда, эту работу можно также выразить как заряд, умноженный на потенциал, или напряжение, или разность потенциалов. Что ж, этот потенциал, или напряжение, является индуцированным напряжением ε . Итак, у нас есть два выражения для работы. Один из них представляет собой ЭДС индукции, умноженную на заряд, а другой равен q x E x 2 πr . Поскольку левые части этих уравнений равны, мы можем приравнять и правые части. При этом мы получим q умножить на ε равно qE умножить на 2 πr . Здесь заряды нейтрализуются с обеих сторон, а ЭДС индукции будет равна E умножить на 2 πr .

Ну, другими словами, произведение величины электрического поля и длины петли, мы можем обобщить это выражение, сказав, что ЭДС индукции равна интегралу по замкнутому пути E точка d л . Причина этого в том, что когда электрическое поле генерируется в результате изменения магнитного поля в регионе, эти силовые линии всегда будут замкнутыми силовыми линиями. Поэтому интеграл по пути будет браться по замкнутому пути или по замкнутому контуру.

Ну, ЭДС индукции также была равна, согласно закону Фарадея, d Φ B над dt, то есть скоростью изменения магнитного потока. Мы можем объединить эти два выражения, чтобы выразить закон Фарадея в его наиболее общей форме, сказав, что интеграл от E точка d l по замкнутому контуру или замкнутому контуру будет равен минусу, и снова мы можно обобщить это N количество терминов, умножив на количество терминов N здесь, умноженное на скорость изменения потока. Итак, это самая общая форма закона индукции Фарадея.

Теперь это просто констатация того, что если магнитный поток изменяется через область, окруженную проводящей петлей, то мы получим индуцированную электродвижущую силу. Теперь, если мы возьмем интеграл E точка d l вдоль замкнутого проводящего контура, это также даст нам индуцированную электродвижущую силу вдоль этого контура. Эта величина будет равна 0, если поток через область, окруженную этой петлей, постоянен. Он будет отличаться от 0, если он меняется, если поток меняется со временем.

Итак, это приведет нас к интересному моменту, который заставит нас по-новому взглянуть на электрический потенциал. Скажем, новый взгляд на концепцию электрического потенциала. А то есть электрический потенциал имеет значение только для электрических полей, создаваемых статическими зарядами. Оно не имеет никакого значения для электрических полей, создаваемых индукцией. Отметим это, сказав, что электрический потенциал имеет значение только для электрических полей, создаваемых статическими зарядами. Это не имеет значения для электрических полей, созданных индукцией.

Теперь, что касается статических зарядов, у нас в какой-то момент были собраны положительные заряды, а затем в какой-то момент собрались отрицательные заряды, вот так. Как только мы получаем таким образом разделение зарядов или поляризацию, мы немедленно получаем результирующее электрическое поле, направленное от положительного заряда к отрицательному заряду, и, как вы помните, поскольку потенциал, связанный с положительным зарядом, больше, чем связанный с ним потенциал. с отрицательным зарядом или отрицательным точечным зарядом, то мы получаем определенную разность потенциалов В вольт между этими двумя точками, и это было равно Vf минус В i , и что было равно работе, выполненной при перемещении заряда из начальной в конечную точку. Допустим, это начальное, это конечное, на единицу заряда, а это тоже было равно минусу, минусу E точка d l , интегрированному от начальной до конечной точки.

Итак, в случае индукции мы получаем замкнутые силовые линии электрического поля. Другими словами, для статических зарядов силовые линии электрического поля всегда являются открытыми силовыми линиями, исходящими из положительного входа в отрицательный полюс. Но с помощью индукции, как мы видели несколько минут назад, мы получаем вот такие замкнутые силовые линии. И электрическое поле касается этих силовых линий в каждой точке.

Что ж, в этом случае, если мы посмотрим на разность потенциалов между двумя точками, она будет равна интегралу с минусом E точка d l по замкнутому контуру, потому что линия поля представляет собой замкнутый контур. Это означает, что мы начнем с определенной точки, начальной точки, а затем закончим той же точкой. Конечная точка будет той же точкой, с которой мы начали. Следовательно, потенциал между начальной и конечной точкой будет одинаковым, и это всегда даст нам 0. Вот почему электрический потенциал или разность потенциалов не имеют никакого значения для электрического поля, созданного посредством индукции.

Эта величина из закона Фарадея такова, что ЭДС индукции равна интегралу E точка d l по замкнутому контуру, а также минус изменение магнитного потока во времени.