3.13. Что такое индукция?. Логика. Учебное пособие
3.13. Что такое индукция?. Логика. Учебное пособиеВикиЧтение
Логика. Учебное пособие
Гусев Дмитрий Алексеевич
Содержание
3.13. Что такое индукция?
Вспомним, опосредованные умозаключения делятся на дедуктивные, индуктивные и умозаключения по аналогии. Дедуктивные умозаключения, или силлогизмы, разновидности которых мы рассмотрели выше, дают достоверные выводы. Индуктивное умозаключение, или индукция – это умозаключение, в котором из нескольких частных случаев выводится общее правило. В отличие от дедуктивных умозаключений, в индукции рассуждение идет от частного к общему, от меньшего к большему, знание расширяется, в силу чего индуктивные выводы, как правило, вероятностны.
Индукция бывает полной и неполной. В полной индукции перечисляются все объекты из какой-либо группы и делается вывод обо всей этой группе.
Меркурий движется.
Венера движется.
Земля движется.
Марс движется.
……………………
Плутон движется.
Меркурий, Венера, Земля, Марс, …, Плутон – это крупные
планеты солнечной системы.
Все крупные планеты солнечной системы движутся.
В неполной индукции перечисляются некоторые объекты из какой-либо группы и делается вывод обо всей этой группе. Например, если в посылках индуктивного умозаключения перечисляются не все девять крупных планет солнечной системы, а только три из них, то такая индукция является неполной:
Меркурий движется.
Венера движется.
Земля движется.
Меркурий, Венера, Земля – это крупные планеты солнечной системы.
Все крупные планеты солнечной системы движутся.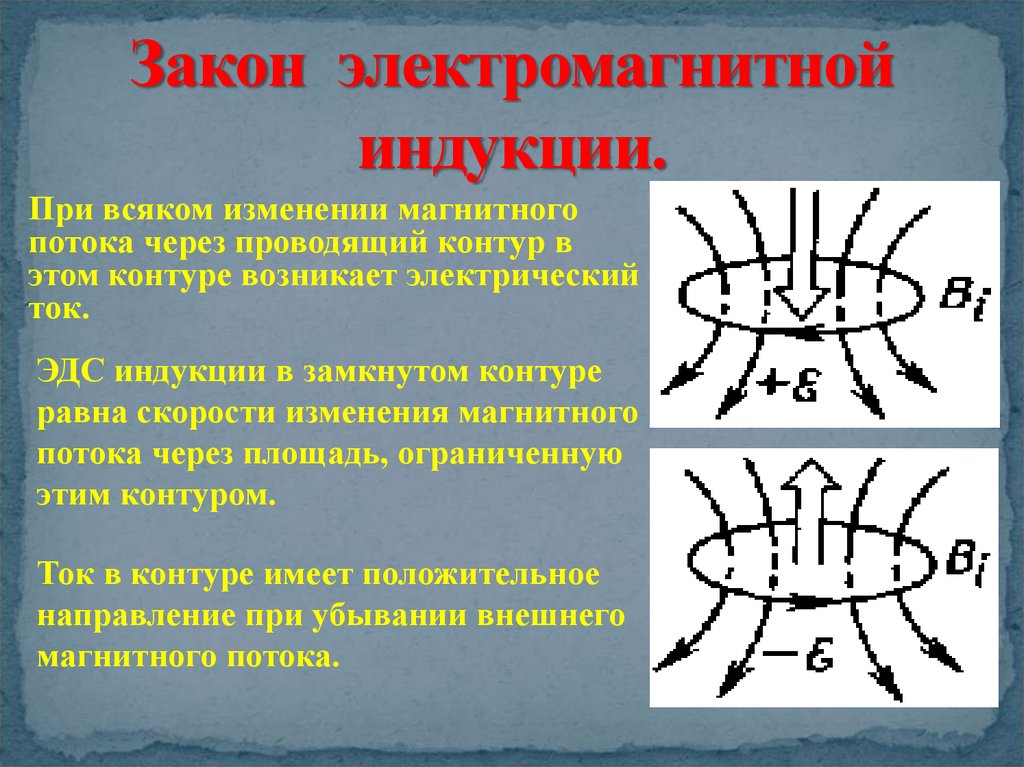
Понятно, что выводы полной индукции достоверны, а неполной – вероятностны, однако полная индукция встречается редко, и поэтому под индуктивными умозаключениями обычно подразумевается неполная индукция.
Неполная индукция бывает  Мы, как и первобытные люди, наблюдаем каждодневный восход солнца на востоке, но, в отличие от них, знаем причину этого явления: Земля вращается вокруг своей оси в одном и том же направлении с неизменной скоростью, в силу чего солнце появляется каждое утро в восточной стороне неба. Поэтому то умозаключение, которое делаем мы, представляет собой научную индукцию и выглядит примерно так:
Мы, как и первобытные люди, наблюдаем каждодневный восход солнца на востоке, но, в отличие от них, знаем причину этого явления: Земля вращается вокруг своей оси в одном и том же направлении с неизменной скоростью, в силу чего солнце появляется каждое утро в восточной стороне неба. Поэтому то умозаключение, которое делаем мы, представляет собой научную индукцию и выглядит примерно так:
Данный текст является ознакомительным фрагментом.
Научная индукция и ее методы
 В этом случае индуктивные рассуждения дополняются объяснениями, опирающимися на законы или принципы. Например: люди в прошлом многократно наблюдали, что при трении
В этом случае индуктивные рассуждения дополняются объяснениями, опирающимися на законы или принципы. Например: люди в прошлом многократно наблюдали, что при трении§ 2. ПОПУЛЯРНАЯ ИНДУКЦИЯ
§ 2. ПОПУЛЯРНАЯ ИНДУКЦИЯ В процессе многовековой деятельности люди наблюдали устойчивую повторяемость многих явлений, которые обобщались и использовались в объяснении наступивших и предсказании будущих событий.Такого рода обобщения связаны с наблюдениями над погодой,
§ 3. НАУЧНАЯ ИНДУКЦИЯ
§ 3. НАУЧНАЯ ИНДУКЦИЯ Научной индукцией называют умозаключение, в котором обобщение строится путем отбора необходимых и исключения случайных обстоятельств.В зависимости от способов исследования различают: (1) индукцию методом отбора (селекции) и (2) индукцию методом
Глава V.
 Индукция
ИндукцияГлава V. Индукция Другой, кроме дедукции, наиболее общий тип умозаключений — это индукция. В ней заключено глубокое своеобразие, и она находится в тесных взаимоотношениях с дедукцией. В реальной практике мышления ее сущность проявляется тоже в многообразных
2. Полная индукция
2. Полная индукция Полной индукция получается в том случае, если, во-первых, исследованы все элементы класса предметов и, во-вторых, если установлено, что каждому из них принадлежит (или не принадлежит) одно и то же общее свойство (отношение).В простейшем случае это выглядит
3. Неполная индукция
3. Неполная индукция
Неполной индукцией называется умозаключение обо всем классе предметов в целом на основе изучения лишь части предметов данного класса.Формула неполной индукции:S1 — PS2 — P….
Глава V. Индукция
Глава V. Индукция 1. Индукция как тип умозаключения Выразите структуру следующих индуктивных умозаключений в схематической форме и определите характер вывода: «Возьмем, например, исследование Роджера Бэкона о происхождении цветов радуги. Сначала у него, как кажется,
1. Индукция как тип умозаключения
§ 6. Математическая индукция
§ 6. Математическая индукция
«Но не забываете ли вы, что в математике также имеет место индукция?» – может возразить читатель. «Вы описывали математику как типичную дедуктивную науку, в которой все теоремы являются необходимыми следствиями аксиом. Однако вы ведь не
«Вы описывали математику как типичную дедуктивную науку, в которой все теоремы являются необходимыми следствиями аксиом. Однако вы ведь не
Глава XIV. Вероятность и индукция
Глава XIV. Вероятность и индукция 1. Проанализируйте следующий аргумент от аналогии, который использовал Бесиан Аррэ, доктор Сорбонны, в 1671 году:«Теология учит нас тому, что Солнце было создано для того, чтобы освещать Землю. Однако для того, чтобы освещать дом, нужно
НЕПОЛНАЯ ИНДУКЦИЯ
НЕПОЛНАЯ ИНДУКЦИЯ Индуктивное умозаключение, результатом которого является общий вывод обо всем классе предметов на основании знания лишь некоторых предметов данного класса, принято называть неполной или популярной индукцией. Например, из того, что инертные газы
1. ЧТО ТАКОЕ МАТЕРИЯ? ЧТО ТАКОЕ ОПЫТ?
1. ЧТО ТАКОЕ МАТЕРИЯ? ЧТО ТАКОЕ ОПЫТ?
С первым из этих вопросов постоянно пристают идеалисты, агностики, и в том числе махисты, к материалистам; со вторым — материалисты к махистам. Попытаемся разобраться, в чем тут дело.Авенариус говорит по вопросу о материи:«Внутри
ЧТО ТАКОЕ МАТЕРИЯ? ЧТО ТАКОЕ ОПЫТ?
С первым из этих вопросов постоянно пристают идеалисты, агностики, и в том числе махисты, к материалистам; со вторым — материалисты к махистам. Попытаемся разобраться, в чем тут дело.Авенариус говорит по вопросу о материи:«Внутри
Популярная индукция
Популярная индукция Популярная, она же народная индукция — это индукция через перечисление. Та самая, про которую мы говорили вчера. «Если три моих знакомых еврея хитры, то и все евреи хитры».Популярная индукция — одно из любимых орудий демагогов. Например: Василий
Научная индукция
Научная индукция Научная индукция работает иначе. Научная индукция объясняет свои выводы. Вернёмся к нашему примеру с хитрыми евреями. Научная индукция для этого примера может выглядеть так:«Мозг этих трёх евреев имеет особый отдел мозга, отвечающий за хитрость, и этот
Индукция (Induction)
Индукция (Induction)
Вид доказательства, в классическом понимании определяемый как переход от частного к общему, или от фактов к закону. Тем самым противостоит дедукции, которая обычно идет от общего к частному, от принципа к следствиям.Нетрудно догадаться, что индукция,
Тем самым противостоит дедукции, которая обычно идет от общего к частному, от принципа к следствиям.Нетрудно догадаться, что индукция,
Индукция родов у женщин с нормальной беременностью сроком 37 недель или более
Снижает ли политика стимулирования родов при сроке беременности 37 недель или более риски для младенцев и их матерей по сравнению с политикой выжидания до более позднего гестационного срока или до тех пор, пока не появятся показания к стимуляции родов?
Этот обзор был первоначально опубликован в 2006 году и впоследствии обновлен в 2012 и 2018 годах.
В чем суть проблемы?
Средняя беременность длится 40 недель с начала последнего менструального периода у женщины. Беременность, продолжающаяся более 42 недель, описывается как «переношенная», и поэтому женщина и её врач могут принять решение о родах путем индукции. К факторам, связанным с перенашиванием беременности и запоздалыми родами, относятся ожирение, первые роды и возраст матери более 30 лет.
К факторам, связанным с перенашиванием беременности и запоздалыми родами, относятся ожирение, первые роды и возраст матери более 30 лет.
Почему это важно?
Затянувшаяся (переношенная) беременность может увеличить риски для младенцев, в том числе `больший риск смерти (до или вскоре после рождения). Однако индукция (стимулирование или вызывание) родов может также создавать риски для матерей и их младенцев, особенно если шейка матки женщины не готова к родам. Современные методы диагностики не могут предсказать риски для младенцев или их матерей как таковые, и во многих больницах придерживаются определенной политики в отношении того, как долго может продолжаться беременность.
Какие доказательства мы обнаружили?
Мы провели поиск доказательств (17 июля 2019) и выявили 34 рандомизированных контролируемых испытания в 16 различных странах с участием более 21 500 женщин (в основном с низким риском осложнений). В ходе испытаний сравнивали политику индукции родов на сроке после 41 полной недели беременности (> 287 дней) с политикой выжидания (выжидательная тактика).
В ходе испытаний сравнивали политику индукции родов на сроке после 41 полной недели беременности (> 287 дней) с политикой выжидания (выжидательная тактика).
Политика стимулирования родов была связана с меньшим числом перинатальных смертей (22 испытания, 18 795 младенцев). Четыре перинатальных смерти произошли в группе политики стимулирования родов по сравнению с 25 случаями перинатальной смерти в группе выжидательной тактики. Меньше мертворождений произошло в группе индукции родов (22 испытания, 18 795 младенцев): два случая — в группе индукции и 16 — в группе выжидательной тактики.
У женщин из групп индукции родов во включенных исследованиях вероятность родоразрешения кесаревым сечением была, вероятно, меньше, чем в группах выжидательной тактики (31 исследование, 21 030 женщин), и, вероятно, была минимальная разница или её не было вообще при сравнении с ассистированными вагинальными родами (22 исследования, 18 584 женщины).
Меньше младенцев поступило в отделение реанимации и интенсивной терапии новорожденных (ОРиИТН) в группе политики индукции родов (17 испытаний, 17 826 младенцев; доказательства высокой определённости). Простой тест состояния здоровье ребенка (оценка по шкале Апгар) на пятой минуте после рождения, вероятно, был более благоприятным в группах индукции по сравнению с выжидательной тактикой (20 испытаний, 18 345 младенцев).
Простой тест состояния здоровье ребенка (оценка по шкале Апгар) на пятой минуте после рождения, вероятно, был более благоприятным в группах индукции по сравнению с выжидательной тактикой (20 испытаний, 18 345 младенцев).
Политика индукции может мало или вообще не ничего изменить для женщин, перенёсших травму промежности, и, вероятно, влияет мало или вообще не влияет на число женщин с послеродовым кровотечением или кормящих грудью при выписке из больницы. У нас нет определённости о влиянии индукции или выжидательной тактики на продолжительность пребывания в родильном доме из-за очень низкой определённости доказательств.
Среди новорожденных число детей с травмой или энцефалопатией было одинаковым в обеих группах (умеренная и низкая определенность доказательств соответственно). Ни в одном из исследований не сообщили о развитии проблем со стороны нервной системы (нейроразвитии) при последующем наблюдении за детьми и послеродовой депрессии у женщин. Только в трех испытаниях сообщили о некоторых показателях материнской удовлетворенности.
Что это значит?
Политика индукции родов по сравнению с выжидательной тактикой связана с меньшим числом смертей младенцев и, вероятно, с меньшим числом кесаревых сечений; и вероятно, мало влияет или вообще не влияет на ассистированные вагинальные роды. Определение наилучшего времени, когда можно предложить женщинам индукцию родов со сроком беременности 37 недель или больше, требует дальнейшего изучения, так же как и дальнейшее изучение профилей риска женщин и их ценностей и предпочтений. Обсуждение рисков индукции родов, включая пользу и вред, может помочь женщинам сделать информированный (осознанный) выбор между индукцией родов, особенно если беременность длится более 41 недели, или выжидательной тактикой — ожиданием начала родов и/или ожиданием до индукции родов. Понимание женщинами индукции, процедур, их рисков и пользы, важно для влияния на их выбор и удовлетворенность.
Заметки по переводу:
Перевод: Алексеева Лада Игоревна. Редактирование: Просюкова Ксения Олеговна и Зиганшина Лилия Евгеньевна. Координация проекта по переводу на русский язык: Кокрейн Россия — Cochrane Russia, Cochrane Geographic Group Associated to Cochrane Nordic. По вопросам, связанным с этим переводом, пожалуйста, обращайтесь к нам по адресу: [email protected]
Редактирование: Просюкова Ксения Олеговна и Зиганшина Лилия Евгеньевна. Координация проекта по переводу на русский язык: Кокрейн Россия — Cochrane Russia, Cochrane Geographic Group Associated to Cochrane Nordic. По вопросам, связанным с этим переводом, пожалуйста, обращайтесь к нам по адресу: [email protected]
Индукция овуляции =>что это и где пройти
ЭКО
Список услуг
Овуляцией называют процесс выхода выход яйцеклетки из фолликула яичника, что происходит у большинства женщин в середине менструального цикла. Если яйцеклетка по каким либо причинам не может этого сделать, то говорят об ановуляции – одной из распространенных причин бесплодия. Индукция овуляция — создание благоприятного гормонального фона для роста фолликула и выхода из него яйцеклетки, что достигается обычно с помощью специальных медикаментов.
Показания к процедуре
Индукция овуляции применяется как в рамках программ ВРТ, так и как самостоятельный метод преодоления эндокринных форм бесплодия. Помимо этого, процедура рекомендована после устранения непроходимости маточных труб при трубном бесплодии и когда причины нарушения фертильности установить не удалось.
Помимо этого, процедура рекомендована после устранения непроходимости маточных труб при трубном бесплодии и когда причины нарушения фертильности установить не удалось.
Как проводится индукция овуляции
В абсолютном большинстве индукция овуляции осуществляется медикаментозно одним или сразу несколькими препаратами. К их числу относятся цитрат кломифена, хорионический гонадотропин, фоллитропин, бромокриптин, каберголин и целый ряд других веществ. Схем лечения существует достаточно много и они подбираются с учетом возраста, заболевания,б которое вызвало бесплодие и других факторов.
Важно знать, что какая бы схема не применялась, стимуляция овуляции всегда проходит под ультразвуковым и гормональным мониторингом, что позволяет отследить процесс и предотвратить гиперстимуляцию яичников — главное осложнение процедуры.
Существует и другой подход и лечению — лапароскопический дриллинг. Его суть заключается в малоинвазивной операции с целью уменьшения стромы яичника, что приводит к снижению концентрации андрогенов и способствует наступлению овуляции. Вместе с тем, данные об эффективности этого метода достаточно противоречивы, а он сам в любом случае представляет собой хирургическое вмешательство со своими рисками осложнений.
Вместе с тем, данные об эффективности этого метода достаточно противоречивы, а он сам в любом случае представляет собой хирургическое вмешательство со своими рисками осложнений.
Индукция овуляции в клинике «Красная горка»
- Профессионализм. С заболеваниями эндокринной системы в нашем Центре борется врач-эндокринолог высшей категории Наталья Александровна Сухова — кандидат медицинских наук и автор свыше 40 работ по медицине.
- Приверженность принципам доказательной медицины. Наши специалисты назначают только те диагностические тесты и лечебные мероприятия, которые доказали свою эффективность.
- Современное оборудование. Мы обладаем всем необходимым, чтобы процедура индукции овуляции прошла максимально качественно и комфортно.
Лечение бесплодия — это не всегда ЭКО. В некоторых случаях, осуществить свою мечту и стать счастливой мамой можно намного проще. Однако, по мере прогрессирования основного заболевания шансы на благоприятный исход лечения снижаются, поэтому не затягивайте с решением этого вопроса и пройдите обследование в нашем Центре.
Врачи, ведущие приём:
-
Тришкин Алексей Геннадьевич
Зав. отделением ВРТ, акушер-гинеколог, репродуктолог, гинеколог-эндокринолог, врач ультразвуковой диагностики, Зав кафедрой «Новых репродуктивных технологий» КемГу, доцент, доктор медицинских наук
Записаться на прием
Имя
Номер телефона
Вопрос
Я посещаю клинику в первый раз
У меня есть карта
Выберите врачаБарашов А. Ю.Дроздик О. В.Иванова А. В.Шамин М. В.Вальшин Т. Ю.Брагин-Мальцев А. И.Соломатина О. А.Массон И. Л.Демченко Д. О.Лунева Е. В.Соловьев В. Б.Неверова Ю. Н.Животовский А. С.Быкова Ю. А.Григоричева Е. В.Дудкина О. А.Кофанова Е. С.Вялова К. В.Жаркова О. Н.Каминская Т. В.Губанков М. В.Корнев В. П.Сохарева И. Г.Корнева О. В.Тришкина Н. Н.Терновая А. С.Власова И. В.Сагателян Г. Р.Фролова Н. А.Лобанова О. Г.Помешкин Е. В.Бушмакин А. Д.Маруев М. Б.Лесников А. И.Безденежных А. В.Сурцев К. С.Шлегель Е. Г.Пискунов А. С.Григорьева О. В.Володина С. С.Изместьев К. В.Кузьмина Т. С.Курганова Л. В.Притчина С. С.Зуева Г. П.Степанова О. В.Бурков А. Н.Барашова Л. П.Стопичева С. Л.Шипицына О. А.Голитенко Е. Ю.Медведева Ю. Д.Сухова Н. А.Елманов А. В.Бочкарникова А. Г.Тришкин А. Г.Луговой К. А.
Ю.Дроздик О. В.Иванова А. В.Шамин М. В.Вальшин Т. Ю.Брагин-Мальцев А. И.Соломатина О. А.Массон И. Л.Демченко Д. О.Лунева Е. В.Соловьев В. Б.Неверова Ю. Н.Животовский А. С.Быкова Ю. А.Григоричева Е. В.Дудкина О. А.Кофанова Е. С.Вялова К. В.Жаркова О. Н.Каминская Т. В.Губанков М. В.Корнев В. П.Сохарева И. Г.Корнева О. В.Тришкина Н. Н.Терновая А. С.Власова И. В.Сагателян Г. Р.Фролова Н. А.Лобанова О. Г.Помешкин Е. В.Бушмакин А. Д.Маруев М. Б.Лесников А. И.Безденежных А. В.Сурцев К. С.Шлегель Е. Г.Пискунов А. С.Григорьева О. В.Володина С. С.Изместьев К. В.Кузьмина Т. С.Курганова Л. В.Притчина С. С.Зуева Г. П.Степанова О. В.Бурков А. Н.Барашова Л. П.Стопичева С. Л.Шипицына О. А.Голитенко Е. Ю.Медведева Ю. Д.Сухова Н. А.Елманов А. В.Бочкарникова А. Г.Тришкин А. Г.Луговой К. А.
Выберите клиникуНа СувороваНа Двужильного
Я согласен на обработку персональных данных
Индукция овуляции
Лечение бесплодия
Для зачатия требуется овуляция.
 Однако, менструальный/овуляторный цикл чрезвычайно чувствителен и может быть легко нарушен. Проблемы, связанные с овуляцией, встречаются очень часто, на них приходится около 25% случаев бесплодия у женщин.1
Однако, менструальный/овуляторный цикл чрезвычайно чувствителен и может быть легко нарушен. Проблемы, связанные с овуляцией, встречаются очень часто, на них приходится около 25% случаев бесплодия у женщин.1Что такое индукция овуляции?
Стимуляция яичников и стимуляция овуляции представляют собой два разных процесса, проведение которых может требоваться у различных женщин в ходе лечения бесплодия.
Стимуляция яичников применяется для получения нескольких яйцеклеток (также называемых ооцитами). Это позволяет репродуктологу выбрать яйцеклетку наилучшего качества в ходе лечения с применением ВРТ, поскольку качество яйцеклеток может отличаться.1,2
Индукция овуляции применяется с целью индуцирования созревания и овуляции фолликулов для высвобождения как минимум одной яйцеклетки. Затем яйцеклетка может быть оплодотворена в организме естественным образом, в ходе полового акта или с применением искусственного оплодотворения с внутриматочной инсеминацией (ВМИ). 1
1
Когда необходима стимуляция овуляции?
У некоторых женщин овуляция не происходит (ановуляция) или происходит нерегулярно (олигоовуляция). Это может являться следствием многих факторов, включая:1
- Нарушения гормонального баланса
- Синдром поликистозных яичников (СПКЯ)
- Избыточную или недостаточную массу тела
- Слишком частую/избыточную физическую нагрузку
Обычно овуляция достигается только приемом лекарственных препаратов от бесплодия, и применение вспомогательных репродуктивных технологий, таких как ЭКО и ИКСИ, не требуется. В зависимости от пациента для индукции овуляции могут использоваться кломифена цитрат или гонадотропины:
- Кломифена цитрат — применяется в качестве первичной терапии1
- Гонадотропины — препараты, которые могут назначаться отдельным пациенткам при ИО, которым требуется более эффективная стимуляция яичников в тех случаях, когда кломифена цитрат не дал положительных результатов.
 1
1
Для предотвращения преждевременного высвобождения яйцеклеток (овуляции) врач может назначить гормональные препараты для подавления естественного менструального цикла1 (См. регулирование цикла ниже)
Лечение
Если женщина прежде не проходила лечение от бесплодия или если она страдает синдромом поликистозных яичников, вероятнее всего, врач назначит ей препарат для начального лечения бесплодия — кломифена цитрат.3 Он представляет собой пероральные таблетки, которые принимают в течение пяти дней на ранней стадии менструального цикла для стимуляции роста фолликулов. Это провоцирует мозг на продукцию гонадотропин-рилизинг-гормона (ГнРГ), стимулирующего выработку фолликулостимулирующего гормона (ФСГ) и лютеинизирующего гормона (ЛГ).1,4 Указанные гормоны стимулируют рост фолликулов и овуляцию яйцеклеток.
Побочные эффекты от приема кломифена цитрата включают: приливы, головные боли или нечёткость зрения, резкие перемены настроения, болезненность молочных желез и тошноту. 1 Поскольку кломифена цитрат стимулирует рост фолликулов, существует повышенный риск развития кист яичников, а также риск многоплодной беременности.1
1 Поскольку кломифена цитрат стимулирует рост фолликулов, существует повышенный риск развития кист яичников, а также риск многоплодной беременности.1
В зависимости от реакции вашего организма на кломифена цитрат ваш врач обсудит с вами другие препараты для лечения бесплодия, такие как гонадотропины.1
Гонадотропины представляют собой естественным образом вырабатывающиеся в организме женщины гормоны. Лечение с применением гонадотропинов состоит в инъекциях указанных гормонов для стимуляции созревания яйцеклеток и овуляции.
Инъекции ФСГ вводятся на ранней стадии менструального цикла, обычно в течение недели или дольше.1 Активируется старт созревания нескольких фолликулов. Инъекции ЛГ могут вводиться параллельно с ФСГ для дальнейшей стимуляции и созревания яйцеклеток. Когда яйцеклетки почти созрели, большинству женщин вводят одну стимулирующую инъекцию хорионического гонадотропина человека (ХГЧ).1 Это в свою очередь стимулирует яичники для полного созревания и высвобождения яйцеклеток. 1
1
Тесты на беременность измеряют уровень ХГЧ в моче или крови; поэтому важно проходить тест на беременность только по рекомендации вашего врача и не ранее, поскольку тест может среагировать на ХГЧ в стимулирующей инъекции и показать ложноположительный результат.1
Поскольку гонадотропины оказывают более сильное воздействие, чем кломифена цитрат, существуют повышенный риск возникновения:1
- Синдрома гиперстимуляции яичников (СГЯ) — состояния, при котором развивается большое количество фолликулов. СГЯ обычно обнаруживается быстро, но около 2% женщин может потребоваться обратиться за помощью в стационар.
- Многоплодная беременность — рождение двойняшек или тройняшек может показаться привлекательным, однако это может привести к серьезным рискам для здоровья матери и детей.
При росте слишком большого числа фолликулов врач может принять меры и отрегулировать дозировку ГТ во избежание возникновения многоплодной беременности и также назначить препараты, контролирующие стимулированный цикл.
Существуют два типа препаратов, используемых для управления циклом: агонисты и антагонисты. Оба типа препаратов являются высокоэффективными, специалист назначит наилучший препарат в каждом конкретном случае.1
Что дальше?
Внутриматочная инсеминация (ВМИ)
Что необходимо при использовании внутриматочной инсеминации?
Узнайте больше
Стимуляция овуляции
Узнайте какие препараты используются при ВРТ
Узнайте больше
Математика в деталях: how to математическая индукция
Начнем с того, что такое математическая индукция.
Математическая индукция – метод математического доказательства, который используется, чтобы доказать истинность некоторого утверждения для всех натуральных чисел, согласно Wikipedia. Говоря простыми словами, у нас есть какое-то математическое высказывание о натуральных числах, и мы хотим доказать/опровергнуть его истинность.
Разные источники дают разное определение натуральных чисел. В моем университете один профессор включает ноль во множество N, а по определению другого натуральные числа начинаются с единицы. Дело вкуса 😉 Но очень важно понять, с каким именно множеством вы работаете. Позже узнаете, почему.
Конечно, если наше математическое высказывание (формула) относится к маленькому множеству чисел, то гораздо легче просто высчитать ответ в уме или ввести данные в Wolfram – на этом всё, пускайте титры.
Например, вы, убивая время в интернете, где-то прочли, что сумма положительных натуральных чисел от 1 до n, то есть, 1+2+3+...+n, вычисляется по формуле n*(n+1)/2. Допустим, у вас проблемы с доверием, и вы хотите проверить, работает ли эта формула на самом деле, или это просто часть всемирного заговора?
Эту формулу можно применить к маленьким множествам, так как вы можете легко вычислить сумму чисел от 1 до 10, от 1 до 20, от 1 до 50, а если вас замучила бессонница, то попробуйте посчитать не овечек, а сумму чисел от 1 до 100. Помогает. Иногда.
Помогает. Иногда.
Потом остается только подставить значения в формулу и сравнить.
Но если мы говорим о множестве с большим количеством элементов или о бесконечном множестве, то именно тут и пригодится индукция.
Проверка высказывания для наименьшего числа – это начало индукции.
Мы начинаем с базиса (база, base case) – нам дано наименьшее число, для которого нужно проверить истинность высказывания. Обычно это 1, но могут быть и другие варианты, которые обязательно указываются в условии. Например, можно начать с 4 или 5. Это не так важно. Но иногда этот базис не указывается эксплицитно. В этом случае вы начинаете с наименьшего числа вашего множества. Поэтому важно знать, с чего начать. Уточните, включается ноль в N или нет. В примерах в этой статье множество натуральных чисел начинается с единицы.
Затем мы утверждаем, что выражение истинно для любого n>=1. Мы не знаем этого наверняка, конечно. Но мы предполагаем, что если утверждение истинно для любого n, то оно будет верно и для n+1. Это называется шагом индукции. А так как n – это любое число из множества N, то мы можем проверить математическое высказывание для очень-очень-очень больших чисел.
Итак, вернёмся к нашей формуле вычисления суммы чисел от 1 до n.
Начало индукции: проверяем, верна ли формула для n=1: n*(n+1)/2=> 1*(1+1)/2=1*(2)/2=1
Так как сумма чисел от 1 до 1 равна 1, то высказывание истинно для n=1.
Затем мы утверждаем, что математическое высказывание истинно для любого n>=1. То есть 1+2+3+...+n = n*(n+1)/2.
Переходим к шагу индукции – если высказывание верно для n, то оно истинно и для n + 1.
1+2+3+...+n + (n+1) = (n+1)(n+1 + 1)/2.
Левая часть уравнения – это сумма чисел от 1 до n+1. Мы заменили все n в правой части на n+1, так как мы больше не рассматриваем n, а доказываем, что высказывание истинно именно для n+1.
Если вы помните, то сумма чисел от 1 до n вычисляется по формуле n*(n+1)/2. Поэтому часть выражения справа (а именно 1+2+3+...+n) можно заменить на n*(n+1)/2.
У нас остается n*(n+1)/2 + (n+1) = (n+1)(n+1 + 1)/2. Нам нужно доказать или опровергнуть равенство этих двух выражений.
Всё, что происходит дальше – это чистая алгебра. Нам надо всего лишь упростить эти выражения, так как немного трудно что-либо сказать об их равенстве, просто посмотрев на них. 2 + 2n + 1
2 + 2n + 1
Правая и левая часть уравнения совпадают. Значит, математическое высказывание истинно.
Математическую индукцию еще сравнивают с эффектом домино. Если косточки домино выстроены в ряд, и какая-то упадёт, приложившись к следующей и опрокинув её, то та, в свою очередь, опрокинет следующую, и за ней последуют все остальные. А если мы опрокинем первую косточку, то упадёт весь ряд.
В индукции, если высказывание истинно для натурального числа, с которого мы начинаем, например, 8, то оно истинно для 9. Если оно истинно для 9, то оно верно для 10. И так далее. До бесконечности. Это мы и пытаемся доказать. Есть задачи, которые имею несколько базисов. Например, вам надо проверить какое-то высказывание для n=4, n=5, n=6 в начале индукции. Попадаются и задачи, где база дана в рекурсивной форме.
Попадаются и задачи, где база дана в рекурсивной форме.
Потренируйтесь на других примерах. Основным скилом для решения подобных задач является умение находить паттерны. Вы также должны понимать, что именно вы хотите доказать? Что описывает формула? Очень важно знать и уметь применять некоторые формулы, которые помогут вам упростить выражения. Например, те же самые формулы сокращённого умножения. Они очень часто встречаются в математической индукции. Очень многие допускают ошибки именно в конце, когда надо подключить свои знания алгебры.
Помните, что математическая индукция применяется только к высказываниям с натуральными числам. Ваш n не может равняться -10 или 8.5. Дискриминация по отношению к действительным и комплексным числам? Вполне может быть.
Для чего же это всё?
Во-первых, решая подобные задачи, вы развиваете логику и алгоритмическое мышление, что играет не последнюю роль в программировании. Вы учитесь распознавать всякого рода паттерны.
Вы учитесь распознавать всякого рода паттерны.
Во-вторых, если вы внимательнее посмотрите на принцип математической индукции, вы заметите, что это чистейшая рекурсия. Предполагаю, что вы знакомы с рекурсией, если вы хотя бы немного программируете. Есть base case – условие завершения алгоритма. Также есть правило перехода. И чтобы проверить высказывание для n, нужно решить что-то для n-1, а потом с помощью алгебры дойти до n.
Рекурсию можно или любить, или люто ненавидеть. Но если ее понять и правильно использовать, она может сделать код элегантнее.
Значение, Определение, Предложения . Что такое индукции
Ток в обмотках статора идет только в фазу размагничивания, спада индукции Bi. | |
Поможет ли двойная система индукции? | |
Это потому, что я велел Рому отсоединить матрицу индукции. | |
Они пытаются провести процесс индукции снова. | |
Микросхемы ОРЕОЛ должны быть невесомыми и должны помещаться в полом ядре для предотвращения тепловой индукции. | |
Когда автолюбители хотят увеличить мощность двигателя, они могут добавить некоторый тип принудительной индукции. | |
Теорема следует путем индукции о длине игры из этих двух лемм. | |
Дозы, необходимые для индукции опухоли, чрезвычайно малы. | |
Дэвид Юм выделил эту проблему индукции и доказал, что причинные отношения не являются истинными a priori. | |
Зал славы рок-н-ролла выбрал лекарство для индукции в своем классе 2019 года. | |
Из-за своей быстрой индукции и времени восстановления, пропофол также широко используется для седации младенцев и детей, проходящих МРТ. | |
Провода также скручены вместе, чтобы уменьшить помехи от электромагнитной индукции. | |
Следующее доказательство по случаям опирается непосредственно на хорошо известные правила арифметики, но использует редко используемую технику прямой-обратной индукции. | |
Как и в случае неинвазивного Д&Е или индукции родов во втором триместре, целью Д&Е является прекращение беременности путем удаления плода и плаценты. | |
Существует несколько ошибочных доказательств индукции, в которых один из компонентов, базисный случай или индуктивный шаг, неверен. | |
Это происходит потому, что глюкоза активно препятствует индукции lacZYA. | |
К 1849 году генераторы, основанные на законе индукции Фарадея, стали достаточно развитыми, чтобы заменить оба типа машин, и Берд рекомендовал их в своих лекциях. | |
Его прерыватель работал автоматически с помощью магнитной индукции с достаточно высокой скоростью. | |
В критическом реакторе деления нейтроны, образующиеся при делении атомов топлива, используются для индукции еще большего количества делений, чтобы поддерживать контролируемое количество высвобождаемой энергии. | |
У некоторых животных, однако, другой тип молекулы, называемый фактором роста фибробластов или FGF, также может играть важную роль в индукции. | |
В дополнение к индукции анестезии, Тиопентал натрия исторически использовался для индуцирования медицинских ком. | |
Обычный диапазон доз для индукции анестезии с использованием тиопентала составляет от 3 до 6 мг / кг, однако существует множество факторов, которые могут это изменить. | |
Позже в том же году фон Нейман смог исправить доказательство для системы арифметики без каких-либо аксиом индукции. | |
Затем ZP3 участвует в индукции акросомной реакции, в результате чего сперматозоид высвобождает содержимое акросомального пузырька. | |
Родоразрешение до 39 недель путем индукции родов или кесарева сечения не рекомендуется, если только это не требуется по другим медицинским причинам. | |
Множественные эффекты могут быть сложены путем индукции с несколькими наборами сеток. | |
Цвета эффекта Макколлоу менее насыщены, чем цвета индукции. | |
Если используемый цвет был красным, то после фазы индукции ахроматическая решетка казалась слегка Красной. | |
В 1993 году Cream были введены в Зал славы рок-н-ролла и вновь сформированы для выступления на церемонии индукции. | |
Типичная доза индукции анестезии составляет 0,35 грамма. | |
Именно по этой причине ультракороткодействующие барбитураты, такие как тиопентал, могут быть использованы для длительной индукции медицинской комы. | |
Исторически тиопентал был одним из наиболее часто используемых и изучаемых препаратов для индукции комы. | |
Оставив доказательство на потом, перейдем к индукции. | |
Этот подход может быть подвергнут строгому математическому доказательству с помощью математической индукции и часто используется в качестве примера рекурсии при обучении программированию. | |
Как утверждали многие авторы, индукция сама по себе может быть надежным процессом, который не случайно порождает истинную веру в надежность индукции. | |
Поскольку хорошо известно, что механическим эквивалентом электрического индуктора является масса, это доказывает, что мемристоры невозможны без использования магнитной индукции. | |
Всякий переход от детализации эмпирической индукции к идеальности и универсальности закона есть скачок. | |
Философские основы аналитической индукции берут свое начало от Аристотеля и его концепции индукции. | |
Аналитическая индукция была ответом Знаниецкого на проблему индукции. | |
По индукции 0 равно всем числам, и поэтому любые два натуральных числа становятся равными. | |
Затем они с помощью индукции выстраиваются в более сложные алгоритмы. | |
Лечение рака химиотерапией и облучением убивает клетки-мишени в первую очередь путем индукции апоптоза. | |
Прямой анализ почвы вблизи, включая использование методов электромагнитной индукции, может также использоваться для мониторинга засоления почвы. | |
Другая методология индукции опирается на нанотехнологии и ландшафтную экологию. | |
Это известно как индукция регулярных языков и является частью общей проблемы индукции грамматики в теории вычислительного обучения. | |
Они действуют, чтобы увеличить скорость отверждения и увеличить плотность поперечных связей, но также сокращают время индукции, что может привести к преждевременной вулканизации. | |
Устойчивые равновесия Мертенса удовлетворяют как прямой, так и обратной индукции. | |
Сперматозоид запускает активацию яйцеклетки путем индукции концентрации свободных ионов кальция в цитоплазме яйцеклетки. | |
Например, каждая из этих успешных систем использует метод для введения индукции или выражения все или ничего. | |
У женщин с ановуляцией это может быть альтернативой после 7-12 попыток индукции овуляции, так как последняя является дорогостоящей и более легкой для контроля. | |
Риск стимуляции яичников-это развитие синдрома гиперстимуляции яичников, особенно если ХГЧ используется для индукции окончательного созревания ооцитов. | |
Основным препаратом, используемым для индукции овуляции, является кломифен, и он показал успех у пациентов, которые не овулируют или имеют синдром поликистозных яичников. | |
Значки CVCC были удалены, но система индукции CVCC осталась. | |
Первоначально выпускавшийся с системой индукции карбюратора, он был позже модернизирован до электронного впрыска топлива, с суффиксом-E, добавленным к обозначению двигателя. | |
Вывод усиливается путем подсчета частоты его наблюдения-численной индукции. | |
Когда циклы вложены, переменная индукции во внешнем цикле может быть инвариантом цикла во внутреннем цикле. | |
Уменьшение силы ищет выражения, включающие инвариант цикла и переменную индукции. | |
Из индукции были исключены Ник Симпер, Томми Болин, Джо Линн Тернер, Джо Сатриани, Стив Морс и Дон Эйри. | |
Он утверждал, что открыл космический луч в 1896 году и изобрел способ получения постоянного тока с помощью индукции, и сделал много заявлений о своем механическом осцилляторе. | |
Клеточные стрессоры, такие как временное прерывание синтеза белка и гипоксия, также достаточны для индукции вирусной реактивации. | |
Это один из многих факторов сборки шпинделя, которые играют ключевую роль в индукции сборки и роста микротрубочек во время фазы М. | |
В 2000 году Лемон получил премию Джона Банна, высшую награду, присуждаемую мемориальным баскетбольным Залом славы Нейсмита за пределами индукции. | |
Катушки магнитной индукции обычно состоят из десятков-сотен-тысяч витков проволоки, намотанной вокруг сердечника с очень высокой магнитной проницаемостью. | |
Среди его вкладов в философию-утверждение, что он решил философскую проблему индукции. | |
Я подошел к проблеме индукции через Юма. | |
В отличие от ФСГ, ЛГ имеет меньшую роль в мужской фертильности вне индукции гонадной продукции тестостерона. | |
Он, по-видимому, способствует индукции хорошего Th3-ответа, поэтому полезен для иммунизации против патогенов, которые блокируются антителами. | |
Концепция индукции ремиссии и поддержания ремиссии очень важна. | |
Это известно как проблема индукции. | |
Решение о проведении индукции должно быть принято после взвешивания рисков и преимуществ, но безопаснее после 39 недель. | |
| Другие результаты | |
Введение в ИТ для новых сотрудников: почему это важно?
Введение в ИТ для новых сотрудников: почему это важно?
Защита данных вашей компании — это непрекращающаяся битва, в которой враги находятся как внутри, так и снаружи ваших стен. Ваши собственные войска часто являются самым слабым звеном в вашей цепочке безопасности, потому что человеческая природа не меняется. У всех нас есть естественная склонность делиться информацией в среде, где технологии и хакеры постоянно совершенствуют способы получения этой информации.
Ваши собственные войска часто являются самым слабым звеном в вашей цепочке безопасности, потому что человеческая природа не меняется. У всех нас есть естественная склонность делиться информацией в среде, где технологии и хакеры постоянно совершенствуют способы получения этой информации.
Даже в 21 веке у большинства людей недостаточно навыков управления паролями, и они обычно используют пароли, которые легко угадать. Хакеры настолько хороши в фишинге, что на его долю приходится 90% взломов и что 30% фишинговых сообщений на самом деле открываются ничего не подозревающими, неосведомленными пользователями.
Итак, когда дело доходит до того, чтобы ваши сотрудники не совершали действий, которые могут стоить вам целое состояние, вводный инструктаж и обучение ИТ — это основа кибербезопасности.
Вот почему.
Снижает риск взлома
В 2017 г. в Австралии было зарегистрировано только 18 серьезных инцидентов безопасности.
Ну, в 2018 году это было 308 .
Причиной такого поразительного роста стало принятие схемы уведомляемых об утечке данных (NDB). Он требует от агентств информировать владельцев учетных записей, когда утечка данных может причинить им серьезный вред. Схема NDB касается не только возможности финансового ущерба, но и психологической и даже физической травмы.
Вводный инструктаж по ИТ помогает убедиться, что ваши сотрудники следуют передовым методам информационной безопасности, помогая свести к минимуму риск взлома, который может поставить под угрозу ваши данные.
Это обучение должно включать политику паролей вашей организации, в которой описаны критерии, которым должны соответствовать пароли, и как часто их нужно менять. Методы, которые пользователи должны использовать для защиты своих паролей, также являются важной частью вводного курса ИТ.
Защищает вашу репутацию
Сегодняшний глобальный цикл новостей и все более привередливые клиенты делают защиту репутации вашей компании сложной задачей в обычных обстоятельствах.
Ущерб от нарушения безопасности выходит за рамки стоимости первоначальной очистки, поскольку потеря данных может привести к гораздо большим затратам: вашим отношениям с вашими клиентами.
Почти две трети опрошенных компаний столкнулись с утечкой данных, которая нанесла ущерб их репутации. Единственная утечка данных, которая скомпрометирует данные клиентов, может затруднить полное восстановление репутации даже крупной компании.
Например, цены на акции Facebook резко упали после того, как в начале 2018 года разразился скандал с Cambridge Analytica. Год спустя акции социальной сети по-прежнему дешевели почти на 10%.
Сотрудникам необходимо пройти надлежащее обучение информационным технологиям, чтобы как можно быстрее начать восстанавливать эти отношения. Клиенты хотят полной прозрачности после взлома, даже если этого не требуют законы о конфиденциальности данных. А с обученными сотрудниками ваша компания добьется большего успеха, чем оставить своим клиентам твит, ориентированный на компанию: «Здесь, в компании X, мы все заботимся о безопасности данных, но…»
Это избавит вас от проблем с юридическими
Правительства во всем мире принимают более строгие правила в отношении защиты данных, особенно личной информации. По данным IBM-Ponemon Institute, несоблюдение требований увеличивает среднюю стоимость утечки данных на 11,90 долларов США на душу населения.
По данным IBM-Ponemon Institute, несоблюдение требований увеличивает среднюю стоимость утечки данных на 11,90 долларов США на душу населения.
Таким образом, вводный инструктаж по ИТ должен включать обучение новых сотрудников соблюдению нормативных требований, особенно в жестко регулируемых отраслях, таких как финансы и здравоохранение.
Финансовые услуги находятся под особенно строгим контролем в связи с принятием последнего пруденциального стандарта, выпущенного Австралийским органом пруденциального регулирования (APRA) 1 июля 2019 г. требования. Среди прочих обязательств им необходимо уведомить APRA о несанкционированном раскрытии такой информации в течение 72 часов.
Регулярное использование электронной почты в деловой переписке также создает возможность юридических осложнений. Сообщения электронной почты, как правило, менее формальны, но на них по-прежнему распространяются те же обязательства, что и на письменные документы.
Например, предприятия могут заключать и расторгать контракты по электронной почте и ссылаться на эти сообщения в судебных разбирательствах. Ваша программа ознакомления с ИТ должна предоставить персоналу соответствующие рекомендации по использованию электронной почты, в том числе осознание того, что она обычно считается официальной корреспонденцией.
Ваша программа ознакомления с ИТ должна предоставить персоналу соответствующие рекомендации по использованию электронной почты, в том числе осознание того, что она обычно считается официальной корреспонденцией.
Управляйте методами работы ваших сотрудников
Более 70 % опрошенных организаций сообщают об улучшении своих мер кибербезопасности с 2017 по 2018 год. Основными причинами этого улучшения являются более эффективное управление и практика найма в дополнение к более передовым технологиям безопасности.
Ваша программа ознакомления с ИТ должна гарантировать, что сотрудники понимают, что они несут личную ответственность за внедрение передового опыта. Такой подход поможет свести к минимуму риск финансовых, юридических и репутационных потерь организации.
Последние тенденции в коммерческой ИТ-практике требуют тщательного изучения во время вводного курса по ИТ. Например, в большинстве организаций теперь есть определенный тип политики «Принеси свое собственное устройство на работу» (BYOD).
Эта тенденция стирает границы между домашним и деловым использованием, особенно для сотрудников, работающих дома. Вводный инструктаж по ИТ должен включать специальную подготовку по защите данных фирмы на личных устройствах.
Вывод: повысьте свою ИТ-защиту
Атаки на вашу организацию редко будут столь очевидны, как группа бронированных солдат на уличном параде. Они могут быть настолько тонкими, что вы даже не узнаете, что это происходит, пока данные ваших клиентов не появятся для продажи в даркнете.
Обучение сотрудников в форме вводных инструктажей по ИТ необходимо для разъяснения политики и практики вашей организации в отношении ИТ. И это обучение не будет эффективным, если оно не подкреплено корпоративной культурой, подчеркивающей ценность информационной безопасности.
Готовы ли вы внедрить в своей организации ознакомительную программу по ИТ? Свяжитесь с Blackbird IT сегодня, чтобы узнать больше о том, как мы можем помочь вам защитить информацию вашей компании.
Свяжитесь с Blackbird IT
Или подпишитесь на наш контент ниже
Примечание: для этого контента требуется JavaScript.
Recent Posts
Как часто вы должны обучать сотрудников осведомленности о кибербезопасности?
Может ли отсутствие защиты данных клиентов привести к краху вашего бизнеса?
Полезные советы по повышению уровня вашей кибербезопасности
Тенденции фишинговых атак в 2022 году: что вы можете сделать для защиты своих данных
По указанию персонала Blackbird выберите тип компьютера ниже, чтобы начать загрузку пакета удаленной поддержки Blackbird.
СКАЧАТЬ ДЛЯ MAC
СКАЧАТЬ ДЛЯ WINDOWS
Как создать эффективный план обеспечения непрерывности бизнесаКибербезопасность
Количество кибератак увеличилось на 20%. Защитите свой бизнес с помощью многофакторной аутентификации | 2FA | MFACybersecurity, Интернет, Безопасность
Защитите свой бизнес с помощью многофакторной аутентификации | 2FA | MFACybersecurity, Интернет, Безопасность
Индукционная кулинария: что это такое и как это работает?| Don’s Appliances
Если вы ищете новую варочную панель, у вас есть несколько вариантов. Существует несколько различных методов нагрева, используемых для варочных панелей, включая газ и электричество, но многие люди не знают, что существует третий вариант, известный как индукция. Хотя каждая варочная панель обладает своими уникальными качествами, важно добавить в свой кухонный репертуар продукт, который вы можете уверенно использовать каждый день.
Газовые и электрические плиты являются золотым стандартом большинства домашних кухонь, но мы хотели выделить все более популярную и динамичную тенденцию приготовления пищи: индукцию. Этот метод приготовления пищи в последнее время набирает обороты, потому что потребители ищут более энергоэффективные варианты приготовления пищи.
Если вы часто готовите, то наверняка будете думать об экономии энергии. Индукционная варочная панель может быть разумным выбором, потому что она не только обеспечивает более точный и равномерный нагрев, но и может сэкономить ваши деньги в долгосрочной перспективе, потому что посуда поглощает тепло, а не поверхность вашего прибора.
Индукционная варочная панель может быть разумным выбором, потому что она не только обеспечивает более точный и равномерный нагрев, но и может сэкономить ваши деньги в долгосрочной перспективе, потому что посуда поглощает тепло, а не поверхность вашего прибора.
Однако, как и любая крупная покупка бытовой техники, она требует тщательного изучения и тщательного рассмотрения. Итак, чтобы немного облегчить себе работу, следуйте нашему последнему руководству, чтобы узнать больше об индукционной кулинарии — что это такое, как это работает и чем это может вам помочь.
Что такое индукционная варочная панель?
Начнем с основ. На первый взгляд индукционные варочные панели очень похожи на стандартные электрические варочные панели со стеклянной поверхностью, но индукционная плита использует электромагнитные волны для нагрева посуды, превращая кастрюли и сковородки в собственный источник тепла.
Поскольку поверхность прибора нагревает посуду с помощью электромагнетизма, система очень эффективна, обеспечивая точное управление и быстрое повышение или понижение температуры. Этот контроль температуры обычно приводит к более быстрому нагреву, особенно во время более трудоемких задач, таких как кипячение воды.
Индукционные варочные поверхности, как известно, кипятят воду на 50 процентов быстрее по сравнению с их газовыми и электрическими аналогами, и они поддерживают постоянную температуру, поэтому случайные разливы или выкипания происходят гораздо реже.
Как работает индукционная плита?
Мы упоминали индукционную варку с использованием электромагнитных токов, но давайте рассмотрим этот процесс подробнее. В то время как газовые и электрические приборы могут использовать теплопроводность для передачи тепла от горелки к кастрюле к вашей еде, индукционное приготовление пищи устраняет посредника, работая почти мгновенно, чтобы нагреть саму посуду для приготовления пищи.
Электрический ток проходит через спиральную медную проволоку под варочной поверхностью, создавая магнитный ток по всей посуде. И самое приятное то, что вся варочная панель остается прохладной на ощупь, поэтому ожоги становятся меньше беспокойства. Известно, что индукционное приготовление более эффективно, чем традиционные методы приготовления пищи, потому что в процессе теряется очень мало тепловой энергии, и вы можете нагревать посуду, не нагревая всю кухню.
Каковы преимущества приготовления пищи с помощью индукции?
Помимо быстрого кипячения и точного контроля температуры, индукционные варочные панели обеспечивают легкую очистку поверхности. Поскольку тепло не поглощается горелками, варочная панель остается достаточно прохладной, чтобы можно было легко вытирать разливы и брызги жира до того, как они полностью обуглятся и сгорят на вашей плите. Окружающее тепло от вашей посуды может по-прежнему вызывать повышение температуры на поверхности для приготовления пищи, но она остывает намного быстрее, чем традиционная варочная панель, поэтому вы можете быстро избавиться от беспорядка.
Некоторые производители предлагают индукционные варочные панели с функцией автоматического выбора размера. Эта индукционная варочная панель черного цвета от Frigidaire (FFIC3026TB) оснащена функцией автоматического определения размера сковороды, которая направляет тепло туда, где это необходимо, и автоматически настраивается в соответствии с размером посуды. Готовите ли вы оладьи на завтрак или обжариваете свиную отбивную на ужин, ваша варочная панель определяет размер вашей сковороды (маленькая, средняя или большая) и направляет необходимое количество тепла для используемой сковороды.
Индукция гораздо безопаснее, потому что плита не сильно нагревается. Если у вас есть маленькие дети, которые любят брать все в свои руки, или непослушные домашние животные, которые любят прыгать на кухонных поверхностях, они могут коснуться прибора, не обжегшись.
Разница между газовыми, электрическими и индукционными варочными панелями
Теперь, когда вы знаете немного больше об индукционных варочных панелях, мы посмотрим, как они соотносятся с другими видами топлива.
Газовые
Газовые варочные панели нагревают пищу открытым пламенем. Газ обеспечивает быстрый нагрев и исключительный контроль как при сильном, так и при слабом нагреве. Пламя позволяет легко оценить уровень нагрева и уменьшить его, если кажется, что посуда становится слишком горячей.
Варочные панели с герметичными газовыми конфорками приятны на ощупь, потому что они предотвращают попадание пищи под конфорку, облегчая уборку. Если вы покупаете варочную панель со сплошными решетками, вы можете легко перемещать тяжелые кастрюли и сковороды по варочной панели, не сгибаясь и не поднимая тяжести.
В некоторых газовых варочных панелях, таких как эта варочная панель с нисходящей тягой от KitchenAid (KCGD500GSS), система вентиляции встроена в варочную поверхность, поэтому отдельная вытяжка не требуется. Дым и запахи можно удалять снаружи или фильтровать и рециркулировать внутри. Газовые варочные панели могут выступать в качестве устройства «два в одном», чтобы ваша кухня работала наилучшим образом.
Дым и запахи можно удалять снаружи или фильтровать и рециркулировать внутри. Газовые варочные панели могут выступать в качестве устройства «два в одном», чтобы ваша кухня работала наилучшим образом.
Электрические
Электрические варочные панели нагревают пищу без пламени. Электрические варочные панели бывают двух видов: змеевики и гладкие. Электрические катушки, находящиеся под поверхностью, нагревают варочную панель и передают это тепло вашей посуде. Змеевики располагаются на поверхности варочной панели и более восприимчивы к разливам, но поддоны, расположенные под змеевиками, будут содержать большую часть беспорядка.
Гладкие поверхности оснащены излучающими нагревательными элементами, похожими на змеевики, но вместо того, чтобы располагаться сверху, зоны нагрева расположены под гладкой, легко очищаемой стеклянной поверхностью. Они равномерно нагреваются и придают вашей кухне элегантный вид.
Если вы заинтересованы в покупке электрической варочной панели, у нас есть несколько замечательных функций, которые помогут вам в приготовлении пищи. Двухэлементные горелки имеют внутреннее кольцо для посуды меньшего размера и внешнее кольцо для посуды большего размера. Мостовые элементы представляют собой большое пространство между двумя основными нагревательными элементами, используемое для создания отдельной варочной поверхности для сковородок, а индикаторы горячей поверхности добавляют вашему устройству элемент безопасности, сообщая вам, когда ваша варочная панель активна или еще слишком горячая, чтобы ее можно было коснуться.
Двухэлементные горелки имеют внутреннее кольцо для посуды меньшего размера и внешнее кольцо для посуды большего размера. Мостовые элементы представляют собой большое пространство между двумя основными нагревательными элементами, используемое для создания отдельной варочной поверхности для сковородок, а индикаторы горячей поверхности добавляют вашему устройству элемент безопасности, сообщая вам, когда ваша варочная панель активна или еще слишком горячая, чтобы ее можно было коснуться.
Индукционная плита
Напомним, что индукционные варочные панели — это разновидность электрических плит. Основное отличие заключается в способе передачи тепла. Магнитные катушки нагревают вашу посуду напрямую, поэтому вы можете наслаждаться точными и равномерными результатами без горячей на ощупь поверхности.
Если вы ищете универсальный прибор для приготовления пищи, индукционная варочная панель Bosch серии 800 (NIT8069SUC) имеет 11 конфорок, 17 уровней мощности и использует настройки SpeedBoost и AutoChef для быстрой, мощной и стабильной настройки температуры для точной результаты приготовления. Эта варочная панель может быть установлена в бескаркасной конструкции, чтобы более органично интегрироваться с вашей столешницей, или может быть установлена в раме из нержавеющей стали, чтобы выделяться и гордиться своей кухней.
Эта варочная панель может быть установлена в бескаркасной конструкции, чтобы более органично интегрироваться с вашей столешницей, или может быть установлена в раме из нержавеющей стали, чтобы выделяться и гордиться своей кухней.
Часто задаваемые вопросы о приготовлении пищи на индукции
1. Отличается ли приготовление пищи на индукции?
Приготовление пищи на индукционном приборе ничем не отличается, но может потребоваться начальное обучение. Поскольку посуда нагревается быстрее, общее время приготовления может сократиться. Следите за своей едой, чтобы избежать переваривания, и используйте различные уровни мощности, чтобы адаптироваться к вашим потребностям. В некоторых моделях предусмотрены уровни, обеспечивающие идеальное количество тепла для тушения, варки и обжаривания.
2. Требуется ли для индукции специальная посуда?
Индукционная посуда для работы должна реагировать на электромагнитные поля. Черные металлы, такие как нержавеющая сталь и чугун, подходят для индукционной плиты. Однако посуда из алюминия, стекла, меди или керамики не подходит для индукционных плит.
Черные металлы, такие как нержавеющая сталь и чугун, подходят для индукционной плиты. Однако посуда из алюминия, стекла, меди или керамики не подходит для индукционных плит.
Если вы не уверены, подходит ли ваша посуда для использования, попробуйте магнитный тест. Если к вашей посуде прилипает магнит, значит, она подойдет для индукционной плиты.
3. Легко ли устанавливать индукционные варочные панели?
Установка будет зависеть от выбранной вами марки прибора, а также от текущей электропроводки и источника питания в вашем доме. Если для вашей варочной панели требуются специальные розетки или новая проводка, обратитесь к профессионалу для установки.
Выбор за вами
Когда дело доходит до покупки новой варочной панели, решите, какая модель прибора лучше всего соответствует вашим кулинарным потребностям. Если вы хотите выйти из своей зоны комфорта и инвестировать в уникальный и динамичный прибор, вам подойдет индукционная варочная панель. С более быстрым нагревом, улучшенной энергоэффективностью и улучшенными функциями безопасности это кажется легкой задачей.
С более быстрым нагревом, улучшенной энергоэффективностью и улучшенными функциями безопасности это кажется легкой задачей.
Если у вас есть вопросы или вам нужна дополнительная информация, просмотрите наш онлайн-каталог, позвоните нам или посетите наш магазин Don’s Appliances — вашего ведущего продавца бытовой техники в районе Питтсбурга.
Индукция родов — Клиника Майо
Обзор
Индукция родов — также известная как стимуляция родов — побуждает матку сокращаться во время беременности до того, как роды начнутся сами по себе при вагинальных родах.
Медицинский работник может порекомендовать стимуляцию родов по разным причинам, в первую очередь, когда есть опасения за здоровье матери или ребенка. Важным фактором в прогнозировании успеха индукции является то, насколько мягкой и расширенной является шейка матки (созревание шейки матки). Гестационный возраст ребенка, подтвержденный ранними регулярными ультразвуковыми исследованиями, также важен.
Если поставщик медицинских услуг рекомендует индукцию родов, обычно это происходит потому, что преимущества перевешивают риски. Если вы беременны, понимание того, почему и как проводится индукция родов, может помочь вам подготовиться.
Если вы беременны, понимание того, почему и как проводится индукция родов, может помочь вам подготовиться.
Продукты и услуги
- Книга: Книга здоровья семьи клиники Мэйо, 5-е издание
- Книга: Руководство клиники Мэйо по здоровой беременности
- Информационный бюллетень: Письмо о здоровье клиники Мэйо — цифровое издание
Почему это делается
3 Определить 9 если необходима индукция родов, поставщик медицинских услуг, вероятно, оценит несколько факторов. К ним относятся здоровье матери и состояние шейки матки. Они также включают здоровье ребенка, срок беременности, вес, размер и положение в матке. Причины для стимуляции родов включают:
- Приблизительно на 1–2 недели позже срока родов без начала родов (переношенная беременность).
- Когда роды не начинаются после отхождения вод (предродовое излитие плодных оболочек).
- Инфекция матки (хориоамнионит).
- Когда предполагаемый вес ребенка меньше 10-го процентиля для гестационного возраста (задержка роста плода).

- Когда вокруг ребенка недостаточно амниотической жидкости (маловодие).
- Возможно, диабет развивается во время беременности (гестационный диабет) или диабет существует до беременности.
- Развитие повышенного артериального давления в сочетании с признаками поражения другой системы органов (преэклампсия) во время беременности. Или наличие высокого кровяного давления до беременности, его развитие до 20 недель беременности (хроническое высокое кровяное давление) или развитие состояния после 20 недель беременности (гестационная гипертензия).
- При отслойке плаценты от внутренней стенки матки перед родами частично или полностью (отслойка плаценты).
- Наличие определенных заболеваний. К ним относятся заболевания сердца, легких или почек и ожирение.
Плановая стимуляция родов — это начало родов для удобства, когда нет медицинской необходимости. Это может быть полезно для женщин, которые живут далеко от больницы или родильного дома или у которых в анамнезе были быстрые роды.
Запланированная индукция может помочь избежать родов без посторонней помощи. В таких случаях поставщик медицинских услуг подтвердит, что гестационный возраст ребенка составляет не менее 39 лет.недель или старше до индукции, чтобы снизить риск проблем со здоровьем у ребенка.
В результате недавних исследований женщинам с беременностью низкого риска предлагается родовозбуждение в сроке от 39 до 40 недель. Исследования показывают, что стимуляция родов в это время снижает несколько рисков, включая мертворождение, рождение крупного ребенка и развитие высокого кровяного давления по мере продолжения беременности. Важно, чтобы женщины и их поставщики принимали участие в принятии решений о стимулировании родов в сроке от 39 до 40 недель.
Запись на прием в клинике Майо
Из клиники Мэйо на ваш почтовый ящик
Зарегистрируйтесь бесплатно и будьте в курсе научных достижений, советов по здоровью и актуальных тем, связанных со здоровьем, таких как COVID-19, а также экспертных знаний по управлению здоровьем.
Чтобы предоставить вам самую актуальную и полезную информацию, а также понять, какая информация полезна, мы можем объединить вашу электронную почту и информацию об использовании веб-сайта с другая информация о вас, которой мы располагаем. Если вы пациент клиники Майо, это может включать защищенную информацию о здоровье. Если мы объединим эту информацию с вашей защищенной медицинской информации, мы будем рассматривать всю эту информацию как информацию и будет использовать или раскрывать эту информацию только так, как указано в нашем уведомлении о практики конфиденциальности. Вы можете отказаться от получения сообщений по электронной почте в любое время, нажав на ссылка для отписки в письме.
Риски
Разрезы матки, используемые при кесаревом сечении
Разрезы матки, используемые при кесаревом сечении
Кесарево сечение включает разрез брюшной полости и разрез матки. После разреза брюшной полости медицинский работник сделает разрез в матке. Наиболее распространены низкие поперечные разрезы (вверху слева).
После разреза брюшной полости медицинский работник сделает разрез в матке. Наиболее распространены низкие поперечные разрезы (вверху слева).
Индукция родов сопряжена с различными рисками, в том числе:
- Неудачная индукция. Индукция может считаться неудачной, если используемые методы не приводят к вагинальным родам через 24 или более часов. В таких случаях может потребоваться кесарево сечение.
- Низкий пульс плода. Лекарства, используемые для стимуляции родов — окситоцин или простагландин — могут вызвать слишком сильное сокращение матки, что может уменьшить снабжение ребенка кислородом и снизить частоту сердечных сокращений ребенка.
- Инфекция. Некоторые методы индукции родов, такие как разрыв плодных оболочек, могут увеличить риск инфицирования как матери, так и ребенка. Чем дольше время между разрывом плодных оболочек и родами, тем выше риск инфекции.
Разрыв матки.
 Это редкое, но серьезное осложнение, при котором матка разрывается по линии рубца после предшествующего кесарева сечения или обширной операции на матке. В редких случаях разрыв матки также может произойти у женщин, у которых ранее не было операций на матке.
Это редкое, но серьезное осложнение, при котором матка разрывается по линии рубца после предшествующего кесарева сечения или обширной операции на матке. В редких случаях разрыв матки также может произойти у женщин, у которых ранее не было операций на матке.Экстренное кесарево сечение необходимо для предотвращения опасных для жизни осложнений. Возможно, придется удалить матку.
- Кровотечение после родов. Индукция родов увеличивает риск того, что мышцы матки не будут правильно сокращаться после родов, что может привести к серьезному кровотечению после родов.
Индукция родов подходит не всем. Это может быть не вариант, если:
- У вас было кесарево сечение с классическим разрезом или обширная операция на матке
- Плацента блокирует шейку матки (предлежание плаценты)
- Ваш ребенок лежит сначала ягодицами (тазовое предлежание) или на боку (поперечное положение)
- У вас активная инфекция генитального герпеса
- Пуповина выскальзывает во влагалище перед родами (выпадение пуповины)
Если у вас было кесарево сечение и вас вызвали роды, ваш лечащий врач, скорее всего, будет избегать приема некоторых лекарств, чтобы снизить риск разрыва матки.
Как вы готовитесь
Индукция родов обычно проводится в больнице или родильном доме. Это потому, что там можно наблюдать за матерью и ребенком, а услуги по родовспоможению легко доступны.
Чего ожидать
Во время процедуры
Существуют различные способы стимуляции родов. В зависимости от обстоятельств поставщик медицинских услуг может использовать один из следующих способов или их комбинацию. Провайдер может:
Созревание шейки матки. Иногда простагландины, варианты химических веществ, вырабатываемых организмом естественным путем, вводят во влагалище или принимают внутрь для истончения или смягчения (созревания) шейки матки. После применения простагландинов контролируют сокращения и частоту сердечных сокращений ребенка.
В других случаях в шейку матки вводят небольшую трубку (катетер) с надувным баллоном на конце. Наполнение баллона физиологическим раствором и размещение его внутри шейки матки способствует созреванию шейки матки.

- Очистите оболочки амниотического мешка. С помощью этой техники, также известной как удаление плодных оболочек, медицинский работник проводит пальцем в перчатке по покрытию амниотического мешка рядом с плодом. Это отделяет мешок от шейки матки и нижней стенки матки, что может способствовать началу родов.
Разрыв амниотического мешка. С помощью этой техники, также известной как амниотомия, медицинский работник делает небольшое отверстие в амниотическом мешке. Отверстие заставляет воду прорываться, что может помочь продвижению родов.
Амниотомию делают только в том случае, если шейка частично раскрыта и истончена, а головка ребенка находится глубоко в малом тазу. До и после процедуры контролируют частоту сердечных сокращений ребенка.
- Введите лекарство в вену. В больнице медицинский работник может ввести в вену разновидность окситоцина (питоцина) — гормона, вызывающего сокращения матки.
 Окситоцин более эффективен при ускорении уже начавшихся родов, чем при созревании шейки матки. Медицинский работник контролирует сокращения и частоту сердечных сокращений ребенка.
Окситоцин более эффективен при ускорении уже начавшихся родов, чем при созревании шейки матки. Медицинский работник контролирует сокращения и частоту сердечных сокращений ребенка.
Время, необходимое для начала родов, зависит от того, насколько созрела шейка матки на момент начала индукции, используемых методов индукции и реакции организма на них. Это может занять от минут до часов.
После процедуры
В большинстве случаев индукция родов приводит к вагинальным родам. Неудачная индукция, при которой процедура не приводит к вагинальным родам, может потребовать повторной индукции или кесарева сечения.
Персонал клиники Мэйо
Связанный
Товары и услуги
Проблема индукции (Стэнфордская философская энциклопедия)
1. Проблема Юма
Юм вводит проблему индукции как часть анализа
представления о причине и следствии. Юм работал с картиной, широко распространенной в
ранний современный период, когда разум был населен ментальными
сущности, называемые «идеями». Юм считал, что в конечном счете все
наши идеи восходят к «впечатлениям»
чувственный опыт. В простейшем случае идея приходит в голову путем
«скопировано» с соответствующего оттиска (Т.
1.1.1.7/4). Затем создаются более сложные идеи за счет комбинации
простые идеи (Э. 2.5/19). Юм считал, что существует ряд соотношений
между идеями, включая отношение причинности (Е. 3.2; подробнее
о философии Юма в целом см. Morris & Brown
2014).
Юм считал, что в конечном счете все
наши идеи восходят к «впечатлениям»
чувственный опыт. В простейшем случае идея приходит в голову путем
«скопировано» с соответствующего оттиска (Т.
1.1.1.7/4). Затем создаются более сложные идеи за счет комбинации
простые идеи (Э. 2.5/19). Юм считал, что существует ряд соотношений
между идеями, включая отношение причинности (Е. 3.2; подробнее
о философии Юма в целом см. Morris & Brown
2014).
Для Юма отношение причинности есть единственное отношение посредством что «мы можем выйти за пределы свидетельства нашей памяти и чувства» (Э. 4.1.4, Т. 1.3.2.3/74). Предположим, у нас есть объект представить нашим чувствам: скажем, порох. Затем мы можем сделать вывод об эффекте этого объекта: скажем, взрыв. Причинно-следственная связь связывает наше прошлое и представить опыт нашим ожиданиям о будущем (Э. 4.1.4/26).
Юм утверждает, что мы не можем сделать причинно-следственный вывод только на основании 90 374 а.
априори означает (Э. 4.1.7). Скорее, утверждает он, оно основано на
опыт, и особенно опыт постоянного соединения. Мы
сделать вывод, что порох взорвется на основе прошлого опыта
связи пороха и взрывов.
Скорее, утверждает он, оно основано на
опыт, и особенно опыт постоянного соединения. Мы
сделать вывод, что порох взорвется на основе прошлого опыта
связи пороха и взрывов.
Хьюм хочет узнать больше об основании такого вывода. Если такой вывод делается по «цепочке рассуждений» (Э. 4.2.16), говорит он, он хотел бы знать, что это за рассуждение. В вообще, он утверждает, что выводы зависят от перехода форма:
Я обнаружил, что такой объект всегда сопровождался такой эффект, и я предвижу, что другие предметы, находящиеся в внешний вид, аналогичный, будет сопровождаться аналогичными эффектами . (Э. 4.2.16)
В Трактате Юм говорит, что
если бы Разум определял нас, он исходил бы из этого принципа что случаи, о которых мы не имели опыта, должны напоминать те, о которых мы имели опыт, и что ход природы продолжается всегда одинаково . (Т. 1.3.6.4)
Для удобства мы будем ссылаться на это заявление о сходстве или
сходство между наблюдаемыми и ненаблюдаемыми закономерностями
«Принцип единообразия (УП)». Иногда его также называют
«Принцип сходства» или «Принцип сходства».
Единообразие природы».
Иногда его также называют
«Принцип сходства» или «Принцип сходства».
Единообразие природы».
Затем Юм представляет свой знаменитый аргумент, заключающийся в том, что не может быть никакого обоснования этого принципа. Аргумент принимает вид дилеммы. Юм различает отношения идей и дела по факту. Отношения идей включают геометрические, алгебраические и арифметические предложения, «и, короче говоря, каждое утверждение, что либо интуитивно, либо демонстративно достоверно». «Факты», с другой стороны, являются эмпирическими суждения, которые легко могут быть поняты как иные, чем они есть. Юм говорит, что
Все рассуждения можно разделить на два вида: доказательные рассуждение, или то, что касается отношений идей и морального рассуждения, или то, что касается материи факта и существования. (Э. 4.2.18)
Юм рассматривает возможность каждого из этих типов рассуждений в
свою очередь, и в каждом случае утверждает, что для него невозможно поставить
аргумент в пользу принципа единообразия.
Во-первых, Юм утверждает, что рассуждение не может быть доказательным, потому что демонстративное рассуждение только устанавливает выводы, которые не могут быть задуман как ложный. И, говорит,
это не подразумевает никакого противоречия в том, что течение природы может измениться, и что объект, внешне похожий на те, которые мы испытали, может быть сопровождается различными или противоположными эффектами. (Э. 4.2.18)
Можно, говорит он, ясно и отчетливо представить себе ситуация, когда ненаблюдаемый случай не следует закономерности, поэтому далеко наблюдается (Е. 4.2.18, Т. 1.3.6.5/89).
Во-вторых, Юм утверждает, что рассуждение также не может быть «таким, как рассматривать материю факта и реальное существование». Он также называет это «вероятное» рассуждение. Все подобные рассуждения, утверждает он, «исходить из предположения, что будущее будет сообразным прошлому», иными словами, на единообразии Принцип (Е.4.2.19).
Поэтому, если цепочка рассуждений основана на аргументе этого
вид, что он снова будет полагаться на это предположение, «и принимая
это само собой разумеющееся, о чем и идет речь». (Э.
4.2.19, см. также Т. 1.3.6.7/90). Тогда второй тип рассуждений
не может обеспечить цепочку рассуждений, которая не является круговой.
(Э.
4.2.19, см. также Т. 1.3.6.7/90). Тогда второй тип рассуждений
не может обеспечить цепочку рассуждений, которая не является круговой.
В версии «Трактата» Юм заключает:
Таким образом, не только наш разум подводит нас в открытии конечная связь причин и следствий, но даже после опыт сообщил нам об их постоянная соединение , нам невозможно удовлетвориться наша причина, почему мы должны расширить этот опыт за пределы тех отдельные случаи, попавшие под наше наблюдение. (Т. 1.3.6.11/91–2)
Таким образом, можно сделать вывод, что наша склонность проецировать прошлые закономерности в будущее не подкреплено разумом. Проблема индукции заключается в том, чтобы найти способ избежать этого вывода, несмотря на аргумент.
Поставив проблему, Юм представляет свою собственную.
«решение» поднятых им сомнений (Э. 5, Т.
1.3.7–16). Это состоит в объяснении того, что индуктивная
умозаключениями движет если не разум. В Трактат Юм
ставит проблему индукции явно контрастным способом. Он
спрашивает, произведен ли переход, задействованный в выводе
Он
спрашивает, произведен ли переход, задействованный в выводе
посредством понимания или воображения; будь мы определяется разумом совершить переход или определенным ассоциации и отношения восприятий? (Т. 1.3.6.4)
И он продолжает резюмировать вывод, говоря:
.Поэтому, когда ум уходит от идеи или впечатления об одном возражать против идеи или убеждения другого, оно не определяется причине, а по определенным принципам, которые связывают воедино идеи этих предметов и объединить их в воображении. (Т. 1.3.6.12)
Таким образом, именно воображение считается ответственным за в основе индуктивного вывода, а не разума.
В Inquiry Хьюм предполагает, что шаг, предпринятый ум,
который не поддерживается ни аргументом, ни процессом понимание… должно быть вызвано каким-то другим принципом равный вес и авторитет. (Д.5.1.2)
Этот принцип называется «обычай» или «привычка». идея состоит в том, что если кто-то видел подобные объекты или события постоянно
соединены, то разум склонен ожидать сходной закономерности с
держать в будущем. Склонность или «склонность» к рисованию
такие умозаключения, является следствием обычая:
идея состоит в том, что если кто-то видел подобные объекты или события постоянно
соединены, то разум склонен ожидать сходной закономерности с
держать в будущем. Склонность или «склонность» к рисованию
такие умозаключения, является следствием обычая:
…обнаружив во многих случаях, что любые два вида объекты, пламя и тепло, снег и холод, всегда были соединены вместе; если пламя или снег заново представить чувствам, ум носится по обычаю ожидать тепла или холода, а к верить , что такое качество существует и обнаружится при ближайшем подход. Эта вера является необходимым результатом помещения ума в таких обстоятельствах. Это работа души, когда мы так положение, столь же неизбежное, как чувство страсти любви, когда мы получать льготы; или ненависть, когда мы встречаемся с обидами. Все эти операции являются разновидностью естественных инстинктов, не поддающихся никаким рассуждениям или процесс мышления и понимания способен либо производить, или предотвратить. (Д.
5.1.8)
Юм утверждает, что тот факт, что эти выводы действительно следуют курсу природы есть своего рода «заранее установленная гармония» (Э. 5.2.21). Это своего рода естественный инстинкт, который на самом деле может быть более эффективно делать нас успешными в мире, чем если бы мы полагались на основания для таких выводов.
2. Реконструкция
Аргумент Юма был представлен и сформулирован во многих разные версии. Также идет оживленная дискуссия по поводу историческая интерпретация того, что сам Юм имел в виду под аргумент. Поэтому трудно дать однозначное и бесспорная реконструкция аргумента Юма. Тем не менее, в целях систематизации различных ответов на юмовскую проблема, которая будет обсуждаться в этой статье, следующая реконструкция послужит полезной отправной точкой.
Аргумент Юма касается конкретных индуктивных выводов, таких как как:
Все наблюдаемые экземпляры A были B .
Следующим экземпляром A будет B .
Назовем это «вывод I ». Выводы, которые попадающие под этот тип схемы, теперь часто называют случаями «простая перечислительная индукция».
Собственный пример Хьюма:
Все наблюдаемые экземпляры хлеба (особого вида) были питательный.
Следующим экземпляром хлеба (такого вида) будет питательный.
Аргумент Юма тогда продолжается следующим образом (посылки помечены как P, а подвыводы и выводы как C):
- P1. Есть только два вида аргументов: доказательные и вероятные (юмовское вилка).
- С2. Вывод I предполагает принцип единообразия (UP).
1 St Звуковой сигнал:
- P3. А доказательный аргумент устанавливает вывод, отрицание которого является противоречие.
- С4. отрицание ВП не является противоречием.
- С1. Здесь нет демонстративный аргумент в пользу UP (по P3 и P4).
2 и звуковой сигнал:
- P5.
 Любой
вероятный аргумент в пользу UP предполагает UP.
Любой
вероятный аргумент в пользу UP предполагает UP. - С6. Аргумент ибо принцип не может предполагать тот же самый принцип (нецикличность).
- С2. Есть нет вероятного аргумента в пользу UP (от P5 и P6).
- С3. Есть нет аргумента для UP (по P1, C1 и C2).
Последствия:
- P7. Если там не является аргументом для UP, нет цепочки рассуждений от предпосылок для вывода любого вывода, который предполагает UP.
- С4. Есть отсутствие цепочки рассуждений от предпосылок к заключению вывода I (по P2, C3 и P7).
- стр.8. Если там не является цепочкой рассуждений от посылок к заключению вывод I вывод не обоснован.
- С5. Вывод I не обосновано (по C4 и P8).
Были разные интерпретации того, что Юм имел в виду под
«доказательные» и «вероятные» аргументы.
Иногда «демонстративный» приравнивается к
«дедуктивный» и вероятностный с «индуктивным»
(например, Салмон, 1966). Тогда первый рог дилеммы Юма
исключить возможность дедуктивного рассуждения, а второе
исключает возможность индуктивного аргумента. Однако,
в этой интерпретации,
помещение Р3
не будет состоять, потому что возможно заключение
дедуктивный аргумент, чтобы быть ненужным предложением. Предпосылка P3 может
изменить, чтобы сказать, что демонстративный (дедуктивный) аргумент
устанавливает вывод, который не может быть ложным, если посылки
истинный. Но тогда становится возможным, что предположение о том, что
будущее напоминает прошлое, что не является необходимым предложением, могло бы
быть установлено дедуктивным аргументом из некоторых посылок, хотя и не
от априори помещений (вопреки выводу
С1).
Тогда первый рог дилеммы Юма
исключить возможность дедуктивного рассуждения, а второе
исключает возможность индуктивного аргумента. Однако,
в этой интерпретации,
помещение Р3
не будет состоять, потому что возможно заключение
дедуктивный аргумент, чтобы быть ненужным предложением. Предпосылка P3 может
изменить, чтобы сказать, что демонстративный (дедуктивный) аргумент
устанавливает вывод, который не может быть ложным, если посылки
истинный. Но тогда становится возможным, что предположение о том, что
будущее напоминает прошлое, что не является необходимым предложением, могло бы
быть установлено дедуктивным аргументом из некоторых посылок, хотя и не
от априори помещений (вопреки выводу
С1).
Другое распространенное прочтение — приравнять «демонстративный» к
«дедуктивно действителен с априорными помещениями», и
«вероятно» с «имеющим эмпирическую предпосылку»
(например, Окаша 2001). Это может быть ближе к истине, если подумать, как
Юм, по-видимому, сделал, что предпосылки, которые могут быть познаны 90 374 а
априори не могут быть ложными и, следовательно, необходимы. Если вывод
является дедуктивно верным, то вывод вывода из а
Априори помещения также должны быть необходимы. Какой первый рог
тогда дилемма исключает возможность дедуктивно достоверного
аргумент с априори посылок, а правит второй рожок
любой аргумент (дедуктивный или недедуктивный), который опирается на
эмпирическая предпосылка.
Если вывод
является дедуктивно верным, то вывод вывода из а
Априори помещения также должны быть необходимы. Какой первый рог
тогда дилемма исключает возможность дедуктивно достоверного
аргумент с априори посылок, а правит второй рожок
любой аргумент (дедуктивный или недедуктивный), который опирается на
эмпирическая предпосылка.
Однако недавние комментаторы утверждали, что в исторической
контекст, в котором находился Юм, различие, которое он проводит между
доказательные и вероятные аргументы имеют мало общего с тем,
не аргумент имеет дедуктивную форму (Оуэн 1999; Гаррет 2002). В
Кроме того, класс выводов, которые устанавливают выводы,
отрицание противоречие может включать в себя не только дедуктивно значимые
выводы из 90 374 априорных 90 375 посылок, но любые выводы, которые
можно вывести с помощью априорных рассуждений (то есть рассуждений
где переход от посылок к заключению не вызывает апелляции
тому, что мы узнаем из наблюдений). Похоже, что Хьюм
намерен аргумент первого рога, чтобы исключить любые а
априори рассуждения, так как он говорит, что изменение хода
природа не может быть исключена «никаким доказательным аргументом или
абстрактное рассуждение априори » (Э. 5.2.18). На этом
понимания, априорных аргументов были бы исключены
первый рог дилеммы Юма и эмпирические аргументы
второй рог. Это интерпретация, которую я приму для
цели настоящей статьи.
5.2.18). На этом
понимания, априорных аргументов были бы исключены
первый рог дилеммы Юма и эмпирические аргументы
второй рог. Это интерпретация, которую я приму для
цели настоящей статьи.
В аргументации Юма UP играет центральную роль. Как мы увидим
в
раздел 4.2,
различные авторы сомневались в этом принципе. Версии
Были также сформулированы аргументы Юма, которые не делают
ссылка на УП. Скорее, они прямо решают вопрос о том, что
аргументы могут быть приведены в поддержку перехода от предпосылок
к заключению конкретного индуктивного вывода я . какая
аргументы могут привести нас, например, к заключению, что следующая часть
хлеб будет питательным из наблюдений за питательным хлебом, приготовленным таким образом
далеко? Для первого рога аргумента аргумент Юма может быть
применяется непосредственно. Доказательный аргумент устанавливает вывод
отрицание которого есть противоречие. Отрицание заключения
индуктивный вывод не является противоречием. это не
противоречие, что следующий кусок хлеба не сытный. Таким образом, нет никаких доказательных аргументов в пользу вывода
индуктивный вывод. Во втором роге аргумента
Проблема, которую поднимает Юм, — это замкнутость. Даже если Юм ошибается в том, что все
индуктивные выводы зависят от UP, все еще может быть
проблема цикличности, но, как мы увидим в
раздел 4.1,
необходимо тщательно рассмотреть точный характер циркулярности.
Но главное в настоящее время состоит в том, что аргумент Юма часто
сформулированы без вызова УП.
Таким образом, нет никаких доказательных аргументов в пользу вывода
индуктивный вывод. Во втором роге аргумента
Проблема, которую поднимает Юм, — это замкнутость. Даже если Юм ошибается в том, что все
индуктивные выводы зависят от UP, все еще может быть
проблема цикличности, но, как мы увидим в
раздел 4.1,
необходимо тщательно рассмотреть точный характер циркулярности.
Но главное в настоящее время состоит в том, что аргумент Юма часто
сформулированы без вызова УП.
Поскольку аргумент Юма представляет собой дилемму, есть два основных способа
противостоять этому. Во-первых, взяться за первый рог и утверждать, что
в конце концов, есть демонстративный аргумент, который здесь понимается как
аргумент, основанный на априорных рассуждениях, — который может
обосновать индуктивный вывод. Второй — справиться со вторым
рог и утверждать, что все-таки существует вероятное (или эмпирическое)
аргумент, который может обосновать индуктивный вывод. Мы обсуждаем
разные варианты этих двух подходов в разделах
3
а также
4.
Есть также те, кто оспаривает последствия этой дилеммы. За
например, некоторые недавние комментаторы Юма интерпретируют его как рисунок
единственный вывод
С4,
а не нормативный вывод
С5
(мы обсуждаем эти интерпретации в
раздел 5.1).
Существуют также подходы, которые не согласны с
помещение Р8
и утверждают, что обеспечение цепочки рассуждений от предпосылок к
заключение не является необходимым условием для обоснования
индуктивный вывод (разделы
5.2
а также
5.3).
Наконец, есть некоторые философы, которые принимают скептическую
вывод
С5
и попробуй его приспособить. Например, были попытки
утверждать, что индуктивный вывод не так важен для научного
запрос, как часто думают
(раздел 6).
Также можно утверждать, что, хотя аргумент Юма
устанавливает, что индуктивные выводы не оправданы в
ощущение, что у нас есть основания считать их выводы верными,
тем не менее возможно и более слабое обоснование. Это основано
на идее, что мы можем установить, что следующие индуктивные процедуры
является средством для достижения определенных эпистемологических целей. Мы изучаем традицию
связанный с этим подходом в
раздел 7.
Мы изучаем традицию
связанный с этим подходом в
раздел 7.
3. Решение первой дилеммы Рога Юма
Первый рог аргумента Юма, сформулированный выше, направлен
при установлении того, что нет никакого демонстративного аргумента в пользу UP. А
многие философы считали, что это не окончательно
исключить возможность обоснования индуктивных выводов
на основе показательного аргумента. Есть два основных потенциальных выхода
пути от первого рога дилеммы Юма. Во-первых,
отказываться от
помещение Р3,
что означает допущение возможности синтетического а
априори предложений. Во-вторых, принять вывод
С1,
что нет демонстративного аргумента в пользу UP, но утверждать, что
такой аргумент не является необходимым для оправдания. Действительно, можно было
сказать, что даже не обязательно иметь доказательную аргументацию в пользу
заключение индуктивного вывода. Скорее, мысль в том, что
будет достаточно для обоснования, чтобы иметь аргумент в пользу
Утверждение, что вывод индуктивного вывода вероятно . Мы рассмотрим каждый из этих подходов в следующих двух
разделы.
Мы рассмотрим каждый из этих подходов в следующих двух
разделы.
3.1 Синтетика
априориКак мы видели в секция 1, Юм использует наглядные аргументы, чтобы сделать выводы, которые «отношения идей», тогда как «вероятные» или «моральные» аргументы имеют выводы, которые «по факту». Юмовское различие между «отношения идей» и «факты» предвосхищает различие, проведенное Кантом между «аналитические» и «синтетические» суждения (Кант 1781 г.). Классический пример аналитического предложения: «Холостяки — неженатые мужчины», и синтетическое предложение «Моя велосипедная шина спустила». Для Юма демонстративный аргументы, основанные на априори рассуждение, можно устанавливают только отношения идей или аналитических предложений. связь между приоритетом и аналитичностью лежит в основе помещение Р3, в котором говорится, что наглядный аргумент устанавливает вывод отрицание которого есть противоречие.
Один из возможных ответов на проблему Юма — отрицание
помещение Р3,
допуская возможность того, что априорное рассуждение может
порождают синтетические предложения. Кант классно возразил в ответ
Юму, что такое синтетическое априори знание возможно
(Кант 1781, 1783). Он делает это, как бы переворачивая
Эмпирическая программа Юма. В то время как Юм пытался
понять, как концепция причинной или необходимой связи может
быть основанным на опыте, Кант вместо этого утверждал, что опыт приходит только
через понятия или «категории»
понимание. По его мнению, можно получить априорных знаний.
этих понятий, включая понятие причинности,
трансцендентный аргумент относительно необходимых предпосылок
опыт. Более подробный отчет об ответе Канта Юму
можно найти в de Pierris and Friedman 2013.
Кант классно возразил в ответ
Юму, что такое синтетическое априори знание возможно
(Кант 1781, 1783). Он делает это, как бы переворачивая
Эмпирическая программа Юма. В то время как Юм пытался
понять, как концепция причинной или необходимой связи может
быть основанным на опыте, Кант вместо этого утверждал, что опыт приходит только
через понятия или «категории»
понимание. По его мнению, можно получить априорных знаний.
этих понятий, включая понятие причинности,
трансцендентный аргумент относительно необходимых предпосылок
опыт. Более подробный отчет об ответе Канта Юму
можно найти в de Pierris and Friedman 2013.
3.2 Обоснование вероятного вывода
Первый рог дилеммы Юма подразумевает, что не может быть
доказательный аргумент к заключению индуктивного вывода
потому что можно представить себе отрицание вывода.
Например, вполне возможно представить себе, что следующий фрагмент
хлеб, который я ем, скорее отравит меня, чем напитает. Однако это делает
не исключаю возможности доказательного аргумента, что
устанавливает только то, что хлеб, скорее всего, насытит, а не то, что
это определенно будет. Существует несколько подходов, которые пытаются
привести наглядный аргумент, что заключение индуктивного
вывод вероятен, хотя и не бесспорен. Если это удается, цепь
рассуждений, основанных на доказательных аргументах из предпосылок
вывод I к предположению, что заключение вероятно
не исключается аргументом Юма. Тогда можно было бы бросить вызов
помещение P8,
говоря, что для обоснования индуктивного
умозаключение иметь цепочку рассуждений от его предпосылок к его
вывод. Скорее было бы достаточно, если бы у нас был аргумент от
предпосылок к утверждению, что вывод является вероятным или вероятным. затем априорное обоснование индуктивного вывода было бы
были предоставлены.
Существует несколько подходов, которые пытаются
привести наглядный аргумент, что заключение индуктивного
вывод вероятен, хотя и не бесспорен. Если это удается, цепь
рассуждений, основанных на доказательных аргументах из предпосылок
вывод I к предположению, что заключение вероятно
не исключается аргументом Юма. Тогда можно было бы бросить вызов
помещение P8,
говоря, что для обоснования индуктивного
умозаключение иметь цепочку рассуждений от его предпосылок к его
вывод. Скорее было бы достаточно, если бы у нас был аргумент от
предпосылок к утверждению, что вывод является вероятным или вероятным. затем априорное обоснование индуктивного вывода было бы
были предоставлены.
3.2.1 Номолого-объяснительный раствор
Первым из этих подходов является
«Номологически-объяснительное» решение, которое было поставлено
вперед Армстронга, BonJour и Фостера (Armstrong 1983; BonJour
1998 год; Фостер 2004). Это решение обращается к Inference to the Best
Объяснение (IBE), в котором говорится, что мы должны заключить, что гипотеза
который обеспечивает лучшее объяснение доказательств, вероятно, верно. Сторонники этого подхода принимают вывод за лучшее объяснение
быть способом вывода, который отличается от типа
«экстраполяционный» индуктивный вывод, который Юм пытался
оправдывать. Они также рассматривают его как тип вывода, который, хотя
недедуктивный, оправдан априори . Например, Армстронг
говорит: «Сделать вывод о наилучшем объяснении — это часть того, что значит
быть рациональным. Если это не рационально, то что?» (Армстронг 1983:
59).
Сторонники этого подхода принимают вывод за лучшее объяснение
быть способом вывода, который отличается от типа
«экстраполяционный» индуктивный вывод, который Юм пытался
оправдывать. Они также рассматривают его как тип вывода, который, хотя
недедуктивный, оправдан априори . Например, Армстронг
говорит: «Сделать вывод о наилучшем объяснении — это часть того, что значит
быть рациональным. Если это не рационально, то что?» (Армстронг 1983:
59).
априорное обоснование проводится в два этапа.
Во-первых, утверждается, что мы должны признать, что определенные наблюдаемые
закономерности требуют объяснения с точки зрения некоторого основного закона.
Например, если монета постоянно выпадает орлом при повторных подбрасываниях,
то становится все менее правдоподобным, что это произошло только что
из-за «случайности». Скорее, мы должны сделать вывод к лучшему
объяснение того, что монета имеет определенный уклон. Сказать, что монета
земли головы не только для наблюдаемых случаев, но и для
ненаблюдаемые случаи, не дает объяснения наблюдаемым
регулярность. Таким образом, простого юмовского постоянного соединения недостаточно.
Что необходимо для объяснения, так это «не-юмовский,
метафизически обоснованная концепция объективной закономерности».
(Бонжур 1998), который рассматривается как связанный с фактическим естественным
необходимость (Армстронг, 1983; Фостер, 2004).
Таким образом, простого юмовского постоянного соединения недостаточно.
Что необходимо для объяснения, так это «не-юмовский,
метафизически обоснованная концепция объективной закономерности».
(Бонжур 1998), который рассматривается как связанный с фактическим естественным
необходимость (Армстронг, 1983; Фостер, 2004).
Как только было установлено, что должно быть какое-то метафизическое
надежное объяснение наблюдаемой закономерности, второй шаг состоит в том, чтобы
утверждают, что из всех возможных метафизически надежных объяснений
«прямое» индуктивное объяснение является лучшим, где
прямое объяснение экстраполирует наблюдаемую частоту на
более широкое население. Например, учитывая, что у монеты есть некоторая цель
вероятность выпадения орла, лучшее объяснение того факта, что \(m/n\)
головы до сих пор наблюдались, заключается в том, что объективная вероятность
решка монеты приземления равна \(m/n\). И эта объективная случайность определяет
что происходит не только в наблюдаемых случаях, но и в ненаблюдаемых
случаи.
Номологически-объяснительное решение основано на принятии МБП в качестве рациональная, априорная форма вывода, отличная от индуктивные выводы, такие как вывод I . Однако можно в качестве альтернативы рассматривайте индуктивные выводы как частный случай IBE (Harman, 1968), или принять IBE просто как альтернативный способ характеризующий индуктивный вывод (Henderson 2014). Если любой из эти взгляды верны, МБП не обладает необходимой независимостью от индуктивного вывода, чтобы обеспечить нециклическое обоснование Это.
Можно возразить и против номолого-объяснительного подхода к оснований на том, что закономерности не обязательно требуют объяснения в с точки зрения необходимых связей или надежных метафизических законов. Жизнеспособность подхода также зависит от устойчивости Неюмистская концепция законов. Было несколько серьезных попытки разработать такое объяснение (Armstrong 1983; Tooley 1977; Dretske 1977), но и много критики (см. J. Carroll 2016).
Еще одно критическое возражение состоит в том, что номолого-объяснительная
решение просто вызывает вопрос, даже если оно считается
правомерно использовать IBE для обоснования индукции. В
На первом этапе рассуждения мы заключаем закон или закономерность, которая
выходит за пределы пространственно-временной области, в которой проводятся наблюдения.
сделано до сих пор, чтобы предсказать, что произойдет в
будущее. Но почему мог бы закон, применимый только к наблюдаемому
пространственно-временная область не может быть столь же хорошим объяснением? Главный
ответ, кажется, что мы можем видеть априори что законы с
временные или пространственные ограничения были бы менее хорошим объяснением.
Фостер утверждает, что причина в том, что это приведет к большему
тайны:
В
На первом этапе рассуждения мы заключаем закон или закономерность, которая
выходит за пределы пространственно-временной области, в которой проводятся наблюдения.
сделано до сих пор, чтобы предсказать, что произойдет в
будущее. Но почему мог бы закон, применимый только к наблюдаемому
пространственно-временная область не может быть столь же хорошим объяснением? Главный
ответ, кажется, что мы можем видеть априори что законы с
временные или пространственные ограничения были бы менее хорошим объяснением.
Фостер утверждает, что причина в том, что это приведет к большему
тайны:
Ибо мне кажется, что закон, действие которого ограничено некоторыми конкретный период более загадочен, по своей сути более загадочен, чем тот, который является темпорально универсальным. (Фостер 2004)
3.2.2 Байесовское решение
Другой способ, которым можно попытаться сконструировать априори аргумент, что предпосылки индуктивного вывода делают его
вывод вероятностный, заключается в использовании формализма вероятности
сама теория. В то время, когда писал Юм, вероятности использовались для
анализировать азартные игры. И вообще, они использовались для решения
проблема того, что мы ожидаем увидеть, учитывая, что определенная причина была
известно, что он действующий. Это так называемая проблема «прямого
вывод». Однако проблема индукции касается
«обратная» задача определения причины или общего
гипотеза, учитывая конкретные наблюдения.
В то время, когда писал Юм, вероятности использовались для
анализировать азартные игры. И вообще, они использовались для решения
проблема того, что мы ожидаем увидеть, учитывая, что определенная причина была
известно, что он действующий. Это так называемая проблема «прямого
вывод». Однако проблема индукции касается
«обратная» задача определения причины или общего
гипотеза, учитывая конкретные наблюдения.
Один из первых и наиболее важных методов борьбы с «обратная» задача с использованием вероятностей была разработана Томас Байес. Эссе Байеса, содержащее основные результаты, было опубликовано после его смерти в 1764 г. (Байес, 1764 г.). Тем не менее, это возможно, что работа была выполнена значительно раньше и фактически написано в ответ на публикацию «Исследования Юма». в 1748 г. (см. Zabell 1989: 290–93, обсуждение того, что известно об истории).
Мы проиллюстрируем байесовский метод, используя задачу рисования
шары из урны. Предположим, что у нас есть урна с белым
и черные шары в неизвестной пропорции. Рисуем образец шаров
из урны, вынув шар, отметив его цвет, а затем положив
назад, прежде чем рисовать снова.
Рисуем образец шаров
из урны, вынув шар, отметив его цвет, а затем положив
назад, прежде чем рисовать снова.
Рассмотрим сначала проблему прямого вывода. Учитывая пропорцию белых шаров в урне, какова вероятность различных исходов для выборки наблюдений заданного размера? Предположим, пропорция белых шаров в урне равно \(\theta = 0,6\). Вероятность вытягивание одного белого шара из выборки равно \(p(W; \theta = 0,6) = 0,6\). Мы также можем вычислить вероятность других исходов, таких как как вытягивание двух белых шаров из выборки из двух по правилам исчисление вероятностей (см. раздел 1 Hájek 2011). В общем, вероятность того, что \(n_w\) белых шаров будет извлечена в выборке размера 9{(1-n_w)} \]
Это конкретный пример «выборочного распределения»,
\(p(E\mid H)\), что дает вероятность определенных свидетельств E в выборке, в предположении, что некоторая гипотеза H верно. Расчет выборочного распределения может
вообще сделать априори , учитывая правила вероятности
исчисление.
Однако задача индукции является обратной задачей. Мы хотим делать вывод не о том, на что будет похожа выборка, с известной гипотезой, скорее мы хотим вывести гипотезу об общей ситуации или населения, основанное на наблюдении за ограниченной выборкой. Затем вероятности гипотез-кандидатов могут быть использованы для информирования предсказания о дальнейших наблюдениях. В случае с урной для например, мы хотим знать, что наблюдение конкретного образца частота белых шаров, \(\frac{n_w}{N}\), говорит нам о \(\theta\), доля белых шаров в урне.
Идея байесовского подхода заключается в назначении вероятностей не только к событиям, которые составляют свидетельство, но также и к гипотезам. Один начинается с распределения «априорной вероятности» по соответствующие гипотезы \(p(H)\). Узнав некоторые улики E , Байесовский обновляет априорную \(p(H)\) до условной вероятности \(р(Н\середина Е)\). Это правило обновления называется «правилом условность». Условная вероятность \(p(H\mid E)\) называется «апостериорной вероятностью» и рассчитывается по правилу Байеса:
\[ p(H\mid E) = \frac{p(E\mid H) p(H)}{p(E)} \]
Здесь выборочное распределение можно принять за условное
вероятность \(p(E\mid H)\), известная как
«вероятность» гипотезы H по доказательствам Е .
Затем можно перейти к вычислению прогностического распределения для пока еще ненаблюдаемые данные \(E’\), данные наблюдений E . Предиктивный распределение в байесовском подходе определяется как
\[ p(E’\mid E) = \sum_{H} p(E’\mid H) p(H\mid E) \]
где сумма становится интегралом в случаях, когда H является непрерывная переменная.
Для примера с урной мы можем вычислить апостериорную вероятность
\(p(\theta\mid n_w)\) по правилу Байеса, а вероятность
дано биномиальным распределением выше. Для этого мы также
необходимо присвоить априорное распределение вероятностей параметру
\(\тета\). Один естественный выбор, сделанный ранее Байесом
себя и Лапласа, состоит в том, чтобы установить равномерный априор над параметром
\(\тета\). Собственное обоснование Байеса для этого выбора заключалось в том, что тогда
если вы вычислите вероятность каждого значения для количества белых
в выборке, основанной только на априорных данных, до того, как будут наблюдаться какие-либо данные,
все эти вероятности равны.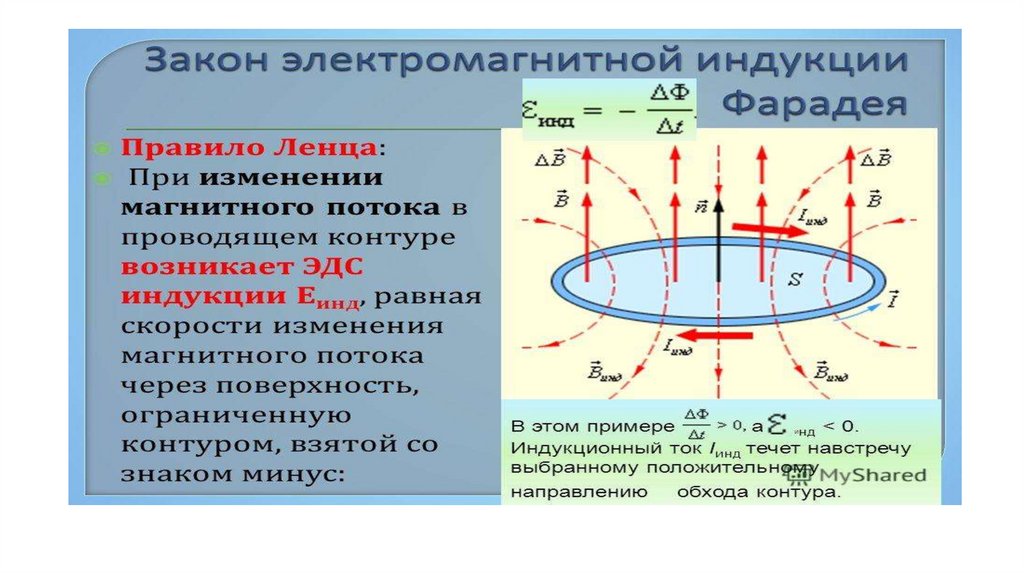 У Лапласа было другое.
обоснование, основанное на принципе безразличия. Этот принцип
утверждает, что если у вас нет никаких оснований отдавать предпочтение одной гипотезе
над другим, вы должны назначить им все равные вероятности.
У Лапласа было другое.
обоснование, основанное на принципе безразличия. Этот принцип
утверждает, что если у вас нет никаких оснований отдавать предпочтение одной гипотезе
над другим, вы должны назначить им все равные вероятности.
При выборе равномерного априора апостериорная вероятность и прогнозное распределение может быть рассчитано. Оказывается, вероятность того, что следующий шар будет белым, учитывая, что \(n_w\) из N розыгрыш был белым, указан
\[ p (ш \ середина n_w) = \ frac {n_w + 1} {N + 2} \]
Это знаменитое «правило последовательности» Лапласа.
(1814 г.). Предположим, на основании наблюдения за 90 белыми шарами из 100,
вычисляем по правилу последовательности, что вероятность
следующий белый шар равен \(91/102=0,89\). Вполне возможно, что
следующий шар может быть черным. Даже в том случае, когда все 100 балов
были белыми, так что вероятность того, что следующий шар будет белым
равно 0,99, все еще существует небольшая вероятность того, что следующий шар не
белый.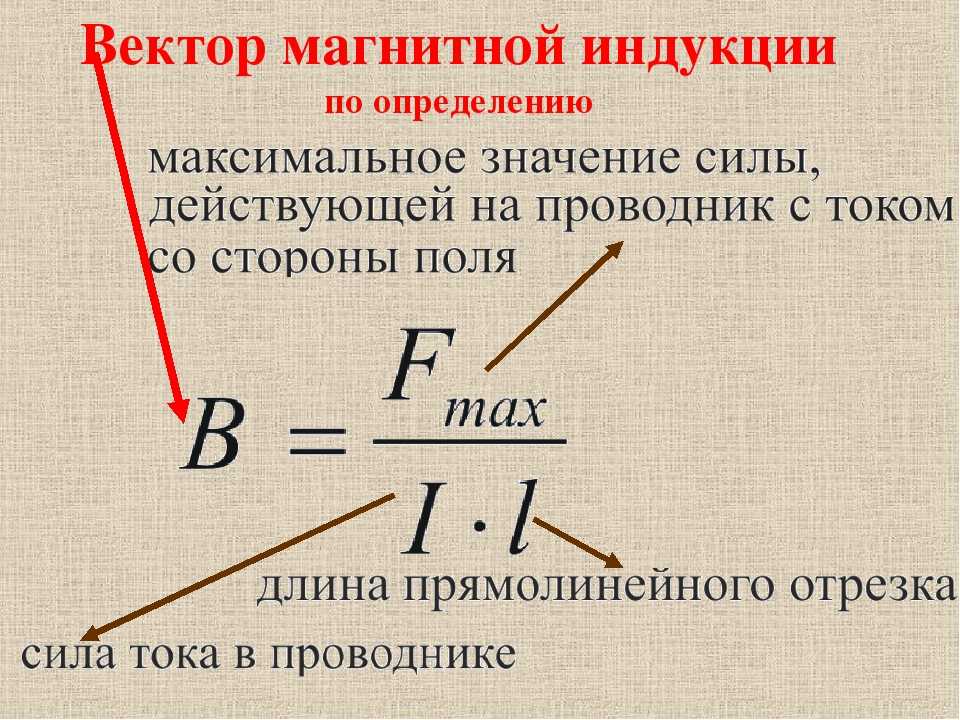 То, что предлагает вероятностное рассуждение, не является
аргумент к выводу, что следующий шар будет определенного цвета,
но аргумент для вывода о том, что определенные будущие наблюдения
очень вероятно учитывая то, что наблюдалось в прошлом.
То, что предлагает вероятностное рассуждение, не является
аргумент к выводу, что следующий шар будет определенного цвета,
но аргумент для вывода о том, что определенные будущие наблюдения
очень вероятно учитывая то, что наблюдалось в прошлом.
В целом, аргумент Байеса-Лапласа в случае с урной обеспечивает пример того, как вероятностные рассуждения могут увести нас от свидетельств о наблюдения в прошлом к предсказанию того, насколько вероятно определенное будущее наблюдения есть. Вопрос в том, какое решение, если таковое имеется, тип расчета обеспечивает задачу индукции. Во-первых зрения, так как это всего лишь математический расчет, выглядит так, как будто это действительно обеспечивает априорный аргумент из предпосылок индуктивного вывода к утверждению, что определенный вывод вероятно.
Однако, чтобы установить это окончательно, необходимо
что все компоненты и допущения аргумента а
Priori , и это требует дальнейшего изучения как минимум трех
важные вопросы.
Во-первых, аргумент Байеса-Лапласа опирается на правила исчисление вероятностей. Каков статус этих правил? Делает следующие за ними составляют априорных рассуждений? Ответ на это частично зависит от того, как интерпретируется сама вероятность. широко говоря, существуют известные интерпретации вероятности согласно к которым правила правдоподобно имеют априори статус и может составляют основу доказательной аргументации. К ним относятся классическая интерпретация, первоначально разработанная Лапласом (1814 г.), логическая интерпретация, расцвет которой пришелся на работы Кейнса. (1921), Джонсон (1921), Джеффрис (1939) и Карнап (1950), а также субъективистская интерпретация Рэмси (1926), Сэвиджа (1954) и де Финетти (1964). Попытки аргументировать вероятностный а Априори решение проблемы индукции было прежде всего связаны с этими интерпретациями.
Во-вторых, в случае урны аргумент Байеса-Лапласа основан
на конкретной вероятностной модели — биномиальной модели. Этот
предполагает, что существует параметр, описывающий
неизвестная пропорция \(\theta\) шаров в урне, и что данные
составляет независимые выборки из распределения по этому параметру.
Что лежит в основе этих предположений? Обобщаются ли они на другие
случаи, выходящие за рамки фактического корпуса урны, т. е. можем ли мы увидеть наблюдения
вообще как аналог розыгрыша из «Урны Природы»?
Существует постоянное беспокойство по поводу того, что такого рода предположения,
в то время как разумно применительно к случаю извлечения шаров из
urn, не будет выполняться для других случаев индуктивного вывода. Таким образом
вероятностное решение проблемы индукции может быть
относительно ограниченный объем. По крайней мере, есть предположения
переходя к выбору модели здесь, которые необходимо сделать явными.
Этот
предполагает, что существует параметр, описывающий
неизвестная пропорция \(\theta\) шаров в урне, и что данные
составляет независимые выборки из распределения по этому параметру.
Что лежит в основе этих предположений? Обобщаются ли они на другие
случаи, выходящие за рамки фактического корпуса урны, т. е. можем ли мы увидеть наблюдения
вообще как аналог розыгрыша из «Урны Природы»?
Существует постоянное беспокойство по поводу того, что такого рода предположения,
в то время как разумно применительно к случаю извлечения шаров из
urn, не будет выполняться для других случаев индуктивного вывода. Таким образом
вероятностное решение проблемы индукции может быть
относительно ограниченный объем. По крайней мере, есть предположения
переходя к выбору модели здесь, которые необходимо сделать явными.
В-третьих, аргумент Байеса-Лапласа опирается на конкретный выбор
априорное распределение вероятностей. Каков статус этого задания,
и может ли он быть основан на принципах априори ? Исторически сложилось так,
Выбор байесовско-лапласовского равномерного априора, а также всей концепции
классической вероятности, основанной на принципе безразличия. Этот принцип рассматривался многими как априорный .
принцип. Тем не менее, он также подвергался значительной критике в
на том основании, что это может привести к противоречивой вероятности
задания (Бертран 1888; Борель 1909; Кейнс 1921). Такой
несоответствия возникают из-за того, что существует более одного способа вырезания
пространство альтернатив, и различные варианты выбора порождают
противоречивые назначения вероятностей. Одна попытка спасти
Принцип безразличия заключался в том, чтобы апеллировать к объяснительству, и
утверждают, что этот принцип следует применять только к резьбе
пространство на «самом объяснительном базовом уровне», где это
уровень идентифицируется в соответствии с априорным понятием
объяснительный приоритет (Huemer 2009).
Этот принцип рассматривался многими как априорный .
принцип. Тем не менее, он также подвергался значительной критике в
на том основании, что это может привести к противоречивой вероятности
задания (Бертран 1888; Борель 1909; Кейнс 1921). Такой
несоответствия возникают из-за того, что существует более одного способа вырезания
пространство альтернатив, и различные варианты выбора порождают
противоречивые назначения вероятностей. Одна попытка спасти
Принцип безразличия заключался в том, чтобы апеллировать к объяснительству, и
утверждают, что этот принцип следует применять только к резьбе
пространство на «самом объяснительном базовом уровне», где это
уровень идентифицируется в соответствии с априорным понятием
объяснительный приоритет (Huemer 2009).
Поиск априорного аргумента для присвоения
предыдущий был в значительной степени заброшен. Для многих субъективист
основы, разработанные Рэмси, де Финетти и Сэвиджем, обеспечивают более
удовлетворительная основа для понимания вероятности. С этой точки
мнению, было бы ошибкой пытаться ввести какие-либо дополнительные а
априорные 90 375 ограничений на вероятности, выходящие за рамки тех, которые диктуются
правила вероятности сами по себе. Скорее присвоение априорных
отражать личное мнение или базовые знания, и никакие предварительные априори неразумный выбор.
С этой точки
мнению, было бы ошибкой пытаться ввести какие-либо дополнительные а
априорные 90 375 ограничений на вероятности, выходящие за рамки тех, которые диктуются
правила вероятности сами по себе. Скорее присвоение априорных
отражать личное мнение или базовые знания, и никакие предварительные априори неразумный выбор.
До сих пор мы рассматривали вероятностные аргументы, вероятности над гипотезами в пространстве гипотез, а также наблюдения. Существует также традиция попыток определить, что распределения вероятностей, которые мы должны были бы получить, учитывая некоторые наблюдения, от начальной точки совместного распределения вероятностей по всем наблюдаемые переменные. Тогда можно постулировать аксиомы непосредственно на это распределение по наблюдаемым, и изучить последствия для предиктивное распределение. Большая часть развития индукции логика, в том числе влиятельная программа Карнапа, протекала в таким образом (Карнап 1950, 1952).
Такой подход помогает прояснить роль допущений, лежащих в основе
вероятностные модели. Одно фундаментальное предположение, которое можно сделать
о наблюдениях заключается в том, что они «заменяемы».
Это означает, что совместное распределение случайных величин равно
инвариантен относительно перестановок. Неформально это означает, что порядок
наблюдения не влияют на вероятность. Например, в
В нашем случае это означало бы, что вытягивание сначала белого шара, а затем
черный шар столь же вероятен, как и выпадение сначала черного, а затем
белый. Де Финетти доказал общую теорему о представлении, что если
совместное распределение вероятностей бесконечной последовательности случайных
переменные предполагаются взаимозаменяемыми, то его можно записать в виде
смесь функций распределения, от каждой из которых данные ведут себя
как если бы они были независимыми случайными розыгрышами (де Финетти 1964). В этом случае
примера с урной теорема показывает, что число равно данные представляют собой независимые случайные выборки из биномиального распределения по
параметр \(\theta\), который сам имеет априорную вероятность
распределение.
Одно фундаментальное предположение, которое можно сделать
о наблюдениях заключается в том, что они «заменяемы».
Это означает, что совместное распределение случайных величин равно
инвариантен относительно перестановок. Неформально это означает, что порядок
наблюдения не влияют на вероятность. Например, в
В нашем случае это означало бы, что вытягивание сначала белого шара, а затем
черный шар столь же вероятен, как и выпадение сначала черного, а затем
белый. Де Финетти доказал общую теорему о представлении, что если
совместное распределение вероятностей бесконечной последовательности случайных
переменные предполагаются взаимозаменяемыми, то его можно записать в виде
смесь функций распределения, от каждой из которых данные ведут себя
как если бы они были независимыми случайными розыгрышами (де Финетти 1964). В этом случае
примера с урной теорема показывает, что число равно данные представляют собой независимые случайные выборки из биномиального распределения по
параметр \(\theta\), который сам имеет априорную вероятность
распределение.
Предположение об обмене можно рассматривать как естественное формализация предположения Юма о том, что прошлое напоминает будущее. Это интуитивно понятно, поскольку допущение взаимозаменяемости означает думая, что порядок наблюдений, как прошлых, так и будущих, делает не имеет значения для вероятностных назначений.
Однако разработка программы индуктивной логики выявила что возможны многие обобщения. Например, Джонсон предложил принять аксиому, которую он назвал «достаточностью постулат». Это означает, что результаты могут быть из ряда разных типов, и что условная вероятность того, что следующий результат типа i зависит только от количества предыдущих испытаний и количество предыдущих исходов типа и (Джонсон 1932). Принятие постулата достаточности для трех и более типов дает общее прогнозирующее распределение, соответствующее «Континуум индуктивных методов» Карнапа (Carnap 1952). Это предиктивное распределение имеет вид:
\[ p(i\mid N_1,N_2,\ldots N_t)= \frac{N_i + k}{N_1 +N_2 + \cdots + N_t + kt} \]
для некоторого положительного числа k . Это сводится к
правило наследования при \(t=2\) и \(k=1\).
Это сводится к
правило наследования при \(t=2\) и \(k=1\).
Обобщения понятия взаимозаменяемости, такие как «частичная взаимозаменяемость» и «марковская взаимозаменяемость», были исследованы, и их можно считать как формы предположения о симметрии (Zabell 1988; Skyrms 2012). Как меньше предполагаются ограничительные аксиомы о вероятностях наблюдаемых, результатом является то, что больше нет уникального результата для вероятность предсказания, а целый класс возможных вероятностей, определяемых обобщенным правилом последовательности, таким как над. Поэтому в этой традиции, как и в Байесовско-Лапласовском подхода, мы отошли от создания аргумента, который производит уникальный априорно-вероятностный ответ на проблему Юма.
Тогда можно подумать, что присвоение предшествующего или соответствующего
соответствующие постулаты о наблюдаемом распределении вероятностей,
именно там, где эмпирические предположения входят в индуктивное
выводы. Вероятностные расчеты — это эмпирические аргументы,
а не априори единиц. Если это верно, то
вероятностная структура в конце концов не предоставила а
априори решение проблемы индукции, но оно имеет скорее
позволило нам прояснить, что могло означать утверждение Юма о том, что
индуктивные выводы основаны на принципе единообразия.
Если это верно, то
вероятностная структура в конце концов не предоставила а
априори решение проблемы индукции, но оно имеет скорее
позволило нам прояснить, что могло означать утверждение Юма о том, что
индуктивные выводы основаны на принципе единообразия.
Некоторые думают, что, хотя проблема индукции не решена,
в некотором смысле частичное решение, которое было названо
«логическое решение». Хаусон, например, утверждает, что
« Индуктивное рассуждение оправдано в той мере, в какой оно
звук, учитывая соответствующие помещения » (Howson 2000: 239, его
акцент). Согласно этой точке зрения, никуда не деться.
эмпирическая предпосылка для индуктивных выводов, но мы все еще можем думать
байесовского обусловливания как своего рода логики или
«ограничение согласованности», которое «генерирует
предсказания из предположений и наблюдений вместе»
(Ромейн 2004: 360). Когда у нас есть эмпирическое предположение,
конкретизируется в априорной вероятности, а наблюдения, байесовские
обусловленность говорит нам, какова результирующая прогностическая вероятность
раздача должна быть.
3.2.3 Комбинаторный подход
Альтернативная попытка использовать вероятностные рассуждения для получения априорным обоснованием индуктивных выводов является так называемое «комбинаторное» решение. Это было впервые поставлено нападающий Дональда С. Уильямса (1947), а затем разработанный Дэвидом Печь (1986).
Подобно аргументу Байеса-Лапласа, решение в значительной степени зависит от
идея о том, что можно выполнить простые априорные вычисления в «прямом выводе» от совокупности к выборке. Как мы
видели, учитывая определенную частоту населения, вероятность
получение разных частот в образце можно рассчитать
непосредственно на основе правил вероятностного исчисления.
Аргумент Байеса-Лапласа основывался на инвертировании вероятности
распределения с использованием правила Байеса, чтобы получить из выборки
распределение к апостериорному распределению. Вместо этого Уильямс предлагает
что обратный вывод может быть основан на определенном логическом
силлогизм: пропорциональный (или статистический) силлогизм.
Пропорциональный или статистический силлогизм выглядит следующим образом:
- Из всего, что есть M , \(m/n\) есть P .
- это М
Следовательно, a равно P с вероятностью \(m/n\).
Например, если 90% кроликов в популяции белые и мы наблюдать за кроликом a , то пропорциональный силлогизм говорит, что мы делаем вывод, что и белые с вероятностью 90%. Уильямс утверждает, что пропорциональный силлогизм является недедуктивным логическим силлогизм, который эффективно интерполирует между силлогизмом для следствие
- Все M являются P
- это М
Следовательно, a равно P .
А силлогизм противоречия
- Нет М есть Р
- а это М
Следовательно, a — это не P .
Этот силлогизм можно комбинировать с наблюдением за поведением все более крупных выборок. Из расчетов выборки распределение, можно показать, что с увеличением размера выборки вероятность того, что частота дискретизации находится в диапазоне, близко аппроксимирует популяционную частоту, также увеличивается. Фактически, Закон больших чисел Бернулли гласит, что вероятность что частота выборки приближается к частоте генеральной совокупности. до единицы, когда размер выборки стремится к бесконечности. Уильямс утверждает, что такие результаты поддерживают «общую общую предпосылку, общую для всех индукции, что образцы «соответствуют» своим популяциям». (Уильямс 1947: 78).
Затем мы можем применить пропорциональный силлогизм к образцам из населения, чтобы получить следующий аргумент:
- Большинство выборок соответствует своей совокупности
- S является образцом.
Таким образом, S соответствует своей популяции с высокой вероятностью.
Это пример пропорционального силлогизма, и он использует общий результат о выборках, соответствующих популяциям в качестве первого крупного помещение.
Следующим шагом является утверждение, что если мы наблюдаем, что образец содержит пропорция \(m/n\) F s, то можно сделать вывод, что поскольку эта выборка с высокой вероятностью соответствует своей генеральной совокупности, т.е. популяции, с высокой вероятностью, имеет популяционную частоту, которая аппроксимирует частоту дискретизации \(m/n\). И Уильямс, и Стоув утверждают, что это составляет логическое априорное решение проблема индукции.
Ряд авторов высказали мнение, что метод Вильямса-Стоува
Аргумент действителен только в том случае, если выборка S взята случайным образом из
совокупность возможных выборок, т. е. любая выборка
вероятно, будет нарисовано, как и любое другое (Браун 1987; Будет 1948; Джакинто
1987). Иногда это представляется как возражение против заявления.
пропорциональный силлогизм. Утверждается, что пропорциональная
Силлогизм действителен только в том случае, если и взяты случайным образом из
население M чел. Однако был получен ответ, что существует
не нужно знать, что выборка выбрана случайным образом, чтобы подать заявку
силлогизм (Maher 1996; Campbell 2001; Campbell & Franklin
2004). Конечно, если у вас есть основания полагать, что ваша выборка
процедура с большей вероятностью привлечет определенных лиц, чем
других — например, если вы знаете, что находитесь в определенном
место, где есть больше определенного типа, то вы должны
не применять пропорциональный силлогизм. Но если у вас нет таких причин,
утверждают защитники, применять его вполне рационально. Конечно это
всегда возможно, что вы берете нерепрезентативную выборку — это означает
один из немногих сэмплов, в котором частота дискретизации не совпадает
популяционная частота — но поэтому вывод только
вероятно и не точно.
Утверждается, что пропорциональная
Силлогизм действителен только в том случае, если и взяты случайным образом из
население M чел. Однако был получен ответ, что существует
не нужно знать, что выборка выбрана случайным образом, чтобы подать заявку
силлогизм (Maher 1996; Campbell 2001; Campbell & Franklin
2004). Конечно, если у вас есть основания полагать, что ваша выборка
процедура с большей вероятностью привлечет определенных лиц, чем
других — например, если вы знаете, что находитесь в определенном
место, где есть больше определенного типа, то вы должны
не применять пропорциональный силлогизм. Но если у вас нет таких причин,
утверждают защитники, применять его вполне рационально. Конечно это
всегда возможно, что вы берете нерепрезентативную выборку — это означает
один из немногих сэмплов, в котором частота дискретизации не совпадает
популяционная частота — но поэтому вывод только
вероятно и не точно.
Более проблематичным шагом в аргументации является последний шаг, который
выводит нас из утверждения, что выборки соответствуют их популяциям с высокой
вероятность утверждения, что, увидев конкретный образец
частота, популяция, из которой взята выборка, имеет частоту
близкой к частоте дискретизации с высокой вероятностью. Проблема здесь
это тонкий сдвиг в том, что подразумевается под «высокой вероятностью»,
что легло в основу распространенного неправильного прочтения
Теорема Бернулли. Взлом (1975: 156–59).) ставит
точку в следующих терминах. Теорема Бернулли разрешает
утверждают, что гораздо чаще, чем нет, небольшой интервал вокруг
частота выборки будет включать истинную частоту населения. В других
словами, весьма вероятно в смысле «обычно
правильно», чтобы сказать, что выборка соответствует своей генеральной совокупности. Но это
не означает, что утверждение о том, что небольшой интервал вокруг
выборка будет содержать истинную популяционную частоту с высокой вероятностью
в смысле «заслуживающий доверия в каждом случае использования». Этот
будет означать, что для любого данного образца весьма вероятно, что
выборка соответствует своей совокупности. Вполне совместимо с утверждением
что «обычно верно», что выборка соответствует
населения, чтобы сказать, что есть некоторые выборки, которые не соответствуют их
населения вообще.
Проблема здесь
это тонкий сдвиг в том, что подразумевается под «высокой вероятностью»,
что легло в основу распространенного неправильного прочтения
Теорема Бернулли. Взлом (1975: 156–59).) ставит
точку в следующих терминах. Теорема Бернулли разрешает
утверждают, что гораздо чаще, чем нет, небольшой интервал вокруг
частота выборки будет включать истинную частоту населения. В других
словами, весьма вероятно в смысле «обычно
правильно», чтобы сказать, что выборка соответствует своей генеральной совокупности. Но это
не означает, что утверждение о том, что небольшой интервал вокруг
выборка будет содержать истинную популяционную частоту с высокой вероятностью
в смысле «заслуживающий доверия в каждом случае использования». Этот
будет означать, что для любого данного образца весьма вероятно, что
выборка соответствует своей совокупности. Вполне совместимо с утверждением
что «обычно верно», что выборка соответствует
населения, чтобы сказать, что есть некоторые выборки, которые не соответствуют их
населения вообще. Таким образом, из бернуллиевских
теорема о том, что для любой заданной частоты дискретизации мы должны назначать высокие
вероятность того, что небольшой интервал вокруг выборки
частота будет содержать истинную частоту населения. Но это
именно тот слайд, который Уильямс делает на последнем шаге своего
аргумент. Махер (1996) аналогичным образом утверждает, что последний шаг
Аргумент Уильямса-Стоува ошибочен. На самом деле, если человек хочет
сделать выводы о вероятности популяционной частоты
учитывая частоту дискретизации, правильный способ сделать это — использовать
Байесовский метод, описанный в предыдущем разделе. Но, как мы там
видел, это требует присвоения априорных вероятностей, и это
объясняет, почему многие думают, что комбинаторное решение
каким-то незаконным образом предполагалось такое предположение, как принцип
безразличие. Аргумент Вильямса-Стоува на самом деле не дает нам
альтернативный способ инвертирования вероятностей, который каким-то образом обходит
все проблемы, с которыми сталкивались байесовцы.
Таким образом, из бернуллиевских
теорема о том, что для любой заданной частоты дискретизации мы должны назначать высокие
вероятность того, что небольшой интервал вокруг выборки
частота будет содержать истинную частоту населения. Но это
именно тот слайд, который Уильямс делает на последнем шаге своего
аргумент. Махер (1996) аналогичным образом утверждает, что последний шаг
Аргумент Уильямса-Стоува ошибочен. На самом деле, если человек хочет
сделать выводы о вероятности популяционной частоты
учитывая частоту дискретизации, правильный способ сделать это — использовать
Байесовский метод, описанный в предыдущем разделе. Но, как мы там
видел, это требует присвоения априорных вероятностей, и это
объясняет, почему многие думают, что комбинаторное решение
каким-то незаконным образом предполагалось такое предположение, как принцип
безразличие. Аргумент Вильямса-Стоува на самом деле не дает нам
альтернативный способ инвертирования вероятностей, который каким-то образом обходит
все проблемы, с которыми сталкивались байесовцы.
4. Решение второй дилеммы Рога Юма
До сих пор мы рассматривали способы, которыми первый рог Юма дилемма может быть решена. Но, конечно, также можно взять на себя вместо него второй рог.
Можно возразить, что вероятный аргумент не будет, несмотря на то, что Юм говорит, быть круговым проблематичным образом (мы рассматриваем ответы этого добрый в раздел 4.1). Или можно попытаться доказать, что вероятные аргументы не круговой вообще (раздел 4.2).
4.1 Индуктивные обоснования индукции
Один из способов решения второго рога дилеммы Юма состоит в том, чтобы отказаться от помещение Р6, что исключает циклические аргументы. Некоторые утверждали, что определенные виды круговых аргументов обеспечили бы приемлемое оправдание для индуктивного вывода. Так как оправдание тогда само быть индуктивным, этот подход часто называют «индуктивное обоснование индукции».
Прежде всего, мы должны исследовать, как именно юмовская циркулярность якобы
возникает. Возьмем простой случай перечислительного индуктивного вывода, который
следует следующему шаблону ( х ):
Возьмем простой случай перечислительного индуктивного вывода, который
следует следующему шаблону ( х ):
Наиболее часто наблюдаемыми F были G s
. Следовательно: Большинство F s являются G s.
Хьюм утверждает, что такие аргументы предполагают принцип единообразия. (ВВЕРХ). По помещениям Р7 а также Р8, это предположение также должно быть подкреплено аргументом, чтобы чтобы индуктивный вывод был оправдан. Естественная идея состоит в том, что мы можно привести доводы в пользу принципа единообразия на том основании, что «это работает». Мы знаем, что это работает, потому что прошлые случаи аргументы, которые опирались на него, оказались успешными. Только это однако недостаточно, если у нас нет оснований полагать, что такое аргументы также будут успешными в будущем. Это утверждение должно сам по себе может быть поддержан индуктивным аргументом ( С ):
Большинство аргументов формы X , которые полагаются на UP, преуспели в
мимо.
Следовательно, большинство аргументов формы X , основанных на UP преуспеть.
Но сам этот аргумент зависит от UP, которая является самой предположение, которое мы пытались оправдать.
Как мы видели в раздел 2, некоторые отвергают утверждение Юма о том, что все индуктивные выводы предполагают УП. Однако аргумент о том, что в основе обоснования индуктивного вывода о вероятном аргументе приведет к циркулярность не обязательно должна полагаться на это утверждение. Проблема циркулярности может оформляться в более общем виде. Если аргумент S зависит от что-то , что уже предполагается в выводе X , тогда аргумент S не может быть использован для обоснования вывода X . Однако вопрос в том, что именно есть нечто.
Некоторые авторы утверждали, что на самом деле S не опирается ни на какие
предпосылка или даже предположение, которое потребовало бы, чтобы мы уже знали
вывод X . S не является «предпосылкой
круговой» аргумент. Скорее, утверждают они, это
«круговое правило» — оно опирается на правило вывода в
чтобы прийти к выводу, что это самое правило является надежным. Предполагать
мы принимаем правило R , в котором говорится, что, когда наблюдается, что
большинство F являются G , мы должны сделать вывод, что большинство F являются Г с. Тогда вывод X опирается на правило R . Мы хотим
показать, что правило R надежно. Мы могли бы апеллировать к тому факту, что R работало в прошлом, и, следовательно, по индукции, оно будет
также работать в будущем. Назовите этот аргумент S *:
Скорее, утверждают они, это
«круговое правило» — оно опирается на правило вывода в
чтобы прийти к выводу, что это самое правило является надежным. Предполагать
мы принимаем правило R , в котором говорится, что, когда наблюдается, что
большинство F являются G , мы должны сделать вывод, что большинство F являются Г с. Тогда вывод X опирается на правило R . Мы хотим
показать, что правило R надежно. Мы могли бы апеллировать к тому факту, что R работало в прошлом, и, следовательно, по индукции, оно будет
также работать в будущем. Назовите этот аргумент S *:
Большинство выводов по правилу R прошли успешно
Следовательно, большинство выводов, следующих за R , успешны.
Поскольку сам этот аргумент использует правило R , его использование для установления что R надежен, является круговым правилом.
Затем некоторые авторы утверждали, что, хотя цикличность предпосылок
порочный, правило-цикличность — нет (Cleve 1984; Papineau 1992). Один
причина думать, что правило-циркулярность не порочна, была бы, если бы она
нет необходимости знать или даже обоснованно полагать, что правило Р является надежным, чтобы перейти к обоснованному выводу, используя правило.
Это заявление экстерналистов об оправдании (Cleve 1984).
Говорят что пока R по факту надежен, один
может сформировать обоснованное убеждение в заключении аргумента, опираясь на
на R , если кто-то имеет обоснованную веру в помещение.
Один
причина думать, что правило-циркулярность не порочна, была бы, если бы она
нет необходимости знать или даже обоснованно полагать, что правило Р является надежным, чтобы перейти к обоснованному выводу, используя правило.
Это заявление экстерналистов об оправдании (Cleve 1984).
Говорят что пока R по факту надежен, один
может сформировать обоснованное убеждение в заключении аргумента, опираясь на
на R , если кто-то имеет обоснованную веру в помещение.
Если экстерналистское утверждение не убеждает, можно попытаться утверждают, что циркулярность правил полезна в другом отношении. За Например, требование, чтобы правило было показано как надежное без любая циркулярность правила может показаться неразумной, когда правило очень принципиальный характер. Как говорит Ланге:
Можно предположить, что, хотя циклический аргумент обычно невозможно обосновать свой вывод, круговой аргумент приемлем в случай обоснования фундаментальной формы рассуждения.
После всего, принципиального больше некуда свернуть, так что все что можно разумно Требование фундаментальной формы рассуждения состоит в том, чтобы она подтверждала сама себя. (Ланге 2011: 56)
Сторонники этой точки зрения указывают, что даже дедуктивное
вывод нельзя обосновать дедуктивно. Рассмотрим Льюиса
Диалог Кэрролла между Ахиллесом и черепахой (Кэрролл
1895). Ахиллес спорит с черепахой, которая отказывается выступать модус поненс . Черепаха принимает допущение, что p ,
и посылка, что p подразумевает q , но он не примет д . Как Ахиллес может убедить его? Ему удается уговорить его
принять другую посылку, а именно «если p и p подразумевает q , затем q ”. Но Черепаха еще не готова
вывести q . Ахиллес продолжает добавлять новые помещения
то же самое, но безрезультатно. Тогда получается, что модус поненс не может быть оправдано тому, кто еще не готов использовать это
правило.
Это могло бы показаться странным, если бы циркулярность предпосылок была порочной, а правило цикличности не было, учитывая, что, по-видимому, обмен между правилами и посылками. Ведь правило всегда может, как в рассказе Льюиса Кэрролла, добавить в качестве предпосылки к аргументу. Но история Кэрролла, по-видимому, также указывает на то, что существует действительно фундаментальное различие между готовностью принять посылка, устанавливающая правило (Черепаха с удовольствием это делает), и будучи готовы использовать это правило (это то, что Черепаха отказывается делать).
Предположим, мы допускаем, что индуктивный аргумент, такой как S (или S *) может поддерживать индуктивный вывод X без порочного округлость. Тем не менее, возможное возражение состоит в том, что аргумент просто не дает полного обоснования X . Ведь меньше разумные правила вывода, такие как контриндукция, могут поддерживать сами себя аналогичным образом. Контриндуктивное правило CI:
Наиболее наблюдаемые A s являются B с.
Следовательно, это не тот случай, когда большинство A являются B s.
Тогда рассмотрим следующий аргумент CI*:
Большинство аргументов CI не увенчались успехом
Следовательно, дело не в том, что большинство аргументов КИ безуспешны, т. е. многие аргументы CI успешны.
Таким образом, этот аргумент устанавливает надежность CI в круговая мода (см. Salmon 1963).
Аргумент S можно использовать для поддержки вывода х , но только для тех, кто уже готов к индуктивным выводам, используя С . Она не может убедить скептика, который не готов полагаться на на это правило в первую очередь. Тогда можно подумать, что аргумент просто не достигает очень многого.
Ответом на эти опасения является то, что, по выражению Папино,
аргумент: «не предполагалось, что делает очень много»
(Папино 1992: 18). Тот факт, что контриндуктивистский аналог
аргумент существует, верен, но неуместен. Допускается, что
Аргумент не может убедить ни контриндуктивиста, ни скептика. Тем не менее, сторонники индуктивного обоснования утверждают, что
есть еще некоторая дополнительная ценность в демонстрации того, что индуктивные выводы
надежны, даже когда мы уже принимаем, что нет ничего
проблематично о них. Индуктивное обоснование индукции
обеспечивает своего рода важную проверку согласованности наших существующих
убеждения.
Тем не менее, сторонники индуктивного обоснования утверждают, что
есть еще некоторая дополнительная ценность в демонстрации того, что индуктивные выводы
надежны, даже когда мы уже принимаем, что нет ничего
проблематично о них. Индуктивное обоснование индукции
обеспечивает своего рода важную проверку согласованности наших существующих
убеждения.
4.2 Нет правил
Можно пойти еще дальше в попытке разобрать Юмовская цикличность. Может быть, индуктивные умозаключения даже не имеют правила в общем. Что, если каждый индуктивный вывод по существу уникален? Окаша, например, утверждает, что проблема цикличности Юма может можно избежать, если за индукцией нет «правил» (Окаша 2005а,б). Нортон выдвигает аналогичную идею о том, что все индуктивные умозаключения материальны и не имеют ничего формального общего (Нортон 2003).
Сторонники таких взглядов подвергли критике утверждение Юма о том, что
является UP, на котором основаны все индуктивные выводы. Там давно
были жалобы на расплывчатость принципа единообразия
(Сэлмон, 1953). Будущее лишь в некоторых отношениях напоминает прошлое,
но не другие. Предположим, что во все мои дни рождения я был
моложе 40 лет. Это не дает мне оснований ожидать, что я
в мой следующий день рождения будет меньше 40 лет. Кажется, тогда есть
главный пробел в изложении Юма. Он мог объяснить или
описал, как мы делаем индуктивный вывод, исходя из предположения, что
это один мы можно нарисовать. Но он оставляет нетронутым вопрос
того, как мы различаем случаи, когда мы экстраполируем закономерность
законно, рассматривая это как закон, и случаи, когда мы этого не делаем.
Будущее лишь в некоторых отношениях напоминает прошлое,
но не другие. Предположим, что во все мои дни рождения я был
моложе 40 лет. Это не дает мне оснований ожидать, что я
в мой следующий день рождения будет меньше 40 лет. Кажется, тогда есть
главный пробел в изложении Юма. Он мог объяснить или
описал, как мы делаем индуктивный вывод, исходя из предположения, что
это один мы можно нарисовать. Но он оставляет нетронутым вопрос
того, как мы различаем случаи, когда мы экстраполируем закономерность
законно, рассматривая это как закон, и случаи, когда мы этого не делаем.
Часто считается, что Нельсон Гудман сделал это утверждение в
особенно яркая форма с его «новой загадкой индукции»
(Гудман 1955: 59-83). Предположим, мы определяем предикат «grue» в
следующим образом. Объект является «грубым», когда он зеленый, если
наблюдается до времени t и синий в противном случае. Гудман считает
мысленный эксперимент, в котором мы наблюдаем кучу зеленых изумрудов
до времени т . Мы могли бы описать наши результаты, сказав, что все
наблюдаемые изумруды зеленые. Используя простой перечислительный индуктивный
схеме, мы могли бы заключить из результата, что все наблюдаемые изумруды
зеленый, что все изумруды зеленые. Но в равной степени мы могли бы описать
те же самые результаты, говоря, что все наблюдаемые изумруды являются грубыми. Затем с помощью
той же схеме, мы могли бы сделать вывод, что все наблюдаемые
изумруды гру, что все изумруды гру. В первом случае мы
ожидайте изумруд, наблюдаемый через время t быть зеленым, тогда как в
второй, мы ожидаем, что он будет синим. Таким образом, два прогноза
несовместимый. Гудман утверждает, что Юм упустил возможность дать
любое объяснение того, почему мы проецируем такие предикаты, как
«зеленый», но не такие предикаты, как «grue». Этот
это «новая загадка», которую часто принимают за дальнейшую
проблема индукции, которую Юм не рассматривал.
Мы могли бы описать наши результаты, сказав, что все
наблюдаемые изумруды зеленые. Используя простой перечислительный индуктивный
схеме, мы могли бы заключить из результата, что все наблюдаемые изумруды
зеленый, что все изумруды зеленые. Но в равной степени мы могли бы описать
те же самые результаты, говоря, что все наблюдаемые изумруды являются грубыми. Затем с помощью
той же схеме, мы могли бы сделать вывод, что все наблюдаемые
изумруды гру, что все изумруды гру. В первом случае мы
ожидайте изумруд, наблюдаемый через время t быть зеленым, тогда как в
второй, мы ожидаем, что он будет синим. Таким образом, два прогноза
несовместимый. Гудман утверждает, что Юм упустил возможность дать
любое объяснение того, почему мы проецируем такие предикаты, как
«зеленый», но не такие предикаты, как «grue». Этот
это «новая загадка», которую часто принимают за дальнейшую
проблема индукции, которую Юм не рассматривал.
Одна мораль, которую можно почерпнуть у Гудмана, состоит в том, что не существует
общий принцип единообразия, на который опираются все вероятные аргументы
(трезвый 1988; Нортон 2003; Окаша 2001, 2005а,б). Скорее каждый индуктивный
умозаключение предполагает некоторую более конкретную эмпирическую предпосылку. А
конкретный индуктивный вывод зависит от определенного способа, которым
будущее похоже на прошлое. Тогда это может быть оправдано другим
индуктивный вывод, основанный на совершенно иных эмпирических
требовать. Это, в свою очередь, должно быть оправдано еще одним
индуктивный вывод. Природа проблемы Юма во втором
Таким образом, рог трансформируется. Циркулярности нет. Скорее есть
регресс индуктивных обоснований, опирающихся каждое на свое собственное
эмпирические предпосылки (Sober 1988; Нортон 2003; Окаша 2001,
2005а,б).
Скорее каждый индуктивный
умозаключение предполагает некоторую более конкретную эмпирическую предпосылку. А
конкретный индуктивный вывод зависит от определенного способа, которым
будущее похоже на прошлое. Тогда это может быть оправдано другим
индуктивный вывод, основанный на совершенно иных эмпирических
требовать. Это, в свою очередь, должно быть оправдано еще одним
индуктивный вывод. Природа проблемы Юма во втором
Таким образом, рог трансформируется. Циркулярности нет. Скорее есть
регресс индуктивных обоснований, опирающихся каждое на свое собственное
эмпирические предпосылки (Sober 1988; Нортон 2003; Окаша 2001,
2005а,б).
Один из способов выразить это — сказать, что аргумент Юма основывается на
об ошибке сдвига квантора (Sober 1988; Okasha 2005a). Юм говорит
что существует общее предположение для всех индуктивных
выводов, тогда как он должен был бы сказать, что для каждого индуктивного
вывод, есть некоторая предпосылка. Различные индуктивные
выводы основываются на различных эмпирических предпосылках, и
проблема цикличности обходится.
Каким же будет последствие предположения, что юмовское проблема действительно должна была быть регрессом, а не замкнутым кругом? Тут возможны разные мнения. С одной стороны, можно подумать что регресс все же приводит к скептическому заключению. Таким образом, хотя точная форма, в которой Юм сформулировал свою проблему, неверна, вывод существенно не отличается (Sober 1988). Другая возможность заключается в том, что преобразование смягчает или даже устраняет скептическая проблема. Например, Нортон утверждает, что результатом является растворение проблемы индукции, поскольку регресс оправдания мягко обрываются (Norton 2003). И еще Окаша мягко предполагает, что даже если регресс бесконечен, «Возможно, в конце концов, бесконечный регресс не так страшен, как порочный круг». (Окаша 2005b: 253).
Любое растворение юмовской цикличности зависит не только от
утверждая, что UP следует заменить эмпирическими предпосылками
которые специфичны для каждого индуктивного вывода. Это также необходимо
установить, что индуктивные выводы не имеют общих
правил — иначе все равно будут хоть какие-то
правило-цикличность. Окаша предполагает, что байесовская модель
обновление убеждений является иллюстрацией того, как можно охарактеризовать индукцию
без правил, но это проблематично, так как в этой модели все
индуктивные выводы по-прежнему разделяют общее правило Байеса
условность. Материальная теория индукции Нортона подробнее
действительно обещает свободную от правил характеристику индукции, но
не ясно, действительно ли можно избежать какой-либо роли по общим правилам
(Ахинштайн, 2010; Уорролл, 2010).
Окаша предполагает, что байесовская модель
обновление убеждений является иллюстрацией того, как можно охарактеризовать индукцию
без правил, но это проблематично, так как в этой модели все
индуктивные выводы по-прежнему разделяют общее правило Байеса
условность. Материальная теория индукции Нортона подробнее
действительно обещает свободную от правил характеристику индукции, но
не ясно, действительно ли можно избежать какой-либо роли по общим правилам
(Ахинштайн, 2010; Уорролл, 2010).
5. Необходимые условия обоснования
Юм обычно читается как выносящий отрицательный вердикт
возможность обоснования вывода I с помощью такой посылки, как
стр.8.
Однако есть некоторые, кто сомневается, что Юм лучше всего интерпретируется
как вывод об обоснованности вывода I при
все (мы обсудим эти интерпретации в
раздел 5.1).
Есть также те, кто по-разному задается вопросом,
помещение Р8
действительно дает действительное необходимое условие для оправдания
вывод I (секции
5. 2
а также
5.3).
2
а также
5.3).
5.1 Интерпретация вывода Юма
Некоторые ученые отрицают, что Юма следует понимать как призыв к
предпосылка такая
помещение Р8
вообще. Они утверждают, что причина в том, что он не стремился к
явно нормативный вывод об обосновании, такой как
С5.
Юм определенно ищет «цепочку рассуждений» от
предпосылок индуктивного вывода к заключению, и он думает
что аргумент для UP необходим для завершения цепочки.
Однако можно было бы подумать, что нет никаких дальнейших предпосылок относительно
обоснование, и поэтому вывод его аргумента просто
С4:
нет цепочки рассуждений от посылок к заключению
индуктивный вывод. Тогда Юм мог бы быть, как Дон Гаррет и Дэвид
Оуэн, выдвигая «тезис о когнитивных
психологии», а не делать нормативные заявления о
оправдание (Оуэн 1999; Гаррет 2002). Диссертация посвящена
характер познавательного процесса, лежащего в основе вывода. Согласно с
Гаррета, главный результат аргументации Юма состоит в том, что может быть
нет процесса рассуждений, который устанавливает UP. Для Оуэна это сообщение
что вывод не делается через цепочку идей, связанных
опосредующие связи, как было бы характерно для способности
причина.
Для Оуэна это сообщение
что вывод не делается через цепочку идей, связанных
опосредующие связи, как было бы характерно для способности
причина.
Есть также интерпретаторы, которые утверждают, что Юм просто пытается исключить особый вид обоснования индукции, основанный на концепция разума, господствовавшая среди рационалистов его времени, а не оправдание вообще (Бошан и Розенберг 1981; Байер 2009). В частности, утверждалось, что это «попытка опровергнуть рационалистическую веру в то, что по крайней мере некоторые индуктивные аргументы демонстративны» (Beauchamp & Розенберг 1981: xviii). Согласно этой интерпретации, помещение Р8 следует изменить на что-то вроде:
- Если нет цепочки рассуждений, основанных на доказательных аргументах из предпосылок к заключению вывода I , то вывод I не обоснован.
Однако такие интерпретации противоречат тому факту, что
Аргумент Юма представляет собой явно двоякую атаку, которая
касается не только доказательных аргументов, но и вероятных
аргументы.
Вопрос о том, насколько экспансивный нормативный вывод следует отнести к
Юм сложный человек. Отчасти это зависит от интерпретации
Собственное решение Юма своей проблемы. Как мы видели в
секция 1,
Юм приписывает основу индуктивного вывода принципам
воображение в «Трактате» и в «Исследовании
«обычай», «привычка», понимаемый как своего рода
естественный инстинкт. Тогда возникает вопрос, является ли эта альтернатива
дает любое обоснование для вывода, даже если ни одно
на основании разума. На первый взгляд кажется, что Юм
предполагая, что индуктивные выводы исходят из совершенно рационального
основа. Он явно не думает, что у них не получается производить хорошие
результаты. На самом деле Юм даже предполагает, что эта работа разума
может быть даже менее «подвержен ошибкам и заблуждениям», чем если бы
были доверены «ошибочным умозаключениям нашего разума,
который медлителен в своих действиях» (Е. 5.2.22). Это также не
Ясно, что он видит работу воображения как полностью
лишен рациональности. Во-первых, Юм говорит о воображении
как регулируется принципы . Позже в Трактате он
даже дает «правила» и «логику» для
характеризуя то, что следует считать хорошим причинным выводом (Т.
1.3.15). Он также ясно видит возможность провести различие между
лучшие формы такого «рассуждения», как он продолжает называть
Это. Таким образом, могут быть основания утверждать, что Юм не пытался
утверждают, что индуктивные выводы не имеют рационального основания
что бы то ни было, а только то, что они не имеют определенного типа
рациональное основание, которое коренится в способности Разума.
Во-первых, Юм говорит о воображении
как регулируется принципы . Позже в Трактате он
даже дает «правила» и «логику» для
характеризуя то, что следует считать хорошим причинным выводом (Т.
1.3.15). Он также ясно видит возможность провести различие между
лучшие формы такого «рассуждения», как он продолжает называть
Это. Таким образом, могут быть основания утверждать, что Юм не пытался
утверждают, что индуктивные выводы не имеют рационального основания
что бы то ни было, а только то, что они не имеют определенного типа
рациональное основание, которое коренится в способности Разума.
Все это указывает на то, что есть место для споров о предполагаемом
масштаб собственного вывода Юма. А значит, есть место и для
дебаты о том, что именно формирует посылку (например,
помещение P8)
который связывает остальную часть его аргумента с нормативным выводом
должен взять. Кто бы в этом ни был прав, факт
остается, что Юм на протяжении всей истории преимущественно читался как
аргумент в пользу индуктивного скептицизма.
5.2 Постулаты и шарниры
Даже если кто-то приписывает нормативный вывод Юму, он может подвергнуть сомнению его аргумент, спросив, помещение Р8 правда. Это может подтолкнуть к общему размышлению о том, что необходимо для обоснование вывода в первую очередь, и что такое Юм даже просят.
Например, Витгенштейн усомнился в том, имеет смысл спрашивать об основаниях для индуктивных выводов.
Если бы кто-нибудь сказал, что информация о прошлом не смогла бы его убедить что что-то произойдет в будущем, я не должен понять его. Его можно было бы спросить: а что же вы ожидаете услышать в таком случае? Какой вид информации вы называете основанием для такого убеждения? … Если это не основания, то что такое основания? не являются основанием, то вы обязательно должны быть в состоянии указать, что должно быть случае, чтобы мы имели право сказать, что есть основания для наше предположение…. (Витгенштейн 1953: 481)
Можно, например, и не думать, что должна быть цепочка
рассуждений, в которых каждый шаг или предположение поддерживается
аргумент. Витгенштейн считал, что существуют некоторые принципы, поэтому
важно, чтобы они не нуждались в дополнительной поддержке
аргумент. Они являются «шарнирами», на которых исследование
повороты.
Витгенштейн считал, что существуют некоторые принципы, поэтому
важно, чтобы они не нуждались в дополнительной поддержке
аргумент. Они являются «шарнирами», на которых исследование
повороты.
Из идей Витгенштейна развилось общее понятие «право», которое является своего рода рациональным основанием для удержания определенные предложения, которые не соответствуют тем же требованиям, что и «оправдание». Право предоставляет эпистемологические права на придерживайтесь предложения, не беря на себя ответственность основывать веру в него на спор. Криспин Райт (2004) утверждал, что определенные принципы, в том числе принцип единообразия, которым мы вправе в этом смысле удерживать.
Некоторые философы ставили перед собой задачу определить множество или
наборы постулатов, которые составляют правдоподобную основу для индуктивных
выводы. Бертран Рассел, например, утверждал, что пять постулатов
лежат в основе индуктивных рассуждений (Russell, 1948). Артур Бёркс,
с другой стороны, предположил, что набор постулатов не уникален,
но может быть несколько наборов постулатов, соответствующих
различные индуктивные методы (Беркс, 1953, 1955).
Главное возражение против всех этих взглядов состоит в том, что они на самом деле не решают проблема индукции таким образом, чтобы адекватно закреплять столбы на котором основан индуктивный вывод. Как говорит Салмон, «допущение необоснованных и необоснованных постулатов к делу с проблемой равносильно превращению научного метода в веры» (Лосось 1966: 48).
5.3 Растворение обычного языка
Вместо того чтобы позволить незащищенным эмпирическим постулатам дать нормативные поддержку индуктивного вывода, можно было бы вместо этого привести доводы в пользу совершенно иное понимание того, что связано с оправданием. Подобно Витгенштейну, более поздние философы обыденного языка, особенно П.Ф. Стросон также задался вопросом, что именно означает «просить обоснование индуктивных выводов (Strawson 1952). Это стало известный как «распад обыденного языка» проблема индукции.
Стросон указывает, что было бы целесообразно обратиться к дедуктивному методу.
обоснование индуктивных выводов. Но не ясно, что это
полезно, поскольку это фактически «требование, чтобы индукция
должно быть показано, что это своего рода дедукция» (Strawson 1952:
230). Скорее, говорит Стросон, когда мы спрашиваем о том,
индуктивный вывод оправдан, мы обычно судим, является ли он
соответствует нашим обычным индуктивным стандартам. Предположим, говорит он, кто-то
путем индуктивного вывода сформировал убеждение, что все ф составляют г . Стросон говорит, что если этого человека спросят об их
оснований или причин для такого убеждения,
Но не ясно, что это
полезно, поскольку это фактически «требование, чтобы индукция
должно быть показано, что это своего рода дедукция» (Strawson 1952:
230). Скорее, говорит Стросон, когда мы спрашиваем о том,
индуктивный вывод оправдан, мы обычно судим, является ли он
соответствует нашим обычным индуктивным стандартам. Предположим, говорит он, кто-то
путем индуктивного вывода сформировал убеждение, что все ф составляют г . Стросон говорит, что если этого человека спросят об их
оснований или причин для такого убеждения,
Я думаю, что это было бы удовлетворительным ответом, если бы он ответил: «Ну, при всем моем богатом и разнообразном опыте я пришел среди бесчисленных случаев f и ни одного случая f что не было случаем г ». Говоря это, он явно претендуя на индуктивную поддержку , индуктивное доказательство определенного рода в пользу его веры. (Стросон 1952)
Именно потому, что индуктивный носитель, как его обычно понимают,
просто состоит в том, что вы наблюдали много положительных примеров в широком
разнообразные условия.
По сути, этот подход отрицает, что создание цепочки рассуждений необходимое условие оправдания. Скорее индуктивная. вывод оправдан, если он соответствует обычным стандартам индуктивное обоснование. Но есть ли в этом что-то еще? Можем ли мы не спрашивать по какой причине мы должны полагаться на эти индуктивные стандарты?
Конечно, имеет смысл спросить, является ли конкретный индуктивный вывод оправдано. Но ответ на него достаточно прост. Иногда у людей достаточно доказательств для своих выводов и иногда нет. Имеет ли смысл также спросить о том, индуктивные процедуры вообще оправданы? Стросон рисует аналогия между вопросом о том, является ли конкретный акт законным. Мы можем ответьте на такой вопрос, говорит он, ссылаясь на закон страны.
Но вообще нет смысла спрашивать, является ли закон земля, правовая система в целом, является или не является законным. Для чего правовые нормы мы апеллируем? (Стросон 1952: 257)
По словам Стросона,
Это аналитическое утверждение, что разумно иметь степень веры в утверждение, которая пропорциональна силе доказательства в его пользу; и это аналитическое предложение, хотя и не утверждение математики, что при прочих равных условиях доказательства обобщения убедительны пропорционально количеству благоприятные случаи и разнообразие обстоятельств, в которых они были найдены, это здорово.
Таким образом, чтобы спросить, разумно ли размещать полагаться на индуктивные процедуры — все равно, что спрашивать, разумно соизмерять степень своих убеждений с сила доказательств. Это то, что «быть разумно» означает в таком контексте. (Строусон 1952: 256–57)
Таким образом, согласно этой точке зрения, не может быть и речи о спросить о том, разумно ли полагаться на индуктивное выводы.
Философы обычного языка явно не выступают против Юма помещение П8. Но на самом деле то, что они делают, предлагает совершенно другое история о том, что значит быть оправданным, веря в вывод индуктивных выводов. Что нужно, так это просто соответствие индуктивным стандартам, и нет никакого реального смысла просить дальнейшее обоснование тех.
Основное возражение против этой точки зрения состоит в том, что соответствие обычному
стандартов недостаточно для обеспечения необходимого обоснования. Что мы
нужно знать, является ли вера в вывод индуктивного
вывод является «эпистемически разумным или оправданным в том смысле,
что … есть основания полагать, что это, вероятно, будет
правда» (BonJour 1998: 198). Проблема, поднятая Юмом, состоит в том,
ли, несмотря на тот факт, что индуктивные выводы имеют тенденцию
сделать верные выводы в прошлом, у нас есть основания думать, что
вывод индуктивного вывода, который мы сейчас делаем, вероятно, будет верным.
Можно утверждать, что установление того, что индуктивный вывод является рациональным в
смысла в том, что он следует индуктивным стандартам, недостаточно, чтобы
установить, что его заключение, вероятно, будет верным. На самом деле Стросон
допускает, что возникает вопрос о том, будет ли «индукция
продолжать быть успешными», что отличается от вопроса
рациональна ли индукция. Этот вопрос он ставит на петлю
по «случайному, фактическому вопросу» (Strawson 1952: 262).
Но если именно этот вопрос волновал Юма, то это не ответ на
установить, что индукция рациональна, если это утверждение не понято
включать или подразумевать, что индуктивный вывод, выполненный в соответствии с
к рациональным стандартам, скорее всего, будет иметь верный вывод.
Проблема, поднятая Юмом, состоит в том,
ли, несмотря на тот факт, что индуктивные выводы имеют тенденцию
сделать верные выводы в прошлом, у нас есть основания думать, что
вывод индуктивного вывода, который мы сейчас делаем, вероятно, будет верным.
Можно утверждать, что установление того, что индуктивный вывод является рациональным в
смысла в том, что он следует индуктивным стандартам, недостаточно, чтобы
установить, что его заключение, вероятно, будет верным. На самом деле Стросон
допускает, что возникает вопрос о том, будет ли «индукция
продолжать быть успешными», что отличается от вопроса
рациональна ли индукция. Этот вопрос он ставит на петлю
по «случайному, фактическому вопросу» (Strawson 1952: 262).
Но если именно этот вопрос волновал Юма, то это не ответ на
установить, что индукция рациональна, если это утверждение не понято
включать или подразумевать, что индуктивный вывод, выполненный в соответствии с
к рациональным стандартам, скорее всего, будет иметь верный вывод.
6.
 Жизнь с индуктивным скептицизмом
Жизнь с индуктивным скептицизмомДо сих пор мы рассматривали различные способы, которыми мы могли бы попытаться решить проблему индукции, сопротивляясь той или иной предпосылке Аргумент Юма. Однако некоторые философы видели его аргумент как неопровержимый, и, таким образом, признали, что он ведет к индуктивный скептицизм, вывод о том, что индуктивные выводы не могут быть оправданным. Задача состоит в том, чтобы найти способ жить с такими радикальный вывод. Похоже, мы полагаемся на индуктивный вывод повсеместно в повседневной жизни, и также обычно считается, что лежит в основе научного метода. Можем ли мы продолжить все это, в то же время серьезно думая, что ничто из этого не оправдано какой-нибудь рациональный аргумент?
Один из вариантов здесь — утверждать, как это делает Николас Максвелл, что
задача индукции поставлена в чрезмерно ограничительном
контекст. Максвелл утверждает, что проблема не возникает, если мы принимаем
иная концепция науки, чем «стандартная
эмпирический», который он называет «целеустремленным». эмпиризм» (Максвелл, 2017).
эмпиризм» (Максвелл, 2017).
Другой вариант здесь — думать, что значение проблемы индукция каким-то образом ограничена скептическим контекстом. сам Хьюм кажется, думал в этом направлении. Например, он говорит:
Природа всегда будет отстаивать свои права и в конце концов возьмет верх над любые абстрактные рассуждения. Хотя мы должны сделать вывод, для например, как и в предыдущем разделе, что во всех рассуждениях от опыта, есть шаг, сделанный разумом, который не подкрепляется любым аргументом или процессом понимания; нет никакой опасности, что эти рассуждения, от которых зависит почти все знание, когда-либо быть затронутым таким открытием. (Д.5.1.2)
Цель Юма явно не в том, чтобы утверждать, что мы не должны
индуктивных умозаключений в повседневной жизни, да и весь его метод и
система описания разума в натуралистических терминах зависит от
индуктивные выводы насквозь. Проблема индукции
следует рассматривать как проблему, которая возникает только на уровне
философское размышление.
Другой способ смягчить силу индуктивного скептицизма состоит в том, чтобы ограничивать его объем. Карл Поппер, например, рассматривал проблему индукции как непреодолимой, но он утверждал, что наука на самом деле не вообще не основаны на индуктивных выводах (Popper 1935 [1959]). Скорее он представил дедуктивистский взгляд на науку, согласно которому делает смелые предположения, а затем пытается фальсифицировать эти домыслы. В простейшем варианте этой учетной записи, когда гипотеза делает предсказание, которое оказывается ложным в эксперимента гипотеза отвергается как фальсифицированная. Логика этого процедура является полностью дедуктивной. Гипотеза влечет за собой предсказание, а ложность предсказания опровергает гипотезу по модусу толленс. Таким образом, Поппер утверждал, что наука не основывается на экстраполяционные выводы, рассмотренные Юмом. Следствием этого является что не так важно, по крайней мере для науки, если эти выводы не будет иметь рационального основания.
Рассказ Поппера кажется неполным в важном смысле. Всегда есть много гипотез, которые еще не опровергнуты
доказательства, и они могут противоречить друг другу. Согласно
строго дедуктивной основе, поскольку ни одна из них еще не фальсифицирована, они
все в равных условиях. Тем не менее, ученые, как правило, хотят сказать
что одно лучше подтверждается доказательствами, чем другие. Мы кажемся
нуждаться в чем-то большем, чем просто дедуктивное рассуждение для поддержки практических
принятие решений (Лосось 1981). Поппер действительно апеллировал к понятию
одна гипотеза лучше или хуже «подтверждается»
доказательство. Но, возможно, это увело его от строго дедуктивного
взгляд на науку. Представляется сомнительным, что чистый дедуктивизм может
дать адекватный отчет о научном методе.
Всегда есть много гипотез, которые еще не опровергнуты
доказательства, и они могут противоречить друг другу. Согласно
строго дедуктивной основе, поскольку ни одна из них еще не фальсифицирована, они
все в равных условиях. Тем не менее, ученые, как правило, хотят сказать
что одно лучше подтверждается доказательствами, чем другие. Мы кажемся
нуждаться в чем-то большем, чем просто дедуктивное рассуждение для поддержки практических
принятие решений (Лосось 1981). Поппер действительно апеллировал к понятию
одна гипотеза лучше или хуже «подтверждается»
доказательство. Но, возможно, это увело его от строго дедуктивного
взгляд на науку. Представляется сомнительным, что чистый дедуктивизм может
дать адекватный отчет о научном методе.
7. Средства и цели Решения
Аргумент Юма можно считать окончательно исключающим
своего рода обоснование индуктивных выводов, которое он искал
за. То есть это может исключать обоснование, которое дает основания для
полагать, что заключение конкретного индуктивного вывода является правильным,
или даже может быть правильным. Однако также возможно перемещение
от акцента на обосновании конкретных индуктивных выводов, и
рассмотреть индуктивные методы в более общем виде. В простых случаях
перечислительная индукция, «индуктивный метод» или
Индуктивный принцип, как его иногда называют,
правило, как экстраполировать наблюдаемые случаи. Например,
это могло бы быть правилом, что следует сделать вывод об универсальном
обобщение, после определенного количества положительных примеров и
отвергнуть универсальное обобщение после наблюдения
контрэкземпляры. Или его можно сформулировать как так называемый
«прямое правило», которое гласит, что следует проецировать
наблюдаемая частота признака в популяции в целом,
включая будущие экземпляры. Может быть, дело в том, что генерал
свойства индуктивного метода дают основание использовать
метод, даже если у нас нет оснований полагать, что этот метод
привести к правильному ответу в любом конкретном приложении? Учитывая
конкретной индуктивной задачи, мы можем искать оптимальный метод, или
средства для обеспечения решения.
Однако также возможно перемещение
от акцента на обосновании конкретных индуктивных выводов, и
рассмотреть индуктивные методы в более общем виде. В простых случаях
перечислительная индукция, «индуктивный метод» или
Индуктивный принцип, как его иногда называют,
правило, как экстраполировать наблюдаемые случаи. Например,
это могло бы быть правилом, что следует сделать вывод об универсальном
обобщение, после определенного количества положительных примеров и
отвергнуть универсальное обобщение после наблюдения
контрэкземпляры. Или его можно сформулировать как так называемый
«прямое правило», которое гласит, что следует проецировать
наблюдаемая частота признака в популяции в целом,
включая будущие экземпляры. Может быть, дело в том, что генерал
свойства индуктивного метода дают основание использовать
метод, даже если у нас нет оснований полагать, что этот метод
привести к правильному ответу в любом конкретном приложении? Учитывая
конкретной индуктивной задачи, мы можем искать оптимальный метод, или
средства для обеспечения решения. Такой аргумент целей и средств может затем
составляют основу для следования методу даже при отсутствии
причины верить в его успех в конкретных случаях.
Такой аргумент целей и средств может затем
составляют основу для следования методу даже при отсутствии
причины верить в его успех в конкретных случаях.
7.1 Прагматичная защита
Одной из первых первых попыток в этом направлении была «прагматический» подход Райхенбаха (1938 [2006]). Рейхенбах действительно считал аргумент Юма неопровержимым, но тем не менее он попытался предоставить более слабое оправдание для индукция. Для того, чтобы подчеркнуть отличие от вида оправдание, которое искал Юм, некоторые дали ему другой термин и ссылаться на решение Рейхенбаха как на «оправдание», а не обоснование индукции (Фейгл 1950; Лосось 1963).
В соответствии с этим подходом у нас есть определенная цель сделать индуктивную
выводы. Даже если мы не можем быть уверены, что сможем достичь цели, мы можем
по-прежнему утверждают, что если цель и может быть достигнута, то только путем следования
обычные принципы индуктивного вывода. Это дает повод для
делать обычные индуктивные выводы. Райхенбах делает
сравнение с ситуацией, когда человек страдает от болезни,
и врач говорит: «Я не знаю, будет ли операция
спасите человека, но если есть какое-то средство, это операция».
(Райхенбах 1938 [2006: 349]). Это как-то оправдывает
оперировать человека, даже если он не знает, что операция
преуспеет.
Райхенбах делает
сравнение с ситуацией, когда человек страдает от болезни,
и врач говорит: «Я не знаю, будет ли операция
спасите человека, но если есть какое-то средство, это операция».
(Райхенбах 1938 [2006: 349]). Это как-то оправдывает
оперировать человека, даже если он не знает, что операция
преуспеет.
Рейхенбах применил эту стратегию к общей форме
«статистическая индукция», в которой мы наблюдаем относительную
частота \(f_n\) конкретного события в n наблюдениях и
затем сформируйте ожидания относительно частоты, которая возникнет, когда будет больше
делаются наблюдения. Тогда «индуктивный принцип»
утверждает, что если после определенного числа случаев наблюдаемое
частота \(m/n\) наблюдается при любом продолжении ряда
наблюдений частота будет по-прежнему находиться в пределах небольшого
интервал \(м/п\). Случаи, подобные рассмотренным Юмом, представляют собой частный случай
этого принципа, где наблюдаемая частота равна 1. Например, в
Дело о хлебе Юма, предположим, что хлеб насыщает n раз из n (т. е. наблюдаемая частота 100%),
то по принципу индукции мы ожидаем, что, поскольку мы
наблюдать больше экземпляров, частота питающих будет продолжаться
быть в пределах очень небольшого интервала 100%. После этого индуктивного
принцип также иногда упоминается как следование
«прямое правило». Проблема в том, чтобы обосновать использование
это правило.
е. наблюдаемая частота 100%),
то по принципу индукции мы ожидаем, что, поскольку мы
наблюдать больше экземпляров, частота питающих будет продолжаться
быть в пределах очень небольшого интервала 100%. После этого индуктивного
принцип также иногда упоминается как следование
«прямое правило». Проблема в том, чтобы обосновать использование
это правило.
Рейхенбах утверждал, что даже если Юм прав, полагая, что мы не можем иметь право думать о любом конкретном применении правила что вывод, вероятно, будет верным, для целей практические действия нам не нужны, чтобы установить это. Мы можем вместо этого рассматривать индуктивное правило как результат «позита», или утверждение, с которым мы поступаем так, как если бы оно было истинным. Мы постулируем определенный частота ф на основании наших показаний, а это как бы делая ставку или пари, что частота на самом деле f .
Цель индуктивного вывода, по Рейхенбаху, состоит в том,
» , чтобы найти серию событий, частота возникновения которых
сходится к пределу ” (1938 [2006: 350]). это
Возможно, мир настолько беспорядочный, что мы не можем построить
серии с такими ограничениями. Но если есть предел, то есть какой-то
элемент ряда наблюдений, за пределами которого действует принцип
индукция приведет к истинному значению предела. Хотя
Индуктивное правило может дать совершенно неправильные результаты в начале последовательности, так как
следует за случайными флуктуациями частоты дискретизации, это
гарантированно в конечном итоге приблизится к предельной частоте, если такая
предел существует. Следовательно, правило индукции оправдано как
инструмент постулирования, потому что это метод, о котором мы знаем, что если
можно делать заявления о будущем мы их найдем
с помощью этого метода (Рейхенбах 1949: 475). Это оправдание
воспринимается как прагматичный, поскольку, хотя он и не дает знания
будущего события, оно дает достаточную причину для действия
(Рейхенбах 1949: 481).
это
Возможно, мир настолько беспорядочный, что мы не можем построить
серии с такими ограничениями. Но если есть предел, то есть какой-то
элемент ряда наблюдений, за пределами которого действует принцип
индукция приведет к истинному значению предела. Хотя
Индуктивное правило может дать совершенно неправильные результаты в начале последовательности, так как
следует за случайными флуктуациями частоты дискретизации, это
гарантированно в конечном итоге приблизится к предельной частоте, если такая
предел существует. Следовательно, правило индукции оправдано как
инструмент постулирования, потому что это метод, о котором мы знаем, что если
можно делать заявления о будущем мы их найдем
с помощью этого метода (Рейхенбах 1949: 475). Это оправдание
воспринимается как прагматичный, поскольку, хотя он и не дает знания
будущего события, оно дает достаточную причину для действия
(Рейхенбах 1949: 481).
У этого прагматичного подхода есть несколько проблем. Одна забота
заключается в том, что предлагаемое им обоснование слишком сильно привязано к
в долгосрочной перспективе, не допуская практически никаких ограничений на то, что может быть
складывается в краткосрочном периоде. Тем не менее, именно в краткосрочной перспективе индуктивная
практика действительно имеет место и там, где она действительно нуждается в обосновании
(Бонжур 1998: 194; Лосось 1966: 53).
Тем не менее, именно в краткосрочной перспективе индуктивная
практика действительно имеет место и там, где она действительно нуждается в обосновании
(Бонжур 1998: 194; Лосось 1966: 53).
С этим связано опасение, что обоснование слабо в в том смысле, что оно применимо ко многим другим правилам вывода, а также так называемое «прямое правило» (Salmon 1966: 53). Это относится, фактически к любому методу, который асимптотически сходится к прямой правило. К легко определяемому классу таких правил относятся те, которые добавляют к правило индукции функция \(c_n\), в которой \(c_n\) сходятся к ноль с увеличением n .
Райхенбах делает два предложения, направленных на то, чтобы избежать этой проблемы. На
с одной стороны, утверждает он, поскольку у нас нет реальной возможности выбирать между
методы, мы могли бы также просто использовать индуктивное правило, поскольку оно
«легче обращаться, благодаря его описательной простоте».
Он также утверждает, что метод, воплощающий в себе «наименьший
риск» следует правилу индуктивности (Reichenbach 1938 [2006:
355–356]).
Другая проблема заключается в том, действительно ли Рейхенбах установил, что не может быть лучшего правила, чем прямое правило. Например, несмотря на все сказанное, мог бы найтись прорицатель или экстрасенс, который способен надежно предсказывать будущие события. Здесь Рейхенбах рассуждает что, используя индукцию, мы могли бы признать надежность альтернативный метод, изучив его послужной список. Эта мысль была позже подхватили и развили в предположение, что «метаиндуктивист», применяющий индукцию не только в уровня «объекта» к наблюдениям, но и к успеху чужие методы, могли бы с помощью этих средств сделать то же самое предиктивно как альтернативный метод (Schurz 2008; см. раздел 7.3 для более подробного обсуждения метаиндукции).
Можно также задаться вопросом, действительно ли прагматический аргумент может
предоставить универсальное, общее обоснование для следования
индуктивное правило. Безусловно, прагматичное решение должно учитывать
различия в выплатах, которые зависят от обстоятельств. Например,
Райхенбах предлагает следующий аналог своей прагматической
обоснование:
Например,
Райхенбах предлагает следующий аналог своей прагматической
обоснование:
Мы можем сравнить наше положение с положением человека, который хочет ловить рыбу в неизведанная часть моря. Некому сказать ему, есть он или нет. в этом месте есть рыба. Закинет ли он свою сеть? Ну, если он хочет ловить рыбу в этом месте, я бы посоветовал ему закинуть сеть, взять хотя бы шанс. Предпочтительнее пробовать даже в условиях неопределенности, чем не пытаться и быть уверенным, что ничего не получит. (Райхенбах 1938 [2006: 362–363])
Как указывает Ланге, аргумент здесь «предполагает, что существует
не стоит пытаться». В такой ситуации «рыбак
имеет все, чтобы выиграть и ничего не потерять, закинув свою сеть»
(Ланге 2011: 77). Но если
есть некоторые значительные затраты на попытку, это может быть не так
Ясно, что самый рациональный образ действий — закинуть сеть.
Точно так же, имеет ли смысл проводить политику
не делать никаких прогнозов, а не придерживаться политики следования
индуктивное правило, может зависеть от того, за какие практические наказания
ошибаться. Прагматичное решение может быть не в состоянии предложить
обоснование следования правилу индуктивности, которое применимо во всех
обстоятельства.
Прагматичное решение может быть не в состоянии предложить
обоснование следования правилу индуктивности, которое применимо во всех
обстоятельства.
7.2 Формальная теория обучения
Как мы видели выше, одной из проблем Райхенбаха было то, что слишком много правил, которые сходятся в пределе к истинной частоте. Какой из них мы должны выбрать в краткосрочной перспективе? можно расширить общую стратегию Рейхенбаха, рассмотрев то, что происходит, если у нас есть другие эпистемологические цели, помимо долгосрочной конвергенции. Могут ли другие цели накладывать ограничения на то, какие методы следует использовать в краткосрочный? Область формальной теории обучения развилась ответы на эти вопросы (Келли 1996; Шульте 1999; также см. Шульте 2017).
В частности, теоретики формального обучения считают целью
докопаться до истины как можно эффективнее или быстрее, а также
как цель свести к минимуму количество изменений в сознании или опровержений
по пути. Затем было показано, что обычный индуктивный метод,
который характеризуется предпочтением более простых гипотез
(бритва Оккама), может быть оправдано, поскольку это единственный метод
который соответствует стандартам для достижения истины в долгосрочной перспективе, поскольку
максимально эффективно, с минимальным количеством ретракций (Шульте
1999).
Теорию формального обучения можно рассматривать как своего рода расширение Программа Рейхенбаха. Он не предлагает обоснования индуктивные умозаключения в смысле объяснения причин, по которым они должны быть восприняты как способные привести к истинному заключению. Скорее он предлагает причин для следования конкретным методам, основанным на их оптимальности в достижения определенных желаемых эпистемологических целей, даже если нет гарантировать, что на любом этапе расследования результаты, которые они дают, вообще близки к истине. Однако недавно «Сталь» (2010) предположил, что формальная теория обучения предлагает больше и действительно обеспечивает решение задачи индукции. Это утверждение основано на довольно ограничительная интерпретация «проблемы Юма» как проблема: «Что является основанием для создания индуктивной вообще обобщения?» (2010: 182), а не как проблема обоснования данного индуктивного вывода. стали претензии были оспорены Колином Хоусоном (2011).
7.3 Метаиндукция
Другой подход к выполнению широко рейхенбаховской программы состоит в том, чтобы
перейти на уровень метаиндукции. Мы можем провести различие между
применение индуктивных методов на уровне событий — т. н.
индукция «на уровне объекта» и применение индуктивных методов
на уровне конкурирующих методов прогнозирования — так называемых
«метаиндукция». В то время как индуктивные методы на уровне объекта
делать прогнозы на основе наблюдаемых событий
происходят, метаиндуктивные методы делают прогнозы на основе агрегирования
прогнозы различных доступных методов прогнозирования в соответствии с
их показатели успешности. Здесь определяется вероятность успеха метода
в соответствии с каким-то точным способом подсчета успеха в создании
предсказания.
Мы можем провести различие между
применение индуктивных методов на уровне событий — т. н.
индукция «на уровне объекта» и применение индуктивных методов
на уровне конкурирующих методов прогнозирования — так называемых
«метаиндукция». В то время как индуктивные методы на уровне объекта
делать прогнозы на основе наблюдаемых событий
происходят, метаиндуктивные методы делают прогнозы на основе агрегирования
прогнозы различных доступных методов прогнозирования в соответствии с
их показатели успешности. Здесь определяется вероятность успеха метода
в соответствии с каким-то точным способом подсчета успеха в создании
предсказания.
Тогда возникает вопрос, может ли существовать метаиндуктивный метод.
который является «прогнозно оптимальным» в том смысле, что
следуя этому методу, лучше всего удается прогнозировать среди всех конкурирующих
методы, независимо от того, какие данные получены. Герхард Шурц
выдвинул на первый план результаты основанной на сожалении системы обучения
Чеза-Бьянки, что существует метаиндуктивная стратегия, которая
прогностически оптимален среди всех доступных прогностических методов
к эпистемологическому агенту (Cesa-Bianchi & Lugosi 2006; Schurz 2008,
предстоящий). Эта метаиндуктивная стратегия, которую Шурц называет
«wMI» предсказывает средневзвешенное значение прогнозов
доступные методы, где веса
«привлекательности», которые измеряют разницу между
собственный показатель успеха метода и показатель успеха wMI.
Эта метаиндуктивная стратегия, которую Шурц называет
«wMI» предсказывает средневзвешенное значение прогнозов
доступные методы, где веса
«привлекательности», которые измеряют разницу между
собственный показатель успеха метода и показатель успеха wMI.
Основной результат состоит в том, что стратегия WMI оптимальна в долгосрочной перспективе. в том смысле, что он сходится к максимальной вероятности успеха доступного методы предсказания. Наихудшие оценки для краткосрочной производительности могут также быть выведены. Результат оптимальности формирует основу для a априори обоснование средств и целей для использования wMI. А именно мысль в том, что разумно использовать wMI, так как он достигает наилучшего вероятность успеха возможна в долгосрочной перспективе из данных методов.
Шурц также утверждает, что это априорное обоснование wMI,
вместе с тем случайным фактом, что индуктивные методы до сих пор
оказался гораздо более успешным, чем неиндуктивные методы, порождает апостериорное обоснование индукции. Поскольку WMI будет
достичь в долгосрочной перспективе максимального успеха из доступных
методы прогнозирования, целесообразно его использовать. Но что касается
на самом деле максимальный успех достигается индуктивными методами.
Следовательно, поскольку это априори использование wMI оправдано, это
тоже априори оправдано использовать максимально удачный
метод на объектном уровне. Так как получается, что максимально
успешным методом является индукция, то целесообразно использовать
индукция.
Поскольку WMI будет
достичь в долгосрочной перспективе максимального успеха из доступных
методы прогнозирования, целесообразно его использовать. Но что касается
на самом деле максимальный успех достигается индуктивными методами.
Следовательно, поскольку это априори использование wMI оправдано, это
тоже априори оправдано использовать максимально удачный
метод на объектном уровне. Так как получается, что максимально
успешным методом является индукция, то целесообразно использовать
индукция.
Теоремы Шурца об оптимальности wMI применимы к случаю где существует конечное число методов прогнозирования. Одна точка дискуссия заключается в том, составляет ли это важное ограничение на его претендует на полное решение проблемы индукции (Экхардт 2010).
Экстраамниотический простагландин Е2 для индукции родов в срок
. 1974 г., январь; 81 (1): 39–46.
doi: 10. 1111/j.1471-0528.1974.tb00362.x.
1111/j.1471-0528.1974.tb00362.x.
А. А. Колдер, М. П. Эмбри, К. Хиллиер
- PMID: 4818315
- DOI: 10.1111/j.1471-0528.1974.tb00362.x
А. А. Колдер и соавт. J Obstet Gynaecol Br Commonw. 1974 Январь
. 1974 г., январь; 81 (1): 39–46.
doi: 10.1111/j.1471-0528.1974.tb00362.x.
Авторы
А. А. Колдер, М. П. Эмбри, К. Хиллиер
- PMID: 4818315
- DOI:
10.
 1111/j.1471-0528.1974.tb00362.x
1111/j.1471-0528.1974.tb00362.x
Абстрактный
Картинка в картинке: В этом исследовании изучается возможность того, что прямой внутриматочный путь введения простагландинов E2 (PGE2) может быть осуществим для стимуляции родов в ближайшем будущем, подобно тому, как это наблюдается при прерывании беременности в середине триместра. Обследовано 40 пациенток, 26 первобеременных и 14 нерожавших. Срок беременности колебался от 38 до 42 недель; возрастной диапазон от 17 до 41 года. Оценка «индуцируемости» определялась с использованием модифицированной системы подсчета очков Бишопа. Пациенты с оценкой индуцируемости от 2 до 5 считались неблагоприятными для индукции, тогда как пациенты с оценкой от 6 до 8 были благоприятными. ПГЕ2, приготовленный в физиологическом растворе в концентрации 1,5 мкг ПГЕ2/мл, вводили со скоростью 20 мкг/час и увеличивали каждые 15 минут на 10 мкг/час до установления родовой деятельности. Самая высокая мощность дозы, использованная в серии, составила 150 мкг/час. При необходимости пациентам вводили седативные препараты. Роды устанавливались, когда схватки на 35 мм рт. ст. или выше происходили с интервалами в 2 1/2 минуты или меньше, а при влагалищном исследовании обнаруживались признаки сглаживания или раскрытия шейки матки. Роды были установлены во всех случаях, средний интервал времени 1,9часы. Средний интервал между индукцией и родоразрешением составил 9,8 часа (11,7 часа в неблагоприятной группе; 8,1 часа в благоприятной группе). Общий средний интервал между индукцией и родами составил 9,3 часа, за исключением 4 случаев кесарева сечения. Средняя общая доза PGE2 составила 550 мкг. Никаких явных побочных эффектов у матерей и их младенцев не наблюдалось. Уровень успеха этого подхода выгодно отличается от традиционных методов индукции родов. Это может быть полезно в ситуациях, когда желательно сохранить неповрежденными плодные оболочки. Следует провести дальнейшие исследования этого метода, чтобы установить его эффективность и определить его побочные эффекты, если таковые имеются.
Самая высокая мощность дозы, использованная в серии, составила 150 мкг/час. При необходимости пациентам вводили седативные препараты. Роды устанавливались, когда схватки на 35 мм рт. ст. или выше происходили с интервалами в 2 1/2 минуты или меньше, а при влагалищном исследовании обнаруживались признаки сглаживания или раскрытия шейки матки. Роды были установлены во всех случаях, средний интервал времени 1,9часы. Средний интервал между индукцией и родоразрешением составил 9,8 часа (11,7 часа в неблагоприятной группе; 8,1 часа в благоприятной группе). Общий средний интервал между индукцией и родами составил 9,3 часа, за исключением 4 случаев кесарева сечения. Средняя общая доза PGE2 составила 550 мкг. Никаких явных побочных эффектов у матерей и их младенцев не наблюдалось. Уровень успеха этого подхода выгодно отличается от традиционных методов индукции родов. Это может быть полезно в ситуациях, когда желательно сохранить неповрежденными плодные оболочки. Следует провести дальнейшие исследования этого метода, чтобы установить его эффективность и определить его побочные эффекты, если таковые имеются.
Похожие статьи
Индукция родов экстраамниотическими простагландинами.
Миллер А.В., Мак Д.С. Миллер А.В. и др. J Obstet Gynaecol Br Commonw. 1974 г., сен; 81 (9): 706–708. doi: 10.1111/j.1471-0528.1974.tb00545.x. J Obstet Gynaecol Br Commonw. 1974. PMID: 4413846
Сравнение внутривенного введения простагландина Е2 и внутривенного введения окситоцина для стимуляции родовой деятельности, осложненной задержкой.
Клегг Д.Р., Флинн А.М., Келли Дж. Клегг Д.Р. и соавт. J Obstet Gynaecol Br Commonw. 1974 декабрь; 81 (12): 995-9. doi: 10.1111/j.1471-0528.1974.tb00421.x. J Obstet Gynaecol Br Commonw. 1974. PMID: 4452929
Индукция родов таблетками простагландина Е2.

Тьери М., Сиан А.И., Де Хемптинн Д., Дером Р., Мартенс С., Ван Кетс Х.В., Эми Дж.Дж. Тьери М. и др. J Obstet Gynaecol Br Commonw. 1974 апреля; 81 (4): 303-6. doi: 10.1111/j.1471-0528.1974.tb00464.x. J Obstet Gynaecol Br Commonw. 1974. PMID: 4824688
Мизопростол для индукции родов: систематический обзор.
Хофмейр Г.Дж., Гюльмезоглу А.М., Альфиревич З. Хофмейр Г.Дж. и соавт. Br J Obstet Gynaecol. 1999 г., август; 106 (8): 798-803. doi: 10.1111/j.1471-0528.1999.tb08400.x. Br J Obstet Gynaecol. 1999. PMID: 10453829 Обзор.
Гель с простагландином Е2 для созревания шейки матки и индукции родов: критический анализ.
Рейберн ВФ. Рейберн ВФ. Am J Obstet Gynecol. 1989 март; 160(3):529-34.
 doi: 10.1016/s0002-9378(89)80020-1.
Am J Obstet Gynecol. 1989.
PMID: 2648830
Обзор.
doi: 10.1016/s0002-9378(89)80020-1.
Am J Obstet Gynecol. 1989.
PMID: 2648830
Обзор.
Посмотреть все похожие статьи
Цитируется
Двойные баллонные катетеры: перспективный инструмент для индукции родов у повторнородящих женщин с неблагоприятным состоянием шейки матки.
Тюлек Ф., Гемичи А., Сойлемез Ф. Тюлек Ф. и др. J Turk Ger Gynecol Assoc. 2019 28 ноября; 20 (4): 231-235. doi: 10.4274/jtgga.galenos.2018.2018.0084. Epub 2018 17 сентября. J Turk Ger Gynecol Assoc. 2019. PMID: 30222124 Бесплатная статья ЧВК.
Результат индукции родов у нерожавших женщин после замены Цервидила Простином.
Басу А., Элгей С., Харан М. Басу А. и др. Журнал «Научный мир».
 2012;2012:325968. дои: 10.1100/2012/325968. Epub 2012 30 апр.
Журнал «Научный мир». 2012.
PMID: 22666106
Бесплатная статья ЧВК.
2012;2012:325968. дои: 10.1100/2012/325968. Epub 2012 30 апр.
Журнал «Научный мир». 2012.
PMID: 22666106
Бесплатная статья ЧВК.Индукция родов вагинальным пессарием с простагландином Е2 пролонгированного действия.
Embrey MP, Graham NB, McNeill ME. Эмбри М.П. и др. Br Med J. 1980, 4 октября; 281 (6245): 901-2. doi: 10.1136/bmj.281.6245.901. Бр Мед Дж. 1980. PMID: 7427502 Бесплатная статья ЧВК.
Сравнительное исследование вагинального геля эстрадиола и простагландина Е2 для созревания неблагоприятной шейки матки перед индукцией родов.
Троманс П.М., Бизли Дж., Шенуда П.И. Троманс П.М. и др. Br Med J (Clin Res Ed). 1981 28 февраля; 282(6265):679-81. doi: 10.1136/bmj.282.6265.679. Br Med J (Clin Res Ed).
 1981.
PMID: 6781613
Бесплатная статья ЧВК.
Клиническое испытание.
1981.
PMID: 6781613
Бесплатная статья ЧВК.
Клиническое испытание.Созревание шейки матки: сравнительная эффективность таблеток Ламицел и простагландин Е2.
Кэхилл Диджей, Кларк Х.С., Мартин Д.Х. Кэхилл Д.Дж. и др. Ir J Med Sci. 1988 г., апрель; 157 (4): 113-4. doi: 10.1007/BF02950366. Ir J Med Sci. 1988 год. PMID: 3164309Клиническое испытание. Аннотация недоступна.
Просмотреть все статьи «Цитируется по»
термины MeSH
вещества
Индукция
\(\def\d{\displaystyle}
\def\курс{Математика 228}
\ новая команда {\ f} [1] {\ mathfrak # 1}
\ новая команда {\ s} [1] {\ mathscr # 1}
\def\N{\mathbb N}
\def\B{\mathbf{B}}
\def\circleA{(-.5,0) круг (1)}
\ деф \ Z {\ mathbb Z}
\def\circleAlabel{(-1. {-1}}
\def\nrml{\triangleleft}
\ деф \ ст {:}
\ деф \ ~ {\ широкая тильда}
\def\rem{\mathcal R}
\def\sigalg{$\sigma$-алгебра }
\def\Гал{\mbox{Гал}}
\def\iff{\leftrightarrow}
\def\If{\Leftrightarrow}
\ деф \ земля {\ клин}
\def\И{\bigwedge}
\защита\вход{\вход}
\def\AAnd{\d\bigwedge\mkern-18mu\bigwedge}
\def\Ви{\bigvee}
\def\VVee{\d\Vee\mkern-18mu\Vee}
\ деф \ имп {\ стрелка вправо}
\def\Imp{\Rightarrow}
\def\Fi{\Leftarrow}
\def\var{\mbox{var}}
\def\Th{\mbox{Th}}
\защита\вход{\вход}
\def\sat{\mbox{Sat}}
\def\con{\mbox{Con}}
\def\iffmodels{\bmodels\models}
\def\dbland{\bigwedge \!\!\bigwedge}
\def\дом{\mbox{дом}}
\def\rng{\mbox{диапазон}}
\def\isom{\cong}
\DeclareMathOperator{\wgt}{wgt}
\newcommand{\vtx}[2]{узел[заливка,круг,внутренний интервал=0pt, минимальный размер=4pt,метка=#1:#2]{}}
\ новая команда {\ va} [1] {\ vtx {выше} {# 1}}
\ новая команда {\ vb} [1] {\ vtx {ниже} {# 1}}
\ новая команда {\ vr} [1] {\ vtx {право} {# 1}}
\ новая команда {\ vl} [1] {\ vtx {слева} {# 1}}
\renewcommand{\v}{\vtx{выше}{}}
\def\circleA{(-.
{-1}}
\def\nrml{\triangleleft}
\ деф \ ст {:}
\ деф \ ~ {\ широкая тильда}
\def\rem{\mathcal R}
\def\sigalg{$\sigma$-алгебра }
\def\Гал{\mbox{Гал}}
\def\iff{\leftrightarrow}
\def\If{\Leftrightarrow}
\ деф \ земля {\ клин}
\def\И{\bigwedge}
\защита\вход{\вход}
\def\AAnd{\d\bigwedge\mkern-18mu\bigwedge}
\def\Ви{\bigvee}
\def\VVee{\d\Vee\mkern-18mu\Vee}
\ деф \ имп {\ стрелка вправо}
\def\Imp{\Rightarrow}
\def\Fi{\Leftarrow}
\def\var{\mbox{var}}
\def\Th{\mbox{Th}}
\защита\вход{\вход}
\def\sat{\mbox{Sat}}
\def\con{\mbox{Con}}
\def\iffmodels{\bmodels\models}
\def\dbland{\bigwedge \!\!\bigwedge}
\def\дом{\mbox{дом}}
\def\rng{\mbox{диапазон}}
\def\isom{\cong}
\DeclareMathOperator{\wgt}{wgt}
\newcommand{\vtx}[2]{узел[заливка,круг,внутренний интервал=0pt, минимальный размер=4pt,метка=#1:#2]{}}
\ новая команда {\ va} [1] {\ vtx {выше} {# 1}}
\ новая команда {\ vb} [1] {\ vtx {ниже} {# 1}}
\ новая команда {\ vr} [1] {\ vtx {право} {# 1}}
\ новая команда {\ vl} [1] {\ vtx {слева} {# 1}}
\renewcommand{\v}{\vtx{выше}{}}
\def\circleA{(-. 5,0) круг (1)}
\def\circleAlabel{(-1.5,.6) узел[выше]{$A$}}
\def\circleB{(.5,0) круг (1)}
\def\circleBlabel{(1.5,.6) узел[выше]{$B$}}
\def\circleC{(0,-1) круг (1)}
\def\circleClabel{(.5,-2) узел[справа]{$C$}}
\def\twosetbox{(-2,-1.4) прямоугольник (2,1.4)}
\def\threesetbox{(-2.5,-2.4) прямоугольник (2.5,1.4)}
\def\ansfilename{практика-ответы}
\def\shadowprops{{fill=black!50,shadow xshift=0.5ex,shadow yshift=0.5ex,path fading={круг с размытым краем 10 процентов}}}
\ новая команда {\ hexbox} [3] {
\def\x{-cos{30}*\r*#1+cos{30}*#2*\r*2}
\def\y{-\r*#1-sin{30}*\r*#1}
\рисовать (\х,\у) +(90:\r) — +(30:\r) — +(-30:\r) — +(-90:\r) — +(-150:\r) — +(150: \r) — цикл;
\draw (\x,\y) узел{#3};
}
\renewcommand{\bar}{\overline}
\newcommand{\card}[1]{\left| #1 \справа|}
\newcommand{\twoline}[2]{\begin{pmatrix}#1 \\ #2 \end{pmatrix}}
\новая команда{\lt}{<}
\новая команда{\gt}{>}
\newcommand{\amp}{&}
\)
5,0) круг (1)}
\def\circleAlabel{(-1.5,.6) узел[выше]{$A$}}
\def\circleB{(.5,0) круг (1)}
\def\circleBlabel{(1.5,.6) узел[выше]{$B$}}
\def\circleC{(0,-1) круг (1)}
\def\circleClabel{(.5,-2) узел[справа]{$C$}}
\def\twosetbox{(-2,-1.4) прямоугольник (2,1.4)}
\def\threesetbox{(-2.5,-2.4) прямоугольник (2.5,1.4)}
\def\ansfilename{практика-ответы}
\def\shadowprops{{fill=black!50,shadow xshift=0.5ex,shadow yshift=0.5ex,path fading={круг с размытым краем 10 процентов}}}
\ новая команда {\ hexbox} [3] {
\def\x{-cos{30}*\r*#1+cos{30}*#2*\r*2}
\def\y{-\r*#1-sin{30}*\r*#1}
\рисовать (\х,\у) +(90:\r) — +(30:\r) — +(-30:\r) — +(-90:\r) — +(-150:\r) — +(150: \r) — цикл;
\draw (\x,\y) узел{#3};
}
\renewcommand{\bar}{\overline}
\newcommand{\card}[1]{\left| #1 \справа|}
\newcommand{\twoline}[2]{\begin{pmatrix}#1 \\ #2 \end{pmatrix}}
\новая команда{\lt}{<}
\новая команда{\gt}{>}
\newcommand{\amp}{&}
\)
Математическая индукция — это метод доказательства, мало чем отличающийся от прямого доказательства или доказательства от противного или комбинаторного доказательства. 3 Возможно, вы еще не знакомы с ними. Мы рассмотрим их в главе 3. Другими словами, индукция — это стиль аргументации, который мы используем, чтобы убедить себя и других в том, что математическое утверждение всегда верно. Многие математические утверждения можно доказать, просто объяснив, что они означают. Другие очень трудно доказать — на самом деле, есть относительно простые математические утверждения, которые еще никто не знает, как доказать. Чтобы облегчить поиск доказательств, важно быть знакомым с некоторыми стандартными стилями аргументации. Индукция — один из таких стилей. Начнем с примера:
3 Возможно, вы еще не знакомы с ними. Мы рассмотрим их в главе 3. Другими словами, индукция — это стиль аргументации, который мы используем, чтобы убедить себя и других в том, что математическое утверждение всегда верно. Многие математические утверждения можно доказать, просто объяснив, что они означают. Другие очень трудно доказать — на самом деле, есть относительно простые математические утверждения, которые еще никто не знает, как доказать. Чтобы облегчить поиск доказательств, важно быть знакомым с некоторыми стандартными стилями аргументации. Индукция — один из таких стилей. Начнем с примера:
ПодразделМарки
¶Расследуй!22
Вам нужно отправить посылку, но вы еще не знаете, сколько вам потребуется почтовых расходов. У вас есть большой запас 8-центовых и 5-центовых марок. Какие суммы почтовых расходов вы можете сделать, используя именно эти марки? Какие суммы невозможно заработать?
Возможно, при рассмотрении вышеописанной проблемы вы выбрали некоторую сумму почтовых расходов, а затем выяснили, можно ли получить эту сумму, используя только 8-центовые и 5-центовые марки. Возможно, вы сделали это для того, чтобы: вы можете сделать 1 цент почтовых расходов? Вы можете сделать 2 цента? 3 цента? И так далее. Если это то, что вы сделали, вы на самом деле ответили на последовательность вопросов. У нас есть методы работы с последовательностями. Посмотрим, поможет ли это.
Возможно, вы сделали это для того, чтобы: вы можете сделать 1 цент почтовых расходов? Вы можете сделать 2 цента? 3 цента? И так далее. Если это то, что вы сделали, вы на самом деле ответили на последовательность вопросов. У нас есть методы работы с последовательностями. Посмотрим, поможет ли это.
На самом деле мы будем составлять не последовательность вопросов, а последовательность утверждений. Пусть \(P(n)\) будет утверждением «вы можете заработать \(n\) центов на почтовых расходах, используя только 8-центовые и 5-центовые марки». Поскольку для каждого значения \(n\text{,}\) \(P(n)\) есть утверждение, оно либо истинно, либо ложно. Итак, если мы сформируем последовательность операторов
\begin{уравнение*} П(1), П(2), П(3), П(4), \ldots \end{уравнение*}последовательность будет состоять из символов \(T\) (истинно) и \(F\) (ложно). В нашем конкретном случае последовательность начинается с
. \begin{уравнение*} F,F,F,F,T,F,F,T,F,F,T,F,F,T,\ldots \end{уравнение*}, потому что \(P(1), P(2), P(3), P(4)\) все ложные (вы не можете получить 1, 2, 3 или 4 цента почтовых расходов), но \(P(5 )\) верно (используйте одну 5-центовую марку) и так далее.
Давайте немного подумаем, как найти значение \(P(n)\) для некоторого конкретного \(n\) («значение» будет либо \(T\), либо \(F\)). Как мы нашли значение \(n\)-го члена последовательности чисел? Как мы нашли \(a_n\text{?}\) Это можно было сделать двумя способами: либо существовала закрытая формула для \(a_n\text{,}\), чтобы мы могли подставить \(n\) в формулу и получить наше выходное значение, или у нас было рекурсивное определение последовательности, поэтому мы могли использовать предыдущие члены последовательности для вычисления \(n\)-го члена. При работе с последовательностями операторов мы также можем использовать любой из этих методов. Возможно, есть способ использовать саму \(n\), чтобы определить, можем ли мы заработать \(n\) центов на почтовых расходах. Это было бы что-то вроде закрытой формулы. Или вместо этого мы могли бы использовать предыдущие термины в последовательности (утверждений), чтобы определить, можем ли мы заработать \(n\) центов на почтовых расходах. То есть, если мы знаем значение \(P(n-1)\text{,}\), можем ли мы перейти от этого к значению \(P(n)\text{?}\) Это было бы что-то как рекурсивное определение последовательности. Помните, найти рекурсивные определения для последовательностей часто было проще, чем найти замкнутые формулы. То же самое и здесь.
Помните, найти рекурсивные определения для последовательностей часто было проще, чем найти замкнутые формулы. То же самое и здесь.
Предположим, я сказал вам, что \(P(43)\) верно (так и есть). Можете ли вы по этому факту определить значение \(P(44)\) (истинно оно или ложно)? Да, ты можешь. Даже если мы не знаем, как именно мы сделали 43 цента из 5-центовых и 8-центовых марок, мы знаем, что каким-то образом это можно было сделать. Что, если бы таким образом использовалось как минимум три 5-центовых марки (составляя 15 центов)? Мы могли бы заменить эти три марки по 5 центов двумя марками по 8 центов (получив 16 центов). Общие почтовые расходы увеличились на 1, поэтому у нас есть способ заработать 44 цента, так что \(P(44)\) верно. Конечно, мы предполагали, что у нас есть как минимум три 5-центовых марки. Что, если бы мы этого не сделали? Тогда у нас должно быть как минимум три марки по 8 центов (что составляет 24 цента). Если мы заменим эти три марки по 8 центов пятью марками по 5 центов (получив 25 центов), то снова мы увеличим нашу сумму на 1 цент, так что мы сможем получить 44 цента, поэтому \(P(44)\) верно.
Обратите внимание, что мы не сказали, как заработать 44 цента, просто сказали, что можем, исходя из того, что можем заработать 43 цента. Откуда мы знаем, что можем заработать 43 цента? Возможно, потому, что мы знаем, что можем заработать \(42\) цента, а мы знаем, что можем сделать, потому что знаем, что можем заработать 41 цент, и так далее. Это рекурсия! Как и в случае рекурсивного определения числовой последовательности, мы должны указать наше начальное значение. В этом случае начальное значение — «\(P(1)\) — ложь». Это нехорошо, так как наше рекуррентное соотношение просто говорит, что \(P(k+1)\) верно , если \(P(k)\) также верно. Нам нужно начать процесс с истинного \(P(k)\text{.}\) Поэтому вместо этого мы можем использовать «\(P(31)\) верно» в качестве начального условия.
Собрав все это вместе, мы приходим к следующему факту: можно (точно) сделать любую сумму почтовых расходов больше 27 центов, используя только 5-центовые и 8-центовые марки. 4 Это не означает, что не существует сумм менее 27 центов, которые также можно заработать. Другими словами, \(P(k)\) верно для любого \(k \ge 28\text{.}\). Чтобы доказать это, мы могли бы сделать следующее:0005
Другими словами, \(P(k)\) верно для любого \(k \ge 28\text{.}\). Чтобы доказать это, мы могли бы сделать следующее:0005
Докажите, что \(P(28)\) верно.
Докажите, что если \(P(k)\) истинно, то \(P(k+1)\) истинно (для любого \(k \ge 28\)).
Предположим, мы сделали это. Тогда мы знаем, что 28-й член приведенной выше последовательности является \(T\) (используя шаг 1, начальное условие или базовый случай ), и что каждый член после 28-го также является \(T\) (используя шаг 2, рекурсивная часть или индуктивный случай ). Вот как на самом деле выглядело бы доказательство.
Доказательство
Пусть \(P(n)\) будет утверждением «можно заработать ровно \(n\) центов почтовых расходов, используя 5-центовые и 8-центовые марки». Мы покажем, что \(P(n)\) верно для всех \(n \ge 28\text{.}\)
Во-первых, мы показываем, что \(P(28)\) верно: \(28 = 4 \cdot 5+ 1\cdot 8\text{,}\), поэтому мы можем получить \(28\) центов, используя четыре 5 -центовые марки и одна 8-центовая марка.
Теперь предположим, что \(P(k)\) верно для некоторого произвольного \(k \ge 28\text{.}\). Тогда можно сделать \(k\) центов, используя 5-центовые и 8-центовые марки. . Обратите внимание, что поскольку \(k \ge 28\text{,}\) не может быть, чтобы мы использовали менее трех 5-центовых марок и меньше, чем три марки по 8 центов: использование двух марок каждой даст только 26 центов. Теперь, если мы заработали \(k\) центов, используя не менее трех марок по 5 центов, замените три марки по 5 центов на две марки по 8 центов. Это заменяет 15 центов почтовых расходов на 16 центов, переходя от общей суммы \(k\) центов к \(k+1\) центов. Таким образом, \(P(k+1)\) верно. С другой стороны, если мы заработали \(k\) центов, используя по крайней мере три марки по 8 центов, то мы можем заменить три марки по 8 центов на пять марок по 5 центов, перейдя от 24 центов к 25 центам, что даст всего \(k+1\) центов почтовых расходов. Так что и в этом случае \(P(k+1)\) верно.
Следовательно, по принципу математической индукции \(P(n)\) истинно для всех \(n \ge 28\text{. }\)
}\)
Подраздел Оформление доказательств
¶То, что мы сделали в примере с маркой выше, работает для многих типов задач. Доказательство по индукции полезно при попытке доказать утверждения обо всех натуральных числах или всех натуральных числах, больших некоторого фиксированного первого случая (например, 28 в приведенном выше примере), а также в некоторых других ситуациях. В частности, индукцию следует использовать, когда есть какой-то способ перейти от одного случая к другому — когда вы можете видеть, как всегда «делать еще один».
Это отличная идея. Размышление о проблеме индуктивно может дать новое понимание проблемы. Например, чтобы по-настоящему понять проблему марки, вы должны подумать о том, как может быть произведена любая сумма почтовых расходов (более 28 центов) (это неиндуктивное рассуждение), а также как способы оплаты изменяются . по мере увеличения суммы (индуктивное рассуждение). Когда вас просят представить доказательство по индукции, вас просят подумать над проблемой динамически ; как увеличение \(n\) меняет проблему?
Но есть и другая сторона доказательств по индукции. В математике недостаточно понять проблему, вы также должны уметь сообщить о проблеме другим. Как и любая дисциплина, математика имеет стандартный язык и стиль, что позволяет математикам эффективно делиться своими идеями. Доказательства по индукции имеют определенный формальный стиль, и умение писать в этом стиле очень важно. Это позволяет нам систематизировать наши идеи и может даже помочь нам сформулировать доказательство.
В математике недостаточно понять проблему, вы также должны уметь сообщить о проблеме другим. Как и любая дисциплина, математика имеет стандартный язык и стиль, что позволяет математикам эффективно делиться своими идеями. Доказательства по индукции имеют определенный формальный стиль, и умение писать в этом стиле очень важно. Это позволяет нам систематизировать наши идеи и может даже помочь нам сформулировать доказательство.
Вот общая структура доказательства по математической индукции:
Конструкция с защитой от индукции
Начните с того, что скажите, какое утверждение вы хотите доказать: «Пусть \(P(n)\) будет утверждением…». Чтобы доказать, что \(P(n)\) истинно для всех \(n \ge 0 \text{,}\) вы должны доказать два факта:
Базовый случай: Докажите, что \(P(0)\) верно. Вы делаете это напрямую. Часто это легко.
Индуктивный случай: Докажите, что \(P(k) \imp P(k+1)\) для всех \(k \ge 0\text{.}\) То есть, докажите, что для любого \(k \ge 0\) если \(P(k)\) истинно, то \(P(k+1)\) также истинно.
 Это доказательство утверждения if… then…, так что вы можете предположить, что \(P(k)\) истинно (\(P(k)\) называется индуктивная гипотеза ). Затем вы должны объяснить, почему \(P(k+1)\) также верно, учитывая это предположение.
Это доказательство утверждения if… then…, так что вы можете предположить, что \(P(k)\) истинно (\(P(k)\) называется индуктивная гипотеза ). Затем вы должны объяснить, почему \(P(k+1)\) также верно, учитывая это предположение.
Предполагая, что вы успешно выполнили обе указанные выше части, вы можете сделать вывод: «Поэтому по принципу математической индукции утверждение \(P(n)\) верно для всех \(n \ge 0\text{.}\ )”
Иногда утверждение \(P(n)\) будет истинным, например, только для значений \(n \ge 4\text{,}\) или некоторых других значений. В таких случаях замените все 0 выше на 4 (или другое значение).
Другое преимущество формализации индуктивных доказательств состоит в том, что это позволяет нам проверить правильность логики, лежащей в основе этого стиля рассуждений. Почему индукция работает? Представьте себе ряд костяшек домино, стоящих на ребрах. Мы хотим доказать, что через минуту все костяшки домино упадут. Для этого вам нужно будет толкнуть первую костяшку домино. Это базовый случай. Также должно быть так, чтобы костяшки домино были расположены достаточно близко друг к другу, чтобы при падении какого-либо конкретного костяшка домино падало следующее. Это индуктивный случай. Если оба этих условия соблюдены, вы толкаете первую костяшку, и каждая костяшка заставит упасть следующую, тогда все костяшки домино упадут.
Это базовый случай. Также должно быть так, чтобы костяшки домино были расположены достаточно близко друг к другу, чтобы при падении какого-либо конкретного костяшка домино падало следующее. Это индуктивный случай. Если оба этих условия соблюдены, вы толкаете первую костяшку, и каждая костяшка заставит упасть следующую, тогда все костяшки домино упадут.
Индукция мощная! Подумайте, насколько легче опрокидывать костяшки домино, когда вам не нужно толкать каждую костяшку самостоятельно. Вы просто запускаете цепную реакцию и полагаетесь на относительную близость костяшек домино, чтобы позаботиться обо всем остальном.
Подумайте о нашем изучении последовательностей. Легче найти рекурсивные определения последовательностей, чем замкнутые формулы. Переходить от одного случая к другому легче, чем переходить непосредственно к конкретному делу. Вот чем так хороша индукция. Вместо того, чтобы переходить непосредственно к (произвольному) случаю для \(n\text{,}\), нам просто нужно сказать, как перейти от одного случая к другому.
Когда вас просят доказать утверждение с помощью математической индукции, вы должны сначала подумать о том, почему это утверждение верно, используя индуктивное рассуждение. Объясните, почему индукция — это правильно, и примерно, почему индуктивный случай будет работать. Затем сядьте и напишите тщательное формальное доказательство, используя приведенную выше структуру.
ПодразделПримеры
¶Вот несколько примеров доказательства по математической индукции.
Пример 2.5.1
Докажите для каждого натурального числа \(n \ge 1\), что \(1 + 2 + 3 + \cdots + n = \frac{n(n+1)}{2}\text{.}\)
Решение
Во-первых, давайте поразмышляем над этим уравнением. На самом деле, мы знаем, что это верно по другим причинам (на ум приходит reverse и add). Но почему индукция может быть применима? В левой части складываются числа от 1 до \(n\text{.}\). Если бы мы знали, как это сделать, добавить еще один член (\(n+1\)) было бы не так сложно. Например, если \(n = 100\text{,}\) предположим, что мы знаем, что сумма первых 100 чисел равна \(5050\) (таким образом, \(1 + 2 + 3 + \cdots + 100 = 5050\). text{,}\), что верно). Теперь, чтобы найти сумму первых 101 числа, имеет смысл просто прибавить 101 к 5050, а не вычислять всю сумму заново. У нас было бы \(1 + 2 + 3 + \cdots + 100 + 101 = 5050 + 101 = 5151\text{.}\) На самом деле всегда было бы легко добавить еще один термин. Вот почему мы должны использовать индукцию.
Например, если \(n = 100\text{,}\) предположим, что мы знаем, что сумма первых 100 чисел равна \(5050\) (таким образом, \(1 + 2 + 3 + \cdots + 100 = 5050\). text{,}\), что верно). Теперь, чтобы найти сумму первых 101 числа, имеет смысл просто прибавить 101 к 5050, а не вычислять всю сумму заново. У нас было бы \(1 + 2 + 3 + \cdots + 100 + 101 = 5050 + 101 = 5151\text{.}\) На самом деле всегда было бы легко добавить еще один термин. Вот почему мы должны использовать индукцию.
Теперь формальное доказательство:
Доказательство
Пусть \(P(n)\) будет утверждением \(1 + 2 + 3 + \cdots + n = \frac{n(n+2)}{2}\text{.}\) Мы покажем, что \(P(n)\) верно для всех натуральных чисел \(n \ge 1\text{.}\)
Базовый случай: \(P(1)\) — это утверждение \(1 = \frac{1(1+1)}{2}\), которое явно верно.
Индуктивный случай: Пусть \(k \ge 1\) — натуральное число. Предположим (по индукции), что \(P(k)\) истинно. Это означает, что \(1 + 2 + 3 + \cdots + k = \frac{k(k+1)}{2}\text{. }\) Мы докажем, что \(P(k+1)\) верно также. То есть мы должны доказать, что \(1 + 2 + 3 + \cdots + k + (k+1) = \frac{(k+1)(k+2)}{2}\text{.}\) Чтобы доказать это уравнение, начните с добавления \(k+1\) к обеим частям индуктивной гипотезы:
}\) Мы докажем, что \(P(k+1)\) верно также. То есть мы должны доказать, что \(1 + 2 + 3 + \cdots + k + (k+1) = \frac{(k+1)(k+2)}{2}\text{.}\) Чтобы доказать это уравнение, начните с добавления \(k+1\) к обеим частям индуктивной гипотезы:
Теперь, упростив правую часть, получим:
\начать{выравнивать*} \frac{k(k+1)}{2} + k+1 \amp = \frac{k(k+1)}{2} + \frac{2(k+1)}{2}\\ \amp = \frac{k(k+1) + 2(k+1)}{2}\\ \amp = \frac{(k+2)(k+1)}{2}. \конец{выравнивание*}Таким образом, \(P(k+1)\) истинно, поэтому по принципу математической индукции \(P(n)\) истинно для всех натуральных чисел \(n \ge 1\text{.}\)
Обратите внимание, что в части доказательства, в которой мы доказывали \(P(k+1)\) из \(P(k)\text{,}\), мы использовали уравнение \(P(k)\text{ .}\) Это была индуктивная гипотеза. Увидеть, как использовать индуктивные гипотезы, обычно несложно при доказательстве факта о сумме, подобной этой. В других доказательствах это может быть менее очевидно, где оно подходит. 92\) на единицу больше, чем кратное 5). Как выглядят числа, которые на единицу больше, чем кратны 5? Они должны иметь последнюю цифру 1 или 6. Что произойдет, если умножить такое число на 6? Зависит от числа, но в любом случае последняя цифра нового числа должна быть 6. И тогда, если вычесть 1, вы получите последнюю цифру 5, то есть число, кратное 5.
В других доказательствах это может быть менее очевидно, где оно подходит. 92\) на единицу больше, чем кратное 5). Как выглядят числа, которые на единицу больше, чем кратны 5? Они должны иметь последнюю цифру 1 или 6. Что произойдет, если умножить такое число на 6? Зависит от числа, но в любом случае последняя цифра нового числа должна быть 6. И тогда, если вычесть 1, вы получите последнюю цифру 5, то есть число, кратное 5.
Дело в том, что каждый раз, когда мы умножив еще на одну шестерку, мы по-прежнему получим число с последней цифрой 6, поэтому вычитание 1 дает нам число, кратное 5. Теперь формальное доказательство: 9n\) для всех целых чисел \(n \ge 5\text{.}\)
Решение
Во-первых, идея аргумента. Что произойдет, если мы увеличим \(n\) на 1? В левой части увеличиваем основание квадрата и переходим к следующему номеру квадрата. В правой части мы увеличиваем степень числа 2. Это означает, что мы удваиваем число. Итак, вопрос в том, как удвоение числа связано с увеличением до следующего квадрата? Подумайте, как выглядит разница двух последовательных квадратов. 2\text{.}\) Эти факторы: 9{k+1}\text{,}\) другими словами, \(P(k+1)\text{.}\) Следовательно, по принципу математической индукции \(P(n)\) верно для all \(n \ge 5\text{.}\)
2\text{.}\) Эти факторы: 9{k+1}\text{,}\) другими словами, \(P(k+1)\text{.}\) Следовательно, по принципу математической индукции \(P(n)\) верно для all \(n \ge 5\text{.}\)
Предыдущий пример может напомнить вам принцип ипподрома из исчисления, который гласит, что если \(f(a) \lt g(a)\text{ ,}\) и \(f'(x) \lt g'(x)\) для \(x > a\text{,}\), то \(f(x) \lt g(x)\) для \(x > a\text{.}\) Та же идея: большая функция увеличивается быстрее, чем меньшая, поэтому большая функция останется большей. В дискретной математике у нас нет производных, поэтому мы смотрим на различия. Таким образом, индукция — это путь.
Предупреждение:
С большой силой приходит большая ответственность. Индукция — это не магия. Предполагать, что \(P(k)\) истинно, кажется очень мощным. В конце концов, мы пытаемся доказать, что \(P(n)\) истинно, и единственная разница заключается в переменной: \(k\) против \(n\text{.}\) Мы предполагаем, что то, что мы хотите доказать, что это правда? Не совсем. Мы предполагаем, что \(P(k)\) истинно только для того, чтобы доказать, что \(P(k+1)\) истинно.
Мы предполагаем, что \(P(k)\) истинно только для того, чтобы доказать, что \(P(k+1)\) истинно.
Тем не менее вы можете начать верить, что с помощью индукции можно доказать что угодно. Рассмотрим это неверное «доказательство» того, что у всех канадцев одинаковый цвет глаз: пусть \(P(n)\) будет утверждением, что у всех \(n\) канадцев одинаковый цвет глаз. \(P(1)\) верно, так как у всех такой же цвет глаз, как и у них самих. Теперь предположим, что \(P(k)\) истинно. То есть предположим, что в любой группе \(k\) канадцев у всех одинаковый цвет глаз. Теперь рассмотрим произвольную группу из \(k+1\) канадцев. Первые \(k\) из них должны иметь одинаковый цвет глаз, так как \(P(k)\) верно. Кроме того, последнее \(k\) из них должно иметь одинаковый цвет глаз, так как \(P(k)\) верно. Так что на самом деле у всех в группе должен быть одинаковый цвет глаз. Таким образом, \(P(k+1)\) верно. Таким образом, по принципу математической индукции \(P(n)\) верно для всех \(n\text{.}\)
Очевидно, что-то пошло не так. Проблема в том, что доказательство того, что \(P(k)\) влечет \(P(k+1)\), предполагает, что \(k \ge 2\text{.}\) Мы только показали \(P(1 )\) правда. На самом деле \(P(2)\) ложно.
Проблема в том, что доказательство того, что \(P(k)\) влечет \(P(k+1)\), предполагает, что \(k \ge 2\text{.}\) Мы только показали \(P(1 )\) правда. На самом деле \(P(2)\) ложно.
ПодразделСильная индукция
¶Расследуй!23
Начните с квадратного листа бумаги. Вы хотите разрезать этот квадрат на более мелкие квадраты, не оставляя отходов (каждый лист бумаги, который у вас получится, должен быть квадратным). Очевидно, что можно разрезать квадрат на 4 квадрата. Вы также можете разрезать его на 9квадраты. Оказывается, можно разрезать квадрат на 7 квадратов (правда, не все одинакового размера). Какое еще количество квадратов вы могли бы получить?
Иногда, чтобы доказать истинность \(P(k+1)\), полезно знать, что \(P(k)\) и \(P(k-1)\) и \(P(k-2)\) верны. Рассмотрим следующую головоломку:
.У вас есть прямоугольная плитка шоколада, состоящая из \(n\) одинаковых плиток шоколада. Вы можете взять такую планку и разбить ее по любой строке или столбцу.
Сколько раз вам придется ломать плитку, чтобы превратить ее в \(n\) одиночных шоколадных квадратиков?
Сначала этот вопрос может показаться невозможным. Возможно, я хотел попросить наименьшее необходимое количество разрывов? Давайте исследовать.
Начните с небольших кейсов. Если \(n=2\text{,}\) у вас должен быть прямоугольник \(1\times 2\), который можно разбить на отдельные части за один раз. С \(n=3\text{,}\) у нас должна быть полоса \(1\times 3\), которая требует двух разрывов: первый разрыв создает один квадрат и полосу \(1\times 2\) , который, как мы знаем, требует одного (большего) перерыва.
Как насчет \(n=4\text{?}\) Теперь у нас может быть полоса \(2\times 2\) или полоса \(1 \times 4\). В первом случае разбейте такт на два \(2\x 2\) такта, каждый из которых требует еще одного перерыва (всего требуется три перерыва). Если мы начали с такта \(1 \times 4\), у нас есть выбор для нашего первого перерыва. Мы могли бы разбить полосу пополам, создав две полоски \(1\times 2\), или мы могли бы разорвать один квадрат, оставив полосу \(1\times 3\). Но в любом случае нам нужно еще два перерыва, всего три.
Но в любом случае нам нужно еще два перерыва, всего три.
Начинает казаться, что независимо от того, как мы разбиваем планку (и как бы \(n\) квадратов ни складывались в прямоугольник), у нас всегда будет одинаковое количество требуемых разрывов. Также похоже, что это число на единицу меньше, чем \(n\text{:}\)
Гипотеза 2.5.4
Если дана прямоугольная плитка шоколада размером \(n\)-квадратов, всегда требуется \(n-1\) разбиений, чтобы уменьшить плитку до одиночных квадратов.
Имеет смысл доказать это по индукции, потому что, сломав планку один раз, у вас останется меньше плиток шоколада. Сведение к более мелким случаям — вот что такое индукция. Мы можем индуктивно предположить, что уже знаем, как обращаться с этими меньшими барами. Проблема в том, что если мы пытаемся доказать индуктивный случай о \((k+1)\)-квадратном бруске, мы не знаем, что после первого разрыва оставшийся брусок будет иметь \(k\) квадратов. Поэтому нам действительно нужно предположить, что наша гипотеза верна для всех случаев, меньших \(k+1\text{. }\)
}\)
Можно ли сделать это более сильное предположение? Помните, в индукции мы пытаемся доказать, что \(P(n)\) истинно для всех \(n\text{.}\). Что, если бы это было не так? Тогда было бы некоторое первое \(n_0\), для которого \(P(n_0)\) было ложным. Так как \(n_0\) это первый контрпример, мы знаем, что \(P(n)\) верно для всех \(n \lt n_0\text{.}\). Теперь мы приступим к доказательству того, что \(P(n_0)\) действительно верно , исходя из предположения, что \(P(n)\) верно для всех меньших \(n\text{.}\)
Это большое преимущество: теперь у нас есть более сильная индуктивная гипотеза. Можно предположить, что \(P(1)\text{,}\) \(P(2)\text{,}\) \(P(3)\text{,}\) … \(P(k) \) верно, просто чтобы показать, что \(P(k+1)\) верно. Ранее для этой цели мы просто предполагали \(P(k)\).
Будет немного проще, если мы изменим наши переменные для сильной индукции. Вот как будет выглядеть формальное доказательство:
Прочная конструкция с защитой от индукции
Опять же, начните с того, что скажите то, что вы хотите доказать: «Пусть \(P(n)\) будет утверждением…». Затем установите два факта:
Затем установите два факта:
Базовый случай: Докажите, что \(P(0)\) верно.
Индуктивный случай: предположим, что \(P(k)\) истинно для всех \(k \lt n\text{.}\). Докажите, что \(P(n)\) истинно.
Вывод: «следовательно, по сильной индукции \(P(n)\) верно для всех \(n \gt 0\text{.}\)»
Конечно, можно заменить 0 на больший базовый корпус, если это необходимо. 5 Технически сильная индукция не требует доказательства отдельного базового случая. Это связано с тем, что при доказательстве индуктивного случая вы должны показать, что \(P(0)\) истинно, предполагая, что \(P(k)\) истинно для всех \(k \lt 0\text{.}\) Но это не поможет, так что вы все равно докажете \(P(0)\). Чтобы быть в безопасности, мы всегда будем включать базовый случай отдельно.
Докажем нашу догадку о головоломке с плиткой шоколада:
Доказательство
Пусть \(P(n)\) будет утверждением «требуется \(n-1\) разбиений, чтобы сократить \(n\)-квадратную плитку шоколада до одиночных квадратов».
Базовый случай: Рассмотрим \(P(2)\text{.}\) Квадраты должны быть расположены в виде прямоугольника \(1\times 2\), и нам нужны \(2-1 = 1\) разрывы, чтобы уменьшить это к одиночным квадратам.
Индуктивный случай: Зафиксируйте произвольное \(n\ge 2\) и предположите, что \(P(k)\) истинно для всех \(k \lt n\text{.}\). Рассмотрим \(n\)- квадратная прямоугольная плитка шоколада. Разбейте планку один раз вдоль любой строки или столбца. Это приводит к двум плиткам шоколада, скажем, размеров \(a\) и \(b\text{.}\). То есть у нас есть \(a\)-квадратная прямоугольная плитка шоколада, квадратная прямоугольная плитка шоколада и \(a+b = n\text{.}\)
Мы также знаем, что \(a \lt n\) и \(b \lt n\text{,}\), поэтому по нашему индуктивному предположению \(P(a)\) и \(P(b)\) верны. Чтобы сократить \(a\)-квадратную полосу до отдельных квадратов, требуется \(a-1\) разрывов; чтобы уменьшить \(b\)-квадратную полосу до отдельных квадратов, требуется \(b-1\) перерывов. Это приводит к тому, что наша исходная полоса сокращается до отдельных квадратов. Все вместе потребовалось начальный перерыв, плюс \(a-1\) и \(b-1\) перерывы, в общей сложности \(1+a-1+b-1 = a+b-1 = n -1\) ломается. Таким образом, \(P(n)\) верно.
Все вместе потребовалось начальный перерыв, плюс \(a-1\) и \(b-1\) перерывы, в общей сложности \(1+a-1+b-1 = a+b-1 = n -1\) ломается. Таким образом, \(P(n)\) верно.
Следовательно, по сильной индукции \(P(n)\) истинно для всех \(n \ge 2\text{.}\)
Вот более математически релевантный пример:
Пример 2.5.5
Докажите, что любое натуральное число больше 1 либо простое, либо может быть представлено в виде произведения простых чисел.
Решение
Во-первых, идея: если мы возьмем некоторое число \(n\text{,}\), возможно, оно простое. Если это так, мы закончили. Если нет, то оно составное, то есть является произведением двух меньших чисел. Каждый из этих множителей меньше \(n\) (но не менее 2), поэтому мы можем повторить рассуждения с этими числами. Мы сократили до меньшего случая.
Теперь формальное доказательство:
Доказательство
Пусть \(P(n)\) будет утверждением «\(n\) либо простое число, либо может быть записано как произведение простых чисел». Мы докажем, что \(P(n)\) истинно для всех \(n \ge 2\text{.}\)
Мы докажем, что \(P(n)\) истинно для всех \(n \ge 2\text{.}\)
Базовый случай: \(P(2)\) верно, потому что \(2\) действительно простое число.
Индуктивный случай: предположим, что \(P(k)\) истинно для всех \(k \lt n\text{.}\). Мы хотим показать, что \(P(n)\) истинно. То есть мы хотим показать, что \(n\) либо простое число, либо произведение простых чисел. Если \(n\) простое, мы закончили. Если нет, то \(n\) имеет более 2 делителей, поэтому мы можем написать \(n = m_1 \cdot m_2\text{,}\) с \(m_1\) и \(m_2\) меньше, чем \( n\) (и больше 1). По индуктивному предположению, \(m_1\) и \(m_2\) являются либо простыми, либо могут быть записаны как произведение простых чисел. В любом случае мы имеем, что \(n\) записывается как произведение простых чисел.
Таким образом, по сильной индукции \(P(n)\) истинно для всех \(n \ge 2\text{.}\)
Используете ли вы обычную или сильную индукцию, зависит от утверждения, которое вы хотите доказать . Если вы хотите быть в безопасности, вы всегда можете использовать сильную индукцию. Это действительно сильнее , так что может сделать все, что может «слабая» индукция. Тем не менее, использовать обычную индукцию часто проще, поскольку есть только одно место, где вы можете использовать индукционную гипотезу. Также есть что сказать по элегантность в пробах. Если вы можете доказать утверждение с помощью более простых инструментов, это хорошо.
Это действительно сильнее , так что может сделать все, что может «слабая» индукция. Тем не менее, использовать обычную индукцию часто проще, поскольку есть только одно место, где вы можете использовать индукционную гипотезу. Также есть что сказать по элегантность в пробах. Если вы можете доказать утверждение с помощью более простых инструментов, это хорошо.
В качестве окончательного контраста между двумя формами индукции рассмотрим еще раз задачу о штампе. Обычная индукция работала, показывая, как увеличить почтовые расходы на один цент (либо заменив три марки по 5 центов двумя марками по 8 центов, либо три марки по 8 центов на пять марок по 5 центов). Мы могли бы привести немного другое доказательство, используя сильную индукцию. Во-первых, мы могли бы показать пять базовых случаев : можно сделать 28, 292 \amp \text{разложением на множители} \конец{выравнивание*}
Таким образом, выполняется \(P(k+1)\), поэтому по принципу математической индукции \(P(n)\) верно для всех \(n \ge 1\text{. }\)
}\)
4
Докажите, что \(F_0 + F_2 + F_4 + \cdots + F_{2n} = F_{2n+1} — 1\), где \(F_n\) — \(n\)-е число Фибоначчи.
Решение
Доказательство
Пусть \(P(n)\) будет утверждением \(F_0 + F_2 + F_4 + \cdots + F_{2n} = F_{2n+1} — 1\text{.}\) Мы покажем, что \( P(n)\) верно для всех \(n \ge 0\text{.}\) Во-первых, базовый случай прост, потому что \(F_0 = 0\) и \(F_1 = 1\), поэтому \(F_0 = F_1 — 1\text{.}\) Теперь рассмотрим индуктивный случай. Предположим, что \(P(k)\) верно, то есть предположим, что \(F_0 + F_2 + F_4 + \cdots + F_{2k} = F_{2k+1} — 1\text{.}\) Чтобы установить \ (P(k+1)\) работаем слева направо: 9{k+1} \lt (k+1)!\), поэтому мы установили \(P(k+1)\text{.}\) Таким образом, по принципу математической индукции \(P(n)\) есть верно для всех \(n \ge 4\text{.}\)
6
Докажите методом математической индукции, что \(F_0 + F_1 + F_2 + \cdots + F_{n} = F_{n+2} — 1\text{,}\), где \(F_n\) — это \(n \)-е число Фибоначчи (\(F_0 = 0\text{,}\) \(F_1 = 1\) и \(F_n = F_{n-1} + F_{n-2}\)).
7
Зомби Эйлер и Зомби Коши, два известных математика-зомби, только что зарегистрировались в Твиттере. Через день у Зомби Коши больше последователей, чем у Зомби Эйлера. Каждый последующий день количество новых последователей Зомби-Коши точно равно количеству новых последователей Зомби-Эйлера (и ни один из них не теряет последователей). Объясните, как доказательство с помощью математической индукции может показать, что каждый день после первого дня у Зомби Коши будет больше последователей, чем у Зомби Эйлера. То есть объясните, что такое базовый случай и индуктивный случай, и почему они вместе доказывают, что у Зомби Коши будет больше последователей на 4-й день. 92 = \ гидроразрыва {n (n + 1) (2n + 1)} {6} \end{уравнение*}
10
Что не так со следующим «доказательством» «факта» того, что \(n+3 = n+7\) для всех значений \(n\) (кроме, конечно, того, что то, что оно пытается доказать, ложно? )?
Доказательство
Пусть \(P(n)\) будет утверждением, что \(n + 3 = n + 7\text{. }\) Мы докажем, что \(P(n)\) истинно для всех \(n \ in \N\text{.}\) Предположим для индукции, что \(P(k)\) истинно. То есть \(k+3 = k+7\text{.}\) Мы должны показать, что \(P(k+1)\) верно. Теперь, поскольку \(k + 3 = k + 7\text{,}\), добавьте 1 к обеим сторонам. Это дает \(k + 3 + 1 = k + 7 + 1\text{.}\) Перегруппировка \((k+1) + 3 = (k+1) + 7\text{.}\) Но это просто \(P(k+1)\text{.}\) Таким образом, по принципу математической индукции \(P(n)\) верно для всех \(n \in \N\text{.}\)
}\) Мы докажем, что \(P(n)\) истинно для всех \(n \ in \N\text{.}\) Предположим для индукции, что \(P(k)\) истинно. То есть \(k+3 = k+7\text{.}\) Мы должны показать, что \(P(k+1)\) верно. Теперь, поскольку \(k + 3 = k + 7\text{,}\), добавьте 1 к обеим сторонам. Это дает \(k + 3 + 1 = k + 7 + 1\text{.}\) Перегруппировка \((k+1) + 3 = (k+1) + 7\text{.}\) Но это просто \(P(k+1)\text{.}\) Таким образом, по принципу математической индукции \(P(n)\) верно для всех \(n \in \N\text{.}\)
Решение
Единственная проблема в том, что мы так и не установили базовый вариант. Конечно, когда \(n = 0\text{,}\) \(0+3 \ne 0+7\text{.}\)
11
Доказательство предыдущей задачи не работает. Но если мы изменим «факт», мы сможем получить рабочее доказательство. Докажите, что \(n + 3 \lt n + 7\) для всех значений \(n \in \N\text{.}\). Вы можете сделать это доказательство с помощью алгебры (без индукции), но цель этого упражнения состоит в том, чтобы выписать корректное индукционное доказательство.
Решение
Доказательство
Пусть \(P(n)\) будет утверждением, что \(n + 3 \lt n + 7\text{.}\) Мы докажем, что \(P(n)\) истинно для всех \(n \in \N\text{.}\) Во-первых, обратите внимание, что выполняется базовый случай: \(0+3 \lt 0+7\text{.}\) Теперь предположим для индукции, что \(P(k)\) правда. То есть \(k+3 \lt k+7\text{.}\) Мы должны показать, что \(P(k+1)\) верно. Теперь, поскольку \(k + 3 \lt k + 7\text{,}\), добавьте 1 к обеим сторонам. Это дает \(k + 3 + 1 \lt k + 7 + 1\text{.}\) Перегруппировка \((k+1) + 3 \lt (k+1) + 7\text{.}\) Но это просто \(P(k+1)\text{.}\) Таким образом, по принципу математической индукции \(P(n)\) верно для всех \(n \in \N\text{.}\ )
12
Найдите ошибку в следующем «доказательстве» того «факта», что \(n \lt 100\) для каждого \(n \in \N\text{.}\)
Доказательство
Пусть \(P(n)\) будет утверждением \(n \lt 100\text{.}\) Мы докажем, что \(P(n)\) верно для всех \(n \in \N\text {. }\) Сначала мы устанавливаем базовый случай: когда \(n = 0\text{,}\) \(P(n)\) верно, потому что \(0 \lt 100\text{.}\) Теперь для индуктивного шага предположим, что \(P(k)\) верно. То есть \(k \lt 100\text{.}\) Теперь, если \(k \lt 100\text{,}\), то \(k\) — это некоторое число, например 80. Конечно, \(80+ 1 = 81\), что все же меньше 100. Значит, и \(k +1 \lt 100\). Но это то, что утверждает \(P(k+1)\), поэтому мы показали, что \(P(k) \imp P(k+1)\text{.}\) Таким образом, по принципу математической индукции, \(P(n)\) истинно для всех \(n \in \N\text{.}\)
}\) Сначала мы устанавливаем базовый случай: когда \(n = 0\text{,}\) \(P(n)\) верно, потому что \(0 \lt 100\text{.}\) Теперь для индуктивного шага предположим, что \(P(k)\) верно. То есть \(k \lt 100\text{.}\) Теперь, если \(k \lt 100\text{,}\), то \(k\) — это некоторое число, например 80. Конечно, \(80+ 1 = 81\), что все же меньше 100. Значит, и \(k +1 \lt 100\). Но это то, что утверждает \(P(k+1)\), поэтому мы показали, что \(P(k) \imp P(k+1)\text{.}\) Таким образом, по принципу математической индукции, \(P(n)\) истинно для всех \(n \in \N\text{.}\)
Решение
Проблема здесь в том, что хотя \(P(0)\) истинно, и пока \(P(k) \imp P(k+1)\) для некоторые значений \(k\ text{,}\) существует по крайней мере одно значение \(k\) (а именно \(k = 99\)), когда это следствие не выполняется. Для действительного доказательства по индукции \(P(k) \imp P(k+1)\) должно быть истинным для всех значений \(k\), больших или равных базовому случаю.
13
Пока приведенное выше доказательство не работает (лучше не работать, так как утверждение, которое оно пытается доказать, ложно!) мы можем доказать что-то подобное. Докажите, что существует строго возрастающая последовательность \(a_1, a_2, a_3, \ldots\) чисел (не обязательно целых) такая, что \(a_n \lt 100\) для всех \(n \in \N\text{. }\) (К в строгом возрастании мы имеем в виду \(a_n \lt a_{n+1}\) для всех \(n\text{.}\) Таким образом, каждое слагаемое должно быть больше предыдущего.)
Докажите, что существует строго возрастающая последовательность \(a_1, a_2, a_3, \ldots\) чисел (не обязательно целых) такая, что \(a_n \lt 100\) для всех \(n \in \N\text{. }\) (К в строгом возрастании мы имеем в виду \(a_n \lt a_{n+1}\) для всех \(n\text{.}\) Таким образом, каждое слагаемое должно быть больше предыдущего.)
Решение
Доказательство
Пусть \(P(n)\) будет утверждением «существует строго возрастающая последовательность \(a_1, a_2, \ldots, a_n\) с \(a_n \lt 100\text{.}\)». Мы докажем \(P(n)\) истинно для всех \(n \ge 1\text{.}\) Сначала мы установим базовый случай: \(P(1)\) говорит, что существует единственное число \(a_1\ ) с \(a_1 \lt 100\text{.}\) Это верно – возьмем \(a_1 = 0\text{.}\) Теперь для индуктивного шага предположим, что \(P(k)\) верно. То есть существует строго возрастающая последовательность \(a_1, a_2, a_3, \ldots, a_k\) с \(a_k \lt 100\text{.}\). Теперь рассмотрим эту последовательность плюс еще один член, \(a_{ k+1}\), которое больше \(a_k\), но меньше \(100\text{. }\) Такое число существует, например, среднее между \(a_k\) и 100. Тогда \ (P(k+1)\) верно, поэтому мы показали, что \(P(k) \imp P(k+1)\text{.}\) Таким образом, по принципу математической индукции \(P( n)\) верно для всех \(n \in \N\text{.}\) 92 + п\) четно».
}\) Такое число существует, например, среднее между \(a_k\) и 100. Тогда \ (P(k+1)\) верно, поэтому мы показали, что \(P(k) \imp P(k+1)\text{.}\) Таким образом, по принципу математической индукции \(P( n)\) верно для всех \(n \in \N\text{.}\) 92 + п\) четно».
16
Докажите, что существует последовательность положительных действительных чисел \(a_0, a_1, a_2, \ldots\) такая, что частичная сумма \(a_0 + a_1 + a_2 + \cdots + a_n\) строго меньше \(2\ ) для всех \(n \in \N\text{.}\) Подсказка: подумайте, как бы вы могли определить, что такое \(a_{k+1}\), чтобы аргумент индукции работал.
Решение
Идея состоит в том, чтобы определить последовательность так, чтобы \(a_n\) было меньше, чем расстояние между предыдущей частичной суммой и 2. Таким образом, когда вы добавляете ее к следующей частичной сумме, частичная сумма все еще меньше, чем 2. Вы можете сделать это заранее или использовать хитрое \(P(n)\) в доказательстве по индукции.
Доказательство
Пусть \(P(n)\) будет утверждением «существует последовательность положительных действительных чисел \(a_0, a_1, a_2, \ldots, a_n\) такая, что \(a_0 + a_1 + a_2 + \cdots + a_n \lt 2\text{.}\)”
Базовый вариант: выберите любой \(a_0 \lt 2\text{.}\)
Индуктивный случай: Предположим, что \(a_1 + a_2 + \cdots + a_k \lt 2\text{.}\) Пусть теперь \(a_{k+1} = \frac{2- a_1 + a_2 + \cdots + a_k }{2}\text{.}\) Затем \(a_1 + a_2 + \cdots +a_k + a_{k+1} \lt 2\text{.}\)
Следовательно, по принципу математической индукции \(P(n)\) истинно для всех \(n \in \N\) 9x\) мы записали \(n\) как сумму различных степеней числа 2.
Следовательно, по принципу (сильной) математической индукции \(P(n)\) истинно для всех \(n \ge 1\text{.}\)
18
Докажите, используя сильную индукцию, что каждое натуральное число является либо числом Фибоначчи, либо может быть записано как сумма различных чисел Фибоначчи.
19
Используйте индукцию, чтобы доказать, что если \(n\) человек пожимают друг другу руки, то общее количество рукопожатий равно \(\frac{n(n-1)}{2}\text{. }\)
}\)
Решение
Заметьте, мы уже доказали это без использования индукции, но индуктивное рассмотрение проливает свет на проблему (и это весело).
Доказательство
Пусть \(P(n)\) будет утверждением «когда \(n\) человек пожимают друг другу руки, всего происходит \(\frac{n(n-1)}{2}\) рукопожатий ».
Базовый случай: когда \(n=2\text{,}\) будет одно рукопожатие и \(\frac{2(2-1)}{2} = 1\text{.}\) Таким образом \ (P(2)\) верно.
Индуктивный случай: предположим, что \(P(k)\) верно для произвольного \(k\ge 2\) (что число рукопожатий среди \(k\) людей равно \(\frac{k(k-1) }{2}\text{.}\) Что произойдет, если появится \(k+1\)-й человек? Сколько 9k) + \log(a) = k\log(a) + \log(a) \end{уравнение*}
с последним равенством по индуктивному предположению. Но это упрощается до \((k+1) \log(a)\text{,}\), устанавливая \(P(k+1)\text{.}\). Поэтому по принципу математической индукции \(P (n)\) истинно для всех \(n \ge 2\text{. }\)
}\)
24
Пусть \(f_1, f_2,\ldots, f_n\) — дифференцируемые функции. Докажите по индукции, что
\begin{уравнение*} (f_1 + f_2 + \cdots + f_n)’ = f_1′ + f_2′ + \cdots + f_n’ \end{уравнение*}Вы можете считать \((f+g)’ = f’ + g’\) для любых дифференцируемых функций \(f\) и \(g\text{.}\)
Подсказка
Вам разрешено исходить из базового случая. Для индуктивного случая сгруппируйте все функции, кроме последней, как одну сумму функций, затем примените обычное правило суммы производных, а затем индуктивную гипотезу.
25
Предположим, \(f_1, f_2, \ldots, f_n\) — дифференцируемые функции. Используйте математическую индукцию, чтобы доказать обобщенное правило произведения:
\begin{уравнение*} (f_1 f_2 f_3 \cdots f_n)’ = f_1′ f_2 f_3 \cdots f_n + f_1 f_2′ f_3 \cdots f_n + f_1 f_2 f_3′ \cdots f_n + \cdots + f_1 f_2 f_3 \cdots f_n’ \end{уравнение*} Вы можете предположить, что правило произведения для двух функций верно.


 1
1 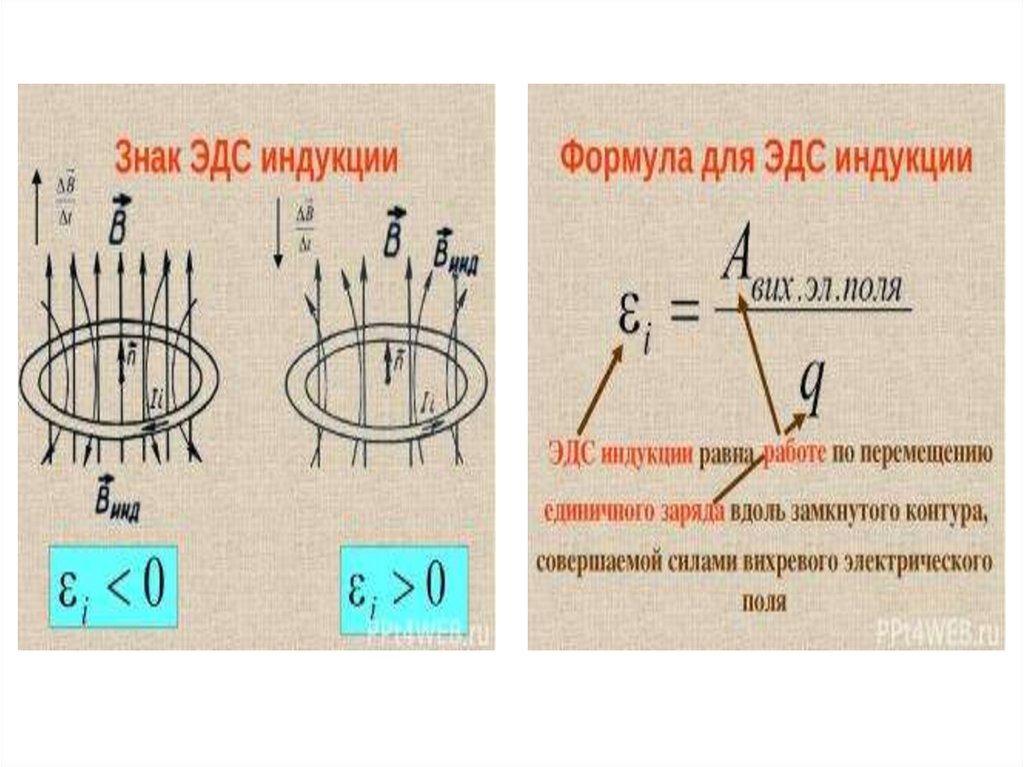

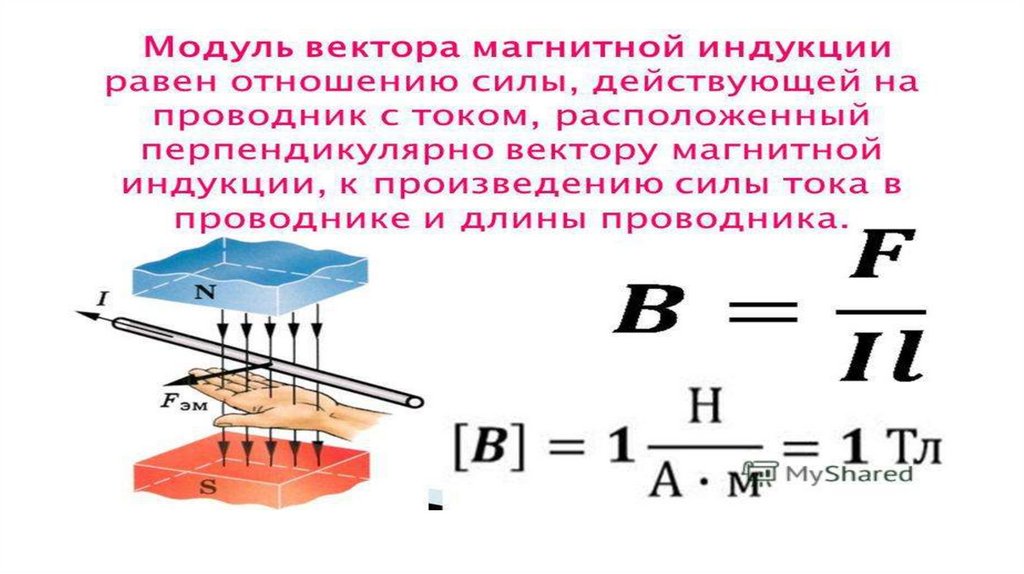




 Это редкое, но серьезное осложнение, при котором матка разрывается по линии рубца после предшествующего кесарева сечения или обширной операции на матке. В редких случаях разрыв матки также может произойти у женщин, у которых ранее не было операций на матке.
Это редкое, но серьезное осложнение, при котором матка разрывается по линии рубца после предшествующего кесарева сечения или обширной операции на матке. В редких случаях разрыв матки также может произойти у женщин, у которых ранее не было операций на матке.
 Окситоцин более эффективен при ускорении уже начавшихся родов, чем при созревании шейки матки. Медицинский работник контролирует сокращения и частоту сердечных сокращений ребенка.
Окситоцин более эффективен при ускорении уже начавшихся родов, чем при созревании шейки матки. Медицинский работник контролирует сокращения и частоту сердечных сокращений ребенка. 5.1.8)
5.1.8) Любой
вероятный аргумент в пользу UP предполагает UP.
Любой
вероятный аргумент в пользу UP предполагает UP.