Олимпиадные задания для школьного этапы олимпиады по информатике 8 класс
Задания первого (школьного) этапа Всероссийской предметной олимпиады школьников по информатике и ИКТ 2014/2015 учебный год 8 классЗадача 1. “Вертолет” – 10 баллов
Исполнитель “Вертолет” перемещается в трехмерном пространстве. Для его управления используется следующая система команд:
Вперед F – вертолет перемещается на F единиц расстояния вперед
Назад B — вертолет перемещается на B единиц расстояния назад
Влево L — вертолет перемещается на L единиц расстояния влево
Вправо R — вертолет перемещается на R единиц расстояния вправо
Вверх U — вертолет перемещается на U единиц расстояния вверх
Вниз D — вертолет перемещается на D единиц расстояния вниз
Переменные F, B, L, R, U, D
Известно, что вертолет выполнил программу из 18 команд, в которой:
Команд Вправо 2 на две больше чем команд Вверх 3
Команд Назад 2 на одну больше чем команд Вниз 2
Команд Влево 4 на одну меньше чем команд Назад 2
Команд Вперед 4 на две меньше чем команд Вправо 2
Команд Вниз 2 на одну больше чем команд Вверх 3
Никакие команды кроме перечисленных в программе не использовались.
На какую одну команду можно заменить эту программу? В ответе указать название команды (направление движения) и через пробел величину смещения в этом направлении (например “Вверх 3”).
Задача 2. “Маска” – 10 баллов
В каталоге присутствуют восемь файлов с перечисленными ниже именами.
Отметьте те из них, которые будут выделяться при использовании маски ?a*?b?*.*c?
где * обозначает любую последовательность символов, даже пустую, а ? – один любой символ
1. abcabc.abc
2. babc.bca
3. babcba.bca
4. aabbcc.aabbcc
5. cacbcc.cccc
6. ababcb.cca
7. cabbac.bacba
8. aaccbb.cca
Задача 3. “Решение логических задач” – 10 баллов
Задача 4. “Диаграммы в электронных таблицах” – 20 баллов
После определения победителей и призеров олимпиад по математике, физике и информатике были построены две диаграммы. В таблице с данными, на основе которых построены диаграммы, содержатся данные о количестве участников, получивших дипломы первой, второй и третьей степени по каждой олимпиаде. Сколько всего было выдано дипломов всех степеней по трем олимпиадам? В ответе укажите целое число.
Задача 5. “Системы счисления” – 20 баллов
Даны простые логические высказывания:
А = {Принтер –устройство вывода информации},
В = {Процессор –устройство хранения информации},
D = {Клавиатура –устройство обработки информации},
Е = {Сканер –устройство хранения информации}.
Последовательность САBCЕD была записана в виде двоичной последовательности (ноль соответствовал ложности, а единица –истинности соответствующего высказывания), а затем переведена в десятичную систему счисления. Какое значение получилось? В ответе укажите целое число.
Задача 6. “Кодовый замок” – 30 баллов




Имеется кодовый замок с четырьмя цветными кнопками. Для открытия замка необходимо нажать одновременно две кнопки определенного цвета. Петя для подбора цветового шифра попробовал множество комбинаций и записал результат своих опытов с кнопками в виде нескольких логических утверждений-инструкций, определяющих состояние замка:
1.«если нажата красная или зеленая кнопка, то следует нажать синюю кнопку» = замок не откроется;
2.«если нажата красная или синяя кнопка, то следует нажать желтую кнопку» = замок не откроется;
3.«нажата зеленая и желтая кнопка» = замок не откроется
4.«нажата зеленая или желтая кнопка» = замок откроется.
Определите цвета кнопок, которые необходимо нажать для открытия кодового замка. (В ответе укажите только первые буквы цветов этих кнопок)
Ключи к заданиям первого (школьного) этапа Всероссийской предметной олимпиады школьников по информатике и ИКТ 2010/2011 учебный годОтвет – Влево 4
Задача 2. “ “Маска” – 10 баллов
Ответ – 3, 4, 5, 8
Задача 4. “Диаграммы в электронных таблицах” – 20 баллов
Ответ – 300
Задача 5. “Системы счисления” – 20 баллов
Ответ – 52
Задача 6. “Кодовый замок” – 30 баллов
Ответ: ЗК, КЗ
На космическом корабле незнайка встретил кодовый замок с четырьмя цветными кнопками. для открытия замка необходимо нажать одновременно две кнопки определенного цвета. незнайка для подбора цветового шифра попробовал множество комбинаций и записал результат своих опытов с кнопками в виде нескольких логических утверждений-инструкций, определяющих состояние замка: 1. «если нажата красная или зеленая кнопка, то следует нажать синюю кнопку» = замок не откроется; 2. «если нажата красная или синяя кнопка, то следует нажать желтую кнопку» = замок не откроется; 3. «нажата зеленая и желтая кнопка» = замок не откроется 4. «нажата зеленая или желтая кнопка» = замок откроется. незнайке, определите цвета кнопок, которые необходимо нажать для открытия кодового замка. в текстовом файле в первой строке укажите только первые буквы цветов этих кнопок. затем, начиная со второй строки, объясните свое решени
клинописьдата рождения ~3300 г. до н. э. место рождения — междуречье. происхождение — оригинальная письменность. состав — 300 — 900 знаков для слоговой и идеографической систем; порядка 30 букв для фонетической адаптации на восточном побережье средиземного моря; 36 букв для старо-персидского слогового алфавита. чтение — изначально справа налево, колонками; затем слева направо строками (начиная с 2400-2350 гг. до н. э. для рукописных текстов; со ii тыс. до н. э. для монументальных надписей). языки — полтора десятка языков и диалектов: шумерский, эламский, хурритский, ханаанский, угаритский, урартский, хеттский, старо-персидский и т. д. наиболее старые известные документы — таблички с административными документами шумерского царства. последний известный документ на вавилонском яз. относится к 75 г. н. э. самые старые письменные документы, найденные на раскопках древнего города урук, относятся к 3300 году до н. э. появление письменности совпадает по времени с развитием городов и сопутствующей этому полной перестройкой общества. в то же время в месопотамии появляется колесо и знание о плавке меди.между тигром и евфратом находилось шумерское царство, а на востоке — царство элам. в городах этих довольно урбанизированных государств жили , торговцы, ремесленники. вне городов — крестьяне и пастухи.как торговые, так и адиминистративные контакты всех этих групп необходимо было запечатлеть в какой-то форме. именно из этой необходимости и появилась письменность.первыми систему записи создали шумеры. элам, где использовали в то время лишь набор разрозненных пиктограмм, адаптировал шумерскую письменность под свой язык.от счета — к письмудля учёта имущества в шумере и эламе использовали систему глиняных шариков. изначально каждый шарик обозначал один объект (корову, барана и т. п.) затем размер и форма комочка стали значащими. а вскоре на них стали появляться пометки (след пальца, засечка), изменяющие их «вес». эти шарики складывались в глиняный контейнер, который запечатывался цилиндрической печатью, идентифицирующей владельца. таким образом, например, если контейнер содержал информацию о количестве голов скота в стаде, его необходимо было разбить, чтобы провести подсчёт находящихся в нём шариков.к 3300 г. до н. э. на поверхности контейнера вместе с печатью владельца стало появляться краткое описание его содержимого. при этом необходимость разбивать контейнер при каждой проверке отпала. постепенно ставшие бесполезными шарики исчезли, контейнер из сферического стал плоским. так появились первые глиняные таблички с первыми числами: кружочками и уголками, выдавленными в глине, форма и размер которых указывали на обозначаемый объект и его количество. таким образом, первые символы письменности имели форму считаемых объектов (товаров). например, знак «коза». играя роль «символа-картинки», они по определению были пиктограммами.впоследствии стали образовываться устойчивые сочетания пиктограмм, смысл которых постепенно отходил от суммы смыслов картинок. например, знак «птица» вместе со знаком «яйцо» дали сочетание «плодовитость» не только в применении к птицам, но как абстрактный термин. эти сочетания уже были идеограммами («символ-идея»).к 3000 г. до н. э. получавшиеся пиктограммы и идеограммы стали использовать фонетически, составляя из этих символов («символ-звук») слова, не имеющие порой никакого, даже косвенного, отношения к изображённым предметам.одновременно изменяется и стиль письма. для записи все символы разложены на короткие отрезки (клинья — откуда название письменности), которые уже не надо было вырезать в глине, а можно было просто наносить при калама — специальной палочки с заострённым концом треугольной формы. параллельно с этим происходит разворот существующих символов на 90° против часовой стрелки.начиная со ii тыс. до н. э. клинопись распространяется по всему ближнему востоку.
Задача «Вертолет» 10 баллов — Задания 7-8 кл
Задания первого (школьного) этапа
7-8 класс
Задача 1. “Вертолет” – 10 баллов
Исполнитель “Вертолет” перемещается в трехмерном пространстве. Для его управления используется следующая система команд:
Вперед F – вертолет перемещается на F единиц расстояния вперед
Назад B — вертолет перемещается на B единиц расстояния назад
Влево L — вертолет перемещается на L единиц расстояния влево
Вправо R — вертолет перемещается на R единиц расстояния вправо
Вверх U — вертолет перемещается на U единиц расстояния вверх
Вниз D — вертолет перемещается на D единиц расстояния вниз
Переменные F, B, L, R, U, D могут принимать любые положительные значения.
Известно, что вертолет выполнил программу из 18 команд, в которой:
Команд Вправо 2 на две больше чем команд Вверх 3
Команд Назад 2 на одну больше чем команд Вниз 2
Команд Влево 4 на одну меньше чем команд Назад 2
Команд Вперед 4 на две меньше чем команд Вправо 2
Команд Вниз 2 на одну больше чем команд Вверх 3
Никакие команды кроме перечисленных в программе не использовались.
На какую одну команду можно заменить эту программу? В ответе указать название команды (направление движения) и через пробел величину смещения в этом направлении (например “Вверх 3”).
Задача 2. “Маска” – 10 баллов
В каталоге присутствуют восемь файлов с перечисленными ниже именами.
Отметьте те из них, которые будут выделяться при использовании маски ?a*?b?*.*c?
где * обозначает любую последовательность символов, даже пустую, а ? – один любой символ
1. abcabc.abc
2. babc.bca
3. babcba.bca
4. aabbcc.aabbcc
5. cacbcc.cccc
6. ababcb.cca
7. cabbac.bacba
8. aaccbb.cca
Задача 3. “Решение логических задач” – 10 баллов
В классе 36 человек. Ученики этого класса посещают математический, исторический и географический кружки, причем математический кружок посещают 18 человек, исторический – 14 человек, географический – 10 человек. Кроме того, известно, что 2 человека посещают все три кружка, 8 человек – математический и исторический, 3 – исторический и географический, 5 – математический и географический. Сколько человек из класса не посещают никаких кружков?
Задача 4. “Диаграммы в электронных таблицах” – 20 баллов
После определения победителей и призеров олимпиад по математике, физике и информатике были построены две диаграммы. В таблице с данными, на основе которых построены диаграммы, содержатся данные о количестве участников, получивших дипломы первой, второй и третьей степени по каждой олимпиаде. Сколько всего было выдано дипломов всех степеней по трем олимпиадам?
Задача 5. “Системы счисления” – 20 баллов
Даны простые логические высказывания:
А = {Принтер –устройство вывода информации},
В = {Процессор –устройство хранения информации},
С = {Монитор –устройство вывода информации},
D = {Клавиатура –устройство обработки информации},
Е = {Сканер –устройство хранения информации}.
Последовательность САBCЕD была записана в виде двоичной последовательности (ноль соответствовал ложности, а единица –истинности соответствующего высказывания), а затем переведена в десятичную систему счисления. Какое значение получилось? В ответе укажите целое число.
Задача 6. “Кодовый замок” – 30 баллов
Имеется кодовый замок с четырьмя цветными кнопками. Для открытия замка необходимо нажать одновременно две кнопки определенного цвета. Петя для подбора цветового шифра попробовал множество комбинаций и записал результат своих опытов с кнопками в виде нескольких логических утверждений-инструкций, определяющих состояние замка:
1.«если нажата красная или зеленая кнопка, то следует нажать синюю кнопку» = замок не откроется;
2.«если нажата красная или синяя кнопка, то следует нажать желтую кнопку» = замок не откроется;
3.«нажата зеленая и желтая кнопка» = замок не откроется
4.«нажата зеленая или желтая кнопка» = замок откроется.
Определите цвета кнопок, которые необходимо нажать для открытия кодового замка. (В ответе укажите только первые буквы цветов этих кнопок)
Ключи
к заданиям первого (школьного) этапа
Задача1. “Вертолет” – 10 баллов
Ответ – Влево 4
Задача 2. “ “Маска” – 10 баллов
Ответ – 3, 4, 5, 8
Задача 4. “Диаграммы в электронных таблицах” – 20 баллов
Ответ – 300
Задача 5. “Системы счисления” – 20 баллов
Ответ – 52
Задача 6. “Кодовый замок” – 30 баллов
Ответ: ЗК, КЗ
Поделитесь с Вашими друзьями:
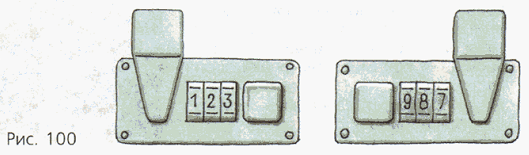
Математика 6 класс Никольский, Потапов, Решетников Номер 947
Папа купил себе дипломат с двумя кодовыми замками. На каждом из этих замков устанавливают код − набор из трёх цифр от 0 до 9 (рис.100). Дипломат закрывают и на его наружной панели устанавливают произвольные наборы цифр. Каждый замок откроется лишь тогда, когда будет правильно набран его код.
а) Саша установил новый код на каждый замок, но забыл сообщить об этом папе и ушел в школу. Сколько времени может занять открывание замков у папы в худшем случае, если он будет последовательно проверить коды для каждого замка и на проверку каждого кода будет тратить 1 с?
б) Какова вероятность открыть с первой попытки один кодовый замок? оба замка?
в) Саша установил новый код на каждый замок и через некоторое время забыл, в каком порядке цифры 1,2 и 3 образуют эти два кода. Сколько кодов в худшем случае придётся проверить Саше, чтобы открыть оба замка?
г) Саша установил два новых кода на замках дипломата и чрез некоторое время забыл их. Он помнит, что в каждый код входят цифры 1, 2 и какая−то третья цифра (не 1 и не 2). Сколько кодов в худшем случае придётся проверить Саше, чтобы открыть один замок? оба замка?

Решение а
Решение:
10 * 10 * 10 = 1000 равновозможных случаев, одно из которых обязательно произойдет при правильном подборе цифр на одном замке.
1000 * 1 = 1000 секунд может потребоваться, чтобы открыть один замок,
1000 * 2 = 2000 секунд может потребоваться, чтобы открыть оба замка.
Ответ: 2000 секунд.
Решение б
Решение:10 * 10 * 10 = 1000 числу всех равновозможных случаев, одно из которых обязательно произойдет при правильном подборе цифр.
11000
− вероятность подбора правильного набора цифр в одном замке, а следовательно и вероятность открытия первого замка с одной попытки.11000∗11000=11000000
− вероятность открытия обоих замков с одной попытки.Ответ:
11000
− вероятность открытия первого замка с одной попытки.11000000
− вероятность открытия обоих замков с одной попытки.Решение в
Ответ:
Код состоит из цифр 1,2,3, при чем цифры не повторяются, тогда:
для 1−ого диска мы можем выбрать цифру 3 способами;
для 2−ого диска мы можем выбрать цифру 2 способами;
для 3−ого диска мы можем выбрать цифру 1 способом.
3 * 2 * 1 = 6 способами, в худшем случае, можно подобрать код на одном замке,
6 * 2 = 12 способами, в худшем случае, можно подобрать код на обоих замках.
Ответ: 12 кодов.
Решение г
Решение:
Код состоит из цифр 1,2, и третьей цифры, при чем цифры не повторяются, тогда:
для 1−ого диска мы можем выбрать цифру 3 способами;
для 2−ого диска мы можем выбрать цифру 2 способами;
для 3−ого диска мы можем выбрать цифру 1 способом.
3 * 2 * 1 = 6 способами можно установить цифры для одного замка.
В каждом из способов два диска уже заняты цифрами 1 и 2, и только для третьего диска может быть выбрано 8 вариантов цифр, поэтому каждый из 6 способов может иметь 8 вариантов цифр.
6 * 8 = 48 кодов будет необходимо подобрать в худшем случае, чтобы открыть один замок.
48 * 2 = 96 кодов будет необходимо подобрать в худшем случае, чтобы открыть оба замка.
Ответ:
48 кодов будет необходимо подобрать в худшем случае, чтобы открыть один замок.
96 кодов будет необходимо подобрать в худшем случае, чтобы открыть оба замка.
Если Вы нашли ошибку, неточность или просто не согласны с ответом, пожалуйста сообщите нам об этом
кодовый замок на логике / Habr
Сразу предупреждаю, что этот проект реализован очень нерационально и особого практического смысла в себе не несёт. Я расскажу о такой, казалось бы простой вещи, как кодовый замок, но реализован он не на микроконтроллере, как это обычно делается, а на логических микросхемах. Ведь взять микроконтроллер и прошить, это слишком просто, здесь есть какой-то подвох! Давайте лучше городить логику, как истинные джедаи!
Итак, приступим. Первоначальная схема была взята из журнала «Радио» 2 2005 года выпуска, но я внёс в неё некоторые изменения.
Схема построена на триггерах — логических элементах, в которые можно записывать 1 бит информации. Если подать плюс на вход триггера С, то он запомнит логический уровень на входе D. Если же подать плюс на вход R, то триггер будет очищен — запомнит ноль, а вход S, соответственно, служит для того, чтобы записывать в триггер единицу, но он в схеме не используется. Записанное в триггер значение выводится на двух выходах — Q и неQ, неQ всегда будет противоположно Q.
Именно принцип работы триггера и лежит в основе этого кодового замка. При включении замка за счёт зарядки конденсатора на входах R возникает импульс высокого уровня, устанавливающий все триггеры в положение 0. Увеличив емкость конденсатора и сопротивление резистора идущего к нему, можно повысить секретность замка. При этом при нажатии на ошибочные кнопки повторный ввод верного кода будет возможен лишь через некоторое время, определяемое цепью RC.
Кнопки нужно нажимать в строго определённом порядке, иначе последний триггер не активируется и замок не откроется. Сигнал с выхода Q каждого триггера поступает на вход D следующего, а нажимая кнопку мы осуществляем запись этого уровня в триггер. Таким образом эта единица с первого триггера «переезжает» на последний сквозь все остальные. Также, если нажать неверную кнопку, то подадите + на входы R всех триггеров, схема сбросит код и нужно будет вводить его сначала.
Отличие старой схемы в том, что в ней нет вспомогательных элементов И, поэтому код легче подобрать. В моём же случае, если вы будете нажимать на верные кнопки, но в неправильном порядке, то элементы И, опять же, сбросят код. Это повышает его надёжность. Они работают следующим образом: элемент И считывает сигнал с кнопки, идущей к триггеру и входу -Q предыдущего триггера. Если кнопка, идущая к триггеру нажата, а предыдущий триггер не активен, то на оба входа элемента И поступает плюс, на выходе получается тоже плюсовой уровень, который уже идёт на входы R и сбрасывает весь код.
Я считаю главным недостатком такой конструкции то, что цифры в коде не могут повторяться, но в остальном работа устройства очень радует.
Помимо основных деталей в схему добавлены светодиоды-индикаторы. Шесть в середине показывают активность каждого из триггеров, а два светодиода сбоку — активность всего замка (красный — закрыто, зелёный — открыто). Не обошлось и без ошибок, кое-где схема перепаяна, но в файле печатной платы я исправил эти ошибки.
На этом всё, печатную плату и схему оставляю здесь, если кто-то захочет её собрать, то я только за.
Использованы микросхемы: К561ТМ2, К155ЛИ1, К155ЛН1.
Печатная плата и схема: yadi.sk/d/p56qGpVDjJXpo
Источник первоначальной схемы: www.radioelectronika.ru/?mod=cxemi&sub_mod=full_cxema&id=661
Как открыть кодовый замок, если забыл код
Замок с кодом – это хорошее средство защиты неприкосновенности жилища или имущества. Ключ от него невозможно потерять или забыть в другом пальто. Код, служащий ключом хранится только в голове владельца. Но бывают такие ситуации, когда он либо «вылетает» из памяти, либо кодовый запор необходимо открыть во что бы, то, ни стало.

Как открыть навесной кодовый замок
Для открытия кодового замка необходимо знание отпирающей комбинации цифр, которую можно либо спросить у его владельца, либо просто подобрать.
Подбор заключается в переборе всех возможных комбинаций цифр, которых в зависимости от модели замка может быть и 64000. В этом случае перебор займет больше недели круглосуточной работы по проверке комбинаций цифр. Но подходит такой способ только при наличии «вагона» времени.
В том же случае если время не терпит можно поискать другие варианты. Например, вскрытие такого замка возможно при помощи алюминиевой банки из-под пива. Для этого ее разрезают, и из тонкого мягкого алюминия вырезают пластинку. Далее, обернув эту пластину вокруг оттянутой дужки устройства, пробуют ее вставить в щель, чтобы отжать его запирающий язычок.
Открытие замков на чемодане/кейсе/сумке
Очень часто люди забывают код запирающих механизмов собственных чемоданов, сумок или кейсов и в панике или какой-нибудь срочности, теряя голову, начинают их просто рвать, резать или ломать подручными средствами.
На самом деле запоры на них, как правило, не очень надежны и имеют малое количество комбинаций. Поэтому совсем не стоит в пылу страстей портить собственное имущество, ведь в большинстве случаев даже не зная или не помня кода, открыть их можно за несколько минут.
Для этого необходимо понять принцип действия таких устройств, заключающийся в том, что при вводе нужной цифры напротив нее срабатывает паз запирающего механизма. Часто этот паз можно даже увидеть сбоку от цифрового колесика, особенно если отжать его в сторону отверткой или ножом. Таким образом, подбираются все цифры, напротив которых виден паз, и замок гарантированно отмыкается, без физического взлома и порчи имущества.
В случае слабости зрения, отсутствия отвертки или высококачественной подгонки деталей агрегата, когда щели между деталями слишком малы, и паз нельзя увидеть, можно подобрать код на слух.
Ведь даже если не видно механизма, шум от его работы и характерный щелчок от срабатывания паза все равно можно услышать, особенно в дешевых моделях устройств.
Правда, для этого как минимум нужна абсолютная тишина, а как максимум стетоскоп. Однако и он может не помочь, если необходимо отрыть дорогой чемодан с фирменным замком, не издающим никаких звуков при подборе комбинации.Как открыть дверной кодовый замок
Кодовые замки на дверях очень хорошо знакомы любому кто хоть раз пытался попасть в подъезд многоквартирного дома, где очень часто на входной двери стоит такой «страж». Как правило, при его установке оставляется заводская комбинация отпирающего шифра, которую можно узнать даже из интернета просто пробив по поиску модель замка и его заводские настройки.
Еще можно воспользоваться дедуктивным методом Шерлока Холмса:

- если внимательно посмотреть на клавиши и область возле каждой из них, то можно определить какие из них используются, а какие нет, например, некоторые из них могут быть заполированы, стерты или вымазаны из-за частого использования;
- еще часто нажимаемые кнопки сильно гуляют и легче поддаются или даже западают при нажатии, из-за чего при использовании не издают щелчка в отличие от неиспользуемых клавиш;
- часто для облегчения набора комбинации в темное время суток или людям с плохим зрение, комбинацию выставляют таким образом, чтобы ее можно было нажать, просто собрав несколько пальцев вместе, такой код, вообще, можно подобрать наугад так называемым методом тыка.
Способы открытия
Практически для всего, что может быть закрыто, запаролено или зашифровано, существует только два метода вскрытия: подбор, угадывание ключ-кода, или физический взлом самого замка, механизма или системы при помощи технических средств.
Подбор
Метод подбора заключает в переборе разных комбинаций цифр. Он может быть осуществлен как довольно быстро, ориентируясь на внешний вид, особенности замка, щелчки и видимое движение запорного механизма, или при забытом пароле оставшиеся в памяти его части, так и полным перебором всех возможных комбинаций.

Например, для перебора всех комбинаций замка с четырьмя числовыми колесиками теоретически нужно по очереди ввести все значения от 0000 до 9999, однако на практике пароль подбирается, конечно, раньше.
Полный перебор подходит для трех-четырехзначных кодов, так как время, затрачиваемое на подбор кода с большими значениями, возрастает в геометрической прогрессии с каждым следующим символом.
Поэтому если замок сложный с множеством цифр и не известно ни начало, ни конец комбинации, на его перебор может уйти от нескольких дней до нескольких недель, что мало кого устроит.
Технический взлом
Метод физического взлома предусматривает как использование отмычек типа пластинок, проволочек, ножей и ножниц, а также прочих тонких приспособлений для размыкания запора. Для чего ими пытаются, проникнут в какие-либо технологические щели замка, и усилием разомкнуть запирающий паз его внутреннего механизма.
Проводить эту операцию нужно очень аккуратно, иначе есть риск либо повредить внутренние детали замка, либо заклинить внутри него кусок от отмычки. В обоих случаях замок, скорее всего, придет в полную негодность, и открыть его можно будет, только полностью разломав.

Для этого применяют еще более грубые методы физического воздействия, на запор подразумевающие, взлом его внешнего корпуса, включая дужки, петли и крепления, при помощи демонтажных инструментов. Чаще всего это отсоединение от него дужки, например, при помощи: мощных кусачек, молотка, зубила, лома, фомки, ножовки или болгарки по металлу.
Используя ножовку или болгарку, просто перепиливают дужку, а в случае с молотком им ударяют по зубилу, наставленному острым концом на дужку замка в самом тонком ее месте.
Эффективность этих методов сильно зависит от мощности и качества замка, так как дужку в дешевых замках можно сбить, даже ударив по ней обычным булыжником, а вот наиболее дорогие изделия из высокопрочных сплавов может быть трудно и долго перепиливать даже электрической болгаркой. Замок после таких манипуляций уже ни на что не годится и его, скорее всего, придется выбросить.
Преимущества и недостатки способов
В большинстве случае рекомендуется метод подбора ведь он позволяет открывать практически любые кодовые замки почти голыми руками без повреждения самого запирающего механизма. Однако такому взлому поддаются не все замки, и эта операция в большинстве случаев требует значительного времени и усидчивости, которые не у всех есть.
Технический взлом оптимален для критических ситуаций, когда необходимо срочно, что-либо открыть и время идет на секунды или минуты. Также этот вариант спасает в самых безвыходных ситуациях, когда замок слишком сложен и надежен.
Однако в пылу гнева или паники не стоит сразу хвататься за кувалду, ведь после такого физического вмешательства в конструкцию любого запирающего механизма, он, скорее всего, придет в негодность. Лучше действовать постепенно, увеличивая степень воздействия на запор.
Советы и рекомендации
- На заводе изготовителе на новые замки, как правило, по умолчанию в качестве кода устанавливают самые простые комбинации цифр, например, «000» или «111» и другие варианты с одним повторяющимся символом.
- Пароль, устанавливаемый на любое кодовое устройство желательно всегда соотносить с реальными цифрами, присутствующими в повседневности, например, с датами дней рождения, серией или номером паспорта и так далее.
- Забытый пароль – это не потерянный ключ, он всегда с человеком, даже если и в подсознании, из которого его можно извлечь, просто вспомнив обстоятельства установки шифра, часто он является датой рождения или просто счастливым числом.
- По возможности, рекомендуется использовать методы открытия замка начиная с самого бережного – подбором, и только в самом конце, когда нет других вариантов и то, что скрывается под замком как минимум ценнее его самого, можно приступать к физическому взлому запирающего механизма.
Статья была полезна?
0,00 (оценок: 0)
1.2. Классическое определение вероятности
… Из этой первой лекции по теории вероятностей я запомнил только полузнакомый термин «математическое ожидание». Незнакомец употреблял этот термин неоднократно, и каждый раз я представлял себе большое помещение, вроде зала ожидания, с кафельным полом, где сидят люди с портфелями и бюварами и, подбрасывая время от времени к потолку монетки и бутерброды, сосредоточенно чего-то ожидают. До сих пор я часто вижу это во сне. Но тут незнакомец оглушил меня звонким термином «предельная теорема Муавра — Лапласа» и сказал, что все это к делу не относится.
Аркадий и Борис Стругацкие, Стажеры.
Предположим, что мы имеем дело с дискретным пространством элементарных исходов, то есть пространством, состоящим из конечного или счетного числа элементов:
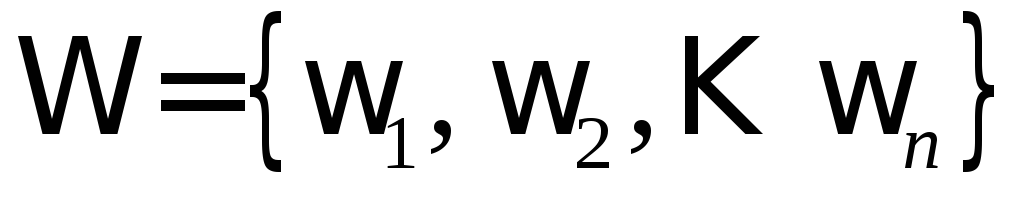 .
.
Поставим каждому
элементарному исходу 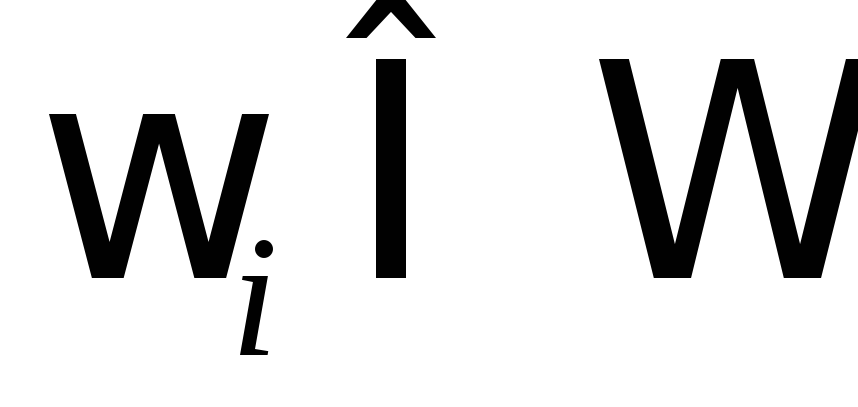 в соответствие число
в соответствие число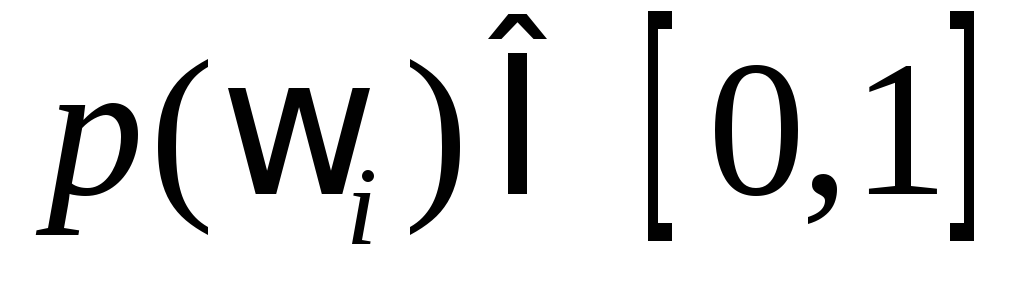 так, что
так, что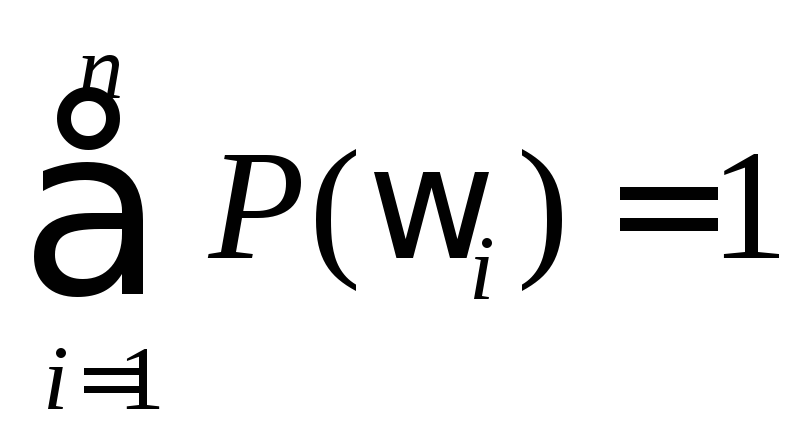 .
.
Назовем число 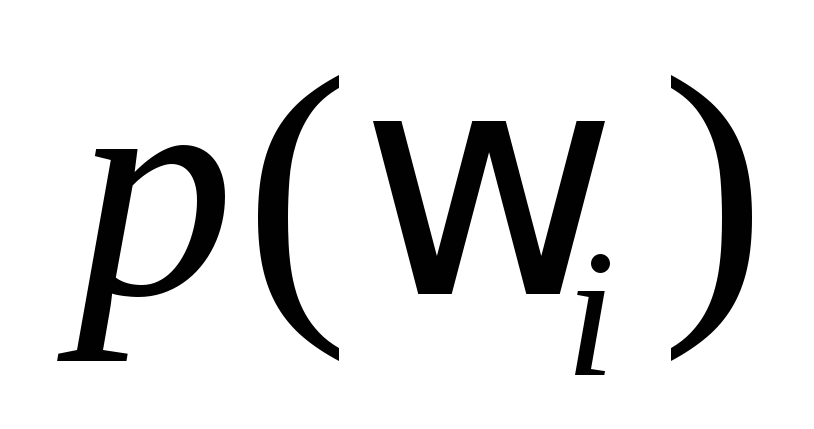 вероятностью элементарного исхода
вероятностью элементарного исхода  .
.
Вероятностью события  называется
число
называется
число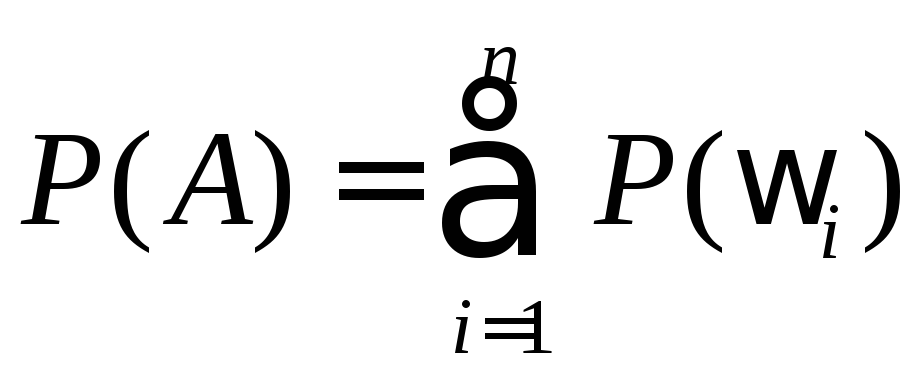 ,
,
равное
сумме вероятностей элементарных исходов,
входящих в событие  .
.
Множество элементарных событий образует полную группу событий, если в результате испытания появиться хотя бы одно из них.
События называются равновозможными, если ни одно из них не является более возможным, чем другое.
Например, при бросании игральной кости выпадение чисел 1,2, …6 – события равновозможные.
Предположим, что
мы имеем дело с пространством элементарных
исходов, состоящим из конечного числа N элементов, образующих полную группу
событий: 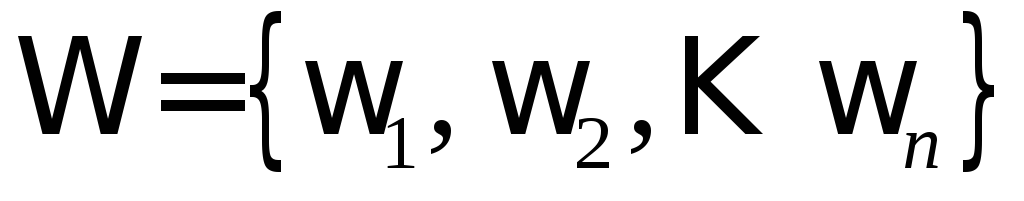 .
Более того, будем считать все элементарные
исходыравновозможными. Тогда вероятность любого из них
принимается равной
.
Более того, будем считать все элементарные
исходыравновозможными. Тогда вероятность любого из них
принимается равной 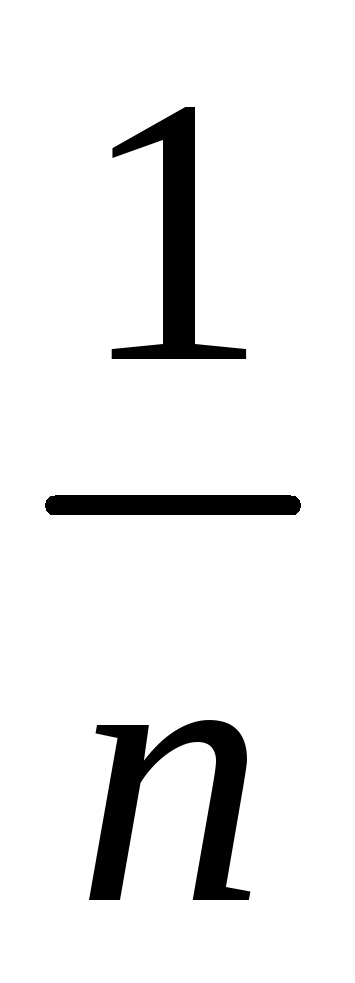 .
.
Если событие  состоит из
состоит из 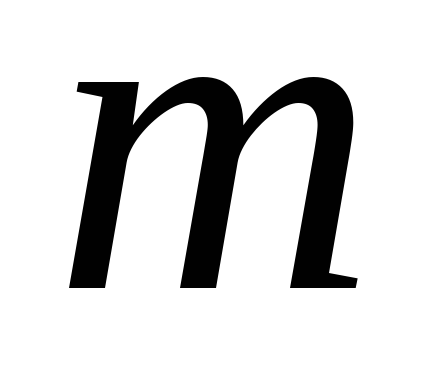 элементарных исходов (благоприятствующих появлению события
элементарных исходов (благоприятствующих появлению события  ),
то вероятность этого события равняется
),
то вероятность этого события равняется
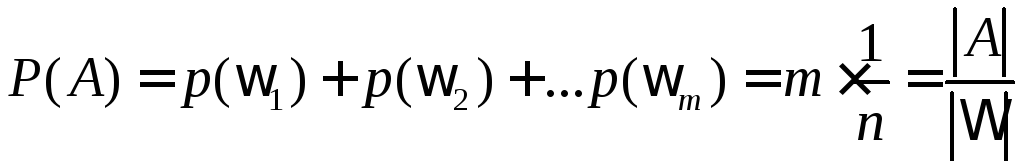 ,
,
где
символом  обозначено число элементарных исходов
обозначено число элементарных исходов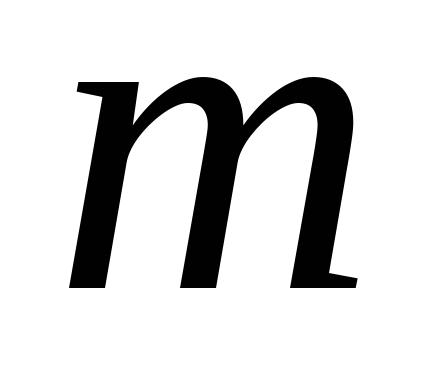 ,
в которых событие
,
в которых событие произошло.
произошло.
В этом случае
вероятность любого события  вычисляется по формуле
вычисляется по формуле
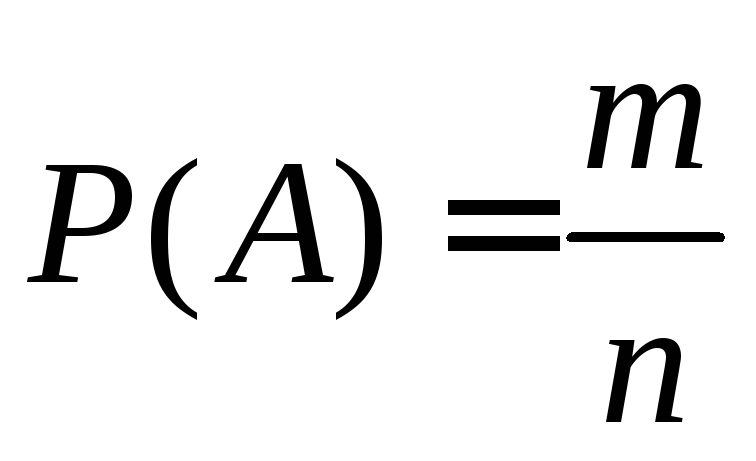 ,
,
называемой классическим
определением вероятности. Эта
формула читается так: «вероятность
события  равна отношению числа исходов,благоприятствующих событию
равна отношению числа исходов,благоприятствующих событию  ,
к общему числу исходов».
,
к общему числу исходов».
Свойства вероятности:
1. 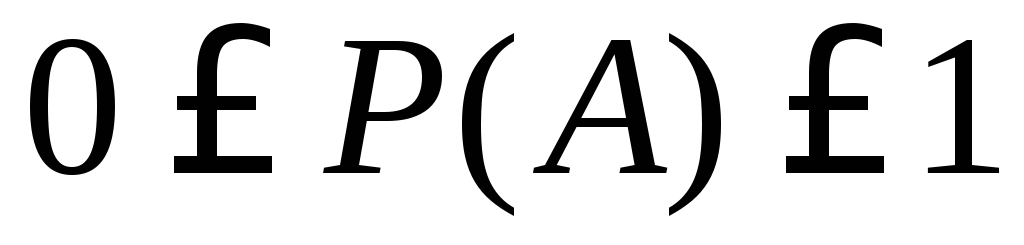 – вероятность любого события есть
положительное число, заключенное от 0
до 1.
– вероятность любого события есть
положительное число, заключенное от 0
до 1.
2.  – вероятность невозможного события
равна 0.
– вероятность невозможного события
равна 0.
3. 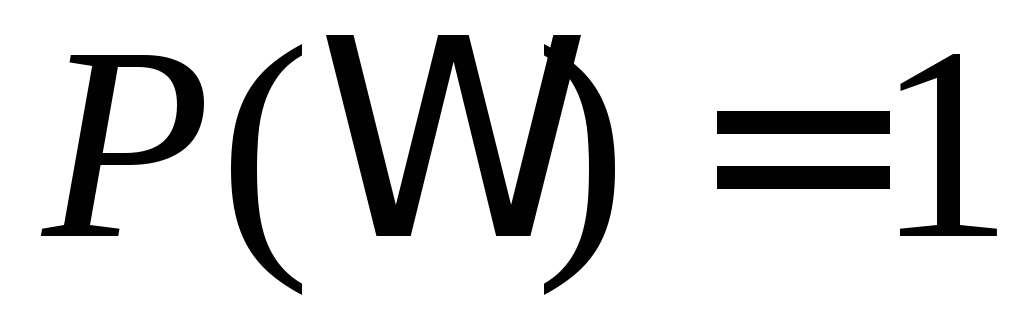 – вероятность достоверного события
равна 1.
– вероятность достоверного события
равна 1.
Пример. В урне 12 шаров: 3 белых, 4 черных, 5 красных. Какова вероятность вынуть из урны черный шар?
Решение.
Эксперимент состоит в случайном выборе
из закрытой урны одного шара. Элементарным
исходом опыта является номер шара и его
цвет. Поскольку все исходы равновероятны,
можно использовать классическое
определение вероятности. Общее число
элементарных исходов 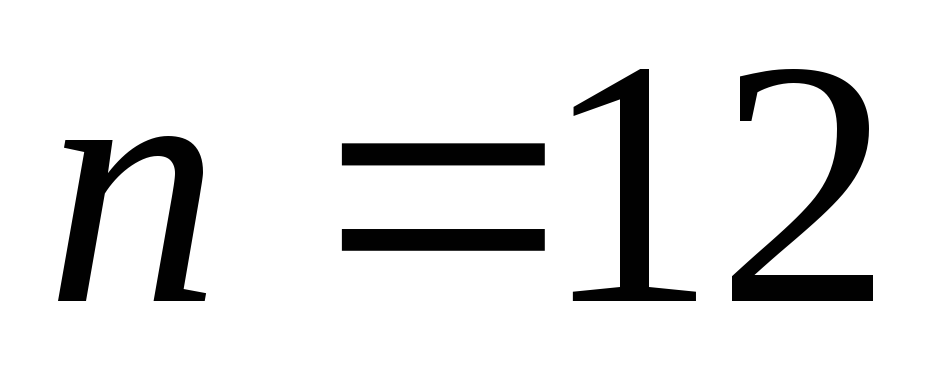 (количество шаров в урне). Событию
(количество шаров в урне). Событию ={извлекли
черный шар} благоприятствуют
={извлекли
черный шар} благоприятствуют 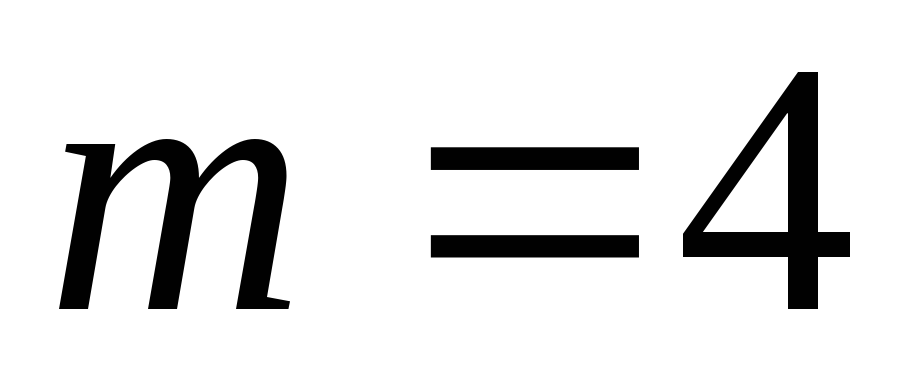 исходов (количество черных шаров).
Получаем, что
исходов (количество черных шаров).
Получаем, что
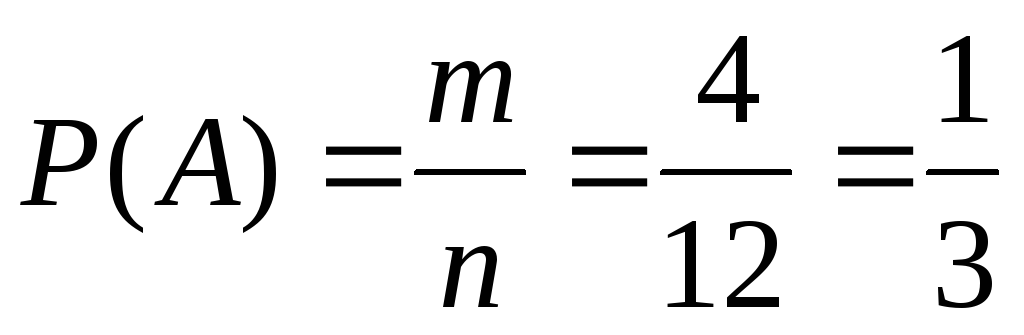 .
.
1.3. Формулы комбинаторики
Комбинаторика – раздел математики, в котором изучаются задачи выбора элементов из заданного множества и расположения их в группы по заданным правилам, в частности задачи о подсчете числа комбинаций, получаемых из элементов данного множества.
Многие комбинаторные задачи могут быть решены с помощью следующих двух важных правил, называемых соответственно правилами суммы и произведения.
Правило суммы:
Если объект  может быть выбран из совокупности
объектов
может быть выбран из совокупности
объектов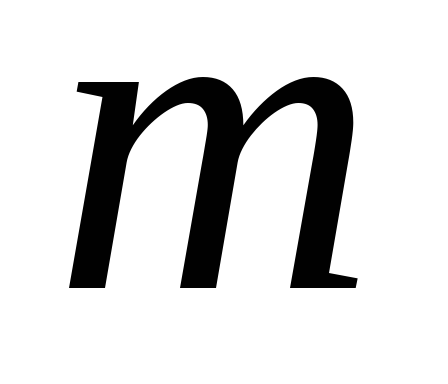 способами, и после каждого такого выбора
объект
способами, и после каждого такого выбора
объект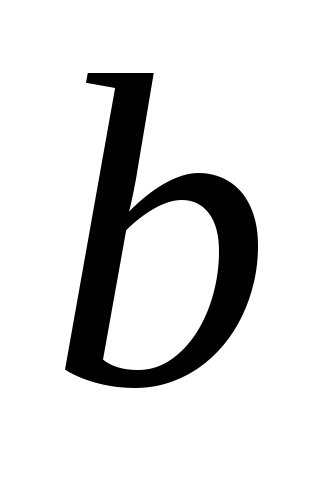 может быть выбран
может быть выбран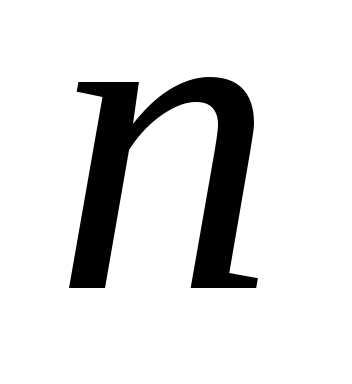 способами, то выбрать либо
способами, то выбрать либо ,
либо
,
либо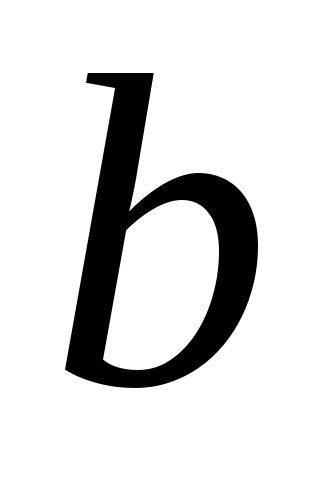 можно
можно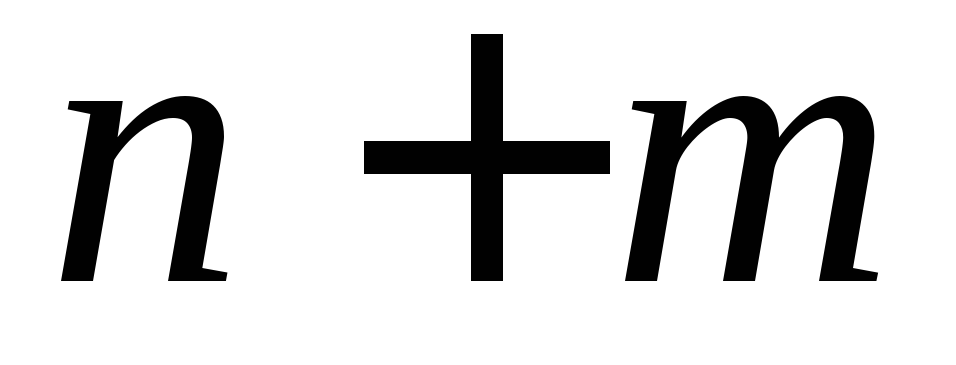 способами.
способами.
Правило
произведения:
Если объект  может быть выбран из совокупности
объектов
может быть выбран из совокупности
объектов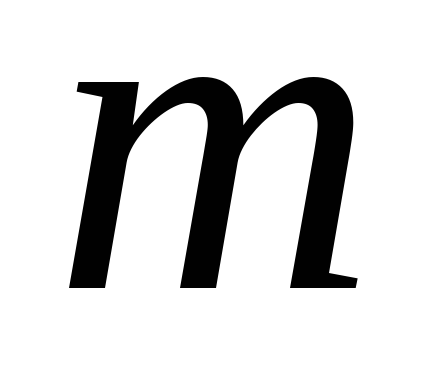 способами, и после каждого такого выбора
объект
способами, и после каждого такого выбора
объект может быть выбран
может быть выбран способами, то пару объектов
способами, то пару объектов ,
,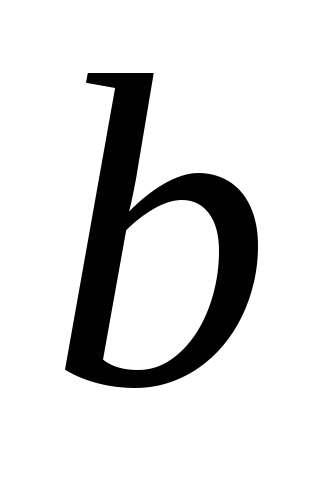 в указанном порядке можно выбрать
в указанном порядке можно выбрать способами.
способами.
Пример 5. В студенческой группе 14 девушек и 6 юношей. Сколькими способами можно выбрать, для выполнения различных заданий, двух студентов одного пола?
Решение.
По правилу произведения двух девушек
можно выбрать 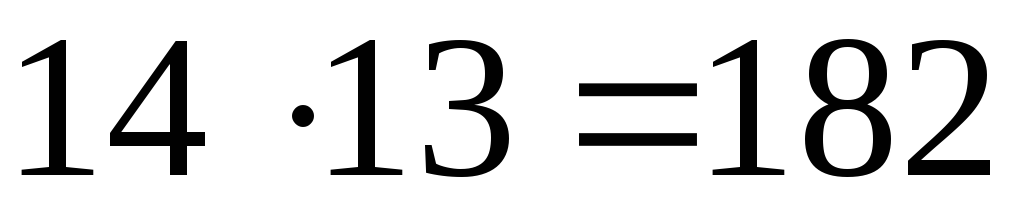 способами, а двух юношей –
способами, а двух юношей –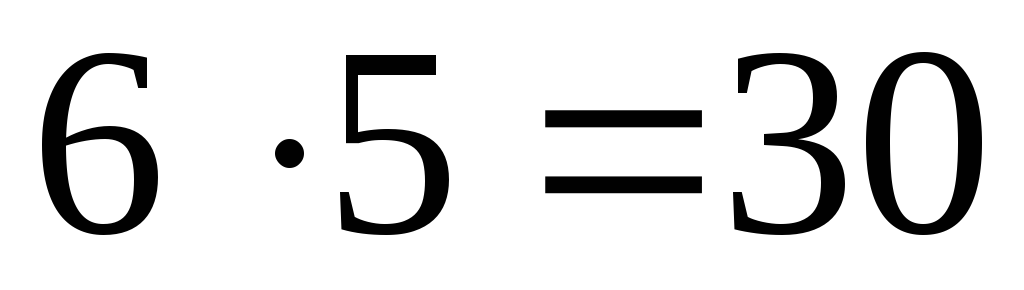 способами. Следует выбрать двух студентов
одного пола: двух девушек или двух
юношей. Согласно правилу сложения число
таких способов выбора будет: 182+30=212.
способами. Следует выбрать двух студентов
одного пола: двух девушек или двух
юношей. Согласно правилу сложения число
таких способов выбора будет: 182+30=212.
Перестановки.
Перестановками называют комбинации, составленные из 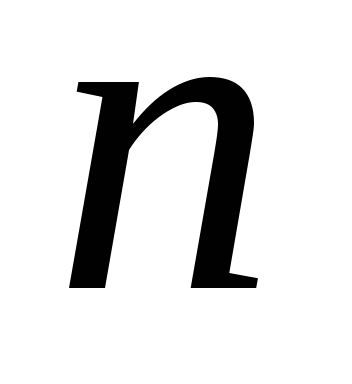 различных элементов и отличающиеся
друг от друга только порядком расположения
элементов.
различных элементов и отличающиеся
друг от друга только порядком расположения
элементов.
Число
всех перестановок из 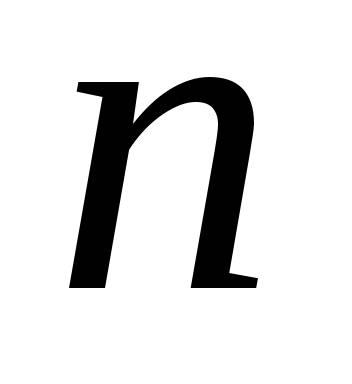 элементов вычисляется по формуле
элементов вычисляется по формуле
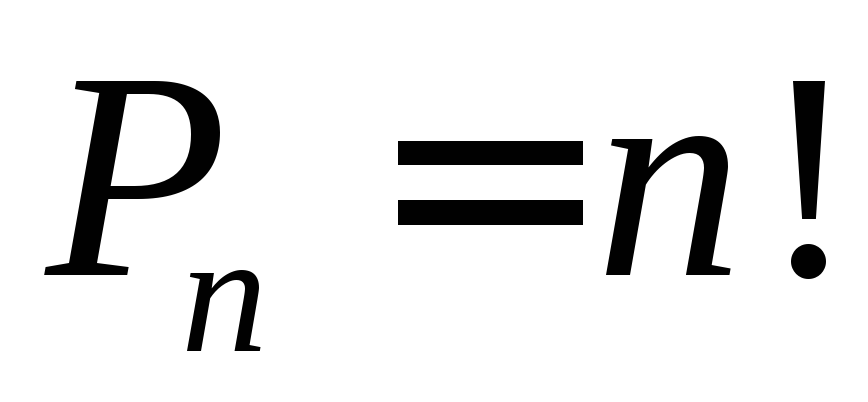
Перестановки
с повторениями:
если один элемент повторяется 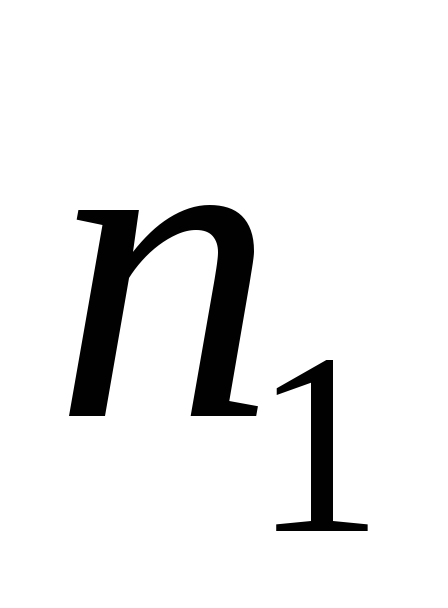 раз, второй элемент повторяется
раз, второй элемент повторяется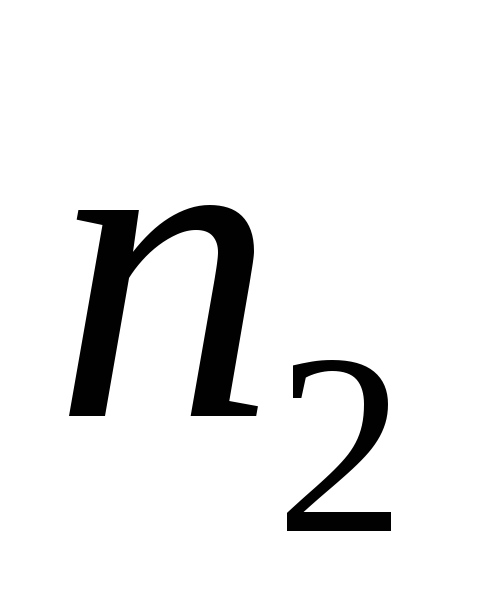 раз,к-тый
элемент повторяется
раз,к-тый
элемент повторяется  раз, а всего элементов
раз, а всего элементов ,
то число комбинаций будет равно:
,
то число комбинаций будет равно:
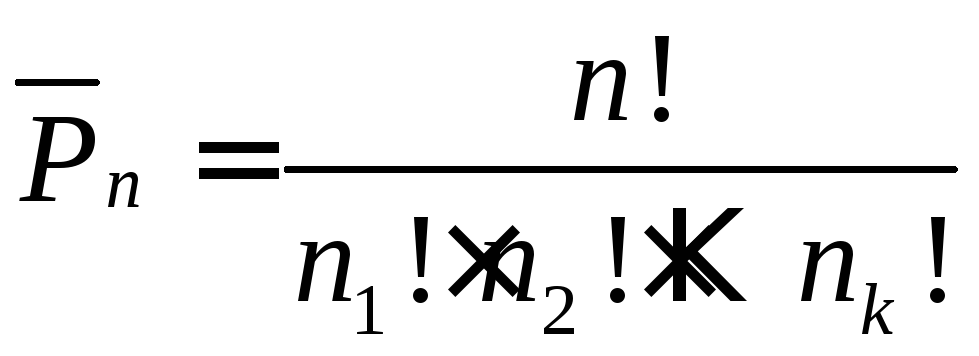 .
.
Пример. Порядок выступления 7 участников конкурса определяется жребием. Сколько различных вариантов жеребьевки при этом возможно?
Решение. Так как каждый вариант жеребьевки отличается только порядком выступления участников, то для подсчета числа различных вариантов следует воспользоваться формулой перестановок:
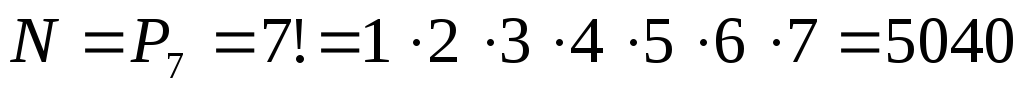 ,
то есть 5040 перестановок.
,
то есть 5040 перестановок.
Пример. Сколько различных пятизначных чисел можно составить из цифр 3, 3, 5, 5, 8?
Решение. Каждое
пятизначное число отличается только
порядком следования цифр, причем цифра
3 встречается 2 раза, цифра 5 – 2 раза, а
цифра 8 – 1 раз, то есть  ,
,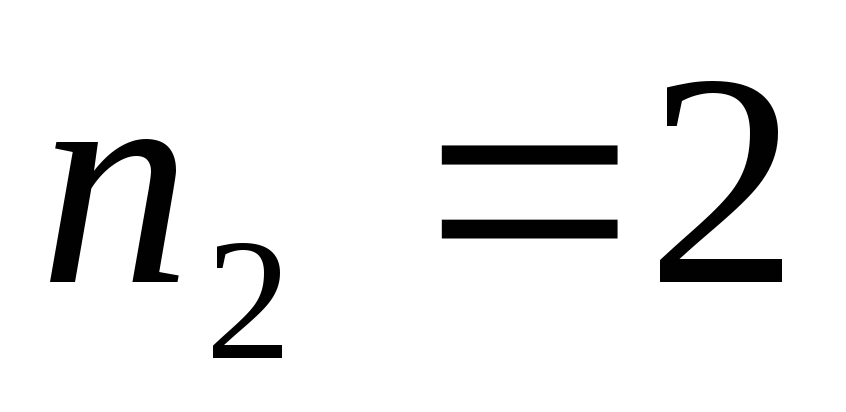 ,
,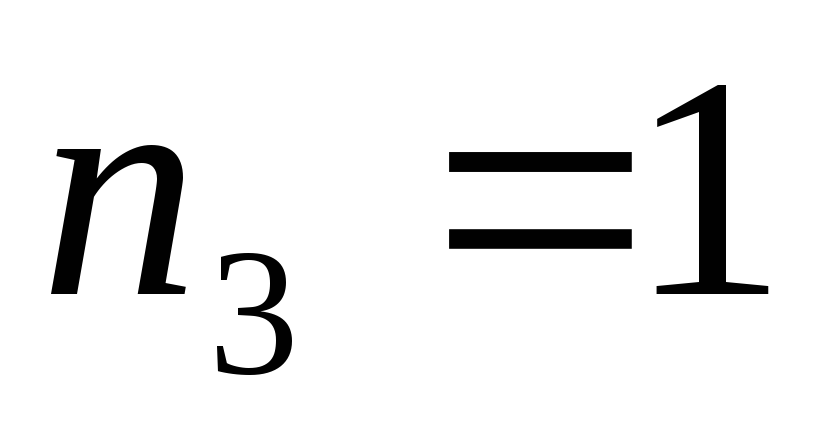 ,
,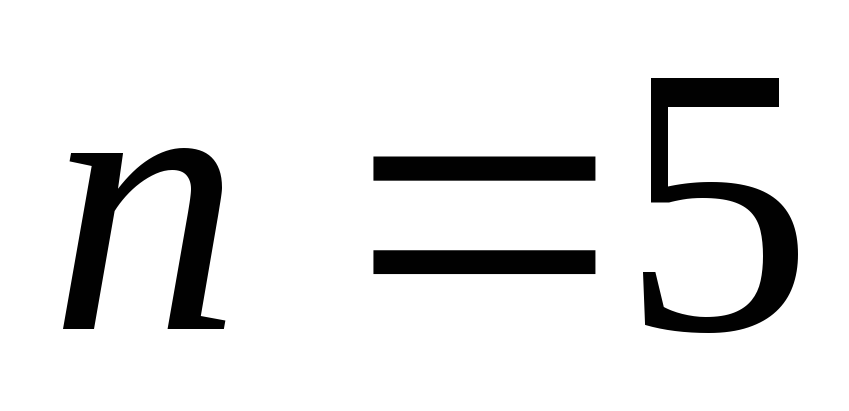 .
Для подсчета числа различных пятизначных
чисел следует воспользоваться формулой
перестановок с повторениями:
.
Для подсчета числа различных пятизначных
чисел следует воспользоваться формулой
перестановок с повторениями:
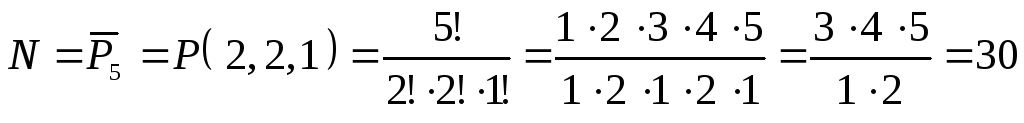 ,
то есть
,
то есть
30 различных пятизначных цифр.
2. Размещения.
Размещениями называются комбинации, составленные
из n различных элементов по 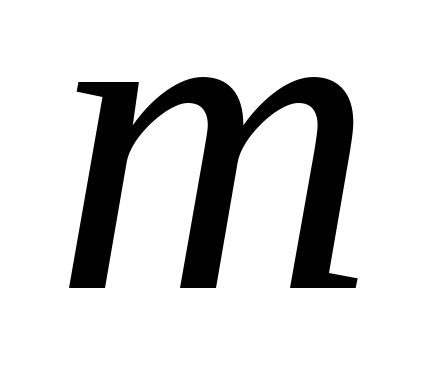 различным элементам, которые отличаются
либосоставом элементов, либо порядком их расположения.
различным элементам, которые отличаются
либосоставом элементов, либо порядком их расположения.
Число
различных размещений из n элементов по 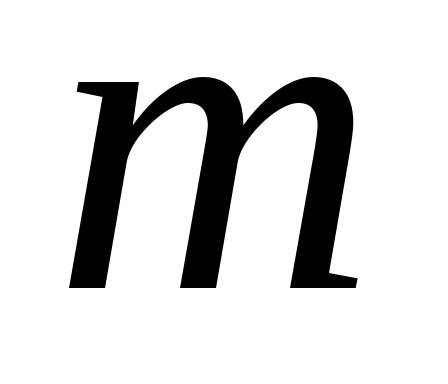 элементам определяется формулой:
элементам определяется формулой:
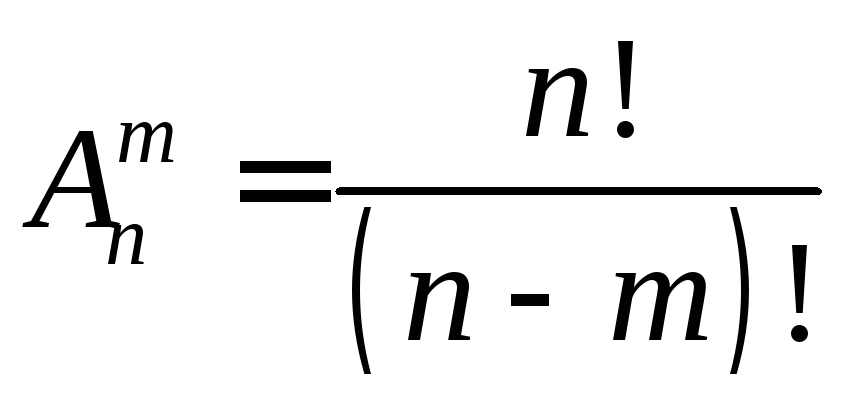 .
.
Размещения
с повторениями:
если каждый элемент может быть использован  раз, то число размещений с повторениями
будет равно:
раз, то число размещений с повторениями
будет равно:
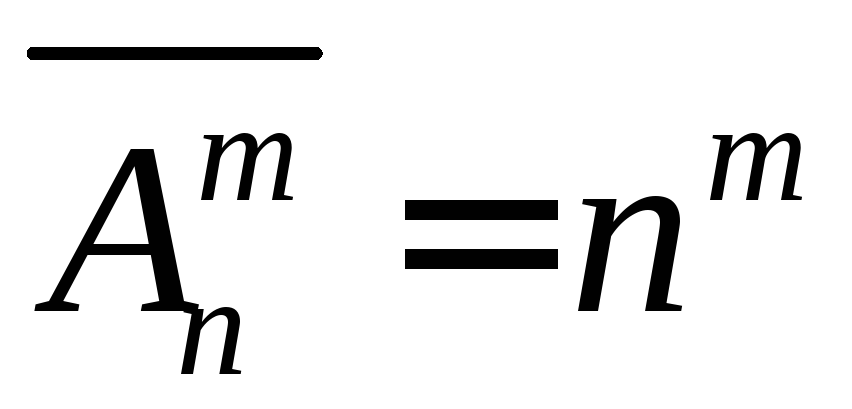 .
.
Пример. На кодовом замке 10 кнопок. Код состоит из трех различных цифр. Сколько различных кодов можно набрать?
Решение. Так как при наборе трехзначного кода можно набирать 3 цифры из имеющихся 10 в любом порядке, то есть коды могут отличаться либо составом цифр, либо порядком их расположения, то для подсчета числа различных кодов воспользуемся формулой размещений:
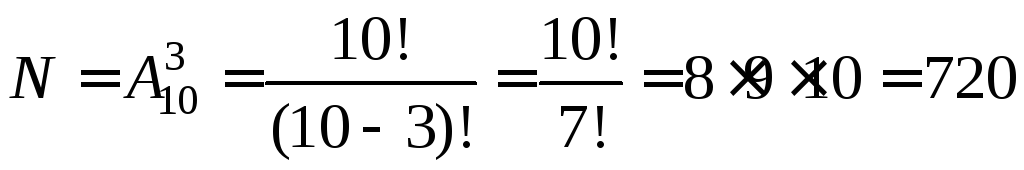 ,
то есть
,
то есть
720 различных кодов.
Пример. Пять человек вошли в лифт на первом этаже девятиэтажного дома. Сколькими способами пассажиры могут выйти из лифта на нужных этажах?
Решение. Каждый из пяти пассажиров может выйти на любом из восьми этажей со 2-го по 9-й включительно. Так как все пассажиры могут выйти на разных этажах, а могут на каком-то этаже выйти несколько пассажиров (например, на втором этаже вышел один пассажир, на четвертом – один, и трое вышли на восьмом этаже), то для подсчета числа способов выхода 5 пассажиров из лифта следует воспользоваться формулой размещения с повторениями:
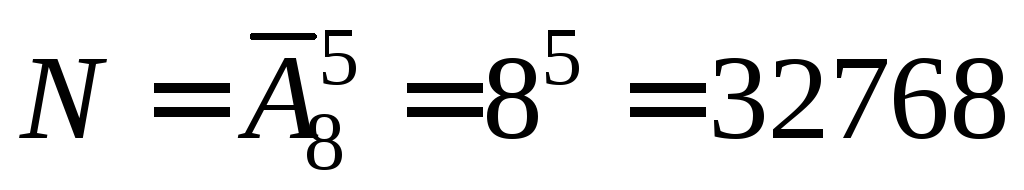 .
.
Такой
же результат можно получить, используя
правило умножения: для первого пассажира
имеется 8 вариантов выхода на этаже, для
второго тоже 8, и для третьего – 8, и для
четвертого – 8, и для пятого – 8. Всего
получается: 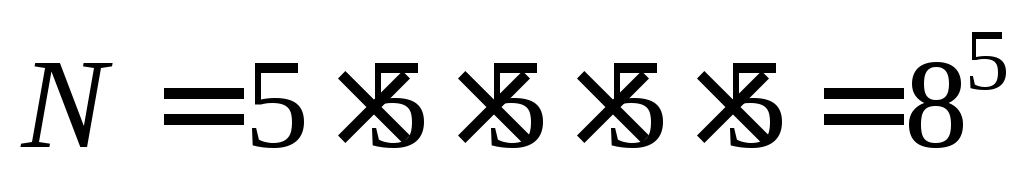 вариантов выхода 5-ти пассажиров.
вариантов выхода 5-ти пассажиров.
3. Сочетания.
Сочетаниями называются комбинации, составленные из n различных элементов по m элементам, отличающиеся друг от друга только составом элементов.
В сочетаниях, в отличие от размещений, не учитывается порядок элементов. Число сочетаний из n элементов по m элементов вычисляется по формуле
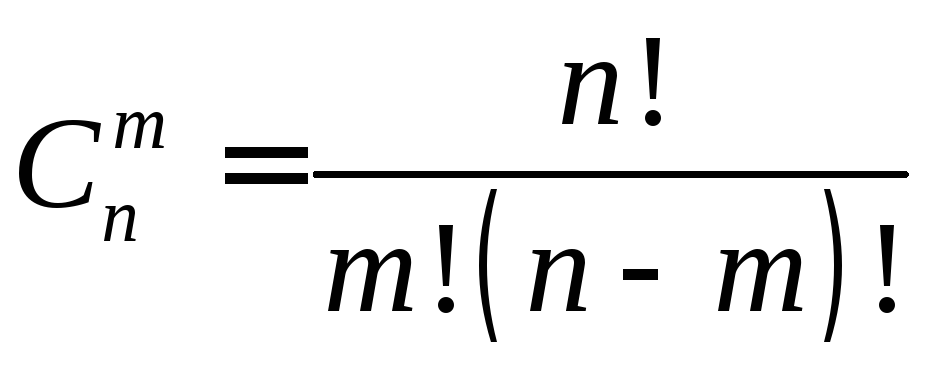 .
.
Сочетания с повторениями: если каждый элемент из n элементов может быть использован m раз, то число сочетаний с повторениями будет равно:
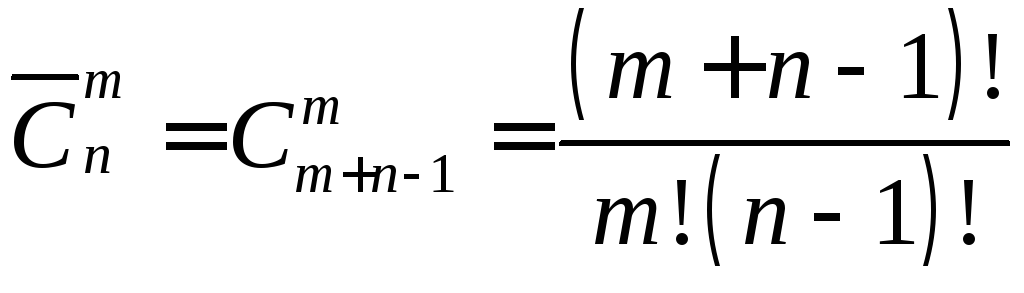 .
.
Пример. Сколькими способами можно выбрать 3 цветка из вазы, в которой стоят 10 красных и 4 розовых гвоздики? Сколькими способами можно выбрать 1 красную гвоздику и 2 розовых?
Решение. Так как
порядок выбора цветов не имеет значение,
то выбрать 3 цветка из вазы, в которой
стоят 14 гвоздик, можно  способами.
способами.
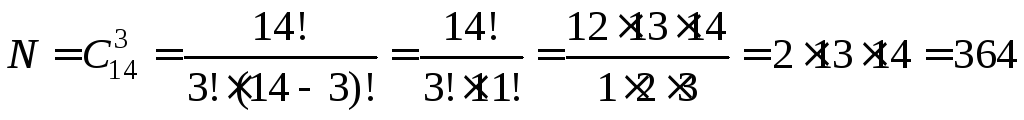 .
.
Красную
гвоздику из 10 имеющихся можно выбрать
10 способами или 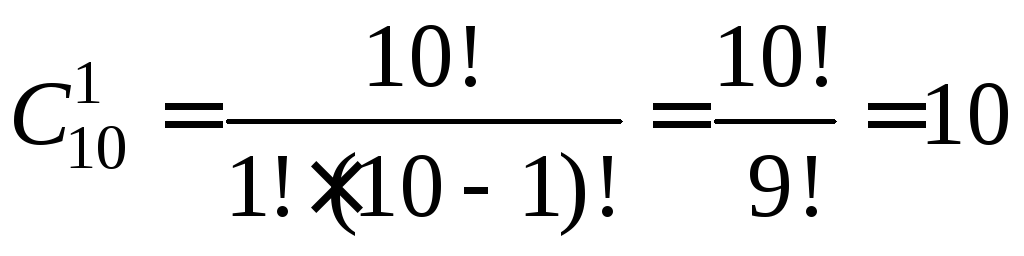 .
Выбрать две розовые гвоздики из имеющихся
четырех можно
.
Выбрать две розовые гвоздики из имеющихся
четырех можно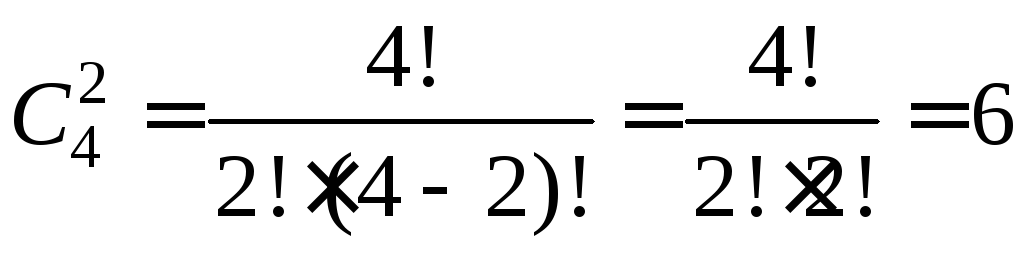 способами. Поэтому букет из одной красной
и двух розовых гвоздик можно составить
(по правилу умножения)
способами. Поэтому букет из одной красной
и двух розовых гвоздик можно составить
(по правилу умножения)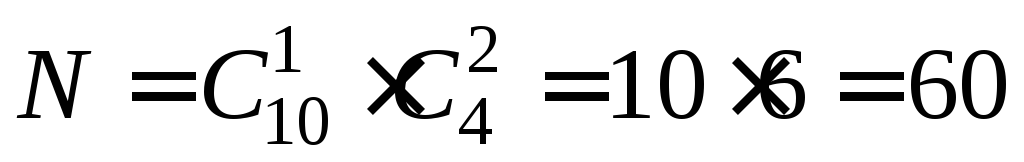 способами.
способами.
Пример. В магазине имеется 7 видов тортов. Сколькими способами можно составить набор, содержащий 3 торта? А если имеются 3 вида тортов, а нужен набор из 7 тортов?
Решение. Поскольку порядок расположения тортов в наборе не играет роли, то искомое число наборов равно числу сочетаний с повторениями из 7 элементов по 3 в каждом:
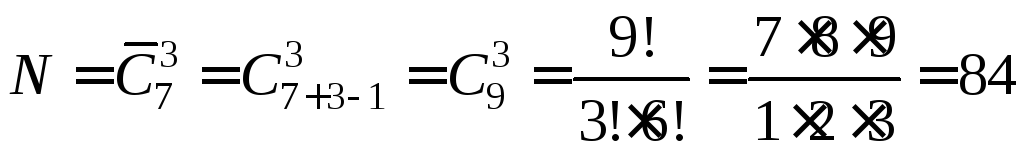 ;
;
Если имеется 3 вида тортов, а нужен набор из 7 тортов, то число возможных наборов равно:
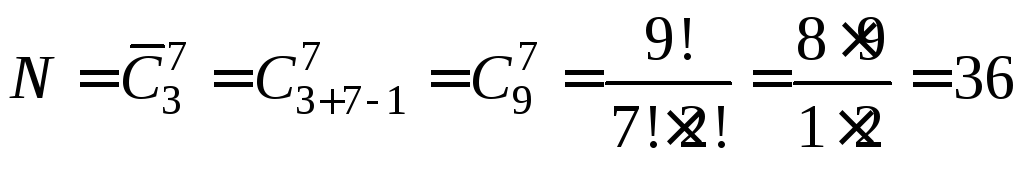 .
.