Логический элемент ИЛИ-НЕ, Логический элемент «исключающее ИЛИ» — Проектирование цифровых устройств
Содержание
- Примеры основных логических элементов
- Что такое логический элемент
- 3. Логические элементы
- Где применяются логические элементы
- Классификация логических элементов
- Логический элемент «и»
- Логический элемент «или»
- Логический элемент «или-не»
- Логический элемент «и-не»
- Логический элемент «исключающий или»
- Логический элемент «не»
- Логический элемент или
- Логический элемент и-не
- Обозначения логических элементов на схеме
Примеры основных логических элементов
На чипах с логической функцией выполняют основные операции:
- конъюнкция — умножение;
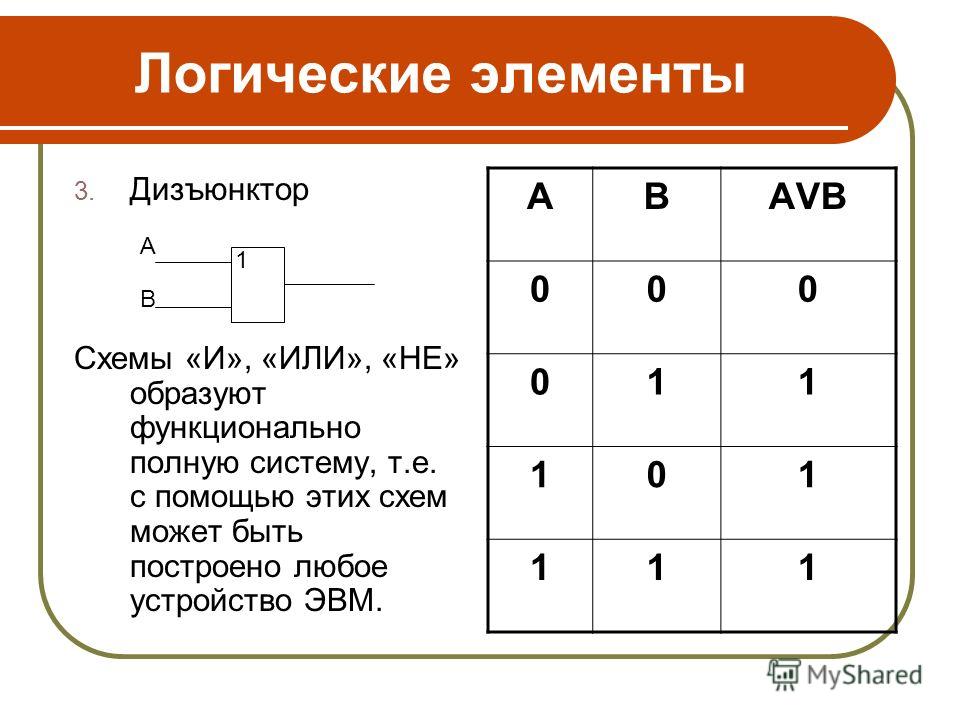
- дизъюнкция — сложение;
- инверсия — отрицание;
- сложение по модулю 2.
Что такое логический элемент
Логический элемент — это интегральная схема, выполняющая логические операции с входной информацией.
Этот электронный чип обеспечивает определенную взаимосвязь между сигналами входа и выхода.
3. Логические элементы
Все, абсолютно все электронные компоненты, обрабатывающие цифровые сигналы, состоят из небольшого набора одинаковых «кирпичиков». В микросхемах малой степени интеграции могут быть единицы и десятки таких элементов, а в современных процессорах их может быть очень и очень много.
Они называются логические элементы. Логическим элементом называется электрическая схема, предназначенная для выполнения какой-либо логической операции с входными данными. Логический элемент — элемент, осуществляющий определенные логические зависимость между входными и выходными сигналами.
Входные данные представляются здесь в виде напряжений различных уровней, и результат логической операции на выходе — также получается в виде напряжения определенного уровня. Логические элементы обычно используются для построения логических схем вычислительных машин, дискретных схем автоматического контроля и управления.
Тем не менее, принцип работы цифровой логики остается неизменным – на входе логического элемента (входов может быть несколько) должен быть цифровой сигнал (сигналы, если входов несколько), который однозначно определяет сигнал на выходе логического элемента.
Конечно, логические элементы строятся, в свою очередь, из уже рассмотренных в предыдущих уроках резисторов, транзисторов и других электронных компонентов, но с точки зрения разработки цифровых схем именно логический элемент является их «элементарной» частицей.
При анализе работы логических элементов используется так называемая булева алгебра . Начала этого раздела математики было изложено в работах Джорджа Буля – английского математика и логика 19-го века, одного из основателей математической логики. Основами булевой алгебры являются высказывания, логические операции, а также функции и законы.
Еще несколько замечаний. Логические элементы (как, впрочем, и другие элементы электронных схем) принято обозначать так, чтобы входы были слева, а выходы справа.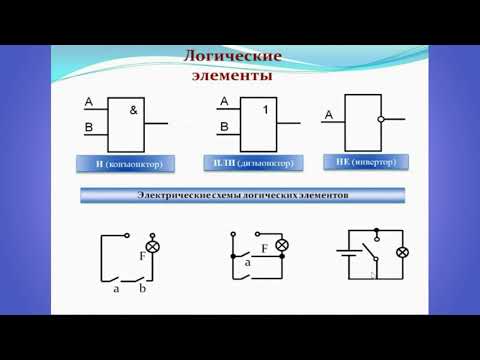 Число входов может быть, вообще говоря, любым, отличным от нуля. Реальные цифровые микросхемы могут иметь до 8 входов, но мы ограничимся двумя – этого достаточно для понимания. Условные обозначения соответствуют отечественному ГОСТу, в других стандартах они могут быть иными.
Число входов может быть, вообще говоря, любым, отличным от нуля. Реальные цифровые микросхемы могут иметь до 8 входов, но мы ограничимся двумя – этого достаточно для понимания. Условные обозначения соответствуют отечественному ГОСТу, в других стандартах они могут быть иными.
Какие же бывают логические элементы?
Логические элементы имеют один или несколько входов и один или два (обычно инверсных друг другу) выхода. Значения «нулей» и «единиц» выходных сигналов логических элементов определяются логической функцией, которую выполняет элемент, и значениями «нулей» и «единиц» входных сигналов, играющих роль независимых переменных. Существуют элементарные логические функции, из которых можно составить любую сложную логическую функцию.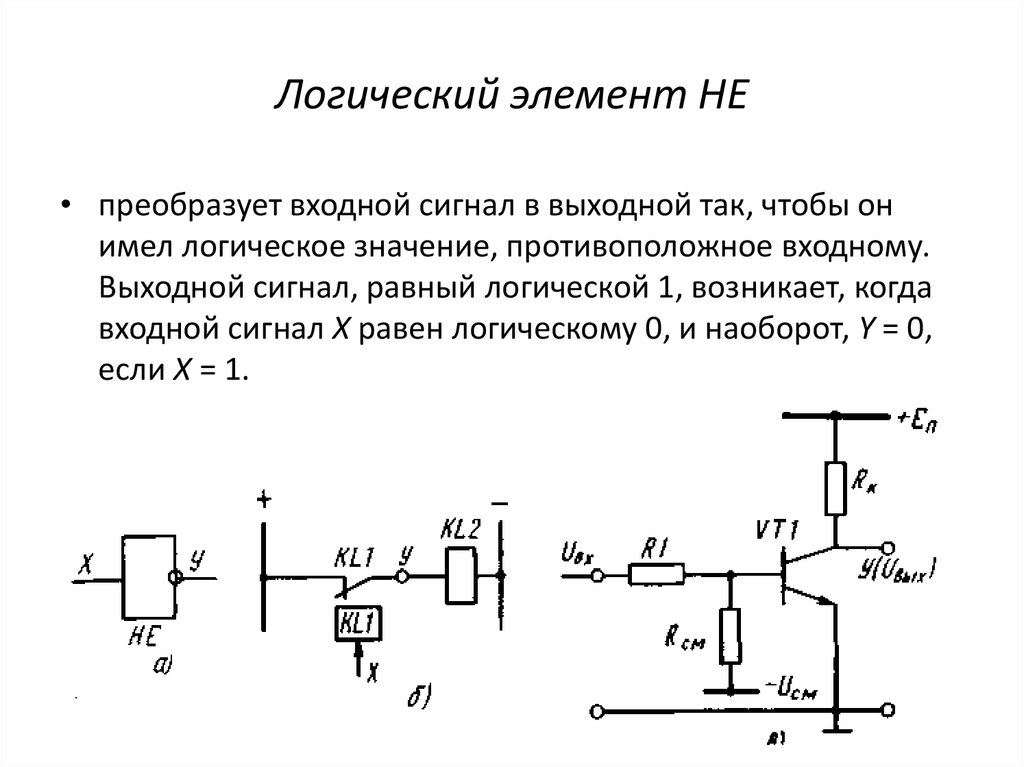
Элемент «И» (AND), он же конъюнктор, выполняет операцию логического умножения:
Условное обозначение – Таблица истинности
Здесь изображен логический элемент «2И» (цифра перед буквой «И» означает число входов). Знак & (амперсант) в левом верхнем углу прямоугольника указывает, что это логический элемент «И». Первые две буквы обозначения DD1.2 указывают на то, что это цифровая микросхема (Digital), цифра слева от точки указывает номер микросхемы на принципиальной схеме, а цифра справа от точки – номер логического элемента в составе данной микросхемы. Одна микросхема может содержать несколько логических элементов.
Состояние входов в таблице обозначаются «0» и «1» («ложь» и «истина»). Из таблицы видно, что выход «Y» будет иметь состояние «1» только в том случае, когда на обоих входах «Х1» и «Х2» будут «1». Это легко запомнить: умножение на «0» всегда дает «0».
Элемент «ИЛИ» (OR), он же дизъюнктор, выполняет операцию логического сложения:
Условное обозначение – Таблица истинности
Состояние «1» на выходе будет всегда, пока есть хотя бы одна «1» на входах.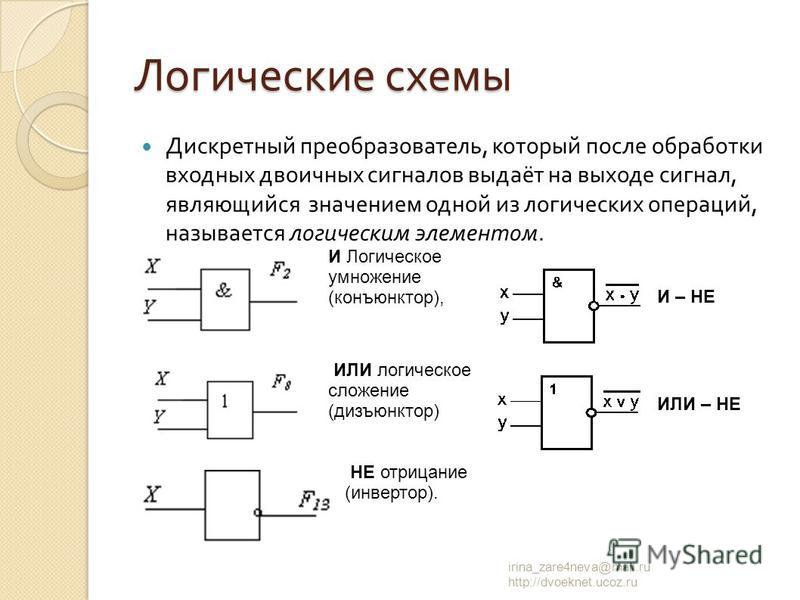
Элемент «НЕ» (NOT), он же инвертор, выполняет операцию логического отрицания:
Условное обозначение – Таблица истинности
Состояние на входе обратно состоянию на входе.
Вот из этих трех элементов строятся все цифровые устройства!
Рассмотрим еще три логических элемента, которые можно получить, комбинируя уже рассмотренные. В силу исторически сложившихся схемотехнических решений эти скомбинированные схемы тоже считаются логическими элементами.
Элемент «И-НЕ» (NAND), конъюнктор с отрицанием:
Условное обозначение – Таблица истинности
Элемент И-НЕ работает точно так же как «И», только выходной сигнал противоположен. Там где у элемента «И» на выходе должен быть «0», у элемента «И-НЕ» будет единица. И наоборот.
Элемент «ИЛИ-НЕ» (NOR), дизъюнктор с отрицанием:
Условное обозначение – Таблица истинности
Элемент работает так же как и «ИЛИ», но с инверсией выхода.
Элемент «Исключающее ИЛИ» (XOR), сумматор по модулю 2:
Условное обозначение – Таблица истинности
В этом элемента «1» на выходе будет только тогда, когда на входах разные состояния.
На таких элементах строят сумматоры двоичных многоразрядных чисел. Для этого используется еще один дополнительный выход, на котором при появлении на входах двух «1» появляется сигнал переноса разряда.
Мы рассмотрели логические элементы, которые применяются в цифровой технике для построения логических схем любого уровня сложности, но рассмотренные нами элементы не могут делать одну крайне важную работу – они не умеют хранить информацию. Для хранения используется более сложный класс устройств, называемый элементами с памятью или конечными автоматами.
Где применяются логические элементы
Логические элементы могут служить автономными частями схемы и составными частями более сложной схемы. В качестве самостоятельного элемента микросхему используют для управления устройством. Также чип с логической опцией имеет назначение генератора импульсов в радиодеталях.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Если нет возможности написать самому, закажите тут.
В комбинационных цифровых схемах рассматриваемые элементы составляют часть больших и сверхбольших интегральных схем, шифраторов и дешифраторов. В триггерах, регистрах, счетчиках и других схемах с памятью также применяют микросхемы с функцией логических действий.
Классификация логических элементов
В зависимости от вида используемых сигналов микросхемы с логическим действием бывают:
- Потенциальные: данные на входе представляют собой напряжения различных уровней. Высокое напряжение — это логическая единица, означающая истину. Низкое напряжение называется логическим нулем и считается ложным значением. В зависимости от подачи напряжения на входе и выполненной операции на выходе получается истина или ложь.
- Импульсные: отсутствие импульсов = логический ноль, наличие импульса = логическая единица.
- Импульсно-потенциальные: Наличие положительного импульса заданной амплитуды означает логическую единицу, его отсутствие — логический ноль.

В зависимости от типа используемых материалов выделяют следующие разновидности микросхем:
- Диодно-резисторная логика. Использование схем, разработанных по этой технологии, возможно только с полупроводниковыми триодами. Для самостоятельного применения этих элементов характерны большие потери.
- Диодно-транзисторная логика. Операции при этой технологии реализуются посредством диодных цепей, а усиление и инверсия сигнала происходят благодаря транзистору.
- Резисторно-транзисторная логика. Данный класс чипов базируется на резисторах и биполярных транзисторах.
- Транзисторно-транзисторная логика. За триодом, выполняющим логическую операцию, подключают выходной инвертор для четкости сигнала на выходе.
Логический элемент «и»
Микросхема «И» выполняет конъюнкцию над входной информацией. Элемент «И» имеет 2-8 входов и один выход.
Логический элемент «или»
Действие сложения над входными данными выполняет элемент «ИЛИ». У этого устройства может быть 2 и более входов и лишь один выход.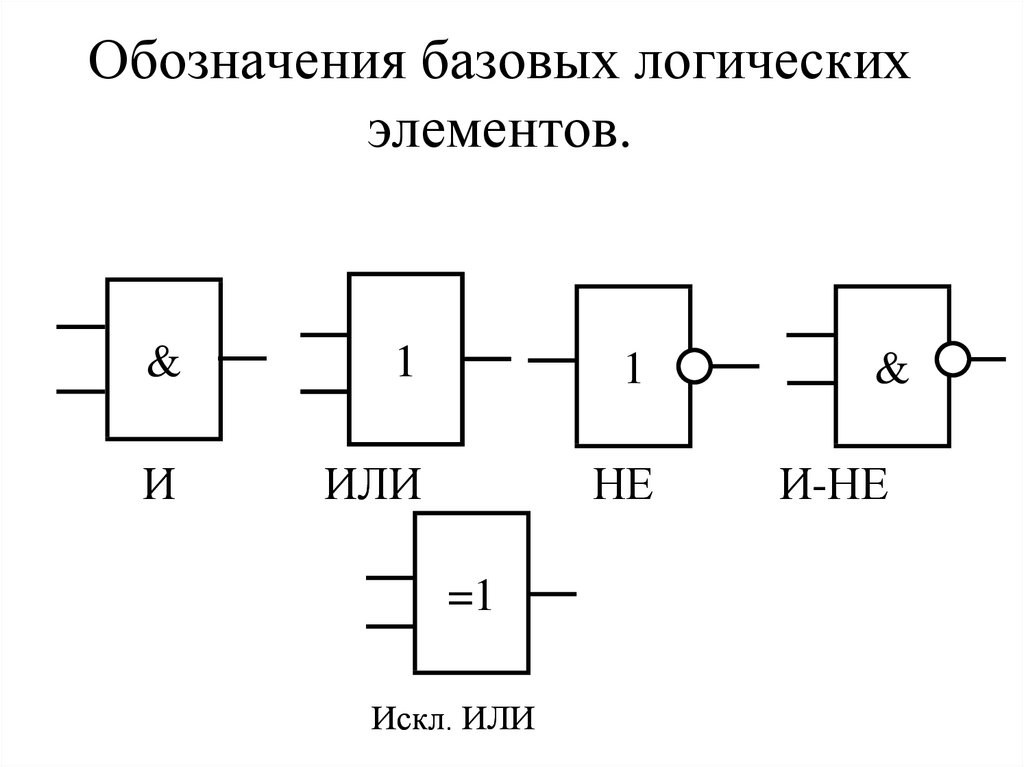
Логический элемент «или-не»
Комбинация «ИЛИ-НЕ» выполняет операцию отрицания дизъюнкции. Данный элемент является противоположным элементу «ИЛИ», соответственно, значения входа и выхода для этих элементов тоже будут обратными друг другу.
Логический элемент «и-не»
«И-НЕ» выполняет функцию отрицания результата конъюнкции. Название следует из принципа работы элемента: «И-НЕ» представляет собой элемент «И», который дополнен элементом «НЕ». Следовательно, «И-НЕ» осуществляет операцию, обратную для элемента «И».
Логический элемент «исключающий или»
Элемент с функцией сложения по модулю 2 называется «исключающем ИЛИ», другое его название — «неравнозначность». Данная микросхема имеет два входа и один выход.
Истинное значение будет в случае разных сигналов на входах. Если на обоих входах будет высокий потенциал, на выходе получится низкий. При одновременной подаче низкого уровня сигнала на каждый вход на выходе также будет низкий уровень.
Логический элемент «не»
Операцию отрицания осуществляет элемент «НЕ». Поскольку он имеет по одному входу и выходу, его называют инвертором.
Для элемента «НЕ» характерно обращение входной информации. При подаче на вход логической единицы выйдет логический ноль, и наоборот, при подаче нуля выйдет единица.
Логический элемент или
Логический элемент ИЛИ выполняет операцию «дизъюнкция», или «логическое сложение». Логические элементы ИЛИ могут иметь 2 и более входов.
Для операции ИЛИ справедливы следующие аксиомы:
Функциональное назначение элемента ИЛИ в российском стандарте обозначают цифрой 1, а в американском — надписью, например, OR3 — элемент ИЛИ с тремя входами (рис. 6.6). Элемент ИЛИ, имеющий 3 входа, описывает логическая функция: у = a v b v с.
Рис. 6.6. Обозначения элементов ИЛИ для трех входов
Таблица истинности логического элемента ИЛИ (табл. 6.4) позволяет сформулировать правило для определения выходного сигнала, справедливое для логических элементов с любым числом входов: выходной сигнал элемента ИЛИ равен нулю, если все входные сигналы равны нулю.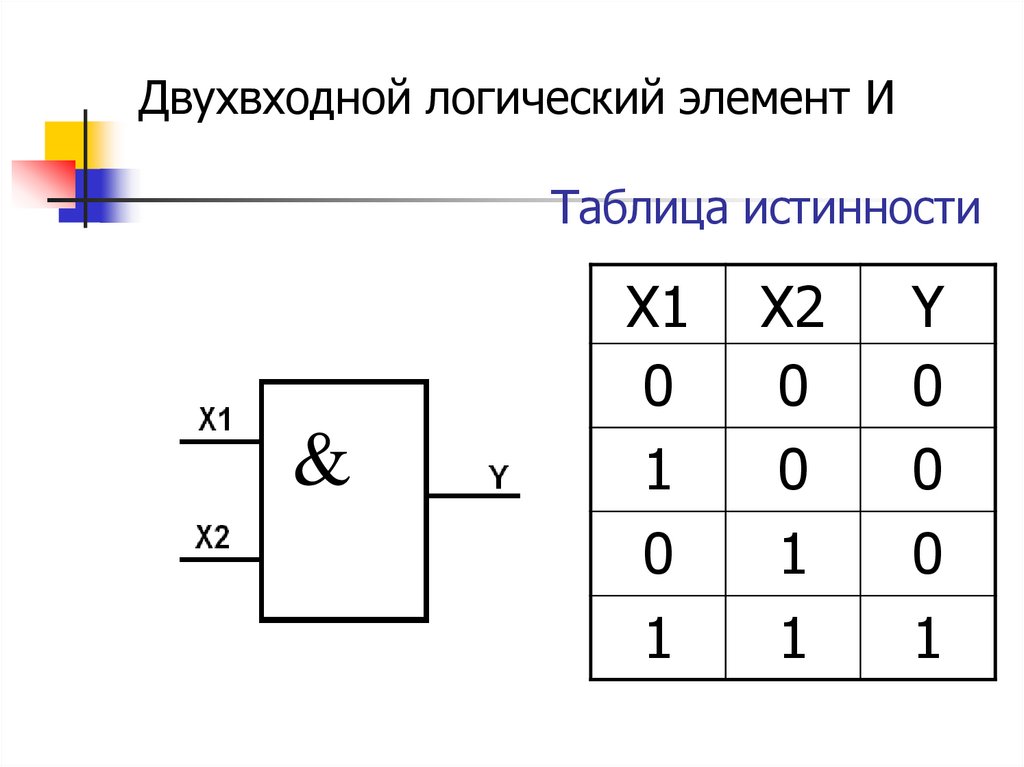
Таблица 6.4
а | b | с | У |
1 | 1 | ||
1 | 1 | ||
1 | 1 | 1 | |
1 | 1 | ||
1 | 1 | 1 | |
1 | 1 | 1 | |
1 | 1 | 1 | 1 |
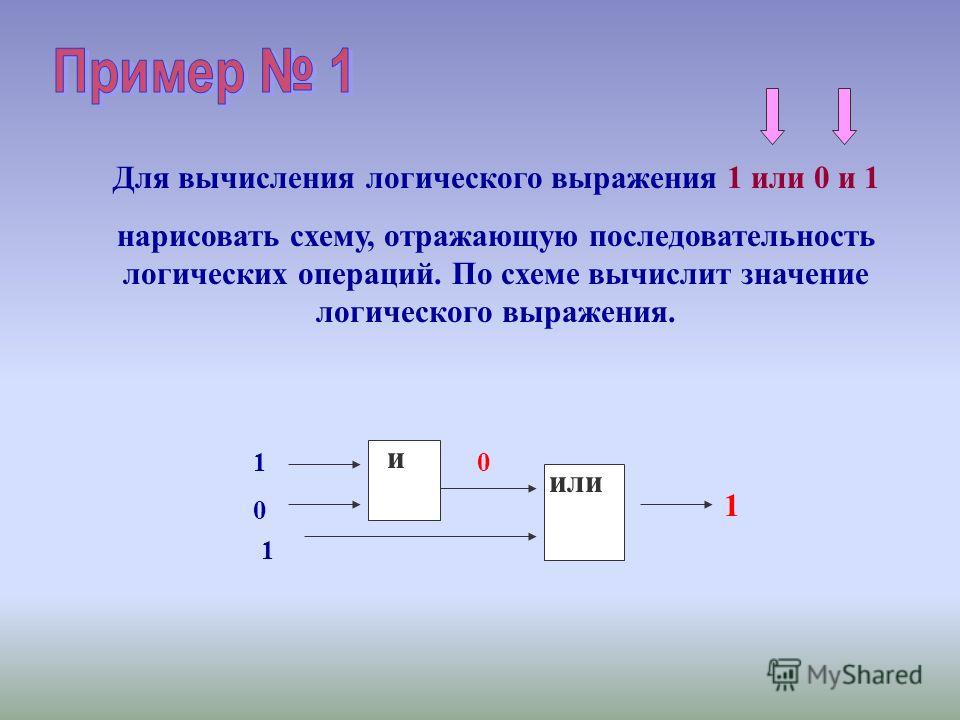
Работу элемента ИЛИ поясняют временные диаграммы (рис. 6.7).
Рис. 6.7. Диаграммы, поясняющие работу элемента ИЛИ
Если один из входов (а) использован как информационный, а два других входа (b, с) как управляющие, то сигнал с входа а будет передаваться на выход у только при Ь-с- 0. Схема стробирования на элементе ИЛИ пропускает отрицательные импульсы при отрицательных управляющих сигналах (интервал времени tx—t2).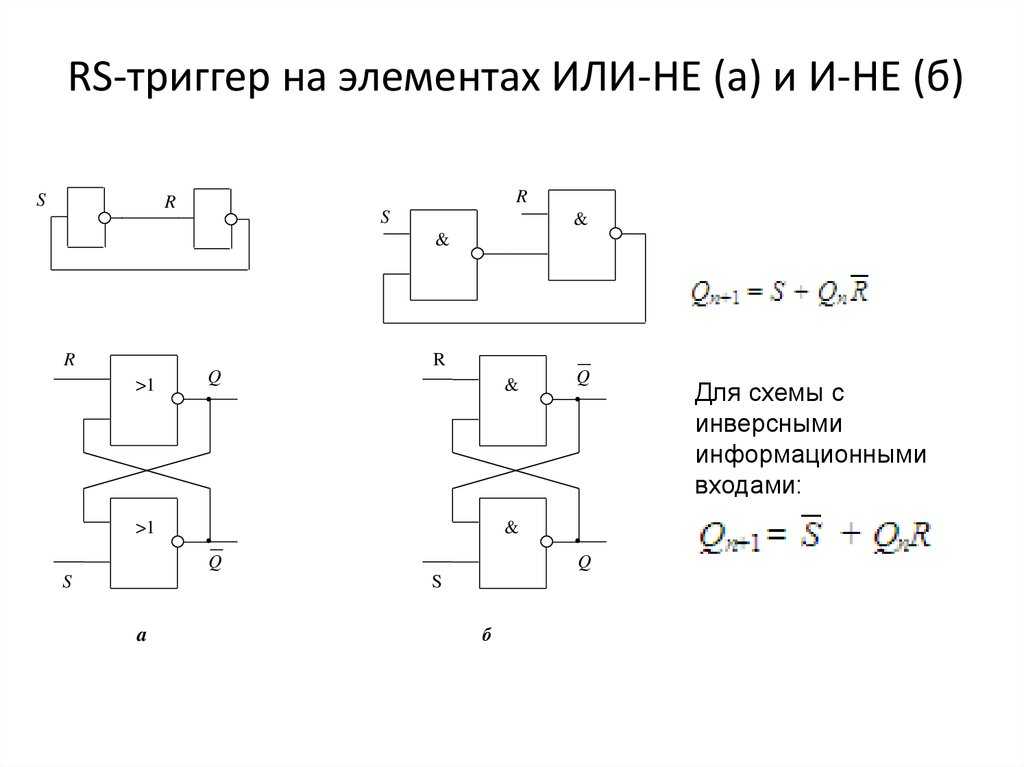 ).
).
Логический элемент и-не
Выполняет операцию «штрих Шеффера» или отрицание конъюнкции и описывается формулой: у = а ? b ? с. Условные графические обозначения элементов И-НЕ отличаются от обозначений элемента И наличием кружка на выходе, что означает инверсию выходного сигнала (рис. 6.4).
Рис. 6.4. Обозначения элементов И-НЕ для трех входов
Таблица истинности (табл. 6.3) позволяет сформулировать правило определения выходного сигнала, независимо от числа входов: на выходе элемента И-НЕ имеем 0, если на все входы подан сигнал 1.
Таблица 6.3
а | b | с | у |
1 | |||
1 | 1 | ||
1 | 1 | ||
1 | 1 | 1 | |
1 | 1 | ||
1 | 1 | 1 | |
1 | 1 | 1 | |
1 | 1 | 1 |
Элементы данного типа использовались как основные в интегральных схемах типа ТТЛ. В сериях интегральных схем малой степени интеграции, например 1533, содержатся элементы И-НЕ, имеющие 2, 3, 4, и 8 входов.
В сериях интегральных схем малой степени интеграции, например 1533, содержатся элементы И-НЕ, имеющие 2, 3, 4, и 8 входов.
Схема стробирования на элементе И-НЕ, как и схема И пропускает положительные импульсы при положительных управляющих сигналах, но выдает инвертированный выходной сигнал (рис. 6.5). При объединении отрицательных импульсов на выходе формируются положительные импульсы.
Рис. 6.5. Временные диаграммы, поясняющие работу элемента И-НЕ
Обозначения логических элементов на схеме
Устройство «И» имеет разное условное обозначение в зависимости от числа входов на устройстве: 2И — чип с двумя входами, «3И» — микросхема с тремя входами и т.д. На схеме это выглядит так:
Элемент «ИЛИ» обозначается подобно интегральной схеме с функцией умножения: «2ИЛИ» = 2 входа, «3ИЛИ» = 3 входа и т.д.:
Чип, осуществляющий отрицание, обозначается схематически так:
На чертеже изображен пример обозначения «2И-НЕ»:
Условное обозначение «2ИЛИ-НЕ» выглядит следующим образом:
История, Теория, Применение.» src=»https://www.youtube.com/embed/bXdiYU3IUJA?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>«Исключающее ИЛИ» принято изображать так:
Логические элементы
Логические элементыЛогические элементы
Логическим элементом
называется электрическая схема,
выполняющая какую-либо логическую
операцию (операции) над входными
данными, заданными в виде уровней
напряжения, и возвращающая
результат операции в виде
выходного уровня напряжения. Так
как операнды логических операций
задаются в двоичной системе
счисления, то логический элемент
воспринимает входные данные в виде
высокого и низкого уровней
напряжения на своих входах.
Соответственно, высокий уровень
напряжения (напряжение логической
1) символизирует истинное значение
операнда, а низкий (напряжение
логического 0) — ложное. Значения
высокого и низкого уровней
напряжения определяются
электрическими параметрами схемы
логического элемента и одинаковы
как для входных, так и для выходных
сигналов. Обычно, логические
элементы собираются как отдельная
интегральная микросхема. К числу
логических операций, выполняемых
логическими элементами относятся
конъюнкция (логическое умножение,
И), дизъюнкция (логическое сложение,
ИЛИ), отрицание (НЕ) и сложение по
модулю 2 (исключающее ИЛИ).
Рассмотрим основные типы
логических элементов.
Значения
высокого и низкого уровней
напряжения определяются
электрическими параметрами схемы
логического элемента и одинаковы
как для входных, так и для выходных
сигналов. Обычно, логические
элементы собираются как отдельная
интегральная микросхема. К числу
логических операций, выполняемых
логическими элементами относятся
конъюнкция (логическое умножение,
И), дизъюнкция (логическое сложение,
ИЛИ), отрицание (НЕ) и сложение по
модулю 2 (исключающее ИЛИ).
Рассмотрим основные типы
логических элементов.
Элемент И
Логический элемент И
выполняет операцию логического
умножения (конъюнкция) над своими
входными данными и имеет от 2 до 8
входов и один выход (как правило,
выпускаются элементы с двумя,
тремя, четырьмя и восемью входами).
На рис. 1. изображены условные
графические обозначения (УГО)
логических элементов И с двумя,
тремя и четырьмя входами
соответственно. Элементы И
обозначаются как NИ, где N —
количество входов логического
элемента (например, 2И, 3И, 8И и т.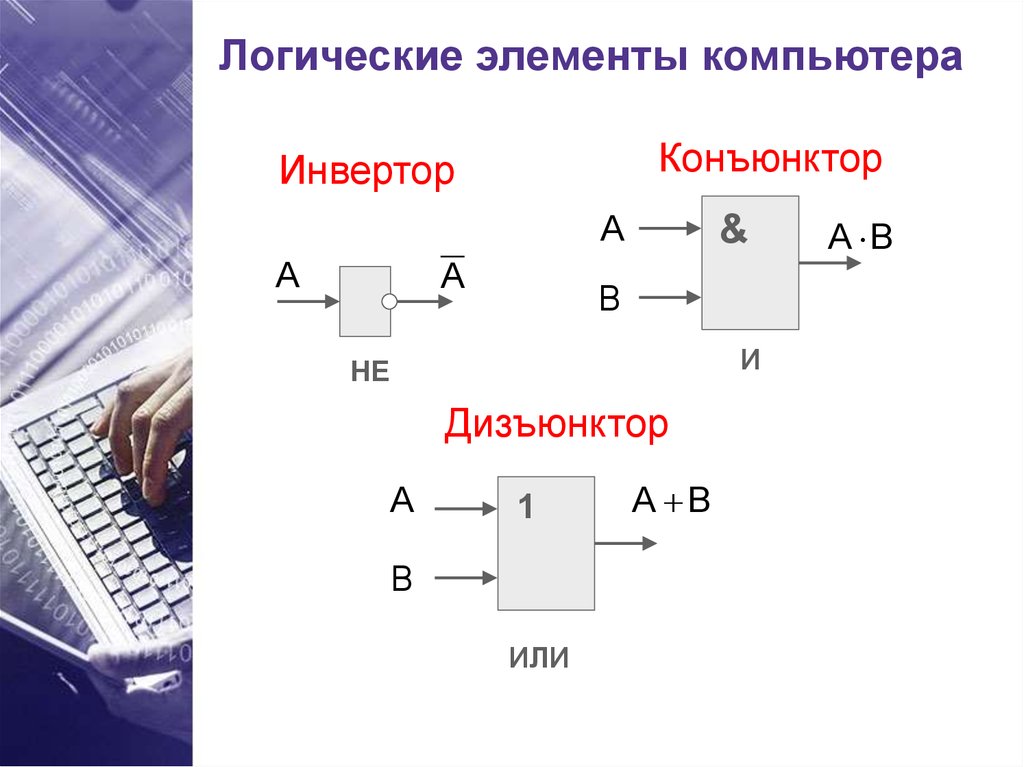
| Рис. 1 |
Элемент ИЛИ
Логический элемент ИЛИ выполняет операцию логического сложения (дизъюнкция) над своими входными данными и, также как и логический элемент И, имеет от 2 до 8 входов и один выход. На рис. 2. изображены УГО логических элементов ИЛИ с двумя, тремя и четырьмя входами соответственно. Элементы ИЛИ обозначаются также, как и элементы И (2ИЛИ, 4ИЛИ и т.д.).
| Рис. 2 |
Элемент НЕ (инвертор)
Логический элемент НЕ
выполняет операцию логического
отрицания над своими входными
данными и имеет один вход и один
выход. Иногда его называют
инвертор, так как он инвертирует
входной сигнал.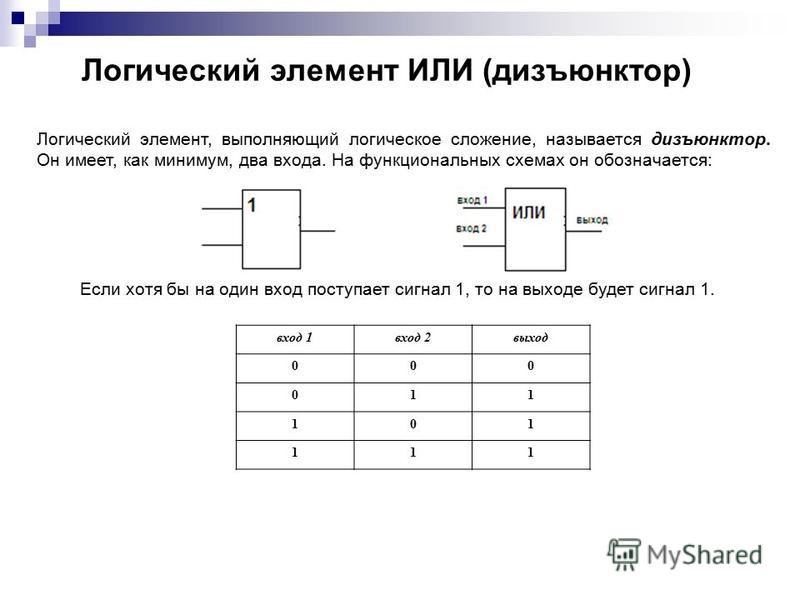
| Рис. 3 |
Элемент И-НЕ
Логический элемент И-НЕ выполняет операцию логического умножения над своими входными данными, а затем инвертирует (отрицает) полученный результат и выдаёт его на выход. Таким образом, можно сказать, что логический элемент И-НЕ — это элемент И с инвертором на выходе. УГО элемента 3И-НЕ приведено на рис. 4.
Элемент ИЛИ-НЕ
Логический элемент ИЛИ-НЕ
выполняет операцию логического
сложения над своими входными
данными, а затем инвертирует
(отрицает) полученный результат и
выдаёт его на выход. Таким образом,
можно сказать, что логический
элемент ИЛИ-НЕ — это элемент ИЛИ с
инвертором на выходе. УГО элемента 3ИЛИ-НЕ
приведено на рис. 5.
Таким образом,
можно сказать, что логический
элемент ИЛИ-НЕ — это элемент ИЛИ с
инвертором на выходе. УГО элемента 3ИЛИ-НЕ
приведено на рис. 5.
| Рис. 5 |
Этот логический элемент выполняет логическую операцию сложения по модулю 2 и, как правило, имеет 2 входа и один выход. Такой элемент, в основном, используется в схемах аппаратного контроля. УГО элемента приведено на рис. 6.
| Рис. 6 |
Комбинационные логические элементы
Существуют и более сложные
логические элементы, выполняющие
несколько логических операций над
своими входными данными.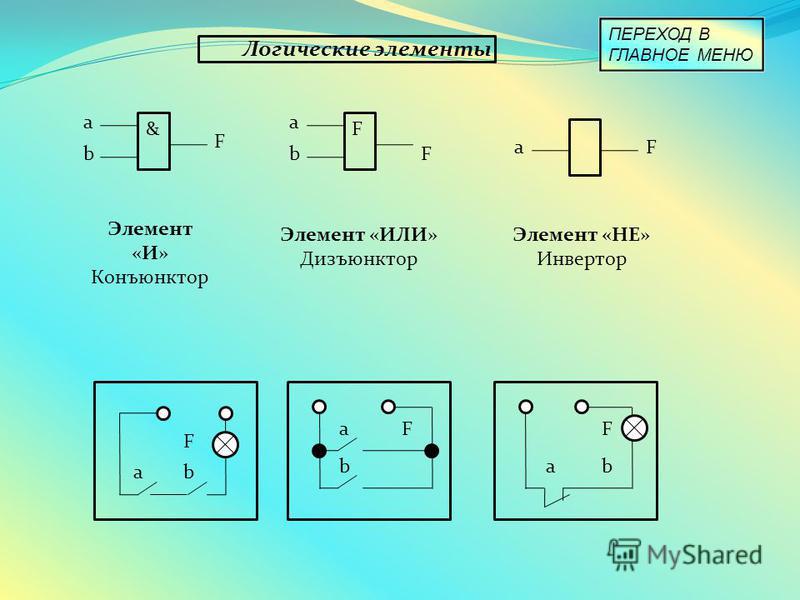
| Рис. 7 |
| Рис. 8 |
Универсальные логические элементы
Универсальные логические
элементы могут использоваться для
выполнения разнообразных операций
над своими входными данными.
Конкретная операция зависит от
того, какие сигналы поданы на
управляющие входы. Чтобы
синтезировать такой универсальный
логический элемент, обычно
пользуются СКНФ или СДНФ, как и в
синтезе комбинационных логических
схем.
Электрические принципиальные схемы логических элементов
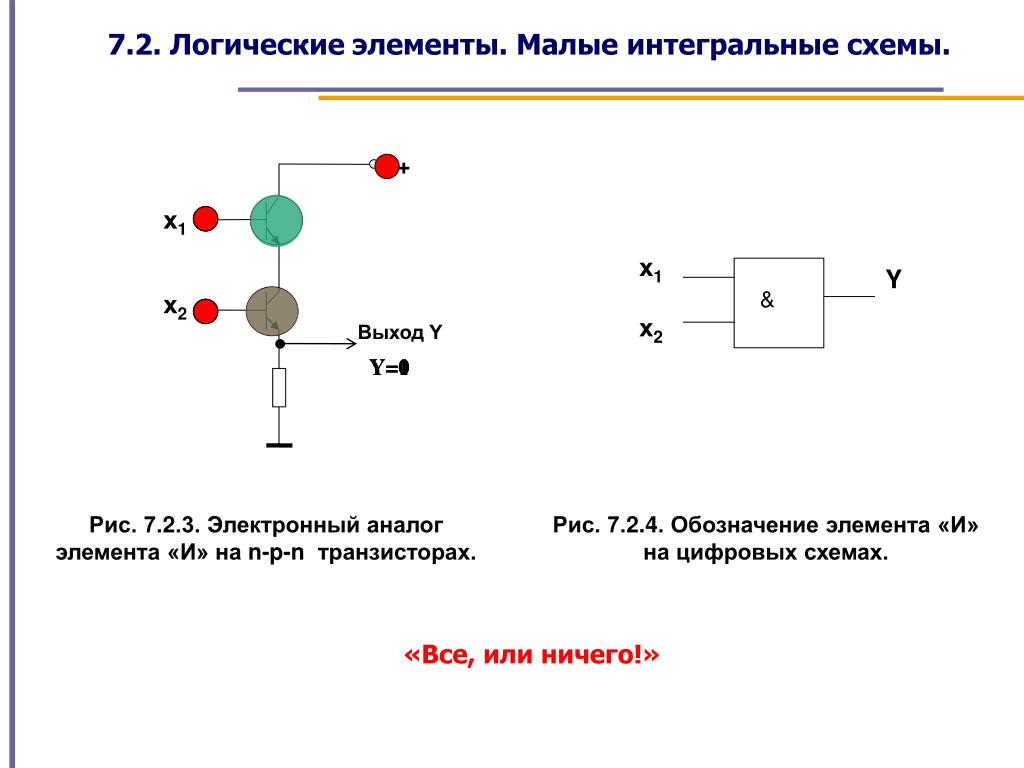
Рассмотрим электрические принципиальные схемы логического элемента И-НЕ с n входами — ДТЛ (рис. 9) и логического элемента И-НЕ с n входами — ТТЛ (рис. 10).
| Рис. 9 |
| Рис. 10 |
На рисунках +U обозначает положительный потенциал источника питания, а -U — отрицательный.
Рассмотрим сначала работу
схемы на рис. 9. Если к одному из
входных диодов приложено
напряжение логического 0, то этот
диод открыт и на базу транзистора
подаётся напряжение логического 0. Транзистор закрывается и на выходе
Транзистор закрывается и на выходе
Теперь рассмотрим работу
схемы на рис. 10. Вызывает некоторый
интерес необычный транзистор на
входе и схема его включения. Такие
многоэмиттерные транзисторы
всегда используются на входах
логических элементов ТТЛ.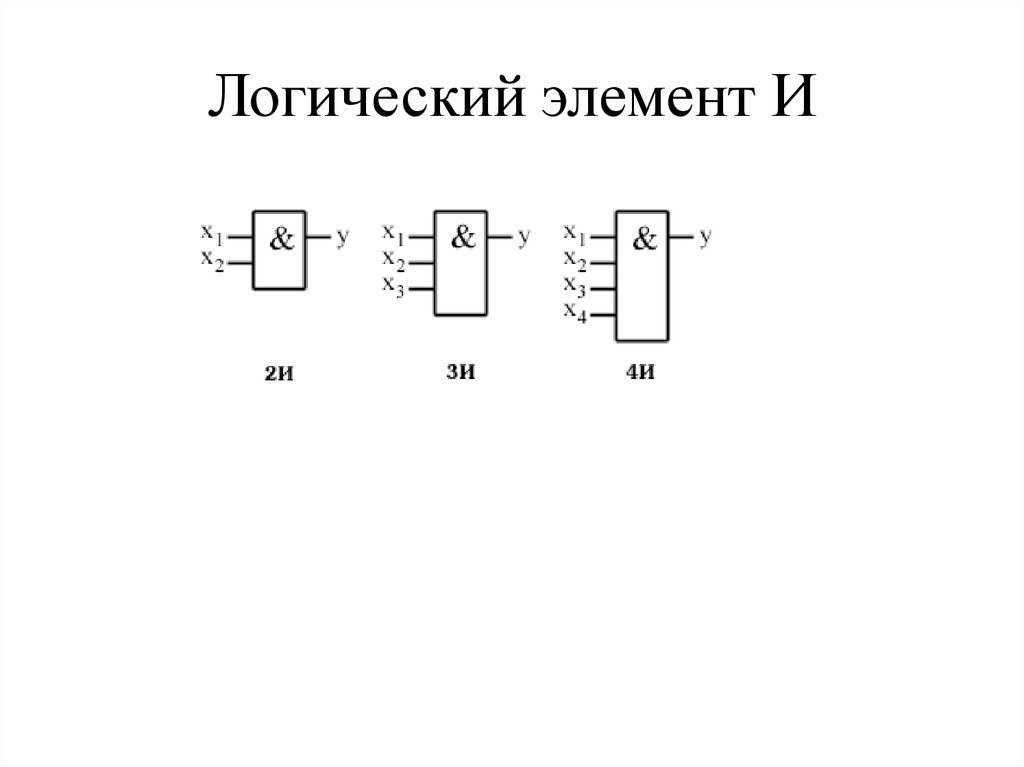 Сам
транзистор выполняет логическую
операцию И. При подаче на один из
входов напряжения логического
нуля, транзистор открывается и,
таким образом, на коллекторе
устанавливается напряжение
логического 0. Напряжение
логической 1 будет на коллекторе
только тогда, когда на всех входах
будет напряжение логической 1.
Подобный транзистор можно
рассматривать как много n-p
переходов, а соответственно, как
много диодов. Таким образом такое
включение транзистора в цепь
эквивалентно диодной сборке на
входе логического элемента И на
рис. 9.
Сам
транзистор выполняет логическую
операцию И. При подаче на один из
входов напряжения логического
нуля, транзистор открывается и,
таким образом, на коллекторе
устанавливается напряжение
логического 0. Напряжение
логической 1 будет на коллекторе
только тогда, когда на всех входах
будет напряжение логической 1.
Подобный транзистор можно
рассматривать как много n-p
переходов, а соответственно, как
много диодов. Таким образом такое
включение транзистора в цепь
эквивалентно диодной сборке на
входе логического элемента И на
рис. 9.
Применение логических элементов
Логические элементы могут
использоваться как
самостоятельные части схемы, так и
входить в состав более сложной
цифровой комбинационной схемы или
схемы с памятью. Как
самостоятельные части схемы,
логические элементы могут
применяться в качестве управляющей
логики какого-либо устройства, а
также в качестве генератора
прямоугольных импульсов с
подключённой ёмкостью или
кварцевым резонатором.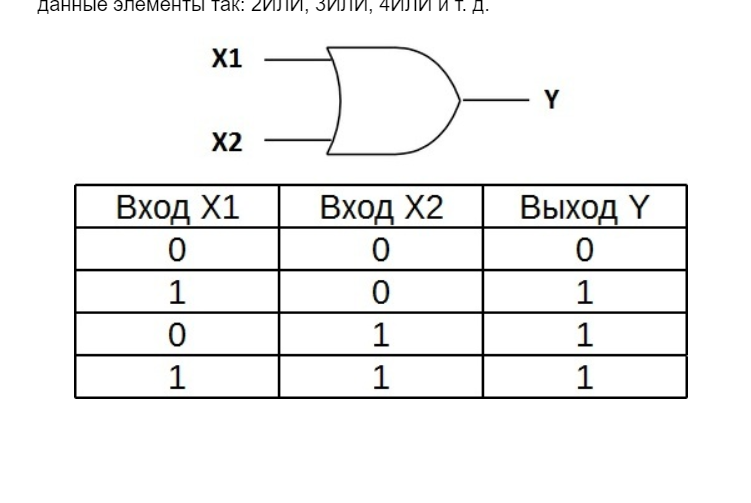 В качестве
комбинационных схем логические
элементы используются в составе
микросхем БИС и СБИС, а также в
дешифраторах и шифраторах,
выполненных в виде отдельных
микросхем. Также, логические
элементы могут входить в состав
схем с памятью (триггеры, регистры,
счётчики и т.д.), выполненных в виде
отдельной микросхемы или в составе
других микросхем.
В качестве
комбинационных схем логические
элементы используются в составе
микросхем БИС и СБИС, а также в
дешифраторах и шифраторах,
выполненных в виде отдельных
микросхем. Также, логические
элементы могут входить в состав
схем с памятью (триггеры, регистры,
счётчики и т.д.), выполненных в виде
отдельной микросхемы или в составе
других микросхем.
Применение исключающее или. Элементы исключающее или. Приоритет логических операций
В Булевой алгебре, на которой базируется вся цифровая техника, электронные элементы должны выполнять ряд определённых действий. Это так называемый логический базис. Вот три основных действия:
ИЛИ — логическое сложение (дизъюнкция ) — OR ;
И — логическое умножение (конъюнкция ) — AND ;
НЕ — логическое отрицание (инверсия ) — NOT .
Примем за основу позитивную логику, где высокий уровень будет «1», а низкий уровень примем за «0».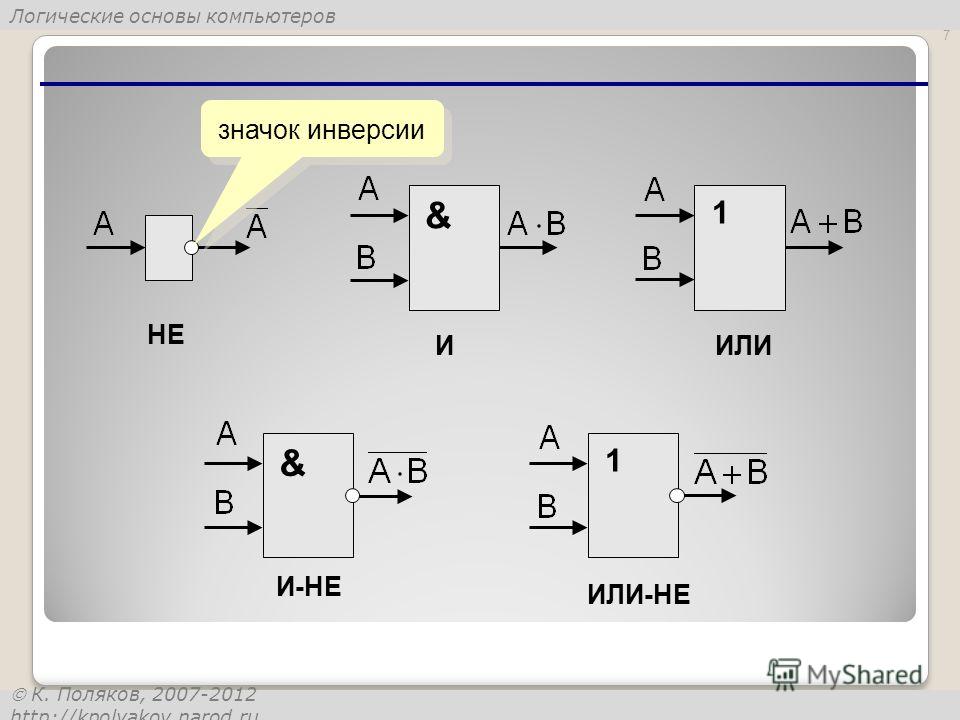 Чтобы можно было более наглядно рассмотреть выполнение логических операций, существуют таблицы истинности для каждой логической функции. Сразу нетрудно понять, что выполнение логических функций «и» и «или» подразумевают количество входных сигналов не менее двух, но их может быть и больше.
Чтобы можно было более наглядно рассмотреть выполнение логических операций, существуют таблицы истинности для каждой логической функции. Сразу нетрудно понять, что выполнение логических функций «и» и «или» подразумевают количество входных сигналов не менее двух, но их может быть и больше.
Логический элемент И.
На рисунке представлена таблица истинности элемента «И » с двумя входами. Хорошо видно, что логическая единица появляется на выходе элемента только при наличии единицы на первом входе и на втором. В трёх остальных случаях на выходе будут нули.
| Вход X1 | Вход X2 | Выход Y |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
На принципиальных схемах логический элемент «И» обозначают так.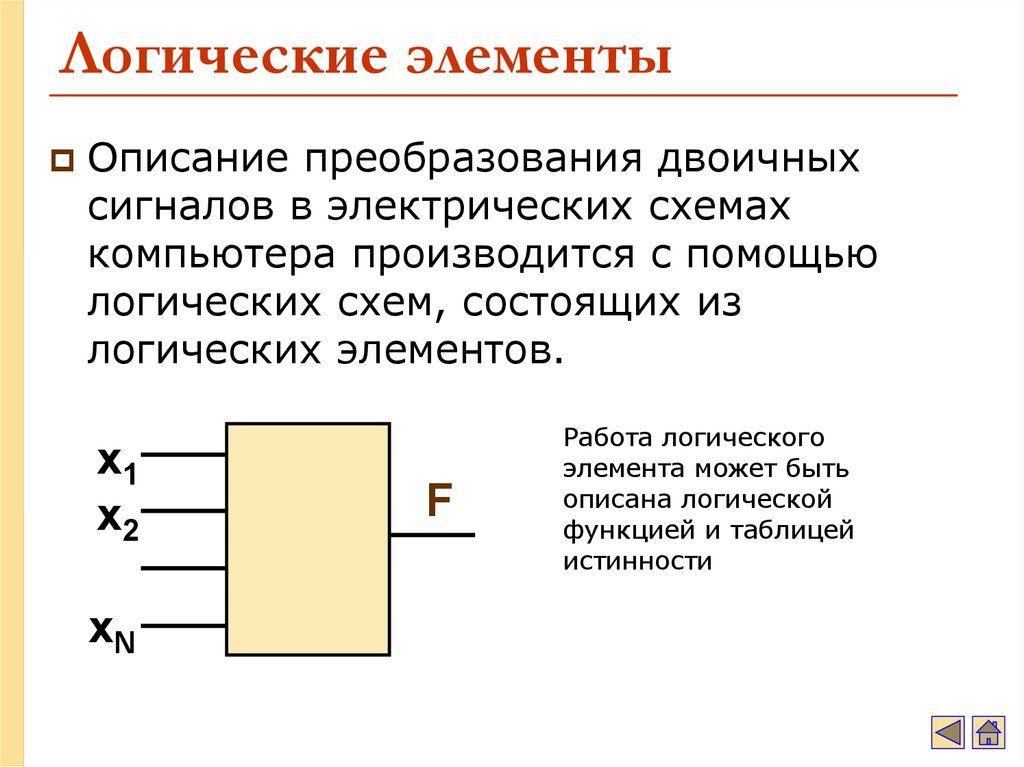
На зарубежных схемах обозначение элемента «И» имеет другое начертание. Его кратко называют AND .
Логический элемент ИЛИ.
Элемент «ИЛИ » с двумя входами работает несколько по-другому. Достаточно логической единицы на первом входе или на втором как на выходе будет логическая единица. Две единицы так же дадут единицу на выходе.
| Вход X1 | Вход X2 | Выход Y |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
На схемах элемент «ИЛИ» изображают так.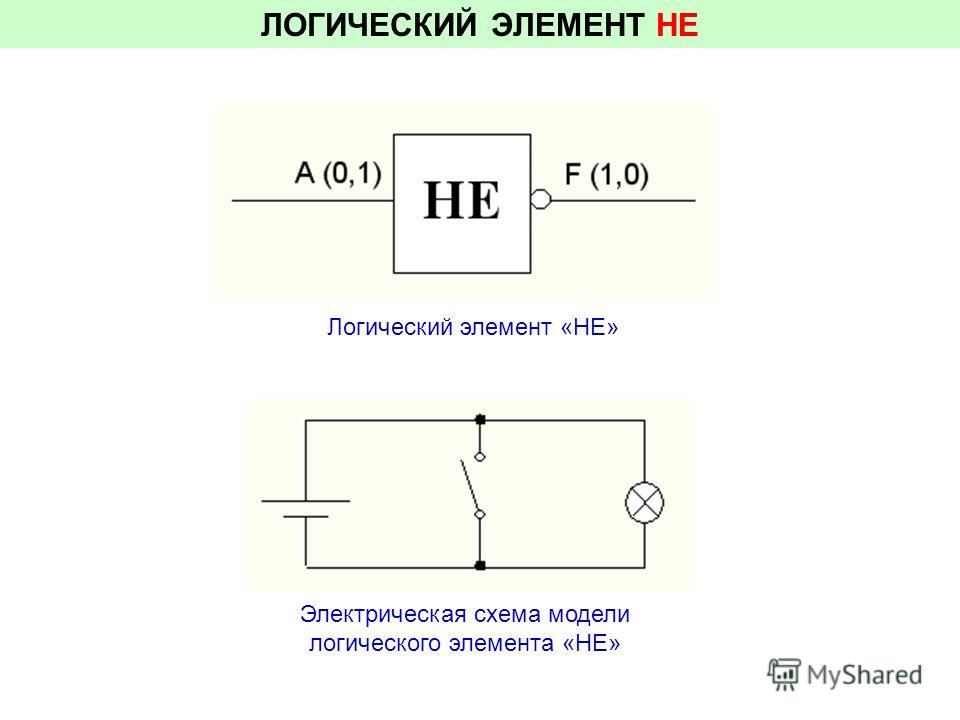
На зарубежных схемах его изображают чуть по-другому и называют элементом OR .
Логический элемент НЕ.
Элемент, выполняющий функцию инверсии «НЕ » имеет один вход и один выход. Он меняет уровень сигнала на противоположный. Низкий потенциал на входе даёт высокий потенциал на выходе и наоборот.
| Вход X | Выход Y |
|---|---|
| 0 | 1 |
| 1 | 0 |
Вот таким образом его показывают на схемах.
В зарубежной документации элемент «НЕ» изображают следующим образом. Сокращённо называют его NOT .
Все эти элементы в интегральных микросхемах могут объединяться в различных сочетаниях. Это элементы: И-НЕ, ИЛИ-НЕ, и более сложные конфигурации. Пришло время поговорить и о них.
Это элементы: И-НЕ, ИЛИ-НЕ, и более сложные конфигурации. Пришло время поговорить и о них.
Логический элемент 2И-НЕ.
Рассмотрим несколько реальных логических элементов на примере серии транзисторно-транзисторной логики (ТТЛ) К155 с малой степенью интеграции. На рисунке когда-то очень популярная микросхема К155ЛА3, которая содержит четыре независимых элемента 2И — НЕ . Кстати, с помощью её можно собрать простейший маячок на микросхеме .
Цифра всегда обозначает число входов логического элемента. В данном случае это двухвходовой элемент «И» выходной сигнал которого инвертируется. Инвертируется, это значит «0» превращается в «1», а «1» превращается в «0». Обратим внимание на кружочек на выходах — это символ инверсии . В той же серии существуют элементы 3И-НЕ, 4И-НЕ, что означает элементы «И» с различным числом входов (3, 4 и т.д.).
Как вы уже поняли, один элемент 2И-НЕ изображается вот так.
По сути это упрощённое изображение двух объёдинённых элементов: элемента 2И и элемента НЕ на выходе.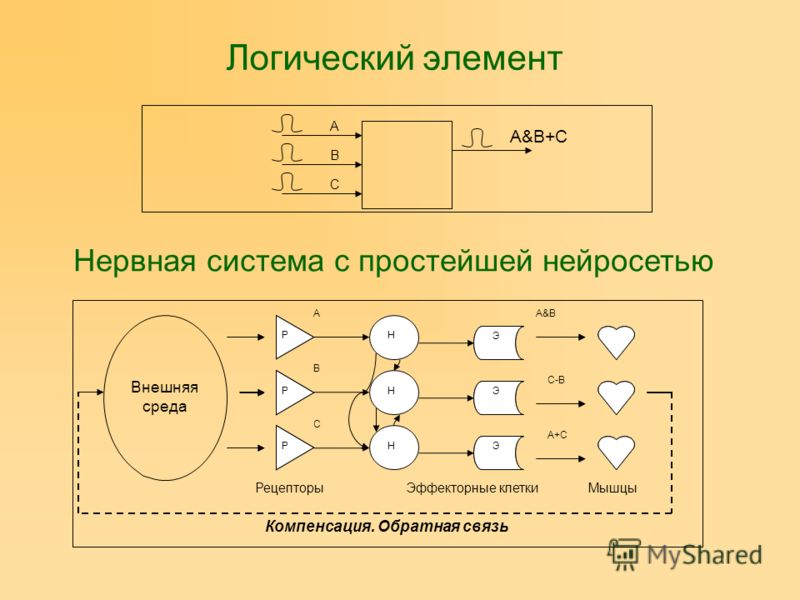
Зарубежное обозначение элемента И-НЕ (в данном случае 2И-НЕ). Называется NAND .
Таблица истинности для элемента 2И-НЕ.
| Вход X1 | Вход X2 | Выход Y |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
В таблице истинности элемента 2И — НЕ мы видим, что благодаря инвертору получается картина противоположная элементу «И». В отличие от трёх нулей и одной единицы мы имеем три единицы и ноль. Элемент «И — НЕ» часто называют элементом Шеффера.
В отличие от трёх нулей и одной единицы мы имеем три единицы и ноль. Элемент «И — НЕ» часто называют элементом Шеффера.
Логический элемент 2ИЛИ-НЕ.
Логический элемент 2ИЛИ — НЕ представлен в серии К155 микросхемой 155ЛЕ1. Она содержит в одном корпусе четыре независимых элемента. Таблица истинности так же отличается от схемы «ИЛИ» применением инвертирования выходного сигнала.
Таблица истинности для логического элемента 2ИЛИ-НЕ.
| Вход X1 | Вход X2 | Выход Y |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 0 |
Изображение на схеме.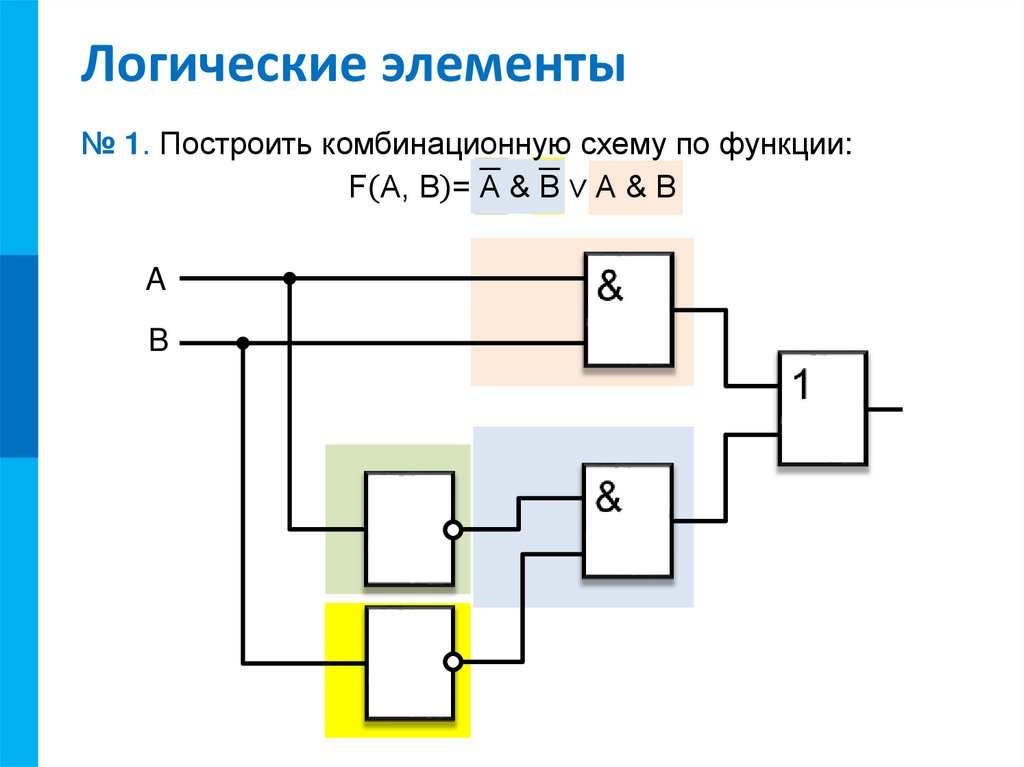
На зарубежный лад изображается так. Называют как NOR .
Мы имеем только один высокий потенциал на выходе, обусловленный подачей на оба входа одновременно низкого потенциала. Здесь, как и на любых других принципиальных схемах, кружочек на выходе подразумевает инвертирование сигнала. Так как схемы И — НЕ и ИЛИ — НЕ встречаются очень часто, то для каждой функции имеется своё условное обозначение. Функция И — НЕ обозначается значком «& «, а функция ИЛИ — НЕ значком «1 «.
Для отдельного инвертора таблица истинности уже приведена выше. Можно добавить, что количество инверторов в одном корпусе может достигать шести.
Логический элемент «исключающее ИЛИ».
К числу базовых логических элементов принято относить элемент реализующий функцию «исключающее ИЛИ». Иначе эта функция называется «неравнозначность».
Высокий потенциал на выходе возникает только в том случае, если входные сигналы не равны. То есть на одном из входов должна быть единица, а на другом ноль.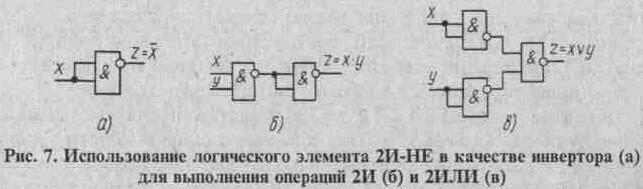 Если на выходе логического элемента имеется инвертор, то функция выполняется противоположная — «равнозначность». Высокий потенциал на выходе будет появляться при одинаковых сигналах на обоих входах.
Если на выходе логического элемента имеется инвертор, то функция выполняется противоположная — «равнозначность». Высокий потенциал на выходе будет появляться при одинаковых сигналах на обоих входах.
Таблица истинности.
| Вход X1 | Вход X2 | Выход Y |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
Эти логические элементы находят своё применение в сумматорах. «Исключающее ИЛИ» изображается на схемах знаком равенства перед единицей «=1 «.
«Исключающее ИЛИ» изображается на схемах знаком равенства перед единицей «=1 «.
На зарубежный манер «исключающее ИЛИ» называют XOR и на схемах рисуют вот так.
Кроме вышеперечисленных логических элементов, которые выполняют базовые логические функции очень часто, используются элементы, объединённые в различных сочетаниях. Вот, например, К555ЛР4. Она называется очень серьёзно 2-4И-2ИЛИ-НЕ.
Её таблица истинности не приводится, так как микросхема не является базовым логическим элементом. Такие микросхемы выполняют специальные функции и бывают намного сложнее, чем приведённый пример. Так же в логический базис входят и простые элементы «И» и «ИЛИ». Но они используются гораздо реже. Может возникнуть вопрос, почему эта логика называется транзисторно-транзисторной.
Если посмотреть в справочной литературе схему, допустим, элемента 2И — НЕ из микросхемы К155ЛА3, то там можно увидеть несколько транзисторов и резисторов. На самом деле ни резисторов, ни диодов в этих микросхемах нет.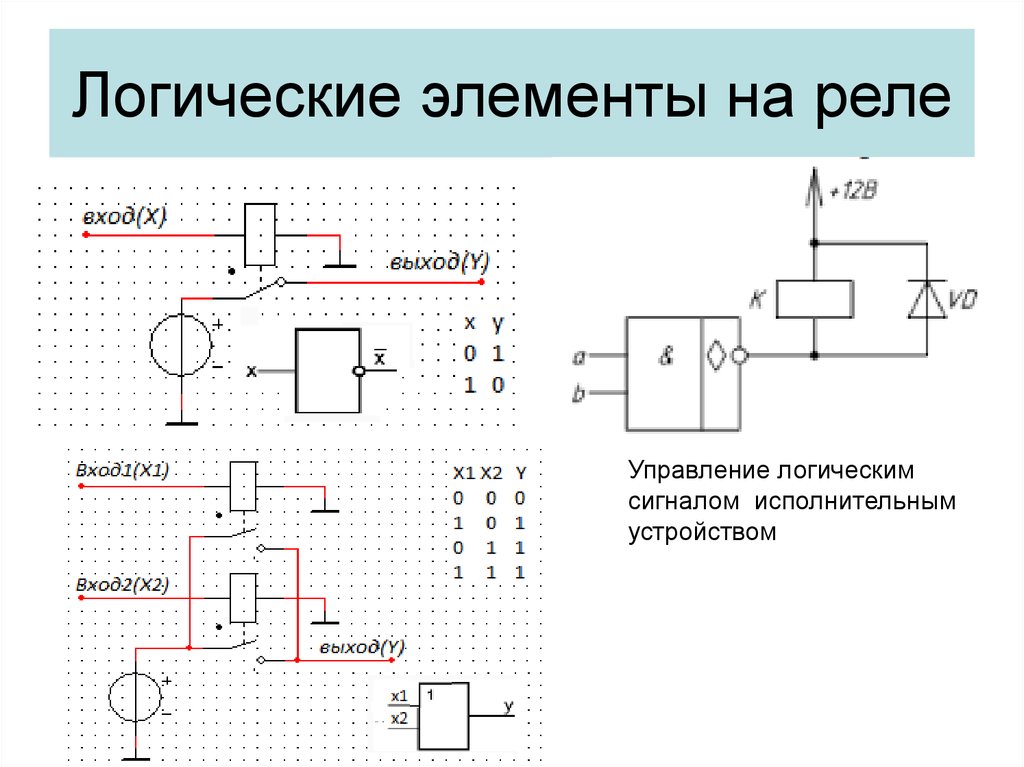 На кристалл кремния через трафарет напыляются только транзисторы, а функции резисторов и диодов выполняют эмиттерные переходы транзисторов. Кроме того в ТТЛ логике широко используются многоэмиттерные транзисторы. Например, на входе элемента 4И стоит четырёхэмиттерный
На кристалл кремния через трафарет напыляются только транзисторы, а функции резисторов и диодов выполняют эмиттерные переходы транзисторов. Кроме того в ТТЛ логике широко используются многоэмиттерные транзисторы. Например, на входе элемента 4И стоит четырёхэмиттерный
Электрическая схема, предназначенная для выполнения какой-либо логической операции с входными данными, называется логическим элементом. Входные данные представляются здесь в виде напряжений различных уровней, и результат логической операции на выходе — также получается в виде напряжения определенного уровня.
Операнды в данном случае подаются — на вход логического элемента поступают сигналы в форме напряжения высокого или низкого уровня, которые и служат по сути входными данными. Так, напряжение высокого уровня — это логическая единица 1 — обозначает истинное значение операнда, а напряжение низкого уровня 0 — значение ложное. 1 — ИСТИНА, 0 — ЛОЖЬ.
Логический элемент
— элемент, осуществляющий определенные логические зависимость между входными и выходными сигналами.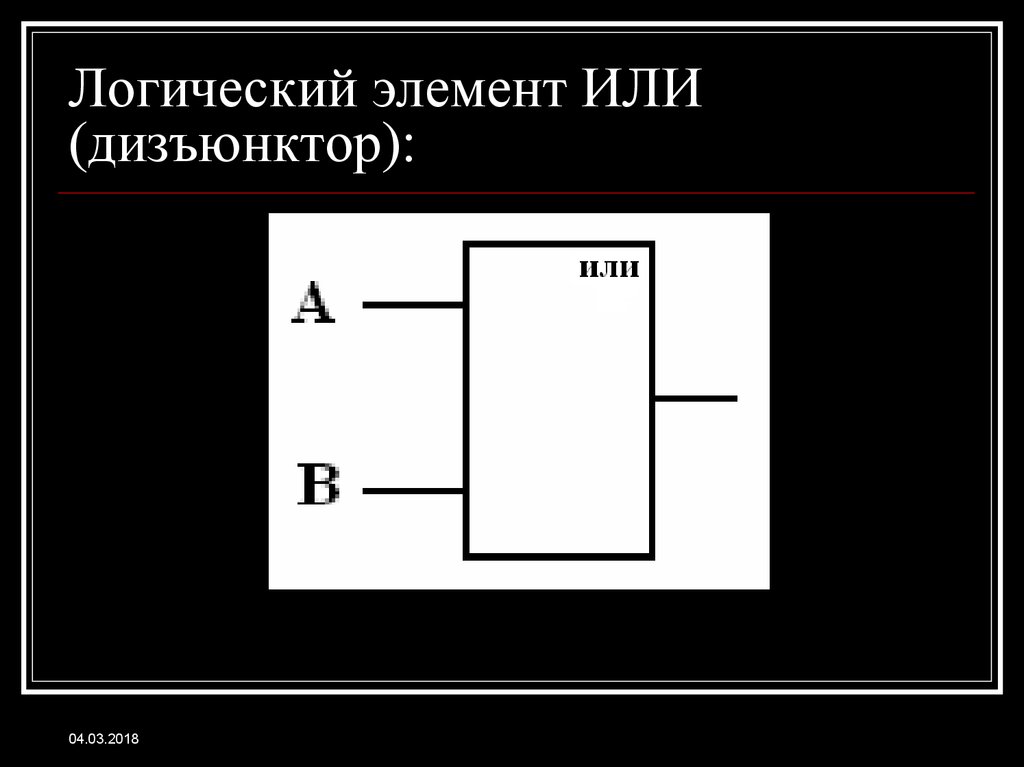 Логические элементы обычно используются для построения логических схем вычислительных машин, дискретных схем автоматического контроля и управления. Для всех видов логических элементов, независимо от их физической природы, характерны дискретные значения входных и выходных сигналов.
Логические элементы обычно используются для построения логических схем вычислительных машин, дискретных схем автоматического контроля и управления. Для всех видов логических элементов, независимо от их физической природы, характерны дискретные значения входных и выходных сигналов.
Логические элементы имеют один или несколько входов и один или два (обычно инверсных друг другу) выхода. Значения «нулей» и «единиц» выходных сигналов логических элементов определяются логической функцией, которую выполняет элемент, и значениями «нулей» и «единиц» входных сигналов, играющих роль независимых переменных. Существуют элементарные логические функции, из которых можно составить любую сложную логическую функцию.
В зависимости от устройства схемы элемента, от ее электрических параметров, логические уровни (высокие и низкие уровни напряжения) входа и выхода имеют одинаковые значения для высокого и низкого (истинного и ложного) состояний.
Традиционно логические элементы выпускаются в виде специальных радиодеталей — интегральных микросхем. Логические операции, такие как конъюнкция, дизъюнкция, отрицание и сложение по модулю (И, ИЛИ, НЕ, исключающее ИЛИ) — являются основными операциями, выполняемыми на логических элементах основных типов. Далее рассмотрим каждый из этих типов логических элементов более внимательно.
Логические операции, такие как конъюнкция, дизъюнкция, отрицание и сложение по модулю (И, ИЛИ, НЕ, исключающее ИЛИ) — являются основными операциями, выполняемыми на логических элементах основных типов. Далее рассмотрим каждый из этих типов логических элементов более внимательно.
Логический элемент «И» — конъюнкция, логическое умножение, AND
«И» — логический элемент, выполняющий над входными данными операцию конъюнкции или логического умножения. Данный элемент может иметь от 2 до 8 (наиболее распространены в производстве элементы «И» с 2, 3, 4 и 8 входами) входов и один выход.
Условные обозначения логических элементов «И» с разным количеством входов приведены на рисунке. В тексте логический элемент «И» с тем или иным числом входов обозначается как «2И», «4И» и т. д. — элемент «И» с двумя входами, с четырьмя входами и т. д.
Таблица истинности для элемента 2И показывает, что на выходе элемента будет логическая единица лишь в том случае, если логические единицы будут одновременно на первом входе И на втором входе.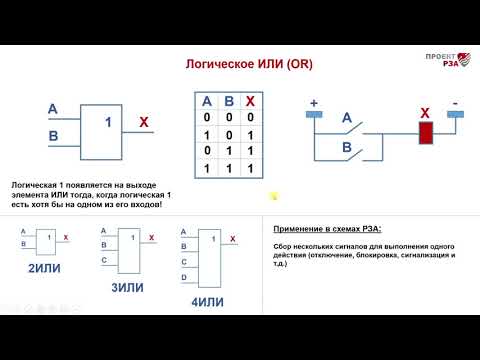 В остальных трех возможных случаях на выходе будет ноль.
В остальных трех возможных случаях на выходе будет ноль.
На западных схемах значок элемента «И» имеет прямую черту на входе и закругление на выходе. На отечественных схемах — прямоугольник с символом «&».
Логический элемент «ИЛИ» — дизъюнкция, логическое сложение, OR
«ИЛИ» — логический элемент, выполняющий над входными данными операцию дизъюнкции или логического сложения. Он так же как и элемент «И» выпускается с двумя, тремя, четырьмя и т. д. входами и с одним выходом. Условные обозначения логических элементов «ИЛИ» с различным количеством входов показаны на рисунке. Обозначаются данные элементы так: 2ИЛИ, 3ИЛИ, 4ИЛИ и т. д.
Таблица истинности для элемента «2ИЛИ» показывает, что для появления на выходе логической единицы, достаточно чтобы логическая единица была на первом входе ИЛИ на втором входе. Если логические единицы будут сразу на двух входах, на выходе также будет единица.
На западных схемах значок элемента «ИЛИ» имеет закругление на входе и закругление с заострением на выходе.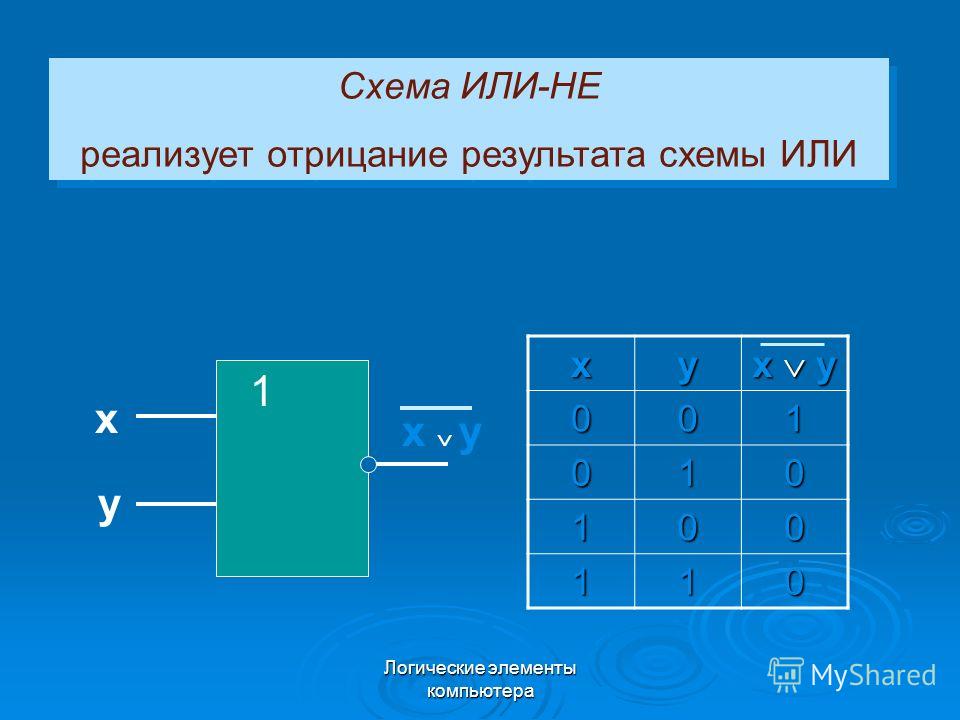 На отечественных схемах — прямоугольник с символом «1».
На отечественных схемах — прямоугольник с символом «1».
Логический элемент «НЕ» — отрицание, инвертор, NOT
«НЕ» — логический элемент, выполняющий над входными данными операцию логического отрицания. Данный элемент, имеющий один выход и только один вход, называют еще инвертором, поскольку он на самом деле инвертирует (обращает) входной сигнал. На рисунке приведено условное обозначение логического элемента «НЕ».
Таблица истинности для инвертора показывает, что высокий потенциал на входе даёт низкий потенциал на выходе и наоборот.
На западных схемах значок элемента «НЕ» имеет форму треугольника с кружочком на выходе. На отечественных схемах — прямоугольник с символом «1», с кружком на выходе.
Логический элемент «И-НЕ» — конъюнкция (логическое умножение) с отрицанием, NAND
«И-НЕ» — логический элемент, выполняющий над входными данными операцию логического сложения, и затем операцию логического отрицания, результат подается на выход.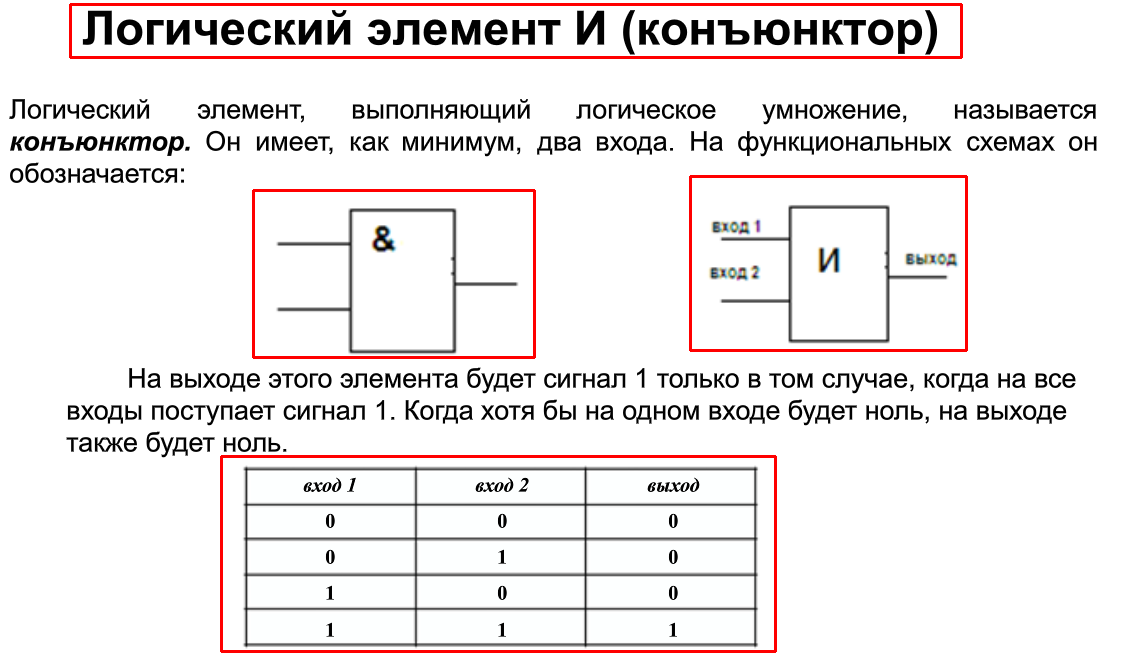 Другими словами, это в принципе элемент «И», дополненный элементом «НЕ». На рисунке приведено условное обозначение логического элемента «2И-НЕ».
Другими словами, это в принципе элемент «И», дополненный элементом «НЕ». На рисунке приведено условное обозначение логического элемента «2И-НЕ».
Таблица истинности для элемента «И-НЕ» противоположна таблице для элемента «И». Вместо трех нулей и единицы — три единицы и ноль. Элемент «И-НЕ» называют еще «элемент Шеффера» в честь математика Генри Мориса Шеффера, впервые отметившего значимость этой в 1913 году. Обозначается как «И», только с кружочком на выходе.
Логический элемент «ИЛИ-НЕ» — дизъюнкция (логическое сложение) с отрицанием, NOR
«ИЛИ-НЕ» — логический элемент, выполняющий над входными данными операцию логического сложения, и затем операцию логического отрицания, результат подается на выход. Иначе говоря, это элемент «ИЛИ», дополненный элементом «НЕ» — инвертором. На рисунке приведено условное обозначение логического элемента «2ИЛИ-НЕ».
Таблица истинности для элемента «ИЛИ-НЕ» противоположна таблице для элемента «ИЛИ».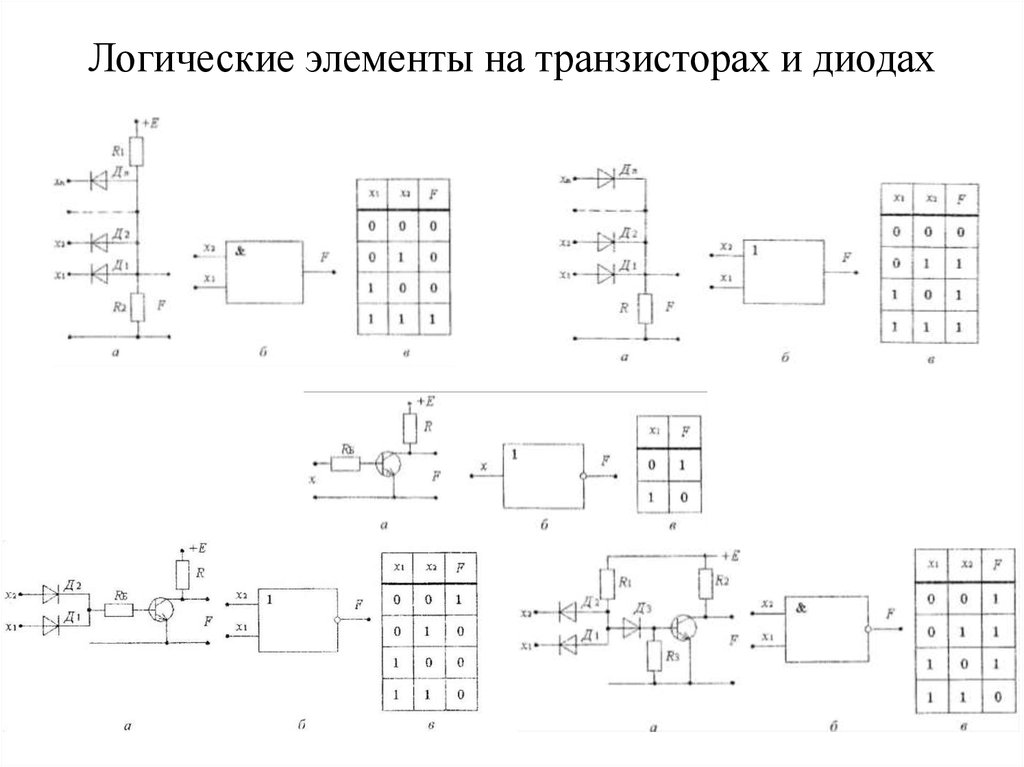 Высокий потенциал на выходе получается лишь в одном случае — на оба входа подаются одновременно низкие потенциалы. Обозначается как «ИЛИ», только с кружочком на выходе, обозначающим инверсию.
Высокий потенциал на выходе получается лишь в одном случае — на оба входа подаются одновременно низкие потенциалы. Обозначается как «ИЛИ», только с кружочком на выходе, обозначающим инверсию.
Логический элемент «исключающее ИЛИ» — сложение по модулю 2, XOR
«исключающее ИЛИ» — логический элемент, выполняющий над входными данными операцию логического сложения по модулю 2, имеет два входа и один выход. Часто данные элементы применяют в схемах контроля. На рисунке приведено условное обозначение данного элемента.
Изображение в западных схемах — как у «ИЛИ» с дополнительной изогнутой полоской на стороне входа, в отечественной — как «ИЛИ», только вместо «1» будет написано «=1».
Этот логический элемент еще называют «неравнозначность». Высокий уровень напряжения будет на выходе лишь тогда, когда сигналы на входе не равны (на одном единица, на другом ноль или на одном ноль, а на другом единица) если даже на входе будут одновременно две единицы, на выходе будет ноль — в этом отличие от «ИЛИ».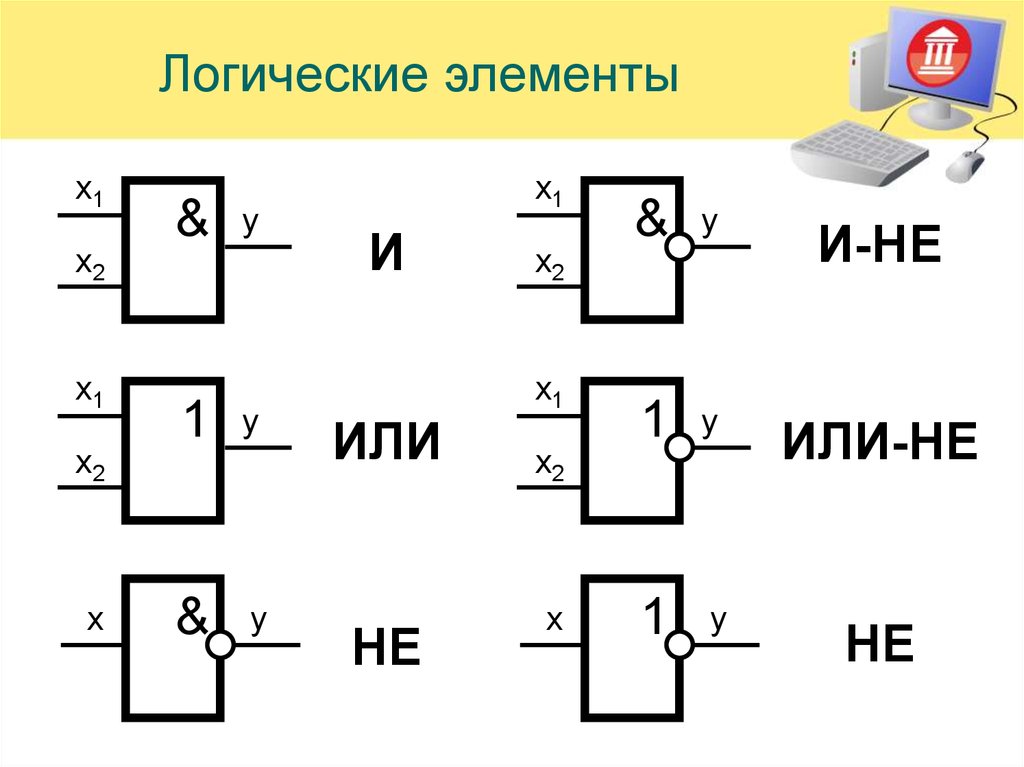 Данные элементы логики широко применяются в сумматорах.
Данные элементы логики широко применяются в сумматорах.
Поведение
Элементы Исключающее ИЛИ, Исключающее ИЛИ-НЕ, Нечётность и Чётность вычисляют соответствующую функцию от значений на входах и выдают результат на выход.
По умолчанию, неподключенные входы игнорируются — то есть, если входы действительно не имеют ничего подключенного к ним — даже провода. Таким образом, вы можете добавить 5-входовый элемент, но подключить только два входа, и он будет работать как 2-входовый элемент; это избавляет вас от необходимости беспокоиться о настройке количества входов каждый раз при создании элемента. (Если все входы не подключены, то на выходе значение ошибки X .) Некоторые пользователи, однако, предпочитают, чтобы Logisim настаивал, чтобы все входы были подключены, поскольку это соответствует реальным элементам. Вы можете включить это поведение, выбрав меню Проект > Параметры…, перейдя на вкладку Моделирование, и выбрав вариант Ошибка для неопределённых входов для Выход элемента при неопределённости.
Двухвходовая таблица истинности для элементов следующая.
| x | y | Исключающее ИЛИ | Исключающее ИЛИ-НЕ | Нечётность | Чётность |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 | 1 |
Как вы можете видеть, элементы Нечётность и Исключающее ИЛИ ведут себя одинаково в случае двух входов; аналогично, элементы Чётность и Исключающее ИЛИ-НЕ ведут себя одинаково. Но если входов с определённым значением больше двух, то элемент Исключающее ИЛИ будет давать на выходе 1, когда единица строго на одном входе, тогда как элемент Нечётность даст на выходе 1, когда единица на нечётном количестве входов. Элемент Исключающее ИЛИ-НЕ будет давать на выходе 1, когда входов с единицей строго не один, тогда как элемент Чётность даст 1, когда входов с единицей чётное количество. Элементы Исключающее ИЛИ и Исключающее ИЛИ-НЕ имеют атрибут, названный Многовходовое поведение, который позволяет настроить их на использование поведения элементов Нечётность и Чётность.
Но если входов с определённым значением больше двух, то элемент Исключающее ИЛИ будет давать на выходе 1, когда единица строго на одном входе, тогда как элемент Нечётность даст на выходе 1, когда единица на нечётном количестве входов. Элемент Исключающее ИЛИ-НЕ будет давать на выходе 1, когда входов с единицей строго не один, тогда как элемент Чётность даст 1, когда входов с единицей чётное количество. Элементы Исключающее ИЛИ и Исключающее ИЛИ-НЕ имеют атрибут, названный Многовходовое поведение, который позволяет настроить их на использование поведения элементов Нечётность и Чётность.
Если на каких-либо входах значение ошибки (например, если противоречивые значения поступают на один и тот же провод) или плавающее значение, то на выходе будет значение ошибки.
Многобитные версии каждого элемента будут выполнять свои однобитные преобразования над входами поразрядно.
Примечание: многие специалисты утверждают, что поведение фигурного элемента Исключающее ИЛИ должно соответствовать поведению элемента Нечётность, но по этому вопросу нет согласия.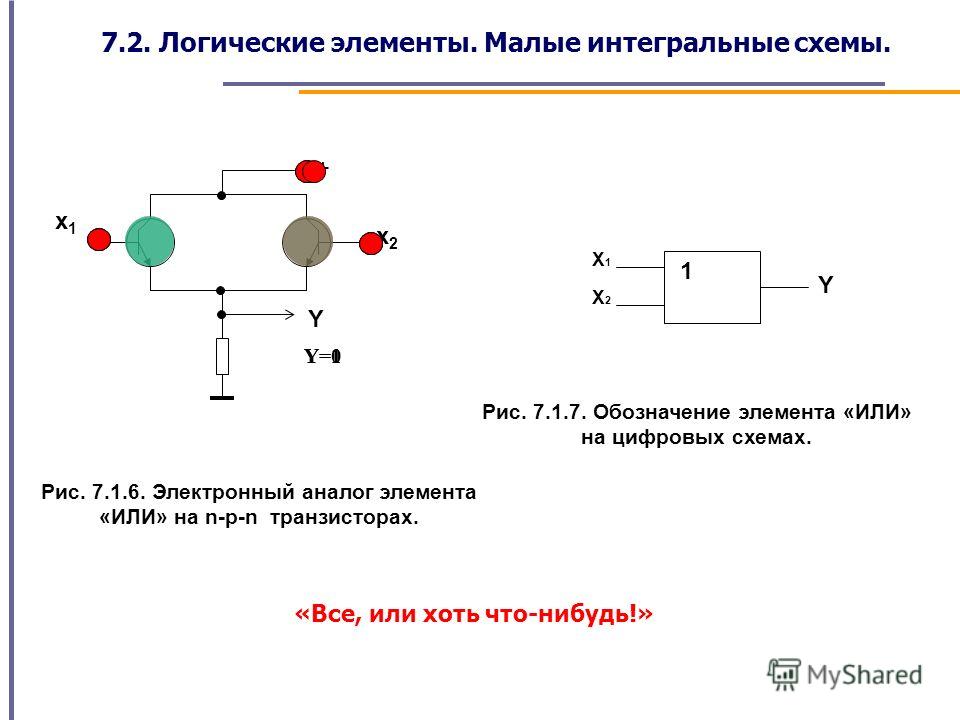 Поведение Logisim по умолчанию для элемента Исключающее ИЛИ основано на стандарте IEEE 91. Это также согласуется с интуитивным пониманием термина Исключающее ИЛИ : официант, спрашивающий, хотите вы гарнир из картофельного пюре, моркови, зеленого горошка, или шинкованной капусты, примет только один выбор, а не три, независимо от того, что вам могут сказать некоторые специалисты. (Должен признать, однако, что я не подвергал это заявление серьезным испытаниям.) Вы можете настроить элементы Исключающее ИЛИ и Исключающее ИЛИ-НЕ на использование одного из вариантов, меняя его атрибут Многовходовое поведение.
Поведение Logisim по умолчанию для элемента Исключающее ИЛИ основано на стандарте IEEE 91. Это также согласуется с интуитивным пониманием термина Исключающее ИЛИ : официант, спрашивающий, хотите вы гарнир из картофельного пюре, моркови, зеленого горошка, или шинкованной капусты, примет только один выбор, а не три, независимо от того, что вам могут сказать некоторые специалисты. (Должен признать, однако, что я не подвергал это заявление серьезным испытаниям.) Вы можете настроить элементы Исключающее ИЛИ и Исключающее ИЛИ-НЕ на использование одного из вариантов, меняя его атрибут Многовходовое поведение.
Контакты (предполагается, что компонент направлен на восток)
Западный край (входы, разрядность соответствует атрибуту Биты данных)
Входы компонента. Их будет столько, сколько указано в атрибуте Количество входов.
Заметьте, что если вы используете фигурные элементы, то западный край элементов Исключающее ИЛИ и Исключающее ИЛИ-НЕ будет искривлён. Тем не менее, входные контакты расположены вряд. Logisim отрисовывает короткие отрезки чтобы показать это; если вы перекроете отрезок, программа будет без предупреждений предполагать, что вы не хотели перекрыть его. При использовании «Вида для печати», эти отрезки не будут отрисованы, если не подключены к проводам.
Тем не менее, входные контакты расположены вряд. Logisim отрисовывает короткие отрезки чтобы показать это; если вы перекроете отрезок, программа будет без предупреждений предполагать, что вы не хотели перекрыть его. При использовании «Вида для печати», эти отрезки не будут отрисованы, если не подключены к проводам.
Восточный край (выход, разрядность соответствует атрибуту Биты данных)
Выход элемента, значение на котором вычисляется на основании текущих значений на входах, как описано выше.
Атрибуты
Когда компонент выбран, или уже добавлен, клавиши от 0 до 9 меняют его атрибут Количество входов, комбинации от Alt-0 до Alt-9 меняют его атрибут Биты данных, а клавиши со стрелками меняют его атрибут Направление.
Направление
Направление компонента (его выхода относительно его входов).
Биты данных
Разрядность входов и выходов компонента.
Размер элемента
Определяет, следует отрисовывать широкую или узкую версию компонента. Это не влияет на количество входов, которое определяется атрибутом Количество входов; правда, если количество входов превышает 3 (для узкого компонента) или 5 (для широкого), то элемент будет отрисовываться с «крыльями», чтобы вместить запрошенное количество входов.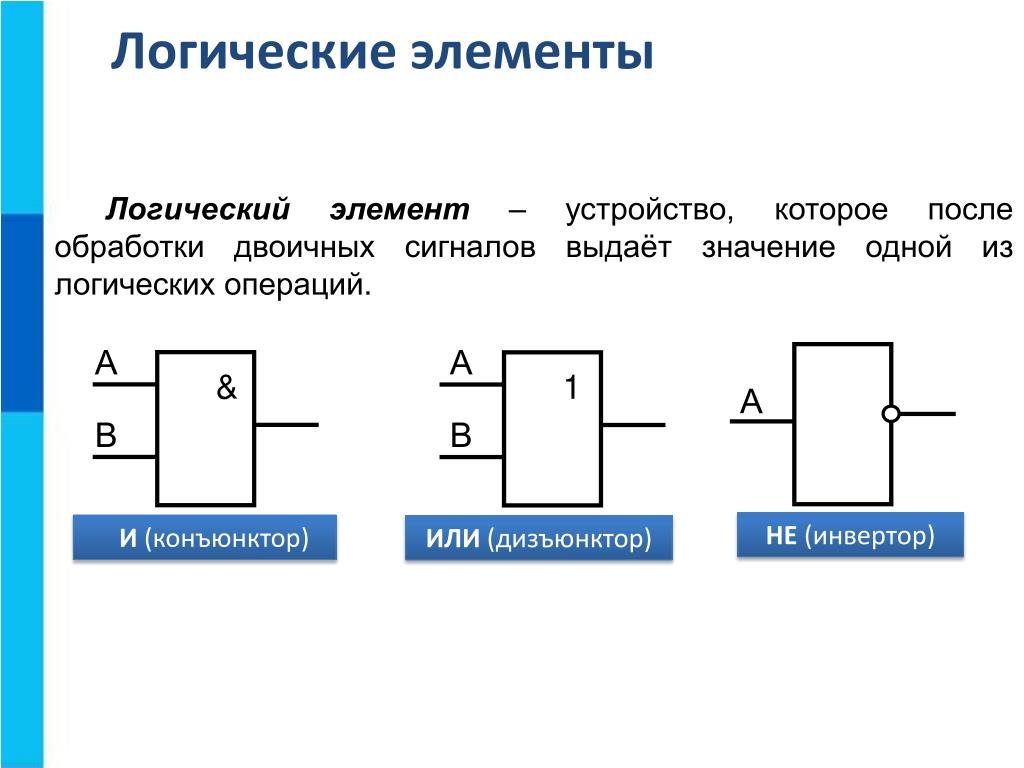 Количество входов
Определяет, сколько контактов на западном крае будет иметь компонент.
Многовходовое поведение (только для Исключающее ИЛИ и Исключающее ИЛИ-НЕ)
Когда входов три или более, то значение на выходе элементов Исключающее ИЛИ и Исключающее ИЛИ-НЕ будет основано или на том, что 1 строго на одном входе (по умолчанию), или на нечётном количестве входов.
Количество входов
Определяет, сколько контактов на западном крае будет иметь компонент.
Многовходовое поведение (только для Исключающее ИЛИ и Исключающее ИЛИ-НЕ)
Когда входов три или более, то значение на выходе элементов Исключающее ИЛИ и Исключающее ИЛИ-НЕ будет основано или на том, что 1 строго на одном входе (по умолчанию), или на нечётном количестве входов.
Бит — это минимальная единица измерения объёма информации, так как она хранит одно из двух значений — 0 (False) или 1 (True). False и True в переводе на русский ложь и истина соответственно. То есть одна битовая ячейка может находиться одновременно лишь в одном состоянии из возможных двух. Напомню, два возможных состояния битовой ячейки равны — 1 и 0.
Есть определённые операции, для манипуляций с битами. Эти операции называются логическими или булевыми операциями, названные в честь одного из математиков — Джорджа Буля (1815-1864), который способствовал развитию этой области науки.
Все эти операции могут быть применены к любому биту, независимо от того, какое он имеет значение — 0(нуль) или 1(единицу).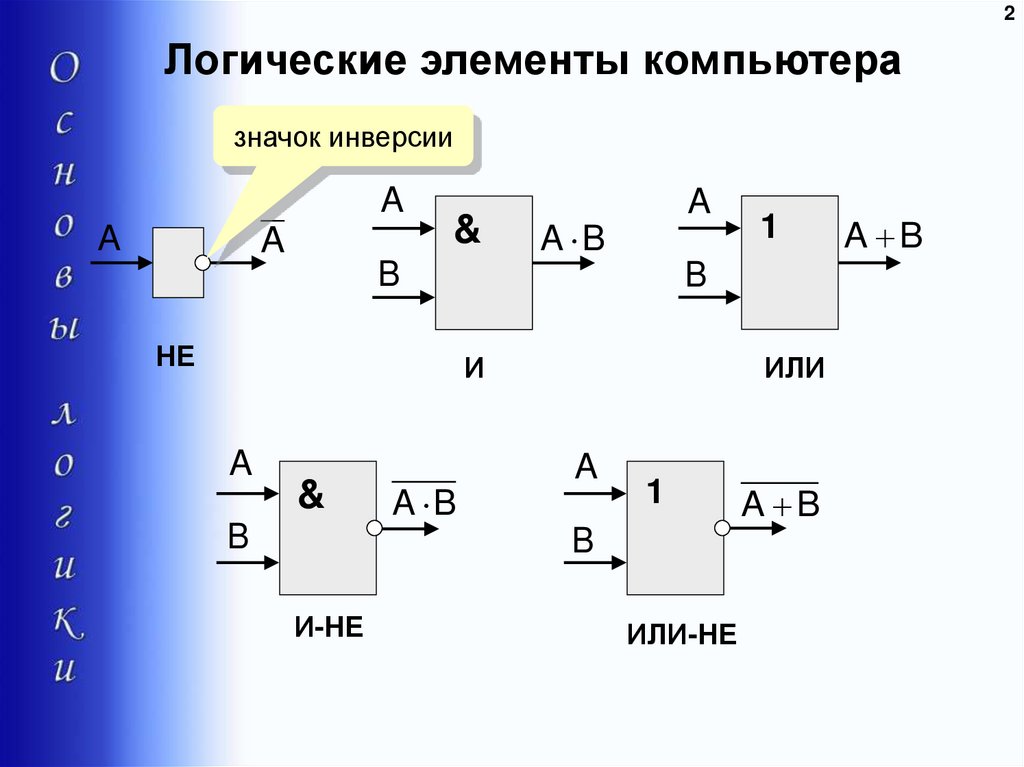 Ниже приведены основные логические операции и примеры их использования.
Ниже приведены основные логические операции и примеры их использования.
Логическая операция И (AND)
Обозначение AND: &
Логическая операция И выполняется с двумя битами, назовем их a и b. Результат выполнения логической операции И будет равен 1, если a и b равны 1, а во всех остальных (других) случаях, результат будет равен 0. Смотрим таблицу истинности логической операции and.
| a(бит 1) | b(бит 2) | a(бит 1) & b(бит 2) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Логическая операция ИЛИ (OR)
Обозначение OR: |
Логическая операция ИЛИ выполняется с двумя битами (a и b). Результат выполнения логической операции ИЛИ будет равен 0, если a и b равны 0 (нулю), а во всех остальных (других) случаях, результат равен 1 (единице). Смотрим таблицу истинности логической операции OR. b(бит 2)
b(бит 2)
Логическая операция НЕ (not)
Обозначение NOT: ~
Логическая операция НЕ выполняется с одним битом. Результат выполнения этой логической операции напрямую зависит от состояния бита. Если бит находился в нулевом состоянии, то результат выполнения NOT будет равен единице и наоборот. Смотрим таблицу истинности логической операции НЕ.
| a(бит 1) | ~a(отрицание бита) |
|---|---|
| 0 | 1 |
| 1 | 0 |
Запомните эти 4 логические операции. Используя эти логические операции, мы можем получить любой возможный результат. Подробно об использовании логических операций в С++ читаем .
Элементы Исключающее ИЛИ (по-английски — Exclusive-OR) также можно было бы отнести к простейшим элементам, но функция, выполняемая ими, несколько сложнее, чем в случае элемента И или элемента ИЛИ.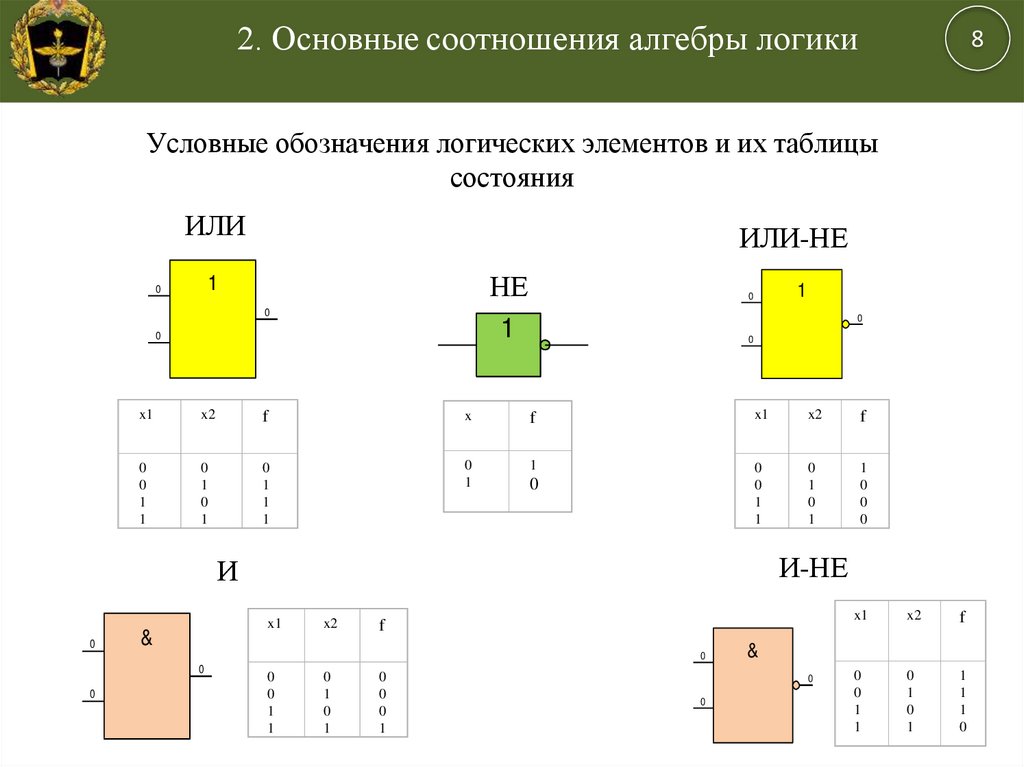 Все входы элементов Исключающее ИЛИ равноправны, однако ни один из входов не может заблокировать другие входы, установив выходной сигнал в уровень единицы или нуля.
Все входы элементов Исключающее ИЛИ равноправны, однако ни один из входов не может заблокировать другие входы, установив выходной сигнал в уровень единицы или нуля.
Рис. 4.1. Обозначения элементов Исключающее ИЛИ: зарубежные (слева) и отечественные (справа)
Под функцией Исключающее ИЛИ понимается следующее: единица на выходе появляется тогда, когда только на одном входе присутствует единица. Если единиц на входах две или больше, или если на всех входах нули, то на выходе будет нуль. Таблица истинности двухвходового элемента Исключающее ИЛИ приведена в табл. 4.1. Обозначения, принятые в отечественных и зарубежных схемах, показаны на рис. 4.1. Надпись на отечественном обозначении элемента Исключающее ИЛИ «=1» как раз и обозначает, что выделяется ситуация, когда на входах одна и только одна единица.
Элементов Исключающее ИЛИ в стандартных сериях немного. Отечественные серии предлагают микросхемы ЛП5 (четыре двухвходовых элемента с выходом 2С), ЛЛ3 и ЛП12, отличающиеся от ЛП5 выходом ОК.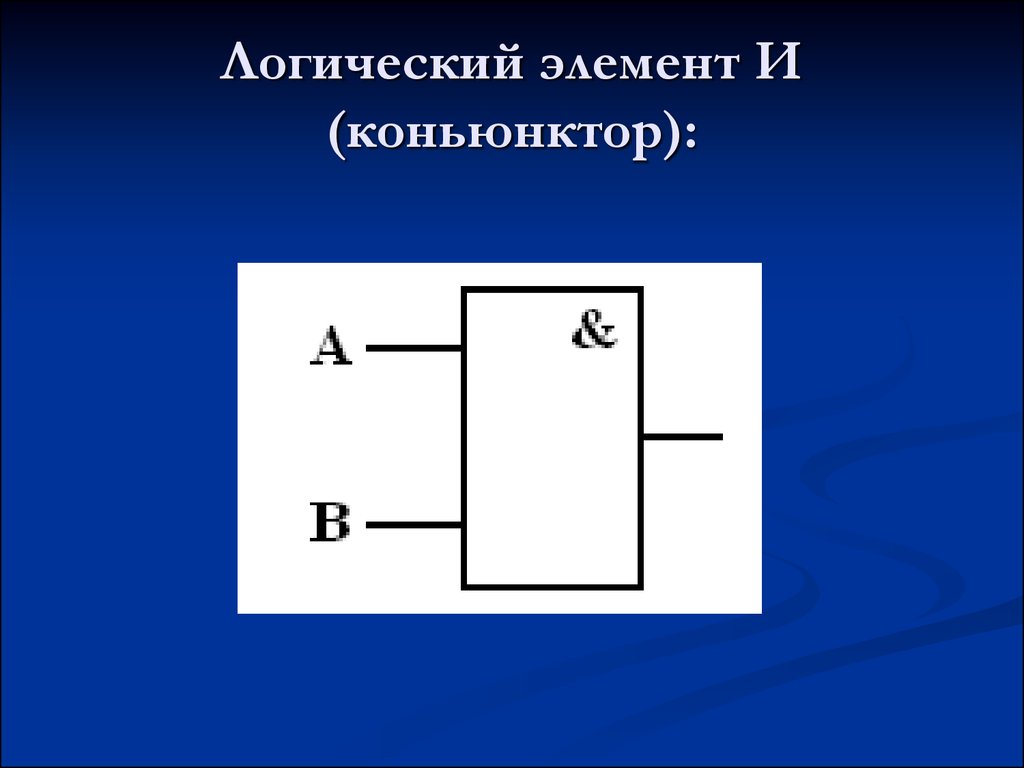 Слишком уж специфическая функция реализуется этими элементами.
Слишком уж специфическая функция реализуется этими элементами.
С точки зрения математики, элемент Исключающее ИЛИ выполняет операцию так называемого суммирования по модулю 2. Поэтому эти элементы также называются сумматорами по модулю два. Как уже отмечалось в предыдущей лекции, обозначается суммирование по модулю 2 знаком плюса, заключенного в кружок.
Основное применение элементов Исключающее ИЛИ, прямо следующее из таблицы истинности, состоит в сравнении двух входных сигналов. В случае, когда на входы приходят две единицы или два нуля (сигналы совпадают), на выходе формируется нуль (см. табл. 4.1). Обычно при таком применении на один вход элемента подается постоянный уровень, с которым сравнивается изменяющийся во времени сигнал, приходящий на другой вход. Но значительно чаще для сравнения сигналов и кодов применяются специальные микросхемы компараторов кодов, которые будут рассмотрены в следующей лекции.
В качестве сумматора по модулю 2 элемент Исключающее ИЛИ используется также в параллельных и последовательных делителях по модулю 2, служащих для вычисления циклических контрольных сумм.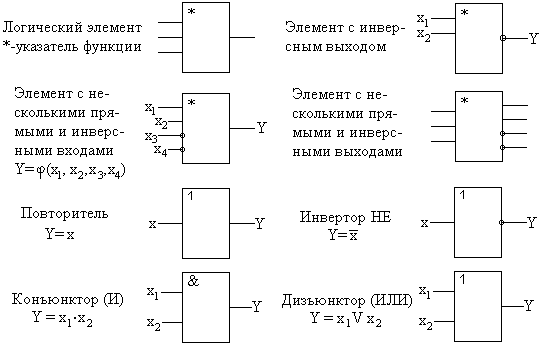 Но подробно эти схемы будут рассмотрены в лекциях 14,15.
Но подробно эти схемы будут рассмотрены в лекциях 14,15.
Важное применение элементов Исключающее ИЛИ — это управляемый инвертор (рис. 4.2). В этом случае один из входов элемента используется в качестве управляющего, а на другой вход элемента поступает информационный сигнал. Если на управляющем входе единица, то входной сигнал инвертируется, если же нуль — не инвертируется. Чаще всего управляющий сигнал задается постоянным уровнем, определяя режим работы элемента, а информационный сигнал является импульсным. То есть элемент Исключающее ИЛИ может изменять полярность входного сигнала или фронта, а может и не изменять в зависимости от управляющего сигнала.
Рис. 4.2. Элемент Исключающее ИЛИ как управляемый инвертор
В случае, когда имеется два сигнала одинаковой полярности (положительные или отрицательные), и при этом их одновременный приход исключается, элемент Исключающее ИЛИ может быть использован для смешивания этих сигналов (рис. 4.3). При любой полярности входных сигналов выходные сигналы элемента будут положительными.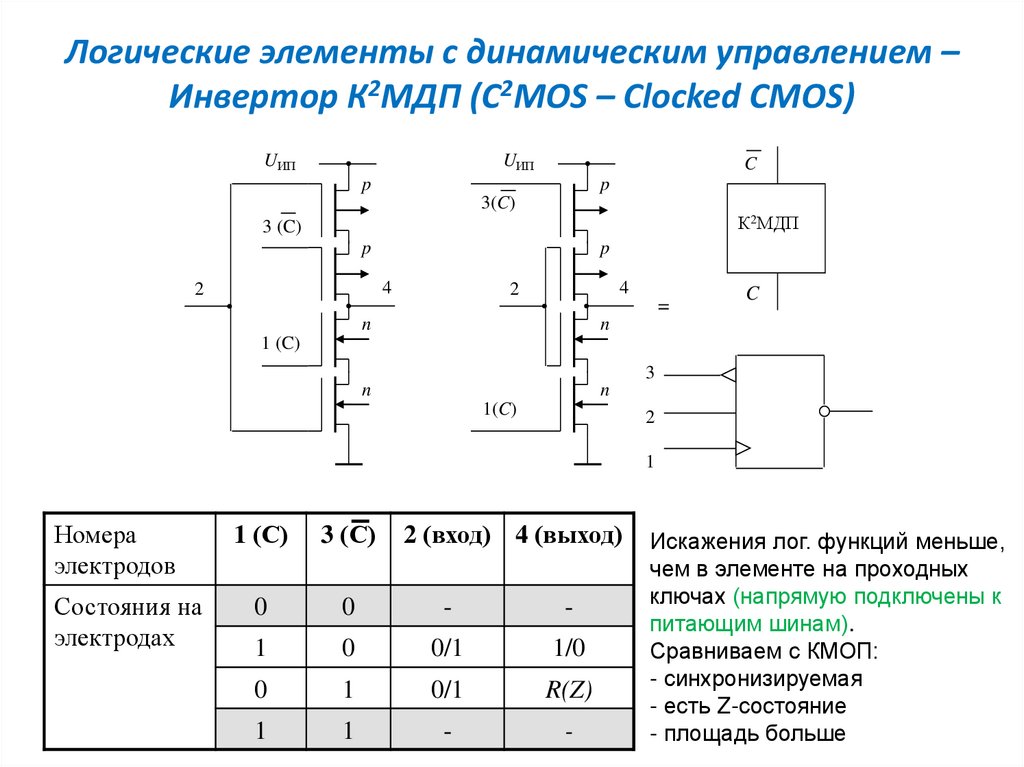 При положительных входных сигналах элемент Исключающее ИЛИ будет работать как элемент 2ИЛИ, а при отрицательных он будет заменять элемент 2И-НЕ. Такие замены могут быть полезны в тех случаях, когда в схеме остаются неиспользованными некоторые элементы Исключающее ИЛИ. Правда, при этом надо учитывать, что задержка распространения сигнала в элементе Исключающее ИЛИ обычно несколько больше (примерно в 1,5 раза), чем задержка в простейших элементах И, И-НЕ, ИЛИ, ИЛИ-НЕ.
При положительных входных сигналах элемент Исключающее ИЛИ будет работать как элемент 2ИЛИ, а при отрицательных он будет заменять элемент 2И-НЕ. Такие замены могут быть полезны в тех случаях, когда в схеме остаются неиспользованными некоторые элементы Исключающее ИЛИ. Правда, при этом надо учитывать, что задержка распространения сигнала в элементе Исключающее ИЛИ обычно несколько больше (примерно в 1,5 раза), чем задержка в простейших элементах И, И-НЕ, ИЛИ, ИЛИ-НЕ.
Рис. 4.3. Применение элемента Исключающее ИЛИ для смешивания двух неодновременных сигналов
Рис. 4.4. Выделение фронтов входного сигнала с помощью элемента Исключающее ИЛИ
Еще одно важнейшее применение элемента Исключающее ИЛИ — формирование коротких импульсов по любому фронту входного сигнала (рис. 4.4). В данном случае не важно, положительный фронт входного сигнала или отрицательный, на выходе все равно формируется положительный импульс. Входной сигнал задерживается с помощью конденсатора или цепочки элементов, а затем исходный сигнал и его задержанная копия поступают на входы элемента Исключающее ИЛИ.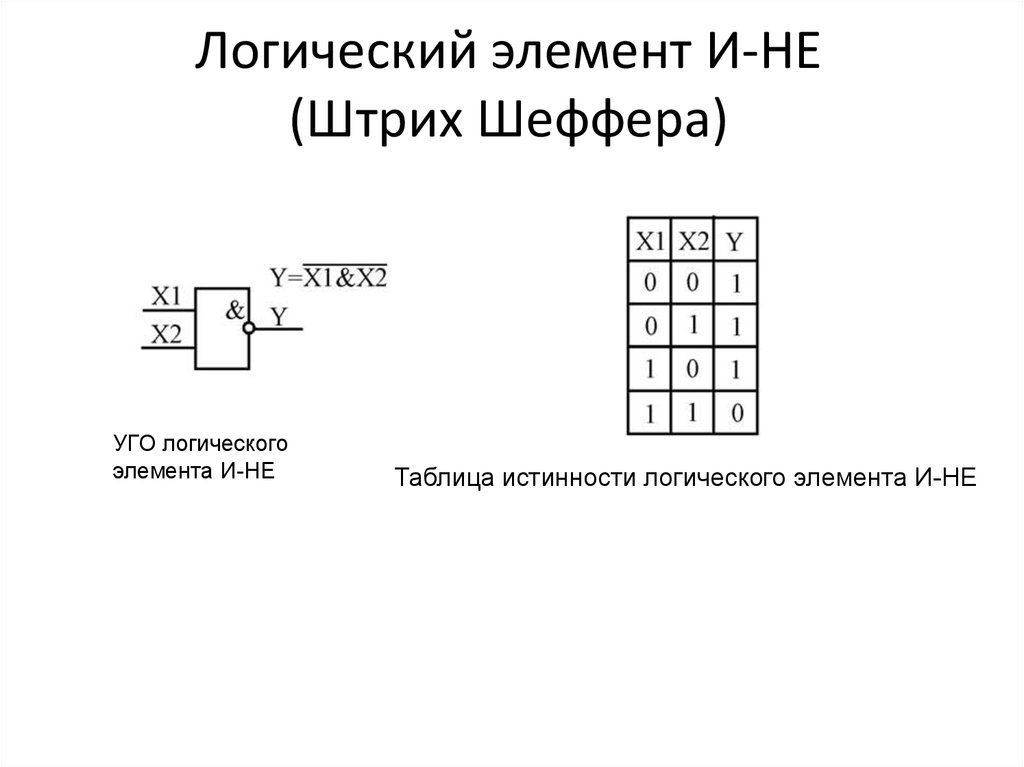 В обеих схемах в качестве элементов задержки используются также двувходовые элементы Исключающее ИЛИ в неинвертирующем включении (на неиспользуемый вход подается нуль). В результате такого преобразования можно говорить об удвоении частоты входного сигнала, так как выходные импульсы следуют вдвое чаще, чем входные.
В обеих схемах в качестве элементов задержки используются также двувходовые элементы Исключающее ИЛИ в неинвертирующем включении (на неиспользуемый вход подается нуль). В результате такого преобразования можно говорить об удвоении частоты входного сигнала, так как выходные импульсы следуют вдвое чаще, чем входные.
Логические элементы и их типы, микросхемы и основы цифровой электроники
Существует три основных типа логических схем:
- Схема отрицания НЕ — инвертор. Схема является одновходовой, на выходе которой сигнал «Y» возникает при отсутствии сигнала «х» на входе. На принципиальных схемах элемент НЕ изображается в виде прямоугольников (рис. 20.1). Его условным символом служит цифра 1, расположенная внутри прямоугольника в левом верхнем углу, и кружок, обозначающий линию выхода. Расположенная возле изображения логического элемента таблица истинности позволяет сделать вывод, каким будет сигнал на выходе при определенной комбинации логических сигналов на входе.
- Схема совпадения И представляет собой многовходовую схему, на выходе которой сигнал «Y» возникает только при наличии сигналов «Хі, х2 .
 .. хп» одновременно на всех выходах. На рис. 20.2 приведено графическое изображение логического элемента с двумя входами -2И и его таблица истинности. Характерным отличием этого элемента на схемах, является наличие внутри прямоугольника английского знака «&» (английский союз «и» — логическое умножение), в левом верхнем углу.
.. хп» одновременно на всех выходах. На рис. 20.2 приведено графическое изображение логического элемента с двумя входами -2И и его таблица истинности. Характерным отличием этого элемента на схемах, является наличие внутри прямоугольника английского знака «&» (английский союз «и» — логическое умножение), в левом верхнем углу.
- Схема сборки ИЛИ — многовходовая схема, сигнал «у» на выходе которой, появляется при наличии сигнала хотя бы на одном из входов. На рис. 20.3 представлено графическое изображение схемы и ее таблица истинности.
Рис. 20.1. Условное графическое обозначение логического элемента НЕ (а) и таблица истинности (б)
Рис. 20.2. Условное графическое обозначение логического элемента И (а) и таблица истинности (б)
Рис. 20.3. Условное графическое обозначение логического элемента ИЛИ (а) и таблица истинности (б)
Существуют и более сложные логические схемы, представляющие собой соединение нескольких простейших схем. Для запоминания результатов преобразований, которые выполняются логическими схемами применяют элемент памяти — триггер. Его схема имеет два выхода (единичный и нулевой) и несколько входов. Триггер может находиться в одном из возможных состояний: единичном или нулевом. Состояние триггера зависит от вида (1 или 0) дискретного сигнала, поступающего на его вход.
Для запоминания результатов преобразований, которые выполняются логическими схемами применяют элемент памяти — триггер. Его схема имеет два выхода (единичный и нулевой) и несколько входов. Триггер может находиться в одном из возможных состояний: единичном или нулевом. Состояние триггера зависит от вида (1 или 0) дискретного сигнала, поступающего на его вход.
Микросхемы серии 155
Большой популярностью среди радиолюбителей пользуются микросхемы серии 155, которые построены на основе так называемой транзисторно-транзисторной логики (ТТЛ). Эта серия включает многовходовые элементы И-НЕ, триггеры, счетчики, дешифраторы, запоминающие устройства и т.д. Напряжение питания микросхем серии 155 составляет 5±0,25 В, которое подается на выводы 14 (+5 В) и 7 (общий провод). При изображении логических элементов на принципиальных схемах подключение к ним источника питания, как правило, не показывают. Рассмотрим практическое использование в радиоэлектронных конструкциях микросхем серии 155.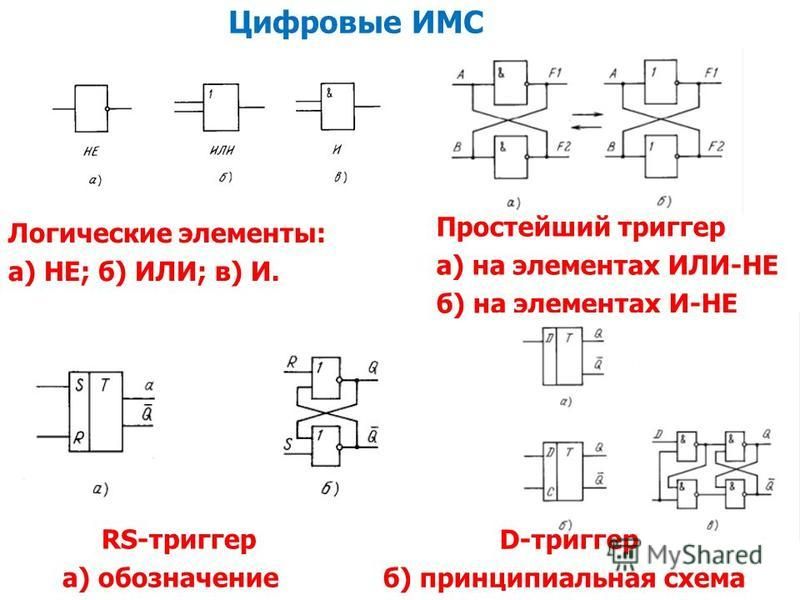 Наиболее часто в конструкциях используется микросхема K155ЛA3. Условное графическое изображение K155JIA3 приведено на рис. 20.4.а. В состав микросхемы входит четыре элемента 2И-НЕ, каждый из которых выполняет операцию логического умножения сигналов по двум входам с последующей инверсией результата на выходе. Следует отметить, что логический элемент, входящий в микросхему, может работать отдельно независимо от других, в связи с этим на принципиальных схемах элементы, составляющие микросхему, изображаются отдельно один от другого. На принципиальных схемах этот факт отмечают в буквенно-цифровом обозначении, например, DD1.1, DD1.2, DD1.3 и DD1.4 (рис. 20.4.6). Принципиальная схема одного логического элемента дана на рис. 20.5.
Наиболее часто в конструкциях используется микросхема K155ЛA3. Условное графическое изображение K155JIA3 приведено на рис. 20.4.а. В состав микросхемы входит четыре элемента 2И-НЕ, каждый из которых выполняет операцию логического умножения сигналов по двум входам с последующей инверсией результата на выходе. Следует отметить, что логический элемент, входящий в микросхему, может работать отдельно независимо от других, в связи с этим на принципиальных схемах элементы, составляющие микросхему, изображаются отдельно один от другого. На принципиальных схемах этот факт отмечают в буквенно-цифровом обозначении, например, DD1.1, DD1.2, DD1.3 и DD1.4 (рис. 20.4.6). Принципиальная схема одного логического элемента дана на рис. 20.5.
Рис. 20.4. Условное графическое изображение интегральной микросхемы К155ЛАЗ: а — без деления на элементы, б — с выделением входящих элементов 2И-НЕ
Как видно из представленной схемы, входящие в нее транзисторы имеют непосредственную связь. В схеме транзистор VT1 имеет два эмиттера и выполняет логическое умножение, VT2 — усиление, ѴТЗ — усиление, a ѴТ4 — инверсию сигнала.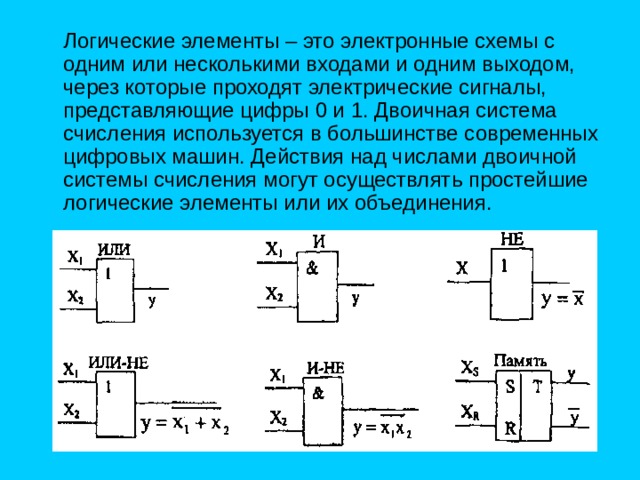 Необходимый режим работы транзисторов задается резисторами R1…R4. Диоды VD1…VD3 предназначены для защиты цепей от напряжения обратной полярности. В момент поступления напряжения на один или оба входа логического элемента (выводы 1 и 2), транзистор VT1 открыт. В то время, как транзистор VT2 закрыт, на базу транзистора VT4 поступает напряжение низкого логического уровня, которое закрывает этот транзистор. В то же время, транзистор ѴТЗ открыт, так как напряжение на его базе, наоборот, соответствует уровню логической 1.
Необходимый режим работы транзисторов задается резисторами R1…R4. Диоды VD1…VD3 предназначены для защиты цепей от напряжения обратной полярности. В момент поступления напряжения на один или оба входа логического элемента (выводы 1 и 2), транзистор VT1 открыт. В то время, как транзистор VT2 закрыт, на базу транзистора VT4 поступает напряжение низкого логического уровня, которое закрывает этот транзистор. В то же время, транзистор ѴТЗ открыт, так как напряжение на его базе, наоборот, соответствует уровню логической 1.
Рис. 20.5. Принципиальная схема логического элементов 2И-НЕ, входящего в интегральную микросхему К155ЛАЗ
В итоге на выходе (вывод 3) элемента оказывается напряжение высокого логического уровня и через нагрузку проходит ток. Если подать на оба входа элемента сигнал, соответствующий логической единицы, то транзистор VT1 закроется, a ѴТ2 откроется. Транзисторы ѴТЗ и ѴТ4 переключатся в противоположные состояния, на выходе появится логический 0 и через нагрузку не будет идти ток. Основными параметрами логической микросхемы, состоящей из элементов И-НЕ, являются:
Основными параметрами логической микросхемы, состоящей из элементов И-НЕ, являются:
- Напряжение питания Un.
- Потребляемая от источника питания номинальная мощность Рном.
- Пороговое напряжение Unop переключения логического элемента из одного состояния в другое.
- Выходное напряжение Uвых логического 0 и единицы.
- Время включения tвкл и выключения tвыкл.
- Коэффициент разветвления по выходу Краз показывающий, какую из микросхем можно подключить к выходу данного элемента.
Литература: В.М. Пестриков. Энциклопедия радиолюбителя.
Урок N 16. Логические элементы и логические функции.
Элементы математической логики.
Логическая функция — это функция логических переменных, которая
может принимать только два значения : 0 или 1. В свою очередь,
сама логическая переменная (аргумент логической функции) тоже может
принимать только два значения : 0 или 1. n.
n.
Логические функции одной переменной
Таблица истинности функции одной переменной Y=f(X) содержит всего
2 строки, а число функций одной переменной равно 4.
1. Функция константа 0, Y=0. Техническая реализация этой функции —
соединение вывода Y с общей шиной с нулевым потенциалом.
Таблица истинности функции константа 0 имеет вид:
2. Функция Y=f(X)=X — функция повторения. Техническая реализация
этой функции — соединение между собой выводов X и Y.
Таблица истинности функции повторения имеет вид:
3. Функция Y=f(X)=NOT(X) — отрицание НЕ или инверсия (NOT(X) — это НЕ X).
Техническая реализация этой функции — инвертор на любом транзисторе
или логическом элементе, или транзисторный ключ.
Таблица истинности функции отрицания имеет вид:
Логический элемент НЕ обозначается на схемах следующим образом:
(пишется X c чертой сверху)
4. Функция константа 1, Y=1. Техническая реализация этой функции —
Функция константа 1, Y=1. Техническая реализация этой функции —
соединение вывода Y с источником питания.
Таблица истинности функции константа 1 имеет вид:
Важнейшей функцией одной переменной является отрицание НЕ,
остальные функции являются тривиальными.
Логические функции двух переменных
Таблица истинности функции двух переменных Y=f(X1,Х2) содержит 4
строки, а число функций двух переменных равно 16.
Мы рассмотрим только несколько основных функций двух переменных.
1. Логическое ИЛИ (логическое сложение, дизъюнкция):
Y= X1 + X2 = X1VX2
Техническая реализация этой функции — два параллельно соединенных
ключа:
Таблица истинности логического ИЛИ имеет вид:
Логический элемент ИЛИ обозначается на схемах следующим образом:
2. Логическое И (логическое умножение, конъюнкция, схема совпаде-
Логическое И (логическое умножение, конъюнкция, схема совпаде-
ний): Y = X1X2 = X1&X2
Техническая реализация этой функции — два последовательно сое-
диненных ключа:
Таблица истинности логического И имеет вид:
Логический элемент И обозначается на схемах следующим образом:
3. Функция стрелка Пирса (ИЛИ-НЕ): Y = NOT(X1+X2)
Таблица истинности функции ИЛИ-НЕ имеет вид:
Логический элемент ИЛИ-НЕ обозначается на схемах следующим образом
:
4. Функция штрих Шеффера (И-НЕ): Y = X1|X2 = NOT(X1X2)
Таблица истинности функции И-НЕ имеет вид:
Логический элемент И-НЕ обозначается на схемах следующим образом:
Есть ещё три логические функции двух переменных, имеющие специ-
альные названия: импликация, эквивалентность, неравнозначность
(исключающее ИЛИ, сложение по модулю 2).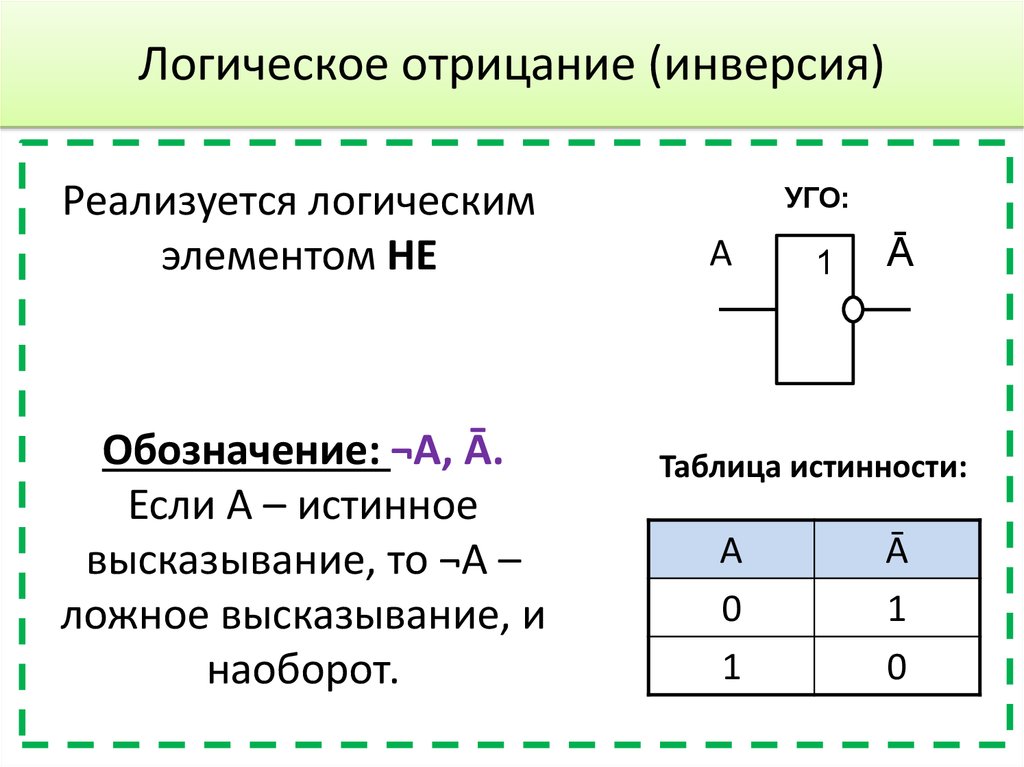 Последние две функции
Последние две функции
являются взаимно обратными, также как, например, функция И и
функция штрих Шеффера.
Элемент памяти — RS-триггер
Триггер — это логическое устройство, способное хранить 1 бит ин-
формации. К триггерам относятся устойства, имеющие два устойчивых
состояния. Простейший триггер — RS-триггер, образован из двух
элементов И-НЕ (или ИЛИ-НЕ). Он позволяет запоминать 1 бит инфор-
мации, поскольку информация в компьютере представляется в двоич-
ном виде. Его схема приведена ниже.
Действие RS-триггера поясняется в приведенной ниже таблице ис-
тинности. S-вход установки (Set), R-вход сброса (Reset).
В обычном (исходном) состоянии на входы триггера поданы 1. Для
записи информации на вход R подан 0. Для сброса информации и под-
готовки к приёму новой информации на вход S подается 0 и триггер
вернётся в исходное состояние.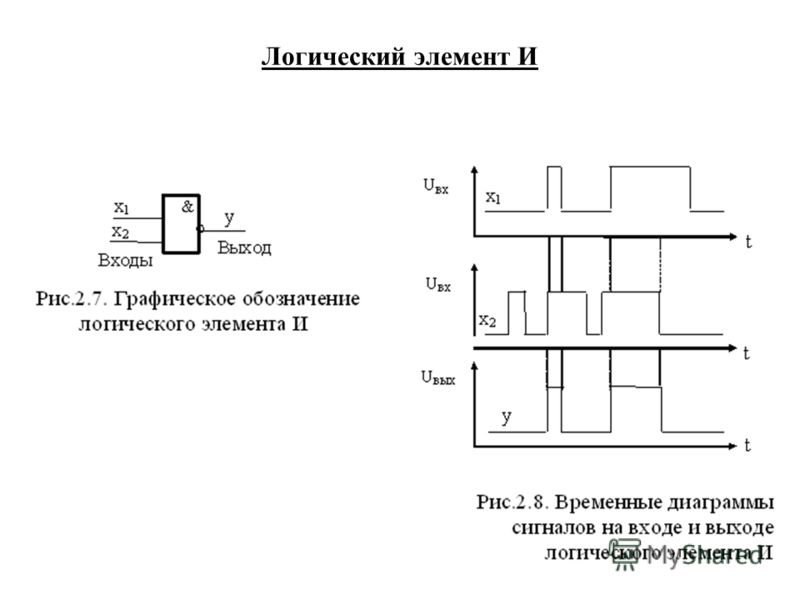
Поскольку один триггер запоминает 1 бит информации, то для запо-
минания 1 байта (8 бит) нужно 8 триггеров, для запоминания 1 Кб
(1024 байт) надо 8192 триггеров. Современные микросхемы ОЗУ спо-
собны запоминать десятки мегабайт информации.
Элементы математической логики
Существуют такие наборы логических функций, с помощью которых
можно выразить любые другие логические функции. Они называются
функционально полными или базисами. Наиболее известный базис —
это набор функций И, ИЛИ, НЕ. Функция штрих Шеффера является ба-
зисной, также как и функция стрелка Пирса. Поэтому, с помощью ло-
гических элементов ИЛИ-НЕ или И-НЕ можно собрать любую логическую
схему. На таких элементах собран микропроцессор компьютера и дру-
гие логические устройства. Логические схемы состоят из логических
элементов, осуществляющих логические операции.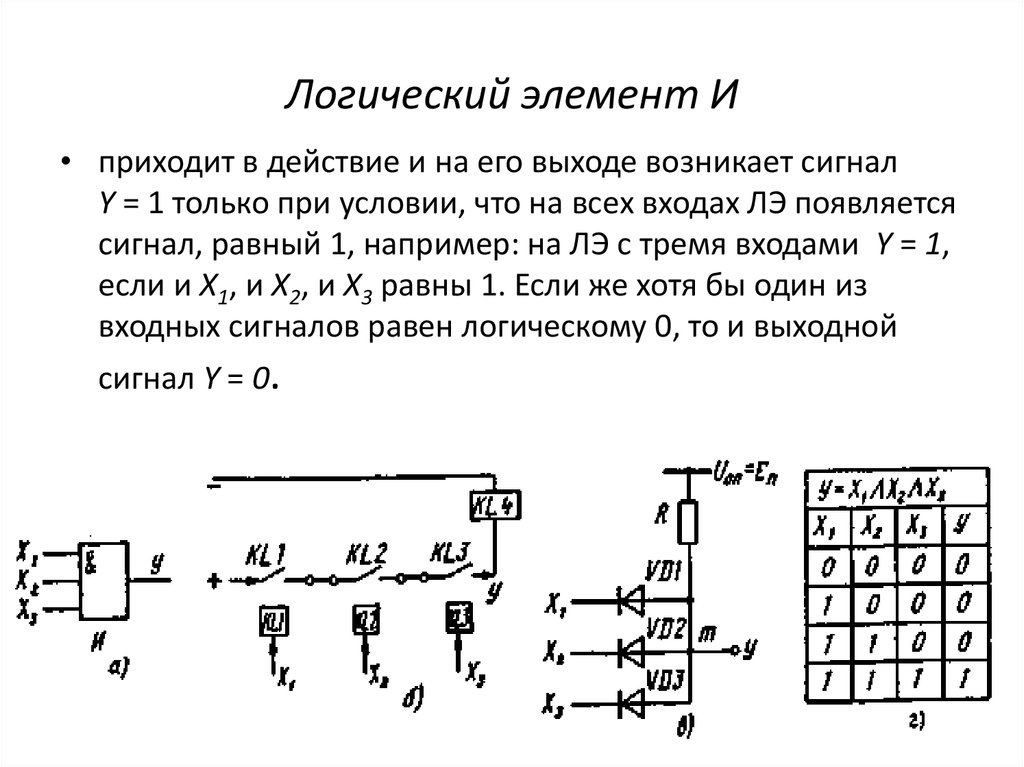
Логика — наука, изучающая методы установления истинности или лож-
ности одних высказываний на основе истинности или ложности других
высказываний (утверждений). Логика изучает методы доказательств и
опровержений. Логика составляет основу всякого управления, в том
числе технологическими процессами.
Математическая логика — современная форма логики, опирающаяся на
формальные математические методы.
Основные объекты логики — высказывания, то есть предложения, ко-
торые могут быть либо истинными, либо ложными. Существуют два
подхода установления истинности высказываний: эмпирический (опыт-
ный) и логический. При эмпирическом подходе истинность высказыва-
ний устанавливается на основе наблюдений, экспериментов, докумен-
тов и других фактов. При логическом подходе истинность высказыва-
ний доказывается на основе истинности других высказываний, то
есть чисто формально, на основе рассуждений без обращения к фак-
там.
В языках программирования QBasic и Turbo Pascal логические функ-
ции И, ИЛИ, НЕ реализуются в виде логических операций OR (ИЛИ),
AND (И), NOT (НЕ).
Множество всех логических функций, на котором определены три ло-
гические операции И, ИЛИ, НЕ называется булевой алгеброй (по име-
ни основоположника математической логики английского математика
Джорджа Буля). Упрощение формул в булевой алгебре производится на
основе эквивалентных преобразований, опирающихся на следующие ос-
новные законы (эквивалентные соотношения):
Кроме того, применяются ещё три соотношения:
Законы 1,2,3,7 показывают, что свойства конъюнкции очень похожи
на свойства умножения, поэтому её часто называют логическим умно-
жением. Из законов 6 и 8 следует, что используя отрицание, дизъ-
юнкцию можно выразить через конъюнкцию, и наоборот:
Это означает, что наборы И-НЕ и ИЛИ-НЕ также являются функцио-
нально полными или базисными.
Вопросы
1. Что такое логическая функция и логический элемент?
2. Что такое таблица истинности и сколько в ней строк?
3. Какие функции одной переменной Вы знаете? Какая из них являет-
ся важнейшей?
4. Как зависит число функций от числа переменных?
5. Что такое конъюнкция и дизъюнкция? Как они реализуются?
6. Что такое функция стрелка Пирса? Какова её таблица истинности?
7. Что такое функция штрих Шеффера? Какова её таблица истинности?
8. Что такое базисная функция и какие базисы Вы знаете?
9. Что такое логика? Какие два подхода существуют в логике?
10. Как доказывается истинность или ложность высказываний? Приве-
дите примеры из практики.
11. Что такое булева алгебра?
12. Какие законы булевой алгебры Вы знаете? Где они применяются?
13. Что такое триггер? Как работает RS-триггер?
14. Сколько надо триггеров, чтобы запомнить 1 Мб информации?
Сколько надо триггеров, чтобы запомнить 1 Мб информации?
⇐ ПредыдущаяСтр 12 из 12
Обозначение его на зарубежных схемах NOR.
11.7. СЛОЖНЫЙ ЛОГИЧЕСКИЙ ЭЛЕМЕНТ «2Х2И-2ИЛИ-НЕ»
Данный логический элемент является комбинацией простых логических элементов, которыми реализуется сложная логическая функция с 4 входами и одним выходом рис. 11.7. Реализация сложного логического элемента на простых элементах показана на рис. 11.7 а. Условное обозначение элемента на схемах показано на рис. 11.7, б. Таблица истинности (рис.11.7, в) имеет незаконченный вид для самостоятельной работы. Ее следует заполнить самостоятельно (рис. 11.7, г). Такой сложный логический элемент описывается следующим логическим уравнением: Получить таблицу истинности можно, анализируя работу простых элементов описанных выше. На практике можно встретить и другие комбинации логических элементов, реализующие сложные функции, но приведенные выше логические элементы наиболее часто встречаются в цифровых схемах и являются базовыми для построения сложных логических схем.
12. ИНТЕГРАЛЬНЫЕ ТРИГГЕРЫ
12.1. ОБЩИЕ ВОПРОСЫ
В вычислительной технике особая роль отводится элементам памяти, т.е. элементам, способным хранить информацию. Для построения схем памяти можно применить простые и сложные логические элементы, которые способны запоминать введенную в них информацию при определенной схеме их включения. Активными логическими уровнями для элемента ИЛИ-НЕ является логическая единица, а для элемента И-НЕ – логический ноль. Такие логические уровни, которые, действуя на одном из входов элемента, однозначно задают логический уровень, на его выходе независимо от уровней на других входах называются активными логическими уровнями. Уровни, обратные активным, называются пассивными уровнями. Определенная схема включения простых элементов с содержанием обратных связей способна хранить информацию. Такая схема называется триггером. Триггер (от англ. Trigger ) – спусковой крючок. Триггеры имеют два выхода, один из которых называется прямым Q, а второй инверсным . Триггеры снабжаются различными типами входов, которые приведены ниже. R — (от англ. RESET) –раздельный вход установки прямого выхода триггера в состояние 0. S — (от англ. SET) –раздельный вход установки выхода триггера в состояние 1. К – вход установки выхода универсального триггера в состояние 0. J — вход установки универсального выхода триггера в состояние 1 Т — счетный вход. D — (от англ. DELAY) информационный вход установки выхода триггера в состояние, соответствующее уровню на этом входе. С — исполнительный управляющий (синхронизирующий) вход. V — разрешающий, управляющий вход. По характеру реакции на входные сигналы триггеры делятся на 2 типа: асинхронные и синхронные.
12.2. АСИНХРОННЫЙ RS – ТРИГГЕР С ПРЯМЫМИ ВХОДАМИ В современной электронике широкое распространение получили интегральные триггеры, особенностью которых является совмещение в одном корпусе интегральной микросхемы нескольких логических элементов рис. Рассмотрим работу интегрального триггера, построенного на логических элементах 2ИЛИ-НЕ (рис. 12.1). Пусть на входах S и R действуют пассивные для логического элемента ИЛИ-НЕ уровни логического 0, которые не влияют на состояние триггера. Пусть в состоянии нуля находится выход Q и в состоянии единицы выход . При подаче на вход S логической единицы произойдет опрокидывание элемента на противоположное состояние, т.е. в состояние логического нуля, тогда на входах второго элемента окажутся два логических нуля, которые переведут этот триггер в состояние логической единицы. Триггер опрокинется и состояния его выходов окажутся противоположными предыдущему т.е. Q =1 и Значок «П» означает предыдущее состояние. Значок (´) означает запрещенную комбинацию входных переменных для данного типа триггера. Логическая функция выходного сигнала может быть записана Эта функция описывает элемент памяти, коим и является триггер. Для записи логического нуля на выход Q необходимо на вход R подать логическую единицу. При комбинации триггер переходит в неопределенное состояние, и состояние выхода может оказаться произвольным после прекращения одновременной подачи логических единиц на вход триггера.
12.3. АСИНХРОННЫЙ RS –ТИРГГЕР С ИНВЕРСНЫМИ ВХОДАМИ Данный тип триггера строится на базовых логических элементах И-НЕ, активными уровнями которого являются логические нули. Для того, чтобы активными были, как и в предыдущем случае, входные сигналы и , будем считать, что на входы подаются инверсии и . При подаче активного уровня ( ) на выходах первого триггера установиться уровень , на выходе второго элемента =0 и триггер оказывается установленным в состояние логической единицы. При подаче активного уровня ( ) триггер установится в состояние логического нуля, как и в случае триггера с прямыми входами. В данном триггере активными уровнями являются логические нули, в то время как в предыдущем триггере активными уровнями были логические единицы. Логическая функция выходного сигнала может быть записана Функция имеет признаки элемента памяти, которым и является триггер.
12.4. СИНХРОННЫЙ ОДНОТАКТНЫЙ RS–ТРИГГЕР Синхронным считают такой триггер, запись информации в который производится с разрешения синхроимпульса по входу С (рис. 12.3.) Существуют синхронные RS–триггеры в которых активные уровни – логические единицы, но можно управлять этим триггером и как асинхронным RS–триггером с инверсными входами (рис.12.3, б). Диаграмма состояний такого триггера изображена на рис 12.3, в. Шины триггера с инверсными входами (показаны пунктиром на рис 12.3, а). Синхронный RS-триггер можно построить по несколько иной схеме. Основной RS-триггер (рис. 12.3, а) построен на элементах 2И-НЕ, но можно установить схему на элементах 2ИЛИ-НЕ, но входные элементы 2И-НЕ следует заменить на элементы 2И. Диаграмма состояний и таблица истинности в обоих схемах одинаковы.
12.5. ДВУХТАКТНЫЙ RS – ТРИГГЕР
Двухтактный триггер строится на двух интегральных синхронных RS–триггерах, схема которых приведена на рис 12.5. С приходом синхроимпульса на вход С первого триггера информация записывается в первый триггер. При наличии синхроимпульса (логической единицы) на первом входе на выходе логического элемента НЕ — логический ноль, т.е. во второй триггер информация не записывается. При спаде синхроимпульса на первом входе (с логической единицы на логический ноль) на выходе логического элемента НЕ (на синхровходе второго триггера) появляется логическая единица. Выходы первого триггера подключены ко входу второго триггера, поэтому информация с первого триггера перезапишется во второй. Запись информации на входе двухтактного триггера запишется на его выход в два этапа. На рис 12.3, б. представлена диаграмма состояний двухтактного синхронного RS–триггера. Синхровход первого триггера на диаграмме состояний обозначен С1, а прямой выход первого триггера обозначен Q1. Диаграмма состояний синхровхода второго триггера обозначена С2 и диаграмма состояний прямого выхода второго триггера обозначена Q2. 12.6. D — ТРИГГЕРЫ D –
D-триггеры применяются для приема информации по одному входу, который называется информационным. D – триггеры осуществляют задержку записи информации на выход триггера (от англ. Delay – задержка) рис. 12.6. Реализовать функцию задержки записи информации и притом только с одного входа с разрешения синхроимпульса можно с использованием асинхронного RS-триггера рис. 12.6. D – триггер можно сформировать и на основе синхронного RS–триггера (рис. 12.7.). Для исключения запрещенной комбинации введен инвертор. Диаграммы состояний обоих D–триггеров выглядят одинаково Вход D является информационным, связанным с входом S синхронного RS–триггера. При подаче на синхровход С логической единицы RS–триггер запишет на выход то, что в данный момент поступает на информационный вход. При логической единице на информационном входе на выход запишется логическая единица, а при логическом нуле — на вход R поступает логическая единица через инвертор и на выход Q запишется логический ноль.
12.7. ДВУХТАКТНЫЙ D -ТРИГГЕР
12.8. DV — ТРИГГЕР DV-триггер кроме входа синхронизации имеет вход разрешения синхронизации – V. Схема простейшего варианта DV–триггера представлена на рис. 12.9. ДВУХТАКТНЫЙ DV — ТРИГГЕР
12.10. СТАИЧЕСКИЕ И ДИНАМИЧЕСКИЕ ТРИГГЕРЫ Если с приходом синхроимпульса опрокидывание триггера происходит в момент появления фронта, то такой триггер называется динамичсеким. Известно, что активными уровнями синхроимпульса могут быть как логические единицы так и логические нули. Для того, чтобы отличать эти триггеры друг от друга вводятся следующие обозначения рис.12.11.
В случае рис. Триггеры, не имеющие на синхровходе наклонной черты, являются статическими и опрокидывание таких триггеров происходит после окончания синхроимпульса.
12.11. Т – ТРИГГЕРЫ
Т–триггеры называют делителями на 2 или счетными триггерами. Существует несколько схем Т– триггеров. Работу некоторых из них мы рассмотрим. Т–триггер имеет один вход, называемый счетным. Работа такого триггера основана на перезаписи информации в триггер, которая становится инверсной по отношению к той, которая была записана в предыдущем случае. Рассмотрим работу Т–триггера на основе схемы рис. 12.12, а. Пусть на выходе Q находился логический ноль, тогда на инверсном выходе находилась логическая единица, которая передается на вход S и с приходом синхроимпульса триггер опрокинется и запишет на выход Q логическую единицу. После опрокидывания триггера логическая единица окажется на входе R, который соединен перемычкой с выходом Q. С приходом синхроимпульса триггер опрокинется в состояние инверсное предыдущему. Работа D–триггера в режиме счетного триггера почти не отличается от работы синхронного RS–триггера. Информационный вход D соединен с инверсным выходом Q триггера. Такая коммутация приводит к тому, что информационном входе D–триггера всегда находится состоянии, инверсном выходному состоянию триггера на данный момент времени. Если на прямом выходе триггера логический ноль то на информационном входе логическая единица, взятая с инверсного выхода. С приходом синхроимпульса триггер опрокинется и запишет на прямой выход логический ноль, а на входе D появиться логическая единица для последующей ее записи в триггер. Диаграмма состояний такого триггера показана на рис. 12.15, в.
12.12. ДВУХТАКТНЫЕ Т – ТРИГГЕРЫ Такие триггеры строятся на основе двух однотактных триггеров, в которых запись информации происходит в первый триггер, а затем перезапись информации во второй триггер рис.
12.13. JК-ТРИГГЕРЫ JK-триггер считают универсальным. На его основе можно построить любой из выше перечисленных триггеров. Структура такого триггера приведена на рис. 12.14 из которого следует, что состояние Q, в котором устанавливается триггер, определяется не только уровнями на информационных входах J и K, но и предыдущим состоянием . Это обстоятельство позволяет построить триггер с применением двух RS-триггеров. Один из триггеров хранит предыдущее состояние Q0. Снимаемые с его выхода уровни Q и совместно с информационными сигналами входов J и К используются для формирования состояния Q во втором RS-триггере. Из рис. 12.14, а видно, что два RS-триггера с элементами И на входе образуют синхронные RS-триггеры. При уровне триггер Т1 не реагирует на входные сигналы входов J и К. На синхронизирующий вход второго триггера подается логическая единица, и триггеру Т2 передается состояние первого триггера. При на синхронизирующий вход второго триггера через инвертор подается 0 и логическая связь между триггерами прекращается. На первом триггере остается предыдущее состояние.
Универсальный JK-триггер можно построить и на совер шенно иной элементной базе, при этом управление таким триггером будет осуществляться не логическими единицами а логическими нулями, являющимися для данного триггера активными уровнями. Разнообразие триггеров очень велико. Это могут быть комбинированные триггеры, собранные на базе одной интегральной микросхемы или состоящие из разнотипных триггеров. Могут быть собраны триггеры и с различным активными уровнями управления – логическими единицами или нулями. JK-триггеры могут быть и двухтактными. На рис. 12.16 приведены схемы, по которым может быть реализован любой тип триггера на основе универсального JK-триггера. а) D-триггер, б) синхронный Т-триггер, в) асинхронный Т-триггер, д) синхронный RS-триггер, г) – асинхронный RS-триггер с инверсными входами. Функцию переходов JK-триггера можно представить в виде логических Булевых функций
При , т.е. при запрещенных комбинациях входных переменных, триггер переходит в состояние противоположное предыдущему. Многообразие интегральных триггеров позволяет формировать схемы со сложными функциями. Учитывая то, что любой интегральный триггер является элементом памяти, можно построить схемы быстродействующей – оперативной памяти. Для управления работой объектов регулирования можно построить такие схемы, на основе которых объект будет управляться по заданной программе. В дальнейшем будет рассмотрен вопрос применения интегральных триггеров в организации различных видов памяти. В разделе «Интегральные триггеры» мы рассмотрели работу различных простых и комбинированных триггеров. Несмотря на универсальность JK-триггеров они не так популярны как другие триггеры. Наиболее часто применяются D-триггеры, не имеющие запрещенных комбинаций входов. Часто применяются комбинированные интегральные триггеры содержащие D-триггер и асинхронный RS-триггер. Сложность применения JK-триггеров в том, что они имеют много комбинаций входных сигналов. Зачастую не все комбинации этих сигналов можно предусмотреть при работе триггера.
⇐ Предыдущая3456789101112 ©2015 arhivinfo.ru Все права принадлежат авторам размещенных материалов. |
логических операторов, поэлементно и | ~ (функции MATLAB)
Логические операторы, поэлементно & | ~ (функции MATLAB)| Справочник по функциям MATLAB |
Поэлементные логические операции над массивами
Синтаксис
A и B А | Б ~ А
Описание
Символы и , | и ~ являются логическими операторами массива И , ИЛИ и НЕ . Они работают с массивами поэлементно, где 0 представляет логическую ложь (
Они работают с массивами поэлементно, где 0 представляет логическую ложь ( F ), а все, что не равно нулю, представляет логическую истину ( T ). Логические операторы возвращают логический массив с элементами, для которых установлено значение true ( 1 ) или false ( 0 ), в зависимости от ситуации.
Оператор и делает логическую И , | Оператор выполняет логическое ИЛИ , а ~A дополняет элементы A . Функция xor(A,B) реализует исключительную операцию ИЛИ . Таблица истинности для этих операторов и функций показана ниже.
| Входы | и | или | не | хор | |
А | Б | А и Б | А | Б | ~А | xor(A,B) |
0 | 0 | 0 | 0 | 1 | 0 |
0 | 1 | 0 | 1 | 1 | 1 |
1 | 0 | 0 | 1 | 0 | 1 |
1 | 1 | 1 | 1 | 0 | 0 |
Приоритет логических операторов по отношению друг к другу:
| Оператор | Операция | Приоритет |
~ | НЕ | Самый высокий |
и | Поэлементно И | |
| | Поэлементно ИЛИ | |
&& | Короткое замыкание И | |
|| | Короткое замыкание ИЛИ | Самый низкий |
Примечания
MATLAB всегда дает оператору и приоритет над оператором | оператор. Хотя MATLAB обычно оценивает выражения слева направо, выражение
Хотя MATLAB обычно оценивает выражения слева направо, выражение a|b&c оценивается как а|(б и в) . Рекомендуется использовать круглые скобки, чтобы явно указать предполагаемый приоритет операторов, содержащих комбинации и и | .
Эти логические операторы имеют эквиваленты функций М-файла, как показано.
| Логическая операция | Эквивалентная функция |
А и Б | и(А,Б) |
А | Б | или (А, В) |
~А | не(А) |
Примеры
Этот пример показывает логическое ИЛИ элементов в векторе u с соответствующими элементами в векторе v :
См.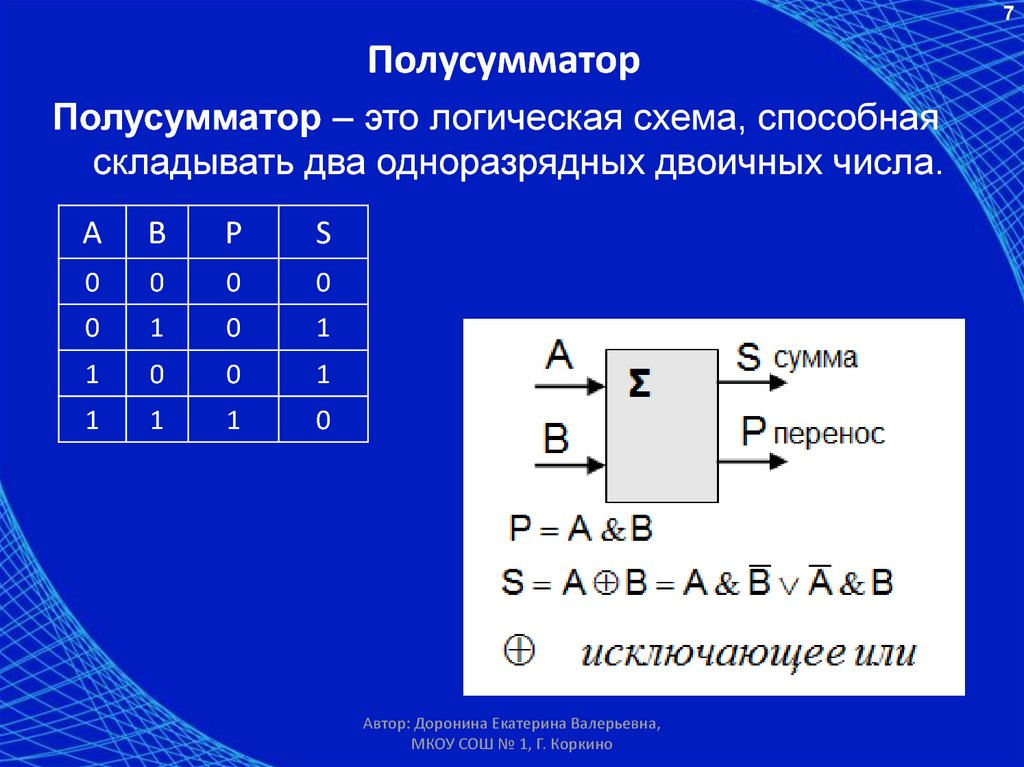 также
также
все , любые , найти , логические , xor , истина , ложь
Логические операторы, короткое замыкание: && , ||
Реляционные операторы: < , <= , > , >= , == , ~=
| Операции сравнения < > <= >= == ~= | Логические операторы, короткое замыкание && || |
Что такое логические теги в HTML?
Посмотреть обсуждение
Улучшить статью
Сохранить статью
- Уровень сложности: Easy
- Последнее обновление: 15 мар, 2021
Посмотреть обсуждение
Улучшить статью
Сохранить статью
Логические теги используются, чтобы сообщить браузеру, какой текст записывается внутри тегов.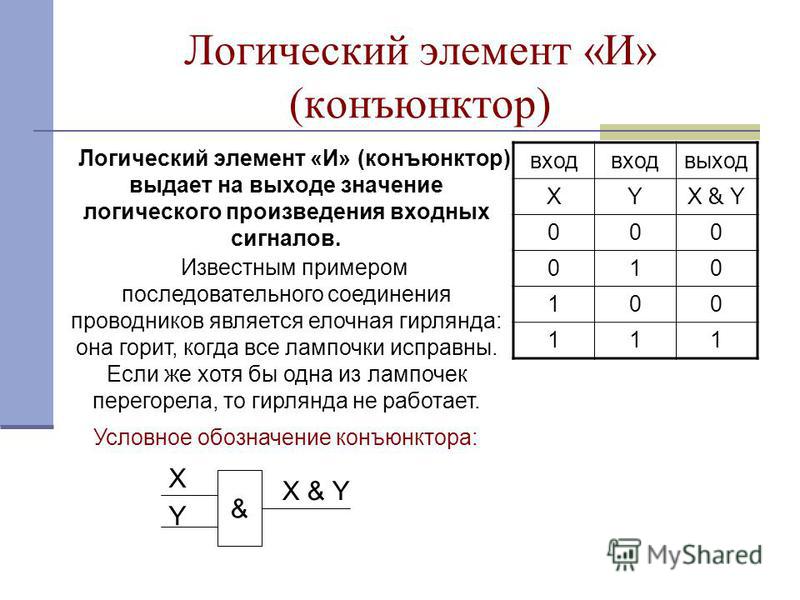 Они отличаются от физических тегов, поскольку физические теги используются для определения внешнего вида текста и не предоставляют никакой информации о тексте.
Они отличаются от физических тегов, поскольку физические теги используются для определения внешнего вида текста и не предоставляют никакой информации о тексте.
Логические теги используются для указания слабовидящему человеку на то, что в тексте есть что-то более важное, или для выделения текста.
Некоторые случаи, когда мы могли бы использовать логические теги:
- Когда мы хотим написать код на нашем веб-сайте.
- Когда мы хотим выделить текст.
- Когда мы хотим отобразить аббревиатуру на веб-странице.
- Когда мы хотим отобразить какую-нибудь известную цитату на нашей веб-странице.
- Когда мы хотим написать некоторую математическую формулу в терминах переменных.
Существует много видов логического текста, вот список некоторых из них:
| Тег | Описание |
|---|---|
7 | |
| <акроним> | Определяет аббревиатуру.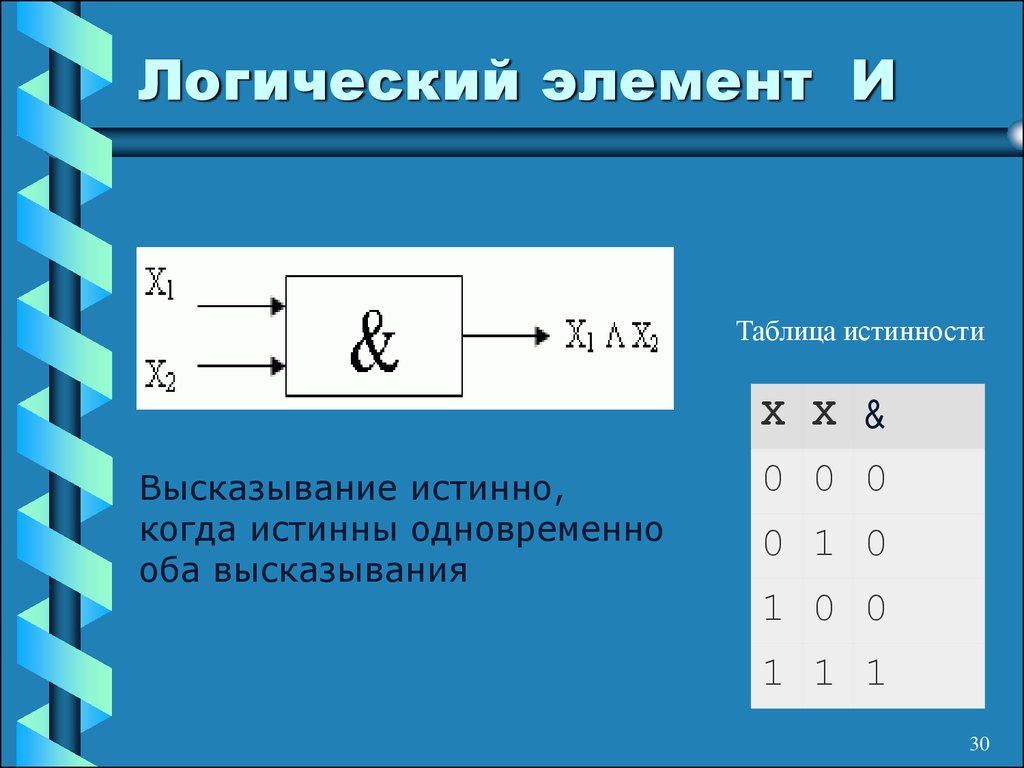 |
| <адрес> | контактные данные лица или организации. |
| Определяет цитирование. Он отображает текст курсивом. | |
| <код> | Определяет фрагмент компьютерного кода. |
| Определяет длинную цитату. | |
| | Определяет удаленный текст и используется для пометки части текста, которая была удалена из документа. |
| Определяет элемент определения и используется для представления определяющего экземпляра в HTML. | |
| Определяет вставленный текст. | |
| Определяет ввод текста с клавиатуры. | |
| Определяет блок предварительно отформатированного текста, который сохраняет текстовые пробелы, разрывы строк, символы табуляции и другие символы форматирования, которые игнорируются веб-браузерами. | |
| | Определяет краткую цитату.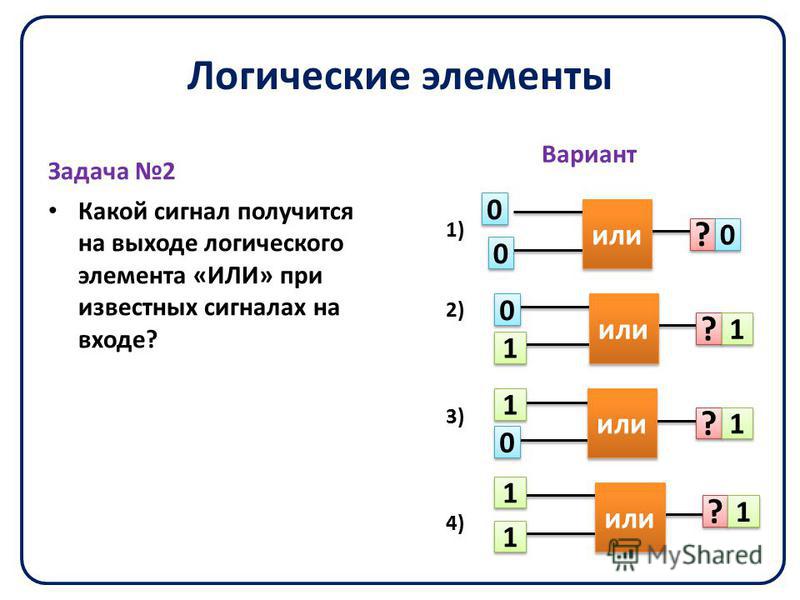 |
| Определяет образец выходного текста из компьютерной программы. | |
| Определяет сильный текст, т.е. показывает важность текста. | |
| Определяет переменную в математическом уравнении или в компьютерной программе. |
Теперь давайте реализуем некоторые вышеперечисленные теги в примерах
1. Тег : Тег означает двунаправленное переопределение. Этот тег используется для изменения направления текста. Он принимает атрибут «dir», который определяет направление текста.
Syntax:
Statements...
HTML
|
Вывод:
Этот текст будет идти справа налево скиGfofskeeG Этот текст будет идти слева направо GeeksforGeeks
2.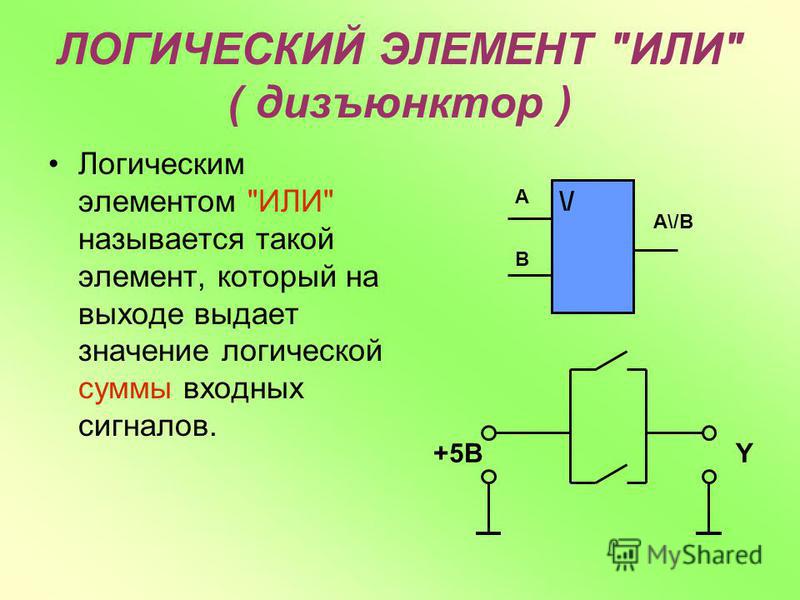 Тег
Тег : Тег рисует линию, обрезающую текст, которая показывает, что текст неверен или удален.
Syntax:
Statements...
HTML
|
Вывод:
3.
3. . в документ. Браузеры обычно показывают вставленные теги подчеркнутыми.
в документ. Браузеры обычно показывают вставленные теги подчеркнутыми.
Syntax:
Statements...
HTML
. |
Output:
4. Тег : Тег используется, чтобы сообщить браузеру, что текст внутри этого тега имеет большое значение и значение. Браузер отображает этот текст жирным шрифтом.
Syntax:
Statements...
HTML
. |
Вывод:
5. Tag: . код некоторого языка программирования. Содержимое внутри этого тега отображается моноширинным шрифтом.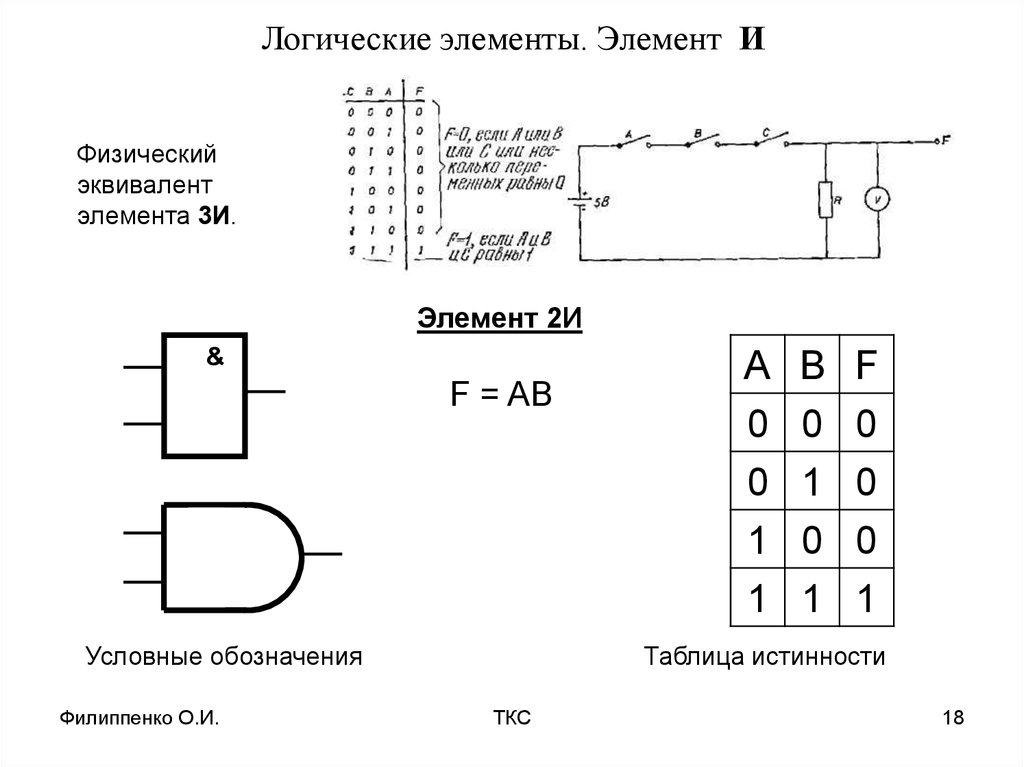
Синтаксис:
Утверждения... HTML
|
. вводится с клавиатуры. Содержимое внутри отображается моноширинным шрифтом.
Содержимое внутри отображается моноширинным шрифтом.
Синтаксис:
Утверждения...
HTML
|
Вывод:
Рекомендуемые статьи
Страница :
Изучение логических элементов.
 Изучение логики работы. логические элементы. Краткая информация из теории
Изучение логики работы. логические элементы. Краткая информация из теорииДля описания алгоритма работы логических схем используется математический аппарат логической алгебры. Алгебра логики оперирует двумя понятиями: событие истинно (логическая «1») или событие ложно (логический «0»). События в алгебре логики могут быть связаны двумя операциями: сложением (дизъюнкцией), обозначаемым знаком U или +, и умножением (конъюнкцией), обозначаемым знаком & или точкой. Отношение эквивалентности обозначается знаком =, а отрицание — чертой или апострофом (") над соответствующим символом.
Логическая схема имеет n входов, которые соответствуют n входным переменным X 1 , … X n, и один или несколько выходов, которые соответствуют выходным переменным Y 1 …. Ю м . Входная и выходная переменные могут принимать два значения X i = 1 или X i = 0.
Функция переключения (SF) логической схемы соединяет входные переменные и одну из выходных переменных с помощью логических операций.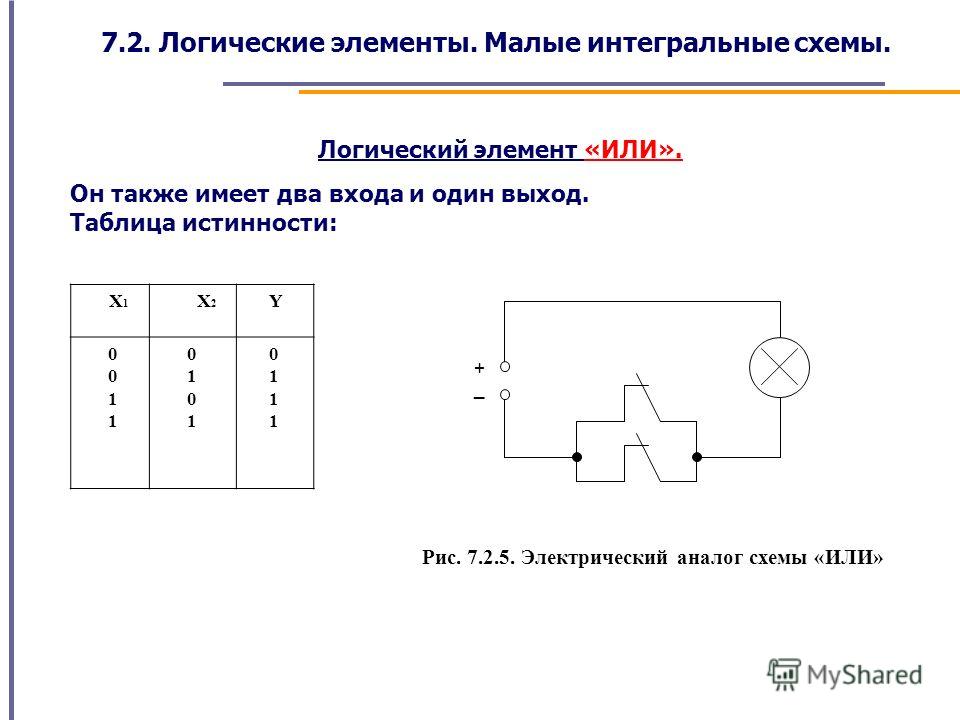 Количество ПФ равно количеству выходных переменных, при этом ПФ может принимать значения 0 или 1.
Количество ПФ равно количеству выходных переменных, при этом ПФ может принимать значения 0 или 1.
Логические операции . Наибольший практический интерес представляют следующие элементарные операции (функции).
Булево умножение (конъюнкция),
Логическое сложение (дизъюнкция),
Булево умножение с инверсией,
Логическое сложение с инверсией,
Суммирование по модулю 2,
Эквивалентность.
Логические элементы . Существуют цифровые интегральные схемы, соответствующие основным логическим операциям. Логическому умножению соответствует логический элемент «И». Логическому сложению соответствует логический элемент «ИЛИ». Логическое умножение с инверсией - логический элемент "И-НЕ". Логическое сложение с инверсией - логический элемент "ИЛИ-НЕ". Операция инверсии соответствует логическому элементу «НЕ». Существуют микросхемы, реализующие множество других логических операций.
таблицы истинности . Основным способом задания ФП является составление таблицы истинности, в которой для каждого набора входных переменных указывается значение ФП (0 или 1).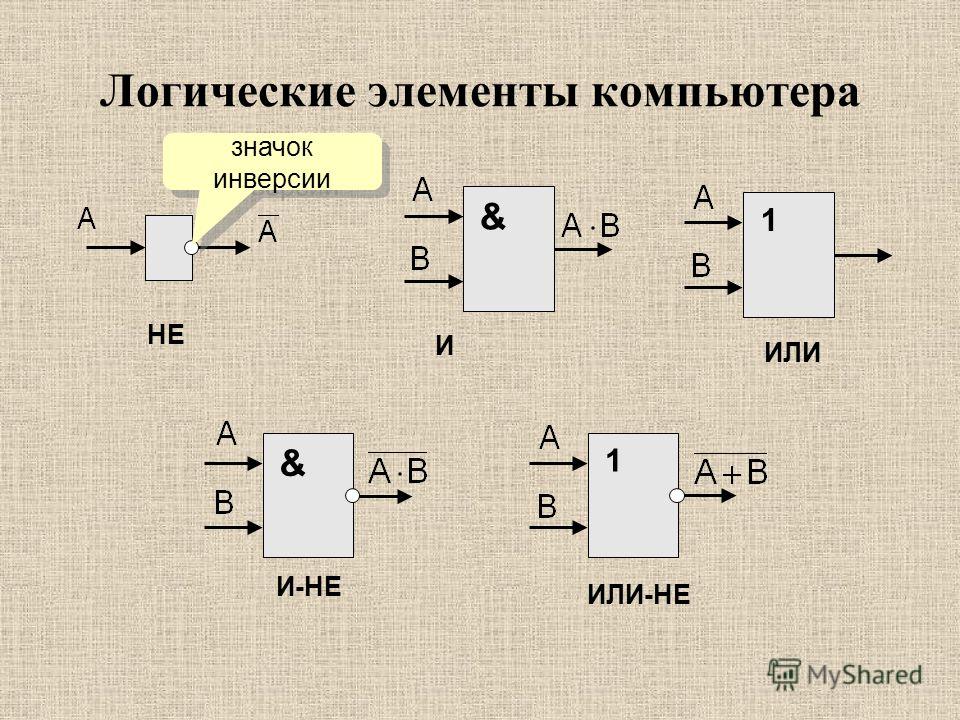 Таблица истинности для логического элемента «НЕ» (логическая операция) равна
Таблица истинности для логического элемента «НЕ» (логическая операция) равна
| Вход X | Выход Y |
1.1. Изучение характеристик логического элемента «ИЛИ-НЕ»
Схема изучения логического элемента «ИЛИ-НЕ» представлена на рис. один.
На схеме рис. 1 входы вентиля «ИЛИ НЕТ» подключены к генератору слов, формирующему последовательность двоичных чисел 00, 01, 10 и 11. Правой (младшей) двоичной цифре каждого числа соответствует к логической переменной Х1, левый (старший) - к логической переменной Х2. К входам логического элемента также подключены логические пробники , которые загораются красным цветом при поступлении на этот вход логической «1». Выход логического элемента подключен к логическому пробнику, который загорается красным при появлении на выходе логической «1».
Построение схемы исследования логического элемента "ИЛИ-НЕ"
Запустить программу с помощью ярлыка на рабочем столе Windows Electronics Workbench .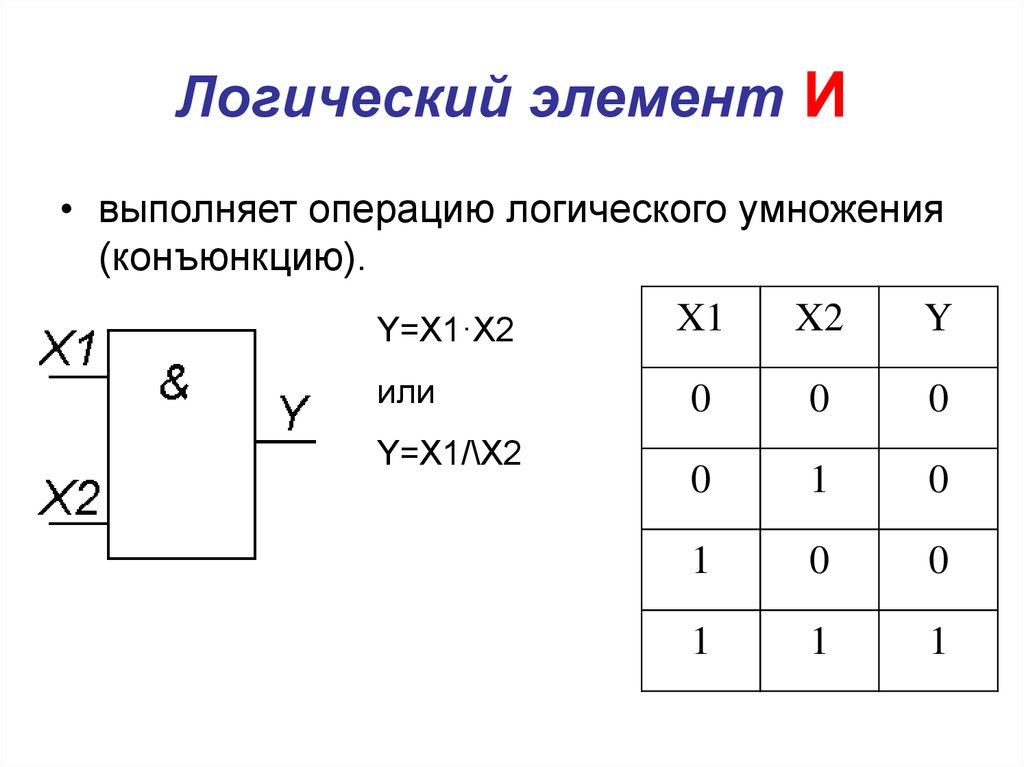
Конструкция схемы рис. 1 будем делать в два этапа: сначала разместим его так, как показано на рис. 1 пиктограммы элементов, а затем соединить их последовательно.
1. Нажмите кнопку
библиотеки компонентов и инструментальные панели. Из появившегося окна логического элемента вытащите значок логического элемента НОР ("ИЛИ НЕТ").
2. Нажмите кнопку
В появившемся окне последовательно вытащите значки логических пробников.
3. Разверните логические щупы, как показано на рис. 1. Для этого на функциональной панели используйте кнопку поворота
4. Нажмите кнопку
библиотеки компонентов и инструментальные панели. Из появившегося окна индикатора вытащите иконку генератор слов
5. Расположите иконки элементов методом буксировки, как показано на рис. 1 и соедините элементы согласно рисунку.
6. Дважды щелкните, чтобы открыть переднюю панель генератора слов .
В левой части панели генератора слов кодовых комбинаций отображаются в шестнадцатеричном коде, а внизу - в двоичном.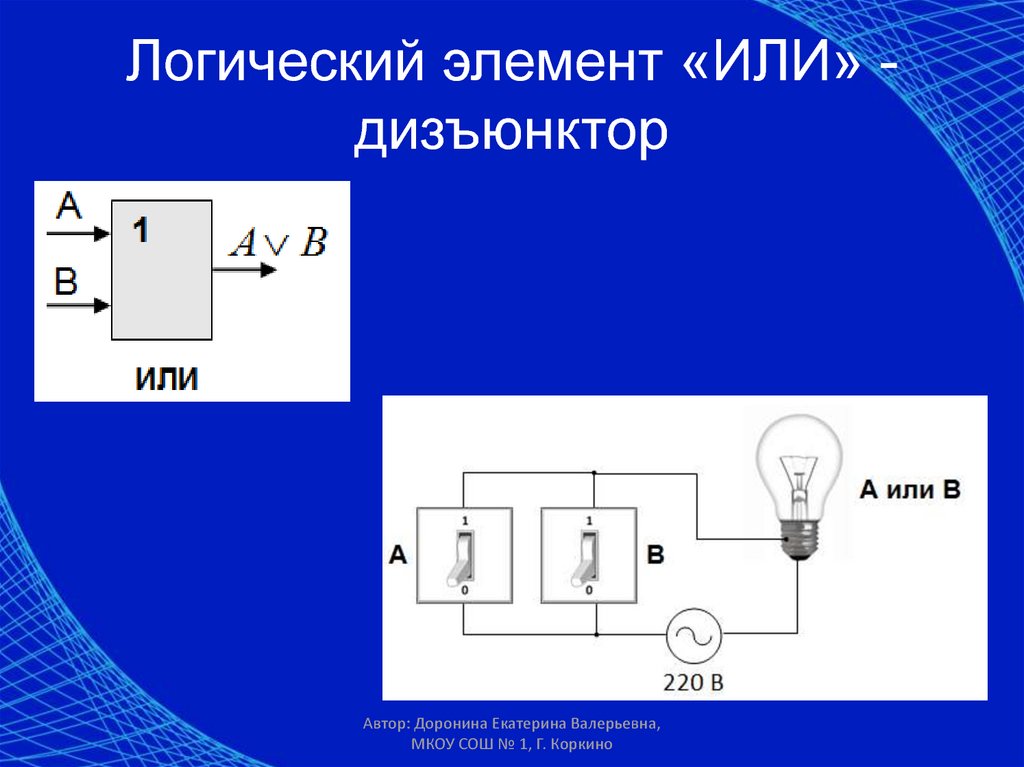
7. Заполните окно шестнадцатеричного кода кодовыми комбинациями, начиная с 0 в верхней нулевой ячейке и добавляя 1 в каждую последующую ячейку. Для этого нажмите на кнопку, в появившемся окне включите опцию Up counter и нажмите на кнопку принять .
8. В окне Частота установить частоту генерации шаблона 1 Гц.
Последовательности двоичных чисел 00, 01, 10 и 11 соответствуют в шестнадцатеричном коде - 0, 1, 2, 3. Запрограммируем генератор на периодическую генерацию заданной последовательности чисел.
9. Набрать в окне Окончательный номер 0003 нажмите на кнопку цикл .
10. Запустите процесс имитации с помощью переключателя. Следите за тем, при каких комбинациях входных сигналов на выходе логического элемента появится «1». Нажав кнопку шаг , заполнить таблицу истинности для элемента "ИЛИ-НЕ" в Отчете. Остановите процесс моделирования с помощью переключателя.
11. Сохраните файл в папке с вашей Фамилией под именем Zan_17_01 .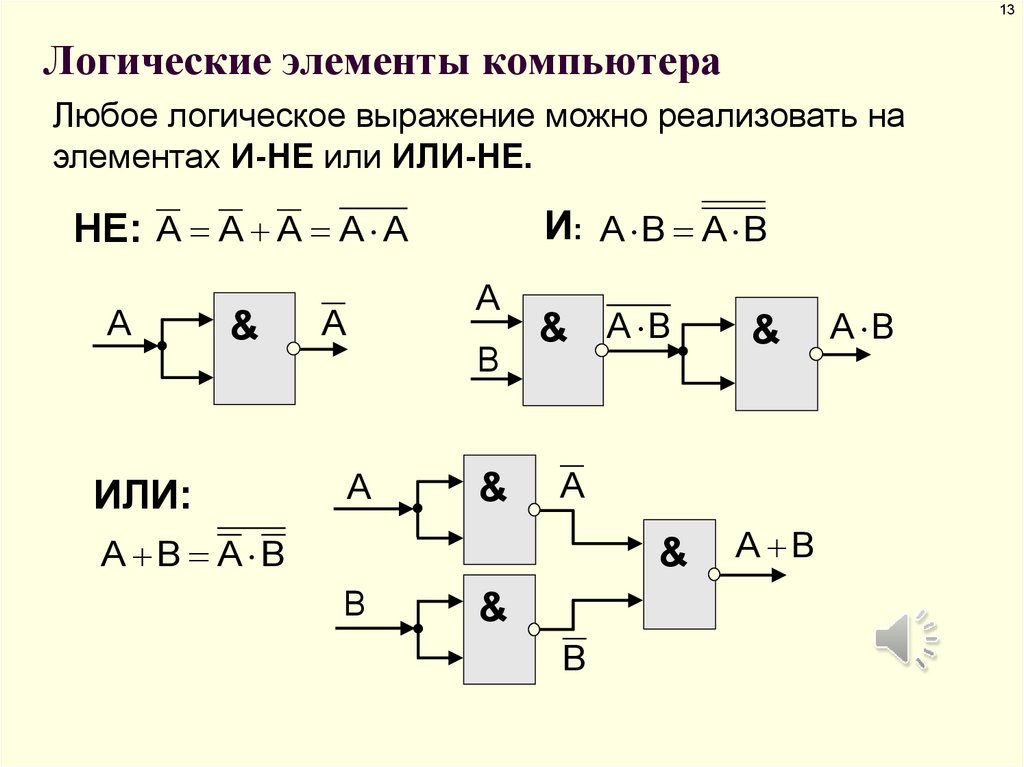
Этот набор позволяет изучить логику основных типов логических элементов. Набор помещен в пластиковую коробку черного цвета размером 200 х 170 х 100 мм.
Установка содержит четыре модуля типоразмера 155 х 95 х 30 мм. Кроме того, должны быть соединительные провода, но в экземпляре, с которым имел дело автор, они отсутствовали, а инструкция по эксплуатации сохранилась.
Логический элемент И
Первый модуль - логический элемент И , на его выходе сигнал появляется только в том случае, если сигнал поступает на оба его информационных входа.
Стандартный модуль представляет собой печатную плату, закрытую сверху прозрачной пластиковой крышкой, закрепленной двумя винтами.
Модуль легко разбирается, что позволяет детально осмотреть печатную плату устройства. С обратной стороны печатные проводники закрыты непрозрачной пластиковой крышкой.
Вентиль ИЛИ
Практически аналогично устроен логический элемент ИЛИ , на его выходе появляется сигнал при условии поступления сигнала на любой из его информационных входов.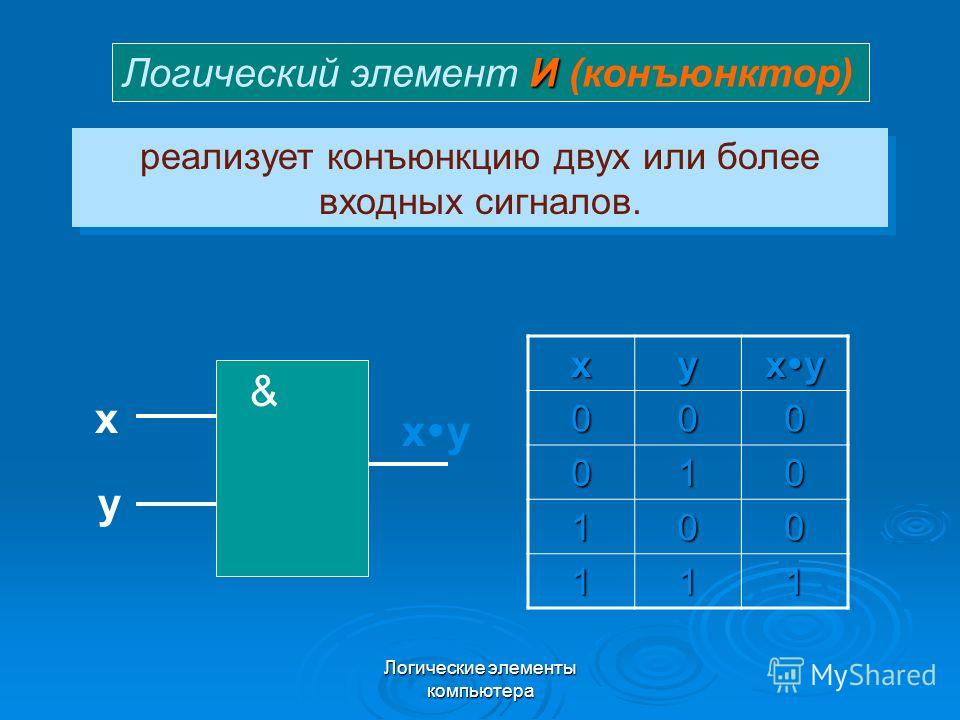
Логический элемент НЕ
Логический элемент НЕ . Входные и выходные сигналы этого элемента всегда имеют противоположные значения.
Триггер
Триггер - логическое устройство с двумя устойчивыми состояниями, используемое как основа для всех видов устройств, требующих хранения информации.
В общем, этот комплект цифровой электроники похож на комплект электронного усилителя. Конечно, реализация логических элементов, представленных в наборе, далеко не единственная. По сути, здесь реализованы логические элементы, как это было сделано в 60-х годах XX века. При этом важно, что при работе с этим набором можно непосредственно изучить пример простейшей схемы, лежащей в основе самой основы цифровой полупроводниковой электроники. Таким образом, отдельный логический элемент перестает быть «черным ящиком», действующим на чистой магии. Хорошо видимая и в то же время защищенная электрическая схема, это как раз то, что нужно для изучения основ электроники.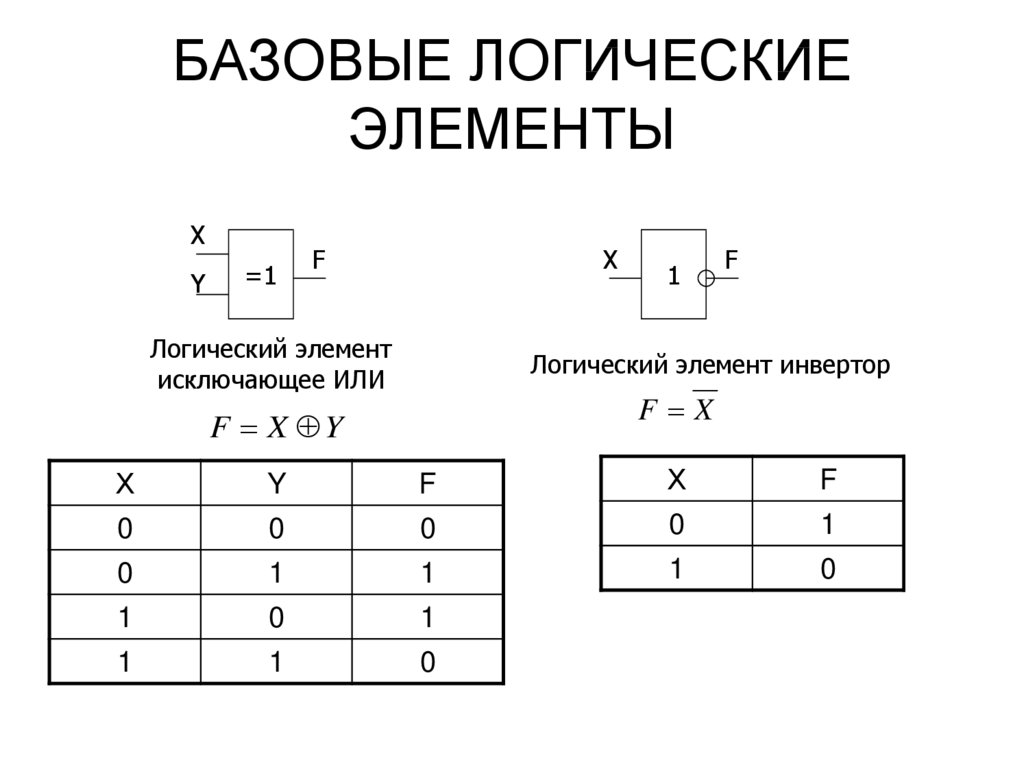 Автор обзора Денев.
Автор обзора Денев.
Транзистор представляет собой компонент из полупроводникового материала, позволяющий управлять достаточно большим электрическим током в цепи путем изменения меньшего тока на управляющем электроде.
Бывают биполярные и полевые транзисторы. Отличаются они тем, что в биполярном транзисторе перенос заряда осуществляется как основными, так и второстепенными носителями заряда - дырками и электронами. В полевых транзисторах перенос заряда осуществляется только одним типом носителей.
Синтез и исследование элементов на основе транзисторно-транзисторной логики (ТТЛ). Схемы ТТЛ основаны на биполярных транзисторах npn. Биполярные транзисторы названы так потому, что перенос зарядов в них осуществляется двумя типами носителей - электронами и дырками. Базовым элементом этой технологии является схема NAND. Логическое умножение осуществляется за счет свойств многоэмиттерного транзистора.
Элемент ИЛИ-НЕ.
Реализация логического элемента ИЛИ-НЕ на биполярных транзисторах показана на рисунке 1. 1.
1.
Логическая функция ИЛИ-НЕ может быть выражена с помощью функций И и НЕ с использованием правил де Моргана: отрицание дизъюнкции есть конъюнкция отрицаний. В схеме имеется два инвертора VT1 и VT2, питание которых осуществляется с помощью ключей и напряжения противоположной полярности. При подаче логического нуля на оба входа («земля») в p-области транзистора происходит разряд, он становится закрытым, при этом ток начинает протекать через транзисторы VT3, VT4, выполняющие функцию И, уровень напряжения достаточен для обеспечения логической единицы. Если хотя бы на один вход подать логическую единицу («плюс»), то на одном из выходов инверторов будет падение напряжения, напряжения на выходе И будет недостаточно для обеспечения логической единицы.
Рисунок 1.1 – Логический элемент ИЛИ-НЕ на биполярных транзисторах
Рисунок 1.2 – Логические нули подаются на входы элемента ИЛИ-НЕ
На рисунке 1.2 показан вариант работы транзисторной схемы, когда логические нули подаются на входы, в результате на выходе будет значение логической единицы.
Элемент ИЛИ-НЕ формирует следующую таблицу истинности (см. Таблицу 1.1):
Таблица 1.1 - Таблица истинности элемента ИЛИ-НЕ
Элемент НЕ.
Элемент НЕ на TTL показан на рис. 1.3.
Рисунок 1.3 – Логический инвертор (функция логическое НЕ)
При установке переключателя в сторону «плюс» протекает небольшой эмиттерный ток, этот ток позволяет открыть транзистор, происходит падение напряжения и индикатор не гаснет загораются, что соответствует логическому нулю. При установке ключа на сторону «земли» блокирующий слой расширяется, сопротивление транзистора становится намного больше сопротивления резистора, транзистор закрыт, падения напряжения нет, что соответствует логической единице.
Таблица истинности элемента НЕ (см. табл. 1.2).
Таблица 1.2 - Таблица истинности элемента НЕ
При питании логических единиц замыканием ключей и через транзисторы вокруг этих ключей протекает достаточный ток и на вход инвертирующего транзистора подается достаточное напряжение для его открытия, ток течет свободно, сопротивление инвертирующего транзистора мало, напряжение на резисторе у инвертора падает, на выходе логический ноль.
Когда в ключах либо единица, либо ноль, либо оба нуля, выходного напряжения на инвертор недостаточно для его открытия, его сопротивление велико и на его коллекторе формируется высокий уровень напряжения, на выходе логический ноль.
Схема элемента И-НЕ со сложным инвертором показана на рисунке 1.5.
Рисунок 1.5 – Элемент И-НЕ со сложным инвертором
Таблица истинности для этого элемента соответствует таблице 1.3.
Этот элемент состоит из трех каскадов: входного (R1, VT1, VT2 - многоэмиттерная модель транзистора), фазоинверсного (VT3, R2, R4) и выходного усилительного (VT4, VT5, VD3, R3).
При подаче на входы х 1 и х 2 логических единиц на транзисторах VT1, VT2 возникает коллекторный ток и течет в базу транзистора VT3, открывая его. Часть эмиттерного тока VT3 поступает на транзистор VT5, он открывается, на выходе у устанавливается низкий уровень напряжения, при этом VT4 закрыт (недостаточно напряжения через переход база-эмиттер VT4 и VD1). При подаче хотя бы одного логического нуля ток коллектора транзисторов VT1, VT2 прекращается, VT3 и VT5 закрываются, VT4 открывается. Так как VT5 закрыт, на выходе формируется высокий уровень напряжения.
При подаче хотя бы одного логического нуля ток коллектора транзисторов VT1, VT2 прекращается, VT3 и VT5 закрываются, VT4 открывается. Так как VT5 закрыт, на выходе формируется высокий уровень напряжения.
Синтез и исследование элементов на МДП-транзисторах.
Развитие схемотехники ЭВМ на МОП-транзисторах началось с появлением в 1962 г. полевого транзистора с индуцированным каналом. Схемы на МОП-транзисторах отличаются относительной простотой изготовления, компактностью, малым энергопотреблением, высокой помехоустойчивостью к изменениям напряжения питания. МОП-транзисторы имеют структуру металл-диэлектрик-полупроводник и обычно называются МДП-транзисторами. Поскольку диэлектрик реализован на основе оксида SiO 2 , используется название MOSFET (униполярные, канальные). Металлический электрод, на который подается управляющее напряжение, называется затвором (G), а два других электрода называются истоком (I) и стоком (C). Ток течет от истока к стоку. Для p-канала полярность стока отрицательная, а для p-канала положительная. Основная полупроводниковая пластина называется облицовкой (П). Канал — это приповерхностный проводящий слой между истоком и стоком, в котором величина тока определяется с помощью электрического поля.
Основная полупроводниковая пластина называется облицовкой (П). Канал — это приповерхностный проводящий слой между истоком и стоком, в котором величина тока определяется с помощью электрического поля.
Процессы инжекции и диффузии в канале отсутствуют. Рабочий ток в канале обусловлен дрейфом в электрическом поле электронов в n-каналах и дырок в p-каналах.
При нулевом значении управляющего напряжения канал отсутствует и ток не течет. Канал, который образуется под действием внешнего управляющего напряжения, называется индуцированным. Напряжение, при котором формируется канал, называется пороговым напряжением. Канал с начальной дополнительной концентрацией зарядов называется встроенным. Быстродействие n-МОП-транзисторов в 5-8 раз превышает быстродействие p-МОП-транзисторов, так как подвижность электронов намного больше, чем дырок. В МОП-схемах полностью исключены резисторы, их роль выполняют МОП-транзисторы.
Элемент ИЛИ-НЕ.
Схема элемента ИЛИ-НЕ представлена на рисунке 1. 6.
6.
Рисунок 1.6 – Элемент ИЛИ-НЕ на МОП-транзисторах
Транзистор VT1 выполняет роль резистора, т.к. МОП-транзисторы имеют высокое сопротивление, для того чтобы он пропускал ток, исток подключается к положительному полюсу истока. При одновременной подаче логических нулей на транзисторы VT2 и VT3 они закрываются, создавая нагрузку после транзистора VT1, уровень этого напряжения соответствует логической единице. Таблица истинности этого элемента соответствует таблице 1.1. Если на вход подать хотя бы одну или обе логические единицы, один из транзисторов VT2 и VT3 (или оба) откроются, произойдет падение напряжения, на выходе будет логический ноль.
Элемент И-НЕ.
Элемент И-НЕ показан на рис. 1.7.
Рисунок 1.7 – Элемент И-НЕ на МОП-транзисторах
Элемент ИЛИ.
Элемент I.
Синтез и исследование элементов на структурах CMDP.
Элемент ИЛИ-НЕ.
Элемент И-НЕ.
Синтез и исследование элементов на основе эмиттерно-связанной логики (ЭСЛ).
Схемотехника элементов ЭСЛ основана на использовании дифференциального усилителя в режиме коммутации тока. Элементы ESL появились в 1967 и в настоящее время являются самыми быстрыми среди полупроводниковых элементов на основе кремния. Задержки распространения сигналов в элементах ЗЭС уменьшились до субнаносекундного диапазона (примерно 1 нс).
Сверхбыстрая работа элементов ЭСЛ достигается за счет использования ненасыщаемого режима работы транзисторов, выходных эмиттерных повторителей и малых амплитуд логических сигналов (около 0,8 В). Логические элементы ЭСЛ имеют парафазный выход, что позволяет одновременно получать прямое и обратное значение реализуемой функции. Это дает заметное снижение общего количества микросхем в аппаратуре.
Особенности схемы ESL и ее характеристики:
Возможность объединения выходов нескольких элементов для формирования новых функций;
Возможность работы на низкоомную нагрузку за счет наличия эмиттерных повторителей;
Низкая величина работы переключения и независимость потребляемой мощности от частоты переключения;
Высокая стабильность динамических параметров при изменении температуры и напряжения питания;
Использование отрицательного источника питания и заземления коллектора, что снижает зависимость выходных сигналов от помех в шинах питания.
К недостаткам элементов ЭСЛ можно отнести сложность схем, значительное энергопотребление и трудности согласования с микросхемами ТТЛ и ТТЛШ.
Элемент I.
Элемент ИЛИ.
Элемент И-НЕ.
Элемент ИЛИ-НЕ.
Синтез и исследование элемента НЕ на МДП транзисторах () в положительной и отрицательной логике.
СЕРГИЕВ ПОСАД
Лаборатория №1
Логические функции, ЭЛЕМЕНТЫ и схемы
Цель
Изучение логических функций, логических элементов и схем.
Устройства и элементы
Логический преобразователь.
Генератор слов.
Вольтметр.
Логические датчики.
Источник напряжения +5 В.
Источник сигнала "логическая единица".
Двухпозиционный переключатель.
Двухвходовые элементы И, И-НЕ, ИЛИ, ИЛИ-НЕ.
Микросхемы 74 серии.
Краткая информация из теории
Аксиомы алгебры логики
Переменные, рассматриваемые в алгебре логики, могут принимать только два значения - 0 или 1. В алгебре логики отношением эквивалентности является определенные (обозначаемые знаком =), операции сложения (дизъюнкции), обозначаемые знаком, умножения (конъюнкции), обозначаемые знаками &, или точкой, и отрицания (или инверсии), обозначаемые знаком подчеркивания или апостроф."
В алгебре логики отношением эквивалентности является определенные (обозначаемые знаком =), операции сложения (дизъюнкции), обозначаемые знаком, умножения (конъюнкции), обозначаемые знаками &, или точкой, и отрицания (или инверсии), обозначаемые знаком подчеркивания или апостроф."
Алгебра логики определяется следующей системой аксиом:
х = 1, если х 0; х = 0, если х 1;
0&0 = 0; 1 1 = 1
1&1 = 1; 0 0 =0;
1&0 = 0&1 = 0; 0 1 = 1 0 = 1;
Логические выражения
Логические выражения обычно записываются в конъюнктивных или дизъюнктивных нормальных формах. В дизъюнктивной форме логические выражения записываются как логическая сумма логических произведений, в конъюнктивной форме - как логическое произведение логических сумм. Процедура такая же, как и в обычных алгебраических выражениях. Булевы выражения связывают значение логической функции со значениями булевых переменных.
Логические законы и тождества
При преобразовании логических выражений используются следующие логические законы и тождества
Логические функции
Любое логическое выражение, составленное из n логических переменных с использованием конечного числа алгебраических операций рассматривается как некоторая функция от n переменных. Такая функция называется логической функцией. В соответствии с аксиомами алгебры логики функция может принимать значение 0 или 1 в зависимости от значения переменных. Функция n логических переменных может быть определена для 2 n значений переменных, соответствующих всем возможным значениям n-битных двоичных чисел. Следующие функции двух переменных x и at
Такая функция называется логической функцией. В соответствии с аксиомами алгебры логики функция может принимать значение 0 или 1 в зависимости от значения переменных. Функция n логических переменных может быть определена для 2 n значений переменных, соответствующих всем возможным значениям n-битных двоичных чисел. Следующие функции двух переменных x и at
f 1 (x, y) = x & y = x y = x - логическое умножение (соединение),
f 2 (x, y) = x y - логическое сложение (дизъюнкция),
f 3 (x,y ) = = – Ход Шеффера,
f 4 (x,y) = = – Стрелка прокола,
f 5 (x,y) = x y = – сложение по модулю 2,
f 6 (x, y) = - эквивалентность.
Логика
Логическим элементом называется физическое устройство, реализующее одну из операций алгебры логики или простейшую логическую функцию. Цепь, составленная из конечного числа логических элементов по определенным правилам, называется логической схемой. Основные логические функции соответствуют элементам схемы, которые их выполняют.
таблица истинности
Так как область определения любой функции от n переменных конечна (2 n значений), то такую функцию можно задать таблицей значений f(i), которые она принимает в точках i, где i= 0,…,2 n -1. Такие таблицы называются таблицами истинности. В таблице 1 представлены таблицы истинности, определяющие вышеуказанные функции.
Таблица 1
Переменные значения | ||||||||
| х | в | f1 | f2 | f 3 | f4 | f5 | f6 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
| 2 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| 3 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 |
Карты Карно
Если количество логических переменных не превышает 5-6, логические уравнения удобно преобразовывать с помощью карт Карно. Цель преобразований — получить компактное логическое выражение (минимизация). Минимизация осуществляется путем объединения соседних множеств (термов). Объединенные наборы должны иметь одинаковые значения признаков (все 0 или все 1). Для наглядности рассмотрим пример: пусть требуется найти логическое выражение для функции большинства f m трех переменных x, y, z, описываемой таблицей истинности, приведенной в табл. 2.
Цель преобразований — получить компактное логическое выражение (минимизация). Минимизация осуществляется путем объединения соседних множеств (термов). Объединенные наборы должны иметь одинаковые значения признаков (все 0 или все 1). Для наглядности рассмотрим пример: пусть требуется найти логическое выражение для функции большинства f m трех переменных x, y, z, описываемой таблицей истинности, приведенной в табл. 2.
Таблица 2
Функция большинства
| № | x | у | г | м |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 |
| 3 | 0 | 1 | 1 | 1 |
| 4 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 1 |
| 6 | 1 | 1 | 0 | 1 |
| 7 | 1 | 1 | 1 | 1 |
Здесь номер строки равен числу i= 2 2 x+2 1 y+2 0 z, образованному значениями переменных.
Давайте составим карту Карно. Это что-то похожее на таблицу, в которой названия столбцов и строк представляют собой значения переменных, причем переменные расположены в таком порядке, что при переходе к соседнему столбцу или строке значение только одной переменной изменяется . Например, в строке xy таблицы 3 значения переменных xy могут быть представлены следующими последовательностями 00,01,11,10 или 00,10,11,01. Таблица заполняется значениями функций, соответствующими комбинациям значений переменных. В результате таблица выглядит так, как показано ниже (таблица 3).
Таблица 3
Карта Карно
Функция большинства
| xy z | 00 | 01 | 11 | 10 |
| 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 | 1 |
На карте Карно отмечены группы, состоящие из 2k соседних ячеек (2,4,8,) и содержащие 1, так как они описываются простыми логическими выражениями. Три овала в таблице определяют логические выражения xy, xz, yz. Каждый овал, соединяющий две клетки, соответствует логическим преобразованиям:
Три овала в таблице определяют логические выражения xy, xz, yz. Каждый овал, соединяющий две клетки, соответствует логическим преобразованиям:
Компактное выражение, описывающее функцию, есть дизъюнкция логических выражений, полученных с помощью карт Карна. В результате получаем выражение в дизъюнктивной нормальной форме
f m = xy v xz v yz .
Если объединить 0, то получится выражение в конъюнктивной нормальной форме
f m = (x v y)(x v z)(y v z).
При реализации мажоритарной функции трех логических переменных получаем схему, которая при подаче на ее входы трех сигналов будет формировать на выходе сигнал, равный сигналу на большинстве входов (2 из 3 или 3 из 3). Эта схема используется для восстановления истинного значения сигналов, поступающих на 3 входа, если возможна ошибка на одном из входов.
Для реализации этой функции на элементах 2И-НЕ необходимо провести следующие преобразования:
Для ДНФ получается более простое выражение, поэтому его следует реализовать. Соответствующая схемная реализация показана на рис. один.
Соответствующая схемная реализация показана на рис. один.
| |
Рис. один
ИЗУЧЕНИЕ ЭЛЕМЕНТОВ ЛОГИКИ
Отправить свою хорошую работу в базу знаний просто. Воспользуйтесь формой ниже
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
HTML версии работы пока нет.
Вы можете скачать архив работы, перейдя по ссылке ниже.
Аналогичные документы
Основные аксиомы и тождества алгебры логики. Аналитическая форма представления булевых функций. Элементарные функции алгебры логики. Функции алгебры логики одного аргумента и формы ее реализации. Свойства, особенности и виды логических операций.
реферат, добавлен 06.12.2010
Системы цифровой обработки информации. Понятие булевой алгебры. Обозначения логических операций: дизъюнкция, конъюнкция, инверсия, импликация, эквивалентность. Законы и тождества булевой алгебры. Логические основы компьютеров. Преобразование структурных формул.
Законы и тождества булевой алгебры. Логические основы компьютеров. Преобразование структурных формул.
презентация, добавлена 11.10.2014
Булевы алгебры — это решетки особого вида, используемые при изучении логики (как логики человеческого мышления, так и логики цифровых компьютеров), а также коммутационных цепей. Минимальные формы булевых многочленов. Теоремы абстрактной булевой алгебры.
Курсовая работа, добавлена 12.05.2009
Свойства операций над множествами. Формулы пропозициональной алгебры. Функции алгебры логики. Существенные и фиктивные переменные. Проверка правильности рассуждений. Алгебра операторов и релейно-контактные схемы. Способы установки графика. Матрицы для графиков.
туториал, добавлен 27.10.2013
Основы формальной логики Аристотеля. Понятия инверсии, конъюнкции и дизъюнкции. Основные законы алгебры логики. Основные законы, допускающие идентичные преобразования логических выражений. Эквивалентные преобразования логических формул.
презентация, добавлена 23.12.2012
Основные понятия алгебры логики. Дизъюнктивные и конъюнктивные нормальные формы. Сущность теоремы Шеннона. Булевы функции двух переменных. Последовательное и параллельное соединение двух выключателей. Свойства элементарных функций алгебры логики.
тест, добавлен 29.11.2010
Понятие об алгебре логики, ее сущность и признаки, основные понятия и определения, предмет и методика изучения. Законы алгебры логики и следствия из них, способы построения формул по заданной таблице истинности. Формы представления булевых функций.
туториал, добавлен 29.04.2009
Логический стиль | использование структурных элементов, которые делают вашу страницу более доступной
Путь // www.yourhtmlsource.com → Доступность → ЛОГИЧЕСКИЙ СТИЛЬ
Росс Шеннон
Многие авторы HTML не знают о различиях между логическими (структурными) элементами и их представлением аналоги, и какой элемент более уместен в различных обстоятельствах. Здесь вы познакомитесь с терминологией и методологией создания логических структур страниц.
Здесь вы познакомитесь с терминологией и методологией создания логических структур страниц.
Навигация по страницам:
Блочные и встроенные элементы
| Логические и презентационные элементы
· Пейзаж
· Использование логического стиля
· Добавление глубины
Последнее обновление этой страницы 21 августа 2012 г.
Блочные и встроенные элементы
Большинство элементов HTML попадают в одну из двух групп: это либо блочных элементов , либо встроенных элементов. . Это важное различие. Элементы уровня блока используются для форматирования целых блоков текста — они выделяются сами по себе, охватывая доступную ширину экрана и обычно добавляя разрывы строк до и после себя. Строчные элементы можно вводить вдоль обычного потока текста, не вызывая серьезных помех, и их можно использовать для воздействия на отдельные символы.
Элементы блочного уровня:
-
<адрес> -
<цитата> -
<дел> -
<набор полей> -
— -
<час> -
<легенда> -
-
<пред> -
Остальные элементы являются встроенными элементами. Правила, управляющие этими двумя типами элементов, просты, но важны:
Правила, управляющие этими двумя типами элементов, просты, но важны:
- Блочные элементы могут содержать другие блочные элементы и встроенные элементы
- Встроенные элементы не могут содержать элементы блочного уровня.
Например, элемент a не может иметь внутри h2 , но заголовок может содержать ссылку. Табличные элементы не относятся строго ни к одному из типов, но могут содержать блочные или встроенные элементы. Элемент — еще один особый случай. Это строго встроенный структурный тип элемента, но поскольку он все равно не может содержать никакого дополнительного контента, это не имеет большого значения. С этими правилами легко ошибиться, поэтому вам следует проверять свои страницы с помощью валидатора W3C ».
Можно изменить способ отображения элемента с помощью его свойства отображения CSS.
Логические и презентационные элементы
Существует еще один метод группировки, который разделяет элементы форматирования текста HTML на две группы — логические или презентационные . Логические элементы представляют функцию текста на странице. То, как они отображаются, зависит от браузера (хотя к настоящему времени браузеры в значительной степени стандартизировали то, как это делается), что означает, что они не зависят от платформы. Презентационные элементы существуют для создания определенного визуального эффекта, но не несут никакого намека на содержание текста.2217 семантическое значение.
Логические элементы представляют функцию текста на странице. То, как они отображаются, зависит от браузера (хотя к настоящему времени браузеры в значительной степени стандартизировали то, как это делается), что означает, что они не зависят от платформы. Презентационные элементы существуют для создания определенного визуального эффекта, но не несут никакого намека на содержание текста.2217 семантическое значение.
Поскольку людям постоянно нужны напоминания; исходные спецификации HTML содержали почти исключительно логические элементы. HTML был структурным языком , а не языком дизайна. Он предназначался для передачи информации максимально простым способом. С тех пор Netscape и Microsoft создали опасную ситуацию, которая была у нас год или два назад, добавив презентационные расширения, такие как элемент шрифта . Файлы HTML стали смехотворно большими из-за избыточных тегов и хаков с презентациями. К счастью, спецификации HTML 4.01 и XHTML 1. 0 отказались от многих элементов представления (заменив их таблицами стилей) и добавили много новых логических элементов, которые добавляют глубины вашей информации. HTML-код снова может быть чистым и простым.
0 отказались от многих элементов представления (заменив их таблицами стилей) и добавили много новых логических элементов, которые добавляют глубины вашей информации. HTML-код снова может быть чистым и простым.
Ландшафт
В прежние времена, когда было не так просто контролировать внешний вид вашей страницы (сейчас для всего этого у нас есть CSS), было приемлемо использовать презентационные элементы для всего и оставлять страницы без какой-либо сортировки. логической структуры. Все были одержимы тем, как выглядели их страницы , не говоря уже о «проблемах» доступности. Люди не использовали элементы заголовков, потому что они выглядели ужасно; легко и просто.
Это был неправильный подход. Поток графических редакторов WYSIWYG в то время сделал эту культуру эстетики по сравнению с совместимостью совершенно бесполезной, и редакторы разослали тысячи страниц, полных шрифт теги и без заголовков.
Проблема: презентационных элементов могут означать только одно . Например, элемент
Например, элемент означает «жирный текст». Что происходит, когда текстовый или аудиобраузер читает этот элемент? В этом контексте это бессмысленно, и поэтому любой акцент, который вы, возможно, хотели показать, используя элемент в первую очередь, теряется для этого читателя. Если вы используете , , каждый браузер может выбрать свою собственную обработку , и представить его результат соответствующим образом — сделав текст жирным, или произнося слова громче и т. д.
Дизайнеры использовали большие шрифты вместо заголовков, чтобы избежать разрывов строк. При интерпретации через любое устройство, кроме графического браузера, эти страницы теряли большую часть своего смысла. Какое название? Где начинаются разделы страницы? Программам, которые пытаются построить структурную схему вашего документа, не с чем будет работать. Кроме того, большинство поисковых систем пытаются выбрать заголовки для лучшего ранжирования.
Недавно произошел возврат к использованию логических элементов, замаскированных таблицей стилей, поэтому ваша страница выглядит так, как вы хотите, но элементы, из которых она состоит, на самом деле делают больше, чем просто придают странице определенный вид. Они позволяют читать страницу в любом количестве типов браузеров, таких как слуховые браузеры, текстовые браузеры, дисплеи Брайля и т. д., и при этом отображаться надлежащим образом.
Использование логического стиля
Так что же такое логические элементы и как они будут выглядеть по умолчанию в графическом браузере?
-
 Вы можете удалить поля с помощью CSS.
Вы можете удалить поля с помощью CSS. -
-
-
<код>подходит для примера компьютерного кода и обычно отображается моноширинным шрифтом. Эквивалентно -
-
-

-
доне является строго логическим элементом, но его использование часто необходимо. -
-
del, используется для отображения текста, вставленного во время редактирования. Обычно отображается с подчеркиванием. -
<адрес>должен содержать контактную информацию, включая адреса электронной почты. -
 Обычно он отображается шрифтом фиксированной ширины.
Обычно он отображается шрифтом фиксированной ширины. -
-
Добавление глубины
Атрибут title позволяет вам добавить всплывающую подсказку к любому элементу вашей страницы . Они особенно полезны применительно к ссылкам, поскольку помогают читателю оценить, что он может найти, если щелкнет ссылку. Вы должны добавить информационные заголовки к как можно большему количеству ссылок, следуя этим » рекомендациям по заголовкам.
Есть еще три элемента, представленные в HTML 4, которые позволяют вам добавлять дополнительную информацию во всплывающую подсказку, используя этот атрибут.
-
используется для обозначения сокращения. Раскройте полное значение аббревиатуры во всплывающей подсказке. Этот тег не применяет собственного форматирования.
Раскройте полное значение аббревиатуры во всплывающей подсказке. Этот тег не применяет собственного форматирования.
-
используется для включения аббревиатуры (например, ASCII) с полным значением во всплывающей подсказке (которую вы должны попытаться определить по крайней мере для первого экземпляра каждой аббревиатуры на странице). Обычно форматирование не применяется.
-
используется для определения сложного слова. Напишите собственное определение во всплывающей подсказке. Обычно отображается курсивом.
исходный код: Поскольку эти элементы были введены совсем недавно, большинство веб-пользователей не заметят их. Кроме того, некоторые из них не делают свое присутствие очень очевидным, поэтому вам следует использовать собственное форматирование (с помощью CSS, конечно), чтобы помочь вашим читателям найти их. Добавить
abbr, acronym, dfn {cursor: help; нижняя граница: пунктирная известь 1px; }
в вашу таблицу стилей, чтобы курсор превратился в курсор справки, и добавьте цветную рамку к трем элементам, составляющим селектор. Этого должно быть достаточно, чтобы большинство пользователей поняли, что им следует на мгновение задержать мышь.
Этого должно быть достаточно, чтобы большинство пользователей поняли, что им следует на мгновение задержать мышь.
Логические операторы: Elementwise & | ~ (функции MATLAB)
логические операторы: поэлементно & | ~ (функции MATLAB)
Справочник по функциям MATLAB
Логические операторы: Elementwise & | ~
Поэлементные логические операции над массивами
Синтаксис
-
A и B
А | Б
~ А
Описание
Символы и , | и ~ являются логическими операторами массива И , ИЛИ и НЕ . Они работают поэлементно в массивах, где логический 0 представляет false , а логический 1 или любой ненулевой элемент представляет верно . Логические операторы возвращают логический массив
Логические операторы возвращают логический массив с элементами, установленными на 1 ( true ) или 0 ( false ), в зависимости от ситуации.
Оператор и выполняет логическое И , | Оператор выполняет логическое ИЛИ , а ~A дополняет элементы A . Функция xor(A,B) реализует исключительную операцию ИЛИ . Таблица истинности для этих операторов и функций показана ниже.
Входы
и
или
не
xor
А
Б
А и Б
А | Б
~А
xor(A,B)
0
0
0
0
1
0
0
1
0
1
1
1
1
0
0
1
0
1
1
1
1
1
0
0
Приоритет логических операторов по отношению друг к другу:
Оператор
Эксплуатация
Приоритет
~
НЕ
Самый высокий
и
Поэлементно И
|
Поэлементно ИЛИ
&&
Короткое замыкание И
||
Короткое замыкание ИЛИ
Самый низкий
Примечания
MATLAB всегда дает 9приоритет оператора 0031 и
над оператором | оператор. Хотя MATLAB обычно оценивает выражения слева направо, выражение
Хотя MATLAB обычно оценивает выражения слева направо, выражение a|b&c оценивается как a|(b&c) . Рекомендуется использовать круглые скобки, чтобы явно указать предполагаемый приоритет операторов, содержащих комбинации и и | .Эти логические операторы имеют эквиваленты функций М-файла, как показано.
| Логическая операция | Эквивалентная функция |
А и Б | и(А,В) |
А | Б | или (А, В) |
~А | не(А) |
Примеры
В этом примере показано логическое ИЛИ элементов вектора u с соответствующими элементами вектора v :
См. Также
Также
Все , Любое , Найти , Logical , XOR , TRUE , FALSE
TRUE , FALES Логические операторы, короткое замыкание, && , ||
Реляционные операторы < , <= , > , >= , == , ~=
логический Логические операторы: короткое замыкание && ||
© 1994-2005 The MathWorks, Inc.
Использовать исключительное или. Элементы эксклюзивные или. Приоритет логических операций
В булевой алгебре, на которой основана вся цифровая техника, электронные элементы должны выполнять ряд определенных действий. Это так называемая логическая основа. Вот три основных шага:
Это так называемая логическая основа. Вот три основных шага:
ИЛИ — логическое сложение ( дизъюнкция ) — ИЛИ ;
И - логическое умножение ( соединение ) - И ;
НЕ-логическое отрицание ( инверсия )- НЕ .
Возьмем за основу положительную логику, где высокий уровень будет "1", а низкий уровень будет принят за "0". Для того, чтобы можно было более наглядно рассмотреть выполнение логических операций, для каждой логической функции существуют таблицы истинности. Сразу легко понять, что выполнение логических функций «и» и «или» предполагает количество входных сигналов не менее двух, но может быть и больше.
Логический элемент I.
На рисунке показана таблица истинности элемента « И » с двумя входами. Хорошо видно, что логическая единица появляется на выходе элемента только при наличии единицы на первом входе и на втором. В остальных трех случаях на выходе будут нули.
Вход X1 Вход X2 Выход Y 0 0 0 1 0 0 0 1 0 1 1 1
На принципиальных схемах логический элемент «И» обозначается следующим образом.
На зарубежных схемах обозначение элемента «И» имеет другой стиль. Кратко называется И .
Логический элемент ИЛИ.
Элемент " ИЛИ " с двумя входами работает несколько иначе. Логической единице на первом входе достаточно или на втором так как на выходе будет логическая единица. Две единицы также дадут единицу на выходе.
Вход X1 Вход X2 Выход Y 0 0 0 1 0 1 0 1 1 1 1 1
На схемах элемент «ИЛИ» изображается следующим образом.
На зарубежных схемах изображается немного иначе и называется элементом ИЛИ .
Логический элемент НЕ.
Элемент, выполняющий функцию инвертирования» НЕ имеет один вход и один выход. Он реверсирует уровень сигнала. Низкий потенциал на входе дает высокий потенциал на выходе и наоборот.
Вход X Выход Y 0 1 1 0
Так это показано на схемах.
В зарубежной документации элемент «НЕ» изображается следующим образом. Они называют это для краткости НЕ .
Все эти элементы в интегральных схемах могут комбинироваться в различных комбинациях. Это элементы: И-НЕ, ИЛИ-НЕ и более сложные конфигурации. Пришло время поговорить о них.
Это элементы: И-НЕ, ИЛИ-НЕ и более сложные конфигурации. Пришло время поговорить о них.
Логический элемент 2И-НЕ.
Рассмотрим несколько реальных логических элементов на примере серии транзисторно-транзисторной логики (ТТЛ) К155 с низкой степенью интеграции. На рисунке показана очень популярная когда-то микросхема К155ЛА3, содержащая четыре независимых элемента 2И - НЕ . Кстати, с его помощью можно собрать простейший маячок на микросхеме.
Число всегда обозначает количество входов стробирования. В данном случае это двухвходовой элемент «И», выходной сигнал которого инвертирован. Перевернутое, что означает, что «0» становится «1», а «1» становится «0». Обратим внимание на кружок на выходах это символ инверсии . В этой же серии есть элементы 3И-НЕ, 4И-НЕ, а значит элементы «И» с разным количеством входов (3, 4 и т. д.).
Как вы уже поняли, один элемент 2И-НЕ изображается так.
По сути, это упрощенное изображение двух объединенных элементов: элемента 2И и элемента НЕ на выходе.
Иностранное обозначение элемента И-НЕ (в данном случае 2И-НЕ). называется NAND .
Таблица истинности для элемента 2И-НЕ.
Вход X1 Вход X2 Выход Y 0 0 1 1 0 1 0 1 1 1 1 0
В таблице истинности элемента 2И - НЕ мы видим, что благодаря инвертору получается картина, противоположная элементу "И". В отличие от трех нулей и одной единицы, у нас есть три единицы и ноль. Элемент И-НЕ часто называют элементом Шеффера.
В отличие от трех нулей и одной единицы, у нас есть три единицы и ноль. Элемент И-НЕ часто называют элементом Шеффера.
Логический элемент 2ИЛИ-НЕ.
Логический элемент 2ИЛИ - НЕ представлен в серии К155 микросхемой 155ЛЕ1. Он содержит четыре независимых элемента в одном корпусе. Таблица истинности также отличается от схемы «ИЛИ» инвертированием выходного сигнала.
Таблица истинности для логического элемента 2ИЛИ-НЕ.
Вход X1 Вход X2 Выход Y 0 0 1 1 0 0 0 1 0 1 1 0
Изображение на схеме.
На иностранный лад его изображают следующим образом. Вызывается как NOR .
У нас на выходе только один высокий потенциал, за счет подачи низкого потенциала на оба входа одновременно. Здесь, как и на любых других принципиальных схемах, кружок на выходе подразумевает инверсию сигнала. Так как схемы И-НЕ и ИЛИ-НЕ очень распространены, каждая функция имеет свой символ. Функция И НЕ обозначается значком " & ", а функция ИЛИ НЕ со значком " 1 ".
Для одиночного инвертора таблица истинности уже приводилась выше. Можно добавить, что количество инверторов в одном корпусе может быть до шести.
Логический элемент "исключающее ИЛИ".
К числу основных логических элементов принято относить элемент, реализующий функцию «исключающее ИЛИ». В противном случае эта функция называется «неэквивалентностью».
Высокий выходной потенциал возникает только в том случае, если входные сигналы не равны. То есть один из входов должен быть единицей, а другой нулевым. Если на выходе логического элемента стоит инвертор, то выполняется обратная функция — «эквивалентность». Высокий потенциал на выходе появится при одинаковых сигналах на обоих входах.
Если на выходе логического элемента стоит инвертор, то выполняется обратная функция — «эквивалентность». Высокий потенциал на выходе появится при одинаковых сигналах на обоих входах.
Таблица истинности.
Вход X1 Вход X2 Выход Y 0 0 0 1 0 1 0 1 1 1 1 0
Эти логические элементы находят свое применение в сумматорах. «Исключающее ИЛИ» изображается на диаграммах знаком равенства перед единицей « =1». ».
«Исключающее ИЛИ» изображается на диаграммах знаком равенства перед единицей « =1». ».
На иностранный манер «исключающее ИЛИ» называется XOR и на схемах рисуют так. используются элементы, совмещенные в различных комбинациях.Вот например К555ЛР4.Называется очень серьезно 2-4И-2ИЛИ-НЕ.
Таблица его истинности не приводится, так как микросхема не является базовым логическим элементом. Такие микросхемы выполняют специальные функции и намного сложнее приведенного примера. В логическую основу также входят простые элементы «И» и «ИЛИ». Но используются они гораздо реже. Может возникнуть вопрос, почему эта логика называется транзисторно-транзисторной.
Если поискать в справочной литературе схему, скажем, элемента 2И - НЕ из микросхемы К155ЛА3, то там можно увидеть несколько транзисторов и резисторов. На самом деле ни резисторов, ни диодов в этих микросхемах нет. На кристалл кремния через трафарет нанесены только транзисторы, а функции резисторов и диодов выполняют эмиттерные переходы транзисторов. Кроме того, в ТТЛ-логике широко используются многоэмиттерные транзисторы. Например, на входе элемента 4И имеется четырехэмиттерный
Кроме того, в ТТЛ-логике широко используются многоэмиттерные транзисторы. Например, на входе элемента 4И имеется четырехэмиттерный
Электрическая схема, предназначенная для выполнения какой-либо логической операции над входными данными, называется логическим элементом. Входные данные здесь представляются в виде напряжений различного уровня, а результат логической операции на выходе также получается в виде напряжения определенного уровня.
Операнды в данном случае подаются - на вход логического элемента поступают сигналы в виде напряжения высокого или низкого уровня, которые по сути служат входными данными. Так, напряжение высокого уровня — логическая единица — указывает на истинное значение операнда, а напряжение низкого уровня 0 — на ложное значение. 1 - ИСТИНА, 0 - ЛОЖЬ.
Логический элемент - элемент, реализующий определенные логические связи между входными и выходными сигналами. Логические элементы обычно используются для построения логических схем ЭВМ, дискретных схем автоматического контроля и управления. Для всех типов логических элементов, независимо от их физической природы, характерны дискретные значения входных и выходных сигналов.
Для всех типов логических элементов, независимо от их физической природы, характерны дискретные значения входных и выходных сигналов.
Логические элементы имеют один или несколько входов и один или два (обычно обратных друг другу) выхода. Значения «нулей» и «единиц» выходных сигналов логических элементов определяются логической функцией, которую выполняет элемент, а значения «нулей» и «единиц» входных сигналов, которые играют роль независимых переменных. Существуют элементарные логические функции, из которых можно составить любую сложную логическую функцию.
В зависимости от устройства схемы элемента, от его электрических параметров логические уровни (высокий и низкий уровни напряжения) входа и выхода имеют одинаковые значения для высокого и низкого (истинного и ложного) состояний.
Традиционно логические элементы выпускаются в виде специальных радиодеталей - интегральных схем. Логические операции, такие как конъюнкция, дизъюнкция, отрицание и сложение по модулю (И, ИЛИ, НЕ, исключающее ИЛИ) являются основными операциями, выполняемыми над логическими элементами базовых типов. Рассмотрим подробнее каждый из этих типов логических элементов.
Рассмотрим подробнее каждый из этих типов логических элементов.
Логический элемент "И" - конъюнкция, логическое умножение, И
"И" - логический элемент, выполняющий операцию конъюнкции или логического умножения над входными данными. Этот элемент может иметь от 2 до 8 (наиболее распространены в производстве элементы «И» с 2, 3, 4 и 8 входами) входов и один выход.
Символы логических элементов «И» с разным количеством входов показаны на рисунке. В тексте логический элемент «И» с тем или иным количеством входов обозначается как «2И», «4И» и т. д. - элемент «И» с двумя входами, с четырьмя входами и т. д.
Таблица истинности для элемента 2И показывает, что на выходе элемента будет логическая единица только в том случае, если логические единицы будут одновременно на первом входе И на втором входе. В остальных трех возможных случаях выход будет равен нулю.
В западных схемах иконка элемента «И» имеет прямую на входе и закругление на выходе. На отечественных схемах — прямоугольник с символом «&».
На отечественных схемах — прямоугольник с символом «&».
Логический элемент "ИЛИ" - дизъюнкция, логическое сложение, ИЛИ
"ИЛИ" - логический элемент, выполняющий операцию дизъюнкции или логического сложения над входными данными. Он, как и элемент «И», бывает с двумя, тремя, четырьмя и т. д. входами и одним выходом. На рисунке показаны символы логических элементов «ИЛИ» с разным количеством входов. Эти элементы обозначаются следующим образом: 2ИЛИ, 3ИЛИ, 4ИЛИ и т. д.
Таблица истинности для элемента «2ИЛИ» показывает, что для появления на выходе логической единицы достаточно, чтобы на первом входе ИЛИ на втором входе. Если логические единицы находятся сразу на двух входах, выход тоже будет один.
В западных схемах значок элемента «ИЛИ» имеет закругленный вход и закругленный заостренный выход. На отечественных схемах — прямоугольник с символом «1».
Логический элемент "НЕ" - отрицание, инвертор, НЕ
"НЕ" - логический элемент, выполняющий операцию логического отрицания над входными данными. Этот элемент, имеющий один выход и только один вход, еще называют инвертором, так как он фактически инвертирует (инвертирует) входной сигнал. На рисунке изображен символ логического элемента «НЕ».
Этот элемент, имеющий один выход и только один вход, еще называют инвертором, так как он фактически инвертирует (инвертирует) входной сигнал. На рисунке изображен символ логического элемента «НЕ».
Таблица истинности инвертора показывает, что высокий входной потенциал дает низкий выходной потенциал и наоборот.
В западных схемах значок элемента «НЕ» имеет форму треугольника с кружком на выходе. На отечественных схемах — прямоугольник с символом «1», с кружком на выходе.
Логический элемент «И-НЕ» - конъюнкция (логическое умножение) с отрицанием, И-НЕ
«И-НЕ» - логический элемент, выполняющий над входными данными операцию логического сложения, а затем операцию логического отрицания, результат выводится. Другими словами, это в основном элемент «И», дополненный элементом «НЕ». На рисунке изображено условное обозначение логического элемента «2И-НЕ».
Таблица истинности для элемента «И-НЕ» противоположна таблице для элемента «И». Вместо трех нулей и единицы - три единицы и ноль. Элемент «И-НЕ» также называют «элементом Шеффера» в честь математика Генри Мориса Шеффера, впервые отметившего значение этого в 1913 году. Обозначается как «I», только с кружочком на выходе.
Вместо трех нулей и единицы - три единицы и ноль. Элемент «И-НЕ» также называют «элементом Шеффера» в честь математика Генри Мориса Шеффера, впервые отметившего значение этого в 1913 году. Обозначается как «I», только с кружочком на выходе.
Логический элемент "ИЛИ-НЕ" - дизъюнкция (логическое сложение) с отрицанием, НЕ-ИЛИ
"ИЛИ-НЕ" - логический элемент, который выполняет операцию логического сложения над входными данными, а затем операцию логического отрицания, результат выводится. Другими словами, это элемент «ИЛИ», дополненный элементом «НЕ» — инвертором. На рисунке изображен символ логического элемента «2ИЛИ-НЕ».
Таблица истинности для элемента "ИЛИ-НЕ" противоположна таблице для элемента "ИЛИ". Высокий потенциал на выходе получается только в одном случае - на оба входа одновременно подаются низкие потенциалы. Обозначается как «ИЛИ», только с кружком на выходе, указывающим на инверсию.
Логический элемент "исключающее ИЛИ" - сложение по модулю 2, исключающее ИЛИ
"исключающее ИЛИ" - логический элемент, выполняющий операцию логического сложения по модулю 2 над входными данными, имеет два входа и один выход. Часто эти элементы используются в схемах управления. На рисунке показано условное обозначение этого элемента.
Часто эти элементы используются в схемах управления. На рисунке показано условное обозначение этого элемента.
Изображение в западных схемах как у "ИЛИ" с дополнительной изогнутой полосой со стороны входа, в отечественных - как у "ИЛИ", только вместо "1" будет написано "=1".
Этот логический элемент также называют «неэквивалентностью». Высокий уровень напряжения будет на выходе только тогда, когда сигналы на входе не равны (на одном единица, на другом ноль или на одном ноль, а на другом один) даже если на входе две единицы при при этом на выходе будет ноль - в этом отличие от "ИЛИ". Эти логические элементы широко используются в сумматорах.
Поведение
Элементы XOR, XOR-NOT, Odd и Even вычисляют соответствующую функцию от значений на входах и выдают результат на выход.
По умолчанию неподключенные входы игнорируются - то есть, если к входам действительно ничего не подключено - даже провода. Таким образом, вы можете добавить элемент с 5 входами, но подключить только два входа, и он будет работать как элемент с 2 входами; это избавляет вас от необходимости беспокоиться об установке количества входных данных каждый раз, когда вы создаете элемент. (Если все входы не подключены, то выходное значение ошибки равно X .) Однако некоторые пользователи предпочитают, чтобы Logisim настаивал на том, чтобы все входы были подключены, поскольку это соответствует реальным элементам. Вы можете включить это поведение, выбрав меню «Проект» > «Параметры…», перейдя на вкладку «Моделирование» и выбрав параметр «Ошибка для неопределенных входных данных» для параметра «Вывод элемента при неопределенности».
(Если все входы не подключены, то выходное значение ошибки равно X .) Однако некоторые пользователи предпочитают, чтобы Logisim настаивал на том, чтобы все входы были подключены, поскольку это соответствует реальным элементам. Вы можете включить это поведение, выбрав меню «Проект» > «Параметры…», перейдя на вкладку «Моделирование» и выбрав параметр «Ошибка для неопределенных входных данных» для параметра «Вывод элемента при неопределенности».
Таблица истинности с двумя входами для элементов выглядит следующим образом.
x у Исключающее ИЛИ Эксклюзивное НЕ-ИЛИ нечетное Четность 0 0 0 1 0 1 0 1 1 0 1 0 1 0 1 0 1 0 1 1 0 1 0 1
Как видите, элементы Odd и XOR ведут себя одинаково в случае двух входов; аналогичным образом элементы Parity и XOR ведут себя одинаково. Но если имеется более двух входов с определенным значением, то элемент XOR выдаст 1, когда единица находится строго на одном входе, а элемент Odd выдаст 1, когда единица находится на нечетном количестве входов. Элемент XOR выдаст на выходе 1, когда входные данные с единицей строго равны 9.3539, а не один, в то время как элемент Parity даст 1, когда есть четное количество входов с одним. Элементы XOR и XOR имеют атрибут Multi-Input Behavior, который позволяет настроить их для использования поведения нечетных и четных элементов.
Но если имеется более двух входов с определенным значением, то элемент XOR выдаст 1, когда единица находится строго на одном входе, а элемент Odd выдаст 1, когда единица находится на нечетном количестве входов. Элемент XOR выдаст на выходе 1, когда входные данные с единицей строго равны 9.3539, а не один, в то время как элемент Parity даст 1, когда есть четное количество входов с одним. Элементы XOR и XOR имеют атрибут Multi-Input Behavior, который позволяет настроить их для использования поведения нечетных и четных элементов.
Если какие-либо входы имеют значение ошибки (например, если конфликтующие значения находятся на одном проводе) или плавающее значение, то на выходе будет значение ошибки.
Многобитовые версии каждого элемента будут выполнять однобитовые преобразования входных данных побитно.
Примечание: многие специалисты утверждают, что поведение фигурного элемента XOR должно соответствовать поведению элемента Odd, но единого мнения по этому вопросу нет. Поведение Logisim по умолчанию для элемента XOR основано на стандарте IEEE 91. Это также согласуется с интуитивным пониманием термина XOR : официант, спрашивающий, хотите ли вы гарнир из картофельного пюре, моркови, зеленого горошка или салата, примет только один вариант, а не три, независимо от того, что некоторые эксперты может сказать вам. (Должен признаться, однако, что я не проверял это утверждение.) Вы можете настроить элементы XOR и XOR на использование одной из опций, изменив атрибут Multi-Input Behavior.
Поведение Logisim по умолчанию для элемента XOR основано на стандарте IEEE 91. Это также согласуется с интуитивным пониманием термина XOR : официант, спрашивающий, хотите ли вы гарнир из картофельного пюре, моркови, зеленого горошка или салата, примет только один вариант, а не три, независимо от того, что некоторые эксперты может сказать вам. (Должен признаться, однако, что я не проверял это утверждение.) Вы можете настроить элементы XOR и XOR на использование одной из опций, изменив атрибут Multi-Input Behavior.
Контакты (при условии, что компонент обращен на восток)
Западный край (входы, разрядность соответствует атрибуту Биты данных)
Входы компонента. Их будет столько, сколько указано в атрибуте Количество входов.
Обратите внимание, что если вы используете фигурные элементы, то западный край элементов XOR и XOR будет искривлен. Однако входные контакты расположены с трудом. Logisim рисует короткие сегменты, чтобы показать это; если вы перекроете сегмент, программа молчаливо предположит, что вы не хотели его перекрывать. При использовании «Вид для печати» эти сегменты не будут отображаться, если они не подключены к проводам.
При использовании «Вид для печати» эти сегменты не будут отображаться, если они не подключены к проводам.
Восточный край (выход, разрядность соответствует атрибуту Data Bits)
Вывод элемента, значение которого вычисляется на основе текущих значений входов, как описано выше.
Атрибуты
Когда компонент выбран или уже добавлен, клавиши от 0 до 9 изменяют его атрибут Количество входов, комбинации Alt-0 до Alt-9 изменяют его атрибут Биты данных, а клавиши со стрелками изменяют его атрибут Направление.
Направление Направление компонента (его выход относительно его входов). Биты данных Биты входов и выходов компонента. Размер элемента Указывает, отображать ли широкую или узкую версию компонента. Это не влияет на количество записей, которое определяется атрибутом Количество записей; однако, если количество входных данных превышает 3 (для узкого компонента) или 5 (для широкого компонента), элемент будет отображаться с «крыльями» для размещения запрошенного количества входных данных. Количество входов Определяет, сколько контактов на западном крае будет иметь компонент. Поведение с несколькими входами (только XOR и XOR-NOT) При наличии трех или более входов выходное значение элементов XOR и XOR-NOR будет основано либо на том факте, что 1 находится строго на одном входе (по умолчанию), либо на нечетном числе входов.
Количество входов Определяет, сколько контактов на западном крае будет иметь компонент. Поведение с несколькими входами (только XOR и XOR-NOT) При наличии трех или более входов выходное значение элементов XOR и XOR-NOR будет основано либо на том факте, что 1 находится строго на одном входе (по умолчанию), либо на нечетном числе входов.
Бит — наименьшая единица информации, так как он хранит одно из двух значений — 0 (Ложь) или 1 (Истина). Ложь и Истина в переводе на русский язык - ложь и правда соответственно. То есть одна битовая ячейка может находиться одновременно только в одном состоянии из двух возможных. Напомню, что два возможных состояния битовой ячейки — 1 и 0.
Существуют определенные операции по манипулированию битами. Эти операции называются логическими или булевыми операциями по имени одного из математиков — Джорджа Буля (1815—1864), внесшего вклад в развитие этой области науки.
Все эти операции можно применять к любому биту, независимо от того, имеет ли он значение 0 (ноль) или 1 (единица). Ниже приведены основные логические операции и примеры их использования.
Ниже приведены основные логические операции и примеры их использования.
Логическая операция И (И)
Обозначение И: &
Логическая операция И выполняется над двумя битами, назовем их a и b. Результат выполнения логической операции И будет равен 1, если а и b равны 1, а во всех остальных (остальных) случаях результат будет равен 0. Смотрим таблицу истинности логической операции и .
а(бит 1) б (бит 2) а (бит 1) и б (бит 2) 0 0 0 0 1 0 1 0 0 1 1 1
Логическая операция ИЛИ (ИЛИ)
Обозначение ИЛИ: |
Логическая операция ИЛИ выполняется над двумя битами (a и b). Результатом выполнения логической операции ИЛИ будет 0, если a и b равны 0 (нулю), а во всех остальных (прочих) случаях результат равен 1 (единице). Смотрим таблицу истинности логической операции ИЛИ. 9б (бит 2)
Смотрим таблицу истинности логической операции ИЛИ. 9б (бит 2)
0 0 0 0 1 1 1 0 1 1 1 0 Логическая операция НЕ (не)
Обозначение НЕ: ~
Логическая операция НЕ выполняется над одним битом. Результат этой логической операции напрямую зависит от состояния бита. Если бит был в нулевом состоянии, то результат выполнения НЕ будет равен единице и наоборот. Смотрим таблицу истинности логической операции НЕ.
а(бит 1) ~a(битовое отрицание) 0 1 1 0
Запомните эти 4 логические операции. Используя эти логические операции, мы можем получить любой возможный результат. Узнайте больше об использовании логических операций в C++.
Элементы Исключающее ИЛИ (по-английски - Exclusive-OR) можно было бы отнести и к простейшим элементам, но выполняемая ими функция несколько сложнее, чем в случае элемента И или элемента ИЛИ. Все входы элементов XOR равны, однако ни один из входов не может блокировать другие входы, установив выходной сигнал равным единице или нулю.
Рис. 4.1. Обозначения элементов XOR: зарубежный (слева) и отечественный (справа)
Функция XOR означает следующее: единица на выходе появляется, когда единица есть только на одном входе. Если на входах две и более единиц, или если все входы нули, то на выходе будет ноль. Таблица истинности двухвходового элемента XOR приведена в табл. 4.1. Обозначения, принятые в отечественных и зарубежных схемах, показаны на рис. 4.1. Надпись на отечественном обозначении элемента Исключающее ИЛИ "=1" как раз и означает, что высвечивается ситуация, когда на входах находится одна и только одна единица.
В стандартной серии мало элементов XOR. Отечественные серии предлагают микросхемы ЛП5 (четыре двухвходовых элемента с выходом 2С), ЛЛ3 и ЛП12, отличающиеся от ЛП5 выходом ОК. Слишком специфическая функция реализуется этими элементами.
Отечественные серии предлагают микросхемы ЛП5 (четыре двухвходовых элемента с выходом 2С), ЛЛ3 и ЛП12, отличающиеся от ЛП5 выходом ОК. Слишком специфическая функция реализуется этими элементами.
С математической точки зрения элемент XOR выполняет операцию так называемого суммирования по модулю 2. Поэтому эти элементы также называют сумматорами по модулю два. Как отмечалось в предыдущей лекции, суммирование по модулю 2 обозначается знаком плюс, заключенным в кружок.
Основное использование элементов XOR, которое непосредственно следует из таблицы истинности, заключается в сравнении двух входных сигналов. В случае, когда на входы поступают две единицы или два нуля (сигналы одинаковые), на выходе формируется ноль (см. табл. 4.1). Обычно в этом приложении на один вход элемента подается постоянный уровень, с которым сравнивается изменяющийся во времени сигнал, поступающий на другой вход. Но гораздо чаще для сравнения сигналов и кодов используются специальные микросхемы компараторов кодов, о которых речь пойдет в следующей лекции.
В качестве сумматора по модулю 2 элемент XOR также используется в параллельных и последовательных делителях по модулю 2, которые используются для вычисления циклических контрольных сумм. Но эти схемы будут подробно рассмотрены в лекциях 14,15.
Важным применением элементов XOR является управляемый инвертор (рис. 4.2). При этом один из входов элемента используется как управляющий, а на другой вход элемента подается информационный сигнал. Если управляющий вход один, то входной сигнал инвертируется, если нулевой, то не инвертируется. Чаще всего управляющий сигнал задается постоянным уровнем, определяющим режим работы элемента, а информационный сигнал является импульсным. То есть элемент XOR может изменить или не изменить полярность входного сигнала или фронта в зависимости от управляющего сигнала.
Рис. 4.2. Элемент XOR в качестве управляемого инвертора
В случае, когда имеется два сигнала одной полярности (положительный или отрицательный) и при этом исключается их одновременное поступление, для смешивания этих сигналов можно использовать элемент XOR (рис. 4.3). При любой полярности входных сигналов выходные сигналы элемента будут положительными. При положительных входных сигналах элемент XOR будет работать как элемент 2ИЛИ, а при отрицательных входных сигналах заменит элемент 2И-НЕ. Такие замены могут быть полезны в тех случаях, когда некоторые элементы исключающего ИЛИ не используются в схеме. Правда, следует учитывать, что задержка распространения сигнала в элементе XOR обычно несколько больше (примерно в 1,5 раза), чем задержка в простейших элементах И, И-НЕ, ИЛИ, ИЛИ-НЕ.
4.3). При любой полярности входных сигналов выходные сигналы элемента будут положительными. При положительных входных сигналах элемент XOR будет работать как элемент 2ИЛИ, а при отрицательных входных сигналах заменит элемент 2И-НЕ. Такие замены могут быть полезны в тех случаях, когда некоторые элементы исключающего ИЛИ не используются в схеме. Правда, следует учитывать, что задержка распространения сигнала в элементе XOR обычно несколько больше (примерно в 1,5 раза), чем задержка в простейших элементах И, И-НЕ, ИЛИ, ИЛИ-НЕ.
Рис. 4.3. Использование элемента XOR для смешивания двух неодновременных сигналов
Рис. 4.4. Выделение фронтов входного сигнала с помощью элемента XOR
Еще одним важным применением элемента XOR является формирование коротких импульсов на любом фронте входного сигнала (рис. 4.4). При этом не имеет значения, положительный фронт входного сигнала или отрицательный, на выходе все равно формируется положительный импульс.


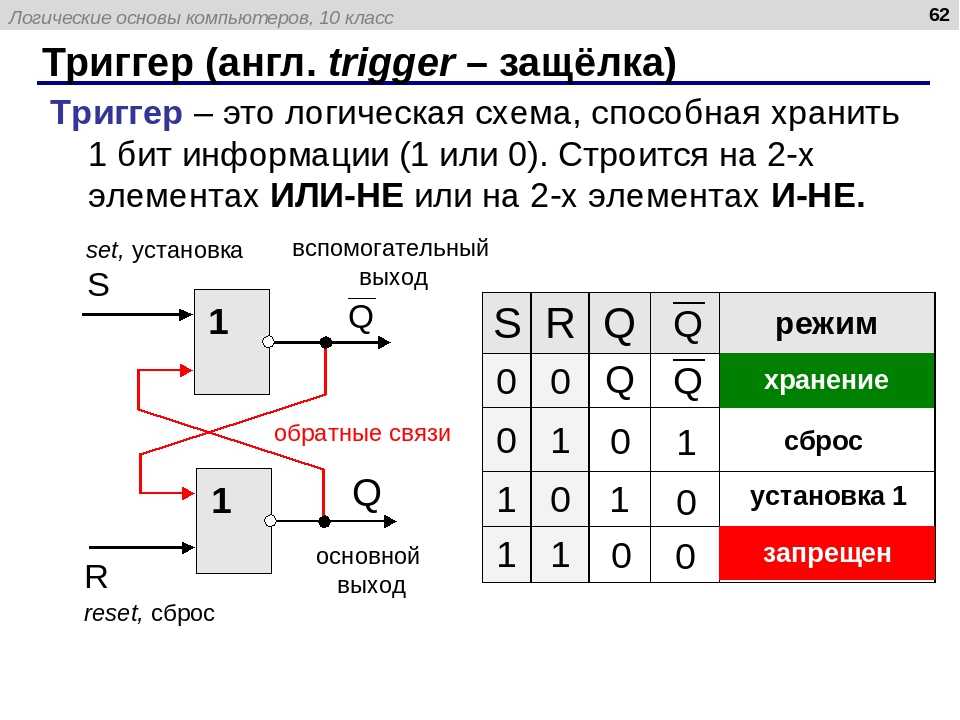
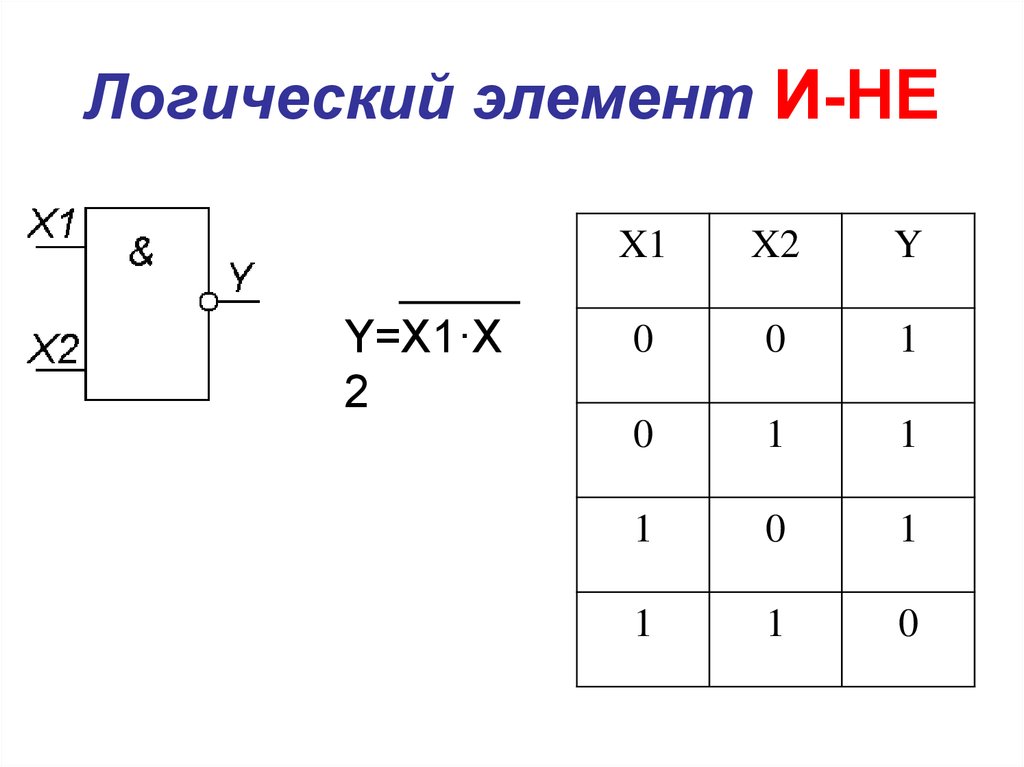 .. хп» одновременно на всех выходах. На рис. 20.2 приведено графическое изображение логического элемента с двумя входами -2И и его таблица истинности. Характерным отличием этого элемента на схемах, является наличие внутри прямоугольника английского знака «&» (английский союз «и» — логическое умножение), в левом верхнем углу.
.. хп» одновременно на всех выходах. На рис. 20.2 приведено графическое изображение логического элемента с двумя входами -2И и его таблица истинности. Характерным отличием этого элемента на схемах, является наличие внутри прямоугольника английского знака «&» (английский союз «и» — логическое умножение), в левом верхнем углу.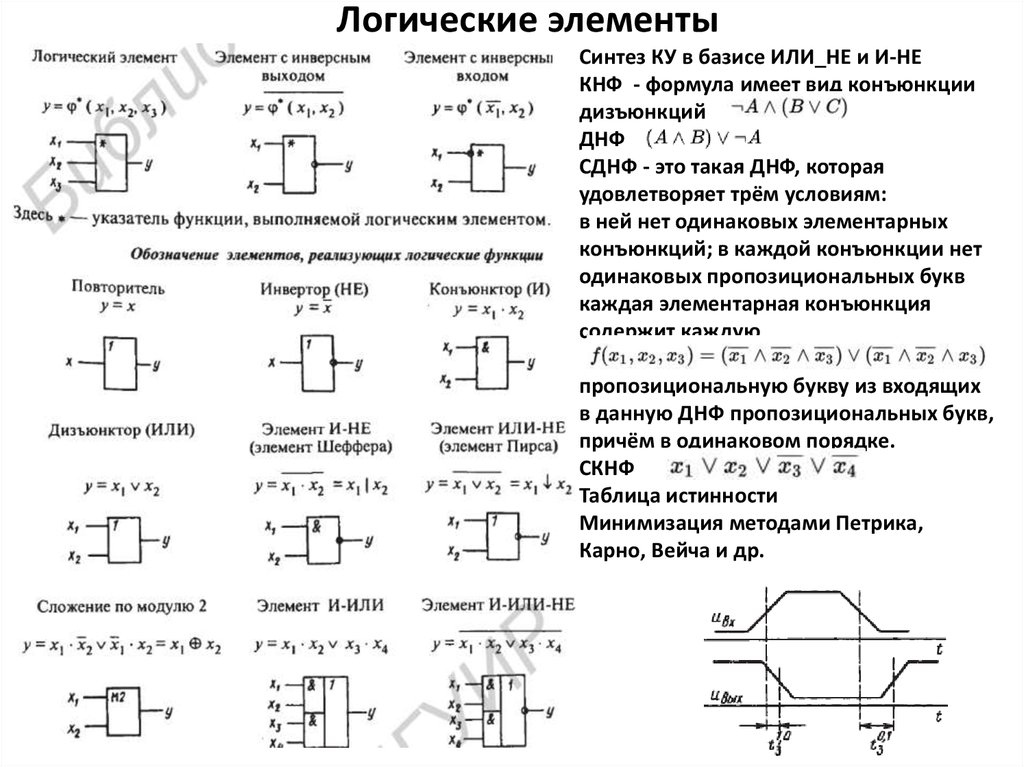

 Состояние обоих выходов триггера всегда противофазно т.е. если на одном из выходов логический ноль, то на втором выходе единица или наоборот.
Состояние обоих выходов триггера всегда противофазно т.е. если на одном из выходов логический ноль, то на втором выходе единица или наоборот.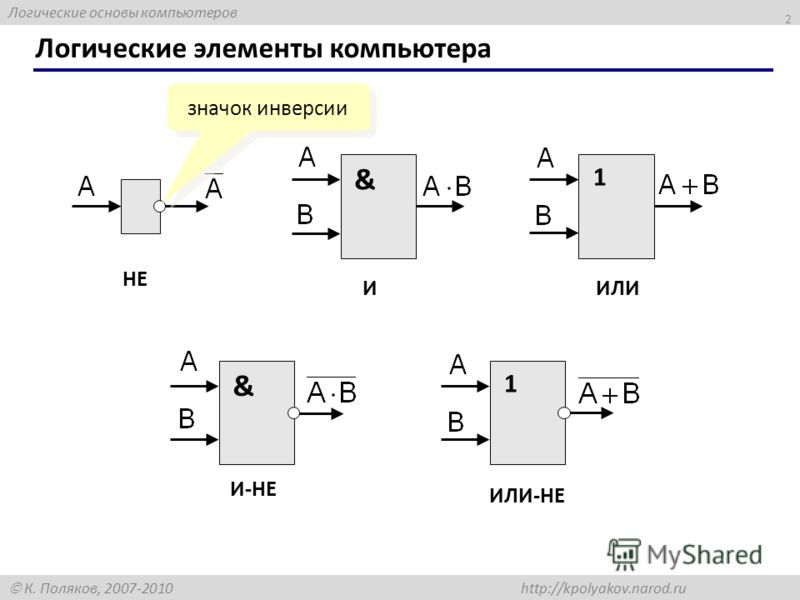 12.1, а.
12.1, а.
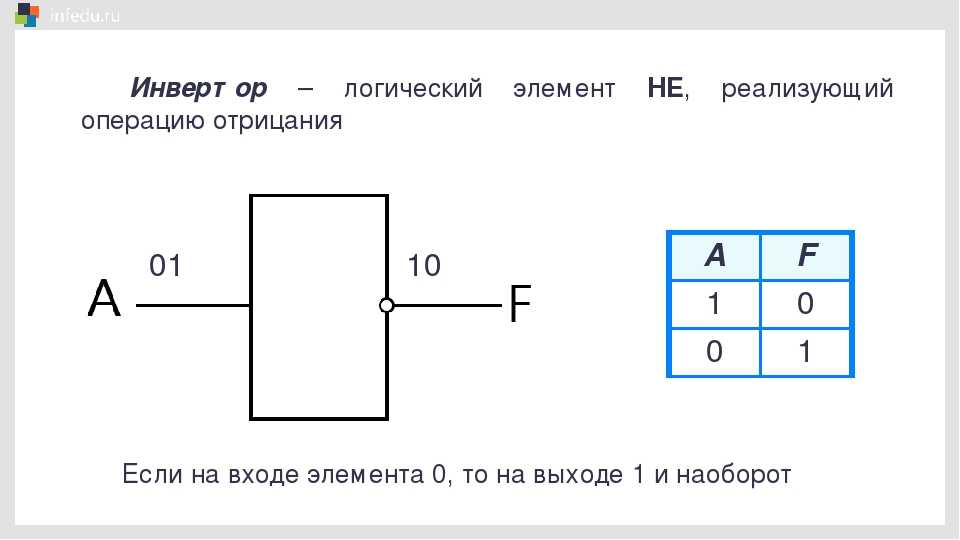 Одновременная подача активных уровней (логического нуля) на оба входа запрещена из-за непредсказуемости выходного состояния. Диаграмма состояний и таблица истинности приведены ниже на рис. 12.2, г.
Одновременная подача активных уровней (логического нуля) на оба входа запрещена из-за непредсказуемости выходного состояния. Диаграмма состояний и таблица истинности приведены ниже на рис. 12.2, г.
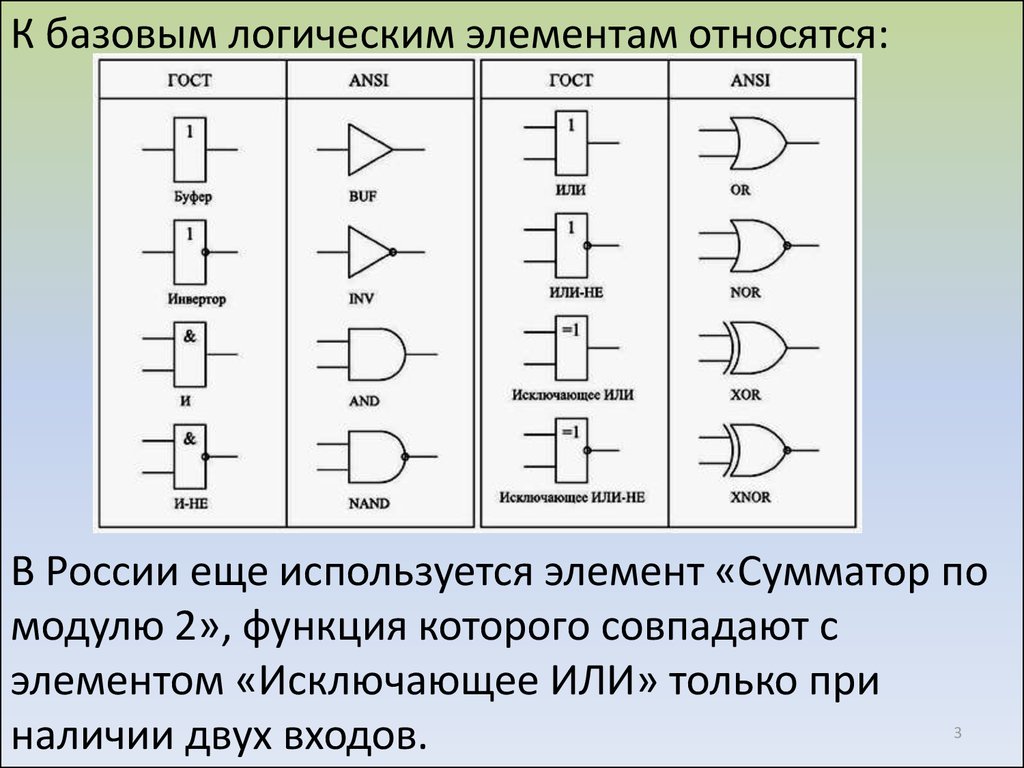
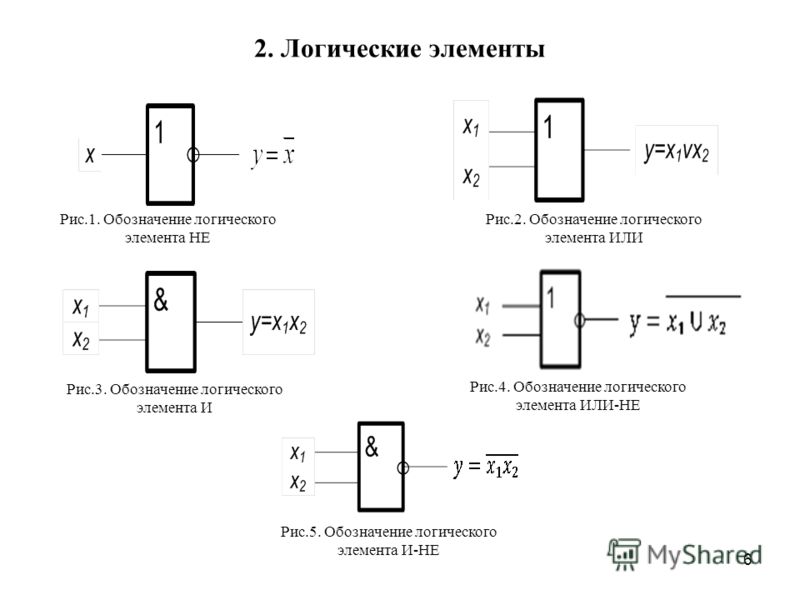
 Выход первого триггера является входом второго триггера S.
Выход первого триггера является входом второго триггера S.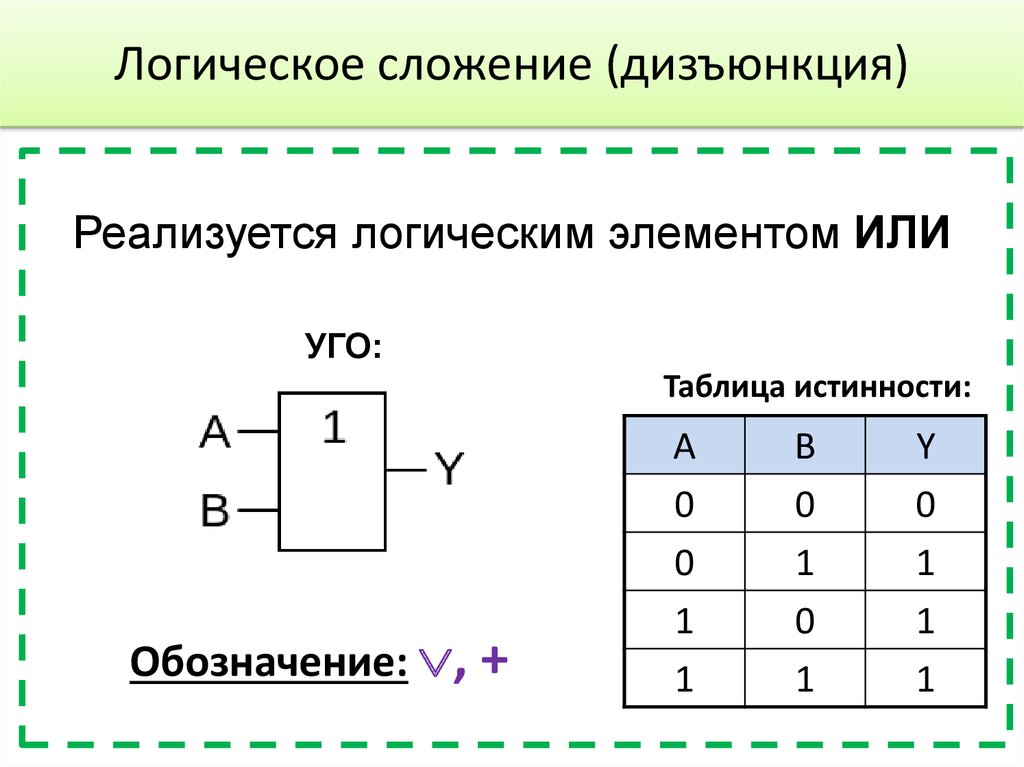 Инвертор, включенный между входами S и R позволяет избежать запрещенной комбинации .
Инвертор, включенный между входами S и R позволяет избежать запрещенной комбинации .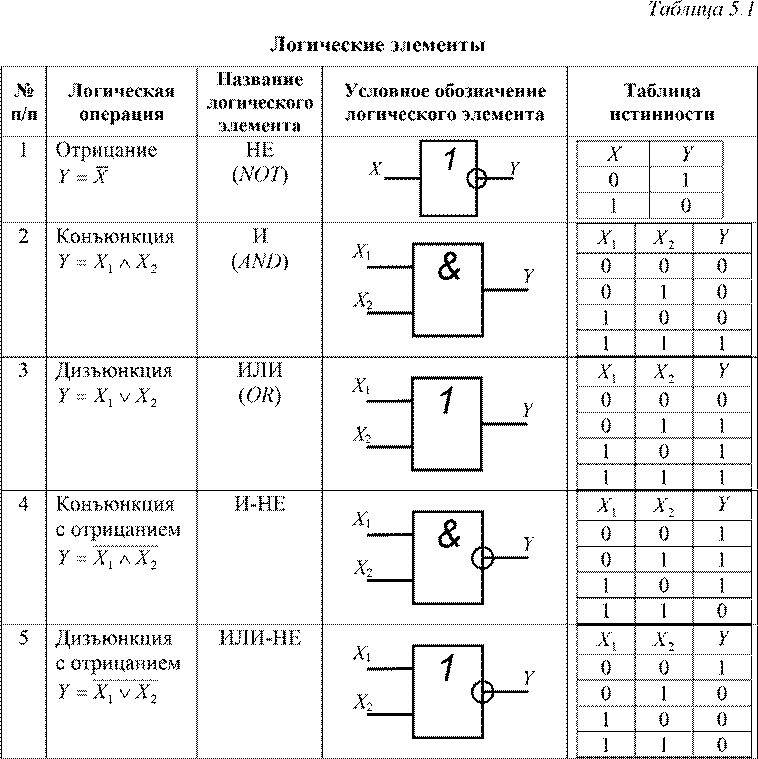 12.9. Логический элемент И разрешает прохождение синхроимпульсов на вход триггера. Внимательное изучение диаграммы состояний позволяет сделать заключение – триггер переключается не только с разрешения синхронизирующего входа, но и работает с разрешения входа V.
12.9. Логический элемент И разрешает прохождение синхроимпульсов на вход триггера. Внимательное изучение диаграммы состояний позволяет сделать заключение – триггер переключается не только с разрешения синхронизирующего входа, но и работает с разрешения входа V.
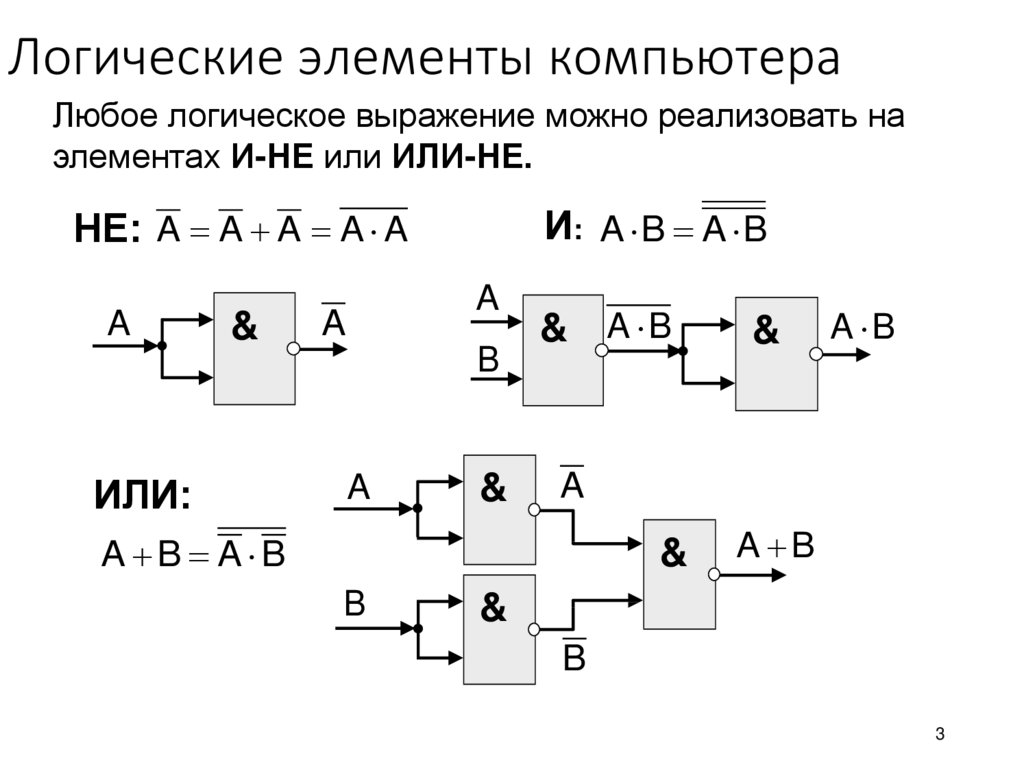 12.11, б на синхровходе C D–триггера всегда находится логическая единица и момент ее спада является сигналом синхронизации для управления работой D -триггера.
12.11, б на синхровходе C D–триггера всегда находится логическая единица и момент ее спада является сигналом синхронизации для управления работой D -триггера.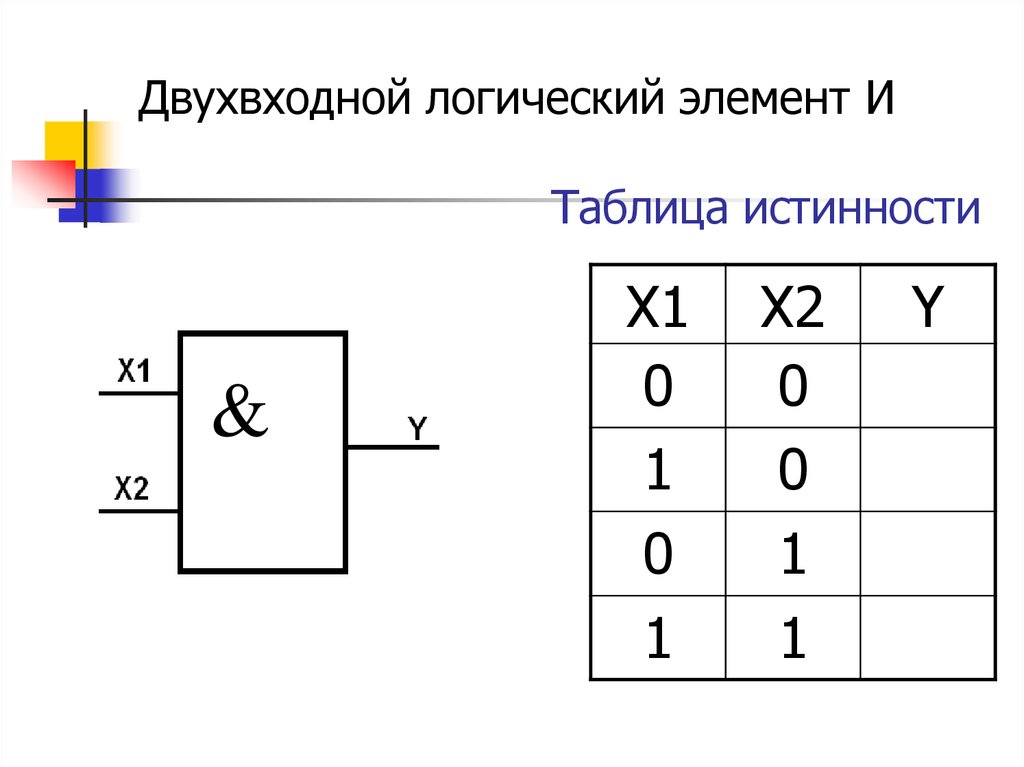
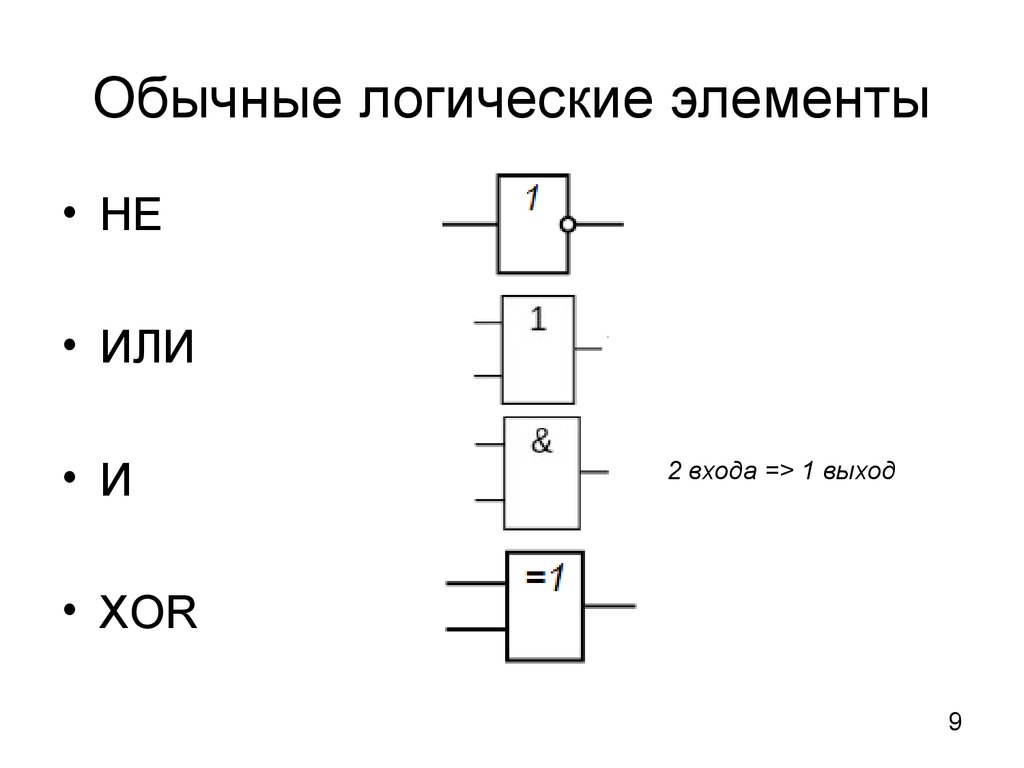 12.13.
12.13.
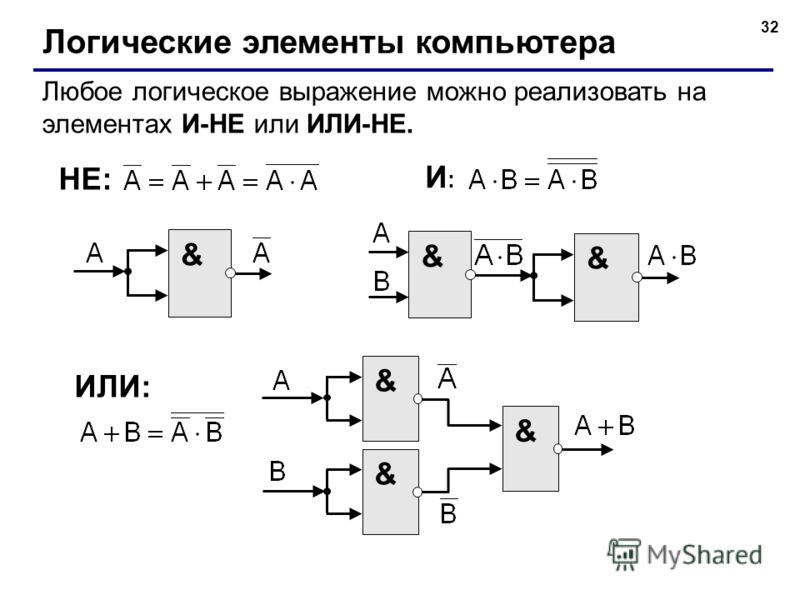 Состояния обоих триггеров совпадают.
Состояния обоих триггеров совпадают. Рассмотрим вариант использования двухтактного JK-триггера в качестве различных типов других триггеров:
Рассмотрим вариант использования двухтактного JK-триггера в качестве различных типов других триггеров: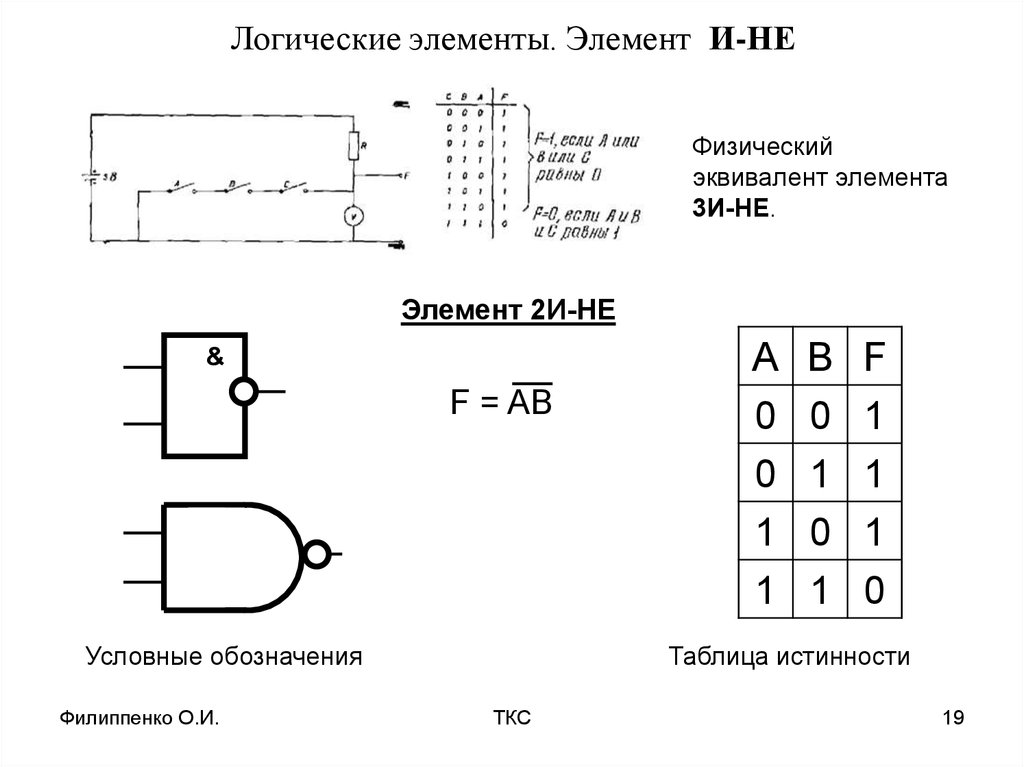
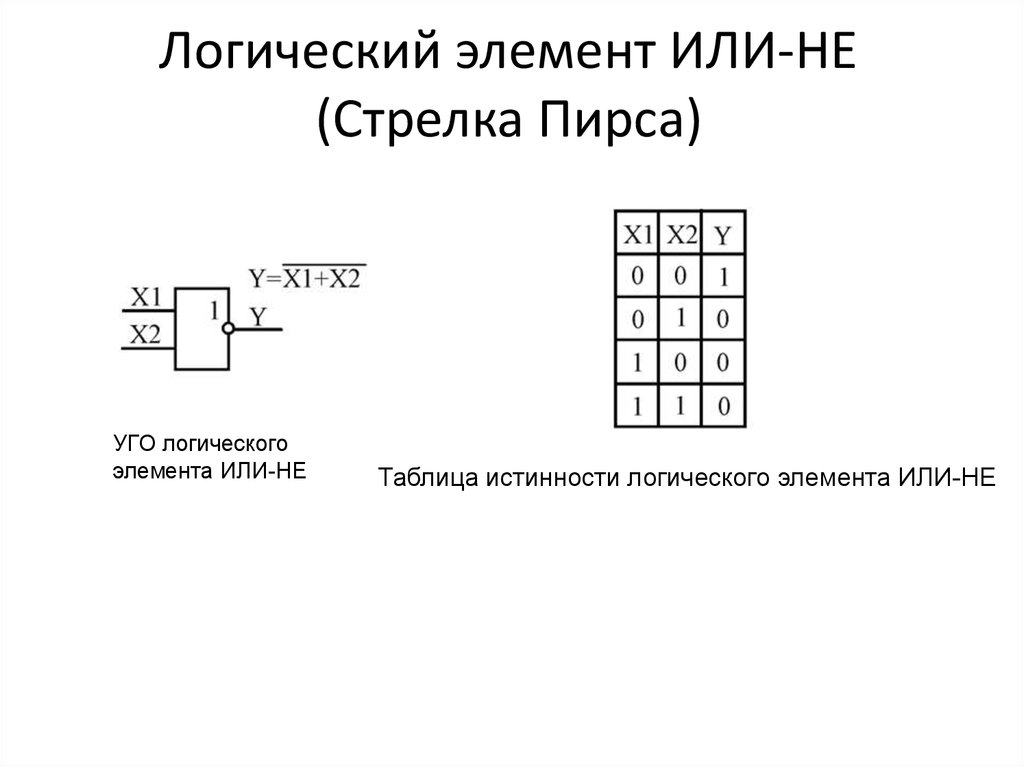 0675
0675 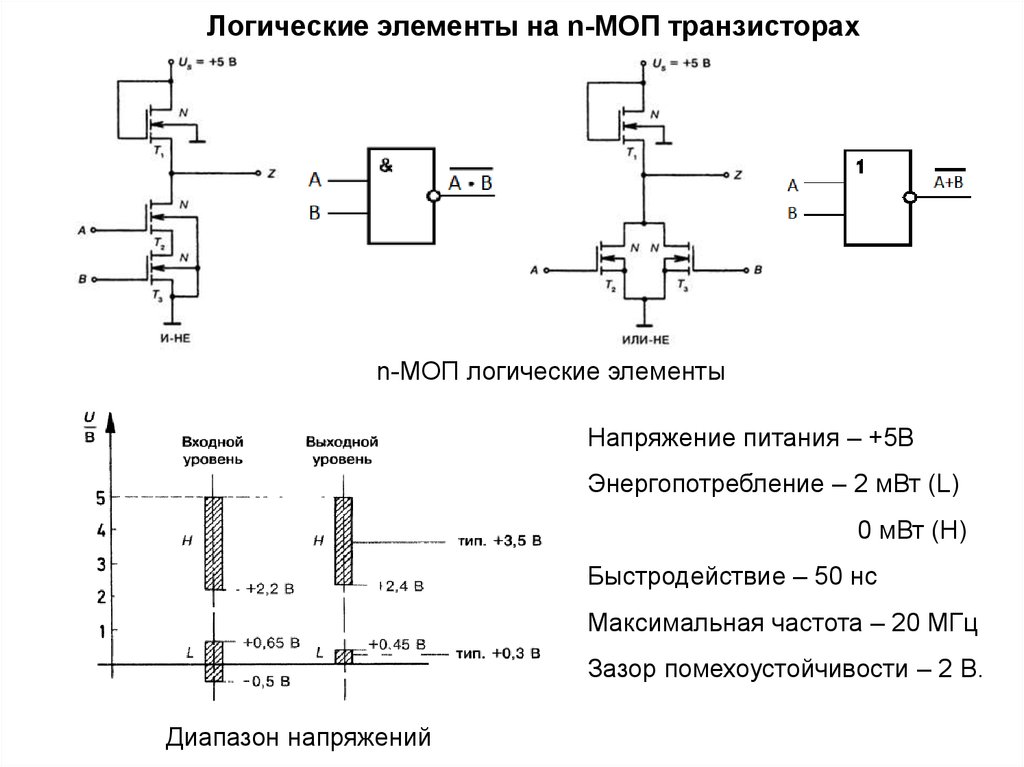 0031 del
0031 del 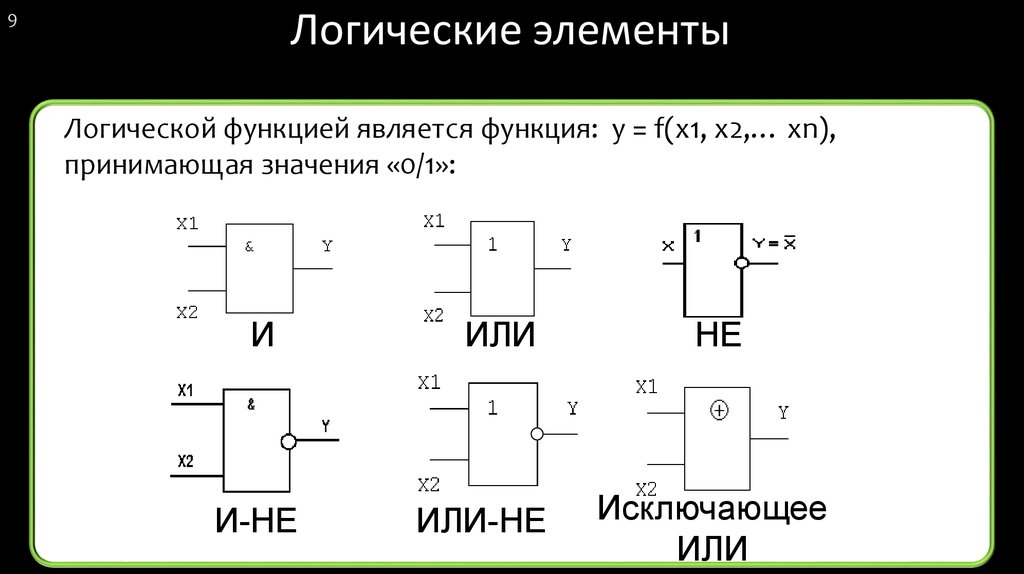 .
.