Логические элементы и таблицы истинности

Абсолютно все цифровые микросхемы состоят из одних и тех же логических элементов – «кирпичиков» любого цифрового узла. Вот о них мы и поговорим сейчас.

Логический элемент – это такая схемка, у которой несколько входов и один выход. Каждому состоянию сигналов на входах, соответствует определенный сигнал на выходе.

Итак, какие бывают элементы?

Элемент «И» (AND)

Иначе его называют «конъюнктор».

Для того, чтобы понять как он работает, нужно нарисовать таблицу, в которой будут перечислены состояния на выходе при любой комбинации входных сигналов. Такая таблица называется «таблица истинности». Таблицы истинности широко применяются в цифровой технике для описания работы логических схем.

Вот так выглядит элемент «И» и его таблица истинности:

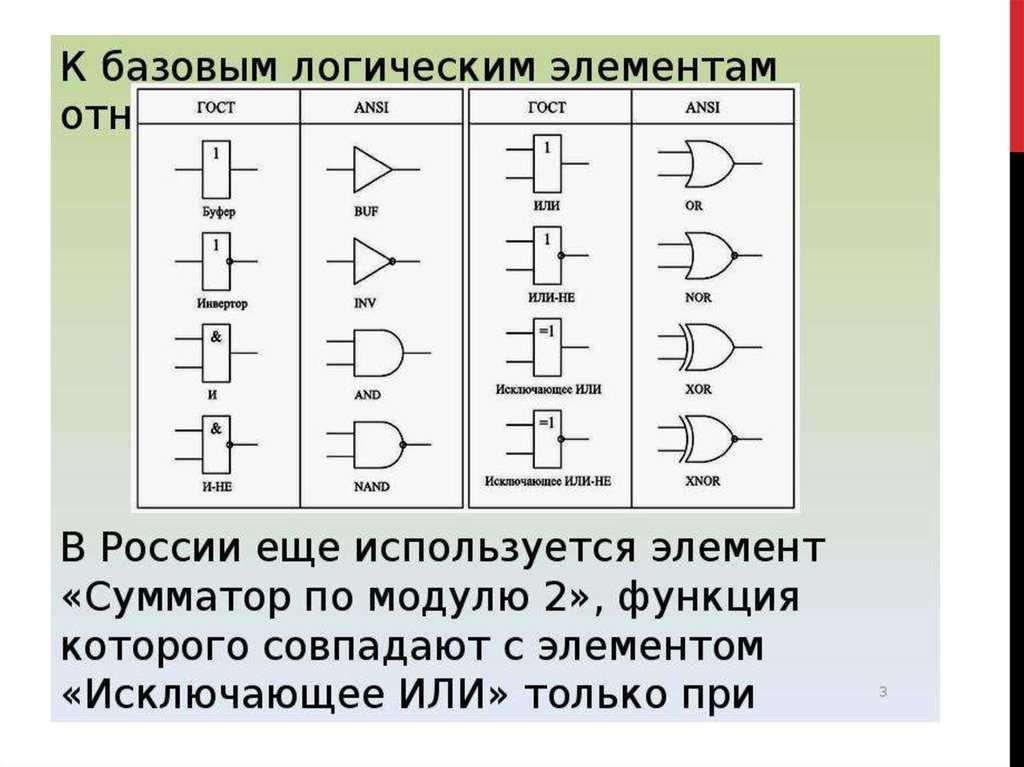
Поскольку вам придется общаться как с русской, так и с буржуйской тех. документацией, я буду приводить условные графические обозначения (УГО) элементов и по нашим и по не нашим стандартам.

Смотрим таблицу истинности, и проясняем в мозгу принцип. Понять его не сложно: единица на выходе элемента «И» возникает только тогда, когда на оба входа поданы единицы. Это объясняет название элемента: единицы должны быть И на одном, И на другом входе.

Если посмотреть чуток иначе, то можно сказать так: на выходе элемента «И» будет ноль в том случае, если хотя бы на один из его входов подан ноль. Запоминаем. Идем дальше.

Элемент «ИЛИ» (OR)

По другому, его зовут «дизъюнктор».

Любуемся:

Опять же, название говорит само за себя.

На выходе возникает единица, когда на один ИЛИ на другой ИЛИ на оба сразу входа подана единица. Этот элемент можно назвать также элементом «И» для негативной логики: ноль на его выходе бывает только в том случае, если и на один и на второй вход поданы нули.

Едем дальше. Дальше у нас очень простенький, но очень необходимый элемент.

Элемент «НЕ» (NOT)

Чаще, его называют «инвертор».

Надо чего-нибудь говорить по поводу его работы?

Ну тогда поехали дальше. Следующие два элемента получаются путем установки инвертора на выход элементов «И» и «ИЛИ».

Элемент «И-НЕ» (NAND)

Элемент И-НЕ работает точно так же как «И», только выходной сигнал полностью противоположен. Там где у элемента «И» на выходе должен быть «0», у элемента «И-НЕ» — единица. И наоборот. Э то легко понять по эквивалентной схеме элемента:

 

Элемент «ИЛИ-НЕ» (NOR)

 

Та же история – элемент «ИЛИ» с инвертором на выходе.

Следующий товарищ устроен несколько хитрее:
Элемент «Исключающее ИЛИ» (XOR)

Он вот такой:

Операция, которую он выполняет, часто называют «сложение по модулю 2». На самом деле, на этих элементах строятся цифровые сумматоры.

Смотрим таблицу истинности. Когда на выходе единицы? Правильно: когда на входах разные сигналы. На одном – 1, на другом – 0. Вот такой он хитрый.

Эквивалентная схема примерно такая:

Ее запоминать не обязательно.

Собственно, это и есть основные логические элементы. На их основе строятся абсолютно любые цифровые микросхемы. Даже ваш любимый Пентиум 4.

Далее мы позанудствуем о том, как синтезировать цифровую схему, имея ее таблицу истинности. Это совсем несложно, а знать надо, ибо пригодится (еще как пригодится) нам в дальнейшем.

Ну и напоследок – несколько микросхем, внутри которых содержатся цифровые элементы. Около выводов элементов обозначены номера соответствующих ног микросхемы. Все микросхемы, перечисленные здесь, имеют 14 ног. Питание подается на ножки 7 (-) и 14 (+). Напряжение питания – смотри в таблице в предыдущем параграфе.

Источник: radiokot.ru

Работа простейших логических элементов, триггеров, счетчиков, дешифраторов, шифраторов, компараторов, регистров сдвига

 

Простейшие логические элементы, триггеры, счетчики, дешифраторы, шифраторы, компараторы, регистры сдвига, сумматоры

Аналоги логических микросхем

Продаю платы и наборы микросхем на Орион 128, куплю микросхемы ПЗУ и ОЗУ.

Магазин запчастей ПК Орион-128

Логические элементы выпускаются в виде — интегральных микросхем. Логические операции, такие как конъюнкция, дизъюнкция, отрицание и сложение по модулю (И, ИЛИ, НЕ, исключающее ИЛИ) — являются основными операциями, выполняемыми на логических элементах основных типов. И так:

Логический элемент «И» — конъюнкция, логическое умножение, AND.

 Логический элемент И «И» — логический элемент, выполняющий над входными данными операцию конъюнкции или логического умножения. Данный элемент может иметь от 2 до 8 (наиболее распространены в производстве элементы «И» с 2, 3, 4 и 8 входами) входов и один выход. Условные обозначения логических элементов «И» с разным количеством входов приведены на рисунке. В тексте логический элемент «И» с тем или иным числом входов обозначается как «2И», «4И» и т. д. — элемент «И» с двумя входами, с четырьмя входами и т.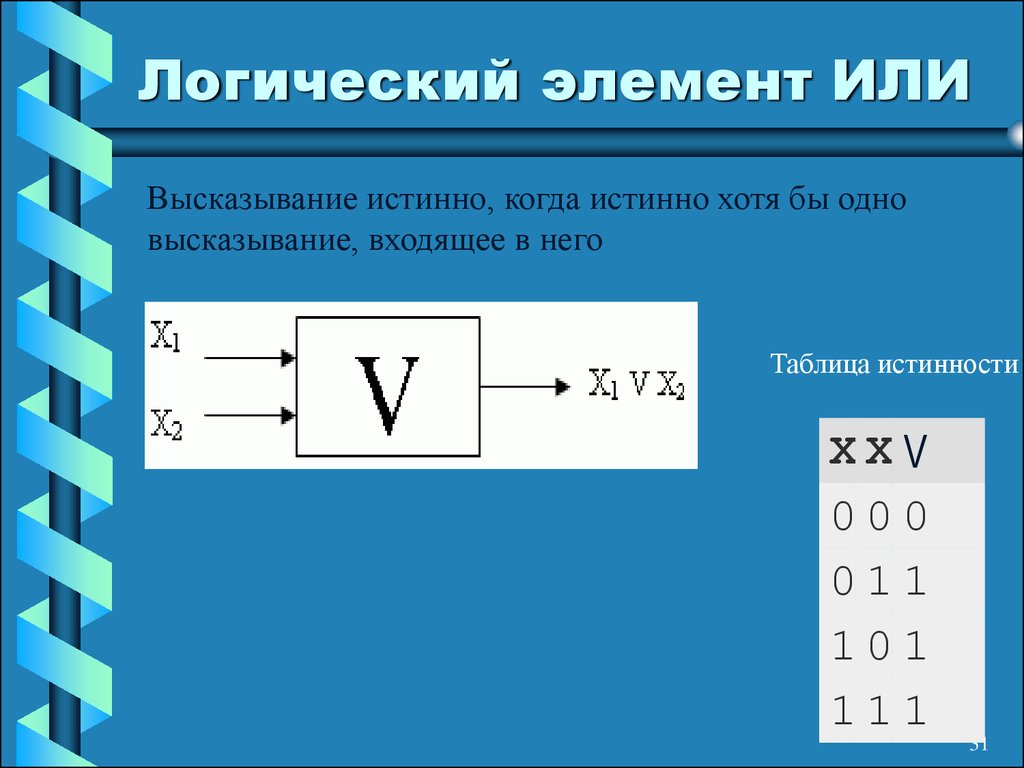

д.

Таблица истинности для элемента 2И

 Таблица истинности для элемента 2И показывает, что на выходе элемента будет логическая единица лишь в том случае, если логические единицы будут одновременно на первом входе И на втором входе. В остальных трех возможных случаях на выходе будет ноль. На западных схемах значок элемента «И» имеет прямую черту на входе и закругление на выходе. На отечественных схемах — прямоугольник с символом «&».

Логический элемент «ИЛИ» — дизъюнкция, логическое сложение, OR

Логический элемент ИЛИ «ИЛИ» — логический элемент, выполняющий над входными данными операцию дизъюнкции или логического сложения.

 Он так же как и элемент «И» выпускается с двумя, тремя, четырьмя и т. д. входами и с одним выходом. Условные обозначения логических элементов «ИЛИ» с различным количеством входов показаны на рисунке. Обозначаются данные элементы так: 2ИЛИ, 3ИЛИ, 4ИЛИ и т. д.

Таблица истинности для элемента  2ИЛИ

Таблица истинности для элемента «2ИЛИ» показывает, что для появления на выходе логической единицы, достаточно чтобы логическая единица была на первом входе ИЛИ на втором входе. Если логические единицы будут сразу на двух входах, на выходе также будет единица. На западных схемах значок элемента «ИЛИ» имеет закругление на входе и закругление с заострением на выходе. На отечественных схемах — прямоугольник с символом «1».

Логический элемент «НЕ» — отрицание, инвертор, NOT

 Логический элемент НЕ «НЕ» — логический элемент, выполняющий над входными данными операцию логического отрицания.

 Данный элемент, имеющий один выход и только один вход, называют еще инвертором, поскольку он на самом деле инвертирует (обращает) входной сигнал.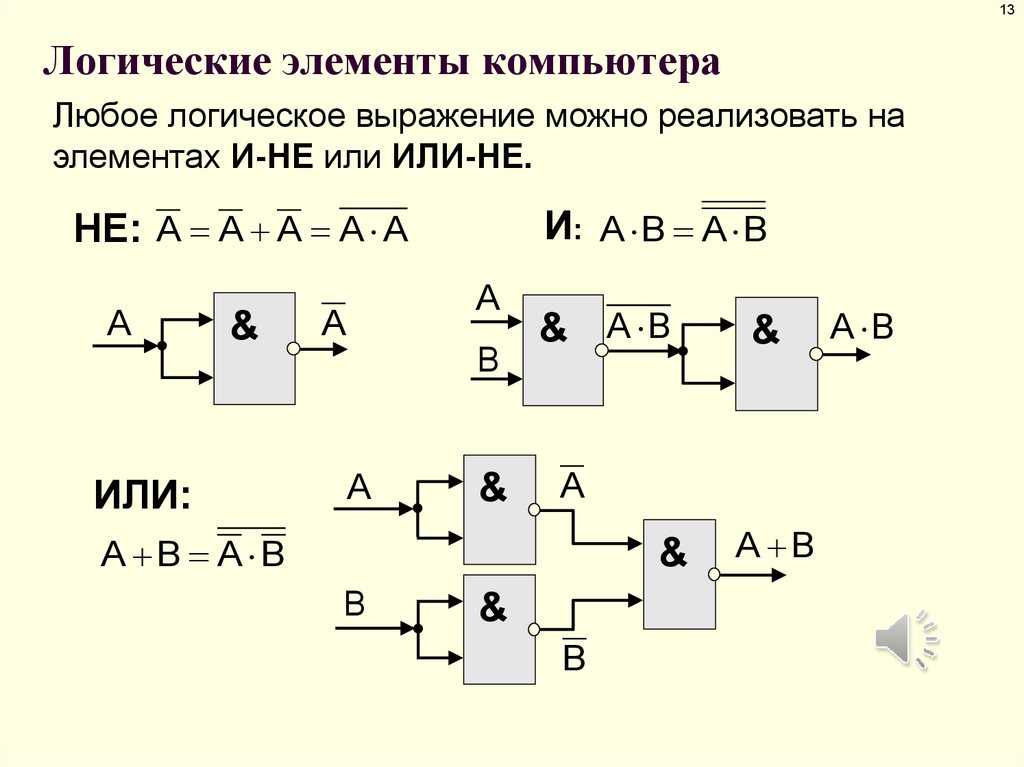

На рисунке приведено условное обозначение логического элемента «НЕ».

Таблица истинности для элемента НЕ

 Таблица истинности для инвертора показывает, что высокий потенциал на входе даёт низкий потенциал на выходе и наоборот. На западных схемах значок элемента «НЕ» имеет форму треугольника с кружочком на выходе. На отечественных схемах — прямоугольник с символом «1», с кружком на выходе.

Логический элемент «И-НЕ» — конъюнкция (логическое умножение) с отрицанием, NAND

Логический элемент И-НЕ «И-НЕ» — логический элемент, выполняющий над входными данными операцию логического сложения, и затем операцию логического отрицания, результат подается на выход.

Другими словами, это в принципе элемент «И», дополненный элементом «НЕ». На рисунке приведено условное обозначение логического элемента «2И-НЕ».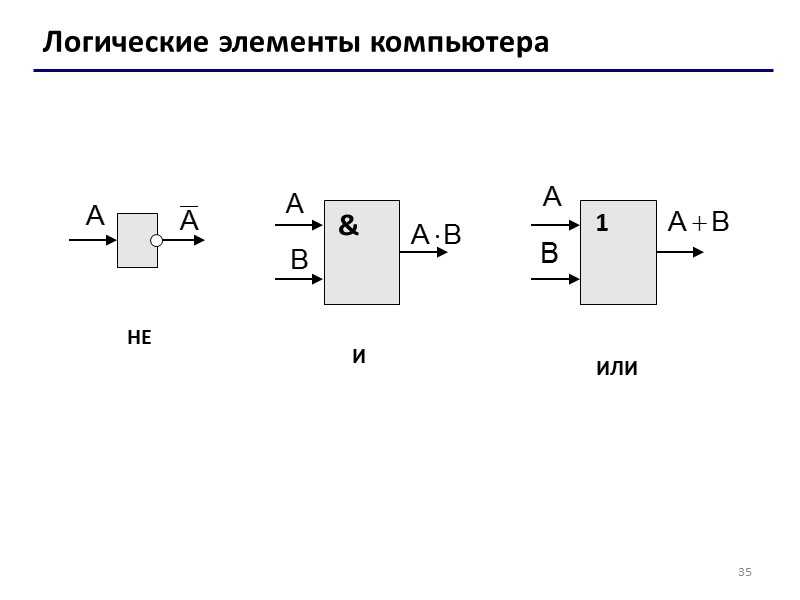

Таблица истинности для элемента И-НЕ

Таблица истинности для элемента «И-НЕ» противоположна таблице для элемента «И». Вместо трех нулей и единицы — три единицы и ноль. Элемент «И-НЕ» называют еще «элемент Шеффера» в честь математика Генри Мориса Шеффера, впервые отметившего значимость этой логической операции в 1913 году. Обозначается как «И», только с кружочком на выходе.

Логический элемент «ИЛИ-НЕ» — дизъюнкция (логическое сложение) с отрицанием, NOR

Логический элемент ИЛИ-НЕ «ИЛИ-НЕ» — логический элемент, выполняющий над входными данными операцию логического сложения, и затем операцию логического отрицания, результат подается на выход.

Иначе говоря, это элемент «ИЛИ», дополненный элементом «НЕ» — инвертором. На рисунке приведено условное обозначение логического элемента «2ИЛИ-НЕ».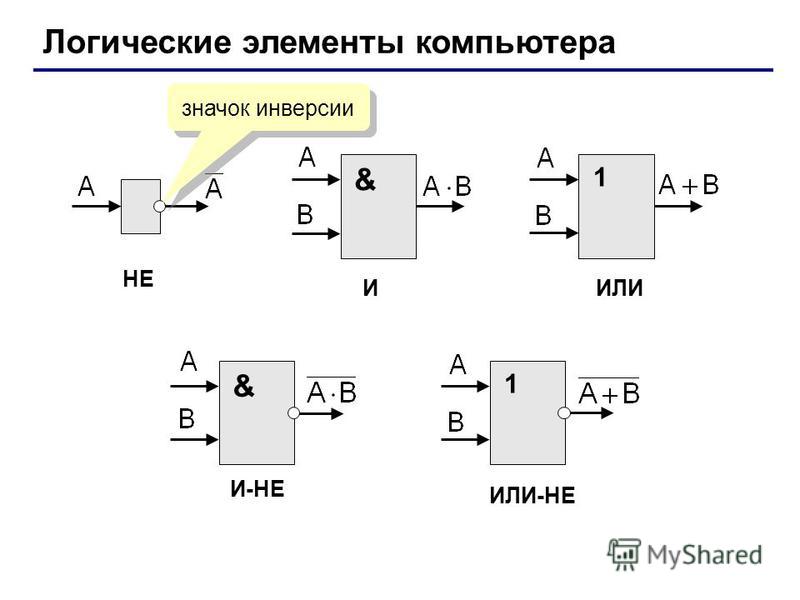

Таблица истинности для элемента ИЛИ-НЕ

Таблица истинности для элемента «ИЛИ-НЕ» противоположна таблице для элемента «ИЛИ». Высокий потенциал на выходе получается лишь в одном случае — на оба входа подаются одновременно низкие потенциалы. Обозначается как «ИЛИ», только с кружочком на выходе, обозначающим инверсию.

Логический элемент «исключающее ИЛИ» — сложение по модулю 2, XOR

Логический элемент исключающее ИЛИ «исключающее ИЛИ» — логический элемент, выполняющий над входными данными операцию логического сложения по модулю 2, имеет два входа и один выход.

Часто данные элементы применяют в схемах контроля. На рисунке приведено условное обозначение данного элемента. Изображение в западных схемах — как у «ИЛИ» с дополнительной изогнутой полоской на стороне входа, в отечественной — как «ИЛИ», только вместо «1» будет написано «=1».

Таблица истинности исключающее ИЛИ

 Этот логический элемент еще называют «неравнозначность». Высокий уровень напряжения будет на выходе лишь тогда, когда сигналы на входе не равны (на одном единица, на другом ноль или на одном ноль, а на другом единица) если даже на входе будут одновременно две единицы, на выходе будет ноль — в этом отличие от «ИЛИ». Данные элементы логики широко применяются в сумматорах.

Операнды в данном случае подаются в двоичной системе счисления — на вход логического элемента поступают сигналы в форме напряжения высокого или низкого уровня, которые и служат по сути входными данными. Так, напряжение высокого уровня — это логическая единица 1 — обозначает истинное значение операнда, а напряжение низкого уровня 0 — значение ложное. 1 — ИСТИНА, 0 — ЛОЖЬ.

Продолжение следует….

Генератор с кварцевой стабилизацией, схемотехника

 

Купить платы, наборы микросхем на Орион128, КР565РУ5В, КР565ру7В, к565ру5г AU, к565ру7г Au в позолоте, куплю микросхемы

 

Полезные и интересные статьи

На предыдущую страницу  На главную страницу  На следующую страницу

 

логических операторов, поэлементно и | ~ (функции MATLAB)

Логические операторы, поэлементно & | ~ (функции MATLAB)

Справочник по функциям MATLAB

Логические операторы, поэлементные & | ~

Поэлементные логические операции над массивами

Синтаксис

•  A и B
  А | Б
  ~ А
   

Описание

Символы и , |

и ~ являются логическими операторами массива И , ИЛИ и НЕ .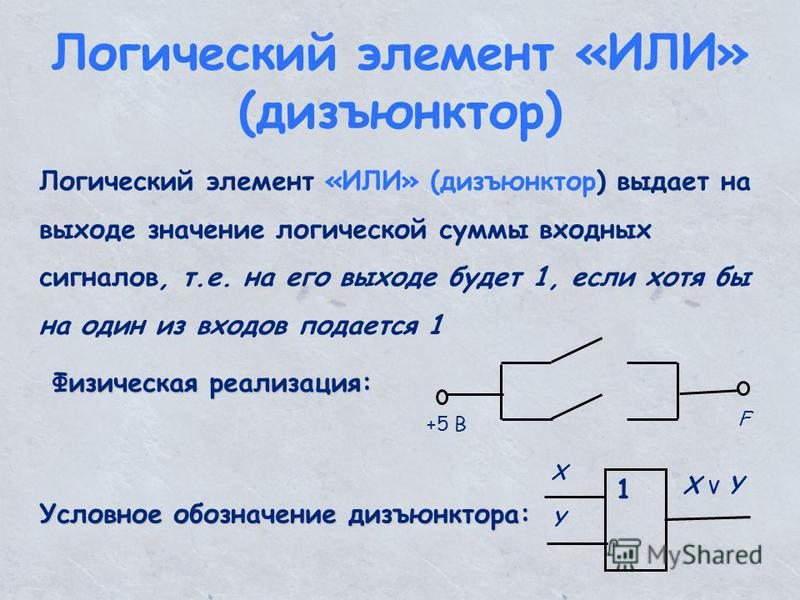 Они работают с массивами поэлементно, где 0 представляет логическую ложь ( F ), а все, что не равно нулю, представляет логическую истину ( T ). Логические операторы возвращают логический массив с элементами, для которых установлено значение true ( 1 ) или false ( 0 ), в зависимости от ситуации.

Оператор и делает логическую И , | Оператор выполняет логическое ИЛИ , а ~A дополняет элементы A . Функция xor(A,B) реализует исключительную операцию ИЛИ . Таблица истинности для этих операторов и функций показана ниже.

Входы		и	или	не	хор
А	Б	А и Б	А | Б	~А	xor(A,B)
0	0	0	0	1	0
0	1	0	1	1	1
1	0	0	1	0	1
1	1	1	1	0	0

Приоритет логических операторов по отношению друг к другу:

Оператор	Операция	Приоритет
~	НЕ	Самый высокий
и	Поэлементно И
|	Поэлементно ИЛИ
&&	Короткое замыкание И
||	Короткое замыкание ИЛИ	Самый низкий

Примечания

MATLAB всегда дает оператору и приоритет над оператором | оператор.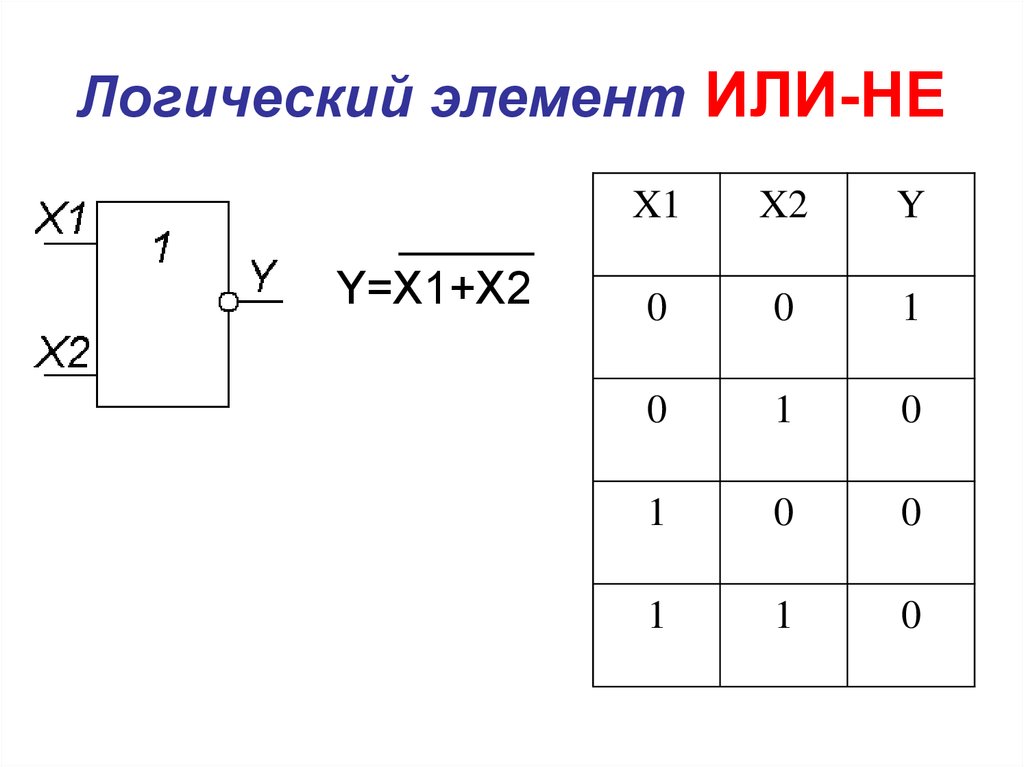 Хотя MATLAB обычно оценивает выражения слева направо, выражение a|b&c оценивается как а|(б и в) . Рекомендуется использовать круглые скобки, чтобы явно указать предполагаемый приоритет операторов, содержащих комбинации и и | .

Эти логические операторы имеют эквиваленты функций М-файла, как показано.

Логическая операция	Эквивалентная функция
А и Б	и(А,Б)
А | Б	или (А, В)
~А	не(А)

Примеры

Этот пример показывает логическое ИЛИ элементов в векторе u с соответствующими элементами в векторе v :

См.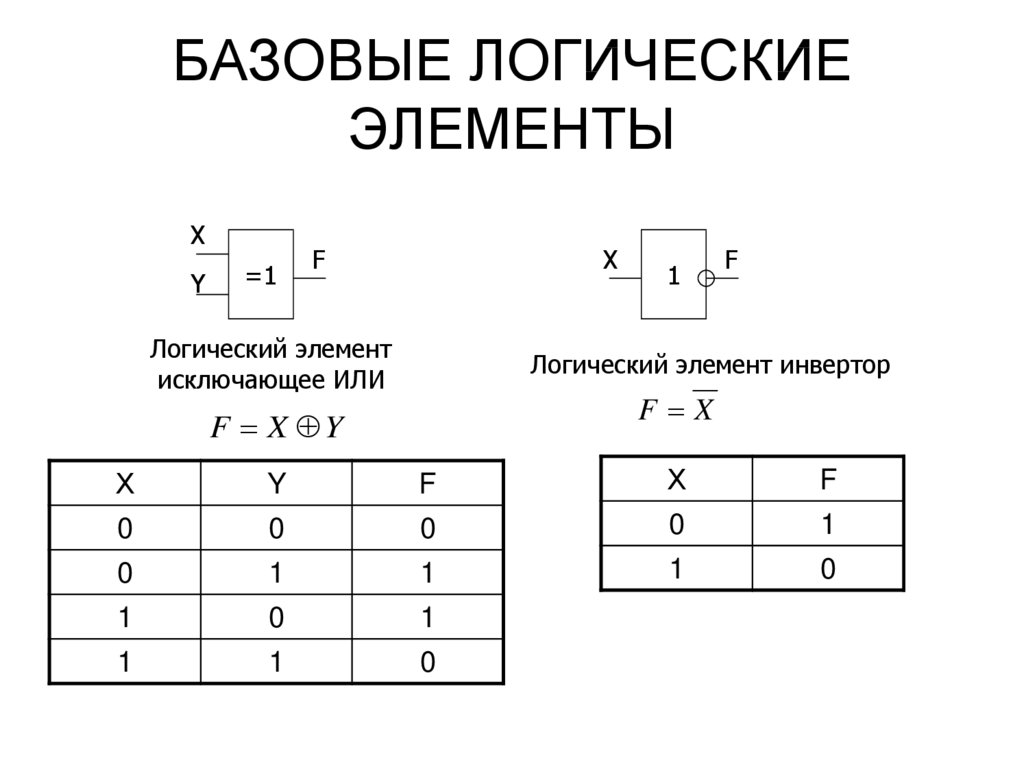 также

все , любые , найти , логические , xor , истина , ложь

Логические операторы, короткое замыкание: && , ||

Реляционные операторы: < , <= , > , >= , == , ~=

Операции сравнения < > <= >= == ~=

Логические операторы, короткое замыкание && ||

Статья о логике+элемент из The Free Dictionary

Логика+элемент | Статья о логике+элемент от The Free Dictionary

Логика+элемент | Статья о логике+элемент The Free Dictionary

---

Слово, не найденное в Словаре и Энциклопедии.