Физика Силы в природе. Гравитационное взаимодействие. Закон всемирного тяготения
Материалы к уроку
Конспект урока
Много ли различных сил существует в природе?
На земле и вне ее существует огромное количество различных тел. Все они взаимодействуют по-разному. Так, например, яблоко с дерева падает на Землю; человек толкает тележку; нога человека бьет по мячу; эбонитовая палочка, которую потерли о мех, притягивает к себе легкие бумажки; магнит собирает вокруг себя железные опилки; проводник с током вращает стрелку компаса; Луна совершает вращательное движение вокруг Земли, а вместе они вращаются вокруг Солнца; взаимодействуют также звезды и звездные системы. Этот ряд примеров можно продолжать бесконечно долго. Означает ли это, что в природе существует бесконечное количество сил? Вовсе нет!
В безграничных просторах Вселенной, на нашей планете и на любой другой, в любом веществе, в каждом живом организме, в атомах, в атомных ядрах и в мире элементарных частиц при взаимодействиях различных тел существуют четыре вида сил:
гравитационные, электромагнитные, ядерные (сильные) и слабые.
Силы гравитации, или иными словами силы всемирного тяготения, действуют между всеми телами — все они притягиваются друг с другом. Но это притяжение может быть заметно только лишь тогда, когда хотя бы одно из этих тел так велико, как, например, Земля или Луна. Иначе эти силы настолько малы, что ими можно пренебрегать.
Электромагнитные силы действуют между электрически заряженными телами. Их действие очень разнообразно. В атомах, молекулах, твердых, жидких и газообразных телах, живых организмах именно электромагнитные силы являются главными. Велика их роль в атомах.
Ядерные силы заметны лишь внутри атомных ядер, они действуют только на очень малых расстояниях – в десятки раз меньших размеров атома.
Ядерные силы — самые мощные в природе. В сотни раз меньше интенсивность электромагнитных сил, еще менее интенсивны слабые взаимодействия.
 Наименее мощные гравитационные силы.
Наименее мощные гравитационные силы. Сильные (ядерные) и слабые взаимодействия проявляются на таких малых расстояниях, когда законы механики Ньютона, а с ними вместе и понятие механической силы теряют свой смысл. В разделе механики мы рассмотрим только гравитационные и электромагнитные взаимодействия.
Силы тяготения. Земной шар сообщает всем телам у поверхности Земли одно и то же ускорение — ускорение свободного падения. Но если земной шар сообщает телу ускорение, то согласно второму закону Ньютона он действует на тело с некоторой силой. Эту силу называют силой тяжести.
Из второго закона Ньютона, ускорение по модулю равно отношению силы, действующей на тело, к массе тела.

Подставляя это выражение для силы тяжести во второй закон
Ньютона, получаем, что для всех тел ускорение равно ускорению свободного падения.
Ньютон был первым человеком, который доказал, что причина падения дождевой капли на Землю, движение Луны и искусственных спутников вокруг Земли и планет вокруг звезд одна и та же. Это сила тяготения, которая действует между всеми телами во Вселенной.

Как и любым другим телам, Земля должна сообщать Луне ускорение, которое не зависит от массы Луны. Траектория движения Луны достаточно хорошо известна, иными словами мы можем легко определить местоположение Луны относительно Земли в любой момент времени. Используя эти данные, можно определить ее ускорение. Оно оказывается примерно в 3600 или 60 в квадрате раз меньше, чем ускорение свободного падения у поверхности Земли. Расстояние до Луны приблизительно равно 60 земным радиусам. Отсюда нетрудно сделать вывод: ускорение, которое сообщает телам сила притяжения к Земле, убывает обратно пропорционально квадрату расстояния до центра Земли. Где c1 — некоторый коэффициент пропорциональности, одинаковый для всех тел.
 Используя эти законы, Ньютон определил, что Солнце сообщает всем планетам ускорение, обратно пропорциональное квадрату расстояния от них до Солнца.
Используя эти законы, Ньютон определил, что Солнце сообщает всем планетам ускорение, обратно пропорциональное квадрату расстояния от них до Солнца.Постоянный коэффициент c2 одинаков для любой планеты, но не совпадает с постоянным коэффициентом c1 для ускорения, который сообщается телам земным шаром.
Учитывая тот факт, что сила всемирного тяготения сообщает всем телам одно и то же ускорение вне зависимости от их массы, то она должна быть пропорциональна массе тела, на которое она оказывает воздействие. Но поскольку некоторое тело, к примеру, Земля действует на свой спутник с силой, пропорциональной массе спутника, то и сам спутник по третьему закону Ньютона должен действовать на Землю с той же силой. Причем эта сила должна быть пропорциональна массе Земли. Если сила тяготения является действительно универсальной, то со стороны данного тела на любое другое тело должна действовать сила, пропорциональная массе этого другого тела.
Впервые гравитационную постоянную удалось измерить английскому физику Генри Кавендишу в 1798 г. Он получил следующее значение для гравитационной постоянной: 6,67 на десять в минус одиннадцатой степени метров квадратных на килограмм в квадрате.
Ускорение свободного падения тел зависит от географической широты. Одной из причин увеличения ускорения свободного падения при перемещении точки, где находится тело, от экватора к полюсам, является то, что земной шар немного сплюснут у полюсов и расстояние до центра Земли в этом месте несколько меньше, чем на экваторе.

Самым необычным свойством гравитационных сил является то, что они сообщают всем телам, совершенно не завися от их масс, одинаковое ускорение. Чтобы лучше осознать это, представьте, что человек, ударяя ногой по футбольному мячу, придает ему такое же ускорение, что и тяжелой гире, которую он также ударит ногой. Разумеется, это невозможно. Земля является именно таким «необыкновенным человеком» с небольшой разницей, которая заключается в том, что действие ее на тела не носит характера кратковременного удара, а продолжается непрерывно в течение многих лет.
Это необычное свойство гравитационных сил объясняется тем, что эти силы пропорциональны массам обоих взаимодействующих тел. Этот факт обязательно вызовет удивление, если над ним хорошо задуматься. Ведь масса тела, входящая во второй закон Ньютона, определяет инертные свойства тела, иными словами его способность приобретать определенное ускорение под действием данной силы.

Массу, которая определяет способность тел притягиваться друг к другу, называют гравитационной массой.
Из механики Ньютона вовсе не следует, что инертная и гравитационная массы это одно и то же. Это равенство подтверждается благодаря опыту. Оно означает, что можно говорить просто о массе тела как о количественной мере как инертных, так и гравитационных его свойств.
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитора
2.10. Гравитационные силы. Закон всемирного тяготения
Все тела в
природе взаимно притягивают друг друга. Закон, которому подчиняется это
притяжение, был установлен Ньютоном и
носит название закона всемирного
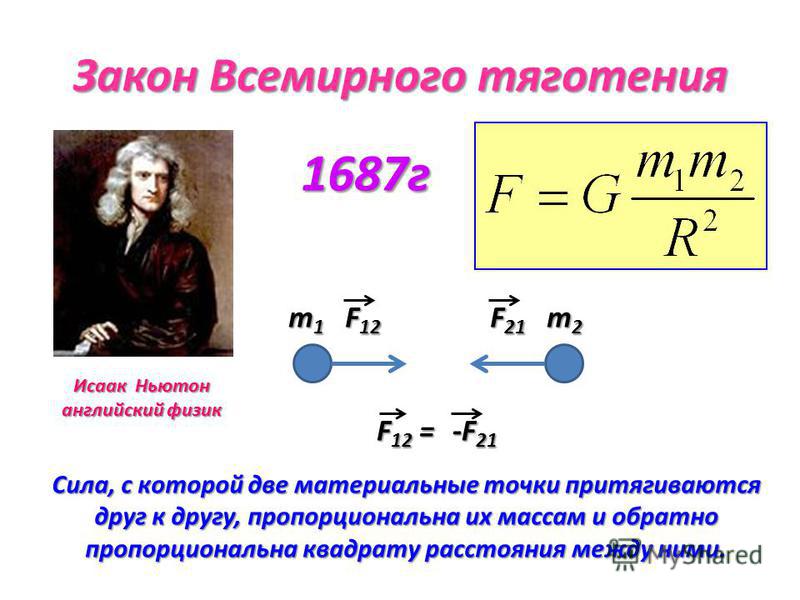
тяготения: сила, с которой две материальные
точки притягивают друг друга,
пропорциональна массам этих точек и
обратно пропорциональна квадрату
расстояния между ними:
Здесь– гравитационная постоянная. Сила
направлена вдоль прямой, проходящей
через взаимодействующие материальные
точки (рис.2.11).
Закон, которому подчиняется это
притяжение, был установлен Ньютоном и
носит название закона всемирного
тяготения: сила, с которой две материальные
точки притягивают друг друга,
пропорциональна массам этих точек и
обратно пропорциональна квадрату
расстояния между ними:
Здесь– гравитационная постоянная. Сила
направлена вдоль прямой, проходящей
через взаимодействующие материальные
точки (рис.2.11).
В векторной форме сила, с которой вторая материальная точка действует на первую, равна
(2.21)
где -единичный вектор, имеющий направление от первой материальной точки ко второй (рис.2.11). Заменив вектор вектором , получим силу, действующую на вторую материальную точку.
Для определения
силы взаимодействия протяженных тел
их нужно разбить на элементарные массы
,
каждую из которых можно было бы принять
за материальную точку (рис.2.12). Согласно
выражению (2.23),
—
я элементарная масса тела 1 притягивается
к -й элементарной массе тела 2 с силой
(2. 22)
22)
где –расстояние между элементарными массами.
Просуммировав (2.22) по всем значениям индекса , получим силу, действующию со стороны тела 2 на принадлежащую телу 1 элементарную массу :
(2.23)
Далее просуммировав (2.23) по всем значениям индекса , т.е. сложив силы, приложенные ко всем элементарным массам первого тела, получим силу, с которой тело 2 действует на тело 1:
Это суммирование сводится к интегрированию и является очень сложной математической задачей. В ряде практических задач взаимодействие тел сводится к взаимодействию материальных точек.
Под действием
силы притяжения к Земле все тела падают
с одинаковым относительно поверхности
Земли ускорением
.
Это означает, что в системе отсчета,
связанной с Землей, на всякое тело массы
действует
сила,
называемая силой тяжести. Когда тело
покоится относительно поверхности
Земли, силауравновешивается реакцией подвеса или опоры, удерживающих тело
от падения
.
По третьему закону Ньютона тело в этом
случае действует на подвес или опору с
силой равной -,
т. е. с силой
.
е. с силой
.
Сила , с которой тело действует на подвес или опору, называется весом тела. Эта сила равна лишь в том случае, когда тело и опора (или подвес) неподвижны относительно Земли. В случае их движения с ускорениемвес не будет равен . Рассмотрим пример (рис.2.13). Подвес в виде укрепленной на рамке пружины движется вместе с телом с ускорением. Уравнение движения тела имеет вид
,
где – реакция подвеса, т.е. сила, с которой пружина действует на тело. По третьему закону Ньютона тело действует на пружину с силой –, которая по определению представляет собой вес тела . Тогда
. (2.24)
Эта формула определяет вес тела в общем случае.
Предположим, что тело и подвес движутся в вертикальном направлении (демонстрация 5). Спроектировав (2.24) на направление отвеса, получаем:
.
Знак «+»
соответствует ускорению, направленному
вверх, а знак «- » — ускорению, направленному
вниз. При свободном падении рамки и
=0.
Тело находится в невесомости.
При свободном падении рамки и
=0.
Тело находится в невесомости.
Не следует путать силу тяжести и вес. Эти силы приложены к разным телам: –к телу, а – к опоре. Сила всегда равна, независимо от того, движется тело или покоится, сила же веса зависит от ускорения, с которым движутся опора и тело, и может быть как больше, так и меньше .
Лекция 18: Ньютоновская гравитация
Лекция 18: Ньютоновская гравитация| Астрономия 161: Введение в астрономию Солнечной системы |
Ключевые идеи:
Закон падающих тел (Галилей)- Все падающие тела испытывают одинаковые гравитационные ускорение
- Гравитация — это сила притяжения между всеми парами массивные объекты
- Гравитационная сила пропорциональна массам, и обратно пропорциональна квадрату расстояния между ними.
ПРИМЕЧАНИЕ:
Эта и следующая лекция, вероятно, являются наиболее математическими из всех лекции, которые будут прочитаны в этом классе.Я призываю вас всех прочтите эти заметки заранее и постарайтесь следовать приведенным в них аргументам. В будет легче следить за ходом лекции. [рвп]
Закон падающих тел
До своих телескопических работ Галилей выполнял фундаментальные исследование движения.Исследовал скорость падения тел, сбрасывая разные гири или сдвигая их по наклонным плоскостям.
Закон падающих тел
- При отсутствии воздуха тяжелые предметы и легкие предметы падают с одинаковым постоянным ускорением.
Универсальное взаимное тяготение
Исаак Ньютон в своих Principia сформулировал закон Универсальное взаимное тяготение:- Гравитация — это Привлекательная сила:
- Сближает массивные объекты.
- Гравитация Универсальная сила:
- Действует повсюду во Вселенной.
- Гравитация есть Взаимная сила:
- Работает между парами массивных объектов.
Гравитационная сила
Сила притяжения между любыми двумя объектами зависит только от:масс двух объектов:
- Более массивные объекты оказывают более сильное гравитационное воздействие.

Расстояние между ними:
- Сила становится на сильнее по мере того, как два объекта приближаются друг к другу.
- Сила становится слабее по мере того, как два объекта удаляются друг от друга.
Оно не зависит от форм, цветов или композиций объекты.
- Сила гравитационного притяжения между любыми двумя массивных тел пропорциональна их массам и обратно пропорциональна квадрату расстояния между их центры.
Математически говоря, сила тяжести между двумя массивными тела это:
- Где:
- F = сила тяжести.
- M 1 = масса первого тела
- M 2 = масса второго тела
- d = расстояние между их центрами.
- Г = Постоянная гравитационной силы
Постоянная силы гравитации
Силовая постоянная, G, представляет собой число, которое дает размер гравитационная связь между двумя массивными объектами.
G очень мало, в метрических единицах:
- G=6,7×10 -11 Ньютон-метр 2 / килограмм 2
- 4,41 Ньютона = 1 фунт
 Подобно Ньютону, Кавендиш ставил свои задачи так, чтобы G математически сокращалась. Мы будем делать то же самое на этом уроке, поэтому вам никогда не понадобится знать G на практике для экзаменов или домашних заданий.
Лишь намного позже (почти 75 лет спустя) его экспериментальные данные были использованы другими для получения значения G. Только во второй половине XIX в.века, что астрономам нужно было знать G, чтобы они могли, среди прочего, вычислять плотности небесных тел, таких как Луна и Солнце.]
Подобно Ньютону, Кавендиш ставил свои задачи так, чтобы G математически сокращалась. Мы будем делать то же самое на этом уроке, поэтому вам никогда не понадобится знать G на практике для экзаменов или домашних заданий.
Лишь намного позже (почти 75 лет спустя) его экспериментальные данные были использованы другими для получения значения G. Только во второй половине XIX в.века, что астрономам нужно было знать G, чтобы они могли, среди прочего, вычислять плотности небесных тел, таких как Луна и Солнце.]Падение яблока.
Встаньте на землю и бросьте яблоко.Какова сила Земли на яблоко?
- F = GM земля M яблоко /R земля 2
Каково ускорение яблока (второй закон Ньютона):
- a яблоко = F/M яблоко = GM земля /R земля 2 = 9,8 м/с 2
 Это означает, что ускорение свободного падения равно независимых от массы яблока, как показал Галилей
ранее.
Это означает, что ускорение свободного падения равно независимых от массы яблока, как показал Галилей
ранее.Равные и противоположные реакции
Но третий закон Ньютона утверждает, что все силы входят в число равных, но противоположных парКакую силу применяет яблоко в ответ на Землю?
- F = GM земля M яблоко /R земля 2
С какой скоростью Земля приближается к яблоку?
- a земля = F/M земля = GM яблоко /R земля 2
- a земля = a яблоко x (M яблоко /M земля )

Масса Земли
Мы можем напрямую измерить ускорение свободного падения на поверхности на Землю, сбрасывая предметы и определяя время их падения (например, как это было сделано по Галилею). Мы нашли- а = 9,8 м/с 2
Мы также можем измерить радиус Земли, используя геометрию (Эратосфен):
- R земля = 6378 километров = 6 378 000 метров
Объединив их вместе, используя формулу Ньютона для гравитационного Сила позволяет нам оценить массу Земли следующим образом:
Орбита Луны
Падающие яблоки — это одно, а как насчет Луны?- Что удерживает Луну на орбите вокруг Земли?
Закон инерции (Ньютон Первый закон движения) предсказывает:
- Если бы между
Луна и Земля, Луна будет двигаться по прямой с постоянной скоростью .

- Отклоняется от прямолинейного пути сила тяжести .
Падение Луны
Какое расстояние Луна проходит вокруг Земли за 1 секунду? Какое расстояние падает яблоко на Землю за первую секунду? Ньютон также знал, что:- Луна находится примерно в 60 земных радиусах от Земли.
Суммируя цифры:
Луна:
- Расстояние, на которое Луна падает на Землю за 1 секунду: x Луна = 0,00136 метра
- Расстояние от Луны до центра Земли: d Луна = 60 R Земля
- Ускорение Луны: a луна = GM земля /d луна 2 = GM земля / (60R земля ) 2
Apple :
- Расстояние, на которое яблоко падает на Землю за 1 секунду: x яблоко = 4,9 метра
- Расстояние от яблока до центра Земли: d яблоко = 1 R земля
- Ускорение Apple: a яблоко = GM земля /d яблоко 2 = GM земля /R земля 2
Соотношение отклонений Яблока и Луны за 1 секунду отношение их ускорений:
Объединив всю имеющуюся у нас информацию, мы получим следующее:

Наблюдения против предсказания
Это правильно?
Ранее мы установили из наблюдений, что отклонения Луна и яблоко за 1 секунду это:
- х луна = 0,00136 метра
- x яблоко = 4,9 метра
Гравитация предсказывает, что
- x яблоко /3600 = 4,9 метра/3600 = 0,00136 метра!!
Соглашение по существу идеально!
Это показывает, что один и тот же закон всемирного тяготения применим к обоим яблоко и луна! Оба чувствуют гравитацию Земли в виде сила, которая становится слабее пропорционально квадрату их расстояния от центра земли.
Так почему же Луна
вращается вокруг Земли? Если Луна немного падает к Земле, как яблоко упала на поверхность, почему Луна движется вокруг Земли по орбите вместо того, чтобы упасть на нее?Чтобы ответить на этот вопрос, нужно сначала рассмотреть, что произошло бы, если бы не действовала гравитация:
- Вопрос :
- Какое расстояние пройдёт Луна по прямой за 1 секунду, если бы не действовала гравитация?
- Ответ :
- Около 1000 метров.

В то же время движение Луны по этому прямолинейному пути также заставит его сместиться на на от Земли.
- Вопрос :
- На какое расстояние от Земли уйдет Луна за 1 во-вторых, если бы не действовала гравитация?
- Ответ :
- Около 0,00136 метра!
Таким образом, мы пришли к поразительному выводу:
- Луна действительно постоянно падает вокруг Земли!
Пока на первый взгляд падение яблока и орбита Луны
кажутся двумя совершенно разными явлениями, если рассматривать их в свете
законы движения Ньютона, на самом деле они являются различными проявлениями
тоже самое! Падение Луны вокруг Земли такое же
движения, как падение яблока на Землю. Оба описаны
одни и те же три закона движения, и оба испытывают гравитационную силу
описывается одним и тем же универсальным законом силы.
Оба описаны
одни и те же три закона движения, и оба испытывают гравитационную силу
описывается одним и тем же универсальным законом силы.
Всемирная гравитация
Закон всемирного тяготения Универсальный :- Управляет падением яблока на Землю.
- Управляет падением Луны вокруг Земли.
- Управляет падением системы Земля/Луна вокруг Солнца.
- Управляет падением Солнца вокруг центра Млечный путь.
- Управляет падением галактик Млечный Путь и Андромеды на их взаимной орбите…
Обновлено: 10 октября 2007 г., Тодд А. Томпсон
Copyright Richard W. Pogge, Все права защищены.
Объяснение урока: Закон тяготения Ньютона
В этом объяснении мы узнаем, как использовать закон тяготения Ньютона для рассчитать силу гравитации между двумя массивными объектами.
Закон всемирного тяготения Ньютона — это основополагающий закон классической физики, описывающий, как объекты с массой
притягиваются друг к другу под действием силы тяжести. Этот закон является универсальным принципом, то есть он применим к все массы в
Вселенная: она говорит нам, что силы, управляющие тем, как объект падает на землю с небольшого расстояния
такие же, как силы, управляющие движением звезд и планет.
Этот закон является универсальным принципом, то есть он применим к все массы в
Вселенная: она говорит нам, что силы, управляющие тем, как объект падает на землю с небольшого расстояния
такие же, как силы, управляющие движением звезд и планет.
Первое, что мы должны отметить о гравитации, это то, что она всегда является притягивающей силой. Сила тяжести заставляет все массы во Вселенной притягиваться ко всем другим массам. Если мы просто рассмотрим две массы в изоляция, сила тяжести воздействует на каждую из них:
Мы видим, что силы, действующие на каждый объект, направлены в противоположные стороны, притягивая два объекта напрямую
вместе. Другими словами, векторы сил, действующих на каждую массу, лежат на линии между двумя массами. Технически мы говорим, что векторы силы направлены вдоль прямой линии, соединяющей центров двух объектов.
массы — центр масс объекта является средним положением всей его массы, а в случае сферического
объект, это лежит в центре. Мы также можем видеть, что силы, действующие на каждый объект, имеют одинаковую
величина 𝐹. Во всех случаях при рассмотрении двух масс сила тяжести действует равные и противоположные силы на обоих
объекты.
Мы также можем видеть, что силы, действующие на каждый объект, имеют одинаковую
величина 𝐹. Во всех случаях при рассмотрении двух масс сила тяжести действует равные и противоположные силы на обоих
объекты.
Пример 1. Определение направлений пары гравитационных сил
На каждом из следующих рисунков показаны две скалы в открытом космосе. Какая фигура правильно показывает направление силы тяжести, действующей на каждый камень?
Ответ
Чтобы ответить на этот вопрос, нам просто нужно помнить, что гравитация всегда привлекательный . Этот
означает, что любая пара масс притягивается друг к другу векторами сил, действующими вдоль линии между
массы, то есть они стянуты непосредственно друг с другом. Просматривая доступные варианты ответов, мы
можно увидеть, что единственный вариант, где это имеет место, — это вариант D. Мы также можем заметить, что хотя
камни выглядят по-разному и могут иметь разную массу, гравитационные силы, действующие на каждый камень
имеют одинаковую величину, 𝐹.
Закон всемирного тяготения Ньютона можно использовать для расчета величины гравитационной силы притяжения действующее между любыми двумя телами, обладающими массой. Начнем с рассмотрения двух тел с массами 𝑚 и 𝑚, разделены расстоянием 𝑟.
Закон всемирного тяготения Ньютона говорит нам, что величина гравитационной силы, действующей на каждое тело, равна пропорциональна как 𝑚, так и 𝑚 и обратно пропорциональна квадрат расстояния 𝑟 между ними. Это отношение может быть выражено следующим утверждением о пропорциональности: 𝐹∝𝑚𝑚𝑟.
Эту пропорциональность можно «преобразовать» в уравнение с помощью введение константы пропорциональности. Эта константа известна как универсальная гравитационная постоянная, 𝐺, и имеет значение 6,674×10 м 3 ⋅кг −1 ⋅с −2 . Используя эту константу, мы можем написать следующее уравнение.
Уравнение: закон всемирного тяготения Ньютона
𝐹=𝐺𝑚𝑚𝑟
Постоянная 𝐺 играет две важные роли в этом уравнении. Во-первых, он масштабирует правую часть уравнения
так, чтобы значение правой части соответствовало размеру гравитационного
создаваемая сила (измеряется в ньютонах). Во-вторых,
это гарантирует, что единицы на каждом
стороны уравнения одинаковы.
Во-первых, он масштабирует правую часть уравнения
так, чтобы значение правой части соответствовало размеру гравитационного
создаваемая сила (измеряется в ньютонах). Во-вторых,
это гарантирует, что единицы на каждом
стороны уравнения одинаковы.
Давайте посмотрим, как мы можем использовать это уравнение для расчета гравитационной силы между двумя объектами.
Опять же, мы будем рассматривать два тела, разделенные определенным расстоянием, как выше. На этот раз мы скажем каждый тело имеет массу 1 кг, и оба находятся на расстоянии 1 м друг от друга.
Здесь 𝑚=1кг, 𝑚=1кг, и 𝑟=1м. Таким образом, создаваемая гравитационная сила 𝐹 определяется выражением 𝐹=𝐺1×1(1)=6,674×10⋅⋅×1×1(1)=6,674×10.kgkgmmkgskgkgmN
Мы можем обратить особое внимание на то, как работают единицы, чтобы дать нам
ньютоны. Единицей 𝐺 является м 3 ⋅кг −1 ⋅с −2 . Когда мы умножаем 𝐺 на две массы (выраженные в килограммах) и делим на
квадрат расстояния (выраженный в квадратных метрах), мы имеем
mkgskgkgmmkgkgsmkgmsN⋅⋅××=⋅⋅⋅=⋅⋅=.
Мы также можем заметить, что рассчитанная нами здесь сила очень мала — слишком мала, чтобы быть заметной в повседневная жизнь. На самом деле, как правило, мы замечаем значительные гравитационные силы только тогда, когда мы имеем дело с относительно большие массы, разделенные относительно небольшими расстояниями. Итак, давайте попробуем другой пример с большим массы.
На этот раз мы рассмотрим двух человек, каждый из которых имеет массу 100 кг, разделенных расстояние 1 м.
Применение закона тяготения Ньютона с помощью 𝑚=100кг, 𝑚=100кг, и 𝑟=1м дает нам 𝐹=𝐺100×100(1)=6,674×10⋅⋅×100×100(1)=6,674×10.kgkgmmkgskgkgmN
Даже если эта сила равна 100 раз больше, чем в предыдущем примере, это еще слишком мал, чтобы быть заметным. Это согласуется с нашим повседневным мировосприятием: мы не ожидали бы заметного гравитационного поля. сила между двумя людьми!
Давайте посмотрим на другой пример с еще большей массой.
Пример 2. Расчет величины гравитационной силы между Two Objects
Два объекта, A и B, находятся в глубоком космосе. Расстояние между центрами масс двух объектов составляет 20 м. Объект А имеет масса 30 000 кг а объект B имеет массу 55 000 кг. Что это величина гравитационной силы между ними? Используйте значение 6,67×10 м 3 /кг⋅с 2 для универсальная гравитационная постоянная. Дайте ответ в экспоненциальном представлении с точностью до двух знаков после запятой.
Ответ
Мы знаем, что гравитация действует на оба объекта так, что они притягиваются вместе. Конкретно, эти векторы силы будут равны по модулю, но направлены в противоположные стороны вдоль прямой линия, соединяющая центры масс двух объектов.
Закон всемирного тяготения Ньютона говорит нам, что сила 𝐹, действующая на каждый объект, определяется выражением
𝐹=𝐺𝑚𝑚𝑟.
В этом случае 𝑚=30000кг, 𝑚=55000кг, и 𝑟=20м. Таким образом, создаваемая гравитационная сила 𝐹 определяется выражением 𝐹=𝐺30000×50000(20)=6,67×10⋅⋅×1,65×10400=2,751…×10.kgkgmmkgskgmN
1 окончательный ответ 𝐹=2,75×10Н.Даже эта сила относительно мала, несмотря на то, что объекты имеют массу в несколько тонн каждый. Однако, когда работа с объектами с очень большой массой, такими как звезды, планеты, и луны — силы, производимые гравитация гораздо более очевидна.
Пример 3: расчет величины гравитационной силы между Земля и Луна
Земля имеет массу 5,97×10 кг, а Луна
имеет массу 7,34×10 кг. Среднее расстояние
между центром Земли и центром Луны находится
384 км. Какова величина
сила притяжения между Землей и Луной? Используйте значение
6,67×10 м 3 /кг⋅с 2 для
универсальная гравитационная постоянная. Дайте ответ по научному
обозначение до двух знаков после запятой.
Дайте ответ по научному
обозначение до двух знаков после запятой.
Ответ
Мы знаем, что гравитация действует на Землю и на Землю с одинаковой силой. Луна. Эти силы действовать вдоль прямой линии, соединяющей центры двух объектов массы, то есть между центром Земля и центр Луны.
Мы можем использовать это уравнение для расчета величины силы 𝐹: 𝐹=𝐺𝑚𝑚𝑟.
Вопрос сообщает нам значения 𝑚=5,97×10кг, 𝑚=7,34×10кг, и 𝑟=384000км. Примечание что мы должны преобразовать 𝑑 в стандартную единицу длины, прежде чем подставляя это в наше уравнение: 𝑟=384×10м. Итак, гравитационная сила произвела, 𝐹, дается 𝐹=𝐺5,97×10×7,34×10(384×10)=6,67×10⋅⋅×4,38198×101,47456×10=1,982…×10, kgkgmmkgskgmN
Округлив это до 2 знаков после запятой, мы получим окончательный ответ: 𝐹=1,98×10N.
В следующем примере мы видим, как можно преобразовать уравнение в
найти величины, отличные от силы 𝐹.
Пример 4. Расчет величины гравитационной силы между Сатурн и Титан
Титан — самый большой спутник Сатурна. Он имеет массу 1,35×10 кг. Сатурн имеет массу 5,68×10 кг. Если величина гравитационной силы между ними равна 3,43×10 N, какое расстояние между центрами масс Сатурна и Титана? Используйте значение 6,67×10 м 3 /кг⋅с 2 для универсальная гравитационная постоянная. Дайте ответ в экспоненциальном представлении с точностью до двух знаков после запятой.
Ответ
Здесь мы думаем о гравитационной силе, действующей между Сатурном и его спутником Титаном. Этот время, когда мы были 90 510, учитывая 90 511 величину гравитационной силы, которая притягивает два тела, и мы хочу определить расстояние между ними.
Для этой задачи мы по-прежнему можем использовать то же уравнение, которое описывает закон всемирного тяготения Ньютона:
𝐹=𝐺𝑚𝑚𝑟.
Так как мы хотим найти значение 𝑟, нам нужно изменить уравнение, чтобы сделать 𝑟 тему. Мы можно начать с умножения обеих сторон на 𝑟, чтобы получить 𝐹𝑟=𝐺𝑚𝑚.
Затем обе части делим на 𝐹: 𝑟=𝐺𝑚𝑚𝐹.
Наконец, мы извлекаем квадратный корень из каждой стороны, оставляя нас с 𝑟 с левой стороны: 𝑟=𝐺𝑚𝑚𝐹.
Поскольку мы знаем силу 𝐹 так же, как и каждую массу, теперь нам просто нужно заменить эти ценности в правая часть уравнения. В этом случае мы будем говорить, что 𝑚 — это масса Титана, равно 1,35×10 кг, а 𝑚 — масса Сатурна, равная 5,68×10: 𝑟=6,67×10⋅⋅1,35×10×5,68×103,43×10=1,221…×10,mkgskgkgNm что, округленное до двух знаков после запятой, дает нам окончательный ответ 1,22×10м.
В следующем примере мы думаем о том, как гравитационная сила меняется с расстоянием, и как эта взаимосвязь
можно представить в виде графика.
Пример 5. Распознавание того, как гравитационная сила меняется с расстоянием на График
Какая из линий на графике показывает, как величина гравитационной силы между двумя объектов зависит от расстояния между их центрами масс?
Ответ
Мы ищем линию, которая показывает нам, как гравитационная сила между двумя объектами изменяется с расстояние.
Это соотношение определяется законом всемирного тяготения Ньютона: 𝐹=𝐺𝑚𝑚𝑟.
Поскольку из вопроса становится ясно, что мы говорим о «двух объектах», мы можем Предположим, что каждый из них имеет постоянная масса. Давайте подумаем, что показывает нам это уравнение, когда мы продолжаем 𝑚 и 𝑚 постоянные, но изменить расстояние, 𝑟.
Обратите внимание, что у нас есть 𝑟 в знаменателе в правой части уравнения. Если бы мы увеличит размер 𝑟, тогда размер 𝑟 тоже увеличится. Увеличив таким образом знаменатель
будет уменьшение размер 𝐺𝑚𝑚𝑟. Поскольку это равно 𝐹,
мы знаем, что 𝐹 уменьшится. В других
слов, увеличивая расстояние 𝑟 между
два объекта будут уменьшать величину гравитационного
сила, 𝐹, между ними.
Поскольку это равно 𝐹,
мы знаем, что 𝐹 уменьшится. В других
слов, увеличивая расстояние 𝑟 между
два объекта будут уменьшать величину гравитационного
сила, 𝐹, между ними.
Это говорит нам о том, что мы ищем строку, которая всегда имеет отрицательное значение. градиент, то есть тот, который показывает сила уменьшается по мере увеличения расстояния. Это означает, что мы можем исключить синий и зеленый линий, которые оба имеют положительные градиенты.
Все остальные линии на графике — фиолетовая , красная и черная — показывают уменьшение силы как расстояние увеличивается. Мы можем выяснить, какая строка верна, спросив себя, что происходит с 𝐹 как 𝑟 приближается к нулю.
Глядя на приведенное выше уравнение, мы видим, что уменьшение
𝑟 увеличится 𝐹. Но, более того, мы
можно увидеть, что если мы установим 𝑟 равным нулю, мы столкнемся с проблемой:
𝐹=𝐺𝑚𝑚0=𝐺𝑚𝑚0.
Делим на ноль! Это означает, что результат (т. е. 𝐹) является «неопределенным». Итак, мы знаем, что граф этого уравнения не будет показывать конечное значение 𝐹, когда 𝑟 = 0. Снова взглянув на график, мы можем видим, что из оставшихся вариантов линии фиолетовый и черный не следуют этому правилу: каждый из этих линии просто пересекает вертикальную ось при некотором конечном значении 𝐹. Это оставляет нам только один доступный вариант ответа: красная линия .
Закон всемирного тяготения Ньютона говорит нам, что величина
гравитационная сила 𝐹 стремится
до бесконечности (т. е. становится все больше и больше без ограничений) как расстояние
𝑟 между двумя объектами получает
все ближе и ближе к нулю. Действительно, это обозначено красной линией на
график: при уменьшении 𝑟
градиент красной линии становится все круче и круче, и она никогда не пересекается
𝑦-ось.

