Гравитация Земли: значение гравитационного поля

Солнечная система > Система Земля-Луна > Планета Земля > Гравитация Земли

Гравитационная карта Земли. Красные участки: области повышенной гравитации

Сила гравитации и гравитационное поле Земли. Узнайте точное значение гравитации на экваторе и полюсах планеты, влияние массы, вращения Земли на силу притяжения.

Если бы не гравитация Земли, нас бы всех унесло в космос. Так что не паникуйте, когда я сообщу, что скорость вашего падения по мере приближения к Земле увеличивается до 9.8 м/сек2. К счастью, вас спасает то, что вы находитесь на поверхности планеты. Можете посмотреть на карту, где показана сила притяжения Земли.

Гравитация зависит от массы. Чем больше масса объекта, тем с большей силой гравитация влияет на объекты вокруг него. Сила притяжения Земли, которую вы испытываете при падении, зависит от расстояния. Так, сила притяжения, которую вы ощущаете на поверхности Земли значительно отличается от той, которую бы вы испытывали, находясь на расстоянии до Луны, или еще дальше. На поверхности планеты сила притяжения составляет 9,8 м/с2.

Гравитационная 3D модель Земли

Вы будете удивлены, узнав, что гравитация на Земле меняется в зависимости от того, в какой ее точке вы находитесь. Первая причина — это вращение Земли. Это вращение затягивает вас в космос, но не волнуйтесь, его силы недостаточно. Сила притяжения Земли на экваторе составляет 9.789 м/с2, а на полюсах 9.832 м/с2. Другими словами, ваш вес на полюсах больше, чем на экваторе, из-за центробежной силы.

С увеличением высоты сила земной гравитации уменьшается, так как увеличивается расстояние от центра Земли. При восхождении на гору она достигает минимального значения (на вершине Эвереста сила притяжения уменьшиться 0.28%), но если вы поднимитесь на высоту Международной космической станции, то сила притяжения составит 90 процентов.

Наконец, сила притяжения зависит от того, что находится под вами. Высокая плотность пород меняет силу гравитации, которую вы можете почувствовать, хотя ее величина очень незначительная. В НАСА уже вычислили силу гравитационного поля Земли с невероятной точностью.

Сегодня написано много статьей на тему Земли во Вселенной. Здесь вы можете ознакомиться с полной гравитационной картой нашей планеты.

Читайте также:

---

Строение Земли

Поверхность Земли

Положение и движение Земли

Земное притяжение. Гравитационное поле Земли

Гравитация, она же притяжение или тяготение, – это универсальное свойство материи, которым обладают все предметы и тела во Вселенной. Суть гравитации залучается в том, что все материальные тела притягивают к себе все другие тела, находящиеся вокруг.

Земное притяжение

Если гравитация – это общее понятие и качество, которым обладают все предметы во Вселенной, то земное притяжение – это частный случай этого всеобъемлющего явления. Земля притягивает к себе все материальные объекты, находящиеся на ней. Благодаря этому люди и животные могут спокойно перемещаться по земле, реки, моря и океаны – оставаться в пределах своих берегов, а воздух – не летать по бескрайним просторам Космоса, а образовывать атмосферу нашей планеты.

Возникает справедливый вопрос: если все предметы обладают гравитацией, почему Земля притягивает к себе людей и животных, а не наоборот? Во-первых, мы тоже притягиваем к себе Землю, просто, по сравнению с ее силой притяжения наша гравитация ничтожно мала. Во-вторых, сила гравитации прямо пропорционально зависит от массы тела: чем меньше масса тела, тем ниже его гравитационные силы.

Второй показатель, от которого зависит сила притяжения – это расстояние между предметами: чем больше расстояние, тем меньше действие гравитации. В том числе благодаря этому, планеты движутся на своих орбитах, а не падают друг на друга.

Примечательно, что своей сферической формой Земля, Луна, Солнце и другие планеты обязаны именно силе тяготения. Она действует в направлении центра, подтягивая к нему вещество, составляющее «тело» планеты.

Гравитационное поле Земли

Гравитационное поле Земли – это силовое энергетическое поле, которое образуется вокруг нашей планеты благодаря действию двух сил:

• гравитации;
• центробежной силе, которая своим появление обязана вращению Земли вокруг своей оси (суточное вращение).

Поскольку и гравитация, и центробежная сила действуют постоянно, то и гравитационное поле является постоянным явлением.

Незначительное воздействие на поле оказывают силы тяготения Солнца, Луны и некоторых других небесных тел, а также атмосферных масс Земли.

Закон всемирного тяготения и сэр Исаак Ньютон

Английский физик, сэр Исаак Ньютон, согласно известной легенде, однажды гуляя по саду днем, увидел на небе Луну. В это же время с ветки упало яблоко. Ньютон тогда занимался изучением закона движения и знал, что яблоко падает под воздействием гравитационного поля, а Луна вращается по орбите вокруг Земли.

И тут в голову гениальному ученому, озаренную инсайтом, пришла мысль, что, возможно, яблоко падает на землю, подчиняясь той же силе, благодаря которой Луна находится на своей орбите, а не носится беспорядочно по всей галактике. Так был открыт закон всемирного тяготения, он же Третий закон Ньютона.

На языке математических формул этот закон выглядит так:

F = GMm/D²,

где F – сила взаимного тяготения между двумя телами;

M – масса первого тела;

m – масса второго тела;

D² – расстояние между двумя телами;

G – гравитационная постоянная, равная 6,67х10^-11.

какова сила притяжения нашей земли?

Это сила и есть вес…

достаточно чтобы удержать луну!

силу притяжения земли можно рассматривать на полюсах, на экваторе и т. д. в среднем она равно 9,8 а так колеблется от 9, 78 до 9,82 приблизительно.. . масса и объем тела не играет никакой роли, просмотри опыт галилея про свободное падение тел.

правильно говорить — сила притяжения земли и какого-то тела F = m*g g = 9,8 м/с2

тело массы m притягивается к земле с силой всемирного тяготения F=GMm/R^2. для земли постоянная величина GM/R^2, где G=6,67*10^(-1) Нм^2/кг^2 — универсальная гравитационная постоянная, М=5,976*10^24 кг — масса земли, R=6,378*10^6 м — средний радиус земли примерно равна 9,81 м/с^2, обозначается буквой g и называется ускорением свободного падения. то есть стла притяжения к земле равна F=mg=9,81*m Н

Скорость гравитации — Википедия

Скорость гравитации — скорость распространения гравитационных воздействий, возмущений и волн.

Скорость гравитации в физических теориях[править | править код]

Классическая физика[править | править код]

В теории гравитации Ньютона скорость гравитации не входит ни в одну формулу, считаясь бесконечно большой. В своих трудах по небесной механике^[1]Лаплас показал, что если гравитационное взаимодействие между двумя телами не действует мгновенно (что эквивалентно введению потенциала, зависящего от скоростей), то в системе движущихся планет не будет сохраняться импульс — часть импульса будет передаваться гравитационному полю, аналогично тому, как это происходит при электромагнитном взаимодействии зарядов в электродинамике. С ньютоновой точки зрения, если гравитационное воздействие передаётся с конечной скоростью и не зависит от скоростей тел, то все точки планеты должны притягиваться к точке, где Солнце было несколько раньше, а не к одновременному его месторасположению. На этом основании Лаплас показал, что эксцентриситет и большие полуоси орбит в задаче Кеплера с конечной скоростью гравитации должны расти со временем — испытывать вековые изменения. Из верхних пределов на изменения этих величин, следующие из устойчивости Солнечной системы и движения Луны, Лаплас показал, что скорость распространения гравитационного ньютонова взаимодействия не может быть ниже 50 миллионов скоростей света^[2].

Сообщается ли притяжение от одного тела к другому мгновенно? Время передачи, если бы оно было для нас заметно, обнаружилось бы преимущественно вековым ускорением в движении Луны. Я предлагал это средство для объяснения ускорения, замеченного в упомянутом движении, и нашёл, что для удовлетворения наблюдениям должно приписать притягательной силе скорость в семь миллионов раз большую, чем скорость светового луча. А так как ныне причина векового уравнения — Луны хорошо известна, то мы можем утверждать, что притяжение передаётся со скоростью, по крайней мере в пятьдесят миллионов раз превосходящей скорость света. Поэтому, не опасаясь какой либо заметной погрешности, мы можем принимать передачу тяготения за мгновенную.

— П. С. Лаплас Изложение системы Мира Париж, 1797.^[3]

Метод Лапласа корректен для прямых обобщений ньютоновой гравитации, но может быть не применим к более сложным моделям. Так, например, в электродинамике движущиеся заряды притягиваются/отталкиваются не от видимых положений других зарядов, а от положений, которые они занимали бы в настоящее время, если бы двигались от видимых положений равномерно и прямолинейно — это является свойством потенциалов Лиенара — Вихерта^[4]. Аналогичное рассмотрение в рамках общей теории относительности приводит к такому же результату с точностью до членов порядка (v/c)3{\displaystyle (v/c)^{3}}^[5].

Общая теория относительности и другие релятивистские теории[править | править код]

В Общей теории относительности (ОТО) в пустом пространстве предельная скорость гравитации равна скорости света^[6][7][8]. В ОТО потенциалами гравитационного поля выступают компоненты метрического тензора, так что гравитационное поле отождествляется в сущности с метрическим полем.

В квантовых теориях гравитации под скоростью гравитации подразумевают скорость гравитонов как наименьших частиц (квантов) поля. Обычно она очень близка к скорости света или совпадает с ней.

Во многих альтернативных теориях гравитации скорость её распространения может существенно отличаться от скорости света, так что непосредственное измерение скорости гравитации представляет собой тест на работоспособность этих теорий.

Эксперименты по определению скорости гравитации[править | править код]

Скорость гравитации можно определить по скорости передачи влияния гравитационного поля на результаты каких-либо измерений. Этот путь может быть использован в высокоточных экспериментах по измерению времени задержки прохождения света и радиосигналов в гравитационном поле какого-либо движущегося массивного тела.

Так, в 2002 году Копейкиным и Фомалонтом был проведён эксперимент^[9][10] на основе радиоинтерферометрии со сверхдлинной базой, в котором излучение от далёкого квазара QSO J0842+1835, проходящее вблизи массивного тела — Юпитера, регистрировалось цепью радиотелескопов на Земле^[11].

Вследствие периодического движения Юпитера по орбите вокруг Солнца со средней скоростью 13,1 км/с, в точках отсчёта Солнечной системы происходит периодическое изменение гравитационного поля. Изменение метрики (как за счёт изменения местоположения планеты, так и за счёт скорости её движения) происходит с опозданием, связанным с ограниченной скоростью гравитации. Учёт данного запаздывания при анализе эксперимента даёт скорость гравитации, близкую по величине к скорости света, с точностью порядка 20 %. Полученный результат требует независимого подтверждения, так как не все физики-релятивисты согласны с интерпретацией эксперимента^[12].

11 февраля 2016 года было объявлено об экспериментальном открытии гравитационных волн коллаборациями LIGO и VIRGO^[13][14][15]. Анализ влияния события GW150914 на дисперсию гравитационных волн в зависимости от частоты не противоречит гипотезе о нулевой массе гравитона и совпадении его скорости со скоростью света для гипотетических расширений ОТО (оценка сверху на массу гравитона: m_g ≤ 1,2 × 10⁻²² eV/c², соответствует оценке снизу на скорость для частоты 35 Гц: v_g/c ≤ 1 — 10^-18)^[16]

Другой способ измерения скорости гравитации связан с фиксацией гравитационных волн от далёких звёздных источников одновременно со световым сигналом. Первое такое измерение получили для гравитационной волны GW170817. Судя по этому событию, отклонение скорости гравитационных волн от скорости света, если такое отклонение существует, лежит в пределах от −3×10⁻¹⁵ до +0,7×10⁻¹⁵. Так как ожидаемая разница коэффициентов преломления и дисперсии межгалактической среды незначительна, то, в пределах погрешности, не обнаружено отличий от скорости света^[17].

1. ↑ P. S. Laplасе Mecanique celeste, 4, livre X Paris, 1805.
2. ↑ Богородский А. Ф. Глава 2 // Всемирное тяготение. — Киев: Наукова думка, 1971.
3. ↑ Цитируется по книге: Борис Николаевич Воронцов-Вельяминов. Лаплас. — М.: Жургазоб’единение, 1937.
4. ↑ Фейнман разбирает эту проблему в 6 томе Фейнмановских лекций по физике, глава 21, § 1.
5. ↑ Богородский А. Ф. Глава 5, § 15 // Всемирное тяготение. — Киев: Наукова думка, 1971.
6. ↑ А. Н. Темчин. Разд. 7.1. Волны и характеристические поверхности, скорости распространения волн метрики // Уравнения Эйнштейна на многообразии. — М.: Едиториал УРСС, 1999. — С. 98—102. — 160 с. — ISBN 5-88417-173-0.
7. ↑ Ландау Л. Д., Лифшиц Е. М. Теоретическая физика: Учеб. пособ.: Для вузов. В 10 т. Т. II. Теория поля. — 8-е изд., стереот. — М.: ФИЗМАТЛИТ, 2003. — 536 с. — ISBN 5-9221-0056-4 (Т. II). — § 109. Сильная гравитационная волна.
8. ↑ Yvonne Choquet-Bruhat. General Relativity and the Einstein Equations (англ.). — Oxford University Press, 2009. — P. 170. — 812 p. — (Oxford Mathematical Monographs). — ISBN 978-0199230723.
9. ↑ Измерена скорость гравитации // membrana, 8 января 2003
10. ↑ Фундаментальный предел скорости гравитации и его измерение, С.М. Копейкин
11. ↑ Fomalont E. B., Kopeikin S. M. The Measurement of the Light Deflection from Jupiter: Experimental Results (2003), Astrophys. J., 598, 704. (astro-ph/0302294)
12. ↑ Обзор на сайте университета Сент-Луиса (англ.)
13. ↑ GRAVITATIONAL WAVES DETECTED 100 YEARS AFTER EINSTEIN’S PREDICTION (англ.). VIRGO. Дата обращения 11 февраля 2016.
14. ↑ Emanuele Berti. Viewpoint: The First Sounds of Merging Black Holes (англ.). Physical Review Letters (11 February 2016). Дата обращения 11 февраля 2016.
15. ↑ B. P. Abbott (LIGO Scientific Collaboration and Virgo Collaboration) et al. Observation of Gravitational Waves from a Binary Black Hole Merger (англ.) // Physical Review Letters : journal. — 2016. — Vol. 116, no. 6. — DOI:10.1103/PhysRevLett.116.061102.
16. ↑ Tests of general relativity with GW150914 (неопр.). LIGO (11 февраля 2016). Дата обращения 12 февраля 2016.
17. ↑ Abbott B. P. et al. (LIGO Scientific Collaboration, Virgo Collaboration, Fermi Gamma-ray Burst Monitor, and INTEGRAL). Gravitational Waves and Gamma-Rays from a Binary Neutron Star Merger: GW170817 and GRB 170817A // The Astrophysical Journal. — 2017. — Vol. 848. — P. L13. — DOI:10.3847/2041-8213/aa920c. [исправить]

Альтернативные теории гравитации — Википедия

Альтернативными теориями гравитации принято называть теории гравитации, существующие как альтернативы общей теории относительности (ОТО) или существенно (количественно или принципиально) модифицирующие её. К альтернативным теориям гравитации часто относят вообще любые теории, не совпадающие с общей теории относительности хотя бы в деталях или как-то обобщающие её. Тем не менее, нередко теории гравитации, особенно квантовые, совпадающие с общей теорией относительности в низкоэнергетическом пределе, «альтернативными» не называют.

Классификация альтернативных теорий гравитации[править | править код]

В физике XVII—XIX столетий доминирующей теорией гравитации была теория Ньютона. В настоящее время большинство физиков основной теорией гравитации считают общую теорию относительности (ОТО), поскольку весь существующий массив экспериментов и наблюдений согласуется с ней (см. Тесты общей теории относительности). Однако ОТО имеет ряд существенных проблем, что приводит к попыткам модификации ОТО или к представлению новых теорий. Современные теории гравитации можно разбить на следующие основные классы:

1. Метрические теории. Сюда относятся ОТО, релятивистская теория гравитации (РТГ) Логунова, и другие.
2. Неметрические теории наподобие теории Эйнштейна — Картана.
3. Векторные теории.
4. Скалярно-тензорные теории. Такова, в частности, теория Йордана — Бранса — Дике.
5. Теории, альтернативные классической теории Ньютона. Известными теориями являются гравитация Ле-Сажа и модифицированная ньютоновская динамика (МОНД).
6. Теории квантовой гравитации, представленные целой серией разновидностей.
7. Теории объединения различных физических взаимодействий. Здесь можно указать теорию супергравитации и теорию струн.

Общий список теорий гравитации со ссылками приведён ниже.

Причины создания альтернативных теорий гравитации[править | править код]

Существуют сотни попыток создания идеальной теории гравитации. По мотивации эти попытки попадают в 3 широкие категории:

• Прямые альтернативы общей теории относительности (ОТО), такие как теория Эйнштейна — Картана, скалярно-тензорная теория гравитации (теория Бранса — Дикке), биметрическая теория Розена или релятивистская теория гравитации Логунова;
• Попытки создания квантовой теории гравитации, наиболее известной из которых является петлевая квантовая гравитация;
• Классические единые теории поля, объединяющие гравитацию с электромагнетизмом и, возможно, другими (обычно гипотетическими) силами, например, теория Калуцы-Клейна, теория Шмутцера.

Эта статья описывает лишь прямые альтернативы ОТО, квантовые теории гравитации являются предметом статьи «Квантовая гравитация», единые теории поля описаны в одноимённой статье, как и попытки создания теории всего.

Поводы для создания теорий гравитации изменялись со временем, исторически первыми из них были попытки объяснить движение планет (с этим успешно справилась Ньютоновская гравитация) и спутников, в частности, Луны. Затем наступило время комбинированных теорий гравитации и света, опиравшихся на концепцию эфира или корпускулярную теорию света, как пример можно назвать теорию гравитации Фатио-Лесажа. После того, как вся физика поменяла свой характер после создания специальной теории относительности, возникла необходимость соединить последнюю с гравитационными силами. В это же время экспериментальная физика дошла в своём развитии до проверки оснований теории относительности и гравитации: лоренц-инвариантности, гравитационного отклонения света и эквивалентности инертной и гравитационной массы (эксперимент Этвёша). Эти эксперименты и другие соображения привели в конце концов к общей теории относительности.

После этого мотивация резко сменила характер. Гравитация ушла из основного фокуса приложения сил для развития физики — им стало развитие квантовой механики и квантовой теории поля, вдохновлённое открытиями в атомной, ядерной физике и физике элементарных частиц. Соединение квантовой механики даже со специальной теорией относительности оказалось столь сложным, что квантовая теория поля до сих пор не представляет собой сколь-нибудь законченной отрасли физического знания. Попытки же сочетать принципы квантовой механики с общей теорией относительности не могут быть признаны полностью успешными и описываются в статье «квантовая гравитация».

После создания ОТО предпринимались попытки как улучшить ранние теории, так и разработать новые, учитывающие новые концепции. Использовались различные подходы, например, добавление к ОТО учёта спина, введение расширения Вселенной в рамки основного (невозмущённого) пространства теории, требование отсутствия сингулярностей.

Экспериментальная техника достигала новых высот и выдвигала всё более жёсткие ограничения на теории гравитации. Многие подходы, разработанные вскоре после создания ОТО, были опровергнуты, и общая тенденция носит характер разработки всё более общих форм теорий гравитации, достигших в конце концов известного совершенства в том смысле, что каково бы ни было обнаруженное экспериментально отклонение от ОТО, найдётся теория, его описывающая.

К 1980-м гг. всё возрастающая точность экспериментов привела к полному отклонению всех теорий гравитации, за исключением того их класса, который включает ОТО как предельный случай. Эти же теории могут быть отклонены на основании принципа «бритвы Оккама» до тех пор, пока не будут надёжно обнаружены и подтверждены экспериментально отклонения от предсказаний ОТО. Вскоре физики-теоретики увлеклись струнными теориями, которые выглядели весьма многообещающе. В середине 1980-х гг. несколько экспериментов якобы обнаружили отклонения от ОТО на малых расстояниях (от сотен метров и ниже), которые назвали проявлениями «пятой силы». Следствием явился кратковременный всплеск активности в струнных теориях гравитации, но эти экспериментальные результаты в последующем не нашли подтверждения (в настоящее время ньютоновский характер сил гравитационного притяжения проверен вплоть до шкалы масштабов в десятки микрометров — 2009 год).

Новые попытки разработать альтернативные теории гравитации почти исключительно вдохновляются космологическими причинами, ассоциированными с такими концепциями, как «инфляция», «тёмная материя» и «тёмная энергия», или заменяющими их. Основной идеей при этом является согласие современной гравитации с гравитационным взаимодействием в ОТО, но при предполагаемом сильном отклонении от него в ранней Вселенной. Изучение аномалии Пионеров (англ. en:Pioneer anomaly) в последнее время также вызвало всплеск интереса к альтернативам ОТО, но фиксируемое отклонение, вероятно, слишком велико, чтобы его можно было объяснить с позиций любой из этих новейших теорий.

См. тензорный анализ, дифференциальная геометрия, математические основы общей теории относительности.

Латинские индексы пробегают значения от 1 до 3, греческие — от 0 до 3. Временной индекс, как правило, 0. Используется соглашение Эйнштейна для суммирования по повторяющимся ко- и контравариантным индексам.

ημν{\displaystyle \eta _{\mu \nu }\;} — метрика Минковского, gμν{\displaystyle g_{\mu \nu }\;} — тензор, обычно метрический тензор. Сигнатура метрики (−,+,+,+).{\displaystyle (-,+,+,+)\;.}

Ковариантная производная записывается как ∂μφ{\displaystyle \partial _{\mu }\varphi \;} или как φ;μ.{\displaystyle \varphi _{;\mu }\;.}

Основной источник: Пайс (1989).

Ранние теории гравитации, под которыми подразумеваются все теории, разработанные до ОТО, включают в себя теорию Ньютона (1686), её разнообразные модификации (в частности, Клеро и Хилла), а затем релятивистские теории: теорию Пуанкаре (1905), Эйнштейна (1912a & b), Эйнштейна-Гроссмана (1913), Нордстрёма (1912, 1913) и Эйнштейна-Фоккера (1914).

Теория Ньютона (1686)[править | править код]

В теории Ньютона (1686), переписанной в современных терминах, поле плотности массы ρ{\displaystyle \rho } генерирует скалярное поле гравитационного потенциала φ{\displaystyle \varphi } следующим образом (с точностью до постоянной):

Δφ=4πGρ{\displaystyle \Delta \varphi =4\pi G\rho }, где Δφ=∇2φ=div⁡grad⁡φ{\displaystyle \Delta \varphi =\nabla ^{2}\varphi =\operatorname {div} \operatorname {grad} \varphi }, G{\displaystyle G} — гравитационная постоянная, Δ{\displaystyle \Delta } — оператор Лапласа, квадрат наблы — скалярный.

В частности, для сферически-симметричной массы M{\displaystyle M} (включая точечную), скалярное поле вне её, принимая потенциал на бесконечности равным нулю, равно

φ=−GMr{\displaystyle \varphi =-G{M \over r}}, где r{\displaystyle r} — расстояние от данной точки до центра симметрии.

Скалярное поле, в свою очередь, влияет на траекторию свободно движущейся частицы так:

d2xjdt2+∂φ∂xj=0{\displaystyle {d^{2}x^{j} \over dt^{2}}+{\partial \varphi \over \partial x^{j}}=0} или x¨+grad⁡φ=0{\displaystyle {\ddot {x}}+\operatorname {grad} \varphi =0}.

Потенциальная энергия точечной массы равна:

P=φM{\displaystyle P=\varphi M}, где P{\displaystyle P} — потенциальная энергия, M{\displaystyle M} — величина массы.

Иногда используется формализм с положительным потенциалом, тяготеющие массы в этом случае образуют «потенциальные горбы», а не «ямы», линии градиента потенциала не исходят из тяготеющих масс, а, наоборот, входят в них. В прежних обозначениях:

связь поля потенциала с полем плотности массы: Δφ=∇2φ=div⁡grad⁡φ=−4πGρ{\displaystyle \Delta \varphi =\nabla ^{2}\varphi =\operatorname {div} \operatorname {grad} \varphi =-4\pi G\rho },

случай сферически-симметричной массы: φ=GMr{\displaystyle \varphi =G{M \over r}},

воздействие на материальную точку: d2xjdt2=∂φ∂xj{\displaystyle {d^{2}x^{j} \over dt^{2}}={\partial \varphi \over \partial x^{j}}} или x¨=grad⁡φ{\displaystyle {\ddot {x}}=\operatorname {grad} \varphi },

потенциальная энергия P=−φM{\displaystyle P=-\varphi M}.

Теория Ньютона и её переформулированный Лагранжем вариант (с введением вариационного принципа), естественно, не принимают во внимание релятивистские эффекты, и, соответственно, сейчас не могут рассматриваться как приемлемые теории гравитации. Тем не менее, теория Ньютона как теория, с известной степенью точности подтверждённая экспериментом, согласно принципу соответствия, должна воспроизводиться любой теорией гравитации как предел при слабом гравитационном поле и малых скоростях движения тел.

Механические модели (1650—1900)[править | править код]

Ньютон на вопрос о причинах тяготения отвечал: «Гипотез не измышляю». Его последователи не были столь щепетильны в данном вопросе и выдвинули множество механических версий объяснения тяготения. Из модификаций ньютоновской теории выделяется теория Лесажа (корпускулярная модель) и её модификации. Пуанкаре (1908) сравнил все известные к тому времени теории и пришёл к выводу, что только теория Ньютона корректна. Остальные модели предсказывают очень большие сверхсветовые скорости гравитационного взаимодействия, что в свою очередь должно было бы приводить к очень быстрому разогреву Земли вследствие столкновений её частиц с частицами, вызывающими гравитационное притяжение тел, чего не наблюдается.

Вот краткий список этих теорий:

• Рене Декарт (1644) и Христиан Гюйгенс (1690) привлекали для объяснения гравитации вихри корпускул, заполняющих всё пустое пространство.
• Роберт Гук (1671) и Джеймс Чэллис (1869) предполагали, что каждое тело излучает волны, которые приводят к притяжению им других тел. Никола Фатио де Дюилье (Nicolas Fatio de Duillier) (1690) и Жорж-Луи Ле Саж (Georges-Louis Le Sage) (1748) предложили корпускулярную модель, использующую эффект затенения одного тела другим от потоков корпускул, которые прибывают постоянно со всех сторон (теория гравитации Лесажа). Позднее подобная модель была разработана Хендриком Антоном Лоренцем, однако вместо корпускул он использовал электромагнитные волны.
• Исаак Ньютон (1675) и Риман (1853) утверждали, что притяжение тел является следствием взаимодействия с потоками эфира.
• Ньютон (1717) и Леонард Эйлер (1760) предложили модель, согласно которой эфир возле тел становится разреженным, что приводит к силе, направленной к телу.
• Кельвин (1871) предложил пульсационную модель гравитации и электромагнетизма.

Отклонения в движении небесных тел от рассчитанных по ньютоновской теории приводили к рассмотрению законов тяготения, отличных от ньютоновых. Так например, для объяснения отклонений в движении Луны одно время применялась формула Клеро

F=m1m2(Gr2+Hr4),{\displaystyle F=m_{1}m_{2}\left({\frac {G}{r^{2}}}+{\frac {H}{r^{4}}}\right)\,,}

а затем Хилла (она же, но с другими параметрами, не совпадающими с лунными, использовалась С. Ньюкомом (1895) при разработке теории движения внутренних планет Соленчной системы и составлении Солнечных таблиц (англ.)русск., через которые затем была определена эфемеридная секунда)

F=Gm1m2r2+δ,|δ|≪1.{\displaystyle F=G{\frac {m_{1}m_{2}}{r^{2+\delta }}}\,,\quad |\delta |\ll 1\,.}

По мере развития небесной механики выяснилось, что эти отклонения не требуют модификации теории тяготения, а вызываются другими причинами^[1].

В настоящее время существуют также разнообразные «вихревые» и «эфиродинамические» теории гравитации, а иногда и электромагнетизма (развиваемые Ацюковским, Воронковым, Леоновым, Рыковым и другими авторами). К ним можно приложить в основном всё те же возражения Пуанкаре, поэтому большинство учёных считают такие попытки в настоящее время относящимися к псевдонаучным.

Электрические модели (1870—1900)[править | править код]

Конец XIX столетия ознаменовался распространением теорий тяготения, связанных с полученными законами электромагнитного взаимодействия, таких как законы Вебера, Гаусса, Римана и Максвелла^[2][3]. Эти модели должны были объяснить единственный аномальный результат небесной механики: рассогласование в вычисляемом и наблюдаемом движении перигелия Меркурия. В 1890 году Леви удалось получить стабильные орбиты и нужную величину сдвига перигелия путём комбинации законов Вебера и Римана. Другая успешная попытка была предпринята П. Гербером в 1898 году^[4]. Тем не менее, так как исходные электродинамические потенциалы оказались неверными (например, закон Вебера не вошёл в окончательную теорию электромагнетизма Максвелла), эти гипотезы были отвергнуты как произвольные^[5][6]. Некоторые другие попытки, которые уже использовали теорию Максвелла, (например, теория Х. Лоренца 1900 года) давали слишком малую прецессию^[7][8][9].

Лоренц-инвариантные модели (1905—1910)[править | править код]

Около 1904—1905 годов работы Х. Лоренца, А. Пуанкаре и А. Эйнштейна заложили фундамент специальной теории относительности, исключив возможность распространения любых взаимодействий быстрее, чем со скоростью света. Таким образом, встала задача заменить ньютоновский закон гравитации на другой, совместимый с принципом относительности, но дающий при малых скоростях и гравитационных полях почти ньютоновские эффекты. Такие попытки были сделаны Г. Пуанкаре (1905 и 1906), Г. Минковским (1908) и А. Зоммерфельдом (1910)^[9]. Однако все рассмотренные модели давали слишком малую величину сдвига перигелия^[10]. В 1907 году Эйнштейн пришёл к выводу, что для описания гравитационного поля необходимо обобщить тогдашнюю теорию относительности, сейчас называемую специальной. От 1907 по 1915 год Эйнштейн последовательно шёл к новой теории, используя в качестве путеводного свой принцип относительности.

Эйнштейн (1912), Эйнштейн и Гроссман (1913)[править | править код]

Публикация Эйнштейна 1912 года (в двух частях) важна лишь в историческом плане. К тому времени он знал о гравитационном красном смещении и об отклонении света. Эйнштейн понимал, что преобразования Лоренца в общем случае неверны в присутствии гравитационного поля, но применил их как эвристический приём. Данная теория утверждала, что скорость света является постоянной величиной в свободном от материи пространстве, но изменяется в присутствии материальных тел, создавая этим гравитационный эффект. Теория ограничивалась стационарными гравитационными полями и включала в себя принцип наименьшего действия:

δ∫ds=0,ds2=ημνdxμdxν,ημν=diag{−c2(xi),1,1,1}.{\displaystyle \delta \int ds=0\,,\qquad ds^{2}=\eta _{\mu \nu }dx^{\mu }dx^{\nu }\,,\quad \eta _{\mu \nu }=diag\{-c^{2}(x^{i}),1,1,1\}.}

Затем Эйнштейн и Гроссман (1913) уже использовали псевдориманову геометрию и тензорный анализ:

δ∫ds=0,ds2=gμνdxμdxν.{\displaystyle \delta \int ds=0\,,\qquad ds^{2}=g_{\mu \nu }dx^{\mu }dx^{\nu }\,.}

В их работе уравнения электродинамики уже точно совпадали с уравнениями в ОТО. Кроме того, использовалось дополнительное уравнение (не всегда верное в ОТО)

Tμν=κρdxμdsdxνds,{\displaystyle T^{\mu \nu }=\kappa \rho {dx^{\mu } \over ds}{dx^{\nu } \over ds}\,,}

выражающее тензор энергии-импульса как функцию плотности материи.

Две теории Нордстрёма (1912), (1913)[править | править код]

Первый подход Нордстрёма (1912) состоял в попытке сохранить метрику Минковского и постоянство скорости света c{\displaystyle c} путём введения зависимости массы от потенциала гравитационного поля φ.{\displaystyle \varphi \,.} Предположив, что φ{\displaystyle \varphi } удовлетворяет уравнению

◻φ=ρ,{\displaystyle \Box \varphi =\rho \,,}

где ρ{\displaystyle \rho } представляет собой плотность энергии массы покоя, а ◻{\displaystyle \Box } — даламбертиан, и введя зависимость

m=m0exp⁡(ϕ/c2),{\displaystyle m=m_{0}\exp(\phi /c^{2})\,,}

Нордстрём предложил следующее уравнение

−∂φ∂xμ=u˙μ+uμc2φ˙,{\displaystyle -{\partial \varphi \over \partial x^{\mu }}={\dot {u}}_{\mu }+{u_{\mu } \over c^{2}{\dot {\varphi }}}\,,}

где

Земная гравитация: значение гравитационного поля

Солнечная система > Система Земля-Луна > Планета Земля > Земная гравитация

Модель Geoid 2011

Земля и гравитация – описание гравитационного поля третьей планеты Солнечной системы. Узнайте значение гравитации для Земли и влияние на жизнь планеты с фото.

Среди фундаментальных сил выделяют гравитацию. Если бы не сила в 9.8 м/с², то бы мы давно все отправились в пространство. К тому же, наши кости быстро постарели, мышцы атрофировались, а органы лишились нормальной функциональности. Насколько же сильная гравитация Земли?

Определение земной гравитации

Гравитация – естественная сила, которая заставляет массивные вещи притягиваться, вроде астероидов, планет, скоплений и т.д. Чем больше масса, тем выше гравитационный показатель. Также он зависит от удаленности (уменьшается с отдалением). Можете посмотреть как выглядит сила гравитации Земли на рисунке.

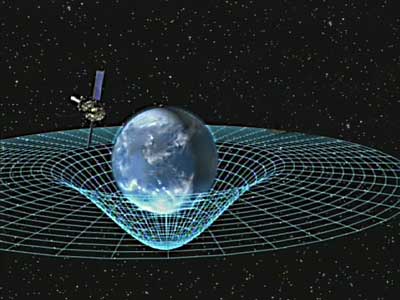
Художественная интерпретация воздействия земной гравитации на пространство-время

Среди четырех фундаментальных сил гравитация выступает самой слабой. Поэтому ей отведена роль воздействия на наименьшие частички – субатомные. А вот в более крупных масштабах она влияет на взаимодействие материи и эволюционный процесс раннего пространства.

Именно гравитация несет ответственность за скопление материи и формирование газового облака, из которого появились первые звезды. Далее она притягивала осколки, создавая планеты и спутники.

Универсальная гравитация Земли и относительность

Энергия и масса соотносятся, поэтому все формы энергии также располагают гравитационной силой. Это отметилось и в общей теории относительности, которая лучше всего характеризует гравитацию. Это не сила, а следствие искривленности пространства и времени, созданное неравномерным распределением массы/энергии.

Художественная интерпретация эффекта перетаскивания, где пространство и время тянутся вокруг массивного объекта

Наиболее экстремальный пример искривленности представлен черной дырой. Это последствие падения сверхмассивной звезды, с которой ничего не может выбраться.

Многие гравитационные моменты также объясняются законом универсальной гравитации Ньютона: существует как притяжение между телами. Силу можно определить математически.

Земная гравитация

В нашем случае она формируется из массы и плотности – 5.9237 х 10²⁴ кг и 5.514 г/см³. Получается, что гравитация Земли равна 9.8 м/с². Однако эта отметка способна меняться в зависимости от вашего расположения на поверхности. На экваториальной линии – 9.789 м/с², а на полюсах – 9.832 м/с².

Международная космическая станция на земной орбите

Также гравитация меняется, основываясь составе небесного тела. Более высокие концентрации материала способны изменить силу. Но эта сумма слишком крошечная, чтобы ее отметить. Вы могли знать, что гравитация иная на большой высоте. Если вы окажитесь на вершине Эвереста, то там сила на 0.28% меньше. На МКС – 90% поверхностной. Но станция пребывает в эффекте свободного падения, поэтому все внутри падает, и вы не ощущаете силы.

Именно гравитация ответственна за то, что скорость побега составляет 11.186 км/ч. Из-за разности в гравитационных показателях с другими объектами приходится готовить астронавтов к сложным условиям и создавать специальные тренажеры и защиту.

Длительное пребывание в микрогравитации негативно сказывается на организме, но НАСА стараются исправить это положение, чтобы без проблем построить марсианские и лунные колонии.

Мы должны быть благодарны за гравитацию Земли, но это и наша ноша, усложняющая процесс освоения чужих миров. Мы прикованы к дому и чувствуем себя здесь прекрасно, но вынуждены ограничивать себя лишь этим шаром.

Читайте также:

---

Строение Земли

Поверхность Земли

Положение и движение Земли

Гравитационный потенциал — Википедия

У этого термина существуют и другие значения, см. Потенциал.

Гравитацио́нный потенциа́л — скалярная функция координат и времени, достаточная для полного описания гравитационного поля в классической механике. Имеет размерность квадрата скорости, обычно обозначается буквой φ{\displaystyle \varphi }. Гравитационный потенциал в точке пространства, задаваемой радиус-вектором r→{\displaystyle {\vec {r}}}, равен отношению потенциальной энергии U(r→){\displaystyle U({\vec {r}})} небольшого тела, помещённого в эту точку, к массе тела m{\displaystyle m}. Как и потенциальная энергия, гравитационный потенциал всегда определяется с точностью до постоянного слагаемого, обычно подбираемого таким образом, чтобы потенциал на бесконечности оказался нулевым.

Впервые понятие гравитационного потенциала ввёл в науку Адриен Мари Лежандр в конце XVIII века.

В современных теориях гравитации роль гравитационного потенциала обычно играют тензорные поля. Так, в стандартной в настоящее время теории гравитации — общей теории относительности — роль гравитационного потенциала играет метрический тензор.

Гравитационный потенциал и уравнения движения[править | править код]

Движение частицы в гравитационном поле в классической механике определяется функцией Лагранжа, имеющей в инерциальной системе отсчета вид:

L=mq˙22−mφ,{\displaystyle L={\frac {m{\dot {q}}^{2}}{2}}-m\varphi ,}

где: m{\displaystyle m} — масса частицы, q{\displaystyle q} — обобщённая координата частицы, φ{\displaystyle \varphi } — потенциал гравитационного поля.

Подставляя выражение для лагранжиана L{\displaystyle L} в уравнения Лагранжа:

ddt∂L∂q˙−∂L∂q=0,{\displaystyle {\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {q}}}}-{\frac {\partial L}{\partial q}}=0,}

получаем уравнения движения

q¨=−grad⁡φ.{\displaystyle {\ddot {q}}=-\operatorname {grad} \varphi .}

Уравнения движения частицы в гравитационном поле в классической механике не содержат массы m{\displaystyle m} или другой величины, характеризующей частицу. Этот факт является отражением принципа эквивалентности сил гравитации и инерции.

Гравитационный потенциал точечной массы и произвольного тела[править | править код]

Гравитационный потенциал, создаваемый точечной массой M{\displaystyle M}, расположенной в начале координат, равен

φ(r→)=−GMr+C,{\displaystyle \varphi ({\vec {r}})=-{\frac {GM}{r}}+C,}

где G{\displaystyle G} — гравитационная постоянная, r{\displaystyle r} — расстояние от начала координат (модуль радиус-вектора r→{\displaystyle {\vec {r}}}). Через C{\displaystyle C} обозначена произвольная константа, опускаемая при выборе φ=0{\displaystyle \varphi =0} на бесконечности.

Эта же формула справедлива для гравитационного потенциала вне любого тела со сферически-симметричным распределением массы. Примером может быть однородный шар или тонкая сфера. (Примечание: внутри сферы потенциал равен потенциалу сферы −GM/a{\displaystyle -GM/a}, где a{\displaystyle a} — радиус сферы).

В общем случае, гравитационный потенциал, создаваемый произвольным распределением массы (плотность ρ{\displaystyle \rho } зависит от координат произвольным образом), удовлетворяет уравнению Пуассона

Δφ(r→)=4πGρ(r→),{\displaystyle \Delta \varphi ({\vec {r}})=4\pi G\rho ({\vec {r}}),}

где Δ{\displaystyle \Delta } — оператор Лапласа. Решение такого уравнения имеет вид

φ(r→)=−G∫V′ρ(r→′)dV′|r→−r→′|+C.{\displaystyle \varphi ({\vec {r}})=-G\int _{V^{\prime }}{\frac {\rho ({\vec {r}}^{\prime })dV^{\prime }}{|{\vec {r}}-{\vec {r}}^{\prime }|}}+C.}

Здесь r→{\displaystyle {\vec {r}}} — радиус-вектор точки, в которой ищется потенциал, а r→′{\displaystyle {\vec {r}}^{\prime }} — радиус-вектор бесконечно малого элемента объёма dV′{\displaystyle dV^{\prime }} с плотностью вещества ρ(r→′){\displaystyle \rho ({\vec {r}}^{\prime })}; интегрирование выполняется по всему объёму тел, создающих поле.

Гравитационный потенциал и гравитационная энергия[править | править код]

Потенциальная энергия частицы, находящейся в гравитационном поле в точке r→{\displaystyle {\vec {r}}}, равна потенциалу поля в этой точке, умноженному на массу частицы m{\displaystyle m}:

U(r→)=mφ(r→).{\displaystyle U({\vec {r}})=m\varphi ({\vec {r}}).}

Под гравитационной энергией системы тел (дискретных частиц) понимается потенциальная энергия, обусловленная взаимным гравитационным тяготением этих частиц. Она равна половине суммы потенциальных энергий отдельных частиц; деление на два позволяет избежать двукратного учёта одних и тех же взаимодействий. Например, для пары материальных точек на расстоянии l{\displaystyle l} друг от друга

Ug=12[U1+U2]=12[−Gm1m2l−Gm2m1l]=−Gm1m2l;{\displaystyle U_{g}={\frac {1}{2}}\left[U_{1}+U_{2}\right]={\frac {1}{2}}\left[-G{\frac {m_{1}m_{2}}{l}}-G{\frac {m_{2}m_{1}}{l}}\right]=-G{\frac {m_{1}m_{2}}{l}};}

здесь U1{\displaystyle U_{1}} — потенциальная энергия первой точки в поле второй, а U2{\displaystyle U_{2}} — второй в поле первой.

Аналогично, для гравитационной энергии непрерывного распределения масс справедливо выражение:

Ug=12∫Vρ(r→)φ(r→)dV,{\displaystyle U_{g}={\frac {1}{2}}\int _{V}\rho ({\vec {r}})\varphi ({\vec {r}})dV,}

где ρ{\displaystyle \rho } — плотность массы, φ{\displaystyle \varphi } — гравитационный потенциал, вычисляемый по формулам из предыдущего раздела, V{\displaystyle V} — объём тела. Так, гравитационная энергия шара массой m{\displaystyle m} и радиуса a{\displaystyle a}, с равномерным распределением плотности, составляет Ug=−3Gm2/5a{\displaystyle U_{g}=-3Gm^{2}/5a}.

Разложения гравитационного потенциала в ряд[править | править код]

В целях вычисления гравитационного потенциала произвольной системы масс на больших расстояниях от неё можно произвести разложение:

φ=−G(MR0+16Dαβ∂2∂Xα∂Xβ1R0+…),{\displaystyle \varphi =-G\left({\frac {M}{R_{0}}}+{\frac {1}{6}}D_{\alpha \beta }{\frac {\partial ^{2}}{\partial {X_{\alpha }}\partial {X_{\beta }}}}{\frac {1}{R_{0}}}+…\right),}

где M=∫ρdV{\displaystyle M=\int \rho dV} — полная масса системы, а величины:

Dαβ=∫ρ(3xαxβ−r2δαβ)dV{\displaystyle D_{\alpha \beta }=\int \rho (3x_{\alpha }x_{\beta }-r^{2}\delta _{\alpha \beta })dV}

формируют тензор квадрупольного момента масс. Он связан с обычным тензором моментов инерции

Jαβ=∫ρ(r2δαβ−xαxβ)dV{\displaystyle J_{\alpha \beta }=\int \rho (r^{2}\delta _{\alpha \beta }-x_{\alpha }x_{\beta })dV}

очевидными соотношениями

Dαβ=Jγγδαβ−3Jαβ.{\displaystyle D_{\alpha \beta }=J_{\gamma \gamma }\delta _{\alpha \beta }-3J_{\alpha \beta }.}

Возможно также разложение по сферическим функциям, применяющееся, в частности, при анализе гравитационных полей космических тел:

φ=−GMr(1−∑n=2∞Jn(Rr)nPn(sin⁡θ)+∑n=2∞∑k=2n(Rr)n(Cnkcos⁡(kλ)+Snksin⁡(kλ))Pnk(sin⁡θ)).{\displaystyle \varphi =-{\frac {GM}{r}}\left(1-\sum _{n=2}^{\infty }J_{n}\left({\frac {R}{r}}\right)^{n}P_{n}(\sin \theta )+\sum _{n=2}^{\infty }\sum _{k=2}^{n}\left({\frac {R}{r}}\right)^{n}(C_{nk}\cos(k\lambda )+S_{nk}\sin(k\lambda ))P_{n}^{k}(\sin \theta )\right).}

Здесь r,θ,λ{\displaystyle r,\theta ,\lambda } — сферические координаты точки наблюдения, Pn{\displaystyle P_{n}} — полином Лежандра n-го порядка, Pnk{\displaystyle P_{n}^{k}} — присоединённые полиномы Лежандра, Jn,Cnk,Snk{\displaystyle J_{n},C_{nk},S_{nk}} — гравитационные моменты^[1].

Гравитационный потенциал и общая теория относительности[править | править код]

Основной источник: ^[2]

В общей теории относительности уравнения движения материальной точки в гравитационном поле имеют вид:

d2xids2+Γrsidxrdsdxsds=0,{\displaystyle {\frac {d^{2}x^{i}}{ds^{2}}}+\Gamma _{rs}^{i}{\frac {dx^{r}}{ds}}{\frac {dx^{s}}{ds}}=0,}

где Γrsi=gik2(dgkrdxs+dgksdxr−dgrsdxk){\displaystyle \Gamma _{rs}^{i}={\frac {g^{ik}}{2}}\left({\frac {dg_{kr}}{dx^{s}}}+{\frac {dg_{ks}}{dx^{r}}}-{\frac {dg_{rs}}{dx^{k}}}\right)} — символы Кристоффеля. Здесь gik{\displaystyle g_{ik}} — метрический тензор, характеризующий гравитационное поле в общей теории относительности.

Из сравнения этих уравнений движения с уравнениями движения ньютоновской механики d2xidt2=−dφdxi{\displaystyle {\frac {d^{2}x^{i}}{dt^{2}}}=-{\frac {d\varphi }{dx^{i}}}} видно, что в общей теории относительности роль гравитационного потенциала φ{\displaystyle \varphi } играет метрический тензор.

В случае скоростей, малых по сравнению со скоростью света, и слабых постоянных гравитационных полей уравнения движения принимают вид

d2xidt2=−c2Γ44i{\displaystyle {\frac {d^{2}x^{i}}{dt^{2}}}=-c^{2}\Gamma _{44}^{i}}

для пространственных координат i=1,2,3{\displaystyle i=1,2,3} и x4=ct{\displaystyle x^{4}=ct} для временной координаты. Пренебрегая производными по времени, вместо Γ44i{\displaystyle \Gamma _{44}^{i}} можно подставить −12dg44dxi{\displaystyle -{\frac {1}{2}}{\frac {dg_{44}}{dx^{i}}}} и таким образом получить ньютоновские уравнения движения

d2xidt2=−dφdxi.{\displaystyle {\frac {d^{2}x^{i}}{dt^{2}}}=-{\frac {d\varphi }{dx^{i}}}.}

Здесь гравитационный потенциал φ{\displaystyle \varphi } и компонента метрического тензора g44{\displaystyle g_{44}} связаны соотношениями

φ=−12c2(g44+1){\displaystyle \varphi =-{\frac {1}{2}}c^{2}(g_{44}+1)}, g44=−(1+2φc2).{\displaystyle g_{44}=-\left(1+{\frac {2\varphi }{c^{2}}}\right).}

В силу того, что элемент мировой линии покоящихся часов равен ds2=g44(dx4)2{\displaystyle ds^{2}=g_{44}(dx^{4})^{2}}, а время t=x4c{\displaystyle t={\frac {x^{4}}{c}}}, замедление хода часов в гравитационном поле будет

tg=t−g44=t1+2φc2≈t(1−φc2).{\displaystyle t_{g}={\frac {t}{\sqrt {-g_{44}}}}={\frac {t}{\sqrt {1+{\frac {2\varphi }{c^{2}}}}}}\approx t\left(1-{\frac {\varphi }{c^{2}}}\right).}

Относительное замедление хода времени в точке с меньшим значением гравитационного потенциала по сравнению с временем в точке с большим значением гравитационного потенциала равно разности гравитационных потенциалов в этих точках, делённой на квадрат скорости света.

• Ландау Л. Д., Лифшиц Е. М. Теоретическая физика, учебное пособие для вузов, в 10 т. / т. 1, «Механика», 5-е изд., стереотип., М.: Физматлит.— 2002.— 224 с., ISBN 5-9221-0055-6 (т. 1), гл. 1 «Уравнения движения», п. 2 «Принцип наименьшего действия», с. 10—14;
• Ландау Л. Д., Лифшиц Е. М. Теоретическая физика, учебное пособие для вузов, в 10 т. / т. 2, «Теория поля», 8-е изд., стереотип., М.: Физматлит.— 2001.— 536 с., ISBN 5-9221-0056-4 (т. 2), гл. 10 «Частица в гравитационном поле», п. 81 «Гравитационное поле в нерелятивистской механике», с. 304—306; гл. 12 «Поле тяготеющих тел», п. 99 «Закон Ньютона», с. 397—401;
• Вейнберг С. Гравитация и космология. Принципы и приложения общей теории относительности, пер. с англ. В. М. Дубовика и Э. А. Тагирова, под ред. Я. А. Смородинского, «Платон», 2000, ISBN 5-80100-306-1, ч. 2 «Общая теория относительности», гл. 3 «Принцип эквивалентности», п. 4 «Ньютоновское приближение», с. 92-93;
• Холшевников К. В., Никифоров И. И. Свойства гравитационного потенциала в примерах и задачах: Учебное пособие. — С-Пб., 2008.— 72 с., ББК 22.6.
• Жарков В. Н. Внутреннее строение Земли и планет. — М.: Наука, 1978. — 192 с.