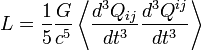Гравитационное поле — это… Что такое Гравитационное поле?

Гравитацио́нное по́ле, или по́ле тяготе́ния — физическое поле, через которое осуществляется гравитационное взаимодействие^[1].

Гравитационное поле в классической физике

Закон тяготения Ньютона

В рамках классической физики гравитационное взаимодействие описывается «законом всемирного тяготения» Ньютона, согласно которому сила гравитационного притяжения между двумя материальными точками с массами и пропорциональна обеим массам и обратно пропорциональна квадрату расстояния между ними:

Здесь  — гравитационная постоянная, приблизительно равная м³/(кг с²), — расстояние между точками.

Для расчёта поля в более сложных случаях, когда тяготеющие массы нельзя считать материальными точками, можно воспользоваться тем фактом, что поле ньютоновского тяготения потенциально. Если обозначить плотность вещества ρ, то потенциал поля φ удовлетворяет уравнению Пуассона:

Недостатки ньютоновской модели тяготения

Практика показала, что классический закон всемирного тяготения позволяет с огромной точностью объяснить и предсказать движения небесных тел. Однако ньютоновская теория содержала ряд серьёзных недостатков. Главный из них — необъяснимое дальнодействие: сила притяжения передавалась неизвестно как через совершенно пустое пространство, причём бесконечно быстро. По существу ньютоновская модель была чисто математической, без какого-либо физического содержания. Кроме того, если Вселенная, как тогда предполагали, евклидова и бесконечна, и при этом средняя плотность вещества в ней ненулевая, то возникает гравитационный парадокс: потенциал поля всюду обращается в бесконечность. В конце XIX века обнаружилась ещё одна проблема: заметное расхождение теоретического и наблюдаемого смещения перигелия Меркурия.

На протяжении более двухсот лет после Ньютона физики предлагали различные пути усовершенствования ньютоновской теории тяготения. Эти усилия увенчались успехом в 1915 году, с созданием общей теории относительности Эйнштейна, в которой все указанные трудности были преодолены. Теория Ньютона оказалась приближением более общей теории, применимым при выполнении двух условий:

1. Гравитационный потенциал в исследуемой системе не слишком велик (много меньше ).
2. Скорости движения в этой системе незначительны по сравнению со скоростью света.

Гравитационное поле в общей теории относительности

В общей теории относительности (ОТО) гравитационное поле является не отдельным физическим понятием, а свойством пространства-времени, появляющимся в присутствии материи. Этим свойством является неевклидовость метрики (геометрии) пространства-времени, и материальным носителем тяготения является пространство-время. Тот факт, что гравитацию можно рассматривать как проявление свойств геометрии четырёхмерного неевклидова пространства, без привлечения дополнительных понятий, есть следствие того, что все тела в поле тяготения получают одинаковое ускорение («принцип эквивалентности» Эйнштейна). Пространство-время при таком подходе приобретает физические атрибуты, которые влияют на физические объекты и сами зависят от них.

Пространство-время ОТО представляет собой псевдориманово многообразие с переменной метрикой. Причиной искривления пространства-времени является присутствие материи, и чем больше её энергия, тем искривление сильнее. Для определения метрики пространства-времени при известном распределении материи надо решить уравнения Эйнштейна. Ньютоновская же теория тяготения представляет собой приближение ОТО, которое получается, если учитывать только «искривление времени», то есть изменение временно́й компоненты метрики, ^[2] (пространство в этом приближении евклидово). Распространение возмущений гравитации, то есть изменений метрики при движении тяготеющих масс, происходит с конечной скоростью, и дальнодействие в ОТО отсутствует.

Другие существенные отличия гравитационного поля ОТО от ньютоновского: возможность нетривиальной топологии пространства, особых точек, гравитационные волны.

Примечания

Литература

• Дубошин Г. Н. Небесная механика. Основные задачи и методы / Глав. ред. физ.-мат. лит. — М.: Наука, 1968. — 800 с.
• Иваненко Д. Д., Сарданашвили Г. А. Гравитация. — 3-е изд. — М.: УРСС, 2008. — 200 с.
• Мизнер Ч., Торн К., Уилер Дж. Гравитация. — М.: Мир, 1977.

Гравитационное поле Земли — это… Что такое Гравитационное поле Земли?

Гравита́ция (всеми́рное тяготе́ние, тяготе́ние) (от лат. gravitas — «тяжесть») — дальнодействующее фундаментальное взаимодействие в природе, которому подвержены все материальные тела. По современным данным, является универсальным взаимодействием в том смысле, что, в отличие от любых других сил, всем без исключения телам независимо от их массы придаёт одинаковое ускорение. Главным образом гравитация играет определяющую роль в космических масштабах. Термин

гравитация используется также как название раздела физики, изучающего гравитационное взаимодействие. Наиболее успешной современной физической теорией в классической физике, описывающей гравитацию, является общая теория относительности, квантовая теория гравитационного взаимодействия пока не построена.

Гравитационное взаимодействие

Гравитационное взаимодействие — одно из четырёх фундаментальных взаимодействий в нашем мире. В рамках классической механики, гравитационное взаимодействие описывается

законом всемирного тяготения Ньютона, который гласит, что сила гравитационного притяжения между двумя материальными точками массы m₁ и m₂, разделёнными расстоянием R, пропорциональна обеим массам и обратно пропорциональна квадрату расстояния — то есть

.

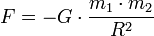Здесь G — гравитационная постоянная, равная примерно 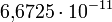м³/(кг•с²). Знак минус означает, что сила, действующая на тело, всегда равна по направлению радиус-вектору, направленному на тело, то есть гравитационное взаимодействие приводит всегда к притяжению любых тел.

Закон всемирного тяготения — одно из приложений закона обратных квадратов, встречающегося так же и при изучении излучений (см. например, Давление света), и являющимся прямым следствием квадратичного увеличения площади сферы при увеличении радиуса, что приводит к квадратичному же уменьшению вклада любой единичной площади в площадь всей сферы.

Поле тяжести потенциально. Это значит, что можно ввести потенциальную энергию гравитационного притяжения пары тел, и эта энергия не изменится после перемещения тел по замкнутому контуру. Потенциальность поля тяжести влечёт за собой закон сохранения суммы кинетической и потенциальной энергии и при изучении движения тел в поле тяжести часто существенно упрощает решение. В рамках ньютоновской механики гравитационное взаимодействие является дальнодействующим. Это означает, что как бы массивное тело ни двигалось, в любой точке пространства гравитационный потенциал зависит только от положения тела в данный момент времени.

Большие космические объекты — планеты, звезды и галактики имеют огромную массу и, следовательно, создают значительные гравитационные поля.

Гравитация — слабейшее взаимодействие. Однако, поскольку оно действует на любых расстояниях и все массы положительны, это тем не менее очень важная сила во Вселенной. Для сравнения: полный электрический заряд этих тел ноль, так как вещество в целом электрически нейтрально.

Также гравитация, в отличие от других взаимодействий, универсальна в действии на всю материю и энергию. Не обнаружены объекты, у которых вообще отсутствовало бы гравитационное взаимодействие.

Из-за глобального характера гравитация ответственна и за такие крупномасштабные эффекты, как структура галактик, черные дыры и расширение Вселенной, и за элементарные астрономические явления — орбиты планет, и за простое притяжение к поверхности Земли и падения тел.

Гравитация была первым взаимодействием, описанным математической теорией. В античные времена Аристотель считал, что объекты с разной массой падают с разной скоростью. Только много позже Галилео Галилей экспериментально определил, что это не так — если сопротивление воздуха устраняется, все тела ускоряются одинаково. Закон всеобщего тяготения Исаака Ньютона (1687) хорошо описывал общее поведение гравитации. В 1915 году Альберт Эйнштейн создал Общую теорию относительности, более точно описывающую гравитацию в терминах геометрии пространства-времени.

Небесная механика и некоторые её задачи

Раздел механики, изучающий движение тел в пустом пространстве только под действием гравитации называется небесной механикой.

Наиболее простой задачей небесной механики является гравитационное взаимодействие двух тел в пустом пространстве. Эта задача решается аналитически до конца; результат её решения часто формулируют в виде трёх законов Кеплера.

При увеличении количества взаимодействующих тел задача резко усложняется. Так, уже знаменитая задача трёх тел (то есть движение трёх тел с ненулевыми массами) не может быть решена аналитически в общем виде. При численном же решении, достаточно быстро наступает неустойчивость решений относительно начальных условий. В применении к Солнечной системе, эта неустойчивость не позволяет предсказать движение планет на масштабах, превышающих сотню миллионов лет.

В некоторых частных случаях удаётся найти приближённое решение. Наиболее важным является случай, когда масса одного тела существенно больше массы других тел (примеры: солнечная система и динамика колец Сатурна). В этом случае в первом приближении можно считать, что лёгкие тела не взаимодействуют друг с другом и движутся по кеплеровым траекториям вокруг массивного тела. Взаимодействия же между ними можно учитывать в рамках теории возмущений, и усреднять по времени. При этом могут возникать нетривиальные явления, такие как резонансы, аттракторы, хаотичность и т. д. Наглядный пример таких явлений — нетривиальная структура колец Сатурна.

Несмотря на попытки описать поведение системы из большого числа притягивающихся тел примерно одинаковой массы, сделать этого не удаётся из-за явления динамического хаоса.

Сильные гравитационные поля

В сильных гравитационных полях, при движении с релятивистскими скоростями, начинают проявляться эффекты общей теории относительности:

Гравитационное излучение

Одним из важных предсказаний ОТО является гравитационное излучение, наличие которого до сих пор не подтверждено прямыми наблюдениями. Однако, имеются косвенные наблюдательные свидетельства в пользу его существования, а именно: потери энергии в двойной системе с пульсаром PSR B1913+16 — пульсаром Халса-Тейлора — хорошо согласуются с моделью, в которой эта энергия уносится гравитационным излучением.

Гравитационное излучение могут генерировать только системы с переменным квадрупольным или более высокими мультипольными моментами, этот факт говорит о том, что гравитационное излучение большинства природных источников направленное, что существенно усложняет его обнаружение. Мощность гравитационного l-польного источника пропорциональна (v / c)^{2l + 2}, если мультиполь имеет электрический тип, и (v / c)^{2l + 4} — если мультиполь магнитного типа ^[1], где v — характерная скорость движения источников в излучающей системе, а c — скорость света. Таким образом, доминирующим моментом будет квадрупольный момент электрического типа, а мощность соответствующего излучения равна:

где Q_ij — тензор квадрупольного момента распределения масс излучающей системы. Константа 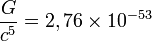 (1/Вт) позволяет оценить порядок величины мощности излучения.

Начиная с 1969 года (эксперименты Вебера (англ.)) и до настоящего времени (февраль 2007) предпринимаются попытки прямого обнаружения гравитационного излучения. В США, Европе и Японии в настоящий момент существует несколько действующих наземных детекторов (GEO 600), а также проект космического гравитационного детектора [2] республики Татарстан.

Тонкие эффекты гравитации

Помимо классических эффектов гравитационного притяжения и замедления времени, общая теория относительности предсказывает существование других проявлений гравитации, которые в земных условиях весьма слабы и их обнаружение и экспериментальная проверка поэтому весьма затруднительны. До последнего времени преодоление этих трудностей представлялось за пределами возможностей экспериментаторов.

Среди них, в частности, можно назвать увлечение инерциальных систем отсчета (или эффект Лензе-Тирринга) и гравитомагнитное поле. В 2005 году автоматический аппарат НАСА Gravity Probe B провёл беспрецедентный по точности эксперимент по измерению этих эффектов вблизи Земли, но его полные результаты пока не опубликованы.

Квантовая теория гравитации

Несмотря на более чем полувековую историю попыток, гравитация — единственное из фундаментальных взаимодействий, для которого пока ещё не построена непротиворечивая перенормируемая квантовая теория. Впрочем, при низких энергиях, в духе квантовой теории поля, гравитационное взаимодействие можно представить как обмен гравитонами — калибровочными бозонами со спином 2.

Стандартные теории гравитации

Подробней см. статью Теории гравитации

В связи с тем, что квантовые эффекты гравитации чрезвычайно малы даже в самых экстремальных экспериментальных и наблюдательных условиях, до сих пор не существует их надёжных наблюдений. Теоретические оценки показывают, что в подавляющем большинстве случаев можно ограничиться классическим описанием гравитационного взаимодействия.

Существует современная каноническая^[3] классическая теория гравитации — общая теория относительности, и множество уточняющих её гипотез и теорий различной степени разработанности, конкурирующих между собой (см. статью Альтернативные теории гравитации). Все эти теории дают очень похожие предсказания в рамках того приближения, в котором в настоящее время осуществляются экспериментальные тесты. Далее описаны несколько основных, наиболее хорошо разработанных или известных теорий гравитации.

Общая теория относительности

В стандартном подходе общей теории относительности (ОТО) гравитация рассматривается изначально не как силовое взаимодействие, а как проявление искривления пространства-времени. Таким образом, в ОТО гравитация интерпретируется как геометрический эффект, причём пространство-время рассматривается в рамках неевклидовой римановой (точнее псевдо-римановой) геометрии. Гравитационное поле (обобщение ньютоновского гравитационного потенциала) иногда называемое также полем тяготения, в ОТО отождествляется с тензорным метрическим полем или метрикой четырехмерного пространства-времени, а напряженность гравитационного поля — с аффинной связностью пространства-времени, определяемой метрикой. Стандартной задачей ОТО является определение компонент метрического тензора, в совокупности задающих метрику пространства-времени, по известному распределению источников энергии-импульса в рассматриваемой системе четырехмерных координат. В свою очередь знание метрики позволяет рассчитывать движение пробных частиц, что эквивалентно знанию свойств поля тяготения в данной системе. В связи с тензорным характером уравнений ОТО, а также со стандартным фундаментальным обоснованием ее формулировки, считается, что гравитация также носит тензорный характер. Одним из следствий является то, что гравитационное излучение должно быть не ниже квадрупольного порядка. Известно, что в ОТО имеются затруднения с объяснением факта неинвариантности энергии гравитационного поля, поскольку данная энергия не описывается тензором. В классической ОТО также возникает проблема описания спин-орбитального взаимодействия. Считается, что существуют определенные проблемы с однозначностью результатов и обоснованием непротиворечивости. Однако экспериментально ОТО считается подтверждающейся до самого последнего времени. Кроме того, многие альтернативные эйнштейновскому, но стандартные для современной физики, подходы к формулировке теории гравитации приводят к результату, совпадающему с ОТО в низкоэнергетическом приближении, которое в основном и доступно экспериментальной проверке.

Теория Эйнштейна-Картана

Теория Эйнштейна-Картана (ЭК) была разработана как расширение ОТО, внутренне включающее в себя описание воздействия на пространство-время кроме энергии-импульса также и спина объектов.^[4] В теории ЭК вводится аффинное кручение, а вместо псевдоримановой геометрии для пространства-времени используется геометрия Римана-Картана. В результате от метрической теории переходят к аффинной теории пространства-времени. Результирующие уравнения для описания пространства-времени распадаются на два класса. Один из них аналогичен ОТО, с тем отличием, что в тензор кривизны включены компоненты с аффинным кручением. Второй класс уравнений задаёт связь тензора кручения и тензора спина материи и излучения. Получаемые поправки к ОТО настолько малы, что пока не видно даже гипотетических путей для их измерения.

Релятивистская теория гравитации

Релятивистская теория гравитации (РТГ) разрабатывается академиком Логуновым А. А. с группой сотрудников. ^[5] В ряде работ они утверждают, что РТГ имеет следующие отличия от ОТО^[6] :

• Гравитация есть не геометрическое поле, а реальное физическое силовое поле, описываемое тензором.

• Гравитационные явления следует рассматривать в рамках плоского пространства Минковского, в котором однозначно выполняются законы сохранения энергии-импульса и момента количества движения. Тогда движение тел в пространстве Минковского эквивалентно движению этих тел в эффективном римановом пространстве.

• В тензорных уравнениях для определения метрики следует учитывать массу гравитона, а также использовать калибровочные условия, связанные с метрикой пространства Минковского. Это не позволяет уничтожить гравитационное поле даже локально выбором какой-то подходящей системы отсчёта.

Как и в ОТО, в РТГ под веществом понимаются все формы материи (включая и электромагнитное поле), за исключением самого гравитационного поля. Следствия из теории РТГ таковы: чёрных дыр как физических объектов, предсказываемых в ОТО, не существует; Вселенная плоская, однородная, изотропная, неподвижная и евклидовая.

C другой стороны, существуют не менее убедительные аргументы противников РТГ, сводящиеся к следующим положениям:

• РТГ есть биметрическая теория, в случае безмассового гравитона эквивалентная так называемой полевой трактовке ОТО как надстройке над ненаблюдаемым пространством Минковского: «В релятивистской теории гравитации… фигурируют в точности те же лагранжианы…, которые приводят к уравнениям гравитационного поля»^[7], «математическое содержание РТГ сводится к математическому содержанию ОТО (в полевой формулировке)» ^[8]. Этот аргумент в таком изложении, правда, по-видимому не учитывает возможных топологических различий между обычной моделью ОТО и такой моделью, или же, по крайней мере, маскирует их.
• Случай массивного гравитона в РТГ не даёт правильного ньютоновского предела при переходе к массе равной 0, и, следовательно, бессмыслен.
• Дополнительные уравнения РТГ представляют собой всего лишь координатные условия: «Весь набор уравнений РТГ в терминах метрики искривленного пространства-времени можно свести к уравнениям Эйнштейна плюс гармоническое координатное условие, столь успешно использовавшееся Фоком» ^[8].
• Вышеприведённые следствия из РТГ являются лишь следствием неточностей: несуществование чёрных дыр — следствием невозможности покрыть одной координатной картой, эквивалентной пространству-времени Минковского, пространство-время сколлапсировавшего в чёрную дыру объекта; космологических предсказаний — следствием принятых координатных условий в сочетании с совершенно произвольным дополнительным допущением о вложенности световых конусов реального пространства в конусы пространства Минковского. (Как видим, этот аргумент явно противоречит первому, показывая расхождение РТГ и ОТО, которые вполне ощутимы; и, если оставить соображения, очевидно исходящие просто изнутри обычной логики ОТО, или суждения о произвольности постулатов, то решение о верности одного из этих подходов остается за экспериментом, если конечно не будет всё же доказана достаточно неочевидная их полная эквивалентность в области наблюдаемого).
(adsbygoogle = window.adsbygoogle || []).push({});

Теория Бранса — Дикке

В скалярно-тензорных теориях, самой известной из которых является теория Бранса — Дикке (или Йордана — Бранса — Дикке), гравитационное поле как эффективная метрика пространства-времени определяется воздействием не только тензора энергии-импульса материи, как в ОТО, но и дополнительного гравитационного скалярного поля. Источником скалярного поля считается свёрнутый тензор энергии-импульса материи. Следовательно, скалярно-тензорные теории, как ОТО и РТГ, относятся к метрическим теориям, дающим объяснение гравитации, используя только геометрию пространства-времени и его метрические свойства. Наличие скалярного поля приводит к двум тензорным уравнениям для метрики. Теория Бранса — Дикке вследствие наличия скалярного поля может рассматриваться также как действующая в пятимерном многообразии, состоящем из пространства-времени и скалярного поля.

[9]

Подобное имеет место и в РТГ, где второе тензорное уравнение вводится для учёта связи между неевклидовым пространством и пространством Минковского^[10]. Благодаря наличию безразмерного подгоночного параметра в теории Йордана — Бранса — Дикке, появляется возможность выбрать его так, чтобы результаты теории совпадали с результатами гравитационных экспериментов.

Теории гравитации

Источники и примечания

1. ↑ См. аналогии между слабым гравитационным полем и электромагнитным полем в статье гравитомагнетизм
2. ↑ http://dulkyn.org.ru/ru/about.html
3. ↑ Канонической эта теория является в том смысле, что она наиболее хорошо разработана и широко используется в современной небесной механике, астрофизике и космологии, причём количество надёжно установленных противоречащих ей экспериментальных результатов практически равно нулю.
4. ↑ Иваненко Д. Д., Пронин П. И., Сарданашвили Г. А., Калибровочная теория гравитации. — М., Изд. МГУ, 1985.
5. ↑ Логунов А. А., Мествиришвили М. А. Релятивистская теория гравитации. — М: Наука, 1989.
6. ↑ Логунов А. А., Мествиришвили М. А. Тензор энергии-импульса материи как источник гравитационного поля. — Теоретическая и математическая физика, 1997, Т. 110, Вып. 1, Стр. 5 — 24.
7. ↑ Зельдович Я. Б., Грищук Л. П. ТЯГОТЕНИЕ, ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ И АЛЬТЕРНАТИВНЫЕ ТЕОРИИ. УФН, 1986, Т. 149, № 4, с. 695—707. С. 704.
8. ↑ ^{1 2} Зельдович Я. Б., Грищук Л. П. Общая теория относительности верна! УФН, 1988, Т. 155, № 3, с. 517—527. С. 521, 524.
9. ↑ Brans, C. H.; Dicke, R. H. (November 1 1961). «Mach’s Principle and a Relativistic Theory of Gravitation». Physical Review 124 (3): 925—935. DOI:10.1103/PhysRev.124.925. Retrieved on 2006-09-23.
10. ↑ С ортодоксальной точки зрения это уравение представляет собой координатное условие, см. выше.

Литература

• Визгин В. П. Релятивистская теория тяготения (истоки и формирование, 1900—1915). М.: Наука, 1981. — 352c.
• Визгин В. П. Единые теории в 1-й трети ХХ в. М.: Наука, 1985. — 304c.
• Иваненко Д. Д., Сарданашвили Г. А. Гравитация, 3-е изд. М.:УРСС, 2008. — 200с.

См. также

Ссылки

Wikimedia Foundation. 2010.

Напряжённость гравитационного поля — Википедия

Материал из Википедии — свободной энциклопедии

Напряжённость гравитацио́нного по́ля — векторная величина, характеризующая гравитационное поле в данной точке и численно равная отношению силы тяготения F→{\displaystyle {\vec {F}}}, действующей на тело, помещённое в данную точку поля, к гравитационной массе этого тела mG{\displaystyle m_{G}}:

E→=F→mG.{\displaystyle {\vec {E}}={\frac {\vec {F}}{m_{G}}}.}

Если источником гравитационного поля является некое гравитирующее тело, то согласно закону всемирного тяготения:

E=GmGMGR2mG=GMGR2,{\displaystyle E={\frac {G{\frac {m_{G}M_{G}}{R^{2}}}}{m_{G}}}=G{\frac {M_{G}}{R^{2}}},}

где

• G{\displaystyle G} — гравитационная постоянная;
• MG{\displaystyle M_{G}} — гравитационная масса тела-источника поля;
• R{\displaystyle R} — расстояние от исследуемой точки пространства до центра масс тела-источника поля.

Применяя второй закон Ньютона и принцип эквивалентности гравитационной и инерционной масс:

{mI=mGF=mIgF=GmGMGR2E→=F→mG⇒{g=GMGR2E=GMGR2⇒E=g,{\displaystyle {\begin{cases}m_{I}=m_{G}\\F=m_{I}g\\F=G{\frac {m_{G}M_{G}}{R^{2}}}\\{\vec {E}}={\frac {\vec {F}}{m_{G}}}\end{cases}}\Rightarrow {\begin{cases}g=G{\frac {M_{G}}{R^{2}}}\\E=G{\frac {M_{G}}{R^{2}}}\end{cases}}\Rightarrow E=g,}

то есть напряжённость гравитационного поля численно (и по размерности) равна ускорению свободного падения в этом поле.

• Сивухин Д. В. Общий курс физики. — Изд. 4-е, стереотипное. — М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2004. — Т. I. Механика. — 576 с.

Материально ли гравитационное поле?

Материально ли гравитационное поле?     Вопрос о материальности гравитационного поля может показаться тривиальным. С философской точки зрения материальность эквивалентна объективной реальности. Но объективная реальность гравитационного поля подтверждается всей нашей повседневной жизнью. Благодаря гравитации мы удерживаемся на поверхности земли, строим здания. Состояние весомости обусловливает ритм работы нашего организма. Гравитация не только служит человеку, но и является фактором, с которым человек ведет постоянную «борьбу»: для преодоления сил тяготения человек создает подъемные краны, космические ракеты и т. д. То есть имеется нечто объективное, действующее на нас и предметы окружающего мира. Но сами по себе такого рода явления еще не доказывают реальности гравитации как физического ноля. Вопрос о природе гравитации, и в частности о ее объективности, можно рассматривать лишь в рамках определенной физической теории. Именно в теории упомянутые факты получают определенный смысл, доказательную силу. Повседневный опыт действительно является убедительным свидетельством объективности гравитации как физического поля, если, однако, мы будем рассматривать его в рамках физики Ньютона. С точки зрения этой физики гравитация является реальным силовым полем, которое подчиняется закону всемирного тяготения. Если на землю падает какой-либо предмет, то мы говорим, что на него действуют реальные силы тяготения. Реальность таких сил проявляется в реальности самого процесса падения. Однако ньютоновская теория оказалась неадекватной природе тяготения. Она не объясняла целый ряд эмпирических фактов, которые получили объяснение в общей теории относительности. Но теория относительности совершенно иначе трактует гравитацию и связанные с нею явления. Свободное падение тел под действием гравитационных сил представляется в ней как их равномерное движение в искривленном пространстве по геодезическим линиям. Гравитация утрачивает значение силового поля: она выступает как кривизна пространства, т. е. как геометрический феномен. И вот здесь сразу же обнаруживается нетривиальность вопроса об объективности гравитации. Для решения его ссылки на «очевидность фактов» недостаточно. В общей теории относительности гравитационное поле характеризуется функциями gik, которые отождествляются с потенциалами поля. Но эти же функции появляются и при описании эвклидова пространства, т. е. пространства, имеющего нулевую кривизну, и следовательно, лишенного гравитации в криволинейных координатах. В результате мы получаем «гравитацию», которая обязана своим существованием применяемому нами способу описания пространства. Возникает проблема различения «истинного» и «фиктивного» гравитационных полей. «Истинное» гравитационное поле выражается кривизной пространства, которая является инвариантом и не может быть создана или устранена никаким преобразованием координат. Такое гравитационное поле не зависит от способа нашего описания и в этом смысле имеет объективный характер. Таким образом, к выводу об объективности истинного гравитационного поля мы можем прийти не просто на основе наблюдения фактов, например фактов падения предметов на землю, а путем теоретического анализа проблемы инвариантности характеризующих его величин. Могут возразить, что здесь смешиваются два разных вопроса: вопрос о том, существует ли гравитация, и вопрос о том, какова ее природа. Ведь переход от классической физики к физике релятивистской ничего не изменил в утверждении об объективной реальности гравитации, истинность которого удостоверена повседневным опытом. Здесь изменились лишь наши представления о природе гравитации. Эти возражения представляются несостоятельными. Нельзя говорить об объективности гравитации как физического поля (а не просто вызываемых ею чувственно воспринимаемых эффектов) вне определенной ее природы. Гравитационное поле, из которого исключена его природа, есть явление без сущности, т. е. представляет собой фиктивный феномен. Но природа гравитационного поля не дана нам непосредственно, а раскрывается в рамках определенных теоретических представлений. Конечно, и общая теория относительности не ревизовала утверждение об объективной сущности гравитационного поля. Но в ее рамках это утверждение является более тонким, чем в ньютоновской теории гравитации, а потому нуждается в более тщательном разъяснении и обосновании. Вопрос о материальности гравитационного поля имеет и другую сторону, с которой связаны еще более сложные проблемы. Мы используем понятие «материальность» как эквивалент понятия «объективная реальность». Однако понятие «объективная реальность» является слишком общим понятием и не позволяет нам различить объективно реальный субстрат и формы его существования, например, пространство и время, которые также являются объективно реальными. Выше поставленный вопрос можно было бы поэтому переформулировать следующим образом: является ли гравитационное поле видом материи подобно другим полям, например электромагнитному, или же оно аналогично пространству-времени как таковому? Бросим ретроспективный взгляд на понятие поля. Оно было введено в связи с исследованиями электромагнетизма и рассматривалось как тождественное понятие электромагнитного поля. Максвелл показал, что оно оказывается не только удобным описанием действия электромагнитных сил на расстоянии, но и плодотворным в научном отношении. Пользуясь этим представлением, он сформулировал свои знаменитые уравнения, в которых содержался ряд новых идей, предвосхитивших опыт. Обстоятельством, определившим эволюцию понятия поля, послужила не только его научная плодотворность, но и обнаруженные у поля конкретные физические свойства. Так, при исследовании поля было обнаружено, что оно обладает энергией. После введения понятия электромагнитного поля было установлено, что оно имеет волновую природу, причем электромагнитные волны регистрировались экспериментально. Наконец, важным аргументом в пользу представления о физической реальности поля явилось открытие квантов электромагнитного поля — фотонов. Гравитационное поле существенно отличается от электромагнитного и других видов полей. Геометрический характер гравитации выделяет ее из всех физических полей и в некотором смысле отдаляет ее от них. Правда, нам могут сказать, что связь гравитационного поля с геометрией указывает на физический смысл геометрии. Геометрия перестает рассматриваться только как математический способ описания пространства, а становится объективным элементом структуры физического явления — гравитационного поля. Но, с другой стороны, эта связь может интерпретироваться (и действительно интерпретируется некоторыми физиками) как «поглощение» геометрией гравитационного поля. Физический статус гравитационного поля стал бы более естественным и очевидным, если бы у него, помимо геометрической структуры, были обнаружены другие физические свойства, например энергия, масса, волны, кванты и т. п. Вот почему внимание многих физиков-релятивистов обращено на исследования и поиски внегеометрических аспектов гравитационного поля. Однако на этом пути ученых подстерегают трудности. Все эти внегеометрические аспекты гравитации до сих пор принадлежат лишь к области догадок. Гравитация (в рамках общей теории относительности) до сего времени предстает перед нами только как геометрия пространства. Геометрический характер гравитационного поля обусловливает специфику проблемы его энергии. Гравитационное поле, вообще говоря, имеет энергию. Казалось бы, наличие у него такого важного физического свойства, как энергия, уже утверждает его физический статус. Но дело в том, что энергия гравитационного поля существенно отличается от энергии других видов полей, например электромагнитного. Величины, характеризующие ее, являются неинвариантными и образуют не тензор, а псевдотензор. Простым переходом от одной системы координат к другой мы можем «создать» гравитацию в данной точке и, наоборот, «устранить» ее. Причем это относится не только к «фиктивным», но и «истинным» гравитационным полям. Геометрическое описание гравитации и отмеченные особенности гравитационной энергии вызвали к жизни концепцию, в которой гравитационное поле не относится к видам материи. По мнению ученых, гравитационное поле (в отличие от электромагнитного) нельзя считать видом материи. Оно не имеет субстратного характера, а принадлежит к пространству-времени и является, как и последнее, формой существования материи. Трактовка гравитации как чисто геометрической формы, вообще говоря, логически допустима. Кроме того, она в большей степени, чем какая-либо другая концепция, опирается на современные релятивистские представления о гравитации. Однако ей присущи существенные дефекты. Во-первых, ее сторонники, отождествляя гравитацию с кривизной пустого пространства, полагают, что именно в этом виде она выступает как форма существования материи. Но в действительности такое понимание гравитации и пространства лишает их статуса форм существования материи. В философии диалектического материализма понятие «форма существования материи», отнесенное к пространству, означает нераздельность пространства и материи, недопустимость существования пространства самого по себе. Поэтому изложенную концепцию гравитации следует рассматривать не как утверждение гравитации и пространства в качестве формы существования материи, а, наоборот, как отрицание их статуса форм существования материи. Во-вторых, полагая, что гравитационное поле полностью сводится к геометрии пространства-времени, ученые считают необоснованными любые попытки поиска его физических свойств, выявления общих черт поля. В частности, они делают вывод о бесперспективности стремления создать квантовую теорию гравитации. Особый характер гравитационных и инерциальных полей должен быть принят во внимание в проблеме квантования этих полей. Само гравитационное поле не обладает массой энергии и импульсом в том смысле, в каком этими величинами обладают другие поля. В заключение коснемся еще двух вопросов. Первый из них можно сформулировать так: не противоречит ли трактовка гравитационного поля как вида материи общей теории относительности? При ответе на него следует иметь в виду, что существуют два утверждения: а) гравитация проявляется в геометрии пространства и времени и б) гравитация полностью сводится к геометрии пространства-времени. Эти утверждения не противоречат одно другому. Более того, второе является более сильным, так как из него можно получить в качестве следствия первое, но не наоборот. Общая теория относительности жестко связана с первым утверждением. Отказ от него является отказом и от общей теории относительности. Кроме того, некоторые физики-релятивисты принимают второе утверждение. Но поскольку второе утверждение не связано жестко с первым в том смысле, что не является его следствием, в рамках общей теории относительности логически допустим отказ от него. Этот отказ может состоять в переходе от концепции гравитационного поля как геометрической структуры пространства-времени к концепции гравитационного поля как вида материи, для которого геометрическая структура пространства-времени является важным, хотя и не единственным, аспектом. Следует отметить, что некоторые физики высказывают мнение, что гравитация — это вид материи. Известный специалист в области общей теории относительности А. 3. Петров писал: «Всякая попытка философского осмысления проблемы гравитации прежде всего сталкивается с фундаментальным вопросом: является ли поле гравитации особым видом материи? В зависимости от того или иного ответа на этот вопрос следуют соответствующие выводы философского характера, с одной стороны, и далеко идущие физические конструктивные следствия, приводящие к таким понятиям, как потенциал, напряженность поля и т. д., — с другой. Мы здесь исходим из того, что поле гравитации есть особый вид материи». Второй вопрос. Когда мы утверждаем, что открытие конкретных физических свойств гравитационного поля может явиться вкладом в обоснование тезиса об его материальности, то не смешиваем ли мы философское понятие материи с естественнонаучными представлениями о ее строении? Действительно, понятие материи фиксирует в явлениях мира лишь одно свойство — свойство объективной реальности. Для того, чтобы считать данное явление материальным, достаточно, чтобы оно обладало свойством объективного бытия. При этом совершенно безразлично, наделено оно или нет теми или иными конкретными свойствами. В данном вопросе имеется один важный момент, который не всегда учитывается. Зададим такой вопрос: что собой представляет свойство бытия? Казалось бы, на этот вопрос можно ответить так: это такое свойство предмета, которое остается у него, если мы отвлечемся от всех конкретных его свойств, за исключением его существования. Но на самом деле в результате этой процедуры мы приходим, выражаясь языком Гегеля, не просто к понятию бытия, а к понятию «чистого бытия», которое оказывается эквивалентным «ничто». Свойство реальности в чистом виде без связи с конкретными наличными свойствами есть не просто абстракция, но абстракция бессодержательная. Бытие вещи имеет характер наличной реальности только через наличие у нее конкретных свойств: оно есть функция от конкретных свойств. С философской точки зрения неважно, что собой представляют эти свойства. Характер их устанавливается посредством опыта и данных конкретных наук. Но наличие каких-либо конкретных свойств вещи является необходимым условием ее бытия. Исходя из всего вышеизложенного, можно сделать вывод, что, хотя положение о материальности гравитации не связано жестко с определенным набором конкретных физических свойств, сам процесс познания их является вкладом в обоснование положения о ее материальности.

ГРАВИТАЦИОННОЕ ПОЛЕ ЗЕМЛИ • Большая российская энциклопедия

• 
• 
• 

  В книжной версии

  Том 7. Москва, 2007, стр. 575-576

• 

  Скопировать библиографическую ссылку:

  ---

Авторы: В. Л. Пантелеев, Л. В. Зотов

ГРАВИТАЦИО́ННОЕ ПО́ЛЕ ЗЕМЛИ́, в ас­тро­но­мии по­ни­ма­ет­ся как по­ле тя­го­те­ния (при­тя­же­ния), в гео­де­зии и гео­фи­зи­ке – как по­ле тя­же­сти.

По­ле тя­го­те­ния есть по­ле сил, ко­то­рые под­чи­ня­ют­ся все­мир­но­го тя­го­те­ния за­ко­ну. Г. п. З. как по­ле тя­го­те­ния ис­поль­зу­ет­ся в за­да­чах ас­тро­но­мии для по­строе­ния ор­бит кос­мич. тел (как ес­те­ст­вен­ных, так и ис­кус­ст­вен­ных) в ок­ре­ст­но­сти пла­не­ты Зем­ля.

По­ле тя­же­сти оп­ре­де­ля­ет­ся во вра­щаю­щей­ся сис­те­ме ко­ор­ди­нат с учё­том сил не­гра­ви­та­ци­он­ной при­ро­ды (уп­ру­гих, элек­тро­ста­тич., маг­нит­ных и др.), ко­то­рые удер­жи­ва­ют проб­ное те­ло не­под­виж­ным от­но­си­тель­но по­верх­но­сти Зем­ли (т. н. ре­ак­ция опо­ры). Рав­но­дей­ст­вую­щая сил ре­ак­ции опо­ры и при­тя­же­ния со­об­ща­ет проб­но­му те­лу цен­тро­ст­ре­ми­тель­ное ус­ко­ре­ние. Вслед­ст­вие не­инер­ци­аль­но­сти вра­щаю­щей­ся сис­те­мы от­счё­та воз­ни­ка­ет цен­тро­беж­ное ус­ко­ре­ние, об­рат­ное по на­прав­ле­нию цен­тро­стре­ми­тель­но­му и вы­зы­вае­мое цен­тро­беж­ной си­лой (см. Си­ла инер­ции). Под си­лой тя­же­сти по­ни­ма­ют рав­но­дей­ст­вую­щую сил при­тя­же­ния Зем­ли и цен­тро­беж­ной си­лы, пом­ня, что по­след­няя яв­ля­ет­ся лишь эф­фек­том ис­поль­зо­ва­ния не­инер­ци­аль­ной сис­те­мы от­счё­та. Не­зна­чи­тель­ный вклад в по­ле тя­же­сти вно­сит так­же дей­ст­вую­щее в ок­ре­ст­но­стях Зем­ли при­тя­же­ние Солн­ца, Лу­ны, пла­нет и др. тел. Г. п. З. как по­ле тя­же­сти – пред­мет изу­че­ния гра­ви­мет­рии.

Функ­ци­ей, опи­сы­ваю­щей Г. п. З., яв­ля­ет­ся гра­ви­тац. по­тен­ци­ал. Наи­бо­лее удоб­ная для из­ме­ре­ния ха­рак­те­ри­сти­ка Г. п. З. – его на­пря­жён­ность (си­ла, с кото­рой по­ле дей­ст­ву­ет на еди­нич­ную то­чеч­ную мас­су), яв­ляю­щая­ся пер­вой про­из­вод­ной гра­ви­тац. по­тен­циа­ла. Эта удель­ная си­ла име­ет раз­мер­ность ус­ко­ре­ния и во вра­щаю­щей­ся сис­те­ме от­счёта, свя­зан­ной с по­верх­но­стью Зем­ли, сов­па­да­ет с ус­ко­ре­ни­ем сво­бод­но­го па­де­ния проб­но­го те­ла. В гра­ви­мет­рии сло­во «удель­ная», как пра­ви­ло, опус­ка­ют и си­лу тя­же­сти измеряют в мил­ли­га­лах (1 мГал=10^–5 м/с²). Др. ре­ги­ст­ри­руе­мые ха­рак­те­ри­сти­ки Г. п. З. – вто­рые про­из­вод­ные гра­витационного по­тен­циа­ла. Еди­ни­цей из­ме­ре­ния вто­рых про­из­вод­ных гра­ви­тац. по­тен­циа­ла слу­жит эт­веш, рав­ный 10^–9 с^–2. Со­б­ран­ную ин­фор­ма­цию о Г. п. З. хра­нят в ви­де карт ано­ма­лий си­лы тя­же­сти (гра­ви­тац. ано­ма­лий) или ка­та­ло­гов гра­ви­мет­рич. пунк­тов.

Г. п. З. мо­жет быть ло­каль­ным, от­ра­жаю­щим рас­пре­де­ле­ние си­лы тя­же­сти на ог­ра­ни­чен­ных пло­ща­дях, или ре­гио­наль­ным. Ло­каль­ное Г. п. З. ши­ро­ко ис­поль­зу­ет­ся для ре­ше­ния за­дач гра­ви­та­ци­он­ной раз­вед­ки, ко­то­рая изу­ча­ет не­од­но­род­но­сти рас­пре­де­ле­ния масс в верх­них сло­ях зем­ной ко­ры, что при­ме­ня­ет­ся в т. ч. и для по­ис­ков по­лез­ных ис­ко­пае­мых. Ме­то­ды, раз­ра­бо­тан­ные для изу­че­ния ло­каль­но­го Г. п. З., ис­поль­зу­ют­ся так­же при ис­сле­до­ва­нии строе­ния верх­них сло­ёв др. пла­нет и Лу­ны. Напр., в 1968 амер. учё­ные У. Сьёг­рен и П. Мюл­лер, ис­сле­дуя лу­че­вые ус­ко­ре­ния (со­став­ляю­щие ус­ко­ре­ния, на­прав­лен­ные по лу­чу зре­ния на­блю­да­те­ля) ис­кус­ст­вен­ных спут­ни­ков Лу­ны, об­на­ру­жи­ли до­воль­но зна­чи­тель­ные по­ло­жи­тель­ные гра­ви­тац. ано­ма­лии над лун­ны­ми мо­ря­ми, что мож­но объ­яс­нить толь­ко кон­цен­тра­ци­ей масс у по­верх­но­сти Лу­ны. По­доб­ные гео­ло­гич. струк­ту­ры бы­ли на­зва­ны мас­ко­на­ми. При­зна­ки мас­ко­нов на­шли так­же на Мер­ку­рии, Мар­се и да­же на Зем­ле.

Ре­гио­наль­ное Г. п. З. ис­поль­зу­ют пре­ж­де все­го для ре­ше­ния фи­зич. за­дач гео­де­зии, для оп­ре­де­ле­ния па­ра­мет­ров об­ще­го зем­но­го эл­лип­сои­да (ОЗЭ) как те­ла от­счё­та, для по­строе­ния гео­гра­фич. карт, вы­чис­ле­ния вы­сот ква­зи­гео­и­да и ук­ло­не­ний от­вес­ных ли­ний (см. Гео­де­зи­че­ская гра­ви­мет­рия). Па­ра­мет­ры ОЗЭ вхо­дят в ал­го­рит­мы об­ра­бот­ки спут­ни­ко­вых дан­ных для оп­ре­де­ле­ния гео­де­зич. ко­ор­ди­нат в спут­ни­ко­вых сис­те­мах по­зи­цио­ни­ро­ва­ния.

По­тен­ци­ал ре­гио­наль­но­го по­ля тя­го­тения в дан­ной точ­ке за­ви­сит от точ­но­го рас­стоя­ния до цен­тра Зем­ли, гео­гра­фич. ши­ро­ты и дол­го­ты мес­та; его зна­че­ние за­да­ёт­ся в ви­де раз­ло­же­ния в ряд по сфе­ри­че­ским (на по­верх­но­сти Зем­ли) или ша­ро­вым (в про­стран­ст­ве) функ­ци­ям. Ана­ло­гич­ное пред­став­ле­ние по­тен­циа­ла по­ля тя­же­сти вклю­ча­ет так­же допол­ни­тель­ный член ря­да, от­ве­чаю­щий за цен­тро­беж­ные си­лы.

Для удоб­ст­ва ре­ше­ния разл. за­дач Г. п. З. ус­лов­но раз­де­ля­ет­ся на нор­маль­ную и ано­маль­ную час­ти. Нор­маль­ная часть со­от­вет­ст­ву­ет идеа­ли­зи­ро­ван­ной Зем­ле («нор­маль­ной» Зем­ле) про­стой гео­мет­ри­че­ской фор­мы и с про­стым рас­пре­де­ле­ни­ем плот­но­сти внут­ри неё. Ано­маль­ная часть по­ля мень­ше по ве­ли­чи­не и от­ра­жа­ет де­та­ли фи­гу­ры и рас­пре­де­ле­ния плот­но­сти ре­аль­ной Зем­ли. Нор­маль­ным гра­ви­тац. по­тен­циа­лом на­зы­ва­ют при­бли­жён­ное пред­став­ле­ние Г. п. З., за­дан­ное пер­вы­ми чле­на­ми раз­ло­же­ния по­тен­циа­ла в ряд по ша­ро­вым функ­циям. Со­от­вет­ст­вую­щая ему нор­маль­ная си­ла тя­же­сти $γ$, ог­ра­ни­чен­ная точ­но­стью по­ряд­ка квад­ра­та сжа­тия Зем­ли (от­но­ше­ние раз­но­сти эк­ва­то­ри­аль­ной и по­ляр­ной по­лу­осей зем­но­го эл­лип­сои­да к эк­ва­то­ри­аль­ной по­лу­оси), име­ет вид $γ=γ_e(1+β\sin^2B-β_1\sin^22B)$, где $B$ – гео­де­зич. ши­ро­та точ­ки. Чис­лен­ные зна­че­ния ко­эф­фи­ци­ен­тов $β$, $β_1$ и $γ_e$ ут­вер­жда­ют­ся ме­ж­ду­нар. со­об­ще­ст­вом гео­де­зис­тов и гео­фи­зи­ков. Ме­ж­ду­нар. фор­му­ла для нор­маль­ной си­лы тя­же­сти, при­ня­тая на 14-й Ге­не­раль­ной ас­самб­лее гео­де­зии и гео­фи­зи­ки в 1967, име­ет сле­дую­щие ко­эф­фи­ци­ен­ты: $γ_e$= 978031,8 мГал, $β$=0,0053024, $β_1$=0,0000059. При этом сжа­тие пла­не­ты Зем­ля ока­зы­ва­ет­ся рав­ным $α$=1/298,249.

Г. п. З. ха­рак­те­ри­зу­ет­ся сле­дую­щи­ми чи­с­ло­вы­ми зна­че­ния­ми ве­ли­чин: си­ла тя­же­сти на эк­ва­то­ре со­став­ля­ет 978032,78 мГал, на по­лю­се – 983218,53 мГал; максимальная ано­ма­лия си­лы тя­же­сти не пре­выша­ет 400 мГал; нор­маль­ный вер­ти­каль­ный гра­ди­ент си­лы тя­же­сти – 0,3086 мГал/м; максимальное от­кло­не­ние от­весной ли­нии 20″; диа­па­зон пе­рио­дич. лун­но-сол­неч­ных ва­риа­ций си­лы тя­же­сти ме­нее 0,3 мГал; воз­мож­ная ве­ли­чи­на ве­ко­во­го из­ме­не­ния си­лы тя­же­сти ме­нее 0,01 мГал/год.

Г. п. З. ис­поль­зу­ют для оп­ре­де­ле­ния фи­гу­ры геоида – одной из уро­вен­ных по­верх­но­стей Зем­ли. На­прав­ле­ние век­то­ра си­лы тя­же­сти (нор­ма­ли к уро­вен­ной по­верх­но­сти) за­да­ёт по­ло­же­ние ас­тро­но­мич. зе­ни­та. Для мн. за­дач на­ви­га­ции важ­но знать от­кло­не­ние от­вес­ной ли­нии от нор­ма­ли к об­ще­му зем­но­му эл­лип­сои­ду.

Вто­рые про­из­вод­ные по­тен­циа­ла тя­же­сти так­же ис­поль­зу­ют для ре­ше­ния гео­ло­го-раз­ве­доч­ных и гео­де­зич. за­дач. Ано­маль­ная часть вто­рых про­из­вод­ных по ве­ли­чи­не дос­ти­га­ет де­сят­ков, а в го­рах – со­тен эт­веш. Вто­рые про­из­вод­ные гра­ви­тац. по­тен­циа­ла из­ме­ря­ют гра­ви­та­ци­он­ны­ми ва­рио­мет­ра­ми, пер­вые про­из­вод­ные – гра­ви­мет­ра­ми.

Гравитационный потенциал — это… Что такое Гравитационный потенциал?

У этого термина существуют и другие значения, см. Потенциал.

Гравитацио́нный потенциа́л — скалярная функция координат и времени, характеризующая гравитационное поле в классической механике. Имеет размерность квадрата скорости, обычно обозначается буквой . Гравитационный потенциал равен отношению потенциальной энергии материальной точки, помещённой в рассматриваемую точку гравитационного поля, к массе этой точки. Впервые понятие гравитационного потенциала ввёл в науку Адриен Мари Лежандр в конце XVIII века.

Движение частицы в гравитационном поле в классической механике определяется функцией Лагранжа, имеющей в инерциальной системе отсчета вид:

, где:  — масса частицы,  — координата частицы,  — потенциал гравитационного поля.

Подставляя выражение для лагранжиана L в уравнения Лагранжа:

,

получаем уравнения движения

.

Гравитационный потенциал и принцип эквивалентности

Уравнения движения частицы в гравитационном поле в классической механике не содержат массы или другой величины, характеризующей частицу. Это является выражением основного свойства гравитационного поля — принципа эквивалентности.

Гравитационный потенциал точечной частицы и произвольного тела

Гравитационный потенциал точечной частицы равен: , где  — гравитационная постоянная,  — масса частицы,  — расстояние от частицы. Эта же формула справедлива и для гравитационного потенциала любого тела со сферически-симметричным распределением плотности массы внутри него.

Для тела с произвольным распределением плотности массы гравитационный потенциал удовлетворяет уравнению Пуассона: , где  — оператор Лапласа,  — объёмная плотность распределения массы в рассматриваемой точке. Общее решение этого уравнения имеет вид: где r — расстояние от элемента объёма dV до рассматриваемой точки поля, а интегрирование производится по всему объёму тел, создающих поле. Гравитационный потенциал симметричного тела симметричен.

Потенциальная энергия частицы в гравитационном поле равна ее массе, умноженной на потенциал поля. Для потенциальной энергии любого распределения масс справедливо выражение:

где  — плотность массы тела,  — гравитационный потенциал,  — объём тела.

Формула для гравитационного потенциала произвольного тела имеет вид:

где  — полная масса системы, а величины:

можно назвать тензором квадрупольного момента масс. Он связан с обычным тензором моментов инерции

очевидными соотношениями

Гравитационный потенциал планет

Гравитационная энергия тела получается интегрированием выражения (1) по объёму тела с использованием выражения для потенциала (2). Для шара массы m, радиусом a, с равномерным распределением плотности масс, получается значение U гравитационной энергии тела:

В общей теории относительности для случая слабых стационарных гравитационных полей устанавливается связь между компонентом метрического тензора пространства-времени и значением гравитационного потенциала Относительное замедление хода времени в точке с меньшим значением гравитационного потенциала по сравнению с временем в точке с большим значением гравитационного потенциала равно разности гравитационных потенциалов в этих точках, делённой на квадрат скорости света.

См. также

Литература

1. Ландау Л. Д., Лифшиц Е. М. «Теоретическая физика», учебное пособие для вузов, в 10 т. / т. 1, «Механика», 5-е изд., стереотип., М., «Физматлит», 2002, 224 с., ISBN 5-9221-0055-6 (т. 1), гл. 1 «Уравнения движения», п. 2 «Принцип наименьшего действия», с. 10-14;
2. Ландау Л. Д., Лифшиц Е. М. «Теоретическая физика», уче. пособ. для вузов, в 10 т. / т. 2, «Теория поля», 8-е изд., стереотип., М., «Физматлит», 2001, 536 с., ISBN 5-9221-0056-4 (т. 2), гл. 10 «Частица в гравитационном поле», п. 81 «Гравитационное поле в нерелятивистской механике», с. 304—306; гл. 12 «Поле тяготеющих тел», п. 99 «Закон Ньютона», с. 397—401;
3. С. Вейнберг «Гравитация и космология», Принципы и приложения общей теории относительности, пер. с англ. В. М. Дубовика и Э. А. Тагирова, под ред. Я. А. Смородинского, «Платон», 2000, ISBN 5-80100-306-1, ч. 2 «Общая теория относительности», гл. 3 «Принцип эквивалентности», п. 4 «Ньютоновское приближение», с. 92-93;
4. К. В. Холшевников, И. И. Никифоров Свойства гравитационного потенциала в примерах и задачах: Учебное пособие. — С-Пб., 2008. — 72 с., ББК 22.6.

ГРАВИТАЦИОННОЕ ПОЛЕ — это… Что такое ГРАВИТАЦИОННОЕ ПОЛЕ?



ГРАВИТАЦИОННОЕ ПОЛЕ

ГРАВИТАЦИОННОЕ ПОЛЕ (поле тяготения), один из видов поля физического, посредством которого осуществляется гравитационное взаимодействие (притяжение) тел, например Солнца и планет Солнечной системы, планет и их спутников, Земли и находящихся на ней или вблизи нее тел (смотри Всемирного тяготения закон).

Современная энциклопедия. 2000.

• ГРАВИТАЦИОННОЕ ВЗАИМОДЕЙСТВИЕ
• ГРАВИТАЦИОННЫЕ ВОЛНЫ

Смотреть что такое «ГРАВИТАЦИОННОЕ ПОЛЕ» в других словарях:

• ГРАВИТАЦИОННОЕ ПОЛЕ — (поле тяготения) поле физическое, создаваемое любыми физическими объектами; через гравитационное поле осуществляется гравитационное взаимодействие тел …   Большой Энциклопедический словарь

• ГРАВИТАЦИОННОЕ ПОЛЕ — ГРАВИТАЦИОННОЕ ПОЛЕ, пространство вокруг предмета, чья масса способна притягивать другой предмет. Сила этого притяжения, разделенная на массу второго предмета, и есть сила гравитационного поля. Предмет с большой массой, такой как Земля, имеет… …   Научно-технический энциклопедический словарь

• Гравитационное поле — (поле тяготения), один из видов поля физического, посредством которого осуществляется гравитационное взаимодействие (притяжение) тел, например Солнца и планет Солнечной системы, планет и их спутников, Земли и находящихся на ней или вблизи нее тел …   Иллюстрированный энциклопедический словарь

• ГРАВИТАЦИОННОЕ ПОЛЕ — (поле тяготения), (см. ТЯГОТЕНИЕ). Физический энциклопедический словарь. М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983 …   Физическая энциклопедия

• гравитационное поле — [ГОСТ 25645.103 84] Тематики условия физические косм. пространства EN gravity field …   Справочник технического переводчика

• Гравитационное поле — Гравитационное поле, или поле тяготения  физическое поле, через которое осуществляется гравитационное взаимодействие[1]. Содержание 1 Гравитационное поле в классической физике …   Википедия

• гравитационное поле — (поле тяготения), поле физическое, создаваемое любыми физическими объектами; через гравитационное поле осуществляется гравитационное взаимодействие тел. * * * ГРАВИТАЦИОННОЕ ПОЛЕ ГРАВИТАЦИОННОЕ ПОЛЕ (поле тяготения), поле физическое (см. ПОЛЕ… …   Энциклопедический словарь

• гравитационное поле — gravitacijos laukas statusas T sritis Standartizacija ir metrologija apibrėžtis Klasikinės fizikos požiūriu – gravitacinės sąveikos tarpininkas, kai lauko šaltiniai yra sąveikaujančiųjų dalelių ar jų sistemų masės. Bendrosios reliatyvumo teorijos …   Penkiakalbis aiškinamasis metrologijos terminų žodynas

• гравитационное поле — gravitacijos laukas statusas T sritis fizika atitikmenys: angl. gravitational field vok. Gravitationsfeld, n; Schwerefeld, n rus. гравитационное поле, n; поле тяготения, n pranc. champ de gravitation, m; champ de pesanteur, m; champ… …   Fizikos terminų žodynas

• ГРАВИТАЦИОННОЕ ПОЛЕ — (поле тяготения), поле физическое, создаваемое любыми физ. объектами; через Г. п. осуществляется гравитац. взаимодействие тел …   Естествознание. Энциклопедический словарь