11.Что такое главный вектор и главный момент?
Момент, равный геометрической сумме моментов всех сил системы относительно точки О, называется главным моментом системы сил относительно этой точки
Геометрическая сумма всех сил системы называется главным вектором системы сил и в отличие от равнодействующей R обозначается R*.
R*=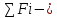 главный
вектор
главный
вектор
M0=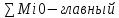 момент
момент
R*=Р1+Р2+Р3= F1+F2+F3
M= M10+M20+M30=M0
12.Чем схожи и различны главный вектор и равнодействующая?
R*≠0, M0≠0, R*перпендикулярно M0 т.к. R* — M0 =0 – в этом случае систему сил можно приводить к равнодействующей. Равной главному вектору этой системы, но приложенной не в центре приведения O, а стоящему от него на расстоянии OC. OC=IM0I/IR*I
13.Зависимость главного момента от центра приведения.
При изменении центра приведения изменяется только главный момент, а главный вектор не изменяется. Влияет на направление главного момента.
14.Инварианты статики.
Инвариант – такие величины которые не зависят от выбора центра приведения.
1)Векторный инвариант I1=R*
2)Скалярный инвариант I2=R*×M
15.Частные случаи приведения произвольной пространственной системы сил.
1)R*=0, M0=0 — в этом случае исходная система является уравновешенной, а тело находится в состоянии покоя.
2) R*=0, M0≠0 – в этом случае исходная система или приводится к чему то или …..
3) R*≠0, M0=0 – в этом случае система сил приводится к равнодействующей R равной главному вектору системы сил R=R*
4) R*≠0, M0≠0, R*перпендикулярно M0 т.к. R* — M0 =0 – в этом случае систему сил можно приводить к равнодействующей. Равной главному вектору этой системы, но приложенной не в центре приведения O, а стоящему от него на расстоянии OC. OC=IM0I/IR*I
5) R*≠0, R*×M0≠0 – в этом случае силу можно привести к динамическому винту(динаме) или к двум скрещивающимися силам.
16.Как находится равнодействующая распределённых сил?
По правилу параллелограмма, метод силового треугольника
17.Какие задачи являются статически определёнными и статически неопределёнными?
18.Как направлены реакции при скольжении тела по шероховатой поверхности.
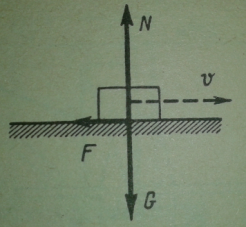
При скольжении тела по шероховатой поверхности к нему приложена сила трения скольжения. Направление этой силы, противодействующей скольжению,
противоположно направлению скорости тела
Модуль силы трения скольжения пропорционален нормальному давлению N:
F = fN.
Коэффициент пропорциональности f называется коэффициентом трения скольжения и определяется опытным путем.
19.Как находится угол трения. Дать понятие конуса трения.
Угол tg которого равен коэф. трения называется углом трения. Tg(альфа) = Fтр./Nа=fNа/Nа=f
Y=arctgf
Геометрическое место всех возможных направлений предельной реакции Ra образует коническую поверхность – конус трения.
20.Сформулировать условие, при котором возможно и не возможно скольжение тела по шероховатой поверхности в зависимости от угла наклона силы к нормали поверхности скольжения.
21.Какие реакции возникают при качении тела по шероховатой поверхности без скольжения.
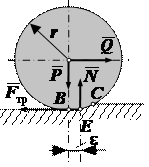
22.Размерность коэф.трения качения и скольжения.
Безразмерный коэффициент f называется коэф. трения скольжения.
23.Как находится центр параллельных сил?
Xc=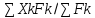
Yc=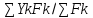
Zc=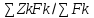
24.Можно ли найти равнодействующую 2 параллельных неравных по модулю сил, направленных в одну сторону? Если да, то чему равна равнодействующая, и где она приложена?
Любую пространственную систему сил в общем случае можно заменить эквивалентной системой, состоящей из одной силы, приложенной в какой-либо точке тела (центре приведения) и равной главному вектору данной системы сил, и одной пары сил, момент которой равен главному моменту всех сил относительно выбранного центра приведения. Поскольку вы имеете дело с двумя параллельными силами, направленными в одну сторону, то на отрезке, соединяющем точки их приложения, найдется точка, относительно которой главный момент этих сил равен нулю. Если в этой точке приложить силу, равную векторной сумме этих двух сил (то есть главный вектор), то она заменит их действие на тело. Таким образом, вы можете найти равнодействующую и точку ее приложения так, что при этом не понадобится дополнительная пара сил.
1 Связи и их реакции
Одним из основных положений механики является принцип освобождаемости от связей, согласно которому несвободное тело можно рассматривать как свободное, если отбросить действующие на него связи и заменить их силами – реакциями связей.
Шарнирно-неподвижная опора
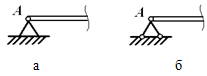
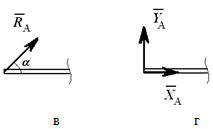
Шарнирно-подвижная опора Реакция направлена по нормали к опорной поверхности
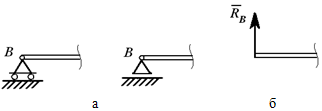 Соединение
стержня и втулки в плоскости–
скользящая заделка.
Соединение
стержня и втулки в плоскости–
скользящая заделка. 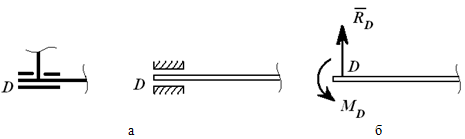 Бискользящая
заделка. В
плоскости данная опора допускает
поступательное перемещение стержня
как по горизонтали, так и по вертикали,
но препятствует повороту (в плоскости).
Реакцией такой опоры будет момент MC
Бискользящая
заделка. В
плоскости данная опора допускает
поступательное перемещение стержня
как по горизонтали, так и по вертикали,
но препятствует повороту (в плоскости).
Реакцией такой опоры будет момент MC 
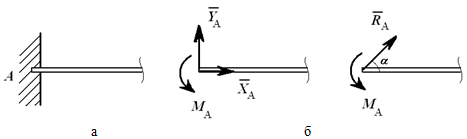 сферический
шарнир
сферический
шарнир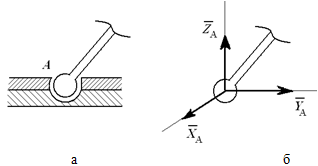
2Главный вектор и главный момент плоской системы сил
Рассмотрим плоскую систему сил (F1, F2, …, Fn),действующих на твердое тело в координатной плоскости Oxy.
Главным вектором системы сил называется вектор R, равный векторной сумме этих сил:
R = F1 + F2 +
… + Fn = 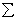 Fi.
Fi.
Для плоской системы сил ее главный вектор лежит в плоскости действия этих сил.
Главным моментом системы сил относительно центра O называется вектор LO, равный сумме векторных моментов этих сил относительно точки О:
LO = MO(F1)
+ MO(F2)
+ … + MO(Fn)
= 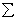
Вектор R не зависит от выбора центра О, а вектор LO при изменении положения центра О может в общем случае изменяться.
Для плоской системы сил вместо векторного главного момента используют понятие алгебраического главного момента. Алгебраическим главным моментом LO плоской системы сил относительно центра О, лежащего в плоскости действия сил, называют сумму алгебраических моментовэтих сил относительно центра О.
Главный вектор и главный момент плоской системы сил обычно вычисляется аналитическими методами.
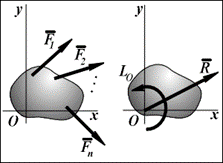
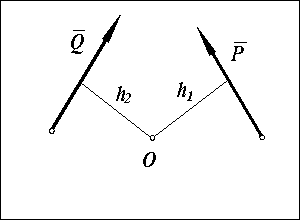
Правило знаков алгебраических моментов сил (в правой системе координат, принятой в механике): момент считается положительным, если сила стремится повернуть тело относительно точки О против хода часовой стрелки, и отрицательной — по ходу часовой стрелки.
Для сил P и Q, изображенных на рисунке, их алгебраические моменты относительно центра О равны: MО = P · h1; MO = -Q · h2.
3-4.Систем тел. Равновесие системы тел. Пример.
Статический расчет системы тел сводится к рассмотрению условий равновесия конструкций, состоящих из тел, соединенных какими-нибудь связями. Связи, соединяющие части конструкции называются внутренними, скрепляющие конструкцию с другими телами, в нее не входящими — внешними.
При решении задач статики реакции связей входят в число неизвестных, которые необходимо определить из уравнений равновесия. Система тел, для которых число неизвестныхреакций связей равно числу уравнений равновесия, называются статически определимыми. Система тел, для которых число неизвестных реакций связей больше числа уравненийравновесия, называются статически неопределимыми.
Если при отбрасывании внешних связей (опор) конструкция остается жесткой, то для нее задача о равновесии решается как для абсолютно твердого тела (при действии плоской системы сил число неизвестных реакций связей не должно быть больше трех).
Если после отбрасывания внешних связей конструкция не считается жесткой, то наиболее рациональным способом решения подобных задач является расчленение на отдельные тела и составление уравнений равновесия для каждого из тел в отдельности.
Для конструкции из n тел, на каждое из которых действует произвольная плоская система сил, получится таким путем 3n уравнений равновесия, позволяющих найти 3nнеизвестных.
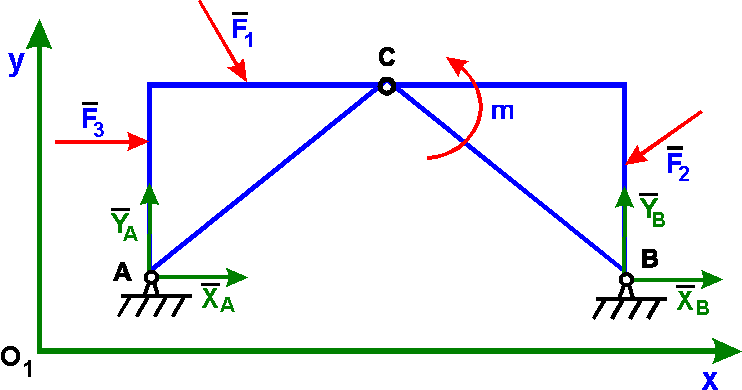 Например, если
отбросить опоры А и В трехшарнирной
арки, то она не будет жесткой: ее части
могут поворачиваться вокруг шарнира С.
Для определения реакций внешних
связей ХА, YА, ХВ, YВ
расчленим конструкцию по соединительному
шарниру С на
две части и рассмотрим равновесие
каждой из частей в отдельности.
Например, если
отбросить опоры А и В трехшарнирной
арки, то она не будет жесткой: ее части
могут поворачиваться вокруг шарнира С.
Для определения реакций внешних
связей ХА, YА, ХВ, YВ
расчленим конструкцию по соединительному
шарниру С на
две части и рассмотрим равновесие
каждой из частей в отдельности.
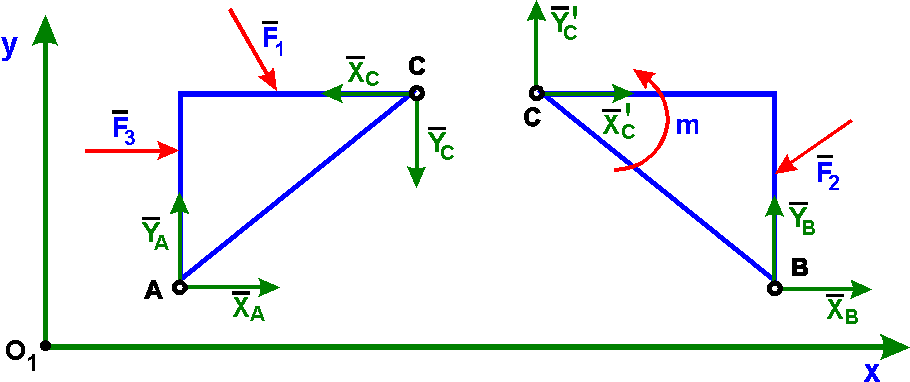
При действии на трехшарнирную арку произвольной плоской системы сил для каждой части можно записать три уравнений равновесия:
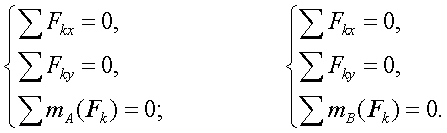 Присоединить к
этой системе шести уравнений на основании
закона о действии и противодействии
уравнения для узла С (ХС = ХСў, YС = YСў),
получим систему уравнений из которой
можно найти реакции внешних связей ХА,
YА, ХВ, YВ и реакции внутренних связей
ХС, YС.
Присоединить к
этой системе шести уравнений на основании
закона о действии и противодействии
уравнения для узла С (ХС = ХСў, YС = YСў),
получим систему уравнений из которой
можно найти реакции внешних связей ХА,
YА, ХВ, YВ и реакции внутренних связей
ХС, YС.
Связь между моментами силы относительно оси и произвольной точки этой оси
Пусть даны сила  и осьl.
Возьмем произвольную точку О на оси l и найдем вектор
и осьl.
Возьмем произвольную точку О на оси l и найдем вектор 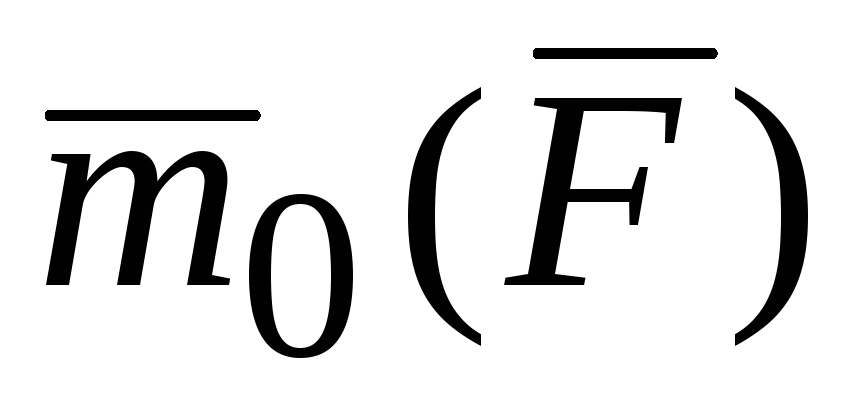 (рис. 2.5). Обозначим γ угол, который
составляет вектор
(рис. 2.5). Обозначим γ угол, который
составляет вектор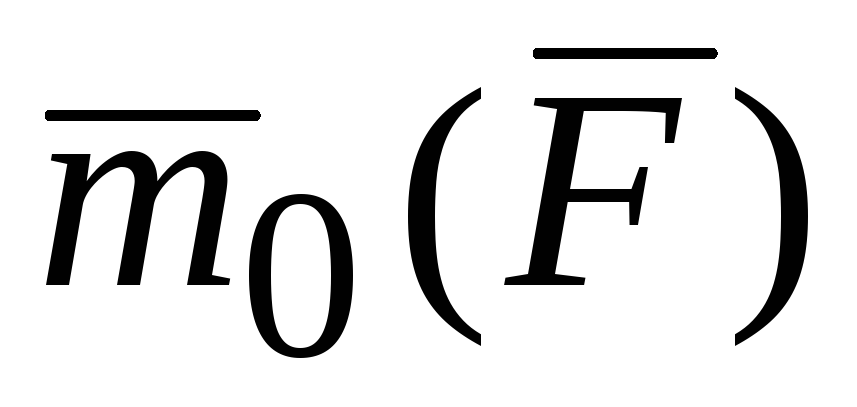 с осьюl.
Возьмем другую точку
с осьюl.
Возьмем другую точку  на осиl и проводим через нее плоскость П
перпендикулярную оси l.
Спроектируем силу
на осиl и проводим через нее плоскость П
перпендикулярную оси l.
Спроектируем силу  на плоскость П. Из геометрии известно,
что если нормали к двум плоскостям
составляют угол γ, то и плоскости
составляют этот угол и для площадей
треугольников справедлива формула:
на плоскость П. Из геометрии известно,
что если нормали к двум плоскостям
составляют угол γ, то и плоскости
составляют этот угол и для площадей
треугольников справедлива формула:
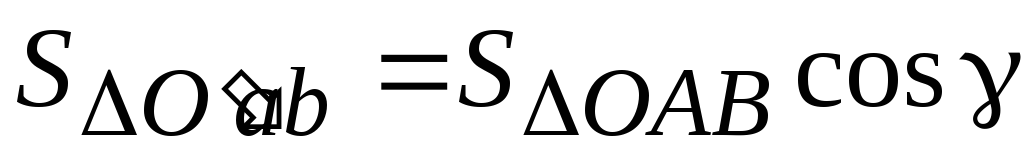 .
(2.8)
.
(2.8)
Д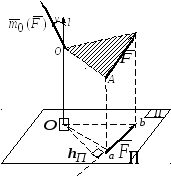 омножим
формулу (2.8) на два:
омножим
формулу (2.8) на два:
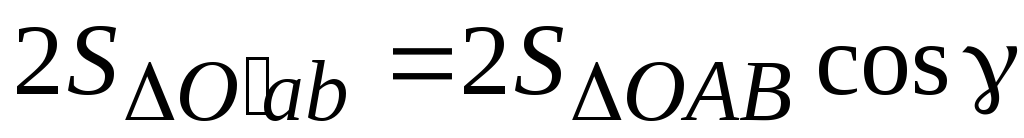 .
(2.9)
.
(2.9)
В формуле (2.9)
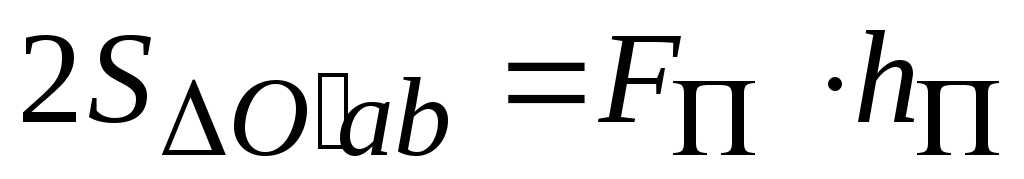 ,
,
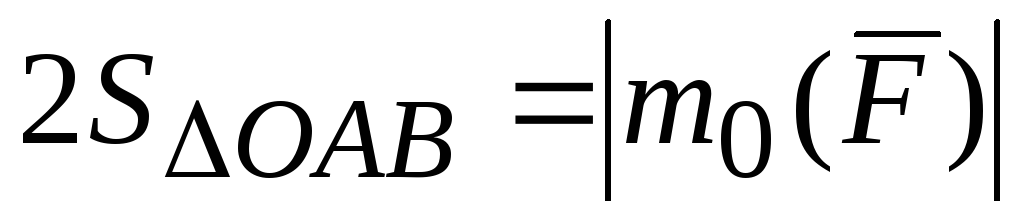 .
.
Следовательно
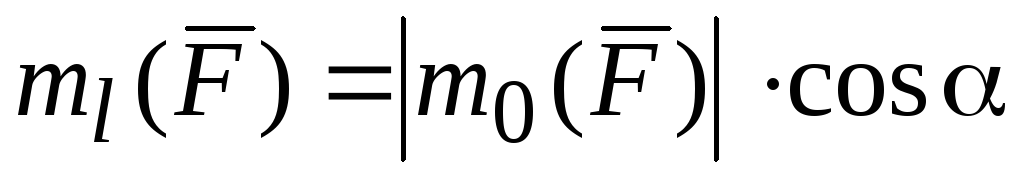 или
или
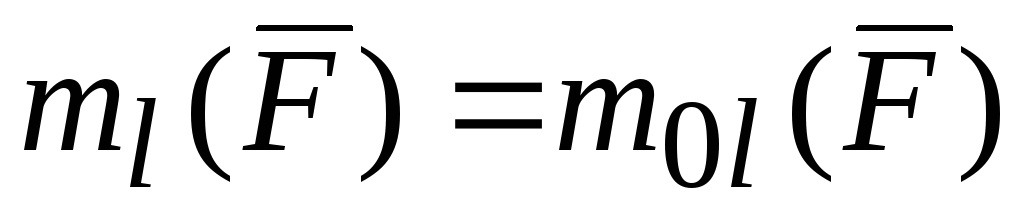 .
.
Рис. 2.5
Момент силы относительно оси равен проекции на эту ось момента силы относительно любой точки этой оси.
Главный вектор системы сил
Пусть дана система
сил 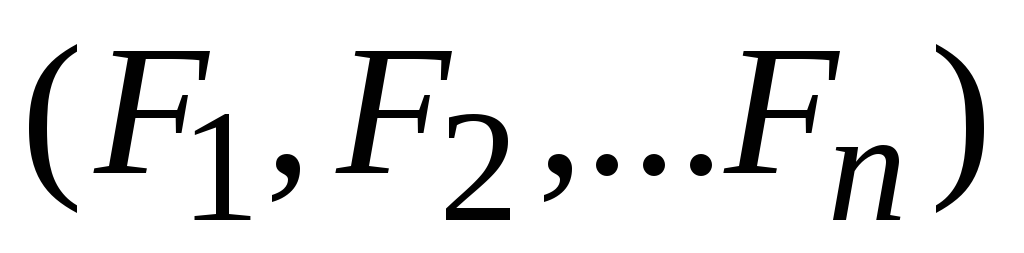 .
.
Определение. Главным вектором системы сил называется вектор, равный геометрический сумме векторов всех сил системы
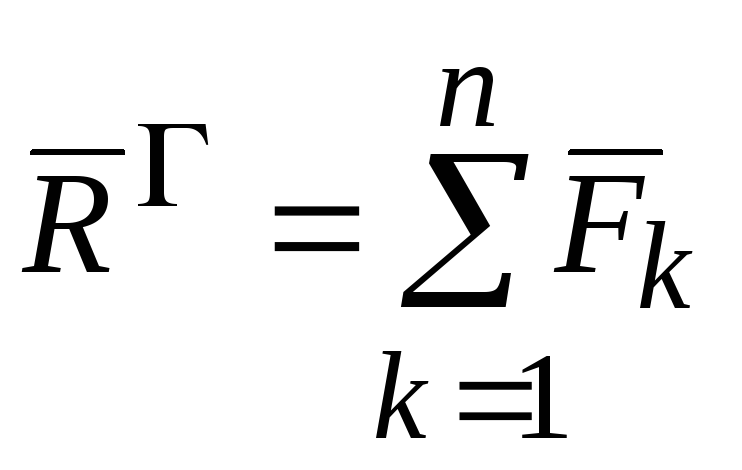 .
(2.10)
.
(2.10)
Главный вектор не является силой. Это свободный вектор, полученный формальным сложением, перенесенных в любую точку векторов сил системы (рис. 2.6).
Способ нахождения главного вектора системы сил
Выберем некоторую
систему координат Oxyz.
По отношению к этой системе координат
силы можно разложить по ортам 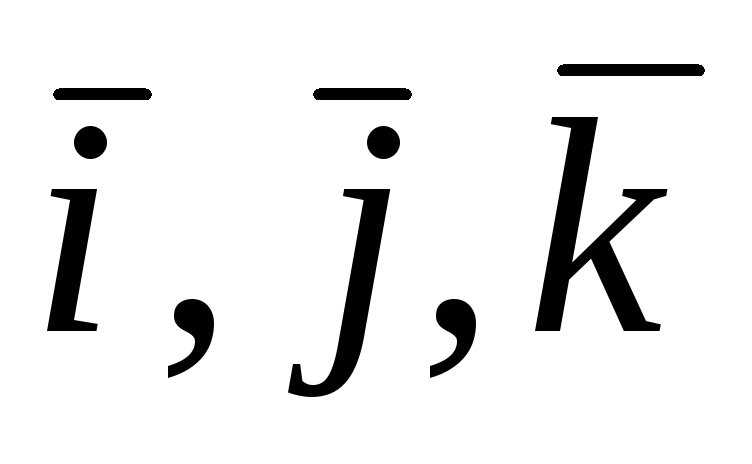 :
:
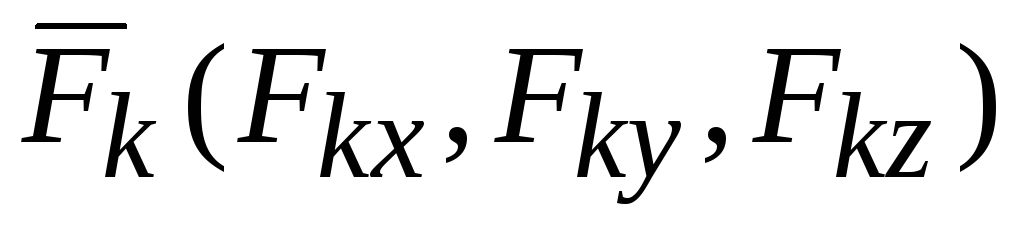 ,
, 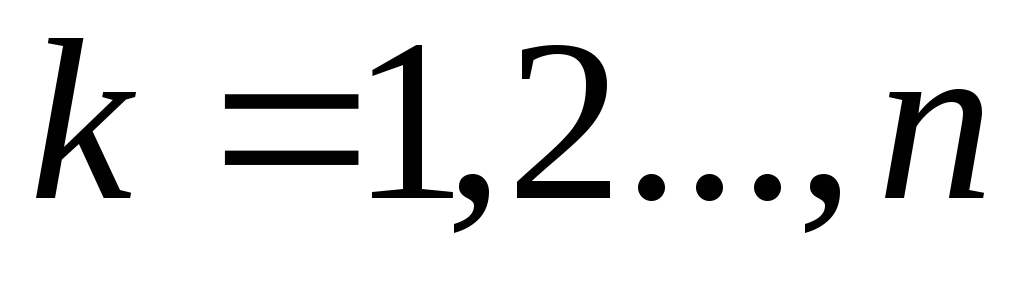 ,
,
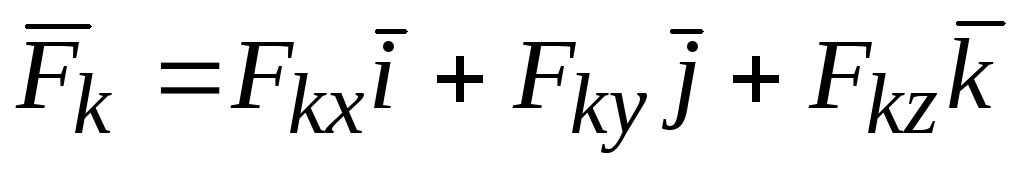 .
(2.11)
.
(2.11)
По определению
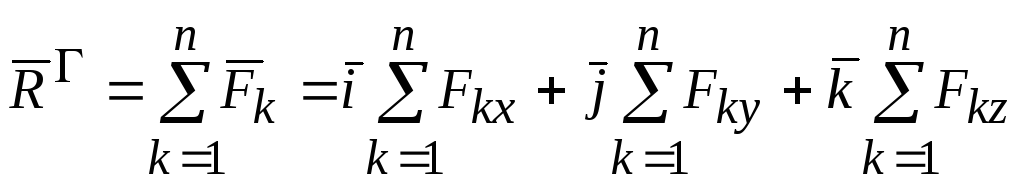 .
(2.12)
.
(2.12)
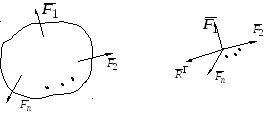
Рис. 2.6
С другой стороны
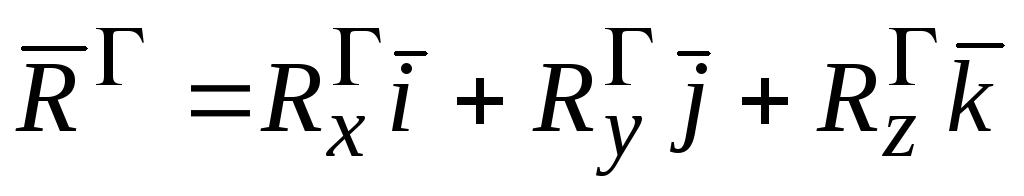 .
(2.13)
.
(2.13)
Сравнивания формулы (3.12) и (3.13), определяем проекции главного вектора системы сил на оси Ox, Оy, Оz:
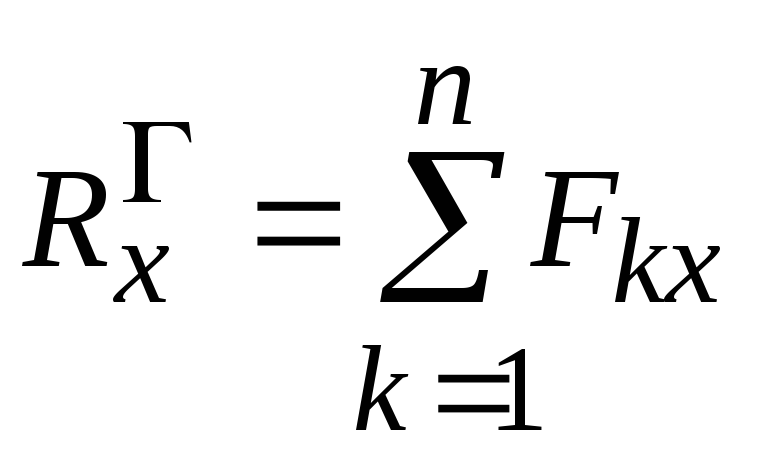 ,
, 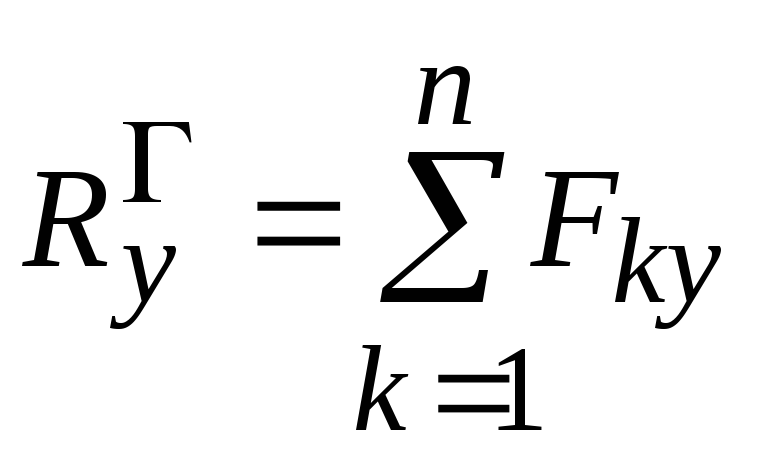 ,
,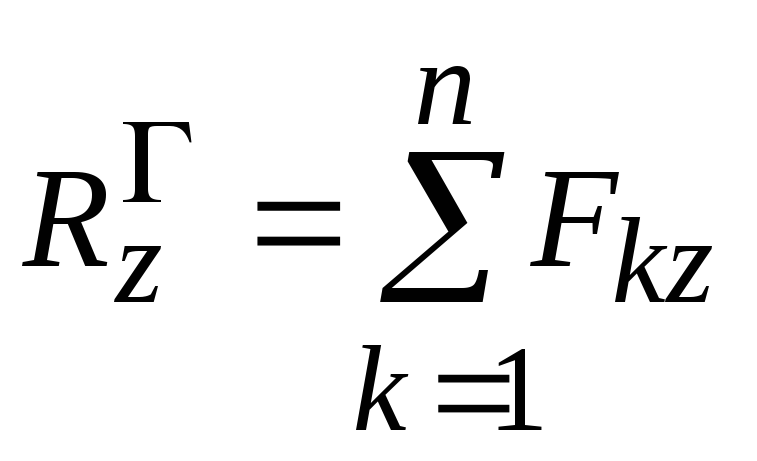 .
.
Тогда по модулю
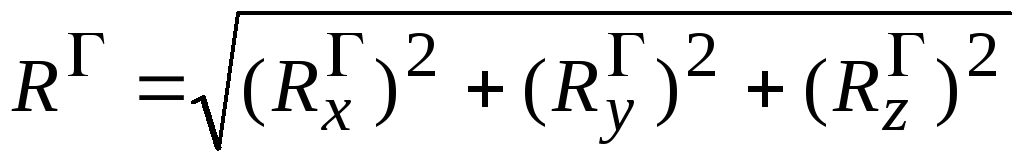 .
(2.14)
.
(2.14)
Направление главного вектора системы сил определяется направляющими векторами:
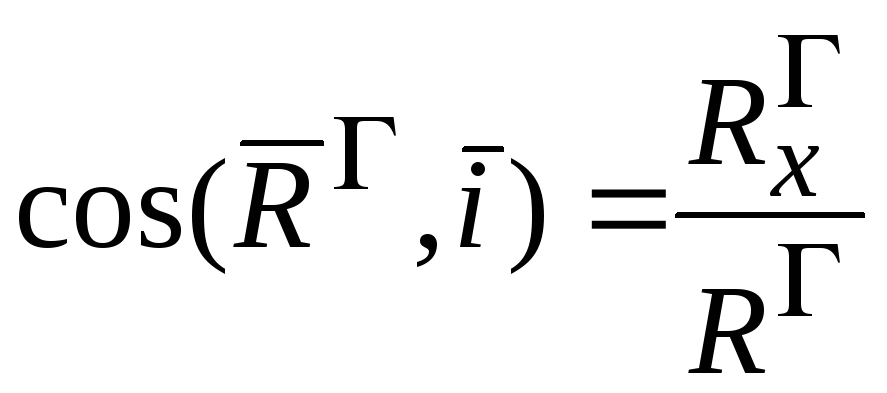 ,
, 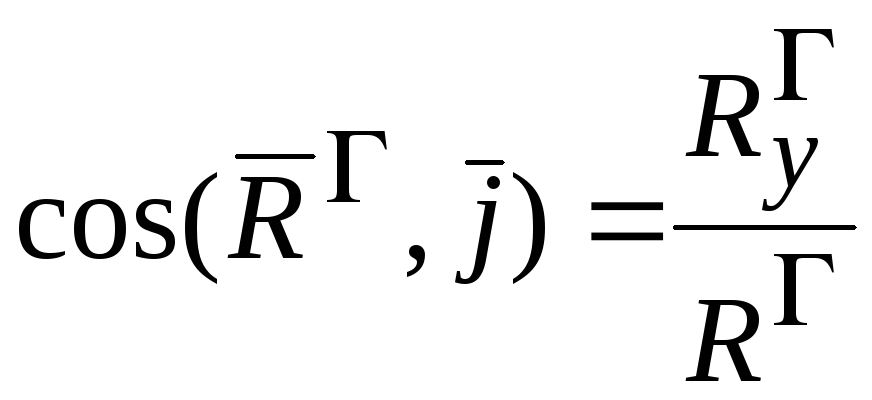 ,
,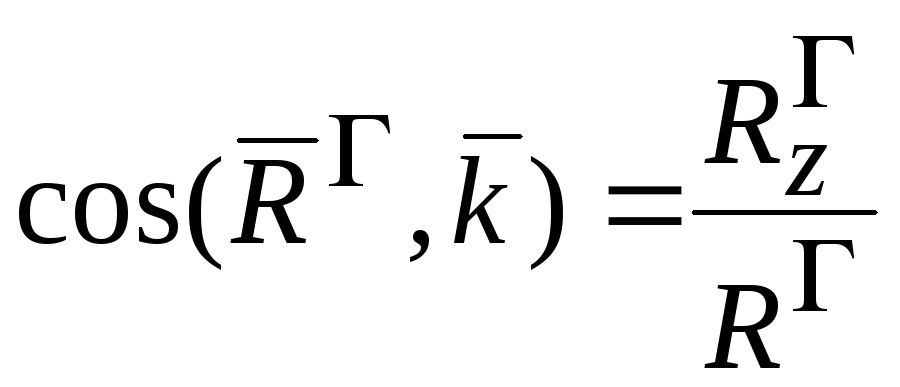 (2.15)
(2.15)
Главный вектор всегда можно найти, в отличие от равнодействующей.
Пример.
Силы
и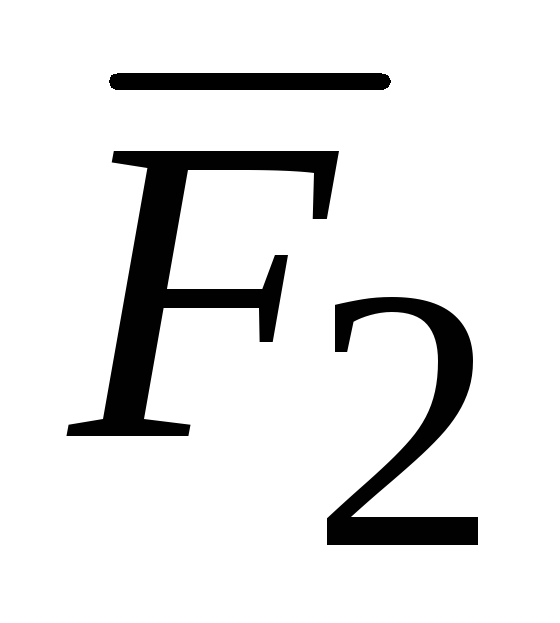 не пересекаются в одной точке,
следовательно, не эквивалентны одной
силе, то есть равнодействующей.
не пересекаются в одной точке,
следовательно, не эквивалентны одной
силе, то есть равнодействующей.
Главный вектор 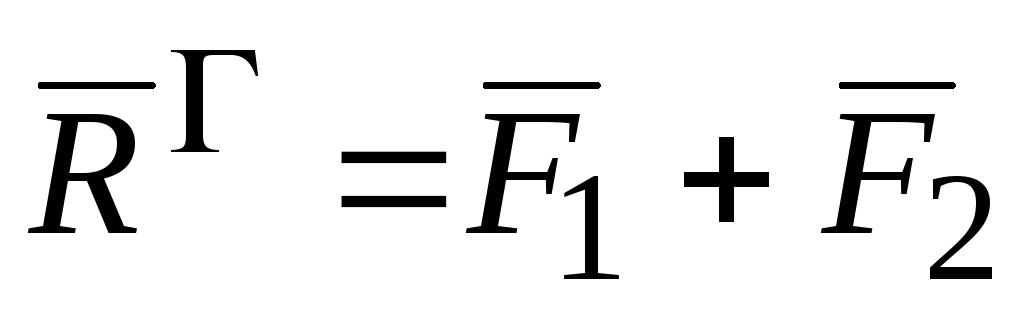 можно взять в любой точке, напримерО (рис.2.7).
можно взять в любой точке, напримерО (рис.2.7).
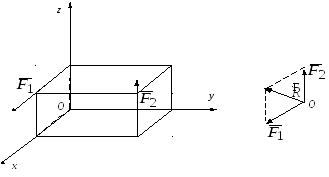 Рис.
2.7
Рис.
2.7
Главный момент системы сил
Пусть имеем систему
сил, действующую на материальный объект 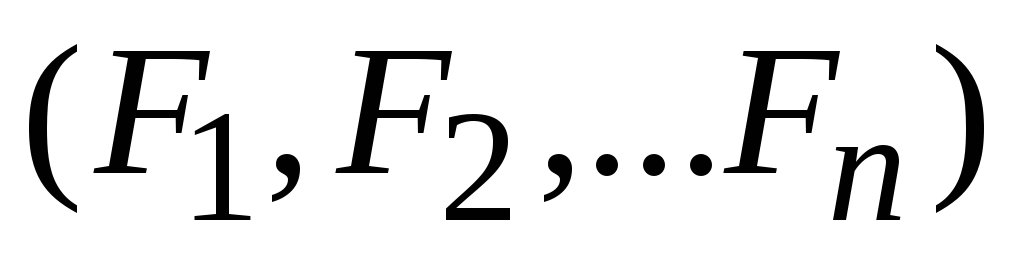 .
Выберем также произвольную, фиксированную
точкуО.
.
Выберем также произвольную, фиксированную
точкуО.
Определение. Главным моментом системы сил относительно некоторой точки О является приложенный в этой точке вектор, равным геометрической сумме моментов всех сил системы относительно этой точки
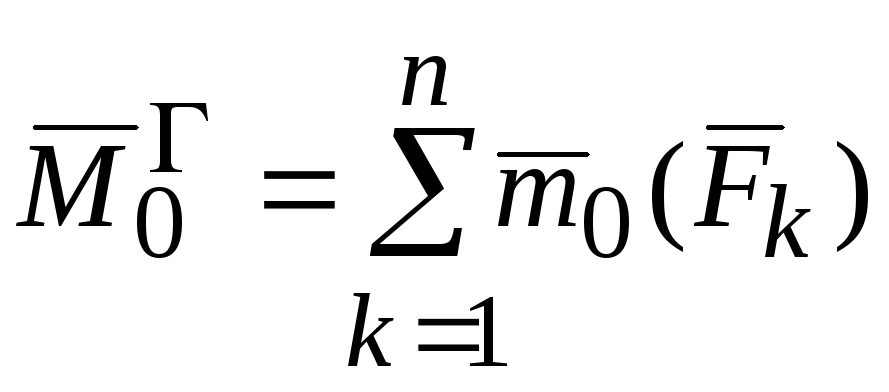 .
(2.16)
.
(2.16)
Способ вычисления главного момента системы сил
В точке О выберем систему координат (рис.2.8). Разложим силы и главный момент системы сил относительно точки О по ортам
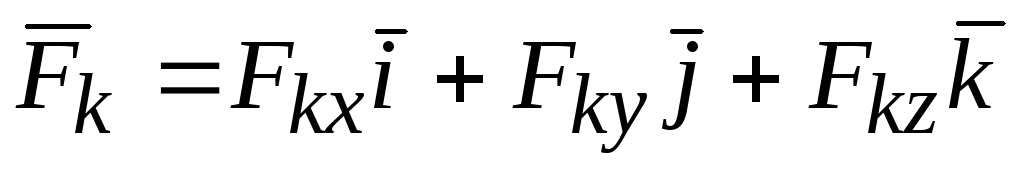 ,
, 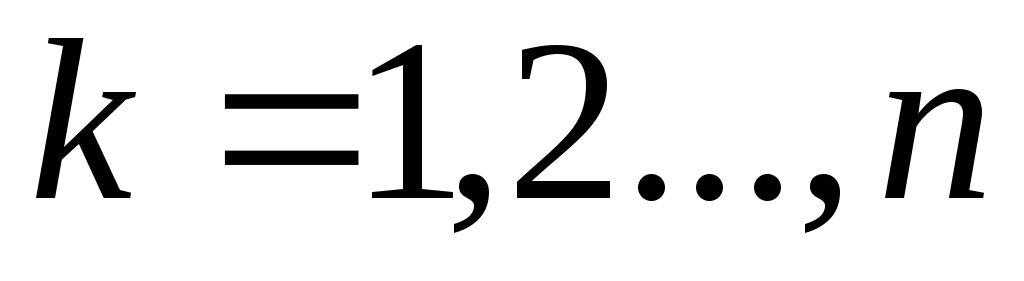 .
.
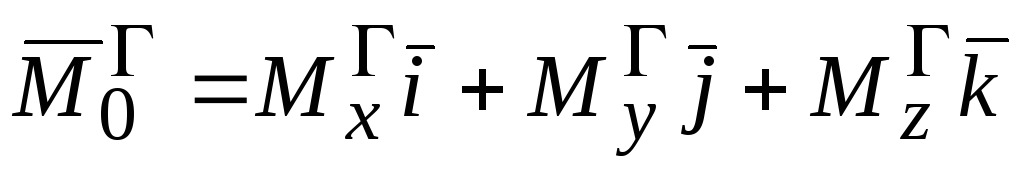 .
(2.17)
.
(2.17)
По определению
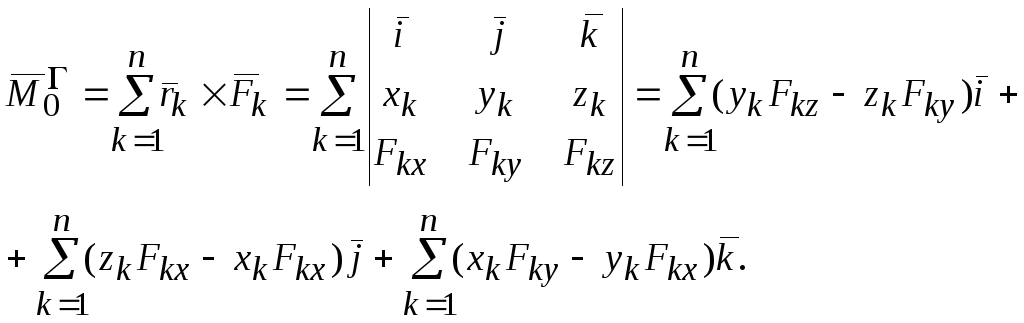 (2.18)
(2.18)

Рис. 2.8
Сравнивая формулы (2.17) и (2.18), получим
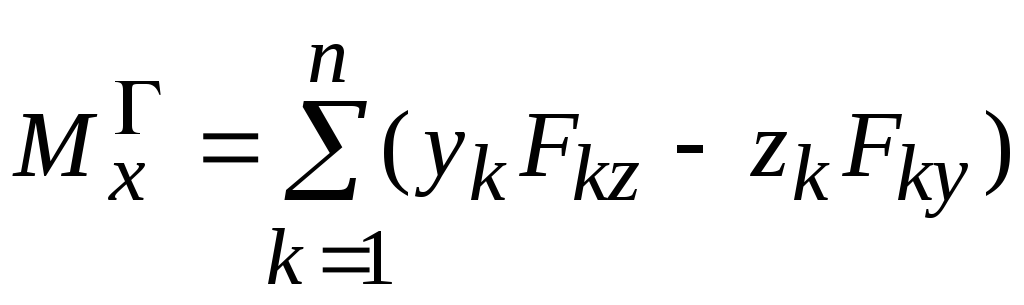 ,
,
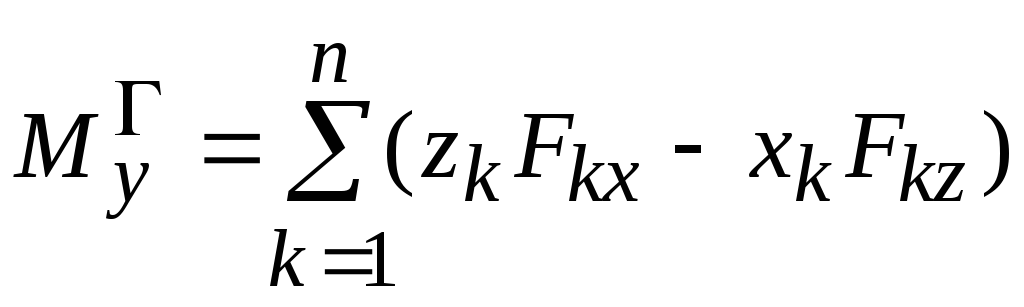 ,
,
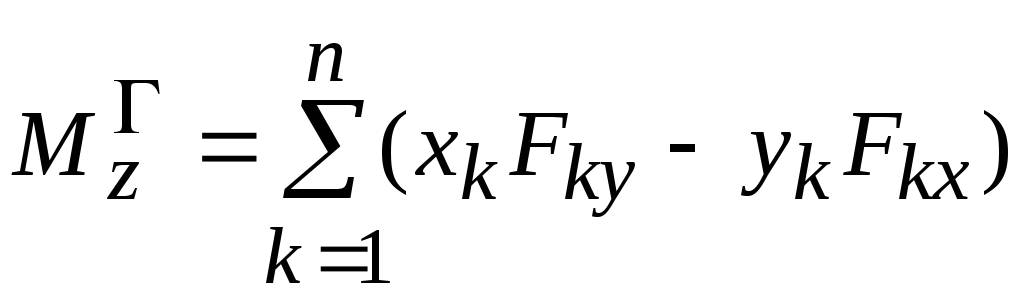 .
.
Тогда модуль главного момента системы сил равен
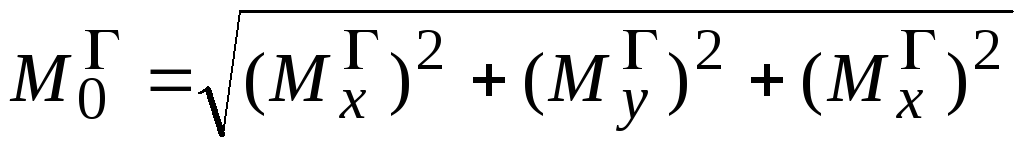 .
.
Направление
главного момента определится направляющими
косинусами 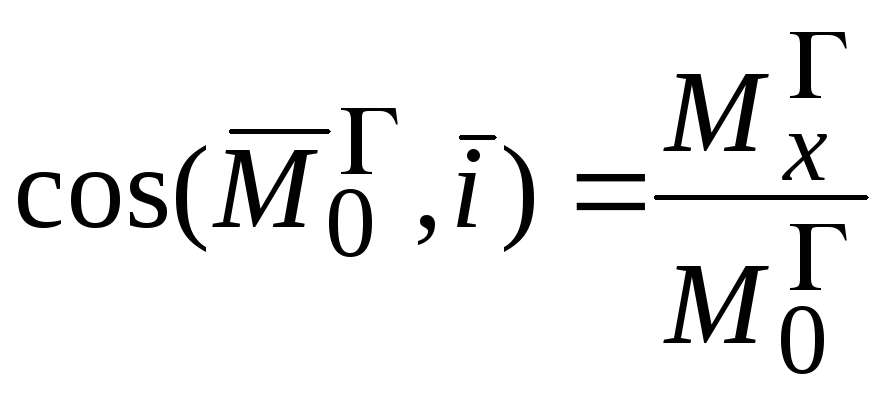 ,
,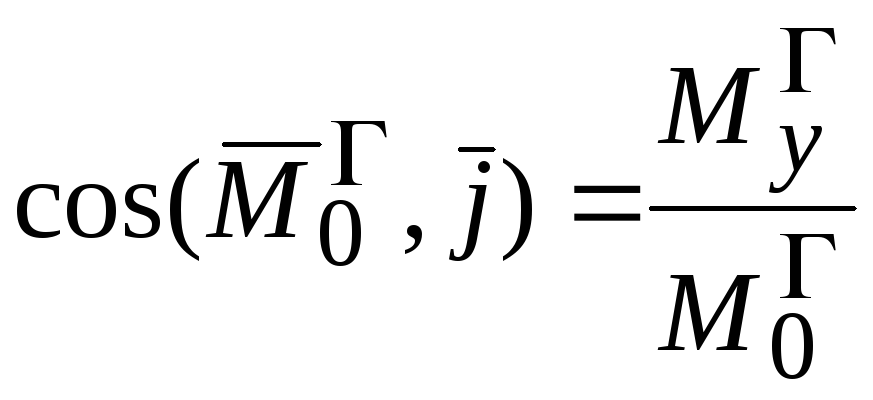 ,
,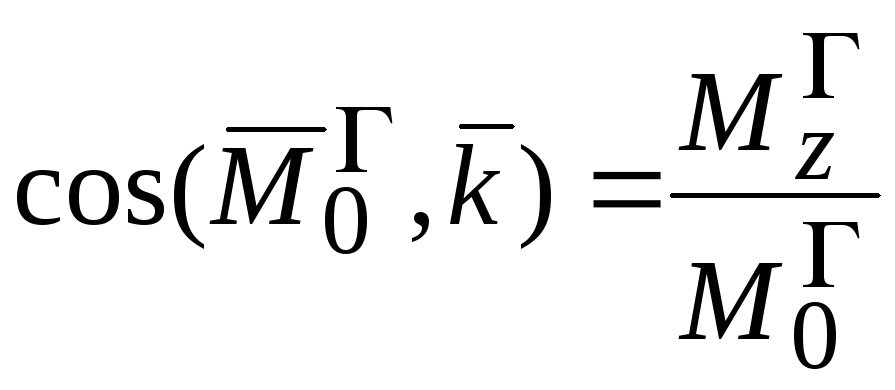 .
.
Главный момент системы сил существенным образом зависит от выбора точки О, в отличие от главного вектора, который от выбора точки О не зависит.
7. Главный вектор и главный момент Главный вектор и главный момент плоской системы сил
Рассмотрим плоскую систему сил (F1, F2, …, Fn),действующих на твердое тело в координатной плоскости Oxy.
Главным вектором системы сил называется вектор R, равный векторной сумме этих сил:
R = F1 + F2 +
… + Fn = 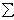 Fi.
Fi.
Для плоской системы сил ее главный вектор лежит в плоскости действия этих сил.
Главным моментом системы сил относительно центра O называется вектор LO, равный сумме векторных моментов этих сил относительно точки О:
LO = MO(F1)
+ MO(F2)
+ … + MO(Fn)
= 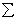 MO(Fi).
MO(Fi).
Вектор R не зависит от выбора центра О, а вектор LO при изменении положения центра О может в общем случае изменяться.
Для плоской системы сил вместо векторного главного момента используют понятие алгебраического главного момента. Алгебраическим главным моментом LO плоской системы сил относительно центра О, лежащего в плоскости действия сил, называют сумму алгебраических моментовэтих сил относительно центра О.
8.Уравнения равновесия плоской системы произвольно расположенных сил
Для равновесия произвольной плоской системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы главный вектор и главный момент этой системы сил равнялись нулю.
Произвольная плоская система сил приводится к главному вектору и главному моменту.
Условия и уравнения равновесия плоской произвольной системы сил
Условия равновесия в векторной форме:
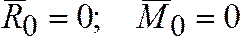 .
.
Первая форма уравнений равновесия:
1. 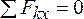 .
.
2. 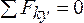 .
.
3. 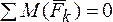 .
.
Третье уравнение составляют относительно произвольной точки. Лучше всего брать точку, в которой имеется больше неизвестных реакций.
Вторая форма уравнений равновесия:
1. 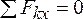 .
.
2. 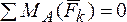 .
.
3. 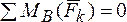 .
.
При использовании второй формы уравнений равновесия необходимо, чтобы ось х не была перпендикулярна прямой АВ.
Третья форма уравнений равновесия:
1. 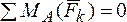 .
.
2. 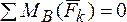 .
.
3. 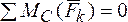 .
.
При использовании третьей формы уравнений равновесия необходимо, чтобы точки А, В, С не лежали на одной прямой.
9.Опоры балок
Балка – это конструктивная деталь в виде прямого бруса, закрепленного на опорах, и изгибаемая приложенными к ней силами.
Высота сечения балки незначительна по сравнению с ее длиной.
Виды нагрузок. По способу приложения нагрузки делятся на сосредоточенные и распределенные. Если реально передача нагрузки происходит на пренебрежимо малой площадке (в точке), нагрузка называется сосредоточенной.
Если нагрузка распределена по значительной площадке или линии (давление воды на плотину, снега на крышу и т. д.), то она является распределенной.
Жесткая заделка (защемление). Опора не допускает перемещений и поворотов. Заделку заменяют двумя составляющими силы RАх и RАу и парой моментов МR.
Шарнирно-подвижная опора. Опора допускает поворот вокруг шарнира и перемещение вдоль опорной поверхности.
Шарнирно-неподвижная опора. Опора допускает поворот вокруг шарнира и может быть заменена двумя составляющими силы вдоль осей координат.
10. Центр тяжести. Статистические моменты площадей

11.Способы задания движения точки
Векторный
При векторном способе задания движения положение точки определяется радиус-вектором, проведенным из неподвижной точки в выбранной системе отсчета.

16. Основная теорема статики о приведении системы сил к заданному центру (теорема Пуансо). Главный вектор и главный момент системы сил.
Всякую пространственную систему сил в общем случае можно заменить эквивалентной системой, состоящей из одной силы, приложенной в какой-либо точке тела (центре приведения) и равной главному вектору данной системы сил, и одной пары сил, момент которой равен главному моменту всех сил относительно выбранного центра приведения.
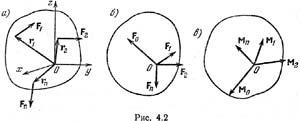
Главным вектором системы сил называется вектор R, равный векторной сумме этих сил:
R = F1 + F2 +
… + Fn = 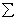 Fi.
Fi.
Для плоской системы сил ее главный вектор лежит в плоскости действия этих сил.
Главным моментом системы сил относительно центра O называется вектор LO, равный сумме векторных моментов этих сил относительно точки О:
LO = MO(F1)
+ MO(F2)
+ … + MO(Fn)
= 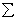 MO(Fi).
MO(Fi).
Вектор R не зависит от выбора центра О, а вектор LO при изменении положения центра О может в общем случае изменяться.
Теорема Пуансо: Произвольную пространственную систему сил можно заменить одной силой главным вектором системы сил и парой сил с главным моментом не нарушая состояния твердого тела. Главный вектор представляет собой геометрическую сумму всех сил действующих на твердое тело и расположен в плоскости действия сил. Главный вектор рассматривается через его проекции на оси координат.
Чтобы привести силы к заданному центру приложенному в некоторой точке твердого тела необходимо: 1) перенести параллельно силу самой себе к заданному центру не изменяя модуля силы; 2) в заданном центре приложить пару сил, векторный момент которой равен векторному моменту перенесенной силы относительного нового центра, эту пару называют присоединенной парой.
Зависимость главного момента от выбора центра приведения. Главный момент относительно нового центра приведения равен геометрической сумме главного момента относительно старого центра приведения и векторного произведения радиуса-вектора, соединяющего новый центр приведения со старым, на главный вектор.
18. Инварианты приведения пространственной системы сил.
Сначала приведем данную систему сил, приложенную к абсолютно твердому
т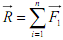 елу,
к центру 0. Тогда получаем эквивалентную
систему, которая характеризуется главным
вектором и главным моментом
елу,
к центру 0. Тогда получаем эквивалентную
систему, которая характеризуется главным
вектором и главным моментом
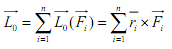
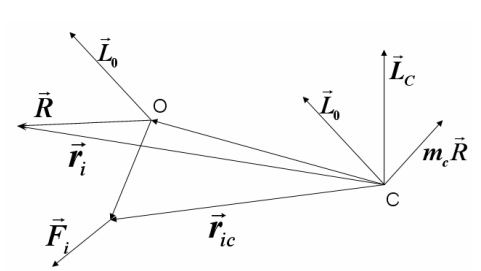
Затем приведем данную систему к новому центру C. Главный вектор системы при этом не изменится. Главный момент изменится, так как относительно нового центра приведения момент каждой из сил системы станет другим. Найдем его изменение.
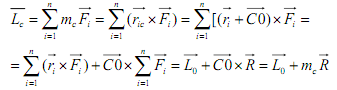
Таким образом, при изменении центра приведения, главный момент изменяется на величину, равную моменту главного вектора относительно нового центра приведения.
Г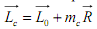 лавный
вектор пространственной системы сил
не изменяется при перемене центра
приведения, т.е. он представляет собой
статический инвариант пространственной
системы сил по отношению к изменению
центра приведения.
лавный
вектор пространственной системы сил
не изменяется при перемене центра
приведения, т.е. он представляет собой
статический инвариант пространственной
системы сил по отношению к изменению
центра приведения.
Спроектируем
равенство на направление главного
вектора R и получим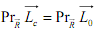
Проекции главных моментов относительно центров приведения O и C на направление главного вектора равны между собой, то есть проекция главного вектора-момента относительно любой точки на направление главного вектора есть второй статический инвариант пространственной системы сил.
Е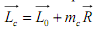 сли
левую и правую части равенства скалярно
умножим на главный вектор R , то
сли
левую и правую части равенства скалярно
умножим на главный вектор R , то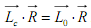
Таким образом, скалярное произведение главного-вектора момента системы относительно любой центра приведения на ее главный вектор дает другое выражение для второго статического инварианта.
Как вычисляются главный вектор и главный момент пространственной системы сил?

центре приведения, и к паре сил с моментом, равным главному моменту всех сил относительно центра приведения.
Модуль и направление главного вектора P определяются по формулам:
P = X 2 +Y 2 + Z 2 ;
cos(P, i )= XP , cos(P, j )= YP , cos(P,k )= ZP ,
X = ∑X k , Y = ∑Yk , Z = ∑Zk .
Модуль и направление главного момента Mo определяется по формулам:
M o =  M x2 + M y2 + M z2 ;
M x2 + M y2 + M z2 ;
|
|
|
|
| M |
|
|
|
|
|
| M y |
|
|
|
|
| M |
|
| |
cos(Mo , i )= | x | , cos(Mo , j )= | , cos(Mo ,k )= | z | , | ||||||||||||||||
| Mo |
| |||||||||||||||||||
|
|
|
|
| Mo |
|
|
|
|
|
|
|
|
|
| Mo |
| ||||
M x = ∑(yk Zk − zkYk ), M y ∑(zk X k − xk Zk ), M z = ∑(xkYk − yk X k ).
Каковы условия равновесия произвольной пространственной системы сил?
Равновесию произвольной пространственной системы сил соответствуют два условия равновесия
M = Mo = 0 , P = 0 ,
которым соответствуют шесть уравнений равновесия
∑X k = 0 , ∑Yk = 0, ∑Zk = 0,
∑M k x = 0 , ∑M k y = 0, ∑M kz = 0
Каковы условия равновесия пространственной системы параллельных сил?
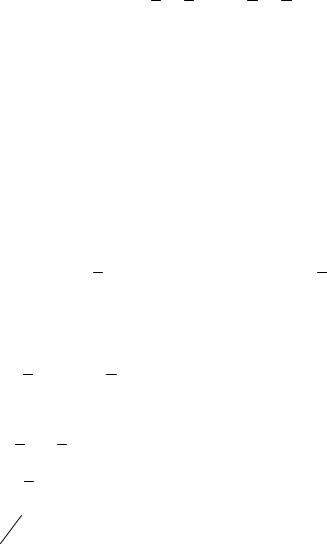
OK = M P
Равновесию пространственной системы параллельных сил соответствуют три условия равновесия:
∑Zk = 0, ∑M k x = 0 , ∑M k y = 0.
Как формулируется теорема Вариньона для пространственной системы мил?
Момент равнодействующей относительно любой точки равен геометрической сумме моментов составляющих сил относительно этой точки, а момент равнодействующей силы относительно любой оси равен алгебраической сумме моментов составляющих сил относительно этой оси.
MO (R)= ∑MO (Fk ).
k
К какому простейшему виду можно привести пространственную систему сил, если главный момент относительно различных точек:
а) имеет одно и то же значение, не равное нулю;
б) равен нулю;
в) имеет различные значения и перпендикулярен к главному вектору;
г) имеет различные значения и не перпендикулярен главному вектору?
а) В случае, если Mo = const , главный вектор P = 0 и силы приводятся к паре сил с моментом равным главному моменту заданных сил относительно центра приведения.
б) Если Mo = 0 , а P ≠ 0 , силы приводятся к равнодействующей силе,
линия действия которой проходит через центр приведения.
в) Если Mo P , силы приводятся к равнодействующей равной главному вектору P и приложенной в точке K , находятся на расстоянии
от точки O .

г) Если Mo не перпендикулярен P , систему сил можно привести к сило-
вому винту – динаме, представляющей собой совокупность силы и пары сил расположенной в плоскости, перпендикулярной к линии действия этой силы, с моментом равным:
M * = Mo cos(Mo , P )= P PMo .
Назовите инварианты системы сил.
а) Главный вектор данной системы сил инвариантен по отношению к центру приведения.
б) Скалярное произведение главного вектора на главный момент данной системы сил инвариантно по отношению к центру приведения:
P Mo = const .
в) Проекция главного момента системы сил относительно любого центра на направление главного вектора есть величина постоянная:
|
|
|
|
|
|
|
|
|
|
|
| ). |
|
|
|
|
|
| |||
|
|
|
|
|
| M | * = M | o cos(M | o , | P |
|
|
|
|
|
| |||||
Запишите уравнение центральной оси системы. |
|
|
|
|
|
| |||||||||||||||
| M | x | −(yZ − zY ) | = | M y −(zX − xZ ) | = | M | z | −(xY − yX ) | = | M | * | . | ||||||||
|
|
| X |
|
|
| Y |
|
|
|
|
| Z |
| R |
| |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||
Что называется параметром динамы?
Постоянная линейная величина, равная p = MP* = P PM2 o , называется па-
раметром винта или динамы.
Каким свойством обладает центр тяжести?
Сила, с которой тело притягивается к Земле, называется центром тяжести. Направление сил притяжения отдельных частиц тела к Земле практически параллельны между собой. Равнодействующая этих параллель-

ных сил, равная их сумме, есть вес тела, а центр этой системы сил, в котором приложен вес тела, называется центром тяжести. В твердом теле центр тяжести не зависит от расположения тела в пространстве.
По каким формулам вычисляется положение центра тяжести однородного тела?
Радиус-вектор и координаты центра тяжести однородного тела определяются по формулам:
r = | ∑rk Pk | или x | = | ∑xk Pk |
| y | = | ∑yk Pk | , z |
| = | ∑zk | Pk | |
k | k | , | k | c | k |
| , | |||||||
|
|
|
|
| ||||||||||
c | P | c |
| P |
| c |
| P |
|
| P |
|
| |
|
|
|
|
|
|
|
|
|
|
| ||||
где rk , xk , yk , zk — радиус-векторы и координаты центров тяжести от-
дельных частей тела.
По каким формулам определяются координаты объема тела, плоских фигур к линии?
Координаты объёма тела определяются по формулам:
r = | 1 |
| r dV или x = | 1 |
| x dV , y = | 1 |
| y dV , z = | 1 |
| z dV . | |
V V∫ | V V∫ | V V∫ | V V∫ | ||||||||||
c | c | c | c |
| |||||||||
|
|
|
|
|
|
|
|
| |||||
Координаты центра тяжести пластинок (плоских фигур) определяются по формулам:
rc = S1 ∫S r dS или xc = S1 ∫S x dS , yc = S1 ∫S y dS .
Координаты центра тяжести линий определяются по формулам:
rc = | 1 | ∫r dAk | или xc = | 1 | ∫x dA, | yc = | 1 | ∫y dA, | zc = | 1 | ∫z dA. |
| A | A |
| A | A |
| A | A |
| A | A |
Что называется статическим моментом площади плоской фигуры относительно оси? Как он вычисляется и какую размерность имеют?
4.5. Главный момент системы сил
Определение.Главным
моментом системы сил относительно
полюса  называется геометрическая сумма моментов
всех сил системы относительно этого
полюса.
называется геометрическая сумма моментов
всех сил системы относительно этого
полюса.
Обозначение: 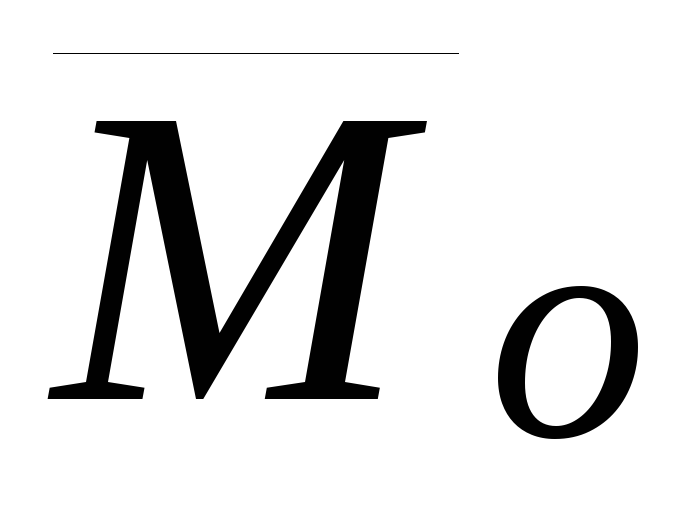 ,
или
,
или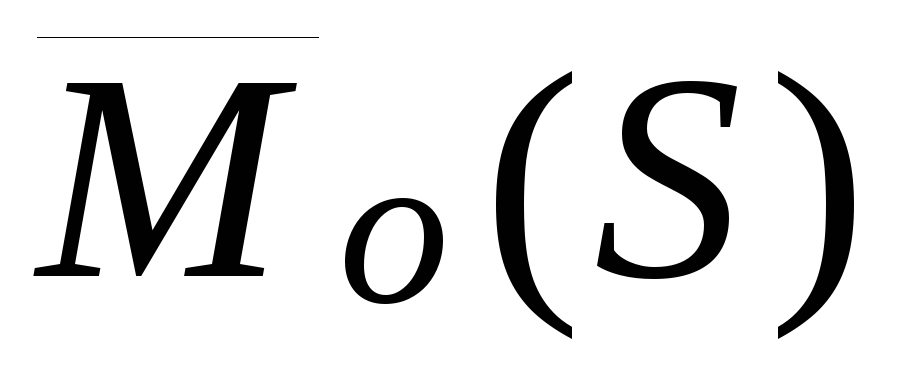 .
Если задана система сил
.
Если задана система сил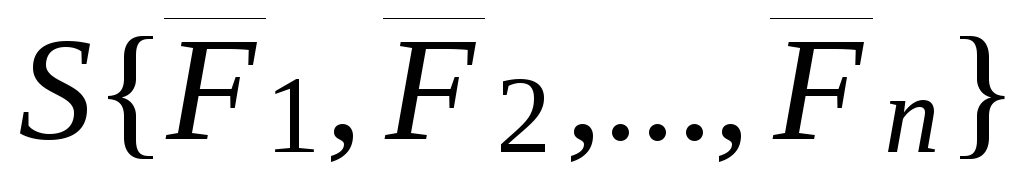 ,
то
,
то
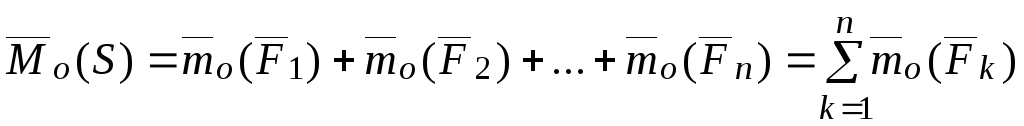 .
.
Определение.Главным
моментом системы сил относительно оси  называется алгебраическая сумма
моментов всех сил системы относительно
этой оси.
называется алгебраическая сумма
моментов всех сил системы относительно
этой оси.
Обозначение: 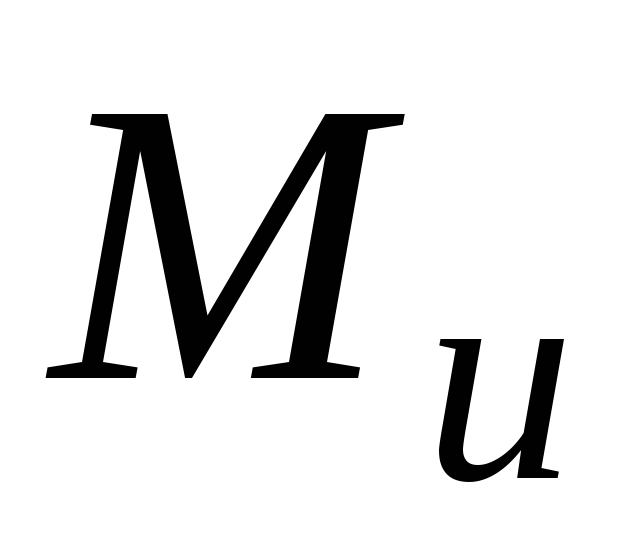 ,
или
,
или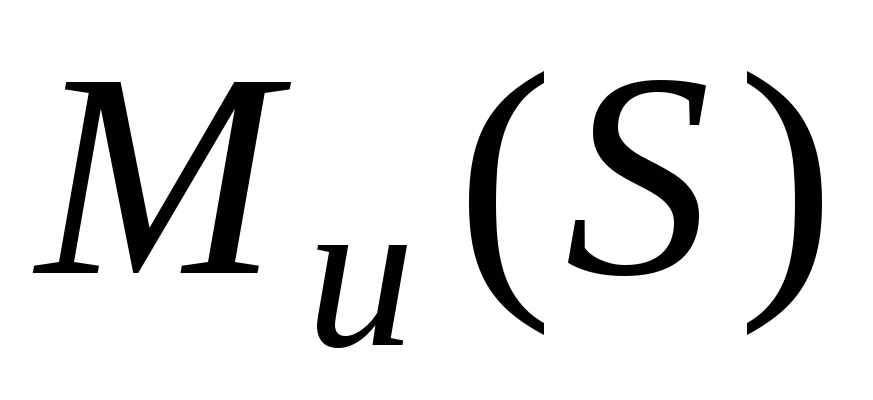
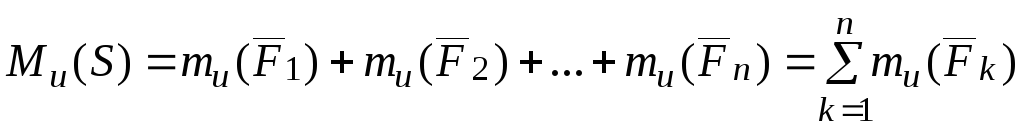 .
.
Теорема.Проекция
главного момента системы сил относительно
полюса  на ось
на ось ,
проходящую через этот полюс, равна
главному моменту сил системы относительно
этой оси, то есть
,
проходящую через этот полюс, равна
главному моменту сил системы относительно
этой оси, то есть
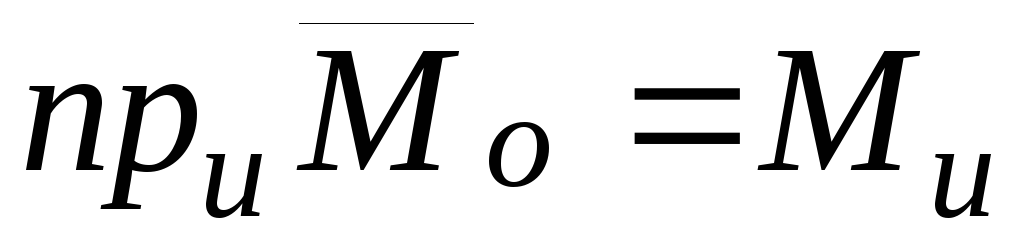 .
.
Доказательство:
Главный
момент системы сил 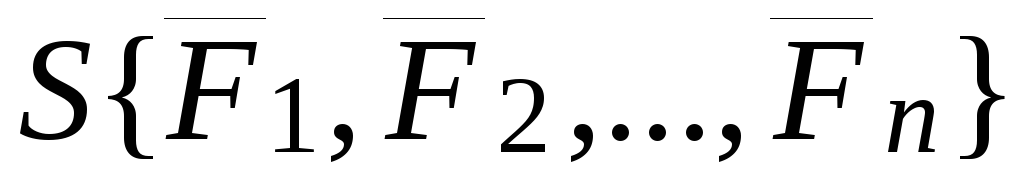 относительно полюса
относительно полюса 
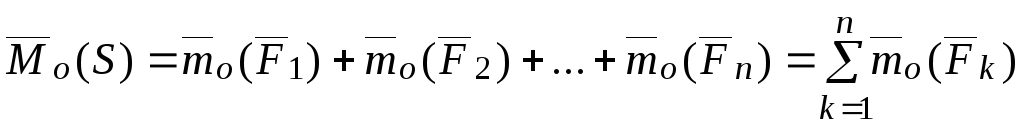 .
.
Спроектируем это
векторное равенство на ось  ,
проходящую через полюс
,
проходящую через полюс  :
:
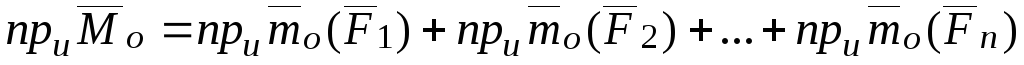 .
.
На основании теоремы о связи между моментом силы относительно полюса и моментом силы относительно оси
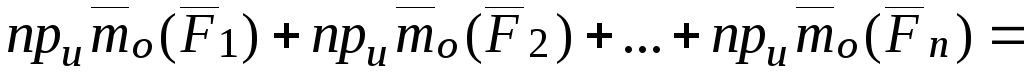
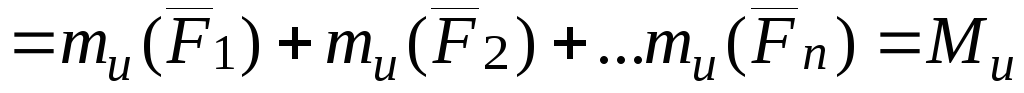 .
.
Следовательно 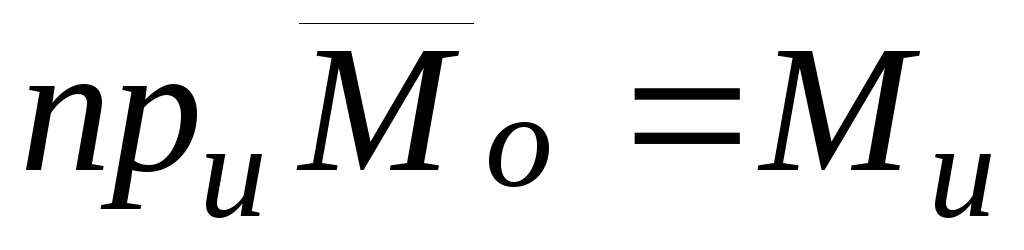 .
.
4.6. Зависимость между главными моментами системы сил относительно двух полюсов
Дана
система сил 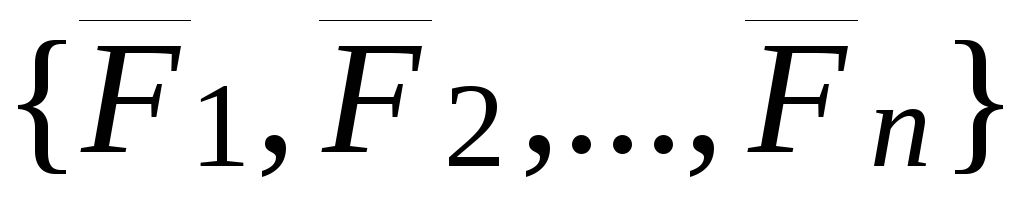 и два полюса: старый
и два полюса: старый  и новый
и новый 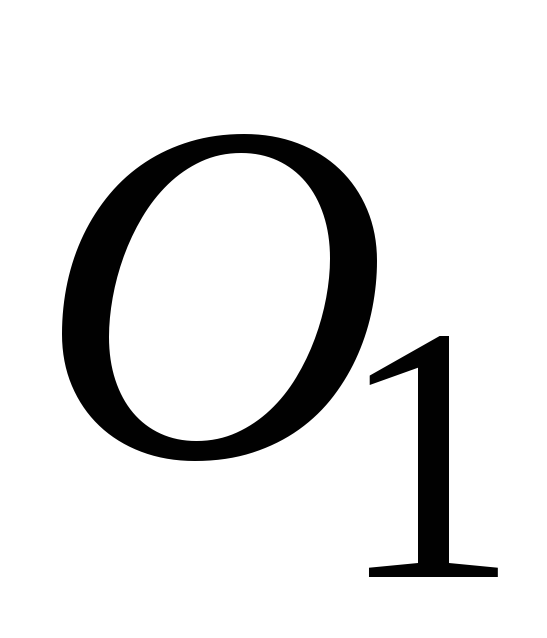 (рис. 23).
(рис. 23).
Главный момент системы сил относительно старого полюса:
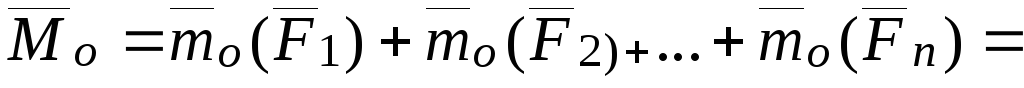
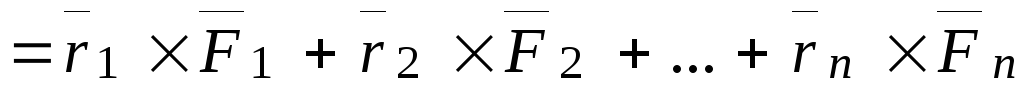 .
.
Главный момент относительно нового полюса:
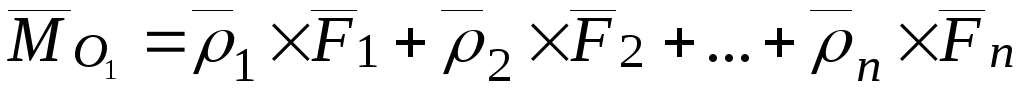 .
.
Здесь 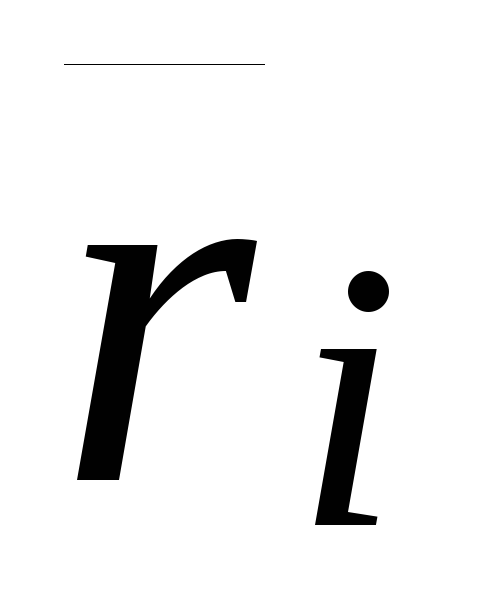 и
и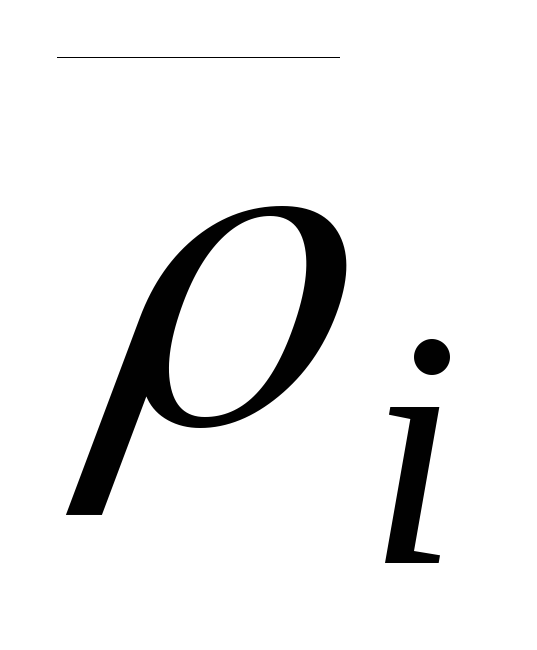 (
(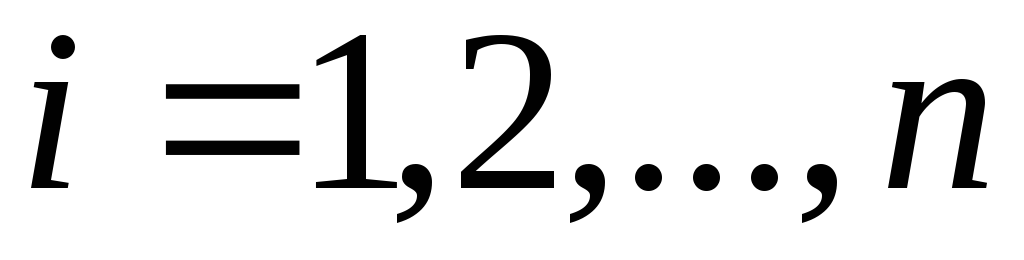 )–радиус-векторы
точки приложения силы
)–радиус-векторы
точки приложения силы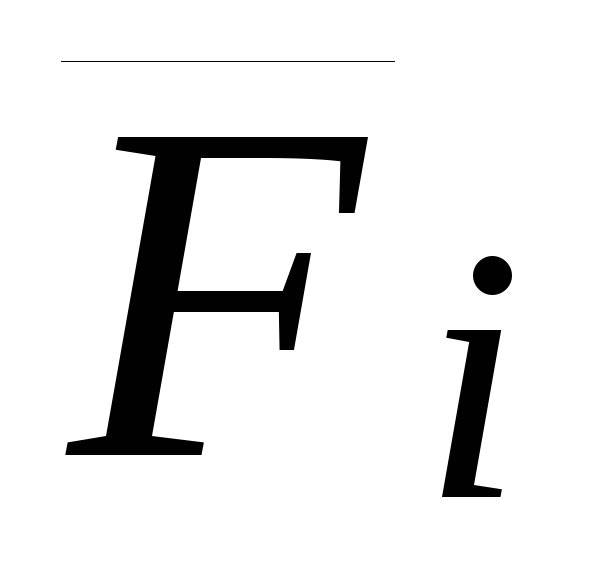 относительно старого и нового полюсов
соответственно.
относительно старого и нового полюсов
соответственно.
Из рисунка видно, что:
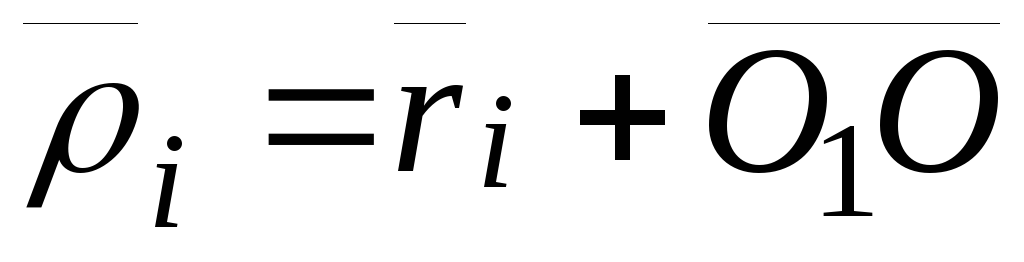
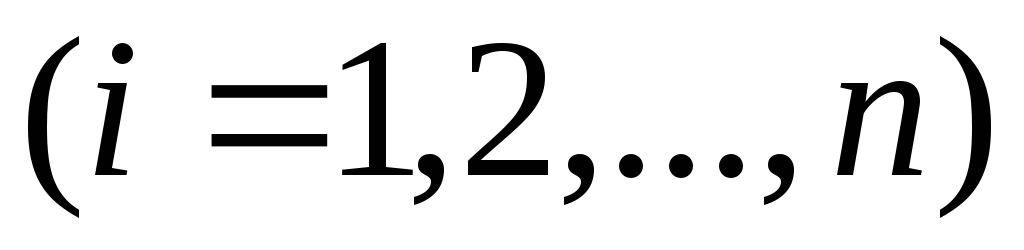 .
.
Тогда
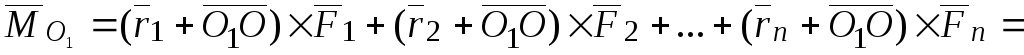
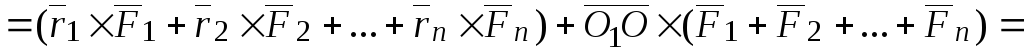
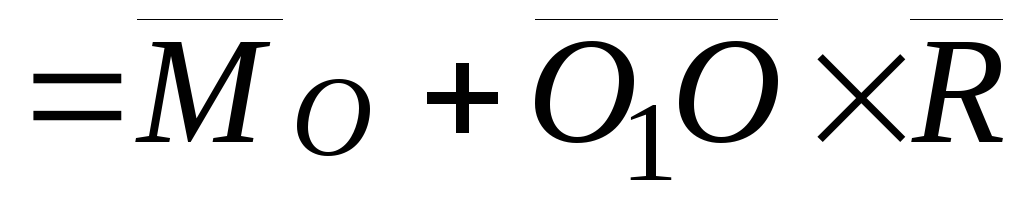 ,
,
где  –главный
вектор. Пришли к теореме о зависимости
между главными моментами системы сил
относительно двух полюсов.
–главный
вектор. Пришли к теореме о зависимости
между главными моментами системы сил
относительно двух полюсов.
Теорема.Главный момент системы сил относительно нового полюса равен сумме главного момента системы сил относительно старого полюса и момента главного вектора, приложенного к старому полюсу относительно нового –полюса, то есть
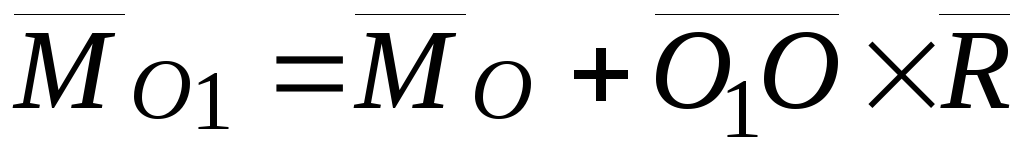 .
.
Следствие
1.Если главный вектор системы
сил равен нулю, то ее главный момент не
зависит от выбора полюса, то есть, если 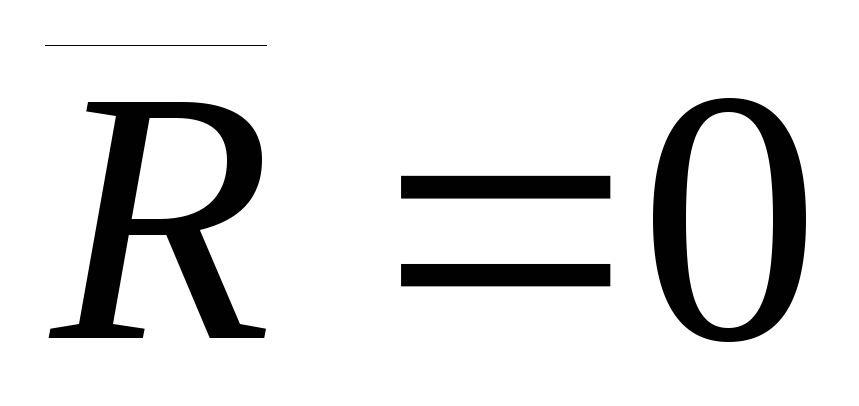 ,
то
,
то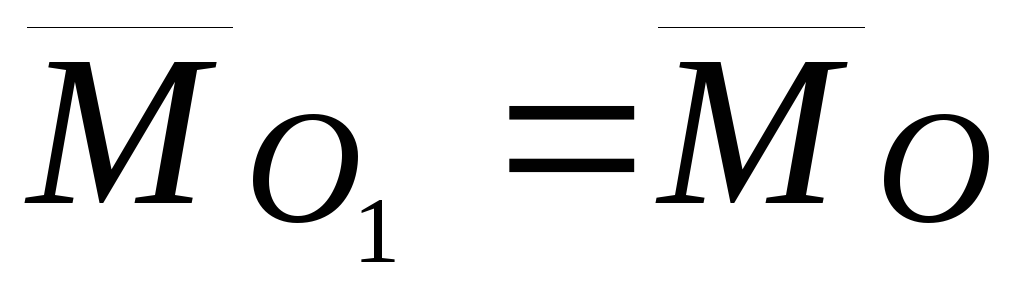 .
.
С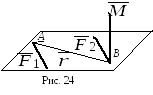 ледствие
2. Главный момент
пары сил не зависит от выбора полюса и
отличен от нуля.
ледствие
2. Главный момент
пары сил не зависит от выбора полюса и
отличен от нуля.
Дана
пара сил {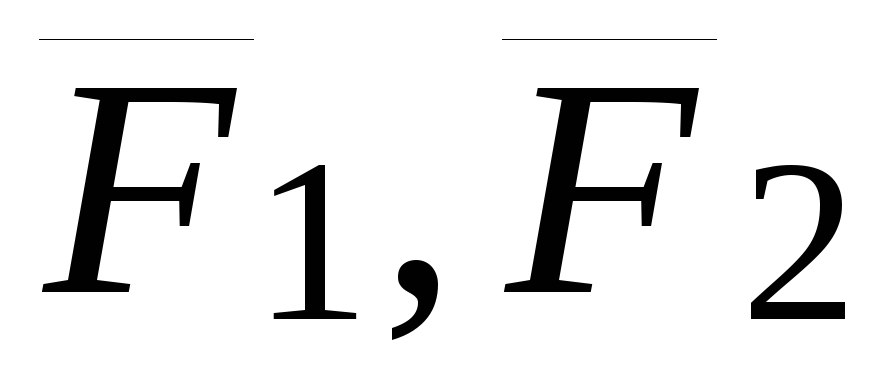 }
(рис. 24).
}
(рис. 24).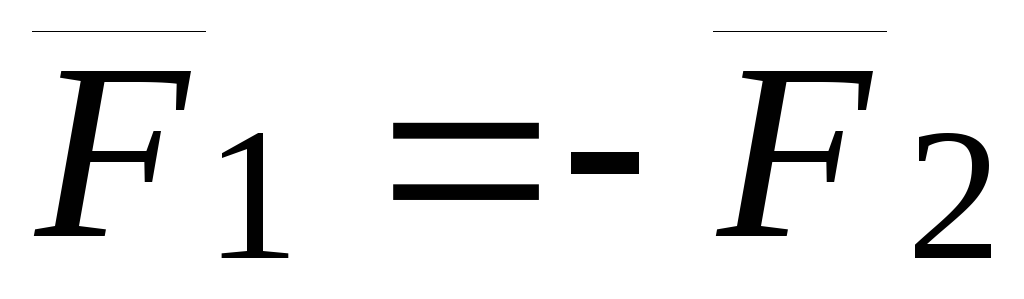 ,
,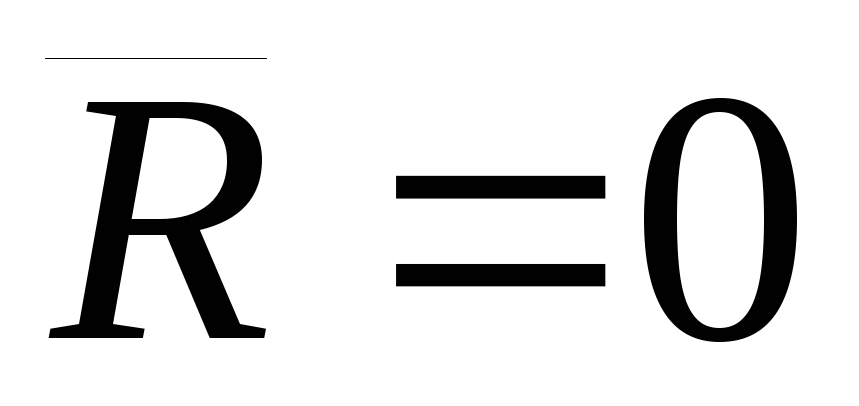 .
Так как главный вектор
.
Так как главный вектор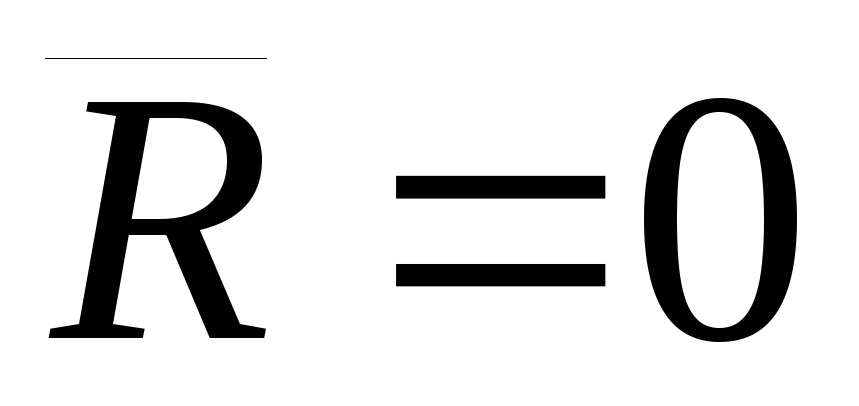 .
То главный момент пары не зависит от
выбора полюса:
.
То главный момент пары не зависит от
выбора полюса:
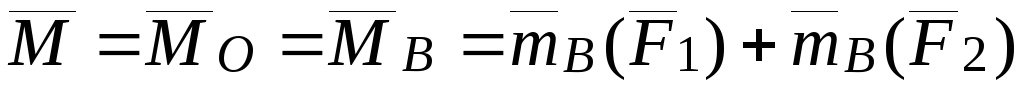 .
.
Линия
действия силы 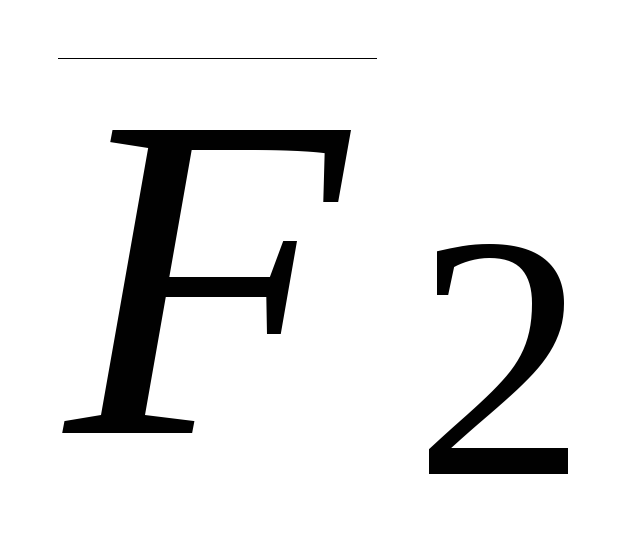 проходит через полюс
проходит через полюс ,
то есть
,
то есть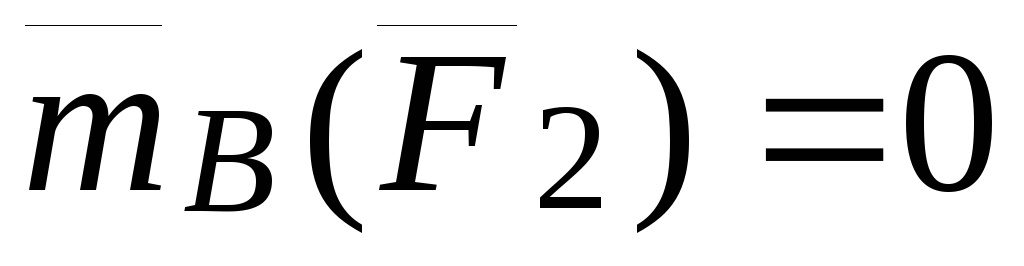 ,
и:
,
и:
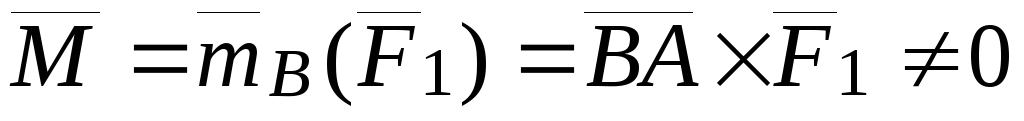 .
.
4.7. Теорема Вариньона (частный случай)
Т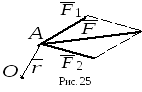 еорема.Если
две силы и их геометрическая сумма
приложены в одной точке, то геометрическая
сумма моментов этих двух сил относительно
произвольного полюса равна моменту их
геометрической суммы относительно того
же полюса.
еорема.Если
две силы и их геометрическая сумма
приложены в одной точке, то геометрическая
сумма моментов этих двух сил относительно
произвольного полюса равна моменту их
геометрической суммы относительно того
же полюса.
Дано: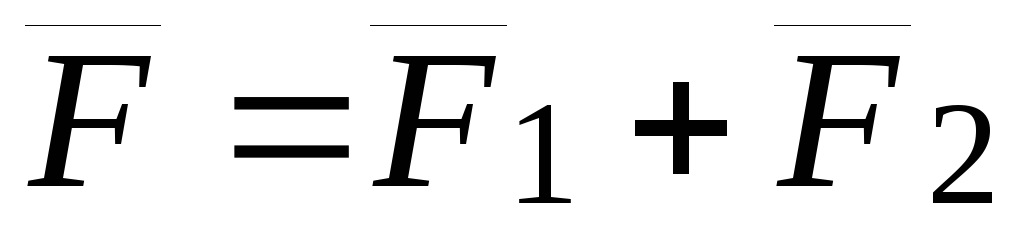 (рис.
25).
(рис.
25).
Доказать: 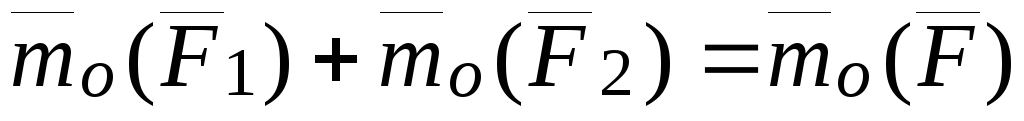 .
.
Доказательство:
Исходя из представления момента силы относительно полюса через векторное произведение:
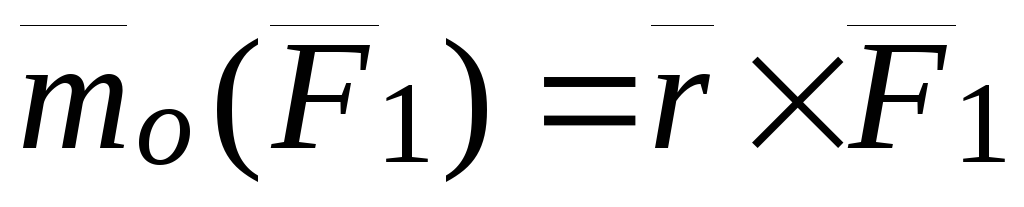 ,
, 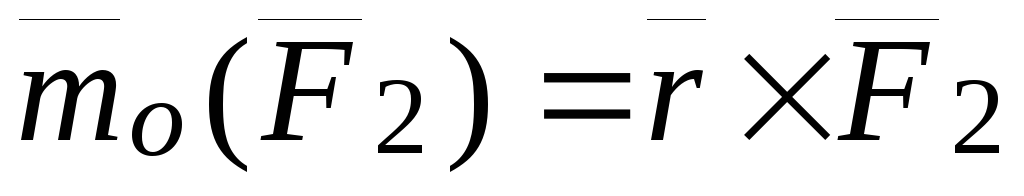 .
.
Тогда
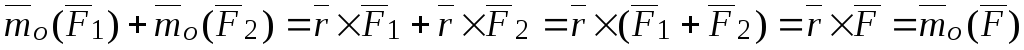 .
.
Элементарные операции статики. Эквивалентные системы сил
Элементарные операции статики
Пусть
к твердому телу приложена система сил 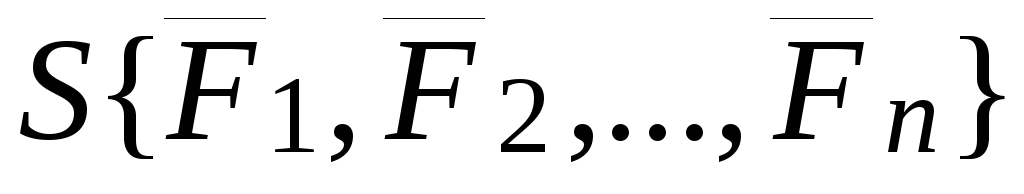 .Элементарными операциями статики называют следующие четыре операции
над силами:
.Элементарными операциями статики называют следующие четыре операции
над силами:
Добавление к системе сил
 двух прямопротивоположных сил.
двух прямопротивоположных сил.Отбрасывание от системы сил
 двух прямопротивоположных сил (если
таковые имеются).
двух прямопротивоположных сил (если
таковые имеются).Замена двух сил (в системе
 ),
приложенных к одной точке (если таковые
имеются) одной силой, равной их
геометрической сумме и приложенной к
этой же точке ( коротко: замена двух
сил, приложенных к одной точке, одной
силой по правилу параллелограмма).
),
приложенных к одной точке (если таковые
имеются) одной силой, равной их
геометрической сумме и приложенной к
этой же точке ( коротко: замена двух
сил, приложенных к одной точке, одной
силой по правилу параллелограмма).Замена любой силы системы
 двумя составляющими силами, полученными
путем разложения этой силы по правилу
параллелограмма.
двумя составляющими силами, полученными
путем разложения этой силы по правилу
параллелограмма.
Первое свойство элементарных операций (физическое свойство).
Элементарные операции над силами, приложенными к твердому телу, не нарушают состояние равновесия тела.
Справедливость этого свойства следует из 2-й и 3-й аксиом статики.
Второе свойство элементарных операций (геометрическое свойство)
Элементарные операции над силами не изменяют главный вектор и главный момент системы сил.
Неизменность главного вектора проверяется непосредственно путем анализа влияния каждой элементарной операции на геометрическую сумму векторов сил системы.
Добавление либо отбрасывание двух прямопротивоположных сил не изменяет главный момент системы сил относительно полюса потому, что сумма моментов двух прямопротивоположных сил относительно одного и того же полюса равна нулю.
Замена по правилу параллелограмма двух сил, приложенных к одной точке, их геометрической суммой, либо замена одной силы ее двумя составляющими, не изменяют главный момент системы сил вокруг полюса по теореме Вариньона (частный случай).


 двух прямопротивоположных сил.
двух прямопротивоположных сил. двух прямопротивоположных сил (если
таковые имеются).
двух прямопротивоположных сил (если
таковые имеются). ),
приложенных к одной точке (если таковые
имеются) одной силой, равной их
геометрической сумме и приложенной к
этой же точке ( коротко: замена двух
сил, приложенных к одной точке, одной
силой по правилу параллелограмма).
),
приложенных к одной точке (если таковые
имеются) одной силой, равной их
геометрической сумме и приложенной к
этой же точке ( коротко: замена двух
сил, приложенных к одной точке, одной
силой по правилу параллелограмма). двумя составляющими силами, полученными
путем разложения этой силы по правилу
параллелограмма.
двумя составляющими силами, полученными
путем разложения этой силы по правилу
параллелограмма.