Векторное произведение векторов.
Векторное произведение векторов.Навигация по странице:
- Определение векторного произведения векторов
- Формулы вычисления векторного произведения векторов
- Свойства векторного произведения векторов
- Примеры задач на вычисления векторного произведения векторов
Онлайн калькулятор. Векторное произведение векторов.
Упражнения на тему векторное произведение векторов.
Определение. Векторным произведением вектора a на вектор b называется вектор c, длина которого численно равна площади параллелограмма построенного на векторах a и b, перпендикулярный к плоскости этих векторов и направленный так, чтоб наименьшее вращение от a к b вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора c (рис. 1).
| рис. 1 |
Формулы вычисления векторного произведения векторов
Векторное произведение
a × b = ijkaxayazbxbybz = i (aybz — azby) — j (axbz — azbx) + k (axby — aybx)
a × b = {aybz — azby; azbx — axbz; axby — aybx
Свойства векторного произведения векторов
Геометрический смысл векторного произведения.

Модуль векторного произведения двух векторов a и b равен площади параллелограмма построенного на этих векторах:
Sпарал = [a × b]
Геометрический смысл векторного произведения.
Площадь треугольника построенного на векторах a и b равна половине модуля векторного произведения этих векторов:
SΔ = 1 |a × b| 2 Векторное произведения двух не нулевых векторов a и b равно нулю тогда и только тогда, когда вектора коллинеарны.
Вектор c, равный векторному произведению не нулевых векторов a и b, перпендикулярен этим векторам.
a × b = -b × a
(k a) × b = a × (k b) = k (a × b)
(a + b) × c = a × c + b × c
Примеры задач на вычисления векторного произведения векторов
Пример 1.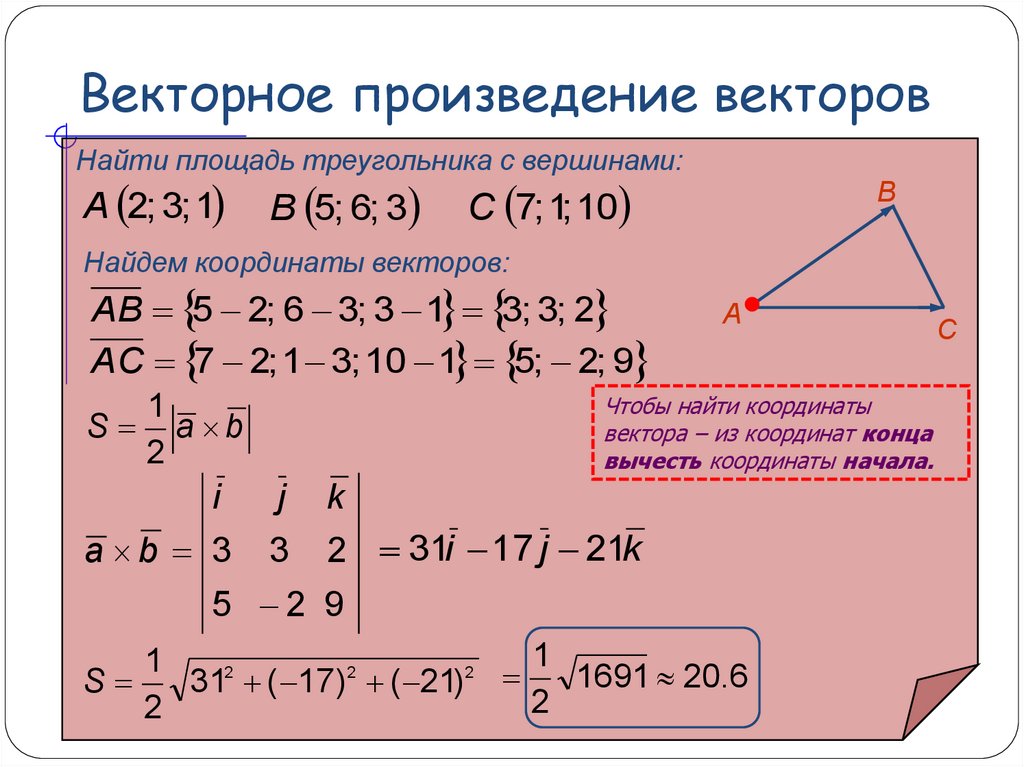 Найти векторное произведение векторов a = {1; 2; 3} и b = {2; 1; -2}.
Найти векторное произведение векторов a = {1; 2; 3} и b = {2; 1; -2}.
Решение:
| a × b = | i | j | k | = |
| 1 | 2 | 3 | ||
| 2 | 1 | -2 |
= i(2 · (-2) — 3 · 1) — j(1 · (-2) — 2 · 3) + k(1 · 1 — 2 · 2) =
= i(-4 — 3) — j(-2 — 6) + k(1 — 4) = -7i + 8j — 3k = {-7; 8; -3}
Пример 2. Найти площадь треугольника образованного векторами a = {-1; 2; -2} и b = {2; 1; -1}.
Решение: Найдем векторное произведение этих векторов:
| a × b = | i | j | k | = |
| -1 | 2 | -2 | ||
| 2 | 1 | -1 |
= i(2 · (-1) — (-2) · 1) — j((-1) · (-1) — (-2) · 2) + k((-1) · 1 — 2 · 2) =
= i(-2 + 2) — j(1 + 4) + k(-1 — 4) = -5j — 5k = {0; -5; -5}
Из свойств векторного произведения:
SΔ =
12|a × b| =
12√02 + 52 + 52 =
12√25 + 25 =
12√50 =
5√22 = 2. 5√2
5√2
Ответ: SΔ = 2.5√2.
Вектора Вектор: определение и основные понятия Определение координат вектора заданного координатами его начальной и конечной точки Модуль вектора. Длина вектора Направляющие косинусы вектора Равенство векторов Ортогональность векторов Коллинеарность векторов Компланарность векторов Угол между векторами Проекция вектора Сложение и вычитание векторов Умножение вектора на число Скалярное произведение векторов Векторное произведение векторов Смешанное произведение векторов Линейно зависимые и линейно независимые вектора Разложение вектора по базису
Онлайн калькуляторы с векторами
Онлайн упражнения с векторами на плоскости
Онлайн упражнения с векторами в пространстве
Векторное произведение векторов. Определение и его смысл
Данная операция определена для двух пространственных векторов, пусть это будут нетленные буквы .
Обозначение: , существуют и другие варианты
И сразу вопрос: в чём отличие векторного произведения от произведения скалярного? Явное отличие, прежде всего, в РЕЗУЛЬТАТЕ:
– Результатом скалярного произведения векторов является ЧИСЛО:
– Результатом векторного произведения векторов является ВЕКТОР:
, то есть, умножаем векторы и получаем снова вектор.
В учебной литературе обозначения тоже могут варьироваться, я буду использовать букву .
Разберём определение «по косточкам»:
1) Исходные векторы , обозначенные красными
стрелками, не коллинеарны.
2) Векторы взяты
3)Геометрический смысл векторного произведения. Это очень важный пункт! ДЛИНА «синего» вектора численно равна ПЛОЩАДИ параллелограмма, построенного на векторах . На рисунке данный параллелограмм заштрихован чёрным цветом. Длина «малинового» вектора , естественно, равна этой же площади.
Примечание: чертёж является схематическим, и поэтому номинальная длина векторного произведения не равна площади параллелограмма.
Вспоминаем одну из геометрических формул: площадь параллелограмма равна произведению смежных сторон на синус угла между ними. Поэтому,
исходя из вышесказанного, справедлива формула вычисления ДЛИНЫ векторного произведения:
Поэтому,
исходя из вышесказанного, справедлива формула вычисления ДЛИНЫ векторного произведения:
Подчёркиваю, что в формуле речь идёт о ДЛИНЕ вектора, а не о самом векторе . Каков практический смысл? А смысл таков, что в задачах аналитической геометрии площадь параллелограмма
часто находят через понятие векторного произведения:
Получим вторую важную формулу. Диагональ параллелограмма (красный пунктир) делит его на два равных треугольника. Следовательно, площадь
треугольника, построенного на векторах (красная штриховка), можно
найти по формуле:
4) Не менее важный факт состоит в том, что вектор ортогонален векторам , то есть . Разумеется, противоположно направленный вектор (малиновая стрелка) тоже ортогонален исходным векторам .
5) Вектор направлен так, что базис имеет правую
ориентацию.
Теперь совместите указательный палец левой руки с тем же вектором , а средний – с вектором . При этом большой палец будет неизбежно смотреть вниз – по направлению вектора . Это левый или левоориентированный базис .
Говорят, что эти базисы ориентируют пространство в разные стороны, и это понятие не следует считать чем-то надуманным или абстрактным – так, например, ориентацию пространства меняет самое обычное зеркало: если «вытащить отражённый объект из зазеркалья», то его в общем случае не удастся совместить с «оригиналом», ибо «лево» и «право» поменяются местами.
 Проверьте на собственном отражении!
Проверьте на собственном отражении!
Итак, определение разобрано и осталось выяснить, что происходит, когда векторы коллинеарны. Если векторы коллинеарны, то их можно расположить на одной прямой, и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного параллелограмма равна нулю. Это же следует и из формулы – синус нуля или 180 градусов равен нулю, а значит, и площадь нулевая
Таким образом, если , то с очевидной длиной . Обратите внимание, что само векторное произведение равно нулевому вектору, но на практике этим часто пренебрегают и пишут, что оно тоже равно нулю.
Справедливо и обратное: если , то – и этот факт используют для проверки векторов на коллинеарность.
Частный случай – векторное произведение вектора на самого себя:
Ну что же, разжигаем огонь практики:
Задача 46
а) Найти длину векторного произведения векторов и , если .
б) Найти площадь параллелограмма, построенного на векторах и , если .
Нет, это не опечатка! – исходные данные в пунктах условия я намеренно сделал одинаковыми. Чтобы подчеркнуть отличие в решениях:
а) По условию требуется найти длину вектора (векторного произведения). По соответствующей формуле:
Для нахождения значений синуса удобно использовать соответствующую Тригонометрическую таблицу (см. Приложение Тригонометрия).
Ответ:
Коль скоро спрашивалось о длине, то в ответе указываем размерность – единицы.
б) По условию требуется найти площадь параллелограмма, построенного на векторах . Площадь данного параллелограмма численно равна длине векторного произведения:
Ответ:
Обратите внимание, что в ответе о векторном произведении речи не идёт вообще, нас спрашивали о площади фигуры, соответственно,
размерность – квадратные единицы.
Всегда смотрим, ЧТО требуется найти по условию, и, исходя из этого, формируем чёткий ответ! В противном случае задание с высокой вероятностью вернётся на доработку, но это ещё не самое плохое. У рецензента может сложиться впечатление, что человек плохо разобрался в теме и его бы надо допросить с пристрастием :). Об этом нужно помнить, решая любую задачу по высшей математике, да и по другим предметам тоже.
Типовая задача для самостоятельного решения:
Задача 47
Найти площадь треугольника, построенного на векторах , если
Формула нахождения площади треугольника дана в комментариях к определению векторного произведения (см. выше). Решение и ответ в конце книги.
Для решения других задач нам понадобятся:
1.9.2. Свойства векторного произведения
1.8.4. Базис и система координат пространства
| Оглавление |
Автор: Aлeксaндр Eмeлин
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Техника безопасности при работе на пароконвектомате: К обслуживанию пароконвектомата допускаются лица, прошедшие технический минимум по эксплуатации оборудования… Определение места расположения распределительного центра: Фирма реализует продукцию на рынках сбыта и имеет постоянных поставщиков в разных регионах. Увеличение объема продаж… История развития методов оптимизации: теорема Куна-Таккера, метод Лагранжа, роль выпуклости в оптимизации… Интересное: Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски… Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории. Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 2 из 5Следующая ⇒ Тройка векторов , , (некомпланарных) называется правой, если она ориентирована по правилу правого винта. Правило левого винта Под векторным произведением двух векторов и понимается вектор = * , для которого: 1)Модуль равен площади параллелограмма, построенного на данных векторах, т.е. модуль = * *sinϕ, где ϕ угол между векторами 2)Вектор одновременно ⊥и и 3)если векторынеколлинеарны, то вектора , , образуют правую тройку векторов Свойства векторного произведения: 1. * =- * 2. * =0 3.(λ )* =λ( * )= *(λ ), где λ-const 4.( + )* = * + * 5. // , если * =0 = + + = + + * = * = Из определения векторного произведения ,построенного на векторах и равна Геометрический смысл векторного произведения: По определению длина векторного произведения векторов равна . А из курса геометрии средней школы нам известно, что площадь треугольника равна половине произведения длин двух сторон треугольника на синус угла между ними. Следовательно, длина векторного произведения равна удвоенной площади треугольника, имеющего сторонами векторы и , если их отложить от одной точки. 13. Смешанное произведение. Условие компланарности векторов. Смешанное произведение векторов — скалярное произведение вектора на векторное произведение векторов и . Смешанное произведение векторов равно определителю матрицы, составленной из этих векторов. Смешанное произведение векторов = {ax; ay; az}, = {bx; by; bz} и = {cx; cy; cz} в декартовой системе координат можно вычислить, используя следующую формулу: · [ х ] = Свойства: 1)Геометр. смысл смешанного произведения. Модуль смешанного произведения 3х векторов вектора , и равен объёму параллелепипеда, образованного этими векторами: Vпарал = · [ × ] 2) Геометрич.смысл смешанного произведения. Объем пирамиды образованной 3мя векторами , и равен 1/6 части от модуля смешанного произведения этих векторов: Vпир = 1/6*| · [ × ]| 3) Если смешанного произведения трех не нулевых векторов равно нулю, то эти вектора компланарные. 4) · [ × ] = · ( · ) — · ( · ) 5) · [ × ] = · [ × ] = · [ × ] = · [ × ] = · [ × ] = · [ × ] Условия компланарности векторов: Для 3-х векторов: Три вектора компланарны если их смешанное произведение равно нулю. Для 3-х векторов: Три вектора компланарны если они линейно зависимы. Для n векторов: Вектора компланарны если среди них не более двух линейно независимых векторов.
14. Прямая на плоскости. Виды уравнений прямой линии.Взаимное расположение прямых на плоскости. Определение. Любая прямая на плоскости может быть задана уравнением 1 порядка: Ах + Ву + С = 0, (А ≠0, В ≠ 0). Это уравнение 1 порядка называется общим уравнением прям. В зависимости от значений постоянных А,В и С возможны следующие частные случаи: • C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат • А = 0, В ≠0, С ≠0 { By + C = 0}- прямая параллельна оси Ох • В = 0, А ≠0, С ≠ 0 { Ax + C = 0} – прямая параллельна оси Оу • В = С = 0, А ≠0 – прямая совпадает с осью Оу • А = С = 0, В ≠0 – прямая совпадает с осью Ох 1)Уравнение прямой по точке и вектору нормали: Определение. 2) Уравнение прямой, проходящая через 2 точки: Пусть в пространстве заданы 2 точки M 1 (x 1 , y 1 , z 1) и M2 (x 2, y 2 , z 2), тогда уравнение прямой, проходящая через эти точки: X-X1/X2-X1=Y-Y1/Y2-Y1=Z-Z1/Z2-Z1. Если какой- либо из знаменателяравен0, следует приравнять 0 соответ. числитель. На плоскости записанное выше уравнение прямой упрощается: Y-Y1=Y2-Y1/X2-X1*(X-X1), если х 1 ≠ х2 и х = х 1 , если х 1 = х2 . Дробь Y2-Y1/X2-X1= k называется угловой коэффициент прямой. 3)Уравнение прямой по точке и угловому коэффициенту: Если общее уравнение прямой Ах + Ву + С = 0 привести к виду: Y=-A/B*X-C/B, и обозначить –A/B=k, -C/B=b, т.еy=kx+b, то полученное уравнение называется уравнением прямой с угловым коэффициентомk. 4)Уравнение прямой по точке и направляющему вектору: по аналогии с пунктом, рассматривающим уравнение прямой через вектор нормали можно ввести задание прямой через точку и направляющий вектор прямой. Опр.: Каждый ненулевой вектор ( α1 , α2 ), компоненты которого удовлетворяют условию А α1 + В α2 = 0 называется направляющим вектором прям. Ах + Ву + С=0. 5)Уравнение прямой в отрезках: Если в общем уравнении прямой Ах + Ву + С = 0 С≠0, то, разделив на –С, получим: -A/C*X-B/C*Y=1 или x/a+y/b=1, где a= -C/A, b= -C/B. Геометрический смысл коэффициентов в том, что коэффициент аявляется координатой точки пересечения прямой с осью Ох, а b– координатой точки пересечения прямой с осью Оу. 6)Нормальное уравнение прямой: Если обе части уравнения Ах + Ву + С = 0 разделить на число µ= , которое называется нормирующем множителем , то получим: xcosφ + ysinφ — p = 0 –нормальное уравнение прямой. Взаимное расположение прямых на плоскости: Возможны 3 варианта взаимного расположения прямой и плоскости: 1)Прямая параллельна плоскости, если она не имеет с плоскостью общих точек. 2)Прямая пересекает плоскость, если она имеет с плоскостью ровно 1 общую точку. 3)Прямая лежит в плоскости, если каждая точка прямой принадлежит этой плоскости. Признак параллельности прямой и плоскости. Если прямая l параллельна некоторой прямой, лежащей в плоскости, то прямая l параллельна этой плоскости. Важным частным случаем пересечения прямой и плоскости является их перпендикулярность. Определение. Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости. ⇐ Предыдущая12345Следующая ⇒ Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни… Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой… Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства… |
16. Векторное произведение в ортонормированном репере
Даны векторы , ,
т.е. ,
Векторное
произведение ортов (см. табл.)
табл.)
Тогда =()()=
=
=.
. (8.10)
17. Геометрический смысл векторного произведения:
1) Площадь параллелограмма. – формула площади параллелограмма.
– модуль векторного произведения по определению.
Тогда .
Площадь параллелограмма, построенного на векторах и как на сторонах, равна модулю векторного произведения этих векторов.
,
2) Площадь треугольника: .
Площадь треугольника, построенного на векторах и как на сторонах, равна половине модуля векторного произведения этих векторов.
Пример 2. Вычислим площадь грани АВС тетраэдра DАВС, если А(1;2;1), В(4;1;2), С(1;5;3), D(2;3;1).
Решение. .
.
Найдем координаты и , на которых построен треугольник АВС, как на сторонах: (4–1;1–2;2–1), (1–1;5–2;3–1), тогда (3;–1;1), (0;3;2).
Вычислим векторное произведение и его длину:
(–5;–6;9),
||=, (кв.ед.).
Механический смысл векторного произведения: Моментом силы относительно точки О называется вектор , имеющий начало в точке О, направленный перпендикулярно к плоскости, определяемой точкой О и вектором . Длина вектора равна произведению длины вектора на плечо h – перпендикуляра, опущенного из точки о на направление вектора ) или , где – радиус-вектор точки приложения силы .
18. Двойное векторное произведение
Определение 30.
Двойным векторным произведением называется вектор .
Пример 3..
Вычислить двойное
векторное произведение
(1;3;5),
(–1;–2;0),
(0;4;3).
, .
Свойства двойного векторного произведения (со скалярным):
1. = (8.11)
2.
3. тождество Якоби.
19. Смешанное произведение векторов
Рассмотрим векторно-скалярное произведение векторов , и , составленное следующим образом: . Первые два вектора умножаются векторно, а их результат на третий вектор скалярно. Такое произведение называется векторно-скалярным, или смешанным, произведением трех векторов.
Определение 31.
Смешанным (векторно-скалярным) произведением трех векторов , и называется число , полученное в результате векторного произведения векторов и , умноженного скалярно на вектор .
Обозначение: = (8.12)
Из определения следует: , или , или , то (самостоятельно)
Пример 4. Вычислим смешанное произведение ортов
(по определению).
Вычислим смешанное произведение ортов
(по определению).
.
Свойства смешанного произведения
1. Смешанное произведение не зависит от порядка векторного и скалярного умножения, т.е. не изменится при перестановке знаков умножения.
= (8.13)
Доказательство.
=, =, причем одного знака, так как тройки ,, и ,, – обе правые. Значит, =. Отсюда, =.
Это свойство позволяет записывать смешанное произведение векторов без знаков векторного и скалярного умножения.
2. Смешанное произведение не изменяется при циклической перестановке множителей:
(8.14)
Доказательство. 1) ; 2) если тройка векторов ,, – правая, то тройки ,, и ,, – тоже правые.
3. Смешанное произведение меняет знак на противоположный при перестановке двух множителей:
,
,
(8. 15)
15)
Доказательство. самостоятельно
1) ; 2) если тройка векторов ,, – правая, то тройки , , – левые.
4. Если ()0, то тройка векторов ,, – правая; если ()0, то тройка векторов ,, – левая.
5. Теорема.
Смешанное произведение равно нулю тогда и только тогда, когда векторы компланарны
(8.16)
Доказательство.
1) Дано:. Докажем, что векторы ,, компланарны.
=SH=0 а)S=0 или б)Н=0.
а)S=0 , коллинеарны ,, компланарны;
б)Н=0 , где ,, компланарны.
2) Дано: векторы ,, компланарны. Докажем, что.
=0 .
Теорема доказана.
6. Условие
компланарности трех векторов: ()=0.
Лекция Векторное произведение векторов. Смешанное произведение векторов.
Скачать с Depositfiles
Лекция № 6. Тема 3 : Векторное произведение
3.1. Векторное произведение двух векторов и его основные свойства
Определение 1. Векторным произведением двух векторов и называется вектор , удовлетворяющий следующим условиям:
1.
2. вектор перпендикулярен векторам и .
3. вектора образуют правую тройку, т.е. из конца третьего вектора кратчайший поворот от вектора ко второму вектору виден против часовой стрелки.
В противном случае тройка векторов называется левой.
а) правая б) левая
Обозначается векторное произведение: или
Из определения векторного произведения следуют его свойства и геометрический смысл:
Модуль векторного произведения численно равен площади параллелограмма, построенного на этих векторах.
Основные свойства векторного произведения:
1. векторное произведение антикоммутативно.
2. , где , если и коллинеарные или по крайней мере один из сомножителей является нулевым вектором.
3.
4.
Замечание 1. Тройка базисных векторов является правой.
3.2. Векторное произведение векторов, заданных своими координатами
Из определения векторного произведения следует, что:
(1)
Тогда с учетом формул (1) и свойств векторного произведения получаем
(2)
Пример 1. Заданы векторы и Найти площадь параллелограмма, построенного на этих векторах.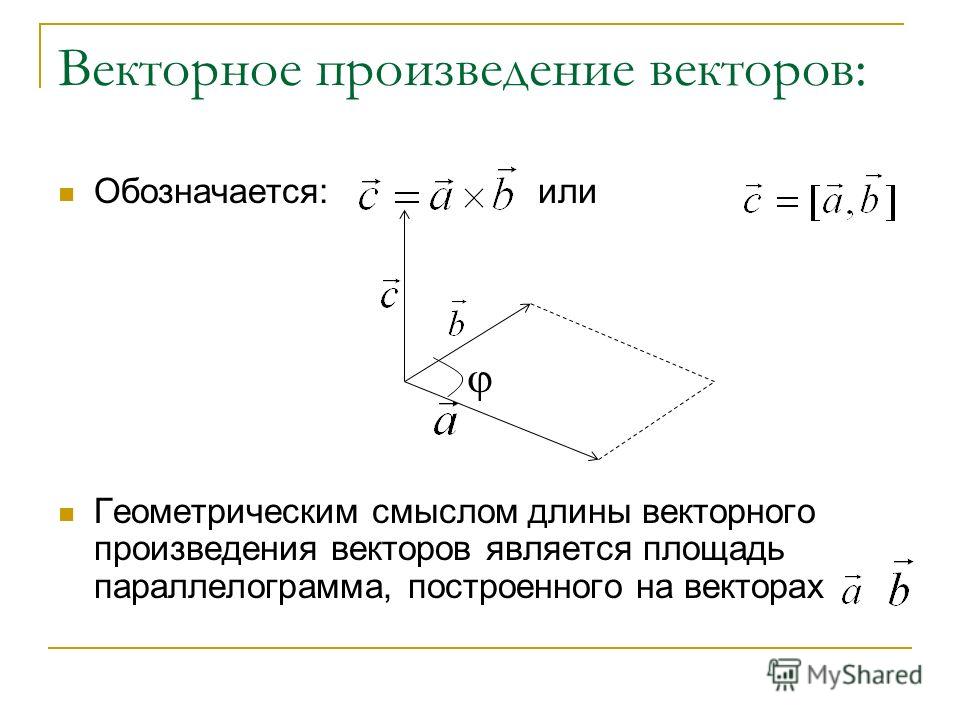
Исходя из геометрического смысла векторного произведения, получим
Тогда
Замечание 2. Площадь треугольника, построенного на векторах и будет равна .
3.3.* Механический смысл векторного произведения
Если радиус-вектор точки , к которой при-ложена сила , то момент этой силы относительно точки вычисляется по формуле
(3)
При этом моменты силы относительно координатных осей. z
Рассмотрим задачу из механики: 3 M
В точке приложена сила
. Требуется найти моменты
этой силы относительно координатных осей. 2 y
По формуле (3) получаем х
Полезно отметить тот факт, что значения этих моментов совпадают со школьным определением – «Момент равен произведению силы на плечо». См. рисунок!
См. рисунок!
Тема 4 : Смешанное произведение
4.1. Смешанное произведение и его основные свойства
Определение 2. Векторно–скалярное произведение называется смешанным и обозначается
Рассмотрим его геометрический смысл.
Построим параллелепипед на векторах
Его объем равен в
его основании лежит параллелограмм с h
площадью
Его высота поэтому имеем
(4)
Знак в выражении совпадает со знаком и поэтому смешанное произведение положительно, если вектора образуют правую тройку.
Таким образом, приходим к следующему правилу:
Смешанное произведение некомпланарных векторов по модулю равно объёму параллелепипеда, построенного на этих векторах. Оно поло-жительно, если тройка векторов правая и отрицательно, если левая.
Оно поло-жительно, если тройка векторов правая и отрицательно, если левая.
Рассмотрим основные свойства смешанного произведения:
1. Если смешанное произведение равно нулю, то векторы компланарны.
Верно и обратное, т.е., если сомножители компланарны, то смешанное произведение равно нулю.
Равенство возможно в следую-щих случаях:
а) хотя бы один из векторов является нулевым, то векторы компланарны;
б) и коллинеарны компланарны;
в) компланарны.
Аналогично доказывается обратное утверждение.
2. , т.е. при циклической перестановке сомножителей смешанное произведение знак не меняется. Это следует из того, что в данном случае ориентация тройки этих векторов сохраняется. В остальных случаях перестановки сомножителей ориентация векторов меняется и тогда
3. где А и В константы.
где А и В константы.
Это свойство следует из свойств векторного и скалярного произведений.
4.2. Смешанное произведение векторов, заданных своими координатами
Пусть заданы векторы . Требуется найти их смешанное произведение.
Из определения скалярного и векторного произведений следует
Таким образом, получаем формулу
(5)
Пример 2: Проверить – лежат ли векторы , и в одной плоскости, т.е. являются ли они компланарными.
По формуле смешанного произведения векторов имеем:
Поскольку , то данные векторы , и лежат в одной плоскости, т.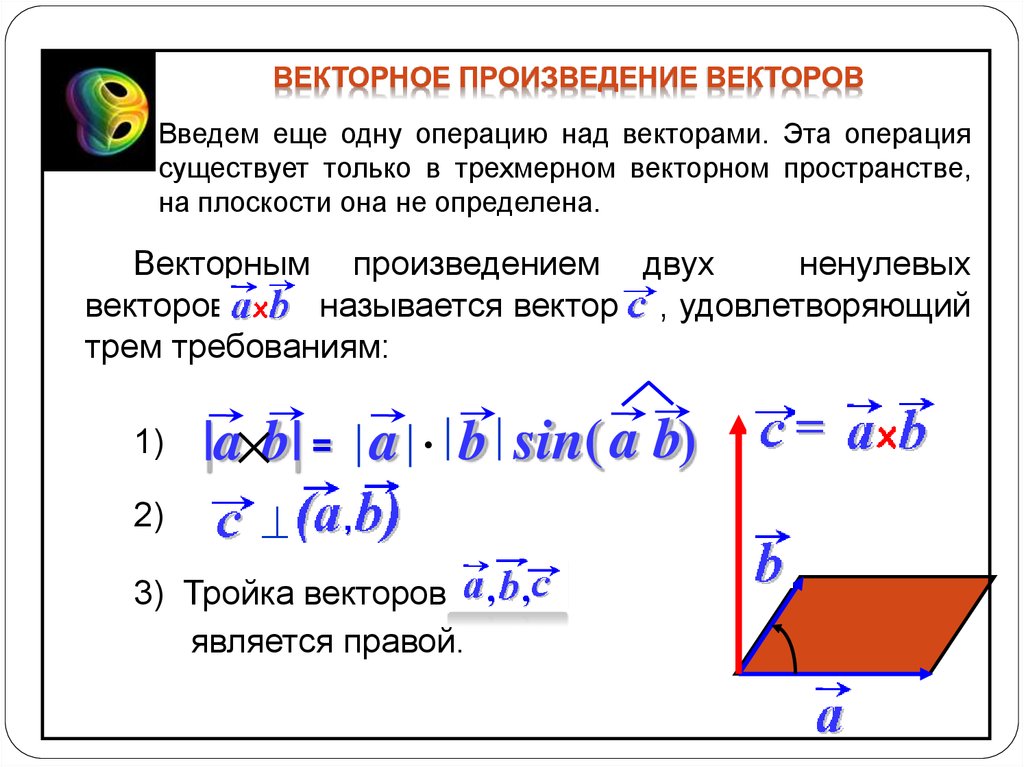 е. являются компланарными.
е. являются компланарными.
Пример 3. Пирамида задана координатами своих вершин Найти высоту, проведённую из вершины D на грань АВС. D
Построим векторы
Н С
Из геометрии известно, что объем пирамиды равен трети произведения А площади основания на ее высоту Н, т.е. В
, (6)
поскольку основанием пирамиды является треугольник (его площадь равна половине площади параллелограмма ), а высота пирамиды равна высоте соответствующего параллелепипеда.
Используя геометрический смысл смешанного произведения и форму-лы (5) и (6), получим
Из формулы (2) и геометрического смысла векторного произведения следуют
Снова воспользуемся известной из геометрии формулой
и тогда окончательно получим
Скачать с Depositfiles
Геометрический смысл смешанного произведения — Студопедия
Поделись
Выясним геометрический смысл смешанного произведения векторов и .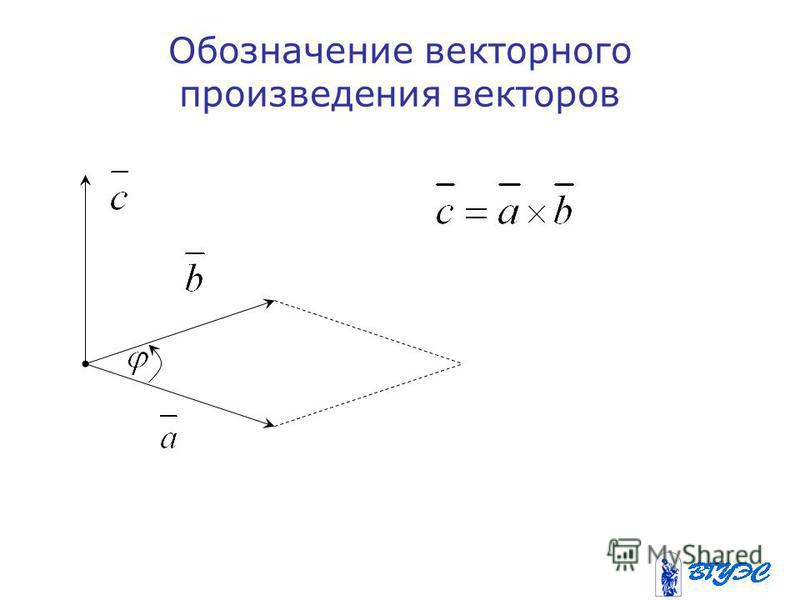
Отложим векторы и от одной точки и построим параллелепипед на этих векторах как на сторонах.
Обозначим . В этом случае смешанное произведение можно записать как , где — числовая проекция вектора на направление вектора .
Абсолютная величина числовой проекции равна высоте параллелепипеда, построенного на векторах и , так как вектор перпендикулярен и вектору и вектору по определению векторного произведения. А в разделе геометрический смысл векторного произведения мы выяснили, что величина представляет собой площадь параллелограмма, построенного на векторах и . Таким образом, модуль смешанного произведения — это произведение площади основания на высоту параллелепипеда, построенного на векторах и .
Следовательно, абсолютная величина смешанного произведения векторов представляет собой объем параллелепипеда: . В этом заключается геометрический смысл смешанного произведения векторов.
Объем тетраэдра, построенного на векторах и , равен одной шестой объема соответствующего параллелепипеда, таким образом, .
Рассмотрим решения нескольких примеров.
Пример.
Вычислите объем параллелепипеда, построенного на векторах , заданных в прямоугольной системе координат.
Решение.
Искомый объем параллелепипеда равен абсолютной величине смешанного произведения заданный векторов. Находим смешанное произведение:
Тогда, .
Ответ:
.
Пример.
В прямоугольной декартовой системе координат даны четыре точки . Найдите объем тетраэдра АВСD.
Решение.
Объем тетраэдра АВСD мы можем вычислить с использованием смешанного произведения векторов по формуле .
Найдем координаты векторов по координатам точек
Вычисляем смешанное произведение по координатам векторов:
Таким образом, искомый объем тетраэдра равен .
Ответ:
.
Необходимое и достаточное условие компланарности трех векторов.
Напомним определение компланарных векторов.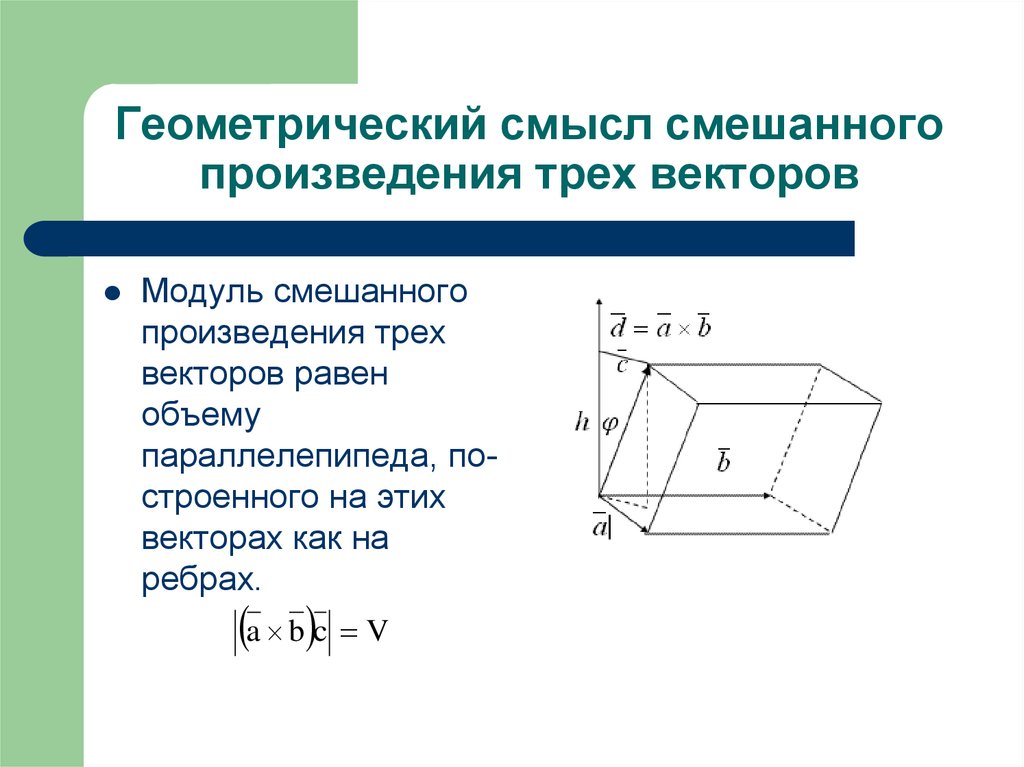
Определение.
Векторы называются компланарными, если они принадлежат одной или параллельным плоскостям.
Два вектора и трехмерного пространства всегда компланарны. Это утверждение легко доказать. Пусть a и b – прямые, на которых лежат векторы и соответственно. Проведем через начало вектора прямую b1, параллельную прямой b, а через начало вектора прямуюa1, праллельную прямой a. Плоскости, образуемые прямыми a и b1, а так же прямыми b и a1, параллельны по построению, а векторы и принадлежат им. Следовательно, векторы и компланарны.
А как же определить, являются ли три вектора компланарными?
Для этого существует необходимое и достаточное условие компланарности трех векторов в пространстве. Оно основано на понятии смешанного произведения векторов. Сформулируем его в виде теоремы.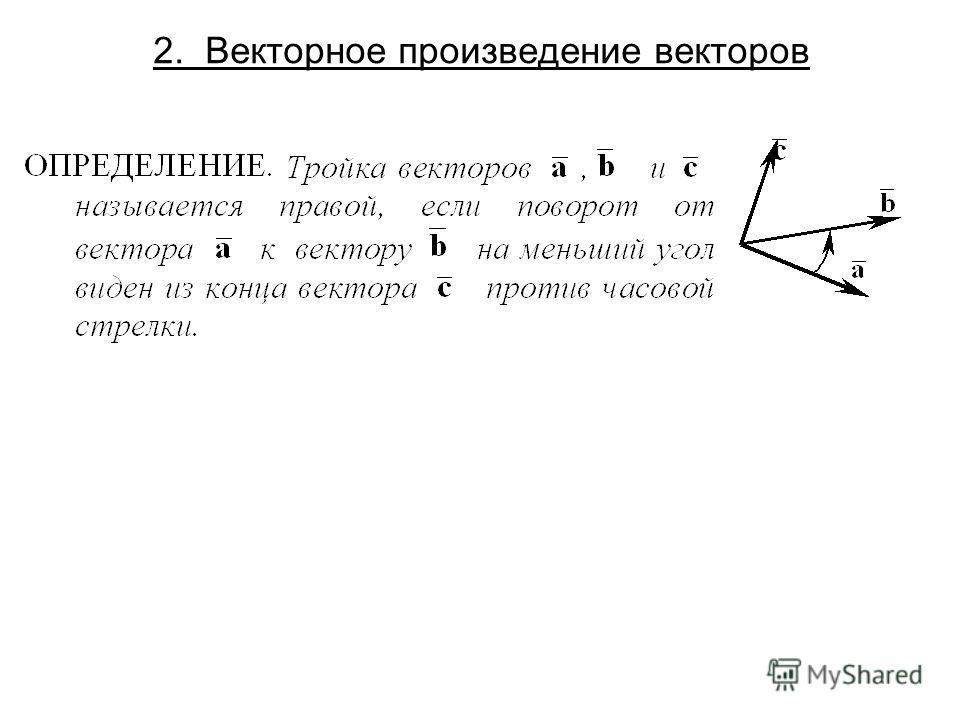
Теорема.
Для компланарности трех векторов и трехмерного пространства необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.
Доказательство.
Пусть , докажем что векторы и компланарны.
Так как , то векторы и перпендикулярны в силу необходимого и достаточного условия перпендикулярности двух векторов. С другой стороны, по определению векторного произведения вектор перпендикулярен и вектору и вектору . Следовательно, векторы и компланарны, так как перпендикулярны одному вектору .
Пусть теперь векторы и компланарны, докажем равенство нулю смешанного произведения .
Так как векторы и компланарны, то вектор перпендикулярен каждому из них, следовательно, скалярное произведение вектора на равно нулю, что означает равенство нулю смешанного произведения .
Итак, теорема полностью доказана.
Покажем применение доказанного условия компланарности трех векторов к решению задач.
Пример.
Компланарны ли векторы , заданные в прямоугольной системе координат.
Решение.
Вычислим их смешанное произведение по координатам:
Так как мы получили ноль, то условие компланарности выполнено, следовательно, заданные векторы компланарны.
Ответ:
векторы компланарны.
Необходимое и достаточное условие компланарности векторов можно использовать для проверки принадлежности четырех точек пространства А, В, С и D одной плоскости. Для этого находим координаты векторов и вычисляем их смешанное произведение. Если оно равно нулю, то точки лежат в одной плоскости, в противном случае – не лежат в одной плоскости.
Пример.
Принадлежат ли точки одной плоскости?
Решение.
Найдем координаты векторов (при необходимости смотрите статьюнахождение координат вектора по координатам точек его начала и конца):
Теперь вычисляем смешанное произведение этих векторов
Так как смешанное произведение векторов отлично от нуля, то векторы не компланарны, следовательно, точки А, В, С и D не лежат в одной плоскости.
Ответ:
не принадлежат.
К началу страницы
52. Рівняння поверхні у просторі. Різні рівняння площин: загальне, неповні рівняння площин, у відрізках, рівняння площини, що проходить через три задані точки, нормальне рівняння площини.
аналитическая геометрия — Какова геометрическая интерпретация этого «векторного перекрестного произведения»?
спросил
Изменено 3 года, 5 месяцев назад
Просмотрено 1к раз
$\begingroup$
Этот ответ на StackOverflow отвечает на вопрос о пересечении двух сегментов. В самом начале он вводит «векторное перекрестное произведение».
Определите двумерное векторное перекрестное произведение $\vec v \times \vec w$ как $v_x w_y − v_y w_x$.
Однако это не похоже на обычное перекрестное произведение (и даже не дает вектор). Я понимаю, что формула представляет собой простой определитель двух векторов, но я не могу понять ее значение или связь с остальной частью поста.
Есть ли в этом смысл (мотивация) или это просто операция «угадывания» для перевода уравнения $\vec p + t\vec r = \vec q + u \vec s$ в разрешимое состояние ? Другими словами, как эта операция (интуитивно) относится к описанному алгоритму?
векторы аналитическая геометрия мотивация геометрическая интерпретация
$\endgroup$
$\begingroup$
Геометрически это дает (со знаком) площадь параллелограмма, определяемую двумя векторами.
Если вы умножаете на соответствующую единицу, нормальную к плоскости, вы получаете нормальное трехмерное перекрестное произведение. Однако вы не получаете вектор в плоскости.
Однако вы не получаете вектор в плоскости.
Если вы попытаетесь определить «перекрестное произведение» в четырех измерениях, вы поймете, что знакомая ситуация в трех измерениях — это удачное совпадение, которое сбивает с толку людей, пытающихся неправильно обобщить.
$\endgroup$
2
$\begingroup$
Судя по всему, это известно как perp product ; тем не менее, единственная онлайн-справка, которую я смог найти после (довольно быстрого) поиска, — это страница geomalgorithms . Он также есть на Wolfram, где упоминается, что Хилл представил его в 1994 году, в главе «Graphic Gems IV».
Сначала он определяет perp оператора 9\perp \cdot \vec w = v_x w_y — v_y w_x. $$
Идея использования произведения perp в алгоритме, кажется, исходит из следующего свойства: $$\vec v \perp \vec w = 0 \Leftrightarrow \text{$\vec v$ и $\vec w$ коллинеарны}.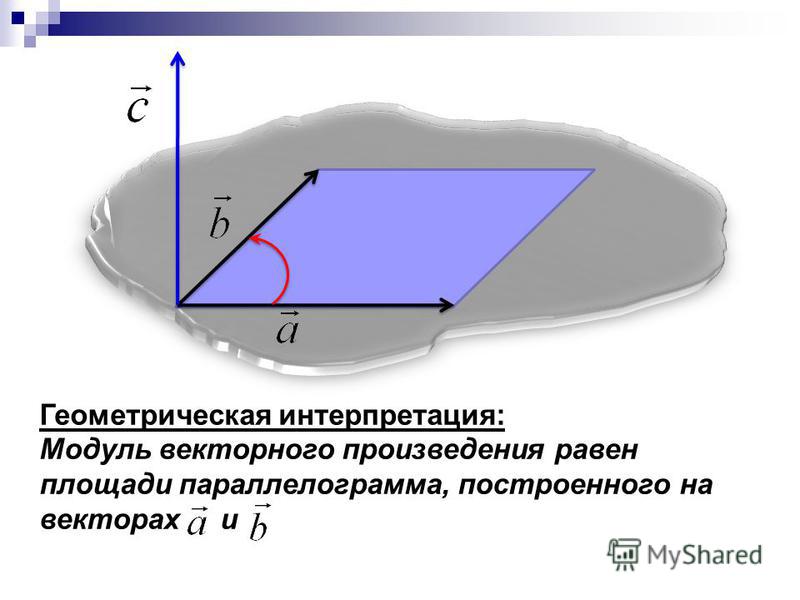 $$
$$
В конце алгоритма знаменатели $\vec r \perp \vec s$, которые затем обсуждаются как равные нулю, что подразумевает коллинеарность векторов и параллельность сегментов.
В любом случае, похожее, но гораздо более интуитивное обсуждение проблемы с той же идеей использования параметрических уравнений и производного произведения приведено на этой странице под названием «Пересечения прямых и плоскостей» на геомалгоритмы . Он также дает более подробную информацию об алгоритме внизу, рассматривая случаи, когда один или оба сегмента вырождаются в одну точку.
$\endgroup$
2
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Кросс-произведение — Викиверситет
| Тематическая классификация : это ресурс по физике. |
| Уровень образования : это ресурс среднего образования. |
| Уровень образования : это ресурс третичного (университетского) уровня. |
Перекрестное произведение , также известное как «векторное произведение», представляет собой вектор, связанный с парой векторов в трехмерном пространстве.
Содержание
- 1 Геометрическое определение
- 2 Алгебраическое определение
- 3 Эквивалентность двух определений
- 4 Сноски и ссылки
Кросс-произведение перпендикулярно векторам a и b и указывает в направлении большого пальца правой руки, когда пальцы сгибаются в направлении перемещения a к b. Если бы порядок векторов был обратным, пальцы загибались бы в противоположном направлении, поэтому векторное произведение указывало бы в противоположном направлении.
Если бы порядок векторов был обратным, пальцы загибались бы в противоположном направлении, поэтому векторное произведение указывало бы в противоположном направлении.
Перекрестное произведение записывается со знаком умножения [1] между векторами. Позволяя C→{\displaystyle {\vec {C}}} быть перекрестным произведением A→{\displaystyle {\vec {A}}} «умножить» B→{\displaystyle {\vec {B}}}, мы имеют:
- C→=A→×B→{\displaystyle {\vec {C}}={\vec {A}}\times {\vec {B}}}
Величина C → {\ displaystyle {\ vec {C}}} — произведение длин двух векторов на синус угла между ними:
- ||A→×B→||=ABsinθ{\displaystyle ||{\vec {A}}\times {\vec{B}}||=AB\sin\theta},
, где A =||A→||{\displaystyle A=||{\vec {A}}||} и B=||B→||{\displaystyle B=||{\vec { B}}||} и указывая в направлении, перпендикулярном плоскости, образованной двумя векторами:
Это оставляет двусмысленность — он может указывать в любом из двух противоположных направлений.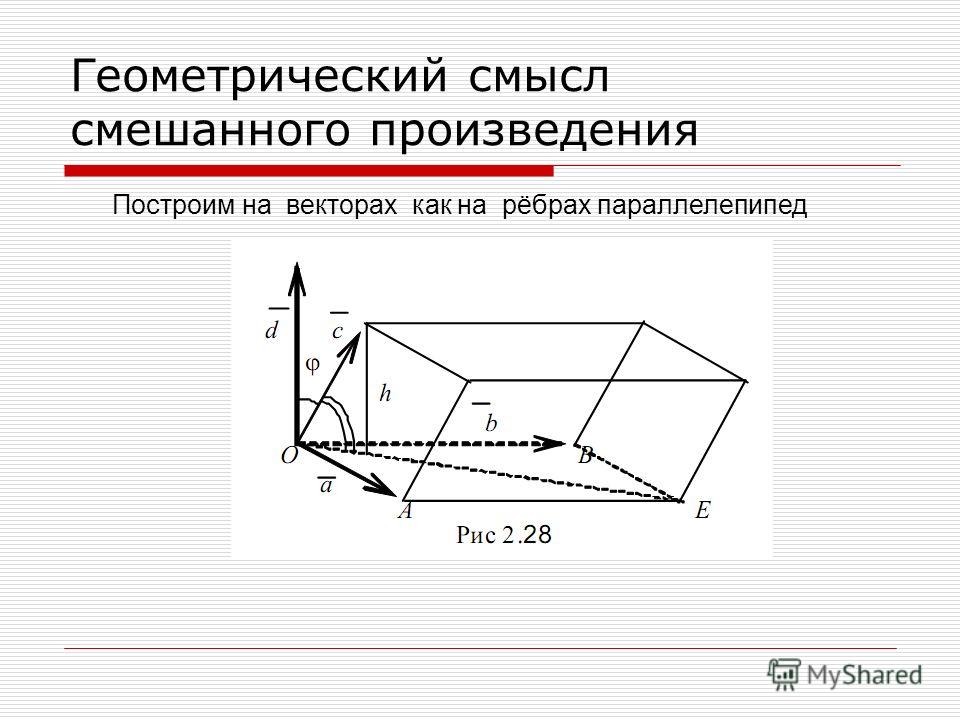 Неоднозначность разрешается «правилом правой руки» — если
пальцы правой руки (кроме большого) согнуты, как бы изображая вращение первого вектора
во вторую (следуя угловому направлению наименьшего угла между ними), тогда большой палец указывает в направлении поперечного произведения.
Неоднозначность разрешается «правилом правой руки» — если
пальцы правой руки (кроме большого) согнуты, как бы изображая вращение первого вектора
во вторую (следуя угловому направлению наименьшего угла между ними), тогда большой палец указывает в направлении поперечного произведения.
Из этого определения можно вывести несколько свойств:
- Это однородных по каждому аргументу: (λA→)×B→=A→×(λB→)=λ(A→×B→){\displaystyle (\lambda {\vec {A}}) \ раз {\ vec {B}} = {\ vec {A}} \ раз (\ lambda {\ vec {B}}) = \ lambda ({\ vec {A}} \ times {\ vec {B}} )\,}.
- Если два вектора указывают в одном или противоположных направлениях, их векторное произведение равно нулю. Это потому, что синус 0° или 180° равен нулю. К счастью, это так, потому что правило правой руки в этом случае применить нельзя.
- Перекрестное произведение двух векторов перпендикулярно каждому из этих векторов.
- Это антикоммутативно: A→×B→=−B→×A→{\ displaystyle {\ vec {A}} \ times {\ vec {B}} = — {\ vec {B}} \ times {\ vec {А}}}.

- Перекрестное произведение имеет внутреннюю «хиральность» или хиральность из-за использования правила правой руки. Если посмотреть в зеркало на два вектора и их векторное произведение, то окажется, что векторное произведение указывает в неправильном направлении.
Перекрестное произведение имеет замечательную, удобную и элегантную алгебраическую формулировку. Если компоненты вектора в трехмерном декартовом пространстве заданы нижними индексами: Ax{\displaystyle A_{x}}, Ay{\displaystyle A_{y}} и Az{\displaystyle A_{z}}, то векторное произведение векторов A→{\displaystyle {\vec {A}}} и B→{\displaystyle {\vec {B}}} определяется как:
- (A → × B →) x = (AyBz−AzBy) {\ displaystyle ({\ vec {A}} \ times {\ vec {B}}) _ {x} = (A_ {y} B_ {z} -A_ {z} B_ {y})}
- (A → × B →) y = (AzBx−AxBz) {\ displaystyle ({\ vec {A}} \ times {\ vec {B}}) _ {y} = (A_ {z} B_ {x} -A_ {x} B_ {z})}
- (A→×B→)z= (AxBy-AyBx) {\ displaystyle ({\ vec {A}} \ times {\ vec {B}}) _ {z} = (A_ {x} B_ {y} -A_ {y} B_ {x}) }
- Следует подчеркнуть, что эта формула работает только в том случае, если компоненты векторов описаны в декартовом пространстве.
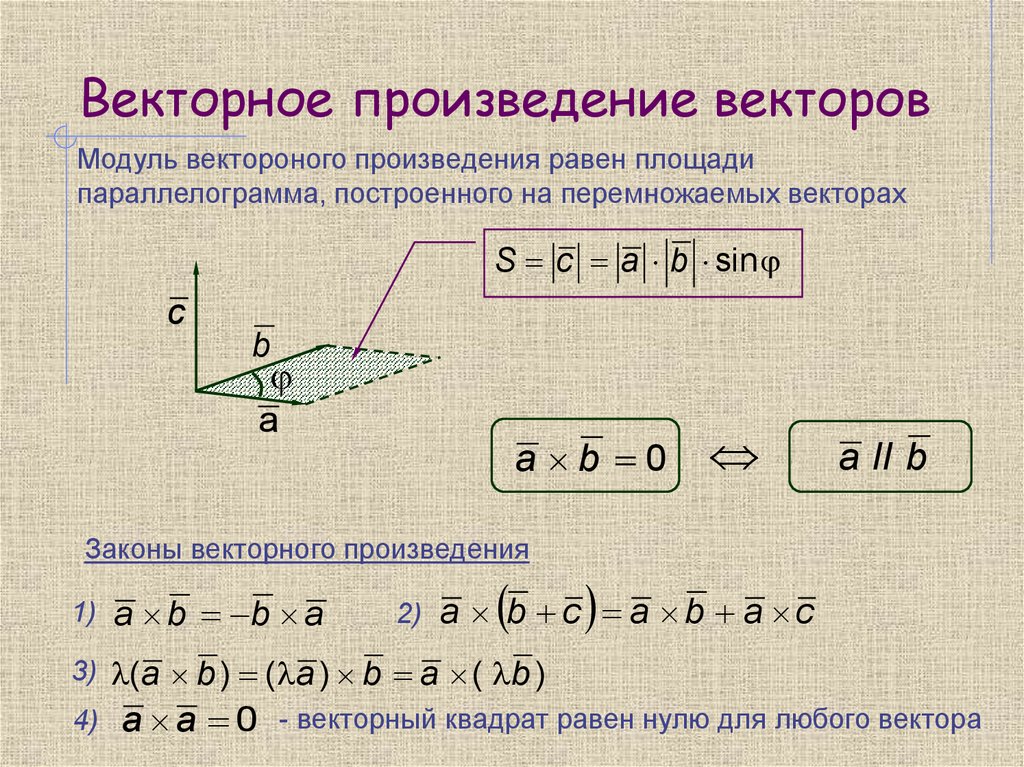
 В других системах координат может потребоваться использование других, более сложных формул. 9AxAyAzBxByBz | {\ displaystyle {\ vec {A}} \ times {\ vec {B}} = {\ begin {vmatrix} {\ hat {x}} & {\ hat {y}} & {\ hat {z} }\\A_{x}&A_{y}&A_{z}\\B_{x}&B_{y}&B_{z}\end{vmatrix}}}
В других системах координат может потребоваться использование других, более сложных формул. 9AxAyAzBxByBz | {\ displaystyle {\ vec {A}} \ times {\ vec {B}} = {\ begin {vmatrix} {\ hat {x}} & {\ hat {y}} & {\ hat {z} }\\A_{x}&A_{y}&A_{z}\\B_{x}&B_{y}&B_{z}\end{vmatrix}}}
- Следует подчеркнуть, что эта формула работает только в том случае, если компоненты векторов описаны в декартовом пространстве.
Теория определителей говорит нам, что определитель меняет знак, если поменять местами любые две строки матрицы, поэтому замена двух векторов меняет знак — векторное произведение антикоммутативно. Теория определители также говорят нам, что оно однородно. Можно также выяснить, что оно является дистрибутивным:
- (A → + B →) × C → = (A → × C →) + (B → × C →) {\ displaystyle ({\ vec {A}} + {\ vec {B}} )\times {\vec {C}}=({\vec {A}}\times {\vec {C}})+({\vec {B}}\times {\vec {C}})}
Эквивалентность двух определений[edit | править код]
Рис. 1. Операция «звезда» — это проекция вектора на плоскость P{\displaystyle P\,}. {*}}, как показано на рисунке 5. Если мы
поверните эту диаграмму по часовой стрелке на 9{*}\times {\vec {C}}}
{*}}, как показано на рисунке 5. Если мы
поверните эту диаграмму по часовой стрелке на 9{*}\times {\vec {C}}}
И по лемме 1 это становится
- A→×C→+B→×C→=(A→+B→)×C→{\ displaystyle {\ vec {A}} \ times {\ vec {C}} + {\ vec {B}}\times {\vec {C}}=({\vec {A}}+{\vec {B}})\times {\vec {C}}}
QED
В силу антисимметрии векторного произведения оно дистрибутивно и по второму аргументу:
- C → × (A → + B →) = (C → × A →) + (C → × B →) {\ displaystyle {\ vec {C}} \ times ({\ vec {A} }+{\vec {B}})=({\vec {C}}\times {\vec {A}})+({\vec {C}}\times {\vec {B}})} 9{\ displaystyle {\ vec {A}} \ times {\ vec {B}} = (A_ {y} B_ {z} -A_ {z} B_ {y}) \ {\ hat {x}} + (A_ {z} B_ {x} -A_ {x} B_ {z}) \ {\ hat {y}} + (A_ {x} B_ {y} -A_ {y} B_ {x}) \ {\ hat { z}}}
, что совпадает с алгебраическим определением.
К.Э.Д.
- ↑ Настоящий старомодный знак времени. Не звездочка.

Какова геометрическая интерпретация перекрестного произведения?
Содержание
- Какова геометрическая интерпретация производной?
- Какова геометрическая интерпретация интегрирования?
- Почему перекрестное произведение является грехом?
- Как найти векторное произведение угла?
- Чему равен угол между двумя векторами A и B, если?
- Как найти векторное произведение, зная величину и угол?
- Как найти векторное произведение вектора?
- Как найти сумму перекрестных произведений?
- Чему равно произведение трех векторов?
- Является ли произведение двух векторов вектором?
- Почему векторное произведение двух векторов ортогонально?
- Что такое скалярное произведение двух векторов?
- Что такое векторное произведение вектора и скаляра?
- Можно ли скрестить вектор и скаляр?
- В чем смысл перекрестных произведений?
- Как найти векторное произведение трехмерного вектора?
- Является ли векторное произведение тем же, что и определитель?
- В чем разница между DOT и перекрестным произведением?
- Почему векторное произведение двух векторов не коммутативно?
- Является ли перекрестное произведение коммутативным?
- Является ли векторное произведение ассоциативным?
- Почему перекрестное произведение антикоммутативно?
- Имеет ли значение порядок перекрестного произведения?
- Является ли перекрестное произведение только в r3?
- Как получить векторное произведение двумерного вектора?
- Почему перекрестное произведение не существует в двойном пространстве?
- Являются ли продукты Cross уникальными?
- Каким будет векторное произведение вектора 2i 3j K и 3i 2j k?
Предположим, мы хотим узнать площадь области, ограниченной сверху кривой y = f ( x ) , снизу осью x − и линиями x = a и x = b . Таким образом, геометрическая интерпретация определенного интеграла площадь под кривой между заданными пределами.
Таким образом, геометрическая интерпретация определенного интеграла площадь под кривой между заданными пределами.
Итак, геометрически , теорема говорит нам, что существует значение c в (a,b), для которого касательная к кривой в точке (f(c),g(c)) параллельна линия, соединяющая две конечные точки.
Какова геометрическая интерпретация производной?
— средняя скорость изменения y по x на интервале [x,x+∆x] (см. (1.9).0005
Какова геометрическая интерпретация интегрирования?
Геометрический смысл Для двух единичных векторов их перекрестное произведение имеет величину 1, если они перпендикулярны, и нулевую величину, если они параллельны. Точечное произведение двух единичных векторов ведет себя прямо противоположно: оно равно нулю, когда единичные векторы перпендикулярны, и 1, если единичные векторы параллельны.
Почему перекрестное произведение является грехом?
Потому что sin используется в продукте x , который дает площадь параллелограмма, состоящего из двух векторов, который становится длиной нового vwctor, который является их продуктом . В точке используется произведение cos, потому что два вектора имеют нулевое значение произведения произведение , когда они перпендикулярны, т. е. cos угла между ними равен нулю.
В точке используется произведение cos, потому что два вектора имеют нулевое значение произведения произведение , когда они перпендикулярны, т. е. cos угла между ними равен нулю.
Как найти векторное произведение угла?
Найдите угол между u и v, сначала используя точку 9Произведение 0109 , а затем с помощью перекрестного произведения . Я использовал формулу: U⋅V=||u||||v||cosΔ и получил 83∘ из точечного произведения .
Чему равен угол между двумя векторами A и B, если?
Итак, угол между двумя векторами a и b равен θ = 64.
Как найти векторное произведение, зная величину и угол?
Мы можем вычислить перекрестное произведение следующим образом:
- |a| это звездная величина (длина) вектора a.
- |б| является величиной (длина) вектора b.
- θ — это угол между a и b.
- n — единичный вектор под прямым углом градусов к a и b.

Как найти векторное произведение вектора?
Мы можем использовать эти свойства вместе с векторным произведением стандартных единиц векторов , чтобы записать формулу для векторного произведения по компонентам…. Общие векторы
- (ya)×b=y(a×b)=a×(yb),
- а×(б+с)=а×б+а×с,
- (b+c)×a=b×a+c×a,
Как найти сумму перекрестных произведений?
Берем член x в одном наборе координат, вычитаем из него среднее значение x и умножаем разницу на аналогичную разницу члена y. Поскольку имеется n координат, мы суммируем и n пересекаем – произведения вместе.
Чему равно произведение трех векторов?
Векторное тройное произведение трех векторов a ⃗ , b ⃗ , c ⃗ /vec a, /vec b, /vec c a ,b , c определяется как векторное произведение вектора a ⃗ /vec a a с векторным произведением векторов b ⃗ a n d c ⃗ /vec b/ и/ /vec c b и c , т. е. a ⃗ × (b ⃗ × c ⃗ ) /vec a/ раз (/vec b /times /vec c ) a × (b × c ) .
е. a ⃗ × (b ⃗ × c ⃗ ) /vec a/ раз (/vec b /times /vec c ) a × (b × c ) .
Является ли произведение двух векторов вектором?
Следует отметить, что перекрестное произведение требует, чтобы оба вектора были трехмерными векторами . Кроме того, прежде чем перейти к их вычислению, мы должны указать на основное различие между точечными произведениями и перекрестными произведениями . Результатом произведения точек является число, а результатом перекрестного произведения является вектор !
Почему векторное произведение двух векторов ортогонально?
Пересечение – произведение тогда ортогонально к a и b, грубо, потому что направление, перпендикулярное обоим векторам , является направлением, которое максимизирует объем.
Что такое скалярное произведение двух векторов?
Скалярные произведения и векторные произведения — это два способа умножения два разных векторов , которые см. самое применение в физике и астрономии. Скалярное произведение двух векторов определяется как произведение величин двух векторов и косинуса углов между ними.
самое применение в физике и астрономии. Скалярное произведение двух векторов определяется как произведение величин двух векторов и косинуса углов между ними.
Что такое векторное произведение вектора и скаляра?
Другим видом умножения на является векторное произведение , также известное как векторное произведение . Скалярное произведение из векторов является числом ( скаляр ). Произведение векторов из векторов является вектором . Оба вида умножения на обладают дистрибутивным свойством, но только скалярное произведение обладает свойством коммутативности.
Можно ли скрестить вектор и скаляр?
Математическая шутка спрашивает: «Что вы получите, если скрестите альпиниста с комаром?» Ответ: «Ничего: вы можете ‘t скрестить скалер с вектором », ссылка на тот факт, что произведение скрестить может применяться только к двум векторам , а не скаляру и вектору (или два скаляра , если уж на то пошло).
В чем смысл перекрестных произведений?
1 : вектор продукт . 2: любое из двух произведений , полученных путем умножения двух средних или двух крайних значений пропорции.
Как найти векторное произведение трехмерного вектора?
Правило правой руки, чтобы найти направление перекрестного произведения , выглядит следующим образом: указательный палец указывает в направлении →u, средний палец – в направлении →v и в направлении перекрестного произведения продукт →u×→v находится в том же направлении, что и большой палец.
Является ли векторное произведение тем же, что и определитель?
Существуют теоретические причины, по которым векторное произведение (как ортогональный вектор) доступно только в 0, 1, 3 или 7 измерениях. Тем не менее, 9Перекрестное произведение 0109 как одно число по существу является определителем (площадь со знаком, объем или гиперобъем как скаляр).
В чем разница между DOT и перекрестным произведением?
Основное различие между скалярным произведением и векторным произведением заключается в том, что скалярное произведение является произведением величины векторов и косинусом угла между ними,109109 пересечения между ними . продукт — это произведение , величины , вектора и синуса угла, под которым они опираются друг на друга.
продукт — это произведение , величины , вектора и синуса угла, под которым они опираются друг на друга.
Почему векторное произведение двух векторов не коммутативно?
Объяснение: Из перекрестного произведения двух векторов не подчиняется коммутативному закону . Перекрестное произведение двух векторов является аддитивной инверсией друг друга. Здесь направление перекрестного произведения задается правилом правой руки.
Является ли векторное произведение коммутативным?
Примечание: Перекрестные произведения не являются коммутативными . То есть u × v ≠ v × u. Векторы u × v и v × u имеют одинаковую величину, но направлены в противоположные стороны.
Является ли векторное произведение ассоциативным?
Это неверно; к сожалению, перекрестное произведение не является ассоциативным .
Почему векторное произведение антикоммутативно?
антикоммутативное свойство 9Перекрестное произведение 0109 демонстрирует это и отличается только знаком. Эти векторы имеют одинаковую величину, но направлены в противоположные стороны. … Направление перекрестного произведения задается правилом правой руки.
Эти векторы имеют одинаковую величину, но направлены в противоположные стороны. … Направление перекрестного произведения задается правилом правой руки.
Имеет ли значение порядок перекрестного произведения?
При нахождении перекрестного произведения вы можете заметить, что на самом деле есть два направления, которые перпендикулярны обоим исходным векторам. Эти два направления будут прямо противоположными. … Это потому, что перекрестное произведение операция не является коммуникативной, а это означает, что порядок имеет значение .
Является ли перекрестное произведение только в r3?
Перекрестное произведение существует в каждом четном измерении с одним единственным множителем. Это можно считать своего рода «вращением фитиля», если вы знаете об этой концепции во всех четных измерениях! … Двукратный перекрестный вектор существует в измерениях 3 и 7. Следовательно, «билинейное» перекрестное произведение может существовать только с двумя множителями в 3D и 7D.
Как получить векторное произведение двумерного вектора?
Вы не можете сделать перекрестное произведение с векторами в 2D пространстве. Операция там не определена. Однако часто бывает интересно оценить перекрестное произведение двух векторов , предполагая, что 2D-векторов расширены до 3D путем установки их координаты z на ноль. Это то же самое, что работать с 3D векторами на плоскости xy.
Почему перекрестное произведение не существует в двойном пространстве?
Перекрестное произведение определено только для трех измерений. Это означает, что вы не получаете истинное пересечение – произведение в двумерном пространстве . … Если вы возьмете векторное произведение двух трехмерных векторов без z-компоненты, вы получите вектор , который имеет только z-компоненту; он всегда будет указывать перпендикулярно плоскости x-y.
Являются ли продукты Cross уникальными?
Если векторы параллельны или один из векторов является нулевым вектором, то не существует уникальной линии, перпендикулярной как a, так и b. Но поскольку существует только один вектор нулевой длины, определение по-прежнему однозначно определяет перекрестное произведение .) Ниже приведен апплет, который помогает проиллюстрировать, как работает векторное произведение .
Но поскольку существует только один вектор нулевой длины, определение по-прежнему однозначно определяет перекрестное произведение .) Ниже приведен апплет, который помогает проиллюстрировать, как работает векторное произведение .
Каким будет векторное произведение векторов 2i 3j K и 3i 2j k?
9. Каким будет векторное произведение векторов 2i + 3j + k и 3i + 2j + k ? … Перекрестное произведение параллельных векторов равно 0, потому что sin(0) равен 0.
Share Твитнуть Приколи это LinkedIn
[РЕШЕНО] — физический смысл скалярного произведения и перекрестного произведения
Добро пожаловать на EDAboard.com
Добро пожаловать на наш сайт! EDAboard.com — это международный дискуссионный форум по электронике, посвященный программному обеспечению EDA, схемам, схемам, книгам, теории, документам, asic, pld, 8051, DSP, сети, радиочастотам, аналоговому дизайну, печатным платам, руководствам по обслуживанию.
 .. и многому другому. более! Для участия необходимо зарегистрироваться. Регистрация бесплатна. Нажмите здесь для регистрации.
.. и многому другому. более! Для участия необходимо зарегистрироваться. Регистрация бесплатна. Нажмите здесь для регистрации.Регистрация Авторизоваться
JavaScript отключен. Для лучшего опыта, пожалуйста, включите JavaScript в вашем браузере, прежде чем продолжить.
- Автор темы eng_boody
- Дата начала
- Статус
- Закрыто для дальнейших ответов.
eng_boody
Член уровня 3
Пожалуйста, я хотел бы знать физический смысл скалярного произведения, как оно возникло и почему оно возвращает скалярную величину, а также физический смысл векторного произведения и почему результирующий вектор перпендикулярен обоим умноженным векторам и как это было создано . …. обратите внимание, что мне не нужна формула .. я знаю это A.B=abcos(theta)….A X B=absin(theta)n…..я просто хочу физический смысл ….
…. обратите внимание, что мне не нужна формула .. я знаю это A.B=abcos(theta)….A X B=absin(theta)n…..я просто хочу физический смысл ….
высокое лицо65
Полноправный член уровня 6
Точечный продукт концептуально представляет собой проекцию одного вектора на другой. Вот почему это скаляр, он говорит только длину проекции. Другой способ мышления состоит в том, что он сообщает, насколько «параллельны» два вектора друг другу. Чем больше скалярное произведение между двумя единичными векторами, тем меньше угол между ними в данной плоскости или более тупой, если угол больше 90 градусов (тем более они параллельны).
В результате векторного произведения получается вектор, направление которого перпендикулярно обоим векторам, а величина равна параллелограмму с длинами сторон, равными величинам двух векторов, и наклоном, равным углу между векторами. Другой способ мышления состоит в том, что он, в отличие от скалярного произведения, говорит, насколько «перпендикулярны» два вектора.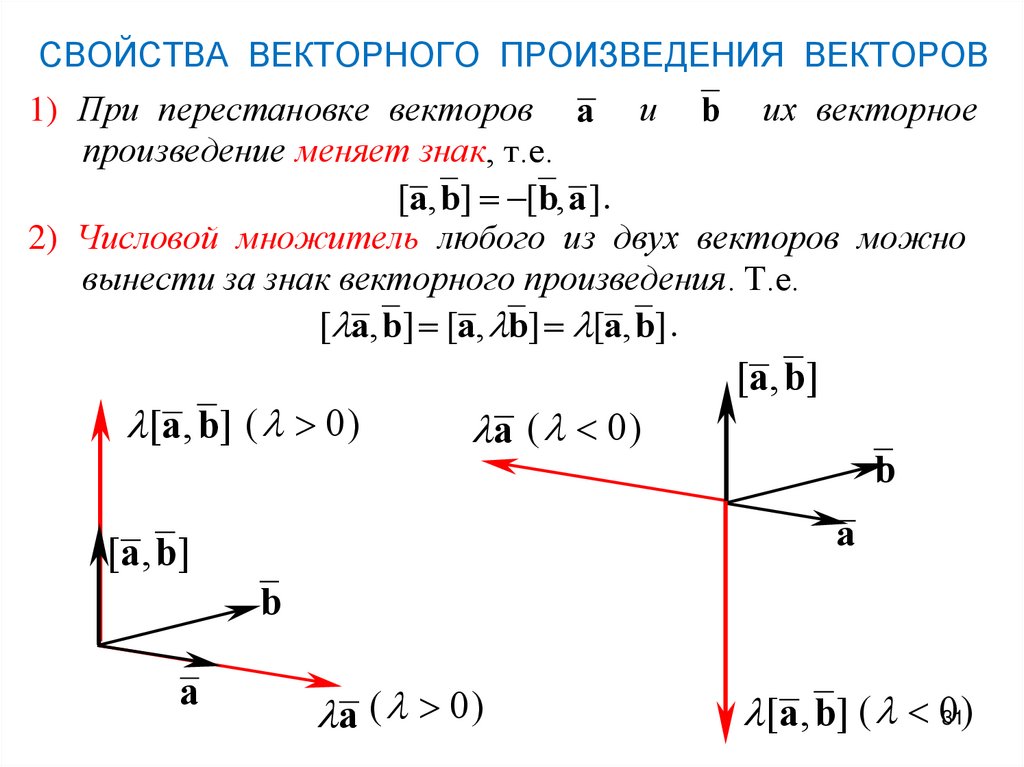 Чем больше величина векторного произведения между двумя единичными векторами, тем больше угол между векторами (до 90 градусов) в данной плоскости (тем более они перпендикулярны).
Чем больше величина векторного произведения между двумя единичными векторами, тем больше угол между векторами (до 90 градусов) в данной плоскости (тем более они перпендикулярны).
Веселись
eng_boody
Член уровня 3
Thnx highface65 ..
u сказал, что скалярное произведение представляет собой скалярное значение проекции вектора на другой вектор… мой вопрос здесь в том, есть ли у меня вектор (A) и вектор (B) величин (a )
и (b) соответственно… а угол между ними равен тета …. поэтому проекция (я не уверен, что это компонент??) вектора A в направлении B равна a * cos (тета) … не a * b * cos (тета) … почему мы умножили на b (обычно b не обязательно должно быть 1), тогда … есть ли разница между проекцией и компонентом вектора (конечно, в каком-то направлении)…… или в чем причина умножения на b .
спасибо
цвет
Расширенный член уровня 2
Проекция B в направлении A равна
\[B\cos(\theta)\]
Проекция A в направлении B равна
\[A\cos(\theta)\]
как во многом эти два вектора указывают в одном и том же направлении. ?
?
вычисляется как произведение этих двух
как \[AB\cos(\theta)\]
h**p://behindtheguesses.blogspot.com/2009/04/dot-and-cross-products.html
Последнее редактирование:
eng_boody
Член уровня 3
большое спасибо ..
- Статус
- Закрыто для дальнейших ответов.
Скалярное произведение и векторное произведение
- Автор Диша Карнатаки
- Ответов: 2
Математика и физика
Дж
Изобретение векторного произведения
- Автор Джон
- Ответов: 3
Математика и физика
Как представлено перекрестное произведение !!
- Автор kalaianand
- Ответов: 13
Математика и физика
Б
Сомнение в векторном анализе с использованием скалярного произведения…
- Автор Bhanumurthy
- Ответов: 4
Математика и физика
Физический смысл операторов Curl и Div
- Автор: safwatonline
- Ответов: 1
Математика и физика
Делиться:
Фейсбук Твиттер Реддит Пинтерест Тамблер WhatsApp Эл. адрес Делиться Ссылка на сайт
Верх
Узнать о перекрестном произведении
Определение перекрестного произведения
Перекрестное произведение — это бинарная операция над двумя векторами в трехмерном пространстве. Символ, который используется для обозначения перекрестного произведения, — ×. Его также называют векторным произведением. Иногда его называют прямым произведением площади, чтобы подчеркнуть геометрическое значение.
Обзор перекрестного произведения
Математически вектор — это величина, которая имеет как направление, так и величину (т. е. длину). Предположим, что a⃗\vec{a}a и b⃗\vec{b}b — два линейно независимых вектора в трехмерном пространстве, тогда перекрестное произведение a⃗\vec{a}a и b⃗\vec{b}b равно обозначается как a⃗×b⃗\vec{a}\times \vec{b}a×b и произносится как ′′a⃗ крест b⃗»»\vec{a}\text{ крест}\vec{b} »’крест’ б» . Кроме того, «a⃗ перекресток b⃗»»\vec{a}\text{ cross }\vec{b}»»a перекресток b» перпендикулярен обоим векторам и b и, следовательно, нормален к плоскости содержащие их. Его не следует путать с скалярным произведением (проекционным произведением) векторов.
е. длину). Предположим, что a⃗\vec{a}a и b⃗\vec{b}b — два линейно независимых вектора в трехмерном пространстве, тогда перекрестное произведение a⃗\vec{a}a и b⃗\vec{b}b равно обозначается как a⃗×b⃗\vec{a}\times \vec{b}a×b и произносится как ′′a⃗ крест b⃗»»\vec{a}\text{ крест}\vec{b} »’крест’ б» . Кроме того, «a⃗ перекресток b⃗»»\vec{a}\text{ cross }\vec{b}»»a перекресток b» перпендикулярен обоим векторам и b и, следовательно, нормален к плоскости содержащие их. Его не следует путать с скалярным произведением (проекционным произведением) векторов.
Если два вектора либо прямо противоположны друг другу по направлению, т.е. не являются линейно независимыми, либо имеют одинаковое направление, если один из них имеет нулевую длину, то их векторное произведение равно нулю.
Есть вопрос по этой теме?
Что вы узнаете:
- Определение векторного произведения
- Обзор векторного произведения
- Формула векторного произведения
- Свойства векторного произведения
- Матричное представление векторного произведения
Формула перекрестного произведения
Перекрестное произведение любых двух векторов может быть определено только в трехмерном пространстве.
Пусть a⃗\vec{a}a и b⃗\vec{b}b — два вектора, тогда векторное произведение этих векторов определяется формулой:
a⃗×b⃗=∣a⃗∣∣b⃗∣sin θn\vec{a}\times \vec{b}=\left| {\vec{а}} \право|\лево| {\vec{b}} \right|\sin \theta na×b=∣a∣∣∣∣∣b∣∣∣∣sinθn
Здесь,
∣a⃗∣=\left| {\vec{a}} \right|=∣a∣= Величина вектора a
∣b⃗∣=\влево| {\vec{b}} \right|=∣∣∣∣b∣∣∣∣= Величина вектора b
θ = Угол между a и b
n = Единичный вектор, который находится под прямым углом к a и b
Эти термины ясно видны из рисунка ниже.
Направление векторного произведения двух векторов также можно проиллюстрировать с помощью правила правой руки. Это можно показать следующим образом.
На приведенном выше рисунке показано направление векторов в трехмерном пространстве. 9
Свойства перекрестного произведения
Перекрестное произведение двух векторов является антикоммутативным.
 б × а = -(а × б)
б × а = -(а × б)Углы между двумя векторами находятся в диапазоне от 0° до 180°.
Векторное произведение двух векторов всегда перпендикулярно (т.е. ортогонально) обоим заданным векторам.
Когда два вектора параллельны, то модуль векторного произведения таких векторов равен 0, т. е. |a × b| = 0
Когда два вектора ортогональны, то величина векторного произведения таких векторов максимальна, т.е. |a × b| = |а| |б|.
Распределительное свойство трех векторов a, b и c: a × (b + c) = a × b + a × c
Скалярное умножение векторного произведения векторов равно (ka) × b = a × (kb) = k(a × b)
Комбинация точечного и векторного произведения векторов — это а. (б × с) = (а × б) . с = б. (а × в) 9
Важным свойством векторного произведения векторов с точки зрения определителя матрицы является:
Продолжайте учиться
Что изучать дальше на основе учебной программы колледжа
Копланарные векторыПлощадь треугольникаСкалярное тройное произведениеПлощадь параллелограммаПравая рука ПравилоПерекрестное произведение векторовСвойства перекрестного произведенияВекторное произведение
Перекрестное произведение двух векторов
Перекрестное произведение двух векторовНавигация по странице:
- Определение перекрестного произведения
- Формулы перекрестного произведения
- Свойства перекрестного произведения
- Примеры перекрестных произведений
Калькулятор перекрестного произведения.

Упражнения. Перекрестное произведение двух векторов.
Определение. Векторное произведение ( векторное произведение ) вектора a на вектор b есть вектор c, длина которого численно равна площади параллелограмма, построенного на векторах a и b, перпендикулярных плоскости этих векторов и направление так, чтобы наименьший поворот от а к b вокруг вектора с осуществлялся против часовой стрелки, если смотреть из конечной точки с (рис. 1).
Рис. 1 Формулы перекрестного произведения
Перекрестное произведение двух векторов a = {a x ; а и ; a z } и b = {b x ; б у ; b z } в декартовых координатах — это вектор, значение которого можно вычислить по следующим формулам: а × б =
i j k = i (a y b z — a z b y ) — j (a x b z — a z b x ) + k (a x b y — a y b x ) а x г b x b y b z a × b = {a y b z — a z b y ; a z b x — a x b z ; a x b y — a y b x }
Свойства векторного произведения
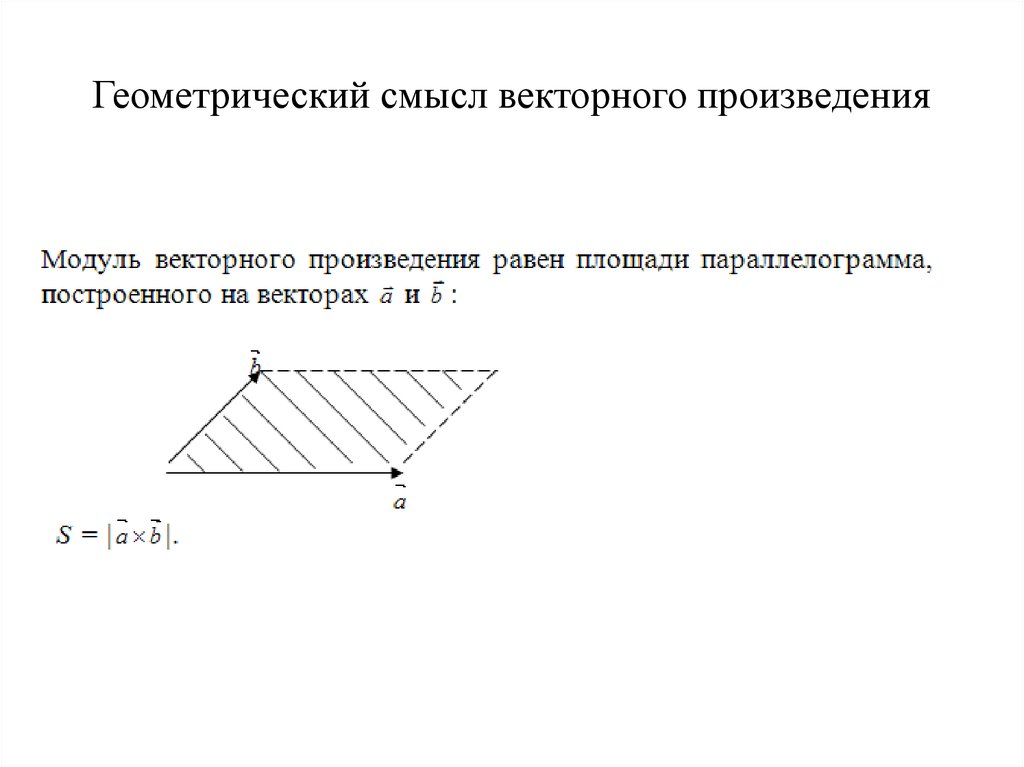
Геометрическая интерпретация.

Модуль векторного произведения двух векторов a и b равен площади параллелограмма, построенного на этих векторах:
А p = |a × b|
Геометрическая интерпретация.
Площадь треугольника, построенного на векторах a и a, равна половине величины векторного произведения этих векторов:
A Δ = 1 |a × b| 2 Перемножение двух ненулевых векторов a и b равно нулю тогда и только тогда, когда векторы коллинеарны.
Вектор c, равный векторному произведению ненулевых векторов a и b, перпендикулярен этим векторам.
c = a × b => c ┴ a и c ┴ b
а × b = -b × а
(k a) × b = a × (k b) = k (a × b)
(а + б) х с = а х с + б х с
Примеры перекрестных произведений
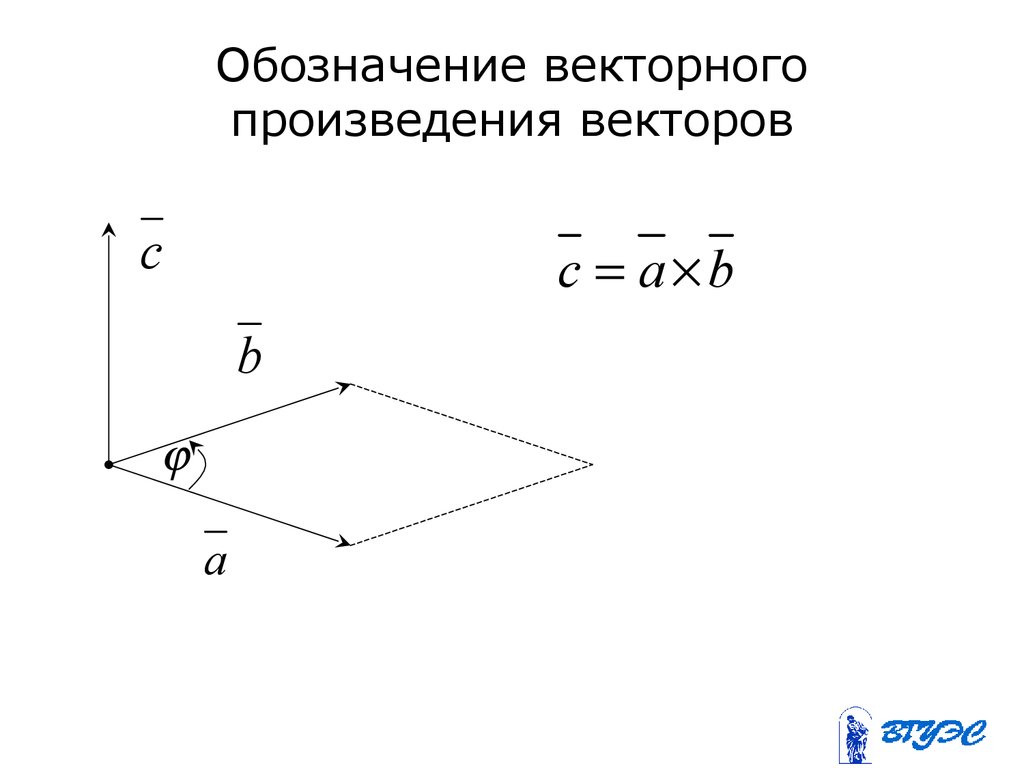
Пример 1.
 Найдите векторное произведение a = {1; 2; 3} и б = {2; 1; -2}.
Найдите векторное произведение a = {1; 2; 3} и б = {2; 1; -2}.Решение:
а × б = я к к = 1 2 3 2 1 -2 = i (2 · (-2) — 3 · 1) — j (1 · (-2) — 2 · 3) + k (1 · 1 — 2 · 2) =
= i (-4 — 3) — j (-2 — 6) + k (1 — 4) = -7 i + 8 j — 3 k = {- 7; 8; -3}
Пример 2. Найдите площадь треугольника, образованного векторами a = {-1; 2; -2} и b = {2; 1; -1}.
Решение: Вычислить векторное произведение этих векторов:
а × б = я к к = -1 2 -2 2 1 -1 = i (2 · (-1) — (-2) · 1) — j ((-1) · (-1) — (-2) · 2) + k ( (-1) · 1 — 2 · 2) =
= i (-2 + 2) — j (1 + 4) + k (-1 — 4) = -5 j — 5 к = {0; -5; -5}
Из свойств векторного произведения:
A Δ = 1 |a × b| = 1 √0 2 + 5 2 + 5 2 = 1 √25 + 25 = 1 √50 = 5√2 2 2 2 2 2 Ответ: A Δ = 2,5√2.




 Геометрический смысл векторного произведения. — КиберПедия
Геометрический смысл векторного произведения. — КиберПедия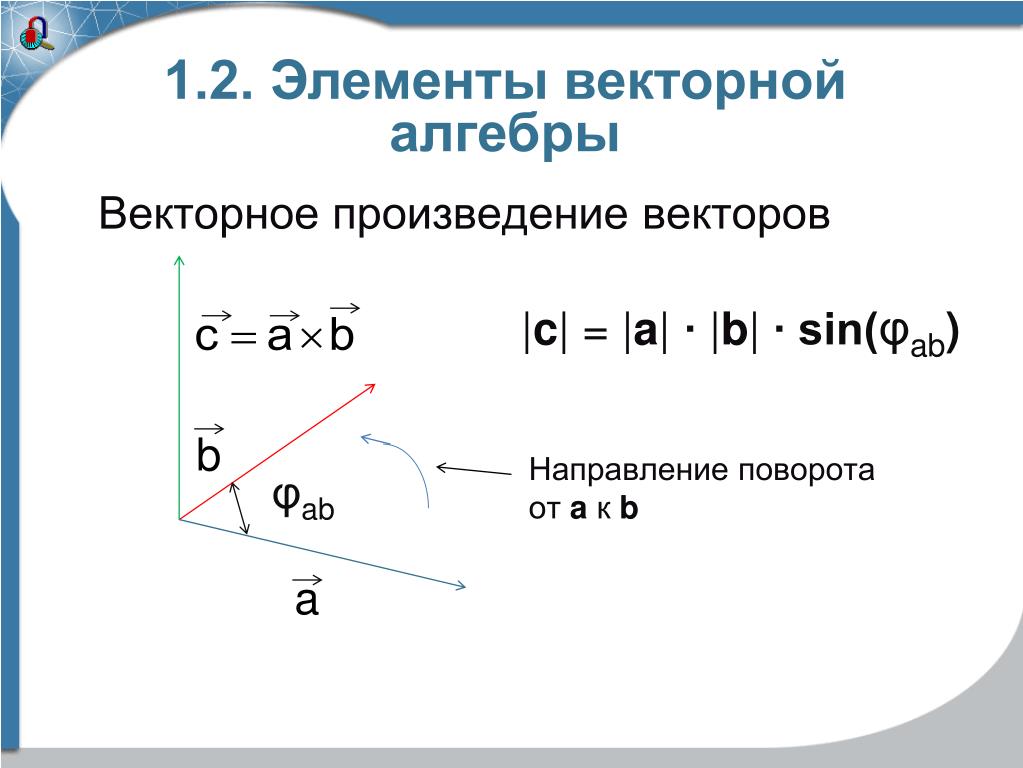 ..
..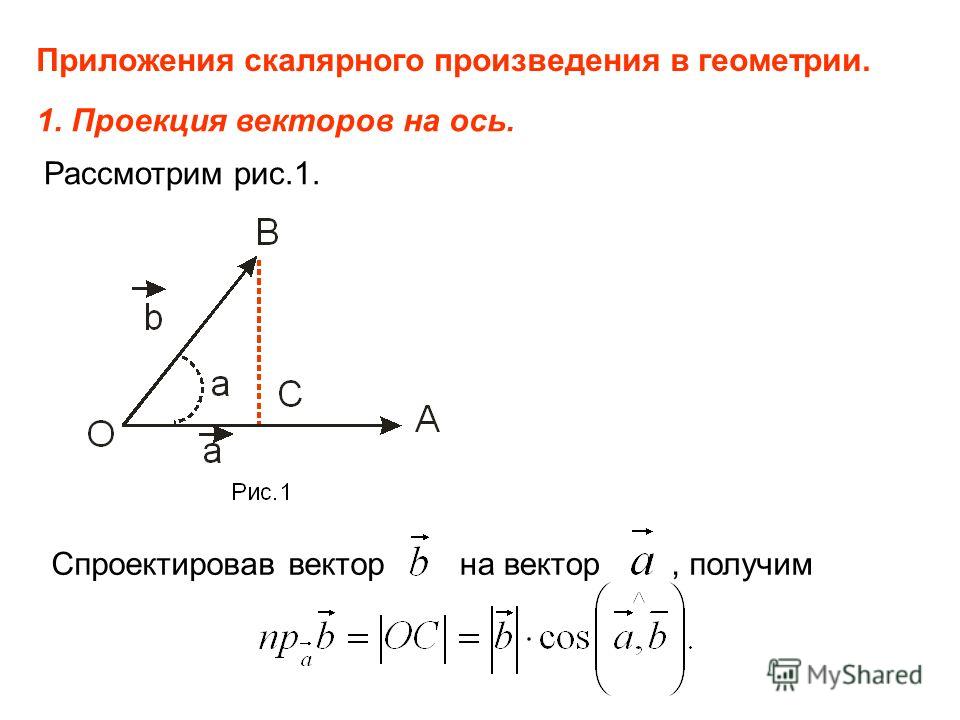
 Другими словами, длина векторного произведения векторов и равна площади параллелограмма со сторонами и и углом между ними, равным . В этом состоит геометрический смысл векторного произведения.
Другими словами, длина векторного произведения векторов и равна площади параллелограмма со сторонами и и углом между ними, равным . В этом состоит геометрический смысл векторного произведения.
 В декартовой прямоугольной системе координат вектор с компонентами (А, В) перпендикулярен прямой , заданной уравнением Ах + Ву + С = 0.
В декартовой прямоугольной системе координат вектор с компонентами (А, В) перпендикулярен прямой , заданной уравнением Ах + Ву + С = 0.
 Знак ± нормирующего множителя надо выбирать так, чтобы μ * С < 0. р – длина перпендикуляра, опущенного из начала координат на прямую, а φ — угол, образованный этим перпендикуляром с положительным направлением оси Ох.
Знак ± нормирующего множителя надо выбирать так, чтобы μ * С < 0. р – длина перпендикуляра, опущенного из начала координат на прямую, а φ — угол, образованный этим перпендикуляром с положительным направлением оси Ох.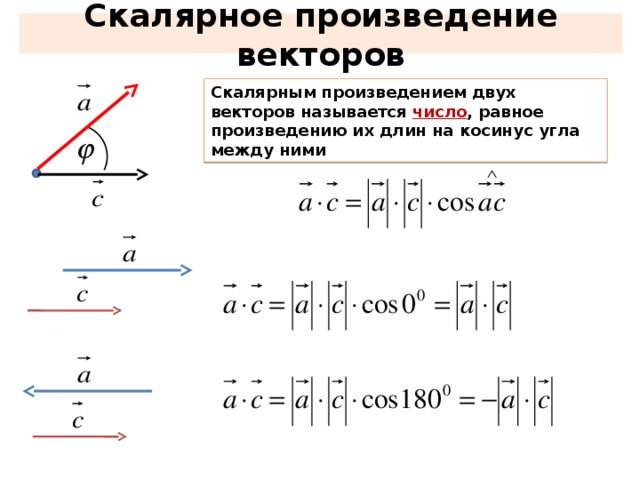 Признак перпендикулярности прямой и плоскости. Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна этой плоскости.
Признак перпендикулярности прямой и плоскости. Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна этой плоскости.
 В других системах координат может потребоваться использование других, более сложных формул. 9AxAyAzBxByBz | {\ displaystyle {\ vec {A}} \ times {\ vec {B}} = {\ begin {vmatrix} {\ hat {x}} & {\ hat {y}} & {\ hat {z} }\\A_{x}&A_{y}&A_{z}\\B_{x}&B_{y}&B_{z}\end{vmatrix}}}
В других системах координат может потребоваться использование других, более сложных формул. 9AxAyAzBxByBz | {\ displaystyle {\ vec {A}} \ times {\ vec {B}} = {\ begin {vmatrix} {\ hat {x}} & {\ hat {y}} & {\ hat {z} }\\A_{x}&A_{y}&A_{z}\\B_{x}&B_{y}&B_{z}\end{vmatrix}}}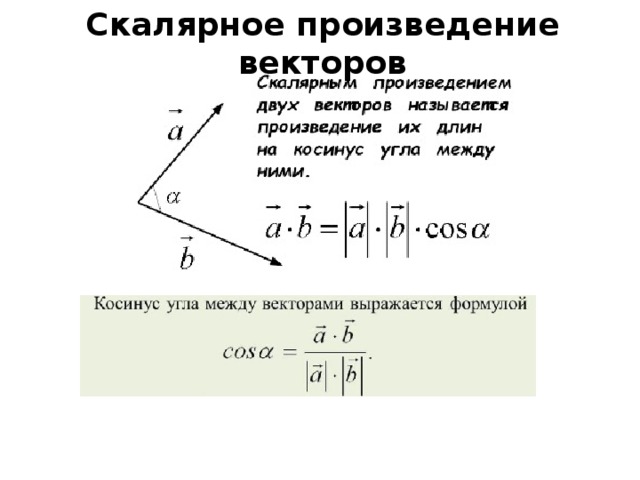

 б × а = -(а × б)
б × а = -(а × б)
 Найдите векторное произведение a = {1; 2; 3} и б = {2; 1; -2}.
Найдите векторное произведение a = {1; 2; 3} и б = {2; 1; -2}.