10. Определение правой тройки векторов. Векторное произведение векторов, его свойства, геометрический смысл.
Тройка
векторов 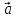 ,
,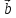 и
и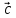 называется правой, если
называется правой, если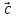 направлен так, что из его конца кратчайший
поворот от
направлен так, что из его конца кратчайший
поворот от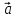 к
к происходит против часовой стрелки.
происходит против часовой стрелки.
Векторным
произведением вектора 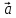 на вектор
на вектор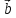
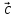 который обладает следующими свойствами:
который обладает следующими свойствами:Его длина равна

Вектор
 перпендикулярен к плоскости, в которой
лежат вектора
перпендикулярен к плоскости, в которой
лежат вектора и
и
Вектор
 направлен так, что поворот от вектора
направлен так, что поворот от вектора к вектору
к вектору осуществляется против часовой стрелки,
если смотреть из конца вектора
осуществляется против часовой стрелки,
если смотреть из конца вектора (тройка векторов
(тройка векторов ,
,
 – правая).
– правая).
Основные свойства векторного произведения:
1)
Векторное произведение 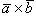 равно
нулю, если векторы
равно
нулю, если векторы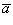 и
и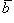 коллинеарны
или какой-либо из перемножаемых векторов
является нулевым.
коллинеарны
или какой-либо из перемножаемых векторов
является нулевым.
2)
При перестановке местами векторов
сомножителей векторное произведение
меняет знак на противоположный 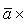
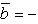
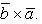
Геометрический смысл векторного произведения: модуль векторного произведения векторов численно равен площади параллелограмма, построенного на этих векторах как на сторонах.
11. Смешанное произведение 3-х векторов, его свойства. Геометрический смысл. Вычисление в координатах. Необходимое и достаточное условие компланарности 3-х векторов.
Смешанным произведением векторов  ,
,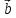 ,
,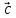
 *
*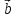 )*
)*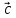 = (
= (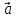 ,
,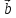 ,
,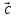 )
) Модуль смешанного произведения векторов 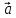
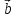 ,
,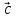 равен объёму параллелепипеда, построенного
на векторах
равен объёму параллелепипеда, построенного
на векторах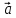 ,
,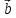 ,
,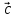 .
.Свойства:
1)
(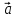 *
*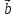
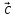 =
= *(
*(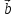 *
*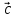 )
) 2)
(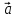 ,
,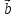 ,
,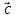 )
= (
)
= (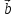
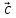 ,
,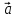 )
= (
)
= ( ,
,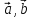 )
= — (
)
= — (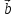 ,
,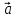 ,
,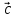
3) 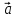 ,
,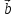 ,
,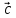 – компланарны (
– компланарны (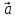 ,
,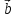 ,
,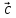 )
= 0
)
= 0
4) 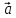
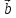 ,
, – правая (
– правая (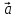 ,
,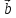 ,
,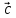 )
> 0
)
> 0 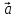 ,
, 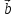 ,
,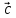
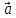 ,
,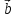 ,
,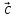 )
< 0
)
< 0 5)
(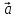 1+
1+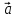 2,
2,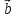 ,
,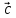
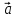 1,
1,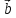 ,
, )
+ (
)
+ ( 2,
2,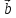 ,
,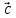 ) (α*
) (α*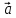
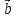 ,
,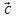 )
= α(
)
= α(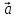 ,
,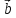 ,
,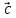 )
) Вычисление
в координатах: 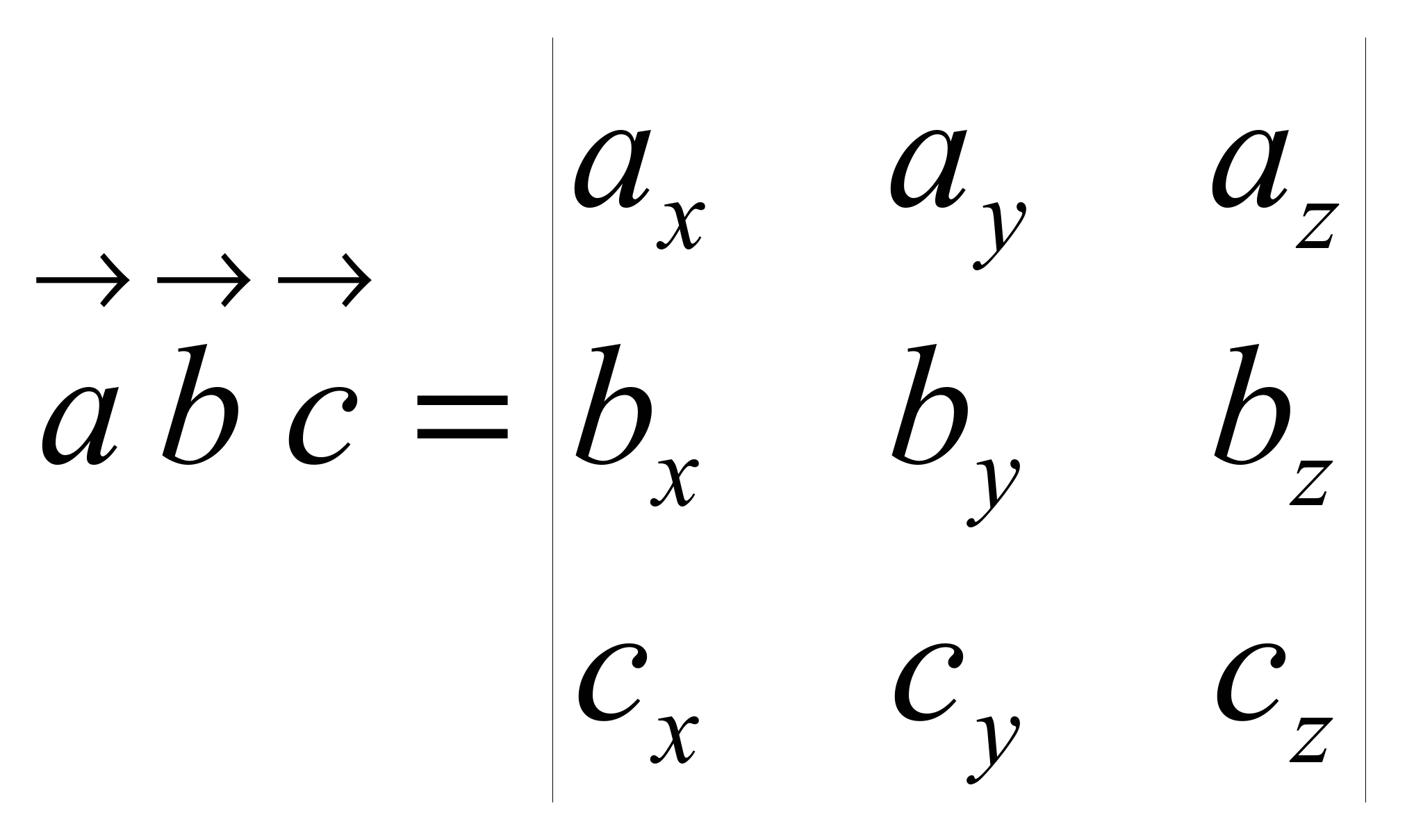
Необходимое
и достаточное условие компланарности
3-х векторов :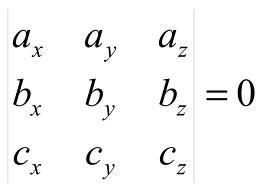
Аналитическая геометрия
12. Виды уравнений прямой на плоскости. Расстояние от точки до прямой.

Виды:
1) Общее уравнение прямой: Ax + By + C = 0
2)
Уравнение прямой в отрезках: 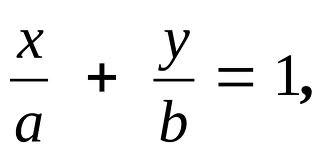
3) Уравнение прямой с угловым коэффициентом: y = kx + b
4)
Каноническое уравнение прямой на
плоскости: 
5)
Параметрические уравнения прямой на
плоскости: 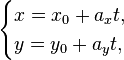
6)
Нормальное уравнение прямой: 
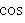
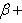
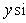
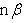

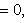 p— длина перпендикуляра,
опущенного из начала координат на
прямую, β- угол наклона этого перпендикуляра к
осиO.
p— длина перпендикуляра,
опущенного из начала координат на
прямую, β- угол наклона этого перпендикуляра к
осиO.
Расстояние точки A(x1, y1) до прямой Ax + By + C = 0 есть длина перпендикуляра, опущенного из этой точки на прямую. Она определяется по формуле:
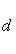
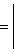
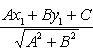
13. Взаимное расположение двух прямых на плоскости, угол между прямыми.
Если
прямые 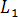 и
и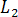 заданы
общими уравнениями
заданы
общими уравнениями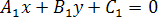 и
и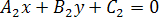 ,
,
тогда
угол между ними находится по формуле: 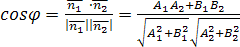
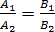 –условие параллельности
прямых
–условие параллельности
прямых  и
и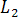 ;
;
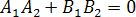 –условие перпендикулярности
прямых
–условие перпендикулярности
прямых 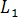 и
и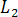 .
.
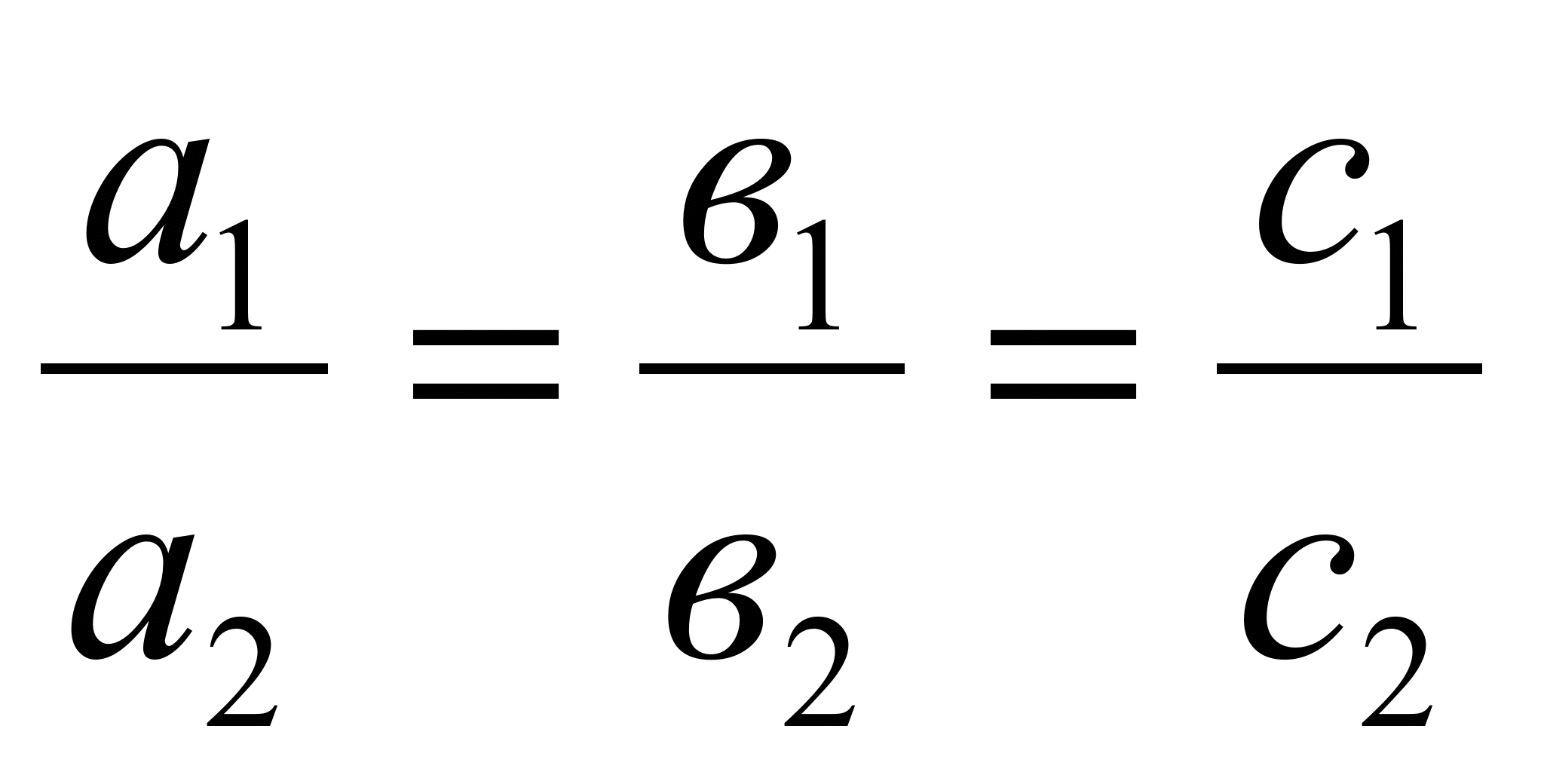 — прямые совпадают.
— прямые совпадают.
14. Виды уравнений плоскости. Расстояние от точки до плоскости.
Виды уравнений плоскости:
1) Общее: Ax + By + Cz + D = 0
2)
В отрезках: 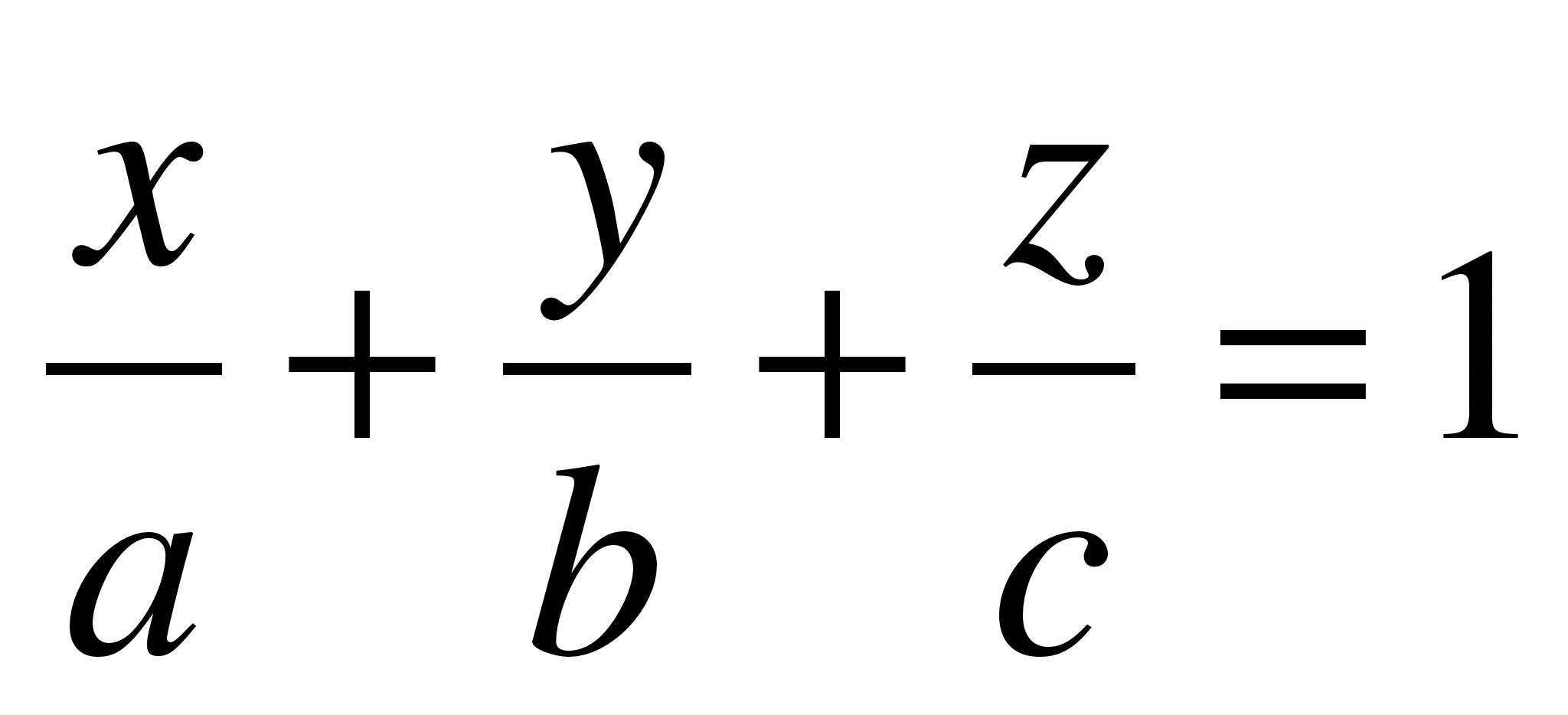
3)
Нормальное: 
Пусть плоскость  задана
уравнениемAx
+ By
+ Cz
+ D
= 0 и дана
точка
задана
уравнениемAx
+ By
+ Cz
+ D
= 0 и дана
точка  .
Тогда расстояниеp
от точки Moдо плоскости
.
Тогда расстояниеp
от точки Moдо плоскости  определяется
по формуле
определяется
по формуле
|
15. Взаимное расположение двух плоскостей, угол между плоскостями.
Взаимное расположение двух плоскостей характеризуется двумя возможностями^
1) Две плоскости не имеют общих точек, и , в таком случае, они называются параллельными
2) Две плоскости имеют хотя бы одну общую точку, и в таком случае они называются пересекающимися.
Пусть
наши плоскости 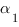 и
и заданы
уравнениями:
заданы
уравнениями:
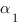 :
:
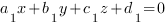
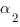 :
: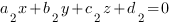
Косинус
угла 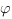 между плоскостями находится по такой
формуле:
между плоскостями находится по такой
формуле:
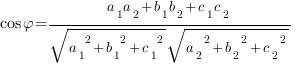
1)
Плоскости параллельны: 
2) Плоскости совпадают, если выполняются следующие условия:

a2*x0 + b2*y0 + c2*z0 + d2 = 0
существует точка M0(x0,y0,z0), принадлежащая плоскости П1
Свойства векторного произведения
10 Векторное произведение равно нулю, если векторы коллинеарны или один из них равен нулю.
 следует
из определения модуля векторного
произведения:
следует
из определения модуля векторного
произведения: 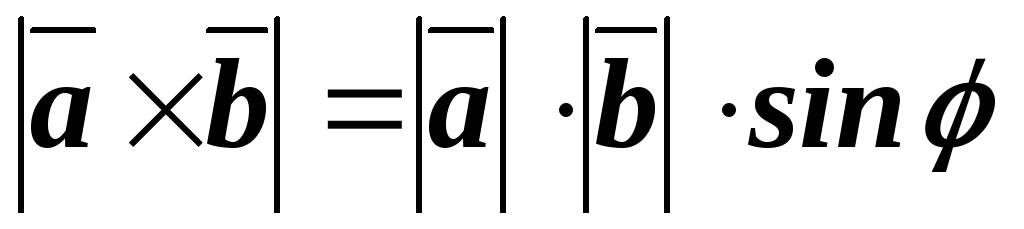 .
.
Модуль равен нулю, если:
1) 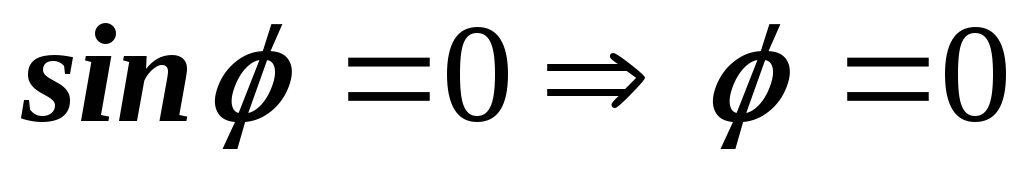 или
или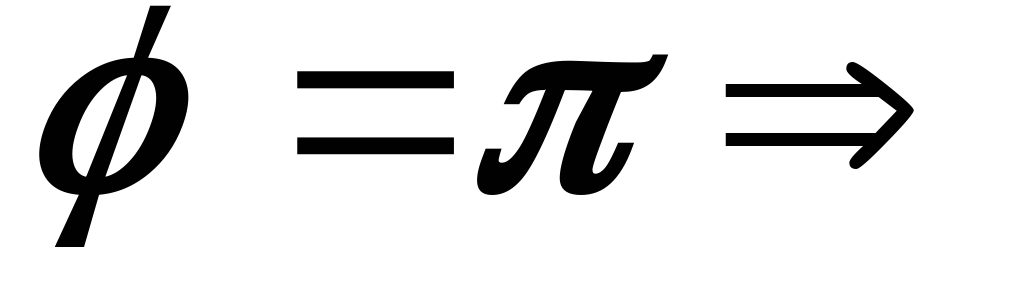 векторы
векторы коллинеарны.
коллинеарны.
2) 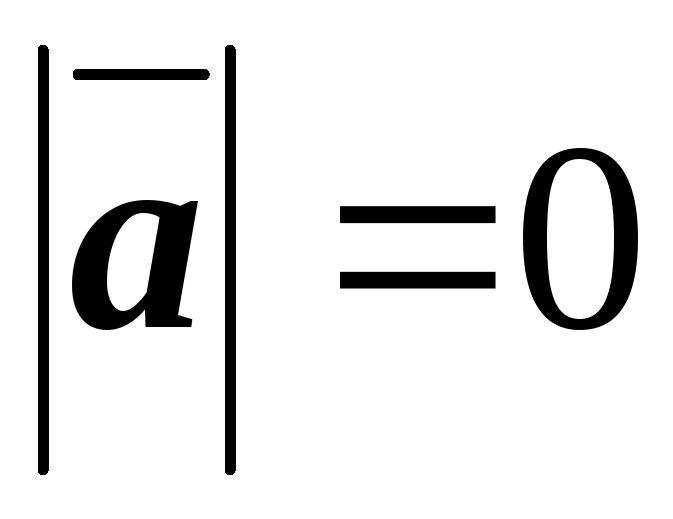 или
или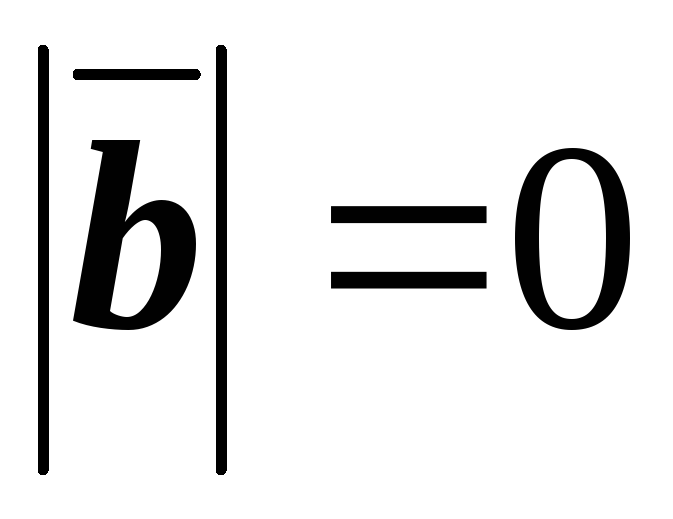 .
.
20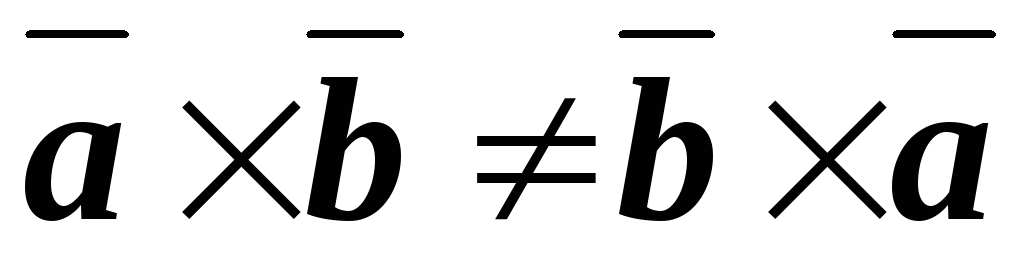 ,
т.е. векторное произведение не коммутативно.
,
т.е. векторное произведение не коммутативно.
30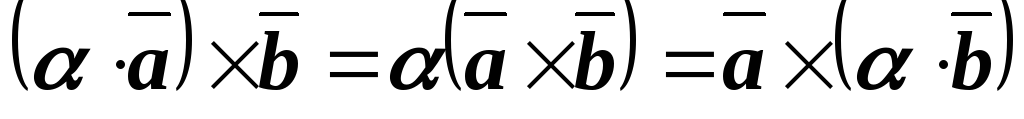 (сочетательный закон относительно
числового множителя).
(сочетательный закон относительно
числового множителя).
40. (распределительный закон относительно
суммы и произведения).
(распределительный закон относительно
суммы и произведения).
Векторное произведение векторов, заданных координатами
Пусть
заданы векторы 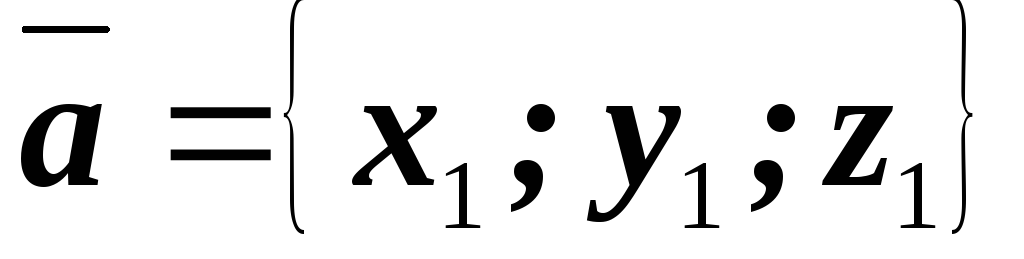 и
и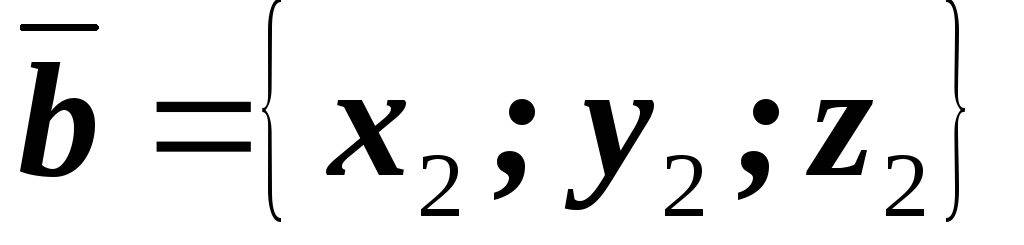 .
.
Векторное
произведение векторов, заданных
координатами, равно определителю
третьего порядка, первой строкой которого
являются единичные векторы 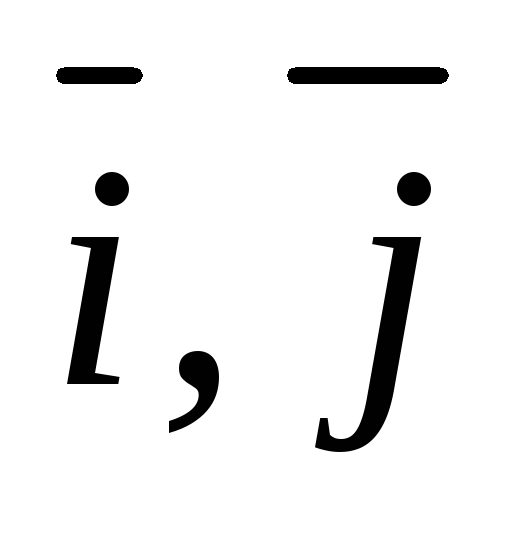 и
и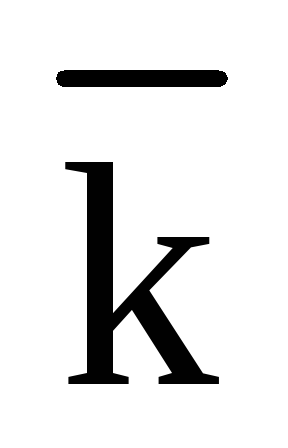 ,
второй- координаты первого перемножаемого
вектора, третьей – координаты второго
вектора:
,
второй- координаты первого перемножаемого
вектора, третьей – координаты второго
вектора:
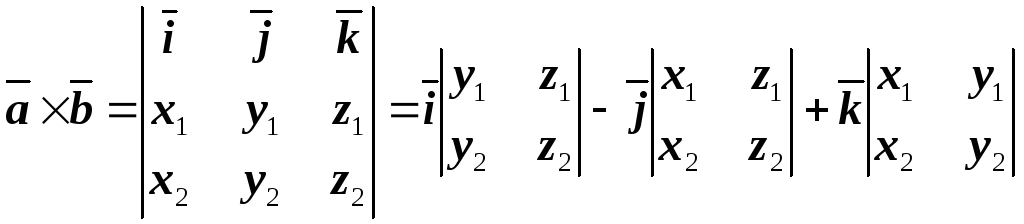 .
(4.10)
.
(4.10)
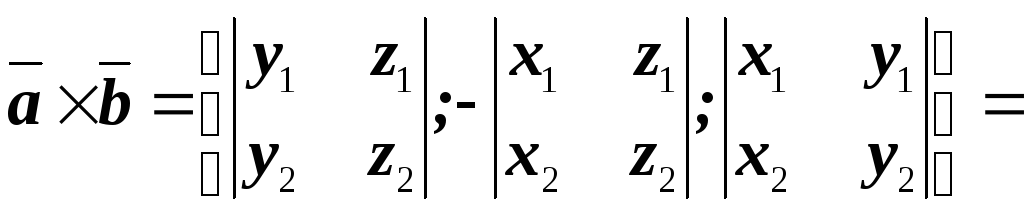
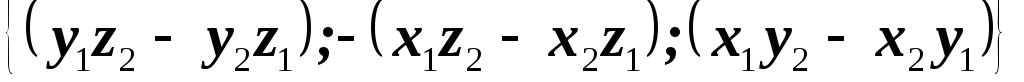 .
(4.11)
.
(4.11)
Практический способ вычисления векторного произведения
Записать векторы один под другим

и, вычёркивая последовательно столбцы одноимённых координат, получаем определители второго порядка, которые являются координатами векторного произведения. При вычислении второй координаты перед определителем изменить знак.
Составить выражение из координат:
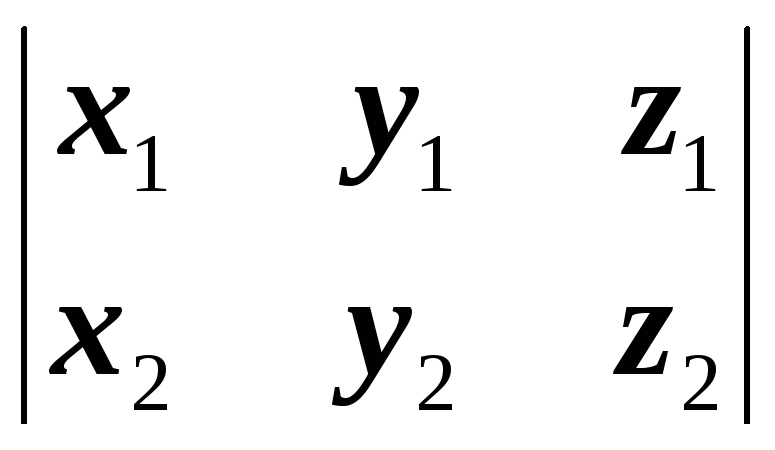 .
(4.12)
.
(4.12)
Для получения координат векторного произведения в выражении (4.12) поочередно вычеркивать столбцы.
Для получения первой координаты x вычеркнуть 1-й столбец:
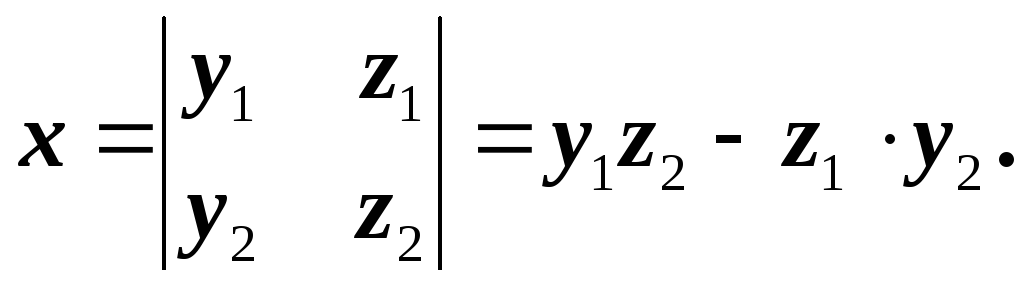
Для получения y вычеркнуть второй столбец, перед оставшимся минором взять знак « — »:
 .
.
Для z вычеркнуть 3-й столбец:

4.3 Смешанное (векторно-скалярное) произведение векторов, его геометрический смысл
Опр 4 Смешанным произведением векторов называется число, полученное в результате векторного произведения двух векторов, скалярно умноженного на третий.
Обозначается 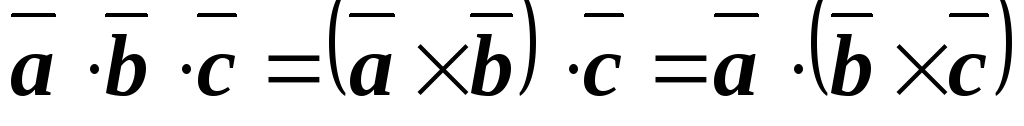 .(4.13)
.(4.13)
Геометрический смысл его выражается теоремой.
Теорема. Смешанное произведение представляет
собой число, абсолютная величина которого
равна объёму параллелепипеда, построенного
на векторах  как на составляющих, т.е.
как на составляющих, т.е.
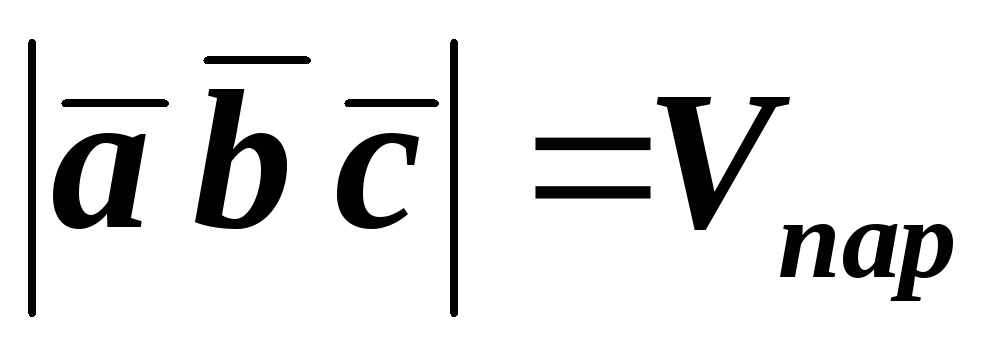 .
(4.14)
.
(4.14)
Подставляя эти значения в формулу (*), получим, что и требовалось доказать.
Свойства смешанного произведения
10 Смешанное произведение равно нулю, если
векторы 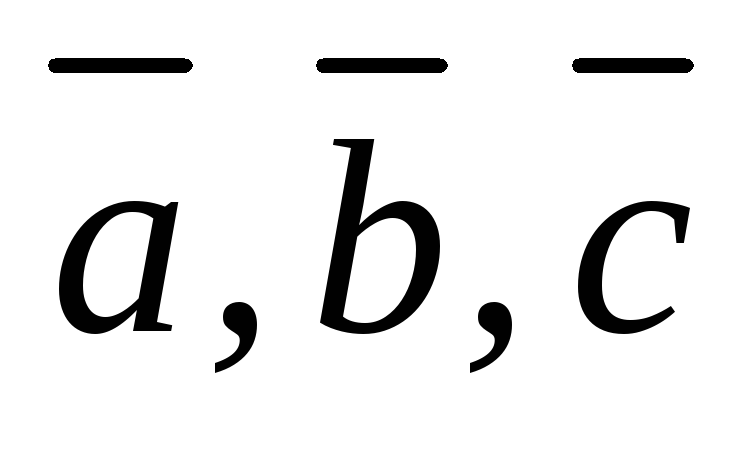 —
компланарны, один из них нулевой или
какие-либо два из них коллинеарные.
—
компланарны, один из них нулевой или
какие-либо два из них коллинеарные.
20 Можно ли переставлять местами сомножители в смешанном произведении?
Там, где произведение скалярное, там можно, а где векторное– нельзя.
 ;
;
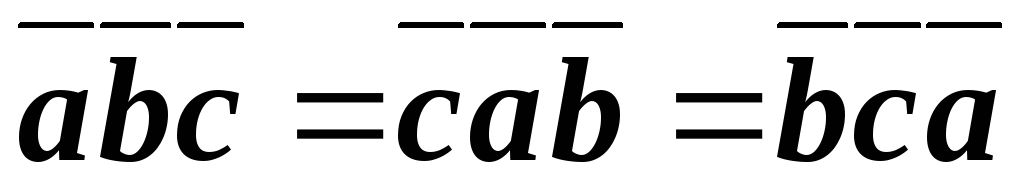 ;
;
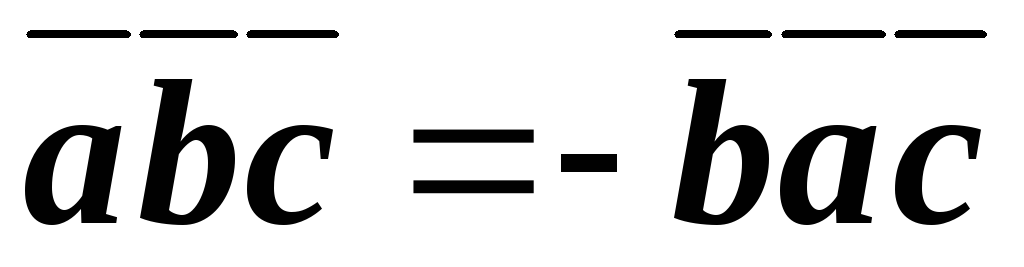 ;
; 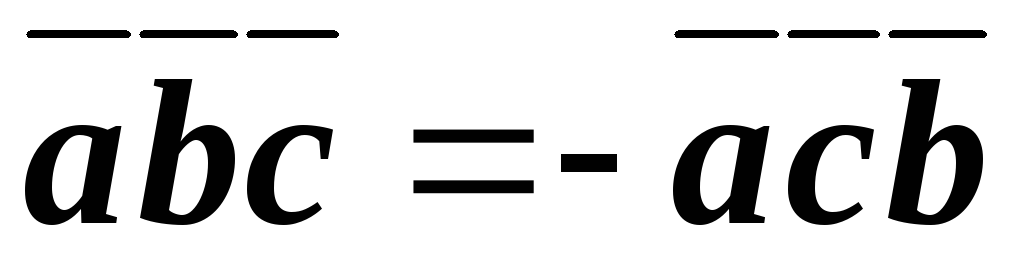 ;
;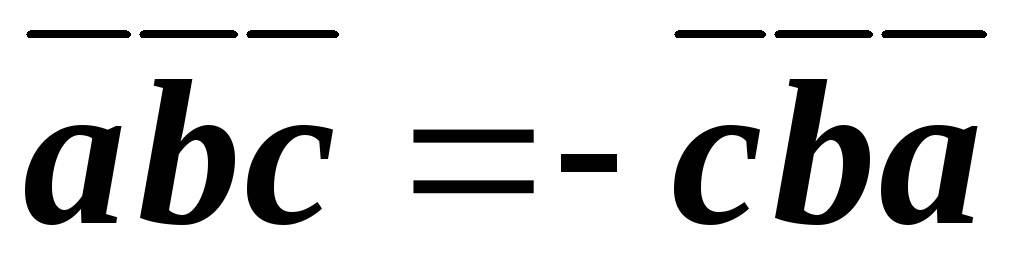 .
.
Если расположить векторы по координатным осям, то, делая круговой поворот их против часовой стрелки (рисунок 20), смешанное произведение не меняет знак.
 .
.
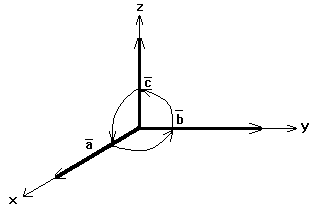 Рис.
20
Рис.
20
Если вращать векторы по ходу часовой стрелки, то смешанное произведение меняет знак на противоположный (рисунок 21).
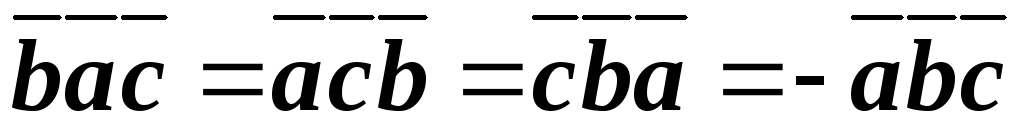 .
.
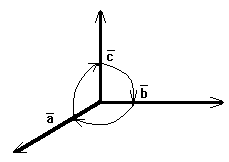 Рис.
21
Рис.
21
Смешанное произведение векторов, заданных координатами
Пусть
векторы 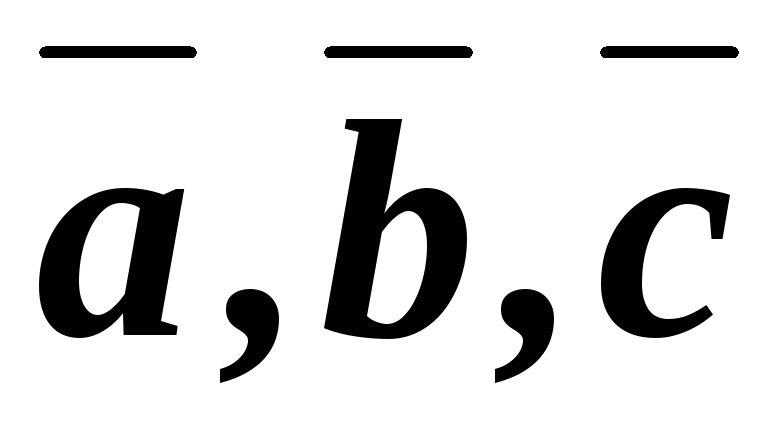 заданы координатами
заданы координатами 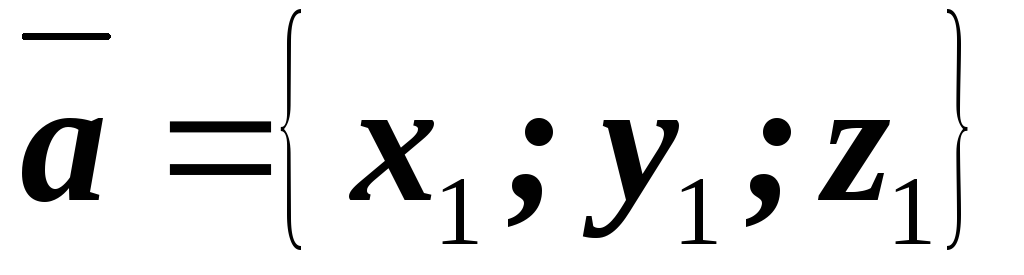 ,
,  ,
,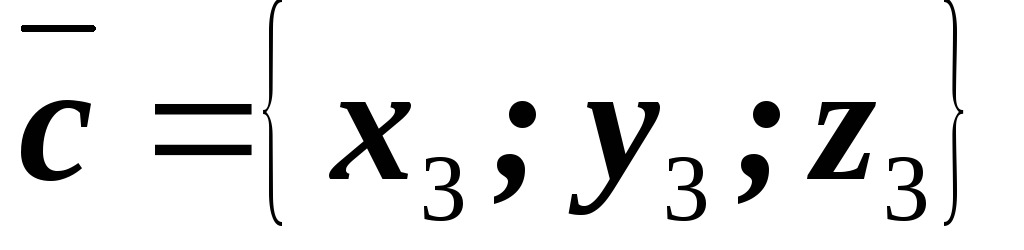 .
.
Тогда смешанное произведение их вычисляется с помощью определителя третьего порядка, строками которого являются координаты перемножаемых векторов.
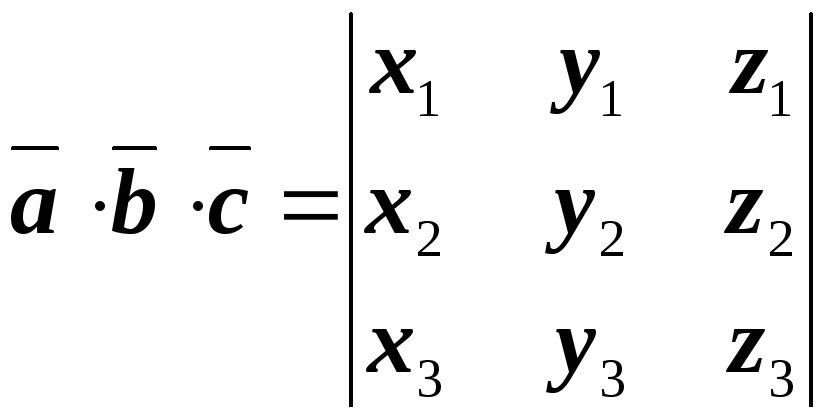 . (4.15)
. (4.15)
Векторное произведение
Ориентация тройки векторов. Упорядоченная тройка некомпланарных векторов называется правой (левой), если из конца третьего вектора кратчайший поворот от первого вектора ко второму виден против часовой стрелки (по часовой стрелке). Начала векторов тройки предполагаются при этом совмещенными. Очевидно, любая тройка некомпланарных векторов является либо правой, либо левой.
Векторное произведение. Векторным произведением вектора a на вектор b называется вектор c , удовлетворяющий трем условиям:
1) 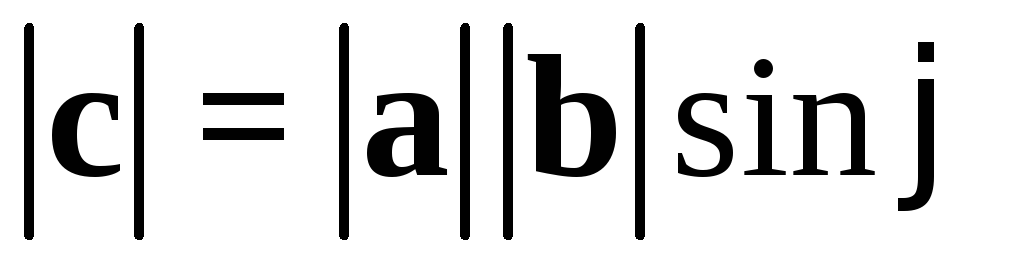 ,
,  ,
,
2)  и
и  ,
,
3) если a не параллелен  ,
то тройка векторов
,
то тройка векторов 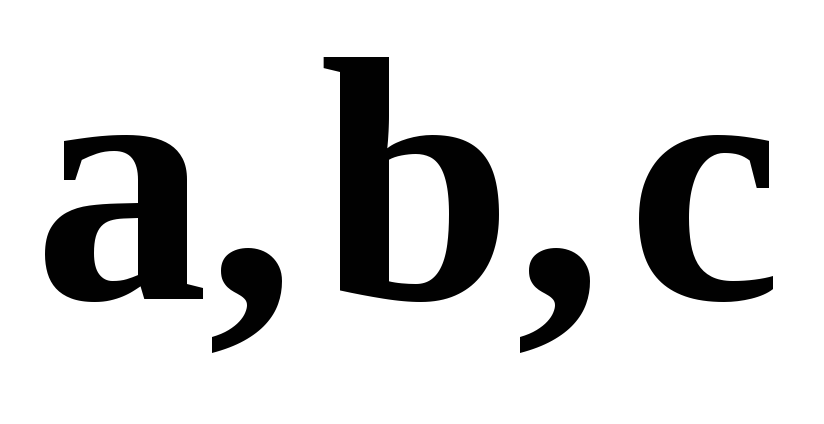 правая. Векторное произведение (рис. 5)
векторовa и b обозначают
правая. Векторное произведение (рис. 5)
векторовa и b обозначают  или
или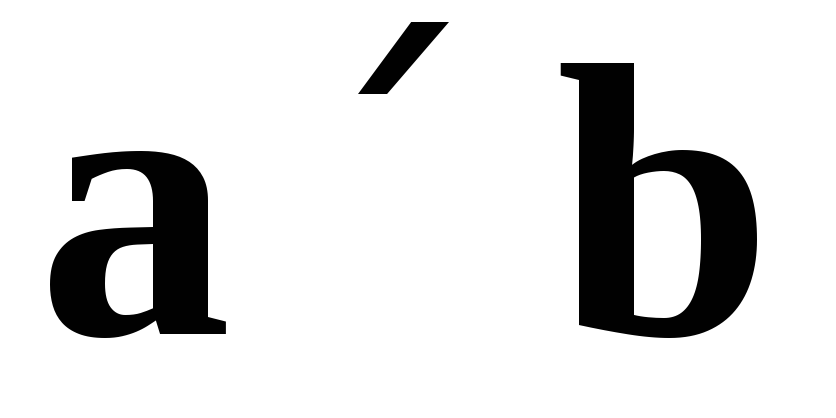 .
Мы будем придерживаться первого
обозначения.
.
Мы будем придерживаться первого
обозначения.
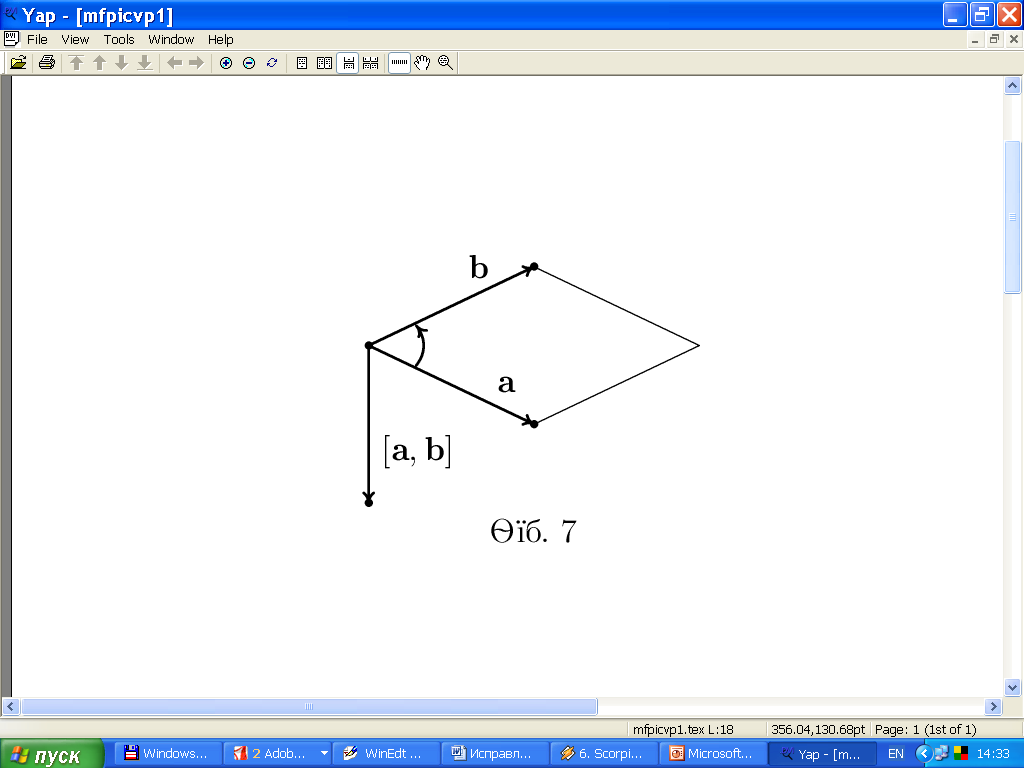
Рис. 5. Векторное произведение
Понятие векторного
произведения родилось в механике. Момент
силы F,
приложенной к точке  ,
относительно точки
,
относительно точки равен векторному произведению
равен векторному произведению 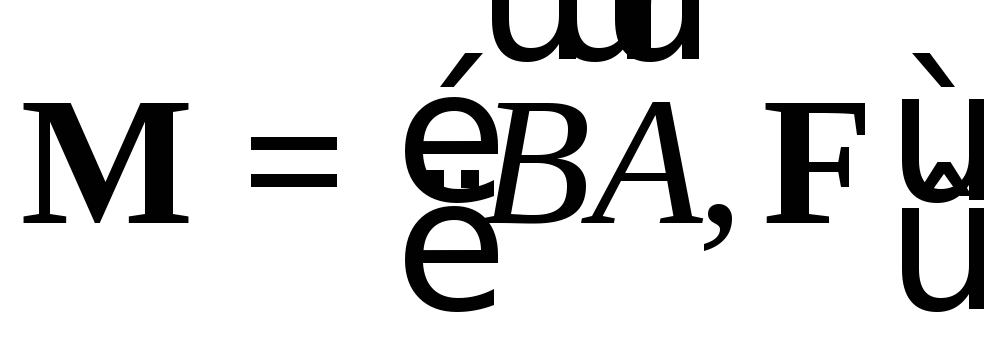 .
.
Геометрические свойства векторного произведения. Из определения векторного произведения нетрудно получить следующие свойства:
1. 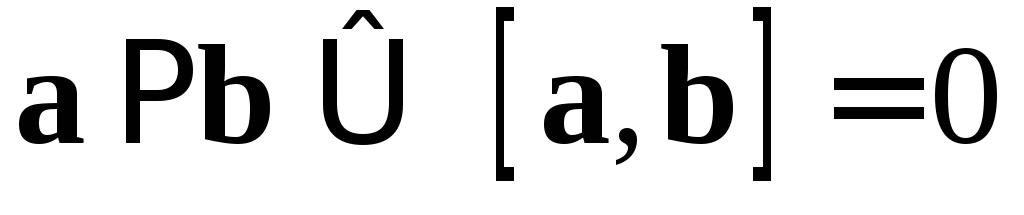 .
.
2. Модуль векторного произведения равен площади параллелограмма, построенного на векторах, приведенных к общему началу.
Докажем свойство
2). Для площади 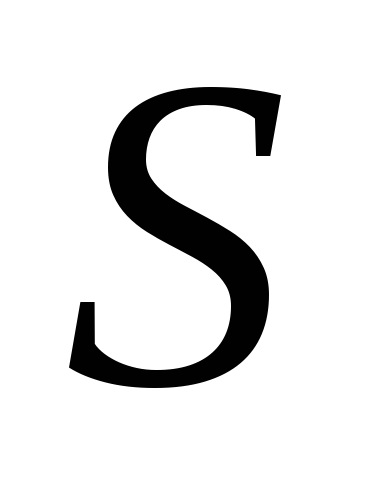 параллелограмма имеем
параллелограмма имеем 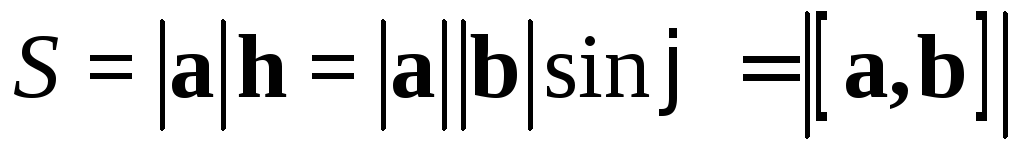 ,
что и требовалось.
,
что и требовалось.
Алгебраические свойства векторного произведения. К таковым относят следующие свойства:
1)  – антикоммутативность;
– антикоммутативность;
2) 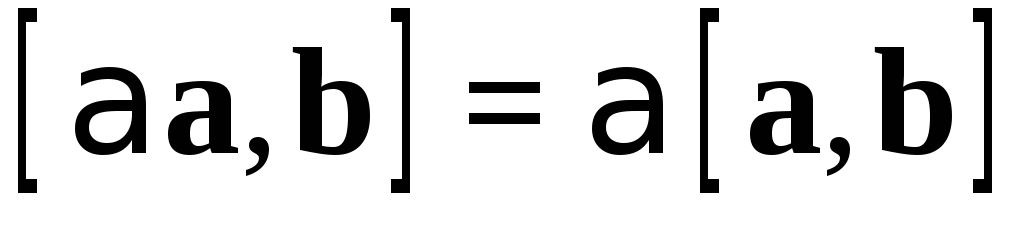 – однородность;
– однородность;
3) 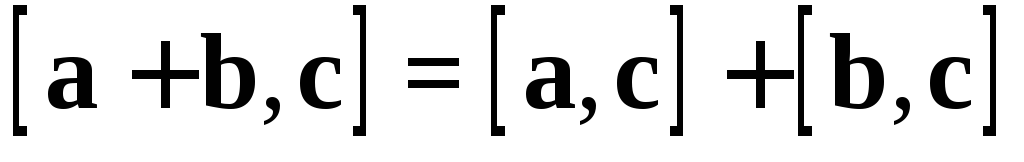 – дистрибутивность;
– дистрибутивность;
4)  – идемпотентность.
– идемпотентность.
Свойства 1, 2, 4 легко следуют из определения. Свойство 3 нуждается в доказательстве; мы получим его после введения базиса.
Получим на векторном
языке выражение для площади параллелограмма  ,
построенного на векторахa и b,
приведенных к общему началу. С одной
стороны,
,
построенного на векторахa и b,
приведенных к общему началу. С одной
стороны,  .
С другой —
.
С другой —
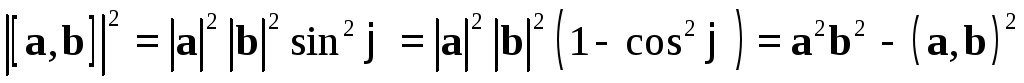 .
.
Или
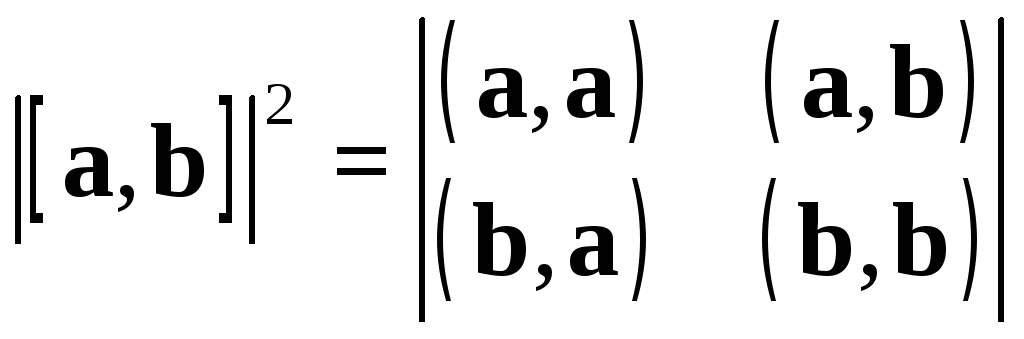 .
(2.15)
.
(2.15)
Таким образом,
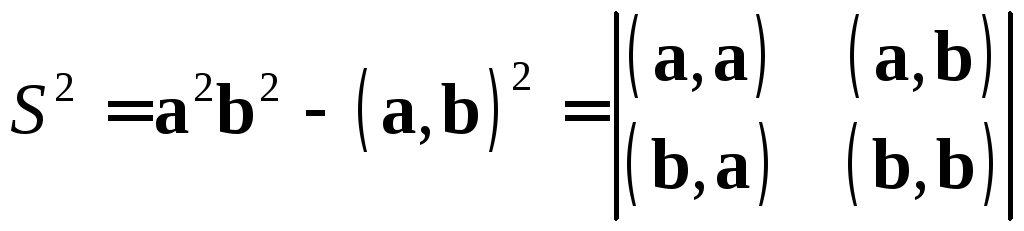 .
(2.16)
.
(2.16)
Определитель в правой части формулы (2.16) называется определителем Грама пары векторов a,b.
Полученный результат можно переписать в виде
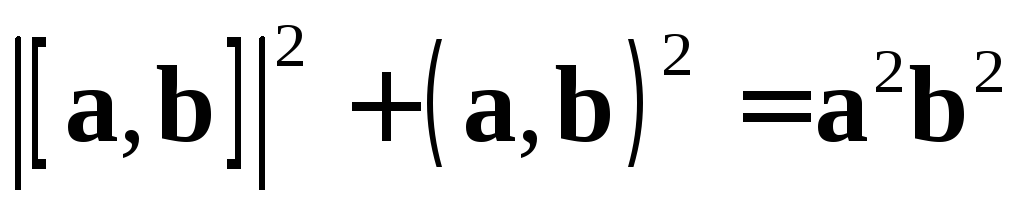 .
.
Докажем известную
со школы теорему синусов.
Рассмотрим треугольник из векторов
таких, что  .
Помножим векторно на
.
Помножим векторно на обе части этого равенства:
обе части этого равенства:
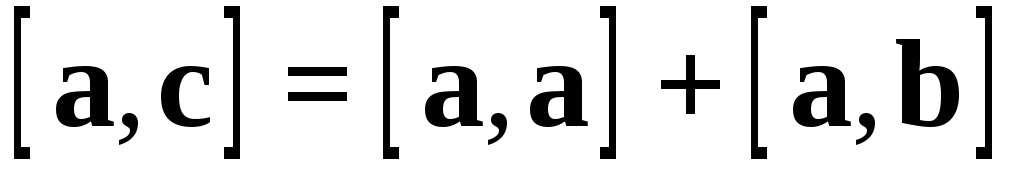 .
.
Так как 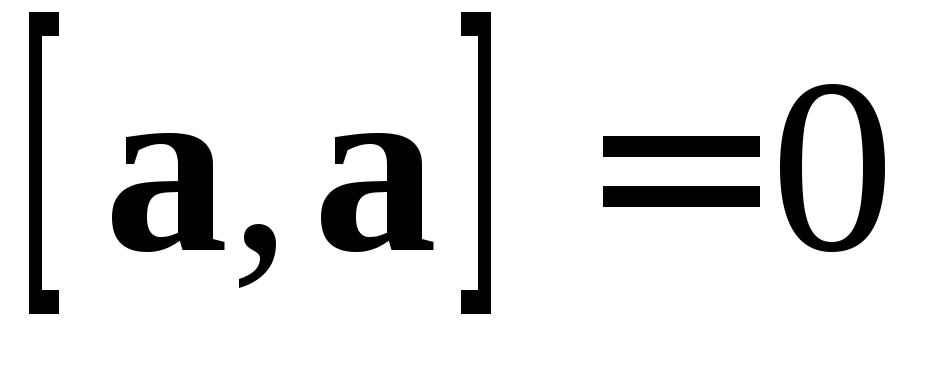 ,
то
,
то 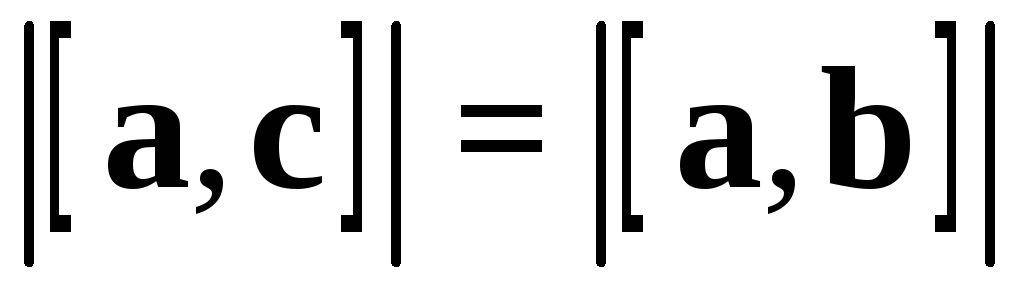 .
Отсюда
.
Отсюда
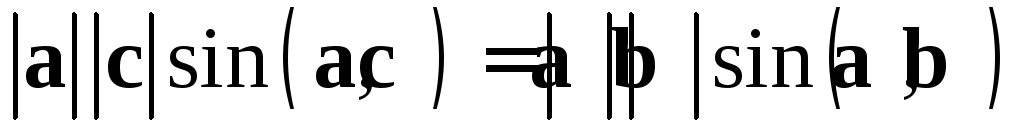 ,
,
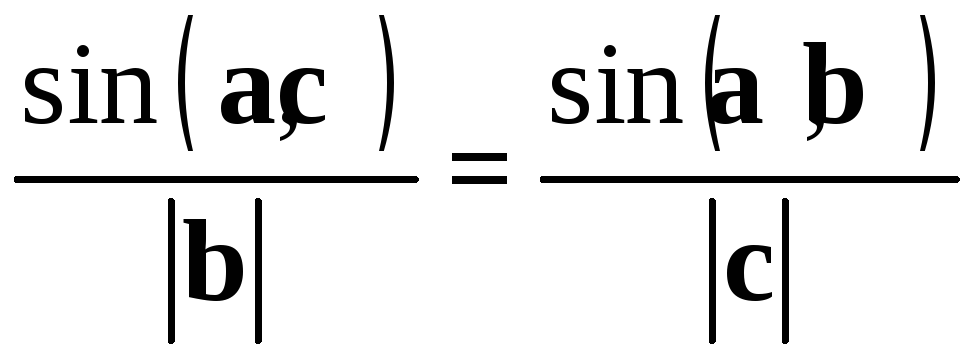 ,
,
что и требовалось.
Смешанное произведение
Смешанное произведение есть тернарная, т.е. трехместная, операция, в отличие, например, от двухместной операции скалярного произведения. Смешанное произведение (и это оправдывает название) определяется через векторное и скалярное произведения.
Смешанным
произведением трех векторов 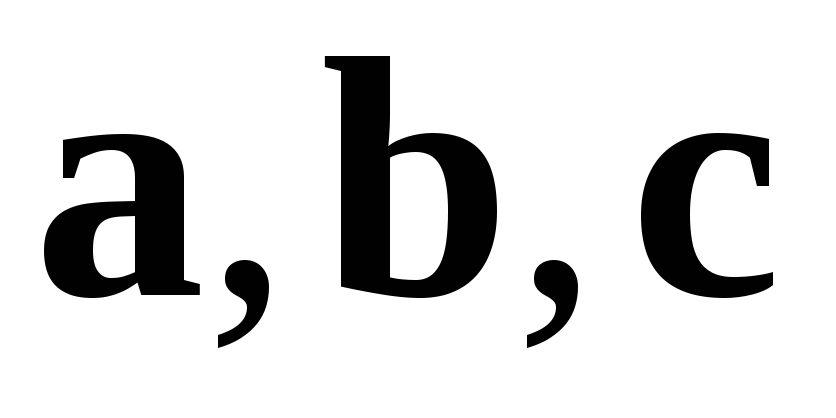 называется число
называется число
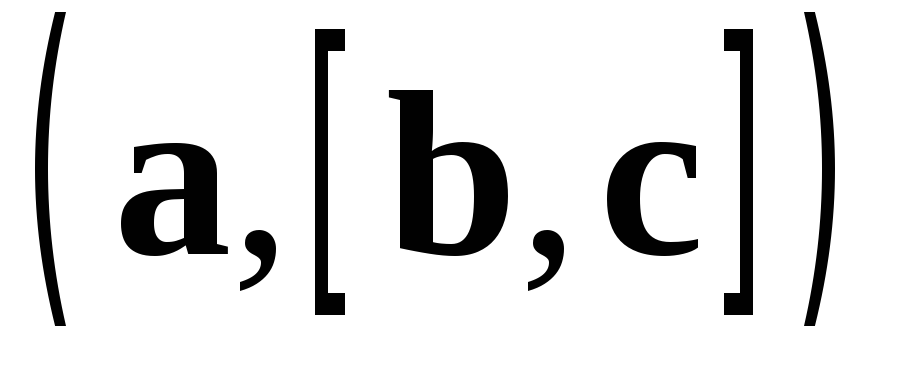 .
.
Смешанное
произведение имеет четкий геометрический
смысл. Ориентированным объемом параллелепипеда,
построенного на упорядоченной тройке
векторов 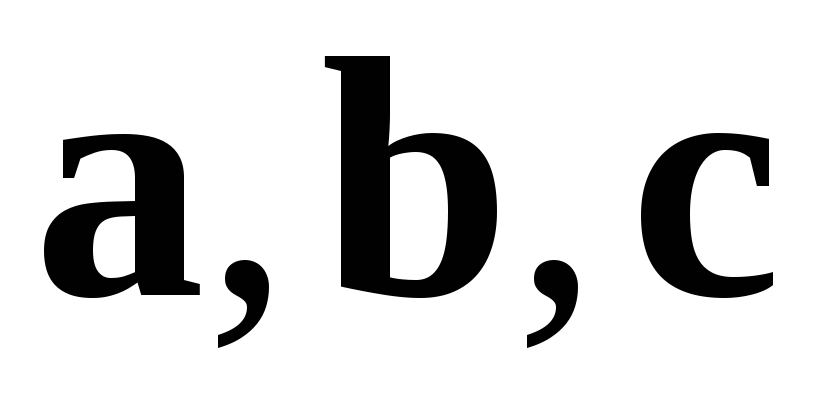 ,
приведенных к общему началу, называется
число, обозначаемое
,
приведенных к общему началу, называется
число, обозначаемое  и равное
объему этого параллелепипеда, взятому
со знаком «плюс», если эта тройка
правая, и со знаком «минус» – в
противном случае.
и равное
объему этого параллелепипеда, взятому
со знаком «плюс», если эта тройка
правая, и со знаком «минус» – в
противном случае.
Лемма. 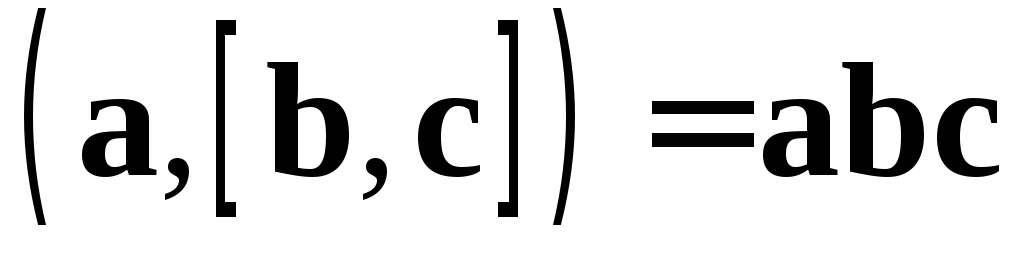 .
.
Доказательство. Объем параллелепипеда (рис.6) равен
произведению площади его основания 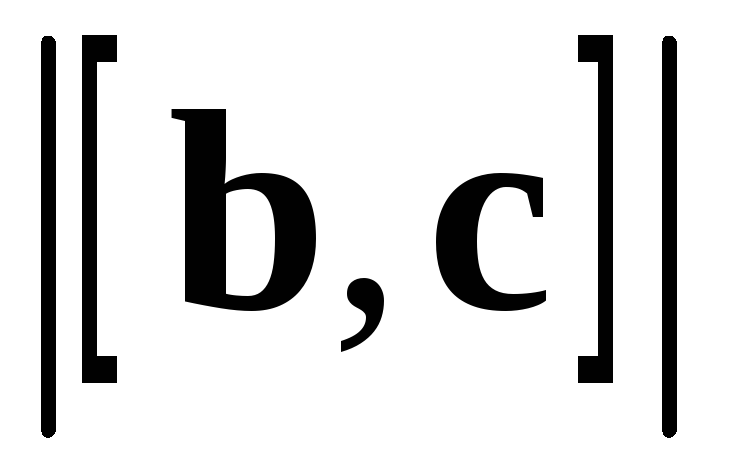 на высоту
на высоту .
.
Поэтому
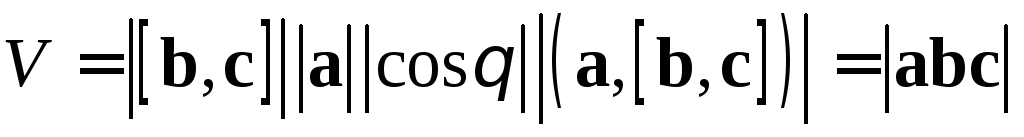 .
.
Теперь вместо  .
Можно писать
.
Можно писать .
.
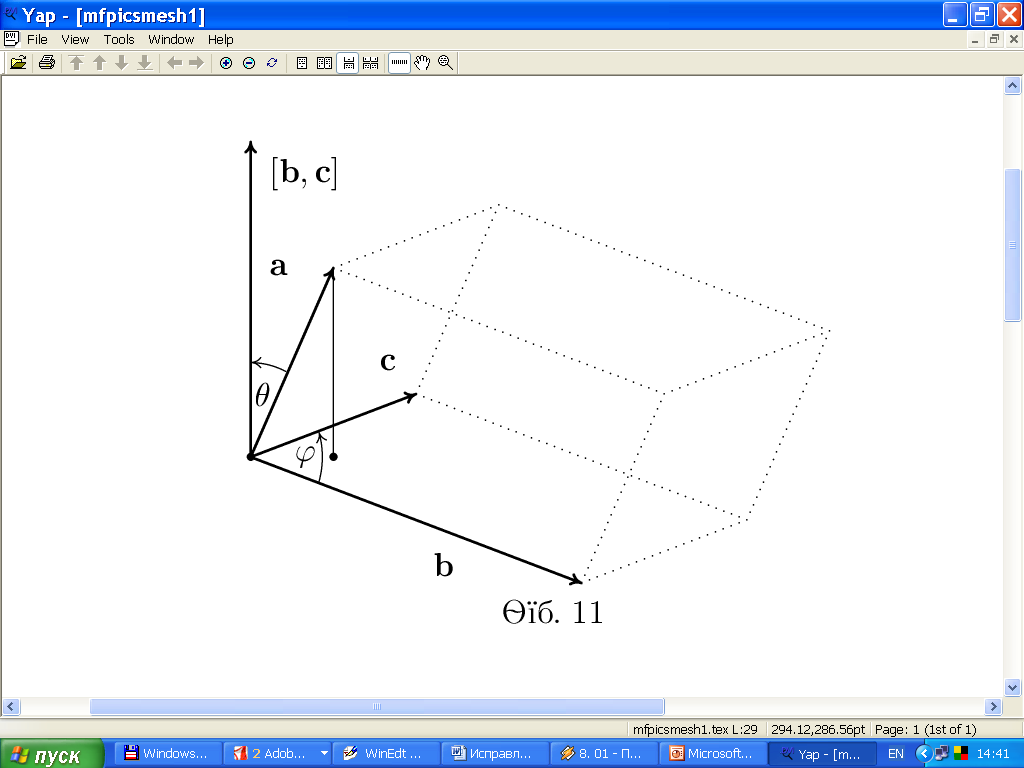
Рис. 6. Смешанное произведение
Следствие 1. 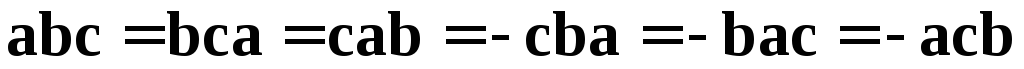 .
.
Следствие 2. Три вектора 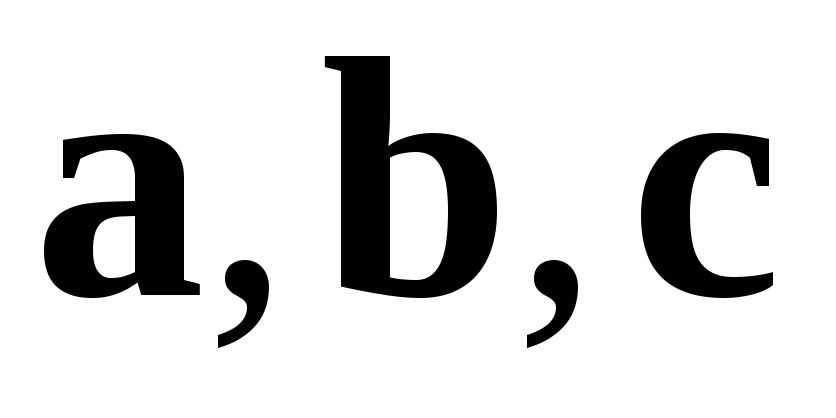 компланарны тогда и только тогда, когда
компланарны тогда и только тогда, когда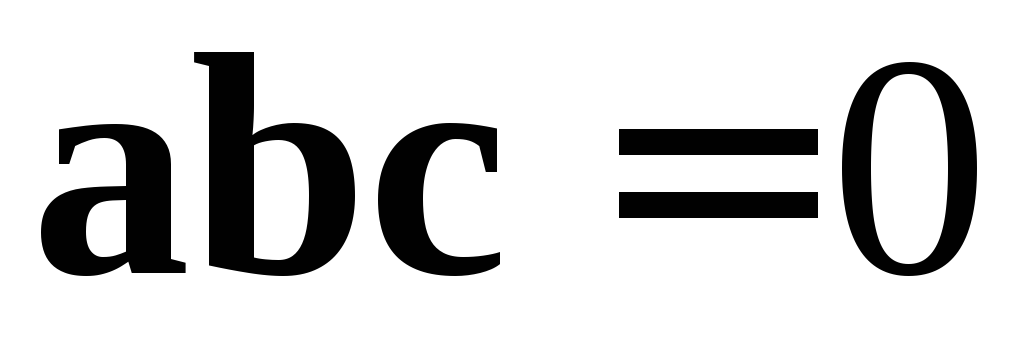 .
.
Предложение. Если вектора 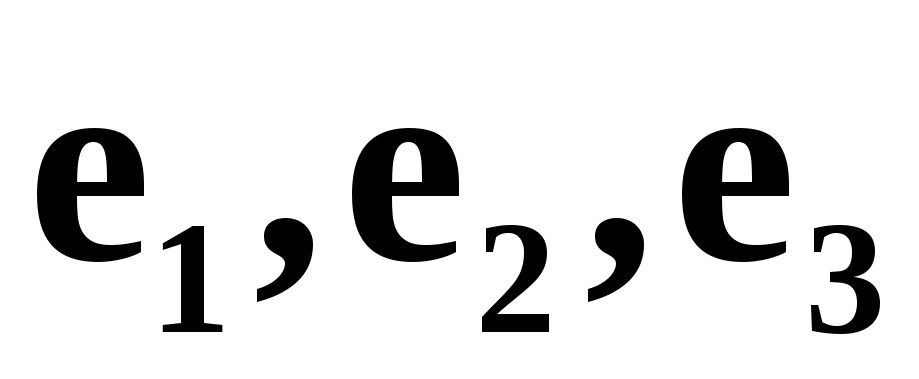 некомпланарные, то и вектора
некомпланарные, то и вектора 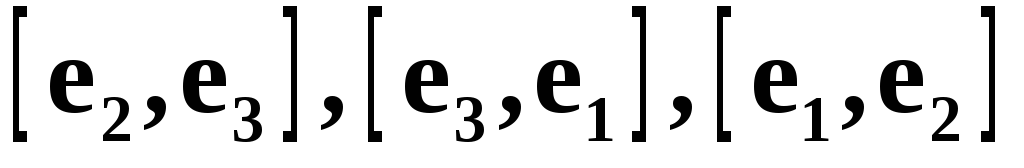 некомпланарные.
некомпланарные.
Доказательство. Предположим
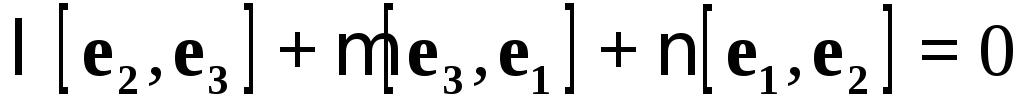
и, например,  .
Умножив обе части равенства скалярно
на
.
Умножив обе части равенства скалярно
на ,
мы получим
,
мы получим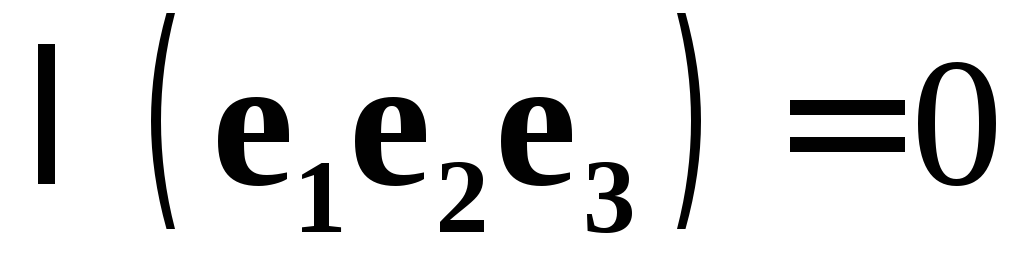 ,
что противоречит некомпланарности
векторов базиса.
,
что противоречит некомпланарности
векторов базиса.
50. Теорема 6. Для
того, чтобы векторы
Дано: Доказать: Доказательство. Из определения
компланарности следует, что векторы
Дано: Доказать: Доказательство. Если |
Свойства скалярного произведения.
Скалярное произведение двух векторов обладает переместительным свойством:
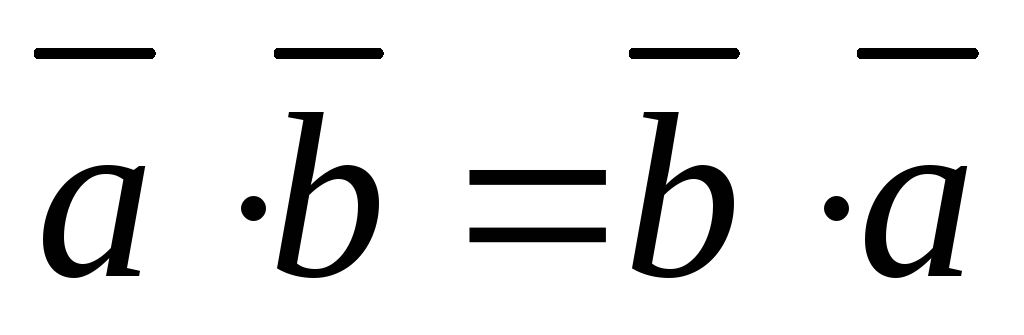 .
.
Скалярное произведение обладает распределительным свойством и сочетательным свойством относительно скалярного множителя:
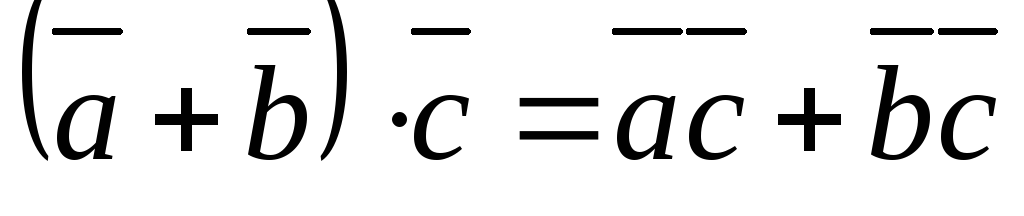 ,
,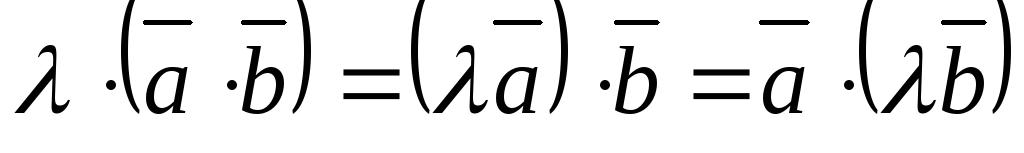 .
.
Пример 1.
Найти угол между векторами 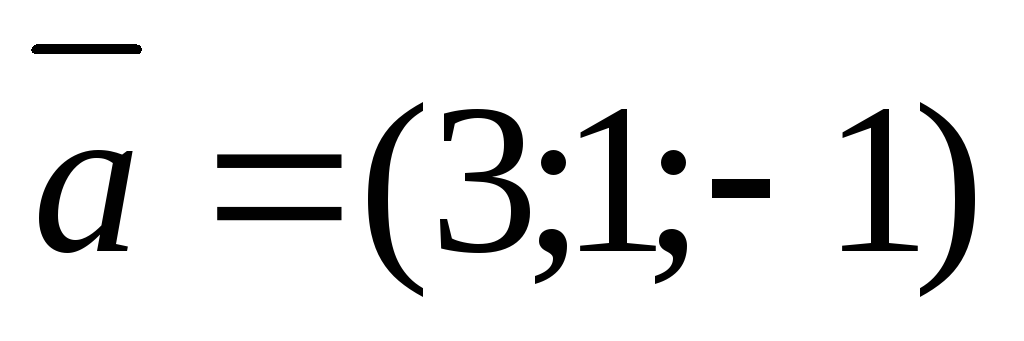 и
и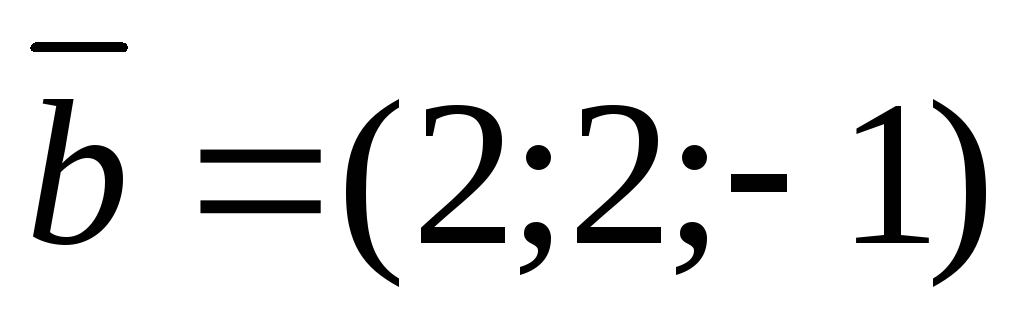 .
.
Решение.
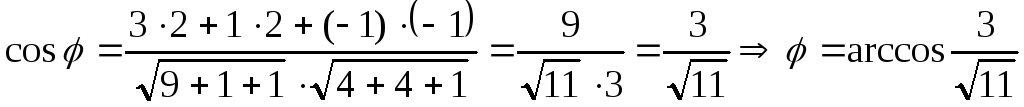 .
.
Пример 2.
Определить, при каком  вектор
вектор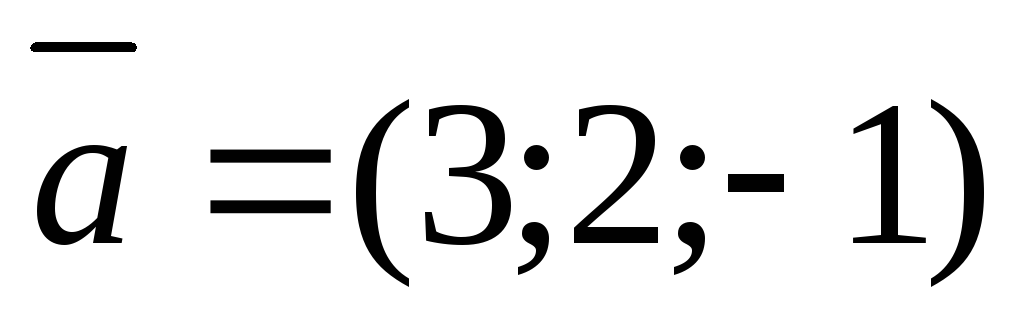 перпендикулярен вектору
перпендикулярен вектору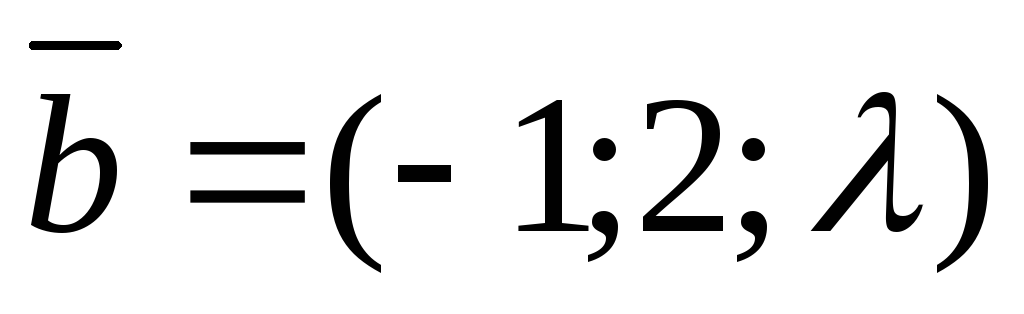 .
.
Решение.

Пример 3.
Вычислить проекцию вектора 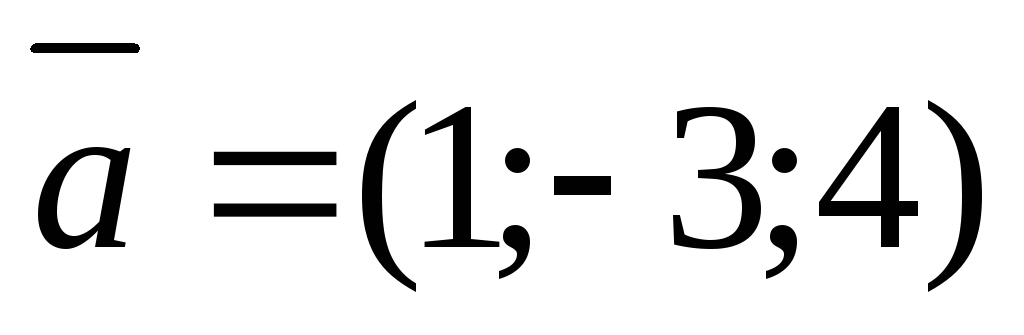 на вектор
на вектор ,
если
,
если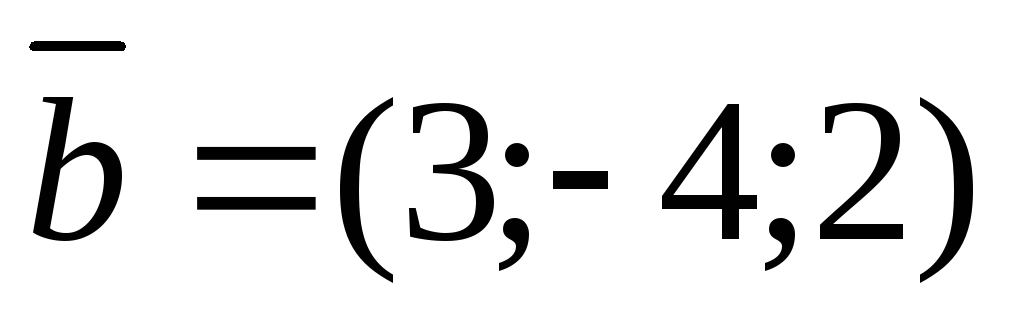 и
и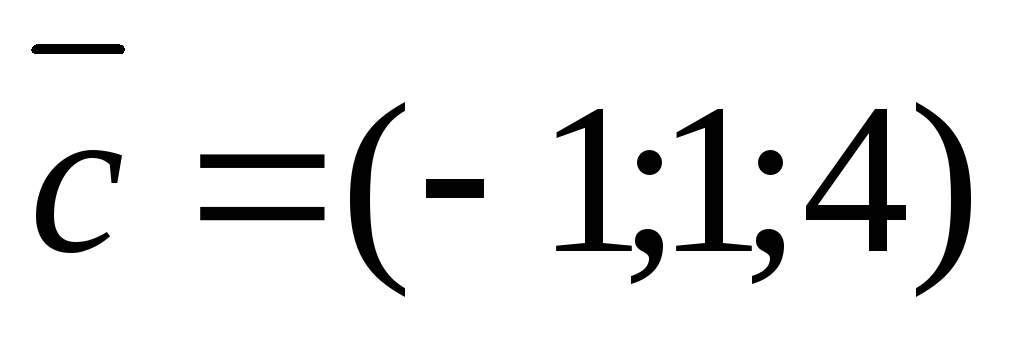 .
.
Решение.
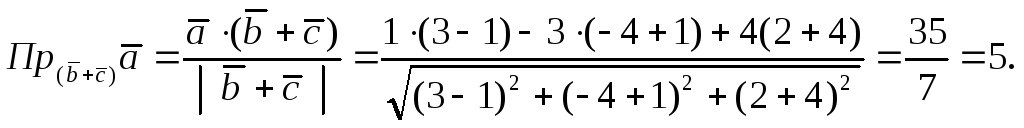
Упражнения.
1.Векторы  и
и образуют угол
образуют угол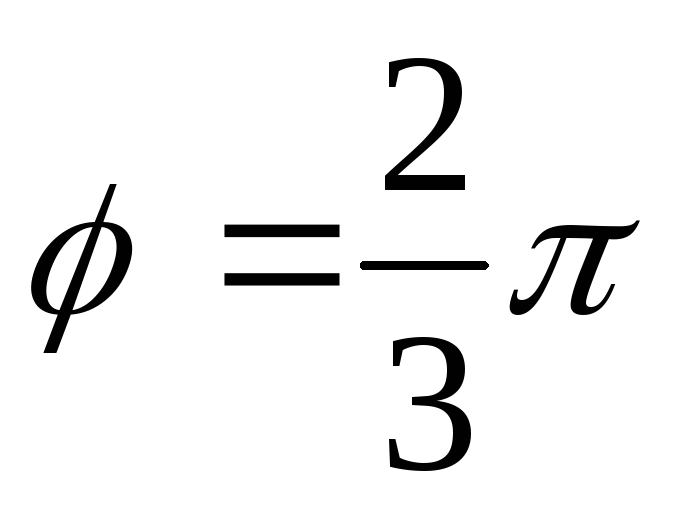 ;
зная, что
;
зная, что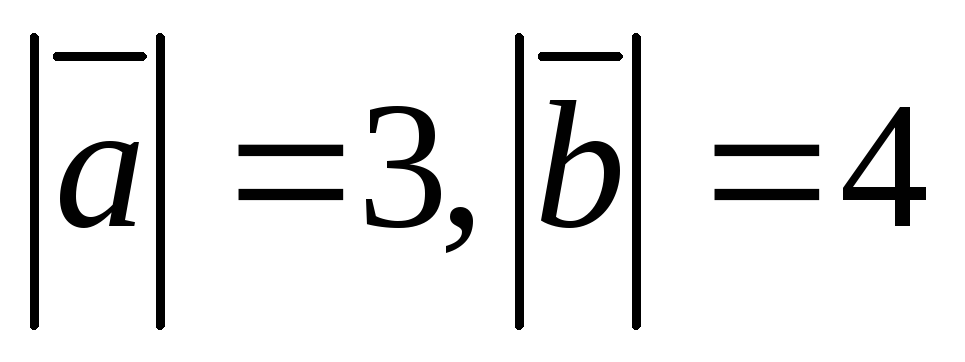 .
.
Вычислить:
1) 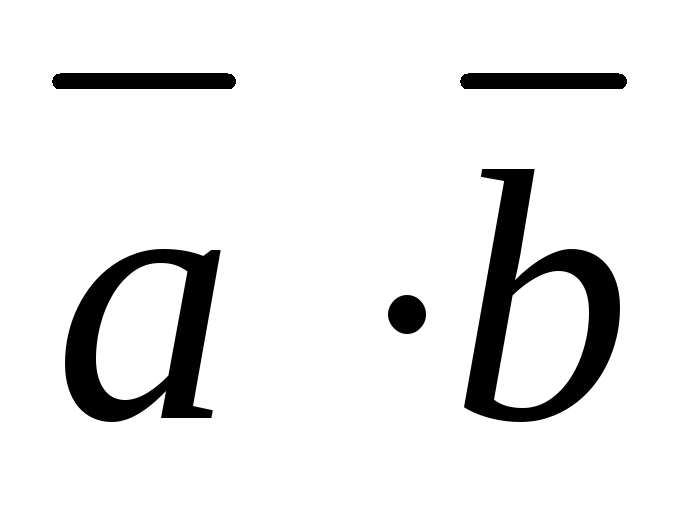 ;
2)
;
2)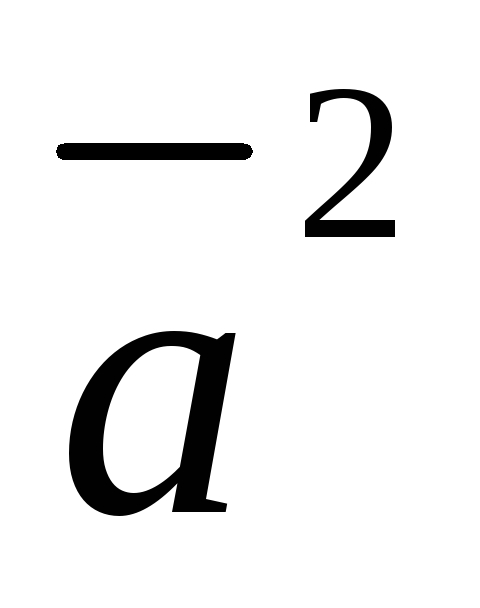 ;
3)
;
3)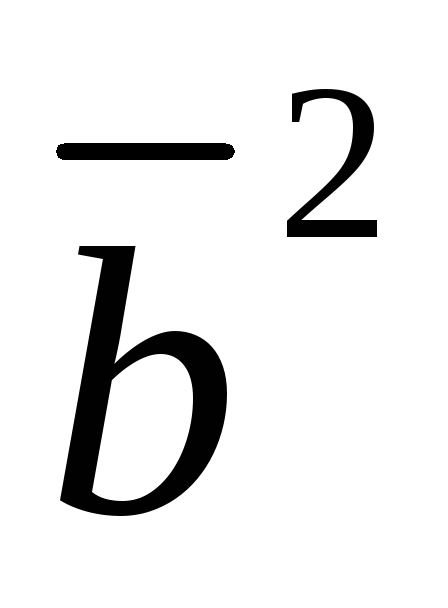 ;
4)
;
4)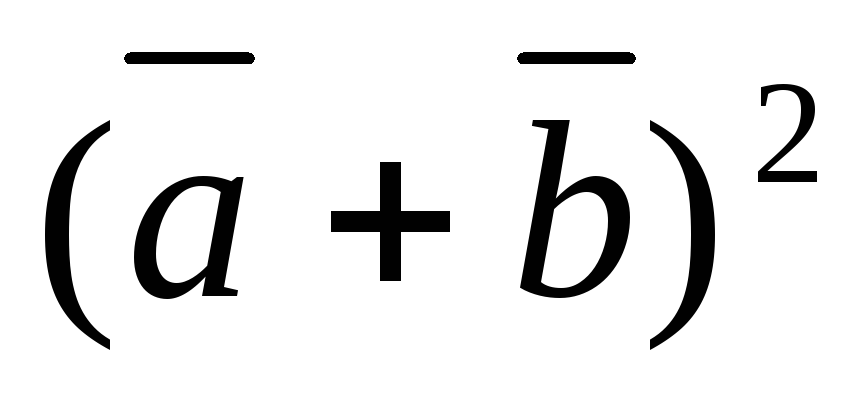 ;
;
5) 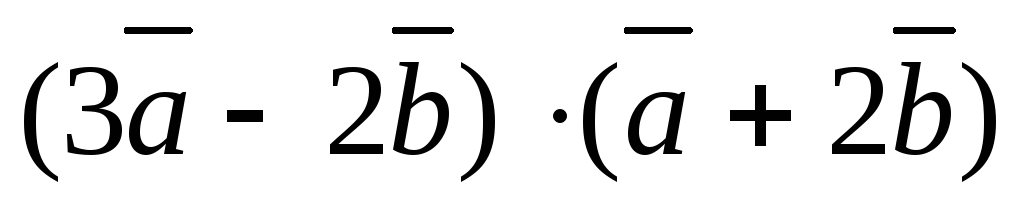 ;
6)
;
6)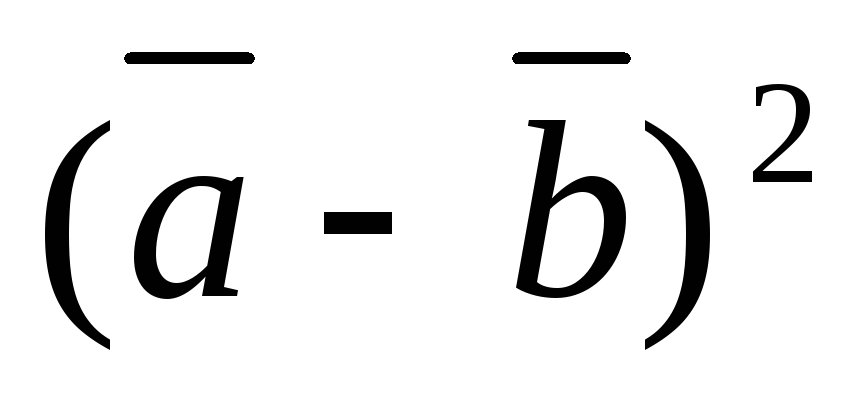 .
.
2.Даны
векторы 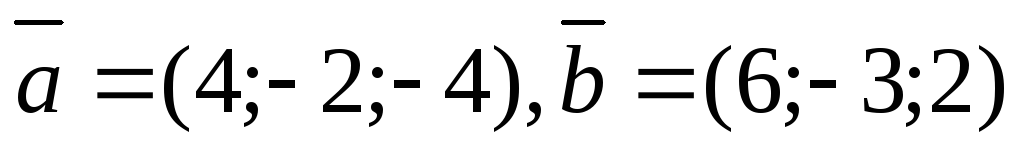 .
.
Вычислить: 1) 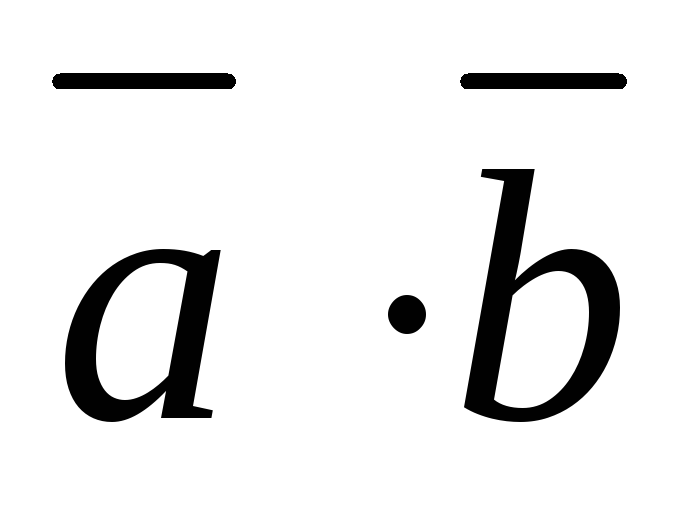 ;
2)
;
2)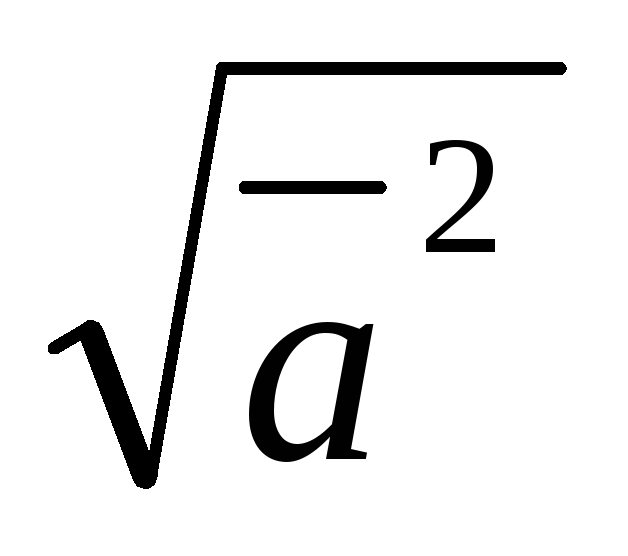 ;
3)
;
3)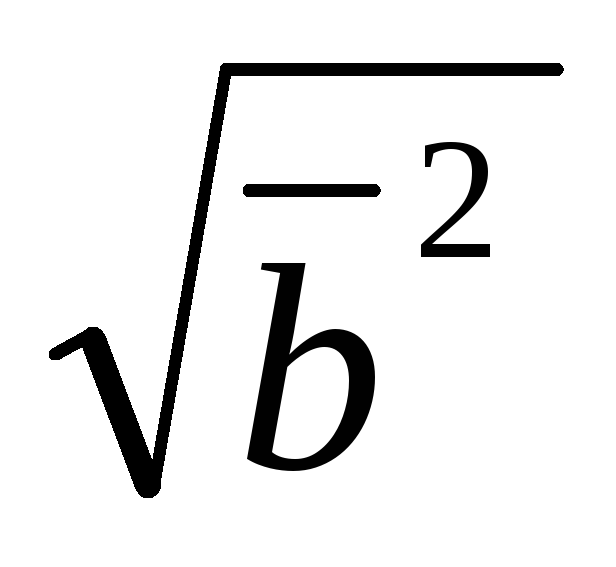 ;
4)
;
4)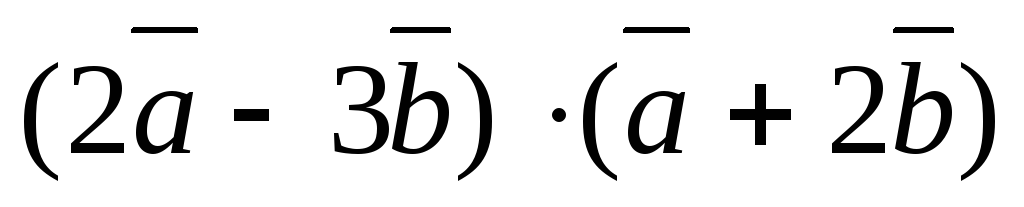 ;
5)
;
5)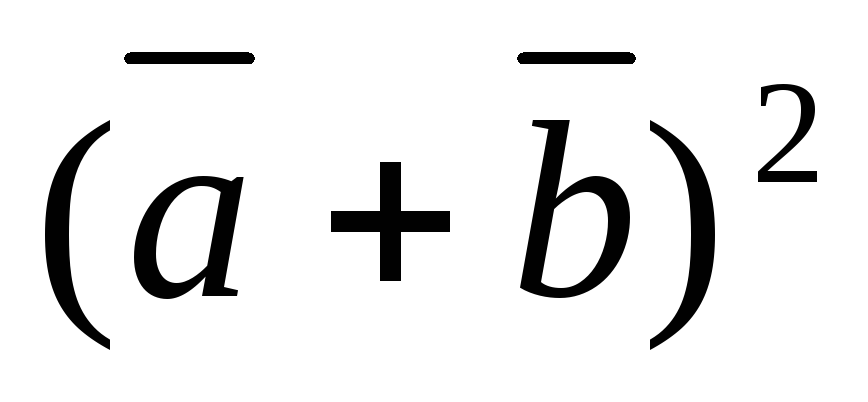 ;
6)
;
6)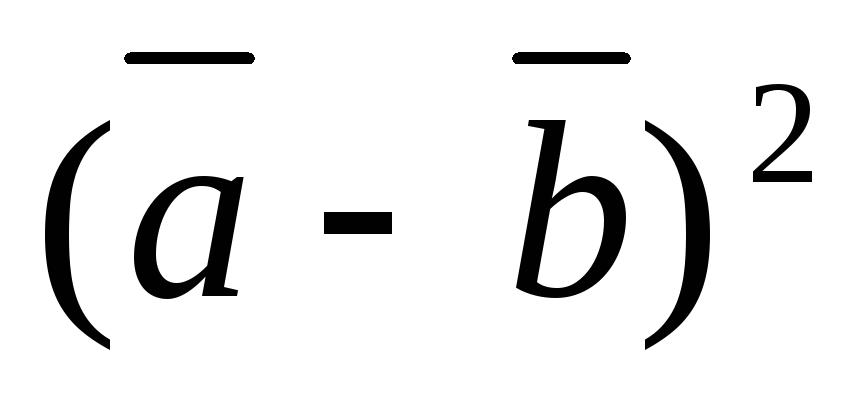 .
.
3.
Вычислить косинус угла, образованного
векторами
и .
.
4. Даны
вершины треугольника 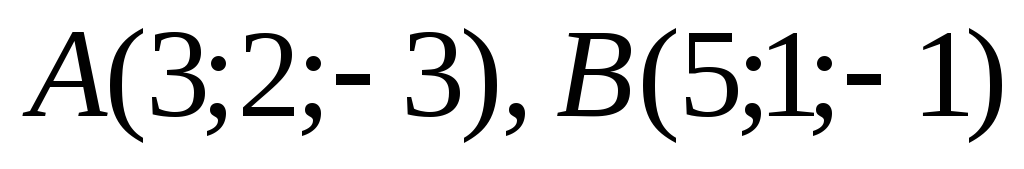 и
и .
.
Определить его внутренний угол при вершине А.
5. Вектор 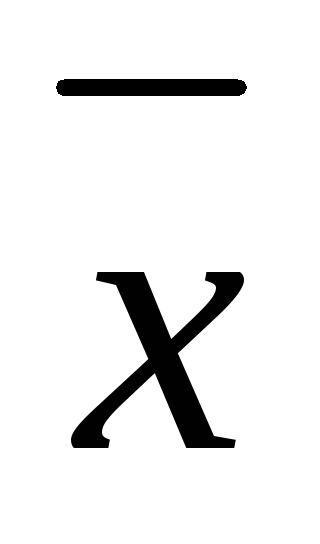 ,
коллинеарный вектору
,
коллинеарный вектору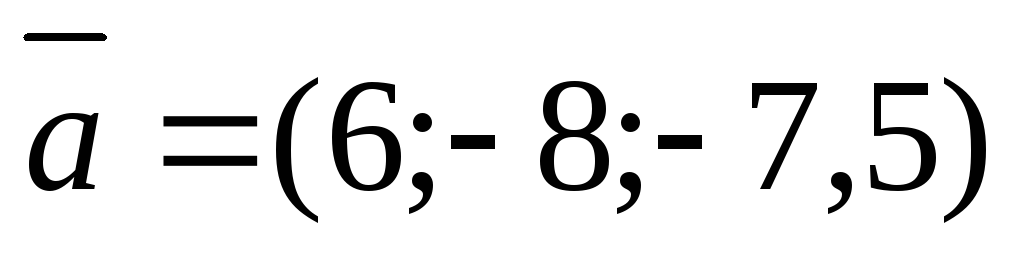 ,
образует острый угол с осьюOZ.
Зная, что
,
образует острый угол с осьюOZ.
Зная, что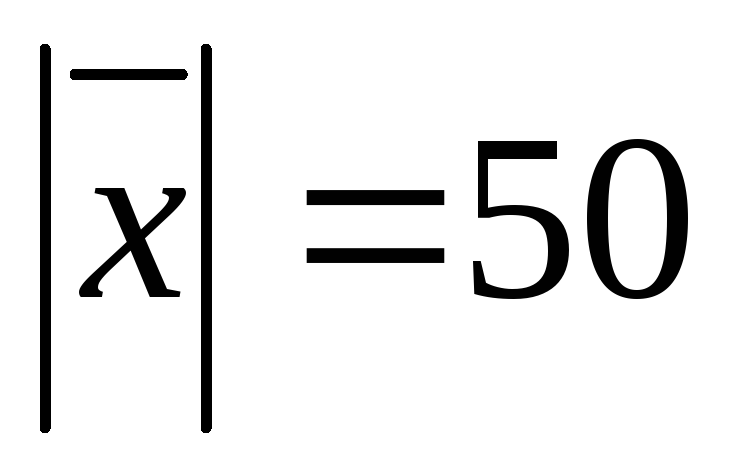 ,
найти его координаты.
,
найти его координаты.
6.
Вычислить проекцию вектора 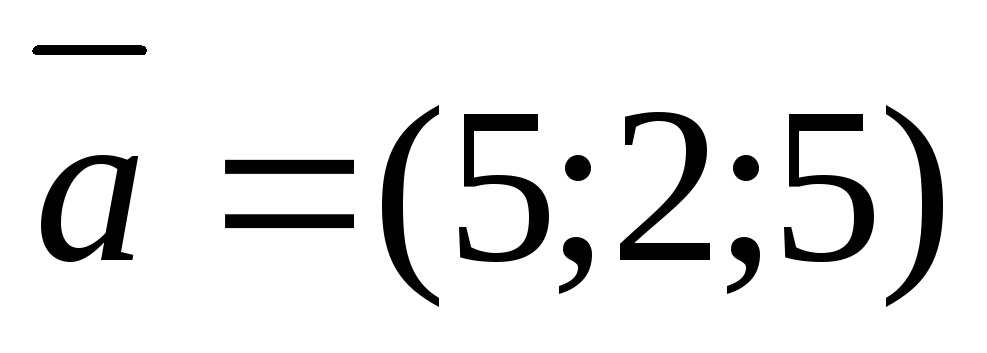 на ось вектора
на ось вектора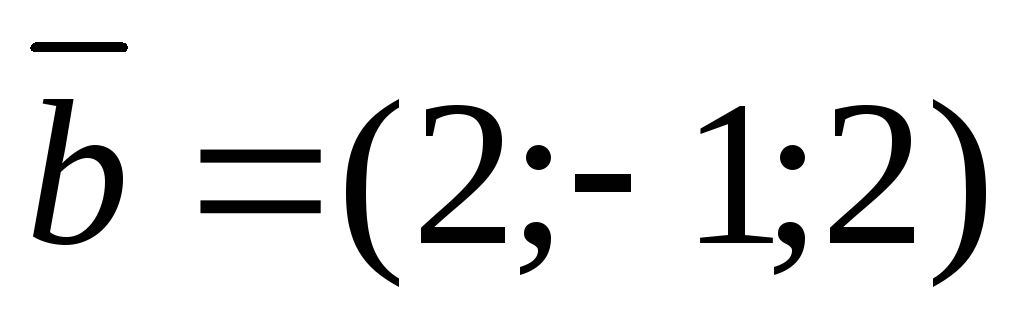 .
.
7. Даны
две точки 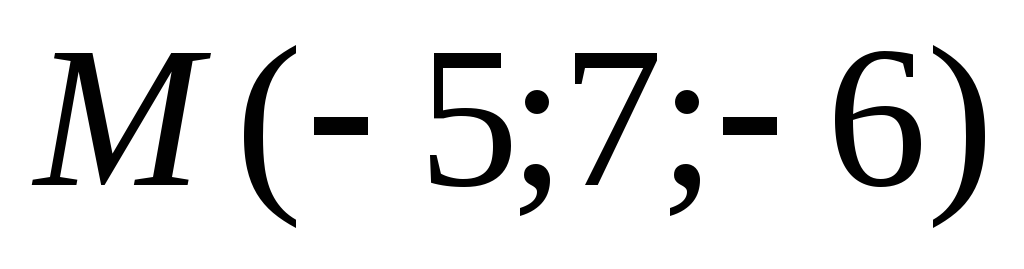 и
и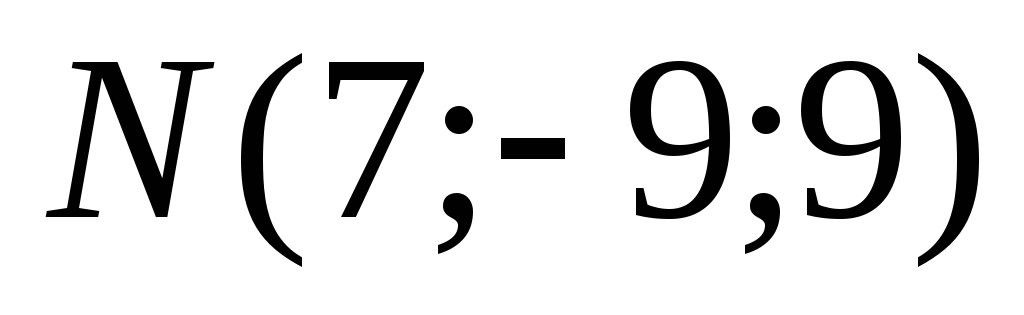 .
.
Вычислить
проекцию вектора 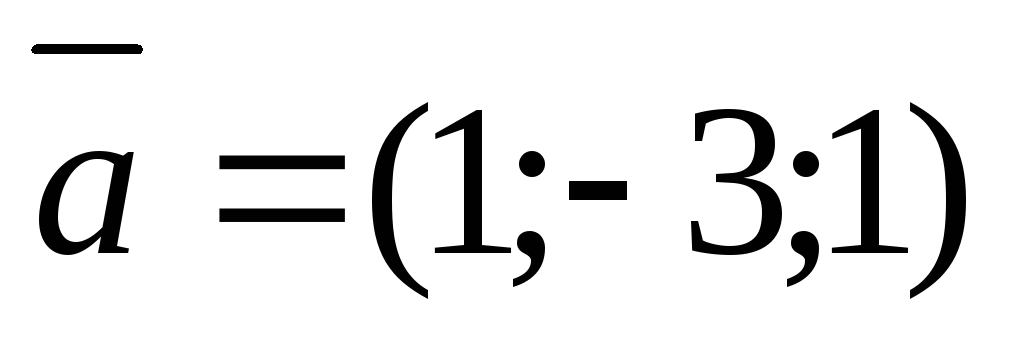 на
ось вектора
на
ось вектора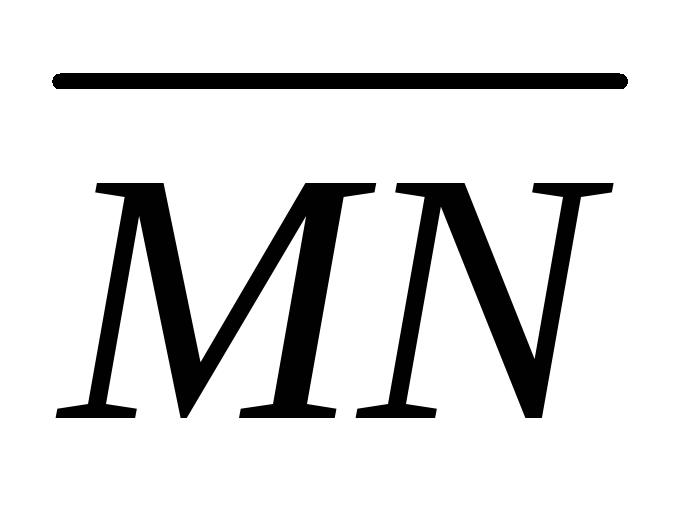 .
.
8.Найти
модуль вектора  ,
если
,
если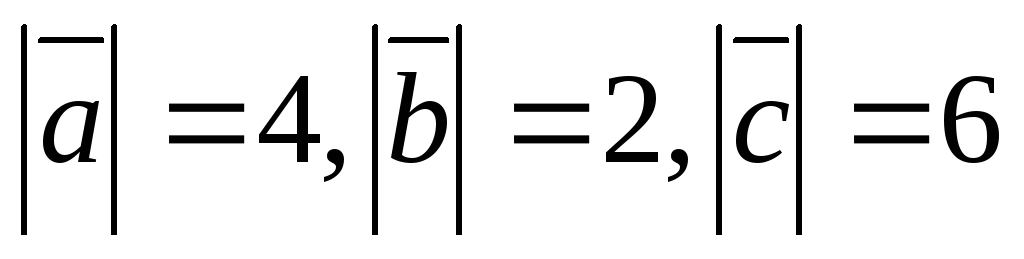 и векторы
и векторы образуют друг с другом углы
образуют друг с другом углы .
.
9.При
каких значениях mвекторы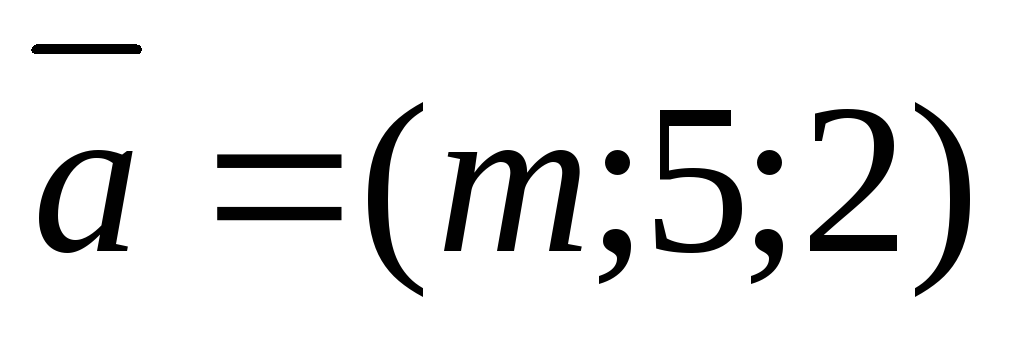 и
и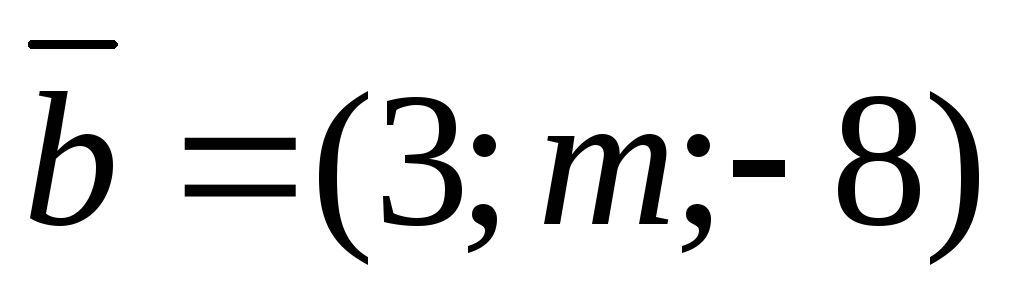 перпендикулярны?
перпендикулярны?
10. Даны
три последовательные вершины
параллелограмма:  .
Найти его четвертую вершинуDи угол между векторами
.
Найти его четвертую вершинуDи угол между векторами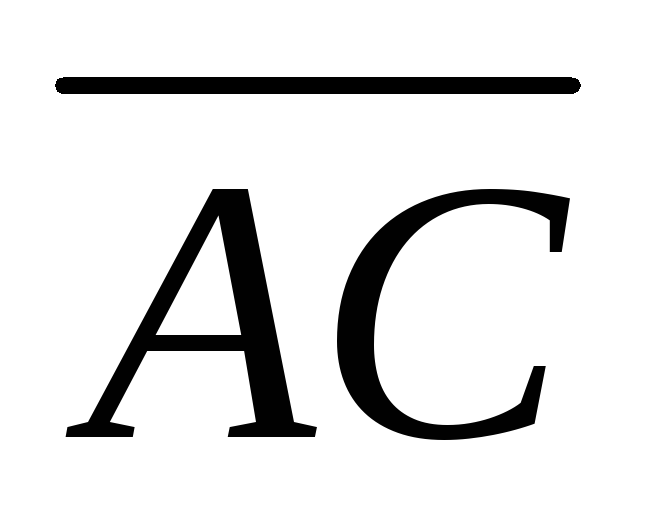 и
и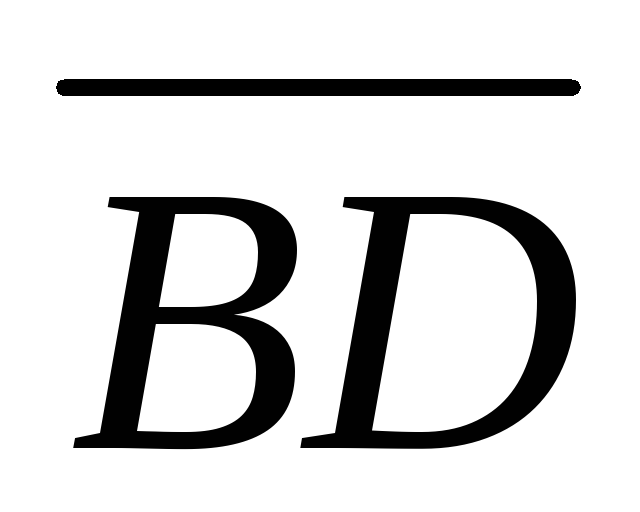 .
.
§6 . Векторное произведение векторов.
Векторным
произведением вектора  на вектор
на вектор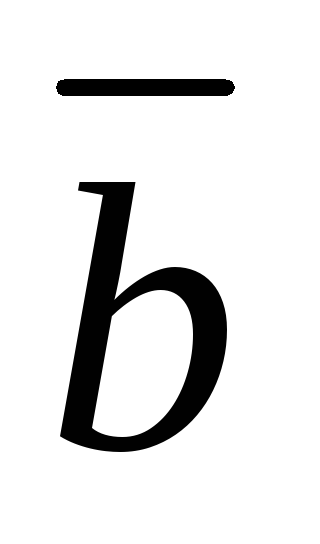 называется вектор обозначаемый символом
называется вектор обозначаемый символом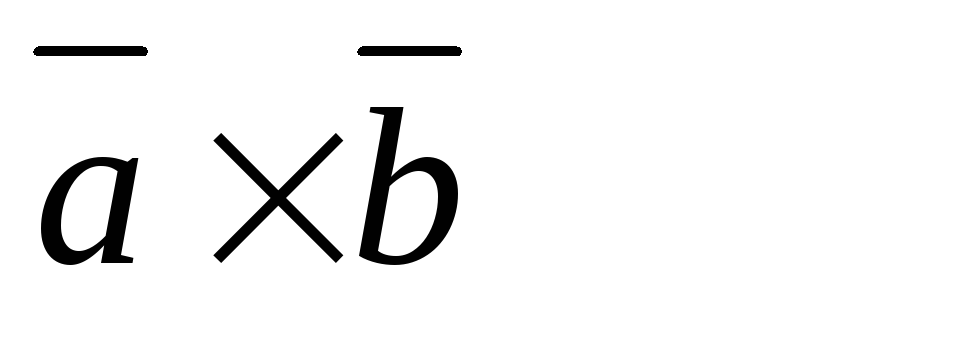 и определяемый следующими тремя
условиями:
и определяемый следующими тремя
условиями:
Модуль вектора
 равен
равен ,
где
,
где — угол между векторами
— угол между векторами и
и ,
т.е.
,
т.е. ;
;
вектор
 перпендикулярен
к каждому из векторов
перпендикулярен
к каждому из векторов и
и ;
;
направление вектора
 таково,
что упорядоченная тройка векторов
таково,
что упорядоченная тройка векторов
 является правой (т.е. если «смотреть»
с конца вектора
является правой (т.е. если «смотреть»
с конца вектора ,
то вращение от
,
то вращение от к
к по кратчайшему пути совершается против
движения часовой стрелки).
по кратчайшему пути совершается против
движения часовой стрелки).
Замечание.Если один из векторов и
и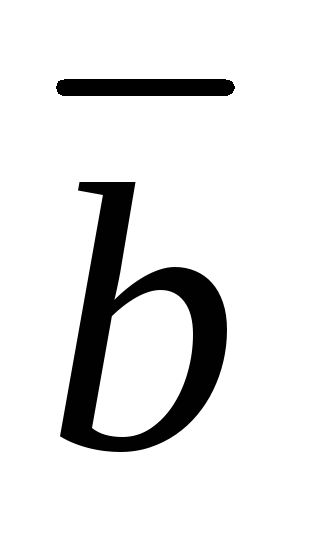 нулевой, то полагаем
нулевой, то полагаем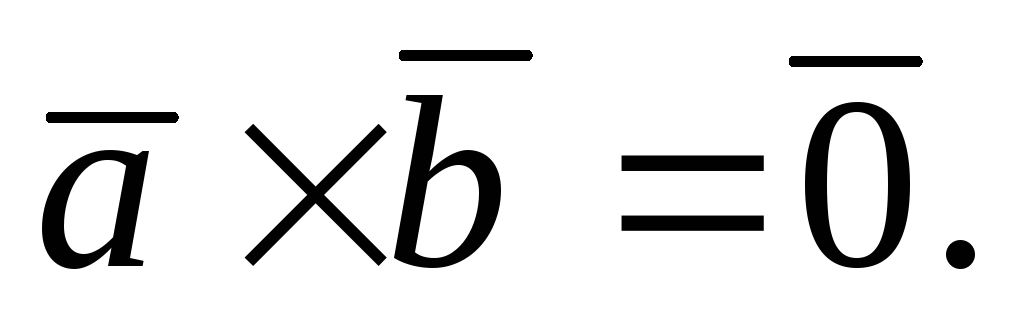
Свойства векторного произведения.
1. 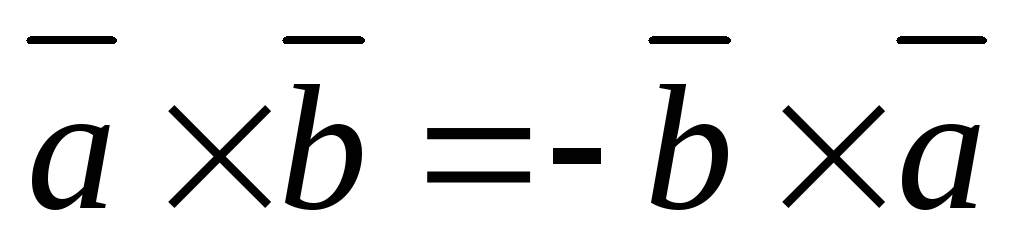 .
.
2. 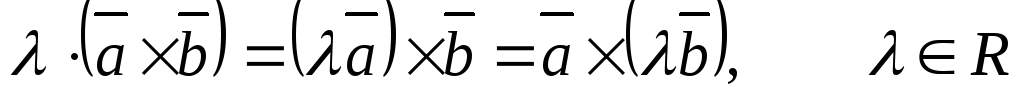 .
.
3. 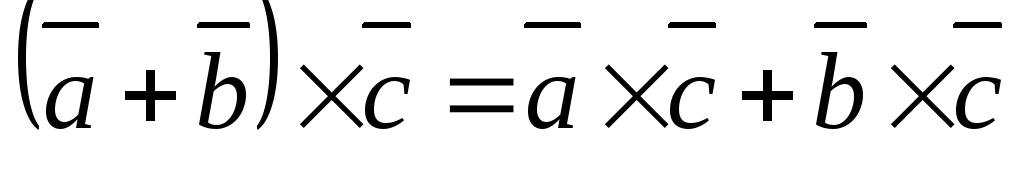
Если
 и
и коллинеарны, то
коллинеарны, то
Геометрический смысл модуля векторного произведения: длина векторного произведения численно равна площадипараллелограмма, построенного на векторахикак на сторонах.
Пример 1.
Найти
площадь параллелограмма, построенного
на векторах 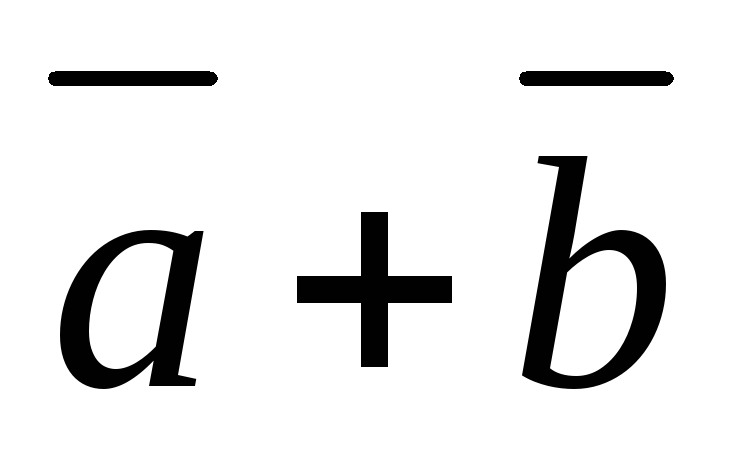 и
и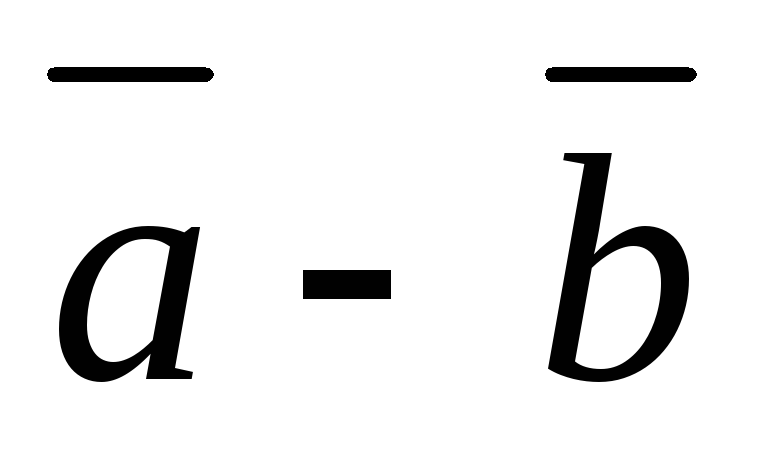 как на сторонах, если
как на сторонах, если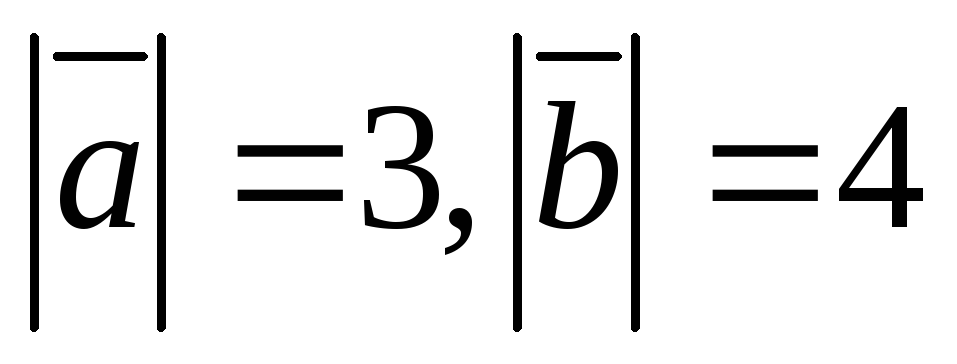 и угол между векторами
и угол между векторами и
и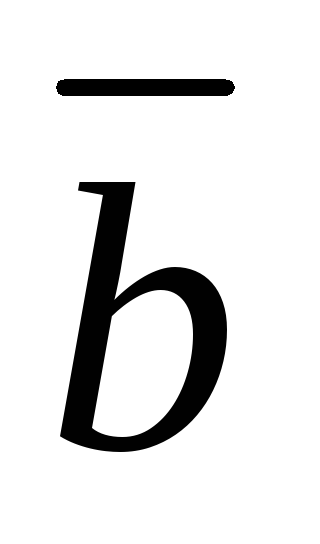 равен
равен .
.
Решение.
Площадь Sискомого параллелограмма равна модулю векторного произведения.
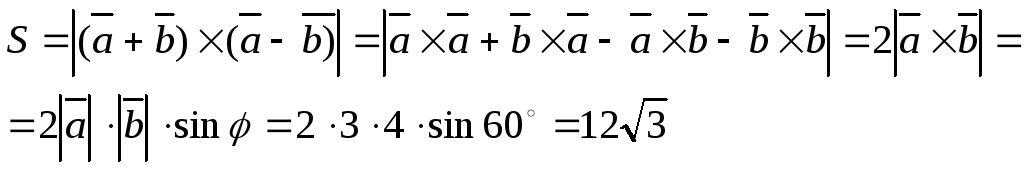
Упражнения.
1. Векторы  и
и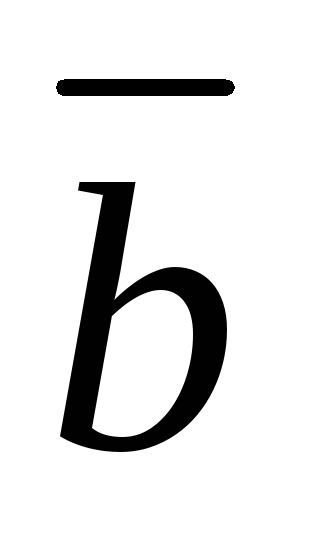 образуют угол
образуют угол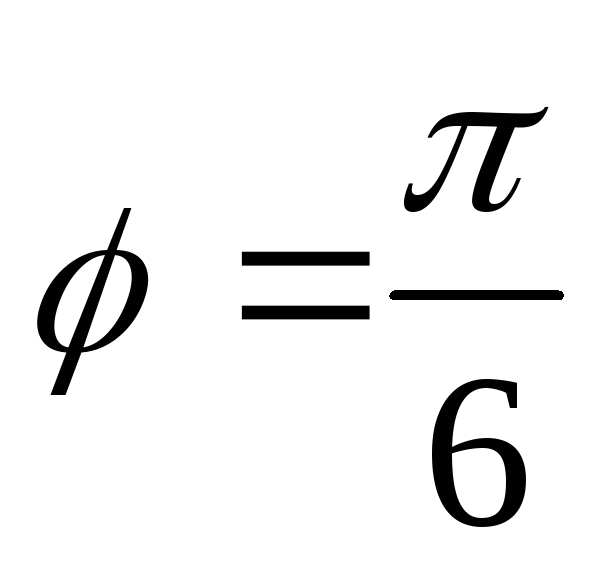 .
Зная, что
.
Зная, что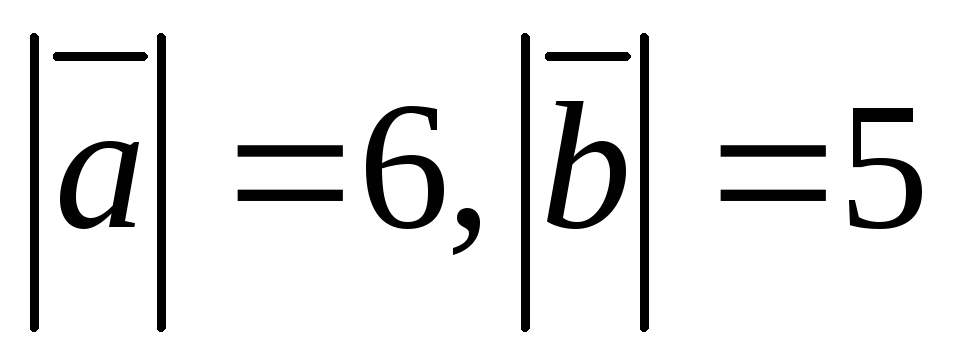 ,
вычислить
,
вычислить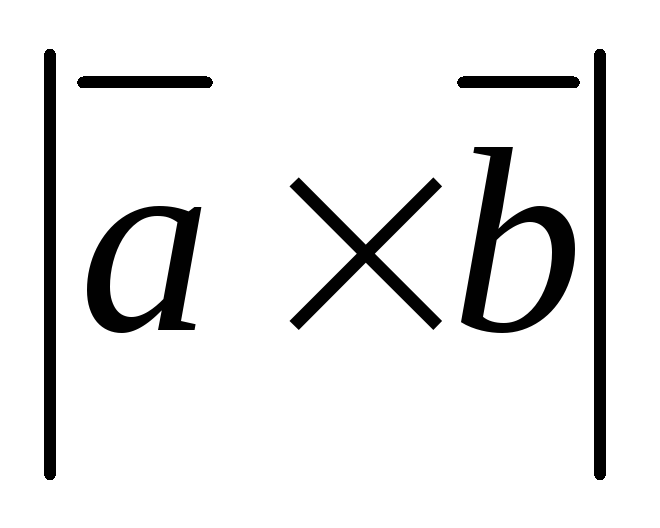 .
.
2. Даны 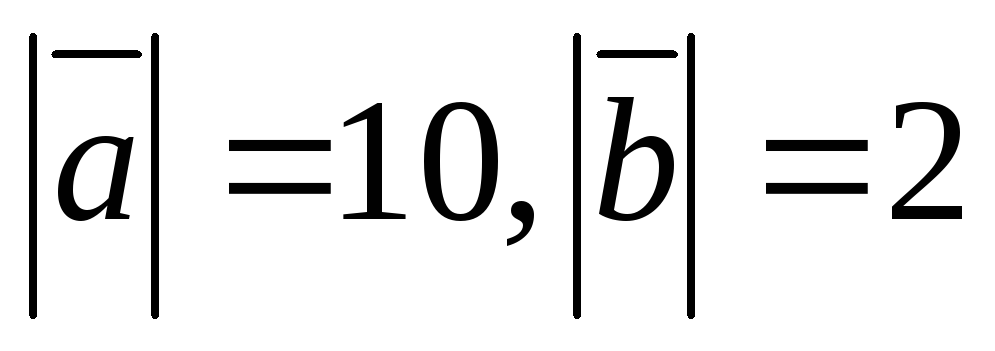 и
и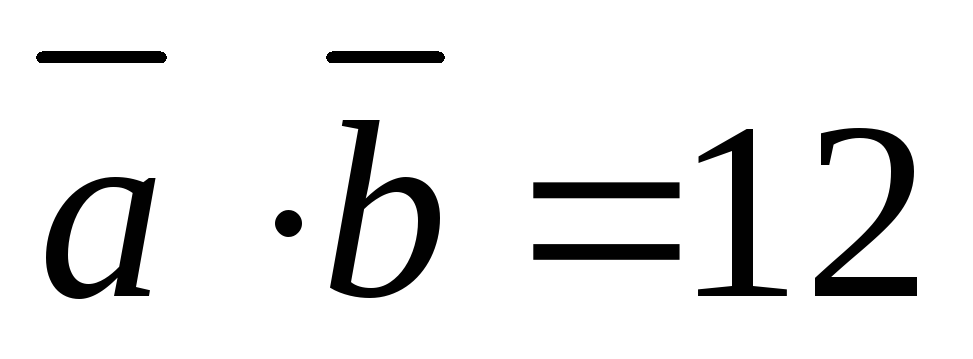 .
Вычислить
.
Вычислить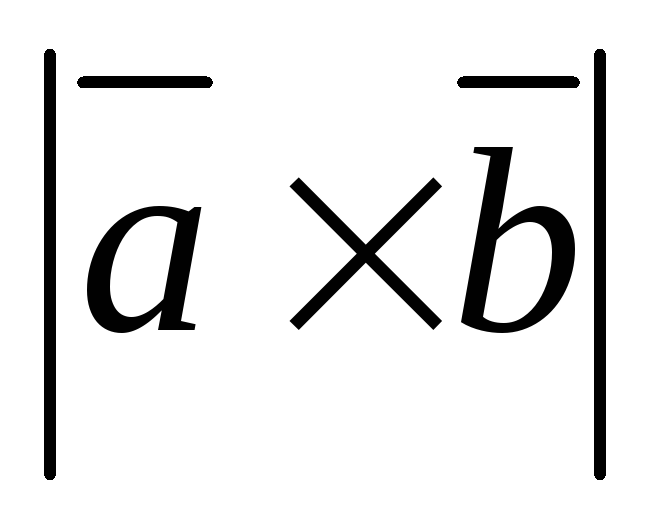 .
.
3. Векторы  и
и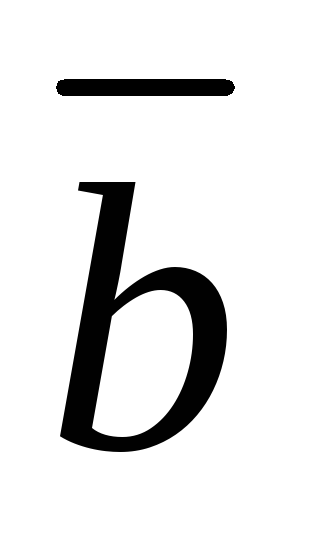 взаимно перпендикулярны. Зная, что
взаимно перпендикулярны. Зная, что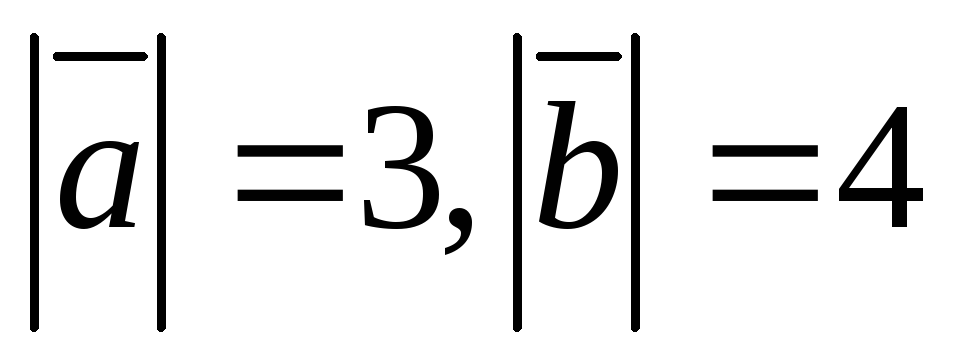 ,
вычислить:
,
вычислить:
1) ;
;
2) 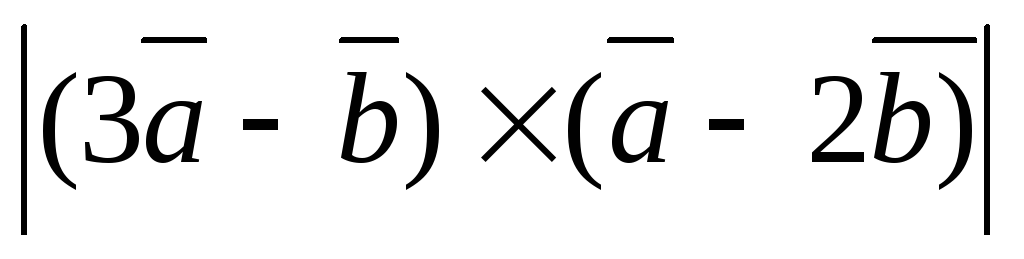 .
.
Векторное произведение в координатной форме.
Пусть
даны два вектора  и
и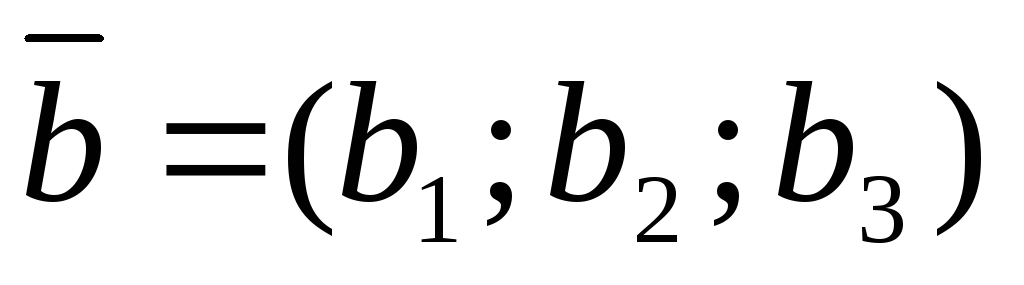 .
.
Векторное произведение равно:

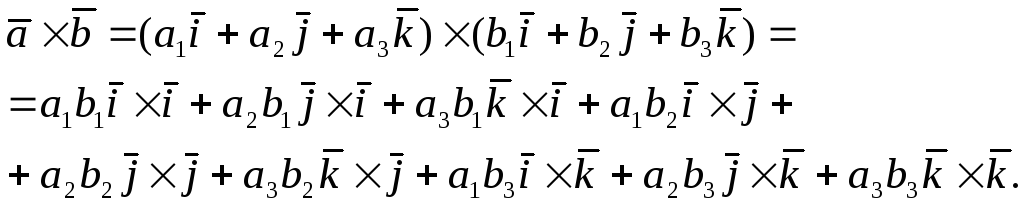
Учитывая
свойство 4,получаем 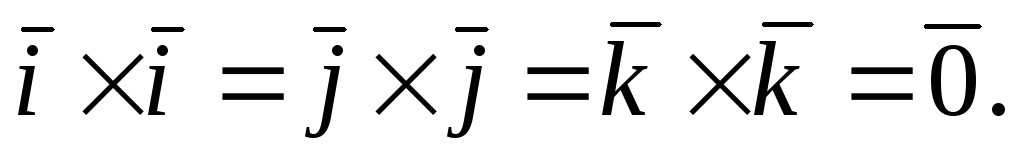

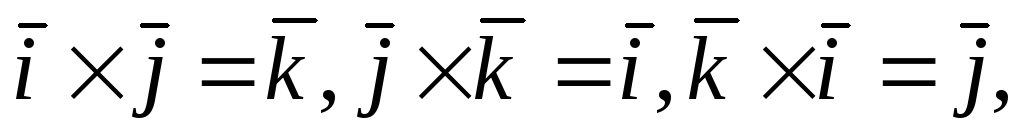


 Тогда
Тогда
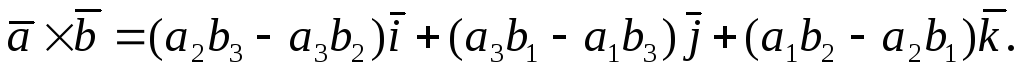
 Разности,
стоящие в скобках, представляют собой
определители второго порядка.
Разности,
стоящие в скобках, представляют собой
определители второго порядка.
 Поэтому
Поэтому
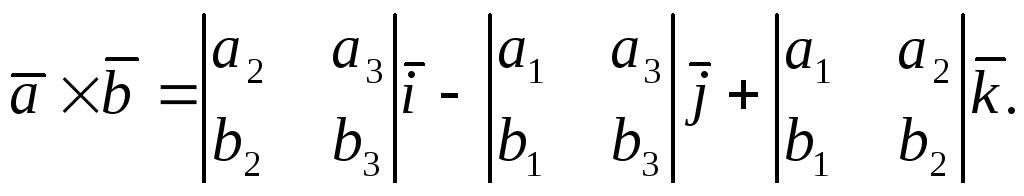
Полученное выражение на основании
формулы разложения определителя третьего
порядка по элементам первой строки
можно символически записать в виде:

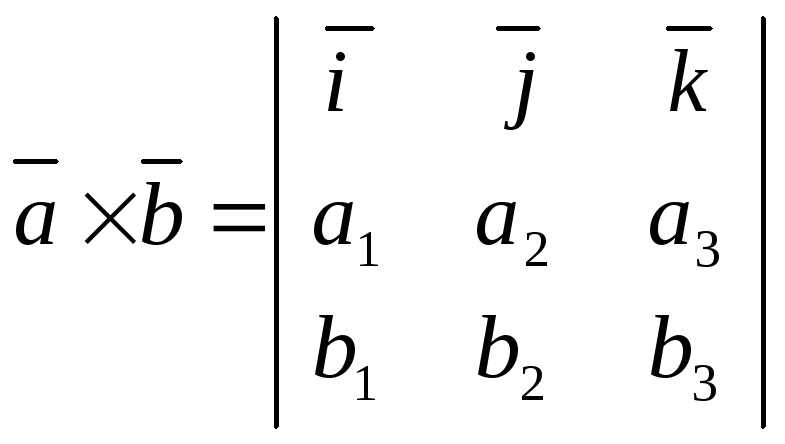 .
.
Следствие.Площадь треугольника, построенного на векторах
треугольника, построенного на векторах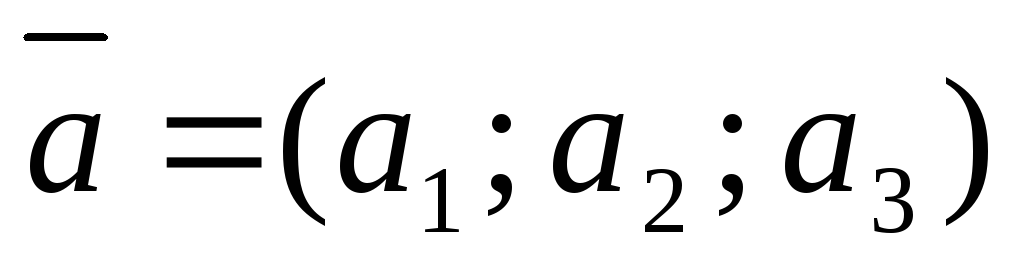 и
и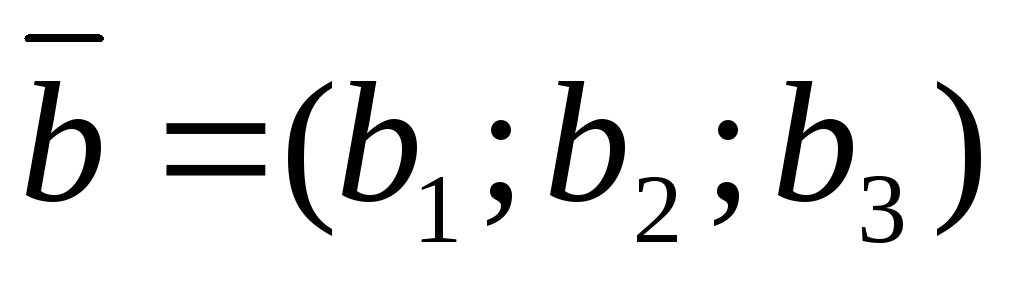 как на сторонах, определяется равенством:
как на сторонах, определяется равенством:
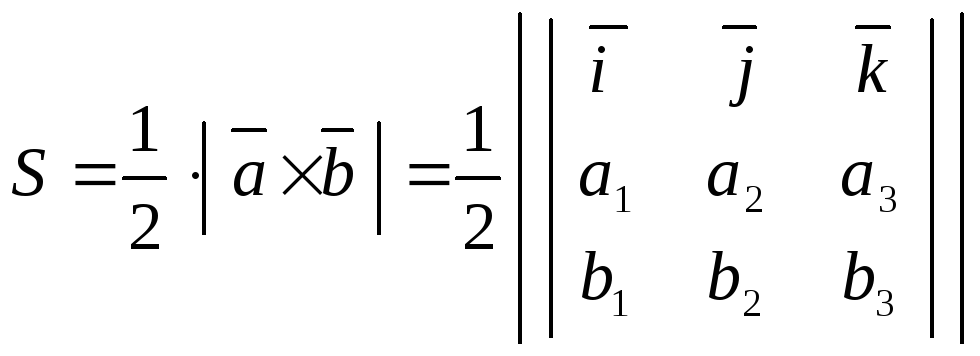 .
.
Пример.
Найти
площадь треугольника, вершины которого
находятся в точках  ,
, ,
,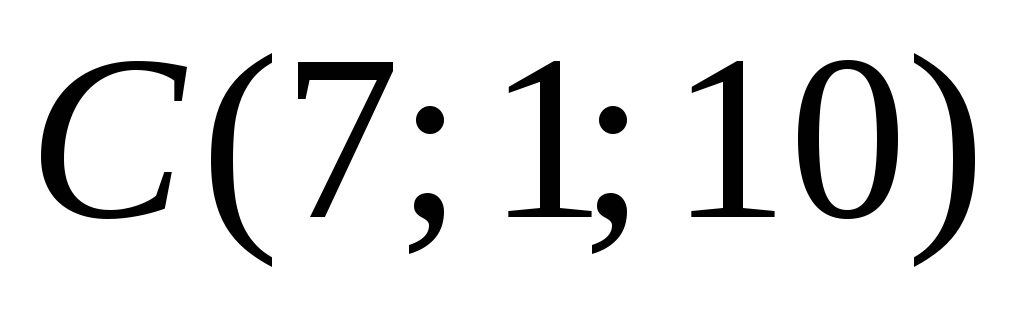 .
.
Решение.
Рассмотрим векторы  и
и ,
совпадающие со сторонами треугольника:
,
совпадающие со сторонами треугольника: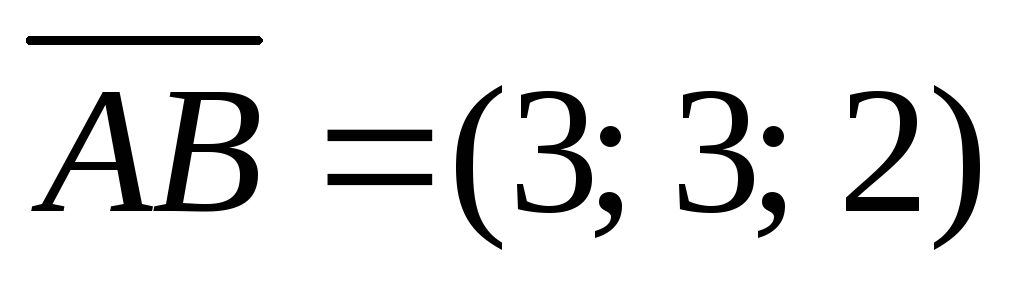 ;
;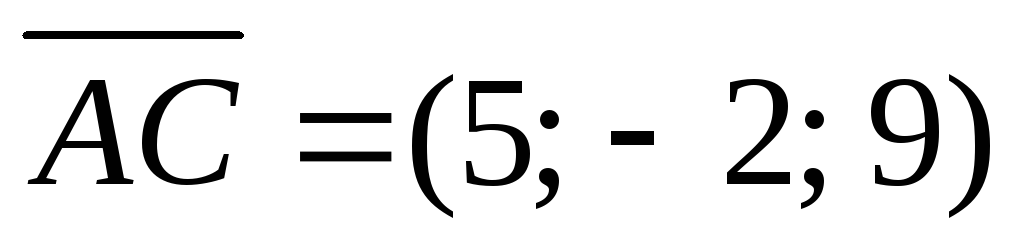 .
.
Найдем сначала их векторное произведение:
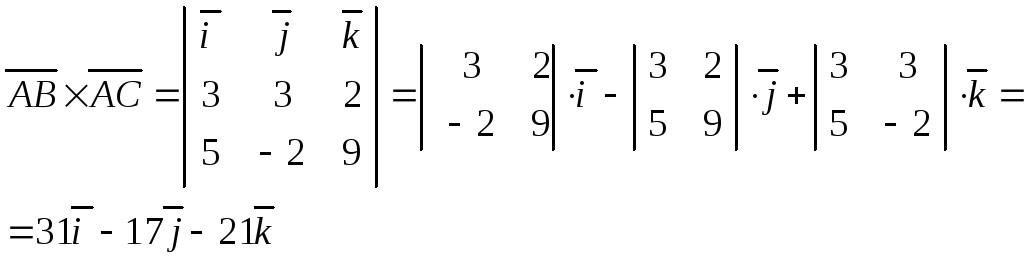 .
.
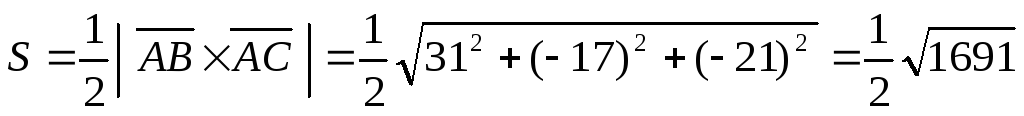 .
.
Упражнения.
1. Даны
векторы 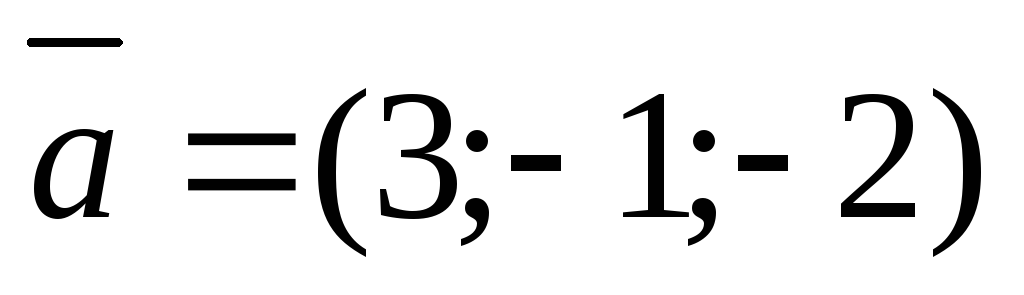 и
и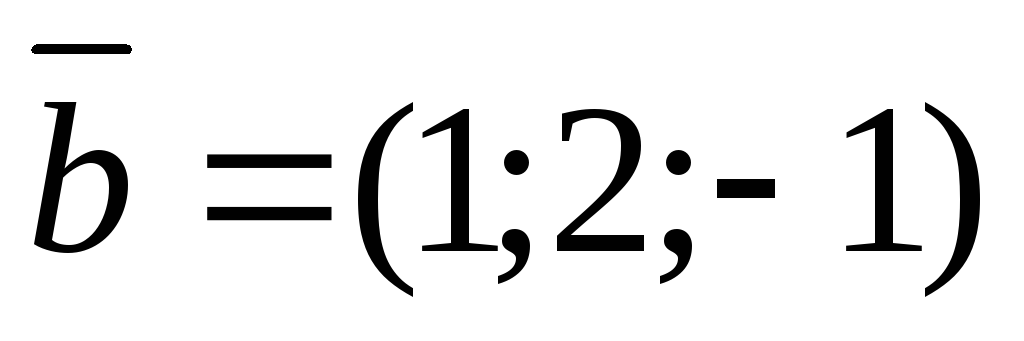 .
Найти координаты векторных произведений:
.
Найти координаты векторных произведений:
1) 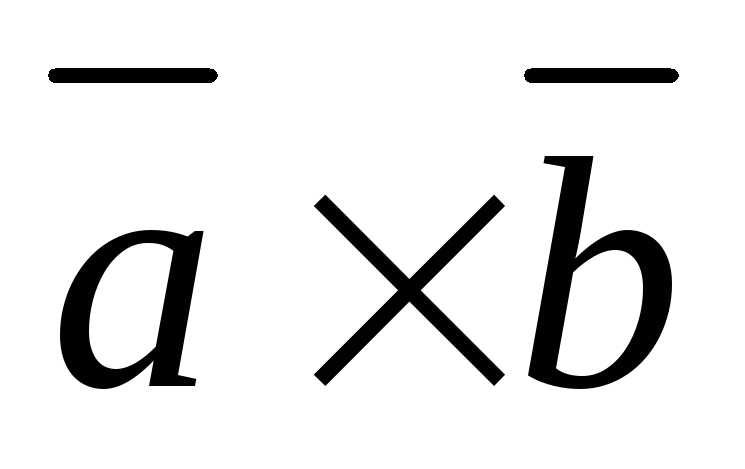 ;
2)
;
2)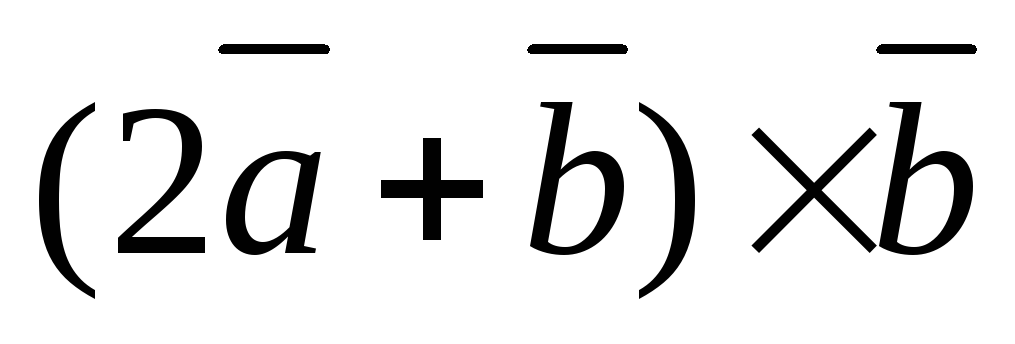 ;
3)
;
3)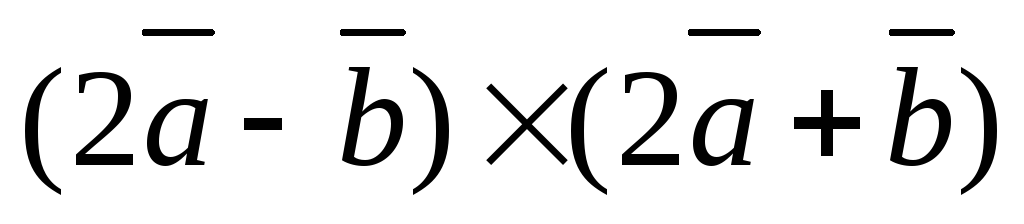 .
.
2. Даны
точки 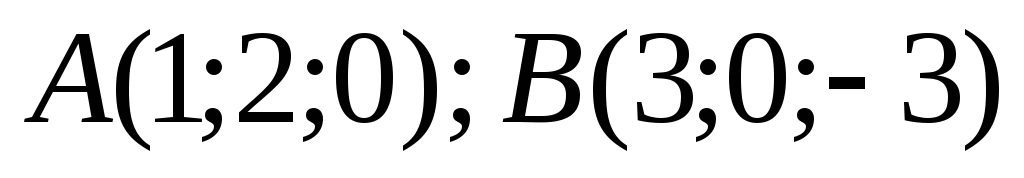 и
и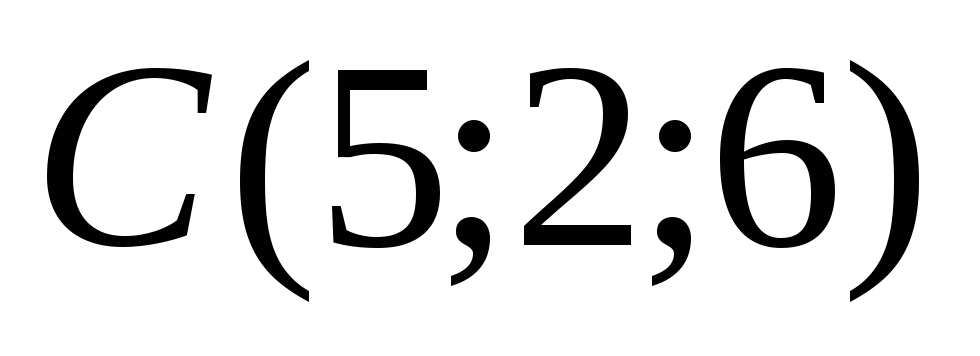 .
Вычислить площадь треугольника
.
Вычислить площадь треугольника .
.
3.Даны
вершины треугольника 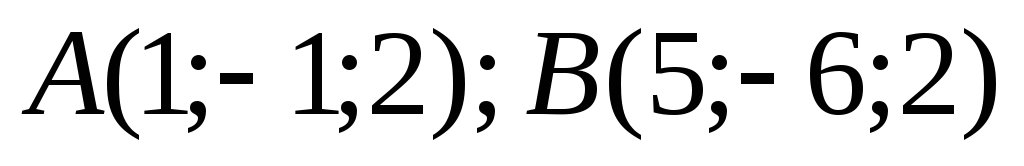 и
и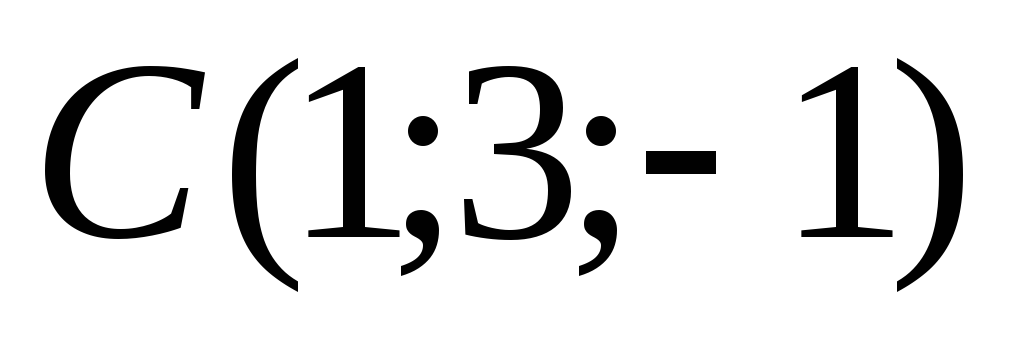 .
Вычислить длину его высоты, опущенной
из вершиныBна сторону
АС.
.
Вычислить длину его высоты, опущенной
из вершиныBна сторону
АС.
4.
Вычислить синус угла, образованного
векторами 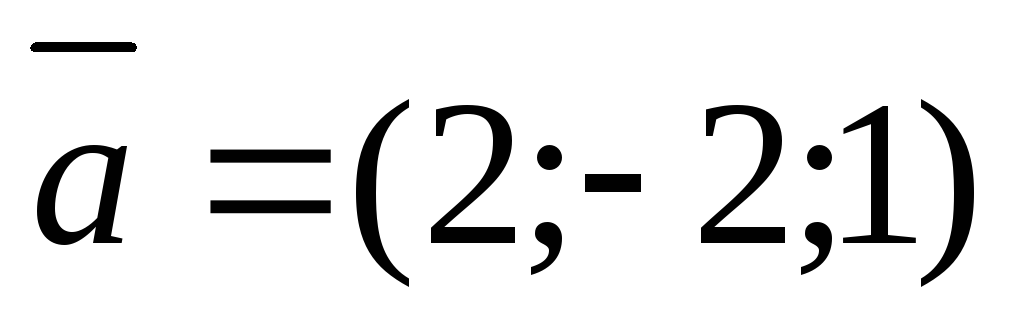 и
и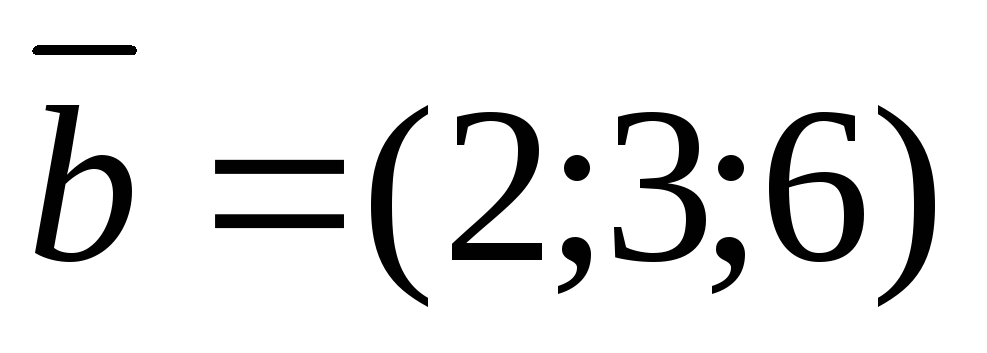 .
.
5.
Вычислить площадь параллелограмма,
построенного на векторах  и
и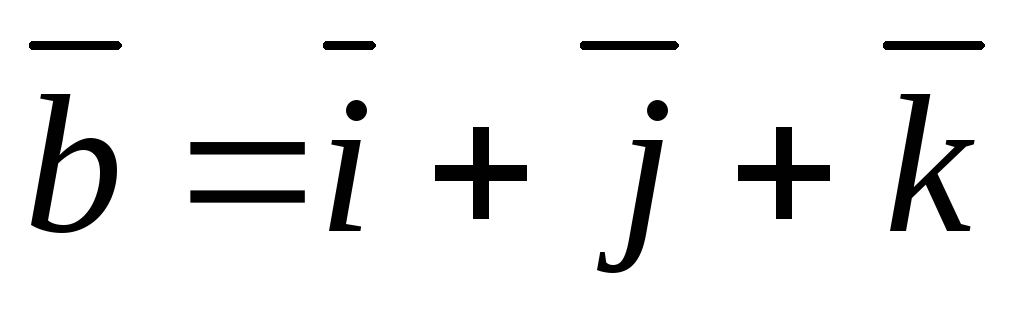 .
.
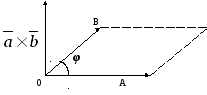
5.2. Векторное произведение двух векторов.
Определение векторного произведения.
О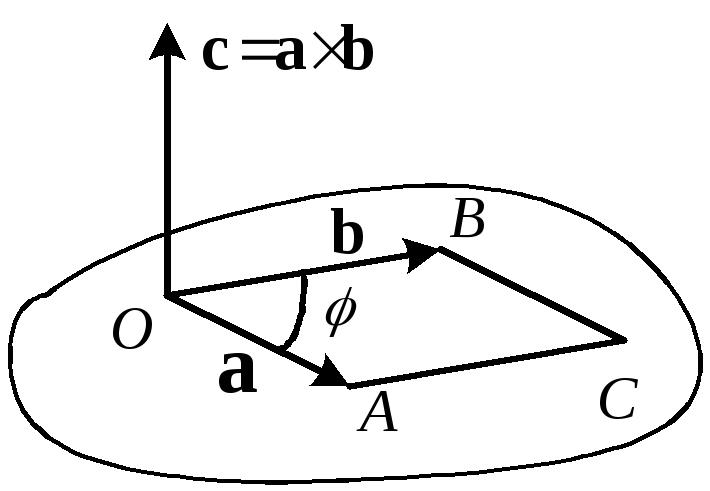 пределение.
Векторным произведением двух векторов
пределение.
Векторным произведением двух векторов  и
и называется вектор
называется вектор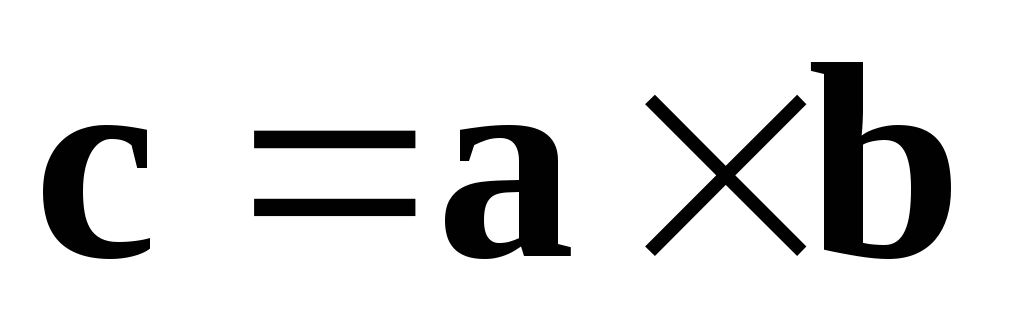 ,
удовлетворяющий следующим условиям:
,
удовлетворяющий следующим условиям:
а) вектор 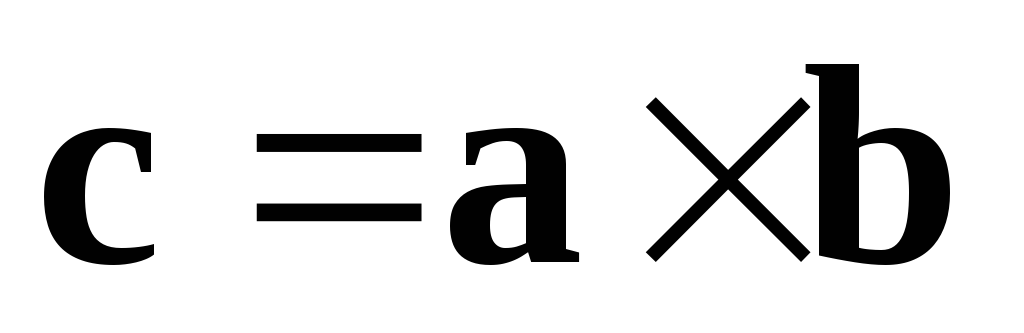 перпендикулярен плоскости векторов
перпендикулярен плоскости векторов  и
и и направлен так, что тройка векторов
и направлен так, что тройка векторов ,
, ,
, правая;
правая;
б) длина вектора 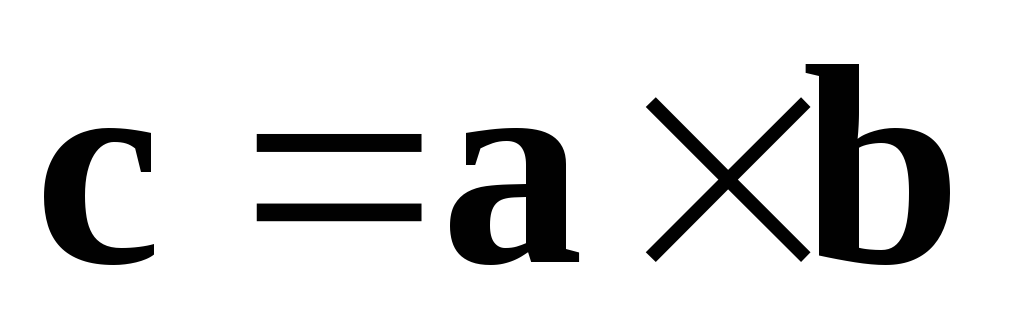 численно равна площади
численно равна площади
Рис. 2.19
параллелограмма,
построенного на векторах  и
и ,
т.е.
,
т.е.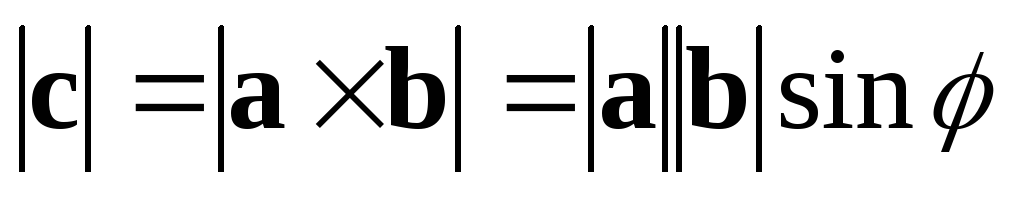 ,
где
,
где —
угол между векторами
—
угол между векторами и
и (рис. 2.19).
(рис. 2.19).
Очевидно, что  ,
, ,
,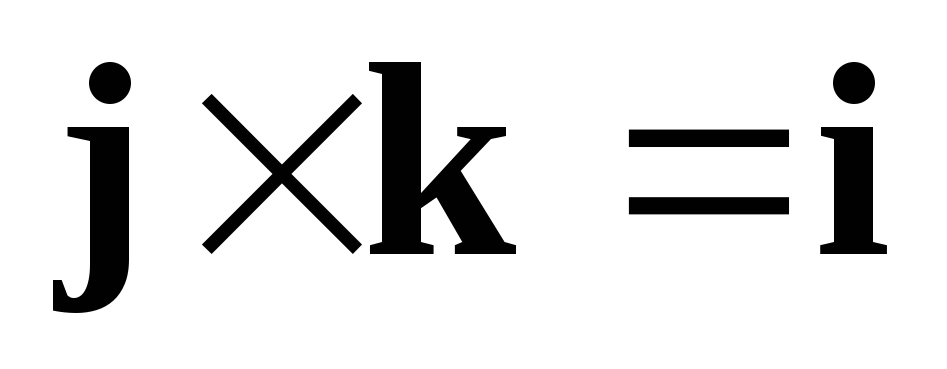 ,
, ,
,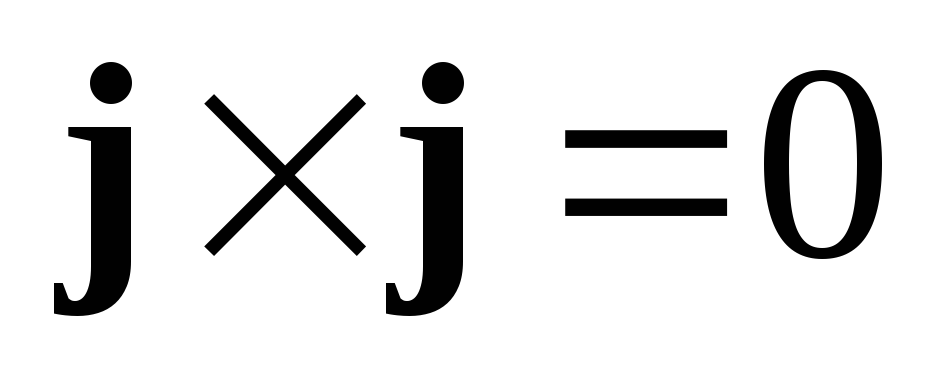 ,
, .
.
Пример 11. Проверить справедливость равенства 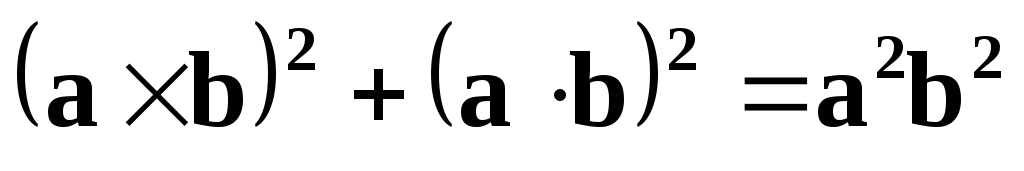 .
.
Решение.  ,
, ,
,
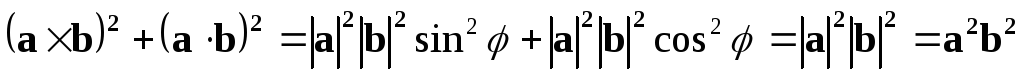 .
.
Метод Жуковского.
Рассмотрим метод
Жуковского построения вектора 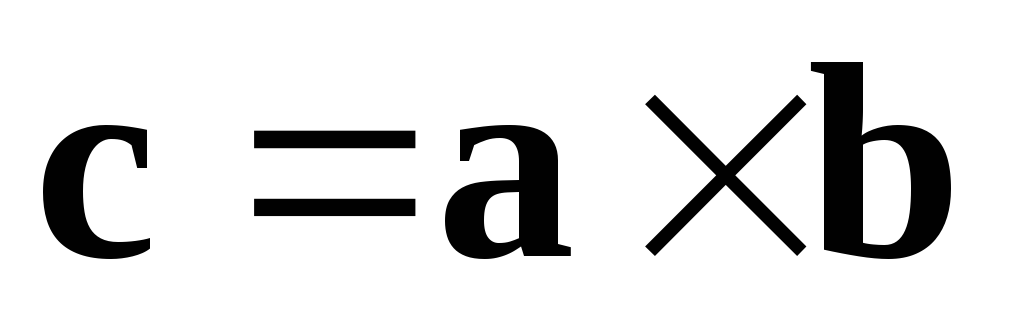 .
.
Пусть угол между
векторами  и
и равен
равен .
.
Векторы  и
и приложим к общему началу
приложим к общему началу (рис. 2.20).
Через точку
(рис. 2.20).
Через точку перпендикулярно вектору
перпендикулярно вектору проведем плоскость
проведем плоскость .
Из конца вектора
.
Из конца вектора опустим перпендикуляр на плоскость
опустим перпендикуляр на плоскость . Точку пересечения этого перпендикуляра
и плоскости обозначим через
. Точку пересечения этого перпендикуляра
и плоскости обозначим через .
Проведем в плоскости
.
Проведем в плоскости вектор
вектор и построим вектор
и построим вектор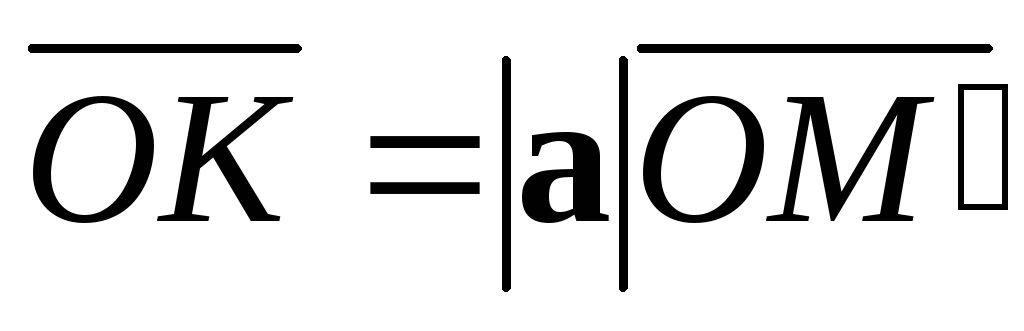 .
.
Рис. 2.20
П окажем,
что вектор
окажем,
что вектор .
.
а) Из построения
следует, что вектор 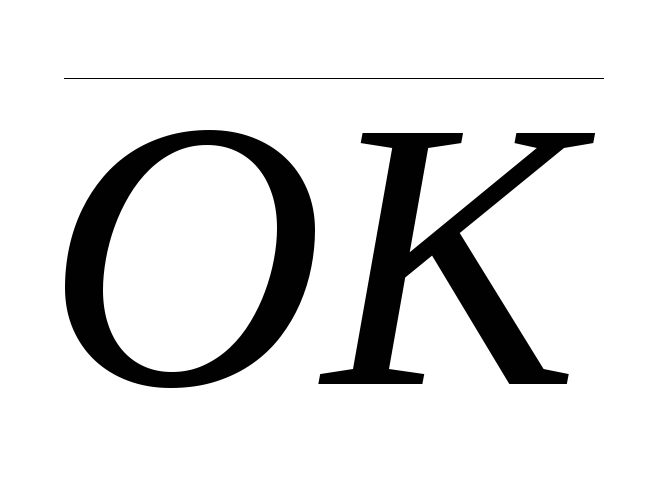 перпендикулярен
векторам
перпендикулярен
векторам ,
, ,
и векторы
,
и векторы ,
, ,
, образуют правую тройку.
образуют правую тройку.
б)  .
.
Из а) и б) следует,
что 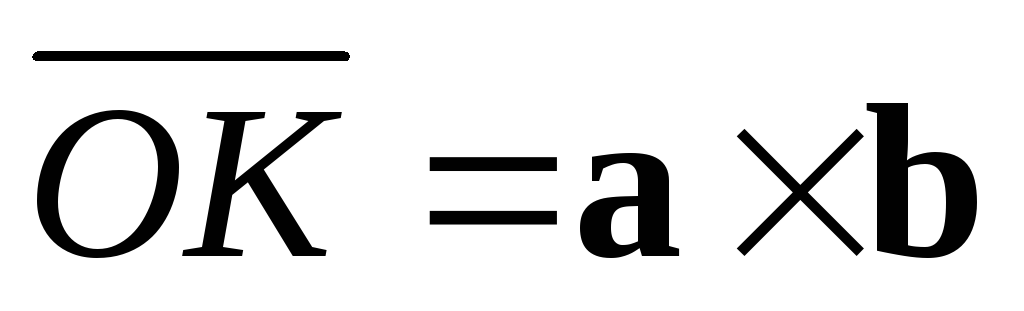 .
.
Если проекцию
вектора  на плоскость
на плоскость обозначить
через
обозначить
через
 ,
то
,
то
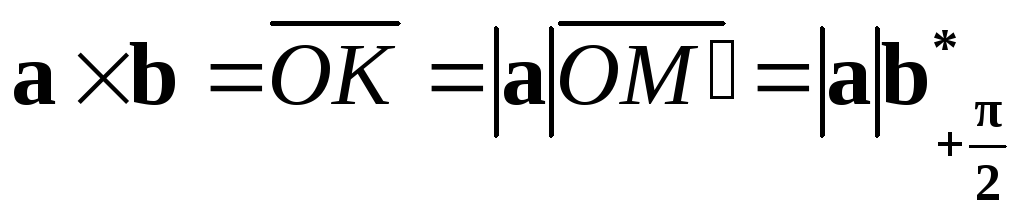 .
.
Свойства векторного произведения.
Векторное произведение двух векторов обладает следующими свойствами:
1) 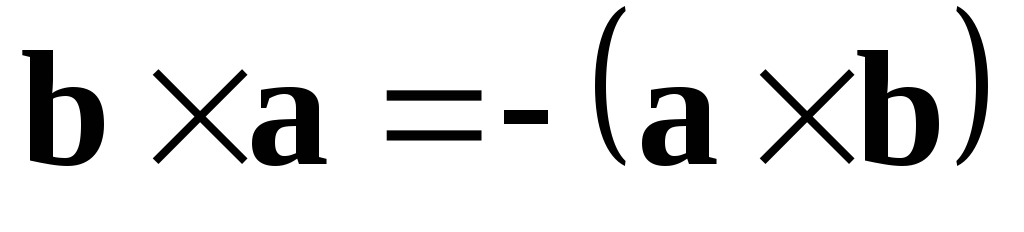 (векторное произведениеантикоммутативно,
т.е. при перестановке сомножителей
направление вектора меняется на
противоположное, при этом его модуль
остаётся неизменным).
(векторное произведениеантикоммутативно,
т.е. при перестановке сомножителей
направление вектора меняется на
противоположное, при этом его модуль
остаётся неизменным).
Это свойство
следует из определения векторного
произведения. Если тройка векторов  правая, то тройка
правая, то тройка —
левая.
—
левая.
2) 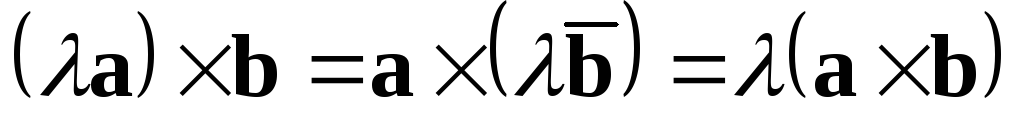 (ассоциативный
закон).
Это
свойство легко доказывается из определения
векторного произведения.
(ассоциативный
закон).
Это
свойство легко доказывается из определения
векторного произведения.
3) 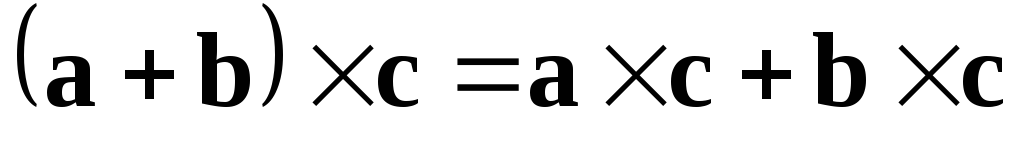 (дистрибутивный
закон.)
►
(дистрибутивный
закон.)
►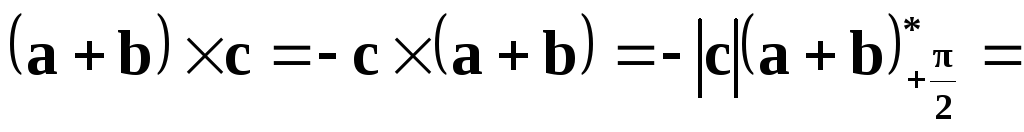
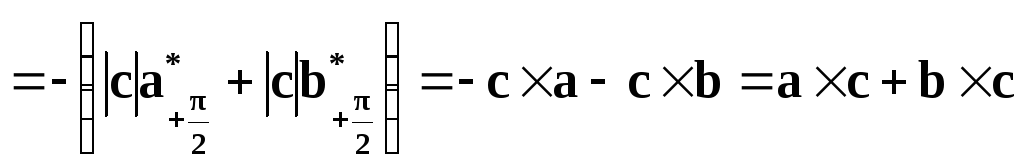 .◄
.◄
4) 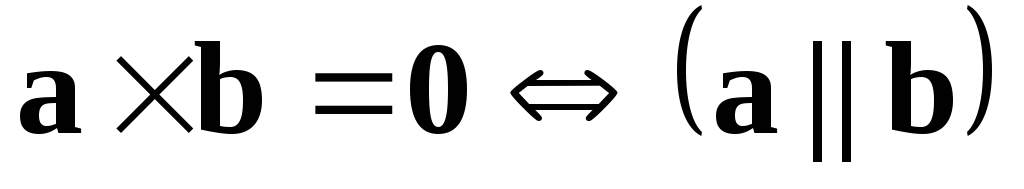 .
Это свойство следует из определения
векторного произведения, а именно из
того, что модуль векторного произведения
равен площади параллелограмма,
построенного на векторах
.
Это свойство следует из определения
векторного произведения, а именно из
того, что модуль векторного произведения
равен площади параллелограмма,
построенного на векторах и
и .
Это свойство дает возможность записать в удобной форме параллельность двух векторов.
.
Это свойство дает возможность записать в удобной форме параллельность двух векторов.
Например, 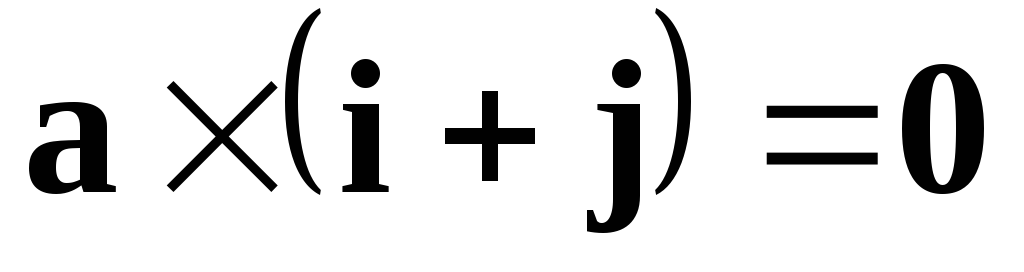 означает, что вектор
означает, что вектор коллинеарен биссектрисе первого
координатного угла.
коллинеарен биссектрисе первого
координатного угла.
Векторное произведение в координатной форме.
Пользуясь свойствами
векторного произведения и равенствами 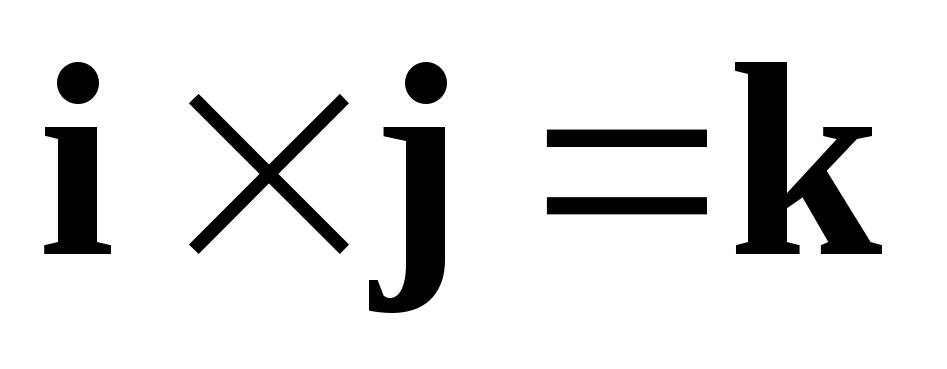 ,
,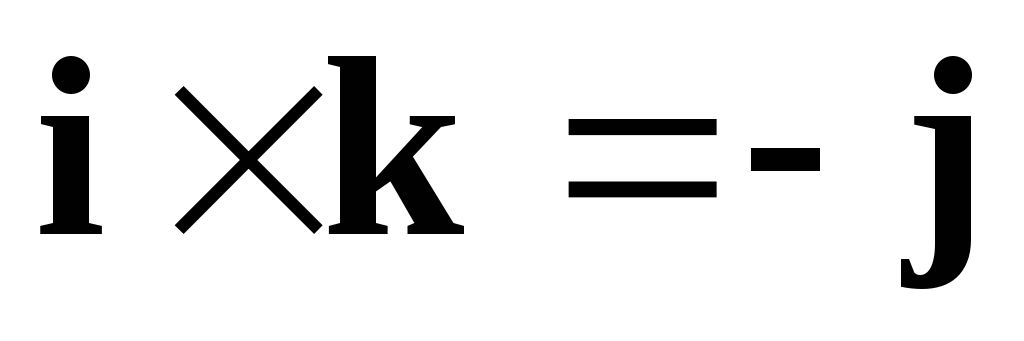 ,
,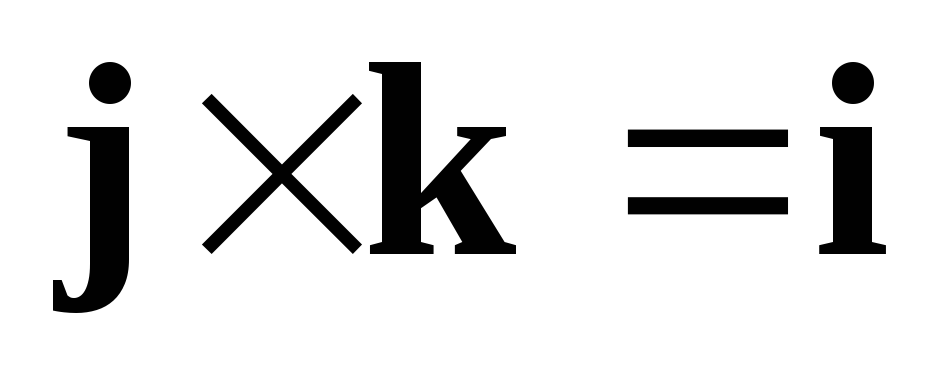 ,
, ,
, ,
, ,
вычислим
,
вычислим
 =
=
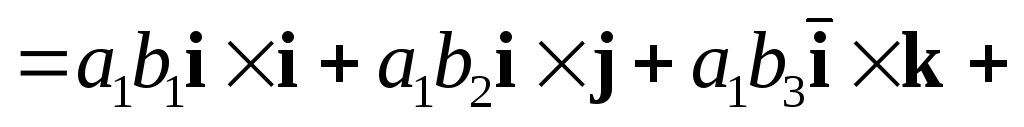
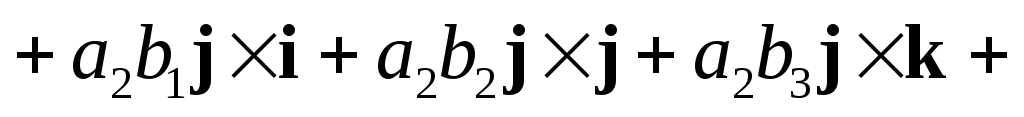
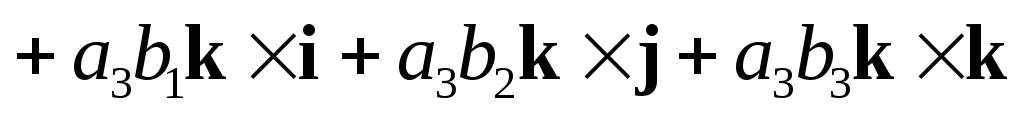 =
=
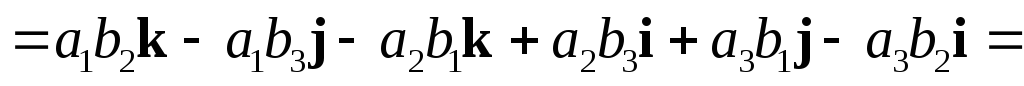
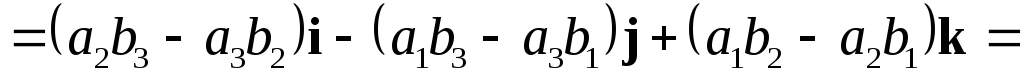

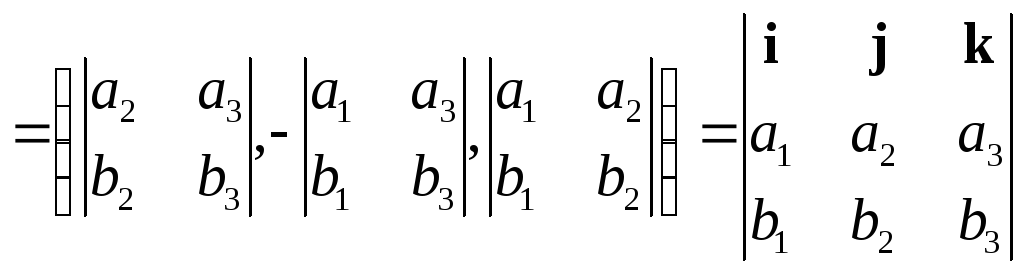 ,
т.е.
,
т.е. 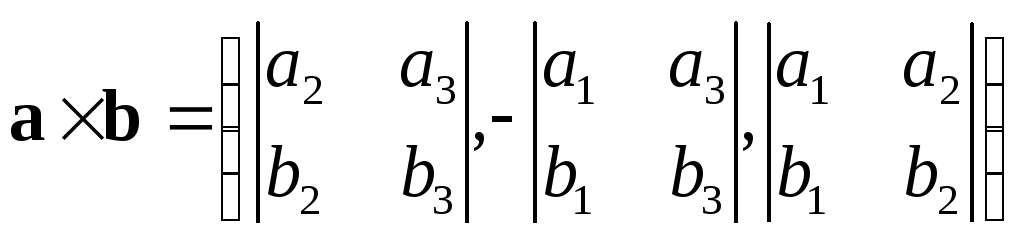 или
или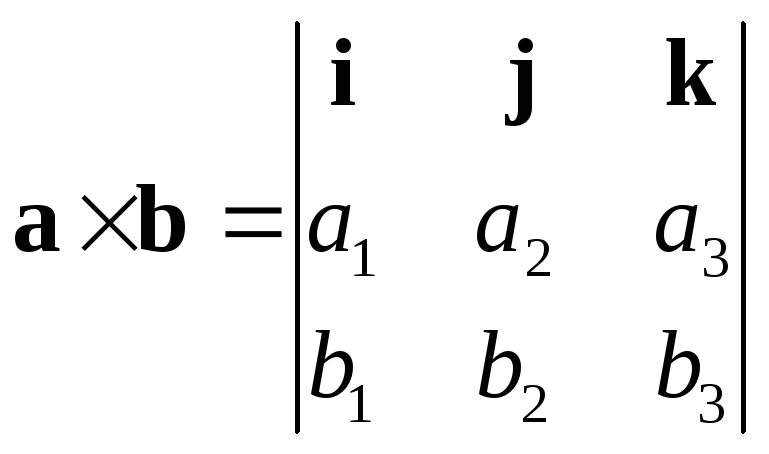 .
.
Применение векторного произведения.
Векторное
произведение векторов  и
и применяется:
применяется:
для нахождения
площади параллелограмма, построенного
на векторах  и
и ;
;
для нахождения
площади треугольника, построенного на
векторах  и
и ;
;
для нахождения
синуса угла между векторами  и
и ;
;
для нахождения
вектора, перпендикулярного векторам  и
и .
.
1) Площадь  параллелограмма, построенного на
векторах
параллелограмма, построенного на
векторах и
и ,
может быть вычислена по формуле
,
может быть вычислена по формуле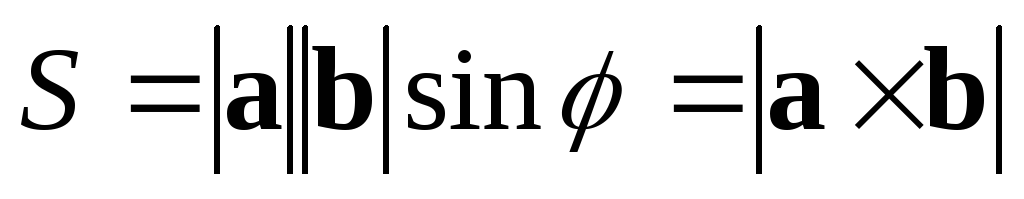 ,
где-
угол между векторами
,
где-
угол между векторами и
и .
.
Замечание. Если 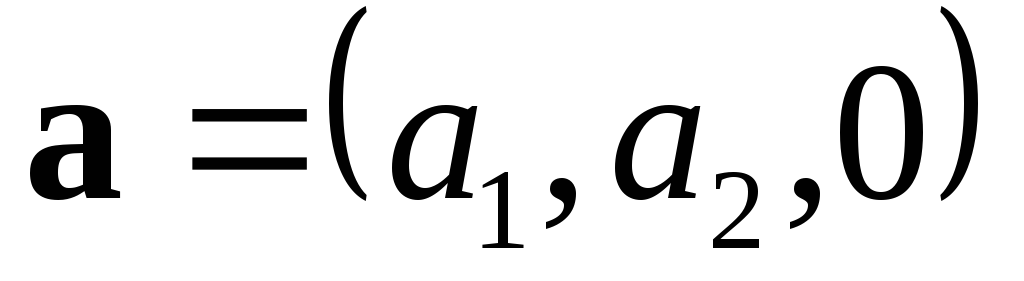 и
и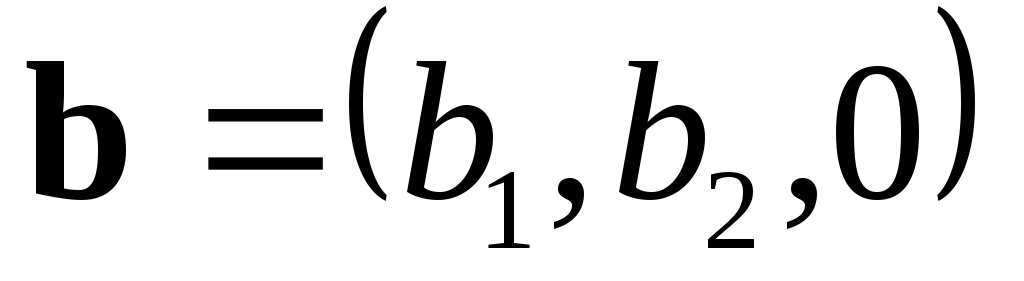 ,
то
,
то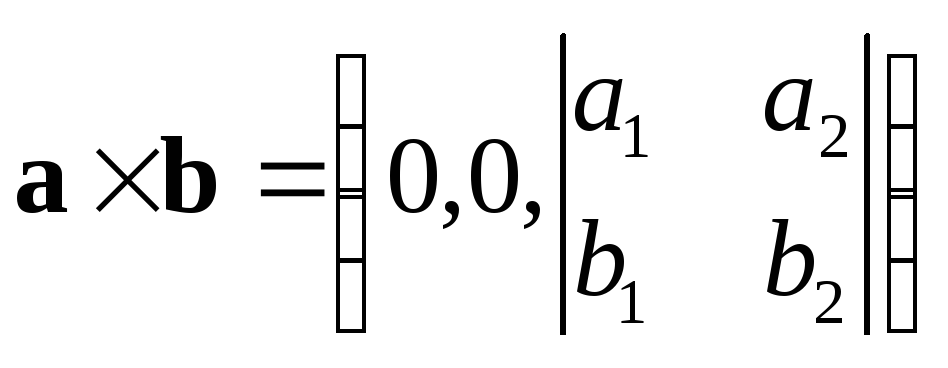 и
и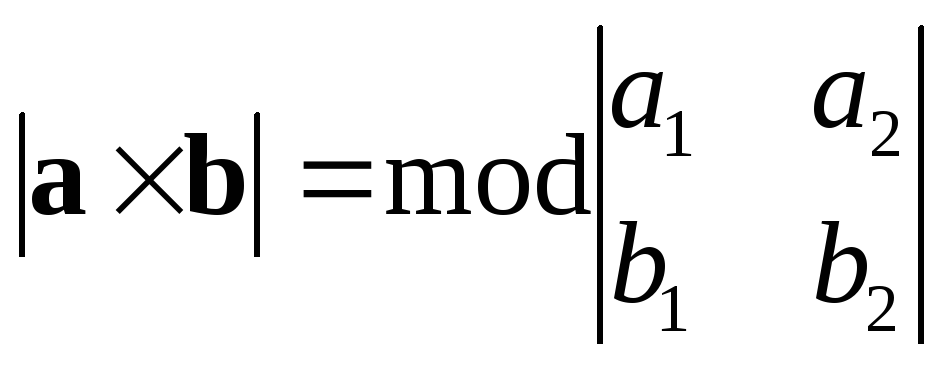 .
Отсюда следует, чтомодуль
определителя второго порядка численно равен площади параллелограмма,
построенного на векторах
.
Отсюда следует, чтомодуль
определителя второго порядка численно равен площади параллелограмма,
построенного на векторах 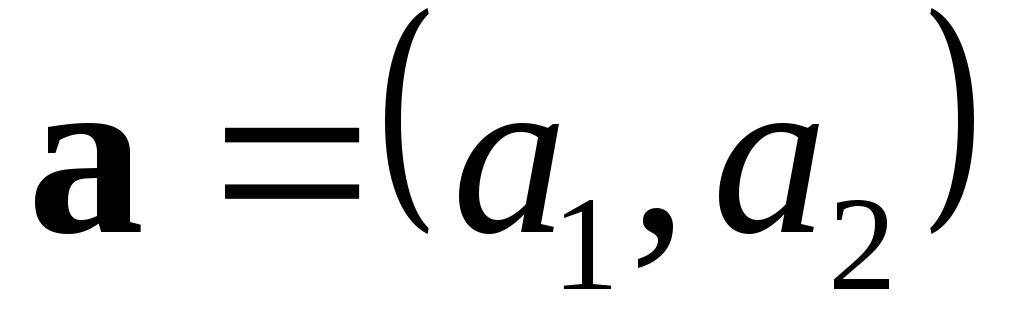 и
и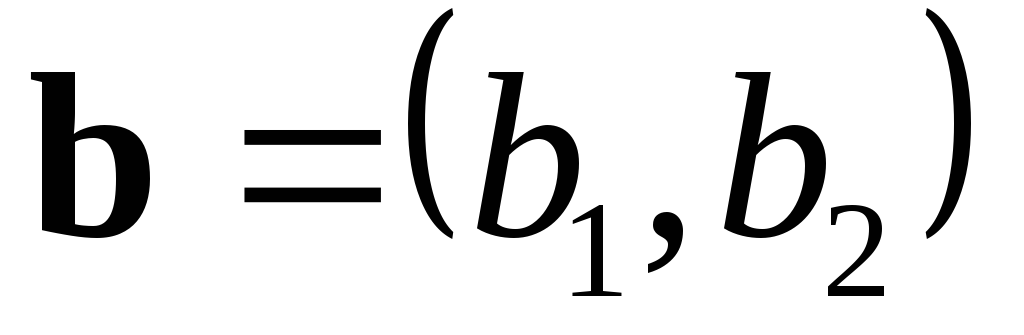 .
.
2) Площадь  треугольника, построенного на векторах
треугольника, построенного на векторах и
и ,
равна половине площади параллелограмма,
построенного на этих же векторах, т.е.
,
равна половине площади параллелограмма,
построенного на этих же векторах, т.е.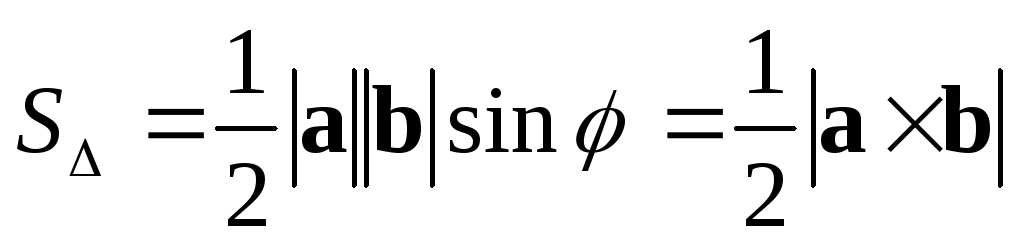 ,
где
,
где —
угол между векторами
—
угол между векторами и
и .
.
3) Синус угла между
векторами  и
и может быть вычислен по формуле
может быть вычислен по формуле .
.
4) Вектор 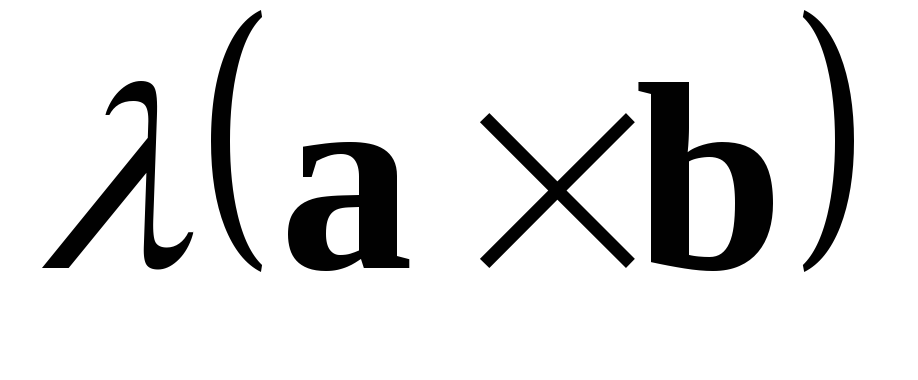 перпендикулярен вектору
перпендикулярен вектору и вектору
и вектору .
.
Замечание. Векторное произведение может быть
использовано при решении системы
линейных однородных уравнений вида 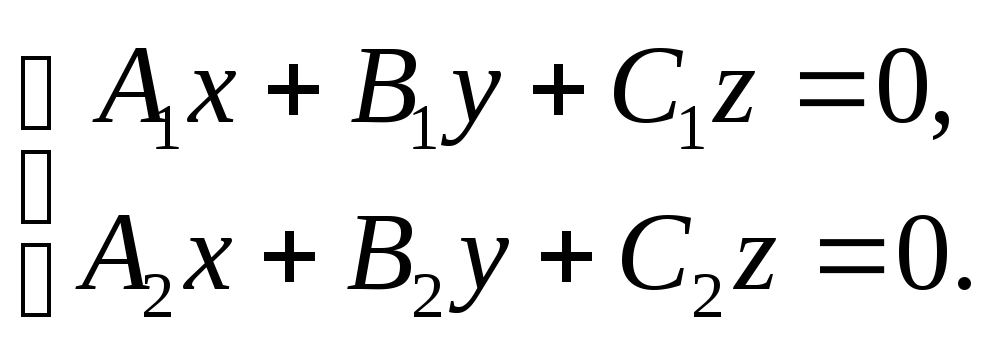 Если векторы
Если векторы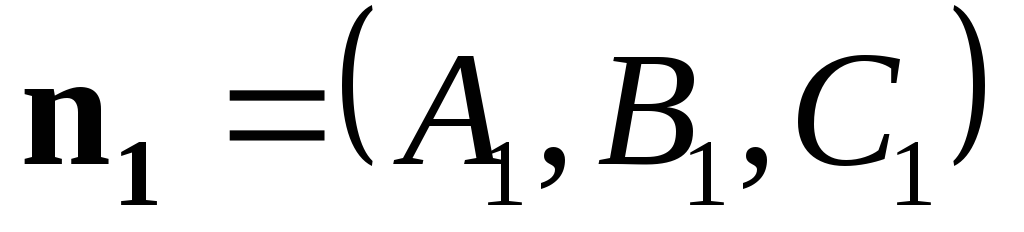 и
и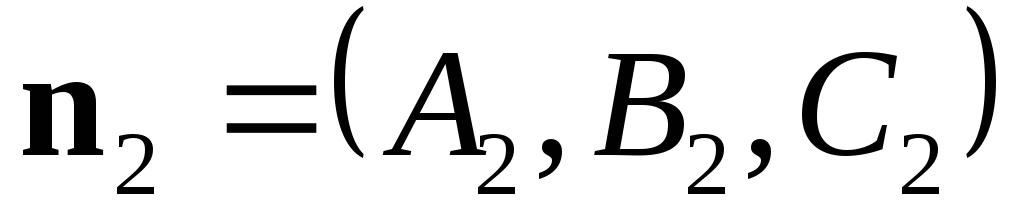 неколлинеарны, то
неколлинеарны, то является
решением исходной системы.
является
решением исходной системы.
►Действительно,
из системы уравнений следует, что вектор  перпендикулярен векторам
перпендикулярен векторам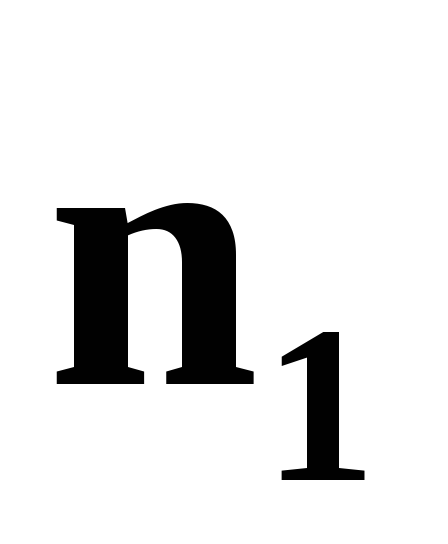 и
и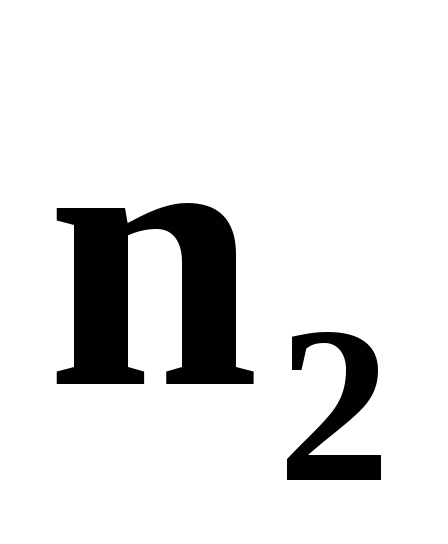 ,
а, следовательно,
,
а, следовательно,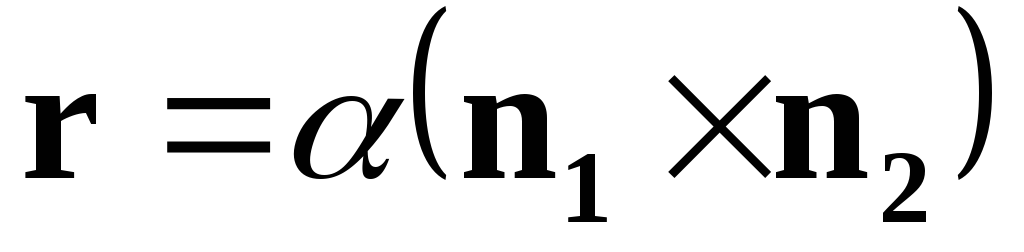 .◄
.◄
● Пример 12. Дано: 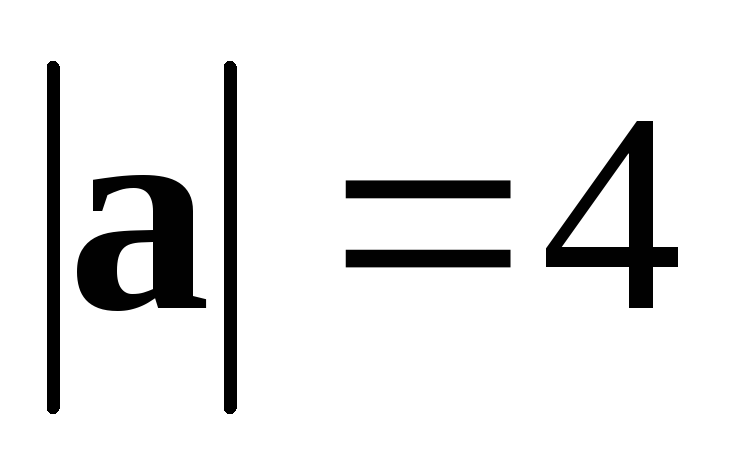 ,
,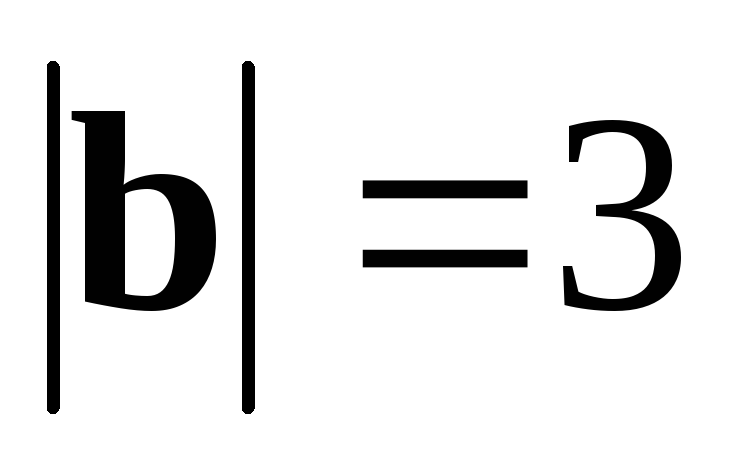 ,
,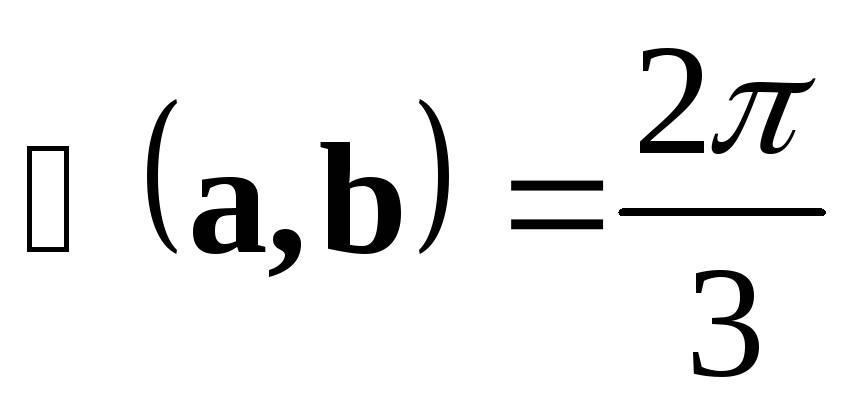 ,
, ,
, .
.
Найти площадь
параллелограмма, построенного на
векторах  и
и .
.
Найти синус угла  между векторами
между векторами и
и .
.
Решение.
Площадь параллелограмма, построенного
на векторах  и
и равнамодулю векторного произведения векторов
равнамодулю векторного произведения векторов  и
и ,
т.е.
,
т.е.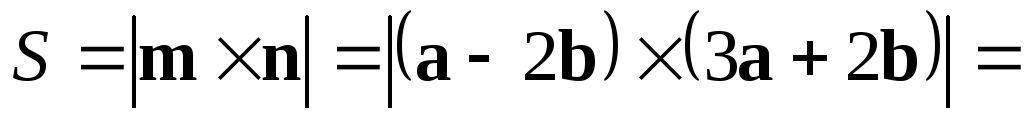
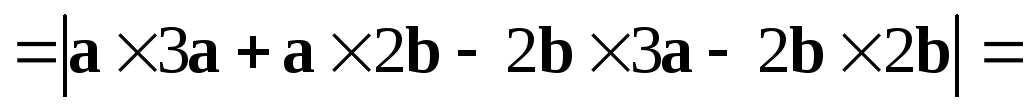
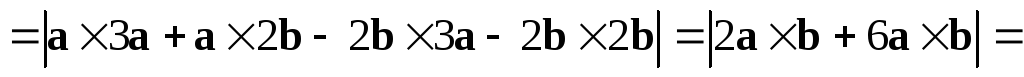
 .
.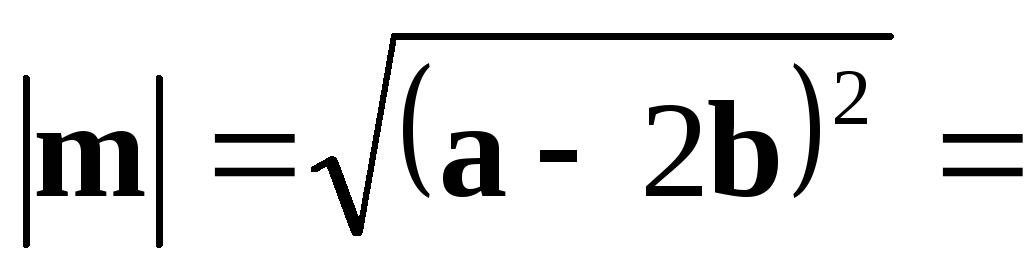
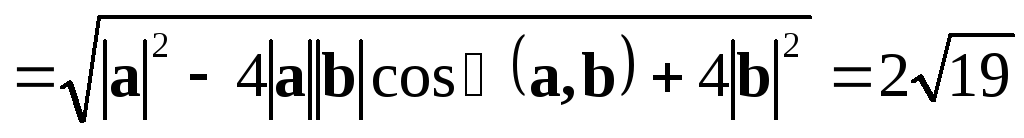 .
.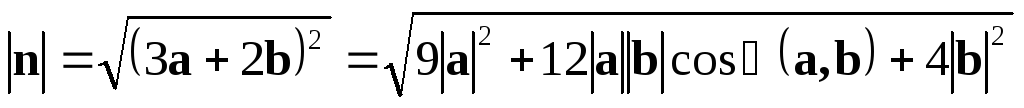 =
= .
.
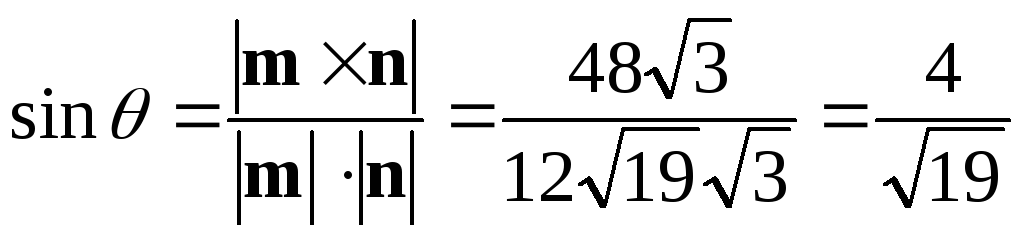 .
.
Ответ: 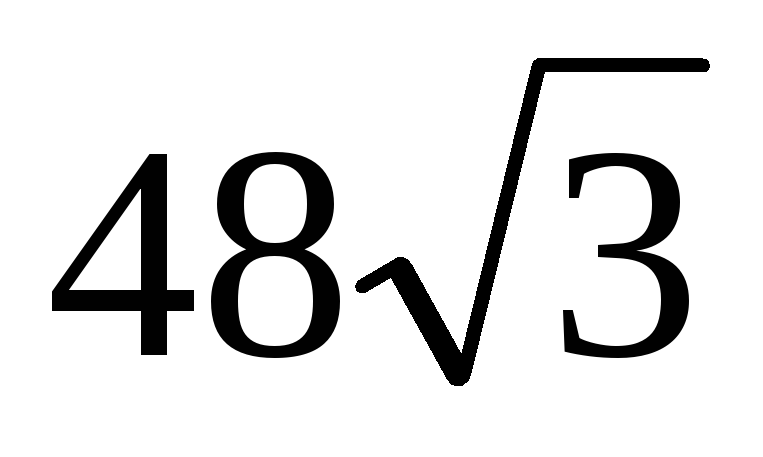 ,
, .
.
● Пример 13. Дано: 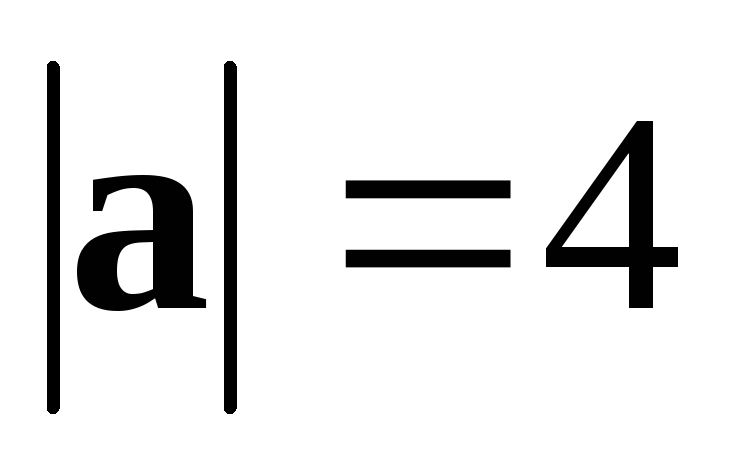 ,
,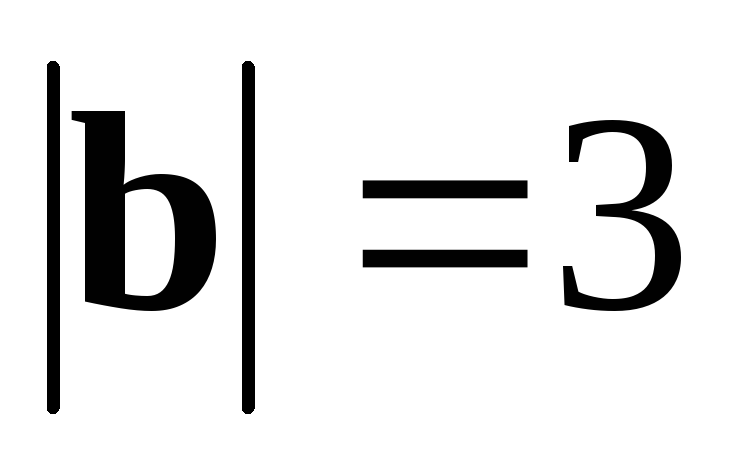 ,
,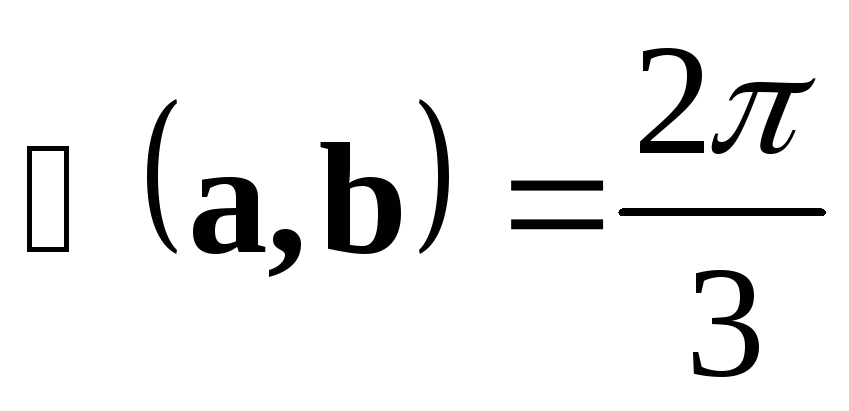 ,
,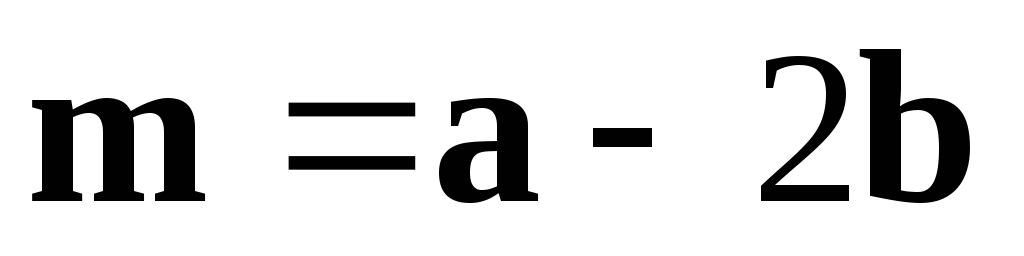 ,
,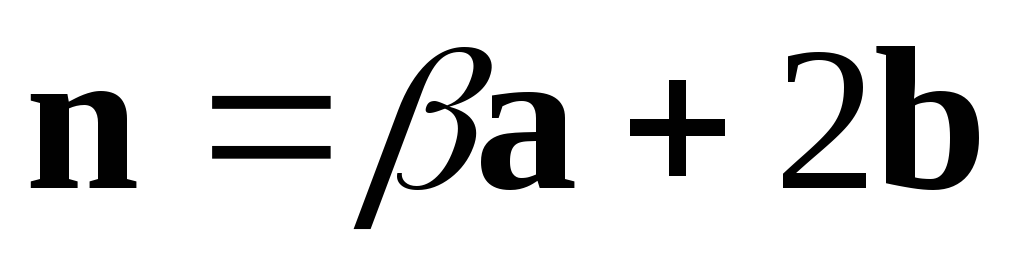 .
.
Найти значение
параметра  ,
при котором векторы
,
при котором векторы и
и коллинеарны.
коллинеарны.
Решение. Первый способ. Так как векторы  и
и коллинеарны, то их векторное произведение
равно нулю.
коллинеарны, то их векторное произведение
равно нулю.
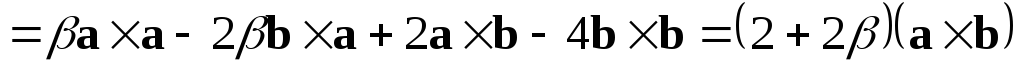 =0,
а так как
=0,
а так как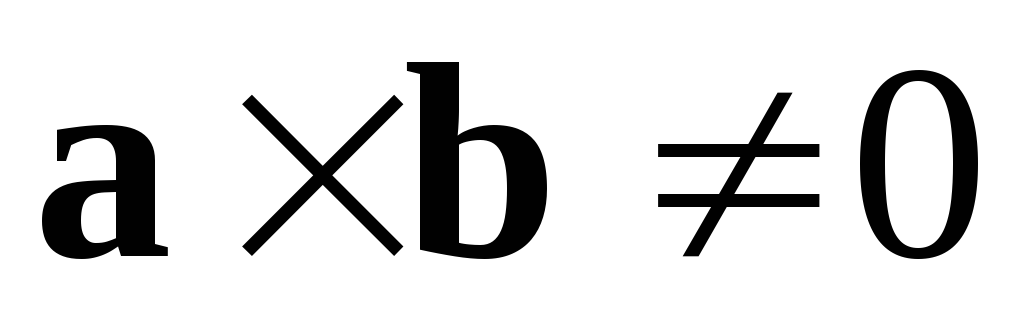 ,
то
,
то и
и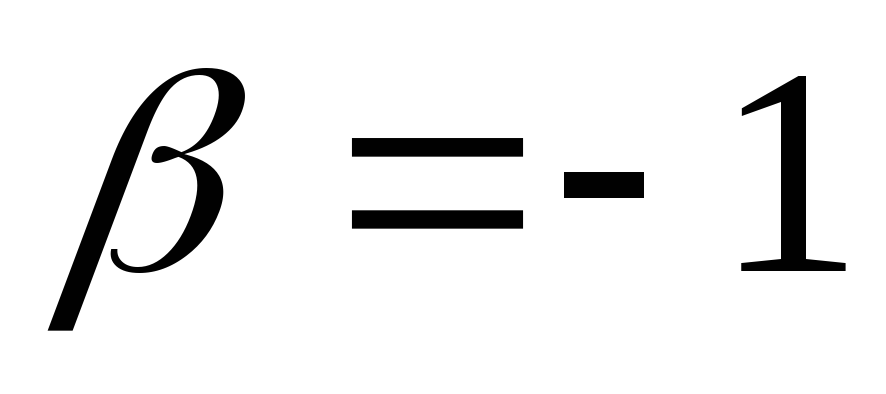 .
.
Второй способ.
Векторы  и
и составляют базис системы векторов
составляют базис системы векторов ,
, ,
,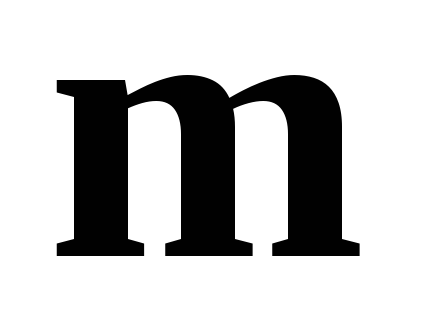 и
и .
В базисе
.
В базисе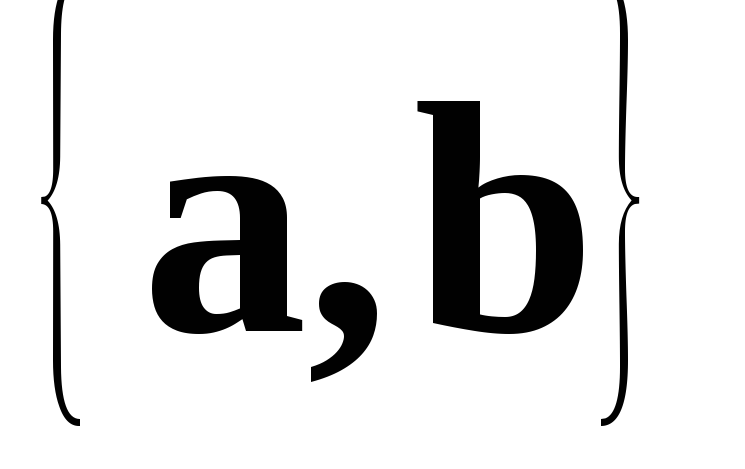
 и
и .
Так как векторы
.
Так как векторы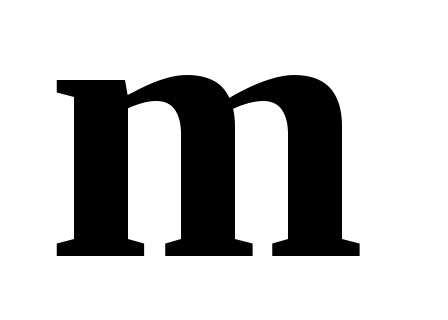 и
и коллинеарны, то
коллинеарны, то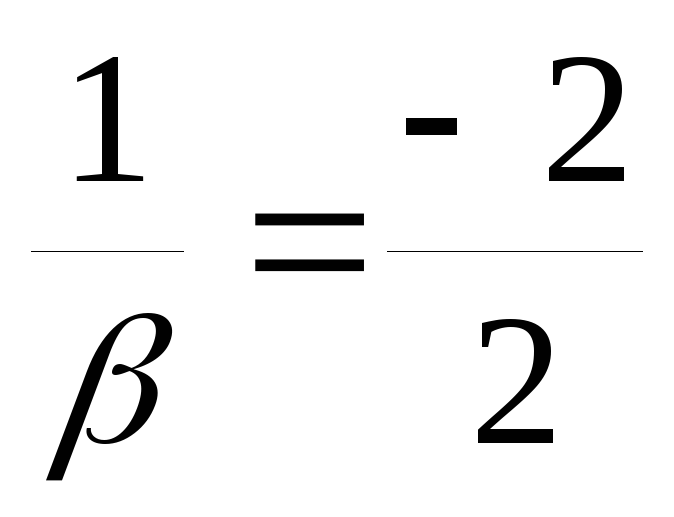 ,
откуда
,
откуда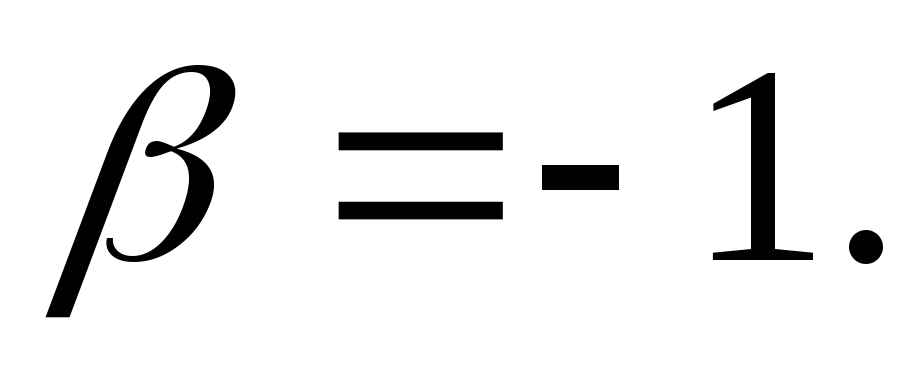 ●
●
● Пример 14. Найти координаты вектора  ,
длина которого равна 15, зная, что он
перпендикулярен оси
,
длина которого равна 15, зная, что он
перпендикулярен оси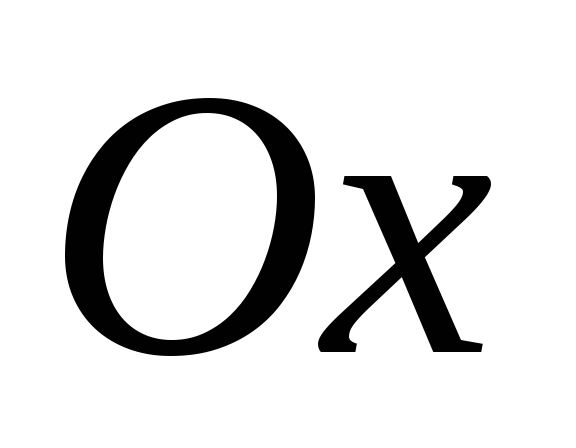 и вектору
и вектору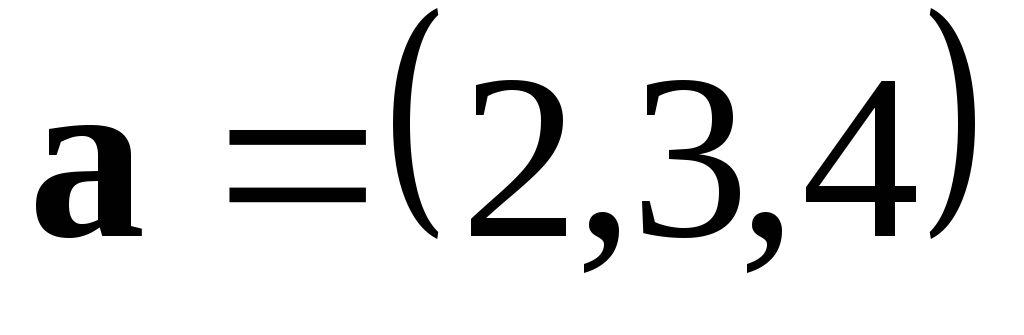 и образует острый угол с осью
и образует острый угол с осью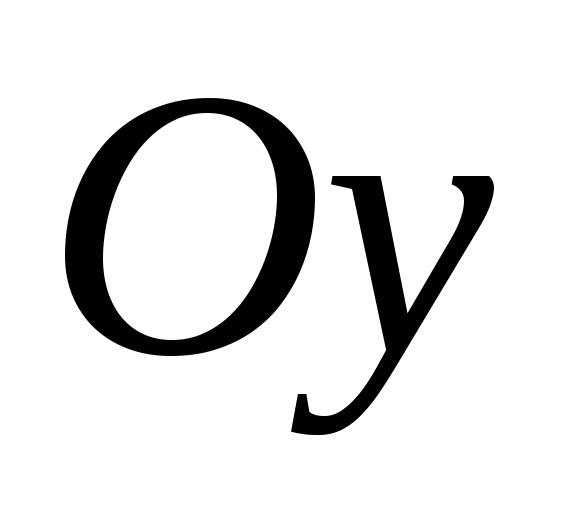 .
.
Решение. 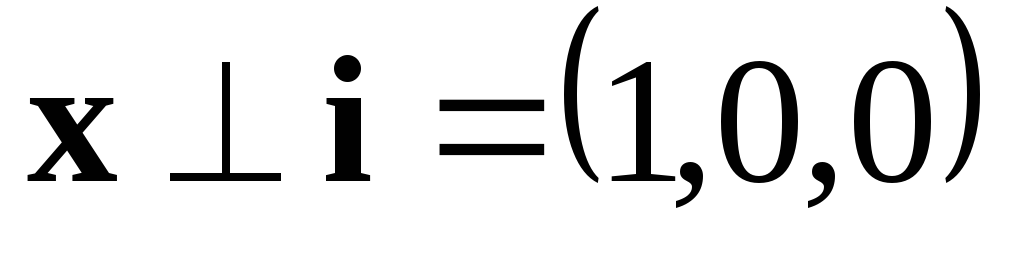 и
и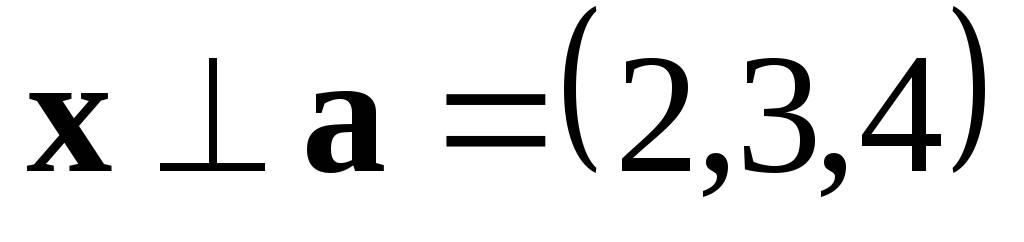 ,
поэтому
,
поэтому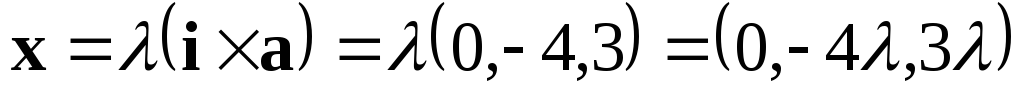 .
.
 ,
откуда
,
откуда 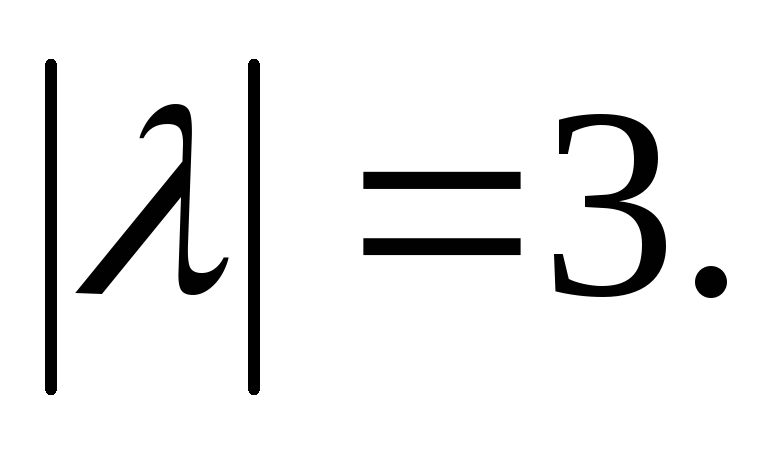
Так как вектор  образует острый угол с осью
образует острый угол с осью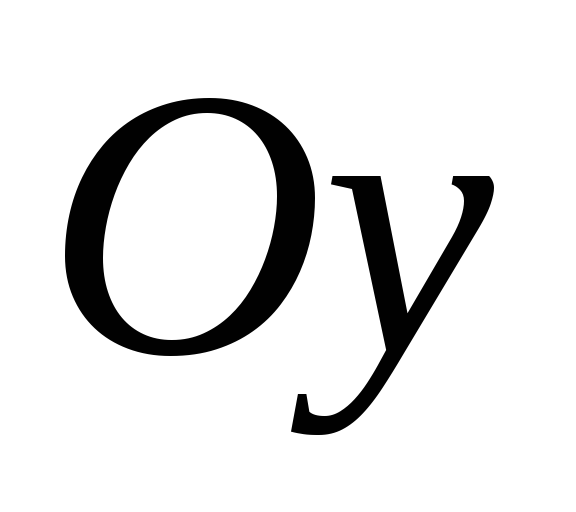 ,
то вторая его координата положительна,
тогда
,
то вторая его координата положительна,
тогда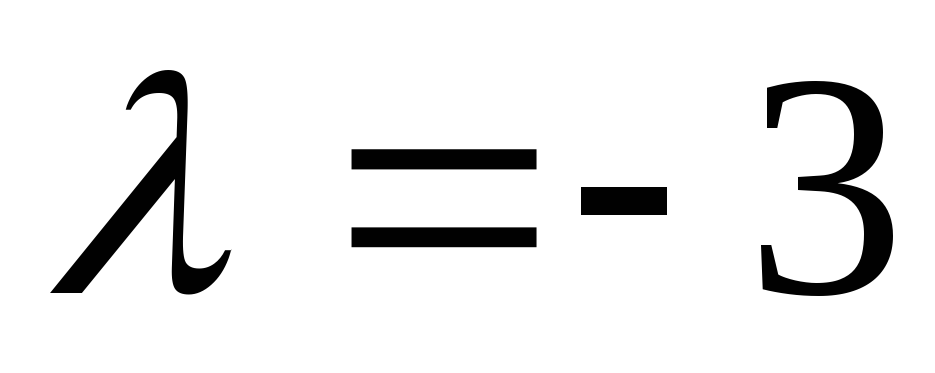 и
и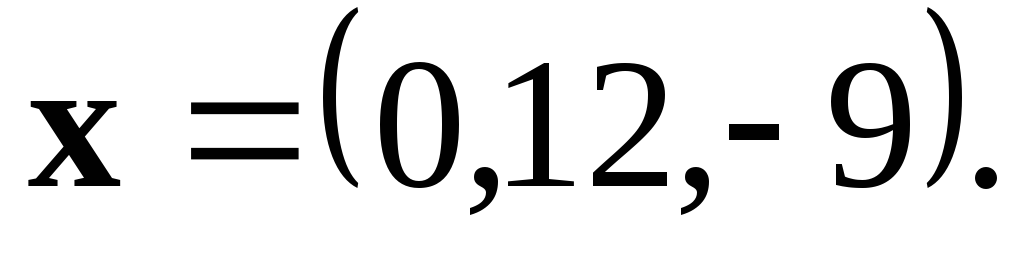 ●
●
● Пример 15. Найти
площадь параллелограмма 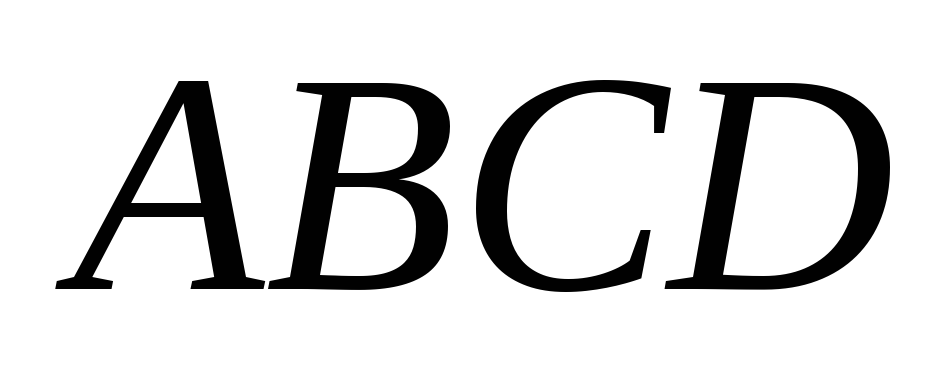 ,
если известны координаты трёх его вершин
,
если известны координаты трёх его вершин ,
,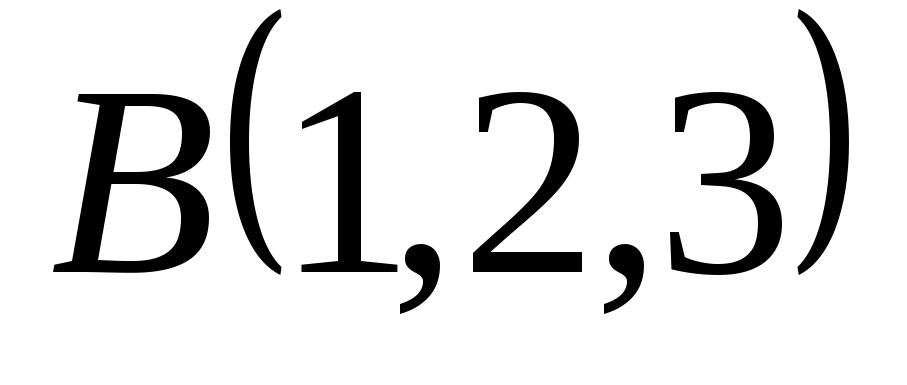 и
и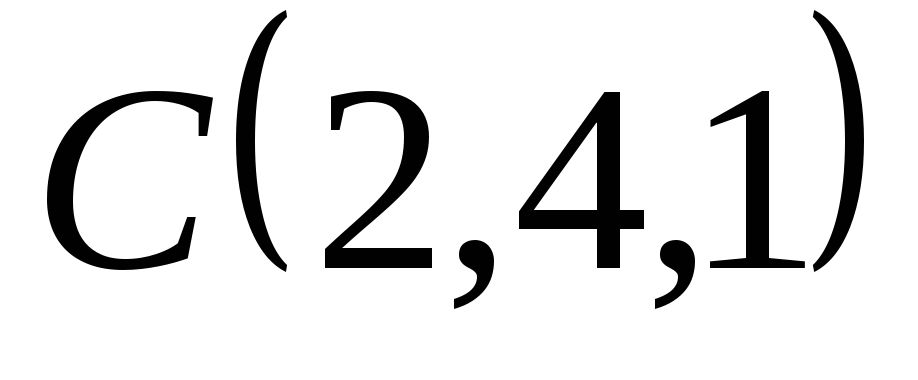 .
.
Решение. 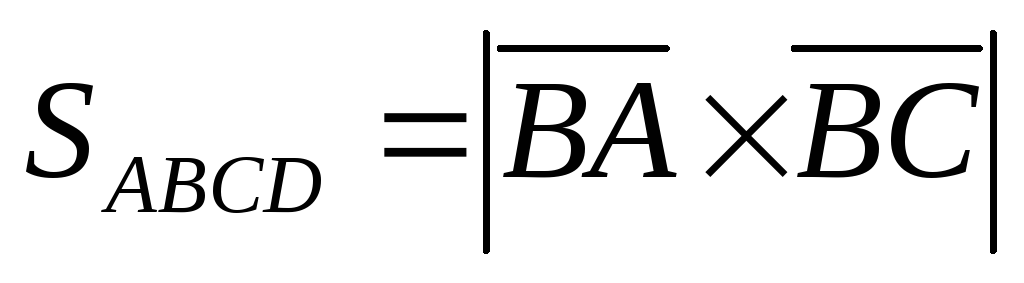 .
. ,
,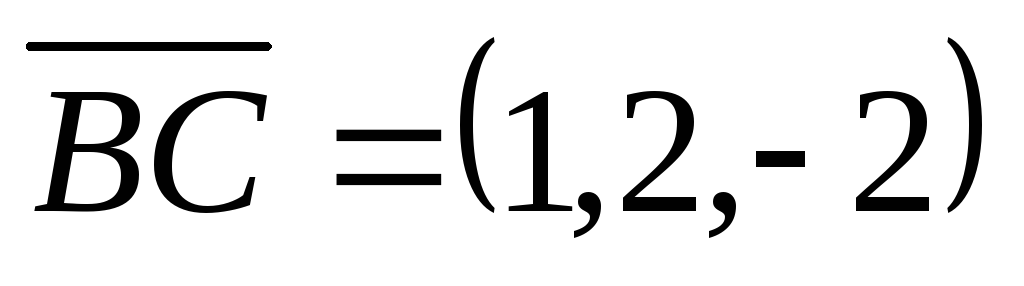 ,
,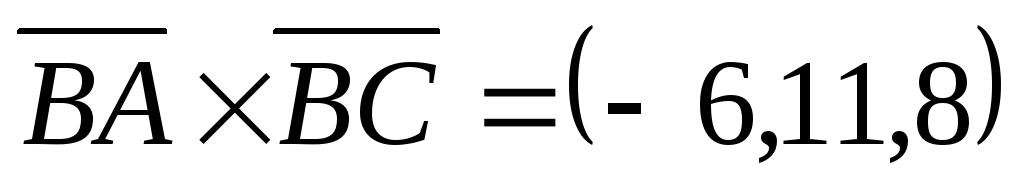 ,
,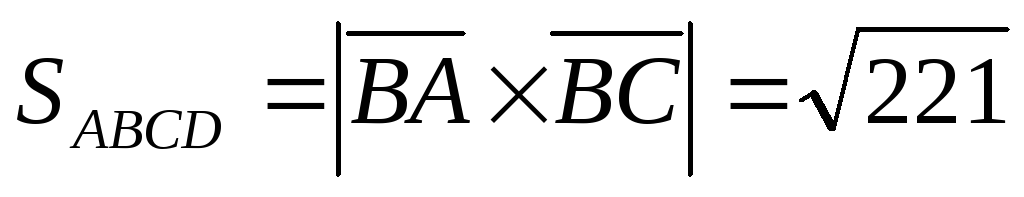 .
.
● Пример 16. 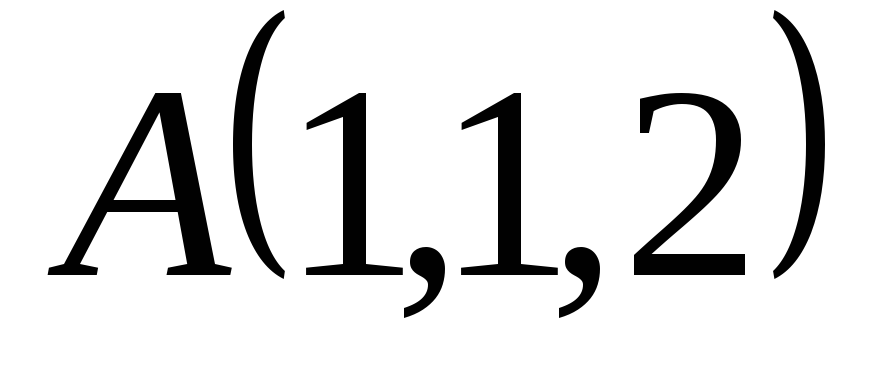 ,
,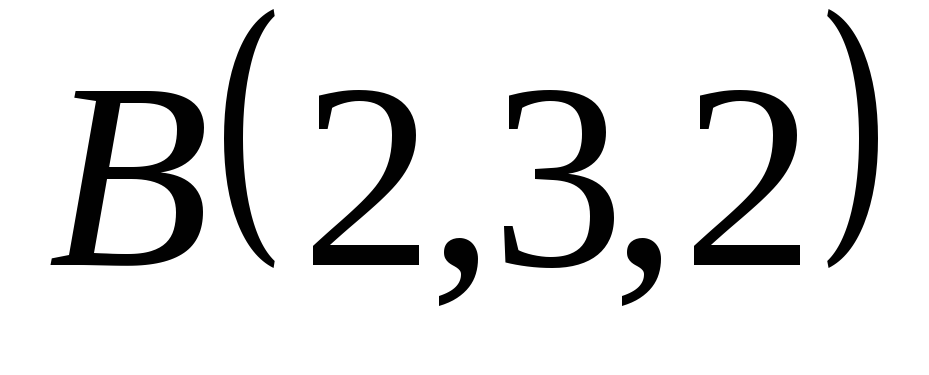 ,
, — вершины треугольника
— вершины треугольника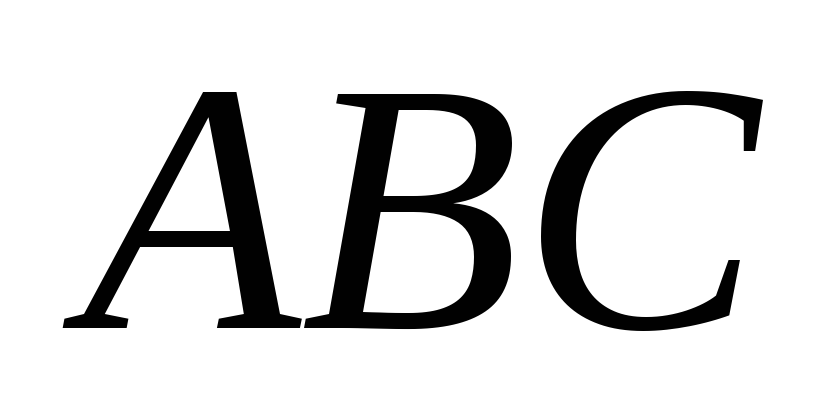 .
Найти недостающую координату
.
Найти недостающую координату точки
точки .
если площадь треугольника
.
если площадь треугольника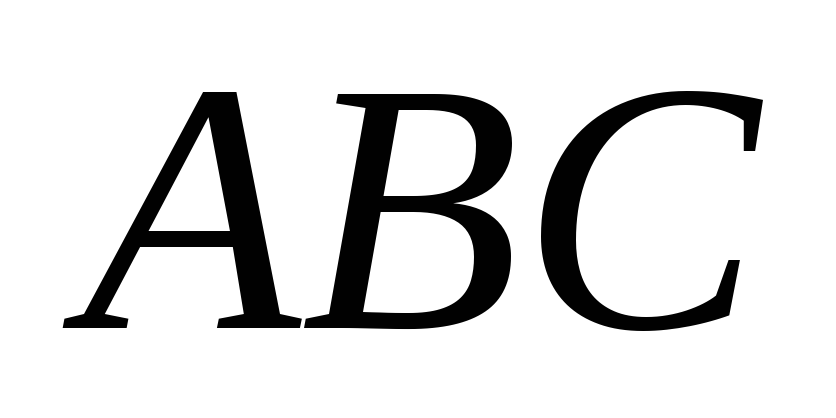 равна 3.
равна 3.
Решение. Площадь 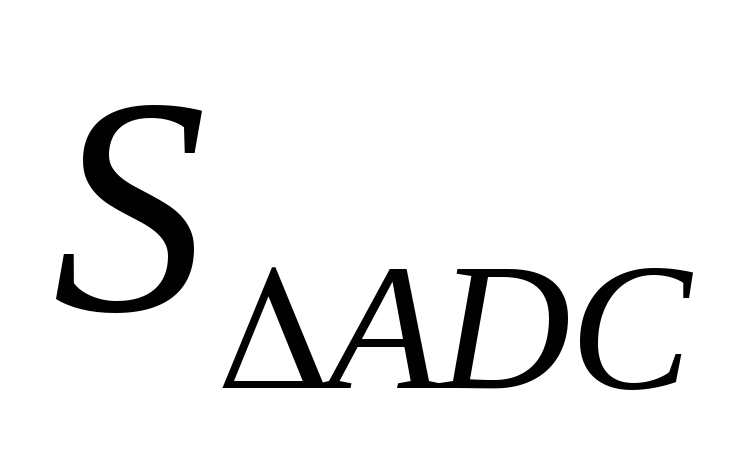 равна половине площади параллелограмма,
построенного на векторах
равна половине площади параллелограмма,
построенного на векторах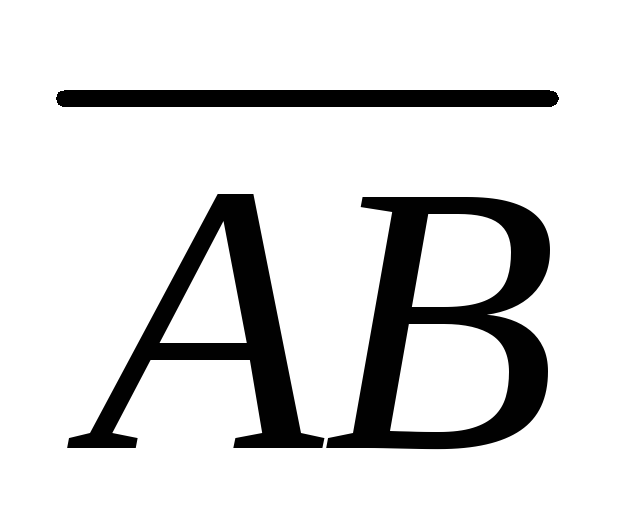 и
и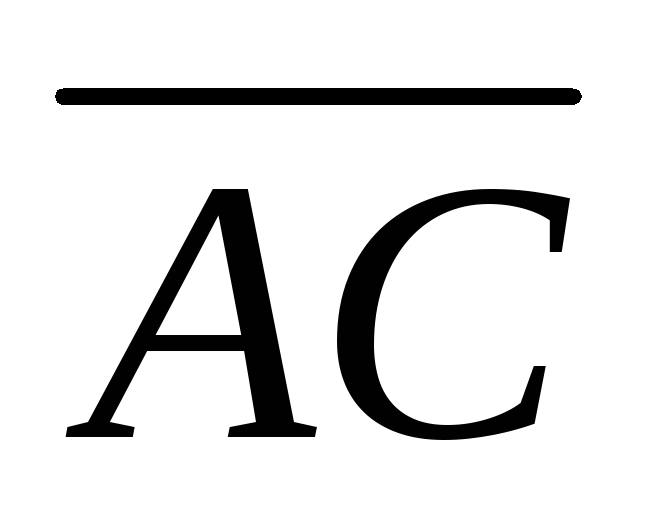 ,
т.е.
,
т.е.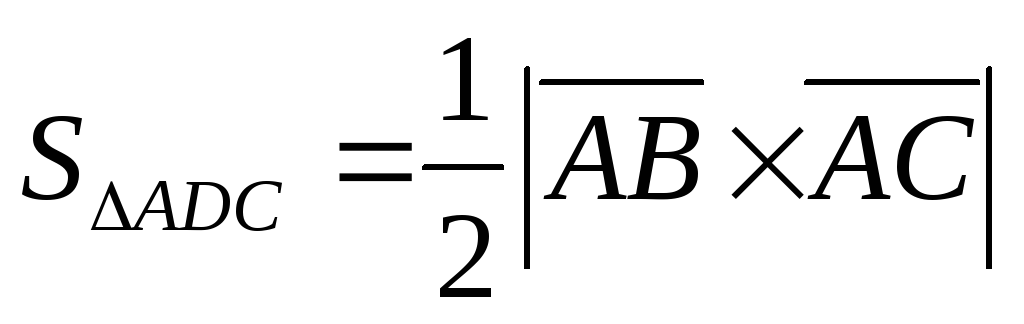 .
.
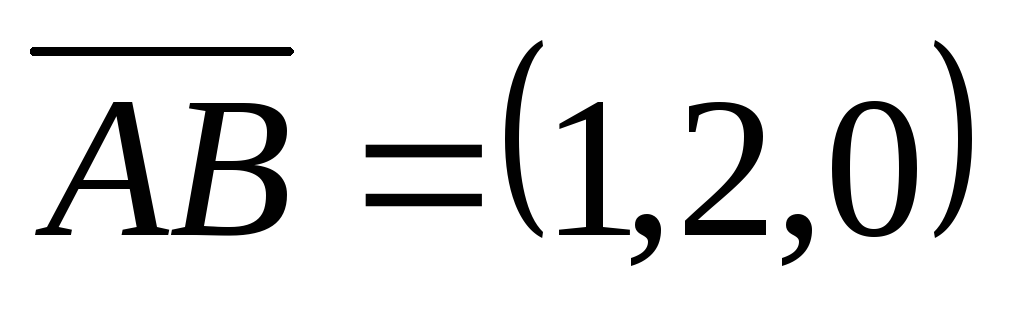 ,
, 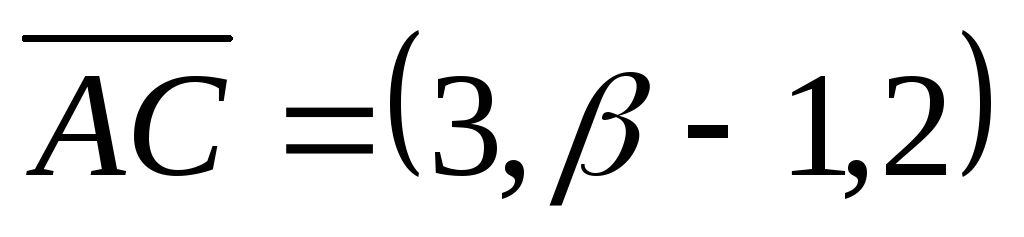 ,
,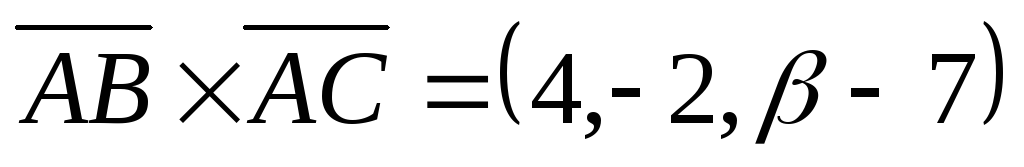 .,
откуда
.,
откуда 16,
16,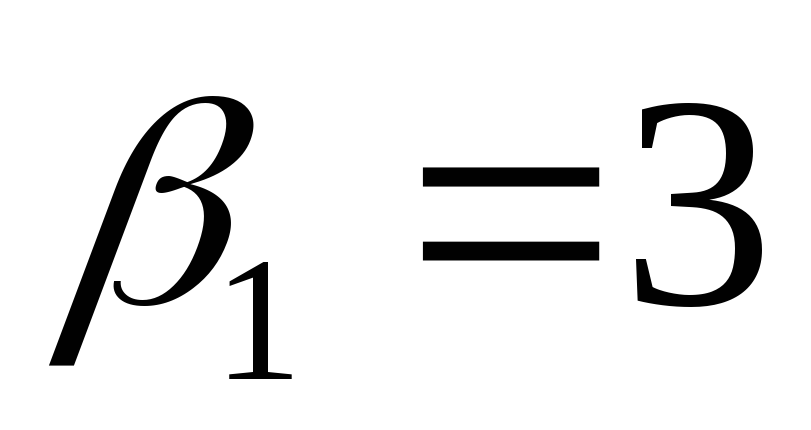 и
и .
.
Ответ: 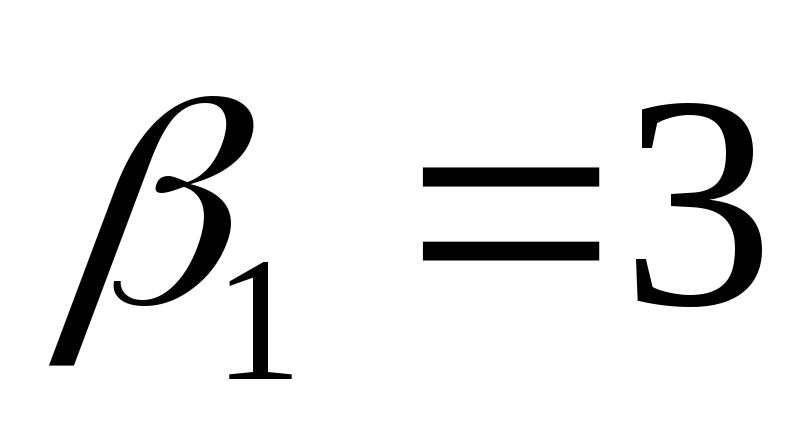 или
или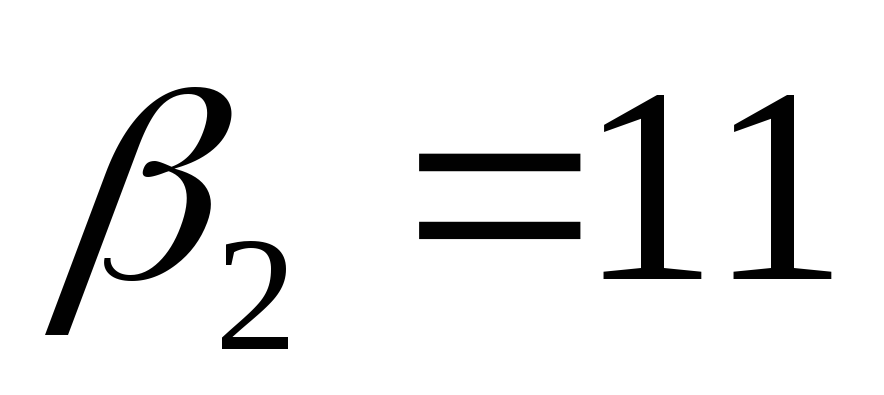 .
.
● Пример 17. Решить систему 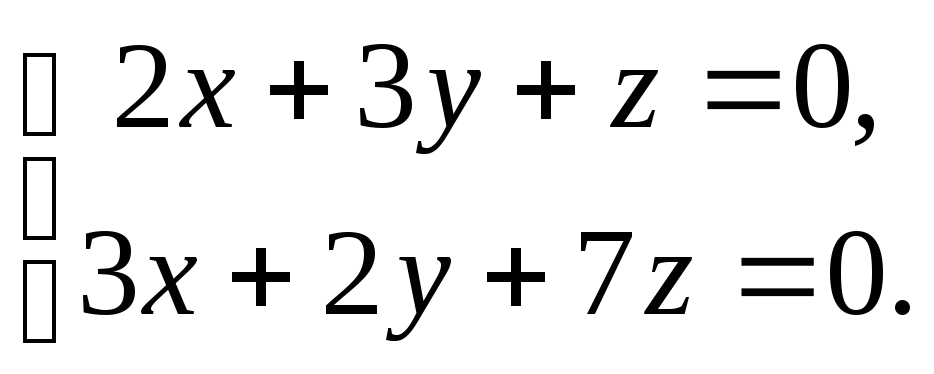
Решение.
Из уравнений системы следует, что вектор 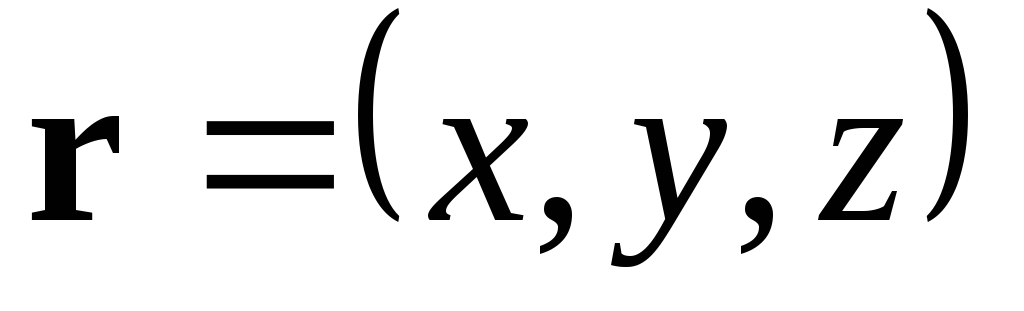 перпендикулярен векторам
перпендикулярен векторам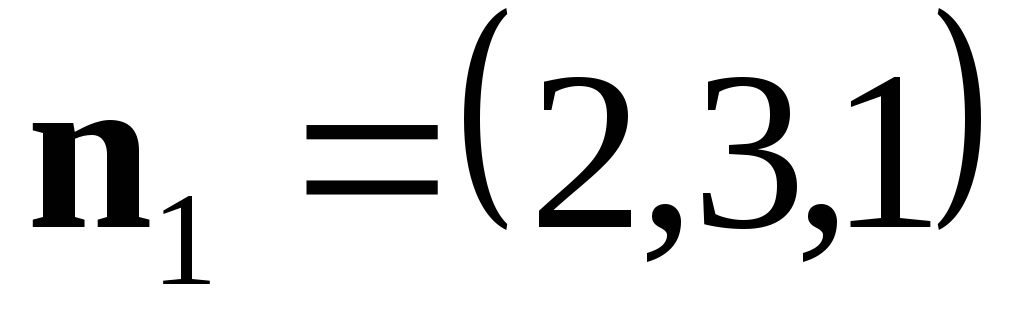 и
и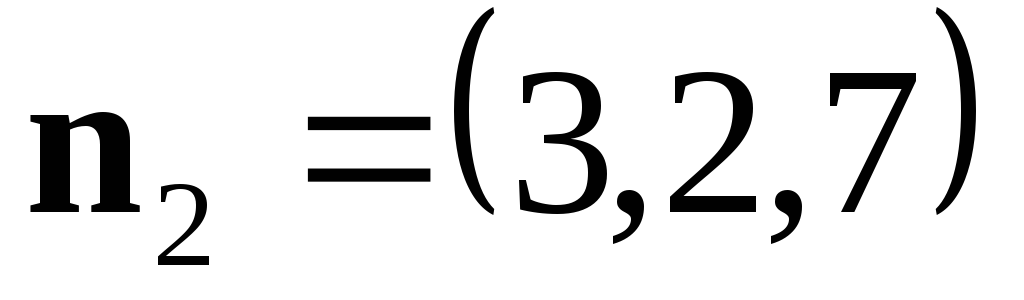 .
Тогда
.
Тогда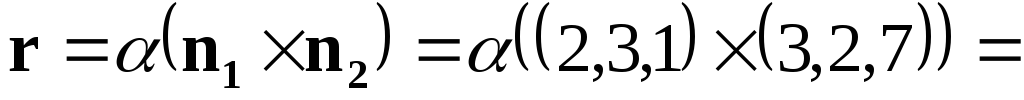
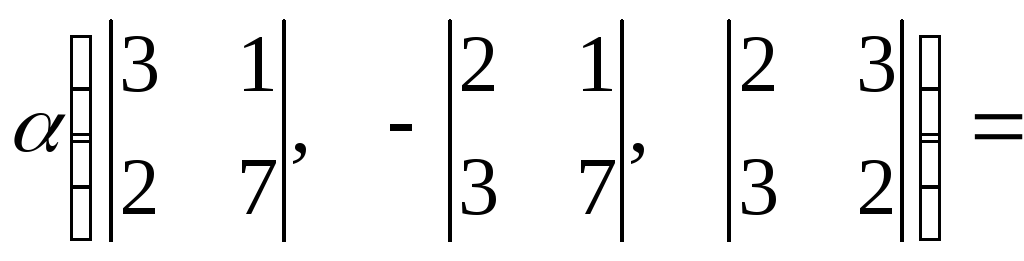
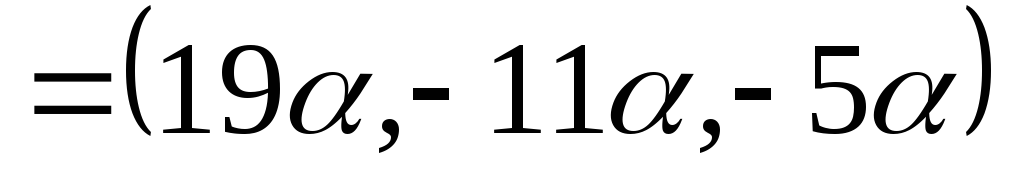 — решение данной системы. ●
— решение данной системы. ●
Векторное произведение векторов — это… Что такое Векторное произведение векторов?
Правые и левые тройки векторов
Три вектора называются упорядоченной тройкой, если указано, какой из этих векторов является первым, какой — вторым, а какой — третьим.
Тройка некомпланарных векторов 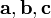 называется правой (левой), если, будучи приведёнными к общему началу, эти векторы располагаются так, как могут быть расположены соответственно большой, несогнутый указательный и средний пальцы правой (левой) руки.
называется правой (левой), если, будучи приведёнными к общему началу, эти векторы располагаются так, как могут быть расположены соответственно большой, несогнутый указательный и средний пальцы правой (левой) руки.
Определение
Векторным произведением вектора 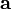 на вектор
на вектор 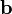 называется вектор
называется вектор 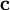 , удовлетворяющий следующим требованиям:
, удовлетворяющий следующим требованиям:
- длина вектора
 равна произведению длин векторов
равна произведению длин векторов  и
и  на синус угла
на синус угла  ; между ними
; между ними
Обозначение:
В различных учебных заведениях определение векторного произведения даётся по-разному. Например, в качестве определения даётся описанное далее выражение векторного произведения в координатах. А далее выводится данное выше определение.
Свойства
Геометрические свойства векторного произведения
Алгебраические свойства векторного произведения
Выражение для векторного произведения в декартовых координатах
Если два вектора 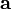 и
и 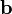 определены своими прямоугольными декартовыми координатами, а говоря точнее — представлены в ортонормированном базисе
определены своими прямоугольными декартовыми координатами, а говоря точнее — представлены в ортонормированном базисе
то их векторное произведение имеет вид
Для запоминания этой формулы удобно использовать определитель:
или
где 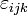 — символ Леви-Чивиты.
— символ Леви-Чивиты.
Обобщения
Кватернионы
Векторное произведение можно также записать в кватернионной форме, поэтому буквы 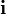 ,
, 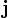 ,
, 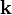 — стандартные обозначения для ортов в
— стандартные обозначения для ортов в 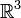 : они рассматриваются как воображаемые кватернионы.
: они рассматриваются как воображаемые кватернионы.
Заметим, что соотношения через векторное произведение между 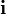 ,
, 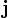 и
и 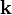 соответствуют правилам умножения для кватернионов i, j и k. Если представить вектор
соответствуют правилам умножения для кватернионов i, j и k. Если представить вектор 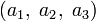 как кватернион a1i + a2j + a3k, то векторное произведение двух векторов получается взятием векторной части от произведения соответствующих им кватернионов. Скалярное произведение этих векторов противоположно скалярной части произведения этих кватернионов.
как кватернион a1i + a2j + a3k, то векторное произведение двух векторов получается взятием векторной части от произведения соответствующих им кватернионов. Скалярное произведение этих векторов противоположно скалярной части произведения этих кватернионов.
Преобразование к матричной форме
Векторное произведение двух векторов можно записать как произведение кососимметрической матрицы и вектора:
где
Пусть 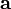 равен векторному произведению:
равен векторному произведению:
тогда
Такая форма записи позволяет обобщить векторное произведение на высшие размерности, представляя псевдовекторы (угловая скорость, индукция и т. п.) как такие кососимметричные матрицы. Ясно, что такие физические величины будут иметь n(n − 1) / 2 независимых компонент в n-мерном пространстве. В трёхмерном пространстве получаются три независимые компоненты, поэтому такие величины можно представлять как векторы этого пространства.
С такой формой записи также зачастую проще работать (например, в en:epipolar geometry).
Из общих свойств векторного произведения следует, что
![[\mathbf{a}]_{\times} \, \mathbf{a} = \mathbf{0}](//rc74.ru/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif) и
и ![\mathbf{a}^{T} \, [\mathbf{a}]_{\times} = \mathbf{0}](//rc74.ru/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif)
а так как ![[\mathbf{a}]_{\times}](/800/600/https/dic.academic.ru/pictures/wiki/files/100/d00b55ad4c7fdd0a1f2a424e0ca572ef.png) кососимметрична, то
кососимметрична, то
В такой форме записи легко доказывается тождество Лагранжа (правило «бац минус цаб»).
Распространение на матрицы
В 3-хмерном случае можно определить векторное произведение матриц и произведение матрицы на вектор. Это делает очевидным указанный выше изоморфизм и позволяет упростить многие выкладки. Представим матрицу A как столбец векторов, тогда
Умножение матрицы на вектор слева определяется аналогично, если представить A как строку векторов. Транспонирование матрицы, соответственно, переводит строку векторов в столбец векторов, и наоборот. Легко обобщить многие соотношения для векторов на соотношения для векторов и матриц, например (A — матрица, 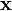 ,
, 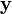 — векторы):
— векторы):
После этого можно изменить форму записи для векторного произведения:
E — единичная матрица. Отсюда очевидны существование и вид матрицы, соответствующей векторному умножению на вектор слева. Аналогично можно получить выражение для матрицы умножения на вектор справа. Распространяя операции над векторами на матрицы покомпонентно, представляя их как «векторы из векторов», стандартные соотношения для векторов легко обобщаются на матрицы. Например, теорема Стокса в 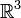 примет вид:
примет вид:
где ротор матрицы A вычисляется как векторное произведение матрицы A на оператор Гамильтона слева. В этих обозначениях очень легко доказать, например, следующие формы теоремы Стокса:
Размерности, не равные трём
Пусть D — размерность пространства.
Векторное произведение, обладающее всеми свойствами обычного трёхмерного векторного произведения, то есть бинарное билинейное антисимметричное невырожденное отображение 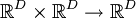 , можно ввести только для размерности 3.
, можно ввести только для размерности 3.
Однако есть простое обобщение на остальные натуральные размерности, начиная с 3, а если нужно — и на размерность 2 (последнее, правда, сравнительно специфическим образом). Тогда это обобщение, в отличие от невозможного, описанного чуть выше, вводится не для пары векторов, а лишь для набора (D − 1) векторов-сомножителей. Вполне аналогично смешанному произведению, естественно обобщаемому в D-мерном пространстве на операцию с D сомножителями. Используя символ Леви-Чивиты 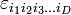 с D индексами, можно явно записать такое (D − 1)-валентное векторное произведение как
с D индексами, можно явно записать такое (D − 1)-валентное векторное произведение как
Такое обобщение дает гиперплощадь размерности (D − 1).
Если нужно ввести операцию именно для двух сомножителей, имеющую геометрический смысл, предельно близкий к смыслу векторного произведения (то есть представляющую ориентированную площадь), то результат уже не будет вектором, так как при D < > 3 не найдется единственной, однозначно определённой нормали к двумерной плоскости, натянутой на множители. Можно ввести бивектор, компоненты которого равны проекциям ориентированной площади параллелограмма, натянутого на пару векторов, на координатные плоскости:
 .
.
Эта конструкция называется внешним произведением.
Для двумерного случая эта операция называется псевдоскалярным произведением, так как получающееся пространство одномерно и результат можно отождествить с псевдоскаляром.
Алгебра Ли векторов
Векторное произведение вводит на 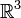 структуру алгебры Ли (поскольку оно удовлетворяет обеим аксиомам — антисимметричности и тождеству Якоби). Эта структура соответствует отождествлению
структуру алгебры Ли (поскольку оно удовлетворяет обеим аксиомам — антисимметричности и тождеству Якоби). Эта структура соответствует отождествлению 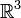 с касательной алгеброй Ли so(3) к группе Ли SO(3) ортогональных линейных преобразований трёхмерного пространства.
с касательной алгеброй Ли so(3) к группе Ли SO(3) ортогональных линейных преобразований трёхмерного пространства.
См. также
Произведения векторов
Другое
Ссылки
Литература
- Кочин Н. Е. Введение в векторный и тензорный анализ.
Wikimedia Foundation. 2010.


 перпендикулярен к плоскости, в которой
лежат вектора
перпендикулярен к плоскости, в которой
лежат вектора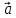 и
и
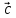 направлен так, что поворот от вектора
направлен так, что поворот от вектора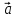 к вектору
к вектору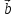 осуществляется против часовой стрелки,
если смотреть из конца вектора
осуществляется против часовой стрелки,
если смотреть из конца вектора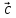 (тройка векторов
(тройка векторов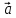 ,
,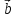
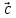 – правая).
– правая).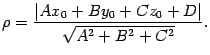
 были
компланарны, необходимо и достаточно,
чтобы их смешанное произведение было
равно нулю, т.е.
были
компланарны, необходимо и достаточно,
чтобы их смешанное произведение было
равно нулю, т.е.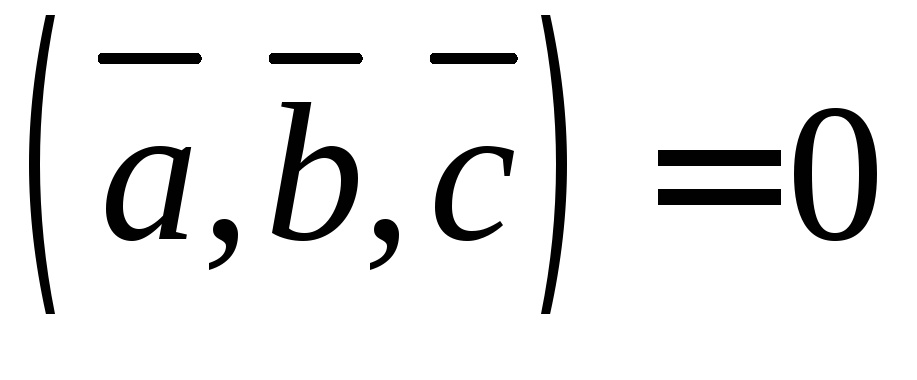 .
Докажем эту теорему.
.
Докажем эту теорему.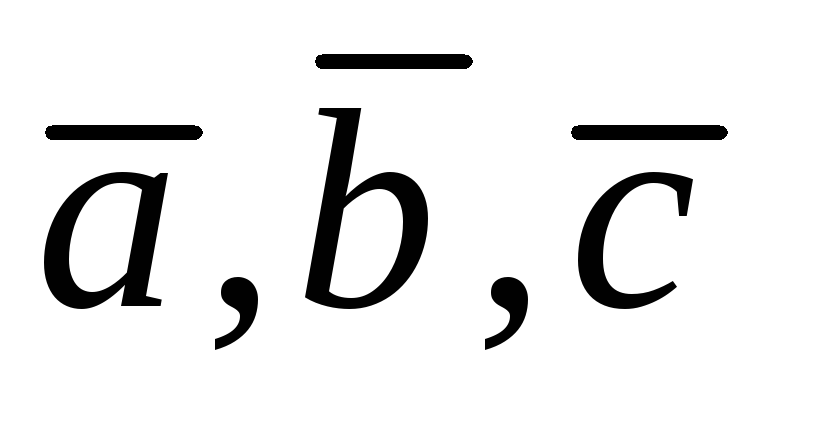
 компланарны,
компланарны,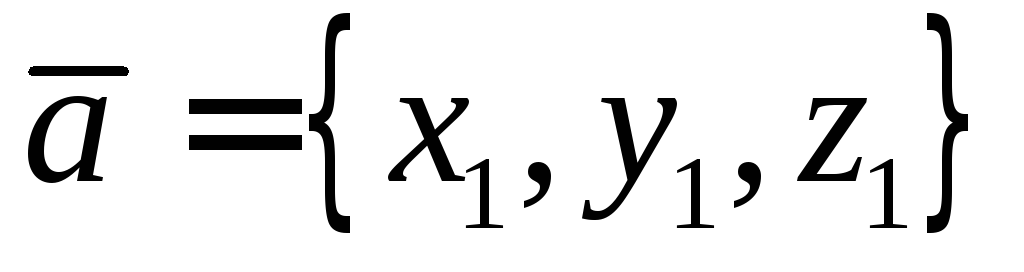 ,
,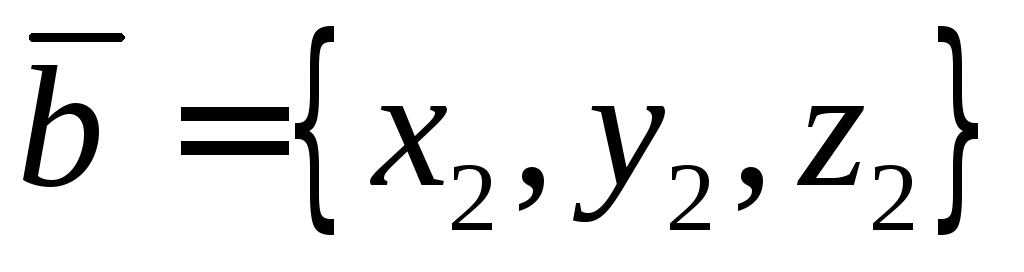 ,
,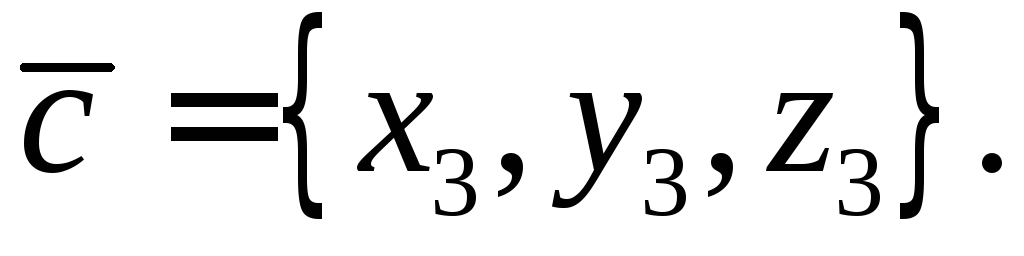
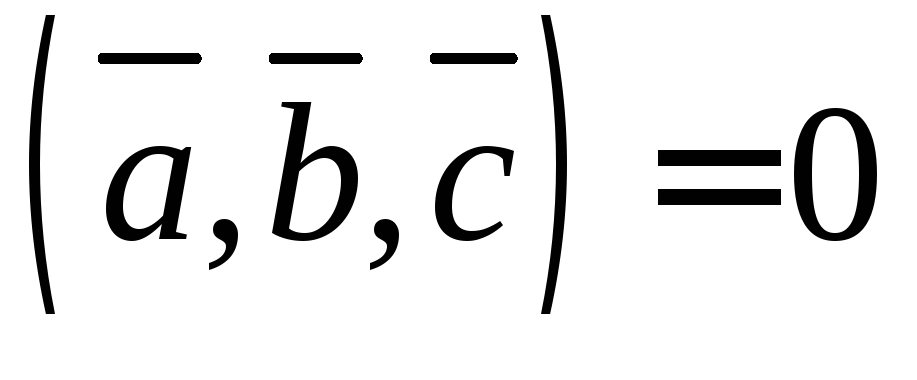 .
.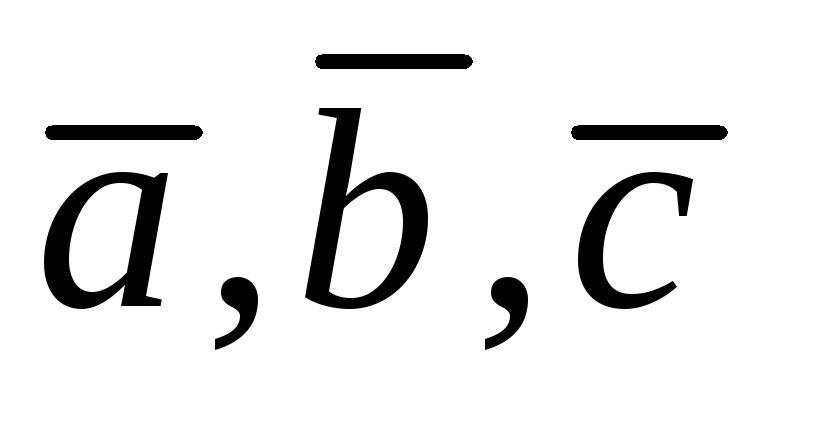 лежат в одной плоскости, тогда один
из векторов, например,
лежат в одной плоскости, тогда один
из векторов, например, линейно выражается через векоры
линейно выражается через векоры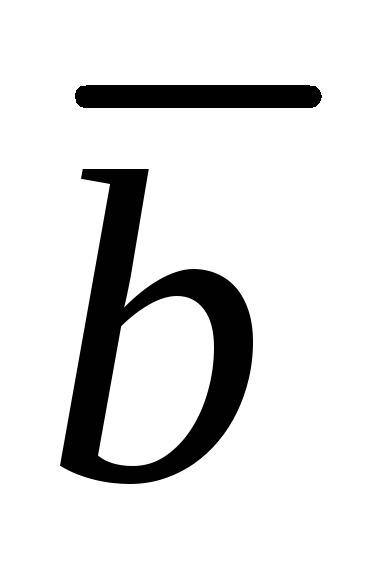 и
и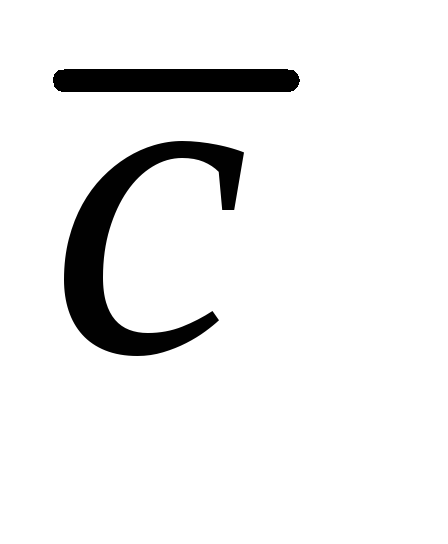 ,
т.е.
,
т.е.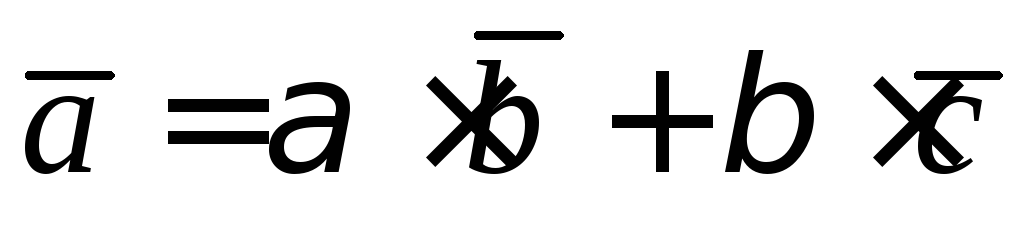 .
Тогда в определителе из координат
векторов строки линейно зависимы.
Следовательно, определитель равен
нулю. Это означает, что
.
Тогда в определителе из координат
векторов строки линейно зависимы.
Следовательно, определитель равен
нулю. Это означает, что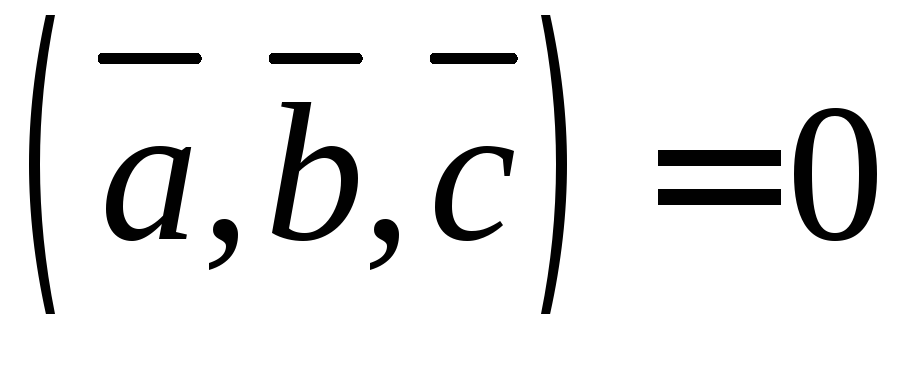 ,
ч.т.д.
,
ч.т.д. .
.
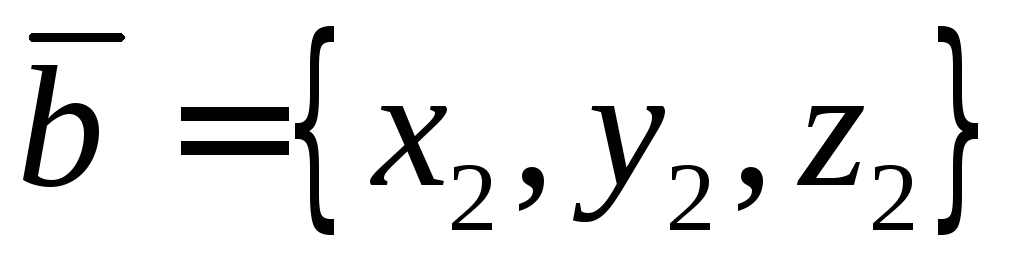
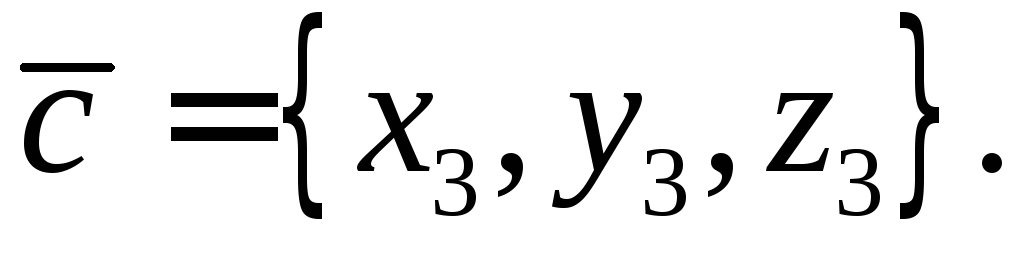

 копланарны.
копланарны.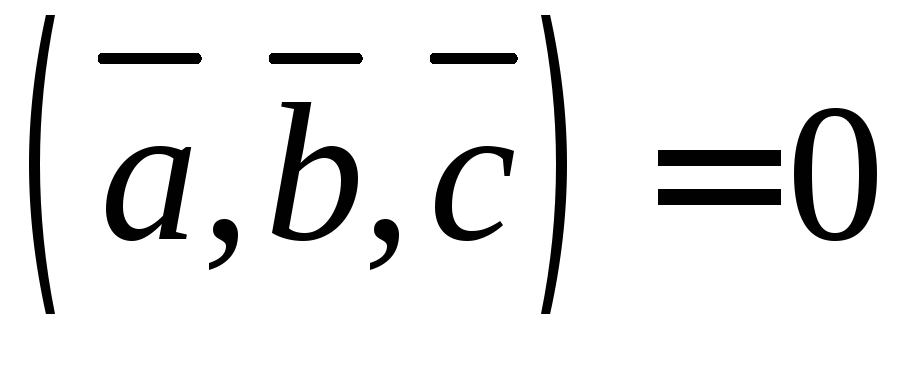 ,
то определитель из координат векторов
равен нулю
,
то определитель из координат векторов
равен нулю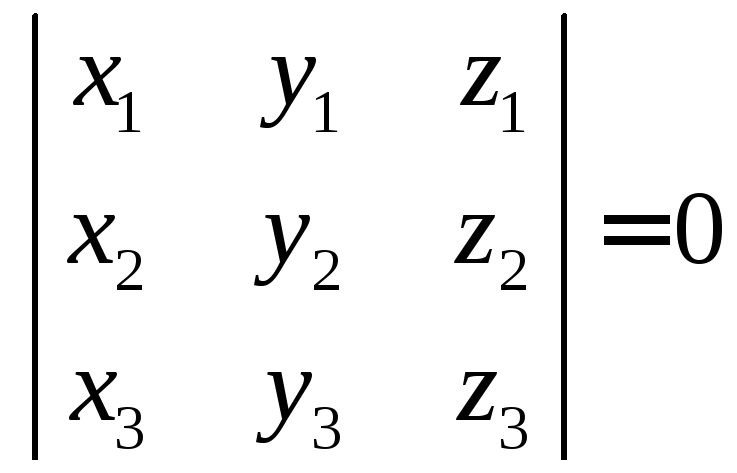 .
Из этого следует, что строки определителя
линейно зависимы. Тогда векторы так
же линейно зависимы, например,
.
Из этого следует, что строки определителя
линейно зависимы. Тогда векторы так
же линейно зависимы, например,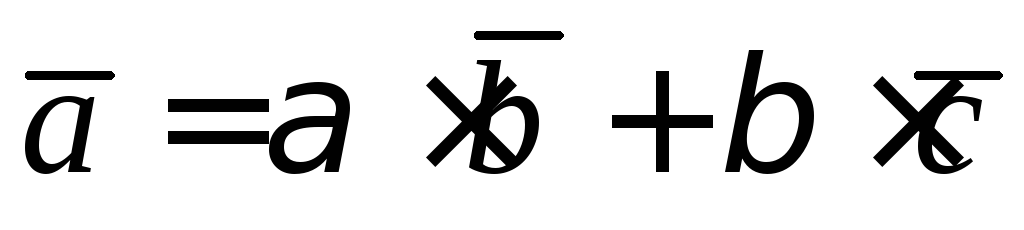 .
Это возможно, лишь в случае, когда
векторы
.
Это возможно, лишь в случае, когда
векторы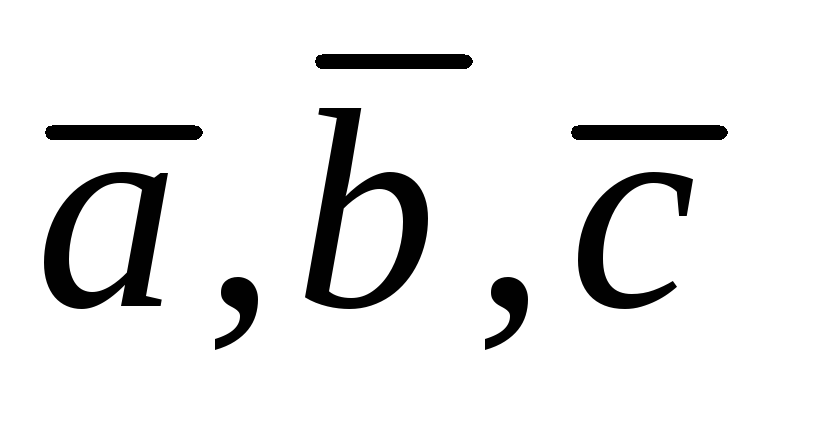 лежат
в одной плоскости, т.е. компланарны,
ч.т.д.
лежат
в одной плоскости, т.е. компланарны,
ч.т.д.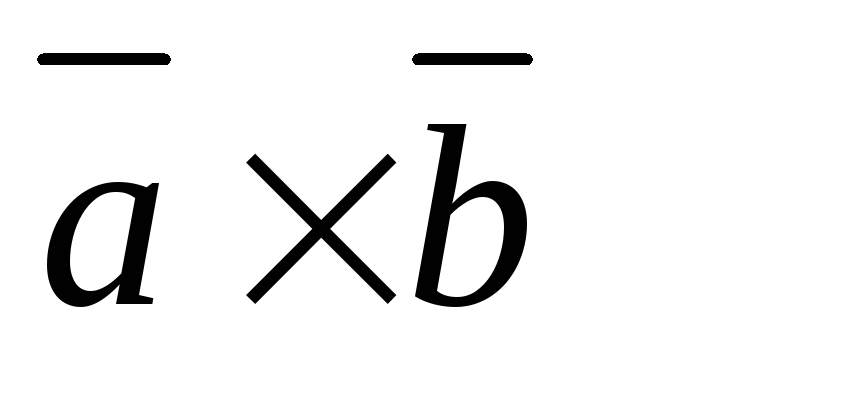 равен
равен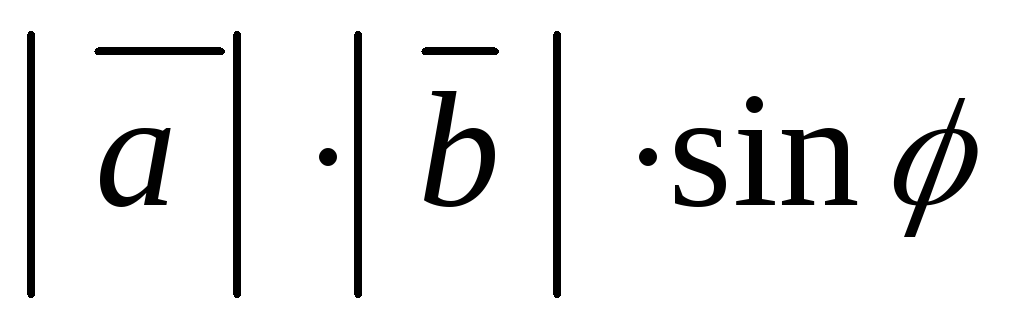 ,
где
,
где — угол между векторами
— угол между векторами и
и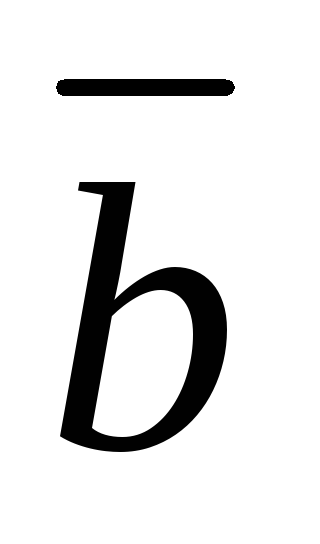 ,
т.е.
,
т.е.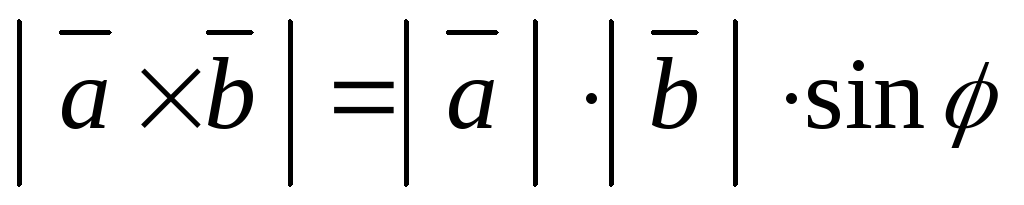 ;
;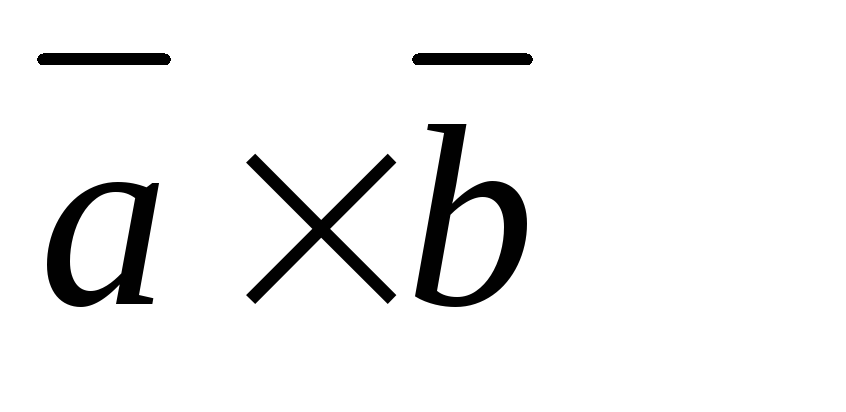 перпендикулярен
к каждому из векторов
перпендикулярен
к каждому из векторов и
и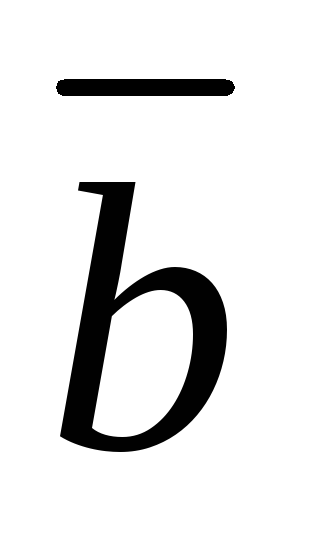 ;
;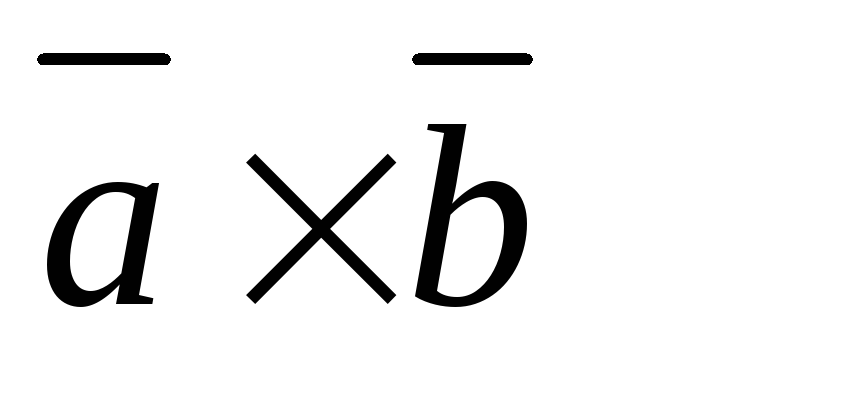 таково,
что упорядоченная тройка векторов
таково,
что упорядоченная тройка векторов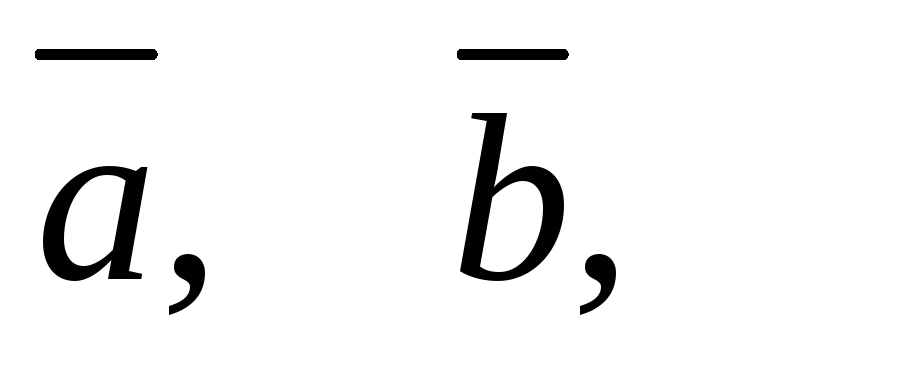
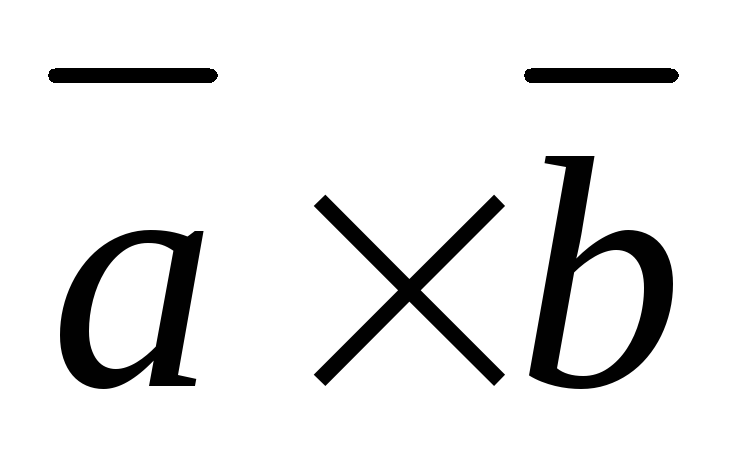 является правой (т.е. если «смотреть»
с конца вектора
является правой (т.е. если «смотреть»
с конца вектора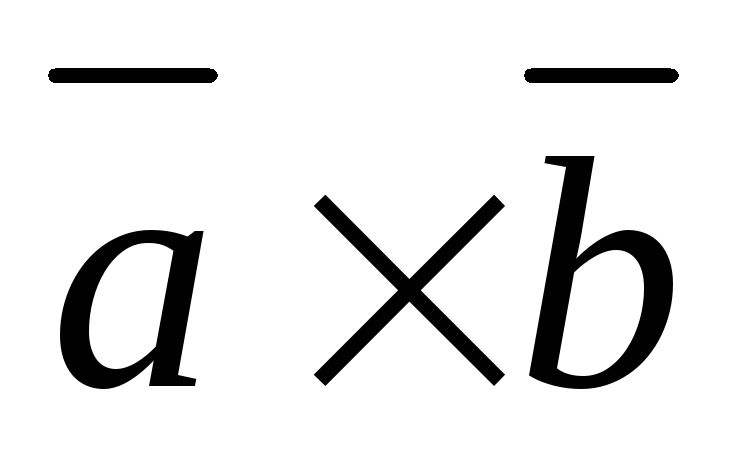 ,
то вращение от
,
то вращение от к
к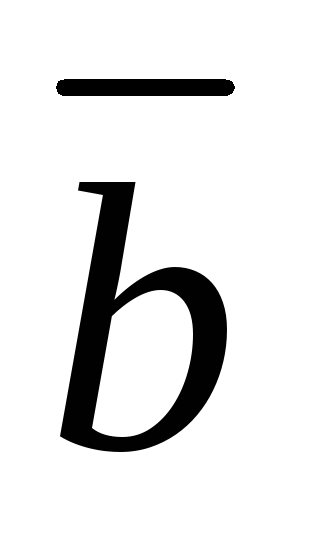 по кратчайшему пути совершается против
движения часовой стрелки).
по кратчайшему пути совершается против
движения часовой стрелки). и
и коллинеарны, то
коллинеарны, то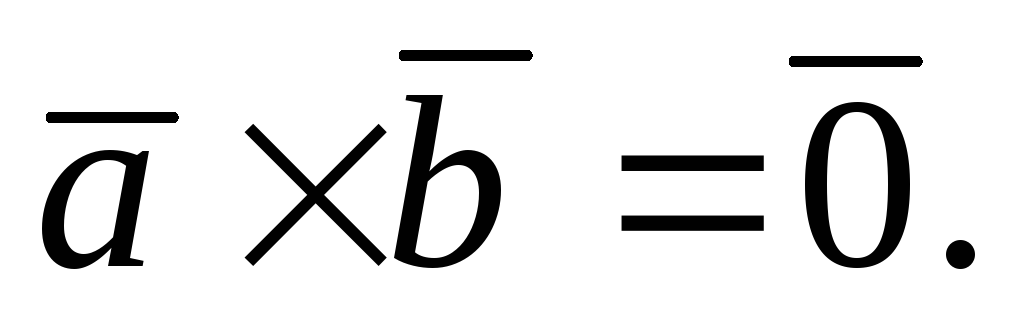
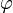 ; между ними
; между ними
![\mathbf c = \left[ \mathbf a \mathbf b \right] = \left[ \mathbf a,\; \mathbf b \right] = \mathbf a \times \mathbf b](/800/600/https/dic.academic.ru/pictures/wiki/files/101/ed09d9154faf68b1a7783004b4cbc46c.png)
![[ \mathbf a,\; \mathbf b ] = S\, \mathbf e](/800/600/https/dic.academic.ru/pictures/wiki/files/50/28395f1def81662c027a8cbd7f6f8aa9.png)
![\left[ \mathbf a,\; \mathbf c \right] = \mathrm{Pr}_{ \mathbf e }\, \mathbf a \left](/800/600/https/dic.academic.ru/pictures/wiki/files/48/04002beabcb294e180266aa94180d9b9.png)
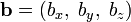
![[ \mathbf a,\; \mathbf b ] = (a_y b_z - a_z b_y,\; a_z b_x - a_x b_z,\; a_x b_y - a_y b_x).](/800/600/https/dic.academic.ru/pictures/wiki/files/52/4c3df91a2cfe53408b07f333a175565a.png)
![[ \mathbf a,\; \mathbf b ] = \begin{vmatrix} \mathbf i &amp; \mathbf j &amp; \mathbf k \\ a_x &amp; a_y &amp; a_z \\ b_x &amp; b_y &amp; b_z \end{vmatrix}](/800/600/https/dic.academic.ru/pictures/wiki/files/49/16ea255c911b3e4c07cc2adae3d7626e.png)
![[ \mathbf a,\; \mathbf b ]_i = \sum_{j,k=1}^3 \varepsilon_{i j k} a_j b_k,](/800/600/https/dic.academic.ru/pictures/wiki/files/55/7c8e6ab7e9c7e3607e920bb75caae299.png)
![\mathbf{a} \times \mathbf{b} = [\mathbf{a}]_{\times} \mathbf{b} = \begin{bmatrix}\,0&amp;\!-a_3&amp;\,\,a_2\\ \,\,a_3&amp;0&amp;\!-a_1\\-a_2&amp;\,\,a_1&amp;\,0\end{bmatrix}\begin{bmatrix}b_1\\b_2\\b_3\end{bmatrix}](/800/600/https/dic.academic.ru/pictures/wiki/files/98/bb0828317b64e54d924e3d9dabb54234.png)
![\mathbf{b} \times \mathbf{a} = \mathbf{b}^T [\mathbf{a}]_{\times} = \begin{bmatrix}b_1&amp;b_2&amp;b_3\end{bmatrix}\begin{bmatrix}\,0&amp;\!-a_3&amp;\,\,\,a_2\\\,\,\,a_3&amp;\,0&amp;\!-a_1\\-a_2&amp;\,\,a_1&amp;\,0\end{bmatrix}](/800/600/https/dic.academic.ru/pictures/wiki/files/97/a1999aed4c7add8bb1d9f291beb9a7e9.png)
![[\mathbf{a}]_{\times} \stackrel{\rm def}{=} \begin{bmatrix}\,\,0&amp;\!-a_3&amp;\,\,\,a_2\\\,\,\,a_3&amp;0&amp;\!-a_1\\\!-a_2&amp;\,\,a_1&amp;\,\,0\end{bmatrix}](/800/600/https/dic.academic.ru/pictures/wiki/files/52/42367ea2bfc38aaf3870e9a3aba428bb.png)
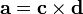
![[\mathbf{a}]_{\times} = (\mathbf{c}\mathbf{d}^T)^T - \mathbf{c}\mathbf{d}^T.](/800/600/https/dic.academic.ru/pictures/wiki/files/53/55d46afc14c256de89aa56b17ef38491.png)
![[\mathbf{a}]_{\times} \, \mathbf{a} = \mathbf{0}](/800/600/https/dic.academic.ru/pictures/wiki/files/98/b00e919750be3b08a60e4757f3cf9cf9.png) и
и ![\mathbf{a}^{T} \, [\mathbf{a}]_{\times} = \mathbf{0}](/800/600/https/dic.academic.ru/pictures/wiki/files/55/762d1d364c16664eff7d042f99842e70.png)
![\mathbf{b}^{T} \, [\mathbf{a}]_{\times} \, \mathbf{b} = 0.](/800/600/https/dic.academic.ru/pictures/wiki/files/98/b0e7a57333b3ebbdf3c81c827152e5fa.png)
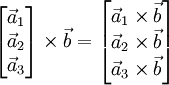
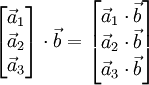
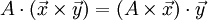
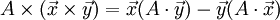
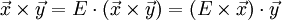
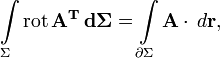
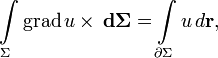
![\int\limits_{\Sigma} \left[ \mathbf{d\Sigma}; \left[ \nabla; \vec a \right] \right] = \int\limits_{\partial\Sigma} \vec a \times d \mathbf{r}.](/800/600/https/dic.academic.ru/pictures/wiki/files/53/552f7432c2a90d787f641f23287017c2.png)
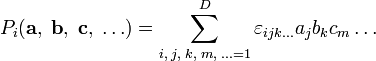
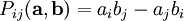 .
.