Применение двоичной системы счисления | Образовательная социальная сеть
Министерство образования и науки
Новые применения двоичной системы счисления
Выполнила:
ученица 8 класса
школы №111
Бубнова Елизавета
Руководитель:
Иванова Ю.Н.
учитель математики
Барнаул — 2013
Содержание
- Введение……………………………………………………………………….3
- Понятие систем счисления……………………………………………………4
- Двоичная система счисления……………………………………………..….7
- Применение двоичной системы счисления……………………………..…..8
- Заключение…………………………………………………………………..12
- Список литературы………………………………………………………….13
Введение
Тема «Системы счисления» имеет прямое отношение к математической теории чисел. Однако в школьном курсе математике она, как правила, не изучается. Необходимость изучения этой темы в курсе информатики связана с тем фактом, что числа в памяти компьютера представлены в двоичной системе счисления, а для внешнего представления содержимого памяти, адресов памяти используют шестнадцатеричную или восьмеричную систему счисления. Являясь смежной с математикой, данная тема вносит вклад в фундаментальной математическое школьное образование. Различные системы счисления используются всегда, когда появляется потребность в числовых расчётах, начиная с вычислений младшеклассника, выполняемых карандашом на бумаге, кончая вычислениями, выполняемыми на суперкомпьютерах. В работе изложена и занимательно описана одна из наиболее популярных систем счисления — двоичная, а также ее применения, как старые, так и новые, как забавные, так и серьёзные. Объект исследования – системы счисления. Главное достоинство двоичной системы — простота алгоритмов сложения, вычитания умножения и деления. Изучение двоичной системы счисления, которая используется в компьютерах, важно для понимания того, каким образом производится обработка числовых данных в ЭВМ. Поэтому данная тема является актуальной.
Являясь смежной с математикой, данная тема вносит вклад в фундаментальной математическое школьное образование. Различные системы счисления используются всегда, когда появляется потребность в числовых расчётах, начиная с вычислений младшеклассника, выполняемых карандашом на бумаге, кончая вычислениями, выполняемыми на суперкомпьютерах. В работе изложена и занимательно описана одна из наиболее популярных систем счисления — двоичная, а также ее применения, как старые, так и новые, как забавные, так и серьёзные. Объект исследования – системы счисления. Главное достоинство двоичной системы — простота алгоритмов сложения, вычитания умножения и деления. Изучение двоичной системы счисления, которая используется в компьютерах, важно для понимания того, каким образом производится обработка числовых данных в ЭВМ. Поэтому данная тема является актуальной.
Предметом исследования является двоичная система счисления.
Целью исследования является – рассмотрение применений двоичной системы счисления в жизни.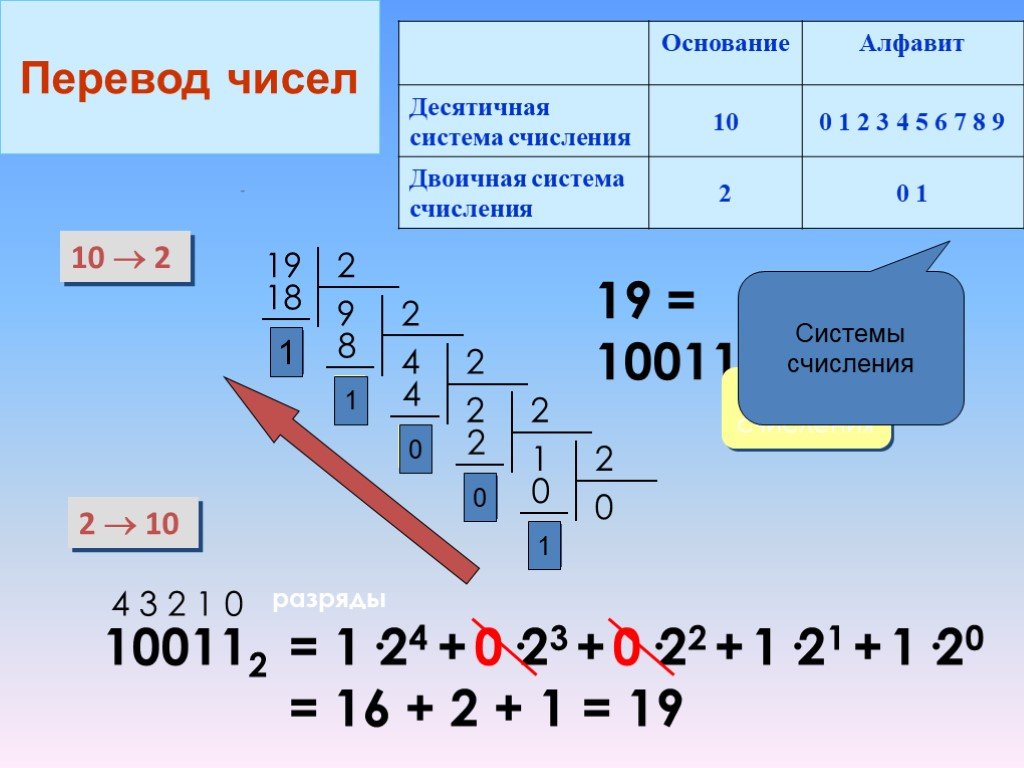
Задачи исследования:
- Рассмотреть понятие систем счисления и их виды
- Изучить двоичную систему счисления, выделить ее достоинства;
- Рассмотреть применение двоичной системы счисления в жизни человека и в компьютерной технике.
Методы исследования:
- Анализ и синтез;
- Сравнение.
Понятие систем счисления
Понятие «число» является ключевым как для математики, так и для информатики. Люди всегда считали и записывали числа, даже 5 тысяч лет назад. Но записывали их по другим правилам, хотя в любом случае число изображалось с помощью любого или нескольких символов, которые назывались цифрами.
Язык чисел, как и любой другой, имеет свой алфавит. В том языке чисел, которым мы обычно пользуемся, алфавитом служат десять цифр – от 0 до 9. Это десятичная система счисления.
Системой счисления мы будем называть способ представления числа символами некоторого алфавита, которые называют цифрами.
Системы счисления делятся на различные группы:
— Анатомического происхождения: десятеричная, пятеричная, двенадцатеричная, двадцатеричная.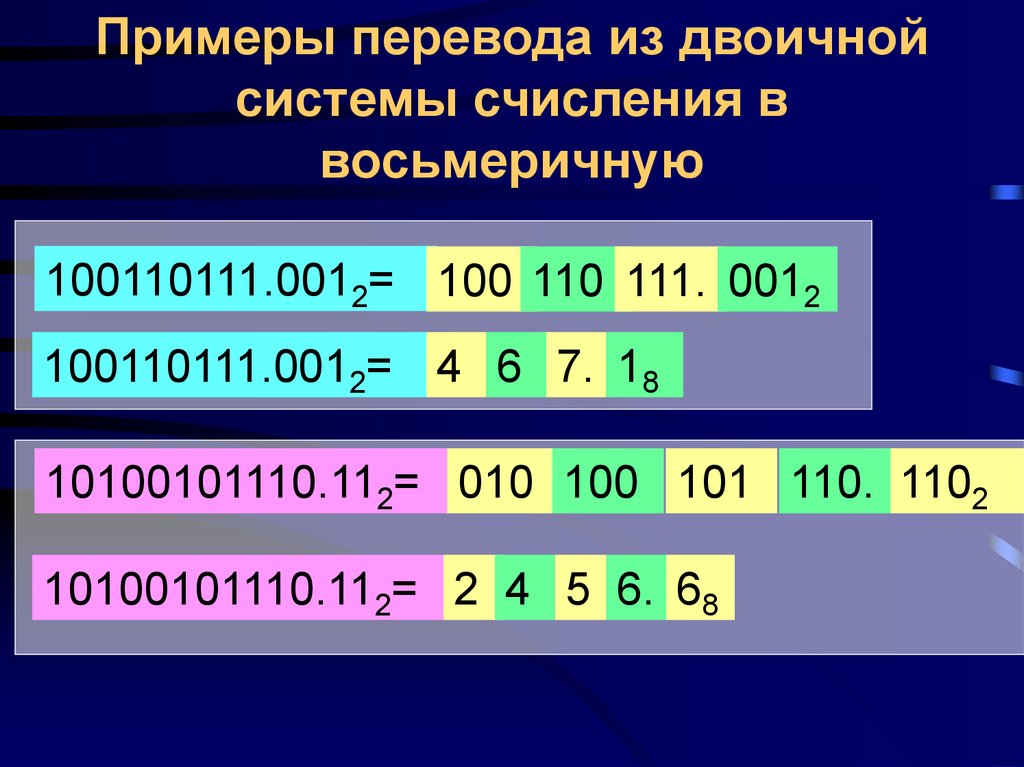
— Алфавитные: древнеармянская, древнегрузинская, древнегреческая, ионическая, славянская.
— Машинные: двоичная, восьмеричная, шестнадцатеричная.
— Прочие: Римская, Вавилонская, Египетская нумерация, Китайская нумерация и другие.
Также различают позиционные и непозиционные системы счисления.
Непозиционные системы счисления. В непозиционных системах счисления значение числа определяется как сумма или разность цифр в числе. В непозиционных системах счисления считать трудно. Древние греки построили геометрию, которую сегодня изучают в школе, доказали важные теоремы теории чисел, но считать они не умели.
Примеры непозиционных систем счисления:
1. У многих народов использовалась система, алфавит которой состоял из одного символа – палочки. Для изображения какого-то числа в этой системе нужно записать определенное множество палочек, равное данному числу: ||||| – число пять.
2. Египтяне применяли для записи чисел иероглифы.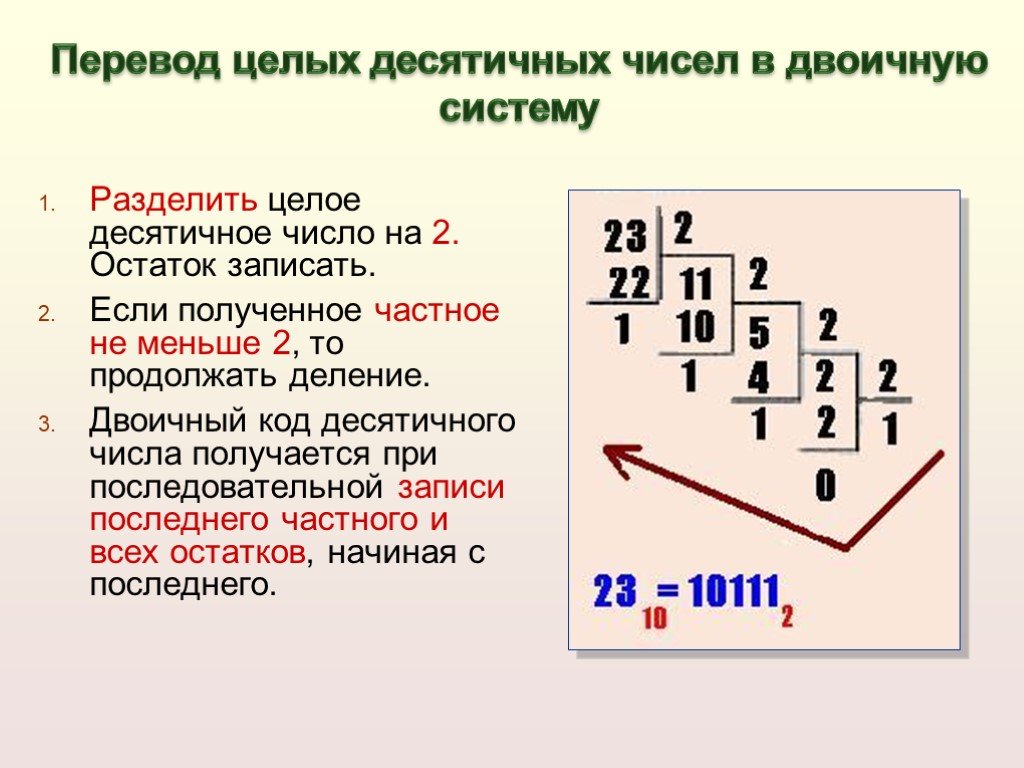 Единицу обозначали одной вертикальной чертой, а для обозначения чисел, меньших 10, нужно было поставить соответствующее число вертикальных штрихов. Если штрихов нужно изобразить несколько, то их объединяли в группы из трех или четырех черт и изображали в несколько рядов, причем в нижнем должно быть столько же штрихов сколько и в верхнем, или на одну больше.
Единицу обозначали одной вертикальной чертой, а для обозначения чисел, меньших 10, нужно было поставить соответствующее число вертикальных штрихов. Если штрихов нужно изобразить несколько, то их объединяли в группы из трех или четырех черт и изображали в несколько рядов, причем в нижнем должно быть столько же штрихов сколько и в верхнем, или на одну больше.
Для обозначения числа 10, основания системы, египтяне вместо десяти вертикальных черт ввели новый коллективный символ, напоминающий по своим очертаниям подкову или крокетную дужку.
Если нужно изобразить несколько десятков, то иероглиф повторяли нужное количество раз. Тоже самое относится и к остальным иероглифам.
Множество из десяти подковообразных символов, т.е. число 100, они заменили другим новым символом, напоминающим силки; десять силков, т.е. число 1 000, египтяне обозначили стилизованным изображением лотоса. Продолжая в том же духе, египтяне обозначили десять лотосов согнутым пальцем, десять согнутых пальцев – волнистой линией и десять волнистых линий – фигуркой удивленного человека. В итоге древние египтяне могли представлять числа до миллиона.
В итоге древние египтяне могли представлять числа до миллиона.
10 | 100 | 1 000 | 10 000 | 100 000 | 1 000 000 | 10 000 000 |
Рис 3. Египетская система счисления
Самым распространенным примером непозиционной системы счисления является римская система счисления
Рис 4. Римская система счисления
Позиционные системы счисления. Позиционной называется такая система счисления, в которой величина, обозначаемая цифрой в записи числа, зависит от ее позиции.
Французский математик Пьер Симон Лаплас (1749— 1827) такими словами оценил «открытие» позиционной системы счисления: «Мысль выражать все числа немногими знаками, придавая им, кроме значения но форме, еще значение по месту, настолько проста, что именно из-за этой простоты трудно оценить, насколько она удивительна».
Первая известная нам система, основанная на позиционном принципе – шестидесятeричная вавилонская. Например, число 59 в данной системе записывается следующим образом:
, т.е. 59 = 5 · 10 + 9.
Запись чисел в позиционных системах счисления осуществляется следующим образом: множество цифр, используемых для записи чисел в позиционных системах счисления, образует алфавит. Количество используемых цифр называется основанием системы счисления. Место каждой цифры в числе – позиция. Сущность позиционного представления чисел отражается в развернутой форме записи числа.
Основание (n) | Название | Алфавит |
n=2 | двоичная | 0, 1 |
n=3 | троичная | 0, 1, 2 |
n=5 | пятеричная | 0, 1, 2, 3, 4 |
n=8 | восьмеричная | 0, 1, 2, 3, 4, 5, 6, 7 |
n=10 | десятичная | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
n=16 | шестнадцатеричная | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F |
Основные достоинства любой позиционной системы счисления – простота выполнения арифметических операций и ограниченное количество символов, необходимых для записи любого числа.
Двоичная система счисления
Двоичная система счисления — система счисления, построенная на позиционном принципе записи чисел, с использованием только двух знаков — цифр 0 и 1. Главное достоинство двоичной системы — простота алгоритмов сложения, вычитания умножения и деления. Таблица умножения в ней совсем не требует ничего запоминать: ведь любое число, умноженное на нуль равно нулю, а умноженное на единицу равно самому себе. И при этом никаких переносов в следующие разряды, а они есть даже в троичной системе. Таблица деления сводится к двум равенствам 0/1 = 0, 1/1 = 1, благодаря чему деление столбиком многозначных двоичных чисел делается гораздо проще, чем в десятичной системе, и по существу сводится к многократному вычитанию.
Таблица сложения, как ни странно, чуть сложнее, потому что 1+1 = 10 и возникает перенос в следующий разряд. В общем виде операцию сложения однобитовых чисел можно записать в виде x+y = 2w+v, где w, v — биты результата. Внимательно посмотрев на таблицу сложения, можно заметить, что бит переноса w — это просто произведение xy, потому что он равен единице лишь когда x и y равны единице. А вот бит v равен x+y, за исключением случая x = y = 1, когда он равен не 2, а 0. Операцию, с помощью которой по битам x, y вычисляют бит v, называют по-разному. Мы будем использовать для неё название «сложение по модулю 2» и символ . Таким образом, сложение битов выполняется фактически не одной, а двумя операциями.
А вот бит v равен x+y, за исключением случая x = y = 1, когда он равен не 2, а 0. Операцию, с помощью которой по битам x, y вычисляют бит v, называют по-разному. Мы будем использовать для неё название «сложение по модулю 2» и символ . Таким образом, сложение битов выполняется фактически не одной, а двумя операциями.
Если отвлечься от технических деталей, то именно с помощью этих операций и выполняются все операции в компьютере.
Для выполнения сложения однобитовых чисел делают обычно даже специальный логический элемент с двумя входами x, y и двумя выходами w, v, как бы составленный из элемента умножения (его часто называют конъюнкцией, чтобы не путать с умножением многозначных чисел) и элемента сложения по модулю 2. Этот элемент часто называют полусумматором.
Применения двоичной системы счисления
1. «Книга перемен»
Двоичная система по существу была известна в Древнем Китае. В классической книге «И цзин» («Книга перемен») приведены так называемые «гексаграммы Фу-си», первая из которых имеет вид , а последняя (64-я) – вид , причем они расположены по кругу и занумерованы в точном соответствии с двоичной системой (нулями и единицами соответствуют сплошные и прерывистые линии). Китайцы не поленились придумать для этих диаграмм специальные иероглифы и названия (например, первая из них называлась «кунь», а последняя – «цянь», сплошной линии сопоставляется мужское начало янь, а прерывистой линии – женское начало инь).
Китайцы не поленились придумать для этих диаграмм специальные иероглифы и названия (например, первая из них называлась «кунь», а последняя – «цянь», сплошной линии сопоставляется мужское начало янь, а прерывистой линии – женское начало инь).
Каждая гексаграмма состоит из двух триграмм (верхней и нижней), им тоже соответствуют определенные иероглифы и названия. Например, триграмме из трех сплошных линий сопоставлен образ-атрибут «небо, творчество», а триграмме из трех прерывистых линий сопоставлен образ-атрибут «земля, податливость, восприимчивость».
2. Азбука Морзе
Сэмюель Морзе – изобретатель азбуки, но его самое главное достижение – изобретение телеграфа (а азбука Морзе понадобилась ему для использования телеграфа). Точка и тире оказались самыми элементарными символами, которые мог передавать его телеграф. Они соответствовали коротким и длинным импульсам электрического тока, передаваемым по телеграфным проводам. Длина импульса определялась нажатием руки телеграфиста на ключ телеграфа. Прием сигнала осуществляло реле, которое после появления в нем импульса тока включало электромагнит, который либо заставлял стучать молоточек, либо прижимал колесико с красящей лентой к бумажной ленте, на которой отпечатывались либо точка, либо тире в зависимости от длины импульса.
Прием сигнала осуществляло реле, которое после появления в нем импульса тока включало электромагнит, который либо заставлял стучать молоточек, либо прижимал колесико с красящей лентой к бумажной ленте, на которой отпечатывались либо точка, либо тире в зависимости от длины импульса.
Азбука Морзе сопоставляет каждой букве алфавита последовательность из точек и тире. Естественней всего использовать такие последовательности длины 6, их всего 64 и хватит даже на русский алфавит. Но Морзе понимал, что длину сообщения желательно уменьшить, насколько возможно, поэтому он решил использовать последовательности длины не более 4, их всего 2 + 4 + 8 + 16 = 30. в русском алфавите пришлось не использовать буквы «э» и «ё» и отождествить мягкий и твердый знаки. Кроме того, наиболее часто используемых буквами он предложил давать самые короткие коды, чтобы уменьшить среднюю длину передаваемого сообщения.
3. Штрих-коды
Примером применения двоичного кодирования в современной технике служат штрих-коды. В супермаркетах на упаковках товаров можно увидеть штрих-код. Для чего он нужен, и как его прочитать?
В супермаркетах на упаковках товаров можно увидеть штрих-код. Для чего он нужен, и как его прочитать?
Нужен он только для автоматического занесения информации в кассовый аппарат. Сам штрих-код состоит из тридцати черных полос переменой толщины, разделенной промежутками тоже переменой толщины. Толщина полос может принимать четыре значения – от самой тонкой до самой толстой. Такую же толщину могут иметь и промежутки. Когда по сканеру проводят штрих-кодом, он воспринимает каждую черную полоску как последовательность единиц длины от одной до четырех и также воспринимает промежутки между полосами, но при этом вместо единиц сканер видит нули. Полностью весь штрих-код сканер воспринимает как последовательность из 95 цифр 0 или 1 (их давно уже принято называть битами). Что же содержит этот код? Он кодирует 13-разрядное десятичное число, совершенно открыто написанное под самим штрих-кодом. Если сканер не смог распознать штрих-код, то это число кассир вводит в аппарат вручную. Штрих-код нужен лишь для облегчения распознавания сканером изображения. Распознавать цифры, к тому же повернутые боком, может только сложная программа распознавания на универсальном компьютере, да и то не очень надежно, а не кассовый аппарат.
Распознавать цифры, к тому же повернутые боком, может только сложная программа распознавания на универсальном компьютере, да и то не очень надежно, а не кассовый аппарат.
Рис 5. Расшифровка штрих-кода
Какую же информацию содержит это 13-значное число? Этот вопрос к математике никакого отношения не имеет. Первые две цифры задают страну – производителя товара. Следующие пять цифр – это код производитель, а следующие пять цифр – код самого продукта в принятой этим производителем кодировке. Последняя цифра – это код проверки. Он однозначно вычисляется по предыдущим 12 цифрам, следующим образом. Нужно сложить все цифры с нечетными номерами, утроить сумму, к ней прибавить сумму оставшихся цифр, а полученный результат вычесть из ближайшего кратного 10 числа.
4. Компьютерная техника и информационные технологии
Столь привычная для нас десятичная система оказалась неудобной для ЭВМ. Если в механических вычислительных устройствах, использующих десятичную систему, достаточно просто применить элемент с множеством состояний (колесо с девятью зубьями), то в электронных машинах надо было бы иметь 10 различных потенциалов в цепях. Наиболее просто реализуется элементы с двумя состояниями — триггеры. Поэтому естественным был переход на двоичную систему. В этой системе всего две цифры — 0 и 1 . Каждая цифра называется двоичной (от английского binary digit — двоичная цифра). Сокращение от этого выражения привело к появлению термина бит, ставшего названием разряда двоичного числа.
Наиболее просто реализуется элементы с двумя состояниями — триггеры. Поэтому естественным был переход на двоичную систему. В этой системе всего две цифры — 0 и 1 . Каждая цифра называется двоичной (от английского binary digit — двоичная цифра). Сокращение от этого выражения привело к появлению термина бит, ставшего названием разряда двоичного числа.
Бит — это минимальная единица измерения информации (0 mini). За битом следует байт, состоящий из восьми бит, затем килобайт (кбайт) — 1024 байта, мегабайт (мбайт) — 1024 кбайта, гигобайт (гбайт) — 1024мбайт.
В компьютере для представления информации используется двоичное кодирование, так как удалось создать надежные работающие технические устройства, которые могут со стопроцентной надежностью сохранять и распознавать не более двух различных состояний (цифр). Все виды информации в компьютере кодируются на машинном языке, в виде логических последовательностей нулей и единиц.
Целые числа в компьютере хранятся в ячейках памяти, в этом случае каждому разряду ячейки памяти соответствует всегда один и тот же разряд числа.
Для хранения целых неотрицательных чисел отводится одна ячейка памяти, состоящая из восьми бит.
Например, число 1910 будет выглядеть:
0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
Для хранения целых чисел со знаком (отрицательных) отводиться две ячейки памяти (16 битов), причем старший (левый) разряд отводиться под знак числа (если число положительное, то в знаковый разряд записывается 0, если отрицательное — 1).
Например, число -9810 будет выглядеть:
1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 |
Начиная с конца 60-х годов, компьютеры все больше использовать для обработки текстовой информации и в настоящее время большая часть компьютеров в мире занято именно обработкой текстовой информации.
Традиционно для кодирования одного символа используется количество информации равное 1 байту, то есть 8 бит. Если рассматривать символы как возможные события, то получаем, что количество различных символов, которые можно закодировать, будет равно 256. Такое количество символов вполне достаточно для представления текстовой информации, включая прописные и строчные буквы русского и латинского алфавитов, а так же цифры, знаки препинания и математических операций, графические символы и так далее. Но способов построения таких кодов очень много, рассмотрим один из них:
Алфавитное неравномерное двоичное кодирование
При алфавитном способе двоичного кодирования символы некоторого первичного алфавита (например, русского) кодируются комбинациями символов двоичного алфавита (т.е. 0 и 1), причем, длина кодов и, соответственно, длительность передачи отдельного кода, могут различаться. Оптимизировать кодирование можно за счет суммарной длительности сообщения. Суммарная длительность сообщения будет меньше, если применить следующий подход: чем буква первичного алфавита, встречается чаще, то присваиваем ей более короткой по длине код. Следовательно, коды букв, вероятность появления которых в сообщении выше, следует строить из возможно меньшего числа элементарных сигналов.
Следовательно, коды букв, вероятность появления которых в сообщении выше, следует строить из возможно меньшего числа элементарных сигналов.
Возможны различные варианты двоичного кодирования, при этом важно, чтобы закодированное сообщение могло быть однозначно декодировано, т.е. чтобы в последовательности 0 и 1, которая представляет собой многобуквенное кодированное сообщение, всегда можно было бы различить обозначения отдельных букв.
Рассмотрим пример построения двоичного кода для символов русского алфавита:
Заключение
В данной работе мы
- рассмотрели понятие систем счисления, выделили их виды,
- рассмотрели двоичную систему счисления;
- выделили применения двоичной системы счисления в жизни человека.
Двоичная система счисления удобна в использовании, что доказывают разнообразные сферы ее применения. В данной работе рассмотрены не все сферы применения двоичной системы счисления и работа в данной области может быть продолжена.
Список используемой литературы
1. Занимательные материалы по математике. 7 – 8 классы. / Составитель Галаева Е.А. – Волгоград: Издательско-торговый дом «Корифей», 2006. – 80 с.
2. Системы счисления и их применение. (Серия: «Библиотека «Математическое просвещение»») / Гашков С.Б. – Москва: Издательство Московского центра непрерывного математического образования, 2004. – 52 с., ил.
3. Раздел информатика, 2001 – 2007. Теле — школа. Интернет – школа «Просвещение.ru»
4. Биографический словарь деятелей в области математики. / Бородин А.И., Бугай А.С. – Киев: «Радянська школа», 1979.
5. Системы счисления. – 5-е издание. / Фомин С.В. — Москва: «Наука». Главная редакция физико-математической литературы, 1987. – 48 с. – (Популярные лекции по математике).
6. Сайт http://numeration.ru/bin.html
СИСТЕМЫ СЧИСЛЕНИЯ | Наука и жизнь
В повседневной жизни мы, как правило, пользуемся десятичной системой счисления. Но это лишь одна из многих систем, которая получила свое распространение, вероятно, по той причине, что у человека на руках 10 пальцев. Однако эта система не всегда удобна. Так, в вычислительной технике применяется двоичная система счисления.
Однако эта система не всегда удобна. Так, в вычислительной технике применяется двоичная система счисления.
Системой счисления называют совокупность приемов и правил наименования и обозначения чисел, с помощью которых можно установить взаимно однозначное соответствие между любым числом и его представлением в виде совокупности конечного числа символов.
В разные исторические периоды развития человечества для подсчетов и вычислений использовались те или иные системы счисления. Например, довольно широко была распространена двенадцатеричная система. Многие предметы (ножи, вилки, тарелки, носовые платки и т. д.) и сейчас считают дюжинами. Число месяцев в году двенадцать. Двенадцатеричная система счисления сохранилась в английской системе мер (например, 1 фут = 12 дюймам) и в денежной системе (1 шиллинг = 12 пенсам).
В древнем Вавилоне существовала весьма сложная шестидесятеричная система. Она, как и двенадцатеричная система, в какой-то степени сохранилась и до наших дней (например, в системе измерения времени: 1 час = 60 минутам, 1 минута = 60 секундам, аналогично в системе измерения углов: 1 градус = 60 минутам, 1 минута = 60 секундам).
У некоторых африканских племен была распространена пятеричная система счисления, у ацтеков и народов майя, населявших в течение многих столетий обширные области американского континента, — двадцатеричная система. У некоторых племен Австралии и Полинезии встречалась двоичная система.
Десятичная система возникла в Индии. Впоследствии ее стали называть арабской потому, что она была перенесена в Европу арабами. Цифры, которыми мы теперь пользуемся, — арабские.
В разное время существовали и другие записи цифр, в настоящее время почти забытые. Однако до сих пор мы иногда встречаемся с записью чисел с помощью букв латинского алфавита, например на циферблатах часов, в книгах для обозначения глав или частей, на деловых бумагах для обозначения месяцев и т.д.
В вычислительной технике применяется двоичная система счисления. Основанием этой системы является число 2. Это означает, что для представления любого числа используются только две цифры, 0 и 1. Целесообраз ность применения двоичной системы в цифровой электронике объясняется тем, что базовый элемент любой электронной схемы имеет два состояния, которым можно приписать значения 0 и 1.
Рассмотрим для примера двоичное число 110010. Единицы и нули в двоичном числе называют разрядами (битами), а положение каждого бита определяет величину показателя степени основания 2, причем старший значащий разряд находится в числе слева, как и в десятичной системе, а младший — справа. Таким образом двоичное число 110010 в десятичной системе равно 1
Двоичная система счисления – определение, преобразование и примеры
Двоичная система счисления – это один из четырех типов системы счисления. В компьютерных приложениях, где двоичные числа представлены только двумя символами или цифрами, то есть 0 (ноль) и 1 (один).
Содержание:
|
Система счисления — это способ представления чисел в компьютерной архитектуре. Существует четыре различных типа системы счисления, например: 9.0005
- Двоичная система счисления (основание 2)
- Восьмеричная система счисления (основание 8)
- Десятичная система счисления (основание 10)
- Шестнадцатеричная система счисления (основание 16).

В этой статье давайте подробно обсудим, что такое двоичная система счисления, преобразование из одной системы в другую, таблицу, позиции, двоичные операции, такие как сложение, вычитание, умножение и деление, использование и решенные примеры.
Что такое двоичная система счисления?
Двоичная система счисления: Согласно цифровой электронике и математике, двоичное число определяется как число, выраженное в двоичной системе счисления или системе счисления с основанием 2. Он описывает числовые значения двумя отдельными символами; 1 (один) и 0 (ноль). Система с основанием 2 — это позиционная система счисления с основанием 2.
Двоичная система применяется внутри почти всех новейших компьютеров и компьютерных устройств из-за ее непосредственной реализации в электронных схемах с использованием логических вентилей. Каждая цифра обозначается как
Пример: Преобразовать 4 в двоичный код.
Решение:
4 в двоичном виде равно (100) 2 .
Здесь 4 представлено в десятичной системе счисления, где мы можем представить число, используя цифры от 0 до 9. Однако в двоичной системе счисления мы используем только две цифры, например 0 и 1.
Теперь давайте обсудим, как преобразовать 4 в двоичную систему счисления. Следующие шаги помогут преобразовать 4 в двоичный код.
Шаг 1: Сначала разделите число 4 на 2. Используйте целое частное, полученное на этом шаге, в качестве делимого для следующего шага. Продолжайте этот шаг, пока частное не станет равным 0,
.Дивиденд | Остаток |
4/2 = 2 | 0 |
2/2 = 1 | 0 |
1/2 = 0 | 1 |
Шаг 2: Теперь запишите остаток в обратном хронологическом порядке.
Здесь младший значащий бит (LSB) равен 0, а старший значащий бит (MSB) равен 1.
Следовательно, десятичное число 4 в двоичной системе равно 100 2
Итак, если мы хотим найти, сколько битов имеет 4 в двоичном формате? мы должны посчитать количество нулей и единиц.
Итак, 4 в двоичном формате равно 100 2 . Здесь 2 нуля и 1 единица. Следовательно, у нас есть 3 бита.
Следовательно, число битов в двоичном коде 4 равно 3.
Что такое бит в двоичном числе?
Одна двоичная цифра называется « бит». Двоичное число состоит из нескольких битов. Примеры:
- 10101 — пятибитное двоичное число .
- 100001 — шестибитное двоичное число 9.0014
Факты, которые следует помнить:
|
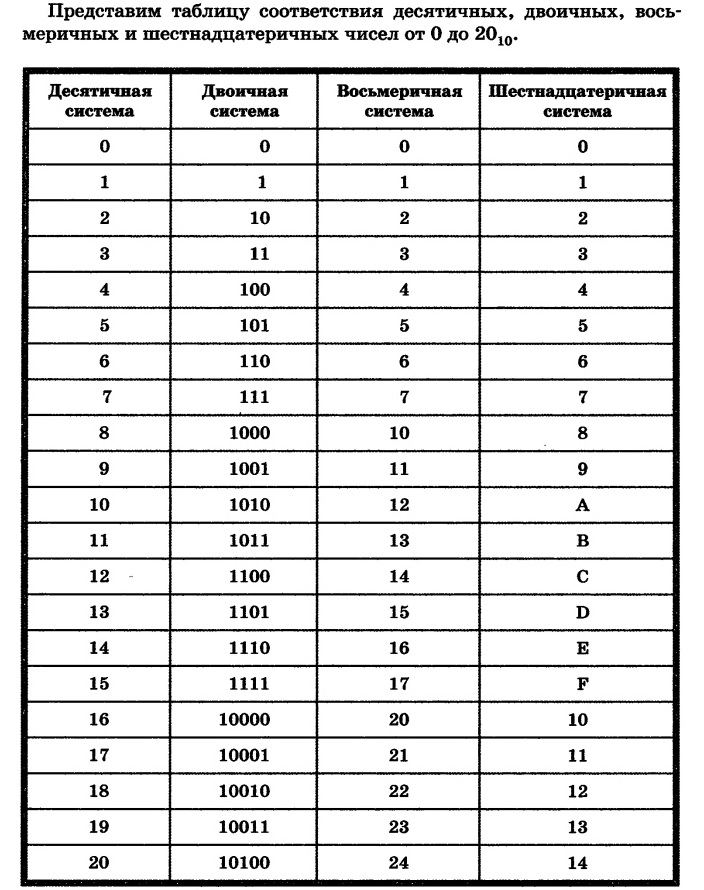
Таблица двоичных чисел
Некоторые двоичные обозначения списков десятичных чисел от 1 до 30 упомянуты в приведенном ниже списке.
| Номер | Двоичный номер | Номер | Двоичный номер | Номер | Двоичный номер |
| 1 | 1 | 11 | 1011 | 21 | 10101 |
| 2 | 10 | 12 | 1100 | 22 | 10110 |
| 3 | 11 | 13 | 1101 | 23 | 10111 |
| 4 | 100 | 14 | 1110 | 24 | 11000 |
| 5 | 101 | 15 | 1111 | 25 | 11001 |
| 6 | 110 | 16 | 10000 | 26 | 11010 |
| 7 | 111 | 17 | 10001 | 27 | 11011 |
| 8 | 1000 | 18 | 10010 | 28 | 11100 |
| 9 | 1001 | 19 | 10011 | 29 | 11101 |
| 10 | 1010 | 20 | 10100 | 30 | 11110 |
Как вычислять двоичные числа
Например, номер для операции 1235.
| Тысячи | Сотни | Десятки | Единицы |
| 1 | 2 | 3 | 5 |
Это означает,
1235 = 1 × 1000 + 2 × 100 + 3 × 10 + 5 × 1
Дано,
| 1000 | = 10 3 = 10 × 10 × 10 |
| 100 | = 10 2 = 10 × 10 |
| 10 | = 10 1 = 10 |
| 1 | = 10 0 (любое значение в нулевой степени равно единице) |
Приведенную выше таблицу можно описать как
.| Тысячи | Сотни | Десятки | Единицы |
| 10 3 | 10 2 | 10 1 | 10 0 |
| 1 | 2 | 3 | 5 |
Следовательно,
1235 = 1 × 1000 + 2 × 100 + 3 × 10 + 5 × 1
= 1 × 10 3 + 2 × 10 2 + 3 × 10 1 + 5 × 10 0
Десятичная система счисления работает с основанием 10, где цифры от 0 до 9 представляют числа.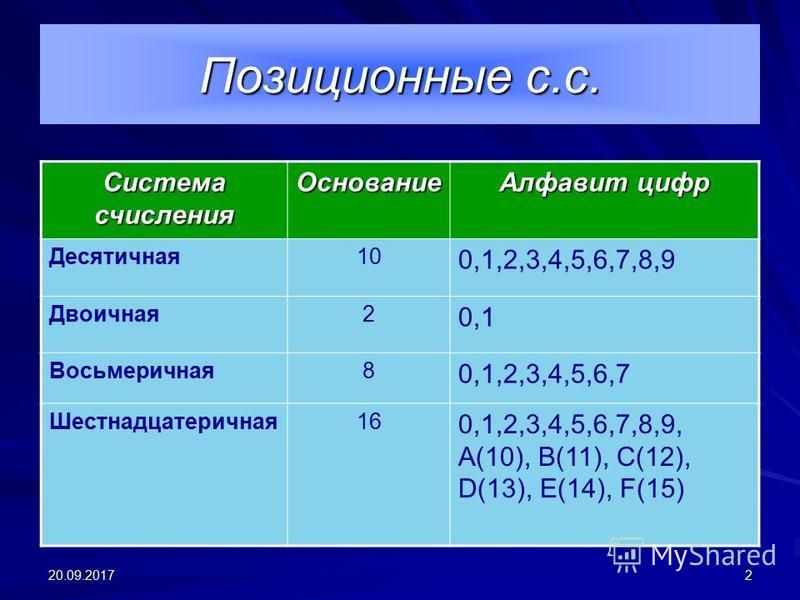 В двоичной системе используется основание 2, а цифры 0-1 представляют числа, а основание известно как основание 9.0011 . Иными словами, приведенную выше таблицу также можно представить следующим образом.
В двоичной системе используется основание 2, а цифры 0-1 представляют числа, а основание известно как основание 9.0011 . Иными словами, приведенную выше таблицу также можно представить следующим образом.
| Тысячи | Сотни | Десятки | Единицы | |
| Десятичный | 10 3 | 10 2 | 10 1 | 10 0 |
| Двоичный | 2 3 | 2 2 | 2 1 | 2 0 |
Размещаем цифры в столбцах 10 0 , 10 1 и так далее по основанию 10. Когда есть необходимость поставить значение больше 9 в виде 10 (n+1) например, чтобы добавить 10 к столбцу 10 0 , вам нужно добавить 1 к столбцу 10 1 .
Размещаем цифры в столбцах 2 0 , 2 1 и так далее по основанию 2. Чтобы поместить значение больше 1 в 2 n , нужно добавить 2 (n+1) . Например, чтобы добавить 3 к столбцу 2 0 , вам нужно добавить 1 к столбцу 2 1 .
Позиция в двоичной системе счисления
В двоичной системе у нас есть единицы, двойки, четверки и т. д.
Например 1011.110
Отображается так:
1 × 8 + 0 × 4 + 1 × 2 + 1 + 1 × ½ + 1 × ¼ + 0 × 1/8
= 11,75 в десятичном формате
Чтобы показать значения больше или меньше единицы, числа можно поместить слева или справа от точки.
Для версии 10.1 10 — это целое число слева от десятичной дроби, и чем дальше мы движемся влево, тем больше разряд становится (в два раза).
Первая цифра справа всегда Половина ½, и по мере продвижения вправо число становится меньше (в два раза больше).
В приведенном выше примере:
- «10» показывает «2» в десятичном формате.

- «.1» показывает «половину».
- Итак, «10,1» в двоичном формате равно 2,5 в десятичном.
Двоичные арифметические операции
Точно так же, как мы выполняем арифметические операции над числами, мы можем выполнять операции сложения, вычитания, умножения и деления над двоичными числами. Давайте изучим их один за другим.
Двоичное сложение
Сложение двух двоичных чисел даст нам само двоичное число. Это самый простой метод. Сложение двух однозначных двоичных чисел приведено в таблице ниже.
| Двоичные числа | Дополнение | |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0; Носить →1 |
Возьмем в качестве примера два двоичных числа и сложим их.
Например: Добавьте 1101 2 и 1001 2 .
Решение:
Двоичное вычитание
Вычитание двух двоичных чисел даст нам само двоичное число. Это также прямой метод. Вычитание двух однозначных двоичных чисел приведено в таблице ниже.
| Двоичные числа | Вычитание | |
| 0 | 0 | 0 |
| 0 | 1 | 1; Занять 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Возьмем в качестве примера два двоичных числа и вычтем их.
Пример: Вычесть 1101 2, и 1010 2 .
Решение: 1101 2 – 1010 2 = 0011 2
Двоичное умножение
Процесс умножения для двоичных чисел такой же, как и для цифр. Давайте разберемся на примере.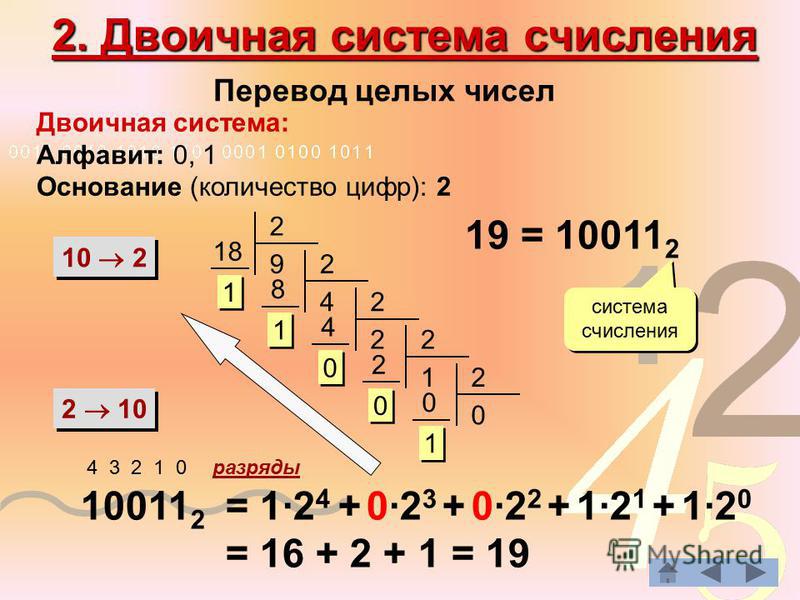
Пример: Умножить 1101 2 и 1010 2 .
Решение:
Двоичный раздел
Двоичное деление аналогично десятичному делению. Мы будем учиться на примере здесь.
Пример: Разделить 1010 2 на 10 2
Решение:
Использование двоичной системы счисления
Двоичные числа обычно используются в компьютерных приложениях. Все коды и языки в компьютерах, такие как C, C++, Java и т. д., используют двоичные цифры 0 и 1 для написания программы или кодирования любых цифровых данных. Компьютер понимает только закодированный язык. Поэтому эта 2-значная система счисления используется для представления набора данных или информации в дискретных битах информации.
Проблемы и решения
Давайте попрактикуемся в некоторых задачах для лучшего понимания:
Вопрос 1 : Что такое двоичное число 1. 1 в десятичном виде?
1 в десятичном виде?
Решение:
Шаг 1: 1 слева соответствует позиции единицы, поэтому это 1.
Шаг 2: Тот, что справа, разделен пополам, так что это
.1 × ½
Шаг 3: , значит, 1,1 = 1,5 в десятичной системе.
Вопрос 2: Напишите 10.11 2 в десятичном формате?
Решение:
10,11 = 1 x (2) 1 + 0 (2) 0 + 1 (½) 1 + 1 (½) 2
= 2 + 0 + ½ + ½
= 2,75
Итак, 10,11 равно 2,75 в десятичном формате.
Продолжайте посещать BYJU’S, чтобы исследовать и узнавать больше о таких темах, связанных с математикой, в увлекательной и увлекательной форме.
Часто задаваемые вопросы о двоичной системе счисления
Что такое двоичная система счисления?
Система счисления, в которой число представлено только двумя цифрами (0 и 1) с основанием 2, называется двоичной системой счисления. Например, 1001 2 — это двоичное число.
Например, 1001 2 — это двоичное число.
Что такое бит?
Бит — это одна цифра в двоичном числе. Например, 101 — это трехбитные двоичные числа, где 1, 0 и 1 — биты.
Как преобразовать десятичное число в двоичное? Приведите пример.
Чтобы преобразовать десятичное число в эквивалентное ему двоичное число, мы каждый раз делим десятичное число на 2, пока не получим 0 в качестве делимого. Возьмем пример для преобразования 13 10 в двоичное число.
13 ÷ 2: 6 и остаток 1
6 ÷ 2: 3 и остаток 0
3 ÷ 2: 1 и остаток 1
1 ÷ 2: 0 и остаток 1
Теперь возьмем биты от последнего остатка к первому остатку, т. е. (от MSB до LSB). Следовательно,
13 10 = 1101 2
Для чего нужны двоичные числа?
Двоичные числа обычно используются в компьютерной архитектуре. Поскольку компьютер понимает только язык двух цифр 0 и 1, поэтому программирование выполняется с использованием двоичной системы счисления.
Чему равно число 163 в двоичном формате?
Значение 163 в двоичном формате равно 10100011.
Как 200 представлено в двоичном формате?
200 — десятичное число. Двоичная форма числа 200: 11001000 2 .
Двоичная система счисления | Почему компьютер использует двоичный номер, логические ворота
Двоичная система счисления
Компьютерная система понимает только двоичную систему счисления. И поэтому нам нужно общаться с компьютером только с помощью Binary Code
Двоичный код также называют машинным языком или машинным кодом. В двоичной системе счисления все числа представляются с использованием только двух числовых чисел: либо 0 (ноль), либо 1 (единица).
Все компьютерные программы, написанные на любом языке программирования высокого уровня, должны быть сначала преобразованы в машинный код в двоичном формате, который может быть непосредственно выполнен центральным процессором компьютера — ЦП.
В этом уроке мы подробно обсудим и найдем ответы на некоторые важные темы в двоичной системе счисления.
Эти вопросы включают в себя: почему компьютер понимает только двоичный код, почему двоичный код состоит только из двух чисел: 0 (ноль) и 1 (единица), различные типы систем счисления, что такое логические вентили и булева алгебра.
Как работает компьютер?
Система двоичных чисел
Содержание
Что такое системы счисления?
Двоичная система счисления
Как данные представлены в двоичном виде
Двоичные числа и логические элементы
Типы систем счисления
Почему компьютер использует двоичные числа?
Двоичный код и двоичные единицы
Двоичная и булева алгебра
Система двоичных чисел и логические вентили
Вопросы для интервью
- Что такое двоичная система счисления?
- Какие существуют типы систем счисления?
- Почему компьютерная система использует только двоичную систему счисления?
- Почему компьютерные программы компилируются?
- Как данные представлены в двоичном виде?
- Двоичный код и двоичные единицы
- Двоичные числа и логические элементы
- Двоичное число и булева алгебра
Изучение информатики в настоящее время считается одним из лучших вариантов карьеры. Карьера в области компьютерных наук дает возможность не только работать с некоторыми первоклассными корпоративными компаниями, но и работать в качестве предпринимателя.
Карьера в области компьютерных наук дает возможность не только работать с некоторыми первоклассными корпоративными компаниями, но и работать в качестве предпринимателя.
Карьера в области компьютерных наук также дает вам возможность ускорить свою карьеру с отличным финансовым вознаграждением.
Что такое система счисления?
Мы все знакомы с широко используемой числовой системой счисления (десятичной системой счисления, в которой используются цифры от 0 до 9), которую мы все используем в нашей повседневной жизни.
Однако существует множество систем счисления, которые можно использовать при общении с компьютерной системой и которые поддерживаются большинством языков программирования.
Система счисления — это система, которой следует определять набор значений, используемых для измерения количества. С помощью системы счисления мы можем выразить количественное измерение любого объекта.
Например, чтобы выразить вес 75 кг, возраст как 26 лет, расстояние как 100 км и так далее.
Однако из-за аппаратной архитектуры компьютерной системы обычно используемая десятичная система счисления не подходит.
Из-за ограничений аппаратной архитектуры компьютера десятичная система не может быть реализована для функционирования компьютерной системы.
Типы системы счисления
Система счисления определяется как система, которая позволяет представить любое число с помощью набора комбинаций символов, цифр и алфавитов. Центральный процессор компьютерной системы может интерпретировать и выполнять только инструкции машинного кода в двоичном формате.
И поэтому весь программный код на любом языке должен быть преобразован в машинный код в двоичном виде с помощью компилятора. Однако большинство языков программирования поддерживают эти четыре системы счисления при написании программного кода.
Двоичная система счисления
Двоичная система счисления использует только две цифры: 0 и 1 . В двоичной системе счисления любое число представляется двумя цифрами: 0 и 1.
Двоичная система счисления имеет основание 2, потому что в ней всего две цифры для представления любого числа.
Восьмеричная система счисления
Восьмеричная система счисления использует только восемь ( 8 ) цифр от 0 до 7 для представления любого числа. В восьмеричной системе счисления любое число (значение) может быть представлено комбинацией любых 8 цифр (0,1,2,3,4,5,6, 7).
Восьмеричная система счисления имеет основание 8, поскольку в ней всего 8 цифр для представления любого числа
Десятичная система счисления
Десятичная система счисления является наиболее часто используемой системой счисления, которая использует десять ( 10 ) цифр от 0 до 9 для представления любого числа.
В десятичной системе любое число может быть представлено комбинацией 10 цифр (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). Десятичная система счисления имеет основание 10, потому что в ней есть 10 цифр для представления любого числа 9.0005
Шестнадцатеричная система счисления
Шестнадцатеричная система счисления имеет шестнадцать ( 16 ) буквенно-цифровых значений от 0 до 9 и от A до F для представления любого числа.
В шестнадцатеричной системе счисления используются девять (10) цифр (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) и семь (6) букв алфавита (A, B, C, D, E, F ) для представления любого числа в этой системе счисления.
Шестнадцатеричная система счисления имеет основание 16, так как использует 16 буквенно-цифровых значений.
Двоичная система счисления
В математике и цифровой электронике двоичное число — это число, выраженное с использованием двоичной системы счисления или системы счисления с основанием 2.
Двоичная система счисления представляет любые числовые значения, используя комбинацию только двух возможных значений, то есть 0 (ноль) и 1 (единица). В цифровой электронике это лучше всего подходит для представления двух состояний: ВКЛ или ВЫКЛ.
Двоичная система счисления использует только две цифры для представления любого числа . Из-за простой реализации в цифровых электронных схемах с использованием логических вентилей двоичная система используется внутри почти всех современных компьютеров и компьютерных устройств.
Таким образом, компьютерная система представляет собой цифровое электронное устройство, которое может понимать и выполнять программные инструкции, передаваемые в двух состояниях: ВКЛ или ВЫКЛ. Эти два состояния лучше всего можно представить с помощью двоичной системы счисления.
Почему компьютер использует двоичную систему счисления
Компьютеры были изобретены благодаря их высокой вычислительной мощности. Компьютеры используются для обработки больших объемов данных с молниеносной скоростью. Компьютерная система состоит из ряда компонентов.
Каждый из этих компонентов выполняет определенную задачу. Одним из наиболее важных компонентов компьютерной системы является ЦП.
ЦП (центральный процессор) в компьютерной системе отвечает за выполнение всех арифметических вычислений и логических решений.
ЦП также называют микропроцессором, микросхемой процессора или просто процессором.
Микросхема процессора состоит из миллионов крошечных электронных компонентов, называемых транзисторами. Транзистор является основным строительным блоком для всех цифровых электронных устройств, включая компьютеры.
Транзистор является основным строительным блоком для всех цифровых электронных устройств, включая компьютеры.
Транзистор изготовлен из кремния, полупроводникового материала. Транзисторы используются в качестве микропереключателя, который может быть либо включен, либо выключен.
Процессор компьютера, который является мозгом компьютерной системы, состоит из миллионов этих транзисторов.
И, следовательно, процессор компьютера может понимать и выполнять инструкции, передаваемые только в виде двух состояний: включено или выключено.
И поэтому для связи с компьютерной системой нам нужна система счисления, способная представить любое число, используя только две цифры.
Двоичная система счисления идеально соответствует этому условию, потому что в двоичной системе счисления мы используем только две цифры, то есть 0 и 1.
В двоичном формате включенное состояние представлено 1 (единица), а выключенное состояние представлено 0 (ноль).
И по этой причине архитектура компьютера поддерживает двоичную систему счисления, и все компьютерные программы должны быть сначала скомпилированы в инструкции машинного кода в двоичном формате, которые может выполнять ЦП компьютера.
Почему компьютер использует двоичную систему счисления
Как данные представлены в двоичном виде
Компьютер хранит всю информацию и программные данные только в двоичном цифровом виде. Это означает, что все данные, будь то текст, фотографии, аудио, видео или что-то еще, состоят только из наборов единиц и нулей.
Однако операционная система представляет эти данные в графическом формате в графическом интерфейсе, удобном для чтения человеком.
Двоичный код и двоичные единицы
Поскольку ЦП компьютера может выполнять только инструкции машинного кода и работать с данными в двоичном формате, весь программный код и данные должны быть представлены в двоичной форме.
Процессор обрабатывает данные, и результат этой операции может быть отправлен либо на устройство вывода (монитор, принтер и т.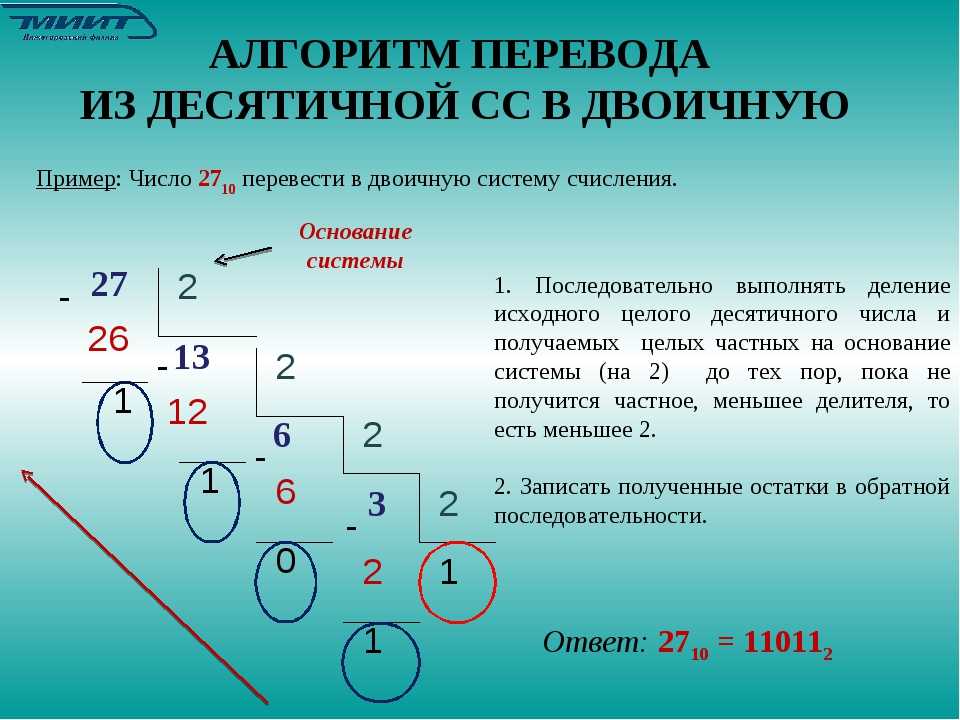 д.), либо сохранен в постоянном запоминающем устройстве для использования в будущем.
д.), либо сохранен в постоянном запоминающем устройстве для использования в будущем.
Фундаментальным строительным блоком цифровой информации является двоичная цифра или бит, который представляет одно состояние 0 (ноль) или 1 (единица). Это представлено битом в памяти компьютера, который является наименьшей единицей памяти.
Для представления большого объема данных биты могут быть организованы в группы по четыре, восемь, шестнадцать, 32 или 64 бита, называемые полубайтами/полубайтами, байтами, словами, длинными словами и очень длинными словами соответственно. Они называются двоичными единицами измерения.
Компьютеры распознают только два дискретных состояния: включено и выключено. Эти состояния могут быть представлены двумя цифрами: 0 и 1. Каждый 0 или 1 называется битом в двоичной системе. Бит — это наименьшая единица данных, которую может обработать компьютер.
A Бит — это сокращение от двоичной цифры. Двоичная система имеет основание 2 с двумя цифрами (0 и 1).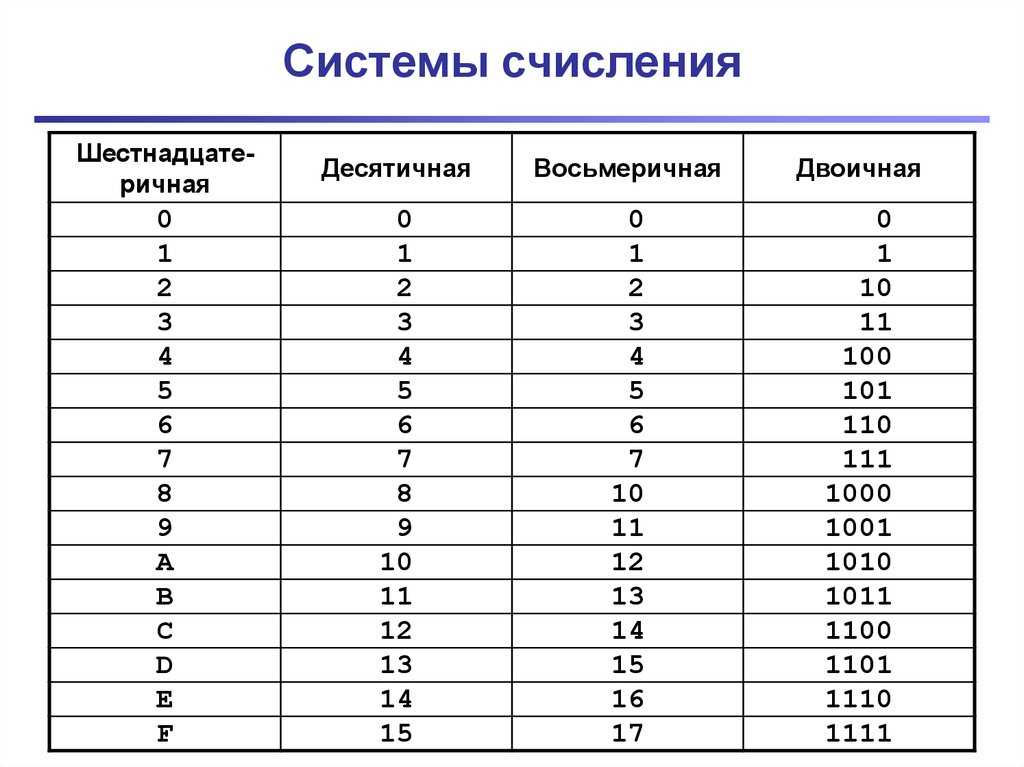 Используя комбинации нулей и единиц, мы можем представлять большие числа.
Используя комбинации нулей и единиц, мы можем представлять большие числа.
Двоичные числа и логические элементы
Компьютерная система выполняет различные задания, выполняя инструкции программы в соответствии с логикой программы. ЦП — это основной компонент внутри компьютерной системы, который выполняет все арифметические вычисления, а также логические операции.
ЦП компьютера отвечает за выполнение как арифметических вычислений, так и логических операций. Центральный процессор состоит из миллионов крошечных схем, называемых транзисторами, которые могут функционировать как микропереключатели.
Логические элементы сконструированы с использованием транзисторов внутри микросхемы процессора, которые в основном используются ЦП для выполнения логических операций.
Компьютеры — это цифровые машины, а логические элементы — основные компоненты цифровой электроники. Логические элементы используются для создания цифровых схем и даже сложных интегральных схем.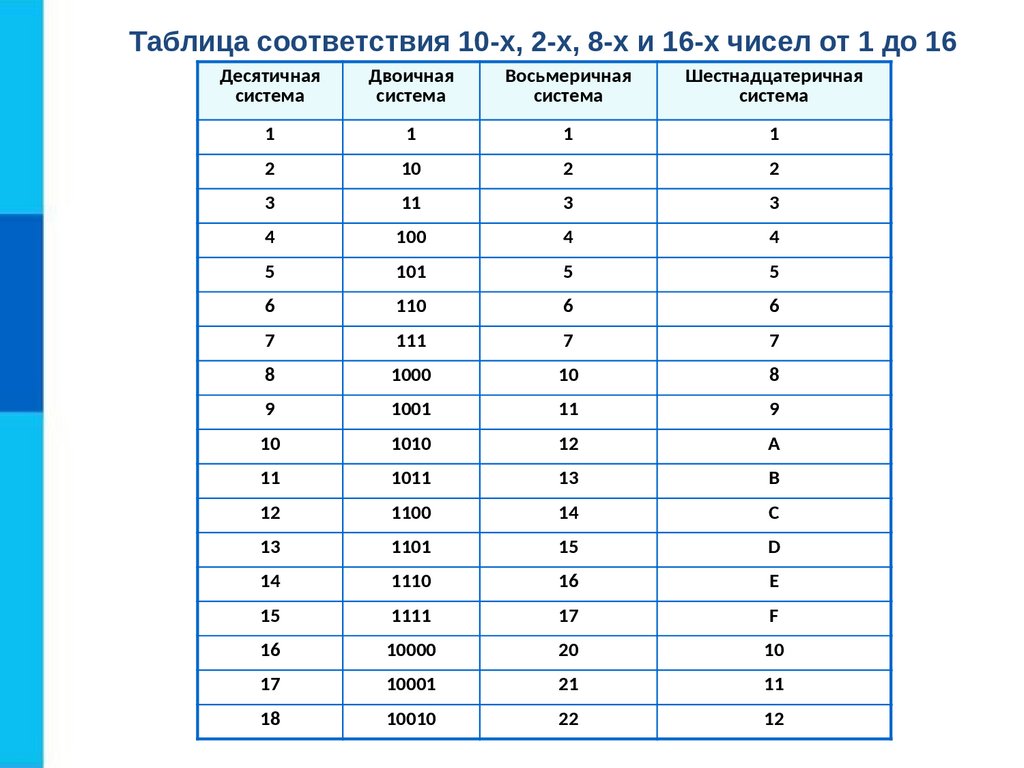
ЦП компьютера состоит из миллионов этих крошечных схем, которые позволяют ЦП выполнять логические операции.
Процессор работает, реагируя на ввод 0 и 1 определенным образом, а затем возвращая вывод на основе решения.
Само решение происходит в схеме, называемой логическим вентилем, для каждого из которых требуется как минимум один транзистор с входами и выходами, расположенными по-разному для разных операций.
Двоичные числа и логическая алгебра
В математике и математической логике булева алгебра — это ветвь алгебры, в которой значения переменных являются истинными значениями ( истина и ложь ) и это обычно обозначается в двоичном формате 1 и 0 соответственно.
Булева алгебра была введена Джорджем Булем в 1854 году, британским математиком. Булева алгебра сыграла фундаментальную роль в развитии цифровой электроники.
В алгебре мы используем десятичные числа, тогда как в булевой алгебре используются значения истинности, истина (1) и ложь (0).