Восьмеричная система счисления – как переводить, таблица

4.6

Средняя оценка: 4.6

Всего получено оценок: 106.

4.6

Средняя оценка: 4.6

Всего получено оценок: 106.

Числа можно представлять не только в десятичном формате, но и в системе счисления с основанием 8, которая использует для обозначения символы 0, 1, 2, 3, 4, 5, 6, 7. О том, как переводить в восьмеричную систему счисления числа из десятичной и двоичной системы и обратно, рассказано в данной статье.

Восьмеричная система счисления

Восьмеричная система счисления имеет вспомогательный характер, ее удобно использовать для сокращенной записи бинарных комбинаций чисел. Она более удобна в работе чем двоичная, так как использует меньшее количество разрядов. Восьмеричная система применялась в свое время для программирования на машинном языке, а также в устройствах подготовки данных, вышедших из употребления с появлением персональных компьютеров.

Алфавит восьмеричной системы составляют восемь цифр от 0 до 7, соответственно основание равно 8.

Числовой ряд восьмеричных чисел: 1, 2, 3, 4, 5, 6, 7,10, 11, 12, 13, 14, 15, 16, 17, 20.

Следует обратить внимание, что после 7 в числовом ряду идет 10, а после 17 число 20.

Число 8 имеет символический смысл, является первым кубом двойки и отождествляется с трехмерным измерением. Для многих древних народов восьмёрка сакральное число. Внешне выглядит как символ бесконечности. В информатике один байт равен 8 битам.

Рис. 1. Символ бесконечности.

Перевод 8 – 2

Перенос восьмеричного числа в двоичный формат – это самый простой способ перевода чисел. Каждой восьмеричной цифре ставится в соответствие группа двоичных цифр в количестве трех. Эта группа называется триадой.

И, наоборот, при переводе двоичного числа в восьмеричный формат производится замена трех двоичных цифр одной восьмеричной. Разбивка целого двоичного числа на трехзначные звенья производится справа налево. Когда крайняя триада получается неполной, то ее дополняют нулями.

Для более быстрого перевода чисел используется таблица записи восьмеричных чисел двоичным форматом.

Рис. 2. Таблица соответствия восьмеричных и двоичных чисел.

Например, 34₈ = 011100₂. Ноль впереди числа отбрасываем и получаем в итоге 11100₂.

И обратный перевод, например: 1101101

2 = (001)(101)(101) = 155₈. В старшей триаде не хватило разрядов, она дополнилась слева двумя нулями.

Перевод 8 – 10

Преобразование чисел из восьмеричного формата в десятичную форму выполняется с использованием правила перевода: целая часть числа последовательно делится на основание новой системы счисления, то есть 8, и остатки от деления записываются начиная с последнего частного в обратном направлении. Например:

246 / 8 = 30 и в остатке 6

30 / 8 = 3 и в остатке 6

3 меньше 8, деление завершено.

Таким образом, 246₁₀ = 366₈.

Обратный перевод выполняется путем разложения числа в развернутую форму:

366₈ = 3*8² + 6*8¹ + 6*8⁰ = 3*64 + 6*8 + 6*1 = 192 + 48 + 6 = 246₁₀

Арифметические действия

Арифметические действия в системе счисления с основанием 8 выполняются также как и в десятичной. Удобнее всего складывать и вычитать большие числа столбиком. Только следует помнить, что после 7 идет 10, то есть сумма восьмеричных чисел 3 + 5 = 10, а не восемь. Удобнее всего при вычислениях пользоваться таблицей сложения восьмеричных чисел.

Рис. 3. Таблица сложения восьмеричных чисел.

Например, сумма 34 + 25 = 61. Это получилось следующим образом. Сначала складываются младшие разряды 4 + 5 = 11 (смотрят по таблице). Единица остается в младшем разряде, а вторая единица переносится в старший разряд и добавляется к сумме чисел 3 + 2 = 5. Итого получилось 61.

Что мы узнали?

Восьмеричная система счисления удобна для представления бинарных кодов и записи машинных команд в программировании. Основание этой системы равно 8. Для перевода чисел из двоичной системы счисления в восьмеричную и обратно используются триады. Перевод восьмеричных чисел в десятичную систему выполняется путем поочередного деления частного числа и записи остатков от деления. Обратный перевод выполняется через раскрытие числа в развернутую форму.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Елена Кетросан

  10/10

Оценка статьи

4.6

Средняя оценка: 4.6

Всего получено оценок: 106.

---

А какая ваша оценка?

Восьмеричная система счисления

Восьмеричная система (система с основанием 8) использовалась для кодирования команд во многих компьютерах 1950-1980-х годов (например, в американской серии PDP-11, советских компьютерах серий ДВК, СМ ЭВМ, БЭСМ). В ней используются цифры от 0 до 7.

Для перевода десятичного числа в восьмеричную проще всего систему использовать стандартный алгоритм для позиционных систем (деление на 8, выписывание остатков в обратном порядке). Например,

рис. 2.26

рис. 2.27

Для перевода из восьмеричной системы в десятичную значение каждой цифры умножают на 8 в степени, равной разряду этой цифры, и полученные произведения складывают:

разряды  2 1 0

144₈ = 18² + 48¹ + 48⁰

= 64 + 48 + 4 = 100.

Более интересен перевод из восьмеричной системы в двоичную и обратно. Конечно, можно перевести число сначала в десятичную систему, а потом – в двоичную. Но для этого требуется выполнить две непростых операции, в каждой из них легко ошибиться.

Оказывается, можно сделать перевод из восьмеричной системы в двоичную напрямую, используя тесную связь между этими системами: их основания связаны равенством 2³ = 8. Покажем это на примере восьмеричного числа 753₈. Запишем его в развернутой форме:

753₈ = 78² + 58¹ + 38⁰ = 72⁶

+ 52³ + 32⁰.

Теперь переведем отдельно каждую цифру в двоичную систему:

7 = 111₂ = 12² + 12¹ + 12⁰, 5 = 101₂ = 12² + 12⁰, 3 = 11₂ = 12¹ + 12⁰.

И подставим эти выражения в предыдущее равенство:

753₈ = (12² + 12¹ + 12⁰)2⁶ + (12² + 12⁰)2³ + (12

1 + 12⁰)2⁰.

Раскрывая скобки, мы получим разложение исходного числа по степеням двойки, то есть его запись в двоичной системе счисления (здесь добавлены нулевые слагаемые для отсутствующих степеней числа 2):

7 53₈ =  1 2⁸ + 1 2⁷ + 1 2⁶ + 1 2⁵ + 0 2⁴ + 1 2³ + 0 2² + 1 2¹ + 1 2⁰.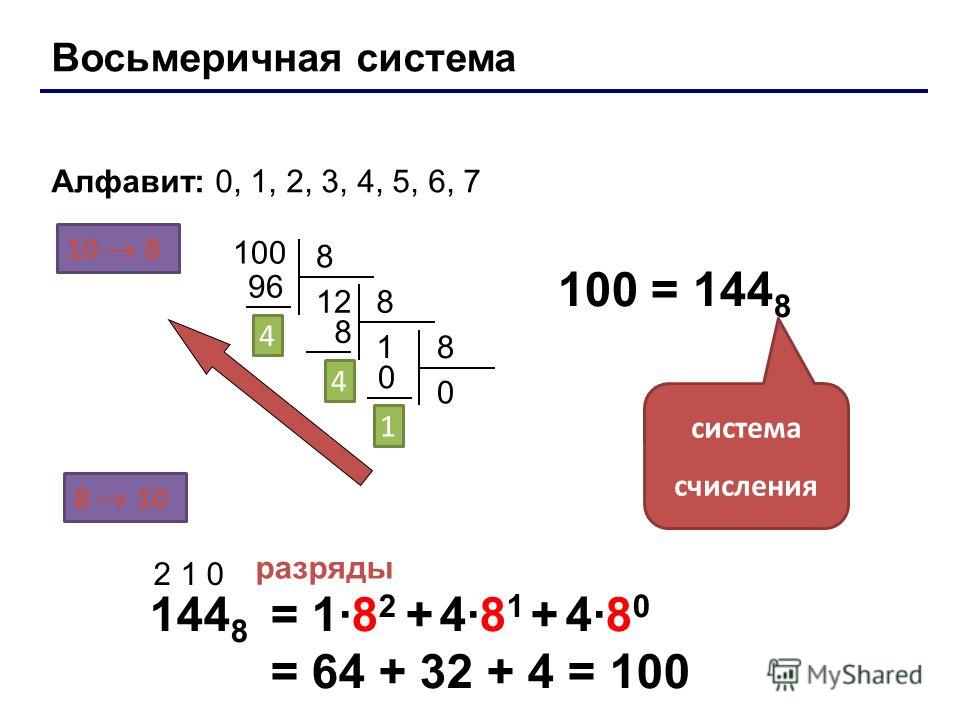

0	000
1	001
2	010
3	011
4	100
5	101
6	110
7	111

Т аким образом, 753₈ = 111 101 011₂.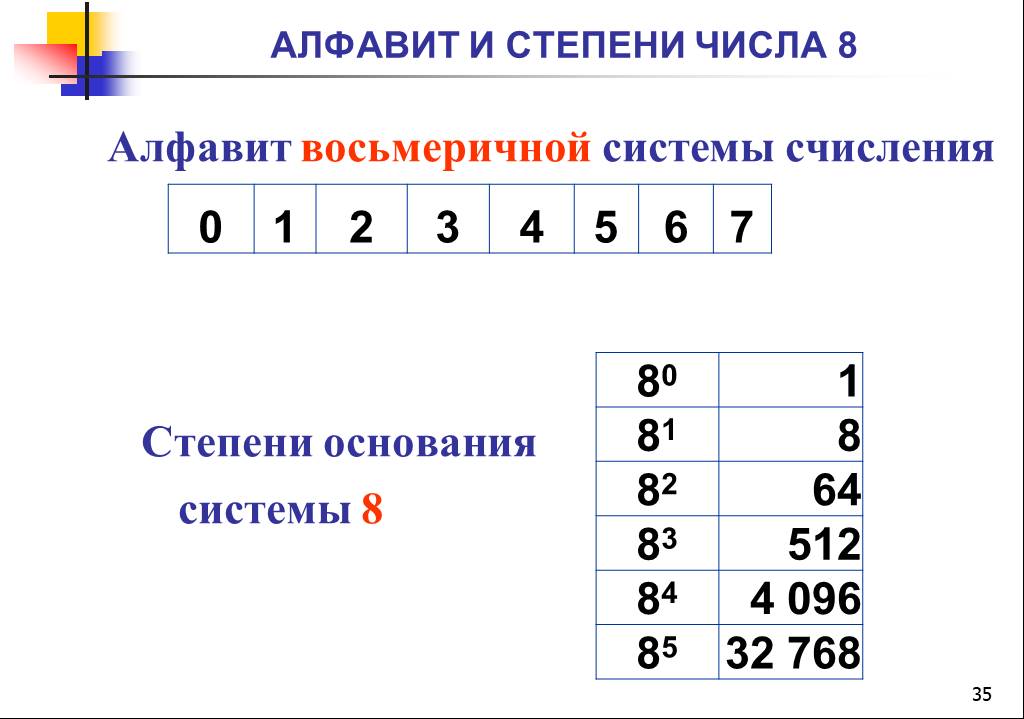 Двоичная запись разбита на триады (группы из трех цифр), каждая триада – это двоичная запись одной цифры исходного восьмеричного числа.

Алгоритм перевода восьмеричного числа в двоичную систему счисления. Перевести каждую цифру (отдельно) в двоичную систему. Записать результаты в виде триады, добавив, если нужно, нули в начале (см. таблицу справа). Соединить триады в одно «длинное» двоичное число.

Например, 35721₈ = 11 101 111 010 001₂. В этой записи триады специально отделены друг от друга пробелом. Обратите внимание, что все триады дополнены спереди нулями до трех цифр:

2 = 10₂ = 010₂, 1 = 1₂ = 001₂.

Для самой первой триады это делать не обязательно, потому что лидирующие нули в записи числа никак его не меняют.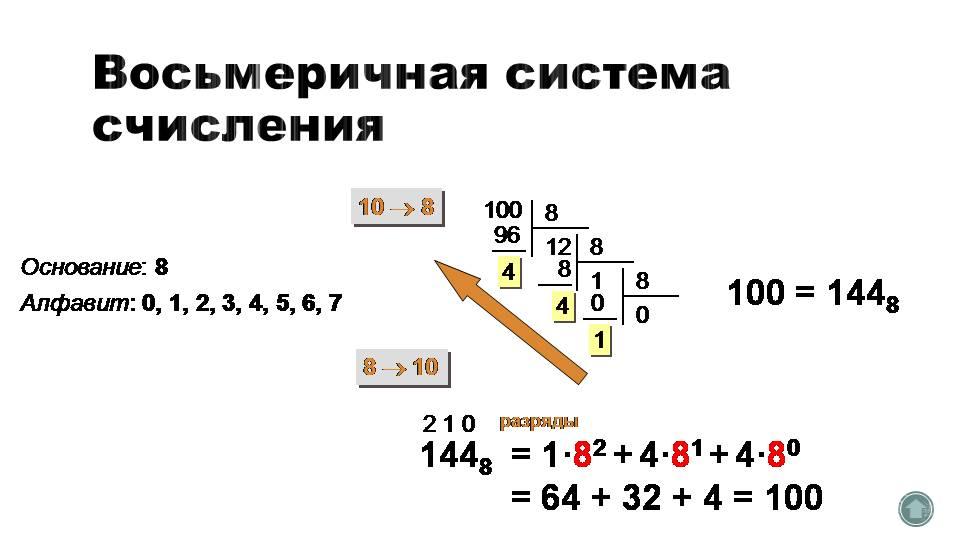 Напротив, если «потерять» нули в середине числа, получится неверный результат.

Алгоритм перевода двоичного числа в восьмеричную систему счисления. Разбить двоичное число на триады, начиная справа. В начало самой первой триады добавить лидирующие нули, если это необходимо. Перевести каждую триаду в восьмеричную (= десятичную) систему. Соединить полученные цифры в одно «длинное» число.

Например, переведем в восьмеричную систему число 1010011100101110111₂. Разобьем его на триады (начиная справа), к первой триаде нужно добавить два нуля (они подчеркнуты):

1010011100101110111₂ = 001 010 011 100 101 110 111₂

Далее по таблице (см. выше) переводим каждую триаду в восьмеричную систему:

1010011100101110111₂ = 1234567₈.

Теперь представьте себе объем вычислений, который потребуется для решения этой задачи через десятичную систему.

П

рис. 2.28

ри вычислениях в восьмеричной системе нужно помнить, что максимальная цифра – это 7. Перенос при сложении возникает тогда, когда сумма в очередном разряде получается больше 7. Заем из старшего разряда равен 10₈ = 8, а все «промежуточные» разряды заполняются цифрой 7 – старшей цифрой системы счисления. Приведем примеры сложения и вычитания:

В примере на сложение запись 18 + 2 означает, что получилась сумма, большая 7, которая не помещается в один разряд. Единица идет в перенос, а двойка остается в этом разряде. При вычитании «– 1» означает, что из этого разряда раньше был заем (его значение уменьшилось на 1), а «+ 8» – заем из следующего разряда.

С помощью восьмеричной системы удобно кратко записывать содержимое областей памяти, содержащих, количество бит, кратное трем. Например, 6-битные данные «упаковываются» в две восьмеричные цифры. Некоторые компьютеры 1960-х годов использовали 24-битные и 36-битные данные, они записывались соответственно с помощью 8 и 12 восьмеричных цифр. Восьмеричная система использовалась даже для компьютеров с 8-битным байтом (PDP-11, ДВК), но позднее была почти вытеснена шестнадцатеричной системой (см. далее).

Сейчас восьмеричная система применяется, например, для установки прав на доступ к файлу в Linux (и других Unix-системах) с помощью команды chmod. Режим доступа кодируется тремя битами, которые разрешают чтение (r, read, старший бит), запись (w, write) и выполнение файла (x, execute, младший бит). Код 7 = 111₂ (rwx) означает, что все биты установлены (полный доступ), а код 5 = 101₂ (r—x) разрешает чтение и выполнение файла, но запрещает его изменение.

языковых агностиков — В каких ситуациях используется восьмеричная база?

спросил 12 лет, 9 месяцев назад

Изменено 11 месяцев назад

Просмотрено 21к раз

Я часто встречал двоичные и шестнадцатеричные числа, но никогда не использовал восьмеричные. Тем не менее, восьмеричное число имеет свое собственное соглашение для использования в некоторых языках (например, начальный 0 указывает на восьмеричное основание). Когда используется восьмеричное число? Каковы некоторые типичные ситуации, когда можно было бы использовать восьмеричное или восьмеричное число, о котором было бы легче рассуждать? Или это просто дело вкуса?

• независимо от языка
• восьмеричное

Восьмеричное используется, когда количество битов в одном слове кратно 3, или если группировка битов имеет смысл для записи группами по 3. Примеры:

• древние системы с 18-битными размерами слов (в основном исторические)
• систем с 9-битными байтами (в основном исторические)
• права доступа к файлу unix с 9 битами (3 * 3 бита, «rwxr-x—» 0750)
• права доступа к файлам unix с 12 битами (такие же, как 9битовая версия, но с добавлением трех битов впереди для setuid, setgid и sticky, 01777, но буквы здесь сложнее)

За 25 лет работы в ИТ я не сталкивался ни с каким использованием восьмеричного кода, кроме битов доступа к файлу unix.

Если количество битов в вашем слове кратно 4, однако , пожалуйста, используйте шестнадцатеричное , во что бы то ни стало.

1

Octal используется как сокращение для представления прав доступа к файлам в системах UNIX. Например, файловый режим rwxr-xr-x будет 0755 .

4

Octal используется, когда синтаксис является пережитком прошлого, когда он, возможно, имел смысл на какой-то платформе (системные слова не всегда были кратны 8 битам). В настоящее время hex — это то, что нужно использовать.

Не об этом подумал, а о цифровых дисплеях!

Несколько других применений из: http://en.wikipedia.org/wiki/Восьмеричный

Одна из основных причин, по которой восьмеричная система использовалась чаще, заключалась в том, что проще преобразовать восьмеричную в двоичную в уме, чем шестнадцатеричную в двоичную: вам нужно только запомнить двоичное представление 8 восьмеричных цифр (0-7).

В те дни, когда отладка означала чтение содержимого регистров из ряда светодиодов или ввод данных с помощью массива тумблеров, это было большой проблемой. Панели на многих из этих ранних компьютеров сгруппировали светодиоды и переключатели в группы по три, чтобы облегчить это.

Однако шестнадцатеричный формат начал побеждать, поскольку размеры слов, кратные 8-битным байтам, стали побеждать, и необходимость чтения и ввода данных в двоичном виде стала ненужной (с текстовым интерфейсом консоли и более поздними отладчиками графического интерфейса).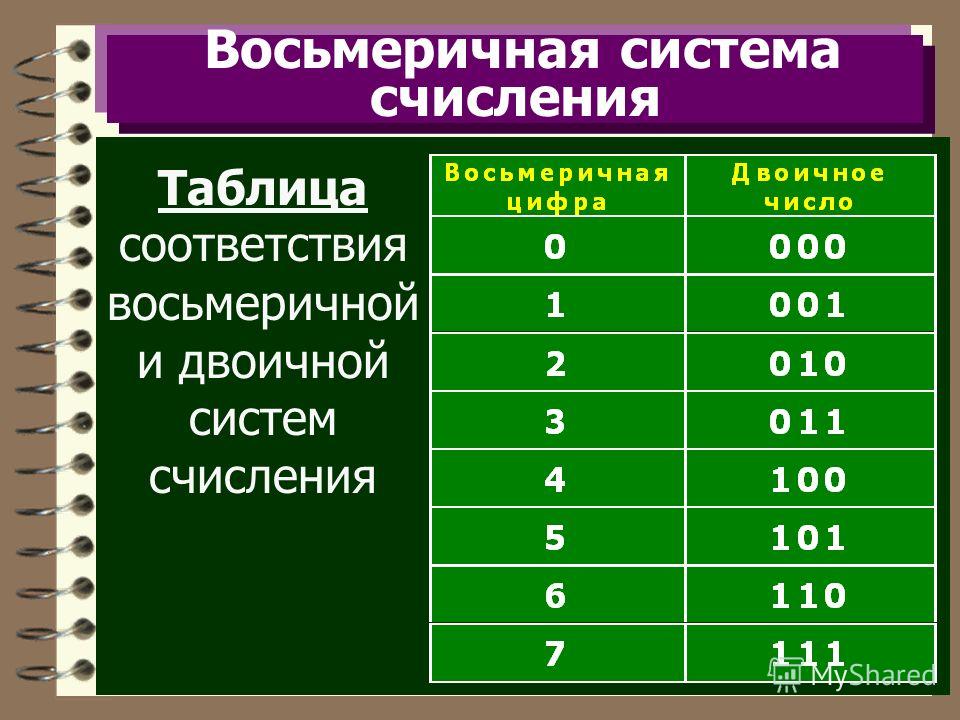

Если бы птицы умели считать, я бы предположил, что они используют восьмеричное число. В то время как у большинства птиц на оперенных «руках» 3 пальца, большинство из них тетрадактилии, то есть по 4 пальца на каждой ноге.

1

В авионике метки слов ARINC 429 почти всегда выражаются в восьмеричном формате.

Музыка, пока вы держитесь подальше от (большинства) диезов и бемолей.

2

К вашему сведению, есть несколько мест, где Windows и javascript автоматически решают, что число с префиксом нуля является восьмеричным, и преобразуют число.

В Windows, если вы выполняете ping и адрес типа 10.0.2.010, он фактически будет пинговать 10.0.2.8

Windows также делает это, если вы вводите его как IP/DNS-адрес для компьютера

Хотя это устарело, Javascript делает это с помощью по умолчанию для некоторых функций, таких как parseInt, если вы не укажете систему счисления http://www. w3schools.com/jsref/jsref_parseint.asp

3

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя адрес электронной почты и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

java — Для чего используются восьмеричные числа (основание 8)?

спросил 3 года 3 месяца назад

Изменено 3 года, 2 месяца назад

Просмотрено 3к раз

Java предоставляет способы записи числовых литералов в основаниях 2, 8, 10 и 16.

Мне интересно, почему основание 8 включено, например. инт х = 0123; ?

Я думаю, что может быть что-то вроде того, что в шестнадцатеричном формате размер одного байта равен FF+1 и так далее.

• Java
• литералы
• восьмеричные

2

Этот ответ был написан на исходный вопрос: «Почему полезно писать число в системе счисления 8?»

Это должно было сделать язык знакомым тем, кто знал Си и т.д. Тогда вопрос зачем поддерживать его в тех!

Были архитектуры (различные PDP), которые использовали 18-битные слова (а другие использовали 36-битные слова), поэтому были бы полезны литералы, в которых цифра имеет ширину 3 бита.

Практически единственное место, где я видел его использование в коде Java, — это указание разрешений в стиле unix, например. 0777 , 0644 и т. д.

(ироничный ответ на вопрос, почему он поддерживается, — «чтобы получить положительные отзывы по этому вопросу»).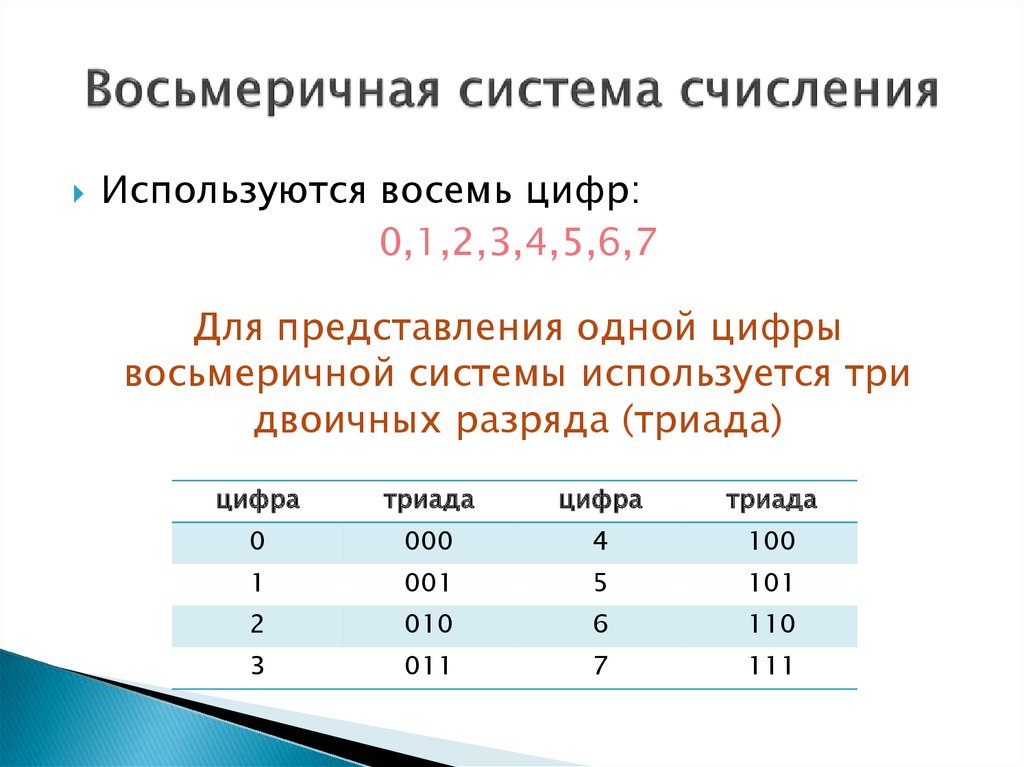

4

«Восьмеричные числа не так распространены, как раньше. Однако восьмеричные числа используются, когда количество битов в одном слове кратно 3. Они также используются в качестве сокращения для представления прав доступа к файлам в системах UNIX и представление чисел UTF8 и т. д.»

Откуда: https://www.tutorialspoint.com/octal-number-system

1

История ЭВМ (наука). Для представления группы битов основание 10 не подходит, основание 8 = 2 ³ для 3 битов, а основание 16 = 2 ⁴ для 4 битов подходит лучше.

Преимущество основания 8 состоит в том, что все цифры на самом деле являются цифрами: 0-7, тогда как основание 16 имеет «цифры» 0-9A-F.

Для 8 битов байта основание 16 (шестнадцатеричное) лучше подходит и победило. Для восьмеричной системы Unix с основанием 8 часто до сих пор используется для 9. 0039 rwx бит (чтение, запись, выполнение) для пользователя, группы и др.; следовательно, восьмеричные числа, такие как 0666 или 0777.

Шестнадцатеричное число распространено повсеместно, не в последнюю очередь из-за размеров слов компьютеров в настоящее время. несколько байтов. То, что 8-битный байт стал стандартом, — это другая, сложная связанная история (2 ³ бит и адресация).

Оригинальный ответ на вопрос «Для чего используются восьмеричные числа (основание 8)?»

• Как сокращение от двоичного: Для вычислительных машин (таких как UNIVAC 1050, PDP-8, ICL 1900 и т. д.) восьмеричный используется как сокращение от двоичного, поскольку размер их слова делится на три (каждая восьмеричная цифра представляет три двоичных разряда). Таким образом, две, четыре, восемь или двенадцать цифр могут кратко отображать целое машинное слово. Это также позволило сократить расходы, позволив использовать трубки Nixie, семисегментные дисплеи и калькуляторы для консолей операторов, где двоичные дисплеи были слишком сложны для использования, десятичные дисплеи требовали сложного оборудования для преобразования корневых и шестнадцатеричных дисплеев, необходимых для отображения большего количества цифр. .

• Представление 16-, 32- или 62-битных слов: Все современные вычислительные платформы используют 16-, 32- или 64-битные слова, далее разделенные на восьмибитные байты. В таких системах потребуется три восьмеричных цифры на байт, при этом старшая восьмеричная цифра представляет две двоичные цифры (плюс один бит следующего значащего байта, если он есть). Восьмеричное представление 16-битного слова требует 6 цифр, но самая значащая восьмеричная цифра представляет (довольно неэлегантно) только один бит (0 или 1). Это представление не дает возможности легко прочитать самый старший байт, потому что он размазан по четырем восьмеричным цифрам. Поэтому сегодня в языках программирования чаще используется шестнадцатеричный формат, поскольку две шестнадцатеричные цифры точно определяют один байт. Некоторые платформы с размером слова, равным степени двойки, по-прежнему имеют подслова команд, которые легче понять, если они отображаются в восьмеричном формате; это включает семейство PDP-11 и Motorola 68000. Современная вездесущая архитектура x86 также относится к этой категории, но восьмеричная архитектура редко используется на этой платформе.

• Описание кодирования: Некоторые свойства двоичного кодирования кодов операций в современной архитектуре x86 становятся более очевидными при отображении в восьмеричном формате, например. байт ModRM, который разделен на поля из 2, 3 и 3 бит, поэтому восьмеричное может быть полезно при описании этих кодировок.

• Вычисления и права доступа к файлам: Восьмеричная иногда используется в вычислениях вместо шестнадцатеричной, возможно, чаще всего в наше время в сочетании с правами доступа к файлам в системах Unix (в разрешении доступа к chmod). Его преимущество заключается в том, что он не требует никаких дополнительных символов в качестве цифр (шестнадцатеричная система с основанием 16, поэтому требуется шесть дополнительных символов после 0–9).).

• Цифровые дисплеи: Восьмеричные числа также используются при отображении цифрового контента на экране, поскольку в нем меньше символов, используемых для представления.

• Графическое представление байтовых строк: Некоторые языки программирования (C, Perl, Postscript и т. д.) имеют представление текстов/графики в восьмеричном формате с экранированием как \nnn. Восьмеричное представление особенно удобно для байтов, отличных от ASCII, в кодировке UTF-8, которая кодирует группы из 6 бит, и где любой начальный байт имеет восьмеричное значение \3nn, а любой байт продолжения имеет восьмеричное значение \2nn.

• Ранняя арифметика с плавающей запятой: Octal также использовался для вычислений с плавающей запятой в компьютерах Ferranti Atlas (1962 г.), Burroughs B5500 (1964 г.), Burroughs B5700 (1971 г.), Burroughs B6700 (1971 г.) и Burroughs B7700 (1972 г.). .

• В транспондерах: Самолет передает код, выраженный в виде четырех восьмеричного числа, при запросе наземным радаром. Этот код используется для различения различных самолетов на экране радара.

Дополнительная литература: https://en.