Восьмеричная система счисления
☰
При описании двоичной системы счисления было упомянуто, почему современное «железо» понимает только двоичную систему. Однако человеку трудно воспринимать длинные записи нулей и единиц, а переводить числа из двоичной в десятичную систему и обратно трудоемко.
Поэтому в программировании иногда используют другие системы счисления – восьмеричную и шестнадцатеричную. Поскольку 8 и 16 являются степенями двойки,
8 = 23, 16 = 24
преобразование двоичного числа в эти системы, также как обратная операция, выполняются просто.
В восьмеричной системе счисления используется восемь знаков-цифр (от 0 до 7). Каждой цифре соответствует число из трех цифр в двоичной системе счисления:
000 – 0 001 – 1 010 – 2 011 – 3 100 – 4 101 – 5 110 – 6 111 – 7
Для преобразования двоичного числа в восьмеричное надо разбить его на тройки цифр и заменить каждую тройку соответствующей ей одной цифрой из восьмеричной системы счисления.
1011101 = 1 011 101 = 001 011 101 = 1 3 5 = 135
В примере число 1011101 в двоичной системе приводится к числу 135 в восьмеричной системе счисления.
10111012 = 1358
Обратный перевод, когда восьмеричное число переводится в двоичное, выполняется аналогично. Только здесь на место восьмеричных цифр подставляются двоичные числа, состоящие из трех цифр.
135 = 001 011 101
Как перевести восьмеричное число в десятичное? Здесь действует тот же алгоритм, как при преобразовании двоичного числа в десятичное. Вспомним его:
11012 = 1 * 23 + 1 * 22 + 0 * 21 + 1 * 20 = 8 + 4 + 0 + 1 = 1310
Однако в случае восьмеричного числа за основание степени берется десятичное число 8:
1358 = 1 * 82 + 3 * 81 + 5 * 80 = 64 + 24 + 5 = 9310
Преобразование десятичного числа в восьмеричное также похоже на перевод в двоичное, за исключением того, что делить надо на 8:
93 / 8 = 11, остаток 5 11 / 8 = 1, остаток 3 1 / 8 = 0, остаток 1
Собираем остатки с конца и получаем число 135 в восьмеричной системе счисления.
«Зачем нужна восьмеричная система счисления в 21 веке?» – Яндекс.Кью
Работа в восьмеричной системе может быть полезна в случае операций с битовыми флагами и масками по причине простоты вычисления таких значений.
Случай с правами доступа в *nix системах — как раз пример применения битовых масок на практике.
Для последовательности из 3 битов очень удобно применять цифры от 0 до 7 (все цифры восьмеричной системы), а операции для вычисления восьмеричного числа очень простые.
Рассмотрим пример с установкой битов от 000 до 111:
установка правого крайнего бита (младшего) увеличит восьмеричное число на 1
установка среднего бита увеличит восьмеричное число на 2
установка старшего бита увеличит восьмеричное число на 4
То есть, нужно определить состояние каждого бита и соответствуюшее ему число, а затем просуммировать биты в состоянии 1.
Расставим биты и соответствующие им цифры, как описано выше:
1 1 1
4 2 1
Теперь когда мы устаналиваем какой-то бит, к итоговой сумме просто прибавляем соответствующую цифру.
Таким образом, если мы хотим установить значение, например, 101, мы суммирует 4 и 1 (я для наглядности указываю цифры для суммы в той последователности, в какой идут биты, от страшего к младшему разряду, то есть слева направо) — получаем 5, или например 110 => 4+2 = 6
111 => 4+2+1 = 7
Эта математика очень проста для вычисления в уме, именно потому и применяется в системе маркировки прав доступа к файлам в *nix.
Теперь добавим ещё немного сложности, и рассмотрим систему из 8 битов, т.е. полноценный байт.
Его можно разбить на 3 секции по битам, и я приведу соответствующие цифры восьмеричной системы:
11 111 111
21 421 421
Теперь, правило такое: в рамках 3 битов в группе числа суммируются, как раньше с 3 битами, но цифры каждой отдельной группы пишутся каждая в своём разряде.
Рассмотрим пример:
10 111 101
Начнём вычисления справа налево (от младшего разряда, отсчитывая по 3 бита):
101 => 4 + 1 = 5
111 = 4 + 2 + 1 = 7
10 => 2
Наглядно:
10 111 101
2 7 5
Значит, итоговое число будет 275 в восьмеричной системе. Фактически, мы отдельно работаем с каждой группой битов (по 3 бита в группе), а потом просто записываем их в нужном порядке.
Фактически, мы отдельно работаем с каждой группой битов (по 3 бита в группе), а потом просто записываем их в нужном порядке.
То есть, если программисту нужно установить битовую последовательность 10111101, достаточно определить в коде переменную с восьмеричным значением 275
Во многих языках программирования нет специального синтаксиса для зависи двоичных значений, например в наиболее распространённых языках C и C++, и удобная запись в восьмеричной системе очень помогает.
В C/C++ и ряде других языков, например Go, восьмеричное число 275 записывается как 0275 (ноль в начале означает, что это восьмеричная система)
Приведу простейший пример на Go (его можно запустить онлайн в https://play.golang.org)
package main
import «fmt»
func main() {
bitmap := 0275 // в Go восьмеричные числа начинаются с нуля, как и в C
fmt.Printf(«%b\n», bitmap)
}
А теперь, как тот же код можно написать используя операции битового сдвига:
package main
import «fmt»
func main() {
bitmap := 1 << 7 + 1 << 5 + 1 << 4 + 1 << 3 + 1 << 2 + 1
fmt.Printf(«%b\n», bitmap)
}
Так же просто в уме производится обратное преобразование из восьмеричной системы в двоичную.
Например, если у нас есть число больше 4 — значит ставим старший (левый крайний бит) равным 1, и отнимаем от числа 4, затем если число всё ещё больше 2 — ставим средний бит и отнимаем от числа 2, и затем проверяем равно ли число 1 (тогда славим правый, младший, бит) или 0 — готово!
Рассмотрим число 7:
7 > 4 значит ставим 100, отнимаем: 7 — 4 = 3
3 > 2 значит ставим 110, отнимаем 3 — 2 = 1
1 значит ставим 111
Для 5:
5 > 4 значит ставим 100, отнимаем: 5 — 4 = 1
1 < 2 значит оставляем 100 и ничего не отнимаем
1 остаётся, значит ставим 101
двоичная, восьмеричная, шестнадцатеричная — урок. Информатика, 8 класс.
Для кодирования информации в компьютере вместо привычной десятичной системы счисления используется двоичная система счисления.
Двоичной системой счисления люди начали пользоваться очень давно. Древние племена Австралии и островов Полинезии использовали эту систему в быту. Так, полинезийцы передавали необходимую информацию, выполняя два вида ударов по барабану: звонкий и глухой. Это было примитивное представление двоичной системы счисления.
Древние племена Австралии и островов Полинезии использовали эту систему в быту. Так, полинезийцы передавали необходимую информацию, выполняя два вида ударов по барабану: звонкий и глухой. Это было примитивное представление двоичной системы счисления.
Алфавит: \(0\) и \(1\).
Для обозначения системы счисления, в которой представляется число, используют нижний индекс, указывающий основание системы. Например, 110112 — число в двоичной системе счисления.
Цифры в двоичном числе являются коэффициентами его представления в виде суммы степеней с основанием \(2\), например:
1012=1 ·22+0 ·21+1 ·20.
Выполнив операции умножения и сложения, получим число в десятичной системе счисления:
1012=4+0+1=5.
Для перевода целого десятичного числа в двоичную систему счисления нужно последовательно выполнять деление данного числа и получаемых целых частных на \(2\) до тех пор, пока не получим частное, равное нулю.
Пример:
Переведём десятичное число \(13\) в двоичную систему счисления. Рассмотренную выше последовательность действий (алгоритм перевода) можно изобразить так:
Получили 1310=11012.
Пример:
Если десятичное число достаточно большое, то более удобен следующий способ записи рассмотренного выше алгоритма:
\(224\) | \(112\) | \(56\) | \(28\) | \(14\) | \(7\) | \(3\) | \(1\) |
\(0\) | \(0\) | \(0\) | \(0\) | \(0\) | \(1\) | \(1\) | \(1\) |
22410=111000002.
Восьмеричной системой счисления называется позиционная система счисления с основанием \(8\).
Алфавит: \(0\), \(1\), \(2\), \(3\), \(4\), \(5\), \(6\), \(7\).
Для перевода целого восьмеричного числа в десятичную систему счисления нужно перейти к его развёрнутой записи и вычислить значение получившегося выражения.
Для перевода целого десятичного числа в восьмеричную систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на 8 до тех пор, пока не получим частное, равное нулю. Исходное число в восьмеричной системе счисления составляется последовательной записью полученных остатков, начиная с последнего.
Пример:
Переведём восьмеричное число 154368 в десятичную систему счисления.
154368=1 ·84+5 ·83+4 ·82+3 ·81+6 ·80=694210
Пример:
Переведём десятичное число \(94\) в восьмеричную систему счисления.
9410=1368
Шестнадцатеричной системой счисления называется позиционная система счисления с основанием \(16\).
Алфавит: \(0\), \(1\), \(2\), \(3\), \(4\), \(5\), \(6\), \(7\), \(8\), \(9\), A, B, C, D, E, F. Буквы A, B, C, D, E, F имеют значения 1010, 1110, 1210, 1310, 1410, 1510.
Для перевода шестнадцатеричного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа.
Для перевода целого десятичного числа в шестнадцатеричную систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на \(16\) до тех пор, пока не получим частное, равное нулю. Исходное число в системе счисления составляется последовательной записью полученных остатков, начиная с последнего.
Пример:
Переведём шестнадцатеричное число \(2\)\(A7\) в десятичное. В соответствии с вышеуказанными правилом представим его в виде суммы степеней с основанием \(16\):
2A716=2
·162+10
·161+7
·160=512+160+7=679.
Пример:
Переведём десятичное число \(158\) в шестнадцатеричную систему счисления.
15810=9E16.
Для перевода числа из любой позиционной системы счисления в десятичную необходимо использовать развернутую формулу числа, заменяя, если это необходимо, буквенные обозначения соответствующими цифрами.
Для перевода целых чисел десятичной системы счисления в число любой системы счисления последовательно выполняют деление нацело на основание системы счисления, пока не получат нуль. Числа, которые возникают как остаток от деления на основание системы счисления, представляют собой последовательную запись разрядов числа в выбранной системе счисления от младшего разряда к старшему. Поэтому для записи самого числа остатки от деления записывают в обратном порядке.
таблица и алфавит, история, применение в информатике
Восьмеричная система счисления — позиционная целочисленная система счисления с основанием 8. Является одной из самых популярных в информатике, наряду с двоичной, десятичной и шестнадцатеричной.
Немного истории
Возникновение восьмеричной системы счисления связывают с техникой счета на пальцах. Однако, если классический счет на пальцах, подразумевает задействование всех десяти, то эта техника использует не пальцы, а промежутки между ними, которых — 8.
Основание и алфавит
Восьмеричная система является традиционной системой счисления с основанием 8. Алфавит состоит их цифр от 0 до 7.
Развернутая форма записи числа будет выглядеть следующим образом:
an-1an-2…a1a0 = an-1 ∙ 8n-1 + an-2 ∙ 8n-2 + ∙∙∙ + a0 ∙ 80
Например:
3678=3 ∙ 82 + 6 ∙ 81 + 7 ∙ 80 = 3 ∙ 64 + 6 ∙ 8 + 7 ∙ 1 = 192 + 48 + 7 = 24710
Применение восьмеричной системы счисления
Многие знают, что компьютеры используют двоичную систему счисления. Однако простому человеку использовать её не удобно, из-за больших вычислений и переводов. В этом случае, гораздо удобнее воспользоваться более емкими системами, такими как восьмеричная или шестнадцатеричная. Восьмеричная очень схожа с десятичной, за исключение двух цифр в алфавите (8,9). Благодаря этому – легка в восприятии. С её помощью можно легко переводить числа с одной системы счисления в другую и совершать арифметические действия.
В этом случае, гораздо удобнее воспользоваться более емкими системами, такими как восьмеричная или шестнадцатеричная. Восьмеричная очень схожа с десятичной, за исключение двух цифр в алфавите (8,9). Благодаря этому – легка в восприятии. С её помощью можно легко переводить числа с одной системы счисления в другую и совершать арифметические действия.
Практическое применение восьмеричная система находила в программировании, однако с развитием компьютерных технологий, практически полностью уступила — шестнадцатеричной. На сегодняшний день, частичное использование можно встретить в Linux-системах.
Таблица десятичных чисел в восьмеричной системе
| Десятичное число | Восьмеричное число |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 10 |
| 9 | 11 |
| 10 | 12 |
| 11 | 13 |
| 12 | 14 |
| 13 | 15 |
| 14 | 16 |
| 15 | 17 |
| 16 | 20 |
| 17 | 21 |
| 18 | 22 |
| 19 | 23 |
| 20 | 24 |
Таблица восьмеричных чисел в двоичной системе
| Восьмеричное число | Двоичное число |
|---|---|
| 0 | 000 |
| 1 | 001 |
| 2 | 010 |
| 3 | 011 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
Оцените материал:
Загрузка. ..
..Поделиться с друзьями:
Восьмеричная система счисления
Содержание:Что такое восьмеричная система счисления
Как перевести целое десятичное число в восьмеричную систему счисления
Как перевести десятичную дробь в восьмеричную систему счисления
Как перевести число из восьмеричной системы счисления в десятичную
Как перевести дробное восьмеричное число в десятичное
Таблица значений десятичных чисел от 0 до 100 в восьмеричной системе счисления
Что такое восьмеричная система счисления
Восьмеричная система счисления, является позиционной системой счисления, то есть имеется зависимость от позиции цифры в записи числа. Для записи числа в восьмеричной системе счисления используется восемь цифр 0, 1, 2, 3, 4, 5, 6 и 7. Для определения в какой системе счисления записано число, внизу, справа от числа ставят цифру, которая называется основанием системы счисления. Например, 72318 или 45568
Например, 72318 или 45568Если вам необходимо перевести число любой системы счисления в другую систему счисления, воспользуйтесь калькулятором систем счисления с подробным решением онлайн.
Как перевести целое десятичное число в восьмеричную систему счисления
Для того, чтобы перевести целое десятичное число в восьмеричную систему счисления нужно десятичное число делить на 8 до тех пор, пока неполное частное не будет равно нулю. В результате будет получено число из остатков деления записанное справа налево.Например, переведем число 36910 в восьмеричную систему счисления:
369 : 8 = 46 остаток: 1
46 : 8 = 5 остаток: 6
5 : 8 = 0 остаток: 5
36910 = 5618
Как перевести десятичную дробь в восьмеричную систему счисления
Для того чтобы перевести десятичную дробь в восьмеричную систему счисления необходимо сначала перевести целую часть десятичной дроби в восьмеричную систему счисления, а затем дробную часть, последовательно умножать на 8, до тех пор, пока в дробной части произведения не получиться ноль (результатом произведения будет целое число) или не будет достигнуто необходимое количество знаков после запятой. Если в результате умножения целая часть не равна нулю, тогда необходимо заменить значение целой части на ноль.
В результате будет получено число из целых частей произведений, записанное слева направо.
Если в результате умножения целая часть не равна нулю, тогда необходимо заменить значение целой части на ноль.
В результате будет получено число из целых частей произведений, записанное слева направо.Например, переведем десятичное число 0.210 в восьмеричную систему счисления:
Переведем целую часть
010 = 08
Переведем дробную часть
0.2 · 8 = 1.6
0.6 · 8 = 4.8
0.8 · 8 = 6.4
0.4 · 8 = 3.2
0.2 · 8 = 1.6
0.6 · 8 = 4.8
0.8 · 8 = 6.4
0.4 · 8 = 3.2
0.2 · 8 = 1.6
0.6 · 8 = 4.8
0.210 = 0.14631463148
Восьмеричные дроби, как и десятичные могут быть как конечными, так и бесконечными. Не всегда конечная десятичная дробь может быть представлена конечной восьмеричной.
В данном примере получается бесконечная периодическая восьмеричная дробь, поэтому умножение на 8 можно производить бесконечное число раз и все равно дробная часть частного не будет равна нулю.![]() В данном случае десятичная дробь 0.2 не может быть точно представлена в восьмеричной системе счисления.
К примеру, дробь 1.510 может быть представлена в восьмеричной системе счисления в виде конечной 2.510 = 1.48.
В данном случае десятичная дробь 0.2 не может быть точно представлена в восьмеричной системе счисления.
К примеру, дробь 1.510 может быть представлена в восьмеричной системе счисления в виде конечной 2.510 = 1.48.
Как перевести число из восьмеричной системы счисления в десятичную
Для того, чтобы перевести число из восьмеричной системы счисления в десятичную систему счисления, необходимо записать позиции каждой цифры в числе с права на лево начиная с нуля. Каждая позиция цифры будет степенью числа 8, так как система счисления 8-ичная. Необходимо последовательно умножить каждое число на 8 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.Например, переведем число 753108 в десятичную систему счисления:
| Позиция в числе | 4 | 3 | 2 | 1 | 0 |
| Число | 7 | 5 | 3 | 1 | 0 |
753108 = 7 ⋅ 84 + 5 ⋅ 83 + 3 ⋅ 82 + 1 ⋅ 81 + 0 ⋅ 80 = 3143210
Как перевести дробное восьмеричное число в десятичное
Для того, чтобы перевести дробное восьмеричное число в десятичное, необходимо записать дробное восьмеричное число, убрав точку и затем сверху расставить индексы. Индексы в дробной части числа начинаются от -1 и продолжаются на уменьшение вправо, индексы в целой части начинаются с 0 и ставятся с права на лево по возрастанию.
Каждая позиция цифры (индекс) будет степенью числа 8, так как система счисления 8-ичная. Необходимо последовательно умножить каждое число на
8 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.
Индексы в дробной части числа начинаются от -1 и продолжаются на уменьшение вправо, индексы в целой части начинаются с 0 и ставятся с права на лево по возрастанию.
Каждая позиция цифры (индекс) будет степенью числа 8, так как система счисления 8-ичная. Необходимо последовательно умножить каждое число на
8 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.Например, переведем дробное восьмеричное число 12.368 в десятичное:
| Позиция в числе | 1 | 0 | -1 | -2 |
| Число | 1 | 2 | 3 | 6 |
12.368 = 1 ⋅ 81 + 2 ⋅ 80 + 3 ⋅ 8-1 + 6 ⋅ 8-2 = 10.4687510
Таблица значений десятичных чисел от 0 до 100 в восьмеричной системе счисления
| Значение числа в десятичной системе счисления | Значение числа в восьмеричной системе счисления |
| 010 | 08 |
| 110 | 18 |
| 210 | 28 |
| 310 | 38 |
| 410 | 48 |
| 510 | 58 |
| 610 | 68 |
| 710 | 78 |
| 810 | 108 |
| 910 | 118 |
| 1010 | 128 |
| 1110 | 138 |
| 1210 | 148 |
| 1310 | 158 |
| 1410 | 168 |
| 1510 | 178 |
| 1610 | 208 |
| 1710 | 218 |
| 1810 | 228 |
| 1910 | 238 |
| 2010 | 248 |
| 2110 | 258 |
| 2210 | 268 |
| 2310 | 278 |
| 2410 | 308 |
| 2510 | 318 |
| 2610 | 328 |
| 2710 | 338 |
| 2810 | 348 |
| 2910 | 358 |
| 3010 | 368 |
| 3110 | 378 |
| 3210 | 408 |
| 3310 | 418 |
| 3410 | 428 |
| 3510 | 438 |
| 3610 | 448 |
| 3710 | 458 |
| 3810 | 468 |
| 3910 | 478 |
| 4010 | 508 |
| 4110 | 518 |
| 4210 | 528 |
| 4310 | 538 |
| 4410 | 548 |
| 4510 | 558 |
| 4610 | 568 |
| 4710 | 578 |
| 4810 | 608 |
| 4910 | 618 |
| 5010 | 628 |
| Значение числа в десятичной системе счисления | Значение числа в восьмеричной системе счисления |
| 5110 | 638 |
| 5210 | 648 |
| 5310 | 658 |
| 5410 | 668 |
| 5510 | 678 |
| 5610 | 708 |
| 5710 | 718 |
| 5810 | 728 |
| 5910 | 738 |
| 6010 | 748 |
| 6110 | 758 |
| 6210 | 768 |
| 6310 | 778 |
| 6410 | 1008 |
| 6510 | 1018 |
| 6610 | 1028 |
| 6710 | 1038 |
| 6810 | 1048 |
| 6910 | 1058 |
| 7010 | 1068 |
| 7110 | 1078 |
| 7210 | 1108 |
| 7310 | 1118 |
| 7410 | 1128 |
| 7510 | 1138 |
| 7610 | 1148 |
| 7710 | 1158 |
| 7810 | 1168 |
| 7910 | 1178 |
| 8010 | 1208 |
| 8110 | 1218 |
| 8210 | 1228 |
| 8310 | 1238 |
| 8410 | 1248 |
| 8510 | 1258 |
| 8610 | 1268 |
| 8710 | 1278 |
| 8810 | 1308 |
| 8910 | 1318 |
| 9010 | 1328 |
| 9110 | 1338 |
| 9210 | 1348 |
| 9310 | 1358 |
| 9410 | 1368 |
| 9510 | 1378 |
| 9610 | 1408 |
| 9710 | 1418 |
| 9810 | 1428 |
| 9910 | 1438 |
| 10010 | 1448 |
Восьмеричная система — счисление — Большая Энциклопедия Нефти и Газа, статья, страница 1
Восьмеричная система — счисление
Cтраница 1
Восьмеричная система счисления применяется для записи программы вычислений на ЭВМ благодаря простоте перевода чисел из восьмеричной в двоичную систему и обратно. [1]
[1]
Восьмеричная система счисления играет в ЭВМ вспомогательную роль и используется для компактной записи двоичных кодов чисел и машинных команд ЭВМ, в различных периферийных устройствах и устройствах подготовки данных. Разбиение двоичного числа на триады осуществляется влево и вправо от запятой, отделяющей целую часть числа от дробной. Если крайние триады получаются неполными, то они дополняются нулями. [2]
Восьмеричная система счисления способствует компактности записи двоичного числа во внешней форме. Двоичный код, подлежащий переводу в восьмеричный, разбивают по триадам, начиная с младших разрядов, и каждой триаде ставят в соответствие разряд восьмеричного числа. [3]
Восьмеричная система счисления удобна тем, что от нее легко можно перейти к двоичной системе счисления. После того как данные записаны в восьмеричной системе, их в процессе ввода в машину чисто механическим путем переводят в двоичную систему счисления. [4]
[4]
Восьмеричная система счисления является наиболее распространенной для кодирования команд машины. [5]
Восьмеричная система счисления применяется программистами для записи вручную программы, а именно для кодирования команд и адресов. Для этой цели восьмеричная система удобна в том отношении, что она более экономична ( требует меньшего числа разрядов, чем двоичная) и в то же время перевод из восьмеричной системы в двоичную очень прост. Одному разряду восьмеричной системы соответствуют три разряда двоичной системы. Поэтому каждый разряд восьмеричной системы переводится в двоичную систему в отдельности. [6]
Восьмеричная система счисления, так же как и шестнадцатеричная, вследствие простоты перевода в двоичную систему широко применяется для представления команд в программе при подготовке задач. [7]
Восьмеричная система счисления имеет основанием число восемь.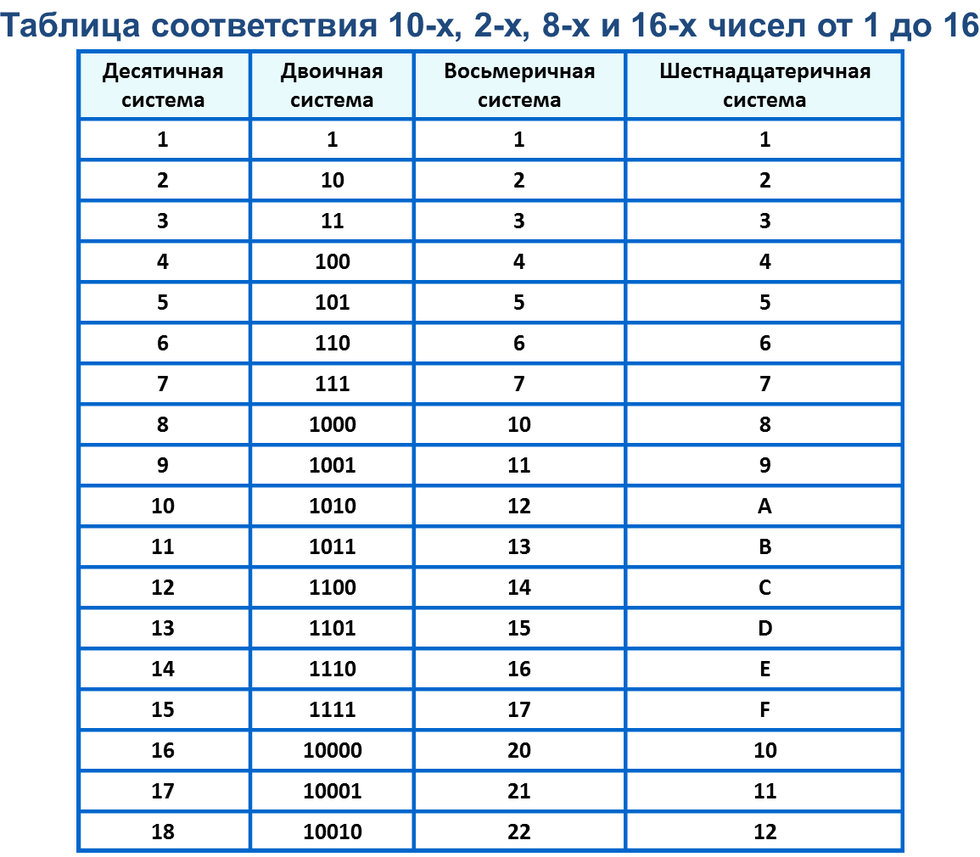 [8]
[8]
Восьмеричная система счисления удобна при выполнении вручную перевода чисел из десятичной системы счисления в двоичную. При этом перевод выполняется в следующем порядке: десятичное число — восьмеричное число — двоичное число. [9]
Восьмеричная система счисления является наиболее распространенной для кодирования команд машины. [10]
Восьмеричная система счисления используется для кодирования операций, нумерации ячеек оперативной и внешней памяти. [11]
Восьмеричная система счисления применяется в ЭВМ в основном для составления программ, так как позволяет производить более короткую и удобную запись двоичных чисел. [12]
Восьмеричную систему счисления используют при подготовке задачи к решению ( программировании), для записи на бланках порядковых номеров команд, кодов операций и адресов в командах. Данная система удобна тем, что в ней запись числа короче в три раза, чем в двоичной системе счисления. Перевод из восьмеричной системы счисления в двоичную и обратно несложен, поскольку он может выполняться при помощи простых электронных и электромеханических схем.
[13]
Данная система удобна тем, что в ней запись числа короче в три раза, чем в двоичной системе счисления. Перевод из восьмеричной системы счисления в двоичную и обратно несложен, поскольку он может выполняться при помощи простых электронных и электромеханических схем.
[13]
Однако восьмеричная система счисления ( так же как двоичная) не используется ни в экономике, ни в технике, и поэтому исходные данные в этой системе не задаются. Тем не менее преимущества восьмеричной системы используются при работе ЭВМ для задания машине программы обработки данных и ряда констант. Команды, образующие программу, кодируются в восьмеричной системе. [14]
Основание восьмеричной системы счисления записывается как 10 ( восемь), оно больше единицы в восемь раз. [15]
Страницы: 1 2 3 4
Информатик БУ — Кратко о системах счисления
Система счисления – это способ записи чисел с помощью символов. Мы все привыкли использовать десять различных знаков для записи чисел: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Такая система счисления называется десятичной. Один знак числа называется цифрой.
Мы все привыкли использовать десять различных знаков для записи чисел: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Такая система счисления называется десятичной. Один знак числа называется цифрой.
Основание системы счисления – это количество знаков, используемых для записи числа в этой системе. Основанием системы счислений, как правило, может являться любое натуральное число (например, шумеры использовали шестидесятеричную систему счисления), но сегодня наиболее распространены (кроме десятичной) двоичная, восьмеричная и шестнадцатеричная. Основание системы счисления указывается подстрочным знаком после числа, например 1012.
Разряд числа – это место цифры в числе. В зависимости от количества разрядов мы называем числа двузначными, трёхзначными, четырёхзначными и т.д.
Двоичная система счисления
Популярность двоичной системы в информатике обусловлена тем, что для записи чисел используется всего две цифры: 0 и 1.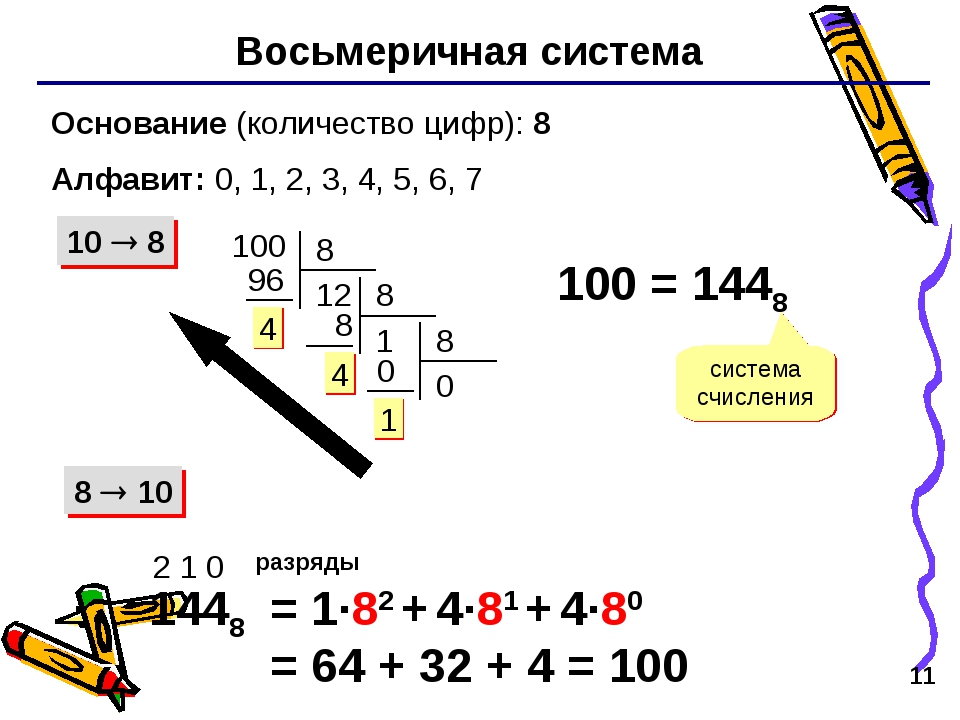 Это соответствует значению одного бита, который тоже может принимать значения 0 и 1. Поэтому во многих случаях один разряд двоичного числа называют битом. А так как в вычислительной технике информация передаётся в битах, то и числа удобнее передавать в виде двоичного (бинарного) кода.
Это соответствует значению одного бита, который тоже может принимать значения 0 и 1. Поэтому во многих случаях один разряд двоичного числа называют битом. А так как в вычислительной технике информация передаётся в битах, то и числа удобнее передавать в виде двоичного (бинарного) кода.
Простой пример. IP-адрес компьютера состоит из четырёх байт, разделенных точками, к примеру:
192.168.0.1
Почему байты записаны в виде чисел? Если перевести байты этого IP-адреса в биты (двоичную систему), мы получим четыре восьмизначных двоичных числа:
11000000. 10101000.00000000.00000001
Двоичные числа состоят из восьми разрядов, а байт равен восьми битам.
Восьмеричная система счисления
Двоичная система счисления удобна для компьютера, но не очень удобна для людей, так как числа, записанные в ней, получаются очень большими по размеру. Представьте, десятичное число 10000000 в двоичной системе выглядит как 100110001001011010000000, не очень удобно, согласитесь?
Поэтому была введена восьмеричная система счисления. Восьмеричная система отличается от десятичной тем, что двоичные числа очень удобно приводить к основанию 8, а восьмеричные – к основанию 2. С десятичной всё немного сложнее. Для перевода используется таблица триад (в правом нижнем углу сайта есть кнопочка, можете посмотреть, а почитать про правила перевода можно здесь).
Восьмеричная система отличается от десятичной тем, что двоичные числа очень удобно приводить к основанию 8, а восьмеричные – к основанию 2. С десятичной всё немного сложнее. Для перевода используется таблица триад (в правом нижнем углу сайта есть кнопочка, можете посмотреть, а почитать про правила перевода можно здесь).
Шестнадцатеричная система счисления
Помните, что один разряд двоичной системы – это один бит? А два разряда шестнадцатеричной системы – это один байт. В современных компьютерах информация кодируется в байтах, поэтому во многих случаях удобно использовать шестнадцатеричную систему.
В шестнадцатеричной системе шестнадцать разрядов: цифры от 0 до 9, и буквы от A до F (где буквы от A до F – десятичные числа от 10 до 15 соответственно).
Шестнадцатеричную систему используют в низкоуровневом программировании, в компьютерном дизайне широко используются шестнадцатеричные коды цвета, в некоторых кодировках символы кодируются именно с помощью шестнадцатеричной системы… В общем, штука полезная:).
Одно из заданий ЕГЭ предыдущих лет было как раз на знание шестнадцатеричных цветовых кодов.
Пример: нужно определить, какой цвет зашифрован кодом #00FF00 в палитре RGB.
Решение: Данный код является кодом цвета в палитре RGB, то есть первые два разряда – Red, вторые два разряда – Green, третьи два разряда – Blue:
#00FF00
Получается, что красного цвета — 0, синего цвета – 0, а зелёного – FF, то есть 255 в десятичной системе счисления (максимальное двузначное шестнадцатеричное число). То есть это код чистого зелёного цвета.
Подобные коды вы можете встретить, к примеру, в палитре цветов Adobe Photoshop, или при разработке внешнего вида сайта, когда для различных элементов дизайна необходимо указать код цвета.
Что такое восьмеричная система счисления? — Определение, восьмеричное в десятичное и десятичное преобразование в восьмеричное
Определение: Система счисления, основание которой равно 8 , известна как восьмеричная система счисления . База 8 означает, что система использует 8 цифр от 0 до 7. Все восемь цифр от 0 до 8 имеют то же физическое значение, что и десятичные числа. Следующая цифра восьмеричного числа представлена числами 10, 11, 12, 13, 14, 15, 16, 17, которые представляют собой десятичные цифры 8, 9, 10, 11, 12, 13, 14, 15.Таким образом, восьмеричное число 20 представляет собой десятичное число 16, а затем 21, 22, 23… .октальные числа будут отображать десятичные цифры 17, 18, 19… и т. Д. И так далее.
Основным недостатком восьмеричной системы счисления является то, что компьютер не понимает восьмеричной системы счисления. Таким образом, для цифровых систем, преобразующих восьмеричное число в двоичное, требуется дополнительная схема. В миникомпьютере используется восьмеричная система счисления.
Восьмеричное преобразование в десятичное
В восьмеричной системе счисления каждая позиция цифры имеет весовую восьмерку относительно степенной восьмерки , показанную на рисунке ниже.
Пример — Рассмотрим восьмеричное число 354,42 в его эквивалентное десятичное число. Целочисленная часть 354 преобразуется в восьмеричную, как показано ниже.
А дробные части 0,42 преобразуются в восьмеричные
В десятичной системе счисления 236,53125.
Преобразование десятичного числа в восьмеричное
Для преобразования десятичного числа в восьмеричное используется восьмеричный метод .В восьмеричном двойном методе целое восьмеричное число равно , разделенному на цифру 8. А для преобразования дробного десятичного числа в восьмеричное число оно умножается на цифру 8 и записывает перенос. Когда эти переносы считываются вниз, получается дробное восьмеричное число.
Пример: Рассмотрим преобразование десятичного числа 236,53. Преобразование целой части показано ниже.
А дробная часть
Таким образом, восьмеричное число равно 354.4172.
систем счисления. Десятичное, двоичное, восьмеричное и шестнадцатеричное | Анны Ромса | Startup
Десятичная, двоичная, восьмеричная и шестнадцатеричная система
Система счисления (или система счисления ) представляет собой систему записи для выражения чисел; то есть математическое обозначение для представления чисел данного набора с использованием цифр или других символов согласованным образом. Число, которое представляет цифра, называется ее значением.Изучая JavaScript, я заинтересовался системами счисления при использовании функции parseInt ().Функция parseInt () используется для преобразования строки в целое число. Эта функция принимает два аргумента: первый аргумент — это строка, которую вы хотите проанализировать, а второй аргумент — это основание .
Основание или основание — это количество уникальных цифр, используемых для представления чисел в позиционной системе счисления. Основание системы счисления в функции parseInt () может быть любым числом 2–36 и по умолчанию не имеет основания 10. Давайте рассмотрим несколько систем подсчета, которые мы используем сегодня.
Уникальные цифры = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
База 10 — это система подсчета, с которой большинство из нас привыкло работать, поэтому мы начнем с нее. Основное / основание системы счисления — 10, потому что оно состоит из 10 цифр. Давайте посмотрим на число 974 210. В приведенном ниже примере 0 находится в «позиции единицы», 1 — в «позиции десятки», 2 — в «позиции сотни», 4 — в «позиции тысячи» и так далее. Каждое число стоит в десять раз больше, чем цифра справа.
Интересный факт: Многие древние цивилизации использовали основание 10 для обозначения чисел. Ходят слухи, что это связано с тем, что люди начинают считать на своих 10 пальцах.
Уникальные цифры = 0, 1
В двоичной системе есть только две цифры для представления каждого числа, поэтому каждая позиция стоит в два раза больше, чем позиция справа от нее.
Если бы мы вели счет в двоичном формате, поскольку у нас есть только две цифры для работы, мы начинаем с 0, затем 1, затем 10, 11, 100, 101 и так далее.Например, здесь двоичная система сравнивается с десятичной:
Интересный факт: Современная двоичная система счисления изучалась в Европе в 16-17 веках, однако системы, связанные с двоичными числами, появились раньше во многих культурах, включая Древний Египет, Китай. и Индия.
Уникальные цифры = 0, 1, 2, 3, 4, 5, 6, 7
У нас есть 8 уникальных цифр для представления значений в восьмеричной системе. Когда мы дойдем до 7, следующим числом будет 10, затем 11 и так далее.После того, как все символы / цифры были использованы, мы снова начинаем с 0 и увеличиваем цифру слева на 1.
Интересный факт: Люди Юки, уроженцы Калифорнии, используют восьмеричную систему, потому что они считают, используя промежутки между пальцами.
Уникальные цифры = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
В шестнадцатеричном формате у нас есть 16 цифр (10 чисел и 6 букв) для обозначения значений. Когда мы достигаем 9, следующее число обозначается буквой A, затем буквой от B до F.После F идет 10 и так далее.
Интересный факт: Шестнадцатеричное число часто используется для представления цветов на веб-страницах в формате #RRGGBB (RR = красные, GG = зеленые, BB = синие). Знак # (или octothorp) указывает, что число было записано в шестнадцатеричном формате. Каждая шестнадцатеричная цифра также известна как полубайт, который представляет четыре двоичных цифры или половину байта.
Теперь, когда мы рассмотрели несколько наиболее часто используемых систем счисления, давайте вернемся к parseInt ().Большую часть времени мы хотим использовать по умолчанию основу 10, особенно при использовании функции parseInt (), поэтому можно с уверенностью сказать, что мы можем полагаться на установку аргумента radix на основе 10. Имейте в виду, что parseInt () по умолчанию не имеет основание 10, поэтому не забудьте установить систему счисления при использовании parseInt ().
parseInt (myNumber, 10)
Чтобы лучше понять 4 системы подсчета, которые мы обсуждали выше, я перечисляю их рядом до 100 в десятичном виде.
Восьмеричные факты для детей
Восьмеричная система счисления — это система счисления с основанием 8.В нем используются цифры от 0 до 7. Система аналогична двоичной (основание 2) и шестнадцатеричной (основание 16). Восьмеричные числа записываются с использованием буквы o перед цифрой, например o04 или o1242. Восьмеричные числа также иногда пишутся с маленькой восьмеркой в правом нижнем углу, как в 1242 8 .
Когда-то восьмеричная система использовалась в основном для работы с компьютерами. Это обеспечило более простой способ работы с двоичными числами. Когда компьютеры перешли от использования 24-битных систем к 32- и 64-битным системам, шестнадцатеричные числа заменили восьмеричные для большинства применений.Некоторые группы, например, коренные американцы, использующие язык юки в Калифорнии и памейские языки в Мексике, также используют восьмеричную систему счисления. Они делают это, потому что, когда они считают, они используют промежутки между пальцами вместо того, чтобы считать настоящие пальцы.
Восьмеричное и двоичное
В восьмеричной системе счисления используется «трехбитное» двоичное кодирование. Каждая цифра восьмеричного числа совпадает с тремя цифрами двоичного числа. Группировка двоичных цифр выполняется справа налево.Первые три двоичные цифры справа сгруппированы в последнюю часть восьмеричного числа, затем следующие три цифры образуют следующую за последней частью числа.
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Восьмеричное и десятичное
В десятичной системе (основание 10) каждая восьмеричная цифра равна этой цифре, умноженной на показатель степени 8, который равен ее положению минус один.
| Место нахождения | ||||||
|---|---|---|---|---|---|---|
| 6 | 5 | 4 | 3 | 2 | 1 | |
| Значение | 32768 (8 5 ) | 4096 (8 4 ) | 512 (8 3 ) | 64 (8 2 ) | 8 (8 1 ) | 1 (8 0 ) |
Пример: o3425 в десятичной системе счисления
|
Восьмеричное и шестнадцатеричное
Octal похож на шестнадцатеричный, потому что они оба легко конвертируются в двоичную.Где восьмеричный равен трехзначному двоичному, шестнадцатеричный равен четырехзначному двоичному. Если восьмеричные числа начинаются с буквы «о», шестнадцатеричные числа заканчиваются буквой «h». Самый простой способ преобразовать одну в другую — преобразовать в двоичную, а затем в другую систему.
| восьмеричный | двоичный | Шестнадцатеричный | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| трехзначный | четырехзначный | |||||||||
| o4 | 100 | 0100 | 04ч | |||||||
| o15 | 001 | 101 | 1101 | 0Dh | ||||||
| o306 | 011 | 000 | 110 | 1100 | 0110 | C6h | ||||
| o54253 | 101 | 100 | 010 | 101 | 011 | 0101 | 1000 | 1010 | 1011 | 58ABh |
Связанные страницы
Основания чисел: восьмеричные и шестнадцатеричные
Purplemath
восьмеричный
Старая компьютерная система счисления — восьмеричная или восьмеричная.Цифры в восьмеричной математике: 0, 1, 2, 3, 4, 5, 6 и 7. Значение «восемь» записывается как «1 восемь и 0 единиц», или 10 8 .
С технической точки зрения существует очень много различных компьютерных протоколов для восьмеричного числа, но мы будем использовать простую математическую систему.
MathHelp.com
Несколько племен Нового Света использовали систему счисления по основанию 8; они считали, используя восемь промежутков между пальцами, а не сами десять пальцев. Синие туземцы в фильме «Аватар» использовали восьмеричное число, потому что на их руках было всего четыре пальца.
Давайте копаем сразу:
Преобразует 357
10 в соответствующее число по основанию восемь.
Я сделаю обычное последовательное деление, на этот раз делю на 8 на каждом шаге:
Как только я добрался до «5» сверху, мне пришлось остановиться, потому что 8 не делится на 5.
Тогда соответствующее восьмеричное число будет 545 8 .
Преобразует 545
8 в соответствующее десятичное число.
Я буду следовать обычной процедуре, перечисляя цифры в одной строке, а затем отсчитывая цифры справа в следующей строке, начиная с нуля:
Затем сделаю обычное сложение и умножение:
5 × 8 2 + 4 × 8 1 + 5 × 8 0
= 5 × 64 + 4 × 8 + 5 × 1
= 320 + 32 + 5
= 357
Тогда соответствующее десятичное число будет 357 10 .
Шестнадцатеричный
Если вы работаете с компьютерным программированием или компьютерной инженерией (или компьютерной графикой, о которой мы поговорим позже), вы столкнетесь с основанием шестнадцати, или шестнадцатеричной, математикой.
Как упоминалось ранее, десятичная математика не имеет одной единственной цифры, представляющей значение «десять». Вместо этого мы используем две цифры, 1 и 0: «10».Но в шестнадцатеричной математике столбцы означают число, кратное шестнадцати! То есть в первом столбце указано, сколько у вас единиц, во втором столбце указано количество шестнадцати, в третьем столбце указано, сколько двести пятьдесят шесть (шестнадцать раз по шестнадцать) и так далее.
В базе десять у нас были цифры от 0 до 9. В базе восемь у нас были цифры от 0 до 7. В базе 4 у нас были цифры от 0 до 3. В любой базовой системе у вас будут цифры от 0 до единицы меньше чем -ваша-база.Это означает, что в шестнадцатеричном формате нам нужны «цифры» от 0 до 15. Для этого нам потребуются отдельные одиночные цифры, обозначающие значения «десять», «одиннадцать», «двенадцать», «тринадцать», «четырнадцать» и «пятнадцать». Но мы этого не делаем. Поэтому вместо этого мы используем буквы. То есть, считая в шестнадцатеричном формате, шестнадцать «цифр» равны:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
Другими словами, A — это «десять» в «обычных» числах, B — «одиннадцать», C — «двенадцать», D — «тринадцать», E — «четырнадцать» и «F» — пятнадцать.Именно это использование букв для цифр делает шестнадцатеричные числа поначалу такими странными. Но преобразования работают обычным образом.
Преобразует 357
10 в соответствующее шестнадцатеричное число.
Здесь я буду делить несколько раз на 16, отслеживая остатки по ходу дела. (Вы можете использовать для этого бумагу для заметок.)
Считывая цифры, начиная сверху и заканчивая правой стороной, я вижу, что:
Преобразует 165
16 в соответствующее десятичное число.
Перечислите цифры и отсчитайте их справа, начиная с нуля:
Помните, что каждая цифра в шестнадцатеричном числе представляет, сколько копий вам нужно от этой шестнадцатой степени, и преобразуйте это число в десятичное:
1 × 16 2 + 6 × 16 1 + 5 × 16 0
= 1 × 256 + 6 × 16 + 5 × 1
= 256 + 96 + 5
= 357
Тогда 165 16 = 357 10 .
Преобразует 63933
10 в соответствующее шестнадцатеричное число.
Я буду делить несколько раз на 16, отслеживая остатки:
Из последовательного деления выше я вижу, что шестнадцатеричное число будет иметь «пятнадцать» в столбце с шестнадцатью квадратами, «девять» в столбце с шестнадцатью квадратами, «одиннадцать» в столбце с шестнадцатью квадратами и « тринадцать дюймов в колонке единиц.Но я не могу записать шестнадцатеричное число как «15
Тогда 63933 10 = F9BD 16 .
Преобразует F9BD в десятичную систему счисления.
Я перечислю цифры и отсчитаю их справа, начиная с нуля:
На самом деле, вероятно, будет полезно переделать это, преобразовав буквенные шестнадцатеричные «цифры» в соответствующие им «обычные» десятичные значения:
Теперь сделаю умножение и сложение:
15 × 16 3 + 9 × 16 2 + 11 × 16 1 + 13 × 16 0
= 15 × 4096 + 9 × 256 + 11 × 16 + 13 × 1
= 61440 + 2304 + 176 + 13
= 63933
Как и ожидалось, F9BD 16 = 63933 10 .
Компьютерная графика
Если вы работаете с веб-страницами и графическими программами, вам может быть полезно преобразовать значения RGB (для изображения в графической программе) в шестнадцатеричные значения (для соответствующего цвета фона на веб-странице).
Графические программы работают со значениями RGB (красный-зеленый-синий) для цветов. Каждый из этих компонентов данного цвета имеет значения от 0 до 255.Эти значения могут быть преобразованы в шестнадцатеричные значения от 00 до FF. Если вы перечислите компоненты RGB цвета в виде строки из трех чисел, вы можете получить, скажем, R: 204, G: 51, B: 255, что переводится в светло-пурпурный # CC33FF в кодировке HTML. Обратите внимание, что 204 10 = CC 16 , 51 10 = 33 16 и 255 10 = FF 16 .
Партнер
С другой стороны, если у вас есть код для # 9
, это будет преобразовано в темно-красноватый R: 153, G: 0, B: 51 в вашей графической программе.То есть, чтобы преобразовать вашу графическую программу в кодировку веб-страницы, используйте шестнадцатеричное число не как одно шестизначное число, а как три двузначных числа, и преобразуйте эти пары цифр в соответствующие значения RGB.Для обсуждения истории «безопасных для Интернета» цветов, в том числе того, почему они включают только шестнадцатеричные эквиваленты 0, 51, 102, 153, 204 и 255, смотрите здесь. Для демонстрации различных цветов текста и фона в HTML посмотрите здесь.
URL: https://www.purplemath.com/modules/numbbase3.htm
Двоичная, шестнадцатеричная и восьмеричная система счисления
Двоичная, шестнадцатеричная и восьмеричная системы относятся к разным системам счисления. Тот, который мы обычно используем, называется десятичным. Эти системы счисления относятся к количеству символов, используемых для представления чисел.В десятичной системе мы используем десять различных символов: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. С помощью этих десяти символов мы можем представить любую величину. Например, если мы видим 2, значит, мы знаем, что есть два чего-то. Например, в конце предложения две точки.
Когда у нас заканчиваются символы, мы переходим к размещению следующей цифры. Чтобы представить единицу больше 9, мы используем 10, что означает одну единицу из десяти и ноль единиц. Это может показаться элементарным, но очень важно понимать нашу систему счисления по умолчанию, если вы хотите понимать другие системы счисления.
Например, когда мы рассматриваем двоичную систему, в которой используются только два символа, 0 и 1, когда у нас заканчиваются символы, нам нужно перейти к размещению следующей цифры. Итак, мы будем считать в двоичном формате 0, 1, 10, 11, 100, 101 и так далее.
В этой статье более подробно рассматриваются двоичная, шестнадцатеричная и восьмеричная системы счисления и объясняется их использование.
Системы счисления используются для описания количества чего-либо или представления определенной информации. В связи с этим могу сказать, что слово «калькулятор» состоит из десяти букв.Наша система счисления, десятичная система, использует десять символов. Следовательно, десятичным считается Base Ten . Описывая системы с помощью оснований, мы можем понять, как работает эта конкретная система.
Когда мы считаем по базе десять, мы считаем, начиная с нуля и заканчивая девятью по порядку.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9,…
Когда мы дойдем до последнего символа, мы создадим новое размещение перед первым и посчитаем его.
8, 9, 1 0, 11, 12,…, 19, 2 0,…
Это продолжается, когда у нас заканчиваются символы для этого места размещения.Итак, после 99 мы переходим к 100.
Размещение символа указывает, сколько он стоит. Каждое дополнительное размещение дает дополнительную степень 10. Рассмотрим число 2853. Мы знаем, что это число довольно велико, например, если оно относится к количеству яблок в корзине. Это много яблок. Как мы узнаем, что он большой? Смотрим количество цифр.
Каждое дополнительное размещение — это дополнительная степень 10, как указано выше. Рассмотрим эту диаграмму.| 10 3 | 10 2 | 10 1 | 10 0 |
|---|---|---|---|
| цифра | цифра | цифра | цифра |
| * 1000 | * 100 | * 10 | * 1 |
Каждая дополнительная цифра представляет все большее и большее количество.Это применимо как для Base 10, так и для других баз. Знание этого поможет вам лучше понять другие основы.
двоичный
Binary — это еще один способ сказать Base Two. Итак, в двоичной системе счисления для представления чисел используются только два символа: 0 и 1. Когда мы считаем с нуля в двоичной системе счисления, символы заканчиваются гораздо чаще.
Отсюда символов больше нет. Мы не переходим к 2, потому что в двоичном формате 2 не существует. Вместо этого мы используем 10.В двоичной системе 10 равно 2 в десятичной системе счисления.
Мы можем считать дальше.
| Двоичный | 0 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | 1001 | 1010 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Десятичное число | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 6 | 2 5 | 2 4 | 2 3 | 2 2 | 2 1 | 2 0 |
|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| 64 + 0 + 0 + 8 + 4 + 0 + 1 | ||||||
| 77 | ||||||
Однако, поскольку это основание два, числа не становятся такими большими, как в десятичном.Тем не менее, двоичное число из 10 цифр будет больше 1000 в десятичном.
Двоичная система используется в информатике и электротехнике. Транзисторы работают от двоичной системы, и транзисторы можно найти практически во всех электронных устройствах. 0 означает отсутствие тока, а 1 означает разрешение тока. Когда различные транзисторы включаются и выключаются, сигналы и электричество отправляются для выполнения различных действий, например, для совершения звонка или вывода этих букв на экран.
Компьютеры и электроника работают с байтами или восьмизначными двоичными числами. Каждый байт содержит закодированную информацию, которую компьютер способен понять. Многие байты объединяются в цепочки для формирования цифровых данных, которые можно сохранить для дальнейшего использования.
восьмеричный
Восьмеричная система счисления — это еще одна система счисления, в которой используется меньше символов, чем в нашей традиционной системе счисления. Восьмеричный формат является модным для Base Eight, что означает, что восемь символов используются для представления всех величин. Это 0, 1, 2, 3, 4, 5, 6 и 7.Когда мы считаем единицу из 7, нам нужно новое размещение, чтобы представить то, что мы называем 8, поскольку 8 не существует в Octal. Итак, после 7 будет 10.
| восьмеричный | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 10 | 11 | 12… | 17 | 20… | 30… | 77 | 100 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Десятичное число | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10… | 15 | 16… | 24… | 63 | 64 |
Так же, как мы использовали степень десяти в десятичной системе и степень двойки в двоичной системе, для определения значения числа мы будем использовать степень восьмерки, поскольку это основание восемь.Рассмотрим число 3623 по основанию восемь.
| 8 3 | 8 2 | 8 1 | 8 0 |
|---|---|---|---|
| 3 | 6 | 2 | 3 |
| 1536 + 384 + 16 + 3 | |||
| 1939 | |||
Каждое дополнительное размещение слева имеет большую ценность, чем в двоичном формате. Третья цифра справа в двоичном формате представляет только 2 3-1 , то есть 4.В восьмеричном формате это 8 3-1 , что равно 64.
Шестнадцатеричный
Шестнадцатеричная система счисления — основание шестнадцати. Как следует из основания, эта система счисления использует шестнадцать символов для представления чисел. В отличие от двоичного и восьмеричного, шестнадцатеричный имеет шесть дополнительных символов, которые он использует помимо обычных, найденных в десятичном. Но что будет после 9? 10 — это не одна цифра, а две … К счастью, по соглашению, когда необходимы дополнительные символы помимо обычных десяти, должны использоваться буквы.Итак, в шестнадцатеричном формате общий список используемых символов составляет 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E и F. На цифровом дисплее , числа B и D строчные.
При шестнадцатеричном счете вы считаете 0, 1, 2 и так далее. Однако, когда вы достигнете 9, вы перейдете прямо к A. Затем вы считаете B, C, D, E и F. Но что дальше? У нас закончились символы! Когда у нас заканчиваются символы, мы создаем новое расположение цифр и идем дальше. Таким образом, после F будет 10. Вы продолжаете считать, пока не дойдете до 19. После 19 следующее число — 1A.Это продолжается вечно.
| Шестнадцатеричный | 9 | А | B | С | D | E | F | 10 | 11… | 19 | 1A | 1Б | 1С… | 9F | A0 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Десятичное число | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 25 | 26 | 27 | 28 | 159 | 160 |
Цифры объясняются степенью 16.Рассмотрим шестнадцатеричное число 2DB7.
| 16 3 | 16 2 | 16 1 | 16 0 |
|---|---|---|---|
| 2 | D | B | 7 |
| 8192 + 3328 + 176 + 7 | |||
| 11703 | |||
Как видите, размещение в шестнадцатеричной системе счисления намного дороже, чем в любой из трех других систем счисления.
Важно знать, что 364 в восьмеричной системе счисления — это , а не , равное обычному 364.Это похоже на то, как 10 в двоичном формате определенно не является 10 в десятичном. 10 в двоичном формате (с этого момента будет записываться как 10 2 ) равно 2. 10 8 равно 8. Откуда мы это знаем? Что такое 20C.38F 16 и как нам узнать?
Вот почему важно понимать, как работают системы счисления. Используя нашу степень основного числа, становится возможным преобразовать любое число в десятичное, а из десятичного в любое.
Десятичное основание
Итак, мы знаем, что 364 8 не равно десятичному числу 364.{p-1} + … + v_1B + v_0 \ end {формула}
Где V 10 — десятичное значение, v — цифра в расположении, p — это размещение справа от числа, предполагая, что крайнее правое размещение равно 0, а B — начальная база. Не пугайтесь формулы! Мы собираемся пройти через это шаг за шагом.
Итак, допустим, у нас есть простое шестнадцатеричное число 2B. Мы хотим знать, что это за число в десятичной системе, чтобы лучше понять его. как нам это сделать?
Воспользуемся формулой выше.Сначала определите каждую переменную. Мы хотим найти V 10 , так что это неизвестно. Число 2B 16 имеет две позиции, так как оно состоит из двух цифр. Следовательно, p на единицу меньше этого значения, поэтому p равно 1. Число в базе 16, поэтому B равно 16. Наконец, мы хотим знать, что такое v, но есть несколько v. У вас v 1 и v 0 . Это относится к значению цифры в позиции индекса. v 1 относится к цифре в первой позиции (вторая цифра справа).0) \\ V_ {10} = 2 (16) +11 (1) \\ V_ {10} = 32 + 11 \\ V_ {10} = 43 \\ \ end {align}
Следовательно, 2B 16 равно 43.
Теперь позвольте мне объяснить, как это работает. Помните, как расположение цифр влияет на фактическое значение? Например, в десятичном числе 123 «1» представляет 100, что составляет 1 * 10 2 . «2» — это 20 или 2 * 10 1 . Аналогично, в числе 2B 16 цифра «2» — это 2 * 16 1 , а буква B — 11 * 16 0 .
Таким образом мы можем определить значение чисел.Для числа 364 8 мы создадим диаграмму, которая показывает десятичное значение каждой отдельной цифры. Затем мы можем сложить их, чтобы получить целое. Число состоит из трех цифр, поэтому, начиная справа, у нас есть позиция 0, позиция 1 и позиция 2. Поскольку это основание восемь, мы будем использовать степень 8.
Сейчас 8 2 64. 8 1 8. 8 0 1. Что дальше?
Помните, что мы сделали с десятичным числом 123? Мы взяли значение цифры , умноженное на соответствующей степени.Итак, учитывая это дальше…
Теперь мы складываем значения вместе, чтобы получить 244. Следовательно, 364 8 равно 244 10 .
Точно так же, как для 123, мы говорим, что есть одна группа по 100, две группы по 10 и три группы по 1, для восьмеричной системы и числа 364 существуют три группы по 64, шесть групп по 8 и четыре группы по 1.
от десятичной дроби к основанию
Так же, как мы можем преобразовать из любого основания в десятичное, можно преобразовать десятичное в любое основание.p \\ (4) \ hspace {6pt} Повторяйте шаги \ hspace {4pt} с \ hspace {4pt} 1 \ hspace {4pt} через \ hspace {4pt} 3 \ hspace {4pt}, пока \ hspace {4pt} p = 0 \\ \ end {align}
Сначала этот алгоритм может показаться запутанным, но давайте рассмотрим пример, чтобы увидеть, как его можно использовать. Мы хотим представить 236 в двоичном, восьмеричном и шестнадцатеричном формате. Итак, давайте сначала попробуем преобразовать его в двоичный код.
Первый шаг — сделать p равным $ \ operatorname {int} (\ sqrt [B] {V}) $. B — это база, в которую мы хотим преобразовать 2.V — это число, которое мы хотим преобразовать, 236. По сути, мы извлекаем квадратный корень из 236 и игнорируем десятичную часть. В результате p становится равным 7.
Шаг второй говорит, что пусть v равно нашему числу V, деленному на B p . B p равно 2 7 , или 128, а целая часть 236, деленная на 128, равна 1. Следовательно, наша первая цифра слева равна 1. Теперь мы фактически меняем V, чтобы стать V минус цифра, умноженная на В стр . Итак, V теперь будет 236-128 или 108.
Мы просто повторяем процесс до тех пор, пока p не станет равным нулю. Когда p становится равным нулю, мы завершаем шаги в последний раз, а затем заканчиваем.
Итак, поскольку V теперь 108, p становится 6. P \ end {уравнение}
На человеческом языке: значение шифра в числе равно значению самого шифра, умноженному на основание системы счисления в степень позиции шифра слева направо в числе, начиная с при 0.Прочтите это несколько раз и попытайтесь понять.
Таким образом, значение цифры в двоичном формате удваивается каждый раз, когда мы перемещаемся влево. (см. таблицу ниже)
Из этого следует, что каждый шестнадцатеричный шифр можно разбить на 4 двоичных разряда. На компьютерном языке: кусочек. Теперь взгляните на следующую таблицу:
| Двоичные числа | ||||||
|---|---|---|---|---|---|---|
| 8 | 4 | 2 | 1 | Шестнадцатеричное значение | Десятичное значение | |
| 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 1 | 1 | 1 | |
| 0 | 0 | 1 | 0 | 2 | 2 | |
| 0 | 0 | 1 | 1 | 3 | 3 | |
| 0 | 1 | 0 | 0 | 4 | 4 | |
| 0 | 1 | 0 | 1 | 5 | 5 | |
| 0 | 1 | 1 | 0 | 6 | 6 | |
| 0 | 1 | 1 | 1 | 7 | 7 | |
| 1 | 0 | 0 | 0 | 8 | 8 | |
| 1 | 0 | 0 | 1 | 9 | 9 | |
| 1 | 0 | 1 | 0 | А | 10 | |
| 1 | 0 | 1 | 1 | B | 11 | |
| 1 | 1 | 0 | 0 | С | 12 | |
| 1 | 1 | 0 | 1 | D | 13 | |
| 1 | 1 | 1 | 0 | E | 14 | |
| 1 | 1 | 1 | 1 | F | 15 | |
Еще один интересный момент: посмотрите на значение в верхней части столбца.Тогда посмотрите на значения. Вы понимаете, о чем я? Да, ты прав! Биты включаются и выключаются в зависимости от своего значения. Значение первой цифры (начиная справа) выглядит следующим образом: 0,1,0,1,0,1,0,1,0,1,… Вторая цифра: 0,0,1,1,0 , 0,1,1,0,0,1,1,0,0… Третья цифра (значение = 4): 0,0,0,0,1,1,1,1,0,0,0,0 , 1,1,1,1,… И так далее…
А как насчет больших чисел? Поэтому нам понадобится дополнительная цифра. (но я думаю, вы догадались сами). Для значений начиная с 16 наша таблица выглядит так:
| Двоичные числа | |||||||
|---|---|---|---|---|---|---|---|
| 16 | 8 | 4 | 2 | 1 | Шестнадцатеричное значение | Десятичное значение | |
| 1 | 0 | 0 | 0 | 0 | 10 | 16 | |
| 1 | 0 | 0 | 0 | 1 | 11 | 17 | |
| 1 | 0 | 0 | 1 | 0 | 12 | 18 | |
| 1 | 0 | 0 | 1 | 1 | 13 | 19 | |
| 1 | 0 | 1 | 0 | 0 | 14 | 20 | |
| 1 | 0 | 1 | 0 | 1 | 15 | 21 | |
| 1 | 0 | 1 | 1 | 0 | 16 | 22 | |
| 1 | 0 | 1 | 1 | 1 | 17 | 23 | |
| 1 | 1 | 0 | 0 | 0 | 18 | 24 | |
| 1 | 1 | 0 | 0 | 1 | 19 | 25 | |
| 1 | 1 | 0 | 1 | 0 | 1A | 26 | |
| 1 | 1 | 0 | 1 | 1 | 1Б | 27 | |
| 1 | 1 | 1 | 0 | 0 | 1С | 28 | |
| 1 | 1 | 1 | 0 | 1 | 1D | 29 | |
| 1 | 1 | 1 | 1 | 0 | 1E | 30 | |
| 1 | 1 | 1 | 1 | 1 | 1 этаж | 31 | |
| Двоичные числа | |||||
|---|---|---|---|---|---|
| 4 | 2 | 1 | Восьмеричное значение | Десятичное значение | |
| 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 1 | 1 | |
| 0 | 1 | 0 | 2 | 2 | |
| 0 | 1 | 1 | 3 | 3 | |
| 1 | 0 | 0 | 4 | 4 | |
| 1 | 0 | 1 | 5 | 5 | |
| 1 | 1 | 0 | 6 | 6 | |
| 1 | 1 | 1 | 7 | 7 | |
В последней теме я объяснил логику двоичной, шестнадцатеричной и восьмеричной систем счисления.Теперь я объясню кое-что более практичное. Если вы полностью поняли предыдущее, можете пропустить эту тему.
Из десятичного числа в двоичное
- Шаг 1. Убедитесь, что ваш номер нечетный или четный.
- Шаг 2: Если четный, напишите 0 (двигаясь в обратном направлении, добавляя двоичные цифры слева от результата).
- Шаг 3: В противном случае, если он нечетный, напишите 1 (таким же образом).
- Шаг 4: Разделите ваше число на 2 (отбрасывая любую дробь) и вернитесь к шагу 1. Повторяйте, пока ваше исходное число не станет 0.
Пример:
Преобразование 68 в двоичное:
- 68 четное, поэтому пишем 0.
- Разделив 68 на 2, получим 34.
- 34 тоже четное, поэтому пишем 0 (пока результат — 00)
- Разделив 34 на 2, получим 17.
- 17 является нечетным, поэтому мы пишем 1 (результат пока — 100 — не забудьте добавить его слева)
- Разделив 17 на 2, мы получим 8,5, или всего 8.
- 8 четное, поэтому пишем 0 (пока результат — 0100)
- Разделив 8 на 2, получим 4.
- 4 четное, поэтому пишем 0 (пока результат — 00100)
- Разделив 4 на 2, получим 2.
- 2 чётно, поэтому пишем 0 (пока результат — 000100)
- Разделив 2 на 2, получим 1.
- 1 нечетное, поэтому пишем 1 (пока результат — 1000100)
- Разделив на 2, мы получим 0,5 или просто 0, так что все готово.
- Конечный результат: 1000100
Из двоичного в десятичный
- Запишите значения в таблицу, как показано выше. (или сделайте это мысленно)
- Добавьте значение в заголовке столбца к своему номеру, если цифра включена (1).
- Пропустите, если значение в заголовке столбца выключено (0).
- Переходите к следующей цифре, пока не закончите все.
Пример:
Преобразование 101100 в десятичное:
- Наивысшая цифра значения: 32. Текущий номер: 32
- Пропустите цифру «16», ее значение равно 0. Текущий номер: 32
- Добавить 8. Текущий номер: 40
- Добавить 4. Текущий номер: 44
- Пропустите цифры «2» и «1», так как их значение равно 0.
- Окончательный ответ: 44
Из десятичного в шестнадцатеричный.
ЭТО ТОЛЬКО ОДИН ИЗ МНОГИХ СПОСОБОВ!
- Преобразуйте десятичное число в двоичное
- Разделить на 4 полубайта, начиная с конца
- Посмотрите на первую таблицу на этой странице и напишите правильный номер вместо полубайта
(вы можете добавить нули в начале, если количество бит не делится на 4, потому что, как и в десятичном, это не имеет значения)
Пример:
Преобразование 39 в шестнадцатеричное:
- Сначала преобразуем в двоичный (см. Выше).Результат: 100111
- Затем мы разбиваем его на полубайты: 0010/0111 (Примечание: я добавил два нуля, чтобы прояснить тот факт, что это полубайты)
- После этого преобразуем полубайты отдельно.
- Окончательный результат: 27
Из шестнадцатеричного в десятичный
* Проверьте формулу в первом абзаце и используйте ее для шифров в шестнадцатеричном числе. (это действительно работает для любого преобразования в десятичную систему счисления)
Пример:
Преобразование 1AB в десятичное:
- Значение B = 16 0 × 11.Это дает 11, очевидно,
- Значение A = 16 1 × 10. Это дает 160. Наш текущий результат — 171.
- Значение 1 = 16 2 × 1. Это дает 256.
- Окончательный результат: 427
От десятичной к восьмеричной
- Преобразовать в двоичный.
- Разделить на части по 3 цифры, начиная справа.
- Преобразование каждой части в восьмеричное значение от 0 до 7
Пример: преобразование 25 в восьмеричное
- Сначала преобразуем в двоичный.Результат: 11001
- Далее мы разделились: 011/001
- Преобразование в восьмеричное: 31
От восьмеричного к десятичному
Снова применим формулу сверху
Пример: преобразовать 42 в десятичное
- Значение 2 = 8 0 × 2 = 2
- Значение 4 = 8 1 × 4 = 32
- Результат: 34
Хорошо, это может быть не на 100% «забавным», но тем не менее интересно.
- Вы склонны видеть числа, начинающиеся с 0x? Это обычная нотация для указания шестнадцатеричных чисел, поэтому вы можете увидеть что-то вроде:
0x000000
0x000002
0x000004
Эта нотация чаще всего используется для перечисления адресов компьютеров, а это совсем другая история.
- Это довольно очевидно, но вы можете «писать» слова, используя шестнадцатеричные числа. Например:
- CAB = 3243 в десятичной системе счисления.
Вы все поняли? Если вы так думаете, проверьте себя:
| Корзина | декабрь | шестигранник |
|---|---|---|
| … | … | 3A |
| … | 76 | … |
| 101110 | … | … |
| … | 88 | … |
| 1011110 | … | … |
| … | … | 47 |
Сделайте несколько упражнений самостоятельно, если хотите еще.
Восьмеричная система счисления— определение и преобразование
Под названием «Восьмеричная система счисления» мы можем понять, что это разновидность системы счисления. Итак, прежде чем мы узнаем восьмеричную систему счисления, позвольте нам сначала узнать, что такое система счисления? Система счисления, также известная как система счисления, представляет собой систему именования, представления или выражения чисел. В математике мы можем называть или представлять числа в различных формах.Четыре основных способа представления чисел — это двоичная система счисления, десятичная система счисления, шестнадцатеричная система счисления и восьмеричная система счисления. Теперь дайте нам знать все концепции системы счисления вместе с их типами, преобразованиями и примерами.
Что такое система счисления?
Система счисления — это способ или система письма, которую мы используем для выражения чисел. Это математическое обозначение, используемое для представления чисел данного набора с использованием цифр или других символов в логической манере.Система счисления позволяет нам представить каждое число уникальным образом. Он представляет собой арифметическую и алгебраическую структуру фигур. Не только это, но также позволяет нам выполнять арифметические операции, такие как сложение, вычитание и деление.
Значение цифры в числе обычно определяется следующим образом:
Типы систем счисления
В математике мы можем представлять числа в различных типах, но четыре основные системы счисления:
Десятичная система счисления (Base- 10)
Двоичная система счисления (Base- 2)
Восьмеричная система счисления (Base-8)
Шестнадцатеричная система счисления (Base- 16)
Восьмеричное число Система
Восьмеричная система счисления — это система с основанием восемь и числа от 0 до 7.Это одна из классификаций систем счисления, помимо двоичных, десятичных и шестнадцатеричных чисел. Символ восьмеричного числа используется для обозначения чисел с основанием 8. Существуют различные применения и важность восьмеричных чисел. Одно из наиболее распространенных его применений — основы работы с компьютером. Мы можем преобразовать восьмеричные числа в десятичные числа, двоичные числа в восьмеричные числа, где нам сначала нужно преобразовать двоичное число в десятичное число, а десятичное число в восьмеричное число.Итак, давайте сначала обсудим восьмеричное число с его определением, таблицей, примером и применением.
Что такое восьмеричная система счисления?
Система счисления с основанием «восемь» известна как восьмеричная система счисления и использует числа от 0 до 7, то есть 0, 1, 2, 3, 4, 5, 6 и 7. Мы можем взять пример. , чтобы лучше понять концепцию. Как мы уже знаем, любое число с основанием 8 называется восьмеричным числом, например \ [24_ {8} \], \ [109_ {8} \], \ [55_ {8} \] и т. Д.
Просто как восьмеричные числа представлены с основанием 8, таким же образом двоичное число представлено с основанием 2, десятичное число с основанием 10 и шестнадцатеричное число представлено с основанием 16.{-3} \] …… и т. Д.
↑
Восьмеричная точка
Чтобы преобразовать восьмеричное число в двоичное, преобразование должно выполняться путем преобразования каждого числа из восьмеричной цифры в двоичную. Каждая цифра должна быть преобразована в 3-битное двоичное число, и результат будет двоичным эквивалентом восьмеричного числа.
Преобразование из восьмеричного в двоичное
Восьмеричный символ | Двоичный эквивалент | |||||
0 | 00016 | 00016 | ||||
2 | 010 | |||||
3 | 011 | |||||
4 | 100 3 | 100 3 | 101 | |||
6 | 110 | |||||
7 | 111 |
Пример 1) Преобразовать \ [(145056) _ {8} \]
Решение 1) Чтобы преобразовать восьмеричное в двоичное и наоборот, нам понадобится эта таблица преобразования. Согласно таблице восьмеричное значение \ [(145056) _ {8} \] может быть преобразовано в двоичное как
\ [(001 \: 100 \: 101 \:. 101 \: 110) _ {2} \ ]
Преобразование двоичного числа в восьмеричное
Мы можем использовать ту же таблицу для преобразования двоичного числа в восьмеричное. И для этого мы сначала должны сгруппировать двоичное число в группу из трех бит и записать его восьмеричный эквивалент.
Пример 2) Преобразование двоичного числа \ [(11001111) _ {2} \] в восьмеричное
Решение 2) Трехбитовая группа двоичных чисел может быть записана как 011 001 111, потому что мы должны добавить ноль перед каждым числом, чтобы завершите группировку в виде трех двоичных цифр.Следовательно, восьмеричные числа будут 3, 1, 7, т. Е. \ [(317) _ {8} \]
Преобразование восьмеричного числа в десятичное
Метод, который мы используем для преобразования восьмеричного числа в его десятичный эквивалент, чрезвычайно просто. {0} \] = 207
Преобразование десятичного числа в восьмеричное
Мы можем преобразовать число из десятичного в восьмеричное, разделив число на 8 с помощью повторного деления. метод, который обычно известен как метод двойного прикосновения.Делаем повторное деление и находим остаток. Вот пример.
Пример 4) Преобразуйте десятичное число 158 в восьмеричное.
Решение 4) Мы должны разделить число 158 на 8 следующим образом:
Изображение будет загружено в ближайшее время
Следовательно, в восьмеричном формате значение будет \ [236_ {8} \]
Преобразовать восьмеричное в base-8 • Конвертер чисел • Обычные конвертеры единиц • Компактный калькулятор • Онлайн-конвертеры единиц
Конвертер длины и расстояния Конвертер массы Конвертер сухого объема и общих измерений при варке Конвертер скоростиКонвертер углового КПД, расхода топлива и экономии топливаКонвертер чиселПреобразователь единиц информации и хранения данныхКурсы валютЖенская одежда и размеры обувиМужская одежда и размеры обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияУгловое ускорение Конвертер ионов Конвертер плотности Конвертер удельного объема Конвертер момента инерции Конвертер момента силы Конвертер крутящего момента Конвертер удельной энергии, теплоты сгорания (на единицу массы) Конвертер удельной энергии, теплоты сгорания (на единицу объема) Конвертер плотности потока Конвертер коэффициентов теплопередачиКонвертер объемного расходаКонвертер массового расходаМолярный расходПреобразователь массового потокаКонвертер молярной концентрацииМассовая концентрация в раствореКонвертер динамической (абсолютной) вязкостиКинематический конвертер вязкости Конвертер поверхностного натяженияПреобразователь уровня проницаемости, проницаемости, паропроницаемости Конвертер уровня трансмиссии звука и пара (SPL) Converter Конвертер уровня звукового давления с выбираемым эталонным параметром Pr essureПреобразователь яркостиПреобразователь яркостиПреобразователь разрешения цифрового изображенияПреобразователь частоты и длины волныПреобразователь оптической мощности (диоптрий) в фокусное расстояниеПреобразователь оптической мощности (диоптрий) в увеличение (X )Преобразователь электрического зарядаПреобразователь линейной плотности зарядаПреобразователь плотности поверхностного зарядаПреобразователь плотности электрического токаПреобразователь плотности электрического тока Конвертер электрического потенциала и напряженияПреобразователь электрического сопротивленияПреобразователь электрического сопротивленияПреобразователь электрической проводимостиПреобразователь электрической проводимостиПреобразователь емкостиПреобразователь индуктивностиПреобразователь реактивной мощности переменного токаПреобразователь американского калибра проводовПреобразование уровней в дБм, дБВ, ваттах и других единицахПреобразователь магнитодвижущей силы Преобразователь магнитной индукции магнитного поля Преобразователь магнитной индукции Конвертер ставокRa диактивность.Конвертер радиоактивного распада Конвертер радиоактивного облученияРадиация. Конвертер поглощенной дозы Конвертер метрических префиксов Конвертер передачи данных Конвертер единиц типографии и цифровых изображений Конвертер единиц измерения объема древесиныКалькулятор молярной массыПериодическая таблица
Обзор
Приложение калькулятора iPhone
Число — это абстрактное математическое понятие, представляющее величину. Используется при подсчете. Числа использовались с древних времен, сначала в виде счетных отметок — царапин на дереве или кости, а затем в качестве более абстрактных систем.Есть несколько способов выражения чисел в числовых системах. Некоторые из них сегодня не используются.
Различные способы представления чисел
Некоторые исследователи считают, что понятие числа возникло независимо в разных регионах. Первоначально письменные представления чисел с помощью символов развивались независимо, но когда торговля между странами и континентами стала широко распространенной, люди учились и заимствовали друг у друга, а системы счисления, используемые в настоящее время, были созданы на основе коллективного знания.
Индусско-арабские цифры
Индо-арабская система счисления является одной из наиболее широко используемых в современном мире. Первоначально он был разработан в Индии и усовершенствован персидскими и арабскими математиками. В средние века он распространился на западный мир через торговлю, заменив римскую систему счисления. Он был дополнительно модифицирован и широко принят во всем мире из-за европейской торговли и колонизации. Это система с основанием 10, что означает, что она основана на десятичных числах и использует десять символов для представления всех чисел.
Десять — это обычное число, которое используют для счета, потому что у людей десять пальцев, а исторически часто для счета использовались части тела. Даже сегодня люди, которые учатся считать или хотят проиллюстрировать в разговоре какую-либо мысль о счете, часто используют пальцы. В некоторых культурах для счета также использовались пальцы ног, промежутки между пальцами и суставы. Любопытно, что числа представлены «цифрами» — тем же словом, которое используется для обозначения пальцев рук и ног в английском и многих других языках.
Надпись на латыни и римскими цифрами на Адмиралтейской арке в Лондоне.Он гласит: ANNO: DECIMO: EDWARDI: SEPTIMI: REGIS: VICTORIÆ: REGINÆ: CIVES: GRATISSIMI: MDCCCCX: (На десятом году правления короля Эдуарда VII королеве Виктории от самых благодарных граждан, 1910).
Римские
Римские цифры использовались в Римской империи и Европе до 14 века. Они все еще используются сегодня в некоторых контекстах, например, в часах, для обозначения часов. Римские цифры основаны на семи числах, написанных буквами латинского алфавита:
Порядок важен в римской системе, потому что большее число, за которым следует меньшее, означает, что нужно сложить два, но меньшее число перед больший означает, что меньшее число вычитается из большего.Например, XI равно 11, а IX равно 9. Правило вычитания не универсальное, оно работает только для этих чисел: IV, IX, XL, XC, CD и CM. В некоторых случаях правила вычитания не используются, а вместо них последовательно пишутся цифры.
Системы в других культурах
Люди во многих географических регионах имели системы представления чисел, похожие на римские или индуистско-арабские. Например, некоторые славяне использовали кириллицу для обозначения чисел, таких как от 1 до 9, кратных 10 и кратных 100, со специальными символами для больших чисел, а также символами, чтобы отличать цифры от букв.В еврейской системе счисления используется еврейский алфавит для обозначения чисел от одного до десяти, кратных десяти, 100, 200, 300 и 400. Остальные числа представлены в виде кратных или сумм. Греческая система счисления также похожа.
В некоторых культурах используются более простые представления, такие как вавилонская система, в которой всего два клинописных символа: один (несколько напоминающий букву «Т») и десять (немного похожий на букву «С»). Так, например, 32 будет записано (с использованием соответствующих символов) как CCCTT.Египетская система была очень похожа, за исключением того, что были дополнительные символы для нуля, ста, одной тысячи, десяти тысяч, ста тысяч и одного миллиона, а также специальные обозначения для дробей. Числа в культуре майя имели символы нуля, единицы и пяти, со специальными обозначениями для чисел больше девятнадцати.
Унарная система счисления. Счетные отметки в различных культурах
Унарный
В унарной системе каждое число представляет собой то же количество символов, что и его значение.Эти символы обычно одинаковы, поэтому, если 1 представлен как A, то 5 будет представлен как AAAAA. Когда дети учатся считать, их учителя часто используют эту систему, чтобы помочь установить связь между конкретной, простой для понимания системой и более абстрактным представлением чисел. Эта система также иногда используется в играх и других простых вычислениях. В разных странах для этого могут использоваться разные типы представительств. Например, при подсчете очков команд-победителей или подсчете пунктов или дней люди в западном мире и некоторых других регионах часто пишут четыре вертикальные линии, затем пересекают их пятой горизонтальной линией и повторяют процесс.Например, в части A) на картинке человек, считающий до четырех, зачеркнул его, затем снова дошел до четырех, зачеркнул и продолжал ставить счетные отметки, пока не сумел до двенадцати. Люди, которые используют или исторически использовали китайские иероглифы в своих системах письма, например, в Китае, Японии и Корее, используют определенный китайский иероглиф с пятью штрихами, чтобы сделать то же самое. В части B) на картинке человек считает до пяти, завершая образ, а затем начинает новый персонаж, продолжая счет до семи.Порядок штриха задан заранее, как показано на рисунке. Унарная система также используется в информатике.
Арифмометр, использующий десятичную систему, и микросхему микропроцессора, которая использует двоичную систему.
Позиционная система
Позиционная система работает с основанием. Например, в базе 10 мы имеем следующее:
- Первая позиция предназначена для чисел от нуля до девяти, то есть число в первой позиции должно быть умножено на десять в степени нуля.
- Число во второй позиции умножается на десять в степени единицы.
- Число в третьей позиции умножается на десять в степени двойки и так далее, пока числа во всех позициях не будут исчерпаны.
Чтобы получить окончательное значение представленного числа, необходимо сложить все значения в каждой позиции. Это удобный способ представления чисел, поскольку он позволяет работать с числами, имеющими относительно большие значения, без использования большого пространства для их записи.
Пример: 3102 = 3 × 10³ + 1 × 10² + 0 × 10¹ + 2 × 10⁰
Двоичная
Двоичная система счисления широко используется в математике и информатике. Он основан на двух символах «0» и «1» для представления всех возможных чисел. Другими словами, это система base-2. Числа представлены следующим образом: 0 = 0, 1 = 1, а от 2 используется принцип сложения. Добавление в основании-2 аналогично добавлению в основании-10. Чтобы увеличить число на единицу:
Художественное представление двоичных чисел
- Если число заканчивается на ноль, последний ноль заменяется единицей: e.грамм. 100 (4) + 1 (1) = 101 (5). Здесь для сравнения в скобках используются десятичные числа.
- Если число заканчивается единицей, но не все единицы, первый ноль справа заменяется единицей, а все следующие за ним справа становятся нулями: 1011 (11) + 1 (1) = 1100.
- Если исходное число — все единицы, то все они заменяются нулями, а впереди добавляется единица: 111 (7) + 1 (1) = 1000 (8).
Чтобы сложить два числа, они выравниваются друг относительно друга, и для каждого места 0 + 0 дает 0, 1 + 0 дает 1, а 1 + 1 дает 10, где 0 помещается в эту позицию, а 1 переносится на следующую позицию.Например:
11111 (31)
+1011 (11)
———————————
101010 (42)
В этом случае, работая справа налево:
- 1 + 1 дает 0, один переносится
- 1 + 1 + 1 дает 1, один переносится
- 1 + 1 дает 0, один переносится
- 1 + 1 + 1 дает 1, один переносится
- 1 +1 дает 10
Итак, сложив это вместе, мы получаем 101010.
Вычитание работает по тому же принципу, за исключением того, что вместо переноса мы «заимствуем».Умножение также похоже на умножение по основанию 10. Умножение на 0 дает 0, а умножение 1 на 1 дает 1. Так, например:
101 (5)
× 10 (2)
————————————
000
101
———————————
1010 (10)
Деление и вычисление квадратных корней также очень похоже на основание 10.
Классификация номеров
Все номера можно разделить на подмножества. Некоторые из приведенных ниже подмножеств частично перекрываются.
Долг — отрицательное число
Отрицательные числа
Отрицательные числа — это числа, представляющие отрицательное значение.Перед ними ставится знак минус. Например, если у человека A нет денег, и он должен 5 долларов человеку B, то у человека A -5 долларов. Здесь –5 — отрицательное число.
Рациональные числа
Рациональные числа — это числа, которые могут быть выражены в виде дробей, где знаменатель — натуральное число, не равное нулю, а числитель — целое число. Например, и 3/4, и -10/5 (то же, что и -2) являются рациональными числами.
Натуральные числа
Натуральные числа — это положительные числа (включая 0), а не дроби, например 7 или 86 766 575 675 456.
Целые числа
Целые числа включают ноль, отрицательные и положительные числа, не являющиеся дробями. Примеры включают -65 и 11 223.
Комплексные числа
Комплексные числа — это все числа, которые являются суммой одного действительного числа и произведения другого действительного числа и квадратного корня из отрицательного числа.
Простые числа
Простые числа — это натуральные числа больше единицы, которые дают целое число только при делении на единицу или само по себе. Некоторые примеры: 3, 5 и 11.2 57 885 161 −1 — наибольшее известное простое число на зиму 2013 года. Оно состоит из 17 425 170 цифр. Простые числа используются в криптографии с открытым ключом, системе кодирования данных, часто используемой при безопасном онлайн-обмене данными, например, в онлайн-банкинге.
Интересные факты о числах
Китайские номера для защиты от мошенничества
Числа для защиты от мошенничества
Для предотвращения мошенничества при написании чисел в бизнесе и торговле в китайском языке используются специальные сложные символы, которые трудно подделать, добавив лишние штрихи.Это сделано потому, что часто используемые китайские символы для чисел слишком просты, и их значение легко изменить, добавив штрихи.
Современный счет в торговле
Некоторые языки в странах, где в настоящее время используется система счисления с основанием 10, по-прежнему отражают то, что в прошлом были распространены другие системы счисления. Например, в английском языке есть специальное слово для двенадцати, «дюжина» — в настоящее время оно используется в основном для подсчета яиц, выпечки, вина и цветов. В кхмерском есть особые слова, основанные на древней системе 20, для подсчета фруктов.
Группировка цифр
И в Китае, и в Японии принята индийско-арабская система счисления, но большие числа сгруппированы по 10 000, и это отражено в языке. Например, в английском языке есть слово «1000», а одно указывает, сколько их тысяч, вплоть до 999 999. Затем следует слово «миллион», обозначающее 1 000 000. В японском языке есть слово, обозначающее 10 000, после чего приращение продолжается до 99 999 999, за которым следует специальное слово для 100 000 000.
Несчастливые числа
Леонардо да Винчи. Последний ужин. Церковь Пресвятой Богородицы (Санта-Мария-делле-Грацие), Милан, Италия.
В западной традиции число 13 считается несчастливым. Многие считают, что это заимствовано из иудео-христианской традиции, где тринадцать было числом учеников Иисуса Христа во время последней вечери, после которой тринадцатый ученик, Иуда, предал Иисуса. Среди викингов также существовало суеверие, что один из тринадцати собравшихся умрет в следующем году.
В России и многих странах бывшего СССР все четные числа считаются несчастливыми. Возможно, эта традиция возникла из убеждения, что четные числа полны, стабильны и статичны, неподвижны и, следовательно, не являются живыми. С другой стороны, нечетные числа представляют собой изменение, движение, сущность, которая нуждается в завершении и развитии, и жизнь. Согласно этому поверью, дарить живым людям четное количество цветов считается невезением — эти числа обычно предназначаются для похорон.
В странах, говорящих на китайском, японском и корейском языках, число 4 считается несчастливым, потому что оно произносится так же, как «смерть». В некоторых случаях все числа, в которых есть четверка, считаются несчастливыми. Например, в здании может не быть этажей 4, 14 и 24. В Китае номер 7 тоже несчастлив, потому что он представляет духовный мир и призраков. Седьмой месяц в китайском календаре называется «месяцем призрака», когда открыта связь между мирами живых и духов.В Японии другое неудачное число — 9 , которое имеет то же произношение, что и «страдание».
В Италии 17 — неудачное число, потому что, когда его римское представление «XVII» переставляется, оно читается как VIXI или «vixi», что переводится с латыни как «Я жил». Это означает, что жизнь окончена, и относится к смерти.
666 — еще одно неудачное число, которое в Библии называется «Число зверя». Иногда считается, что это 616, но чаще встречается 666.Это относится к антихристу или сатане. Его происхождение спорно, но некоторые ученые считают, что 666 — это транслитерация на иврит, а 616 — на латынь имени императора Нерона, который ассоциируется с гонениями на христиан и с тираническим и кровавым правлением. Некоторые также считают, что Нерон был поджигателем во время большого пожара в Риме, хотя его причастность оспаривается историками.
В Афганистане, особенно в Кабуле и его окрестностях 39 считается проклятым или постыдным числом, связанным с проституцией.Это связано с историей о сутенере, у которого на номерном знаке и в номере квартиры был номер 39. Некоторые обвиняют власти и подразделения организованной преступности в распространении этого суеверия с целью получения прибыли от покупки и продажи автомобилей с «оскорбительными» номерными знаками. Суеверие настолько сильны, что люди насмехаются и иным образом оскорбляют тех, у кого номер 39 в номере, квартире или номере телефона. По слухам, один из таких случаев насмешек привел к трагедии, когда против кандидата в депутаты, внесенного в бюллетень для голосования, издевались проезжающие мимо водители, что привело к дорожно-транспортному происшествию.


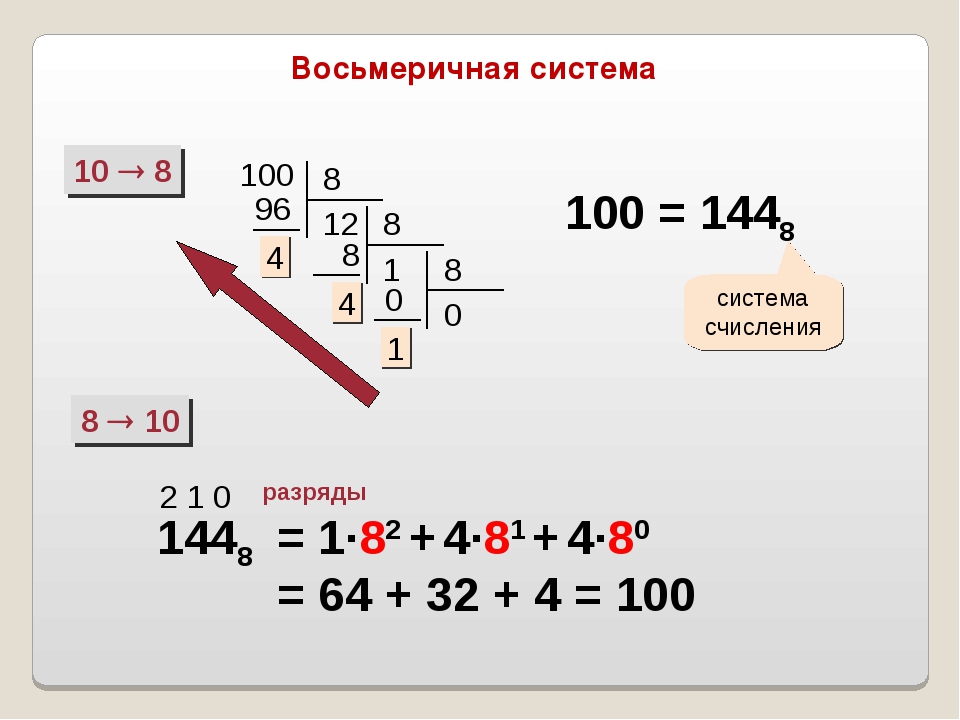 Printf(«%b\n», bitmap)
Printf(«%b\n», bitmap)