Восьмеричная система счисления — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 31 декабря 2018; проверки требуют 6 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 31 декабря 2018; проверки требуют 6 правок.

Системы счисления в культуре
Индо-арабская
Арабская Тамильская Бирманская	Кхмерская Лаосская Монгольская Тайская
Восточноазиатские
Китайская Японская Сучжоу Корейская	Вьетнамская Счётные палочки
Алфавитные
Абджадия Армянская Ариабхата Кириллическая Греческая	Грузинская Эфиопская Еврейская Акшара-санкхья
Другие
Вавилонская Египетская Этрусская Римская Дунайская	Аттическая Кипу Майяская Эгейская Символы КППУ
Позиционные
2, 3, 4, 5, 6, 8, 10, 12, 16, 20, 60
Нега-позиционная
Симметричная
Смешанные системы
Фибоначчиева
Непозиционные
Единичная (унарная)

Восьмери́чная систе́ма счисле́ния — позиционная целочисленная система счисления с основанием 8. Для представления чисел в ней используются цифры от 0 до 7.

Восьмеричная система чаще всего используется в областях, связанных с цифровыми устройствами. Характеризуется лёгким переводом восьмеричных чисел в двоичные и обратно, путём замены восьмеричных чисел на триплеты двоичных. Широко использовалась в программировании и компьютерной документации, однако позднее была почти полностью вытеснена шестнадцатеричной.

Восьмеричная система применяется при выставлении прав доступа к файлам и прав исполнения для участников в Linux-системах^[1][2].

Таблица перевода восьмеричных чисел в двоичные[править | править код]

08  = 0002
18  = 0012
2 8  = 0102
38  = 0112
48  = 1002
58  = 1012
68  = 1102
78  = 1112

Для перевода восьмеричного числа в двоичное необходимо заменить каждую цифру восьмеричного числа на триплет двоичных цифр. Например: 2541₈ = [ 2₈ | 5₈ | 4₈ | 1₈ ] = [ 010₂ | 101₂ | 100₂ | 001₂ ] = 010101100001₂.

Использование в естественных языках[править | править код]

Языки юки^[3] и паме^[4] используют восьмеричную систему счисления.

Ряд языков программирования, в частности, Си/С++, Ada, Perl, Java и Python (до 3.0), имеют специальный синтаксис (аналогичный использованию префикса «0x» для шестнадцатеричных констант) для записи восьмеричных констант с применением ведущего нуля, например, 0644 представляет собой запись литеральной константы со десятичным значением 420

10.

По статистике, применение восьмеричных констант в программах на языке Си чрезвычайно низко (около 0,1 % от всех литеральных констант, без учета константы «0», технически также восьмеричной). Определенную популярность такие константы сохраняют в случае описания прав на файлы в Unix/POSIX стиле (0666, 0750), и при отдельных случаях работы с битовыми масками, когда программисту проще представлять битовое представление восьмеричных чисел, а не шестнадцатиричных или, тем более, десятичных

[5].

Подобные правила указания системы счисления могут быть неочевидны для программистов и приводят к ошибкам. В некоторых языках существуют рекомендации не использовать такую запись^[6], в других языках такая записи восьмеричных констант запрещена (например, в Python с версии 3 используется префикс 0o^[7][8]) или не используется (например Rust и D^[7]).

Некоторые версии языка Бейсик используют для записи восьмеричных констант префикс &O, например &O644. Здесь O — это не ноль, а буква латинского алфавита, обозначающая английское слово Octal (восьмеричный).

двоичная, восьмеричная, шестнадцатеричная — урок. Информатика, 8 класс.

Для кодирования информации в компьютере вместо привычной десятичной системы счисления используется двоичная система счисления.

Двоичной системой счисления люди начали пользоваться очень давно. Древние племена Австралии и островов Полинезии использовали эту систему в быту. Так, полинезийцы передавали необходимую  информацию, выполняя два вида ударов по барабану: звонкий и глухой. Это было примитивное представление двоичной системы счисления.

Двоичной системой счисления называется позиционная система счисления с основанием \(2\).

Для записи чисел в ней использовали только две цифры:  \(0\) и \(1\).

Для обозначения системы счисления, в которой представляется число, используют нижний индекс, указывающий основание системы. Например, 110112 —  число в двоичной системе счисления.

 

Цифры в двоичном числе являются коэффициентами его представления в виде суммы степеней с основанием \(2\), например:

 

1012=1 ·22+0 ·21+1 ·20.

 

В десятичной системе счисления это число будет выглядеть так:

 

1012=4+0+1=5.

 

Для перевода целого десятичного числа в двоичную систему счисления нужно последовательно выполнять деление данного числа и получаемых целых частных на \(2\) до тех пор, пока не получим частное, равное нулю. Исходное число в двоичной системе счисления составляется последовательной записью полученных остатков, начиная с последнего.

Пример:

Переведём десятичное число \(13\) в двоичную систему счисления. Рассмотренную выше последовательность действий (алгоритм перевода) можно изобразить так:

 

 

Получили 1310=11012.

Пример:

Если десятичное число достаточно большое, то более удобен следующий способ записи рассмотренного выше алгоритма:

 

\(224\)	\(112\)	\(56\)	\(28\)	\(14\)	\(7\)	\(3\)	\(1\)
\(0\)	\(0\)	\(0\)	\(0\)	\(0\)	\(1\)	\(1\)	\(1\)

 

22410=111000002.

Восьмеричной системой счисления называется позиционная система счисления с основанием \(8\).

 

Для записи чисел в восьмеричной системе счисления используются цифры:  \(0\), \(1\), \(2\), \(3\), \(4\), \(5\), \(6\), \(7\).

Для перевода целого восьмеричного числа в десятичную систему счисления следует перейти к его развёрнутой записи и вычислить значение получившегося выражения.

Для перевода целого десятичного числа в восьмеричную систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на 8 до тех пор, пока не получим частное, равное нулю. Исходное число в восьмеричной системе счисления составляется последовательной записью полученных остатков, начиная с последнего.

Пример:

Переведём восьмеричное число  154368 в десятичную систему счисления.

154368=1 ·84+5 ·83+4 ·82+3 ·81+6 ·80=694210

Пример:

Переведём десятичное число \(94\) в восьмеричную систему счисления.

 

 

9410=1368

Шестнадцатеричной системой счисления называется позиционная система счисления с основанием \(16\).

 

Для записи чисел в шестнадцатеричной системе счисления используются цифры:  \(0\), \(1\), \(2\), \(3\), \(4\), \(5\), \(6\), \(7\), \(8\), \(9\) и латинские буквы A, B, C, D, E, F. Буквы A, B, C, D, E, F имеют значения 1010, 1110, 1210, 1310, 1410, 1510.

Для перевода шестнадцатеричного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа.

Для перевода целого десятичного числа в шестнадцатеричную  систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на \(16\) до тех пор, пока не получим частное, равное нулю. Исходное число в системе счисления составляется последовательной записью полученных остатков, начиная с последнего.

Пример:

Переведём шестнадцатеричное число \(2\)\(A7\) в десятичное. В соответствии с вышеуказанными правилом представим его в виде суммы степеней с основанием \(16\):

2A716=2 ·162+10 ·161+7 ·160=512+160+7=679.

Пример:

Переведём десятичное число \(158\) в шестнадцатеричную систему счисления.

 

 

15810=9E16.

Для перевода числа из любой позиционной системы счисления в десятичную необходима использовать развернутую формулу числа, заменяя, если это необходимо, буквенные обозначения соответствующими цифрами.

Для перевода целых чисел десятичной системы счисления в число любой системы счисления последовательно выполняют деление нацело на основание системы счисления, пока не получат нуль. Числа, которые возникают как остаток от деления на основание системы счисление, представляют собой последовательную запись разрядов числа в выбранной системе счисления от младшего разряда к старшему. Поэтому для записи самого числа остатки от деления записывают в обратном порядке.

«Зачем нужна восьмеричная система счисления в 21 веке?» – Яндекс.Знатоки

Работа в восьмеричной системе может быть полезна в случае операций с битовыми флагами и масками по причине простоты вычисления таких значений.

Случай с правами доступа в *nix системах — как раз пример применения битовых масок на практике.

Для последовательности из 3 битов очень удобно применять цифры от 0 до 7 (все цифры восьмеричной системы), а операции для вычисления восьмеричного числа очень простые.

Рассмотрим пример с установкой битов от 000 до 111:

установка правого крайнего бита (младшего) увеличит восьмеричное число на 1

установка среднего бита увеличит восьмеричное число на 2

установка старшего бита увеличит восьмеричное число на 4

То есть, нужно определить состояние каждого бита и соответствуюшее ему число, а затем просуммировать биты в состоянии 1.

Расставим биты и соответствующие им цифры, как описано выше:

1 1 1

4 2 1

Теперь когда мы устаналиваем какой-то бит, к итоговой сумме просто прибавляем соответствующую цифру.

Таким образом, если мы хотим установить значение, например, 101, мы суммирует 4 и 1 (я для наглядности указываю цифры для суммы в той последователности, в какой идут биты, от страшего к младшему разряду, то есть слева направо) — получаем 5, или например 110 => 4+2 = 6

111 => 4+2+1 = 7

Эта математика очень проста для вычисления в уме, именно потому и применяется в системе маркировки прав доступа к файлам в *nix.

Теперь добавим ещё немного сложности, и рассмотрим систему из 8 битов, т.е. полноценный байт.

Его можно разбить на 3 секции по битам, и я приведу соответствующие цифры восьмеричной системы:

11 111 111

21 421 421

Теперь, правило такое: в рамках 3 битов в группе числа суммируются, как раньше с 3 битами, но цифры каждой отдельной группы пишутся каждая в своём разряде.

Рассмотрим пример:

10 111 101

Начнём вычисления справа налево (от младшего разряда, отсчитывая по 3 бита):

101 => 4 + 1 = 5

111 = 4 + 2 + 1 = 7

10 => 2

Наглядно:

10 111 101

2 7 5

Значит, итоговое число будет 275 в восьмеричной системе. Фактически, мы отдельно работаем с каждой группой битов (по 3 бита в группе), а потом просто записываем их в нужном порядке.

То есть, если программисту нужно установить битовую последовательность 10111101, достаточно определить в коде переменную с восьмеричным значением 275

Во многих языках программирования нет специального синтаксиса для зависи двоичных значений, например в наиболее распространённых языках C и C++, и удобная запись в восьмеричной системе очень помогает.

В C/C++ и ряде других языков, например Go, восьмеричное число 275 записывается как 0275 (ноль в начале означает, что это восьмеричная система)

Приведу простейший пример на Go (его можно запустить онлайн в https://play.golang.org)

package main
import «fmt»
func main() {
bitmap := 0275 // в Go восьмеричные числа начинаются с нуля, как и в C
fmt.Printf(«%b\n», bitmap)
}

А теперь, как тот же код можно написать используя операции битового сдвига:

package main
import «fmt»
func main() {
bitmap := 1 << 7 + 1 << 5 + 1 << 4 + 1 << 3 + 1 << 2 + 1
fmt.Printf(«%b\n», bitmap)
}

Так же просто в уме производится обратное преобразование из восьмеричной системы в двоичную.

Например, если у нас есть число больше 4 — значит ставим старший (левый крайний бит) равным 1, и отнимаем от числа 4, затем если число всё ещё больше 2 — ставим средний бит и отнимаем от числа 2, и затем проверяем равно ли число 1 (тогда славим правый, младший, бит) или 0 — готово!

Рассмотрим число 7:

7 > 4 значит ставим 100, отнимаем: 7 — 4 = 3

3 > 2 значит ставим 110, отнимаем 3 — 2 = 1

1 значит ставим 111

Для 5:

5 > 4 значит ставим 100, отнимаем: 5 — 4 = 1

1 < 2 значит оставляем 100 и ничего не отнимаем

1 остаётся, значит ставим 101

Восьмеричная система счисления — Программирование на C, C# и Java

Оглавление:
Перевод из десятичной системы счисления в восьмеричную
Перевод из восьмеричной системы счисления в десятичную
Перевод из двоичной системы счисления в восьмеричную
Перевод из восьмеричной системы счисления в двоичную
Перевод из восьмеричной системы счисления в шестнадцатеричную и из шестнадцатеричной системы в восьмеричную
Применение восьмеричной системы счисления

Восьмеричная система – одна из основных систем счислений наряду с двоичной, десятичной и шестнадцатеричной, применяемая в информационных технологиях.

Как мы знаем, компьютеры «воспринимают» лишь двоичную систему счисления, состоящую только из нулей и единиц. Однако человеку довольно непривычно и неудобно работать с такими числами. Например, привычное нам десятичное число 2 143 в двоичной системе будет выглядеть как 100001011111.  Переводить числа из двоичной системы в десятеричную также не очень удобно и бывает довольно муторно.

В итоге было решено использовать альтернативные и более простые системы счисления: восьмеричную и шестнадцатеричную. Числа 8 и 16 являются степенями двойки (2 в третьей и 2 в четвёртой степени соответственно), поэтому выполнять преобразования из двоичной системы и наоборот гораздо легче, чем при десятичной системе счисления, которая не может похвастаться своей причастностью к степеням числа 2.

Кроме того, числа в восьмеричной системе как минимум более приятны глазу и гораздо короче, чем их аналоги в двоичной системе. Так, например, в восьмеричной системе то же число 2 143 будет записываться как 4137.

В восьмеричной системе счисления, как уже можно было догадаться, основанием является цифра 8 и, соответственно, она вмещает в себя только восемь цифр: от 0 до 7. Поэтому числа в восьмеричной системе счисления очень похожи на десятичные, в отличие от шестнадцатеричных, где присутствуют буквы латинского алфавита или двоичных, состоящих только из двух цифр. Отличают эти две системы тем, что в восьмеричной отсутствуют цифры 8 и 9, а также, очевидно, нижними индексами: у числа в десятичной системе прибавляют нижний индекс с цифрой 10, а к числам в восьмеричной системе приписывают цифру 8, например:

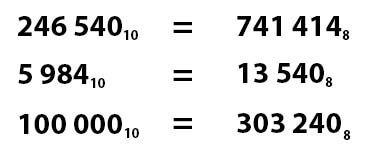 Теперь давайте научимся переводу чисел в восьмеричную систему счисления и наоборот.

Перевод из десятичной системы счисления в восьмеричную

Давайте попробуем изучить перевод десятичного числа в восьмеричное на примере. После этого примера вы без проблем сможете переводить любые числа в эту систему.

Возьмём десятичное число 15 450 и попробуем перевести его в восьмеричную систему счисления.

Для начала нам необходимо разделить исходное число на основание системы, в которую мы хотим это число перевести. Для восьмеричной системы это число 8. То есть мы делим 15 450 на 8.

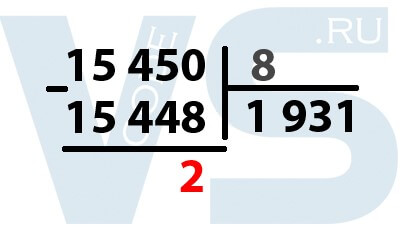
Происходит деление в столбик, но, в отличие от стандартного деления, мы не находим неполные частные, а делим сразу всё делимое на 8. Наибольшим числом, при котором 15 450 делится без остатка на 8 будет число 1 931. 1931 * 8 = 15 448. Теперь мы вычитаем из 15 450 полученное число 15 448, у нас получился остаток 2. Выделяем эту двойку, так как это уже кусочек нашего числа в восьмеричной системе.
Продолжаем: теперь делим полученное на предыдущем шаге частное на 8:

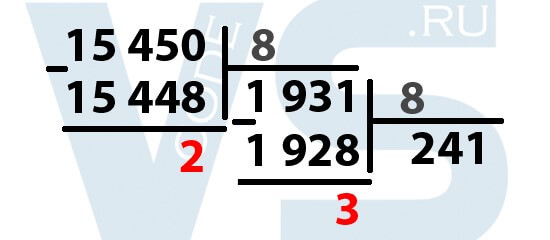
Всё точно так же: наибольшим числом, при котором 1 931 делится без остатка на 8 будет число 241. При умножении 241 на 8 получается число 1 928. Ищем разность между 1 931 и 1928 – получается 3. Выделяем её. Далее делим 241 на 8.

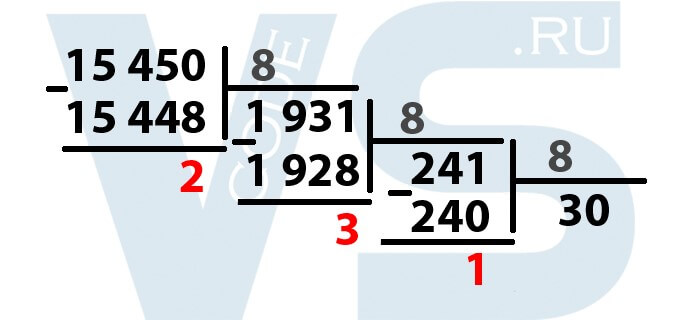
Получается число 30, умножив его на 8, получаем 240. Вычитаем из 241 это число, получается 1. Выделяем единицу.
Продолжаем деление до тех пор, пока частное не станет меньше 8!

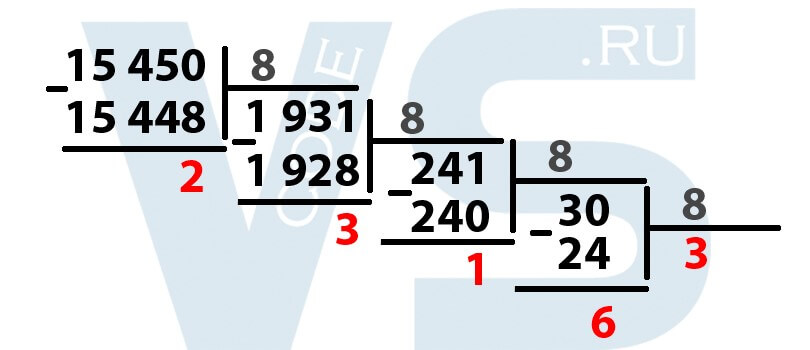Итак, делим 30 на 8, получается 3,75, отбрасываем дробную часть, получается 3. Умножаем 3 на 8, получается 24. 30 – 24 = 6. Выделяем шестёрку. Мы закончили деление так как 3 меньше 8. Обязательно выделяем последнее частное тоже (у нас это цифра 3).

Выделенные красным цифры – это и есть наше число в восьмеричной системе, НО они написаны наоборот. То есть, чтобы правильно прочитать число в восьмеричной системе, необходимо сделать это справа налево.

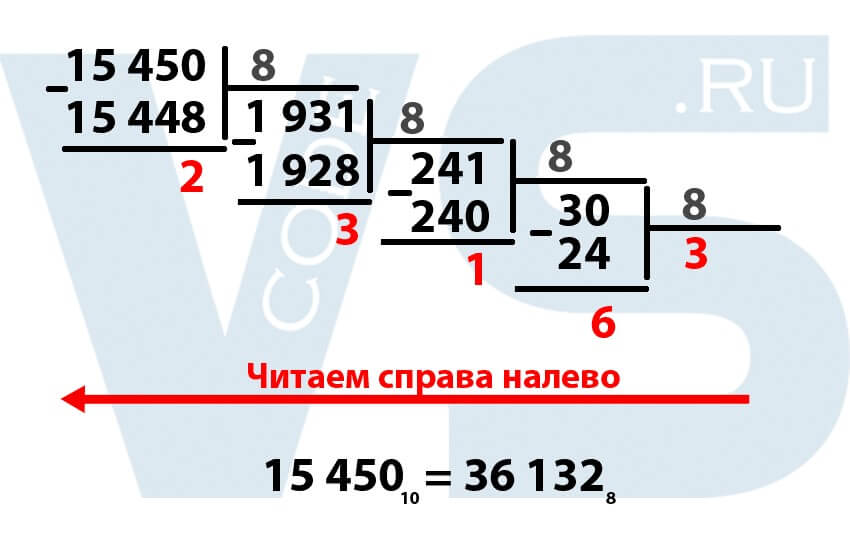
Таким образом, десятичное число 15 450₁₀ в восьмеричной системе будет выглядеть как 36 132₈.

Итого, алгоритм перевода чисел из десятичной системы в восьмеричную следующий:

1. Разделить исходное число на 8. Найти максимальное частное и убрать дробную часть от него. Например, исходное число 20 : 8 = 2,5. Значит в частное мы записываем число 2.
2. Умножить полученное частное на 8. Записать его под исходным числом.
3. Найти остаток между этими числами и выделить его – это кусочек переведённого в восьмеричную систему числа.
4. Затем разделить в столбик полученное частное на 8, записать ответ и проделать шаги 2 и 3.
5. Производить деление до тех пор, пока делимое не станет меньше 8. Выделить это делимое тоже.
6. Выписать все выделенные числа справа налево (т.е. последнее делимое будет на первом месте, затем идёт остаток, найденный на последнем шаге, затем остаток, найденный на предпоследнем шаге и т.д.). Полученное при такой записи число и будет нашим искомым восьмеричным.

Теперь перейдём к переводу восьмеричного числа в десятичную систему счисления.

Перевод из восьмеричной системы счисления в десятичную

Перевести восьмеричное число в десятичное даже проще, чем наоборот. Давайте рассмотрим пример: переведём восьмеричное число 3607₈ в десятичное.

Для начала мы делаем такую запись: с конца берём каждую цифру нашего исходного числа, каждое из них умножаем на 8, и все в целом складываем. Должно получиться примерно так:

Однако, это ещё не всё! После того, как мы сделали подобную запись, ко всем числам 8, на которые умножаются цифры исходного числа, необходимо добавить степени в порядке возрастания: 0, 1, 2 и т.д. Обязательно необходимо начинать с нулевой степени!

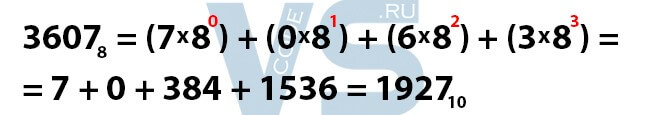
Всё, что остаётся после этого – просто посчитать. В итоге у нас получилось число 1927 в десятичной системе.

Перевод из двоичной системы счисления в восьмеричную

Перевод чисел из двоичной системы счисления в восьмеричную – довольно необычное дело для тех, кто никогда с этим не сталкивался. Однако на деле всё не так пугающе, как может показаться с первого раза.

Давайте попробуем. Допустим, у нас есть двоичное число 1010010001011101100.

Для начала нам необходимо разбить это число на триады – группы из трёх цифр. Почему именно три цифры? Как мы знаем, у систем счислений имеются основания. И у двоичной системы основание – 2. Нам необходимо перевести двоичное число в восьмеричную систему с основанием 8. Математически это можно записать так:

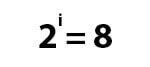
Найти i, пожалуй, не составит труда: i = 3, то есть, для записи одного восьмеричного числа в двоичной системе необходимо 3 бита или, говоря иначе – 3 двоичные цифры. Поэтому мы и будем разбивать двоичное число на триады. Однако надо запомнить, что делать это надо с младшего бита. Бит – это одна цифра в двоичном числе. Чем дальше бит от начала числа, тем он младше. Самый младший бит – это последняя цифра двоичного числа. Иными словами, мы разбиваем число на триады, начиная с конца.

Внимание: если старшая триада не заполнена, до конца, перед ней необходимо дописать столько нулей, чтобы получилась полноценная триада.

Теперь всё, что нам остаётся – это перевести каждую из этих триад из двоичной системы счисления в восьмеричную. Это можно сделать самостоятельно:

Для этого в каждой отдельной триаде (начиная с первой) нужно каждую цифру (начиная с последней) умножить на 2, возведённую в степени от 0 до 2, и сложить полученные три числа.

Затем, полученные результаты по каждой отдельной триаде надо выписать, начиная с самой первой. Записанное число и будет нашим конечным результатом в восьмеричной системой счисления.

Однако можно сильно облегчить себе задачу, не высчитывая все триады числа, а просто сверяя каждую из них по таблице соответствия двоичных чисел восьмеричным, например, по такой:

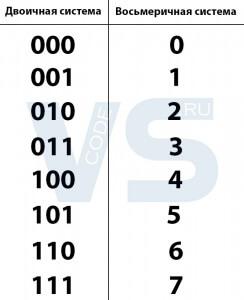
Теперь можно просто смотреть на триаду, сверять её с таблицей и записывать число, соответствующее ей в восьмеричной системе.

Перевод из восьмеричной системы счисления в двоичную

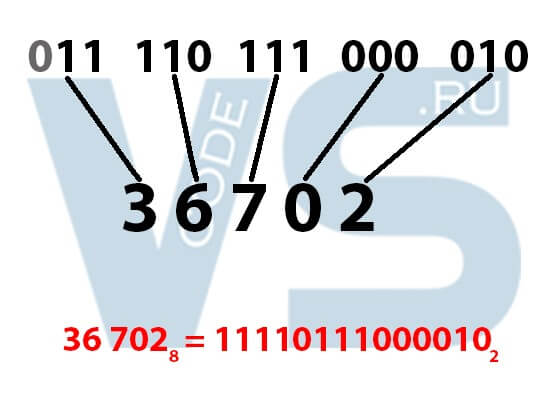
Самым удобным способом перевода из восьмеричной системы счисления в двоичную является использование таблицы соответствий. Итак, допустим, мы хотим перевести восьмеричное число 36702 в двоичную систему. Что же нам делать? Мы берём первую цифру нашего исходного числа – 3. Ищем её по таблице соответствия – в двоичной системе это 011. Берём следующую цифру – 6 и ищем её в таблице, находим 110, и так далее. Продолжаем, пока не переведём все восьмеричные цифры в триады. В итоге у нас получится необходимое двоичное число.

Внимание: Если в старших битах (то есть в самом начале двоичного числа) имеются нули, необходимо убрать их до первой единицы. Например, как на изображении ниже. В старшем бите у нас получился ноль при переводе восьмеричной тройки, и мы убрали его. Это делается для удобства, потому что зачем хранить и писать незначащие цифры.

Перевод из восьмеричной системы счисления в шестнадцатеричную и из шестнадцатеричной системы в восьмеричную

К сожалению, несмотря на то, что эти системы счисления близки друг к другу, напрямую перевести друг в друга нельзя. Легче всего при переводе этих двух систем друг в друга воспользоваться посредничеством двоичной системы. То есть, перевести восьмеричную систему счисления в двоичную, разделив число на триады и воспользовавшись таблицей соответствий, а затем перевести это число из двоичной системы в шестнадцатеричную с помощью тетрад. И наоборот: перевести число из шестнадцатеричной системы в двоичную, а затем уже из двоичной системы в восьмеричную описанными выше способами.

Применение восьмеричной системы счисления

В прошлом веке выпускались компьютеры, в которых использовались 12-ти, 24-х и 36-битные слова. Это, например, модель ICT 1900 (1964 год), а также PDP-8, выпущенная в 1965 году – это коммерчески довольно успешная модель миникомпьютера в своё время. Кроме того, некоторые мейнфреймы от компании IBM использовали восьмеричную систему. В компьютерах, размер машинного которых кратен тройке, очень удобно использовать систему с основанием восемь, поскольку всегда все биты из слова можно представить в виде целого количества цифр в восьмеричной системе. Например, слово из 24-х бит, можно записать в виде 8-ми восьмеричных чисел.

Если говорить про использование восьмеричной системы в жизни людей, то известно, что в индейских языках Юки (Калифорния) и Паме (Мексика) использовалась данная система. Индейцы считали предметы не по количеству пальцев на руках, а по количеству промежутков между ними.

 

Восьмеричная система счисления

5 (100%) 12 votes

Поделиться в соц. сетях:

Восьмеричная система счисления — это… Что такое Восьмеричная система счисления?

Системы счисления в культуре
Индо-арабская система счисления
Арабская Индийские Тамильская Бирманская	Кхмерская Лаоская Монгольская Тайская
Восточноазиатские системы счисления
Китайская Японская Сучжоу Корейская	Вьетнамская Счётные палочки
Алфавитные системы счисления
Абджадия Армянская Ариабхата Кириллическая	Греческая Эфиопская Еврейская Катапаяди
Другие системы
Вавилонская Египетская Этрусская Римская	Аттическая Кипу Майская
Позиционные системы счисления
Десятичная система счисления (10)
2, 3, 4, 5, 6, 7, 8, 9, 12, 16, 20, 60
Нега-позиционная система счисления
Симметричная система счисления
Смешанные системы счисления
Фибоначчиева система счисления
Непозиционные системы счисления
Единичная (унарная) система счисления
Список систем счисления

Восьмери́чная систе́ма счисле́ния — позиционная целочисленная система счисления с основанием 8. Для представления чисел в ней используются цифры от 0 до 7.

Восьмеричная система часто используется в областях, связанных с цифровыми устройствами. Характеризуется лёгким переводом восьмеричных чисел в двоичные и обратно, путём замены восьмеричных чисел на триплеты двоичных. Ранее широко использовалась в программировании и вообще компьютерной документации, однако в настоящее время почти полностью вытеснена шестнадцатеричной.

Таблица перевода восьмеричных чисел в двоичные

08  = 0002
18  = 0012
28  = 0102
38  = 0112
48  = 1002
58  = 1012
68  = 1102
78  = 1112

Для перевода восьмеричного числа в двоичное необходимо заменить каждую цифру восьмеричного числа на триплет двоичных цифр. Например: 2541₈ = [ 2₈ | 5₈ | 4₈ | 1₈ ] = [ 010₂ | 101₂ | 100₂ | 001₂ ] = 010101100001₂

Ссылки

Система счисления — Википедия

Системы счисления в культуре
Индо-арабская
Арабская Тамильская Бирманская	Кхмерская Лаосская Монгольская Тайская
Восточноазиатские
Китайская Японская Сучжоу Корейская	Вьетнамская Счётные палочки
Алфавитные
Абджадия Армянская Ариабхата Кириллическая Греческая	Грузинская Эфиопская Еврейская Акшара-санкхья
Другие
Вавилонская Египетская Этрусская Римская Дунайская	Аттическая Кипу Майяская Эгейская Символы КППУ
Позиционные
2, 3, 4, 5, 6, 8, 10, 12, 16, 20, 60
Нега-позиционная
Симметричная
Смешанные системы
Фибоначчиева
Непозиционные
Единичная (унарная)

Систе́ма счисле́ния (англ. numeral system или system of numeration) — символический метод записи чисел, представление чисел с помощью письменных знаков.

Система счисления:

Системы счисления подразделяются на:

В позиционных системах счисления один и тот же числовой знак (цифра) в записи числа имеет различные значения в зависимости от того места (разряда), где он расположен. Изобретение позиционной нумерации, основанной на поместном значении цифр, приписывается шумерам и вавилонянам; развита была такая нумерация индусами и имела неоценимые последствия в истории человеческой цивилизации. К числу таких систем относится современная десятичная система счисления, возникновение которой связано со счётом на пальцах. В средневековой Европе она появилась через итальянских купцов, в свою очередь заимствовавших её у арабов.

Под позиционной системой счисления обычно понимается b{\displaystyle b}-ичная система счисления, которая определяется целым числом b>1{\displaystyle b>1}, называемым основанием системы счисления. Целое число без знака x{\displaystyle x} в b{\displaystyle b}-ичной системе счисления представляется в виде конечной линейной комбинации степеней числа b{\displaystyle b}:

x=∑k=0n−1akbk{\displaystyle x=\sum _{k=0}^{n-1}a_{k}b^{k}}, где ak{\displaystyle a_{k}} — это целые числа, называемые цифрами, удовлетворяющие неравенству 0≤ak≤(b−1){\displaystyle 0\leq a_{k}\leq (b-1)}.

Каждая степень bk{\displaystyle b^{k}} в такой записи называется весовым коэффициентом разряда. Старшинство разрядов и соответствующих им цифр определяется значением показателя k{\displaystyle k} (номером разряда). Обычно в записи ненулевых чисел начальные нули опускаются.

Если не возникает разночтений (например, когда все цифры представляются в виде уникальных письменных знаков), число x{\displaystyle x} записывают в виде последовательности его b{\displaystyle b}-ичных цифр, перечисляемых по убыванию старшинства разрядов слева направо:

x=an−1an−2…a0.{\displaystyle x=a_{n-1}a_{n-2}\dots a_{0}.}

Например, число сто три представляется в десятичной системе счисления в виде:

103=1⋅102+0⋅101+3⋅100.{\displaystyle 103=1\cdot 10^{2}+0\cdot 10^{1}+3\cdot 10^{0}.}

Наиболее часто употребляемыми в настоящее время позиционными системами являются:

В позиционных системах чем больше основание системы счисления, тем меньшее количество разрядов (то есть записываемых цифр) требуется при записи числа.

Смешанная система счисления является обобщением b{\displaystyle b}-ичной системы счисления и также зачастую относится к позиционным системам счисления. Основанием смешанной системы счисления является возрастающая последовательность чисел {bk}k=0∞{\displaystyle \{b_{k}\}_{k=0}^{\infty }}, и каждое число x{\displaystyle x} в ней представляется как линейная комбинация:

x=∑k=0n−1akbk{\displaystyle x=\sum _{k=0}^{n-1}a_{k}b_{k}}, где на коэффициенты ak{\displaystyle a_{k}}, называемые как и прежде цифрами, накладываются некоторые ограничения.

Записью числа x{\displaystyle x} в смешанной системе счисления называется перечисление его цифр в порядке уменьшения индекса k{\displaystyle k}, начиная с первого ненулевого.

В зависимости от вида bk{\displaystyle b_{k}} как функции от k{\displaystyle k} смешанные системы счисления могут быть степенными, показательными и т. п. Когда bk=bk{\displaystyle b_{k}=b^{k}} для некоторого b{\displaystyle b}, смешанная система счисления совпадает с показательной b{\displaystyle b}-ичной системой счисления.

Наиболее известным примером смешанной системы счисления является представление времени в виде количества суток, часов, минут и секунд. При этом величина «d{\displaystyle d} дней, h{\displaystyle h} часов, m{\displaystyle m} минут, s{\displaystyle s} секунд» соответствует значению d⋅24⋅60⋅60+h⋅60⋅60+m⋅60+s{\displaystyle d\cdot 24\cdot 60\cdot 60+h\cdot 60\cdot 60+m\cdot 60+s} секунд.

Факториальная система счисления[править | править код]

В факториальной системе счисления основаниями являются последовательность факториалов bk=k!{\displaystyle b_{k}=k!}, и каждое натуральное число x{\displaystyle x} представляется в виде:

x=∑k=1ndkk!{\displaystyle x=\sum _{k=1}^{n}d_{k}k!}, где 0≤dk≤k{\displaystyle 0\leq d_{k}\leq k}.

Факториальная система счисления используется при декодировании перестановок списками инверсий: имея номер перестановки, можно воспроизвести её саму следующим образом: номер перестановки (нумерация начинается с нуля) записывается в факториальной системе счисления, при этом коэффициент при числе i!{\displaystyle i!} будет обозначать число инверсий для элемента i+1{\displaystyle i+1} в том множестве, в котором производятся перестановки (число элементов меньших i+1{\displaystyle i+1}, но стоящих правее его в искомой перестановке).

Пример: рассмотрим множество перестановок из 5 элементов, всего их 5! = 120 (от перестановки с номером 0 — (1,2,3,4,5) до перестановки с номером 119 — (5,4,3,2,1)), найдём перестановку с номером 100:

100=4!⋅4+3!⋅0+2!⋅2+1!⋅0=96+4;{\displaystyle 100=4!\cdot 4+3!\cdot 0+2!\cdot 2+1!\cdot 0=96+4;}

положим ti{\displaystyle t_{i}} — коэффициент при числе i!{\displaystyle i!}, тогда t4=4{\displaystyle t_{4}=4}, t3=0{\displaystyle t_{3}=0}, t2=2{\displaystyle t_{2}=2}, t1=0{\displaystyle t_{1}=0}, тогда: число элементов меньших 5, но стоящих правее равно 4; число элементов меньших 4, но стоящих правее равно 0; число элементов меньших 3, но стоящих правее равно 2; число элементов меньших 2, но стоящих правее равно 0 (последний элемент в перестановке «ставится» на единственное оставшееся место) — таким образом, перестановка с номером 100 будет иметь вид: (5,3,1,2,4) Проверка данного метода может быть осуществлена путём непосредственного подсчёта инверсий для каждого элемента перестановки.

Фибоначчиева система счисления[править | править код]

Фибоначчиева система счисления основывается на числах Фибоначчи. Каждое натуральное число n{\displaystyle n} в ней представляется в виде:

n=∑kfkFk{\displaystyle n=\sum _{k}f_{k}F_{k}}, где Fk{\displaystyle F_{k}} — числа Фибоначчи, fk∈{0,1}{\displaystyle f_{k}\in \{0,1\}}, при этом в коэффициентах fk{\displaystyle f_{k}} есть конечное количество единиц и не встречаются две единицы подряд.

В непозиционных системах счисления величина, которую обозначает цифра, не зависит от положения в числе. При этом система может накладывать ограничения на положение цифр, например, чтобы они были расположены в порядке убывания.

Биномиальная система счисления[править | править код]

В биномиальной системе счисления (англ.) число x представляется в виде суммы биномиальных коэффициентов:

x=∑k=1n(ckk){\displaystyle x=\sum _{k=1}^{n}{c_{k} \choose k}}, где 0≤c1<c2<⋯<cn.{\displaystyle 0\leq c_{1}<c_{2}<\dots <c_{n}.}

При всяком фиксированном значении n{\displaystyle n} каждое натуральное число представляется уникальным образом.^[1]

Система остаточных классов (СОК)[править | править код]

Представление числа в системе остаточных классов основано на понятии вычета и китайской теореме об остатках. СОК определяется набором попарно взаимно простых модулей (m1,m2,…,mn){\displaystyle (m_{1},m_{2},\dots ,m_{n})} с произведением M=m1⋅m2⋅⋯⋅mn{\displaystyle M=m_{1}\cdot m_{2}\cdot \dots \cdot m_{n}} так, что каждому целому числу x{\displaystyle x} из отрезка [0,M−1]{\displaystyle [0,M-1]} ставится в соответствие набор вычетов (x1,x2,…,xn){\displaystyle (x_{1},x_{2},\dots ,x_{n})}, где

x≡x1(modm1);{\displaystyle x\equiv x_{1}{\pmod {m_{1}}};}

x≡x2(modm2);{\displaystyle x\equiv x_{2}{\pmod {m_{2}}};}

…

x≡xn(modmn).{\displaystyle x\equiv x_{n}{\pmod {m_{n}}}.}

При этом китайская теорема об остатках гарантирует однозначность представления для чисел из отрезка [0,M−1]{\displaystyle [0,M-1]}.

В СОК арифметические операции (сложение, вычитание, умножение, деление) выполняются покомпонентно, если про результат известно, что он является целочисленным и также лежит в [0,M−1]{\displaystyle [0,M-1]}.

Недостатками СОК является возможность представления только ограниченного количества чисел, а также отсутствие эффективных алгоритмов для сравнения чисел, представленных в СОК. Сравнение обычно осуществляется через перевод аргументов из СОК в смешанную систему счисления по основаниям (m1,m1⋅m2,…,m1⋅m2⋅⋯⋅mn−1){\displaystyle (m_{1},m_{1}\cdot m_{2},\dots ,m_{1}\cdot m_{2}\cdot \dots \cdot m_{n-1})}.

Система счисления Штерна-Броко[править | править код]

Система счисления Штерна-Броко — способ записи положительных рациональных чисел, основанный на дереве Штерна-Броко.

Шестнадцатеричная система счисления — Википедия

Материал из Википедии — свободной энциклопедии

Системы счисления в культуре
Индо-арабская
Арабская Тамильская Бирманская	Кхмерская Лаосская Монгольская Тайская
Восточноазиатские
Китайская Японская Сучжоу Корейская	Вьетнамская Счётные палочки
Алфавитные
Абджадия Армянская Ариабхата Кириллическая Греческая	Грузинская Эфиопская Еврейская Акшара-санкхья
Другие
Вавилонская Египетская Этрусская Римская Дунайская	Аттическая Кипу Майяская Эгейская Символы КППУ
Позиционные
2, 3, 4, 5, 6, 8, 10, 12, 16, 20, 60
Нега-позиционная
Симметричная
Смешанные системы
Фибоначчиева
Непозиционные
Единичная (унарная)

Шестнадцатеричная система счисления — позиционная система счисления по целочисленному основанию 16. В качестве цифр этой системы счисления обычно используются цифры от 0 до 9 и латинские буквы от A до F. Буквы A, B, C, D, E, F имеют значения 10₁₀, 11₁₀, 12₁₀, 13₁₀, 14₁₀, 15₁₀ соответственно.

Широко используется в низкоуровневом программировании и компьютерной документации, поскольку в современных компьютерах минимальной адресуемой единицей памяти является 8-битный байт, значения которого удобно записывать двумя шестнадцатеричными цифрами. Такое использование началось с системы IBM/360, где вся документация использовала шестнадцатеричную систему, в то время как в документации других компьютерных систем того времени (даже с 8-битными символами, как, например, PDP-11 или БЭСМ-6) использовали восьмеричную систему.

В стандарте Юникода номер символа принято записывать в шестнадцатеричном виде, используя не менее 4 цифр (при необходимости — с ведущими нулями).

Шестнадцатеричный цвет — запись трёх компонентов цвета (R, G и B) в шестнадцатеричном виде.

В математике[править | править код]

В математике основание системы счисления принято указывать в десятичной системе в нижнем индексе. Например, десятичное число 1443 можно записать как 1443₁₀ или как 5A3₁₆.

В языках программирования[править | править код]

В разных языках программирования для записи шестнадцатеричных чисел используют различный синтаксис:

• В Ада и VHDL такие числа указывают так: «16#5A3#».
• В Си и языках схожего синтаксиса, например, в Java, используют префикс «0x». Например, «0x5A3».
• В некоторых языках ассемблера используют букву «h», которую ставят после числа. Например, «5A3h». При этом, если число начинается не с десятичной цифры, то для отличия от имён идентификаторов (например, констант) впереди ставится «0» (ноль)^[1]: «0FFh» (255₁₀)
• Другие ассемблеры (AT&T, Motorola), а также Паскаль и некоторые версии Бейсика используют префикс «$». Например, «$5A3».
• В ассемблерах для IBM mainframe (Assembler F, Assembler 2, Assembler H) используется запись X’xx..xx’. Например X’05A3′.
• Некоторые иные платформы, например ZX Spectrum в своих ассемблерах (MASM, TASM, ALASM, GENS и т. д.) использовали запись #5A3, обычно выровненную до одного или двух байт: #05A3.
• Другие версии Бейсика, например Turbo Basic, используют для указания шестнадцатеричных цифр сочетание «&h» или «&H» перед числом. Например, «&h5A3».
• В Unix-подобных операционных системах (и многих языках программирования, имеющих корни в Unix/linux) непечатные символы при выводе/вводе кодируются как 0xCC, где CC — шестнадцатеричный код символа.

Перевод чисел из одной системы счисления в другую[править | править код]

Перевод чисел из шестнадцатеричной системы в десятичную[править | править код]

Для перевода шестнадцатеричного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа.

Например, требуется перевести шестнадцатеричное число 3A5 в десятичное. В этом числе 3 цифры. В соответствии с вышеуказанным правилом представим его в виде суммы степеней с основанием 16:

3A5₁₆ = 3·16²+10·16¹+5·16⁰=
= 3·256+10·16+5·1 = 768+160+5 = 933₁₀

При переводе чисел, следует помнить, что в шестнадцатеричной системе счисления: A=10; B=11; C=12; D=13; E=14; F=15.

Перевод чисел из двоичной системы в шестнадцатеричную и наоборот[править | править код]

Для перевода многозначного двоичного числа в шестнадцатеричную систему нужно разбить его на тетрады справа налево и заменить каждую тетраду соответствующей шестнадцатеричной цифрой. Для перевода числа из шестнадцатеричной системы в двоичную нужно заменить каждую его цифру на соответствующую тетраду из нижеприведённой таблицы перевода.

Например:

010110100011₂ = 0101 1010 0011 = 5A3₁₆

Таблица перевода чисел[править | править код]

	0hex	=	0dec	=	0oct		0	0	0	0
	1hex	=	1dec	=	1oct		0	0	0	1
	2hex	=	2dec	=	2oct		0	0	1	0
	3hex	=	3dec	=	3oct		0	0	1	1
	4hex	=	4dec	=	4oct		0	1	0	0
	5hex	=	5dec	=	5oct		0	1	0	1
	6hex	=	6dec	=	6oct		0	1	1	0
	7hex	=	7dec	=	7oct		0	1	1	1
	8hex	=	8dec	=	10oct		1	0	0	0
	9hex	=	9dec	=	11oct		1	0	0	1
	Ahex	=	10dec	=	12oct		1	0	1	0
	Bhex	=	11dec	=	13oct		1	0	1	1
	Chex	=	12dec	=	14oct		1	1	0	0
	Dhex	=	13dec	=	15oct		1	1	0	1
	Ehex	=	14dec	=	16oct		1	1	1	0
	Fhex	=	15dec	=	17oct		1	1	1	1