Почему компьютеры используют двоичную систему счисления

Люди предпочитают десятичную систему, вероятно, потому, что с древних времен считали по пальцам, а пальцев у людей по десять на руках и ногах. Не всегда и не везде люди пользуются десятичной системой счисления. В Китае, например, долгое время пользовались пятеричной системой счисления.

А компьютеры используют двоичную систему потому, что она имеет ряд преимуществ перед другими системами:

• для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток — нет тока, намагничен — не намагничен и т.п.), а не, например, с десятью, — как в десятичной;

• представление информации посредством только двух состояний надежно и помехоустойчиво;

• возможно применение аппарата булевой алгебры для выполнения логических преобразований информации;

• двоичная арифметика намного проще десятичной.

Недостаток двоичной системы — быстрый рост числа разрядов, необходимых для записи чисел.

Применение восьмеричной и шестнадцатеричной систем счисления

Двоичная система, удобная для компьютеров, для человека неудобна из-за ее громоздкости и непривычной записи.

Перевод чисел из десятичной системы в двоичную и наоборот выполняет машина. Однако, чтобы профессионально использовать компьютер, следует научиться понимать слово машины. Для этого и разработаны восьмеричная и шестнадцатеричная системы.

Числа в этих системах читаются почти так же легко, как десятичные, требуют соответственно в три (восьмеричная) и в четыре(шестнадцатеричная) раза меньше разрядов, чем в двоичной системе

 (ведь числа 8 и 16 — соответственно, третья и четвертая степени числа 2).

Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему очень прост: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр).

Например:

Чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную, его нужно разбить влево и вправо от запятой на

триады (для восьмеричной) или тетрады (для шестнадцатеричной) и каждую такую группу заменить соответствующей восьмеричной (шестнадцатеричной) цифрой.

Например,

Перевод чисел из десятичной системы счисления в другие позиционные системы счисления

При переводе целого десятичного числа в систему с основанием q его необходимо последовательно делить на q до тех пор, пока не останется остаток, меньший или равный q-1. Число в системе с основанием q записывается как последовательность остатков от деления, записанных в обратном порядке, начиная с последнего.

Пример:

 Перевести число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

Ответ: 75₁₀ = 1 001 011₂ = 113₈ = 4B₁₆.

Перевод простой десятичной дроби в другие позиционные системы счисления

Пpи переводе правильной десятичной дpоби в систему счисления с основанием q необходимо сначала саму дробь, а затем дробные части всех последующих произведений последовательно умножать на q, отделяя после каждого умножения целую часть пpоизведения. Число в новой системе счисления записывается как последовательность полученных целых частей пpоизведения.

Умножение пpоизводится до тех поp, пока дpобная часть пpоизведения не станет pавной нулю. Это значит, что сделан точный пеpевод. В пpотивном случае пеpевод осуществляется до заданной точности. Достаточно того количества цифp в pезультате, котоpое поместится в ячейку.

Пример: Перевести число 0,35 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

Ответ: 0,35₁₀ = 0,01011₂ = 0,263₈ = 0,59₁₆ .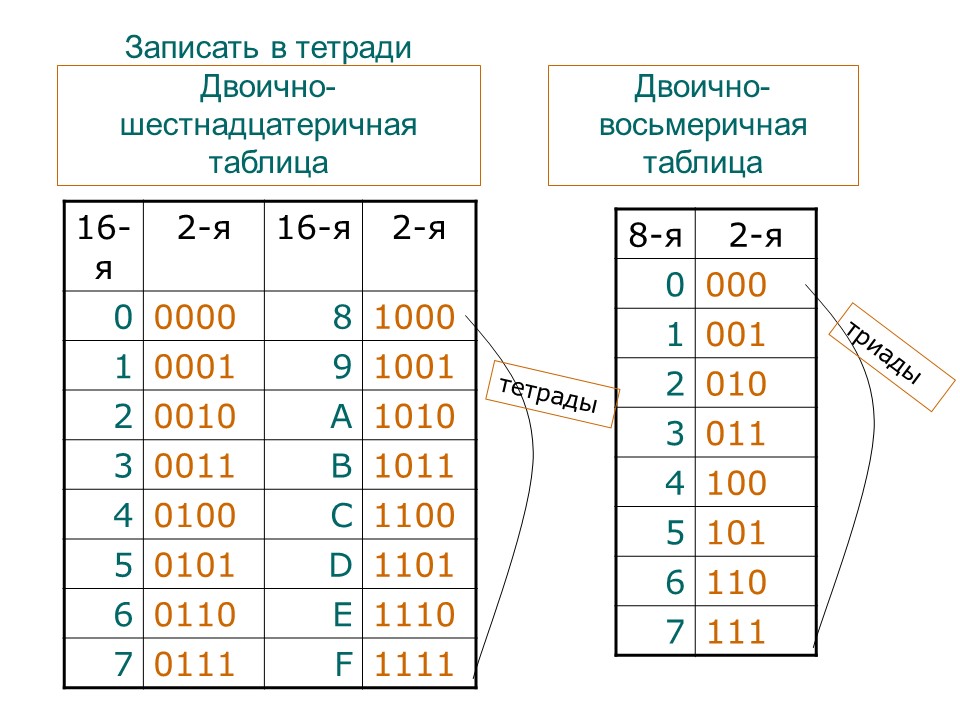

Почему в ЭВМ используется двоичная система счисления

В отличие от человека – ЭВМ не умеют мыслить. Они не способны подрожать человеческому воображению. Однако компьютеры могут очень быстро выполнять сложные математические расчеты и решать за секунды задачи, на которые у нас могли уходить целые недели. Все данные, которые есть в ПК, записаны в цифровом коде, алфавит которого состоит из двух символов – нуля и единицы. В этой статье вы узнаете ответ на вопрос — почему в ЭВМ используется двоичная система счисления.

Содержание статьи

1. Ликвидация безграмотности
2. Введение для чайников
3. Цифровая арифметика в информатике
4. Почему в ЭВМ используется двоичная система счисления
5. Почему использовалась в начале эры ЭВМ?
6. Почему мы пользуемся ей сейчас?
7. Вывод

Ликвидация безграмотности

Введение для чайников

Итак, для того чтобы понять почему двоичный код используется в ЭВМ нужно иметь о нем базовое представление. Все Вы знакомы с десятичным представлением чисел – в нем используются знаки (цифры) от нуля до девяти. После того, как вы использовали цифры от 0 до 9, разряд единиц обнуляется и идет переход к следующему порядку — получается число 10. Использовав все комбинации из двух цифр (отсчитав до 99), вы переходите к разряду сотен.

Отсюда можно сделать вывод, что в десятичной форме записи – цифра следующего разряда всегда в десять раз больше, чем предыдущая (1,10,100,1000 и т.д.). Аналогичное правило применимо и к двоичному коду, состоящему из последовательности нулей и единиц – каждый следующий разряд в два раза больше предыдущего. Чтобы вам было понятнее, покажем это наглядно.

Цифровая арифметика в информатике

В двоичном счислении, исходя из предыдущего раздела, 1 будет представлена, как 1, 2-10,4-100,8-1000. Именно в таком двоичном представлении компьютер работает с вашими данными и неважно, какую форму они имеют – графическую, музыкальную или текстовую. Абсолютно вся информация в корпусе вашего ПК зашита в виде комбинации из нулей и единиц.

Один нолик или однёрка называется единицей информации, или как его еще принято называть – «бит». Наверное, каждый, кто работал с ЭВМ или увлекался информатикой, слышал про магическое число 256. Почему оно так называется? Это количество знаков, которое может распознать компьютер по их коду. Сюда входят кириллический алфавит, латинские буквы цифры и другие символы вроде знаков препинания. Для того чтобы кодировать один символ в ЭВМ нужно 8 бит памяти. Почему?

А 8 бит, принято в информатике называть, как один байт – количество памяти необходимое для хранения одного символа. Зная всё это можно перейти к главному вопросу:

Почему в ЭВМ используется двоичная система счисления

Почему использовалась в начале эры ЭВМ?

Ответ прост — на это повлияли законы физики и особенности развития аппаратного обеспечения. Вспомните, как выглядели первые ЭВМ – большие установки, которые занимали по площади размер, сопоставимый с теннисным кортом.

Для отображения битов и проведения операций с ними использовались обычные лампочки «Ильича» (лампы накаливания). Если на лампу подавался ток, то она обозначала единицу, если ток не подавался, и лампа не горела – 0. Всё это управлялось с помощью электронного реле

. Почему разработчики приняли решение реализовать все именно так? Здесь можно выделить несколько главных причин:

1. Простота технической реализации;
   Есть всего два состояния, а это значит, что можно подобрать большое количество физических процессов, для представления данных. Например, ток (подается или нет), магнитная дорожка (отрезок дорожки намагничен или нет).
2. Большая надежность;
3. Высокая помехоустойчивость.

Второй и третий плюс вытекают из первого. Да и в то время технологии были не настолько развиты, чтобы можно было предложить более практичное решение. Революция произошла в конце пятидесятых, начале шестидесятых годов, когда были выпущены первые кремниевые транзисторы.

Почему мы пользуемся ей сейчас?

Сейчас будет сложно, так что приготовьтесь. Процессоры всех современных компьютеров и других цифровых устройств работают на основе схемотехнических элементов, которые называются транзисторы.

Итак, что это такое? Если говорить просто, то это элемент, который позволяет управлять электрическим током. Рассмотрим принцип его действия.

Элемент состоит из трех частей:

1. Полупроводниковой подложки;
2. Области P-типа:
3. Области N-типа.

Здесь вам нужно знать несколько моментов. В N области содержатся частицы с отрицательным зарядом (электроны). В P области содержатся носители положительного заряда, так называемые «дырки»

. Между ними располагается так называемый обедненный слой. В нем содержится некоторое количество электронов.

Если подать одноименное напряжение на источник и минусовое на управляющую ногу, то потечет ток в сторону выхода – это будет 1, а если наоборот, то ток идти не будет – что будет равно 0. Менять свое состояние устройство может ОЧЕНЬ быстро. Если вы не поняли, как это работает — не страшно. Главное поймите, что элемент делает.

Однако грош цена была бы этому изобретению – если с помощью транзистора можно было выводить только нуль и единицу. Почему? Какой смысл от букв и цифр, если мы не можем с ними выполнять различные операции.

Однако подключив два транзистора определенным образом, мы сможем выполнять логические действия, такие как «или» (сложение) и «и» (умножение). Также можно менять значения на выходе, меняя напряжения на входе. Таким образом, получаются различные комбинации нулей и единиц.

Вывод

А теперь подумайте, какую еще систему можно использовать в компьютере и почему? Например, возьмем следующее по счету — троичное счисление. Система должна находиться в одном из трех состояний. Какой физический процесс подойдет для отображения данных?

Если же брать три уровня тока, то какое устройство сможет быстро производить с ними операции? Правильно, такого не существует. На данный момент, как и раньше, нет более удобного и простого аналога представления информации – это и будет являться ответом на вопрос: почему в ЭВМ используется двоичная система счисления.

Почему компьютеры используют двоичные числа?

Почему компьютеры используют двоичный код?

Пожалуйста, включите JavaScript

Почему компьютеры используют двоичный код?

Двоичная система счисления используется в вычислительной технике и электронике, потому что это самый простой доступный метод подсчета. Кроме того, двоичная система счисления используется для кодирования всего, от памяти до изображений на экране. Таким образом, он является основой для хранения и передачи данных в большинстве цифровых электронных устройств.

Чтобы понять, как это возможно, важно сначала понять двоичную систему счисления и ее работу.

Реклама

Двоичные и десятичные числа

Двоичные числа означают одно или другое.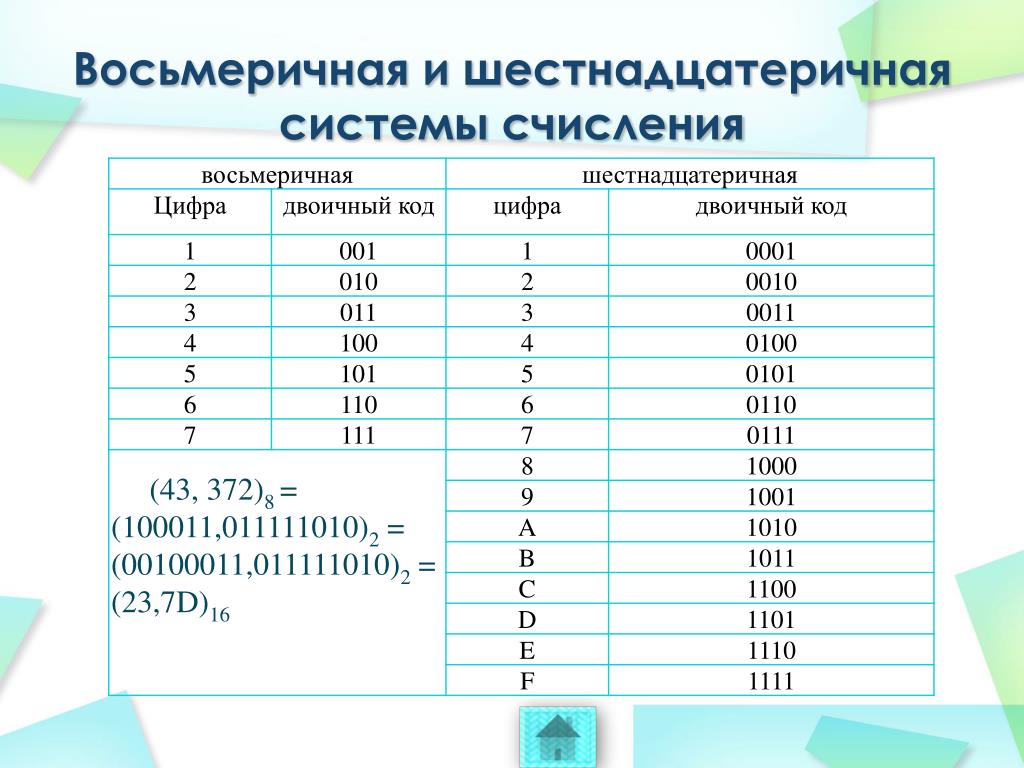 Бинарный выбор, например, предполагает выбор одного из двух возможных вариантов. Двоичное число описывается с помощью системы счисления с основанием 2, в которой используются только два разных символа или цифры: обычно 0 и 1. Все числа в системе счисления с основанием 2 обозначаются с использованием одного или другого из этих символов. Каждая отдельная цифра называется битом.

В повседневной жизни мы не считаем по системе счисления по основанию 2. Вместо этого мы используем десятичную систему счисления с основанием 10. Это означает, что у нас есть 10 различных символов или цифр, доступных для представления различных чисел. Мы можем считать от 0 до 9 до того, как у нас закончатся разные символы, поэтому, когда мы доходим до десяти, мы представляем их, комбинируя 1 и 0.

В нашей системе счета с основанием 10 одна цифра называется единица. Вторая цифра — десятка. Таким образом, символ десяти (10) часто означает 1 лот, а не единицы. Двадцать один (21), написанный цифрами, означает две партии по десять и одну единицу. Каждая дополнительная цифра, которую мы добавляем в нашу систему счисления с основанием 10, представляет собой число, кратное десяткам. Например, мы можем обозначить до 99 (девять лотов по десять и девять единиц), прежде чем нам придется добавить еще одну цифру. Десять лотов часто обозначают как 100, и мы называем это число сотней.

Advertisements

Двоичный счет

Система счисления с основанием 2 работает так же, но вместо десяти различных символов, доступных перед добавлением еще одной цифры, их всего два. Это связано с тем, что в двоичной системе мы можем считать только 0 и 1, прежде чем закончатся символы и нам придется повторно использовать их во второй строке цифр. Следовательно, 0010 равняется двум (одна партия из двух и ни одного бита), 0101 обозначает пять (одна партия из четырех, без двоек и один бит) и так далее.

Наша обычная система счета использует единицы, десятки, сотни и тысячи для представления дополнительных рядов цифр.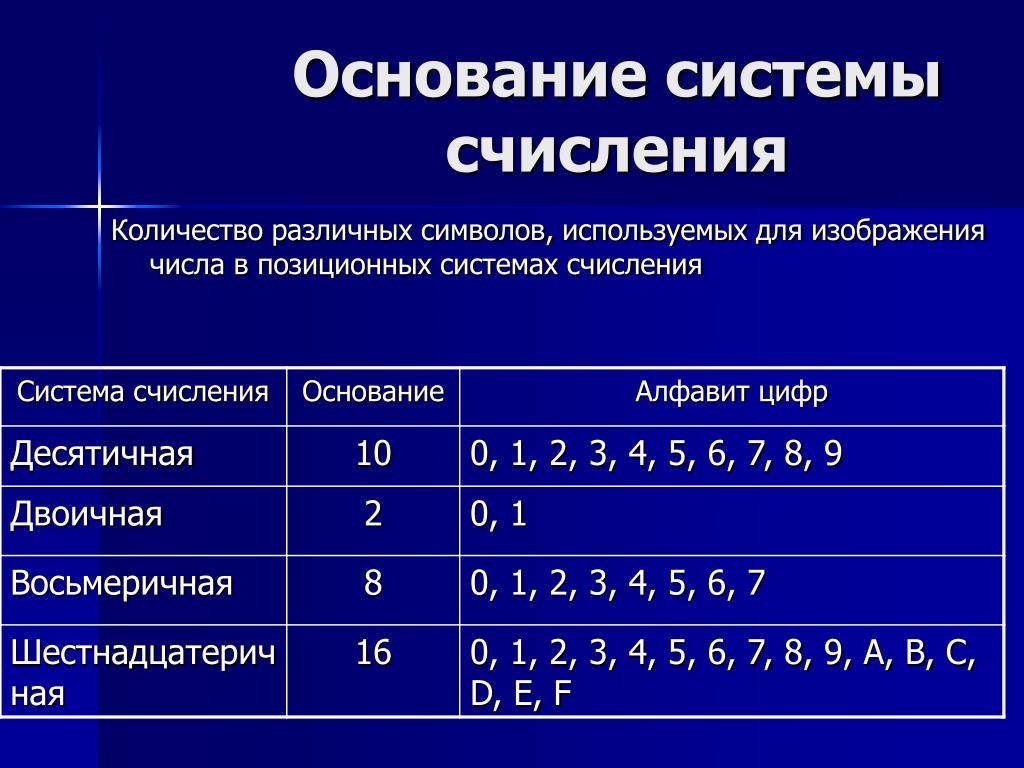 В двоичной системе используются биты, двойки, четверки, восьмерки, шестнадцати и так далее. Таким образом, двоичные числа обычно состоят как минимум из четырех или восьми цифр, в зависимости от того, насколько велико число. Но помимо того, что для выражения гораздо меньших чисел требуется больше цифр (например, шестнадцать описывается как 16 в десятичной системе и 00010000 в двоичной), концепция остается той же.

Почему компьютеры используют двоичные числа?

Основная причина, по которой в вычислениях используется двоичная система счисления, заключается в ее простоте. Компьютеры не понимают язык или числа так, как мы. Все, с чем они действительно могут работать, — это переключатели и электрические сигналы, включенные или выключенные. Для кодирования инструкций или сохранения значений с помощью переключателей, которые могут быть либо выключены, либо включены, двоичная система является вашим очевидным выбором. В двоичном коде «выключено» представлено 0, а «включено» представлено 1.

Компьютеры используют транзисторы в качестве электронных переключателей. Небольшое количество тока, поступающего на транзистор, может генерировать гораздо более высокий выходной ток: меньший ток включает более высокий ток. Если тока нет, выключатель остается выключенным. Это фундаментальное объяснение того, как работают микрочипы.

Значения сохраняются в двоичном формате с помощью этих переключателей, устанавливая их в положение «включено» (1) или «выключено» (0). Один переключатель эквивалентен одному биту, поэтому бит также представляет наименьший объем информации, который можно настроить. Восемь переключателей, т. е. восемь битов, составляют байт. Поскольку каждый переключатель представляет собой строку цифр в двоичной системе счета, восемь переключателей представляют любое значение от 0 до 256. Инструкции состоят из строк этих битов, которые может считывать соответствующее оборудование.

В настоящее время на одном микрочипе можно разместить миллионы транзисторов, но в ранних вычислениях транзисторы должны были быть намного больше. Возможно, система счета, использующая больше чисел, позволит хранить больше значений, используя гораздо меньше места. Так почему же мы до сих пор используем только двоичную систему?

Рекламные объявления

Тернарный компьютер

Добавление еще одной цифры в систему кодирования означало бы добавление возможности определять мощность (т. е. напряжение) электрического сигнала, а не только то, был ли он включен или выключен. Но, конечно, вам также понадобится способ вычисления трех цифр, что потребует использования совершенно нового оборудования.

Аппаратное обеспечение для троичных вычислений — расчеты с тремя возможными значениями — уже существует. Первый компьютер, способный выполнять такие вычисления, был создан в 1840 году, а первая современная электрическая версия — троичный компьютер — была построена в Советском Союзе в 1958 году. Хотя троичный компьютер потенциально дешевле в производстве и в некоторых отношениях потенциально более эффективен , похоже, темпы массового производства бинарных компьютеров затормозили дальнейшее развитие.

Двоичная логика

Сказав это, вероятно, то, как устроены транзисторы и как они выполняют вычисления, является настоящей причиной, по которой мы так долго придерживаемся двоичной системы. Двоичная математика гораздо легче для понимания компьютером, чем троичная математика.

Если сложить транзисторные переключатели вместе, получится логический вентиль. Гейт сравнивает два разных типа входных данных (т. е. включен или выключен каждый из переключателей), чтобы определить свой выход. Следовательно, в вычислениях доступны три типа вентилей и три различных операции: И, ИЛИ и НЕ. Именно так компьютеры принимают решения, и это является основным принципом компьютерного программирования, когда программа состоит из логических наборов инструкций. Примером того, как это работает в реальной жизни, может быть: «Если я уйду вовремя И нет пробок, я сяду на поезд.

Эти операции основаны на разделе математики, называемом булевой алгеброй. Булева логика утверждает, что есть четыре возможных результата, если у вас есть два возможных входа (как в двоичной системе). Каждая операция логического вентиля может быть выражена в виде таблицы истинности:

Реклама

Резюме

Компьютеры используют двоичные числа, потому что это самый простой и простой способ записи и обработки электрических токов, протекающих через их оборудование. Если есть электрический ток, транзисторный переключатель включен. Транзисторный переключатель выключен, если нет электрического тока. Выключатель обозначается цифрой 1, а выключатель — цифрой 0,9.0004

Каждый переключатель представляет один бит информации, а восемь битов называются байтом. Так информация хранится в памяти компьютера.

Тернарные системы существуют, но не используются повсеместно. В будущем они могут стать более распространенными, но в настоящее время невозможно воспроизвести аппаратное обеспечение в столь мелком масштабе, который необходим для того, чтобы троичные транзисторы были жизнеспособны на рынке.

Информатика: Двоичный

Урок 3: Двоичный

/en/computer-science/hardware-and-software/content/

Двоичный

На протяжении всей истории почти каждая цивилизация использовала десятичную систему счисления с 10 цифрами : от нуля до девяти. Все числа, которые мы можем придумать, используют некоторую комбинацию этих 10 цифр.

Однако компьютеры работают иначе. Вместо этого они используют систему счисления, в которой состоит всего из двух цифр : единицы и нуля. Эта система называется двоичной , и ваш компьютер использует ее все время.

Посмотрите видео ниже, чтобы узнать больше о том, как компьютеры используют двоичные файлы.

Компьютерам нужна информация, чтобы делать то, что они делают. Эта цифровая информация, или данных , состоит из чего-то, называемого битами . Бит — это сокращение от двоичной цифры , что означает, что каждый бит на самом деле представляет собой просто одно число: либо один , либо ноль .

Эти биты можно комбинировать для создания более крупных единиц, таких как байты, мегабайты и т. д., которые мы используем для измерения наших файлов. Чем больше файл, тем больше в нем битов. Так что что-то вроде видео высокого разрешения на самом деле состоит из миллионов и миллионов единиц и нулей.

Но как именно эти единицы и нули объединяются и позволяют компьютеру функционировать? Давайте подумаем о двоичном коде как о выключателе света . Представьте, что единица представляет собой выключатель света на , а ноль представляет на . В бинарном режиме свет либо включен, либо выключен, без каких-либо других возможных состояний.

Эти биты связаны вместе как различные комбинации единиц и нулей, и они образуют своего рода код . Затем ваш компьютер быстро обрабатывает этот код и переводит его в данные, сообщая ему, что делать.

Вам может быть интересно, почему компьютеры используют двоичную систему вместо десятичной, которую мы используем для счета в нашей повседневной жизни.