Закон (принцип) конкурентного исключения Г.Ф. Гаузе
«Ряд интересных экспериментов на простейших и микроорганизмах провел советский ученый Г.Ф. Гаузе. Два простейших организма одного семейства, но разных видов он поместил в общий стеклянный сосуд с ограниченным количеством пищи.
Крошечные существа умудрились сотрудничать, делились пищей и оба выжили.
Затем Гаузе поместил в сосуд с таким же количеством пищи два организма одного вида. На этот раз подопытные начали драться и оба погибли. […]
Кстати, Ч. Дарвин предвосхитил результаты эксперимента Гаузе в главе III «Происхождения видов путем естественного отбора»:
«Борьба [за существование] почти неизбежно будет самой суровой между индивидами одного вида, потому что они населяют одни и те же районы, требуют одной и той же пищи и подвергаются одним и тем же опасностям… Так же как виды одного рода имеют обычно… некоторое сходство в привычках и строении и всегда в структуре, борьба обычно происходит более жестокая между видами одного рода, когда они начинают конкурировать друг с другом, чем между видами разных родов.
.. мы смутно понимаем, почему конкуренция должна быть более жестокой между близкими формами, которые заполняют почти одно и то же пространство в экономике природы».
Кроме того, эксперименты привели Г.Ф. Гаузе к выводу о том, что два конкурирующих вида могут сосуществовать только при наличии более чем одного скудного ресурса.
Две популяции вступают в соревнование, если одна понижает уровень роста другой. Они могут сделать это, поедая обеды соперников, вторгаясь на их территорию или включая свои магнитофоны на такую громкость, чтобы все соперники лишили себя жизни. Вариантов достаточно.
Г.Ф. Гаузе определил три возможных результата войн простейших организмов: Два вида вторгаются на территорию друг друга одновременно. Границы между ними стираются, и они приходят к сосуществованию на одном и том же пространстве.
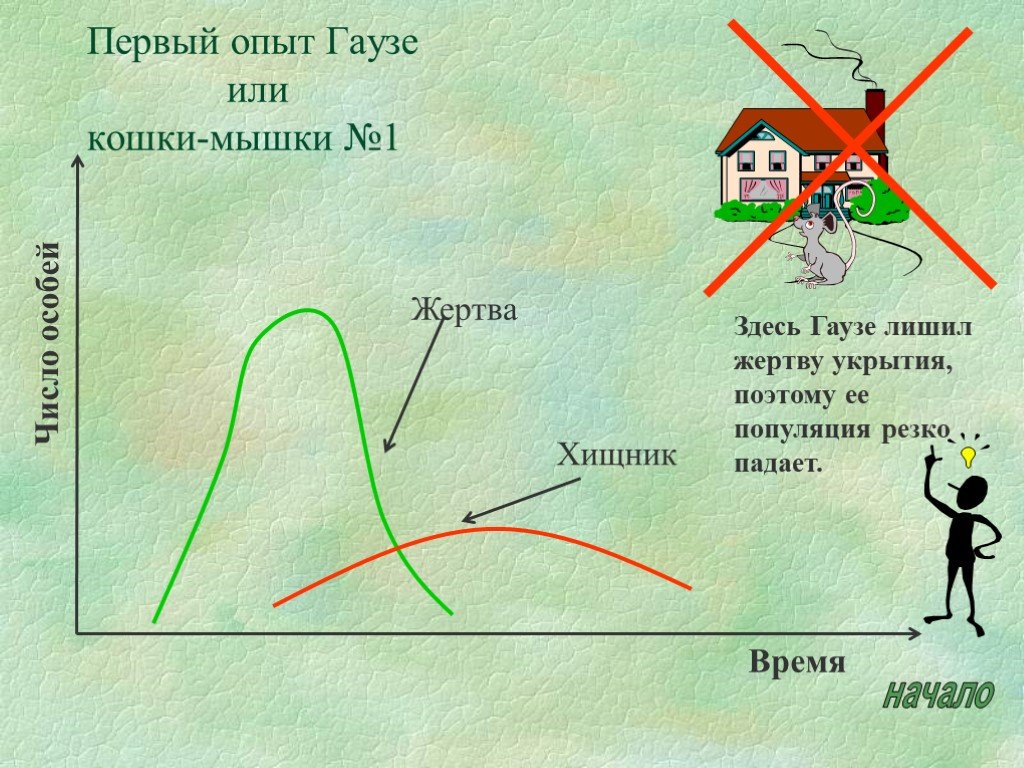
Только один вид вторгается на территорию другого. В результате он становится господствующим. Оккупированный вид уничтожается.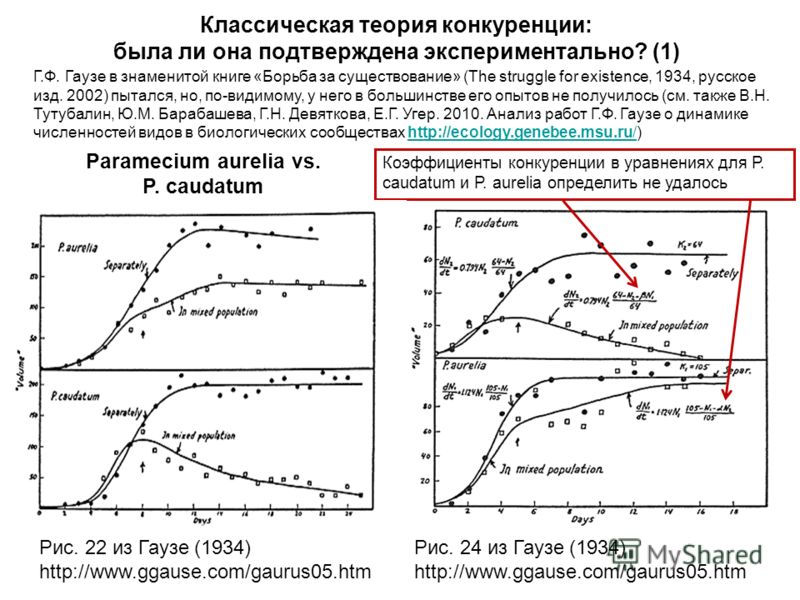
Ни один из видов не переходит границу. Так же как во время недавней «гонки вооружений», между ними существует баланс сил, обеспечивающий мир. Биологи называют это состояние бистабильностью».
Ричард Кох, Законы Силы, Минск, «Попурри», 2003 г., с. 90-92.
«Выражение «закон Гаузе» появилось в 1940-х гг., после того как Гаузе в экспериментах на простейших (1931-1935) показал, что два вида не могут устойчиво существовать в ограниченном пространстве, если они конкурируют за ресурс, ограниченность которого является непосредственным и единственным фактором, лимитирующим обе видовые популяции.
Иногда закон Гаузе формулируется в терминах экологической ниши: два вида не могут сосуществовать, если они занимают одну экологическую нишу. Представления об экологической нише существовали давно. Так, американский натуралист Дж. Гринелл (Grinell, 1917), впервые предложивший термин «экологическая ниша», характеризовал его как пространственное распределение видов. Экологическая ниша определялась в качестве понятия, близкого к местообитанию.
[…]
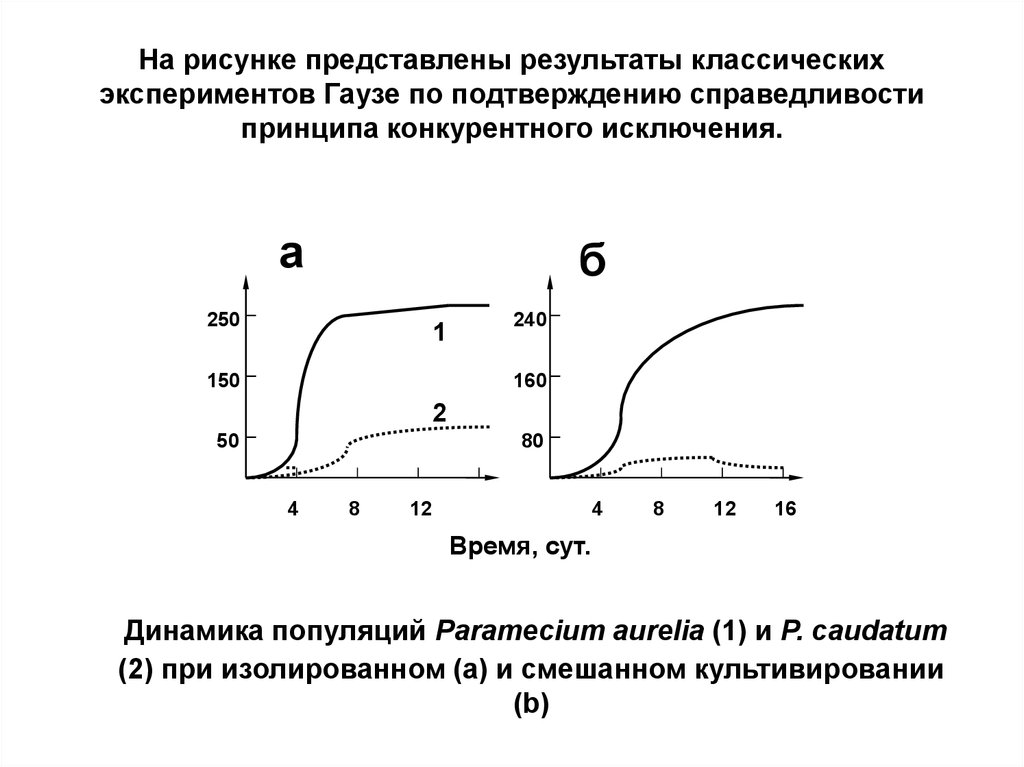
Вначале для экспериментов объектами исследований служили Paramecium aurelia и P. caudatum. Был изучен рост каждого вида в чистой культуре, вычислены коэффициенты размножения, внутривидовой конкуренции, максимальная численность популяции в определенном объеме среды обитания.
Затем были созданы смешанные культуры из двух видов, в которых определялся уровень межвидовой конкуренции, и выяснялись причины вытеснения видов. В этих исследованиях небольшая часть популяции ежедневно изымалась при помощи платиновой петли, и, следовательно, искусственная смертность приближала ситуацию к естественным условиям, в которых часть организмов всегда погибает.
Конкуренция между двумя видами инфузорий, которые питались одним из видов дрожжей и обитали в одном пространстве, всегда заканчивалась вытеснением одного из видов. При этом исход конкуренции зависел не только от факторов среды, но также и от наличия продуктов обмена веществ конкурирующих видов.
Это было новым и важным выводом, поскольку теоретические расчёты Вольтерры — Лотки обычно основывались лишь на учете исходных биологических свойств взаимодействующих видов.
Совсем по-иному складывались конкурентные отношения между P. aurelia и P. bursaria. Хотя и в этих опытах инфузории конкурировали за пищу и пространство, ни один из видов не исчезал, оба могли существовать неопределенно долгое время. Поскольку пищей для инфузорий в этой серии опытов служил смешанный корм, состоящий из дрожжей и бактерий, причину сосуществования видов можно было усмотреть в их пищевой специализации, которая должна была ослабить интенсивность конкуренции.
Действительно, оказалось, что P. bursaria обитала в основном на дне пробирки и питалась оседающими дрожжевыми клетками, а P. aurelia находилась в верхней части пробирки и питалась преимущественно бактериями. Однако и на корме, состоящем из одних только дрожжевых клеток, достигалось равновесие между видами, но при одном условии: если пробирка интенсивно освещалась.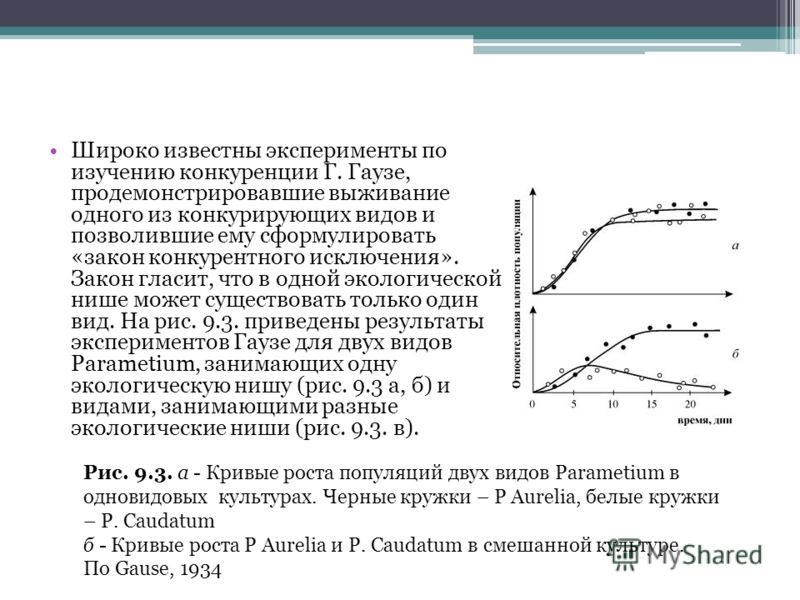
Объяснялось это тем, что вид, обитающий на дне пробирки, неминуемо исчез бы не от недостатка пищи, а от недостатка кислорода. Но этого не происходило, так как вид существовал в симбиозе с водорослью зоохлореллой, которая при ярком освещении снабжала его кислородом. Вид, более чувствительный к недостатку кислорода, обитал в верхней части пробирки, где его было вполне достаточно.
Следовательно, каждый вид существовал в своей собственной зоне, но выживание одного из них обеспечивалось симбиозом с водорослью.
На основании этих экспериментов Гаузе предложил свою концепцию экологической ниши, в которой объединил положение вида в пространстве и его функциональную роль в сообществе. Эти опыты по конкурентному вытеснению видов составили экспериментальную основу положения, вошедшего в мировую литературу под названием закона Гаузе, или принципа конкурентного исключения».
Галл Я.М., Г.Ф. Гаузе: от борьбы за существование к антибиотикам, синтез экологии и теории эволюции, в Сб.
: Создатели современного эволюционного синтеза / Отв. ред. Э.И. Колчинский, СПб, «Нестор-История», 2012 г., с. 639-640.
Принцип конкурентного исключения • Джеймс Трефил, энциклопедия «Двести законов мироздания»
200 законов мироздания > Науки о жизни
Если в стабильной среде сосуществуют два конкурирующих вида, это происходит в результате дифференциации ниш. Если такой дифференциации нет, один из видов обречен на вымирание.
Самое важное понятие в экологии — это понятие экологической ниши. Под нишей подразумевают совокупность факторов окружающей среды, в пределах которых данный вид может развиваться и воспроизводиться. Например, у растения ниша может включать в себя количество осадков, солнечного света и почвенных минералов, необходимых для его роста. У животного-хищника к нише можно отнести климатические факторы, наличие подходящей жертвы и количество эндемичных заболеваний в данной местности.
Принцип конкурентного исключения гласит: если два вида конкурируют за одну нишу, есть только два возможных исхода.
Либо эти два вида немного изменятся и каждый займет немного другую нишу (
В экологии есть много примеров сосуществования видов, но почти во всех таких примерах можно выявить дифференциацию ниш. Если же такая дифференциация не обнаружена, это можно объяснить как нарушением принципа, так и тем, что ученые пока не нашли, что именно изменилось, — например, им надо было исследовать наличие калия, а не фосфора. Но поскольку в других ситуациях значительно больше фактов в пользу конкуренции и поскольку есть теоретические основания полагать, что конкуренция в природе есть, экологи склонны считать, что и в этих случаях действует принцип конкурентного исключения.
См. также:
1964 | Коэволюция |
6
Показать комментарии (6)
Свернуть комментарии (6)
Принцип конкурентного исключения еще называют «законом Гаузе» – в честь Георгия Францевича Гаузе (1910–1986) – выдающегося российского эколога, эволюциониста, специалиста по антибиотикам. Но Дж.Эвелин Хатчинсон предложил именовать это правило «приципом Вольтерры–Гаузе», что вполне справедливо. Итальянский математик Вито Вольтерра на математических моделях (системе дифференциальных уравнений) показал, что два вида, потребляющие одну пищу и этой пищей ограниченные, не могут устойчиво сосуществовать: один вид вытесняет другой. Гаузе же, еще будучи студентом, заинтересовался этими работами и провел эксперименты с простейшими, подтвердив данное правило эмпирически.
Ответить
Lev_Kalmykov 02.01.2013 18:29 Ответить
Принцип конкурентного исключения в явном виде был сформулирован Хардиным (Hardin, 1960). Интересно, что Хардин подчеркнул принципиальную невозможность доказать этот принцип экспериментально.
Еще одна проблема заключается в том, что теоретически принцип конкурентного исключения является недоказанным до сих пор. Модель Лотки-Вольтерры говорит нам о том, что виды сосуществуют, если для обоих видов внутривидовая борьба является более напряженной, чем межвидовая. Однако дальнейшая интерпретация данной интерпретации, которой является принцип конкурентного исключения, не имеет доказательства.
Эта сложная ситуация привела к появлению нейтральной теории Хаббела. Однако даже сами сторонники нейтральной теории говорят о том, что “реальный мир не нейтрален” (Rosindell et al., 2012). Просто нейтральная модель позволяет в некоторых случаях получить правдоподобные результаты без понимания механизмов откуда эти результаты берутся в природе.
Интересная дискуссия на тему является ли нейтральная модель полезной или отражает состояние невежества о механизмах биоразнообразия прошла в 2012 году в Cell Press:
http://news.cell.com/discussions/trends-in-ecology-and-evolution/ecological-neutral-theory-useful-model-or-statement-of- ignorance Garrett J. Hardin. (1960). The Competitive Exclusion Principle. Science 131 (3409): 1292–1297. DOI: 10.1126/science.131.3409.1292
James Rosindell, Stephen P. Hubbell, Fangliang He, Luke J. Harmon, Rampal S. Etienne. (2012) The case for ecological neutral theory.
Ответить
Lev_Kalmykov 19.09.2013 11:24 Ответить
ПРОВЕРКА И ПЕРЕФОРМУЛИРОВАНИЕ ПРИНЦИПА КОНКУРЕНТНОГО ИСКЛЮЧЕНИЯ
Аннотация статьи (авторский перевод)
“Сохранение биоразнообразия становится все более актуальной задачей. Важно найти механизмы конкурентного сосуществования видов с различной приспособленностью в особо неблагоприятных условиях — на одном ограниченным ресурсе, в изолированной стабильной среде обитания, без каких-либо трейдофов и кооперативных взаимодействий. Здесь мы показываем такой механизм конкурентного сосуществования на основе солитоноподобного поведения популяционных волн. Мы смоделировали его логическим аксиоматическим детерминированным индивидуально-ориентированным клеточно-автоматным методом. Наши механистические модели популяционной и экосистемной динамики являются моделями типа белого (прозрачного) ящика и поэтому они обеспечивают прямое понимание изучаемых механизмов.
Переформулированный принцип конкурентного исключения:
«Если каждый без исключения индивид менее приспособленного вида при любой попытке использовать лимитирующий ресурс всегда имеет прямой конфликт интересов с индивидом более приспособленного вида и всегда проигрывает, то при прочих равных условиях для всех индивидов конкурирующих видов, эти виды не смогут сосуществовать неопределенно долго и менее приспособленный вид будет вытеснен из данного местообитания в долгосрочной перспективе».[1]
[1] Kalmykov L.V., Kalmykov V.L. Verification and reformulation of the competitive exclusion principle // Chaos, Solitons & Fractals. 2013. Т. 56. — C. 124-131. doi:http://dx.doi.org/10.1016/j.chaos.
2013.07.006Ответить
Лев Калмыков 08.06.2015 17:31 Ответить
Обобщённый принцип конкурентного исключения для произвольного числа ресурсных конкурентов [1]:
If a competitor completely prevents any use of at least one necessary resource by all its competitors, and itself always has access to all necessary resources and the ability to use them, then, all other things being equal, all its competitors will be excluded.
[1] Kalmykov, L. & Kalmykov, V. A Solution to the Biodiversity Paradox by Logical Deterministic Cellular Automata. Acta Biotheoretica 63, 203-221, doi:10.1007/s10441-015-9257-9 (2015).
Ответить
taras 15.08.2019 12:33 Ответить
Обречённый вид мы могли просто застать до вымирания, пару видов, имеющих тенденцию изменения для занятия более узких ниш, – до того, как они так изменятся.
Насколько долго виды конкурируют в одной и той же нише и в одном и том же ареале? Вот какой вопрос надо задать себе первым при обнаружении нескольких конкурирующих видов.Ответить
jozeppe 24.10.2020 22:50 Ответить
Прямо как в маркетинге.
Есть такая классическая книжка по маркетингу — «Дифференцируйся (отличайся) или умрай» Джека Траута и Эла Райса. Если попытаться ужать всю книгу в один тезис, то можно сформулировать примерно так: для того чтобы выжить в конкурентной борьбе, ты должен отличаться от конкурентов, то есть дифференцировать ниши. Иначе, если твоя ниша совпадает с нишами конкурентов, то ты будешь раздавлен более сильными конкурентами.
Прямо тот же самый принцип конкурентного исключения, но только в применении к бизнесу.
Ответить
Виды могут жить бок о бок, если они не различаются экологически, а наоборот – очень близки. Такова выдвинутая Стивеном Хаббелом (Stephen P. Hubbell) «гипотеза нейтральности», используемая, в частности, для объяснения сосуществования множества видов деревьев в тропическом лесу.
2013.07.006
Насколько долго виды конкурируют в одной и той же нише и в одном и том же ареале? Вот какой вопрос надо задать себе первым при обнаружении нескольких конкурирующих видов.Написать комментарий
? | Зависимость количества видов от площади экосистемы |
около 1900 | Территориальность у животных |
1926 | Отношения хищник—жертва |
1934 | Принцип конкурентного исключения |
1966 | Теория оптимального фуражирования |
1970-е | Дифференциальное использование ресурсов |
1976 | Теорема о маргинальных значениях |
XVI в.
Принцип Коперника
1924
Принцип запрета Паули
Новостная рассылка
«Элементы» в соцсетях:
Применение теоремы Гаусса для количественной оценки локализованных поверхностных выбросов по данным аэродинамических измерений ветра и газовых примесей
Статьи | Том 10, выпуск 9
Атмос. Изм. Тех., 10, 3345–3358, 2017
https://doi.org/10.5194/amt-10-3345-2017
© Автор(ы) 2017. Работа распространяется на условиях
лицензии Creative Commons Attribution 3.0 .
Исследовательская статья 13 сентября 2017 г.
Исследовательская статья | 13 сентября 2017 г.
Stephen Conley 1,6 ,Ian Faloona 1 ,Shobhit Mehrotra 1 ,Maxime Suard 1 ,Donald H. Lenschow 2 ,Colm Sweeney 4 ,Scott Herndon 3 ,Stefan Schwietzke 4 ,5 , Габриэль Петрон 4,5 , Джастин Пайфер 6 , Эрик А.
Корт 7 и Рассел Шнелл 5 Стивен Конли и др.
Стивен Конли 1,6 ,Ian Faloona 1 ,Shobhit Mehrotra 1 ,Maxime Suard 1 ,Donald H. Lenschow 2 ,Colm Sweeney 4 ,Scott Herndon 3 ,Stefan Schwietzke 4,5 , Габриэль Петтрон 4,5 , Джастин Пифер 6 , Эрик А. Корт 7 и Рассел Шнелл 5
Столовые детали. Ресурсы, Калифорнийский университет, Дэвис, Калифорния 95616, США
, Боулдер, Колорадо, СШАПолучено: 24 февраля 2017 г. – Начало обсуждения: 18 апреля 2017 г. – Пересмотрено: 11 августа 2017 г. – Принято: 16 августа 2017 г. – Опубликовано: 13 сентября 2017 г.
Аннотация. Оценки выбросов парниковых газов в воздухе становятся все более распространенными с появлением быстрой коммерческой разработки приборов для обнаружения следов газов, отличающихся повышенной точностью, точностью и частотой измерений, а также с растущим интересом к проверке текущих кадастров выбросов. Многочисленные исследования с воздуха показали, что кадастры выбросов могут недооценивать некоторые источники выбросов углеводородов в нефте- и газодобывающих бассейнах США. Следовательно, правильная оценка точности этих бортовых методов имеет решающее значение для интерпретации значения таких расхождений.
Мы представляем новый метод отбора проб поверхностных источников любых газовых примесей, для которого могут быть выполнены быстрые и точные измерения, и применяем его к метану, этану и углекислому газу в пространственных масштабах ∼ 1000 м, когда последовательные петли облетают целевой источник. области на нескольких высотах. Используя разложение Рейнольдса для скалярных концентраций вместе с теоремой Гаусса, мы показываем, что метод точно учитывает мелкомасштабную турбулентную дисперсию локального шлейфа, которая часто игнорируется в других средних массовый баланс
методы. С помощью моделирования больших вихрей (LES) мы также показываем, как можно оптимизировать радиус вращения по кругу для микрометеорологических условий, возникающих во время любого полета. Кроме того, взяв пробы контролируемых выбросов метана и этана на землю, мы можем убедиться, что точность метода в соответствующих метеорологических условиях часто превышает 10 %, а пределы обнаружения ниже 5 кг·ч −1 для обоих метановых и этан.
Из-за того, что минимальная безопасная высота полета, установленная FAA, составляет 150 м, размещение самолета имеет решающее значение для предотвращения прохождения значительной части шлейфа выбросов ниже минимальной высоты отбора проб самолета, которая обычно является основным источником неопределенности в этих измерениях. Наконец, мы показываем, как точность метода сильно зависит от количества циклов отбора проб и/или времени, затрачиваемого на отбор проб исходного шлейфа.
Загрузить
Краткий обзор
В этом документе описывается новый метод количественного определения поверхностных выбросов газовых примесей (например, метана) от небольших самолетов (например, Mooney, Cessna) примерно за 30 мин. Этот метод значительно повышает нашу способность быстро реагировать в случае катастрофических сбоев, таких как Aliso Canyon и Deep Water Horizon.
Подробнее
Закон Гаусса | Brilliant Math & Science Wiki
Агнишом Чаттопадхьяй, Абхиджит Ватс, Сатьябрата Даш, и
способствовал
Содержимое
- Утверждение теоремы
- Закрытые поверхности
- Поток векторного поля
- Дивергенция векторного поля.
- Закон Гаусса для электрического поля
- Закон Гаусса для других важных полей
- Эквивалентность с законом Кулона
- Приложения
Замкнутая поверхность — это поверхность, которая компактна и не имеет границ . Другими словами, замкнутая поверхность — это поверхность, которая делит пространство (за исключением самого себя) на две непересекающиеся части: внешнюю и внутреннюю. Некоторые простые примеры закрытых поверхностей включают неповрежденные пузыри, сферы Дайсона или корпус, внутри которого можно было бы оказаться, если бы они залезли в спальный мешок и зашили отверстие.
Лист бумаги Пустая бутылка из-под газировки Чаша Надувная трубка для плавания
Закон Гаусса — очень мощный метод определения электрического поля из-за распределения зарядов. Математическое выражение для закона Гаусса: E⋅dA=ϵ0Qenc,
где SSS — поверхность, E⃗\vec{E}E — вектор электрического поля, dA⃗\vec{dA}dA — бесконечно малый элемент площади, QencQ_{enc}Qenc — заряд, заключенный в S,S,S , а ϵ0\epsilon_0ϵ0 — константа.
Чтобы применить закон Гаусса, нам нужно понять, что означает каждая из частей этого выражения. Этот набор задач поможет вам понять каждый из компонентов. Начнем с ССС. Вы можете быть более знакомы с интегралами как с пределом суммы функции на линейном интервале, который дает «площадь под кривой». Интеграл по поверхности функции — это просто сумма этой функции по всем точкам на поверхности.
Поверхность по закону Гаусса представляет собой замкнутую двумерную поверхность , такую как поверхность сферы или поверхность куба. Замкнутая поверхность — это поверхность, которая делит пространство на внутреннее и внешнее, причем под делением мы понимаем, что нет пути, идущего изнутри наружу, который не проникал бы сквозь поверхность. Рассмотрим НДС поверхности нижележащих объектов. Для какого из объектов НДС является замкнутой поверхностью?
Грубо говоря, поток поля через поверхность — это суммарный поток через нее. Мы развиваем эту интуицию в примере ниже.
Подумайте об этой аналогии:
Предположим, вы вставили хлопчатобумажную мембрану в середину трубы, по которой течет вода. Какой поток воды через мембрану?
Конечно, ответом будет средняя нормальная составляющая скорости умноженная на площадь мембраны .
Это то, что мы называем потоком через мембрану!
Почему мы берем нормальный компонент? Потому что выравнивание мембраны по направлению потока имеет значение. Что, если и мембрана, и поток выровнены горизонтально?
Φ=∮SE→⋅dA→. \Phi = \oint_{\mathcal{S}} \overrightarrow{E} \cdot d \overrightarrow{A}.Φ=∮SE⋅dA.
Дивергенция векторного поля в точке — это величина источника или стока поля в этой точке.
Конечно, это то же самое, что утверждать, что дивергенция представляет собой объемную плотность внешнего потока векторного поля из бесконечно малого объема вокруг данной точки.
Формально указанное выше переводится как
9, \overrightarrow{E}(x \widehat{i} + y \widehat{j} + z \widehat{k}) = u \widehat{i} + v \widehat{j} + w \widehat{k}, E(xi+yj+zk)=ui+vj+wk,
, затем
дел E→=∇⋅E→=∂u∂x+∂v∂y+∂w∂z. \operatorname{div}\,\overrightarrow{E} = \nabla \cdot \overrightarrow{E} = \frac{\partial{u}}{\partial{x}}+\frac{\partial{v}}{ \partial{y}}+\frac{\partial{w}}{\partial{z}} .divE=∇⋅E=∂x∂u+∂y∂v+∂z∂w.
Интегральная форма
Если SSS является замкнутой поверхностью, в которой заключен заряд QQQ, то поток ΦE\Phi_EΦE через SSS равен
ΦE=∮SE→⋅dA→=Qε0. \Phi_E = \oint_{\mathcal{S}} \overrightarrow{E} \cdot d \overrightarrow{A} =\frac{Q}{\varepsilon_0}. ΦE=∮SE⋅dA=ε0Q.
Дифференциальная форма
Если ρ(r→) \rho \left(\overrightarrow{r}\right)ρ(r) объемная плотность заряда при r→\overrightarrow{r}r, то дивергенция электрического поля E→\overrightarrow{E}E при r→\overrightarrow{r}r равно
∇⋅E→(r→)=ρ(r→)ε0.
\nabla \cdot \overrightarrow{E}\left(\overrightarrow{r}\right) = \frac{\rho \left(\overrightarrow{r}\right) }{\varepsilon_0} .∇⋅E(r)= ε0ρ(r).
Приведенное выше обсуждение потоков и дивергенций должно прояснить, почему эти две формы эквивалентны. Тем не менее эта эквивалентность вытекает из теоремы Гаусса или теоремы о расходимости.
Аналогичное утверждение, такое как электрический закон Гаусса, может быть сделано для нескольких других полей. Вот таблица таких выражений, где символы имеют свои обычные значения.
| Поле | Интегральная форма | Дифференциальная форма |
| Гравитационное\hпространство{20мм} | ∮g→⋅dA→=−4πGM\oint \overrightarrow{g} \cdot d \overrightarrow{A} = -4 \pi G M∮g⋅dA=−4πGM\hspace{20mm} | ∇⋅g →=−4πGρ \nabla \cdot \overrightarrow{g} =-4 \pi G \rho ∇⋅g=−4πGρ |
| Магнитное | ∮B→⋅dA→=0\oint \overrightarrow{B} \cdot d \overrightarrow{A} = 0∮B⋅dA=0 | ∇⋅B→=0\nabla \cdot \overrightarrow{B} = 0 ∇⋅B=0 |
Вывод кулоновских чисел из Гаусса :
Рассмотрим заряд QQQ и сферу радиуса rrr.
, что является законом Гаусса, как и хотелось. □_\квадрат□.
Примечание : Предлагаемое доказательство работает только для сферических поверхностей; более общее доказательство заканчивается использованием векторного исчисления и функций Грина/Дельта. Не стесняйтесь делать снимок в общем случае.
9dA=∮r2γdA=r2γ∮dA=r2γ4πr2=4πγ=ε0q,Закон Гаусса — мощное утверждение о полях обратных квадратов. Он нашел свое место не только в решении задач, но и в четырех уравнениях Максвелла, а также в гравитации. 92}4πϵ0x2λ
Предположим, что бесконечно длинный прямой проводник с током имеет однородную линейную плотность заряда λ.\lambda.λ. Пусть этот провод находится на оси yyy плоскости xyxyxy, и пусть x>0x > 0x>0 будет расстоянием между осью yyy и точкой PPP на плоскости xyxyxy. Какова напряженность электрического поля в точке P?P?P?
Примечание: ϵ0\epsilon_0 ϵ0 в вариантах ниже обозначает электрическую постоянную.
