Кривизна Гаусса — Википедия
Слева направо: поверхность с отрицательной гауссовой кривизной (гиперболоид), поверхность с нулевой гауссовой кривизной (цилиндр), и поверхность с положительной гауссовой кривизной (сфера).Гауссова кривизна — мера искривления поверхности в окрестности какой-либо её точки. Гауссова кривизна является объектом внутренней геометрии поверхностей, в частности, не изменяется при изометрических изгибаниях.
Кривизна Гаусса для двумерной поверхности[править | править код]
Обозначим нормальные кривизны в главных направлениях (главные кривизны) в рассматриваемой точке поверхности κ1{\displaystyle \kappa _{1}} и κ2{\displaystyle \kappa _{2}}. Величина:
- K=κ1κ2{\displaystyle K=\kappa _{1}\kappa _{2}}
называется гауссовой кривизной, полной кривизной или просто кривизной поверхности. Встречается также термин скаляр кривизны, который подразумевает результат свёртки тензора кривизны; при этом скаляр кривизны вдвое больше, чем гауссова кривизна.
Гауссова кривизна может быть вычислена через метрику поверхности, и поэтому она является объектом внутренней геометрии (отметим, что главные кривизны к внутренней геометрии не относятся). По знаку кривизны можно классифицировать точки поверхности (см. рисунок). Кривизна плоскости равна нулю. Кривизна сферы радиуса R всюду равна 1R2{\displaystyle {\frac {1}{R^{2}}}}. Существует и поверхность постоянной отрицательной кривизны — псевдосфера.
Кривизна Гаусса для гиперповерхности[править | править код]
Кривизна n-мерной гиперповерхности в точке полностью описывается её главными кривизнами k(1),k(2),…,k(n){\displaystyle k^{(1)},k^{(2)},\dots ,k^{(n)}} и соответствующими главными направлениями.
Рассмотрим (с точностью до знака) симметрические многочлены, составленные из чисел
- (1)k(1),k(2),…,k(n):{\displaystyle (1)\qquad k^{(1)},k^{(2)},\dots ,k^{(n)}:}
- (2){K[1]=−(k(1)+k(2)+⋯+k(n))=−∑ik(i)K[2]=k(1)k(2)+k(1)k(3)+⋯+k(n−1)k(n)=∑i<jk(i)k(j)⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯K[n]=(−1)nk(1)k(2)⋯k(n){\displaystyle (2)\qquad \left\{{\begin{array}{rcl}K^{[1]}&=&-(k^{(1)}+k^{(2)}+\dots +k^{(n)})=-\sum \limits _{i}k^{(i)}\\K^{[2]}&=&k^{(1)}k^{(2)}+k^{(1)}k^{(3)}+\dots +k^{(n-1)}k^{(n)}=\sum \limits _{i<j}k^{(i)}k^{(j)}\\\cdots &\cdots &\cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \\K^{[n]}&=&(-1)^{n}k^{(1)}k^{(2)}\cdots k^{(n)}\\\end{array}}\right.}
Назовем вышеприведенные величины кривизнами Гаусса соответствующей степени. Общая формула кривизны Гаусса степени m запишется так:
- (3)K[m]=∑i1<i2<⋯<imk(i1)k(i2)⋯k(im){\displaystyle (3)\qquad K^{[m]}=\sum _{i_{1}<i_{2}<\dots <i_{m}}k^{(i_{1})}k^{(i_{2})}\cdots k^{(i_{m})}}
Кривизны Гаусса являются коэффициентами характеристического многочлена для матрицы тензора полной кривизны гиперповерхности:
- (4)det(λδji−bji)=λn+K[1]λn−1+⋯+K[n−1]λ+K[n]{\displaystyle (4)\qquad \det(\lambda \delta _{j}^{i}-b_{j}^{i})=\lambda ^{n}+K^{[1]}\lambda ^{n-1}+\dots +K^{[n-1]}\lambda +K^{[n]}}
Тензорная формула для кривизны Гаусса[править | править код]
Формула (3) определяет кривизну Гаусса через собственные числа тензора полной кривизны гиперповерхности bij{\displaystyle b_{ij}}. Попробуем выразить эти величины через компоненты самого тензора bij{\displaystyle b_{ij}} в любой системе координат. Для вычисления определителя произвольного тензора второго ранга мы имеем такую формулу с использованием тензора метрической матрешки (см. Абсолютно антисимметричный единичный тензор):
- (5)det(aji)=1n!gj1j2…jni1i2…inai1j1ai2j2⋯ainjn{\displaystyle (5)\qquad \det(a_{j}^{i})={1 \over n!}g_{j_{1}j_{2}\dots j_{n}}^{i_{1}i_{2}\dots i_{n}}a_{i_{1}}^{j_{1}}a_{i_{2}}^{j_{2}}\cdots a_{i_{n}}^{j_{n}}}
Подставим в эту формулу aji=λδji−bji{\displaystyle a_{j}^{i}=\lambda \delta _{j}^{i}-b_{j}^{i}}, чтобы вычислить левое выражение формулы (4), тогда имеем:
- (6)n!det(λδji−bji)=gj1j2…jni1i2…in(λδi1j1−bi1j1)⋯(λδinjn−binjn){\displaystyle (6)\qquad n!\det(\lambda \delta _{j}^{i}-b_{j}^{i})=g_{j_{1}j_{2}\dots j_{n}}^{i_{1}i_{2}\dots i_{n}}(\lambda \delta _{i_{1}}^{j_{1}}-b_{i_{1}}^{j_{1}})\cdots (\lambda \delta _{i_{n}}^{j_{n}}-b_{i_{n}}^{j_{n}})}
Раскроем скобки в формуле (6). Поскольку тензор метрической матрешки gj1j2…jni1i2…in{\displaystyle g_{j_{1}j_{2}\dots j_{n}}^{i_{1}i_{2}\dots i_{n}}} не меняется при синхронной перестановке верхних и нижних индексов, то все слагаемые при одинаковой степени λm{\displaystyle \lambda ^{m}} будут одинаковыми (их количество равно биномиальному коэффициенту Cnm{\displaystyle C_{n}^{m}}), и мы получаем:
- (7)n!det(λδji−bji)=λngs1s2…sns1s2…sn−Cn1λn−1gjs2…snis2…snbij+Cn2λn−2gj1j2…sni1i2…snbi1j1bi2j2−…{\displaystyle (7)\qquad n!\det(\lambda \delta _{j}^{i}-b_{j}^{i})=\lambda ^{n}g_{s_{1}s_{2}\dots s_{n}}^{s_{1}s_{2}\dots s_{n}}-C_{n}^{1}\lambda ^{n-1}g_{js_{2}\dots s_{n}}^{is_{2}\dots s_{n}}b_{i}^{j}+C_{n}^{2}\lambda ^{n-2}g_{j_{1}j_{2}\dots s_{n}}^{i_{1}i_{2}\dots s_{n}}b_{i_{1}}^{j_{1}}b_{i_{2}}^{j_{2}}-\dots }
Поскольку последовательные свертки тензора метрической матрешки равны:
- (8)gj1j2…jmsm+1sm2…sni1i2…imsm+1sm+2…sn=(n−m)!gj1…jmi1…im{\displaystyle (8)\qquad g_{j_{1}j_{2}\dots j_{m}s_{m+1}s_{m_{2}}\dots s_{n}}^{i_{1}i_{2}\dots i_{m}s_{m+1}s_{m+2}\dots s_{n}}=(n-m)!\,g_{j_{1}\dots j_{m}}^{i_{1}\dots i_{m}}}
То из формулы (7) и формулы для биномиальных коэффициентов Cnm=n!m!(n−m)!{\displaystyle C_{n}^{m}={n! \over m!(n-m)!}} находим такую формулу для характеристического многочлена (разделив обе стороны уравнения (7) на n!{\displaystyle n!}):
- (9)det(λδji−bji)=λn−λn−11!gjibij+λn−22!gj1j2i1i2bi1j1bi2j2−…{\displaystyle (9)\qquad \det(\lambda \delta _{j}^{i}-b_{j}^{i})=\lambda ^{n}-{\lambda ^{n-1} \over 1!}g_{j}^{i}b_{i}^{j}+{\lambda ^{n-2} \over 2!}g_{j_{1}j_{2}}^{i_{1}i_{2}}b_{i_{1}}^{j_{1}}b_{i_{2}}^{j_{2}}-\dots }
Сравнивая формулы (9) и (4), находим такую формулу для кривизны Гаусса:
- (10)K[m]=(−1)mm!gj1j2…jmi1i2…imbi1j1bi2j2…bimjm{\displaystyle (10)\qquad K^{[m]}={(-1)^{m} \over m!}g_{j_{1}j_{2}\dots j_{m}}^{i_{1}i_{2}\dots i_{m}}b_{i_{1}}^{j_{1}}b_{i_{2}}^{j_{2}}\dots b_{i_{m}}^{j_{m}}}
Для скалярной кривизны гиперповерхности мы имеем такую формулу
- (11)R=gikgjlRijkl=2∑i<jk(i)k(j)=2K[2]{\displaystyle (11)\qquad R=g^{ik}g^{jl}R_{ijkl}=2\sum _{i<j}k^{(i)}k^{(j)}=2K^{[2]}}
Чтобы обобщить эту формулу для более высоких степеней, попробуем заменить произведение двух метрических тензоров в формуле (11) на тензор метрической матрешки четвертого ранга:
- (12)gijklRijkl=|gikgilgjkgjl|Rijkl=(gikgjl−gilgjk)Rijkl=2R=4K[2]{\displaystyle (12)\qquad g^{ijkl}R_{ijkl}={\begin{vmatrix}g^{ik}&g^{il}\\g^{jk}&g^{jl}\end{vmatrix}}R_{ijkl}=(g^{ik}g^{jl}-g^{il}g^{jk})R_{ijkl}=2R=4K^{[2]}}
Для дальнейших вычислений мы перейдем в локальную декартову систему координат в одной из точек многообразия P, и ориентируем её вдоль главных направлений гиперповерхности. В точке P матрица метрического тензора будет единичной:
- (13)gij=δij={1,i=j0,i≠j{\displaystyle (13)\qquad g_{ij}=\delta _{ij}={\begin{cases}1,&i=j\\0,&i\neq j\end{cases}}}
а потому мы можем численно не различать ковариантные и соответствующие контравариантные компоненты тензоров (верхние и нижние индексы). Тензор Римана в точке P{\displaystyle P} будет в некотором смысле диагональным, а именно, его ненулевые компоненты будут равны:
- (14)Rijij=−Rijji=k(i)k(j)(i≠j){\displaystyle (14)\qquad R_{ijij}=-R_{ijji}=k^{(i)}k^{(j)}\qquad (i\neq j)}
и равны нулю все те компоненты Rijkl{\displaystyle R_{ijkl}}, где вторая пара индексов (kl){\displaystyle (kl)} не совпадает с (ij){\displaystyle (ij)} с точностью до перестановки в паре.
Левая часть формулы (12) является линейной формой от тензора Римана, а коэффициентами этой формы служат компоненты тензора метрической матрешки. Очевидным обобщением является рассмотрение билинейной формы и форм высших степеней от компонента тензора Римана. Проведем вычисления формулы (12) еще раз и таким образом, чтобы эти вычисления можно было легко обобщить. Имеем, учитывая диагональность тензора Римана:
- (15)gklijRijkl=∑i,j(∑k,lgklijRijkl)=∑i,j(gijijRijij+gjiijRijji){\displaystyle (15)\qquad g_{kl}^{ij}R_{ij}^{kl}=\sum _{i,j}\left(\sum _{k,l}g_{kl}^{ij}R_{ij}^{kl}\right)=\sum _{i,j}\left(g_{ij}^{ij}R_{ij}^{ij}+g_{ji}^{ij}R_{ij}^{ji}\right)}
Далее, два слагаемых в правой части формулы (15) одинаковы вследствие антисимметрии по индексам внутри пары как тензора метрической матрешки, так тензора Римана. Кроме того, диагональная компонента метрической матрешки равна единице, поскольку (в следующей формуле сложения по одинаковым индексам не производится, а индексы i,j{\displaystyle i,j} разные):
- (16)gijij=|δiiδjiδijδjj|=|1001|=1{\displaystyle (16)\qquad g_{ij}^{ij}={\begin{vmatrix}\delta _{i}^{i}&\delta _{j}^{i}\\\delta _{i}^{j}&\delta _{j}^{j}\end{vmatrix}}={\begin{vmatrix}1&0\\0&1\end{vmatrix}}=1}
Учитывая вышесказанное и формулу (14), превращаем формулу (15) далее:
- (17)gklijRijkl=2∑i≠j1⋅k(i)k(j)=2⋅2!∑i<jk(i)k(j)=2⋅2!K[2]{\displaystyle (17)\qquad g_{kl}^{ij}R_{ij}^{kl}=2\sum _{i\neq j}1\cdot k^{(i)}k^{(j)}=2\cdot 2!\sum _{i<j}k^{(i)}k^{(j)}=2\cdot 2!K^{[2]}}
Теперь перейдем к вычислению следующей квадратичной формы:
- (18)Φ2(R)=gk1l1k2l2i1j1i2j2Ri1j1k1l1Ri2j2k2l2{\displaystyle (18)\qquad \Phi _{2}(R)=g_{k_{1}l_{1}k_{2}l_{2}}^{i_{1}j_{1}i_{2}j_{2}}R_{i_{1}j_{1}}^{k_{1}l_{1}}R_{i_{2}j_{2}}^{k_{2}l_{2}}}
Коэффициентами этой формы служат компоненты тензора метрической матрешки восьмого ранга. Этот тензор имеет две группы индексов, и является антисимметричным по перестановке индексов внутри этих групп. Вычисляем аналогично формуле (15).
- (19)Φ2(R)=∑i1,j1,i2,j2(∑k1,l1,k2,l2gk1l1k2l2i1j1i2j2Ri1j1k1l1Ri2j2k2l2)=22∑i1,j1,i2,j2gi1j1i2j2i1j1i2j2Ri1j1i1j1Ri2j2i2j2{\displaystyle (19)\qquad \Phi _{2}(R)=\sum _{i_{1},j_{1},i_{2},j_{2}}\left(\sum _{k_{1},l_{1},k_{2},l_{2}}g_{k_{1}l_{1}k_{2}l_{2}}^{i_{1}j_{1}i_{2}j_{2}}R_{i_{1}j_{1}}^{k_{1}l_{1}}R_{i_{2}j_{2}}^{k_{2}l_{2}}\right)=2^{2}\sum _{i_{1},j_{1},i_{2},j_{2}}g_{i_{1}j_{1}i_{2}j_{2}}^{i_{1}j_{1}i_{2}j_{2}}R_{i_{1}j_{1}}^{i_{1}j_{1}}R_{i_{2}j_{2}}^{i_{2}j_{2}}}
Обозначим индексы i1,j1,i2,j2{\displaystyle i_{1},j_{1},i_{2},j_{2}} как i,j,k,l{\displaystyle i,j,k,l} для упрощения записи:
- (19a)Φ2(R)=22∑i,j,k,lgijklijklRijijRklkl=224!∑i,j,k,lalldifferentgijklijklk(i)k(j)k(k)k(l){\displaystyle (19a)\qquad \Phi _{2}(R)=2^{2}\sum _{i,j,k,l}g_{ijkl}^{ijkl}R_{ij}^{ij}R_{kl}^{kl}=2^{2}4!\sum _{i,j,k,l \over all\;different}g_{ijkl}^{ijkl}k^{(i)}k^{(j)}k^{(k)}k^{(l)}}
Все четыре индекса i,j,k,l{\displaystyle i,j,k,l} должны быть попарно различными, поскольку компоненты тензора метрической матрешки равны нулю при наличии двух одинаковых индексов в одной группе. В правой сумме формулы (19a) стоят диагональные компоненты тензора метрической матрешки, которые равны единице (аналогично формуле 16).
- (19b)Φ2(R)=22∑i,j,k,lalldifferentk(i)k(j)k(k)k(l)=22⋅4!∑i<j<k<lk(i)k(j)k(k)k(l)=22⋅4!K[4]{\displaystyle (19b)\qquad \Phi _{2}(R)=2^{2}\sum _{i,j,k,l \over all\;different}k^{(i)}k^{(j)}k^{(k)}k^{(l)}=2^{2}\cdot 4!\sum _{i<j<k<l}k^{(i)}k^{(j)}k^{(k)}k^{(l)}=2^{2}\cdot 4!K^{[4]}}
Множитель 4! при переходе ко второй сумме в формуле (19a) возник вследствие того, что для одного слагаемого в правой сумме, характеризующегося фиксированным набором четырех различных чисел i<j<k<l{\displaystyle i<j<k<l}, соответствует 4! = 24 одинаковых по величине слагаемого в левой сумме, характеризующихся перестановками этих четырех чисел.
Формулы (19), (19a), (19b) легко обобщаются на формы высших степеней. Таким образом получаем общую формулу для нахождения кривизны Гаусса парной степени 2m{\displaystyle 2m}:
- (20)K[2m]=12m(2m)!gk1l1…kmlmi1j1…imjmRi1j1k1l1⋯Rimjmkmlm{\displaystyle (20)\qquad K^{[2m]}={1 \over 2^{m}(2m)!}g_{k_{1}l_{1}\dots k_{m}l_{m}}^{i_{1}j_{1}\dots i_{m}j_{m}}R_{i_{1}j_{1}}^{k_{1}l_{1}}\cdots R_{i_{m}j_{m}}^{k_{m}l_{m}}}
Альтернативный вывод формулы кривизны Гаусса для парной степени[править | править код]
Воспользуемся следующим выражением тензора Римана через тензор полной кривизны
- (21)Rijkl=bikbjl−bjkbil{\displaystyle (21)\qquad R_{ij}^{kl}=b_{i}^{k}b_{j}^{l}-b_{j}^{k}b_{i}^{l}}
и начнем в формуле (10) группировать сомножители по два, например начиная с первых двух (здесь мы считаем, что степень 2m{\displaystyle 2m} кривизны Гаусса не меньше двух (m≥1{\displaystyle m\geq 1}), и для упрощения записи опустим обозначения m{\displaystyle m}):
- (22)(2m)!K=gkl…ij…bikbjl⋯=−gkl…ji…bikbjl⋯{\displaystyle (22)\qquad (2m)!K=g_{kl\dots }^{ij\dots }b_{i}^{k}b_{j}^{l}\cdots =-g_{kl\dots }^{ji\dots }b_{i}^{k}b_{j}^{l}\cdots }
Последнее преобразование справедливо вследствие антисимметрии тензора метрической матрешки относительно индексов в верхней группе. Далее, в последнем выражении поменяем местами индексы i,j{\displaystyle i,j}
Gaussian поверхность — Gaussian surface
 Цилиндрическая гауссова поверхность обычно используются для расчета электрического заряда бесконечно длинной, прямой, «идеальной» проволоки.
Цилиндрическая гауссова поверхность обычно используются для расчета электрического заряда бесконечно длинной, прямой, «идеальной» проволоки.Гауссова поверхность (иногда сокращенно GS) представляет собой замкнутую поверхность в трехмерном пространстве , через которое поток из векторного поля вычисляется; как правило, гравитационное поле , то электрическое поле или магнитное поле. Это произвольная замкнутая поверхность S = ∂ V ( граница из 3- х мерной области V ) , используемая в сочетании с законом Гаусса для соответствующего поля ( закон Гаусса , Ряда Гаусса или закон Гаусса для гравитации ), выполняя поверхность интеграла , чтобы вычислить общее количество количества исходного закрытого; например, количество гравитационной массы в качестве источника гравитационного поля или количества электрического заряда в качестве источника электростатического поля, или наоборот: вычисления поля для распределения источника.
Для конкретности, электрическое поле рассматривается в этой статье, так как это наиболее частый тип поля концепция поверхность используется.
Гауссовские поверхности, как правило , тщательно подобраны , чтобы использовать симметрии из ситуации , чтобы упростить вычисление поверхностного интеграла . Если гауссова поверхность выбирается таким образом, что для каждой точки на поверхности компонента электрического поля вдоль вектора нормали является постоянной, то расчет не требует трудной интеграции , как константы , которые возникают могут быть выведены из интеграла.
Общие гауссовских поверхности
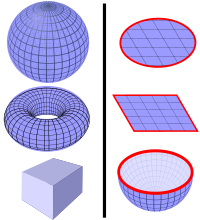 Примеры действительных (слева) и недействительных (справа) гауссовых поверхностей. Слева: Некоторые допустимые гауссовских поверхности включают поверхность сферы, поверхность тора, и поверхность куба. Они замкнутые поверхности , которые полностью ограждают 3D — объем. Справа: Некоторые поверхности , которые НЕ МОГУТ быть использованы в качестве гауссовых поверхностей, таких как поверхности диска , квадратуры или поверхности полусферы. Они не в полной мере приложить 3D объема, и имеют границы (красный). Обратите внимание , что бесконечные плоскости можно аппроксимировать гауссовую поверхность.
Примеры действительных (слева) и недействительных (справа) гауссовых поверхностей. Слева: Некоторые допустимые гауссовских поверхности включают поверхность сферы, поверхность тора, и поверхность куба. Они замкнутые поверхности , которые полностью ограждают 3D — объем. Справа: Некоторые поверхности , которые НЕ МОГУТ быть использованы в качестве гауссовых поверхностей, таких как поверхности диска , квадратуры или поверхности полусферы. Они не в полной мере приложить 3D объема, и имеют границы (красный). Обратите внимание , что бесконечные плоскости можно аппроксимировать гауссовую поверхность.- ΦЕзнак равно{\ Displaystyle \ Phi _ {E} = \, \!}
 S{\ Displaystyle \ scriptstyle S \!} Е⋅dAзнак равноQеNсε0,{\ Displaystyle \ mathbf {Е} \; \ CDOT \ mathrm {d} \ mathbf {A} = {\ гидроразрыва {Q_ {прил}} {\ varepsilon _ {0}}} \, \.!}
S{\ Displaystyle \ scriptstyle S \!} Е⋅dAзнак равноQеNсε0,{\ Displaystyle \ mathbf {Е} \; \ CDOT \ mathrm {d} \ mathbf {A} = {\ гидроразрыва {Q_ {прил}} {\ varepsilon _ {0}}} \, \.!}
Таким образом Q ENC является электрический заряд приложен к гауссовой поверхности.
Это закон Гаусса, сочетающее в себе как теорему о дивергенции и закон Кулона .
Сферическая поверхность
Сферическая гауссова поверхность используется при нахождении электрического поля или поток , полученный любым из следующих:
Сферическая Gaussian поверхность выбрана так, что она концентрический с распределением заряда.
В качестве примера рассмотрит заряженную сферическую оболочку S в незначительной толщине, с равномерно распределенным зарядом Q и радиусом R . Мы можем использовать закон Гаусса , чтобы найти величину результирующего электрического поля
С тем же самым, например, с использованием большей гауссова поверхностью вне оболочки , где г > R , закон Гаусса будет производить электрическое поле ненулевого. Это определяется следующим образом .
Поток из сферической поверхности S является:
- ΦЕзнак равно{\ Displaystyle \ Phi _ {E} = \, \!}
 ∂S{\ Displaystyle \ scriptstyle \ парциальное S \, \!} Е⋅dAзнак равно∫∫сЕdAсоз0∘знак равноЕ∫∫SdA{\ Displaystyle \ mathbf {E} \ CDOT d \ mathbf {A} = \ int \! \! \! \! \ Int _ {с} EdA \ соз 0 ^ {\ CIRC} = E \ int \! \! \! \! \ int _ {S} дА \, \!}
∂S{\ Displaystyle \ scriptstyle \ парциальное S \, \!} Е⋅dAзнак равно∫∫сЕdAсоз0∘знак равноЕ∫∫SdA{\ Displaystyle \ mathbf {E} \ CDOT d \ mathbf {A} = \ int \! \! \! \! \ Int _ {с} EdA \ соз 0 ^ {\ CIRC} = E \ int \! \! \! \! \ int _ {S} дА \, \!}
Площадь поверхности сферы радиуса г является
- ∫∫SdAзнак равно4πр2{\ Displaystyle \ int \! \! \! \! \ Int _ {S} дА = 4 \ пи г ^ {2}}
что означает
- ΦЕзнак равноЕ4πр2{\ Displaystyle \ Phi _ {Е} = Е4 \ пи г ^ {2}}
По закону Гаусса поток также
- ΦЕзнак равноQAε0{\ Displaystyle \ Phi _ {Е} = {\ гидроразрыва {Q_ {А}} {\ varepsilon _ {0}}}}
наконец , приравнивание выражения для Ф Е дает величину Е — поля в положении г :
- Е4πр2знак равноQAε0⇒Езнак равноQA4πε0р2,{\ Displaystyle Е4 \ пи г ^ {2} = {\ гидроразрыва {Q_ {А}} {\ varepsilon _ {0}}} \ четырехъядерных \ Rightarrow \ четырехъядерных Е = {\ гидроразрыва {Q_ {А}} {4 \ пи \ varepsilon _ {0} г ^ {2}}}.}
Этот нетривиальный результат показывает , что любое сферическое распределение заряда действует как точечный заряд при наблюдении со стороны распределения заряда; это на самом деле проверка закона Кулона . И, как уже упоминалось, любые внешние расходы не учитываются.
Цилиндрическая поверхность
Цилиндрическая гауссова поверхность используется при нахождении электрического поля или поток , полученный любым из следующих:
- бесконечно длинная линия равномерного заряда
- бесконечная плоскость равномерного заряда
- бесконечно длинный цилиндр равномерного заряда
В качестве примера «поле вблизи бесконечной линии заряда» приведено ниже;
Рассмотрим точку P на расстоянии г от линии заряда бесконечной , имеющего плотность заряда (заряд на единицу длины) Х. Представьте себе замкнутую поверхность в виде цилиндра, ось вращения является линия заряда. Если ч длина цилиндра, то заряд , заключенный в цилиндре
- Qзнак равноλчас{\ Displaystyle д = \ Lambda H},
где Q является заряд , заключенный в гауссовой поверхности. Есть три поверхности , б и гр , как показано на рисунке. Дифференциальный вектор площадь является д , на каждой поверхности , б и гр .
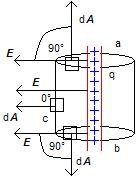
Закрытая поверхность в виде цилиндра , имеющего заряд линии в центре и показаны дифференциальные зоны d всех трех поверхностей.
Вынесение потока состоит из трех вкладов:
- ΦЕзнак равно{\ Displaystyle \ Phi _ {E} = \, \!}
 A{\ Displaystyle \ scriptstyle A \, \!} Е⋅dAзнак равно∫∫aЕ⋅dA+∫∫бЕ⋅dA+∫∫сЕ⋅dA{\ Displaystyle \ mathbf {E} \ CDOT d \ mathbf {A} = \ int \! \! \! \! \ Int _ {а} \ mathbf {E} \ CDOT d \ mathbf {A} + \ int \ ! \! \! \! \ Int _ {B} \ mathbf {E} \ CDOT д \ mathbf {A} + \ Int \! \! \! \! \ Int _ {C} \ mathbf {E} \ CDOT д \ mathbf {A}}
A{\ Displaystyle \ scriptstyle A \, \!} Е⋅dAзнак равно∫∫aЕ⋅dA+∫∫бЕ⋅dA+∫∫сЕ⋅dA{\ Displaystyle \ mathbf {E} \ CDOT d \ mathbf {A} = \ int \! \! \! \! \ Int _ {а} \ mathbf {E} \ CDOT d \ mathbf {A} + \ int \ ! \! \! \! \ Int _ {B} \ mathbf {E} \ CDOT д \ mathbf {A} + \ Int \! \! \! \! \ Int _ {C} \ mathbf {E} \ CDOT д \ mathbf {A}}
Для поверхностей а и б, Е и г будут перпендикулярны . Для поверхности с, Е и д будет параллельны , как показано на рисунке.
- ΦЕзнак равно∫∫aЕdAсоз90∘+∫∫бЕdAсоз90∘+∫∫сЕdAсоз0∘знак равноЕ∫∫сdA{\ Displaystyle {\ начать {выравниваются} \ Phi _ {E} & = \ int \! \! \! \! \ Int _ {а} EdA \ соз 90 ^ {\ CIRC} + \ int \! \! \ ! \! \ int _ {Ь} EdA \ соз 90 ^ {\ CIRC} + \ int \! \! \! \! \ int _ {C} EDA \ соз 0 ^ {\ CIRC} \\ & = E \ ИНТ \! \! \! \! \ int _ {с} дА \\\ конец {выравниваются}}}
Площадь поверхности цилиндра является
- ∫∫сdAзнак равно2πрчас{\ Displaystyle \ int \! \! \! \! \ Int _ {с} дА = 2 \ пи отн}
что означает
- ΦЕзнак равноЕ2πрчас{\ Displaystyle \ Phi _ {E} = E2 \ Pi} RH
По закону Гаусса
- ΦЕзнак равноQε0{\ Displaystyle \ Phi _ {Е} = {\ гидроразрыва {д} {\ varepsilon _ {0}}}}
приравнивания для Ф Е выходов
- Е2πрчасзнак равноλчасε0⇒Езнак равноλ2πε0р{\ Displaystyle Е2 \ пи отн = {\ гидроразрыва {\ Lambda ч} {\ varepsilon _ {0}}} \ четырехъядерных \ Rightarrow \ четырехъядерных Е = {\ гидроразрыва {\ Lambda} {2 \ пи \ varepsilon _ {0} р}}}
Gaussian дОТ
Эта поверхность наиболее часто используется для определения электрического поля из — за бесконечный лист заряда с равномерной плотностью заряда, или плитой заряда с некоторой конечной толщиной. Дот имеет цилиндрическую форму, и можно рассматривать как состоящие из трех компонентов: диск на одном конце цилиндра с площадью πR², диском на другом конце с равной площадью, так и на стороне цилиндра. Сумма электрического потока через каждый компонент поверхности пропорциональна приложенный заряд дота, как продиктовано законом Гаусса. Поскольку поле близко к листу может быть аппроксимировано постоянная, дот ориентирован таким образом , так что силовые линии проникают диски на концах поля под прямым углом , и сторона цилиндра параллельна силовые линии ,
Смотрите также
Рекомендации
- Перселла, Эдвард М. (1985). Электричество и магнетизм . McGraw-Hill. ISBN 0-07-004908-4 .
- Джексон, Джон Д. (1998). Классическая электродинамика (3 — е изд.) . Wiley. ISBN 0-471-30932-X .
дальнейшее чтение
- Электромагнетизм (второе издание) , IS Грант, WR Филлипс, Манчестер Physics, John Wiley & Sons, 2008, ISBN 978-0-471-92712-9
внешняя ссылка
- Поля — глава из учебника онлайн
Закон Гаусса для магнитного и электрического поля, определение
В статье расскажем про определение потока электрического поля, подробно узнаете про закон Гаусса, его отличия от закона Кулона, а так же рассмотрим на примерах применение закона Гаусса для расчета электрического поля. В дополнении к этому, рассмотрим линии и потоки магнитного поля, закон Гаусса для поля B.
Определение потока электрического поля
Если электрическое поле однородно и когда плоскость с площадью A установлена перпендикулярно линии этого поля E , то поток электрического поля ΦE,пронизывающий эту поверхность, равен:


Если теперь эта поверхность отклонена на угол φ от предыдущей позиции, поток изменит свое значение и будет:


Поскольку поток имеет скалярный размер, это соотношение для однородного поля можно записать как произведение скалярного вектора поля E и вектора поверхности A:
ΦE = Е * А
В общем случае, когда поле неоднородно, а поверхность не плоская, приближенное выражение для поля E через участок изогнутой поверхности получается путем деления этого куска на количество из n небольших плоских панелей, каждая из которых имеет небольшую, но конечную поверхность ΔA i . Электрическое поле, проходящее через поверхность ΔA i, имеет приблизительно постоянное значение E i, а приблизительное значение поля E потока получается суммированием потоков через отдельные плоские лепестки.


Поток Е (гомогенная или гетерогенный) через бесконечно малый элемент поверхности d А называются скалярное произведение:


Поток поля E, проходящий через участок области A, будет получен после замены суммы путем интегрирования по всей плоскости A:


Поток поля E, проходящий через замкнутую поверхность A, описывается интегралом (целочисленный символ с кружком)


Вектор dА мы выбираем так , что он обращен к наружной поверхности:


Поток векторного поля может быть проиллюстрирован графически с использованием силовых линий этого поля:


Общее количество силовых линий в телесном угле при 2R такое же, как и на расстоянии R. Напряженность поля обратно пропорциональна R2 , но площадь A прямо пропорциональна R2 . Таким образом, произведение этих двух величин, 1 / R2 × R2 , не зависит от R.
Если внутри замкнутой поверхности на чертеже , обозначенном A1, разместить положительный заряд +Q, поток электронов через поверхность будет положительным. После того, как внутри другой замкнутой поверхности А2 будет размещать груз с тем же значением, но с противоположным знаком, -Q, поток будет отрицательным (линии поля входят внутрь), но абсолютное значение потока через поверхность A2 будет таким же, как для поверхности A1.


Значение потока не зависит от формы замкнутой поверхности, а зависит только от величины нагрузки, заключенной внутри этой поверхности. Следовательно, поток поля, исходящий из электрического диполя внутри любой замкнутой поверхности, будет равен нулю (поскольку алгебраическая сумма +Q и -Q равна нулю).


Если бы заряды не были одинаковыми, поток поля не мог быть нулевым. Если, например, отрицательный заряд больше положительного, поток поля через закрытую поверхность является отрицательным, как на рисунке:


Закон Гаусса для электрического поля
Закон Гаусса, один из важнейших в электродинамике, определяет, что поток электрического поля E через замкнутую поверхность определяется только алгебраической суммой всех электрических зарядов Q, содержащихся в этой поверхности. Неважно, как эти нагрузки распределяются внутри этой поверхности.


Символ Q является алгебраической суммой зарядов внутри замкнутой поверхности A, после чего мы интегрируем поток; g0 — электрическая проницаемость вакуума.
Не имеет значения, как распределяются заряды внутри поверхности A. В то же время на величину общего потока электрического поля не влияют никакие заряды, которые находятся за пределами поверхности А, даже те, которые прилипли к ее внешней стороне.
Закон Гаусса для электрического поля представляет собой обобщенную формулировку взаимосвязи между зарядами и электрическими полями и является одним из четырех уравнений Максвелла, описывающих все электрические и магнитные явления.
Применение закона Гаусса для расчета электрического поля
Имея данное распределение заряда, мы можем использовать закон Гаусса для электрического поля, чтобы вычислить значение электрического поля в конкретной точке или области. Ключевое действие — окружить соответствующую зону нагрузки подходящим образом выбранной закрытой поверхностью. Хотя закон Гаусса выполняется для каждой замкнутой грани А, выбор этой поверхности должен быть таким, чтобы его интегрирование было наиболее простым. В приведенных примерах предлагаемая поверхность Гаусса отмечена красным контуром на рисунке.
1. Закон Кулона содержится в законе Гаусса, но он сам является экспериментальной зависимостью, которую мы использовали для получения закона Гаусса.
Таким образом, закон Гаусса является более общим, чем закон Кулона: закон Гаусса не может быть выведен из закона Кулона, но закон Кулона легко получается из закона Гаусса. Достаточно найти силу F = q * E , действующую на точечный заряд q, расположенный на расстоянии r от другого точечного заряда Q. Чтобы определить F, нам нужно знать только E. Поместим нагрузку Q в центр сферы с радиусом r, как на рисунке:


Поле Е от заряда Q на поверхности сферы имеют то же значение, всюду на поверхности вектора E параллельно вектору dА. После применения закона Гаусса мы получаем:


или


Поскольку вектор E направлен вдоль радиуса r , то:


Согласно определению поля E, сила, действующая на нагрузку q, равна:


Поэтому мы получили закон Кулона от закона Гаусса:


2. Поле заряженной проводящей сферы с радиусом r (внутри сферы нет зарядов):


В соответствии с законом Гаусса, поле вне сферы на расстоянии R от центра , или:


Внутри поля сферы (Q = 0): E = 0.
3. Поле однородно заряженной диэлектрической сферы. Общая нагрузка, содержащаяся в шаре, составляет Q.


При расчете поля E на расстоянии x от центра сферы обозначим через q заряд, содержащийся в сфере с радиусом x. От прямой линии мы получаем:


На основании закона Гаусса искали поле Е внутри шара. Таким образом, поле внутри сферы линейно растет с увеличением x. Вне сферы поле уменьшается с увеличением расстояния от центра:


4. Линейное зарядное поле и заряженный проводящий цилиндр с плотностью заряда 8 [С / м]:


На участке L имеется нагрузка Q = 8 L, поэтому мы получаем закон Гаусса . Отсюда мы находим искомую область:


5. Поле заряженного бесконечного плоского слоя.


Поле является однородным и простирается в обоих направлениях перпендикулярно поверхности пластины (проходит только через основание цилиндра). Мы получаем закон Гаусса:


6. Поле заряженной бесконечной плоской проводящей пластины.


Нагрузка на проводящую пластину распределяется на обе поверхности. Поскольку у нас есть два слоя нагрузки с плотностью заряда σ каждый, то напряженность поля будет в два раза выше в зависимости от результата предыдущего примера.


7. Поле между противоположно заряженными параллельными проводящими пластинами:


В качестве гауссовой поверхности мы выбираем прямоугольную призму с одним основанием, погруженным в металлическую пластину, где нет ни заряда, ни поля E. Поле проникает только в основание прямоугольной призмы, которое находится в пространстве между пластинами. Из закона Гаусса мы получаем:


Снаружи пластин поле равно нулю.
Линии магнитного поля
Магнитные силовые линии , как правило, кривые, иллюстрирующие направления магнитного поля B. Это означает, что в каждой точке линии поля имеется вектор B, касательный к этой линии. В однородном поле B линии поля образуют пучок параллельных прямых. Линий поля B бесконечно много, потому что одна линия проходит через каждую точку поля.
Из предыдущей статьи мы знаем, что источниками поля B являются движущиеся электрические заряды (электрический ток). Другими широко известными источниками магнитного поля являются постоянные магниты, часто сделанные в форме подковы или стержня. Каждый магнит имеет два полюса, обычно называемых северным и южным (в соответствии с их ориентацией к полюсам Земли). Эти полюса нельзя отделить друг от друга. Стержневой магнит, разрезанный на две части, даст два стержневых магнита, каждый из которых будет иметь собственный набор полюсов N и S. Такие умножающие магниты можно продолжать без надежды на отделение полюсов друг от друга. Каждый магнит, полученный таким образом, будет биполярной системой ( магнитный диполь). Хотя ни один закон природы не запрещает магнитным полюсам появляться отдельно в качестве магнитных монополей, ни в природе, ни в экспериментальных исследованиях магнитных монополей пока не найдено. Поиски продолжаются.
Как мы видели ранее, линии электрического поля генерируются на отдельных зарядах или в системах нагрузки и могут легко исчезать. В случае поля B линии поля образуют замкнутые петли. Такие линии, идущие от одного полюса, могут проникать через различные объекты в непосредственной близости от магнита, но они обязательно должны возвращаться к другому полюсу.


Изображение распределения поля B вокруг стержневого магнита показано на фотографии стеклянной пластины, обсыпанной ферромагнитным порошком и помещенной на магнит. Порошковый слой уплотняется в областях, где поле B сильнее. В непосредственной близости от полюсов, где поле является самым сильным, ферромагнитный порошок энергично натягивается на полюса магнита, заставляя слой истончаться на стекле.


Поскольку линии поля B образуют замкнутые петли, такие линии, пересекающие замкнутую поверхность, обязательно должны давать нулевую сумму — число линий, покидающих эту область, точно равно числу обратных линий.


Отличным местом для всех, кто интересуется природой и экспериментальными исследованиями, является Exploratorium в Сан-Франциско, расположенный во дворце рядом со знаменитым мостом Золотые Ворота и островом тюрьмы Алькатрас (ныне музей). Из более чем ста исследовательских стендов, особенно осажденных детьми, есть станция с магнитом, покрытым ферромагнитными зернами (называемым там «песком»). Магнитное поле, проникая через тело, строит свои структуры в пространстве, вызывая, среди прочего, выращивание ферромагнитных деревьев на поверхности ладони, как показано на фотографиях.




Поток магнитного поля
Поток B определяется аналогично вектору потока любого размера, и, в частности , потока электрического поля Е. Элементарный поток поля В , проходящих через бесконечно малый элемент поверхности d А определяются как скалярное произведение между этими двумя значениями:


Таким образом, поток поля B, проходящий через макроскопический поверхностный слой A:


Единица магнитного потока в системе СИ составляет 1 Вебер (1 Вб) = 1 Н · м · А -1 . Таким образом, магнитное поле B иногда называют плотностью потока и 1T = 1 Вт · м -2 .
Закон Гаусса для магнитного поля
Закон Гаусса для поля B определяет, что поток магнитного поля через закрытую поверхность равен нулю, т.е. :


Обратите внимание на очень важный символ интеграла с кружком, который говорит, что интеграция должна происходить на замкнутой поверхности. В случае электрического поля плотность электрического заряда находится справа от аналогичного уравнения. Поскольку в природе нет магнитных монополей, полюса N и S должны быть в одном и том же числе, что дает алгебраически ноль. По этой причине справа от уравнения, описывающего закон Гаусса для B , ноль. Закон Гаусса для магнитного поля является одним из четырех уравнений Максвелла (в интегральной форме), описывающих совокупность электрических и магнитных явлений в природе.
Теорема Гаусса
Экспериментально установленные закон Кулона и принцип суперпозиции позволяют полностью описать электростатическое поле заданной системы зарядов в вакууме. Однако, свойства электростатического поля можно выразить в другой, более общей форме, не прибегая к представлению о кулоновском поле точечного заряда.
Введем новую физическую величину, характеризующую электрическое поле – поток Φ вектора напряженности электрического поля. Пусть в пространстве, где создано электрическое поле, расположена некоторая достаточно малая площадка ΔS. Произведение модуля вектора на площадь ΔS и на косинус угла α между вектором 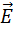 и нормалью
и нормалью  к площадке называется элементарным потоком вектора напряженности через площадку ΔS (рис. 1.3.1):
к площадке называется элементарным потоком вектора напряженности через площадку ΔS (рис. 1.3.1):
| ΔΦ = E ΔS cos α = En ΔS, |
где En – модуль нормальной составляющей поля 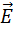
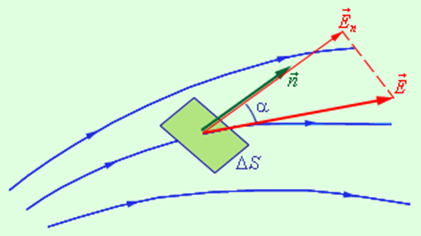 |
| Рисунок 1.3.1. К определению элементарного потока ΔΦ |
Рассмотрим теперь некоторую произвольную замкнутую поверхность S. Если разбить эту поверхность на малые площадки ΔSi, определить элементарные потоки ΔΦi поля 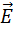 через эти малые площадки, а затем их просуммировать, то в результате мы получим поток Φ вектора
через эти малые площадки, а затем их просуммировать, то в результате мы получим поток Φ вектора 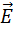 через замкнутую поверхность S (рис. 1.3.2):
через замкнутую поверхность S (рис. 1.3.2):
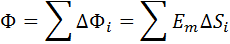
В случае замкнутой поверхности всегда выбирается внешняя нормаль.
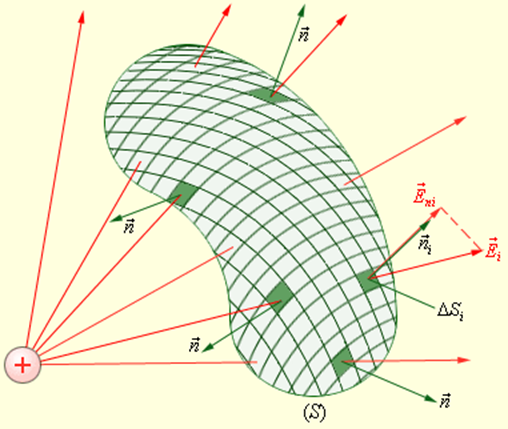 |
| Рисунок 1.3.2. Вычисление потока Ф через произвольную замкнутую поверхность S |
Теорема Гаусса утверждает:
Поток вектора напряженности электростатического поля  через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε0.
через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε0.
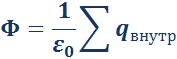
Для доказательства рассмотрим сначала сферическую поверхность S, в центре которой находится точечный заряд q. Электрическое поле в любой точке сферы перпендикулярно к ее поверхности и равно по модулю
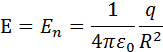
где R – радиус сферы. Поток Φ через сферическую поверхность будет равен произведению E на площадь сферы 4πR2. Следовательно, 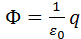
Окружим теперь точечный заряд произвольной замкнутой поверхностью S и рассмотрим вспомогательную сферу радиуса R0 (рис. 1.3.3).
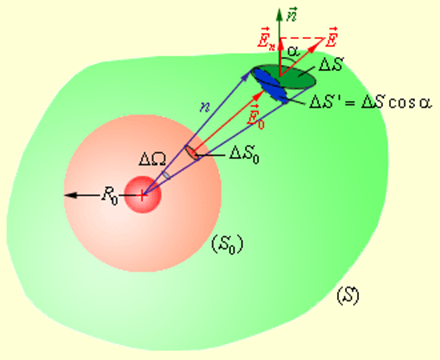 |
| Рисунок 1.3.3. Поток электрического поля точечного заряда через произвольную поверхность S, окружающую заряд |
Рассмотрим конус с малым телесным углом ΔΩ при вершине. Этот конус выделит на сфере малую площадку ΔS0, а на поверхности S – площадку ΔS. Элементарные потоки ΔΦ0 и ΔΦ через эти площадки одинаковы. Действительно,
| ΔΦ0 = E0ΔS0, ΔΦ = EΔS cos α = EΔS ‘. |
Здесь ΔS’ = ΔS cos α – площадка, выделяемая конусом с телесным углом ΔΩ на поверхности сферы радиуса n.
Так как 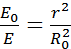 , a
, a 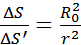 , следовательно
, следовательно 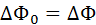 Отсюда следует, что полный поток электрического поля точечного заряда через произвольную поверхность, охватывающую заряд, равен потоку Φ0 через поверхность вспомогательной сферы:
Отсюда следует, что полный поток электрического поля точечного заряда через произвольную поверхность, охватывающую заряд, равен потоку Φ0 через поверхность вспомогательной сферы:

Аналогичным образом можно показать, что, если замкнутая поверхность S не охватывает точечного заряда q, то поток Φ = 0. Такой случай изображен на рис. 1.3.2. Все силовые линии электрического поля точечного заряда пронизывают замкнутую поверхность S насквозь. Внутри поверхности S зарядов нет, поэтому в этой области силовые линии не обрываются и не зарождаются.
Обобщение теоремы Гаусса на случай произвольного распределения зарядов вытекает из принципа суперпозиции. Поле любого распределения зарядов можно представить как векторную сумму электрических полей 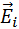 точечных зарядов. Поток Φ системы зарядов через произвольную замкнутую поверхность S будет складываться из потоков Φi электрических полей отдельных зарядов. Если заряд qi оказался внутри поверхности S, то он дает вклад в поток, равный
точечных зарядов. Поток Φ системы зарядов через произвольную замкнутую поверхность S будет складываться из потоков Φi электрических полей отдельных зарядов. Если заряд qi оказался внутри поверхности S, то он дает вклад в поток, равный  если же этот заряд оказался снаружи поверхности, то вклад его электрического поля в поток будет равен нулю.
если же этот заряд оказался снаружи поверхности, то вклад его электрического поля в поток будет равен нулю.
Таким образом, теорема Гаусса доказана.
Теорема Гаусса является следствием закона Кулона и принципа суперпозиции. Но если принять утверждение, содержащееся в этой теореме, за первоначальную аксиому, то ее следствием окажется закон Кулона. Поэтому теорему Гаусса иногда называют альтернативной формулировкой закона Кулона.
Используя теорему Гаусса, можно в ряде случаев легко вычислить напряженность электрического поля вокруг заряженного тела, если заданное распределение зарядов обладает какой-либо симметрией и общую структуру поля можно заранее угадать.
Примером может служить задача о вычислении поля тонкостенного полого однородно заряженного длинного цилиндра радиуса R. Эта задача имеет осевую симметрию. Из соображений симметрии электрическое поле должно быть направлено по радиусу. Поэтому для применения теоремы Гаусса целесообразно выбрать замкнутую поверхность S в виде соосного цилиндра некоторого радиуса r и длины l, закрытого с обоих торцов (рис. 1.3.4).
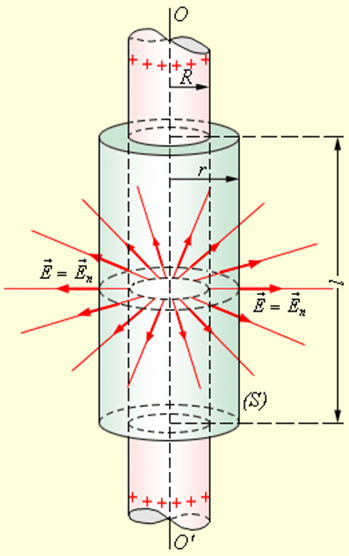 |
| Рисунок 1.3.4. Вычисление поля однородно заряженного цилиндра. OO’ – ось симметрии |
При r ≥ R весь поток вектора напряженности будет проходить через боковую поверхность цилиндра, площадь которой равна 2πrl, так как поток через оба основания равен нулю. Применение теоремы Гаусса дает:
 |
где τ – заряд единицы длины цилиндра. Отсюда
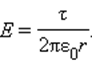 |
Этот результат не зависит от радиуса R заряженного цилиндра, поэтому он применим и к полю длинной однородно заряженной нити.
Для определения напряженности поля внутри заряженного цилиндра нужно построить замкнутую поверхность для случая r < R. В силу симметрии задачи поток вектора напряженности через боковую поверхность гауссова цилиндра должен быть и в этом случае равен Φ = E 2πrl. Согласно теореме Гаусса, этот поток пропорционален заряду, оказавшемуся внутри замкнутой поверхности. Этот заряд равен нулю. Отсюда следует, что электрическое поле внутри однородно заряженного длинного полого цилиндра равно нулю.
Аналогичным образом можно применить теорему Гаусса для определения электрического поля в ряде других случаев, когда распределение зарядов обладает какой-либо симметрией, например, симметрией относительно центра, плоскости или оси. В каждом из таких случаев нужно выбирать замкнутую гауссову поверхность целесообразной формы. Например, в случае центральной симметрии гауссову поверхность удобно выбирать в виде сферы с центром в точке симметрии. При осевой симметрии замкнутую поверхность нужно выбирать в виде соосного цилиндра, замкнутого с обоих торцов (как в рассмотренном выше примере). Если распределение зарядов не обладает какой-либо симметрией и общую структуру электрического поля угадать невозможно, применение теоремы Гаусса не может упростить задачу определения напряженности поля.
Рассмотрим еще один пример симметричного распределения зарядов – определение поля равномерно заряженной плоскости (рис. 1.3.5).
 |
| Рисунок 1.3.5. Поле равномерно заряженной плоскости. σ – поверхностная плотность заряда. S – замкнутая гауссова поверхность |
В этом случае гауссову поверхность S целесообразно выбрать в виде цилиндра некоторой длины, закрытого с обоих торцов. Ось цилиндра направлена перпендикулярно заряженной плоскости, а его торцы расположены на одинаковом расстоянии от нее. В силу симметрии поле равномерно заряженной плоскости должно быть везде направлено по нормали. Применение теоремы Гаусса дает:
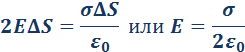
где σ – поверхностная плотность заряда, т. е. заряд, приходящийся на единицу площади.
Полученное выражение для электрического поля однородно заряженной плоскости применимо и в случае плоских заряженных площадок конечного размера. В этом случае расстояние от точки, в которой определяется напряженность поля, до заряженной площадки должно быть значительно меньше размеров площадки.
гауссова кривизна — Gaussian curvature
 Слева направо: поверхности отрицательной гауссовой кривизны ( гиперболоид ), поверхность нулевого гауссовой кривизны ( цилиндр ), и поверхность положительной гауссовой кривизны ( сферы ).
Слева направо: поверхности отрицательной гауссовой кривизны ( гиперболоид ), поверхность нулевого гауссовой кривизны ( цилиндр ), и поверхность положительной гауссовой кривизны ( сферы ). 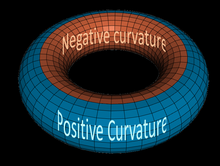 Некоторые точки на торе имеют положительный, некоторые из них отрицательный, а некоторые имеют нулевой гауссовой кривизны.
Некоторые точки на торе имеют положительный, некоторые из них отрицательный, а некоторые имеют нулевой гауссовой кривизны.В дифференциальной геометрии , то гауссова кривизна или Гаусс кривизны Κ из поверхности в точке , это произведение главных кривизн , каппа 1 и каппа 2 , в данной точке:
- Кзнак равноκ1κ2,{\ Displaystyle \ mathrm {K} = \ каппа _ {1} \ каппа _ {2}.}
Например, сфера радиуса г имеет гауссовой кривизны 1 / г 2 везде, и плоскую плоскость и цилиндр имеют гауссова кривизна 0 всюду. Гауссова кривизна может также быть отрицательным, как и в случае гиперболоида или внутренней стороне тора .
Гауссова кривизна является внутренней мерой кривизны , зависящей только от расстояния, измеряемые на поверхности, а не на том , как она изометрически вложенной в евклидовом пространстве. Это содержание egregium Theorema .
Гауссова кривизна имени Карл Фридрих Гаусс , который опубликовал egregium Theorema в 1827 году.
Неформальное определение
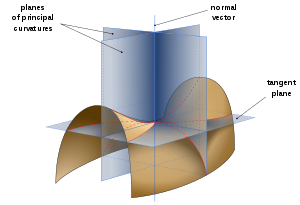
В любой точке на поверхности, мы можем найти нормальный вектор , который под прямым углом к поверхности; плоскости , содержащие вектор нормали, называются нормальными плоскости . Пересечение нормальной плоскости и поверхности образуют кривую называется нормальным сечением , а кривизна этой кривой является нормальная кривизна . Для большинства точек на большинстве поверхностей, различные нормальные сечения будут иметь различную кривизну; максимальные и минимальные значения они называются главными кривизны , назовут их каппа 1 , каппа 2 . Гауссова кривизна представляет собой произведение двух главных кривизн Κ = каппа 1 κ 2 .
Знак гауссовой кривизны может быть использован для характеристики поверхности.
- Если обе главные кривизны имеют одинаковый знак: каппа 1 К 2 > 0 , то гауссова кривизна положительна , а поверхность , как говорят, эллиптическую точку. В таких точках, поверхность будет купол , как, локально лежащих на одной стороне ее касательной плоскости. Все секционные кривизны будут иметь один и тот же знак.
- Если главные кривизны имеют разные знаки: каппа 1 К 2 <0 , то гауссова кривизна является отрицательным , и поверхность , как говорят, гиперболическую или седловой точки . В таких точках, поверхность будет седловой форме. Поскольку одна главная кривизна отрицательна, одна положительно, а нормальная кривизна изменяется непрерывно , если вращать плоскость , ортогональные к поверхности вокруг нормали к поверхности в двух направлениях, нормальные кривизны будут равна нуль давая асимптотические кривые для этой точки.
- Если одна из главных кривизн равна нулю: каппа 1 К 2 = 0 , гауссова кривизна равна нулю , а поверхность называется иметь параболическую точку.
Большинство поверхностей будут содержать участки положительной гауссовой кривизны (эллиптические точки) и области отрицательной гауссовой кривизны , разделенную кривые точки с нулевой гауссовой кривизной называется параболическая линией .
Отношение к геометрии
Когда поверхность имеет постоянную нулевую гауссовую кривизну, то это развертывающаяся поверхность и геометрия поверхности является геометрией Евклида .
Когда поверхность имеет постоянную положительную гауссову кривизну, то это сфера и геометрия поверхности является сферической геометрией .
Когда поверхность имеет постоянную отрицательную гауссову кривизны, то это псевдосферическая поверхность и геометрия поверхности является гиперболической геометрией .
Дальнейшее неформальное обсуждение
В дифференциальной геометрии , две главные кривизны в данной точке поверхности являются собственными значениями этого оператора формы в точке. Они измеряют , как поверхность прогибается различными количествами в различных направлениях в этой точке. Представим поверхность по теореме о неявной функции как график функции, е , из двух переменных, таким образом , что точка р является критической точкой, то есть, градиент
Альтернативные определения
Он также дается
- Кзнак равно⟨(∇2∇1-∇1∇2)е1,е2⟩йег,{\ Displaystyle \ mathrm {K} = {\ гидроразрыва {\ Лангле (\ набла _ {2} \ набла _ {1} — \ набла _ {1} \ набла _ {2}) \ mathbf {е} _ {1 }, \ mathbf {е} _ {2} \ rangle} {\ Det г}}}
где это производная ковариантной и
В точке р на регулярной поверхности в R 3 , гауссова кривизна также дается
- К(п)знак равнойе(S(п)),{\ Displaystyle К (\ mathbf {р}) = \ Det (S (\ mathbf {р})),}
где S является оператором формы .
Полезная формула для гауссовой кривизны является уравнением Лиувилля в терминах лапласиана в изотермических координатах .
Общая кривизна
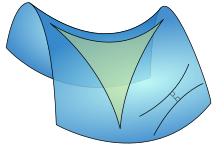
Поверхностный интеграл гауссовой кривизны по некоторой области поверхности, называется полной кривизной . Общая кривизна геодезического треугольника равна отклонение суммы его углов от я. Сумма углов треугольника на поверхности положительной кривизны превысит п, в то время как сумма углов треугольника на поверхности отрицательной кривизны будет меньше , чем π. На поверхности нулевой кривизны, такие как евклидовой плоскости , углы подведут точно П радианах.
- Σязнак равно13θязнак равноπ+∬TКdA,{\ Displaystyle \ сумма _ {= 1} ^ {3} \ тета _ {я} = \ Pi + \ IINT _ {T}, К \, дА.}
Более общий результат является теорема Гаусса-Бонне .
Важные теоремы
Theorema egregium
Гаусс Theorema Egregium (латы «замечательная теорема») утверждает , что гауссова кривизна поверхности может быть определена из измерений длины на самой поверхности. В самом деле, можно найти , учитывая полное знание первой фундаментальной формы и выразил с помощью первой фундаментальной формы и ее частных производных первого и второго порядка. Эквивалентно, то определитель из второй фундаментальной формы поверхности в R 3 может быть выражен так. «Замечательно», и удивительно, особенность этой теоремы является то , что хотя определение гауссовой кривизны поверхности S в R — конечно зависит от способа , в котором поверхность расположена в пространстве, конечный результат, сам гауссовой кривизна , определяются внутренней метрикой поверхности без каких — либо дальнейших ссылок на окружающее пространство: это внутренний инвариантно . В частности, гауссова кривизна инвариантна относительно изометрических деформаций поверхности.
В современной дифференциальной геометрии , «поверхностный», рассматривается абстрактно, является двумерный дифференцируемым многообразием . Для подключения этой точки зрения с классической теорией поверхностей , такая абстрактная поверхность вкладываются в R 3 и снабженная римановой метрикой , заданной первой фундаментальной формой. Предположим , что образ вложения представляет собой поверхность S в R 3 . Локальная изометрия является Диффеоморфизм F : U → V между открытыми областями R 3 , ограничение которого на S ∩ U является изометрией на образ. Theorema Egregium затем формулируется следующим образом :
- Гауссова кривизна вложенной гладкой поверхности в R 3 инвариантна относительно локальной изометрии.
Например, гауссова кривизна цилиндрической трубки равна нуль, то же самое, что и для «развернутых» трубок (который является плоским). С другой стороны, так как сфера радиуса R имеет постоянной положительной кривизны R -2 и плоскую плоскость имеет постоянную кривизну 0, эти две поверхности не изометрическим, даже локально. Таким образом , любое плоское представление даже части шара должны искажать расстояния. Поэтому ни картографическая проекция не является совершенной.
Теорема Гаусса-Бонне
Теорема Гаусс-Бонн связывает общую кривизну поверхности в ее Эйлере характеристику и обеспечивает важную связь между локальными геометрическими свойствами и глобальными топологическими свойствами.
Поверхности постоянной кривизны
- Миндинг теорема «s (1839) утверждаетчто все поверхности с той же постоянной кривизной К локально изометрическим. Следствием теоремы Миндинга является точто любая поверхность, кривизна которой тождественно равна нулю может быть построена путем изгиба некоторой плоской области. Такие поверхности называются развертывающиеся поверхности . Миндинг также поднял вопрос оли замкнутая поверхность с постоянной положительной кривизной обязательно жесткая.
- Либман теорема «s (1900) ответилвопрос Миндинга в. Единственный регулярные (класс C 2 ) замкнутые поверхности в R 3 с постоянной положительной гауссовой кривизной являются сферами . Если сфера деформируется, она не остается сферой, доказываячто сфера является жесткой. Стандартное доказательство использует Гильберт лемму , что не- пупочной точка крайней главной кривизны имеет неположительна гауссова кривизну.
- Теорема Гильберта (1901) утверждаетчто не существует полной аналитической (класс C & omega ) регулярная поверхность в R 3 постоянной отрицательной гауссовой кривизны. В самом деле, заключение справедливо также для поверхностей класса C 2 , погруженных в R 3 , но ломается для C 1 -поверхностей. Псевдосфера имеет постоянную отрицательную гауссову кривизныкроме его особого острия .
Альтернативные формулы
- Кзнак равнойе(яя)йе(я)знак равноLN-M2Ег-F2,{\ Displaystyle K = {\ гидроразрыва {\ йе (\ mathrm {I \! I})} {\ йе (\ mathrm {I})}} = {\ гидроразрыва {LN-M ^ {2}} {EG- F ^ {2}}}.}
- Формула Brioschi дает гауссовую кривизну исключительно в терминах первой фундаментальной формы:
- Кзнак равно|-12Еvv+FUv-12гUU12ЕUFU-12ЕvFv-12гUЕF12гvFг|-|012Еv12гU12ЕvЕF12гUFг|(Ег-F2)2{\ Displaystyle К = {\ гидроразрыва {{\ начинаются {vmatrix} — {\ гидроразрыва {1} {2}} Е- {ст} + Р- {уф} — {\ гидроразрыва {1} {2}} G_ {уу} & {\ гидроразрыва {1} {2}} Е- {и} & Р- {и} — {\ гидроразрыва {1} {2}} Е- {v} \\ Р- {v} — {\ гидроразрыва {1} {2} } G_ {и} & Е & Р \\ {\ гидроразрыва {1} {2}} G_ {v} & Р & С \ конец {vmatrix}} — {\ начинаются {vmatrix} 0 & {\ гидроразрыва {1} {2}} Е- {v } & {\ гидроразрыва {1} {2}} G_ {и} \\ {\ гидроразрыва {1} {2}} Е- {v} & Е & Р \\ {\ гидроразрыва {1} {2}} G_ {и} & Р & G \ конец {vmatrix}}} {(ЭГ-F ^ {2}) ^ {2}}}}
- Кзнак равно-12Ег(∂∂UгUЕг+∂∂vЕvЕг),{\ Displaystyle К = — {\ гидроразрыва {1} {2 {\ SQRT {Е.}}}} \ влево ({\ гидроразрыва {\ парциальное} {\ парциальное и}} {\ гидроразрыва {G_ {и}} {\ SQRT {Е.}}} + {\ гидроразрыва {\ парциальное} {\ парциальное V}} {\ гидроразрыва {Е- {v}} {\ SQRT {Е.}}} \ справа).}
- Для поверхности , описанной в графе функции г = Р (х, у) , гауссова кривизна:
- Кзнак равноFИксИкс⋅FYY-FИксY2(1+FИкс2+FY2)2{\ Displaystyle К = {\ гидроразрыва {Р- {хх} \ CDOT Р- {уу} -F_ {ху} ^ {2}} {(1 + Р- {х} ^ {2} + Р- {у} ^ {2} ) ^ {2}}}}
- Для неявно определенной поверхности, Р (х, у, г) = 0, гауссова кривизна может быть выражена в терминах градиента и матрицы Гессе :∇F{\ Displaystyle \ набла F} ЧАС(F){\ Displaystyle Н (Р)}
- Кзнак равно-|ЧАС(F)∇FT∇F0||∇F|4знак равно-|FИксИксFИксYFИксZFИксFИксYFYYFYZFYFИксZFYZFZZFZFИксFYFZ0||∇F|4{\ Displaystyle К = — {\ гидроразрыва {\ начинают {vmatrix} Н (Р) & \ набла Р ^ {\ mathsf {T}} \\\ набла Р & 0 \ конец {vmatrix}} {| \ набла F | ^ { 4}}} = — {\ гидроразрыва {\ начинают {vmatrix} Р- {хх} & Р- {х} & Р- {XZ} & Р- {х} \\ Р- {х} & Р- {уу} & Р- {уг} & Р- {у} \ \ F_ {XZ} и Р- {уг} и Р- {ZZ} и Р- {г} \\ Р- {х} и Р- {у} и Р- {г} & 0 \\\ конец {vmatrix}} {| \ набла F | ^ {4} }}}
- Для поверхности с метрикой конформной к евклидовой, так что F = 0 и E = G = е сг , кривизна Гаусса задается формулой (Δ быть обычный оператор Лапласа ):
- Кзнак равно-12еσΔσ,{\ Displaystyle К = — {\ гидроразрыва {1} {2e ^ {\ Sigma}}} \ Delta \ Sigma,}
- Гауссова кривизной является ограничивающей разницей между окружностью геодезической окружности и окружностью в плоскости:
- Кзнак равноИтр→0+32πр-С(р)πр3{\ Displaystyle К = \ Пт _ {г \ к 0 ^ {+}} 3 {\ гидроразрыва {2 \ пи гС (г)} {\ пи г ^ {3}}}}
- Гауссова кривизна является ограничивающим разность между площадью геодезического диска и диска в плоскости:
- Кзнак равноИтр→0+12πр2-A(р)πр4{\ Displaystyle К = \ Пт _ {г \ к 0 ^ {+}} 12 {\ гидроразрыва {\ пи г ^ {2} -А (г)} {\ пи г ^ {4}}}}
- Кзнак равно-1Е(∂∂UΓ122-∂∂vΓ112+Γ121Γ112-Γ111Γ122+Γ122Γ122-Γ112Γ222){\ Displaystyle К = — {\ гидроразрыва {1} {Е}} \ влево ({\ гидроразрыва {\ парциальное} {\ частичного и}} \ Gamma _ {12} ^ {2} — {\ гидроразрыва {\ парциальное} {\ парциальное v}} \ Gamma _ {11} ^ {2} + \ Gamma _ {12} ^ {1} \ Gamma _ {11} ^ {2} — \ Gamma _ {11} ^ {1} \ Гамма _ {12} ^ {2} + \ Gamma _ {12} ^ {2} \ Gamma _ {12} ^ {2} — \ Gamma _ {11} ^ {2} \ Gamma _ {22} ^ {2} \право)}
Смотрите также
Рекомендации
книги
- P.Grinfeld (2014). Введение в тензорный анализ и Исчисление движущихся поверхностей . Springer. ISBN 1-4614-7866-9 .
внешняя ссылка
Кривизна Гаусса — это… Что такое Кривизна Гаусса?
Слева направо: поверхность с отрицательной гауссовой кривизной (гиперболоид), поверхность с нулевою гауссовой кривизной (цилиндр), и поверхность с положительной гауссовой кривизной (сфера).Гауссова кривизна — мера искривления поверхности в окрестности какой-либо её точки.
Определение
Кривизна Гаусса для двумерной поверхности
Обозначим нормальные кривизны в главных направлениях (главные кривизны) в рассматриваемой точке поверхности и . Величина:
называется гауссовой кривизной, полной кривизной или просто кривизной поверхности. Встречается также термин скаляр кривизны, который подразумевает результат свёртки тензора кривизны; при этом скаляр кривизны вдвое больше, чем гауссова кривизна.
Гауссова кривизна может быть вычислена через метрику поверхности, и поэтому она является объектом внутренней геометрии (отметим, что главные кривизны к внутренней геометрии не относятся). По знаку кривизны можно классифицировать точки поверхности (см. рисунок). Кривизна плоскости равна нулю. Кривизна сферы радиуса R всюду равна . Существует и поверхность постоянной отрицательной кривизны — псевдосфера.
Кривизна Гаусса для гиперповерхности
Кривизна n-мерной гиперповерхности в точке полностью описывается главными кривизнами:
и соответствующими главными направлениями.
Рассмотрим (с точностью до знака) симметрический многочлен, составленный из чисел :
Назовем вышеприведенные величины кривизнами Гаусса соответствующей степени. Общая формула кривизны Гаусса степени m запишется так:
Кривизны Гаусса являются коэффициентами характеристического многочлена для матрицы тензора полной кривизны гиперповерхности:
Тензорная формула для кривизны Гаусса
Формула (3) определяет кривизну Гаусса через собственные числа тензора полной кривизны гиперповерхности . Попробуем выразить эти величины через компоненты самого тензора в любой системе координат. Для вычисления определителя произвольного тензора второго ранга мы имеем такую формулу с использованием тензора метрической матрешки (см. Абсолютно антисимметричный единичный тензор):
Подставим в эту формулу , чтобы вычислить левое выражение формулы (4), тогда имеем:
Раскроем скобки в формуле (6). Поскольку тензор метрической матрешки не меняется при синхронной перестановке верхних и нижних индексов, то все слагаемые при одинаковой степени будут одинаковыми (их количество равно биномиальному коэффициенту ), и мы получаем:
Поскольку последовательные свертки тензора метрической матрешки равны:
То из формулы (7) и формулы для биномиальных коэффициентов находим такую формулу для характеристического многочлена (разделив обе стороны уравнения (7) на ):
Сравнивая формулы (9) и (4), находим такую формулу для кривизны Гаусса:
Выражение через тензор Римана
Для скалярной кривизны гиперповерхности мы имеем такую формулу
Чтобы обобщить эту формулу для более высоких степеней, попробуем заменить произведение двух метрических тензоров в формуле (11) на тензор метрической матрешки четвертого ранга:
Для дальнейших вычислений мы перейдем в локальную декартову систему координат в одной из точек многообразия P, и ориентируем ее вдоль главных направлений гиперповерхности. В точке P матрица метрического тензора будет единичной:
а потому мы можем численно не различать ковариантные и соответствующие контравариантные компоненты тензоров (верхние и нижние индексы). Тензор Римана в точке будет в некотором смысле диагональным, а именно, его ненулевые компоненты будут равны:
и равны нулю все те компоненты , где вторая пара индексов не совпадает с с точностью до перестановки в паре.
Левая часть формулы (12) является линейной формой от тензора Римана, а коэффициентами этой формы служат компоненты тензора метрической матрешки. Очевидным обобщением является рассмотрение билинейной формы и форм высших степеней от компонента тензора Римана. Проведем вычисления формулы (12) еще раз и таким образом, чтобы эти вычисления можно было легко обобщить. Имеем, учитывая диагональность тензора Римана:
Далее, два слагаемых в правой части формулы (15) одинаковы вследствие антисимметрии по индексам внутри пары как тензора метрической матрешки, так тензора Римана. Кроме того, диагональная компонента метрической матрешки равна единице, поскольку (в следующей формуле сложения по одинаковым индексам не производится, а индексы разные):
Учитывая вышесказанное и формулу (14), превращаем формулу (15) далее:
Теперь перейдем к вычислению следующей квадратичной формы:
Коэффициентами этой формы служат компоненты тензора метрической матрешки восьмого ранга. Этот тензор имеет две группы индексов, и является антисимметричным по перестановке индексов внутри этих групп. Вычисляем аналогично формуле (15).
Обозначим индексы как для упрощения записи:
Все четыре индекса должны быть попарно различными, поскольку компоненты тензора метрической матрешки равны нулю при наличии двух одинаковых индексов в одной группе. В правой сумме формулы (19a) стоят диагональные компоненты тензора метрической матрешки, которые равны единице (аналогично формуле 16).
Множитель 4! при переходе ко второй сумме в формуле (19a) возник вследствие того, что для одного слагаемого в правой сумме, характеризующегося фиксированным набором четырех различных чисел , соответствует 4! = 24 одинаковых по величине слагаемого в левой сумме, характеризующихся перестановками этих четырех чисел.
Формулы (19), (19a), (19b) легко обобщаются на формы высших степеней. Таким образом получаем общую формулу для нахождения кривизны Гаусса парной степени :
Альтернативный вывод формулы кривизны Гаусса для парной степени
Воспользуемся следующим выражением тензора Римана через тензор полной кривизны
и начнем в формуле (10) группировать сомножители по два, например начиная с первых двух (здесь мы считаем, что степень кривизны Гаусса не меньше двух (), и для упрощения записи опустим обозначения ):
Последнее преобразование справедливо вследствие антисимметрии тензора метрической матрешки относительно индексов в верхней группе. Далее, в последнем выражении поменяем местами индексы :
Теперь добавим уравнение (22) и (23), при этом учтя (21). Получаем, опять изменив обозначение индексов:
Множитель 2 в левой части уравнения (24) появился в результате группировки двух множителей . Очевидно, мы можем аналогичным образом сгруппировать попарно и остальные сомножители, тогда в левой части мы получим множитель , а в правой — выражение, в котором участвует только тензор Римана и тензор метрической матрешки, т.е. мы получим формулу (20).
Кривизна Гаусса нечетной степени
Кривизна Гаусса нечетной степени также связана с тензором Римана, но более сложными формулами, чем (20). К тому же из этих формул кривизна Гаусса выражается неоднозначно.
Значение кривизны Гаусса
В начале было дано определение кривизны Гаусса только для гиперповерхности (формулы 2, 3). Но формула (20), как и формулы для нахождения кривизны Гаусса нечетной степени, позволяют распространить это понятие на произвольные (абстрактные) многообразия. Таким образом мы можем рассматривать кривизны Гаусса как скалярные инварианты тензора Римана.
Внутренняя кривизна многообразия полностью описывается тензором Римана.
Кривизну Гаусса как скаляр можно интегрировать по объему всего многообразия (смотрите статью Интегралы Гаусса). Интеграл от K [n] является топологическим инвариантом n-мерного многообразия (не меняется при непрерывной деформации многообразиях).
Литература
См. также
Отображение Гаусса — Википедия
Материал из Википедии — свободной энциклопедии
Отображение Гаусса ставит в соответствие каждой точке поверхности вектор единичной нормали в этой точке. Концы всех таких векторов, отложенных от одной точки, лежат на сфере единичного радиуса. Эта статья об отображении поверхности в сферу; об отображении единичного отрезка в себя см. Преобразование Гаусса.Отображение Гаусса (гауссово отображение, сферическое отображение) — отображение из гладкой поверхности в трёхмерном евклидовом пространстве в единичную сферу, при котором точка поверхности отображается в вектор единичной нормали в этой точке. Названо в честь Карла Фридриха Гаусса.
- Отображение Гаусса естественно обобщается на случай гиперповерхности в евклидовом пространстве произвольной размерности.
- Для подмногообразия евклидова пространства произвольной размерности и коразмерности естественным аналогом отображения Гаусса является отображение, сопоставляющее точке подмногообразия точку грассманиана, соответствующую касательному пространству в этой точке.
- Б. А. Дубровин, С. П. Новиков, А. Т. Фоменко. Современная геометрия. — Любое издание.
- П. К. Рашевский. Риманова геометрия и тензорный анализ. — Любое издание.
- Д. Гильберт, С. Кон-Фоссен. Наглядная геометрия. — Любое издание.
- Топоногов В. А. Дифференциальная геометрия кривых и поверхностей. — Физматкнига, 2012. — ISBN 9785891552135.


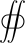 S{\ Displaystyle \ scriptstyle S \!} Е⋅dAзнак равноQеNсε0,{\ Displaystyle \ mathbf {Е} \; \ CDOT \ mathrm {d} \ mathbf {A} = {\ гидроразрыва {Q_ {прил}} {\ varepsilon _ {0}}} \, \.!}
S{\ Displaystyle \ scriptstyle S \!} Е⋅dAзнак равноQеNсε0,{\ Displaystyle \ mathbf {Е} \; \ CDOT \ mathrm {d} \ mathbf {A} = {\ гидроразрыва {Q_ {прил}} {\ varepsilon _ {0}}} \, \.!}