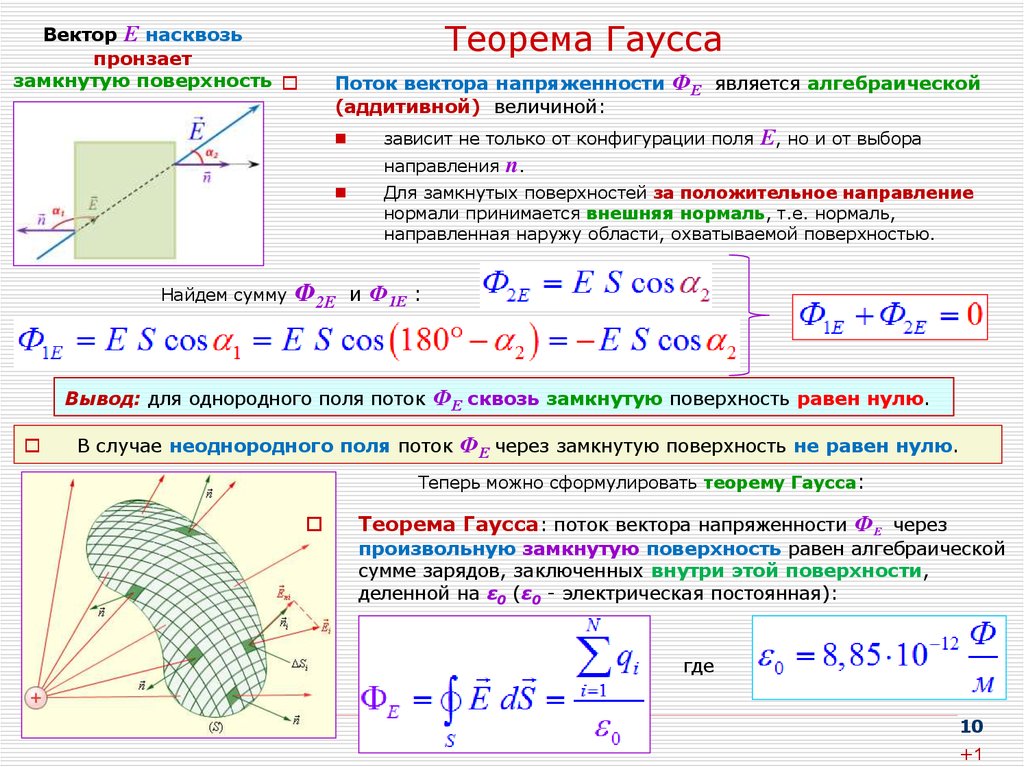
Теорема Гаусса в дифференциальной форме

Теорема Гаусса в интегральной форме

С помощью теоремы Гаусса в интегральной форме нельзя определить, как связан исток линий вектора электрического смещения в данной точке поля с плотностью свободных зарядов в этой же точке. Чтобы узнать это, рассмотрим дифференциальную форму теоремы Гаусса. Для этого разделим обе части уравнения интегральной формы записи теоремы Гаусса на одну и туже скалярную величину V (объем), находящийся внутри замкнутой поверхности:

.

Это выражение справедливо для V любой величины, устремим V к 0.

Предел отношения потока вектора электрического смещения сквозь замкнутую поверхность, ограничивающую некоторый объем, к объему называют дивергенцией вектора электрического смещения.

Или вместо слова «дивергенция» употребляют термины «расхождение».

,

где – объемная плотность заряда:

.

1. Если объемная плотность зарядов >0 в данной точке поля положительна, то из бесконечно малого объема окружающего данную точку поля, линии вектора электрического смещения исходят (исток).

2. Если объемная плотность зарядов <0 в данной точке поля отрицательна, то в бесконечно малый объем окружающий данную точку поля, линии вектора электрического смещения входят (сток).

3. Если объемная плотность зарядов =0 в данной точке поля равна нулю, то в данной точке поля нет ни стока, ни истока. Линии вектора электрического смещения проходят через данную точку пространства.

Силовые линии начинаются и заканчиваются на зарядах.

Теорема Гаусса в дифференциальной форме

Если среда однородна и изотропна, то ее и тогда:

.

Разложим дивергенцию в декартовой системе координат:

;

;

.

Если два проводящих тела разделены диэлектриком и несут на себе равные по значению и противоположные по знаку заряды, то в пространстве между ними создается электрическое поле.

Под емкостью С между двумя телами, на которых имеются равные и противоположные по знаку заряды, понимают абсолютную величину отношения заряда на одном из тел к разности потенциалов между телами.

.

Емкость измеряется в Фарадах .

Емкостью обладают любые два тела, разделенные диэлектриком.

Техническое устройство определенной емкости – это конденсатор.

Емкость линейного конденсатора не зависит от заряда и разности потенциалов, а зависит от геометрических размеров конденсатора и свойств диэлектрика находящегося между пластинами.

Методика расчёта ёмкости тела правильной формы:

Условно считают заряд известным, через него выражают напряжение и подставляют в формулу для емкости, где заряд сокращают.

Емкость плоского конденсатора

Применим теорему Гаусса в интегральной форме:

.

Поле плоского конденсатора равномерно, поэтому можно убрать знак интеграла:

.

Заряд равномерно распределен по поверхности пластин, поэтому в расчетах удобно пользоваться понятием поверхностной плотности заряда.

;

;

.

Зная напряженность электростатического поля найдем напряжение:

.

Тогда

.

Ёмкость цилиндрического конденсатора

(коаксиального кабеля)

Напряженность поля цилиндрического конденсатора (см. применение теоремы Гаусса):

.

Зная напряженность электростатического поля найдем напряжение:

.

Заряд распределен по длине.

,

где l – длина кабеля.

Тогда емкость цилиндрического конденсатора:

.

Ёмкость двух проводной линии

Если d >> R_{n ,} то .

Если d ≈ R_{n ,} то .

Ёмкость сферического конденсатора

.

Если R₂ устремить к бесконечности, то получим формулу для шара:

.

Ёмкость двухслойного цилиндрического конденсатора

Поверхность каждого слоя эквипотенциальна, поэтому её можно заменить металлической поверхностью, сообщив некоторый потенциал (второе следствие теоремы единственности решения).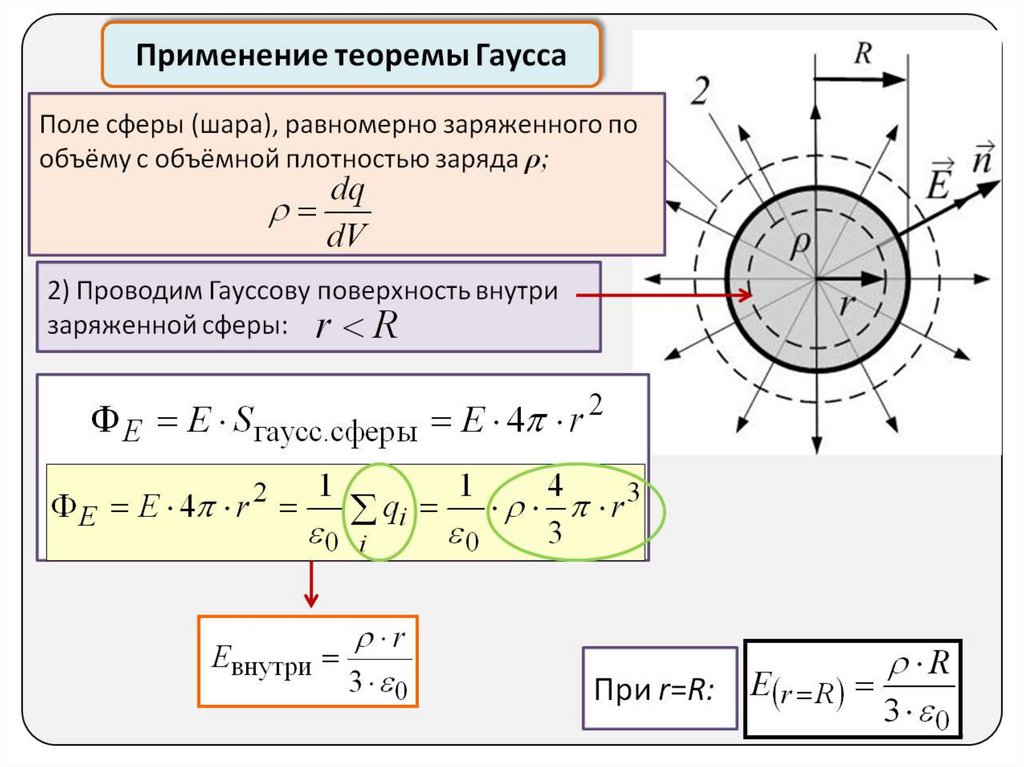 Получим два конденсатора один внутри другого.

+

Конденсаторы соединим последовательно:

;

;;

;.

PhysBook:Электронный учебник физики — PhysBook

Содержание

• 1 Учебники
• 2 Механика
  • 2.1 Кинематика
  • 2.2 Динамика
  • 2.3 Законы сохранения
  • 2.4 Статика
  • 2.5 Механические колебания и волны
• 3 Термодинамика и МКТ
  • 3. 1 МКТ
  • 3.2 Термодинамика
• 4 Электродинамика
  • 4.1 Электростатика
  • 4.2 Электрический ток
  • 4.3 Магнетизм
  • 4.4 Электромагнитные колебания и волны
• 5 Оптика. СТО
  • 5.1 Геометрическая оптика
  • 5. 2 Волновая оптика
  • 5.3 Фотометрия
  • 5.4 Квантовая оптика
  • 5.5 Излучение и спектры
  • 5.6 СТО
• 6 Атомная и ядерная
  • 6.1 Атомная физика. Квантовая теория
  • 6.2 Ядерная физика
• 7 Общие темы
• 8 Новые страницы

Здесь размещена информация по школьной физике:

1. материалы из учебников, лекций, рефератов, журналов;
2. разработки уроков, тем;
3. flash-анимации, фотографии, рисунки различных физических процессов;
4. ссылки на другие сайты

и многое другое.

Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.

Учебники

Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –

Механика

Кинематика

Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве

Динамика

Законы Ньютона – Силы в механике – Движение под действием нескольких сил

Законы сохранения

Закон сохранения импульса – Закон сохранения энергии

Статика

Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика

Механические колебания и волны

Механические колебания – Механические волны

---

Термодинамика и МКТ

МКТ

Основы МКТ – Газовые законы – МКТ идеального газа

Термодинамика

Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение

---

Электродинамика

Электростатика

Электрическое поле и его параметры – Электроемкость

Электрический ток

Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках

Магнетизм

Магнитное поле – Электромагнитная индукция

Электромагнитные колебания и волны

Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны

---

Оптика.

СТО

Геометрическая оптика

Прямолинейное распространение света. Отражение света – Преломление света – Линзы

Волновая оптика

Свет как электромагнитная волна – Интерференция света – Дифракция света

Фотометрия

Фотометрия

Квантовая оптика

Квантовая оптика

Излучение и спектры

Излучение и спектры

СТО

СТО

---

Атомная и ядерная

Атомная физика. Квантовая теория

Строение атома – Квантовая теория – Излучение атома

Ядерная физика

Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы

---

Общие темы

Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике

Новые страницы

Запрос не дал результатов.

Закон Гаусса

Закон Гаусса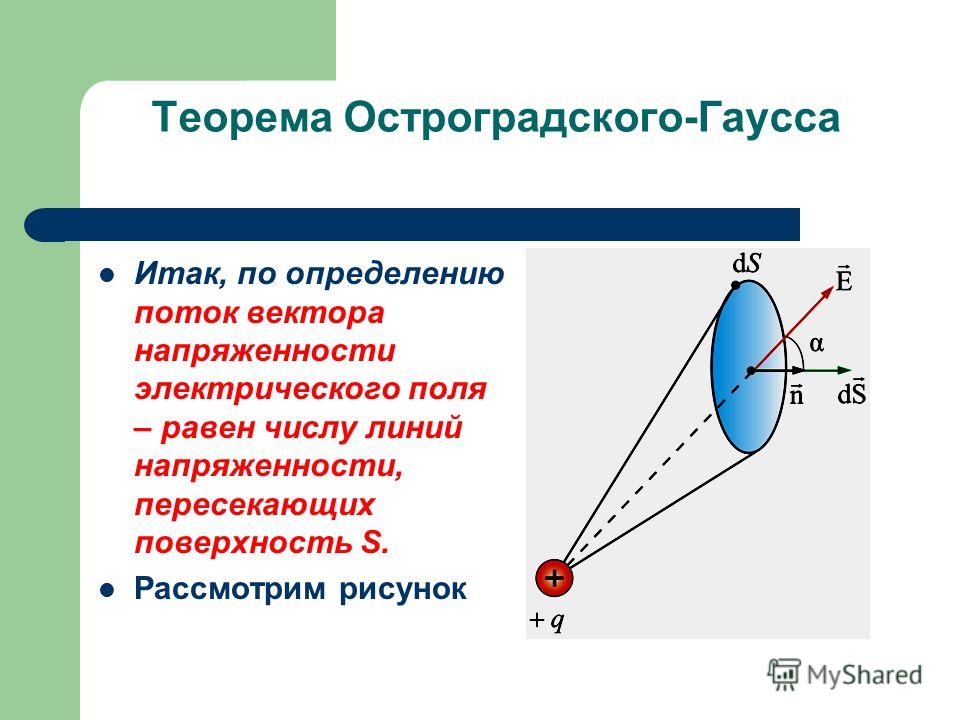

Суммарный электрический поток, исходящий от замкнутой поверхности, равен заключенному заряду, деленному на диэлектрическую проницаемость. Электрический поток через площадь определяется как электрическое поле, умноженное на площадь поверхности, спроецированной на плоскость, перпендикулярную полю. Закон Гаусса — это общий закон, применимый к любой замкнутой поверхности. Это важный инструмент, поскольку он позволяет оценить количество заключенного заряда путем отображения поля на поверхности вне распределения заряда. Для геометрий достаточной симметрии это упрощает вычисление электрического поля. Другой способ наглядно представить это — рассмотреть датчик площади A, который может измерять электрическое поле, перпендикулярное этой области. Если он выберет любую закрытую поверхность и перешагнет через нее, измерив перпендикулярное поле, умноженное на его площадь, он получит меру суммарного электрического заряда внутри поверхности, независимо от того, как сконфигурирован этот внутренний заряд. Приложения Более формальное утверждение Закон Гаусса для магнетизма

Индекс Концепции электрического поля

Гиперфизика***** Электричество и магнетизм R Ступица

Назад

Интеграл площади электрического поля над любой замкнутой поверхностью равен суммарному заряду, заключенному в поверхности, деленному на диэлектрическую проницаемость пространства. Закон Гаусса – это форма одного из Максвелла уравнения, четыре фундаментальные уравнения на электричество и магнетизм. Закон Гаусса позволяет оценить электрического поля во многих практических ситуации, образуя симметричную Гауссова поверхность, окружающая распределение заряда и оценка электрический поток через эту поверхность. Приложения

Индекс Концепции электрического поля

Гиперфизика***** Электричество и магнетизм R Ступица

Назад

Понятие электрического потока полезно в сочетании с законом Гаусса. Электрический поток через плоскую область определяется как произведение электрического поля на составляющую площади, перпендикулярную полю. Если площадь не плоская, то для оценки потока обычно требуется интеграл площади, поскольку угол будет постоянно изменяться. Когда площадь A используется в такой векторной операции, подразумевается, что величина вектора равна площади, а направление вектора перпендикулярно площади. Магнитный поток

Индекс Концепции электрического поля

Гиперфизика***** Электричество и магнетизм R Ступица

Назад

8

Закон Гаусса является мощным инструментом для расчета электрических полей, когда они возникают из распределения зарядов достаточной симметрии для его применения. Закон Гаусса Гауссовы поверхности Если распределение заряда недостаточно симметрично для применения закона Гаусса, то поле должно быть найдено путем суммирования полей точечных зарядов отдельных элементов заряда. Примеры: Конечный линейный заряд Заряженное кольцо Заряженный диск	Индекс Электрическое поле Концепции электрического поля
Гиперфизика***** Электричество и магнетизм R Ступица
Назад

Закон Гаусса. Введение, вывод, приложения к теореме Гаусса

Закон Гаусса определяется как общий поток, исходящий от замкнутой поверхности, равен потоку, заключенному на поверхности, деленному на диэлектрическую проницаемость. Анализируется закон Гаусса, который анализирует электрический заряд, поверхность и вопрос электрического потока. Давайте узнаем больше о законе и о том, как он действует, чтобы мы могли понять уравнение закона.

Что такое закон Гаусса?

Согласно закону Гаусса, полный электрический поток, выходящий из замкнутой поверхности, равен содержащемуся в ней заряду, деленному на диэлектрическую проницаемость. Электрический поток в данной области рассчитывается путем умножения электрического поля на площадь поверхности, спроецированной на плоскость, перпендикулярную полю. Полный поток, связанный с замкнутой поверхностью, равен 1 ⁄ ε ₀ раз больше заряда, охваченного замкнутой поверхностью, в соответствии с законом Гаусса.

∮ E.ds = q ⁄ ε _o

Например, точечный заряд q помещен в куб с ребром а. Поток через каждую грань куба теперь равен q ⁄ 6ε _o в соответствии с законом Гаусса. Электрическое поле является наиболее фундаментальной концепцией в понимании электричества. В общем, электрическое поле поверхности вычисляется с использованием закона Кулона; однако понимание идеи закона Гаусса требуется для расчета распределения электрического поля на замкнутой поверхности. Он описывает, как электрический заряд заключен в замкнутой поверхности или как электрический заряд присутствует в закрытой поверхности, которая заключена.

Формула закона Гаусса

Согласно формуле закона Гаусса, общий электрический заряд, заключенный в замкнутой поверхности, пропорционален общему потоку, заключенному в этой поверхности. Как следствие, полный электрический заряд Q, содержащийся на поверхности, равен: если ε ₀ — электрическая постоянная, а ϕ — полный поток.

Q = ϕ ε _o

Формула закона Гаусса:0011

• ε _o — электростатическая постоянная,
• Q — общий заряд на данной поверхности, а
• ϕ — поток, окружающий поверхность.

Теорема Гаусса

Теорема Гаусса связывает «поток» линий электрического поля (поток) с зарядами внутри замкнутой поверхности простыми словами. Суммарный заряд в объеме, содержащемся на замкнутой поверхности, точно пропорционален чистому потоку через замкнутую поверхность.

ϕ = E.dA = q _net ⁄ ε _o

Чистый электрический поток остается равным 0, если на поверхности нет зарядов. Количество линий электрического поля, входящих в поверхность, равно количеству силовых линий, выходящих из поверхности.

Следствие утверждения теоремы Гаусса:

Электрический поток от любой замкнутой поверхности возникает только из-за источников и стоков электрических полей, окруженных поверхностью. На электрический поток не влияют никакие заряды вне поверхности. Более того, только электрические заряды могут действовать как источники или поглотители электрического поля. Важно отметить, что изменяющееся магнитное поле не может действовать как источник или поглотитель электрического поля.

 

Поскольку он заключает в себе чистый заряд, чистый поток для поверхности слева отличен от нуля. Поскольку правая поверхность не содержит заряда, чистый поток равен нулю. Закон Гаусса есть не что иное, как повторение закона Кулона. Закон Кулона легко получить, применяя теорему Гаусса к точечному заряду, окруженному сферой.

Примечание: Закон Гаусса и закон Кулона тесно связаны. Если применить закон Гаусса к точечному заряду в сфере, это будет то же самое, что применить закон Кулона.

Уравнение закона Гаусса

Уравнение закона Гаусса можно понять с помощью интегрального уравнения. Закон Гаусса в интегральной форме приведен ниже:

∫E.dA = Q/ε ₀ ⇢ (1)

Где

• E — электрическое поле,
• Q — электрический заряд
• ε ₀ — электрическая проницаемость свободного пространства
• A — направленный наружу вектор площади нормали

Поток — это мера напряженности поля, проходящего через поверхность. Электрический поток определяется как:

Φ = ∫E⋅dA ⇢ (2)

Применение закона Гаусса

Существуют различные формулы, полученные из применения закона Гаусса для различных условий. Ниже приведены некоторые известные применения закона Гаусса:

• В среде с диэлектрической проницаемостью К напряженность электрического поля вблизи плоского заряженного проводника E = σ ⁄ K ε _o . E _воздух = σ ⁄ ε _o , когда диэлектрической средой является воздух.
• На расстоянии r в случае бесконечной линии заряда E = (1 ⁄ 4 × π r ε ₀ ) (2π ⁄ r) = λ ⁄ 2π r ε _o , где λ — линейная плотность заряда.
• В конденсаторе поле между двумя параллельными пластинами равно E = σ ⁄ ε ₀ , где σ — поверхностная плотность заряда.
• Напряженность электрического поля вблизи плоского слоя заряда составляет E = σ ⁄ 2K ε _o , где σ — поверхностная плотность заряда.
• Для заряженного кольца радиусом ‘R’, от центра кольца на расстоянии ‘x’, здесь электрическое поле принимает вид: электрическое поле, вызванное бесконечным проводом, предположим, что заряд на единицу бесконечно длинного провода равен λ. Электрическое поле радиально удалено от всех точек провода, и ни одна компонента не параллельна линии заряда. Теперь предположим, что проволока представляет собой цилиндр (с радиусом «r» и длиной «l») с центром на линии заряда в качестве гауссовой поверхности.

   

  Электрическое поле перпендикулярно цилиндру. Следовательно, угол между электрическим полем и вектором площади равен 0°. Итак, cosθ = 1. Верх и низ цилиндра параллельны электрическому полю. Следовательно, вектор площади здесь равен 90 ° по отношению к электрическое поле. Следовательно, cosθ = 0. Отсюда можно сказать, что электрический поток возникает только за счет искривленной поверхности цилиндра. По закону Гаусса:

  ϕ = E.d ⇢ A

  ϕ _чистая = ϕ _{изогнутая} + ϕ _верх + ϕ _низ

  ϕ = E.d ⇢ A = ∫E.dA cos0 + ∫E.dA cos90 + ∫E.dA cos90

  равноудален от линии заряда из-за его радиальной симметрии. Итак, электрическое поле на поверхности имеет постоянное значение по всей поверхности.

  ϕ = ∫E.dA = ∫E. 2πrl

  Суммарный заряд, заключенный в поверхности:

  q _net = λ.l

  Теперь, используя теорему Гаусса:

  ϕ = ∫E. 2πrl = д _net ⁄ ε _o = λ. l/ε _o 

  ∫E. 2πrl = λ.l/ε _o

  E = λ/2πrε _o

  Решенные примеры по закону Гаусса

  Пример 1. В направлении x существует однородное электрическое поле величиной E = 50 Н⁄К. Рассчитайте поток этого поля через плоскую квадратную площадку со стороной 5 см в плоскости y-z, используя теорему Гаусса. Предположим, что нормаль положительна вдоль положительной оси x.

  Решение:

  Дано:

  Электрическое поле, E = 50 Н⁄Кл

  Длина края квадрата, a = 5 см = 0,05 м

  Поток поля через плоский квадрат, ϕ = ∫ E cosθ ds

  Поскольку нормаль к площади указывает вдоль электрического поля, θ = 0,

  Кроме того, E является однородным, поэтому Φ = E ΔS = (50 Н⁄C) (0,05 м) ² = 0,125 Н м ² С ^-1 .

  Отсюда поток данного поля равен 0,125 Н·м ² C ^-1 .

  Пример 2: Имеются три заряда, q ₁ , q ₂ и q _3, , имеющие заряды 4 Кл, 7 Кл и 2 Кл, заключенные в поверхность. Найдите полный поток, заключенный на поверхности.

  Решение:

  Общий заряд Q,

  Q = Q ₁ + Q ₂ + Q ₃

  = 4 C + 7 C + 2 C

  = 13 C

  = 4 C + 7 C + 2 C

  = 13 C

  = 4 C + 7 C + 2 C

  = 13 C

  1111110 Полный поток, ϕ = Q ⁄ ε ₀

  ϕ = 13 C ⁄ (8,854×10 ⁻¹² F ⁄ м)

  ϕ = 1,468 Н·м ² C ^-1

  м, общий поток равен 8 04 N м1. 2 С ^-1 .

  Пример 3: Две проводящие пластины с зарядами Q ₁ и Q ₂ расположены параллельно друг другу. Найдите распределение на всех четырех поверхностях.

  Решение:

  Из рисунка видно, что две грани лежат внутри проводника при E = 0. Поток также равен 0. Грани, которые снаружи, параллельны электрическому полю, поток там тоже будет 0. Следовательно, полный поток электрического поля равен 0,

  По закону Гаусса общий заряд внутри замкнутой поверхности должен быть равен 0. Следовательно, заряд на внутренней стороне одной пластины должен быть равен заряду на другой стороне.

  Используя уравнение E = σ/2ε ₀ , электрическое поле в точке P:

  • Из-за заряда Q ₁ – q = (Q ₁ – q)/2Aε ₀ (вниз) .
  • Из-за заряда +q = +q/ε ₀ (вверх).
  • В связи со сбором Q ₂ + q = (Q ₂ + q)/2Aε ₀ (вверх)
  • За счет заряда -q = -q/ε ₀ (вниз).

  Результирующее электрическое поле направлено вниз: 0 + +Q/ε ₀

  Q ₁ -Q +Q -Q ₂ = 0

  Q = (Q ₁ -Q ₂ )/2

  Q ₁ – q = (Q ₁ + Q ₂ )/2

  Q ₂ + q = (Q ₁ + Q ₂ )/2

  Пример 4. Какова дифференциальная форма теоремы Гаусса?

  Решение:

  Электрическое поле связано с распределением заряда в определенном месте пространства дифференциальной версией закона Гаусса. Для пояснения, согласно закону, дивергенция электрического поля (E) равна объемной плотности заряда (ρ) в данной позиции. Написано так:

  ΔE = ρ ⁄ ε ₀

  Здесь ε ₀ — диэлектрическая проницаемость свободного пространства.

  Пример 5: Имеются три концентрические сферические оболочки A, B и C с радиусами a, b и c. Заряды присутствуют на оболочках А и С (соответственно q и -q), а оболочка В заземлена. Найдите суммарные заряды на B и C.

   

  Решение:

  Поскольку внутренняя поверхность оболочки B должна иметь заряд -q, предположим, что внешняя поверхность B имеет заряд x. Тогда внутренняя поверхность C должна иметь заряд «-x».

  Потенциал, обусловленный зарядом «q» на A = q/4πε ₀ b

  Потенциал, обусловленный «-q» на внутренней поверхности B = -q/4πε ₀ b

  Потенциал, обусловленный «x» на внешней поверхности B = x/4πε ₀ b

  Потенциал из-за «-x» на внутренней поверхности C = -x/4πε ₀ c

  Потенциал из-за «x – q» на внутренней поверхности C = x – q/4πε ₀ c

  Теперь суммарный потенциал: VB = x/4πε ₀ b – q/4πε ₀ c

  Этот потенциал равен 0, так как оболочка B заземлена. .

  Следовательно, x = qb/c

  Ниже приведен рисунок, показывающий заряды на каждой поверхности:

   

  Часто задаваемые вопросы по закону Гаусса

  Вопрос 1: Укажите закон Гаусса.

  Ответ:

  Закон Гаусса гласит, что суммарный поток электрического поля прямо пропорционален заряду, заключенному в замкнутой поверхности.

  Вопрос 2: Как выбрать подходящую поверхность Гаусса для различных случаев?

  Решение:

  Чтобы выбрать приемлемую поверхность Гаусса, мы должны учитывать тот факт, что отношение заряда к диэлектрической проницаемости обеспечивается (двумерным) поверхностным интегралом по электрическому полю распределения заряда. симметрия.

  Нам нужно знать о трех возможных сценариях.

  • Когда распределение заряда сферически симметрично, оно называется сферическим.
  • Когда распределение заряда цилиндрически симметрично, оно называется цилиндрическим.
  • Когда распределение заряда демонстрирует трансляционную симметрию вдоль плоскости, это называется дотом.

  В зависимости от того, где мы хотим вычислить поле, мы можем определить размер поверхности. Теорема Гаусса полезна для определения направления поля при наличии симметрии, поскольку она сообщает нам, как поле направлено.

  Вопрос 3. Закон Гаусса в электростатике.

  Решение:

  Закон Гаусса в электростатике гласит, что электрический поток через любую замкнутую поверхность равен суммарному заряду, заключенному в поверхности, деленному на диэлектрическую проницаемость свободного пространства. Обычно закон Гаусса используется для расчета электрическое поле симметричных распределений заряда. При использовании этого закона для решения проблемы электрического поля требуется множество процессов. Вот подробности:

  1. Во-первых, мы должны определить пространственную симметрию распределения заряда.
  2. Следующим шагом является выбор правильной поверхности Гаусса, которая имеет ту же симметрию, что и распределение заряда. Его разветвления также должны быть определены.
  3. Рассчитайте поток через поверхность, оценив интеграл ϕ _с E по поверхности Гаусса.
  4. Рассчитайте количество заряда, содержащегося на поверхности Гаусса.
  5. Рассчитайте электрическое поле распределения заряда.

  Однако, чтобы определить электрическое поле, учащиеся должны помнить о трех формах симметрии. Ниже приведены несколько форм симметрии:

  • Симметрия на сфере
  • Симметрия в цилиндрической форме
  • Симметрия на плоскости

  Вопрос 4: Каковы применения закона Гаусса?

  Ответ:

  Сложные электростатические задачи, связанные с симметрией, такой как цилиндрическая, сферическая и т. д., могут быть решены с использованием закона Гаусса. Это также помогает найти электрическое поле, которое требует сложных вычислений.

  Вопрос 5: Что такое поверхность Гаусса?

  Ответ:

  Поверхность Гаусса – это поверхность, через которую рассчитывается электрический поток.

  Вопрос 6: Укажите закон Гаусса для магнетизма.