Компенсация высших гармоник активными динамическими фильтрами.
Активные динамические фильтры прекрасно справляются с задачей компенсации высших гармоник, обусловленных работой преобразователей частоты, выпрямителей, регуляторов напряжения и т.п. Преобразователи могут быть с различными входными дросселями, без дросселей, с входными фильтрами 5 и 7 гармоник (“tuned filters”) и др.
Вариант подключения активного фильтра в электроустановке с преобразователями частоты.
Активные фильтры компенсируют высшие гармоники до 49 порядка включительно, при этом пользователь может произвольно выбирать требуемую степень компенсации по каждой гармонике. Это оптимизирует ресурсы фильтров и снижает стоимость оборудования.
На этом видео показан пример компенсации нелинейного тока, потребляемого из сети.
Активные динамические фильтры могут работать в «слабых» сетях, при малой мощности источника электроэнергии. Это позволяет использовать их в системах бесперебойного питания, когда применение пассивных фильтров малоэффективно.
Вариант подключения активного фильтра на шины гарантированного питания.
Пример. Ответственные потребители компрессорной станции подключены к источнику бесперебойного питания (ИБП) мощностью 80 кВА. В составе потребителей особой группы есть частотно-регулируемые приводы. При включении преобразователей частоты коэффициент нелинейных искажений по напряжению (на шинах бесперебойного питания) достигает 17 %.
Нелинейные искажения при включении частотно-регулируемого привода от шин гарантированного питания.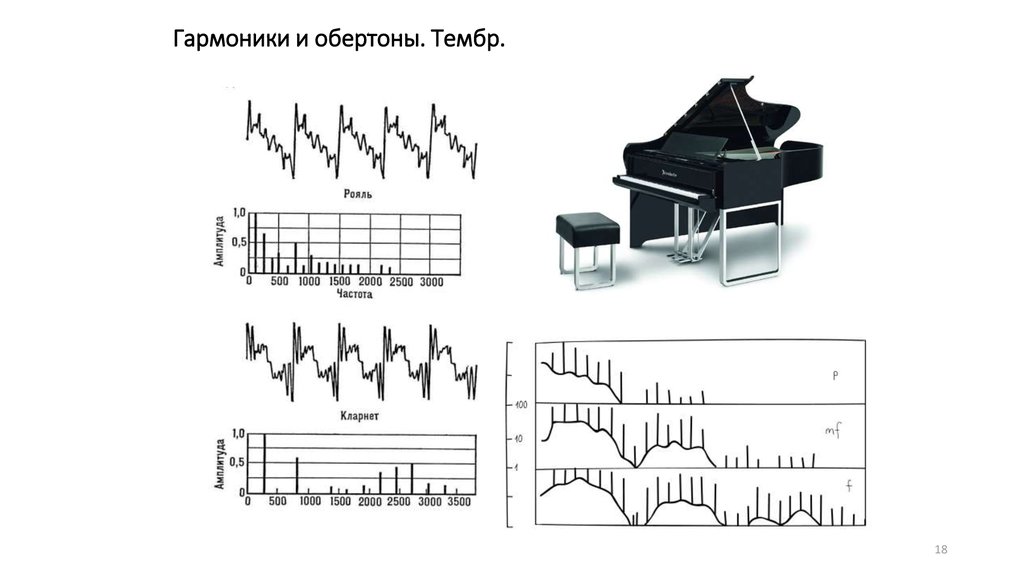
ИБП не может синхронизироваться с сетью при восстановлении электроснабжения и переходит в аварийный режим.
Аварийный режим источника бесперебойного питания, возникающий вследствие нелинейных искажений на шинах.
Потребители продолжают работать от ИБП до полного разряда аккумуляторной батареи, что является нештатной ситуацией.
Подключение активного фильтра на шины гарантированного питания снимает проблему синхронизации.
Активные фильтры во многих случаях являются выгодной альтернативой применения 12-пульсных схем выпрямления и преобразователей частоты AFE (Active Front End), поскольку:
- параллельное подключение к нагрузке позволяет компенсировать высшие гармоники группы преобразователей разного типа и мощности;
- небольшие размеры АДФ позволяют интегрировать их в существующие электроустановки;
- выборочная компенсация «опасных» гармоник обеспечивает оптимальное соотношение «цена-качество».
Предложения Инженерного центра «АРТ».
Полный комплекс работ по созданию систем динамической компенсации высших гармоник и реактивной мощности на базе активных фильтров.
Контактная информация.
Техника сверхвысоких частот. Том 1
Техника сверхвысоких частот. Том 1
ОглавлениеПРЕДИСЛОВИЕ РЕДАКТОРАГЛАВА 1. РАСПРОСТРАНЕНИЕ ВОЛН В ЦЕПЯХ 1.1. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ СВЕРХВЫСОКИХ ЧАСТОТ КАК ЭЛЕКТРОМАГНИТНОЕ ИЗЛУЧЕНИЕ 1.2. СВОЙСТВА МАТЕРИАЛОВ 1.2.2. Металлические проводники 1.2.3. Полупроводники 1.3. ВОЛНЫ С ЧИСТО ПОПЕРЕЧНЫМИ ПОЛЯМИ 1.3.2. Плоскопараллельные линии сверхвысоких частот 1.3.3. Коаксиальные линии 1.4. ВОЛНЫ В ПОЛЫХ ПРОВОДЯЩИХ ТРУБАХ 1.4.2. Круглые волноводы 1.5. СЛОЖНЫЕ ВОЛНОВОДЫ 1.5.2. Гребневые волноводы 1.5.3. Волноводы, содержащие диэлектрик ГЛАВА 2. ПРАКТИЧЕСКИЕ ЛИНИИ ПЕРЕДАЧИ 2.1. ТЕОРИЯ ЛИНИИ ПЕРЕДАЧИ 2.1.2. Круговая диаграмма 2.1.3. Широкополосное согласование 2.2. РАБОЧИЕ ПАРАМЕТРЫ 2.2.1. Перекрытие по частоте 2.2.3. Допустимая мощность 2.3. СТАНДАРТНЫЕ ВОЛНОВОДЫ 2.3.1. Прямоугольные волноводы 2.3.2. Круглые волноводы 2.3.3. Широкополосные и компактные волноводы 2.  4. МЕТОДЫ СОЕДИНЕНИЯ2.4.1. Выравнивание волноводов 2.4.2. Контактные прокладки и дроссели 2.4.3. Крепежные и зажимные устройства 2.5. УПЛОТНЕНИЕ И ГЕРМЕТИЗАЦИЯ 2.5.1. Волноводные системы 2.5.2. Соединители и сочленения 2.6. ПРОСТЫЕ ПЕРЕХОДЫ 2.6.1. Изгибы, уголки и скрутки 2.6.2. Переходы и преобразователи 2.7. ГИБКИЕ ВОЛНОВОДЫ 2.7.2. Позвонковая модель 3.1.2. Отверстия связи 3.1.3. Параллельные и последовательные тройники 3.2. ПРЕОБРАЗОВАТЕЛИ ВИДОВ КОЛЕБАНИЙ 3.2.1. Коаксиально-волноводные переходы 3.2.2. Переходы с прямоугольного волновода на круглый 3.2.3. Переход от линейной поляризации к круговой 3.3. НАПРАВЛЕННЫЕ ОТВЕТВИТЕЛИ 3.3.2. Распределенная связь 3.3.3. Системы с полной передачей мощности 3.4. ГИБРИДНЫЕ СОЕДИНЕНИЯ 3.4.1. Тип соединения с фазами, находящимися в квадратуре 3.4.2. Синфазные гибридные соединения 3.4.3. Различные гибридные соединения 3.  3.5.2. Подвижные вставки 3.5.3. Фазовращатели 3.6. ВРАЩАЮЩИЕСЯ СОЧЛЕНЕНИЯ 3.6.1. Вращающиеся сочленения с колебаниями кругового магнитного вида 3.6.2. Вращающиеся сочленения различных типов 3.7. МЕХАНИЧЕСКИЕ ПЕРЕКЛЮЧАТЕЛИ 3.7.1. Механические переключатели с ручным управлением 3.7.2. Быстродействующие переключатели ГЛАВА 4. МЕТОДЫ ИЗМЕРЕНИЙ И ПРИБОРЫ 4.1. ИЗМЕРЕНИЕ МОЩНОСТИ 4.1.2. Методы измерений, основанные на преобразовании мощности в тепловую энергию 4.1.3. Эффект Холла и давление излучения 4.2. ИЗМЕРЕНИЕ ЗАТУХАНИЯ 4.2.2. Фиксированные аттенюаторы и оконечные нагрузки 4.3. ИЗМЕРЕНИЕ ПОЛНЫХ СОПРОТИВЛЕНИЙ 4.3.2. Картина стоячей волны 4.3.3. Мостовые методы ГЛАВА 5. РЕЗОНАТОРЫ И ФИЛЬТРЫ 5.1.2. Свойства цепей 5.1.3. Измерения характеристик 5.2. ИЗМЕРЕНИЕ ДЛИНЫ ВОЛНЫ 5.2.1. Волномеры с объемными резонаторами 5.2.2. Волноводные интерферометры 5.  3. ФИЛЬТРУЮЩИЕ ЦЕПИ5.3.2. Связанные резонаторы 5.3.3. Четвертьволновая связь ГЛАВА 6. ХАРАКТЕРИСТИКИ МАТЕРИАЛОВ И МЕТОДЫ ИХ ИЗМЕРЕНИЙ 6.1.2. Методы измерений в свободном пространстве и в линии передачи 6.1.3. Методы измерений в объемном резонаторе 6.2. ЭКСПЕРИМЕНТЫ И РЕЗУЛЬТАТЫ 6.2.3. Твердые тела 6.3. ПРОВОДИМОСТЬ МЕТАЛЛОВ 6.3.2. Аномальное поведение 6.3.3. Сверхпроводимость ГЛАВА 7. СПЕКТРОМЕТРИЯ ДИЭЛЕКТРИКОВ 7.1.2. Форма линии и интенсивность 7.1.3. Сверхтонкая структура 7.1.4. Явления Штарка и Зеемана 7.2. СПЕКТРОМЕТРЫ 7.2.2. Поглощающие ячейки 7.2.3. Типы спектрометров 7.3. ПАРАМАГНИТНЫЙ РЕЗОНАНС В ТВЕРДЫХ ТЕЛАХ 7.3.2. Техника измерения 7.3.3. Типичные материалы 7.3.4. Времена релаксации 7.4. ЦИКЛОТРОННЫЙ РЕЗОНАНС 7.4.2. Определение эффективной массы носителей ГЛАВА 8. СВОЙСТВА И ПРИМЕНЕНИЕ ГИРОМАГНИТНЫХ СРЕД 8.1.2. Распространение электромагнитных волн в неограниченной среде 8.  8.2.2. Ферромагнитный резонанс 8.2.3. Нелинейные эффекты и нестабильность 8.3. РАСПРОСТРАНЕНИЕ В НАПРАВЛЯЮЩИХ СИСТЕМАХ 8.3.2. Прямоугольный волновод 8.3.3. Ферритовые устройства в качестве элементов схем 8.4. ИЗМЕРЕНИЯ ПАРАМЕТРОВ ФЕРРИТОВЫХ МАТЕРИАЛОВ 8.4.2. Резонансные методы 8.4.3. Волноводные методы 8.5. РЕЗОНАНСНЫЕ ВЕНТИЛИ 8.6. УСТРОЙСТВА, РАБОТАЮЩИЕ СО СЛАБЫМИ ПОЛЯМИ 8.6.2. Устройства с поперечным полем 8.6.3. Прочие узлы ГЛАВА 9. ПЛОСКОПАРАЛЛЕЛЬНЫЕ СИСТЕМЫ 9.2. СИММЕТРИЧНЫЕ ПОЛОСКОВЫЕ ЛИНИИ 9.2.1. Линии типа «диэлектрических сэндвичей» 9.3. НЕСИММЕТРИЧНЫЕ ПОЛОСКОВЫЕ ЛИНИИ 9.3.2. Несимметричная полосковая линия с твердым диэлектриком 9.4. ЭЛЕМЕНТЫ И УЗЛЫ 9.4.2. Переходные устройства 9.4.3. Узлы полосковых систем 9.5. ЦЕПИ И СИСТЕМЫ 9.5.3. Частотные фильтры 9.5.4. Цепи питания антенн 9.6. МАТЕРИАЛЫ И МЕТОДЫ ПРОИЗВОДСТВА 9.  6.2. Техника изготовления печатных схемГЛАВА 10. ПЕРИОДИЧЕСКИЕ И НАПРАВЛЯЮЩИЕ СТРУКТУРЫ 10.1. ВОЛНЫ В ПЕРИОДИЧЕСКИ НАГРУЖЕННЫХ ЛИНИЯХ 10.1.2. Пространственные гармоники 10.1.3. Многократно-периодические структуры 10.2. МЕТАЛЛИЧЕСКИЕ СТРУКТУРЫ С ДИЭЛЕКТРИЧЕСКИМ ПОКРЫТИЕМ 10.2.2. Радиальные волны над плоскими поверхностями 10.2.3. Продольные цилиндрические волны 10.3. ЛИНИИ ПЕРЕДАЧИ ПОВЕРХНОСТНЫХ ВОЛН 10.3.2. Влияние кривизны 10.3.3. Возбудители и другие устройства 10.4. ВОЛНЫ В ДИЭЛЕКТРИЧЕСКИХ ЛИНИЯХ 10.4.2. Цилиндрические стержни 10.4.3. Многослойные среды 10.4.4. Линии с зеркальным изображением 10.5. СТРУКТУРЫ ИЗ СВЯЗАННЫХ РЕЗОНАТОРОВ 10.5.2. Объемные резонаторы 10.6. СПИРАЛЬНЫЕ СТРУКТУРЫ 10.6.2. Практические варианты ГЛАВА 11. ЛАМПЫ С СЕТОЧНЫМ УПРАВЛЕНИЕМ И ЛАМПЫ С ПРОСТРАНСТВЕННЫМ ЗАРЯДОМ 11.1.2. Лампы с сеточным управлением 11.2. ВЗАИМОДЕЙСТВИЕ ПУЧКА И РЕЗОНАТОРА 11.2.2. Усилительные клистроны 11. 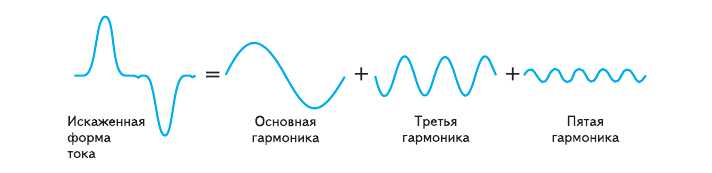 2.3. Отражательные клистроны11.3. ВЗАИМОДЕЙСТВИЕ ПУЧКА И КОНТУРА 11.3.1. Электронно-волновые лампы 11.3.2. Лампы с бегущей волной 11.3.3. Лампы обратной волны ГЛАВА 12. ЛАМПЫ СО СКРЕЩЕННЫМИ ПОЛЯМИ И ГЕНЕРАЦИЯ ВОЛН МИЛЛИМЕТРОВОГО ДИАПАЗОНА 12.1.2 Карсинотрон типа М 12.2. МАГНЕТРОНЫ 12.2.2. Резонаторные системы 12.2.3. Взаимодействие между электронным потоком и резонансной системой 12.2.4. Рабочие характеристики 12.3. ГЕНЕРАЦИЯ ВОЛН МИЛЛИМЕТРОВОГО ДИАПАЗОНА 12.3.2. Высокочастотный предел когерентного излучения 12.4. ИСТОЧНИКИ ЭЛЕКТРОНОВ 12.4.1. Термоэлектронные катоды 12.4.2. Фокусированные пучки ГЛАВА 13. ТЕХНИКА ОПТИЧЕСКОГО ТИПА 13.1.2. Типы дифракции 13.1.3. Рассеяние 13.2. ИСКУССТВЕННЫЕ ДИЭЛЕКТРИКИ 13.2.2. Структуры волноводного типа 13.3. КОНТРОЛЬ ОТРАЖЕНИЙ ОТ ПОВЕРХНОСТИ 13.3.2. Неотражающие поглотители 13.3.3. Увеличение отражающей способности 13.4. ПРИБОРЫ И СИСТЕМЫ 13.4.1. Спектрометры 13.  4.2. Интерферометры13.4.3. Устройство с делением пучка |
Что такое гармоники? Изучение ткани музыки — Блог
Иллюстрация: Franco Égalité
Гармоники могут не занимать наше внимание, когда мы играем на инструменте или сочиняем музыку.
Тем не менее, они представляют собой фундаментальный аспект звука, объясняющий саму суть музыки — почему музыка — это . Сегодня давайте рассмотрим, что такое гармоники и как вы можете извлечь пользу из понимания их как музыканта.
Простейший звук
Чтобы понять гармоники, нам нужно сначала изучить самый простой из всех звуков: синусоидальную волну . Если вы когда-либо играли синусоиду, глядя на многополосный эквалайзер, вы увидите, что вся энергия сконцентрирована вокруг одной частоты, соответствующей проигрываемой ноте:
Частотный спектр синусоидальной волны, воспроизводимой D4
Звук, который мы слышим
Между тем, если вы сыграете ту же ноту, используя прямоугольную волну, вы увидите нечто совсем другое; есть еще частотный контент на ~293 Гц (частота, соответствующая D4), чем где-либо еще, но помимо этого происходит гораздо больше:
Частотный спектр прямоугольной волны при воспроизведении D4
Звук, который мы слышим
Все более мягкие частоты видимые по всему спектру прямоугольной волны — это то, что мы называем ее гармониками, и именно они позволяют нам слышать прямоугольную волну и распознавать ее как нечто, отличающееся от синусоидальной волны, даже если они воспроизводят точную такая же заметка.
Гармоники существуют в разной степени для каждого тонального звука (кроме синусоидальных волн), и именно поэтому многие люди называют синусоидальную волну «самым простым звуком».0007
Так что же такое гармоники?
Приведенное выше исследование подводит нас к следующему пункту: всякий раз, когда вы слышите тон, вы почти никогда не слышите просто этот тон — скорее, вы слышите его плюс смесь множества других более высоких и тихих звуков. высоты тона, которые известны как гармоники .
Гармоники возникают на частотах, кратных основной частоте , что является самой громкой высотой тона, воспринимаемой нашими ушами (в нашем предыдущем примере с прямоугольной волной основная частота будет равна 29).3 Гц).
Итак, например, если у нас есть основная частота 100 Гц, гармоники будут существовать на частотах 200 Гц, 300 Гц, 400 Гц, 500 Гц и т. д. ссылаться на них).
Гармоники и тембр
Независимо от того, слышите ли вы прямоугольную волну, фортепиано, скрипку или любой другой звук, до тех пор, пока играемая нота постоянна, все они будут иметь одну и ту же основную частоту.
Как указывалось ранее, что позволяет каждому инструменту различать свой уникальный звуковой характер, или timbre , насколько громкой или тихой является каждая из гармоник.
Прямоугольная волна имеет очень математический метод определения баланса гармоник. Он состоит только из нечетных целых чисел, полностью исключая четные. Кроме того, амплитуда каждого обертона уменьшается в зависимости от того, где он расположен в ряду (например, третья гармоника будет иметь только треть амплитуды основной частоты, пятая гармоника будет иметь одну пятую амплитуды основной частоты и т. д.).
Между тем, более органичный звук, такой как человеческий голос, будет иметь гораздо менее линейный и более сложный спектр гармоник. В отличие от синусоидальных и прямоугольных волн, большинство звуков также не являются идеально периодическими по своей природе, а нюансы тембра меняются по мере удержания ноты — это означает, что в большинстве случаев точный баланс гармоник для звука также постоянно колеблется.
Применение понимания гармоник к музыке
Если вы понимаете, что гармоники лежат в основе тембра всех звуков, вы можете использовать эти знания самым универсальным образом, когда дело доходит до звукового дизайна. Например, если вы хотите, чтобы инструмент звучал более «синусоидально», вы можете использовать встроенный эквалайзер вашей DAW, чтобы повысить основную частоту или обрезать гармонический контент, который находится над ней. Если вы хотите, чтобы звук казался менее тональным и более «шумовым», вы можете рассмотреть возможность искажения сигнала, чтобы ввести больше негармонические частичные — обертоны, которые не соответствуют ожидаемым целым кратным основным тонам.
Если вы хотите выйти на новый уровень, есть также несколько специальных плагинов и инструментов, которые позволяют вам тонко манипулировать гармониками. Например, Pigments 3 от Arutria имеет специальный движок Harmonic, который отображает содержание обертонов синтезированных звуков с помощью динамичной и привлекательной визуализации.
Используя такие параметры, как Tilt Offset и Parity, вы можете хирургически манипулировать балансом между нечетными и четными обертонами, скоростью их появления и многим другим, что открывает совершенно новый подход к звуковому дизайну:
Узнайте больше обо всех возможностях синтеза в Pigments 3 из нашего руководства по функциям
Феномен природы
Одна из самых крутых вещей в гармониках заключается в том, что они не были изобретены людьми, а являются акустическим принципом. что существует столько времени. Однако, если вы внимательно посмотрите на то, как гармоники распределяются в ряду, вы начнете понимать, что целые числа, кратные основной гармонике, определяют многие интервалы, которые являются ключевыми для музыки, которую мы знаем и любим — первый обертон ровно на октаву выше первого. основной тон, второй обертон — чистая квинта, четвертый обертон — другая октава, пятый обертон — мажорная терция и так далее.
Это явление означает, что древние цивилизации могли бессознательно реконструировать музыку из природы задолго до того, как мы поняли математику волновых форм.
Такие понятия, как созвучие и музыкальные гаммы, в некотором смысле являются социальными, различающимися в зависимости от культуры и периода времени, но в некотором смысле они также интуитивны и универсальны, судя по тому, как вы можете проследить их происхождение до частотных отношений, существующих в гармониках. Гармоники открывают нам, что музыка одновременно остро математическая и неописуемо мистическая — и возможность пройти через это пересечение в качестве создателей музыки — это действительно особый опыт.
Погрузитесь глубже в мир гармоник с Arturia’s Pigments 3:
Попробуйте Pigments 3 бесплатно
22 мая 2021 г.
Что такое гармоники? — Бет Роарс
В своем блоге «Что происходит, когда мы издаем звук» я заявляю: «Когда мы издаем звук, воздушный поток проходит между двумя сросшимися голосовыми связками. Эти складки мягкие и приходят в вибрацию от проходящего воздушного потока, вспомните, когда вы в детстве дули на траву. Они очень быстро вибрируют от 100 до 3000 раз в секунду, в зависимости от высоты издаваемого нами звука.
Сколько раз в секунду вибрируют голосовые связки в зависимости от того, какая высота поется, т.е. 100 раз в секунду — это 100 Гц». но это не вся история.
Голосовые связки и, следовательно, воздух вибрируют сразу на нескольких частотах. Эти более быстрые вибрации называются гармониками или обертонами и вместе с формантами являются частью того, что определяет ваш тон. Возможно, вы уже сталкивались с идеей обертонного пения у таких людей, как Ави Каплан из Pentatonix, в котором флажолет усиливается, чтобы создать эффект одновременного пения двух нот. Послушайте фантастический пример обертонного пения ниже.
Все в природе имеет гармоники и вибрирует сразу на нескольких нотах. Единственный способ воспроизвести звук без гармоник — это использовать камертон или электронный синтезатор.
ЧТО МЫ ПОНИМАЕМ ПОД ФУНДАМЕНТАЛЬНЫМ ЗВУКОМ? Говоря о гармониках, вы часто будете слышать термин «основной тон». Это означает изначальную, самую низкую и самую сильную вибрацию.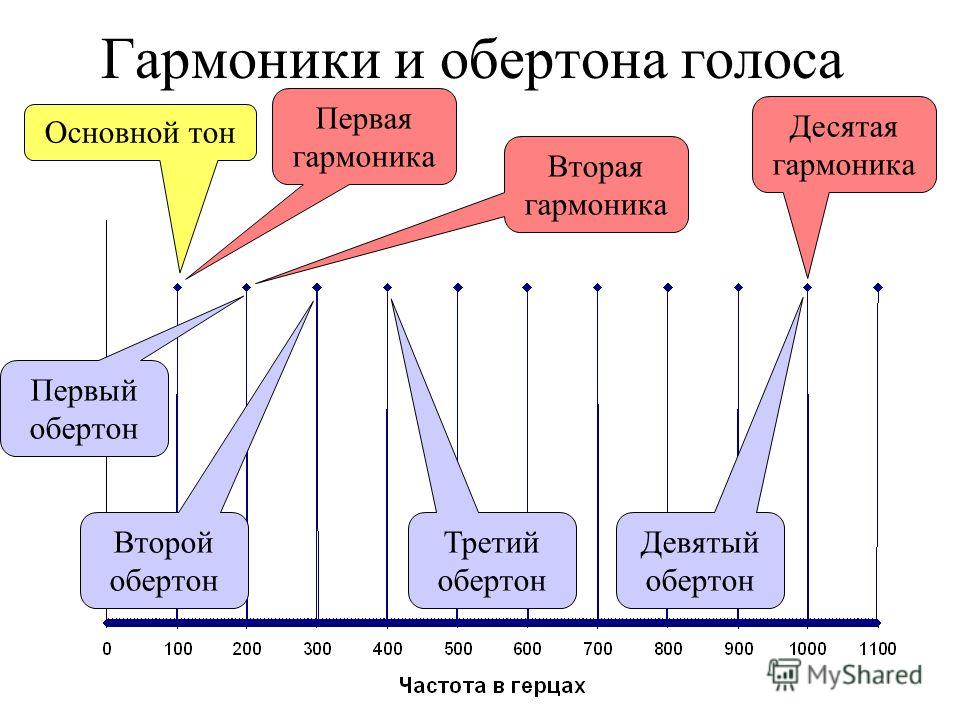
Это то, что мы называем высотой, которую мы поем.
Возможно, вы сталкивались с термином форманты и задавались вопросом, чем они отличаются от гармоник. Гармоники исходят от голосовых связок, а форманты формируются в голосовом тракте. Поэтому вы изменяете гармоники, изменяя форму голосовых связок, и форманты, изменяя форму голосового тракта.
ГАРМОНИЧЕСКАЯ СЕРИЯЕсли первоначальная вибрация (основной тон) и голосовые связки вибрируют периодически, то более высокие вибрации будут иметь предсказуемую частоту.
Если бы основной тон был 100 Гц, голосовые связки создавали бы все гармоники ниже, как показано на нотоносце.
Основная высота тона : C2 или 65 Гц.
Вторая гармоника : на октаву выше основного тона. Он вибрирует в два раза быстрее основного тона. C3 или 130 Гц.
Третья гармоника: На октаву и квинту выше основного тона.
