пилообразный сигнал — это… Что такое пилообразный сигнал?

Если сигнал периодический с частотой следования f, то частоты, составляющие этот сигнал, кратны f, то есть f, 2f, 3f, 4f и т.д.

что такое гармоника сигнала???

Эти частоты называются гармониками. Первая гармоника есть f, вторая гармоника — 2f, третья гармоника — 3f, и так далее. Первую гармонику, f, часто называют основной частотой (fundamental frequency).

 

 

РИСУНОК 11-7

Пример гармоник. Ассиметричное искажение, показанное в (с), вызывают четные и нечетные гармоники (d), Симметричные искажения, показанные в (е), приводят только к четным гармоникам (f).

 

На рисунке 11-7 показан пример гармоник. Рисунок (а) чистая синусоида, (b) – ее ДПФ, одиночный пик. В (с) синусоида искажена в верхней части. В (d) показан результат этого искажения в частотной области. Так как искаженный сигнал периодический с той же самой частотой, как и исходный, частотная область состоит из того же пика плюс гармоники. Гармоники могут быть любой амплитуды, однако они обычно становятся меньше с увеличением их частоты. Как и для любого сигнала,

резкие края приводят к высоким частотам. Например, рассмотрим обычный генератор квадратных волн частотой 1 кГц на элементах ТТЛ логики. Резкий подъем за несколько наносекунд даст гармоники около 100 МГц, десять тысяч гармоник!

Рисунок (е) демонстрирует тонкий гармонический анализ. Если сигнал симметричен относительно горизонтальной оси, то есть верхние лепестки есть зеркальное отражение нижних лепестков, то все четные гармоники будут равны нулю. Как показано в (f), сигнал состоит из основной частоты, третьей гармоники, пятой гармоники и т.д.

 

 

РИСУНОК 11-8

Наложение гармоник. Рисунки (а) и (b) показывают искажение синусной волны и ее частотный спектр, соответственно. Гармоник выше, чем 0,5, будут накладываться между 0 и 0,5. Рисунок (с) показывает частотный спектр в логарифмическом масштабе, вскрывая множество пиков наложения с очень маленькой амплитудой.

 

Все непрерывные периодические сигналы могут быть представлены суммой гармоник, как было описано. Дискретные периодические сигналы имеют проблему, которая нарушает это простое отношение. Как вы, возможно, догадались проблема в

наложении. Рисунок 11-8а показывает синусную волну, искаженную в верхней части так же, как был искажен предыдущий сигнал. Этот сигнал выглядит менее регулярным и сглаженным чем в предыдущем примере, поскольку синусная волна имеет много более высокую частоту, что дает всего несколько отсчетов на цикл. Рисунок (b) показывает частотный спектр этого сигнала. Как и ожидается, вы можете определить основную частоту и гармоники. Этот пример показывает, что гармоники могут простираться до частот много больше, чем 0,5 частоты дискретизации, и накладываться между 0 и 0,5. Вы не заметите их в (b) потому, что амплитуды их слишком малы. Рисунок (с) показывает частотный спектр в логарифмическом масштабе, демонстрируя наложение этих малых пиков. На первый взгляд этот спектр выглядит похожим на случайный шум. Но это не так, это результат перекрытия многих гармоник при их наложении.

Важно понимать, что этот пример предполагает искажение сигнала после того, как он был представлен в цифровом виде. Если это искажение происходит с аналоговым сигналом, вы можете удалить ненужные гармоники антиэлайзинговым фильтром перед оцифровкой.

Гармоники наложения являются проблемой только тогда, когда нелинейные операции выполняются непосредственно над дискретным сигналом. Даже в этом случае амплитуда этих гармоник наложения достаточно мала, и их можно игнорировать.

Концепция гармоник так же полезна по другой причине: она объясняет, почему ДПФ рассматривает временную и частотную области как периодические. В частотной области N-точечное ДПФ состоит из N/2+1 равномерно расположенных частот. Вы можете рассматривать частоты между этими отсчетами как (1) имеющими нулевую величину или (2) не существующими. В любом случае они не вносят вклад в синтез сигнала временной области. Другими словами, дискретный частотный спектр состоит из гармоник, а не из непрерывного уровня частот. Это требует, что бы сигнал временной области был периодический с частотой равной самой низкой частоте из синусоид в частотной области, то есть основной частоте. Пренебрегая величиной постоянного тока (DC), самая низкая частота, представленная в частотной области, делает один полный цикл колебаний каждые N отсчетов, что делает период временной области равной N. Другими словами, если одна область

дискретная, другая должна быть периодической, и наоборот. Это имеет силу для всех четырех членов семейства преобразования Фурье. Поскольку ДПФ рассматривает обе области как дискретные, то их необходимо рассматривать и как периодические.

Отсчеты в каждой области представляют гармоники периода противоположной области.

РадиоКот :: Жучки, передатчики и приемники: основные термины

РадиоКот >Обучалка >Аналоговая техника >Жучки, передатчики и приемники: что о них надо знать >

Жучки, передатчики и приемники: основные термины

 

Итак, для начала – краткий глоссарий по приемопередающей технике.

Передатчик – устройство, передающее сигнал.

Приемник – устройство, принимающее сигнал 🙂

Антенна – элемент электрической схемы, преобразующий принимаемые электромагнитные колебания в электрический сигнал (приемная антенна), или наоборот – электрический сигнал в электромагнитные колебания (передающая антенна). Одна и та же антенна может быть и передающей и принимающей, причем даже одновременно.

Сопротивление антенны – величина, грубо говоря, указывающая насколько «тяжело» энергия уходит с антенны в эфир. Знать это сопротивление необходимо для правильного расчета излучаемой мощности: чем выше сопротивление антенны – тем больше должно быть напряжение подаваемого на нее сигнала для получения одной и той же мощности.

В приемных антеннах знание сопротивления необходимо для правильного расчета входного каскада приемника.

Фидер – линия, по которой передается высокочастотная энергия. Чаще всего в качестве фидера юзается коаксиальный кабель.

Волновое сопротивление – величина, определяемая соотношением погонной емкости и погонной индуктивности кабеля. Зависит от типа кабеля – обычно указывается в названии. Стандартные значения ВС: 50 Ом, 75 Ом, 300 Ом. Его необходимо знать для правильного согласования устройств, соединенных этим кабелем (например – передатчика и антенны).

Выходное сопротивление – величина сопротивления, которое нужно подключить к выходу устройства для получения номинальной мощности.

Входное сопротивление – сопротивление, которым обладает вход устройства.

Согласование устройств

– выравнивание входного/выходного сопротивлений двух соединяемых устройств. Для эффективной передачи энергии между двумя устройствами, необходимо чтоб выходное сопротивление передающего устройства было равно входному сопротивлению принимающего.

Резонансная частота антенны – частота, на которой антенна обладает наименьшим сопротивлением.

Широкополосность / узкополосность антенны – термин, говорящий о том, как антенна относится к частотам, которые больше и меньше резонансной. То есть, насколько резко уменьшается ее эффективность при уходе от резонансной частоты в ту или другую сторону. То есть, какова ее полоса пропускания.

Диаграмма направленности антенны – кривая, показывающая пространственное распределение излучаемой мощности / чувствительности антенны для различных углов относительно основной оси. Обычно используют круговые диаграммы, которые выглядят примерно так, как показано на рисунке. Кривая при этом получается в виде «лепестков». Поэтому часто можно услышать термин «лепесток направленности»

Чувствительность приемника – величина, характеризующая способность принимать слабые электрические сигналы. Чем меньше напряжение сигнала, который еще может принять приемник, тем лучше чувствительность. Выражается в микровольтах (мкВ) – если входной сигнал – электрический, или микровольтах на метр (мкВ/м) – если входной сигнал – электромагнитные колебания (при этом измеряется не напряжение а напряженность электромагнитного поля).

Модуляция – это, надеюсь, понятно – метод запаковки информативного низкочастотного модулирующего сигнала (например — звука) в высокочастотную несущую (сигнал, передаваемый в эфир). Модуляция бывает амплитудная (АМ), частотная (ЧМ или FM ), фазовая, широтно-импульсная или какая-то другая. Нас интересуют первые две. При амплитудной модуляции низкочастотный сигнал управляет амплитудой несущей, при частотной – частотой (в небольших пределах).

Девиация – порог отклонения частоты несущей от состояния покоя при частотной модуляции. Состояние покоя – это когда модулирующий (низкочастотный) сигнал равен 0.

Гармоники – частотные составляющие сигнала, кратные его основной частоте. Обычно, гармоники бывают выше основной частоты. Во сколько раз гармоника больше основной частоты – такой ее номер. То есть, если она в три раза больше – то ее зовут «3-я гармоника», если в пять раз – «5-я гармоника» и т.д. Гармоники возникают в результате нелинейных искажений сигнала, их можно выделить из сигнала при помощи полосовых частотных фильтров или колебательных контуров.

Гармоники широко применяют в радиотехнике, как в передатчиках, так и в приемниках.

В передатчиках их используют для получения больших частот из маленьких. Например, есть кварц на 20,57 МГц, а нам надо получить сигнал со стабильной частотой 144 МГц. Что мы делаем? Мы делаем генератор на 20,57 МГц, затем выделяем 7-ю гармонику его сигнала и усиливаем ее. Вот вам и 144МГц!

На основе гармоник также строятся гетеродинные приемники.

Однако, гармоники бывают и вредны. Например, нельзя передавать в эфир сигнал, содержащий много гармоник, потому что гармоники будут забивать кратные частоты и могут помешать работе других радиостанций.

Линейные искажения – искажения сигнала, которые позволяют впоследствии восстановить исходный сигнал из искаженного. К ним относится регулировка амплитуды (мощности), частотного спектра, фазового угла и т.п.

Нелинейные искажения – искажения сигнала, после которых невозможно восстановить исходный сигнал. К ним относятся, например, перемодуляция – искажение, возникающее при избыточной амплитуде сигнала: у сигнала «срезаются верхушки».

Колебательный контур – схема, состоящая из параллельно или последовательно включенных конденсатора и катушки индуктивности. При ударном возбуждении, в КК возникают затухающие синусоидальные (гармонические) колебания некоторой частоты, которая называется «резонансная частота», определяется емкостью конденсатора и индуктивностью катушки и рассчитывается по формуле:

Подробнее про КК читаем в обучалке по аналоговой технике, в статье «Как заколебать ток»

КК используется в генераторе передатчика для получения требуемой частоты, в приемнике – для выделения из принятого радиосигнала определенной частоты.

Частотный фильтр – схема, которая позволяет ослабить или усилить определенный диапазон частот.

—Поехали дальше—>>

---

Как вам эта статья?	Заработало ли это устройство у вас?

Практическое применение преобразования Фурье для анализа сигналов. Введение для начинающих

1. Преобразование Фурье и спектр сигнала

Во многих случаях задача получения (вычисления) спектра сигнала выглядит следующим образом. Имеется АЦП, который с частотой дискретизации Fd преобразует непрерывный сигнал, поступающий на его вход в течение времени Т, в цифровые отсчеты — N штук. Далее массив отсчетов подается в некую программку, которая выдает N/2 каких-то числовых значений (программист, который утянул из инета написал программку, уверяет, что она делает преобразование Фурье).

Чтобы проверить, правильно ли работает программа, сформируем массив отсчетов как сумму двух синусоид sin(10*2*pi*x)+0,5*sin(5*2*pi*x) и подсунем программке. Программа нарисовала следующее:

рис.1 График временной функции сигнала

рис.2 График спектра сигнала

На графике спектра имеется две палки (гармоники) 5 Гц с амплитудой 0.5 В и 10 Гц — с амплитудой 1 В, все как в формуле исходного сигнала. Все отлично, программист молодец! Программа работает правильно.

Это значит, что если мы подадим на вход АЦП реальный сигнал из смеси двух синусоид, то мы получим аналогичный спектр, состоящий из двух гармоник.

Итого, наш реальный измеренный сигнал, длительностью 5 сек, оцифрованный АЦП, то есть представленный дискретными отсчетами, имеет дискретный непериодический спектр.

С математической точки зрения — сколько ошибок в этой фразе?

Теперь начальство решило мы решили, что 5 секунд — это слишком долго, давай измерять сигнал за 0.5 сек.


рис.3 График функции sin(10*2*pi*x)+0,5*sin(5*2*pi*x) на периоде измерения 0.5 сек

рис.4 Спектр функции

Что-то как бы не то! Гармоника 10 Гц рисуется нормально, а вместо палки на 5 Гц появилось несколько каких-то непонятных гармоник. Смотрим в интернетах, что да как…

Во, говорят, что в конец выборки надо добавить нули и спектр будет рисоваться нормальный.

рис.5 Добили нулей до 5 сек

рис.6 Получили спектр

Все равно не то, что было на 5 секундах. Придется разбираться с теорией. Идем в Википедию — источник знаний.

2. Непрерывная функция и представление её рядом Фурье

Математически наш сигнал длительностью T секунд является некоторой функцией f(x), заданной на отрезке {0, T} (X в данном случае — время). Такую функцию всегда можно представить в виде суммы гармонических функций (синусоид или косинусоид) вида:

(1), где:

k — номер тригонометрической функции ( номер гармонической составляющей, номер гармоники)
T — отрезок, где функция определена (длительность сигнала)
Ak — амплитуда k-ой гармонической составляющей,
θk- начальная фаза k-ой гармонической составляющей

Что значит «представить функцию в виде суммы ряда»? Это значит, что, сложив в каждой точке значения гармонических составляющих ряда Фурье, мы получим значение нашей функции в этой точке.

(Более строго, среднеквадратичное отклонение ряда от функции f(x) будет стремиться к нулю, но несмотря на среднеквадратичную сходимость, ряд Фурье функции, вообще говоря, не обязан сходиться к ней поточечно. См. https://ru.wikipedia.org/wiki/Ряд_Фурье.)

Этот ряд может быть также записан в виде:

(2),
где , k-я комплексная амплитуда.

или

(3)

Связь между коэффициентами (1) и (3) выражается следующими формулами:

и

Отметим, что все эти три представления ряда Фурье совершенно равнозначны. Иногда при работе с рядами Фурье бывает удобнее использовать вместо синусов и косинусов экспоненты мнимого аргумента, то есть использовать преобразование Фурье в комплексной форме. Но нам удобно использовать формулу (1), где ряд Фурье представлен в виде суммы косинусоид с соответствующими амплитудами и фазами. В любом случае неправильно говорить, что результатом преобразования Фурье действительного сигнала будут комплексные амплитуды гармоник. Как правильно говорится в Вики «Преобразование Фурье (ℱ) — операция, сопоставляющая одной функции вещественной переменной другую функцию, также вещественной переменной.»

Итого:
Математической основой спектрального анализа сигналов является преобразование Фурье.

Преобразование Фурье позволяет представить непрерывную функцию f(x) (сигнал), определенную на отрезке {0, T} в виде суммы бесконечного числа (бесконечного ряда) тригонометрических функций (синусоид и\или косинусоид) с определёнными амплитудами и фазами, также рассматриваемых на отрезке {0, T}. Такой ряд называется рядом Фурье.

Отметим еще некоторые моменты, понимание которых требуется для правильного применения преобразования Фурье к анализу сигналов. Если рассмотреть ряд Фурье (сумму синусоид) на всей оси Х, то можно увидеть, что вне отрезка {0, T} функция представленная рядом Фурье будет будет периодически повторять нашу функцию.

Например, на графике рис.7 исходная функция определена на отрезке {-T\2, +T\2}, а ряд Фурье представляет периодическую функцию, определенную на всей оси х.

Это происходит потому, что синусоиды сами являются периодическими функциями, соответственно и их сумма будет периодической функцией.

рис.7 Представление непериодической исходной функции рядом Фурье

Таким образом:

Наша исходная функция — непрерывная, непериодическая, определена на некотором отрезке длиной T.
Спектр этой функции — дискретный, то есть представлен в виде бесконечного ряда гармонических составляющих — ряда Фурье.
По факту, рядом Фурье определяется некоторая периодическая функция, совпадающая с нашей на отрезке {0, T}, но для нас эта периодичность не существенна.

Далее.

Периоды гармонических составляющих кратны величине отрезка {0, T}, на котором определена исходная функция f(x). Другими словами, периоды гармоник кратны длительности измерения сигнала. Например, период первой гармоники ряда Фурье равен интервалу Т, на котором определена функция f(x). Период второй гармоники ряда Фурье равен интервалу Т/2. И так далее (см. рис. 8).

рис.8 Периоды (частоты) гармонических составляющих ряда Фурье (здесь Т=2π)

Соответственно, частоты гармонических составляющих кратны величине 1/Т. То есть частоты гармонических составляющих Fk равны Fk= к\Т, где к пробегает значения от 0 до ∞, например к=0 F0=0; к=1 F1=1\T; к=2 F2=2\T; к=3 F3=3\T;… Fk= к\Т (при нулевой частоте — постоянная составляющая).

Пусть наша исходная функция, представляет собой сигнал, записанный в течение Т=1 сек. Тогда период первой гармоники будет равен длительности нашего сигнала Т1=Т=1 сек и частота гармоники равна 1 Гц. Период второй гармоники будет равен длительности сигнала, деленной на 2 (Т2=Т/2=0,5 сек) и частота равна 2 Гц. Для третьей гармоники Т3=Т/3 сек и частота равна 3 Гц. И так далее.

Шаг между гармониками в этом случае равен 1 Гц.

Таким образом сигнал длительностью 1 сек можно разложить на гармонические составляющие (получить спектр) с разрешением по частоте 1 Гц.
Чтобы увеличить разрешение в 2 раза до 0,5 Гц — надо увеличить длительность измерения в 2 раза — до 2 сек. Сигнал длительностью 10 сек можно разложить на гармонические составляющие (получить спектр) с разрешением по частоте 0,1 Гц. Других способов увеличить разрешение по частоте нет.

Существует способ искусственного увеличения длительности сигнала путем добавления нулей к массиву отсчетов. Но реальную разрешающую способность по частоте он не увеличивает.

3. Дискретные сигналы и дискретное преобразование Фурье

С развитием цифровой техники изменились и способы хранения данных измерений (сигналов). Если раньше сигнал мог записываться на магнитофон и храниться на ленте в аналоговом виде, то сейчас сигналы оцифровываются и хранятся в файлах в памяти компьютера в виде набора чисел (отсчетов).

Обычная схема измерения и оцифровки сигнала выглядит следующим образом.

рис.9 Схема измерительного канала

Сигнал с измерительного преобразователя поступает на АЦП в течение периода времени Т. Полученные за время Т отсчеты сигнала (выборка) передаются в компьютер и сохраняются в памяти.

рис.10 Оцифрованный сигнал — N отсчетов полученных за время Т

Какие требования выдвигаются к параметрам оцифровки сигнала? Устройство, преобразующее входной аналоговый сигнал в дискретный код (цифровой сигнал) называется аналого-цифровой преобразователь (АЦП, англ. Analog-to-digital converter, ADC) ( Wiki).

Одним из основных параметров АЦП является максимальная частота дискретизации (или частота семплирования, англ. sample rate) — частота взятия отсчетов непрерывного во времени сигнала при его дискретизации. Измеряется в герцах. (( Wiki))

Согласно теореме Котельникова, если непрерывный сигнал имеет спектр, ограниченный частотой Fмакс, то он может быть полностью и однозначно восстановлен по его дискретным отсчетам, взятым через интервалы времени , т.е. с частотой Fd ≥ 2*Fмакс, где Fd — частота дискретизации; Fмакс — максимальная частота спектра сигнала. Другими слова частота оцифровки сигнала (частота дискретизации АЦП) должна как минимум в 2 раза превышать максимальную частоту сигнала, который мы хотим измерить.

А что будет, если мы будем брать отсчеты с меньшей частотой, чем требуется по теореме Котельникова?

В этом случае возникает эффект «алиасинга» (он же стробоскопический эффект, муаровый эффект), при котором сигнал высокой частоты после оцифровки превращается в сигнал низкой частоты, которого на самом деле не существует. На рис. 11 красная синусоида высокой частоты — это реальный сигнал. Синяя синусоида более низкой частоты — фиктивный сигнал, возникающий вследствие того, за время взятия отсчета успевает пройти больше, чем пол-периода высокочастотного сигнала.

Рис. 11. Появление ложного сигнала низкой частоты при недостаточно высокой частоте дискретизации

Чтобы избежать эффекта алиасинга перед АЦП ставят специальный антиалиасинговый фильтр — ФНЧ (фильтр нижних частот), который пропускает частоты ниже половины частоты дискретизации АЦП, а более высокие частоты зарезает.

Для того, чтобы вычислить спектр сигнала по его дискретным отсчетам используется дискретное преобразование Фурье (ДПФ). Отметим еще раз, что спектр дискретного сигнала «по определению» ограничен частотой Fмакс, меньшей половине частоты дискретизации Fd. Поэтому спектр дискретного сигнала может быть представлен суммой конечного числа гармоник, в отличие от бесконечной суммы для ряда Фурье непрерывного сигнала, спектр которого может быть неограничен. Согласно теореме Котельникова максимальная частота гармоники должна быть такой, чтобы на нее приходилось как минимум два отсчета, поэтому число гармоник равно половине числа отсчетов дискретного сигнала. То есть если в выборке имеется N отсчетов, то число гармоник в спектре будет равно N/2.

Рассмотрим теперь дискретное преобразование Фурье (ДПФ).

Сравнивая с рядом Фурье

видим, что они совпадают, за исключением того, что время в ДПФ имеет дискретный характер и число гармоник ограничено величиной N/2 — половиной числа отсчетов.

Формулы ДПФ записываются в безразмерных целых переменных k, s, где k – номера отсчетов сигнала, s – номера спектральных составляющих.
Величина s показывает количество полных колебаний гармоники на периоде Т (длительности измерения сигнала). Дискретное преобразование Фурье используется для нахождения амплитуд и фаз гармоник численным методом, т.е. «на компьютере»

Возвращаясь к результатам, полученным в начале. Как уже было сказано выше, при разложении в ряд Фурье непериодической функции (нашего сигнала), полученный ряд Фурье фактически соответствует периодической функции с периодом Т. (рис.12).

рис.12 Периодическая функция f(x) с периодом Т0, с периодом измерения Т>T0

Как видно на рис.12 функция f(x) периодическая с периодом Т0. Однако из-за того, что длительность измерительной выборки Т не совпадает с периодом функции Т0, функция, получаемая как ряд Фурье, имеет разрыв в точке Т. В результате спектр данной функции будет содержать большое количество высокочастотных гармоник. Если бы длительность измерительной выборки Т совпадала с периодом функции Т0, то в полученном после преобразования Фурье спектре присутствовала бы только первая гармоника (синусоида с периодом равным длительности выборки), поскольку функция f(x) представляет собой синусоиду.

Другими словами, программа ДПФ «не знает», что наш сигнал представляет собой «кусок синусоиды», а пытается представить в виде ряда периодическую функцию, которая имеет разрыв из-за нестыковки отдельных кусков синусоиды.

В результате в спектре появляются гармоники, которые должны в сумме изобразить форму функции, включая этот разрыв.

Таким образом, чтобы получить «правильный» спектр сигнала, являющегося суммой нескольких синусоид с разными периодами, необходимо чтобы на периоде измерения сигнала укладывалось целое число периодов каждой синусоиды. На практике это условие можно выполнить при достаточно большой длительности измерения сигнала.

Рис.13 Пример функции и спектра сигнала кинематической погрешности редуктора

При меньшей длительности картина будет выглядеть «хуже»:

Рис.14 Пример функции и спектра сигнала вибрации ротора

На практике бывает сложно понять, где «реальные составляющие», а где «артефакты», вызванные некратностью периодов составляющих и длительности выборки сигнала или «скачками и разрывами» формы сигнала. Конечно слова «реальные составляющие» и «артефакты» не зря взяты в кавычки. Наличие на графике спектра множества гармоник не означает, что наш сигнал в реальности из них «состоит». Это все равно что считать, будто число 7 «состоит» из чисел 3 и 4. Число 7 можно представить в виде суммы чисел 3 и 4 — это правильно.

Так и наш сигнал… а вернее даже не «наш сигнал», а периодическую функцию, составленную путем повторения нашего сигнала (выборки) можно представить в виде суммы гармоник (синусоид) с определенными амплитудами и фазами. Но во многих важных для практики случаях (см. рисунки выше) действительно можно связать полученные в спектре гармоники и с реальными процессами, имеющими циклический характер и вносящими значительный вклад в форму сигнала.

Некоторые итоги

1. Реальный измеренный сигнал, длительностью T сек, оцифрованный АЦП, то есть представленный набором дискретных отсчетов (N штук), имеет дискретный непериодический спектр, представленный набором гармоник (N/2 штук).

2. Сигнал представлен набором действительных значений и его спектр представлен набором действительных значений. Частоты гармоник положительны. То, что математикам бывает удобнее представить спектр в комплексной форме с использованием отрицательных частот не значит, что «так правильно» и «так всегда надо делать».

3. Сигнал, измеренный на отрезке времени Т определен только на отрезке времени Т. Что было до того, как мы начали измерять сигнал, и что будет после того — науке это неизвестно. И в нашем случае — неинтересно. ДПФ ограниченного во времени сигнала дает его «настоящий» спектр, в том смысле, что при определенных условиях позволяет вычислить амплитуду и частоту его составляющих.

Использованные материалы и другие полезные материалы.

FourierScope — программа для построения радио сигналов и их спектрального анализа.
Graph — программа с открытым кодом, предназначенная для построения математических графиков.
ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ – КАК ЭТО ДЕЛАЕТСЯ
Дискретное преобразование Фурье (ДПФ)

Амплитудно-частотная характеристика (АЧХ). Спектр сигнала.

При обсуждении переменного тока в одной из предыдущих статей (ссылка) мы познакомились с понятием гармонической (синусоидальной) функции. А бывают ли негармонические функции и сигналы и как с ними работать? В этом нам и предстоит сегодня разобраться 🙂 Кроме того, мы рассмотрим важнейшее понятие – амплитудно-частотную характеристику (АЧХ) сигналов.

Гармонические и негармонические сигналы.

И для начала давайте чуть подробнее разберемся, как же классифицируются сигналы. В первую очередь нас интересуют гармонические сигналы. Их форма повторяется через определенный интервал времени T, называемый периодом. Периодические сигналы в свою очередь делятся на два больших класса – гармонические и негармонические. Гармонический сигнал – это сигнал, который можно описать следующей функцией:

y = A cos(wt + \phi)

Здесь A – амплитуда сигнала, w – циклическая частота, а \phi – начальная фаза. Вы спросите – а как же синус? Разве синусоидальный сигнал не является гармоническим? Конечно, является, дело в том, что sin\alpha = cos(\frac{\pi}{2}\medspace-\medspace \alpha) – то есть сигналы отличаются начальной фазой, соответственно, синусоидальный сигнал не противоречит определению, которое мы дали для гармонических колебаний 🙂

Вторым подклассом периодических сигналов являются негармонические колебания. Вот пример негармонического сигнала:

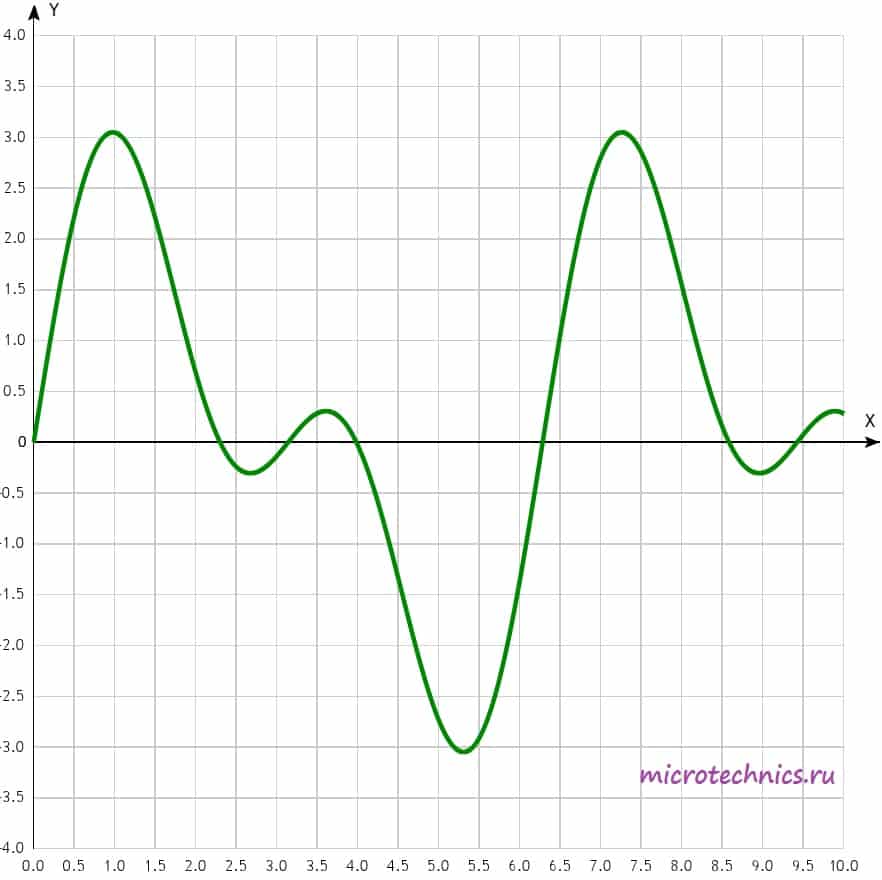
Как видите, несмотря на “нестандартную” форму, сигнал остается периодическим, то есть его форма повторяется через интервал времени, равный периоду.

Для работы с такими сигналами и их исследования существует определенная методика, которая заключается в разложении сигнала в ряд Фурье. Суть методики состоит в том, что негармонический периодический сигнал (при выполнении определенных условий) можно представить в виде суммы гармонических колебаний с определенными амплитудами, частотами и начальными фазами. Важным нюансом является то, что все гармонические колебания, которые участвуют в суммировании, должны иметь частоты, кратные частоте исходного негармонического сигнала. Возможно это пока не совсем понятно, так что давайте рассмотрим практический пример и разберемся чуть подробнее 🙂 Для примера используем сигнал, который изображен на рисунке чуть выше. Его можно представить следующим образом:

u(t) = u_1(t) + u_2(t) = 2 sin(t) + 1.5 sin(2t)

Давайте изобразим все эти сигналы на одном графике:

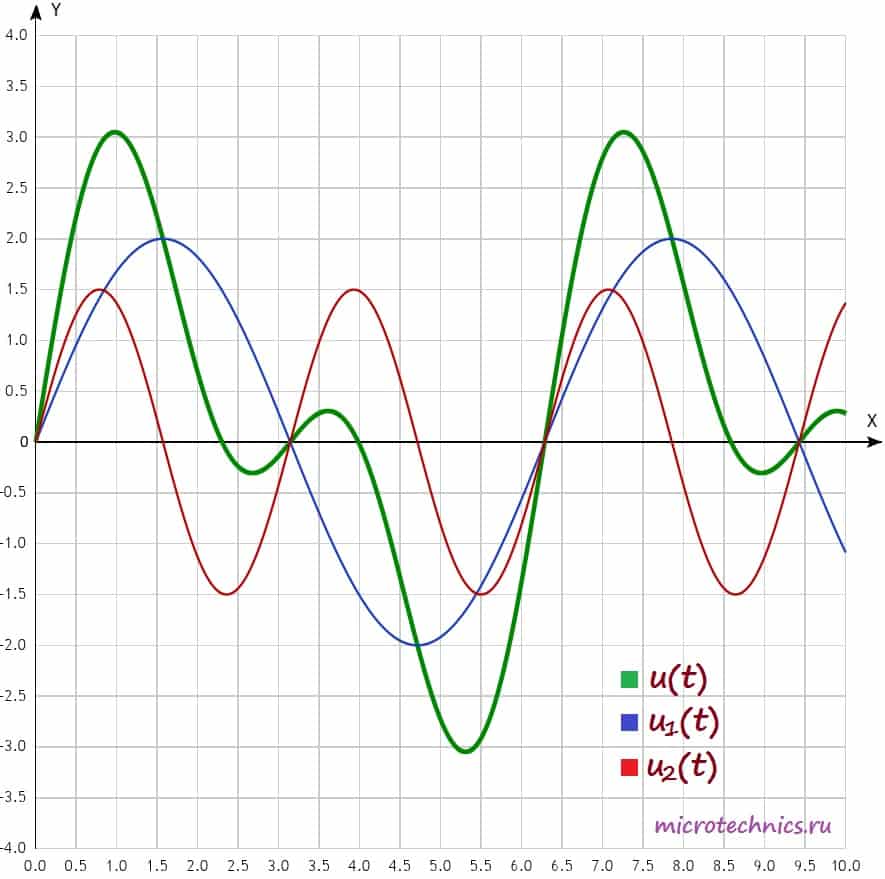
Функции u_1(t), u_2(t) называют гармониками сигнала, а ту из них, период которой равен периоду негармонического сигнала, называют первой или основной гармоникой. В данном случае первой гармоникой является функция u_1(t) (ее частота равна частоте исследуемого негармонического сигнала, соответственно, равны и их периоды). А функция u_2(t) = 1.5 sin(2t) представляет из себя ни что иное как вторую гармонику сигнала (ее частота в два раза больше). В общем случае, негармонический сигнал раскладывается на бесконечное число гармоник:

u(t) = U_0 + \sum_{i=0}^{\infty}{U_{k}\thinspace sin(\thinspace kwt + \phi_k\thinspace )}

В этой формуле U_k – амплитуда, а \phi_k – начальная фаза k-ой гармоники. Как мы уже упомянули чуть ранее, частоты всех гармоник кратны частоте первой гармоники, собственно, это мы и видим в этой формуле 🙂 U_0 – это нулевая гармоника, ее частота равна 0, она равна среднему значению функции за период. Почему среднему? Смотрите – среднее значения функции синуса за период равно 0, а значит при усреднении в этой формуле все слагаемые, кроме U_0 будут равны 0.

Амплитудный спектр сигнала.

Совокупность всех гармонических составляющих негармонического сигнала называют спектром этого сигнала. Различают фазовый и амплитудный спектр сигнала:

• фазовый спектр сигнала – совокупность начальных фаз всех гармоник
• амплитудный спектр сигнала – амплитуды всех гармоник, из которых складывается негармонический сигнал

Давайте рассмотрим амплитудный спектр поподробнее. Для визуального изображения спектра используют диаграммы, представляющие из себя набор вертикальных линий определенной длины (длина зависит от амплитуды сигналов). На горизонтальной оси диаграммы откладываются частоты гармоник:

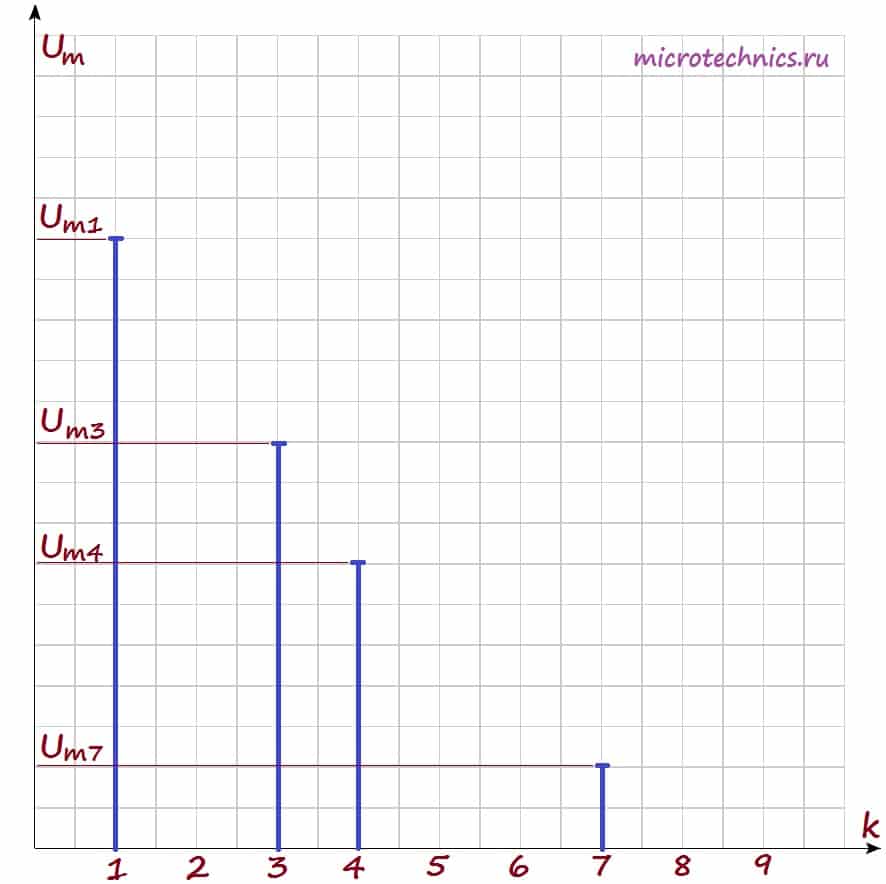
По горизонтальной оси могут откладываться как частоты в Гц, так и просто номера гармоник, как в данном случае. А по вертикальной оси – амплитуды гармоник, тут все понятно. Давайте построим амплитудный спектр сигнала для негармонического колебания, которое мы рассматривали в качестве примера в самом начале статьи. Напоминаю, что его разложение в ряд Фурье выглядит следующим образом:

u(t) = u_1(t) + u_2(t) = 2 sin(t) + 1.5 sin(2t)

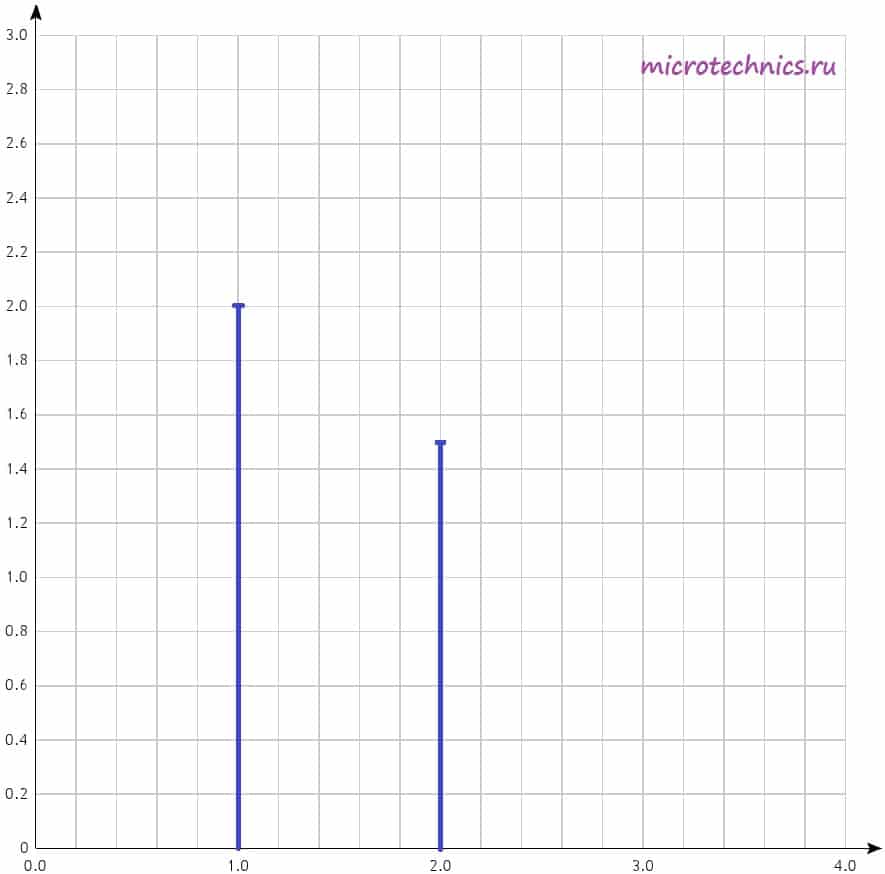
У нас есть две гармоники, амплитуды которых равны, соответственно, 2 и 1.5. Поэтому на диаграмме две линии, длины которых соответствуют амплитудам гармонических колебаний. Фазовый спектр сигнала строится аналогично, за той лишь разницей, что используются начальные фазы гармоник, а не амплитуды.

Итак, с построением и анализом амплитудного спектра сигнала мы разобрались! Давайте перейдем к следующей теме сегодняшней статьи – к понятию амплитудно-частотной характеристики.

Амплитудно-частотная характеристика (АЧХ).

АЧХ является важнейшей характеристикой многих цепей и устройств – фильтров, усилителей звука и т. д. Даже простые наушники имеют свою собственную амплитудно-частотную характеристику. Что же она показывает?

АЧХ – это зависимость амплитуды выходного сигнала от частоты входного сигнала. Как мы выяснили в первой части статьи, негармонический периодический сигнал можно разложить в ряд Фурье. Но нас сейчас интересует, в первую очередь, аудио-сигнал, и выглядит он следующим образом:

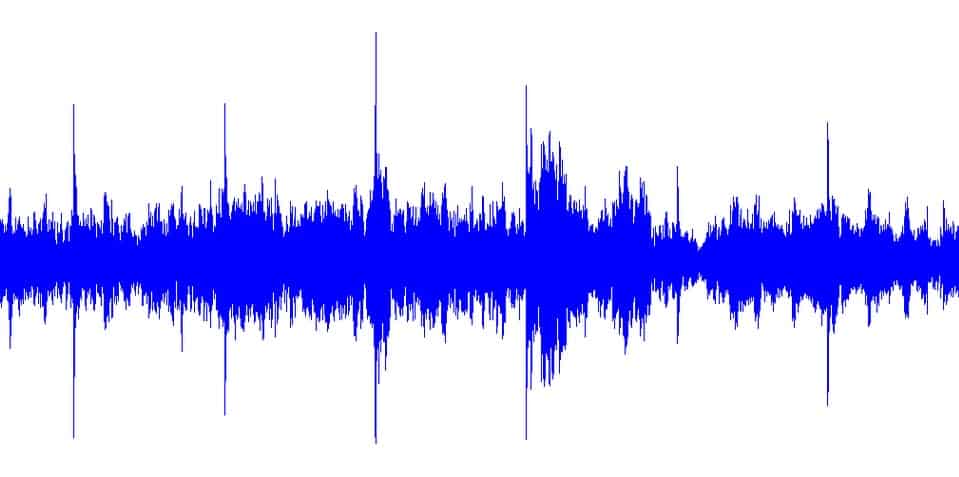
Как видите, ни о какой периодичности здесь не идет и речи! Но, к счастью, существуют специальные алгоритмы, которые позволяют представить звуковой сигнал в виде спектра входящих в него частот. Мы сейчас не будем подробно разбирать эти алгоритмы, это тема для отдельной статьи 🙂 Просто примем тот факт, что они позволяют нам осуществить такое преобразование с аудио-сигналом.

Соответственно, мы можем построить диаграмму амплитудного спектра звукового сигнала. А пройдя через какую-либо цепь (к примеру, через наушники при воспроизведении звука) сигнал будет изменен. Так вот амплитудно-частотная характеристика как раз и показывает, какие изменения будет претерпевать входной сигнал при прохождении через ту или иную цепь. Давайте обсудим этот момент чуть поподробнее…

Итак, на входе мы имеем ряд гармоник. Амплитудная-частотная характеристика показывает, как изменится амплитуда той или иной гармоники при прохождении через цепь. Рассмотрим пример АЧХ:

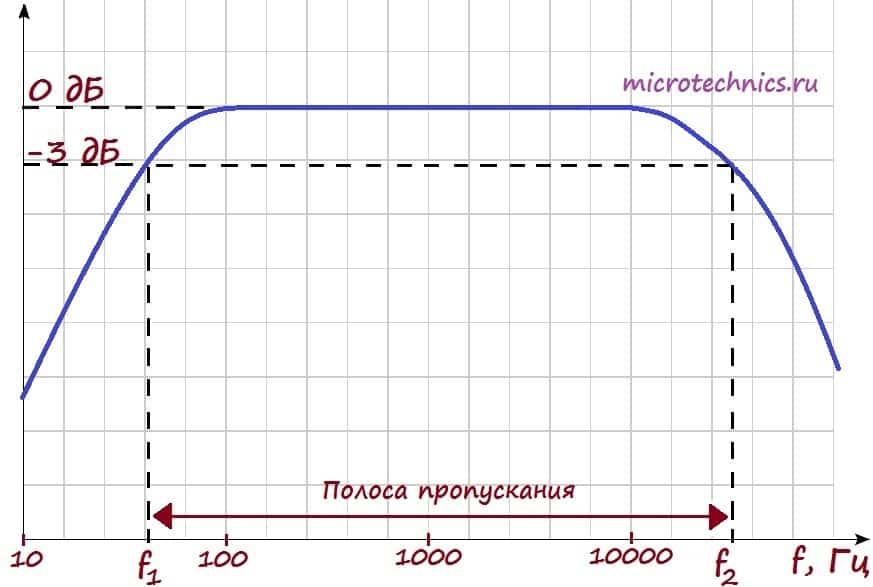
Разберемся поэтапно, что же тут изображено… Начнем с осей графика АЧХ. По оси y мы откладываем величину выходного напряжения (или коэффициента усиления, как на данном рисунке). Коэффициент усиления мы откладываем в дБ, соответственно величина, равная 0 дБ, соответствует усилению в 1 раз, то есть амплитуда сигнала остается неизменной.

По оси x откладываются частоты входного сигнала. Таким образом, в рассматриваемом случае для всех гармоник, частоты которых лежат в интервале от 100 до 10000 Гц, амплитуда не изменится. А сигналы всех остальных гармоник будут ослаблены.

На графике отдельно отмечены частоты f_1 и f_2. Их отличительной особенностью является то, что сигнал гармоник данных частот будет ослаблен в 1.41 раза (3 дБ) по напряжению. Это соответствует уменьшению по мощности в 2 раза . Полосу частот между f_1 и f_2 называют полосой пропускания. Получается следующая ситуация – сигналы всех гармоник, частоты которых лежат в пределах полосы пропускания устройства/цепи будут ослаблены менее, чем в 2 раза по мощности.

Практические примеры АЧХ аудио-устройств.

Частотный диапазон аудио-устройств обычно разбивают на низкие, средние и высокие частоты. Приблизительно это выглядит так:

• 20 Гц – 160 Гц – область низких частот
• 160 Гц – 1.28 КГц – область средних частот
• 1.28 КГц – 20.5 КГц – область высоких частот

Именно такую терминологию обычно можно встретить в разных программах-эквалайзерах, используемых для настройки звука. Теперь вы знаете, что красивые графики из таких программ являются именно амплитудно-частотными характеристиками, с которыми мы познакомились в сегодняшней статье 🙂

В завершении статьи посмотрим на пару АЧХ, полученных в программном эквалайзере:

Здесь мы можем видеть амплитудно-частотную характеристику усилителя. Причем усилены будут преимущественно средние частоты диапазона.

А здесь ситуация совсем другая – низкие и верхние частоты усиливаются, а в области средних частот для гармоник с частотой 500 Гц мы наблюдаем значительное ослабление.

А здесь усиливаются только низкие частоты. Аудио-аппаратура с такой АЧХ будет обладать высоким уровнем басов 🙂

На этом мы заканчиваем нашу сегодняшнюю статью… Спасибо за внимание и ждем вас на нашем сайте снова!

Теория радиоволн: аналоговая модуляция / Хабр

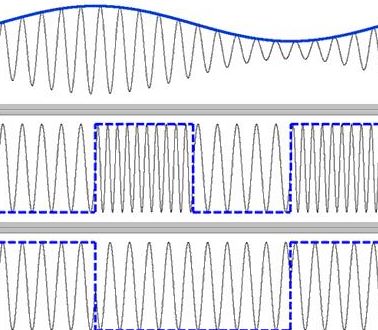
Продолжаем серию общеобразовательных статей, под общим названием «Теория радиоволн».
В предыдущих статьях мы познакомились с радиоволнами и антеннами:

Давайте ближе познакомимся с модуляцией радиосигнала.

В рамках этой статьи, будет рассмотрена аналоговая модуляция следующих видов:

• Амплитудная модуляция
• Амплитудная модуляция c одной боковой полосой
• Частотная модуляция
• Линейно-частотная модуляция
• Фазовая модуляция
• Дифференциально-фазовая модуляция

Амплитудная модуляция

При амплитудной модуляции, огибающая амплитуд несущего колебания изменяется по закону, совпадающему с законом передаваемого сообщения. Частота и фаза несущего колебания при этом не меняется.

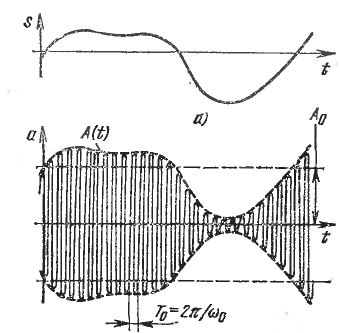
Одним из основных параметров АМ, является коэфициент модуляции(M).
Коэффициент модуляции — это отношение разности между максимальным и минимальным значениями амплитуд модулированного сигнала к сумме этих значений(%).
Проще говоря, этот коэффициент показывает, насколько сильно значение амплитуда несущего колебания в данный момент отклоняется от среднего значения.
При коэффициенте модуляции больше 1, возникает эффект перемодуляции, в результате чего происходит искажение сигнала.

Спектр АМ

Данный спектр свойственен для модулирующего колебания постоянной частоты.

На графике, по оси Х представлена частота, по оси У — амплитуда.
Для АМ, кроме амплитуды основной частоты, находящейся в центре, представлены также значения амплитуд справа и слева от частоты несущей. Это так называемые левая и правая боковые полосы. Они отнесены от частоты несущей на расстояние равное частоте модуляции.
Расстояние от левой до правой боковой полосы называют ширина спектра.
В нормальном случае, при коэффициенте модуляции <=1, амплитуды боковых полос меньше или равны половине амплитуды несущей.
Полезная информация заключена только в верхней или нижней боковых полосах спектра. Основная спектральная составляющая — несущая, не несет полезной информации. Мощность передатчика при амплитудной модуляции в большей части расходуется на «обогрев воздуха», за счет не информативности самого основного элемента спектра.

Амплитудная модуляция с одной боковой полосой

В связи с неэффективностью классической амплитудной модуляции, была придумана амплитудная модуляция с одной боковой полосой.
Суть ее заключается в удалении из спектра несущей и одной из боковых полос, при этом вся необходимая информация передается по оставшейся боковой полосе.

Но в чистом виде в бытовом радиовещании этот вид не прижился, т.к. в приемнике нужно синтезировать несущую с очень высокой точностью. Используется в аппаратуре уплотнения и любительском радио.
В радиовещании чаще используют АМ с одной боковой полосой и частично подавленной несущей:

При такой модуляции соотношение качество/эффективность наилучшим образом достигается.

Частотная модуляция

Вид аналоговой модуляции, при которой, частота несущей изменяется по закону модулирующего низкочастотного сигнала. Амплитуда при этом остается постоянной.

а) — несущая частота, б) модулирующий сигнал, в) результат модуляции

Наибольшее отклонение частоты от среднего значения, называется девиацией.
В идеальном варианте, девиация должна быть прямо пропорционально амплитуде модулирующего колебания.

Спектр при частотной модуляции выглядит следующим образом:

Состоит из несущей и симметрично отстающей от нее вправо и влево гармоник боковых полос, на частоту кратную частоте модулирующего колебания.
Данный спектр представляет гармоническое колебание. В случае реальной модуляции, спектр имеет более сложные очертания.
Различают широкополосную и узкополосную ЧМ модуляцию.
В широкополосной — спектр частот, значительно превосходит частоту модулирующего сигнала. Применяется в ЧМ радиовещании.
В радиостанциях применяют в основном узкополосную ЧМ модуляцию, требующую более точной настройки приемника и соответственно более защищенную от помех.
Спектры широкополосной и узкополосной ЧМ представлены ниже

Спектр узкополосной ЧМ напоминает амплитудную модуляцию, но если учесть фазу боковых полос, то окажется, что эти волны имеют постоянную амплитуду и переменную частоту, а не постоянную частоту и переменную амплитуду (AM). При широкополосной ЧМ амплитуда несущей может быть очень малой, что обусловливает высокую эффективность ЧМ; это значит, что большая часть передаваемой энергии содержится в боковых частотах, несущих информацию.

Основные преимущества ЧМ, перед АМ — энергоэффективность и помехоустойчивость.

Как разновидность ЧМ, выделяют Линейно-частотную модуляцию.
Суть ее заключается в том, что частота несущего сигнала изменяется по линейному закону.

Практическая значимость линейно-частотно-модулированных (ЛЧМ) сигналов заключается в возможности существенного сжатия сигнала при приеме с увеличением его амплитуды над уровнем помех.
ЛЧМ находят применение в радиолокации.

Фазовая модуляция

В реальности, больше применяют термин фазовая манипуляция, т.к. в основном производят модуляцию дискретных сигналов.
Смысл ФМ таков, что фаза несущей, изменяется скачкообразно, при приходе очередного дискретного сигнала, отличного от предыдущего.

Из спектра можно видеть, почти полное отсутствие несущей, что указывают на высокую энергоэффективность.
Недостаток данной модуляции в том, что ошибка в одном символе, может привести к некорректному приему всех последующих.

Дифференциально-фазовая манипуляция

В случае этой модуляции, фаза меняется не при каждом изменении значения модулирующего импульса, а при изменении разности. В данном примере при приходе каждой «1».

Преимущество этого вида модуляции в том, что в случае возникновения случайной ошибки в одном символе, это не влечет дальнейшую цепочку ошибок.

Стоит отметить, что существуют также фазовые манипуляции такие как квадратурная, где используется изменение фазы в пределах 90 градусов и ФМ более высоких порядков, но их рассмотрение выходит за рамки данной статьи.

PS: хочу еще раз отметить, что цель статей не заменить учебник, а рассказать «на пальцах» об основах радио.
Рассмотрены лишь основные виды модуляций для создания у читателя представления о теме.

Характеристики периодических гармонических сигналов — Студопедия

Сигнал называется периодическим, если его значение повторяется через определенный интервал времени. Этот интервал называется периодом измерения сигнала. Форма сигнала может быть произвольной.

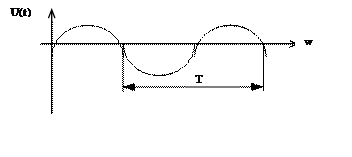Рис. Периодическая форма сигнала.

Удобнее период прохождения сигнала определить по точкам перехода через ноль. Гармоническим будем называть сигнал, который можно представить, как сумму гармоник основной частоты сигнала.

U (t) = U₁sin wt + U₂sin2 wt + U₃ sin3 wt + ……….+ U_n sin n wt — аддитивная модель сигнала;

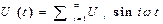— ряд Фурье. В зависимости от характеристики сигнала в нем присутствуют те или иные высшие гармоники. Например, если сигнал симметричный (т.е. U(t) = = — U(-t)), то в его составе нечетные гармоники.

Эквивалентно разложению в ряд Фурье для сигнала вводят понятие спектральной плотности сигнала.

Спектральная плотность сигнала — графическое представление разложения Фурье, на графике указывается основная составляющая, амплитуда которой пропорциональна амплитуде ряда Фурье, а также высшие гармоники: 2w, 3w, 4w и т.д.

Амплитуды убывают. Принято изменение большинства амплитуд спектров представлять экспонентой.

В разложении Фурье число гармоник стремится к бесконечности. На практике это невозможно, поэтому вводят искусственно ограничения на ширину спектра. Считают верхней крайней гармоникой спектра такую, амплитуда которой 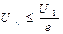; где U₁ – амплитуда основной гармоники.

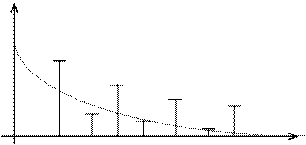
Чтобы можно было реализовать то или иное преобразование, мы должны вводить эти ограничения, то есть мы искусственно ограничиваем спектр основной частотой. Часто для гармонических сигналов используют другое ограничение на порядок больше w_в » 10 w (для близких к синусоидальным сигналов).

Форма спектра, как и набор составляющих преобразований Фурье, зависит от “испорченности” сигнала.

Так, идеальная синусоида U(t) = U_n (sin wt) +0 отображается на спектре в виде I.

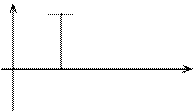G(w)

w

Рис. Отображение идеальной синусоиды на спектре.

Если U(t) = U_n (sin wt) cos W t (W — другая частота)

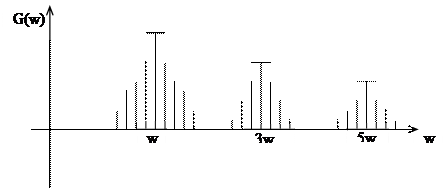
Рис. Спектр амплитудно-модулированного сигнала

Характеристики электрических сигналов определены нормативными документами, определяющими качество электрической энергии, показателями качества. Там более 50 параметров, основными из которых считаются различные формы описания напряжения (тока) сигнала: U_м — амплитуда или max. за период значение напряжения, U (t) — мгновенное значение напряжения – величина в определенный момент времени.

Поскольку разложение сигнала в ряд Фурье на составляющие гармоники – теоретическое предположение, гипотеза, его можно проверить путем анализа сигнала специальными приборами – анализаторами спектра. Прибор представляет приемник с перестраиваемым входным контуром. Усиленный сигнал подается на ЭЛТ. На экране трубки просматривается сигнал.

Анализатор спектра позволяет наглядно убедиться в том, что сложный периодический сигнал есть сумма составляющих, то есть на экране регистрируются сигналы с различной интенсивностью. Не периодический сигнал (например, переходный процесс при выключении линии) анализируют с помощью устройств, имеющих память: запоминающих осциллографов, анализаторов спектра с памятью, путем ввода информации в ЭВМ и ее обработки.

Любой сигнал — периодический и не периодический можно представить с помощью некоторой функции времени. Как правило, полного равенства часто не бывает, поскольку согласно разложению Фурье, число составляющих стремиться к бесконечности. Но в измерительной технике вынуждены ограничивать число составляющих шириной спектра.

U(t) @ F(t)

Форма сигнала может быть представлена самописцем (быстродействующий прибор для записи формы сигнала). Например. Сигнал преобразуется в световой зайчик и пишется на фотобумаге. Более распространенный прибор—осциллограф. В любой момент периода мы можем зафиксировать значение ординаты:Форма сигнала может быть представлена и набором дискретных значений U(t_j)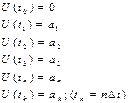

Те же объяснения можно применить и для i(t). Поскольку электрические сигналы изменяются быстро, записать форму, определить их мгновенное значение возможно только с помощью автоматических электронных средств, поэтому используют другие производные значения ( производные мгновенных значений ).

Амплитудное значение сигнала есть максимальное из мгновенных значений на интервале периода.

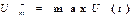
Поскольку сигнал может быть двуполярным, амплитуда ²+² и ²-² полуволн.

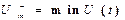
Размах – это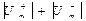

Для измерения амплитудного значения применяют амплитудные вольтметры. Мы можем измерить амплитуду с помощью соответствующего прибора. Пиковое значение напряжения U_n – наибольшая величина амплитудного значения на интервале t, значительно превышающем период сигнала. Пиковое значение используют для анализа электрической прочности изоляторов, воздушных промежутков и т.д. Пиковый вольтметр зафиксирует это значение за измеряемый интервал времени.

Амплитудный вольтметр усредняет значение, а пиковый – максимизирует.

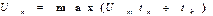
В энергетике амплитудное значение не является первостепенным параметром, т.к. основная цель передача электрической энергии. Эту процедуру характеризует действующее или среднеквадратическое значение напряжения.

Действующим значением напряжения переменного тока называют такую величину напряжения постоянного тока, которая на такой тже нагрузке выделяет одинаковую мощность.

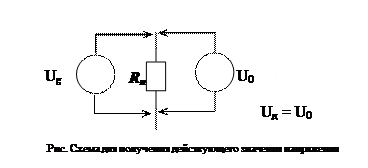
Математически действующее значение вычисляется как:

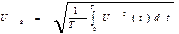
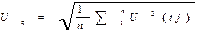
Средневыпрямленное значение напряжения используют при преобразовании переменного тока в постоянный, когда форма напряжения однополярна и определен интеграл.

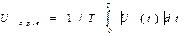
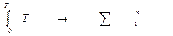
Постоянная составляющая напряжения U₀ определяется как разность между U(t) и U_n .

U₀ = U(t) — U_n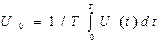

Постоянная составляющая сигнала показывает, что сигнал следует представить из двух величин

U (t) = U₀+U_n

Для обобщающей характеристики электрических сигналов применяют коэффициенты, характеризующие форму сигнала:

Коэффициент амплитуды

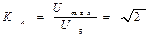
Коэффициент формы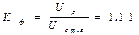

Для синусоидального сигнала значение K_A и K_F cсоответственно и 1.11. Если форма сигнала отличается от синусоиды, это отражается на коэффициентах K_A и K_F . С ростом числа гармоник в составе сигнала коэффициенты K_F уменьшаются.

Коэффициенты K_А в зависимости от составляющих сигнала изменяются не однозначно. График выглядит так:

График изменения коэффициента К_А от гармоник проходит N номинальное значение. Поэтому номинальная величина 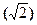встречается не только у чистой синусоиды. Совокупный анализ К_А и К_Ф может послужить инструментом для определения: есть ли в сигнале верхние гармоники. Помимо двух коэффициентов также используют коэффициенты гармоник и искажений.

Как правило, измерительные приборы стрелочные, проградуированы в единицах измерения действующего значения напряжений или тока, поэтому форма сигнала оказывает заметное влияние на действительное значение. С увеличением числа верхних гармоник форма изменяется не однозначно, что приводит к различным вариантам действительного значения.

Поскольку к качеству электрической энергии предъявляются строгие требования, измерения основных параметров должны проводиться с высокой точностью. Оптимально это выполняется на автоматизированных установках.

Большинство вольтметров измеряют действующее значение, которое зависит от состава гармоник .

ещё немного о «магических» свойствах ТЛЗ для музыкантов и аудиофилов / Блог компании Pult.ru / Хабр

Одним из самых популярных материалов нашего блога на GT стал пост “Сеанс теплой ламповой магии с разоблачением”. Он коснулся расхожих стереотипов при оценке УМЗЧ с полупроводниковой и ламповой схемотехникой. Кроме того, бурным и живым стало обсуждение поста о гитарном ламповом усилении и цифровой эмуляции ламповых эффектов.

Некоторые из моих оппонентов в холиварах на эти темы заявили, что я, дескать, мало знаю о ТЛЗ, и все прелести оного совсем не в гармониках, а в трансформаторах, операционных усилителях и т.п. Оппоненты непрозрачно намекали, что нет подробных исследований спектрального состава искажений для ламповых и транзисторных усилителей.

В тех материалах я писал о том, что рано ставить точку в вопросе лампового звука, теперь, полагаю, пора. Совсем недавно мне попалось относительно свежее исследование физика Дэвида Кипортса, которое окончательно закрывает вопрос о природе и эффектах так называемого ТЛЗ (по крайней мере в вопросе гитарного усиления).

Психоакустика восприятия искажений

Как мы уже писали, в исследованиях Флетчера, Войшвилло и Алдошиной была выявлена разница между субъективным восприятием разных гармоник. В частности, исследования показали, что гармоники высокого порядка воспринимаются как выраженные неприятные искажения, а низкого, как более благозвучные или по крайней мере менее заметные.

Также в исследованиях отмечалось, что нечетные гармоники (3-я, 5-я, 7-я, 15-я и т.п.) создают диссонирующие тоны и поэтому воспринимаются как неблагозвучные или дисгармоничные. Тоны, генерируемые четными гармониками, напротив, гармонично сочетаются основным звуком.
На этих исследованиях базируется большинство утверждений о том, что приятным для человеческого уха является звук тёплых (в прямом смысле) ламповых усилителей. Полупроводниковые уступают им в благозвучности искажений. Именно благозвучность ламп с успехом используется музыкантами и иногда ценится аудиофилами.

При этом доказано, что т.н. “честность” (верность воспроизведения) у современных “каменных” усилителей выше, т.к. уровень искажений в них значительно ниже. В 70-е ламповая техника имела преимущества, так как коэффициент гармоник был приблизительно равен для транзисторных и ламповых систем. Сегодня ситуация существенно отличается, так как большинство ламповых изделий десятки, а порой и в сотни раз сильнее искажает звук, по сравнению с аналогичным по цене полупроводниковым УМЗЧ.

Точка Дэвида Кипортса

Дэвид Кипортс, работающий в американском колледже Миллса, не придумал ничего нового. Но именно этого человека будут помнить как физика, препарировавшего ламповую ”магию” и доказавшего физическую природу психоакустических эффектов.

На всякий случай упрощенно опишу появление гармонических искажений при звукоусилении. Транзисторы (микросхемы) или вакуумные лампы позволяют увеличить электрическую мощность. В случае со звуком процесс усиления мощности сопряжен с появлением дополнительных сигналов другими частотами — т.е. гармоническими искажениями. Например, при усилении сигнала 300 Гц появляются сигналы 600, 900, 1 200 Гц, соответственно, вторая, третья и четвертая гармоники.

Дэвид Кипортс испытывал гитарные усилители, так как его интересовали именно любовь гитаристов. С т.н. аудиофильской лампой он не работал, и судя по его статье, он о ней не очень знает.

Ученый исследовал и сравнил гармонические искажения в усилителях Fender Pro Jr и Bugera BC15. Первый — полностью ламповый (на триодах реализованы предусилитель и оконечник), второй построен как гибрид (ламповое предусиление и транзисторный оконечник).
Ученый определил ряд закономерностей, которые касались этих усилителей.

Например, Fender Pro Jr в режиме работы без перегрузки был характерен низкий Кг, значительное преобладание четных гармоник, были выражены гармоники низкого порядка 2-я, 4-я. Режим перегрузки приводил к усилению 5-й гармоники по сравнению с 6-й, и ослаблению четных гармоник, на фоне некоторого усиления нечетных. Bugera BC15 в обоих режимах продемонстрировала выраженность нечетных гармоник, в основном 3-й и 5-й.

Кратко можно охарактеризовать выводы экспериментатора как то, что реализация усиления на транзисторах способствует появлению в результирующем сигнале большего количества неблагозвучных нечетных гармоник.

При этом появления гармоник высокого порядка, на которые ссылались авторы похожих публикаций в 70-е, не наблюдаются. Напротив, как в ламповом, так и в транзисторном усилителях порядок гармоних ограничен 6-й.

В своем исследовании физик даёт и психоакустическое обоснование благозвучности четных и неблагозвучности нечетных гармоник, а также называет причины, по которым ламповое усиление ценится у гитаристов.

Так усиливающийся сигнал электрогитар уже богат гармоническим содержанием. К исходным гармоникам этого сигнала перегруженный ламповый тракт способен добавить дополнительные гармоники к каждой из исходных. При этом наиболее выраженными из них будут четные, что и гарантирует необходимый эстетический музыкальный эффект.

Сухой остаток

Отраженные в исследовании Кипортса данные позволяют говорить о том, что известные эффекты благозвучности лампового звука имеют исключительно гармоническую природу. Также исследование свидетельствует о том, что ламповая техника в настоящий момент наиболее применима именно в качестве гитарного усиления, а также создания эстетически ценных музыкальных эффектов.

При этом классическую “лампу” сегодня можно эффективно заменить цифровыми эмуляциями (так как никакой проблемы в создании гармонических искажений при цифровой обработке сигнала сейчас нет). Отмечу, что последние пока не находят широкого концертного и репетиционного применения, в силу непривычности эксплуатации (многим проще купить лампу), однако все больше используются в студийной работе.

В HI-FI и Hi End лампы постепенно умирают, в связи со схемотехнической сложностью для достижения высокой верности воспроизведения, а также возможностью точной и недорогой цифровой имитации т. н. лампового звучания.

В этих сегментах ламповое усиление остаётся актуальным для создания уникальных и неоправданно дорогих аутентичных схемотехнических шедевров, рассчитанных на узкий круг ценителей. Также лампы эффективны в специализированном усилении для наушников, особенно для электростатических.

Джинса
В нашем каталоге предствален широкий ассортимент гитраных усилителей, а также ламповых УМЗЧ для воспроизведения музыки.

свободных гармонических сигналов — финансовое решение FxMath

Гармонические ценовые паттерны выводят геометрические ценовые паттерны на новый уровень, используя числа Фибоначчи для определения точных поворотных точек. В отличие от других методов торговли, Harmonic trading пытается предсказать будущие движения. Это резко контрастирует с обычными методами, которые являются реакционными, а не прогнозирующими. Давайте посмотрим на несколько примеров того, как гармонические ценовые модели используются для торговли валютами на валютном рынке.

Объединить геометрию и числа Фибоначчи

Гармоническая торговля объединяет модели и математику в метод торговли, который является точным и основан на предположении, что модели повторяются.В основе методологии лежит первичный коэффициент или производная от него (0,618 или 1,618). Дополняющие отношения включают: 0,382, 0,50, 1,41, 2,0, 2,24, 2,618, 3,14 и 3,618. Первичное соотношение обнаруживается почти во всех природных и экологических структурах и явлениях; он также встречается в искусственных сооружениях. Поскольку эта закономерность повторяется в природе и в обществе, соотношение также наблюдается на финансовых рынках, на которые влияет среда и общества, в которых они торгуют.

Находя паттерны различной длины и величины, трейдер может затем применить к паттернам отношения Фибоначчи и попытаться предсказать будущие движения.Этот метод торговли в значительной степени приписывается Скотту Карни, хотя другие внесли свой вклад или обнаружили модели и уровни, которые повышают производительность.

Проблемы с гармониками

Гармонические ценовые паттерны чрезвычайно точны, требуя, чтобы паттерн демонстрировал движения определенной величины, чтобы при развертывании паттерна можно было точно определить точку разворота. Трейдер может часто видеть паттерн, который выглядит как гармонический паттерн, но уровни Фибоначчи не будут выровнены в паттерне, что делает паттерн ненадежным с точки зрения Гармонического подхода.Это может быть преимуществом, поскольку требует от трейдера терпения и ожидания идеальных настроек.

Гармонические паттерны могут определять, как долго продлится текущее движение, но их также можно использовать для выделения точек разворота. Опасность возникает, когда трейдер занимает позицию в области разворота и паттерн не работает. Когда это происходит, трейдер может попасть в сделку, где тренд быстро развернется против него. Следовательно, как и во всех торговых стратегиях, необходимо контролировать риск.

Важно отметить, что паттерны могут существовать внутри других паттернов, и также возможно, что негармонические паттерны могут (и, вероятно, будут) существовать в контексте гармонических паттернов.Их можно использовать для повышения эффективности гармонического паттерна и улучшения характеристик входа и выхода. В пределах одной гармонической волны также могут существовать несколько ценовых волн (например, волна CD или волна AB). Цены постоянно меняются; поэтому важно сосредоточиться на более широкой картине торгуемого периода времени. Фрактальная природа рынков позволяет применять теорию от самых маленьких до самых больших временных рамок.

Чтобы использовать этот метод, трейдер получит выгоду от графической платформы, которая позволяет трейдеру строить множественные уровни восстановления Фибоначчи для измерения каждой волны.

Некоторые важные гармонические паттерны

• Крабовый узор
• AB = образец CD
• Образец акулы
• Паттерн Гартли
• Узор бабочки
• Выкройка летучей мыши
• Модель с тремя приводами
• 5-0 Шаблон

Получение бесплатных сигналов гармонической диаграммы по электронной почте

Вы можете подписаться на наши бесплатные сигналы гармонического шаблона по электронной почте.Каждый сигнал включает время торговли, пару, временные рамки, название паттерна, цену входа, тейк-профит и стоп-лосс.

Образцы сигналов

Время сигнала (GMT): 2015.09.28 10:13

Пара: XAUUSD

Таймфрейм: h5

Паттерн: бычий 121

Сделка: покупка (длинная)

OpenЦена: 1133.31

TakeProfit: 1142,37

StopLoss: 1124.2721

Время сигнала (GMT): 2015.09.25 08:03

Пара: USDJPY

Таймфрейм: h5

Паттерн: Медвежий COL Поручик

Сделка: Продажа (Продажа)

OpenЦена: 120.84

TakeProfit: 120,159

Стоплосс: 121.2252

.

гармонический сигнал — это … Что такое гармонический сигнал?

Гармонический анализ — раздел математики, изучающий представление функций или сигналов в виде суперпозиции основных волн. В нем исследуются и обобщаются понятия рядов Фурье и преобразований Фурье. Основные волны называются гармониками…… Wikipedia

Гармоники и отдельные линии и шум — (HILN) — параметрический кодек для звука. Основная предпосылка кодировщика заключается в том, что большая часть звука, и особенно речь, может быть синтезирована только из синусоид и шума.Кодировщик описывает отдельные синусоиды с амплитудой и частотой,…… Wikipedia

Harmonic Vector Excitation Coding — (HVXC) ist ein auf die Übertragung von Sprache optimiertes Verfahren zur Kompression von Audiodaten. Trotz sehr geringer Bitraten sind HVXC kodierte Daten für die Übermittlung von Sprache in einer akzeptablen Qualität geeignet. Eingesetzt wird es… Deutsch Wikipedia

Harmonic Foldback — Hammond Orgel Классификация Elektrophon Tasteninstrument Tonumfang C1 fis5 Verwandte Instrumente Orgel Klangbeispiel… Deutsch Wikipedia

Гармоническое вейвлет-преобразование — В математике обработки сигналов гармоническое вейвлет-преобразование, введенное Дэвидом Эдвардом Ньюландом в 1993 году, представляет собой линейное преобразование заданной функции на основе вейвлетов в представление временной частоты.Он сочетает в себе преимущества…… Wikipedia

Гармонический осциллятор — Эта статья о гармоническом осцилляторе в классической механике. Для его использования в квантовой механике см квантовый гармонический осциллятор. Классическая механика… Википедия

Harmonic — Эта статья о компонентах периодических сигналов. Для использования в других целях, см Гармоника (значения). Узлы колеблющейся струны — гармоники. Гармоника волны — это составляющая частоты сигнала, которая является целым числом, кратным… Wikipedia

Отношение сигнал / шум — Отношение сигнал / шум в статистике см. В Cohen s d.Отношение сигнал / шум (часто сокращенно SNR или S / N) — это показатель, используемый в науке и технике, который сравнивает уровень полезного сигнала с уровнем фонового шума. Это определяется…… Википедия

Подпространство сигнала — При обработке сигналов методы подпространства сигнала представляют собой эмпирические линейные методы уменьшения размерности и уменьшения шума. В последнее время эти подходы вызвали значительный интерес и исследования в контексте улучшения речи,…… Wikipedia

гармоническое искажение — существительное: искажение, при котором гармоники входного сигнала производятся в усилителе и появляются на выходе вместе с усиленным входным сигналом… Полезный английский словарь

гармоника — Переменный сигнал, частота которого является целым кратным основной основной частоты… ИТ-глоссарий терминов, акронимов и сокращений

.

Технические характеристики органа Hammond

Эта страница предназначена для ознакомления с некоторыми ключевыми техническими аспектами органа B3 Hammond, которые вносят вклад в «звук Hammond». Лично я склоняюсь к копированию этого звука с помощью других технологий. Возможно, однажды я построю орган «колесо-клон», но опять же, Clavia могла бы его прибить! Тем не менее, создание органа было бы неплохим проектом.

Содержание

Тяги

Гармоники, кадры и ноты, используемые на дышлах Hammond, показаны ниже:

Как можно видеть, для каждой ноты гармоники идут на три октавы выше и на одну октаву ниже.

Основная высота звука инструмента изменяется от тона 13 до тона 73. Эта высота обеспечивается 3-м тягой, основной.

5⅓ ‘кадры странным образом расположены в качестве второй тяги, а не в ее логическом положении между основной и 2-й гармониками, предположительно потому, что она обозначена как «суб-3-я гармоника».

Фолдбек

Harmonic foldback используется для уменьшения необходимого количества звуков на обоих концах клавиатуры. Он влияет на 3-ю и последующие гармоники вверху и субфундаментальную гармонику внизу.Это показано в следующей таблице, в которой показаны тонколесные диски (1-91), используемые для каждой гармоники

.

	Нижний фолдбек		Верхняя складка
Субфундаментальный	13-24	13-61
Субтретий		20-80
Фундаментальный		13-73
Секунда		25-85
Третий		31-91	80
Четвертый		37-91	80-85
Пятая		41-91	80-89
Шестой		44-91	80-91	80
Восьмая		49-91	80-91	80-85

Третья гармоника повторяет высшую С.4-я гармоника повторяется из тона 56, G верхней октавы. 5-я гармоника повторяется из тона 52, D # верхней октавы. 7-я гармоника повторяется из тона 49, нижнего до верхней октавы. 8-я гармоника повторяется с тона 44, G в четвертой октаве. Обратите внимание, что 6-я и 8-я гармоники фактически повторяют некоторые тона дважды.

Поскольку нижние тембры, которые загнуты назад, фактически присутствуют в инструменте для педалей, можно перенастроить Hammond для получения настоящего баса, без нижнего загиба.Причуда в том, что самая низкая октава тонколес имеет более сложную форму и обеспечивает форму волны, которая ближе к прямоугольной, с присутствием некоторых 3-й и 5-й гармоник.

На диаграмме ниже показано влияние гармонического фолдбэка на верхние и нижние ноты клавиатуры. Самая низкая нота имеет субфундамент, загнутый назад, даже если тон-генератор идет достаточно низко, что представлено шириной серых полос. Вверху есть пять тонов, которые «выходят за пределы» генератора и загибаются обратно на предусмотренную верхнюю октаву.Обратите внимание: это означает, что если вы играете верхнюю до, она фактически включает два одинаковых тона (тоны 80 и 85) три раза!

Теоретически для полных 5 октав клавиатуры B3 потребуется 61 основной тон, плюс 3 октавы выше для гармоник и на одну октаву ниже для субфундаментальной гармоники. Это дает в общей сложности девять октав, или 61 + 36 + 12 = 109 тонов. Поскольку доступен только 91 тон, необходимость в фолдбеке очевидна.

Нажмите кнопку

Контакты механических клавиш на B3 имеют сигналы уровня звука.Их прямое переключение на выход вызывало слышимые щелчки. Эти щелчки стали характерной частью звука Hammond. Щелчок вызван комбинацией девяти ключевых контактов, которые не замыкаются одновременно, и дребезг контактов, усугубляемый грязными контактами. Это вызывает случайное быстрое переключение сигнала в начальной части ноты. Поскольку это переключение вводит переходные процессы, мы слышим это как звук со случайным высокочастотным содержимым — щелчок. Это можно смоделировать либо добавлением переходного шума, либо электронным моделированием дребезга контакта.

Гармоническая утечка

Генератор тонколесного колеса Hammond содержит серию металлических разделителей, которые разбивают генератор на «бункеры». Каждый бункер содержит 2 тонных колеса, которые связаны с одной и той же ведомой шестерней. Между тонами, находящимися в одном бункере, существует определенная магнитная утечка, поэтому можно услышать утечку гармоник на четыре октавы выше или ниже требуемого тона. Хорошие копии Хаммонда включают эту утечку.

Сканер хоруса / вибрато

Схема хоруса / вибрато Hammond стала известна сама по себе, поскольку органы, имеющие «настоящее» вибрато на основе сканера, более ценны, чем органы без него.Так что же это за схема и как она работает?

Короче говоря, это 9-ступенчатая линия задержки. Задержка производится с помощью схем фазового сдвига LC. Он может производить только очень короткую задержку около 1 мс. Для вибрато или хоруса требуется переменная задержка, которая создается вращающимся рычагом сканера, который по очереди улавливает сигналы с каждой стадии задержки. Из-за способа, которым это сделано (по сути, конденсатора с воздушным зазором), эффект заключается в переходе от одного каскада к другому. Сканер настроен на сканирование каждого нажатия от 1 до 9, а затем снова от 9 до 1.Это эквивалентно треугольной волновой модуляции времени задержки. Полный цикл, от 1 до 9 и обратно, составляет 16 шагов. Несмотря на то, что для каждого из двух эффектов доступны три настройки глубины (VIB1, VIB2, VIB3, CHORUS1, CHORUS2, CHORUS3) на B3, нет управления скоростью, которая установлена ​​на постоянное значение 7 Гц. Любая хорошая копия должна обеспечивать такую ​​скорость.

Юрген Хейбле потратил некоторое время на копирование оригинальной схемы сканера Hammond и создание современной копии. К сожалению, его схема в настоящее время недоступна в Интернете.В нем используется настоящая LC-линия задержки с фазовым сдвигом, соединенная с парой VCA и другими схемами для замирания от одного каскада к другому. Очевидно, это дает очень точную копию исходного звука без каких-либо движущихся частей.

Другие, менее строгие копии возможны с использованием устройств BBD. Проблема с ними будет заключаться в чрезвычайно коротком необходимом времени задержки. У большинства микросхем будет слишком много ступеней и слишком медленные часы, чтобы получить необходимое время. Они также обеспечивают одинаковую задержку для всех частот, а не то, что является особенностью задержки сдвига фазы LC от Hammond.

Возможно, более многообещающим было бы использование фазовращателей на базе 9 операционных усилителей и последующее сканирование между их выходами с использованием схемы, очень похожей на схему Юргена.

Проблемы с копированием B3

Есть разные проблемы с копированием B3. Их:

Создание 91 индивидуального синусоидального тона

Это сделать не так-то просто, а при разумной цене — еще сложнее. В идеале волны не должны иметь фиксированных фазовых соотношений между связанными нотами, хотя они имеют достаточно фиксированные отношения в исходном органе.Пружинные соединения между ступенями тон-генератора придают этому некоторую плавность. Это фиксированное, но не фиксированное фазовое соотношение — еще один интересный аспект технологии, но с неизвестным влиянием на звук.

Переключение тонов на шины

Оригинальные органы имеют по девять контактов под каждой клавишей. Даже этого недостаточно, так как они отнимают у гармоники один контакт при включении перкуссии. Для каждой нажатой клавиши (как минимум) девять отдельных частот должны быть переданы на девять отдельных выходных микшеров, а сигнал должен быть передан в схему перкуссии.Это дает в общей сложности 61 × 10 контактов, необходимых для каждого из двух руководств (без учета педалей!), Всего 1220 переключающих контактов, хотя, как уже упоминалось, Хаммонд немного уменьшил это.

Если есть способ соединить это соединение, чтобы оно не выглядело как паутина паука, страдающего обсессивно-компульсивным расстройством, я его не видел. Даже мультиплексирование, похоже, не помогает, поскольку оно просто перемещает проблему обратно, превращаясь в вопрос получения правильных тонов на мультиплексоры.

Это основная проблема любого полностью полифонического органа — и всех лучших из них.

Легкие части B3

Выходные схемы довольно просты. Шины представляют собой простые схемы смесителя, которые суммируют все нажатые ноты, а тяги регулируют выходную громкость смесителя каждой гармоники. Эти гармоники затем смешиваются в конечном выходном смесителе перед усилением.

Заставить это звучать как B3 — это вопрос тона и технологии — использование ламп, а не транзисторов и так далее. Если все остальное в порядке с вашим органом clonewheel, и вы подключите его к громкоговорителю Leslie с ламповым усилителем, он будет звучать как Hammond.

Определение частот используемых тонов

Частота определенного тона зависит от ряда факторов:

• M — Скорость главного двигателя, 20 об / сек (1200 об / мин)
• T — Количество зубьев на тонколесе
• R — Передаточное число. Это равно количеству зубьев ведущей шестерни / количеству зубьев ведомой шестерни.

Соотношения в Hammond следующие:

Примечание	Привод (A)	Приводной (B)	Соотношение (A / B)
С	85	104	0.817307692
С #	71	82	0,865853659
D	67	73	0,917808219
D #	105	108	0,972222222
E	103	100	1.030000000
F	84	77	1.090909091
F #	74	64	1.156250000
G	98	80	1,225000000
G #	96	74	1,297297297
А	88	64	1,375000000
A #	67	46	1.456521739
B	108	70	1,542857143

Формула точной частоты тона:

Частота F (Гц) = M * T * R

Таким образом, для среднего A:

20 * 16 * (88/64) = 440 Гц

As — единственные ноты на Hammond, которые точно соответствуют шкале равного темперирования.Ноты с наибольшим отклонением от высоты тона в первых семи октавах — это G #. Они равны 0,69 цента от правильной подачи.

Для C # = 4434 Гц: 20 * 192 * (74/64) = 4440 Гц

По сути, передаточные числа определяют ноту, в то время как количество зубцов на колесе тона определяет октаву. Следовательно, все тона в одной октаве используют колеса с одинаковым количеством зубцов. Тональный генератор 91 частоты использует:

• Колеса с 2 зубьями 12 тонн
• 12-ти тонные колеса 4 зуба
• Колеса 8 зубьев 12 тонн
• Колеса 16 зубьев 12 тонн
• 12-тонные колеса 32 зуба
• 12-ти тонные колеса 64 зуба
• 12-ти тонные колеса 128 зубьев
• 7-тонные колеса 192 зуба

Последняя (верхняя) октава необычна, поскольку Хаммонд не умел резать колеса с 256 зубьями.Вместо этого они использовали колеса со 192 зубьями и использовали передаточное число от буквы F снизу вверх. Это означает, что верхняя половина октавы находится дальше от высоты тона из-за количества зубцов на тонколесе, не равного 256. В верхней половине октавы C # является самым дальним отклонением от высоты звука, примерно 1,93 цента резкостью. Это все еще меньше, чем 6 центов, которые должны быть минимально заметной разницей в высоте тона.

Настройка с равным темпом означает, что невозможно найти точные гармоники на клавиатуре — каждый тон является «наилучшим подходом», а не точным значением.Однако Hammond не использует истинную настройку равной темперации, а использует собственное приближение. В случае 6-й, 3-й и суб-3-й гармоник это приводит к тому, что они немного ближе к истинному значению, чем равная темперация, а в случае 5-й — немного хуже. Различия есть, но очень незначительные и, вероятно, незначительные. Если не учитывать верхнюю половину октавы, которая сильно отличается, результаты представлены в таблице ниже:

Гармоника	Истинный коэффициент гармоник	Соотношение темпераментов	Коэффициент Хаммонда
Субфундамент	0.5	0,5	0,5
Фундаментальный	1	1	1
Дополнительный 3-й	1,5	1.498307077	1.498823530
2-я	2	2	2
3-й	3	2,996614154	2.997647060
4-я	4	4	4
5-я	5	5.039684200	5.040941178
6-й	6	5,993228307	5.995294120
8-й	8	8	8

Какие частоты используются?

Нижняя октава находится в диапазоне от 32,69 Гц до 65,38 Гц. Эти тона представляют собой сложные тонколесные диски и доступны только на педалях.

Тональные сигналы для руководств идут от 65,38 Гц (самый низкий C) до 2092.31 Гц (самый высокий C). Тон-генератор также генерирует гармоники на другую октаву и немного выше этого, до C выше (4184,62 Гц) и, наконец, до F # выше этого (5924,62 Гц). Это самая высокая высота в органе.

.

Вычислить полное гармоническое искажение (THD) сигнала

Вычислить полное гармоническое искажение (THD) сигнала

Библиотека

Simscape / Электрооборудование / Специализированные системы питания / Управление и измерения / Измерения

Simscape / Электрооборудование / Специализированные энергосистемы / Основные блоки / Измерения / Дополнительные измерения

×

Описание

Блок THD вычисляет полное гармоническое искажение (THD) периодический искаженный сигнал.Сигналом может быть измеренное напряжение. или текущий.

THD определяется как среднеквадратическое значение (RMS) общие гармоники сигнала, деленные на среднеквадратичное значение его основной гармоники сигнал. Например, для токов THD определяется как

полное гармоническое искажение (THD) = IHIFIH = I22 + I32 +… + In2 In: среднеквадратичное значение гармоники nIF: среднеквадратичное значение основного тока

THD имеет нулевое значение значение для чисто синусоидального напряжения или тока.

Параметры

Основная частота входного сигнала (Гц)

Укажите частоту в герцах основного сигнала.По умолчанию 60 .

Время выборки

Укажите время выборки блока в секундах. Установить 0 на реализовать непрерывный блок. По умолчанию 0 .

Характеристики

Время выборки	Указано в Время выборки параметр Непрерывно, если Время выборки = 0
Скалярное расширение	Да, из параметров
Размерный	Да

Примеры

Модель power_RMS_THD использует блок THD для вычисления THD сигнала 60 Гц со вторым гармоника и смещение постоянного тока.

Время выборки модели параметрируется набором переменных Ts. значение по умолчанию 50e-6 с. Задайте для Ts значение 0 в командном окне, чтобы моделируйте модель в непрерывном режиме.

Представлен в R2013a

.