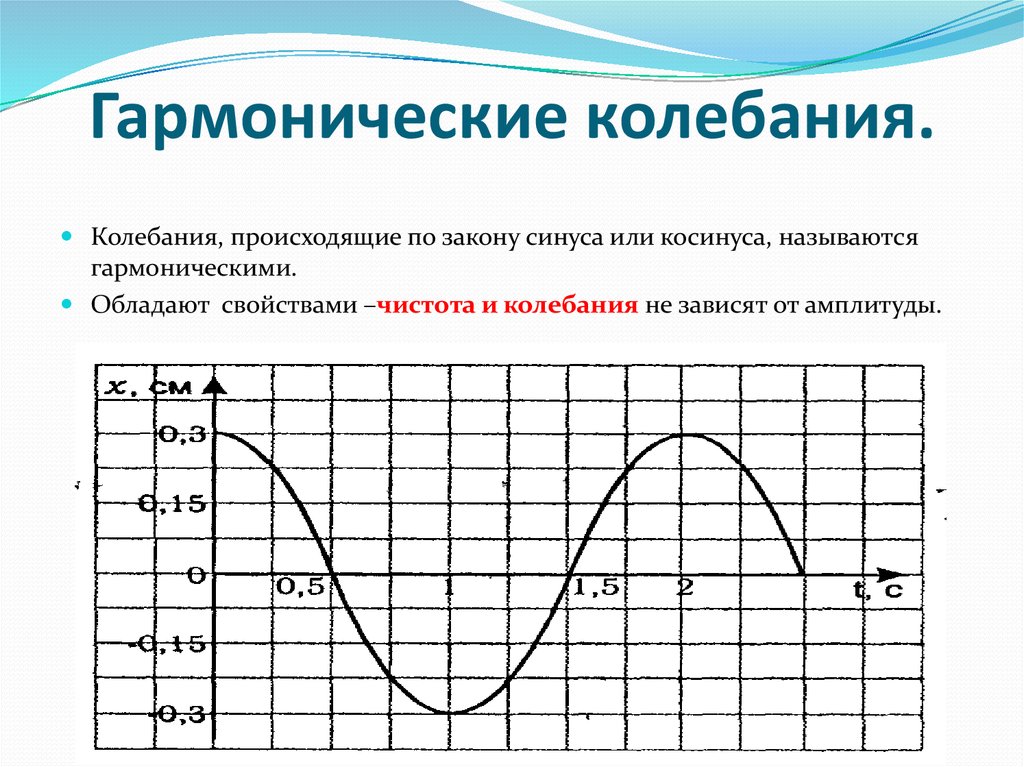
Гармонические колебания

Определение 1

Техника и окружающий мир являются примерами того, что существуют такие процессы, которые повторяются через определенные промежутки времени, то есть периодически. Их называют колебательными.

Колебательные движения. Формулы

Такие движения относят к явлениям с разной физической природой с подчинением общим закономерностям. Запись колебания тока в электрической цепи и математического маятника производится одним и тем же уравнением. Различная природа колебательных движений позволяет рассматривать их с единой точки зрения, исходя из общности закономерностей.

Определение 2

Механические колебания – это периодические или непериодические изменения физической величины, описывающей механическое движение (скорость, перемещение и так далее).

Когда в заданной среде атомы располагаются очень близко или молекулы испытывают силовое воздействие, наблюдается возбуждение механических колебаний. Это говорит о том, что процесс будет иметь конечную скорость, зависящую от свойств среды, которая распространяется от точки к точке.

Так возникают механические волны. Явный пример – звуковые волны в воздухе.

Волновые процессы и колебания разной природы имеют много общего, а их распространение может быть описано аналогичными математическими уравнениями. Это подтверждает единство материального мира.

Гармонические колебания. Определение

В механике предусмотрено движение поступательно, вращательно и с наличием колебаний.

Определение 3

Механические колебания – это движения тел, которые повторяются точно или приблизительно за определенные одинаковые временные промежутки.

Функция x=f(t) объясняет закон движения тела с наличием колебаний. При графическом изображении дается представление о протекании колебательного процесса во времени. Рисунок 2.1.1 наглядно показывает принцип простых колебательных систем груза на пружине или математического маятника.

Рисунок 2.1.1. Механические колебательные системы.

Механические колебания подразделяют на свободные и вынужденные.

Определение 4

Действия внутренних сил системы после выведения из равновесия порождают свободные колебания. Примером могут служить колебания груза на пружине или маятника. Если их действие происходит под воздействием внешних сил, тогда их называют вынужденными.

Простейшим видом колебаний являются гармонические колебания, которые описываются уравнением x=xmcos (ωt+φ0), где x– смещение тела от положения равновесия, xm – амплитуда колебаний, ω– циклическая или круговая частота, t – время.

Величина, располагаемая под знаком косинуса, получила название фазы гармонического процесса: φ=ωt+φ0. Если t=0, φ=φ0, тогда φ0 рассматривается в качестве начальной фазы.

Период колебаний Т – это минимальный промежуток времени, через который происходят повторения движения тела. Величина, обратная периоду колебаний, называют частотой колебаний f=1T.

Частота гармонических колебаний показывает их количество, совершаемое за единицу времени, измеряемая в герцах (Г).

Связь с циклической частотой ω и периодом T выражается с помощью формулы:

ω=2πf=2πT.

Рисунок 2.1.2 показывает гармонические колебания тел с разными положениями тел. Данный эксперимент наблюдается в специальных условиях при наличии периодических вспышек освещения, называемого стробоскопическим. Для изображения векторов скорости тела в разные моменты времени используют стрелки.

Рисунок 2.1.2. Стробоскопическое изображение гармонических колебаний. Начальная фаза φ0=0. Интервал времени между последовательными положениями тела τ = T12.

На графике 2.1.3. показаны изменения, происходящие во время гармонического процесса, при изменении амплитуды колебаний xm, или периода Т (частоты f), или начальной фазы φ0.

Рисунок 2.1.3. Во всех трех случаях для синих кривых φ0=0: a – красная кривая отличается от синей только большей амплитудой (x’m>xm); b – красная кривая отличается от синей только значением периода (T’=T2); с – красная кривая отличается от синей только значением начальной фазы  φ0’=-π2 рад.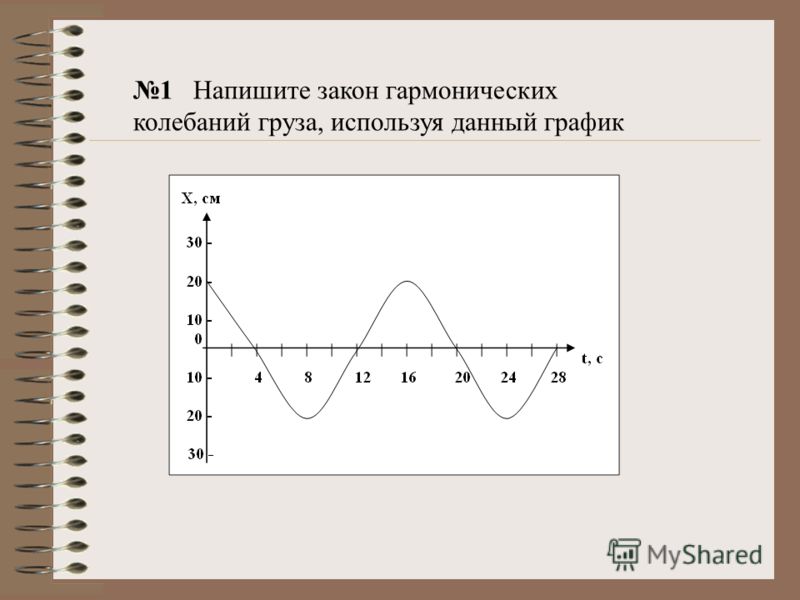

Гармонический закон

Если колебания совершаются вдоль прямой Ох, тогда направление вектора скорости аналогично. Определение скорости движения тела υ=υx определяют из выражения υ=∆x∆t; ∆t→0.

Отношение ∆x∆t при ∆t→0 математика трактует как вычисление производной функции x(t) за определенное время t. Обозначение принимает вид dx (t)dt, x'(t) или x˙.

Гармонический закон движения записывается в качестве x=xmcos (ωt+φ0). После вычисления производной формула приобретает вид:

υ=x˙(t)=-ωxmsin (ωt+φ0)=ωxmcos ωt+φ0+π2.

Слагаемое +π2 считают изменением начальной фазы. Достижение максимального значения скорости по модулю υ=ωxmпроизводится при прохождении тела через положение равновесия, то есть x=0. Аналогично определяют ускорение a=ax. Тогда a=∆υ∆t, ∆t→0. Отсюда следует, что a равняется производной функции υ(t) за время t или второй производной функции x(t). Подставив выражения, получим

a=υ˙(t)=x¨(t)=-ω2xmcos (ωt+φ0)=-ω2x(t).

Наличие отрицательного знака указывает на то, что ускорение a(t) имеет противоположный смещению x(t) знак. Исходя из второго закона Ньютона, сила, которая заставляет совершать колебательные движения, направляется в сторону положения равновесия x=0.

На рисунке 2.1.4 изображены графики, где имеются зависимости скорости, ускорения, совершающие гармонические колебания.

Рисунок 2.1.4. Графики координаты x (t), скорости υ (t) и ускорения a (t) тела, совершающего гармонические колебания.

Рисунок 2.1.5. Модель гармонических колебаний.

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р.

Реферат от 1 дня / от 700 р.

КЕПЛЕРА ЗАКОНЫ | Энциклопедия Кругосвет

Содержание статьи

• Закон 1.
• Закон 2.
• Закон 3.

КЕПЛЕРА ЗАКОНЫ, принципы движения планет, сформулированные в начале 17 в. И.Кеплером (1571–1630) на основе многолетних наблюдений Т.Браге (1546–1601). Они используются в небесной механике и формулируются так:

1. Орбита любой планеты есть эллипс, в одном из фокусов которого находится Солнце.

2. Планета движется так, что ее радиус-вектор за равные интервалы времени заметает равные площади. (Закон площадей.)

3. Квадраты периодов любых двух планет соотносятся как кубы их средних расстояний от Солнца. (Гармонический закон.)

Замечательно, что законы Кеплера, составляющие базис небесной механики, выведены из наблюдений Тихо, выполненных без телескопа.

Закон 1.

Тихо поставил перед Кеплером задачу создания научной теории движения Марса. Следуя методике тех лет, Кеплер перепробовал множество комбинаций эпициклов и эксцентриков, но не смог найти подходящую для точного предвычисления наблюдаемого положения планеты. Наконец, он предположил, что орбита Марса эллиптическая, и увидел, что эта кривая хорошо описывает наблюдения, если Солнце поместить в один из фокусов эллипса. Затем Кеплер предположил (хотя и не мог точно доказать этого), что все планеты движутся по эллипсам, в фокусе которых находится Солнце. А орбиту Луны он описал эллипсом, в фокусе которого расположена Земля.

Действительно, орбиты всех больших планет – эллипсы, причем у Венеры орбита наиболее округлая (эксцентриситет е = 0,0068), а у Плутона наиболее вытянута (е = 0,2485). Орбиты малых планет – астероидов – тоже эллипсы; наиболее круглая орбита у астероида 1177 Гоннезия (е = 0,0063), а наиболее эксцентричная у 944 Идальго (е = 0,656).

Закон 2.

Законы Кеплера полностью эмпирические, они выведены из наблюдений. Чтобы получить закон площадей, Кеплер трудился около восьми лет, проделав громадный объем вычислений. Чем ближе планета к Солнцу, тем быстрее она движется по орбите. Каждый год в начале января Земля, проходя через перигелий, движется быстрее; поэтому видимое перемещение Солнца по эклиптике к востоку также происходит быстрее, чем в среднем за год. В начале июля Земля, проходя афелий, движется медленно, поэтому и перемещение Солнца по эклиптике замедляется. Закон площадей указывает, что сила, управляющая орбитальным движением планет, направлена к Солнцу.

Закон 3.

Третий, или гармонический, закон Кеплера связывает среднее расстояние планеты от Солнца (a) с ее орбитальным периодом (t):

где индексы 1 и 2 соответствуют любым двум планетам.

Пример: найти среднее расстояние от Солнца планеты Уран, имеющей период 84,015 лет. Из приведенной выше формулы, взяв период Земли за 1 год и ее расстояние от Солнца за 1 а.е.,

Ньютон (1643–1727) установил, что гравитационное притяжение планеты определенной массы зависит только от расстояния до нее, а не от других свойств, таких, как состав или температура. Он показал также, что закон Кеплера не совсем точен; что в действительности в него входит и масса планеты:

где M – масса Солнца, а m₁ и m₂ – массы планет. Поскольку движение и масса оказались связаны, эту комбинацию гармонического закона Кеплера и закона тяготения Ньютона используют для определения массы планет и спутников, если известны их расстояния и орбитальные периоды.

Проверь себя!
Ответь на вопросы викторины «Астрономия»

Какая планета солнечной системы была открыта последней?

Пройти тест

Самый быстрый словарь в мире | Vocabulary.

com

ПЕРЕЙТИ К СОДЕРЖАНИЮ

0. гармонический закон закон, утверждающий, что отношение квадрата периода обращения (в годах) к кубу оси орбиты (в астрономических единицах) одинаково для всех планет

1. гармонически по отношению к гармонии

2. гармонические, включающие или характеризующиеся гармонией

3. среднее гармоническое среднее n чисел, выраженное как обратное значение среднего арифметического обратных чисел

4. гармоника небольшой прямоугольный инструмент, в который вдувается воздух

5. 67″>

   гармонично гармонично

6. гармонические, включающие или характеризующиеся гармонией

7. гармонизируемый, способный быть гармоничным или последовательным

8. гармоники изучение музыкального звука

9. термоэмиссионный клапан электронное устройство, состоящее из системы электродов, расположенных в вакуумированной стеклянной или металлической оболочке

10. герметично воздухонепроницаемым способом

11. гармонический анализ анализ периодической функции в виде суммы простых синусоидальных составляющих

12. 24″>

    гармоническое движение Периодическое движение, при котором смещение либо симметрично относительно точки, либо является суммой таких движений

13. гормональные или связанные с гормонами или вызванные ими

14. отшельнический, характеризующийся аскетическим уединением

15. гармоничные, демонстрирующие эквивалентность или соответствие между составляющими

16. Рамон-и-Кахаль Испанский гистолог, известный своими работами по строению нервной системы (1852-1934)

17. гармония совместимость во мнениях и поступках

18. очаровательно в очаровательной манере

19. 8″>

    термоядерное оружие, использующее ядерное оружие, основанное на синтезе, в отличие от деления

Третий закон Кеплера: движение планет Солнечной системы

Третий закон Кеплера раскрыл тайны движения в нашей Солнечной системе. (Изображение предоставлено: Getty Images)

Третий закон Кеплера — последняя революционная теорема немецкого астронома Иоганна Кеплера, объясняющая орбиты планет вокруг Солнца.

До того, как Кеплер изложил свои законы движения планет в начале 17 века, знания человечества о Солнечной системе и за ее пределами находились в зачаточном состоянии и в значительной степени оставались загадкой. Во времена Кеплера считалось, что Земля является центром Солнечной системы и, возможно, самой Вселенной.

Даже более точные гелиоцентрические модели Солнечной системы, в которых Солнце помещалось в их центр, были неполными, предполагая, что планеты движутся по аккуратным кругам вокруг своих звезд.

Связанный: Планеты Солнечной системы: Орден 8 (или 9) планет

Законы Кеплера вместо этого немного сдвигают звезду из центра этой модели в фокусную точку, сглаживая орбиты планет, и предлагают что эти планетарные тела движутся со скоростями, которые варьируются в зависимости от близости к их звезде.

Иоганн Кеплер

Первые семена законов Кеплера были посажены до его рождения в 1571 году в Вольном имперском городе Вайль-дер-Штадт, который сейчас является частью Штутгартского региона в немецкой земле Баден-Вюртемберг отцу Генриху Кеплеру и матери Катарина Гульденманн.

Они предшествовали его наблюдению Великой кометы в 1577 году, что воспитало в молодом человеке увлечение астрономией, которое продлится всю его жизнь. Или его наблюдение за лунным затмением в 1580 году, которое укрепило эту озабоченность.

Более знаменательное событие для Кеплера произошло в 1543 году, еще до его рождения, когда Николай Коперник опубликовал свою теорию о вращении Земли вокруг Солнца в книге «Об обращениях небесных сфер».

Эта теория зажжет крупную научную революцию  , метко названную революцией Коперника. Кеплер и другие в конечном итоге оседлали эту волну и, опираясь на работу Коперника, опровергли геоцентрические модели, предполагавшие, что Солнце и другие тела Солнечной системы вращаются вокруг Земли.

Иоганн Кеплер был немецким астрономом и математиком, родившимся в 1571 году. (Изображение предоставлено Getty Images) известный астроном Тихо Браге.

Браге считался в то время автором самых точных наблюдений в астрономии, и он видел потенциал исследований Кеплера. Это не означало, что он полностью доверял своему новому помощнику.

Кеплеру была представлена ​​только часть планетарных данных Браге, чтобы он не затмил своего нового наставника. Этот страх перед потенциалом Кеплера вполне мог побудить Браге поставить перед ним задачу лучше понять орбиту Марса . Пока Кеплер работал над этой проблемой, Браге приступил к совершенствованию собственной геоцентрической модели Солнечной системы с Землей в ее центре.

Орбита Марса не только не соответствовала геоцентрической модели, но и была проблемой для ранних моделей Коперника, предполагавших, что орбиты планет представляют собой идеальные окружности.

Таким образом, Кеплер пришел к выводу, что орбиты планет не круговые, а представляют собой сплющенные круги или эллипсы.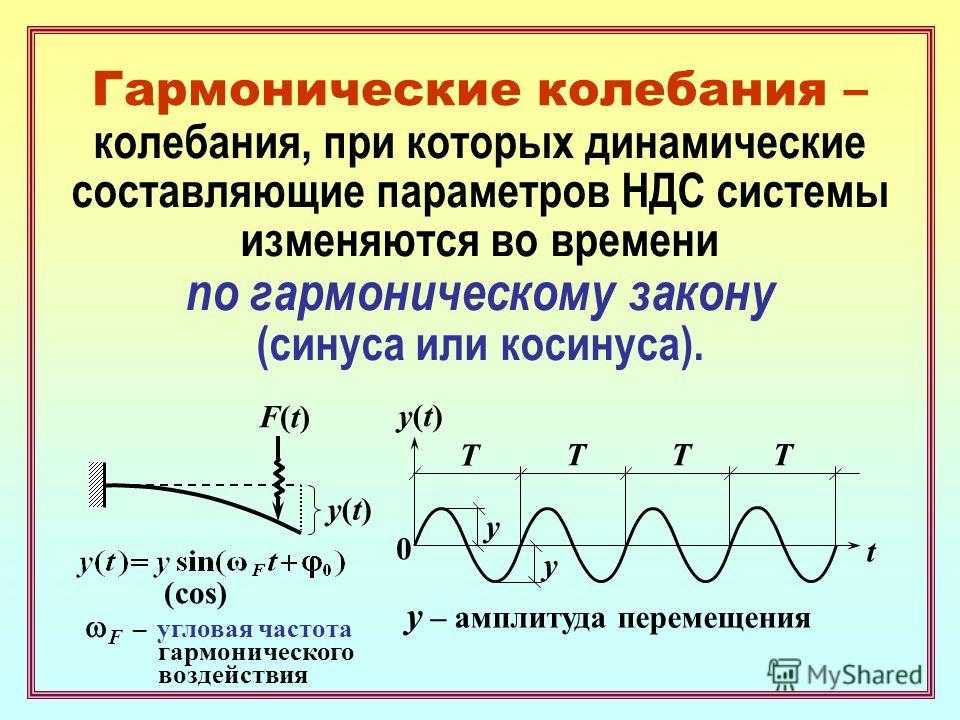 Поручив Кеплеру исследование орбиты Марса  — «самой эллиптической планетарной орбиты », — Браге невольно распутал свою собственную геоцентрическую модель еще до ее завершения и способствовал созданию законов, которые помогут закрепить гелиоцентризм как общепринятую модель Солнечной системы.

Схема геоцентрической траектории Марса. Исследование Кеплером орбиты Красной планеты привело к его первым двум планетарным законам. (Изображение предоставлено Иоганном Кеплером/PD-US)

Свойства первого и второго законов эллипсов

Один из ключей к пониманию кеплеровских законов движения планет лежит в свойствах эллипсов.

Первое свойство эллипсов состоит в том, что они определяются двумя фокусными точками — фокусами. Сумма расстояний до любой точки эллипса всегда постоянна. Для орбит планет это приводит к первому закону Кеплера: «Орбита планеты представляет собой эллипс с Солнцем в одном из двух фокусов».

Это означает, что планета и ее звезда вращаются вокруг общего центра масс, но поскольку масса звезды намного больше массы ее планеты, этот центр масс не просто ближе к звезде, он часто находится под ее поверхностью.

Второе свойство эллипса определяет отличие этой формы от круга. Эллипс — это сплющенный круг, эта «плоскостность» определяется как эксцентриситет и принимает значение от 0 до 1. Таким образом, идеальный круг можно рассматривать как эллипс с эксцентриситетом, равным 0. Парабола — это эллипс с эксцентриситетом из 1. 

Связанные: Что такое астрономия? Определение и история

Для второго закона Кеплера представьте планету на эллиптической орбите с линией, соединяющей ее с родительской звездой. По мере движения планеты линия вычерчивает область, которая всегда остается неизменной.

Период обращения планеты определяется путем измерения времени, прошедшего между пролетами Земли и Солнца. Как только период обращения известен, третий закон Кеплера применяется для определения среднего расстояния планеты от ее звезд. (Изображение предоставлено NASA Ames)

Однако из-за эксцентриситета, когда планета находится ближе к своей звезде, линия между ними становится короче. Это означает, что область, которую он отслеживает, более мелкая. Таким образом, чтобы нанести на карту ту же область за то же время, планета должна двигаться быстрее.

Итак, второй закон Кеплера говорит нам, что когда планета находится ближе всего к своей звезде — «точке, называемой перигелием», — она движется быстрее всего. С другой стороны, когда планета находится дальше всего от своей звезды — «в афелии», — планета движется медленнее всего.

Естественно сгруппировать эти два закона вместе, поскольку они родились из тщательно охраняемых наблюдений Браге и были опубликованы вместе в работе 1609 года Astronomia nova (Новая астрономия).

На формулировку третьего закона Кеплера, также известного как Закон Гармонии, ушло еще десять лет. Опубликовано в 1619 г., это раскрыло бы механику Солнечной системы в беспрецедентных деталях.

Гармонический третий закон

«Квадрат периода обращения планеты пропорционален кубу большой полуоси ее орбиты».

Это третий закон Кеплера в двух словах, и он вытекает из третьего физического свойства эллипсов, связанного с различными точками их осей.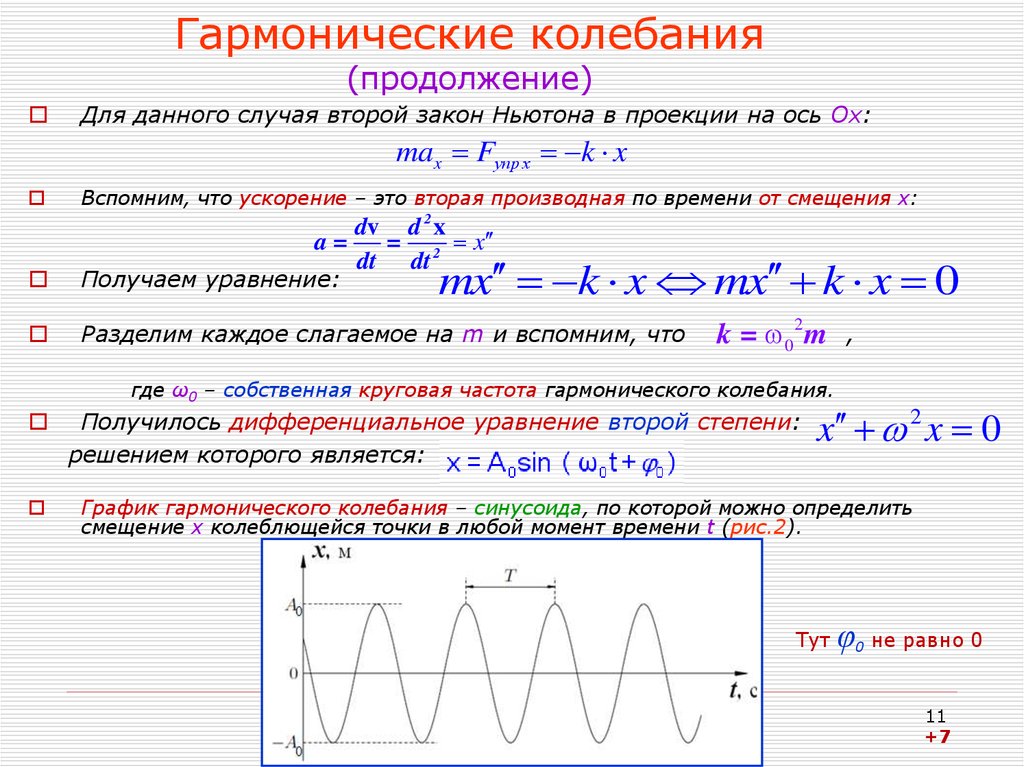 Самая длинная ось эллипса называется большой осью, а самая короткая ось называется малой осью. Половина большой оси называется большой полуосью.

Уравнение третьего закона Кеплера: P² = a³, поэтому квадрат периода орбиты планеты (P) равен размеру большой полуоси орбиты (a) в кубе, если он выражен в астрономических единицах.

На самом деле третий закон Кеплера сравнивает орбитальный период и радиус орбиты планеты с другими планетами. Таким образом, в отличие от первого и второго законов Кеплера, описывающих характеристики движения одной планеты, третий закон астронома сравнивает движение разных планет и вычисляет гармонии планет.

Это сравнение принимает форму отношения квадратов периодов (T²) к кубам их средних расстояний от солнца (R³), обнаружив, что оно одинаково для каждой из планет.

Благодаря этому закону, если мы знаем расстояние планеты от ее звезды, мы можем вычислить период ее обращения и наоборот. Поскольку расстояние между Землей и Солнцем (1 а. е.) составляет около 92 960 000 миль (149 600 000 километров), а один земной год составляет 365 дней, расстояние и период обращения других планет можно рассчитать, если известна только одна переменная.

Для Солнечной системы это дает нам точную картину обращения каждой планеты вокруг Солнца.

По мере увеличения расстояния планеты от Солнца время, необходимое им для обращения вокруг Солнца, быстро увеличивается.

Например, Меркурий — ближайшая к Солнцу планета — совершает полный оборот за 88 дней. Третья планета от Солнца, Земля, совершает оборот вокруг Солнца примерно за 365 дней. А Сатурн , шестая планета Солнечной системы от своей звезды, занимает 10 759. Конечно, Гармонический Закон говорит нам не только об орбитах планет.

Использование третьего закона Кеплера

В третьем законе Кеплера вы можете заметить одну вещь: в нем не упоминается масса объекта. Тем не менее, благодаря применению ньютоновских законов гравитации , физики пришли к более обобщенной форме уравнения.

Связанный: Что такое квантовая гравитация?

Эту обобщенную форму уравнения третьего закона можно использовать для нахождения масс тел, входящих в описываемую систему. При заданной массе 1 (m1) и массе 2 (m2) массы двух тел, m1, описывающих звезду, обычно настолько значительно больше, чем m2, что массой вращающегося тела можно пренебречь.

Имея это в виду, Гармонический закон был успешно использован для расчета масс планет в нашей Солнечной системе с точными массами и средними плотностями, найденными для Марса, Юпитера, Сатурна, Урана и Нептуна .

Это выходит за рамки планет и звезд и может применяться к планетам и их лунам и даже к искусственным спутникам, размещенным на орбите вокруг них.

Недавнее размещение искусственных спутников вокруг Венеры позволило точно определить массу и среднюю плотность Венеры. Кроме того, общая масса системы Плутон-Харон была определена с использованием гармонического закона.

Астрономы успешно использовали третий закон для измерения высокоэллиптических орбит комет вокруг Солнца.

Но третий закон Кеплера полезен не только в Солнечной системе.

Третий закон Кеплера за пределами Солнечной системы

Астрономы открыли более 4000 планет за пределами Солнечной системы и благодаря законам Кеплера могут рассчитать их орбиты и массы.

Поскольку другие звезды имеют массу, отличную от массы Солнца, третий закон Кеплера подвергается небольшой корректировке для расчета масс их планет. Для экзопланет , формула изменена, чтобы учесть изменение массы звезды по сравнению с нашим Солнцем. Поэтому астрономы используют R = (T² x Ms)¹/3, где Ms — масса звезды по отношению к массе нашего Солнца, для расчета массы экзопланеты.

Художественная концептуальная иллюстрация экзопланеты 55 Cancri e, вращающейся вокруг двойной звездной системы. Третий закон Кеплера сыграл жизненно важную роль в исследовании таких звездных систем. (Изображение предоставлено NASA/JPL-Caltech)

Третий закон Кеплера в сочетании со вторым законом позволил нам определить массы звезд в двойных системах, что жизненно важно для понимания как структуры, так и эволюции звезд.

Для этого астрономы используют бинарную функцию масс, которая выводится из третьего закона Кеплера и того факта, что тела вращаются вокруг общего центра тяжести. При рассмотрении звезд и планет это намного ближе, чем звезда, из-за гораздо меньшей массы планеты. Однако для двойных звезд мы не можем делать те же предположения и не можем просто игнорировать m2, потому что в этих случаях оно гораздо ближе к m1. К счастью, для двойных звезд, если астрономы знают период звезд (T) и их среднее расстояние (a), они все же могут вычислить сумму масс двух звезд.

Это означает, что Закон Гармонии теперь используется в планетарных системах, сильно отличающихся от нашей. Системы, о которых Кеплер едва ли мог мечтать, когда он начинал с Великой кометы в 16 веке.

Иоганн Кеплер умер 15 ноября 1630 года.

Помимо его законов движения планет, его наследие живет в форме космических телескопов Кеплера, которые внесли жизненно важный вклад в открытие планет за пределами Солнечной системы и кратеров на и Луна, и Марс среди множества других вещей.

Конечно, ни одному астроному или ученому нельзя приписать наше понимание Вселенной. Самым большим пробелом в законах Кеплера был тот факт, что первоначальный астроном не мог объяснить силу, удерживающую планеты, взаимосвязью, которую он наблюдал.

Точно так же, как Кеплер построил на основе работы Коперника, Исаак Ньютон в конечном итоге пришел и использовал законы Кеплера для построения своей теории гравитации. И Альберт Эйнштейн в конечном итоге использовал эту работу для разработки своей общей теории относительности.

Весьма вероятно, что когда Ньютон знаменито сказал: «Если я и видел дальше, то потому, что стоял на плечах гигантов», он думал о Кеплере и его законах движения планет.

Additional resources

• Harmonies Of The World
• Johannes Kepler: And the New Astronomy (Oxford Portraits in Science)
• NASA : Законы движения планет Кеплера, описанные с использованием спутников Земли (открывается в новой вкладке)

Присоединяйтесь к нашим космическим форумам, чтобы продолжать обсуждать последние миссии, ночное небо и многое другое! А если у вас есть новость, исправление или комментарий, сообщите нам об этом по адресу: [email protected].

Роберт Ли – научный журналист из Великобритании, чьи статьи были опубликованы в журналах Physics World, New Scientist, Astronomy Magazine, All About Space, Newsweek и ZME Science. Он также пишет о научной коммуникации для Elsevier и European Journal of Physics. Роб имеет степень бакалавра наук в области физики и астрономии Открытого университета Великобритании.