Паронимы «гармонический» и «гармоничный» — значение и разница слов
Паронимы «гармонический» и «гармоничный» — значение и разница слов
- Словарь паронимов
- Г
- гармонический — гармоничный
Слова «гармонический» и «гармоничный» являются паронимами — созвучными и схожими в написании словами, но имеющими разное значение. Слова образуют паронимическую пару части речи имя прилагательное. Тип паронимов: полные. Объясним значение, покажем разницу слов на примерах.
ПечататьРазница в написании и ударении: гармони́ческий и гармони́чный.
гармонический
- Значение
- (спец.). Относящийся к тармонии; основанный на принципах гармонии.
- Примеры словосочетаний
- • в музыке — гармонический обертон, ряд, мажор, диссонанс;
• гармоническое построение, сопровождение;
• гармонические ноты, колебания, тоны;
• в математике — гармонический ряд, синтезатор, анализатор, баланс;
• гармоническое среднее деление;
• гармонические колебания. - Примеры предложений
- Я много понаделал всяких гармонических задач, гармонизируя сначала цифровые басы, потом мелодии и хоралы. (Н.Римский-Корсаков, «Летопись моей музыкальной жизни»)Разложение числа a на два слагаемых b и a — b называется гармоническим делением, или золотым сечением. («СЭС»)
гармоничный
- Значение
- Содержащий элементы гармонии; обладающий согласованностью, слаженностью, взаимным соответствием разных качеств предметов, явлений, частей целого.
- Примеры словосочетаний
- • гармоничный голос, тембр;
• гармоничная мелодия, музыка;
• гармоничное пение, движение, расположение, построение;
• гармоничный человек;
• гармоничная личность, фигура. - Примеры предложений
- У бабушки доброта была гармоничная. (В.Вересаев, «В юные годы»)Ведь картина должна быть цельной и, несмотря на весь ужас изображённого, гармоничной …. (В.Ярошенко, «Люди и сокровища»)Легко, просто, без натуги, свободно звучал гармоничный, огромной силы и необыкновенной красоты бас. (Скиталец, «Кандалы»)
Гармонический ряд — ПриМат
Гармоническим называется ряд:$$\sum_{n=1}^{\infty}\frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n}+\cdots,$$ т.е. гармонический ряд состоит из членов, обратных числам натурального ряда.Проверим гармонический ряд на сходимость:Обобщённым гармоническим рядом называется ряд:$$\sum_{n=1}^{\infty}\frac{1}{n^{\alpha }}=1+\frac{1}{2^{\alpha }}+\frac{1}{3^{\alpha }}+\cdots +\frac{1}{n^{\alpha }}+\cdots$$ Обобщённый гармонический ряд расходится при [latex]\alpha\leq 1[/latex] и сходится при[latex]\alpha>1[/latex]
Лимит времени: 0
Информация
Тест на проверку знаний по данной теме.
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
| Место | Имя | Записано | Баллы | Результат |
|---|---|---|---|---|
| Таблица загружается | ||||
| Нет данных | ||||
- С ответом
- С отметкой о просмотре
Гармонический ряд — это… Что такое Гармонический ряд?
В математике гармонический ряд представляет собой сумму, составленную из бесконечного количества членов, обратных последовательным числам натурального ряда[1]:
- .
Ряд назван гармоническим, так как складывается из «гармоник»: -я гармоника, извлекаемая из скрипичной струны, — это основной тон, производимый струной длиной от длины исходной струны.[2]
Сумма первых n членов ряда
Отдельные члены ряда стремятся к нулю, но его сумма расходится. n-ной частичной суммой sn гармонического ряда называется n-ное гармоническое число:
Некоторые значения частичных сумм
Формула Эйлера
В 1740 году Л. Эйлером было получено асимптотическое выражение для суммы первых n членов ряда[1]:
- ,
где — постоянная Эйлера — Маскерони, а — натуральный логарифм.
При значение , следовательно, для больших n:
- — формула Эйлера для суммы первых n членов гармонического ряда.
| , (%) | |||
| 10 | 2,93 | 2,88 | 1,7 |
| 25 | 3,82 | 3,80 | 0,5 |
Более точная асимптотическая формула для частичной суммы гармонического ряда:
- , где — числа Бернулли.
Данный ряд расходится, однако ошибка вычислений по нему никогда не превышает половины первого отброшенного члена.
Теоретико-числовые свойства частичных сумм
Сходимость ряда
- при
Гармонический ряд расходится очень медленно (для того, чтобы частичная сумма превысила 100, необходимо около 10
Расходимость гармонического ряда можно продемонстрировать, сравнив его с телескопическим рядом:
- ,
частичная сумма которого, очевидно, равна:
- .
Доказательство Орема
Доказательство расходимости можно построить, группируя слагаемые следующим образом:
Последний ряд, очевидно, расходится. Это доказательство принадлежит средневековому учёному Николаю Орему (ок. 1350).
Альтернативное доказательство расходимости
Предположим, что гармонический ряд сходится к сумме :
Тогда, перегруппируя дроби, получим:
Вынесем из второй скобки :
Заменим вторую скобку на :
Перенесём в левую часть:
Подставим обратно вместо сумму ряда:
Это равенство, очевидно, неверно, так как единица больше одной второй, одна треть больше одной четвёртой, и так далее. Таким образом, наше предположение о сходимости ряда ошибочно, и ряд расходится.
- не равно 0, т.к. каждая из скобок положительная.
Это означает, что S — есть бесконечность и наши операции по добавлению или вычитанию ее из обоих сторон равенства недопустимы.
Частичные суммы
n-ая частичная сумма гармонического ряда,
называется n-ым гармоническим числом
Разница между n-м гармоническим числом и натуральным логарифмом n сходится к постоянной Эйлера-Маскерони.
Разница между различными гармоническими числами никогда не равна целому числу и никакое гармоническое число, кроме , не является целым[3].
Связанные ряды
Ряд Дирихле
Обобщенным гармоническим рядом (или рядом Дирихле) называют ряд[1][4]
- .
Обобщенный гармонический ряд расходится при α≤1 и сходится при α>1[4].
Сумма обобщённого гармонического ряда порядка α равна значению дзета-функции Римана:
Для чётных это значение явно выражается через число пи, например, , а уже для α=3 его значение аналитически неизвестно.
Знакопеременный ряд
Первые 14 частичных сумм знакочередующегося гармонического ряда (чёрные отрезки), показывающие сходимость к натуральному логарифму от 2 (красная линия).В отличие от гармонического ряда, у которого все слагаемые берутся со знаком «+», ряд
сходится по признаку Лейбница. Поэтому говорят, что такой ряд обладает условной сходимостью. Его сумма равна натуральному логарифму 2:
Эта формула — частный случай ряда Меркатора (англ.), ряда Тейлора для натурального логарифма.
Похожий ряд может быть получен из ряда Тейлора для арктангенса:
Это известно как ряд Лейбница.
Случайный гармонический ряд
Бирон Шмуланд из Университета Альберты рассмотрел[5][6] свойства случайного ряда
где sn независимые, одинаково распределённые случайные величины, которые принимают значения +1 и −1 с одинаковой вероятностью ½. Показано, что этот ряд сходится с вероятностью 1, и сумма ряда есть случайная величина с интересными свойствами. Например, функция плотности вероятности, вычисленная в точках +2 или −2 имеет значение 0,124 999 999 999 999 999 999 999 999 999 999 999 999 999 7642 …, отличаясь от на менее чем 10−42. Статья Шмуланда объясняет, почему эта величина близка, но не равна 1/8.
«Истончённый» гармонический ряд
- Ряд Кемпнера (англ.)
Если рассмотреть гармонический ряд, в котором оставлены только слагаемые, знаменатели которых не содержат цифры 9, то окажется, что оставшаяся сумма сходится к числу <80[7]. Более того, доказано, что если оставить слагаемые, не содержащие любой заранее выбранной последовательности цифр, то полученный ряд будет сходиться. Однако из этого будет ошибочно заключать о сходимости исходного гармонического ряда, т.к. с ростом разрядов в числе n, все меньше слагаемых берется для суммы «истонченного» ряда. Т.е. в конечном счете мы отбрасываем подавляющее большинство членов образующих сумму гармонического ряда, чтобы не превзойти ограничивающую сверху геометрическую прогрессию.
Примечания
- ↑ 1 2 3 Математический энциклопедический словарь. / Гл. ред. Ю. В. Прохоров; Ред. кол.: С. И. Адян, Н. С. Бахвалов, В. И. Битюцков и др. — М.: Сов. энциклопедия, 1988. — 847 с. стр. 139.
- ↑ Р.Грэхэм, Д.Кнут, О.Паташник Конкретная математика. Основание информатики — М.: Мир; БИНОМ. Лаборатория знаний, 2006. — стр. 47. — С. 703 ISBN 503003773X
- ↑ Harmonic Number — from Wolfram MathWorld
- ↑ 1 2 Справочник по математике для инженеров и учащихся втузов. Бронштейн И. Н., Семендяев К. А. М.: Наука. Главная редакция физико-математической литературы, 1981, 718 с.
- ↑ «Random Harmonic Series», American Mathematical Monthly 110, 407—416, May 2003
- ↑ Schmuland’s preprint of Random Harmonic Series
- ↑ Nick’s Mathematical Puzzles: Solution 72
Гармонический ряд — ПриМат
Гармоническим называется ряд:$$\sum_{n=1}^{\infty}\frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n}+\cdots,$$ т.е. гармонический ряд состоит из членов, обратных числам натурального ряда.Проверим гармонический ряд на сходимость:Общий член гармонического ряда стремится к 0.$$\lim_{n\rightarrow \infty }\frac{1}{n}=0$$ Это показывает, что необходимое условие сходимости ряда выполняется. Для доказательства сходимости гармонического ряда будем использовать критерий Коши. По критерию Коши для того чтобы ряд сходился необходимо и достаточно чтобы:$$\forall \varepsilon >0, \exists N_{\varepsilon },\forall n>N_{\varepsilon },\forall p > 0:\left | \frac{1}{n+1}+\frac{1}{n+2}+\cdots +\frac{1}{n+p} \right |$$$$>\left | \frac{1}{2n}+\frac{1}{2n}+\cdots +\frac{1}{2n} \right |=\frac{1}{2}=\varepsilon$$ Из этого следует что гармонический ряд не удовлетворяет критерию Коши. Иначе говоря гармонический ряд расходится.
Обобщённым гармоническим рядом называется ряд:$$\sum_{n=1}^{\infty}\frac{1}{n^{\alpha }}=1+\frac{1}{2^{\alpha }}+\frac{1}{3^{\alpha }}+\cdots +\frac{1}{n^{\alpha }}+\cdots$$ Обобщённый гармонический ряд расходится при [latex]\alpha\leq 1[/latex] и сходится при[latex]\alpha>1[/latex]
Лимит времени: 0
Информация
Тест на проверку знаний по данной теме.
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
| Место | Имя | Записано | Баллы | Результат |
|---|---|---|---|---|
| Таблица загружается | ||||
| Нет данных | ||||
- С ответом
- С отметкой о просмотре
Обобщённый гармонический ряд — ПриМат
Обобщённым гармоническим рядом называют ряд:$$\sum_{n=1}^{\infty }\frac{1}{n^{\alpha}}=1+\frac{1}{2^{\alpha}}+\frac{1}{3^{\alpha}}+\cdots +\frac{1}{n^{\alpha}}+\cdots $$
$$\sum_{n=1}^{\infty }\frac{1}{n^{\alpha }},$$ где [latex]\alpha>0[/latex]. При [latex]\alpha=1[/latex] получаем гармонический ряд, а он как известно расходится.При [latex]0
Теперь рассмотрим случай [latex]\alpha>1[/latex]. Выберем такое натуральное [latex]m[/latex], что [latex]n1[/latex] имеем [latex]S_{n}(\alpha)\leq \frac{1}{1-2^{1-\alpha}}[/latex], т.е. последовательность частичных сумм ограниченна сверху, и по теореме о сходимости рядов с неотрицательными членами ряд сходится при [latex]\alpha>1[/latex].
Лимит времени: 0
Информация
Тест на проверку знаний по данной теме.
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
Правильных ответов: 0 из 2
Ваше время:
Время вышло
Вы набрали 0 из 0 баллов (0)
Рубрики
- Математический анализ 0%
- С ответом
- С отметкой о просмотре
Гармонический ряд Википедия
Гармони́ческий ряд — сумма, составленная из бесконечного количества членов, обратных последовательным числам натурального ряда:
- ∑ k = 1 ∞ 1 k = 1 + 1 2 + 1 3 + 1 4 + ⋯ + 1 k + ⋯ {\displaystyle \sum _{k=1}^{\mathcal {\infty }}{\frac {1}{k}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+\cdots +{\frac {1}{k}}+\cdots } .
Ряд назван гармоническим, так как складывается из «гармоник»: k {\displaystyle k} -я гармоника, извлекаемая из скрипичной струны, — это основной тон, производимый струной длиной 1 k {\displaystyle {\frac {1}{k}}} от длины исходной струны[1]. Кроме того, каждый член ряда, начиная со второго, представляет собой среднее гармоническое двух соседних членов.
Суммы первых n членов ряда (частичные суммы)[ | ]
Отдельные члены ряда стремятся к нулю, но его сумма расходится. Частичная сумма n первых членов гармонического ряда называется n-м гармоническим числом:
- H n = ∑ k = 1 n 1 k = 1 + 1 2 + 1 3 + 1 4 + ⋯ + 1 n {\displaystyle H_{n}=\sum _{k=1}^{n}{\frac {1}{k}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+\cdots +{\frac {1}{n}}}
Разница между n {\displaystyle n}
Числовой ряд. Необходимый признак сходимости
204
1.1. Числовой ряд и его сумма
Определение 1. Пусть дана числовая последовательность  .
Образуем выражение
.
Образуем выражение
 (1)
(1)
которое
называется числовым
рядом. Числа  называютсячленами
ряда,
а выражение
называютсячленами
ряда,
а выражение 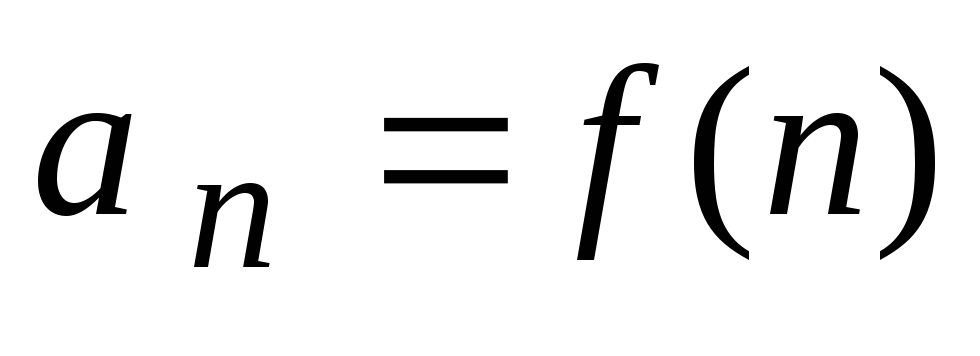 общим
членом ряда.
общим
членом ряда.
Пример
1. Найти общий член ряда 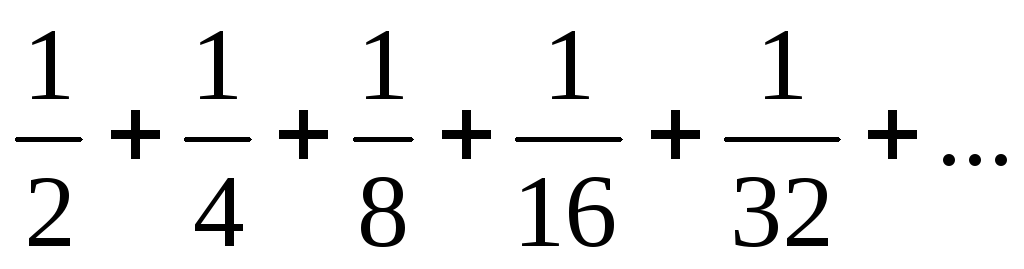 .
.
При  ,
,
при  ,
,
при 
Нетрудно
заметить, что общий член ряда  .
.
Поэтому искомый ряд можно записать следующим образом
 .
.
Построим из членов ряда (1) последовательность таким образом:
 ;
;
 ;
;
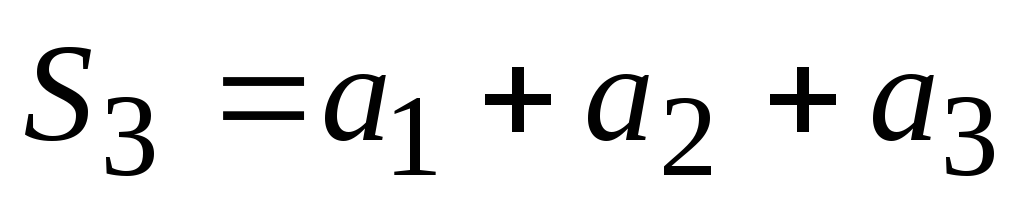 ;
;
…
 .
.
Каждый член этой последовательности представляет собой сумму соот-ветствующего числа первых членов числового ряда.
Определение 2. Сумма первых п членов ряда (1) называется n-ой частичной суммой числового ряда.
Определение
3. Числовой ряд  называетсясходящимся,
если
называетсясходящимся,
если 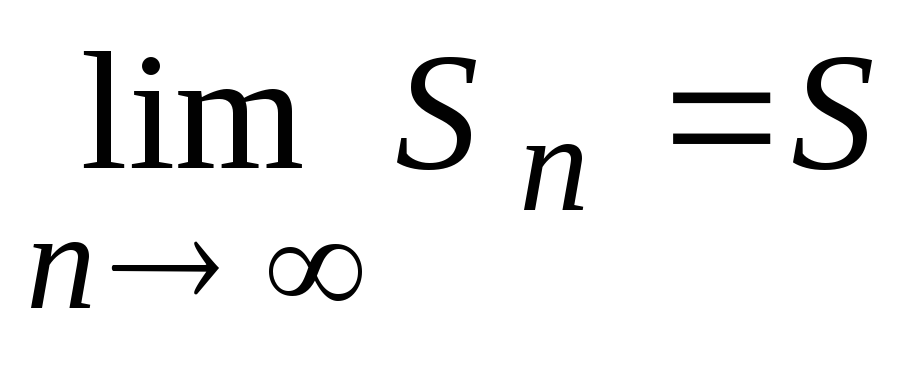 ,
где число
,
где число называетсясуммой
ряда,
и пишут
называетсясуммой
ряда,
и пишут 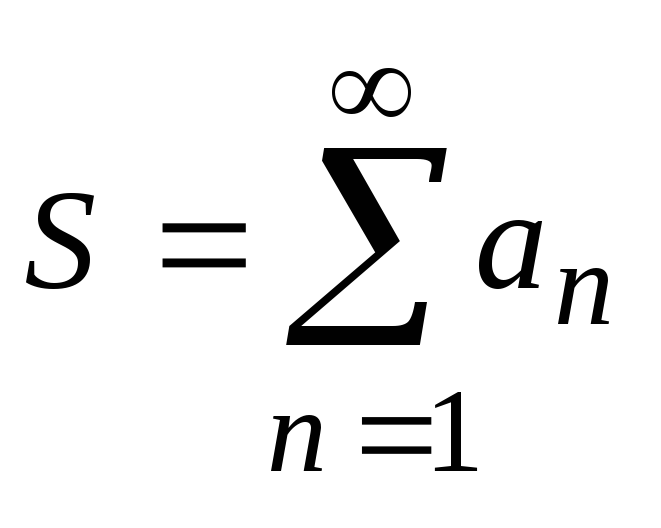 . Если
. Если
предел частичных сумм бесконечен или не существует, то ряд называется расходящимся.
Пример
2. Проверить
на сходимость ряд  .
.
Для
того, чтобы вычислить n-ю
частичную сумму  представим общий член
представим общий член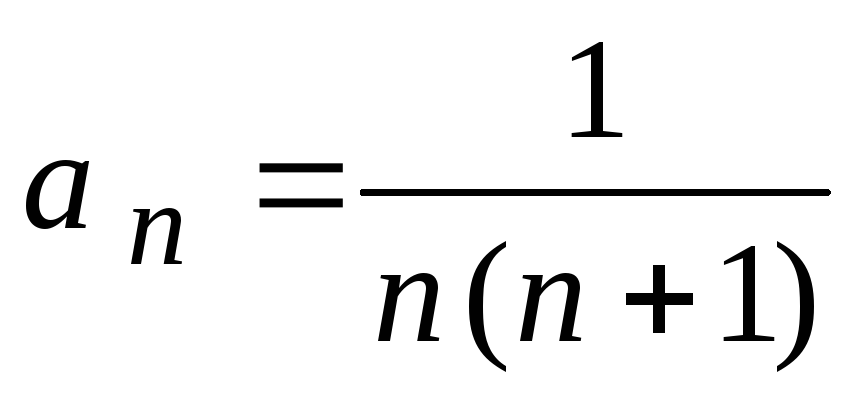 ряда
ряда в виде суммы простейших дробей
в виде суммы простейших дробей

Сравнивая коэффициенты при одинаковых степенях n, получим систему линейных алгебраических уравнений относительно неизвестных коэффици-ентов А и В

Отсюда
находим, что  ,
а
,
а .
.
Следовательно,
общий член ряда имеет вид 
Тогда
частичную сумму 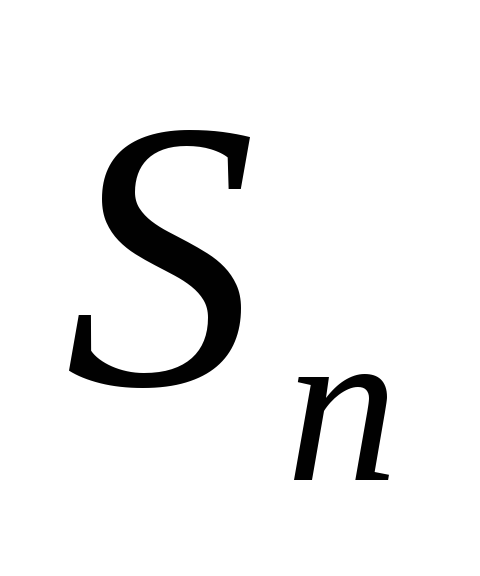 можно представить в виде
можно представить в виде
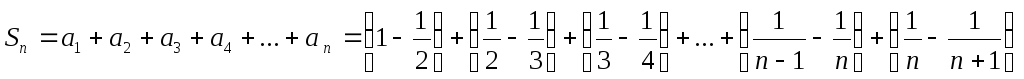 .
.
После раскрытия скобок и приведения подобных членов, она примет вид
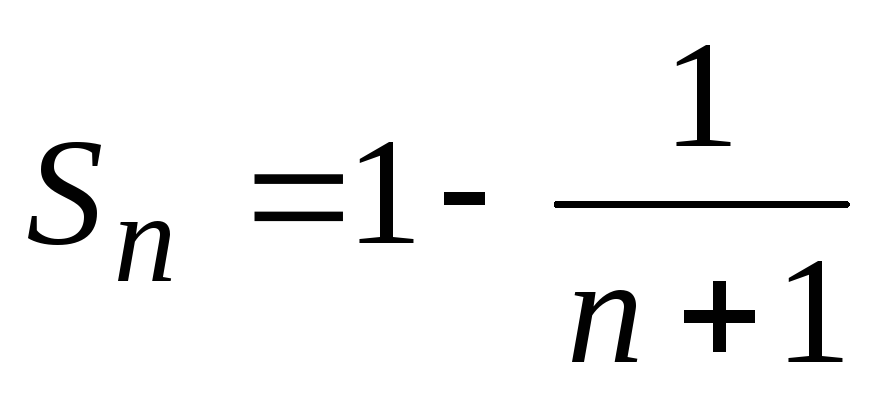 .
.
Вычислим сумму ряда

Так как предел равен конечному числу, то данный ряд сходится.
Пример
2. Проверить
на сходимость ряд 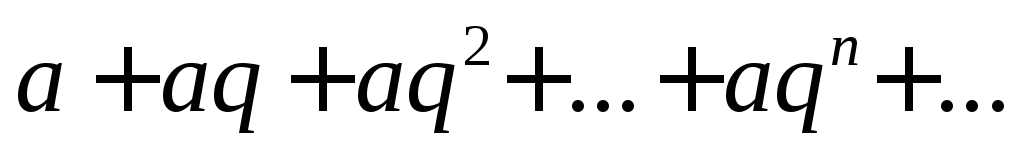
бесконечную геометрическую прогрессию.
Как
известно, сумма первых п членов геометрической прогрессии при q  1
равна
1
равна  .
.
Тогда имеем следующие случаи:
1.
Если 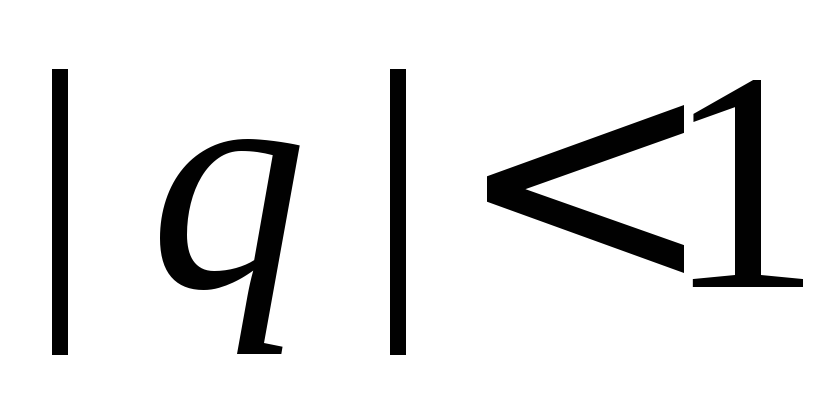 ,
то
,
то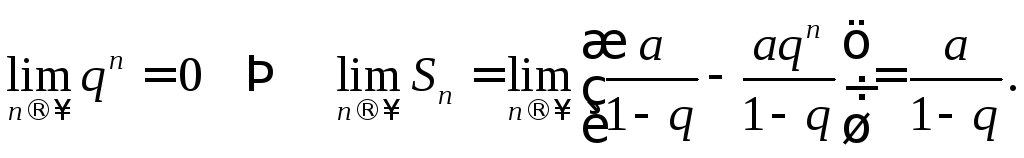
2.
Если 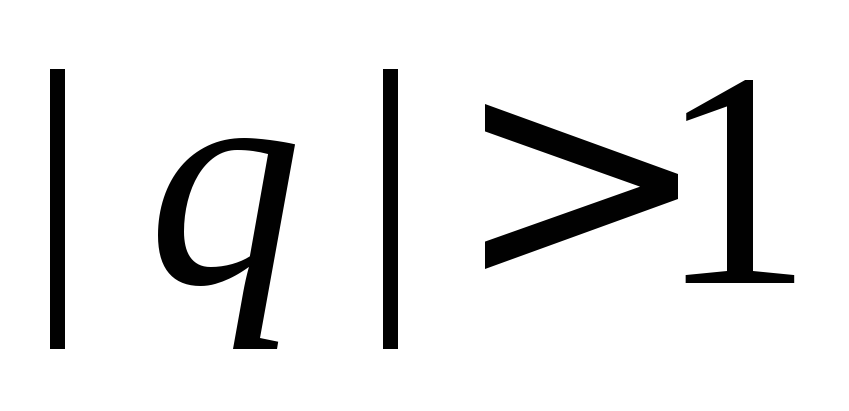 ,
то
,
то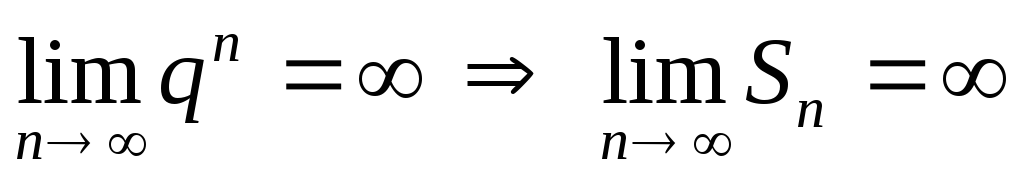 ,
т.е. ряд расходится.
,
т.е. ряд расходится.
3.
Если  ,
то ряд имеет вид
,
то ряд имеет вид и тогда
и тогда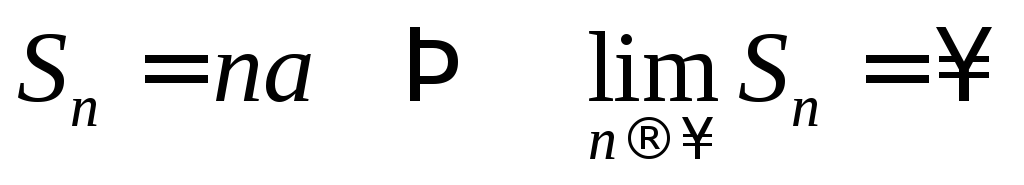 ,
т.е. ряд расходится.
,
т.е. ряд расходится.
4.
Если 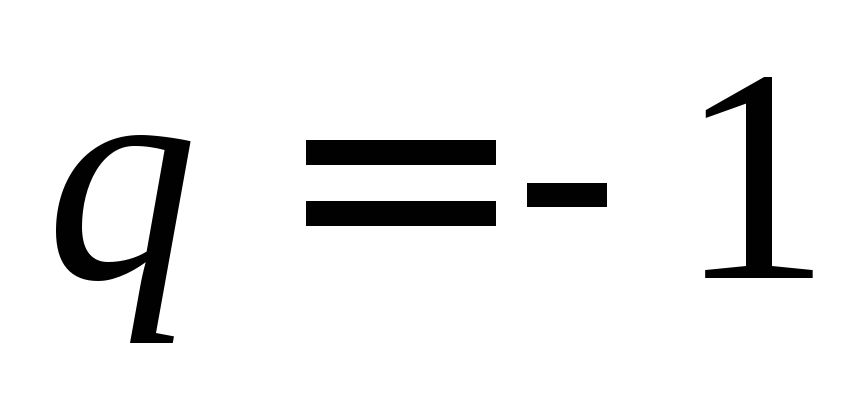 ,
то ряд имеет вид
,
то ряд имеет вид и тогда
и тогда ,
если частичная сумма имеет четное число
членов и
,
если частичная сумма имеет четное число
членов и ,
если нечётное число, т.е.
,
если нечётное число, т.е. не существует, следовательно, ряд
расходится.
не существует, следовательно, ряд
расходится.
Определение
4. Разность между суммой ряда S и частичной суммой 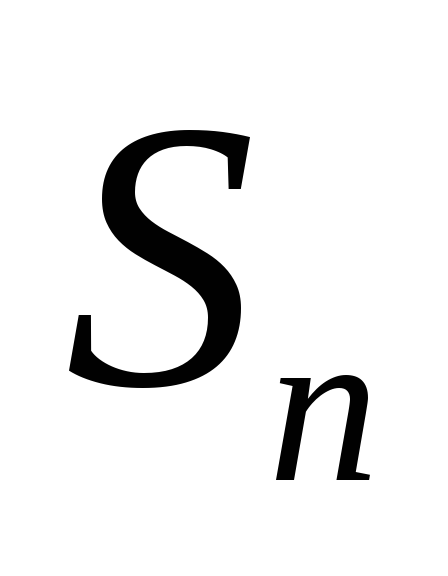 называетсяостатком
ряда и обозначается
называетсяостатком
ряда и обозначается 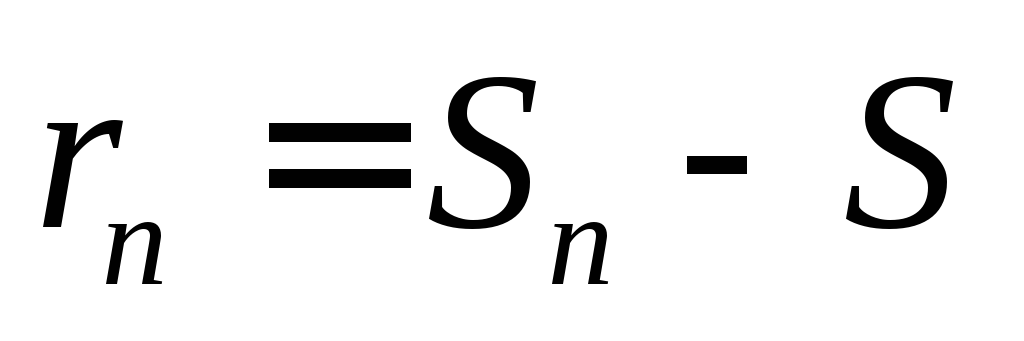 ,
т.е.
,
т.е. .
.
Так
как для сходящихся рядов  ,
то
,
то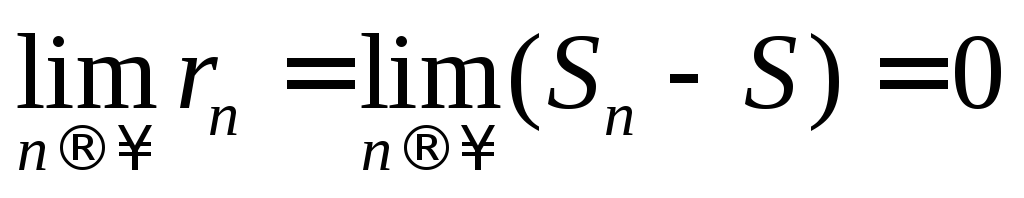 ,
,
т.е.  будет б.м.в. при
будет б.м.в. при .
Таким образом, значение
.
Таким образом, значение является приближенным значением суммы
ряда.
является приближенным значением суммы
ряда.
Из определения суммы ряда следуют свойства сходящихся рядов:
1. Если ряды  и
и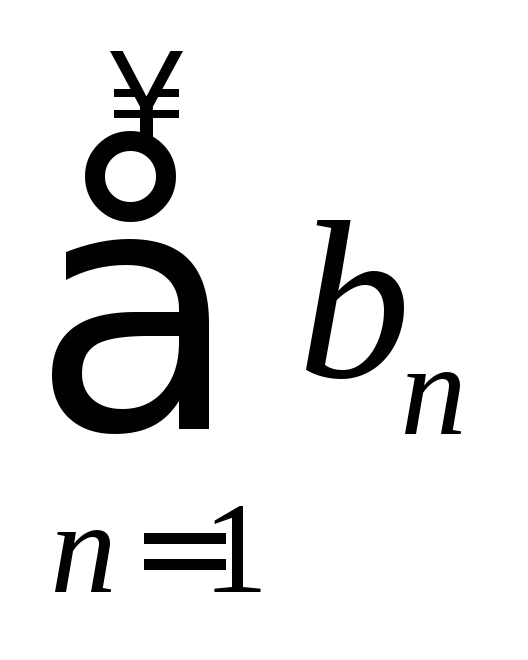 сходятся, т.е. имеют соответственно
суммыS и Q,
то сходится ряд
сходятся, т.е. имеют соответственно
суммыS и Q,
то сходится ряд  ,
где
,
где ,
а его сумма равнаA S + B Q.
,
а его сумма равнаA S + B Q.
2. Если
сходится
ряд  ,
то сходится и ряд, полученный из данного
,
то сходится и ряд, полученный из данного
ряда отбрасыванием или добавлением конечного числа членов. Верно и обратное.
1.2. Необходимый признак сходимости. Гармонический ряд
Теорема.
Если ряд 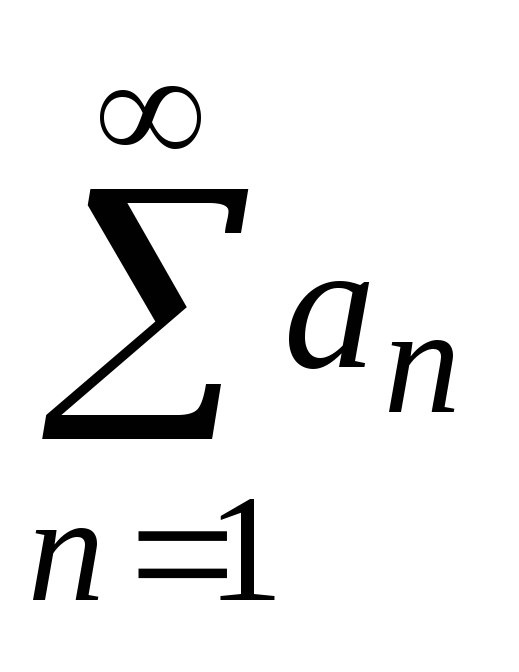 сходится,
то общий член ряда стремится
к
нулю
при
сходится,
то общий член ряда стремится
к
нулю
при 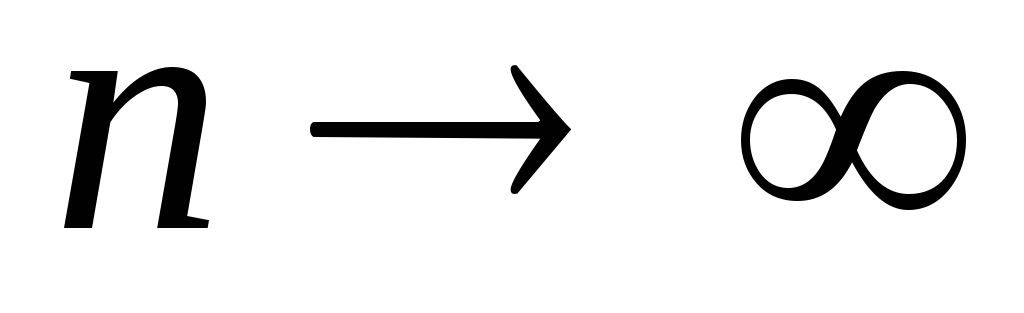 ,
т.е.
,
т.е. .
.
Действительно, имеем
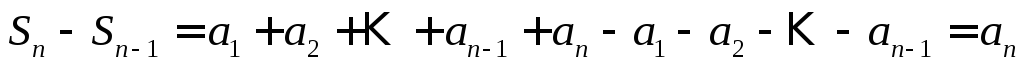 ,
,
тогда  , что
и требовалось доказать.
, что
и требовалось доказать.
Следствие. Если
же  ,
то ряд расходится. Обратное, вообще говоря, неверно, что
будет показано ниже.
,
то ряд расходится. Обратное, вообще говоря, неверно, что
будет показано ниже.
Определение
5. Ряд вида  называется гармоническим.
называется гармоническим.
Для
этого ряда выполняется необходимый
признак, так как  .
.
В то же время он является расходящимся. Покажем это
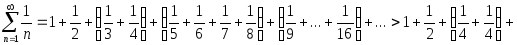

Таким образом, гармонический ряд расходится.
Тема 2 : Достаточные признаки сходимости рядов
с положительными членами
2.1. Признаки сравнения
Пусть даны два ряда с положительными членами:
 (1)
(1)
 (2)
(2) Признак
сравнения. Если для всех членов рядов (1) и (2), начиная
с некоторого номера, выполняется
неравенство 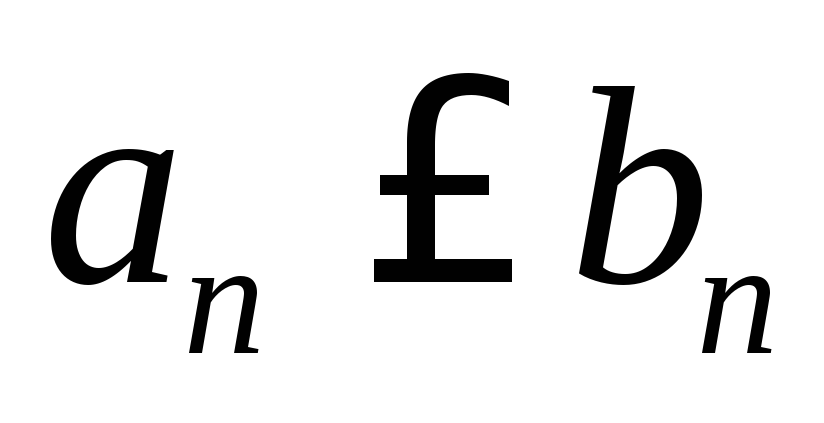 и ряд (2) сходится, то сходится и ряд (1).
Аналогично, если
и ряд (2) сходится, то сходится и ряд (1).
Аналогично, если и ряд (2) расходится, то расходится и
ряд (1).
и ряд (2) расходится, то расходится и
ряд (1).
Пусть 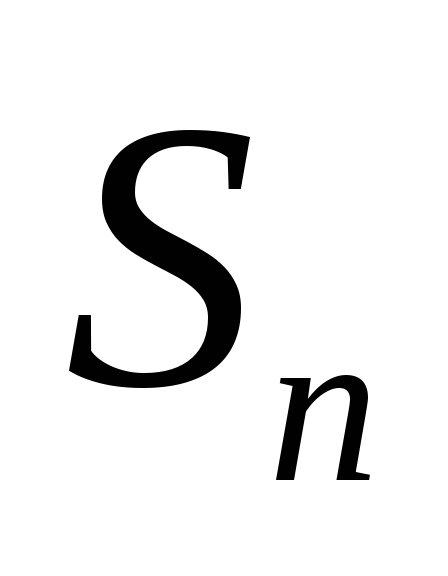 и
и
 .
.
Так
как  и ограничена, то
и ограничена, то ,
т.е. ряд (1) сходится.
,
т.е. ряд (1) сходится.
Аналогично доказывается и вторая часть признака.
Пример 3. Исследовать на сходимость ряд
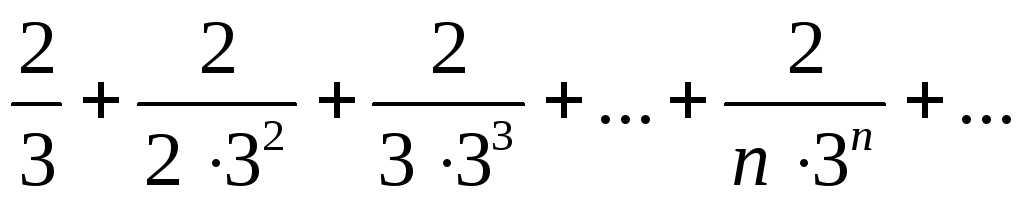 .
.
Сравним
с членами ряда 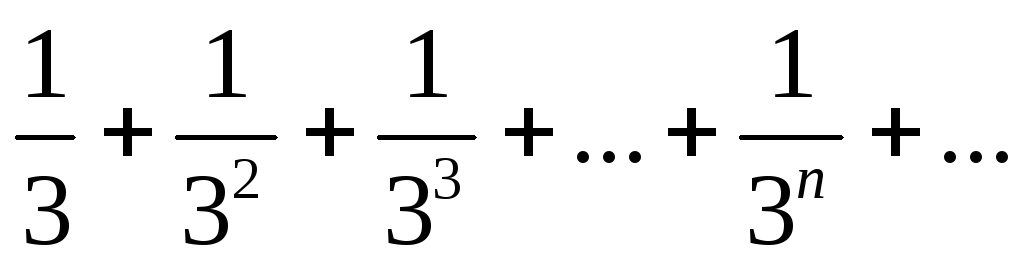 .
.
Начиная
с  ,
имеем
,
имеем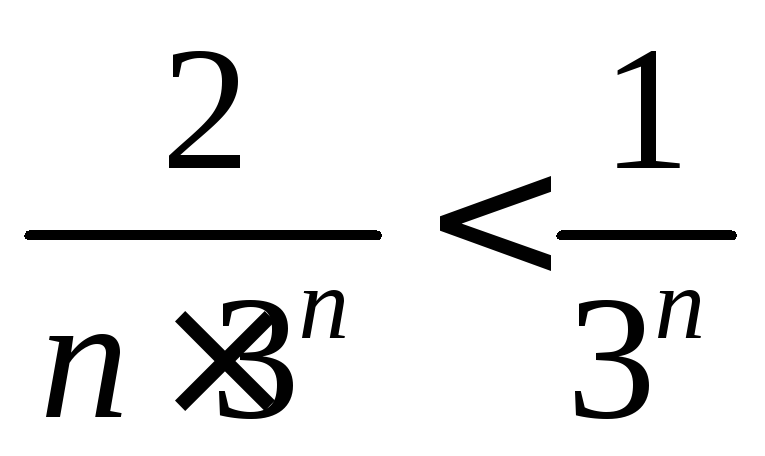 .
.
Так
как
ряд  сходится
сходится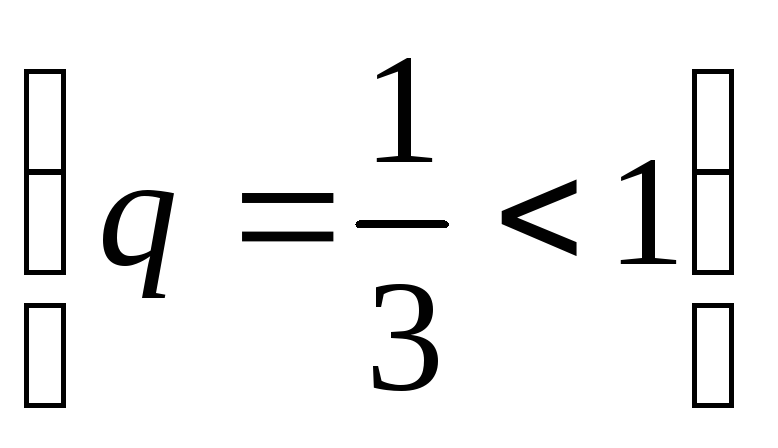 ,
то
данный
ряд
также
сходится.
,
то
данный
ряд
также
сходится.
На практике часто более удобно пользоваться так называемым предельным признаком сравнения, который вытекает из предыдущего.
Предельный
признак сравнения.
Если
для двух рядов (1-2) с положи-тельными
членами выполняется условие 
 ,
то
,
то
из сходимости ряда (1) следует сходимость ряда (2), а из расходимости ряда (1) следует расходимость ряда (2), т.е. ряды ведут себя одинаково.
Пример
4. Исследовать на сходимость ряд  .
.
В
качестве ряда для сравнения возьмем
гармонический ряд  ,
,
который является расходящимся.
Тогда

а, следовательно, наш ряд расходится.
Замечание. Часто для сравнения удобно использовать
так называемый обобщённый
гармонический ряд  ,
который, как будет показано ниже,
сходится при
,
который, как будет показано ниже,
сходится при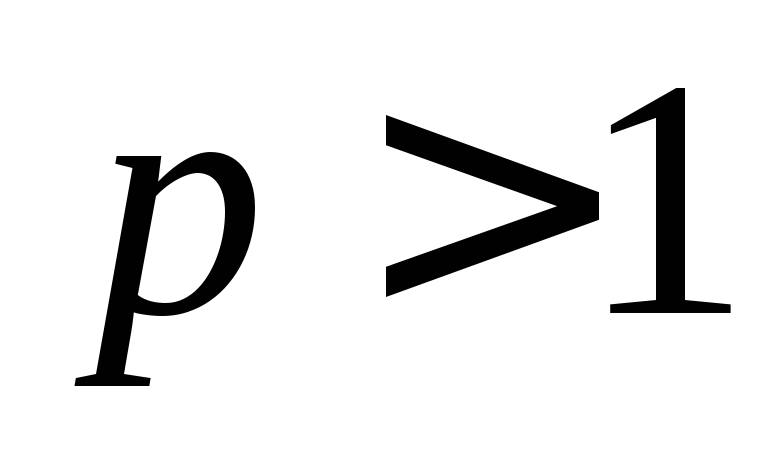 и расходится при
и расходится при .
.
Артикул: гармонический ряд
Ссылка: гармонический рядteoria.com использует файлы cookie. Используя наш сайт, вы соглашаетесь на использование файлов cookie. Прочтите нашу политику конфиденциальности для получения дополнительной информации. Закрыть
Когда мы слышим звук, издаваемый музыкальным инструментом, мы на самом деле слышим множество звуков, которые образуют гармонический ряд. В семнадцатом веке француз Жозеф Совер (1653-1716) и англичанин Томас Пиго (1657-1686) отметили, что струны колеблются по частям — феномен, который объясняет, почему одна струна производит такое множество звуков.
На видео ниже показан спектральный анализ C на две октавы ниже среднего C (C2):
Примечания:
- Мы написали ноты, соответствующие первым 16 гармоникам серии. Очевидно, что за этими первыми гармониками следует много гармоник.
- Первая гармоника или основная гармоника не обязательно является самой сильной гармоникой.
- Баланс между гармониками постоянно меняется. Это вкупе с огромным количеством гармоник объясняет трудности, с которыми мы сталкиваемся при синтезе звуков.
Важность гармонического ряда
Гармонический ряд определяет многие из наших интервалов. Ниже перечислены октава, пятая, четвертая, мажорная треть и минорная седьмая:
. 
Мы можем вычислить математическое соотношение (или размер), разделив частоты нот. Здесь мы используем частоту некоторых гармоник для вычисления размера интервалов:

| Интервал | Передаточное отношение | По гармоникам |
|---|---|---|
| Октава | 130/65 = 2 | 1 и 2 |
| Пятая | 195/130 = 1.5 | 2 и 3 |
| Четвертый | 260/195 = 1,33 | 3 и 4 |
| Большой третий | 325/260 = 1,25 | 4 и 5 |
| Малая седьмая | 455/260 = 1,75 | 4 и 7 |
Интересно, что мы можем вычислить значения, используя номера гармоник:
| Интервал | Передаточное отношение | По гармоникам |
|---|---|---|
| Октава | 2/1 = 2 | 1 и 2 |
| Пятая | 3/2 = 1.5 | 2 и 3 |
| Четвертый | 4/3 = 1,33 | 3 и 4 |
| Большой третий | 5/4 = 1,25 | 4 и 5 |
| Малая седьмая | 7/4 = 1,75 | 4 и 7 |
Расчет частот
Математические соотношения могут использоваться для расчета частоты нот.Из A 440 мы вычисляем частоту C #, E и G:
| А | C # (основная треть) | E (идеальный пятый) | G (второстепенная седьмая) |
| 440 | 440 х 1,25 = 550 | 440 х 1,5 = 660 | 440 x 1,75 = 770 |
Если разделить на математическое соотношение, мы получим убывающие интервалы.Здесь мы вычисляем частоту F, большая треть ниже A:

Чирикать Follow @teoriaEng ,
определение гармоничного по The Free Dictionary
Разве я не чувствую в своей душе, что являюсь частью этого огромного гармоничного целого? Его несогласованные столкновения поднимаются вверх в одном гармоничном тоне, который сливается с музыкой других миров, чтобы завершить оркестр Бога. Спенсерианская строфа с ее богатым разнообразием движения и его гармоничное завершение, надолго закрыли для меня «Чайльд Гарольд», и всякий раз, когда я находил в какой-либо книге стихотворение, в котором вторая строка не рифмулась с первой, я читал его неохотно или не читал вообще.«Как может быть полностью гармоничный союз без сочетания четырех в одном, а именно. Я сам спрошу его об этой книге жизни, но я хочу, чтобы вы сказали ему, что рассказали мне историю о потерянной Маргарет, и спросите если он позволит мне использовать это как романтическую нить, чтобы сплести истории из книги жизни в гармоничное целое ».« Ее сияющие локоны, разделенные на две части, опоясывают гармоничный контур ее белых и нежных щек. Однако люди не столь гармоничны в своих высказываниях и, возбужденные по любому поводу, доводят себя до состояния своего рода словесного пароксизма, во время которого проецируются все описания грубых звуков. из их уст, с поразительной силой и быстротой.Только со времени нашего последнего путешествия туда стены приобрели более серый оттенок, а кирпичная кладка приобрела более гармоничный медный оттенок; деревья выросли, и многие из них, которые тогда только протягивали свои тонкие ветви вдоль вершин живой изгороди, теперь были кустистыми, сильными и пышными, раскидывались под ветвями, набухшими от сока, огромными тенями цветущих плодов на благо путешественника … «Таким образом, Кедмон, помня все, что он слышал, и, так сказать, жевал жвачку, преобразовал то же самое в наиболее гармоничный стих; и, сладко повторяя то же самое, сделал своих хозяев, в свою очередь, своими слушателями.Мы такие гармоничные, а вы были кузнецом — не возражаете? »Затем, чтобы гармонии, естественно, будут следовать ритмы, и они должны подчиняться тем же правилам, поскольку нам не следует искать сложные системы измерения , или метры любого рода, а лучше выяснить, какие ритмы являются выражением мужественной и гармоничной жизни; и когда мы их найдем, мы адаптируем ступню и мелодию к словам, имеющим такой же дух, а не слова к Это можно было увидеть в линиях ее фигуры, в движениях рук, в плавности платья, в распущенных волосах, бессознательном, но гармоничном и столь же привлекательном для многих, как и сама красота.,4.6 Гармоники серии II: гармоники, интервалы и инструменты
Названия различных интервалов и то, как они написаны на нотоносце, в основном являются результатом долгой истории развития музыкальной нотации и теории. Но настоящие интервалы — то, как звучат ноты — не являются случайностью истории. Как и октавы, другие интервалы также производятся гармоническим рядом. Напомним, что частоты любых двух высот, разнесенных на октаву, имеют соотношение 2: 1.(См. «Гармонические серии I», чтобы рассмотреть это.) Любой другой интервал, о котором говорят музыканты, также можно описать как имеющий определенное соотношение частот. Чтобы найти эти отношения, посмотрите на гармонический ряд, записанный в общепринятых обозначениях.
Рисунок 4.53. Гармонический ряд, записанный в виде нот
Посмотрите на третью гармонику на рисунке 4.53. Его частота в три раза больше частоты первой гармоники (соотношение 3: 1). Помните, что частота второй гармоники в два раза больше частоты первой гармоники (соотношение 2: 1).Другими словами, есть две волны высшей C для каждой волны низшей C и три волны третьей гармоники G для каждой волны основной гармоники. Таким образом, соотношение частот второй гармоники к третьей составляет 2: 3. (Другими словами, две волны до на каждые три из G.) Из гармонического ряда, показанного выше, вы можете видеть, что интервал между этими двумя нотами составляет идеальную квинту. Соотношение частот всех идеальных квинт — 2: 3.
Упражнение 4.6.1. (Перейти к решению)
Интервал между четвертой и шестой гармониками (соотношение частот 4: 6) также является пятой. Вы можете это объяснить?
Какие еще гармоники имеют пятый интервал?
Какие гармоники имеют интервал четвертой?
Какое соотношение частот для интервала четверти?
Если вы внимательно изучили приведенный выше гармонический ряд, то, возможно, заметили, что некоторые ноты, написанные для одного и того же интервала, имеют разные соотношения частот.Например, интервал между седьмой и восьмой гармониками является основной секундой, как и интервалы между 8 и 9, между 9 и 10 и между 10 и 11. Но 7: 8, 8: 9, 9:10, и 10:11, хотя они довольно близки, не совсем то же самое. Фактически, современная западная музыка использует систему настройки равных темпераментов, которая делит октаву на двенадцать нот, которые находятся на равном расстоянии друг от друга. (У них действительно одинаковые соотношения частот, в отличие от полушагов в гармоническом ряду.) Положительный аспект равной темперации (и причина, по которой она используется) заключается в том, что инструмент будет одинаково настроен во всех тональностях.Отрицательный аспект заключается в том, что это означает, что все интервалы, кроме октав, немного расстроены относительно фактического гармонического ряда. Для получения дополнительной информации о равномерном темпераменте см. «Системы настройки». Интересно, что музыканты имеют тенденцию возвращаться к истинным гармоникам, когда это возможно (другими словами, когда легко настроить каждую ноту). Например, хоровая группа a capella или ансамбль духовых инструментов может петь или играть безупречные четверти и квинты, «сокращенные» мажорные трети и «расширенные» минорные трети, а также половину и целые шаги слегка различающихся размеров.
Гармонический ряд особенно важен для медных духовых инструментов. Пианист или ксилофонист получает только одну ноту от каждой клавиши. Струнный исполнитель, которому нужна другая нота из струны, крепко держит струну в другом месте. По сути, это делает вибрирующую струну новой длины с новой основой.
Но медник, не меняя длины инструмента, получает разные ноты, фактически играя на гармониках инструмента.Деревянные духовые инструменты тоже делают это, хотя и не в такой степени. Большинство деревянных духовых инструментов могут иметь две разные октавы с практически одинаковой аппликатурой; нижняя октава является основой столба воздуха внутри инструмента при этой аппликатуре. Верхняя октава — первая гармоника.
ЗаметкаВ некоторых деревянных духовых инструментах, таких как кларнет, верхняя «октава» может фактически быть третьей гармоникой, а не второй, что усложняет аппликатуру этих инструментов. Пожалуйста, см. «Стоячие волны» и «Духовые инструменты» для объяснения этого явления.
Это медные инструменты, которые позволяют извлекать разные ноты из трубки одинаковой длины. Звук духовых инструментов начинается с вибраций губ исполнителя. Вибрируя губами с разной скоростью, игрок может заставить звучать гармонику столба воздуха вместо основной. Таким образом, горностай может сыграть любую ноту в гармонической последовательности инструмента, которая находится в пределах диапазона музыканта. Сравните эти хорошо известные звуковые сигналы с гармоническим рядом выше.
Рисунок 4.54. Горн звонит
Несмотря на то, что горн ограничен тем, что может воспроизводить только одну гармоническую серию, он все же может воспроизводить многие хорошо известные мелодии.
На протяжении веков все медные духовые инструменты были бесклапанными. Духовой инструмент мог играть только ноты одного гармонического ряда. (Важным исключением был тромбон и его родственники, которые могут легко изменять свою длину и гармонический ряд с помощью слайда.) Верхние октавы ряда, где ноты расположены достаточно близко друг к другу, чтобы сыграть интересную мелодию, часто было трудно играть , и некоторые гармоники звучат совершенно не в гармонии с ушами, ожидающими такого же темперамента.Решение этих проблем, когда латунные клапаны были усовершенствованы, заключалось в добавлении к прибору нескольких клапанов; трех обычно достаточно. Каждый клапан открывает дополнительную длину трубки, что делает инструмент немного длиннее и делает доступным совершенно новую серию гармоник. Обычно один клапан дает гармонический ряд на полшага ниже, чем бесклапанный ввод; другой, на целую ступень ниже; а третий — на полторы ступеньки ниже. Клапаны также можно использовать в комбинации, что делает доступным еще больше гармонических последовательностей.Таким образом, духовой инструмент с клапаном может найти в удобной середине своего диапазона (его средний регистр ) комбинацию клапанов, которая даст достаточно настроенную версию для каждой ноты хроматической гаммы. (Подробнее об истории клапанной латуни см. В разделе «История валторны». Подробнее о том, как и почему создаются гармоники в духовых инструментах, см. «Стоячие волны и духовые инструменты»)
ЗаметкаТромбоны до сих пор используют слайд вместо клапанов, чтобы сделать их инструмент длиннее.Но основной принцип все тот же. В каждой «позиции» слайда инструмент получает новый гармонический ряд. Ноты между позициями не являются частью хроматической гаммы, поэтому они обычно используются только для специальных эффектов, таких как глиссандо (скользящие ноты).
Рисунок 4.55. Серии гармоник с перекрытием в духовых инструментах
Эти гармонические серии предназначены для медного инструмента, у которого есть основная гармоника «C», когда не используются никакие клапаны — например, труба C.Помните, что для каждой основной гармоники существует целый ряд гармоник, и любая нота может быть основной. Вам просто нужно найти латунную трубку подходящей длины. Таким образом, труба или туба могут получить один гармонический ряд без использования клапанов, другой на полшага ниже с использованием одного клапана, другой на целый ряд ниже с использованием другого клапана и т. К тому времени, когда будут использованы все комбинации клапанов, есть способ получить настроенную версию каждой ноты, которая им нужна.
Упражнение 4.6.2. (Перейти к решению)
Запишите ряд гармоник для прибора выше, когда и первый, и второй клапаны открыты. (Вы можете использовать этот PDF-файл, если вам нужна нотная бумага.) Какие новые ноты добавлены в средний диапазон инструмента? Какие-нибудь заметки все еще отсутствуют?
ЗаметкаВалторна имеет репутацию «сложного» инструмента для игры. Это тоже из-за гармонического ряда. Большинство медных духовых инструментов играют в первых нескольких октавах гармонического ряда, где ноты расположены дальше друг от друга, и требуется довольно большая разница во рту и губах (амбушюр, произносится как AHM-buh-sher), чтобы получить другую ноту.Диапазон валторны выше в гармоническом ряду, где ноты расположены ближе друг к другу. Таким образом, очень небольшие различия во рту и губах могут означать, что выходит неправильная гармония.
Игра гармоник на струнных
Струнные исполнители также используют гармоники, хотя и не так много, как медные. Гармоники на струнах имеют очень отличный тембр от обычных струнных звуков. Они дают более тихий, тонкий, более похожий на колокольчик тон и обычно используются как своего рода особый эффект, привлекающий ухо.
Обычно струнный исполнитель держит струну очень плотно. Это укорачивает длину колеблющейся части струны, фактически делая (временно) более короткую колеблющуюся струну, которая имеет свой собственный полный набор гармоник.
Чтобы «сыграть гармонику», вместо этого нужно очень, очень легко касаться струны. Длина строки не меняется. Вместо этого легкое прикосновение мешает всем вибрациям, у которых нет узла в этом месте.
Рисунок 4.56.Струнные гармоники
Более тонкий и тихий звук «играющих гармоник» вызван тем фактом, что большая часть гармонического ряда отсутствует в звуке, что, конечно, влияет на тембр. Легкое прикосновение к струне в большинстве мест приведет к отсутствию звука. Этот метод хорошо работает только в тех местах на струне, где основная гармоника (одна из более длинных и громких гармоник с нижним номером) имеет узел. Некоторые исполнители на струнах могут получить больше гармоник, удерживая струну в одном месте и слегка касаясь ее в другом месте, но это продвинутая техника.
,Гармоническая серия| 예문
사전> гармонический ряд 에 대한 예문гармонический ряд 아직 Кембриджский словарь 에 없습니다. 사용자 여러분 의 참여 를 기다 립니다
Добавление клапанов позволило играть низко на гармонике серии инструмента и при этом иметь полный набор нот.Википедия
에서 이 예문 은 Википедия 에서 온 출처. 당신 은 CC BY-SA 라이센스 보호 하에서 재사용 가능 합니다. Каждый раз, когда игрок приводит в движение струну, определенный набор частот резонирует на основе гармоники серии .Википедия
에서 이 예문 은 Википедия 에서 온 출처. 당신 은 CC BY-SA 라이센스 보호 하에서 재사용 가능 합니다. Другой вид мультифонизма может быть получен путем одновременного проигрывания двух соседних нот гармоники серии .Википедия
에서 이 예문 은 Википедия 에서 온 출처. 당신 은 CC BY-SA 라이센스 보호 하에서 재사용 가능 합니다. Закрытый цилиндр вибрирует только на нечетных элементах своей гармоники серии .Википедия
에서 이 예문 은 Википедия 에서 온 출처. 당신 은 CC BY-SA 라이센스 보호 하에서 재사용 가능 합니다. Соответствующая гармоника серия растет без ограничений, хотя и очень медленно, примерно приближаясь к функции натурального логарифма.Википедия
에서 이 예문 은 Википедия 에서 온 출처. 당신 은 CC BY-SA 라이센스 보호 하에서 재사용 가능 합니다. Любопытно, что в работе, столь богатой спектральным мышлением, это единственное слышимое присутствие естественной гармоники серии во всем произведении.Для прямоугольных объектов модальные частоты образуют отдельные гармоники серии на основе каждого из размеров. На нем играют палкой, которая может ударять по струне в разных положениях, создавая легкие вариации в содержании гармоники серии . На рисунке 4 представлено взвешивание гармоники серии в зависимости от относительного тона, а сумма весов нормализована.Из-за природы металлических звуков спектральные составляющие обычно не связаны с гармоникой серии . Это излучает интервалы только интонации естественной гармоники серии , часто описываемой как небесные, гармонические и согласные в других музыкальных практиках. Каждый раз, когда в большом цикле встречаются более низкие гармоники, они сопровождаются собственной гармоникой серии .То же самое верно для всех гармоник в цикле, достаточно низких, чтобы производить слышимую гармонику серии самостоятельно. Гармоника Серия , полученная из данной ноты, представляет собой заданный тон, состоящий из основного тона и тонов высших гармоник. Harmonic series , как правило, очень изменчивы, как и модели шума, основанные на заданной изменяющейся во времени спектральной огибающей.Игроки должны были смягчить своенравную интонацию естественной гармоники серии и отточить свою технику, чтобы соответствовать требованиям композиторов и разборчивых слушателей. В этом случае регулярные текстуры соответствуют звукам с гармонически связанными частотными частями, тогда как возрастающее отклонение от гармоники серии связано с увеличением неравномерности текстур.Это удлиняет колеблющийся столб воздуха, тем самым понижая основной тон и связанную с ним гармонику серии , создаваемую инструментом.Википедия
에서 이 예문 은 Википедия 에서 온 출처. 당신 은 CC BY-SA 라이센스 보호 하에서 재사용 가능 합니다. С точки зрения того, что мы слышим, каждая октава в гармонике серии делится на все более мелкие и более многочисленные интервалы.Википедия
에서 이 예문 은 Википедия 에서 온 출처. 당신 은 CC BY-SA 라이센스 보호 하에서 재사용 가능 합니다. Без клапанов доступны только примечания в пределах гармоники серии .Википедия
에서 이 예문 은 Википедия 에서 온 출처. 당신 은 CC BY-SA 라이센스 보호 하에서 재사용 가능 합니다.예문 에 나오는 어떤 견해 나 의견 Cambridge Dictionary 편찬자, Cambridge University Press, 교열 관 의 의견 을 표현 하는 것은 아닙니다.
гармонический ряд 단어 가 Cambridge Dictionary 에 아직 등재 되어 있지 않습니다. 등재 시키 겠습니까?
{{#сообщение}}{{message}}
{{/сообщение}} {{^ Сообщение}}일부 연설 을 선택 하고 정의 를 넣는 칸 에 입력 해서 제안 하기.
{{/сообщение}} 품사명사 의 선택, 동사, 등등. 형용사 부사 감탄사 명사 번호 접두사 접미사 동사
정의
보내세요 취소
,
