Гармонический осциллятор — это… Что такое Гармонический осциллятор?

У этого термина существуют и другие значения, см. Осциллятор.

Гармони́ческий осцилля́тор (в классической механике) — система, которая при смещении из положения равновесия испытывает действие возвращающей силы F, пропорциональной смещению x (согласно закону Гука):

где k — коэффициент жёсткости системы.

Если F — единственная сила, действующая на систему, то систему называют простым или консервативным гармоническим осциллятором. Свободные колебания такой системы представляют собой периодическое движение около положения равновесия (гармонические колебания). Частота и амплитуда при этом постоянны, причём частота не зависит от амплитуды.

Если имеется ещё и сила трения (затухание), пропорциональная скорости движения (вязкое трение), то такую систему называют затухающим или диссипативным осциллятором. Если трение не слишком велико, то система совершает почти периодическое движение — синусоидальные колебания с постоянной частотой и экспоненциально убывающей амплитудой. Частота свободных колебаний затухающего осциллятора оказывается несколько ниже, чем у аналогичного осциллятора без трения.

Если осциллятор предоставлен сам себе, то говорят, что он совершает свободные колебания. Если же присутствует внешняя сила (зависящая от времени), то говорят, что осциллятор испытывает вынужденные колебания.

Механическими примерами гармонического осциллятора являются математический маятник (с малыми углами отклонения), груз на пружине, торсионный маятник и акустические системы. Среди других аналогов гармонического осциллятора стоит выделить электрический гармонический осциллятор (см. LC-цепь).

Свободные колебания

Консервативный гармонический осциллятор

В качестве модели консервативного гармонического осциллятора возьмём груз массы m, закреплённый на пружине жёсткостью k.

Пусть x — смещение груза относительно положения равновесия. Тогда, согласно закону Гука, на него будет действовать возвращающая сила:

Используя второй закон Ньютона, запишем

Обозначая и заменяя ускорение a на вторую производную от координаты по времени напишем:

Это дифференциальное уравнение описывает поведение консервативного гармонического осциллятора. Коэффициент называют циклической частотой осциллятора. (Здесь имеется в виду круговая частота, измеряющаяся в радианах в секунду. Чтобы перевести её в частоту, выражающуюся в Герцах, надо разделить круговую частоту на )

Будем искать решение этого уравнения в виде:

Здесь A — амплитуда, ω — частота колебаний (пока не обязательно равная собственной частоте), φ — начальная фаза.

Подставляем в дифференциальное уравнение.

Амплитуда сокращается. Значит, она может иметь любое значение (в том числе и нулевое — это означает, что груз покоится в положении равновесия). На синус также можно сократить, так как равенство должно выполняться в любой момент времени t. Таким образом, остаётся условие на частоту колебаний:

Отрицательную частоту можно отбросить, так как произвол в выборе этого знака покрывается произволом выбора начальной фазы.

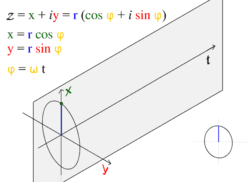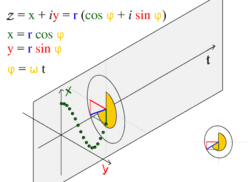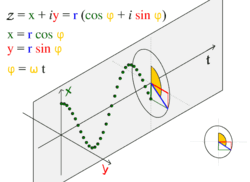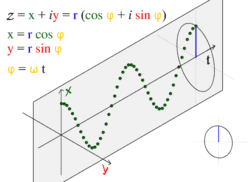движение по кругу и движение гармоническое

Общее решение уравнения записывается в виде:

где амплитуда A и начальная фаза φ — произвольные постоянные. Эта запись исчерпывает все решения дифференциального уравнения, так как позволяет удовлетворить любым начальным условиям (начальному положению груза и его начальной скорости).

Итого, консервативный гармонический осциллятор может совершать чисто гармонические колебания с частотой, равной его собственной частоте, с амплитудой любой величины и с произвольной начальной фазой.

Кинетическая энергия записывается в виде

и потенциальная энергия есть

тогда полная энергия имеет постоянное значение

Простое гармоническое движение

Простое гармоническое движение — это движение простого гармонического осциллятора, периодическое движение, которое не является ни вынужденным, ни затухающим. Тело в простом гармоническом движении подвергается воздействию единственной переменной силы, которая по модулю прямо пропорциональна смещению

x от положения равновесия и направлена в обратную сторону.

Это движение является периодическим: тело колеблется около положения равновесия по синусоидальному закону. Каждое последующее колебание такое же, как и предыдущее, и период, частота и амплитуда колебаний остаются постоянными. Если принять, что положение равновесия находится в точке с координатой, равной нулю, то смещение x тела от положения равновесия в любой момент времени даётся формулой:

где A — амплитуда колебаний, f — частота, φ — начальная фаза.

Частота движения определяется характерными свойствами системы (например, массой движущегося тела), в то время как амплитуда и начальная фаза определяются начальными условиями — перемещением и скоростью тела в момент начала колебаний. Кинетическая и потенциальная энергии системы также зависят от этих свойств и условий.

Простое гармоническое движение. На этой анимированной картинке по вертикальной оси отложена координата частицы (x в формуле), а по горизонтальной оси отложено время (t).

Простое гармоническое движение может быть математическими моделями различных видов движения, таких как колебание пружины. Другими случаями, которые могут приближённо рассматриваться как простое гармоническое движение, являются движение маятника и вибрации молекул.

Простое гармоническое движение является основой некоторых способов анализа более сложных видов движения. Одним из таких способов является способ, основанный на преобразовании Фурье, суть которого сводится к разложению более сложного вида движения в ряд простых гармонических движений.

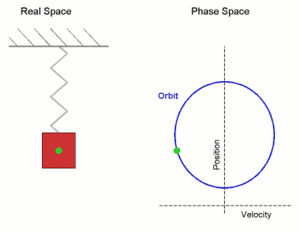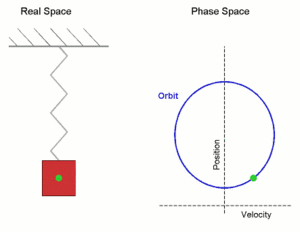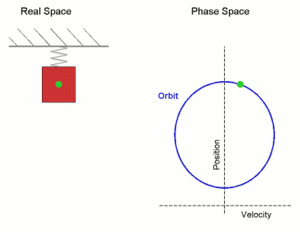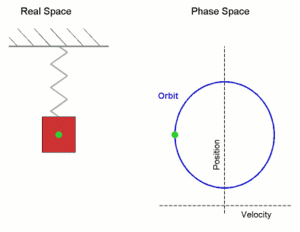Простое гармоническое движение, показанное одновременно в реальном пространстве и в фазовом пространстве. Здесь ось скорости и ось положения показаны иначе по сравнению с обычным изображением осей координат — это сделано для того, чтобы оба рисунка соответствовали друг другу. Real Space — реальное пространство; Phase Space — фазовое пространство; velocity — скорость; position — положение (позиция).

Типичным примером системы, в которой происходит простое гармоническое движение, является идеализированная система груз-пружина, в которой груз присоединён к пружине. Если пружина не сжата и не растянута, то на груз не действует никаких переменных сил, и груз находится в состоянии механического равновесия. Однако, если груз вывести из положения равновесия, пружина деформируется, и с её стороны на груз будет действовать сила, которая будет стремиться вернуть груз в положение равновесия. В случае системы груз-пружина такой силой является сила упругости пружины, которая подчиняется закону Гука:

где

F — возвращающая сила,

x — перемещение груза (деформация пружины),

k — коэффициент жёсткости пружины.

Любая система, в которой происходит простое гармоническое движение, обладает двумя ключевыми свойствами:

1. Когда система выведена из состояния равновесия, должна существовать возвращающая сила, стремящаяся вернуть систему в равновесие.
2. Возвращающая сила должна в точности или приближённо быть пропорциональна перемещению.

Система груз-пружина удовлетворяет обоим этим условиям.

Однажды смещённый груз подвергается действию возвращающей силы, ускоряющей его, и стремящейся вернуть в начальную точку, то есть, в положение равновесия. По мере того, как груз приближается к положению равновесия, возвращающая сила уменьшается и стремится к нулю. Однако в положении x = 0 груз обладает некоторым количеством движения (импульсом), приобретённым благодаря действию возвращающей силы. Поэтому груз проскакивает положение равновесия, начиная снова деформировать пружину (но уже в противоположном направлении). Возвращающая сила будет стремиться замедлить его, пока скорость не станет равной нулю; и сила вновь будет стремиться вернуть груз в положение равновесия.

Пока в системе нет потерь энергии, груз будет колебаться как описано выше; такое движение называется периодическим.

Дальнейший анализ покажет, что в случае системы груз-пружина движение является простым гармоническим.

Динамика простого гармонического движения

Для колебания в одномерном пространстве, учитывая Второй закон Ньютона (F = m d²x/dt²) и закон Гука (F = −kx, как описано выше), имеем линейное дифференциальное уравнение второго порядка:

где

m — масса тела,

x — его перемещение относительно положения равновесия,

k — постоянная (коэффициент жёсткости пружины).

Решение этого дифференциального уравнения является синусоидальным; одно из решений таково:

где A, ω и φ — постоянные величины, и положение равновесия принимается за начальное.^[1] Каждая из этих постоянных представляет собой важное физическое свойство движения: A — это амплитуда, ω = 2πf — круговая частота, и φ — начальная фаза.^[2]

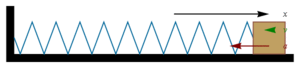Положение, скорость и ускорение гармонического осцилятора

Используя приёмы дифференциального исчисления, скорость и ускорение как функция времени могут быть найдены по формулам:

Положение, скорость и ускорение простого гармонического движения на фазовой плоскости

Ускорение может быть также выражено как функция перемещения:

Поскольку ma = −mω²x = −kx, то

Учитывая, что ω = 2πf, получим

и поскольку T = 1/f, где T — период колебаний, то

Эти формулы показывают, что период и частота не зависят от амплитуды и начальной фазы движения.

Энергия простого гармонического движения

Кинетическая энергия K системы в зависимости от времени t такова:

и потенциальная энергия есть

Полная механическая энергия системы, однако, имеет постоянное значение

Примеры

Система груз-пружина без затухания, в которой происходит простое гармоническое движение.

Простое гармоническое движение представлено в различных простых физических системах, и ниже приведены некоторые примеры.

Груз на пружине

Масса m, прикреплённая к пружине с постоянной жёсткостью k, является примером простого гармонического движения в пространстве. Формула

показывает, что период колебаний не зависит от амплитуды и ускорения свободного падения.

Универсальное движение по окружности

Простое гармоническое движение в некоторых случаях можно рассматривать как одномерная проекция универсального движения по окружности. Если объект движется с постоянной угловой скоростью ω по окружности радиуса r, центром которой является начало координат плоскости x − y, то такое движение вдоль каждой из координатных осей является простым гармоническим с амплитудой r и круговой частотой ω.

Груз как простой маятник

Движение маятника, не имеющего затуханий, можно приближённо рассматривать как простое гармоническое движение, если амплитуда колебаний очень мала в сравнении с длиной стержня.

В приближении малых углов движение простого маятника является близким к простому гармоническому. Период колебаний такого маятника, прикреплённого к стержню длиной ℓ с ускорением свободного падения g даётся формулой

Это показывает, что период колебаний не зависит от амплитуды и массы маятника, но зависит от ускорения свободного падения g, поэтому при той же самой длине маятника, на Луне он будет качаться медленнее, так как там слабее гравитация и меньше значение ускорения свободного падения.

Указанное приближение является корректным только при небольших углах отклонения, поскольку выражение для углового ускорения пропорционально синусу координаты:

где

I — момент инерции; в данном случае I = m ℓ ².

Когда угол θ мал, можно считать, что sin θ ≈ θ, и выражение принимает вид:

что делает угловое ускорение прямо пропорциональным углу θ, а это удовлетворяет определению простого гармонического движения.

Затухающий гармонический осциллятор

Взяв за основу ту же модель, добавим в неё силу вязкого трения. Сила вязкого трения направлена против скорости движения груза относительно среды и пропорциональна этой скорости. Тогда полная сила, действующая на груз, записывается так:

Проводя аналогичные действия, получаем дифференциальное уравнение, описывающее затухающий осциллятор:

Здесь введено обозначение: . Коэффициент носит название постоянной затухания. Он тоже имеет размерность частоты.

Решение же распадается на три случая.

• При малом трении () общее решение записывается в виде:

, где  — частота свободных колебаний.

• Затухание называют критическим. Начиная с такого значения показателя затухания, осциллятор будет совершать так называемое неколебательное движение. В граничном случае движение происходит по закону:

• При сильном же трении решение выглядит следующим образом:

, где

Критическое затухание примечательно тем, что именно при критическом затухании осциллятор быстрее всего стремится в положение равновесия. Если трение меньше критического, он дойдёт до положения равновесия быстрее, однако «проскочит» его по инерции, и будет совершать колебания. Если трение больше критического, то осциллятор будет экспоненциально стремиться к положению равновесия, но тем медленнее, чем больше трение.

Поэтому в стрелочных индикаторах (например, в амперметрах) обычно стараются ввести именно критическое затухание, чтобы прочитать его показания можно было максимально быстро.

Затухание осциллятора также часто характеризуют безразмерным параметром, называемым добротностью. Добротность обычно обозначают буквой . По определению, добротность равна:

Чем больше добротность, тем медленнее затухают колебания осциллятора.

У осциллятора с критическим затуханием добротность равна 0,5. Соответственно, добротность указывает характер поведения осциллятора. Если добротность больше 0,5, то свободное движение осциллятора представляет собой колебания; со временем он пересечёт положение равновесия неограниченное количество раз. Добротность, меньшая или равная 0,5, соответствует неколебательному движению осциллятора; в свободном движении он пересечёт положение равновесия не более одного раза.

Добротность иногда называют коэффициентом усиления осциллятора, так как при некоторых способах возбуждения при совпадении частоты возбуждения с резонансной амплитуда колебаний оказывается примерно в раз больше, чем при возбуждении на низкой частоте.

Также добротность примерно равна количеству колебательных циклов, за которое амплитуда колебаний уменьшается в раз, умноженному на .

В случае колебательного движения затухание ещё характеризуют такими параметрами, как:

• Время жизни колебаний (оно же время затухания, оно же время релаксации) τ — время, за которое амплитуда колебаний уменьшится в e раз.

Это время рассматривается как время, необходимое для затухания (прекращения) колебаний (хотя формально свободные колебания продолжаются бесконечно долго).

• Логарифмический декремент затухания. Определяется как логарифм отношения двух последовательных максимальных отклонений в одну сторону: Величина, обратная d, есть количество колебаний, которое пройдёт за время затухания τ.

Вынужденные колебания

Колебания осциллятора называют вынужденными, когда на него производится некоторое дополнительное воздействие извне. Это воздействие может производиться различными средствами и по различным законам. Например, силовым возбуждением называется воздействие на груз силой, зависящей только от времени по определённому закону. Кинематическим возбуждением называют воздействие на осциллятор движением точки закрепления пружины по заданному закону. Возможно также воздействие трением, когда, например, среда, с которой груз испытывает трение, совершает движение по заданному закону.

Литература

Бутиков Е. И. Собственные колебания линейного осциллятора. Учебное пособие

См. также

Примечания

1. ↑ Решение приведённого дифференциального уравнения можно записать с помощью функции синуса:
   И это тоже верное решение, поскольку известно общее равенство cos θ = sin(π/2 — θ). Используя тригонометрические соотношения, можно записать
   и таким образом
   также является верным решением при соответствующим образом выбранных постоянных a и b.
2. ↑ Максимальное перемещение (то есть амплитуда), x_max, имеет место, когда cos(ωt + φ) = 1, и таким образом, когда x_max = A. Таким образом, A является амплитудой.
   Поскольку
   то величина 2π/ω является периодом T (время, за которое совершается одно полное колебание). Также, поскольку T = 1/f, ω = 2πf является угловой скоростью.

Гармонический осциллятор — Студопедия

Систему, описываемую уравнением 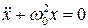, где 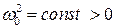, будем называть гармоническим осциллятором. Решение этого уравнения, как известно, имеет вид:

.

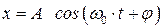Следовательно, гармонический осциллятор представляет собой систему, которая совершает гармонические колебания около положения равновесия.

Для гармонического осциллятора справедливы все результаты, полученные ранее для гармонического колебания.

Рассмотрим и обсудим ещё дополнительно к ним два вопроса.

Найдем импульс гармонического осциллятора. Продифференцируем выражение 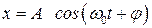по t и, умножив полученный результат на массу осциллятора, получим:

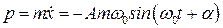. (8.8)

В каждом положении, характеризуемом отклонением “x”, осциллятор имеет некоторое значение ”p”. Чтобы найти ”p” как функцию ”x”, нужно исключить ”t” из написанных для ”p” и ”x” уравнений, Представим эти уравнения в виде:

(8.9)

Возведя эти выражения в квадрат и складывая, получим:

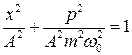. (8.10)

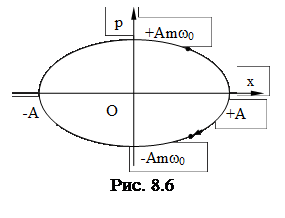Нарисуем график, показывающий зависимость ”p” импульса гармонического осциллятора от отклонения ”x” (рис. 8.6). Координатную плоскость (”p”, ”x”) принято называть фазовой плоскостью, а соответствующий график – фазовой траекторией. Фазовая траектория гармонического осциллятора представляет собой эллипс с полуосями “A” и ”A·m·w₀”. Каждая точка фазовой траектории изображает состояние осциллятора для некоторого момента времени (т.е. его отклонение и импульс). С течением времени точка, изображающая состояние, перемещается по фазовой траектории, совершая за период колебания полный обход. Причем это перемещение совершается по часовой стрелке [а именно, если в некоторый момент времени t¢ x=A, p=0, то в следующий момент времени ”x” будет уменьшаться, а ”p” принимать все возрастающие по модулю отрицательные значения, т.е. движение изобразительной точки (т.е. точки изображающей состояние) будет происходить по часовой стрелке].

Найдем теперь площадь эллипса . Или

.

Здесь , где n₀ – собственная частота осциллятора, являющаяся для данного осциллятора величиной постоянной.

Следовательно, . Откуда

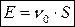. (8.11)

Таким образом, полная энергия гармонического осциллятора пропорциональна площади эллипса, причем коэффициентом пропорциональности служит собственная частота осциллятора.

8.6. Малые колебания системы вблизи положения равновесия.

Рассмотрим произвольную механическую систему, положение которой может быть задано с помощью одной величины “x”. Величиной ”x”, определяющей положение системы может быть угол, отсчитываемый от некоторой плоскости или расстояние, отсчитываемое вдоль заданной кривой.

Потенциальная энергия такой системы будет функцией одной переменной ”x”: E_p=E_p(x).

Выберем начало отсчета таким образом, чтобы в положении равновесия x=0. Тогда функция E_p(x) будет иметь минимум при x=0.

Далее разложим функцию E_p(x) в ряд по степеням “x”, причем ограничимся случаем малых колебаний, поэтому высшими степенями “x” можно пренебречь. По формуле Маклорена:

.

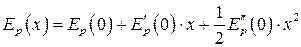(ввиду малости “x” остальными членами пренебрегаем)

Так как E_p(x) при x=0 имеет минимум, то 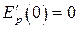, а 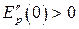. Обозначим E_p(x) = b и , тогда .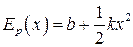

Это выражение идентично с выражением для потенциальной энергии системы, в которой действует квазиупругая сила (константу “b” можно положить равной 0).

Сила, действующая на систему, может быть определена по формуле: . Получено с учетом, что работа совершается за счет убыли потенциальной энергии .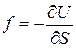

Итак, потенциальная энергия системы при малых отклонениях от положения равновесия оказывается квадратичной функцией смещения, а сила, действующая на систему, имеет вид квазиупругой силы. Следовательно, при малых отклонениях от положения равновесия любая механическая система будет совершать колебания, близкие к гармоническим.

8.7. Математический маятник.

ОПРЕДЕЛЕНИЕ: математическим маятником будем называть идеализированную систему, состоящую из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке.

Отклонение маятника от положения равновесия будет характеризоваться углом j (рис. 8.7). При отклонении маятника от положения равновесия возникает вращательный момент 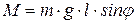, он имеет такое направление, что стремится вернуть маятник в положение равновесия, поэтому моменту M и угловому смещению j нужно приписать разные знаки.

Следовательно,

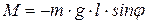. (8.12)

Напишем теперь для маятника уравнение динамики вращательного движения (учитывая, что b – угловое ускорение равно 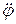, а ).

Рассмотрим малые колебания ( ) и введем величину , тогда получим

Решением этого уравнения будет функция

Следовательно, при малых колебаниях угловое отклонение математического маятника изменяется по гармоническому закону.

Как следует из формулы , частота колебаний математического маятника зависит только от его длины и величины “g” и не зависит от массы маятника. Учитывая, что 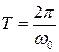получим

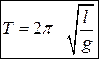. (8.13)

Гармонический осциллятор Википедия

У этого термина существуют и другие значения, см. Осциллятор.

Гармони́ческий осцилля́тор (в классической механике) — система, которая при выведении её из положения равновесия испытывает действие возвращающей силы F, пропорциональной смещению x:

F = − k x {\displaystyle F=-kx} ,

где k — постоянный коэффициент.

Если F — единственная сила, действующая на систему, то систему называют простым или консервативным гармоническим осциллятором. Свободные колебания такой системы представляют собой периодическое движение около положения равновесия (гармонические колебания). Частота и амплитуда при этом постоянны, причём частота не зависит от амплитуды.

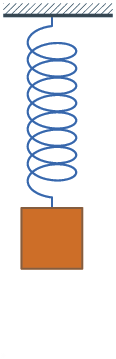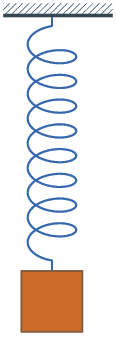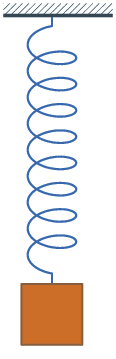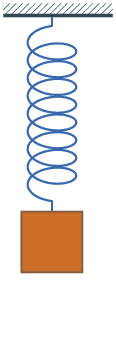
Свободные колебания системы груз—пружина без затухания.

Если имеется ещё и сила трения (затухание), пропорциональная скорости движения (вязкое трение), то такую систему называют затухающим или диссипативным осциллятором. Если трение не слишком велико, то система совершает почти периодическое движение — синусоидальные колебания с постоянной частотой и экспоненциально убывающей амплитудой. Частота свободных колебаний затухающего осциллятора оказывается несколько ниже, чем у аналогичного осциллятора без трения.

Если осциллятор предоставлен сам себе, то говорят, что он совершает свободные колебания. Если же присутствует внешняя сила (зависящая от времени), то говорят, что осциллятор испытывает вынужденные колебания.

Механическими примерами гармонического осциллятора являются математический маятник (с малыми углами отклонения), груз на пружине, торсионный маятник и акустические системы. Среди немеханических аналогов гармонического осциллятора можно выделить электрический гармонический осциллятор (см. LC-цепь).

Свободные колебания консервативного гармонического осциллятора[ | ]

Уравнение и его решения[ | ]

Пусть x — смещение материальной точки относительно её положения равновесия, а F — действующая на точку возвращающая сила любой природы вида

F = − k x {\displaystyle F=-kx} ,

где k = const. Тогда, используя

Идеальный гармонический осциллятор. Уравнение идеального осциллятора и его решение. Амплитуда, частота и фаза колебаний

КОЛЕБАНИЯ

Лекция 1

ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ

Идеальный гармонический осциллятор. Уравнение идеального осциллятора и его решение. Амплитуда, частота и фаза колебаний

Колебание – один из самых распространённых процессов в природе и технике. Колебания – это процессы, повторяющиеся во времени. Колеблются высотные здания и высоковольтные провода под действием ветра, маятник заведённых часов и автомобиль на рессорах во время движения, уровень реки в течение года и температура человеческого тела при болезни. Звук – это колебания давления воздуха, радиоволны – периодические изменения напряжённости электрического и магнитного поля, свет – это тоже электромагнитные колебания. Землетрясения – колебания почвы, приливы и отливы – изменение уровней морей и океанов, вызываемые притяжением луны и т.д.

Колебания бывают механические, электромагнитные, химические, термодинамические и др. Несмотря на такое многообразие, все колебания описываются одними и теми же дифференциальными уравнениями.

Первыми учёными, изучавшими колебания, были Галилео Галилей и Христиан Гюйгенс. Галилей установил независимость периода колебаний от амплитуды. Гюйгенс изобрёл часы с маятником.

Любая система, которая, будучи слегка выведена из положения равновесия, совершает устойчивые колебания, называется гармоническим осциллятором. В классической физике такими системами являются математический маятник в пределах малых углов отклонения, груз в пределах малых амплитуд колебаний, электрический контур, состоящий из линейных элементов ёмкости и индуктивности.

       Гармонический осциллятор можно считать линейным, если смещение от положения равновесия прямо пропорционально возмущающей силе. Частота колебаний гармонического осциллятора не зависит от амплитуды. Для осциллятора выполняется принцип суперпозиции — если действуют несколько возмущающих сил, то эффект их суммарного действия может быть получен как результат сложения эффектов от действующих сил в отдельности.

Гармонические колебания описываются уравнением (рис.1.1.1)

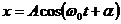            (1.1.1)

где х  -смещение колеблющейся величины от положения равновесия, А – амплитуда колебаний, равная величине максимального смещения, 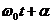 — фаза колебаний, определяющая смещение в момент времени 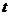,  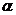— начальная фаза, определяющая величину смещения  в начальный момент времени, 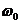 — циклическая частота колебаний.

Время одного полного колебания называется периодом, 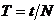, где 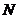 — число колебаний, совершенных за время .

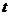Частота колебаний 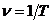 определяет число колебаний, совершаемых в единицу времени, она связана с циклической частотой соотношением , тогда период .

Скорость колеблющейся материальной точки

,

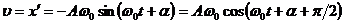ускорение

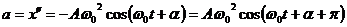.                      (1.1.2)

Таким образом, скорость и ускорение гармонического осциллятора также изменяются по гармоническому закону с амплитудами  и 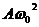 соответственно. При этом скорость опережает по фазе смещение на 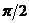, а ускорение – на  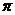(рис.1.1.2).

Из сопоставления уравнений движения гармонического осциллятора (1.1.1) и (1.1.2) следует, что 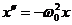, или

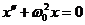.                                                      (1.1.3)

Это дифференциальное уравнение второго порядка называется уравнением гармонического осциллятора. Его решение содержит два постоянные а и 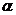, которые определяются заданием начальных условий

.

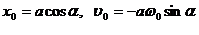Отсюда  .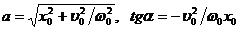

Если периодически повторяющийся процесс описывается уравнениями, не совпадающими с (1.1.1), он н6азывается ангармоническим. Система, совершающая ангармонические колебания, называется ангармоническим осциллятором.

 

1.1.2. Свободные колебания систем с одной степенью свободы. Комплексная форма представления гармонических колебаний

       В природе очень распространены малые колебания, которые система совершает вблизи своего положения равновесия. Если система, выведенная из положения равновесия, предоставлена себе, то есть на неё не действуют внешние силы, то такая система будет совершать свободные незатухающие колебания. Рассмотрим систему с одной степенью свободы.

       Устойчивому равновесию соответствует такое положение системы, в котором её потенциальная энергия 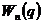 имеет минимум (q – обобщённая координата системы). Отклонение системы от положения равновесия приводит к возникновению силы 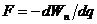, которая стремится вернуть систему обратно. Значение обобщённой координаты, соответствующей положению равновесия, обозначим 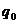, тогда отклонение от положения равновесия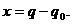

       Будем отсчитывать потенциальную энергию от минимального значения 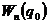. Примем 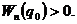Полученную функцию  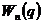разложим в ряд Маклорена и оставим первый член разложения, имеем: о

,

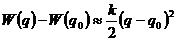где 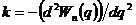. Тогда с учётом введённых обозначений:

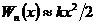 ,                                                   (1.1.4)

С учётом выражения (1.1.4) для силы, действующей на систему, получаем:

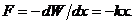
Согласно второму закону Ньютона, уравнение движения системы имеет вид: ,      

тогда

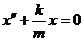,                                                              (1.1.5)

Выражений (1.1.5) совпадает с уравнением (1.1.3) свободных гармонических колебаний при условии, что

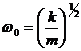,                                                                            (1.1.6)

и имеет два независимых решения:  и 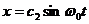, так что общее решение:

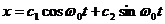,  или

,                             

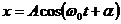где

       Из формулы (1.1.6) следует, что частота определяется только собственными свойствами механической системы и не зависит от амплитуды и от начальных условий движения.

       Зависимость координаты колеблющейся системы от времени можно определить в виде вещественной части комплексного выражения 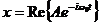       , где A=Xe-iα – комплексная амплитуда, её модуль совпадает с обычной амплитудой, а аргумент – с начальной фазой.

 

1.1.3. Примеры колебательных движений различной физической природы

Квантовый гармонический осциллятор — это… Что такое Квантовый гармонический осциллятор?

Гармонический осциллятор в квантовой механике представляет собой квантовый аналог простого гармонического осциллятора, при этом рассматривают не силы, действующие на частицу, а гамильтониан, то есть полную энергию гармонического осциллятора, причём потенциальная энергия предполагается квадратично зависящей от координат. Учёт следующих слагаемых в разложении потенциальной энергии по координате ведёт к понятию ангармонического осциллятора.

Задача о гармоническом осцилляторе в координатном представлении

Гамильтониан квантового осциллятора массы m, собственная частота которого ω, выглядит так:

В координатном представлении , . Задача об отыскании уровней энергии гармонического осциллятора сводится к нахождению таких чисел E при которых следующее дифференциальное уравнение в частных производных

имеет решение в классе квадратично интегрируемых функций.

Для

решение имеет вид:

функции  — полиномы Эрмита:

Данный спектр значений E заслуживает внимания по двум причинам: во-первых, уровни энергии дискретны и равноотстоящи, то есть разница в энергии между двумя соседними уровнями постоянна и равна , во-вторых наименьшее значение энергии равно . Этот уровень называют основным, вакуумом, или уровнем нулевых колебаний.

Операторы рождения и уничтожения

Гораздо проще спектр гармонического осциллятора можно получить с помощью операторов рождения и уничтожения, сопряжённых друг другу.

Оператор рождения:

Оператор уничтожения:

Их коммутатор равен

С помощью операторов рождения и уничтожения гамильтониан квантового осциллятора записывается в компактном виде:

,

где  — оператор номера уровня (чисел заполнения). Собственные вектора такого гамильтониана являются фоковскими состояниями, а представление решения задачи в таком виде называется «представлением числа частиц».

Ангармонический осциллятор

Под ангармоническим осциллятором понимают осциллятор с неквадратичной зависимостью потенциальной энергии от координаты. Простейшим приближением ангармонического осциллятора является приближение потенциальной энергии до третьего слагаемого в ряде Тейлора:

Точное решение задачи о спектре энергии такого осциллятора довольно трудоёмкое, однако можно вычислить поправки к энергии, если предположить, что кубическое слагаемое мало по сравнению с квадратичным, и воспользоваться теорией возмущений.

В представлении операторов рождения и уничтожения (представление вторичного квантования), кубическое слагаемое равно

Этот оператор имеет нулевые диагональные элементы, а потому первая поправка теории возмущений отсутствует. Вторая поправка к энергии произвольного невакуумного состояния равна

Многочастичный квантовый осциллятор

В простейшем случае взаимодействия нескольких частиц можно применить модель многочастичного квантового осциллятора, подразумевая взаимодействие соседних частиц по квадратичному закону:

Здесь под и подразумеваются отклонение (от положения равновесия) и импульс -той частицы. Суммирование ведётся только по соседним частицам.

Такая модель приводит к теоретическому обоснованию фононов — бозе-квазичастиц, наблюдающихся в твёрдом теле.

Переходы под влиянием внешней силы

Под влиянием внешней силы квантовый осциллятор может переходить с одного уровня энергии () на другой (). Вероятность этого перехода для осциллятора без затухания даётся формулой:

,

где функция определяется как:

,

а  — полиномы Лагерра.

См. также

Литература

Ландау, Л. Д., Лифшиц, Е. М. Квантовая механика (нерелятивистская теория). — Издание 3-е, переработанное и дополненное. — М.: Наука, 1974. — 752 с. — («Теоретическая физика», том III).

4. 3. Гармонический осциллятор. Примеры гармонических осцилляторов. @

Тела, которые при движении совершают гармонические ко­лебания, называют гармоническими осциляторами. Рассмотрим ряд примеров гармонических осциляторов.

Пример1. Пружинный маятник – это тело массой m, способное совершать колебания под действием силы упругости невесомой (m_{пружины}m_тела) пружины (рис.4.2).

Т

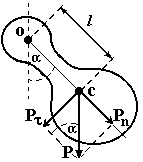
Рис.4.3. Физический маятник.

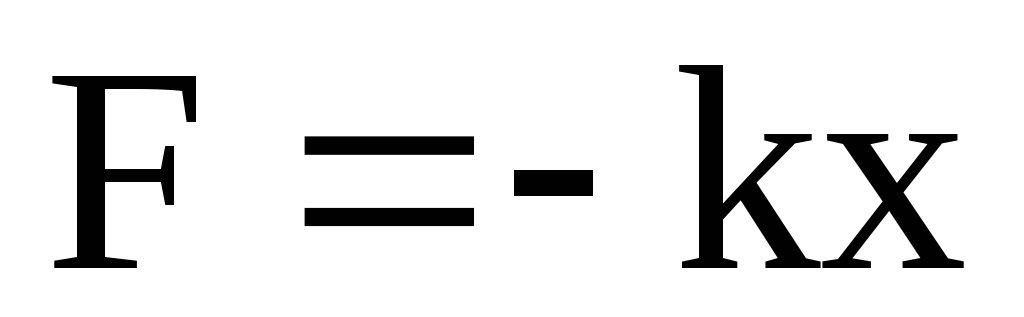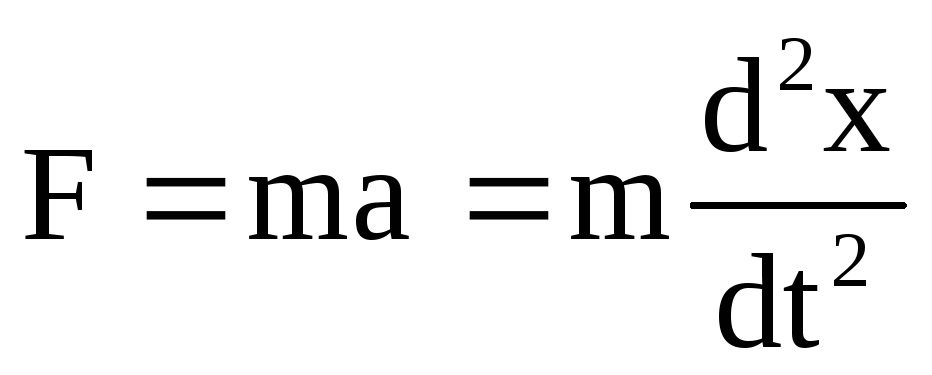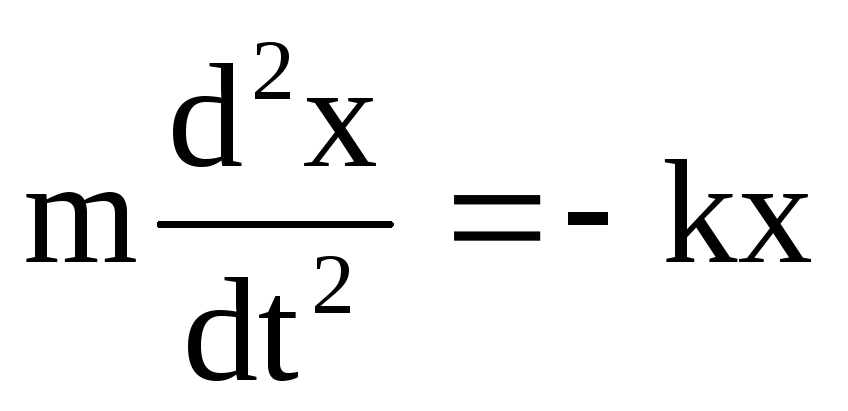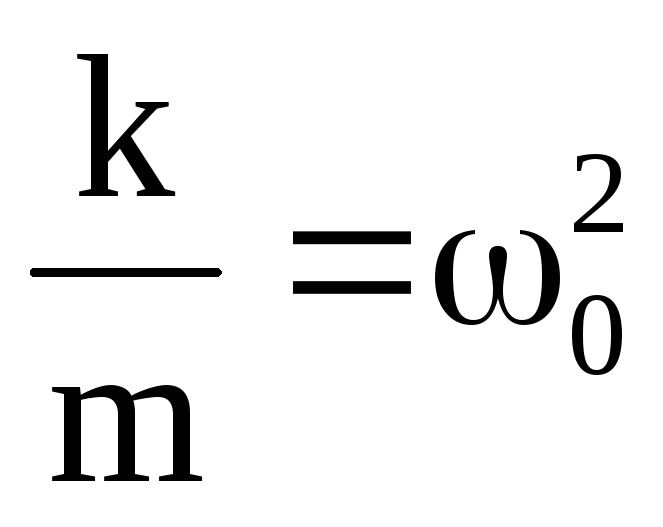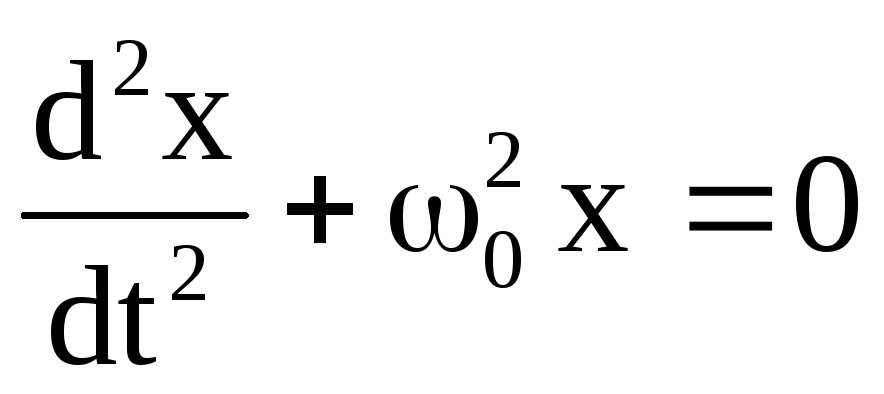рением в системе пренебрегаем. При смещении тела на расстояние х от положе­ния равновесия О на него дейст­вует сила уп­ругости пружины, направленная к положению равновесия:, гдеk — коэффициент упругости (жесткости) пружины. По второму закону Ньютона . От­сюдаи, если обозначить, тогда получимдифференциальное урав­нение гармонических колебаний. Его решения имеют вид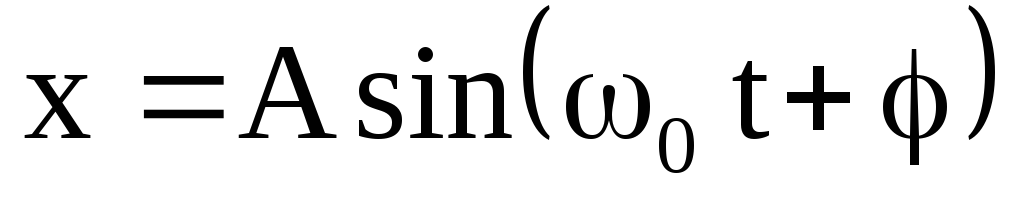либо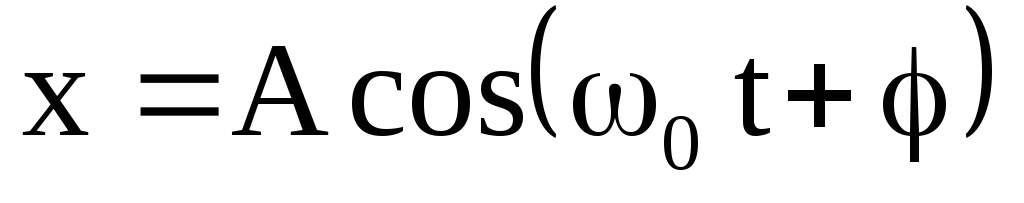. Таким образом, колебания пружинного маятника — гармонические с циклической час­тотой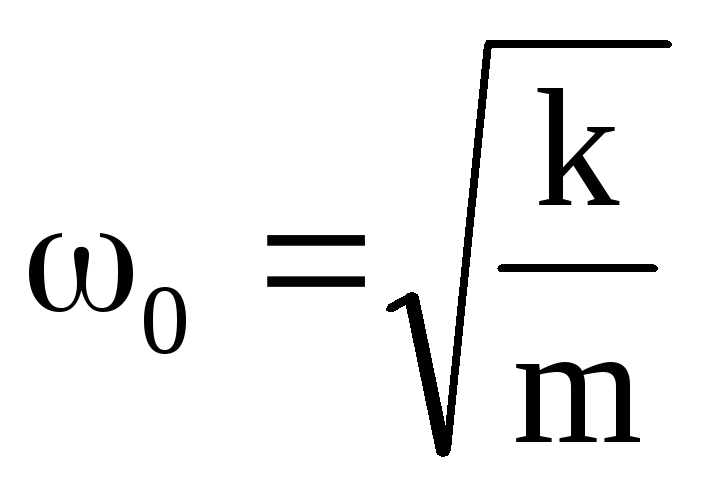и периодом.

Пример 2. Физический маятник — это твердое тело, совер­шаю­щее колебания под действием силы тяжести вокруг подвижной го­ризон­тальной оси, не совпадающей с его цен­тром тяжести С (рис. 4. 3). Ось проходит через точку О. Если маятник откло­нить от положения равновесия на малый угол  и отпус­тить, он будет совершать ко­лебания, следуя основному уравнению динамики вращательного движения твердого тела 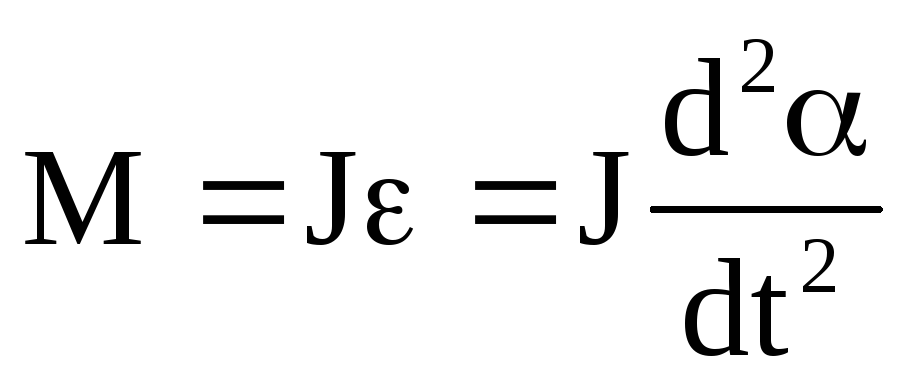, гдеJ — момент инерции маятника относительно оси, М ‑ момент силы, возвращающей физический маятник в поло­жение равно­весия. 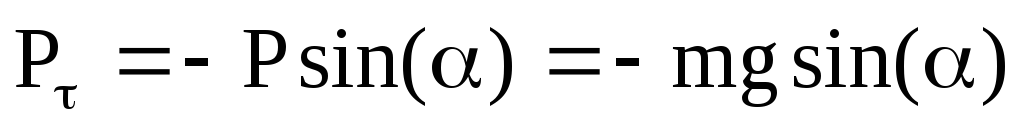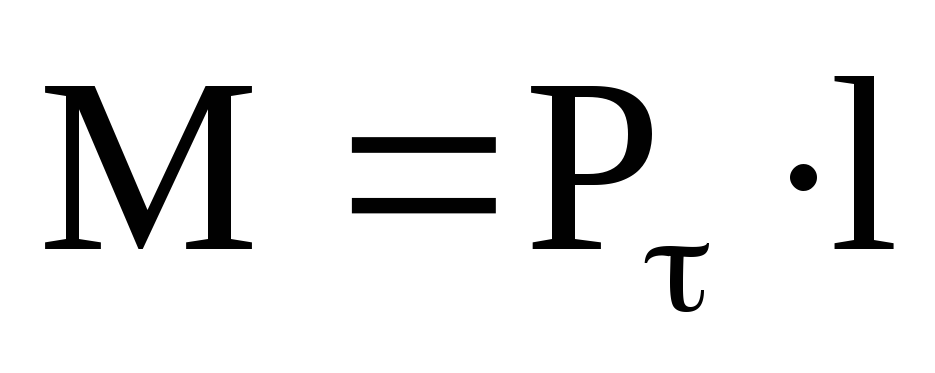Он создается силой тяжести , ее момент равен(l=ОС). В результате получаем 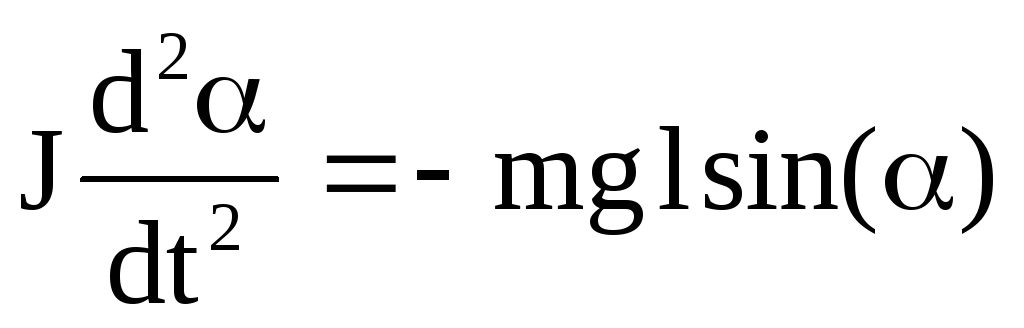.     Это дифференциальное уравнение колебаний для произвольных углов отклонения. При малых углах, когда 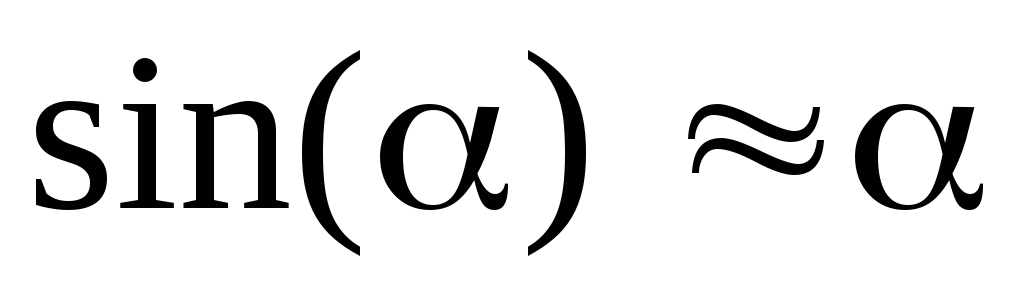,или, принимая, получим дифференциальное уравнение колебания физического маятника. Его решения имеют вид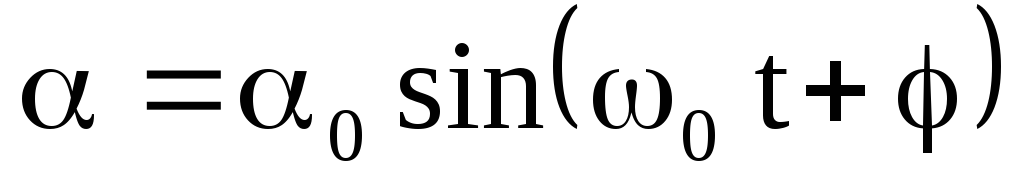или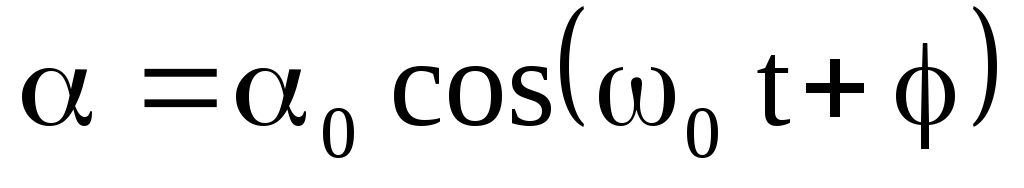. Таким образом, при малых отклонениях от положения равновесия физический маят­ник совершает гармонические колебания с циклической частотойи периодом.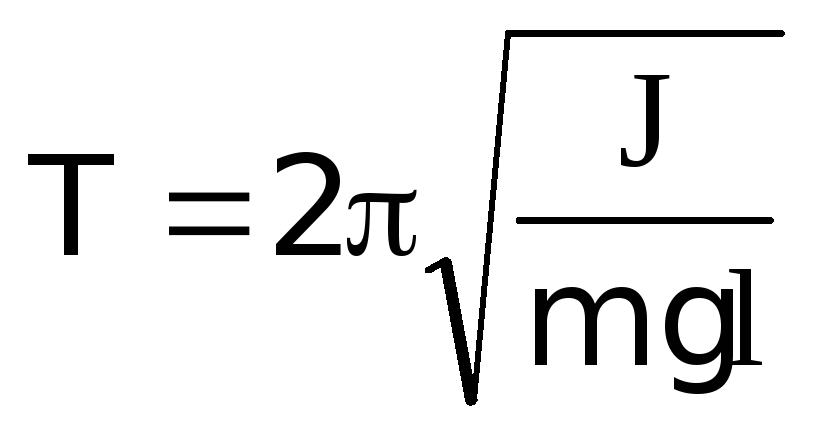

Пример3. Математический маятник — это материальная точка с массой m (тяжелый шарик малых размеров), подвешенная на невесомой (по сравнению с m шарика), уп­ругой, нерастяжимой нити длинною l. Если вывести шарик из положения равновесия, отклонив его от вертикали на небольшой угол , а затем отпустить, он будет совершать колебания. Если рассматривать данную систему как физический маятник с моментом инерции материальной точки J = ml², то из формул для физического маятника получим выражения для циклической частоты и периода колебаний математического маятника

, .

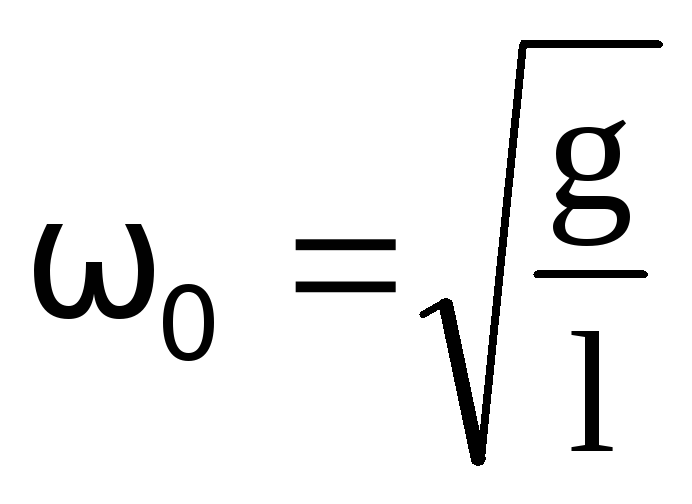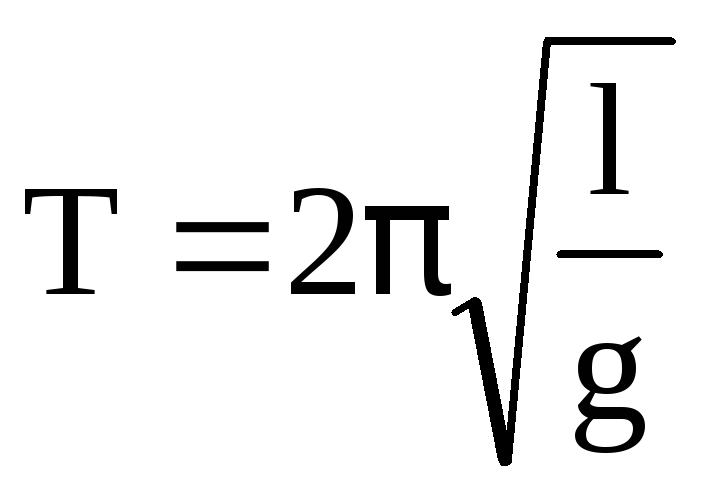4. 4. Затухающие колебания. @

В рассмотренных примерах гармонических колебаний единственной силой, действующей на материальную точку (тело), была квазиупругая сила F и не учитывались силы сопротивления, которые присутству­ют в лю­бой реальной системе. Поэтому рассмотренные колебания можно назвать идеальными незатухающими гармоническими колебаниями.

Наличие в реальной колебательной системе силы сопротивления среды при­во­дит к уменьшению энергии системы. Если убыль энергии не пополнять за счет работы внешних сил, колебания будут затухать. Затухающими называются колеба­ния с уменьшающейся во времени амплитудой.

Рассмотрим свободные затухающие колебания. При небольших скоростях сила сопротивления F_C пропорциональна скорости v и обратно пропорциональна ей по направлению 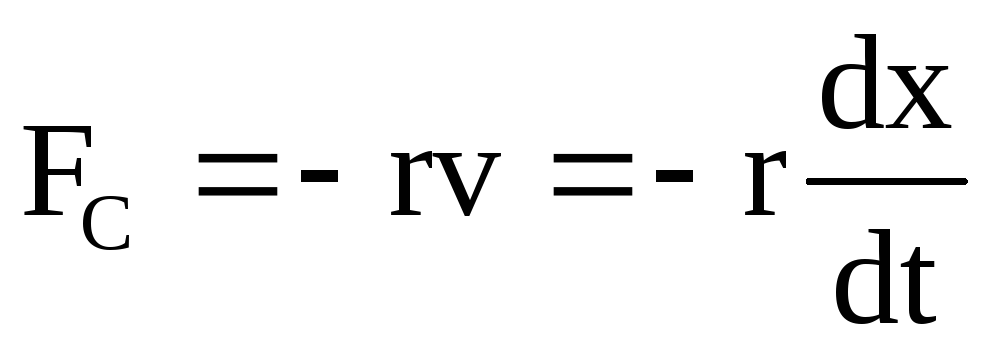, гдеr — коэффициент сопротивления среды. Используя второй закон Ньютона, получим дифференциальное уравнение затухающих колебаний ,,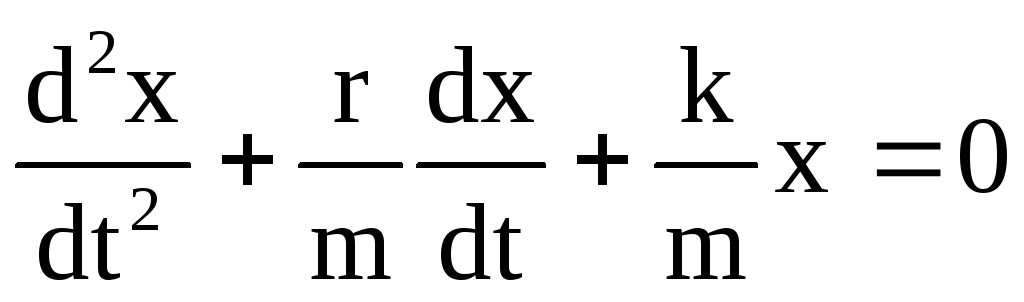. Обозначим,. Тогда дифференциальное уравнение приобретает вид:

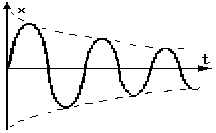
Рис.4.4. Зависимость смеще­ния и амплитуды затухаю­щих колебаний от времени.

.

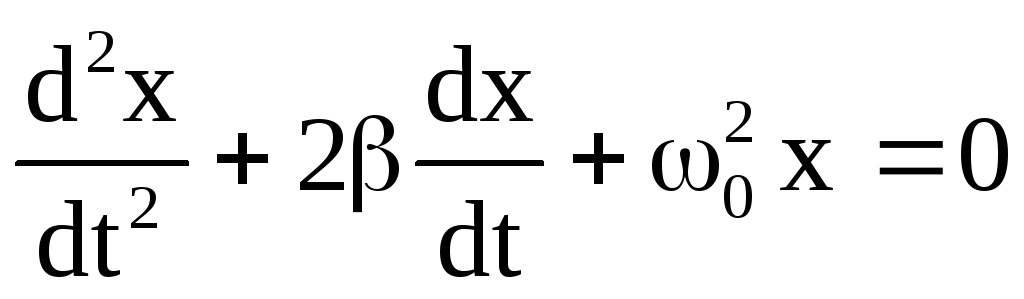Это дифференциальное уравнение затухающих колебаний. Здесь ₀ — собственная частота колеба­ний системы, т.е. частота свободных колебаний при r=0,  — коэффициент зату­хания оп­ределяет скорость убывания амплитуды. Решениями этого уравнения при условии ₀ являются

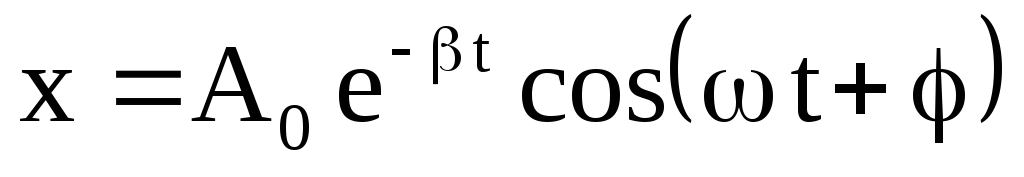либо .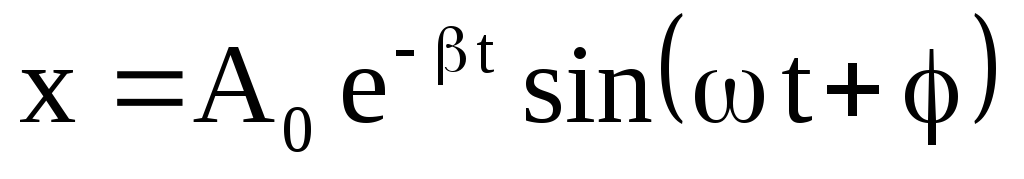

График последней функции представлен на рис.4.4. Верхняя пунктирная линия дает график функции 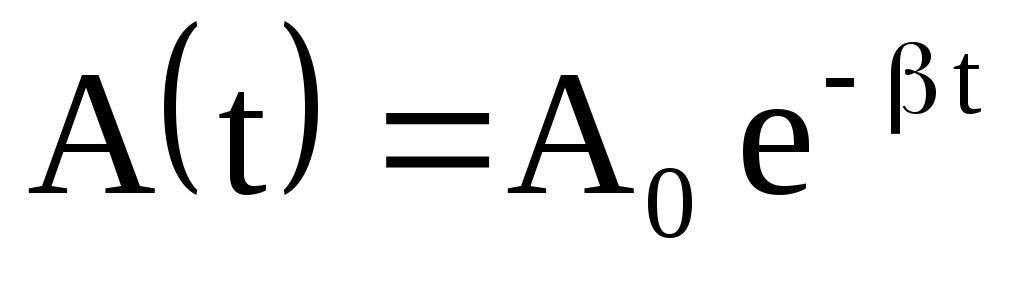, А₀ — амплитуда в начальный момент времени. Амплитуда во времени убывает по экспоненциальному закону,  — коэффициент зату­хания по величине обратен времени релакса­ции , т.е. вре­мени за которое амплитуда уменьшается в e раз, так как

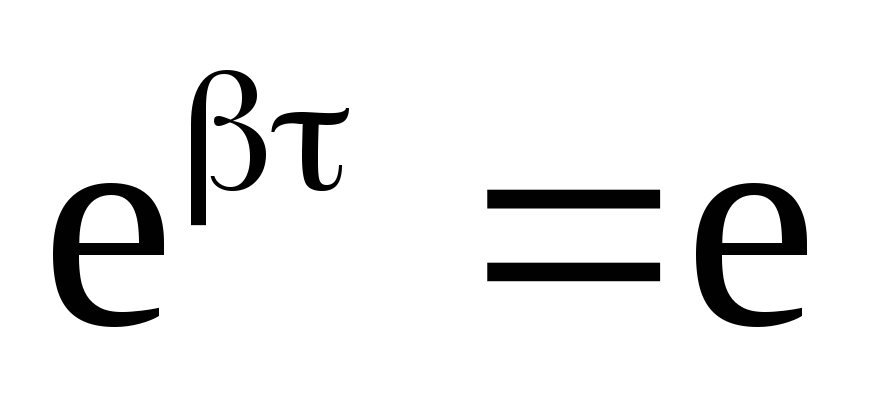, , = 1, 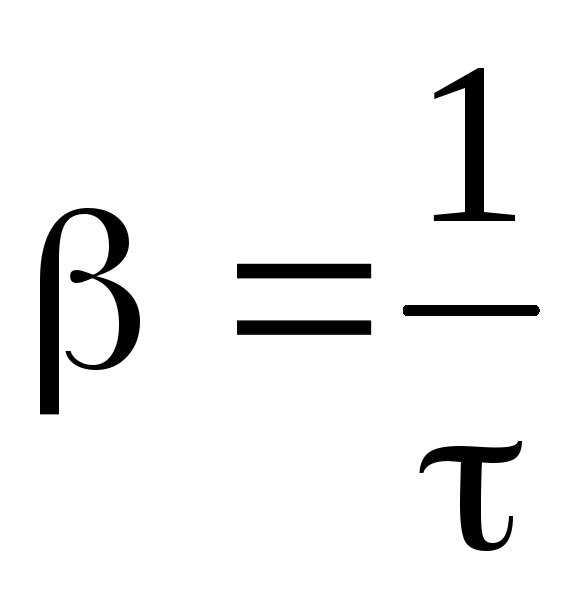. Частота и период затухающих колебаний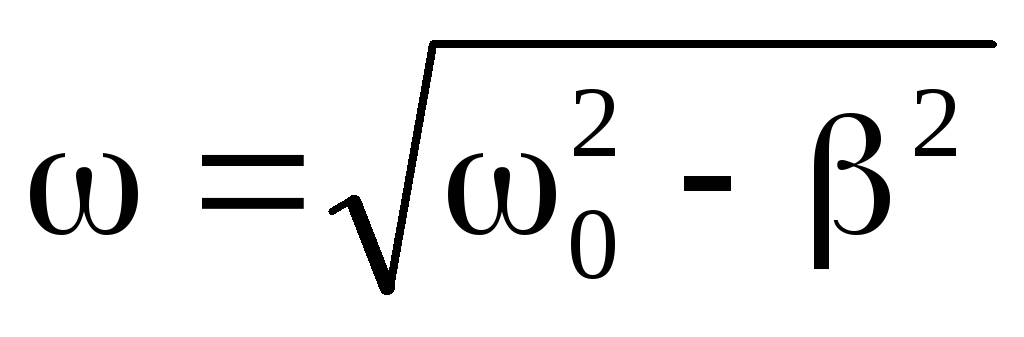,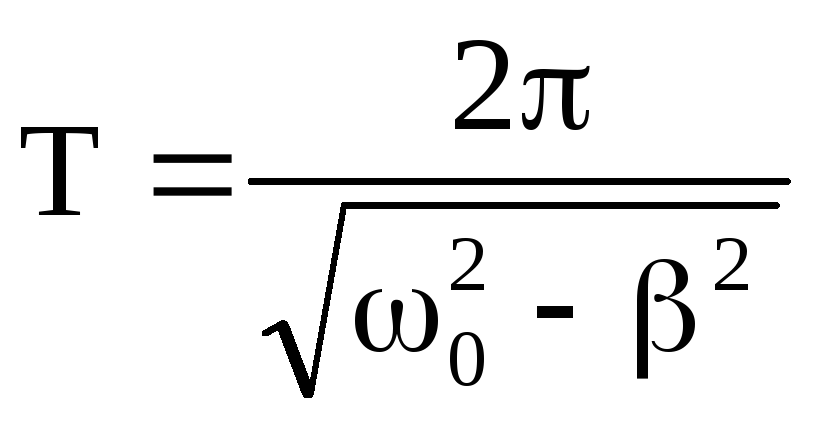; при очень малом сопротивлении среды (²₀²) период колебаний практически ра­вен 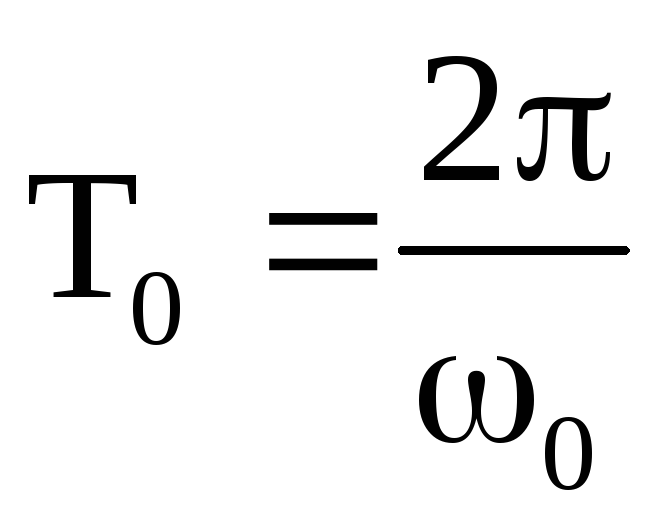. С ростом период колебаний увеличивается и при >₀ решение дифференциального уравнения показывает, что колебания не совершаются, а происходит монотонное движение системы к положению равновесия. Такое движение называют апериодическим.

Для характеристики скорости затухания колебаний служат еще два параметра : декремент затухания D и логарифмический декремент . Декремент затуха­ния показывает во сколько раз уменьшается амплитуда колебаний за время од­ного периода Т.

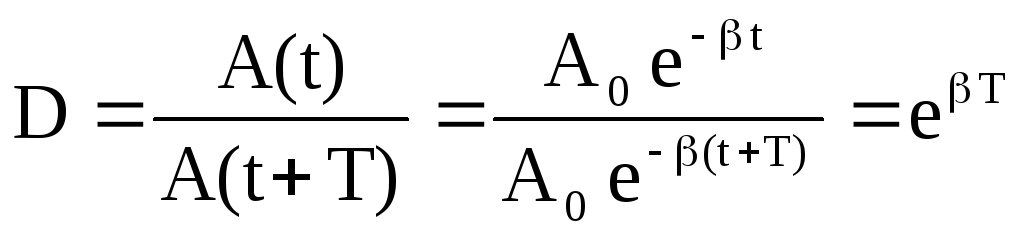
Н

Рис.4.5. Вид резонансных кривых.

атуральный логарифм от декремента затухания есть логарифмический декремент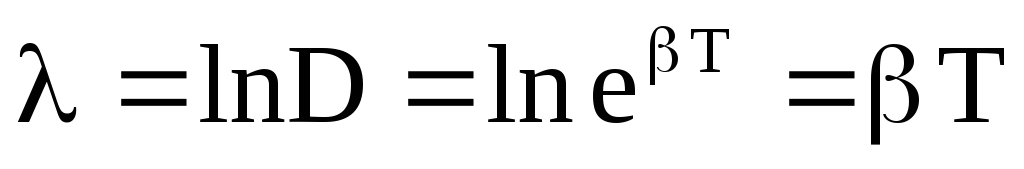

. Так как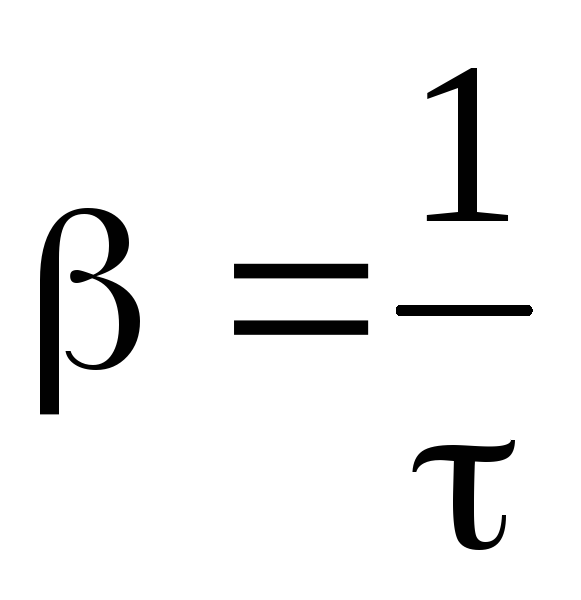, то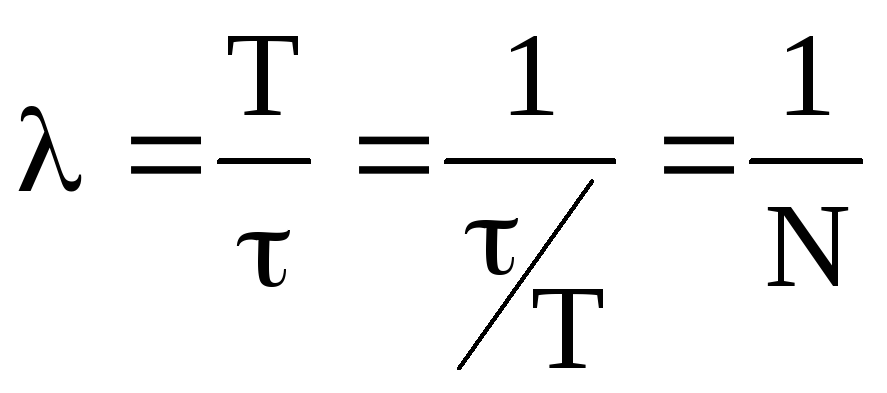, гдеN — число колебаний за время.

гармонический осциллятор — это… Что такое гармонический осциллятор?



гармонический осциллятор

 

гармонический осциллятор
—
[Я.Н.Лугинский, М.С.Фези-Жилинская, Ю.С.Кабиров. Англо-русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.]

Тематики

• электротехника, основные понятия

Справочник технического переводчика. – Интент. 2009-2013.

• гармонический корректор аппаратуры системы передачи с ЧРК
• гармонический преобразователь частоты

Смотреть что такое «гармонический осциллятор» в других словарях:

• Гармонический осциллятор — У этого термина существуют и другие значения, см. Осциллятор. Гармонический осциллятор (в классической механике)  система, которая при смещении из положения равновесия испытывает действие возвращающей силы F, пропорциональной смещению x… …   Википедия

• гармонический осциллятор — harmoninis osciliatorius statusas T sritis fizika atitikmenys: angl. harmonic oscillator vok. harmonischer Oszillator, m rus. гармонический осциллятор, m pranc. oscillateur harmonique, m …   Fizikos terminų žodynas

• Квантовый гармонический осциллятор — Гармонический осциллятор в квантовой механике представляет собой квантовый аналог простого гармонического осциллятора, при этом рассматривают не силы, действующие на частицу, а гамильтониан, то есть полную энергию гармонического осциллятора,… …   Википедия

• Осциллятор (значения) — Осциллятор (от лат. oscillo  качаюсь)  система, совершающая колебания, то есть показатели которой периодически повторяются во времени. Физика Понятие осциллятора играет важную роль в теории твёрдого тела, электромагнитных излучений,… …   Википедия

• ОСЦИЛЛЯТОР — ОСЦИЛЛЯТОР, в электронике система, испытывающая колебания. Цепь осциллятора преобразует постоянный ток в высокочастотный переменный ток. Гармонический осциллятор генерирует синусоидальные колебания. см. также ЭЛЕКТРИЧЕСКИЙ ТОК …   Научно-технический энциклопедический словарь

• ОСЦИЛЛЯТОР ГАРМОНИЧЕСКИЙ — система с одной степенью свободы, колебания к рой описываются уравнением вида Фазовые траектории окружности, период колебаний не зависит от амплитуды. Потенциальная энергия О. г. квадратично зависит от х: Примеры О. г.: малые колебания маятника,… …   Математическая энциклопедия

• Осциллятор — (от лат. oscillo  качаюсь)  система, совершающая колебания, то есть показатели которой периодически повторяются во времени. Физика Понятие осциллятора играет важную роль в физике и достаточно повсеместно используется, например, в… …   Википедия

• ОСЦИЛЛЯТОР — (Oscillator) в широком смысле любая колебательная система. В современной теоретической физике особое значение имеет т. наз. гармонический О., под которым разумеют электрическую систему, совершающую гармонические колебания и порождающую в… …   Морской словарь

• Осциллятор Дуффинга — У этого термина существуют и другие значения, см. Осциллятор. Отображение Пуанкаре для вынужденных колебаний осциллятора Дуффинга, демонстрирующее хаотическое поведение Осциллятор Дуффинга (англ. Duffing oscillator) простейшая одномерна …   Википедия

• осциллятор — а; м. [от лат. oscillum качание, колебание] Спец. Система тел, способная совершать колебания (механические, электромагнитные и т.п.). Энергия осциллятора. Гармонический о. (при малых колебаниях). * * * осциллятор (от лат. oscillo  качаюсь),… …   Энциклопедический словарь

Глава 5: Гармонический осциллятор — Химия LibreTexts

Гармонический осциллятор — это модель, которая имеет несколько важных приложений как в классической, так и в квантовой механике. Он служит прототипом для математической обработки таких разнообразных явлений, как упругость, акустика, цепи переменного тока, колебания молекул и кристаллов, электромагнитные поля и оптические свойства материи.

Классический осциллятор

Простая реализация гармонического осциллятора в классической механике — это частица, на которую действует возвращающая сила, пропорциональная ее смещению из положения равновесия.Если рассматривать движение в одном измерении, это означает

\ [F = −kx \ label {1} ​​\]

Такая сила может исходить от пружины, которая подчиняется закону Гука, как показано на рисунке \ (\ PageIndex {1} \). Согласно закону Гука, который применяется к реальным пружинам при достаточно малых смещениях, восстанавливающая сила пропорциональна смещению — растяжению или сжатию — из положения равновесия.

Рисунок \ (\ PageIndex {1} \): пружина подчиняется закону Гука.

Силовая постоянная \ (k \) — это мера жесткости пружины.2 \ Equiv \ dfrac {k} {m} \]

Точечная запись (введенная самим Ньютоном) используется вместо простых чисел, когда независимой переменной является время. Общее решение уравнения \ (\ ref {3} \) —

\ [x (t) = A \ sin ωt + B \ cos ωt \ label {4} \]

, который представляет периодическое движение с синусоидальной зависимостью от времени. Это известно как простое гармоническое движение , а соответствующая система известна как гармонический осциллятор . Колебание происходит с постоянной угловой частотой

\ [\ omega = \ sqrt {\ dfrac {k} {m}} \; \ text {радиан в секунду} \ label {5} \]

Это называется собственной частотой генератора .Соответствующая круговая (или угловая) частота в Герцах (циклах в секунду) равна

.

\ [\ nu = \ dfrac {\ omega} {2 \ pi} = \ dfrac {1} {2 \ pi} \ sqrt {\ dfrac {k} {m}} \; \ text {Hz} \ label {6} \]

Общее соотношение между силой и потенциальной энергией в консервативной системе в одном измерении равно

.

\ [F = \ dfrac {−dV} {dx} \ label {7} \]

Таким образом, потенциальная энергия гармонического осциллятора равна

.

\ [V (x) = \ dfrac {1} {2} kx ^ 2 \ label {8} \]

, имеющий форму параболы, как показано на рисунке \ (\ PageIndex {2} \).{2} \), а кинетическая энергия на мгновение равна нулю. Напротив, когда осциллятор движется мимо \ (x = 0 \), кинетическая энергия достигает своего максимального значения, а потенциальная энергия равна нулю.

Рисунок \ (\ PageIndex {2} \): функция потенциальной энергии и несколько первых уровней энергии для гармонического осциллятора.

Гармонический осциллятор в квантовой механике

Учитывая потенциальную энергию в уравнении \ (\ ref {8} \), мы можем записать уравнение Шредингера для одномерного гармонического осциллятора:

\ [- \ dfrac {\ hbar ^ {2}} {2m} \ psi » (x) + \ dfrac {1} {2} kx ^ 2 \ psi (x) = E \ psi (x) \ label {9} \]

Впервые мы сталкиваемся с дифференциальным уравнением с непостоянными коэффициентами , решить которое гораздо сложнее.2 \ alpha} {2m} = \ dfrac {1} {2} \ hbar \ sqrt {\ dfrac {k} {m}} = \ dfrac {1} {2} \ hbar \ omega \ label {17} \]

где \ (\ omega \) — собственная частота осциллятора согласно классической механике. Функция в уравнении \ (\ ref {16} \) имеет форму гауссианы, колоколообразной кривой, столь любимой в социальных науках. Функция не имеет узлов, что приводит нас к выводу, что это основное состояние системы. Основное состояние обычно обозначается квантовым числом \ (n = 0 \) (частица в коробке является исключением, с \ (n = 1 \) обозначение основного состояния).{2} / 2} \ label {24} \]

Используя интегралы, указанные в таблице в Приложении 5 к интегралам Гаусса, мы определяем, что с \ (a = \ dfrac {1} {2} \) делает \ (\ psi_ {2} (x) \) ортогональным \ (\ psi_ {0} (x) \) и \ (\ psi_ {1} (x) \). Проверяем, что это еще одна собственная функция, соответствующая

\ [E_ {2} = \ dfrac {5} {2} \ hbar \ omega \ label {25} \]

Общий результат, который следует из более продвинутого математического анализа, дает следующую формулу для нормированных собственных функций:

\ [\ psi_ {n} (x) = (\ dfrac {\ sqrt {\ alpha}} {2 ^ {n} n! \ Sqrt {\ pi}}) ^ {1/2} H_ {n} ( \ sqrt {\ alpha} x) e ^ {- \ alpha x ^ {2} / 2} \ label {26} \]

, где \ (H_ {n} (\ xi) \) представляет полином Эрмита степени \ (n \).{3} -12 \ xi \ label {27} \]

Четыре собственные функции низшего гармонического осциллятора показаны на рисунке \ (\ PageIndex {3} \). Обратите внимание на топологическое сходство с соответствующими собственными функциями «частицы в ящике».

Рисунок \ (\ PageIndex {3} \): Собственные функции гармонического осциллятора для n = 0, 1, 2, 3.

Собственные значения даются простой формулой

\ [E_ {n} = \ left (n + \ dfrac {1} {2} \ right) \ hbar \ omega \ label {28} \]

Они показаны на рисунке \ (\ PageIndex {2} \) в том же масштабе, что и потенциальная энергия.Энергия основного состояния \ (E_ {0} = \ dfrac {1} {2} \ hbar \ omega \) больше, чем классическое значение нуля, что снова является следствием принципа неопределенности. Это означает, что осциллятор всегда колеблется.

Примечательно, что разница между последовательными собственными значениями энергии имеет постоянное значение

\ [\ Delta E = E_ {n + 1} -E_ {n} = \ hbar \ omega = h \ nu \ label {29} \]

Это напоминает формулу Планка для энергии фотона. Поэтому неудивительно, что квантовая теория излучения имеет структуру сборки осцилляторов, каждый из которых представляет собой моду электромагнитных волн определенной частоты.

,

Одномерный гармонический осциллятор

Одномерный гармонический осциллятор

Одномерный гармонический осциллятор

Гармонический осциллятор — чрезвычайно важная физическая проблема . Многие потенциалы выглядят как гармонический осциллятор около своего минимума. Это первый непостоянный потенциал, для которого мы будем решать Уравнение Шредингера.

Гамильтониан гармонического осциллятора определяется выражением

что делает уравнение Шредингера для собственных состояний энергии

Обратите внимание, что этот потенциал также имеет симметрию четности.Потенциал нефизичен, потому что он не стремится к нулю на бесконечности, однако, часто это очень хорошее приближение, и этот потенциал можно точно решить.

Стандартно удалить жесткость пружины из гамильтониана, заменив его на классический генератор с частотой .

Гармонический осциллятор гамильтониан становится. Решаемое дифференциальное уравнение :

к решить уравнение гармонического осциллятора, сначала перейдем к безразмерным переменным, затем найдите форму решения для , затем умножьте это решение на полином, выведите рекурсивное соотношение между коэффициентами многочлена, показывают, что ряд многочленов должен завершиться, если решения должны быть нормализуемыми, вывести энергию собственные значения, а затем, наконец, вывести функции, которые являются решениями.

Собственные значения энергии — это

для , Существует счетное число решений с равными энергетическими интервалами. Мы были вынуждены квантовать энергии требованием, чтобы волновые функции нормируемы.

Волновая функция основного состояния равна.

Это распределение Гаусса (минимальная неопределенность).Поскольку потенциал HO обладает симметрией четности, решения имеют четную или нечетную четность . Основное состояние — четность.

Первое возбужденное состояние является состоянием нечетной четности с полиномом первого порядка умножения тот же гауссовский.

Второе возбужденное состояние — это четность с полиномом второго порядка, умножающим тот же гауссовский.

Обратите внимание, что равно количеству нулей волновой функции.Это обычная тенденция. С большим количеством нулей волновая функция имеет большую кривизну и, следовательно, большую кинетическую энергию.

Общее решение можно записать как

с коэффициентами, определяемыми рекурсивным соотношением и безразмерная переменная предоставлено. Ряд заканчивается последним ненулевым членом, имеющим ,

Джим Брэнсон 2013-04-22

,

Простой гармонический осциллятор | Физика в двух словах

Если бы меня спросили: «Есть ли в физике концепция, которая появляется снова и снова во время исследований? Что-то, на что, несомненно, стоит потратить некоторое время вначале, чтобы получить глубокое понимание с самого начала?» Ну, первое, что определенно пришло мне в голову, это концепция гармонического осциллятора . Гармонический осциллятор — это простейшая модель физического колебательного процесса, и он применим во многих различных областях физики — колебания есть везде!

Для просмотра анимации колебаний включите JavaScript. Реализация простого гармонического осциллятора: масса $ m $ прикреплена к пружине и колеблется без трения или внешнего воздействия.

Допущения

Интуитивно понятный пример колебательного процесса — это груз, прикрепленный к пружине (см. Рис. 1). Существует положение равновесия массы, при котором ее полная потенциальная энергия имеет минимум. Это означает, что любое смещение массы из этого равновесия вызывает восстанавливающую силу, которая стремится вернуть массу в ее равновесное положение. Простой гармонический осциллятор — это идеализированная система, в которой восстанавливающая сила прямо пропорциональна смещению от равновесия (что делает его гармоникой ) и где нет ни трения, ни внешнего воздействия (что делает его простым ).

Установка простого гармонического осциллятора: подобный частице объект массы $ m $ прикреплен к системе пружин с жесткостью пружины $ k $. Существует положение равновесия, в котором нет результирующей силы, действующей на массу $ m $. Однако, если частица смещается из состояния равновесия, возникает возвращающая сила $ f (x) = -k x $, которая стремится вернуть частицу в ее положение равновесия.

Уравнение движения

Уравнение движения задается вторым законом Ньютона, который связывает ускорение частицы $ \ ddot {x} (t) $ с возвращающей силой $ -k \, x (t) $ (заданной законом Гука ) где $ k $ — жесткость пружины: ^{[1] [2]} \ begin {align} & m \, \ ddot {x} (t) = — k \, x (t) \ nonumber \\ \ Leftrightarrow \ quad & m \, \ ddot {x} (t) + k \, x (t) = 0 \ label {eq: Equation-motion} \ end {align}

Это дифференциальное уравнение со следующим properties: ^[3]

• Это обычное : Есть только одна независимая переменная, $ t $.
• линейный : Если $ x_1 (t) $ и $ x_2 (t) $ — решения, а $ a $ и $ b $ — некоторые коэффициенты, то $ a \, x_1 (t) + b \, x_2 (t) $ — тоже решение.
• однородный : Все встречающиеся члены кратны x (t) или одной из его производных.
• и второго порядка : Наивысшая производная имеет порядок 2.

Если вы новичок в решении дифференциальных уравнений: нет жестких или быстрых общих правил, как найти решение для конкретного случая и вы даже не можете быть уверены, что есть решение.Поэтому решение дифференциальных уравнений требует некоторого опыта, тщательного изучения свойств уравнений, а также хорошей интуиции. К счастью, тот, который мы сейчас изучаем, — один из простых случаев!

Решение

Согласно теореме существования и единственности, для этого дифференциального уравнения существует единственное решение для каждой пары начальных условий. ^[4] Начальными условиями являются положение $ x_0: = x (t_0) $ и скорость $ v_0: = \ dot {x} (t_0) $ массы $ m $ в некоторый начальный момент времени $ t_0 $.Для удобства можно установить $ t_0 = 0 $, чтобы упростить последующие уравнения (без потери общности). Теперь цель состоит в том, чтобы найти функцию, которая решает уравнение. \ eqref {eq: формула движения} для все возможные начальные условия . Такая функция называется общим решением .

Гадание на решение

В уравнении движения \ eqref {eq: Equation-motion} $ \ ddot {x} (t) $ кратно $ x (t) $. Это означает, что желаемая функция остается неизменной до постоянного множителя при взятии двух производных.2: = к / м $. То же самое можно найти и для функции косинуса.

Мы уже нашли некоторые частные решения дифференциального уравнения (например, $ x (t) = \ sin (\ omega_0t) $ и $ x (t) = \ cos (\ omega_0 t) $). Однако пока эти решения обслуживают только отдельные пары начальных условий: \ begin {align} x (t) = \ sin (\ omega_0 t) \ quad & \ Rightarrow \ quad \ begin {pmatrix} x (0) \\ \ точка {x} (0) \ end {pmatrix} = \ begin {pmatrix} \ sin (\ omega_0 \ cdot 0) \\ \ omega_0 \ cos (\ omega_0 \ cdot 0) \ end {pmatrix} = \ begin {pmatrix } 0 \\ \ omega_0 \ end {pmatrix} \\ [2ex] x (t) = \ cos (\ omega_0 t) \ quad & \ Rightarrow \ quad \ begin {pmatrix} x (0) \\ \ dot {x } (0) \ end {pmatrix} = \ begin {pmatrix} \ cos (\ omega_0 \ cdot 0) \\ — \ omega_0 \ sin (\ omega_0 \ cdot 0) \ end {pmatrix} = \ begin {pmatrix} 1 \\ 0 \ end {pmatrix} \ end {align}

Согласно общей теории линейных дифференциальных уравнений, множество решений этого ОДУ второго порядка образует двумерное векторное пространство.Таким образом, общее решение может быть получено линейной комбинацией двух линейно независимых частных решений. Поскольку две тригонометрические функции линейно независимы друг от друга, можно записать: \ begin {align} x (t) = a \, \ sin (\ omega_0 t) + b \, \ cos (\ omega_0 t) \ quad \ текст {with} \ quad \ omega_0 = \ sqrt {\ frac {k} {m}} \ label {eq: general-solution-sin} \ end {align} Здесь $ a, b \ in \ mathbb {R} $ — произвольные коэффициенты, которые можно настроить для воспроизведения любого набора начальных условий: ^[5] \ begin {align} a: = \ frac {v_0} {\ omega_0} \ quad \ text {и} \ quad b: = x_0 \ end {align}

Общее решение простого гармонического осциллятора зависит от начальных условий $ x_0 = x (t = 0) $ и $ v_0 = \ dot {x} (t ​​= 0) $ колеблющегося объекта как а также его масса $ m $ и жесткость пружины $ k $.Он задается следующим образом: \ begin {align} x (t) = \ frac {v_0} {\ omega_0} \, \ sin (\ omega_0 t) + x_o \, \ cos (\ omega_0 t) \ quad \ text {с } \ quad \ omega_0 = \ sqrt {\ frac {k} {m}} \ end {align}

Экспоненциальная функция

Как было отмечено выше, не только функции синуса и косинуса пропорциональны своим вторым производным, но и то же самое верно и для экспоненциальной функции, и поэтому можно построить общее решение и из экспоненциальной функции. Опять же, мы начинаем с вставки анзаца $ x (t) = e ^ {\ lambda \, t} $ в уравнение движения \ eqref {eq: Equation-motion}, чтобы убедиться, что это решение: \ begin {align} \ left (m \, \ lambda ^ 2 + k \, \ right) \, e ^ {\ omega_0 t} & = 0 \ nonumber \\ \ Rightarrow \ lambda = \ pm \ sqrt {- \ frac {k} {m}} & = \ pm i \, \ omega_0 t \ end {align} Это дает два возможных (комплексных) значения для свободного параметра $ \ lambda $, которые зависят от конкретных свойств настройки ( постоянная пружины $ k $ и масса $ m $).{-i \ omega_0 t} \ nonumber \\ & = a \ left [\ cos (\ omega_0 t) + i \ sin (\ omega_0 t) \ right] + b \ left [\ cos (\ omega_0 t) — i \ sin (\ omega_0 t) \ right] \ nonumber \\ & = \ left (a + b \ right) \ cos (\ omega_0 t) + i \ left (ab \ right) \ sin (\ omega_0 t) \ label {eq: general-solution-exp} \ end {align} Здесь тождество Эйлера использовалось для того, чтобы переписать комплексную экспоненту в терминах тригонометрических функций. Теперь x (t) должен быть действительным числом, поскольку он описывает (реальное) смещение частицы.* \ label {eq: b-комплексно-сопряженный} \ end {align} Таким образом, на самом деле остается только один комплексный параметр $ a $ с двумя независимыми действительными компонентами $ \ Re {a} $ и $ \ Im {a} $, которые снова может быть определено начальными условиями. Поэтому нужно вставить \ eqref {eq: b-complex-conugated} в \ eqref {eq: general-solution-exp} и вычислить x (t) и его производную в $ t = 0 $: \ begin {align} \ begin { pmatrix} x (t = 0) \\ \ dot {x} (t ​​= 0) \ end {pmatrix} & \ stackrel {\ eqref {eq: general-solution-exp}} {=} \ begin {pmatrix} a + a ^ * \\ i (aa ^ *) \, \ omega_0 \ end {pmatrix} = \ begin {pmatrix} x_0 \\ v_0 \ end {pmatrix} \ end {align} Поскольку $ \ Re {a} = \ frac {a + a ^ *} {2} = \ frac {x_0} {2} $ и $ \ Im {a} = \ frac {aa *} {2i} = — \ frac {v_0} {\ omega_0} $ ^[6] , можно найти: \ begin {align} \ Leftrightarrow \ quad a & = \ frac {1} {2} \, \ left (x_0 — i \ frac {v_0} {\ omega_0} \ right) \ end {align} Решение становится — аналогично результату в предыдущем разделе: \ begin {align} x (t) = \ frac {v_0} {\ omega_0} \, \ sin (\ omega_0 t) + x_0 \, \ cos (\ omega_0 t) \ end {align}

Систематический подход: степенной ряд Ansatz

Когда я впервые изучал дифференциальные уравнения, я не был очень доволен fi поиск решения, просто угадав его.Я имею в виду — в течение всего моего математического образования я научился систематически находить решения математических задач, применяя общие правила. И теперь я должен был просто угадать решение?

Мне было интересно, есть ли способ на самом деле получить это решение. И я рад вам сказать: есть! Но не в общем, а по крайней мере для дифференциальных уравнений, подобных рассмотренному.

Метод работает следующим образом. Неизвестная функция $ x (t) $ записывается в виде степенного ряда, чтобы получить более конкретное представление.Подставляя его в дифференциальное уравнение, можно затем вывести условия для коэффициентов и, таким образом, идентифицировать функцию решения.

При этом неявно предполагается, что желаемая функция в первую очередь может быть представлена ​​в виде степенного ряда. Однако ради компактности я не хочу обсуждать математические требования для этого. Однако если при таком подходе будет найдено верное решение, то метод будет оправдан ретроспективно.

Представление $ x (t) $ в виде степенного ряда (при центрировании в $ t = 0 $) определяется как ^[7] \ begin {align} x (t) = \ sum_ {n = 0} ^ {\ infty} a_n \, t ^ n \ quad \ text {with} \ quad n \ in \ mathbb {N} \ quad \ text {и} \ quad a_n \ in \ mathbb {R} \ label {eq: power -series-represantation} \ end {align} и имеет следующие производные: \ begin {align} \ dot {x} (t) & = \ sum_ {n = 1} ^ {\ infty} n \, a_n \, t ^ {n-1} = \ sum_ {n = 0} ^ {\ infty} (n + 1) \, a_ {n + 1} \, t ^ n \ label {eq: power-series-производная} \\ \ ddot {x} (t) & = \ sum_ {n = 2} ^ {\ infty} n \, (n-1) \, a_n \, t ^ {n-2} = \ sum_ {n = 0} ^ {\ infty} (n + 2) (n + 1) \, a_ {n + 2} \, t ^ n \ label {eq: power-series-sec-производный} \\ \ end {align} Вставка этих выражения в ур.n = 0 \ end {align}

Это выражение истинно, только если член в квадратных скобках исчезает. ^[8] Это обеспечивает условие на выбор коэффициентов степенного ряда: \ begin {align} m \, (n + 2) (n + 1) \, a_ {n + 2} + k \, a_n = 0 \ nonumber \\ \ Leftrightarrow \ quad a_ {n + 2} = — \ frac {k} {m} \ frac {a_n} {(n + 2) (n + 1)} \ label {eq: рекурсия -rule} \ end {align} Первое, на что следует обратить внимание, это то, что $ a_2 $ — это коэффициент с наименьшим индексом, который фактически может быть вычислен с помощью рекуррентного отношения \ eqref {eq: recursion-rule}.{\ frac {n-1} {2}} \ frac {a_1} {n} \ qquad n \ text {нечетное} \ end {case} \ end {align}, и если вы настроены скептически, вы можете проверить это, индукция. ^[9] И, основываясь на предыдущих разделах, с этого момента обозначение $ \ omega_0: = \ frac {k} {m} $ будет использоваться снова, чтобы термины были компактными. Выражения для коэффициентов $ a_n $ теперь можно использовать для записи более конкретного представления ряда $ x (t) $: ^[10] \ begin {align} x (t) & = x_ \ text {odd} ( t) + x_ \ text {even} (t) \ qquad \ text {with} \\ [2ex] x_ \ text {even} (t): & = \ sum_ {n \ text {even}} a_0 \ left ( — \ omega_0 ^ 2 \ right) ^ {\ frac {n} {2}} \ frac {t ^ n} {n!} \ qquad \ left | \ quad j: = \ frac {n} {2} \ right.{2j + 1}} {(2j + 1)!} \ Nonumber \\ & = \ frac {a_1} {\ omega_0} \, \ sin (\ omega_0 t) \ end {align} Кроме того, на основе ур. \ eqref {eq: power-series-производная} и \ eqref {eq: power-series-represantation} легко увидеть, что остальные коэффициенты определяются начальными условиями \ begin {align} x (t = 0) = a_0 = x_0 \ quad \ text {и} \ quad \ dot {x} (t ​​= 0) = a_1 = v_0 \ end {align}, так что решение дается \ begin {align} x (t) = x_0 \, \ cos (\ omega_0 t) + \ frac {v_0} {\ omega} \, \ sin (\ omega_0 t) \ end {align}, который воспроизводит результаты предыдущих разделов.

В некоторых случаях подход степенных рядов обеспечивает хороший способ фактически вывести решения дифференциальных уравнений, не делая необоснованных предположений о конкретной форме функции решения. Однако даже в этом довольно простом примере он включает в себя довольно много шагов и, возможно, не так элегантен, как метод угадывания . Вот почему это обычно не лучший метод обучения решению дифференциальных уравнений. И в большинстве случаев вы будете намного быстрее, используя, например, экспоненциальный подход, а не метод степенных рядов.

,

Гармонический осциллятор в одном измерении

Классическая механика против квантовой: гармонический осциллятор в одном измерении
Далее: Вероятность (x): Где находится Up: intro_simulation Предыдущая: Статистическая механика — Расчет Гармонический осциллятор — это модельная система модельных систем. Мы изучаем его здесь, чтобы охарактеризовать различия в динамическом поведении. предсказывается классической и квантовой механикой, подчеркивая концепции и результаты.Более подробную информацию и математический аппарат можно найти в учебники [1,2]. Наша модельная система представляет собой одиночную частицу, движущуюся в размере x , соединенную пружиной с фиксированной точкой. Его потенциальная энергия равна , где k — жесткость пружины. Жесткие пружины описываются большими цифрами k .

Классический , этот генератор подвергается синусоидальным колебаниям амплитуды и частота , где E — полная энергия, потенциальная плюс кинетическая.В состоянии равновесия при температуре T его средняя потенциальная энергия и кинетическая энергия равны; они зависят только от температуры, а не от частоты движения.

Квантово-механически , вероятность найти частицу в данном месте получается из решения Уравнение Шредингера, дающее собственные значения и собственные функции. Для одномерного гармонического осциллятора энергии оказываются , где — постоянная Планка, f — классическая частота движения (см. выше), а n может принимать целые значения от От 0 до бесконечности.Оказывается, это действительные функции, содержащие полиномов Эрмита . Из уравнения 1 только основное состояние () заполняется как температура , Энергия идет не в ноль, а в. Соответствующее движение нулевой точки является квантово-механическим явлением. Классически движения нет, так как , Таким образом, мы ожидаем, что квантовая механика предсказывает больше движения, чем классическая механика, особенно при низких температурах.

---

Подразделы

---

Далее: Вероятность (x): Где находится Up: intro_simulation Предыдущая: Статистическая механика — Расчет

Стейнбах 2019-02-01

,