Site Loader
Posted on 23.01.2021

Содержание

Гармоническое число — Википедия

Материал из Википедии — свободной энциклопедии

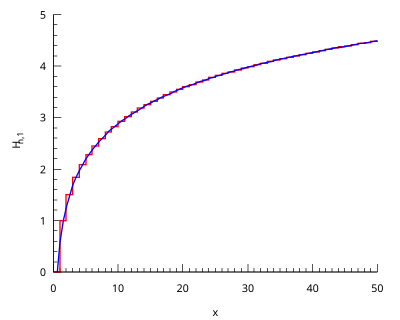Гармоническое число Hn,1{\displaystyle H_{n,1}}, где n=⌊x⌋{\displaystyle n=\lfloor {x}\rfloor } (красная линия) и его асимптотический предел γ+ln⁡(x){\displaystyle \gamma +\ln(x)} (синяя линия).

В математике n-м гармоническим числом называется сумма обратных величин первых n последовательных чисел натурального ряда:

Hn=∑k=1n1k=1+12+13+⋯+1n.{\displaystyle H_{n}=\sum _{k=1}^{n}{\frac {1}{k}}=1+{\frac {1}{2}}+{\frac {1}{3}}+\cdots +{\frac {1}{n}}.}

Гармонические числа являются частичными суммами гармонического ряда.

Изучение гармонических чисел началось в античности. Они имеют важное значение в различных областях теории чисел и теории алгоритмов и, в частности, тесно связаны с дзета-функцией Римана.

  • Гармонические числа можно определить рекуррентно следующим образом:
    {Hn=Hn−1+1nh2=1{\displaystyle {\begin{cases}H_{n}=H_{n-1}+{\frac {1}{n}}\\H_{1}=1\end{cases}}}
  • Также верно соотношение:
    Hn=γ+ψ(n+1)=Γ′(n)Γ(n)+1n+γ{\displaystyle H_{n}=\gamma +\psi (n+1)={\frac {\Gamma ‘(n)}{\Gamma (n)}}+{\frac {1}{n}}+\gamma },
    где ψ(n){\displaystyle \psi (n)} — дигамма-функция, γ=−ψ(1){\displaystyle \gamma =-\psi (1)} — постоянная Эйлера — Маскерони.
  • Еще одно соотношение:
    Hn=∑k=1n(nk)(−1)k+1k{\displaystyle H_{n}=\sum _{k=1}^{n}{\binom {n}{k}}{\frac {(-1)^{k+1}}{k}}}

Дополнительные представления[править | править код]

Нижеследующие формулы могут быть использованы для вычисления гармонических чисел (в том числе и в точках, отличных от точек натурального ряда):

  • интегральные представления:
    Hx=∫011−tx1−tdt,Re(x)>−1{\displaystyle H_{x}=\int _{0}^{1}{\frac {1-t^{x}}{1-t}}dt,\quad Re(x)>-1}
  • предельные представления:
    Hx=limn→∞(ln⁡(n)−∑k=0n1x+k+1)+γ{\displaystyle H_{x}=\lim _{n\to \infty }\left(\ln(n)-\sum _{k=0}^{n}{\frac {1}{x+k+1}}\right)+\gamma }
    Hx=x∑k=0∞1(k+1)(x+k+1){\displaystyle H_{x}=x\sum _{k=0}^{\infty }{\frac {1}{(k+1)(x+k+1)}}};
  • разложение в ряд Тейлора в точке x=0{\displaystyle x=0}:
    Hx=∑k=1∞(−1)k+1ζ(k+1)xk=ζ(2)x−ζ(3)x2+ζ(4)x3−ζ(5)x4+⋯,{\displaystyle H_{x}=\sum _{k=1}^{\infty }(-1)^{k+1}\zeta (k+1)x^{k}=\zeta (2)x-\zeta (3)x^{2}+\zeta (4)x^{3}-\zeta (5)x^{4}+\cdots ,}
    где ζ(x){\displaystyle \zeta (x)} — дзета-функция Римана;
  • асимптотическое разложение:
    Hx=γ+ln⁡(x)+12x−112×2+1120×4−1252×6+1240×8−1132×10+⋯{\displaystyle H_{x}=\gamma +\ln(x)+{\frac {1}{2x}}-{\frac {1}{12x^{2}}}+{\frac {1}{120x^{4}}}-{\frac {1}{252x^{6}}}+{\frac {1}{240x^{8}}}-{\frac {1}{132x^{10}}}+\cdots }.

∑k=1∞Hkzk=−ln⁡(1−z)1−z{\displaystyle \sum _{k=1}^{\infty }H_{k}z^{k}=-{\frac {\ln(1-z)}{1-z}}}

Значения от нецелого аргумента[править | править код]

  • h2/2=2−2ln⁡2{\displaystyle H_{1/2}=2-2\ln 2}
  • h2/3=3−3ln⁡32−π23{\displaystyle H_{1/3}=3-{\frac {3\ln 3}{2}}-{\frac {\pi }{2{\sqrt {3}}}}}
  • h2/4=4−3ln⁡2−π2{\displaystyle H_{1/4}=4-3\ln 2-{\frac {\pi }{2}}}
  • h2/5=5−5ln⁡54−121+25π−52ln⁡φ,{\displaystyle H_{1/5}=5-{\frac {5\ln 5}{4}}-{\frac {1}{2}}{\sqrt {1+{\frac {2}{\sqrt {5}}}}}\pi -{\frac {\sqrt {5}}{2}}\ln \varphi ,}
где φ{\displaystyle \varphi } — золотое сечение.
  • h2/7=7−ln⁡14−π2ctgπ7−2cos⁡(π7)ln⁡(cos⁡π14)+2sin⁡(3π14)ln⁡(sin⁡π7)−2sin⁡(π14)ln⁡(cos⁡3π14){\displaystyle H_{1/7}=7-\ln 14-{\frac {\pi }{2}}\mathrm {ctg} {\frac {\pi }{7}}-2\cos \left({\frac {\pi }{7}}\right)\ln \left(\cos {\frac {\pi }{14}}\right)+2\sin \left({\frac {3\pi }{14}}\right)\ln \left(\sin {\frac {\pi }{7}}\right)-2\sin \left({\frac {\pi }{14}}\right)\ln \left(\cos {\frac {3\pi }{14}}\right)}

Суммы, связанные с гармоническими числами[править | править код]

Тождества, связанные с гармоническими числами[править | править код]

Приближённое вычисление[править | править код]

С помощью формулы суммирования Эйлера-Маклорена получаем следующую формулу:

Hn=ln⁡n+γ+12n+∑k=1mB2k2kn2k−θm,nB2m+2(2m+2)n2m+2,{\displaystyle H_{n}=\ln n+\gamma +{\frac {1}{2n}}+\sum \limits _{k=1}^{m}{\frac {B_{2k}}{2kn^{2k}}}-\theta _{m,n}{\frac {B_{2m+2}}{(2m+2)n^{2m+2}}},}

где 0<θm,n<1{\displaystyle 0<\theta _{m,n}<1}, γ{\displaystyle \gamma } — постоянная Эйлера, которую можно вычислить быстрее из других соображений[каких?], а Bk{\displaystyle B_{k}} — числа Бернулли.

Теоретико-числовые свойства[править | править код]

  • Теорема Вольстенхольма утверждает, что для всякого простого числа p>3{\displaystyle p>3} выполняется сравнение:
    Hp−1≡0(modp2).{\displaystyle H_{p-1}\equiv 0{\pmod {p^{2}}}.}

Некоторые значения гармонических чисел[править | править код]

h2=1h3=32=1,5h4=116≈1,833h5=2512≈2,083H5=13760≈2,283{\displaystyle {\begin{matrix}H_{1}&=&1\\\\H_{2}&=&{\frac {3}{2}}&=&1{,}5\\\\H_{3}&=&{\frac {11}{6}}&\approx &1{,}833\\\\H_{4}&=&{\frac {25}{12}}&\approx &2{,}083\\\\H_{5}&=&{\frac {137}{60}}&\approx &2{,}283\end{matrix}}}H6=4920=2,45H7=363140≈2,593H8=761280≈2,718h203≈7,484h206≈14,393{\displaystyle {\begin{matrix}H_{6}&=&{\frac {49}{20}}&=&2{,}45\\\\H_{7}&=&{\frac {363}{140}}&\approx &2{,}593\\\\H_{8}&=&{\frac {761}{280}}&\approx &2{,}718\\\\H_{10^{3}}&\approx &7{,}484\\\\H_{10^{6}}&\approx &14{,}393\end{matrix}}}

Числитель и знаменатель несократимой дроби, представляющей собой n-e гармоническое число, являются n-ми членами целочисленных последовательностей A001008 и A002805, соответственно.

В 2002 году Lagarias доказал[1], что гипотеза Римана о нулях дзета-функции Римана эквивалентна утверждению, что неравенство

σ(n)≤Hn+ln⁡(Hn)eHn{\displaystyle \sigma (n)\leq H_{n}+\ln(H_{n})e^{H_{n}}}

верно при всех целых n≥1{\displaystyle n\geq 1} со строгим неравенством при n>1{\displaystyle n>1}, где σ(n){\displaystyle \sigma (n)} — сумма делителей числа n{\displaystyle n}.

Гармоническое число — это… Что такое Гармоническое число?

  • Гармоническое среднее —         число (у), обратное которому есть Арифметическое среднее чисел, обратных данным числам (а1, a2,…, an):          …   Большая советская энциклопедия

  • ГАРМОНИЧЕСКОЕ СРЕДНЕЕ — число (у), обратное к рому есть арифметич. среднее чисел, обратных данным числам (a1 a2,…,an) …   Большой энциклопедический политехнический словарь

  • Число 666 — 666 шестьсот шестьдесят шесть 663 · 664 · 665 · 666 · 667 · 668 · 669 Факторизация: 2⋅32⋅37 Римская запись: DCLXVI Двоичное: 1010011010 Восьмеричное: 1232 Шестнадцатеричное: 29A …   Википедия

  • ГАРМОНИЧЕСКОЕ СРЕДНЕЕ — чисел число, обратная величина к рого является средним арифметическим обратных величин данных чисел, т. е. число Например, является Г. с. дробей и , Г. с. чисел не превосходит их арифметич. среднего. Л. Д. Кудрявцев …   Математическая энциклопедия

  • Среднее гармоническое — Средним гармоническим нескольких положительных чисел называется число, обратное среднему арифметическому их обратных, то есть число Содержание 1 Свойства 2 Приложения и примеры …   Википедия

  • 666 (число) — 666 шестьсот шестьдесят шесть 663 · 664 · 665 · 666 · 667 · 668 · 669 Факторизация: Римская запись: DCLXVI Двоичное: 1010011010 Восьмеричное: 1232 Шестнадцатеричное: 29A …   Википедия

  • Гармонический ряд — В математике гармонический ряд представляет собой сумму, составленную из бесконечного количества членов, обратных последовательным числам натурального ряда[1]: . Ряд назван гармоническим, так как складывается из «гармоник»: я гармоника,… …   Википедия

  • Задача о джипе

    — (англ. Jeep problem, desert crossing problem, exploration problem)  математическая задача, целью которой является максимизация пути, который можно преодолеть на джипе с полным баком топлива в труднопреодолимых условиях, к примеру, в… …   Википедия

  • Биномиальный коэффициент — В математике биномиальные коэффициенты  это коэффициенты в разложении бинома Ньютона по степеням x. Коэффициент при обозначается или и читается «биномиальный коэффициент из n по k» (или «це из n по k»): В …   Википедия

  • Гипотеза Римана — Задачи тысячелетия Равенство классов P и NP Гипотеза Ходжа Гипотеза Пуанкаре Гипотеза Римана Квантовая теория Янга  Миллса Существование и гладкость  решений уравнений Навье Стокса Гипотеза Бёрча Свиннертон Дайера Гипотеза Римана о… …   Википедия

    • Среднее гармоническое — Википедия

    Материал из Википедии — свободной энциклопедии

    Сре́днее гармони́ческое — один из способов, которым можно понимать «среднюю» величину некоторого набора чисел. Его можно определить следующим образом: пусть даны положительные числа x1,…,xn{\displaystyle x_{1},\ldots ,x_{n}}, тогда их средним гармоническим будет такое число H{\displaystyle H}, что

    nH=1×1+…+1xn{\displaystyle {\frac {n}{H}}={\frac {1}{x_{1}}}+\ldots +{\frac {1}{x_{n}}}}.

    Можно получить явную формулу для среднего гармонического:

    H(x1,…,xn)=n1x1+1×2+⋯+1xn=11n∑i=1n1xi{\displaystyle H(x_{1},\ldots ,x_{n})={\frac {n}{{\frac {1}{x_{1}}}+{\frac {1}{x_{2}}}+\cdots +{\frac {1}{x_{n}}}}}={\frac {1}{{\frac {1}{n}}\sum \limits _{i=1}^{n}{\frac {1}{x_{i}}}}}},

    т. е. среднее гармоническое есть обратная величина к среднему от обратных к числам x1,…,xn{\displaystyle x_{1},\ldots ,x_{n}}.

    • Среднее гармоническое действительно является «средним», в том смысле что min(x1,…,xn)⩽H(x1,…,xn)⩽max(x1,…,xn){\displaystyle \min(x_{1},\ldots ,x_{n})\leqslant H(x_{1},\ldots ,x_{n})\leqslant \max(x_{1},\ldots ,x_{n})}.
    • Вообще, среднее гармоническое является средним степени -1.
    • Среднее гармоническое двойственно среднему арифметическому в следующем смысле:
    H(x1,…,xn)=A−1(x1−1,…,xn−1){\displaystyle H(x_{1},\ldots ,x_{n})=A^{-1}(x_{1}^{-1},\ldots ,x_{n}^{-1})} и
    A(x1,…,xn)=H−1(x1−1,…,xn−1){\displaystyle A(x_{1},\ldots ,x_{n})=H^{-1}(x_{1}^{-1},\ldots ,x_{n}^{-1})} (когда последнее определено).
    H≤G≤A≤S,{\displaystyle H\leq G\leq A\leq S,}
    где H{\displaystyle H} — среднее гармоническое;
    G{\displaystyle G} — среднее геометрическое;
    A{\displaystyle A} — среднее арифметическое;
    S{\displaystyle S} — среднее квадратическое.

    Пусть есть набор неотрицательных чисел x1,…,xn{\displaystyle x_{1},\ldots ,x_{n}} и набор чисел w1,…,wn{\displaystyle w_{1},\ldots ,w_{n}}, где wi{\displaystyle w_{i}}называется весом величины xi{\displaystyle x_{i}}. Тогда их взвешенным средним гармоническим называется число

    H(x1,…,xn;w1,…,wn)=w1+…+wnw1x1+…+wnxn{\displaystyle H(x_{1},\ldots ,x_{n};w_{1},\ldots ,w_{n})={\frac {w_{1}+\ldots +w_{n}}{{\frac {w_{1}}{x_{1}}}+\ldots +{\frac {w_{n}}{x_{n}}}}}}.

    Легко заметить, что при w1=…=wn≠0{\displaystyle w_{1}=\ldots =w_{n}\neq 0}(то есть когда все величины «равноправны») получается обычное среднее гармоническое.

    У трапеции длина отрезка, проходящего через точку пересечения диагоналей параллельно основаниям, равна среднему гармоническому длин оснований[1] Диаметры заполненных аквамариновым цветом кругов, называемых кругами-близнецами[en], одинаковые и равны среднему гармоническому радиусов полуокружностей, построенных на отрезках AB и BC как на диаметрах.

    В статистике среднее гармоническое применяется в случае, когда наблюдения, для которых требуется получить среднее арифметическое, заданы обратными значениями.

    В формуле тонкой линзы удвоенное фокусное расстояние равно среднему гармоническому расстояния от линзы до предмета и расстояния от линзы до изображения. Подобным образом среднее гармоническое входит и в аналогичную формулу для сферического зеркала.

    Средняя скорость на пути, разделенном на равные участки, скорость на которых постоянна, равна среднему гармоническому скоростей на этих участках пути. Более обще, если путь разбит на участки, скорость на каждом из которых постоянна, то средняя скорость будет равна взвешенному среднему гармоническому скоростей (каждая скорость идет с весом, равным длине соответствующего ей отрезка).

    Средняя плотность сплава равна взвешенному среднему гармоническому плотностей сплавляемых веществ (веса — массы частей соответствующих веществ).

    Сопротивление, получающееся при параллельном подключении нескольких резисторов, равно среднему гармоническому их сопротивлений, деленному на их количество. Аналогичное утверждение верно для емкостей последовательно соединенных конденсаторов.

    • Weisstein, Eric W. Harmonic Mean / MathWorld—A Wolfram Web Resource

    Гармонический ряд — Википедия

    Гармони́ческий ряд — сумма, составленная из бесконечного количества членов, обратных последовательным числам натурального ряда:

    ∑k=1∞1k=1+12+13+14+⋯+1k+⋯{\displaystyle \sum _{k=1}^{\mathcal {\infty }}{\frac {1}{k}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+\cdots +{\frac {1}{k}}+\cdots }.

    Ряд назван гармоническим, так как складывается из «гармоник»: k{\displaystyle k}-я гармоника, извлекаемая из скрипичной струны, — это основной тон, производимый струной длиной 1k{\displaystyle {\frac {1}{k}}} от длины исходной струны[1]. Кроме того, каждый член ряда, начиная со второго, представляет собой среднее гармоническое двух соседних членов.

    Суммы первых n членов ряда (частичные суммы)[править | править код]

    Отдельные члены ряда стремятся к нулю, но его сумма расходится. Частичная сумма n первых членов гармонического ряда называется n-м гармоническим числом:

    Hn=∑k=1n1k=1+12+13+14+⋯+1n{\displaystyle H_{n}=\sum _{k=1}^{n}{\frac {1}{k}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+\cdots +{\frac {1}{n}}}

    Разница между n{\displaystyle n}-м гармоническим числом и натуральным логарифмом n{\displaystyle n} сходится к постоянной Эйлера — Маскерони γ=0,5772…{\displaystyle \gamma =0{,}5772…}.

    Разница между различными гармоническими числами никогда не равна целому числу и никакое гармоническое число, кроме h2=1{\displaystyle H_{1}=1}, не является целым: ∀n>1∑k=1n1k∉N{\displaystyle \forall n>1\;\;\;\;\sum _{k=1}^{n}{\frac {1}{k}}\notin \mathbb {N} }[2].

    Некоторые значения частичных сумм[править | править код]

    h2=1h3=32=1,5h4=116≈1,833h5=2512≈2,083H5=13760≈2,283{\displaystyle {\begin{matrix}H_{1}&=&1\\\\H_{2}&=&{\frac {3}{2}}&=&1{,}5\\\\H_{3}&=&{\frac {11}{6}}&\approx &1{,}833\\\\H_{4}&=&{\frac {25}{12}}&\approx &2{,}083\\\\H_{5}&=&{\frac {137}{60}}&\approx &2{,}283\end{matrix}}}H6=4920=2,45H7=363140≈2,593H8=761280≈2,718h203≈7,484h206≈14,393{\displaystyle {\begin{matrix}H_{6}&=&{\frac {49}{20}}&=&2{,}45\\\\H_{7}&=&{\frac {363}{140}}&\approx &2{,}593\\\\H_{8}&=&{\frac {761}{280}}&\approx &2{,}718\\\\H_{10^{3}}&\approx &7{,}484\\\\H_{10^{6}}&\approx &14{,}393\end{matrix}}}

    Формула Эйлера[править | править код]

    В 1740 году Эйлером было получено асимптотическое выражение для суммы первых n{\displaystyle n} членов ряда:

    Hn=ln⁡n+γ+εn{\displaystyle H_{n}=\ln n+\gamma +\varepsilon _{n}},

    где γ=0,5772…{\displaystyle \gamma =0{,}5772…} — постоянная Эйлера — Маскерони, а ln{\displaystyle \ln } — натуральный логарифм.

    При n→∞{\displaystyle n\rightarrow \infty } значение εn→0,{\displaystyle \varepsilon _{n}\rightarrow 0,} следовательно, для больших n{\displaystyle n}

    Hn≈ln⁡n+γ{\displaystyle H_{n}\approx \ln n+\gamma } — формула Эйлера для суммы первых n{\displaystyle n} членов гармонического ряда.
    Пример использования формулы Эйлера
    n{\displaystyle n}Hn=∑k=1n1k{\displaystyle H_{n}=\sum _{k=1}^{n}{\frac {1}{k}}}ln⁡n+γ{\displaystyle \ln n+\gamma }εn{\displaystyle \varepsilon _{n}}, (%)
    102,932,881,7
    253,823,800,5

    Более точная асимптотическая формула для частичной суммы гармонического ряда:

    Hn≍ln⁡n+γ+12n−112n2+1120n4−1252n6⋯=ln⁡n+γ+12n−∑k=1∞B2k2kn2k,{\displaystyle H_{n}\asymp \ln n+\gamma +{\frac {1}{2n}}-{\frac {1}{12n^{2}}}+{\frac {1}{120n^{4}}}-{\frac {1}{252n^{6}}}\dots =\ln n+\gamma +{\frac {1}{2n}}-\sum _{k=1}^{\infty }{\frac {B_{2k}}{2k\,n^{2k}}},} где B2k{\displaystyle B_{2k}} — числа Бернулли.

    Данный ряд расходится, однако ошибка вычислений по нему никогда не превышает половины первого отброшенного члена[источник не указан 554 дня].

    Гармонический ряд расходится: sn→∞{\displaystyle s_{n}\rightarrow \infty } при n→∞,{\displaystyle n\rightarrow \infty ,} однако очень медленно (для того, чтобы частичная сумма превысила 100, необходимо около 1043 элементов ряда).

    Расходимость гармонического ряда можно продемонстрировать, сравнив его со следующим телескопическим рядом, который получается из логарифмирования (1+1n)n<e{\displaystyle \left(1+{\frac {1}{n}}\right)^{n}<e}:

    vn=ln⁡(n+1)−ln⁡n=ln⁡(1+1n)<1n.{\displaystyle v_{n}=\ln(n+1)-\ln n=\ln \left(1+{\frac {1}{n}}\right)<{\frac {1}{n}}.}

    Частичная сумма этого ряда, очевидно, равна ∑i=1nvi=ln⁡(n+1).{\displaystyle \sum _{i=1}^{n}v_{i}=\ln(n+1).} Последовательность таких частичных сумм расходится; следовательно, по определению телескопический ряд расходится, но тогда из признака сравнения рядов следует, что гармонический ряд тоже расходится.

    Доказательство через предел последовательности частичных сумм[3][править | править код]

    Рассмотрим последовательность Hn=∑k=1n1k=1+12+13+14+⋯+1n.{\displaystyle H_{n}=\sum _{k=1}^{n}{\frac {1}{k}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+\cdots +{\frac {1}{n}}.} Покажем, что эта последовательность не является фундаментальной, то есть, что ∃ε>0:∀k∈N ∃n>k,∃p∈N:|Hn+p−Hn|≥ε.{\displaystyle \exists \varepsilon >0:\forall k\in \mathbb {N} \ \exists n>k,\exists p\in \mathbb {N} :\left\vert H_{n+p}-H_{n}\right\vert \geq \varepsilon .} Оценим разность|Hn+p−Hn|=1n+1+⋯+1n+p≥1n+p+⋯+1n+p=pn+p.{\displaystyle \left\vert H_{n+p}-H_{n}\right\vert ={\frac {1}{n+1}}+\cdots +{\frac {1}{n+p}}\geq {\frac {1}{n+p}}+\cdots +{\frac {1}{n+p}}={\frac {p}{n+p}}.} Пусть p≐n.{\displaystyle p\doteq n.} Тогда ∀n∈N:|h3n−Hn|≥12.{\displaystyle \forall n\in \mathbb {N} :\left\vert H_{2n}-H_{n}\right\vert \geq {\frac {1}{2}}.} Следовательно, данная последовательность не является фундаментальной и по критерию Коши расходится. Тогда по определению ряд также расходится.

    Доказательство Орема[править | править код]

    Доказательство расходимости можно построить, если сравнить гармонический ряд с другим расходящимся рядом, в котором знаменатели дополнены до степени двойки:

    ∑k=1∞1k=1+[12]+[13+14]+[15+16+17+18]+[19+⋯]+⋯>1+[12]+[14+14]+[18+18+18+18]+[116+⋯]+⋯=1+ 12   +12 + 12  +  12 + ⋯.{\displaystyle {\begin{aligned}\sum _{k=1}^{\infty }{\frac {1}{k}}&{}=1+\left[{\frac {1}{2}}\right]+\left[{\frac {1}{3}}+{\frac {1}{4}}\right]+\left[{\frac {1}{5}}+{\frac {1}{6}}+{\frac {1}{7}}+{\frac {1}{8}}\right]+\left[{\frac {1}{9}}+\cdots \right]+\cdots \\&{}>1+\left[{\frac {1}{2}}\right]+\left[{\frac {1}{4}}+{\frac {1}{4}}\right]+\left[{\frac {1}{8}}+{\frac {1}{8}}+{\frac {1}{8}}+{\frac {1}{8}}\right]+\left[{\frac {1}{16}}+\cdots \right]+\cdots \\&{}=1+\ {\frac {1}{2}}\ \ \ +\quad {\frac {1}{2}}\ \quad +\ \qquad \quad {\frac {1}{2}}\qquad \ \quad \ +\quad \ \ {\frac {1}{2}}\ \quad +\ \cdots .\end{aligned}}}

    Это доказательство принадлежит средневековому учёному Николаю Орему (ок. 1350).

    Обобщённый гармонический ряд[править | править код]

    Обобщённым гармоническим рядом (частный случай ряда Дирихле) называют ряд[4]

    ∑k=1∞1kα=1+12α+13α+14α+⋯+1kα+⋯{\displaystyle \sum _{k=1}^{\infty }{\frac {1}{k^{\alpha }}}=1+{\frac {1}{2^{\alpha }}}+{\frac {1}{3^{\alpha }}}+{\frac {1}{4^{\alpha }}}+\cdots +{\frac {1}{k^{\alpha }}}+\cdots }.

    Этот ряд расходится при α⩽1{\displaystyle \alpha \leqslant 1} и сходится при α>1{\displaystyle \alpha >1}[4].

    Сумма обобщённого гармонического ряда порядка α{\displaystyle \alpha } равна значению дзета-функции Римана:

    ∑k=1∞1kα=ζ(α){\displaystyle \sum _{k=1}^{\infty }{\frac {1}{k^{\alpha }}}=\zeta (\alpha )}

    Для чётных это значение явно выражается через число пи — например, сумма ряда обратных квадратов ζ(2)=π26{\displaystyle \zeta (2)={\frac {\pi ^{2}}{6}}}. Но уже для α=3 его значение (константа Апери) аналитически неизвестно.

    Другой иллюстрацией расходимости гармонического ряда может служить соотношение ζ(1+1n)∼n.{\displaystyle \zeta (1+{\frac {1}{n}})\sim n.}

    Знакопеременный ряд[править | править код]

    Первые 14 частичных сумм знакочередующегося гармонического ряда (чёрные отрезки), показывающие сходимость к натуральному логарифму от 2 (красная линия)

    В отличие от гармонического ряда, у которого все слагаемые берутся со знаком «+», ряд

    ∑n=1∞(−1)n+1n=1−12+13−14+15−⋯{\displaystyle \sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}\;=\;1\,-\,{\frac {1}{2}}\,+\,{\frac {1}{3}}\,-\,{\frac {1}{4}}\,+\,{\frac {1}{5}}\,-\,\cdots }

    сходится по признаку Лейбница. Поэтому говорят, что такой ряд обладает условной сходимостью. Его сумма равна натуральному логарифму 2:

    1−12+13−14+15−⋯=ln⁡2.{\displaystyle 1\,-\,{\frac {1}{2}}\,+\,{\frac {1}{3}}\,-\,{\frac {1}{4}}\,+\,{\frac {1}{5}}\,-\,\cdots \;=\;\ln 2.}

    Эта формула — частный случай ряда Меркатора, то есть ряда Тейлора для натурального логарифма.

    Похожий ряд может быть получен из ряда Тейлора для арктангенса:

    ∑n=0∞(−1)n2n+1=1−13+15−17+⋯=π4.{\displaystyle \sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}\;\;=\;\;1\,-\,{\frac {1}{3}}\,+\,{\frac {1}{5}}\,-\,{\frac {1}{7}}\,+\,\cdots \;\;=\;\;{\frac {\pi }{4}}.}

    Это соотношение известно как ряд Лейбница.

    Случайный гармонический ряд[править | править код]

    В 2003 году изучены[5][6] свойства случайного ряда

    ∑n=1∞snn,{\displaystyle \sum _{n=1}^{\infty }{\frac {s_{n}}{n}},}

    где sn{\displaystyle s_{n}} — независимые, одинаково распределённые случайные величины, которые принимают значения +1 и −1 с одинаковой вероятностью ½. Показано, что этот ряд сходится с вероятностью 1, и сумма ряда есть случайная величина с интересными свойствами. Например, функция плотности вероятности, вычисленная в точках +2 или −2 имеет значение:

    0,124 999 999 999 999 999 999 999 999 999 999 999 999 999 7 642…,

    отличаясь от ⅛ на менее чем 10−42.

    «Истончённый» гармонический ряд[править | править код]

    См. Ряд Кемпнера[en]

    Если рассмотреть гармонический ряд, в котором оставлены только слагаемые, знаменатели которых не содержат цифры 9, то окажется, что оставшийся ряд сходится, и его сумма меньше 80[7]. Позже была найдена более точная оценка, ряд Кемпнера сходится к 22,92067661926415034816{\displaystyle 22{,}92067661926415034816} (последовательность A082838 в OEIS). Более того, доказано, что если оставить слагаемые, не содержащие любой заранее выбранной последовательности цифр, то полученный ряд будет сходиться. Из этого можно сделать ошибочное заключение о сходимости исходного гармонического ряда, что не верно, поскольку с ростом разрядов в числе n{\displaystyle n} всё меньше слагаемых берётся для суммы «истончённого» ряда. То есть, в конечном счёте отбрасывается подавляющее большинство членов, образующих сумму гармонического ряда, чтобы не превзойти ограничивающую сверху геометрическую прогрессию.

    1. ↑ Грэхэм Р., Кнут Д., Паташник О. Конкретная математика. Основание информатики. — М.: Мир; БИНОМ. Лаборатория знаний, 2006. — С. 47. — 703 с. ISBN 5-03-003773-X
    2. ↑ Harmonic Number — from Wolfram MathWorld
    3. ↑ Кудрявцев Н. Л. Лекции по математическому анализу. — 2013. — С. 35.
    4. ↑ 1 2 Бронштейн И. Н., Семендяев К. А. Справочник по математике для инженеров и учащихся втузов. М.: Наука. Главная редакция физико-математической литературы, 1981, 718 с.
    5. ↑ «Random Harmonic Series», American Mathematical Monthly 110, 407—416, May 2003
    6. ↑ Schmuland’s preprint of Random Harmonic Series
    7. ↑ Nick’s Mathematical Puzzles: Solution 72

    Гармоническое число — Википедия

    Материал из Википедии — свободной энциклопедии

    Гармоническое число Hn,1{\displaystyle H_{n,1}}, где n=⌊x⌋{\displaystyle n=\lfloor {x}\rfloor } (красная линия) и его асимптотический предел γ+ln⁡(x){\displaystyle \gamma +\ln(x)} (синяя линия).

    В математике n-м гармоническим числом называется сумма обратных величин первых n последовательных чисел натурального ряда:

    Hn=∑k=1n1k=1+12+13+⋯+1n.{\displaystyle H_{n}=\sum _{k=1}^{n}{\frac {1}{k}}=1+{\frac {1}{2}}+{\frac {1}{3}}+\cdots +{\frac {1}{n}}.}

    Гармонические числа являются частичными суммами гармонического ряда.

    Изучение гармонических чисел началось в античности. Они имеют важное значение в различных областях теории чисел и теории алгоритмов и, в частности, тесно связаны с дзета-функцией Римана.

    Альтернативные определения

    • Гармонические числа можно определить рекуррентно следующим образом:
      {Hn=Hn−1+1nh2=1{\displaystyle {\begin{cases}H_{n}=H_{n-1}+{\frac {1}{n}}\\H_{1}=1\end{cases}}}
    • Также верно соотношение:
      Hn=γ+ψ(n+1)=Γ′(n)Γ(n)+1n+γ{\displaystyle H_{n}=\gamma +\psi (n+1)={\frac {\Gamma ‘(n)}{\Gamma (n)}}+{\frac {1}{n}}+\gamma },
      где ψ(n){\displaystyle \psi (n)} — дигамма-функция, γ=−ψ(1){\displaystyle \gamma =-\psi (1)} — постоянная Эйлера — Маскерони.
    • Еще одно соотношение:
      Hn=∑k=1n(nk)(−1)k+1k{\displaystyle H_{n}=\sum _{k=1}^{n}{\binom {n}{k}}{\frac {(-1)^{k+1}}{k}}}

    Дополнительные представления

    Нижеследующие формулы могут быть использованы для вычисления гармонических чисел (в том числе и в точках, отличных от точек натурального ряда):

    • интегральные представления:
      Hx=∫011−tx1−tdt,Re(x)>−1{\displaystyle H_{x}=\int _{0}^{1}{\frac {1-t^{x}}{1-t}}dt,\quad Re(x)>-1}
    • предельные представления:
      Hx=limn→∞(ln⁡(n)−∑k=0n1x+k+1)+γ{\displaystyle H_{x}=\lim _{n\to \infty }\left(\ln(n)-\sum _{k=0}^{n}{\frac {1}{x+k+1}}\right)+\gamma }
      Hx=x∑k=0∞1(k+1)(x+k+1){\displaystyle H_{x}=x\sum _{k=0}^{\infty }{\frac {1}{(k+1)(x+k+1)}}};
    • разложение в ряд Тейлора в точке x=0{\displaystyle x=0}:
      Hx=∑k=1∞(−1)k+1ζ(k+1)xk=ζ(2)x−ζ(3)x2+ζ(4)x3−ζ(5)x4+⋯,{\displaystyle H_{x}=\sum _{k=1}^{\infty }(-1)^{k+1}\zeta (k+1)x^{k}=\zeta (2)x-\zeta (3)x^{2}+\zeta (4)x^{3}-\zeta (5)x^{4}+\cdots ,}
      где ζ(x){\displaystyle \zeta (x)} — дзета-функция Римана;
    • асимптотическое разложение:
      Hx=γ+ln⁡(x)+12x−112×2+1120×4−1252×6+1240×8−1132×10+⋯{\displaystyle H_{x}=\gamma +\ln(x)+{\frac {1}{2x}}-{\frac {1}{12x^{2}}}+{\frac {1}{120x^{4}}}-{\frac {1}{252x^{6}}}+{\frac {1}{240x^{8}}}-{\frac {1}{132x^{10}}}+\cdots }.

    Производящая функция

    ∑k=1∞Hkzk=−ln⁡(1−z)1−z{\displaystyle \sum _{k=1}^{\infty }H_{k}z^{k}=-{\frac {\ln(1-z)}{1-z}}}

    Свойства

    Значения от нецелого аргумента

    • h2/2=2−2ln⁡2{\displaystyle H_{1/2}=2-2\ln 2}
    • h2/3=3−3ln⁡32−π23{\displaystyle H_{1/3}=3-{\frac {3\ln 3}{2}}-{\frac {\pi }{2{\sqrt {3}}}}}
    • h2/4=4−3ln⁡2−π2{\displaystyle H_{1/4}=4-3\ln 2-{\frac {\pi }{2}}}
    • h2/5=5−5ln⁡54−121+25π−52ln⁡φ,{\displaystyle H_{1/5}=5-{\frac {5\ln 5}{4}}-{\frac {1}{2}}{\sqrt {1+{\frac {2}{\sqrt {5}}}}}\pi -{\frac {\sqrt {5}}{2}}\ln \varphi ,}
    где φ{\displaystyle \varphi } — золотое сечение.
    • h2/7=7−ln⁡14−π2ctgπ7−2cos⁡(π7)ln⁡(cos⁡π14)+2sin⁡(3π14)ln⁡(sin⁡π7)−2sin⁡(π14)ln⁡(cos⁡3π14){\displaystyle H_{1/7}=7-\ln 14-{\frac {\pi }{2}}\mathrm {ctg} {\frac {\pi }{7}}-2\cos \left({\frac {\pi }{7}}\right)\ln \left(\cos {\frac {\pi }{14}}\right)+2\sin \left({\frac {3\pi }{14}}\right)\ln \left(\sin {\frac {\pi }{7}}\right)-2\sin \left({\frac {\pi }{14}}\right)\ln \left(\cos {\frac {3\pi }{14}}\right)}

    Суммы, связанные с гармоническими числами

    Тождества, связанные с гармоническими числами

    Приближённое вычисление

    С помощью формулы суммирования Эйлера-Маклорена получаем следующую формулу:

    Hn=ln⁡n+γ+12n+∑k=1mB2k2kn2k−θm,nB2m+2(2m+2)n2m+2,{\displaystyle H_{n}=\ln n+\gamma +{\frac {1}{2n}}+\sum \limits _{k=1}^{m}{\frac {B_{2k}}{2kn^{2k}}}-\theta _{m,n}{\frac {B_{2m+2}}{(2m+2)n^{2m+2}}},}

    где 0<θm,n<1{\displaystyle 0<\theta _{m,n}<1}, γ{\displaystyle \gamma } — постоянная Эйлера, которую можно вычислить быстрее из других соображений[каких?], а Bk{\displaystyle B_{k}} — числа Бернулли.

    Теоретико-числовые свойства

    • Теорема Вольстенхольма утверждает, что для всякого простого числа p>3{\displaystyle p>3} выполняется сравнение:
      Hp−1≡0(modp2).{\displaystyle H_{p-1}\equiv 0{\pmod {p^{2}}}.}

    Некоторые значения гармонических чисел

    h2=1h3=32=1,5h4=116≈1,833h5=2512≈2,083H5=13760≈2,283{\displaystyle {\begin{matrix}H_{1}&=&1\\\\H_{2}&=&{\frac {3}{2}}&=&1{,}5\\\\H_{3}&=&{\frac {11}{6}}&\approx &1{,}833\\\\H_{4}&=&{\frac {25}{12}}&\approx &2{,}083\\\\H_{5}&=&{\frac {137}{60}}&\approx &2{,}283\end{matrix}}}H6=4920=2,45H7=363140≈2,593H8=761280≈2,718h203≈7,484h206≈14,393{\displaystyle {\begin{matrix}H_{6}&=&{\frac {49}{20}}&=&2{,}45\\\\H_{7}&=&{\frac {363}{140}}&\approx &2{,}593\\\\H_{8}&=&{\frac {761}{280}}&\approx &2{,}718\\\\H_{10^{3}}&\approx &7{,}484\\\\H_{10^{6}}&\approx &14{,}393\end{matrix}}}

    Числитель и знаменатель несократимой дроби, представляющей собой n-e гармоническое число, являются n-ми членами целочисленных последовательностей A001008 и A002805, соответственно.

    Приложения

    В 2002 году Lagarias доказал[1], что гипотеза Римана о нулях дзета-функции Римана эквивалентна утверждению, что неравенство

    σ(n)≤Hn+ln⁡(Hn)eHn{\displaystyle \sigma (n)\leq H_{n}+\ln(H_{n})e^{H_{n}}}

    верно при всех целых n≥1{\displaystyle n\geq 1} со строгим неравенством при n>1{\displaystyle n>1}, где σ(n){\displaystyle \sigma (n)} — сумма делителей числа n{\displaystyle n}.

    См. также

    Примечания

    Гармоническое число — Википедия. Что такое Гармоническое число

    Гармоническое число Hn,1{\displaystyle H_{n,1}}, где n=⌊x⌋{\displaystyle n=\lfloor {x}\rfloor } (красная линия) и его асимптотический предел γ+ln⁡(x){\displaystyle \gamma +\ln(x)} (синяя линия).

    В математике n-м гармоническим числом называется сумма обратных величин первых n последовательных чисел натурального ряда:

    Hn=∑k=1n1k=1+12+13+⋯+1n.{\displaystyle H_{n}=\sum _{k=1}^{n}{\frac {1}{k}}=1+{\frac {1}{2}}+{\frac {1}{3}}+\cdots +{\frac {1}{n}}.}

    Гармонические числа являются частичными суммами гармонического ряда.

    Изучение гармонических чисел началось в античности. Они имеют важное значение в различных областях теории чисел и теории алгоритмов и, в частности, тесно связаны с дзета-функцией Римана.

    Альтернативные определения

    • Гармонические числа можно определить рекуррентно следующим образом:
      {Hn=Hn−1+1nh2=1{\displaystyle {\begin{cases}H_{n}=H_{n-1}+{\frac {1}{n}}\\H_{1}=1\end{cases}}}
    • Также верно соотношение:
      Hn=γ+ψ(n+1)=Γ′(n)Γ(n)+1n+γ{\displaystyle H_{n}=\gamma +\psi (n+1)={\frac {\Gamma ‘(n)}{\Gamma (n)}}+{\frac {1}{n}}+\gamma },
      где ψ(n){\displaystyle \psi (n)} — дигамма-функция, γ=−ψ(1){\displaystyle \gamma =-\psi (1)} — постоянная Эйлера — Маскерони.
    • Еще одно соотношение:
      Hn=∑k=1n(nk)(−1)k+1k{\displaystyle H_{n}=\sum _{k=1}^{n}{\binom {n}{k}}{\frac {(-1)^{k+1}}{k}}}

    Дополнительные представления

    Нижеследующие формулы могут быть использованы для вычисления гармонических чисел (в том числе и в точках, отличных от точек натурального ряда):

    • интегральные представления:
      Hx=∫011−tx1−tdt,Re(x)>−1{\displaystyle H_{x}=\int _{0}^{1}{\frac {1-t^{x}}{1-t}}dt,\quad Re(x)>-1}
    • предельные представления:
      Hx=limn→∞(ln⁡(n)−∑k=0n1x+k+1)+γ{\displaystyle H_{x}=\lim _{n\to \infty }\left(\ln(n)-\sum _{k=0}^{n}{\frac {1}{x+k+1}}\right)+\gamma }
      Hx=x∑k=0∞1(k+1)(x+k+1){\displaystyle H_{x}=x\sum _{k=0}^{\infty }{\frac {1}{(k+1)(x+k+1)}}};
    • разложение в ряд Тейлора в точке x=0{\displaystyle x=0}:
      Hx=∑k=1∞(−1)k+1ζ(k+1)xk=ζ(2)x−ζ(3)x2+ζ(4)x3−ζ(5)x4+⋯,{\displaystyle H_{x}=\sum _{k=1}^{\infty }(-1)^{k+1}\zeta (k+1)x^{k}=\zeta (2)x-\zeta (3)x^{2}+\zeta (4)x^{3}-\zeta (5)x^{4}+\cdots ,}
      где ζ(x){\displaystyle \zeta (x)} — дзета-функция Римана;
    • асимптотическое разложение:
      Hx=γ+ln⁡(x)+12x−112×2+1120×4−1252×6+1240×8−1132×10+⋯{\displaystyle H_{x}=\gamma +\ln(x)+{\frac {1}{2x}}-{\frac {1}{12x^{2}}}+{\frac {1}{120x^{4}}}-{\frac {1}{252x^{6}}}+{\frac {1}{240x^{8}}}-{\frac {1}{132x^{10}}}+\cdots }.

    Производящая функция

    ∑k=1∞Hkzk=−ln⁡(1−z)1−z{\displaystyle \sum _{k=1}^{\infty }H_{k}z^{k}=-{\frac {\ln(1-z)}{1-z}}}

    Свойства

    Значения от нецелого аргумента

    • h2/2=2−2ln⁡2{\displaystyle H_{1/2}=2-2\ln 2}
    • h2/3=3−3ln⁡32−π23{\displaystyle H_{1/3}=3-{\frac {3\ln 3}{2}}-{\frac {\pi }{2{\sqrt {3}}}}}
    • h2/4=4−3ln⁡2−π2{\displaystyle H_{1/4}=4-3\ln 2-{\frac {\pi }{2}}}
    • h2/5=5−5ln⁡54−121+25π−52ln⁡φ,{\displaystyle H_{1/5}=5-{\frac {5\ln 5}{4}}-{\frac {1}{2}}{\sqrt {1+{\frac {2}{\sqrt {5}}}}}\pi -{\frac {\sqrt {5}}{2}}\ln \varphi ,}
    где φ{\displaystyle \varphi } — золотое сечение.
    • h2/7=7−ln⁡14−π2ctgπ7−2cos⁡(π7)ln⁡(cos⁡π14)+2sin⁡(3π14)ln⁡(sin⁡π7)−2sin⁡(π14)ln⁡(cos⁡3π14){\displaystyle H_{1/7}=7-\ln 14-{\frac {\pi }{2}}\mathrm {ctg} {\frac {\pi }{7}}-2\cos \left({\frac {\pi }{7}}\right)\ln \left(\cos {\frac {\pi }{14}}\right)+2\sin \left({\frac {3\pi }{14}}\right)\ln \left(\sin {\frac {\pi }{7}}\right)-2\sin \left({\frac {\pi }{14}}\right)\ln \left(\cos {\frac {3\pi }{14}}\right)}

    Суммы, связанные с гармоническими числами

    Тождества, связанные с гармоническими числами

    Приближённое вычисление

    С помощью формулы суммирования Эйлера-Маклорена получаем следующую формулу:

    Hn=ln⁡n+γ+12n+∑k=1mB2k2kn2k−θm,nB2m+2(2m+2)n2m+2,{\displaystyle H_{n}=\ln n+\gamma +{\frac {1}{2n}}+\sum \limits _{k=1}^{m}{\frac {B_{2k}}{2kn^{2k}}}-\theta _{m,n}{\frac {B_{2m+2}}{(2m+2)n^{2m+2}}},}

    где 0<θm,n<1{\displaystyle 0<\theta _{m,n}<1}, γ{\displaystyle \gamma } — постоянная Эйлера, которую можно вычислить быстрее из других соображений[каких?], а Bk{\displaystyle B_{k}} — числа Бернулли.

    Теоретико-числовые свойства

    • Теорема Вольстенхольма утверждает, что для всякого простого числа p>3{\displaystyle p>3} выполняется сравнение:
      Hp−1≡0(modp2).{\displaystyle H_{p-1}\equiv 0{\pmod {p^{2}}}.}

    Некоторые значения гармонических чисел

    h2=1h3=32=1,5h4=116≈1,833h5=2512≈2,083H5=13760≈2,283{\displaystyle {\begin{matrix}H_{1}&=&1\\\\H_{2}&=&{\frac {3}{2}}&=&1{,}5\\\\H_{3}&=&{\frac {11}{6}}&\approx &1{,}833\\\\H_{4}&=&{\frac {25}{12}}&\approx &2{,}083\\\\H_{5}&=&{\frac {137}{60}}&\approx &2{,}283\end{matrix}}}H6=4920=2,45H7=363140≈2,593H8=761280≈2,718h203≈7,484h206≈14,393{\displaystyle {\begin{matrix}H_{6}&=&{\frac {49}{20}}&=&2{,}45\\\\H_{7}&=&{\frac {363}{140}}&\approx &2{,}593\\\\H_{8}&=&{\frac {761}{280}}&\approx &2{,}718\\\\H_{10^{3}}&\approx &7{,}484\\\\H_{10^{6}}&\approx &14{,}393\end{matrix}}}

    Числитель и знаменатель несократимой дроби, представляющей собой n-e гармоническое число, являются n-ми членами целочисленных последовательностей A001008 и A002805, соответственно.

    Приложения

    В 2002 году Lagarias доказал[1], что гипотеза Римана о нулях дзета-функции Римана эквивалентна утверждению, что неравенство

    σ(n)≤Hn+ln⁡(Hn)eHn{\displaystyle \sigma (n)\leq H_{n}+\ln(H_{n})e^{H_{n}}}

    верно при всех целых n≥1{\displaystyle n\geq 1} со строгим неравенством при n>1{\displaystyle n>1}, где σ(n){\displaystyle \sigma (n)} — сумма делителей числа n{\displaystyle n}.

    См. также

    Примечания

    Гармоническое число — Википедия

    Материал из Википедии — свободной энциклопедии

    Гармоническое число Hn,1{\displaystyle H_{n,1}}, где n=⌊x⌋{\displaystyle n=\lfloor {x}\rfloor } (красная линия) и его асимптотический предел γ+ln⁡(x){\displaystyle \gamma +\ln(x)} (синяя линия).

    В математике n-м гармоническим числом называется сумма обратных величин первых n последовательных чисел натурального ряда:

    Hn=∑k=1n1k=1+12+13+⋯+1n.{\displaystyle H_{n}=\sum _{k=1}^{n}{\frac {1}{k}}=1+{\frac {1}{2}}+{\frac {1}{3}}+\cdots +{\frac {1}{n}}.}

    Гармонические числа являются частичными суммами гармонического ряда.

    Изучение гармонических чисел началось в античности. Они имеют важное значение в различных областях теории чисел и теории алгоритмов и, в частности, тесно связаны с дзета-функцией Римана.

    Альтернативные определения

    • Гармонические числа можно определить рекуррентно следующим образом:
      {Hn=Hn−1+1nh2=1{\displaystyle {\begin{cases}H_{n}=H_{n-1}+{\frac {1}{n}}\\H_{1}=1\end{cases}}}
    • Также верно соотношение:
      Hn=γ+ψ(n+1)=Γ′(n)Γ(n)+1n+γ{\displaystyle H_{n}=\gamma +\psi (n+1)={\frac {\Gamma ‘(n)}{\Gamma (n)}}+{\frac {1}{n}}+\gamma },
      где ψ(n){\displaystyle \psi (n)} — дигамма-функция, γ=−ψ(1){\displaystyle \gamma =-\psi (1)} — постоянная Эйлера — Маскерони.
    • Еще одно соотношение:
      Hn=∑k=1n(nk)(−1)k+1k{\displaystyle H_{n}=\sum _{k=1}^{n}{\binom {n}{k}}{\frac {(-1)^{k+1}}{k}}}

    Дополнительные представления

    Нижеследующие формулы могут быть использованы для вычисления гармонических чисел (в том числе и в точках, отличных от точек натурального ряда):

    • интегральные представления:
      Hx=∫011−tx1−tdt,Re(x)>−1{\displaystyle H_{x}=\int _{0}^{1}{\frac {1-t^{x}}{1-t}}dt,\quad Re(x)>-1}
    • предельные представления:
      Hx=limn→∞(ln⁡(n)−∑k=0n1x+k+1)+γ{\displaystyle H_{x}=\lim _{n\to \infty }\left(\ln(n)-\sum _{k=0}^{n}{\frac {1}{x+k+1}}\right)+\gamma }
      Hx=x∑k=0∞1(k+1)(x+k+1){\displaystyle H_{x}=x\sum _{k=0}^{\infty }{\frac {1}{(k+1)(x+k+1)}}};
    • разложение в ряд Тейлора в точке x=0{\displaystyle x=0}:
      Hx=∑k=1∞(−1)k+1ζ(k+1)xk=ζ(2)x−ζ(3)x2+ζ(4)x3−ζ(5)x4+⋯,{\displaystyle H_{x}=\sum _{k=1}^{\infty }(-1)^{k+1}\zeta (k+1)x^{k}=\zeta (2)x-\zeta (3)x^{2}+\zeta (4)x^{3}-\zeta (5)x^{4}+\cdots ,}
      где ζ(x){\displaystyle \zeta (x)} — дзета-функция Римана;
    • асимптотическое разложение:
      Hx=γ+ln⁡(x)+12x−112×2+1120×4−1252×6+1240×8−1132×10+⋯{\displaystyle H_{x}=\gamma +\ln(x)+{\frac {1}{2x}}-{\frac {1}{12x^{2}}}+{\frac {1}{120x^{4}}}-{\frac {1}{252x^{6}}}+{\frac {1}{240x^{8}}}-{\frac {1}{132x^{10}}}+\cdots }.

    Производящая функция

    ∑k=1∞Hkzk=−ln⁡(1−z)1−z{\displaystyle \sum _{k=1}^{\infty }H_{k}z^{k}=-{\frac {\ln(1-z)}{1-z}}}

    Свойства

    Значения от нецелого аргумента

    • h2/2=2−2ln⁡2{\displaystyle H_{1/2}=2-2\ln 2}
    • h2/3=3−3ln⁡32−π23{\displaystyle H_{1/3}=3-{\frac {3\ln 3}{2}}-{\frac {\pi }{2{\sqrt {3}}}}}
    • h2/4=4−3ln⁡2−π2{\displaystyle H_{1/4}=4-3\ln 2-{\frac {\pi }{2}}}
    • h2/5=5−5ln⁡54−121+25π−52ln⁡φ,{\displaystyle H_{1/5}=5-{\frac {5\ln 5}{4}}-{\frac {1}{2}}{\sqrt {1+{\frac {2}{\sqrt {5}}}}}\pi -{\frac {\sqrt {5}}{2}}\ln \varphi ,}
    где φ{\displaystyle \varphi } — золотое сечение.
    • h2/7=7−ln⁡14−π2ctgπ7−2cos⁡(π7)ln⁡(cos⁡π14)+2sin⁡(3π14)ln⁡(sin⁡π7)−2sin⁡(π14)ln⁡(cos⁡3π14){\displaystyle H_{1/7}=7-\ln 14-{\frac {\pi }{2}}\mathrm {ctg} {\frac {\pi }{7}}-2\cos \left({\frac {\pi }{7}}\right)\ln \left(\cos {\frac {\pi }{14}}\right)+2\sin \left({\frac {3\pi }{14}}\right)\ln \left(\sin {\frac {\pi }{7}}\right)-2\sin \left({\frac {\pi }{14}}\right)\ln \left(\cos {\frac {3\pi }{14}}\right)}

    Суммы, связанные с гармоническими числами

    Тождества, связанные с гармоническими числами

    Приближённое вычисление

    С помощью формулы суммирования Эйлера-Маклорена получаем следующую формулу:

    Hn=ln⁡n+γ+12n+∑k=1mB2k2kn2k−θm,nB2m+2(2m+2)n2m+2,{\displaystyle H_{n}=\ln n+\gamma +{\frac {1}{2n}}+\sum \limits _{k=1}^{m}{\frac {B_{2k}}{2kn^{2k}}}-\theta _{m,n}{\frac {B_{2m+2}}{(2m+2)n^{2m+2}}},}

    где 0<θm,n<1{\displaystyle 0<\theta _{m,n}<1}, γ{\displaystyle \gamma } — постоянная Эйлера, которую можно вычислить быстрее из других соображений[каких?], а Bk{\displaystyle B_{k}} — числа Бернулли.

    Теоретико-числовые свойства

    • Теорема Вольстенхольма утверждает, что для всякого простого числа p>3{\displaystyle p>3} выполняется сравнение:
      Hp−1≡0(modp2).{\displaystyle H_{p-1}\equiv 0{\pmod {p^{2}}}.}

    Некоторые значения гармонических чисел

    h2=1h3=32=1,5h4=116≈1,833h5=2512≈2,083H5=13760≈2,283{\displaystyle {\begin{matrix}H_{1}&=&1\\\\H_{2}&=&{\frac {3}{2}}&=&1{,}5\\\\H_{3}&=&{\frac {11}{6}}&\approx &1{,}833\\\\H_{4}&=&{\frac {25}{12}}&\approx &2{,}083\\\\H_{5}&=&{\frac {137}{60}}&\approx &2{,}283\end{matrix}}}H6=4920=2,45H7=363140≈2,593H8=761280≈2,718h203≈7,484h206≈14,393{\displaystyle {\begin{matrix}H_{6}&=&{\frac {49}{20}}&=&2{,}45\\\\H_{7}&=&{\frac {363}{140}}&\approx &2{,}593\\\\H_{8}&=&{\frac {761}{280}}&\approx &2{,}718\\\\H_{10^{3}}&\approx &7{,}484\\\\H_{10^{6}}&\approx &14{,}393\end{matrix}}}

    Числитель и знаменатель несократимой дроби, представляющей собой n-e гармоническое число, являются n-ми членами целочисленных последовательностей A001008 и A002805, соответственно.

    Приложения

    В 2002 году Lagarias доказал[1], что гипотеза Римана о нулях дзета-функции Римана эквивалентна утверждению, что неравенство

    σ(n)≤Hn+ln⁡(Hn)eHn{\displaystyle \sigma (n)\leq H_{n}+\ln(H_{n})e^{H_{n}}}

    верно при всех целых n≥1{\displaystyle n\geq 1} со строгим неравенством при n>1{\displaystyle n>1}, где σ(n){\displaystyle \sigma (n)} — сумма делителей числа n{\displaystyle n}.

    См. также

    Примечания

    alexxlab

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *