7. Тема: Переменный ток
7.1 Основные формулы и указания к решению задачи
7.1.1. Переменный ток, текущий через резистор сопротивлением R
Если к концам участка цепи (рис. 7.1а) приложено напряжение U=Umсost, то сила тока определяется законом ОмаI=U/R= (Um/R) сost= =Imсost, гдеI– амплитуда силы тока. Векторная диаграмма (рис. 7.1б) амплитудных значений токаImи напряженияUmна резисторе показывает, что сдвиг фаз междуImиUmравен нулю.
а б
Рис. 7.1. Схема цепи переменного тока (а) и
векторная диаграмма, соответствующая
данной цепи (б).
7.1.2. Переменный ток, текущий через катушку индуктивностью L
Если в цепи (рис. 7.2а) приложено переменное напряжение U = Um сos t,то сила тока в такой цепиI=Imсos(t–/2). ВеличинаRL=Lназывается индуктивным сопротивлением. Векторная диаграмма (рис. 7.2б) показывает, что падение напряженияUопережает по фазе токI, текущий через катушку на/2.
а б
Рис. 7.2. Схема цепи переменного тока (а) и
векторная диаграмма, соответствующая данной цепи (б).
7.1.3. Переменный ток, текущий через конденсатор емкостью С
Если переменное
напряжение приложено к конденсатору
(рис. 7.3а), то он все время перезаряжается,
и в цепи течет переменный ток. Если все
внешнее напряжение приложено к
конденсатору, а сопротивлением подводящих
проводов можно пренебречь, то U=Umсost.
Сила токаI=Imсos(t +/2),
гдеIm=U
Если все
внешнее напряжение приложено к
конденсатору, а сопротивлением подводящих
проводов можно пренебречь, то U=Umсost.
Сила токаI=Imсos(t +/2),
гдеIm=U
Величина RC= 1/(C) называется емкостным сопротивлением.
Падение напряжения на конденсаторе U отстает по фазе от текущего через конденсатор тока I на /2. Это показано на векторной диаграмме (рис. 7.3б).
А б
Рис. 7.3. Схема цепи переменного тока (а) и
векторная диаграмма, соответствующая данной цепи (б).
7.1.4. Цепь переменного тока, содержащая последовательно включенные резистор, катушку индуктивности и конденсатор
Рассмотрим цепь
переменного тока, содержащую последовательно
включенные резистор, катушку и конденсатор
(рис.
. (7.1)
Из прямоугольного треугольника получаем
, (7.2)
откуда амплитуда силы тока имеет значение
. (7.3)
Следовательно, если напряжение в цепи изменяется по закону
U=Umсost, то в цепи течет токI=Imсos(t–).
А б
Рис. 7.4. Схема цепи переменного тока (а) и
векторная диаграмма, соответствующая
данной цепи (б).
Действующие значения тока и напряжения для синусоидального тока соответственно равны:
I=Im/U=Um/(7.4)
7.2 Примеры решения задач
Пример 1.В цепи переменного тока (
Дано: U= 127В;f= 50Гц;C= 2410-6Ф;L= 0,6Гн;R= 100Ом.
I= ?
Решение. Начертим схему соединения приборов (рис. 7.5а) и построим векторную диаграмму токов (рис. 7.5б). При параллельном соединении элементов на каждом из них напряжение одинаковое, поэтому за основное направление возьмем вектор амплитуды напряжения.
а | б |
Рис. 7.5. Схема цепи переменного
тока (а) и
7.5. Схема цепи переменного
тока (а) и
векторная диаграмма, соответствующая данной цепи (б).
Амплитуда тока в конденсаторе ImСопережает амплитуду напряжения на/2, амплитуда тока в дросселеImdотстает от амплитуды напряжения на угол
. (7.5)
Векторная сумма токов ImCиImdопределяет подводимый токI. Из векторной диаграммы очевидно, что
I 2m = I 2mC + I 2md – 2ImCImd соs(90 – ) = I 2mC + I 2m – 2 ImCImd sin . (7.6)
Перейдем к действующим значениям тока:
I
 7)
7)Токи ICиIdнайдем, применив закон Ома к каждому участку отдельно:
IC = UC, , = 2f. (7.8)
Расчеты дают: sin = 0,8832; IC = 0,96 A, Id = 0,562 A; I = 0,515 A.
Выполним проверку единиц измерения величин.
(7.9)
Пример 2.В цепь переменного тока (f= 50Гц) с действующим значением силы тока 10Авключены последовательно конденсатор емкостьюC= 18мкФ, активное сопротивлениеR1= 10Оми дроссель индуктивностьюL= 0,6Гни активным сопротивлениемR2= 109Ом. Определить действующее в цепи напряжение.
Дано: f= 50Гц;I= 10А;C= 1810-6мкФ;R1= 10Ом;L= 0,6Гн;R2= 100Ом.
U– ?
Решение. Начертим схему включения приборов (рис. 7.6а) и построим векторную диаграмму напряжений (рис. 7.6б).
а | б |
Рис. 7.6 Схема цепи переменного тока (а) и
векторная диаграмма соответствующая данной цепи (б).
При последовательном соединении через все элементы идет одинаковый ток, поэтому за основное направление возьмем вектор амплитуды тока
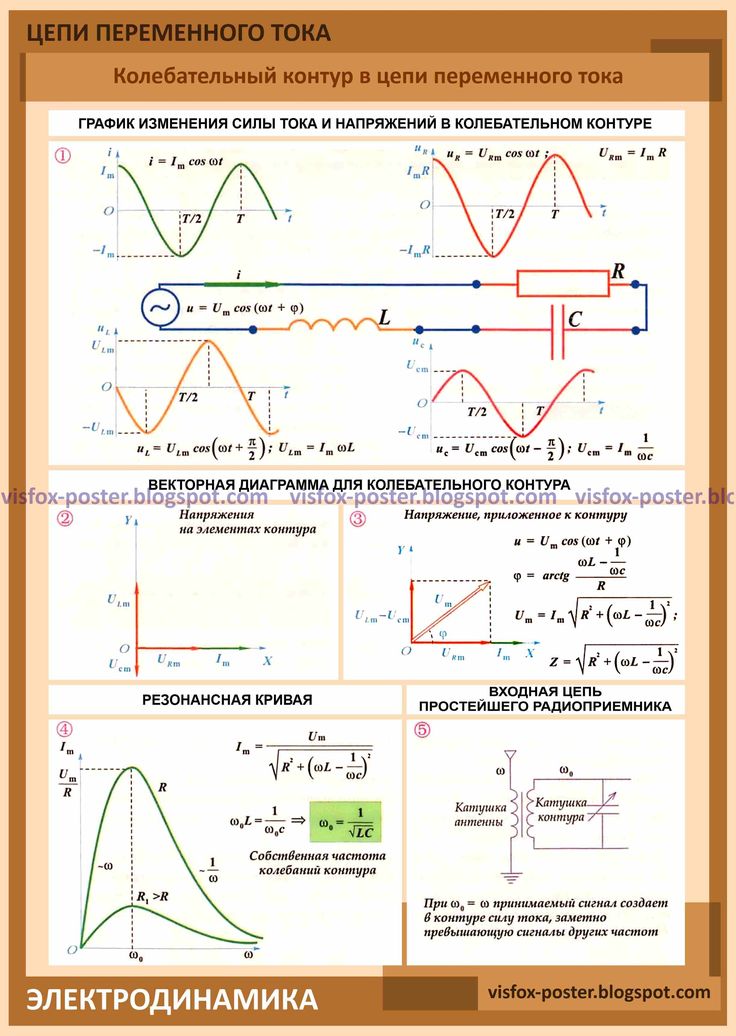 Амплитуда напряжения на резистореUmRсовпадает с амплитудой тока (колеблется
в фазе с током). Амплитуда полного
напряжения в цепи равна векторной сумме
напряжений
Амплитуда напряжения на резистореUmRсовпадает с амплитудой тока (колеблется
в фазе с током). Амплитуда полного
напряжения в цепи равна векторной сумме
напряженийАмплитуда напряжения, совпадающего по фазе с током:
U1m = UmR + U‘md = ImR1 + ImR2. (7.10)
Амплитуда напряжения, опережающего ток на /2:
U2m=U»md – UmC,. (7.11)
Амплитуда полного напряжения
. (7.12)
Перейдем к действующим значениям напряжения и тока
,= 2f. (7.13)
Подставим численные данные
U = 220 В.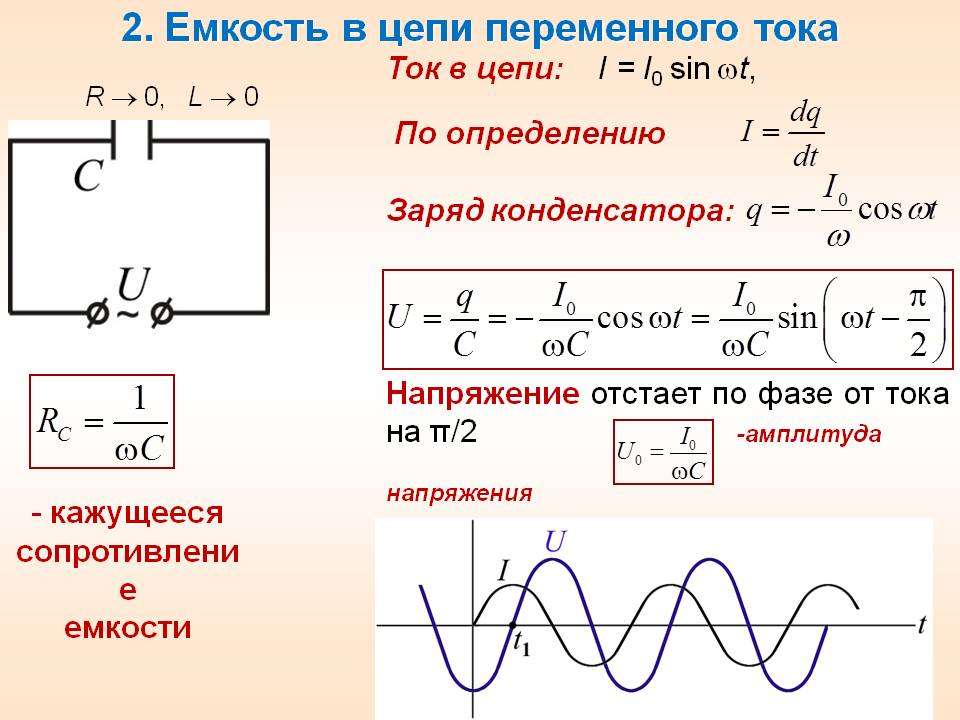
Выполним проверку единиц измерения величин.
(7.14)
Определение, формулы, термины, типы и применение
Электрическая цепь представляет собой замкнутый путь или петлю, по которой непрерывно протекают заряды или электрический ток. Это замкнутый проводящий путь для электронов, который также известен как электрическая цепь или электрическая сеть. В электричестве цепи могут быть различных типов, таких как разомкнутые, замкнутые, последовательные, параллельные и т. д. Цепь переменного тока — это тип электрической цепи.
В этой статье основное внимание уделяется цепи переменного тока. Читайте дальше, чтобы узнать, что такое цепь переменного тока, термины, используемые в цепи переменного тока, ее типы, использование и чем она отличается от цепи постоянного тока с часто задаваемыми вопросами.
Цепь переменного тока
Величина, которая непрерывно изменяется по величине от нуля до максимального значения с переменным направлением через равные промежутки времени, известна как переменная величина, такая как ток (I) или напряжение (V).
Цепи переменного тока питаются от источника переменного тока, такого как переменный ток или напряжение, которые являются синусоидальными и периодически изменяются по направлению и величине. Другими словами, напряжение или ток колеблются в виде синусоидальной волны и меняются со временем.
Такой ток представлен \( i=i_0 sin(\omega t + \phi) \)
Ток повторяет свое значение через каждый интервал времени T=2π/⍵. Это называется периодом тока. В условиях переменного тока половину времени этот ток остается положительным, а другую половину периода времени становится отрицательным.
Цепь переменного тока состоит из трех основных компонентов; резистор, конденсатор и катушка индуктивности, которые уникальным образом сопротивляются потоку электрического тока. Это пассивные компоненты цепи переменного тока, поскольку они продолжают потреблять электрическую энергию. Эти компоненты в электрической цепи могут использоваться в бесконечном количестве комбинаций и конструкций.
- Цепь переменного тока с резистором показана на рисунке выше. Такая цепь также известна как чисто резистивная цепь. Не забудьте обратить внимание на символ источника переменного тока. Если ток в момент времени t равен I, согласно петлевому закону Кирхгофа \(V_0sin\omega t = R_i\)
Или, \(i=V_0sin\omega R\)
\(i=i_0 sin\omega t\)
\(i_0=V_0/R\)
Когда напряжение и ток одновременно достигают своих максимальных значений, они считаются синфазными. Если используются среднеквадратичные (RMS) значения тока и напряжения, считается, что закон Ома действителен для этого условия. Эти значения также называются действующими значениями тока и напряжения, а ток также известен как виртуальный ток. Следовательно, отношения будут;
\(l_{rms}=\frac{l_{\max}}{\sqrt{2}}и\ V_{rms}=\frac{V_{\max}}{\sqrt{2}}\)
Следовательно, закон Ома может быть выражен как \(V_{rms\ }=I_{rms}\times RI\)
Также ознакомьтесь с нашей статьей о токе и электричестве
Формулы цепи переменного тока
Вот некоторые формулы Цепи переменного тока:
| Параметр | Формула | |||
| Переменное напряжение | 5\(v=V_0sin)0049 | Переменный ток | \(i=I_0sin\omega t\) | |
| Емкостное реактивное сопротивление | \( X_c=\frac{1}{2\pi fc} \(\) | \(\)V_{rms}=\frac{V_0}{ \sqrt{2}}\) | ||
| действующее значение тока | \(I_r_m_s=\frac{I_0}{\sqrt{2}}\) | |||
| Индуктивное сопротивление | \( X_L=\frac{V_L}{I_L}\ =\omega L = 2 \pi fL \left (\Omega\right) \) | |||
| Фазовый угол ряда RLC схема 92_{rms}R \) |
Также читайте о вихревых токах и токах смещения здесь
Термины, используемые в цепях переменного тока
Различные термины, используемые в цепях переменного тока: пиковое значение или максимальное значение — это наивысшее положительное или отрицательное значение, полученное при изменении количества за один полный цикл.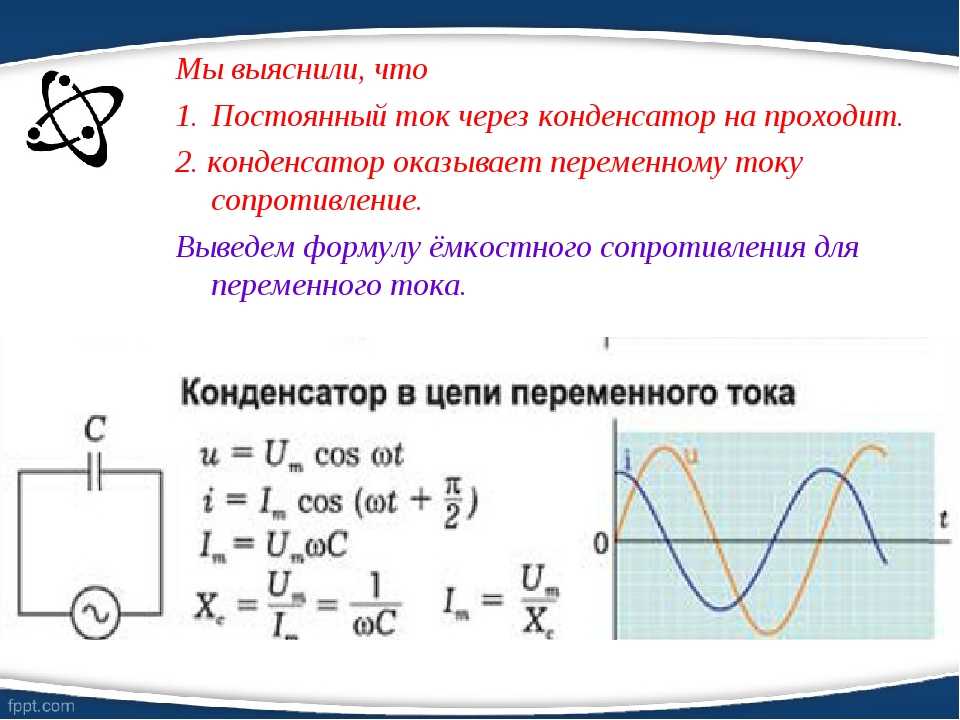 \(E_m\) или \(V_m\) и \(I_m\) обозначают максимальные значения напряжения и тока соответственно.
\(E_m\) или \(V_m\) и \(I_m\) обозначают максимальные значения напряжения и тока соответственно.

Узнайте больше о Wattleless Current здесь
Типы цепей переменного тока
Существуют различные типы цепей переменного тока с различными комбинациями, которые могут быть разработаны. Некоторыми из наиболее распространенных являются полностью резистивные, полностью емкостные, полностью индуктивные, RC-цепи, RL-цепи, LC-цепи и RLC-цепи последовательно, а также в параллельных комбинациях.
Рассмотрим некоторые из них подробнее.
Полностью резистивная
Полностью резистивная цепь имеет очень низкую индуктивность, поэтому ее реактивным сопротивлением можно пренебречь по сравнению с сопротивлением при нормальной частоте. Кроме того, этот тип схемы полностью использует напряжение для преодоления омического сопротивления цепи. Следовательно, его также называют безиндуктивной цепью. Резисторы, используемые в этой цепи, контролируют, регулируют и задают путь движения тока или напряжения в цепи. Следует помнить, что значение сопротивления резистора остается постоянным независимо от частоты питания.
Резисторно-индукторная (RL) цепь переменного тока
RL-цепь состоит из катушки (индуктора) с чистой индуктивностью L-индуктора, резистора и источника переменного тока, соединенных последовательно. В этой схеме в катушке индуктивности возникает обратная ЭДС, когда ключ остается замкнутым. Следовательно, току требуется больше времени, чтобы достичь своего максимального значения, но величина протекающего тока остается такой же, поскольку резистор и индуктор соединены последовательно. Постоянная времени этой цепи называется индуктивной постоянной времени и предлагается как T=L/R
Резистор-индуктор-конденсатор (RLC) Цепь переменного тока
В цепи переменного тока RLC резистор с сопротивлением R, катушка индуктивности с индуктивностью L и конденсатор с емкостью C соединены последовательно или параллельно. Синусоидальный отклик последовательной RLC-цепи будет меняться с частотой, потому что индуктивное и емкостное сопротивления \(X_L\) и \(X_C\) являются функциями частоты питания.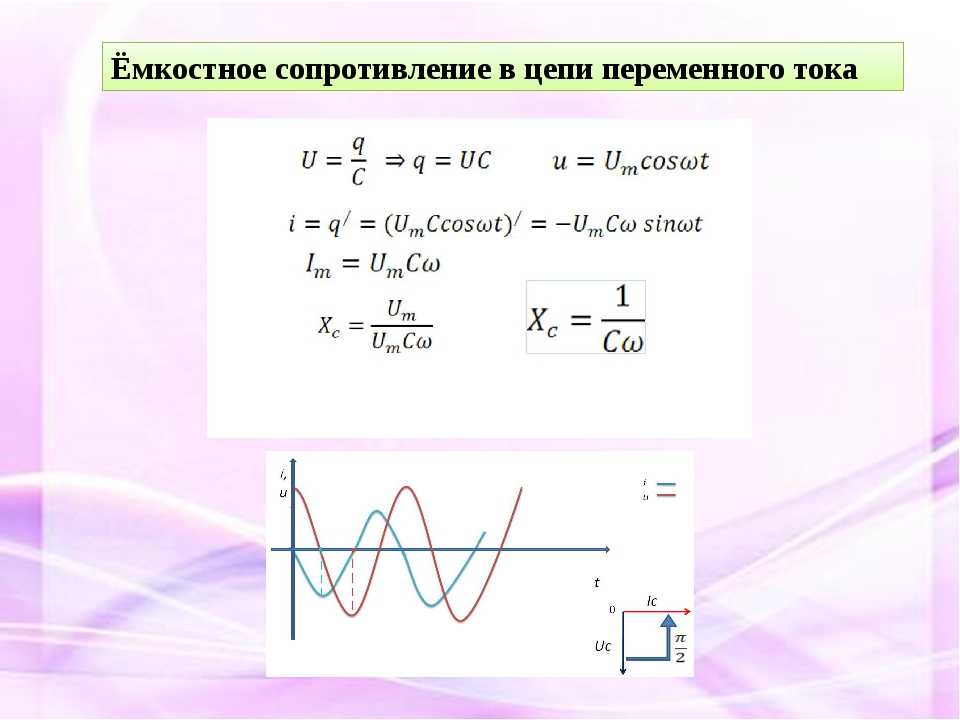 Уникальные падения напряжения на каждом элементе цепи R, L и C будут, таким образом, «в противофазе» друг с другом, и соотношение фаз можно описать следующим образом:
Уникальные падения напряжения на каждом элементе цепи R, L и C будут, таким образом, «в противофазе» друг с другом, и соотношение фаз можно описать следующим образом:
\(V_R\) — мгновенное напряжение на чистом резисторе, которое находится «в фазе» с током.
\(V_L\) — мгновенное напряжение на чистом индукторе, и оно «опережает» ток на 90 градусов.
\(V_C\), мгновенное напряжение на чистом конденсаторе на 90 градусов отстает от тока.
В результате \(V_L\) и \(V_C\) сдвинуты по фазе на 180 градусов и противостоят друг другу.
Узнайте больше о законах Кирхгофа о цепях здесь
Анализ цепи переменного тока
Анализ цепи — это процесс нахождения всех токов и напряжений в сети, состоящей из соединенных компонентов. Системы, в которых напряжение источника часто колеблется, обычно синусоидально, известны как системы переменного тока (AC). Источник напряжения системы переменного тока создает напряжение, которое рассчитывается на основе времени, пикового напряжения и угловой частоты. Ток в простой цепи рассчитывается путем деления напряжения на сопротивление. Пиковый ток (полученный путем деления пикового напряжения на сопротивление), угловая частота и время используются для расчета переменного тока.
Ток в простой цепи рассчитывается путем деления напряжения на сопротивление. Пиковый ток (полученный путем деления пикового напряжения на сопротивление), угловая частота и время используются для расчета переменного тока.
Узнайте больше об электрическом сопротивлении здесь
Теория цепи переменного тока
Принцип выработки энергии переменного тока в цепи переменного тока основан на вращении магнита вдоль стационарного набора проводов или катушек в постоянном магнитном поле.
Математическое исследование стационарного поведения электрических цепей, в которых токи и напряжения регулярно колеблются во времени, известно как теория переменного тока. В анализ включаются только синусоидальные колебания, которые не ограничены, поскольку любая общая периодическая форма волны может быть представлена в виде суммы таких значений, т. е. в виде ряда Фурье.
Знайте больше о электрической мощности здесь
Разница между AC и током AC и DC
Различия между AC и CURE CUPH:
| DC Схема | AC Схема | AC.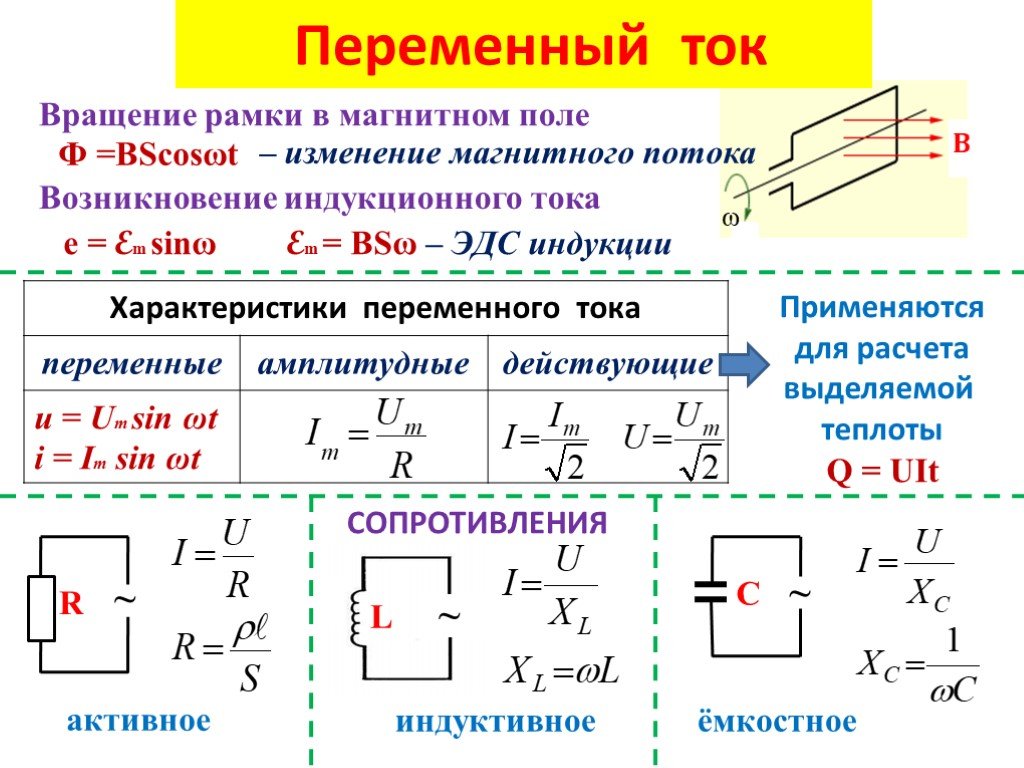 течет в одном направлении в цепи постоянного тока течет в одном направлении в цепи постоянного тока | Ток течет в переменных направлениях в цепи переменного тока. |
| Напряжение постоянного тока и источник питания не могут перемещаться далеко, так как они часто теряют энергию. | Считается более безопасным для передачи электричества на большие расстояния, чтобы обеспечить большую мощность |
| Электроны устойчиво движутся в одном направлении. | Электроны непрерывно переключают направление потока между движением вперед и назад |
| Батареи или элементы используются в цепи постоянного тока в качестве источника питания | Генераторы переменного тока используются в качестве источника энергии в цепи переменного тока |
| Частота тока в цепь постоянного тока остается нулевой | Частота тока варьируется от 50 до 60 Гц в зависимости от страны |
Также прочтите Магнитный эффект электрического тока
Использование цепи переменного тока
Цепи переменного тока постоянно используются дома, в офисах и на предприятиях магазины. Это связано с тем, что производить и передавать переменный ток на большие расстояния достаточно просто. Передача электроэнергии теряет меньше энергии при высоких напряжениях, например выше 110 кВ. Более низкие токи являются результатом более высоких напряжений, а более низкие токи приводят к меньшему теплу, выделяемому в линии электропередачи из-за сопротивления. Трансформаторы упрощают преобразование переменного тока из высокого напряжения.
Это связано с тем, что производить и передавать переменный ток на большие расстояния достаточно просто. Передача электроэнергии теряет меньше энергии при высоких напряжениях, например выше 110 кВ. Более низкие токи являются результатом более высоких напряжений, а более низкие токи приводят к меньшему теплу, выделяемому в линии электропередачи из-за сопротивления. Трансформаторы упрощают преобразование переменного тока из высокого напряжения.
Электродвигатели также могут питаться от сети переменного тока. Единственная разница между двигателями и генераторами заключается в том, что двигатели преобразуют электрическую энергию в механическую. Это полезно для многих крупных бытовых приборов, работающих от сети переменного тока, таких как холодильники, посудомоечные машины и т. д.
Цепи переменного тока используются везде, от транспорта до домов, производящих электроэнергию, и всего электрооборудования, используемого в обычном домашнем хозяйстве.
Мы надеемся, что эта статья о цепи переменного тока была полезна для вашей подготовки к экзамену. Кандидаты могут найти дополнительную информацию по физике в Testbook. Testbook предлагает обновления, касающиеся различных государственных экзаменов. Загрузите приложение Testbook, чтобы найти лучшие доступные предложения.
Кандидаты могут найти дополнительную информацию по физике в Testbook. Testbook предлагает обновления, касающиеся различных государственных экзаменов. Загрузите приложение Testbook, чтобы найти лучшие доступные предложения.
Часто задаваемые вопросы о цепи переменного тока
В.1 Для чего используются цепи переменного тока?
Ans.1 Цепи переменного тока, используемые для доступа к электроснабжению домашних хозяйств, предприятий и промышленности на большие расстояния без потери мощности.
В.2 Как работают цепи переменного тока?
Ans.2 Цепи переменного тока питаются от генератора переменного тока, имеющего колебания электрического поля. Этим переменным источником может быть подаваемый ток или напряжение в цепи.
Q.3 Что такое простая цепь переменного тока?
Ответ 3 Простая цепь переменного тока состоит из резистора, конденсатора или катушки индуктивности, соединенных с источником питания переменного тока. Простая цепь переменного тока обычно имеет резистор в качестве пассивного элемента.
Простая цепь переменного тока обычно имеет резистор в качестве пассивного элемента.
В.4 Почему переменный ток используется вместо постоянного?
Ans.4 Колебания тока в переменном токе позволяют эффективно путешествовать на большие расстояния с меньшими потерями мощности, также считается удобным легко повышать или понижать напряжение.
В.5. Солнечные панели относятся к переменному или постоянному току?
Ans.5 Солнечные панели производят постоянный ток, потому что, когда солнечный свет падает, заряды панели начинают двигаться в определенном направлении устойчиво без каких-либо колебаний.
Скачать публикацию в формате PDF| Значение журнала 10 с использованием общего журнала и натурального журнала с примерами |
| Значение e: шаги по поиску и его важность с решенными примерами |
| Узловой анализ: определение, типы, этапы применения, свойства, примеры решений , Примеры и значение |
| |||||
| | |||||
| ПОЛЕЗНЫЕ ФОРМУЛЫ кондиционера ПЕРИОД ВРЕМЯ (t) ЧАСТОТА (f) СРЕДНЕЕ НАПРЯЖЕНИЕ ИЛИ ТОК ЭФФЕКТИВНОЕ ЗНАЧЕНИЕ НАПРЯЖЕНИЯ ИЛИ ТОКА МАКСИМАЛЬНОЕ НАПРЯЖЕНИЕ ИЛИ ТОК ЗАКОН ОМА ДЛЯ ЦЕПИ ПЕРЕМЕННОГО ТОКА, СОДЕРЖАЩЕЙ ТОЛЬКО СОПРОТИВЛЕНИЕ ПОСТОЯННАЯ ВРЕМЕНИ Л/П (TC) ВЗАИМНАЯ ИНДУКТИВНОСТЬ (М) ОБЩАЯ ИНДУКТИВНОСТЬ (L T ) Серия без магнитной муфты ОБЩАЯ ИНДУКТИВНОСТЬ (L T ) ПАРАЛЛЕЛЬНАЯ (без магнитной связи) ЕМКОСТЬ (Кл) ПОСТОЯННАЯ ВРЕМЕНИ RC (t) ОБЩАЯ ЕМКОСТЬ (C T ) СЕРИЯ ОБЩАЯ ЕМКОСТЬ (C T ) ПАРАЛЛЕЛЬНАЯ ИНДУКТИВНАЯ РЕАКТИВНОСТЬ (X L ) ЕМКОСТНАЯ РЕАКТИВНОСТЬ (X C ) ИМПЕДАНС (Z) ЗАКОН ОМА ДЛЯ РЕАКТИВНЫХ ЦЕПЕЙ ЗАКОН ОМА ДЛЯ ЦЕПЕЙ, СОДЕРЖАЩИХ СОПРОТИВЛЕНИЕ И РЕАКТИВНОЕ СОПРОТИВЛЕНИЕ РЕАКТИВНАЯ МОЩНОСТЬ ПОЛНАЯ МОЩНОСТЬ КОЭФФИЦИЕНТ МОЩНОСТИ (PF) НАПРЯЖЕНИЕ ВО ВТОРИЧНОЙ ОПЕРАТИВНОЙ ОПЕРАЦИОННОЙ ОПЕРАЦИОННОЙ ОПЕРАЦИИ (E s ) НАПРЯЖЕНИЕ НА ПЕРВИЧНОЙ СЕТИ (E p ) ТОК ВО ВТОРИЧНОМ (I s ) ТОК ПО ПЕРВИЧНОЙ СЕТИ (I p ) ЭФФЕКТИВНОСТЬ ТРАНСФОРМАТОРА ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ В прямоугольном треугольнике есть несколько соотношений, которые всегда выполняются. Понимание этих взаимосвязей, называемых тригонометрическими функциями, необходимо для решения проблем в цепях переменного тока, таких как коэффициент мощности, импеданс, падение напряжения и так далее. Чтобы быть ПРЯМОУГОЛЬНЫМ треугольником, треугольник должен иметь «квадратный» угол; тот, в котором между двумя сторонами ровно 90. Тригонометрические функции не применяются к любой другой тип треугольника. Этот тип треугольника показан на рисунке V-1. С помощью тригонометрических функций можно определить НЕИЗВЕСТНУЮ длину одной или нескольких сторон треугольника или количество градусов в НЕИЗВЕСТНЫХ углах, в зависимости от о том, что в настоящее время известно о треугольнике. Например, если длины любых двух сторон известны, то третья сторона и оба угла
& тета; (тета) и Φ (фи) можно определить. Рисунок V-1. — Прямоугольный треугольник. Первый основной факт треугольников состоит в том, что В ЛЮБОМ ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ СУММА ТРЕХ ТРЕУГОЛЬНИКОВ УГЛЫ, ОБРАЗОВАННЫЕ ВНУТРИ ТРЕУГОЛЬНИКА, ДОЛЖНЫ ВСЕГДА РАВНЫ 180. Если один угол всегда равен 90 (a прямой угол), то сумма двух других углов всегда должна быть 90. таким образом, если угол &thetas; известно, Φ можно быстро определить. Например, если &thetas; 30 м, что такое Φ ? Также, если &thetas; известно, Φ можно определить таким же образом. Второй основной факт, который вы должны понять, это то, что ДЛЯ КАЖДОЙ РАЗЛИЧНОЙ КОМБИНАЦИИ
УГЛЫ В ТРЕУГОЛЬНИКЕ ИМЕЮТ ОПРЕДЕЛЕННОЕ СООТНОШЕНИЕ МЕЖДУ ДЛИНАМИ ТРЕХ СТРАН. Рисунок V-2. — Треугольник 30-60-90. Если угол &thetas; 30, Φ должно быть 60. С &thetas; равно 30, отношение длины стороны B к стороне C равно 0,866 к 1. То есть, если гипотенуза равна 1 дюйма, сторона, примыкающая к &thetas;, сторона B, имеет длину 0,866 дюйма. Кроме того, с & тета; равным 30, отношение стороны А к стороне С равно 0,5 к 1. То есть при гипотенуза длиной 1 дюйм, сторона, противоположная &thetas; (сторона А) имеет длину 0,5 дюйма. С & тета; все еще в 30 лет сторона А составляет 0,5774 длины стороны В. С комбинацией даны углы (30-60-90) это ЕДИНСТВЕННЫЕ соотношения длин, которые будут «соответствует» образующему прямоугольный треугольник. Обратите внимание, что для заданного значения &thetas; показаны три соотношения:
отношение B\C, которое всегда называют отношением КОСИНУС &thetas;, отношением A\C,
которое всегда является отношением SINE &thetas;, и отношением A\B, которое всегда является
ТАНГЕНТНОЕ отношение &thetas;. Существует набор коэффициентов для каждого приращения от 0 до 90. Эти угловые отношения, или функции синуса, косинуса и тангенса, перечислены для каждой степени и десятой доли степень в таблице в конце этого приложения. В этой таблице длина гипотенузы треугольника считается неподвижным. Таким образом, приведенные соотношения длин относятся к тому, как в какие стороны А и В изменяются по отношению друг к другу и по отношению к стороне С, как угол & тета; варьируется от 0 до 90. Решение задач по тригонометрии (решение треугольников намного проще, когда таблица тригонометрических функций используется правильно. Наиболее распространенные способы его будет показано путем решения ряда примерных задач. Задача 1: Если гипотенуза треугольника (сторона C) на рисунке V-3 имеет длину 10 дюймов, и угол &thetas; равно 33, какой длины стороны B и A? Рисунок V-3. Решение: Отношение B/C является функцией косинуса. Сверившись с таблицей функций, Вы обнаружит, что косинус числа 33 равен 0,8387. Это означает, что длина B равна 0,8387 длины длина стороны C. Если длина стороны C составляет 10 дюймов, то сторона B должна быть 10 X 0,8387 или 8,387 дюймов в длину. Чтобы определить длину стороны А, используйте функцию синуса, отношение А\С. Снова сверившись с таблицей функций, вы обнаружите, что синус числа 33 равен 0,5446. Таким образом, сторона А должна быть 10 х 0,5446 или 5,446 дюйма в длину. Задача 2: треугольник на рисунке V-4 имеет длину основания 74,2 фута и гипотенузу 100 ноги длинные. Что такое &thetas; и какова длина стороны A? Рисунок V4. — Задача 2. Решение: если углы не заданы, вы всегда должны сначала найти известный угол.
отношение B\C — косинус неизвестного угла &thetas;; следовательно, 74,2/100 или 0,742 равно
косинус неизвестного угла. То есть &thetas; = 42,1. С помощью &тета; известно, сторона A решается с помощью отношение синусов A/C. Синус 42,1, согласно таблице, равен 0,6704. Следовательно, сторона А имеет размеры 100 х 0,6704 или 67,04 фута в длину. Задача 3: В треугольнике на рисунке V-5 длина основания равна 3 единицам, а высота равна 4 единицы. Что такое &thetas; и какой длины гипотенуза? Решение: С данной информацией тангенс &thetas; может быть определено. Тан &thgr; = А/В = 4/3 = 1,33. Рисунок V-5. — Задача 3. Найдя значение 1,33 как значение тангенса в таблице функций, вы обнаружите, что оно тангенс 53.1. Следовательно, &thetas; = 53,1. Однажды &thetas; известна, то для определения можно использовать отношение синуса или косинуса.
длина гипотенузы. Косинус 53,1 равен 0,6004. | |||||


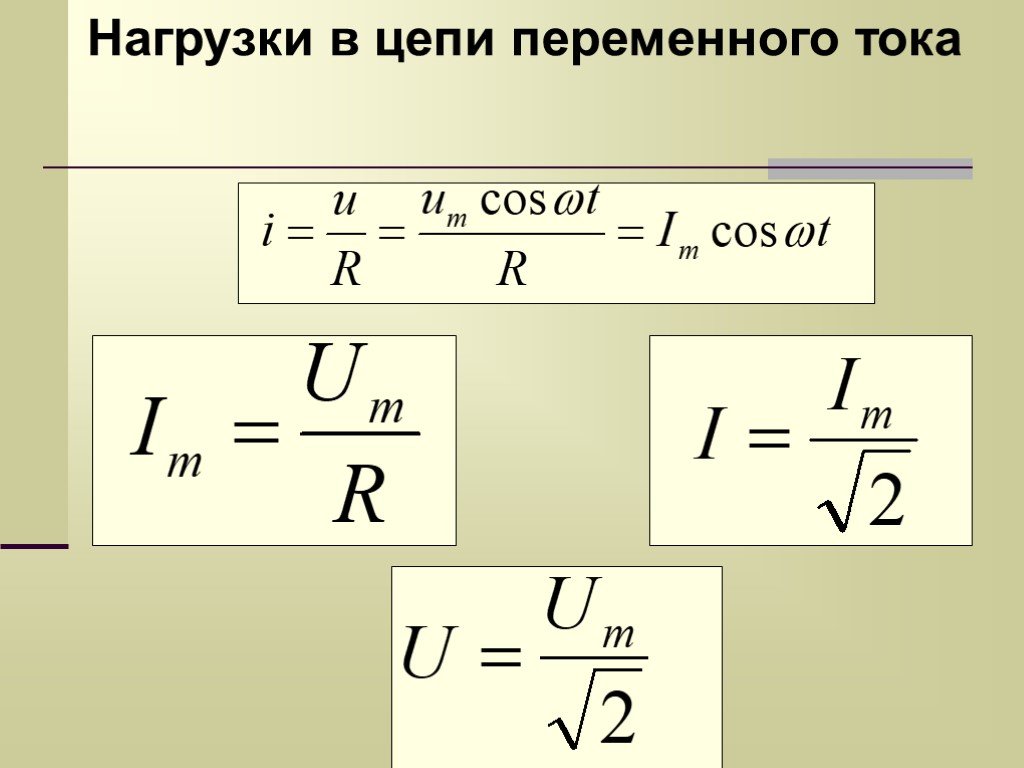 Эти
отношения касаются длины сторон прямоугольного треугольника и того, как
длины зависят от углов между ними.
Эти
отношения касаются длины сторон прямоугольного треугольника и того, как
длины зависят от углов между ними. Треугольник также может быть
решена, если длина любой стороны и одного из углов (&thetas; или Φ в
инжир. V-1) известны.
Треугольник также может быть
решена, если длина любой стороны и одного из углов (&thetas; или Φ в
инжир. V-1) известны. Рассмотрим треугольник на рисунке V-2, состоящий из основания, стороны B; высота, сторона А;
и гипотенуза, сторона C. (Гипотенуза всегда самая длинная сторона, и всегда
напротив 90 угол.)
Рассмотрим треугольник на рисунке V-2, состоящий из основания, стороны B; высота, сторона А;
и гипотенуза, сторона C. (Гипотенуза всегда самая длинная сторона, и всегда
напротив 90 угол.) Если &тета; изменяется, изменяются все три отношения, так как
длины сторон (основания и высоты) меняются.
Если &тета; изменяется, изменяются все три отношения, так как
длины сторон (основания и высоты) меняются. — Задача 1.
— Задача 1. Найдя 0,742 в качестве значения косинуса в таблице, вы обнаружите
что это косинус 42,1.
Найдя 0,742 в качестве значения косинуса в таблице, вы обнаружите
что это косинус 42,1.