Формулы сопротивления воздуха для нескольких сценариев с примером —
Трение между воздухом и другим объектом называется сопротивлением воздуха. Рассмотрим, как определить сопротивление воздуха при падении объекта.
Сопротивление воздуха падающего объекта можно рассчитать, умножив плотность воздуха на коэффициент сопротивления, умноженный на площадь, на два, а затем умножив на скорость.
Сила тяжести и сопротивление воздуха — две силы естественного поля, которые двигают все на Земле. Формула сопротивления воздуха для сферы, доказательство формулы сопротивления воздуха, формула сопротивления воздуха для свободного падения и то, как получить среднее сопротивление воздуха, будут рассмотрены более подробно.
Как рассчитать сопротивление воздуха падающего предмета?Скорость, площадь и форма объекта, проходящего через воздух, влияют на сопротивление воздуха. Проверим, как оценить сопротивление воздуха падающего предмета.
Чтобы определить, какое сопротивление воздуха будет испытывать падающий предмет, используйте формулу FD = 1 / 2 ρv2CDА. В этом уравнении FD означает перетаскивание, ρ — плотность жидкости, v для относительной скорости объекта относительно жидкости, CD для коэффициента лобового сопротивления и A для площади поперечного сечения.
Задача: Огромный пассажирский самолет летит со скоростью 250.0 метров в секунду. A = 500 квадратных метров крыльев самолета подвергаются ветру. Коэффициент аэродинамического сопротивления CD = 0.024. Плотность воздуха ρ = 0.4500 кг на кубический метр на высоте самолета. Какому сопротивлению воздуха подвергается пассажирский самолет?
Решение: Даны данные,
А = 500 квадратных метров
CD = 0.024
ρ = 0.4500 кг на кубический метр
Сопротивление воздуха падающего предмета определяется выражением
FD = 1/2 ρv2CDA
FD =(0. 4500 кг/м3 × 0.025 × 510.0 м2)/2 (250.0 м/с) 2
4500 кг/м3 × 0.025 × 510.0 м2)/2 (250.0 м/с) 2
FD = (0.4500 кг/м3 × 0.025 × 510.0 м2)/2 (62500 м2/s2)
FD = 179296 кг.м/с2
Как рассчитать сопротивление воздуха при движении снаряда?Объект или частица называется снарядом, а его движение называется движением снаряда. Посмотрим, как можно рассчитать сопротивление воздуха при движении снаряда.
Скорость, ускорение, и перемещение должно быть включено при описании движения снаряда в целом, как описано ниже,
- По осям x и y мы должны расположить их составные части. Предположим, что все силы, кроме силы тяжести, ничтожны.
- Компоненты ускорения тогда чрезвычайно прямолинейны, если положительное направление определено как восходящее, ay = -g = — 0.98 м / с.2 (-32 фут/с2).
- Поскольку гравитация вертикальна,x = 0.
 аx = 0 указывает, что vx = V0x, или что начальная и конечная скорости в направлении x равны.
аx = 0 указывает, что vx = V0x, или что начальная и конечная скорости в направлении x равны. - При этих ограничениях на ускорение и скорость кинематическое уравнение x (t) = x0 + (вx) среднийt для движения в униформе гравитационное поле можно записать через уравнение v2y (т) = v2oy + 2аy (г — г0), куда входят и остальные кинематические уравнения движения с ускорением с постоянным ускорением.
- Кинематические уравнения движения в однородном гравитационном поле переходят в кинематические уравнения сy = -г, аx = 0.
- Горизонтальное движение, v0x= Vx, х = х0 + Vxt.
- Вертикальное движение, у = у0 + ½ (в0y + Vy)т; вy = Voy – гт; у = уo + Voyт – ½ гт2, v2y = V2oy – 2г (у – уo).

Задача: Снаряд взлетает в воздух во время фейерверка под углом 75.00 над горизонтом с начальной скоростью 70.0 м/с. Снаряд рассчитан так, что взрыватель сработает именно тогда, когда он будет на максимальной высоте над землей.
- а. Рассчитайте высоту взрыва снаряда.
- б. Через какое время снаряд выстрелит и взорвется?
- в. Что происходит с горизонтальным положением снаряда при его взрыве?
- д. Как далеко в целом продвинулся объект от места запуска до самой высокой точки?
Решение: (а) Под «высотой» мы подразумеваем высоту над начальной точкой или высоту. Когда vy = 0 достигается высшая точка любой траектории, известная как вершина. Мы используем следующее уравнение, чтобы получить y, потому что мы знаем начальное местоположение, начальную и конечную скорости и начальное положение:
v2y = V2oy – 2г (у – у0)
Уравнение упрощается тем, что yo и vy оба равны нулю.
0 = в2oy – 2г.
Вычислив y, мы получаем, y = v2oy/ 2г.
Теперь нам нужно выяснить, какова начальная компонента скорости y, или v0y, является. Его можно рассчитать по формуле v0y=v0sin θ, где v0 обозначает начальную скорость 70.0 м/с и θo=75° обозначает начальный угол. Таким образом-
v0y=v0sin θ = (70.0 м/с) sin750 = 67.6 м/с и-
у = (67.6 м/с)2 / 2(9.80 м/с2)
у = 233 м.
Начальная вертикальная скорость и максимальная высота положительны, потому что вверх положительна, а ускорение, вызванное силой тяжести, отрицательно. Снаряд с начальной вертикальной составляющей скорости 67.6 м/с достигнет максимальной высоты 233 м. Также имейте в виду, что максимальная высота зависит только от вертикальной составляющей начальной скорости (без учета сопротивления воздуха).
(b) Существуют различные способы определить, когда снаряд достигает высшей точки, как и во многих физических задачах. Самый простой подход в этой ситуации — использовать vy=v0y -гт. Это уравнение становится vy= 0 на вершине
Самый простой подход в этой ситуации — использовать vy=v0y -гт. Это уравнение становится vy= 0 на вершине
0 = в0y− гт
или,
т = voy/g = (67.6 м/с) / (9.80 м/с2)
t = 6.90 с.
Другой способ найти время — использовать y = yo + ½ (в0y + Vy) т.
в) Сопротивление воздуха мало, следовательно, ах и ау равны нулю. И, как упоминалось ранее, горизонтальная скорость постоянна. Как показывают уравнения x=x0+vxт, где х0 равно нулю, горизонтальное перемещение равно горизонтальной скорости, умноженной на время. Таким образом,
х = vxt,
Когда vx — компонент x скорости, определяется выражением
vx = V0cosθ = (70.0 м/с) cos75°=18.1 м/с.
Поскольку оба движения имеют одинаковое время t, x равно
х = (18.1 м/с) × 6.90 с = 125 м.
Без сопротивления воздуха горизонтальное движение имеет постоянную скорость. Горизонтальное смещение, наблюдаемое здесь, может помочь предотвратить травму зрителей от падающих пиротехнических фрагментов. Немалую роль при взрыве снаряда играет сопротивление воздуха, и многие осколки падают сразу внизу.
Горизонтальное смещение, наблюдаемое здесь, может помочь предотвратить травму зрителей от падающих пиротехнических фрагментов. Немалую роль при взрыве снаряда играет сопротивление воздуха, и многие осколки падают сразу внизу.
(d) Нахождение размера и направления смещения в самой высокой точке — это все, что здесь требуется, поскольку горизонтальная и вертикальная составляющие смещения уже рассчитаны:
s→ = 125 см + 233 см; |ŝ|=√ (1252 + 2332) = 264 м; Φ = загар -1 (233/125) = 61.8°
Как рассчитать сопротивление воздуха при конечной скорости?Сопротивление воздуха по величине эквивалентно весу падающего тела с предельной скоростью. Рассмотрим метод расчета сопротивления воздуха при предельной скорости.
- Используя второй закон Ньютона для падающего объекта в качестве отправной точки, мы можем определить сопротивление воздуха при конечной скорости: Fg + Far = ма.

- Для определения сопротивления воздуха при заданной скорости используются следующие два типа сопротивления воздуха: Far = – bv альтернативно, Far = — бв2.
- Для расчета сопротивления воздуха при конечной скорости используется закон Ньютона для определения сопротивления воздуха при конечной скорости, поскольку ускорение равно нулю. мг – бв = 0; мг – бв2 = 0.
- Чтобы определить сопротивление воздуха при заданной скорости, ответом на задачу о скорости является vT = мг/б. Альтернативой является то, что vT = √(мг/б).
Если m представляет массу в килограммах, g — квадрат ускорения свободного падения, а b — произвольная величина.
Задача: При падении из состояния покоя объект массой 55 кг испытывает силу сопротивления воздуха, определяемую Far = -15В2. Определить конечную скорость объекта.
Решение: используйте формулу vT = √ (мг/б) для определения конечной скорости силы сопротивления вида Far = -bv2. Добавляя к уравнению, получаем,
Добавляя к уравнению, получаем,
vT = √(55) × (9.81)/15)
vT = 5.99 м / с
Как рассчитать коэффициент сопротивления воздуха?Коэффициент сопротивления изменяется как квадратное отношение относительной скорости объекта. Рассмотрим метод расчета коэффициента сопротивления воздуха.
Коэффициент сопротивления воздуха рассчитывается по уравнению с = Fвоздух /v2. В расчете Фвоздух — силовое сопротивление, а c — силовая постоянная в этом уравнении. Жидкости, обычно вода в спортивной среде, также подвержены силе трения, которая не ограничивается только воздухом.
Сопротивление жидкости, сопротивление воздуха и сопротивление — все это относится к одному и тому же.
Проблема: Если объект движется со скоростью 22 мс-1 столкнуться с сопротивлением воздуха 50 Н, какова постоянная силы?
Решение: Даны данные,
v = 22 мс-1
Fвоздух = 50 Н
Формула для коэффициента сопротивления воздуха:
с = Fвоздух /v2
Замените указанные значения в формуле выше. Затем,
Затем,
с = 50/(22)2
с = 0.103
Как рассчитать аэродинамическое сопротивление парашюта?Вес пульсирует на шнуре, когда парашют раскрывается. Рассмотрим, как определить аэродинамическое сопротивление парашюта.
- Чтобы определить аэродинамическое сопротивление парашюта. Уравнение для силы сопротивления парашюта, также известной как его сила сопротивления ветру, имеет вид F.D = 1 / 2 ρv2CDА. Где, ФD — сила сопротивления, r — плотность воздуха, Cd — коэффициент лобового сопротивления, A — площадь парашюта, а v — скорость в воздухе.
- Чтобы определить сопротивление воздуха парашюта по квадрату скорости, сопротивление возрастает.
- Чтобы определить сопротивление воздуха парашюта, нет никакой чистой силы, действующей на ракету, когда сопротивление равно весу. F = D – W = 0.
- Cd = 2 Фd / ρв2A = W для определения аэродинамического сопротивления парашюта.

- И, наконец, V = sqrt (2W/Cdρ A) используется для определения аэродинамического сопротивления парашюта.
При сравнении двух предметов те, у которых больший вес, меньший коэффициент лобового сопротивления, меньшая плотность газа или меньшая площадь, движутся с большей скоростью.
Как найти сопротивление воздуха через массу и ускорение?Единственной силой, воздействующей на людей поначалу, является гравитация, которая толкает их со скоростью -9.8 м/с2. Давайте посмотрим, как можно рассчитать сопротивление воздуха, используя массу и ускорение.
- Чтобы найти сопротивление воздуха с массой и ускорением, мы можем использовать некоторую алгебру, чтобы получить ускорение объекта с точки зрения чистой внешней силы и массы объекта (a = F/m).
- Чистая внешняя сила (F = W – D) равна разнице между силами веса и силы сопротивления. Тогда ускорение объекта определяется выражением a = (W – D) / m.

Задача: Автомобиль массой около 29 кг движется из Калькутты в Раджастхан со скоростью 50 метров в секунду, а гусеница нагружена железом и весит 84 кг. Определить силу сопротивления автомобиля.
Решение: Даны данные,
Ускорение = 50 м/с2
Вес = 84 кг
Масса = 29 кг
Мы знаем, что a = (W – D) / m
50 = (84 – Д)/ 29
1450 = 84 – Д
-Д = 1450 – 84
Д = – 1366 Н
График сопротивления воздухаКогда частички воздуха сталкиваются с передней частью объекта, он замедляется. Давайте проверим этот график сопротивления воздуха.
Кредит изображения — График сопротивления воздуха by Кропоткино 113 (говорить) (CC-BY-SA-3.0)За счет уменьшения угла выпуска можно свести к минимуму влияние сопротивления воздуха на горизонтальную составляющую траектории снаряда. Расстояние и скорость, или скорость, обратно пропорциональны.
Как рассчитать сопротивление воздуха по скорости?Чем больше частиц воздуха воздействует на объект, тем больше его общее сопротивление увеличивается с площадью поверхности. Давайте рассмотрим, как определить сопротивление воздуха на основе скорости.
Давайте рассмотрим, как определить сопротивление воздуха на основе скорости.
Формула, используемая для определения сопротивления воздуха по скорости: c = Fv.2. Сила сопротивления воздуха представлена в технике буквой F, постоянная силы представлена буквой c, а скорость объекта представлена буквой v. Существует линейная зависимость между сопротивлением воздуха и величиной сопротивления воздуха. плотность.
Между скоростью и сопротивлением воздуха создается квадратичная зависимость. Площадь передней кромки объекта, движущегося по воздуху, определяет, какое сопротивление воздуха он будет испытывать. Сопротивление воздуха увеличивается с увеличением площади.
Задача: Если сопротивление воздуха тела равно 34 Н, а силовая постоянная равна 0.04, какова его скорость?
Данные приведены, Fвоздух = 34 Н и с = 0.04
Формула сопротивления воздуха:
Fвоздух = резюме2
v2 = 34 / 0.04
v2 = 850
v = 29. 15 м / с.
15 м / с.
Сила сопротивления воздуха измеряется в Ньютонах (Н). Рассмотрим, как определить силу сопротивления воздуха.
Fвоздух = — резюме2 уравнение, используемое для определения силы сопротивления воздуха. Фвоздух — силовое сопротивление, а c — силовая постоянная в этом уравнении. Знак минус показывает, что объект движется в направлении, противоположном направлению сопротивления воздуха.
Задача: силовая постоянная для самолета, движущегося со скоростью 50 мс.-1 составляет 0.05. Определить сопротивление воздуха.
Решение: Даны данные,
Скорость воздуха, v = 50
Силовая постоянная, c = 0.05
Сила воздуха определяется выражением
F = – резюме2
F = (-) 0.05 × 50 × 50
F = – 125 Н.
Формула сопротивления воздуха для шараЗависимость между силой сопротивления, действующей на тело, и сопротивлением воздуха обратная. Давайте посмотрим на формулу сопротивления воздуха шара.
Давайте посмотрим на формулу сопротивления воздуха шара.
Коэффициент сопротивления воздуха для сферических материалов можно рассчитать по следующей формуле: Cd = 2 Фd / ρв2A, где для сферических материалов-
- Cd = коэффициент сопротивления воздуха,
- Fd сопротивление воздуха по Ньютону,
- А — площадь формы в плане в квадратных метрах,
- ρ = плотность сферы, выраженная в килограммах на кубический метр,
- А вязкость вещества, выраженная в метрах в секунду, известна как v.
Задача: Плотность воздуха 0.4500 кг/м3, а самолет, летящий на высоте, имеет скорость 250 м/с. 500 м2 Крылья самолета открыты ветру. На самолет действует сила сопротивления воздуха 168750 Н. Выполните расчет коэффициента лобового сопротивления.
Решение: Приведенные данные, Сопротивление воздуха для сферических материалов, Fd = 168750 Н
Плотность, ρ = 0. 4500 кг/м3
4500 кг/м3
Площадь поперечного сечения, А = 500 м2
Скорость, v = 250 м/с
Мы знаем, что для сферических материалов
Cd = 2 Фd / ρв2A
Cd = 2 × 168750 / (0.4500 × 2502 × 500)
Cd = 0.025
Как рассчитать среднее сопротивление воздуха?Сопротивление воздуха — это разновидность жидкостного трения, которое влияет на падающие в воздухе предметы. Давайте посмотрим, как определить среднее сопротивление воздуха.
Умножив плотность воздуха, коэффициент сопротивления, площадь и скорость на два, можно рассчитать среднее сопротивление воздуха, которое будет испытывать падающий объект. Гравитация заставляет объекты двигаться вниз, в отличие от трения воздуха, которое действует противоположным образом и замедляет скорость.
Сопротивление воздуха возрастает по мере увеличения площади поверхности, на которую падают предметы.
ЗаключениеСопротивление воздуха — это сила, которую испытывает объект при прохождении через воздух, где, если человек движется быстрее, сила сопротивления воздуха возрастает. Безразмерный коэффициент сопротивления CD, который рассчитывается как CD = ФD/1/2 ρАв2 где ρ — плотность жидкости (в данном случае воздуха). Площадь поперечного сечения объекта A = (1/4) ΠD2, а его скорость v.
Безразмерный коэффициент сопротивления CD, который рассчитывается как CD = ФD/1/2 ρАв2 где ρ — плотность жидкости (в данном случае воздуха). Площадь поперечного сечения объекта A = (1/4) ΠD2, а его скорость v.
Механика жидкости и газа
Механика жидкости и газа
ОглавлениеПРЕДИСЛОВИЕВВЕДЕНИЕ § 1. Предмет механики жидкости и газа. Основные свойства «макромодели» жидкости и газа: сплошность и подвижность § 3. Краткий очерк исторического развития механики жидкости и газа. От гидромеханики древних до установления воззрений ньютонианской эпохи § 4. Эпоха Эйлера и Бернулли. Гидроаэродинамика в XIX в. § 5. Современный этап развития механики жидкости и газа ГЛАВА I. ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ § 6. Поле физической величины. Скалярное и векторное поля. Поверхности уровня. Векторные линин и трубки § 7. Мера однородности поля в данном направлении и в дайной точке. Градиевт скалярного поля и дифференциальный тензор векторного поля как меры неоднородности поля § 9.  Поле ускорений. Разложение ускорения частицы на локальную и конвективную составляющие Поле ускорений. Разложение ускорения частицы на локальную и конвективную составляющие§ 10. Скоростное поле сплошной среды в окрестности данной точки. Угловая скорость и вихрь. Тензор скоростей деформаций и его компоненты § 11. Скорость объемного расширения жидкости. Интегральные представления дифференциальных операторов поля. Основные интегральные формулы § 12. Вихревые линии и трубки. Вторая теорема Гельмгольца. Интенсивность вихревой трубки § 13. Выражение интенсивности вихревой трубки через циркуляцию вектора по контуру, охватывающему трубку. Теорема об изменении циркуляции скорости во времени § 14. Распределение массы в сплошной среде. Плотность и удельный вес. Напряжения. Тензор напряженности и его симметричность § 15. Общие уравнения динамики сплошной среды. Уравнение неразрывности. Уравнения динамики в напряжениях § 16. Тепловые явления в жидкостях и газах. Закон сохранения энергии и уравнение баланса энергии § 17.  Общие уравнения равновесного состояния жидкости и газа. Равновесие воздуха в атмосфере. Приближенные барометрические формулы. Стандартная атмосфера Общие уравнения равновесного состояния жидкости и газа. Равновесие воздуха в атмосфере. Приближенные барометрические формулы. Стандартная атмосфера§ 19. Давление тяжелой несжимаемой жидкости на поверхность тела. Сила и момент, приложенные к телу, плавающему в тяжелой жидкости. Случай вращающейся жидкости ГЛАВА III. ДИНАМИКА ИДЕАЛЬНОЙ ЖИДКОСТИ И ГАЗА. ОСНОВНЫЕ УРАВНЕНИЯ И ОБЩИЕ ТЕОРЕМЫ § 20. Идеальная жидкость. Основные уравнения движения § 21. Закон сохранения энергии в движущейся идеальной жидкости. Адиабатическое движение. Сохранение энтропии § 22. Эйлерово представление конвективного изменения объемного интеграла. Перенос величины сквозь контрольную поверхность § 24. Теорема об изменении кинетической энергии.  Работа и мощность внутренних сил. Эйлерова форма уравнения изменения кинетической энергии Работа и мощность внутренних сил. Эйлерова форма уравнения изменения кинетической энергии§ 25. Теорема Бернулли о сохранении полной механической энергии при стационарном баротропном движении идеальной жидкости и газа ГЛАВА IV. ОДНОМЕРНЫЙ ПОТОК ИДЕАЛЬНОЙ ЖИДКОСТИ § 26. Одномерное течение идеальной сжимаемой жидкости. Линеаризированные уравнения. Скорость распространения малых возмущений в жидкости или газе § 28. Распространение непрерывных возмущений конечной интенсивности. Характеристики. Образование разрывной ударной волны § 29. Стоячая ударная волна или скачок уплотнения. Ударная адиабата § 30. Критические величины в одномерном потоке газа. Связь между скоростями до и после скачка. Изменение давления, плотности и температуры в скачке уплотнения § 31. Скорость распространения ударной волны.  § 32. Влияние интенсивности скачка уплотнения на сжатие газа. Измерение скоростей и давлений в до- и сверхзвуковых потоках § 33. Одномерное движение газа по трубе переменного сечения. Истечение из резервуара большой емкости сквозь сходящееся сопло § 34. Одномерное течение в сопле Лаваля. Движение газа с притоком тепла ГЛАВА V. БЕЗВИХРЕВОЕ ДВИЖЕНИЕ ЖИДКОСТИ. ПЛОСКОЕ ДВИЖЕНИЕ НЕСЖИМАЕМОЙ ЖИДКОСТИ § 35. Сохранение циркуляции скорости в потоке идеальной жидкости. Теорема Кельвина и Лаграижа. Безвихревое движение. Потенциал скоростей § 36. Интеграл Лагранжа — Коши уравнений безвихревого движения. Теорема Бернулли. Некоторые общие свойства безвихревого движения идеальной несжимаемой жидкости в односвязной области § 38. Построение полей течения по заданной характеристической Функции.  Простейшие плоские потоки и их наложение Простейшие плоские потоки и их наложение§ 39. Бесциркуляционное и циркуляционное обтекания круглого цилиндра § 40. Применение криволинейных координат. Бесциркуляционное и циркуляционное обтекания эллиптического цилиндра и пластинки. Задача Жуковского об обтекании решетки пластин. § 42. Прямая задача в теории плоского движения идеальной несжимаемой жидкости. Применение метода конформных отображений. Гипотеза Чаплыгина о безотрывном обтекании задней кромки профиля. Формула циркуляции § 43. Теорема Жуковского о подъемной силе крыла. Зависимость подъемной силы от угла атаки. Коэффициент подъемной силы § 44. Применение метода комплексных переменных к выводу теоремы Жуковского. Формулы Чаплыгина для главного вектора и момента сил давления потока на крыло  Независимость от угла атаки момента относительно фокуса. Парабола устойчивости Независимость от угла атаки момента относительно фокуса. Парабола устойчивости§ 46. Частные случаи конформного отображения крылового профиля на круг. Преобразование Жуковского-Чаплыгина. Теоретические крыловые профили § 47. Задача об обтекании слабо изогнутой дужки произвольной формы (теория тонкого крыла) § 48. Определение обтекания крылового профиля произвольной формы § 49. Обобщение теоремы Жуковского на случай плоской решетки с бесчисленным множеством профилей ГЛАВА VI. ПЛОСКОЕ БЕЗВИХРЕВОЕ ДВИЖЕНИЕ СЖИМАЕМОГО ГАЗА 51. Линеаризированный до- и сверхзвуковой газовый поток вдоль волнистой стенки § 52. Тонкое крыло в линеаризированном до- и сверхзвуковом потоках. Влияние сжимаемости газа на коэффициент подъемной силы в дозвуковом потоке. Коэффициенты подъемной силы и волнового сопротивления при сверхзвуковом потоке § 53. Нелинеаризированные уравнения движения идеального сжимаемого газа.  Переход в плоскость годографа. Уравнения Чаплыгина Переход в плоскость годографа. Уравнения Чаплыгина§ 54. Метод С. А. Христиановича. Приближенные формулы учета влияния сжимаемости на распределение давления § 56. Решетка профилей в плоском докритическом потоке сжимаемого газа. Обобщение теоремы Жуковского § 56. Решетка профилей в плоском докритическом потоке сжимаемого газа. Обобщение теоремы Жуковского § 57. Нелинеаризированный сверхзвуковой поток. «Характеристики» уравнений плоского сверхзвукового потока. Линин возмущения и их основные свойства § 58. Обтекание выпуклого угла сверхзвуковым потоком. Влияние угла поворота струи на ее газодинамические элементы ГЛАВА VII. ПРОСТРАНСТВЕННОЕ БЕЗВИХРЕВОЕ ДВИЖЕНИЕ § 60.  Ортогональные криволинейные координаты в пространстве. Основные дифференциальные операторы поля в криволинейных координатах Ортогональные криволинейные координаты в пространстве. Основные дифференциальные операторы поля в криволинейных координатах§ 61. Потенциал скоростей. Поле источника и диполя. Непрерывное распределение источников и диполей. Ньютонов потенциал. Потенциал простого и двойного слоев § 62. Поле скоростей вокруг заданной системы вихрей. Формула Био – Савара. Потенциал скоростей замкнутой вихревой нити. Аналогия с потенциалом двойного слоя § 63. Функция тока и ее связь с векторным потенциалом скоростей. Функции тока простейших течений § 64. Обтекание сферы. Давление однородного стационарного потока идеальной несжимаемой жидкости на погруженное в нее тело. Парадокс Даламбера § 65. Общие уравнения осесимметричного движения. Применение цилиндрических координат. Течение сквозь каналы § 66. Осесимметричное продольное обтекание тел вращения. Случай эллипсоида вращения § 67. Поперечное обтекание тел вращения. Пример эллипсоида вращения § 68. Продольное и поперечное обтекание тел вращения большого удлинения.  Приближенные выражения граничных условий. Применение тригонометрических сумм для определения коэффициентов … Приближенные выражения граничных условий. Применение тригонометрических сумм для определения коэффициентов …§ 69. Метод «особенностей». Применение непрерывно распределенных источников (стоков) и диполей для решения задачи о продольном и поперечном обтекании тел вращения § 70. Общий случай движения твердого тела сквозь несжимаемую идеальную жидкость. Определение потенциала скоростей. Главный вектор и главный момент сил давления потока на тело § 71. Коэффициенты «присоединенных масс». Свойство симметрии. «Присоединенная» кинетическая энергия. Определение «присоединенных масс» поступательно движущегося цилиндра, шара и эллипсоида § 72. Элементы теории крыла конечного размаха. Вихревая система крыла. Гипотеза плоских сечеиий. Геометрические и действительные углы атаки. Подъемная сила и «индуктивное сопротивление» § 73. Основные формулы теории «несущей линии». «Индуктивная скорость» и «индуктивный угол». Прямая задача определения подъемной силы и индуктивного сопротивления по заданному распределению циркуляции § 74.  Крыло с минимальным индуктивным сопротивлением. Эллиптическое распределение циркуляции. Связь между коэффициентами индуктивного сопротивления и подъемной силы. Основное уравнение теории крыла и понятие о его интегрировании Крыло с минимальным индуктивным сопротивлением. Эллиптическое распределение циркуляции. Связь между коэффициентами индуктивного сопротивления и подъемной силы. Основное уравнение теории крыла и понятие о его интегрированииГЛАВА VIII. ДИНАМИКА ВЯЗКОЙ ЖИДКОСТИ И ГАЗА § 75. Внутреннее трение и теплопроводность в жидкостях и газах. Законы Ньютона и Фурье. Влияние температуры на коэффициенты вязкости и теплопроводности. Число «сигма» § 76. Обобщение закона Ньютона на случай произвольного движения среды. Закон линейной связи между тензорами напряжений и скоростей деформации § 77. Общие уравнения движения вязкой жидкости. Динамические уравнения и уравнение баланса энергии. Граничные условия движения жидкости с треннем и теплопроводностью § 78. Понятие о подобии гидродинамических явлений. Безразмерные уравнения движения вязкой жидкости и газа. Условия подобия § 79. Ламинарное движение вязкой несжимаемой жидкости по цилиндрической трубе § 80. Обтекание шара при очень малых значениях числа Рейнольдса.  Формула сопротивления шара по Стоксу и ее обобщения Формула сопротивления шара по Стоксу и ее обобщения§ 81. Вихревые линии в идеальной и вязкой жидкости. Сохраняемость вихревых линий при отсутствии внутреннего трения. Диффузия вихря в вязкой жидкости § 82. Одномерное прямолинейное движение сжимаемого вязкого газа. Движение внутри скачка уплотнения. Понятие о толщине скачка § 83. Работа внутренних сил и диссипация механической энергии в движущейся вязкой среде § 84. Обтекание тел жидкостью и газом при больших значениях числа Рейнольдса. Основные уравнения теории ламинарного пограничного слоя § 85. Ламинарный пограничный слой на пластинке, продольно обтекаемой несжимаемой жидкостью. Неизотермическое движение § 86. Ламинарный пограничный слой при степенном задании скорости внешнего потока § 87. Ламинарный пограничный слой в общем случае задания скорости внешнего потока. Применение уравнения импульсов для приближенного расчета ламинарного пограничного слоя § 88. Способы определения функций … Приближенный метод расчета ламинарного пограничного слоя § 89.  Ламинарный пограничный слой на пластинке, продольно обтекаемой сжимаемым газом при больших скоростях. Случай линейной зависимости коэффициента вязкости от температуры (n = 1) Ламинарный пограничный слой на пластинке, продольно обтекаемой сжимаемым газом при больших скоростях. Случай линейной зависимости коэффициента вязкости от температуры (n = 1)§ 90. Ламинарный пограничный слой на пластинке при любом законе связи между вязкостью и температурой и при числе … Обтекание крылового профиля потоком больших скоростей ГЛАВА IX. ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ § 91. Переход ламинарного движения в турбулентное. Критическое рейнольдсово число § 92. Область и «точка» перехода. Явление «кризиса обтекания» § 93. Основные уравнения осреднеиного турбулентного движения. Тензор турбулентных напряжений § 94. Турбулентное движение жидкости в плоской и круглой трубе. Логарифмические формулы скоростей § 95. Формулы сопротивления гладких труб при турбулентном движении жидкости. Ламинарный подслой § 96. Влияние шероховатости стенок трубы на ее сопротивление. Предельные режимы течения. Режим установившейся шероховатости § 97. Турбулентный пограничный слой на продольно обтекаемой пластине.  Сопротивление пластины Сопротивление пластины§ 98. Турбулентный пограничный слой на крыловом профиле при малом продольном перепаде давлений § 99. Турбулентный пограничный слой на крыловом профиле при значительных продольных перепадах давления § 100. Профильное сопротивление крыла. Разложение профильного сопротивления на сопротивление трения и сопротивление давлений. Обратное влияние пограничного слоя на распределение давлений по поверхности обтекаемого профиля § 101. Приближенные формулы профильного сопротивления крыла и крылового профиля в решетке § 102. Основные закономерности «свободной турбулентности». Плоская турбулентная струя в пространстве, заполненном той же жидкостью § 103. Турбулентный след за обтекаемым телом § 104. Рассеяние турбулентных возмущений в жидкости. Случай изотропной и однородной турбулентности. Закон сохранения момента возмущений |
Формулы сопротивления воздуха для нескольких сценариев с примером —
Трение между воздухом и другим объектом называется сопротивлением воздуха. Рассмотрим, как определить сопротивление воздуха при падении объекта.
Рассмотрим, как определить сопротивление воздуха при падении объекта.
Сопротивление воздуха падающего объекта можно рассчитать, умножив плотность воздуха на коэффициент сопротивления и площадь на два, а затем умножив на скорость.
Гравитация и сопротивление воздуха — две силы естественного поля, которые двигают все на Земле. Формула сопротивления воздуха для сферы, доказательство формулы сопротивления воздуха, формула сопротивления воздуха для свободного падения и то, как получить среднее сопротивление воздуха, будут рассмотрены более подробно.
Как рассчитать сопротивление воздуха падающего предмета?Скорость, площадь и форма объекта, проходящего через воздух, влияют на сопротивление воздуха. Проверим, как оценить сопротивление воздуха падающего предмета.
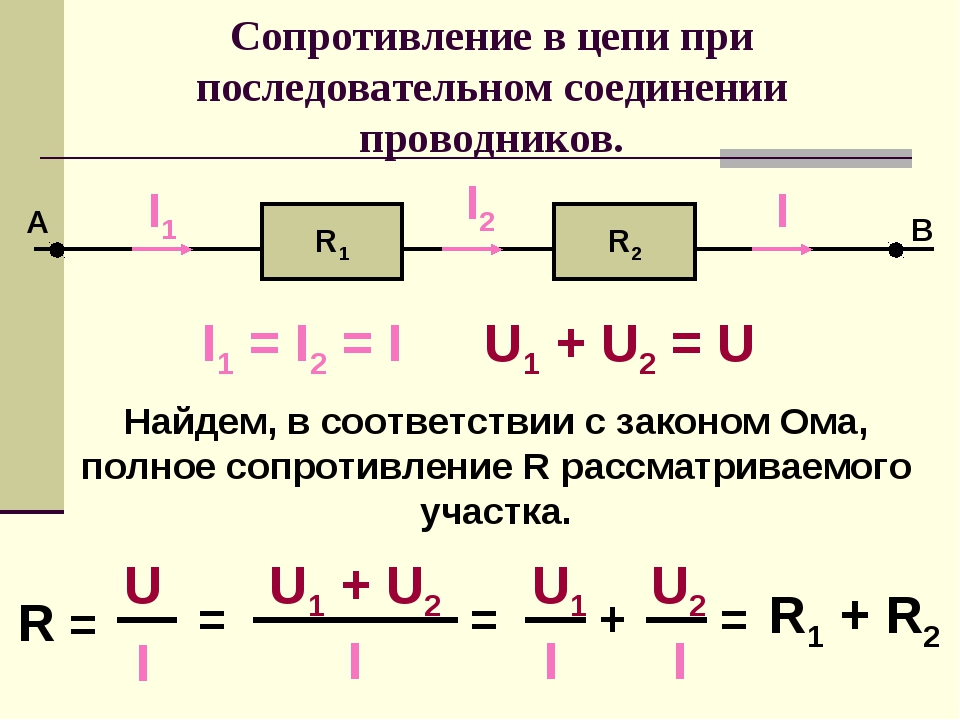
Чтобы определить, какое сопротивление воздуха будет испытывать падающий предмет, используйте формулу F D = 1/2 ρ v 2 C D A. В этом уравнении F D означает перетаскивание, ρ — плотность жидкости, v — относительная скорость объекта относительно жидкости, C D — коэффициент сопротивления и A — площадь поперечного сечения.
В этом уравнении F D означает перетаскивание, ρ — плотность жидкости, v — относительная скорость объекта относительно жидкости, C D — коэффициент сопротивления и A — площадь поперечного сечения.
Задача: Огромный пассажирский самолет летит со скоростью 250 метров в секунду. A = 500 квадратных метров крыльев самолета подвергаются ветру. Коэффициент аэродинамического сопротивления C D = 0,024. Плотность воздуха ρ = 0,4500 кг на кубический метр на высоте самолета. Какому сопротивлению воздуха подвергается пассажирский самолет?
Решение: Даны следующие данные:
A = 500 квадратных метров
C D = 0,024
ρ = 0,4500 кг на кубический метр 1/2 ρv 2 C D A
F D =(0.4500 kg/m 3 × 0.025 × 510.0 m 2 )/2 (250.0 m/s) 2
F D = (0,4500 кг/м 3 × 0,025 × 510,0 м 2 )/2 (62500 м 2 /с 2 )
F D = 179296 кг·м/с 2
Как рассчитать сопротивление воздуха при движении снаряда? Объект или частица называется снарядом, а его движение называется движением снаряда. Посмотрим, как можно рассчитать сопротивление воздуха при движении снаряда.
Посмотрим, как можно рассчитать сопротивление воздуха при движении снаряда.
Скорость, ускорение и смещение должны быть включены при описании движения снаряда в целом, как описано ниже,
- По осям x и y мы должны расположить их составные части. Предположим, что все силы, кроме силы тяжести, ничтожны.
- Компоненты ускорения тогда чрезвычайно прямолинейны, если положительное направление определено как восходящее, ay = -g = – 0,98 м/с 2 (-32 фут/с 2 ).
- Поскольку гравитация вертикальна, a x = 0. a x = 0 означает, что v x = v 0x , или что начальная и конечная скорости в направлении x равны.
- При этих ограничениях на ускорение и скорость кинематическое уравнение x (t) = x 0 + (v x ) avg t для движения в однородном гравитационном поле может быть записано через уравнение v 2 y (t) = v 2 oy + 2a y (y – y 0 ), куда входят и остальные кинематические уравнения движения с ускорением с постоянным ускорением.

- Кинематические уравнения для движения в однородном гравитационном поле становятся кинематическими уравнениями с х = х 0 + v х t.
- Вертикальное движение, y = y 0 + ½ (v 0y + v y )t; v y = v oy – гт; y = y o + v oy t – ½ gt 2 , v 2 y = v 2 oy – 2g (y – y o ).
Задача: Во время фейерверка под углом 75,0 0 над горизонтом с начальной скоростью 70,0 м/с пущен снаряд. Снаряд рассчитан так, что взрыватель сработает именно тогда, когда он будет на максимальной высоте над землей.
- а. Рассчитайте высоту взрыва снаряда.
- б. Через какое время снаряд выстрелит и взорвется?
- г. Что происходит с горизонтальным положением снаряда при его взрыве?
- д. Как далеко в целом продвинулся объект от места запуска до самой высокой точки?
Решение: (a) Под «высотой» мы подразумеваем высоту над начальной точкой или высоту. Когда v y = 0, достигается высшая точка любой траектории, известная как вершина. Мы используем следующее уравнение, чтобы получить y, потому что мы знаем начальное местоположение, начальную и конечную скорости и начальное положение:
Когда v y = 0, достигается высшая точка любой траектории, известная как вершина. Мы используем следующее уравнение, чтобы получить y, потому что мы знаем начальное местоположение, начальную и конечную скорости и начальное положение:
V 2 Y = V 2 OY — 2G (Y — Y 0 )
Уравнение стало проще из -за того, что Y O и v Y оба являются Zero. .
0 = v 2 oy – 2gy.
Вычислив y, мы получим y = v 2 oy /2g.
Теперь нам нужно выяснить, какова начальная компонента y скорости, или v 0y . Его можно рассчитать по формуле v 0y =v 0 sin θ, где v 0 обозначает начальную скорость 70,0 м/с, а θ o =75° обозначает начальный угол. Таким образом-
v 0y =v 0 sin θ = (70,0 м/с) sin75 0 = 67,6 м/с и-
y = (67,6 м/с) 2 929,28 / м/с 2 )
y = 233 м.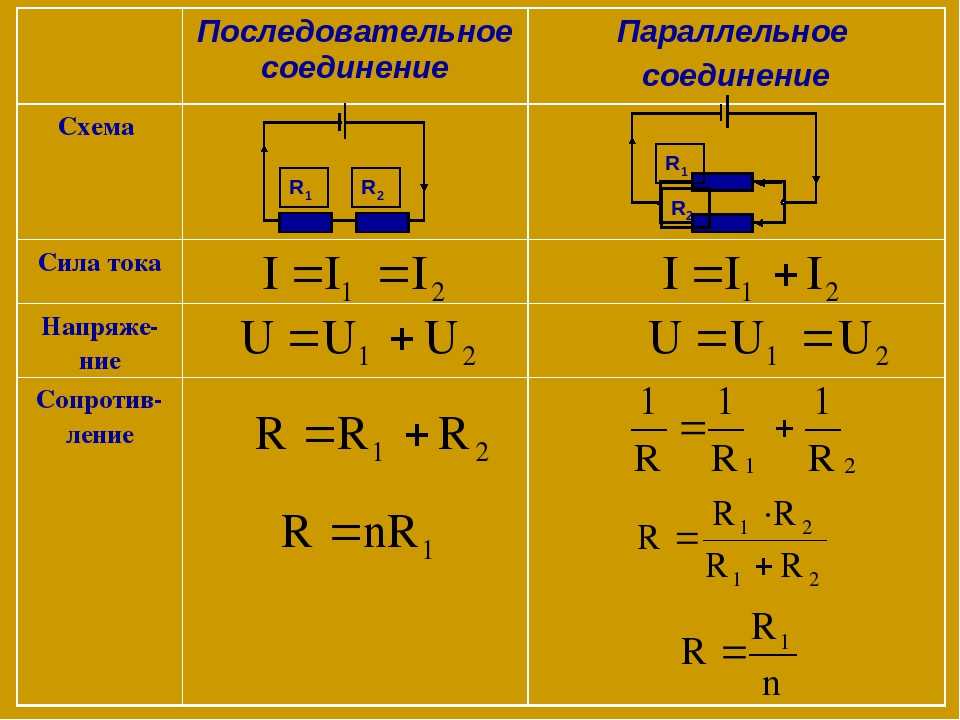
Начальная вертикальная скорость и максимальная высота положительны, потому что вверх положителен, а ускорение, вызванное силой тяжести, отрицательно. Снаряд с начальной вертикальной составляющей скорости 67,6 м/с достигнет максимальной высоты 233 м. Также имейте в виду, что максимальная высота зависит только от вертикальной составляющей начальной скорости (без учета сопротивления воздуха).
(b) Существуют различные способы определить, когда снаряд достигает высшей точки, как и во многих физических задачах. Самый простой подход в этой ситуации — использовать v y =v 0y -gt. Это уравнение принимает вид v y = 0 на вершине
0 = v 0y − gt
или,
t = v oy /g = (67,6 м/с) / (9,80 м/с 2 )
t = 6,90 с.
Другой способ определения времени — использование y = y o + ½ (v 0y + v y ) t.
(c) Сопротивление воздуха мало, следовательно, ax и ay равны нулю. И, как упоминалось ранее, горизонтальная скорость постоянна. Как показывают уравнения x=x 0 +v x t, где x 0 равно нулю, горизонтальное перемещение равно горизонтальной скорости, умноженной на время. Таким образом,
И, как упоминалось ранее, горизонтальная скорость постоянна. Как показывают уравнения x=x 0 +v x t, где x 0 равно нулю, горизонтальное перемещение равно горизонтальной скорости, умноженной на время. Таким образом,
x = v x t,
.0003
v x = v 0 cosθ = (70,0 м/с) cos75°=18,1 м/с.
Поскольку оба движения имеют одинаковое время t, x равно
x = (18,1 м/с) × 6,90 с = 125 м.
Горизонтальное движение без сопротивления воздуха имеет постоянную скорость. Горизонтальное смещение, наблюдаемое здесь, может помочь предотвратить травму зрителей от падающих пиротехнических фрагментов. Немалую роль при взрыве снаряда играет сопротивление воздуха, и многие осколки падают сразу внизу.
(d) Здесь требуется только найти величину и направление смещения в самой высокой точке, так как горизонтальная и вертикальная составляющие смещения уже рассчитаны:
с → = 125 х + 233 х; |ŝ|=√ (125 2 + 233 2 ) = 264 м; Φ = tan -1 (233/125) = 61,8°
Как рассчитать сопротивление воздуха при конечной скорости? Сопротивление воздуха эквивалентно по величине весу падающего объекта при конечной скорости. Рассмотрим метод расчета сопротивления воздуха при предельной скорости.
Рассмотрим метод расчета сопротивления воздуха при предельной скорости.
- Используя второй закон Ньютона для падающего объекта в качестве отправной точки, мы можем определить сопротивление воздуха при конечной скорости: F g + F ar = ma .
- Для определения сопротивления воздуха при заданной скорости используются следующие два типа сопротивления воздуха: F ar = – bv альтернативно, F ar = – bv 2 .
- Для расчета сопротивления воздуха при предельной скорости используется закон Ньютона для определения сопротивления воздуха при предельной скорости, поскольку ускорение равно нулю, мг – бв = 0; mg – bv 2 = 0.
- Чтобы определить сопротивление воздуха при заданной скорости, ответом на задачу скорости является v T = mg/b. Альтернативой является то, что v T = √(мг/б).

Если m представляет массу в килограммах, g — квадрат ускорения свободного падения, а b — произвольная величина.
Проблема: При падении из состояния покоя объект массой 55 кг испытывает силу сопротивления воздуха, определяемую F ар = -15В 2 . Определить конечную скорость объекта.
Решение: Используйте формулу v T = √ (мг/б) для определения конечной скорости силы сопротивления вида Far = -bv 2 . Складывая в уравнение, получаем
v T = √(55) × (9,81)/15)
v T = 5,99 м/с
Как рассчитать коэффициент сопротивления воздуха?Коэффициент лобового сопротивления зависит от квадрата относительной скорости объекта. Рассмотрим метод расчета коэффициента сопротивления воздуха.
Коэффициент сопротивления воздуха рассчитывается по уравнению c = F воздух /v 2 . В расчете F воздух является силовым сопротивлением, а c является силовой константой в этом уравнении. Жидкости, обычно вода в спортивной среде, также подвержены силе трения, которая не ограничивается только воздухом.
Жидкости, обычно вода в спортивной среде, также подвержены силе трения, которая не ограничивается только воздухом.
Сопротивление жидкости, сопротивление воздуха и сопротивление — все это относится к одному и тому же.
Проблема: Если объект, движущийся со скоростью 22 мс -1 , встречает сопротивление воздуха 50 Н, какова постоянная силы?
Решение: Даны данные:
v = 22 мс -1
F воздух = 50 Н
Формула для коэффициента сопротивления воздуха:
Замените указанные значения в приведенной выше формуле. Тогда
с = 50/(22) 2
с = 0,103
Как рассчитать аэродинамическое сопротивление парашюта?При раскрытии парашюта груз пульсирует вниз. Рассмотрим, как определить аэродинамическое сопротивление парашюта.
- Для определения аэродинамического сопротивления парашюта Уравнение силы сопротивления парашюта, также известной как сила сопротивления ветру, имеет вид F D = 1/2 ρ v 2 C D
1 A.
 Где, F D – сила сопротивления, r – плотность воздуха, C d — коэффициент лобового сопротивления, A — площадь парашюта, а v — скорость в воздухе.
Где, F D – сила сопротивления, r – плотность воздуха, C d — коэффициент лобового сопротивления, A — площадь парашюта, а v — скорость в воздухе. - Чтобы определить сопротивление воздуха парашюта как квадрат скорости, сопротивление возрастает.
- Для определения аэродинамического сопротивления парашюта нет никакой чистой силы, действующей на ракету, когда сопротивление равно весу. F = D – W = 0,
- C d = 2 F d / ρv 2 A = W для определения аэродинамического сопротивления парашюта.
- И, наконец, V = sqrt (2W/C d ρ A) используется для определения аэродинамического сопротивления парашюта.
При сравнении двух предметов те, у которых больший вес, меньший коэффициент сопротивления, меньшая плотность газа или меньшая площадь, движутся с большей скоростью.
Как найти сопротивление воздуха через массу и ускорение? Единственной силой, воздействующей на людей поначалу, является гравитация, которая толкает их со скоростью -9,8 м/с2. Давайте посмотрим, как можно рассчитать сопротивление воздуха, используя массу и ускорение.
Давайте посмотрим, как можно рассчитать сопротивление воздуха, используя массу и ускорение.
- Чтобы найти сопротивление воздуха с массой и ускорением, мы можем использовать некоторую алгебру, чтобы получить ускорение объекта с точки зрения чистой внешней силы и массы объекта (a = F/m).
- Суммарная внешняя сила (F = W – D) равна разнице между силами веса и сопротивления. Тогда ускорение объекта определяется выражением a = (W – D) / m.
Проблема: Автомобиль массой около 29 кг движется из Калькутты в Раджастхан со скоростью 50 метров в секунду, а гусеница нагружена железом и весит 84 кг. Определить силу сопротивления автомобиля.
Решение: Даны данные:
Ускорение = 50 м/с 2
Вес = 84 кг
Масса = 29 кг
Мы знаем, что a = (W – D) / m
2
(84 – D)/ 29
1450 = 84 – D
-D = 1450 – 84
D = – 1366 N
График сопротивления воздуха При столкновении частиц воздуха с объектом фронт замедляется . Давайте проверим этот график сопротивления воздуха.
Давайте проверим этот график сопротивления воздуха.
За счет уменьшения угла выпуска можно минимизировать влияние сопротивления воздуха на горизонтальную составляющую траектории снаряда. Расстояние и скорость, или скорость, обратно пропорциональны.
Как рассчитать сопротивление воздуха по скорости?Чем больше частиц воздуха воздействует на объект, тем больше его общее сопротивление с увеличением площади поверхности. Давайте рассмотрим, как определить сопротивление воздуха на основе скорости.
Формула, используемая для определения сопротивления воздуха по скорости: c = Fv 2 . Сила сопротивления воздуха представлена в технике буквой F, постоянная силы представлена буквой c, а скорость объекта представлена буквой v. Существует линейная зависимость между сопротивлением воздуха и плотностью воздуха.
Между скоростью и сопротивлением воздуха создается квадратичная зависимость. Площадь передней кромки объекта, движущегося по воздуху, определяет, какое сопротивление воздуха он будет испытывать. Сопротивление воздуха увеличивается с увеличением площади.
Задача: Если сопротивление воздуха объекта равно 34 Н, а силовая постоянная равна 0,04, какова его скорость?
Данные: F AIR = 34 N и C = 0,04
Формула для сопротивления воздуха,
F AIR = CV 2
V 2 = 34/0,04
V. 2 = 850v = 29,15 м/с.
Как рассчитать силу сопротивления воздуха?Сила сопротивления воздуха измеряется в Ньютонах (Н). Рассмотрим, как определить силу сопротивления воздуха.
F воздух = – cv 2 – уравнение, используемое для определения силы сопротивления воздуха. F air — силовое сопротивление, а c — силовая постоянная в этом уравнении. Знак минус показывает, что объект движется в направлении, противоположном направлению сопротивления воздуха.
Знак минус показывает, что объект движется в направлении, противоположном направлению сопротивления воздуха.
Задача: Силовая постоянная для самолета, движущегося со скоростью 50 мс, -1 равна 0,05. Определить сопротивление воздуха.
Решение: Даны данные,
Скорость воздуха, v = 50
Постоянная силы, c = 0,05
Сила воздуха определяется выражением,
F = – cv 2
F = (-) 0,05 × 50 90 × 0 50 F = – 125 Н.
Формула сопротивления воздуха для шараЗависимость между силой сопротивления, действующей на тело, и сопротивлением воздуха обратная. Давайте посмотрим на формулу сопротивления воздуха шара.
Коэффициент сопротивления воздуха для сферических материалов можно рассчитать по следующей формуле: C D = 2 F D / ρv 2 A, где для материалов в форме сфера-
- C D = Коэффициент сопротивления воздуха,
- F D 9008 основанное на сопротивлении воздуха,
- A — площадь формы в плане в квадратных метрах,
- ρ = плотность сферы, выраженная в килограммах на кубический метр,
- А вязкость вещества, выраженная в метрах в секунду, известна как т.

Задача: Плотность воздуха 0,4500 кг/м 3 , и самолет, летящий на высоте, имеет скорость 250 м/с. 500 м 2 крыльев самолета открыты ветру. На самолет действует сила сопротивления воздуха 168750 Н. Выполните расчет коэффициента лобового сопротивления.
Решение: Приведенные данные, Сопротивление воздуха для сферических материалов, F d = 168750 Н
Плотность, ρ = 0,4500 кг/м 3
Площадь поперечного сечения, A = 500 м 2
Скорость, V = 250 м/ с
Мы знаем, что для материалов в форме сферы
C D = 2 F D / ρv 2 A
C D = 2 × 168750 / (0,4500 × 250 2 × 500)
C d = 0,025
Как рассчитать среднее сопротивление воздуха? Сопротивление воздуха — это разновидность жидкостного трения, воздействующая на падающие в воздухе предметы. Давайте посмотрим, как определить среднее сопротивление воздуха.
Умножая плотность воздуха, коэффициент сопротивления, площадь и скорость на два, можно вычислить среднее сопротивление воздуха, которое испытывает падающий объект. Гравитация заставляет объекты двигаться вниз, в отличие от трения воздуха, которое действует противоположным образом и замедляет скорость.
Сопротивление воздуха увеличивается по мере увеличения площади поверхности для падающих предметов.
ЗаключениеСопротивление воздуха — это сила, которую испытывает объект при прохождении через воздух, где, если человек движется быстрее, сила сопротивления воздуха возрастает. Безразмерный коэффициент лобового сопротивления C D , который рассчитывается как C D = F D /1/2 ρAv 2 , где ρ — плотность жидкости (в данном случае воздуха). Площадь поперечного сечения объекта A = (1/4) ΠD 2 , скорость v
Использование формулы сопротивления Блазиуса для оценки эффективного диаметра эндотрахеальных трубок
. 1992 г., октябрь; 146 (4): 974-9.
1992 г., октябрь; 146 (4): 974-9.
doi: 10.1164/ajrccm/146.4.974.
Ф Лофасо 1 , B Louis, L Brochard, A Harf, D Isabey
принадлежность
- 1 Национальный институт здравоохранения и медицинских исследований INSERM U.296, Медицинский факультет, Кретей, Франция.
- PMID: 1416427
- DOI: 10.1164/ajrccm/146.4.974
F Лофасо и соавт. Ам преподобный Респир Дис. 1992 окт.
. 1992 г., октябрь; 146 (4): 974-9.
1992 г., октябрь; 146 (4): 974-9.
doi: 10.1164/ajrccm/146.4.974.
Авторы
Ф Лофасо 1 , Б. Луи, Л. Брошар, А. Харф, Д. Изабей
принадлежность
- 1 Национальный институт здравоохранения и медицинских исследований INSERM U.296, Медицинский факультет, Кретей, Франция.
- PMID: 1416427
- DOI: 10.1164/ajrccm/146.4.974
Абстрактный
Для раннего обнаружения отложения слизи в эндотрахеальных трубках (ЭТТ) мы предлагаем использовать геометрический, независимый от потока параметр, то есть диаметр ЭТТ, основанный на точном знании режима потока ЭТТ, вместо использования классического сопротивления ЭТТ, зависящего от потока. на основе эмпирического нелинейного уравнения Рорера. Исходя из предполагаемого наклона -0,24, полученного из диаграмм Муди, характеризующих соотношение давление-поток в ЭТТ с различными внутренними диаметрами (D), мы сначала оценили, что наклон формулы сопротивления Блазиуса -0,25 может быть применен к ЭТТ взрослого размера, что означает, что поток остается полностью развитым, турбулентным и гидравлически гладким (на 0,5 л/с меньше или равно V меньше или равно 1,4 л/с). Введение в ЭТТ напорного катетера (внешний диаметр: d) для стимуляции измерений in vivo не изменило эти результаты при условии, что гидравлический диаметр D* = D — d был заменен на D в формуле Блазиуса. Формула Блазиуса затем использовалась для определения на основании измерений давления и потока in vitro в ЭТТ перед интубацией и в ЭТТ, выстланной сухими слизистыми выделениями, эффективный диаметр, который, как показано здесь, сильно коррелирует с фактическим диаметром, измеренным с помощью объемного вытеснения воды. Эффективный диаметр ЭТТ был измерен у восьми пациентов на разных этапах после оральной или назальной интубации.
на основе эмпирического нелинейного уравнения Рорера. Исходя из предполагаемого наклона -0,24, полученного из диаграмм Муди, характеризующих соотношение давление-поток в ЭТТ с различными внутренними диаметрами (D), мы сначала оценили, что наклон формулы сопротивления Блазиуса -0,25 может быть применен к ЭТТ взрослого размера, что означает, что поток остается полностью развитым, турбулентным и гидравлически гладким (на 0,5 л/с меньше или равно V меньше или равно 1,4 л/с). Введение в ЭТТ напорного катетера (внешний диаметр: d) для стимуляции измерений in vivo не изменило эти результаты при условии, что гидравлический диаметр D* = D — d был заменен на D в формуле Блазиуса. Формула Блазиуса затем использовалась для определения на основании измерений давления и потока in vitro в ЭТТ перед интубацией и в ЭТТ, выстланной сухими слизистыми выделениями, эффективный диаметр, который, как показано здесь, сильно коррелирует с фактическим диаметром, измеренным с помощью объемного вытеснения воды. Эффективный диаметр ЭТТ был измерен у восьми пациентов на разных этапах после оральной или назальной интубации. По сравнению с фактическим диаметром ЭТТ, измеренным до введения, эффективный диаметр был немного уменьшен (2,6 ± 2,5%) в течение первой недели интубации и сильно уменьшен (12,2 ± 2,8%) в течение второй недели. В 250 СЛОВ)
По сравнению с фактическим диаметром ЭТТ, измеренным до введения, эффективный диаметр был немного уменьшен (2,6 ± 2,5%) в течение первой недели интубации и сильно уменьшен (12,2 ± 2,8%) в течение второй недели. В 250 СЛОВ)
Похожие статьи
Оценка перепада давления на вдохе в неонатальных и детских эндотрахеальных трубках.
Жарро П.Х., Луи Б., Дасье Г., Десфрер Л., Бланшар П.В., Мориетт Г., Изабей Д., Харф А. Jarreau PH и соавт. J Appl Physiol (1985). 1999 г., июль; 87 (1): 36–46. doi: 10.1152/jappl.1999.87.1.36. J Appl Physiol (1985). 1999. PMID: 10409556
Неинвазивная оценка работы дыхания за счет эндотрахеальной трубки.
Хейер Л., Луис Б., Изабей Д., Лофасо Ф., Брошар Л., Фредберг Дж.Дж., Харф А.
 Хейер Л. и соавт.
Анестезиология. 1996 декабрь; 85 (6): 1324-33. doi: 10.1097/00000542-199612000-00013.
Анестезиология. 1996.
PMID: 8968179
Хейер Л. и соавт.
Анестезиология. 1996 декабрь; 85 (6): 1324-33. doi: 10.1097/00000542-199612000-00013.
Анестезиология. 1996.
PMID: 8968179Акустический метод оценки продольного профиля эндотрахеальных трубок.
Ван Сурелл С., Луис Б., Лофасо Ф., Бейдон Л., Брошар Л., Харф А., Фредберг Дж., Изабей Д. Ван Сурелл С. и др. Am J Respir Crit Care Med. 1994 г., январь; 149 (1): 28–33. doi: 10.1164/ajrccm.149.1.8111593. Am J Respir Crit Care Med. 1994. PMID: 8111593
Сопротивление детских и неонатальных эндотрахеальных трубок: влияние скорости потока, размера и формы.
Манчур Т., Гриноу А., Николсон Г.П., Рафферти Г.Ф. Манчур Т. и др. Крит Уход Мед. 2000 май; 28 (5): 1595-8. doi: 10.1097/00003246-200005000-00056.
 Крит Уход Мед. 2000.
PMID: 10834718
Крит Уход Мед. 2000.
PMID: 10834718Вентилятор-ассоциированная пневмония: новые определения и профилактические стратегии.
Миетто К., Пинчироли Р., Патель Н., Берра Л. Миетто С. и др. Уход за дыханием. 2013 июнь; 58 (6): 990-1007. doi: 10.4187/respcare.02380. Уход за дыханием. 2013. PMID: 23709196 Обзор.
Посмотреть все похожие статьи
Цитируется
Поддержка низкого давления в сравнении с автоматической компенсацией трубки во время пробного самостоятельного дыхания при отлучении от груди.
Герен С., Терзи Н., Мезиди М., Бабой Л., Чебиб Н., Йонис Х., Арго Л., Хенкс Л., Луис Б. Герен С. и др. Энн Интенсивная терапия. 2019 13 декабря; 9 (1): 137.
 doi: 10.1186/s13613-019-0611-y.
Энн Интенсивная терапия. 2019.
PMID: 31836913
Бесплатная статья ЧВК.
doi: 10.1186/s13613-019-0611-y.
Энн Интенсивная терапия. 2019.
PMID: 31836913
Бесплатная статья ЧВК.Физиологические предикторы потребности в респираторной и кашлевой помощи после экстубации.
Терци Н., Лофасо Ф., Массон Р., Бере П., Норманд Х., Думановски Э., Фалез Л., Сонеф Б., Добин С., Брюне Дж., Аннан Д., Париенти Дж. Дж., Орликовски Д. Терзи Н. и др. Энн Интенсивная терапия. 2018 5 февраля; 8 (1): 18. doi: 10.1186/s13613-018-0360-3. Энн Интенсивная терапия. 2018. PMID: 29404723 Бесплатная статья ЧВК.
Роль размера трубки и интраназального сжатия назотрахеальной трубки в снижении давления при дыхании во время назотрахеальной интубации: лабораторное исследование.
Футагава К., Такасуги Ю., Кобаяши Т.
 , Моришита С., Окуда Т.
Футагава К. и др.
БМС Анестезиол. 2017 17 октября; 17 (1): 141. doi: 10.1186/s12871-017-0432-1.
БМС Анестезиол. 2017.
PMID: 2
, Моришита С., Окуда Т.
Футагава К. и др.
БМС Анестезиол. 2017 17 октября; 17 (1): 141. doi: 10.1186/s12871-017-0432-1.
БМС Анестезиол. 2017.
PMID: 211 Бесплатная статья ЧВК.
Взаимосвязь между сопротивлением дыхательных путей до и после наркоза у пациентов, подвергающихся общей анестезии: проспективное обсервационное исследование.
Икеда Т., Учида К., Ямаути Ю., Нагасэ Т., Оба К., Ямада Ю. Икеда Т. и др. ПЛОС Один. 17 февраля 2017 г .; 12 (2): e0172421. doi: 10.1371/journal.pone.0172421. Электронная коллекция 2017. ПЛОС Один. 2017. PMID: 28212451 Бесплатная статья ЧВК.
Роль эндотрахеальных трубок и скользящих соединений в снижении давления при дыхании: лабораторное исследование.
Такасуги Ю.



 аx = 0 указывает, что vx = V0x, или что начальная и конечная скорости в направлении x равны.
аx = 0 указывает, что vx = V0x, или что начальная и конечная скорости в направлении x равны.





 Где, F D – сила сопротивления, r – плотность воздуха, C d — коэффициент лобового сопротивления, A — площадь парашюта, а v — скорость в воздухе.
Где, F D – сила сопротивления, r – плотность воздуха, C d — коэффициент лобового сопротивления, A — площадь парашюта, а v — скорость в воздухе. 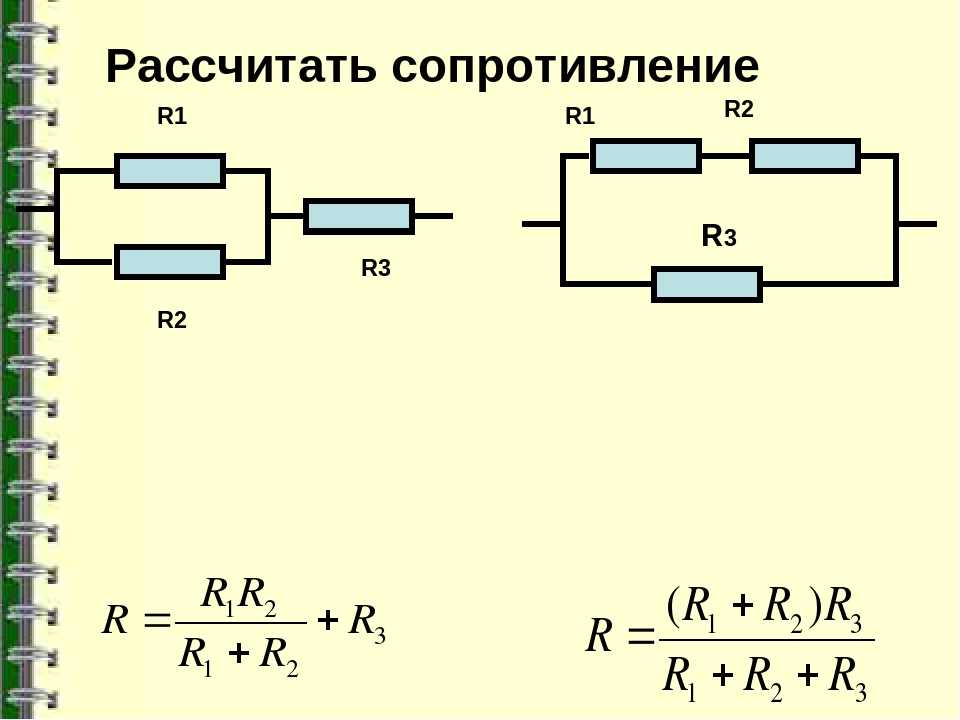
 Хейер Л. и соавт.
Анестезиология. 1996 декабрь; 85 (6): 1324-33. doi: 10.1097/00000542-199612000-00013.
Анестезиология. 1996.
PMID: 8968179
Хейер Л. и соавт.
Анестезиология. 1996 декабрь; 85 (6): 1324-33. doi: 10.1097/00000542-199612000-00013.
Анестезиология. 1996.
PMID: 8968179 Крит Уход Мед. 2000.
PMID: 10834718
Крит Уход Мед. 2000.
PMID: 10834718 doi: 10.1186/s13613-019-0611-y.
Энн Интенсивная терапия. 2019.
PMID: 31836913
Бесплатная статья ЧВК.
doi: 10.1186/s13613-019-0611-y.
Энн Интенсивная терапия. 2019.
PMID: 31836913
Бесплатная статья ЧВК. , Моришита С., Окуда Т.
Футагава К. и др.
БМС Анестезиол. 2017 17 октября; 17 (1): 141. doi: 10.1186/s12871-017-0432-1.
БМС Анестезиол. 2017.
PMID: 2
, Моришита С., Окуда Т.
Футагава К. и др.
БМС Анестезиол. 2017 17 октября; 17 (1): 141. doi: 10.1186/s12871-017-0432-1.
БМС Анестезиол. 2017.
PMID: 2