«Как проявляется действие силы Лоренца в разных системах отсчета?» — Яндекс Кью
Физика
Популярное
Сообщества
Как известно, сила Лоренца зависит от скорости, и соответственно если мы можем наблюдать траекторию заряженной частицы, то в разных системах отсчета она будет разной из-за изменения силы Лоренца. Но ведь это парадоксально, тогда заряженная частица в разных, в том числе и инерциальных, системах отсчета будет оказывать разное действие на окружающую среду, что идёт в противоречие как принципу относительности, так и вприцнипе здравому смыслу. В чем объяснение — очередной эффект теории относительности, или что то ещё?
ФизикаНаука+2
Михаил Лепихин
Физика·
3,7 K
Ответить2УточнитьЛучший
Вадим Романский
Физика
7,0 K
младший научный сотрудник ФТИ им. Иоффе · 16 дек 2022 ·
Иоффе · 16 дек 2022 ·
astropolytech
Эта проблема решается преобразованием электрических и магнитных полей друг через друга при переходе в системы отсчета. И в классическом пределе никакие релятивистские формулы не нужны.
Просто в движущейся системе появляется электрическое поле E = -vxB/c
астрофизическое образование
Перейти на vk.com/astropolytechАндрей О. Федотов
17 декабря 2022
А электрическое поле в классике появится? У Фейнмана речь о изменении длин (плотности заряда)
Комментировать ответ…Комментировать…
Антон Фурс
Физика
476
программист, интересны квантовая механика, теория относительности и астрономия · 9 часов назад
Извиняюсь за придирку, хочу лишь поправить вас. «Если мы можем наблюдать траекторию заряженной частицы, то в разных системах отсчета она будет разной из-за изменения силы Лоренца». Траектория любого тела в разных СО конечно будет разной =). Вы наверно имели ввиду, что изменение траектории не будет определяться лишь сложением скорости частицы со скоростью движущейся СО… Читать далее
Траектория любого тела в разных СО конечно будет разной =). Вы наверно имели ввиду, что изменение траектории не будет определяться лишь сложением скорости частицы со скоростью движущейся СО… Читать далее
Комментировать ответ…Комментировать…
Топ-20
E Karell
4,1 K
Довольно широкий круг интересов и компетенции, разнообразный опыт · 16 дек 2022
Да, именно теория относительности, а точнее ее постулат о предельной скорости распространения взаимодействия, не зависящей от системы отсчета и равной скорости света в вакууме и решает эту проблему. Более того, именно такие соображения: что законы физики не должны зависеть от системы отсчета, и привели к этому самому постулату. Если ввести в уравнения Максвелла… Читать далее
1 эксперт согласен
Михаил Лепихин
16 декабря 2022
Просто меня смущает, что этот эффект неинвариантности силы может проявляется и на малых скоростях, а согласно.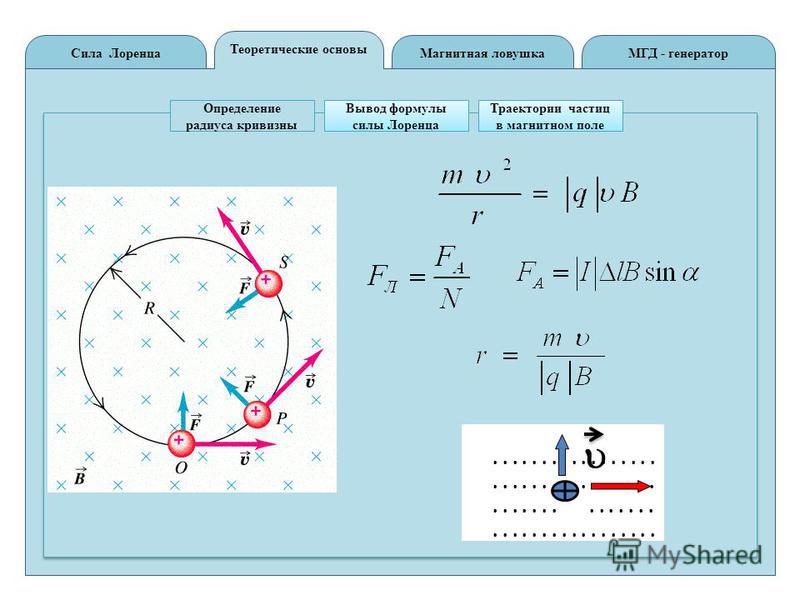 .. Читать дальше
.. Читать дальше
Комментировать ответ…Комментировать…
Кумашский Игорь
138
Физика т/т, производственник, к Нижнему с любовью. · 17 дек 2022
Наблюдая из разных систем отсчета за камерой Вильсона с траекториями частиц, мы ничего необычного не заметим, сама камера и траектории внутри неë будут выглядеть в соответствии с ОТО и релятивистской формулой силы Лоренца.
1 эксперт согласен
Александр
8 февраля
Уточните пожалуйста, какова траектория движения двух однонаправленных электронов? Спиралеобразная?
Комментировать ответ…Комментировать…
Дмитрий Кравченко
2,7 K
По образованию физик, работаю программистом · 16 дек 2022
Так и есть, классическая электродинамика нарушает Лоренц-инвариантность. Это и послужило одной их причин создания Специальной теории относительности.
Stephen Walker
20 декабря 2022
Неподвижную волну типа TM01 можно возбудить в запредельном волноводе разомкнутым концом коаксиальной линии: Элект… Читать дальше
Комментировать ответ…Комментировать…
Александр
-13
Частный предприниматель · 5 янв
Сила Лоренца появится в любой инерциальной СО (системе отсчета). Т.к. даже в СО, где изначально заряды были неподвижны для наблюдателя, под действием кулоновской силы они начнут двигаться, и в тоже мгновение наблюдатель зафиксирует лоренцовское взаимодействие.
Stephen Walker
6 января
Пусть два положительных заряда по оному кулону, на расстоянии 1 м друг от друга движутся в противоположные стороны. .. Читать дальше
.. Читать дальше
Вы знаете ответ на этот вопрос?
Поделитесь своим опытом и знаниями
Войти и ответить на вопрос
О сообществе
Физика
Сообщество экспертов-физиков — общаемся, обсуждаем новости и отвечаем на самые интересные вопросы современной науки. Присоединяйтесь!
5.1: Квантование закона силы Лоренца
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 34659
- Ю. Д. Чонг
- Наньянский технологический университет 9{-19}\,\mathrm{C}\) — элементарный заряд. Для описания частиц с произвольным электрическим зарядом \(q\) просто выполните замену \(e \rightarrow -q\) в формулах, с которыми вы столкнетесь впоследствии.

Мы хотим сформулировать гамильтониан, управляющий квантовой динамикой такой частицы, с учетом двух упрощающих предположений: (i) частица имеет заряд и массу, но в остальном она «бесхарактерна» (т. е. мы игнорируем спиновый угловой момент и магнитный диполь момента, которым обладают реальные электроны), и (ii) электромагнитное поле рассматривается как классическое поле, что означает, что электрическое и магнитное поля являются определенными величинами, а не операторами. (Позже мы увидим, как выйти за пределы этих упрощений.)
Классически электромагнитное поле действует на частицу по закону силы Лоренца,
\[\mathbf{F}(\mathbf{r},t) = -e\Big(\mathbf{E}(\mathbf{ r},t) + \dot{\mathbf{r}}\times \mathbf{B}(\mathbf{r},t)\Big),\]
, где \(\mathbf{r}\) и \(\dot{\mathbf{r}}\) обозначают положение и скорость частицы, \(t\) — время, а \(\mathbf{E}\) и \(\mathbf{B}\ ) — электрическое и магнитное поля. Если другие силы отсутствуют, второй закон Ньютона дает уравнение движения
\[m\ddot{\mathbf{r}} = -e\Big(\mathbf{E}(\mathbf{r},t) + \dot{\mathbf{r}} \times \mathbf{B }(\mathbf{r},t)\Big), \label{eom}\]
, где \(m\) — масса частицы.

Введем электромагнитный скалярный и векторный потенциалы \(\Phi(\mathbf{r},t)\) и \(\mathbf{A}(\mathbf{r},t)\):
\[ \begin{align} \mathbf{E}(\mathbf{r},t) &= — \nabla \Phi(\mathbf{r},t) — \frac{\partial\mathbf{A}}{\partial t}, \\ \mathbf{B}(\mathbf{r},t) &= \nabla \times \mathbf{A}(\mathbf{r},t). \label{Bfield}\end{align}\] 92 + e \Big[\Phi(\mathbf{r},t) — \dot{\mathbf{r}} \cdot \mathbf{A}(\mathbf{r},t) \Big]. \label{Lag}\]
Это следует обычному рецепту для лагранжиана как кинетическая энергия минус потенциальная энергия, где \(-e\Phi\) служит функцией потенциальной энергии, за исключением \(-e\dot{ \mathbf{r}} \cdot \mathbf{A}\) термин. Чтобы увидеть, работает ли этот лагранжиан, подставьте его в уравнения Эйлера-Лагранжа
\[\frac{\partial L}{\partial r_i} = \frac{d}{dt} \frac{\partial L}{\partial \точка{r}_i}. \label{Эйлер-Лагранж}\]
Частные производные лагранжиана:
\[\begin{align} \begin{align} \frac{\partial L}{\partial r_i} &= e\Big[\partial_i \Phi — \dot{ r}_j \,\partial_i A_j \Big]\\ \frac{\partial L}{\partial \dot{r}_i} &= m\dot{r}_i — e A_i.
 \end{aligned}\end{align}\]
\end{aligned}\end{align}\]Теперь мы хотим взять полных производных по времени от \(\partial L /\partial \dot{r}_i\). При этом обратите внимание, что поле \(\mathbf{A}\) имеет свою собственную \(t\)-зависимость, а также меняется в зависимости от \(t\)-зависимого положения частицы. Таким образом,
\[\begin{align} \begin{align} \frac{d}{dt} \frac{\partial L}{\partial \dot{r}_i} &= m\ddot{r}_i — e \, \frac{d}{dt} A_i(\mathbf{r}(t),t) \\ &= m\ddot{r}_i — e\, \partial_t A_i — e\, \dot{r} _j \partial_j A_i. \end{aligned}\end{align}\]
(В приведенных выше уравнениях \(\partial_i \equiv \partial/\partial r_i\), где \(r_i\) — это \(i\)-й компонента вектора положения, в то время как \(\partial_t \equiv \partial/\partial t\).) Подстановка этих выражений в уравнения Эйлера-Лагранжа \(\eqref{EulerLagrange}\) дает
\[\begin{align} \begin{align} m\ddot{r}_i &= -e\Big[\Big(-\partial_i \Phi — \partial_t A_i\Big) + \dot{r}_j \Big( \partial_i A_j — \partial_j A_i\Big) \Big] \\ &= -e \Big[E_i(\mathbf{r},t) + \big(\dot{\mathbf{r}} \times \mathbf{B}(\mathbf{r},t) \big)_i\, \Big].
 2}{2m} + e\Phi — \ frac{e}{m}(\mathbf{p}+e\mathbf{A})\cdot \mathbf{A}\right). \end{выравнивание}\end{выравнивание}\] 92}{2m} + V(\mathbf{r},t).\]
2}{2m} + e\Phi — \ frac{e}{m}(\mathbf{p}+e\mathbf{A})\cdot \mathbf{A}\right). \end{выравнивание}\end{выравнивание}\] 92}{2m} + V(\mathbf{r},t).\]В уравнении \(\eqref{H0}\) член \(-e\Phi\) действует как потенциальная энергия, которая нет ничего удивительного. Что еще более интересно, векторный потенциал появляется в результате замены
\[\mathbf{p} \rightarrow \mathbf{p} + e\mathbf{A}(\mathbf{r},t).\]
Что это значит? иметь в виду? Подумайте о том, что означает «импульс» для заряженной частицы в электромагнитном поле. Теорема Нётер утверждает, что каждая симметрия системы (классическая или квантовая) связана с законом сохранения. Импульс — это величина, сохраняющаяся, когда система симметрична при пространственных переносах. Одно из уравнений Гамильтона утверждает, что
\[\frac{dp_i}{dt} = \frac{\partial H}{\partial r_i},\]
, что означает, что если \(H\) равно \(\mathbf{r}\)- независимыми, то \(d\mathbf{p}/dt = 0\). Но когда электромагнитные потенциалы \(\mathbf{r}\)-независимы, величина \(m\dot{\mathbf{r}}\) (которую мы обычно называем импульсом) не обязательно сохраняется! Возьмем потенциалы
\[\Phi(\mathbf{r}, t) = 0, \;\;\; \mathbf{A}(\mathbf{r}, t) = Ct \hat{z},\]
, где \(C\) — некоторая константа.
 Эти потенциалы \(\mathbf{r}\)-независимы, но векторный потенциал зависит от времени, поэтому член \(-\dot{\mathbf{A}}\) в уравнении \(\eqref{Bfield} \) дает неисчезающее электрическое поле:
Эти потенциалы \(\mathbf{r}\)-независимы, но векторный потенциал зависит от времени, поэтому член \(-\dot{\mathbf{A}}\) в уравнении \(\eqref{Bfield} \) дает неисчезающее электрическое поле:\[\mathbf{E}(\mathbf{r},t) = — C\hat{z}, \;\;\;\mathbf{B}(\mathbf{r},t) = 0. \]
Тогда закон силы Лоренца говорит, что
\[\frac{d}{dt}(m\dot{\mathbf{r}}) = eC\hat{z},\]
и, следовательно, \ (m\dot{\mathbf{r}}\) не сохраняется. С другой стороны, величина \(\mathbf{p} = m\dot{\mathbf{r}} — e \mathbf{A}\) сохраняется в :
\[\frac{d}{dt }(m\dot{\mathbf{r}} — e\mathbf{A}) = eC\hat{z} — eC\hat{z} = 0.\]
Следовательно, это подходящий канонический импульс для частица в электромагнитном поле. 92}{2m} — e\Phi(\hat{\mathbf{r}},t). \label{quantumH}\]
Примечание
Оператор импульса, как обычно, равен \(\hat{\mathbf{p}} = -i\hbar\nabla\) в представлении волновой функции.
Калибровочная симметрия
Гамильтониан \(\eqref{quantumH}\) обладает тонким свойством, известным как калибровочная симметрия .
 Предположим, мы изменили скалярный и векторный потенциалы с помощью замен
Предположим, мы изменили скалярный и векторный потенциалы с помощью замен\[\begin{align} \Phi(\mathbf{r},t) &\rightarrow \Phi(\mathbf{r},t) — \dot{\ Лямбда}(\mathbf{r},t) \label{gauge-subst-1} \\ \mathbf{A}(\mathbf{r},t) &\стрелка вправо \mathbf{A}(\mathbf{r} ,t) + \nabla{\Lambda}(\mathbf{r},t), \label{gauge-subst-2}\end{align}\] 92}{2m} — e\Phi(\hat{\mathbf{r}},t) \right]\psi(\mathbf{r},t).\]
Тогда можно показать, что волновая функция \ (\psi\, \exp(-ie\Lambda/\hbar)\) автоматически удовлетворяет уравнению Шредингера для преобразованного гамильтониана \(\hat{H}_\Lambda\):
\[i\hbar\frac{ \partial}{\partial t} \left[\psi(\mathbf{r},t) \, \exp\left(-\frac{ie\Lambda(\mathbf{r},t)}{\hbar} \right)\right] = \hat{H}_\Lambda(t) \left[\psi(\mathbf{r},t) \, \exp\left(-\frac{ie\Lambda(\mathbf{ r},t)}{\hbar}\right)\right]. \label{gaugeschrod}\]
Чтобы доказать это, посмотрите, как производные по времени и пространству действуют на новую волновую функцию:
\[\begin{align} \begin{align} \frac{\partial}{\partial t} \left[\psi \, \exp\left(-\frac{ie\Lambda}{\hbar}\right)\right] &= \left[\frac{\partial\psi}{\partial t} \;-\; \frac{ie}{\hbar} \dot{\Lambda}\, \psi \,\, \right] \exp\left(\frac{ie\Lambda}{\hbar}\right)\\ \nabla \ влево[\psi \, \exp\left(-\frac{ie\Lambda}{\hbar}\right)\right] &= \left[\nabla \psi — \frac{ie}{\hbar} \nabla \Lambda \,\psi \right] \exp\left(\frac{ie\Lambda}{\hbar}\right).
 \end{выравнивание}\end{выравнивание}\]
\end{выравнивание}\end{выравнивание}\]Когда дополнительные члены, порожденные фактором \(\exp(ie\Lambda/\hbar)\), вставляются в уравнение Шредингера, они сокращают калибровочные члены в скалярном и векторном потенциалах. Например,
\[\begin{align} \Big(-i\hbar\nabla + e\mathbf{A} + e\nabla\Lambda\Big) \left[\psi \, \exp\left(- \frac{ie\Lambda}{\hbar}\right)\right] &= \Big[\left(-i\hbar\nabla + e\mathbf{A}\right)\psi\Big]\; \exp\left(-\frac{ie\Lambda}{\hbar}\right) \label{first_gauge_action}\end{align}\]
92}{2m} — e\Phi(\hat{\mathbf{r}})\]имеет тот же энергетический спектр \(\{E_m\}\) с собственными функциями \(\{\,\psi_m( \mathbf{r}) \exp[-ie\Lambda(\mathbf{r})/\hbar]\,\}\).
Эффект Ааронова-Бома
В квантовой электродинамике именно электромагнитный скалярный и векторный потенциалы появляются непосредственно в гамильтониане, а не в электрическом и магнитном полях. Это имеет глубокие последствия. Например, даже если заряженная квантовая частица находится в области с нулевым магнитным полем, она может ощутить влияние ненулевого векторных потенциалов , создаваемых магнитными потоками в другом месте в космосе, явление, называемое эффектом Ааронова-Бома .

Простая установка для наблюдения эффекта Ааронова-Бома показана на рисунке ниже. Частица захватывается в кольцеобразную область («кольцо») радиусом \(R\) и шириной \(d \ll R\). Вне кольца мы устанавливаем \(-e\Phi\rightarrow\infty\) так, чтобы волновая функция обращалась в нуль; внутри кольца положим \(\Phi = 0\). Мы игнорируем \(z\)-зависимость всех полей и волновых функций, так что задача становится двумерной. Определим полярные координаты \((r,\phi)\) с началом в центре кольца.
Рисунок \(\PageIndex{1}\)Теперь предположим, что мы проводим магнитный поток (например, с помощью соленоида) через начало координат, которое находится в области, ограниченной кольцом. Этот поток можно описать векторным потенциалом
\[\mathbf{A}(r,\phi) = \frac{\Phi_B}{2\pi r} \, \mathbf{e}_\phi, \label {Asolenoid}\]
, где \(\mathbf{e}_\phi\) — единичный вектор, указывающий в азимутальном направлении. Мы можем проверить из уравнения \(\eqref{Asolenoid}\), что полный магнитный поток через любую петлю радиуса \(r\), охватывающую начало координат, равен \((\Phi_B/2\pi r)(2\pi r) = \Phi_B\).
 Тот факт, что это не зависит от \(r\), означает, что плотность магнитного потока сосредоточена в инфинитезимальной области, окружающей начало координат, и равна нулю во всех остальных местах. Однако векторный потенциал \(\mathbf{A}\) везде отличен от нуля. 9{i k R \phi}, & r \in [R-d/2, R + d/2] \\ 0 & \textrm{иначе}. \end{cases}\]
Тот факт, что это не зависит от \(r\), означает, что плотность магнитного потока сосредоточена в инфинитезимальной области, окружающей начало координат, и равна нулю во всех остальных местах. Однако векторный потенциал \(\mathbf{A}\) везде отличен от нуля. 9{i k R \phi}, & r \in [R-d/2, R + d/2] \\ 0 & \textrm{иначе}. \end{cases}\]Описывает «волноводную моду» с полуволновым профилем волны в направлении \(r\) (чтобы обращаться в нуль при \(r = R \pm d/2\)) , путешествуя в азимутальном направлении с волновым числом \(k\). Константа нормализации \(\psi_0\) не имеет значения. Нам нужно, чтобы волновая функция была однозначной при изменении \(2\pi\) азимутальной координаты, поэтому
\[k \cdot 2\pi R = 2\pi n \;\;\;\Rightarrow \ ;\;\; k = \frac{n}{R}, \;\;\;\mathrm{where}\;\; n \in \mathbb{Z}.\] 92}. \label{abcurves}\end{align}\]
Эти энергетические уровни показаны в зависимости от магнитного потока \(\Phi_B\) на рисунке ниже:
Рисунок \(\PageIndex{2}\)Каждый энергетический уровень имеет квадратичная зависимость от \(\Phi_B\).
 2\), фундаментальная единица магнитного потока, называемая квант магнитного потока . Другими словами, изменение \(\Phi_B\) на число, кратное \(h/e\), оставляет энергетический спектр неизменным! Это свойство инвариантности, не зависящее ни от ширины кольца, ни от каких-либо других геометрических параметров системы, можно объяснить с помощью калибровочной симметрии. Когда дополнительный поток \(nh/e\) (где \(n\in\mathbb{Z}\)) проходит через кольцо, уравнение \(\eqref{Asolenoid}\) говорит нам, что изменение вектора потенциал равен \(\Delta\mathbf{A} = (n\hbar/ e r) \mathbf{e}_\phi\). Но мы можем отменить последствия этого с помощью калибровочного поля 9.{дюйм\фи}. \end{cases}\]
2\), фундаментальная единица магнитного потока, называемая квант магнитного потока . Другими словами, изменение \(\Phi_B\) на число, кратное \(h/e\), оставляет энергетический спектр неизменным! Это свойство инвариантности, не зависящее ни от ширины кольца, ни от каких-либо других геометрических параметров системы, можно объяснить с помощью калибровочной симметрии. Когда дополнительный поток \(nh/e\) (где \(n\in\mathbb{Z}\)) проходит через кольцо, уравнение \(\eqref{Asolenoid}\) говорит нам, что изменение вектора потенциал равен \(\Delta\mathbf{A} = (n\hbar/ e r) \mathbf{e}_\phi\). Но мы можем отменить последствия этого с помощью калибровочного поля 9.{дюйм\фи}. \end{cases}\]Обратите внимание, что это \(\Lambda\) не является однозначным, но это не проблема! И \(\nabla\Lambda\), и фазовый множитель \(\exp(-ie\Lambda/\hbar)\) являются однозначными, и это величины, которые входят в соотношения калибровочной симметрии \(\ eqref{gauge-subst-1}\)–\(\eqref{gauge-subst-2}\).

Эта страница под названием 5.1: Квантование закона силы Лоренца распространяется в соответствии с лицензией CC BY-SA 4.0 и была создана, изменена и/или курирована YD Chong через исходный контент, который был отредактирован в соответствии со стилем и стандартами LibreTexts. Платформа; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Ю. Д. Чонг
- Лицензия
- CC BY-SA
- Версия лицензии
- 4,0
- Показать оглавление
- нет
- Теги
- Эффект Ааронова-Бома
- измерительное поле
- калибровочная симметрия
- преобразование датчика
- сила Лоренца
- источник@http://www1.
 spms.ntu.edu.sg/~ydchong/teaching.html
spms.ntu.edu.sg/~ydchong/teaching.html
Gale Apps — Технические трудности
Приложение, к которому вы пытаетесь получить доступ, в настоящее время недоступно. Приносим свои извинения за доставленные неудобства. Повторите попытку через несколько секунд.
Если проблемы с доступом сохраняются, обратитесь за помощью в наш отдел технической поддержки по телефону 1-800-877-4253. Еще раз спасибо, что выбрали Gale, обучающую компанию Cengage.
org.springframework.remoting.RemoteAccessException: невозможно получить доступ к удаленной службе [authorizationService@theBLISAuthorizationService]; вложенным исключением является com.zeroc.Ice.UnknownException unknown = «java.lang.IndexOutOfBoundsException: индекс 0 выходит за границы для длины 0 в java.base/jdk.internal.util.Preconditions.outOfBounds(Preconditions.java:64) в java.base/jdk.internal.util.Preconditions.outOfBoundsCheckIndex(Preconditions.
 java:70)
в java.base/jdk.internal.util.Preconditions.checkIndex(Preconditions.java:248)
в java.base/java.util.Objects.checkIndex(Objects.java:372)
в java.base/java.util.ArrayList.get(ArrayList.java:458)
в com.gale.blis.data.subscription.dao.LazyUserSessionDataLoaderStoredProcedure.populateSessionProperties(LazyUserSessionDataLoaderStoredProcedure.java:60)
в com.gale.blis.data.subscription.dao.LazyUserSessionDataLoaderStoredProcedure.reQuery(LazyUserSessionDataLoaderStoredProcedure.java:53)
в com.gale.blis.data.model.session.UserGroupEntitlementsManager.reinitializeUserGroupEntitlements(UserGroupEntitlementsManager.java:30)
в com.gale.blis.data.model.session.UserGroupSessionManager.getUserGroupEntitlements(UserGroupSessionManager.java:17)
в com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.getProductSubscriptionCriteria(CrossSearchProductContentModuleFetcher.
java:70)
в java.base/jdk.internal.util.Preconditions.checkIndex(Preconditions.java:248)
в java.base/java.util.Objects.checkIndex(Objects.java:372)
в java.base/java.util.ArrayList.get(ArrayList.java:458)
в com.gale.blis.data.subscription.dao.LazyUserSessionDataLoaderStoredProcedure.populateSessionProperties(LazyUserSessionDataLoaderStoredProcedure.java:60)
в com.gale.blis.data.subscription.dao.LazyUserSessionDataLoaderStoredProcedure.reQuery(LazyUserSessionDataLoaderStoredProcedure.java:53)
в com.gale.blis.data.model.session.UserGroupEntitlementsManager.reinitializeUserGroupEntitlements(UserGroupEntitlementsManager.java:30)
в com.gale.blis.data.model.session.UserGroupSessionManager.getUserGroupEntitlements(UserGroupSessionManager.java:17)
в com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.getProductSubscriptionCriteria(CrossSearchProductContentModuleFetcher. java:244)
на com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.getSubscribedCrossSearchProductsForUser(CrossSearchProductContentModuleFetcher.java:71)
на com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.getAvailableContentModulesForProduct(CrossSearchProductContentModuleFetcher.java:52)
на com.gale.blis.api.authorize.strategy.productentry.strategy.AbstractProductEntryAuthorizer.getContentModules(AbstractProductEntryAuthorizer.java:130)
на com.gale.blis.api.authorize.strategy.productentry.strategy.CrossSearchProductEntryAuthorizer.isAuthorized(CrossSearchProductEntryAuthorizer.java:82)
на com.gale.blis.api.authorize.strategy.productentry.strategy.CrossSearchProductEntryAuthorizer.authorizeProductEntry(CrossSearchProductEntryAuthorizer.java:44)
на com.gale.blis.api.authorize.strategy.ProductEntryAuthorizer.authorize(ProductEntryAuthorizer.
java:244)
на com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.getSubscribedCrossSearchProductsForUser(CrossSearchProductContentModuleFetcher.java:71)
на com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.getAvailableContentModulesForProduct(CrossSearchProductContentModuleFetcher.java:52)
на com.gale.blis.api.authorize.strategy.productentry.strategy.AbstractProductEntryAuthorizer.getContentModules(AbstractProductEntryAuthorizer.java:130)
на com.gale.blis.api.authorize.strategy.productentry.strategy.CrossSearchProductEntryAuthorizer.isAuthorized(CrossSearchProductEntryAuthorizer.java:82)
на com.gale.blis.api.authorize.strategy.productentry.strategy.CrossSearchProductEntryAuthorizer.authorizeProductEntry(CrossSearchProductEntryAuthorizer.java:44)
на com.gale.blis.api.authorize.strategy.ProductEntryAuthorizer.authorize(ProductEntryAuthorizer. java:31)
в com.gale.blis.api.BLISAuthorizationServiceImpl.authorize_aroundBody0(BLISAuthorizationServiceImpl.java:57)
на com.gale.blis.api.BLISAuthorizationServiceImpl.authorize_aroundBody1$advice(BLISAuthorizationServiceImpl.java:61)
на com.gale.blis.api.BLISAuthorizationServiceImpl.authorize(BLISAuthorizationServiceImpl.java:1)
в com.gale.blis.auth.AuthorizationService._iceD_authorize(AuthorizationService.java:97)
в com.gale.blis.auth.AuthorizationService._iceDispatch(AuthorizationService.java:406)
в com.zeroc.IceInternal.Incoming.invoke(Incoming.java:221)
в com.zeroc.Ice.ConnectionI.invokeAll(ConnectionI.java:2706)
на com.zeroc.Ice.ConnectionI.dispatch(ConnectionI.java:1292)
в com.zeroc.Ice.ConnectionI.message(ConnectionI.java:1203)
в com.zeroc.IceInternal.ThreadPool.run(ThreadPool.java:412)
в com.zeroc.IceInternal.ThreadPool.
java:31)
в com.gale.blis.api.BLISAuthorizationServiceImpl.authorize_aroundBody0(BLISAuthorizationServiceImpl.java:57)
на com.gale.blis.api.BLISAuthorizationServiceImpl.authorize_aroundBody1$advice(BLISAuthorizationServiceImpl.java:61)
на com.gale.blis.api.BLISAuthorizationServiceImpl.authorize(BLISAuthorizationServiceImpl.java:1)
в com.gale.blis.auth.AuthorizationService._iceD_authorize(AuthorizationService.java:97)
в com.gale.blis.auth.AuthorizationService._iceDispatch(AuthorizationService.java:406)
в com.zeroc.IceInternal.Incoming.invoke(Incoming.java:221)
в com.zeroc.Ice.ConnectionI.invokeAll(ConnectionI.java:2706)
на com.zeroc.Ice.ConnectionI.dispatch(ConnectionI.java:1292)
в com.zeroc.Ice.ConnectionI.message(ConnectionI.java:1203)
в com.zeroc.IceInternal.ThreadPool.run(ThreadPool.java:412)
в com.zeroc.IceInternal.ThreadPool. access$500(ThreadPool.java:7)
в com.zeroc.IceInternal.ThreadPool$EventHandlerThread.run(ThreadPool.java:781)
в java.base/java.lang.Thread.run(Thread.java:834)
»
org.springframework.remoting.ice.IceClientInterceptor.convertIceAccessException(IceClientInterceptor.java:348)
org.springframework.remoting.ice.IceClientInterceptor.invoke(IceClientInterceptor.java:310)
org.springframework.remoting.ice.MonitoringIceProxyFactoryBean.invoke(MonitoringIceProxyFactoryBean.java:71)
org.springframework.aop.framework.ReflectiveMethodInvocation.proceed(ReflectiveMethodInvocation.java:186)
org.
access$500(ThreadPool.java:7)
в com.zeroc.IceInternal.ThreadPool$EventHandlerThread.run(ThreadPool.java:781)
в java.base/java.lang.Thread.run(Thread.java:834)
»
org.springframework.remoting.ice.IceClientInterceptor.convertIceAccessException(IceClientInterceptor.java:348)
org.springframework.remoting.ice.IceClientInterceptor.invoke(IceClientInterceptor.java:310)
org.springframework.remoting.ice.MonitoringIceProxyFactoryBean.invoke(MonitoringIceProxyFactoryBean.java:71)
org.springframework.aop.framework.ReflectiveMethodInvocation.proceed(ReflectiveMethodInvocation.java:186)
org. springframework.aop.framework.JdkDynamicAopProxy.invoke(JdkDynamicAopProxy.java:215)
com.sun.proxy.$Proxy151.authorize(Неизвестный источник)
com.gale.auth.service.BlisService.getAuthorizationResponse(BlisService.java:61)
com.gale.apps.service.impl.MetadataResolverService.resolveMetadata(MetadataResolverService.java:65)
com.gale.apps.controllers.DiscoveryController.resolveDocument(DiscoveryController.java:57)
com.gale.apps.controllers.DocumentController.redirectToDocument(DocumentController.java:22)
jdk.
springframework.aop.framework.JdkDynamicAopProxy.invoke(JdkDynamicAopProxy.java:215)
com.sun.proxy.$Proxy151.authorize(Неизвестный источник)
com.gale.auth.service.BlisService.getAuthorizationResponse(BlisService.java:61)
com.gale.apps.service.impl.MetadataResolverService.resolveMetadata(MetadataResolverService.java:65)
com.gale.apps.controllers.DiscoveryController.resolveDocument(DiscoveryController.java:57)
com.gale.apps.controllers.DocumentController.redirectToDocument(DocumentController.java:22)
jdk. internal.reflect.GeneratedMethodAccessor310.invoke (неизвестный источник)
java.base/jdk.internal.reflect.DelegatingMethodAccessorImpl.invoke(DelegatingMethodAccessorImpl.java:43)
java.base/java.lang.reflect.Method.invoke(Method.java:566)
org.springframework.web.method.support.InvocableHandlerMethod.doInvoke(InvocableHandlerMethod.java:205)
org.springframework.web.method.support.InvocableHandlerMethod.invokeForRequest(InvocableHandlerMethod.java:150)
org.springframework.web.servlet.mvc.method.annotation.ServletInvocableHandlerMethod.invokeAndHandle(ServletInvocableHandlerMethod.
internal.reflect.GeneratedMethodAccessor310.invoke (неизвестный источник)
java.base/jdk.internal.reflect.DelegatingMethodAccessorImpl.invoke(DelegatingMethodAccessorImpl.java:43)
java.base/java.lang.reflect.Method.invoke(Method.java:566)
org.springframework.web.method.support.InvocableHandlerMethod.doInvoke(InvocableHandlerMethod.java:205)
org.springframework.web.method.support.InvocableHandlerMethod.invokeForRequest(InvocableHandlerMethod.java:150)
org.springframework.web.servlet.mvc.method.annotation.ServletInvocableHandlerMethod.invokeAndHandle(ServletInvocableHandlerMethod. java:117)
org.springframework.web.servlet.mvc.method.annotation.RequestMappingHandlerAdapter.invokeHandlerMethod (RequestMappingHandlerAdapter.java:895)
org.springframework.web.servlet.mvc.method.annotation.RequestMappingHandlerAdapter.handleInternal (RequestMappingHandlerAdapter.java:808)
org.springframework.web.servlet.mvc.method.AbstractHandlerMethodAdapter.handle(AbstractHandlerMethodAdapter.java:87)
org.springframework.web.servlet.DispatcherServlet.doDispatch(DispatcherServlet.java:1067)
org.springframework.web.servlet.DispatcherServlet.doService(DispatcherServlet.
java:117)
org.springframework.web.servlet.mvc.method.annotation.RequestMappingHandlerAdapter.invokeHandlerMethod (RequestMappingHandlerAdapter.java:895)
org.springframework.web.servlet.mvc.method.annotation.RequestMappingHandlerAdapter.handleInternal (RequestMappingHandlerAdapter.java:808)
org.springframework.web.servlet.mvc.method.AbstractHandlerMethodAdapter.handle(AbstractHandlerMethodAdapter.java:87)
org.springframework.web.servlet.DispatcherServlet.doDispatch(DispatcherServlet.java:1067)
org.springframework.web.servlet.DispatcherServlet.doService(DispatcherServlet. java:963)
org.springframework.web.servlet.FrameworkServlet.processRequest(FrameworkServlet.java:1006)
org.springframework.web.servlet.FrameworkServlet.doGet(FrameworkServlet.java:898)
javax.servlet.http.HttpServlet.service(HttpServlet.java:626)
org.springframework.web.servlet.FrameworkServlet.service(FrameworkServlet.java:883)
javax.servlet.http.HttpServlet.service(HttpServlet.java:733)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:227)
org.
java:963)
org.springframework.web.servlet.FrameworkServlet.processRequest(FrameworkServlet.java:1006)
org.springframework.web.servlet.FrameworkServlet.doGet(FrameworkServlet.java:898)
javax.servlet.http.HttpServlet.service(HttpServlet.java:626)
org.springframework.web.servlet.FrameworkServlet.service(FrameworkServlet.java:883)
javax.servlet.http.HttpServlet.service(HttpServlet.java:733)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:227)
org. apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.apache.tomcat.websocket.server.WsFilter.doFilter(WsFilter.java:53)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.apache.catalina.filters.HttpHeaderSecurityFilter.doFilter(HttpHeaderSecurityFilter.java:126)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.
apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.apache.tomcat.websocket.server.WsFilter.doFilter(WsFilter.java:53)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.apache.catalina.filters.HttpHeaderSecurityFilter.doFilter(HttpHeaderSecurityFilter.java:126)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org. apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.servlet.resource.ResourceUrlEncodingFilter.doFilter(ResourceUrlEncodingFilter.java:67)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.RequestContextFilter.doFilterInternal (RequestContextFilter.java:100)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.
apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.servlet.resource.ResourceUrlEncodingFilter.doFilter(ResourceUrlEncodingFilter.java:67)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.RequestContextFilter.doFilterInternal (RequestContextFilter.java:100)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org. apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:102)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
com.gale.common.http.filter.SecurityHeaderFilter.doFilterInternal(SecurityHeaderFilter.java:29)
org.
apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:102)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
com.gale.common.http.filter.SecurityHeaderFilter.doFilterInternal(SecurityHeaderFilter.java:29)
org. springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:102)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.
springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:102)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org. owasp.validation.GaleParameterValidationFilter.doFilterInternal(GaleParameterValidationFilter.java:97)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.boot.web.servlet.support.ErrorPageFilter.doFilter(ErrorPageFilter.java:126)
org.springframework.boot.web.servlet.support.ErrorPageFilter.access$000(ErrorPageFilter.java:64)
org.
owasp.validation.GaleParameterValidationFilter.doFilterInternal(GaleParameterValidationFilter.java:97)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.boot.web.servlet.support.ErrorPageFilter.doFilter(ErrorPageFilter.java:126)
org.springframework.boot.web.servlet.support.ErrorPageFilter.access$000(ErrorPageFilter.java:64)
org. springframework.boot.web.servlet.support.ErrorPageFilter$1.doFilterInternal(ErrorPageFilter.java:101)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.springframework.boot.web.servlet.support.ErrorPageFilter.doFilter(ErrorPageFilter.java:119)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.FormContentFilter.doFilterInternal (FormContentFilter.java:93)
org.
springframework.boot.web.servlet.support.ErrorPageFilter$1.doFilterInternal(ErrorPageFilter.java:101)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.springframework.boot.web.servlet.support.ErrorPageFilter.doFilter(ErrorPageFilter.java:119)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.FormContentFilter.doFilterInternal (FormContentFilter.java:93)
org. springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.boot.actuate.metrics.web.servlet.WebMvcMetricsFilter.doFilterInternal (WebMvcMetricsFilter.java:96)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.
springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.boot.actuate.metrics.web.servlet.WebMvcMetricsFilter.doFilterInternal (WebMvcMetricsFilter.java:96)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain. java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.CharacterEncodingFilter.doFilterInternal (CharacterEncodingFilter.java:201)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.
java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.CharacterEncodingFilter.doFilterInternal (CharacterEncodingFilter.java:201)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org. apache.catalina.core.StandardWrapperValve.invoke(StandardWrapperValve.java:202)
org.apache.catalina.core.StandardContextValve.invoke(StandardContextValve.java:97)
org.apache.catalina.authenticator.AuthenticatorBase.invoke(AuthenticatorBase.java:542)
org.apache.catalina.core.StandardHostValve.invoke(StandardHostValve.java:143)
org.apache.catalina.valves.ErrorReportValve.invoke(ErrorReportValve.java:92)
org.apache.catalina.valves.AbstractAccessLogValve.invoke(AbstractAccessLogValve.java:687)
org.
apache.catalina.core.StandardWrapperValve.invoke(StandardWrapperValve.java:202)
org.apache.catalina.core.StandardContextValve.invoke(StandardContextValve.java:97)
org.apache.catalina.authenticator.AuthenticatorBase.invoke(AuthenticatorBase.java:542)
org.apache.catalina.core.StandardHostValve.invoke(StandardHostValve.java:143)
org.apache.catalina.valves.ErrorReportValve.invoke(ErrorReportValve.java:92)
org.apache.catalina.valves.AbstractAccessLogValve.invoke(AbstractAccessLogValve.java:687)
org. apache.catalina.core.StandardEngineValve.invoke(StandardEngineValve.java:78)
org.apache.catalina.connector.CoyoteAdapter.service(CoyoteAdapter.java:357)
org.apache.coyote.http11.Http11Processor.service(Http11Processor.java:374)
org.apache.coyote.AbstractProcessorLight.process(AbstractProcessorLight.java:65)
org.apache.coyote.AbstractProtocol$ConnectionHandler.process(AbstractProtocol.java:893)
org.apache.tomcat.util.net.NioEndpoint$SocketProcessor.doRun(NioEndpoint.java:1707)
org.apache.
apache.catalina.core.StandardEngineValve.invoke(StandardEngineValve.java:78)
org.apache.catalina.connector.CoyoteAdapter.service(CoyoteAdapter.java:357)
org.apache.coyote.http11.Http11Processor.service(Http11Processor.java:374)
org.apache.coyote.AbstractProcessorLight.process(AbstractProcessorLight.java:65)
org.apache.coyote.AbstractProtocol$ConnectionHandler.process(AbstractProtocol.java:893)
org.apache.tomcat.util.net.NioEndpoint$SocketProcessor.doRun(NioEndpoint.java:1707)
org.apache.




 \end{aligned}\end{align}\]
\end{aligned}\end{align}\]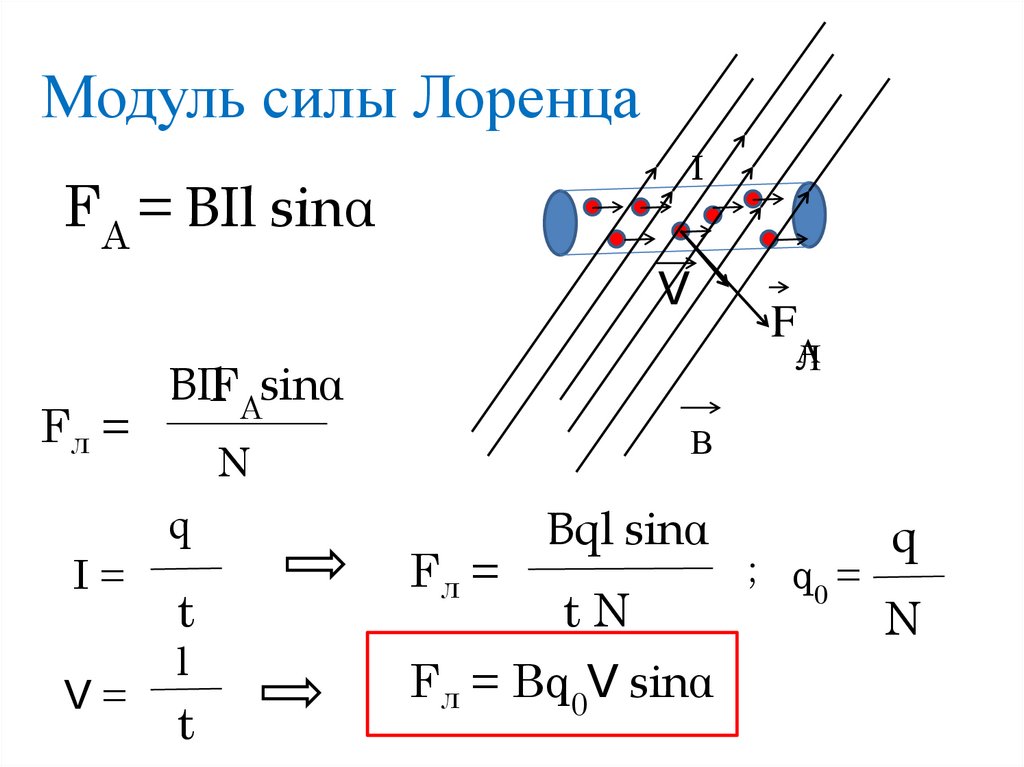 2}{2m} + e\Phi — \ frac{e}{m}(\mathbf{p}+e\mathbf{A})\cdot \mathbf{A}\right). \end{выравнивание}\end{выравнивание}\] 92}{2m} + V(\mathbf{r},t).\]
2}{2m} + e\Phi — \ frac{e}{m}(\mathbf{p}+e\mathbf{A})\cdot \mathbf{A}\right). \end{выравнивание}\end{выравнивание}\] 92}{2m} + V(\mathbf{r},t).\] Эти потенциалы \(\mathbf{r}\)-независимы, но векторный потенциал зависит от времени, поэтому член \(-\dot{\mathbf{A}}\) в уравнении \(\eqref{Bfield} \) дает неисчезающее электрическое поле:
Эти потенциалы \(\mathbf{r}\)-независимы, но векторный потенциал зависит от времени, поэтому член \(-\dot{\mathbf{A}}\) в уравнении \(\eqref{Bfield} \) дает неисчезающее электрическое поле: Предположим, мы изменили скалярный и векторный потенциалы с помощью замен
Предположим, мы изменили скалярный и векторный потенциалы с помощью замен \end{выравнивание}\end{выравнивание}\]
\end{выравнивание}\end{выравнивание}\]
 Тот факт, что это не зависит от \(r\), означает, что плотность магнитного потока сосредоточена в инфинитезимальной области, окружающей начало координат, и равна нулю во всех остальных местах. Однако векторный потенциал \(\mathbf{A}\) везде отличен от нуля. 9{i k R \phi}, & r \in [R-d/2, R + d/2] \\ 0 & \textrm{иначе}. \end{cases}\]
Тот факт, что это не зависит от \(r\), означает, что плотность магнитного потока сосредоточена в инфинитезимальной области, окружающей начало координат, и равна нулю во всех остальных местах. Однако векторный потенциал \(\mathbf{A}\) везде отличен от нуля. 9{i k R \phi}, & r \in [R-d/2, R + d/2] \\ 0 & \textrm{иначе}. \end{cases}\] 2\), фундаментальная единица магнитного потока, называемая квант магнитного потока . Другими словами, изменение \(\Phi_B\) на число, кратное \(h/e\), оставляет энергетический спектр неизменным! Это свойство инвариантности, не зависящее ни от ширины кольца, ни от каких-либо других геометрических параметров системы, можно объяснить с помощью калибровочной симметрии. Когда дополнительный поток \(nh/e\) (где \(n\in\mathbb{Z}\)) проходит через кольцо, уравнение \(\eqref{Asolenoid}\) говорит нам, что изменение вектора потенциал равен \(\Delta\mathbf{A} = (n\hbar/ e r) \mathbf{e}_\phi\). Но мы можем отменить последствия этого с помощью калибровочного поля 9.{дюйм\фи}. \end{cases}\]
2\), фундаментальная единица магнитного потока, называемая квант магнитного потока . Другими словами, изменение \(\Phi_B\) на число, кратное \(h/e\), оставляет энергетический спектр неизменным! Это свойство инвариантности, не зависящее ни от ширины кольца, ни от каких-либо других геометрических параметров системы, можно объяснить с помощью калибровочной симметрии. Когда дополнительный поток \(nh/e\) (где \(n\in\mathbb{Z}\)) проходит через кольцо, уравнение \(\eqref{Asolenoid}\) говорит нам, что изменение вектора потенциал равен \(\Delta\mathbf{A} = (n\hbar/ e r) \mathbf{e}_\phi\). Но мы можем отменить последствия этого с помощью калибровочного поля 9.{дюйм\фи}. \end{cases}\]
 spms.ntu.edu.sg/~ydchong/teaching.html
spms.ntu.edu.sg/~ydchong/teaching.html java:70)
в java.base/jdk.internal.util.Preconditions.checkIndex(Preconditions.java:248)
в java.base/java.util.Objects.checkIndex(Objects.java:372)
в java.base/java.util.ArrayList.get(ArrayList.java:458)
в com.gale.blis.data.subscription.dao.LazyUserSessionDataLoaderStoredProcedure.populateSessionProperties(LazyUserSessionDataLoaderStoredProcedure.java:60)
в com.gale.blis.data.subscription.dao.LazyUserSessionDataLoaderStoredProcedure.reQuery(LazyUserSessionDataLoaderStoredProcedure.java:53)
в com.gale.blis.data.model.session.UserGroupEntitlementsManager.reinitializeUserGroupEntitlements(UserGroupEntitlementsManager.java:30)
в com.gale.blis.data.model.session.UserGroupSessionManager.getUserGroupEntitlements(UserGroupSessionManager.java:17)
в com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.getProductSubscriptionCriteria(CrossSearchProductContentModuleFetcher.
java:70)
в java.base/jdk.internal.util.Preconditions.checkIndex(Preconditions.java:248)
в java.base/java.util.Objects.checkIndex(Objects.java:372)
в java.base/java.util.ArrayList.get(ArrayList.java:458)
в com.gale.blis.data.subscription.dao.LazyUserSessionDataLoaderStoredProcedure.populateSessionProperties(LazyUserSessionDataLoaderStoredProcedure.java:60)
в com.gale.blis.data.subscription.dao.LazyUserSessionDataLoaderStoredProcedure.reQuery(LazyUserSessionDataLoaderStoredProcedure.java:53)
в com.gale.blis.data.model.session.UserGroupEntitlementsManager.reinitializeUserGroupEntitlements(UserGroupEntitlementsManager.java:30)
в com.gale.blis.data.model.session.UserGroupSessionManager.getUserGroupEntitlements(UserGroupSessionManager.java:17)
в com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.getProductSubscriptionCriteria(CrossSearchProductContentModuleFetcher. java:244)
на com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.getSubscribedCrossSearchProductsForUser(CrossSearchProductContentModuleFetcher.java:71)
на com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.getAvailableContentModulesForProduct(CrossSearchProductContentModuleFetcher.java:52)
на com.gale.blis.api.authorize.strategy.productentry.strategy.AbstractProductEntryAuthorizer.getContentModules(AbstractProductEntryAuthorizer.java:130)
на com.gale.blis.api.authorize.strategy.productentry.strategy.CrossSearchProductEntryAuthorizer.isAuthorized(CrossSearchProductEntryAuthorizer.java:82)
на com.gale.blis.api.authorize.strategy.productentry.strategy.CrossSearchProductEntryAuthorizer.authorizeProductEntry(CrossSearchProductEntryAuthorizer.java:44)
на com.gale.blis.api.authorize.strategy.ProductEntryAuthorizer.authorize(ProductEntryAuthorizer.
java:244)
на com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.getSubscribedCrossSearchProductsForUser(CrossSearchProductContentModuleFetcher.java:71)
на com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.getAvailableContentModulesForProduct(CrossSearchProductContentModuleFetcher.java:52)
на com.gale.blis.api.authorize.strategy.productentry.strategy.AbstractProductEntryAuthorizer.getContentModules(AbstractProductEntryAuthorizer.java:130)
на com.gale.blis.api.authorize.strategy.productentry.strategy.CrossSearchProductEntryAuthorizer.isAuthorized(CrossSearchProductEntryAuthorizer.java:82)
на com.gale.blis.api.authorize.strategy.productentry.strategy.CrossSearchProductEntryAuthorizer.authorizeProductEntry(CrossSearchProductEntryAuthorizer.java:44)
на com.gale.blis.api.authorize.strategy.ProductEntryAuthorizer.authorize(ProductEntryAuthorizer. java:31)
в com.gale.blis.api.BLISAuthorizationServiceImpl.authorize_aroundBody0(BLISAuthorizationServiceImpl.java:57)
на com.gale.blis.api.BLISAuthorizationServiceImpl.authorize_aroundBody1$advice(BLISAuthorizationServiceImpl.java:61)
на com.gale.blis.api.BLISAuthorizationServiceImpl.authorize(BLISAuthorizationServiceImpl.java:1)
в com.gale.blis.auth.AuthorizationService._iceD_authorize(AuthorizationService.java:97)
в com.gale.blis.auth.AuthorizationService._iceDispatch(AuthorizationService.java:406)
в com.zeroc.IceInternal.Incoming.invoke(Incoming.java:221)
в com.zeroc.Ice.ConnectionI.invokeAll(ConnectionI.java:2706)
на com.zeroc.Ice.ConnectionI.dispatch(ConnectionI.java:1292)
в com.zeroc.Ice.ConnectionI.message(ConnectionI.java:1203)
в com.zeroc.IceInternal.ThreadPool.run(ThreadPool.java:412)
в com.zeroc.IceInternal.ThreadPool.
java:31)
в com.gale.blis.api.BLISAuthorizationServiceImpl.authorize_aroundBody0(BLISAuthorizationServiceImpl.java:57)
на com.gale.blis.api.BLISAuthorizationServiceImpl.authorize_aroundBody1$advice(BLISAuthorizationServiceImpl.java:61)
на com.gale.blis.api.BLISAuthorizationServiceImpl.authorize(BLISAuthorizationServiceImpl.java:1)
в com.gale.blis.auth.AuthorizationService._iceD_authorize(AuthorizationService.java:97)
в com.gale.blis.auth.AuthorizationService._iceDispatch(AuthorizationService.java:406)
в com.zeroc.IceInternal.Incoming.invoke(Incoming.java:221)
в com.zeroc.Ice.ConnectionI.invokeAll(ConnectionI.java:2706)
на com.zeroc.Ice.ConnectionI.dispatch(ConnectionI.java:1292)
в com.zeroc.Ice.ConnectionI.message(ConnectionI.java:1203)
в com.zeroc.IceInternal.ThreadPool.run(ThreadPool.java:412)
в com.zeroc.IceInternal.ThreadPool. access$500(ThreadPool.java:7)
в com.zeroc.IceInternal.ThreadPool$EventHandlerThread.run(ThreadPool.java:781)
в java.base/java.lang.Thread.run(Thread.java:834)
»
org.springframework.remoting.ice.IceClientInterceptor.convertIceAccessException(IceClientInterceptor.java:348)
org.springframework.remoting.ice.IceClientInterceptor.invoke(IceClientInterceptor.java:310)
org.springframework.remoting.ice.MonitoringIceProxyFactoryBean.invoke(MonitoringIceProxyFactoryBean.java:71)
org.springframework.aop.framework.ReflectiveMethodInvocation.proceed(ReflectiveMethodInvocation.java:186)
org.
access$500(ThreadPool.java:7)
в com.zeroc.IceInternal.ThreadPool$EventHandlerThread.run(ThreadPool.java:781)
в java.base/java.lang.Thread.run(Thread.java:834)
»
org.springframework.remoting.ice.IceClientInterceptor.convertIceAccessException(IceClientInterceptor.java:348)
org.springframework.remoting.ice.IceClientInterceptor.invoke(IceClientInterceptor.java:310)
org.springframework.remoting.ice.MonitoringIceProxyFactoryBean.invoke(MonitoringIceProxyFactoryBean.java:71)
org.springframework.aop.framework.ReflectiveMethodInvocation.proceed(ReflectiveMethodInvocation.java:186)
org. springframework.aop.framework.JdkDynamicAopProxy.invoke(JdkDynamicAopProxy.java:215)
com.sun.proxy.$Proxy151.authorize(Неизвестный источник)
com.gale.auth.service.BlisService.getAuthorizationResponse(BlisService.java:61)
com.gale.apps.service.impl.MetadataResolverService.resolveMetadata(MetadataResolverService.java:65)
com.gale.apps.controllers.DiscoveryController.resolveDocument(DiscoveryController.java:57)
com.gale.apps.controllers.DocumentController.redirectToDocument(DocumentController.java:22)
jdk.
springframework.aop.framework.JdkDynamicAopProxy.invoke(JdkDynamicAopProxy.java:215)
com.sun.proxy.$Proxy151.authorize(Неизвестный источник)
com.gale.auth.service.BlisService.getAuthorizationResponse(BlisService.java:61)
com.gale.apps.service.impl.MetadataResolverService.resolveMetadata(MetadataResolverService.java:65)
com.gale.apps.controllers.DiscoveryController.resolveDocument(DiscoveryController.java:57)
com.gale.apps.controllers.DocumentController.redirectToDocument(DocumentController.java:22)
jdk. internal.reflect.GeneratedMethodAccessor310.invoke (неизвестный источник)
java.base/jdk.internal.reflect.DelegatingMethodAccessorImpl.invoke(DelegatingMethodAccessorImpl.java:43)
java.base/java.lang.reflect.Method.invoke(Method.java:566)
org.springframework.web.method.support.InvocableHandlerMethod.doInvoke(InvocableHandlerMethod.java:205)
org.springframework.web.method.support.InvocableHandlerMethod.invokeForRequest(InvocableHandlerMethod.java:150)
org.springframework.web.servlet.mvc.method.annotation.ServletInvocableHandlerMethod.invokeAndHandle(ServletInvocableHandlerMethod.
internal.reflect.GeneratedMethodAccessor310.invoke (неизвестный источник)
java.base/jdk.internal.reflect.DelegatingMethodAccessorImpl.invoke(DelegatingMethodAccessorImpl.java:43)
java.base/java.lang.reflect.Method.invoke(Method.java:566)
org.springframework.web.method.support.InvocableHandlerMethod.doInvoke(InvocableHandlerMethod.java:205)
org.springframework.web.method.support.InvocableHandlerMethod.invokeForRequest(InvocableHandlerMethod.java:150)
org.springframework.web.servlet.mvc.method.annotation.ServletInvocableHandlerMethod.invokeAndHandle(ServletInvocableHandlerMethod. java:117)
org.springframework.web.servlet.mvc.method.annotation.RequestMappingHandlerAdapter.invokeHandlerMethod (RequestMappingHandlerAdapter.java:895)
org.springframework.web.servlet.mvc.method.annotation.RequestMappingHandlerAdapter.handleInternal (RequestMappingHandlerAdapter.java:808)
org.springframework.web.servlet.mvc.method.AbstractHandlerMethodAdapter.handle(AbstractHandlerMethodAdapter.java:87)
org.springframework.web.servlet.DispatcherServlet.doDispatch(DispatcherServlet.java:1067)
org.springframework.web.servlet.DispatcherServlet.doService(DispatcherServlet.
java:117)
org.springframework.web.servlet.mvc.method.annotation.RequestMappingHandlerAdapter.invokeHandlerMethod (RequestMappingHandlerAdapter.java:895)
org.springframework.web.servlet.mvc.method.annotation.RequestMappingHandlerAdapter.handleInternal (RequestMappingHandlerAdapter.java:808)
org.springframework.web.servlet.mvc.method.AbstractHandlerMethodAdapter.handle(AbstractHandlerMethodAdapter.java:87)
org.springframework.web.servlet.DispatcherServlet.doDispatch(DispatcherServlet.java:1067)
org.springframework.web.servlet.DispatcherServlet.doService(DispatcherServlet. java:963)
org.springframework.web.servlet.FrameworkServlet.processRequest(FrameworkServlet.java:1006)
org.springframework.web.servlet.FrameworkServlet.doGet(FrameworkServlet.java:898)
javax.servlet.http.HttpServlet.service(HttpServlet.java:626)
org.springframework.web.servlet.FrameworkServlet.service(FrameworkServlet.java:883)
javax.servlet.http.HttpServlet.service(HttpServlet.java:733)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:227)
org.
java:963)
org.springframework.web.servlet.FrameworkServlet.processRequest(FrameworkServlet.java:1006)
org.springframework.web.servlet.FrameworkServlet.doGet(FrameworkServlet.java:898)
javax.servlet.http.HttpServlet.service(HttpServlet.java:626)
org.springframework.web.servlet.FrameworkServlet.service(FrameworkServlet.java:883)
javax.servlet.http.HttpServlet.service(HttpServlet.java:733)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:227)
org. apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.apache.tomcat.websocket.server.WsFilter.doFilter(WsFilter.java:53)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.apache.catalina.filters.HttpHeaderSecurityFilter.doFilter(HttpHeaderSecurityFilter.java:126)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.
apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.apache.tomcat.websocket.server.WsFilter.doFilter(WsFilter.java:53)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.apache.catalina.filters.HttpHeaderSecurityFilter.doFilter(HttpHeaderSecurityFilter.java:126)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org. apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.servlet.resource.ResourceUrlEncodingFilter.doFilter(ResourceUrlEncodingFilter.java:67)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.RequestContextFilter.doFilterInternal (RequestContextFilter.java:100)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.
apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.servlet.resource.ResourceUrlEncodingFilter.doFilter(ResourceUrlEncodingFilter.java:67)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.RequestContextFilter.doFilterInternal (RequestContextFilter.java:100)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org. apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:102)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
com.gale.common.http.filter.SecurityHeaderFilter.doFilterInternal(SecurityHeaderFilter.java:29)
org.
apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:102)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
com.gale.common.http.filter.SecurityHeaderFilter.doFilterInternal(SecurityHeaderFilter.java:29)
org. springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:102)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.
springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:102)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org. owasp.validation.GaleParameterValidationFilter.doFilterInternal(GaleParameterValidationFilter.java:97)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.boot.web.servlet.support.ErrorPageFilter.doFilter(ErrorPageFilter.java:126)
org.springframework.boot.web.servlet.support.ErrorPageFilter.access$000(ErrorPageFilter.java:64)
org.
owasp.validation.GaleParameterValidationFilter.doFilterInternal(GaleParameterValidationFilter.java:97)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.boot.web.servlet.support.ErrorPageFilter.doFilter(ErrorPageFilter.java:126)
org.springframework.boot.web.servlet.support.ErrorPageFilter.access$000(ErrorPageFilter.java:64)
org. springframework.boot.web.servlet.support.ErrorPageFilter$1.doFilterInternal(ErrorPageFilter.java:101)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.springframework.boot.web.servlet.support.ErrorPageFilter.doFilter(ErrorPageFilter.java:119)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.FormContentFilter.doFilterInternal (FormContentFilter.java:93)
org.
springframework.boot.web.servlet.support.ErrorPageFilter$1.doFilterInternal(ErrorPageFilter.java:101)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.springframework.boot.web.servlet.support.ErrorPageFilter.doFilter(ErrorPageFilter.java:119)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.FormContentFilter.doFilterInternal (FormContentFilter.java:93)
org. springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.boot.actuate.metrics.web.servlet.WebMvcMetricsFilter.doFilterInternal (WebMvcMetricsFilter.java:96)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.
springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.boot.actuate.metrics.web.servlet.WebMvcMetricsFilter.doFilterInternal (WebMvcMetricsFilter.java:96)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain. java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.CharacterEncodingFilter.doFilterInternal (CharacterEncodingFilter.java:201)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.
java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.CharacterEncodingFilter.doFilterInternal (CharacterEncodingFilter.java:201)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org. apache.catalina.core.StandardWrapperValve.invoke(StandardWrapperValve.java:202)
org.apache.catalina.core.StandardContextValve.invoke(StandardContextValve.java:97)
org.apache.catalina.authenticator.AuthenticatorBase.invoke(AuthenticatorBase.java:542)
org.apache.catalina.core.StandardHostValve.invoke(StandardHostValve.java:143)
org.apache.catalina.valves.ErrorReportValve.invoke(ErrorReportValve.java:92)
org.apache.catalina.valves.AbstractAccessLogValve.invoke(AbstractAccessLogValve.java:687)
org.
apache.catalina.core.StandardWrapperValve.invoke(StandardWrapperValve.java:202)
org.apache.catalina.core.StandardContextValve.invoke(StandardContextValve.java:97)
org.apache.catalina.authenticator.AuthenticatorBase.invoke(AuthenticatorBase.java:542)
org.apache.catalina.core.StandardHostValve.invoke(StandardHostValve.java:143)
org.apache.catalina.valves.ErrorReportValve.invoke(ErrorReportValve.java:92)
org.apache.catalina.valves.AbstractAccessLogValve.invoke(AbstractAccessLogValve.java:687)
org. apache.catalina.core.StandardEngineValve.invoke(StandardEngineValve.java:78)
org.apache.catalina.connector.CoyoteAdapter.service(CoyoteAdapter.java:357)
org.apache.coyote.http11.Http11Processor.service(Http11Processor.java:374)
org.apache.coyote.AbstractProcessorLight.process(AbstractProcessorLight.java:65)
org.apache.coyote.AbstractProtocol$ConnectionHandler.process(AbstractProtocol.java:893)
org.apache.tomcat.util.net.NioEndpoint$SocketProcessor.doRun(NioEndpoint.java:1707)
org.apache.
apache.catalina.core.StandardEngineValve.invoke(StandardEngineValve.java:78)
org.apache.catalina.connector.CoyoteAdapter.service(CoyoteAdapter.java:357)
org.apache.coyote.http11.Http11Processor.service(Http11Processor.java:374)
org.apache.coyote.AbstractProcessorLight.process(AbstractProcessorLight.java:65)
org.apache.coyote.AbstractProtocol$ConnectionHandler.process(AbstractProtocol.java:893)
org.apache.tomcat.util.net.NioEndpoint$SocketProcessor.doRun(NioEndpoint.java:1707)
org.apache.