11.1. Три формулы мощности.
PBm | Q | S | ||
1 | RI2 | XI2 | ZI2 | последоват |
2 | GU2 | BU2 | YU2 | параллельн |
3 | UIcos | UI | символич | |
Активная мощность | Реактивная мощность | Полная мощность |
Выражение
мощности в символической форме.
Главное условие разности фаз:
-возьмём другой знак перед j.
— значит для получения мощности в символической форме достаточно умножить на , тогда действительная часть выражает активную мощность, а мнимая реактивную.
Условие передачи максимальн мощности от источн энергии приёмнику.
— нам задано, и менять его нельзя.
Тогда выберем такое X, чтобы наблюдался резонанс и ток в цепи был максимальным, это возможно, когда: X=Xi.
Значит должно выполнять условие:
А это условие получилось таким же как и в цепи постоянного тока. Таким образом максимальная мощность получается:
КПД при выполнении этого условия следующий
В
электроэнергетических установках
режим передачи max
P
не выгоден вследствие больших потерь
энергии. В устройствах автоматики,
радиотехники, связи обычно никакого
значения не имеет, т.к. кол-во передаваемой
энергии меньше. И обычно специально
создают условия для передачи максимальной
энергии приёмнику от передатчика.
В устройствах автоматики,
радиотехники, связи обычно никакого
значения не имеет, т.к. кол-во передаваемой
энергии меньше. И обычно специально
создают условия для передачи максимальной
энергии приёмнику от передатчика.
В
тех случаях, когда изменение тока в
одной цепи вызывает явление индукции
не только в одной цепи, но и в соседней,
то говорят, что эти цепи индуктивно
связаны. Явление наз.
-поток рассеивания первичной обмотки
— поток взаимной индукции
-совокупность магнитных силовых линий (линий магнитной индукции), пронизывающих только первичную обмотку и вызываемых током первичной обмотки.
— поток взаимной индукции, сцепляющийся с вторичной обмоткой и определяемый током в первичной обмотке.
Замкнем вторичн обмотку, ток будет также переменным и создаст свои силовые линии
-поток самоиндукции -поток самоиндукции
-потокосцепление самоиндукции -потокосцепл. вз. индукции
Коэф,
характеризующие индуктивносвязанную
систему
Индуктивностью наз коэф пропорциональности между суммой потокосцеплений самоиндукций обмотки и ее током, при условии, что остальные обмотки разомкнуты (L).
Взаимной индукцией наз коэф пропорциональности между суммой потокосцеплений разомкнутой обмотки и током, создающим магнитное поле (М).
Коэф трансформации – это отношение ЭДС, индуктирующаяся во вторичной разомкнутой обмотке к ЭДС, индуктирующаяся в первичной обмотке (U).
К оэф связи – среднее геом. Коэф трансформации (К)
Согласное и встречное включение катушек.
Согласное включение – включение катушек, при заданных положительных направлениях токов, потоки самоиндукции и взаимоиндукции складываются.
Мощность моторов в сезонах Формулы 1
27 декабря 2011, 13:57
Ferrari – единственная команда, выступающая в Формуле 1 с первого сезона. Кроме того, итальянская команда – самостоятельный производитель моторов, что позволяет проследить тенденцию изменения мощности двигателей с 1950 по 2011 год…
| Год | Шасси | Формула двигателя | Мощность |
| 1950 | Ferrari 375 | 4. |
350 сил |
| 1951 | Ferrari 375 | 4.5 литра V12 | 350 сил |
| 1952 | Ferrari 500 | 2 литра, рядный 4 (по регламенту F2) | 185 сил |
| 1953 | Ferrari 500 | 2 литра, рядный 4 (по регламенту F2) | 185 сил |
| 1954 | Ferrari 553 | F1 2.5 литра, рядный 4 | 260 сил |
| 1955 | Ferrari 555 | F1 2.5 литра, рядный 4 | 260 сил |
| 1956 | Ferrari D50 | 2.5 литра, V8 | 265 сил |
| 1957 | Ferrari 801 | 2. 5 литра, V8 5 литра, V8 |
275 сил |
| 1958 | Ferrari 246 | 2.5 литра, V6 | 280 сил |
| 1959 | Ferrari 256 | 2.5 литра, V6 | 280 сил |
| 1960 | Ferrari 246 P | 2.5 литра, V6 | 263 сил |
| 1961 | Ferrari 156 | 1.5 литра, V6 | 190 сил |
| 1962 | Ferrari 156 | 1.5 литра, V6 | 190 сил |
| 1963 | Ferrari 156 F1-63 | 1.5 литра V6 | 205 сил |
| 1964 | Ferrari 158 | 1. 5 литра, V8 5 литра, V8 |
210 сил |
| 1965 | Ferrari 512 | 1.5 литра, оппозитный 12 | 220 сил |
| 1966 | Ferrari 312 F1-66 | 3 литра V12 | 360 сил |
| 1967 | Ferrari 312 F1-67 | 390 сил | |
| 1968 | Ferrari 312 F1-68 | 3 литра V12 | 410 сил |
| 1969 | Ferrari 312 F1-69 | 3 литра V12 | 436 сил |
| 1970 | Ferrari 312 B | 3 литра оппозитный 12 | 450 сил |
| 1971 | Ferrari 312 B2 | 3 литра оппозитный 12 | 470 сил |
| 1972 | 3 литра оппозитный 12 | 470 сил | |
| 1973 | Ferrari 312 B3-73 | 3 литра оппозитный 12 | 485 сил |
| 1974 | Ferrari 312 B3-74 | 3 литра оппозитный 12 | 490 сил |
| 1975 | Ferrari 312 T | 3 литра оппозитный 12 | 495 сил |
| 1976 | Ferrari 312 T2 | 3 литра оппозитный 12 | |
| 1977 | Ferrari 312 T2 | 3 литра оппозитный 12 | 500 сил |
| 1978 | Ferrari 312 T3 | 3 литра оппозитный 12 | 510 сил |
| 1979 | Ferrari 312 T4 | 3 литра оппозитный 12 | 515 сил |
| 1980 | Ferrari 312 T5 | 3 литра оппозитный 12 | 515 сил |
| 1981 | Ferrari 126 CK | 1.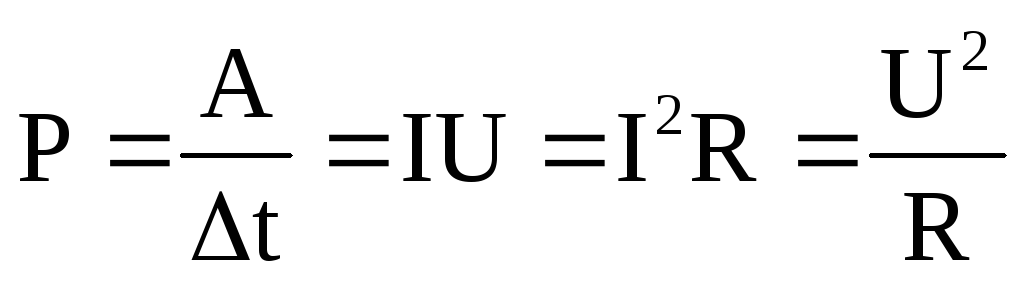 5 литра V6 турбо 5 литра V6 турбо |
540 сил |
| 1982 | Ferrari 126 C2 | 1.5 литра V6 турбо | 580 сил |
| 1983 | Ferrari 126 C3 | 1.5 литра V6 турбо | 600 сил |
| 1984 | Ferrari 126 C4 | 1.5 литра V6 турбо | 660 сил |
| 1985 | Ferrari 156-85 | 1.5 литра V6 турбо | 780 сил |
| 1986 | Ferrari F1-86 | 1.5 литра V6 турбо | 850 сил |
| 1987 | Ferrari F1-87 | 1.5 литра V6 турбо | 880 сил |
| 1988 | Ferrari F1-87/88C | 1. 5 литра V6 турбо 5 литра V6 турбо |
620 сил |
| 1989 | Ferrari F1-89 | 3.5 литра V12 | 600 сил |
| 1990 | Ferrari F1-90 | 3.5 литра V12 | 680 сил |
| 1991 | Ferrari F1-91 | 3.5 литра V12 | 725 сил |
| 1992 | Ferrari F92 A | 3.5 литра V12 | 735 сил |
| 1993 | Ferrari F93 A | 3.5 литра V12 | 745 сил |
| 1994 | Ferrari 412 T1 | 3.5 литра V12 | 750 сил |
| 1995 | Ferrari 412 T2 | 3 литра V12 | 690 сил |
| 1996 | Ferrari F310 | 3 литра V10 | 715 сил |
| 1997 | Ferrari F310 B | 3 литра V10 | 730 сил |
| 1998 | Ferrari F300 | 3 литра V10 | 805 сил |
| 1999 | Ferrari F399 | 3 литра V10 | 790 сил |
| 2000 | Ferrari F1-2000 | 3 литра V10 | 805 сил |
| 2001 | Ferrari F2001 | 3 литра V10 | 825 сил |
| 2002 | Ferrari F2002 | 3 литра V10 | 835 сил |
| 2003 | Ferrari F2003-GA | 3 литра V10 | 845 сил |
| 2004 | Ferrari F2004 | 3 литра V10 | 865 сил |
| 2005 | Ferrari F2005 | 3 литра V10 | 865 сил |
| 2006 | Ferrari 248 F1 | 2. 4 литра V8 4 литра V8 |
725 сил |
| 2007 | Ferrari F2007 | 2.4 литра V8 | 730 сил |
| 2008 | Ferrari F2008 | 2.4 литра V8 | 740 сил |
| 2009 | Ferrari F60 | 2.4 литра V8 | 750 сил |
| 2010 | Ferrari F10 | 2.4 литра V8 | 760 сил |
| 2011 | Ferrari 150° Italia | 2.4 литра V8 | 770 сил |
- Ferrari
Нашли опечатку?
Выделите её и нажмите Ctrl+Enter!
Нашли опечатку? Выделите её и нажмите кнопку поиска.
Текст: Дмитрий Бухаров. Источник: по материалам F1Racing
Использование материалов без письменного разрешения редакции F1News.ru запрещено.
Функция POWER в Excel (формула, примеры)
В математике у нас были показатели степени, степень данного основного числа. В Excel у нас есть аналогичная встроенная функция, известная как функция СТЕПЕНЬ, которая используется для вычисления мощности данного числа или основания. Чтобы использовать эту функцию, мы можем использовать ключевое слово =POWER( в ячейке и указать два аргумента, один как число, а другой как степень.
Например, предположим, что основание 4 возведено в степень 3, т.е. , 4 куб.=4*4*4 = 64.
СТЕПЕНЬ в Excel — это математическая/тригонометрическая функция, которая вычисляет и возвращает результат возведения числа в степень. Функция POWER Excel принимает два аргумента: основание (любое действительное число) и показатель степени (степень , означающая, сколько раз данное число будет умножено само на себя) . Например, 5, умноженное на степень 2, равно 5 х 5.
Например, 5, умноженное на степень 2, равно 5 х 5.
Содержание
- Power в Excel
- Формула POWER Функция
- Объяснение функции СТЕПЕНЬ в Excel
- Как использовать функцию СТЕПЕНЬ в Excel
- СТЕПЕНЬ в Excel, пример №1
- СТЕПЕНЬ, в Excel, пример №2
- СТЕПЕНЬ, в Excel, пример №3 POWER
- СТЕПЕНЬ, в примере Excel №4
- Рекомендуемые статьи
Формула функции СТЕПЕНЬ
Объяснение функции СТЕПЕНЬ в Excel
Функция СТЕПЕНЬ в Excel принимает оба аргумента в виде числового значения. Следовательно, передаваемые аргументы имеют целочисленный тип, где число является базовым числом, а СТЕПЕНЬ — показателем степени. Оба аргумента являются обязательными и необязательными.
Мы можем использовать функцию СТЕПЕНЬ в Excel разными способами, например, для математических операций. Например, мы можем использовать уравнение функции СТЕПЕНЬ для вычисления реляционных алгебраических функций.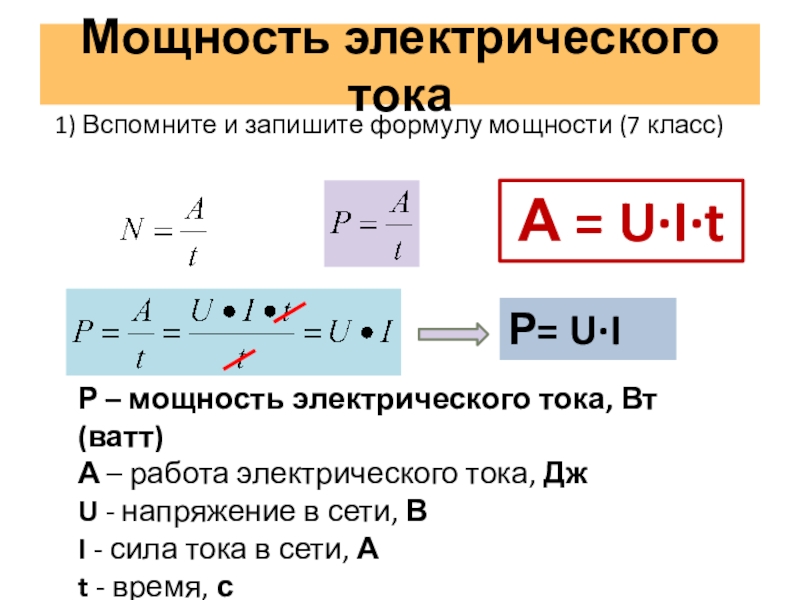
Как использовать функцию POWER в Excel
Функция POWER в Excel очень проста и удобна в использовании. Давайте разберемся с работой POWER в Excel на некоторых примерах.
Вы можете скачать этот шаблон Excel функции POWER здесь — Шаблон Excel функции POWER
POWER в Excel, пример № 1 92 (=POWER(10,2)
Теперь, выбрав значения x и y из диапазона B4:K5, выберите график (в этом примере мы выбрали график рассеяния с плавными линиями) из «Вставить
Итак, мы получаем линейный экспоненциальный график для заданного уравнения функции СТЕПЕНЬ.
СТЕПЕНЬ в Excel, пример №2
В алгебре у нас есть уравнение квадратичной функции СТЕПЕНЬ, представленное как ax2+bx+c= 0, где x неизвестен, а a, b и c — коэффициенты.Решение этого уравнения функции СТЕПЕНЬ дает корни уравнения, которые являются значениями x.
Корни уравнения квадратичной функции СТЕПЕНИ вычисляются по следующей математической формуле:
- x = (-b+ (b 2 -4ac) 1/2 )/2a
- x = (-b+ (b 2 -4ac) b- (b 2 -4ac) 1/2 )/2a
b2-4ac называется дискриминантом и описывает число корней уравнения квадратичной функции POWER.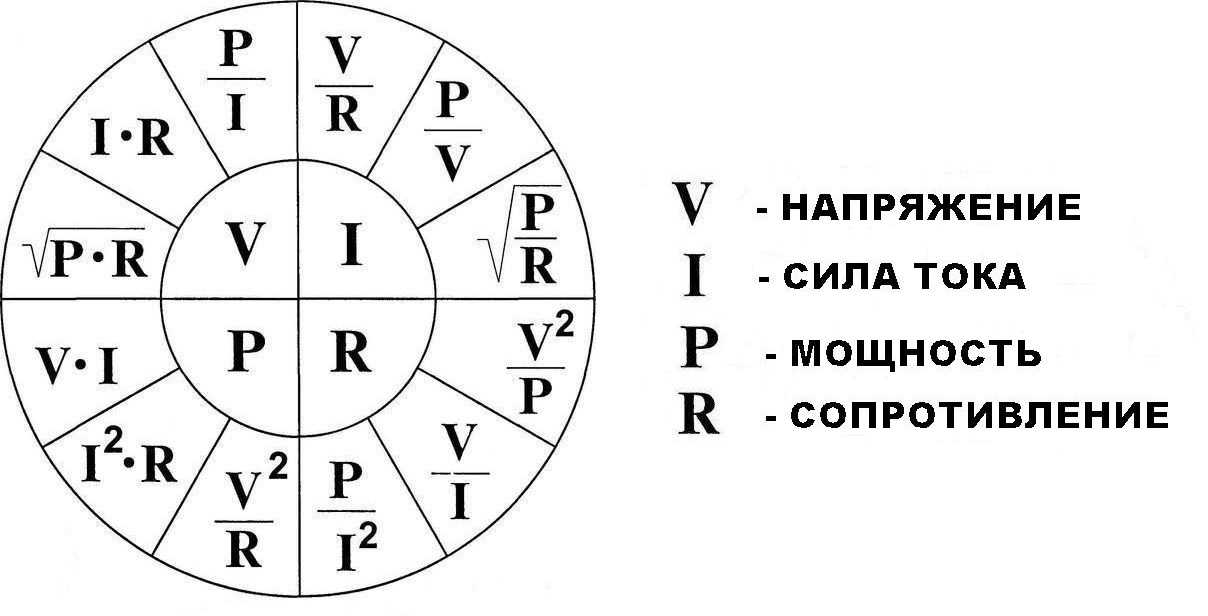
Теперь у нас есть список уравнений квадратичной функции СТЕПЕНЬ, приведенный в столбце A. Но сначала нам нужно найти корни уравнений. 92.
У нас есть пять квадратичных уравнений функции СТЕПЕНЬ, и мы будем решать их, используя формулу с помощью функции СТЕПЕНЬ в Excel, чтобы найти корни.
В первом уравнении функции СТЕПЕНЬ a=4, b=56 и c = -96. Если мы решим их математически, используя приведенную выше формулу, мы получим корни -15,5 и 1,5.
Чтобы реализовать это в формуле Excel, мы будем использовать функцию СТЕПЕНЬ в Excel, и формула будет:
- = ((-56+СТЕПЕНЬ(СТЕПЕНЬ(56,2)-(4*4*(-9)3)),1/2)))/(2*4) даст первый корень и
- = ((-56-СТЕПЕНЬ(СТЕПЕНЬ(56,2)-(4*4*(-93) ),1/2)))/(2*4) даст второй корень уравнения
Таким образом, полная формула будет,
= «Корни уравнений» &» «&(( -56+МОЩНОСТЬ(МОЩНОСТЬ(56,2)-(4*4*(-93)),1/2)))/(2*4)&” , “&((-56-МОЩНОСТЬ(МОЩНОСТЬ(56) ,2)-(4*4*(-93)),1/2)))/(2*4)
Формулы объединяются строкой «Корни уравнения».
Используя ту же формулу для других уравнений функции СТЕПЕНЬ, мы имеем:
Вывод:
СТЕПЕНЬ в Excel Пример №3
Итак, мы можем использовать функцию СТЕПЕНЬ в Excel для различных математических расчетов.
Предположим, нам нужно определить сложный процент. Сложный процент. Сложный процент — это процент, начисляемый на сумму основной суммы и общего процента, начисленного на нее до сих пор. Это играет решающую роль в получении более высокой прибыли от инвестиций. Подробнее, для которых формула:
Сумма = Основная сумма (1 + r/n) nt
- Где r — процентная ставка, n — количество начислений процентов в год, а t — время.
- Если сумма в размере 4000 долларов США депонирована на счет (сберегательный) с процентной ставкой 5% годовых, ежемесячно начисляемой на сложные проценты, стоимость инвестиции через 5 лет может быть рассчитана с использованием приведенной выше формулы сложных процентов.
- Когда основная сумма = 4000 долларов США, ставка = 5/100, т.
 е. 0,05, n = 12 (ежемесячное начисление сложных процентов), время = 5 лет.
е. 0,05, n = 12 (ежемесячное начисление сложных процентов), время = 5 лет.
У нас есть формула, использующая формулу сложных процентов и реализующая ее в формуле Excel с помощью функции POWER.
=B2*(POWER((1+(B3/B5)),(B4*B5)))
Таким образом, баланс инвестиций через 5 лет составляет 5 133,43 доллара.
POWER в Excel Example #4
Согласно закону тяготения Ньютона, два тела на расстоянии r от их центра тяжести притягиваются друг к другу во Вселенной в соответствии с формулой гравитационной POWER Excel.
F = (G*M*m)/r 2
Когда F — величина гравитационной силы, G называется гравитационной постоянной, M — масса первого тела, m — масса второго второго тела, а r — расстояние между телами от их центра тяжести. 930 будет представлено как 1,98*степень (10,30), аналогично другим значениям.
 *POWER(10,11),2)
*POWER(10,11),2) Так как значение, полученное как сила, является большим числом, Excel выразил его научным представлениемExcel выразил его научным представлениемВ Excel научное обозначение представляет собой особый стиль записи чисел в научной и экспоненциальной формах. Экспоненциальная запись помогает компактно отображать значения, позволяя нам сравнивать и использовать их в расчетах.Подробнее. Чтобы преобразовать его в дробь, измените формат на дробь.
Вывод:
Итак, Солнце притягивает Землю с силой 35229150283107
0000 Ньютон.
Рекомендуемые статьи
Эта статья представляет собой руководство по функции POWER в Excel. Здесь мы обсуждаем формулу POWER в Excel и способы использования функции POWER Excel, а также примеры Excel и загружаемые шаблоны Excel. Вы также можете посмотреть на эти полезные функции в Excel: –
- Excel против AccessExcel против. AccessExcel и Access — два самых мощных инструмента Microsoft для анализа данных и создания отчетов, но между ними есть существенные различия.
 Excel — более старый продукт Microsoft, тогда как Access — самый продвинутый и сложный продукт Microsoft. В Excel очень легко создавать информационные панели и формулы, тогда как в Access очень легко создавать базы данных и соединения.Подробнее
Excel — более старый продукт Microsoft, тогда как Access — самый продвинутый и сложный продукт Microsoft. В Excel очень легко создавать информационные панели и формулы, тогда как в Access очень легко создавать базы данных и соединения.Подробнее - GetPivotData в Excel
- НЕ Функция
Формула мощности. Что такое формула мощности?
Формула силы
Подобно энергии, мы часто слышим слово «сила». В повседневной жизни у него много значений, но в физике он имеет очень конкретное значение — это мера скорости, с которой выполняется работа (или, аналогично, с которой передается энергия).
Способность точно измерять мощность была одним из ключевых навыков, позволивших инженерам в свое время разработать паровые двигатели, которые привели в действие промышленную революцию. По-прежнему крайне важно понять, как лучше всего использовать энергетические ресурсы, питающие современный мир.
Формула мощности применима не только к механической энергии, но также к электричеству и химии.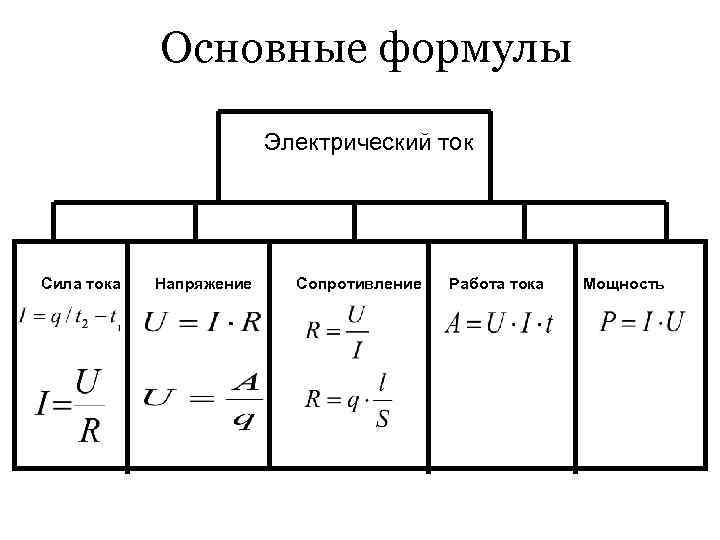 Формула мощности также позволяет рассчитать тепловую энергию (например, формула мощности в электронике представляет собой произведение силы тока и напряжения — P=Ul).
Формула мощности также позволяет рассчитать тепловую энергию (например, формула мощности в электронике представляет собой произведение силы тока и напряжения — P=Ul).
Формула мощности, в случае электрической цепи постоянного тока, определяется по закону Ома. Тогда формула мощности будет следующей: P=12R или P=U2/R
Формула мощности
По определению, один ватт равен одному джоулю работы, совершаемой в секунду. Итак, если P представляет собой мощность в ваттах, Delta E — это изменение энергии (количество джоулей), а Delta t — это время в секундах, , то формула мощности:
P = ΔE/Δt
Существует еще одна единица измерения мощности, которая до сих пор широко используется – лошадиная сила. Обычно это обозначается символом л.с. и берет свое начало в 17 веке, когда оно относилось к мощности типичной лошади, используемой для поворота лебедки. С тех пор лошадиная сила определяется как мощность, необходимая для подъема груза массой 75 кг на расстояние 1 метр за 1 секунду. Итак, сколько это мощность в ваттах?
Итак, сколько это мощность в ваттах?
Итак, мы знаем, что при подъеме против силы тяжести масса приобретает гравитационную потенциальную энергию – Ep = m⋅g⋅h.
Применение формулы мощности
На практике формулу мощности можно использовать, например, при выборе подходящего резистора для электрической системы. Его также можно использовать для расчета, достаточно ли конкретной максимальной мощности этой модели для данного проекта. Если расчет неверен, компонент схемы или даже вся схема могут быть повреждены. Автоматизация, робототехника, электроника — основные области, где часто используется формула мощности и информация о мощности. Инженерия и наука основывают большую часть своих исследований на энергетике.
Как измерить переменную мощность?
Во многих ситуациях, когда используются энергоресурсы, скорость потребления меняется со временем. Одним из таких примеров является типичное потребление электроэнергии в домах. Мы наблюдаем минимальное использование в течение дня, затем максимальное использование во время приготовления пищи и длительный период интенсивного использования для вечернего освещения и обогрева.
Здесь уместно выразить по крайней мере три способа выражения мощности: мгновенная мощность, средняя мощность и пиковая мощность. Электроэнергетическая компания должна следить за всем этим. На самом деле, для решения каждой из них часто используются разные энергетические ресурсы.
— Мгновенная мощность — это мощность, измеренная в данный момент. Если вы рассмотрите формулу мощности P = ΔE / ΔtP, это измерение, которое вы получите, когда Δt очень мало. Если вам посчастливилось иметь график зависимости мощности от времени, мгновенная мощность — это просто значение, которое вы можете прочитать на графике в любое время.
— Средняя мощность — это мощность, измеренная за длительный период (т. е. когда Δt в формуле мощности очень велико). Один из способов вычислить это — найти площадь под кривой зависимости мощности от времени (которая дает общую проделанную работу) и разделить ее на общее время. Обычно это лучше всего делать с помощью дифференциального исчисления, но часто можно довольно точно оценить, используя только геометрию.


 е. 0,05, n = 12 (ежемесячное начисление сложных процентов), время = 5 лет.
е. 0,05, n = 12 (ежемесячное начисление сложных процентов), время = 5 лет. Excel — более старый продукт Microsoft, тогда как Access — самый продвинутый и сложный продукт Microsoft. В Excel очень легко создавать информационные панели и формулы, тогда как в Access очень легко создавать базы данных и соединения.Подробнее
Excel — более старый продукт Microsoft, тогда как Access — самый продвинутый и сложный продукт Microsoft. В Excel очень легко создавать информационные панели и формулы, тогда как в Access очень легко создавать базы данных и соединения.Подробнее