Электродвижущая сила — формулы и определение с примерами
Электродвижущая сила:
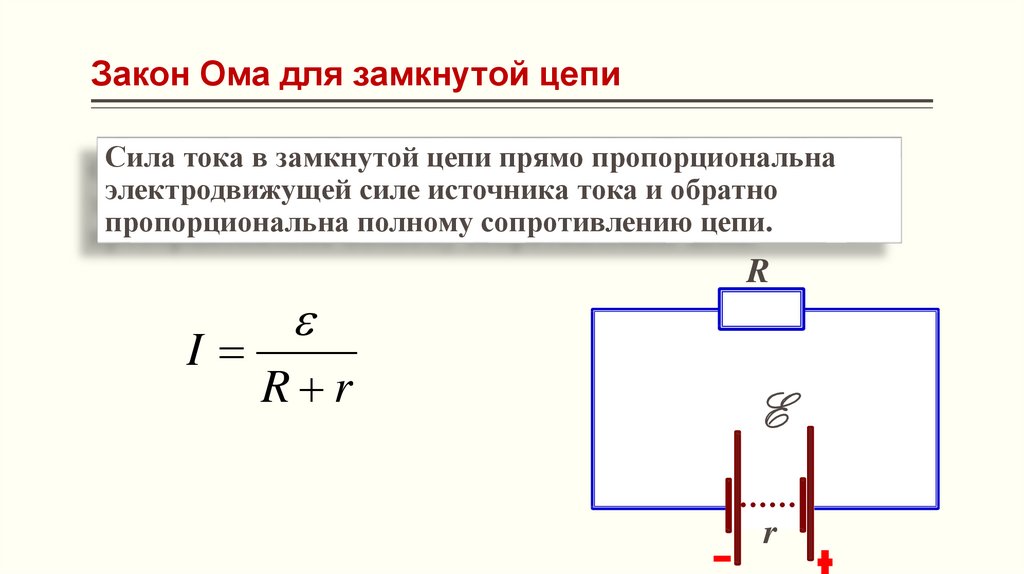
Простейшая электрическая цепь состоит из источника тока, потребителей (электробытовые приборы, лампочки, резисторы, электроизмерительные приборы), соединительных проводов и выключателя.
Для существования постоянного тока в цепи необходимо поддерживать постоянную разность потенциалов между полюсами электрической цепи. Можно сказать иначе — следует непрерывно разделять электрические заряды противоположных знаков, которые под действием сил Кулона стремятся соединиться. Для этой цели необходимы силы иной природы, так называемые сторонние силы, работа которых по замкнутому контуру, в отличие от потенциальных кулоновских сил, не равна нулю.
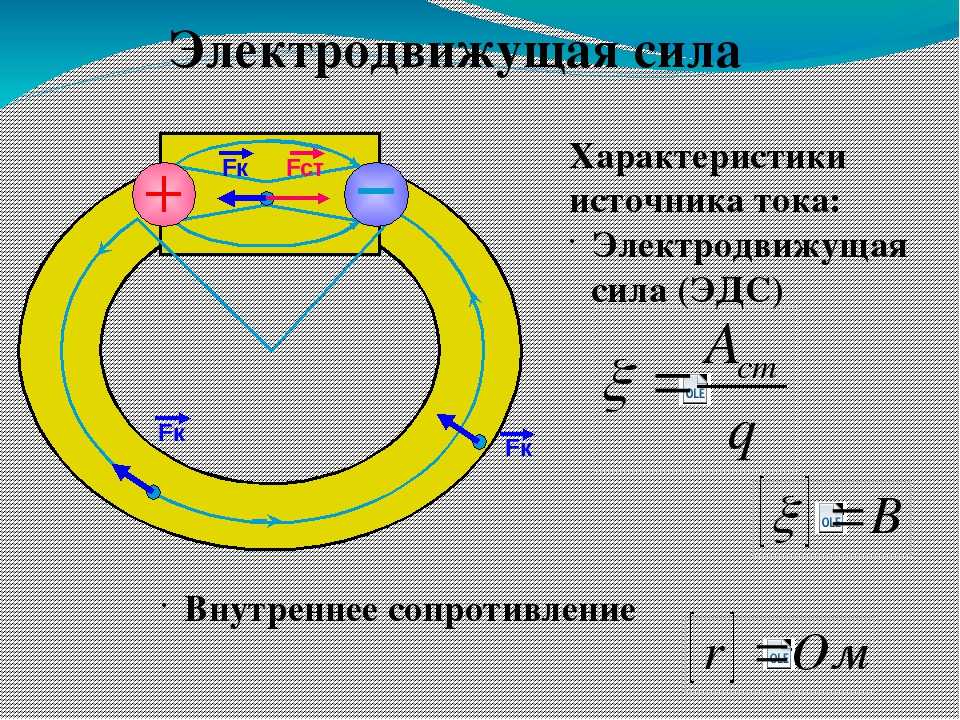
Характеристикой действия сторонних сил является электродвижущая сила (ЭДС), которая численно равна работе сторонних сил по перемещению единичного положительного заряда внутри источника тока:
Термин «электродвижущая сила» был введен Ампером в 1822 г.
Работа сторонних сил осуществляется внутри источника тока (рис. 113), обеспечивающего непрерывное разделение электрических зарядов в цепи. Внутри источника тока под действием сторонних сил электрические заряды движутся против направления действия кулоновских сил (см. рис. ИЗ).
Именно за счет работы, совершаемой сторонними силами внутри источника тока, восстанавливается энергия электрического поля, расходуемая в различных элементах замкнутой электрической цепи.
Таким образом, источник тока обеспечивает замкнутое движение электрических зарядов в одном направлении. Проводник, соединяющий клеммы источника снаружи, называют
Устройство, способное поддерживать разность потенциалов между концами электрической цепи и обеспечивать упорядоченное движение электрических зарядов во внешней цепи, называется источником тока.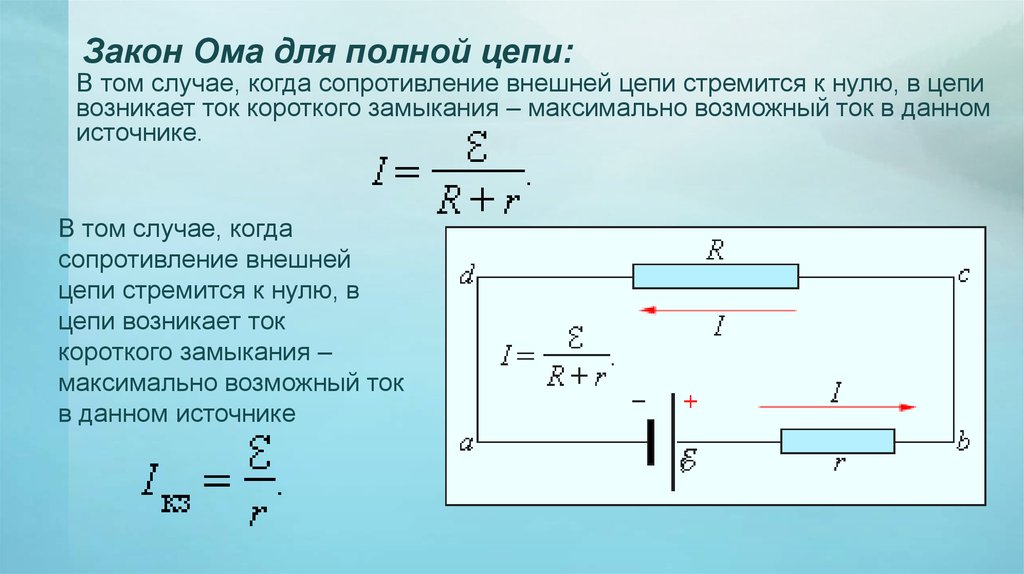
Отметим, что источники ЭДС, вообще говоря, делятся на два вида: источники тока, у которых и источники напряжения, у которых где r — внутреннее сопротивление источника, R — сопротивление внешнего участка цепи. Так, розетка бытовой сети является источником напряжения, поскольку сопротивление лампы накаливания мощностью Р = 60 Вт (R~400 0м) гораздо больше внутреннего сопротивления (r~0,1 Ом).
Источник электрического тока имеет два полюса (две клеммы), к которым присоединяются концы проводников, образующих внешний участок цепи.
На электрических схемах источник тока обозначается так, как показано на рисунке 114.
Положительный полюс (клемма) источника тока условно изображается более длинной чертой, чем отрицательный. Основные характеристики источника тока — величину ЭДС и его внутреннее сопротивление r — также указывают на электрических схемах.
Положительный полюс (клемма) источника тока имеет наибольшее значение электрического потенциала в цепи. Поскольку на каждом из элементов цепи, обладающих сопротивлением, происходит некоторое падение напряжения, то чем дальше точка внешней части цепи от положительного полюса источника, тем ниже ее потенциал относительно данного полюса.
Поскольку на каждом из элементов цепи, обладающих сопротивлением, происходит некоторое падение напряжения, то чем дальше точка внешней части цепи от положительного полюса источника, тем ниже ее потенциал относительно данного полюса.
Иными словами, потенциал уменьшается (падает) вдоль внешней части цепи от точки к точке в направлении прохождения тока. Соответственно, наименьший потенциал в цепи имеет отрицательный полюс источника тока.
Схема распределения потенциала вдоль цепи, содержащей источник тока, может быть представлена при помощи механической аналогии с катящимся шариком, изображенной на рисунке 115.
Внешняя часть замкнутой цепи соответствует участку АВС контура, внутренняя (источник тока) — участку СА. Самостоятельно шарик будет катиться только от точки А к точке С, а для подъема его от точки С к точке А необходимо действие сторонних сил.
Сравнивая электрический ток с течением жидкости в трубах, можно отметить, что потенциал является аналогом гидростатического давления в жидкости. Действительно, распределение гидростатического давления в трубе, по которой течет вода, аналогично распределению потенциалов вдоль проводника с током. Как течение воды обусловлено разностью гидростатических давлений (напором) на участке трубы, так и ток обусловлен разностью потенциалов
Действительно, распределение гидростатического давления в трубе, по которой течет вода, аналогично распределению потенциалов вдоль проводника с током. Как течение воды обусловлено разностью гидростатических давлений (напором) на участке трубы, так и ток обусловлен разностью потенциалов
Участок цепи, на котором есть источник тока, является неоднородным участком цепи.
Электрические заряды внутри источника тока (на внутреннем участке цепи)
движутся против кулоновских сил под действием сторонних сил, а во всей остальной цепи (на внешнем участке цепи) их приводит в движение электрическое поле, создаваемое источником.
- Заказать решение задач по физике
Продолжая аналогию между течением электрического тока и течением жидкости по трубам, можно сказать, что источник тока является аналогом насоса, подающего воду под давлением в трубы (рис. 116).
В разомкнутой цепи разность потенциалов между клеммами источника тока равна его ЭДС, которую в этом случае можно измерить с помощью вольтметра (рис.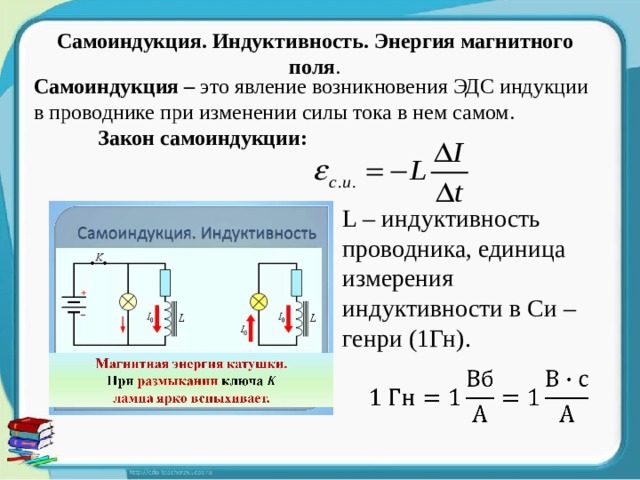 117).
117).
В настоящее время выпускается множество различных источников ЭДС — от маленьких батареек (сухих элементов) для часов и калькуляторов до мощных промышленных генераторов.
Простейшая батарея (гальванический элемент) состоит из двух электродов (пластин или стержней) из разнородных металлов, погруженных в разбавленную кислоту (электролит). В сухом элементе электролит представляет собой желеобразную массу. При соединении проводником электродов в замкнутой цепи будет проходить ток вследствие возникновения ЭДС на границе соприкосновения различных проводников. Кроме того, один из проводников меняет химический состав под действием электрического тока. В результате химических превращений внутренняя (химическая) энергия тел, составляющих цепь, уменьшается, и таким образом поддерживается ток в цепи. Гальванический элемент является химическим источником тока, так как в нем происходит прямое преобразование химической энергии в электрическую.
На рисунке 118 приведено устройство наиболее широко распространенного марганцево-цинкового сухого элемента. В цинковый корпус 1, выполняющий роль отрицательного электрода, помещен угольный стержень 2, являющийся положительным электродом батареи. Свободное пространство 3 между электродами заполнено вязким раствором щелочи или раствором хлорида аммония.
В цинковый корпус 1, выполняющий роль отрицательного электрода, помещен угольный стержень 2, являющийся положительным электродом батареи. Свободное пространство 3 между электродами заполнено вязким раствором щелочи или раствором хлорида аммония.
Перечислим наиболее распространенные источники тока.
Гальванические элементы (1—2 В) и аккумуляторы (2—20 В) расходуют химическую энергию веществ, способных взаимодействовать с растворами кислот, щелочей, солей.
Для промышленного производства электроэнергии используются мощные генераторы (динамо-машины), дающие напряжение до 15 кВ за счет использования механической энергии, производимой турбинами (рис. 119), двигателями внутреннего сгорания и т. д.
В последнее время широкое распространение получили так называемые альтернативные источники электроэнергии. К ним относятся термоэлементы, использующие энергию теплового движения заряженных частиц, а также фотоэлементы, создающие ток за счет энергии электромагнитного излучения (рис. 120).
120).
Описание лабораторной установки и вывод расчетной формулы
,
где – сопротивление вольтметра;
r – внутреннее сопротивление источника тока.
Тогда
,
отсюда напряжение , которое показывает вольтметр,
,
т.е. вольтметр покажет значение напряжения меньше ЭДС на величину Ir падения напряжения на внутреннем сопротивлении источника тока.
Если >>r, то это отличие незначительное.
Для измерения ЭДС
источника надо применить метод, при
котором ток в источнике тока отсутствует.
Это компенсационный метод, который
позволяет ЭДС элемента компенсировать
известным падением напряжения на участке
цепи.
Схема электрической цепи компенсационного метода изображена на рис. 3.3. Здесь – батарея с ЭДС, превосходящей ЭДС исследуемого элемента и поддерживающая постоянный ток I1 в цепи реохорда АВ, проволока которого натянута на масштабную линейку. К подвижному контакту реохорда
Рис. 3.3.
По условиям измерения замыкание цепи батареи должно предшествовать замыканию цепи гальванометра. Это достигается с помощью двойного ключа К1.
Компенсация ЭДС
возможна только в том случае, если
батарея и исследуемый
элемент х включены одноименными полюсами навстречу
друг другу.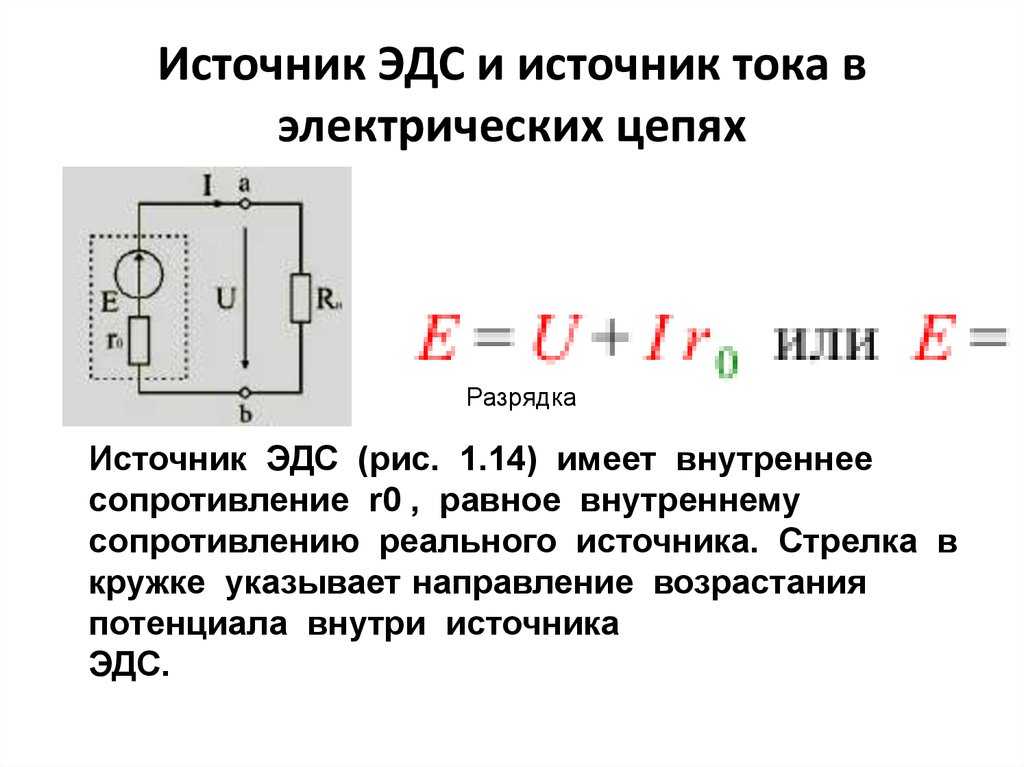 Если ЭДС батареи больше ЭДС исследуемого элемента х,
то на реохорде всегда можно найти такую
точку С,
когда стрелка гальванометра будет
стоять на нуле, т.е. в ветви АGС тока не окажется.
Если ЭДС батареи больше ЭДС исследуемого элемента х,
то на реохорде всегда можно найти такую
точку С,
когда стрелка гальванометра будет
стоять на нуле, т.е. в ветви АGС тока не окажется.
Согласно обобщенному закону Ома для ветви АGС
x ,
где rx– внутреннее сопротивление источникаx;
Rr – сопротивление гальванометра;
А – С– разность потенциалов между точками А и С реохорда.
Аналогично для ветви АС
,
где – сопротивление участка реохорда.
Из двух последних равенств имеем:
x.
Когда ток, проходящий через гальванометр, I2=0, то
x. (3.10)
В этом случае падение напряжения на АС, создаваемое батареей, равно ЭДС исследуемого элемента х.
Заменим исследуемый элемент нормальным, ЭДС которого известна и строго постоянна. Тогда компенсация произойдет в некоторой новой точке D. Ток в цепи гальванометра отсутствует, а в цепи АВ остается неизменным (I1). Тогда согласно выражению (3.10)
n. (3.11)
Из выражений (3.10) и (3.11) получим
xn.
Для калиброванной проволоки реохорда сопротивление участков пропорционально их длинам, поэтому
xn,
(3.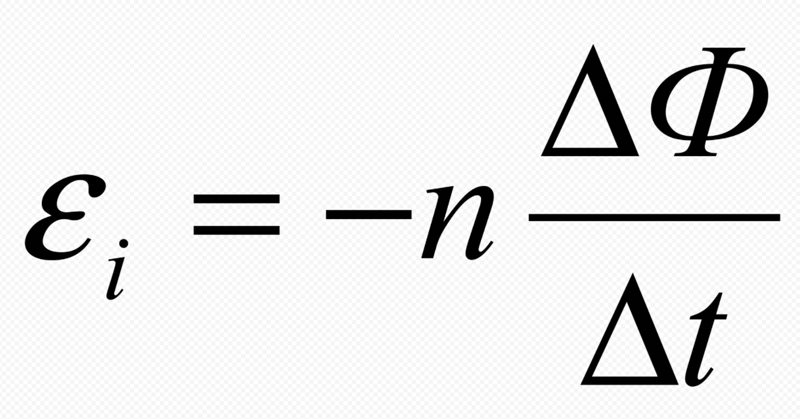 12)
12)
где и– длины участковАС и АD.
В данной работе в качестве эталонной ЭДС служит нормальный элемент Вестона, представляющий собой гальванический ртутно-кадмиевый элемент, ЭДС которого при 20оС равна n =1,0183 В. При работе с нормальным элементом его нельзя встряхивать, переворачивать, пропускать токи, превышающие 10–6 А.
1. Изучите электрическую схему лабораторной установки.
2. Убедитесь, что источник тока с ЭДС (источник питания ИЭПП-1) присоединен к точкам А и В реохорда соответствующими полюсами.
3. С помощью проводников присоедините к установке первый исследуемый источник тока и ключом К2 включите его в цепь (положение ).
4. Включите источник питания ИЭПП-1 в сеть и установите на его выходных зажимах напряжение 7 В.
5. Установите
подвижный контакт реохорда вблизи
среднего положения. Замыкая на короткое
время двойной ключ К1 и перемещая движок (точка С)
по реохорду, добейтесь отсутствия тока
в цепи гальванометра. Отметьте длину
участка lx (АС)
и результаты запишите в табл. 7.
Установите
подвижный контакт реохорда вблизи
среднего положения. Замыкая на короткое
время двойной ключ К1 и перемещая движок (точка С)
по реохорду, добейтесь отсутствия тока
в цепи гальванометра. Отметьте длину
участка lx (АС)
и результаты запишите в табл. 7.
6. Аналогичные измерения произведите еще два раза, устанавливая на выходных зажимах источника питания ИЭПП-1 напряжение 6 и 5 В. Результаты запишите в табл. 7.
7. Выключите источник питания, отсоедините первый исследуемый источник тока. На его место присоедините второй источник тока. Проделайте операции, описанные в п. 4–6, со вторым исследуемым элементом.
8. С помощью ключа К2 включите в цепь нормальный элемент
(положение n).
Для этого элемента повторите указания
п. 4–6. Отметьте длину участка реохорда ln (АD),
на котором произошла компенсация, и
запишите полученные данные в табл. 7.
7.
9. Используя полученные данные, рассчитайте по формуле (3.12) ЭДС первого и второго источников тока. Результаты расчетов запишите в табл. 7.
10. Соедините элементы х1 и х2 последовательно (рис.3.4, а), подсоедините к установке и произведите измерения согласно указаниям п. 4–6. Результаты измерений запишите в табл. 8.
а) б)
Рис. 3.4.
11. Соедините элементы х1 и х2 параллельно (рис.3.4, б), подсоедините к установке и произведите измерения согласно указаниям п. 4–6. Результаты измерений запишите в табл. 8.
12. Используя
полученные данные, рассчитайте по
формуле (3.12) ЭДС при последовательном
и параллельном соединениях источников
тока. Соответствующие значения ln возьмите из табл. 7. Результаты расчетов
запишите в табл. 8.
Соответствующие значения ln возьмите из табл. 7. Результаты расчетов
запишите в табл. 8.
Т а б л и ц а 7. Результаты измерений и вычислений
Номер опыта | U, В | Первый элемент | Второй элемент | Нормальный элемент | |||
lx, мм | x, В | lx, мм | x, В | ln, мм | n, В | ||
1 | 7 | 1,018 | |||||
2 | 6 | ||||||
3 | 5 | ||||||
Среднее значение | |||||||
Т
а б л и ц а 8. Результаты
измерений и вычислений
Результаты
измерений и вычислений
Номер опыта | U, В | Последовательное соединение | Параллельное соединение | ||
lx, мм | x, В | lx, мм | x, В | ||
1 | 7 | ||||
2 | 6 | ||||
3 | 5 | ||||
Среднее значение | |||||
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 3 из 3 Алгоритм решения задач по теме «Электромагнитная индукция»: 1. Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур. 2. Записать формулу:
3. Записать выражение для изменения магнитного потока и подставить в формулу закона электромагнитной индукции. 4. Записать математически все дополнительные условия (чаще всего это формулы закона Ома для полной цепи, силы Ампера или силы Лоренца, формулы кинематики и динамики). 5. Решить полученную систему уравнений относительно искомой величины. 6. Решение проверить. Электромагнитная индукция. Правило Ленца Явление электромагнитной индукции заключается в том, что в результате изменения во времени магнитного потока, который пронизывает замкнутый проводящий контур, в контуре возникает электрический ток. Открыто это явление было физиком из Великобритании Максом Фарадеем в 18311831 году. Формула магнитного потока Введем обозначения, необходимые нам для записи формулы. Для обозначения магнитного потока используем букву ФФ, площади контура – SS, модуля вектора магнитной индукции – BB, αα – это угол между вектором →BB→ и нормалью →nn→ к плоскости контура. Магнитный поток, который проходит через площадь замкнутого проводящего контура, можно задать следующей формулой: Φ=B⋅S⋅cos αΦ=B·S·cos α, Проиллюстрируем формулу. Рисунок 1.20.11.20.1. Магнитный поток через замкнутый контур. Направление нормали →nn→ и выбранное положительное направление →ll→ обхода контура связаны правилом правого буравчика. За единицу магнитного потока в СИСИ принят 11 вебер (Вб)(Вб). Магнитный поток, равный 1 Вб1 Вб, может быть создан в плоском контуре площадью 1 м21 м2 под воздействием магнитного поля с индукцией 1 Тл1 Тл, которое пронизывает контур по направлению нормали. 1 Вб=1 Тл⋅м21 Вб=1 Тл·м2 Закон Фарадея Изменение магнитного потока приводит к тому, что в проводящем контуре возникает ЭДС индукции δиндδинд. Она равна скорости, с которой происходит изменение магнитного потока через ограниченную контуром поверхность, взятой со знаком минус. Впервые экспериментально установил это Макс Фарадей. Он же записал свое наблюдение в виде формулы ЭДС индукции, которая теперь носит название Закона Фарадея: Определение 1 Закон Фарадея: δинд=−ΔΦΔtδинд=-∆Φ∆t Правило Ленца Определение 2 Согласно результатам опытов, индукционный ток, который возникает в замкнутом контуре в результате изменения магнитного потока, всегда направлен определенным образом. Проиллюстрируем правило Ленца рисунком, на котором изображен неподвижный замкнутый проводящий контур, помещенный в однородное магнитное поле. Модуль индукции увеличивается во времени. Пример 1 Рисунок 1.20.2.1.20.2. Правило Ленца Здесь ΔΦΔt>0∆Φ∆t>0, а δинд<0δинд<0 < 0. Индукционный ток IиндIинд протекает навстречу выбранному положительному направлению →ll→ обхода контура. Благодаря правилу Ленца мы можем обосновать тот факт, что в формуле электромагнитной индукции δиндδинд и ΔΦΔt∆Φ∆t противоположны по знакам. Если задуматься о физическом смысле правила Ленца, то это частный случай Закона сохранения энергии. Мы помогаем студентам с дипломными, курсовыми, контрольнымиУзнать стоимость ⇐ Предыдущая123 Читайте также: Как правильно слушать собеседника Типичные ошибки при выполнении бросков в баскетболе Принятие христианства на Руси и его значение Средства массовой информации США |
|
Последнее изменение этой страницы: 2020-12-17; просмотров: 1030; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
электромагнетизм — Какая формула дает ЭДС
Вопрос
Изменено 3 года, 5 месяцев назад
Просмотрено 122 раза
$\begingroup$
Недавно я изучал уравнения Максвелла и не смог правильно понять ЭДС $\zeta$. Математически имеем $\zeta=-\dfrac{d\Phi_B}{dt}$, где $\Phi_B$ — магнитный поток поверхности $\Sigma$.
Сначала нас учили, что также имеем: $\zeta=\oint_{\partial\Sigma} \overrightarrow{E}\cdot \overrightarrow{dl}$, где $\overrightarrow{E}$ — электрическое поле и $\overrightarrow{dl}$ является элементом $\partial\Sigma$, и, наконец, что: $\zeta=\oint_{\partial\Sigma} (\overrightarrow{v}\times\overrightarrow{B})\ cdot \overrightarrow{dl}$, где $\overrightarrow{B}$ — магнитное поле, а $\overrightarrow{v}$ — скорость (это скорость элемента $\partial\Sigma$?).
Но после некоторых исследований я думаю, что первая формула используется, когда $\Sigma$ находится в состоянии покоя (когда она не движется), а вторая используется, когда $\Sigma$ движется и $\overrightarrow{B }$ постоянен во времени.
Не могли бы вы дать мне формулу, обобщающую эти две формулы? и можем ли мы вывести его из $\zeta=-\dfrac{d\Phi_B}{dt}$
- электромагнетизма
- уравнений Максвелла
$\endgroup$
$\begingroup$
Правильный способ записи — использовать определение потока
$$\oint_{\partial R} \mathbf{E}\cdot d\mathbf{r} = -\frac{d\Phi_B}{dt } $$
Используя определение потока, мы имеем отношение
$$ \frac{d\Phi_B}{dt} = \frac{d}{dt}\iint_{R}\mathbf{B}\cdot d\mathbf{A}. $$
Следовательно, мы имеем
$$ \boxed{ \oint_{\partial R} \mathbf{E}\cdot d\mathbf{r} = \frac{d}{dt}\iint_{R}\mathbf {B}\cdot d\mathbf{A}}$$
Это следует понимать очень похоже на закон Ампера. Вы рисуете некоторую кривую $\partial R$, охватывающую область $R$ (обычно называемую «петлей Фарадиана»), а затем поле E вдоль $\partial R$ задается производная по времени от потока, заключенного в через $\partial R$.
Вы рисуете некоторую кривую $\partial R$, охватывающую область $R$ (обычно называемую «петлей Фарадиана»), а затем поле E вдоль $\partial R$ задается производная по времени от потока, заключенного в через $\partial R$.
$\endgroup$
$\begingroup$
ЭДС для сегмента пути представляет собой интеграл силы на единицу заряда, которая действовала бы на него, если бы заряд был размещен последовательно во всех точках этого пути.
Например, ЭДС индукции является интегралом индуцированного электрического поля. Это соленоидальное поле, сопровождающее изменяющееся магнитное поле.
Другим видом ЭДС является ЭДС движения. Это интеграл силы на единицу заряда, заставляющей заряды двигаться относительно проводника, когда этот проводник движется в магнитном поле. Эта электродвижущая сила возникает из-за внешнего магнитного поля, но на самом деле больше похожа на силу ограничения из механики (заряды не могут двигаться по кругу в проводнике, потому что они ограничены его стенками).
Другим примером является химическая ЭДС в ячейке Вольта: на макроскопическом уровне это макроскопическая сила, возникающая в результате химических реакций; он указывает в направлении, противоположном направлению макроскопического кулоновского электрического поля.
Во всех случаях путь обычно выбирается как представляющий интерес проводящий путь, такой как провод или путь через элемент Вольта. Но это может быть любой путь в пространстве. В частности, мы можем выбрать путь вне магнита, в воздухе или в вакууме. Путь может быть даже замкнутым — это часто рассматривается при рассмотрении индуцированного электрического поля в электрической цепи.
Во всех случаях EMF определяет чистую работу, которая была бы выполнена на единицу заряда, если бы ее тянули по пути, а все остальные вещи были бы заморожены. Таким образом, при выполнении интеграции интегрированная величина должна оцениваться за один раз. Итак, ЭДС — функция того времени.
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
ЭДС – Чтение Фейнмана
ОК. Побег невозможен. Это часть физики. Я не собираюсь вдаваться в подробности всего этого (потому что это блог о физике, а не о технике), но полезно рассмотреть основы, которые, по сути, являются правилами Кирхгофа 9.0096 . Для протокола: Густав Кирхгоф был немецким гением, который сформулировал эти законов об окружном движении , когда он был еще студентом, когда ему было лет 20 или около того. Он сделал это в рамках семинара 170 лет назад, а затем превратил в докторскую диссертацию. Наводит на мысли об этой песне Dire Straits — Вот как это делается — Эти парни не тупые. 🙂
Так что этот пост, по сути, просто «объяснение» изложения Фейнманом правил Кирхгофа, поэтому я пишу этот пост в основном для себя, чтобы ничего не упустить. Откровенно говоря, использование Фейнманом системы обозначений при работе с комплексными числами иногда сбивает с толку, поэтому да, я кое-что «перепишу». Прелесть фейнмановского представления электрических цепей в том, что он придерживается законов Максвелла при описании всех идеальных элементов цепи, поэтому продолжает использовать линейные интегралы электрического поля 9.0044 E вокруг замкнутых путей (вот что такое цепь) для описания так называемых пассивных элементов цепи, а также резюмирует идею электродвижущей силы при обсуждении так называемых активных элементов цепи , так это генератор. Это хорошо, потому что это связывает все это с тем, что мы узнали до сих пор, то есть с основными принципами , выраженными в системе уравнений Максвелла. Сказав это, я не буду делать эту ссылку здесь, в этом посте, потому что я чувствую, что это делает весь подход довольно тяжелым.
Прелесть фейнмановского представления электрических цепей в том, что он придерживается законов Максвелла при описании всех идеальных элементов цепи, поэтому продолжает использовать линейные интегралы электрического поля 9.0044 E вокруг замкнутых путей (вот что такое цепь) для описания так называемых пассивных элементов цепи, а также резюмирует идею электродвижущей силы при обсуждении так называемых активных элементов цепи , так это генератор. Это хорошо, потому что это связывает все это с тем, что мы узнали до сих пор, то есть с основными принципами , выраженными в системе уравнений Максвелла. Сказав это, я не буду делать эту ссылку здесь, в этом посте, потому что я чувствую, что это делает весь подход довольно тяжелым.
ОК. Давай сделаем это. Давайте сначала вспомним понятие импеданса .
Концепция импеданса Существует три идеальных (пассивных) элемента схемы: резистор, конденсатор и катушка индуктивности. Реальные элементы схемы обычно сочетают в себе характеристики всех из них, даже если они предназначены для работы как идеальные элементы схемы. В совокупности эти идеальные (пассивные) элементы схемы обозначаются как импедансы 9 .0096 , потому что… Ну… Потому что у них сопротивление . На самом деле, вы должны заметить, что если мы зарезервируем термины, оканчивающиеся на -ance, для свойства элементов схемы, а термины, оканчивающиеся на -или, для самих объектов, то мы должны называть их импедорами . Однако этот термин, похоже, не прижился.
Реальные элементы схемы обычно сочетают в себе характеристики всех из них, даже если они предназначены для работы как идеальные элементы схемы. В совокупности эти идеальные (пассивные) элементы схемы обозначаются как импедансы 9 .0096 , потому что… Ну… Потому что у них сопротивление . На самом деле, вы должны заметить, что если мы зарезервируем термины, оканчивающиеся на -ance, для свойства элементов схемы, а термины, оканчивающиеся на -или, для самих объектов, то мы должны называть их импедорами . Однако этот термин, похоже, не прижился.
Вы уже знаете, что такое импеданс. Я объяснял это раньше, особенно в своем посте о тонкостях, связанных с собственной и взаимной индуктивностью. Импеданс в основном расширяет концепцию сопротивление , как мы знаем это от цепей постоянного тока (постоянного тока) до цепей переменного тока (переменного тока). Проще говоря, когда задействованы переменные токи – то есть, когда поток заряда периодически меняет направление на противоположное – тогда вполне вероятно, что из-за свойств схемы сигнал тока будет отставать от напряжения сигнал , и поэтому у нас будет фаза разность говорит нам, на сколько. Итак, сопротивление — это просто действительное число R — это отношение между (1) напряжением, приложенным к резистору, и (2) током через него, поэтому мы пишем R = V/I — и у него есть величина, только , но импеданс — это «число», которое имеет как величину, так и фазу, так что это комплексное число или вектор.
Итак, сопротивление — это просто действительное число R — это отношение между (1) напряжением, приложенным к резистору, и (2) током через него, поэтому мы пишем R = V/I — и у него есть величина, только , но импеданс — это «число», которое имеет как величину, так и фазу, так что это комплексное число или вектор.
В технике такие «числа» с величиной и фазой называются векторов . Вектор представляет напряжения, токи и импедансы как фазы e vect или (обратите внимание на полужирный курсив pha 9096 pha : они объясняют, как мы получили фазы). На самом деле это просто , вращающийся вектор . Таким образом, вектор имеет различных магнитуд (A) и фазу (φ), которая определяется (1) примерно максимальной величиной A 0 , (2) примерно угловая частота ω и (3) некоторая начальная фаза (θ). Таким образом, мы можем записать амплитуду A как:
Таким образом, мы можем записать амплитуду A как:
A = A(φ) = A 0 · cos(φ) = A 0 · cos(ωt + θ)
Как обычно, в Википедии есть хороший анимация для него:
Если вам интересно, почему я использую функцию косинуса , а не синуса , ответ таков: это не имеет значения: синус и косинус — это одна и та же функция, за исключением Разность фаз π/2: просто поверните анимацию выше на 90 градусов, или подумайте о формуле: sinφ = cos(φ−π/2). 🙂
Таким образом, A = A 0 · cos(ωt + θ) — амплитуда . Это может быть напряжение, ток или любая другая реальная переменная. Сам вектор фазы представлен комплексным числом , т. е., так сказать, двумерным числом, которое можно записать в виде всего следующего: e i φ = A 0 ·cosφ + i ·A 0 ·sinφ = A 0 ·cos(ωt+θ) + i ·A 0 0 0 9 9 0 0 0 9 0 9 0 9 0 9 0 9 0 9 0 9 0 9 ( 0 0 9 1 9 7 ·sin) A 0 · E I (ωt+θ) = 0 · E I θ · E9096 I θ · E9096 θ · E9096 θ · θ · θ · 9096 θ · 9096 θ . · e i ωt с A 0 = A 0 · e i θ
· e i ωt с A 0 = A 0 · e i θ
Это просто формула Эйлера, и я боюсь, что должен отослать вас на мою страницу, посвященную основам , если вы этого не понимаете. Я знаю, о чем вы думаете: зачем нам векторное представление? Почему мы не можем просто удовлетвориться формулой A = A 0 · cos(ωt+θ)? Правдивый ответ: это просто для упрощения вычислений: с экспонентами работать проще, чем с косинусами или синусами. Например, написав e i (ωt + θ) = e i θ · e i ωt проще, чем писать cos(ωt + θ) = … […] Ну? […] Хмм… 🙂
Смотрите! Вы уже застряли. Вам придется использовать формулу cos(α+β) = cosα·cosβ − sinα·sinβ: вы получите те же результаты (просто сделайте это для простого расчета импеданса ниже), но это займет много времени. больше времени, и легче сделать ошибку. Сказав, почему запись комплексных чисел великолепна, я также должен предупредить вас. Есть несколько вещей, на которые вы должны обратить внимание. Одной из таких вещей является нотация. Другой тип математических операций, которые мы можем выполнять: обычно это нормально, но нам нужно быть осторожными с i 2 = –1 вещь при умножении комплексных чисел. Однако я не буду говорить об этом здесь, потому что это только еще больше запутает вас. 🙂
больше времени, и легче сделать ошибку. Сказав, почему запись комплексных чисел великолепна, я также должен предупредить вас. Есть несколько вещей, на которые вы должны обратить внимание. Одной из таких вещей является нотация. Другой тип математических операций, которые мы можем выполнять: обычно это нормально, но нам нужно быть осторожными с i 2 = –1 вещь при умножении комплексных чисел. Однако я не буду говорить об этом здесь, потому что это только еще больше запутает вас. 🙂
Просто для обозначения, позвольте мне отметить, что Фейнман написал бы A 0 как A 0 с маленькой шляпой или символом вставки (∧) поверх него, чтобы указать сложный коэффициент не переменная. Итак, он пишет A 0 9019.7 как Â 0 = A 0 · e i θ . Однако меня это сбивает с толку, и поэтому я предпочитаю использовать полужирный шрифт для любого комплексного числа, независимо от того, является оно переменным или нет.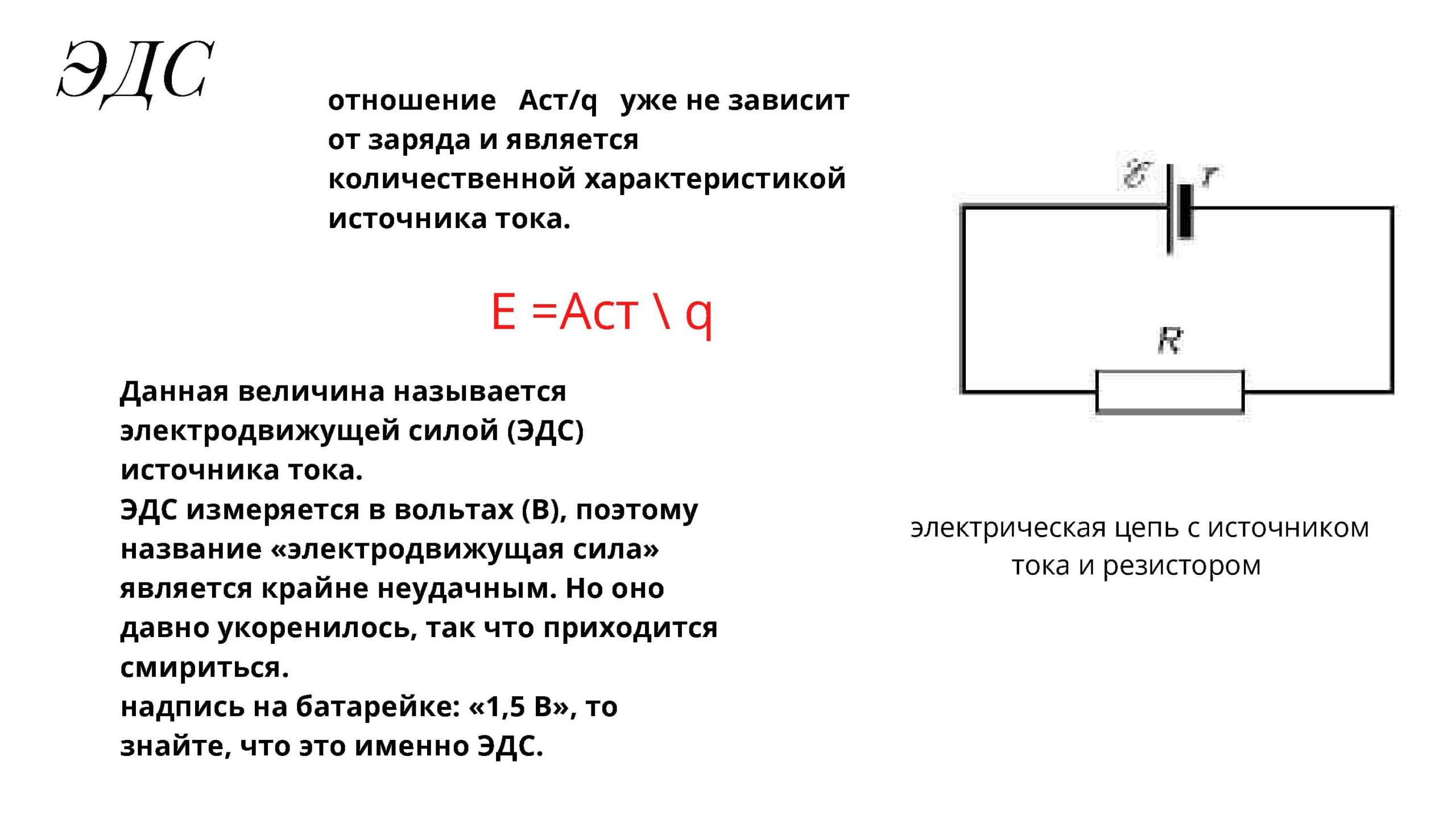 Недостатком является то, что нам нужно помнить, что коэффициент перед экспонентой — это , а не переменная: это комплексное число, но не переменная . В самом деле, посмотрите на это A 0 = A 0 · e i θ равенство осторожно : A 0 – это конкретное комплексное число , которое охватывает начальную фазу θ. Так что это , а не величина самого вектора, т.е. | А | = А 0 . На самом деле, амплитуда, амплитуда, фаза… Здесь мы используем много запутанной терминологии, поэтому вам нужно «понимать» математику.
Недостатком является то, что нам нужно помнить, что коэффициент перед экспонентой — это , а не переменная: это комплексное число, но не переменная . В самом деле, посмотрите на это A 0 = A 0 · e i θ равенство осторожно : A 0 – это конкретное комплексное число , которое охватывает начальную фазу θ. Так что это , а не величина самого вектора, т.е. | А | = А 0 . На самом деле, амплитуда, амплитуда, фаза… Здесь мы используем много запутанной терминологии, поэтому вам нужно «понимать» математику.
Полное сопротивление также не является переменной величиной. Это какая-то константа. При этом эта константа будет зависеть от угловой частоты ω. Итак… Ну… Просто подумайте об этом, пока будете читать дальше. 🙂 Значит импеданс около номер , как и сопротивление, но это сложный номер . Обозначим его через Z и, еще раз используя формулу Эйлера, запишем так:
Обозначим его через Z и, еще раз используя формулу Эйлера, запишем так:
Z = | З | e i θ = В / I = | В | e i (ωt + θ В ) /| я | e i (ωt + θ I ) = [| В |/| I |] · E I ( θ V — θ I ) , , , , , , , , , , , , , , , , , , , , , , , , θ, θ. сложное отношение , точно так же, как R = V/I было некоторым реальным отношением : это комплексное отношение , потому что оно имеет величину и направление, очевидно. Также обратите внимание, что, как я уже упоминал, импеданс, как правило, является некоторой функцией частоты ω, о чем свидетельствует член ωt в экспоненте, но поэтому мы не рассматриваем ω как переменную: V и Я переменные, и поэтому они зависят от ω, поэтому вы должны рассматривать ω как некоторый параметр. Я знаю, что я должен, возможно, , а не , будьте так откровенны в том, что происходит, но я хочу убедиться, что вы понимаете.
Также обратите внимание, что, как я уже упоминал, импеданс, как правило, является некоторой функцией частоты ω, о чем свидетельствует член ωt в экспоненте, но поэтому мы не рассматриваем ω как переменную: V и Я переменные, и поэтому они зависят от ω, поэтому вы должны рассматривать ω как некоторый параметр. Я знаю, что я должен, возможно, , а не , будьте так откровенны в том, что происходит, но я хочу убедиться, что вы понимаете.
Так что же происходит? Иллюстрация ниже (снова ссылка на Википедию) объясняет. Это довольно общий вид очень простой цепи переменного тока. Так что нам все равно, что такое импеданс: это может быть катушка индуктивности или конденсатор, или их комбинация, но нам все равно: мы просто называем это импедансом или импедансом или , если хотите. 🙂 Дело в том, что если мы применим переменный ток, то ток и напряжение будут расти и падать, но 9Токовый сигнал 0095 будет отставать от сигнала напряжения , и некоторый фазовый коэффициент θ говорит нам, насколько сильно, поэтому θ будет разностью фаз .
Теперь мы делим одно комплексное число на другое в этой формуле Z = V / I выше, и деление одного комплексного числа на другое не все и просто, поэтому позвольте мне повторить — запишите эту формулу для Z выше как:
V = I ∗ Z = I ∗| З | e i θ
Теперь, хотя формула V = I ∗ Z напоминает формулу V = I·R , следует обратить внимание на выделенный жирным шрифтом шрифт для 9004 и 9044. I и символ *, который я использую здесь для умножения. Жирный шрифт для V и I означает, что они являются векторами или комплексными числами. Что касается символа ∗, то он показывает, что мы не говорим о векторном векторном произведении 9.0044 A × B здесь, но произведение двух комплексных чисел. [Очевидно, что не векторное произведение точек на , потому что скалярное произведение векторов дает действительное число, а не какой-то другой вектор.] их:
[Очевидно, что не векторное произведение точек на , потому что скалярное произведение векторов дает действительное число, а не какой-то другой вектор.] их:
- В = | В | e i (ωt + θ V ) = V 0 · e i (ωt + θ В )
- I = | я | e i (ωt + θ I ) = I 0 · e i (ωt + θ I )
θ V и θ I являются, очевидно, так называемыми начальными фазами напряжения и тока соответственно. Этих «начальных» фаз не независимы: мы говорим о фазе разности действительно, между напряжением и токовым сигналом, и она определяется свойствами цепи. Фактически, в этом весь смысл: импеданс является свойством схемы и определяет, как сигнал тока изменяется в зависимости от сигнала напряжения. Фактически, мы часто выбираем точку t = 0 так, что θ V , и тогда нам нужно найти θ I . […] ХОРОШО. Давайте продолжим. Выписывая все факторы в В = I ∗ Z = I ∗| З | e i θ уравнение дает:
Фактически, в этом весь смысл: импеданс является свойством схемы и определяет, как сигнал тока изменяется в зависимости от сигнала напряжения. Фактически, мы часто выбираем точку t = 0 так, что θ V , и тогда нам нужно найти θ I . […] ХОРОШО. Давайте продолжим. Выписывая все факторы в В = I ∗ Z = I ∗| З | e i θ уравнение дает:
В = | В | e i (ωt + θ V ) = 4 04 09 Z= 9 04 09 9004 5 я | e i (ωt + θ I ) ∗| З | и я θ = | I || З | e i (ωt + θ I + θ)
должны выполняться равенства:
- | В | = | I || З | ⇔ | З | = | В |/| я |
- ωt + θ В = ωt + θ I + θ ⇔ θ = θ V − θ I
Готово!
Конечно, вы еще раз пожалуетесь на эти комплексные числа: напряжение и ток — это что-то реальное, не так ли? Итак, что такое на самом деле в этих комплексных числах? Ну… я могу просто сказать то, что уже сказал. Ты прав. Я использовал комплексную нотацию только для упрощения исчисления, поэтому учитывается только действительная часть тех комплекснозначных функций.
Ты прав. Я использовал комплексную нотацию только для упрощения исчисления, поэтому учитывается только действительная часть тех комплекснозначных функций.
ОК. Мы закончили с импедансом. Теперь мы можем обсудить импедансов , включая резисторы (для которых у нас не будет такого отставания или разности фаз, но понятие импеданса тем не менее применимо).
Однако, прежде чем я начну, вы должны подумать о том, что я сделал выше: я объяснил понятие импеданса, но мало что сделал с ним. Реальная проблема обычно заключается в том, что вы получаете напряжение как функцию времени, а затем вам нужно рассчитать импеданс цепи, а затем ток как функцию времени. Так что я просто показал фундаментальные отношения, но в реальной жизни вы не будете знать, что такое θ и θ I может быть. Что ж… Позвольте мне исправить это утверждение: мы дадим вам формулы для θ, когда мы будем обсуждать различные элементы схемы и их импеданс ниже, и тогда вы сможете использовать эти формулы для расчета θ I . 🙂
🙂
Начнем с того, что кажется самым простым : резистор. Реальный резистор на самом деле , а не , который легко понять, потому что он требует от нас понимания свойств настоящие материалов. Действительно, это может вас удивить или не удивить, но линейная зависимость между напряжением и током для реальных материалов является лишь приблизительной. Кроме того, понять, как резисторы рассеивают энергию , непросто. Действительно, в отличие от катушек индуктивности и конденсаторов, то есть двух других пассивных компонентов электрической цепи, резистор не накапливает , а рассеивает энергии, как показано ниже.
Это хорошая анимация (спасибо за нее еще раз в Википедии), так как она показывает, как энергия используется в электрической цепи. Обратите внимание, что небольшие движущиеся плюс соответствуют соглашению о том, что ток определяется как движение положительных зарядов, поэтому мы пишем I = dQ/dt вместо I = −dQ/dt. Это также объясняет направление линии поля E, которая была добавлена, чтобы показать, что заряды движутся вместе с полем, которое генерируется источником питания (которое здесь не показано). Итак, что мы имеем здесь, так это то, что на одной стороне цепи около 9 0095 генератор или источник напряжения будут создавать ЭДС , выталкивая заряды, и поэтому анимация показывает, как некоторые нагрузят – т. потерять своих толчков (что видно по изменению цвета с желтого на черный). Таким образом, мощность , то есть энергии в единицу времени , поставляется, а затем потребляется.
Это также объясняет направление линии поля E, которая была добавлена, чтобы показать, что заряды движутся вместе с полем, которое генерируется источником питания (которое здесь не показано). Итак, что мы имеем здесь, так это то, что на одной стороне цепи около 9 0095 генератор или источник напряжения будут создавать ЭДС , выталкивая заряды, и поэтому анимация показывает, как некоторые нагрузят – т. потерять своих толчков (что видно по изменению цвета с желтого на черный). Таким образом, мощность , то есть энергии в единицу времени , поставляется, а затем потребляется.
Чтобы увеличить ток в цепи выше, вам нужно увеличить напряжение, но увеличение обоих равнозначно увеличению мощность , потребляемая в цепи. Электрическая мощность — это напряжение, умноженное на ток, поэтому P = V·I (или v·i, если я использую строчные буквы, используемые в двух анимациях ниже). Теперь закон Ома (I = V/R) говорит, что если мы хотим удвоить ток, нам нужно удвоить напряжение, и поэтому мы учетверяем мощность, тогда: P 2 = V 2 · I 2 = (2·V 1 )·(2·I 1 ) = 4·V 1 ·I 1 = 2 · P 0196 1 . Итак, у нас есть закон квадрата-куба для мощности, который мы получаем, подставляя V вместо R·I или подставляя I вместо V/R, так что мы можем записать мощность P как P = V 2 /R = I 2 ·Р. Этот закон квадрата-куба говорит то же самое: если вы хотите удвоить напряжение или ток, вам фактически придется удвоить и то, и другое, и, следовательно, вы увеличите мощность в четыре раза.
Итак, у нас есть закон квадрата-куба для мощности, который мы получаем, подставляя V вместо R·I или подставляя I вместо V/R, так что мы можем записать мощность P как P = V 2 /R = I 2 ·Р. Этот закон квадрата-куба говорит то же самое: если вы хотите удвоить напряжение или ток, вам фактически придется удвоить и то, и другое, и, следовательно, вы увеличите мощность в четыре раза.
Но вернемся к импедансу : Закон Ома равен Z = В / I Закон для резисторов, но мы можем упростить его, потому что мы знаем, что напряжение на резисторе и ток, проходящий через на , равен в фазе . Следовательно, θ V и θ I идентичны и, следовательно, З | e i θ равно нулю и, следовательно, Z = | З |. Теперь | З | = | В |/| я | = V 0 / I 0 . Таким образом, полное сопротивление Z — это просто некоторое действительное число R = V 0 /I 0 , которое мы также можем записать как: E I (ωt +α ) )/(I 0 · E I (ωt +α ) ) ) ) ). где α = θ V = θ I
Таким образом, полное сопротивление Z — это просто некоторое действительное число R = V 0 /I 0 , которое мы также можем записать как: E I (ωt +α ) )/(I 0 · E I (ωt +α ) ) ) ) ). где α = θ V = θ I
Приведенное выше уравнение выходит из R = V 0 /I 0 к R = V(t)/I(t) = V/I. Обратите внимание на то же самое: второе уравнение говорит, что в любой момент времени напряжение и ток будут пропорциональны друг другу, с R или его обратной величиной в качестве константы пропорциональности. В любом случае, у нас есть формула для Z здесь:
Z = R = V/I = V 0 / I 0
Итак, это просто. Прежде чем мы перейдем к следующему, позвольте мне отметить, что сопротивление реальный резистор может зависеть от его температуры , поэтому в реальных приложениях желательно поддерживать его температуру как можно более стабильной. Вот почему реальные резисторы имеют номинальную мощность и рекомендуемые рабочие температуры. На изображении ниже показано, как так называемые резисторы радиатора могут быть установлены на радиаторе с помощью простого пружинного зажима, чтобы обеспечить отвод рассеиваемого тепла. Эти радиаторные резисторы довольно малы (всего 10 на 15 мм), но рассчитаны на 35 ватт — так что это довольно много для такой мелочи — , если правильно смонтировать.
Вот почему реальные резисторы имеют номинальную мощность и рекомендуемые рабочие температуры. На изображении ниже показано, как так называемые резисторы радиатора могут быть установлены на радиаторе с помощью простого пружинного зажима, чтобы обеспечить отвод рассеиваемого тепла. Эти радиаторные резисторы довольно малы (всего 10 на 15 мм), но рассчитаны на 35 ватт — так что это довольно много для такой мелочи — , если правильно смонтировать.
Как уже упоминалось, линейная зависимость между напряжением и током только приблизительно , и наблюдаемая зависимость также имеет место только для частот, которые не являются «слишком высокими», потому что, если частота становится очень высокой, свободное электроны начнут излучать энергию, поскольку они производят электромагнитное излучение. Так что всегда нужно смотреть на допуски реальных резисторов, которые могут составлять ± 5%, ± 10% или что-то еще. В любом случае… Далее.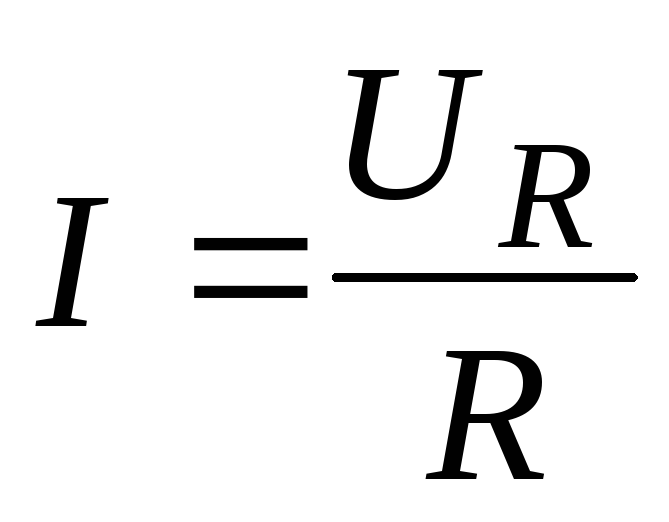
C = Q/V
Здесь легко спутать букву C с буквой C для кулон , которую я тоже сейчас использую, и так… Ну… Только не надо! 🙂 Значение символа обычно очевидно из контекста.
Что касается объяснения этой зависимости, то оно довольно простое: конденсатор состоит из двух отдельных проводников в пространстве, с положительным зарядом на одном и равным и противоположным (т.е. отрицательным) зарядом на другом. Итак, логика суперпозиции полей подразумевает, что если мы удвоим заряды, мы также удвоим поля, и поэтому работа, которую нужно совершить, чтобы перенести единичный заряд с одного проводника на другой, также удвоится! Вот почему разность потенциалов между проводниками пропорциональна заряду.
Формула C = Q/V фактически измеряет способность конденсатора хранить электрического заряда и, следовательно, хранить энергии , поэтому термин емкость действительно вполне уместен. Я дам вам погуглить несколько иллюстраций, подобных приведенной ниже, на которых показано, как на самом деле заряжается конденсатор в цепи. Обычно в цепи присутствует некоторое сопротивление, чтобы ограничить ток при подключении к источнику напряжения, и, следовательно, как вы можете видеть, коэффициент R, умноженный на C (R·C), определяет, насколько быстро или медленно конденсатор заряжается и/или разряжается. Также обратите внимание, что ток равен скорости изменения заряда во времени: I = dQ/dt.
Я дам вам погуглить несколько иллюстраций, подобных приведенной ниже, на которых показано, как на самом деле заряжается конденсатор в цепи. Обычно в цепи присутствует некоторое сопротивление, чтобы ограничить ток при подключении к источнику напряжения, и, следовательно, как вы можете видеть, коэффициент R, умноженный на C (R·C), определяет, насколько быстро или медленно конденсатор заряжается и/или разряжается. Также обратите внимание, что ток равен скорости изменения заряда во времени: I = dQ/dt.
В вышеупомянутом посте мы также приводим несколько формул для емкости конкретных типов конденсаторов. Например, для конденсатора с параллельными пластинами формула была C = ε 0 A/ d . Мы также упомянули его единицу измерения, которая составляет кулонов / вольт , очевидно, но — в честь Майкла Фарадея, который дал нам закон Фарадея и много других интересных формул — он называется фарад : 1 Ф = 1 Ц/В. C здесь кулон , конечно. Извините, нам приходится использовать C для обозначения двух разных вещей, но, как я уже говорил, значение символа обычно ясно из контекста.
C здесь кулон , конечно. Извините, нам приходится использовать C для обозначения двух разных вещей, но, как я уже говорил, значение символа обычно ясно из контекста.
В этом посте мы также говорили о том, как на самом деле работают диэлектрики, но мы говорили , а не об импедансе конденсатора, так что давайте сделаем это сейчас. Расчет довольно прост. Его интерпретация несколько меньше. Но… Что ж… Давайте попробуем.
Это ток, который заряжает конденсатор (извините, я продолжаю использовать оба термина взаимозаменяемо), и мы знаем, что ток — это скорость изменения заряда во времени (I = dQ/dt). Теперь вы помните, что в общем случае мы запишем вектор A as A = A 0 · e i ωt with A 0 = A 0 · e i θ , so A 0 — комплексный коэффициент, включающий начальную фазу, которую мы записали как θ V и θ I для напряжения и тока соответственно. Итак, мы будем представлять напряжение и ток, используя эти обозначения, поэтому напишем: V = V 0 · E I ωt и I = I 0 · E9096
Итак, мы будем представлять напряжение и ток, используя эти обозначения, поэтому напишем: V = V 0 · E I ωt и I = I 0 · E9096
I = dQ/dt = d(C·V)/dt = C·dV/dt
Что такое dV/dt? О… Вы скажете: V — это величина V , значит, она равна | В | = | В 0 · e i ωt | = | В 0 |·| e i ωt | = | В 0 | = |V 0 · e i θ | = |V 0 |·| и я θ | = |V 0 | = В 0 . Итак… Ну… Что? V 0 здесь какая-то константа! Это максимальная амплитуда V, так что… Ну… Его производная по времени равна нулю: dV 0 /dt = 0.
Итак… Ну… Что? V 0 здесь какая-то константа! Это максимальная амплитуда V, так что… Ну… Его производная по времени равна нулю: dV 0 /dt = 0.
Да. Верно. Мы сделали что-то очень неправильно здесь! Вам действительно нужно быть начеку с этой записью комплексных чисел, и вам нужно думать о том, что вы делаете. V — это не величина V , а его (изменяющаяся) амплитуда . Таким образом, это действительное напряжение V, которое меняется со временем: оно равно V 0 · cos(ωt + θ V ), что является реальной частью нашего вектора V . А? Да. Просто задержитесь на некоторое время. Я знаю, что это сложно, и, честно говоря, Фейнман нам здесь не особо помогает. Давайте сделаем один шаг назад, и поэтому — вы сразу поймете, почему я это делаю — давайте вычислим производную по времени нашего вектора В вместо производной по времени нашего реального напряжения В. Итак, мы вычисляем d V /dt, что равно:
Итак, мы вычисляем d V /dt, что равно:
d V /dtd( V 0 · e i ωt )/dt = V 0 · D ( E I ωt )/DT = V 0 · ( I V 0 · ( I V 0 · ( I V 0 · ( I V 0 · ( I V 0 · ( I V 0 · ( I V 0 ). ωt = I ω · V 0 · E I ωt = I ω · V
Примечание. Мы берем производную по времени от нашего вектора, и результатом является сам вектор, умноженный на i ω. Ну да. Это общее свойство экспонент, но все же… Замечательно! Мы получили бы то же самое с I , но пока нам это не нужно. Что мы делаем должны сделать, так это перейти от нашего отношения I = C·dV/dt, которое связывает действительных частей I и V друг с другом, к I = C·d V /dt отношение, которое связывает (комплекс) фазоров . Итак, мы пишем:
Что мы делаем должны сделать, так это перейти от нашего отношения I = C·dV/dt, которое связывает действительных частей I и V друг с другом, к I = C·d V /dt отношение, которое связывает (комплекс) фазоров . Итак, мы пишем:
I = C·dV/dt ⇔ I = C·d В /dt
Можем ли мы это сделать? Просто так? Мы просто заменяем I и V на I и V ? Да, можем. Почему? Ну… Мы знаем, что I является реальной частью I , поэтому мы можем написать I = Re ( I )+ Im ( I ) · i = I +
Im ( I )· i , и тогда мы можем записать правую часть уравнения как (C·d V /dt)· i . Теперь два комплексных числа равны, если и только если , их действительная и мнимая части совпадают, так что… Ну… Запишите все это, если хотите, используя формулу Эйлера, и вы увидите, что все это действительно имеет смысл.
Итак, что мы получаем? I = C·d V /dt дает нам:
I = C·d V /dt = C·( i ω)· V
4 Из этого /V
= C·( i ω) и, следовательно, окончательно получаем – – ! — что нам нужно получить:Z = V / I = 1/( i ωC)
если вы проверите на этом Фейнмана, вы увидите, что он — или, что более вероятно, его помощники — просто катаются по этому, не слишком заботясь о математической строгости. ХОРОШО. Теперь осталось интерпретировать это «число» Z = 1/( i ωC). Это чисто воображаемое число , и это действительно константа, хотя и сложный постоянный. Его можно переписать как:
Z = 1/( i ωC) = i -1 /(ωC) = – i /(ωC) = (1/ωC) · e − i ·π/2
[Извините. Я не могу быть здесь более откровенным. Это просто из чудес комплексных чисел: i -1 = — i. Просто проверьте один из моих постов о комплексных числах для получения более подробной информации.] Теперь — i множитель соответствует повороту минус 90 градусов, и это дает вам истинный смысл того, что обычно говорят о цепи с конденсатором: напряжение на конденсаторе будет отставать от ток с разностью фаз равной π/2, как показано ниже. Конечно, поскольку напряжение определяет ток, мы должны сказать, что ток отстает с разностью фаз 3 π/2, а не наоборот! Действительно, i -1 = – i = –1· i = i 2 · i = i 3 , так что это составляет три «оборота» фазы в направлении против по часовой стрелке, т.е. направление, в котором «поворачивается» наш угол ωt.
Я не могу быть здесь более откровенным. Это просто из чудес комплексных чисел: i -1 = — i. Просто проверьте один из моих постов о комплексных числах для получения более подробной информации.] Теперь — i множитель соответствует повороту минус 90 градусов, и это дает вам истинный смысл того, что обычно говорят о цепи с конденсатором: напряжение на конденсаторе будет отставать от ток с разностью фаз равной π/2, как показано ниже. Конечно, поскольку напряжение определяет ток, мы должны сказать, что ток отстает с разностью фаз 3 π/2, а не наоборот! Действительно, i -1 = – i = –1· i = i 2 · i = i 3 , так что это составляет три «оборота» фазы в направлении против по часовой стрелке, т.е. направление, в котором «поворачивается» наш угол ωt.
Это замечательный результат. На приведенном выше рисунке предполагается, что максимальная амплитуда напряжения и тока одинаковы, поэтому | З | = | В |/| я | = 1, но что, если их не то же самое? Что такое настоящих бит? Я вас слышу, правда: «К черту жирные буквы: что такое V и I? Что на самом деле?»
Ну… V и I — настоящие биты V = | В | e i (ωt+ θ V ) = V 0 · e i (ωt+ θ V ) and of I = | я | e i (ωt+ θ I ) = I 0 · e i (ωt+θ V −θ ) = I 0 · e i (ωt− θ ) = I 0 · e i (ωt+ π/2 ) respectively so, assuming θ V = 0 (как было сказано выше, это просто вопрос выбора удобной точки t = 0), получаем:
- В = В 0 ·cos(ωt)
- I = I 0 · cos(ωt + π/2)
Таким образом, разность фаз π/2 есть (со знаками надо быть осторожнее, конечно: θ = −π/2, но, похоже, здесь ток опережает ), но V 0 /I 0 отношение не обязательно должно быть равно единице, поэтому реальное напряжение и ток могут выглядеть примерно так, как показано ниже, где максимальная амплитуда тока составляет только половину 0095 максимум амплитуда напряжения.
Итак, давайте быстро проанализируем это: отношение V 0 /I 0 равно | З | = | В |/| я | = V 0 /I 0 = 1/ωC = (1/ω)(1/C) (обратите внимание, что не равно V/I = V(t)/I(t), что равно отношение, которое не имеет смысла, потому что I(t) проходит через ноль, когда ток переключает направление). И что? Ну… Это означает, что отношение обратно пропорционально как частоте ω, так и емкости C, как показано ниже. Подумайте об этом: если ω стремится к нулю, V 0 /I 0 переходит в ∞, что означает, что для заданного напряжения ток должен стремиться к нулю. Это имеет смысл, потому что мы говорим о постоянном токе, когда ω → 0, и конденсатор заряжается, и все: токов больше нет. Теперь, если C стремится к нулю, то есть мы говорим о конденсаторах практически без емкости, мы также получим крошечных токов. И наоборот, для больших C мы получим огромные токи, так как конденсатор может принимать практически любой заряд, который вы на него набрасываете, так что для малых V 0 /I 0 соотношения. Самое интересное, что нужно учитывать, это то, что ω стремится к бесконечности, так как отношение V 0 /I 0 также довольно мало. Что случается? Конденсатор не успевает зарядиться, поэтому он всегда находится в таком состоянии, когда в него втекают и вытекают большие токи, так как он не может создать напряжение , которое противодействовало бы электродвижущей силе, создаваемой источник напряжения.
Самое интересное, что нужно учитывать, это то, что ω стремится к бесконечности, так как отношение V 0 /I 0 также довольно мало. Что случается? Конденсатор не успевает зарядиться, поэтому он всегда находится в таком состоянии, когда в него втекают и вытекают большие токи, так как он не может создать напряжение , которое противодействовало бы электродвижущей силе, создаваемой источник напряжения.
ОК. Вот и все. Давайте обсудим последний (пассивный) элемент.
Катушки индуктивностиМы немного испортили вечеринку этой иллюстрацией выше, так как она уже дает разность фаз для катушки индуктивности: · π/2 , с L Индуктивностью из катушки
Итак, снова , предполагая, что θ V = 0, мы можем рассчитать I AS:
999 999 99999999. Of course, вам нужно еще раз связать это с реальным напряжением и реальный ток, поэтому давайте запишем действительные части наших фазоров : Просто чтобы убедиться, что вы не заснете во время чтения, я сделал еще один график того, как все может выглядеть. Итак, теперь это сигнал тока , который отстает сигнал напряжения с разностью фаз , равной θ = π/2. Кроме того, для полноты картины я должен показать вам, как отношение V 0 /I 0 теперь зависит от L и ω. Как теперь получить формулу Z = i ωL? В моем посте об индуктивности я объяснил, что такое катушка индуктивности : в основном это катушка провода. Его определяющая характеристика состоит в том, что изменяющийся ток вызовет в нем изменяющееся магнитное поле и, следовательно, некоторое изменение потока магнитного поля. Теперь закон Фарадея говорит нам, что это вызовет некоторую циркуляцию электрического поля в катушке , что составляет индуцирует разность потенциалов, которая называется электродвижущей силой (ЭДС). V = −Ɛ = L·(dI/dt) Теперь это очень похоже на соотношение I = C·dV/dt, которое мы получили для конденсаторов, и оно действительно полностью аналогично: нам просто нужно поменять местами I и V, C и L символы. V = L·dI/dt⇔ V = L·d I /dt Теперь d I /dt является такой же производной по времени, как и d V /dt. Мы вычисляем это как: d I /dtd( I 0 · e i ωt )/dt = I 0 ·d( e i ωt )/dt = I 0 ·( i ω)· e i ωt = I ω · I 0 · E I ωt = I ω · I SO, что мы получаем 4. = L·d I /dt = i ωL· I Сейчас, Z = В / I , поэтому Z = i ωL действительно! Давайте суммируем то, что мы нашли: Обратите внимание, что полное сопротивление конденсаторов уменьшается по мере увеличения частоты , а для катушек индуктивности наоборот. Мы объяснили это, заставив вас думать о токах: при заданном напряжении мы будем иметь большие токи для высоких частот и, следовательно, маленькое отношение V 0 /I 0 . Вы представляете, что происходит с катушкой индуктивности? , а не , так просто, поэтому я отсылаю вас к приложению ниже для получения дополнительных пояснений. Позвольте мне также отметить, что, как вы видите, импеданс (идеальных) катушек индуктивности и конденсаторов представляет собой чистое мнимое число , так что это комплексное число, не имеющее вещественной части. Однако в реальной жизни импеданс обычно имеет как действительную, так и мнимую часть, так что это будет, так сказать, своего рода смесь. Реальная часть называется «сопротивлением» R, а «мнимая» часть называется «реактивным сопротивлением» X. Формула для обоих приведена ниже: Но здесь я должен закончить свой пост на элементы схемы. Получилось довольно длинно, поэтому буду обсуждать правила Кирхгофа в моем следующем посте. Катушки индуктивности понять не просто — интуитивно , т.е. Вот почему я потратил так много времени на то, чтобы написать о них в своем другом посте о них, на который я должен вас здесь отослать. | я | e i (ωt+ θ I ) = I 0 · e i (ωt+θ V −θ ) = I 0 · e i (ωt− θ ) = I 0 · e i (ωt− π/2 )
| я | e i (ωt+ θ I ) = I 0 · e i (ωt+θ V −θ ) = I 0 · e i (ωt− θ ) = I 0 · e i (ωt− π/2 )  Действительно, здесь также можно написать, что | З | = | В |/| я | = V 0 /I 0 , но здесь мы находим, что V 0 /I 0 = ωL, поэтому здесь мы имеем простую линейную пропорциональность! Например, для данного напряжения V 0 у нас будет меньших токов по мере увеличения ω, так что это противоположно тому, что происходит с нашими идеальными конденсаторами. Я позволю вам подумать об этом… 🙂
Действительно, здесь также можно написать, что | З | = | В |/| я | = V 0 /I 0 , но здесь мы находим, что V 0 /I 0 = ωL, поэтому здесь мы имеем простую линейную пропорциональность! Например, для данного напряжения V 0 у нас будет меньших токов по мере увеличения ω, так что это противоположно тому, что происходит с нашими идеальными конденсаторами. Я позволю вам подумать об этом… 🙂 Теперь получается, что индуцированная ЭДС пропорциональна изменению тока. Итак, у нас здесь есть еще одна константа пропорциональности, так что это похоже на то, как мы определили сопротивление или емкость . Таким образом, во многих отношениях индуктивность — это просто еще один коэффициент пропорциональности. Если обозначить его L – говорят, что этот символ в честь русского физика Генрих Ленц , которого вы знаете из Закона Ленца – тогда определим его как: , а отрицательный знак указывает на то, что ЭДС противодействует изменению тока, поэтому она будет вызывать противодействующий ток . Однако мощность нашего источника напряжения обеспечит эффективное изменение тока, поэтому он будет противодействовать «противоэдс», создаваемой катушкой индуктивности. Если быть точным, то напряжение на выводах нашего индуктора, которое мы обозначим через V, будет равно и противоположно Ɛ, поэтому запишем:
Теперь получается, что индуцированная ЭДС пропорциональна изменению тока. Итак, у нас здесь есть еще одна константа пропорциональности, так что это похоже на то, как мы определили сопротивление или емкость . Таким образом, во многих отношениях индуктивность — это просто еще один коэффициент пропорциональности. Если обозначить его L – говорят, что этот символ в честь русского физика Генрих Ленц , которого вы знаете из Закона Ленца – тогда определим его как: , а отрицательный знак указывает на то, что ЭДС противодействует изменению тока, поэтому она будет вызывать противодействующий ток . Однако мощность нашего источника напряжения обеспечит эффективное изменение тока, поэтому он будет противодействовать «противоэдс», создаваемой катушкой индуктивности. Если быть точным, то напряжение на выводах нашего индуктора, которое мы обозначим через V, будет равно и противоположно Ɛ, поэтому запишем: Итак, мы пишем:
Итак, мы пишем: /I 0
/I 0 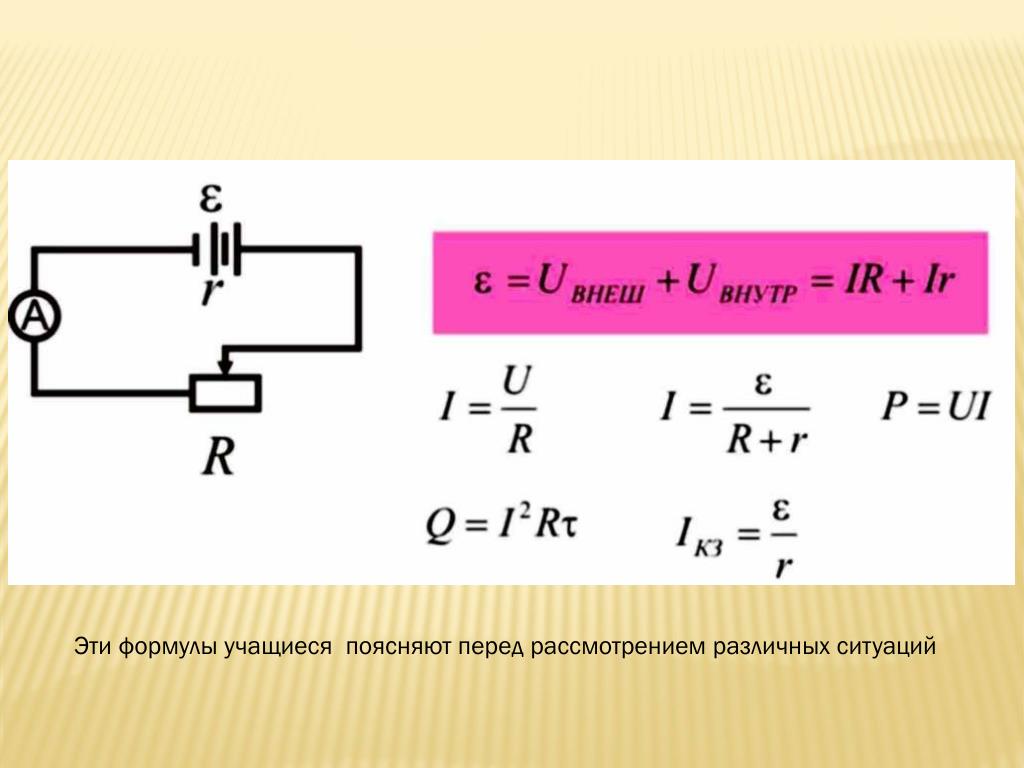 В технике мнимая часть импеданса называется реактивным сопротивлением , поэтому инженеры говорят, что идеальных конденсаторов и катушек индуктивности имеют чисто мнимое реактивное сопротивление .
В технике мнимая часть импеданса называется реактивным сопротивлением , поэтому инженеры говорят, что идеальных конденсаторов и катушек индуктивности имеют чисто мнимое реактивное сопротивление .  Но позвольте мне повторить основные моменты. Ключевая идея заключается в том, что мы накачиваем энергии в катушку индуктивности при подаче тока, и, как вы знаете, скорость изменения во времени равна мощности : P = dW/dt, поэтому мы говорим мощность и здесь, что равно напряжению умножить на ток : P = dW/dt = V·I. На приведенном ниже рисунке показано, что происходит, когда переменный ток подается на цепь с катушкой индуктивности. Таким образом, предполагается, что ток идет в одном, а затем в другом направлении, поэтому I > 0, а затем I < 0 и так далее. Мы также предполагаем некоторую красивую синусоидальную кривую для тока здесь (т.0044 красная кривая
Но позвольте мне повторить основные моменты. Ключевая идея заключается в том, что мы накачиваем энергии в катушку индуктивности при подаче тока, и, как вы знаете, скорость изменения во времени равна мощности : P = dW/dt, поэтому мы говорим мощность и здесь, что равно напряжению умножить на ток : P = dW/dt = V·I. На приведенном ниже рисунке показано, что происходит, когда переменный ток подается на цепь с катушкой индуктивности. Таким образом, предполагается, что ток идет в одном, а затем в другом направлении, поэтому I > 0, а затем I < 0 и так далее. Мы также предполагаем некоторую красивую синусоидальную кривую для тока здесь (т.0044 красная кривая 
Итак, да, для нарастания тока требуется энергия из какого-то внешнего источника, которая используется для преодоления «противоэдс» в катушке индуктивности, и эта энергия хранится в самой катушке индуктивности. [Если вы все еще задаетесь вопросом, почему он хранится в индукторе, подумайте над другим вопросом: где , иначе будет храниться?] Как хранится ? Посмотрите на график и подумайте: очевидно, она хранится в виде кинетической энергии зарядов. Это объясняет, почему энергия равна нулю, когда ток равен нулю, и почему энергия достигает максимума, когда ток достигает максимума. Так что да, во всем есть смысл! 🙂
Приведу еще один пример. На приведенном ниже графике предполагается, что ток достигает некоторого максимума. Когда он достигнет своего максимума, сохраненных энергии также будут исчерпаны. В этом примере предполагается постоянного тока , так что это цепь постоянного тока: ток нарастает, но затем стабилизируется на каком-то максимуме, который мы можем найти, применяя закон Ома к сопротивлению цепи: I = V/R. Сопротивление? Но мы говорили об идеальном индукторе? Мы. Если в цепи нет другого сопротивления, произойдет короткое замыкание, поэтому предполагается, что у нас действительно есть некоторое сопротивление в цепи, и, следовательно, мы должны также подумать о некоторой потере энергии на тепло от ток в сопротивлении. Если нет, что ж… Ваш источник энергии, очевидно, скоро исчерпает свои возможности. 🙂
Сопротивление? Но мы говорили об идеальном индукторе? Мы. Если в цепи нет другого сопротивления, произойдет короткое замыкание, поэтому предполагается, что у нас действительно есть некоторое сопротивление в цепи, и, следовательно, мы должны также подумать о некоторой потере энергии на тепло от ток в сопротивлении. Если нет, что ж… Ваш источник энергии, очевидно, скоро исчерпает свои возможности. 🙂
Так что же происходит? У нас есть некоторая изменяющаяся сила тока в катушке, но, очевидно, и какая-то инерция: катушка сама сопротивляется изменению тока через «противоэдс». Теперь для преодоления инерции требуется энергия или мощность, так что это мощность, поступающая от нашего источника напряжения: она будет компенсировать «противоэдс», поэтому мы можем эффективно представить небольшую схему с катушкой индуктивности и источник напряжения, как показано ниже.
Но почему мы пишем V = − Ɛ? Наш источник напряжения может иметь любое напряжение, не так ли? Да.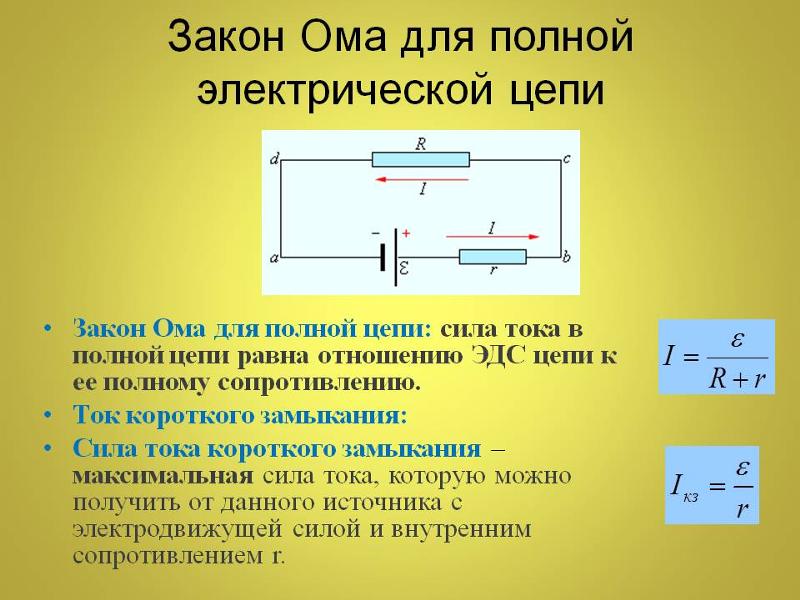 Конечно. Но, таким образом, катушка всегда будет обеспечивать ЭДС , то есть , противоположное этого напряжения. Подумайте об этом: у нас есть некоторое напряжение, которое прикладывается к клеммам катушки индуктивности, и поэтому у нас будет некоторый ток. Ток, который меняет . И именно этот ток будет генерировать ЭДС , что равно Ɛ = –L·(dI/dt). Так что не думайте о Ɛ как о какой-то константе: постоянен коэффициент собственной индуктивности L, а I (и, следовательно, dI/dt) и V являются переменными.
Конечно. Но, таким образом, катушка всегда будет обеспечивать ЭДС , то есть , противоположное этого напряжения. Подумайте об этом: у нас есть некоторое напряжение, которое прикладывается к клеммам катушки индуктивности, и поэтому у нас будет некоторый ток. Ток, который меняет . И именно этот ток будет генерировать ЭДС , что равно Ɛ = –L·(dI/dt). Так что не думайте о Ɛ как о какой-то константе: постоянен коэффициент собственной индуктивности L, а I (и, следовательно, dI/dt) и V являются переменными.
Дело в том, что у нас не может быть никакой разности потенциалов в идеальном проводнике, которым являются клеммы: любая разность потенциалов, то есть любое электрическое поле, на самом деле, вызвала бы огромные токи. Другими словами, напряжение V и ЭДС Ɛ должны уравновешивать друг друга, все время . В противном случае у нас были бы огромные токи в проводах, восстанавливающие равенство V = −Ɛ.
Позвольте мне использовать здесь аргумент Фейнмана.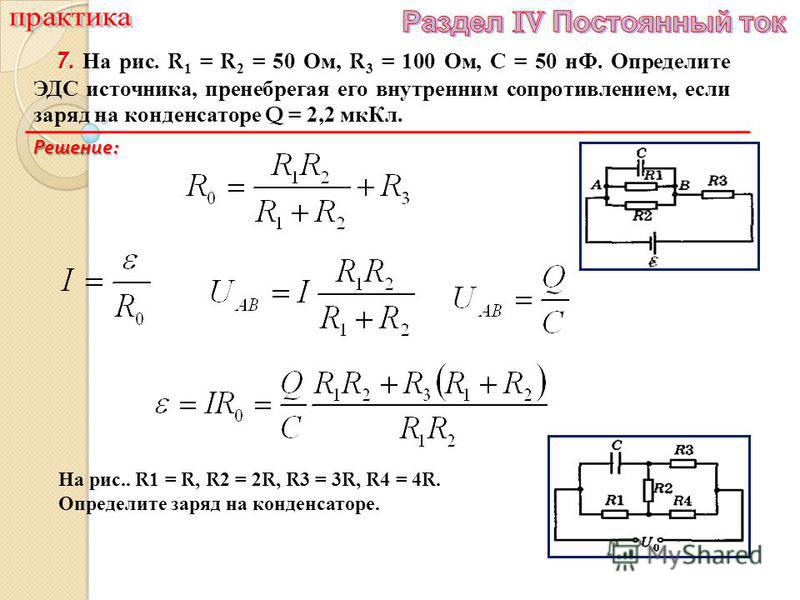 Возможно, это сработает лучше. 🙂 Наша идеальная катушка индуктивности показана ниже: она защищена какой-то металлической коробкой, чтобы гарантировать, что она не взаимодействует с остальной частью схемы. Итак, у нас есть некоторый ток I, который мы принимаем за переменный ток, и мы знаем некоторые напряжение необходимо, чтобы вызвало этот ток, так что это разность потенциалов V между клеммами.
Возможно, это сработает лучше. 🙂 Наша идеальная катушка индуктивности показана ниже: она защищена какой-то металлической коробкой, чтобы гарантировать, что она не взаимодействует с остальной частью схемы. Итак, у нас есть некоторый ток I, который мы принимаем за переменный ток, и мы знаем некоторые напряжение необходимо, чтобы вызвало этот ток, так что это разность потенциалов V между клеммами.
Полная циркуляция E — по всей цепи — может быть записана как сумма двух частей:
Теперь мы знаем, что циркуляция E может быть вызвана только некоторым изменением магнитного поля, что и происходит в катушке индуктивности:
Таким образом, это изменение магнитного потока вызывает «противоэдс», и поэтому интеграл слева фактически равен Ɛ, а не минус Ɛ, но +Ɛ. Теперь второй интеграл равен V, потому что это напряжение V между двумя выводами a и b. Таким образом, весь интеграл равен 0 = Ɛ + V и, следовательно, мы имеем это:
V = − Ɛ = L·dI/dt
Некоторый контент на этой странице был отключен 16 июня 2020 года в результате уведомления об удалении DMCA от Калифорнийского технологического института.
Вы можете узнать больше о DMCA здесь:
https://en.support.wordpress.com/copyright-and-the-dmca/
: Некоторый контент на этой странице был отключен 16 июня 2020 г. в результате уведомления Калифорнийского технологического института о нарушении Закона США «Об авторском праве в цифровую эпоху». Вы можете узнать больше о DMCA здесь:
Узнать определение, формулу, ЭДС и примеры
Таким же образом, когда заряд перемещается из одного места в другое, его потенциальная энергия преобразуется в кинетическую энергию, которая выражается через электрический потенциал как \(KE = Q\times V\). Следовательно, разность потенциалов можно описать как изменение потенциальной энергии и других форм энергии единичного заряда при его перемещении из одной точки А в В по цепи, а разность потенциалов этих двух точек можно представить как \(V_{B}-V_{A} (\Delta V) = \Delta U/q \)
В этой статье мы узнаем о разности потенциалов, формуле для расчета разности потенциалов с шагами и разнице между разностью потенциалов и ЭДС вместе с решенными примерами.
Разность потенциалов
Разность электрических потенциалов между двумя точками, которая определяется как работа, необходимая на единицу заряда для перемещения пробного заряда между двумя точками, известна как напряжение или разность электрических потенциалов.
Когда ток проходит между двумя точками P и Q в электрической цепи, мы учитываем заряд только между точками P и Q, поэтому знание точного потенциала в каждой точке не важно. Знание возможной разницы между двумя точками делает работу. В результате усилие, затрачиваемое на перенос единичного положительного заряда из одного места в другое, равно разности потенциалов между двумя точками. Этот процесс также можно наглядно понять по приведенной ниже диаграмме.
Разность потенциалов измеряется в вольтах (В), которые являются единицей измерения разности потенциалов в системе СИ. Если работа, связанная с переносом заряда в 1 кулон из одного места в другое, составляет 1 джоуль, то говорят, что разность потенциалов между двумя точками равна 1 вольту.
1 вольт = 1 джоуль/1 кулон
Вольт — это единица измерения разности потенциалов, а вольтметр — это прибор, используемый для ее измерения. При подключении вольтметра к цепи убедитесь, что положительный вывод подключен к положительному выводу элемента, а отрицательный вывод подключен к отрицательному выводу элемента.
Согласно закону Ома, разность потенциалов, падающая на фиксированное сопротивление в один ом при протекании через него тока в один ампер, называется вольтом. Другими словами, один вольт равен одному амперу, умноженному на один ом, или V = I×R
Термин «вольт» дан по имени физика Алессандро Вольта, которому приписывают изобретение электрической батареи.
Формула разности потенциалов
Формула для расчета разности потенциалов:
\( \delta v\ =\frac{\delta w}{\delta q} \)
Или,
\( V=\frac{W}{Q} \)
Где,
В = Разность потенциалов между двумя точками
Вт = Работа, выполненная для перемещения заряда между этими двумя точками
Q = Заряд, который необходимо переместить против электрического поля
Разность потенциалов можно рассчитать в разных терминах.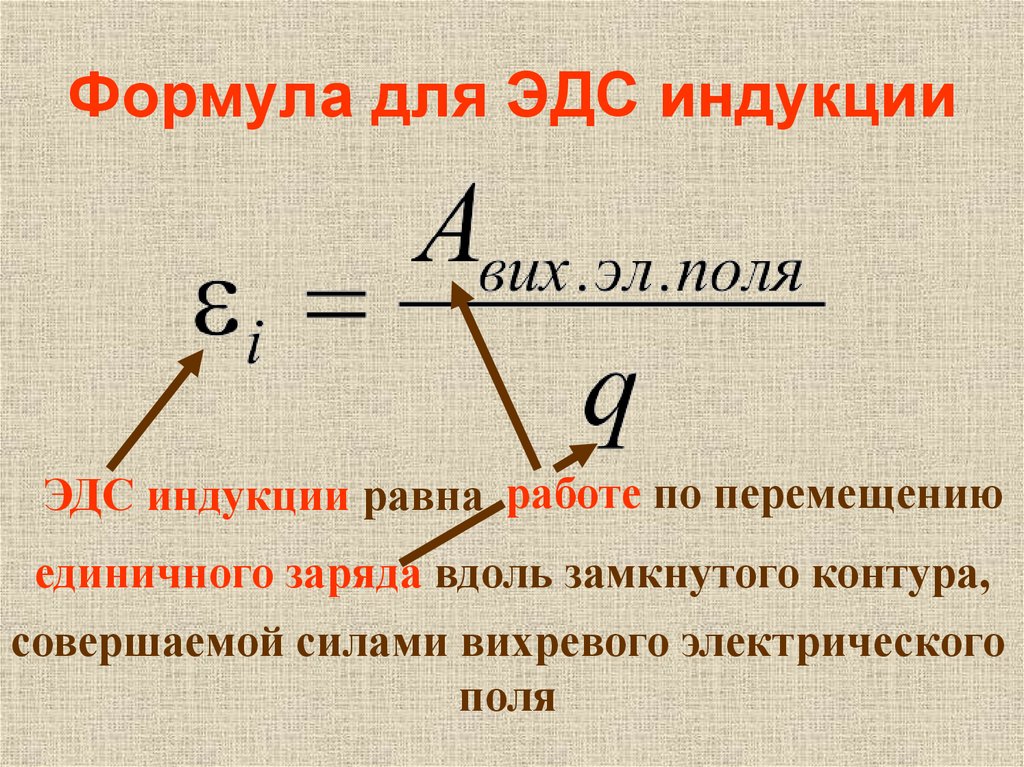 Обсудим некоторые другие формулы для расчета разности потенциалов.
Обсудим некоторые другие формулы для расчета разности потенциалов.
В пересчете на электрическое поле;
Так как, \( E\ =\ \frac{F}{q} \)
и, \( W\ =\ Fdx \)
\( E\ =\ -\frac{\partial V}{ \partial x} \)
Где,
E = электрическое поле
dx = длина пути
dV = разность потенциалов
Здесь отрицательный знак представляет электрический градиент
В соответствии с законом Ома,
2 \ ( V\ =\ I\ \cdot\ R \)
Где,
I = ток, протекающий через резистор
R = сопротивление
В = разность потенциалов
Шаги для нахождения разности потенциалов
В соответствии с формулами, приведенными выше, разность потенциалов можно рассчитать в два простых шага по каждой формуле:
Шаг 1. Определить работу (Вт), необходимую для перемещения заряд (Q).
Шаг 2 . Используйте формулу \( V\ =\ \frac{W}{Q}\) для расчета разности потенциалов.
Кроме того, разность потенциалов также может быть рассчитана, если электростатическая сила для заряда указана в формуле:
Шаг 1. Определить работу (Вт), используя \(W\ =\ Fd x \) и заряд.
Определить работу (Вт), используя \(W\ =\ Fd x \) и заряд.
Шаг 2. Используйте формулу \( V\ =\ \frac{W}{Q} \)или \(- \frac{d V}{dx} \) для расчета разности потенциалов.
Difference between the Potential difference and EMF
The difference between potential difference and EMF is as follows:
| Potential Difference | Electro-Motive Force (EMF) |
| В замкнутой цепи разность потенциалов между любыми двумя точками называется разностью потенциалов. | Максимальная разность потенциалов между двумя электродами элемента, когда цепь разомкнута, т. е. из элемента не поступает ток. |
| Энергия, рассеиваемая при протекании единичного заряда через компоненты, называется разностью потенциалов. | Определяется как энергия, подводимая к заряду ячейкой. |
Разность потенциалов зависит от сопротивления между двумя точками в прямо пропорциональной зависимости. | ЭДС не зависит от сопротивления цепи. |
| Разность потенциалов всегда меньше по величине по сравнению с ЭДС. | Величина ЭДС всегда больше разности потенциалов |
| Наводится только электрическими полями. | Электродвижущая сила может создаваться в электрическом, магнитном и гравитационном полях. |
| Формула для напряжения или разности потенциалов дается как; \( V\ =\ I\cdot R \) | Формула для ЭДС включает также внутреннее сопротивление элемента; \( E\ =\ I\ \left(R\ +r\right) \) |
| Разность потенциалов рассматривается как действие ЭДС. | Считается причиной разделения заряда. |
Разность потенциалов Решенные примеры
Пример 1. Какая работа совершается при перемещении заряда в 4 Кл через две точки с разностью потенциалов 2 В?
Решение: Дано,
Q = 4 Кл
В = 2 вольта
Вт = ?
По формуле;
\( W\ =\ Q\ \cdot V \)
\( W = 4\times 2 \)
W= 8 Дж
Пример 2. Какая разность потенциалов необходима, чтобы совершить работу 120 Дж, чтобы нести заряд 8 Кл между двумя точками?
Какая разность потенциалов необходима, чтобы совершить работу 120 Дж, чтобы нести заряд 8 Кл между двумя точками?
Решение: Дано,
W = 120 Дж
Q = 8 Кл
В = ?
По формуле;
\( W\ =\ Q\ \cdot V \)
В = 120/8
В = 15 вольт
Пример 3. Ток 6 ампер течет по проводу в течение 1 минуты при разности потенциалов 10 вольт подключен через него; вычислить работу, совершенную в этом процессе.
Решение: Дано,
I = 6 А
t = 60 с
В = 10 вольт
Вт = ?
По соотношениям:
\( W\ =\ Q\ \cdot V \)
Q = It
W = VIt
\( W = 10 \times 6 \times 60 \)
W = 3600 Дж
Вы можете просмотреть больше таких удивительных тем по физике. Получите помощь от экспертов, чтобы повысить уровень своей концептуальной игры и подготовиться к экзаменам с помощью выборочных учебных материалов, пробных тестов и ценных идей, которые помогут вам получить более высокие оценки и победить на экзамене. Загрузите бесплатное приложение Testbook, чтобы получить эксклюзивные предложения прямо сейчас!
Загрузите бесплатное приложение Testbook, чтобы получить эксклюзивные предложения прямо сейчас!
Часто задаваемые вопросы о разнице потенциалов
В.1. Что такое напряжение разности потенциалов?
Ответ 1 Согласно закону Ома, разность потенциалов, падающая на фиксированное сопротивление в один ом при протекании через него тока в один ампер, называется вольтом или напряжением. Другими словами, один вольт равен одному амперу, умноженному на один ом или \(V=I\times R\).
Q.2 Какова разность потенциалов между двумя точками?
Ответ 2 Разность потенциалов – это работа или энергия, высвобождаемая при перемещении единицы количества электрического заряда из одной точки в другую. Это представлено разницей потенциалов между этими двумя точками как \(V_{B}-V_{A} (\Delta V) = \Delta U/q \)
Q.3 В чем разница между током и разностью потенциалов?
Ответ 3 Электрический ток возникает в результате движения ионов или электронов внутри провода, а разность потенциалов — это работа, необходимая для переноса единичного положительного заряда из одного места в другое.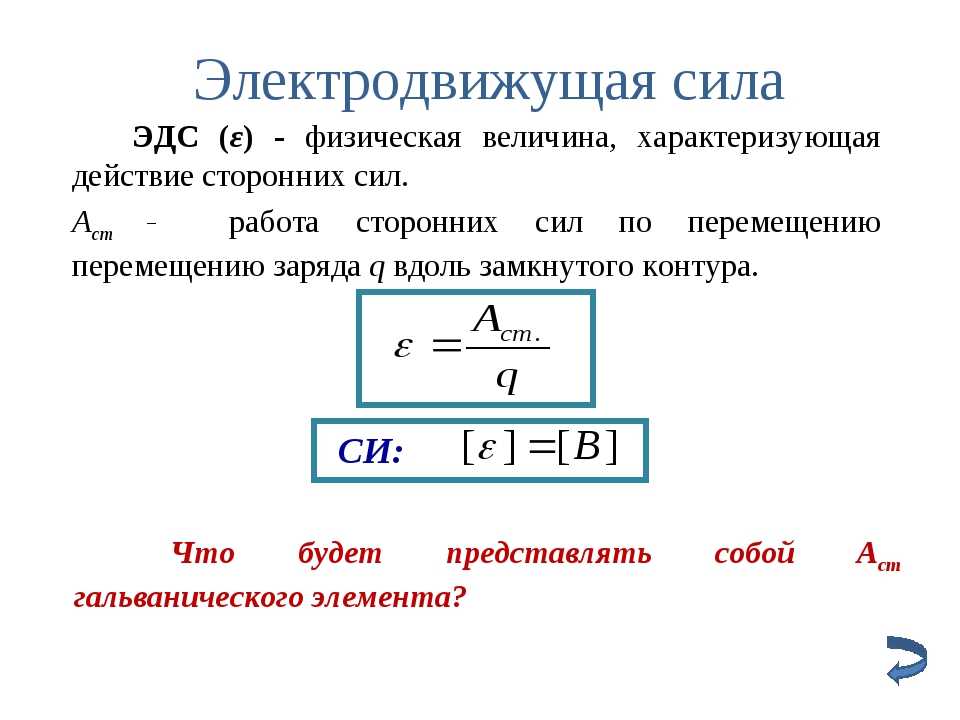


 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления

 Создаваемое индукционным током магнитное поле препятствует изменению вызвавшего этот индукционный ток магнитного потока. Ленц сформулировал это правило в 18331833 году.
Создаваемое индукционным током магнитное поле препятствует изменению вызвавшего этот индукционный ток магнитного потока. Ленц сформулировал это правило в 18331833 году.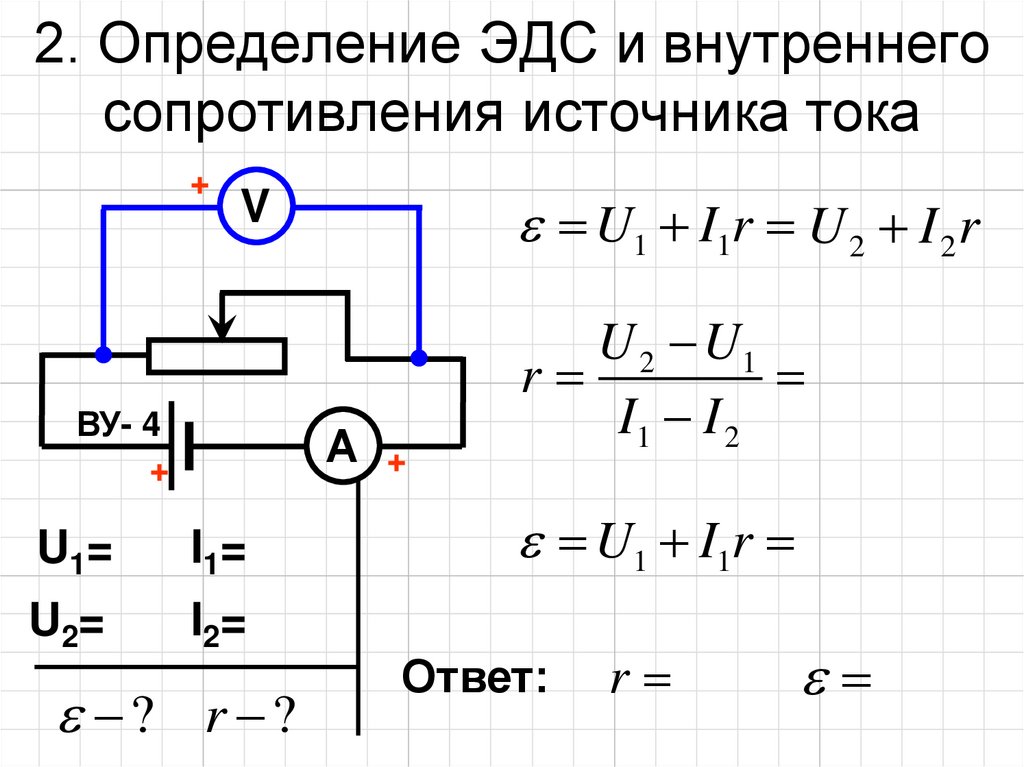 su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.007 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.007 с.) Вы можете узнать больше о DMCA здесь:
Вы можете узнать больше о DMCA здесь: