В Мексике в Ferrari вынуждены снизить мощность двигателей
30 октября 2022, 21:05
В этом сезоне все привыкли, что гонщики Ferrari, прежде всего Шарль Леклер, прекрасно проводят квалификации и регулярно претендуют на поул. Недаром Леклер и Карлос Сайнс 12 раз стартовали с первых позиций в 20 гонках. Но Гран При Мехико они начнут только пятым и седьмым, причём испанцу удалось опередить напарника.
Как пишет Auto Motor und Sport, на высоте 2238 м над уровнем моря могучая силовая установка Ferrari работает уже не столь эффективно, как двигатели соперников, в том числе и потому, что геометрические размеры турбины у неё несколько меньше. В обычных условиях это никак не проявляется, но в Мексике становится проблемой, и чтобы снизить нагрузку на турбонагнетатель, в Ferrari вынуждены несколько снижать мощность.
Из 22-х трасс чемпионата только три находятся заметно выше уровня моря, и мексиканская расположена выше всех, зато на всех остальных у Ferrari подобных проблем нет.
В команде это понимают и, разумеется, не должны удивляться возникающим сложностям. Крылья на F1-75 Сайнса и Леклера отрегулированы на меньший угол атаки по сравнению с соперниками, однако по максимальной скорости красные машины оказались только на 12-й и 16-й строчках соответствующего рейтинга. Только на первом секторе, состоящем в основном из прямых отрезков, гонщики Скудерии теряли до 0,5 секунды.
На то, что в команде понимают причины этого, намекнул Карлос, сказав следующее: «Мы понимаем, почему медленно едем, и на какие компромиссы нам приходится идти, однако в реальности всё оказалось ещё сложнее, чем мы ожидали».
Чтобы хотя бы немного компенсировать дефицит скорости на прямых, в Ferrari снизили уровень прижимной силы, а это привело к тому, что машины начали больше скользить. Резина при этом перегревается, и найти правильный баланс намного сложнее.
Оба гонщика жаловались на недостаточную поворачиваемость в медленных поворотах и избыточную – на быстрых участках круга.
Машина слишком сильно подскакивала на поребриках, и чувствовалось, что Леклер и Сайнс пилотируют менее уверенно, чем обычно.
В любом случае, их задача – добраться до финиша и показать максимально возможные результаты, ведь Mercedes постепенно отыгрывает отставание от итальянской команды. Две команды по-прежнему разделяет 53 очка, но если в Мексике Ferrari не удастся минимизировать возможные потери, то борьба за второе место в Кубке конструкторов серьёзно обострится.
- Карлос Сайнс-младший
- Ferrari
Нашли опечатку?
Выделите её и нажмите Ctrl+Enter!
Нашли опечатку? Выделите её и нажмите кнопку поиска.
Текст: Андрей Лось. Источник: Auto Motor und Sport
Использование материалов без письменного разрешения редакции F1News.ru запрещено.
Основы радиолокации — Импульсная и средняя мощность
Импульсная и средняя мощность
коэффициент заполнения
средняя мощность
импульсная мощность
длительность импульса
период повторения импульсов
Рисунок 1.
К пояснению понятий «коэффициент заполнения», «импульсная мощность», «средняя мощность»
коэффициент заполнения
средняя мощность
импульсная мощность
длительность импульса
период повторения импульсов
Рисунок 1. К пояснению понятий «коэффициент заполнения», «импульсная мощность», «средняя мощность»
Импульсная и средняя мощность
Энергия, излучаемая радиолокатором непрерывного излучения может быть легко определена,
поскольку передатчик такого радиолокатора работает непрерывно.
Однако у импульсного радиолокатора передатчик включается и выключается,
чтобы обеспечить получение информации о дальности цели с каждым импульсом.
Знать количество энергии, излучаемой в таком случае, важно, поскольку оно связано с мощностью на выходе передатчика,
от которой прямо зависит максимальная дальность действия радиолокатора.
Чем большую энергию излучает радиолокатор, тем большей будет дальность обнаружения им цели.
Энергия импульса равна произведению импульсной (пиковой, максимальной) мощности на длительность импульса. Однако измерительные средства (датчики), используемые в радиолокаторах для измерения мощности, выполняют измерение в течение интервала времени, превышающего длительность импульса. По этой причине период повторения импульсов включен в формулы для расчета мощности передатчика. Мощность, измеренная в течение такого периода, называют средней мощностью. Соотношение между средней и импульсной мощностью поясняется на Рисунке 1 и описывается следующей формулой:
| D = | = | τ | mit |
P = средняя мощность Pi = импульсная мощность τ = длительность импульса Τ = период повторения импульсов |
(1) | |
| Pi | Τ |
Импульсная мощность должна вычисляться чаще, чем средняя мощность.
Это вызвано тем, что большинство измерительных средств измеряют среднюю мощность напрямую,
как правило, путем оценки нагрева чувствительного элемента датчика.
Формула (1) определяет общий подход к расчету импульсной мощности по средней мощности и наоборот.
Поскольку некоторое количество энергии накапливается в модуляторе, система электропитания должна обеспечивать потребляемую мощность передатчика, лишь немного большую, чем средняя излучаемая мощность.
Коэффициент заполнения
Произведение длительности импульса (τ) на частоту повторения импульсов (prf), являющуюся величиной, обратной периоду повторения импульсов (Τ) в формуле (1), называют коэффициентом заполнения радиолокатора. Коэффициент заполнения показывает какую часть рабочего периода (периода повторения импульсов) система находится в «активном» состоянии.
Иногда при расчетах импульсной и средней мощности используется величина, обратная коэффициенту заполнения.
Такая величина называется скважностью.
Она показывает сколько импульсов укладывается в интервал времени, равный периоду повторения.
Сущность коэффициента заполнения можно пояснить на таком примере (Рисунок 1). Предположим, передатчик работает в течение 1 микросекунды и выключается на 99 микросекунд, затем снова запускается на 1 микросекунду и так далее. В таком случае передатчик работает в течении одной из ста микросекунд или 1/100 всего рабочего времени, то есть его коэффициент заполнения составляет 1/100 или 1 процент. Значение коэффициента заполнения используется при расчетах как импульсной мощности, так и средней мощности радиолокационной системы.
Формулы для быстрого расчета лошадиных сил и мощности
Формулы для быстрого расчета лошадиных сил и мощности
| ||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
с. =
с. =
с. =
с. (горизонтальная)
с. = мощность в л.с. 
на 2,68
Обзор работы, энергии и мощности: термины и формулы
Условия
Консервативная сила
Любая сила, сохраняющая механическую энергию, в отличие от неконсервативной сила. См. заявление о консервации механических энергия.
Консервативная система
Система, в которой сохраняется энергия.
Энергия
Способность выполнять работу.
Кинетическая энергия
Энергия движения.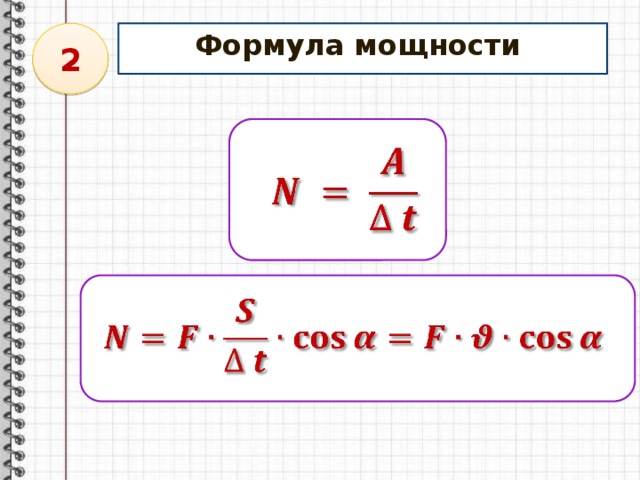
Неконсервативная сила
Любая сила, которая не сохраняет механическую энергию, в отличие от консервативная сила.
Независимость пути
Свойство консервативных сил, утверждающее, что работа, совершаемая на любом пути между двумя заданными баллы одинаковые.
Потенциальная энергия
Энергия конфигурации консервативной системы. Для формул видеть Определение потенциальной энергии, гравитационной потенциальная энергия и Определение потенциальной энергии с учетом позиционно-зависимого сила.
Полная механическая энергия
Сумма кинетической и потенциальной энергии консерванта система. См. определение полной механической энергии.
Работа
Сила, приложенная на расстоянии. Формулы см. в работе, выполняемой константой.
сила, параллельная перемещению, и работа, совершаемая любым
постоянная сила и
работу, совершаемую силой, зависящей от положения.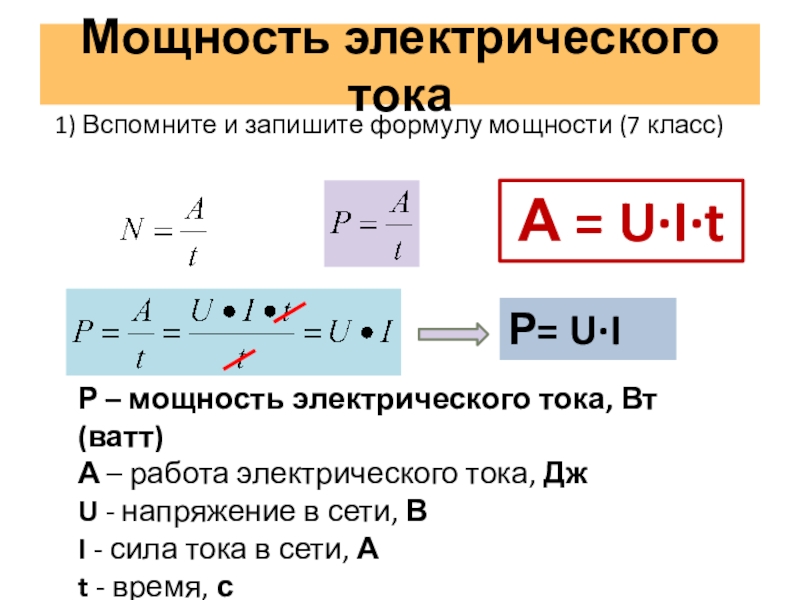
Джоуль
Единицы работы, эквивалентные ньютон-метру. Также единицы энергии.
Сила
Работа, совершаемая в единицу времени. Формулы см. в разделе Формула для среднего. сила, Определение мгновенной мощности и формула для мгновенной мощности.
Ватт
единица мощности; равно джоулю в секунду.
Формулы
| Работа, совершаемая постоянной силой, параллельной перемещению | Вт = Фх |
| Работа, совершаемая любой постоянной силой | Вт = Fx cos θ |
| Теорема о работе-энергии | Вт = ΔK |
| Формула средней мощности | = |
| Определение мгновенной мощности | Р = |
| Формула мгновенной мощности | Р = Fv cos θ |
| Работа, совершаемая силой, зависящей от положения | Вт = F ( x ) дх сила.  |