Формула Кирхгофа — это… Что такое Формула Кирхгофа?

Фо́рмула Кирхго́фа — аналитическое выражение для решения гиперболического уравнения в частных производных (т. н. «волнового уравнения») во всём трёхмерном пространстве. Методом спуска (то есть уменьшением размерности) из него можно получить решения двумерного (Формула Пуассона) и одномерного (Формула Д’Аламбера) уравнения.

Полная формулировка задачи и ответа

Рассмотрим уравнение

, где функции и определены на , а  — оператор Лапласа.

Это уравнение определяет распространение бегущей волны в n-мерной однородной среде со скоростью в моменты времени .

Для того, чтобы решение было однозначным, необходимо определить начальные условия. Начальные условия определяют состояние пространства (или, говорят, «начальное возмущение») в момент времени :

Тогда обобщённая формула Кирхгофа даёт решение этой задачи в трёхмерном случае:

где поверхностные интегралы берутся по сфере .

Сам Кирхгоф рассматривал только трёхмерный случай.

Простой вывод решения основной задачи использует преобразование Фурье.

Физические следствия

Передний и задний волновые фронты от локализованного в пространстве возмущения действуют на наблюдателя в течение ограниченного отрезка времени

Пусть в начальный момент времени на некотором компакте M есть локальное возмущение ( и/или ). Если мы находимся в некоторой точке , то, как видно из формулы (область интегрирования), возмущение мы почувствуем через время .

Вне отрезка времени , где , функция u(x ₀, t) равна нулю.

Таким образом, начальное возмущение, локализованное в пространстве, вызывает в каждой точке пространства действие, локализованное во времени, то есть возмущение распространяется в виде волны, имеющей передний и задний фронты, что выражает принцип Гюйгенса). На плоскости же этот принцип нарушается. Обоснованием этого является тот факт, что носитель возмущения, компактный в , уже не будет компактным в , а будет образовывать бесконечный цилиндр, и, следовательно, возмущение будет неограниченно во времени (у цилиндрических волн отсутствует задний фронт).

[1]

Решение уравнения колебаний мембраны (двумерного пространства)

(функция соответствует вынуждающей внешней силе)

с начальными условиями

задаётся формулой:

.

Решение одномерного волнового уравнения

(функция соответствует вынуждающей внешней силе)

с начальными условиями

имеет вид^[2]

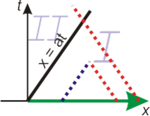В область II приходят характеристики только из одного семейства

При пользовании формулой Д’Аламбера следует учесть, что иногда решение может не быть единственным во всей рассматриваемой области . Решение волнового уравнения представляется в виде суммы двух функций: , то есть оно определяется двумя семействами характеристик: . Пример, показанный на рисунке справа, иллюстрирует волновое уравнение для полубесконечной струны, и начальные условия в нём заданы только на зеленой линии x≥0. Видно, что в область I приходят как ξ-характеристики, так и η-характеристики, в то время как в области II есть только ξ-характеристики. То есть, в области II формула Д’Аламбера не работает.

Применение формул

В общем виде формула Кирхгофа довольно громоздка, а потому решение задач математической физики с её помощью обычно является затруднительным. Однако, можно воспользоваться линейностью волнового уравнения с начальными условиями и искать решение в виде суммы трех функций: , которые удовлетворяют следующим условиям:

Сама по себе такая операция не упрощает пользование формулой Кирхгофа, но для некоторых задач оказывается возможным подбор решения, либо сведение многомерной задачи к одномерной путем замены переменных. Например, пусть . Тогда, сделав замену , уравнение для задачи «С» примет вид:

Таким образом, пришли к одномерному уравнению, а, значит, можно воспользоваться формулой Д’Аламбера:

В силу четности начального условия, решение сохранит свой вид во всей области .

Примечания

1. ↑ КИРХГОФА ФОРМУЛА // Физическая энциклопедия / Д. М. Алексеев, А. М. Балдин, А. М. Бонч-Бруевич, А. С. Боровик-Романов, Б. К. Вайнштейн, С. В. Вонсовский, А. В. Гапонов-Грехов, С. С. Герштейн, И. И. Гуревич, А. А. Гусев, М. А. Ельяшевич, М. Е. Жаботинский, Д. Н. Зубарев, Б. Б. Кадомцев, И. С. Шапиро, Д. В. Ширков; под общ. ред. А. М. Прохорова. — М.: Советская энциклопедия, 1988—1998.
2. ↑ Формула Д’Аламбера в Физической энциклопедии

Литература

• Михайлов В.П., Михайлова Т.В., Шабунин М.И. Сборник типовых задач по курсу Уравнения математической физики. — М.: МФТИ, 2007. — ISBN 5-7417-0206-6

Ссылки

Первый закон Кирхгофа | Все Формулы

   

Первый закон Кирхгофа — Алгебраическая сумма токов, сходящихся в узле, равна нулю.

   

Первый закон Кирхгофа оперирует понятием узел. Узлом называется точка, в которой сходится более чем два проводника. Ток, текущий к узлу, считается положительным, текущий от узла имеет противоположный знак.

Первый закон Кирхгофа

Иными словами, сколько тока втекает в узел, столько из него и вытекает. Данный закон следует из закона сохранения заряда. Если цепь содержит p узлов, то она описывается p − 1 уравнениями токов.

На нашем рисунке два узла, следовательно уравнений будет всего одно. Суммарный ток мы определим, используя первый закон Кирхгофа:

   

Давайте решим более сложную задачу на первое правило Кирхгофа.

Первое правило Кирхгофа 2

В данной схеме у нас четыре узла, следовательно у нас будет всего три уравнения.

Первый узел (а) :

   

Второй узел (b) :

   

Третий узел (c) :

   

Зная некоторые токи, с помощью данного закона, мы можем найти остальные (неизвестные) токи.

В формуле мы использовали :

I — Ток в цепи

Формула дифракции Кирхгофа — Kirchhoff’s diffraction formula

Кирхгофа «с дифракционной формулой (также Френеля-Кирхгофа дифракции формула ) могут быть использованы для моделирования распространения света в широком диапазоне конфигураций, либо аналитически илипомощью численного моделирования . Это дает выражение для волнового возмущениякогда монохроматическая сферическая волна проходит через отверстие в качестве непрозрачного экрана. Уравнение получается путем несколько приближений к интегральной теореме Кирхгоф , которая использует теорему Грина для получения решения однородного волнового уравнения .

Вывод формулы дифракции Кирхгофа

Интегральная теорема Кирхгофа , иногда называют интегральной теоремы Френеля-Кирхгофа, использует тождества Грина , чтобы получить решение однородного волнового уравнения в произвольной точке

Р в терминах значений решения волнового уравнения и его производной первого порядка в все точки на произвольную поверхность, покрывающую P .

Решение , предложенное по интегральной теореме для монохроматического источника:

U(п)знак равно14π∫S[U∂∂N(еяКss)-еяКss∂U∂N]dS,{\ Displaystyle U (P) = {\ гидроразрыва {1} {4 \ пи}} \ Int _ {S} \ влево [U {\ гидроразрыва {\ парциальное} {\ парциальное п}} \ влево ({\ гидроразрыва { E ^ {ИКС}} {S}} \ справа) — {\ гидроразрыв {е ^ {ИКС}} {S}} {\ гидроразрыва {\ парциального U} {\ парциального п}} \ правый] Ds,}

где U представляет собой комплексную амплитуду возмущения на поверхности, к это волновое число , а s представляет собой расстояние от Р до поверхности.

Сделанные предположения являются:

• U и ∂ U / ∂ п являются прерывистыми на границах апертуры,
• расстояние до точечного источника и размерность открытия S намного больше , чем λ.

точечный источник

Геометрическое расположение используется при выводе формулы дифракции Kirchhhoff в

Рассмотрим монохроматического точечного источника при P ₀ , который освещает отверстие в экране. Энергия волны , излучаемой точечного источника убывает как обратный квадрат расстояния, поэтому амплитуда убывает как обратная величина расстояния. Комплексная амплитуда возмущения на расстоянии г дается

U(р)знак равноaеяКрр,{\ Displaystyle и (г) = {\ гидроразрыва {ае ^ {IKR}} {г}}}

где представляет собой величину возмущения в точечном источнике.

Возмущение в точке Р может быть найдено путем применения интегральной теоремы к замкнутой поверхности , образованного пересечение сферы радиуса R с экраном. Интегрирование производится по областям A ₁ , ₂ и ₃ , что дает

U(п)знак равно14π[∫A1+∫A2+∫A3(U∂∂N(еяКss)-еяКss∂U∂N)]dS,{\ Displaystyle U (P) = {\ гидроразрыва {1} {4 \ пи}} \ влево [\ Int _ {А_ {1}} + \ Int _ {А_ {2}} + \ Int _ {А_ {3 }} \ влево (U {\ гидроразрыва {\ парциального} {\ парциального п}} \ влево ({\ гидроразрыв {е ^ {ИКС}} {s}} \ справа) — {\ гидроразрыв {е ^ {ИКС}} {S}} {\ гидроразрыва {\ парциального U} {\ парциального п}} \ справа) \ правый]} Ds.

Для решения уравнения, то предполагается , что значения U и ∂ U / ∂ п в области ₁ являются такими же , как , когда на экране нет, давая в Q :

UA1знак равноaеяКрр,{\ Displaystyle U_ {А_ {1}} = {\ гидроразрыва {ае ^ {IKR}} {г}}}

∂UA1∂Nзнак равноaеяКрр[яК-1р]соз⁡(N,р),{\ Displaystyle {\ гидроразрыва {\ парциального U_ {А_ {1}}} {\ парциального п}} = {\ гидроразрыв {ая ^ {IKR}} {г}} \ левый [ик — {\ гидроразрыв {1} { г}} \ вправо] \ сов (п, г),}

где R представляет собой длину Р ₀ Q , и ( п , г ) угол между Р ₀ Q и нормалью к отверстию.

Кирхгофа предполагает , что значения U и ∂ U / ∂ п в ₂ равны нулю. Это означает , что U и ∂ U / ∂ п являются прерывистыми на краю отверстия. Это не так, и это одна из приближений , используемых при выводе уравнения. Эти предположения иногда называют граничными условиями Кирхгофа.

Вклад от А ₃ к интегралу также предполагается равным нулю. Это может быть оправданно, сделав предположение о том, что источник начинает излучать в определенное время, а затем, сделав R достаточно большим, так что , когда возмущение в Р рассматриваются, вклад от А _— не приехал туда. Не Такая волна уже не монохроматическая , так как монохроматическая волна должна существовать во все времена, но это предположение не является необходимым, и более формальным аргумент избежать его использования был получен.

У нас есть

∂∂N(еяКss)знак равноеяКss[яК-1s]соз⁡(N,s),{\ Displaystyle {\ гидроразрыва {\ парциального} {\ парциального п}} \ влево ({\ гидроразрыв {е ^ {ИКС}} {s}} \ справа) = {\ гидроразрыва {е ^ {ИКС}} {s} } \ левой [ик — {\ гидроразрыва {1} {s}} \ вправо] \ сов (п, з),}

где ( п , s ) представляет собой угол между нормалью к отверстию и PQ .

И, наконец, термины 1 / R и 1 / с предполагаются пренебрежимо малы по сравнению с к , так как г и с , как правило , значительно больше , чем 2л / к , которая равна длине волны . Таким образом, выше интеграл, который представляет собой комплексную амплитуду в P , становится

U(п)знак равно-яa2λ∫A1еяК(р+s)рs[соз⁡(N,р)-соз⁡(N,s)]dA1,{\ Displaystyle U (Р) = — {\ гидроразрыва {IA} {2 \ Lambda}} \ Int _ {А_ {1}} {\ гидроразрыва {е ^ {ик (г + s)}} {RS}} [ \ сов (п, г) -. \ сов (п, з)] \, д {А_ {1}}}

Это формула дифракции Кирхгофа или Френеля-Кирхгофа.

Эквивалентность уравнения Гюйгенса-Френеля

Геометрическое расположение используется, чтобы выразить формулу Кирхгофа в форме, аналогичной Гюйгенса-Френеля

Принцип Гюйгенса-Френеля может быть получена путем интегрирования по другую замкнутую поверхность. Площадь ₁ выше , заменяется на волновой фронт от P ₀ , который почти заполняет отверстие, и часть конуса с вершиной в точке P ₀ , которая наклеена ₄ на диаграмме. Если радиус кривизны волны достаточно велик, вклад от A _— можно пренебречь. У нас также есть

χзнак равноπ-(р0,s),{\ Displaystyle \ х = \ пи — (R_ {0}, с),}

где χ как определено в принципе Гюйгенса-Френеля , и потому ( п , г ) = 1. Комплексная амплитуда волнового фронта при г ₀ задается

U(р0)знак равноaеяКр0р0,{\ Displaystyle U (R_ {0}) = {\ гидроразрыва {ае ^ {ikr_ {0}}} {R_ {0}}}.}

Дифракционная формула приобретает следующий вид

U(п)знак равно-я2λaеяКр0р0∫SеяКss(1+соз⁡χ)dS,{\ Displaystyle U (Р) = — {\ гидроразрыва {я} {2 \ Lambda}} {\ гидроразрыва {ае ^ {ikr_ {0}}} {R_ {0}}} \ Int _ {S} {\ гидроразрыва {е ^ {ИКС}} {S}} (1+ \ соз \ х) \, Д.С..}

Это формула дифракции Кирхгофа, который содержит параметры , которые должны были быть произвольно назначены в выводе Гюйгенса-Френеля уравнения.

Расширенный источник

Предположим , что отверстие освещается расширенной волны источника. Комплексная амплитуда на апертуре задается U ₀ ( г ).

Предполагается, как и прежде, что значения U и ∂ U / ∂ п в области ₁ являются такими же , как , когда на экране нет, то, что значения U и ∂ U / ∂N в A ₂ равны нулю (граничные условия Кирхгофа) и что вклад от а ₃ до интеграла также равны нулю. Кроме того , предполагается , что 1 / с пренебрежимо мала по сравнению с к . Тогда мы имеем

U(п)знак равно-14π∫A1еяКss[яКU0(р)соз⁡(N,s)-∂U0(р)∂N]dS,{\ Displaystyle U (Р) = — {\ гидроразрыва {1} {4 \ пи}} \ Int _ {А_ {1}} {\ гидроразрыва {е ^ {ИКС}} {s}} \ влево [ikU_ {0 } (г) \ сов (N, S) -. {\ гидроразрыва {\ парциального u_ {0} (г)} {\ парциального п}} \ \ вправо], Д.С.}

Это наиболее общая форма дифракционной формулы Кирхгофа. Для решения этого уравнения для протяженного источника, дополнительная интеграция будет необходимо просуммировать вклад отдельных точек в источнике. Если, однако, мы предполагаем, что свет от источника в каждой точке в отверстии имеет четко определенное направление, которое в случае, если расстояние между источником и отверстием значительно больше, чем длиной волны, то можно записать

U0(р)≈a(р)еяКр,{\ Displaystyle U_ {0} (г) \ ок а (г) е ^ {IKR}}

где ( г ) является величина возмущения в точке г в раскрыве. Тогда мы имеем

∂U0(р)∂Nзнак равнояКa(р)соз⁡(N,р){\ Displaystyle {\ гидроразрыва {\ парциальное {U_ {0} (г)}} {\ парциальное п}} = IKA (г) \ соз (п, г)}

и поэтому

U(п)знак равно-я2λ∫Sa(р)еяКss[соз⁡(N,s)-соз⁡(N,р)]dS,{\ Displaystyle U (Р) = — {\ гидроразрыва {я} {2 \ Lambda}} \ int _ {S} A (R) {\ гидроразрыва {е ^ {ИКС}} {S}} [\ соз (п , с) — \ соз (п, г)] \, Д.С.}.

Фраунгофера и Френеля дифракционные уравнения

Несмотря на различные приближения , которые были сделаны в достижении формулы, является достаточной , чтобы описать большинство проблем в инструментальной оптике. Это происходит главным образом потому , что длина волны света намного меньше , чем размеры любых препятствиях. Аналитические решения не представляется возможным для большинства конфигураций, но дифракции Френеля уравнение и дифракции Фраунгофера уравнение, являются приближениями формулы Кирхгофа для ближнего поля и дальнего поля , могут быть применены к очень широкому диапазону оптических систем.

Одним из важных предположений , сделанных в достижении дифракционной формулы Кирхгофа является то , что г и s значительно больше , чем λ. Дальнейшее приближение может быть сделано, что существенно упрощает уравнение далее: это является то , что расстояние Р ₀ Q и QP , значительно больше , чем размеры апертуры. Это позволяет сделать еще два приближения:

• сов ( п, г ) — сов ( п, з ) заменяется 2cos & beta ; , где β угол между Р ₀ Р и нормалью к отверстию. Фактор 1 / RS заменяется на 1 / г « с » , где R « и s » расстояния от P ₀ и P до начала координат, которая расположена в отверстии. Комплексная амплитуда становится:

U(п)знак равно-яaсоз⁡βλр’s’∫SеяК(р+s)ds,{\ Displaystyle U (P) = -. {\ Гидроразрыва {И. \ соз \ бета} {\ Lambda г на}} \ int _ {S} ^ {е К (г + s)} \, DS}

• Предположим , что отверстие лежит в ху плоскости, а координаты Р ₀ , Р и Q (общая точка в отверстии) являются ( х ₀ , у ₀ , г ₀ ), ( х , у , г ) и ( х ‘ у ‘ , 0) соответственно. Тогда мы имеем:

 р2знак равно(Икс0-Икс’)2+(Y0-Y’)2+Z02,{\ Displaystyle ~ г ^ {2} = (X_ {0} -x ‘) ^ {2} + (у- {0} -y’) ^ {2} + z_ {0} ^ {2}}

 s2знак равно(Икс-Икс’)2+(Y-Y’)2+Z2,{\ Displaystyle ~ s ^ {2} = (х-х ‘) ^ {2} + (у-у’) ^ {2} + Z ^ {2}}

 р’2знак равноИкс02+Y02+Z02,{\ Displaystyle ~ г ‘^ {2} = X_ {0} ^ {2} + у- {0} ^ {2} + z_ {0} ^ {2}}

 s’2знак равноИкс2+Y2+Z2,{\ Displaystyle ~ s’^ {2} = х ^ {2} + у ^ {2} + Z ^ {2}.}

Мы можем выразить г и S следующим образом :

рзнак равнор'[1-2(Икс0Икс’+Y0Y’)р’2+Икс’2+Y’2р’2]1/2,{\ Displaystyle г = г ‘\ влево [1 — {\ гидроразрыва {2 (X_ {0} х’ + у- {0} у ‘)} {г’ ^ {2}}} + {\ гидроразрыва {х ‘^ {2} + у ‘^ {2}} {г’ ^ {2}}} \ право] ^ {1/2},}

sзнак равноs'[1-2(ИксИкс’+YY’)s’2+Икс’2+Y’2s’2]1/2,{\ displaystyle S = S ‘\ влево [1 — {\ гидроразрыва {2 (хх’ + уу ‘)} {s’ ^ {2}}} + {\ гидроразрыва {х ‘^ {2} + у’ ^ { 2}} {s’^ {2}}} \ право] ^ {1/2}.}

Они могут быть расширены в виде степенных рядов:

рзнак равнор'[1-12р’2[2(Икс0Икс’+Y0Y’)+(Икс’2+Y’2)]+12р’2[2(Икс0Икс’+Y0Y’)+(Икс’2+Y’2)]2+⋯],{\ Displaystyle г = г ‘\ влево [1 — {\ гидроразрыва {1} {2r’ ^ {2}}} [2 (X_ {0} х ‘+ у- {0} у’) + (х ‘^ { 2} + у ‘^ {2})] + {\ гидроразрыва {1} {2r’ ^ {2}}} [2 (X_ {0} х ‘+ y_ {0} у) + (х’ ^ { 2} + у ‘^ {2})] ^ {2} + \ cdots \ вправо],}

sзнак равноs'[1-12s’2[2(ИксИкс’+YY’)+(Икс’2+Y’2)]+12s’2[2(ИксИкс’+YY’)+(Икс’2+Y’2)]2+⋯],{\ displaystyle S = S ‘\ левый [1 — {\ гидроразрыва {1} {2s’ ^ {2}}} [2 (хх ‘+ уу) + (х ‘^ {2} + у’ ^ {2 })] + {\ гидроразрыва {1} {2с ‘^ {2}}} [2 (хх’ + уу) + (х ‘^ {2} + у’ ^ {2})] ^ {2} + \ cdots \ вправо].}

Комплексная амплитуда на Р теперь может быть выражена как

U(п)знак равно-ясоз⁡βλaеяК(р’+s’)р’s’∫SеяКе(Икс’,Y’)dИкс’dY’,{\ Displaystyle U (P) = — {\ гидроразрыва {я \ соз \ бета} {\ Lambda}} {\ гидроразрыва {ае ^ {ик (г ‘+ s’)}} {г на}} \ int _ { S} е ^ {ИКФ (х», у ‘)} \, dx’dy’,}

где F ( х « у » ) включает в себя все термины в указанных выше для выражений с и г отдельно от первого члена в каждом выражении и может быть записан в виде

е(Икс’,Y’)знак равнос1Икс’+с2Y’+с3Икс’2+с4Y’2+с5Икс’Y’⋯,{\ Displaystyle Р (х ‘у ‘) = C_ {1} х’ + C_ {2} у ‘+ C_ {3} х’ ^ {2} + C_ {4} у’ ^ {2} + C_ { 5} x’y ‘\ cdots}

где с _я константа.

дифракция Фраунгофера

Если все члены в е ( х « у » ) можно пренебречь для членов в исключением х « и у » , мы имеем дифракции Фраунгофера уравнение. Если направляющие косинусы Р ₀ Q и PQ являются

L0знак равно-Икс0/р’,м0знак равно-Y0/р’,Lзнак равноИкс/s’,мзнак равноY/s’,{\ Displaystyle {\ {начинаются выровнены} L_ {0} & = — X_ {0} / г ‘\\ м_ {0} & = — у- {0} / г’, \\ л & = х / с, \\ т & = у / с. \ {конец выровнен}}}

Дифракции Фраунгофера уравнение затем

U(п)знак равноС∫SеяК[(L0-L)Икс’+(м-м0)Y’]dИкс’dY’,{\ Displaystyle U (Р) = С \ Int _ {S} е ^ {ик [(L_ {0} -l) х ‘+ (т-M_ {0}) у’]} \, dx’dy», }

где С является константой. Это также может быть записано в виде

U(п)знак равноС∫Sея(К0-К)⋅р’dр’,{\ Displaystyle U (Р) = С \ Int _ {S} е ^ {я (\ mathbf {K} _ {0} — \ mathbf {K}) \ CDOT \ mathbf {г} ‘} \, д-р’, }

где K ₀ и K являются волновые векторы волн , путешествующих из P ₀ к отверстию и от отверсти к Р , соответственно, и г ‘ является точкой в отверстии.

Если точечный источник заменяется протяженным источником которого комплексная амплитуда на апертуре задается U ₀ ( г» ), то дифракции Фраунгофера уравнение:

U(п)α∫Sa0(р’)ея(К0-К)⋅р’dр’,{\ Displaystyle U (Р) \ propto \ Int _ {S} а_ {0} (\ mathbf {г} «) е ^ {я (\ mathbf {K} _ {0} — \ mathbf {K}) \ CDOT \ mathbf {г} ‘} \, д-р’,}

где ₀ ( г» ), как и прежде, величина возмущения на апертуре.

В дополнение к приближений, сделанных при выводе уравнения Кирхгофа, предполагается, что

• г и s значительно больше , чем размер отверстия,
• второго и более высокого порядка членов в выражении F ( х « у » ) можно пренебречь.

дифракция Френеля

При квадратичные члены нельзя пренебрегать , но все члены более высокого порядка может, уравнение становится дифракции Френеля уравнение. В аппроксимации для уравнения Кирхгофа используются, а также дополнительные предположения:

• г и s значительно больше , чем размер отверстия,
• Третье и члены более высокого порядка в выражении F ( х « у » ) можно пренебречь.

Рекомендации

дальнейшее чтение

• Воан, Graham (2000). Кембриджский Справочник по физике формул . Cambridge University Press. ISBN  9780521575072 .
• Гриффитс, Дэвид Дж (2012). Введение в электродинамике . Pearson Education, Limited. ISBN  978-0-321-85656-2 .
• Группа, Иегуда B. (2006). Свет и материя: электромагнетизм, оптика, спектроскопия и лазеры . John Wiley & Sons . ISBN  978-0-471-89931-0 .
• Кеньон, Ян (2008). Свет Фантастическая: Современное введение в классической и квантовой оптики . Oxford University Press . ISBN  978-0-19-856646-5 .
• Лернер, Rita G .; Джордж Л., Trigg (1991). Энциклопедия физики . VCH. ISBN  978-0-89573-752-6 .
• Сибил П. Паркер (1993). МакГроу-Хилл Энциклопедия физики . McGraw-Hill Ryerson, Limited. ISBN  978-0-07-051400-3 .

Формула Кирхгофа — Википедия

Фо́рмула Кирхго́фа — аналитическое выражение для решения гиперболического уравнения в частных производных (т. н. «волнового уравнения») во всём трёхмерном пространстве. Методом спуска (то есть уменьшением размерности) из него можно получить решения двумерного (Формула Пуассона) и одномерного (Формула Д’Аламбера) уравнения.

Полная формулировка задачи и ответа

Рассмотрим уравнение

∂2u∂t2−a2△u=f{\displaystyle {\frac {\partial ^{2}u}{\partial t^{2}}}-a^{2}\triangle u=f}, где функции u=u(x,t){\displaystyle u=u(\mathbf {x} ,t)} и f=f(x,t){\displaystyle f=f(\mathbf {x} ,t)} определены на (x,t)∈Rn×R+{\displaystyle (\mathbf {x} ,t)\in \mathbb {R} ^{n}\times \mathbb {R} ^{+}}, а △{\displaystyle \triangle } — оператор Лапласа.

Это уравнение определяет распространение бегущей волны в n-мерной однородной среде со скоростью a{\displaystyle a} в моменты времени t>0{\displaystyle t>0}.

Для того, чтобы решение было однозначным, необходимо определить начальные условия. Начальные условия определяют состояние пространства (или, говорят, «начальное возмущение») в момент времени t=0{\displaystyle t=0}:

u|t=0=φ0(x¯),∂u∂t|t=0=φ1(x¯){\displaystyle u|_{t=0}=\varphi _{0}({\bar {x}}),\quad \left.{\frac {\partial u}{\partial t}}\right|_{t=0}=\varphi _{1}({\bar {x}})}

Тогда обобщённая формула Кирхгофа даёт решение этой задачи в трёхмерном случае:

u(x,t)=∂∂t[14πa2t∬Sφ0(y)d2Sn]+14πa2t∬Sφ1(y)d2Sn+14πa2∭|x−y|⩽atf(y,t−|x−y|a)|x−y|d3y{\displaystyle u(\mathbf {x} ,t)={\frac {\partial }{\partial t}}\left[{\frac {1}{4\pi a^{2}t}}\iint \limits _{S}\varphi _{0}(\mathbf {y} )d^{2}S_{n}\right]+{\frac {1}{4\pi a^{2}t}}\iint \limits _{S}\varphi _{1}(\mathbf {y} )d^{2}S_{n}+{\frac {1}{4\pi a^{2}}}\iiint \limits _{\left|\mathbf {x} -\mathbf {y} \right|\leqslant at}{\frac {f\left(\mathbf {y} ,t-{\frac {\left|\mathbf {x} -\mathbf {y} \right|}{a}}\right)}{\left|\mathbf {x} -\mathbf {y} \right|}}d^{3}\mathbf {y} }

где поверхностные интегралы берутся по сфере S:|x−y|=at{\displaystyle S\colon \left|\mathbf {x} -\mathbf {y} \right|=at}.

Сам Кирхгоф рассматривал только трёхмерный случай.

Простой вывод решения основной задачи использует преобразование Фурье.

Физические следствия

Передний и задний волновые фронты от локализованного в пространстве возмущения действуют на наблюдателя в течение ограниченного отрезка времени

Пусть в начальный момент времени t=0{\displaystyle t=0} на некотором компакте M есть локальное возмущение (φ0≠0{\displaystyle \varphi _{0}\neq 0} и/или φ1≠0{\displaystyle \varphi _{1}\neq 0}). Если мы находимся в некоторой точке x¯0∈R3{\displaystyle {\bar {x}}_{0}\in \mathbb {R} ^{3}}, то, как видно из формулы (область интегрирования), возмущение мы почувствуем через время t1=1ainfy¯∈M|y¯−x¯0|{\displaystyle t_{1}={\frac {1}{a}}\inf _{{\bar {y}}\in M}\left|{\bar {y}}-{\bar {x}}_{0}\right|}.

Вне отрезка времени [t1;t2]{\displaystyle \left[t_{1};t_{2}\right]}, где t2=1asupy¯∈M|y¯−x¯0|{\displaystyle t_{2}={\frac {1}{a}}\sup _{{\bar {y}}\in M}\left|{\bar {y}}-{\bar {x}}_{0}\right|}, функция u(x ₀, t) равна нулю.

Таким образом, начальное возмущение, локализованное в пространстве, вызывает в каждой точке пространства действие, локализованное во времени, то есть возмущение распространяется в виде волны, имеющей передний и задний фронты, что выражает принцип Гюйгенса). На плоскости же этот принцип нарушается. Обоснованием этого является тот факт, что носитель возмущения, компактный в R2{\displaystyle \mathbb {R} ^{2}}, уже не будет компактным в R3{\displaystyle \mathbb {R} ^{3}}, а будет образовывать бесконечный цилиндр, и, следовательно, возмущение будет неограниченно во времени (у цилиндрических волн отсутствует задний фронт).^[1]

Решение уравнения колебаний мембраны (двумерного пространства)

utt=a2△u+f{\displaystyle u_{tt}=a^{2}\triangle u+f}

(функция f(x,t){\displaystyle f(x,t)} соответствует вынуждающей внешней силе)

с начальными условиями

u(x,0)=φ(x),ut(x,0)=ψ(x){\displaystyle u(x,0)=\varphi (x),\quad u_{t}(x,0)=\psi (x)}

задаётся формулой:

u(x¯,t)=u(x1,x2,t)=12πa∫0t∬r<a(t−τ)f(y1,y2,τ)dy1dy2dτa2(t−τ)2−(y1−x1)2−(y2−x2)2+∂∂t12πa∬r<atφ(y1,y2)dy1dy2a2t2−(y1−x1)2−(y2−x2)2+12πa∬r<atψ(y1,y2)dy1dy2a2t2−(y1−x1)2−(y2−x2)2{\displaystyle u({\bar {x}},t)=u(x_{1},x_{2},t)={\frac {1}{2\pi a}}\int \limits _{0}^{t}\iint \limits _{r<a(t-\tau )}{\frac {f(y_{1},y_{2},\tau )dy_{1}dy_{2}d\tau }{\sqrt {a^{2}(t-\tau )^{2}-(y_{1}-x_{1})^{2}-(y_{2}-x_{2})^{2}}}}+{\frac {\partial }{\partial t}}{\frac {1}{2\pi a}}\iint \limits _{r<at}{\frac {\varphi (y_{1},y_{2})dy_{1}dy_{2}}{\sqrt {a^{2}t^{2}-(y_{1}-x_{1})^{2}-(y_{2}-x_{2})^{2}}}}+{\frac {1}{2\pi a}}\iint \limits _{r<at}{\frac {\psi (y_{1},y_{2})dy_{1}dy_{2}}{\sqrt {a^{2}t^{2}-(y_{1}-x_{1})^{2}-(y_{2}-x_{2})^{2}}}}}.

Решение одномерного волнового уравнения

utt=a2uxx+f{\displaystyle u_{tt}=a^{2}u_{xx}+f\quad } (функция f(x,t){\displaystyle f(x,t)} соответствует вынуждающей внешней силе)

с начальными условиями

u(x,0)=φ(x),ut(x,0)=ψ(x){\displaystyle u(x,0)=\varphi (x),\quad u_{t}(x,0)=\psi (x)}

имеет вид^[2]

u(x,t)=φ(x+at)+φ(x−at)2+12a∫x−atx+atψ(α)dα+12a∫0t∫x−a(t−τ)x+a(t−τ)f(s,τ)dsdτ{\displaystyle u(x,t)={\frac {\varphi (x+at)+\varphi (x-at)}{2}}+{\frac {1}{2a}}\int \limits _{x-at}^{x+at}{\psi (\alpha )d\alpha }+{\frac {1}{2a}}\int \limits _{0}^{t}\int \limits _{x-a(t-\tau )}^{x+a(t-\tau )}f(s,\tau )dsd\tau }

В область II приходят характеристики только из одного семейства

При пользовании формулой Д’Аламбера следует учесть, что иногда решение может не быть единственным во всей рассматриваемой области R1×[0,T]{\displaystyle \mathbb {R} ^{1}\times [0,T]}. Решение волнового уравнения представляется в виде суммы двух функций: u(x,t)=f(x+at)+g(x−at){\displaystyle u(x,t)=f(x+at)+g(x-at)}, то есть оно определяется двумя семействами характеристик: x+at=ξ, x−at=η{\displaystyle x+at=\xi ,\ x-at=\eta }. Пример, показанный на рисунке справа, иллюстрирует волновое уравнение для полубесконечной струны, и начальные условия в нём заданы только на зеленой линии x≥0. Видно, что в область I приходят как ξ-характеристики, так и η-характеристики, в то время как в области II есть только ξ-характеристики. То есть, в области II формула Д’Аламбера не работает.

Применение формул

В общем виде формула Кирхгофа довольно громоздка, а потому решение задач математической физики с её помощью обычно является затруднительным. Однако, можно воспользоваться линейностью волнового уравнения ∂2u∂t2=a2△u+f(x¯,t){\displaystyle {\frac {\partial ^{2}u}{\partial t^{2}}}=a^{2}\triangle u+f({\bar {x}},t)} с начальными условиями u(x¯,0)=φ0(x¯), ut(x¯,0)=φ1(x¯){\displaystyle u({\bar {x}},0)=\varphi _{0}({\bar {x}}),\ u_{t}({\bar {x}},0)=\varphi _{1}({\bar {x}})} и искать решение в виде суммы трех функций: u(x,t)=A(x,t)+B(x,t)+C(x,t){\displaystyle u(x,t)=A(x,t)+B(x,t)+C(x,t)}, которые удовлетворяют следующим условиям:

∂2A∂t2=a2△A+f(x¯,t),A(x¯,0)=0, At(x¯,0)=0;{\displaystyle {\frac {\partial ^{2}A}{\partial t^{2}}}=a^{2}\triangle A+f({\bar {x}},t),\qquad A({\bar {x}},0)=0,\ A_{t}({\bar {x}},0)=0;}

∂2B∂t2=a2△B,B(x¯,0)=φ0(x¯), Bt(x¯,0)=0;{\displaystyle {\frac {\partial ^{2}B}{\partial t^{2}}}=a^{2}\triangle B,\qquad B({\bar {x}},0)=\varphi _{0}({\bar {x}}),\ B_{t}({\bar {x}},0)=0;}

∂2C∂t2=a2△C,C(x¯,0)=0, Ct(x¯,0)=φ1(x¯).{\displaystyle {\frac {\partial ^{2}C}{\partial t^{2}}}=a^{2}\triangle C,\qquad C({\bar {x}},0)=0,\ {\mathit {C}}_{t}({\bar {x}},0)=\varphi _{1}({\bar {x}}).}

Сама по себе такая операция не упрощает пользование формулой Кирхгофа, но для некоторых задач оказывается возможным подбор решения, либо сведение многомерной задачи к одномерной путём замены переменных. Например, пусть φ1(x,y,z)=11+(x+3y−2z)2{\displaystyle \varphi _{1}(x,y,z)={\frac {1}{1+(x+3y-2z)^{2}}}}. Тогда после замены ξ=x+3y−2z{\displaystyle \xi =x+3y-2z} уравнение для задачи «С» примет вид:

∂2C∂t2=14a2∂2C∂ξ2,C(ξ,0)=0, Ct(ξ,0)=11+ξ2.{\displaystyle {\frac {\partial ^{2}C}{\partial t^{2}}}=14a^{2}{\frac {\partial ^{2}C}{\partial \xi ^{2}}},\qquad {\mathit {C}}(\xi ,0)=0,\ C_{t}(\xi ,0)={\frac {1}{1+\xi ^{2}}}.}

Таким образом, пришли к одномерному уравнению, а, значит, можно воспользоваться формулой Д’Аламбера:

C(ξ,t)=1214a∫ξ−14atξ+14atdη1+η2=1214a(arctg⁡(ξ+14at)−arctg⁡(ξ−14at)).{\displaystyle C(\xi ,t)={\frac {1}{2{\sqrt {14}}a}}\int \limits _{\xi -{\sqrt {14}}at}^{\xi +{\sqrt {14}}at}{\frac {d\eta }{1+\eta ^{2}}}={\frac {1}{2{\sqrt {14}}a}}\left(\operatorname {arctg} (\xi +{\sqrt {14}}at)-\operatorname {arctg} (\xi -{\sqrt {14}}at)\right).}

В силу четности начального условия, решение сохранит свой вид во всей области t>0{\displaystyle t>0}.

Примечания

Литература

• Михайлов В.П., Михайлова Т.В., Шабунин М.И. Сборник типовых задач по курсу Уравнения математической физики. — М.: МФТИ, 2007. — ISBN 5-7417-0206-6.

Ссылки

Формула Кирхгофа — Википедия

Фо́рмула Кирхго́фа — аналитическое выражение для решения гиперболического уравнения в частных производных (т. н. «волнового уравнения») во всём трёхмерном пространстве. Методом спуска (то есть уменьшением размерности) из него можно получить решения двумерного (Формула Пуассона) и одномерного (Формула Д’Аламбера) уравнения.

Полная формулировка задачи и ответа

Рассмотрим уравнение

∂2u∂t2−a2△u=f{\displaystyle {\frac {\partial ^{2}u}{\partial t^{2}}}-a^{2}\triangle u=f}, где функции u=u(x,t){\displaystyle u=u(\mathbf {x} ,t)} и f=f(x,t){\displaystyle f=f(\mathbf {x} ,t)} определены на (x,t)∈Rn×R+{\displaystyle (\mathbf {x} ,t)\in \mathbb {R} ^{n}\times \mathbb {R} ^{+}}, а △{\displaystyle \triangle } — оператор Лапласа.

Это уравнение определяет распространение бегущей волны в n-мерной однородной среде со скоростью a{\displaystyle a} в моменты времени t>0{\displaystyle t>0}.

Для того, чтобы решение было однозначным, необходимо определить начальные условия. Начальные условия определяют состояние пространства (или, говорят, «начальное возмущение») в момент времени t=0{\displaystyle t=0}:

u|t=0=φ0(x¯),∂u∂t|t=0=φ1(x¯){\displaystyle u|_{t=0}=\varphi _{0}({\bar {x}}),\quad \left.{\frac {\partial u}{\partial t}}\right|_{t=0}=\varphi _{1}({\bar {x}})}

Тогда обобщённая формула Кирхгофа даёт решение этой задачи в трёхмерном случае:

u(x,t)=∂∂t[14πa2t∬Sφ0(y)d2Sn]+14πa2t∬Sφ1(y)d2Sn+14πa2∭|x−y|⩽atf(y,t−|x−y|a)|x−y|d3y{\displaystyle u(\mathbf {x} ,t)={\frac {\partial }{\partial t}}\left[{\frac {1}{4\pi a^{2}t}}\iint \limits _{S}\varphi _{0}(\mathbf {y} )d^{2}S_{n}\right]+{\frac {1}{4\pi a^{2}t}}\iint \limits _{S}\varphi _{1}(\mathbf {y} )d^{2}S_{n}+{\frac {1}{4\pi a^{2}}}\iiint \limits _{\left|\mathbf {x} -\mathbf {y} \right|\leqslant at}{\frac {f\left(\mathbf {y} ,t-{\frac {\left|\mathbf {x} -\mathbf {y} \right|}{a}}\right)}{\left|\mathbf {x} -\mathbf {y} \right|}}d^{3}\mathbf {y} }

где поверхностные интегралы берутся по сфере S:|x−y|=at{\displaystyle S\colon \left|\mathbf {x} -\mathbf {y} \right|=at}.

Сам Кирхгоф рассматривал только трёхмерный случай.

Простой вывод решения основной задачи использует преобразование Фурье.

Физические следствия

Передний и задний волновые фронты от локализованного в пространстве возмущения действуют на наблюдателя в течение ограниченного отрезка времени

Пусть в начальный момент времени t=0{\displaystyle t=0} на некотором компакте M есть локальное возмущение (φ0≠0{\displaystyle \varphi _{0}\neq 0} и/или φ1≠0{\displaystyle \varphi _{1}\neq 0}). Если мы находимся в некоторой точке x¯0∈R3{\displaystyle {\bar {x}}_{0}\in \mathbb {R} ^{3}}, то, как видно из формулы (область интегрирования), возмущение мы почувствуем через время t1=1ainfy¯∈M|y¯−x¯0|{\displaystyle t_{1}={\frac {1}{a}}\inf _{{\bar {y}}\in M}\left|{\bar {y}}-{\bar {x}}_{0}\right|}.

Вне отрезка времени [t1;t2]{\displaystyle \left[t_{1};t_{2}\right]}, где t2=1asupy¯∈M|y¯−x¯0|{\displaystyle t_{2}={\frac {1}{a}}\sup _{{\bar {y}}\in M}\left|{\bar {y}}-{\bar {x}}_{0}\right|}, функция u(x ₀, t) равна нулю.

Таким образом, начальное возмущение, локализованное в пространстве, вызывает в каждой точке пространства действие, локализованное во времени, то есть возмущение распространяется в виде волны, имеющей передний и задний фронты, что выражает принцип Гюйгенса). На плоскости же этот принцип нарушается. Обоснованием этого является тот факт, что носитель возмущения, компактный в R2{\displaystyle \mathbb {R} ^{2}}, уже не будет компактным в R3{\displaystyle \mathbb {R} ^{3}}, а будет образовывать бесконечный цилиндр, и, следовательно, возмущение будет неограниченно во времени (у цилиндрических волн отсутствует задний фронт).^[1]

Решение уравнения колебаний мембраны (двумерного пространства)

utt=a2△u+f{\displaystyle u_{tt}=a^{2}\triangle u+f}

(функция f(x,t){\displaystyle f(x,t)} соответствует вынуждающей внешней силе)

с начальными условиями

u(x,0)=φ(x),ut(x,0)=ψ(x){\displaystyle u(x,0)=\varphi (x),\quad u_{t}(x,0)=\psi (x)}

задаётся формулой:

u(x¯,t)=u(x1,x2,t)=12πa∫0t∬r<a(t−τ)f(y1,y2,τ)dy1dy2dτa2(t−τ)2−(y1−x1)2−(y2−x2)2+∂∂t12πa∬r<atφ(y1,y2)dy1dy2a2t2−(y1−x1)2−(y2−x2)2+12πa∬r<atψ(y1,y2)dy1dy2a2t2−(y1−x1)2−(y2−x2)2{\displaystyle u({\bar {x}},t)=u(x_{1},x_{2},t)={\frac {1}{2\pi a}}\int \limits _{0}^{t}\iint \limits _{r<a(t-\tau )}{\frac {f(y_{1},y_{2},\tau )dy_{1}dy_{2}d\tau }{\sqrt {a^{2}(t-\tau )^{2}-(y_{1}-x_{1})^{2}-(y_{2}-x_{2})^{2}}}}+{\frac {\partial }{\partial t}}{\frac {1}{2\pi a}}\iint \limits _{r<at}{\frac {\varphi (y_{1},y_{2})dy_{1}dy_{2}}{\sqrt {a^{2}t^{2}-(y_{1}-x_{1})^{2}-(y_{2}-x_{2})^{2}}}}+{\frac {1}{2\pi a}}\iint \limits _{r<at}{\frac {\psi (y_{1},y_{2})dy_{1}dy_{2}}{\sqrt {a^{2}t^{2}-(y_{1}-x_{1})^{2}-(y_{2}-x_{2})^{2}}}}}.

Решение одномерного волнового уравнения

utt=a2uxx+f{\displaystyle u_{tt}=a^{2}u_{xx}+f\quad } (функция f(x,t){\displaystyle f(x,t)} соответствует вынуждающей внешней силе)

с начальными условиями

u(x,0)=φ(x),ut(x,0)=ψ(x){\displaystyle u(x,0)=\varphi (x),\quad u_{t}(x,0)=\psi (x)}

имеет вид^[2]

u(x,t)=φ(x+at)+φ(x−at)2+12a∫x−atx+atψ(α)dα+12a∫0t∫x−a(t−τ)x+a(t−τ)f(s,τ)dsdτ{\displaystyle u(x,t)={\frac {\varphi (x+at)+\varphi (x-at)}{2}}+{\frac {1}{2a}}\int \limits _{x-at}^{x+at}{\psi (\alpha )d\alpha }+{\frac {1}{2a}}\int \limits _{0}^{t}\int \limits _{x-a(t-\tau )}^{x+a(t-\tau )}f(s,\tau )dsd\tau }

В область II приходят характеристики только из одного семейства

При пользовании формулой Д’Аламбера следует учесть, что иногда решение может не быть единственным во всей рассматриваемой области R1×[0,T]{\displaystyle \mathbb {R} ^{1}\times [0,T]}. Решение волнового уравнения представляется в виде суммы двух функций: u(x,t)=f(x+at)+g(x−at){\displaystyle u(x,t)=f(x+at)+g(x-at)}, то есть оно определяется двумя семействами характеристик: x+at=ξ, x−at=η{\displaystyle x+at=\xi ,\ x-at=\eta }. Пример, показанный на рисунке справа, иллюстрирует волновое уравнение для полубесконечной струны, и начальные условия в нём заданы только на зеленой линии x≥0. Видно, что в область I приходят как ξ-характеристики, так и η-характеристики, в то время как в области II есть только ξ-характеристики. То есть, в области II формула Д’Аламбера не работает.

Применение формул

В общем виде формула Кирхгофа довольно громоздка, а потому решение задач математической физики с её помощью обычно является затруднительным. Однако, можно воспользоваться линейностью волнового уравнения ∂2u∂t2=a2△u+f(x¯,t){\displaystyle {\frac {\partial ^{2}u}{\partial t^{2}}}=a^{2}\triangle u+f({\bar {x}},t)} с начальными условиями u(x¯,0)=φ0(x¯), ut(x¯,0)=φ1(x¯){\displaystyle u({\bar {x}},0)=\varphi _{0}({\bar {x}}),\ u_{t}({\bar {x}},0)=\varphi _{1}({\bar {x}})} и искать решение в виде суммы трех функций: u(x,t)=A(x,t)+B(x,t)+C(x,t){\displaystyle u(x,t)=A(x,t)+B(x,t)+C(x,t)}, которые удовлетворяют следующим условиям:

∂2A∂t2=a2△A+f(x¯,t),A(x¯,0)=0, At(x¯,0)=0;{\displaystyle {\frac {\partial ^{2}A}{\partial t^{2}}}=a^{2}\triangle A+f({\bar {x}},t),\qquad A({\bar {x}},0)=0,\ A_{t}({\bar {x}},0)=0;}

∂2B∂t2=a2△B,B(x¯,0)=φ0(x¯), Bt(x¯,0)=0;{\displaystyle {\frac {\partial ^{2}B}{\partial t^{2}}}=a^{2}\triangle B,\qquad B({\bar {x}},0)=\varphi _{0}({\bar {x}}),\ B_{t}({\bar {x}},0)=0;}

∂2C∂t2=a2△C,C(x¯,0)=0, Ct(x¯,0)=φ1(x¯).{\displaystyle {\frac {\partial ^{2}C}{\partial t^{2}}}=a^{2}\triangle C,\qquad C({\bar {x}},0)=0,\ {\mathit {C}}_{t}({\bar {x}},0)=\varphi _{1}({\bar {x}}).}

Сама по себе такая операция не упрощает пользование формулой Кирхгофа, но для некоторых задач оказывается возможным подбор решения, либо сведение многомерной задачи к одномерной путём замены переменных. Например, пусть φ1(x,y,z)=11+(x+3y−2z)2{\displaystyle \varphi _{1}(x,y,z)={\frac {1}{1+(x+3y-2z)^{2}}}}. Тогда после замены ξ=x+3y−2z{\displaystyle \xi =x+3y-2z} уравнение для задачи «С» примет вид:

∂2C∂t2=14a2∂2C∂ξ2,C(ξ,0)=0, Ct(ξ,0)=11+ξ2.{\displaystyle {\frac {\partial ^{2}C}{\partial t^{2}}}=14a^{2}{\frac {\partial ^{2}C}{\partial \xi ^{2}}},\qquad {\mathit {C}}(\xi ,0)=0,\ C_{t}(\xi ,0)={\frac {1}{1+\xi ^{2}}}.}

Таким образом, пришли к одномерному уравнению, а, значит, можно воспользоваться формулой Д’Аламбера:

C(ξ,t)=1214a∫ξ−14atξ+14atdη1+η2=1214a(arctg⁡(ξ+14at)−arctg⁡(ξ−14at)).{\displaystyle C(\xi ,t)={\frac {1}{2{\sqrt {14}}a}}\int \limits _{\xi -{\sqrt {14}}at}^{\xi +{\sqrt {14}}at}{\frac {d\eta }{1+\eta ^{2}}}={\frac {1}{2{\sqrt {14}}a}}\left(\operatorname {arctg} (\xi +{\sqrt {14}}at)-\operatorname {arctg} (\xi -{\sqrt {14}}at)\right).}

В силу четности начального условия, решение сохранит свой вид во всей области t>0{\displaystyle t>0}.

Примечания

Литература

• Михайлов В.П., Михайлова Т.В., Шабунин М.И. Сборник типовых задач по курсу Уравнения математической физики. — М.: МФТИ, 2007. — ISBN 5-7417-0206-6.

Ссылки

КИРХГОФА ФОРМУЛА — с русского на все языки

formula (pi. formulae, formulas)

•Аналогичные формулы могут быть выписаны для… — Analogous formulas can be written down for…

• Будем руководствоваться формулой… — We are guided by the formula…

• В формулах (2) переменная к предполагается функцией от г. — In the formulas (2), к is assumed to be a function of r.

• В этой формуле мы все еще не предположили, что… — In this formula we have not yet assumed that…

• Данная формула хорошо согласуется с экспериментом. — This formula is in good agreement with the experiment; This formula is in good agreement with with experimental results.

• Для F обычно дается следующая формула: … — The formula usually given for F is…

• Другой способ вывода этих формул основан на… — Another way of deriving these formulas is based on…

• Затем задача заключается в выводе формулы для… — The problem is then to deduce a formula for…

• Здесь мы приводим некоторые формулы для… — Неге we give some formulae for…

• Используя подобные формулы, можно… — Using such formulae, it is possible to…

• Нашей задачей является нахождение общей формулы для… — The problem is to find a general formula for…

• Не существует общей формулы для… — There is no general formula for…

• Очевидным следствием соотношения (1) является формула… — An obvious deduction from (1) is the formula…

• Подобным способом могут быть выведены несколько иные дополнительные формулы. — Still other formulas can be obtained in a similar way.

• Результат, представленный формулой (9), очень полезен при выводе свойств (чего-л). — The result (9) is very useful for deducing properties of…

• Справедливость этой формулы зависит от… — The validity of this formula depends on…

• Теперь мы получим ту же самую формулу из других соображений. — We now obtain the same formula from another point of view.

• Физическим следствием формулы (1) является то, что… — The physical implication of (1) is that…

• Формула (4) может быть выражена в несколько отличной форме посредством… — The result (4) may be expressed in a slightly different form by means of…

• Часто использование альтернативной формулы (2) имеет свои преимущества. — It is often advantageous to use the alternative formula (2).

• Эта формула полезна когда бы ни… — This formula is useful whenever…

• Эта формула четко предсказывает… — This formula clearly predicts…

Формула первого закона Кирхгофа

Все расчеты в сетях постоянного тока можно выполнять, используя закон Ома и закон сохранения заряда. Однако если цепь является сложной, разветвленной, содержит несколько контуров и включает несколько источников ЭДС, то для упрощения расчетов используют правила (законы) Кирхгофа. Правила Кирхгофа применяют для составления системы линейных уравнений, из которых можно найти силы тока, текущие в разных элементах цепи.

Прежде чем записать формулу первого правила Кирхгофа определим, что такое узел в цепи, так как первый закон Кирхгофа называют правилом узлов.

Узлом разветвленной цепи называют точку, в которой сходятся три или более проводников с токами. На (рис.1) точка О является узлом. В нее входят два тока: и и выходят токи и .

Для правильной записи формулы первого правила Кирхгофа важно помнить, при составлении уравнения необходимо учитывать направления течения токов. Следует помнить, что токи, подходящие к узлу и токи, исходящие из узла имеют разные знаки. При решении задачи, для себя нужно решить, какие токи считать положительными, например, входящие в узел, и после этого все токи в данной задаче записывать со знаком плюс.

Теперь сама формула первого закона Кирхгофа:

   

Выражение (1) означает, что алгебраическая сумма токов (сумма с учетом знаков) в любом узле цепи постоянного тока равна нулю.

Для того чтобы не ошибаться со знаками при составлении уравнений на основе первого правила Кирхгофа на схемах направление силы тока изображают при помощи стрелок (см. рис.1).

Первый закон Кирхгофа – это следствие закона сохранения электрического заряда. Сумма токов (с учетом их знаков), которая сходится в узле, есть заряд, проходящий через данный узел в единицу времени. Если токи в узле не изменяются во времени, то сумма токов должна быть равна нулю, иначе потенциал узла был бы переменным, соответственно токи были бы переменными тоже. При постоянном токе ни какая из точек цепи не может накапливать заряд. В противном случае токи станут переменными.

Примеры решения задач по теме «Первый закон Кирхгофа»