Курс высшей математики, Т.2
Курс высшей математики, Т.2
ОглавлениеПРЕДИСЛОВИЕ К ДЕВЯТНАДЦАТОМУ ИЗДАНИЮГЛАВА I. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ § 1. УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА 2.  (n)=f(x).19. Системы обыкновенных дифференциальных уравнений. 20. Примеры. 21. Системы уравнений и уравнения высших порядков. 22. Линейные уравнения с частными производными. 23. Геометрическая интерпретация. 24. Примеры. ГЛАВА II. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ПО ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 25. Линейные однородные уравнения второго порядка. 26. Линейные неоднородные уравнения второго порядка. 27. Линейные уравнения высших порядков. 28. Однородные уравнения второго порядка с постоянными коэффициентами. 29. Линейные неоднородные уравнения второго порядка с постоянными коэффициентами. 30. Частные случаи. 32. Линейные уравнения высших порядков с постоянными коэффициентами. 33. Линейные уравнения и колебательные явления. 34. Собственные и вынужденные колебания. 35. Синусоидальная внешняя сила и резонанс.  36. Предельные задачи. 37. Примеры. 38. Символический метод. 39. Линейные однородные уравнения высших порядков с постоянными коэффициентами. 40. Линейные неоднородные уравнения с постоянными коэффициентами. 41. Пример. 42 Уравнение Эйлера. 43. Системы линейных уравнений с постоянными коэффициентами. § 4. ИНТЕГРИРОВАНИЕ С ПОМОЩЬЮ СТЕПЕННЫХ РЯДОВ 45. Интегрирование линейного уравнения с помощью степенного ряда 46. Примеры. 47. Разложение решения в обобщенный степенной ряд. 48. Уравнение Бесселя 49. Уравнения, приводящиеся к уравнению Бесселя § 5. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ПО ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 50. Метод последовательных приближений для линейных уравнений. 51. Случай нелинейного уравнения. 52. Дополнения к теореме существования и единственности. 53. Сходимость метода Эйлера — Коши. 54. Особые точки дифференциальных уравнений первого порядка. 55. Автономные системы. 56. Примеры. 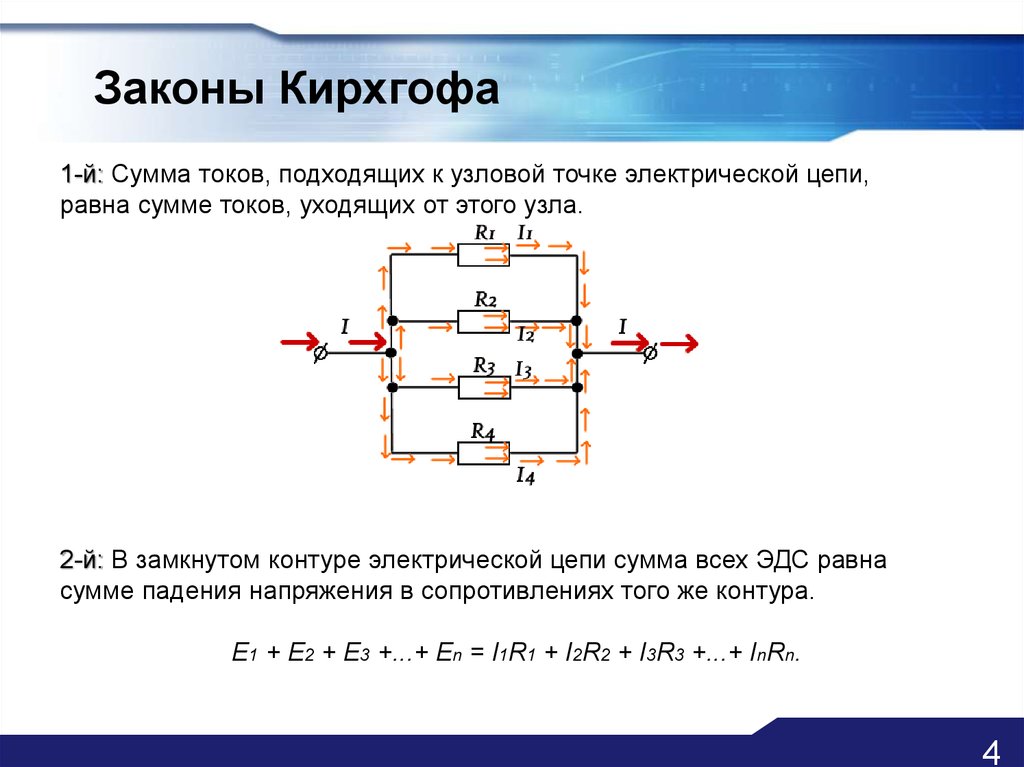 ГЛАВА III. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА § 6. КРАТНЫЕ ИНТЕГРАЛЫ 58. Двукратный интеграл. 59. Вычисление двукратного интеграла. 60. Криволинейные координаты. 61. Трехкратный интеграл 62. Цилиндрические и сферические координаты. 63. Криволинейные координаты в пространстве. 64. Основные свойства кратных интегралов. 65. Площадь поверхности. 66. Интегралы по поверхности и формула Остроградского. 67. Интегралы по определенной стороне поверхности. 68. Моменты. § 7. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ 70. Работа силового поля. Примеры. 71. Площадь и криволинейный интеграл. 72. Формула Грина 73. Формула Стокса. 74. Независимость криволинейного интеграла от пути на плоскости. 75. Случай многосвязной области. 76. Независимость криволинейного интеграла от пути в пространстве. 77. Установившееся течение жидкости. 78.  Интегрирующий множитель.79. Уравнение в полных дифференциалах для случая трех переменных. 80. Замена переменных в двойном интеграле. § 8. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА 82. Формула Дирихле. 83. Дифференцирование под знаком интеграла 84. Примеры. 85. Несобственные интегралы. 86. Неабсолютно сходящиеся интегралы. 87. Равномерно сходящиеся интегралы. 88. Примеры. 89. Несобственные кратные интегралы. 90. Примеры. § 9. МЕРА И ТЕОРИЯ ИНТЕГРИРОВАНИЯ 92. Основные теоремы. 93. Счетные множества. Действия над точечными множествами. 94. Мера Жордана. 95. Квадрируемые множества. 96. Независимость от выбора осей. 97. Случай любого числа измерений. 98. Интегрируемые функции. 99. Вычисление двойного интеграла. 100. n-кратные интегралы. 101. Примеры. 102. Внешняя мера Лебега. 104. Измеримые функции. 105.  Дополнительные сведения.106. Интеграл Лебега. 107. Свойства интеграла Лебега. 108. Интегралы от неограниченных функций. 109. Предельный переход под знаком интеграла. 110. Теорема Фубини. 111. Интегралы по множеству бесконечной меры. ГЛАВА IV. ВЕКТОРНЫЙ АНАЛИЗ И ТЕОРИЯ ПОЛЯ 112. Сложение и вычитание векторов. 113. Умножение вектора на скаляр. Компланарность векторов. 114. Разложение вектора по трем некомпланарным векторам. 115. Скалярное произведение. 116. Векторное произведение. 118. Скорости точек вращающегося твердого тела; момент вектора. § 11 ТЕОРИЯ ПОЛЯ 119. Дифференцирование вектора 120. Скалярное поле и его градиент. 121. Векторное поле; расходимость и вихрь. 122. Потенциальное и соленоидальное поля. 123. Направленный элемент поверхности. 124. Некоторые формулы векторного анализа. 125. Движение твердого тела и малая деформация. 126.  Уравнение непрерывности.127. Уравнения гидродинамики идеальной жидкости. 128. Уравнения распространения звука. 130. Уравнения Максвелла. 131. Выражение оператора Лапласа в ортогональных координатах. 132. Операция дифференцирования для случая переменного поля. ГЛАВА V. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ 133. Плоская кривая, ее кривизна и эволюта. 134. Эвольвента. 135. Естественное уравнение кривой. 136. Основные элементы кривой в пространстве. 137. Формулы Френе. 138. Соприкасающаяся плоскость. 139. Винтовые линии. 140. Поле единичных векторов. § 13. ЭЛЕМЕНТЫ ТЕОРИИ ПОВЕРХНОСТЕЙ 141. Параметрические уравнения поверхности. 142. Первая дифференциальная форма Гаусса. 143. Вторая дифференциальная форма Гаусса. 145. Индикатриса Дюпена и формула Эйлера. 146. Определение главных радиусов кривизны и главных направлений. 147.  Линии кривизны.148. Теорема Дюпена. 149. Примеры. 150. Гауссова кривизна. 151. Вариация элемента площади и средняя кривизна. 152. Огибающая семейства поверхностей и кривых. 153. Развертывающиеся поверхности. ГЛАВА VI. РЯДЫ ФУРЬЕ 154. Ортогональность тригонометрических функций. 155. Теорема Дирихле. 156. Примеры. 157. Разложение в промежутке (0, п). 158. Периодические функции периода 2l. 160. Общие ортогональные системы функций. 161. Класс L2 162. Сходимость в среднем. 163. Ортонормированные системы в L2. § 15. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ РЯДОВ ФУРЬЕ 164. Разложение в ряд Фурье. 165. Вторая теорема о среднем. 166. Интеграл Дирихле. 167. Теорема Дирихле. 168. Приближение к непрерывной функции полиномами. 169. Формула замкнутости. 170. Характер сходимости рядов Фурье. 171. Улучшение сходимости рядов Фурье. 172. Пример. § 16. ИНТЕГРАЛ ФУРЬЕ И КРАТНЫЕ РЯДЫ ФУРЬЕ 173.  Формула Фурье.176. Кратные ряды Фурье. ГЛАВА VII. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ МАТЕМАТИЧЕСКОЙ ФИЗИКИ 176. Уравнение колебаний струны. 177. Решение Даламбера. 178. Частные случаи. 179. Ограниченная струна. 180. Способ Фурье. 181. Гармоники и стоячие волны. 182. Вынужденные колебания. 183. Сосредоточенная сила. 184. Формула Пуассона. 185. Цилиндрические волны. 186. Случай n-мерного пространства. 187. Неоднородное волновое уравнение. 188. Точечный источник. 189. Поперечные колебания мембран. 190. Прямоугольная мембрана. 191. Круглая мембрана. 192. Теорема единственности. 193. Применение интеграла Фурье. 195. Установившиеся процессы. 196. Устанавливающиеся процессы. 197. Примеры. 198. Обобщенное уравнение колебаний струны. 199. Неограниченная цепь в общем случае. 200. Способ Фурье для ограниченной цепи. 201.  Обобщенное волновое уравнение.§ 19. УРАВНЕНИЕ ЛАПЛАСА 202. Гармонические функции. 203. Формула Грина. 204. Основные свойства гармонических функций. 205. Решение задачи Дирихле для круга. 206. Интеграл Пуассона. 207. Задача Дирихле для сферы. 208. Функция Грина. 209. Случай полупространства. 210. Потенциал объемных масс. 211. Уравнение Пуассона. 212. Формула Кирхгофа. § 20. УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ 214. Неограниченный стержень. 215. Стержень, ограниченный с одного конца. 216. Стержень, ограниченный с обоих концов. 217. Дополнительные замечания. 218. Случай сферы. 219. Теорема единственности. |
Расчеты в электротехнике по первому закону Кирхгофа
Сложно представить любую точную науку без использования соответствующих формул. Они присутствуют в различных основополагающих правилах и канонах.
В электротехнике, которая относится к точным наукам, обязательно применяется первый закон Кирхгофа.
Он необходим для проведения грамотных расчетов силы тока на всевозможных участках электрической проводки.
Что собой представляет узел, ветвь и контур
Под электроцепью понимается совокупность нескольких элементов — узлов, ветвей, а также контуров
.
Ветвь — главный элемент электрической цепи
Основным элементом электроцепи считается ветвь. На всей ее протяженности проходит тот же самый ток. Наиболее простой вариант ветви — это некоторый участок провода.
Ветвью называется также электрический прибор, который включен в розетку, и сам кабель, проведенный к данной розетке. На протяжении всей длины каждой ветви могут встречаться узлы, из которых выходят новые разветвления.
На разных участках электропровода эти ветви способны соединяться друг с другом параллельно, последовательно, в том числе образовывать узлы. При последовательном соединении получается новая ветвь, но крупных размеров.
Узел в электрической цепи
Узел — это место, в котором соединяются ветви электросхемы.
В законе Кирхгофа подробно описывается прохождение, а также распределение электрического тока в ветвях, которые подключены в одному узлу.
Под узлом в электропроводке понимается подключение разного количества проводов к одной клемме или проводу, в том числе это применительно к двойной розетке либо целому блоку розеток.
Понятие контура в электросхеме
Каждая электрическая сеть имеет источник питания. Например, в электрическом фонарике батарейку и полностью контур можно увидеть, а в случае с жилым зданием системой электрообеспечения выступает трансформаторная подстанция. Причем совсем необязательно, чтобы она находилась близко. Расстояние между домом и подстанцией может составлять несколько километров.
В подобных электросетях мощность источника электрического тока в несколько раз больше мощности проводки в квартире. Исходя из этого, при составлении схемы электрической цепи опускаются значения трансформатора. Расчеты ведутся исключительно для цепи, содержащей несколько узлов.
Что входит в определение закона Кирхгофа
Данный закон, предназначенный для электроцепи, опирается на правило сохранения заряда либо электроэнергии. В соответствии с такими законами, количество электрического тока, поступающего в узел, равняется значению »электричества», выходящего из этого же узла.
На основе такого правила по электроцепи, сделаны следующие выводы:
- Алгебраическая сумма электрических токов в узлах соответствует нулевой отметке. Такой результат получается при складывании положительного значения тока (со знаком »+» ), который направлен в узел, и отрицательного значения тока (со знаком »-»), выходящим из того же узла. Данная формула с подобными расчетами используется при составлении сложных схем.
- Сумма электрических токов, входящих в узел, равняется сумме выходящих из узла токов. Если не учитывать знак величины, то это является арифметической суммой.
Внимание! В электросетях переменного тока высокой частоты наблюдаются потери.
Они связаны с емкостью сети. Значение потерь нельзя определить прямыми способами. В такой ситуации кажется, что происходит нарушение первого закона Кирхгофа.
Как записывается правило Кирхгофа
Любое правило электротехники записывается в виде формулы. Первый закон Кирхгофа имеет два способа написания. В качестве образца можно представить узел с парой входящих электропроводов и токами в них — I1 и I2, а также исходящими из узла проводами — I3, I4 и I5.
Здесь следует вычисление:
- Алгебраическая сумма. Суммарное значение выводится на основе преобразования предшествующей формулы k-m=0 или I1+I2-I3-I4-I5=0. Запись получила применение при более сложных расчетах электросхем.
- Арифметическая сумма. Формула записывается как k=m или I1+I2=I3+I4+I5. В данном случае k — это приближающиеся к узлу линии, обозначение m — выходящие из узла провода. Предлагаемая форма записи применяется в случае, если необходимо узнать сечение токосодержащих жил для электропроводки с одной фазой либо однолинейной схемы электрообеспечения.
Формула также подходит для определения требуемой мощности блоков электросети.
Внимание! Электрический ток, протекающий в подходящих линиях, является положительным, а в случае исходящих проводов — отрицательным.
Расчеты для трехфазной линии
Для трехфазных линий переменного тока составляется схема, в которой присутствует рабочая нейтраль. В этом случае точкой соединения фазных линий с нулем выступает узел. Здесь используется первый закон Кирхгофа, формула которого записывается в более усложненном виде.
Сложное написание формулы связано с тем, что в электросетях переменного электрического тока помимо активного проходит также другой вид тока — реактивный, емкостной либо индуктивный. Исходя из этого, ток в разнофазных электропроводах оказывается передвинут не на 120 градусов, а другую угловую меру.
Для трехфазной линии ведутся специальные расчеты — строится график с векторами. В процессе определения значения тока в нейтрали суммируется вектор, но никак не величина самого тока.
Подобный расчет имеет свои сложности, поэтому он не проводится. Взамен этому осуществляется равномерное распределение нагрузки по всем фазам с максимальной эффективностью. При этом не требуется выбора профиля нейтрального электропроводника. На практике активно применяется готовая кабельная продукция от различных брендовых компаний.
Как проводятся расчеты электроцепи на основе правила Кирхгофа
Данный закон электроцепи получил применение при определении силы тока, а также профиля электропроводов, мощности блоков питания.
Определение параметра электропроводки
По внешнему виду электропроводка и токопроводящие линии напоминают контуры дерева — это кабель с огромным сечением и силой тока расходится в узле на множество отдельных друг от друга и небольших по сечению ветвей, сравнительно маленькой силой тока.
Запись формулы выглядит таким образом: Iвх=Iвых.
Как найти значение блока питания
Известно, что большая часть электрооборудования, приборов и аппаратов работают при непосредственном их подключении к электросети переменного тока напряжением 220 В.
Однако в продаже имеется немалое количество электроустановок, работающих при более низком значении напряжения. С учетом такой разницы в показателях напряжения, подобные приборы подсоединяются к блокам питания.
Закон Кирхгофа — правило, согласно которому выявляется связь между силой электрического тока во входящих и исходящих кабелях одного узла. Под электрическим током следует понимать исключительно направленное движение заряженных частиц.
В соответствии с действующим правилом о сохранении массы и энергии, сколько компонентов подходит к узлу, столько же и выходит из него. Правило Кирхгофа применяется во время расчетов профиля токосодержащих жил, в том числе мощности источника питания.
Детерминант Кирхгофа и формулы дерева цепей Маркова – Libres pensées d’un mathématicien ordinaire
Густав Роберт Кирхгоф (1824 – 1887) Этот пост посвящен формуле Густава Кирхгофа, выражающей инвариантную меру неприводимой конечной цепи Маркова через пролетные деревья. Многие из нас уже встречали имя Густава Кирхгофа на уроках физики при изучении электричества.
Пусть \( {X={(X_t)}_{t\geq0}} \) — непрерывное время Цепь Маркова 9{tQ}\right)_{i,j}. \]
Недиагональные элементы \( {Q} \) неотрицательны, а строки \( {Q} \) имеют нулевую сумму:
\[ \forall i,j\in V, \ quad i\neq j, \quad Q_{i,j}\geq0, \quad Q_{i,i}=-\sum_{k\neq i}Q_{i,k}. \]
Скелетный граф \( {G=(V,E)} \) of \( {Q} \) — это ориентированный граф , определяемый
\[ (i,j)\in E \quad\mathrm{iff}\quad Q_{i,j}>0. \]
Предположим, что \( {Q} \) является неприводимым , что означает, что \( {G} \) равно 9{(i,i)})=\sum_{T\in\mathcal{T}_i}\prod_{(j,k)\in T}Q_{j,k} \]
, где сумма пробегает набор \( {\mathcal{T}_i} \) остовных деревьев \({G} \) с корнем в \({i} \). Напомним, что остовное дерево или покрывающее дерево из \( {G} \) с корнем \( {i\in V} \) является подграфом \( {G} \) с набором ребер \( {V} \), которое является деревом с корнем \( {i} \). Обратите внимание, что \( {\mathcal{T}_i} \) непусто, так как \({G} \) связно.
Обратите внимание, что \( {\mathcal{T}_1,\ldots,\mathcal{T}_n} \) не обязательно имеют один и тот же кардинал из-за того, что ребра ориентированы: дерево покрытия с корнем в \( {i } \) содержит любой \( {j} \) как вершину, но не обязательно как возможный корень из-за стрелок. 9{(i,s)})\neq0} \).
Случайное блуждание. Предположим теперь, что \( {Q_{i,j}\in\{0,1\}} \) для каждого \( {i,j\in V} \) с \( {i\neq j} \) . Тогда \( {X} \) — это ближайшие соседи случайных блужданий на \( {G} \), диагональ \( {-Q} \) образована последовательностью степеней из \( {G} \), а \( {Q} \) — это лапласиан \( {\Delta_G} \) из \({G} \). В этом случае \( {Q_{j,k}=1} \) для каждого \( {(j,k)\in G} \) и, таким образом, приведенная выше формула Кирхгофа сводится к
\[ \forall i\in V,\quad \mu_i=|\mathcal{T}_i|. \]
Предположим теперь, что \( {Q} \) дополнительно симметрично , что означает, что \( {G} \) не ориентировано в том смысле, что \( {(j,k)\in E} \) тогда и только тогда, когда \( {(k,j)\in E} \).
В этом случае инвариантной вероятностной мерой \({Q}\) будет тогда равномерный закон на \({V}\). Из-за отсутствия ориентации множества \( {\mathcal{T}_1,\ldots,\mathcal{T}_n} \) имеют один и тот же кардинал \( {\kappa} \), который является числом остовных деревья \( {G} \) (без укоренения). У нас есть 9{(i,j)}) =|\mathcal{T}|_i=\каппа. \]
Другими словами, матрица кофакторов лапласиана неориентированного графа имеет постоянные элементы, равные количеству остовных деревьев графа.
Соединим \( {\kappa} \) с собственными значениями симметричной матрицы \( {-Q} \), пронумерованными как
\[ 0=\lambda_1<\lambda_2\leq\cdots\leq \ лямбда_н. \]
Здесь \( {\lambda_1} \) просто, так как \( {Q} \) неприводимо. Характеристический многочлен \( {-Q} \) равен 9{n-2}} \).
Алгоритм Вильсона. Дэвид Уилсон изобрел точный алгоритм для создания остовного дерева \( {G} \), которое следует равномерному распределению на множестве остовных деревьев \( {G} \).
Начиная с вершины \( {1} \), алгоритм состоит в установке \( {A_1=\{1\}} \) и моделировании пути простого случайного блуждания по \( {G} \), начиная с вершине \( {2} \) до тех пор, пока она не достигнет \( {A_1} \). Тогда \( {A_2} \) является объединением \( {A_1} \) и версии этого пути со стертым циклом. Если \( {A_2=V} \), алгоритм останавливается. Если нет, то повторяем то же самое, начиная на этот раз путь из наименьшей вершины не в \({A_2}\), останавливая путь, когда он достигает \({A_2}\), и так далее. Алгоритм Уилсона можно естественным образом связать с функцией Грина случайного блуждания на \({G}\) с граничными условиями Дирихле на подмножестве \({V}\). 9{kQ}\right)_{i,j}. \]
Дополнительная литература.
- Лайонс и Перес, Вероятность на деревьях и сетях (глава 4)
- Лейтон и Ривест, Оценка вероятности с использованием конечной памяти
- Анантарам и Цукас, Доказательство теоремы дерева цепи Маркова конечные цепи Маркова
- Биан и Чапуи, Матрицы Лапласа и остовные деревья древовидных графов
- Розенталь – Примечание о формуле Кирхгофа и алгоритме Уилсона
- Харрис и Херст и Моссингхофф, Комбинаторика и теория графов
Статья о Кирхгофе+формула из The Free Dictionary
Кирхгофа+формула | Статья о формуле Кирхгофа в The Free DictionaryКирхгоф+формула | Статья о формуле Кирхгофа в The Free Dictionary
Слово, не найденное в Словаре и Энциклопедии.
