Формула индукции магнитного поля, B
Онлайн калькуляторы
На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.
Справочник
Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!
Заказать решение
Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!
Главная Справочник Формулы по физике Формула индукции магнитного поля
Направлением вектора магнитной индукции считают направление на север магнитной стрелки, которая может свободно вращаться в магнитном поле. Такое же направление имеет положительная нормаль к замкнутому контуру, по которому течет ток. Положительная нормаль имеет направление, совпадающее с направлением перемещения правого винта (буравчика), если его вращают по направлению тока в контуре.
Модуль вектора магнитной индукции можно установить, используя силу, которая действует на проводники с током, помещенные в магнитное поле (силу Ампера). Тогда модуль вектора равен частному от деления максимальной силы (), с которой магнитное поле оказывает воздействие на отрезок проводника с током (I) к произведению силы тока на длину проводника ():
Рассматривая силу Лоренца, которая действует на заряженную частицу, движущуюся в магнитном поле, получают формулу для магнитной индукции в виде:
где – модуль силы Лоренца; q – заряд частицы, движущейся со скоростью v в магнитном поле; – это угол между векторами и . Направления , векторов и связаны между собой правилом левой руки.
Формулой, которая определяет величину вектора магнитной индукции в данной точке магнитного поля, считают так же следующее выражение:
где – максимальный вращающий момент, действующий на рамку, которая обладает магнитным моментом , равным единице, если нормаль к рамке перпендикулярна направлению поля.
Вращающий момент (M), действующий на контур с током I в однородном магнитном поле можно вычислить как:
где S – площадь, которую обтекает ток I. Следует помнить, что максимальный вращающий момент получается тогда, когда плоскость контура параллельна линиям магнитной индукции поля ().
Принцип суперпозиции магнитных полей
Если магнитное поле получается в результат наложения нескольких магнитных полей то, магнитная индукция поля (), может быть найдена как векторная сумма магнитных индукций отдельных полей ():
Закон Био-Савара-Лапласа, как формула для вычисления величины индукции магнитного поля
Закон Био-Савара – Лапласа является одним из распространенных законов, который позволяет вычислить вектор магнитной индукции () в любой точке магнитного поля, создаваемого в вакууме элементарным проводником с током:
где I – сила тока; – вектор элементарный проводник по модулю он равен длине проводника, при этом его направление совпадает с направлением течения тока; – радиус-вектор, который проводят от элементарного проводника к точке, в которой находят поле; – магнитная постоянная.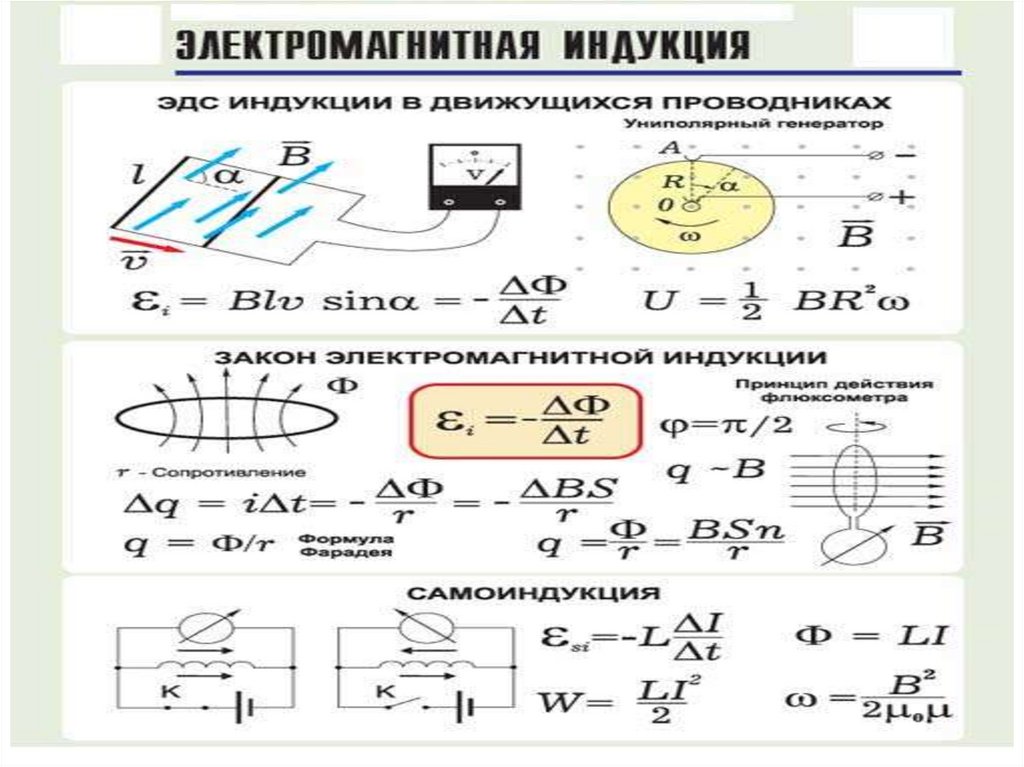
Вектор является перпендикулярным к плоскости, в которой расположены и , конкретное направление вектора магнитной индукции определяют при помощи правила буравчика (правого винта).
Для однородного и изотропного магнетика, заполняющего пространство, вектор магнитной индукции в вакууме( и в веществе (), при одинаковых условиях, связывает формула:
где – относительная магнитная проницаемость вещества.
Частные случаи формул для вычисления модуля вектора магнитной индукции
Формула для вычисления модуля вектора индукции в центре кругового витка с током (I):
где R – радиус витка.
Модуль вектора магнитной индукции поля, которое создает бесконечно длинный прямой проводник с током:
где r – расстояние от оси проводника до точки, в которой рассматривается поле.
В средней части соленоида магнитная индукция поля вычисляется при помощи формулы:
где n – количество витков соленоида на единицу длины; I – сила тока в витке.
Примеры решения задач по теме «Индукция магнитного поля»
| Понравился сайт? Расскажи друзьям! | |||
17. Формулы индукции магнитного поля токов различной формы. Магнитная проницаемость среды.
Если проводник с током создает в вакууме магнитное поле с магнитной индукцией Во, то в другой среде магнитное поле, созданное этим же проводником с током будет иметь индукцию В. Т.е. значение магнитной индукции зависит от среды, в которой существует магнитное поле. Отношение магнитной индукции В поля в данной среде к магнитной индукции Во в вакууме, характеризует магнитные свойства данной среды и называется относительной магнитной проницаемостью вещества — µ.
18. Магнитный поток. Формула тока, изображение и единица измерения.
19. Действия магнитного поля на движущийся заряд. Сила Лоренца.
Из
опыта известно, что магнитное поле
оказывает действие не только на проводники
с током, но и на отдельные заряды, которые
движутся в магнитном поле.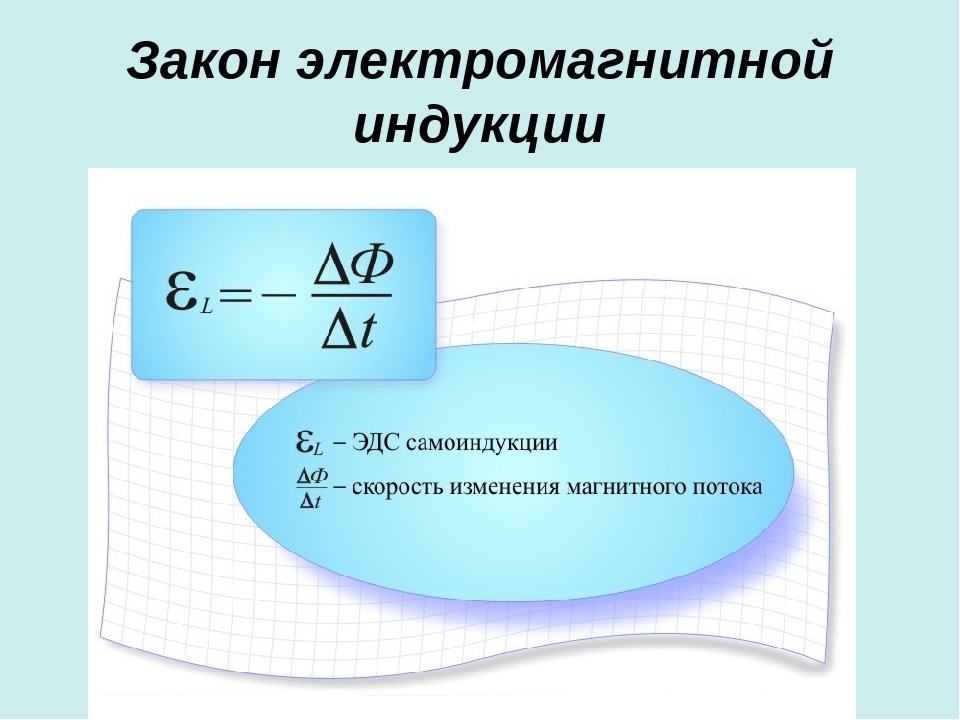
Сила, которая
действует на электрический заряд Q,
движущийся в магнитном поле со скоростью
v, называется силой Лоренца и задается
выражением
Чтобы определить направление силы Лоренца используем правило левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца направить вдоль вектора v (для Q>0 направления I и v совпадают, для Q<0 — противоположны), то отогнутый большой палец покажет направление силы, которая действует на положительный заряд. На рис. 1 продемонстрирована взаимная ориентация векторов v, В (поле имеет направление на нас, на рисунке показано точками) и F для положительного заряда. Если заряд отрицательный, то сила действует в противоположном направлении. Модуль силы Лоренца, как уже известно, равен где α — угол между v и В.
Подчеркнем
еще раз, что магнитное поле не оказывает
действия на покоящийся электрический
заряд. Этим магнитное поле существенно
отличается от электрического.
Поскольку сила Лоренца всегда перпендикулярна скорости движения заряженной частицы, то данная сила может менять только направление этой скорости, не изменяя при этом ее модуля. Значит, сила Лоренца работы не совершает. Другими словами, постоянное магнитное поле не совершает работы над движущейся в этом поле заряженной частицей и, следовательно, кинетическая энергия этой частицы при движении в магнитном поле не изменяется.
В случае, если на движущийся электрический заряд вместе с магнитным полем с индукцией В действует еще и электрическое поле с напряженностью Е, то суммарная результирующая сила F, которая приложена приложенная к заряду, равна векторной сумме сил — силы, действующей со стороны электрического поля, и силы Лоренца:
20.
Магнитные свойства вещества. Кривая намагничивания ферромагнетиков.Формула магнитной индукции – подробное объяснение и часто задаваемые вопросы
Магнитная индукция – это явление генерации электродвижущей силы или ЭДС. в проводнике, относящемся к изменению связанного с ним магнитного потока. Он был открыт ученым Майклом Фарадеем в 1831 году. Позднее закон индукции Фарадея был математически представлен Максвеллом. Магнитная индукция — очень важное научное явление и важнейшая тема физики. Чтобы понять, что означает формула магнитной индукции, давайте разберемся с законом индукции Фарадея. Здесь мы также изучим формулу индуцированной ЭДС, формулу закона Фарадея и некоторые другие важные особенности магнитной индукции.
Закон индукции Фарадея
Формула индукции магнитного поля Фарадея утверждает, что при изменении магнитного потока, связанного с проводником, индуцируется электродвижущая сила (ЭДС). Скорость изменения магнитного потока в замкнутом контуре равна скорости изменения ЭДС.
(Изображение скоро будет загружено)
Согласно экспериментам Фарадея
ε прямо пропорционально изменению потока
ε обратно пропорционально Δt
ε, создаваемое в катушке с N витками, в N раз больше, чем у одиночной катушки с током (ε ∝ N)
Магнитный поток, проходящий через поверхность векторной площади A:
ΦB =B⋅A = BAcosθ
Для переменного магнитного поля магнитный поток dΦB через бесконечно малую площадь dA:
dΦB = B⋅dA
Поверхностный интеграл дает полный магнитный поток через поверхность.
ΦB = ∫∫A B⋅dA
Согласно формуле закона Фарадея, в витке провода с N витками формула ЭДС наведения в замкнутой цепи имеет вид
ЭДС (ε) = — N\[\frac{\Delta \phi }{\Delta t}\]
При изменении потока на Δ за время Δt.
Знак минус показывает, что возникает ток I и магнитное поле B, противоположное направлению изменения потока.
Это известно как закон Ленца.
Формула электромагнитной индукции для движущегося проводника
(Изображение будет загружено в ближайшее время)
Для движущегося стержня N=1 и потока Φ=BAcosθ, θ=0º и cosθ=1, a B перпендикулярна A.
Площадь, заметаемая стержнем, равна ΔA= lΔx
∴ ε = \[\frac{B \Delta A }{\Delta t}\] = \[\frac{Bl \Delta x}{\Delta t}\] = Blv
, где v (скорость) перпендикулярно B (магнитному полю)
(изображение будет загружено в ближайшее время)
В приведенном выше сценарии генератора скорость составляет угол θ с B, так что ее составляющая, перпендикулярная B, равна vsinθ.
ε = Blv sinθ
Где, l = длина проводника,
v = скорость проводника,
θ = угол между магнитным полем и направлением движения.
Таким образом, формула индуцированного тока означает тесную связь между электрическим полем и магнитным полем, которая зависит от определенного изменения во времени.
Заключение
Создание напряжения (или ЭДС) над электрическим проводником, помещенным в переменное магнитное поле, называется электромагнитной индукцией. Индуцированная электродвижущая сила в замкнутом контуре равна скорости изменения магнитного потока, охваченного контуром, в соответствии с законом Фарадея.
Математическая индукция — Темы предварительного исчисления
Темы в
ПРЕДВАРИТЕЛЬНАЯ РАБОТА
Содержание | Дом
27
Принцип математической индукции
НАТУРАЛЬНЫЕ ЧИСЛА счетные числа: 1, 2, 3, 4 и т. д. Математическая индукция — это метод доказательства утверждения (теоремы или формулы), которое утверждается о каждое
Под «каждым» или «всем» натуральными числами мы подразумеваем любое, которое назовем.
Например,
1 + 2 + 3 + . . . + н = ½ н ( н + 1).
Это утверждает, что сумма последовательных чисел от 1 до n задается формулой справа.
Мы хотим доказать, что это будет верно для n = 1, n = 2, n = 3 и так далее. Теперь мы можем проверить формулу для любого заданного числа , скажем, n = 3:
1 + 2 + 3 = ½ · 3 · 4 = 6
— это правда. Это верно и для
1 + 2 + 3 + 4 = ½ · 4 · 5 = 10.
Но как нам доказать это правило для каждого значения n ?
Способ доказательства следующий. Мы показываем, что , если утверждение — правило — истинно для любого конкретного числа k (например, 104), то оно также будет истинным для следующего за ним числа k + 1 (например, 105). Затем мы показываем, что утверждение будет верным для 1. Отсюда следует, что утверждение будет верным для 2. Следовательно, оно будет верным для 3. Оно будет верным для любого натурального числа, которое мы назовем.
Это называется принципом математической индукции.
| Если | ||
| 1) | , когда утверждение истинно для натурального числа n = k , , то оно также будет истинным для его преемника, n = k + 1; | |
| и | ||
| 2) | утверждение верно для n = 1; | |
| то утверждение будет верным для каждого натурального числа | ||
Чтобы доказать утверждение по индукции, мы должны доказать части 1) и 2) выше.
Гипотеза шага 1) — » Утверждение верно для n = k » — называется предположением индукции или гипотезой индукции. это то, что мы предполагают , когда мы доказываем теорему по индукции.
Пример 1. Докажите, что сумма первых n натуральных чисел задается следующей формулой:
| 1 + 2 + 3 + . . . + н | = | n ( n + 1) 2 | . |
Доказательство . Мы выполним шаги 1) и 2) выше. Во-первых, предположим , что формула верна для n = k ; то есть будем считать:
| 1 + 2 + 3 + . . . + к | = | к ( к + 1) 2 | . (1) |
Это предположение индукции. Предполагая это, мы должны доказать, что формула верна для ее преемника, n = k + 1. То есть мы должны показать:
| 1 + 2 + 3 + . . . + ( к + 1) | = | ( к + 1)( к + 2) 2 | . (2) |
Для этого мы просто добавим следующий член ( k + 1) в обе стороны предположения индукции, строка (1):
Это строка (2), которую мы хотели показать в первую очередь.
Далее мы должны показать, что формула верна для n = 1. Имеем:
1 = ½ · 1 · 2
— это правда. Теперь мы выполнили оба условия принципа математической индукции. Таким образом, формула верна для любого натурального числа.
(В приложении к арифметике мы прямо устанавливаем эту формулу.)
Пример 2. Докажите, что это правило показателей верно для любого натурального числа n :
( аб ) н = а н б н 8.
Доказательство . Опять же, мы начинаем с , предполагая, что верно для 9.0083 н = к ; то есть принимаем:
( аб ) к = а к б к .
. . . . . . . (3)
При таком предположении мы должны показать, что правило верно для его преемника, n = ( k + 1). Мы должны показать:
( аб ) к + 1 = a к + 1 б к + 1 . . . . . . . (4)
(При использовании математической индукции учащийся всегда должен писать именно то, что должно быть показано.)
Теперь, учитывая предположение, линия (3), как мы можем получить из нее строку (4)?
Просто умножив обе стороны линии (3) на ab :
| ( аб ) к аб | = | а к б к аб | |
| = | а к а б к б | ||
| так как порядок множителей не имеет значения, | |||
| = | а к + 1 б к + 1 . | ||
Это линия (4), которую мы хотели показать.
Итак, мы показали, что если теорема верна для любого конкретного натурального числа k , то она также верна для следующего за ним числа k + 1,
.Далее мы должны показать, что правило верно для n = 1; то есть тот
( аб ) 1 = а 1 б 1 .
Но ( аб ) 1 = аб ; и a 1 b 1 = ab .
Таким образом, это правило верно для любого натурального числа n .
Пример 3. Сумма последовательных кубов. Докажите этот замечательный факт арифметики:
1 3 + 2 3 + 3 3 + . . . + n 3 = (1 + 2 + 3 + . . . + n ) 2 .
«Сумма n последовательных кубов равна квадрату
суммы первых n чисел.
»
Другими словами, согласно Примеру 1:
| 1 3 + 2 3 + 3 3 + . . . + п 3 | = | n ²( n + 1)² 4 |
Доказательство . Для удобства сумму до n будем обозначать через S ( n ). Предположим, что формула верна для n = k ; то есть тот
| С ( к ) | = | к ²( к + 1)² 4 | (1) |
| Теперь мы должны показать, что формула верна и для n = k + 1; что | |||
| S ( к + 1) | = | ( к + 1)²( к + 2)² 4 | (2) |
| To do that, add the next cube to S ( k ), line (1): | |||
| S ( k + 1) | = | S ( к ) + ( к + 1) 3 | |
| = | к ²( к + 1)² 4 | + ( к + 1) 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| = | к ²( к + 1)² + 4( к + 1)³ 4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| = | ( k + 1)²[ k ² + 4( k + 1)] 4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| — принимая ( k + 1) 2 как общий множитель, | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| = | ( к + 1)²( к ² + 4 к + 4) 4 | ||
| = | ( к + 1)²( к + 2)² 4 | ||
Это линия (2), которую мы хотели показать.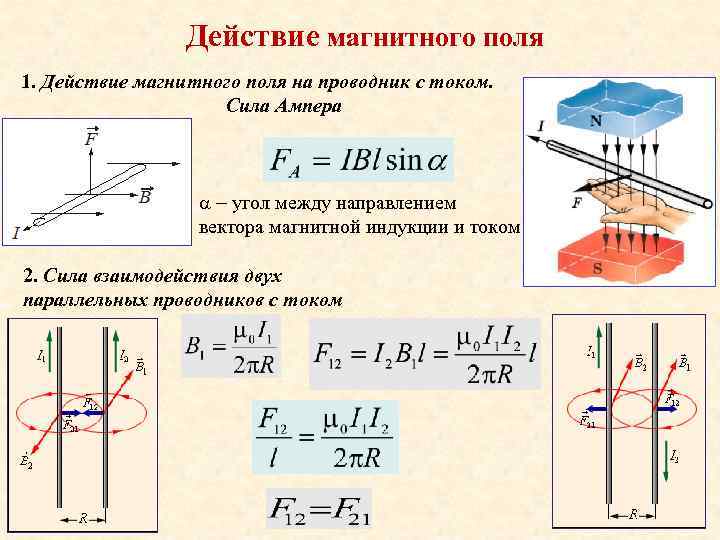
Наконец, мы должны показать, что формула верна для n = 1.
| 1 3 | = | 1² · 2² 4 |
| 1 | = | 1 · 4 4 |
— это правда. Таким образом, формула верна для любого натурального числа.
В Приложении к Арифметике мы прямо показываем, что это верно.
Задача 1. В соответствии с принципом математической индукции доказать утверждение, которое утверждается о каждом натуральном числе 9.0083 n , нужно доказать две вещи.
а) Что первое?
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
Если утверждение истинно для n = k , то оно будет верно и для его преемника, k + 1.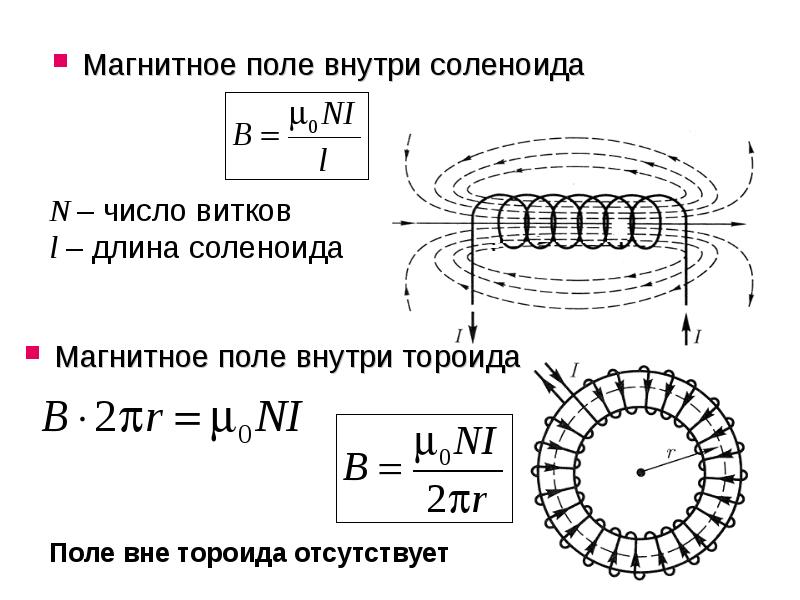
б) Что такое второе?
Утверждение верно для н = 1.
c) Часть a) содержит предположение индукции. Что это?
Утверждение верно для n = k .
Задача 2. Пусть S ( n ) = 2 n − 1. Вычислить
а) S ( к ) = 2 к — 1
б) S ( к + 1) = 2( к + 1) − 1 = 2 k + 2 − 1 = 2 k + 1
Задача 3. Сумма первых n нечетных чисел равна n-му квадрату .
1 + 3 + 5 + 7 + . . . + (2 н — 1) = н 2 .
а) Чтобы доказать с помощью математической индукции, какой будет индукция
а) предположение?
Утверждение верно для n = к :
1 + 3 + 5 + 7 + . . . + (2 к — 1) = к 2 .
б) На основании этого предположения, что мы должны показать?
Утверждение верно для его преемника, k + 1:
1 + 3 + 5 + 7 + .
. . + (2 к — 1) + 2 к + 1 = ( к + 1)².
c) Покажи это.
При добавлении 2 k + 1 к обеим частям предположения индукции:
| 1 + 3 + 5 + 7 + . . . + (2 к − 1) + 2 к + 1 | = | к ² + 2 к + 1 |
| = | ( к + 1) 2 | |
г) Чтобы завершить доказательство с помощью математической индукции, что мы должны показать?
Утверждение верно для n = 1.
д) Покажи это.
1 = 1 2
Задача 4. Докажите методом математической индукции:
Если мы обозначим эту сумму как S ( n ), то предположим, что формула верна для n = k ; то есть предположим
| С ( к ) | = | к 2 к + 1 | . |
Теперь покажите, что формула верна для n = k + 1; то есть показать:
| С ( к + 1) | = | к + 1 2 к + 3 | . |
Начало:
| С ( к + 1) | = | S ( k ) + следующих членов, чей знаменатель является произведением следующих нечетных чисел. |
| = | ||
| = | ||
| = | ||
| = | ||
| = | ||
Далее,
Формула верна для n = 1:
Следовательно, это верно для всех натуральных чисел.
