| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Физический справочник / / Электрические и магнитные величины / / Понятия и формулы для электричества и магнетизма. / / Таблица большая основных формул электричества и магнетизма Поделиться:
| ||||||||||||||||||||||||||
Электромагнетизм Основные формулы
Связь магнитной индукции B с напряженностью H магнитного поля:
,
где — магнитная проницаемость изотропной среды; 0 — магнитная постоянная. В вакууме =1, и тогда магнитная индукция в вакууме
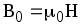
Закон Био-Савара-Лапласа:
 или
или 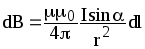 ,
,
где dB — магнитная индукция поля, создаваемого элементом проводника длиной dl с током I; r — радиус-вектор, направленный от элемента проводника к точке, в которой определяется магнитная индукция; — угол между радиус-вектором и направлением тока в элементе проводника.
Магнитная индукция в центре кругового тока:
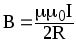
 ,
,
где R — радиус кругового витка.
Магнитная индукция на оси кругового тока:

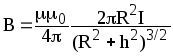 ,
,
где h — расстояние от центра витка до точки, в которой определяется магнитная индукция.
Магнитная индукция поля прямого тока:
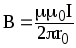 ,
,
где r0 — расстояние от оси проводника до точки, в которой определяется магнитная индукция.
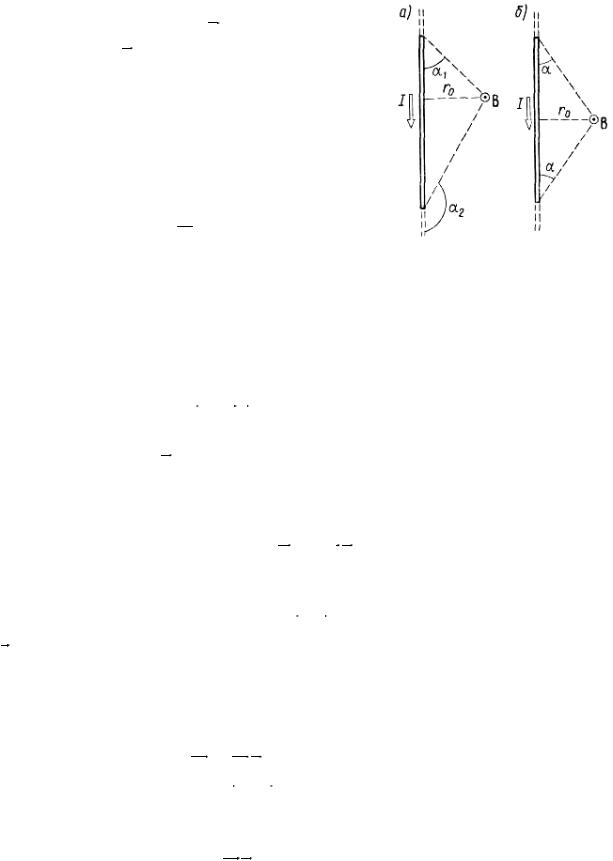
Магнитная индукция поля, создаваемого отрезком провода с током ( см.рис.)
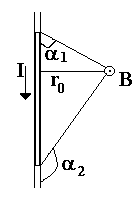
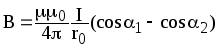
Обозначения ясны из рисунка. Направление вектора магнитной индукции B обозначено точкой — это значит, что B направлен перпендикулярно плоскости чертежа к нам.
При симметричном расположении концов провода относительно точки, в которой определяется магнитная индукция -cos2=cos1, тогда
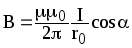
Магнитная индукция поля соленоида:
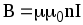 ,
,
где n — отношение числа витков соленоида к его длине.
Сила, действующая на проводник с током в магнитном поле (закон Ампера)
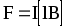 или
или 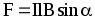 ,
,
где l — длина проводника; — угол между направлением тока в проводнике и вектором магнитной индукции B. Это выражение справедливо для однородного магнитного поля и прямого отрезка проводника. Если поле неоднородно и проводник не является прямым, то закон Ампера можно применять к каждому элементу проводника в отдельности:
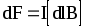 .
.
Сила взаимодействия параллельных проводов с током:
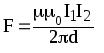 ,
,
где d — расстояние между проводами
Магнитный момент плоского контура с током:
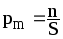 ,
,
где n —единичный вектор нормали к плоскости контура; I — сила тока, протекающего по контуру; S — площадь контура.
Механический (вращательный) момент, действующий на контур с током, помещенный в однородное магнитное поле:
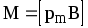 или
или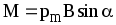 ,
,
где — угол между векторами pm и B
Отношение магнитного момента pm к механическому L (моменту импульса) заряженной частицы, движущейся по круговой орбите:
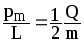 ,
,
где Q — заряд частицы; m- масса частицы.
Сила Лоренца
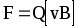 или
или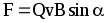 ,
,
где v — скорость заряженность частицы; — угол между векторами v и B.
Магнитный поток:
а) в случае однородного магнитного поля и плоской поверхности:
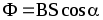 или
или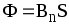 ,
,
где S — площадь контура; — угол между нормалью к плоскости контура и вектором магнитной индукции.
б) в случае неоднородного поля и произвольной поверхности:
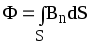 (интегрирование по всей поверхности)
(интегрирование по всей поверхности)
Потокосцепление (полный поток)
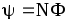
Эта формула верна для соленоида и тороида с равномерной намоткой плотно прилегающих друг к другу N витков.
Работа по перемещению замкнутого контура в магнитном поле:
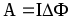
ЭДС индукции:
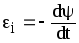 .
.
Разность потенциалов на концах проводника, движущегося со скоростью
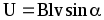 ,
,
где l-длина проводника; — угол между векторами v и B
Заряд, протекающий по замкнутому контуру при изменении магнитного потока, пронизывающего этот контур:
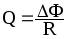 или
или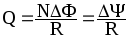 ,
,
где R — сопротивление контура.
Индуктивность контура:
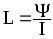
ЭДС самоиндукции:
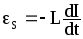 .
.
Индуктивность соленоида:
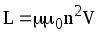 ,
,
где n — отношение числа витков соленоида к его длине; V — объем соленоида.
Мгновенное значение силы тока в цепи, обладающей сопротивлением R и индуктивностью L:
а) 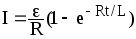 (при замыкании цепи)
(при замыкании цепи)
где — эдс источника тока; t- время, прошедшее после замыкания цепи;
б) 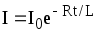 (при размыкании цепи),
(при размыкании цепи),
где I0— сила тока в цепи при t=0; t- время, прошедшее с момента замыкания цепи.
Энергия магнитного поля:
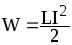
Объемная плотность энергии магнитного поля (отношение энергии магнитного поля соленоида к его объему):
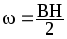 или
или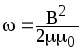 ,
,
где B — магнитная индукция; H- напряженность магнитного поля.
Основные формулы Электромагнетизм
МАГНЕТИЗМ
Методические указания и контрольные задания для самостоятельной работы студентов
Дарибазарон Э.Ч., Санеев Э.Л., Шагдаров В.Б.
Редактор Т.Ю.Артюнина
Подготовлено в печать 2001 г. Формат 6080 1/16
Усл.п.л. 3,72; уч.-изд.л. 3,2; Тираж 150 экз.
___________________________________________________
РИО ВСГТУ, Улан-Удэ, Ключевская, 40а
Отпечатано на ротапринте ВСГТУ, Улан-Удэ,
Ключевская, 42.
Восточно-Сибирский государственный
технологический университет
Министерство образования РФ
ВОСТОЧНО-СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ
ЗАДАНИЯ ПО ФИЗИКЕ
ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТОВ
РАЗДЕЛ: ”МАГНЕТИЗМ»
Составители: Дарибазарон Э.Ч.,
Санеев Э.Л.,
Шагдаров В.Б.
Улан-Удэ 2002
Связь магнитной индукции B с напряженностью H магнитного поля:
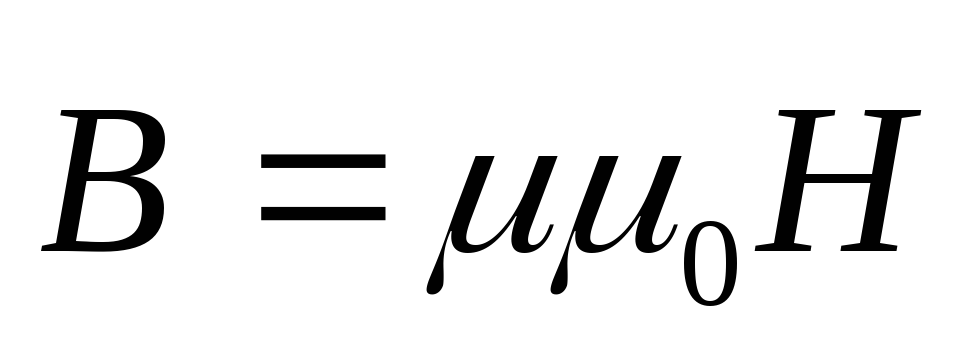
где — магнитная проницаемость изотропной среды; 0 — магнитная постоянная.
В вакууме = 1, и тогда магнитная индукция в вакууме
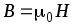
Закон Био-Савара-Лапласа:
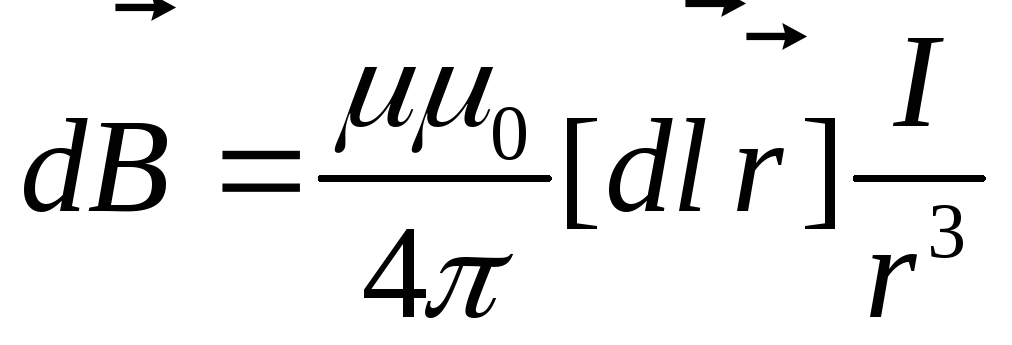 или
или 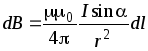
где 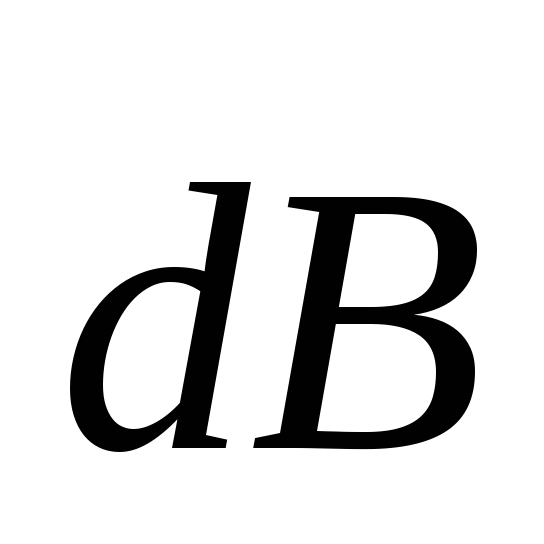 — магнитная индукция поля, создаваемого
элементом проводника длинойdl
с током I;
— магнитная индукция поля, создаваемого
элементом проводника длинойdl
с током I; 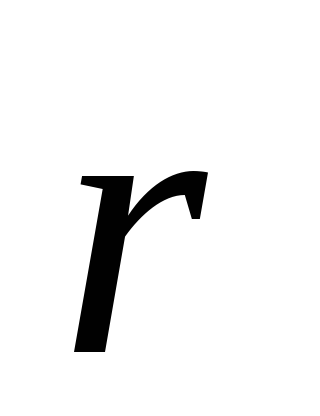 — радиус-вектор,
направленный от элемента проводника к
точке, в которой определяется магнитная
индукция;
— угол между радиусом-вектором и
направлением тока в элементе проводника.
— радиус-вектор,
направленный от элемента проводника к
точке, в которой определяется магнитная
индукция;
— угол между радиусом-вектором и
направлением тока в элементе проводника.
Магнитная индукция в центре кругового тока:
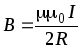
где R — радиус кругового витка.
Магнитная индукция на оси кругового тока:
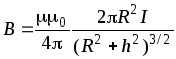
где h — расстояние от центра витка до точки, в которой определяется магнитная индукция.
Магнитная индукция поля прямого тока
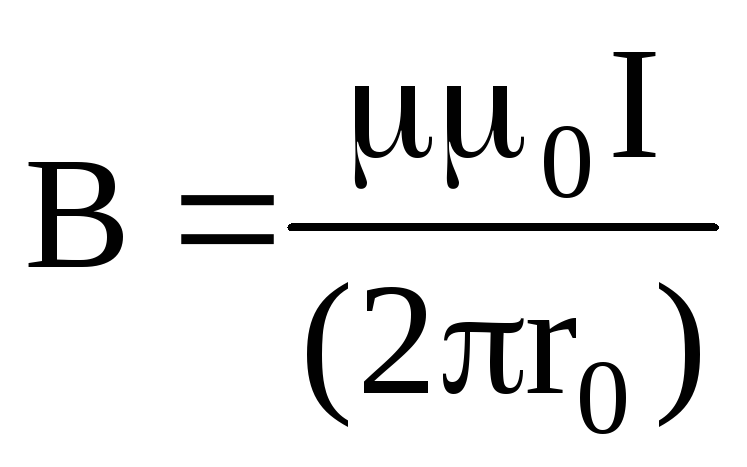
где ro — расстояние от оси проводника до точки, в которой определяется магнитная индукция.
Магнитная индукция поля, создаваемого отрезком провода с током (рис.I,a):
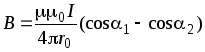
Обозначения
ясны из рисунка. Направление вектора
магнитной индукции 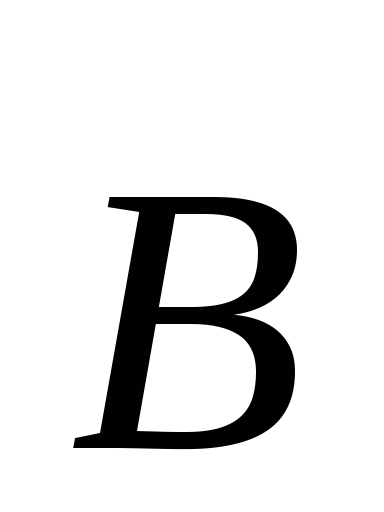 обозначено
точкой — это значит, что
обозначено
точкой — это значит, что 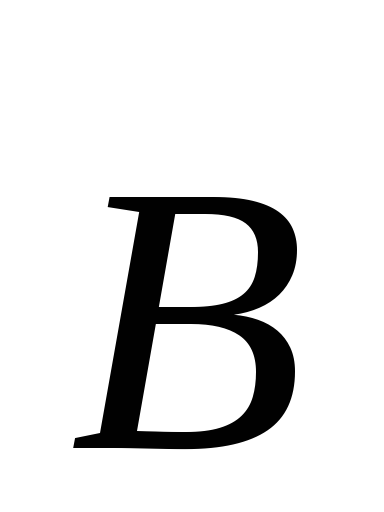 направлен перпендикулярно плоскости
чертежа к нам.
направлен перпендикулярно плоскости
чертежа к нам.
При симметричном расположении концов провода относительно точки, в которой определяется магнитная индукция (рис.I,б):
-cos2 = cos1=cos,
тогда
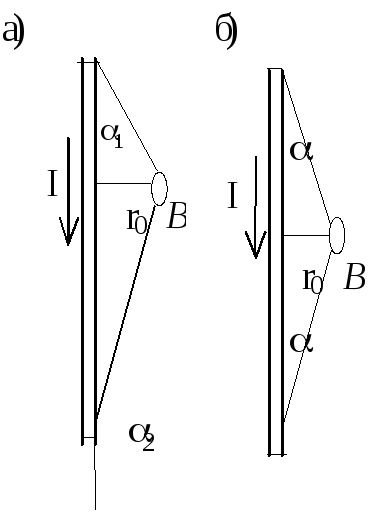
Рис.1
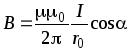
Магнитная индукция поля соленоида
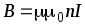
где n — отношение числа витков соленоида к его длине.
Сила, действующая на проводник с током в магнитном поле (закон Ампера):
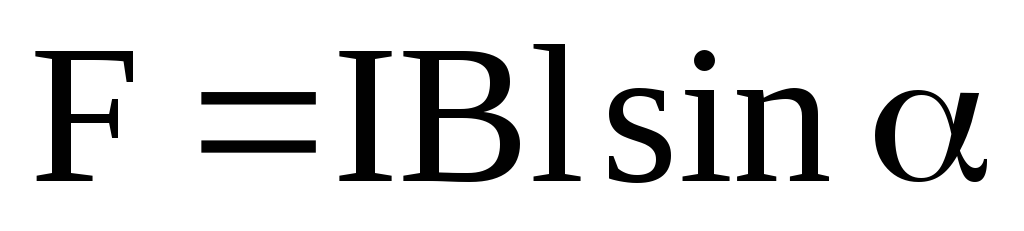
где
l — длина
проводника;
— угол между направлением тока в проводнике
и вектором магнитной индукции  .
Это выражение справедливо для однородного
магнитного поля и прямого отрезка
проводника. Если поле неоднородно и
проводник не является прямым, то закон
Ампера можно применить к каждому элементу
проводника в отдельности:
.
Это выражение справедливо для однородного
магнитного поля и прямого отрезка
проводника. Если поле неоднородно и
проводник не является прямым, то закон
Ампера можно применить к каждому элементу
проводника в отдельности:
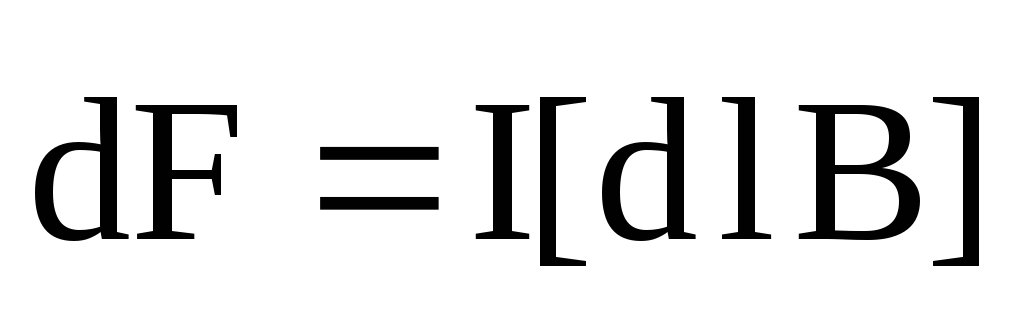
Магнитный момент плоского контура с током:
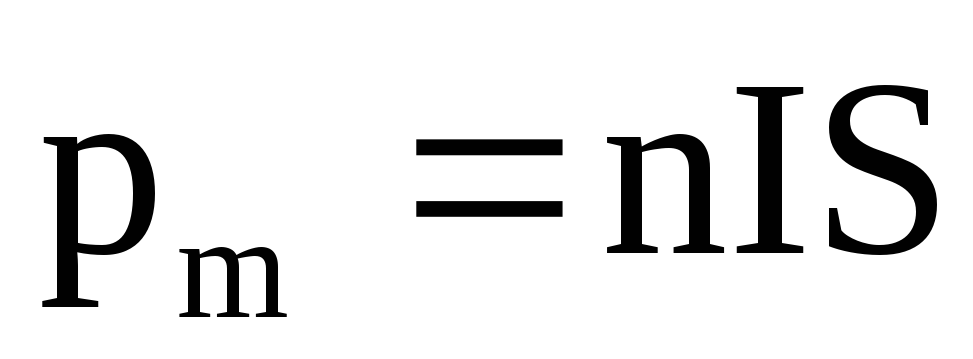
где 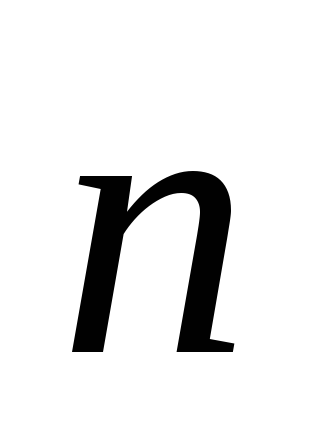 — единичный
вектор нормали (положительный) к плоскости
контура; I
— сила тока, протекающего по контуру; S
— площадь контура.
— единичный
вектор нормали (положительный) к плоскости
контура; I
— сила тока, протекающего по контуру; S
— площадь контура.
Механический (вращательный) момент, действующий на контур с током, помещенный в однородное магнитное поле:
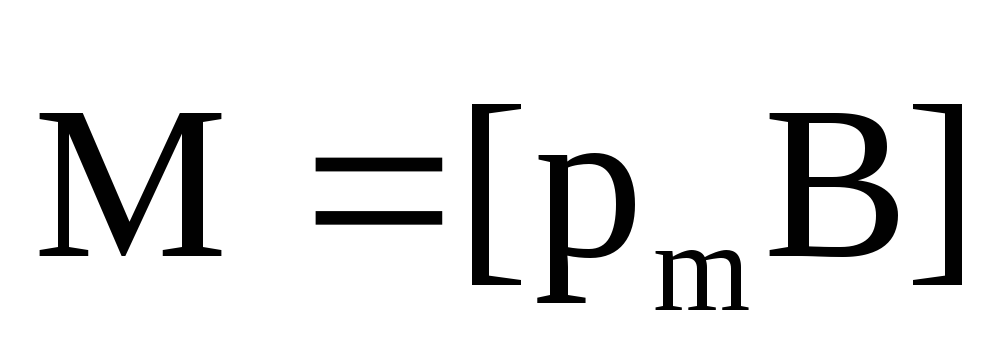
 ,
или
,
или 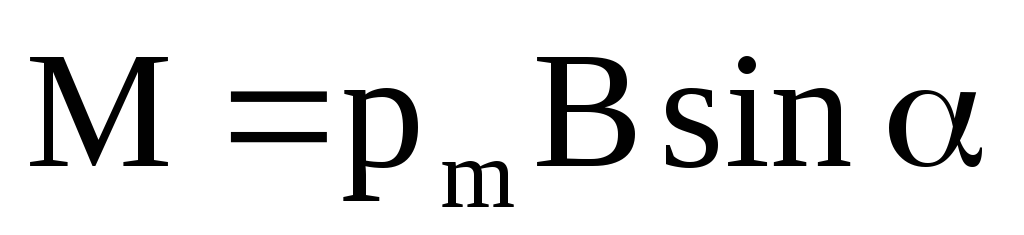
где — угол между
векторами 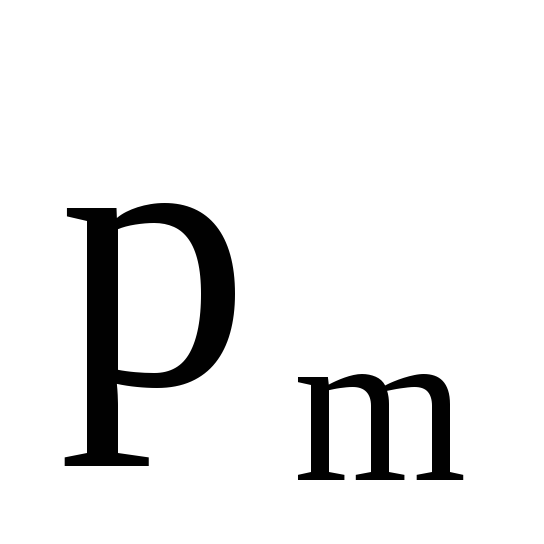 и
и  .
.
Потенциальная энергия (механическая) контура с током в магнитном поле:
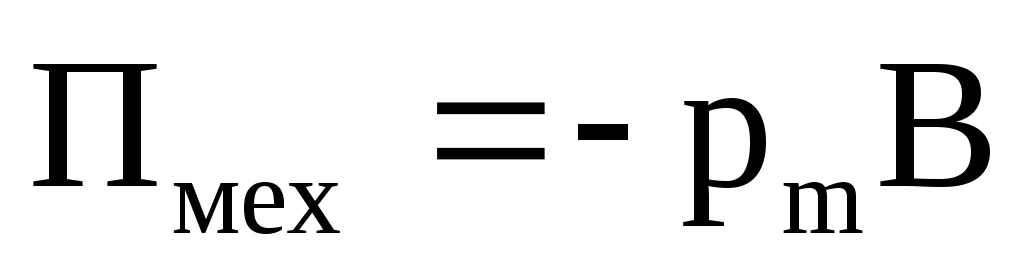 , или
, или 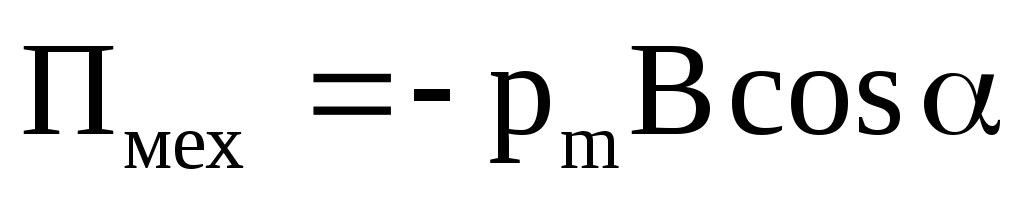


Отношение
магнитного момента 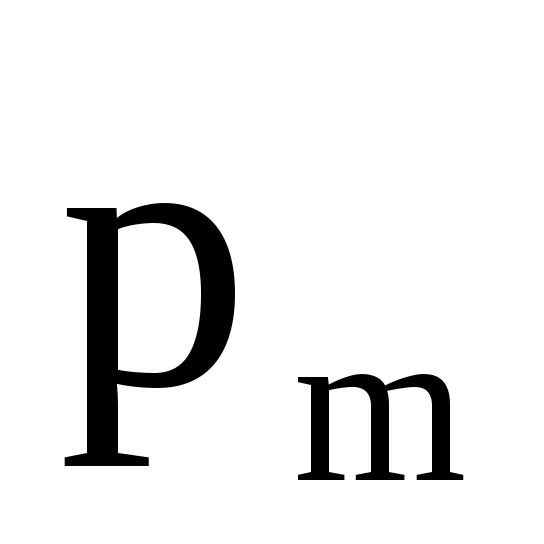 к механическому
к механическому 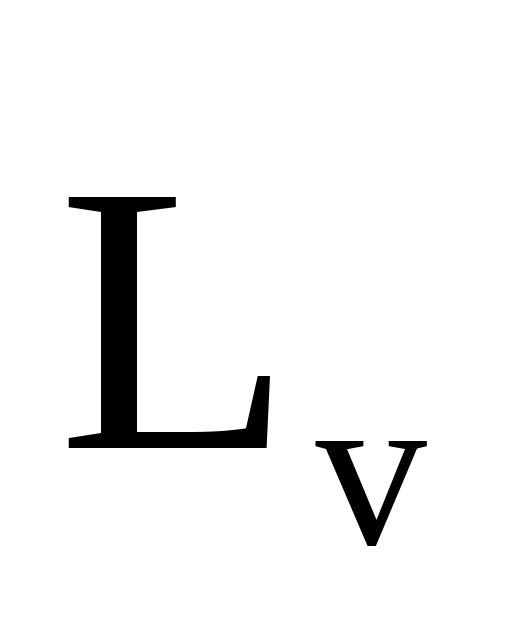 (моменту импульса) заряженной частицы,
движущейся по круговой орбите:
(моменту импульса) заряженной частицы,
движущейся по круговой орбите:
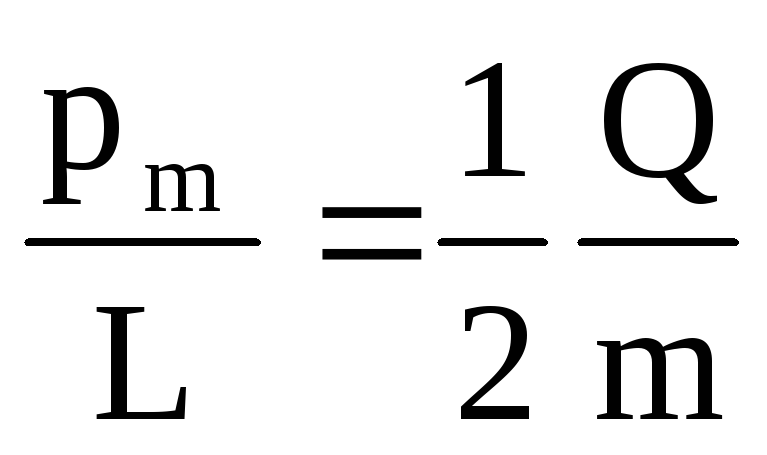
где Q — заряд частицы; m — масса частицы.
Сила Лоренца:
 ,
или
,
или 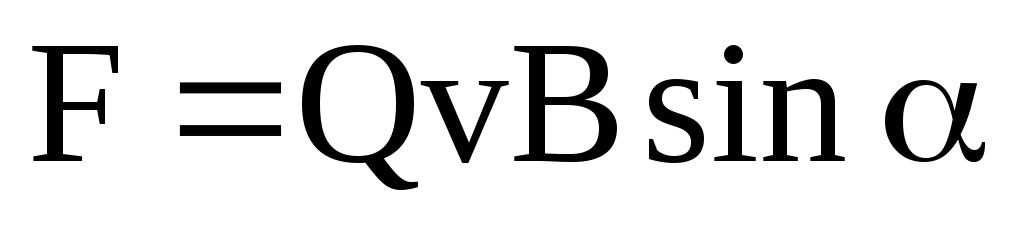
где  —
скорость заряженной частицы;
— угол между векторами
—
скорость заряженной частицы;
— угол между векторами  и
и .
.
Магнитный поток:
а) в случае однородного магнитного поля и плоской поверхности
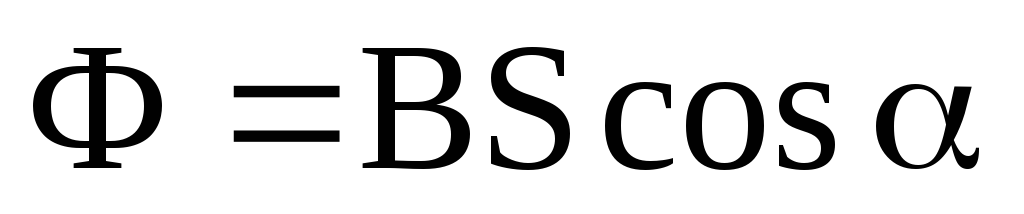 или
или 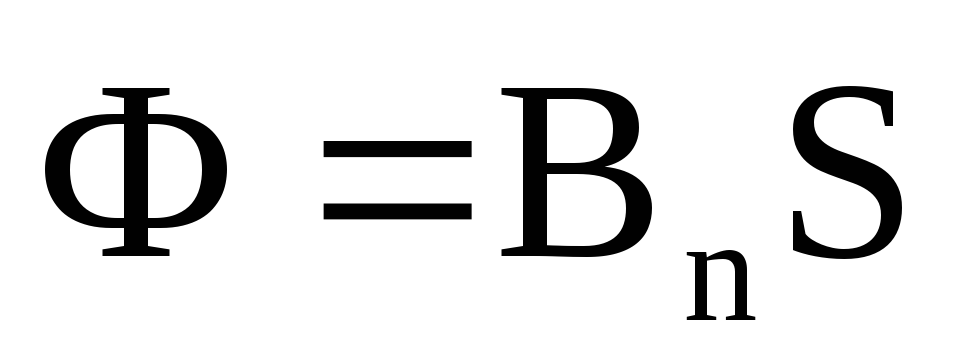
где S — площадь контура; — угол между нормалью к плоскости контура и вектором магнитной индукции;
б) в случае неоднородного поля и произвольной поверхности
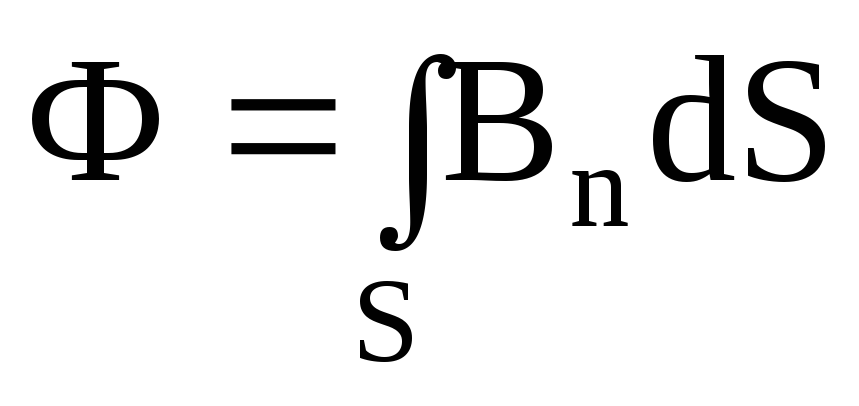
(интегрирование ведется по всей поверхности).
Потокосцепление (полный поток):
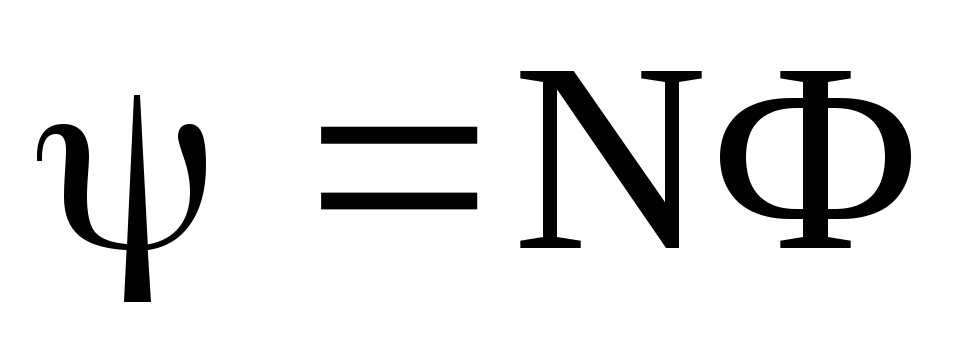
Эта формула верна для соленоида и тороида с равномерной намоткой плотно прилегающих друг к другу N витков.
Работа по перемещению контура в магнитном поле:
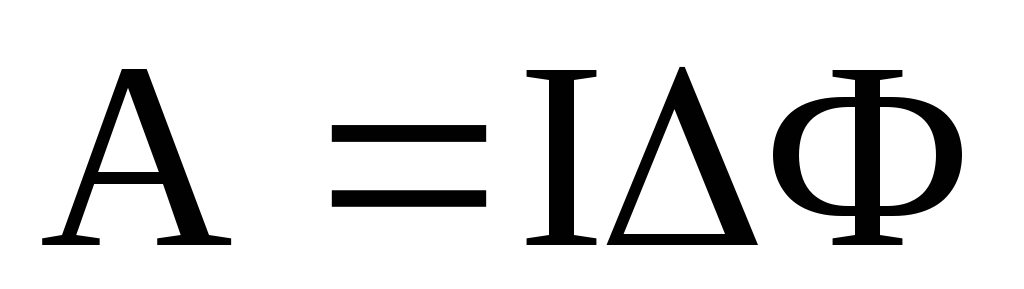
Э.д.с. индукции:
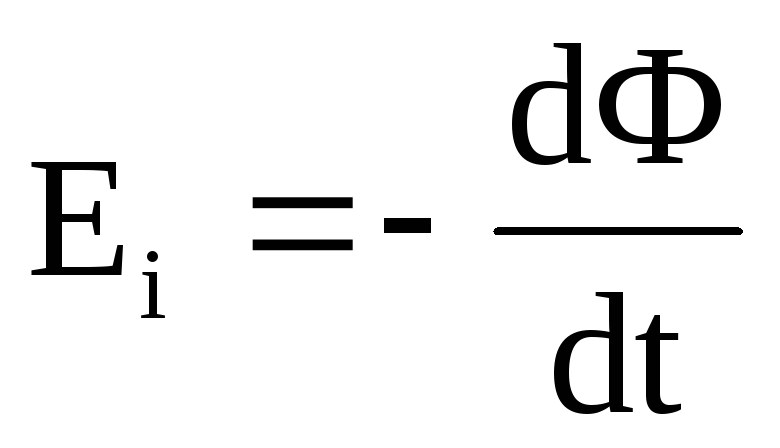
Разность
потенциалов на концах проводника,
движущегося со скоростью  в магнитном
поле:
в магнитном
поле:
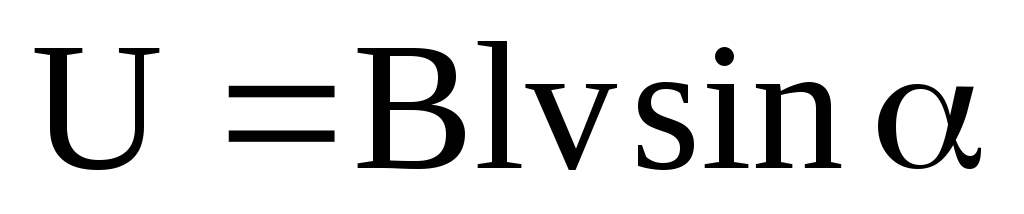
где
l — длина проводника;
— угол между векторами  и
и .
.
Заряд, протекающий по замкнутому контуру при изменении магнитного потока, пронизывающего этот контур:
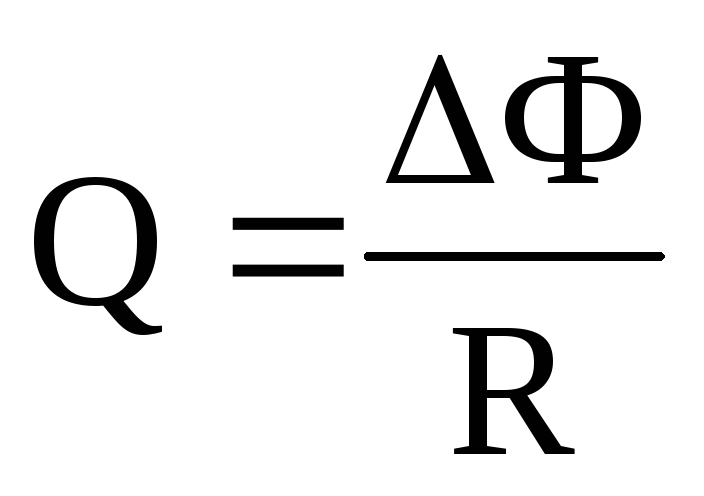 или
или 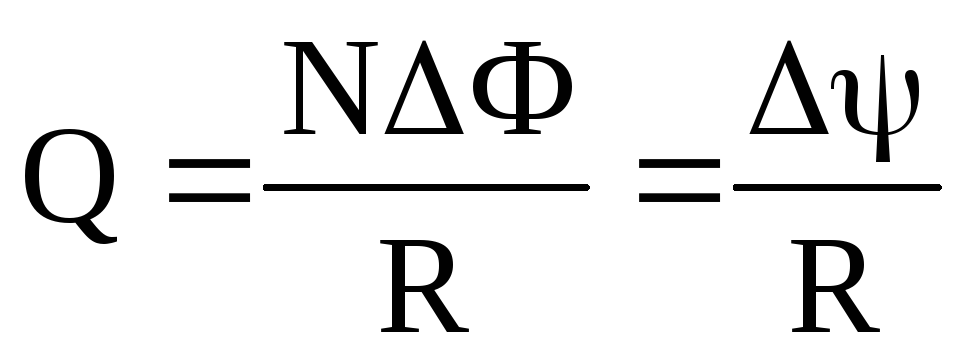
где R — сопротивление контура.
Индуктивность контура:
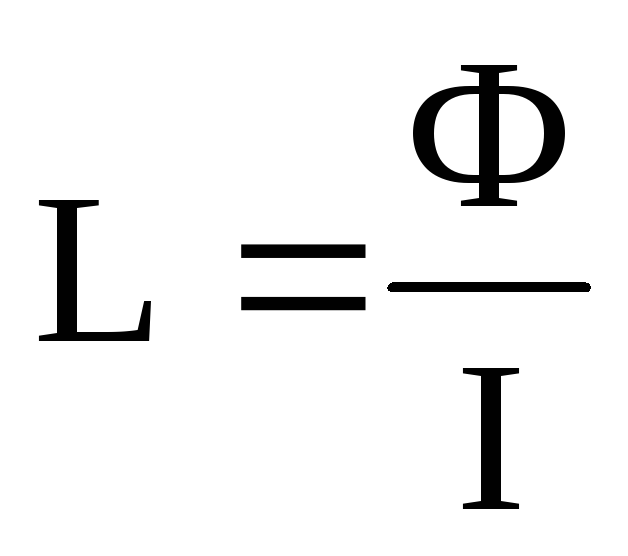
Э.д.с. самоиндукции:
Индуктивность соленоида:
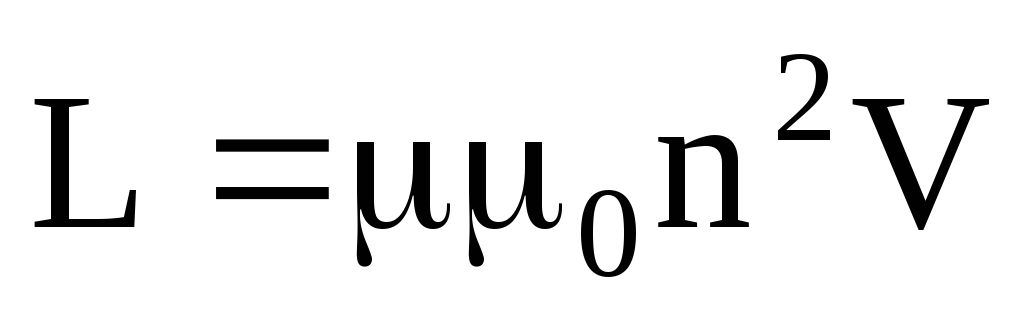
где n — отношение числа витков соленоида к его длине; V — объем соленоида.
Мгновенное значение силы тока в цепи, обладающей сопротивлением R и индуктивностью L:
а) 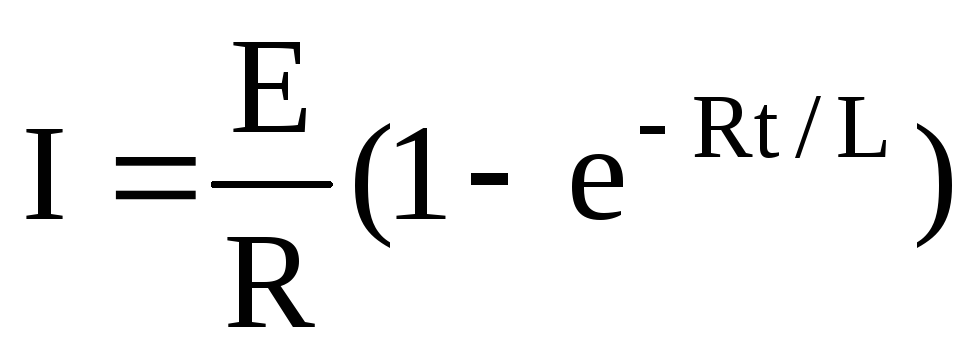 (при
замыкании цепи), где E — э.д.с.
источника тока;
t —
время, прошедшее после замыкания цепи;
(при
замыкании цепи), где E — э.д.с.
источника тока;
t —
время, прошедшее после замыкания цепи;
б) 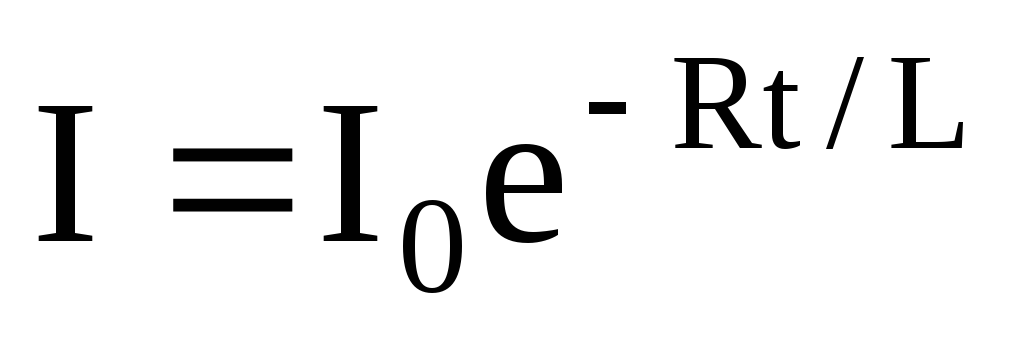 (при размыкании цепи), где Io — сила тока в цепи при
(при размыкании цепи), где Io — сила тока в цепи при t = 0; t
— время, прошедшее с момента размыкания
цепи.
t = 0; t
— время, прошедшее с момента размыкания
цепи.
Энергия магнитного поля:
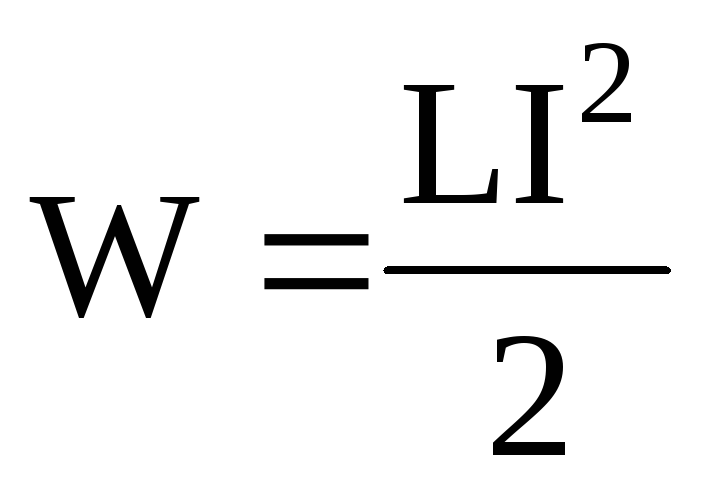
Объемная плотность энергии магнитного поля (отношение энергии магнитного поля соленоида к его объему):
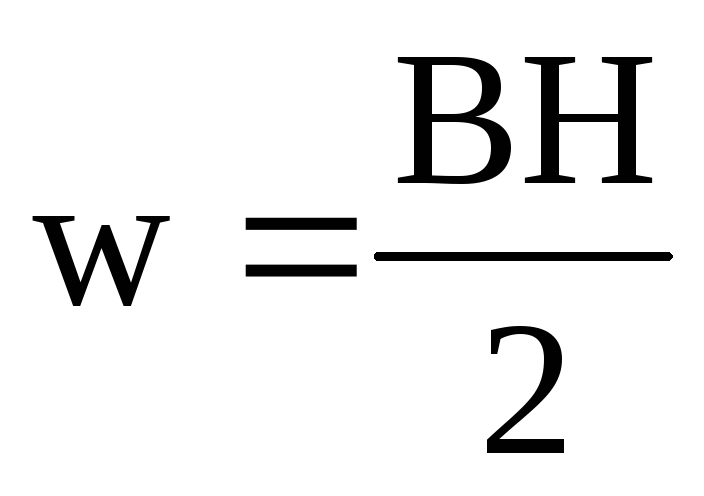 ,
или
,
или 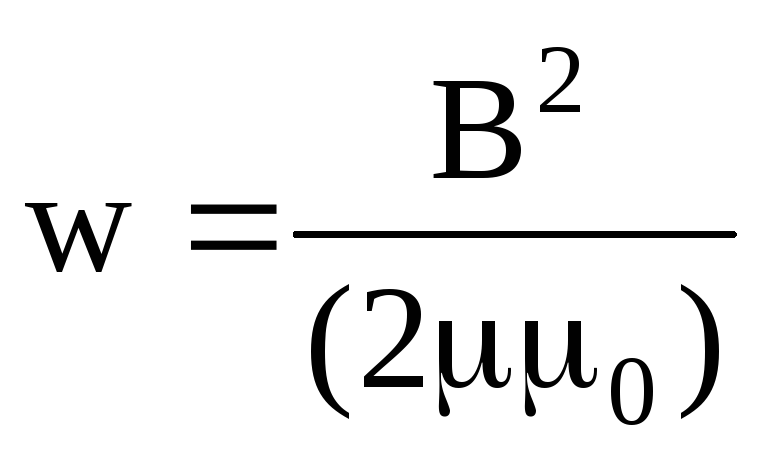 ,
или
,
или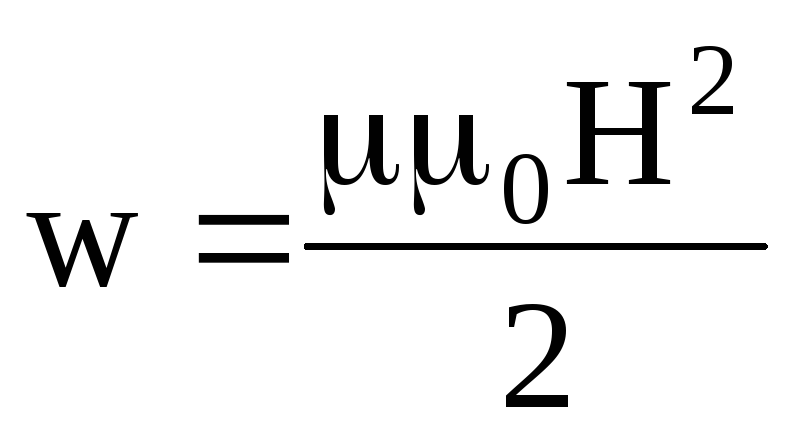
где B — магнитная индукция; H — напряженность магнитного поля.
Электромагнетизм Основные формулы
Индукция магнитного поля
 — векторная величина, численно равная
отношению максимального вращающего
момента
— векторная величина, численно равная
отношению максимального вращающего
момента  ,
действующего на пробный контур тока,
помещенный в данную точку поля к
магнитному моменту контура
,
действующего на пробный контур тока,
помещенный в данную точку поля к
магнитному моменту контура  .
.
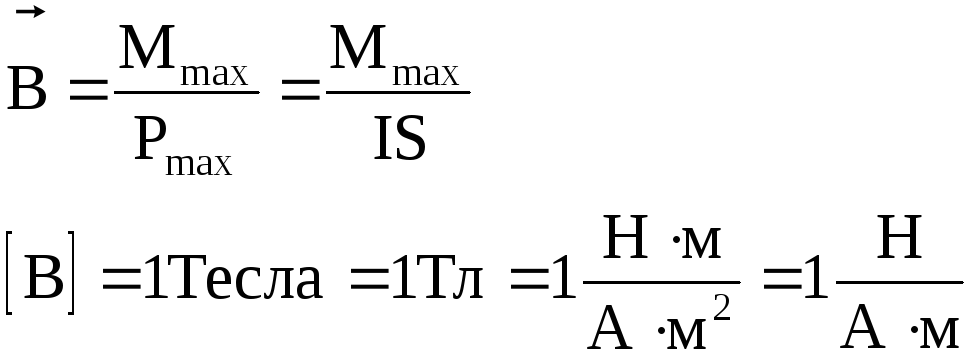
I – сила тока в контуре, S – площадь контура.
Принцип суперпозиции (наложения) магнитных полей
Магнитная
индукция результирующего поля равна: 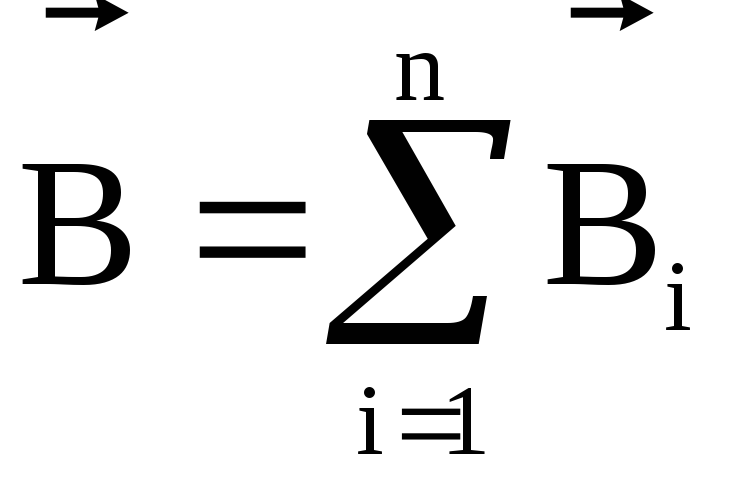
Закон Био-Савара-Лапласа
Магнитная
индукция, создаваемая элементом
проводника  с током I в точке,
находящейся на расстоянии
с током I в точке,
находящейся на расстоянии  от элемента
от элемента  .
.
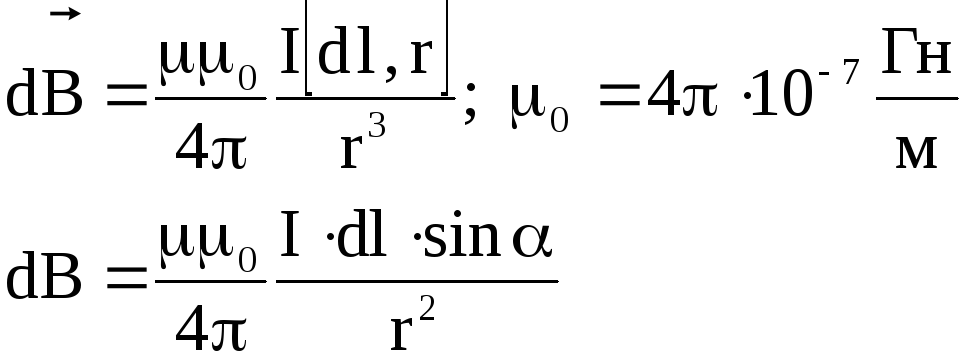
 —
радиус-вектор, проведенный из элемента
—
радиус-вектор, проведенный из элемента 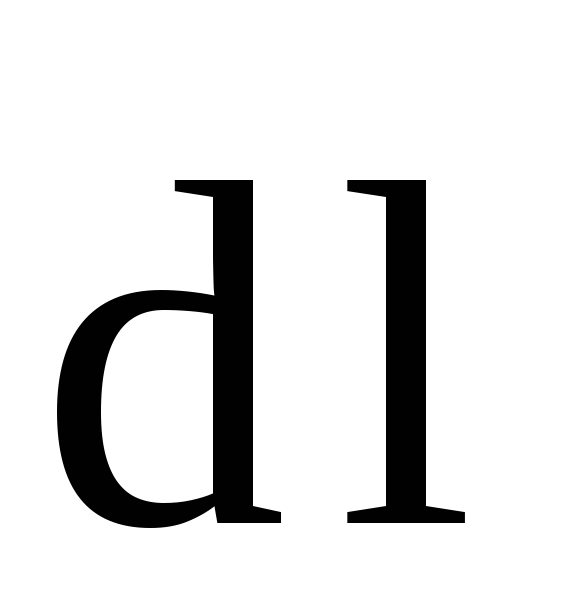 проводника в точку поля;
проводника в точку поля;
 ;
;
 —
угол между векторами
—
угол между векторами  и
и 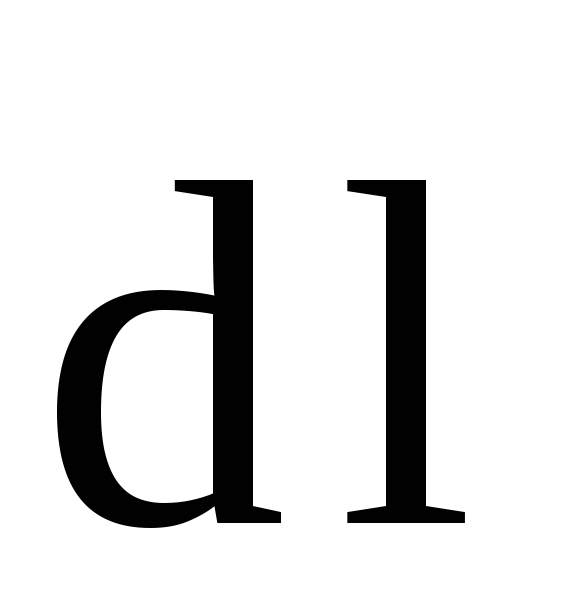 ;
;
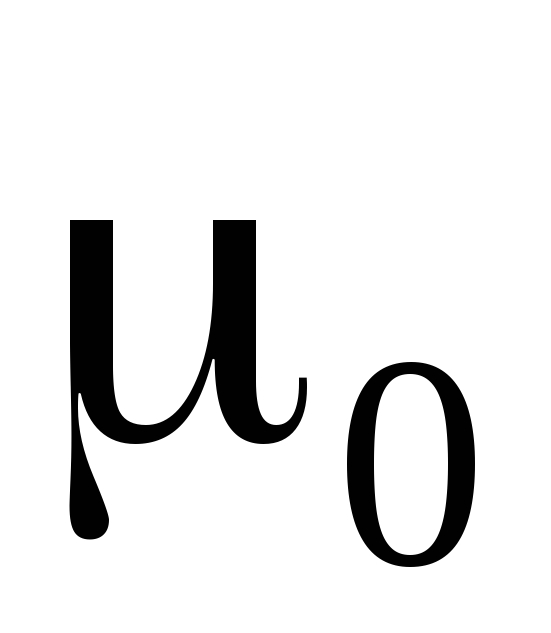 —
магнитная постоянная;
—
магнитная постоянная;  — магнитная проницаемость среды.
— магнитная проницаемость среды.
Вектор  имеет направление движения острия
буравчика при вращении его рукоятки в
плоскости
имеет направление движения острия
буравчика при вращении его рукоятки в
плоскости  от первого сомножителя ко второму.
от первого сомножителя ко второму.
Связь индукции магнитного поля с напряженностью


Индукция магнитного поля бесконечного прямого тока на расстоянии

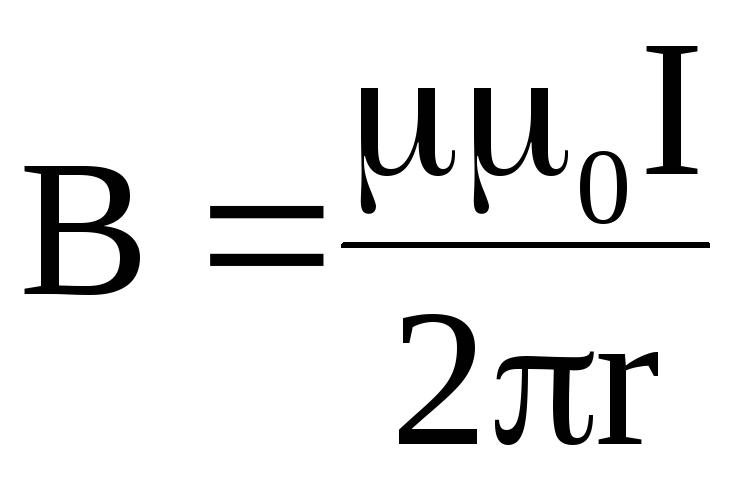
Индукция магнитного поля в центре кругового витка радиусом R
Сила Ампера
Cила
Ампера, действующая на элемент
проводника 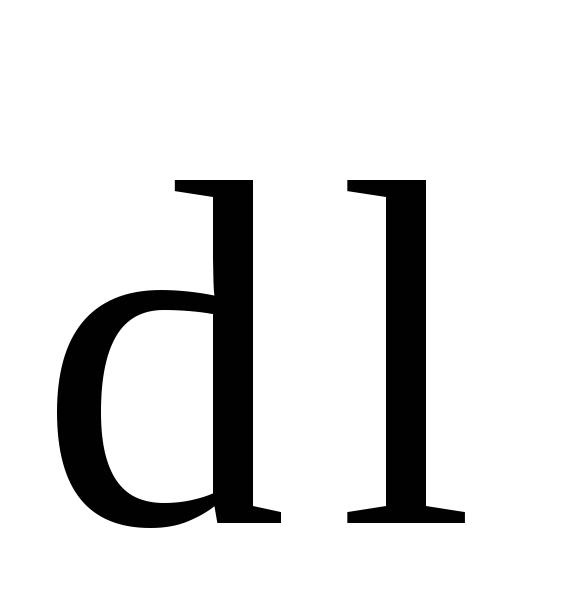 с током I в однородном
магнитном поле с индукцией
с током I в однородном
магнитном поле с индукцией  .
.
 —
угол между векторами
—
угол между векторами  и
и 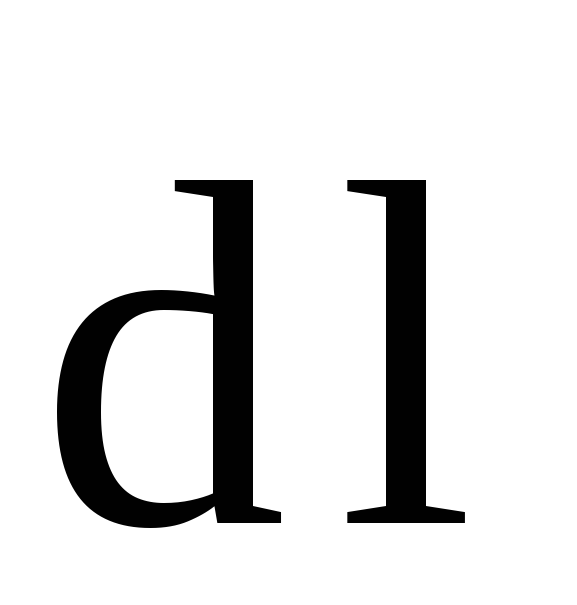 .
.
Cила
Ампера, действующая на прямолинейный
проводник, длиной 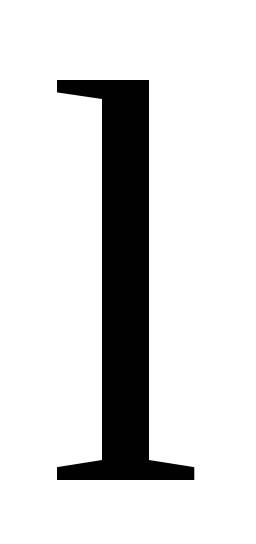 ,
с током I в однородном
магнитном поле с индукцией
,
с током I в однородном
магнитном поле с индукцией  .
.
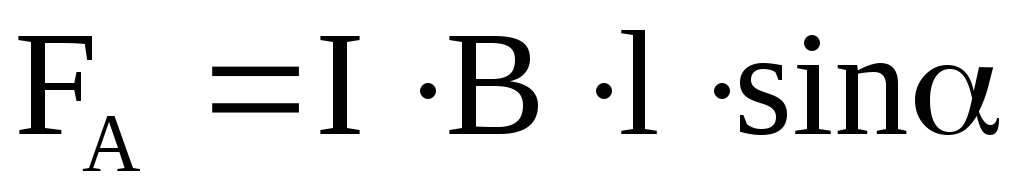
 —
угол между векторами
—
угол между векторами  и
и 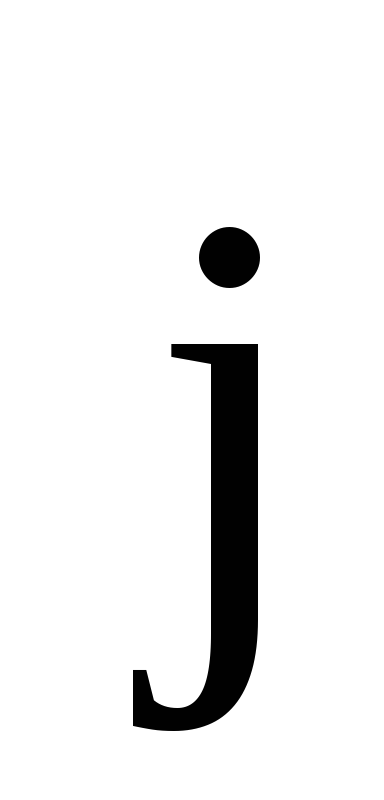 .
.
Взаимодействие параллельных токов
Сила
взаимодействия двух параллельных токов 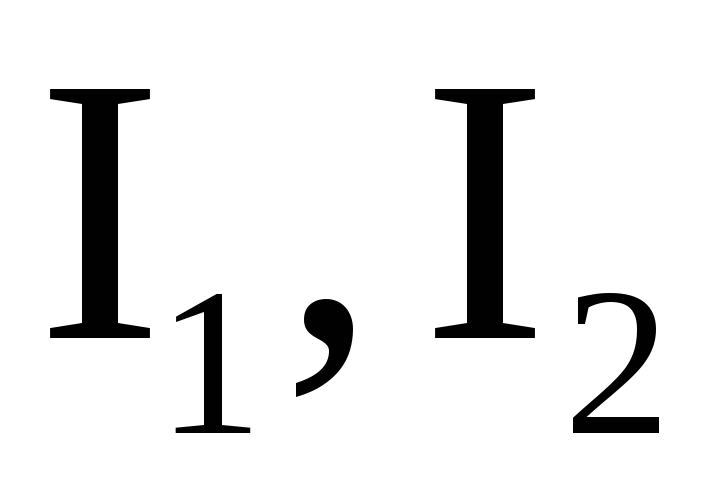 длиной
длиной 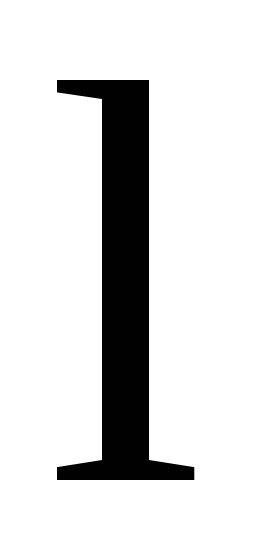 ,
находящихся на расстоянии r друг от друга
,
находящихся на расстоянии r друг от друга
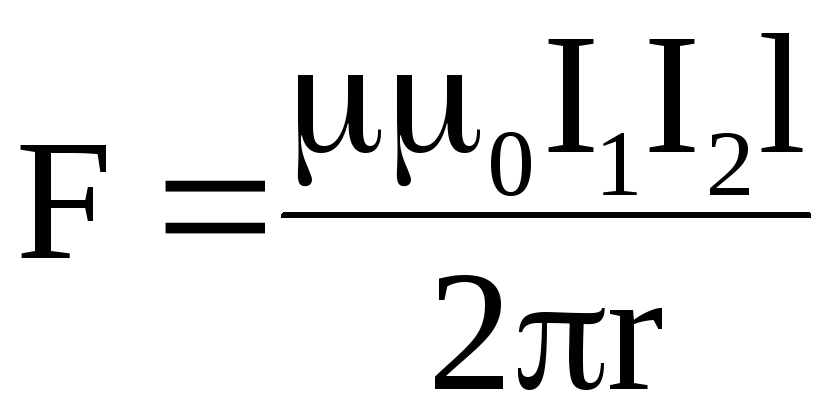
Сила Лоренца. Сила, действующая на заряженную частицу с зарядом q, движущуюся со скоростью
 в однородном магнитном поле с индукцией
в однородном магнитном поле с индукцией  .
.
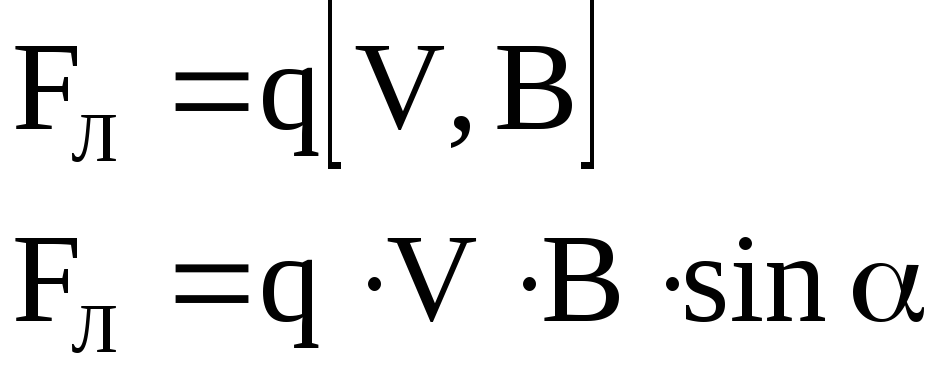
—
угол между векторами  и
и  .
.
Поток вектора магнитной индукции
 через плоский контур площадью S
в случае однородного
магнитного поля
через плоский контур площадью S
в случае однородного
магнитного поля
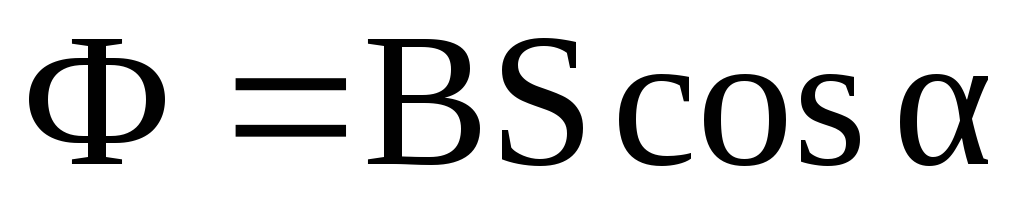
где  — угол между нормалью к плоскости контура
и направлением вектора магнитной
индукции
— угол между нормалью к плоскости контура
и направлением вектора магнитной
индукции  .
.
Закон электромагнитной индукции
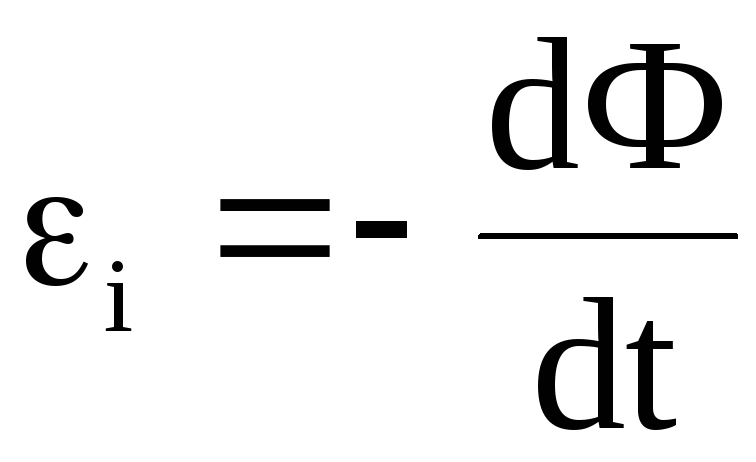
 —
электродвижущая сила индукции
—
электродвижущая сила индукции
Индуктивность контура с током
Магнитный поток сквозь контур и сила тока в нем связаны соотношением:
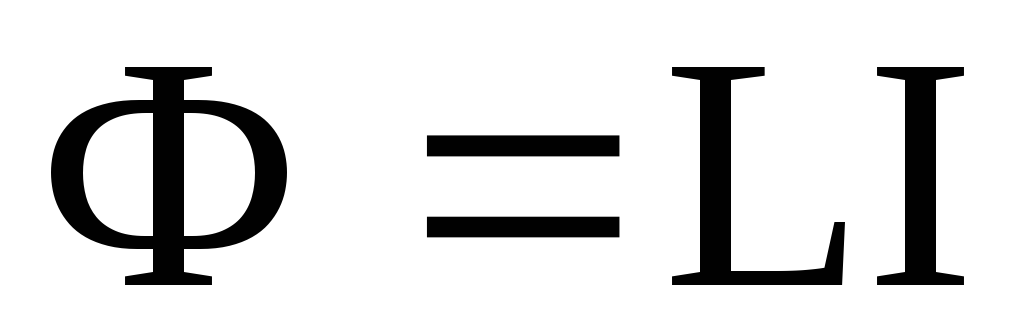
L – индуктивность контура
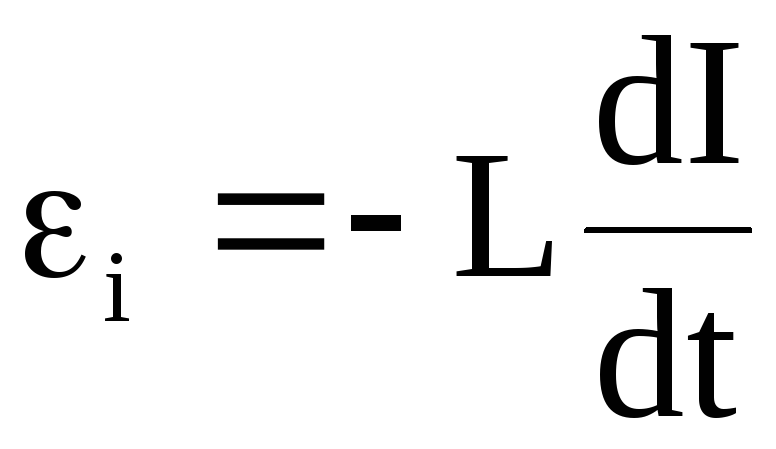
 —
электродвижущая сила самоиндукции,
возникающая в замкнутом контуре при
изменении силы тока в нем.
—
электродвижущая сила самоиндукции,
возникающая в замкнутом контуре при
изменении силы тока в нем.
Энергия магнитного поля
 , создаваемого током в замкнутом
контуре индуктивностью L
, создаваемого током в замкнутом
контуре индуктивностью L
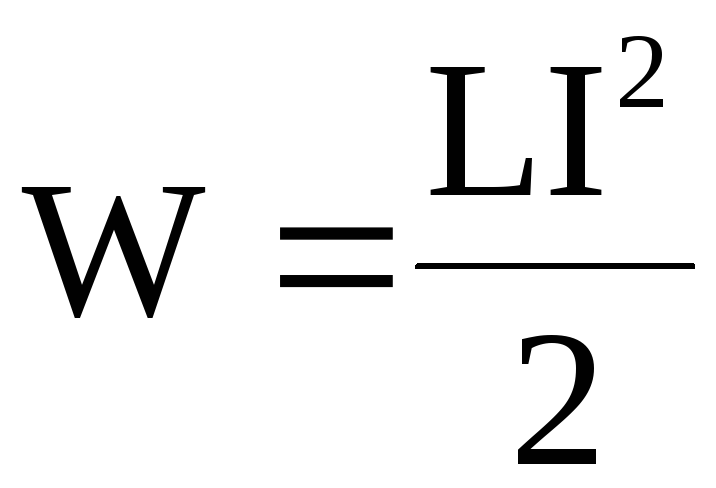
Объемная плотность энергии магнитного поля
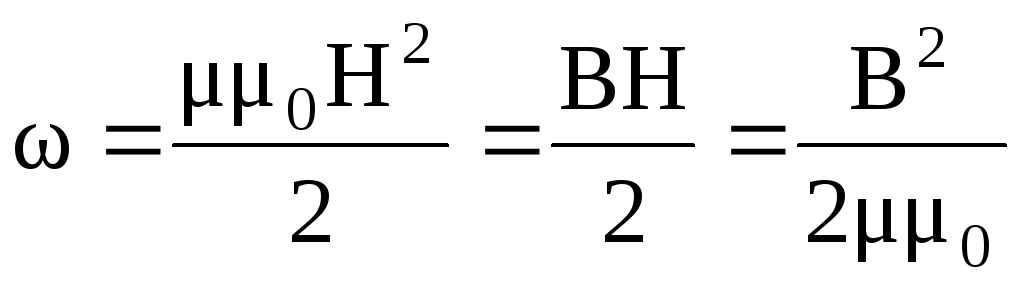 .
.
Примеры решения задач
Пример 1. По двум параллельным прямым проводам длиной 2,5 м каждый, находящимся на расстоянии 0,2 м друг от друга, текут в одинаковом направлении одинаковые токи 1 кА. Вычислить силу взаимодействия токов.
Дано: | Решение: |
| Каждый
ток создает магнитное поле, которое
действует на другой проводник. Найдем
силу |
| Модуль
магнитной индукции поля тока |
Согласно
закону Ампера, на каждый элемент
второго проводника с током Т.к.
отрезок Подставляя
выражение для модуля Силу Вычисления: Проверка размерностей: Ответ: 2,5 Н | |
Пример 2. Электрон двигаясь со скоростью 107 м/с влетает в однородном магнитном поле с индукцией 2.10-3 Тл перпендикулярно его силовым линиям. Чему равен радиус описываемой им окружности?
Дано: | Решение: | ||||||||
| На движущийся в магнитном поле электрон действует сила Лоренца. Вектор силы Лоренца перпендикулярен вектору скорости и, следовательно, по второму закону Ньютона, сообщает электрону нормальное ускорение | ||||||||
| приравнивая правые части выражений (1) и (2) получим | ||||||||
Вычисления: Проверка размерностей: Ответ: Пример 3. При скорости изменения силы тока в соленоиде, равной 50 А/с, на его концах возникает ЭДС самоиндукции 0,08 В. Определить индуктивность соленоида.
Задачи для самостоятельного решения Поле кругового тока. Поле прямого тока
Сила Ампера. Взаимодействие параллельных токов
Движение заряженных частиц в магнитном поле
Электромагнитная индукция
Энергия магнитного поля
| |||||||||
4. Колебания и волны
Электромагнетизм основные формулы
47
РАЗДЕЛIV. ЭЛЕКТРОМАГНЕТИЗМ
Основные формулы
Связь магнитной индукции B с напряженностью H магнитного поля
B = µµ0 H ,
где µ — магнитная проницаемость изотропной среды; µ0 — магнитная постоянная. В вакууме µ = 1, и тогда магнитная индукция в вакууме
|
|
|
|
| B = µ0 H . |
|
|
|
Закон Био—Савара—Лапласа |
|
|
|
| ||||
d B = | µµ | 0 | [dlr] | I | или d B = | µµ0 I sinα | dl , | |
4π |
| r3 | 4π | r 2 | ||||
где d B — магнитная индукция поля, создаваемого элементом провода длиной dl
с током I; r — радиус-вектор, направленный от элемента проводника к точке, в которой определяется магнитная индукция; α — угол между радиусом-вектором и направлением тока в элементе провода.
Магнитная индукция в центре кругового тока
B = µµ2R0 I ,
где R — радиус кругового витка.
Магнитная индукция на оси кругового тока
B = | µµ | 0 2πR2 I | , | ||
|
|
| |||
4π (R2 + h3 )3 / 2 | |||||
|
| ||||
где h — расстояние от центра витка до точки, в которой определяется магнитная индукция.
Магнитная индукция поля прямого тока
B = µµ0 I /(2πr0) ,
где r0 — расстояние от оси провода до точки, в которой определяется магнитная индукция.
Магнитная индукция поля, создаваемого отрезком провода с током
(см. рис. 4.1,а),
B = µµ0 I (cosα1 −cosα2) . 4πr0

48
Обозначения ясны из рисунка. Направление вектора магнитной индукции B обозначено точкой —
это значит, что B направлен перпендикулярно плоскости чертежа к нам.
При симметричном расположении концов провода относительно точки, в которой определяется магнитная индукция (рисунок. 4.1,б), -cosα2 = cosα1 = cosα, тогда
B = µµ0 I cosα . 2π r0
Магнитная индукция поля соленоида | Рисунок 4.1 |
B = µµ0nI , |
|
где п — отношение числа витков соленоида к его длине.
Сила, действующая на провод с током в магнитном поле (закон Ампера),
F = I[l B], или F = IBl sinα ,
где l — длина провода; α — угол между направлением тока в проводе и вектором
магнитной индукции B . Это выражение справедливо для однородного магнитного поля и прямого отрезка провода. Если поле неоднородно и провод не является прямым, то закон Ампера можно применять к каждому элементу провода в отдельности:
d F = I[dl B].
Магнитный момент плоского контура с током pm = nIS ,
где n — единичный вектор нормали (положительной) к плоскости контура; I — сила тока, протекающего по контуру; S — площадь контура.
Механический (вращательный) момент, действующий на контур с током, помещенный в однородное магнитное поле,
M =[pm B], | или | M = pmB sinα , | |
где α — угол между векторами pm и B . |
|
|
|
Потенциальная энергия (механическая)* | контура с током в | ||
магнитном поле |
|
|
|
Пмех = −pm B , | или | Пмех | = −pmB cosα . |
_____________________________________________________________________
* Часть полной потенциальной энергии, которая обусловлена существованием механического (вращательного) момента.

49
Отношение магнитного момента рт к механическому L (моменту импульса) заряженной частицы, движущейся по крутой орбите,
pLm = 12 Qm ,
где Q — заряд частицы; т — масса частицы. Сила Лоренца*
F =Q[νB], или F =QνB sinα ,
где ν — скорость заряженной частицы; α — угол между векторами
ν и B .
Магнитный поток:
а) в случае однородного магнитного поля и плоской поверхности
Ф = BS cosα или Ф=BnS,
где S — площадь контура; α — угол между нормалью к плоскости контура и вектором магнитной индукции;
б) в случае неоднородного поля и произвольной поверхности
Ф = ∫S BndS
(интегрирование ведется по всей поверхности). Потокосцепление (полный поток)
Ψ = NФ.
Эта формула верна для соленоида и тороида с равномерной намоткой плотно прилегающих друг к другу N витков.
Работа по перемещению замкнутого контура в магнитном поле
A = I∆Ф.
ЭДС индукции
εi = −ddtΨ .
Разность потенциалов на концах провода, движущегося со скоростью ν в магнитном поле,
U = Blν sinα ,
где l — длина провода; α — угол между векторами ν и B .
Заряд, протекающий по замкнутому контуру при изменении магнитного потока, пронизывающего этот контур,
Q = ∆Ф/ R , или Q = N∆Ф/ R = ∆Ψ/ R ,
где R — сопротивление контура. Индуктивность контура
L=Ф/I.
ЭДС самоиндукции
εs = −L dIdt .
____________________________________________________________________
* Если частица находится одновременно в электрическом и магнитном полях, то под силой Лоренца понимают выражение F = Q E +Q[ υ B ].
50
Индуктивность соленоида
L=µµ0n2V,
где п — отношение числа витков соленоида к его длине; V — объем соленоида. Мгновенное значение силы тока в цепи, обладающей сопротивлением R
и индуктивностью L:
а) I = | ε | (1 −e−Rt / L ) (при замыкании цепи), где ε — ЭДС источника тока; t — | |
R | |||
|
|
время, прошедшее после замыкания цепи;
б) I = Ioe−Rt / L (при размыкании цепи), где I0 — сила
тока в цепи при t = 0; t — время, прошедшее с момента размыкания цепи. Энергия магнитного поля
W = LI2 2 .
Объемная плотность энергии магнитного поля (отношение энергии магнитного поля соленоида к его объему)
ω = BH / 2, или ω = B2 /(2µµ0) , или ω = µµ0 H 2 / 2 ,
где В — магнитная индукция; H — напряженность магнитного поля.
Раздел III. Электричество и электромагнетизм Основные законы и формулы
где  и
и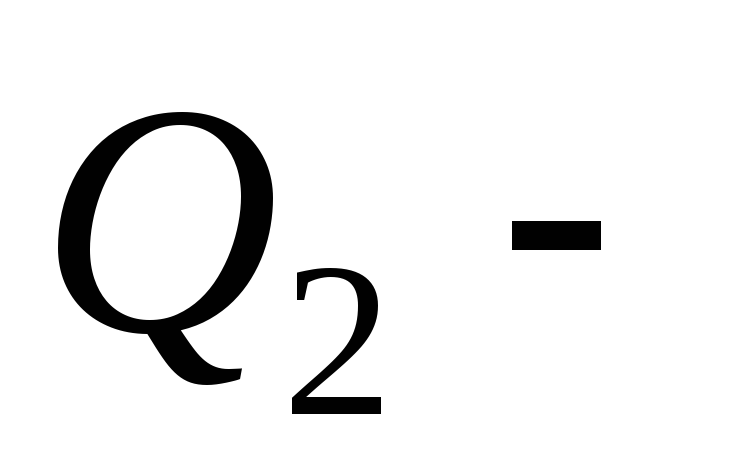 заряды,
заряды,
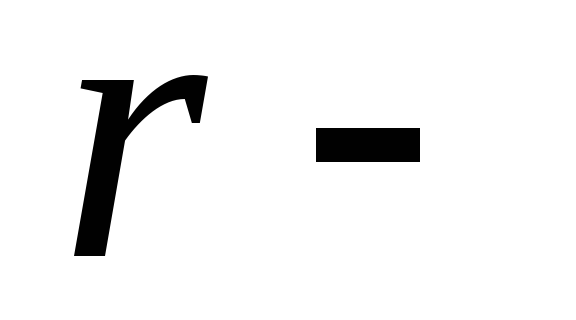 расстояние
между зарядами,
расстояние
между зарядами,
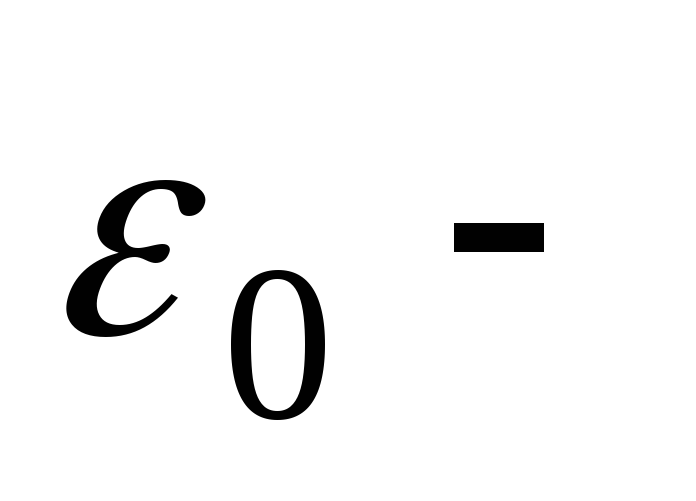 электрическая
постоянная,
электрическая
постоянная,
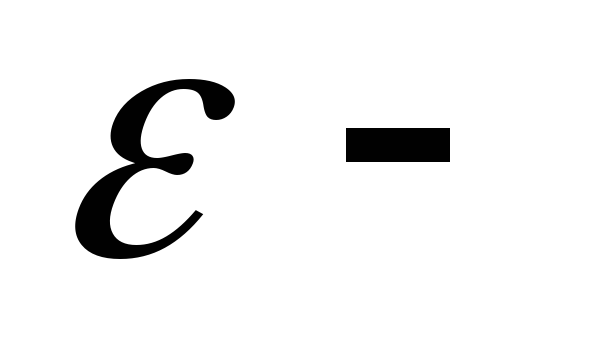 диэлектрическая
проницаемость среды.
диэлектрическая
проницаемость среды.
точечного
заряда 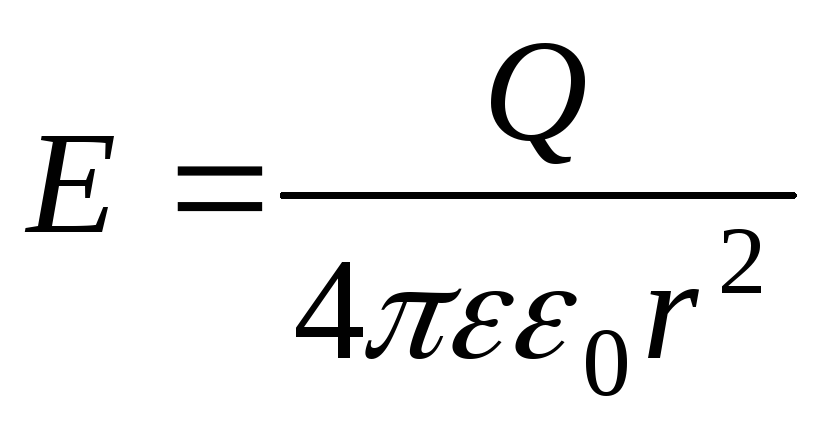 ,
,
бесконечно
длинной заряженной нити 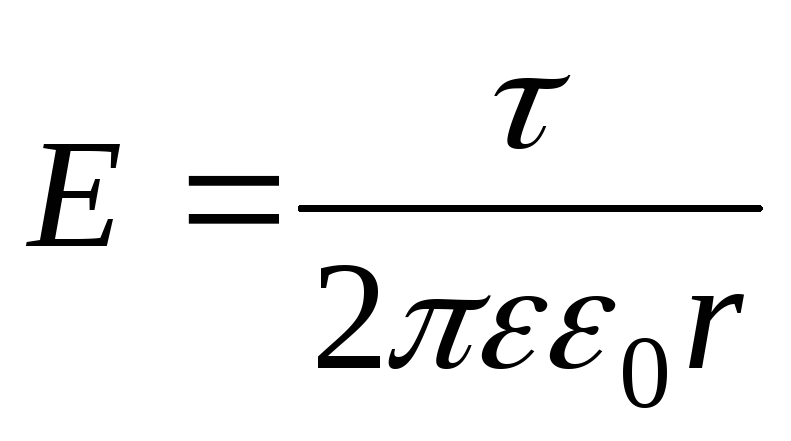 ,
,
равномерно
заряженной плоскости 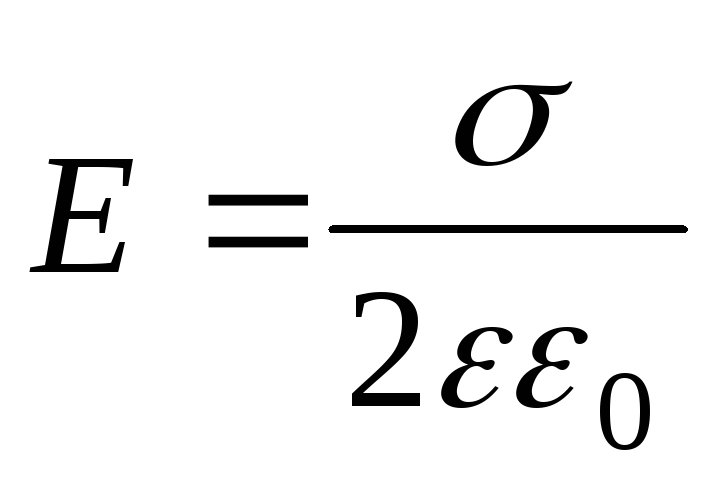 ,
,
между
двумя равномерно и разноименно заряженными
бесконечными плоскостями 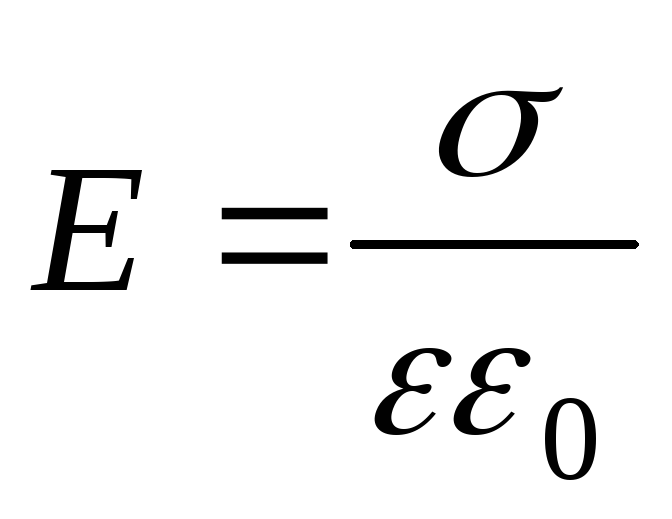 .
.
Принцип суперпозиции
 .
.Объемная, поверхностная и линейная плотности заряда
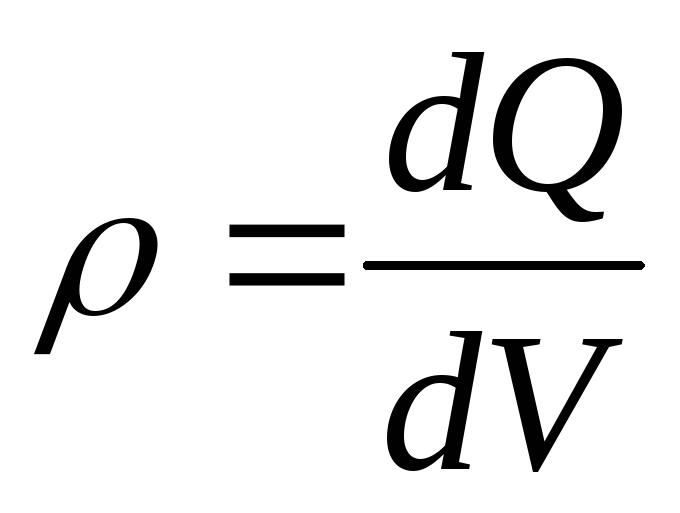 ,
,
,
,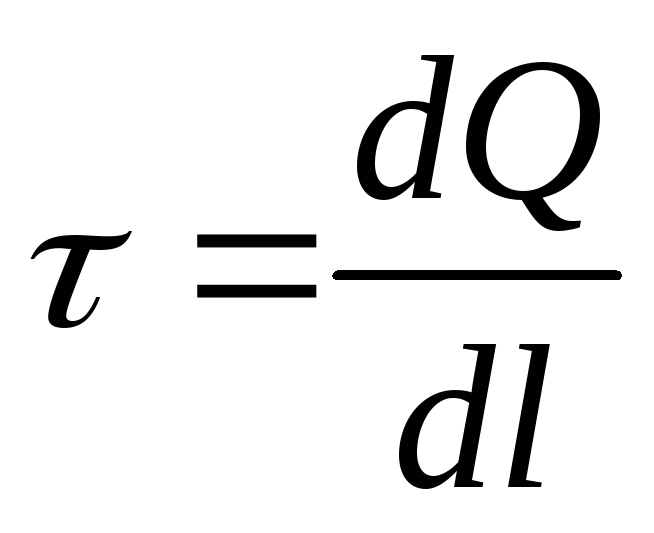 .
.
Напряженность поля, создаваемого равномерно заряженной сферической поверхностью
 ,
, .
.Напряженность поля, создаваемого объемно заряженным шаром
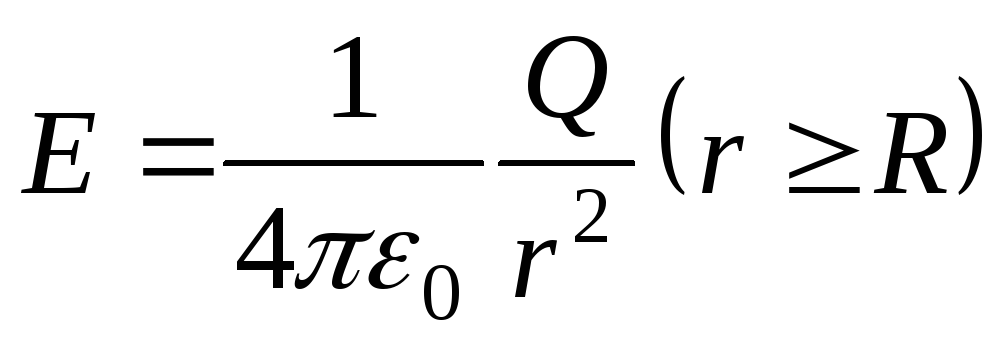 ,
, 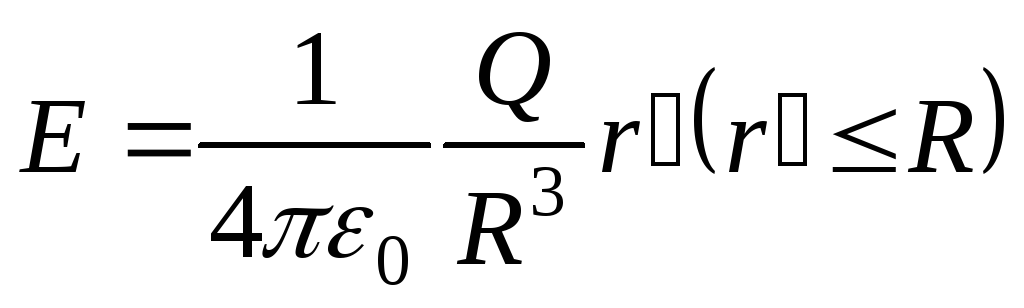 .
.
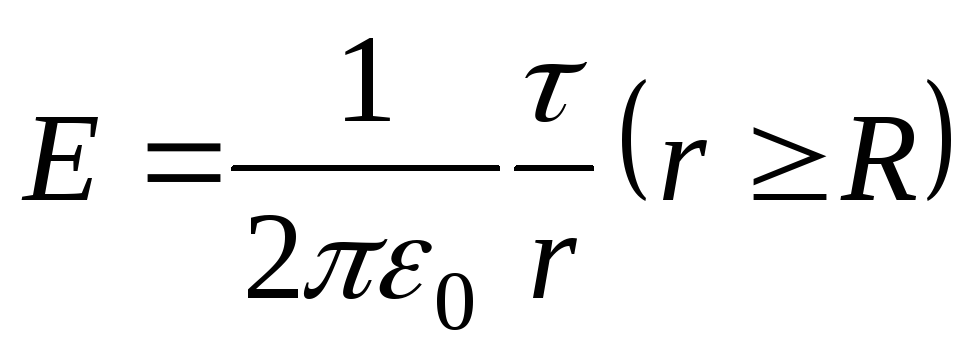 ,
, 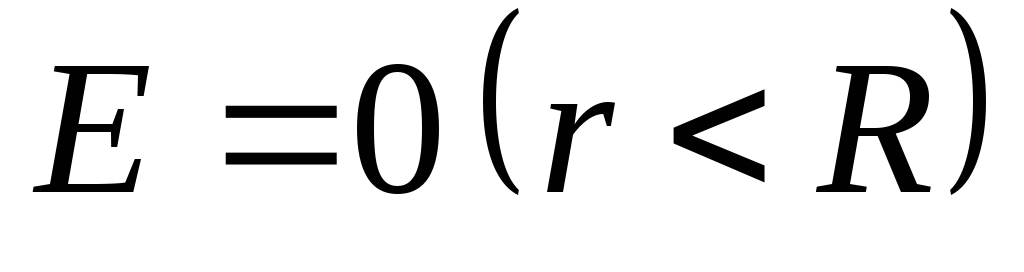 .
.
Потенциал электростатического поля
 .
.Связь между потенциалом электростатического поля и его напряженностью
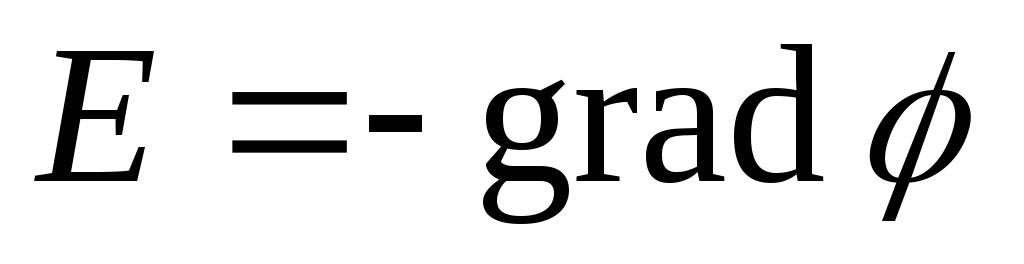 ,
, 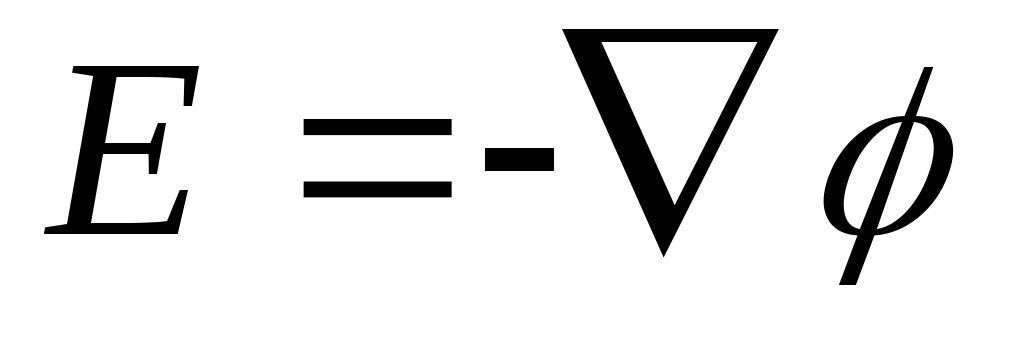 .
.
Примеры решения задач
Пример 1. С какой силой взаимодействуют два заряда по 10 нКл, находящиеся на расстоянии 3 см друг от друга?
Решение. Запишем закон Кулона:
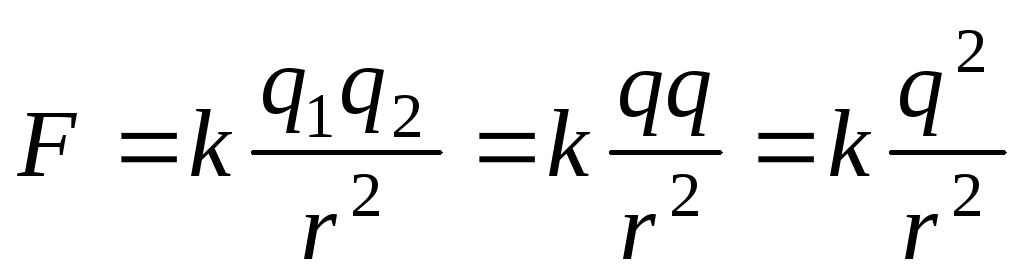 .
.
Итак, 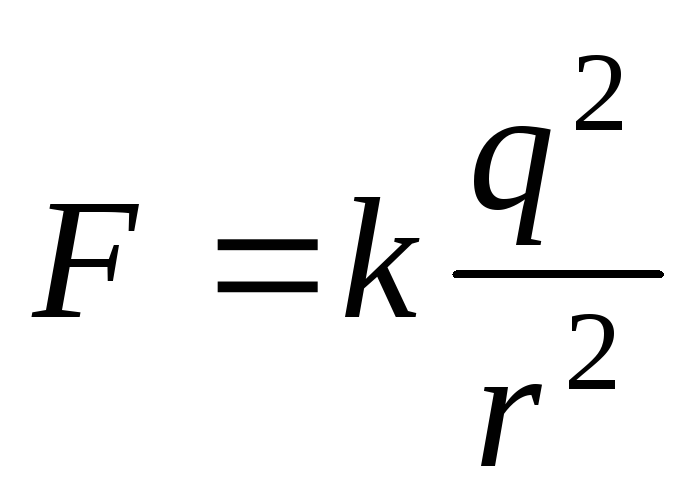 ;
;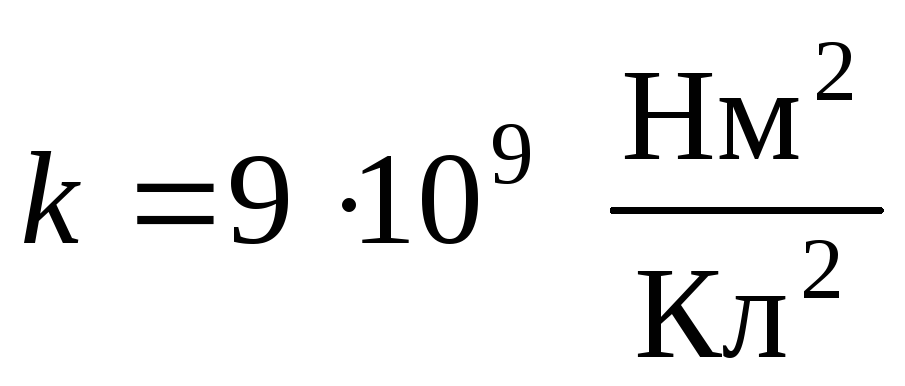 .
.
Вычислим результат:
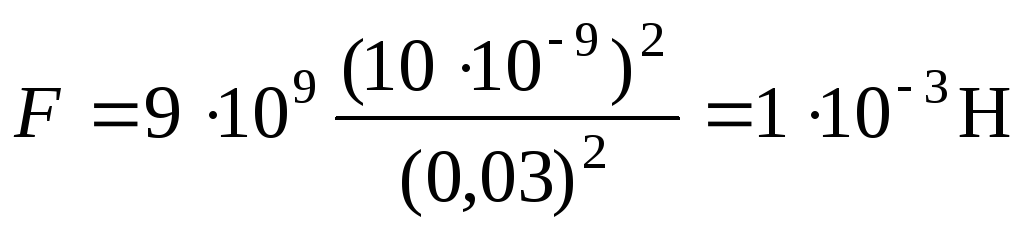 ,
,
Ответ: 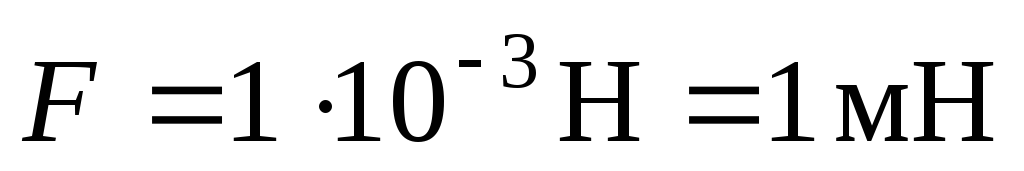 .
.
Пример 2. Заряды 90 и 10 нКл расположены на расстоянии 4 см друг от друга. Где надо поместить третий заряд, чтобы он находился в равновесии?
Решение. Сделаем пояснительный рисунок

Обозначим 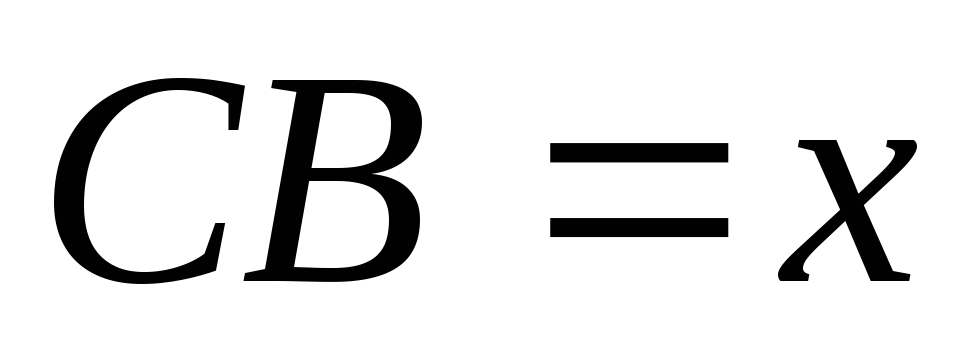 Тогда
Тогда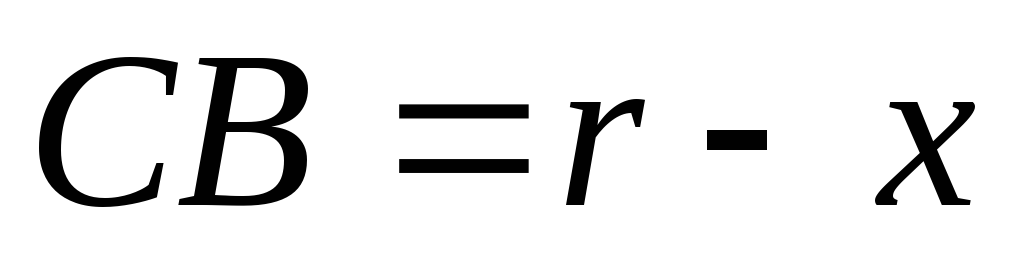 .
Проанализируем задачу для случая, когда
заряд
.
Проанализируем задачу для случая, когда
заряд –
положительный. На заряд
–
положительный. На заряд  действуют силы:
действуют силы:
 сила
отталкивания со стороны заряда
сила
отталкивания со стороны заряда  ;
; сила
отталкивания со стороны заряда
сила
отталкивания со стороны заряда  .
.
Равновесие
заряда  наступит при условии равенства модулей
сил
наступит при условии равенства модулей
сил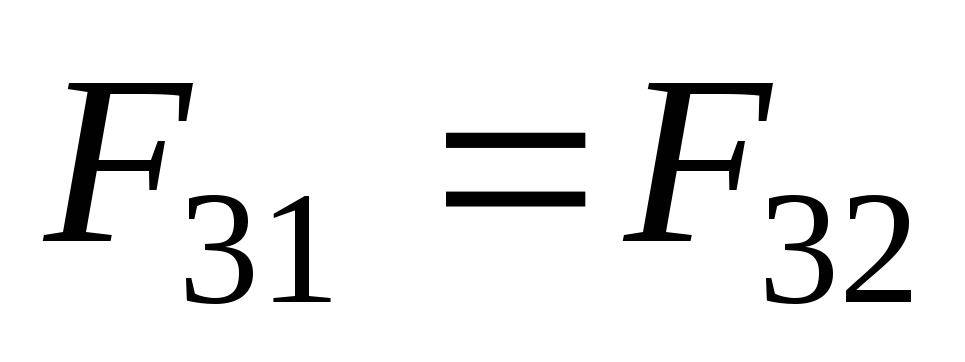 .
Найдем модули действующих на заряд
.
Найдем модули действующих на заряд сил:
сил:
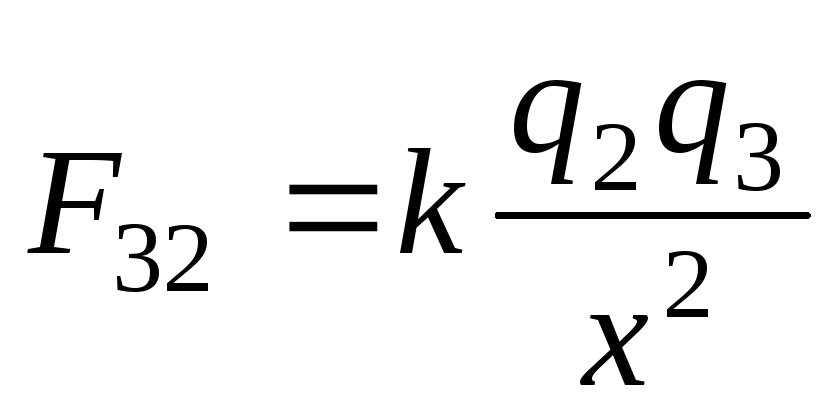 ;
; 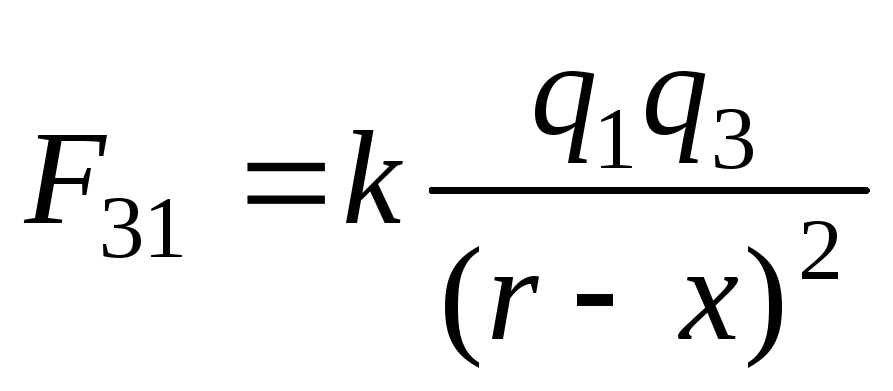 .
.
Приравняем их:
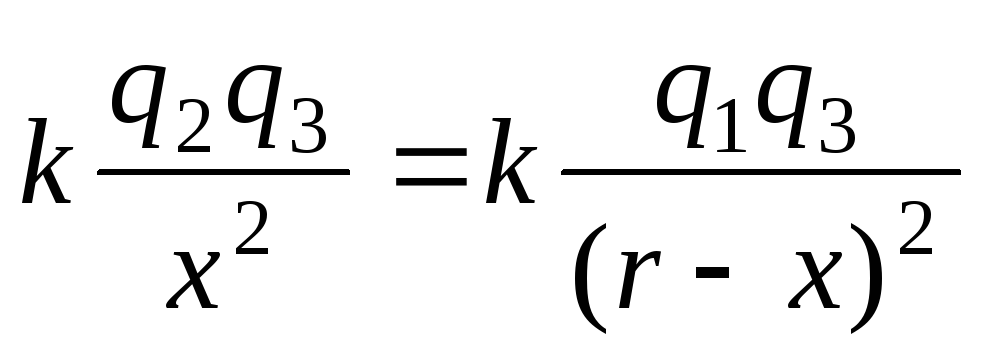 .
.
После
сокращения левой и правой части на
одинаковый множитель 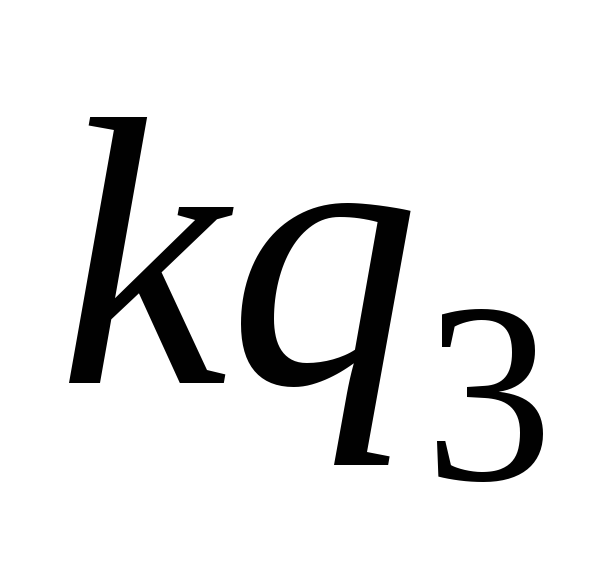 получим:
получим:
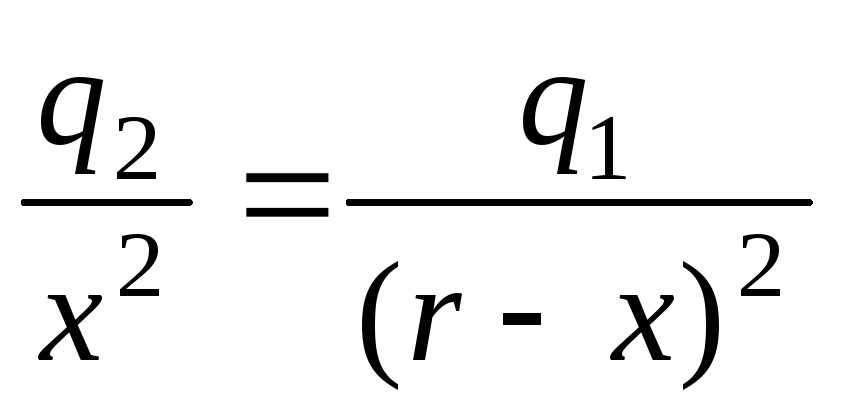 или
или 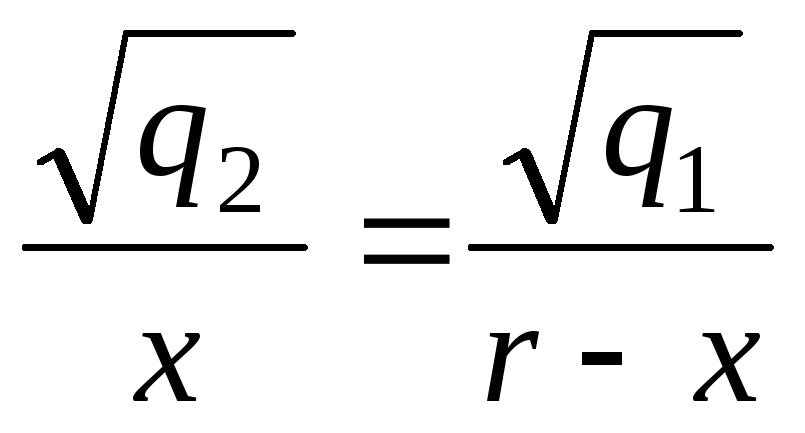 .
.
Воспользуемся
свойством пропорции: 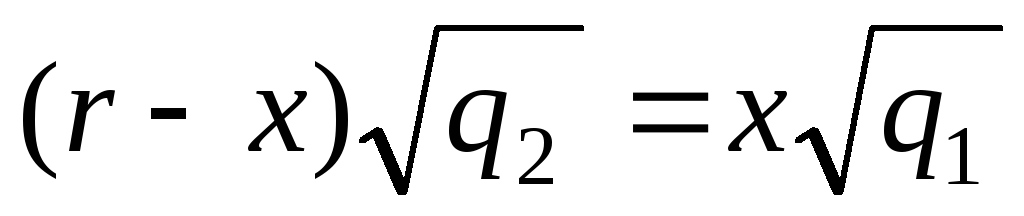 .
.
Выразим отсюда х:
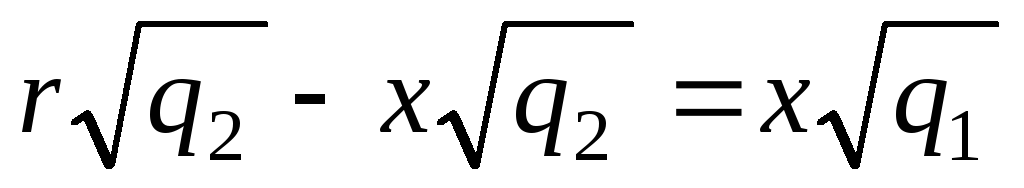 ;
; 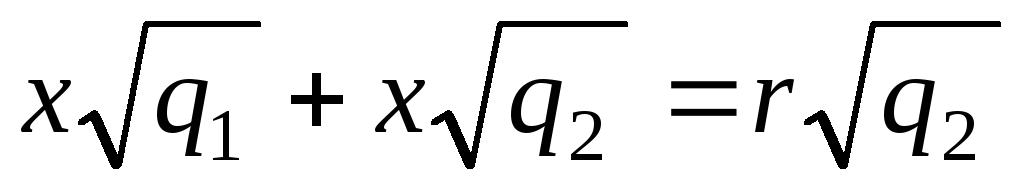 ;
;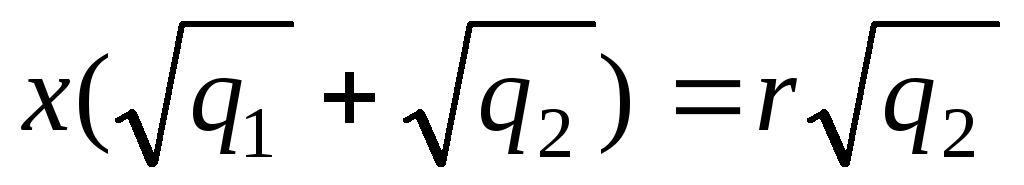 ;
;
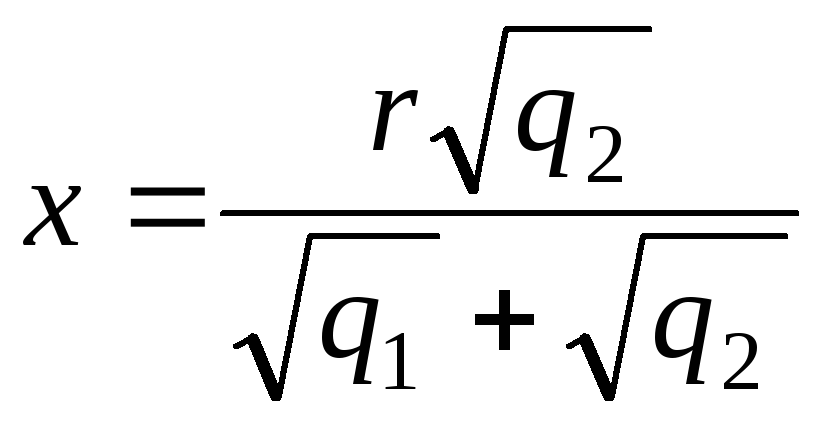 .
.
Вычислим результат:
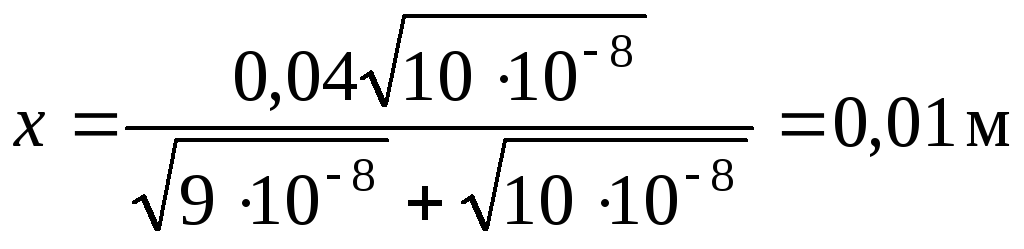 .
.
Результат
не зависит от знака заряда  .
.
Ответ: 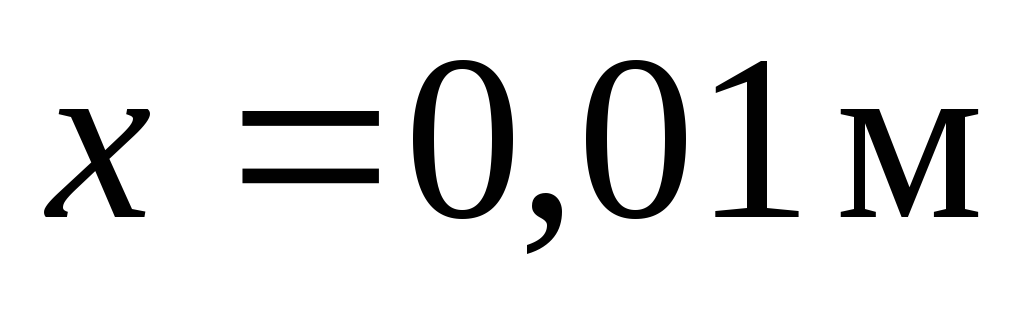 .
.
Пример 3. С каким ускорением движется электрон в поле с напряженностью 10 кВ/м?
Решение.
Из определения напряженности электрического
поля 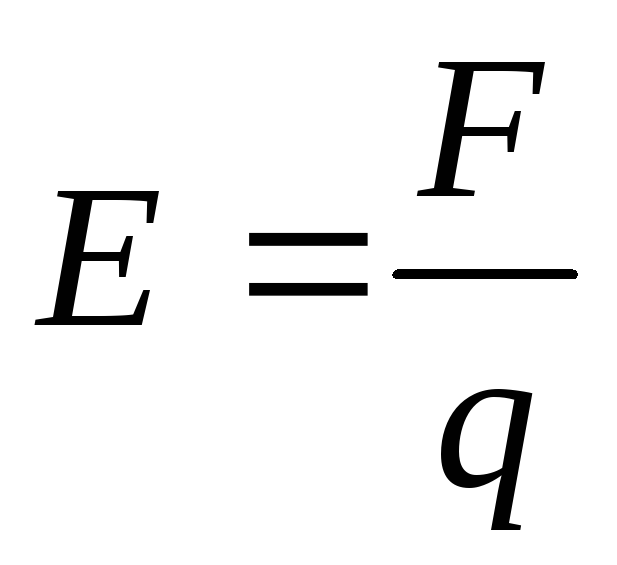 находим выражение для
находим выражение для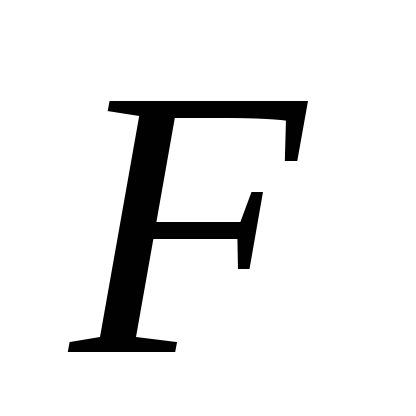 :
: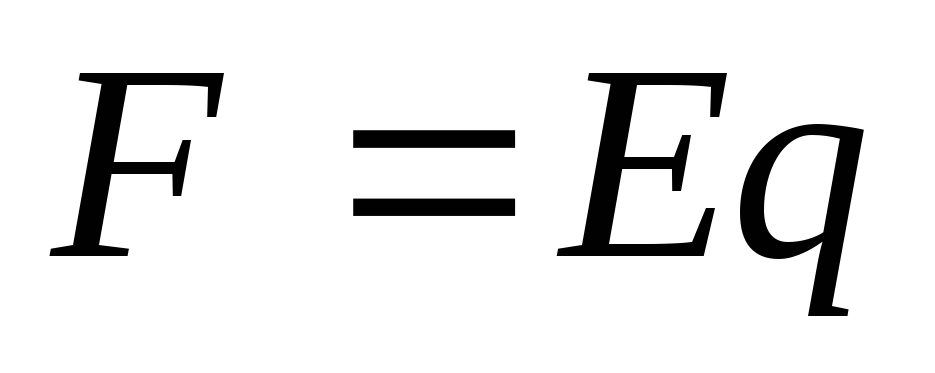 .
С другой стороны, поII
закону Ньютона, сила равна произведению
массы электрона на его ускорение а:
.
С другой стороны, поII
закону Ньютона, сила равна произведению
массы электрона на его ускорение а: 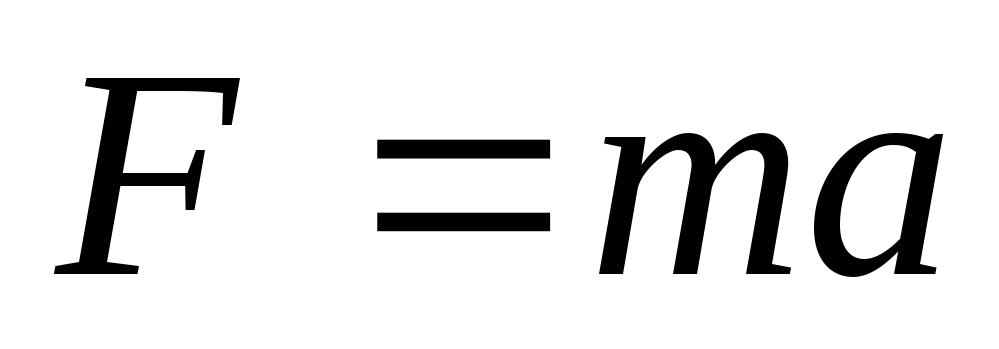 .
.
Итак,
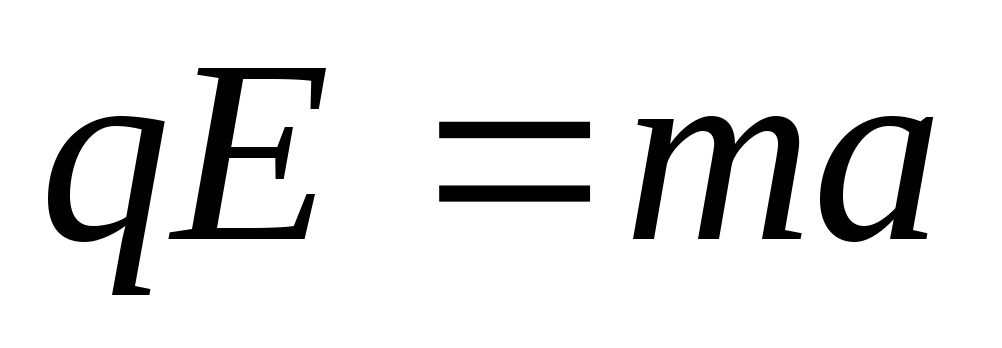 ,
, 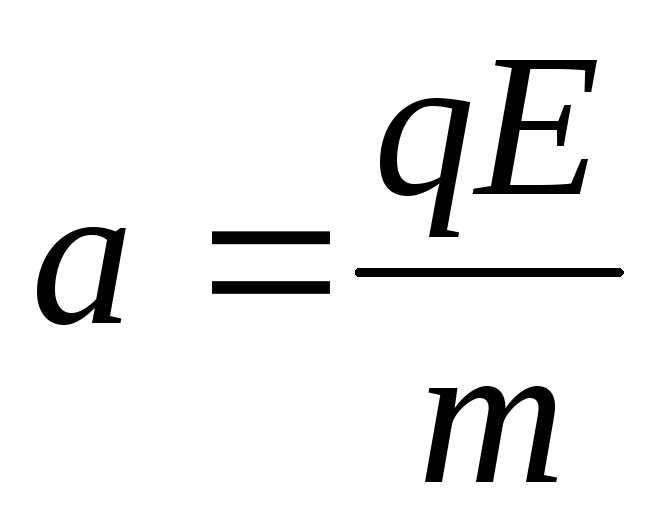 .
.
Вычислим результат:
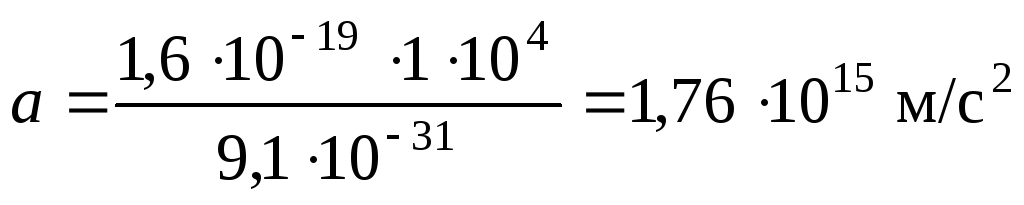 .
.
Ответ: 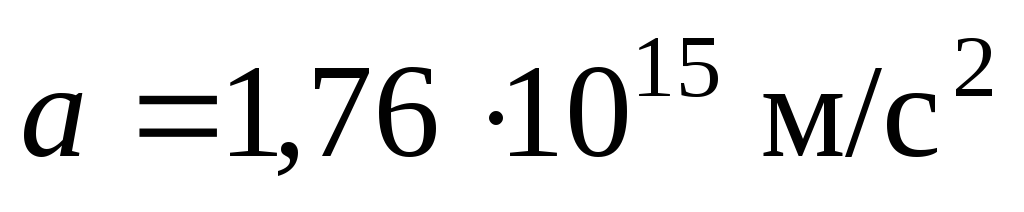 .
.
Пример 4. Медный шар радиусом R = 0,5 см помещен в масло. Плотность масла ρ = 0,8 103 кг/м3. Найти заряд шара, если в однородном электрическом поле шар оказался взвешенным в масле. Электрическое поле направлено вверх и его напряженность Е = 3,6 МВ/м.
Решение. На шар действуют силы: электростатическая сила F (вверх), сила тяжести mg (вниз) и сила Архимеда FA (вверх). Запишем уравнение равновесия:
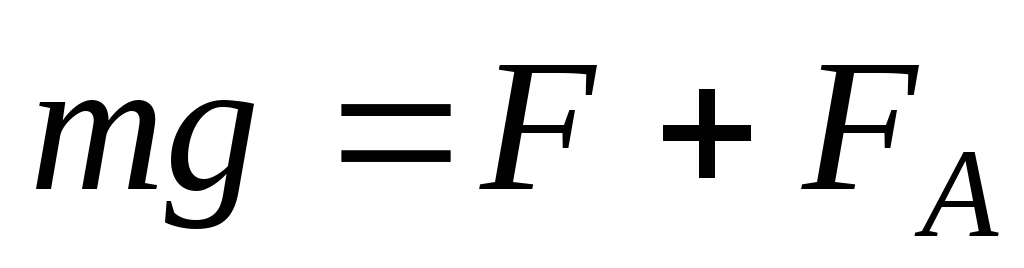 .
.
Здесь
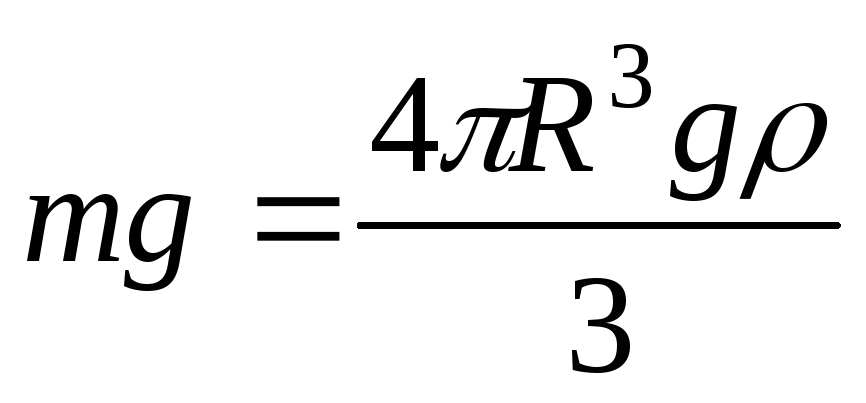 ,
, 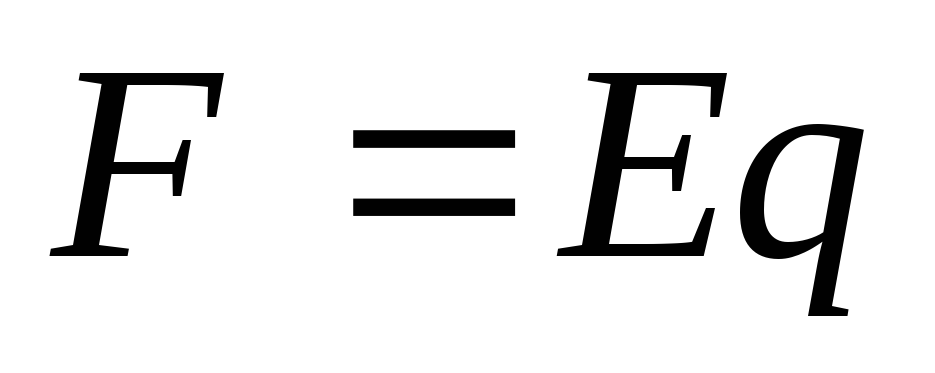 ,
,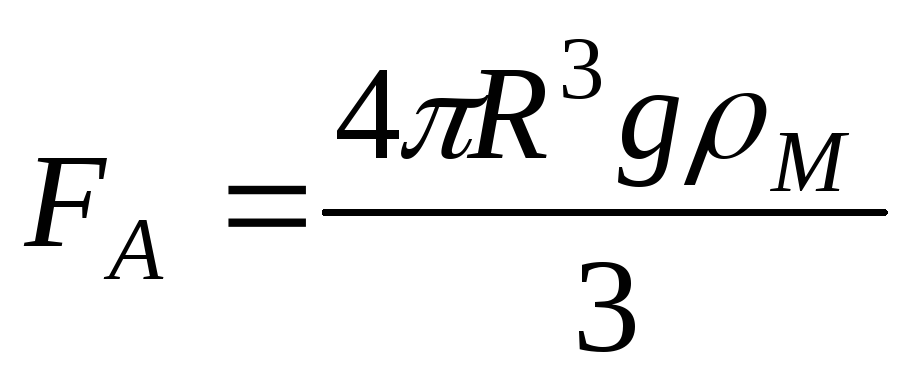 ,
,
где  ,
,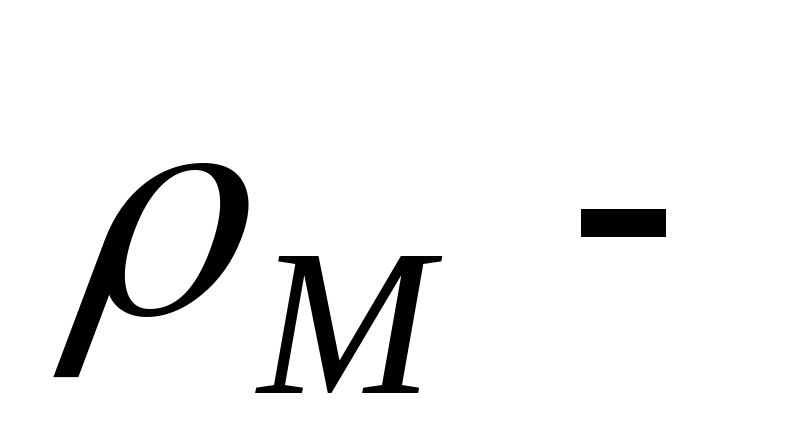 соответственно
плотности меди и масла. Из последних
соотношений имеем
соответственно
плотности меди и масла. Из последних
соотношений имеем
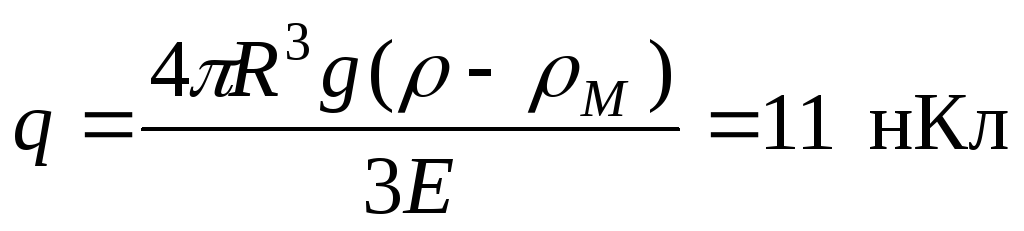 .
.
Ответ: 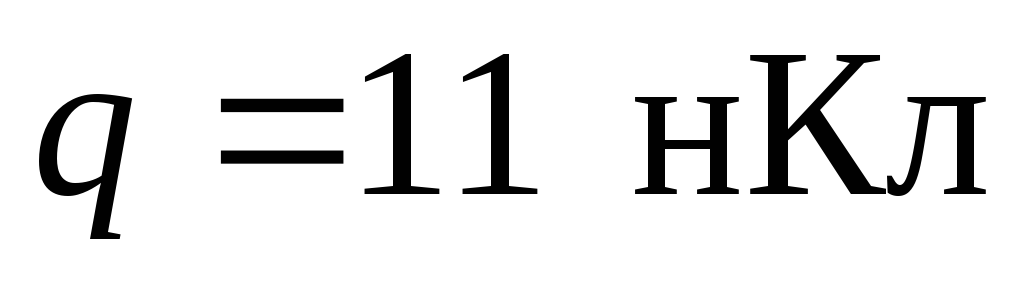 .
.
Пример 5. Электрон переместился в ускоряющем поле из точки с потенциалом 200 В в точку с потенциалом 300 В. Найти кинетическую энергию электрона, изменение потенциальной энергии взаимодействия с полем.
Решение. По закону сохранения энергии работа, совершенная полем над зарядом, идет на изменение кинетической энергии заряда:
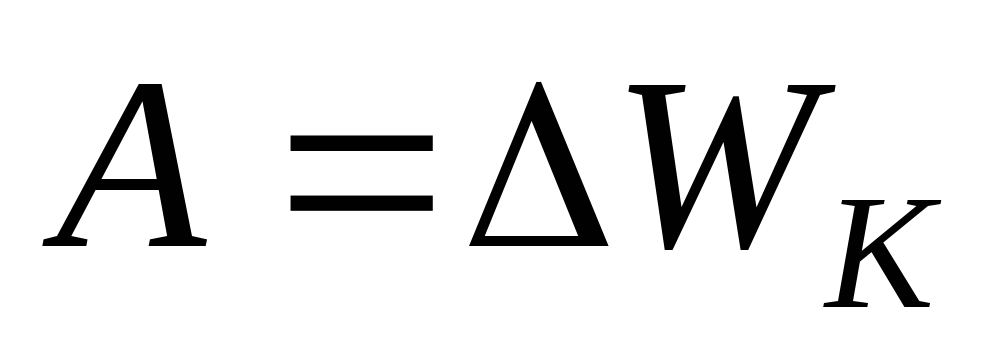 ,
, 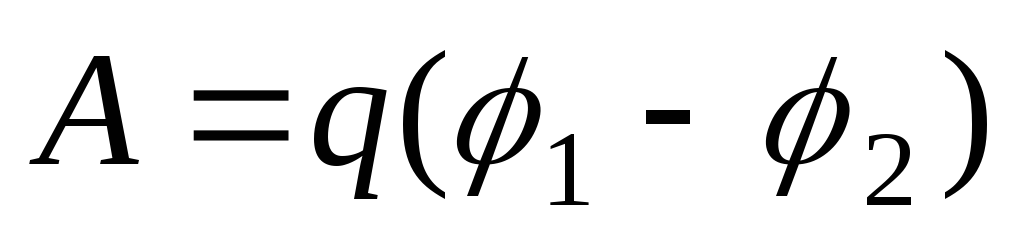 .
.
В
нашем случае 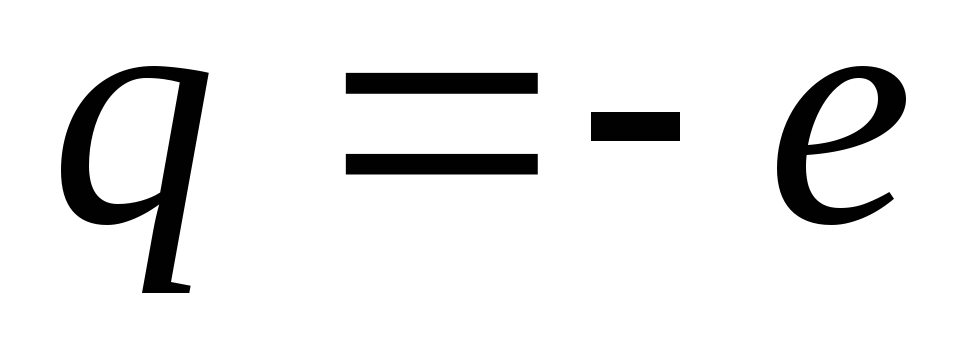 ,
,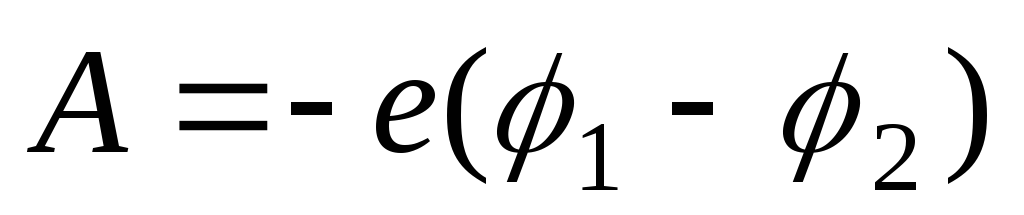 ,
где
,
где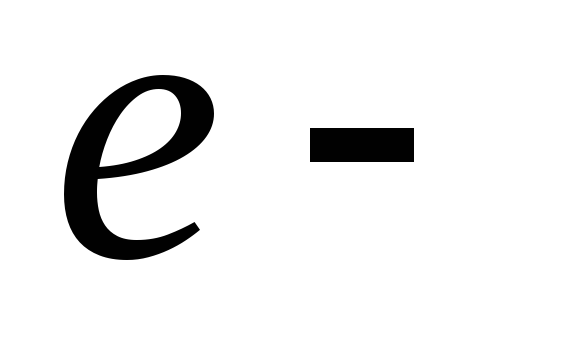 модуль
заряда электрона.
модуль
заряда электрона.
Итак,
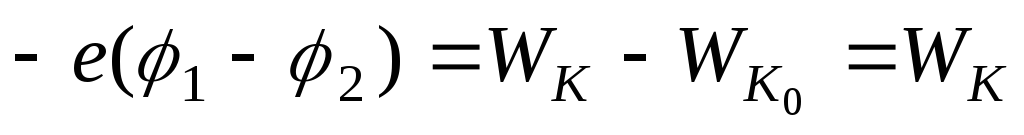 ,
,
так
как 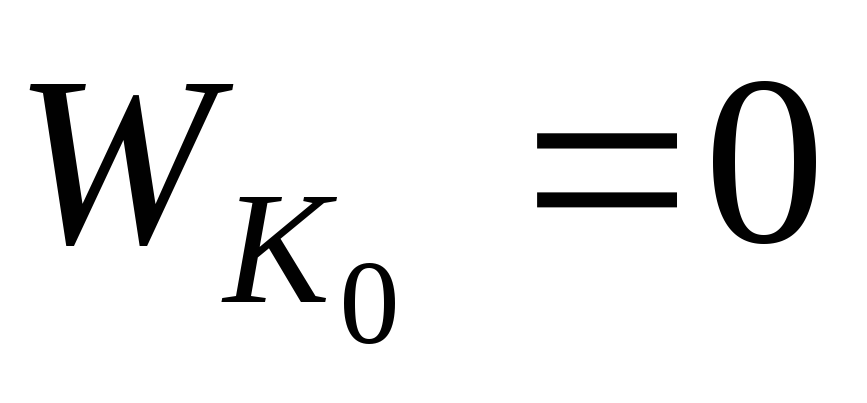 ,
то
,
то
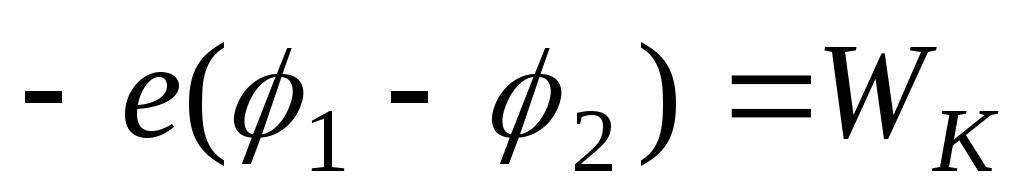 .
.
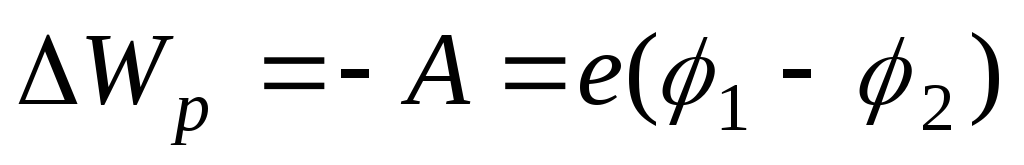 .
.
Вычислим результат:
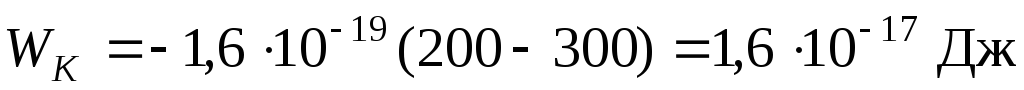 ,
,
 .
.
Ответ: 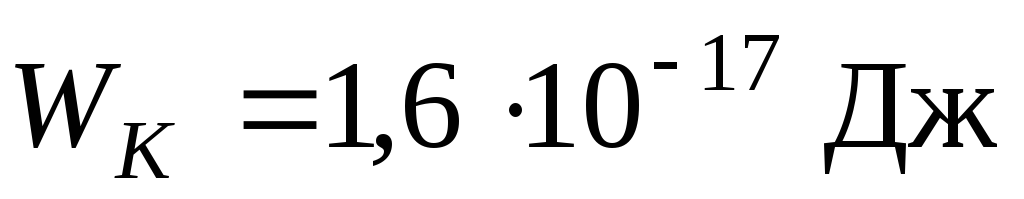 .
.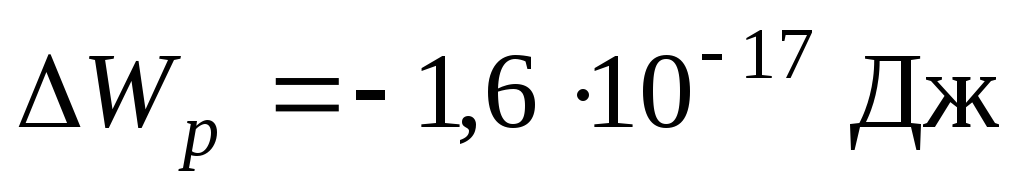 .
.
Пример 6. Заряд конденсатора 1 мкКл, площадь пластин 100 см2, зазор между пластинами заполнен слюдой. Определить объемную плотность энергии поля конденсатора и силу притяжения пластин. (ɛ = 6)
Решение. Сила притяжения между двумя разноименно заряженными обкладками конденсатора равна:
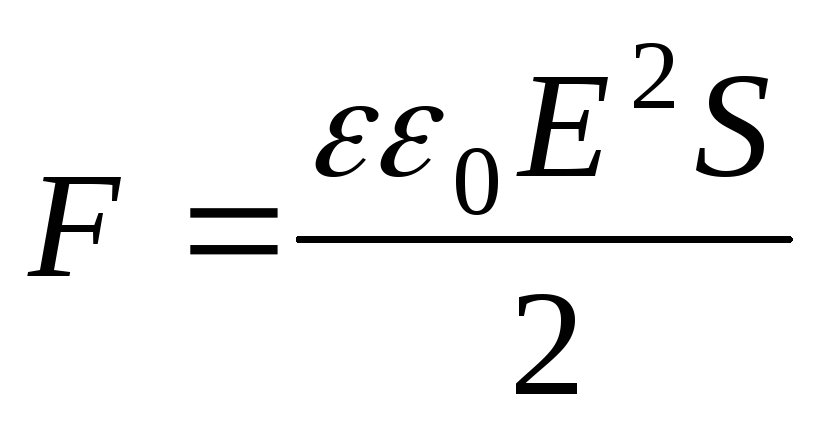 ,
,
где E – напряженность поля конденсатора; S – площадь обкладок конденсатора.
Напряженность однородного поля плоского конденсатора
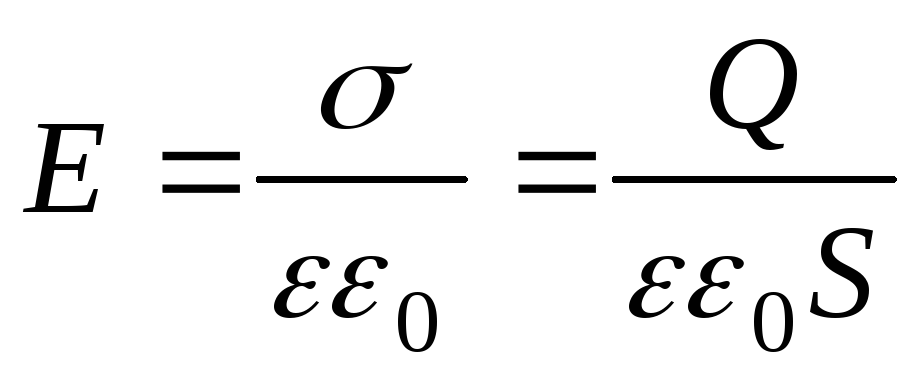 ,
,
где 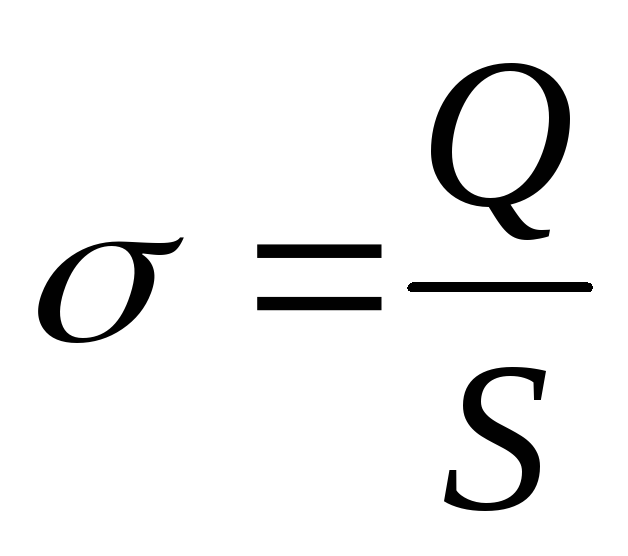 –
поверхностная плотность заряда.
–
поверхностная плотность заряда.
Рассчитаем
силу 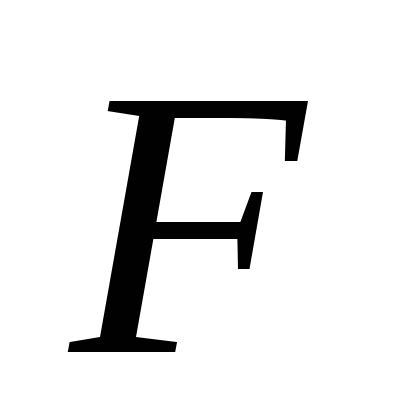 :
:
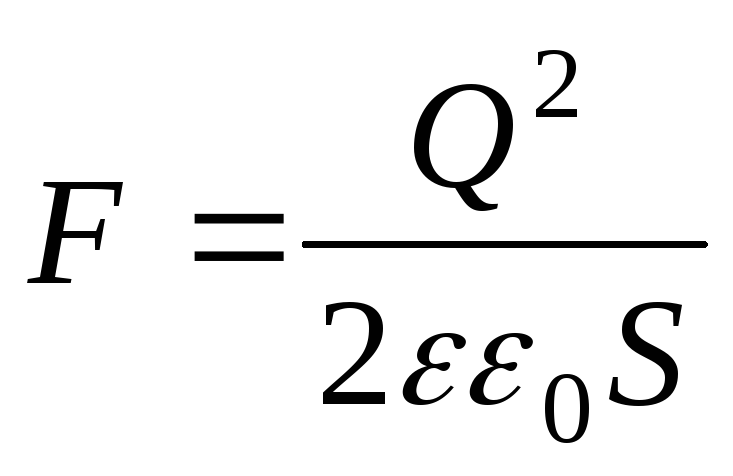 ,
, 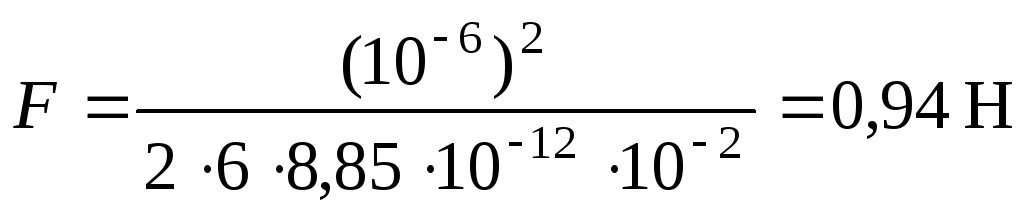 .
.
Объемная плотность энергии электрического поля
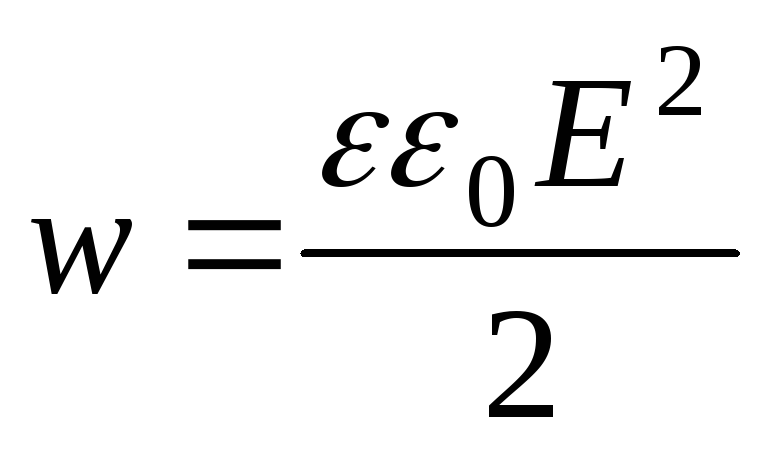 .
.
Преобразуем последнее равенство:
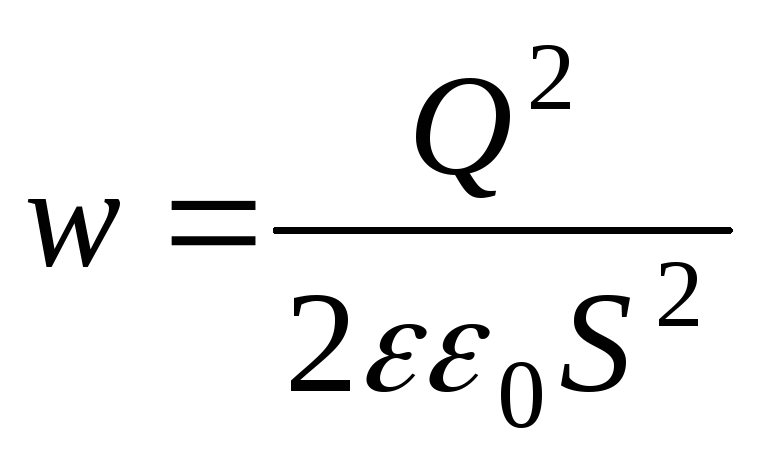 .
.
Вычислим результат:
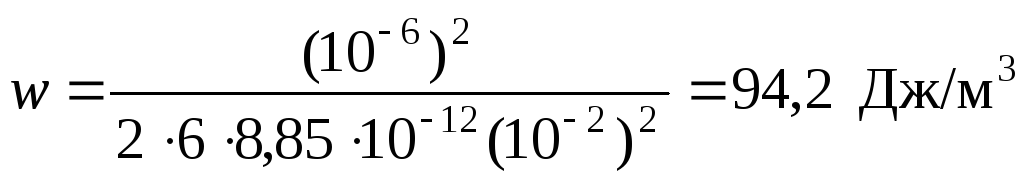 .
.
Ответ: 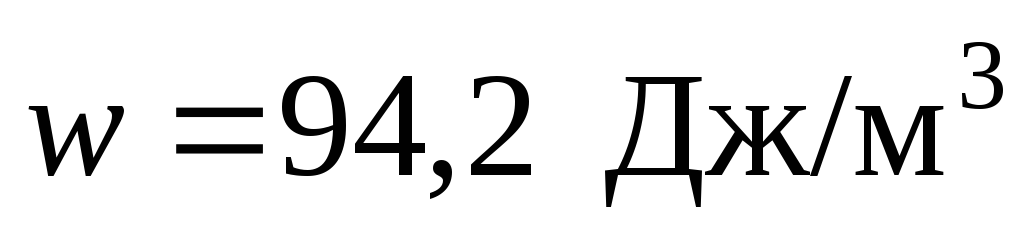 .
.
Пример 7. Определить плотность тока в нихромовом проводнике длиной 5 м, если на концах его поддерживается разность потенциалов 2 В.
Решение.
По закону Ома в дифференциальной форме
плотность тока 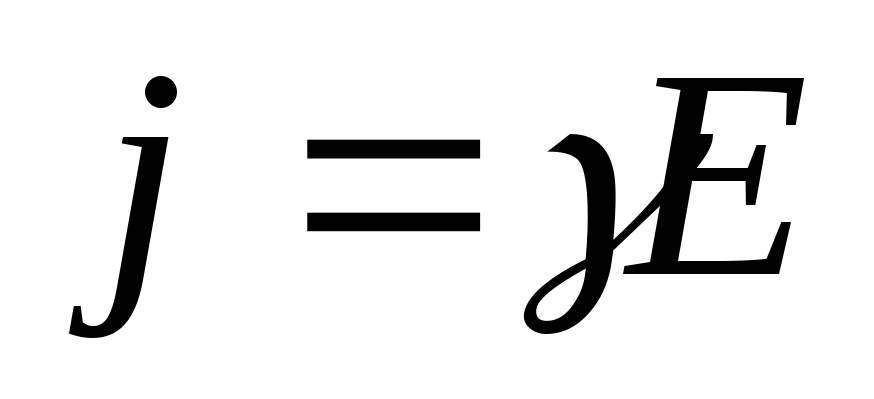 ,
где
,
где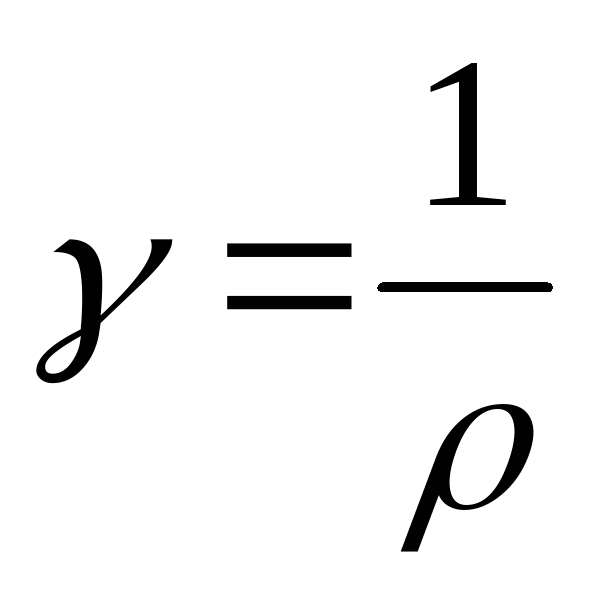 – удельная проводимость, ρ – удельное
сопротивление проводника,
– удельная проводимость, ρ – удельное
сопротивление проводника,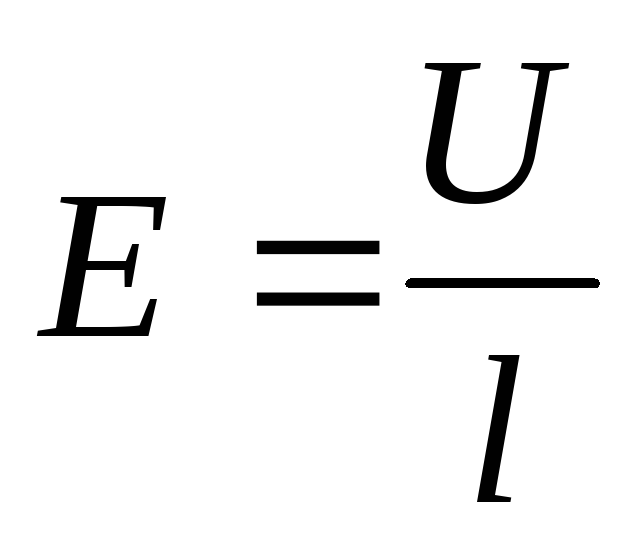 – напряженность поля в проводнике, гдеU
– напряжение на концах проводника
длиной l.
– напряженность поля в проводнике, гдеU
– напряжение на концах проводника
длиной l.
Тогда
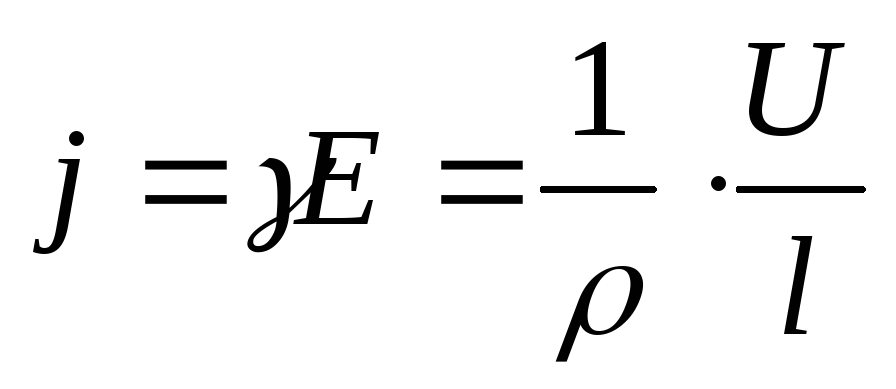 .
.
Вычислим результат:
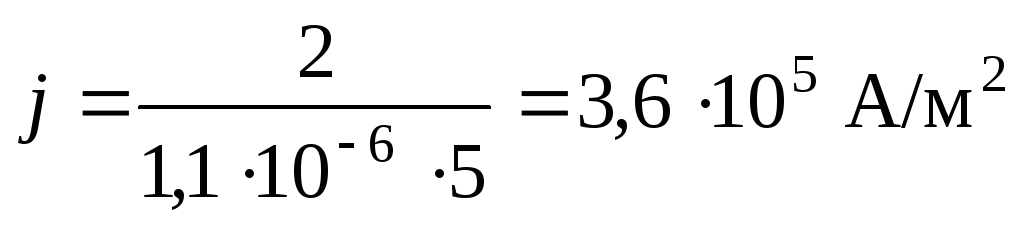 .
.
Ответ: 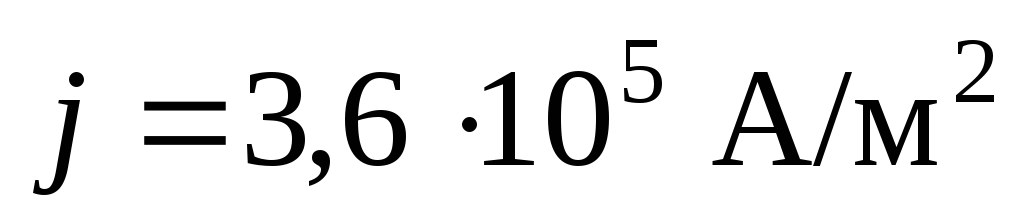 .
.
Пример 8. Под действием однородного магнитного поля перпендикулярно линиям индукции начинает перемещаться прямой проводник массой 2 кг, сила тока в котором 10 А. Какой магнитный поток пересечет этот проводник к моменту времени, когда его скорость станет равна 31,6 м/с?
Решение.
Работа перемещения проводника с током
под действием магнитного поля равна 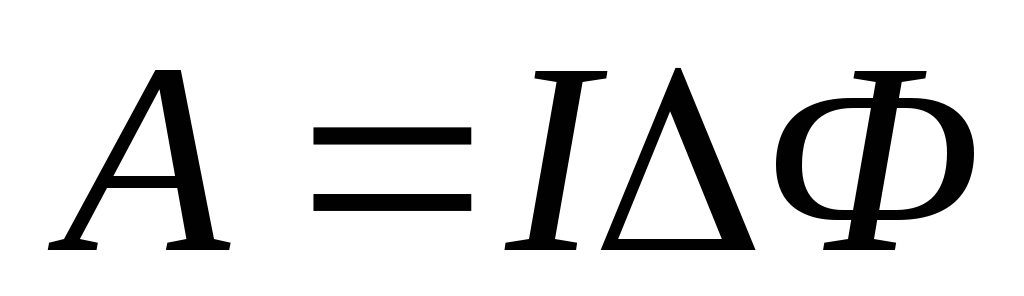 .
Эта работа будет численно равна
кинетической энергии, приобретаемой
проводником:
.
Эта работа будет численно равна
кинетической энергии, приобретаемой
проводником:
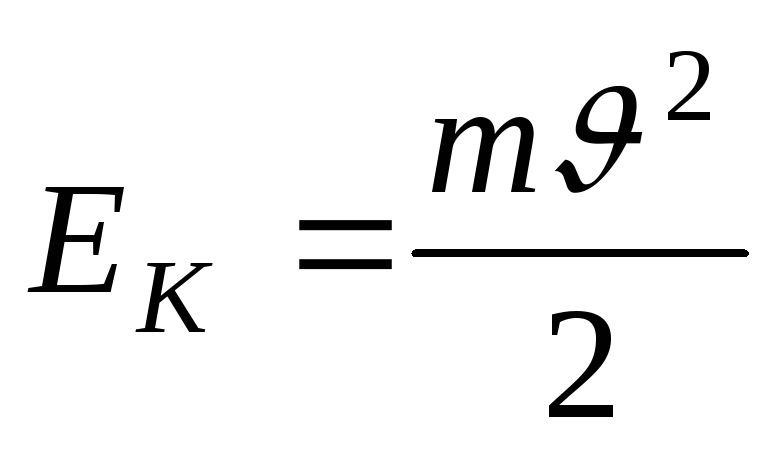 ;
; 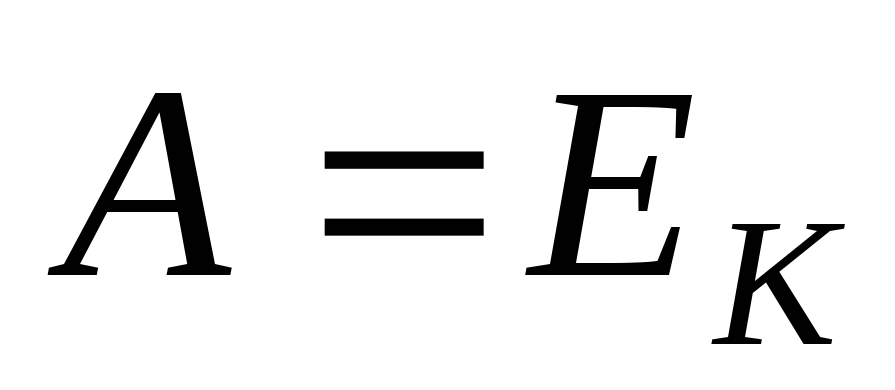 ;
;
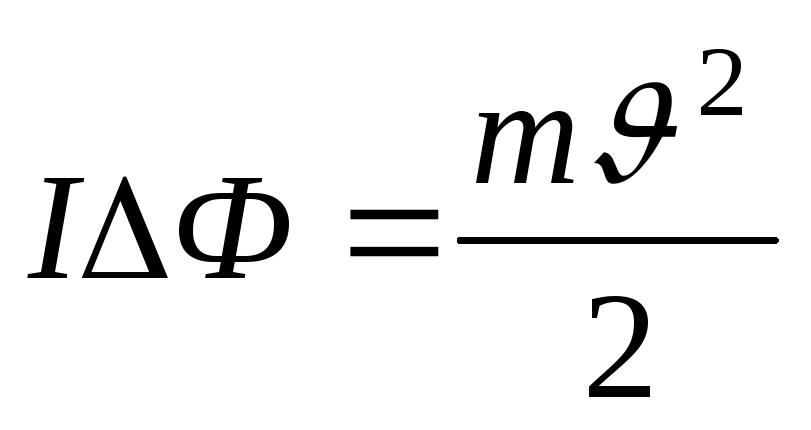 ;
; 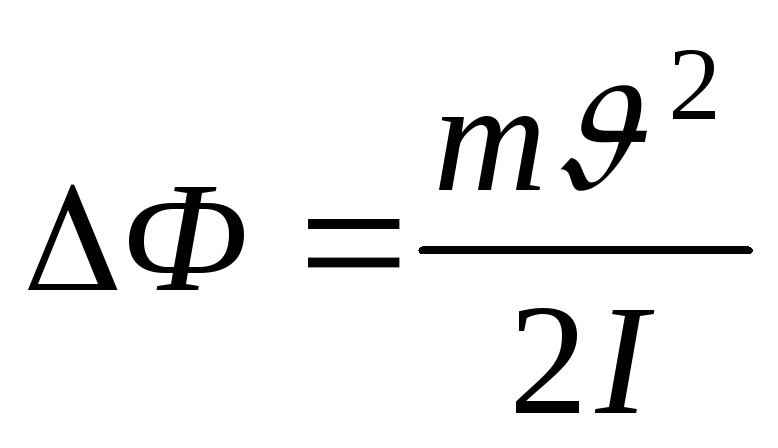 ;
;
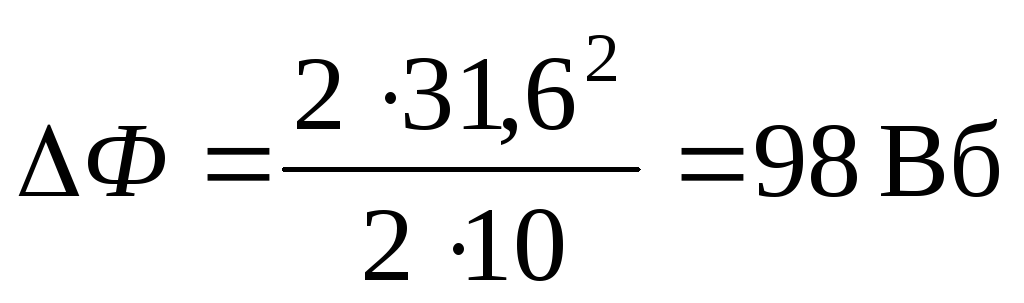 .
.
Ответ: 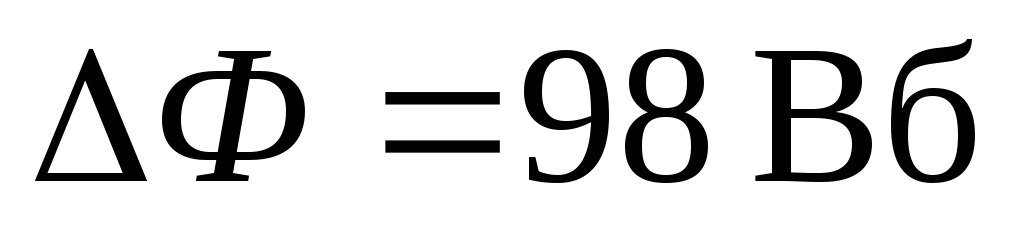 .
.
Пример 9. Обмотка соленоида имеет сопротивление 10 Ом. Какова его индуктивность, если при прохождении тока за 0,05 с в нем выделяется количество теплоты, эквивалентное энергии поля соленоида?
Решение. Энергия магнитного поля соленоида равна:
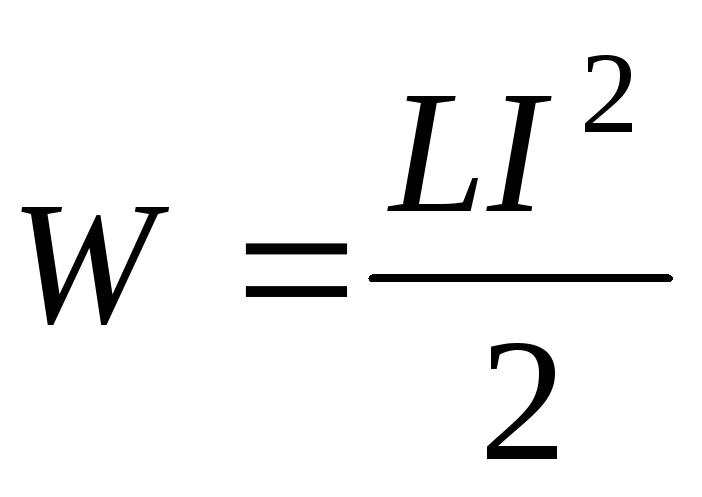 ,
,
а количество теплоты определяется по закону Джоуля – Ленца:
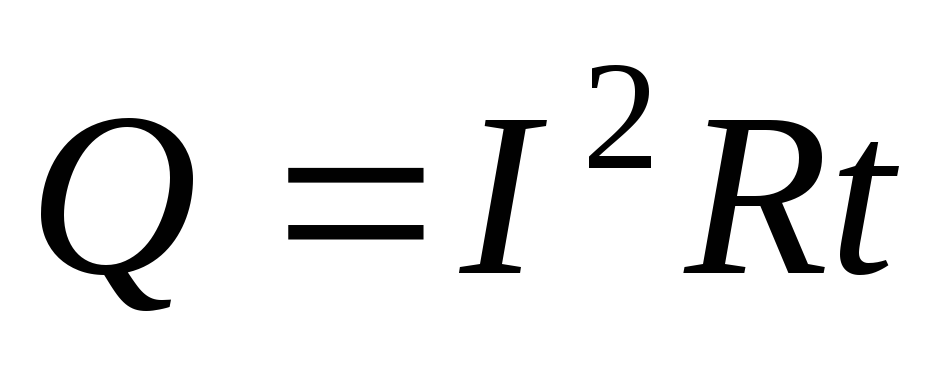 .
.
Так
как 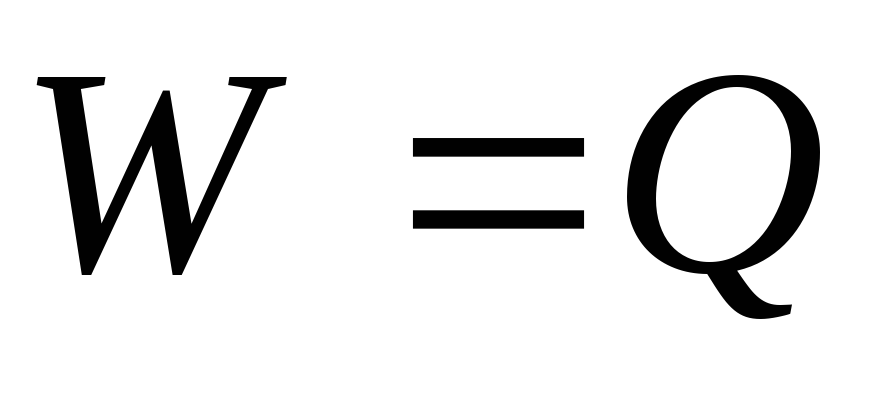 ,
то
,
то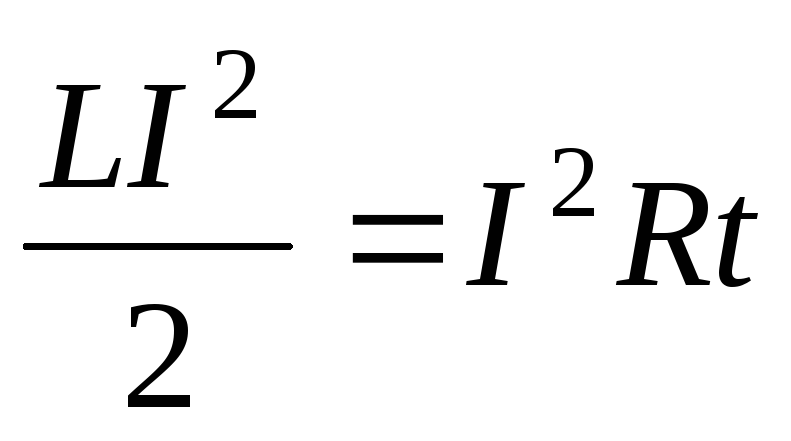 ,
,
откуда
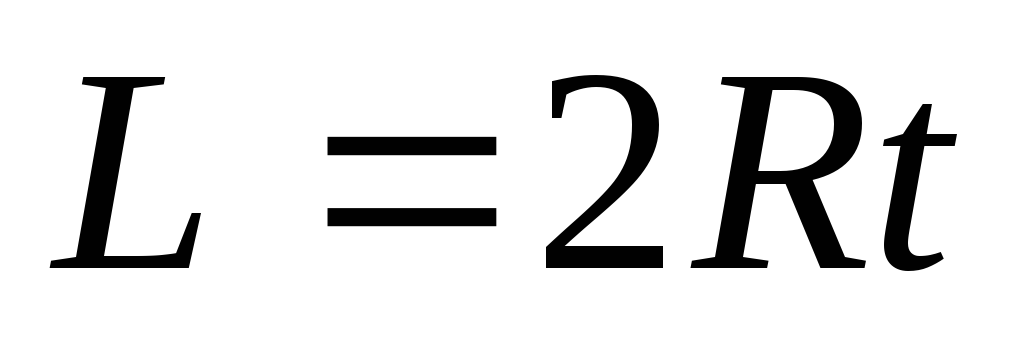 ,
, 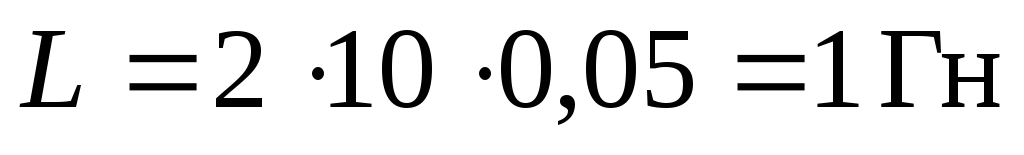 .
.
Ответ: 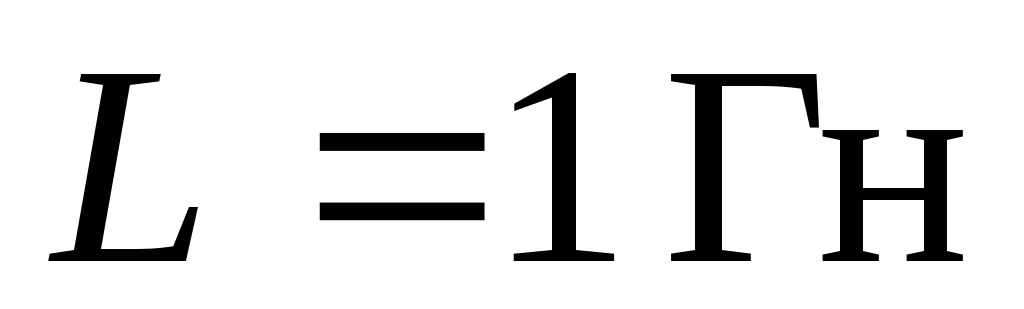 .
.
Таблица вариантов
Номер студента по списку | Номера задач | |||||||
1, 11, 21, 31 2, 12, 22, 32 3, 13, 23, 33 4, 14, 24, 34 5, 15, 25, 35 6, 16, 26, 36 7, 17. 27, 37 8, 18, 28, 38 9, 19, 29, 39 10, 20, 30, 40 | 1 2 3 4 5 6 7 8 9 10 | 11 12 13 14 15 16 17 18 19 20 | 21 22 23 24 25 26 27 28 29 30 | 31 32 33 34 35 36 37 38 39 40 | 41 42 43 44 45 46 47 48 49 50 | 51 52 53 54 55 56 57 58 59 60 | 61 62 63 64 65 66 67 68 69 70 | 71 72 73 74 75 76 77 78 79 80 |
Электромагнетизм
Теория электромагнетизма в ее классическом понимании сформировалась в XIX веке. Это фундаментальное учение о том, как устроен наш мир.
Значение электромагнетизма заключается в том, что:
- Философское и мировоззренческое значение данной теории придает описание электромагнитного поля, как особой формы существования материи.
- Электромагнетизм играл значимую роль в появлении и развитии теории относительности.
- Данный раздел физики играет большую роль в научно – техническом прогрессе.
Замечание 1
Курс «Электромагнетизма» длительное время остается консервативным. Причиной тому служит завершенность теории.
Определение 1
Электромагнетизмом называют раздел физики, который посвящен изучению законов и явлений, связанных с электрическими и магнитными полями, их связью и взаимозависимостью.
Фундаментальными понятиями теории электромагнетизма являются:
- заряд;
- электрическое поле;
- потенциал;
- энергия поля;
- электромагнитное взаимодействие;
- магнитное поле;
- магнитная индукция;
- электромагнитное поле и др.
К основным законам электромагнетизма можно отнести следующие:
- закон Кулона;
- закон Ампера;
- закон Био-Савара-Лапласа;
- закон Ома;
- закон индукции Фарадея;
- уравнения Максвелла.
Закон Кулона
Обобщая результаты экспериментов с крутильными весами, Кулон предложил закон, в соответствии с которым пара точечных зарядов (рис.1) $q_1$ и $q_2$, находящихся в вакууме действуют друг на друга с силами равными $F$, направленными вдоль прямой, которая соединяет рассматриваемые заряды, при этом:
$\vec{F}_{12}=\frac{1}{4\pi \varepsilon_{0}}\frac{q_{1}q_{2}}{\left|r_{2}-r_{1} \right|^{3}}\left( \vec{r}_{2}-\vec{r}_{1}\right)=-\vec{F}_{21}\left( 1 \right)$,
где $ \epsilon_0=8,85\bullet 10^{-12}$ Ф/м – электрическая постоянная; $\vec F_{12 }$ — сила, действующая на заряд $q_2$ со стороны заряда $q_1$.
Рисунок 1. Закон Кулона. Автор24 — интернет-биржа студенческих работ
Замечание 2
Одноименные заряды отталкиваются, противоположные притягиваются.
Закон Кулона – это основной закон электростатики.
Для вычисления сил взаимодействия заряженных тел произвольных форм и размеров используют принцип суперпозиции, который можно сформулировать следующим образом:
Взаимодействие пары точечных зарядов не изменяется, если внести третий заряд. Он будет взаимодействовать с первыми двумя зарядами.
Закон Ампера
Датский физик Г. Эрстед обнаружил, что магнитная стрелка, при нахождении рядом с проводом с током может поворачиваться. Данное открытие стало основанием для вывода о связи магнитных и электрических явлений. Основным в открытии Эрстеда было то, что магнит реагировал на перемещающийся электрический заряд. Появилось понимание того, что магнитное поле создается перемещающимся зарядом.
Проводя анализ экспериментов Эрстеда, А. Ампер выдвинул гипотезу о том, что земной магнетизм порождается токами, которые обтекают нашу планету в направлении с запада на восток.
Вывод был сделан следующий:
Магнитные свойства каждого тела определены замкнутыми электрическими токами в нем.
Ампер установил, что два проводника с токами взаимодействуют. Если токи в параллельных проводниках однонаправленные, то эти проводники притягиваются.
Результатом экспериментов Ампера стал закон, который назвали его именем.
Сила взаимодействия пары контуров с током зависит от силы тока в каждом контуре и уменьшается при увеличении расстояния между рассматриваемыми контурами:
$d\vec{F}_{12}=\frac{\mu_{0}}{4\pi }\frac{I_{1}I_{2}(d\vec{l}_{2}\times(d\vec{l}_{1}\times \vec{r}_{12})}{r_{12}^{3}}\left( 2 \right)$,
где $\mu_0=4\pi\bullet 10^{-7}$ Н/$A^2$ — магнитная постоянная; $ d\vec F_{12}$ – сила, с которой первый элемент с током действует на второй. Выражение (2) содержит двойное векторное произведение; $I_1; I_2$ — силы токов, которые текут в проводниках; $I_1d\vec l_1$; $I_2d\vec l_2$ — элементы токов (рис.2).
Рисунок 2. Закон Ампера. Автор24 — интернет-биржа студенческих работ
Закон Био – Савара – Лапласа
Проводники с током воздействуют друг на друга, посредством магнитных полей, которые их окружают.
Введем векторную величину $\vec B$, которая будет характеристикой магнитного поля. Для этого параметра поля был установлен экспериментально закон, который получил название по именам его первооткрывателей, закон Био – Савара- Лапласа:
$dB=\frac{\mu_{0}}{4\pi }\frac{Idl}{r^{2}}\sin {\alpha \, \left( 3\right),}$,
где $Idl$ — элемент с током, который создает магнитное поле; $r$ — расстояние до точки в которой поле рассматривается поле; $\alpha$ — угол между векторами $d\vec l$ и $\vec r$.
Полученный вектор индукции нормален к векторам $d\vec l$ и $\vec r$, его направление определяют при помощи правила буравчика:
Если правый винт поворачивать по направлению тока, то вектор индукции в каждой точке параллелен направлению бесконечно малого перемещения конца рукоятки буравчика.
Замечание 3
Закон Био – Савара- Лапласа играет такую же роль в магнитостатике, как закон Кулона в электростатике.
Закон Ома
В начале XIX века Г. Ом рассматривая процессы течения электрического тока в цепи, имеющей источник установил, что:
$I=\frac{Ɛ}{r+R}\left( 4 \right)$,
где $I$ — сила тока в цепи; $Ɛ$ — электродвижущая сила источника тока; $r$ — внутреннее сопротивление источника; $R$ — сопротивление цепи (внешнее). Выражение (4) описывает ситуацию в замкнутой цепи.
Если рассматривать участок цепи, по которому течет ток, то закон Ома представляется в виде:
$I=\frac{U}{R}\left( 5 \right)$.
где $U$ — напряжение участка; $R$ — сопротивление участка.
Если участок цепи содержит источник, то закон Ома предстанет в виде:
$IR=Ɛ-Ir$(6).
Выражение (6) означает, что напряжение на нагрузке меньше ЭДС на величину, равную падению напряжения ($Ir$) на внутреннем сопротивлении источника.
Закон Ома в виде (4-6) называют законом в интегральной форме.
Закон Ома в дифференциальной форме можно записать как:
$\vec{j}=\frac{1}{\rho }\vec{E}\left( 7 \right)$,
где $\vec j$ — вектор плотности тока; ρ – удельное сопротивление проводника; $\vec E$ — вектор напряженности электрического поля.
Закон индукции Фарадея
Электромагнитная индукция была открыта Фарадеем в 1881 году.
Фарадей понимал электромагнитную индукцию как возбуждение токов в проводниках под воздействием магнитного поля.
Экспериментально доказано, что электродвижущая сила (ЭДС) ($Ɛ $) индукции в контуре пропорциональна скорости изменения магнитного потока сквозь рассматриваемый контур. В Международной системе единиц (СИ) данный результат выражен формулой:
$Ɛ=-\frac{dФ}{dt}\left( 8 \right)$,
где $Ф$ -переменный магнитный поток через замкнутый контур или его часть.
В общем случае изменение магнитного потока сквозь плоский контур вызвано:
- переменным во времени магнитным полем;
- движением контура в поле и переменой его ориентации.
Уравнения Максвелла
Максвелл доказал, что сущностью электромагнитной индукции стало создание магнитным полем вихревого электрического поля. Индукционный ток является вторичным эффектом, который появляется в проводящих веществах. Трактовка электромагнитной индукции, которую дал Максвелл стала более общей.
Уравнения Максвелла стали математическим основанием классического электромагнетизма.
Запишем их в виде системы:
$rot\, \vec{E}=-\frac{\partial \vec{B}}{\partial t}\left( 9 \right)$,
$rot\, \vec{H}=\vec{j}+\frac{\partial \vec{D}}{\partial t}\left( 10 \right)$,
$div\, \vec{D}=\rho \left( 11 \right)$,
$div\, \vec{B}=0\left( 12 \right)$.
В выражениях (9)- (12) мы имеем: $\vec E$ и $\vec D$ — напряженность и индукция электрического поля;
$\vec H$ и $\vec B$ — напряженность и магнитная индукции;
$\rho$ — объемная плотность электрического заряда;
$\vec j$ — плотность тока.
Уравнения Максвелла у нас представлены в дифференциальной форме. Для однозначного описания электромагнитных полей уравнения Максвелла дополняют материальными уравнениями среды. В общем виде они записываются в виде функций:
$\vec D=\vec D(\vec E)$; $\vec B=\vec B(\vec H)$; $\vec j=\vec j(\vec E)$.


 — векторная величина, численно равная
отношению максимального вращающего
момента
— векторная величина, численно равная
отношению максимального вращающего
момента 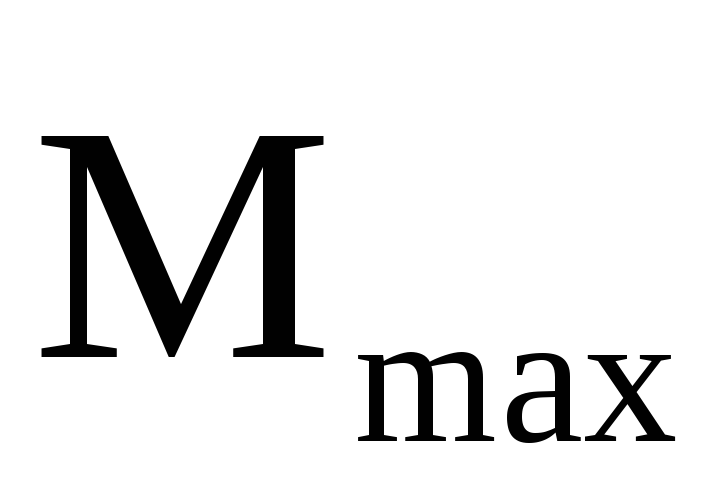 ,
действующего на пробный контур тока,
помещенный в данную точку поля к
магнитному моменту контура
,
действующего на пробный контур тока,
помещенный в данную точку поля к
магнитному моменту контура 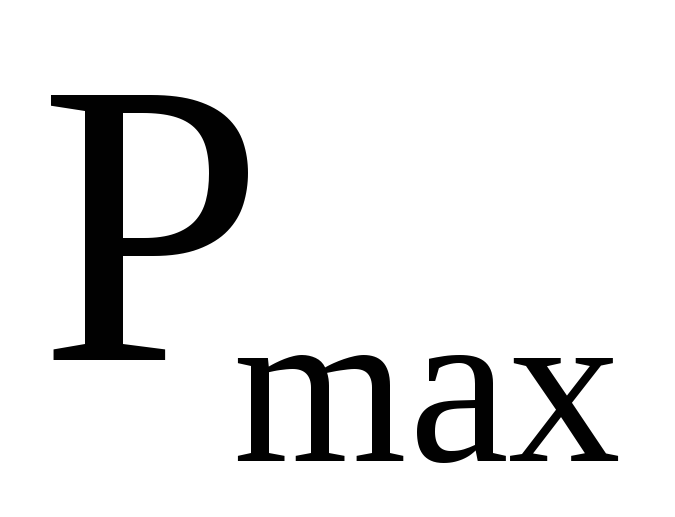 .
.

 в однородном магнитном поле с индукцией
в однородном магнитном поле с индукцией  .
. через плоский контур площадью S
в случае однородного
магнитного поля
через плоский контур площадью S
в случае однородного
магнитного поля , создаваемого током в замкнутом
контуре индуктивностью L
, создаваемого током в замкнутом
контуре индуктивностью L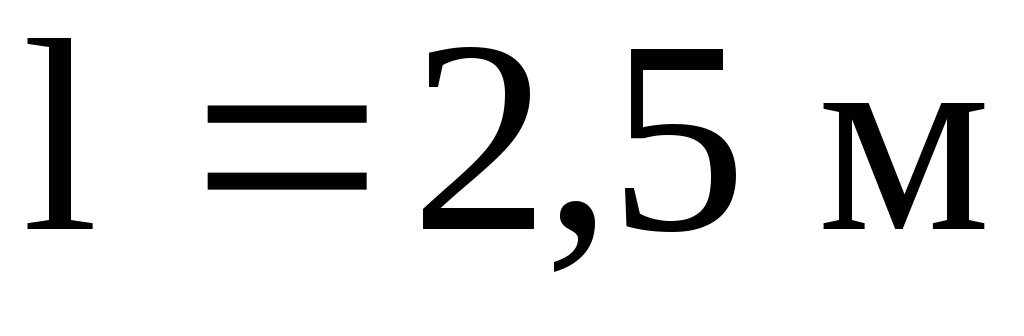
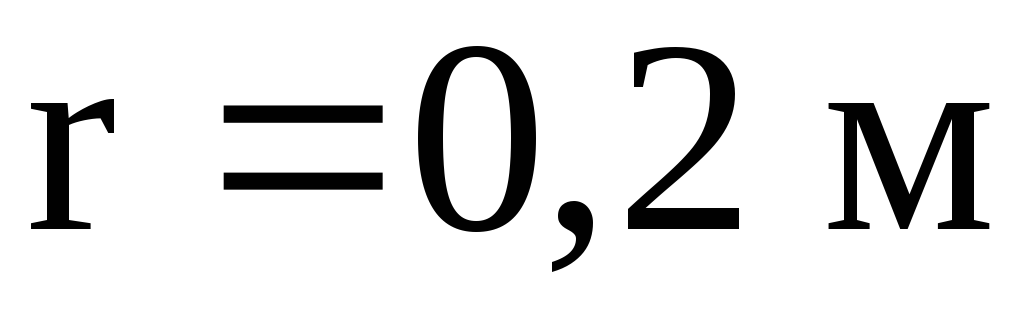
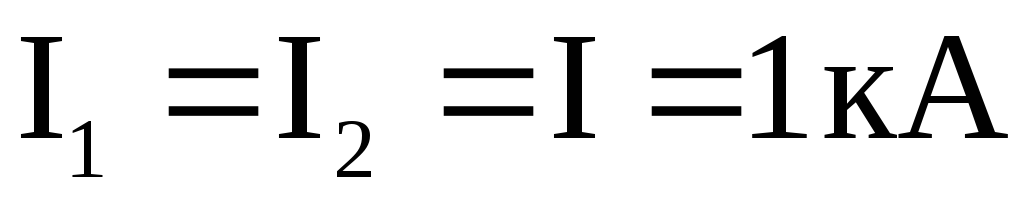
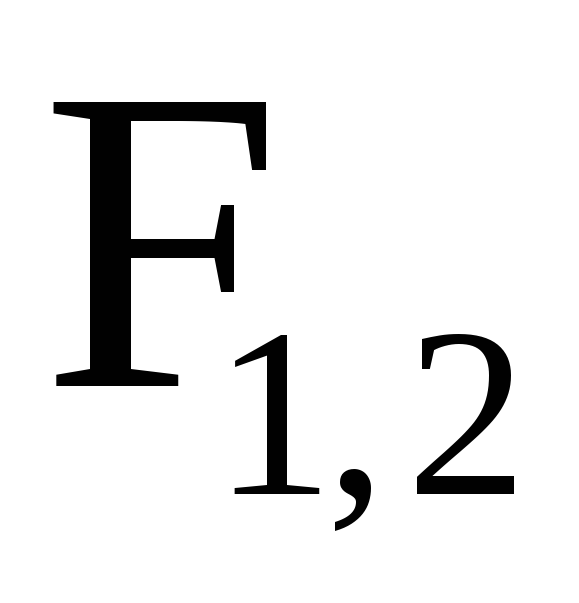 ,
с которой магнитное поле, созданное
током
,
с которой магнитное поле, созданное
током 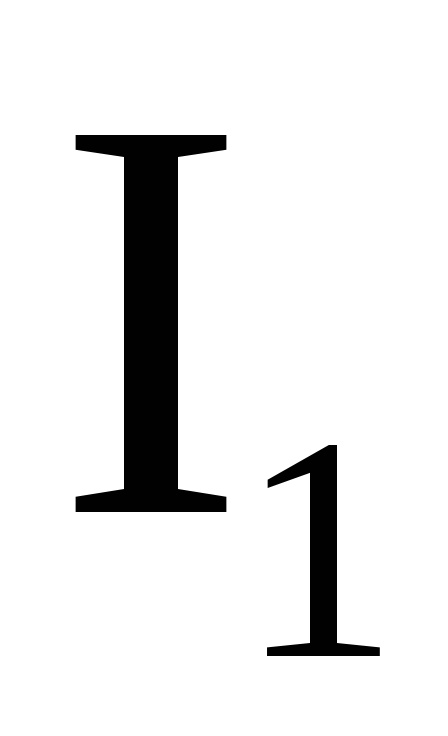 ,
действует на проводник с током
,
действует на проводник с током 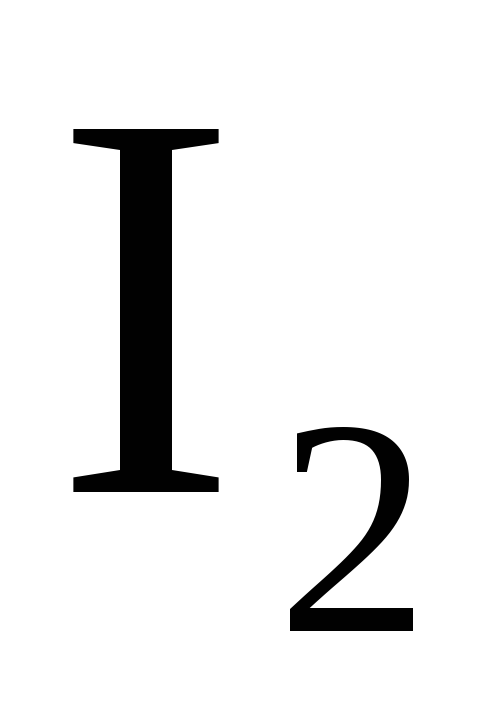 .
.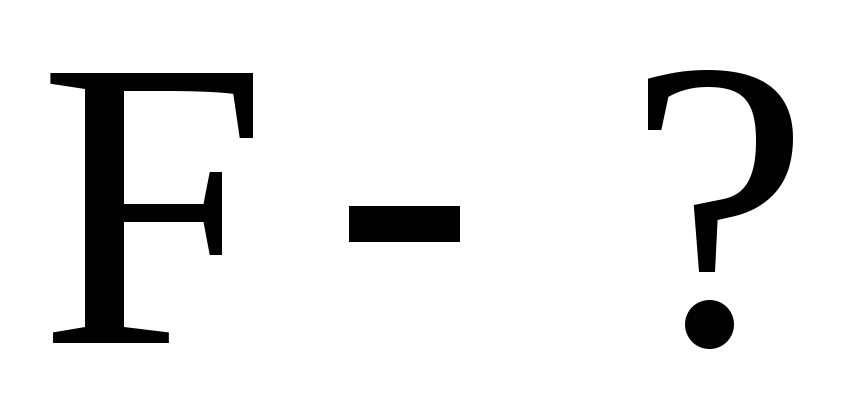
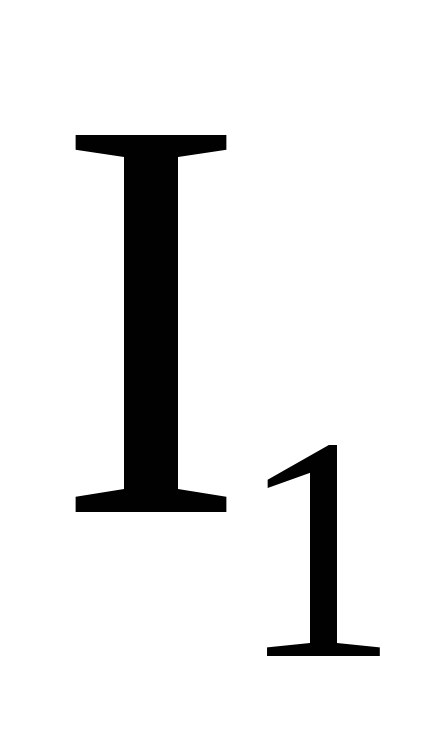 определяется соотношением:
определяется соотношением: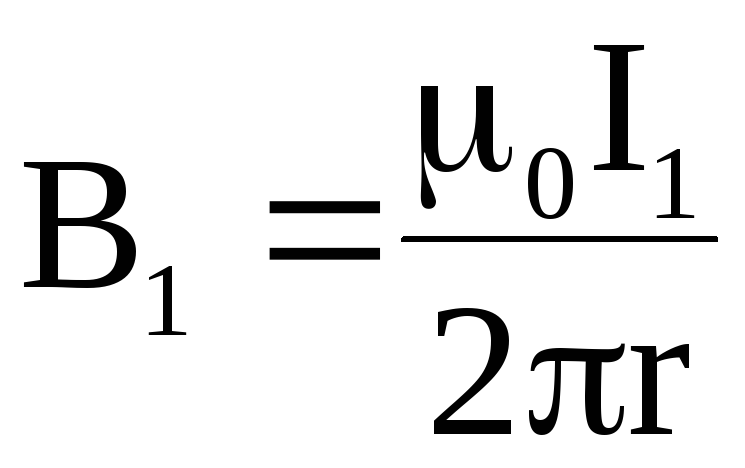 (1)
(1)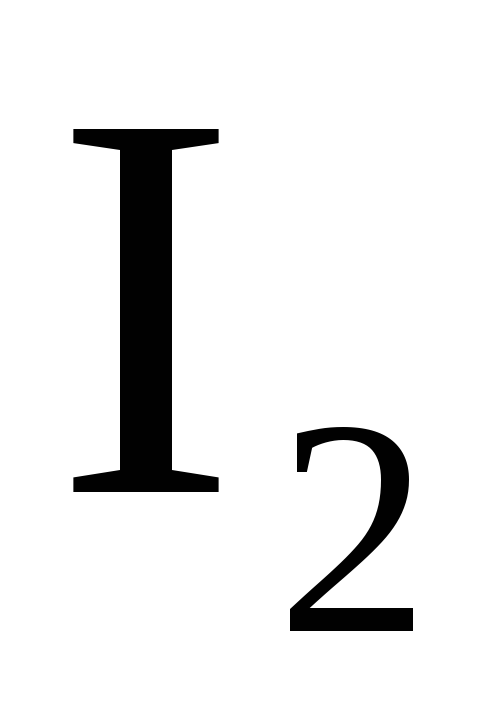 ,
длиной
,
длиной 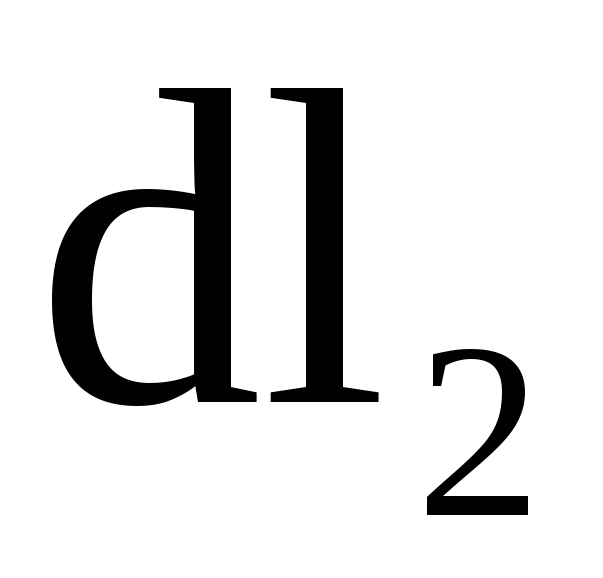 в магнитном поле действует сила:
в магнитном поле действует сила: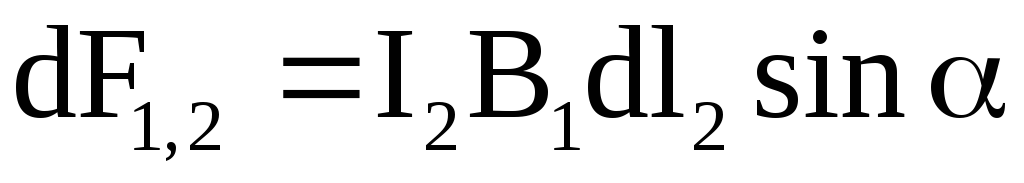 (2)
(2)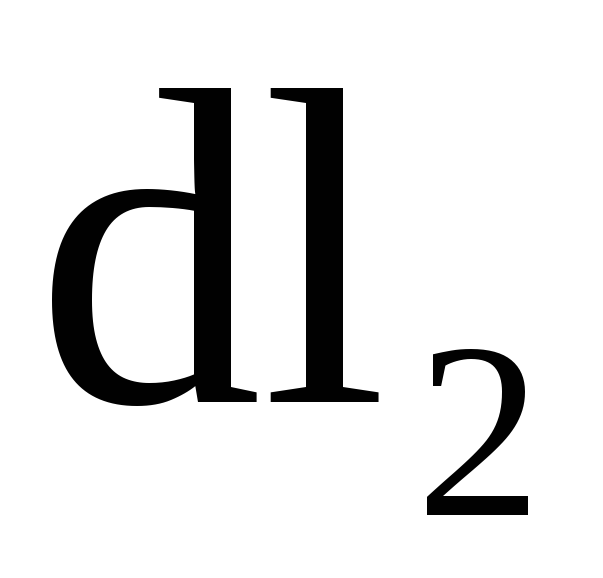 перпендикулярен вектору
перпендикулярен вектору  ,
,  и тогда
и тогда (3)
(3) (1) в (3), получим
(1) в (3), получим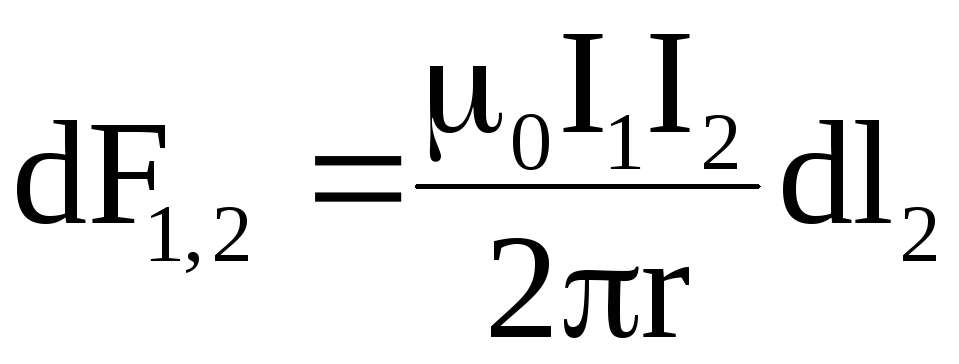 (4)
(4)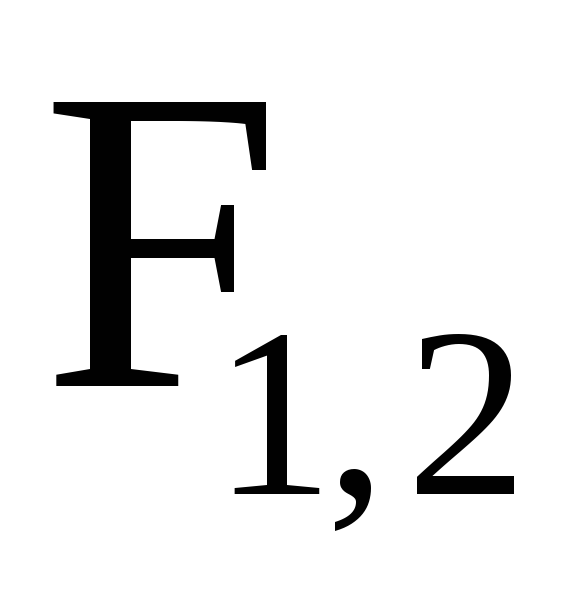 найдем интегрированием по всей длине
второго проводника:
найдем интегрированием по всей длине
второго проводника: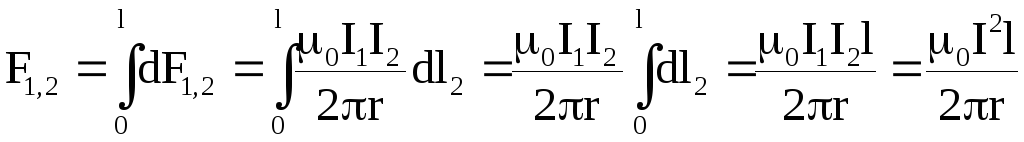 (5)
(5)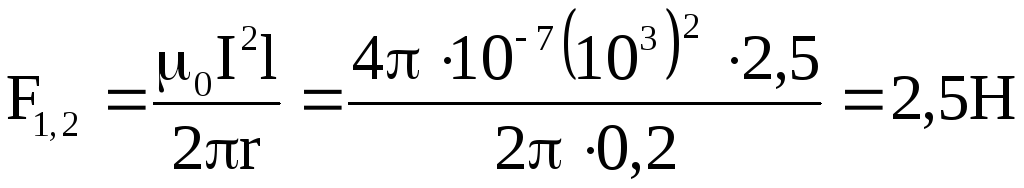
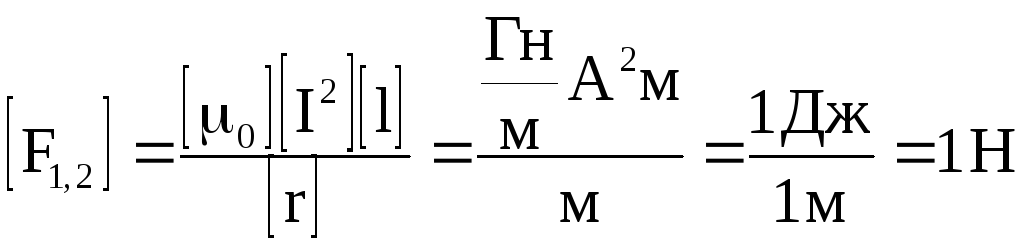
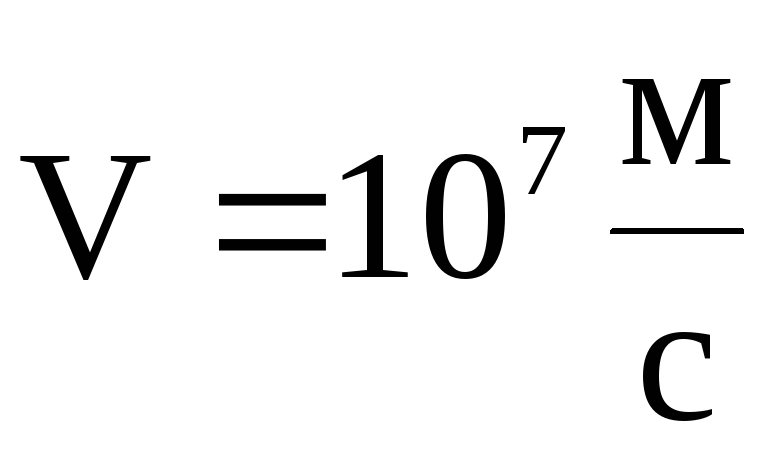
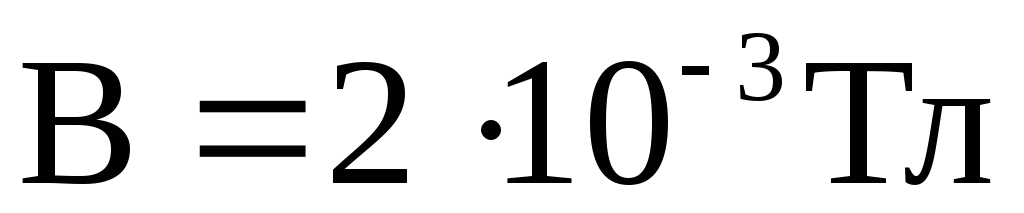
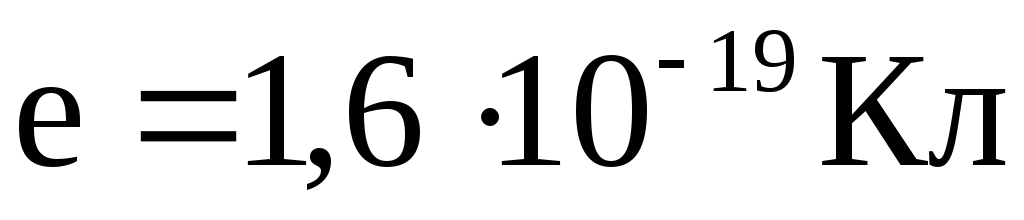
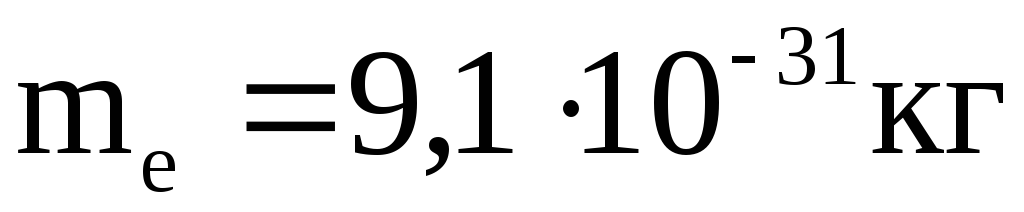
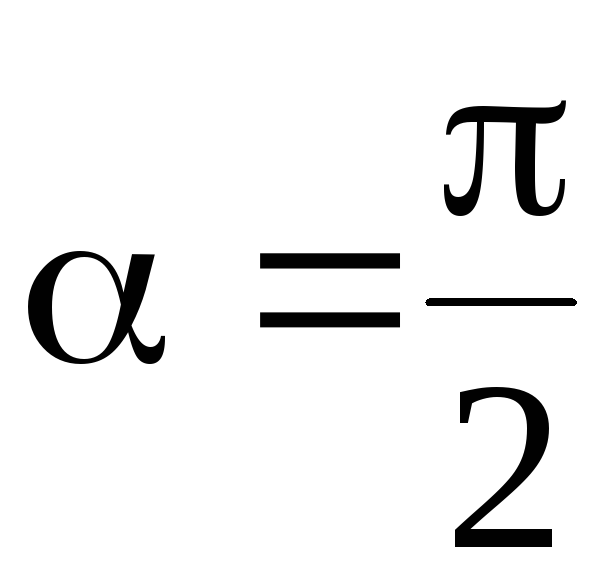
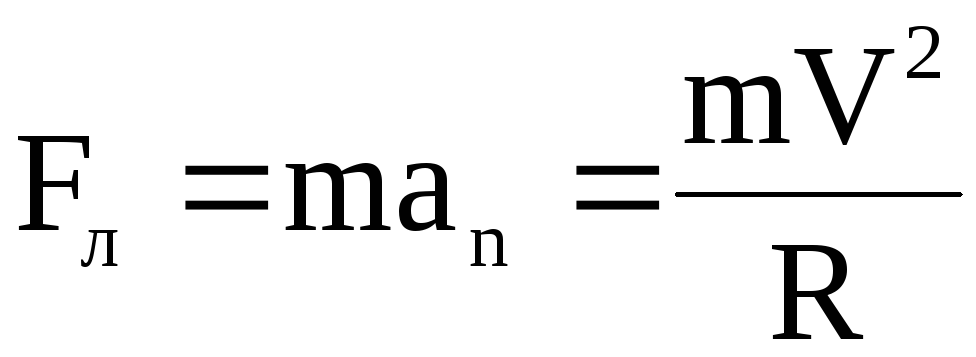 (1)
(1)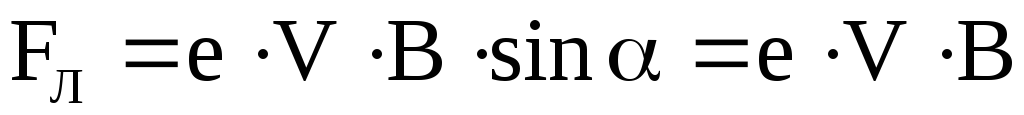 (2)
(2)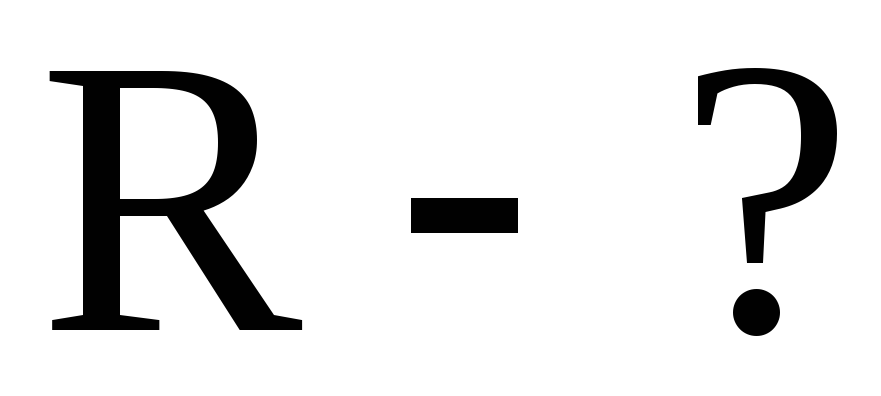
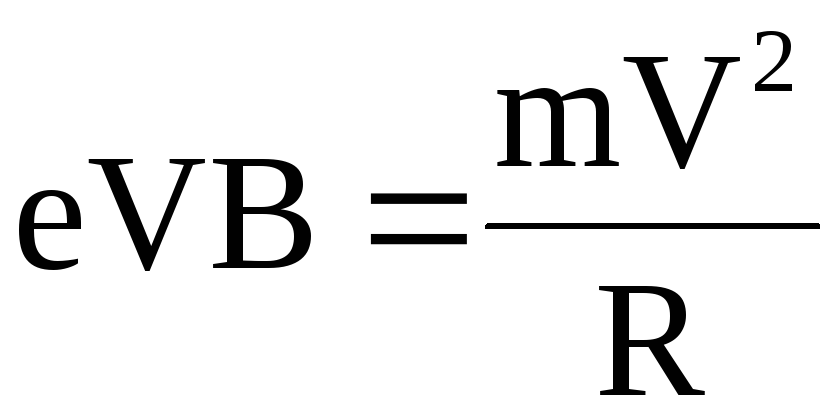 (3)
(3)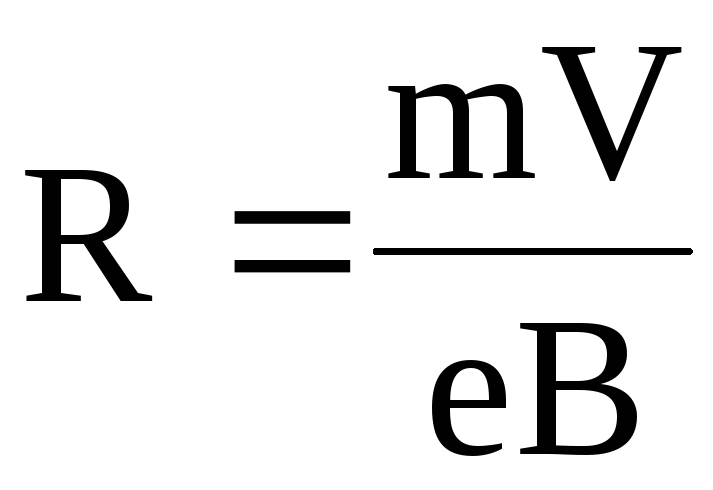 (4)
(4)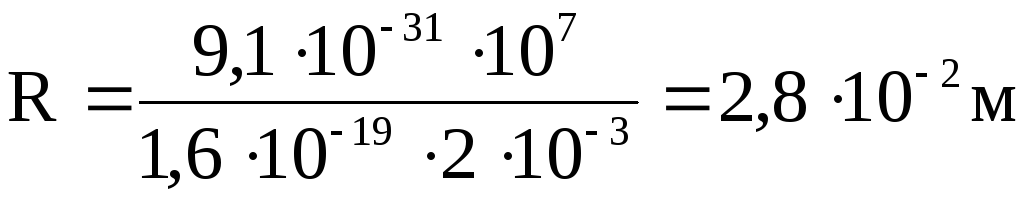
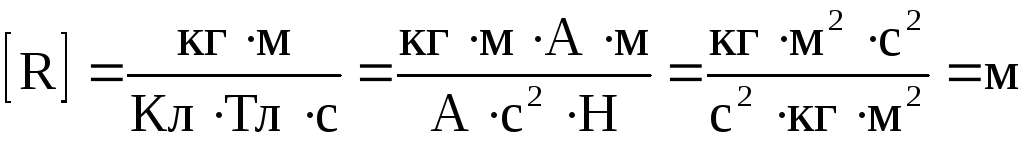
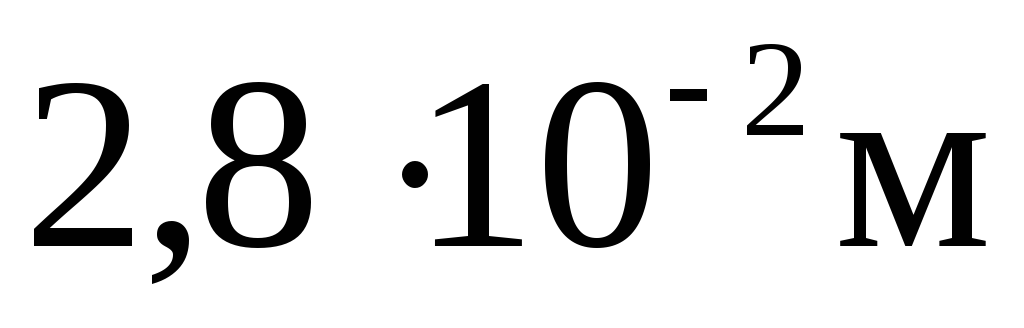
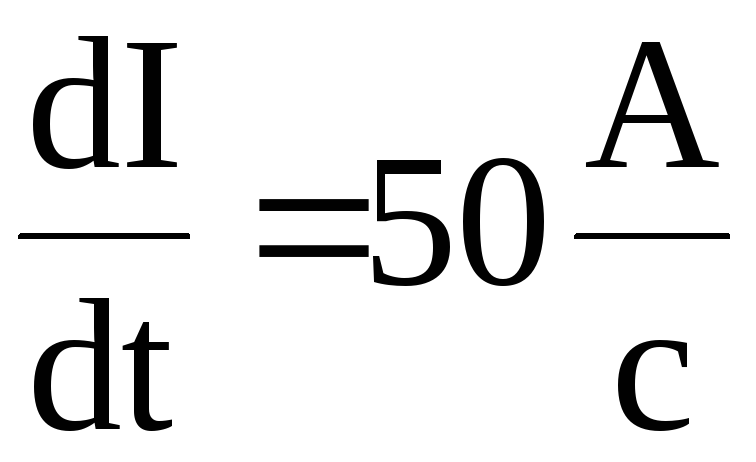
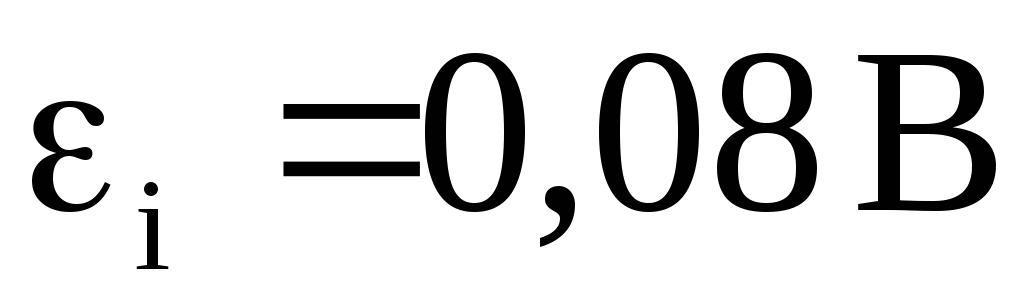
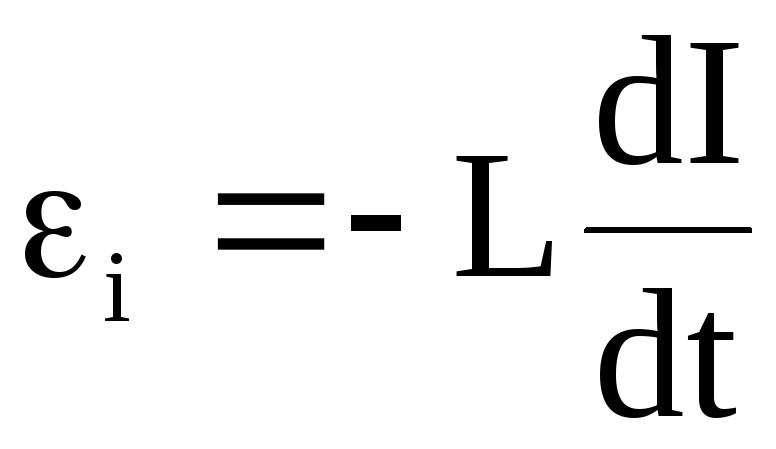 (1)
(1)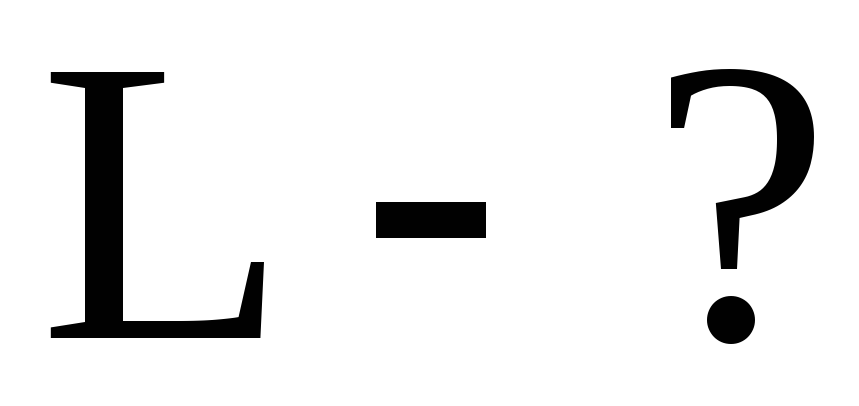
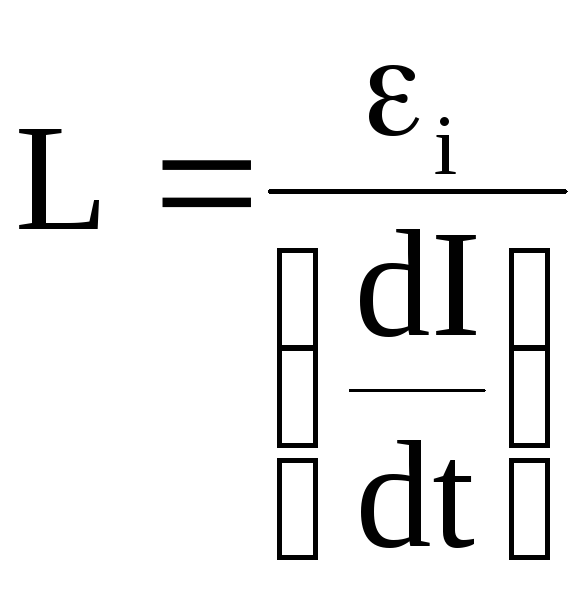 (2)
(2)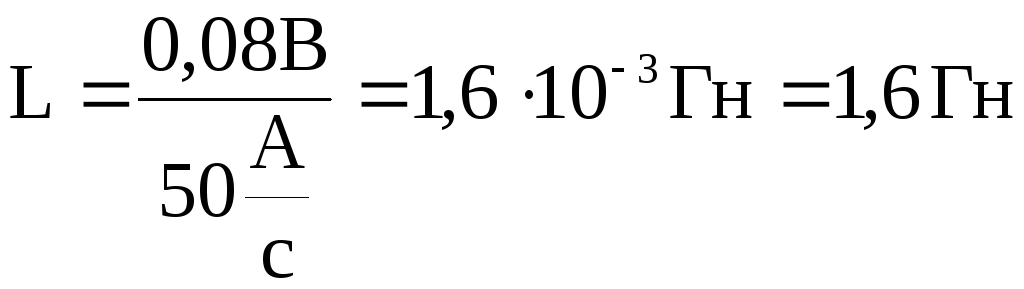
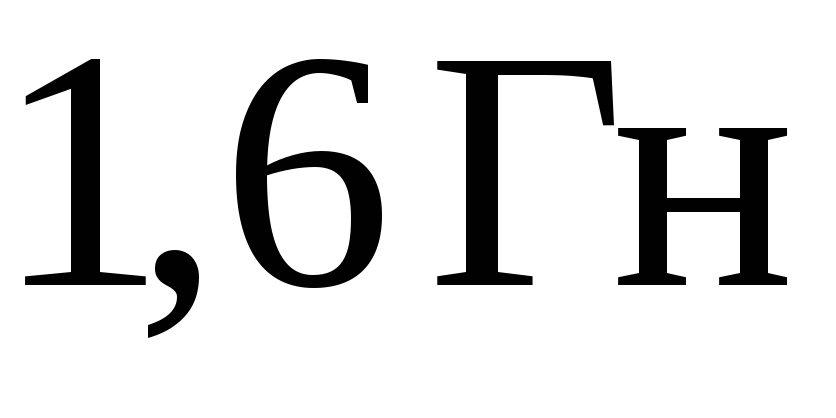
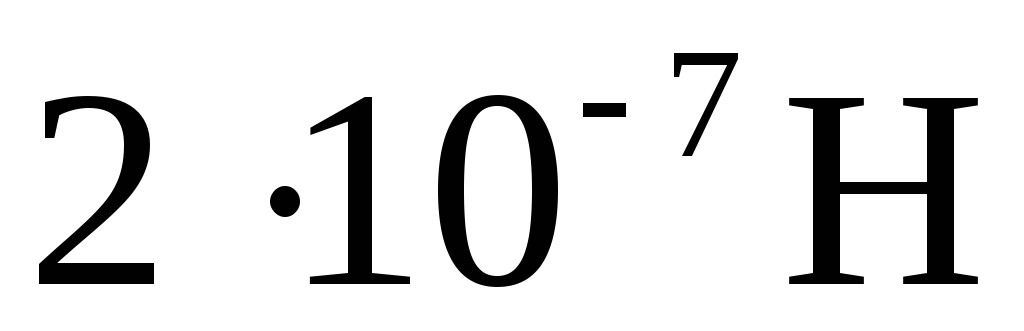 на каждый метр длины.
на каждый метр длины.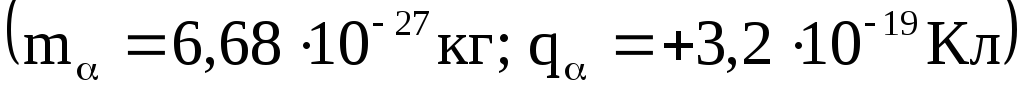 движется
в однородном магнитном поле
напряженностью Н=100 кА/м по окружности
радиусом 10 см. Найти скорость
— частицы.
движется
в однородном магнитном поле
напряженностью Н=100 кА/м по окружности
радиусом 10 см. Найти скорость
— частицы. ,
возникающей в контуре, если магнитный
поток изменится до нуля за время 2 мс.
,
возникающей в контуре, если магнитный
поток изменится до нуля за время 2 мс.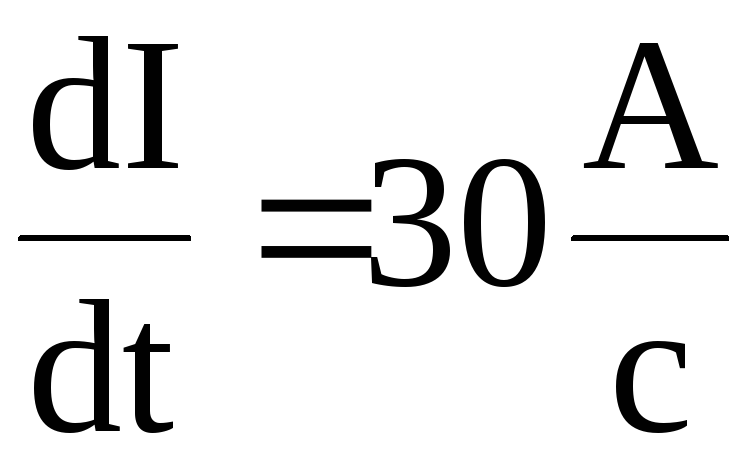 ,
в нем возникает ЭДС самоиндукции
0,09 В. Определить индуктивность контура.
,
в нем возникает ЭДС самоиндукции
0,09 В. Определить индуктивность контура.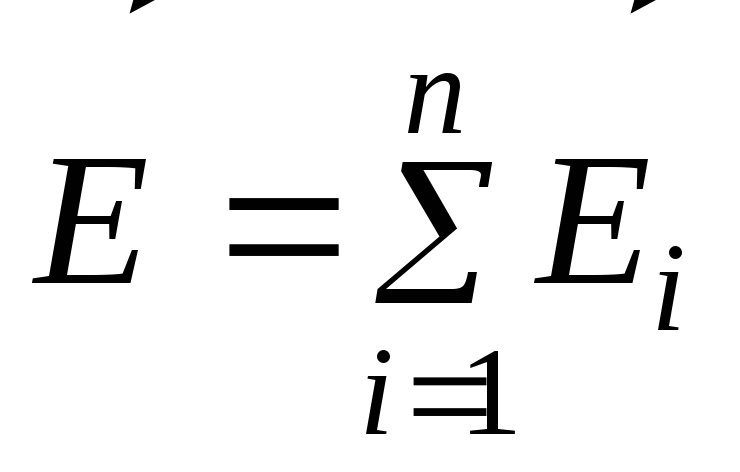 .
.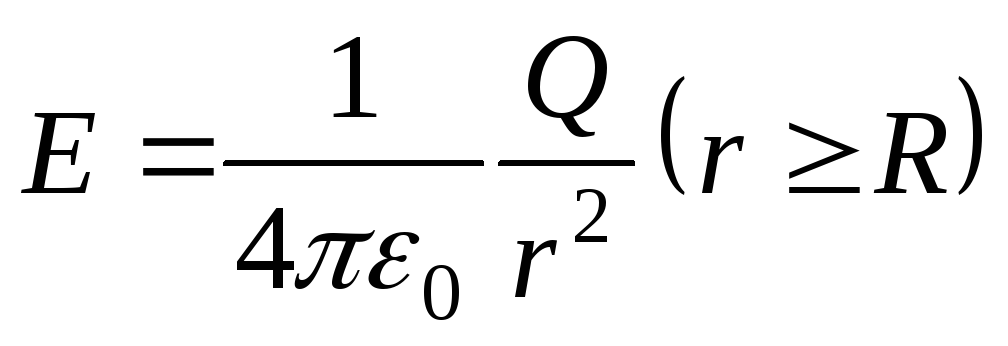 ,
,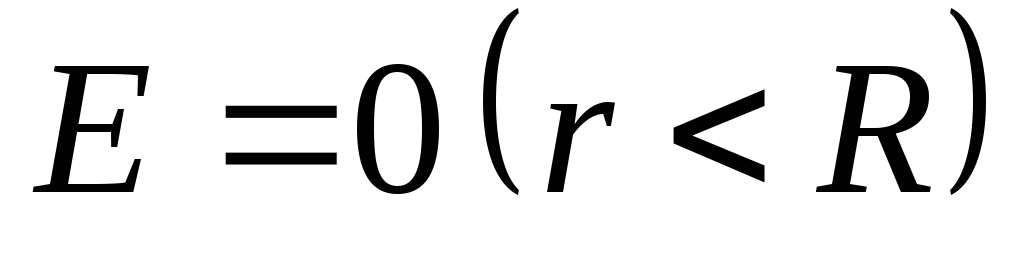 .
.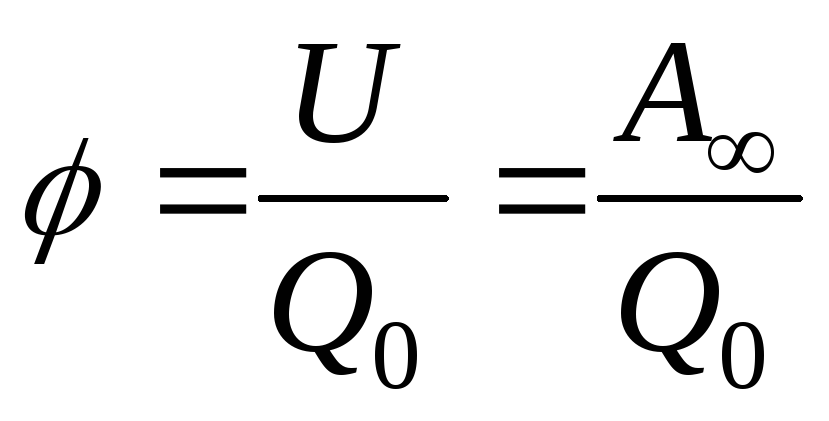 .
. сила
отталкивания со стороны заряда
сила
отталкивания со стороны заряда 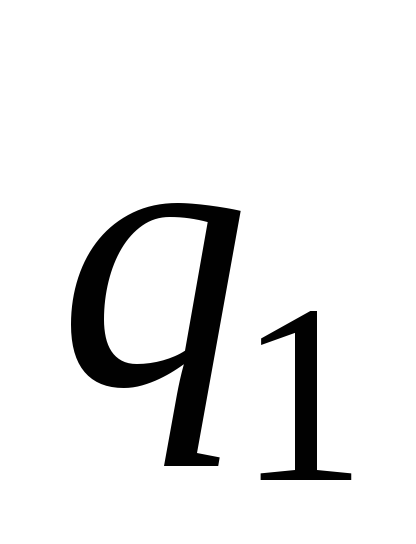 ;
;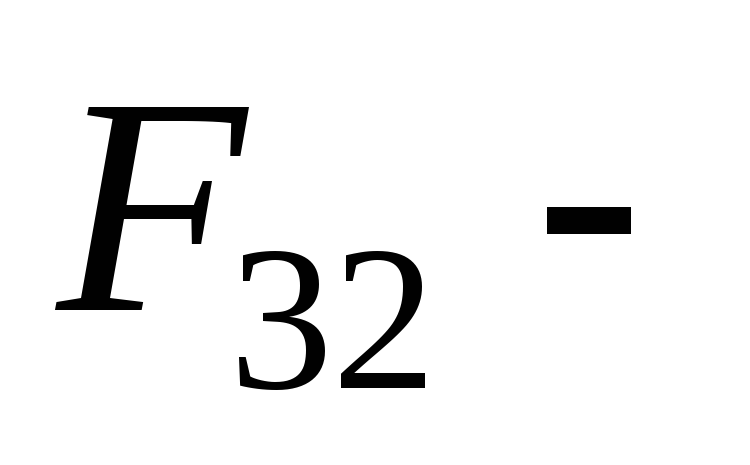 сила
отталкивания со стороны заряда
сила
отталкивания со стороны заряда 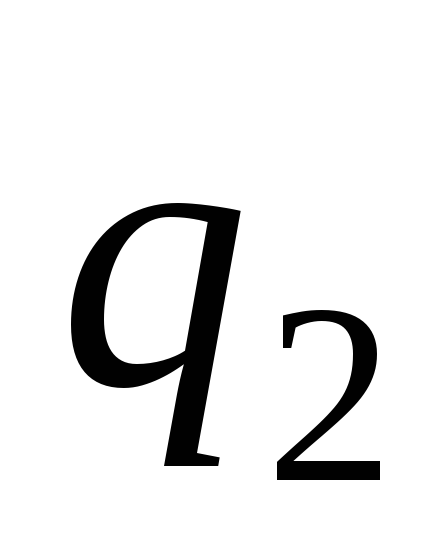 .
.