Электрический ток в металлах | Формулы по физике
Электрический ток в металлах: максимальная скорость электрона
Найти
Известно, что:
v_максeEtm =
Вычислить ‘v_макс’Средняя скорость дрейфа электронов
Найти
Известно, что:
v_средeEtm =
Вычислить ‘v_сред’Сила тока
Найти
Известно, что:
Ien0tSUml =
Вычислить ‘I’Первый закон электролиза фарадея
Известно, что:
mkΔ_q =
Вычислить ‘m’Первый закон электролиза фарадея
Найти
Известно, что:
mkIt =
Вычислить ‘m’Электрохимический эквивалент
Найти
Известно, что:
kmq =
Второй закон электролиза фарадея
Найти
Известно, что:
kMFn =
Вычислить ‘k’Постоянная (число) Фарадея
Найти
Известно, что:
FeN_A =
Вычислить ‘F’Электролиз: масса осаждённого вещества
Найти
Известно, что:
mMItFn =
Вычислить ‘m’Ионизационная работа
Найти
Известно, что:
mvA =
Вычислить ‘m’Кинетическая энергия электрона
Найти
Известно, что:
Диод: сила тока насыщения
Найти
Известно, что:
Ien =
Вычислить ‘I’Основные электрические законы.
Базовые формулы и расчетыСодержание
В предыдущей статье мы познакомились с основными электрическими понятиями, такими как электрический ток, напряжение, сопротивление и мощность. Настал черед основных электрических законов, так сказать, базиса, без знания и понимания которых невозможно изучение и понимание электронных схем и устройств.
Закон Ома
Электрический ток, напряжение, сопротивление и мощность, безусловно, между собой связаны. А взаимосвязь между ними описывается, без сомнения, самым главным электрическим законом – законом Ома. В упрощенном виде этот закон называется: закон Ома для участка цепи. И звучит этот закон следующем образом:
«Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи».
Для практического применения формулу закона Ома можно представить в виде вот такого треугольника, который помимо основного представления формулы, поможет определить и остальные величины.
Работает треугольник следующим образом. Чтобы вычислить одну из величин, достаточно закрыть ее пальцем. Например:
В предыдущей статье мы проводили аналогию между электричеством и водой, и выявили взаимосвязь между напряжением, током и сопротивлением. Также хорошей интерпретацией закона Ома может послужить следующий рисунок, наглядно отображающий сущность закона:
На нем мы видим, что человечек «Вольт» (напряжение) проталкивает человечка «Ампера» (ток) через проводник, который стягивает человечек «Ом» (сопротивление). Вот и получается, что чем сильнее сопротивление сжимает проводник, тем тяжелее току через него проходить («сила тока обратно пропорциональна сопротивлению участка цепи» – или чем больше сопротивление, тем хуже приходится току и тем он меньше). Но напряжение не спит и толкает ток изо всех сил (чем выше напряжение, тем больше ток или – «сила тока в участке цепи прямо пропорциональна напряжению»).
Когда фонарик начинает слабо светить, мы говорим – «разрядилась батарейка».
Что с ней произошло, что значит разрядилась? А значит это, что напряжение батарейки снизилось и оно больше не в состоянии «помогать» току преодолевать сопротивление цепей фонарика и лампочки. Вот и получается, что чем больше напряжение – тем больше ток.
Последовательное подключение – последовательная цепь
При последовательном подключении потребителей, например обычных лампочек, сила тока в каждом потребителе одинаковая, а вот напряжение будет отличаться. На каждом из потребителей напряжение будет падать (снижаться).
А закон Ома в последовательной цепи будет иметь вид:
При последовательном соединении сопротивления потребителей складываются. Формула для расчета общего сопротивления:
Параллельное подключение – параллельная цепь
При параллельном подключении, к каждому потребителю прикладывается одинаковое напряжение, а вот ток через каждый из потребителей, в случае, если их сопротивление отличается – будет отличаться.
Закон Ома для параллельной цепи, состоящей из трех потребителей, будет иметь вид:
При параллельном соединении общее сопротивление цепи всегда будет меньше значения самого маленького отдельного сопротивления.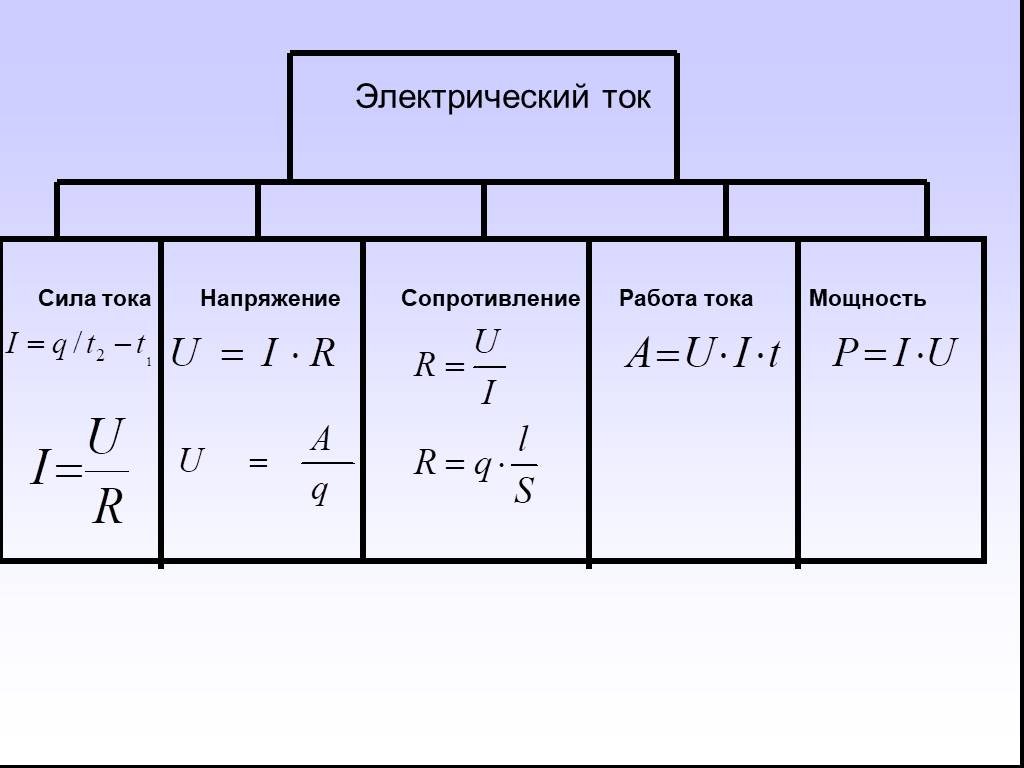
Или еще говорят, что «сопротивление будет меньше наименьшего».
Общее сопротивление цепи, состоящей из двух потребителей, при параллельном соединении:
Общее сопротивление цепи, состоящей из трех потребителей, при параллельном соединении:
Для большего числа потребителей расчет производится исходя из того, что при параллельном соединении проводимость (величина обратная сопротивлению) рассчитывается как сумма проводимостей каждого потребителя.
Электрическая мощность
Мощность – это физическая величина, характеризующая скорость передачи или преобразования электрической энергии. Рассчитывается мощность по следующей формуле:
Таким образом зная, напряжение источника и измерив потребляемый ток, мы можем определить мощность потребляемую электроприбором. И наоборот, зная мощность электроприбора и напряжение сети, можем определить величину потребляемого тока. Такие вычисления порой необходимы. Например, для защиты электроприборов используются предохранители или автоматические выключатели.
Чтобы правильно подобрать средство защиты нужно знать потребляемый ток. Предохранители, применяемые в бытовой технике, как правило подлежат ремонту и для их восстановления достаточно подобрать и заменить проволоку.
Применив закон Ома, можно рассчитать мощность и по другой формуле:
При расчетах надо учитывать, что часть потребляемой электроэнергии расходуется на нагрев и преобразуется в тепло. При работе греются не только электрообогреватели, но и телевизоры, и компьютеры и другая бытовая техника.
И в завершение, в качестве бонуса, вот такая шпаргалка, которая поможет определить любой из основных электрических параметров, по уже известным.
электромагнетизм. Эквивалентные формулы для плотности электрического тока
спросил
Изменено 8 лет, 4 месяца назад
Просмотрено 1к раз
$\begingroup$
Я читаю статью, в которой говорится, что «отношение тока к площади данной поверхности известно как плотность тока» и определяется как 92 А}$.
Это всегда верно по определению.
$J=\sigma E$ — это другое уравнение: оно эквивалентно закону Ома, который вам лучше известен как $V = IR$. Закон Ома не универсален; он работает только для определенных материалов, называемых омическими материалами.
Для омического материала можно показать, что две формулы для $J$ эквивалентны, используя формулу для удельного сопротивления, $R = \rho L/A$, и тот факт, что $\rho = 1/\sigma$, вместе с соотношением $\vec{E} = -\nabla V$.
$\endgroup$
$\begingroup$
Упрощая:
Вы можете рассматривать $J = I/A$ как одно из определений $J$.
Поскольку ток $I$ связан с электрическим полем, то и $J$ должно зависеть от электрического поля. В первом приближении предполагается линейная зависимость между $J$ и $E$. Естественно, это не линейная зависимость, но в некоторых случаях она хорошо работает как аппроксимация (например, твердые и жидкие изотропные материалы).
Поэтому мы говорим:
$$J = \сигма E$$
Константа пропорциональности $\sigma$ линейной зависимости интерпретируется как константа проводимости, поскольку чем больше $\sigma$, тем больше ток $I$, поддерживающий постоянным электрическое поле $E$.
$\endgroup$
0
Зарегистрируйтесь или войдите
Зарегистрироваться через Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Current Electricity Formulas: JEE & NEET Physics
Электрический ток — это скорость потока заряженных частиц, таких как электроны или ионы, через электрический проводник или пространство. Он измеряется в кулонах в секунду, который называется ампер. В этой статье мы увидим некоторые важные текущие формулы электричества, которые также помогут вам в подготовке к конкурсным экзаменам, таким как JEE и NEET. 92RT}{4.2}Калория\)
ЗАКОНЫ КИРХГОФФА Закон тока Кирхгофа (Закон соединения)\(\Sigma I_{in}=\Sigma I_{in}=\Sigma I_{in}s7 Law’s9hoff
Kirchoff 90 (Петлевой закон)\(\Sigma IR+\Sigma EMF=0\)
КОМБИНАЦИЯ СОПРОТИВЛЕНИЙ Сопротивления в серии
{1} R_{3}+….+R_{n}\) (это означает, что \(R_{eq}\) больше любого резистора)) и
\(V=V_{1}+V_{2}+V_{3}+….
+V_{n}\)
\(V_{1}=\frac{R_{1}}{R_{1}+R_{2}+….R_{n}}V;V_{2}=\frac{R_{2}}{R_ {1}+R_{2}+….R_{n}}В\)
\(\frac{1}{R_{eq}}=\frac{1}{R_{1}}+\frac{1}{R_{2}}+\frac{1}{R_{3}}\ )
СЕТЬ УИТСТОУНА: (СЕТЬ С 4 ТЕРМИНАЛАМИ)Когда ток через гальванометр равен нулю (нулевая точка или точка баланса) \(\frac{P}{Q}=\frac{R}{S}\), тогда PS = QR.
ГРУППИРОВАНИЕ ЯЧЕЙ Ячейки в серии
Эквивалент \(EMFE_{eq}=E_{1}+E_{2}+….+E_{n}\) [запишите ЭДС с полярностью]
Эквивалентное внутреннее сопротивление \(r_{eq}=r_{1}+r_{2}+r_{3}+r_{4}….+r_{n}\)
Параллельные ячейки\ (\ frac{1}{r_{eq}}=\frac{1}{r_{1}}+\frac{1}{r_{2}}+\frac{1}{r_{3}}+… .+\frac{1}{r_{n}}\)
АМПЕРМЕТР
Параллельно с гальванометром подключен шунт (малое сопротивление) для преобразования его в амперметр.
Идеальный амперметр имеет нулевое сопротивление.
Амперметр представляется следующим образом –
Если максимальное значение тока, измеряемое амперметром, равно I, то \(I_{g}.R_{g}=(I-I_{g})S\)
\(S=\frac{I_{g}.R_{g}}{I-I_{g}}\) ; \(S=\frac{I_{g}\times R_{g}}{I}\), когда \(I>>I_{g}\)
, где I = максимальный ток, который можно измерить с помощью данного амперметра .
ВОЛЬТМЕТРВысокое сопротивление включено последовательно с гальванометром. Он используется для измерения разности потенциалов на резисторе в цепи.
Для максимальной разности потенциалов \(V=I_{g}.R_{s}+I_{g}R_{g}\)
\(R_{s}=\frac{V}{I_{G}} -R_{G}\) Если \(R_{G}< \(I=\frac{\varepsilon}{r+R}\) \(V_{A}-V_{B}=\frac{\varepsilon}{R+r}. R\) Градиент потенциала \((x)\rightarrow\) Разность потенциалов на единицу длины провода \(x=\frac{V_{A}-V_{B}}{L} =\frac{\ varepsilon }{R+r}. В случае I На рисунке (1) соединяется с (2), тогда длина баланса =\(l_{1}\) \(\varepsilon_{1}=xl_{1}\) ……………….(1) В случае II, На рисунке (3) соединяется с (2), тогда длина баланса = \ (l_{2}\) \(\varepsilon_{2}=xl_{2}\) ……………….(2) \(\ frac{\varepsilon {1}}{\varepsilon {2}}=\frac{l_{1}}{l_{2}}\) Если известно одно из значений \(\varepsilon {1}или \varepsilon {2}\), можно найти другое. Если x известен, то можно найти как \(\varepsilon {1}, так и \varepsilon {2}\). \(V_{A}-V_{C}=xl_{1}\) \(IR_{1}=xl_{1}\) \(I=\frac{xl_{1}} {R_{1}}\) Точно так же мы можем найти и значение \({R_{2}}\). Потенциометр является идеальным вольтметром, потому что он не потребляет ток из цепи в точке баланса. по первому расположению \(\varepsilon ‘=xl_{1}\)……….(1) по второму расположению \(IR=xl_{2}\) \(I=\frac{xl_ {2}}{R}\), а также \(I=\frac{\varepsilon ‘}{r’+R}\) \(\frac{\varepsilon ‘}{r’+R}=\frac{xl_{2}}{R}\Стрелка вправо \frac{xl_{1}}{r’+R}=\frac{xl_ {2}}{R}\) \(r’=\left [\frac{l_{1}-l_{2}}{l_{2}} \right ]R\) (d) Амперметр и вольтметр можно отградуировать потенциометром. Измерительный мост используется для измерения неизвестного сопротивления Если \(AB=lcm,then\) \(BC=(100-l)cm.\) Сопротивление провода между A и B , \(R\propto l\)
\frac{R}{L}\)
Применение потенциометра (a) Найти ЭДС неизвестной ячейки и сравнить ЭДС двух ячеек. 
(e) Амперметр и вольтметр можно калибровать с помощью потенциометра.
ИЗМЕРИТЕЛЬНЫЙ МОСТ
Или \(R =\сигма l\)……….
