Формула нахождения эдс

Электромагнитная индукция. Закон электромагнитной индукции. Правило Ленца Правило Ленца 1.

Поиск данных по Вашему запросу:

Схемы, справочники, даташиты:

Прайс-листы, цены:

Обсуждения, статьи, мануалы:

Дождитесь окончания поиска во всех базах.

По завершению появится ссылка для доступа к найденным материалам.

Содержание:

• Закон Ома для полной (замкнутой) цепи
• Эдс формула и ее расчеты
• Термоэлектричество
• Связь ЭДС и напряжения
• Формула закона Ома
• Переменный ток
• ЭДС при движении проводника в поле

ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Задачи на гальванический элемент. Продукты в ОВР. Ч.5-4.

Закон Ома для полной (замкнутой) цепи

Основные электротехнические формулы. Закон Ома. Электрическая мощность :. Напомним, что любой сигнал, может быть с любой точностью разложен в ряд Фурье, то есть в предположении, что параметры сети частотнонезависимы — данная формулировка применима ко всем гармоникам любого сигнала.

Поиск по сайту TehTab. Техническая информация Раздел. Алфавиты, номиналы, коды Будущим инженерам Инженерные приемы и понятия Математический справочник Материалы — свойства, обозначения Оборудование — стандарты, размеры Перевод единиц измерения Свойства рабочих сред Справочник инженера Таблицы численных значений Технологические понятия и чертежи Физический справочник Справочник Химический справочник.

Дополнительная информация от TehTab. Вы сейчас здесь: Основные электротехнические формулы.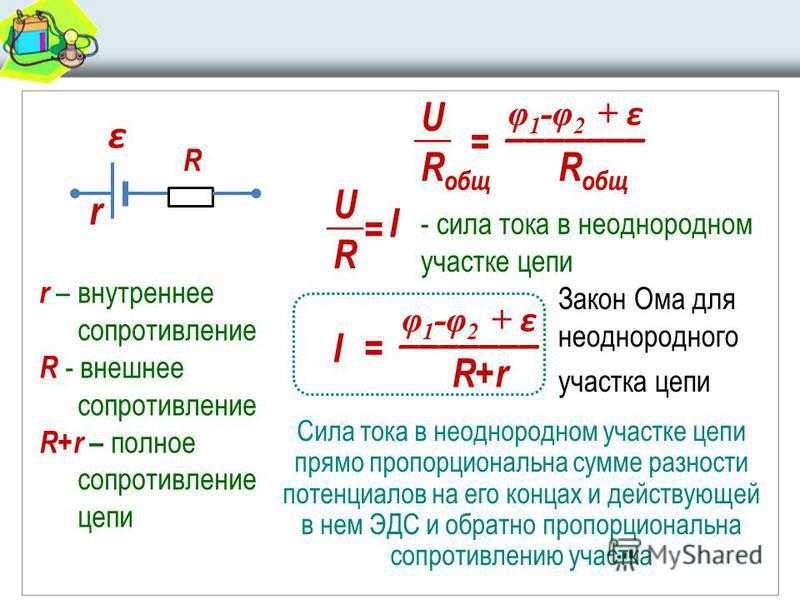 Законы Кирхгофа они же Правила Кирхгофа для тока и напряжения. Коэффициент мощности для трехфазного электродвигателя. Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу.

Навигация по справочнику TehTab. Цепь постоянного тока или, строго говоря, цепь без комплексного сопротивления Применимость формул: пренебрегаем зависимостью сопротивлений от силы тока. Дополнительная информация: Электростатика.

Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.

Эдс формула и ее расчеты

Математические формулы Формулы по физике Поиск. Постоянный ток. Электростатика Постоянный ток Магнитное поле Электромагнитная индукция Механические колебания Механические волны Электромагнитные колебания Переменный ток Электромагнитные волны Фотометрия Геометрическая лучевая оптика Волновая оптика Квантовая оптика Термодинамика Пар, жидкости, твёрдое состояние Теория относительности Атом и ядро атома Кинематика Динамика Статика Законы сохранения механической энергии Давление жидкости и газа Молекулярная кинетика Тепловые явления Электрический ток в металлах. Формулы по физике Постоянный ток Постоянный ток. Электродвижущая сила. I — сила тока q — заряд t — время. I — сила тока e — заряд электрона n — концентрация заряженных частиц v — скорость S — площадь поперечного сечения.

Напряженность электрического поля точечного заряда, – точечный заряд, создающий поле, – радиус-вектор, проведенный из точки нахождения заряда.

Термоэлектричество

В разгар учебного года многим ученым деятелям требуется эдс формула для разных расчетов. Эксперименты, связанные с гальваническим элементом, так же нуждаются в информации об электродвижущей силе. Но для начинающих не так-то просто понять, что же это такое. ЭДС или электродвижущая сила — это параметр характеризующий работу любых сил не электрической природы, работающих в цепях где сила тока как постоянного, так и переменного одинакова по всей длине. В сцепленном токопроводящем контуре ЭДС приравнивается работе данных сил по перемещению единого плюсового положительного заряда вдоль всего контура.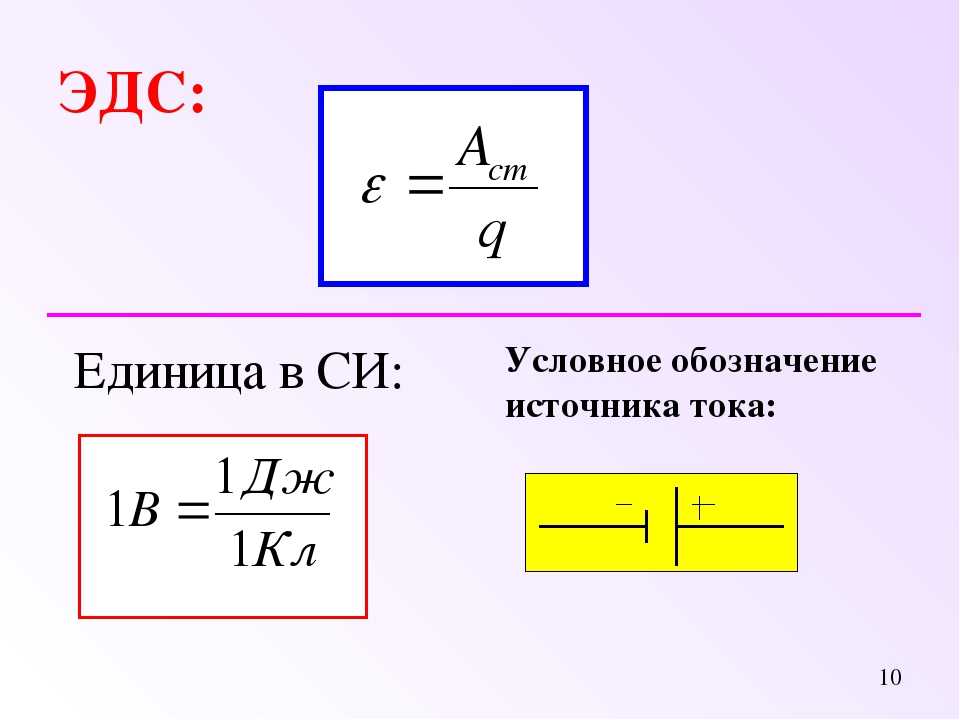 Сторонние силы — это силы которые выполняют разделение зарядов в источнике и в итоге образуют на его полюсах разность потенциалов. Для этой силы единицей измерения является вольт. Только в момент отсутствия тока в батареи, электродвижущая си-а будет равна напряжению на полюсах.

Связь ЭДС и напряжения

Самоиндукция является частным случаем разнообразных проявлений электромагнитной индукции. Рассмотрим контур, подключенный к источнику тока. По контуру протекает электрический ток I. Этот ток создает в окружающем пространстве магнитное поле. В результате контур пронизывается собственным магнитным потоком Ф.

В электротехнике источники питания электрических цепей характеризуются электродвижущей силой ЭДС.

Формула закона Ома

Выведем зависимость ЭДС генератора от параметров машины, скорости вращения якоря и магнитного потока. ЭДС, индуцируемая в каждом витке обмотки, может быть определена по формуле Применительно к машине постоянного тока эта формула и весь последующий вывод значительно упрощается введением понятия средней индукции. Пусть магнитный поток, создаваемый главным полюсом, Ф, тогда при полюсах общий магнитный поток равен. Однако можно с достаточной точностью допустить, что индукция распределена равномерно во всем воздушном зазоре, поэтому для расчетов можно взять ее среднее значение: где d — диаметр сердечника якоря, I — образующая цилиндра якоря длина якоря. Тогда средняя ЭДС одного проводника обмотки при равна где l — длина активной части проводника равна образующей цилиндра якоря ; v — линейная окружная скорость движения проводника. Подставим в формулу 6.

Переменный ток

Некоторые свободные электроны могут покинуть поверхность металла, если их энергия окажется равной или превысит работу выхода. Работа выхода зависит от типа материала. При плотном соединении контакте двух металлических поверхностей электроны из металла с меньшей работой выхода будут переходить в металл с большей работой выхода. При этом возникает контактная разность потенциалов, величина которой зависит от температуры. Термоэлемент состоит из двух таких соединений сваренных или спаянных. Если их температуры одинаковы, то контактные напряжения компенсируются. Если контактные соединения имеют различную температуру, то возникает термо-ЭДС, вызывающая термоток. Его величина зависит от сопротивления цепи, материалов и разности температур.

Данная величина называется электродвижущей силой (ЭДС) источника тока . Согласно формуле (1) источник тока совершает при этом работу.

ЭДС при движении проводника в поле

На нашем сайте собрано более бесплатных онлайн калькуляторов по математике, геометрии и физике. Не можете решить контрольную?! Мы поможем!

Основные электротехнические формулы. Закон Ома. Электрическая мощность :. Напомним, что любой сигнал, может быть с любой точностью разложен в ряд Фурье, то есть в предположении, что параметры сети частотнонезависимы — данная формулировка применима ко всем гармоникам любого сигнала. Поиск по сайту TehTab. Техническая информация Раздел.

Тензор электромагнитного поля Тензор энергии-импульса 4-потенциал 4-ток.

Задача взята из задачника по физике класса, автор А. Правильные ответы: 20 А, в, В, 2 кВт. Напишите ход решения, плиззз. Грабцевич Разделите напряжение на зажимах на сумму сопротивлений ламп 50 ламп включены параллельно и проводов, получите ток в цепи. ЭДС генератора найдете как произведение тока в цепи на полное сопротивление.

До сих пор при изучении электрического тока мы рассматривали направленное движение свободных зарядов во внешней цепи , то есть в проводниках, подсоединённых к клеммам источника тока. Как мы знаем, положительный заряд :. Теперь нашему положительному заряду нужно замкнуть свою траекторию и вернуться на положительную клемму. Для этого ему требуется преодолеть заключительный отрезок пути — внутри источника тока от отрицательной клеммы к положительной.

Внутреннее сопротивление источника постоянного тока формула

Приборы и принадлежности, используемые в работе:

1. Источник электрической энергии.
2. Амперметр.
3. Вольтметр.
4. Реостат.
5. Ключ.
6. Соединительные провода.

Цель работы:

1. Научится собирать, заданную электрическую схему.

2. Используя закон ОМА для всей цепи, определить опытным путём величину внутреннего сопротивления и ЭДС источника электрической цепи.

Формула закона Ома для всей цепи имеет вид:

, (1)

Е – ЭДС источника электрической энергии

R – сопротивление внешней части цепи

r – внутреннее сопротивление источника

I – сила тока в цепи.

Перепишем формулу (I) в виде:

(2)

Величина является напряжением на внешней части цепи. Тогда формула (2) примет вид:

(3)

Если в полной цепи менять внешнее сопротивление, то будут меняться величины I и U (ток в цепи и напряжение на внешней её части). Пусть при силе тока в цепи , напряжение на внешней цепи равно , а при силе тока равно . Тогда дважды запишем формулу (3).

(4)

Левые части у уравнений одинаковые, поэтому приравняем правые части:

и получим формулу для нахождения г внутреннего сопротивления источника:

(5)

Подставив (5) в одно из уравнений системы (4), получим формулу для нахождения Е ЭДС источника:

;

(6)

1. Определить цену деления амперметра и вольтметра.

2. Собрать следующую схему:

При сборке схемы соблюдать следующие требования:

– Собирать схему только при разомкнутом ключе К.

– Приступать к включению схемы и измерениям только после того, как преподаватель или лаборант проверят, правильно ли собрана Ваша схема.

– При замыкании ключа особое внимание обратить на показания амперметра – он не должен зашкаливать.

3. Изменяя величину внешнего сопротивления реостатом, получить 7 различных значений силы тока и напряжения во внешней цепи.

4. По формуле (5) вычислить 7 различных значений внутреннего сопротивления источника.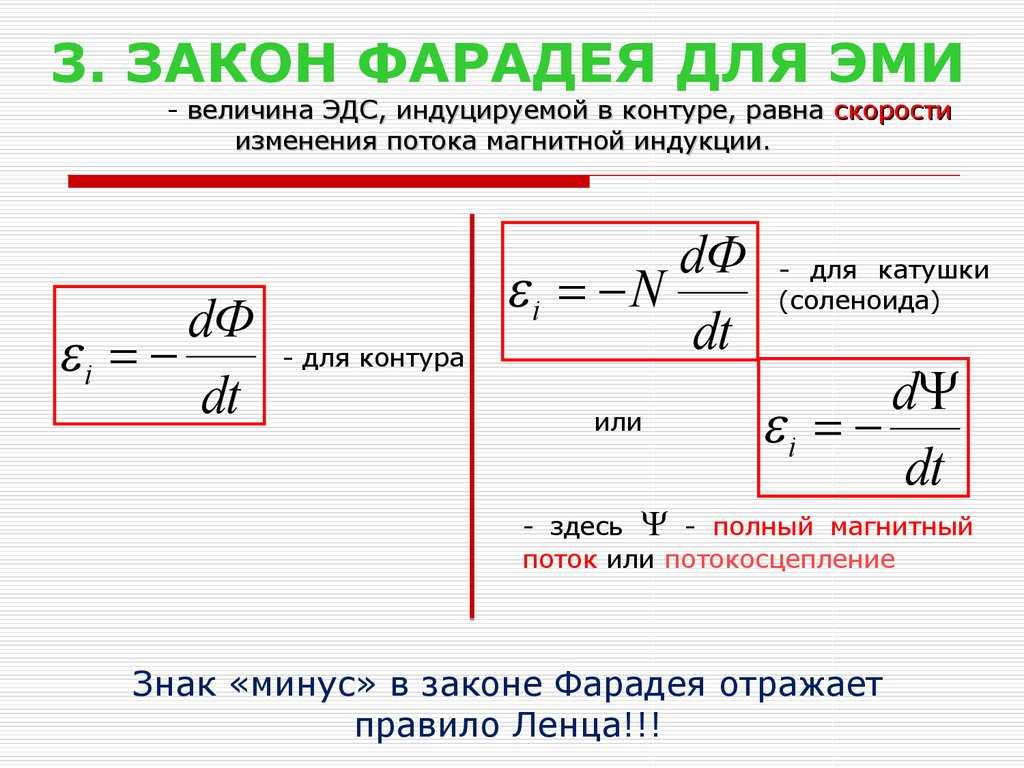

5. По формуле (6) вычислить 7 различных значений ЭДС источника электрической энергии.

6. Результаты измерений I и U, а также вычислений r и Е занести в таблицу.

В таблице n– число делений, на которое отклонилась стрелка амперметра или вольтметра при очередном измерении.

В следующую колонку после n записывается сила тока или напряжение в цепи, которые вычисляются по формуле:

(цена деления);

Таблица результатов измерений и вычислений

Цена одного деления амперметра = .

Цена одного деления вольтметра =.

№

Сила тока

Напряжение

Внутренние сопротивление

ЭДС источника

Дел

I

Дел

U

r

sr

E

sЕ

n

А

n

B

Ом

Ом

Ом

Ом

%

В

В

В

В

%

7. Вычислить погрешности с которыми определены внутреннее сопротивление и ЭДС источника электрической энергии, по формулам:[13]

; s_r = D r_ср/ r_ср × 100%

;

8. Значение погрешностей занести в таблицу и по результатам, полученным в лабораторной работе сделать вывод[14].

КОНТРОЛЬНЫЕ ВОПРОСЫ ПЕРВОГО УРОВНЯ.

1. Закон Ома для всей цепи (формула и формулировка).

2.Закон Ома при параллельном, последовательном и смешанном соединении одинаковых источников электрической энергии (формулы, схемы).

3. Определение цены деления многопредельного прибора.

КОНТРОЛЬНЫЕ ВОПРОСЫ ВТОРОГО И ТРЕТЬЕГО УРОВНЯ.

4.Закон Ома для участка цепи с ЭДС (3 случая и общий закон) и для всей цепи при нескольких ЭДС.

5.Что называется ЭДС источника электрической энергии? Единицы ЭДС.

6. Понятие внутреннего сопротивления источника.

7.Измерительные приборы вольтметр и амперметр[15].
Лабораторная работа № 8.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Как то на паре, один преподаватель сказал, когда лекция заканчивалась – это был конец пары: «Что-то тут концом пахнет». 8424 – | 8039 – или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Величина, характеризующая количество энергетических потерь, возникающих при протекании тока через его источник, определяется как внутреннее сопротивление источника тока. Как и обычное сопротивление, имеет единицу измерения, равную 1 Ом. Ток, двигаясь через источник, теряет часть своей энергии, которая переходит в тепло, точно так же, как на любом нагрузочном сопротивлении. Это значит, что величина напряжения на выводах источника зависит от величины тока, а не от ЭДС.

Если рассмотреть замкнутую электрическую цепь, в которую включён источник тока (батарейка, аккумулятор или генератор), и нагрузку R, то ток течёт и внутри источника. Внутреннее сопротивление источника, обозначаемое буквой r, ему препятствует.

У генератора r – это внутреннее сопротивление обмоток статора, у аккумулятора – сопротивление электролита.

Измерение сопротивления петли фаза-нуль

Петля «фаза – нуль» – это электрическая цепь переменного тока, которая может возникнуть в результате короткого замыкания между проводами: «фаза» и «ноль» или «фаза» и «фаза». Разрушение изоляции, механические повреждения или случайное соединение оголённых участков кабеля между собой могут стать этому причиной. В установках с глухо заземлённой нейтралью нулевой проводник физически связан с нейтралью трансформатора, она подключена к контуру заземления. При замыкании на корпус или соединении фаз между собой образуется цепь (петля).

Главная задача проводимых измерений – узнавать, каким будет величина тока через петлю при КЗ.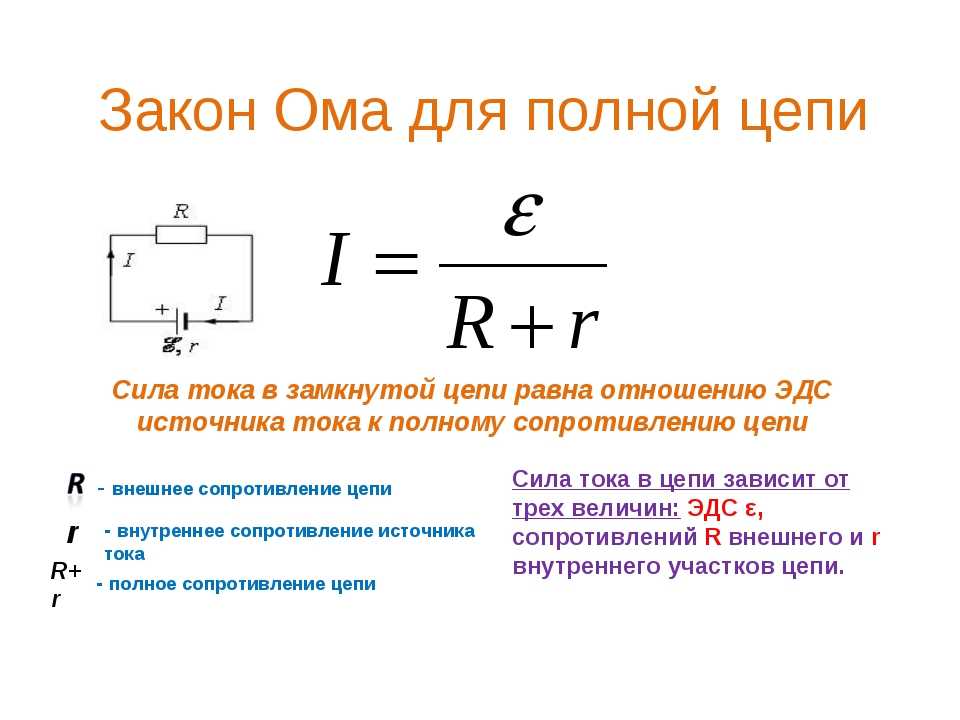 Это обязательно для расчёта и подбора защитного оборудования. Хорошим результатом будет маленькое сопротивление петли, тогда ток Iк.з. будет наибольшим. От его величины зависит, как быстро сработает защитный автоматический выключатель.

Чем меньше времени будет затрачено на отключение повреждённой или закороченной цепи, тем больше шансов предотвратить пожар от возгорания кабельной сети. При попадании человека под удар электрического тока в результате прикосновения или короткого замыкания автоматическое снятие напряжения спасёт ему жизнь.

На предприятиях ежегодно проводится комплекс измерений защитного заземления и сопротивления петли фаза – ноль. При неудовлетворительных результатах проводится ряд мероприятий:

• заменяются участки провода, не отвечающие требованиям по диаметру сечения;
• перекручиваются болтовые соединения с обязательной установкой врезных шайб;
• вскрываются контуры защитных заземлений и осматриваются на предмет целостности сварных соединений и состояния элементов заземления;
• при необходимости в контур защитного заземления добавляются дополнительные элементы;
• исключается последовательное подключение корпусов устройств к общей шине заземления.

После выполнения комплекса мероприятий измерения проводятся повторно.

Нахождение внутреннего сопротивления

Его можно находить двумя путями: рассчитать или измерить. Первым путём идут при работе с электрическими схемами, второй – выбирают, занимаясь с реальными устройствами.

Простой расчёт производится с использованием формулы Закона Ома для участка полной цепи:

Чтобы узнать силу тока, нужно напряжение ЭДС делить на сумму сопротивлений.

Выразив отсюда r, получают формулу для его вычисления:

где:

• r – внутреннее сопротивление источника;
• ε – ЭДС источника;
• I – сила тока в полной цепи;
• R – сопротивление в полной цепи.

Комплекс измерений этого параметра у настоящего устройства не подразумевает непосредственных замеров. Тестируются напряжения на нагрузочном сопротивлении в двух режимах тока: холостом и КЗ.

Так как не любой источник может выдержать даже кратковременный режим замыкания, берётся метод измерения без вычислений.

В схему включается внешнее сопротивление нагрузки в виде подстроечного резистора Rн. Выставляется такое значение, при котором падение напряжения на резисторе равнялось бы 1/2 U холостого хода. Тогда измеренное омметром Rн будет соответствовать внутреннему сопротивлению источника.

Малое внутреннее сопротивление

Малой величины внутреннего сопротивления добиваются применением обратной связи в схемах, куда включён двухполюсник. В стабилизаторах напряжения r достигает значений менее 9*10-4 Ом. Автомобильная АКБ 6СТ-60 обладает сопротивлением около 0,01 Ом. Если произвести измерения петли фаза-ноль бытовой сети, то норма значения лежит в пределах 0,05-1 Ом.

Реактивное внутреннее сопротивление

Кроме гальванических и электролитических двухполюсников, существуют источники питания, схемы которых включают в себя реактивные элементы. При определении их внутреннего сопротивления используют метод комплексных амплитуд. Он подразумевает использовать при расчётах комплексные сопротивления элементов, включённых в схему. Величины токов и напряжений заменяются значениями их комплексных амплитуд. Сам алгоритм вычисления такой же, как при расчёте активного сопротивления.

Процесс измерений r-реактивного немного отличается от измерения активной составляющей сопротивления. Методы зависят от того, какие параметры этой комплексной функции нужно узнать: отдельные составляющие или комплексное число.

На эти параметры влияет частота, поэтому, чтобы при тестировании добиться информации о внутреннем реактивном значении r, нужно убрать частотную зависимость. Это достигается комплексом замеров на всём диапазоне частот, генерируемых таким двухполюсником.

Большое внутреннее сопротивление

Пьезоэлектрические датчики, конденсаторные микрофоны и другие источники импульсов обладают повышенным внутренним импедансом. Чтобы эффективно использовать такие устройства, нужно правильно согласовать схему считывания сигнала. При неудачном согласовании неизбежны потери.

Важно! Удачное согласование по напряжению получается при использовании для снятия сигнала устройства, с большим входным сопротивлением, чем у источника сигнала. В случае высокоомного источника для считывания сигнала применяется буферный усилитель.

Внутреннее сопротивление и импеданс

Импеданс – полное (комплексное) внутреннее сопротивление эквивалентного двухполюсника переменному току. Обозначается буквой Z и так же измеряется в Омах.

Двухполюсник и его эквивалентная схема

Двухполюсник представляет собой электрическую цепь, содержащую две точки присоединения к другим цепям. Бывает два вида электрических цепей:

• цепи, содержащие источник тока или напряжения;
• двухполюсники, не являющиеся источниками.

Первые характеризуются электрическими параметрами: силой тока, напряжением и импедансом. Для расчёта параметров таких двухполюсников предварительно производят замену реальных элементов цепи на идеальные элементы. Комбинация, которая получается в результате подобной замены, называется эквивалентной схемой.

Внимание! При работе со сложными электрическими схемами с учётом того, что устройство работает на одной частоте, допустимо преобразовывать последовательные и параллельные ветви до получения простой схемы, доступной для расчёта параметров.

Второй вид двухполюсников можно охарактеризовать только величиной внутреннего сопротивления.

Влияние внутреннего сопротивления на свойства двухполюсника

Чем оно выше, тем меньшую мощность выдаёт источник при подключении нагрузки. Определить мощность в нагрузке можно по формуле:

где:

• E – напряжение ЭДС;
• R – сопротивление нагрузки;
• r – активное внутреннее сопротивление двухполюсника.

Формула применима к двухполюсникам, не отдающим энергию.

К сведению. Когда величина внутреннего сопротивления двухполюсника приближается по своему значению к сопротивлению нагрузки, передача мощности достигает максимума.

Разрядная емкость источника

Величина, зависящая от силы тока разряда, называется разрядной ёмкостью источника. Это электрический заряд, который отдаёт источник в процессе эксплуатации в зависимости от тока нагрузки. Эту величину можно считать постоянной условно. Так, стартерный аккумулятор, имеющий разрядную ёмкость С = 55 А*ч, при токе разряда 5,5 А проработает 10 часов. При запусках холодного или имеющего неисправность автомобиля аккумулятор можно разрядить за несколько минут.

Для того чтобы найти остаточную разрядную ёмкость, производят циклы «заряд – разряд». Они выполняются при помощи нагрузочных сопротивлений. Разряд на нагрузочное сопротивление производят до минимально допустимых значений плотности электролита. При этом замеряется время работы под нагрузкой. Это актуально при сезонном обслуживании аккумуляторов для выявления процессов саморазряда.

Внутреннее сопротивление источников тока – важная величина. Методы, применяемые для её снижения, являются прямыми путями увеличения отдаваемой мощности источника, значит, повышения производительности двухполюсников. Правильное измерение и вычисление импеданса эквивалентных схем позволяют приблизить двухполюсник к идеальному источнику.

Видео

Величина, характеризующая количество энергетических потерь, возникающих при протекании тока через его источник, определяется как внутреннее сопротивление источника тока. Как и обычное сопротивление, имеет единицу измерения, равную 1 Ом. Ток, двигаясь через источник, теряет часть своей энергии, которая переходит в тепло, точно так же, как на любом нагрузочном сопротивлении. Это значит, что величина напряжения на выводах источника зависит от величины тока, а не от ЭДС.

Если рассмотреть замкнутую электрическую цепь, в которую включён источник тока (батарейка, аккумулятор или генератор), и нагрузку R, то ток течёт и внутри источника. Внутреннее сопротивление источника, обозначаемое буквой r, ему препятствует.

У генератора r – это внутреннее сопротивление обмоток статора, у аккумулятора – сопротивление электролита.

Измерение сопротивления петли фаза-нуль

Петля «фаза – нуль» – это электрическая цепь переменного тока, которая может возникнуть в результате короткого замыкания между проводами: «фаза» и «ноль» или «фаза» и «фаза». Разрушение изоляции, механические повреждения или случайное соединение оголённых участков кабеля между собой могут стать этому причиной. В установках с глухо заземлённой нейтралью нулевой проводник физически связан с нейтралью трансформатора, она подключена к контуру заземления. При замыкании на корпус или соединении фаз между собой образуется цепь (петля).

Главная задача проводимых измерений – узнавать, каким будет величина тока через петлю при КЗ. Это обязательно для расчёта и подбора защитного оборудования. Хорошим результатом будет маленькое сопротивление петли, тогда ток Iк.з. будет наибольшим. От его величины зависит, как быстро сработает защитный автоматический выключатель.

Чем меньше времени будет затрачено на отключение повреждённой или закороченной цепи, тем больше шансов предотвратить пожар от возгорания кабельной сети. При попадании человека под удар электрического тока в результате прикосновения или короткого замыкания автоматическое снятие напряжения спасёт ему жизнь.

На предприятиях ежегодно проводится комплекс измерений защитного заземления и сопротивления петли фаза – ноль. При неудовлетворительных результатах проводится ряд мероприятий:

• заменяются участки провода, не отвечающие требованиям по диаметру сечения;
• перекручиваются болтовые соединения с обязательной установкой врезных шайб;
• вскрываются контуры защитных заземлений и осматриваются на предмет целостности сварных соединений и состояния элементов заземления;
• при необходимости в контур защитного заземления добавляются дополнительные элементы;
• исключается последовательное подключение корпусов устройств к общей шине заземления.

После выполнения комплекса мероприятий измерения проводятся повторно.

Нахождение внутреннего сопротивления

Его можно находить двумя путями: рассчитать или измерить. Первым путём идут при работе с электрическими схемами, второй – выбирают, занимаясь с реальными устройствами.

Простой расчёт производится с использованием формулы Закона Ома для участка полной цепи:

Чтобы узнать силу тока, нужно напряжение ЭДС делить на сумму сопротивлений.

Выразив отсюда r, получают формулу для его вычисления:

где:

• r – внутреннее сопротивление источника;
• ε – ЭДС источника;
• I – сила тока в полной цепи;
• R – сопротивление в полной цепи.

Комплекс измерений этого параметра у настоящего устройства не подразумевает непосредственных замеров. Тестируются напряжения на нагрузочном сопротивлении в двух режимах тока: холостом и КЗ.

Так как не любой источник может выдержать даже кратковременный режим замыкания, берётся метод измерения без вычислений.

В схему включается внешнее сопротивление нагрузки в виде подстроечного резистора Rн. Выставляется такое значение, при котором падение напряжения на резисторе равнялось бы 1/2 U холостого хода. Тогда измеренное омметром Rн будет соответствовать внутреннему сопротивлению источника.

Малое внутреннее сопротивление

Малой величины внутреннего сопротивления добиваются применением обратной связи в схемах, куда включён двухполюсник. В стабилизаторах напряжения r достигает значений менее 9*10-4 Ом. Автомобильная АКБ 6СТ-60 обладает сопротивлением около 0,01 Ом. Если произвести измерения петли фаза-ноль бытовой сети, то норма значения лежит в пределах 0,05-1 Ом.

Реактивное внутреннее сопротивление

Кроме гальванических и электролитических двухполюсников, существуют источники питания, схемы которых включают в себя реактивные элементы. При определении их внутреннего сопротивления используют метод комплексных амплитуд. Он подразумевает использовать при расчётах комплексные сопротивления элементов, включённых в схему. Величины токов и напряжений заменяются значениями их комплексных амплитуд. Сам алгоритм вычисления такой же, как при расчёте активного сопротивления.

Процесс измерений r-реактивного немного отличается от измерения активной составляющей сопротивления. Методы зависят от того, какие параметры этой комплексной функции нужно узнать: отдельные составляющие или комплексное число.

На эти параметры влияет частота, поэтому, чтобы при тестировании добиться информации о внутреннем реактивном значении r, нужно убрать частотную зависимость. Это достигается комплексом замеров на всём диапазоне частот, генерируемых таким двухполюсником.

Большое внутреннее сопротивление

Пьезоэлектрические датчики, конденсаторные микрофоны и другие источники импульсов обладают повышенным внутренним импедансом. Чтобы эффективно использовать такие устройства, нужно правильно согласовать схему считывания сигнала. При неудачном согласовании неизбежны потери.

Важно! Удачное согласование по напряжению получается при использовании для снятия сигнала устройства, с большим входным сопротивлением, чем у источника сигнала. В случае высокоомного источника для считывания сигнала применяется буферный усилитель.

Внутреннее сопротивление и импеданс

Импеданс – полное (комплексное) внутреннее сопротивление эквивалентного двухполюсника переменному току. Обозначается буквой Z и так же измеряется в Омах.

Двухполюсник и его эквивалентная схема

Двухполюсник представляет собой электрическую цепь, содержащую две точки присоединения к другим цепям. Бывает два вида электрических цепей:

• цепи, содержащие источник тока или напряжения;
• двухполюсники, не являющиеся источниками.

Первые характеризуются электрическими параметрами: силой тока, напряжением и импедансом. Для расчёта параметров таких двухполюсников предварительно производят замену реальных элементов цепи на идеальные элементы. Комбинация, которая получается в результате подобной замены, называется эквивалентной схемой.

Внимание! При работе со сложными электрическими схемами с учётом того, что устройство работает на одной частоте, допустимо преобразовывать последовательные и параллельные ветви до получения простой схемы, доступной для расчёта параметров.

Второй вид двухполюсников можно охарактеризовать только величиной внутреннего сопротивления.

Влияние внутреннего сопротивления на свойства двухполюсника

Чем оно выше, тем меньшую мощность выдаёт источник при подключении нагрузки. Определить мощность в нагрузке можно по формуле:

где:

• E – напряжение ЭДС;
• R – сопротивление нагрузки;
• r – активное внутреннее сопротивление двухполюсника.

Формула применима к двухполюсникам, не отдающим энергию.

К сведению. Когда величина внутреннего сопротивления двухполюсника приближается по своему значению к сопротивлению нагрузки, передача мощности достигает максимума.

Разрядная емкость источника

Величина, зависящая от силы тока разряда, называется разрядной ёмкостью источника. Это электрический заряд, который отдаёт источник в процессе эксплуатации в зависимости от тока нагрузки. Эту величину можно считать постоянной условно. Так, стартерный аккумулятор, имеющий разрядную ёмкость С = 55 А*ч, при токе разряда 5,5 А проработает 10 часов. При запусках холодного или имеющего неисправность автомобиля аккумулятор можно разрядить за несколько минут.

Для того чтобы найти остаточную разрядную ёмкость, производят циклы «заряд – разряд». Они выполняются при помощи нагрузочных сопротивлений. Разряд на нагрузочное сопротивление производят до минимально допустимых значений плотности электролита. При этом замеряется время работы под нагрузкой. Это актуально при сезонном обслуживании аккумуляторов для выявления процессов саморазряда.

Внутреннее сопротивление источников тока – важная величина. Методы, применяемые для её снижения, являются прямыми путями увеличения отдаваемой мощности источника, значит, повышения производительности двухполюсников. Правильное измерение и вычисление импеданса эквивалентных схем позволяют приблизить двухполюсник к идеальному источнику.

Видео

Лабораторная работа № 7. Определение внутреннего сопротивления и эдс источника электрического тока.

Приборы и принадлежности, используемые в работе:

1. Источник электрической энергии.

2. Амперметр.

3. Вольтметр.

4. Реостат.

5. Ключ.

6. Соединительные провода.

Цель работы:

1. Научится собирать, заданную электрическую схему.

2. Используя закон ОМА для всей цепи, определить опытным путём величину внутреннего сопротивления и ЭДС источника электрической цепи.

1.Теоретическое введение.

Формула закона Ома для всей цепи имеет вид:

, (1)

где:

Е — ЭДС источника электрической энергии

R — сопротивление внешней части цепи

r — внутреннее сопротивление источника

I — сила тока в цепи.

Перепишем формулу (I) в виде:

(2)

Величина является напряжением на внешней части цепи. Тогда формула (2) примет вид:

(3)

Если в полной цепи менять внешнее сопротивление, то будут меняться величины I и U (ток в цепи и напряжение на внешней её части). Пусть при силе тока в цепи , напряжение на внешней цепи равно , а при силе тока равно . Тогда дважды запишем формулу (3).

(4)

Левые части у уравнений одинаковые, поэтому приравняем правые части:

откуда:

и получим формулу для нахождения г внутреннего сопротивления источника:

(5)

Подставив (5) в одно из уравнений системы (4), получим формулу для нахождения Е ЭДС источника:

;

(6)

2.

Ход работы.

1. Определить цену деления амперметра и вольтметра.

2. Собрать следующую схему:

При сборке схемы соблюдать следующие требования:

— Собирать схему только при разомкнутом ключе К.

— Приступать к включению схемы и измерениям только после того, как преподаватель или лаборант проверят, правильно ли собрана Ваша схема.

— При замыкании ключа особое внимание обратить на показания амперметра — он не должен зашкаливать.

3. Изменяя величину внешнего сопротивления реостатом, получить 7 различных значений силы тока и напряжения во внешней цепи.

4. По формуле (5) вычислить 7 различных значений внутреннего сопротивления источника.

5. По формуле (6) вычислить 7 различных значений ЭДС источника электрической энергии.

6.  Результаты измерений I и U, а также вычислений r и Е занести в таблицу.

В таблице n— число делений, на которое отклонилась стрелка амперметра или вольтметра при очередном измерении.

В следующую колонку после n записывается сила тока или напряжение в цепи, которые вычисляются по формуле:

(цена деления);

U = n_V  (цена деления).

Таблица результатов измерений и вычислений

Цена одного деления амперметра = …

Цена одного деления вольтметра =…

№

Сила тока

Напряжение

Внутренние сопротивление

ЭДС источника

Дел

I

Дел

U

r

r

E

Е

n

А

n

B

Ом

Ом

Ом

Ом

%

В

В

В

В

%

1

2

3

4

5

6

7

7. Вычислить погрешности с которыми определены внутреннее сопротивление и ЭДС источника электрической энергии, по формулам:¹³

; _r =  r_ср/ r_ср  100%

;

8. Значение погрешностей занести в таблицу и по результатам, полученным в лабораторной работе сделать вывод¹⁴.

КОНТРОЛЬНЫЕ ВОПРОСЫ ПЕРВОГО УРОВНЯ.

1. Закон Ома для всей цепи (формула и формулировка).

2.Закон Ома при параллельном, последовательном и смешанном соединении одинаковых источников электрической энергии (формулы, схемы).

3. Определение цены деления многопредельного прибора.

КОНТРОЛЬНЫЕ ВОПРОСЫ ВТОРОГО И ТРЕТЬЕГО УРОВНЯ.

4.Закон Ома для участка цепи с ЭДС (3 случая и общий закон) и для всей цепи при нескольких ЭДС.

5.Что называется ЭДС источника электрической энергии? Единицы ЭДС.

6. Понятие внутреннего сопротивления источника.

Закон Фарадея

Закон Фарадея

Давайте сначала внимательно рассмотрим уравнение 2 уравнений Максвелла. это называется законом индукции Фарадея .

∫ _A B ·d A = Φ _B  является потоком B через площадь, ограниченную кривой Γ.

∂/∂t∫ _A B ·d A = ∂Φ _B /∂t частная производная этого потока по времени.
Взятие частной производной означает взятие производной потока по времени, сохраняя при этом площадь фиксированной.

∮ _Γ E ∙d r – работа, совершаемая на единицу заряда при перемещении пробного заряда один раз вокруг кривая Г.

Закон Фарадея гласит, что абсолютная величина или величина циркуляции электрическое поле E вокруг замкнутого контура равно скорости изменения из магнитный поток через площадь, ограниченную петлей. Приведенное ниже уравнение выражает закон Фарадея в математической форме.

dΦ _B /dt (через фиксированную площадь) = -∫ _{вокруг петли} E ·d r (на фиксированное время)

Знак минус в этом уравнении говорит нам о направлении тираж. (См. ниже.)

Когда магнитный поток через закрытую область заменами петель, ∫ _{вокруг цикла} E ·d r не равно нулю, циркулирует электрическое поле E .
E ∙d r проделанная работа на единицу заряда электрическим полем при перемещении заряда на расстояние d r .
Если петля является реальной проволочной петлей, тогда есть реальная работа, выполненная индуцированным поле на бесплатных сборах.
∫ _{вокруг петли} E ·d r работа на единицу заряда полем при однократном перемещении заряда по контуру.
Это ЭДС индукции равна , и измеряется в вольтах.

dΦ _B /dt (через фиксированную площадь) = ЭДС индукции

Если кривая Γ представляет собой кривую, описываемую проволочной петлей с сопротивлением R, то по проводу будет течь ток I = ЭДС/R.
ЭДС индукции вызывает протекание тока без разность потенциалов из-за разделенных зарядов.

Индуцированное электрическое поле НЕ консервативное поле. Когда вы перемещаете заряд против индуцированного поле один раз вокруг цикла, вы должны сделать работу. Но твоя работа НЕ хранится как потенциальная энергия. Вы не можете позволить электрическому полю выполнять работу по восстановлению энергия, затраченная вами на перемещение заряда. Наведенное электрическое поле исчезает, когда как только магнитный поток перестанет изменяться. Работа, которую вы делаете на заряд против индуцированного поля локально не сохраняется. Энергия может переноситься в виде электромагнитная волна. Электромагнитные волны переносят энергию через свободное пространство.

Каково направление динамического (индуцированного) поля?

Знак минус в уравнении, выражающем закон Фарадея, говорит нам о направление индуцированного поля.
Есть простой способ запомнить это направление. Циркуляция индуцированного поля равна ЭДС.
Любой ток, протекающий в результате этой ЭДС, создает магнитное поле, противодействующее изменения потока, которые его производят.
Это называется Закон Ленца.

ЭДС индукции противостоит ИЗМЕНЕНИЮ потока, который ее вызывает.

Пример:

Магнит быстро движется к проволочной петле, как показано на рисунке.
Поток через проволочную петлю увеличивается в нисходящем направлении.
В контуре начинает течь ток в направлении, указанном стрелкой.
 

Магнитная сила из-за петли на магните замедляет приближающийся магнит.

Прелесть закона Ленца в том, что вам не нужно вглядываться в детали. Если магнитный поток через проводник изменится, токи будут течь в противоположном направлении. все, что вызвало изменение. Если какое-то относительное движение вызывает изменение потока, ток попытается остановить это относительное движение. Если изменение тока в цепь отвечает за изменение потока, то ЭДС индукции будет стремиться предотвратить изменение тока в этой цепи.

Смотрите:  Электромагнитная индукция и Закон Фарадея (Youtube)

Проблема:

Рассмотрим плоскую квадратную катушку с N = 5 витками.
Катушка по 20 см с каждой стороны, имеет магнитное поле через него проходит 0,3 Тл.
Плоскость катушки перпендикулярна магнитное поле: поле направлено за пределы страницы.
(a)  Если ничего не изменить, какова ЭДС индукции?
(б) Магнитное поле равномерно увеличивается от 0,3 Тл до 0,8 Тл за 1 с. Чему равна ЭДС индукции в катушке, пока происходит изменение?
(c) При изменении магнитного поля ЭДС, наводимая в катушке, вызывает ток течь. Течет ток по часовой или против часовой стрелки вокруг катушки?

Решение:

• Рассуждение:
  Если величина магнитного поля B меняется, то поток Φ = BA изменяется, и возникает ЭДС.
• Детали расчета:
  (a) ЭДС индуцируется изменяющимся магнитным потоком. Если ничего изменяется, ЭДС индукции равна нулю.
  (b) Катушка имеет 5 витков. Каждый виток имеет площадь A = (0,2 м) ² . Начальный магнитный поток через каждый виток катушки Φ ₀ = B ₀ A = 0,3*(0,2) ² Тм ² = 0,012 Тм ² .
  Конечный магнитный поток через каждый виток катушки равен Φ _f = B _f A = 0,8*(0,2) ² Tm ² = 0,032 Tm ² .
  Суммарное изменение потока через катушку N(Φ _ф — Φ ₀ ), при N = 5. ЭДС индукции равна
  ЭДС = -N∆Φ/∆t = -N(Φ _f — Φ ₀ )/∆t = [-5*(0,032 -0,012)/1,0] В = -0,1 В.
  (c) При изменении магнитного поля магнитный поток увеличился вне страницы. По закону Ленца ЭДС индукции в контуре благодаря этому изменяющемуся потоку создается ток, который создает поле, противодействующее сдача. Поле, создаваемое током в катушке, направлено в стр., противоположном направлению увеличения потока. Для производства поле на страницу, ток должен течь по часовой стрелке вокруг петли по правилу правой руки.

---

Модуль 8: вопрос 1

Стержневой магнит расположен перед горизонтальной проволочной петлей так, чтобы его северный полюс указывает на петлю. Затем магнит оттягивается от петля. Наведенный ток в петле течет по часовой стрелке или против часовой стрелки?

Обсудите это со своими однокурсниками на форуме!
Визуализируйте магнитное поле стержневого магнита. Как поток этого поле через проволочную петлю изменить?

---

Самоиндукция

Если длинная катушка провода площадью поперечного сечения A и длиной ℓ с N витками подключен или отключен от батареи, изменение магнитного потока через катушка создает ЭДС индукции. Индуцированный ток создает магнитное поле, противодействующее изменению магнитного потока. Величина ЭДС индукции можно рассчитать по закону Фарадея.

• Магнитное поле внутри длинной катушки B = μ ₀ (Н/л)И.
• Поток через катушку равен NBA = μ ₀ (N ² /л)IA.
• Изменение потока в единицу времени составляет мк ₀ (N ² /л)A ∆I/∆t = L*∆I/∆t, так как I — единственная величина, изменяющаяся со временем.
  L = μ ₀ (N ² /л)А называется собственная индуктивность катушки. Единицы индуктивности: Генри (Гн). 1 Гн = 1 Вс/А.
• ЭДС индукции равна ЭДС = -L*dI/dt, где знак минус является следствием закона Ленца.

ЭДС индукции пропорциональна скорости изменения тока в катушка. Оно может в несколько раз превышать напряжение питания. Когда выключатель в цепи с большим током размыкается, уменьшая ток до ноль за очень короткий промежуток времени, это может привести к искре. Все цепи имеют собственную индуктивность, и у нас всегда есть ЭДС = -L*∆I/∆t. Собственная индуктивность L зависит только по геометрии цепи.

Проблема:

Катушка имеет собственную индуктивность 3 мГн, а ток через нее изменяется от 0,2 А до 1,5 А за время 0,2 с. Найдите модуль средней ЭДС индукции в катушке за это время.

Решение:

• Рассуждение:
  ЭДС самоиндукции равна ЭДС = -L*∆I/∆t.
• Детали расчета:
  L = 3 мГн, ∆I/∆t = (1,5–0,2 А)/0,2 с = 6,5 А/с.
  ЭДС = -L*∆I/∆t = -(0,003 Вс/А)(6,5 А/с) = -0,0195 В.
  Знак минус указывает на то, что ЭДС индукции противодействует изменениям потока, которые произвел его.

Проблема:

Круглая катушка из 25 витков диаметром 1 м. Он размещен со своим ось вдоль направления магнитного поля Земли (величина 50 микроТл), а затем за 0,2 с переворачивается на 180 ^o . Какова средняя ЭДС сгенерировано

Решение:

• Рассуждение:
  Ф _B  = B ∙ A  является потоком B через площадь A. Первоначально B и A выровнены, в конце концов они анти-выровнены. Точка знак изменения продукта.
• Детали расчета:
  ЭДС = -∆Φ _B /∆t. Φ _B (исходный) = NAB = 25*π*(0,5 м) ² 50*10 ^-6 Т = 9,82*10 ^-4 Тм ² .
  Φ _B (конечный)  = -Φ _B (начальный), поскольку катушка перевернута.
  |∆Φ _B | = 2Φ _B (исходное).
  |∆Φ _B /∆t| знак равно 2*(9,82*10 ^-4 Тм ² )/(0,2 с) = 9,82*10 ^-3 В.

Проблема:

Катушка радиусом 0,5 м, состоящая из 500 витков, поворачивается на четверть оборота за 4,17 с. мс, первоначально имея плоскость, перпендикулярную однородному магнитному полю. Найти напряженность магнитного поля, необходимую для индукции средней ЭДС 10 000 В.

Решение:

• Обоснование:
  ЭДС = -∆Φ _B /∆t. Φ _B = NABcosθ изменяется от NAB до 0 за 4,17 мс, так как θ изменяется от 0 до 90 ^o за 4,17 мс.
• Детали расчета:
  |∆Φ _В | = NAB = 500*π*(0,5 м) ² *B = (393 м ² ) * Б.
  Хотим
  |ЭДС| = |∆Φ _B /∆t| = (393 м ² )/(4,17*10 ^-3 с) * B = (94174 м ² /с)*B = 10000 ^{В.
  В = 0,1 Вс/м 2 = 0,1 Тл.}

Уравнение ЭДС трансформатора | Коэффициент трансформации трансформатора

Уравнение ЭДС трансформатора очень важно для понимания работы трансформатора. Когда синусоидальное напряжение подается на первичную обмотку трансформатора, он потребляет ток намагничивания, чтобы создать магнитный поток в сердечнике.

Поток соединяется со вторичной обмоткой и создает ЭДС. Мы можем легко вывести уравнение ЭДС трансформатора, рассчитав скорость изменения потока за один цикл формы волны переменного тока. ЭДС индукции в первичной и вторичной обмотках трансформатора также зависит от коэффициента трансформации трансформатора.

Отношение вторичной ЭДС к первичной ЭДС называется коэффициентом преобразования напряжения трансформатора. Отношение витков первичной обмотки к виткам вторичной обмотки называется коэффициентом витков трансформатора (TTR).

Поток, образующийся в сердечнике, связывается с первичной и вторичной обмотками трансформатора. Переменный поток, возникающий в сердечнике при соединении с витками первичной и вторичной обмотки, индуцирует напряжение, называемое ЭДС.

ЭДС, наводимая в обмотке трансформатора, зависит от количества витков и скорости изменения потока. ЭДС, индуцированная между первичной и вторичной обмотками, всегда противодействует приложенному напряжению.

Согласно закону электромагнитной индукции Фарадея, если переменный поток соединяется с катушкой, в катушке индуцируется напряжение. Напряжение, индуцируемое в первичной и вторичной обмотках трансформатора, приведено ниже. Среднеквадратичное значение вторичной ЭДС индукции и первичной ЭДС индукции можно рассчитать с использованием закона электромагнитной индукции Фарадея.

Где,

Знак минус показывает, что напряжение, индуцированное в первичной и вторичной обмотках, противодействует приложенному напряжению.

Вывод уравнения ЭДС трансформатора

Вывод уравнения ЭДС трансформатора можно получить путем расчета скорости изменения потока в сердечнике трансформатора. Поток, создаваемый в сердечнике, синусоидальный.

Поток в активной зоне изменяется от + Ф _м до -Ф _м за 1/2f секунды.

Напряжение, индуцируемое в первичной обмотке, равно 

Поток, индуцируемый в первичной обмотке, обусловлен синусоидальным напряжением, приложенным к первичной обмотке, поэтому поток также изменяется синусоидально. Мгновенное значение потока в трансформаторе равно ;

Подставляя значение потока в уравнение (1)

Максимальное значение напряжения, индуцированного в первичной обмотке, равно 

Среднеквадратичное значение (RMS) индуцированного напряжения в первичной обмотке

Подставляя Ep(max) значение в уравнении (4)

Точно так же среднеквадратичное значение (СКЗ) индуцированного напряжения во вторичной обмотке равно ;

Общее уравнение ЭДС трансформатора:

Коэффициент трансформации напряжения трансформатора  

Отношение витков вторичной обмотки к виткам первичной обмотки известно как коэффициент трансформации напряжения трансформатора и обозначается буквой «К».

 Деление уравнения (6) на уравнение (5)

Если витков вторичной обмотки больше, чем витков первичной обмотки, вторичное напряжение будет выше, чем первичное напряжение, а коэффициент витков (K) больше 1. Трансформатор, который трансформатор с коэффициентом трансформации по напряжению более 1 называется повышающим трансформатором.

Если коэффициент трансформации напряжения (К) меньше 1, трансформатор называется понижающим.

Намагничивающая МДС незначительна, когда в первичной и вторичной обмотках трансформатора протекает значительный ток. Суммарная МДС первичной и вторичной МДС равна намагничивающей МДС. Трансформатор представляет собой машину с постоянным магнитным потоком, пока напряжение и частота остаются постоянными.

При значительной нагрузке трансформатора намагничивающей МДС можно пренебречь.

Знак минус показывает, что направление тока в первичной и вторичной обмотках противоположно току намагничивания. Знак минус можно опустить для расчета коэффициента трансформации трансформатора.

Из уравнений (7) и (8)

Здесь K — коэффициент трансформации трансформатора по напряжению.

Уравнение коэффициента трансформации напряжения (9) трансформатора верно , если поток в сердечнике трансформатора постоянный. Поток в трансформаторе изменяется, если напряжение питания и/или частота отклоняются от расчетного значения.

Коэффициент витков трансформатора

Отношение витков первичной обмотки (Np) к виткам вторичной обмотки (Ns) трансформатора известно как коэффициент витков трансформатора или TTR. Обозначается буквой «а».

Теперь мы можем записать коэффициент трансформации и уравнения преобразования напряжения в виде;

Решенные задачи по уравнению ЭДС трансформатора

Двухобмоточный трансформатор имеет первичную обмотку с 300 витками и вторичную обмотку с 10 витками. Первичная обмотка подключена к сети 3300 В. Рассчитать-

•  Вторичное напряжение без нагрузки
•  Первичный ток, когда 100-амперная нагрузка подключена ко вторичной обмотке
• Отношения полной мощности, протекающей в первичной и вторичной цепях, и коэффициенты преобразования напряжения

• 9013 трансформатора?

Первый закон трансформатора:

Вторичное напряжение без нагрузки :

Вторичное напряжение без нагрузки = 110 Вольт

Второй Закон трансформатора:

Первичный ток, когда нагрузка 100-ампер подключена к вторичному

Первичный ток = 3,33 Ампер

Очевидная сила в первичной цепи

вторичная цепь

Коэффициент трансформации трансформатора (TTR)

Коэффициент трансформации напряжения трансформатора

Читать далее

• Разница между трансформаторами высокого, среднего и низкого напряжения
• Почему сердечник силового трансформатора заземлен?
• Разница между током холостого хода, током возбуждения и током утечки в трансформаторе
• В чем недостаток большого тока возбуждения в трансформаторе?
• Каков класс изоляции трансформаторного масла?
• Почему трансформатор не работает с питанием постоянного тока?
• Почему обмотка НН расположена рядом с сердечником?
• Номинальные характеристики трансформатора
• Соединение трансформатора с открытым треугольником

Связанные сообщения:

Пожалуйста, подпишитесь на нас и поставьте лайк:

ЭДС неизвестной ячейки с использованием потенциометра Калькулятор

✖ЭДС неизвестной ячейки с помощью потенциометра используется для определения ЭДС неизвестной ячейки и сравнения ЭДС двух ячеек. ⓘ ЭДС неизвестной ячейки с помощью потенциометра [ℰ]		AbvoltAttovoltCentivoltDecivoltDekavoltEMU of Electric PotentialESU of Electric PotentialFemtovoltGigavoltHectovoltKilovoltMegavoltMicrovoltMillivoltNanovoltPetavoltPicovoltPlanck VoltageStatvoltTeravoltVoltWatt per AmpereYoctovoltZeptovolt	+10% -10%
✖Length is the measurement or extent of something from end to end.ⓘ Length [ L]		AlnAngstromArpentАстрономическая единицаАттометрAU длиныЯчменьМиллиард световых летБор РадиусКабель (международный)Кабель (Великобритания)Кабель (США)КалибрСантиметрЦепьКубит Рад (Греческий)Кубит (Длинный)Кубит (Великобритания)ДекаметрДециметрРадиус Земли от ЛуныЗемляЭкваториальное расстояние от Солнца Classical)EllExameterFamnFathomFemtometerFermiFinger (ткань)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkMe gameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (Cloth)NanometerNautical League (int)Nautical League UKNautical Mile (International)Nautical Mile (UK)ParsecPerchPetameterPicaPicometerPlanck LengthPointPoleQuarterReedReed (Long)RodRoman ActusRopeRussian ArchinSpan (Cloth)Sun RadiusTerameterTwipVara CastellanaVara ConuqueraVara De TareaYardYoctometerYottameterZeptometerZettameter	+10% -10%
✖final Длина -это измерение или протяженность чего -либо от конца до конца. Окончательная длина [L 2 ]		2 ] 440		9000. ДлинаЯчменьМиллиард Световых Годов Бор РадиусКабель (Международный)Кабель (Великобритания)Кабель (США)КалибрСантиметрЦепьКубит (Греческий)Кубит (Длинный)Кубит (Великобритания)ДекаметрДециметрРасстояние Земли от ЛуныРасстояние Земли от СолнцаЭкваториальный Радиус ЗемлиПолярный Радиус ЗемлиЭлектронный Радиус (Классический)EllExameterFamnFathomFemtooFermiFinger Survey (Finger Survey (Cloth)Finger )FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (Cloth)NanometerNautical League (int)Nautical League UKPautical Mile (International)Parsecer erPlanck LengthPointPoleQuarterReedReed (Long)Roman ActusRopeRussian ArchinSpan (ткань)Sun RadiusTerameterTwipVara CastellanaVara ConuqueraVara De TareaYardYoctometerYottameterZeptometerZettameter	+10% -10%

✖Электродвижущая сила – это способность системы создавать поток заряда. ⓘ ЭДС неизвестной ячейки с использованием потенциометра [ε]

AbvoltAttovoltCentivoltDecivoltDekavoltEMU электрического потенциалаESU электрического потенциалаFemtovoltGigavoltHectovoltKilovoltMegavoltMicrovoltMillivoltNanovoltPetavoltPicovoltPlanck VoltageStatvoltTeravoltVoltWatt per AmpereYoctovoltZeptovolt

⎘ Копировать

👎

Формула

Перезагрузить

👍

ЭДС неизвестной клетки с использованием решения потенциометра

ШАГ 0: Сводка предварительного расчета

ШАГ 1: Преобразование входных данных в базовую единицу

ЭДС неизвестной ячейки с использованием потенциометра: 6 В —> 6 В Преобразование не требуется
Длина: 4 метра —> 4

2,4 вольта —> преобразование не требуется

< 3 калькулятора потенциометров

ЭДС неизвестной клетки с использованием формулы потенциометра

Электродвижущая сила = (ЭДС неизвестной ячейки с использованием потенциометра * длина) / конечная длина
ε = (ℰ*л)/л ₂

Как рассчитывается ЭДС неизвестной ячейки с помощью потенциометра?

Пусть длина баланса 1 равна l ₁ , тогда ε ₁ = xl ₁
пусть длина баланса 2 равна l ₂ , тогда ε ₂ = xl ₂
тогда ε ₁ /ε _{2 = l 1 / l 2}

Как рассчитать ЭДС неизвестной ячейки с помощью потенциометра?

ЭДС неизвестной ячейки с использованием потенциометра Калькулятор использует Электродвижущая сила = (ЭДС неизвестной ячейки с использованием потенциометра * Длина) / Конечная длина для расчета электродвижущей силы, ЭДС неизвестной ячейки с использованием потенциометра используется для определения электродвижущей силы неизвестной ячейки и сравнения электродвижущей силы двух ячеек. Электродвижущая сила обозначается символом ε .

Как рассчитать ЭДС неизвестной ячейки с помощью потенциометра с помощью этого онлайн-калькулятора? Чтобы использовать этот онлайн-калькулятор для ЭДС неизвестной ячейки с помощью потенциометра, введите ЭДС неизвестной ячейки с помощью потенциометра (ℰ) , Длина (L) & Final Length (l ₂ ) и нажмите кнопку расчета. Вот как можно объяснить ЭДС неизвестной ячейки с помощью расчета потенциометра с заданными входными значениями -> 2,4 = (6 * 4)/10 .

Часто задаваемые вопросы

Что такое ЭДС неизвестной ячейки при использовании потенциометра?

ЭДС неизвестной ячейки с использованием потенциометра используется для определения электродвижущей силы неизвестной ячейки и сравнения электродвижущей силы двух ячеек и представляется как ε = (ℰ*L)/l ₂ или Электродвижущая сила = (ЭДС неизвестной ячейки с использованием потенциометра*длина)/конечная длина . ЭДС неизвестной ячейки с использованием потенциометра используется для определения ЭДС неизвестной ячейки и сравнения ЭДС двух ячеек. Длина — это измерение или протяженность чего-либо от конца до конца, а окончательная длина — это измерение или протяженность чего-либо от конца до конца.

Как рассчитать ЭДС неизвестной ячейки с помощью потенциометра?

ЭДС неизвестной ячейки с помощью потенциометра используется для определения электродвижущей силы неизвестной ячейки и сравнения электродвижущей силы двух ячеек рассчитывается с помощью Электродвижущая сила = (ЭДС неизвестной ячейки с использованием потенциометра * длина)/конечная длина . Чтобы рассчитать ЭДС неизвестной ячейки с помощью потенциометра, вам потребуется ЭДС неизвестной ячейки с помощью потенциометра (ℰ) , длины (L) и конечной длины (l ₂ ) . С помощью нашего инструмента вам нужно ввести соответствующее значение ЭДС неизвестной ячейки с помощью потенциометра, длины и конечной длины и нажать кнопку расчета.