Электрическое поле (для школьников). Урок 3
Электрическое поле (для школьников). Урок 3Работа сделана по учебнику физики под редакцией Ландсберга, 2 том.
Внимание! Чтобы увидеть ответы на вопросы, кликните по ним. Чтобы сменить картинку, кликните по кнопке. Если ответ на вопрос вам не ясен, советую хорошо подумать, прежде чем смотреть ответ.
Конденсаторы широко используются в электронике, в электротехнике. В любом электронном устройстве их множество. Можете посмотреть, какие они бывают, в «Яндекс-картинках». Для тех, кто ещё не знает: это устройство, обычно состоящее из двух пластин из проводника и выводов, соединённых с этими пластинами. Пластины расположены близко одна к другой и изолированы друг от друга. Они могут быть плоскими или обе вместе с изолирующим слоем скрученными в рулончик.
Вот на две таких пластины в разрезе. Зарядим левую пластину, например, положительно. В правой пластине под действием электрического поля переместятся заряды.
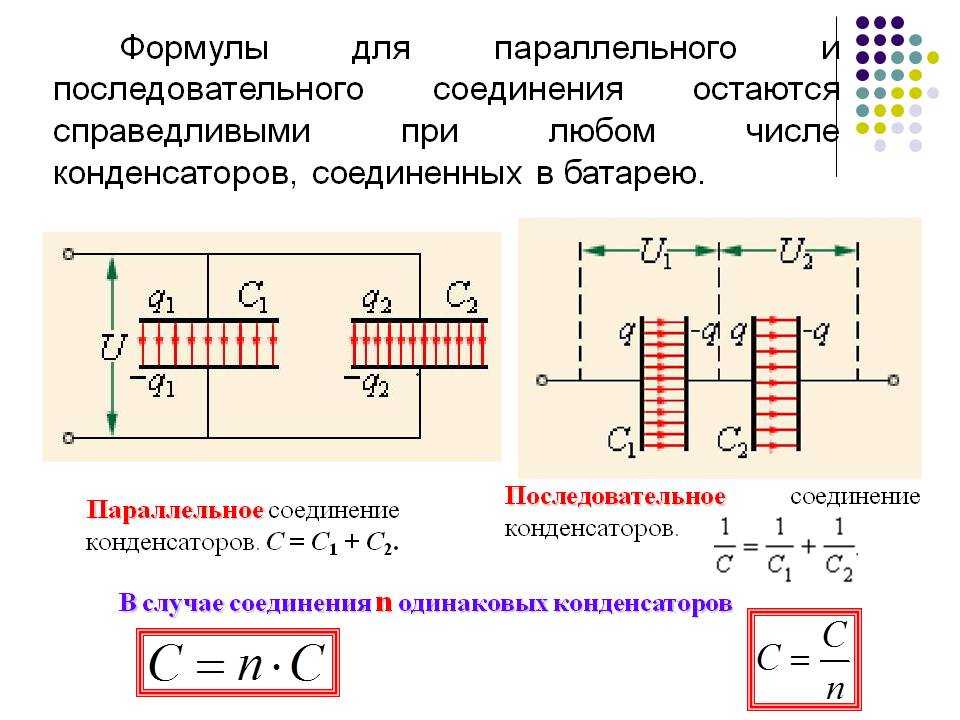
Опыты показывают, что заряд конденсатора прямо пропорционален разнице потенциалов между его пластинами.
q=CU
Коэффициент C характеризует конденсатор. Он называется ёмкостью конденсатора. Чем он больше, тем, при данном напряжении между его пластинами, на них находится больший заряд. Чем больше ёмкость, тем больший заряд можно «залить» в конденсатор (при данном напряжении между его пластинами).
C=q/UЕдиница ёмкости называется фарад. Ёмкостью в один фарад обладает конденсатор, каждая из пластин которого имеет заряд в 1 кулон при напряжении между пластинами в 1 вольт. Для практических целей фарад — слишком большая единица. На практике обычно применяют более мелкие единицы — микрофарад (мкф) и пикофарад (пкф). Микрофарад равен одной миллионной доле фарада, пикофарад равен одной миллионной доле микрофарада.
Ёмкость конденсатора пропорциональна площади его пластин и обратно пропорциональна расстоянию между ними.
Докажите, это так.
Напряжённость поля (а следовательно и густота линий поля) между пластинами конденсатора пропорциональна напряжению между пластинами и обратно пропорциональна расстоянию между ними (смотрите урок 2). Допустим, напряжение нас не меняется. Тогда чем больше площадь пластин, тем больше линий поля там поместится. Чем пластины ближе друг к другу, тем линии поля гуще, следовательно, их больше. Линии поля начинаются от положительных зарядов, заканчиваются на отрицательных.
Ёмкость конденсатора пропорциональна площади его пластин. Если соединить, например, три одинаковых конденсатора параллельно, общая площадь их пластин будет в три раза больше, и общая ёмкость их будет в три раза больше (рис. 2). Вообще, при параллельном соединении конденсаторов их общая ёмкость будет равна сумме емкостей этих конденсаторов. А напряжение на их пластинах будет, разумеется, одинаковым.
Конденсаторы также соединяют последовательно. Посмотрим, что при этом происходит (рис. 3). Подадим на группу последовательно соединённых конденсаторов напряжение U. На левой пластине конденсатора 1 (1л) появится заряд +q, а на правой пластине этого же конденсатора (1п) вследствие индукции появится заряд -q. Но это означает, что на левой пластине конденсатора 2 (2л) появится заряд +q, ведь общий заряд пластин 1п и 2л равен нулю. И таким образом на каждом из конденсаторов появится одинаковый заряд.
Опыты показывают, что ёмкость конденсатора также зависит от материала диэлектрика. Допустим, диэлектриком в конденсаторе является вакуум и ёмкость конденсатора равна C0 . Тогда если вместо вакуума в качестве диэлектрика использовать какое либо вещество, ёмкость конденсатора увеличится в раз.
| воздух | 1.0006 |
| чистая вода | 81 |
| слюда | 6-8 |
| стекло | 4-7 |
| радиотехническая керамика | до 80 |
Из формул (рис. 4-0 позиция 1) следует, что диэлектрик с диэлектрической проницаемостью уменьшает напряжение между пластинами конденсатора в раз. Это в свою очередь означает, что напряжённость поля между пластинами конденсатора уменьшается в раз (рис. 4-0 позиция 2).
Вообще, если пространство между зарядами заполнено диэлектриком с диэлектрической проницаемостью , напряжённость поля между ними уменьшается в раз. Модифицируем также закон Кулона — вставим в его формулу коэффициент диэлектрической проницаемости (рис. 4-0 позиция 3 ).
Теперь объяснение этого явления.
Как известно, атомы состоят из положительно заряженых ядер и отрицательно заряженых электронов. Многие молекулы устроены так, что одна их часть является положительным зарядом, а другая — отрицательным. Положительный и отрицательный заряд равны по модулю, то есть в целом такая молекула является нейтральной. Такие молекулы называют диполями. Мы здесь не будем вдаваться в химию и будем изображать их как на рис. 4, в виде прямоугольников с заряженными концами.
Что происходит, если вещество попадает в электрическое поле? Во первых, дипольные свойства молекулы могут усилиться. Заряды в ней могут смещаться под действием поля. Расстояние между полюсами диполя становится больше (рис. 4).
Во вторых диполи проявляют тенденцию поворачиваться под действием поля. Смотрим рисунок 5 позиция 1. Направление прямоугольников совершенно хаотическое. Когда отсутствует внешнее электрическое поле, хаотическим является и направление диполей в веществе. Появляется поле. Диполи поворачиваются так, что положительный их заряд становится ближе к отрицательному заряду — источнику внешнего поля, а отрицательный заряд диполя становится ближе к положительному заряду — источнику внешнего поля.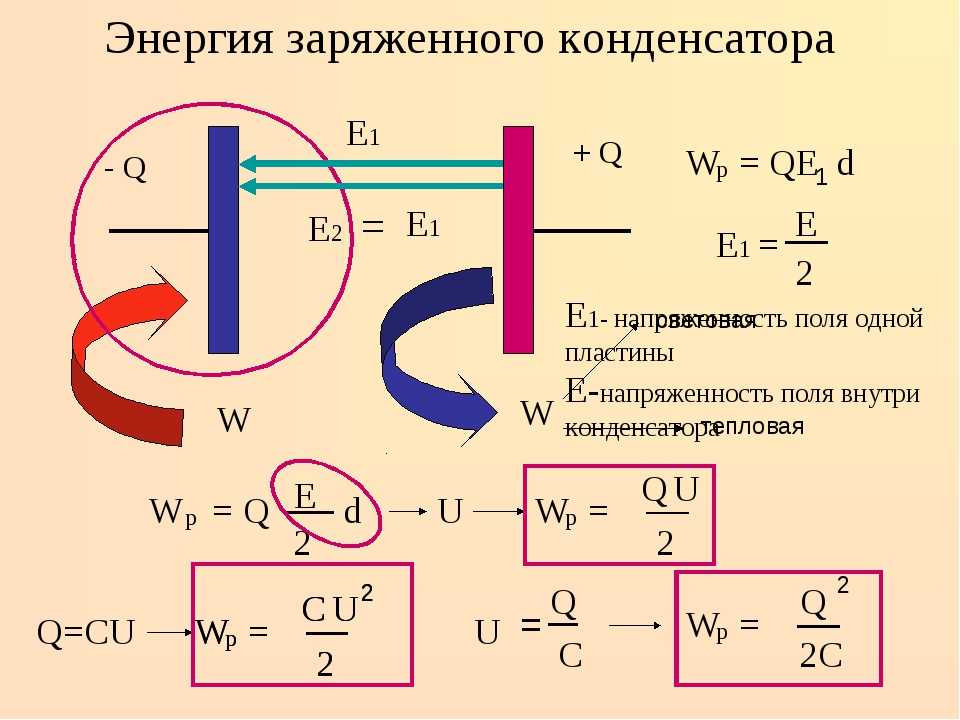
Снова смотрим рис.5 позиция 2 и 3. Под действием поля пластин конденсатора 2 диполи поворачиваются, их полюса сдвигаются. В результате на границе диэлектрика, примыкающей к положительно заряженой пластине конденсатора образуется отрицательный заряд, а на границе, примыкающей к отрицательной пластине образуется положительный заряд. Взаимное поле этих двух зарядов направлено в сторону, противоположную взаимному полю пластин конденсатора. В результате взаимное поле пластин конденсатора ослабляется.
Первый урок     Второй урок     На домашнюю страницу
Курс физики. Том II. Учение об электричестве
Курс физики.
Том II. Учение об электричестве
ОглавлениеЧАСТЬ ТРЕТЬЯ. УЧЕНИЕ ОБ ЭЛЕКТРИЧЕСТВЕ§ 2. Количество электричества. Закон Кулона § 3. Атомное строение электричества § 4. Напряженность электрического поля § 5. Теорема Острогдадского — Гаусса § 6. Вектор электрической индукции § 7. Примеры применения теоремы Остроградского — Гаусса § 8. Потенциал электрического поля § 9. Формулы электростатики в практической системе единиц ГЛАВА II. ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ § 10. Распределение электричества по поверхностй заряженных проводников § 11. Электризация проводников в поле и деформация поля проводниками § 12. Контактная разность потенциалов § 13. Электроемкость § 14. Расчет электроемкости конденсаторов § 15. Электрическая энергия § 16. Энергия поля § 17. Электрометры § 18. О природе электрических явлений ГЛАВА III. ДИЭЛЕКТРИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ § 19. Дипольная и электронная поляризация диэлектриков. Сегнетоэлектрики § 20. Деформация поля диэлектриками § 21. Электрическая восприимчивость § 22.  Электронная теория диэлектриков§ 23. Пьезоэлектрические и пироэлектрические явления § 24. Электроконвекционные явления (электрофорез, электроэндосмос и др.) ГЛАВА IV. ПОСТОЯННЫЙ ТОК § 25. Величина тока. Электродвижущая сила и напряжение § 26. Закон Ома. Законы Кирхгофа § 27. Закон Джоуля — Ленца § 28. Дифференциальная форма законов Ома и Джоуля — Ленца. Соотношение аналогии между проводимостью и емкостью ГЛАВА V. ТОК В МЕТАЛЛАХ § 29. Сведения об электропроводности. Термометры сопротивления, болометры, тензометры § 30. Закон Видемана — Франца. Теория электропроводности металлов § 31. Сверхпроводимость § 32. Термоэлектрические явления и их применение § 33. Зависимость термоэлектродвижущей силы от температуры спаев. Явление Пельтье ГЛАВА VI. ТОК В ПОЛУПРОВОДНИКАХ § 34. Полупроводники § 35. Понятие о зонной теории электропроводности § 36. Применения полупроводников ГЛАВА VII. ТОК В ЭЛЕКТРОЛИТАХ § 37. Электролиз. Законы Фарадея.  Электрохимические эквиваленты. Потенциалы разложения§ 38. Вторичные реакции на электрэдах. Применения электролиза § 39. Подвижность ионов и электропроводность растворов § 40. Гальванические элементы. Электрохимическая природа коррозии § 41. Электродные потенциалы § 42. Аккумуляторы § 43. Свободная энергия гальванической цепи. Концентрационные элементы ГЛАВА VIII. ТОК В ГАЗАХ § 44. Ионизация и электропроводность газов § 45. Типы и механизм разряда в газах § 46. Катодные и анодные лучи § 47. Тлеющий разряд § 48. Дуговой разряд § 49. Искровой разряд. Молния ГЛАВА IX. ТОК ЭЛЕКТРОННОЙ ЭМИССИИ. ЭЛЕКТРОННЫЕ ЛАМПЫ § 50. Термоэлектронная эмиссия. Формула Ричардсона — Дёшмена § 51. Торможение электронного потока. Рентгеновы трубки § 52. Пустотные выпрямители тока (диоды, кенотроны) § 53. Усилительные электронные лампы (триоды) § 54. Фотоэлектрический эффект. Фотоэлементы. Фотореле § 55. Вторичная электронная эмиссия.  Электронные умножители§ 56. Динатронный эффект. Экранированные радиолампы ГЛАВА X. МАГНИТНОЕ ПОЛЕ § 57. Исторические сведения. Закон Кулона для магнитных полюсов § 58. Магнитные величины и соотношения, аналогичные электрическим § 59. Магнитное поле Земли § 60. Магнитное поле тока § 61. Закон Био и Савара § 62. Магнитодвижущая сила. Поток индукции электромагнита § 63. Магнитные свойства веществ и их использование § 64. Электронная теория магнетизма ГЛАВА XI. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ТОК § 65. Формула Ампера и ее трактовка по Фарадею § 66. Работа, производимая током при перемещении проводника в магнитном поле. Электромоторы § 67. Отклоняющее действие магнитного поля на электронный поток (в вакууме и в металле) § 68. Электродинамические измерительные приборы. Гальванометры, Осциллографы § 69. Формулы электродинамики в практической системе единиц ГЛАВА XII. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ § 70. Понятие об электромагнитном поле.  Электромагнитная индукция§ 71. Закон Ленца. Картина электромагнитного поля по Фарадею § 72. Закон Фарадея. Индукционное измерение магнитного потока и магнитодвижущей силы. Вихревые токи § 73. Явление самоиндукции. Индуктивность. Законы нарастания и спада тока при включении и выключении цепи § 74. Энергия магнитного поля тока. Индуктивность и энергия электромагнита. Индуктивность кабеля § 75. Взаимная индуктивность. Энергия взаимодействия токов. Коэффициент взаимной индукции катушек с общим сердечником § 76. Уравнения Максвелла и уравнения Лорентца § 77. Электромагнитное происхождение массы электрона ГЛАВА XIII. ПЕРЕМЕННЫЙ ТОК § 78. Генерирование переменного тока § 79. Работа генератора электрической энергии на нагрузку Эффективные значения напряжения и величины тока § 80. Емкостное сопротивление и индуктивное сопротивление § 81. Активные и реактивные токи. Коэффициент мощности (cos f). Потери (tg b) § 82. Обобщенный закон Ома § 83.  Электрический резонанс§ 84. Трансформация тока § 85. Трехфазный ток. Синхронные и асинхронные моторы ГЛАВА XIV. ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ И ИХ ПРИМЕНЕНИЕ § 86. Индуктор § 87. Колебательный контур § 88. Вибратор Герца (возбуждение колебательного контура индуктором). Токи Тесла § 89. Электромагнитные волны. Вектор Умова — Пойнтинга § 90. Излучение электрического диполя. Волны в двухпроводной линии. Антенны § 91. Распространение электромагнитных волн. Роль ионосферы. «Радиоокно» в космос § 92. Ламповые генераторы электрических колебаний § 93. Модуляция электрических колебаний § 94. Прием, детектирование и усиление радиосигналов. Супергетеродины § 95. Преобразование звуковых колебаний в электрические и электрических в звуковые. Электрозапись и воспроизведение звука § 96. Телевидение § 97. Сантиметровые волны и их распространение в волноводах § 98. Радиолокация. Генерирование ультракоротких волн (клистроны и магнетроны) |
Как работают конденсаторы Как измерить накопленный заряд формулы
Конденсаторы
30.
01.2022 | Просмотров: 2713 | Схемы | автор: ELECTRONOOBS
Доля
Сегодня я буду использовать конденсатор с плоскими пластинами для некоторых экспериментов. Сегодня мы начнем с первого класса и речь пойдет о конденсаторах. Я хочу показать вам, как они работают, некоторые связанные уравнения с конденсаторами, какие типы у нас есть и как площадь, диэлектрик и расстояние между пластинами могут повлиять на характеристики конденсатора. Кроме того, мы увидим, как измерить накопленный заряд внутри конденсатора, используя несколько классных формул.
Часть 1. Как работают конденсаторы?
Итак, как работает доза конденсатора? Что ж, самое простое представление конденсатора — это две проводящие пластины, подобные приведенным ниже, расположенные рядом друг с другом, но никогда не касаются , и обычно между ними находится какой-то диэлектрик , и мы увидим, что такое диэлектрик.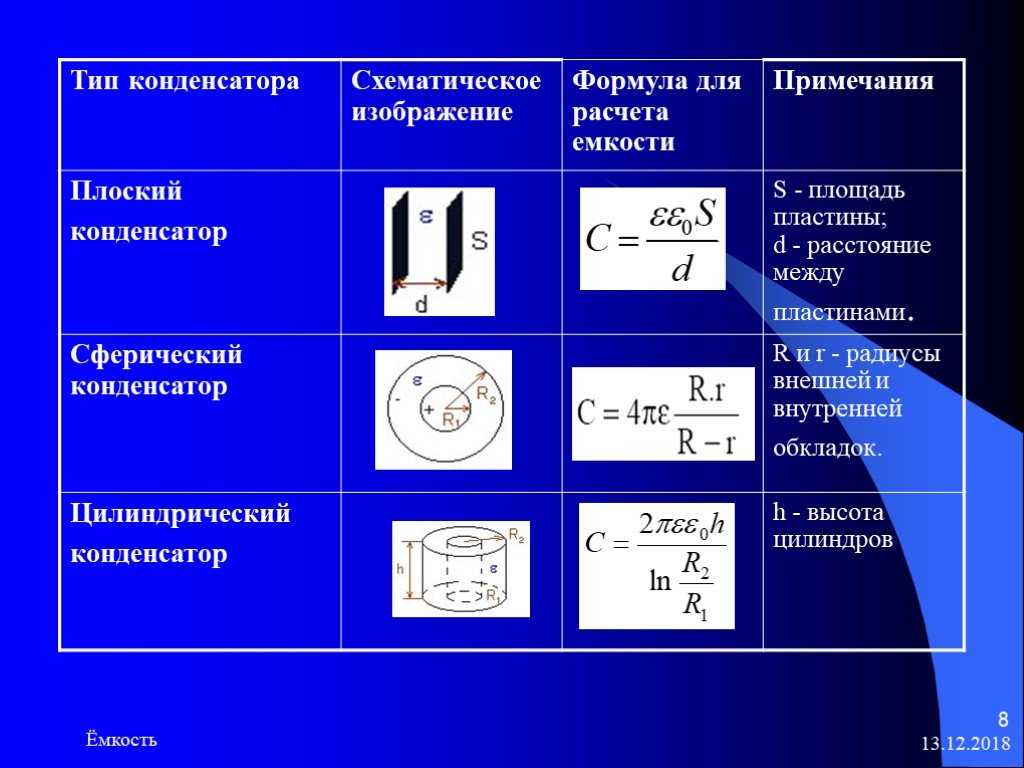
находится в данный момент. С другой стороны, мы знаем, что электроны имеют отрицательный заряд. Отрицательное с отрицательным будет отталкивать друг друга, а положительное с отрицательным притягиваться, все благодаря электрическим полям. Идея конденсатора состоит в том, чтобы хранить эти электроны на своих металлических пластинах. Но вы видите, вы не можете добавить больше электронов к металлу, потому что они будут вытеснены другими электронами, которые уже есть в металле. Если только вы не нанесете положительный заряд на другую сторону, чтобы они притянулись. Эта сила притяжения (электрическое поле) могла бы преодолеть толкающую силу, создаваемую электронами, отталкивающими друг друга, и, таким образом, на металлических пластинах конденсатора накапливался бы больший заряд. Чем больше это электрическое поле, тем больше заряда мы можем передать металлической пластине.
Чтобы создать отрицательный и положительный заряд, мы прикладываем к пластинам перепад напряжения , но пластины никогда не касаются друг друга.
С помощью этой разницы потенциалов мы теперь можем выталкивать электроны на правую пластину и высасывать их из левой пластины, создавая положительный заряд. Поскольку металлические пластины не соприкасаются, электроны не могут перейти на другую сторону, чтобы заполнить положительные отверстия. Но между положительным и отрицательным зарядом существует электрическая сила, и эта сила удерживает их вместе. Так что даже если я отключу подачу напряжения, так как заряду некуда деться, конденсатор сохранит свой заряд. Вот как мы можем хранить энергию внутри конденсатора.
Часть 2. Типы конденсаторов
А что, если я подключу аккумулятор наоборот. У этого идеального конденсатора левая и правая металлические пластины одинаковы, поэтому он будет работать без проблем. Но в зависимости от материалов, которые мы используем для изготовления конденсаторов, это может быть проблемой, и это может случиться с вашим конденсатором. Видите ли, есть несколько типов материалов, которые мы могли бы использовать для изготовления конденсаторов, таких как керамика , тантал, электролит, полимер, слюда, пленка или кремний 9.
0023, и каждый из них имеет свои особенности.
Например, для электролитических и танталовых конденсаторов эти материалы делают их поляризованными, и мы используем такие символы, чтобы обозначить их как поляризованные или неполяризованные. Мы можем видеть электролитический или танталовый конденсатор с линией, указывающей на отрицательный контакт. Если вы разместите их задом наперёд, они могут не сработать или даже взорваться. Посмотрите видео ниже и посмотрите, как взрываются конденсаторы !
Часть 3 — Диэлектрик
Итак, это была основная часть о конденсаторах. До сих пор между металлическими пластинами у нас был воздух. Мы называем материал между пластинами диэлектриком , а в электромагнетизме это электрический изолятор, который может поляризоваться электрическим полем.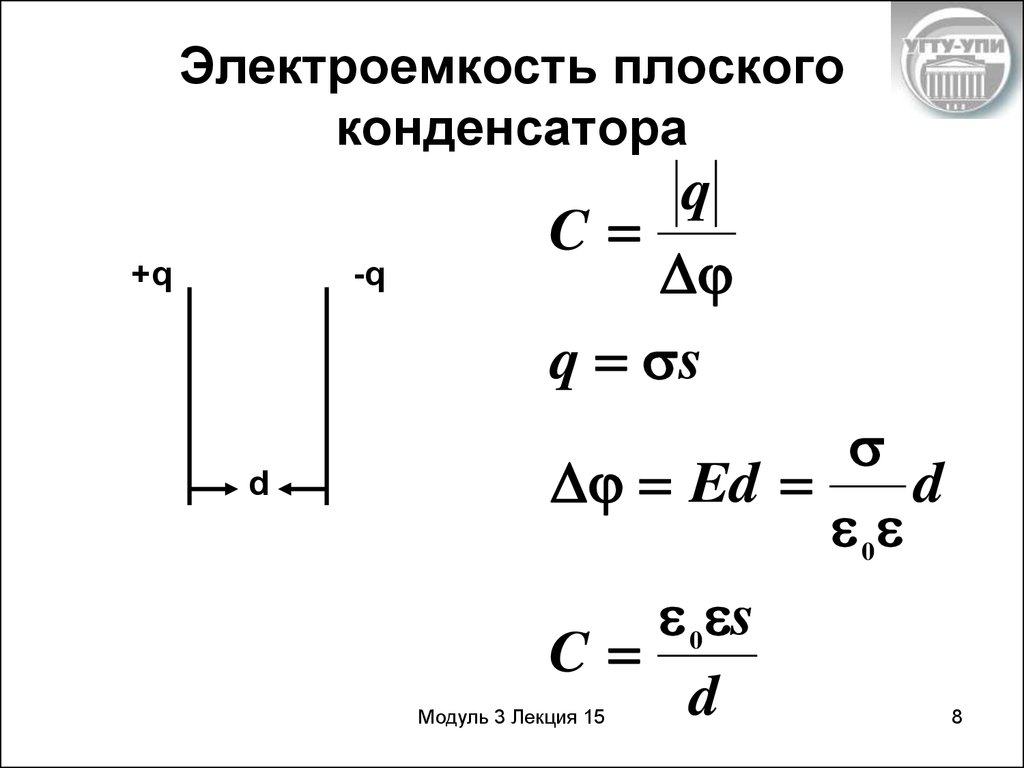
Воздух — это диэлектрик, пластик — еще один диэлектрик, резина может быть диэлектриком, стекло или даже дерево — диэлектриком для конденсаторов. Но в зависимости от используемого материала для диэлектрика свойства конденсатора будут меняться. Единицей измерения конденсаторов является емкость, которая измеряется в фарадах в честь Майкла Фарадея. Эта емкость идеально равна площади пластин, деленной на расстояние между пластинами и умноженной на электростатическую постоянную. Эта константа равна эпсилон 0, умноженному на эпсилон r, где эпсилон 0 — диэлектрическая проницаемость пустоты, а эпсилон r — диэлектрическая проницаемость используемого материала. Таким образом, очевидно, что на емкость конденсатора влияет материал, из которого изготовлен диэлектрик.
Ниже приведена таблица с различными материалами и каждой соответствующей диэлектрической проницаемостью. Как вы можете видеть, воздух имеет диэлектрическую проницаемость 1. Но стекло, например, имеет диэлектрическую проницаемость от 5 до 10, поэтому очевидно, используя формулу выше, если расстояние и площадь остаются прежними, но мы меняем диэлектрик с воздуха на стекла, емкость должна быть выше.
Часть 4 — Расстояние между пластинами
Из той же формулы мы также можем видеть, что емкость может меняться в зависимости от расстояния. Чем меньше расстояние между пластинами, тем выше будет емкость. Опять же, я измеряю емкость этих двух металлических пластин. Теперь я уменьшаю расстояние между ними. Как видите, емкость теперь выше. И он станет ниже, если я увеличу расстояние. Чтобы получить очень высокие значения, производители используют очень тонкие материалы, свернутые вместе, чтобы проводящий материал всегда был изолирован. Таким образом, у нас есть огромная площадь и очень небольшое расстояние между ними, что приводит к высоким значениям емкости.
Часть 5 — Площадь конденсатора
Чем больше общая площадь, тем выше будет емкость.
В этом примере, когда я сдвигаю одну пластину в сторону, общая площадь становится меньше, поэтому, как вы можете видеть, емкость уменьшается.
На самом деле, мы можем видеть это с переменными конденсаторами, такими как этот здесь. Вращением ручки можно разделить большую или меньшую площадь, поэтому значение становится выше или ниже. И, как я уже говорил вам ранее, чтобы получить наибольшую площадь и минимальный объем, производители упаковывают конденсаторы вот так, где проводник и диэлектрик свернуты вместе в цилиндре.
Часть 6. Расчет накопленного заряда
Другая формула состоит в том, что электрическое поле равно приложенному напряжению, деленному на расстояние. Электрическое поле должно быть постоянным, так что произойдет, если я увеличим расстояние с тем же напряжением. Что ж, еще один эксперимент, который мы можем провести с этими пластинами, — вычислить накопленный заряд внутри конденсатора. Что нам нужно сделать, так это зарядить пластины, скажем, до 12 В, когда расстояние составляет 1 мм, а затем отключить источник питания.
Затем увеличиваем расстояние при измерении напряжения и расстояния, и по формуле ранее, так как поле должно быть постоянным, напряжение должно увеличиваться. Мы можем сделать замеры и составить таблицу, где у нас есть напряжение и расстояние в мм. Затем мы передаем эти значения в инвертированные значения, то есть 1 делим на напряжение и 1 делим на расстояние. Мы наносим эти значения на график и делаем линейную регрессию этой линии в Excel. Это даст уравнение, которое мы могли бы использовать, в приведенном ниже примере y = 0,0545x + 0,0336.
Это уравнение на самом деле представляет 1/V = a * 1/d + b. Теперь мы получаем это 0,0545 и называем его, например, «а». Затем из этих двух других формул и предыдущего уравнения мы можем получить, что Q, который представляет собой накопленный заряд, равен эпсилону 0, умноженному на площадь конденсатора, деленному на это число «а». Поскольку мой конденсатор круглый, площадь в моем случае равна пи R в квадрате, где R — радиус моей металлической пластины, и мы можем легко это измерить.
Поместите эту площадь в наше уравнение, и мы получим накопленный заряд.
Часть 7 — Посмотреть полный видеоурок
Я надеюсь, что теперь вы знаете больше о конденсаторах. Если мои видео помогут вам, поддержите мою работу на моем PATREON или сделайте пожертвование на моем PayPal. Еще раз спасибо и увидимся позже, ребята.
Поддержите меня на PayPal
Поддержите меня на PATReon
30.01.2022 | Просмотров: 2713 | Схемы | автор: ELECTRONOOBS
Поделиться
Расчетные уравнения для параллельных пластинчатых конденсаторов Формулы Калькулятор емкости
Расчетные уравнения для параллельных пластинчатых конденсаторов Формулы Калькулятор емкости Решение для емкости.
Примечание:
диэлектрическая проницаемость в свободном пространстве = ε 0 = 8,85 пФ/м
Входные данные:
Преобразование:
диэлектрическая проницаемость (ε)
= 0
фарад/метр 92
Расстояние разделения (S)
= 0
МЕТР
Решение:
емкость (C)
= Не рассчитанное
. Другие единицы:
. Выберите, чтобы найти другое неизвестное
плоский конденсатор
| емкость | |
| диэлектрическая проницаемость | |
| 3 площадь 6 | |
| separation distance |
cylindrical capacitor
| capacitance | |
| permittivity | |
| length of conductors | |
| outer conductor diameter | |
| внутренний диаметр проводника |
емкость
| емкость | |
| electrical charge | |
| potential difference |
stored energy
| stored energy | |
| capacitance | |
| potential difference |
stored energy
| накопленная энергия | |
| емкость | |
| Электрический заряд |
Хранение энергии
| Хранение энергии | |||||
| ЭЛЕКТРИЧЕСКАЯ ЗАПРЕДКА | ЭЛЕКТРИЧЕСКИЙ ЗАПРЕДКИ | ЭЛЕКТРИЧЕСКИЙ ЗАПРЕДНЫЙ
Ссылки — Книги: Типлер, Пол А.  1995. Физика для ученых и инженеров. Стоит Издатели. 3-е изд.Графики роста младенцев — Процентили для младенцев Калькулятор оплаты сверхурочной работы Конвертер зарплаты в почасовую оплату — Вакансии Скидка в процентах — Калькулятор скидок при продаже Калькулятор повышения заработной платы Калькулятор линейной интерполяции Калькулятор возраста собаки Калькулятор закона идеального газа Калькулятор плотности Калькуляторы дизайна, связанные с сабвуфером Калькулятор уравнений звуковой волны Расчетные формулы переменного тока Калькулятор уравнений уровня инфляции Калькулятор уравнений вентиляции сабвуфера Наибольший общий делитель Евклид Калькулятор расчетных формул конденсатора Калькулятор коэффициента безубыточности Калькулятор формул уравнений мощности Калькулятор конструкции циклона Калькулятор уравнений Хазена Вильямса Калькулятор насоса — водная гидравлика Калькулятор процентных уравнений Калькулятор налога с продаж Калькулятор идеальной конструкции реактора Калькулятор импульса импульса Калькулятор закона Ома Управление проектами с добавленной стоимостью Онлайн-веб-приложения, Богатые интернет-приложения, Технические инструменты, Спецификации, Практические руководства, Обучение, Приложения, Примеры, Учебники, Обзоры, Ответы, Ресурсы для просмотра тестов, Анализ, Решения для домашних заданий, Рабочие листы, Справка, Данные и информация для инженеров, Техники, учителя, репетиторы, исследователи, образование K-12, учащиеся колледжей и старших классов, научные выставки и ученые Джимми Рэймонд Контакт: aj@ajdesigner.  |
