Физика Длина волны. Скорость волны
Материалы к уроку
Конспект урока
Хорошей моделью образования волны в шнуре может служить цепочка маленьких шариков (точек), массой m каждый, между которыми действует сила упругости. Мы можем вообразить, что между шариками расположены маленькие пружинки. Пусть точка 1 отведена вверх и
отпущена. Пружинка, связывающая ее с точкой 2, при этом растянется, возникнет сила упругости, которая действует не только на точку 1, но и на точку 2. Начнет, следовательно, колебаться и точка 2. Это приведет к деформации следующей пружинки, так что начнет совершать колебания и точка 3 и т.д. Так как у всех шариков одинаковые массы и у всех пружинок одинаковые жесткости, то все шарики будут колебаться (каждый около своего положения равновесия) с одинаковыми периодами и одинаковыми амплитудами. Однако начнутся эти колебания неодновременно.
Ведь все шарики обладают инертностью (у них есть масса!) и, значит, на изменение их скорости требуется время. Поэтому вторая точка начнет колебаться позже, чем первая, третья — позже, чем вторая, и т.д. Допустим, что к тому моменту времени, когда точка 1 пройдет путь от положения равновесия до крайнего верхнего положения (на это уйдет четверть периода колебаний), успеют начать колебания точки 2 и 3. Точки, правее третьей, еще покоятся. До них не дошла «очередь». К моменту, когда точка 1 вернется в положение равновесия, начнут свои колебания точки 4—6 и т. д. Через промежуток времени, равный периоду колебаний шариков, шарик 1 завершит свое первое колебание. К этому времени соседняя точка 2 этого сделать не успеет, потому что она начала двигаться позже. Она и закончит свое первое колебание позже точки 1. Еще позже это сделают точки 3, 4 и т. д. На некотором расстоянии от точки 1 находится точка,
Эта точка начнет свое первое колебание в тот момент, когда точка 1 начнет свое второе колебание. Обозначим расстояние, на которое колебание распространяется за время Т, греческой буквой λ (лямбда). Называется оно длиной волны.Длина волны — это расстояние, на которое распространяется волна за время, равное одному периоду колебаний. Так как длина волны — это расстояние, пройденное ею, то и найти эту величину можно, как и любое другое расстояние, умножив скорость прохождения на единицу времени. Таким образом, длина волны связана со скоростью распространения волны прямо пропорционально. Найти длину волны можно по формуле:
где λ — длина волны, v — скорость волны, T — период колебаний.
Учитывая, что период колебаний обратно пропорционален частоте этих же колебаний: T=1⁄υ (ню), можно вывести связь скорости распространения волны с частотой колебаний:
v=λυ .
Скорость волны равна произведению частоты колебаний в волне на длину волны.
Частота колебаний волн не меняется при переходе из одной среды в другую. Так, например, частота вынужденных колебаний совпадает с частотой колебаний источника. Частота колебаний не зависит от свойств среды распространений. При переходе из одной среды в другую меняется лишь длина волны и скорость ее распространения. Эти формулы справедливы как для поперечных, так и для продольных волн. При распространении продольных волн длина волны будет расстоянием между двумя ближайшими точками с одинаковым растяжением или сжатием. Она также будет совпадать с расстоянием, пройденным волной за один период колебаний, поэтому формулы будут полностью подходить и в этом случае. Прежде чем, говорить о решении задач, на применение данных формул, обратимся к стандартным единицам измерения данных физических величин, к Системе Интернациональной.Определите, с какой скоростью будет распространяться бегущая волна с частотой 20 Гц и длиной волны 15 м.
Решение. Дана длина волны (лямбда) 15 метров и частота волны (ню) 20 Герц.
Необходимо определить скорость волны V (вэ). Запишем формулу, для расчета скорости волны. Подставляем числовые значения. 15 метров умножить на 20 Герц, получаем ответ. Скорость волны равна 300 метров в секунду.
Задача
На поверхности озера механическая волна движется со скоростью 5,6 м/с. Найдите значение частоты и периода колебаний поплавка удочки, если длина механической волны равна 4 м?
Решение. Скорость волны V (вэ) равна 5,6 метров секунду, длина волны λ (лямбда) равна 4 метрам. Определить период Т (тэ) и частоту волны ν (ню). Запишем формулу для расчета скорости волны. Выразим из данной формулы частоту волны ν (ню). Подставим числовые значения: 5,6 м/с разделить на 4 м. Получим 1,4 Герц. Запишем формулу для расчета периода волны. Период волны (тэ) и частота волны (лямбда) связаны обратно пропорциональной зависимостью. Подставим числовые значения, получим значение периода равное 0,7секунд.
Ответ: частота волны (ню) равна 1,4 Герц, период волны (тэ) равен 0,7 секунды.
Задача
Какая из величин и во сколько раз изменится при переходе звука из воздуха вводу — частота или длина волны? Так как скорость звука в воздухе равна 340 м/с, а в воде 1535 м/с, найдем отношение скоростей в разных средах. Рассчитав, можно сделать вывод о том, что скорость волны больше в воде в 4,5 раза. Между скоростью движения волны V(вэ) и длиной волны λ (лямбда) наблюдается пропорциональная зависимость. Следовательно, длина волны λ в воде больше в 4,5 раза при условии, что частота звуковой волны остается величиной постоянной.
Задача.
На рисунке представлен график механической волны, которая распространяется в воздухе. Используя данные графика, рассчитайте длину данной волны. Период волны Т (тэ) равен 4 секунды; а по условию задачи, волна распространяется в воздухе со скоростью V (вэ), равной 340 м/с. Чтобы определить длину волны λ (лямбда), необходимо скорость волны V (вэ) умножить на период Т (тэ). Подставим числовые значения и получим ответ: длина волны равна 1360 м.
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитораОставить заявку на подбор
Длина звуковой волны – формула
4.1
Средняя оценка: 4.1
Всего получено оценок: 297.
4.1
Средняя оценка: 4.1
Всего получено оценок: 297.
Звук – это механические волны, распространяющиеся в упругих средах, которые могут воспринимать слуховые анализаторы человека. Звук, как и любой другой волновой процесс, имеет ряд характеристик. Рассмотрим такую важную характеристику звука, как длина волны.
Звуковые волны в разных средах
В большинстве случаев мы воспринимаем звук, распространяющийся в воздухе. Воздушная звуковая волна – это ряд распространяющихся в воздухе колебаний плотности – сжатий и разрежений.
То есть, звук представляет собой продольную механическую волну.
Для распространения механической волны необходимо наличие упругой среды, которой является не только воздух. А, значит, звук может распространяться и в других средах – в жидкостях и кристаллах. Однако, упругость жидкостей и кристаллов гораздо выше, чем упругость воздуха, поэтому колебания точек в таких средах среде происходит с гораздо большими внутренними напряжениями. Это приводит к тому, что колебания распространяются намного быстрее.
Длина звуковой волны
Если скорость распространения звука в различных средах различна, а его частота фиксирована, то расстояние между соседними сжатиями или разрежениями будет также различно.
Это расстояние и называется длиной звуковой волны. Поскольку частота и период связаны простой обратной зависимостью, формулу длины звуковой волны можно получить как на основе частоты колебаний, так и на основе периода:
$$\lambda = vT={v\over \nu},$$
где:
Из формулы можно видеть, что длина волны прямо пропорциональна скорости звука в среде.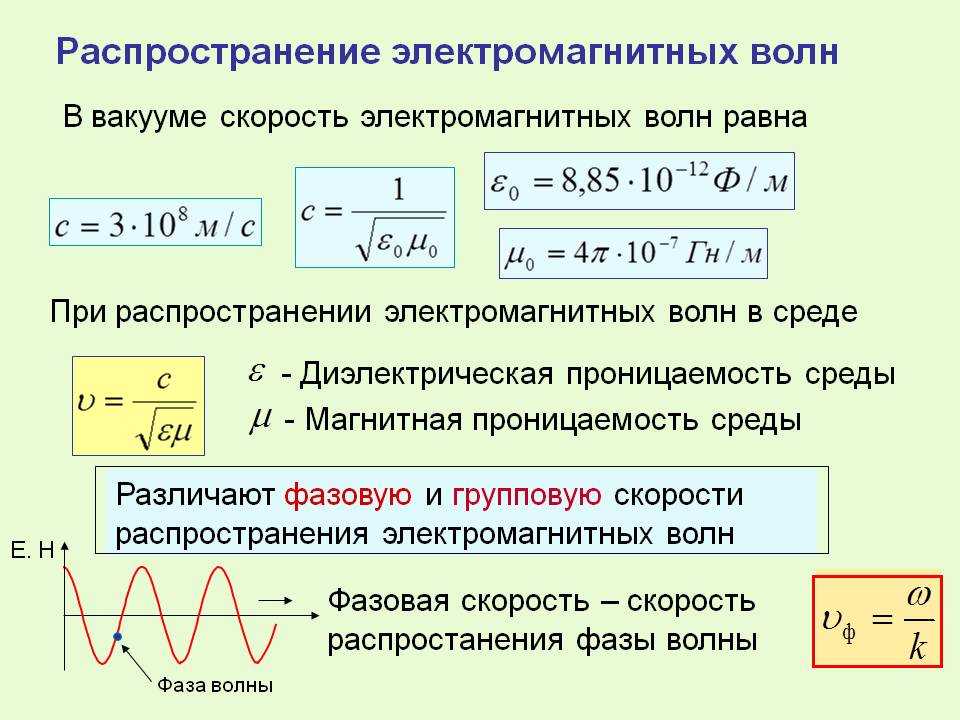
При одной и той же частоте длина волны будет наименьшей в газах при невысоких давлениях, будет больше в жидкостях, и самой большой будет в кристаллах. Например, для частоты 500гц:
Среда | v (м/с) | λ(м) |
Воздух | 330 | 0.66 |
Вода | 3 | |
Металл | 6000 | 12 |
Роль длины звуковой волны
Звуковые волны способны отражаться от границ сред. Это свойство используется в ряде случаев и человеком и Природой. Если в среде есть какие-то неоднородности – то звуковые волны отражаются от них, и по картине отражения можно делать выводы о расположении неоднородностей. Такой процесс называется эхолокацией. Природное использование эхолокации – поведение летучих мышей и дельфинов.
Человек использует эхолокацию в целях дефектоскопии промышленных установок, а также в медицинской практике, для исследования внутренних органов.
Однако, для отражения волны граница между средами должна иметь размеры больше ее длины. Если длина волны будет больше, волна будет просто огибать неоднородность, не отражаясь. Отсюда следует важный вывод, что для обнаружения небольших неоднородностей длина звуковой волны должна быть как можно меньше.
Именно поэтому и человек и Природа для эхолокации использует ультразвук. Малая длина волны ультразвука способствует обнаружению самых мелких неоднородностей.
Что мы узнали?
Звук представляет собой распространяющиеся в среде сжатия и расширения. Длина звуковой волны – это расстояние между ближайшими сжатиями или расширениями. В разных средах длина волны различна, короткие ультразвуковые волны удобны для эхолокации.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.1
Средняя оценка: 4.1
Всего получено оценок: 297.
А какая ваша оценка?
Руководство по изучению скорости волны| Inspirit
Инструменты для творчества скоро появятся, чтобы вдохновить!
Присоединяйтесь к списку рассылки, чтобы узнать, когда мы запустимся.
Физика
Общая физика
Гармоническое движение и волны
Учебное пособие по скорости волн
Джессика
MS-PS4-1
Расстояние, пройденное волной за определенный промежуток времени, называется скоростью волны.
Что такое скорость волны?
Расстояние, которое волна проходит за определенное время, например количество метров, которое волна проходит за секунду, называется скоростью волны.
Защипывание гитарной струны является примером скорости волны.
Если кто-то дернет гитарную струну, кажется, что струны движутся в виде поперечной волны. Хотя звуковая волна представляет собой продольную волну, волна на гитаре поперечная. Частицы в струне движутся перпендикулярно направлению распространения волны.
ФОРМУЛА СКОРОСТИ ВОЛНЫ
Уравнение скорости волны (скорость = длина волны x частота) связывает скорость волны с длиной волны и частотой. Когда длина волны и частота известны, это уравнение можно использовать для расчета скорости волны.
Частота волн — это количество волн, которые движутся в секунду. Кроме того, продолжительность рассчитывается как обратная величина частоты волны. Длина волны — это расстояние между соответствующими точками двух последовательных волн.
ПЕРЕМЕННЫЕ, ВЛИЯЮЩИЕ НА СКОРОСТЬ ВОЛНЫ
- Длина волны
- Скорость
- Расстояние
- Частота
Вышеуказанные четыре переменные влияют на скорость волны.
ЗАВИСИМОСТЬ СРЕДЫ
- Скорость большинства волн зависит от среды, в которой распространяется волна.
- Волны обычно быстрее всего проходят через твердые тела и медленнее всего через газ.
- Это потому, что частицы ближе всего друг к другу в твердом теле, а частицы ближе всего друг к другу в газе.
- Если частицы находятся дальше друг от друга, распределению энергии потребуется больше времени, чтобы пройти через среду от одной частицы к другой.
###Свойства волн
__1. Амплитуда __
Во время волнового движения частицы колеблются вокруг своего среднего положения или положения равновесия, создавая звуковые волны. Максимальное смещение частиц выше или ниже среднего положения называется амплитудой, или можно сказать, что Амплитуда — это максимальная высота выше или ниже среднего положения. Амплитуда обозначается X0, а единицей амплитуды в системе СИ является метр.
__2. Длина волны __
Поперечные волны распространяются в последовательных или последовательных гребнях и впадинах, в то время как продольные волны распространяются в последовательном сжатии и разрежении.
В случае поперечных волн длина последовательной коры и впадины называется ее длиной волны. В то время как в случае продольных волн длина последовательного сжатия и разрежения называется ее длиной волны. Длина волны обозначается греческой буквой лямбда (λ), а ее единицей СИ является метр.
3. Период времени
Чтобы понять концепцию периода времени, мы должны понять концепцию волнового цикла. В случае поперечных волн одна кора и одна впадина образуют один волновой цикл или одно колебание, а в случае продольных волн одно сжатие и одно разрежение образуют один волновой цикл или одно колебание. Общее число волновых циклов зависит от количества корок и впадин в поперечных волнах, тогда как в случае продольных волн оно зависит от числа сжатий и разрежений. Время, за которое колеблющееся тело совершает один волновой цикл или одно колебание, называется периодом времени. Период времени обозначается буквой Т, а его единицей СИ является секунда. Например, если волна завершает свое колебание или один волновой цикл за две секунды, то ее период времени составляет T = 2 секунды.
4. Частота Количество волновых циклов или количество колебаний, совершенных за одну секунду. Частота обозначается f. Единицей частоты в системе СИ является герц. Например, если волна совершает три колебания за одну секунду, то частота этой волны равна трем герцам. Частота обратно пропорциональна периоду времени.
Пример скорости волны
Резюме
- Уравнение скорости волны (скорость = длина волны x частота) связывает скорость волны с длиной волны и частотой.
- Когда известны длина волны и частота, это уравнение можно использовать для расчета скорости волны.
- Частота волны — это количество волн, которые движутся за одну секунду.
- Кроме того, период времени рассчитывается как величина, обратная частоте волны.
- Длина волны — это расстояние между соответствующими точками любых двух последовательных волн.
Часто задаваемые вопросы
В. Что такое скорость волны?
Расстояние, пройденное данной точкой (например, вершиной) волны за данный интервал времени, является скоростью в случае волны.
В. Какова скорость волны с длиной волны 2 м и частотой 1,5 Гц?
Скорость = Длина волны x Частота
Скорость = 2 x 1,5
Скорость = 3 м/сек.
В. Энергия звука распространяется сквозь материю волнами. Звуковые волны распространяются быстрее в воздухе или в воде? Поясните свой ответ.
Жидкости не так плотно упакованы. Газы, с другой стороны, относительно рыхло упакованы. Это позволяет звуку проходить через твердое тело гораздо быстрее, чем через газ. В воде звук распространяется в четыре раза быстрее и дальше, чем в воздухе.
В. Какова формула скорости волны?
Скорость волны = Длина волны x Частота
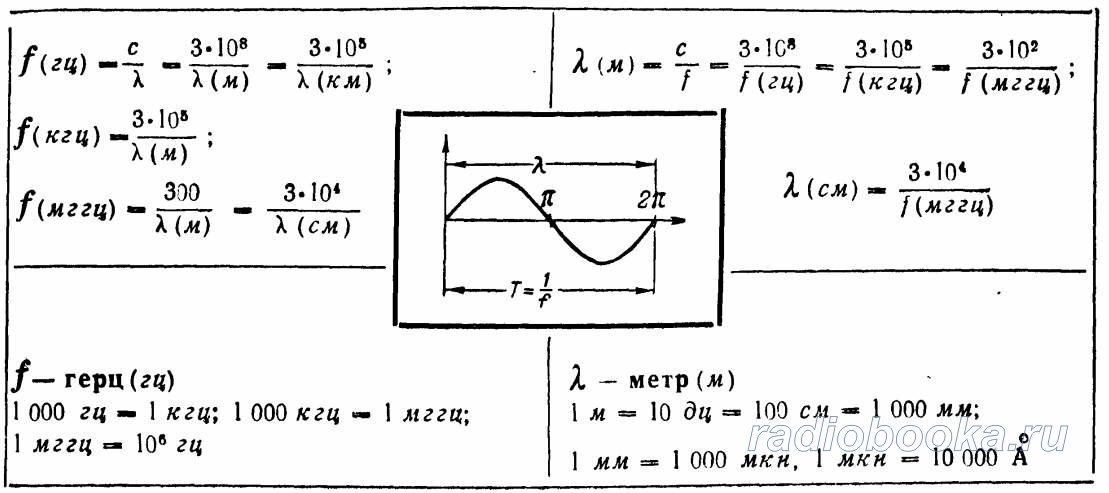
Мы надеемся, что вам понравился этот урок и вы узнали что-то интересное о Скорость волны ! Присоединяйтесь к нашему сообществу Discord, чтобы получить ответы на любые вопросы и пообщаться с другими студентами, такими же, как и вы! Обещаем, это делает учебу намного веселее!0001 17 Физика слуха Звук, как и все волны, распространяется с определенной скоростью и обладает свойствами частоты и длины волны. Вы можете наблюдать прямое свидетельство скорости звука, наблюдая за фейерверком. Вспышка взрыва видна задолго до того, как слышен его звук, что подразумевает как то, что звук распространяется с конечной скоростью, так и то, что он намного медленнее света. Вы также можете непосредственно ощущать частоту звука. Восприятие частоты называется шаг . Длина волны звука непосредственно не ощущается, но косвенные свидетельства обнаруживаются в соотношении размеров музыкальных инструментов с их высотой звука. Зависимость скорости звука, его частоты и длины волны такая же, как и для всех волн: [латекс]\boldsymbol{v_{\textbf{w}}=f\лямбда},[/латекс] , где[latex]\boldsymbol{v_{\textbf{w}}}[/latex]– скорость звука,[latex]\boldsymbol{f}[/latex]– его частота, а[latex]\boldsymbol{ \lambda}[/latex] — его длина волны. Длина волны звука — это расстояние между соседними идентичными частями волны, например, между соседними сжатиями, как показано на рис. 2. Частота такая же, как у источника, и представляет собой количество волн, проходящих через точку на единицу. 2 . Таблица 1 показывает, что скорость звука сильно различается в разных средах. Скорость звука в среде определяется сочетанием жесткости среды (или сжимаемости в газах) и ее плотности. Чем жестче (или менее сжимаема) среда, тем выше скорость звука. Это наблюдение аналогично тому факту, что частота простого гармонического движения прямо пропорциональна жесткости колеблющегося объекта. Чем больше плотность среды, тем медленнее скорость звука. Это наблюдение аналогично тому факту, что частота простого гармонического движения обратно пропорциональна массе колеблющегося объекта. Скорость звука в воздухе мала, потому что воздух сжимаем. Поскольку жидкости и твердые тела относительно жесткие и их очень трудно сжать, скорость звука в таких средах обычно выше, чем в газах. Землетрясения, по существу звуковые волны в земной коре, являются интересным примером того, как скорость звука зависит от жесткости среды. Землетрясения имеют как продольную, так и поперечную составляющую, и они распространяются с разной скоростью. Объемный модуль гранита больше, чем его модуль сдвига. По этой причине скорость продольных волн или волн давления (Р-волн) при землетрясениях в граните значительно выше скорости поперечных или сдвиговых волн (S-волн). Оба компонента землетрясений распространяются медленнее в менее жестком материале, таком как отложения. P-волны имеют скорость от 4 до 7 км/с, а S-волны, соответственно, имеют скорость от 2 до 5 км/с, причем обе они быстрее в более твердом материале. P-волна постепенно опережает S-волну по мере того, как они проходят через земную кору. Время между P- и S-волнами обычно используется для определения расстояния до их источника, эпицентра землетрясения. На скорость звука влияет температура в данной среде. Для воздуха на уровне моря скорость звука равна [латекс]\boldsymbol{v _{\textbf{w}}=(331\textbf{м/с})}[/latex][латекс]\boldsymbol{\sqrt{\frac{T}{273\textbf{ К}}}},[/латекс] , где температура (обозначается как[латекс]\жирныйсимвол{Т})[/латекс]выражается в единицах Кельвина. Скорость звука в газах связана со средней скоростью частиц в газе,[латекс]\жирныйсимвол{v_{\textbf{среднеквадратичное значение}}},[/латекс]и что 9{\circ}\textbf{C}}[/latex] это 343 м/с, увеличение менее чем на 4%. На рис. 3 показано, как летучая мышь использует скорость звука для определения расстояния. Эхо также используется в медицинской визуализации. Одним из наиболее важных свойств звука является то, что его скорость почти не зависит от частоты. Эта независимость, безусловно, верна на открытом воздухе для звуков в слышимом диапазоне от 20 до 20 000 Гц. [латекс]\boldsymbol{v_{\textbf{w}}=f\лямбда}.[/латекс] В данной среде при фиксированных условиях [латекс]\boldsymbol{v _{\textbf{w}}}[/латекс]постоянна, так что существует связь между[латекс]\жирныйсимвол{f}[/латекс] и[латекс]\жирныйсимвол{\лямбда};[/латекс]чем выше частота, тем меньше длина волны. См. рис. 4 и рассмотрим следующий пример. Резюме
Рисунок 1. При взрыве фейерверка световая энергия воспринимается раньше звуковой. Звук распространяется медленнее, чем свет. (кредит: Доминик Алвес, Flickr)
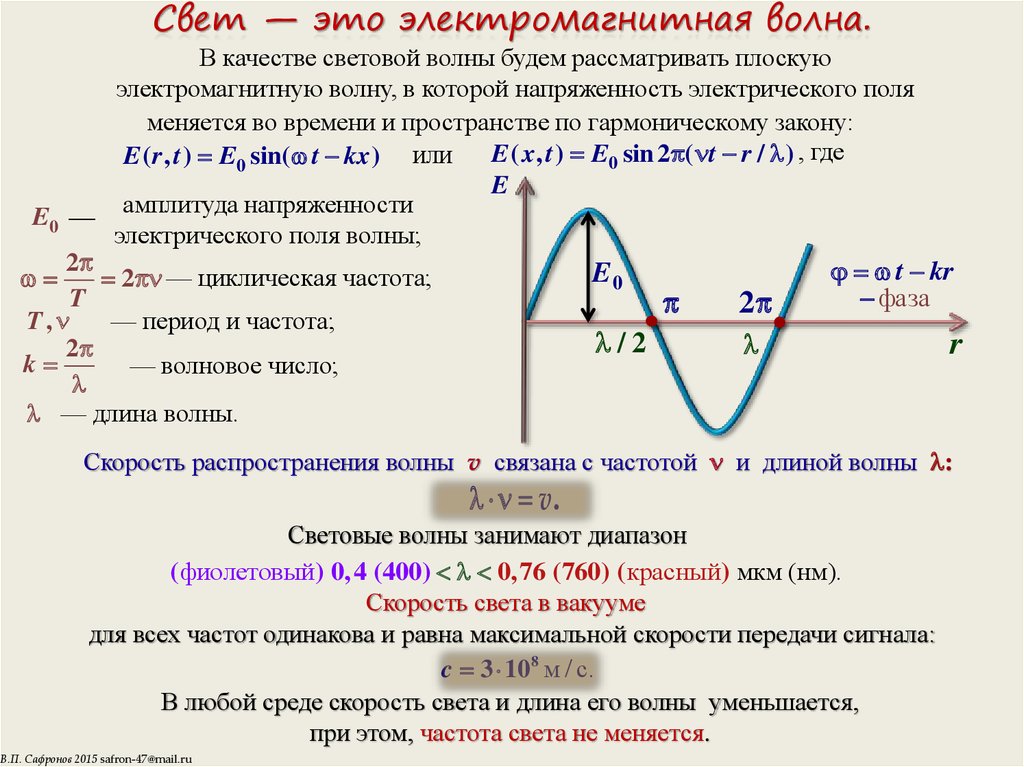Маленькие инструменты, такие как пикколо, обычно издают высокие звуки, в то время как большие инструменты, такие как туба, обычно издают низкие звуки. Высокий тон означает малую длину волны, а размер музыкального инструмента напрямую связан с длиной волны звука, который он производит. Таким образом, небольшой инструмент создает коротковолновые звуки. Аналогичные аргументы утверждают, что большой инструмент создает длинноволновые звуки.
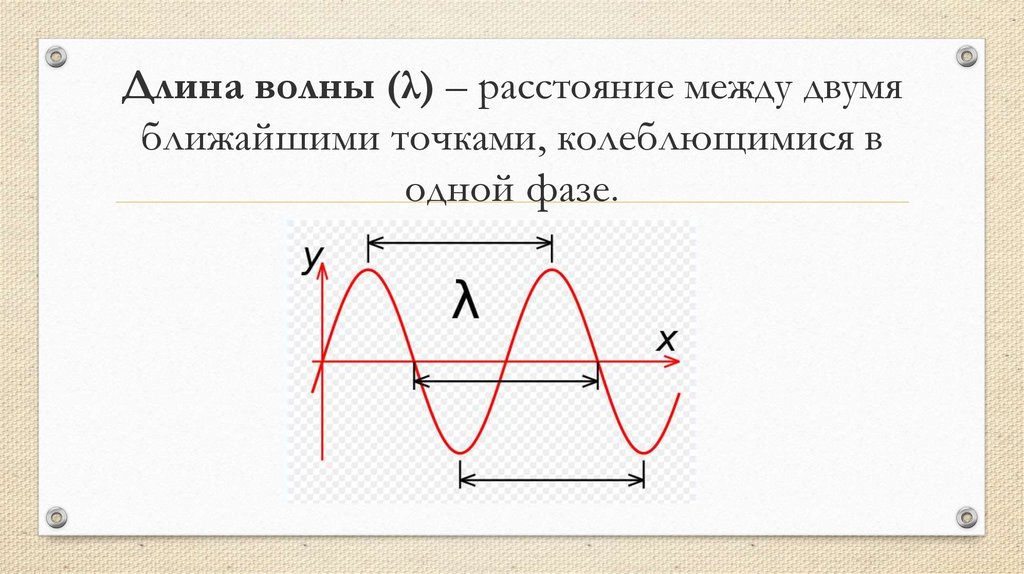время.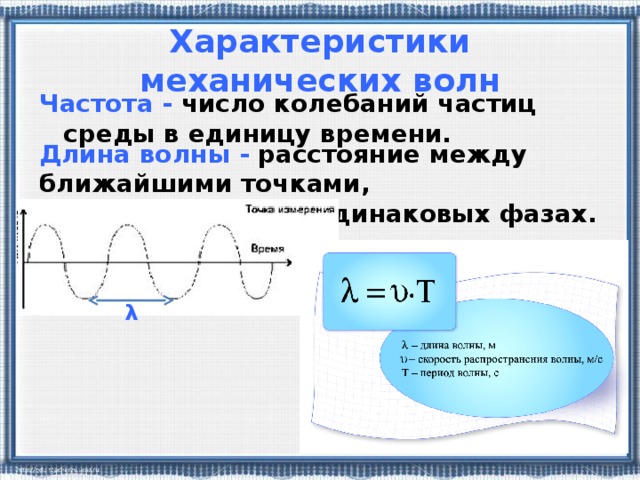
Средний v w (м/с) Газы при 0ºC Воздух 331 Углекислый газ 259 Кислород 316 Гелий 965 Водород 1290 Жидкости при 20ºC Этанол 1160 Меркурий 1450 Вода пресная 1480 Морская вода 1540 Ткань человека 1540 Твердые вещества (продольные или объемные) Вулканизированная резина 54 Полиэтилен 920 Мрамор 3810 Стекло, пирекс 5640 Свинец 1960 Алюминий 5120 Сталь 5960 Таблица 1. 
Скорость звука в различных средах.
Если бы эта независимость не была истинной, вы бы наверняка заметили ее, например, в музыке, которую играет марширующий оркестр на футбольном стадионе. Предположим, что высокочастотные звуки распространяются быстрее — тогда чем дальше вы находитесь от группы, тем больше звук низкочастотных инструментов будет отставать от высокочастотных. Но музыка всех инструментов доносится с ритмом, не зависящим от расстояния, поэтому все частоты должны распространяться почти с одинаковой скоростью. Напомним, что
Здесь низкочастотные звуки излучаются большим динамиком, называемым низкочастотным динамиком, а высокочастотные звуки излучаются маленьким динамиком, называемым твитером. 9{\circ}\textbf{C}}[/latex]воздух. (Предположим, что значения частоты точны до двух значащих цифр.)
Стратегия
Чтобы найти длину волны по частоте, мы можем использовать [латекс]\жирныйсимвол{v_{\textbf{w}}=f\lambda}. [/latex]
Решение
- Определить известные. Значение для[латекс]\жирныйсимвол{v_{\textbf{w}}},[/латекс]задается как
[латекс]\boldsymbol{v _{\textbf{w}}=(331\textbf{м/с})}[/latex][латекс]\boldsymbol{\sqrt{\frac{T}{273\textbf{ К}}}}.[/латекс]
- Преобразуйте температуру в кельвины, а затем введите температуру в уравнение
[латекс]\boldsymbol{v _{\textbf{w}}=(331\textbf{м/с})}[/latex][латекс]\boldsymbol{\sqrt{\frac{303\textbf{K}} {273\textbf{ K}}}}[/latex][latex]\boldsymbol{=348,7\textbf{ м/с}}.[/latex]
- Решите зависимость между скоростью и длиной волны для [латекс]\жирныйсимвол{\лямбда}:[/латекс]
[латекс]\boldsymbol{\lambda\:=}[/латекс][латекс]\boldsymbol{\frac{v _{\textbf{w}}}{f}}.
[/latex] - Введите скорость и минимальную частоту, чтобы получить максимальную длину волны:
[латекс]\boldsymbol{\lambda _{\textbf{max}}\:=}[/latex][латекс]\boldsymbol{\frac{348,7\textbf{м/с}}{20\textbf{Гц}} }[/латекс][латекс]\boldsymbol{=17\textbf{м}}.[/латекс]
- Введите скорость и максимальную частоту, чтобы получить минимальную длину волны:
[латекс]\boldsymbol{\lambda _{\textbf{мин}}=}[/латекс][латекс]\boldsymbol{\frac{348,7\textbf{м/с}}{20 000\textbf{Гц}}}[ /латекс][латекс]\жирныйсимвол{=0,017\textbf{м}=1,7\текстбф{см}}.[/латекс]
[/latex]Обсуждение
Поскольку произведение [латекс]\boldsymbol{f}[/latex], умноженное на [латекс]\boldsymbol{\lambda}[/latex], равно константе, чем меньше[латекс]\boldsymbol{ f}[/latex]есть, тем больше должен быть [латекс]\boldsymbol{\lambda}[/latex], и наоборот.
Скорость звука может изменяться при переходе звука из одной среды в другую. Однако частота обычно остается неизменной, потому что она похожа на возбужденное колебание и имеет частоту исходного источника.
Если [латекс]\boldsymbol{v_{\textbf{w}}}[/latex]изменяется, а [латекс]\boldsymbol{f}[/latex]остается прежним, то длина волны[латекс]\boldsymbol{\lambda} [/latex] должен измениться. То есть, потому что[latex]\boldsymbol{v_{\textbf{w}}=f\lambda}[/latex]чем выше скорость звука, тем больше его длина волны для данной частоты.
Установление связей: домашнее исследование — голос как звуковая волна
Подвесьте лист бумаги так, чтобы верхний край бумаги был зафиксирован, а нижний край мог свободно двигаться. Вы можете приклеить верхний край бумаги к краю стола. Аккуратно подуйте возле края нижней части листа и обратите внимание, как движется лист. Говорите тихо, а затем громче, чтобы звуки касались края нижней части бумаги, и отмечайте, как движется лист. Объясните эффекты.
Зависимость скорости звука[латекс]\boldsymbol{v_{\textbf{w}}},[/latex]его частоты[латекс]\boldsymbol{f},[/latex]и его длины волны[латекс]\ жирныйсимвол{\lambda}[/латекс]равно
[латекс]\boldsymbol{v_{\textbf{w}}=f\лямбда},[/латекс]
, что является одним и тем же соотношением для всех волн.
