Законы кирхгофа 1 и 2 примеры. Первый закон кирхгофа
Большое количество электрических цепей на практике являются сложными. Однако в цепь любого уровня сложности имеет элементы двух простейших видов. Это узлы и замкнутые контуры. Узел — это любая точка разветвления цепи, в которой сошлось три или более проводников, по которым текут токи.
Второе правило (закон) Кирхгофа является следствием обобщенного закона Ома. Так, если в изолированной замкнутой цепи есть один источник ЭДС, то сила тока в цепи будет такой, что сумма падения напряжения на внешнем сопротивлении и внутреннем сопротивлении источника будет равна сторонней ЭДС источника. Если источников ЭДС несколько, то берут их алгебраическую сумму. Знак ЭДС выбирается положительным, если при движении по контуру в положительном направлении первым встречается отрицательный полюс источника. (За положительное направление обхода контура принимают направление обхода цепи либо по часовой стрелке, либо против нее).
Формулировка второго закона Кирхгофа
Произведение алгебраической величины силы тока (I) на сумму вешних и внутренних сопротивлений всех участков замкнутого контура равно сумме алгебраических значений сторонних ЭДС () рассматриваемого контура:
Каждое произведение определяет разность потенциалов, которая существовала бы между концами соответствующего участка, если бы ЭДС в нем была равно нулю. Величину называют падением напряжения, которое вызывается током.
Величину называют падением напряжения, которое вызывается током.
Второй закон Кирхгофа иногда формулируют следующим образом:
Для замкнутого контура сумма падений напряжения есть сума ЭДС в рассматриваемом контуре.
Правила Кирхгофа служат для того, чтобы составить систему уравнений, позволяющих найти силу тока для сложной цепи. Направление положительного обхода выбирают для всех контуров одинаковым. При составлении уравнений, используя правила Кирхгофа необходимо внимательно следить за расстановкой знаков токов и ЭДС.
Система уравнений, которая получается при использовании первого и второго закона Кирхгофа является полной и дает возможность отыскать все токи. При составлении уравнений, используя правила Кирхгофа, надо следить за тем, чтобы новое уравнение имело хотя бы одну величину, которая еще не вошла в предыдущие уравнения. Кроме того, необходимо, чтобы система уравнений имела число уравнений равное количеству неизвестных.
Второй закон Кирхгофа следует из того, что электрическое напряжение по замкнутому контуру равно нулю, то есть это правило является следствием основного свойства электростатического поля, которое заключается в том, что работа поля при движении заряда по замкнутой траектории равна нулю.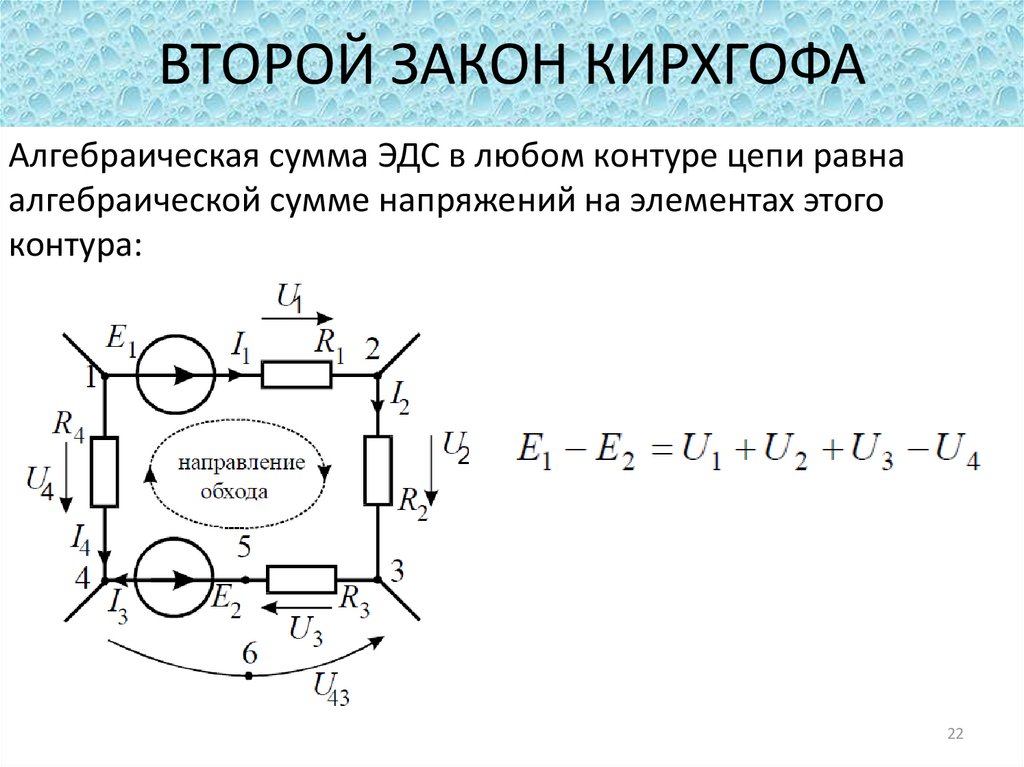
Примеры решения задач
ПРИМЕР 1
| Задание | Примените второе правило Кирхгофа для рис.1 и запишите уравнения рассмотрев контуры: ABDCA; ABFEA |
| Решение | Направление обхода контура зададим при помощи последовательности букв в его обозначении. Так для контура имеем направление обхода по часовой стрелке. Рассматривая эту цепь в дальнейшем направления обхода контуров изменять нельзя. Положительными будем считать токи, которые совпадают с направлением обхода контура. Для контура со знаком плюс будут во второе правило Кирхгофа входить ток: , со знаком минус ток . В соответствии с правилом выбора знака ЭДС, сформулированном в теоретической части, в рассматриваемый контур и будут положительными. Уравнение, соответствующее второму правилу Кирхгофа для контура запишем как: Рассмотрим контур . Ток согласно избранным нами направлениям будет положительным во втором законе Кирхгофа, то — отрицательным. |
| Ответ | Для контура . Для контура получили: |
ПРИМЕР 2
| Задание | Пусть n одинаковых источников ЭДС соединены последовательно и замкнуты на внешнюю цепь (рис.2). Чему равна ЭДС данной цепи, если ЭДС каждого источника равна , внутренне сопротивление каждого источника ? Сопротивление внешней цепи R. |
В цепях, состоящих из последовательно соединенных источника и приемника энергии, соотношения между током, ЭДС и сопротивлением всей цепи или, между напряжением и сопротивлением на каком-либо участке цепи определяется законом Ома .
На практике в цепях, токи, от какой-либо точки, идут по разным путям.
В замкнутой электрической цепи ни в одной ее точке не могут скапливаться электрические заряды так, как это вызвало бы изменение потенциалов точек цепи.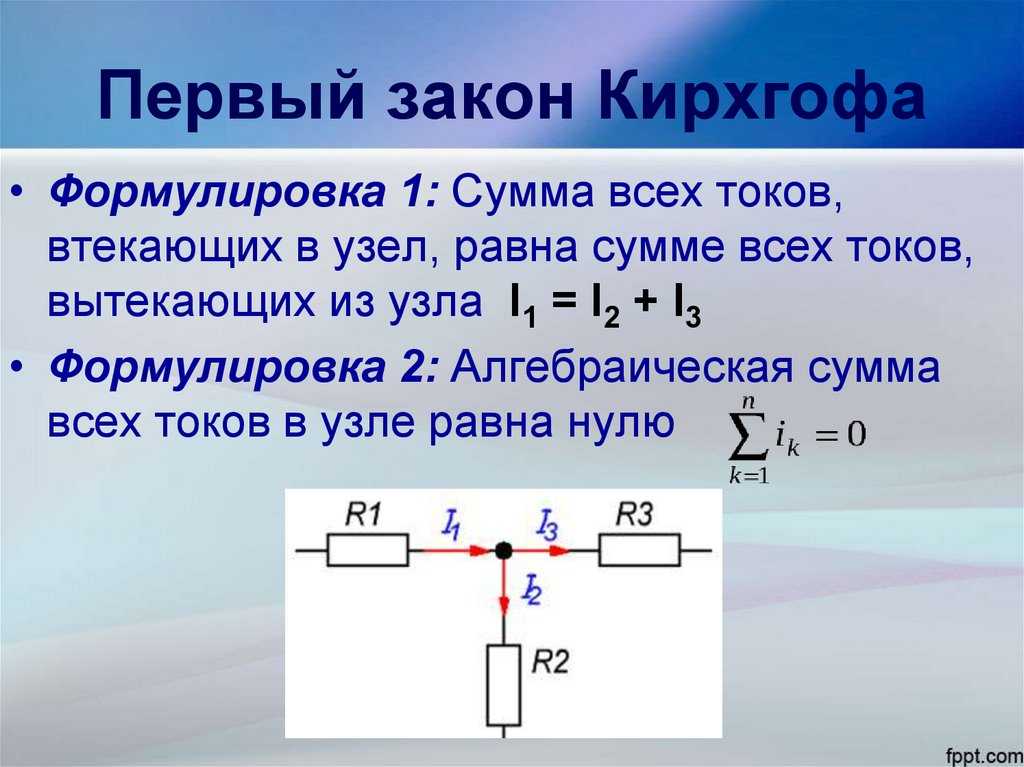 Поэтому электрические заряды притекающие к какому-либо узлу в единицу времени, равны зарядам, утекающим от этого узла за ту же единицу.
Поэтому электрические заряды притекающие к какому-либо узлу в единицу времени, равны зарядам, утекающим от этого узла за ту же единицу.
Разветвлённая цепь.
В узлеА цепь разветвляется на четыре ветви, которые сходятся в узел В .
Обозначим токи в неразветвленной части цепи —
I1 , I2 , I3 , I4 .
У этих токов в такой цепи будет соотношение:
I = I1+I2+I3+I4;
Cумма токов, подходящих к узловой точке электрической цепи,
равна сумме токов, уходящих от этого узла.
При параллельном соединении резисторов ток проходит по четырем направлениям, что уменьшает общее сопротивление или увеличивает общую проводимость цепи, которая равна сумме проводимостей ветвей.
Обозначим силу тока в неразветвленной ветви буквойI .
Силу тока в отдельных ветвях соответственно I1
Напряжение между точками A и B — U .
Общее сопротивление между этими точками — R .
По закону Ома напишем:
I = U/R ; I1 = U/R1 ; I2 = U/R2 ; I3 = U/R3 ; I4 = U/R4 ;
Согласно первому закону Кирхгофа:
I = I1+I2+I3+I4 ; или U/R = U/R1+U/R2+U/R3+U/R4 .
Сократив обе части полученного выражения на U получим:
1/R = 1/R1+1/R2+1/R3+1/R4
Cоотношение для любого числа параллельно соединенных резисторов.
В случае, если в цепи содержится два параллельно соединенных резистора
R1 и R2 , то можно написать равенство:
1/R =1/R1+1/R2 ;
Из этого равенства найдем сопротивление R , которым можно заменить два параллельно соединенных резистора:
Полученное выражение имеет большое практическое применение.
Благодаря этому закону производятся расчёты электрических цепей.
В замкнутом контуре электрической цепи сумма всех эдс равна
сумме падения напряжения в сопротивлениях того же контура.
E1 + E2 + E3 +…+ En = I1R1 + I2R2 + I3R3 +…+ InRn . При составлении уравнений выбирают направление обхода цепи и произвольно задаются направлениями токов.Если в электрической цепи включены два источника энергии, эдс которых совпадают по направлению, т. е. согласно изо1, то эдс всей цепи равна сумме эдс этих источников,
т. е.
E = E1+E2 .Если же в цепь включено два источника, эдс которых имеют противоположные направления, т. е. включены встречно изо2, то общая эдс цепи равна разности эдс этих источников
Е = Е1-Е2 .
При последовательном включении в электрическую цепь нескольких источников энергии с различным направлением эдс общая эдс равна сумме эдс всех источников. Складывая эдс одного направления, берут со знаком плюс, а эдс противоположного направления — со знаком минус.
В нашем случае, при встречном включении, положения щупов пришлись на противоположную полярность источника большего напряжения, поэтому на приборе отрицательный знак.
Благодаря этим законам производятся расчёты электрических цепей.
Существует несколько методов расчёта, один из них «Метод узловых напряжений»
Два приема, которые применяют для упрощения процесса составления уравнений, необходимых при расчетах сложных разветвленных цепей постоянного тока называют законами (вернее было бы сказать правилами) Кирхгофа. Прежде чем перейти к самим правила Кирхгофа введем два необходимых определения.
Разветвлёнными цепями названы цепи, которые имеют несколько замкнутых контуров, несколько источников электродвижущей силы (ЭДС).
Узлом разветвлённой цепи называют точку, в которой сходятся три или более проводников с токами.
Первый закон (правило) Кирхгофа, простыми словами
Первое правило Кирхгофа называют правилом узлов, так как оно касается сил токов в узах цепи. Словесно первый закон Кирхгофа формулируют следующим образом: Алгебраическая сумма сил токов в узле равна нулю. В виде формулы это правило запишем как:
С каким знаком сила тока будет входить в сумму (1), зависит от произвольного выбора. Но при этом следует считать, что все входящие в узел токи имеют одинаковые знаки, а все исходящие из узла токи имеют противоположные входящим, знаки. Пусть все входящие токи мы примем за положительные, тогда все исходящие их этого узла токи будут отрицательными. Если направления токов изначально не заданы, то их задают произвольно. Если при расчетах получено, что сила тока отрицательна, значит, что верное направление тока является противоположным тому, которое предполагали.
Первый закон Кирхгофа является следствием закона сохранения заряда. Если в цепи текут только постоянные токи, то нет в этой цепи точек, которые накапливали бы заряд. Иначе токи не были бы постоянными.
Иначе токи не были бы постоянными.
Первый закон Кирхгофа дает возможность составить независимое уравнение, при наличии в цепи k узлов.
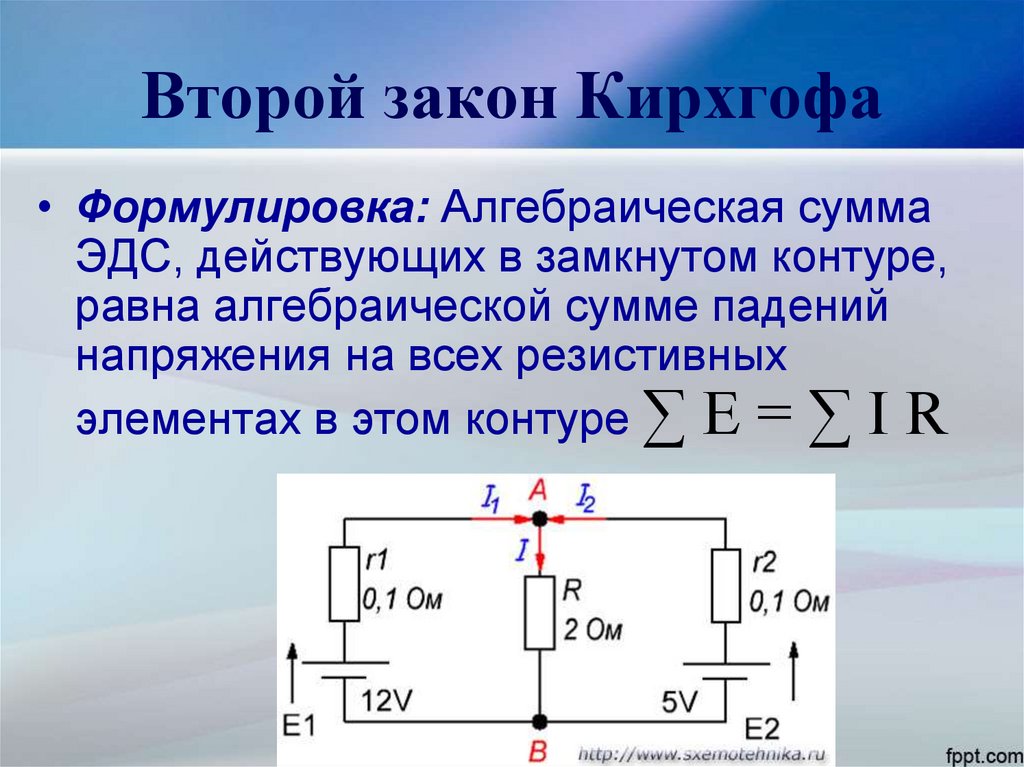
Второй закон (правило) Кирхгофа, простыми словами
Второй закон Кирхгофа относят к замкнутым контурам, поэтому его называют правилом контуров. Согласно этому правилу суммы произведений алгебраических величин сил тока на внешние и внутренние сопротивления всех участков замкнутого контура равны алгебраической сумме величин сторонних ЭДС (), входящих в рассматриваемый контур. В виде формулы второй закон Кирхгофа запишем как:
где величину часто называют падением напряжения; N — число рассматриваемых участков избранного контура. При использовании второго правила Кирхгофа важно помнить о направлении обхода контура. Как это делается? Произвольно выберем направление обхода рассматриваемого в задаче контура (по часовой стрелке или против нее). В случае совпадения направления обхода контура с направлением силы тока в рассматриваемом элементе, величина входит в (2) со знаком плюс. ЭДС войдет в сумму правой части выражения (2) со знаком плюс, если при движении вдоль контура, в соответствии с избранным направлением обхода первым мы встречаем отрицательный полюс источника ЭДС.
ЭДС войдет в сумму правой части выражения (2) со знаком плюс, если при движении вдоль контура, в соответствии с избранным направлением обхода первым мы встречаем отрицательный полюс источника ЭДС.
Используя второе правило Кирхгофа можно получить независимые уравнения для тех контуров цепи, которые не получены наложением уже описанных контуров. Количестов независимых контуров (n) равно:
где p — количество ветвей в цепи; k — число узлов.
Количество независимых уравнений, которые дадут оба правила Кирхгофа равно (s):
Делаем вывод о том, что число независимых уравнений будет равно числу разных токов в исследуемой цепи.
Второе правило Кирхгофа — следствие закона Ома. В принципе любую цепь можно рассчитать, применяя только закон Ома и закон сохранения заряда. Правила Кирхгофа являются всего лишь упрощающими приемами для решения задач, рассматривающих цепи постоянного тока.
Используя правила Кирхгофа для составления уравнений необходимо внимательно следить за расстановкой знаков токов и ЭДС.
Первое и второе правила Кирхгофа дают метод расчета цепи, то есть используя их можно найти все токи в цепи, если известны все ЭДС и сопротивления, в том числе и внутренние сопротивления источников.
Примеры решения задач
ПРИМЕР 1
| Задание | Как следует записать уравнение для токов, используя первое правило Кирхгофа для узла А, изображенного на рис.1 |
| Решение | Прежде чем применять первое правило Кирхгофа определим для себя, что положительными будут токи, которые входят в узел А, тогда выходящие из этого узла токи мы должны будем записать в первом правиле Кирхгофа со знаком минус. Из рис. 1 в узел А входят токи: Из узла А выходят токи: Тогда согласно правилу узлов имеем: |
| Ответ |
ПРИМЕР 2
| Задание | Составьте систему независимых уравнений, используя правила Кирхгофа, которая позволит найти все токи в цепи, представленной на рис. 2, если известны все ЭДС и все сопротивления (они указаны на рисунке)? 2, если известны все ЭДС и все сопротивления (они указаны на рисунке)? |
| Решение | Направления токов выберем произвольно, обозначим их на рис.1. Пусть через сопротивление течет ток . На рис.2 видно, что в нашей цепи два узла. Это точки A и С. Запишем первое правило Кирхгофа для узла А: |
При расчете электрических цепей нам часто приходится встречаться с цепями, которые образуют замкнутые контуры. В состав таких контуров, помимо сопротивлений, могут входить еще электродвижущие силы, то есть источники напряжений. На рисунке 1 представлен участок сложной электрической цепи. Задана полярность всех (э. д. с.). Произвольно выбираем положительные направления токов. Обходим контур от точки А в произвольном направлении, например по часовой стрелке. Рассмотрим участок АБ . На этом участке происходит падение потенциала (ток идет от точки с высшим потенциалом к точке с низшим потенциалом).
На участке АБ :
φ А + E 1 – I 1 × r 1 = φ Б .
На участке БВ :
φ Б – E 2 – I 2 × r 2 = φ В .
На участке ВГ :
φ В – I 3 × r 3 + E 3 = φ Г .
На участке ГА :
φ Г – I 4 × r 4 = φ А .
Складывая почленно четыре приведенных уравнения, получим:
φ А + E 1 – I 1 × r 1 + φ Б – E 2 – I 2 × r 2 + φ В – I 3 × r 3 + E 3 + φ Г – I 4 × r 4 = φ Б + φ В + φ Г + φ А
E 1 – I 1 × r 1 – E 2 – I 2 × r 2 – I 3 × r 3 + E 3 – I 4 × r 4 = 0.
Перенеся произведения I × r в правую часть, получим:
E 1 – E 2 + E 3 = I 1 × r 1 + I 2 × r 2 + I 3 × r 3 + I 4 × r 4 .
В общем виде
Это выражение представляет собой . Формула второго закона Кирхгофа показывает, что во всяком замкнутом контуре алгебраическая сумма э. д. с. равна алгебраической сумме падений напряжений. Бывают случаи, когда в замкнутом контуре отсутствуют источники э. д. с., тогда применимо другое определение второго закона Кирхгофа – алгебраическая сумма падений равна нулю.
Видео 1. Второй закон Кирхгофа
Рассмотрим простой замкнутый контур (рисунок 2).
| Рисунок 2. Простой замкнутый контур |
По второму закону Кирхгофа
E = I × r 0 + I × r = I × (r 0 + r ),
| I 3 = I 1 + I 2 . | (3) |
Имеем три уравнения с тремя неизвестными. Решая их, находим величину и направление токов. Подставляя значение тока I 3 из уравнения (3) в уравнение (1), получим:
Подставляя значение тока I 3 из уравнения (3) в уравнение (1), получим:
6 = 2 × I 1 + 5 × I 1 + 5 × I 2 ;
Сложим уравнения для двух контуров почленно:
(6 = 7 × I 1 + 5 × I 2) + (2 = I 1 – 2 × I 2)
(12 = 14 × I 1 + 10 × I 2) + (10 = 5 × I 1 – 10 × I 2).
Сложив два последних уравнения, имеем:
22 = 19 × I 1 , откуда I 1 = 1,156 А,
подставляем значение I 1 в уравнение (1):
6 = 2 × 1,156 + 5 × I 3 ,
Подставляем значение I 1 в уравнение (2):
2 = 1,156 – 2 × I 2 ,
Знак минус показывает, что действительное направление тока I 2 обратно принятому нами направлению.
Основные законы электротехники. Теоретические основы.
Основные законы
Закон Ома
В популярной форме закон можно сформулировать следующим образом:
чем выше напряжение при одном и том же сопротивлении, тем выше сила тока и, в то же время, чем больше сопротивление участка цепи при одном и том же напряжении, тем меньше сила тока, протекающая через него.
 Георг ОмЗакон Ома для участка цепи гласит: ток прямо пропорционален напряжению и обратно пропорционален сопротивлению. Закон Ома для участка цепи записывается следующей формулой: I = U/R.
Георг ОмЗакон Ома для участка цепи гласит: ток прямо пропорционален напряжению и обратно пропорционален сопротивлению. Закон Ома для участка цепи записывается следующей формулой: I = U/R. В настоящее время невозможно себе представить любой самый элементарный расчет основных электрических величин для любой цепи без использования закона Ома.
Закон Ома для полной цепи добавляет понятие электродвижущей силы (ЭДС). ЭДС — это все, что создает электрический ток, сила, которая толкает электроны в одном направлении в течение продолжительного времени. Это могут быть какие-либо химические элементы питания, наподобие батареек и аккумуляторов. Каждый источник электродвижущей силы обладает своим внутренним сопротивлением RвнЕсли мы присоединим к нашему источнику нагрузку
Rн, то у нас цепь станет замкнутой и в цепи будет течь токА на внутреннем сопротивлении упадет какое-то напряжение, в результате у нас получился делитель напряжения, так как
Rн также имеет какое-то свое сопротивление. По закону Ома, чем больше сила тока в цепи, тем больше будет падение напряжения на внутреннем сопротивлении Rвн.
По закону Ома, чем больше сила тока в цепи, тем больше будет падение напряжения на внутреннем сопротивлении Rвн.Из закона Ома для участка цепи получаем, что
URвн= IRвнUн= IRнзапишем далее
E = URвн + URнE = IRвн + IRн = I(Rвн +Rн)I = E/(Rвн +Rн)Последнее выражение и есть
закон Ома для полной цепиЗакон Кирхгофа по току
Сумма токов, втекающих в точку, равна сумме токов, вытекающих из нее (сохранение заряда).
 Иногда это правило называют законом Кирхгофа для токов. Инженеры любят называть такую точку схемы узлом. Из этого правила вытекает следствие: в последовательной цепи (представляющей собой группу элементов, имеющих по два конца и соединенных этими концами один с другим) ток во всех точках одинаков.Густав Кирхгоф
Иногда это правило называют законом Кирхгофа для токов. Инженеры любят называть такую точку схемы узлом. Из этого правила вытекает следствие: в последовательной цепи (представляющей собой группу элементов, имеющих по два конца и соединенных этими концами один с другим) ток во всех точках одинаков.Густав КирхгофЗакон Кирхгофа для напряжений
При параллельном соединении элементов напряжение на каждом из элементов одинаково. Иначе говоря, сумма падений напряжения между точками
А и В , измеренная по любой ветви схемы, соединяющей эти точки, одинакова и равна напряжению между точками А и В .Иногда это правило формулируется так: сумма падений напряжения в любом замкнутом контуре схемы равна нулю (при отсутствии ЭДС).
При присутствии в замкнутой цепи ЭДС по закону Кирхгофа алгебраическая сумма (с учетом знака) падений напряжений на всех ветвях любого замкнутого контура цепи, равна алгебраической сумме ЭДС ветвей этого контура.

ЭДС, создающие ток в контуре, направление которого совпадает с направление обхода контура записываются со знаком «+», в противном случае ЭДС записываются со знаком «-». Напряжения, падающие на элементах цепи записываются со знаком «+», если ток, протекающий через эти элементы совпадает по направлению с обходом контура, в противном случае напряжения записываются со знаком «-».
Закон Джоуля-Ленца
Эмилий ЛенцЗависимость тепловой энергии от силы тока в проводнике определяется по
закону Джоуля—Ленца. Сформулирован этот закон был в 1841 году английским учёным Д. Джоулем и совершенно отдельно от него в 1842 году известным русским физиком Э. Ленцем. Поэтому он получил своё двойное название — закон Джоуля – Ленца.При прохождении электрического тока по проводнику количество тепла, выделяемого током в проводнике, прямо пропорционально силе тока, взятой во второй степени, величине сопротивления проводника и времени действия тока.
 Джеймс Джоуль
Джеймс ДжоульПри столкновении электронов с молекулами расходуется энергия, которая превращается в тепло.
Любое движение, при котором преодолевается сопротивление, требует затраты определенной энергии.
закон
Джоуля—Ленца можно записать следующим образом: Q = I2Rt,где
Q (Дж) — количество теплоты, создаваемое током,I — ток, протекающий по проводнику,R — сопротивление проводника,t — время, в течение которого ток протекал по проводнику,Джоуля-Ленца влияет на
выбор проводов для цепей. Потому что при неправильном подборе проводов возможен сильный нагрев проводника, а также его возгорание. Это происходит, когда сила тока превышает предельно допустимые значения и выделяется слишком много энергии.Чрезмерный нагрев проводников с током и электрооборудования допускать нельзя.
 Опасен сильный перегрев при коротких замыканиях проводов, когда по проводниках могут протекать достаточно большие токи.
Опасен сильный перегрев при коротких замыканиях проводов, когда по проводниках могут протекать достаточно большие токи.Вывод второго закона Кирхгофа
Мы можем решить простые электрические цепи, применяя закон Ома, то есть
В = IR
Для не слишком сложных цепей мы разрешаем это, используя принцип сохранения энергии или определение разности потенциалов/напряжения между двумя точками в цепи.
Мы рассчитываем сопротивление и разность потенциалов по закону Ома в простых цепях. Но на практике в реальном времени мы сталкиваемся со сложными цепями, включающими множество сопротивлений и несколько источников ЭДС. В таких случаях мы не можем легко определить эффективное сопротивление и ЭДС по закону Ома.
Густав Роберт Кирхгоф дал два правила, известные в его честь как правила Кирхгофа, для лучшего понимания цепей и их эффективного разрешения. Эти правила воплощают принцип сохранения зарядов и энергии.
Законы Кирхгофа о цепях
Прежде чем мы сформулируем эти правила, мы определим следующие термины, которые являются фундаментальными для теории цепей и необходимы в этой связи для удобного понимания электрических цепей. Цепь – это точка, в которой электрически соединены три или более проводников. Соединение также называют узлом или точкой ветвления.
Петля: Петля — это замкнутый путь в электрической цепи. Его еще называют сеткой.
Узел: Узел — это точка на схеме соединения двух или более элементов схемы. (Узел может быть или не быть узлом, но узел будет узлом.)
1-й закон Кирхгофа/Правило тока/Теорема о соединении:
Алгебраическая сумма всех токов, протекающих через любое соединение, равна нулю. или ноль.
То есть
∑I = 0
Кроме того, сумма токов, входящих в любое соединение (∑I)in, должна равняться сумме электрических токов, выходящих из этого соединения (∑I)out.
Условное обозначение:
Токи, текущие к узлу, равны +ve. Токи, оттекающие от соединения, отрицательные, -ve.
Второе правило Кирхгофа/Правило напряжения/Теорема о контуре:
Алгебраическая сумма разности потенциалов, возникающая при обходе замкнутого контура, равна нулю.
То есть ∑V = 0
Этот закон называется правилом напряжения или теоремой о петле.
Правила знаков:
a. Когда мы проходим через источник в направлении – к +, ЭДС считается положительной. Когда мы перемещаемся от + к -, ЭДС отрицательна.
б. Когда мы проходим через резистор в том же направлении, что и предполагаемый ток, напряжение отрицательное, и наоборот.
Второе правило Кирхгофа/Второй закон Расчет/вывод
При применении этого правила человек начинает с точки на петле и идет по ней, чтобы снова достичь начальной или начальной точки. Это движение может быть как по часовой, так и против часовой стрелки.
Это движение может быть как по часовой, так и против часовой стрелки.
Здесь при движении по петле любое встречающееся падение потенциала принимается за положительное, а любое возрастание потенциала за отрицательное. Чистая сумма всех этих разностей потенциалов приведет к нулю.
На рисунке показана петля цепи ABCDEFA. Поскольку мы начинаем с А и идем по петле по часовой стрелке, чтобы достичь начальной точки А, мы получаем следующие разности потенциалов:
Va – Vb = i1R1
Vb – Vc = i2R2
Vc – Vd = -E1
Vd – Ve =i3R3
Ve – Vf = – i4R4
Vb – Va0 = E2 90,002 Складываем все эти 90,002
i1R1 + i2 R2 -E1 + i3R3 – i4R4 + E2 = 0.
Закон петли следует непосредственно, потому что электростатическая сила является консервативной силой в природе и работа, которую она совершает на любом замкнутом пути, равна нулю.
Применение законов цепей
Законы Кирхгофа лежат в основе теории цепей и используются для расчета значений тока, разности потенциалов (напряжения) и внутреннего сопротивления в цепи постоянного тока (постоянного тока).

Мы можем найти применение закона Кирхгофа полезным для определения номинала неизвестных резисторов в цепи, используя принцип моста Уитстона и измерительного моста.
Ограничения законов Кирхгофа
Принцип закона Кирхгофа, то есть KCL (закон тока Кирхгофа) и KVL (закон напряжения Кирхгофа), несовместим с цепями переменного тока (AC) более высоких частот.
Закон Кирхгофа о напряжении больше не остается согласованным в переменном магнитном поле, потому что изменяющееся магнитное поле влечет за собой изменяющееся электрическое поле (из закона Фарадея), которое для замкнутого контура является неконсервативным. Следовательно, линейный интеграл электрического поля не равен нулю, а ведет себя несовместимо с KVL или законом напряжения Кирхгофа.
Заключение
Эти фундаментальные правила теории цепей позволяют нам измерять различные электрические величины с помощью моста Уитстона, измерительного моста или потенциометра.
Правила Кирхгофа
∑I = 0 (правило соединения)
Это следует принципу сохранения заряда.
∑V = 0 (правило цикла)
Это следует принципу сохранения энергии.
Видео с вопросами: Использование законов Кирхгофа для расчета тока в цепи
Стенограмма видео
Рассмотрим данную цепь. Каково значение 𝐼? (A) Девять ампер, (B) шесть ампер, (C) 4,5 ампера, (D) три ампера.
В этом вопросе мы представлены
со следующей схемой, и мы хотим рассчитать значение тока 𝐼
обозначены на схеме. Чтобы ответить на этот вопрос, мы будем
использовать законы Кирхгофа. Напомним, что первый закон Кирхгофа
утверждает, что сумма токов в переходе или узле в цепи должна быть
то же самое, что сумма токов из узла или узла.
Обозначим принципиальную схему с токами в цепи. Мы видим, что текущий 𝐼 входит в узел, выделенный синим, а токи 𝐼 один и 𝐼 два выходят узла, выделенного синим цветом. Таким образом, с помощью Кирхгофа первый закон в этом узле, мы находим, что 𝐼 равно 𝐼 один плюс 𝐼 два. Нам дано значение 𝐼 один. Итак, если мы можем узнать значение текущие 𝐼 два, тогда мы сможем вычислить значение 𝐼.
Чтобы найти значение 𝐼 два, мы
будем использовать второй закон Кирхгофа. Напомним, что второй закон Кирхгофа
утверждает, что сумма разности потенциалов на каждом компоненте в петле равна
равен нулю. Рассмотрим первый цикл, который
мы выделили в схеме. Мы можем обозначить потенциал
разница на пятиомном резисторе равна 𝑉 𝑅 единице, и мы можем обозначить потенциал
разница на резисторе 10 Ом как 𝑉 𝑅 два. Затем, применяя метод Кирхгофа
Второй закон цикла один, мы находим, что 𝑉 𝑅 один плюс 𝑉 𝑅 два равно нулю.
Затем, применяя метод Кирхгофа
Второй закон цикла один, мы находим, что 𝑉 𝑅 один плюс 𝑉 𝑅 два равно нулю.
Мы можем получить выражения для 𝑉 𝑅 один и 𝑉 𝑅 два по закону Ома. Напомним, что закон Ома может быть записывается как 𝑉 равно 𝐼𝑅, где 𝑉 — разность потенциалов, 𝐼 — ток, 𝑅 — сопротивление. Нам также нужно использовать некоторый знак условности при использовании второго закона Кирхгофа. Когда петля проходит через резистора в том же направлении, что и ток, член 𝐼𝑅 отрицателен, потому что ток идет в сторону уменьшения потенциала. Когда петля проходит через резистора в направлении, противоположном току, член 𝐼𝑅 положительный, потому что это означает увеличение потенциала.
Теперь мы можем применить закон Ома. Начнем с пятиомного
резистор. Ток через пятиомный
Резистор — это ток 𝐼, который, как нам сказали, имеет значение три ампера. Заметим также, что цикл проходит
через резистор в том же направлении, что и ток, поэтому наш член 𝐼𝑅 должен быть
отрицательный. Применяя закон Ома, находим
что разность потенциалов на пятиомном резисторе 𝑉 𝑅 единица равна
минус три ампера на пять ом равно минус 15 вольт.
Заметим также, что цикл проходит
через резистор в том же направлении, что и ток, поэтому наш член 𝐼𝑅 должен быть
отрицательный. Применяя закон Ома, находим
что разность потенциалов на пятиомном резисторе 𝑉 𝑅 единица равна
минус три ампера на пять ом равно минус 15 вольт.
Далее рассмотрим 10-омный
резистор. Ток через 10 Ом
резистор ток 𝐼 два. Заметим на этот раз, что петля
проходит через резистор в направлении, противоположном току, поэтому наш 𝐼𝑅
срок положительный. Разность потенциалов на
Резистор 10 Ом 𝑉 𝑅 два будет равно 𝐼 два раза по 10 Ом. Итак, подставив значения 𝑉
𝑅 один и 𝑉 𝑅 два в уравнение, которое мы получили из второго закона Кирхгофа для
петля один, у нас есть уравнение минус 15 вольт плюс 10 Ом умножить 𝐼 два равно
нуль. Добавление 15 вольт к обеим сторонам
уравнение, мы получаем 10 Ом умножить на 𝐼 два равно 15 вольт.




