46. Вращающий момент двигателя постоянного тока

Вращающий момент двигателя постоянного тока создается взаимодействием магнитного потока индуктора Ф с током якоряI_я. При числе параллельных ветвей обмотки якоря 2а сила тока в каждой из них будет равна По формуле вращающий момент, создаваемый каждым стержнем обмотки

где D – диаметр якоря и l – активная длина стержня в м. Полный электромагнитный вращающий момент двигателя в ньютонометрах получим, помножив т на число стержней, в обмотке N:

Обозначив полюсное деление через τ, можем написать:

и окончательно

где постоянный коэффициент 

Вращающий момент двигателя постоянного тока пропорционален произведению магнитного потока индуктора на ток якоря.

Механическая мощность на валу двигателя, согласно равенству , выразится формулой

47 Основной характеристикой для оценки электромеханических свойств электродвигателя является механическая характеристика, представляющая собой зависимость n=f(М) или = f(М). Иногда используется так называемая скоростная характеристика, представляющая собой зависимость n=f(I). или= f(I). 

Рис. 2. Механические характеристики двигателя постоянного тока при различных сопротивлениях цепи якоря (а) и напряжениях (б)

Изменяя сопротивление реостата в цепи якоря можно получить при номинальной нагрузке различные угловые скорости электродвигателя на искусственных характеристиках — ω1, ω2, ω3

Двигатели постоянного тока пускаются в ход с помощью пускового реостата, ограничивающего пусковой ток. Из уравнения электрического равновесия 

Так как в момент пуска n = 0, то E = с Ф n = 0 и, следовательно

Сопротивление якоря R_я очень мало (десятые, а то и сотые доли ома) и потому пусковой ток якоря I_яn получается очень большим, во много раз превышающим номинальный.

Чтобы ограничить пусковой ток, на время пуска последовательно с якорем включается пусковой реостат R_n.

В этом случае

Величина сопротивления R_n выбирается по допустимому пусковому току якоря, обычно

По мере разгона двигателя пусковой реостат ступень за ступенью выводится. Металлические проволочные пусковые реостаты входят в комплект поставки двигателя. При пуске двигателя параллельная обмотка возбуждения включается на полное напряжение, то есть регулировочный реостат 

R_peг в цепи параллельной обмотки выводится полностью, пуск осуществляется при максимальном потоке Ф, что увеличивает пусковой момент и облегчает запуск. Реверсирование — изменение направления вращения двигателя — производится путем изменения направления действия вращающего момента. Для этого требуется изменить направление магнитного потока двигателя постоянного тока, т. е. переключить обмотку возбуждения или якорь, при этом в якоре будет протекать ток другого направления. При переключении и цепи возбуждения, и якоря направление вращения останется прежним.

Момент силы (примеры формула) — Знаешь как

Момент силы это векторная величина, понятие момента силы используется, в основном, в области задач статики и задач, связанных с вращением деталей (рычагов и др.) в технической механике.

Содержание статьи

• 1 Что такое вращательное движение тела Момент силы Момент инерции
  • 1.1 Момент силы
    • 1.1.1 От чего зависит действие силы
  • 1.2 Момент силы относительно центра вращения
    • 1.2.1 Инерция вращающегося тела
  • 1.3 Как увеличить инерцию
  • 1.4 Единицы измерения

Что такое вращательное движение тела Момент силы Момент инерции

Движение, при котором все точки тела описывают окружности, лежащие в параллельных плоскостях, с центрами, расположенными на одной неподвижной прямой, называется вращательным движением тела.

Прямая О’О» (рис. 2, а) называется осью вращения. Угловая скорость для всех точек вращающегося тела одинакова, линейные скорости различны: чем дальше расположена точка от центра вращения, тем больше ее линейная скорость.

Для того чтобы вызвать вращение тела, к нему надо приложить силу F, которая:

1. Действует в плоскости Р, перпендикулярной оси вращения.
2. Не проходит через эту ось.
3. Направлена под прямым углом к радиусу r, проведенному от оси вращения О’О» к точке приложения силы. При этом действие силы тем значительнее, чем дальше расположена точка ее приложения от оси вращения.

Это учитывается с помощью величины, называемой вращающим моментом или просто моментом силы.

Момент силы

Движение тела называется вращательным, если все его точки движутся по окружностям, центры которых расположены на одной прямой, называемой осью вращения.

Колеса всевозможных машин и механизмов могут вращаться вокруг неподвижной оси; пропеллер самолета, колодезный «журавль», дверь на петлях, откидная крышка школьной парты представляют собой примеры того же случая.

Если вначале тело покоится, то, чтобы вызвать вращение, необходимо подействовать на тело с некоторой силой. Однако не всякая приложенная сила вызовет вращение тела.

Силы, одинаковые по величине, но различные по направлению или приложенные в разных точках, могут вызвать весьма различные эффекты.

Оказывается, сила момента сейчас, действующая на тело, закрепленное на оси, только тогда может вызвать его вращение, когда направление силы не проходит через ось.

Сила, направленная параллельно оси вращения, также не вызывает вращение тела, а только стремится изогнуть ось.

От чего зависит действие силы

Вращающее действие силы зависит не только от ее величины, но и от расстояния между осью вращения и прямой, по которой действует сила.

Кратчайшее расстояние от оси вращения до прямой, по которой действует сила, называется плечом силы. 

На рис. плечо силы обозначено буквой l. Величина, характеризующая вращающее действие силы, называется моментом силы и обозначается буквой М.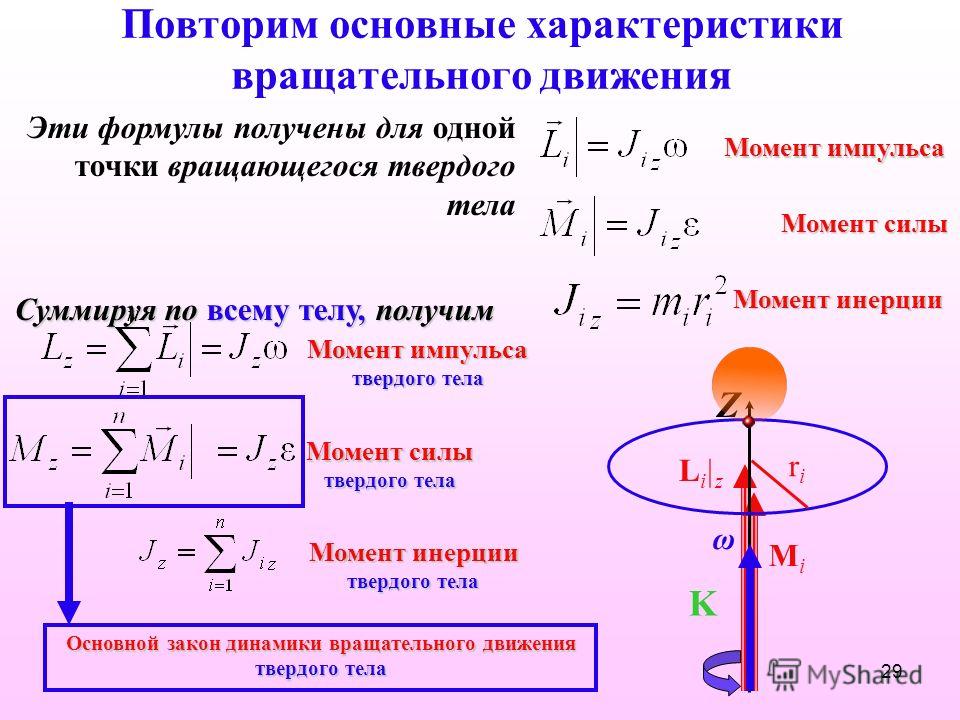 Момент силы измеряется произведением силы на плечо (момент силы формула):

М =Ft.

Момент силы — векторная величина. Направление вектора М определяется поступательным движением буравчика, расположенного вдоль оси вращения, если направление вращения его головки совпадает с направлением действующей силы.

В СИ за единицу момента силы принимается момент силы в один ньютон, имеющий плечо в один метр

1 Н • 1 м = 1 Нм.

Чтобы отличить моменты сил, создающих вращение в противоположные стороны, условились считать моменты сил, вращающих тело против часовой стрелки, положительными, а моменты сил, вращающих тело по часовой стрелке,— отрицательными.

Момент силы, направленной вдоль прямой, проходящей через ось вращения, равен нулю (так как l = 0).

Чтобы получить нужный момент при наименьшем усилии, надо стараться приложить силу как можно дальше от оси вращения, увеличивая тем самым плечо силы и соответственно уменьшая величину силы.

Не случайно дверная ручка закреплена на наибольшем расстоянии от оси вращения

Момент силы относительно центра вращения

Момент силы М  относительно центра вращения в общем случае называют векторную величину, численно равную произведению силы F на длину d перпендикуляра, опущенного из центра вращения на направление силы, который называют плечом силы (рис. 2, б) (в нашем случае плечом силы

F является радиус r, проведенный из центра вращения О к точке приложения силы — рис. 2, а).

Вектор М момента силы приложен к центру О окружности и направлен вдоль оси вращения в направлении, определяемом по «правилу буравчика».

Если под действием момента силы тело по отношению к наблюдателю вращается по часовой стрелке (рис. 2, а), то момент считается положительным, в противном случае — отрицательным.

Если на теле действует несколько моментов сил, то они складываются алгебраически (т.

е. с учетом знака момента).

Для того чтобы тело, имеющее ось вращения, находилось в равновесии, алгебраическая сумма моментов, действующих на него, должна равняться нулю.

Инерция вращающегося тела

Аналогично тому как действие силы при вращательном движении зависит от плеча силы, так и инерция вращающегося тела зависит от расположения его массы относительно оси вращения.

Чем дальше от оси вращения расположена масса тела, тем больше ее инерция. Это можно продемонстрировать с помощью прибора, показанного на рис. 3. На стойке П укреплен блок Б с четырьмя стержнями, по которым могут передвигаться грузы М. 

На блок намотана нить, на конце которой подвешена гиря Г. Натяжение нити создает на оси блока вращающий момент, постоянный по величине, под действием которого блок со стержнями приводится во вращение.

Ускорение блока можно определить путем наблюдения времени, в течение которого гиря Г опускается на определенное расстояние, отмечаемое по шкале Ш.  Это ускорение зависит от инерции блока.

Если грузы М расположены близко от оси вращения, блок имеет небольшую инерцию и гиря опускается очень быстро. Если передвинуть грузы к краям стержней в положение М’, то инерция блока увеличится и гиря будет опускаться заметно медленнее.

Как увеличить инерцию

Для того чтобы учитывать инерцию при вращательном движении тела, пользуются величиной, называемой моментом инерции. 

Момент инерции j для тела достаточно малой массы m относительно оси, находящейся на расстоянии r от центра масс тела (рис. 4), численно равняется произведению этой массы на квадрат расстояния:

j = mr².

Напомним, что центром масс (или центром тяжести) тела называют точку, в которой может быть приложена равнодействующая силы тяжести всех отдельных частей тела.

Для тел сплошных, однородных, правильной геометрической формы центр масс совпадает с геометрическим центром.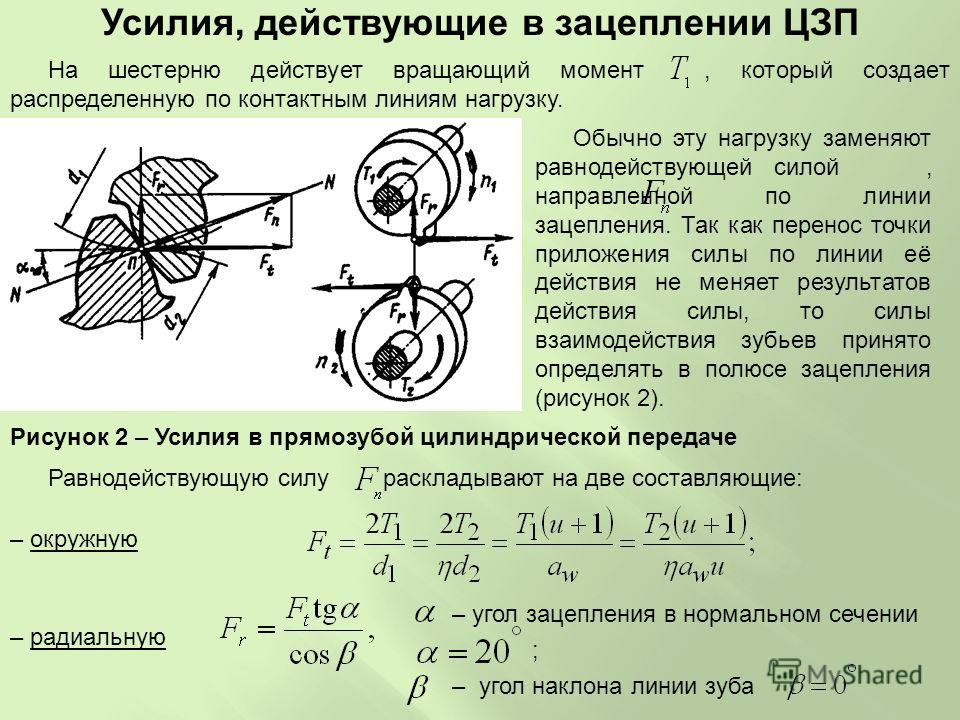

Центр масс тела человека находится в сагиттальной плоскости несколько впереди второго крестцового позвонка.

Вычисление момента инерции

Для вычисления момента инерции какого-либо тела его разделяют на множество достаточно малых по массе элементов, для каждого из них вычисляют момент инерции j относительно заданной оси вращения и затем последние суммируют.

Момент инерции в системе СИ измеряется в кг•м², в СГС — г•см². Моменты инерции однородных тел правильной геометрической формы могут быть вычислены по известным формулам.

Например, для однородного цилиндра относительно продольной оси: J = (1/2) тr², где т — масса иr — радиус цилиндра.

Для однородного шара с массой т и радиусом r момент инерции относительно оси, проходящей через центр шара:

J = (2/5) mr².

Для тел неоднородных или сложной геометрической формы момент инерции обычно определяется опытным путем.

Если вращательное движение тела происходит равноускоренно, то оно характеризуется угловым и линейным ускорениями.

Угловое ускорение ε измеряется отношением изменения ∆ω угловой скорости за достаточно малый промежуток времени ∆t к этому промежутку:

ε = ∆ω/∆t

Единицы измерения

Единицей измерения углового ускорения является рад/сек² или 1/сек².

Линейное ускорение а какой-либо точки тела равняется произведению углового ускорения ε на расстояние r точки от оси вращения:

а = εr = (∆ω/∆t)r.

Единица измерения в системе СГС — см/сек², в системе СИ — м/сек² При равноускоренном вращательном движении угловое ускорение ε прямо пропорционально приложенному моменту силы М и обратно пропорционально моменту инерции J тела:

ε = M/J, откуда М = εJ = J (∆ω/∆t).

Эта зависимость выражает второй закон Ньютона применительно к вращательному движению и называется основным уравнением вращательного движения.

Определим кинетическую энергию Е_к тела достаточно малой массы m, вращающегося равномерно с угловой скоростью ω вокруг неподвижной оси, находящейся на расстоянии г от центра масс тела. По общему правилу:

Eк = (mυ²)/2 = (mω²r²)/2 = j(ω²/2)

Для вычисления кинетической энергии Е_к вращающегося тела с массой М его надо разделить на множество достаточно малых по массе элементов, вычислить для каждого из них кинетическую энергию Е_к и затем суммировать:

Eк = Е’к1 + Е’к2 + … = j1(ω²/2) + j(ω²/2) + … = ω²/2(j₁ + j₂ + …) = J(ω²/2)

Кинетическая энергия тела, вращающегося вокруг неподвижной оси, равняется половине произведения момента инерции тела на квадрат его угловой скорости.

Статья на тему Момент силы

Как рассчитать крутящий момент электродвигателя

Лорен Нагель

Опубликовано: 21 июня 2022 г., последнее обновление 21 июня 2022 г. Его можно использовать для расчета механической мощности и получения электрической мощности. Для дронов и электрических самолетов знание крутящего момента также позволяет рассчитать КПД двигателя отдельно от КПД остальной части системы.

В этой статье мы:

• Используйте формулу крутящего момента электродвигателя для расчета крутящего момента бесщеточного двигателя
• Экспериментальная проверка нашего расчета на испытательном стенде серии 1580.

Рис. 1. Испытательный стенд серии 1580 с бесщеточным двигателем

Как же рассчитать крутящий момент электродвигателя?

Допустим, мы хотим узнать крутящий момент нашего мотора Xoar 2407. Вот что мы знаем:

• Вес: 36 г
• кв: 2300 кв
• Размеры статора: 24 x 7 x 0,15 мм
• Конфигурация: 12N14P

Здесь нет ничего полезного для расчета крутящего момента, поэтому давайте рассмотрим некоторую справочную информацию.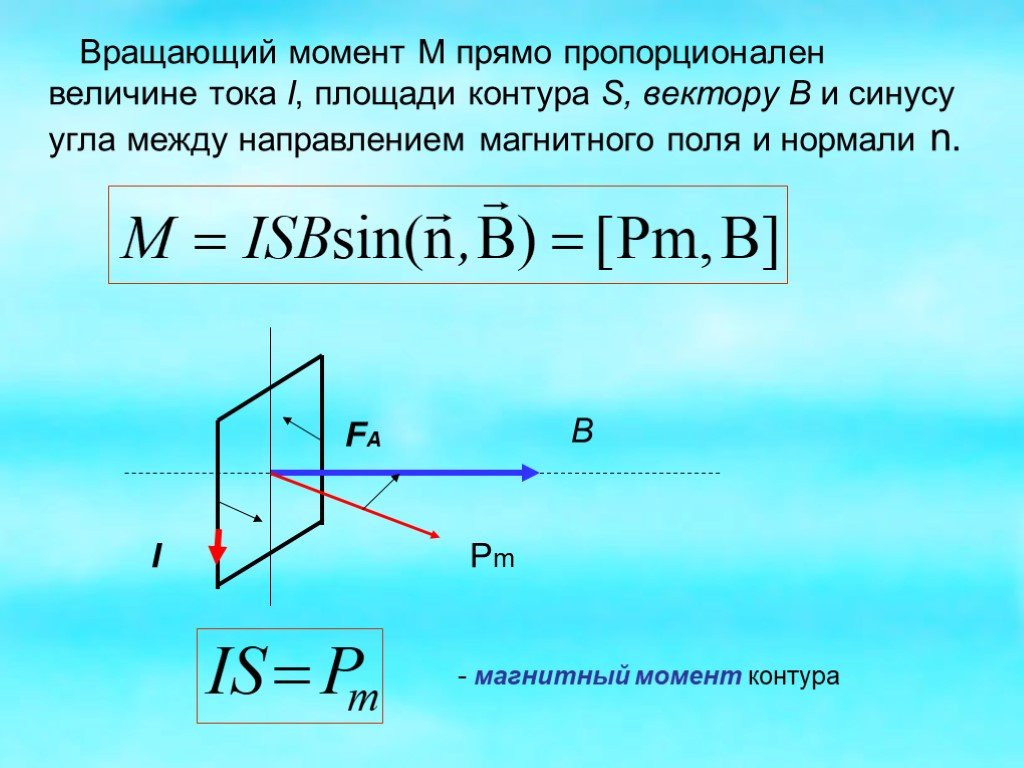

Крутящий момент двигателя связан с несколькими переменными, но наиболее важным для расчета крутящего момента является ток.

Крутящий момент электродвигателя Формула:

«Kt» — это коэффициент крутящего момента двигателя, единицами измерения которого являются Н·м/А (ньютон-метры на ампер). Kt — это отношение крутящего момента к току, и эта зависимость не является идеально линейной.

Сам по себе этот коэффициент не очень полезен для нас, но мы можем использовать предположение, что Kt = 1/Kv, а Kv — это число, которое у нас есть.

Допустим, мы хотим подать на наш двигатель ток 20 А. Мы можем использовать это число и Kv нашего двигателя для расчета теоретического крутящего момента.

Kv двигателя обычно указывается в об/мин/В, но для того, чтобы он работал в нашей формуле, нам нужны единицы СИ, в данном случае (радианы/секунды)/вольты. Для преобразования мы разделим 2300 на 60 с и умножим на 2π.

Более точное объяснение значения Kv двигателя см. в нашей статье: Как рассчитать Kv двигателя

Теперь мы можем подставить наше значение SI Kv в нашу формулу крутящего момента двигателя:

Эта цифра кажется разумной, но нелинейность, вызванная ESC и двигатель могут означать, что теоретические результаты не обязательно отражают реальность. Обычно мы ожидаем разницу в 10–50 % между теоретическим значением и измеренным значением.

Обратите внимание, что это уравнение работает в предположении, что зависимость между крутящим моментом и током является линейной, что не соответствует действительности, поэтому вычисленный крутящий момент не будет абсолютно точным.

Давайте подключим двигатель к нашему испытательному стенду и посмотрим, насколько близко мы подошли к нашему теоретическому значению.

Рис. 2. Испытательный стенд серии 1580 с бесщеточным двигателем и пропеллером

Мы использовали испытательный стенд для проведения простого пошагового испытания, проводя измерения, когда система достигала 20 А.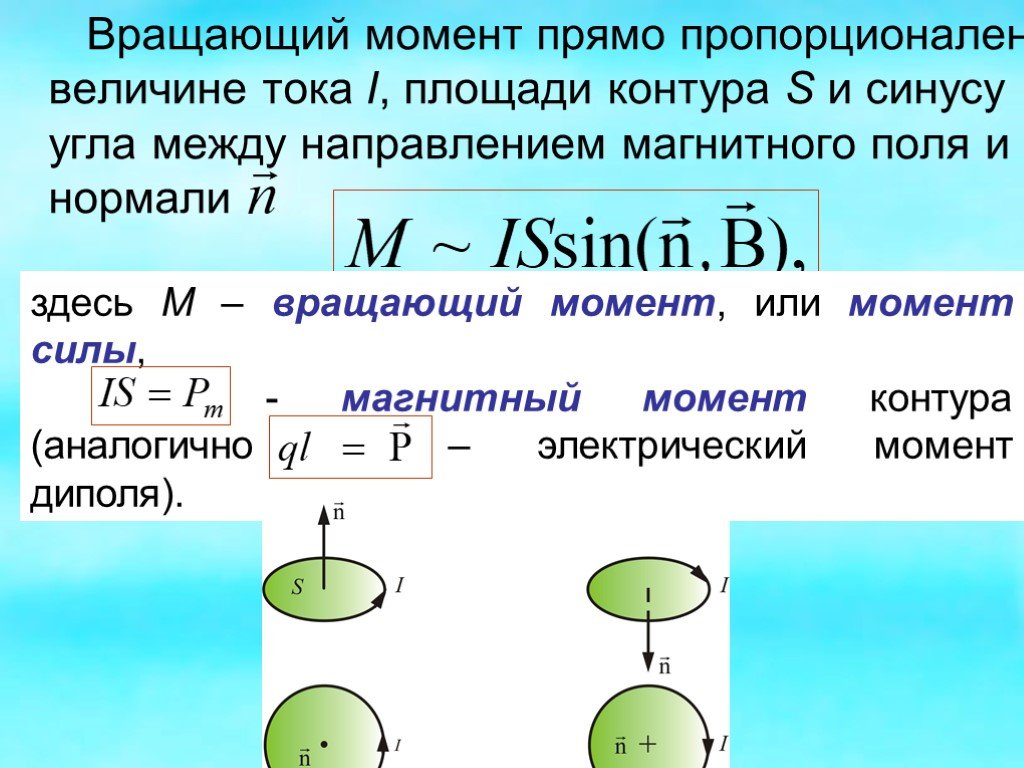 Результаты этого испытания приведены ниже. Рис. 3. Крутящий момент в сравнении с текущими результатами

Как видите, вопреки тому, что предлагает формула, зависимость между током и крутящим моментом не является линейной. Это связано с потерями от ESC и двигателя.

Эти данные показывают, что расчеты крутящего момента могут дать нам только оценку истинного крутящего момента, создаваемого двигателем. Чтобы получить точные данные о крутящем моменте, вам нужен инструмент для его измерения.

Мы знали об этой дилемме в течение достаточно долгого времени, поэтому мы разработали наши стенды для испытаний двигателей, чтобы пользователи могли собирать высокоточные данные о двигателях. В дополнение к измерению крутящего момента наши испытательные стенды также измеряют тягу, число оборотов в минуту, электрическую мощность, механическую мощность, эффективность двигателя и ESC, эффективность гребного винта и общую эффективность системы.

Дополнительная литература: Анализ мощности и эффективности бесщеточного двигателя

Если у вас есть дополнительные вопросы, не стесняйтесь оставлять нам комментарии ниже.

Оставить комментарий

Комментарии будут одобрены перед показом.

Похожие сообщения в блоге

Статическое и динамическое тестирование при измерении данных

Каков средний КПД электродвигателя

Как измерить скорость двигателя с помощью нашего датчика оборотов

Крутящий момент и скорость: в чем разница?

22 ноября 2021 г.

Крутящий момент и скорость: в чем разница? | Телефонная компания

Крутящий момент в зависимости от скорости

Когда вы покупаете новый двигатель или большой набор коммерческих двигателей, необходимо учитывать определенные факторы. Вы должны учитывать такие вещи, как производители, ассортимент и инструменты автоматизации. Вы также должны учитывать такие факторы, как крутящий момент двигателя, сопротивление, крутящий момент, крутящий момент в футах, выходной крутящий момент, требования к крутящему моменту и т. д. 

Одним из наиболее важных факторов, которые следует учитывать при покупке двигателя, является соотношение мощности и крутящего момента, а также взаимосвязь между ними.

В чем разница между скоростью и крутящим моментом?

Прежде чем покупать новый двигатель, вам необходимо изучить разницу между скоростью и крутящим моментом. Многие думают, что крутящий момент электродвигателя связан со скоростью, но это не совсем так.

Чтобы развеять это распространенное заблуждение, вам нужно понять, что крутящий момент и скорость индивидуальны. Крутящий момент относится к вращательной силе электродвигателя, а скорость относится к скорости, с которой двигатель может вращаться.

Это означает, что крутящий момент связан с силой вращения, а скорость связана со скоростью вращения, которую можно рассчитать, исследуя число оборотов в минуту или число оборотов в минуту.

Что лучше: крутящий момент или скорость

Что лучше: больший крутящий момент или большая скорость? Хотя скорость определяет максимальную скорость электродвигателя, больший крутящий момент может помочь вам достичь максимальной скорости за меньшее время. Чтобы определить, лучше ли иметь больший крутящий момент или большую мощность, вам нужно будет подумать о требованиях вашего приложения.

Для приложения, требующего исключительно высоких скоростей, вам нужно сосредоточиться на поиске двигателя с большой мощностью. Если сила вращения является более важным фактором с точки зрения вашего применения, вам понадобится двигатель с большим крутящим моментом.

Как рассчитать крутящий момент скорости?

Когда речь идет о зависимости крутящего момента от скорости, полезно знать формулу. Формула, которая используется для определения выходной мощности двигателя, включая скорость и крутящий момент: мощность (P) = скорость (n) x крутящий момент (M). Крутящий момент электродвигателя обычно рассчитывается в дюйм-фунтах (дюйм-фунтах), ньютон-метрах (Н-м).

Чем больше крутящий момент, тем выше скорость?

Наличие большего крутящего момента не означает, что у вас больше скорость. Скорость рассчитывается по-другому и фокусируется на оборотах в минуту. Тем не менее, крутящий момент может повлиять на время, необходимое для достижения максимальной скорости.

Крутящий момент — это скорость или мощность?

Важно понимать, что крутящий момент — это не скорость, он относится к мощности вашего двигателя с точки зрения силы вращения. Если вам нужна большая скорость двигателя, найдите двигатель с максимальной скоростью, если вам нужно большее усилие вращения, найдите двигатель с максимальным крутящим моментом.

Найдите двигатели мирового класса от поставщика мирового класса, купите Telco Today

Теперь, когда вы знаете больше о зависимости крутящего момента от скорости, пришло время найти лучший двигатель для вашего применения. Некоторые приложения, естественно, требуют большей скорости, в то время как другие требуют большего крутящего момента.